多组分体系热力学3
多相多组分系统热力学--习题及答案

第二章 多相多组分系统热力学习题及答案§2. 1 均相多组分系统热力学(P68)1. 水溶液(1代表溶剂水,2代表溶质)的体积V 是质量摩尔浓度b 2的函数,若V = A +B b 2+C (b 2)2(1)试列式表示V 1和V 2与b 的关系; (2)说明A 、B 、A/n 1的物理意义; (3)溶液浓度增大时V 1和V 2将如何变化解:(1) 由b 2的定义“1kg 溶剂中所含溶质的物质的量”,因此本题中可视溶剂水为1kg ,从而认为将 b 2=n 2。
★112222,,,,2T P n T P n V V V B Cb n b ⎛⎫⎛⎫∂∂===+ ⎪ ⎪∂∂⎝⎭⎝⎭ 据偏摩尔量的集合公式V=n 1V 1+n 2V 2,★V 1 =2211()V n V n -=2211()V b V n - =22222211[A+Bb +C(b )-Bb -2C(b )]n =2211[A-C(b )]n = 2211A C (b )n n - (2)20lim b V A →=,故A 表示当b 2→0,纯溶剂的体积,即1kg 溶剂水的体积;220lim b V B →=,故B 表示当b 2→0,无限稀溶液中溶质的偏摩尔体积;2101lim b AV n →=,A/n 1表示溶剂水的摩尔体积。
(3)由以上V 1和V 2 的表达式可知,溶液浓度(b 2)增大时,V 2 增大,V 1减小。
2. 哪个偏微商既是化学势又是偏摩尔量哪些偏微商称为化学势但不是偏摩尔量答:化学势表达式: ,,c B B T P n G n μ⎛⎫∂= ⎪∂⎝⎭= ,,cB T V n F n ⎛⎫∂ ⎪∂⎝⎭= ,,cB S P n H n ⎛⎫∂ ⎪∂⎝⎭= ,,cB S V n U n ⎛⎫∂ ⎪∂⎝⎭偏摩尔量: ,,c B B T P n G G n ⎛⎫∂= ⎪∂⎝⎭,,,c B B T P n F F n ⎛⎫∂= ⎪∂⎝⎭,,,c B B T P n H H n ⎛⎫∂= ⎪∂⎝⎭,,,cBB T P n U U n ⎛⎫∂= ⎪∂⎝⎭ 可见,只有偏微商,,c B T P n G n ⎛⎫∂ ⎪∂⎝⎭既是化学势又是偏摩尔量,,,c B T V n F n ⎛⎫∂ ⎪∂⎝⎭、,,c B S P n H n ⎛⎫∂ ⎪∂⎝⎭、,,cB S V n U n ⎛⎫∂ ⎪∂⎝⎭称为化学势,但不是偏摩尔量。
南京大学物理化学(第五版)04章_多组分系统热力学
(
Gm p
)T
Vm
对多组分系统,把 Gm 换为 B ,则摩尔体积变为偏
摩尔体积 VB 。
化学势与温度的关系
(
B
T
)
p
,nB
,
nc
[ T
G ( ) ] T , p,nc p,nB ,nc nB
[ nB
G ( T ) p,nB ,nc ]T , p,nc
(S) [ nB ]T , p,nc
nk 0
dnk
k
n1Z1 n2 Z2 nk Zk nBZB B=1
偏摩尔量的加和公式
k
Z= nB ZB
B=1
这就是偏摩尔量的加和公式,说明系统的总 的容量性质等于各组分偏摩尔量的加和。
例如:系统只有两个组分,其物质的量和偏 摩尔体积分别为 n1,V1 和 n2 ,V2 ,则系统的总体积为:
(1)热力学能
设系统中有 1, 2,3, , k 个组分
所含的量分别为 n1, n2, , nk
U U (S,V , n1, n2, , nk )
化学势的定义
U U (S,V , n1, n2, , nk )
其全微分为
dU
U ( S )V ,nB dS
(
U V
)
S
,nB
dV
k U B1 ( nB )S ,V ,nc(cB) dnB
如果转移是在平衡条件下进行,则
dG 0 又
dnB dnB
所以 (B B )dnB 0
化学势在相平衡中的应用
(B B )dnB 0
因为 dnB 0 所以
B B
组分B在α,β两相中,达平衡的条件是该
(完整版)物理化学3-4章练习题

第三章 多组分系统热力学一.选择题:选择正确答案的编号,填在各题后的括号内:1.下面各个偏导式中,哪个是偏摩尔量( ) A.j n T p Bn ,,⎪⎪⎭⎫⎝⎛∂∂μ B.jn V S B n U ,,⎪⎪⎭⎫ ⎝⎛∂∂ C. jn T p B m n S ,,⎪⎪⎭⎫ ⎝⎛∂∂ D. j n T p B n V ,,⎪⎪⎭⎫ ⎝⎛∂∂ 2.下面各个偏导式中,哪个不是化学势( ) A. jn V S B n U ,,⎪⎪⎭⎫⎝⎛∂∂ B. jn p T Bn H ,,⎪⎪⎭⎫ ⎝⎛∂∂ C. jn p T Bn G ,,⎪⎪⎭⎫ ⎝⎛∂∂ D. jn V T Bn F ,,⎪⎪⎭⎫ ⎝⎛∂∂ 3.理想液态混合物中任一组分B,其偏摩尔量和摩尔量的关系为( )A. B H =*B m H , B. B V VBm *≠, C. B G =*B m G , D. B S =*B m S ,4.一定温度下,纯液体A 的饱和蒸汽压为pA*,化学势为*A μ,凝固点为*f T ,当A 中加入少量不挥发性溶质后,上述三个量p A,μA,Tf,它们的关系为( )A, p A*<pA*A μ<μA*f T <TfB. p A*>pA*A μ <μA*f T <TfC. p A*<pA*A μ<μA*f T >T fD.p A*>pA *A μ>μA*f T >Tf5.一定温度和压力下的乙醇水溶液中,若使乙醇的偏摩尔体积的变化dV>0.此时水的偏摩尔体积的变化dV水( )A. >0B.=0C. <0D.不能确定 6.对多组分体系中B 物质的偏摩尔量XB=Bj n p T Bn X ≠⎪⎪⎭⎫⎝⎛∂∂,,,下列叙述中不正确的是( ) A.X B是无限大量体系中B 物质每变化1 mol 时该体系容量性质X 的变化量B.X 为容量性质, XB也为容量性质C.XB不仅取决于T,p,而且取决于浓度D.X=X n B B ∑7.将固体NaCl 投放到水中, NaCl 逐渐溶解,最后达到饱和.开始溶解时溶液中的NaCl 的化学式为µ(a),饱和时溶液中NaCl 的化学势为µ(b),固体NaCl 的化学势为,则( ) A. µ(a)= µ(b)< µ(c) B. µ(a)= µ(b)> µ(c) C. µ(a)> µ(b)= µ(c) D. µ(a)<µ(b)= µ(c) 8.下列物理量中,( )既是偏摩尔量,又是化学势. A. Bj n p T Bn F ≠⎪⎪⎭⎫⎝⎛∂∂,, B. Bj n p S Bn H ≠⎪⎪⎭⎫ ⎝⎛∂∂,, C. Bj n p T Bn G ≠⎪⎪⎭⎫ ⎝⎛∂∂,, D. Bj n p S Bn U ≠⎪⎪⎭⎫ ⎝⎛∂∂,, 9.理想液态混合物的通性是( ) A 、 ΔV 混合=0 ΔH 混合=0 ΔS 混合>0 ΔG 混合<0 B 、 ΔV 混合=0 ΔH 混合=0 ΔS 混合>0 ΔG 混合=0 C 、 ΔV 混合> 0 ΔH 混合> 0 ΔS 混合>0 ΔG 混合<0 D 、 ΔV 混合=0 ΔH 混合=0 ΔS 混合=0 ΔG 混合=0 10.7、298K 时A 和B 两种气体在某一溶剂中溶解的亨利系数分别为kA 和kB ,且kA>kB ,则当A 和B 压力相同时,在该溶剂中溶解的量是 ( ) A 、 A 的量大于B 的量 B 、 A 的量小于B 的量 C 、 A 的量等于B 的量D 、 A 的量和B 的量无法比较11、313K 时纯液体A 的饱和蒸汽压是纯液体B 的21倍,A 和B 能形成理想液态混合物。
计算题多组分热力学

(2)因为 k b = 所以
θ ∆ vap H m =
RTb*2 M 苯
θ ∆ vap H m
RTb*2 M 苯 kb
8.314 × (353.25) 2 × 78.113 × 10 −3 = J ⋅ mol −1 2.58
p O 2 = k O2 CO 2 = k O2
WO 2 V液 M O2
1
TEL:010-64434903
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY
kO2 = p O2 V液 M O 2 WO2 101.325 × 31.9988 × 10 −3 kPa ⋅ mol ⋅ dm −3 = −3 0.045 × 10
* * (1 − xCH 3OH ) p = p CH 3OH + p C 2 H5OH = p CH x + pC 3OH CH 3OH 2 H 5OH * * * = ( p CH − pC ) xCH 3OH + p C =(83.7-47.0)×0.58979kPa+47.0kPa=68.5kPa 3OH 2 H 5OH 2 H 5OH * p CH 3OH = p CH x =83.4×0.58979kPa=49.2kPa 3OH CH 3OH
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY 第四章 多组分系统热力学习题及参考答案
1.60℃时甲醇的饱和蒸气压是 83.4kPa,乙醇的饱和蒸气压是 47.0kPa。二者可形成理 想液态混合物。若混合物的组成为二者的质量分数各 50%,求 60℃时此事物的平衡蒸气组 成,以摩尔分数表示。
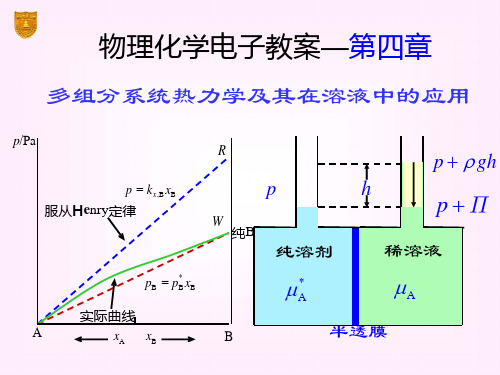
第四章 多组分系统热力学

前两章-单组分均相封闭系统,如:纯物质或某种 理想气体系统。 科学研究及生产实践-多组分系统 纯物质单相封闭系统:确定n(对于单相封闭系统, 此为一定值)、T、p,系统的状态即可确定。此时, 系统的一切性质,不只是强度性质而且全部容量性 质都有了确定值。若以X代表任意一种容量性质, 如V、U、S、G等,对于物质的量固定的纯物质单 相系统,都有: X=f(T,p) 其微小改变量为:
10
XB物理意义为:在恒温、恒压、均相封闭系统中, 只增加任一组分B,同时不引起原来nj改变,且不 发生缔合、沉淀、化学反应时: (1)dnB量B物质的加入,系统容量性质X对nB的变 化率。或在原有nB中加入dnB的B,使X改变了dX的 比值; (2)条件同前,在一个无限大的系统中,加入1 mol 的B物质,引起容量性质X的改变量。 如:向一大缸某白酒中,加入1 mol的水,引起V增 大了17.0 ml (<18.0 ml), 则此时V水=17.0 ml· -1。 mol
X X X dp dX dT d n1 p n T p , ni T , ni 1 T , p , n2 , n3 ,nk
X n 2 X d n2 n T , p , n1 , n3 ,nk k d nk T , p , n1 , n2 ,nk 1
W (乙) 10
W (水) 90
V (乙) 12.67
V (水) 90.36
V 103.30
V (实) 101.84
V 1.19
20 g乙醇+180 g水,其V=2×1.19=2.38 ml
7
描述一多组分均相系统的状态,除指明系统的T和p, 还必须指明系统的组成ni。为此,需要引入偏摩尔 量(XB)来代替单组分系统中的摩尔量(Xm)。 一、偏摩尔量的定义 含有k个组分的均相系统,其任一容量性质X (可为 V, U, H, S, A, G)可写成下列函数式: X=f(T,p,n1,n2,…nk) 2+k个变量 当系统的T、p及各组分的n均发生一微小变化时, 该容量性质X也相应发生微小变化。根据状态函数的 性质,此变化可用全微分表示,即:
04章_多组分系统热力学及其在溶液中的应用解析
类似地还可得到化学势的其他表达式(广义定义):
U H B ( )S ,V ,nc (cB) ( ) S , p ,nc (c B) nB nB A G ( )T ,V ,nc (c B) ( )T , p ,nc (c B) nB nB
2.只有广度性质才有偏摩尔量,而偏摩尔量是强度 性质。 3.纯物质的偏摩尔量就是它的摩尔量。 4.任何偏摩尔量都是T,p和组成的函数。
2018/10/5
偏摩尔量的加和公式
、k个组分组成,则系 设一个均相系统由1、2、 统任一容量性质Z应是T,p及各组分物质的量的函数, 即:
Z Z (T , p, n1 , n2 , , nk )
2018/10/5
Gibbs-Duhem公式——系统中偏摩尔量之间的关系
如果在溶液中不按比例地添加各组分,则溶液浓 度会发生改变,这时各组分的物质的量和偏摩尔量均 会改变。 根据加和公式 对Z进行微分
Z n1 Z1 n2 Z2 nk Zk
dZ n1dZ1 Z1dn1 nkdZk Zkdnk
2018/10/5
溶液
溶液(solution) 溶液以物态可分为固态溶液和液态溶液。根据 溶液中溶质的导电性又可分为电解质溶液和非电解
质溶液。本章主要讨论液态的非电解质溶液。
溶剂(solvent)和溶质(solute) 如果组成溶液的物质有不同的状态,通常将液 态物质称为溶剂,气态或固态物质称为溶质。 如果都是液态,则把含量多的一种称为溶剂, 含量少的称为溶质。
k
B
0
等温等压
这就称为Gibbs-Duhem公式,说明偏摩尔量之间 是具有一定联系的。某一偏摩尔量的变化可从其它偏 摩尔量的变化中求得。
多组分系统热力学补充练习题

第3章多组分系统热力学(一)、填空题1.偏摩尔量是指多组分系统中的任一量X(如、、等)在温度和压力及除了组分B以外其它各组分的物质的量均不变的条件下,由于某一组分B的物质的量的极微小变化而引起系统量X随组分B的物质的量的变化率。
2.理想液态混合物是指在一定温度下,液态混合物中的任意组分在全部的组成范围内都遵守定律的混合物,可以认为此溶液中各种分子的是相同的。
3.物质标准态的规定如下,固态:固体纯物质在的状态;液态:纯液体在的状态;气态: -在任一温度T,标准压力p°下的状态。
在这些状态下物质所具有的化学势为各自的标准化学势。
4. A、B两液体形成理想液态混合物,已知在温度T时纯A和B的饱和蒸气压分别为p A*=40kPa和p B*=120 kPa,若该混合物在温度T及压力100 kPa时开始沸腾,则此时的液相和气相组成为x B= , y B= 。
5.在室温下,一定量的苯和甲苯混合,这一过程所对应△H的大约为。
6.在某温度下,纯液体A的饱和蒸气压是纯液体B的13倍,A和B形成理想液态混合物,若平衡时的气相中A和B的摩尔分数相等,则液相中A 和B的摩尔分数比为。
7.0.5molNaOH固体在288.2K时溶于4.559mol水中形成溶液的蒸气压为1363.9Pa,而此时纯水的蒸气压为1704.9Pa。
则溶液中水的活度为,溶液中溶剂的化学势和纯水的化学势相差。
8.含有某非挥发性溶质的水的稀溶液,在271K时凝固,水的K f为1.86K·kg·mol-1、K b为0.52 K·kg·mol-1,该溶液的正常沸点为,298.15K时的渗透压为。
9. 353.15K时,苯和甲苯的蒸气压分别为100 kPa和38.7kPa,二者形成混合物,其平衡气相的组成为y(苯)为0.30,则液相的组成x(苯)为。
10. 298.15K时,水(A)和丙酮(B)组成溶液,实验测得x B=0.1791,p=21.30kPa,y B=0.8782,已知p B*=30.61kPa,k x,B=185kPa,将该溶液视为液态混合物,则丙酮(B)的活度系数B为,将该溶液视为稀溶液,则丙酮(B)的活度系数x,B为。
多组分系统热力学

多组分系统热力学一、判断题:1 克拉佩龙方程适用于纯物质的任何两相平衡。
()2 克—克方程比克拉佩龙方程的精确度高。
( )3 一定温度下的乙醇水溶液,可应用克—克方程式计算其饱和蒸气压。
()4 将克—克方程的微分式用于纯物质的液气两相平衡,因为 vap H m>0,所以随着温度的升高,液体的饱和蒸气压总是升高的。
()5 二组分理想液态混合物的总蒸气压大于任一纯组分的蒸气压。
()6 理想混合气体中任意组分B的逸度就等于其分压力p B。
()7 因为溶入了溶质,故溶液的凝固点一定低于纯溶剂的凝固点。
()8 溶剂中溶入挥发性溶质,肯定会引起溶液的蒸气压升高。
()9 理想稀溶液中的溶剂遵从亨利定律,溶质遵从拉乌尔定律()10 理想液态混合物与其蒸气成气、液两相平衡时,气相总压力p与液相组成x B呈线性关系。
()11 如同理想气体一样,理想液态混合物中分子间没有相互作用力。
()12 一定温度下,微溶气体在水中的溶解度与其平衡气相分压成正比。
()13 化学势是一广度量。
()14 只有广度性质才有偏摩尔量。
()15 稀溶液的沸点总是高于纯溶剂的沸点。
()16 单组分系统的熔点随压力的变化可用克劳休斯-克拉佩龙方程解释。
()17.公式 d G = -S d T + V d p只适用于可逆过程。
()18.某一体系达平衡时,熵最大,自由能最小。
()19.封闭体系中,由状态1经定温、定压过程变化到状态2,非体积功W/<0,且有W/>∆G 和∆G<0,则此变化过程一定能发生。
()20.根据热力学第二定律,能得出,从而得到。
()21.只有可逆过程的∆G才可以直接计算。
()22.凡是自由能降低的过程一定都是自发过程。
()23.只做体积功的封闭体系,的值一定大于零。
()24.偏摩尔量就是化学势。
()25.在一个多组分溶液中,只有溶质才有偏摩尔量。
()26.两组分混合成溶液时,没有热效应产生,此时形成的溶液为理想溶液。
()27.拉乌尔定律和亨利定律既适合于理想溶液,也适合于稀溶液。
