高中数学北师大版选修1-1学案：第三章章末复习课

合集下载

【优教通,同步备课】高中数学(北师大版)选修1-1教案：第3章导数的概念及其几何意义参考教案

3.2 导数的概念及其几何意义教学目标：1．导数的概念及几何意义；2．求导的基本方法；3．导数的应用.教学重点：导数的综合应用；教学难点：导数的综合应用.一.知识梳理1．导数的概念及几何意义.2．求导的基本方法①定义法：()x f '=()()xx f x x f x y x ∆-∆+=∆∆→∆0lim ②公式法：0c ='（c 为常数）;)(x n ' = 1-n nx (n ∈N) ; )v (u '±=v u '±'3．导数的应用①求曲线切线的斜率及方程；②研究函数的单调性、极值、最值；③研究函数的图象形态、性状；④导数在不等式、方程根的分布（个数）、解析几何等问题中的综合应用．二．基础训练1.函数()13++=x ax x f 有极值的充要条件是 ( )A.0>aB.0≥aC.a<0D.0≤a2.函数()133+-=x x x f 在闭区间[]03，-上的最大值、最小值分别是（）A.1，-1B.1，-17C.3，-17D.9，-193.a>3,则方程x 3-ax 2+1=0在(0,2)上恰好有A 0个根B 1个根C 2个根D 3个根 4. 设函数y=f(x)在其定义域上可导,若)(x f '的图象如图所示,下列判断: q x () = -2⋅cos x ()- 2 - ②x=-1时, f(x)取得极小值;③x=1时, f(x)取得极小值;④f(x)在(-1,1)上是减函数,在(1,2)上是增函数.其中正确的是A ①②B ②③C ③④D ②③④5. 函数f(x) =-x 3+3x 2+ax+c 在(-∞,1]上是单调减函数,则a 的最大值是A -3 B-1 C1 D36．设t≠0，点P(t ，0)是函数f(x)=x 3+ax 与y=bx 2+c 的图象的一个公共点，两函数的图象在点P 处有相同的切线．(I)用t 表示a ，b ，c ；(Ⅱ)若函数y=f(x)-g(x)在(-l ，3)上单调递减，求 t 的取值范围．三．典型例题例1.设a 为实数，函数f(x)=x 3-x 2-x+a ．（I ）求f(x)的极值；（Ⅱ）当a 在什么范围内取值时，曲线y=f(x)与x 轴仅有一个交点．例2已知f(x)=x 3+ax+b 定义在区间[-1，1]上，且．f(0) =f(1)，设x l ，x 2∈[-1，1]，且x 1≠x 2．1)求证：|f(x 1)-f(x 2)|< 2|x 1-x 2|；2)若0<x l <x 2≤1，求证：|f(x 1)-f(x 2)|<1．例3已知抛物线x x y C 221+=：和a x y C +-=22：，如果直线L 同时是1C 和2C 的切线，称L 是1C 和2C 的公切线，公切线上两个切点之间的线段，称为公切线段。

高中数学(北师大版)选修1-1教案：第3章导数应用参考教案

复习总结：导数应用1．了解导数概念的某些实际背景（如瞬时速度，加速度，光滑曲线切线的斜率等）；掌握函数在一点处的导数的定义和导数的几何意义；理解导函数的概念.2. 熟记八个基本导数公式(c,m x (m 为有理数)，x x a e x x a xx log ,ln ,,,cos ,sin的导数)；掌握两个函数和、差、积、商的求导法则，了解复合函数的求导法则，会求某些简单函数的导数.3．理解可导函数的单调性与其导数的关系；了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号)；会求一些实际问题(一般指单峰函数)的最大值和最小值．导数导数的概念导数的求法和、差、积、商、复合函数的导数导数的应用函数的单调性函数的极值函数的最值主要涉及函数单调性、极大（小）值，以及最大（小）值等，遇到有关问题要能自觉地运用导数. 例1．求函数y=12+x 在x 0到x 0+Δx之间的平均变化率.解 ∵Δy=11)(11)(11)(2202020220+++∆+--+∆+=+-+∆+x x x x x x x x x.11)(2,11)()(220200202020+++∆+∆+=∆∆∴+++∆+∆+∆=x x x xx x y x x x x x x变式训练1. 求y=x在x=x 0处的导数解)())((limlim lim00000000000x x x x x x x x x x x x x x x yx x x +∆+∆+∆+-∆+=∆-∆+=∆∆→∆→∆→∆.211lim00x x x x x =+∆+=→∆例2. 求下列各函数的导数：（1）;sin 25x xx x y ++=（2）);3)(2)(1(+++=x x x y（3）;4cos 212sin 2⎪⎭⎫⎝⎛--=x x y （4）.1111xxy ++-=解 (1)∵,sin sin 23232521xx x xxx x x y ++=++=-∴y′.cos sin 2323)sin()()(232252323x x x x x x x x x x-----+-+-='+'+'=（2）方法一 y=（x 2+3x+2）（x+3）=x 3+6x 2+11x+6，∴y′=3x 2+12x+11. 方法二 'y =[])3)(2)(1()3()2)(1('+++++'++x x x x x x=[])2)(1()2(）1（'++++'+x x x x （x+3）+（x+1）（x+2）=（x+2+x+1）（x+3）+（x+1）（x+2）=（2x+3）（x+3）+（x+1）（x+2）=3x 2（3）∵y=,sin 212cos 2sin x x x =⎪⎭⎫ ⎝⎛--∴.cos 21)(sin 21sin 21x x x y ='='⎪⎭⎫ ⎝⎛='（4）xx x x x xxy -=+--++=++-=12)1)(1(111111 ，∴.)1(2)1()1(21222x x x x y -=-'--='⎪⎭⎫ ⎝⎛-=' 变式训练2：求y=tanx 的导数. 解y′.cos 1cos sin cos cos )(cos sin cos )(sin cos sin 22222x x xx x x x x x x x =+='-'='⎪⎭⎫ ⎝⎛=例3. 已知曲线y=.34313+x（1）求曲线在x=2处的切线方程；（2）求曲线过点（2，4）的切线方程.解（1）∵y′=x 2,∴在点P （2，4）处的切线的斜率k='y |x=2∴曲线在点P （2，4）处的切线方程为y-4=4(x-2),即4x-y-4=0.（2）设曲线y=34313+x 与过点P （2，4）的切线相切于点⎪⎭⎫⎝⎛+3431,300x x A ，则切线的斜率k='y |x x ==20x .∴切线方程为),(343102030x x x x y -=⎪⎭⎫ ⎝⎛+-即.34323020+-⋅=x x x y∵点P （2，4）在切线上，∴4=,343223020+-x x即,044,0432020302030=+-+∴=+-x x x x x ∴,0)1)(1(4)1(00020=-+-+x x x x∴(x 0+1)(x 0-2)2=0,解得x 0=-1或x 0=2, 故所求的切线方程为4x-y-4=0或x-y+2=0.变式训练3：若直线y=kx 与曲线y=x 3-3x 2+2x 相切，则k= . 答案 2或41-例4. 设函数bx ax x f ++=1)( (a,b ∈Z )，曲线)(x f y =在点))2(,2(f 处的切线方程为y=3.（1）求)(x f 的解析式；（2）证明：曲线)(x f y =上任一点的切线与直线x=1和直线y=x 所围三角形的面积为定值，并求出此定值. （1）解2)(1)(b x a x f +-='，于是⎪⎪⎩⎪⎪⎨⎧=+-=++,0)2(1,32122b a b a 解得⎩⎨⎧-==,1,1b a 或⎪⎪⎩⎪⎪⎨⎧-==.38,49b a 因为a,b ∈Z ，故.11)(-+=x x x f （2）证明在曲线上任取一点⎪⎪⎭⎫⎝⎛-+11,00x x x ．由200)1(11)(--='x x f 知，过此点的切线方程为)()1(11110200020x x x x x x y -⎥⎦⎤⎢⎣⎡--=-+--．令x=1，得1100-+=x xy ，切线与直线x=1交点为⎪⎪⎭⎫⎝⎛-+11,100x x ．令y=x ，得120-=x y ，切线与直线y=x 的交点为)12,12(00--x x ．直线x=1与直线y=x 的交点为(1,1)．从而所围三角形的面积为22212211121112100000=--=----+x x x x x ．所以，所围三角形的面积为定值2.变式训练4：偶函数f （x ）=ax 4+bx 3+cx 2+dx+e 的图象过点P （0，1），且在x=1处的切线方程为y=x-2，求y=f （x）的解析式解 ∵f （x ）的图象过点P （0，1），∴e=1. ①又∵f （x ）为偶函数，∴f （-x ）=f （x ）故ax 4+bx 3+cx 2+dx+e=ax 4-bx 3+cx 2-dx+ ∴b=0，d=0.②∴f （x ）=ax 4+cx2∵函数f （x ）在x=1处的切线方程为y=x-2，∴可得切点为（1，-1）∴a+c+1=-1. ③∵)1('f =(4ax3+2cx)|x=1=4a+2c ，∴4a+2c=1. ④由③④得a=25，c=29-∴函数y=f （x ）的解析式为.12925)(24+-=x x x f1．理解平均变化率的实际意义和数学意义。

高中数学第3章章末复习课学案北师大版必修1

第3章指数函数和对数函数■｛整敷摘數咸■（无理數曲数斥）—2S―〔图擁和性质］一*——〔运算性质）——（换虧应I〔折数噸蝕、每甫數.对數函数圳丘的出鏈〕指数、对数的运算22 厶 2【例 1 】计算：(1)lg 5 + 3lg 8 + lg 5lg 20 + (lg 2);1(2)3三-276 + 164 -2 x (8 -3 )=2+ lg 5 + lg 2(lg 5 + lg 2)I J_-8-8 +2T+T-2.=2+ lg 5 + lg 2 = 3.1丄(2)原式二3’ -(3‘)石] j_= 3y-3y+23-2x2-+(24)T -2 x (23] 4+ 2y x2y2+ 2’ x (22)1HW；[解](1)原式=2lg 5 + 2lg 2 + ig 5(1=2(lg 2 + lg 5) + lg 5 + lg 2 x lg 5 +2+ lg 2) + (lg 2)2(lg 2)-1(4-5 )1 •指数幕运算的一般原则(1) 有括号的先算括号里的，无括号的先做指数运算. (2) 先乘除后加减，负指数幕化成正指数幕的倒数.(3) 底数是负数，先确定符号，底数是小数，先化成分数，底数是带分数的，先化成假分数. (4) 若是根式，应化为分数指数幕，尽可能用幕的形式表示，运用指数幕的运算性质来解答. 2 •对数运算的常用方法(1) 首先利用幕的运算把底数或真数进行变形，化成分数指数幕的形式，使幕的底数最简,然后正用对数运算性质化简合并.(2) 将对数式化为同底数对数的和、差、倍数运算，然后逆用对数的运算性质，转化为同底对数真数的积、商、幕的运算.51 .已知 a >b >l ，若 log a b + log b a =㊁，a b = b a ，贝U a =5[由 log a b + log b a =空，得 log a b +•••(log a b )2-|log a b + 1 = 0,1 、 1 解得 log a b = 2或 2,又 a >b >1，则 log a b =刁由 a b = b a ，得 b = a log a b ,1 1 1 1 •- log a 2a = 2，即 log + 1 = §,1 1•- log a 2=- 2, 1 1 …a -2= 2，• a = 4, b = 2.]指(对)数函数的图像及应用【例2】已知函数f (x )是定义在R 上的偶函数，当x 》0时，f (x ) = x .1 log a b4,2(1) 画出函数f (X )的图像；(2) 根据图像写出f (x )的单调区间，并写出函数的值域.［解］(1)先作出当x >0时，f (x ) = 2 x 的图像，利用偶函数的图像关于 y 轴对称，再作出f (x )在x € ( —8, 0)时的图像.(2)函数f (x )的单调递增区间为(一^, 0)，单调递减区间为［0 ,+8)，值域为(0,1］.由于指数函数 y = a x a >0,且a 三1 ，对数函数 y = log a x a >0,且a ^l的图像与性质都与a 的取值有密切的关系，a 变化时，函数的图像与性质也随之改变 .因此，在求解问题时，当a 的值不确定时，要对它进行分类讨论 .1 x2 .当0<x w 2时，4 <log a x ，贝U a 的取值范围是()D. ( _2, 2)B ［易知0<a <1,则函数y = 4x 与y = log a x 的大致图像如图，则只需满足log £>2,解得<a <1,故选 B.比较大小【例3】(1)三个数a = 0.67, b =严，c = log 0.76的大小关系为(A . b <c <aB . b <a <c C. c <a <b D. c <b <a()A . b <a <cB . a <b <cC. b <c <aD.c <a <b(1) C (2) A [(1)结合 y = 0.6 x , y = 7x 和 y = log 0.7X 的图象，可知 0<a <1, b >1, c <0,故c <a <b .B .C.(1, 2比较两数式或几个数式大小问题是一个重要题型，它主要是考查幕函数、指数函数、对数函数图像与性质的应用及差值比较法与商值比较法的应用，常用的方法有单调性法、图像法、中间量搭桥法、作差法、作商法、分析转化法等3 .若 a >b >1,0< c <1,则()数的性质可知D 错，故选C.］［1. 已知f (x ) = log a | x |，满足f ( — 5) = 1，试画出函数f (x )的图像. 提示：因为 f ( 一 5) = 1，所以 log a 5 = 1，即卩 a = 5, ［log 5X , x >0,故 f (x ) = log 5| x | = |log 5 — x , x <0. 所以函数y = log 5| x |的图像如图所示.2. 试写出函数f (x ) = log 5| x |的值域及单调区间.提示：由探究1的图像知f (x )的值域为R,递增区间为(0,+^)，递减区间为(一汽 0).3. 把探究1中的函数改为y = log b (x —1)( b >0且b * 1)，试求该函数恒过的定点. 提示：令x — 1 = 1得x = 2,又y = log b 1 = 0，故该函数恒过定点(2,0). 1 imx已知函数f (x ) = log a (a >0,且a * 1)是奇函数. x — 1(1) 求实数m 的值；(2) 探究函数f (x )在(1 ,+s )上的单调性.［思路探究］(1)利用奇函数的定义求解；(2)利用复合函数单调性的判断方法判断. ［解］(1)由 f (x )是奇函数，得 f ( — x ) =— f (x ), 口1 + mx 1 — mx即 log a =— log a-—x — 1x — 1A . c . ca <bc ・ cB . ab <ba C. a log b c <b log a CD. log a C <log b C［对于选项A,考虑幕函数 ccc cy = x ,因为c >0,所以y = x 为增函数，又a >b >1,所以a >b ,A 错.对于选项B,ab c <ba c ? 1 - c <b ，又 y = a x 是减函数，所以B 错.对于选项D,由对数函2 21 — mxa 21 — x•••(1 — m )x 2= o ,2• 1 — m = 0，解得 n ± 1., , 1— mx 1 — x ,,八卄宀又当哙1时，口=冇一 1，故m= 1不合题意・所以m=— 1.x + 1⑵ 由(1)知，f (x ) = log - = log ax I函数u = 1 + x4〒在区间(1 ,+s )上单调递减. •••当a >1时，f (x )在区间(1 ,+s )上单调递减; 当0<a <1时，f (x )在区间(1 ,+s )上单调递增.求解与指对数函数有关的复合函数的问题时，需要弄清楚三个方面的问题:1定义域，所有问题都必须在定义域内讨论； 2底数与1的大小关系；3复合函数的构成，如 y = a f x 是由 y = a 与u = f x 构成的.- -1 +2 + a ・33(1)若f (x )的定义域为(一a, 1)，求a 的值；⑵ 若f (x )在x € ( —a, 1)内恒有意义，求a 的取值范围.［解］(1)由函数f (x )的定义域为(一a, 1)，得关于x 的不等式1 + 2 + a •3x >0的解集为(一a•/ g ( x )在R 上是增函数，•不等式g (1)> g (x )的解集为(一a, 1),•- a = g (1) =— 1.⑵ 由已知得，不等式 1 + 2x + a ・3x >0对x € ( —a,1)恒成立,•••log 1 + mx a_-x — 1 卜log 1 — mxlog 1—mx 21 — x2 =1,4 .已知 f (x ) = lg1+1)，即 a > —g (x )的解集为(一a, 1).g(x)对x € ( —a,1)恒成立; 即a>—故a>g(x)max,T g(x)在区间(一^, 1)上是增函数,-g(x)<g(1) =- 1，二a>- 1.- 7 -。

2018版高中数学北师大版选修1-1学案：第三章变化率与

2．1 导数的概念[学习目标] 1.理解并掌握导数的概念.2.掌握求函数在一点处的导数的方法．知识点一导数的概念设函数y ＝f (x )，当自变量x 从x 0变到x 1时，函数值从f (x 0)变到f (x 1)，函数值y 关于x 的平均变化率为Δy Δx ＝f (x 1)－f (x 0)x 1－x 0＝f (x 0＋Δx )－f (x 0)Δx ，当x 1趋于x 0时，即Δx 趋于0时，如果平均变化率趋于一个固定的值，那么这个值就是函数y ＝f (x )在x 0点的导数．记作f ′(x 0)＝lim x 1→x 0f (x 1)－f (x 0)x 1－x 0＝li m Δx →0f (x 0＋Δx )－f (x 0)Δx .知识点二求在某一点x 0处的导数的步骤 (1)求函数的增量：Δy ＝f (x 0＋Δx )－f (x 0)； (2)求平均变化率：Δy Δx ＝f (x 0＋Δx )－f (x 0)Δx；(3)取极限：求Δx 趋于0时，ΔyΔx所趋近的值，即为函数y ＝f (x )在点x 0处的导数．题型一利用定义求导数例1 求函数f (x )＝3x 2－2x 在x ＝1处的导数．解 Δy ＝3(1＋Δx )2－2(1＋Δx )－(3×12－2×1) ＝3(Δx )2＋4Δx ，∵Δy Δx ＝3(Δx )2＋4Δx Δx＝3Δx ＋4， ∴f ′(1)＝lim Δx→0ΔyΔx ＝lim Δx →0(3Δx ＋4)＝4. 反思与感悟求一个函数y ＝f (x )在x ＝x 0处的导数的步骤如下：(1)求函数值的变化量Δy ＝f (x 0＋Δx )－f (x 0)； (2)求平均变化率Δy Δx ＝f (x 0＋Δx )－f (x 0)Δx ；(3)取极限，得导数f ′(x 0)＝lim Δx→0ΔyΔx. 跟踪训练1 利用导数的定义求函数f (x )＝－x 2＋3x 在x ＝2处的导数．解由导数的定义知，函数在x ＝2处的导数 f ′(2)＝lim Δx→f (2＋Δx )－f (2)Δx ，而f (2＋Δx )－f (2)＝－(2＋Δx )2＋3(2＋Δx )－(－22＋3×2)＝－(Δx )2－Δx ，于是f ′(2)＝lim Δx →0－(Δx )2－ΔxΔx ＝lim Δx →0 (－Δx －1)＝－1.题型二导数概念的应用例2 已知f (x )在x 0处的导数f ′(x 0)＝k ，求下列各式的值： (1)li m Δx→f (x 0)－f (x 0－Δx )2Δx ；(2)li m Δx→f (x 0＋Δx )－f (x 0－Δx )Δx .解 (1)∵li m Δx→0f (x 0)－f (x 0－Δx )x 0－(x 0－Δx )＝f ′(x 0)，即li m Δx→f (x 0)－f (x 0－Δx )Δx ＝f ′(x 0)＝k .∴li m Δx→f (x 0)－f (x 0－Δx )2Δx ＝k2.(2)∵f (x 0＋Δx )－f (x 0－Δx )(x 0＋Δx )－(x 0－Δx )，即f (x 0＋Δx )－f (x 0－Δx )2Δx 为函数f (x )在区间[x 0－Δx ，x 0＋Δx ]上平均变化率．∴当Δx 趋于0时，f (x 0＋Δx )－f (x 0－Δx )2Δx 必趋于f ′(x 0)＝k ，∴li m Δx→f (x 0＋Δx )－f (x 0－Δx )2Δx ＝k ，∴li m Δx→f (x 0＋Δx )－f (x 0－Δx )Δx ＝2k .反思与感悟在导数的定义中，增量Δx 的形式是多种多样的，但不论Δx 选择哪种形式，Δy 也必须选择相应的形式，利用函数f (x )在点x 0处可导的条件，可以将已给定的极限式恒等变形转化为导数定义的结构形式．跟踪训练2 已知f ′(x 0)＝－2，求lim k →0f ⎝⎛⎭⎫x 0－12k －f (x 0)k 的值．解 ∵f ′(x 0)＝lim k →0f ⎣⎡⎦⎤x 0＋⎝⎛⎭⎫－12k －f (x 0)－12k ＝－2.(注：Δx ＝－12k )，∴lim k →0f ⎝⎛⎭⎫x 0－12k －f (x 0)k＝－12lim k →0f ⎝⎛⎭⎫x 0－12k －f (x 0)－12k＝－12f ′(x 0)＝⎝⎛⎭⎫－12×(－2)＝1.导数在实际问题中的应用例3 柏油路是用沥青和大小石子等材料混合后辅成的，铺路工人铺路时需要对沥青加热使之由固体变成黏稠液体状．如果开始加热后第x 小时的沥青温度(单位：℃)为：f (x )＝⎩⎪⎨⎪⎧80x 2＋20，0≤x ≤1，－2049(x 2－2x －224)，1<x ≤8.经过计算开始加热后第15分钟和第4小时沥青温度的瞬时变化率分别为f ′(0.25)＝40，f ′(4)＝－12049，试说明它们的实际意义．分析本例中，f ′(t 0)反映了沥青温度在x ＝t 0附近的变化情况．解由题意知，在第15分钟和第4小时沥青温度的瞬时变化率分别为40，－12049，它表示在加热第15分钟时，沥青温度为40 ℃/h 的速度上升，在第4小时时，沥青温度以12049℃/h的速度下降．也可以说，在加热第15分钟左右，沥青温度大约以40 ℃/h 的速度上升；在第4小时左右，沥青温度大约以12049℃/h 的速度下降．解后反思导数可以描述任何事物的瞬时变化率，一般地，函数f (x )在某点处的导数大小表示在此点附近变化的快慢．1．函数f (x )在x 0处可导，则li m h→f (x 0＋h )－f (x 0)h ( )A ．与x 0、h 都有关B ．仅与x 0有关，而与h 无关C ．仅与h 有关，而与x 0无关D ．与x 0、h 均无关答案 B2．设函数f (x )可导，则lim Δx→f (1＋3Δx )－f (1)3Δx 等于( )A ．f ′(1)B ．3f ′(1) C.13f ′(1) D ．f ′(3) 答案 A 解析 lim Δx→f (1＋3Δx )－f (1)3Δx ＝f ′(1)．3．函数f (x )＝x 3＋2xf ′(1)，则f ′(0)＝( ) A ．－6 B ．6 C ．－4 D ．4 答案 A解析 ∵f (x )＝x 2＋2xf ′(1)， ∴f ′(1)＝lim Δx→f (1＋Δx )－f (1)Δx＝lim Δx →0(1＋Δx )3＋2(1＋Δx )f ′(1)－1－2f ′(1)Δx＝3＋2f ′(1)，解得f ′(1)＝－3，代入原式得f (x )＝x 3－6x ，故f ′(0)＝lim Δx →0(Δx )3－6ΔxΔx ＝－6.4．一做直线运动的物体，其位移s 与时间t 的关系是s ＝3t －t 2，则物体的初速度是________．答案 3 解析 v 初＝lim Δt→0s (0＋Δt )－s (0)Δt ＝lim Δt →0(3－Δt )＝3.5．已知函数f (x )＝1x，则f ′(1)＝________. 答案－12解析 f ′(1)＝lim Δx →0f (1＋Δx )－f (1)Δx ＝lim Δx →011＋Δx －1Δx＝lim Δx →－11＋Δx (1＋1＋Δx )＝－12.利用导数定义求导数三步曲：(1)作差求函数的增量Δy ＝f (x 0＋Δx )－f (x 0)；(2)作比求平均变化率Δy Δx ＝f (x 0＋Δx )－f (x 0)Δx ；(3)取极限得导数f ′(x 0)＝lim Δx→0ΔyΔx. 简记为一差，二比，三极限．。

(北师大版)选修1-1课件：第3章-章末复习课件(1)

1 5 2 求曲线 y＝ x ＋3x ＋4x 在 x＝－1 处的切线的倾斜角． 5
解析： 1 5 ∵y＝f(x)＝5x ＋3x2＋4x，
4
∴f′(x)＝x ＋6x＋4.∴f′(－1)＝－1. 1 5 即曲线 y＝5x ＋3x2＋4x 在 x＝－1 处的切线的斜率 k＝－1，设其倾斜角为 α. 3 ∴tan α＝－1.又∵α∈[0，π)，∴α＝4π.
Δy 如果当 Δx→0 时有极限，我们就说 y＝f(x)在点 x0 处 Δx 可导，并把这个极限叫做 f(x)在点 x0 处的导数(或变化率)，记作 f′(x0) 或 y′|x ＝ x0 ，即 f′(x0) ＝ Δ lim x→0 Δy ＝Δ lim x→0 Δx
fx0－Δx－fx0 .函数 y＝f(x)的导数 f′(x)，就是当 Δx→0 时， Δx Δy 函数的增量 Δy 与自变量的增量 Δx 的比的极限， Δx fx＋Δx－fx Δy 即 f′(x)＝Δ lim lim . x→0 Δx＝Δ x→0 Δx
1 ．以选择题或填空题的形式考查导数的几何意义． 2 ．导数的运算与导数的应用相结合出现在解答题中．
一、导数的概念
对于函数 y＝f(x)，如果自变量 x 在 x0 处有增量 Δx， Δy 那么函数 y 相应地有增量 Δy＝f(x0＋Δx)－f(x0)，比值就叫 Δx Δy 做函数 y＝f(x)在 x0 到 x0＋Δx 之间的平均变化率，即＝ Δx fx0＋Δx－fx0 ， Δx
f1－f1－x 设 f(x)为可导函数且满足条件 lim ＝ 2x －1，求曲线 y＝f(x)在点(1，f(1))处的切线的斜率．
解析： f1－f1－x ∵f(x)为可导函数且 lim ＝－1， 2x
f1－f1－x 1 1 ∴2lim ＝－1，即2f′(1)＝－1， x ∴f′(1)＝－2. 因此 y＝f(x)在点(1，f(1))处的切线的斜率为－2.

高中数学北师大版选修1-1教案：第3章导数与函数的单

导数与函数的单调性一、学习目标1．会从几何直观探索并了解函数的单调性与其导数之间的关系，并会灵活应用；2．会用导数判断或证明函数的单调性；3．通过对函数单调性的研究，加深对函数导数的理解，提高用导数解决实际问题的能力.二、学习重、难点灵活应用导数研究与函数单调性有关的问题，并能运用数形结合的思想方式．三、学习进程1．温习增函数、减函数的概念：一般地，设函数y=)(x f 的概念域为A ，若是对于概念域A 内某个区间I 上的任意两个自变量的值21x x 、，当21x x <时，（1）若都有)()(21x f x f <，那么就说函数)(x f 在区间I 上是（2）若都有)()(21x f x f >，那么就说函数)(x f 在区间I 上是2．函数的单调性与导数的关系（1）设函数y=)(x f ，若在某区间上恒有0)(>'x f ，则)(x f 为该区间上的函数，若在某区间上恒有0)(<'x f ，则)(x f 为该区间上的函数，若是在某区间恒有0)('=x f ，那么)(x f 在该区间为常值函数.即由0)(>'x f 得函数y=)(x f 的单调区间，由0)(<'x f 得函数y=)(x f 的单调区间.（2）若可导函数)(x f 在),(b a 上单调递增⇒ ；若可导函数)(x f 在),(b a 上单调递减⇒ .例1．肯定函数34)(2+-=x x x f 在哪个区间上是增函数，哪个区间上是减函数.例2．求32287y x x =-+的单调区间.例3．肯定函数)2,0(,sin )(π∈=x x x f 的单调减区间.变式：讨论函数x x y sin 2-=在)2,0(π内的单调性．1、当堂反馈1．肯定下列函数的单调区间：（1）3)(x x x f -= （2）31232)(23+-+=x x x x f（3）x x x f cos sin )(+= （4）)3()(2-=x x x f2．证明：x e x f x -=)(在区间)0,(-∞上是减函数.五、小结反思。

[K12配套]2018北师大版高中数学选修1-1学案：第三章章末复习课

学习目标 1.会求函数在某点处的导数.2.理解导数的几何意义，会求曲线上某点处的切线方程.3.能够运用导数公式和求导法则进行求导运算．知识点一函数y ＝f (x )在x ＝x 0处的导数1．函数y ＝f (x )在x ＝x 0处的________________称为函数y ＝f (x )在x ＝x 0处的导数，记作________________，即f ′(x 0)＝lim Δx →ΔyΔx＝________________________. 2．函数y ＝f (x )在点x 0处的导数f ′(x 0)是曲线y ＝f (x )在点P (x 0，f (x 0))处____________，在点P 处的切线方程为________________________．知识点二导函数如果一个函数f (x )在区间(a ，b )上的每一点x 处都有导数，导数值记为________，f ′(x )＝li mΔx →0 f (x ＋Δx )－f (x )Δx，则f ′(x )是关于x 的函数，称f ′(x )为f (x )的导函数，通常也简称为________．知识点三基本初等函数的导数公式设两个函数f (x )，g (x )可导，则类型一利用导数的定义解题例1 利用导数的定义求函数y ＝x 2＋1的导数．反思与感悟 (1)对于导数的定义，必须明白定义中包含的基本内容和Δx 趋于0的方式，函数的改变量Δy 与自变量的改变量Δx 的比趋于一个固定的值．即ΔyΔx ＝lim Δx →0 f (x 0＋Δx )－f (x 0)Δx. (2)在用定义求导数时，必须掌握三个步骤以及用定义求导数的一些简单变形．跟踪训练1 已知s (t )＝t ＋2t ，求li m Δt →0 s (5＋Δt )－s (5)Δt .类型二导数的几何意义例2 函数y ＝f (x )的图像如图，下列数值的排序正确的是( )A ．0<f ′(2)<f ′(3)<f (3)－f (2)B ．0<f ′(3)<f (3)－f (2)<f ′(2)C ．0<f ′(3)<f ′(2)<f (3)－f (2)D ．0<f (3)－f (2)<f ′(2)<f ′(3)反思与感悟导数的几何意义主要应用于切线问题，解决此类问题的关键点是找“切点”，应注意：(1)在表示切线斜率、切线方程时均需用切点坐标；(2)切点既在曲线上又在切线上，因此可用切线方程求切点坐标；(3)若已知点不在曲线上，则该点与切点连线斜率等于在切点处的导数值，这也是求切点坐标的主要方法．跟踪训练2 已知函数f (x )＝x 3－3x 2＋ax ＋2，曲线y ＝f (x )在点(0,2)处的切线与x 轴交点的横坐标为－2.则a 的值是________．类型三导数的计算例3 求下列函数的导数： (1)y ＝x 2－ln x ＋a x ＋π； (2)y ＝33x 4＋4x 3； (3)y ＝(x ＋1)(x ＋2)(x ＋3)； (4)y ＝cos x x 2.反思与感悟有关导数的计算应注意以下两点 (1)熟练掌握公式：熟练掌握简单函数的导数公式及函数的和、差、积、商的导数运算法则． (2)注意灵活化简：当函数式比较复杂时，要将函数形式进行化简，化简的原则是将函数拆分成简单函数的四则运算形式，由于在导数的四则运算公式中，和与差的求导法则较为简洁，因此化简时尽可能转化为和、差的形式，尽量少用积、商求导．跟踪训练3 求下列函数的导数：(1)y ＝3x 2－x x ＋5x －9x ；(2)y ＝cos 2x sin x ＋cos x .类型四导数的综合应用例4 设函数f (x )＝a 2x 2(a >0)，若函数y ＝f (x )图像上的点到直线x －y －3＝0距离的最小值为2，求a 的值．反思与感悟利用基本初等函数的求导公式，结合导数的几何意义可以解决一些与距离、面积相关的几何的最值问题．解题时可先利用图像分析取最值时的位置情况，再利用导数的几何意义准确计算．跟踪训练4 已知直线x －2y －4＝0与抛物线y 2＝x 相交于A 、B 两点，O 是坐标原点，试在抛物线的弧AOB 上求一点P ，使△ABP 的面积最大．1．自由落体的物体在t ＝4 s 时的瞬时速度是指( ) A ．在第4秒末的速度 B ．在第4秒始的速度C ．在第3秒至第4秒的平均速度D ．在第4秒始到第4秒末之间的任何时刻的速度 2．已知函数f (x )＝x 22x ，则f ′(2)等于( ) A ．16＋ln 2 B ．16＋8ln 2 C ．8＋16ln 2D ．16＋16ln 23．若函数y ＝f (x )＝x 3，且f ′(a )＝3，则a 等于( ) A ．1 B ．－1 C ．±1D ．不存在4．若直线y ＝12x ＋b 是曲线y ＝ln x (x >0)的一条切线，则实数b ＝________.5．已知P ，Q 为抛物线x 2＝2y 上两点，点P ，Q 的横坐标分别为4，－2，过P ，Q 分别作抛物线的切线，两切线交于点A ，则点A 的纵坐标为________．1．利用定义求函数的导数是逼近思想的应用． 2．导数的几何意义是曲线在一点的切线的斜率．3．对于复杂函数的求导，可利用导数公式和导数的四则运算法则，减少运算量．答案精析知识梳理知识点一1．瞬时变化率 f ′(x 0)lim Δx →f (x 0＋Δx )－f (x 0)Δx2．切线的斜率 y －f (x 0)＝f ′(x 0)(x －x 0) 知识点二 f ′(x ) 导数知识点三αx α－1 cos x －sin x a x ln a e x 1x ln a 1x 1cos 2x －1sin 2x 知识点四f ′(x )＋g ′(x ) f ′(x )－g ′(x ) f ′(x )g (x )＋f (x )g ′(x ) 题型探究例1 解 y ′＝lim Δx →ΔyΔx＝lim Δx →f (x ＋Δx )－f (x )Δx＝lim Δx →(x ＋Δx )2＋1－x 2＋1Δx＝lim Δx →2x ·Δx ＋(Δx )2Δx [(x ＋Δx )2＋1＋x 2＋1]＝lim Δx →2x ＋Δx (x ＋Δx )2＋1＋x 2＋1＝xx 2＋1. 跟踪训练1 解 ∵lim Δx →0s (5＋Δt )－s (5)Δt＝s ′(5)，又s ′(t )＝1－2t 2，∴lim Δx →s (5＋Δt )－s (5)Δt＝s ′(5)＝1－225＝2325.例2 B [过点(2，f (2))和点(3，f (3))的割线的斜率k ＝Δy Δx ＝f (3)－f (2)3－2＝f (3)－f (2)，又由导数的几何意义并结合题干中的图像可知0<f ′(3)<f (3)－f (2)<f ′(2)，故选B.] 跟踪训练2 1 [∵f ′(0)＝a ， ∴y ＝f (x )在点(0,2)处的切线方程为 y －2＝ax ，由题意知x ＝－2时，y ＝0，可得a ＝1.] 例3 解 (1)y ′＝(x 2－ln x ＋a x ＋π)′ ＝(x 2)′－(ln x )′＋(a x )′＋π′ ＝2x －1x ＋a x ln a .(2)y ′＝(33x 4＋4x 3)′ ＝(33x 4)′＋(4x 3)′ ＝(3·x 43)′＋(4·x 32)′＝4x 13＋6x 12＝43x ＋6x .(3)因为y ＝(x 2＋3x ＋2)(x ＋3) ＝x 3＋6x 2＋11x ＋6，所以y ′＝3x 2＋12x ＋11. (4)y ′＝⎝⎛⎭⎫cos x x 2′＝(cos x )′·x 2－cos x ·(x 2)′x 4＝－sin x ·x 2－cos x ·(2x )x 4＝－x sin x ＋2cos x x 3.跟踪训练3 解 (1)∵y ＝3x 32－x ＋5－9x －12，∴y ′＝⎝⎛⎭⎫3x 32′－x ′＋5′－⎝⎛⎭⎫9x －12′ ＝92x 12－1＋92x －32 ＝92x ⎝⎛⎭⎫1＋1x 2－1. (2)∵y ＝cos 2xsin x ＋cos x＝cos 2x －sin 2x cos x ＋sin x ＝cos x －sin x ， ∴y ′＝(cos x －sin x )′ ＝(cos x )′－(sin x )′ ＝－sin x －cos x .例4 解因为f (x )＝a 2x 2，所以f ′(x )＝2a 2x ，令f ′(x )＝2a 2x ＝1，得x ＝12a 2，此时y ＝14a2，则点⎝⎛⎭⎫12a 2，14a 2到直线x －y －3＝0的距离为2，即2＝|12a 2－14a2－3|2，解得a ＝12或510.跟踪训练4 解设P (x 0，y 0)，过点P 与AB 平行的直线为l ，如图．由于直线x －2y －4＝0与抛物线y 2＝x 相交于A 、B 两点，所以|AB |为定值，要使△ABP 的面积最大，只要P 到AB 的距离最大，而P 点是抛物线的弧AOB 上的一点，因此点P 是抛物线上平行于直线AB 的切线的切点，由图知点P 在x 轴上方，y ＝x ，y ′＝12x ，由题意知k AB ＝12.∴k l ＝12x 0＝12，即x 0＝1，∴y 0＝1.∴P (1,1)．当堂训练1．A 2.D 3.C 4.ln 2－1 5.－4。

高中数学北师大版选修1-1学案：第三章 2 导数的概念及其几何意义

学习目标1.理解导数的概念以及导数和变化率的关系.2.会计算函数在某点处的导数，理解导数的实际意义.3.理解导数的几何意义，会求曲线上某点处的切线方程．知识点一导数的概念思考1平均变化率与瞬时变化率有何区别、联系？梳理知识点二导数的几何意义如图，P n的坐标为(x n，f(x n))(n＝1,2,3,4，…)，P的坐标为(x0，y0)，直线PT为过点P的切线．思考1割线PP n 的斜率k n 是多少？思考2当点P n 无限趋近于点P 时，割线PP n 的斜率k n 与切线PT 的斜率k 有什么关系？梳理(1)切线的定义：当P n 趋近于点P 时，割线PP n 趋近于确定的位置，这个确定位置的直线PT 称为________的切线．(2)导数f ′(x 0)的几何意义：函数f (x )在x ＝x 0处的导数就是切线的斜率k ，即k ＝________________________________________________________________________. (3)切线方程：曲线y ＝f (x )在点(x 0，f (x 0))处的切线方程为________________________．类型一利用定义求导数例1求函数f (x )＝3x 2－2x 在x ＝1处的导数．反思与感悟求一个函数y ＝f (x )在x ＝x 0处的导数的步骤如下： (1)求函数值的变化量Δy ＝f (x 0＋Δx )－f (x 0)； (2)求平均变化率Δy Δx ＝f (x 0＋Δx )－f (x 0)Δx ；(3)取极限，得导数f ′(x 0)＝lim Δx→0ΔyΔx. 跟踪训练1利用导数的定义求函数f (x )＝－x 2＋3x 在x ＝2处的导数．类型二求切线方程命题角度1 求在某点处的切线方程例2已知曲线y ＝2x 2上一点A (1,2)，求： (1)点A 处的切线的斜率； (2)点A 处的切线方程．反思与感悟求曲线在某点处的切线方程的步骤跟踪训练2曲线y ＝x 2＋1在点P (2,5)处的切线与y 轴交点的纵坐标是________．命题角度2 曲线过某点的切线方程例3求抛物线y ＝14x 2过点(4，74)的切线方程．反思与感悟过点(x 1，y 1)的曲线y ＝f (x )的切线方程的求法步骤 (1)设切点(x 0，y 0)；(2)建立方程f ′(x 0)＝y 1－y 0x 1－x 0；(3)解方程得k＝f′(x0)，x0，y0，从而写出切线方程．跟踪训练3求过点(－1，－2)且与曲线y＝2x－x3相切的直线方程．类型三导数的几何意义的综合应用例4已知曲线f(x)＝x2＋1与g(x)＝x3＋1在x＝x0处的切线互相垂直，求x0的值．引申探究若将本例的条件“垂直”改为“平行”，则结果如何？反思与感悟导数的几何意义是曲线的切线的斜率，已知切点可以求斜率，反过来，已知斜率也可以求切点，从而可以与解析几何等知识相联系．跟踪训练4已知直线l：y＝4x＋a与曲线C：y＝x3－2x2＋3相切，求a的值及切点坐标．1．设函数f (x )在点x 0附近有定义，且有f (x 0＋Δx )－f (x 0)＝a Δx ＋b (Δx )2(a ，b 为常数)，则() A ．f ′(x )＝a B ．f ′(x )＝b C ．f ′(x 0)＝a D ．f ′(x 0)＝b2．曲线f (x )＝9x 在点(3,3)处的切线的倾斜角等于()A ．45°B ．60°C ．135°D ．120°3.如图，函数y ＝f (x )的图像在点P (2，y )处的切线是l ，则f (2)＋f ′(2)等于() A ．－4B ．3 C ．－2D ．14．已知函数y ＝ax 2＋b 在点(1,3)处的切线斜率为2，则ba ＝________.5．求曲线y ＝1x 在点⎝⎛⎭⎫2，12处的切线方程．1．导数f ′(x 0)的几何意义是曲线y ＝f (x )在点(x 0，f (x 0))处的切线的斜率，即k ＝lim Δx →0f (x 0＋Δx )－f (x 0)Δx＝f ′(x 0)．2．利用导数求曲线的切线方程，要注意已知点是否在曲线上．如果已知点在曲线上，则以该点为切点的切线方程为y －f (x 0)＝f ′(x 0)(x －x 0)；若已知点不在切线上，则设出切点(x 0，f (x 0))，表示出切线方程，然后求出切点．答案精析问题导学知识点一思考1平均变化率刻画函数值在区间[x 1，x 2]上变化的快慢，瞬时变化率刻画函数值在x 0点处变化的快慢；当Δx 趋于0时，平均变化率ΔyΔx 趋于一个常数，这个常数即为函数在x 0处的瞬时变化率，它是一个固定值．梳理lim Δx→f (x 0＋Δx )－f (x 0)Δx f ′(x 0)瞬时变化率知识点二思考1割线PP n 的斜率 k n ＝f (x n )－f (x 0)x n －x 0.思考2k n 无限趋近于切线PT 的斜率k . 梳理(1)点P 处 (2)li m Δx→f (x 0＋Δx )－f (x 0)Δx ＝f ′(x 0)(3)y －f (x 0)＝f ′(x 0)(x －x 0) 题型探究例1解∵Δy ＝3(1＋Δx )2－2(1＋Δx )－(3×12－2×1) ＝3(Δx )2＋4Δx ，∴Δy Δx ＝3(Δx )2＋4Δx Δx＝3Δx ＋4， ∴f ′(1)＝lim Δx→0ΔyΔx ＝lim Δx →0(3Δx ＋4)＝4. 跟踪训练1解由导数的定义知，函数在x ＝2处的导数 f ′(2)＝lim Δx→f (2＋Δx )－f (2)Δx ，而f (2＋Δx )－f (2)＝－(2＋Δx )2＋3(2＋Δx )－(－22＋3×2)＝－(Δx )2－Δx ，于是f ′(2)＝lim Δx →0－(Δx )2－ΔxΔx＝lim Δx →(－Δx －1)＝－1. 例2解(1)k ＝li m Δx→0Δy Δx＝lim Δx →02(1＋Δx )2－2×12Δx＝lim Δx →04Δx ＋2(Δx )2Δx＝lim Δx →(4＋2Δx )＝4， ∴点A 处的切线的斜率为4.(2)点A 处的切线方程是 y －2＝4(x －1)，即4x －y －2＝0. 跟踪训练2 －3 解析lim Δx→0ΔyΔx＝lim Δx →0(2＋Δx )2＋1－22－1Δx＝lim Δx →(4＋Δx )＝4，曲线y ＝x 2＋1在点(2,5)处的切线方程为 y －5＝4(x －2)，即y ＝4x －3.∴切线与y 轴交点的纵坐标是－3.例3解设切线在抛物线上的切点为(x 0，14x 20)，∵lim Δx →014(x 0＋Δx )2－14x 20Δx＝lim Δx →0 (12x 0＋14Δx )＝12x 0. ∴14x 20－74x 0－4＝12x 0，即x 20－8x 0＋7＝0，解得x 0＝7或x 0＝1，即切线过抛物线y ＝14x 2上的点(7，494)，(1，14)，故切线方程为y －494＝72(x －7)或y －14＝12(x －1)，化简得14x －4y －49＝0或2x －4y －1＝0，即为所求的切线方程．跟踪训练3解lim Δx→0Δy Δx＝lim Δx →02(x ＋Δx )－(x ＋Δx )3－2x ＋x 3Δx＝lim Δx →[2－3x 2－3x Δx －(Δx )2] ＝2－3x 2.设切点坐标为(x 0,2x 0－x 30)． ∴切线方程为y －2x 0＋x 30＝(2－3x 20)(x －x 0)．又∵切线过点(－1，－2)，∴－2－2x 0＋x 30＝(2－3x 20)(－1－x 0)，即2x 30＋3x 20＝0，∴x 0＝0或x 0＝－32.∴切点坐标为(0,0)或⎝⎛⎭⎫－32，38. 当切点坐标为(0,0)时，切线斜率为2，切线方程为y ＝2x ，即2x －y ＝0. 当切点坐标为⎝⎛⎭⎫－32，38时，切线斜率为－194，切线方程为y ＋2＝－194(x ＋1)，即19x ＋4y ＋27＝0.综上可知，过点(－1，－2)且与曲线相切的切线方程为 2x －y ＝0或19x ＋4y ＋27＝0.例4解因为f ′(x 0)＝lim Δx →0(x 0＋Δx )2＋1－(x 20＋1)Δx＝lim Δx →(Δx ＋2x 0)＝2x 0， g ′(x 0)＝lim Δx →0(x 0＋Δx )3＋1－(x 30＋1)Δx＝lim Δx →[(Δx )2＋3x 0Δx ＋3x 20] ＝3x 20，k 1＝2x 0，k 2＝3x 20，因为切线互相垂直，所以k 1k 2＝－1，即6x 30＝－1，解得x 0＝－3366. 引申探究解由例4知，f ′(x 0)＝2x 0，g ′(x 0)＝3x 20，k 1＝2x 0，k 2＝3x 20，由题意知2x 0＝3x 20，得x 0＝0或23. 跟踪训练4解设直线l 与曲线C 相切于点P (x 0，y 0)． ∵lim Δx→f (x ＋Δx )－f (x )Δx＝lim Δx →0(x ＋Δx )3－2(x ＋Δx )2＋3－(x 3－2x 2＋3)Δx＝3x 2－4x ，由题意可知k ＝4，即3x 20－4x 0＝4，解得x 0＝－23或x 0＝2，∴切点的坐标为(－23，4927)或(2,3)．当切点为(－23，4927)时，有4927＝4×(－23)＋a ，a ＝12127. 当切点为(2,3)时，有3＝4×2＋a ， a ＝－5.∴当a ＝12127时，切点坐标为(－23，4927)；当a ＝－5时，切点坐标为(2,3)．当堂训练 1．C2.C3.D4.2 5．解因为lim Δx→f (2＋Δx )－f (2)Δx＝lim Δx →012＋Δx －12Δx＝lim Δx→0－12(2＋Δx )＝－14.所以这条曲线在点⎝⎛⎭⎫2，12处的切线斜率为－14，由直线的点斜式方程可得切线方程为 y －12＝－14(x －2)，即x ＋4y －4＝0.。

高中数学(北师大)选修1-1课件：第3章章末复习课件2

(1 3x)4
例2、已知曲线C1：y
x2
与曲线C2：y
(x
2) 2
，直线l与C1、C2都相切，求直线l的方程。
解：设l与C1相切于点 P1 (x1, y1 )，l与C2相切于点 P2 (x2 , y2 )
直线l的斜率为k。C1：yห้องสมุดไป่ตู้
x 2，y
2x，k
2
x1，P1
(
k 2
,
k2 4
)
C2：y (x 2)2，y 2(
2
x2
1
1
2 ln x3
x
。
（2）∵ y x2 (x 3)( x 3) x4 9x2
∴ y 4x3 18x
（3）∵ y x 1 sin 2x x (sin x cosx)2 x sin x cosx
又∵ x (0, ) 4
∴ y x(cosx sin x) 故 sin x cosx
(ln x)' 1 x
1 ；(loga x)' x log a e ；
(e x )' e x ； (a x )' a x ln a 。
5．导数的四则运算法则：
[u(x) v(x)]' u ' (x) v' (x)
[u(x)v(x)] u '(x)v(x) u(x)v '(x)
[Cu(x)] Cu '(x)
∴ y 1 (cos x sin x) x ( sin x cos x)
(1 x) cos x (1 x) sin x 。
（4）y
(e
2x1
)(1
3x)3 [(1
e2x1[(1 3x)3 ]2

北师大版高中数学选修1-1学案：第三章4

跟踪训练1 求下列函数的导数：
(1)y＝axsin x，其中a>0且a≠1；(2)y＝.
类型二导数运算法则的简单应用
例2 已知函数f(x)＝＋，曲线y＝f(x)在点(1，f(1))处的切线方程为x＋2y－3＝0，求a，b的值．
引申探究
已知函数f(x)＝＋，求曲线y＝f(x)在点(1，f(1))处的切线方程．
反思与感悟 (1)此类问题往往涉及切点、切点处的导数、切线方程三个主要元素．其他的条件可以进行转化，从而转化为这三个要素间的关系．
(2)准确求出已知函数式的导数、切线方程是解决此类问题的关键．
跟踪训练2 若函数f(x)＝exsin x，则此函数图像在点(4，f(4))处的切线的倾斜角为( )
A. B．0 C．钝角 D．锐角
答案精析
问题导学
知识点
思考经计算得：
y＝x2f(x)在x0处的导数为xf′(x0)＋2x0f(x0)．
梳理 f′(x)g(x)＋f(x)g′(x) xgx－fxg′x,g2x) kf′(x)
题型探究
例1 解 (1)因为y＝x3＋x－＋
＝x3＋x－＋sin x·x－2，
所以y′＝(x3＋x－＋sin x·x－2)′
北师大版高中数学选修
学习目标 1.理解导数的乘法与除法法则.2.将导数公式和导数四则运算相结合，灵活解决一些导数问题．
知识点导数的乘法与除法法则
思考设函数y＝f(x)在x0处的导数为f′(x0)，g(x)＝x2，怎样用导数定义求y＝f(x)g(x)＝x2f(x)在x0处的导数？
梳理一般地，若两个函数f(x)和g(x)的导数分别是f′(x)和g′(x)，则[f(x)g(x)]′＝________________________________________________________________________；

北师大版高中数学必修一学案：第三章章末复习课(1)

3．应用指数函数y＝ax和对数函数y＝logax的图像和性质时，若底数含有字母，要特别注意对底数a＞1和0＜a＜1两种情况的讨论．
4．幂函数与指数函数的主要区别：幂函数的底数为变量，指数函数的指数为变量．因此，当遇到一个有关幂的形式的问题时，就要看变量所在的位置从而决定是用幂函数知识解决，还是用指数函数知识去解决．
跟踪训练4 若函数y＝logax(a>0，且a≠1)的图像如图所示，则下列函数图像正确的是( )
1．化简lg a100,2＋பைடு நூலகம்glg a)为( )
A．1 B．2 C．3 D．0
2．在同一直角坐标系中，函数f(x)＝xa(x>0)，g(x)＝logax的图像可能是( )
3．函数f(x)＝x与函数g(x)＝log|x|在区间(－∞,0)上的单调性为( )
1．函数是高中数学极为重要的内容，函数思想和函数方法贯穿整个高中数学的过程，对本章的考查是以基本函数形式出现的综合题和应用题，一直是常考不衰的热点问题．
2．从考查角度看，指数函数、对数函数概念的考查以基本概念与基本计算为主；对图像的考查重在考查平移变换、对称变换以及利用数形结合的思想方法解决数学问题的能力；对幂函数的考查将会从概念、图像、性质等方面来考查．
(1)log0.22，log0.049；
(2)a1.2，a1.3；
(3)30.4,0.43，log0.43.
类型三指数函数、对数函数、幂函数的综合应用
例3 已知函数f(x)＝a·2x＋b·3x，其中常数a，b满足ab≠0.
(1)若ab>0，判断函数f(x)的单调性；
(2)若ab<0，求f(x＋1)>f(x)时的x的取值范围．
例2 解 (1)∵82＝(23)2＝26，

高中数学北师大版选修1-1教案：第3章计算导数参考教

计算导数教学进程：一、温习一、导数的概念；二、导数的几何意义；3、导函数的概念；4、求函数的导数的流程图。

（1）求函数的改变量)()(x f x x f y -∆+=∆（2）求平均转变率xx f x x f x y ∆-∆+=∆∆)()( （3）取极限，得导数/y ＝()f x '=x y x ∆∆→∆0lim 本节课咱们将学习常见函数的导数。

第一咱们来求下面几个函数的导数。

（1）、y=x （2）、y=x 2 （3）、y=x 3问题1：1-=x y ，2-=x y ，3-=x y 呢？问题2：从对上面几个幂函数求导，咱们能发觉有什么规律吗？二、新授一、大体初等函数的求导公式：⑴ ()kx b k '+= (k,b 为常数) ⑵ 0)(='C (C 为常数) ⑶ ()1x '= ⑷ 2()2x x '= ⑸ 32()3x x '= ⑹ 211()x x'=- ⑺ ()2x x '= 由⑶~⑹你能发觉什么规律?⑻ 1()x x ααα-'= （α为常数）⑼ ()ln (01)x x a a a a a '=>≠， ⑽ a a 11(log x)log e (01)x xlnaa a '==>≠，且 ⑾ x x e )(e =' ⑿ x 1)(lnx =' ⒀ cosx )(sinx =' ⒁ sinx )(cosx －=' 从上面这一组公式来看，咱们只要掌握幂函数、指对数函数、正余弦函数的求导就可以够了。

例一、求下列函数导数。

（1）5-=x y （2）x y 4= （3）x x x y =（4）x y 3log = （5）y=sin(2π+x) (6) y=sin 3π （7）y=cos(2π－x) （8）y=(1)f '例2：已知点P 在函数y=cosx 上，（0≤x≤2π），在P 处的切线斜率大于0，求点P 的横坐标的取值范围。

高中数学北师大版选修1-1第三章《导数在实际问题中的应用》word教案1

导数在实际问题中的应用教学目的：1. 进一步熟练函数的最大值与最小值的求法；⒉初步会解有关函数最大值、最小值的实际问题教学重点：解有关函数最大值、最小值的实际问题．教学难点：解有关函数最大值、最小值的实际问题．授课类型：新授课课时安排：1课时教具：多媒体、实物投影仪教学过程：一、复习引入：1.极大值：一般地，设函数f(x)在点x 0附近有定义，如果对x 0附近的所有的点，都有f(x)＜f(x 0)，就说f(x 0)是函数f(x)的一个极大值，记作y 极大值=f(x 0)，x 0是极大值点2.极小值：一般地，设函数f(x)在x 0附近有定义，如果对x 0附近的所有的点，都有f(x)＞f(x 0).就说f(x 0)是函数f(x)的一个极小值，记作y 极小值=f(x 0)，x 0是极小值点3.极大值与极小值统称为极值4. 判别f (x 0)是极大、极小值的方法:若0x 满足0)(0='x f ，且在0x 的两侧)(x f 的导数异号，则0x 是)(x f 的极值点，)(0x f 是极值，并且如果)(x f '在0x 两侧满足“左正右负”，则0x 是)(x f 的极大值点，)(0x f 是极大值；如果)(x f '在0x 两侧满足“左负右正”，则0x 是)(x f 的极小值点，)(0x f 是极小值5. 求可导函数f (x )的极值的步骤:(1)确定函数的定义区间，求导数f ′(x ) (2)求方程f ′(x )=0的根(3)用函数的导数为0的点，顺次将函数的定义区间分成若干小开区间，并列成表格.检查f ′(x )在方程根左右的值的符号，如果左正右负，那么f (x )在这个根处取得极大值；如果左负右正，那么f (x )在这个根处取得极小值；如果左右不改变符号即都为正或都为负，那么f (x )在这个根处无极值6.函数的最大值和最小值:在闭区间[]b a ,上连续的函数)(x f 在[]b a ,上必有最大值与最小值．⑴在开区间(,)a b 内连续的函数)(x f 不一定有最大值与最小值． ⑵函数的最值是比较整个定义域内的函数值得出的；函数的极值是比较极值点附近函数值得出的．⑶函数)(x f 在闭区间[]b a ,上连续，是)(x f 在闭区间[]b a ,上有最大值与最小值的充分条件而非必要条件．(4)函数在其定义区间上的最大值、最小值最多各有一个，而函数的极值可能不止一个，也可能没有一个7.利用导数求函数的最值步骤:⑴求)(x f 在(,)a b 内的极值；⑵将)(x f 的各极值与)(a f 、)(b f 比较得出函数)(x f 在[]b a ,上的最值二、讲解范例：例1在边长为60 cm 的正方形铁片的四角切去相等的正方形，再把它的边沿虚线折起(如图)，做成一个无盖的方底箱子，箱底的边长是多少时，箱底的容积最大？最大容积是多少？解法一：设箱底边长为x cm ，则箱高602xh -=cm ，得箱子容积 260)(322x x h x x V -==)600(<<x ．23()602x V x x '=-)600(<<x令 23()602x V x x '=-＝0，解得 x=0（舍去），x=40，并求得 V(40)=16 000由题意可知，当x 过小（接近0）或过大（接近60）时，箱子容积很小，因此，16 000是最大值答：当x=40cm 时，箱子容积最大，最大容积是16 000cm 3解法二：设箱高为x cm ，则箱底长为(60-2x )cm ，则得箱子容积_ 60x x x V 2)260()(-=)300(<<x ．（后面同解法一，略）由题意可知，当x 过小或过大时箱子容积很小，所以最大值出现在极值点处．事实上，可导函数260)(322x x h x x V -==、xx x V 2)260()(-=在各自的定义域中都只有一个极值点，从图象角度理解即只有一个波峰，是单峰的，因而这个极值点就是最值点，不必考虑端点的函数值例2圆柱形金属饮料罐的容积一定时，它的高与底与半径应怎样选取，才能使所用的材料最省？解：设圆柱的高为h ，底半径为R ，则表面积S=2πRh+2πR 2由V=πR 2h ，得2Vh R π=，则 S(R)= 2πR 2V R π+ 2πR 2=2V R +2πR 2令 22()Vs R R'=-+4πR=0解得，h=2V R π即h=2R因为S(R)只有一个极值，所以它是最小值答：当罐的高与底直径相等时，所用材料最省变式：当圆柱形金属饮料罐的表面积为定值S 时，它的高与底面半径应怎样选取，才能使所用材料最省？提示：S =2Rh π+22R π⇒h =RR S ππ222-⇒V (R )=RR S ππ222-πR 2=3221)2(21R SR R R S ππ-=- )('R V )=026R S π=⇒ ⇒R h R Rh R 222622=⇒+=πππ．例3在经济学中，生产x 单位产品的成本称为成本函数同，记为C(x)，出售x 单位产品的收益称为收益函数，记为R(x)，R(x)－C(x)称为利润函数，记为P(x)。

2019-2020学年度北师大版高中数学选修1-1学案：第三章疑难规律方法

——教学资料参考参考范本——2019-2020学年度北师大版高中数学选修1-1学案：第三章疑难规律方法______年______月______日____________________部门20xx 最新20xx 北师大版高中数学选修1-1学案：第三章疑难规律方法1．求参数例1 设曲线y ＝f(x)＝ax2在点(1，a)处的切线与直线2x －y －6＝0平行，则a ＝________.解析根据导数的定义，＝1＋Δx2－a,Δx)＝Δx2,Δx)＝2a ＋a Δx ，当Δx 无限趋近于0时，2a ＋a Δx 无限趋近于2a ，即f′(1)＝2a.又由曲线f(x)＝ax2在点(1，a)处的切线与直线2x －y －6＝0平行，得2a ＝2，即a ＝1. 答案 1 2．求倾斜角例2 求曲线y ＝f(x)＝x3－x2＋5在x ＝1处的切线的倾斜角．分析要求切线的倾斜角α，先要求切线的斜率k ，再根据斜率k ＝tan α，求出倾斜角α.解设曲线y ＝f(x)＝x3－x2＋5在x ＝1处的切线的倾斜角为α.f(1＋Δx －f1,Δx)＝1＋Δx3－1＋Δx2＋5－⎝ ⎛⎭⎪⎫13－1＋5Δx)()＝Δx3－Δx,Δx)＝(Δx)2－1，当Δx 无限趋近于0时，(Δx)2－1无限趋近于－1，即tan α＝f′(1)＝－1.因为α∈[0，π)，所以α＝.故切线的倾斜角为.评注切线的倾斜角α能通过求切线的斜率得到，在解题过程中，一定要注意切线的倾斜角α的取值范围．3．求曲线的切线例3 求在点P处与曲线y＝x3相切的切线方程．分析要求直线在点P处的切线方程，需求得过点P的切线的斜率k，然后根据点斜式可求得切线方程．解因为点P在曲线y＝x3上，Δy＝(2＋Δx)3－×23＝4Δx＋2(Δx)2＋(Δx)3，所以＝4＋2Δx＋(Δx)2，当Δx无限趋近于0时，Δy无限趋近于4，即k＝4.Δx故所求的切线方程为y－＝4(x－2)，即12x－3y－16＝0.评注求在点P处与曲线相切的切线方程时，可求出切线的斜率，然后再根据点斜式求切线方程．4．求切点的坐标例4 若曲线y＝f(x)＝x3＋1在点P处的切线的斜率为3，求点P的坐标．分析要求点P的坐标，可设点P的坐标为(x0，x＋1)，然后由切线的斜率为3，解方程求得．解设点P的坐标为(x0，x＋1)，因为x0＋Δx－fx0,Δx)＝Δx2＋Δx3,Δx)＝3x＋3x0Δx＋(Δx)2，当Δx无限趋近于0时，上式无限趋近于3x，所以3x＝3.解得x0＝±1.故点P的坐标是(1,2)或(－1,0)．评注值得注意的是切点P的坐标有两个，部分同学误认为只有一个而出错.2 利用导数求切线方程曲线的切线问题是高考的常见题型之一．而导数f′(x0)的几何意义为曲线y＝f(x)在点P(x0，f(x0))处的切线的斜率，所以利用导数解决相切问题是常用的方法．下面对“求过一点的切线方程”的题型做以下归纳．1．已知切点，求曲线的切线方程此类题只需求出曲线的导数f′(x)，并代入点斜式方程即可．例1 曲线f(x)＝x3－3x2＋1在点(1，－1)处的切线方程为( )B．y＝－3x＋2A．y＝3x－4D．y＝4x－5C．y＝－4x＋3 解析由f′(x)＝3x2－6x，知在点(1，－1)处的斜率k＝f′(1)＝－3.所以切线方程为y－(－1)＝－3(x－1)，即y＝－3x＋2.故选B.答案B2．已知过曲线上一点，求切线方程过曲线上一点的切线，该点未必是切点，故应先设切点，再求切点，即用待定切点法．例2 求过曲线f(x)＝x3－2x上的点(1，－1)的切线方程．解设P(x0，y0)为切点，则切线的斜率为f′(x0)＝3x－2.所以切线方程为y－y0＝(3x－2)(x－x0)，即y－(x－2x0)＝(3x－2)(x－x0)．又知切线过点(1，－1)，所以－1－(x－2x0)＝(3x－2)(1－x0)．解得x0＝1，或x0＝－.故所求切线方程为y－(1－2)＝(3－2)(x－1)，或y－(－＋1)＝(－2)(x＋)，即x－y－2＝0，或5x＋4y－1＝0.点评可以发现直线5x＋4y－1＝0并不以(1，－1)为切点，实际上是经过点(1，－1)，且以(－，)为切点的直线．这说明过曲线上一点的切线，该点未必是切点．3．已知过曲线外一点，求切线方程此类题可先设切点，再求切点，即用待定切点法来求解．例3 求过点(2,0)且与曲线f(x)＝相切的直线方程．解设P(x0，y0)为切点，则切线的斜率为f′(x0)＝－.所以切线方程为y－y0＝－(x－x0)，即y－＝－(x－x0)．又已知切线过点(2,0)，把它代入上述方程，得－＝－(2－x0)．解得x0＝1，y0＝＝1，即x＋y－2＝0.点评点(2,0)实际上是曲线外的一点，但在解答过程中却无需判断它的确切位置，这充分反映出待定切点法的高效性．4．求两条曲线的公切线例4 已知曲线C1：y＝x2与C2：y＝－x2＋4x－4，直线l与C1，C2都相切，求直线l的方程．分析设出直线与两条曲线的切点坐标，分别求出曲线在切点处的切线方程，再利用两个方程所表示的直线重合，建立方程组求解．解设l与C1相切于点P(x1，x)，与C2相切于点Q(x2，－x＋4x2－4)．由C1：y＝x2，得y′＝2x，则与C1相切于点P的切线方程为y－x＝2x1(x－x1)，即y＝2x1x－x，由C2：y＝－x2＋4x－4，得y′＝－2x＋4，则与C2相切于点Q的切线方程为y＝－2(x2－2)x＋x－4.因为两切线重合，所以2x1＝－2(x2－2)且－x＝x－4，解得x1＝0，x2＝2或x1＝2，x2＝0.所以直线l的方程为y＝0或y＝4x－4.点评公切线问题的一般解法是分别求出曲线在切点处的切线方程，再利用两直线重合的条件建立方程组求解.3 导数运算中的常见错误1．对f′(x0)与f′(x)理解有误例1 已知函数f(x)＝x2＋2xf′(1)，则f′(0)的值为( )A．0 B．－4 C．－2 D．2错解由f(x)＝x2＋2xf′(1)得f(0)＝0.所以f′(0)＝0.故选A.错因分析解题时没有弄清导函数和其在某点处的导数的关系，求函数在某点处的导数时，应先求导再求函数值，同时要注意f′(1)是常数．正解由f(x)＝x2＋2xf′(1)得，f′(x)＝2x＋2f′(1)．所以f′(1)＝2×1＋2f′(1)．所以f′(1)＝－2.从而f′(x)＝2x－4.所以f′(0)＝－4.故选B.2．切点位置的确定有误例2 求过点P(1,0)且与曲线f(x)＝x3－x相切的直线的方程．错解由题意知点P(1,0)在曲线上．因为f′(x)＝3x2－1，所以f′(1)＝2.所以切线方程为y－0＝2(x－1)，即2x－y－2＝0.错因分析点P(1,0)虽然在曲线上，但不一定是切点，解题时把点P(1,0)当作切点显然是错误的．求曲线的切线方程时，应注意两种“说法”：(1)曲线在点P处的切线方程(一定是以点P为切点)；(2)曲线过点P的切线方程(无论点P是否在曲线上，点P都不一定是切点)．正解设切点为(x0，x－x0)，则过该点的切线方程为y－(x－x0)＝(3x－1)(x－x0)．由切线过点P(1,0)得：0－(x－x0)＝(3x－1)(1－x0)，整理得2x－3x＋1＝0.即(x0－1)2(2x0＋1)＝0，解得x0＝1或x0＝－.所以切线方程为2x－y－2＝0或x＋4y－1＝0.3．对切线定义的理解有误例3 已知曲线C：y＝f(x)＝x3＋，曲线C在点P(2,4)处的切线方程为y＝4x－4，试分析该切线与曲线C是否还有其他公共点？若有，求出公共点的坐标；若没有，说明理由．错解由于直线y＝4x－4与曲线C相切，因此除切点P(2,4)外没有其他的公共点．错因分析“切线与曲线有唯一公共点”，此说法对圆、椭圆这一类特殊曲线是成立的，但对一般曲线不一定成立．正解由消去y整理得：x3－12x＋16＝0，即(x－2)(x2＋2x－8)＝0.所以(x－2)2(x＋4)＝0，解得x＝2或x＝－4.所以交点的坐标为(2,4)，(－4，－20)，所以该切线与曲线的公共点除了切点(2,4)外还有点(－4，－20)．。

高中数学(北师大版)选修1-1教案：第3章疑难解析：导数概念

有关导数概念的几个疑难问题一、导数相关概念1．导数的定义包含了两层意思：可导条件和导数概念。

函数y =)(x f 在x 0点可导是)(x f 在x 0点的性质，因为函数并不是一定在定义域内处处可导的。

如果0lim →∆x xy ∆∆不存在，称函数在x 0点不可导；若0lim →∆x x y ∆∆存在，则称此极限值为函数在该点的导数。

2．y =)(x f 在x 0点可导有以下三个条件：①y =)(x f 在x 0点处及其附近有意义；②左极限-→∆0lim x x y ∆∆及其右极限+→∆0lim x x y ∆∆都存在；③-→∆0lim x x y ∆∆=+→∆0lim x xy ∆∆，即左右极限相等。

三个条件中的任何一个受到破坏，函数在该点就不可导。

3．导函数y =)(x f '与原来的函数y =)(x f 有相同的定义域(a ，b)．4．“函数在一点处的导数”、“导函数”、“导数”三个概念既有联系又有区别： ①．函数在一点处的导数y 0=)(0x f '是一个常数，不是变量．②．函数的导数，是针对某一区间内任意点x 而言的．函数y =)(x f 在区间(a ，b)内每一点都可导，是指对于区间(a ，b)内每一个确定的值x 0，都对应着一个确定的导数y 0=)(0x f '．根据函数的定义，在开区间(a ，b)内就构成了一个新的函数，就是函数y =)(x f 的导函数y =)(x f '．③．函数y =)(x f 在点x 0处的导数y 0=)(0x f '就是导函数y =)(x f '在点x = x 0处的函数值，即)(0x f '=)(x f '|0x x =．5．导数与连续的关系：若函数y =)(x f 在x 0处可导，则此函数在x 0处连续，但逆命题不成立，即函数y =)(x f 在x 0处连续，未必在x 0处可导，也就是说，连续性是函数具有可导性的必要条件，而不是充分条件．因而可导性比连续性要求更高．下面用两个例题说明这个问题．例1 求证：若函数在点x 0处可导，则函数)(x f 在点x 0处连续．证明：∵函数)(x f 在点x 0处可导，∴在点x 0处有： 0lim x x →[)(x f －)(0x f ] =0lim →∆x y ∆=0lim →∆x (x y ∆∆·x ∆) =0lim →∆x x y ∆∆·0lim →∆x x ∆=)(0x f '·0 = 0， ∴0lim x x →)(x f =)(0x f ，即函数)(x f 在点x 0处连续．例2 求证：函数)(x f = | x |在点x 0= 0处连续，但在x 0处不可导．证明：∵①)0(f = 0；②-→∆0lim x | x | =+→∆0lim x | x | =0lim →∆x | x | = 0 ；③0lim →∆x )(x f =)0(f ． ∴)(x f = | x |在点x 0= 0处连续．① 又∵函数)(x f = | x |在点x 0= 0及其附近有意义； ②x y ∆∆=x x f x x f ∆-∆+)()(00=x f x f ∆-∆+)0()0(=x x f ∆∆)(=x x ∆∆||=⎪⎪⎩⎪⎪⎨⎧∆-=∆∆-∆=∆∆0.10,1＜x xx x ＞x x ； ③-→∆0lim x xy ∆∆=－1，+→∆0lim x x y ∆∆=1，即0lim →∆x x y ∆∆不存在，所以)(x f = | x |在点x 0= 0处不可导．综上所述，函数)(x f = | x |在点x 0= 0处连续，但在在x 0处不可导．综上，函数y =)(x f 在点x 0处有定义、有极限、连续、可导是四个不同的概念，它们之间的关系是：)(x f 在点x 0处有定义，不一定在x 0处连续；但)(x f 在点x 0处连续，一定在点x 0处有定义，即)(x f 在点x 0处有定义是)(x f 在点x 0处连续的必要而不充分的条件。

高中数学北师大版选修1-1教案：第3章函数的极值参考

函数的极值
【学习要求】
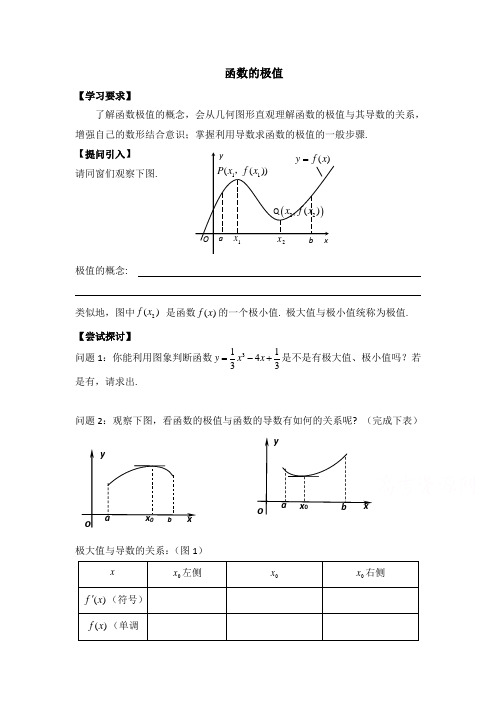
了解函数极值的概念，会从几何图形直观理解函数的极值与其导数的关系，增强自己的数形结合意识；掌握利用导数求函数的极值的一般步骤. 【提问引入】请同窗们观察下图.
极值的概念: 类似地，图中2()f x 是函数()f x 的一个极小值. 极大值与极小值统称为极值. 【尝试探讨】
问题1：你能利用图象判断函数311
433y x x =-+是不是有极大值、极小值吗？若
是有，请求出.
问题2：观察下图，看函数的极值与函数的导数有如何的关系呢? （完成下表）极大值与导数的关系：（图1）
x
0x 左侧 0x 0x 右侧
)(x f '（符号）
)(x f （单调
)(x f y =
O y
x
a
1x b ))((11x f x P ，
2x
Q ()22,()x f x
o
a
x 0
b
x
y
o
a x 0
b
x
y
性）
极小值与导数的关系：（图2）
x
0x 左侧 0x 0x 右侧
)(x f '（符号）
)(x f （单调性）
问题3：请问如何判断0()f x 是极大值或是极小值？
【典型例题】
例3:求函数311
433y x x =-+的极值.
【巩固提高】
1．利用导数知识，求函数2()2f x x x =--的极值．
2．求函数31
()3f x x x =-的极值．
3．函数)(x f 的概念域为R ，导函数)(x f '的图象如图所示，则函数)(x f 的图象上的极值点有个
O。

北师版数学高一-学案第三章章末复习提升

1．本章涉及的概念比较多，要真正理解它们的实质，搞清它们的区别与联系．了解随机事件发生的不确定性和频率的稳定性，要进一步了解概率的意义以及频率与概率的区别． 2．应用互斥事件的概率加法公式，一定要注意首先确定事件彼此是否互斥，然后求出各事件分别发生的概率，再求和．求较复杂的概率通常有两种方法：一是将所求事件转化为彼此互斥的事件的和；二是先求其对立事件的概率，然后再应用公式P (A )＝1－P (A )(事件A 与A 互为对立事件)求解．3．对于古典概型概率的计算，关键要分清基本事件的总数n 与事件A 包含的基本事件的个数m ，再利用公式P (A )＝mn 求出概率．有时需要用列举法把基本事件一一列举出来，在列举时必须按某一顺序做到不重不漏．4．对于几何概型事件概率的计算，关键是求得事件A 所占区域和整个区域的几何度量，然后代入公式求解．5．学习本章的过程中，要重视教材的基础作用，重视过程的学习，重视基本数学思想和数学方法的形成和发展，注意培养分析问题和解决问题的能力．题型一随机事件的概率 1．有关事件的概念(1)必然事件：在条件S下，一定会发生的事件，叫作相对于条件S的必然事件，简称必然事件．(2)不可能事件：在条件S下，一定不会发生的事件，叫作相对于条件S的不可能事件，简称不可能事件．(3)确定事件：必然事件与不可能事件统称为相对于条件S的确定事件，简称确定事件．(4)随机事件：在条件S下可能发生也可能不发生的事件，叫作相对于条件S的随机事件，简称随机事件．(5)事件的表示方法：确定事件和随机事件统称为事件，一般用大写字母A，B，C…表示．2．对于概率的定义应注意以下几点(1)求一个事件的概率的基本方法是通过大量的重复试验．(2)只有当频率在某个常数附近摆动时，这个常数才叫作事件A的概率．(3)概率是频率的稳定值，而频率是概率的近似值．(4)概率反映了随机事件发生的可能性的大小．(5)必然事件的概率为1，不可能事件的概率为0，故0≤P(A)≤1.例1对一批U盘进行抽检，结果如下表：(1)(2)从这批U盘中任抽一个是次品的概率约是多少？(3)为保证买到次品的顾客能够及时更换，要销售2000个U盘，至少需进货多少个U盘？解(1)表中次品频率从左到右依次为0.06,0.04，0.025，0.017,0.02,0.018.(2)当抽取件数a越来越大时，出现次品的频率在0.02附近摆动，所以从这批U盘中任抽一个是次品的概率约是0.02.(3)设需要进货x个U盘，为保证其中有2000个正品U盘，则x(1－0.02)≥2000，因为x是正整数，所以x≥2041，即至少需进货2041个U盘．跟踪训练1某射击运动员为备战奥运会，在相同条件下进行射击训练，结果如下：(1)该射击运动员射击一次，击中靶心的概率大约是多少？(2)假设该射击运动员射击了300次，则击中靶心的次数大约是多少？(3)假如该射击运动员射击了300次，前270次都击中靶心，那么后30次一定都击不中靶心吗？(4)假如该射击运动员射击了10次，前9次中有8次击中靶心，那么第10次一定击中靶心吗？解 (1)由题意得，击中靶心的频率分别为0.8,0.95，0.88，0.92,0.89,0.91，当射击次数越来越多时，击中靶心的频率在0.9附近摆动，故概率约为0.9. (2)击中靶心的次数大约为300×0.9＝270(次)．(3)由概率的意义，可知概率是个常数，不因试验次数的变化而变化．后30次中，每次击中靶心的概率仍是0.9，所以不一定． (4)不一定．题型二古典概型及其应用古典概型是一种最基本的概率模型，也是学习其他概率模型的基础，在高考题中，经常出现此种概率模型的题目．解题时要紧紧抓住古典概型的两个基本特点，即有限性和等可能性．另外，在求古典概型问题的概率时，往往需要我们将所有基本事件一一列举出来，以便确定基本事件总数及事件所包含的基本事件数．这就是我们常说的穷举法．在列举时应注意按一定的规律、标准，不重不漏．例2 海关对同时从A ，B ，C 三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量(单位：件)如下表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.(1)求这6件样品中来自A ，B (2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．解 (1)因为样本容量与总体中的个体数的比是650＋150＋100＝150，所以样本包含三个地区的个体数量分别是 50×150＝1,150×150＝3,100×150＝2.所以这6件样品中来自A ，B ，C 三个地区的数量分别为1,3,2.(2)设6件来自A，B，C三个地区的样品分别为A；B1，B2，B3；C1，C2，则从这6件样品中抽取的2件商品构成的所有基本事件为：{A，B1}，{A，B2}，{A，B3}，{A，C1}，{A，C2}，{B1，B2}，{B1，B3}，{B1，C1}，{B1，C2}，{B2，B3}，{B2，C1}，{B2，C2}，{B3，C1}，{B3，C2}，{C1，C2}，共15个．每个样品被抽到的机会均等，因此这些基本事件的出现是等可能的．记事件D“抽取的这2件商品来自相同地区”，则事件D包含的基本事件有：{B1，B2}，{B1，B3}，{B2，B3}，{C1，C2}，共4个．所以P(D)＝415，即这2件商品来自相同地区的概率为415.跟踪训练2甲、乙、丙3个盒中分别装有大小相等、形状相同的卡片若干张．甲盒中装有2张卡片，分别写有字母A和B；乙盒中装有3张卡片，分别写有字母C，D和E；丙盒中装有2张卡片，分别写有字母H和I.现要从3个盒中各随机取出1张卡片，求：(1)取出的3张卡片中恰好有1张、2张、3张写有元音字母的概率各是多少？(2)取出的3张卡片上全是辅音字母的概率．解根据题意画出如图所示的树状图．由树状图可以得到，所有可能出现的基本事件有12个，它们出现的可能性相等．(1)只有1个元音字母的结果有5个，所以P(1个元音字母)＝512；有2个元音字母的结果有4个，所以P(2个元音字母)＝412＝1 3；有3个元音字母的结果有1个，所以P(3个元音字母)＝112.(2)全是辅音字母的结果有2个，所以P(3个辅音字母)＝212＝1 6.题型三互斥事件与对立事件1．对互斥事件与对立事件的概念的理解(1)互斥事件是不可能同时发生的两个事件；对立事件除要求这两个事件不同时发生外，还要求二者必须有一个发生．因此对立事件一定是互斥事件，但互斥事件不一定是对立事件，对立事件是互斥事件的特殊情况．(2)利用集合的观点来看，如果事件A∩B＝∅，则两事件是互斥的，此时A＋B的概率就可用概率加法公式来求，即为P(A＋B)＝P(A)＋P(B)；如果事件A∩B≠∅，则可考虑利用古典概型的定义来解决，不能直接利用概率加法公式．(3)利用集合的观点来看，如果事件A∩B＝∅，A＋B＝U，则两事件是对立的，此时A＋B就是必然事件，可由P(A＋B)＝P(A)＋P(B)＝1来求解P(A)或P(B)．2．互斥事件概率的求法(1)若A1，A2，…，A n互斥，则P(A1＋A2＋…＋A n)＝P(A1)＋P(A2)＋…＋P(A n)．(2)利用这一公式求概率的步骤：①要确定这些事件彼此互斥；②先求出这些事件分别发生的概率，再求和．值得注意的是：①是公式的使用条件，如不符合，是不能运用互斥事件的概率加法公式的．3．对立事件概率的求法P(Ω)＝P(A＋A)＝P(A)＋P(A)＝1，由公式可得P(A)＝1－P(A)(这里A是A的对立事件，Ω为必然事件)．4．互斥事件的概率加法公式是解决概率问题的重要公式，它能把复杂的概率问题转化为较为简单的概率或转化为其对立事件的概率求解．例3某人在如图所示的直角边长为4m的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获量Y(单位：kg)与它的“相近”作物株数X(单位：株)之间的关系如下表所示：(1)完成下表，并求所种作物的平均年收获量，Y51484542频数4(2)解(1)所种作物的总株数为1＋2＋3＋4＋5＝15，其中“相近”作物株数为1的作物有2株，“相近”作物株数为2的作物有4株，“相近”作物株数为3的作物有6株，“相近”作物株数为4的作物有3株，列表如下：Y51484542频数2463所种作物的平均年收获量为51×2＋48×4＋45×6＋42×315＝102＋192＋270＋12615＝69015＝46.(2)由(1)，知P(Y＝51)＝215，P(Y＝48)＝415.故在所种作物中随机选取一株，它的年收获量至少为48kg的概率为P(Y≥48)＝P(Y＝51)＋P(Y＝48)＝215＋415＝25.跟踪训练3向三个相邻的军火库投一枚炸弹，炸中第一个军火库的概率为0.2，炸中第二个军火库的概率为0.12，炸中第三个军火库的概率为0.28，三个军火库中，只要炸中一个另两个也会发生爆炸，求军火库发生爆炸的概率．解设A.B.C分别表示炸弹炸中第一、第二及第三个军火库这三个事件，事件D表示军火库爆炸，已知P(A)＝0.2，P(B)＝0.12，P(C)＝0.28.又因为只投掷了一枚炸弹，故不可能炸中两个及以上军火库，所以A.B.C是互斥事件，且D＝A＋B＋C，所以P(D)＝P(A＋B＋C)＝P(A)＋P(B)＋P(C)＝0.2＋0.12＋0.28＝0.6，即军火库发生爆炸的概率为0.6.题型四几何概型及其应用若试验同时具有基本事件的无限性和每个事件发生的等可能性两个特点，则此试验为几何概型．由于其结果的无限性，概率就不能应用P (A )＝mn 求解，故需转化为几何度量(如长度、面积、体积等)的比值求解．几何概型同古典概型一样，是概率中最具代表性的试验概型之一，在高考命题中占有非常重要的位置．例4 节日前夕，小李在家门前的树上挂了两串彩灯．这两串彩灯的第一次闪亮相互独立，且都在通电后的4s 内任一时刻等可能发生，然后每串彩灯以4s 为间隔闪亮．那么这两串彩灯同时通电后，它们第一次闪亮的时刻相差不超过2s 的概率是( ) A.14 B.12 C.34 D.78答案 C解析设两串彩灯同时通电后，第一次闪亮的时刻分别为x ，y ，则0≤x ≤4,0≤y ≤4，而事件A “它们第一次闪亮的时刻相差不超过2s ”，即|x －y |≤2，其表示的区域为如图所示的阴影部分．由几何概型概率公式，得P (A )＝42－2×⎝⎛⎭⎫12×2×242＝34.跟踪训练4 如图所示的大正方形面积为13，四个全等的直角三角形围成一个阴影小正方形，较短的直角边长为2，向大正方形内投掷飞镖，则飞镖落在阴影部分的概率为( ) A.413B.213C.113D.313 答案 C解析设阴影小正方形边长为x ，则在直角三角形中有22＋(x ＋2)2＝(13)2，解得x ＝1或x＝－5(舍)，∴阴影部分面积为1，∴飞镖落在阴影部分的概率为1 13.1.关于古典概型，必须要解决好下面三个方面的问题：(1)试验结果是否有限且是等可能的；(2)试验的基本事件有多少个；(3)事件A是什么，它包含多少个基本事件．只有回答好了这三方面的问题，解题才不会出错．2．两个事件互斥，它们未必对立；反之，两个事件对立，它们一定互斥．若事件A1，A2，A3，…，A n彼此互斥，则P(A1＋A2＋…＋A n)＝P(A1)＋P(A2)＋…＋P(A n)．3．几何概型的试验中，事件A的概率P(A)只与子区域A的几何度量(长度、面积或体积)成正比，而与A的位置和形状无关．求试验为几何概型的概率，关键是求得事件所占区域和整个区域Ω的几何度量，然后代入公式即可求解．。

2019-2020高中北师大版数学选修1-1 第3章章末复习课

一、导数的概念1．函数y＝f(x)在x＝x0处的导数(1)定义称函数y＝f(x)在x＝x0处的瞬时变化率limΔx→0ΔyΔx＝limΔx→0f(x0＋Δx)－f(x0)Δx为函数y＝f(x)在x＝x0处的导数，记作f′(x0)，即f′(x0)＝limΔx→0ΔyΔx＝limΔx→0f(x0＋Δx)－f(x0)Δx.(2)几何意义函数f(x)在点x0处的导数f′(x0)的几何意义是在曲线y＝f(x)上点(x0，f(x0))处的切线的斜率．(瞬时速度就是位移函数s(t)对时间t的导数)相应地，切线方程为y－y0＝f′(x0)(x－x0)．2．函数f(x)的导函数称函数f′(x)＝limΔx→0f(x＋Δx)－f(x)Δx为f(x)的导函数．二、基本初等函数的导数公式1．[f(x)±g(x)]′＝f′(x)±g′(x)．2．[f (x )·g (x )]′＝f ′(x )g (x )＋f (x )g ′(x )． 3.⎣⎢⎡⎦⎥⎤f (x )g (x )′＝f ′(x )g (x )－f (x )g ′(x )[g (x )](g (x )≠0)．导数的概念和几何意义【例1】已知曲线y ＝13x 3＋43. (1)求曲线在点P (2,4)处的切线方程； (2)求曲线过点P (2,4)的切线方程； (3)求斜率为1的曲线的切线方程．[解] (1)∵P (2,4)在曲线y ＝13x 3＋43上，且y ′＝x 2， ∴在点P (2,4)处的切线的斜率为k ＝4.∴曲线在点P (2,4)处的切线方程为：y －4＝4(x －2)，即4x －y －4＝0.(2)设曲线y ＝13x 3＋43与过点P (2,4)的切线相切于点 A ⎝ ⎛⎭⎪⎫x 0，13x 30＋43，则切线的斜率为k ＝x 20. ∴切线方程为y －⎝ ⎛⎭⎪⎫13x 30＋43＝x 20(x －x 0)，即y ＝x 20·x －23x 30＋43.∵点P (2,4)在切线上，∴4＝2x 20－23x 30＋43，即x 30－3x 20＋4＝0， ∴x 30＋x 20－4x 20＋4＝0，∴x 20(x 0＋1)－4(x 0＋1)(x 0－1)＝0，∴(x 0＋1)(x 0－2)2＝0，解得x 0＝－1或x 0＝2，故所求的切线方程为：x －y ＋2＝0或4x －y －4＝0. (3)设切点为(x 0，y 0)，则切线的斜率为x 20＝1，x 0＝±1. 切点为(－1,1)或⎝ ⎛⎭⎪⎫1，53，∴切线方程为：y －1＝x ＋1或y －53＝x －1. 即x －y ＋2＝0或3x －3y ＋2＝0.1．导数的概念(1)导数：f ′(x 0)＝lim Δx →0f (x 0＋Δx )－f (x 0)ΔxΔx 是自变量x 在x 0处的改变量，它可正、可负，但不可为零，f ′(x 0)是一个常数．(2)导函数： f ′(x )＝lim Δx →0f (x ＋Δx )－f (x )Δxf ′(x )为f (x )的导函数，是一个函数． 2．导数的概念及几何意义(1)函数f (x )在x ＝x 0处的导数等于曲线在该点处的切线斜率，即k ＝f ′(x 0)． (2)函数f (x )在x ＝x 0处的切线方程是y －f (x 0)＝f ′(x 0)·(x －x 0)．(3)求函数f (x )过某点的切线方程应遵循“设切点——写切线——求切点——得方程”的过程．1．已知曲线f (x )＝x 3－3x ，过点A (0,16)作曲线y ＝f (x )的切线，求该切线方程．[解]设切点坐标M(x0，x30－3x0)．则切线的斜率k＝f′(x0)＝3x20－3，切线方程y＝(3x20－3)x＋16.又因为点M在切线上，所以x30－3x0＝(3x20－3)x0＋16，得x0＝－2.所以切线方程为y＝9x＋16.导数的运算【例2】求下列函数的导数．(1)y＝x＋x5＋x－13x2；(2)y＝11－x＋11＋x；(3)y＝e x ln(2x)；(4)y＝－sin x2⎝⎛⎭⎪⎫1－2cos2x4.[解](1)∵y＝x＋x5＋x－13x2＝x12＋x5＋x－13x2＝x－32＋x3＋x－73，∴y′＝－32x－52＋3x2－73x－103.(2)∵y＝11－x＋11＋x＝21－x，∴y′＝2 (1－x)2.(3)∵y＝e x ln 2x，y＝e x(ln 2＋ln x)＝e x ln 2＋e x ln x，∴y ′＝e xln 2＋e xln x ＋e xx .(4)∵y ＝－sin x 2⎝ ⎛⎭⎪⎫1－2cos 2 x 4＝sin x 2cos x 2＝12sin x ， ∴y ′＝12cos x .求一个函数的导数的基本方法有三种：一是利用定义，二是利用基本初等函数的导数公式，三是把函数分解成为基本初等函数的和、差、积、商的运算，再利用导数的运算法则进行计算，其中以第三种较为常见.在第三种运算中，对不具备求导法则所要求的结构形式的函数要进行适当的变形，比如(1)函数中有两个以上因式乘积的形式，可利用多项式的乘法展开后再求导.(2)利用代数恒等变形，避开商的求导，简化运算.(3)利用三角恒等变形简化求导过程等等.2．求下列函数的导数． (1)y ＝3x 2＋x cos x ； (2)y ＝tan x x ； (3)y ＝x 2－2x ＋5x 3.[解] (1)y ′＝(3x 2)′＋(x cos x )′ ＝6x ＋x ′cos x ＋x (cos x )′ ＝6x ＋cos x －x sin x .(2)法一：y ′＝(tan x )′·x －tan x x 2＝xcos 2x－tan xx 2＝x －cos 2 x ·tan x x 2cos 2 x ＝x －sin x cos xx 2cos 2 x .法二：y ′＝⎝ ⎛⎭⎪⎫sin x x cos x ′＝(sin x )′x cos x －sin x (x cos x )′x 2cos 2 x＝x cos2x－sin x(cos x－x sin x)x2cos2x＝x－sin x cos xx2cos2x.(3)∵y＝1x－2x2＋5x3＝x－1－2x－2＋5x－3，∴y′＝－x－2－2×(－2)x－3＋5×(－3)x－4＝－1x2＋4x3－15x4.方程思想【例3】设抛物线C1：y＝x2－2x＋2与抛物线C2：y＝－x2＋ax＋b在它们的一个交点处的切线互相垂直．(1)求a、b之间的关系；(2)若a>0，b>0，求ab的最大值．思路探究：由两曲线方程可求(表示)出公共点坐标P(x0，y0)，在P处两切线斜率可利用在P处导数表示，建立方程从而解决问题．[解](1)设两抛物线的交点为P(x0，y0)，由题意知x20－2x0＋2＝－x20＋ax0＋b，整理得2x20－(2＋a)x0＋2－b＝0①由导数可得抛物线C1、C2在交点P处的切线斜率为：k1＝2x0－2，k2＝－2x0＋a.因两切线互相垂直，则有k1k2＝－1，即(2x0－2)(－2x0＋a)＝－1，整理得2[2x20－(2＋a)x0]＋2a－1＝0②联立①和②，消去x0得a＋b＝5 2.(2)由(1)知a＋b＝5 2，又a>0，b>0，∴ab ≤⎝ ⎛⎭⎪⎫a ＋b 22＝⎝ ⎛⎭⎪⎪⎫5222＝2516. 当且仅当a ＝b ＝54时取等号，故ab 的最大值为2516.利用方程的思想解题，往往需要根据一些要求，确定某些变量的值，需列出这些量满足的方程(或方程组)，通过解方程(或方程组)求出它们.本章中利用导数处理与切线斜率等有关的问题，通常需要根据已知条件建立相关含参数的方程(组)求解.3．已知函数f (x )＝ax －6x 2＋b的图像在点M (－1，f (－1))处的切线方程为x ＋2y ＋5＝0.求函数y ＝f (x )的解析式．[解] 由函数f (x )的图像在点M (－1，f (－1))处的切线方程为x ＋2y ＋5＝0，知－1＋2f (－1)＋5＝0，即f (－1)＝－2.由切点为M 点得f ′(－1)＝－12. ∵f ′(x )＝a (x 2＋b )－2x (ax －6)(x 2＋b )2.∴⎩⎪⎨⎪⎧－a －61＋b ＝－2，a (1＋b )－2(a ＋6)(1＋b )2＝－12.即⎩⎨⎧a ＝2b －4，a (1＋b )－2(a ＋6)(1＋b )2＝－12.解得a ＝2，b ＝3或a ＝－6，b ＝－1 (由b ＋1≠0，故b ＝－1舍去)．所以所求的函数解析式是f (x )＝2x －6x 2＋3.。

高中数学北师大版选修1-1学案：第三章 章末复习课

【优教通,同步备课】高中数学(北师大版)选修1-1教案：第3章 导数的概念及其几何意义 参考教案

高中数学(北师大版)选修1-1教案：第3章 导数应用 参考教案

高中数学第3章章末复习课学案北师大版必修1

2018版高中数学北师大版选修1-1学案：第三章 变化率与

(北师大版)选修1-1课件：第3章-章末复习课件(1)

高中数学北师大版选修1-1教案：第3章 导数与函数的单

[K12配套]2018北师大版高中数学选修1-1学案：第三章 章末复习课