13矩阵位移法
矩阵位移法和有限元法的异同

矩阵位移法和有限元法的异同矩阵位移法和有限元法是数值计算领域中常用的两种方法,它们都具有非常优秀的数值精度和高度的计算效率。
在工程领域中,它们常常用于解决结构振动、热传导、电场、磁场等问题,因此其应用非常广泛。
本文将从多个角度比较两种方法的异同。
一、基本原理矩阵位移法是基于结构受力平衡公式推导而来,通过建立刚度矩阵,利用矩阵乘法计算结构中各点受力情况,从而得到结构变形情况。
有限元法则是将结构分割成很多有限元,建立每个有限元内部的受力方程,通过组合各个有限元的受力方程形成整个结构的受力方程,从而得到变形情况。
二、精度和适用范围矩阵位移法是一种较为精确的计算方法,适用于较小结构和较短时间内的计算。
而有限元法精度相对较差,但它适用于更为复杂的结构和更长时间内的计算,且可以模拟非线性问题。
三、模型建立和求解在矩阵位移法中,需要先根据实际结构建立刚度矩阵,然后将载荷矩阵和位移矩阵代入方程中求解。
而在有限元法中,需要将结构分割成有限元,并建立每个有限元的受力方程,然后进行求解。
有限元法需要进行剖分后求解,模型的建模过程相对较为复杂,计算量较大。
四、应用领域和优缺点矩阵位移法适用于解决结构较小、较简单的问题,在建模和求解过程中较为简单,计算速度快。
但它的缺点是在处理较复杂的问题时很难得到精确解。
有限元法适用于处理复杂问题,精度相对更高。
但在建模和求解过程中计算量比较大,时间较长,适用于需要高精度计算的问题。
综上所述,矩阵位移法和有限元法都是重要的数值计算方法,适用于不同的领域。
在遇到具体问题时,需要根据问题的特点选择合适的数值计算方法,从而得到更好的计算效果。
矩阵位移法中,结构的原始刚度方程

矩阵位移法是结构分析中常用的一种方法,它通过将结构刚度矩阵和位移向量进行相乘,来求解结构的位移。
在矩阵位移法中,结构的原始刚度方程是一个关键的内容,它描述了结构在外部荷载作用下的位移响应。
一、什么是矩阵位移法矩阵位移法是一种基于矩阵运算的结构分析方法。
它通过建立结构的刚度矩阵和荷载矩阵,将结构的位移表示为荷载、边界条件和材料性质的函数,然后利用矩阵运算的方法求解结构的位移响应。
矩阵位移法的优点是可以较为准确地分析复杂结构的位移响应,适用范围广泛。
二、结构的原始刚度方程在矩阵位移法中,结构的原始刚度方程是描述结构在受到外部荷载作用下的位移响应的重要方程。
它通常表示为Ku=f,其中K是结构的刚度矩阵,u是结构的位移向量,f是结构受到的外部荷载。
结构的刚度矩阵K可以根据结构的几何形状、材料性质和边界条件进行求解。
它包含了结构的刚度信息,可以反映出结构在受到荷载作用时的变形特性。
结构的位移向量u是结构的位移表示,它包含了结构在各个节点的位移信息。
结构受到的外部荷载f可以根据结构所受到的力的大小和作用位置进行求解。
三、矩阵位移法的求解步骤在使用矩阵位移法求解结构的位移响应时,一般可以按照以下步骤进行:1.建立结构的刚度矩阵和荷载矩阵需要根据结构的几何形状、材料性质和边界条件建立结构的刚度矩阵K和荷载矩阵f。
在建立刚度矩阵和荷载矩阵时,需要考虑结构的整体刚度特性和外部荷载的作用情况,确保建立的矩阵能够准确地描述结构的位移响应。
2.确定结构的边界条件和荷载接下来,需要确定结构的边界条件和受到的外部荷载。
结构的边界条件包括固定节点的位移约束和受固定支撑等信息,外部荷载包括施加在结构上的力和力矩等。
3.求解结构的位移响应利用已建立的刚度矩阵和荷载矩阵,结合结构的边界条件和受到的外部荷载,可以通过矩阵运算的方法求解结构的位移响应。
具体的求解方法包括直接求解、迭代法和分解法等,根据实际情况选择合适的方法进行求解。
4.分析结构的位移响应根据求解得到的结构位移向量u,可以分析结构在受到外部荷载作用时的位移响应情况。
矩阵位移法小结

式中K为总刚度矩阵,为结构的结点位移列向量,P
为结点力列向量。
总刚度矩阵K反应了整个结构的刚度,是描述结点 力与结点位移之间关系的系数矩阵。其矩阵的性质与 特点:
总结
( 1 )元素kij的物理意义为:当△j=1而其他位移分量为零 时产生在△i方向的杆端力。
(2)主子块Kii是由结点i的相关单元中与结点i相应的主 子块叠加而得。
3. 弹性支座的处理 通常用主对角元素叠加法处理弹性支座。如果结构的 第j个自由度是弹性约束,那么,把弹性支座的刚度系数 叠加到原始刚度矩阵主对角线的第j个元素上即可得到经 约束处理后的总刚度方程。
总结
4. 总刚度方程和总刚度矩阵的性质与特点 总刚度方程为整体结构的结点荷载与结点位移之间的 关系式,是结构应满足的平衡条件。无论何种结构,其总 刚度方程都具有统一的形式:
总结
对于每个结点位移分量数相同的结构,原始刚度矩阵 的阶数为结构的总结点数乘以结点位移分量的数目,例 如,每个结点位移分量数为3的平面刚架,结构原始刚 度矩阵的阶数为3n×3n 。
总结
(2)边界条件处理
对于刚性支座,用划行划列法处理刚性支座,即直接 划去原始刚度方程中与零位移对应的行和列。这样做有 时要改变原方程的排列顺序,会给编程带来麻烦。为了不 改变原方程的排列顺序,同时又要引入边界条件,采用 “主一副零”法。
的单元刚度方程中求杆端内
力
总结
一、基本概念
结构矩阵分析是采用矩阵方法分析结构力学问题的一种 方法。与传统的力法、位移法相对应,在结构矩阵分析中 也有矩阵力法和矩阵位移法,或柔度法与刚度法。矩阵位 移法易于实现计算过程程序化而被广泛应用。
矩阵位移法是结构力学中的位移法加上矩阵方法。矩阵 位移法的基本未知量也是结点位移——独立的线位移和转 角。但由于有时考虑杆件的轴向变形,且把杆件铰结端的 转角也作为基本未知量,因此,基本未知量数目比传统位 移法的基本未知量多一些。
第十三章 矩阵位移法
0 sin 0 0
0 0 0 0 0 1
坐标转换矩阵(正交矩阵)
T
1
T
T
13-2 整体坐标系下的单元刚度矩阵
同理:
e
T
e
其中:
1 2 3 4 5 6
13-1 概述
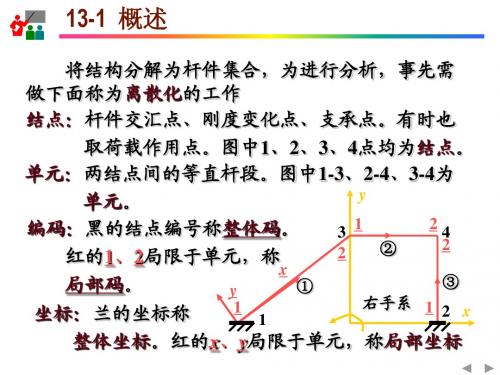
将结构分解为杆件集合,为进行分析,事先需 做下面称为离散化的工作 结点:杆件交汇点、刚度变化点、支承点。有时也 取荷载作用点。图中1、2、3、4点均为结点。 单元:两结点间的等直杆段。图中1-3、2-4、3-4为 y 单元。 24 编码:黑的结点编号称整体码。 3 1 2 ② 2 红的1、2局限于单元,称 x ③ 局部码。 ① y 右手系 1 2 x 1 坐标:兰的坐标称 1 整体坐标。红的x、y局限于单元,称局部坐标
13-2局部坐标系下的单元刚度矩阵
EA EA F1 1 0 0 4 l l 12 EI 6 EI F 2 0 3 2 2 3 0 l l 6 EI 4 EI F 3 0 2 3 0 2 l l EA EA F 4 1 0 0 4 l l 12 EI 6 EI F 5 0 3 2 2 3 0 l l 6 EI 2 EI F 6 0 2 2 3 0 l l
局部坐标下自由单元的单元刚度矩阵
13-2局部坐标系下的单元刚度矩阵
2 单元刚度矩阵的性质
(1)单元刚度系数的意义
(2)单元刚度矩阵是对称矩阵 (3)自由单元刚度矩阵是奇异矩阵 矩阵行列式等于零,逆阵不存在。
单位杆端位移引起的杆端力
反力互等定理
F
e
矩阵位移法——精选推荐

第十二章矩阵位移法12-1 概述用经典的力法和位移法求解超静定结构,随着基本未知量数目的增多,相应需要建立和求解的多元代数方程的个数也增多,计算工作极为冗繁和困难。
由于计算技术的飞速发展,电子计算机广泛应用于结构分析,使力学学科在计算技术上实现了现代化,大大推动了工程设计技术上的改进和结构理论的发展。
基于上述情况,结构矩阵分析方法已从本世纪六十年代迅速发展起来。
在结构矩阵分析中,运用矩阵进行计算,不仅能使公式非常紧凑,而且在形式上规格统一,便于使计算过程程序化,因而适用于电子计算机进行自动化的数学计算。
结构矩阵分析的两种基本方法是矩阵位移法(刚度法)和矩阵力法(柔度法),前者在计算中采用结点位移作为基本未知量,后者则采用多余力作为基本未知量。
对于杆件结构,矩阵位移法比矩阵力法便于编制通用的程序,因而在工程界应用较为广泛。
矩阵位移法与位移法在本质上并无区别,两者的差异仅在于矩阵位移法是从电算这一角度出发,它在解题步骤上以矩阵作为组织运算的数学工具。
在杆件结构的矩阵位移法中,把复杂的结构视为有限个单元(杆件)的集合,各单元彼此在结点处连接而组成整体。
因而先把结构分解成有限个单元和结点,即对结构进行离散化。
继而对单元进行分析,建立单元杆端力与杆端位移之间的关系。
再根据变形谐调条件、静力平衡条件使离散化的结构恢复为原结构,从而形成结构刚度方程,据此不难求解结构的结点位移和单元杆端力。
矩阵位移法的基本思路是“先分后合”,即先将结构离散然后集合,这样一分一合的过程,就把复杂结构的计算问题转化为简单杆件的分析与综合问题了。
因此,它的解题方法可分为两大步骤:(1)单元分析。
研究单元的力学特性。
(2)整体分析。
考虑单元的集合,研究整体方程的组成原理和求解方法。
12一2 单元刚度矩阵一、单元的划分在杆件结构中,一般是把每个杆件作为一个单元。
为了计算方便起见,只采用等截面直杆这种形式的单元,并且还规定荷载只作用于结点处。
矩阵位移法和位移法的异同

矩阵位移法和位移法的异同引言矩阵位移法和位移法是结构力学中常用的分析方法,用于计算结构的变形和应力。
它们在工程领域广泛应用,可以帮助工程师设计和优化各种结构。
本文将介绍矩阵位移法和位移法的基本原理、计算步骤以及它们之间的异同。
矩阵位移法矩阵位移法是一种基于刚体平衡原理和弹性力学理论的结构分析方法。
它通过建立结构的刚度矩阵和载荷向量的关系方程组,求解未知节点位移,从而得到结构的变形、应力等参数。
原理矩阵位移法基于以下两个基本原理: 1. 刚体平衡原理:结构在平衡状态下,任何一个节点受力的合力为零。
2. 弹性力学原理:结构内部材料满足胡克定律,即应力与应变成正比。
计算步骤矩阵位移法主要包括以下几个步骤: 1. 建立单元刚度矩阵:根据单元的几何形状和材料性质,通过积分或近似方法计算出单元的刚度矩阵。
2. 组装整体刚度矩阵:将所有单元的刚度矩阵按照节点自由度的顺序组装成整体刚度矩阵。
3. 施加边界条件:根据实际情况,确定某些节点的位移或受力边界条件。
4. 求解位移向量:根据结构的平衡方程和边界条件,建立节点位移与载荷之间的关系方程组,并求解未知节点位移。
5. 计算应力和变形:根据已知位移和单元刚度矩阵,计算结构中各个点的应力和变形。
优点矩阵位移法具有以下优点: 1. 精确性高:通过建立精确的刚度矩阵和载荷向量关系方程组,可以得到精确的结构变形和应力分布。
2. 适用范围广:适用于各种结构类型,包括梁、板、壳等。
3. 可扩展性强:可以通过增加单元数量或自由度来提高计算精度。
位移法位移法是一种基于虚位移原理的结构分析方法。
它通过假设结构发生微小位移,建立虚位移与内力的关系,从而求解结构的变形和应力。
原理位移法基于以下两个基本原理: 1. 虚位移原理:假设结构发生微小位移,使得结构内部势能函数最小。
2. 弹性力学原理:结构内部材料满足胡克定律,即应力与应变成正比。
计算步骤位移法主要包括以下几个步骤: 1. 建立虚位移场:根据虚位移原理,建立虚位移场,并将其表示为一组未知系数乘以已知基函数的形式。
《结构力学》第十章矩阵位移法

《结构力学》第十章矩阵位移法矩阵位移法是结构力学中的一种重要分析方法,通过将结构的受力分析转化为矩阵运算,可以有效地求解复杂结构的位移和应力分布。
本文将分为四个部分来介绍矩阵位移法的基本原理和应用。
第一部分将介绍矩阵位移法的基本原理。
矩阵位移法基于结构的受力平衡方程和变形条件,建立了适用于不同类型结构的一般形式的位移函数。
通过对这些位移函数进行适当组合,可以得到一个较为简化的位移矩阵方程。
这个方程可以通过矩阵运算求解,从而得到结构的位移和应力分布。
第二部分将介绍矩阵位移法的应用。
矩阵位移法可以用于求解各种类型的结构,包括梁、柱、框架等。
具体应用时,首先需要确定结构的边界条件和受力情况,然后根据结构的几何形状和材料性质,建立相应的位移函数。
之后,将位移函数按照一定的规则组合起来,建立一个位移矩阵方程。
通过解这个方程,可以得到结构的位移和应力分布。
第三部分将介绍矩阵位移法的优点。
相比于传统的力方法,矩阵位移法具有计算简单、准确性高、适用范围广等优点。
这是因为矩阵位移法可以通过矩阵运算将结构的受力分析转化为代数运算,减少了繁琐的计算过程,并且可以应用于各种不规则结构。
第四部分将介绍矩阵位移法的局限性。
矩阵位移法虽然具有很多优点,但也有一些限制。
首先,矩阵位移法对结构的刚度矩阵的求取较为复杂,需要通过精确和谐振数法等途径进行求解。
其次,矩阵位移法不能用于解决非线性和动力问题。
总结起来,矩阵位移法是一种重要的结构力学分析方法,通过将结构的受力分析转化为矩阵运算,可以有效地求解复杂结构的位移和应力分布。
它具有计算简单、准确性高、适用范围广等优点,但也有一些局限性。
因此,在实际应用中需要根据具体情况选择合适的方法。
同时,矩阵位移法的进一步研究和发展也是一个非常重要的方向。
《矩阵位移法》课件

实际工程案例分析
总结词
为了验证矩阵位移法的有效性,可以通过实际工程案例 进行分析。通过与实验结果的对比,可以评估方法的精 度和可靠性。
详细描述
选取具有代表性的实际工程案例,如高层建筑、大跨度 桥梁等,利用矩阵位移法进行计算,并将结果与实验数 据进行对比。通过对比分析,可以评估矩阵位移法的精 度和可靠性,为该方法在实际工程中的应用提供依据。 同时,也可以针对不同工程案例的特点,对矩阵位移法 进行优化和改进,提高其适用性和计算效率。
05
矩阵位移法的优缺点
优点
精确度高
矩阵位移法基于严格的数学推导,能 够精确地计算出结构的位移和内力, 尤其适用于复杂结构的分析。
适用性强
矩阵位移法可以处理多种类型的载荷 ,包括静载、动载以及温度载荷等, 适用范围广泛。
便于计算机化
矩阵位移法的计算过程可以通过计算 机程序实现,便于进行大规模的结构 分析。
多尺度方法
将矩阵位移法应用于多尺度问题 ,考虑不同尺度之间的相互作用 和影响,为复杂系统提供更准确 的模拟结果。
THANKS
感谢观看ts
目录
• 引言 • 矩阵位移法的基本概念 • 矩阵位移法的实施步骤 • 矩阵位移法的应用实例 • 矩阵位移法的优缺点 • 未来展望与研究方向
01
引言
什么是矩阵位移法
矩阵位移法是一种数值分析方法,用 于求解线性方程组和解决各种数值计 算问题。
它通过将原问题转化为矩阵形式,利 用矩阵运算来求解未知数,具有高效 、精确和灵活的特点。
并行计算
利用并行计算技术,将计算任务分解为多个子任务,同时运行在多 个处理器上,加快计算速度。
智能优化
结合人工智能和机器学习技术,自动调整算法参数,实现自适应优 化,提高算法的效率和稳定性。
矩阵位移法

k22坐k11标局k01成部1k029坐200标时kk20与32,3 整局k0体12部45 单k0k20514
0 k26 k26
To 47
k e ke
刚和有何整k关体3k3系单33 ?刚k0k间454535
k35 00
k3k6 36
0 k56
对称对称
kk5544
kk65k66 66
F e FEe k e e
单元杆端位移矩阵
e 1
2
3
4
T e
单元刚度矩阵(应熟记)
12 6l 12 6l
k
e
EI l3
6l
12
4l 2 6l
6l 12
2l
2
6l
6l 2l 2 6l 4l 2
是转角位移方程的矩阵表示
单元等效结点荷载矩阵
根据单跨梁的载常数,可得
向上满跨均布荷载 q 作用
(F FE )e k e e F e FEe k e e
连续梁单元需要 进行坐标转换吗?
连续梁的局部坐标与整 体坐标一致,所以不需 要转换。
第一种做法
桁架单元如何
进行坐标转换? T
力的转换
T
F1
F2
F3
F4
T
cos
0
位移的转换
sin
0
0
cos
0 T F1
sin F2
1 2
3. 坐标转换问题
在搞清单元特性后,像位移法一样,需将单 元拼装回去。在结点处位移自动满足协调条件 的基础上,令全部结点平衡,即可建立求解位 移的方程,这是下一节将讨论的内容。
除连续梁外,一般结构单元不全同方位, 为保证协调和平衡,应将杆端位移和杆端力 都转换成统一的,对整体坐标的量,因此要 先解决坐标转换问题。下面先讨论自由式梁 单元的转换问题。
矩阵位移法基本流程

矩阵位移法基本流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!矩阵位移法基本流程一、结构离散化阶段。
在运用矩阵位移法进行分析之前,首先要对结构进行离散化处理。
矩阵位移法程序化解题方法

矩阵位移法解法步骤解:1)、单元及结点位移分量统一编码单元及结点位移分量编码、整体坐标系如图所示,局部坐标系横轴正向在各单元上标出。
注:编结点位移分量总码时,后处理法和先处理法有区别:采用后处理法编码时暂不考虑边界条件对支座处位移分量的限制,皆视为一般情形处理;采用先处理法时,对已知为零的位移分量总是以零编码。
对于连接于铰结点的杆端编码时,线位移采用同码,而角位移异码。
2)、形成局部坐标中单元刚度矩阵 k e:首先,计算各单元杆件的几何特征:⋯ ⋯各单元的单元刚度矩阵如下:单元①: ⋯ ⋯3)、形成整体坐标中单元刚度矩阵:(计算公式: k e = T T ke T ) 整体坐标系中的各单元刚度矩阵转换如下:单元①: ⋯ ⋯4)、集成整体刚度矩阵 K (单元集成法或直接刚度法):首先,由各单元的局部码与总码的对应关系写出各单元的定位向量如下:λ e = ⋯ ⋯ T其次,将各单元刚度矩阵 k e 按其定位向量 λ e 在整体刚度矩阵 K 中定位并累加 得整体刚度矩阵如下:K =(⋯ ⋯)5)、计算综合等效结点荷载向量 F P :①、计算局部坐标系中各杆件单元的固端力向量:F P e =(F N1F ,F Q1F ,M 1F ,F N2F ,F Q2F ,M 2F )T ②、转换整体坐标系中各杆件单元的固端力向量:{F P }e =(F x1F ,F y1F ,M 1F ,F x2F ,F y2F ,M 2F )T ③、将各杆件单元的固端力反其指向,并按其定位向量 λ e 在综合等效结点荷载向量 F P 定位并累加,得综合等效结点荷载向量如下:F P = ⋯ ⋯ T6)、计入边界条件条件,写出刚度方程并解之:刚度方程: K Δ = F P采用后处理法时,对已知为零的结点位移,在整体刚度矩阵 K 中将其所对应行列的主元素记为1,其余都变为零,然后写出刚度方程,解之。
采用先处理法时,由于在进行位移分量编码时已考虑边界条件,因而无须再计入,只写出刚度方程求解即可。
矩阵位移法

TT T T T T I
Fx1 F y1 M1 单元坐标 转换矩阵 F x2 Fy 2 M 2
e
Hale Waihona Puke eF e TF e
T 1 T T
单元坐标转换矩阵T是一正交矩阵。
EI 25 104 kN m l
0 300 0
5m
0 为了简洁,下面将矩阵 中各元素的单位略去。 12 30 0 12 30 30 100 0 30 50 4 EA 10 0 0 l 0 0 300 0 0 12 30 0 12 30 12 EI 6 EI [k11 ] 0 3 2 30 50 0 30 100 l l 6 EI 4 EI 第一列元素变符号即第四列,第二列元素变符号即第五列 0 ①: 2 ②求整体坐标系中的单刚, k l l 第一行元素变符号即第四行,第二行元素变符号即第五行
3、有限单元法的三个基本环节: ①单元划分:一根等截面直杆作为一个单元,单元间由结点相联。 ②单元分析:建立单元刚度方程,形成单元刚度矩阵(物理关系)。 ③整体分析:由单元刚度矩阵形成整体刚度矩阵,建立结构的 位移法基本方程(几何关系、平衡条件)。
§9-2 单元刚度矩阵(element stiffnessmatrix)(局部坐标系)
T11 T12 T T T 21 22
因此,(a)式的逆转换式为: 同理
F e T TF e
e T e
(b)
e T T e
整体坐标系中的单元刚度矩阵
F e TF e
(a)
e T e
(b)
单元刚度矩阵的性质 设局部坐标系中、整体坐标系中的单元刚度方程分别为: ①单元刚度矩阵是杆端力用杆端位移来表达的联系矩阵。 e e e F k Δ (c) ②其中每个元素称为单元刚度系数,表示由于单位杆端位移引起的杆端力。 ③单元刚度矩阵是对称矩阵。 F e k eΔe (d ) ④第k列元素分别表示当第k个杆端位移=1时引起的六个杆端力分量。 e e e e ⑤一般单元刚度矩阵是奇异矩阵。不存在逆矩阵。因此, 将式(a)、(b)代入式(c) k eT IF T T TTF ke T T 可由单元刚度方程,由杆端位移唯一确定杆端力;但由杆端力反推杆端位移时, 可能无解、可能解不唯一。 k e T T k eT
矩阵位移法

D1 = D2 = 0
; D5 = D6 = 0
则有修正后的总刚度矩阵:
-100 2 [K ] = 100 600
[k11 ] [k12 ] {F1} = {F2 } [k 21 ] [k 22 ]
{D1} {D 2 }
@
单元刚度矩阵的性质:①对称性;②奇异性; ③主对角元恒为正值
3、整体刚度矩阵
K ij :单元仅发生第j个杆端单位位移时,在第
Y2 = QBA
写成矩阵表达式为:
4 EI 2 EI 6 EI q + q + -v ) ( v l 1 l 2 l2 1 2 2 EI 4 EI 6 EI q + q + -v ) ( M2 = v l 1 l 2 l2 1 2 6 EI 12 EI (v1 - v2 ) Y1 = (q1 +q 2 ) + l2 l2 6 EI 12 EI = q + q (v1 - v2 ) Y2 ( 1 2) l2 l2 M1 =
2
3
1 2
Hale Waihona Puke 3-1 50 1 50 50 300 -50 150 -1 -50 2 -100 -1 -50 = 50 150 -100 600 50 150 -1 50 1 50 -50 150 50 300
计入边界条件:因边界结点1和3 为固定端,故有:
0 12EI l3 6 EI - 2 l 0 12EI l3 6 EI - 2 l
@
0 6 EI l2 2 EI l 0 6 EI - 2 l 4 EI l
EA l 0 0
01_结构力学——矩阵位移法1

kij 表示 u j 1 引起的杆端力Fi 的大小。
15 / 48
第十三章 矩阵位移法 第二节 单元分析(局部坐标系下的单元分析 )
3、局部坐标系中的单元刚度矩阵性质
EA 1 1 k11 k12 k l 1 1 k21 k22
1、矩阵位移法的基本思路 b、基本假设和基本原理
线弹性、小变形。满足叠加原理、功能原理
c、正负号规定(采用右手法则)
杆端内力规定当与坐标轴正方向一致时为正;
杆端位移和结点位移规定当与坐标轴正方向一致时为正。
结点外力规定当与坐标轴正方向一致时为正;
8 / 48
第十三章 矩阵位移法 第一节 矩阵位移法概述
杆端内力:
u1 , u2
F1 , F2
13 / 48
第十三章 矩阵位移法 第二节 单元分析(局部坐标系下的单元分析 )
2、局部坐标系中的单元刚度矩阵
EA u1 l EA u2 l
F1e
u1
1 1
EA EA
e
e
2 2
u2
EA u1 l EA u2 l
局部坐标 系下的单 刚方程
e
EA e EA e u1 u2 l l
法
杆件端点位移 结构结点位移
位移法
法 需要选择基本体系和多余约束。所以较多地依赖于结构的具 体情况,不宜实现计算机计算的自动化,但其优点是计算出 的结果就是力。 位移法 是先求结点位移,再换算成力,该法的计算自动化和通用性强, 目前广为采用。 7 / 48 力
第十三章 矩阵位移法 第一节 矩阵位移法概述
x
矩阵位移法

0 cos 0 sin 0
e
0
0 X 1 0 Y 1 0 M 1 0 X 2 0 Y 2 1 M 2
e
简记:
F
e
T
F
T 为单元坐标转换矩阵
22
cos sin 0 T 0 0 0
e e
2、叠加各单元贡献矩阵,得到整体刚度矩阵。 二、单元定位向量 1、定义: 由单元的结点位移总码组成的向量称为“单元定
0 6EI 2 u1 l 2EI v1 1 l 0 u 2 v 2 6EI 2 l 2 4EI l
e
记为
F k
e
12
局部坐标系中的单元刚度方程
e
F 1 F 2 F 3 ... F 4 F 5 F 6
e
7
13.2 单元分析(一)——局部坐标系 中的单元刚度矩阵
定义:单元杆端力和杆端位移之间的转换关
系成为单元刚度方程。
F k
e e
e
e k 其中 称作单元刚度矩阵(简称作单刚)
sin cos 0 0 0 0
0 0 1
0 0 0
0 0 0 sin cos 0
0 cos 0 sin 0 0
0 0 0 0 0 1
23
T 为正交矩阵
T T F T F T T
e e
0 6EI l2 4EI l 0 6EI l2 2EI l
EA l 0 0
0 12EI 3 l 6EI 2 l 0 12EI l3 6EI 2 l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13.4.1 连续梁的整体刚度矩阵
举例13—4
整体刚度方程是整体结构的结点力与结点位移之间的关系式,是通过考虑结构的变形连 续条件和平衡条件建立起来的。无论何种结构,其整体刚度方程都具有统一的形式:
[K]是整体刚度矩阵,{Δ}结构的结点位移列向量,{F}结构的结点力列向量。
13.4.2 整体刚度矩阵的性质
13.5.2 单元定位向量
(1) 结点位移分量的统一编码——总码 平面刚架中的一个结点可能有一个、两个或三个结点位移,在进行结点位移分量编码 时,应考虑每个结点的位移情况,对结构的所有结点位移分量进行统一编码。对每个结点的 三个位移分量,按照先x轴方向,再y轴方向后转动放顺序依次编码,编完一个结点再编下一 个结点。对于已知为零的结点位移分量,其总码均编为0。如图13-10(a)结构的结点位移分量 的统一编码如图中所示。
位置和方位无关;整体坐标系中的单元刚度矩阵 的方位都有关。 计算单元刚度矩阵举例 举例13—3
13.4 连续梁整体分析
整体分析的目的是建立整体刚度方程,即建立结构的结点力与结点位移之间的关系式, 导出整体刚度矩阵。具体作法有两种:一种是传统位移法,另一种是单元集成法(即刚度集 成法或直接刚度法)。 下面以连续梁为例,用传统位移法建立整体刚度方程,进而总结出单元集成法。
端力。如第i行第j列元素代表当第j个杆端位移分量=1(其它位移分量为零)时引起的第i个杆 端力分量的值。 单刚中第j列元素代表当第j个杆端位移分量=1(其它位移分量为零)时引起的六个杆端 力分量的值。 由图13-4可见, v = 1 产生的单元变形及单元的杆端力与 v = −1 产生的单元变形及单元 2 1 的杆端力相同。 由此得到:单元刚度矩阵的第二列元素变符号即第五列元素,第一列元素变符号即第四 列元素。第三列元素不变符号即第六列元素,但要注意 度矩阵是对称矩阵,所以,各行元素之间也具有类似的关系。 (2) 对称性 由反力互等定理可知: kij = k ji ,即单元刚度矩阵是对称矩阵。 (3) 奇异性 一般单元的单元刚度矩阵是奇异矩阵,不存在逆阵。因此,如已知杆端位 移,由单元刚度方程可求出杆端力,且是唯一解。但若已知杆端力,则求不出杆端位移,杆 端位移可能无解,也可能无唯一解。 (4) 分块表示 可按杆端将单元刚度方程写成分块形式: , 。由于单元刚
/jglx/jingpin/chejian/jiben/dianzijiao%27an...
2012-2-26
第十三章 矩阵位移法
页码,7/14
部坐标系中的单元刚度矩阵
,只与单元的几何形状、物理常数有关,而与单元的 ,与单元的几何形状、物理常数及单元
13.1 概 述
矩阵位移法以传统的位移法作为理论基础,以矩阵作为数学表达形式,以电子计算机作 为计算手段,它是一种三位一体的计算方法。采用矩阵进行运算,不仅公式紧凑,而且形式 统一,便于使计算过程规格化和程序化。这些正是适应了电子计算机进行自动化计算的要 求。
13.1.1 矩阵位移法的基本思路
先将结构离散成有限个单元,按照单元的力学性质,建立单元刚度方程,形成单元刚度 矩阵;然后在满足变形条件和平衡条件的前提下,将这些单元集合成整体,即由单元刚度矩 阵集成整体刚度矩阵,建立结构的位移法基本方程,进而求出结构的位移和内力。这样,在 “一拆一搭”的过程中就使一个复杂结构的计算问题转化为有限个简单单元的分析与集成问 题。 因此,矩阵位移法基本环节是:结构的离散化 、单元分析 和整体分析 。
13.2.4 特殊单元的单元刚度矩阵
/jglx/jingpin/chejian/jiben/dianzijiao%27an...
2012-2-26
第十三章 矩阵位移法
量可以指定为任意值。特殊单元的某个或某些杆端位移已知 为零。特殊单元的单元刚度矩阵,可由一般单元刚度矩阵中划去与零位移对应的行和列得 到。 (1) 忽略轴向变形时梁单元在局部坐标系中的单元刚度矩阵(图13-5) 划去一般单元刚度矩阵式(13-4)中第一、四行和第一、四列可得:
第十三章 矩阵位移法
页码,1/14
第13章 矩阵位移法
【13.1 概述】【13.2 单元分析(一)】【13.3 单元分析(二)】【13.4 连续梁整体分 析】 【13.5 刚架整体分析】【13.6 等效结点荷载】【13.7 计算步骤和算例】
学习内容
有限单元法的基本概念,结构离散化。 平面杆系结构的单元分析:局部坐标系下的单元刚度矩阵和整体坐标系下的单元刚度矩 阵。 平面杆系结构的整体分析:结构整体刚度矩阵和结构整体刚度方程。 支承条件的处理,单元内力计算。 利用对称性简化位移法计算。 矩阵位移法的计算步骤和应用举例。
13.1.2 单元划分
在杆件结构矩阵分析中,一般是把杆件的转转折点、汇交 点、边界点、突变点或集中荷载作用点等处作为结点,结点之 间的杆件部分作为单元。如图13-1所示。为了减少基本未知量 的数目,跨间集中荷载作用点处也可不作为结点,但要计算跨间荷载的等效结点荷载。
/jglx/jingpin/chejian/jiben/dianzijiao%27an...
中的各元素在整体刚度矩阵[K]中的位置并累加到[K]。
/jglx/jingpin/chejian/jiben/dianzijiao%27an...
2012-2-26
第十三章 矩阵位移法
页码,9/14
(3) 对所有单元循环一边,最后得到整体刚度矩阵[K]。 举例 13—5
(1) [K]中的元素Kij 称为整体刚度系数 ,它表示当第j个结点位移分量Δj=1(其他结点位 移分量为零)时所产生的第i个结点力Fi。 (2) 对称性 [K]是对称矩阵,是稀疏带状矩阵。 (3) 奇异性 引入支承条件之前是奇异矩阵,引入支承条件之后是非奇异矩阵,存在逆 阵。
13.4.3 整体刚度矩阵的集成
13.5 刚架整体分析
13.5.1 刚架整体分析的特点
刚架的整体分析与连续梁相比,基本思路相同,但情况复杂一些,主要表现在: (1) 刚架中每个结点位移分量增加到三个:角位移和两个方向的线位移。(一般情况下要 考虑刚架各杆的轴向变形); (2) 各杆方向不尽相同,在整体分析中采用整体坐标系,故要进行坐标变换; (3) 刚架中除了刚结点,还要考虑铰结点等其它情况。
13.3.1 单元坐标转换矩阵
整体坐标系如图13-8中的xoy坐标系。 两种坐标系中单元杆端力和杆端位移转换关系为:
其中[T]称为单元的坐标转换矩阵
公式推导 举例13—2
13.3.2 整体坐标系中的单元刚度矩阵
13.3.3 整体坐标系中的单元刚度矩阵的特性
整体坐标系中的单元刚度矩阵与局部坐标系中的单元刚度矩阵有类似的特性。此外,局
v2 θ 2
推导过程 举例13—1
/jglx/jingpin/chejian/jiben/dianzijiao%27an...
2012-2-26
第十三章 矩阵位移法
页码,4/14
13.2.3 单元刚 度矩阵 的特性
(1) 单 元刚度系数的意义 单刚中的每个元素称为单元刚度系数 ,代表由于单位杆端位移引起的杆
/jglx/jingpin/chejian/jiben/dianzijiao%27an...
2012-2-26
第十三章 矩阵位移法
页码,6/14
矩阵的形式简单。但是,在一个复杂的结构中, 各单元的局部坐标系不尽相同,很不统一。为了进行整体分析,必须选一个统一的坐标系 (称为整体坐标系 )。按这个统一的坐标系来建立各单元的刚度矩阵。
学习目的和要求
矩阵位移法是以计算机为计算工具的现代化结构分析方法。基于该法的结构分析程序在 结构设计中得到了广泛的应用。因此,以计算机进行结构分析是本章的学习目的。 矩阵位移法是以位移法为理论基础,以矩阵为表现形式,以计算机作为运算工具的综合 分析方法。引入矩阵运算的目的是使计算过程程序化,便于计算机自动化处理。尽管矩阵位 移法从手算的角度来看运算模式呆板,过程繁杂,但这些正是计算机所需要的和十分容易解 决的。矩阵位移法的特点是用“机算”代替“手算”。因此,学习本章是既要了解它与位移法的 共同点,更要了解它的一些新手法和新思想。 本章的基本要求: 矩阵位移法包含两个基本环节:单元分析和整体分析。 在单元分析中,熟练掌握单元刚度矩阵和单元等效荷载的概念和形成。熟练掌握已知结
/jglx/jingpin/chejian/jiben/dianzijiao%27an...
2012-2-26
第十三章 矩阵位移法
页码,2/14
点位移后求单元杆端力的计算方法。 在整体分析中,熟练掌握结构整体刚度矩阵中元素的物理意义和集成过程,熟练掌握结 构综合结点荷载的集成过程。掌握单元定位向量的建立,支撑条件的处理。 自由式单元的单元刚度矩阵不要求背记,但要领会其物理意义,并会由它来推出特殊单 元的单元刚度矩阵。
由变形连续条件知,结点发生单位位移,交与该结点的各单元的杆端也发生单位位移; 由刚度系数的物理意义知,单位杆端位移产生的杆端力是单元刚度矩阵中的元素,单位结点
/jglx/jingpin/chejian/jiben/dianzijiao%27an...
2012-2-26
13.2.2 局部坐标系中的单元刚度矩阵
在局部坐标系中,杆端力及杆端位移的正方向如图13-2所示。单元刚度方程可表示为:
(13-1) 其中单元的杆端力列阵和杆端位移列阵为:
{F }
单元刚度矩阵为:
e
= X 1 Y1
e
M1
X 2 Y2
M 2
T
T
(13-2) (13-3)
{∆}
= u1 v1 θ1 u 2
(2) 连续梁单元的单元刚度矩阵(图13-6) 划去一般单元刚度矩阵中第一、二、四、五行和相应的列可得:
(3) 桁架单元(图13-7)在局部坐标系中的单元刚度矩阵 划去一般单元刚度矩阵中第二、三、五、六行和相应的列可得:
