第六、八章光学系统的像差理论和像质评价 2012

合集下载

第六章像差与成像质量评价

a A a -y B z b z b C
由于慧差是垂轴像差，当系统结构完全对称，孔径光阑置于系统的中央，且物像放大率=-1时，整个光束结构关于系统的中心点对称（如图所 1 示），系统前半部产生的慧差与后半部产生的慧差绝对值相同、符号相反，慧差完全自动消除。由于一般光学系统的放大率不等于－1，因此，绝对的对称结构并不适合，根据实际系统的物像关系，设计接近对称结构的光学系统，将有利于自动校正慧差。
正弦差越大，说明小视场大孔径光线失对称现象越严重。故视场很小时就要考虑彗差。减小彗差：彗差和透镜
的形状、物点的位置、
光阑的大小和位置有关：
① 物点及光阑的位置（同心原则）：如光阑
过单折射面的球心时不产生彗差。 ② 减小光阑直径
当轴外物点发出一束很细的光束通过入瞳进入系统时，成对的宽光束光线之间的失对称现象将被忽略，球差也不会对细光束有大的影响。但是，光束各截面之间仍然存在着失对称现象，且随着视场的增大而愈加明显。如图所示，轴外B点发出细光束在球面上所截得的曲面显然已不是一个对称的回转曲面，它在不同截面方向上有不同的曲率，并在子午和弧矢这两个相互垂直的截面方向上具有最大或最小的曲率，表现出最大的曲率差。子午和弧矢面上的细光束，虽然各自能会聚于主光线上的一点，但相互并不重合，即一个轴外物点以细光束成像，被聚焦为子午和弧矢两个像，这种像差我们称其为细光束像散。
轴外物点B发出充满入瞳的一束光，这束光以通过入瞳中心的主光线为对称中心。考察主光线z和一对上下光线a、b。折射前，上下光线相对于主光线对称，而折射后，上下光线不再对称于主光线，它们的相交点偏离了主光线。
入瞳
-K' t a' z' b' B't c

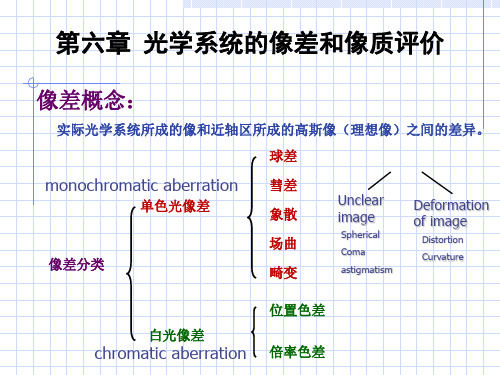
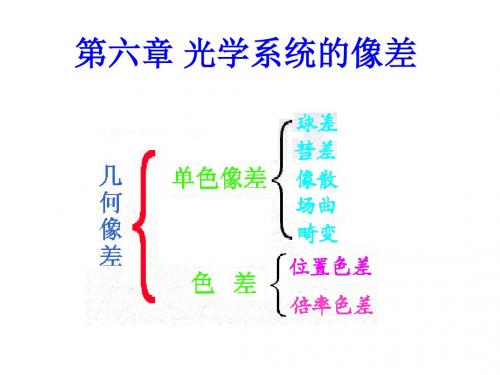
光学系统的像差

3
单色像差
球差——轴上点宽光束像差彗差——轴外点宽光束像差像散——轴外点细光束像差像面弯曲（简称场曲）畸变
4
球差
轴上物点以宽光束成像时产生的像差。不同孔径角的光线所成的像点相对于理想
像点的位置偏离。由于此球差是沿光轴方向度量的，也称为
轴向球差
5
轴上物点的单色像差——球差
30
近轴物近轴光线成像的色差
123
不同波长的光，焦距不同,像的位置不同．在1,2,3三截面上,形成的光环半
径不同.
31
色差严重影响光学系统成像性质，一般光学系统都必须校正色差。可以用正负透镜适当组合来校正位置色差。
32
影响位置色差的主要因素：
随孔径角的增大而增大与光学材料的折射率和色散率有关与透镜的焦距有关
B
37
倍率色差随视场的增大而增大，由于倍率色差的存在，使物体边缘呈现彩色，从而，造成白光所成的像呈现彩色斑。
38
对于一般光学系统来说，球差、慧差和位置色差这三种对对成像性质影响较大，所以首先考虑消除，因人眼具有自动校正色差功能，故影响成像质量主要是球差和慧差。
39
光学设计的意义
50
像散的影响因素
随视场增大而增大与光阑位置有关与系统焦距及透镜表面曲率有关此外，与光束大小也有关
51
像面弯曲（简称场曲）
52
53
场曲
光学系统如存在像散，一个物面将形成两个像面（即子午像面和弧矢像面），两弯曲像面与高斯像面的偏离分别称为子午场曲和弧矢场曲，以符号 xt′和xs′表示之。
理想成像的要求出入射光束为同心光束，只有近轴区成
像才是理想成像。
1

第八章光学系统的像质评价分解

I ( y)

1 1 1 cos y c源自s 3y cos 5y cos 7y 4 3 5 7
其中 2/T称为空间角频率；空间频率 1 T
对光学系统而言，这个分解过程的物理意义是：如果物平面的强度分布是一个周期函数，可以把它看成是由很多频率、振幅和初位相不同的余弦函数合成。
像平面输出的余弦基元为： I ( y' ) 1 a' cos(2' y' ) 物面图形的对比K为
I I 2a K max min a I max I min 2
像面图形的对比K’为
I’(y )
I 'max I 'min 2a' K' a' I 'max I 'min 2
二、中心点亮度光学系统存在像差时，其成像衍射的中心亮度（爱里斑亮度）与不存在像差时衍射斑的中心亮度的比值来表示光学系统的成像质量；这个比值称为中心点亮度，用S.D.表示。斯托列尔（K.Strehl）准则：当S.D. ≥0.8时，认为光学系统的成像质量是完善的。
适用于：小像差光学系统，计算复杂。
第八章光学系统的像质评价
第一节瑞利判断和中心亮度
一、瑞利（Reyleigh）判断
实际波面与参考球面波之间的最大波像差不超过时， 4 此波面可看作是无缺陷的。参考球面选择的标准是使波象差的最大值最小；波像差的最大值允许量不超过 4 。
优点：便于实际应用；
缺点：从光波传播光能的观点看，瑞利判断不够严密；适用于：小像差光学系统，如：望远物镜，显微物镜，微缩物镜，制版物镜等。
1 5
a6 0
矩形周期函数的振幅频谱函数

光学系统成像质量评价

（一）望远镜分辨率（二）照相系统分辨率（三）显微镜分辨率
第九节光学传递函数第十节用光学传递函数评价系统的像质
上一页下一页返回
第一节概述
成像质量评价的方法：成像质量评价的方法：
1、用于在光学系统实际制造完成后对其进行实际测量。用于在光学系统实际制造完成后对其进行实际测量。分辨率检验星点检验用于在光学系统还没制造出来， 2、用于在光学系统还没制造出来，即在设计阶段通过计算就能评定系统质量。系统质量。
上一页
下一页
返回
第二节介质的色散和光学系统的色差
某一种介质对两种不同颜色光线的折射率之差称为该介质对这两种颜色光的色散。光的色散。不同颜色光线的像点沿光轴方向的位置之差称为轴向色差分别表示F 两种波长光线的近轴像距,则轴向色差为：若用 lF ', lC '分别表示F，C两种波长光线的近轴像距,则轴向色差为：
1500 N= F
三、显微镜物镜分辨率：显微镜物镜分辨率：
在显微镜系统中，物体位在近距离，一般以物平面上刚能分开两物体在显微镜系统中，物体位在近距离，间的最短距离σ 间的最短距离σ表示
σ=
0.61λ 0.61λ = nu NA
上一页下一页返回
第九节光学传递函数
一种对设计和使用都适用的统一的像质评价指标图像分解与合成的概念像面与物面对比之比称为对指定空间频率μ的对比传递因子，像面与物面对比之比称为对指定空间频率μ的对比传递因子，用 MTFμ表示表示。 MTFμ表示。称为振幅传递因子
δ L ' = L ' l '
上一页下一页返回
第四节轴外像点的单色相差
如图所示，主光线和光轴决定的平面，称为子午面，如图所示，主光线和光轴决定的平面，称为子午面，过主光线与子午面垂直的平面，称为弧矢面。面垂直的平面，称为弧矢面。

第八章光学系统的像质评价和像差公差

第二节分辨率
★ 分辨率——反映光学系统能分辨物体细节的能力，可用来评价光学系统的成像质量。
★ 瑞利指出“能分辨的两个等亮度点间的距离对应艾里斑的半径”，即一个亮点的衍射图案中心与另一个亮点的衍射图案的第一暗环重合时，这两个亮点则能被分辨。
如图 8-3b 。这时在两个衍射图案光强分布的叠加曲线中有两个极大值和一个极小值，其极大值与极小值之比为 1:0.735 ，这与光能接收器（如眼睛或照相底板）能分辨的亮度差别相当。若两亮点更靠近时，如图8-3c，则光能接收器就不能再分辨出它们是分离开的两个点。
图8-8 光学系统的调制传递函数计算实例
下面简要介绍两种利用调制传递函数评价成像质量的方法。
一、利用MTF曲线来评价成像质量
MTF表示各种不同频率的正弦强度分布函数经光学系统成像后，其对比度(即振幅)的衰减程度。当某一频率的对比度下降到零，说明该频率的光强分布已无
亮度变化，即该频率被截止。这是利用光学传函评价成像质量的主要方法。
瑞利判断和中心点亮度是从不同角度提出的像质评价方法，研究表明，对一些常用的像差形式，当最大波像差为λ/4时，其中心点亮度S.D约等于0.8，表明这两种评价方法是一致的。
斯托列尔准则同样是一种高质量的像质评价标准，也只适用于小像差系统。但由于其计算相当复杂，在实际中不便应用。
现代光学设计软件不仅能计算中心点亮度，而且能绘制任一
★ 任何光学系统都不可能，也没有必要把所有的像差都校正为零，必然还残存有剩余像差，故有必要讨论各种光学系统所允许存在的剩余像差值及像差公差的范围。
第一节瑞利（Reyleigh）判断和中心点亮度
一、瑞利判断
瑞利判断是根据成像波面相对理想球面波的变形程度来判断光学系统的成像质量.瑞利认为“实际波面与参考球面波之间的最大波像差不超过 λ/4 时 , 光学系统的成像质量是良好的”.

光学系统的像差理论和像质评价

20 Engineering Optics
彗差对于大孔径系统和望远系统影响较大彗差的大小与光束宽度、物体的大小、光阑位置、光组内部结构（折射率、曲率、孔径）有关对于某些小视场大孔径的系统（如显微镜），常用 “正弦差”来描述小视场的彗差特性。正弦差等于彗差与像高的比值，用符号SC’表示
SC ' li m Ks '/y '
由子午光束所形成的像是一条垂直子午面的短线t称为子午焦线由弧矢光束所形成的像是一条垂直弧矢面的短线s称为弧矢焦线
t
A
s
24
Engineering Optics
这两条短线不相交但相互垂直且隔一定距离
两条短线间沿光轴方向的距离即表示像散的大小用符号Xts’表示
Xts’=Xt’-Xs’
t
A
s
25
Engineering Optics
入瞳
光学系统
光屏
这种即非对称又不会聚于一点的细光束称为像散光束这两条短线（焦线）光能量最为集中，它们是轴外点的像
Engineering Optics
大孔径产生的球差
11
Engineering Optics
加发散透镜消除球差
12
Engineering Optics
球差
13
Engineering Optics
2、彗差(轴外点宽光束)
了解成像光束光线的全貌：子午平面和弧矢平面由轴外物点和光轴所确定的平面称为子午平面子午平面内的光束称子午光束
第六、八章光学系统的相差理论和像质量评价
Engineering Optics
1
光学系统的像差理想光学系统的分辨率各类光学系统分辨率的表示方法

应用光学第八章光学系统成像质量评价

球差（Spherical aberration) 慧差（Coma）像散（Astigmatism）场曲（Field curvature）畸变（Distortion）
色差（Chromatic aberration）
轴向色差（Axial chromatic aberration）垂轴色差（Chromatic difference of magnification）
球差：不同孔径光线对理想像点的距离称为球差。
L' L'l'
符号规则：光线聚焦点在理想像点右方为正，左方为负。通常用1.0，0.85，0.707，0.5，0.3孔径的球差来描述整个光束的结构。
球差的消除
球差的大小与物点位置和成像光束的孔径角有关。球差的消除：
利用正、负透镜组合，可以消除球差。非球面透镜
弧XS矢’ 。场表曲示：此弧光矢线光对线交对点交与点理B想S’离像理平想面像的平偏面离的程轴度向。距离弧矢慧差：光线对交点BS’离开主光线的垂直距离KS’ 。表
示此光线对交点偏离主光线的程度，即弧矢光线相对于主光线不对称的程度。细想像光平束面弧的矢轴场向曲距：离当x光s’束。的宽度趋于零，其交点Bs’离理轴外弧矢球差：不同宽度弧矢光线对的弧矢场曲和细光束弧矢场曲之差。表示了细光束与宽光束交点前后位置的差。
8-9 光学传递函数
光学系统是一个空间不变的线性系统。
光学
分解
系统
合成
物面
物点
弥散斑
像面
假定每个弥散斑的形状相同，其光强度与相应物点的光强度成正比。这样的系统我们称为空间不变的线性系统。
光学传递函数理论的出发点
分解
光学系统
合成
物面强

像差理论与像质评价

像差基础理论与像质评价2006-03-10实际光学系统中,只有平面反射镜在理论上具有理想光学系统的性质.其它光学系统都不能以一定寛度的光束对一定大小的物体成完善像,即物体上任一点发出的光束通过光学系统后不能会聚为一点,而形成一弥散斑,或者使像不能严格地表现出原物形状,这就是像差.一.像差的分类( 一) 几何像差分为两大类,共七种,如下:1单色像差A.球差B.慧差C.像散D.场曲E.畸变2.色差A.位置色差( 轴向色差)B.倍率色差( 放大率色差或垂轴色差)( 二) 波像差由点光源发出的光应向各方向传播相同的距离,因此,波面应该是中心点与点光源重合的球面,称为球面波.此球面波经光学系统后,由于各个面的折射而改变了曲率.如果光学系统是理想的,那边那么形成一个新的球面波.但是实际上, 光学系统总有剩余像差,使折射以后的波面或多或少地变了形,而不复为球面波.这一变了形的实际波面与理想球面波之间的偏离,称为波像差.( 三) 单色像差又可分为以下两类:1.轴上点像差: A. .球差. B.正弦差.2.轴外点像差: A. 轴外球差. B.慧差 C.像散 D.场曲 E.畸变二.像差的基本概念( 一) 球差δĽ球差δĽ在数值上是轴点发出的不同孔径光线像方截距L’与近轴光截距ℓ’之差值,即:δĽ=L’-ℓ’举例:有一镜头,参数如下:R TC n25.815 4.0 1.5163-25.815-1-垂轴球差: δT'=δL'tgU'由于像平面上的像是由弥散斑组成,所以不能反映物体的细节,球差严重时,像就变得糢糊不清. 所以任何光学系统都必须校正好球差.( 二) 慧差轴外点B发出子午光束,主光线,上光线和下光线不交于一点.在折射前主光线是光束的轴线,而折射后主光线不再是光束的轴线.光线失去了对称性.用上,下光线交点到主光线的垂直光轴方向的偏离来表示这种光束的不对称, 称为子午慧差. K’T=1/2(Y’a+Y'b)-Y'zY’a---上光线在高斯像面上的交点高度.Y'b---下光线在高斯像面上的交点高度Y'z---主光线在高斯像面上的交点高度-2-( 三) 像散当轴外物点B通过有像散的光学系统成像时,使一屏沿光轴移动,在不同位置时,B点的像就会发生很大的变化.在位置1时,为一长轴垂直于子午面的椭圆；移到位置2时为一垂直于子午面的短线；在位置3时又成为一长轴和子午面垂直的椭圆；在位置4时形成一个原斑；在位置5时形成一长轴在子午面内的椭圆；位置6时形成一子午面内的短线；位置7时又扩散成为椭圆。

第八章光学系统的像质评价和像差公差

第八章光学系统的像质评价和像差公差光学系统的像质评价和像差公差是光学设计中非常重要的内容，对于确保光学系统的成像效果和减小像差具有重要意义。

本文将从像质评价和像差公差两个方面进行详细介绍。

第一部分：像质评价在光学系统设计中，像质评价是衡量系统成像效果好坏的一项重要指标。

像质评价可以通过不同的参数来进行，如分辨率、畸变、像场曲率等。

1.分辨率：分辨率是指系统能够分辨出最小细节的能力。

在光学系统中，分辨率受到折射率、孔径、波长等因素的影响。

分辨率的提高可以通过增加系统的孔径、减小像散等方法来实现。

2.畸变：畸变是指光学系统成像时图像相对于参考图像的形变情况。

主要分为径向畸变和切向畸变两种。

径向畸变是指图像中心与边缘的变形情况，切向畸变是指图像的扭曲情况。

畸变的产生主要是由于光学元件的形状和定位误差导致的，可以通过优化元件设计和加强装配精度来减小畸变。

3.像场曲率：像场曲率是指光学系统各个像点的焦距随着物距的变化情况。

如果像场曲率过大，会导致成像不清晰，失去焦点。

可以通过调整透镜曲率半径、引入焦点平面等方法来改善像场曲率。

第二部分：像差公差像差是指光学系统成像时图像与理想像之间的差异，它是光学系统中不可避免的问题。

为了减小像差，需要对光学系统进行像差公差的设计和控制。

1.球面像差：球面像差是由于透镜表面的曲率或者抛物率与光线的入射角度不匹配导致的成像失真。

可以通过优化透镜表面形状和选择合适的材料来减小球面像差。

2.形状像差：形状像差是光学元件的形状不规则或者安装位置偏差导致的成像失真。

可以通过优化元件设计和加强装配精度来减小形状像差。

3.色差：色差是指透镜对不同波长的光具有不同的折射率，从而导致颜色偏差。

色差主要分为色散和像散两种。

色散是指透镜对不同波长的光具有不同的聚焦效果，像散是指不同波长的光成像位置不一致。

可以通过使用多片透镜组合、引入补偿透镜等方法来减小色差。

在光学系统设计中，像质评价和像差公差是重要的内容，对于确保系统的成像效果和减小像差具有重要意义。

第6章像差与成像质量评价(修改)

第六章像差与成像质量评价在几何光学中，我们从理想光学系统的观点讨论了光学系统的成像原理。

但是，实际光学系统只在近轴区才具有理想光学系统的性质，即只有当孔径和视场很小的情况下才能成完善像，而这样的光学系统实际应用意义不大。

第一节:概述通过前面的学习，我们了解到：除平面反射镜外，其他的光学系统都不能成完善像，即系统存在像差。

像差是指实际光学系统的成像与理想光学系统成像之间的差异。

实践和理论都可证明要完全消除像差也是不能的。

但是从另一方面看，由于人眼和其他光接收器本身都具有一定的缺陷，所以也就没有必要把光学系统的像差完全消除。

实际上，只要把影响像质的几个主要像差减小到某种容限范围内,即接收器不能察觉时，就可认为光学系统得到了满意的成像效果。

像差，透镜或反射镜所呈的像与原物面貌并非完全相同的现象。

造成球面像差的原因：是由于一点光源发散的光线被分聚在不同的点上的缘故。

理想光学系统＊如果通过光学系统后仍然是同心光束，则在会聚点成像：完善像点。

＊物面上所有点发出的光束都在像方成完善像点：则系统成完善像。

＊不考虑像差的成像关系即是理想光学系统。

完善成像的物理条件由于物点发出的是球面波，而其完善像点由会聚的球面波形成，而球面波面之间的光程是相等的，所以，完善成像的物理条件是：物点和像点之间所有光线的传播等光程。

完善成像的条件是苛刻的在实际工程中，满足等光程、满足完善成像条件是很困难的。

数学推导得出光学透镜表面是一个4次曲线方程，将该曲线绕光轴旋转得到卵形曲面。

它的加工是十分困难的。

在非完善成像的情况下，成像光束不再是同心光束，得到的像点为一个弥散斑。

实际的光学系统的透镜大多是由球面构成非球面光学加工的复杂性和高难度，相对来说，球面的加工则容易得多，所以，一般光学系统都用球面来代替非球面，只有在特殊要求的情况下，才采用非球面。

采用非球面的情况：⑴航天领域⑵高科技领域⑶能够采用模压镜片的场合（批量生产）v 与近轴区成像比较必然在成像位置和像的大小方面存在一定的差异，被称为像差。

应用光学：第八章光学系统的像质评价和像差

1、光学系统成像：
n
-u A
n’
umax’
A’
2、衍射成像：
通常把实际光学系统与理想光学系统的衍射分辨率的差作为评价实际光学系统成像质量的指标。
如果用望远镜观察到在视场中靠得很近的四颗星星恰能被分辨。
若将该望远镜的物镜孔径限制得更小，则可能分辨不出这是四颗星星。
3、理想光学系统的衍射分辨率公式：
M+
B
Z B
B
M-
-K’T
B’t
B’T -δL’
-（ XT’- xt’) -xt’
-XT’
XT’称为子午场曲， KT’称为子午彗差， xt’称为细光束子午场曲， δLT’＝XT’- xt’为宽光束和细光束子午场曲之差，与轴上点球差类似，也称为轴外子午球差。
2、弧矢像差
M+
B
B
B
Z
M-
-K’S
B’s
2. 影响
• 由于象散的存在，使得轴外视场的象质显著下降，即使光圈开得很小，在子午和弧矢方向均无法同时获得非常清晰的影象。
• 象散的大小仅与视场角有关，而与孔径大小无关。因此，在广角镜头中象散就比较明显，在拍摄时应尽量使被摄体处于画面的中心。
3. 校正方法
• 正负透镜象散相反，胶合后可消除；
4.当光学系统是小视场，由于像高本身较小，慧差很小，用慧差的绝对值不足以说明系统的慧差特征，此时用慧差与像高的比值来描写这种像差，故慧差变成了正弦差，此时初级慧差和初级正弦差之间的关系为：
SC
'
lim
K
' s
y'0 y '
正弦差计算式：
物体无限远时：

光学系统像质评价 [自动保存]

xts xt xs
细光束像散曲线
轴外像点的单色像差
实际光学系统所成的像即使子午像差和弧矢像差都为零，但对应的像高并不一定和理想像高一致，这种像对物的变形像差称为畸变。
' ' ' ' ' ' Ao Bp ( yz ) 是光束的实际像高，Ao Bo ( yo ) 是理想像高，两者之差即为畸变
光学传递函数的评价方法
• 用MTF曲线评价成像质量（所有频率） • 用特征频率传递函数值评价光学系统的质量（根据光学系统使用目的）
• 用MTF阈值进行成像质量评价（分辨率）
• 用MTF曲线的积分值来评价成像质量（中心点亮度） • 用MTF曲线族来进行成像质量评价（焦深）
光学特性参数
孔径光阑或入瞳位置
它是限制轴上物点成像光束立体角（锥角）的光阑
入瞳的位置用从第一面顶点到入瞳面的距离lz表示，符号规则同样是向右为正，向左为负
光学特性参数
渐晕
由于轴外点成像光束部分被遮挡，造成像的边缘部分亮度比像平面中心暗，这种现象叫渐晕。
入窗
入瞳
O
A1
A2
A3
像差
实际成像的典型表现是，一个物点发出的光束经光学系统后不能聚焦成一点而形成弥散斑，垂轴平面的物体也不可能成理想的垂轴平面像而发生像面弯曲，同时物体成像还会产生变形，此外，还有不同波长光源之间的成像差异。实际像与理想像的差异称为像差。像差包括：球差、彗差、像散、场曲、畸变和色差。其中，前五种是单色像差，色差分为垂轴色差和位置色光学特性
成像质量
焦距、物距、像距、放大率、入瞳位置、入瞳距离等
光学系统所包含的像应该足够清晰，并且物像相似，变形要小

光学系统的像质评价和像差公差

科技资讯科技资讯S I N &T NOLOGY I NFORM TI ON2008N O .12SC I ENCE &TEC HN OLO GY I NFO RM ATI O N学术论坛1瑞利判断和中心点亮度1.1瑞利判断定义：实际波面与参考球面波之间的最大波像差不超过4/λ时，此波面可看作是无缺陷的。

优点：便于实际应用缺点：不够严密。

适用范围：是一种较为严格的像质评价方法，适用于小像差光学系统。

1.2中心点亮度1)中心点亮度：光学系统存在像差时，其成像衍射斑的中心亮度和不存在像差时衍射斑的中心亮度之比S.D 来表示光学系统的成像质量。

2)斯托列尔准则：当S.D ≥0.8，认为光学系统的成像质量是完善的。

3)适用范围：是一种高质量的像质评价标准，适用于小像差光学系统。

4)缺点：计算相当复杂，很少作为计算评价方法使用。

2分辨率分辨率反映光学系统分辨物体细节的能力，是一个很重要的指标参数，故也可用分辨率作为光学系统的成像质量评价方法。

2.1分辨率基本公式根据衍射理论，光学系统的最小分辨角为Δθ：Δθ=1.22λ/D对不同类型的光学系统，可由上式得到不同的表示形式。

2.2缺点1)只适用于大像差光学系统；2)与实际情况存在差异；3)存在伪分辨现象.故用分辨率来评价光学系统的成像质量也不是一种严格而可靠的评价方法。

2.3优点其指标单一，便于测量，在光学系统像质检测中得到广泛应用。

3点列图3.1点列图定义在几何光学的成像过程中，由一点发出的许多条光线经光学系统成像后，由于像差的存在，使其与像面的交点不再集中于一点，而是形成一个分布在一定范围内的弥散图形，称为点列图。

3.2适用范围适用于大像差光学系统。

照相物镜的像质评价：利用集中30％以上的点或光线所构成的图形区域作为其实际有效的弥散斑，弥散斑直径的倒数为系统的分辨率。

3.3优缺点优点：简便易行，形象直观。

缺点：工作量非常大，只有利用计算机才能实现。

工程光学第六章像差理论重点讲解

校对公式：
h lu lu nuy nuy J
最后可计算出像点位置和系统各基点位置。
焦点位置及焦距计算：l1 , u1 0
f ' h1 / u'k
2、轴外物点近轴光线光路计算（第二近轴光线）
仍用近轴光线光路计算公式和校对公式,所有量均注以下标z.
已知：物方物位、入瞳位置和物高，即 l, lz , uz 。求解：像方物位、出瞳位置和像高，即 l, lz , uz 。
i
l
r
r
u（当l1
时， u1
0，i1
h1
/
r1）
i' n i
n'
u' u i i'
l' r(1 i' )
u'
l' n'lr
n'l n(l r)
第二节光线的光路计算
对于有k个面的折射系统，需利用根据过渡公式：
过渡公式：
lk lk1 dk 1 uk uk 1 nk nk 1
对于小视场的光学系统，例如望远物镜和显微物镜等，只要求校正与孔径有关的像差，所以只需计算上述第一种光线。对大孔径、大视场的光学系统，如照相物镜等，要求校正所有像差，所以需要计算上述三种光线。
第二节光线的光路计算
由已知条件：
光学系统的结构参数（r,d,n）
物体的位置和大小入瞳的位置和大小
解决问题：
第一节概述
像差校正：
在实际光学系统中，各种像差是同时存在的，像差影响光学系统成像的清晰度、相似性和色彩逼真度等，就降低了成像质量。故像差的大小反映了光学系统质量的优劣。
除了平面镜成像以外，没有像差的光学系统是不存在的。完全消除像、色差是不可能的，针对光学系统的不同用途，只要把像、色差降低在某范围内，使光接收器不能分辨，或者说这种差别只要能骗过光接收器，就可以认为是理想的。

【像差与像质评价】

niL sin U sin I - sin I ' sin I ' - sin U S- 1 1 1 cos I - U cos I ' U cos I I ' 2 2 2
球差对成像质量的影响
球差使像点成为弥散斑，影响成像质量。孔径越大，球差越大，弥散斑越大，像越模糊
2
图6-6 齐明透镜
2 n2 / n3 n 2 1 2 n
由这样两个齐明面组成的透镜叫做齐明透镜
球差的校正
1、正、负透镜组合球差是折射球面的固有像差，单个表面无法校正球差 • 单正透镜产生负球差； • 单负透镜产生正球差。
2、选择高折射率的材料。保证光焦度不变时，提高透镜的折射率能增大球面曲率半径，减小球差。
§6-2 球差
• 球面像差的简称，轴上点唯一的单色像差
轴上点发出的同心光束经光学系统各个球面折射后，不再为同心光束。与光轴成不同孔径角U，或离光轴不同高度h的光线交光轴于不同的位置上，相对于由近铀
光线决定的理想像点有不同偏离。
hmax
-Umax
A
-U
h
A’ L’
A０’
△y’
－δL’
l’
δL’
＝L’ －l’
Y'
y'
此为满足等晕条件的系统。
1 n sin U L' -1 ' ' n' sin U ' L - lz
若系统不满足等晕条件，
不成立
其两端偏差用OSC’表示，即是正弦差。物体在有限远时，其正弦差为
n sin U L' OSC ' - ' ' -1 ' n sin U L - lz

像差理论与像质评价

物、象点与球面中心重合；
LLr
3） siIn siU n 0
I U
siIn nsiIn nLrsiU n
n
n r
L nn r n
siIn nsiIn nLrsiU n
n
nr
L nnr n
不晕透镜（齐明透镜）：两面均满足不晕条件
不晕点
例：设计一齐明透镜，第一面曲率半径r1=-95mm，物点位于第一面曲率中心，第二面满足齐明条件。若该透镜厚度d=5mm，折射率n=1.5，该透镜在空气中，求：
二、场曲（像面弯曲） curvature
1. 轴上点通过光学系统不存在象散。
某一视场的子午象点、弧矢象点相对于高斯象面的距离xt′和xs′分别称为子午象面弯曲和弧矢象面弯曲，简称子午场曲和弧矢场曲。
x t x s
lt l ls l
象散和场曲的关系为: xts xtxs
2. 象散和场曲的关系：
L nn r n
L nnr n
§ 6－3 象散和像面弯曲
一、象散 astigmatism
1. 轴外点无限细光束通过光学系统时，无彗差。有象散、场曲。
Bt′— 轴外点B的子午像 Bs′— 轴外点B的弧矢像
沿主光线方向的距离Bt′Bs′是光学系统的象散。在光学设计中一般以在光轴上的投影来量度光学系统的象散值，以xts′表示。
不再是常数。
B0′
A
YzYzy
A′
2. 畸变的影响：
B
畸变与所有的其它像差不同，它仅由主光线的光路决定，仅引起像的变形，使像对物产生失真，对成像的清晰度并无影响。
当孔阑位置移动，球差的影响，不同视场的主光线与高斯像面交点高度不等于理想像高,其差别就是系统的畸变

第八章光学系统的像质评价和像差公式

第八章光学系统的像质评价和像差公式光学系统的像质评价和像差公式是研究光学系统成像质量的重要工具。

光学系统的像质评价主要通过像差公式来描述光学系统成像的误差，从而提供了评价光学系统成像质量的定量指标。

光学系统的像质评价可以从图像质量和像差两个方面进行。

图像质量是指图像的清晰度、对比度、分辨率等方面，是反映图像信息传递能力的指标。

而像差是指由于光学系统的结构、材料、制造等因素造成的光线偏差，导致图像不完美的情况。

像质评价的目标是通过对图像质量和像差的分析，得到一个综合的定量指标，从而评估光学系统的成像质量。

像差公式是描述光学系统成像误差的数学关系。

常见的像差公式有球差公式、彗差公式、像散公式、畸变公式等。

这些公式通过数学表达了光线经过光学系统后的成像位置与理想位置之间的差异，即描述了光学系统的误差情况。

这些公式的推导通常是基于几何光学的假设和光线传播的物理原理，可以对光线的传播路径进行建模和分析。

光学系统的像差公式一般可表示为：Δx=AΔy+B(Δy)²+C(Δρ)²+D(Δy)³+E(Δy)(Δρ)²+F(Δρ)³+...其中Δx是成像位置的偏差，Δy是入射光线的高度偏差，Δρ是入射光线的径向偏差。

A、B、C、D、E、F等系数则表示了不同像差的贡献程度。

不同的像差对成像质量的影响各不相同，有的像差会导致图像模糊、失真，有的像差会限制系统的分辨率等。

通过分析像差公式，可以得到不同像差与光学系统参数的关系。

这使得我们能够通过调整光学系统的设计参数来减小或消除像差，提高光学系统的成像质量。

例如，如果发现球差对成像质量的影响较大，可以通过改变光学系统的球面曲率来减小球差；如果发现像散对成像质量的影响较大，可以通过引入非球面透镜来减小像散。

像差公式为光学系统的设计和优化提供了理论基础和指导。

总结起来，光学系统的像质评价和像差公式是研究光学系统成像质量的重要工具。

第六章光学系统的像差

第五节像面畸变
• 畸变的定义 • 畸变的形成 • 畸变的度量 • 畸变的影响 • 畸变的校正
畸变的定义
• 理想光学系统物像共轭面上的垂轴放大率为常数，所以像与物相似
• 实际光学系统的一对共轭面上的放大率并不是常数，随视场的增大而变化
• 像对于物的变形像差称为畸变
畸变的形成
• 见附图
畸变的度量
L'FC L'F L'C • 近轴区域的位置色差 l'FC l'F l'C
• 特别指出，以复色光成像的物体即使在近轴区域也存在色差
位置色差的形成
• 见附图
色差曲线
h hm 1 0.85 D C 0.707
0.5
F L'FCD
0.3
-0.1 0 0.1 0.2 0.3 L' b)
• 平面物体成弯曲像面的成像缺陷称为场曲像差
场曲的形成
• 见附图
场曲的度量
子午场曲 xt ' lt 'l'
子午场曲
弧矢场曲 xs ' ls 'l'
场曲曲线
t' s' p
y / ym
p s' t'
y / ym
O x't , x's
O x't , x's
场曲的影响
场曲的校正
• 正负透镜组合 • 厚透镜
参知政事范仲淹等人遭谗离职，欧阳修上书替他们分辩，被贬到滁州做了两年知州。到任以后，他内心抑郁，但还能发挥“宽简而不扰”的作风，取得了某些政绩。《醉翁亭记》就是在这个时期写就的。目标导学二：朗读文章，通文顺字1．初读文章，结合工具书梳理文章字词。2．朗读文章，划分文章节奏，标出节奏划分有疑难的语句。节奏划分示例

第8章光学系统成像质量评价

2
实际上，实际上，绝大多数光学系统以白光或复色光成白光是由不同波长的单色光所组成的，像。白光是由不同波长的单色光所组成的，它们对于光学介质具有不同的折射率，因而白光进入光学于光学介质具有不同的折射率，系统后就会因色散而有不同的传播光路，形成了复系统后就会因色散而有不同的传播光路，形成了复色像差。色像差。这种由不同色光的光路差别引起的像差称为色差。色差有两种，位置色差和倍率色差。为色差。色差有两种，位置色差和倍率色差。白光经光学系统后，由于各种单色光有各自的白光经光学系统后，单色像差，可见白光成像是很复杂的。单色像差，可见白光成像是很复杂的。为了便于对像差的分析，才将白光的像差分成单色像差和色差。像差的分析，才将白光的像差分成单色像差和色差。其中，其中，单色像差是对光能接收器最为灵敏的色光而言的，言的，而色差是对光能接收器的有效波段内两种边缘色光而言的。所谓消像差，缘色光而言的。所谓消像差，也只是消这种色光的单色像差和这两种色光的色差。单色像差和这两种色光的色差。
11
图a
图b
图8－4 －
12
如图8-5，点发出的近轴光线的高斯像点A 的截距l’；如图，从A点发出的近轴光线的高斯像点 0'的截距；点发出的近轴光线的高斯像点的截距孔径角入射光线的共扼光线与光轴交A 点以U1孔径角入射光线的共扼光线与光轴交 1'点，截距为 L1'；以U2孔径角入射光线的共扼光线与光轴交 2'点，孔径角入射光线的共扼光线与光轴交A 点；截距为L2'。A点发出的同心光束不交在同一点。如在像截距为。点发出的同心光束不交在同一点。点发出的同心光束不交在同一点方不论在A 或或处放置光屏都将看到一个弥散斑处放置光屏都将看到一个弥散斑。方不论在 0'或A2'或A1'处放置光屏都将看到一个弥散斑。这是一种球面固有特性而引起的成像缺陷。这是一种球面固有特性而引起的成像缺陷。

第六、八章 光学系统的像差理论和像质评价 2012

第六章像差与成像质量评价

光学系统的像差

第八章 光学系统的像质评价分解

光学系统成像质量评价

第八章 光学系统的像质评价和像差公差

光学系统的像差理论和像质评价

应用光学第八章 光学系统成像质量评价

像差理论与像质评价

第八章光学系统的像质评价和像差公差

第6章 像差与成像质量评价(修改)

应用光学：第八章 光学系统的像质评价 和像差

光学系统像质评价 [自动保存]

光学系统的像质评价和像差公差

工程光学第六章像差理论重点讲解

【像差与像质评价】

像差理论与像质评价

第八章光学系统的像质评价和像差公式

第六章 光学系统的像差

第8章 光学系统成像质量评价

第六、八章光学系统的像差理论和像质评价 2012

第八章光学系统的像质评价分解

第八章光学系统的像质评价和像差公差

应用光学第八章光学系统成像质量评价

第6章像差与成像质量评价(修改)

应用光学：第八章光学系统的像质评价和像差

第六章光学系统的像差

第8章光学系统成像质量评价