第二学期慈溪市七年级数学竞赛模拟试题
数学竞赛试题初一及答案

数学竞赛试题初一及答案一、选择题(每题2分,共10分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 22. 如果a和b是两个非零实数,且a+b=5,那么a-b的最大值是多少?A. 5B. 4C. 3D. 23. 一个数的平方根是它本身,这个数可能是:A. 0B. 1C. -1D. 44. 下列哪个选项是4的倍数?A. 7B. 8C. 9D. 105. 如果一个三角形的内角和为180°,那么一个四边形的内角和是多少度?A. 360°B. 540°C. 720°D. 900°二、填空题(每题2分,共10分)6. 一个数的绝对值是它与____的距离。
7. 圆的周长公式是C=__。
8. 如果一个数的立方等于它本身,那么这个数可能是____。
9. 一个直角三角形的两条直角边分别为3和4,那么它的斜边长是____。
10. 一个数的倒数是1/这个数,那么1的倒数是____。
三、简答题(每题5分,共15分)11. 解释什么是有理数,并给出两个有理数的例子。
12. 什么是质数?请列出前5个质数。
13. 描述如何使用勾股定理来计算直角三角形的斜边长度。
四、计算题(每题10分,共20分)14. 计算下列表达式的值:(2+3)×(2-3)。
15. 解下列方程:2x + 5 = 13。
五、解答题(每题15分,共30分)16. 一个长方形的长是15厘米,宽是10厘米,求它的周长和面积。
17. 一个班级有40名学生,其中1/4是男生,1/3是女生,剩余的是教师。
求男生、女生和教师的人数。
答案:一、选择题1. B2. A3. A4. B5. A二、填空题6. 07. 2πr(或πd,d为直径)8. 0, ±19. 5 10. 1三、简答题11. 有理数是可以表示为两个整数的比的数,例如1/2和3。
12. 质数是大于1的自然数,且除了1和它本身外,不能被其他自然数整除的数。
慈溪七年级下册试卷数学

一、选择题(每题3分,共30分)1. 若a > 0,b < 0,则下列不等式中正确的是()A. a + b > 0B. a - b < 0C. -a < -bD. ab > 02. 若x^2 - 4x + 3 = 0,则x的值为()A. 1 或 3B. -1 或 3C. 1 或 -3D. -1 或 -33. 在直角坐标系中,点A(2,3),点B(-1,-2),则线段AB的中点坐标为()A. (1,1)B. (1,2)C. (2,1)D. (2,2)4. 若一个数的平方根是3,则这个数是()A. 9B. 3C. -9D. -35. 下列函数中,是反比例函数的是()A. y = x^2B. y = 2xC. y = 1/xD. y = 3x + 16. 在△ABC中,若∠A = 60°,∠B = 45°,则∠C的度数是()A. 75°B. 120°C. 135°D. 150°7. 若x + y = 5,x - y = 1,则x的值为()A. 3B. 2C. 4D. 68. 若a > b,下列不等式中正确的是()A. a^2 > b^2B. a^2 < b^2C. a^3 > b^3D. a^3 < b^39. 在平面直角坐标系中,点P(3,4),点Q(-2,-1),则线段PQ的长度是()A. 5B. 6C. 7D. 810. 若x^2 + 2x - 3 = 0,则x的值为()A. 1 或 -3B. 1 或 3C. -1 或 -3D. -1 或 3二、填空题(每题3分,共30分)11. 若a + b = 5,a - b = 1,则ab的值为__________。
12. 在△ABC中,若∠A = 2∠B,∠C = 60°,则∠B的度数是__________。
13. 若一个数的平方根是2,则这个数的立方根是__________。
七年级下册数学慈溪试卷

一、选择题(每题3分,共30分)1. 下列各数中,有理数是()A. √-1B. √3C. πD. 0.1010010001……2. 下列运算正确的是()A. (-3)² = 9B. (-2)³ = -8C. (-5)⁰ = 0D. (-4)⁻² = 163. 如果a < b,那么下列不等式中正确的是()A. a + 2 < b + 2B. a - 2 > b - 2C. 2a < 2bD. 2a > 2b4. 下列函数中,是反比例函数的是()A. y = 2x + 1B. y = 3/xC. y = x² - 4D. y = x³ + 25. 在直角坐标系中,点A(-2,3)关于原点对称的点是()A.(2,-3)B.(-2,-3)C.(3,-2)D.(-3,2)6. 如果等腰三角形底边长为6,腰长为8,那么它的面积是()A. 18B. 24C. 36D. 487. 下列各式中,不是分式的是()A. 1/xB. x²/2xC. x + 1/xD. 2x - 38. 下列各组数中,存在有理数k使得a² + b² = k²的是()A. a = 2,b = 3B. a = 5,b = -12C. a = -4,b = 5D. a = 0,b = 09. 如果a、b是方程x² - 5x + 6 = 0的两个根,那么a + b的值是()A. 5B. 6C. 7D. 810. 下列图形中,是平行四边形的是()A. 矩形B. 菱形C. 等腰梯形D. 等边三角形二、填空题(每题3分,共30分)11. (1)如果a = -3,那么a² + a的值是______。
12. (2)函数y = 2x - 1的图像是一条______。
13. (3)等腰直角三角形的两个锐角是______。
慈溪七年级初中数学试卷

一、选择题(每题3分,共30分)1. 下列各数中,不是有理数的是()A. 3.14B. -5C. √2D. 0.52. 如果a < b,那么下列不等式中正确的是()A. a - 2 < b - 2B. a + 2 > b + 2C. 2a < 2bD. 2a > 2b3. 下列各数中,是正数的是()A. -1B. 0C. 1/2D. -1/24. 下列各数中,绝对值最大的是()A. -3B. 2C. -2D. 35. 下列各数中,不是整数的是()A. 2B. -5C. 1/2D. 06. 下列各数中,是质数的是()A. 4B. 9C. 11D. 157. 如果一个数的平方是25,那么这个数是()A. 5B. -5C. ±5D. 08. 下列各数中,是偶数的是()A. 2B. 3C. 4D. 59. 下列各数中,不是正比例函数图象的是()A. y = 2xB. y = -3xC. y = 5/xD. y = x^210. 下列各图形中,不是轴对称图形的是()A. 正方形B. 等边三角形C. 平行四边形D. 矩形二、填空题(每题3分,共30分)11. √9的值是__________。
12. 3/4与5/6的最小公倍数是__________。
13. 如果a = 2,那么a + 2的值是__________。
14. 下列各数中,是负数的是__________。
15. 如果一个数的倒数是1/5,那么这个数是__________。
16. 下列各数中,是质数的是__________。
17. 如果一个数的平方是49,那么这个数是__________。
18. 下列各数中,是奇数的是__________。
19. 下列各数中,不是正比例函数图象的是__________。
20. 下列各图形中,不是轴对称图形的是__________。
三、解答题(每题10分,共40分)21. 解方程:2x - 3 = 7。
七年级第二学期数学竞赛试题及参考答案
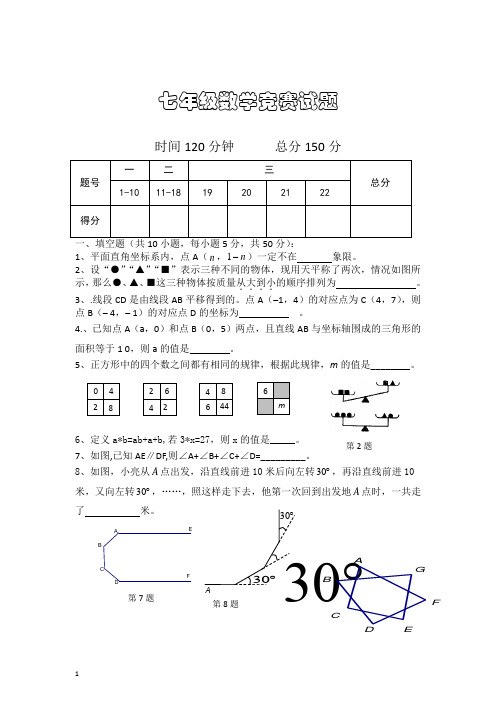
七年级数学竞赛试题时间120分钟 总分150分1、平面直角坐标系内,点A (n ,n -1)一定不在 象限。
2、设“●”“▲”“■”表示三种不同的物体,现用天平称了两次,情况如图所示,那么●、▲、■这三种物体按质量从大到小....的顺序排列为 。
3、.线段CD 是由线段AB 平移得到的。
点A (–1,4)的对应点为C (4,7),则点B (– 4,– 1)的对应点D 的坐标为 。
4.、已知点A (a ,0)和点B (0,5)两点,且直线AB 与坐标轴围成的三角形的面积等于1 0,则a 的值是 。
5、正方形中的四个数之间都有相同的规律,根据此规律,m 的值是_____ 。
6、定义a*b=ab+a+b,若3*x=27,则x 的值是_____。
7、如图,已知AE ∥DF,则∠A+∠B+∠C+∠D=_________。
8、如图,小亮从A 点出发,沿直线前进10米后向左转30︒,再沿直线前进10米,又向左转30︒,……,照这样走下去,他第一次回到出发地A 点时,一共走了 米。
0 2 8 4 2 4 6 2 4 6 8 44 A30︒30︒30︒第8题第2题FEDCBA 第7题ABCDEFG9、方程组12,6x y x y ⎧+=⎪⎨+=⎪⎩的解是________________ 。
10、如上图所示,∠A +∠B +∠C +∠D +∠E +∠F +∠G = _____________度。
二、选择题((共8小题,每小题5分,共40分):11、若点A(m,n)在第二象限,那么点B(-m,│n│)在( ) A 、 第一象限 B 、第二象限 C 、第三象限 D 、第四象限 12、已知关于x 的方程01)2(=-+x b a 无解,那么b a 的值是:A 、负数B 、正数C 、非负数D 、非正数13、当x=-2时, 37ax bx +-的值为9,则当x=2时,37ax bx +-的值是( )A 、-23B 、-17C 、23D 、1714、设△ABC 的三边长分别为a ,b ,c , 其中a ,b 满足0)4(|6|2=+-+-+b a b a , 则第三边c 的长度取值范围是( )A 、3<c<5B 、2<c<4C 、4<c<6D 、5<c<615、 某种商品若按标价的八折出售,可获利20%,若按原价出售,可获利( ) A 、25% B 、40% C 、50% D 、66.7%16、如图,有一块直角三角板XYZ 放置在△ABC 上,恰好三角板XYZ 的两条直角边XY 、XZ 分别经过点B ,C ,若∠A =40°,则∠ABX +∠ACX =( ) A 、25° B 、30° C 、45° D 、50°第16题17、如图△ABC 中已知D 、E 、F 分别为BC 、AD 、CE 的中点,且S △ABC =2Mcm ,则第17题S 阴影的值为:A 、2Mcm 61B 、2Mcm 51C 、2Mcm 41D 、2Mcm 3118、方程198919901989...433221=⨯++⨯+⨯+⨯x x x x 的解是( )A 、1989B 、1990C 、1991D 、1992三、解答题:(共5小题,共60分):19、(10分)已知方程组⎩⎨⎧=+=+4232y ax y x 的解,x 与y 之和为1,求a 的值20、(15分)如图:已知DEF ABC ∆∆与是一副三角板的拼图,在同一条线上D C E A ,,,. 求21∠∠与的度数21、(15分)如图所示,在△ABC 中,∠B=∠C ,∠A DE =∠AED ,︒=∠60BAD ,第23题F求∠EDC的度数;22.(20分)某校师生积极为汶川地震灾区捐款,在得知灾区急需帐篷后,立即到当地的一家帐篷厂采购,帐篷有两种规格:可供3人居住的小帐篷,价格为每顶160元,可供10人居住的大帐篷,价格为每顶400元,学校共花去捐款96000元,正好可供2300人临时居住。
初一数学竞赛测试题及答案

初一数学竞赛测试题及答案【测试题一】题目:计算下列表达式的值:\[ 2^3 + 3^2 - 4 \times 5 \]【答案】首先,按照运算顺序,先计算乘方和乘法,再计算加法和减法。
\[ 2^3 = 8 \]\[ 3^2 = 9 \]\[ 4 \times 5 = 20 \]然后进行加减运算:\[ 8 + 9 - 20 = 17 - 20 = -3 \]所以,表达式的值为 -3。
【测试题二】题目:如果一个数的平方等于这个数本身,这个数是什么?【答案】设这个数为 \( x \),根据题意,我们有:\[ x^2 = x \]这个方程可以重写为:\[ x^2 - x = 0 \]\[ x(x - 1) = 0 \]根据零乘律,\( x = 0 \) 或 \( x - 1 = 0 \),所以 \( x = 0 \) 或 \( x = 1 \)。
【测试题三】题目:一个长方体的长、宽、高分别是 8 厘米、6 厘米和 5 厘米,求这个长方体的体积。
【答案】长方体的体积可以通过长、宽、高的乘积来计算:\[ \text{体积} = 长 \times 宽 \times 高 \]\[ \text{体积} = 8 \times 6 \times 5 = 240 \text{ 立方厘米} \]【测试题四】题目:一个圆的半径是 7 厘米,求这个圆的周长和面积。
【答案】圆的周长公式是 \( C = 2\pi r \),面积公式是 \( A = \pi r^2 \)。
将半径 \( r = 7 \) 厘米代入公式中:\[ C = 2 \times \pi \times 7 \approx 44 \text{ 厘米} \]\[ A = \pi \times 7^2 \approx 153.94 \text{ 平方厘米} \]【测试题五】题目:一个班级有 40 名学生,其中 2/5 是男生,3/5 是女生。
如果班级里增加了 10 名男生,那么班级里男生和女生的比例是多少?【答案】首先,计算原有男生和女生的人数:男生:\( 40 \times \frac{2}{5} = 16 \) 人女生:\( 40 \times \frac{3}{5} = 24 \) 人增加 10 名男生后,男生总数变为 \( 16 + 10 = 26 \) 人,女生人数不变。
慈溪初中竞赛数学试卷

一、选择题(每题5分,共20分)1. 下列各数中,不是有理数的是()A. -3.14B. 0.1010010001…C. √9D. 2/32. 已知 a + b = 5,ab = 6,则a² + b² 的值为()A. 25B. 26C. 27D. 293. 在直角坐标系中,点P(2,3)关于原点对称的点的坐标是()A. (-2,-3)B. (2,-3)C. (-2,3)D. (3,-2)4. 下列命题中,正确的是()A. 平行四边形对边平行B. 矩形对角线相等C. 等腰三角形底角相等D. 所有三角形都是等边三角形5. 已知等差数列的前三项分别为2,5,8,则第10项为()A. 21B. 24C. 27D. 30二、填空题(每题5分,共20分)6. 若x² - 4x + 4 = 0,则 x 的值为______。
7. 若 a,b,c 成等比数列,且 a + b + c = 15,a² + b² + c² = 75,则 bc 的值为______。
8. 在等腰三角形ABC中,AB = AC,AD是BC边上的高,若∠BAC = 30°,则∠ADB的度数为______。
9. 已知函数 y = kx + b 的图象经过点(1,3),则 k 和 b 的值分别为______。
10. 在直角坐标系中,点P(-3,4)到原点的距离为______。
三、解答题(共60分)11. (10分)已知等差数列的前三项分别为3,5,7,求:(1)该数列的通项公式;(2)该数列的前n项和公式。
12. (15分)已知函数y = ax² + bx + c(a≠0)的图象经过点(1,3),且抛物线的顶点坐标为(2,-1)。
(1)求函数的解析式;(2)若抛物线与x轴的交点坐标为(-1,0)和(3,0),求a和b的值。
13. (15分)在等腰三角形ABC中,AB = AC,D是BC边上的高,且∠BAC = 40°。
初一数学竞赛测试题及答案

初一数学竞赛测试题及答案一、选择题(每题2分,共10分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 如果一个数的平方等于这个数本身,那么这个数可能是:A. 0B. 1C. -1D. 2答案:A、B3. 一个数的绝对值是它本身,这个数是:A. 正数B. 负数C. 零D. 正数或零答案:D4. 下列哪个分数是最简分数?A. 4/8B. 5/10C. 3/4D. 6/9答案:C5. 如果一个三角形的三个内角分别为x°,y°和z°,那么x+y+z的值是:A. 180°B. 360°C. 90°D. 270°答案:A二、填空题(每题3分,共15分)6. 一个数的平方根是它本身,这个数可以是______。
答案:0或17. 如果a和b是两个连续的自然数,且a>b,那么a-b的值是______。
答案:18. 一个数的立方等于它本身,这个数可能是______。
答案:1或-1或09. 如果一个数的相反数是它本身,那么这个数是______。
答案:010. 一个数的绝对值等于它本身,这个数是非负数,即这个数是______。
答案:正数或零三、计算题(每题5分,共20分)11. 计算下列各题:(1) (-3) × (-4) = ______。
答案:12(2) 5 - (-3) = ______。
答案:8(3) (-2)² = ______。
答案:4(4) √16 = ______。
答案:4四、解答题(每题10分,共30分)12. 一个直角三角形的两条直角边分别为3厘米和4厘米,求斜边的长度。
答案:根据勾股定理,斜边长度为√(3² + 4²) = √(9 + 16) = √25 = 5厘米。
13. 一个数列的前三项为1, 1, 2,从第四项开始,每一项都是前三项的和。
求第10项的值。
浙江省慈溪市区域性七年级数学竞赛试卷(含答案)浙教版

七年级(下)数学竞赛试题(5月13日下午1:00——3:00 满分120分 可使用函数型计算器) 一、选择题(每小题4分,共40分)1、如图,有三条公路,其中AC 与AB 垂直,小明和小亮分别从A 、B 两地沿AC 、BC 同时出发骑车到C 城,若他们同时到达,则下列判断中正确的是( )A 、小明骑车的速度快B 、小亮的骑车速度快C 、两人一样快D 、因为不知道公路的长度,所以无法判断他们速度的快慢2、把4本两两不同的书全部分给甲、乙两个人,且每人至少分到一本书,则所有不同的的分配方法有( )A 、10B 、12C 、14D 、16 3、设“●,▲,■”分别表示三种不同的物体,如下图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么“?”处应放“■”的个数为 ( )A 、 5B 、 4C 、3D 、 2 4、方程x +y +z =7的正整数解有( )A 、10组B 、12组C 、15组D 、16组5、有如下四个命题:①两个符号相反的分数之间至少有一个正整数; ②两个符号相反的分数之间至少有一个负整数; ③两个符号相反的分数之间至少有一个整数; ④两个符号相反的分数之间至少有一个有理数. 其中真命题的个数为( ) A 、1 B 、2 C 、3 D 、46、已知,,,a b c d 都是整数,x a b b c c d d a =-+-+-+-,那么( ) A 、x 一定是奇数 B 、x 一定是偶数 C 、仅当,,,a b c d 同奇或同偶时, x 是偶数 D 、x 的奇偶性不能确定7、如图,在ABC 中,已知AB=AC ,点D 、E 分别在AC 、AB 上,且BD=BC ,AD=DE=EB ,那么A ∠的度数是( )A 、30°B 、45°C 、35°D 、60°●● ▲■●■▲●▲?(1) (2)(3)学校 姓名 班级 学号----------------------------装--------------------------------------订--------------------------------线-----------------------------------------------CD图78、如图1,在ΔABC 中,AB=AC,∠ABC=40O ,BD 是∠ABC 的平分线,延长BD 至E,使DE=AD,则∠ECA 的度数为( )A 、30OB 、35OC 、40OD 、45O9、 架上有两套同样的教材,每套分上、下两册,在这四册教材中随机抽取两册,恰好组成一套教材的概率是( )A 、32 B 、31 C 、21 D 、6110、如图,“回”字形的道路宽为1米,整个“回”字形的长为8米,宽为7米,…个人从入口点A 沿着道路中央走到终点B ,他共走了( ).A 、55米B 、55.5米C 、56米D 、56.5米二、填空题(每小题4分,共40分)11、已知5,3a b ==,且a b <,则23a b -=12、等腰三角形的一个外角为100°,那么它的底角为 13、学校跑道最内侧由两个直径42米的半圆和直跑道组成,最内侧跑道一圈正好400米,每条跑道宽1.2米。
慈溪七年级试卷数学下册

一、选择题(每题4分,共40分)1. 下列各数中,有理数是()A. √16B. πC. 0.1010010001...D. √-92. 已知a、b是相反数,且a+b=0,那么a等于()A. 0B. 1C. -1D. 无法确定3. 下列各式中,正确的是()A. a^2 = aB. a^3 = aC. (a^2)^3 = a^6D. a^2 a^3 = a^54. 在下列各数中,正数是()A. -3B. 0C. 1/2D. -√25. 下列各对数中,互为倒数的是()A. 2和1/2B. 3和-1/3C. -4和4D. 0和1/06. 已知等腰三角形的底边长为8cm,腰长为10cm,那么这个三角形的面积是()A. 40cm^2B. 32cm^2C. 48cm^2D. 36cm^27. 若x=3,那么代数式2x^2-5x+2的值为()A. 5B. 7C. 11D. 138. 下列各图中,能组成三角形的是()A.B.C.D.9. 下列各式中,符合一元一次方程的是()A. 2x+5=0B. 2x^2+5=0C. 2x^3+5=0D. 2x^2-5x+6=010. 下列各数中,是正比例函数图象上的点的坐标是()A. (2, 4)B. (1, 3)C. (4, 2)D. (3, 1)二、填空题(每题4分,共40分)11. -3的相反数是__________,|-5|的值是__________。
12. 若a=-3,那么2a-5的值是__________。
13. 已知a^2=25,那么a的值是__________。
14. 下列各数中,有理数是__________,无理数是__________。
15. 在直角坐标系中,点P(-2, 3)关于y轴的对称点是__________。
16. 若一个数x满足方程2x-3=7,那么x的值是__________。
17. 等腰三角形的底边长为6cm,腰长为8cm,那么这个三角形的周长是__________cm。
慈溪七年级数学试卷

一、选择题(每题4分,共20分)1. 下列各数中,不是有理数的是()A. -2.5B. 0.333...C. √9D. π2. 下列各式中,正确的是()A. a² + b² = (a + b)²B. (a - b)² = a² - 2ab + b²C. (a + b)² = a² + 2ab + b²D. (a - b)² = a² + 2ab - b²3. 已知等腰三角形底边长为8cm,腰长为10cm,则该三角形的周长是()A. 16cmB. 24cmC. 32cmD. 40cm4. 下列函数中,是反比例函数的是()A. y = 2x + 3B. y = 3/xC. y = x²D. y = √x5. 下列各数中,是正数的是()A. -3/2B. -1.5C. 0D. 3/2二、填空题(每题4分,共20分)6. 已知x + 2 = 5,则x = ________。
7. 若 (a - b)² = 9,且a > b,则a + b = ________。
8. 等腰三角形的底边长为10cm,腰长为8cm,则该三角形的面积是________ cm²。
9. 函数y = 3x - 2的图像是一条直线,其斜率是 ________。
10. 已知数列1, 3, 5, 7, ...的通项公式是 ________。
三、解答题(共60分)11. (12分)解下列方程:(1)2(x - 3) = 5x + 1(2)(x + 2)(x - 5) = 012. (12分)已知一元二次方程x² - 4x + 3 = 0,求:(1)该方程的解(2)该方程的判别式13. (12分)已知等腰三角形底边长为12cm,腰长为10cm,求:(1)该三角形的面积(2)该三角形的高14. (12分)函数y = kx + b的图像经过点(2,3)和(-1,-1),求:(1)该函数的解析式(2)该函数的图像与x轴的交点坐标15. (12分)已知数列1, 4, 7, 10, ...的通项公式是an = 3n - 2,求:(1)该数列的第10项(2)该数列的前10项和答案:一、选择题1. D2. C3. B4. B5. D二、填空题6. 37. 38. 489. 310. 3n - 2三、解答题11. (1)x = 7/3(2)x = 5 或 x = -512. (1)x = 1 或 x = 3(2)判别式 = 16 - 12 = 4 13. (1)面积= 60cm²(2)高 = 6cm14. (1)y = 2x - 1(2)交点坐标为(1/2,0)15. (1)第10项 = 28(2)前10项和 = 155。
慈溪七年级试卷数学答案

一、选择题1. 下列各数中,有理数是()A. √2B. πC. -3/5D. √-1答案:C解析:有理数是可以表示为两个整数之比的数,即形如a/b(a和b都是整数,且b不为0)的数。
在给出的选项中,只有-3/5是两个整数之比,因此是有理数。
2. 下列等式中,正确的是()A. 2^3 = 8B. 3^2 = 9C. (-2)^3 = -8D. 4^2 = 16答案:C解析:根据幂的定义,一个数的n次幂是指这个数连乘n次。
选项A、B、D都是正确的幂运算结果,但题目要求选择正确的等式,因此正确答案是C。
3. 在下列图形中,不是平行四边形的是()A. 正方形B. 矩形C. 菱形D. 三角形答案:D解析:平行四边形是指对边平行且相等的四边形。
在给出的选项中,正方形、矩形、菱形都满足这个条件,而三角形不满足,因此正确答案是D。
4. 下列函数中,是反比例函数的是()A. y = 2x + 3B. y = x^2C. y = k/x (k≠0)D. y = 3x答案:C解析:反比例函数是指函数的图像为双曲线,且满足y=k/x(k为常数,k≠0)的关系。
在给出的选项中,只有C满足这个条件,因此正确答案是C。
5. 下列数中,不是实数的是()A. -3.14B. √9C. πD. -√16答案:C解析:实数包括有理数和无理数。
有理数是可以表示为两个整数之比的数,无理数是不能表示为两个整数之比的数。
在给出的选项中,-3.14、√9、-√16都是有理数,而π是无理数,因此正确答案是C。
二、填空题1. 若a > 0,则a的平方根是()答案:√a解析:平方根是指一个数的平方等于另一个数,即x^2 = a,则x是a的平方根。
因为a > 0,所以a的平方根是√a。
2. 下列函数中,y=3x是一次函数的是()答案:y=3x解析:一次函数是指函数的最高次数为1的多项式函数,即y=ax+b(a和b是常数,且a≠0)。
在给出的选项中,只有y=3x满足这个条件。
慈溪初中数学竞赛试卷

一、选择题(每题4分,共40分)1. 若实数a、b满足a²+b²=1,则a+b的取值范围是()A. [-√2, √2]B. [-1, 1]C. [-√2, √2]D. [-1, 1]2. 若方程x²-4x+3=0的两根为m和n,则m+n和mn的值分别是()A. 4,3B. 4,-3C. -4,3D. -4,-33. 在等腰三角形ABC中,底边BC=6,腰AB=AC=8,则顶角A的度数是()A. 36°B. 45°C. 60°D. 90°4. 若函数f(x)=ax²+bx+c的图像与x轴交于点(1,0),(-1,0),则a、b、c 的值分别是()A. 1,-2,0B. 1,2,0C. -1,-2,0D. -1,2,05. 若一个正方体的体积为64立方厘米,则其表面积是()A. 96平方厘米B. 128平方厘米C. 256平方厘米D. 512平方厘米6. 在直角坐标系中,点A(-2,3),点B(4,1),则线段AB的中点坐标是()A. (1, 2)B. (1, 3)C. (2, 1)D. (2, 2)7. 若等比数列{an}的第一项a₁=3,公比q=2,则第10项a₁₀是()A. 48B. 96C. 192D. 3848. 若方程x²-3x+2=0的根为实数a和b,则a²+b²的值是()A. 4B. 6C. 9D. 129. 在梯形ABCD中,AD∥BC,AD=4,BC=6,AB=CD=5,则梯形的高是()A. 2B. 3C. 4D. 510. 若等差数列{an}的第一项a₁=2,公差d=3,则第n项an的值是()A. 3nB. 3n-1C. 3n+1D. 3n-2二、填空题(每题4分,共20分)11. 若等差数列{an}的第一项a₁=1,公差d=2,则第10项a₁₀的值是______。
12. 若方程x²-6x+9=0的两根为a和b,则a²+b²的值是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011学年第二学期七年级数学竞赛试题考试时间:120分钟,满分120分一、选择题(每小题4分,共24分)1.设a 是无理数,且a ,b 满足01=+--b a ab ,则b 是一个( )(A )小于0的有理数(B )大于0的有理数(C )小于0的无理数(D )大于0的无理数 2.三角形三条边的长a ,b ,c 都是质数,且16=++c b a ,则这个三角形是( ) (A )直角三角形(B )等腰三角形(C )等边三角形(D )直角三角形或等腰三角形 3.现有8根木棒,它们分别是1,2,3,4,5,6,7,8,若从8根木棒中抽取3根拼三角形,要求三角形的最长边为8,另两边之差大于2(以上单位:厘米),那么可以拼成不同三角形的种数为( )(A )2种(B )3种(C )4种(D )5种4.如图,长方形内有两个相邻的正方形,面积分别为2和8,图中阴影部分的面积为( ) (A )1(B )2(C )3(D )45.有一个正方体A ,B,C 的对面分别是z y x ,,三个字母,如图所示,将这个正方体从现有位置依此翻到第1,2,……,12格,这时顶上的字母是( ). (A )x (B )y (C )z (D )A6.我市某区在中心广场要建造一个花圃,花圃分为4个部分(如图),现要求同一个区域内种同一种颜色的花,要求相邻部分不能栽种相同颜色的花,则不同的栽种方法共有( )种(花的颜色共4种). (A )81(B )82(C )83(D )84 二、填空题(每小题5分,共50分)第4题第5题第6题7.已知012=-+a a ,则2011223++a a =.8.甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需325元,若购甲4件,乙10件,丙1件共需410元,那么购甲、乙、丙各1件共需________元.9.已知0,0,aa b><化简=---+-22)4()1(a b b a ___________. 10.已知2a +2b +ab =32,且a +b +3ab =-21,那么a +b +ab 的值为__________.11.如图所示的方格纸中,点A 、B 、C 都是格点(小正方形的顶点),则∠BAC 与∠BCA 度数的和为.12.ABC ∆中,,,900α=∠=∠A ACB 以C 为中心将ABC ∆旋转θ角到C B A 11∆(旋转过程中保持ABC ∆的形状大小不变)B 点恰落在11B A 上,如图,则旋转角θ的大小 为_________.13.在近似计算中,有效数字的个数可以用来衡量近似数的近似程度,使计算简化.但稍一不慎,它也会给我们带来麻烦。
如2100=1267650600228229401496703205376,某次计算中,出现(2100+1010)-2100=0.请指出这次近似计算时取的有效数字的个数最多是. 14.小明某天登录到某中学数学网站,他在首页看到了一个“您是通过什么方式知道网站的”小调查,查看了投票结果,发现投票总人数是800,其中“数学游戏”项的投票占68%,当天他再次登录该网站时,发现“数学游戏”项的投票率上升到72%,则此时投票总人数至少为__________人.15.一辆自行车,前胎行驶5000km 就不能继续使用,后胎行驶3000km 就不能继续使用,若在行驶中合理交换前后胎,则最多可以行驶__________km .第11题第12题θαB 1A 1CB A16.所谓机器洗牌,是将一副扑克牌按一定次序重新排列,即将第一张牌放到第1k 张牌的位置,将第二张牌放到第2k 张牌的位置,将第三张牌放到第3k 张牌的位置,……,等等.设按原先点数的顺序排列的13张红心同色纸牌(正面朝上): A ,2,3,4,5,6,7,8,9,10,J ,Q ,K 经第一次洗牌后,牌的顺序变为3,8,K ,A ,4,10,Q ,J ,5,7,6,2,9 则再经过两次同样方式的洗牌后,牌的顺序应该是.三、解答题(第17题10分、第18、19、20题各12分,共46分)17.已知a ,b ,c 为实数且多项式c bx ax x +++23能被432-+x x 整除. (1)求c a +4的值; (2)求c b a --22的值.18.某租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A 、B 两地收割小麦,其中30台派往A 地,20台派往B 地.两地区与该租赁公司商定的每天的租赁价格如下:(1)设派往A 地x 台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y (元),请用x 表示y ,并注明x 的范围.(2)若使租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案写出.19.有三张点数不同的扑克牌,随意分给甲、乙、丙每人一张,然后收起来洗牌之后再分给他们,这样分了n 次之后,三人累计的点数:甲为16,乙为11,丙为24,已知甲第一次得到的牌是其中点数最大的一张,求这三张牌的点数各是多少?(说明:扑克牌的点数与牌面上的数字相同,对于“A ”、“K ”、“Q ”、“J ”,它们的点数分别是l ,13,12,11)20.如图,已知在△ABC 中,∠BAC 为直角,AB=AC ,D 为AC 上一点,CE ⊥BD 于E . (1)“若BD 平分∠ABC ,则CE=12BD ”,说明这一结论成立的理由;(2)若D 为AC 上一动点,∠AED 如何变化,若变化,求它的变化范围;若不变,求出它的度数,并说明理由.EDC B2011学年第二学期七年级数学竞赛参考答案及评分标准一、选择题(每小题4分,共24分)二、填空题(每小题5分,共50分)7. 2012 ; 8. 155 ; 9.-3 ;10.61; 11. 45°; 12.α2; 13. 20 ;14. 915 ; 15. 3750 ; 16.9,6,5,K ,3,Q ,8,10,A ,2,7,J ,4. 三、解答题(第17题10分、第18、19、20题各12分,共46分)17.已知a ,b ,c 为实数且多项式c bx ax x +++23能被432-+x x 整除. (1)求c a +4的值; (2)求c b a --22的值.解:(1)∵)1)(4(432-+=-+x x x x ,-----------------------------2分∴4+x ,1-x 能整除c bx ax x +++23把4-=x 代入得:041664=+-+-c b a ① 把1=x 代入得: 01=+++c b a ②②⨯4-①得:c a +4=12 ③-----------------------------6分(2)由③得:43c a -=④ 代入②得143-=++-c b c ,即c b 434--=⑤ ∴c b a --22=1423826=-++-c c c -----------------------------10分18.某租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地收割小麦,其中30台派往A地,20台派往B地.两地区与该租赁公司商定的每天的租赁价格如下:(1)设派往A地x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),请用x表示y,并注明x的范围.(2)若使租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案写出.解:(1)y=(30-x)×1800+(x-10)×1600+1600x+(30-x)×1200=200x+74000,------------5分10≤x≤30;-----------------------------7分(2)200x+74000≥79600,解得x≥28,-----------------------------9分三种方案,依次为x=28,29,30的情况①当x=28时,派往A地28台乙型联合收割机,那么派往B地2台乙,派往A地的2台甲型收割机,派往B地18台甲.②当x=29时,派往A地29台乙型联合收割机,那么派往B地1台乙,派往A地的1台甲型收割机,派往B地19台甲.③当x=30时,派往A地30台乙型联合收割机,那么派往B地0台乙,派往A地的0台甲型收割机,派往B地20台甲.-----------------------------12分19.有三张点数不同的扑克牌,随意分给甲、乙、丙每人一张,然后收起来洗牌之后再分给他们,这样分了n 次之后,三人累计的点数:甲为16,乙为11,丙为24,已知甲第一次得到的牌是其中点数最大的一张,求这三张牌的点数各是多少?(说明:扑克牌的点数与牌面上的数字相同,对于“A”、“K”、“Q”、“J”,它们的点数分别是l ,13,12,11)解:设三张牌点数分别为,,,113,a b c c b a ≤<<≤且则()16112451317n a b c ++=++==⨯3216,17,3a b c a b c n ++≥++=++==且则-----------------------------4分甲三次得的点数为232323,,,1617,a x x a x x a b c x x b c ++=<=+++<+则所以---------------6分再由c b ≠得,b x ≠2,b x ≠3,所以c x x ==32-----------------------------8分 由乙得,1y ,2y ,3y 及a y ≠1可得321y y y ++=11<16=c c a ++则推理可得b y y ==32,c y =1得到方程组⎪⎩⎪⎨⎧=+=+=+242112162a b b c c a -----------------------------10分解得 ⎪⎩⎪⎨⎧===3410c b a -----------------------------12分20.如图,已知在△ABC 中,∠BAC 为直角,AB=AC ,D 为AC 上一点,CE ⊥BD 于E . (1)“若BD 平分∠ABC ,则CE=12BD ”,说明这一结论成立的理由;(2)若D 为AC 上一动点,∠AED 如何变化,若变化,求它的变化范围;若不变,求出它的度数,并说明理由. 解:(1)延长BA 、CE 交于F∠BAC 为直角,CE ⊥BD 于E∠∴BAC=∠CAF ,∠ACF=∠DBA AB=AC ∴△ABD ≌△ACF∴BD=CF---------------------------------------------------4分 BD 平分∠ABC ,BE=BE ∴△FEB ≌△CEB∴CE=EF=21CF=21BD------------------------------------------6分(2)不变--------------------------------------------------------------7分 过A 作AG ⊥BE 于G ,作AH ⊥CF 于H在△ABG 与△ACH 中⎪⎩⎪⎨⎧∠=∠∠=∠=AHC AGB ACH ABD ACAB ∴△ABG ≌△ACH∴AG=AH-----------------------------------------------------------------10分在Rt △GAE 与Rt △AHE 中ED C BFGH⎩⎨⎧==AE AE AHAG ∴Rt △GAE ≌Rt △AHE∴∠AED= 45-------------------------------------------------------------------------12分第6题提示:如果1、4相同,则有4×3×3=36种方式;如果1、4不同,则有4×3×2×2=48种方式.那么加起来应该有84种方式. 第13题提示:2100=1267650600228229401496703205376 是一个31位数, l 010= l000 000 0000是一个11位数,由此可见这次近似计算时取的有效数字的个数最多是20. 第14题提示:800×(1-68%)=256人.从极端考虑,后来投票的人都投了“数学游戏”项,设再次登录该网站时“数学游戏”项的投票数为x 人,则x ÷(256+x )=72%,解得x ≈659. 投票总人数至少的人数为:256+659=915人 第15题提示:每只轮胎的磨损总量设为1,每行驶1km 前后胎的损耗度分别为50001,30001, 行驶xkm 后交换,继续行驶ykm 报废.⎪⎪⎩⎪⎪⎨⎧=+=+1500013000113000150001y x y x ,所以,3750=+y x km ∴最多可行驶3750km . 第16题提示: 洗牌的方式是: (1)→(4);(2)→(12);(3)→(1);(4)→(5);(5)→(9);(6)→(11);(7)→(10);(8)→(2);(9)→(13);(10)→(6);(11)→(8);(12)→(7);(13)→(3)。
