人教版八年级数学下册期末培优卷(一)(扫描版 有答案)
人教版八年级下册数学期末培优检测试题(一)含答案.docx

期末培优检测试题(一)1. 根据下列表述,能确定具体目标位置的是(2. 李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量 是()116.64金额18数量升6.48单价/元A.金额B.数量C.单价D.金额和数量3. 要使四边形,8必是平行四边形,则匕4: /B : ZC : NZ?可能为()A. 2: 3: 6: 7B. 3: 4: 5: 6C. 3: 3: 5: 5D. 4: 5: 4: 5 4. 点夕的坐标为(2-a, 3尹6),且到两坐标轴的距离相等,则点P 的坐标为( )A. (3, 3)B. (3, -3)C. (6, -6)D. (3, 3)或(6, -6) 5. 在下列调查中,适宜采用全面调查的是( )A. 了解九(1)班学生校服的尺码情况B. 检测一批电灯泡的使用寿命C. 了解我省中学生的视力情况D. 调查宁波《来发讲啥》栏目的收视率 6. 函数尸吴尸序彳的自变量x 的取值范围是( )C. x 「3如图,在%迎中,AB=2BC,所是彤的中点,则/CMD (_______________ CA.电影院1号厅第2排普宁市大学路 C.东经118° ,北纬68°南偏西45A. xN1B. 是直角 D.度数不能确定8. 今年我市有4万名学生参加中考,为了 了解这些考生的数学成绩,从中抽取2000名考生 的数学成绩进行统计分析.在这个问题中,下列说法正确的是( )A. 这4万名考生的全体是总体B. 每个考生是个体C. 2000名考生是总体的一个样本D. 样本容量是2000 9. 下列判断正确的是()A. 对角线互相垂直的四边形是菱形B. 两组邻边相等的四边形是平行四边形C. 对角线相等的平行四边形是矩形D. 有一个角是直角的平行四边形是正方形 10.已知直线y=k 对b 经过第一、二、三象限,且点(2, 1)在该直线上,设m=2k-b,则0的取值范围是( ) A. 0V/7/V1 B. - 1 </77<1C. 1 </77<2D. - 1 </77<2 11.菱形的两条对角线分别为8和6,则菱形的周长和面积分别是() A. 20, 48B. 14, 48C. 24, 20D. 20, 24 12.已知 A (1, -3) ,(2, -1), ,现将线段祖平移至4岛如果点4 (a, -1) , &(-2, Z?),那么砰6的值是()A. 6B. - 1C. 2D. -2 13.小刘下午5点30分放学匀速步行回家,途中路过鲜花店为过生日的妈妈选购了一束鲜 花,6点20分到家,已知小刘家距学校3千米,下列图象中能大致表示小刘离学校的距 离S (千米)与离校的时间t (分钟)之的关系的是()A.是锐角 C.是钝角s(T^)50 "分钟)14.对于一次函数j/=以-3)对2,"随x 的增大而增大,"的取值范围是()15. 如图,四边形心位;为矩形,点,,。
人教版八年级数学下册期末复习培优练习题(一)及答案

期末复习培优练习题(一)一.选择题1.下列各式计算正确的是()A.3﹣2=B.=×C.=4a(a>0)D.÷=2.式子有意义的x的取值范围是()A.x≥﹣且x≠1B.x≠1C.D.x>﹣且x≠1 3.直角三角形中,两直角边分别是12和5,则斜边上的中线长是()A.34 B.26 C.8.5 D.6.54.下列说法不正确的是()A.平行四边形对边平行B.两组对边平行的四边形是平行四边形C.平行四边形对角相等D.一组对角相等的四边形是平行四边形5.在计算100个数的平均数时,将其中的一个数100错看成了1000,则此时计算出来的平均数比实际结果多()A.9 B.10 C.19 D.26.甲乙两名同学本学期参加了相同的5次数学考试,老师想判断这两位同学的数学成绩谁更稳定,老师需比较这两人5次数学成绩的()A.平均数B.中位数C.众数D.方差7.下列命题中,正确的命题是()A.一组对边平行但不相等的四边形是梯形B.对角线相等的平行四边形是正方形C.有一个角相等的两个等腰三角形相似D.一组对边相等,另一组对边平行的四边形是平行四边形8.在平面直角坐标系中,把直线y=2x﹣3沿y轴向上平移2个单位后,得到的直线的函数表达式为()A.y=2x+2 B.y=2x﹣5 C.y=2x+1 D.y=2x﹣19.若y关于x的函数关系式为y=kx+1,当x=1时,y=2,则当x=﹣3时函数值是()A.﹣1 B.﹣2 C.﹣3 D.﹣410.在四边形中,给出下列四个条件:①四边都相等,有一个内角是直角;②四个内角都相等,有一组邻边相等;③对角线互相垂直,且每一条对角线平分一组对角;④对角线互相垂直平分且相等;其中能判定这个四边形为正方形的所有条件分别为()A.①②B.③④C.①②④D.①②③④11.若一次函数y=kx+3(k为常数且k≠0)的图象经过点(﹣2,0),则关于x的方程k(x ﹣5)+3=0的解为()A.x=﹣5 B.x=﹣3 C.x=3 D.x=512.如图,在直角坐标系中,已知点A(6,0),点B为y轴正半轴上一动点,连接AB,以AB为一边向下作等边△ABC,连接OC,则OC的最小值()A.B.3 C.2D.3二.填空题13.计算:(5+)(5﹣2)=.14.在Rt△ABC中,∠C=90°,AB=15,BC:AC=3:4,则BC=.15.直线y=﹣2x+1不经过第象限.16.若直线y=(m2﹣4m+1)x+(2m+1)与直线y=﹣2x+3平行.则m的值为.17.如图所示的网格是正方形网格,则∠PAB﹣∠PCD=°.(点A,B,C,D,P 是网格线交点)18.如图,已知平行四边形ABCD中,AD=6,AB=,∠A=45°.过点B、D分别作BE⊥AD,DF⊥BC,交AD、BC与点E、F.点Q为DF边上一点,∠DEQ=30°,点P 为EQ的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=EQ,则EM的长等于.三.解答题19.计算:(1)×+(2)2﹣6+20.在平面直角坐标系xOy中,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).(1)求直线AB的解析式;=2,求点C的坐标.(2)若直线AB上的点C在第一象限,且S△BOC21.为了解某校八年级学生科普知识竞赛的情况,现从中随机抽取部分学生的成绩,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:(Ⅰ)本次随机抽样调查的学生人数为,图①中的m的值为;(Ⅱ)求本次抽样调查获取的样本数据的众数、中位数和平均数;(Ⅲ)若该校八年级共有学生300人,如果竞赛成绩达到28分(含28分)及以上为优秀,请估计该校八年级学生在本次科普竞赛中成绩优秀的人数.22.如图,在▱ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:四边形BFDE是平行四边形.23.如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,且点A、B、C均在格点上.(1)请在所给的网格内画出以线段AB、BC为边的菱形并写出点D的坐标;(2)菱形ABCD的周长为;(3)菱形ABCD的面积为.24.某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B 两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B 两市的费用别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.(1)请填写下表A(吨)B(吨)合计(吨)C(吨)240D(吨)x260总计(吨)200 300 500(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m 元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.25.定义:有一个内角为90°,且对角线相等的四边形称为准矩形.(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD=;②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是;(整点指横坐标、纵坐标都为整数的点)(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是.参考答案一.选择题1.A.2.A.3.D.4.D.5.A.6.D.7.A.8.D.9.B.10.C.11.C.12.B.二.填空题13.19.14.9.15.三.16.3.17.4518.1或2三.解答19.解:(1)原式=+4=3+4=7;(2)原式=4﹣6+4=2.20.解:(1)设直线AB的解析式为y=kx+b,把A(1,0),B(0,﹣2)分别代入得,解得,∴直线AB的解析式为y=2x﹣2;(2)设C(t,2t﹣2)(t>1),=2,∵S△BOC∴×2×t=2,解得t=2,∴C点坐标为(2,2).21.解:(Ⅰ)9÷18%=50(人),12÷50=24%;故答案为:50,24;(Ⅱ)∵在这组数据中,18出现14次,出现的次数最多,∴这组数据的众数是18;将这组数据从小到大排列后,处在第25、26位的两个数都是18,因此中位数是18;==17.8;答:平均数为17.8,中位数是18,众数是18;(Ⅲ)300×=174人,答:该校八年级学生在本次科普竞赛中成绩优秀的人数为174人.22.证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵AE=CF,∴AD﹣AE=BC﹣CF,∴ED=BF,又∵AD∥BC,∴四边形BFDE是平行四边形.23.解:(1)以线段AB、BC为边的菱形ABCD是菱形.D(﹣2,1).故答案为D(﹣2,1).(2)∵B(3,﹣4),C(2,0),∴BC==,∴菱形ABCD的周长为4.故答案为4.(3)∵A(﹣1,﹣3),C(2,0),B(3,﹣4),D(﹣2,1),∴AC=3,BD=5,∴S=•5=15.菱形ABCD故答案为15.24.解:(1)∵D市运往B市x吨,∴D市运往A市(260﹣x)吨,C市运往B市(300﹣x)吨,C市运往A市200﹣(260﹣x)=(x﹣60)吨,故答案为:x﹣60、300﹣x、260﹣x;(2)由题意可得,w=20(x﹣60)+25(300﹣x)+15(260﹣x)+30x=10x+10200,∴w=10x+10200(60≤x≤260);(3)由题意可得,w=10x+10200﹣mx=(10﹣m)x+10200,当0<m<10时,x=60时,w取得最小值,此时w=(10﹣m)×60+10200≥10320,解得,0<m≤8,当m>10时,x=260时,w取得最小值,此时,w=(10﹣m)×260+10200≥10320,解得,m≤,∵<10,∴m>10这种情况不符合题意,由上可得,m的取值范围是0<m≤8.25.解:(1)①∵∠ABC=90°,∴BD=AC===,故答案为,②∵A(0,3),B(5,0),∴AB==,设点P(m,n),O(0,0),∴OP==,∵m ,n 都为整数,∴点P (3,5)或(5,3); 故答案为P (3,5)或(5,3); (2)∵四边形ABCD 是正方形, ∴AB =BC ,∠A =∠ABC =90°, ∴∠EBF +∠EBC =90°, ∵BE ⊥CF ,∴∠EBC +∠BCF =90°, ∴∠EBF =∠BCF , ∴△ABE ≌△BCF , ∴BE =CF ,∴四边形BCEF 是准矩形; (3),,∵∠ABC =90°,∠BAC =60°,AB =2, ∴BC =2,AC =4,准矩形ABCD 中,BD =AC =4, ①当AC =AD 时,如图1,作DE ⊥AB ,∴AE =BE =AB =1, ∴DE ===,∴S 准矩形ABCD =S △ADE +S 梯形BCDE =DE ×AE +(BC +DE )×BE =×+(2+)×1 =+;②当AC =CD 时,如图2,作DF ⊥BC , ∴BD =CD , ∴BF =CF =BC =,∴DF ===,∴S 准矩形ABCD =S △DCF +S 梯形ABFD =FC ×DF +(AB +DF )×BF =××+(2+)×=+; ③当AD =CD ,如图3,连接AC 中点和D 并延长交BC 于M ,连接AM ,连接BG ,过B 作BH ⊥DG , 在Rt △ABC 中,AC =2AB =4, ∴BD =AC =4, ∴AG =AC =2, ∵AB =2, ∴AB =AG , ∵∠BAC =60°, ∴∠ABG =60°,∴∠CBG =30°在Rt △BHG 中,BG =2,∠BGH =30°, ∴BH =1,在Rt △BHM 中,BH =1,∠CBH =30°, ∴BM =,HM =,∴CM =, 在Rt △DHB 中,BH =1,BD =4,∴DH =,∴DM =DH ﹣MH =﹣, ∴S 准矩形ABCD =S △ABM +S 四边形AMCD , =BM ×AB +AC ×DM =××2+×4×(﹣) =2; 故答案为+,+,2.。
人教版2020八年级数学下册期末综合复习培优测试卷1(附答案详解)

①体育场离小冬家2.5千米②小冬在体育场锻炼了15分钟
③体育场离早餐店4千米④小冬从早餐店回家的平均速度是3千米/小时
C、当∠A+∠B=∠C时,且∠A+∠B+∠C=180°,所以∠C=90°,所以△ABC为直角三角形;
D、当∠A:∠B:∠C=3:4:5时,可设∠A=3x°,∠B=4x°,∠C=5x°,
12.如图,矩形 的对角线 、 交于点 ,点 是边 上的一个动点, 于 , 于 , ,则 的最大值为__________.
13.在口ABCD中,若∠A+∠C=100°,则∠B=_______.
14.直线 的解析为 ,则原点到直线 的距离为___________.
15.在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到__________.
8.矩形两条对 角线的一个锐角为60°,两条对角线的长度和为20cm,则这个矩形的一条较短边的长度为( )A. B. C. D.
9.下列运算错误的是()
A. B.
C. D.
10.如图,在平行四边形ABCD中,CE是∠DCB的平分线,F是AB的中点,AB=6,BC=4,则AE:EF:FB为( )
A.1:2
参考答案
1.C
【解析】
试题解析: ,
,
,
又 是四边形的四条边,
当 是对边, 是对边时,四边形时平行四边形.
当 是邻边, 是邻边时,四边形的对角线互相垂直.
人教版八年级下册数学 期末综合复习培优卷(含答案)

期末综合复习培优卷满分:120分时间:120分钟一.选择题(满分30分,每小题3分)1.下列式子属于最简二次根式的是()A.B.C.(a>0)D.2.下列运算中正确的是()A.+=B.(﹣)2=5 C.3﹣2=1 D.=±43.如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为()A.3B.5 C.6 D.44.若一组数据为3,5,4,5,6,则这组数据的众数是()A.3 B.4 C.5 D.65.顺次连接一个四边形的各边中点,得到了一个正方形,则这个四边形最可能是()A.平行四边形B.菱形C.矩形D.正方形6.把直线y=2x向下平移3个单位长度得到直线为()A.y=2x+3 B.y=5x C.y=6x D.y=2x﹣37.如图,数轴上的点A表示的数是﹣2,点B表示的数是1,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为()A.B.+2 C.﹣2 D.28.甲、乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米,图中的折线表示甲、乙两人之间的距离y(米)与甲步行时间x(分钟)的函数关系图象,则()A.乙骑自行车的速度是180米/分B.乙到还车点时,甲、乙两人相距850米C.自行车还车点距离学校300米D.乙到学校时,甲距离学校200米9.如图,在▱ABCD中,若∠A+∠C=130°,则∠D的大小为()A.100°B.105°C.110°D.115°10.把直线y=﹣x+2向上平移a个单位后,与直线y=2x+3的交点在第二象限,则a的取值范围是()A.a>1 B.C.﹣D.a<1二.填空题(满分18分,每小题3分)11.已知一组数据1,7,10,8,x,6,0,3,若=5,则x应等于.12.a、b、c是△ABC三边的长,化简+|c﹣a﹣b|=.13.如图,小巷左右两侧是竖直的墙.一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面2m,则小巷的宽度为m.14.如图,在菱形ABCD中,AC与BD交于点O,若AC=8,BD=6,则菱形ABCD的面积为.15.如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,则关于x的不等3x+b>ax ﹣2的解集为.16.甲、乙两人分别从A、B两地相向而行,y与x的函数关系如图,其中x表示乙行走的时间(时),y表示两人与A地的距离(千米),甲的速度比乙每小时快千米.三.解答题17.(6分)计算(1)+﹣﹣(2)(1﹣2)(1+2)(3)(4+3)÷2(4)×÷3﹣×(1﹣)018.(6分)如图,在▱ABCD中,AE=CF,求证:四边形DEBF是平行四边形.19.(7分)已知一次函数y=(2a﹣1)x+a﹣2.(1)若这个函数的图象经过原点,求a的值;(2)若这个函数的图象经过一、三、四象限,求a的取值范围.20.(7分)如图,在△ABC中,∠ABC=15°,AB=,BC=2,以AB为直角边向外作等腰直角△BAD,且∠BAD=90°;以BC为斜边向外作等腰直角△BEC,连接DE.(1)按要求补全图形;(2)求DE长;(3)直接写出△ABC的面积.21.(8分)如图1,A,B,C是郑州市二七区三个垃圾存放点,点B,C分别位于点A的正北和正东方向,AC=40米.八位环卫工人分别测得的BC长度如下表:甲乙丙丁戊戌申辰BC(单位:米)84 76 78 82 70 84 86 80 他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2,图3:(1)求表中BC长度的平均数、中位数、众数;(2)求A处的垃圾量,并将图2补充完整;(3)用(1)中的作为BC的长度,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.(注:=1.732)22.(8分)甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA 表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:(1)当轿车刚到乙地时,此时货车距离乙地千米;(2)当轿车与货车相遇时,求此时x的值;(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.23.(8分)如图,在矩形纸片ABCD中,已知AB=2,BC=2,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.(1)当点E与点C重合时,求DF的长;(2)若B′C′分别交边AD,CD于点F,G,且∠DAE=22.5°,求△DFG的面积;(3)如果点M为CD的中点,那么在点E从点C移动到点D的过程中,求C′M的最小值.24.(10分)如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD,BC 于点E,F,作BH⊥AF于点H,分别交AC,CD于点G,P,连接GE,GF.(1)求证:△OAE≌△OBG;(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由;(3)试求:的值(结果保留根号).25.(12分)如图,直线y=kx+6与x轴、y轴分别相交于点E、F,点E的坐标为(﹣8,0),点A的坐标为(﹣6,0),点P是直线EF上的一个动点.(1)求k的值;(2)点P在第二象限内的直线EF上的运动过程中,写出△OPA的面积S与x的函整表达式,并写出自变量x的取值范围;(3)探究,当点P在直线EF上运动到时,△OPA的面积可能是15吗,若能,请求出点P的坐标;若不能,说明理由.参考答案一.选择题1.B.2.B.3.B.4.C.5.D.6.D.7.C.8.C.9.D.10.C.二.填空题11.5.12.2a13.2.2.14.24.15.x>﹣2.16.0.4.三.解答题17.解:(1)原式=3+2﹣2﹣3=﹣;(2)原式=12﹣(2)2=1﹣8=﹣7;(3)原式=+=2+;(4)原式=﹣×1=2﹣=.18.证明:在▱ABCD中,则AB∥CD,AB=CD,∵AE=CF,∴AB﹣AE=CD﹣CF,∴BE=DF,∵BE∥DF,∴四边形DEBF是平行四边形.19.解:(1)∵y=(2a﹣1)x+a﹣2经过原点,∴a﹣2=0,得:a=2,∴a的值为2;(2)∵y=(2a﹣1)x+a﹣2的图象经过一、三、四象限,∴,解得:<a<2,∴a的取值范围为:<a<2.20.解:(1)如图所示(2)连接DC,交BC于点F,∵△ABD是等腰直角三角形,AB=,∠BAD=90°,∴AB=AD=,∠ABD=45°,∴DB==2∵∠ABC=15°,∴∠DBC=∠ABC+∠ABD=60°,又BC=BD=2,∴△BCD是等边三角形,∴BD=CD=2,∴D点在线段BC的垂直平分线上,又∵△BEC是等腰直角三角形,∴BE=CE,∠CEB=45°,∴E点在线段BC的垂直平分线上,∴DE垂直平分BC,∴BF=BC=1,∠BFE=90°,∵∠FBE=∠BEF=45°,∴BF=EF=1,Rt△BFD中,BF=1,BD=2,由勾股定理得DF=,∴DE=DF+EF=+1,(3)∵AC=AC,BC=CD,AB=AD ∴△ABC≌△ADC(SSS)∴S△ABC =S△ADC,∵S△ABC =(S△BCD﹣S△ABD)∴S△ABC=(×4﹣××)=21.解:(1)==80(米),众数是:84米,中位数是:81米;(2)∵C处垃圾存放量为:320kg,在扇形统计图中所占比例为:50%,∴垃圾总量为:320÷50%=640(千克),∴A处垃圾存放量为:(1﹣50%﹣37.5%)×640=80(kg),占12.5%.补全条形图如下:(2)垃圾总量是:320÷50%=640(千克),则A处的垃圾量是:640×(1﹣50%﹣37.5%)=80(千克),(3)在直角△ABC中,AB===40=69.28(米).∵运送1千克垃圾每米的费用为0.005元,∴运垃圾所需的费用为:69.28×80×0.005≈27(元),答:运垃圾所需的费用为27元.22.解:(1)根据图象信息:货车的速度V货=,∵轿车到达乙地的时间为货车出发后4.5小时,∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米),此时,货车距乙地的路程为:300﹣270=30(千米).所以轿车到达乙地后,货车距乙地30千米.故答案为:30;(2)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).∵C(2.5,80),D(4.5,300)在其图象上,,解得,∴CD段函数解析式:y=110x﹣195(2.5≤x≤4.5);易得OA:y=60x,,解得,∴当x=3.9时,轿车与货车相遇;=150,两车相距=150﹣80=70>20,(3)当x=2.5时,y货由题意60x﹣(110x﹣195)=20或110x﹣195﹣60x=20,解得x=3.5或4.3小时.答:在两车行驶过程中,当轿车与货车相距20千米时,x的值为3.5或4.3小时.23.解:(1)如图,∵四边形ABCD是矩形,∴AB=CD=2,BC=AD=2,∠B=∠BCD=∠D=90°,∴∠ACB=30°,由翻折不变性可知:∠ACB=∠ACF=30°,∠DCF=30°,∴DF=(2)如图2中,∵∠DAE=22.5°,∠BAD=90°,∴∠BAE=∠EAB′=67.5°,∴∠B′AF=45°,∵∠B′=90°,∴∠B′AF=∠B′FA=45°,∵B′A=B′F=2,∴AF=2,∴DF=2﹣2,∵∠AFB′=∠DFG=45°,∴DG=DF=2﹣2,=•(2﹣2)2=∴S△DFG(3)如图3中,连接AM,AC′,MC′.∵AC′=4,AM==,∵C′M≥AC′﹣AM,∴C′M≥4﹣,∴C′M的最小值为4﹣.24.(1)证明:∵四边形ABCD是正方形,∴OA=OB,∠AOE=∠BOG=90°.∵BH⊥AF,∴∠AHG=90°,∴∠GAH+∠AGH=90°=∠OBG+∠AGH,∴∠GAH=∠OBG,即∠OAE=∠OBG.∴在△OAE与△OBG中,,∴△OAE≌△OBG(ASA);(2)四边形BFGE是菱形,理由如下:∵在△AHG与△AHB中,∴△AHG≌△AHB(ASA),∴GH=BH,∴AF是线段BG的垂直平分线,∴EG=EB,FG=FB.∵∠BEF=∠BAE+∠ABE=67.5°,∠BFE=90°﹣∠BAF=67.5°∴∠BEF=∠BFE∴EB=FB,∴EG=EB=FB=FG,∴四边形BFGE是菱形;(3)=﹣1.25.解:(1)点E的坐标为(﹣8,0),且在直线y=kx+6上,则﹣8k+6=0,解得,;(2)∵点P(x,y)是第二象限内的直线上的一个动点,∴,∴;(3)当点P在x轴的上方时,由题意得,=15,整理,得,解得,,则.此时点P的坐标是;当点P在x轴的下方时,y=﹣5,此时综上所述,△OPA的面积是15时,点P的坐标为或.。
人教版数学八年级下册期末培优练习试题(含答案)

八年级下册期末培优练习试题一.选择题1.下列式子为最简二次根式的是( ) A .B .C .D .2.若,则x 可取的整数值有( )A .1个B .2个C .3个D .4个3.如图,A ,B ,C 三点在边长为1的正方形网格的格点上,则∠BAC 的度数为( )A .30°B .45°C .50°D .60°4.下列说法错误的是( )A .平行四边形的内角和与外角和相等B .一组邻边相等的平行四边形是菱形C .对角线互相平分且相等的四边形是矩形D .四条边都相等的四边形是正方形 5.在平面直角坐标系中,直线y =x +与x 轴正方向的夹角度数是( )A .30°B .45°C .60°D .120°6.数据4,3,5,3,6,3,4的众数和中位数是( ) A .3,4B .3,5C .4,3D .4,5 7.小明的作业本上有以下四题:①=4a 2;②•=5a ;③;④,做错的题有( ) A .4个B .3个C .2个D .1个8.一次函数y =2x ﹣3的图象不经过的象限是( ) A .一B .二C .三D .四9.如图,在矩形ABCD 中,O 为AC 中点,EF 过O 点且EF ⊥AC 分别交DC 于F ,交AB 于E ,点G 是AE 中点且∠AOG =30°,则下列结论正确的个数为( )(1)DC =3OG ;(2)OG =BC ;(3)△OGE 是等边三角形;(4)S △AOE =S 矩形ABCD .A .1个B .2个C .3个D .4个10.如图,已知直线y 1=x +b 与y 2=kx ﹣1相交于点P ,点P 的横坐标为﹣1,则关于x 的不等式x +b ≤kx ﹣1的解集在数轴上表示正确的是()A.B.C.D.11.如图,已知平行四边形ABCD中,AB=BC,点M从点D出发,沿D→C→A以1cm/s的速度匀速运动到点A,图2是点M运动时,△MAB的面积y(cm2)随时间x(s)变化的关系图象,则边AB的长为()cm.A.B.C.D.12.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示y与x之间的函数关系,下列说法:①动车的速度是270千米/小时;②点B的实际意义是两车出发后3小时相遇;③甲、乙两地相距1000千米;④普通列车从乙地到达甲地时间是9小时,其中不正确的有()A.1个B.2个C.3个D.4个二.填空题13.函数y=中,自变量x的取值范围是.14.E为▱ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,那么∠ABE=.15.如图,已知▱OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx﹣2与BC、OA分别交于M,N,且将▱OABC的面积分成相等的两部分,则k的值是.16.如图,已知OP平分∠AOB,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.CP=,PD=6.如果点M是OP的中点,则DM的长是.17.如图,在菱形ABCD中,AC=6,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是.三.解答题19.计算:(1);(2)20.树叶有关的问题:如图1,一片树叶的长是指沿叶脉方向量出的最长部分的长度(不含叶柄),树叶的宽是指沿与主叶脉垂直方向量出的最宽处的长度,树叶的长宽比是指树叶的长与树叶的宽的比值.某同学在校园内随机收集了A树、B树、C树三棵的树叶各10片,通过测量得到这些树叶的长y(单位:cm),宽x(单位:cm)的数据,计算长宽比,整理如表:表1A树、B树、C树树叶的长宽比统计表1 2 3 4 5 6 7 8 9 10A树树叶的长宽比 4.0 4.9 5.2 4.1 5.7 8.5 7.9 6.3 7.7 7.9B树树叶的长宽比 2.5 2.4 2.2 2.3 2.0 1.9 2.3 2.0 1.9 2.0C树树叶的长宽比 1.1 1.2 1.2 0.9 1.0 1.0 1.1 0.9 1.0 1.3 表2A树、B树、C树树叶的长宽比的平均数、中位数、众数、方差统计表平均数中位数众数方差A树树叶的长宽比 6.2 6.0 7.9 2.5B树树叶的长宽比 2.2 0.38C树树叶的长宽比 1.1 1.1 1.0 0.02解决下列问题:(1)将表2补充完整;(2)①小张同学说:“根据以上信息,我能判断C树树叶的长、宽近似相等.”②小李同学说:“从树叶的长宽比的平均数来看,我认为,如图3的树叶是B树的树叶.”请你判断上面两位同学的说法中,谁的说法是合理的,谁的说法是不合理的,并给出你的理由;(3)现有一片长103cm,宽52cm的树叶,请将该树叶的数用“★”表示在图2中,判断这片树叶更可能来自于A、B、C中的哪棵树?并给出你的理由.21.学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.(1)根据图象信息,当t=分钟时甲乙两人相遇,甲的速度为米/分钟,乙的速度为米/分钟;(2)图中点A的坐标为;(3)求线段AB所直线的函数表达式;(4)在整个过程中,何时两人相距400米?22.如图,在△ABC中,∠ACB=90°,AC=15.sin∠A=,点D是BC的中点,点P是AB上一动点(不与点B 重合),延长PD至E,使DE=PD,连接EB、EC.(1)求证;四边形PBEC是平行四边形;(2)填空:①当AP的值为时,四边形PBEC是矩形;②当AP的值为时,四边形PBEC是菱形.23.如图,已知直线l1:y=2x﹣3与直线l2:y=﹣x+3相交于点P,分别与y轴相交于点A、B.(1)求点P的坐标;(2)点M(0,k)为y轴上的一个动点,过点M作y轴的垂线交l1和l2于点N,Q,当NQ=2时,求k的值.24.在平面直角坐标系中,点A(a,b﹣1),点B(a+2,b+1),若a、b满足+(2a+b+5)2=0 (1)写出A,B两点的坐标;≤8,求x的取值范围:(2)若点P(x,0)为x轴上一动点,且S△ABP(3)平移线段AB得到EF,点A对应点为E,点B对应点为F,且点E的坐标是方程2x﹣y=10的一个解,点F的坐标是方程x﹣y=7的一个解,例如(2,3)是方程2x+y=7的一个解,点H为线段EF上一点,且点H 到x轴的距离为5,求点H的坐标.25.综合与实践:问题情境:在矩形ABCD中,点E为BC边的中点,将△ABE沿直线AE翻折,使点B与点F重合,直线AF交直线CD于点G.特例探究实验小组的同学发现:(1)如图1,当AB=BC时,AG=BC+CG,请你证明该小组发现的结论;(2)当AB=BC=4时,求CG的长;延伸拓展(3)实知小组的同学在实验小组的启发下,进一步探究了当AB:BC=时,线段AG、BC、CG之间的数量关系,请你直接写出实知小组的结论.参考答案一.选择题1.B.2.B.3.B.4.D.5.C.6.A.7.D.8.B.9.C.10.D.11.A.12.B.二.填空题13.x≠﹣3.14.51°.15.k=.16.5.17.3.三.解答题19.解:(1)原式=4﹣3+=;(2)原式=9﹣8﹣=1﹣3=﹣2.20.解(1)将B树叶的长宽的比从小到大排序处在第5、6位的两个数平均数为(2.0+2.2)÷2=2.1,因此中位数是2.1,出现次数最多的数是2.0,因此众数是2.0,补全的统计表如下:(2)小张同学的说法是合理的,C树叶的长宽比1:1左右;小李同学的说法是不合理的,该树叶来自A树,理由:观察该树叶其长是宽的6倍左右,应该是来自A树叶.(3)图2中,★表示这片树叶的数据,这片树叶来自B树;理由:这片树叶的长为103,宽为52,长宽的比大约为2.0,根据平均数可得它来自B树.21.解:(1)根据图象信息,当t=24分钟时甲乙两人相遇,甲的速度为2400÷60=40(米/分钟).∴甲、乙两人的速度和为2400÷24=100米/分钟,∴乙的速度为100﹣40=60(米/分钟).故答案为:24,40,60;(2)乙从图书馆回学校的时间为2400÷60=40(分钟),40×40=1600,∴A点的坐标为(40,1600).故答案为:(40,1600);(3)设线段AB所表示的函数表达式为y=kt+b,∵A(40,1600),B(60,2400),∴,解得,∴线段AB所表示的函数表达式为y=40t;(4)两种情况:①迎面:(2400﹣400)÷100=20(分钟),②走过:(2400+400)÷100=28(分钟),∴在整个过程中,第20分钟和28分钟时两人相距400米.22.解:∵点D是BC的中点,∴BD=CD,∵DE=PD,∴四边形PBEC是平行四边形;(2)①当∠APC=90°时,四边形PBEC是矩形,∵AC=15.sin∠A=,∴PC=12,由勾股定理得AP=9,∴当AP的值为9时,四边形PBEC是矩形;②∵在△ABC中,∠ACB=90°,AC=15.设BC=4x,AB=5x,则(4x)2+152=(5x)2,解得:x=5,∴AB=5x=25,当PC=PB时,四边形PBEC是菱形,此时点P为AB的重点,所以AP=12.5,∴当AP的值为12.5时,四边形PBEC是菱形.23.解:(1)根据题意,得:,解得:,∴点P的坐标为(2,1).(2)y=2x﹣3中y=k时,2x﹣3=k,解得x=,y=﹣x+3中y=k时,﹣x+3=k,解得x=3﹣k,∵NQ=2,∴|﹣(3﹣k)|=2,解得:k=或k=﹣.24.解:(1)由+(2a+b+5)2=0得:3a+4b=0,且2a+b+5=0解得:a=﹣4,b=3,∴A(﹣4,2)、B(﹣2,4)(2)设过点A(﹣4,2)、B(﹣2,4)的直线解析式为:y=kx+b 则有:﹣4k+b=2,﹣2k+b=4解得:k=1,b=6∴直线AB解析式为:y=x+6分别过点A、B作AN,BM垂直x轴,垂足分别为N、M则AN=2,BM=4设直线AB与x轴的交点为C,令y=0,得x+6=0,解得x=﹣6∴C(﹣6,0)S==|x+6|×4﹣|x+6|×2=|x+6| △ACP≤8又∵S△ABP∴|x+6|≤8,解得:﹣14≤x≤2,且x≠﹣6(3)由题意AB∥EF设直线EF解析式为:y=x+m∵点E也在直线2x﹣y=10上,联立这两个方程可解得x=10+m,y=10+2m,∴E(10+m,10+2m)由平移知识可得:F(12+m,12+2m)∵点F坐标是:x﹣y=7的一个解所以解得:m=﹣8∴E(2,﹣6),F(4,﹣4)则直线EF为:y=x﹣8∵点H到x轴的距离为5,∴|y|=5,可得|x﹣8|=5,x﹣8=5,或x﹣8=﹣5解得:x=13,或x=3∴点H(13,5)或(3,﹣5)25.解:(1)如图1中,连接EG.∵△AEF是由△AEB翻折得到,∴EB=EF=EC,AB=AF,∠AFE=∠B=∠C=90°,在Rt△EGF和Rt△EGC,,∴Rt△EGF≌Rt△EGC(HL),∴FG=GC,∵AB=AF=BC,∴AG=AF+FG=BC+CG.(2)CG=1.(3)如图2中,连接EG.∵△AEB≌△AEF,△EGF≌△EGC,∴AB=AF,BE=EF=EC,FG=GC,∵AB:BC=:2,∴AB=BC,∴AG=AF+FG=AB+CG=BC+CG.即AG=BC+CG.。
人教版八年级下册数学期末试卷(培优篇)(Word版含解析)

人教版八年级下册数学期末试卷(培优篇)(Word版含解析)一、选择题1.要使二次根式3x 有意义,x的值可以是()A.﹣1 B.0 C.2 D.42.如图,正方形网格中的ABC,若小方格边长为1,则ABC的形状为()A.直角三角形B.锐角三角形C.钝角三角形D.以上答案都不对3.下列不能判定四边形ABCD是平行四边形的条件是()A.AB∥CD,AD∥BC B.OA=OC,OB=ODC.AB∥CD,AD=BC D.AB=CD,AD=BC4.一家公司打算招聘一名翻译对甲、乙、丙三名应试者进行了听、说、读、写的英语水平测试,他们各项成绩(百分制)如下表所示:应试者听说读写甲73808283乙85788573丙80828080如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:1:3:4的比确定,从他们的平均成绩(百分制)看,应该录取()A.甲B.乙C.丙D.不确定5.下列命题中:①两条对角线互相平分且相等的四边形是正方形;②菱形的一条对角线平分一组对角;③顺次连接四边形各边中点所得的四边形是平行四边形;④两条对角线互相平分的四边形是矩形;⑤平行四边形对角线相等.假命题的个数是()A.1 B.2 C.3 D.46.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为()A .28°B .52°C .62°D .72°7.如图,在边长为12的等边△ABC 中,D 为边BC 上一点,且BD =12CD ,过点D 作DE ⊥AB 于点E ,F 为边AC 上一点,连接EF 、DF ,M 、N 分别为EF 、DF 的中点,连接MN ,则MN 的长为( )A .3B .2C .23D .48.如图,直线 y 1 与 y 2 相交于点C , y 1 与 x 轴交于点 D ,与 y 轴交于点(0,1), y 2 与 x 轴 交于点 B (3,0),与 y 轴交于点 A ,下列说法正确的个数有( )①y 1的 解 析 式 为12y x =+;② OA = OB ;③22AC BC =;④12y y ⊥;⑤ ∆AOB ≅ ∆BCD . A .2 个B .3个C .4 个D .5 个二、填空题9.代数式2021x -中,字母x 的取值范围是____________.10.如图,菱形ABCD 周长为40,对角线12BD =,则菱形ABCD 的面积为______.11.由四个全等的直角三角形组成如图所示的“赵爽弦图”,若直角三角形两直角边边长的和为3,面积为1,则图中阴影部分的面积为____________ .12.如图,在矩形ABCD 中,点E 在AD 上,且EC 平分BED ∠,若1AB =,45EBC ∠=︒,则DE 的长为__________.13.已知一次函数的图象经过(2,0),(0,4)-两点,则该一次函数解析式是______. 14.如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,点E 、F 分别是AO 、AD 的中点,若AB=5cm ,BC=12cm ,则△AEF 的周长为_______________.15.如图,在平面直角坐标系中,点A 1,A 2,A 3,…,都在x 轴正半轴上,点B 1,B 2,B 3,…,都在直线33y x =上,△A 1B 1A 2,△A 2B 2A 3,△A 3B 3A 4,…,都是等边三角形,且OA 1=1,则点B 6的纵坐标是______________.16.如图,在Rt ABC 中,∠C =90°,AC =4,BC =6,D 是BC 的中点,E 是AC 上一动点,将CDE 沿DE 折叠到C DE '△,连接AC ′,当AEC '△是直角三角形时,CE 的长为_____.三、解答题17.计算:(1)(2+5)(2﹣5); (2)1822+﹣3; (3)(π﹣2021)01112|32|()2-++-+.18.如图,货船和快艇分别从码头A 同时出发.其中,货船沿着北偏西54°方向以15海里/小时的速度匀速航行,快艇沿着北偏东36°方向以36海里/小时的速度航行,1小时后.两船分别到达B 、C 点.求B 、C 两点之间的距离.19.已知,在边长为1的小正方形组成的48⨯网格中,ABC 的顶点均为格点.,请按要求分别作出ABC ,并解答问题.(1)在图1中作钝角ABC ,图2中作直角ABC ,图3中作锐角ABC ,都使5BC =; (2)在图4中作直角ABC ,AB 为斜边,两直角边长度为无理数,并直接写出ABC 的面积.20.如图,在平行四边形ABCD 中,点P 是AB 边上一点(不与A ,B 重合),过点P 作PQ ⊥CP ,交AD 边于点Q ,且∠QPA =∠PCB ,QP =QD .(1)求证:四边形ABCD 是矩形; (2)求证:CD =CP .21.同学们,我们以前学过完全平方公式,a 2±2ab+b 2=(a±b )2,你一定熟练掌握了吧?现在我们又学习了平方根,那么所有的正数和0都可以看作是一个数的平方,比如:2=2(2),3=2(3),7=2(7),02=0,那么我们利用这种思想方法计算下面的题: 例:求332-的算术平方根解:332-=222-+1=2(2)22-+12=2(21)- ∴332-的算术平方根是21-同学们,你看明白了吗?大胆试一试,相信你能做正确! (1)322+ (2)108322++(3)3225267212922011230-+-+-+-+-.22.公交是一种绿色的出行方式,今年我具开通环保电动公交车.公交车在每天发车前需先将蓄电池充满、然后立即开始不间断运行.为保障行车安全,当蓄电池剩余电最低于20KWh 时,需停止运行.在充电和运行过程中,蓄电池的电量y (单位:KWh )与行驶时间x (单位:h )之间的关系如图所示,(1)公交车每小时充电量为 KWh ,公交车运行的过程中每小时耗电量为 KWh ; (2)求公交车运行时,y 关于x 的函数解析式,并写出自变量x 的取值范围. (3)求蓄电池的电量剩余25%时,公交车运行时间x 的值.23.如图1,在一个平面直角三角形中的两直角边的平方之和一定等于斜边的平方。
人教版八年级数学下册期末试卷(培优篇)(Word版含解析)

人教版八年级数学下册期末试卷(培优篇)(Word 版含解析) 一、选择题 1.函数1x y x =-中,自变量x 的取值范围是( ) A .x ≥0B .x ≥0且x ≠1C .x ≠1D .0≤x ≤1 2.下列各组长度的线段能构成直角三角形的是直( ) A .30,40,50 B .7,12,13 C .5,9,12 D .3,4,6 3.如图,在ABCD 中,点,EF 分别在边BC AD ,上.若从下列条件中只选择一个添加到图中的条件中:①//AE CF ;②AE CF =;③BE DF =;④BAE DCF ∠=∠.那么不能使四边形AECF 是平行四边形的条件相应序号是( )A .①B .②C .③D .④ 4.若a 、b 、c 的平均数为7,则1a +、2b +、3+c 的平均数为( )A .7B .8C .9D .10 5.如图,已知矩形ABCD 的对角线AC 的长为10cm ,连结矩形各边中点E 、F 、G 、H 得四边形EFGH ,则四边形EFGH 的周长为( )cm .A .20B .202C .203D .256.如图,在Rt ABC 中,90ABC ∠=︒,点D 在边AC 上,2AB =,BD CD =,2BC AB =.若ABD △与EBD △关于直线BD 对称,则线段CE 的长为( )A .655B .755C .855D .9557.如图所示,2AB =,则数轴上点C 表示的数为( )A .3B .5C .13D .58.小张、小王两个人从甲地出发,去8千米外的乙地,图中线段OA 、PB 分别反映了小张、小王步行所走的路程S (千米)与时间t (分钟)的函数关系,根据图像提供的信息,小王比小张早到乙地的时间是__________分钟.A .4B .6C .16D .10二、填空题9.若式子1x -有意义,则x 的取值范围是_________.10.已知一个菱形有一个内角为120︒,周长为16cm ,那么该菱形的面积等于________ . 11.如图,一个密封的圆柱形油罐底面圆的周长是10m ,高为13m ,一只壁虎在距底面1m 的A 处,C 处有食物,壁虎沿油罐的外侧面爬行到C 处捕食,它爬行的最短路线长为_____m .12.如图,将矩形ABCD 折叠,使点C 和点A 重合,折痕为EF ,EF 与AC 交于点O .若5AE =,3BF =,则AO 的长为______.13.如图,一次函数y kx b =+的图象与坐标轴的交点坐标分别为A (0,2),B (-3,0),下列说法:①y 随x 的增大而减小;②3b =-;③关于x 的方程0kx b +=的解为2x =;④关于x 的不等式<0kx b +的解集<3x -.其中说法正确的有_____________.14.在矩形ABCD 中,3AB =,ABC ∠的平分线BE 交AD 所在的直线于点E ,若2DE =,则AD 的长为__________.15.星期六下午,小张和小王同时从学校沿相同的路线去书店买书,小王出发4分钟后发现忘记带钱包,立即调头按原速原路回学校拿钱包,小王拿到钱包后,以比原速提高20%的速度按原路赶去书店,结果还是比小张晚4分钟到书店(小王拿钱包的时间忽略不计).在整个过程中,小张保持匀速运动,小王提速前后也分别保持匀速运动,如图所示是小张与小王之间的距离y (米)与小王出发的时间x (分钟)之间的函数图象,则学校到书店的距离为________米.16.已知,如图,在ABC ∆中,90106C AB AC CD ∠=︒==,,,是AB 上的中线,如果将BCD ∆沿CD 翻折后,点B 的对应点'B ,那么'BB 的长为__________.三、解答题17.计算下列各式的值(1271462(2183222(3)311232(832(4)2(31)4x -=18.有一架5米长的梯子搭在墙上,刚好与墙 头对齐,此时梯脚与墙的距离是3米(1)求墙的高度?(2)若梯子的顶端下滑1米,底端将水平动多少米?19.如图,4×10长方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B,E,F都在格点上,按下列要求作图,使得所画图形的顶点均在格点上.(1)在图中画出以AB为边的正方形ABCD;(2)在图中画出以EF为边的等腰三角形EFG,且△EFG的周长为1010+;(3)在(1)(2)的条件下,连接CG,则线段CG的长为.20.如图,菱形ABCD的对角线AC和BD交于点O,点E在线段OB上(不与点B,点O 重合),点F在线段OD上,且DF=BE,连接AE,AF,CE,CF.(1)求证:四边形AECF是菱形;(2)若AC=4,BD=8,当BE=3时,判断△ADE的形状,说明理由.21.小明在解决问题:已知23+2a2﹣8a+1的值,他是这样分析与解的:∵23+23(23)(23-+-3∴a﹣2=3∴(a﹣2)2=3,a2﹣4a+4=3∴a2﹣4a=﹣1∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1请你根据小明的分析过程,解决如下问题:(1)化简121++132++143++…+110099+ (2)若a=121-,求4a2﹣8a+1的值. 22.振兴加工厂中甲,乙两组工人同时加工某种零件,乙组在工作中有一段时间停产更换设备,更换设备后,乙组的工作效率是原来的2.5倍.两组各自加工零件的数量y (件)与时间x (时)之间的函数图象如图所示.(1)求甲组加工零件的数量y 与时间x 之间的函数解析式;(2)求出图中a 的值及乙组更换设备后加工零件的数量y 与时间x 之间的函数解析式.23.如图,在▱ABCD 中,连接BD ,AB BD ⊥,且AB BD =,E 为线段BC 上一点,连接AE 交BD 于F .(1)如图1,若22AB =,BE =1,求AE 的长度;(2)如图2,过D 作DH ⊥AE 于H ,过H 作HG ⊥AD 交AD 于G ,交BD 于M ,过M 作MN ∥AD 交AE 于N ,连接BN ,证明:2NH BN =;(3)如图3,点E 在线段BC 上运动时,过D 作DH ⊥AE 于H ,延长DH 至Q ,使得12QH AH =,M 为AD 的中点,连接QM ,若42AD =,当QM 取最大值时,请直接写出△ADH 的面积.24.如图,在平面直角坐标系中,直线2y x =+与x 轴、y 轴分别交A 、B 两点,与直线12y x b =-+相交于点(2,)C m , (1)求点A 、B 的坐标;(2)求m和b的值;(3)若直线12y x b=-+与x轴相交于点D.动点P从点D开始,以每秒1个单位的速度向x轴负方向运动,设点P的运动时间为t秒,①若点P在线段DA上,且ACP∆的面积为10,求t的值;②是否存在t的值,使ACP∆为等腰三角形?若存在,求出t的值;若不存在,请说明理由.25.如图,在矩形 ABCD中, AB=16 , BC=18 ,点 E在边 AB 上,点 F 是边 BC 上不与点B、C 重合的一个动点,把△EBF沿 EF 折叠,点B落在点 B' 处.(I)若 AE=0 时,且点 B' 恰好落在 AD 边上,请直接写出 DB' 的长;(II)若 AE=3 时,且△CDB' 是以 DB' 为腰的等腰三角形,试求 DB' 的长;(III)若AE=8时,且点 B' 落在矩形内部(不含边长),试直接写出 DB' 的取值范围.26.(1)操作发现:如图①,在Rt ABC中,∠C=2∠B=90°,点D是BC上一点,沿AD折叠ADC,使得点C恰好落在AB上的点E处,请写出AB、AC、CD之间的关系?并说明理由.(2)问题解决:如图②,若(1)中∠C≠90°,其他条件不变,请猜想AB、AC、CD之间的关系,并证明你的结论;(3)类比探究:如图③,在四边形ABCD中,∠B=120°,∠D=90°,AB=BC,AD=BC,连接AC,点E是CD上一点,沿AE折叠,使得点D正好落在AC上的点F处,若BC=3,求出DE的长.【参考答案】一、选择题1.B解析:B【分析】根据分式和二次根式有意义的条件进行计算即可.【详解】解:由x≥0且x-1≠0得出x≥0且x≠1,x的取值范围是x≥0且x≠1,故选:B.【点睛】本题考查了函数自变量的取值范围问题,掌握分式和二次根式有意义的条件是解题的关键.2.A解析:A【分析】求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.【详解】解:A、302+402=502,能构成直角三角形,故选项正确;B、72+122≠132,不能构成直角三角形,故选项错误;C、52+92≠122,能构成直角三角形,故选项错误;D、32+42≠62,不能构成直角三角形,故选项错误.故选A.【点睛】本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.3.B解析:B【解析】【分析】利用平行四边形的性质,依据平行四边形的判定方法,即可得出不能使四边形AECF是平行四边形的条件.【详解】解:①∵四边形ABCD平行四边形,∴AD//BC,∴AF//EC,∵AE∥CF,∴四边形AECF是平行四边形;②∵AE=CF不能得出四边形AECF是平行四边形,∴条件②符合题意;③∵四边形ABCD平行四边形,∴AD=BC,AD∥BC,又∵BE=DF,∴AF=EC.又∵AF∥EC,∴四边形AECF是平行四边形.④∵四边形ABCD是平行四边形,∴∠B=∠D,∵∠BAE=∠DCF,∴∠AEB=∠CFD.∵AD∥BC,∴∠AEB=∠EAD.∴∠CFD=∠EAD.∴AE∥CF.∵AF∥CE,∴四边形AECF是平行四边形.综上所述,不能使四边形AECF是平行四边形的条件有1个.故选:B.【点睛】本题考查了平行四边形的性质定理和判定定理,以及平行线的判定定理;熟记平行四边形的判定方法是解决问题的关键.4.C解析:C【解析】【分析】根据a 、b 、c 的平均数为7可得73a b c ++=,再列出计算1a +、2b +、3+c 的平均数的代数式,整理即可得出答案.【详解】 解:∵a 、b 、c 的平均数为7,∴73a b c ++=, ∴1232933a b c a b c +++++++=+=, 故选:C .【点睛】本题考查计算平均数.掌握平均数的计算公式是解题关键.5.A解析:A【分析】连接BD ,根据三角形中位线定理易得四边形EFGH 的各边长等于矩形对角线的一半,而矩形对角线相等,从而算出周长即可.【详解】连接BD ,∵H 、G 是AD 与CD 的中点,∴HG 是△ACD 的中位线,∴HG=12AC=5cm ,同理EF=5cm ,∵四边形ABCD 是矩形,∴根据矩形的对角线相等,即BD=AC=10cm ,∵H 、E 是AD 与AB 的中点,∴EH 是△ABD 的中位线,∴EH=12BD=5cm ,同理FG=5cm ,∴四边形EFGH 的周长为20cm .故选A .【点睛】熟练掌握矩形对角线相等和三角形中位线等于第三边的一半的性质是解决本题的关键. 6.A解析:A【解析】【分析】连接AE ,利用对称的性质得到BD 是线段AE 的垂直平分线,DF 是△AEC 的中位线,利用面积法求得AF 的长,再根据勾股定理求得DF 的长即可求解.【详解】解:连接AE ,∵∠ABC =90°,BD =CD ,∴∠DBC =∠DCB ,∠DBC +∠ABD =90°,∠DCB +∠BAC =90°,∴∠ABD =∠BAC ,∴BD =AD ,则BD =AD =CD ,即D 为AC 中点,∵AB =2,BC =2AB ,∴BC =4,AC 222425+∵△ABD 与△EBD 关于直线BD 对称,∴AF =EF ,BE =AB =2,AD =DE ,∴BD 是线段AE 的垂直平分线,则AF ⊥BD ,BD =AD =CD =DE 5=∴DF 是△AEC 的中位线,∴EC =2DF ,∵S △ABD =12S △ABC , ∴111222BD AF BC AC ⨯=⨯⨯15422AF =⨯⨯, 解得:AF 45 ∴DF 2235AD AF -, ∴EC =2DF 65 故选:A .【点睛】 本题考查了轴对称的性质,三角形中位线定理,线段垂直平分线的判定和性质,勾股定理等,解题的关键是灵活运用所学知识解决问题.7.C解析:C【解析】【分析】根据题意得OB OC =,在Rt ABO 中,利用勾股定理可得13OB =,从而得到13OC OB ==,即可求解.【详解】解:如图,由题意知:3OA =,2AB =,BA OC ⊥,OB OC =.90BAO ∴∠=︒.在Rt ABO 中,90BAO ∠=︒,22223213OB OA AB ∴=++13OC OB ∴=∴数轴上点C 13故选:C .【点睛】本题主要考查了勾股定理,数轴与实数,尺规作图——作一条线段等于已知线段,熟练掌握相关知识点是解题的关键.8.B解析:B【分析】由函数图象求出OA 、PB 解析式,再把8y =代入解析式就可以求出小张、小王所用时间.【详解】解:由图象可知:设OA 的解析式为:y kx =,OA 经过点(60,5),560k ∴=,得112k =, OA ∴函数解析式为:112y x =①, 把8y =代入①得:1812x =, 解得:96x =, ∴小张到达乙地所用时间为96(分钟);设PB 的解析式为:y mx n =+,∴100605m n m n +=⎧⎨+=⎩, 解得:1101m n ⎧=⎪⎨⎪=-⎩, PB ∴的解析式为:1110y x =-②, 把8y =代入②得:18110x =-, 解得:90x =, 则小王到达乙地的时间为小张出发后90(分钟),∴小王比小张早到96906-=(分钟),故选:B .【点睛】本题考查的一次函数的应用,关键是由图象求函数解析式.二、填空题9.1≥x【解析】【分析】根据二次根式有意义的条件即可求得x 的取值范围.【详解】∴10x -≥,解得1≥x .故答案为:1≥x .【点睛】本题考查了二次根式有意义的条件,理解二次根式有意义的条件是解题的关键. 10.E解析:2【解析】【分析】作AE BC ⊥于E ,由三角函数求出菱形的高AE ,再运菱形面积公式=底×高计算即可;【详解】作AE BC ⊥于E ,如图所示,∵四边形ABCD 是菱形,周长为16cm ,120BCD ∠=︒,∴4AB BC cm ==,60B ∠=︒, ∴()3sin 4sin 604232AE AB B cm ==⨯︒=⨯=, ∴菱形的面积()242383BC AE cm ==⨯=. 故答案为283cm .【点睛】本题主要考查了菱形的性质,结合三角函数的计算是解题的关键.11.A解析:13【解析】【分析】根据题意画出圆柱的侧面展开图的平面图形,进而利用勾股定理得出答案.【详解】解:如图所示:由题意可得:AD =5m ,CD =12m ,则AC =2212513+=(m),故答案为:13.【点睛】本题主要考查了平面展开图的最短路径问题,正确画出平面图形是解题的关键. 12.B解析:25【分析】首先根据矩形的性质得出//AD BC ,AD BC =,AB CD =,然后根据平行线的性质及等量代换得出AFE AEF ∠=∠,则5AE AF ==,然后根据折叠的性质得出FC AF =,OA OC =,进而求出BC ,然后利用勾股定理求出AB ,AC ,从而答案可求.【详解】∵四边形ABCD 是矩形,∴//AD BC ,AD BC =,AB CD =,∴EFC AEF ∠=∠,由折叠得,EFC AFE ∠=∠,∴AFE AEF ∠=∠,∴5AE AF ==,由折叠得,FC AF =,OA OC =,∴358BC =+=,在Rt ABF 中,4AB =,在Rt ABC 中,AC∴AO OC ==故答案为:【点睛】本题主要考查矩形的性质,折叠的性质和勾股定理,掌握折叠和矩形的性质及勾股定理是关键.13.④【分析】根据一次函数的性质,一次函数与一元一次方程的关系对各个说法分析判断即可得解.【详解】解:把(0,2)A ,(3,0)B -,代入y kx b =+中,可得:230b k b =⎧⎨-+=⎩, 解得:232k b ⎧=⎪⎨⎪=⎩,所以解析式为:223y x =+; ①y 随x 的增大而增大,故①说法错误;②2b =,故②说法错误;③关于x 的方程0kx b +=的解为3x =-,故③说法错误;④关于x 的不等式0kx b +<的解集3x <-,故④说法正确.故答案是:④.【点睛】本题主要考查了一次函数的性质,以及一次函数与一元一次方程,解题的关键是:利用数形结合求解.14.5或1【分析】当点E 在AD 上时,根据平行线的性质和角平分线的定义可得3AE AB ==,可得AD 的长;当点E 在AD 的延长线上时,同理可求出AD 的长.【详解】解:如图1,当点E在AD上时,四边形ABCD是矩形,∴∠=︒,//A90AD BC,∴∠=∠,AEB CBE∠,BE平分ABC∴∠=∠,ABE CBE∴∠=∠,ABE AEB∴==,3AE ABDE=,2∴=+=+=;325AD AE DEAE=,如图2,当点E在AD的延长线上时,同理3∴=-=-=.AD AE DE321故答案为:5或1.【点睛】本题主要考查了矩形的性质,等腰直角三角形的性质等知识,解题的关键是正确画出两种图形.15.840【分析】结合题意根据最后一段图象可求得根据小王后来的速度,进而可求得小王原来的速度,再根据第一段图象可求得小张的速度,最后根据两人行完全程的时间相差4分钟可得方程,解方程即可求得答案.【解析:840【分析】结合题意根据最后一段图象可求得根据小王后来的速度,进而可求得小王原来的速度,再根据第一段图象可求得小张的速度,最后根据两人行完全程的时间相差4分钟可得方程,解方程即可求得答案.【详解】解:由题意可知:最后一段图象是小张到达书店后等待小王前往书店的图象,则小王后来的速度为:336÷4=84(米/分钟),∴小王原来的速度为:84÷(1+20%)=70(米/分钟),根据第一段图象可知:v 王-v 张=40÷4=10(米/分钟),∴小张的速度为:70-10=60(米/分钟),设学校到书店的距离为x 米, 由题意得:4448460x x ⎛⎫++-= ⎪⎝⎭, 解得:x =840,答:学校到书店的距离为840米,故答案为:840.【点睛】本题考查了函数图象的实际应用,行程问题的基本关系,一元一次方程的应用,有一定的难度,求出两人的速度是解题的关键. 16..【分析】先用勾股定理求得BC ,利用斜边上的中线性质,求得CD ,BD 的长,再利用折叠的性质,引进未知数,用勾股定理列出两个等式,联立方程组求解即可.【详解】如图所示,∵,∴BC==8, 解析:485. 【分析】先用勾股定理求得BC ,利用斜边上的中线性质,求得CD ,BD 的长,再利用折叠的性质,引进未知数,用勾股定理列出两个等式,联立方程组求解即可.【详解】如图所示,∵90,10,6ACB AB AC ∠=︒==,∴,∵CD 是AB 上的中线,∴CD=BD=AD=5,设DE=x ,BE=y ,根据题意,得2225x y +=,22(5)64x y ++=,解得x=75,y=245, ∴4825BB y '==, 故答案为:485.【点睛】本题考查了勾股定理,斜边上中线的性质,方程组的解法,折叠的性质,熟练掌握折叠的性质,正确构造方程组计算是解题的关键.三、解答题17.(1);(2);(3)0;(4)或【分析】(1)根据二次根式的乘除计算法则求解即可;(2)先利用二次根式的性质化简,然后根据二次根式的加减计算法则求解即可;(3)先根据二次根式的性质化简,然解析:(13142)2-;(3)0;(4)1x =或13x =- 【分析】(1)根据二次根式的乘除计算法则求解即可;(2)先利用二次根式的性质化简,然后根据二次根式的加减计算法则求解即可; (3)先根据二次根式的性质化简,然后根据二次根式的混合计算法则求解即可; (4)根据求平方根的方法解方程即可.【详解】(1271462142762=⨯632==;(2==(3)⎛= ⎝⎭3=÷=-0=; (4)∵()2314x -=,∴312x -=或312x -=-,解得1x =或13x =-. 【点睛】本题主要考查了利用二次根式的性质化简,二次根式的乘除计算,二次根式的混合计算,二次根式的加减计算,求平方根法解方程,熟知相关计算法则是解题的关键.18.(1)4米;(2)1米【分析】(1)利用勾股定理可以得出梯子的顶端距离地面的高度.(2)由(1)可以得出梯子的初始高度,下滑4米后,可得出梯子的顶端距离地面的高度,再次使用勾股定理,已知梯子的解析:(1)4米;(2)1米【分析】(1)利用勾股定理可以得出梯子的顶端距离地面的高度.(2)由(1)可以得出梯子的初始高度,下滑4米后,可得出梯子的顶端距离地面的高度,再次使用勾股定理,已知梯子的底端距离墙的距离为7米,可以得出,梯子底端水平方向上滑行的距离.【详解】解:(1)根据勾股定理:墙的高度4AC ==(米);(2)梯子下滑了1米,即梯子距离地面的高度1413ACAC '=-=-=(米).根据勾股定理:4B C '=(米)则431'='-=-=(米),即底端将水平动1米.BB CB CB答:(1)墙的高度是4米;(2)若梯子的顶端下滑1米,底端将水平动1米.【点睛】本题考查了勾股定理的应用,要求熟练掌握利用勾股定理求直角三角形边长.19.(1)见解析;(2)见解析;(3)【解析】【分析】(1)根据正方形的判定画出以AB为边的正方形ABCD即可;(2)画出以EF为边的等腰三角形EFG,且△EFG的周长为等腰三角形即可;(3)解析:(1)见解析;(2)见解析;(3)5【解析】【分析】(1)根据正方形的判定画出以AB为边的正方形ABCD即可;(2)画出以EF为边的等腰三角形EFG,且△EFG的周长为1010+等腰三角形即可;(3)由勾股定理求出CG即可.【详解】解:(1)如图,所作正方形ABCD即为以AB为边的正方形ABCD;(2)如图,所作△EFG即为以EF为边的等腰三角形EFG,且△EFG的周长为1010+;(3)如图,CG=22+=5.12【点睛】本题考查作图-应用与设计,勾股定理,解题的关键是理解题意,根据GE=GF=5画出等腰三角形.20.(1)见解析;(2)直角三角形,理由见解析【分析】(1)根据菱形的性质得出AC⊥BD,AO=CO,BO=DO,求出OE=OF,再根据菱形的判定得出即可;(2)根据菱形的性质求出AO=2,BO=解析:(1)见解析;(2)直角三角形,理由见解析【分析】(1)根据菱形的性质得出AC⊥BD,AO=CO,BO=DO,求出OE=OF,再根据菱形的判定得出即可;(2)根据菱形的性质求出AO=2,BO=DO=4,求出OE和DE,根据勾股定理求出AD2=20,AE2=5,求出AD2+AE2=DE2,再根据勾股定理的逆定理求出答案即可.【详解】解:(1)证明:∵四边形ABCD是菱形,∴AC⊥BC,AO=CO,BO=DO,∵BE=DF,BO=DO,∴BO﹣BE=DO﹣DF,即OE=OF,∵AO=CO,∴四边形AECF是平行四边形,∵AC⊥BD,∴四边形AECF是菱形;(2)解:△ADE是直角三角形,理由是:∵AC=4,BD=8,AO=CO,BO=DO,∴AO=2,BO=DO=4,∵BE=3,∴OE=4﹣3=1,DE=DO+OE=4+1=5,在Rt△AOD中,由勾股定理得:AD2=AO2+DO2=22+42=20,在Rt△AOE中,由勾股定理得:AE2=AO2+OE2=22+12=5,∵DE2=52=25,∴AD2+AE2=DE2,∴∠DAE=90°,即△ADE是直角三角形.【点睛】本题考查了菱形的性质和判定,平行四边形的判定,勾股定理,勾股定理的逆定理等知识点,能熟记菱形的性质和判定是解此题的关键.21.(1)9;(2)5.【解析】【详解】试题分析:(1)此式必须在把分母有理化后才能实现化简,即各分式分子分母同乘以一个因式,使得与分母相乘后,为平方差公式结构,如.(2)先对a值进行化简得解析:(1)9;(2)5.【解析】【详解】试题分析:(1)此式必须在把分母有理化后才能实现化简,即各分式分子分母同乘以一个因式,使得1=.(2)先对a1,若就接着代入求解,计算量偏大.模仿小明做法,可先计算2(1)a-的值,就能较为简单地算出结果;也可对这个二次三项式进行配方,再代入求值.后两种方法都比直接代入计算量小很多.解:(1)原式=1)+++⋯(2)∵1a===,解法一:∵22(1)11)2a-=-=,∴2212a a-+=,即221a a-=∴原式=24(2)14115a a-+=⨯+=解法二∴原式=24(211)1a a-+-+24(1)3a=--211)3=--4235=⨯-=点睛:(1得22=-=-a b,去掉根号,实现分母有理化.(2)当已知量为根式时,求这类二次三项式的值,直接代入求值,计算量偏大,若能巧妙利用完全平方公式或者配方法,计算要简便得多.22.(1)y=70x;(2)a=320,y=100x﹣280【分析】(1)利用待定系数法求一次函数解析式即可;(2)利用乙的原来加工速度得出更换设备后,乙组的工作速度即可.【详解】解:(1)∵解析:(1)y=70x;(2)a=320,y=100x﹣280【分析】(1)利用待定系数法求一次函数解析式即可;(2)利用乙的原来加工速度得出更换设备后,乙组的工作速度即可.【详解】解:(1)∵图象经过原点及(6,420),∴设解析式为:y=kx,∴6k=420,解得:k=70,∴y =70x ;(2)乙3小时加工120件, ∴乙的加工速度是:每小时40件,∴乙组在工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2.5倍. ∴更换设备后,乙组的工作速度是:每小时加工40×2.5=100(件), a =120+100×(6﹣4)=320;乙组更换设备后,乙组加工的零件的个数y 与时间x 的函数关系式为:y =120+100(x ﹣4)=100x ﹣280. 【点睛】本题考查了一次函数的应用,解题的关键是根据题意得出函数关系式以及数形结合.23.(1)见解析;(2)见解析;(3). 【分析】(1)分别过点作,垂足分别为,勾股定理解即可;(2)连接,过点作于点,设,经过角度的变换得出,再证明,得出,,结合已知条件,继而证,得出,,进而得到解析:(1)见解析;(2)见解析;(3)1655. 【分析】(1)分别过点,B E 作,BS AD ER AD ⊥⊥,垂足分别为,S R ,勾股定理解Rt ARE △即可; (2)连接BH ,过点N 作NT AD ⊥于点T ,设BAN α∠=,经过角度的变换得出BAN HDB ∠=∠,再证明ATN △≌HGD △,得出,AN HD =,结合已知条件,继而证BAN ≌BDH △,得出ABN DBH ∠=∠,NB HB =,进而得到NBH △是等腰直角三角形,从而得证;(3)分别作,AD AQ 的中垂线,交于点O ,根据作图,先判断MQ 最大的时候的位置, 进而由12QH AH =,42AD =,构造直角三角形,勾股定理求得,AH HD ,从而求得△ADH 的面积 . 【详解】(1)如图,分别过点,B E 作,BS AD ER AD ⊥⊥,垂足分别为,S RAB BD ⊥,AB BD =,22AB =ABD ∴是等腰直角三角形,ASB △是等腰直角三角形224AD AB BD ∴=+=∴122AS SD AD ===,2BS AS == 四边形ABCD 是平行四边形 //AD BC ∴,BS AD ER AD ⊥⊥,1BE =∴四边形SBER 是矩形 ∴SR BE =1=,2RE SB ==3AR AS SR ∴=+= 在Rt ARE △中22223213AE AR RE =+=+=(2)连接BH ,过点N 作NT AD ⊥于点T ,设BAN α∠=BAD 是等腰直角三角形 45BAD BDA ∴∠=∠=︒45HAD BAD BAN α∴∠=∠-∠=︒-DH AE ⊥,9045ADH HAD α∴∠=︒-∠=︒+4545HDB ADH ADB αα∴∠=∠-∠=︒+-︒=BAN HDB ∴∠=∠ NT AD ⊥9090(45)45ANT HAD αα∴∠=︒-∠=︒-︒-=︒+,90ATN ∠=︒ANT ADH HDG ∴∠=∠=∠ HG AD ⊥ 90HGD ∴∠=︒ ATN HGD ∴∠=∠又45BDA ∠=︒9045DMG MDG ∴∠=︒-∠=︒ GD GM ∴=//MN AD ,HG AD ⊥,NT AD ⊥∴四边形TNMG 是矩形GM TN ∴= TN GD ∴=在ATN △和HGD △中ANT HDG TN GDATN HGD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ATN △≌HGD △(ASA )AN HD ∴=在BAN 和BDH △中 AB BD BAN HDB AN HD =⎧⎪∠=∠⎨⎪=⎩∴BAN ≌BDH △(SAS )ABN DBH ∴∠=∠,NB HB =ABN NBD DBH NBD ∠+∠=∠+∠ 即ABD NBH ∠=∠AB BD ⊥ 90ABD ∴∠=︒90NBH ∴∠=︒NBH ∴△是等腰直角三角形∴222NH BN BH BN =+=即2NH BN =(3)分别作,AD AQ 的中垂线,交于点O ,由题意,当点E 在线段BC 上运动时,AQD ∠不变,AD 的长度不变,则,,A D Q 三点共圆,则点Q 在以O 为圆心OQ 为半径的圆上运动,DH AE ⊥,12QH AH =tan 2AHAQD QH∴∠== 在OMQ 中MQ MO OQ ≤+∴当,,M O Q 三点共线时,MQ 取得最大值,此时情形如图:,AB BD BM AD =⊥∴AM MD =,,M O Q 三点共线,∴点Q 在AB 的垂直平分线上QA QD ∴=DH AE ⊥,tan 2AHAQDQH∠== 设QH x =,则AH 2x = 5AQ x ∴=QD =5DH x x ∴=-42AD =222AH DH AD ∴+= 即222(2)(5)(42)x x x +-=得:255x =-△ADH 的面积12AH DH =⋅ 12(5)2x x x =⨯⋅-2(51)x =165=(51)555=- ∴当QM 取最大值时,△ADH 165【点睛】本题考查了平行四边形的性质,矩形的性质与判定,等腰三角形的性质,垂直平分线的性质,圆的性质,勾股定理,三角形三边关系,三角形全等的证明与性质,动点问题等,本题是一道综合性比较强的题,熟练平面几何的性质定理是解题的关键. 24.(1),;(2);(3)①;②存在,或或或 【解析】 【分析】(1)分别使,,代入,即可求出点、的坐标;(2)把代入直线,可求,可得C 点的坐标,再把C 点坐标代入直线,即可得出的值; (3)①根据解析:(1)(2,0)A -,(0,2)B ;(2)4,5m b ==;(3)①7t =;②存在,4t =或12t =-1242t或8t=【解析】 【分析】(1)分别使0x =,0y =,代入2y x =+,即可求出点A 、B 的坐标;(2)把(2,)C m 代入直线2y x =+,可求m ,可得C 点的坐标,再把C 点坐标代入直线12y x b =-+,即可得出b 的值;(3)①根据ACP ∆的面积公式列等式可得t 的值; ②存在,分三种情况:.a 当AC CP =时,如图①,.b 当AC AP =时,如图②,.c 当AP PC =时,如图③,分别求t 的值即可. 【详解】解(1)在2y x =+中 当0x =时,2y = 当0y =时,2x =-(2,0)A ∴-,(0,2)B(2)点(2,)C m 在直线2y x =+上224m ∴=+=又点(2,4)C 也在直线12y x b =-+上∴即1452x解得5b =(3)在152y x =-+中当0x =时,10x = (10,0)D ∴(2,0)A -12AD ∴=①设PD t =,则12AP t 过C 作CE AP ⊥于E ,则4CE =由ACP ∆的面积为10 得1(12)4102t 解得7t =②过C 作CE AP ⊥于E 则4CE =,4AE =42AC ∴=.a 当AC CP =时,如图①所示则28AP AE4PDAD AP4t ∴=.b 当1242AP AP AC时,如图②所示11242DP t,21242DP t.c 当CP AP =时,如图③所示设EP a 则224CPa ,4AP a2244a a解得0a =4AP ∴=8PD8t ∴=综上所述,当4t =或1242t =-或1242t 或8t =时,ACP ∆为等腰三角形【点睛】本题属于一次函数综合题,涉及的知识有:待定系数法求一次函数解析式,坐标与图形性质,勾股定理,等腰三角形的判定,以及一次函数与坐标轴的交点,熟练掌握性质及定理是解本题的关键,并注意运用分类讨论的思想解决问题.25.(I) ;(II) 16或10;(III) . 【解析】 【分析】(I)根据已知条件直接写出答案即可.(II)分两种情况:或讨论即可.(III)根据已知条件直接写出答案即可.【详解】(I解析:(I) ;(II) 16或10;(III) .【解析】【分析】(I)根据已知条件直接写出答案即可.(II)分两种情况:或讨论即可.(III)根据已知条件直接写出答案即可.【详解】(I) ;(II)∵四边形是矩形,∴,.分两种情况讨论:(i)如图1,当时,即是以为腰的等腰三角形.(ii)如图2,当时,过点作∥,分别交与于点、.∵四边形是矩形,∴∥,.又∥,∴四边形是平行四边形,又,'⊥,∴□是矩形,∴,,即B H CD又,∴,,∵,∴,∴,在Rt ΔEGB '中,由勾股定理得:,∴,在中,由勾股定理得:,综上,的长为16或10.(III) . (或).【点睛】本题主要考查了四边形的动点问题.26.(1),理由见解析;(2),理由见解析;(3) 【分析】(1)由翻折的性质可知:,,然后证明为等腰直角三角形,从而得到,故此可证得;(2)由翻折的性质得到,,,由三角形外角的性质可证明,从而得到解析:(1)AB AC CD =+,理由见解析;(2)AB AC CD =+,理由见解析;(3)3632-【分析】(1)由翻折的性质可知:AE AC =,DE DC =,然后证明BED 为等腰直角三角形,从而得到BE ED =,故此可证得AB AC CD =+;(2)由翻折的性质得到AE AC =,DE DC =,C AED ∠=∠,由三角形外角的性质可证明B EDB ∠=∠,从而得到BE ED =,于是可证明AB AC CD =+;(3)过点B 作BH AC ⊥,垂足为H ,由直角三角形性质和勾股定理可求得CH 的长,从而得到AC 的长,设DE m =,则EF m =,32CE m =,求解即可.根据222CF EF CE +=,建立方程求解即可. 【详解】解:(1)AB AC CD =+.理由如下: 如图①,290C B ∠=∠=︒,45B ∴∠=︒,由翻折的性质可知:AE AC =,DE CD =,90C AED ∠=∠=︒, ∴18090BED AED ∠=︒-∠=︒,45B ∠=︒,90BED ∠=︒,45EDB ∴∠=︒, 45B EDB ∴∠=∠=︒, BE ED ∴=,BE CD ∴=,AB AE BE =+,AB AC CD ∴=+;(2)AB AC DC =+.理由如下:如图②,由翻折的性质得:AE AC =,DE DC =,C AED ∠=∠,B EDB AED ∠+∠=∠,2C B ∠=∠, B BDE ∴∠=∠, BE ED ∴=,BE DC ∴=,AB AE BE =+,AB AC DC ∴=+;(3)如图,过点B 作BH AC ⊥,垂足为H .120B ∠=︒,3AB BC ==,30BCA BAC ∴∠=∠=︒. BH AC ⊥,90BHC,1322BH BC ∴==, 在Rt BCH △中,22223333()2CH BC BH --, AB BC =,BH AC ⊥,CH HA ∴=.332233AC CH ∴== 在Rt ACD △中,3AD BC ==,AC 33=90D ∠=︒,2222(33)332CD AC AD ∴--由折叠得:3AF AD ==,EF DE =,90AFE D ∠=∠=︒,333CF AC AF ∴=-=,18090CFE AFE ∠=︒-∠=︒,设DE m =,则EF m =,32CE m =, 在Rt CEF △中,222CF EF CE +=,222(333)(32)m m ∴+=,解得:3632m -=DE ∴3632- 【点睛】本题是三边形综合题,主要考查的是翻折的性质、三角形外角的性质、等腰三角形三线合一的性质、直角三角形性质,勾股定理的应用,灵活运用相关图形的性质是解题的关键.。
人教版八年级数学下册期末试卷(培优篇)(Word版含解析)

人教版八年级数学下册期末试卷(培优篇)(Word 版含解析)一、选择题1.下列式子中不一定是二次根式的是( )A .3B .4C .aD .2a2.在ABC 中,三边长分别为a ,b ,c ,且2a c b +=,12c a b -=,则ABC 是( )A .直角三角形B .等边三角形C .等腰三角形D .等腰直角三角形3.如图,四边形ABCD 中,对角线AC 、BD 交于点O ,下列条件能证明四边形ABCD 是平行四边形的有( )①AB ∥DC ,AD ∥BC ;②AB =DC ,AD =BC ;③AO =CO ,BO =DO ;④AB ∥DC ,AD =BC ;⑤AB ∥DC ,AB =CD ;⑥∠BAD =∠BCD ,∠ABC =∠AD C .A .3个B .4个C .5个D .6个4.为了解居民用水情况,在某小区随机抽查记录了20户家庭的月用水量,汇总结果如表: 月用水量(吨) 45 6 8 9户数1 2 13 3 1则关于这20户家庭的月用水量,下列说法正确的是( )A .月用水量的众数是9吨 B .月用水量的众数是13吨 C .月用水量的中位数是6吨 D .月用水量的平均数是6吨 5.下列是勾股数的有( )① 3、4、5;② 5、12 、13;③ 9、40 、41;④ 13、14、15;71017、、⑥ 11 、60 、61 A .6组B .5组C .4组D .3组6.如图,在Rt ABC 中,∠C =90°,AC =6,BC =9,点D 为BC 边上的中点,将ACD 沿AD 对折,使点C 落在同一平面内的点C '处,连接BC ',则BC '的长为( )A .92B .275C .32D .237.□ABCD 的对角线AC 、BD 相交于点O ,AE 平分∠BAD 交BC 于点E , 且∠ADC =60°,AB =12BC ,连接OE .有下列结论:①∠CAD =30°; ②S □ABCD = AB ·AC ; ③OB =AB ; ④OE =12AB .其中成立的有( ).A .1个 B .2个C .3个D .4个8.如图1,动点P 从菱形ABCD 的顶点A 出发,沿A →C →D 以1cm /s 的速度运动到点D .设点P 的运动时间为(s ),△PAB 的面积为y (cm 2).表示y 与x 的函数关系的图象如图2所示,则a 的值为( )A 5B .52C .2D .5二、填空题9.(1)当x _____3x - (223a b ==,用含a ,b 0.54________.10.已知一个菱形有一个内角为120︒,周长为16cm ,那么该菱形的面积等于________ . 11.如图,一木杆在离地面1.5m 处折断,木杆顶端落在离木杆底端2m 处,则木杆折断之前的高___(m ).12.如图,在矩形ABCD中,点E在AD上,且EC平分BED∠,若1AB=,45EBC∠=︒,则DE的长为__________.13.已知一次函数y=kx﹣b,当自变量x的取值范围是1≤x≤3时,对应的因变量y的取值范围是5≤y≤10,那么k﹣b的值为_______.14.如图,矩形ABCD中,对角线AC=8cm,rAOB是等边三角形,则AD的长为______cm.15.如图,CD是直线33y x=上的一条动线段,且2CD=,点()23,1A+,连接AC、AD,则ACD∆周长的最小值是_______.16.一条笔直的公路上顺次有、、A B C三地,小军早晨5:00从A地出发沿这条公路骑自行车前往C地,同时小林从B地出发沿这条公路骑摩托车前往A地,小林到地后休息了1个小时, 然后掉头原路原速返回追赶小军,经过一段时间后两人同时到达C 地,设两人行驶的时间为x (小时),两人之间的距离为y (千米), y 与x 之间的函数图像如图所示,下列说法:①小林与小军的速度之比为2:1;②10:00时,小林到达A 地;③21:00时,小林与小军同时到达C 地;④BC 两地相距420千米,其中正确的有_________(只填序号)三、解答题17.计算 (1)()()1202131351274π-⎛⎫---++-- ⎪⎝⎭(2)148348542÷-⨯+ 18.如图,一架长2.5m 的梯子AB 斜靠在墙AC 上,∠C =90°,此时,梯子的底端B 离墙底C 的距离BC 为0.7m(1)求此时梯子的顶端A 距地面的高度AC ;(2)如果梯子的顶端A 下滑了0.9m ,那么梯子的底端B 在水平方向上向右滑动了多远?19.如图,每个小正方形的边长都为1,AB 的位置如图所示. (1)在图中确定点C ,请你连接CA ,CB ,使CB ⊥BA ,AC =5;(2)在完成(1)后,在图中确定点D ,请你连接DA ,DC ,DB ,使CD 10AD =17BD 的长.20.如图,在△ABC 中,AD 是BC 边上的中线,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F ,连接CF . (1)求证:AF =DC ;(2)若AB ⊥AC ,AB =8,AC =6,求BF 的长.21.743+743+7212+437+=,4312⨯=,即:22(4)(3)7+=,4312=2227437212(4)243(3)((43)23++=+⨯+=+=问题:(1423+=__________526-=____________﹔(22m n ±a ,b (a b >),使a b m +=,ab n =,即22(()a b m +=a b n =2m n ±=__________.(3415-22.为丰富同学们的课余活动,某校成立了篮球课外兴趣小组,计划购买一批篮球,需购买A 、B 两种不同型号的篮球共300个.已知购买3个A 型篮球和2个B 型篮球共需340元,购买2个A 型篮球和1个B 型篮球共需要210元. (1)求购买一个A 型篮球、一个B 型篮球各需多少元?(2)若该校计划投入资金W 元用于购买这两种篮球,设购进的A 型篮球为t 个,求W 关于t 的函数关系式;(3)学校在体育用品专卖店购买A 、B 两种型号篮球共300个,经协商,专卖店给出如下优惠:A 种球每个降价8元,B 种球打9折,计算下来,学校共付费16740元,学校购买A 、B 两种篮球各多少个?23.已知如图1,四边形ABCD是正方形,.如图1,若点分别在边上,延长线段CB至G,使得,若求EF的长;如图2,若点分别在边延长线上时,求证:如图3,如果四边形ABCD不是正方形,但满足且,请你直接写出BE 的长.24.如图1,在平面直角坐标系xOy中,直线AB交y轴于点A(0,3),交x轴于点B(﹣4,0).(1)求直线AB的函数表达式;(2)如图2,在线段OB上有一点C(点C不与点O、点B重合),将AOC沿AC折叠,使点O落在AB上,记作点D,在BD上方,以BD为斜边作等腰直角三角形BDF,求点F 的坐标;(3)在(2)的条件下,如图3,在平面内是否存在一点E,使得以点A,B,E为顶点的三角形与ABC全等(点E不与点C重合),若存在,请直接写出满足条件的所有点E的坐标,若不存在,请说明理由.25.如图,在平面直角坐标系中,点A(1,4),点B(3,2),连接OA,OB.(1)求直线OB与AB的解析式;(2)求△AOB的面积.(3)下面两道小题,任选一道作答.作答时,请注明题号,若多做,则按首做题计入总分.①在y轴上是否存在一点P,使△PAB周长最小.若存在,请直接写出....点P坐标;若不存在,请说明理由.②在平面内是否存在一点C,使以A,O,C,B为顶点的四边形是平行四边形.若存在,请直接写出....点C坐标;若不存在,请说明理由.26.在直角坐标系xOy中,四边形ABCD是矩形,点A在x轴上,点C在y轴的正半轴BC=.上,点B,D分别在第一,二象限,且3AB=,4=.(1)如图1,延长CD交x轴负半轴于点E,若AC AE①求证:四边形ABDE为平行四边形②求点A的坐标.(2)如图2,F为AB上一点,G为AD的中点,若点G恰好落在y轴上,且CG平分∠,求AF的长.DCF(3)如图3,x 轴负半轴上的点P 与点Q 关于直线AD 对称,且AP AD =,若BCQ △的面积为矩形ABCD 面积的18,则BQ 的长可为______(写出所有可能的答案).【参考答案】一、选择题 1.C 解析:C 【分析】根据二次根式的性质即可判断. 【详解】342a a a 可能为负数,故不一定是二次根式故选C . 【点睛】此题主要考查二次根式的识别,解题的关键是熟知二次根式的定义.2.A解析:A 【分析】根据平方差公式,可得222c a b -= ,即可求解. 【详解】解:∵2a c b +=,12c a b -=,∴()()122a c c ab b +-=⋅ , 即222c a b -= , ∴222+=a b c , ∴ABC 是直角三角形. 故选: A . 【点睛】本题主要考查了勾股定理的逆定理,平方差公式,熟练掌握若一个三角形的两边的平方和等于第三边的平方是解题的关键.3.C解析:C 【解析】 【分析】由平行四边形的判定方法分别对各个条件进行判断即可. 【详解】解:①∵AB ∥DC ,AD ∥BC , ∴四边形ABCD 是平行四边形; ②∵AB =DC ,AD =BC , ∴四边形ABCD 是平行四边形; ③∵AO =CO ,BO =DO , ∴四边形ABCD 是平行四边形;④由AB ∥DC ,AD =BC ,不能判定四边形ABCD 是平行四边形; ⑤∵AB ∥DC ,AB =CD , ∴四边形ABCD 是平行四边形; ⑥∵∠BAD =∠BCD ,∠ABC =∠ADC , ∴四边形ABCD 是平行四边形;能证明四边形ABCD 是平行四边形的有5个, 故选:C . 【点睛】此题考查的是平行线的判定定理,掌握平行线的判定定理是解题的关键.4.C解析:C 【解析】 【分析】根据表格中的数据,可以得到这组数据的中位数,众数和平均数,从而可以解答本题. 【详解】解:由表格中的数据可得,月用水量的众数是6吨,故选项A 、B 错误;月用水量的中位数是(6+6)÷2=6(吨),故选项C 正确;月用水量的平均数是:4152613839120⨯+⨯+⨯+⨯+⨯=6.25(吨),故选项D错误;故选:C.【点睛】本题考查众数、中位数和加权平均数,解答本题的关键是计算出这组数据的平均数和中位数.5.C解析:C【分析】根据勾股定理的逆定理分别进行计算,然后判断即可.【详解】解:①2223+4=5,故3、4、5是勾股数;②2225+12=13,故5、12 、13是勾股数;③2229+40=41,故9、40 、41是勾股数;④22213+1415≠,故13、14、15不是勾股数;⑤222⑥22211+60=61,故11 、60 、61是勾股数是勾股数的共4组故选:C【点睛】本题考查了了勾股数,关键是找出数据之间的关系,掌握勾股定理逆定理.6.B解析:B【解析】【分析】由折叠的性质可得AD⊥CC',CN=C'N,由勾股定理可求AD,DN的长,即可求BC'的长.【详解】解:如图,连接CC',∵将△ACD沿AD对折,使点C落在同一平面内的点C'处,∴AD⊥CC',CN=C'N,∵点D为BC边上的中点,∴CD=12BC=92152∵S△ACD=12×AC×CD=12×AD×CN ∴CN=185∴DN=2227 = 10CD CN-,∵CN=C'N,CD=DB,∴C'B=2DN=275,故选:B.【点睛】本题考查翻折变换,勾股定理,三角形中位线定理,利用勾股定理可求DN的长是本题的关键.7.C解析:C【解析】【分析】由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=12BC,得到AE=12BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S▱ABCD=AB•AC,故②正确,根据AB=12BC,OB=12BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=12AB,故④正确.【详解】∵四边形ABCD是平行四边形,∴∠ABC=∠ADC=60°,∠BAD=120°,∵AE平分∠BAD,∴∠BAE=∠EAD=60°∴△ABE是等边三角形,∴AE=AB=BE,∵AB=12BC,∴AE=12BC,∴∠BAC=90°,∴∠CAD=30°,故①正确;∵AC⊥AB,∴S▱ABCD=AB•AC,故②正确,∵AB =12BC ,OB =12BD ,∵BD >BC ,∴AB ≠OB ,故③错误;∵CE =BE ,CO =OA ,∴OE =12AB ,故④正确.故①②④正确,共3个.故选C【点睛】本题考查了平行四边形的性质,等边三角形的判定和性质,直角三角形的性质,平行四边形的面积公式,熟练掌握性质定理和判定定理是解题的关键. 8.B解析:B【分析】由图2知,菱形的边长为a ,对角线BD 为当点P 在线段AC 上运动时,y 12=AP 12⨯BD 12=,即可求解. 【详解】解:由图2知,菱形的边长为a ,对角线AC =则对角线BD 为= 当点P 在线段AC 上运动时,y 12=AP 12⨯BD 12=,由图2知,当x =y =a ,即a 12= 解得:a 52=, 故选:B .【点睛】本题考查的是动点图象问题,涉及到函数、解直角三角形等知识,此类问题关键是:弄清楚不同时间段,图象和图形的对应关系,进而求解.二、填空题9. x ≥0且x ≠9310ab 【解析】(1)根据二次根式的被开方数是非负数、分式的分母不为0列出不等式,解不等式即可. (2)利用二次根式的性质进而化简用含a 、b 的式子表示0.54即可. 【详解】 解:(1)∵式子13x -有意义, ∴由题意得,x ≥0,30x -≠,解得,x ≥0且x ≠9;(2)∵2,3a b ==, ∴543632330.54100101010ab ⨯⨯====; 故答案为:x ≥0且x ≠9;310ab . 【点睛】 本题考查的是二次根式有意义的条件、分式有意义的条件,掌握二次根式的被开方数是非负数是解题的关键.10.E解析:283cm【解析】【分析】作AE BC ⊥于E ,由三角函数求出菱形的高AE ,再运菱形面积公式=底×高计算即可;【详解】作AE BC ⊥于E ,如图所示,∵四边形ABCD 是菱形,周长为16cm ,120BCD ∠=︒,∴4AB BC cm ==,60B ∠=︒,∴()3sin 4sin 60423AE AB B cm ==⨯︒=⨯=, ∴菱形的面积()242383BC AE cm ==⨯=. 故答案为283cm .【点睛】本题主要考查了菱形的性质,结合三角函数的计算是解题的关键.11.4【分析】由题意得,在直角三角形中,知道两直角边,运用勾股定理即可求出斜边,从而得出这根木杆折断之前的高度.【详解】解:∵一木杆在离地面1.5m处折断,木杆顶端落在离木杆底端2m处,∴折断的部分长为,∴折断前高度为2.5+1.5=4(m).故答案为4.【点睛】本题考查勾股定理的应用,主要考查学生对勾股定理在实际生活中的运用能力.12.D1【分析】由矩形的性质和角平分线的定义得出∠DEC=∠ECB=∠BEC,推出BE=BC,求得AE=AB=1,然后依据勾股定理可求得BC的长;【详解】解:∵四边形ABCD是矩形,∴AD∥BC,∴∠DEC=∠BCE,∵EC平分∠DEB,∴∠DEC=∠BEC,∴∠BEC=∠ECB,∴BE=BC,∵四边形ABCD是矩形,=∴∠A=90°,AD BC∵∠ABE=45°,∴∠ABE=∠AEB=45°,∴AB=AE=1,由勾股定理得:BE==,∴BC=AD=BE,∴=-,1DE AD AE1.【点睛】本题考查了矩形的性质,等腰三角形的性质与判定,勾股定理的应用;熟练掌握矩形的性质,证出BE=BC是解题的关键.13.5或10【分析】本题分情况讨论①k>0时,x=1时对应y=5;②k>0时,x=1时对应y=10.【详解】解:①k>0时,由题意得:x=1时,y=5,∴k-b=5;②k<0时,由题意得:x=1时,y=10,∴k-b=10;综上,k-b的值为5或10.故答案为:5或10.【点睛】本题考查了待定系数法求函数解析式,注意本题需分两种情况,不要漏解.14.A解析:【详解】∵△AOB是等边三角形,∴∠BAC=60°,∴∠ACB=30°,∵AC=8cm,∴AB=4cm,在Rt△ABC中,,∵AD=BC,∴AD的长为.15.+2.【分析】过点A作AB⊥CD,垂足为点B,当点B为CD的中点时,△ACD的周长最小,利用等腰三角形的性质,勾股定理计算即可.【详解】过点A作AB⊥CD,垂足为点B,当点B为CD的中点时,解析:.【分析】过点A作AB⊥CD,垂足为点B,当点B为CD的中点时,△ACD的周长最小,利用等腰三角形的性质,勾股定理计算即可.【详解】过点A作AB⊥CD,垂足为点B,当点B为CD的中点时,△ACD的周长最小,如图,延长BA交x轴与点E,过点A作AF⊥x轴,垂足为点F,设点M(3y=上一个点,则OM∴∠MOF=30°,∴∠BEF=60°,∠EAF=30°,∵A(1),∴OF AF=1,设AE=2n,则EF=n,根据勾股定理,得2241=+,n n∴EF AE∴OE=OF+EF=2+433,∴BE=12OE=1+233,∴BA=BE-AE=1+233-233=1,∵CB=BD,AB⊥CD,CD=2,∴AC=AD22BC BA+CB=BD=1,∴AC=AD22112+=∴△ACD的周长最小值为2.故答案为:22.【点睛】本题考查了正比例函数的解析式,勾股定理,直角三角形中30°角的性质,等腰三角形的判定和性质,两点间的距离公式,准确确定最小值的情形,并灵活运用勾股定理求解是解题的关键.16.②④【分析】根据第一段图像可求得两人的速度和,结合第二段图像可求得小林的速度,进而可得小军的速度,由此可判断①;根据“时间=路程÷速度”可判断②;根据“时间=路程差÷速度差”可判断③、④.【详解析:②④【分析】根据第一段图像可求得两人的速度和,结合第二段图像可求得小林的速度,进而可得小军的速度,由此可判断①;根据“时间=路程÷速度”可判断②;根据“时间=路程差÷速度差”可判断③、④.【详解】解:由题意可得v林+v军=300÷3=100(千米/小时)200÷100=2(小时)则v林=300÷(2+3)=60(千米/小时)v 军=100-60=40(千米/小时)∴v 林:v 军=60:40=3:2,∴①错误;∵300÷60=5(小时)5+5=10,∴②正确;∵40×(3+2+1)=240(千米)240÷(60-40)=12(小时)5+3+2+1+12=23∴小林和小军在23:00到达C 地,∴③错误;∵12×60-300=420,∴④正确.故答案为:②④.【点睛】本题考查了一次函数的应用,理解函数图象上点的实际意义是解决本题的关键.三、解答题17.(1)2;(2)【分析】(1)原式利用绝对值、有理数的乘方、零指数幂、负整数指数幂以及立方根定义计算即可求出值;(2)根据二次根式的性质化简,然后再进行计算即可;【详解】解:(1)==解析:(1)2;(2)4【分析】(1)原式利用绝对值、有理数的乘方、零指数幂、负整数指数幂以及立方根定义计算即可求出值;(2)根据二次根式的性质化简,然后再进行计算即可;【详解】解:(1))()1020211314π-⎛⎫--++- ⎪⎝⎭=31413-+--=2(2==4-=4【点睛】本题主要考查了实数的运算,关键是熟练掌握立方根和算术平方根.18.(1)2.4米;(2)1.3m【分析】(1)直接利用勾股定理求出AC的长,进而得出答案;(2)直接利用勾股定理得出B′C,进而得出答案.【详解】解:(1)∵∠C=90°,AB=2.5,BC解析:(1)2.4米;(2)1.3m【分析】(1)直接利用勾股定理求出AC的长,进而得出答案;(2)直接利用勾股定理得出B′C,进而得出答案.【详解】解:(1)∵∠C=90°,AB=2.5,BC=0.7,∴AC=(米),2.4答:此时梯顶A距地面的高度AC是2.4米;(2)∵梯子的顶端A下滑了0.9米至点A′,∴A′C=AC−A′A=2.4−0.9=1.5(m),在Rt△A′CB′中,由勾股定理得:A′C2+B′C2=A′B′2,∴1.52+B′C2=2.52,∴B′C=2(m),∴BB′=CB′−BC=2−0.7=1.3(m),答:梯子的底端B在水平方向滑动了1.3m.【点睛】此题主要考查了勾股定理的实际应用,熟练掌握勾股定理是解题关键.19.(1)见解析;(2).【解析】【分析】(1)利用网格即可确定C点位置;(2)由勾股定理在Rt△DBG中,可求BD的长.【详解】解:(1)如图,∴∴BC⊥AB,在Rt△ACH中,A解析:(1)见解析;(2)26.【解析】【分析】(1)利用网格即可确定C点位置;(2)由勾股定理在Rt△DBG中,可求BD的长.【详解】解:(1)如图,222===AB BC AC5,20,25,∴222+=AB BC AC∴BC⊥AB,在Rt△ACH中,AC=5;(2)∵CD=10,AD=17,可确定D点位置如图,∴在Rt△DBG中,BD=26.【点睛】本题考查勾股定理的应用,利用三角形内角和确定C点位置,由勾股定理确定D点的位置是解题的关键.20.(1)见解析;(2)【分析】(1)由“AAS”可证△AFE≌△DBE,可得AF=BD=DC;(2)先证四边形AOFH是矩形,可得AH=FO=4,AO=FH=3,再在直角三角形FHB中,由勾股定解析:(1)见解析;(2)317【分析】(1)由“AAS”可证△AFE≌△DBE,可得AF=BD=DC;(2)先证四边形AOFH是矩形,可得AH=FO=4,AO=FH=3,再在直角三角形FHB中,由勾股定理可求解.【详解】证明:(1)∵AF ∥BC ,∴∠AFE =∠DBE ,∵E 是AD 的中点,AD 是BC 边上的中线,∴AE =DE ,BD =CD ,在AFE △和DBE 中AFE DBE FEA BED AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AFE ≌△DBE (AAS ),∴AF =BD ,∴AF =DC ;(2)解:如图,连接DF 交AC 于点O ,过点F 作FH ⊥AB ,交BA 的延长线于H ,∵AF ∥BC ,AF =CD ,∴四边形ADCF 是平行四边形,∵AB ⊥AC ,AD 是中线,∴AD =CD ,∴四边形ADCF 是菱形,∴AC ⊥DF ,AO =CO =3,OF =O D =12DF ,∵AF ∥BC ,AF =BD ,∴四边形AFDB 是平行四边形,∴DF =AB =8,∴OF =OD =4,∵FH ⊥AB ,AB ⊥AC ,AC ⊥DF ,∴四边形AOFH 是矩形,∴AH =FO =4,AO =FH =3,∴8412BH BA AH =+=+=,∵FH ⊥AB ,∴三角形FHB 是直角三角形,∴在Rt FHB 中,根据勾股定理, 229144317BF FH BH =++=【点睛】本题考查了全等三角形的判定与性质,平行四边形的判定,菱形的判定,矩形的判定,直角三角形的性质,勾股定理,考查知识点较多,综合性较强,解题的关键是要掌握并灵活运用这些知识点.21.(1),;(2);(3)【解析】【分析】(1)根据题目所给的方法将根号下的数凑成完全平方的形式进行计算;(2)根据题目给的a,b与m、n的关系式,用一样的方法列式算出结果;(3)将写成,4解析:(112)a b>;(3【解析】【分析】(1)根据题目所给的方法将根号下的数凑成完全平方的形式进行计算;(2)根据题目给的a,b与m、n的关系式,用一样的方法列式算出结果;(34写成3522+,就可以凑成完全平方的形式进行计算.【详解】解:(11;(2)a b===>;(3.【点睛】本题考查二次根式的计算和化简,解题的关键是掌握二次根式的运算法则.22.(1)一个A型篮球为80元,一个B型篮球为50元;(2)函数解析式为:;(3)A型篮球120个,则B型篮球为180个.【分析】(1)设一个A型篮球为x元,一个B型篮球为y元,根据题意列出方程组求解析:(1)一个A型篮球为80元,一个B型篮球为50元;(2)函数解析式为:()30150000300W t t=+≤≤;(3)A型篮球120个,则B型篮球为180个.【分析】(1)设一个A型篮球为x元,一个B型篮球为y元,根据题意列出方程组求解即可得;(2)A型篮球t个,则B型篮球为()300t-个,根据单价、数量、总价的关系即可得;(3)根据A型篮球与B型篮球的优惠政策求出单价,然后代入(2)解析式中求解即可得.【详解】解:(1)设一个A 型篮球为x 元,一个B 型篮球为y 元,根据题意可得:323402210x y x y +=⎧⎨+=⎩, 解得:8050x y =⎧⎨=⎩, ∴一个A 型篮球为80元,一个B 型篮球为50元;(2)A 型篮球t 个,则B 型篮球为()300t -个,根据题意可得:()()805030030150000300W t t t t =+-=+≤≤,∴函数解析式为:()30150000300W t t =+≤≤;(3)根据题意可得:A 型篮球单价为()808-元,B 型篮球单价为500.9⨯元,则 ()()16740808500.9300t t =-+⨯⨯-,解得:120t =,300180t -=,∴A 型篮球120个,则B 型篮球为180个.【点睛】题目主要考查二元一次方程组及一次函数的应用,理解题意,列出相应方程是解题关键. 23.(1);(2)见解析;(3)【分析】(1)先用SAS 证ABG ≌ADF ,可得AG=AF ,∠BAG=∠DAF ,又可证∠EAG=∠EAF ,故可用SAS 证GAE ≌FAE ,EF=GE ,即EF 长度可求;(解析:(1);(2)见解析;(3) 【分析】(1)先用SAS 证ABG ≌ADF ,可得AG=AF ,∠BAG=∠DAF ,又可证∠EAG=∠EAF ,故可用SAS 证GAE ≌FAE ,EF=GE ,即EF 长度可求;(2)在DF 上取一点G,使得DG=BE, 连接AG ,先用SAS 证ABE ≌ADG ,可得AE=AG ,∠BAE=∠DAG ,又可证∠EAF=∠GAF ,故可用SAS 证AEF ≌AGF ,可得EF=GF ,且DG=BE ,故EF=DF-DG=DF-BE ; (3)在线段DF 上取BE=DG ,连接AG ,求证∠ABE=∠ADC ,即可用SAS 证ABE ≌ADG ,可得AE=AG ,∠BAE=∠DAG ,又可证∠EAF=∠GAF ,故可用SAS 证AEF ≌AGF ,可得EF=GF ,设BE=x ,则CE= 7+x ,EF=18-x ,根据勾股定理:,即可求得BE 的长度.【详解】解:(1)证明:如图1所示,在正方形ABCD 中,AB=AD ,∠BAD=90°,在ABG 和ADF 中,∴ABG≌ADF(SAS),∴AG=AF,∠BAG=∠DAF,又∵∠DAF+∠FAB=∠FAB+∠BAG=90°,且∠EAF=45°,∴∠EAG=∠FAG-∠EAF=45°=∠EAF,在GAE和FAE中,∴GAE≌FAE(SAS),∴EF=GE=GB+BE=2+3=5;(2)如下图所示,在DF上取一点G,使得DG=BE, 连接AG,∵四边形ABCD是正方形,故AB=AD,∠ABE=∠ADG=90°,在ABE和ADG中,∴ABE≌ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠BAG+∠DAG=90°,故∠BAG+∠BAE=90°,∵∠EAF=45°,故∠GAF=45°,∠EAF=∠GAF=45°,在AEF和AGF中,∴AEF≌AGF(SAS),∴EF=GF,且DG=BE,∴EF=DF-DG=DF-BE;(3)BE=5,如下图所示,在线段DF上取BE=DG,连接AG,∵∠BAD=∠BCD=90°,故∠ABC+∠ADC=180°,且∠ABC+∠ABE=180°,∴∠ABE=∠ADC,在ABE和ADG中,∴ABE≌ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠BAG+∠DAG=90°,故∠BAG+∠BAE=90°,∵∠EAF=45°,故∠GAF=45°,∠EAF=∠GAF=45°,在AEF和AGF中,∴AEF≌AGF(SAS),∴EF=GF,设BE=x,则CE=BC+BE =7+x,EF=GF=DC+CF-DG= DC+CF-BE=18-x,在直角三角形ECF中,根据勾股定理:,即:,解得x=5,∴BE=x=5.【点睛】本题主要考察了全等三角形的证明及性质、勾股定理,解题的关键在于添加辅助线,找出全等三角形,并用对应边/对应角相等的定理,解决该题.24.(1);(2);(3)或或【解析】【分析】(1)直接利用待定系数法,即可得出结论;(2)先求出AD=3,AB=5,进而求出点D的坐标,再构造出△BMF≌△FND,得出BM=FN,FM=DN,解析:(1)334y x =+;(2)197(,)55F -;(3)5(,3)2E -或3312(,)105-或73(,)105- 【解析】【分析】 (1)直接利用待定系数法,即可得出结论;(2)先求出AD =3,AB =5,进而求出点D 的坐标,再构造出△BMF ≌△FND ,得出BM =FN ,FM =DN ,设F (m ,n ),进而建立方程组求解,即可得出结论;(3)分两种情况,①当ABC ABE '≌时,利用中点坐标公式求解,即可得出结论;②当ABC BAE ≌时,当点E 在AB 上方时,根据AE ∥BC ,AE BC =即可得出结论;③当点E 在AB 下方时,过点E ''作E Q y ''⊥轴于Q ,过点B 作BP x ⊥轴,过点E '作E P BP '⊥,证明QAE PBE '''△≌△,即可得出结论.【详解】(1)设直线AB 的函数表达式为y kx b =+,直线AB 交y 轴于点A (0,3),交x 轴于点B (﹣4,0),403k b b -+=⎧∴⎨=⎩343k b ⎧=⎪∴⎨⎪=⎩ ∴直线AB 的函数表达式为334y x =+; (2)如图,过点D 分别引,x y 轴的垂线,交,x y 轴于,G H 两点,∵点A (0,3),点B (-4,0),∴OA =3,OB =4,∴AB 2234+=5,由折叠知,AD =OA =3,532DB ∴=-=设(,)D a b -(0,0)a b >>,DG b DH a ∴==,4,3BG a AH b =-=-222222,AD DH AH DB BG DG =+=+∴()()2222223342a b a b ⎧+-=⎪⎨-+=⎪⎩解得:436a b -=D 在334y x =+上,334b a ∴=-+ 4363412a b a b -=⎧∴⎨+=⎩ 解得12565a b ⎧=⎪⎪⎨⎪=⎪⎩, 126(,)55D ∴-, 过点F 作FM ⊥x 轴于M ,延长HD 交FM 于N ,∴∠BMF =∠FND =90°,∴∠BFM +∠FBM =90°,∵△BFD 是等腰直角三角形,∴BF =DF ,∠BFD =90°,∴∠BFM +∠DFN =90°,∴∠FBM =∠DFN ,∴△BMF ≌△FND (AAS ),∴BM =FN ,FM =DN ,设F (m ,n ), 则125645n m n m ⎧=--⎪⎪⎨⎪-=+⎪⎩ 19575m n ⎧=-⎪⎪∴⎨⎪=⎪⎩ 197(,)55F ∴-; (3)设OC =a ,则BC =4-a ,由折叠知,∠BDC =∠ADC =∠AOC =90°,CD =OC =a ,在Rt △BDC 中,222BC CD BD =+,∴()2244a a -=+, ∴a =32, 335(,0),,222C OC BC ∴-==, ∵点A ,B ,E 为顶点的三角形与△ABC 全等,①当△ABC ≌△ABE '时,∴BE '=BC ,∠ABC =∠ABE ',连接CE '交AB 于D ,则CD =E 'D ,CD ⊥AB ,由(1)知, 126(,)55D -设E '(b ,c ),∴131216(),(0)22525b c -=-+= ∴3312,105b c =-=, ∴3312(,)105E '-; ②当△ABC ≌BAE 时,当点E 在AB 上方时,∴AC =BE ,BC =AE ,EAB CBA =∠∠,∴AE ∥BC ,∴5(,3)2E -; ③当点E 在AB 下方时,AC =BE '',BC =AE '',ABC ABE '△≌△,∴BC BE '=,当ABC BAE ''△≌△时,ABE BAE '''∴△≌△,AE BE '''∴=,BAE ABE '''∠=∠,过点E ''作E Q y ''⊥轴于Q ,过点B 作BP x ⊥轴,过点E '作E P BP '⊥,//PB AQ ∴,90P AQE ''∠=∠=︒,PBA QAB ∴∠=∠,PBA ABE QAB BAE '''∴∠-∠=∠-,即PBE QAE '''∠=∠,90P AQE ''∠=∠=︒,QAE PBE '''∴△≌△,,PE QE AQ PE ''''∴==, 点3312(,)105E '-,(4,0)B -, ∴AQ PB ==125,PE QE '''==33741010-+=, 123355OQ ∴=-=, ∴73(,)105E ''-, ∴满足条件的点E 的坐标为5(,3)2E -或3312(,)105-或73(,)105-. 【点睛】本题考查了待定系数法,折叠的性质,等腰直角三角形的性质,全等三角形的判定和性质,平移的性质,勾股定理,中点坐标公式,构造出全等三角形,分类讨论是解题的关键.25.(1)直线OB 的解析式为,直线AB 的解析式为y= -x+5(2)5;(3)①存在,(0,);②存在,(2,-2)或(4,6)或(-2,2)【分析】(1)根据题意分别设出两直线的解析式,代入直线上解析:(1)直线OB 的解析式为23y x =,直线AB 的解析式为y = -x +5(2)5;(3)①存在,(0,72);②存在,(2,-2)或(4,6)或(-2,2)【分析】(1)根据题意分别设出两直线的解析式,代入直线上两点坐标即可求出直线OB 与AB 的解析式;(2)延长线段AB 交x 轴于点D ,求出D 的坐标,分别求出AOD S ∆、BOD S ∆由AOB AOD BOD S S S ∆∆∆=-即可求得;(3)①根据两点之间线段最短,A 、B 在y 轴同侧,作出点A 关于y 的对称点A ',连接A 'B 与y 轴的交点即为所求点P ;②使以A ,O ,C ,B 为顶点的四边形是平行四边形,则分三种情况分析,分别以OA 、AB 、OB 为对角线作出平行四边形,利用中点坐标公式代入求解即可.【详解】解:(1)设直线OB 的解析式为y =mx ,∵点B (3,2), ∴2223,,33m m y x === , ∴直线OB 的解析式为23y x =, 设直线AB 的解析式为y =kx +b ,根据题意可得:432k b k b +=⎧⎨+=⎩ 解之得15k b =-⎧⎨=⎩∴直线AB 的解析式为y = -x +5.故答案为:直线OB 的解析式为23y x =,直线AB 的解析式为y = -x +5; (2)如图,延长线段AB 交x 轴于点D ,当y =0时,-x +5=0,x =5,∴点D 横坐标为5,OD =5,∴11541022AOD A S OD y ∆=⨯⨯=⨯⨯=, 11525,22BOD B S OD y ∆=⨯⨯=⨯⨯= ∴5AOB AOD BOD S S S ∆∆∆=-=,故答案为:5.(3)①存在,(0,72); 过点A 作y 轴的对称点A ',连接A 'B ,交y 轴与点P ,则点P 即为使△PAB 周长最小的点, 由作图可知,点A '坐标为(1,4)-,又点B (3,2)则直线A 'B 的解析式为:1722y x =-+, ∴点P 坐标为7(0,)2, 故答案为:7(0,)2;②存在. (2,2)- 或(4,6)或(2,2)-.有三种情况,如图所示:设点C 坐标为(,)x y ,当平行四边形以AO 为对角线时,由中点坐标公式可知,AO 的中点坐标和BC 中点坐标相同,∴310240x y +=+⎧⎨+=+⎩解得22x y =-⎧⎨=⎩ ∴点1C 坐标为(2,2)-,当平行四边形以AB 为对角线时,AB 的中点坐标和OC 的中点坐标相同,则 031024x y +=+⎧⎨+=+⎩46x y =⎧⎨=⎩ ∴点2C 的坐标为(4,6),当平行四边形以BO 为对角线时,BO 的中点坐标和AC 的中点坐标相同,则 130420x y +=+⎧⎨+=+⎩解得22x y =⎧⎨=-⎩∴点3C 坐标为(2,2)-,故答案为:存在,(2,2)-或(4,6)或(2,2)-.【点睛】本题考查了直线解析式的求法,列二元一次方程组求解问题,割补法求三角形的面积,两点之间线段最短,“将军饮马”模型的应用,添加点构造平行四边形,利用中点坐标公式求点坐标题型.26.(1)①见解析;②;(2);(3)或【分析】(1)①利用三线合一定理证明ED=CD ,即可得到ED=AB ,由矩形的性质可以得到AE=AC=BD ,即可证明;②设A (a ,0),C (0,b ),利用勾股定解析:(1)①见解析;②7,05A ⎛⎫ ⎪⎝⎭;(2)43AF =;(34610【分析】(1)①利用三线合一定理证明ED =CD ,即可得到ED =AB ,由矩形的性质可以得到AE =AC =BD ,即可证明;②设A (a ,0),C (0,b ),利用勾股定理求出225AC AE AB BC ==+,则CE =CD +DE =6,E (a -5,0),则()222225102536EC a b a a b =-+=-++=,22225AC a b =+=,由此即可求解; (2)延长BA 到M 于y 轴交于M ,先证明△DGC ≌△AGM ,得到∠DCG =∠AMG ,AM =CD =AB =3,再由角平分线的定义即可推出CF =MF ,设AF =m ,则CF =MF =3+m ,BF =AB -AF =3-m ,由222CF CB BF =+,得到()()222343m m +=+-,解方程即可;(3)分Q 在矩形ABCD 内部和外部两种情况求解即可.【详解】解:(1)①∵四边形ABCD 是矩形,∴∠ADC =90°,AC =BD ,DC =AB∵AC =AE ,∴CD =ED ,AE =BD∴ED =AB ,∴四边形ABDE 是平行四边形;②设A (a ,0),C (0,b ),∵四边形ABCD 是矩形,∴∠ABC =90°,CD =AB =DE =3, ∴225AC AE AB BC ==+=,CE =CD +DE =6,∴E (a -5,0),∴()222225102536EC a b a a b =-+=-++=,22225AC a b =+=, ∴25102536a -+=,解得75a =, ∴7,05A ⎛⎫ ⎪⎝⎭;(2)如图,延长BA 到M 于y 轴交于M ,∵G 为AD 中点,∴AG =DG ,∵四边形ABCD 是矩形,∴∠D =∠DAB =∠GAM =∠B =90°,又∵∠DGC =∠AGM ,∴△DGC ≌△AGM (ASA ),∴∠DCG =∠AMG ,AM =CD =AB =3∵CG 平分∠DCF ,∴∠DCG =∠FCM =∠AMG ,∴CF =MF ,设AF =m ,则CF =MF =3+m ,BF =AB -AF =3-m ,∵222CF CB BF =+,∴()()222343m m +=+-解得43m =, ∴43AF =;(3)当Q 在矩形内部时,如图所示,过点Q 作QE ⊥BC 于E ,延长EQ 交AD 于F ,连接AQ∵111===288BCQ ABCD S BC EQ S BC AB ⋅⋅△矩形, ∴1344EQ AB ==; ∵BC ∥AD ,EF ⊥AD ,BA ⊥AD ,∴EF ∥AB ,∴四边形ABEF 是矩形,∴EF =AB =3,BE =AF ,∴94FQ EF EQ =-=, ∵点P 与点Q 关于直线AD 对称,且AP =AD ,∴AP =AD =AQ =4∴222281=1616AF BE AQ FQ =-=-,22281923=1616162BQ BE EQ +=-+=, ∴462BQ =;当Q 在矩形ABCD 的外部时,如图所示过点Q 作QE ⊥BC 于E ,延长QE 交AD 于F ,连接AQ同理求得1344EQ AB ==,154FQ EF EQ =+=, ∴2222225=1616AF BE AQ FQ =-=-, ∴22222595=1616162BQ BE EQ +=-+=, ∴10BQ = ∴综上所述,46BQ =10 4610 【点睛】 本题主要考查了矩形的性质,勾股定理,两点距离公式,等腰三角形的性质与判定,平行四边形的判定等等,解题的关键在于能够熟练掌握相关知识进行求解.。
人教版八年级下册数学期末试卷(培优篇)(Word版含解析)

人教版八年级下册数学期末试卷(培优篇)(Word 版含解析) 一、选择题 1.式子2x -在实数范围内有意义,则x 的取值范围是( )A .0x ≥B .0x <C .2x ≤D .2x ≥ 2.下列各比值中,是直角三角形的三边之比的是( )A .1:2:3B .2:3:4C .3:4:5D .1:3:1 3.下列命题:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线相等的四边形是矩形;③对角线互相垂直平分的四边形是菱形;④对角线互相垂直的矩形是正方形.其中真命题的个数是( )A .1B .2C .3D .44.某校对八年级8个班学生平均一周的课外阅读时间进行了统计,分别为(单位:h ):3.5,4,3,4,3,3.5,3,5.这组数据的中位数和众数是( )A .3.5,3B .4,3C .3,4D .3,3.5 5.如图的网格中,每个小正方形的边长为1,A ,B ,C 三点均在格点上,结论错误的是( )A .AB=25B .∠BAC=90°C .ABC S 10=D .点A 到直线BC 的距离是2 6.如图,在菱形ABCD 中,M ,N 分别在AB ,CD 上,且AM =CN ,MN 与AC 交于点O ,连接BO .若∠DAC =28°,则∠OBC 的度数为( )A .28°B .52°C .62°D .72°7.如图,在ABC 中,点D E 、分别是AB AC 、的中点,10,AC =点F 是DE 上一点,1DF =.连接AF CF 、,若90,AFC ∠︒=则BC 的长度为( )A .8B .10C .12D .148.甲、乙两位同学住在同一小区,学校与小区相距2700米.一天甲从小区步行出发去学校,12分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米,图中的折线表示甲、乙两人之间的距离y (米)与甲步行时间x (分钟)的函数关系图象.则( )A .乙骑自行车的速度是180米/分B .乙到还车点时,甲,乙两人相距850米C .自行车还车点距离学校300米D .乙到学校时,甲距离学校200米二、填空题9.化简:()()2223x x ---=______10.若菱形的周长为20cm ,一个内角为60︒,则菱形的面积为___________. 11.如图 ,在△ ABC 中,∠C =90°,∠ABC 的平分线 BD 交 AC 于点 D .若 BD =10cm ,BC =8cm ,则点 D 到直线 AB 的距离= ________.12.如图,在Rt ABC △中,90ACB ∠=︒,CD AB ⊥于点D ,3ACD BCD ∠=∠,点E 是斜边AB 的中点,若2CD =,则CE 的长为_____.13.在平面直角坐标中,点A (﹣3,2)、B (﹣1,2),直线y =kx (k ≠0)与线段AB 有交点,则k 的取值范围为___.14.在矩形ABCD 中,∠B 的平分线BE 与AD 交于点E ,∠BED 的平分线EF 与DC 交于点F ,若AB =9,DF =2FC ,则BC =___________.(结果保留根号)15.如图,在平面直角坐标系中,函数y =2x 和y =﹣x 的图象分别为直线l 1,l 2,过点(1,0)作x 轴的垂线交l l 于点A 1,过点A 1作y 轴的垂线交l 2于点A 2,过点A 2作x 轴的垂线交l 1于点A 3,过点作y 轴的垂线交l 2于点A 4,…依次进行下去.则点A 4的坐标为__;点6A 的坐标为_____;点A 2021的坐标为____.16.如图,在平面直角坐标系中,直线334y x =+交x 轴于点A 、交y 轴于点B ,C 点与A 点关于y 轴对称,动点P 、Q 分别在线段AC 、AB 上(点P 不与点A 、C 重合),满足BPQ BAO ∠=∠.当PQB △为等腰三角形时,点P 的坐标是_____.三、解答题17.计算:(1)(520+|25(﹣1)2021;(26363147.18.小王与小林进行遥控赛车游戏,终点为点A ,小王的赛车从点C 出发,以4米/秒的速度由西向东行驶,同时小林的赛车从点B 出发,以3米/秒的速度由南向北行驶(如图).已知赛车之间的距离小于或等于25米时,遥控信号会产生相互干扰,AC =40米,AB =30米.出发3秒钟时,遥控信号是否会产生相互干扰?19.如图,每个小正方形的边长都为1,AB 的位置如图所示.(1)在图中确定点C ,请你连接CA ,CB ,使CB ⊥BA ,AC =5;(2)在完成(1)后,在图中确定点D ,请你连接DA ,DC ,DB ,使CD =10,AD =17,直接写出BD 的长.20.在△ABC 中,∠ACB =90°,∠BAC =30°,D 为AB 的中点,四边形BCED 为平行四边形,DE ,AC 相交于F .连接DC ,AE .(1)试确定四边形ADCE 的形状,并说明理由.(2)若AB =16,AC =12,求四边形ADCE 的面积.(3)当△ABC 满足什么条件时,四边形ADCE 为正方形?请给予证明.21.阅读下列材料,然后回答问题: 3+1,通常有如下两种方法将其进一步化简: 方法一()())()22231231313+13+13131==--方法二:()()()22313+1312=31 3+13+13+1--==-(1)请用两种不同的方法化简:253 +;(2)化简:2222 42648620122010 +++⋅⋅⋅+++++.22.甲、乙两个服装厂加工同种型号的防护服,甲厂每天加工的数量是乙厂每天加工的数量的1.5倍,两厂各加工600套防护服,甲厂比乙厂少用4天.(1)求甲、乙两厂每天各加工多少套防护服?(2)已知甲、乙两厂加工这种防护服每天的费用分别是150元和120元.期间,某医院急需3000套这种防护服,甲厂单独加工一段时间后另有安排,剩下的任务只能由乙厂单独完成.设甲厂加工m天,乙厂加工y天.①求y关于m的函数关系式.②如果加工总费用不超过6360元,那么甲厂至少要加工多少天?23.如图平行四边形ABCD,E,F分别是AD,BC上的点,且AE=CF,EF与AC交于点O.(1)如图①.求证:OE=OF;(2)如图②,将平行四边形ABCD(纸片沿直线EF折叠,点A落在A1处,点B落在点B1处,设FB交CD于点G.A1B分别交CD,DE于点H,P.请在折叠后的图形中找一条线段,使它与EP相等,并加以证明;(3)如图③,若△ABO是等边三角形,AB=4,点F在BC边上,且BF=4.则=(直接填结果).24.如图1,直线y=kx+b经过第一象限内的定点P(3,4).(1)若b=7,则k=_______;(2)如图2,直线y=kx+b与y轴交于点C,已知点A(6,t),过点A作AB//y轴交第一象限内的直线y=kx+b于点B,连接OB,若BP平分∠OBA.①证明OBC是等腰三角形;②求k的值;(3)如图3,点M是x轴正半轴上的一个动点,连接PM,把线段PM绕点M顺时针旋转90°至线段NM(∠PMN=90°且PM=MN),连接OP,ON,PN,当OPN周长最小时,求点N的坐标;25.如图,在矩形 ABCD中, AB=16 , BC=18 ,点 E在边 AB 上,点 F 是边 BC 上不与点B、C 重合的一个动点,把△EBF沿 EF 折叠,点B落在点 B' 处.(I)若 AE=0 时,且点 B' 恰好落在 AD 边上,请直接写出 DB' 的长;(II)若 AE=3 时,且△CDB' 是以 DB' 为腰的等腰三角形,试求 DB' 的长;(III)若AE=8时,且点 B' 落在矩形内部(不含边长),试直接写出 DB' 的取值范围.26.已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.试探究下列问题:(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.【参考答案】一、选择题1.D解析:D【分析】由二次根式的性质可以得到x-2≥0,由此即可求解.【详解】解:依题意得:x-2≥0,∴x≥2.故选D.【点睛】此题主要考查了二次根式有意义的条件,根据被开方数是非负数即可解决问题.2.C解析:C【分析】先分别设三角形的三边,依据勾股定理的逆定理列式计算即可判断.【详解】解:A、设三边分别为x、2x、3x,∵222x x x+≠,(2)(3)∴三边比为1:2:3的三角形不是直角三角形;B、设三边分别为2x、3x、4x,∵222+≠,x x x(2)(3)(4)∴三边比为2:3:4的三角形不是直角三角形;C、设三边分别为3x、4x、5x,∵222+=,(3)(4)(5)x x x∴三边比为3:4:5的三角形是直角三角形;D、设三边分别为x、3x、x,∵222+≠,(3)x x x∴三边比为1:3:1的三角形不是直角三角形;故选:C.【点睛】此题考查应用勾股定理的逆定理判断三角形是否是直角三角形,熟记定理并应用解决问题是解题的关键.3.B解析:B【解析】【分析】根据平行四边形、矩形、菱形和正方形的判定直接进行判断即可.【详解】解:①一组对边平行且相等的四边形是平行四边形,原命题是假命题;②对角线相等的平行四边形是矩形,原命题是假命题;③对角线互相垂直平分的四边形是菱形,是真命题;④对角线互相垂直的矩形是正方形,是真命题;故选:B.【点睛】本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.4.A解析:A【解析】【分析】据众数和中位数的定义求解即可,中位数:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.众数:在一组数据中出现次数最多的数.【详解】将3.5,4,3,4,3,3.5,3,5从小到大排列为:3,3,3,3.5,3.5,4,4,5.其中3出现的次数最多,则众数为3,中位数为:3.5 3.53.52+=.故选A.【点睛】本题考查了求众数和中位数,理解众数和中位数的定义是解题的关键.5.C解析:C【分析】根据勾股定理以及其逆定理和三角形的面积公式逐项分析即可得到问题答案.【详解】解:A正确,不符合题意;∵AC=BC5==,∴22252025AC AB BC+=+==,∴△ACB是直角三角形,∴∠CAB=90°,故选项B正确,不符合题意;S△ABC111442421345222=⨯-⨯⨯-⨯⨯-⨯⨯=,故选项C错误,符合题意;点A到直线BC的距离25525AC ABBC===,故选项D正确,不符合题意;故选:C.【点睛】本题考查了勾股定理以及逆定理的运用,在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么 222+=a b c .熟记勾股定理的内容是解题得关键.6.C解析:C【解析】【分析】根据菱形的性质以及AM =CN ,利用ASA 可得△AMO ≌△CNO ,可得AO =CO ,然后可得BO ⊥AC ,继而可求得∠OBC 的度数.【详解】解:∵四边形ABCD 为菱形,∴AB ∥CD ,AB =BC ,∴∠MAO =∠NCO ,∠AMO =∠CNO ,在△AMO 和△CNO 中,∵ MAO NCO AM CN AMO CNO ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AMO ≌△CNO (ASA ),∴AO =CO ,∵AB =BC ,∴BO ⊥AC ,∴∠BOC =90°,∵∠DAC =28°,∴∠BCA =∠DAC =28°,∴∠OBC =90°﹣28°=62°.故选:C .【点睛】本题考查了菱形的性质和全等三角形的判定和性质,注意掌握菱形对边平行以及对角线相互垂直的性质.7.C解析:C【解析】【分析】根据直角三角形的性质求出EF ,进而求出DE ,根据三角形中位线定理计算,得到答案.【详解】解:90AFC ∠=︒,点E 是AC 的中点,10AC =,1110522EF AC ∴==⨯=, 1DF =,6DE DF EF ∴=+=,点D 、E 分别是AB 、AC 的中点,212BC DE ∴==,故选:C .【点睛】本题考查的是直角三角形的性质、三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.8.C解析:C【分析】根据函数图象中的数据可以求得甲步行的速度、乙骑自行车的速度、乙一共所用的时间,从而得出乙步行的速度、自行车还车点与学校的距离,求出乙到还车点时,甲、乙所用的时间,即可得出路程差,根据乙到学校时,所用时间为19分,此时甲所用的时间为31分,则可求出甲距学校的路程.【详解】由图可得:甲步行的速度为:960÷12=80(米/分),乙骑自行车的速度为:[960+(20-12)×80]÷(20-12)=200(米/分),故A 错误; 乙步行的速度为:80-5=75(米/分)乙一共所用的时间:31-12=19(分)设自行车还车点距学校x 米,则:27001920075x x ++= 解得:x =300.故C 正确;乙到还车点时,乙所用时间为:(2700+300)÷200=15(分)乙到还车点时,甲所用时间为:12+15=27(分)路程差=2700+300-80×27=840(米),故B 错误;乙到学校时,所用时间为19分,而甲所用的时间=12+19=31(分),甲距学校的路程=2700-80×31=220(米),故D 错误.故选C .【点睛】本题考查了根据函数图象获取信息,解答本题的关键是明确题意,利用数形结合的思想解答.二、填空题9.-1【解析】【分析】根据二次根式有意义的条件,求出x 的范围,再根据二次根式的性质和绝对值的性质化简,即可得到答案.【详解】由2x -可知20x -≥,∴2x ≤,30x ∴-<()()222323x x x x ---=---,∴()2323231x x x x x x ---=---=--+=-故答案为:1-.【点睛】本题考查了二次根式化简求值,正确掌握二次根式有意义的条件,二次根式的性质,绝对值的性质是解题关键.10.A解析:2253cm 2【解析】【分析】由菱形的性质和已知条件得出AB =BC =CD =DA =5cm ,AC ⊥BD ,由含30°角的直角三角形的性质得出BO =12AB =52cm ,由勾股定理求出OA ,可得BD ,AC 的长度,由菱形的面积公式可求解.【详解】解:如图所示:∵四边形ABCD 是菱形,∴AB =BC =CD =DA ,∠BAO =12∠BAD =30°,AC ⊥BD ,OA =12AC ,BO =DO ∵菱形的周长为20cm ,∴AB =BC =CD =DA =5cm ,∴BO =12AB =52cm , ∴OA 22AB OB -532cm ), ∴AC =2OA =53cm ,BD =2BO =5cm∴菱形ABCD 的面积=12AC ×BD 2253.故答案是:2253cm 2. 【点睛】 本题考查了菱形的性质、含30°角的直角三角形的性质、勾股定理;熟练掌握菱形的性质,并能进行推理计算是解决问题的关键.11.D 解析:6cm【解析】【分析】过点D 作DE ⊥AB 于E ,利用勾股定理列式求出CD ,再根据角平分线上的点到角的两边距离相等可得DE=CD 即可求解.【详解】如图,过点D 作DE ⊥AB 于E ,∵∠C=90°,BD=10cm ,BC=8cm ,∴226BD BC -cm ,∵∠C=90°,BD 是∠ABC 的平分线,∴DE=CD=6cm ,即点D 到直线AB 的距离是6cm .故答案为:6cm .【点睛】本题考查了勾股定理、角平分线的性质、点到直线的距离等知识,在解题时要能灵活应用各个知识点是本题的关键.12.2【分析】根据角之间的关系求得45DEC ∠=︒,从而求得CE 的长.【详解】解:∵3ACD BCD ∠=∠,90ACB ∠=︒∴22.5BCD ∠=︒又∵CD AB ⊥∴9022.5BCD B BAC ∠=︒-∠=∠=︒,90CDE ∠=︒又∵点E 是斜边AB 的中点∴CE AE =∴22.5ECA BAC ∠=∠=︒∴45BEC ∠=︒∴CDE △为等腰直角三角形 ∴2CE故答案为2.【点睛】此题主要考查了直角三角形的有关性质,熟练掌握勾股定理、斜边中线等于斜边一半等性质是解题的关键.13.B 解析:2-2-3k ≤≤【分析】分别把B 点和A 点坐标代入y =kx (k ≠0)可计算出对应的k 的值,从而得到k 的取值范围.【详解】解:∵直线y =kx (k ≠0)与线段AB 有交点,∴当直线y =kx (k ≠0)过B (-1,2)时,k 值最小,则有-k =2,解得k =-2,当直线y =kx (k ≠0)过A (-3,2)时,k 值最大,则-3k =2,解得k =2-3, ∴k 的取值范围为2-2-3k ≤≤ 故答案为:2-2-3k ≤≤ 【点睛】本题考查了一次函数的应用和性质,解题的关键是运用数形结合的思想进行转化解题. 14.E解析:3【分析】先延长EF 和BC ,交于点G ,再根据条件可以判断三角形ABE 为等腰直角三角形,并求得其斜边BE 的长,然后根据条件判断三角形BEG 为等腰三角形,最后根据△EFD ∽△GFC 得出CG 与DE 的倍数关系,并根据BG=BC+CG 进行计算即可.【详解】延长EF 和BC ,交于点G .∵矩形ABCD 中,∠B 的角平分线BE 与AD 交于点E ,∴∠ABE=∠AEB=45°,∴AB=AE=9,∴直角三角形ABE 中,又∵∠BED 的角平分线EF 与DC 交于点F ,∴∠BEG=∠DEF .∵AD ∥BC ,∴∠G=∠DEF ,∴∠BEG=∠G ,∴BG=BE=92. 由∠G=∠DEF ,∠EFD=∠GFC ,可得△EFD ∽△GFC ,∴122CG CF CF DE DF CF ===. 设CG=x ,DE=2x ,则AD=9+2x=BC .∵BG=BC+CG ,∴92=9+2x+x ,解得x=32-3,∴BC=9+2(32-3)=62+3.故答案为62+3.考点:矩形的性质;等腰三角形的判定;相似三角形的判定与性质.15.(4,﹣4) (﹣8,8) (21010,21011)【分析】根据一次函数图象上点的坐标特征可得出点A1、A2、A3、A4、A5、A6、A7、A8等的坐标,根据坐标的变化找出解析:(4,﹣4) (﹣8,8) (21010,21011)【分析】根据一次函数图象上点的坐标特征可得出点A 1、A 2、A 3、A 4、A 5、A 6、A 7、A 8等的坐标,根据坐标的变化找出变化规律“A 4n+1(22n ,22n+1),A 4n+2(-22n+1,22n+1),A 4n+3(-22n+1,-22n+2),A 4n+4(22n+2,-22n+2)(n 为自然数)”,依此规律结合6=1×4+2;2021=505×4+1即可找出点A 2021的坐标.【详解】解:观察,发现规律:A 1(1,2),A 2(-2,2),A 3(-2,-4),A 4(4,-4),A 5(4,8),…,∴“A 4n+1(22n ,22n+1),A 4n+2(-22n+1,22n+1),A 4n+3(-22n+1,-22n+2),A 4n+4(22n+2,-22n+2)(n 为自然数)”,∵6=1×4+2,A 6(﹣8,8)∵2021=505×4+1,∴A 2021的坐标为(21010,21011).故答案为:(4,﹣4); (﹣8,8);(21010,21011).【点睛】本题考查了一次函数图象上点的坐标特征以及规律型中坐标的变化,解题的关键是找出变化规律“A 4n+1(22n ,22n+1),A 4n+2(-22n+1,22n+1),A 4n+3(-22n+1,-22n+2),A 4n+4(22n+2,-22n+2)(n 为自然数)”.16.(1,0),(−,0)【分析】分三种情况考虑:当PQ =PB 时,可得△APQ ≌△CBP ,确定出此时P 的坐标;当BQ =BP 时,利用外角性质判断不可能;当BQ =PQ 时,设OP=x ,则AP =4+x ,BP解析:(1,0),(−78,0) 【分析】分三种情况考虑:当PQ =PB 时,可得△APQ ≌△CBP ,确定出此时P 的坐标;当BQ =BP时,利用外角性质判断不可能;当BQ =PQ 时,设OP=x ,则AP =4+x ,BP 而求出此时P 的坐标即可.【详解】 解:对于直线334y x =+,令x =0,得到y =3;令y =0,得到x =−4,∴A (−4,0),B (0,3),即OB =3,∵A 与C 关于y 轴对称,∴C (4,0),即OC =4,则根据勾股定理得:BC =5=;∵C 点与A 点关于y 轴对称,∴∠BAO=∠BCO ,∵BPQ BAO ∠=∠,∴∠BPQ=∠BCO ,又∵∠BCO+∠CBP=∠BPQ+∠APQ ,∴∠CBP =∠APQ ,(i )当PQ =PB 时,则△APQ ≌△CBP ,∴AP =CB =5,∴OP =1,∴此时点P (1,0);(ii )当BQ =BP 时,∠BQP =∠BPQ ,∵∠BQP 是△APQ 的外角,∴∠BQP >∠BAP ,又∵∠BPQ=∠BAO,∴这种情况不可能;(iii)当BQ=PQ时,∠QBP=∠QPB,又∵∠BPQ=∠BAO,∴∠QBP=∠BAO,∴AP=BP,设OP=x,则AP=4+x,BP∴4+x解得:x=−78.此时点P的坐标为:(−78,0).综上,P的坐标为(1,0),(−78,0).故答案是:(1,0),(−78,0).【点睛】此题属于一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,坐标与图形性质,等腰三角形的性质,全等三角形的判定与性质,熟练掌握性质与判定是解本题的关键.三、解答题17.(1)﹣2;(2)3+.【分析】(1)先化简零指数幂,绝对值,有理数的乘方,然后再计算;(2)先利用平方差公式,二次根式的除法运算法则计算乘除,最后算加减.【详解】解:(1)原式=1+﹣2解析:(12;(2)【分析】(1)先化简零指数幂,绝对值,有理数的乘方,然后再计算;(2)先利用平方差公式,二次根式的除法运算法则计算乘除,最后算加减.【详解】解:(1)原式=2﹣12;(2)22=6﹣=【点睛】本题考查二次根式的混合运算,零指数幂,掌握二次根式混合运算的运算顺序和计算法则及平方差公式(a +b )(a ﹣b )=a 2﹣b 2的结构是解题关键.18.不会【分析】根据题意可分别求出出发3秒钟时小王和小林的赛车行驶的路程,从而可分别求出他们的赛车距离终点的距离,再结合勾股定理即可求出出发3秒钟时他们赛车的距离,和遥控信号会产生相互干扰的距离小于解析:不会【分析】根据题意可分别求出出发3秒钟时小王和小林的赛车行驶的路程,从而可分别求出他们的赛车距离终点的距离,再结合勾股定理即可求出出发3秒钟时他们赛车的距离,和遥控信号会产生相互干扰的距离小于或等于25米作比较即可得出答案.【详解】解:如图,出发3秒钟时,11423CC =⨯=米,1393BB =⨯=米,∵AC =40米,AB =30米,∴AC 1=28米,AB 1=21米,∴在11Rt AB C 中,22221111282135B C AC AB =+=+=米>25米,∴出发3秒钟时,遥控信号不会产生相互干扰.【点睛】本题考查勾股定理的实际应用.读懂题意,将实际问题转化为数学问题是解答本题的关键.19.(1)见解析;(2).【解析】【分析】(1)利用网格即可确定C 点位置;(2)由勾股定理在Rt △DBG 中,可求BD 的长. 【详解】解:(1)如图,∴∴BC ⊥AB ,在Rt △ACH 中,A解析:(1)见解析;(226【分析】(1)利用网格即可确定C点位置;(2)由勾股定理在Rt△DBG中,可求BD的长.【详解】解:(1)如图,222===AB BC AC5,20,25,∴222+=AB BC AC∴BC⊥AB,在Rt△ACH中,AC=5;(2)∵CD=10,AD=17,可确定D点位置如图,∴在Rt△DBG中,BD=26.【点睛】本题考查勾股定理的应用,利用三角形内角和确定C点位置,由勾股定理确定D点的位置是解题的关键.20.(1)四边形ADCE是菱形,见解析;(2);(3)当AC=BC时,四边形ADCE为正方形,见解析.【分析】(1)先证明四边形ADCE为平行四边形,进而证明AC⊥DE,即可证明四边形ADCE为菱形解析:(1)四边形ADCE是菱形,见解析;(2)2473)当AC=BC时,四边形ADCE为正方形,见解析.【分析】(1)先证明四边形ADCE为平行四边形,进而证明AC⊥DE,即可证明四边形ADCE为菱形;(2)勾股定理求得BC=7BC=DE,进而根据菱形的面积等于对角线乘积的一半进行求解即可;(3)根据∠ADC=90°,D为AB的中点,即可得AC=BC.解:(1)四边形ADCE是菱形理由:∵四边形BCED为平行四边形,∴CE//BD,CE=BD,BC//DE,∵D为AB的中点,∴AD=BD∴CE=AD又∵CE//AD,∴四边形ADCE为平行四边形∵BC//DF,∴∠AFD=∠ACB=90°,即AC⊥DE,∴四边形ADCE为菱形.(2)在Rt△ABC中,∵AB=16,AC=12,∴BC=∵四边形BCED为平行四边形,∴BC=DE,∴DE=∴四边形ADCE的面积=1AC·DE=2(3)当AC=BC时,四边形ADCE为正方形证明:∵AC=BC,D为AB的中点,∴CD⊥AB,即∠ADC=90°,∴四边形ADCE为矩形又∵BCED为平行四边形,∴BC=DE∴DE=AC∴四边形ADCE为正方形.【点睛】本题考查了平行四边形的性质,菱形的判定,正方形的性质与判定,勾股定理,掌握以上四边形的性质与判定是解题的关键.21.(1);(2)【解析】【分析】(1)首先理解题意,根据题目的解析,即可利用两种不同的方法化简求得答案;(2)结合题意,可将原式化为,继而求得答案.【详解】解:(1)方法一:方法二:;解析:(1(2)【解析】【分析】(1)首先理解题意,根据题目的解析,即可利用两种不同的方法化简求得答案;(2+2012-案.【详解】解:(1()()2222==-22-==(2)原式+2012-【点睛】本题考查了分母有理化的知识.此题难度较大,解题的关键是理解题意,掌握分母有理化的两种方法.22.(1)甲厂每天加工75套防护服,乙厂每天加工50套防护服;(2)①y =﹣m+60;②甲厂至少要加工28天【分析】(1)设乙厂每天加工x套防护服,则甲厂每天加工1.5x套防护服,根据“两厂各加工6解析:(1)甲厂每天加工75套防护服,乙厂每天加工50套防护服;(2)①y=﹣32m+60;②甲厂至少要加工28天【分析】(1)设乙厂每天加工x套防护服,则甲厂每天加工1.5x套防护服,根据“两厂各加工600套防护服,甲厂比乙厂要少用4天”列出方程,解之即可;(2)①根据“某医院急需3000套这种防护服”和“设甲厂加工m天,乙厂加工y天”列出方程,即可得到y关于m的函数关系式;②根据“甲、乙两厂加工这种防护服每天的费用分别是150元和120元”和“总加工费不超过6360元”列出不等式,求出m的取值范围即可.【详解】解:(1)设乙厂每天加工x套防护服,则甲厂每天加工1.5x套防护服.根据题意得:60060041.5x x=-,解得x=50,经检验:x=50是原方程的解,且符合题意,∴1.5x=1.5×50=75,答:甲厂每天加工75套防护服,乙厂每天加工50套防护服;(2)①根据题意得:75m+50y=3000,∴y=32-m+60;②根据题意得:150m+120×(32-m+60)≤6360,解得m≥28,答:甲厂至少要加工28天.【点睛】本题考查了分式方程与不等式的应用,关键是理清楚题目意思,建立方程或不等式求解.注意解分式方程后要验根.23.(1)见解析;(2)FG=EP,理由见解析;(3)【分析】(1)证△ODE≌△OFB(ASA),即可得出OE=OF;(2)连AC,由(1)可知OE=OF,OB=OD,证△AOE≌△COF(SA解析:(1)见解析;(2)FG=EP,理由见解析;(3【分析】(1)证△ODE≌△OFB(ASA),即可得出OE=OF;(2)连AC,由(1)可知OE=OF,OB=OD,证△AOE≌△COF(SAS),得AE=CF,由折叠性质得AE=A1E=CF,∠A1=∠BAD=∠BCD,∠B=∠B1,则∠D=∠B1,证△A1PE≌△CGF (AAS),即可得出FG=EP;(3)作OH⊥BC于H,证四边形ABCD是矩形,则∠ABC=90°,得∠OBC=30°,求出AC=8,由勾股定理得BC=,则CF=-4,由等腰三角形的性质得BH=CH=12BC=HF=,OH=12OB=2,由勾股定理得OF=,进而得出答案.【详解】解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠ODE=∠OBF,∠OED=∠OFB,∵AE=CF,∴AD-AE=BC-CF,即DE=BF,在△ODE和△OFB中,,∴△ODE≌△OFB(ASA),∴OE=OF;(2)FG=EP,理由如下:连AC,如图②所示:由(1)可知:OE=OF,OB=OD,∵四边形ABCD是平行四边形,∴AC过点O,OA=OC,∠BAD=∠BCD,∠D=∠B,在△AOE和△COF中,,∴△AOE≌△COF(SAS),∴AE=CF,由折叠性质得:AE=A1E=CF,∠A1=∠BAD=∠BCD,∠B=∠B1,∴∠D=∠B1,∵∠A1PE=∠DPH,∠PHD=∠B1HG,∴∠DPH=∠B1GH,∵∠B1GH=∠CGF,∴∠A1PE=∠CGF,在△A1PE和△CGF中,,∴△A1PE≌△CGF(AAS),∴FG=EP;(3)作OH⊥BC于H,如图③所示:∵△AOB是等边三角形,∴∠ABO=∠AOB=∠BAO=60°,OA=OB=AB=4,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∴AC=BD,∴四边形ABCD是矩形,∴∠ABC=90°,∴∠OBC=∠OCB=30°,∵AB=OB=BF=4,∴AC=BD=2OB=8,由勾股定理得:BC==,∴CF=-4,∵OB=OC,OH⊥BC,∴BH=CH=12BC=23,∴HF=4-23,OH=12OB=2,在Rt△OHF中,由勾股定理得:OF===,∴,故答案为:2.【点睛】本题是四边形综合题,考查了平行四边形的性质、矩形的判定与性质、翻折变换的性质、全等三角形的判定与性质、等腰三角形的性质、含30°角的直角三角形的性质、等边三角形的性质、勾股定理等知识;本题综合性强,解题的关键是准确寻找全等三角形解决问题,学会添加常用辅助线,属于中考压轴题.24.(1)-1;(2)①证明见详解;②;(3)(,)【解析】【分析】(1)把P(3,4),b=7代入y=kx+b中,可得k=-1(2)①根据平行的性质:内错角相等,证明∠OCB=∠OBC,由等角解析:(1)-1;(2)①证明见详解;②34-;(3)(7715,2815-)【解析】【分析】(1)把P(3,4),b=7代入y=kx+b中,可得k=-1(2)①根据平行的性质:内错角相等,证明∠OCB=∠OBC,由等角对等边得到OBC是等腰三角形②根据坐标证明P是BC的中点,由等腰三角形三线合一性质得OP⊥BC,求出OP函数关系式中k的值,根据两个一次函数图像互相垂直时k的关系,求解出直线BC的表达式中的k=3 4 -(3)根据动点M的运动情况分析出N的轨迹函数,然后证明△OHG是等腰直角三角形,根据中点坐标公式求得直线O’P的表达式,联立方程求出N点坐标【详解】(1)把P(3,4),b=7代入y=kx+b中,可得4=3k+7解得k=-1故答案为-1(2)①∵AB∥y轴∴∠ABC=∠OCB∵BP平分∠OBA∴∠OBC=∠ABC∴∠OCB=∠OBC∴OBC是等腰三角形②如图4所示,连接OP∵AB//y轴,A(6,t)∴B点横坐标是6∵P横坐标是3∴P是BC的中点∴OP⊥BC设直线OP的表达式为y=kx将P(3,4)代入得4=3k解得k= 43,则设直线BC的表达式中的k=3 4 -.故答案为3 4 -.(3)①如图5-1,当点M与O重合时,作PE⊥y轴于点E,作NF⊥y轴于点F∵PM ⊥NM∴∠PMN=90°∴∠PME+∠NMF=90°∵∠FMN+∠FNM=90°∴∠PME=∠MNF在△PEM △MFN 中=PME MNF PEM MFN PM MN ∠=∠⎧⎪∠∠⎨⎪=⎩∴△PEO ≌△OFN (AAS )∴MF=PE=3,FN=ME=4则N 点的坐标为(4,-3)②如图5-2所示,,当PM ⊥x 轴时,N 点在x 轴上,则MN=PM=3,ON=OM+MN=7,∴N 的坐标为(7,0)综上所述得点N 在直线y=x-7的直线上运动设直线y=x-7与坐标轴分别交于点G 、H ,作O 关于直线HG 的对称点O`,连接O`P 交直线HG 于点N ,此时ON+PN 有最小值,最小值为线段O`P 的长度.如图5-3所示.当直线y=x-7可得H(0,-7),G(7,0),OG=OH,△OHG是等腰直角三角形,当OQ⊥HG时,Q是HG的中点,由中点坐标公式可得Q(72,-72),∵O`与O对称∴Q是OO`的中点由中点坐标公式可得O’(7,-7),∴可得直线O’P的表达式为1149y x44=-+联立方程1149447x xy x⎧=+⎪⎨⎪=-⎩﹣,解得77152815 xy⎧=⎪⎪⎨⎪=-⎪⎩∴N点坐标为(7715,2815-)∴当△OPN周长最小时,点N的坐标为(7715,2815-)故答案为(7715,2815-)【点睛】本题考查的是一次函数综合运用,涉及到三角形全等、角平分线的性质,平行的性质等,熟练掌握数形结合的解题方法是解决此题目的关键,综合性强,难度较大.25.(I) ;(II) 16或10;(III) .【解析】【分析】(I)根据已知条件直接写出答案即可.(II)分两种情况:或讨论即可.(III)根据已知条件直接写出答案即可.【详解】(I解析:(I) ;(II) 16或10;(III) .【解析】【分析】(I)根据已知条件直接写出答案即可.(II)分两种情况:或讨论即可.(III)根据已知条件直接写出答案即可.【详解】(I) ;(II)∵四边形是矩形,∴,.分两种情况讨论:(i)如图1,当时,即是以为腰的等腰三角形.(ii)如图2,当时,过点作∥,分别交与于点、.∵四边形是矩形,∴∥,.又∥,∴四边形是平行四边形,又,'⊥,∴□是矩形,∴,,即B H CD又,∴,,∵,∴,∴,在RtΔEGB 中,由勾股定理得:,∴,在中,由勾股定理得:,综上,的长为16或10.(III) . (或).【点睛】本题主要考查了四边形的动点问题.26.(1)成立;(2)成立,理由见试题解析;(3)正方形,证明见试题解析.【详解】试题分析:(1)因为四边形ABCD为正方形,CE=DF,可证△ADF≌△DCE (SAS),即可得到AF=DE,∠DA解析:(1)成立;(2)成立,理由见试题解析;(3)正方形,证明见试题解析.【详解】试题分析:(1)因为四边形ABCD为正方形,CE=DF,可证△ADF≌△DCE(SAS),即可得到AF=DE,∠DAF=∠CDE,又因为∠ADG+∠EDC=90°,即有AF⊥DE;(2)∵四边形ABCD为正方形,CE=DF,可证△ADF≌△DCE(SAS),即可得到AF=DE,∠E=∠F,又因为∠ADG+∠EDC=90°,即有AF⊥DE;(3)设MQ,DE分别交AF于点G,O,PQ交DE于点H,因为点M,N,P,Q分别为AE,EF,FD,AD的中点,可得MQ=PN=12DE,PQ=MN=12AF,MQ∥DE,PQ∥AF,然后根据AF=DE,可得四边形MNPQ是菱形,又因为AF⊥DE即可证得四边形MNPQ是正方形.试题解析:(1)上述结论①,②仍然成立,理由是:∵四边形ABCD为正方形,∴AD=DC,∠BCD=∠ADC=90°,在△ADF和△DCE中,∵DF=CE,∠ADC=∠BCD=90°,AD=CD,∴△ADF≌△DCE(SAS),∴AF=DE,∠DAF=∠CDE,∵∠ADG+∠EDC=90°,∴∠ADG+∠DAF=90°,∴∠AGD=90°,即AF⊥DE;(2)上述结论①,②仍然成立,理由是:∵四边形ABCD为正方形,∴AD=DC,∠BCD=∠ADC=90°,在△ADF和△DCE中,∵DF=CE,∠ADC=∠BCD=90°,AD=CD,∴△ADF≌△DCE(SAS),∴AF=DE,∠E=∠F,∵∠ADG+∠EDC=90°,∴∠ADG+∠DAF=90°,∴∠AGD=90°,即AF⊥DE;(3)四边形MNPQ是正方形.理由是:如图,设MQ,DE分别交AF于点G,O,PQ交DE于点H,∵点M,N,P,Q分别为AE,EF,FD,AD的中点,∴MQ=PN=12DE,PQ=MN=12AF,MQ∥DE,PQ∥AF,∴四边形OHQG是平行四边形,∵AF=DE,∴MQ=PQ=PN=MN,∴四边形MNPQ是菱形,∵AF⊥DE,∴∠AOD=90°,∴∠HQG=∠AOD=90°,∴四边形MNPQ是正方形.。
人教版八年级数学下册期末试卷(培优篇)(Word版含解析)

人教版八年级数学下册期末试卷(培优篇)(Word 版含解析)一、选择题1.要使二次根式1x +有意义,则x 的取值范围是( )A .1≥xB .1x >C .1x ≥-D .1x >- 2.要做一个直角三角形的木架,以下面各组木棒为三边,刚好能做成的是( ) A .5,6,7B .10,4,8C .10,26,24D .9,15,173.在四边形ABCD 中,连接对角线AC ,已知AB =CD ,现增加一个条件,不能判断该四边形是平行四边形的是( ) A .AB ∥CD B .AD =BCC .∠B =∠DD .∠BAC =∠ACD4.某校进行广播操比赛,如图是20位评委给某班的评分情况统计图,则该班平均得分( )A .9B .6.67C .9.1D .6.745.如图,在Rt △ABC 中,∠BAC =90°,AB =3,AC =4,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 的中点,则AM 的最小值是( )A .2.4B .2C .1.5D .1.26.规定:菱形与正方形的接近程度叫做“接近度”,并用d 表示.设菱形的两个相邻内角分别为°α、°β,菱形的接近度定义为180d αβ=--.则下列说法不正确的是( ) A .接近度d 越大的菱形越接近于正方形 B .有一个内角等于100°的菱形的接近度160d = C .接近度d 的取值范围是0180d ≤≤ D .当180d =时,该菱形是正方形7.如图,在ABC 中,点D E 、分别是AB AC 、的中点,10,AC =点F 是DE 上一点,1DF =.连接AF CF 、,若90,AFC ∠︒=则BC 的长度为( )A .8B .10C .12D .148.如图1,在矩形ABCD 的边AD 上取一点E ,连接BE .点M ,N 同时以1cm/s 的速度从点B 出发,分别沿折线B -E -D -C 和线段BC 向点C 匀速运动.连接MN ,DN ,设点M 运动的时间为t s ,△BMN 的面积为S cm 2,两点运动过程中,S 与t 的函数关系如图2所示,则当点M 在线段ED 上,且ND 平分∠MNC 时,t 的值等于( )A .2+25B .4+25C .14﹣25D .12﹣25二、填空题9.若121xx -+有意义,则x 的取值范围为_______________. 10.若菱形的两条对角线的长分别为6和10,则菱形的面积为__________. 11.图中阴影部分是一个正方形,则此正方形的面积为_______ .12.如图,点E 是矩形纸片ABCD 的边BC 上的一动点,沿直线AE 折叠纸片,点B 落在点B '位置,连接C B '.若AB =3,BC =6,则线段C B '长度的最小值为 ________________.13.直线y kx b =+与x 轴、y 轴的交点分别为(1,0)-、(0,3)则这条直线的解析式为__________.14.如图,在ABC 中,点D 、E 、F 分别在边AB 、BC 、CA 上,且DE ∥CA ,DF ∥BA ,下列四种说法:①四边形AEDF 是平行四边形;②如果∠BAC =90°,那么四边形AEDF 是菱形;③如果AD 平分∠BAC ,那么四边形AEDF 是菱形;④如果AB =AC ,那么四边形AEDF 是菱形.其中,正确的有_____.(只填写序号)15.直线y =22x +3与两坐标轴围成的三角形面积是 __________________. 16.如图,在平面直角坐标系中,直线AB y ⊥轴,且()0,16A ,12AB =,过点B 作直线l 与y 轴负半轴交于点D .已知点A 关于直线l 的对称点为1A ,连结1BA ,并延长交x 轴于点C .当20BC =时,则点D 的坐标为_______.三、解答题17.计算 (1)18232+- (2)123273+-(3)(57)(57)2-++ (4)0214(37)8(12)2++⨯-- 18.学校需要测量升旗杆的高度.同学们发现系在旗杆顶端的绳子垂到了地面,并多出了段,但这条绳子的长度未知.经测量,绳子多出的部分长度为2m ,将绳子沿地面拉直,绳子底端距离旗杆底端6m (如图所示),求旗杆的高度.19.如图所示,在77⨯的方格纸中,每个小正方形的边长均为1,线段AB 的端点A 、B 均在小正方形的顶点上.(1)在图中画出以AB 为边的菱形ABCD ,菱形的面积为8;(2)在图中画出腰长为5的等腰三角形ABE ,且点E 在小正方形顶点上; (3)连接CE ,请直接写出线段CE 的长.20.如图,在△ABC 中,AD 是BC 边上的中线,点E 是AD 的中点,过点A 作AF ∥BC 交BE 的延长线于F ,连接CF . (1)求证:△AEF ≌△DEB ;(2)若∠BAC =90°,试判断四边形ADCF 的形状,并证明你的结论.21.[阅读材料]我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,为三角形和多边形的面积计算提供了新的方法和思路,在知道三角形三边的长而不知道高的情况下使用秦九韶公式可以更简便地求出面积,比如说在测量土地的面积的时候,不用测三角形的高,只需测两点间的距离,就可以方便地求出答案,即三角形的三边长分别为a 、b 、c ,则其面积S 2222221()42a b c a b ⎡⎤+--⎢⎥⎣⎦出一辙,即三角形的三边长分别为a 、b 、c ,记p =2a b c++,则其面积S =()()()p p a p b p c ---价的,计算各有优劣,它填补了中国数学史中的一个空白,从中可以看出中国古代已经具有很高的数学水平. [解决问题](1)当三角形的三边a =7,b =8,c =9时,请你从上面两个公式里,选择合适的公式计算出三角形的面积.(2)当三角形的三边a =7,b =22,c =3时,请你从上面两个公式里,选择合适的公式计算出三角形的面积.22.黄埔区某游泳馆推出以下两种收费方式. 方式一:顾客不购买会员卡,每次游泳付费40元.方式二:顾客先购买会员卡,每张会员卡800元,仅限本人一年内使用,凭卡游泳,每次游泳再付费20元.设你在一年内来此游泳馆游泳的次数为x 次,选择方式一的总费用为y 1(元),选择方式二的总费用为y 2(元). (1)请分别写出y 1,y 2与x 之间的函数表达式;(2)如果你在一年内来此游泳馆游泳的次数超过60次,为省钱,你选择哪种方式? 23.在菱形ABCD 中,点E 为边BC 的中点,,垂足为点, 垂足为点G .(1)如图①,求证:;(2)如图②,如图③,请分别写出线段之间的数量关系,不需要证明;(3)在(1)(2)的条件下,若菱形ABCD 的面积为,菱形ABCD 的周长为,四边形的面积为 ,线段DF 的长为 .24.如图,一次函数5y x =-+与坐标轴交于,A B 两点,将线段OB 以点O 为中心逆时针旋转一定角度,点B 的对应点落在第二象限的点C 处,且OBC 的面积为10.(1)求点C 的坐标及直线BC 的表达式;(2)点D 在直线AB 上第二象限内一点,在BCD △中有一个内角是45︒,求点D 的坐标; (3)过原点О的直线,与直线AB 交于点P ,与直线BC 交于点Q ,在,,O P Q 三点中,当其中一点是另外两点所连线段的中点时,求OCP △的面积.25.如图,已知平面直角坐标系中,1,0A 、()0,2C ,现将线段CA 绕A 点顺时针旋转90︒得到点B ,连接AB .(1)求出直线BC 的解析式;(2)若动点M 从点C 出发,沿线段CB 以每分钟10个单位的速度运动,过M 作//MN AB 交y 轴于N ,连接AN .设运动时间为t 分钟,当四边形ABMN 为平行四边形时,求t 的值. (3)P 为直线BC 上一点,在坐标平面内是否存在一点Q ,使得以O 、B 、P 、Q 为顶点的四边形为菱形,若存在,求出此时Q 的坐标;若不存在,请说明理由.26.在正方形ABCD 中,AB =4,点E 是边AD 上一动点,以CE 为边,在CE 的右侧作正方形CEFG ,连结BF .(1)如图1,当点E 与点A 重合时,则BF 的长为 . (2)如图2,当AE =1时,求点F 到AD 的距离和BF 的长. (3)当BF 最短时,请直接写出此时AE 的长.【参考答案】一、选择题 1.C 解析:C 【分析】根据二次根式有意义的条件可得x +1≥0,再解即可. 【详解】解:由题意得:x +1≥0, 解得:x ≥−1, 故选:C . 【点睛】此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.2.C解析:C【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.【详解】解:A、因为222567+≠,故不能作为直角三角形三边长度,不符合题意;B、因为2224810+≠,故不能作为直角三角形三边长度,不符合题意;C、因为222102426+=,故能作为直角三角形三边长度,符合题意;D、因为22291517+≠,故不能作为直角三角形三边长度,不符合题意.故选:C.【点睛】本题考查勾股定理的逆定理的应用,解题的关键是判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.3.C解析:C【解析】【分析】根据平行四边形的判定定理对各个选项进行判断即可.【详解】解:A、∵AB=CD,AB∥CD,∴四边形ABCD是平行四边形,不符合题意;B、∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,不符合题意;C、∵AB=CD,∠B=∠D,不能判定四边形ABCD是平行四边形,符合题意;D、∵∠BAC=∠ACD,∴AB∥CD,∵AB=CD,∴四边形ABCD是平行四边形,不符合题意;故选C.【点睛】本题主要考查了平行四边形的判定定理,解题的关键在于能够熟练掌握平行四边形的判定定理.4.C解析:C【解析】【分析】根据加权平均数的定义列式计算即可.【详解】解:该班平均得分5889710587⨯+⨯+⨯++=9.1(分),故选:C.【点睛】本题主要考查了加权平均数,解题的关键是掌握加权平均数的定义.5.D解析:D【分析】首先连接AP,由在Rt△ABC中,∠BAC=90°,PE⊥AB于E,PF⊥AC于F,可证得四边形AEPF是矩形,即可得AP=EF,即AP=2AM,然后由当AP⊥BC时,AP最小,即可求得AM的最小值.【详解】解:连接AP,∵PE⊥AB,PF⊥AC,∴∠AEP=∠AFP=90°,又∵∠BAC=90°,∴四边形AEPF是矩形,∴AP=EF,∵∠BAC=90°,M为EF中点,∴AM=12EF=12AP,∵在Rt△ABC中,∠BAC=90°,AB=3,AC=4,∴BC=22AB AC=5,当AP⊥BC时,AP值最小,此时S△BAC=12×3×4=12×5×AP,解得AP=2.4,∴AP的最小值为2.4,∴AM的最小值是1.2,故选:D.【点睛】本题考查了矩形的性质的运用,勾股定理的运用,三角形的面积公式的运用,垂线段最短的性质的运用,解答时求出AP的最小值是关键.6.C解析:C【解析】【分析】根据接近度的意义,逐项计算判断即可.【详解】解:菱形的两个相邻内角°α、°β越接近,菱形越接近于正方形,也就是说αβ-的值越小,菱形越接近于正方形,即接近度d 越大的菱形越接近于正方形,故A 正确,不符合题意;有一个内角等于100°的菱形的两个邻角的度数分别为100°和80°,180********d =--=,故B 正确,不符合题意;∵菱形的两个相邻内角分别为°α、°β,∴0180αβ≤-<,d 的取值范围是0180d <≤,故C 错误,符合题意; 当180d =时,90αβ==︒,所以该菱形是正方形,故D 正确,不符合题意; 故选:C . 【点睛】本题考查了菱形与正方形的性质,正方形的判定,正确理解“接近度”的意思是解决问题的关键.7.C解析:C 【解析】 【分析】根据直角三角形的性质求出EF ,进而求出DE ,根据三角形中位线定理计算,得到答案. 【详解】解:90AFC ∠=︒,点E 是AC 的中点,10AC =,1110522EF AC ∴==⨯=, 1DF =,6DE DF EF ∴=+=,点D 、E 分别是AB 、AC 的中点,212BC DE ∴==,故选:C . 【点睛】本题考查的是直角三角形的性质、三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.8.D解析:D 【分析】分析图像得出BE 和BC ,求出AB ,作EH ⊥BC 于H ,作EF ∥MN ,M 1N 2∥EF ,作DG ⊥M 1N 2于点G ,求出EF 和M 1N 2,在△DM 1N 2中,利用面积法列出方程,求出t 值即可. 【详解】解:由题意可得:点M 与点E 重合时,t =5,则BE =5, 当t =10时,点N 与点C 重合,则BC =10, ∵当t =5时,S =10,∴5102AB⨯=,解得:AB =4, 作EH ⊥BC 于H ,作EF ∥MN ,M 1N 2∥EF ,作DG ⊥M 1N 2于点G ,则EH =AB =4,BE =BF =5, ∵∠EHB =90°, ∴BH 2254-, ∴HF =2,∴EF 222425+ ∴M 1N 2=25设当点M 运动到M 1时,N 2D 平分∠M 1N 2C , 则DG =DC =4,M 1D =10-AE -EM 1=10-3-(t -5)=12-t , 在△DM 1N 2中,1121122DM AB M N DG ⨯⨯=⨯⨯, 即()1112425422t ⨯-⨯=⨯, 解得:1225t =- 故选D . 【点睛】本题考查了动点问题的函数图像,矩形的性质,勾股定理,面积法,解题的关键是读懂图象,了解图象中每个点的实际含义.二、填空题9.12x ≤且1x ≠- 【解析】 【分析】根据二次根式和分式有意义的条件:被开方数大于等于0,分母不等于0,列不等式求解. 【详解】解:由题意得:120x -≥,且10x +≠ 解得:12x ≤且1x ≠- 故答案为:12x ≤且1x ≠- 【点睛】本题考查了分式有意义的条件和二次根式有意义的条件,掌握:分式有意义,分母不为0;二次根式的被开方数是非负数是解题的关键.【解析】【分析】因为菱形的对角线互相垂直,互相垂直的四边形的面积等于对角线乘积的一半.【详解】解:菱形的面积为:1610302⨯⨯=.故答案为:30.【点睛】本题考查菱形的性质,关键知道菱形的对角线互相垂直,然后根据面积等于对角线乘积的一半求出结果.11.36cm2【解析】【分析】利用勾股定理求正方形边长,从而求正方形的面积.【详解】解:由题意可知:正方形的边长为:221086-=∴正方形的面积为:6²=36故答案为:36 cm2.【点睛】本题考查勾股定理解直角三角形,题目比较简单,正确计算是解题关键.12.A解析:35﹣3【分析】连接AC,当A、B'、C共线时,C B'的值最小,进而解答即可.【详解】解:如图,连接AC.∵折叠,∴AB=A B'=3,∵四边形ABCD是矩形,∴∠B=90°,∴AC22223635AB BC++=∵C B'≥AC﹣A B',∴当A、B'、C共线时,C B'的值最小为:53,故答案为:53.本题考查翻折变换、矩形的性质、勾股定理等知识,解题的关键是熟练掌握基本知识,作出正确的辅助线,属于中考常考题型.13.y=3x+3.【分析】把(-1,0)、(0,3)代入y=kx+b 得到03k b b -+=⎧⎨=⎩,然后解方程组可. 【详解】解:根据题意得03k b b -+=⎧⎨=⎩, 解得33k b =⎧⎨=⎩, 所以直线的解析式为y=3x+3.故答案为y=3x+3.【点睛】本题考查了待定系数法求一次函数的解析式:设一次函数的解析式为y=kx+b (k 、b 为常数,k≠0),然后把函数图象上两个点的坐标代入得到关于k 、b 的方程组,然后解方程组求出k 、b ,从而得到一次函数的解析式.14.D解析:①③【分析】根据平行四边形的判定和菱形的判定解答即可.【详解】解:∵DE ∥CA ,DF ∥BA ,∴四边形AEDF 是平行四边形,故①正确;∵∠BAC =90°,四边形AEDF 是平行四边形,∴四边形AEDF 是矩形,故②错误;∵AD 平分∠BAC ,四边形AEDF 是平行四边形,∴四边形AEDF 是菱形,故③正确;∵AB =AC ,四边形AEDF 是平行四边形,不能得出AE =AF ,故四边形AEDF 不一定是菱形,故④错误;故答案为:①③.【点睛】此题考查菱形的判定,关键是就平行四边形的判定和菱形的判定解答.15.【分析】利用一次函数图象上点的坐标特征,可求出直线与两坐标轴的交点坐标,再利用三角形的面积计算公式,即可求出直线y =x+3与两坐标轴围成的三角形面积.解:当x =0时,y =3,∴直线【分析】利用一次函数图象上点的坐标特征,可求出直线与两坐标轴的交点坐标,再利用三角形的面积计算公式,即可求出直线y +3与两坐标轴围成的三角形面积. 【详解】解:当x =0时,y =3,∴直线y +3与y 轴的交点坐标为(0,3);当y =0+3=0,解得:x =﹣∴直线y2x +3与x 轴的交点坐标为(﹣0).∴直线y+3与两坐标轴围成的三角形面积为12×|﹣【点睛】 本题考查了一次函数图象上点的坐标特征以及三角形的面积,牢记直线上任意一点的坐标都满足函数关系式y =kx +b 是解题的关键.16.【分析】先根据已知条件得出B 的坐标(12,16),然后根据等腰三角形和勾股定理得出E 点坐标(4,0),利用待定系数法可求得直线BD 的解析式,即可求出D 点坐标.【详解】作BF ⊥OC,垂足为F解析:()0,8-【分析】先根据已知条件得出B 的坐标(12,16),然后根据等腰三角形和勾股定理得出E 点坐标(4,0),利用待定系数法可求得直线BD 的解析式28y x =-,即可求出D 点坐标.【详解】作BF ⊥OC,垂足为F∵()0,16A ,12AB =∴B(12,16)∵AB y ⊥∴AB ∥OC∴∠ABE=∠BEC∵A 关于直线l 的对称点为1A∴∠ABE=∠EBC∴∠BEC=∠EBC∴BC=EC=20在Rt △BFC 中2222201612CF BC BF =--=∴EF=20-12=8∴OE=12-8=4∴E(4,0)设直线BD 的解析式为y=kx+b ,把点B ,E 代入解析式得121640k b k b +=⎧⎨+=⎩ 解得28k b =⎧⎨=-⎩∴直线BD 的解析式为28y x =- ;所以D ()0,8-;故答案:()0,8-【点睛】本题考查了一次函数的解析式及交点、位置、勾股定理、对称等问题,掌握一次函数解析式和交点及找出等腰三角形是解题的关键.三、解答题17.(1)1;(2);(3)0;(4).【分析】(1)先运用分母有理化化简,然后再计算即可;(2)先运用二次根式的性质化简,然后再计算即可;(3)先运用平方差公式计算,然后再化简即可;(4)先解析:(1)1;(2;(3)0;(4)3+ 【分析】(1)先运用分母有理化化简,然后再计算即可;(2)先运用二次根式的性质化简,然后再计算即可;(3)先运用平方差公式计算,然后再化简即可;(4)先运用零次幂、二次根式的性质、完全平方公式化简,然后再计算即可.【详解】解:(133=6232+- =4-3=1;(2)=;(3)2+ =5-7+2=0;(4)02(1+=41(12)⨯+-=423+-+=3+【点睛】本题主要考查了二次根式的运算,掌握分母有理化、二次根式的性质成为解答本题的关键.18.8m【分析】由题可知,旗杆,绳子与地面构成直角三角形,根据题中数据,用勾股定理即可解答.【详解】解:设旗杆的长度为xm,则绳子的长度为:(x+2)m,在Rt△ABC中,由勾股定理得:x2+解析:8m【分析】由题可知,旗杆,绳子与地面构成直角三角形,根据题中数据,用勾股定理即可解答.【详解】解:设旗杆的长度为x m,则绳子的长度为:(x+2)m,在Rt△ABC中,由勾股定理得:x2+62=(x+2)2,解得:x=8,答:旗杆的高度为8m.【点睛】本题考查的是勾股定理的应用,根据题意得出直角三角形是解答此题的关键.19.(1)见解析;(2)见解析;(3).【解析】【分析】(1)根据菱形的性质:菱形的四边都相等,利用网格画出对应的菱形即可;(2)根据图中所给的AB计算出AB的长不等于5,即AB为底,然后利用勾解析:(1)见解析;(2)见解析;(3)CE【解析】【分析】(1)根据菱形的性质:菱形的四边都相等,利用网格画出对应的菱形即可;(2)根据图中所给的AB计算出AB的长不等于5,即AB为底,然后利用勾股定理找出E点即可;(3)利用勾股定理进行相应的计算即可得到答案.【详解】解:(1) 根据菱形的性质:菱形的四边都相等,菱形的面积为8,画出的图形如下图所示(2)如图所示22105∵=+=≠AB BP AP∴AB为等腰三角形ABE的底∴AE=BE=5225∵=+==BE BT ET AE∴下图即为所求(3)如图所示,连接EC则由题意得2217+=CE CH EH【点睛】本题主要考查了应用设计与作图,正确利用网格结合勾股定理是解题的关键.20.(1)见解析;(2)四边形ADCF 是菱形,理由见解析.【分析】(1)由“AAS”可证△AEF ≌△DEB ;(2)先证四边形ADCF 是平行四边形,由直角三角形的性质可得AD =CD ,可得结论.【详解析:(1)见解析;(2)四边形ADCF 是菱形,理由见解析.【分析】(1)由“AAS ”可证△AEF ≌△DEB ;(2)先证四边形ADCF 是平行四边形,由直角三角形的性质可得AD =CD ,可得结论.【详解】证明:(1)∵AD 是BC 边上的中线,∴BD =CD ,∵点E 是AD 的中点,∴AE =ED ,∵AF ∥BC ,∴∠AFE =∠EBD ,在△AEF 和△DEB 中,AFE DBE FEA BED AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AEF ≌△DEB (AAS ),(2)四边形ADCF 是菱形,理由如下:∵△AEF≌△DEB,∴AF=BD,又∵BD=CD,∴AF=CD,∵AF∥BC,∴四边形ADCF是平行四边形,∵∠BAC=90°,AD是BC边上的中线,∴AD=CD,∴四边形ADCF是菱形.【点睛】本题考查了全等三角形的判定和性质,菱形的判定和性质.证明四边形ADCF是平行四边形是解题的关键.21.(1)S=12;(2)S=【解析】【分析】(1)利用三角形的三边均为整数,可选择海伦公式进行计算;(2)利用三角形的三边中有无理数,可选择秦九韶公式进行计算.【详解】解:(1),由海伦解析:(1)S2)S【解析】【分析】(1)利用三角形的三边均为整数,可选择海伦公式进行计算;(2)利用三角形的三边中有无理数,可选择秦九韶公式进行计算.【详解】解:(1)789122p++==,∴由海伦公式得:S===(2)由秦九韶公式得:S==【点睛】本题主要考查了数学常识,三角形的面积,二次根式的应用,根据三角形三边数字的特征选择恰当的公式是解题的关键.22.(1)y1=40x,y2=20x+800;(2)在一年内来此游泳馆游泳的次数超过60次,为省钱,应选择方式二【分析】(1)根据题意可以写出y1,y2与x之间的函数表达式;(2)将x=15代入(解析:(1)y1=40x,y2=20x+800;(2)在一年内来此游泳馆游泳的次数超过60次,为省钱,应选择方式二【分析】(1)根据题意可以写出y1,y2与x之间的函数表达式;(2)将x=15代入(1)中函数关系式,求出相应的函数值,然后比较大小即可解答本题.【详解】解:(1)当游泳次数为x时,方式一费用为:y1=40x,方式二的费用为:y2=20x+800;(2)若一年内来此游泳馆游泳的次数为60次,方式一的费用为:y1=40×60=2400(元),方式二的费用为:y2=20×60+800=2000(元),∵2400>2000,∴在一年内来此游泳馆游泳的次数超过60次,为省钱,应选择方式二.【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,求出y1,y2与x之间的函数表达式,利用一次函数的性质解答.23.(1)见解析;(2),理由见解析;(3)78,或【分析】(1)如图①中,如图1中,过点作于.证明可得结论.(2)如图②中,结论:.如图③中,结论:.利用全等三角形的性质解决问题即可.(3)根解析:(1)见解析;(2),理由见解析;(3)78,或【分析】(1)如图①中,如图1中,过点D作于.证明可得结论.(2)如图②中,结论:.如图③中,结论:.利用全等三角形的性质解决问题即可.(3)根据菱形的周长求出菱形的边长,利用菱形的面积公式求出菱形的高EF,再利用勾股定理求出,利用(2)中结论解决问题即可.【详解】解:(1)如图①中,如图1中,过点D作于.四边形ABCD是菱形,,//AD BC,,,,,,,∴四边形是平行四边形,,=,,,AB AC,,,,,.(2)如图②中,结论:.理由:过点D作于.同法可证,,,.如图③中,结论:.理由:过点D作于.同法可证,,,.(3)菱形ABCD的周长为52,,菱形ABCD的面积,,,,,四边形的面积.,,,如图②中,,如图③,故答案为78,或.【点睛】本题属于四边形综合题,考查了菱形的性质,解直角三角形,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.24.(1);(2),或;(3)5或0或【解析】【分析】(1)由的面积,求出,由,进而求解;(2)①当为时,证明,得到点的坐标为,进而求解;②当时,过点作轴于点,当时,,即可求解;(3)分点是中解析:(1)152y x =+;(2)5(2-,15)2或(4,9)-;(3)5或0或5517 【解析】【分析】(1)由OBC ∆的面积11||5()1022C C OB x x =⨯⨯=⨯⨯-=,求出4C x =-,由22222(4)525OC t OB =-+===,进而求解; (2)①当DCB ∠为45︒时,证明()HMR CNH AAS ∆≅∆,得到点R 的坐标为(7,6)--,进而求解;②当45CD A ∠'=︒时,过点D '作D K x '⊥轴于点K ,当4x =-时,59y x =-+=,即可求解;(3)分点O 是中点、点P 是中点、点Q 是中点三种情况,利用一次函数的性质,求出点P 的坐标,进而求解.【详解】解:(1)一次函数5y x =-+与坐标轴交于A ,B 两点,故点A 、B 的坐标分别为(5,0)、(0,5),则5OB =,则OBC ∆的面积11||5()1022C C OB x x =⨯⨯=⨯⨯-=,解得4C x =-,则设点C 的坐标为(4,)t -,则22222(4)525OC t OB =-+===,解得3t =,故点C 的坐标为(4,3)-,设BC 的表达式为y kx b =+, 则345k b b =-+⎧⎨=⎩,解得125k b ⎧=⎪⎨⎪=⎩, 故直线BC 的表达式为152y x =+; (2)令1502y x =+=,解得10x =-, 设直线BC 交x 轴于点(10,0)H -,在BCD ∆中有一个内角是45︒,这个角不可能是DBC ∠,①当DCB ∠为45︒时,过点H 作RH CD ⊥于点R ,过点H 作y 轴的平行线NM ,交过点R 与x 轴的平行线于点M ,交过点C 与x 轴的平行线于点N ,45HCR DCB ∠=∠=︒,CHR ∴∆为等腰直角三角形,则90CHR ∠=︒,CH CR =,90RHM CHN ∠+∠=︒,90CHN HCN ∠+∠=︒,RHM HCN ∴∠=∠,90HMR CNH ∠=∠=︒,CH RH =,()HMR CNH AAS ∴∆≅∆,4106HM CN ∴==-+=,3MR NH ==,故点R 的坐标为(7,6)--,由点C 、R 坐标,同理可得,直线CR 的表达式为315=+y x ,联立315=+y x 和5y x =-+并解得52152x y ⎧=-⎪⎪⎨⎪=⎪⎩, 故点D 的坐标为5(2-,15)2; ②当45CD A ∠'=︒时, 过点D '作D K x '⊥轴于点K ,当4x =-时,59y x =-+=,即点(4,9)D '-;综上,点D 的坐标为5(2-,15)2或(4,9)-; (3)设点P 的坐标为(,5)m m -+,则OP 的表达式为5m y x m -=, 联立上式与152y x =+并解得10103m x m =-, 即点Q 的横坐标为10103m m -, ①当点O 是中点时,则点P 、Q 的横坐标互为相反数,即10103m m m =--, 解得0m =(舍去)或20,故点P 的坐标为(20,15)-,②当点P 是中点时,同理可得:102103m m m=-, 解得0m =(舍去)或53, 故点P 的坐标为5(3,10)3; ③当点Q 是中点时,同理可得,点10(3P -,25)3; 当点P 的坐标为5(3,10)3时,如图2,设直线CP 交y 轴于点K ,由点C 、P 的坐标得:直线CP 的表达式为1551717y x =+, 故5517OK =, 则OCP ∆的面积1155555()(4)221736P C OK x x =⨯⨯-=⨯⨯+=; 当点P 的坐标为(20,15)-时,同理可得:OCP ∆的面积0=;当点P 的坐标为10(3-,25)3时, 同理可得:OCP ∆的面积5=,综上,OCP ∆的面积为5或0或5517. 【点睛】本题考查的是二次函数综合运用,涉及到一次函数的性质、等腰三角形的性质、三角形全等、面积的计算等,其中(3),要注意分类求解,避免遗漏.25.(1);(2)t=s时,四边形ABMN是平行四边形;(3)存在,点Q坐标为:或或或.【分析】(1)如图1中,作BH⊥x轴于H.证明△COA≌△AHB(AAS),可得BH=OA=1,AH=OC=2解析:(1)123y x=-+;(2)t=23s时,四边形ABMN是平行四边形;(3)存在,点Q坐标为:618,55⎛⎫⎪⎝⎭或(3,1)-或(3,1)-或155,88⎛⎫-⎪⎝⎭.【分析】(1)如图1中,作BH⊥x轴于H.证明△COA≌△AHB(AAS),可得BH=OA=1,AH=OC=2,求出点B坐标,再利用待定系数法即可解决问题.(2)利用平行四边形的性质求出点N的坐标,再求出AN,BM,CM即可解决问题.(3)如图3中,当OB为菱形的边时,可得菱形OBQP,菱形OBP1Q1.菱形OBP3Q3,当OB为菱形的对角线时,可得菱形OP2BQ2,点Q2在线段OB的垂直平分线上,分别求解即可解决问题.【详解】(1)如图1中,作BH⊥x轴于H.∵A(1,0)、C(0,2),∴OA=1,OC=2,∵∠COA=∠CAB=∠AHB=90°,∴∠ACO+∠OAC=90°,∠CAO+∠BAH=90°,∴∠ACO=∠BAH,∵AC=AB,∴△COA≌△AHB(AAS),∴BH=OA=1,AH=OC=2,∴OH=3,∴B(3,1),设直线BC的解析式为y=kx+b,则有231 bk b=⎧⎨+=⎩,解得:132kb⎧=-⎪⎨⎪=⎩,∴123y x =-+; (2)如图2中,∵四边形ABMN 是平行四边形,∴AN ∥BM ,∴直线AN 的解析式为:1133y x =-+, ∴10,3N ⎛⎫ ⎪⎝⎭, ∴103BM AN ==, ∵B (3,1),C (0,2),∴BC=10,∴2103CM BC BM =-=, ∴21021033t =÷=, ∴t=23s 时,四边形ABMN 是平行四边形; (3)如图3中,如图3中,当OB 为菱形的边时,可得菱形OBQP ,菱形OBP 1Q 1.菱形OBP 3Q 3, 连接OQ 交BC 于E ,∵OE ⊥BC ,∴直线OE 的解析式为y=3x ,由3123y xy x=⎧⎪⎨=-+⎪⎩,解得:3595xy⎧=⎪⎪⎨⎪=⎪⎩,∴E(35,95),∵OE=OQ,∴Q(65,185),∵OQ1∥BC,∴直线OQ1的解析式为y=-13x,∵OQ1,设Q1(m,-1m3),∴m2+19m2=10,∴m=±3,可得Q1(3,-1),Q3(-3,1),当OB为菱形的对角线时,可得菱形OP2BQ2,点Q2在线段OB的垂直平分线上,易知线段OB的垂直平分线的解析式为y=-3x+5,由3513y xy x=-+⎧⎪⎨=-⎪⎩,解得:15858xy⎧=⎪⎪⎨⎪=-⎪⎩,∴Q2(158,58-).综上所述,满足条件的点Q坐标为:618,55⎛⎫⎪⎝⎭或(3,1)-或(3,1)-或155,88⎛⎫-⎪⎝⎭.【点睛】本题属于一次函数综合题,考查了平行四边形的判定和性质,菱形的判定和性质,一次函数的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.26.(1);(2)点F到AD的距离为3,BF=;(3)2【分析】(1)连接DF,证明△ADF≌△CDA,得出CDF共线,然后用勾股定理即可;(2)过点F作FH⊥AD交AD的延长线于点H,FH⊥BC解析:(1)2)点F到AD的距离为3,BF3)2【分析】(1)连接DF,证明△ADF≌△CDA,得出CDF共线,然后用勾股定理即可;(2)过点F作FH⊥AD交AD的延长线于点H,FH⊥BC交BC的延长线于K,证明△EHF≌△CDE,再用勾股定理即可;(3)当B ,D ,F 共线时,此时BF 取最小值,求出此时AE 的值即可.【详解】解:(1)如图,连接DF ,∵∠CAF =90°,∠CAD =45°,∴∠DAF =45°,在△CAD 和△FAD 中,AF AC CAD FAD AD AD =⎧⎪∠=∠⎨⎪=⎩, ∴△CAD ≌△FAD (SAS ),∴DF =CD ,∴∠ADC =∠ADF =90°,∴C ,D ,F 共线,∴BF 2=BC 2+CF 2=42+82=80,∴BF =45,故答案为:45;(2)如图,过点F 作FH ⊥AD 交AD 的延长线于点H ,FH ⊥BC 交BC 的延长线于K ,∵四边形CEFG 是正方形,∴EC =EF ,∠FEC =90°,∴∠DEC +∠FEH =90°,又∵四边形ABCD 是正方形,∴∠ADC =90°,∴∠DEC +∠ECD =90°,∴∠ECD =∠FEH ,又∵∠EDC =∠FHE =90°,在△ECD 和△FEH 中,FHE EHC FEH ECD EF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ECD ≌△FEH (AAS ),∴FH =ED ,∵AD =4,AE =1,∴ED =AD -AE =4-1=3,∴FH =3,即点F 到AD 的距离为3,∴∠DHK =∠HDC =∠DCK =90°,∴四边形CDHK 为矩形,∴HK =CD =4,∴FK =FH +HK =3+4=7,∵△ECD ≌△FEH ,∴EH =CD =AD =4,∴AE =DH =CK =1,∴BK =BC +CK =4+1=5,在Rt △BFK 中,BF(3)∵当A ,D ,F 三点共线时,BF 的最短,∴∠CBF =45°,∴FH =DH ,由(2)知FH =DE ,EH =CD =4,∴ED =DH =4÷2=2,∴AE =2.【点睛】本题主要考查正方形的性质和全等三角形的判定,关键是要作辅助线构造全等的三角形,在正方形和三角形中辅助线一般是垂线段,要牢记正方形的两个性质,即四边相等,四个内角都是90°.。
人教版数学八年级下册数学期末试卷(培优篇)(Word版含解析)

人教版数学八年级下册数学期末试卷(培优篇)(Word 版含解析) 一、选择题1.要使12021x-有意义,x 的取值范围是( ).A .2021x ≥B .2021x ≤C .2021x >D .2021x < 2.下列各组数中,能构成直角三角形的三边的是( ) A .3,5,6 B .1,1,2C .6,8,11D .5,12,163.在下列条件中,不能判定四边形为平行四边形的是( )A .对角线互相平分B .一组对边平行且相等C .两组对角分别相等D .对角线互相垂直4.某商场招聘员工一名,现有甲、乙、丙三人竞聘,通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示,若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2,3,5,那么从成绩看,应该录取( ) 应试者 计算机 语言 商品知识 甲 60 70 80 乙 80 70 60 丙708060A .甲B .乙C .丙D .任意一人都可5.如图,在正方形ABCD 中,取AD 的中点E ,连接EB ,延长DA 至F ,使EF =EB ,以线段AF 为边作正方形AFGH ,交AB 于点H ,则AHAB的值是( )A .512- B .512+ C .352D .126.如图,在菱形ABCD 中,∠D =140°,则∠1的大小为( )A.15°B.20°C.25°D.30°BC=,7.如图,在四边形ABCD中,E、F分别是AB、AD的中点,若6EF=,13△的面积为()CD=,则BCD5A.60 B.48 C.30 D.158.如图,等腰直角三角形△OAB的边OA和矩形OCDE的边OC在x轴上,OA=4,OC=1,OE=2.将矩形OCDE沿x轴正方向平移t(t>0)个单位,所得矩形与△OAB公共部分的面积记为S(t).将S(t)看作t的函数,当自变量t在下列哪个范围取值时,S(t)是t的一次函数()A.1<t<2 B.2<t<3C.3<t<4 D.1<t<2或4<t<5二、填空题9.已知552=-+--,则y x=________.y x x10.菱形两条对角线长分别为2、6,则这个菱形的面积为_________.11.如图,在△ABC中,∠ACB=90°,以它的三边为边分别向外作正方形,面积分别为S1,S2,S3,已知S1=5,S2=12,则S3=_____.12.如图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知==,则BF=______.AD AB4,313.已知一次函数的图象过点(3,5)与点(-4,-9),则这个一次函数的解析式为____________.14.如图,在四边形ABCD 中AB ∥CD ,若加上AD ∥BC ,则四边形ABCD 为平行四边形.若E 、F 为BD 上两点,且BE=DF.现在请你给□ABCD 添加一个适当的条件________,使得四边形AECF 为菱形.15.如图所示,直线2y x =+与两坐标轴分别交于A 、B 两点,点C 是OB 的中点,D 、E 分别是直线AB 、y 轴上的动点,当CDE ∆周长最小时,点D 的坐标为_____.16.如图,直角三角形纸片的两直角边长分别为6,8,按如图那样折叠,使点A 与点B 重合,折痕为DE ,则:BCEBDESS等于____________.三、解答题17.计算: (12340100.15(2)()()()201515112283π-⎛⎫-+--+---+ ⎪⎝⎭18.如图,一架梯子AB 斜靠在一竖直的墙OA 上,这时AO =3m ,∠OAB =30°,梯子顶端A 沿墙下滑至点C ,使∠OCD =60°,同时,梯子底端B 也外移至点D .求BD 的长度.(结果保留根号)[补充:直角三角形中,30°所对的直角边是斜边的一半]19.如图,在4×4的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形或四边形.(绘图要求:①所绘图形不得超出正方形网格;②必须用直尺和中性笔绘图,确保所绘图形的顶点必须在格点上)(1)在图①中,画一个直角三角形,使它的三边长都是有理数;(2)在图②中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数; (3)在图③中,画一个直角三角形,使它的三边长都是无理数; (4)在图④中,画一个正方形,使它的面积为10.20.如图1,在ABC 中,AD BC ⊥于点D ,AD BD =,点E 为边AD 上一点,且DE DC =,连接BE 并延长,交AC 于点F .(1)求证:BED AEF ∽;(2)过点A 作//AG BC 交BF 的延长线于点G ,连接CG ,如图2.若2DE AE AD =⋅,求证:四边形ADCG 是矩形.21.743+743+化为7212+﹐由于437+=,4312⨯=,即:22(4)(3)7+=,4312⨯=,所以2227437212(4)243(3)((43)23+=+=+⨯+=+=+,问题:(1)填空:423+=__________,526-=____________﹔(2)进一步研究发现:形如2m n ±的化简,只要我们找到两个正数a ,b (a b >),使a b m +=,ab n =,即22()()a b m +=,a b n ⨯=﹐那么便有:2m n ±=__________.(3)化简:415-(请写出化简过程)22.某超市以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种干果销售量y (千克)与每千克降价x (元)(0<x <20)之间满足一次函数关系,其图象如图所示. (1)求y 与x 之间的函数关系式;(2)当每千克干果降价3元时,超市获利多少元?23.社团活动课上,数学兴趣小组的同学探索了这样的一个问题: 如图1,,点为边上一定点,点B 为边上一动点,以AB 为一边在∠MON 的内部作正方形ABCD ,过点C 作,垂足为点F (在点O 、之间),交BD 与点E ,试探究的周长与的长度之间的等量关系该兴趣小组进行了如下探索:(动手操作,归纳发现) (1)通过测量图1、2、3中线段、、EF 和的长,他们猜想的周长是长的_____倍.请你完善这个猜想(推理探索,尝试证明)为了探索这个猜想是否成立,他们作了如下思考,请你完成后续探索过程:(2)如图,过点C作,垂足为点G则又四边形ABCD正方形,,则在与中,(类比探究,拓展延伸)(3)如图,当点F在线段的延长线上时,直接写出线段、EF、与长度之间的等量关系为.24.在平面直角坐标系中,O为坐标原点,直线y=x+b交x轴的负半轴于点A,交y轴的正半轴于点B,AB=2,点C在x轴的正半轴上,OC=2.(1)如图1,求直线BC的解析式;(2)如图2,点D在第四象限的直线C上,DE⊥AB于点E,DE=AB,求点D的坐标;(3)在(2)的条件下,请在平面内找一点P,使得四边形PDBE是平行四边形,直接写出这样的点P的坐标;(4)如图3,在(2)的条件下,点F在线段OA上,点G在线段OB上,射线FG交直线BC于点H,若∠FGO=2∠AEF,FG=5,求点H的坐标.25.如图,菱形纸片ABCD 的边长为2,60,BAC ∠=︒翻折,,B D ∠∠使点,B D 两点重合在对角线BD 上一点,,P EF GH 分别是折痕.设()02AE x x =<<.(1)证明:AG BE =;(2)当02x <<时,六边形AEFCHG 周长的值是否会发生改变,请说明理由; (3)当02x <<时,六边形AEFCHG 的面积可能等于534吗?如果能,求此时x 的值;如果不能,请说明理由.26.如图,在正方形ABCD 中,点E 、F 是正方形内两点,BE DF ∥,EF BE ⊥,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:(1)在图1中,连接BD ,且BE DF =①求证:EF 与BD 互相平分; ②求证:222()2BE DF EF AB ++=;(2)在图2中,当BE DF ≠,其它条件不变时,222()2BE DF EF AB ++=是否成立?若成立,请证明:若不成立,请说明理由.(3)在图3中,当4AB =,135DPB ∠=︒,2246BP PD +=时,求PD 之长.【参考答案】一、选择题 1.D 解析:D 【分析】根据二次根式有意义的条件:被开方数要大于等于0和分式有意义的条件:分母不能为0,进行求解即可得到答案. 【详解】 解:∵2021x-有意义,∴2021020210x x ⎧-≥⎪⎨-≠⎪⎩, ∴2021x <, 故选D . 【点睛】本题主要考查了二次根式和分式有意义的条件,解题的关键在于能够熟练掌握相关知识进行求解.2.B解析:B 【分析】根据勾股定理逆定理:222+=a b c ,将各个选项逐一代数计算即可得出答案. 【详解】 解:A 、222356,∴不能构成直角三角形,故A不符合题意;B 、∵22211+=,∴能构成直角三角形,故B 符合题意;C 、∵2226811+≠,∴不能构成直角三角形,故C 不符合题意;D 、22251216+≠,∴不能构成直角三角形,故D 不符合题意. 故选B . 【点睛】此题主要考查学生对勾股定理的逆定理的理解和掌握,要求学生熟练掌握这个逆定理.3.D解析:D 【解析】 【分析】利用平行四边形的判定可求解. 【详解】解:A 、对角线互相平分的四边形是平行四边形,故该选项不符合题意; B 、一组对边平行且相等的四边形是平行四边形,故该选项不符合题意; C 、两组对角分别相等的四边形是平行四边形,故该选项不符合题意; D 、对角线互相垂直的四边形不一定是平行四边形,故该选项符合题意; 故选:D . 【点睛】本题考查了平行四边形的判定,熟练掌握平行四边形的判定是本题的关键.4.A解析:A 【解析】 【分析】分别按照2,3,5的赋权计算甲,乙,丙的平均数,再录取最高分即可. 【详解】解:根据题意,甲的最终成绩为60270380573235⨯+⨯+⨯=++(分),乙的最终成绩为80270360567235⨯+⨯+⨯=++(分),丙的最终成绩为70280360568235⨯+⨯+⨯=++(分),所以应该录取甲, 故选:A .【点睛】本题考查的是加权平均数的含义与计算,理解赋权2,3,5的含义是解题的关键.5.A解析:A 【分析】设AB =2a ,根据四边形ABCD 为正方形,E 点为AD 的中点,可得EF 的长,进而可得结果. 【详解】 解:设AB =2a , ∵四边形ABCD 为正方形, ∴AD =2a , ∵E 点为AD 的中点, ∴AE =a ,∴BE==, ∴EF =,∴AF =EF ﹣AE 1)a ,∵四边形AFGH 为正方形, ∴AH =AF 1)a ,∴)12a AH ABa==. 故选:A . 【点睛】本题考查了正方形的性质,解决本题的关键是掌握正方形的性质.6.B解析:B 【解析】 【分析】由菱形的性质得到DA =DC ,∠DAC =∠1,由等腰三角形的性质得到∠DAC =∠DCA =∠1,根据三角形的内角和定理求出∠DAC ,即可得到∠1. 【详解】解:∵四边形ABCD 是菱形, ∴DA =DC ,∠DAC =∠1, ∴∠DAC =∠DCA =∠1, 在△ABD 中,∵∠D =140°,∠D +∠DAC +∠DCA =180°,∴∠DAC =∠DCA =12(180°﹣∠D )=12×(180°﹣140°)=20°, 故选B . 【点睛】本题主要考查了菱形的性质,角平分线的性质,等腰三角形的性质,解题的关键在于能够熟练掌握相关知识进行求解.7.C解析:C【解析】【分析】连接BD ,根据三角形中位线定理求出BD ,根据勾股定理的逆定理得到∠BDC =90°,然后求得面积即可.【详解】解:连接BD ,∵E 、F 分别是A B 、AD 中点,∴BD =2EF =12,∵CD 2+BD 2=25+144=169,BC 2=169,∴CD 2+BD 2=BC 2,∴∠BDC =90°,∴S △DBC =12BD •CD =12×12×5=30,故选:C .【点睛】本题考查的是三角形中位线定理、勾股定理的逆定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键. 8.D解析:D【分析】分12t <<,,24t <<,45t <<,5t >讨论即可得出结果.【详解】解:4=OA ,1OC =,2OE =,∴当矩形OCDE 在12t <<范围内移动时,()S t 由0变为2,()S t 随t 的增大而增大, 当矩形OCDE 在24t <<范围内移动时,()S t 为定值2,当矩形OCDE 在45t <<范围内移动时,()S t 由2变为0,()S t 随t 的增大而减小, 当矩形OCDE 在5t >时,()S t 为0,综上所述,矩形OCDE 在12t <<或45t <<范围内移动时,()S t 是t 的一次函数, 故选:D .【点睛】本题考查了图形的平移、一次函数的定义,抓住一次函数的定义分类讨论是解决本题的关键.二、填空题9.125【解析】【分析】根据二次根式的非负性求出x ,y ,即可得解;【详解】 ∵2y =,∴550x x -=-=,∴5x =,∴2y =-, ∴21525y x -==; 故答案是125. 【点睛】本题主要考查了利用二次根式的非负性化简求值,准确计算是解题的关键.10【解析】【分析】根据菱形的面积等于两对角线乘积的一半求出其面积即可.【详解】解:∵∴这个菱形的面积12=【点睛】本题考查的是菱形的面积计算,熟知菱形的面积等于两对角线乘积的一半是解题的关键. 11.A解析:17【解析】【分析】根据勾股定理即可得到结论.【详解】解:∵∠ACB =90°,S 1=5,S 2=12,∴AC 2=5,BC 2=12,∴AB 2=AC 2+BC 2=5+12=17,∴S 3=17,故答案为:17.【点睛】本题考查了勾股定理,正方形的面积,正确的识别图形是解题的关键.12【分析】根据折叠的性质,4AD AF ==,再根据勾股定理即可求解.【详解】解:根据折叠的性质,4AD AF ==,在Rt ABF 中,由勾股定理得:BF =【点睛】本题考查了折叠的性质、勾股定理,解题的关键是掌握折叠的性质.13.2 1.y x =-【分析】设一次函数的解析式为:y kx b =+,利用待定系数法把已知点的坐标代入解析式,解方程组即可得答案.【详解】解:设一次函数的解析式为:y kx b =+,3549k b k b +=⎧∴⎨-+=-⎩解得:21k b =⎧⎨=-⎩所以这个一次函数的解析式为:2 1.y x =-故答案为:2 1.y x =-【点睛】本题考查的是利用待定系数法求解一次函数的解析式,掌握待定系数法是解题的关键. 14.A解析:AB=AD【分析】由菱形的性质可得AE=AF ,∠AEF=∠AFE ,即可得到∠AEB=∠AFD ,利用SAS 即可证明△ABE ≌△ADF ,可得AB=AD ,即可得答案.【详解】∵四边形AECF 为菱形,∴AE=AF ,∠AEF=∠AFE ,∴∠AEB=∠AFD ,在△ABE和△ADF中,AE AFAEB AFD BE DF=⎧⎪∠=∠⎨⎪=⎩,∴△ABE≌△ADF,∴AB=AD,∴可添加AB=AD,使得四边形AECF为菱形.故答案为:AB=AD【点睛】本题考查了菱形的性质及全等三角形的判定与性质,利用菱形性质得出△ABE≌△ADF是解题关键.15.【分析】作点C关于AB的对称点F,关于AO的对称点G,连接DF,EG,由轴对称的性质,可得DF=DC,EC=EG,故当点F,D,E,G在同一直线上时,△CDE的周长=CD+DE+CE=DF+DE解析:53 (,)44 -【分析】作点C关于AB的对称点F,关于AO的对称点G,连接DF,EG,由轴对称的性质,可得DF=DC,EC=EG,故当点F,D,E,G在同一直线上时,△CDE的周长=CD+DE+CE=DF +DE+EG=FG,此时△DEC周长最小,然后求出F、G的坐标从而求出直线FG的解析式,再求出直线AB和直线FG的交点坐标即可得到答案.【详解】解:如图,作点C关于AB的对称点F,关于AO的对称点G,连接FG分别交AB、OA于点D、E,由轴对称的性质可知,CD=DF,CE=GE,BF=BC,∠FBD=∠CBD,∴△CDE的周长=CD+CE+DE=FD+DE+EG,∴要使三角形CDE的周长最小,即FD+DE+EG最小,∴当F、D、E、G四点共线时,FD+DE+EG最小,∵直线y=x+2与两坐标轴分别交于A、B两点,∴B(-2,0),∴OA=OB,∴∠ABC =∠ABD =45°,∴∠FBC =90°,∵点C 是OB 的中点,∴C (1-,0),∴G 点坐标为(1,0),1BF BC ==,∴F 点坐标为(-2,1),设直线GF 的解析式为y kx b =+,∴021k b k b +=⎧⎨-+=⎩, ∴1313k b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴直线GF 的解析式为1133y x =-+, 联立11332y x y x ⎧=-+⎪⎨⎪=+⎩, 解得5434x y ⎧=-⎪⎪⎨⎪=⎪⎩, ∴D 点坐标为(54-,34) 故答案为:(54-,34). 【点睛】本题主要考查了轴对称-最短路线问题,一次函数与几何综合,解题的关键是利用对称性在找到△CDE 周长的最小时点D 、点E 位置,凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.16.14:25【分析】在中利用勾股定理计算出,根据折叠的性质得到,,设,则,,在中根据勾股定理计算出,则,利用三角形面积公式计算出,在中利用勾股定理计算出,利用三角形面积公式计算出,然后求出两面积的解析:14:25【分析】在Rt BEC △中利用勾股定理计算出10AB =,根据折叠的性质得到5AD BD ==,EA EB =,设AE x =,则BE x =,8EC x =-,在Rt BEC △中根据勾股定理计算出254x =,则257844EC ,利用三角形面积公式计算出1172162244BCE S BC CE ,在Rt BED △中利用勾股定理计算出222515()544ED ,利用三角形面积公式计算出11157552248BDE S BD DE ∆==⨯⨯=,然后求出两面积的比. 【详解】 解:在Rt BAC 中,6BC =,8AC =,10AB ∴=,把ABC ∆沿DE 使A 与B 重合,AD BD ∴=,EA EB =,152BD AB ∴==, 设AE x =,则BE x =,8EC x =-, 在Rt BEC △中,222BE EC BC ,即222(8)6x x =-+, 254x ∴=, 2578844ECx , 1172162244BCE S BC CE , 在Rt BED △中,222BE ED BD , 222515()544ED , 11157552248BDE S BD DE ∆∴==⨯⨯=, 2175::14:2548BCE BDE S S ∆∆∴==. 故答案为:14:25.【点睛】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等,对应角相等.也考查了勾股定理.三、解答题17.(1);(2)−7+3【分析】(1)先把各二次根式化为最特意二次根式,再合并即可得到答案;(2)分别根据平方差公式、负整数指数幂的运算法则,绝对值的代数意义,零指数幂的运算法则以及二次根式的性解析:(1);(2)−【分析】(1)先把各二次根式化为最特意二次根式,再合并即可得到答案;(2)分别根据平方差公式、负整数指数幂的运算法则,绝对值的代数意义,零指数幂的运算法则以及二次根式的性质代简各项后再合并即可得到答案.【详解】解:(1= (2))()20111123π-⎛⎫--+- ⎪⎝⎭=51911---+=7-+【点睛】本题主要考查了二次根式的加减以及实数的混合运算,熟练掌握运算法则是解答本题的关键.18.3﹣(m )【分析】先在Rt △OAB 中,OA =3m ,∠OAB =30°,求出梯子AB 的长,在滑动过程中梯子的长是不变的,再根据已知条件证明出△AOB ≌△DOC ,即可求出BD 长.【详解】解:在Rt解析:3m )【分析】先在Rt △OAB 中,OA =3m ,∠OAB =30°,求出梯子AB 的长,在滑动过程中梯子的长是不变的,再根据已知条件证明出△AOB ≌△DOC ,即可求出BD 长.【详解】解:在Rt △ABO 中,∵AO =3m ,∠OAB =30°,12BO AB ∴=AO ∴=OB ∴=∴AB =,∵∠OCD =60°,∴∠ODC =30°,在△AOB 和△DOC 中,OAB ODC AOB DOC AB DC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AOB≌△DOC(AAS),∴OA=OD,OC=OB,∴BD=OD﹣OB=3﹣3(m).【点睛】本题考查了勾股定理解直角三角形,三角形全等的性质与判定,求出BO的长是解题的关键.19.(1)见解析;(2)见解析;(3)见解析;(4)见解析;【解析】【分析】根据勾股定理即可得.【详解】解:(1)如图①所示,三边分别为:3,4,5;(2)如图②所示,三边分别为:,,2或解析:(1)见解析;(2)见解析;(3)见解析;(4)见解析;【解析】【分析】根据勾股定理即可得.【详解】解:(1)如图①所示,三边分别为:3,4,5;(2)如图②所示,三边分别为:2,2,2或22,22,4 ;(3如图③所示,三边分别为:5,5,10或2,22,10或10,10,25;(4)如图④所示,正方形的边长为:10,则面积:(10)2=10.【点睛】本题考查了勾股定理,解题的关键是掌握勾股定理.20.(1)见解析;(2)见解析【分析】(1)先证,得,又因为,可证;(2)先证,得,又因为,利用边与边的关系,得,又因为,可证得四边形ADCG是平行四边形,又因为,四边形ADCG是矩形.【详解】解析:(1)见解析;(2)见解析【分析】(1)先证ACD BED △≌△,得EBD CAD ∠=∠,又因为BED AEF ∠=∠,可证BED AEF ∽;(2)先证AEG DCA ∽,得AE AG DC AD=,又因为2DE AE AD =⋅,利用边与边的关系,得DC AG =,又因为//AG DC ,可证得四边形ADCG 是平行四边形,又因为AD BC ⊥,四边形ADCG 是矩形.【详解】(1)证明:∵AD BC ⊥,∴90ADC BDE ∠=∠=︒.∵AD BD =,DC DE =,∴ACD BED △≌△.∴EBD CAD ∠=∠.∵BED AEF ∠=∠,∴BED AEF ∽.(2)证明:∵//AG BC ,∴∠=∠AGE EBD ,由(1)知EBD CAD ∠=∠,∴AGE CAD ∠=∠,∵AEG BED ACD ∠=∠=∠,∴AEG DCA ∽, ∴AE AG DC AD=, ∴AE AD DC AG ⋅=⋅,∵2DE AE AD =⋅,DE DC =,∴22DC AG DE DC ⋅==,∴DC AG =,∵//AG DC ,∴四边形ADCG 是平行四边形,∵AD BC ⊥,∴四边形ADCG 是矩形.【点睛】本题考查了相似三角形的判定与性质,全等的判定和性质、平行四边形、矩形的判定,能利用相似和全等找到边与边的关系是解题的关键.21.(1),;(2);(3)【解析】【分析】(1)根据题目所给的方法将根号下的数凑成完全平方的形式进行计算; (2)根据题目给的a ,b 与m 、n 的关系式,用一样的方法列式算出结果; (3)将写成,4解析:(112)a b >;(3【解析】【分析】(1)根据题目所给的方法将根号下的数凑成完全平方的形式进行计算;(2)根据题目给的a ,b 与m 、n 的关系式,用一样的方法列式算出结果;(34写成3522+,就可以凑成完全平方的形式进行计算. 【详解】解:(11;(2)a b ===>;(3. 【点睛】本题考查二次根式的计算和化简,解题的关键是掌握二次根式的运算法则. 22.(1)y=10x+100(0<x <20);(2)当每千克干果降价3元时,超市获利2210元【分析】(1)由待定系数法即可得到函数的解析式;(2)根据(1)的解析式将x=3代入求出销售量,再根据解析:(1)y =10x +100(0<x <20);(2)当每千克干果降价3元时,超市获利2210元【分析】(1)由待定系数法即可得到函数的解析式;(2)根据(1)的解析式将x =3代入求出销售量,再根据每千克利润×销售量=总利润列式求解即可.【详解】解:(1)设y 与x 之间的函数关系式为:y =kx +b ,把(2,120)和(4,140)代入得,21204140k b k b +=⎧⎨+=⎩, 解得:10100k b =⎧⎨=⎩, ∴y 与x 之间的函数关系式为:y =10x +100(0<x <20);(2)根据题意得,销售量y=10×3+100=130,(60-3-40)×130=2210(元),答:当每千克干果降价3元时,超市获利2210元.【点睛】本题考查的是一次函数的应用,解题的关键是利用待定系数法求出y与x之间的函数关系式,此类题目主要考查学生分析、解决实际问题能力,又能较好的考查学生“用数学”的意识.23.(1)2;(2)证明见解析过程;(3)AE+EF-AF=2OA.【分析】(1)通过测量可得;(2)过点C作CG⊥ON,垂足为点G,由AAS可证△ABO≌△BCG,可得BG=AO,BO=CG,由解析:(1)2;(2)证明见解析过程;(3)AE+EF-AF=2OA.【分析】(1)通过测量可得;(2)过点C作CG⊥ON,垂足为点G,由AAS可证△ABO≌△BCG,可得BG=AO,BO=CG,由SAS可证△ABE≌△CBE,可得AE=CE,由线段的和差关系可得结论;(3)过点C作CG⊥ON,垂足为点G,由AAS可证△ABO≌△BCG,可得BG=AO,BO=CG,由SAS可证△ABE≌△CBE,可得AE=CE,可得结论.【详解】解:(1)△AEF的周长是OA长的2倍,故答案为:2;(2)如图4,过点C作CG⊥ON,垂足为点G,则∠CGB=90°,∴∠GCB+∠CBG=90°,又∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°,∠DBC=∠DBA=45°,则∠CBG+∠ABO=90°,∴∠GCB=∠ABO,在△BCG与△ABO中,,∴△BCG≌△ABO(AAS),∴BG=AO,CG=BO,∵∠AOB=90°=∠CGB=∠CFO,∴四边形CGOF是矩形,∴CF=GO,CG=OF=OB,在△ABE和△CBE中,,∴△ABE≌△CBE(SAS),∴AE=CE,∴△AEF的周长=AE+EF+AF=CE+EF+AF=CF+AF=GO+AF=BG+BO+AF=2AO;(3)如图5,过点C作CG⊥ON于点G,则∠CGB=90°,∴∠GCB+∠CBG=90°,又∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°,∠DBC=∠DBA=45°,则∠CBG+∠ABO=90°,∴∠GCB=∠ABO,在△BCG与△ABO中,∴△BCG≌△ABO(AAS),∴BG=AO,BO=CG,∵∠AOB=90°=∠CGB=∠CFO,∴四边形CGOF 是矩形,∴CF=GO ,CG=OF=OB ,在△ABE 和△CBE 中,,∴△ABE ≌△CBE (SAS ),∴AE=CE ,∴AE+EF-AF=EF+CE-AF=NB+BO-(OF-AO )=OA+OB-(OB-OA )=2OA .【点睛】本题是四边形综合题,考查了全等三角形的判定和性质,正方形的性质,矩形的判定和性质,添加恰当的辅助线构造全等三角形是本题的关键.24.(1);(2)D (3,3);(3)点P 的坐标有:(6,0)或(0,)或(,12);(4)H (,).【解析】【分析】(1)由题意表达出点A 和点B 的坐标,然后用勾股定理建立等式可求出b 的值,从而得 解析:(1)36y x =-+;(2)D (3,-3);(3)点P 的坐标有:(6,0)或(0,6-)或(6-,12);(4)H (45,185). 【解析】【分析】(1)由题意表达出点A 和点B 的坐标,然后用勾股定理建立等式可求出b 的值,从而得到点B 的坐标,结合点C 的坐标,进而求出直线BC 的解析式;(2)过点D 作DK ∥y 轴交直线AB 于点K ,设出点D 的坐标,表达出点K 的坐标,结合DE =AB ,建立等式,可求出点D 的坐标;(3)由题意,要使四边形PDBE 是平行四边形,则要进行分类讨论,可分为3种情况进行分析;先求出点E 的坐标,然后利用平行四边形的性质,平移的性质,即可求出点P 的所有点的坐标;(4)由题意可得AE =OE ,且∠AEO =90°,可将△AEF 绕点E 旋转,构造全等三角形;表达出线段长,利用勾股定理建等式,求解参数的值,进而求出点H 的坐标.【详解】解:(1)∵直线y =x +b 交x 轴的负半轴于点A ,交y 轴的正半轴于点B ,∴A (-b ,0),B (0,b ),∴OA =OB =b ,在△OAB 中,∠AOB =90°,AB =由勾股定理可得,b 2+b 2=2,解得,b =6(b =-6舍去),∴OA =OB =6,∴点A为(6-,0),点B为(0,6);∵OC=2,∴C(2,0),设直线BC的解析式为y=kx+6,∴2k+6=0,k=-,解得:3∴直线BC的解析式为36=-+.y x(2)过点D作DK∥y轴交直线AB于点K,∴∠ABO=∠K=45°,∵AB=DE=2∴DK=12,设点D的横坐标为t,则D(t,-3t+6),K(t,t+6),∴DK=t+6-(-3t+6)=12,解得:t=3,∴D(3,-3).(3)根据题意,要使四边形PDBE是平行四边形,则要进行分类讨论,可分为3种情况进行分析;如图所示:①当点P 在点1P 的位置时,此时四边形1BEDP 是矩形;∵∠ABO =45°,DE ⊥AB ,∴△OBE 是等腰直角三角形,∵OB =6,∴BE =OE =32∴点E 是AB 的中点,∴点E 的坐标为(3-,3);∵点B 为(0,6),点D 为(3,-3),由平移的性质,则点1P 的坐标为(6,0);②当点P 在点2P 的位置时,此时四边形2BEP D 是平行四边形,则BD ∥EP 2,BE ∥DP 2;∵点E 的坐标为(3-,3),点B 为(0,6),点D 为(3,-3),由平移的性质,则点2P 的坐标为(0,6-);③当点P 在点3P 的位置时,此时四边形3BP ED 是平行四边形,则BP 3∥DE ,DB ∥EP 3;∵点E 的坐标为(3-,3),点B 为(0,6),点D 为(3,-3),由平移的性质,则点3P 的坐标为(6-,12);综合上述,点P 的坐标有:(6,0)或(0,6-)或(6-,12);(4)过点E 作EL ⊥DK 于点L ,连接OD ,过点E 作EM ⊥x 轴于点M ,如图:则AM =OM =3=EM =3,∴EM =AM ,∴∠MEO =∠EOM =45°,∴∠AEO =90°,在OG 上截取ON =AF ,连接EN ,∵∠EAF =∠EON ,∴△EAF ≌△EON (AAS ),∴EF =EN ,∠AEF =∠OEN ,∴∠FEN =∠FEO +∠OEN =∠FEO +∠AEF =∠AEO =90°,∴∠EFN =45°,∵∠EFO =∠AEF +∠EAO =∠EFN +∠NFO ,又∵∠EAO =∠EFN =45°,∴∠NFO =∠AEF ,∴∠FGO =2∠AEF =2∠NFO ,设∠AEF =α,则∠NFO =α,∠FNO =90°-α,∠FGO =2α,在y 轴负半轴上截取OP =ON ,连接FP ,则OF 垂直平分NP ,∴FN =FP ,∴∠FPO =90°-α,∴∠GFP =180°-2α-(90°-α)=90°-α=∠GPF ,∴FG =GP =5,设AF =m ,则ON =OP =m ,则OG =5-m ,OF =6-m ,在Rt △OGF 中,由勾股定理可得,(5-m )2+(6-m )2=52,解得:m =2,(m =9舍去),∴OG =3,OF =4,∴F (-4,0),G (0,3),设直线FG 的解析式为y =ax +c ,∴340c a c =-⎧⎨-+=⎩,解得343a c ⎧=⎪⎨⎪=⎩,∴直线FG 的解析式为:334y x =+,∵H 是直线334y x =+与直线y =-3x +6的交点, ∴33436y x y x ⎧=+⎪⎨⎪=-+⎩,解得45185x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴H (45,185). 【点睛】本题是一次函数与几何综合问题,考查了一次函数的性质,平行四边形的性质,平移的性质,勾股定理,等腰三角形的性质等知识,解题的关键是熟练掌握所学的知识,正确作出合适的辅助线,运用分类讨论的思想进行解题.25.(1)见解析;(2)不变,见解析;(3)能,或【分析】(1)由折叠的性质得到BE=EP ,BF=PF ,得到BE=BF ,根据菱形的性质得到AB ∥CD ∥FG ,BC ∥EH ∥AD ,于是得到结论;(2)由解析:(1)见解析;(2)不变,见解析;(3)能,1x =1【分析】(1)由折叠的性质得到BE=EP ,BF=PF ,得到BE=BF ,根据菱形的性质得到AB ∥CD ∥FG ,BC ∥EH ∥AD ,于是得到结论;(2)由菱形的性质得到BE=BF ,AE=FC ,推出△ABC 是等边三角形,求得∠B=∠D=60°,得到∠B=∠D=60°,于是得到结论;(3)记AC 与BD 交于点O ,得到∠ABD=30°,解直角三角形得到AO=1,S 四边形ABCDAEFCHG时,得到S △BEF +S △DGHGH 与BD 交于点M ,求得GM=12x ,根据三角形的面积列方程即可得到结论. 【详解】解:()1折叠后B 落在BD 上,,BE EP ∴=BF PF = BD 平分,ABC ∠BE BF ∴=,∴四边形BEPF 为菱形,同理四边形GDHP 为菱形,////,// //,AB CD FG BC EH AD ∴∴四边形AEPG 为平行四边形,AG EP BE ∴==.()2不变.理由如下:由()1得.AG BE =四边形BEPF 为菱形,,.BE BF AE FC ∴==60,BAC ABC ∠=︒为等边三角60B D ∴∠=∠=︒,,,EF BE GH DG ∴==36AEFCHG C AE EF FC CH GH AG AB ∴=+++++==六边形为定值.()3记AC 与BD 交于点O .2,60,AB BAC =∠=30,ABD ∴∠=1,AO ∴=3,BO12332ABC S ∴=⨯23ABCD S ∴=四边形当六边形AEFCHG 534 53233344DEF DGH S S +=由()1得BE AG =AE DG ∴=DG x =2BE x ∴=-记GH 与BD 交于点,M12GM x ∴=,3DM = 23DHGS x ∴= 同理)2233233BEF Sx x =-= 223333334x x +化简得22410,x x -+= 解得121x =221x = ∴当21x =21AEPCHG 534 【点睛】此题是四边形的综合题,主要考查了菱形的性质,等边三角形的判定和性质,三角形的面积公式,菱形的面积公式,解本题的关键是用x 表示出相关的线段,是一道基础题目. 26.(1)①详见解析;②详见解析;(2)当BE≠DF 时,(BE+DF )2+EF2=2AB2仍然成立,理由详见解析;(3)【分析】(1)①连接ED 、BF ,证明四边形BEDF 是平行四边形,根据平行四边形 解析:(1)①详见解析;②详见解析;(2)当BE ≠DF 时,(BE +DF )2+EF 2=2AB 2仍然成立,理由详见解析;(3)2622PD =-【分析】(1)①连接ED 、BF ,证明四边形BEDF 是平行四边形,根据平行四边形的性质证明;②根据正方形的性质、勾股定理证明;(2)过D 作DM ⊥BE 交BE 的延长线于M ,连接BD ,证明四边形EFDM 是矩形,得到EM=DF,DM=EF,∠BMD=90°,根据勾股定理计算;(3)过P作PE⊥PD,过B作BELPE于E,根据(2)的结论求出PE,结合图形解答.【详解】(1)证明:①连接ED、BF,∵BE∥DF,BE=DF,∴四边形BEDF是平行四边形,∴BD、EF互相平分;②设BD交EF于点O,则OB=OD=12BD,OE=OF=12EF.∵EF⊥BE,∴∠BEF=90°.在Rt△BEO中,BE2+OE2=OB2.∴(BE+DF)2+EF2=(2BE)2+(2OE)2=4(BE2+OE2)=4OB2=(2OB)2=BD2.在正方形ABCD中,AB=AD,BD2=AB2+AD2=2AB2.∴(BE+DF)2+EF2=2AB2;(2)解:当BE≠DF时,(BE+DF)2+EF2=2AB2仍然成立,理由如下:如图2,过D作DM⊥BE交BE的延长线于M,连接BD.∵BE∥DF,EF⊥BE,∴EF⊥DF,∴四边形EFDM是矩形,∴EM=DF,DM=EF,∠BMD=90°,在Rt△BDM中,BM2+DM2=BD2,∴(BE+EM)2+DM2=BD2.即(BE+DF)2+EF2=2AB2;(3)解:过P作PE⊥PD,过B作BE⊥PE于E,则由上述结论知,(BE+PD)2+PE2=2AB2.∵∠DPB=135°,∴∠BPE=45°,∴∠PBE=45°,∴BE=PE.∴△PBE是等腰直角三角形,∴BP2BE,∵2+2PD=6,∴2BE+2PD=6,即BE+PD=6∵AB=4,∴(6)2+PE2=2×42,解得,PE=2∴BE=2∴PD=6﹣2.【点睛】本题考查的是正方形的性质、等腰直角三角形的性质以及勾股定理的应用,正确作出辅助性、掌握正方形的性质是解题的关键.。
人教版八年级下册数学期末试卷(培优篇)(Word版含解析)
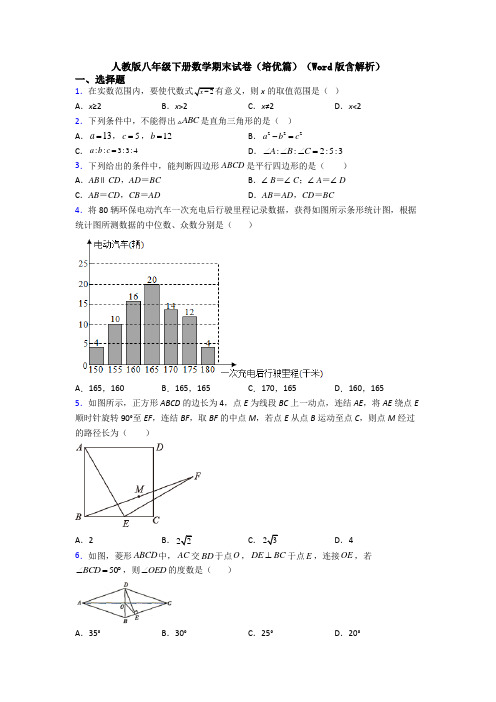
人教版八年级下册数学期末试卷(培优篇)(Word 版含解析)一、选择题1.在实数范围内,要使代数式2x -有意义,则x 的取值范围是( )A .x ≥2B .x >2C .x ≠2D .x <22.下列条件中,不能得出ABC 是直角三角形的是( )A .13a =,5c =,12b =B .222a c b -=C .::3:3:4a b c =D .::2:5:3A B C ∠∠∠=3.下列给出的条件中,能判断四边形ABCD 是平行四边形的是( )A .AB ∥CD ,AD =BC B .∠B =∠C ;∠A =∠DC .AB =CD ,CB =AD D .AB =AD ,CD =BC4.将80辆环保电动汽车一次充电后行驶里程记录数据,获得如图所示条形统计图,根据统计图所测数据的中位数、众数分别是( )A .165,160B .165,165C .170,165D .160,165 5.如图所示,正方形ABCD 的边长为4,点E 为线段BC 上一动点,连结AE ,将AE 绕点E 顺时针旋转90°至EF ,连结BF ,取BF 的中点M ,若点E 从点B 运动至点C ,则点M 经过的路径长为( )A .2B .22C .23D .46.如图,菱形ABCD 中,AC 交BD 于点O ,DE BC ⊥于点E ,连接OE ,若50BCD ∠=︒,则OED ∠的度数是( )A .35°B .30°C .25°D .20°7.如图,有一个圆柱,底面圆的直径AB =16π,高BC =12cm ,P 为BC 的中点,一只蚂蚁从A 点出发沿着圆柱的表面爬到P 点的最短距离为( )A .9cmB .10cmC .11cmD .12cm8.小张、小王两个人从甲地出发,去8千米外的乙地,图中线段OA 、PB 分别反映了小张、小王步行所走的路程S (千米)与时间t (分钟)的函数关系,根据图像提供的信息,小王比小张早到乙地的时间是__________分钟.A .4B .6C .16D .10二、填空题9.二次根式9x +在实数范围内有意义,则x 的取值范围是__.10.在菱形ABCD 中,AB =m ,AC +BD =n ,则菱形ABCD 的面积为_________.(用含m 、n 的代数式表示)11.如图,数字代表所在正方形的面积,则A 所代表的正方形的面积为_________.12.如图,点P 在矩形ABCD 的对角线AC 上,且不与点A C 、重合,过点P 分别作边AB AD 、的平行线,交两组对边于点E F 、和G H 、.四边形PEDH 和四边形PFBG 都是矩形并且面积分别为S 1,S 2,则S 1,S 2之间的关系为__________.13.直线y=kx+b的图象如图所示,则代数式2k﹣b的值为 _____.14.如图,O是矩形ABCD的对角线AC、BD的交点,OM⊥AD,垂足为M,若AB=8,则OM长为_______.15.如图1,点P从ABC的顶点A出发,沿A→B→C匀速运动到点C,图2是点P运动时线段CP的长度y随时间x变化的关系图象,其中点Q为曲线部分的最低点,则ABC的边AB的长度为___.16.如图,四边形ABCD是矩形纸片,AD=10,CD=8.在CD边上取一点E,将纸片沿AE 翻折,使点D落在BC边上的点F处.则AF=__;CF=__;DE=__.三、解答题17.计算:(1)2(3)-+(﹣2)﹣2﹣116+(π﹣2)0; (2)(3﹣2)2×12+613. 18.如图,一架2.5m 长的梯子AB 斜靠在一面竖直的墙AC 上,这时梯子的底端B 到墙的底端C 的距离为0.7m ,如果梯子的顶端沿墙下滑0.4m ,那么梯子的底端将向外移多少米?19.如图,每个小正方形的边长都是1,△ABC 的三个顶点分别在正方形网格的格点上. (1)求AB ,BC 的长;(2)判断△ABC 的形状,并说明理由.20.请在横线上添加一个合适的条件,并写出证明过程:如图,平行四边形ABCD 对角线上有两点E ,F ,AE =CF , ,连接EB ,ED ,FB ,FD .求证:四边形EBFD 为菱形.21.阅读,并回答下列问题:公元322r a r a a+≈+2的近似值. (12211+1321212≈+=⨯2看23124⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭2≈___________≈______________;依次算法,所得2的近似值会越来越精确.(2)按照上述取近似值的方法,当2取近似值577408时,求近似公式中的a和r的值.22.在乡村道路建设过程中,甲、乙两村之间需要修建水泥路,甲、乙两村合作完成.已知甲村需要水泥70吨,乙村需要水泥110吨,A厂可提供100吨水泥,B厂可提供80吨水泥,两厂到两村的运费如表:目的地运费/(元/吨)甲村乙村A厂240180B厂250160(1)设从A厂运往甲村水泥x吨,求运送的总费用y(元)与x(吨)之间的函数关系式,并写出自变量x的取值范围;(2)请你设计出运费最低的运送方案,并求出最低运费.23.如图,正方形ABCD的顶点C处有一等腰直角三角形CEP,∠PEC=90°,连接AP,BE.(1)若点E在BC上时,如图1,线段AP和BE之间的数量关系是;(2)若将图1中的△CEP顺时针旋转使P点落在CD上,如图2,则(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)在(2)的基础上延长AP,BE交于F点,若DP=PC=2,求BF的长.24.在平面直角坐标系xOy中,对于任意三点A,B,C的“矩积”,给出如下定义:“横底”a:任意两点横坐标差的最大值;“纵高”h:任意两点纵坐标差的最大值;则“矩积”S=ah.例如:三点坐标分别为A(1,﹣2),B(2,2),C(﹣1,﹣3),则“横底”a=3,“纵高”h=5,“矩积”S=ah=15.已知点D(﹣2,3),E(1,﹣1).(1)若点F在x轴上.①当D,E,F三点的“矩积”为24,则点F的坐标为;②直接写出D,E,F三点的“矩积”的最小值为;(2)若点F在直线y=mx+4上,使得D,E,F三点的“矩积”取到最小值,直接写出m的取值范围是.25.矩形ABCD 中,AB =3,BC =4.点E ,F 在对角线AC 上,点M ,N 分别在边AD ,BC 上.(1)如图1,若AE =CF =1,M ,N 分别是AD ,BC 的中点.求证:四边形EMFN 为矩形.(2)如图2,若AE =CF =0.5,02AM CN x x ==<<(),且四边形EMFN 为矩形,求x 的值.26.如图1,ABC ∆中,CD AB ⊥于D ,且::2:3:4BD AD CD =;(1)试说明ABC ∆是等腰三角形;(2)已知Δ40ABC S =cm 2,如图2,动点M 从点B 出发以每秒1cm 的速度沿线段BA 向点A 运动,同时动点N 从点A 出发以相同速度沿线段AC 向点C 运动,当其中一点到达终点时整个运动都停止.设点M 运动的时间为t (秒).①若DMN ∆的边与BC 平行,求t 的值;②在点N 运动的过程中,ADN ∆能否成为等腰三角形?若能,求出t 的值;若不能,请说明理由.【参考答案】一、选择题1.A解析:A【分析】根据二次根式有意义,被开方数为非负数,列一元一次不等式,解不等式即可得.【详解】解:根据题意,得20x -≥,∴2x ≥,故选:A .【点睛】本题考查了二次根式有意义条件、一元一次不等式解法;解题的关键是熟练掌握二次根式有意义的条件是解题关键.2.C解析:C【分析】根据三角形内角和定理可分析出D 的正误;根据勾股定理逆定理可分析出A 、B 、C 的正误.【详解】解:A 、∵22251213+= ,∴能构成直角三角形,故此选项不符合题意;B 、∵222a c b -=,∴222a b c =+ ,∴能构成直角三角形,故此选项不符合题意;C 、∵()()()222334x x x +≠,∴不能构成直角三角形,故此选项符合题意;D 、设∠A =2x °,∠B =5x °,∠C =3x °,3x +2x +5x =180,解得:x =18,则5x °=90°,△ABC 是直角三角形,故此选项不符合题意;故选:C.【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.3.C解析:C【解析】【分析】平行四边形的判定定理①两组对边分别相等的四边形是平行四边形,②一组对边平行且相等的四边形是平行四边形,③两组对角分别相等的四边形是平行四边形,④对角线互相平分的四边形是平行四边形,判断即可.【详解】解:A、根据AD∥CD,AD=BC不能判断四边形ABCD是平行四边形,故本选项错误;B、根据∠B=∠C,∠A=∠D不能判断四边形ABCD是平行四边形,故本选项错误;C、根据AB=CD,AD=BC,得出四边形ABCD是平行四边形,故本选项正确;D、根据AB=AD,BC=CD,不能判断四边形ABCD是平行四边形,故本选项错误;故选:C.【点睛】本题考查了对平行四边形的判定定理的应用,关键是能熟练地运用平行四边形的判定定理进行推理,此题是一道比较容易出错的题目.4.B解析:B【解析】【分析】由中位数和众数的定义结合条形统计图即可得出答案.【详解】根据题意有80辆电动汽车为偶数个,根据统计图可知最中间的两个数都为165,故中位数=1651651652+=,165出现了20次,为最多,即众数为165.故选:B.【点睛】本题考查中位数和众数的定义,从条形统计图中获取必要的信息是解答本题的关键.5.B解析:B【分析】已知EF⊥AE,当E点在线段BC上运动到两端时,正好是M点运动的两个端点,由此可以判断M点的运动轨迹是BC、CD中点的连线长.【详解】解:取BC 、CD 的中点G 、H ,连接GH ,连接BD∴GH 为△BCD 的中位线,即12GH BD = ∵将AE 绕点E 顺时针旋转90°至EF ,∴EF ⊥AE ,当E 点在B 处时,M 点在BC 的中点G 处,当E 点在C 点处时,M 点在CD 中点处, ∴点M 经过的路径长为GH 的长,∵正方形ABCD 的边长为4,∴2242BD BC CD =+=∴1222GH BD ==, 故选B .【点睛】本题主要考查了正方形的性质,勾股定理和中位线定理,解题的关键在于找到M 点的运动轨迹.6.C解析:C【解析】【分析】根据直角三角形的斜边中线性质可得OE BE OD ==,根据菱形性质可得1652DBE ABC ︒∠=∠=,从而得到OEB ∠度数,再依据90OED OEB ︒∠=-∠即可. 【详解】解:∵四边形ABCD 是菱形,50BCD ︒∠=,∵O 为BD 中点,1652DBE ABC ︒∠=∠=. DE BC ⊥,∴在 Rt BDE ∆中,OE BE OD ==,65OEB OBE ︒∴∠=∠=.906525OED ︒︒︒∴∠=-=.故选C .【点睛】本题主要考查了菱形的性质、直角三角形斜边中线的性质,解决这类问题的方法是四边形转化为三角形.7.B解析:B【解析】【分析】把圆柱的侧面展开,连接AP ,利用勾股定理即可得出AP 的长,即蚂蚁从A 点爬到P 点的最短距离.【详解】解:如图:展开后线段AB 的长度是圆柱中半圆AB 的周长, 圆柱底面直径16cm π、高12BC cm =,P 为BC 的中点,∴6BP cm =, 1168,2AB cm ππ∴=⨯⨯= 在Rt ABP 中,22228610()AP AB PB cm ++=,∴蚂蚁从A 点爬到P 点的最短距离为10cm ,故选:B .【点睛】本题考查的是平面展开-最短路径问题,根据题意画出圆柱的侧面展开图,利用勾股定理求解是解答此题的关键.8.B解析:B【分析】由函数图象求出OA 、PB 解析式,再把8y =代入解析式就可以求出小张、小王所用时间.【详解】解:由图象可知:设OA 的解析式为:y kx =, OA 经过点(60,5),560k ∴=, 得112k =, OA ∴函数解析式为:112y x =①,把8y =代入①得:1812x =, 解得:96x =, ∴小张到达乙地所用时间为96(分钟);设PB 的解析式为:y mx n =+,∴100605m n m n +=⎧⎨+=⎩, 解得:1101m n ⎧=⎪⎨⎪=-⎩, PB ∴的解析式为:1110y x =-②, 把8y =代入②得:18110x =-, 解得:90x =, 则小王到达乙地的时间为小张出发后90(分钟),∴小王比小张早到96906-=(分钟),故选:B .【点睛】本题考查的一次函数的应用,关键是由图象求函数解析式.二、填空题9.x ≥﹣9【解析】【分析】由二次根式的非负性可得x +9≥0,即可求解.【详解】解:∵∴x +9≥0,∴x ≥﹣9,故答案为x ≥﹣9.【点睛】)0a ≥的式子叫二次根式,熟练掌握二次根式成立的条件是解答本题的关键.10.A 解析:2214n m - 【解析】【分析】根据菱形的性质及勾股定理计算即可;【详解】解:在菱形ABCD 中,AB =m ,AC +BD =n , ∴22221122AC BD AB m ⎛⎫⎛⎫+== ⎪ ⎪⎝⎭⎝⎭, ∴AC 2+BD 2=4m 2, ∴菱形ABCD 的面积=()()22211222AC BD AC BD AC BD +-+=⨯, =221422n m -⨯, =2214n m -, 故答案为:2214n m -. 【点睛】本题主要考查了菱形的性质,勾股定理,准确计算是解题的关键.11.A解析:【解析】【分析】三个正方形的边长正好构成直角三角形的三边,根据勾股定理得到字母A 所代表的正方形的面积A =36+64=100.【详解】解:由题意可知,直角三角形中,一条直角边的平方=36,一条直角边的平方=64,则斜边的平方=36+64.故答案为:100.【点睛】本题考查了正方形的面积公式以及勾股定理.12.S 1=S 2【分析】由矩形的性质找出90D B ∠=∠=︒,结合对边互相平行即可证出四边形PEDH 和四边形PFBG 都是矩形,再根据矩形的性质可得出三对三角形的面积相等,由此即可得结果.【详解】解:∵四边形ABCD 为矩形,∴90D B ∠=∠=︒.又∵////EF AB CD ,////GH AD BC ,∴四边形PEDH 和四边形PFBG 都是矩形.∵//EF AB ,//HG BC ,四边形ABCD 为矩形,∴四边形AEPG 和四边形PHCF 也是矩形,∴ACD ABC SS =,PHC PCF S S =,AEP APG S S =, ∴ACD PHC AEP ABC PCF APG S S S S S S --=--,∴12S S故答案为:12S S .【点睛】本题考查了矩形的性质与判定,掌握矩形的性质与判定是解题的关键.13.-3【分析】将点(2,3)P -代入y kx b =+即可求解.【详解】解:y kx b =+的图象经过点(2,3)P -,32k b ∴=-+,23k b ∴-=-,故答案为3-.【点睛】本题考查一次函数图象上点的特征,熟练掌握点与一次函数解析式的关系是解题的关键. 14.A解析:4【解析】【分析】根据三角形的中位线即可求解.【详解】∵O 是矩形ABCD 的对角线AC 、BD 的交点,∴O 是AC 中点,又OM ⊥AD ,AD ⊥CD ∴12∥OM CD ,又AB=CD=8 故OM=4故填:4【点睛】此题主要考查矩形的性质,解题的关键是熟知三角形中位线的性质.15.10【分析】根据图2中的曲线可得,当点P 在△ABC 的顶点A 处,运动到点B 处时,图1中的AC=BC=13,当点P 运动到AB 中点时,此时CP ⊥AB ,根据图2点Q 为曲线部分的最低点,可得CP=12,根解析:10【分析】根据图2中的曲线可得,当点P 在△ABC 的顶点A 处,运动到点B 处时,图1中的AC =BC =13,当点P 运动到AB 中点时,此时CP ⊥AB ,根据图2点Q 为曲线部分的最低点,可得CP =12,根据勾股定理可得AP =5,再根据等腰三角形三线合一可得AB 的长.【详解】根据题图②可知:当点P 在点A 处时,13CP AC ==,当点P 到达点B 时,13CP CB ==,∴ABC 为等腰三角形,当点P 在AB 上运动且CP 最小时,CP AB ⊥时,12CP =,∴ABC 的AB 边的高为12,如解图,当CP AB ⊥时,12CP =,在Rt ACP 中,2213125AP =-=,∴2510AB =⨯=.故答案为:10.【点睛】本题主要考查了动点问题的函数图象,解决本题的关键是综合利用两个图形给出的条件. 16.4 5【分析】先根据矩形的性质得AB=CD=8,在RtΔABF 中,利用勾股定理计算BF=6,再根据矩形的性质得AD=CB=10 ,则CF=BC−BF=4;设DE=x ,则EF=x解析:4 5【分析】先根据矩形的性质得AB=CD=8,在RtΔABF 中,利用勾股定理计算BF=6,再根据矩形的性质得AD=CB=10 ,则CF=BC−BF=4;设DE=x ,则EF=x , EC=8−x ,然后在 RtΔECF 中根据勾股定理得到42+(8−x)2=x 2 ,再解方程即可得到DE 的长.【详解】解:根据折叠可得AF =AD =10,∵四边形ABCD 是矩形,∴BC =AD =10,在Rt △ABF 中, AB 2+FB 2=AF 2,∴FB=6.∴FC =10﹣6=4,设DE =x ,则EF =x ,EC =8﹣x ,在Rt △ECF 中,∵CE 2+FC 2=EF 2,∴42+(8﹣x )2=x 2,解得x =5.则DE =5.故答案为:10,4,5.【点睛】本题考查了图形的折叠,矩形的性质和勾股定理,关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.三、解答题17.(1)4;(2)【分析】(1)根据二次根式的性质,零指数幂和负指数幂的性质计算即可;(2)根据二次根式的乘法运算计算即可;【详解】(1)原式;(2)原式;【点睛】本题主要考查了二次根解析:(1)4;(2)24【分析】(1)根据二次根式的性质,零指数幂和负指数幂的性质计算即可;(2)根据二次根式的乘法运算计算即可;【详解】(1)原式1131444=+-+=;(2)原式()342424=-⨯+;【点睛】本题主要考查了二次根式的混合运算,结合负指数幂,零指数幂计算是解题的关键. 18.米.【分析】先在中,利用勾股定理出的长,再根据线段的和差可得的长,然后在中,利用勾股定理求出的长,最后根据即可得出答案.【详解】解:由题意得:,则,在中,,则,答:梯子的底解析:0.8米.【分析】先在Rt ABC 中,利用勾股定理出AC 的长,再根据线段的和差可得1A C 的长,然后在11Rt A B C 中,利用勾股定理求出1B C 的长,最后根据11BB B C BC =-即可得出答案.【详解】解:由题意得:11112.5m,0.7m,0.4m,AB A B BC AA AC B C ====⊥,在Rt ABC 中, 2.4(m)AC ==,则11 2.40.42(m)AC AC AA =-=-=,在11Rt A B C 中,1 1.5(m)B C =, 则11 1.50.70.8(m)BB B C BC =-=-=,答:梯子的底端将向外移0.8米.【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题关键.19.(1)AB =2,BC =,(2)△ABC 是直角三角形,见解析.【解析】【分析】(1)先利用勾股定理分别计算两边的长即可;(2)利用勾股定理的逆定理得到三角形为直角三角形.【详解】解:(1)解析:(1)AB =BC 2)△ABC 是直角三角形,见解析.【解析】【分析】(1)先利用勾股定理分别计算两边的长即可;(2)利用勾股定理的逆定理得到三角形为直角三角形.【详解】解:(1)AB =BC(2)AC =5, ∵2225+=,∴AB 2+BC 2=AC 2,∴△ABC 是直角三角形.此题考查了勾股定理和勾股定理的逆定理,熟练掌握勾股定理是解本题的关键. 20.,见解析【分析】根据题意和图形,可以在空格处填一个条件,注意填写的条件不唯一,只要可以证明结论成立即可,然后根据菱形的判定方法证明即可.【详解】补充条件:AB =BC ,证明:连接BD 交AC 于解析:AB BC =,见解析【分析】根据题意和图形,可以在空格处填一个条件,注意填写的条件不唯一,只要可以证明结论成立即可,然后根据菱形的判定方法证明即可.【详解】补充条件:AB =BC ,证明:连接BD 交AC 于点O ,如图所示,∵四边形ABCD 是平行四边形,∴OB =OD ,OA =OC ,∵AE =CF ,∴OE =OF ,∴四边形EBFD 是平行四边形,∵AB =BC ,∴∠BAE =∠BCF ,在△BAE 和△BCF 中,BA BC BAE BCF AE CF =⎧⎪∠=∠⎨⎪=⎩, ∴△BAE ≌△BCF (SAS ),∴BE =BF ,∴平行四边形EBFD 是菱形,即四边形EBFD 为菱形.故答案为:AB =BC .【点睛】本题考查菱形的判定、平行四边形的性质、全等三角形的判定与性质,利用数形结合的思想解答是解答本题的关键.21.(1);(2)或 ;或【解析】【分析】根据近似公式计算出近似值的过程和方法计算的近似值和确定a 和r 的值.【详解】(1)根据近似公式可知:≈故答案为;(2)∵∴∴∴整理,解析:(1)1343222-+⨯;1712(2)1712a =或2417;1144r =-或2289 【解析】【分析】的近似值和确定a 和r 的值.【详解】(1≈1343222-+⨯≈1712故答案为1343222-+⨯;1712(2)∵2r a a≈≈+ ∴225772408a r r a a ⎧+=⎪⎨+=⎪⎩∴5772()408r a a =⨯- ∴25772()2408a a a +⨯-= 整理,22045774080a a -+= 解得:1712a = 或2417a =∴1144r =-或2289r = 故答案为1712a =或2417 ;1144r =-或2289 【点睛】本题考查二次根式的估算,审清题意,根据题目所给的近似公式计算是解题关键. 22.(1)y =﹣30x+37100(0≤x≤70);(2)最低运送方案为A 厂运往甲村水泥70吨,运往乙村水泥30吨:B 厂运往甲村水泥0吨,B 厂运往乙村水泥80吨,最低运费为35000元.【分析】(1解析:(1)y =﹣30x +37100(0≤x ≤70);(2)最低运送方案为A 厂运往甲村水泥70吨,运往乙村水泥30吨:B 厂运往甲村水泥0吨,B 厂运往乙村水泥80吨,最低运费为35000元.【分析】(1)由从A 厂运往甲村水泥x 吨,根据题意首先求得从A 厂运往乙村水泥(100-x )吨,B 厂运往甲村水泥(70-x )吨,B 厂运往乙村水泥吨,然后根据表格求得总运费y (元)关于x (吨)的函数关系式;(2)根据(1)中的一次函数解析式的增减性,即可知当x =70时,总运费y 最省,然后代入求解即可求得最低运费.【详解】(1)设从A 厂运往甲村水泥x 吨,则A 厂运往乙村水泥(100﹣x ) 吨,B 厂运往甲村水泥(70﹣x )吨,B 厂运往乙村水泥110﹣(100﹣x )=(10+x )吨,∴y =240x +180(100﹣x )+250(70﹣x )+160(10+x )=﹣30x +37100,x 的取值范围是0≤x ≤70,∴y =﹣30x +37100(0≤x ≤70);(2)∵y =﹣30x +37100(0≤x ≤70),﹣30<0,∴y 随x 的增大而减小,∵0≤x ≤70,∴当x =70时,总费用最低,最低运费为:﹣30×70+37100=35000 (元),∴最低运送方案为A 厂运往甲村水泥70吨,运往乙村水泥30吨:B 厂运往甲村水泥0吨,B 厂运往乙村水泥80吨,最低运费为35000元.【点睛】本题主要考查了一次函数的实际应用问题,解决本题的关键是理解题意,读懂表格,求得一次函数解析式,然后根据一次函数的性质求解.23.(1)AP=BE ;(2)成立,理由见解析;(3)【分析】(1)首先说明A ,P ,C 三点共线,设正方形ABCD 的边长为1,CE=x ,根据正方形和等腰直角三角形的性质求出AP和BE的长,即可判断;(解析:(1)AP=2BE;(2)成立,理由见解析;(3)810 5【分析】(1)首先说明A,P,C三点共线,设正方形ABCD的边长为1,CE=x,根据正方形和等腰直角三角形的性质求出AP和BE的长,即可判断;(2)过点B作BH⊥BE,且BH=BE,连接AH,EH,证明△ABH≌△BEC,得到AH=EC=PE,∠AHB=∠CEB,从而证明四边形AHEP是平行四边形,同理可得AP=EH=2BE;(3)过B,D分别作AF的垂线,垂足为K,M,证明△ABK≌△DAM,得到BK=AM,求出AP,在△ADP中利用面积法求出DM,可得AM和BK,再利用勾股定理求出BF即可.【详解】解:(1)∵点E在BC上,△PEC为等腰直角三角形,∴PE=CE,∠PCE=45°,∵四边形ABCD是正方形,∴∠ACB=45°,∴A,P,C三点共线,设正方形ABCD的边长为1,CE=x,∴PE=x,PC=2x,AC=22112+=,∴AP=AC-PC=()2221x x-=-,BE=BC-CE=1-x,∴AP=2BE;(2)成立,如图,过点B作BH⊥BE,且BH=BE,连接AH,EH,∵∠ABC=∠EBH=90°,∴∠CBE+∠ABE=∠ABH+∠ABE=90°,∴∠CBE=∠ABH,又∵BH=BE,AB=BC,∴△ABH≌△BEC(SAS),∴AH=EC=PE,∠AHB=∠CEB,∴∠AHE=∠AHB-∠EHB=∠CEB-45°,∵∠HEP=360°-∠CEB-∠HEB-∠CEP=360°-∠CEB-45°-90°=225°-∠CEB,∴∠AHE +∠HEP =∠CEB -45°+225°-∠CEB =180°,∴AH ∥PE ,∴四边形AHEP 是平行四边形,∴AP =EH =2BE ;(3)如图,过B ,D 分别作AF 的垂线,垂足为K ,M ,∵∠BAD =∠BAK +∠DAM =90°,∠ABK +∠BAK =90°,∴∠ABK =∠DAM ,又∵AB =AD ,∠AKB =∠AMD =90°,∴△ABK ≌△DAM (AAS ),∴BK =AM ,∵四边形ABCD 是正方形,DP =PC =2,∴AD =CD =4,∠AHE =90°,∴AP 2225AD DP +∴S △ADP =1122AD DP AP DM ⨯⨯=⋅,∴11422522DM ⨯⨯=⨯, ∴45DM = ∴AM 22458545⎛⎫- ⎪ ⎪⎝⎭, 由(2)可知:△EBH 为等腰直角三角形,HE ∥AP ,∴∠KBF =12∠HBE =45°, ∴∠F =45°,∴BF 852810 【点睛】本题考查了正方形的性质,等腰直角三角形的判定和性质,勾股定理,全等三角形的判定和性质,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.24.(1)①(﹣5,0)或(4,0);②12;(2)或【解析】【分析】(1)①已知F 在x 轴上,故“纵高”=4,根据“矩积”的定义,可知“横底”=6,应分三种情况进行分类讨论,当a<-2时、当-2≤解析:(1)①(﹣5,0)或(4,0);②12;(2)12m≥或1m≤-【解析】【分析】(1)①已知F在x轴上,故“纵高”=4,根据“矩积”的定义,可知“横底”=6,应分三种情况进行分类讨论,当a<-2时、当-2≤a≤1时、当a>1时;②将F点的横坐标仍按照三类情况进行讨论,根据“矩积”的定义可求解;(2)使直线过点D(-2,3)或点H(1,3),求出该特殊位置时m的值,即可求解.【详解】解:(1)设点F坐标为(a,0),①∵D,E,F三点的“矩积”为24,“纵高”=4,∴“横底”=6,当a<-2时,则“横底”=1-a=6,∴a=-5;当-2≤a≤1时,则“横底”=3≠6,不合题意舍去;当a>1时,则“横底”=a-(-2)=6;∴a=4,∴点F(﹣5,0)或(4,0),故答案为:(﹣5,0)或(4,0);②当a<-2时,则1-a>3,∴S=4(1-a)>12,当﹣2≤a≤1时,S=3⨯4=12,当a>1时,则a-(-2)>3,∴S=4⨯[a-(-2)]>12,∴D,E,F三点的“矩积”的最小值为12,故答案为:12;(2)由(1)可知:设点F(a,0),当﹣2≤a≤1时,D,E,F三点的“矩积”能取到最小值,如图下图所示,直线y=mx+4恒过点(0,4),使该直线过点D(-2,3)或点H(1,3),当F 在点D或点H时,D,E,F三点的“矩积”的最小值为12,当直线y=mx+4过点D(-2,3)时,∴3=-2m+4,∴解得:1m=2,当直线y=mx+4过点H(1,3)时,∴3=m+4,∴m=-1,∴当m≥12或m≤-1时,D,E,F三点的“矩积”能取到最小值.【点睛】本题主要考察了一次函数的几何应用,提出了“矩积”这个全新的概念,解题的关键在于通过题目的描述,知道“矩积”的定义,同时要注意分类讨论.25.(1)见详解;(2)【分析】(1)连接MN,由勾股定理求出AC=5,证出四边形ABNM是矩形,得MN=AB=3,证△AME≌△CNF(SAS),得出EM=FN,∠AEM=∠CFN,证EM∥FN,解析:(1)见详解;(2)72x=【分析】(1)连接MN,由勾股定理求出AC=5,证出四边形ABNM是矩形,得MN=AB=3,证△AME≌△CNF(SAS),得出EM=FN,∠AEM=∠CFN,证EM∥FN,得四边形EMFN是平行四边形,求出MN=EF,即可得出结论;(2)连接MN,作MH⊥BC于H,则MH=AB=3,BH=AM=x,得HN=BC-BH-CN=4-2x,由矩形的性质得出MN=EF=AC-AE-CF=4,在Rt△MHN中,由勾股定理得出方程,解方程即可.【详解】(1)证明:连接MN,如图1所示:∵四边形ABCD 是矩形,∴AD ∥BC ,AD=BC ,∠B=90°,∴∠EAM=∠FCN ,AC=2222345AB BC +=+=,∵M ,N 分别是AD ,BC 的中点,∴AM=DM=BN=CN ,AM ∥BN ,∴四边形ABNM 是平行四边形,又∵∠B=90°,∴四边形ABNM 是矩形,∴MN=AB=3,在△AME 和△CNF 中,AM CN EAM FCN AE CF =⎧⎪∠=∠⎨⎪=⎩, ∴△AME ≌△CNF (SAS ),∴EM=FN ,∠AEM=∠CFN ,∴∠MEF=∠NFE ,∴EM ∥FN ,∴四边形EMFN 是平行四边形,又∵AE=CF=1,∴EF=AC-AE-CF=3,∴MN=EF ,∴四边形EMFN 为矩形.(2)解:连接MN ,作MH ⊥BC 于H ,如图2所示:则四边形ABHM 是矩形,∴MH=AB=3,BH=AM=x ,∴HN=BC-BH-CN=4-2x ,∵四边形EMFN为矩形,AE=CF=0.5,∴MN=EF=AC-AE-CF=4,在Rt△MHN中,由勾股定理得:32+(4-2x)2=42,解得:x=2,∵0<x<2,∴x=2-【点睛】本题考查了矩形的判定与性质、平行四边形的判定与性质、全等三角形的判定与性质、平行线的判定、勾股定理等知识;熟练掌握矩形的判定与性质和勾股定理是解题的关键.26.(1)证明见解析;(2)①t值为5或6;②点N运动的时间为6s,,或时,为等腰三角形. 【分析】(1)设BD=2x,AD=3x,CD=4x,则AB=5x,由勾股定理求出AC,即可得出结论;(2解析:(1)证明见解析;(2)①t值为5或6;②点N运动的时间为6s,365s,或5s时,ΔADN为等腰三角形.【分析】(1)设BD=2x,AD=3x,CD=4x,则AB=5x,由勾股定理求出AC,即可得出结论;(2)①由△ABC的面积求出BD、AD、CD、AC;再分当MN∥BC时,AM=AN和当DN∥BC时,AD=AN两种情况得出方程,解方程即可;②分三种情况:AD=AN;DA=DN;和ND=NA,三种情况讨论即可【详解】解:(1)设BD=2x,AD=3x,CD=4x,则AB=5x,在Rt△ACD中,AC5x,∴AB=AC,∴△ABC是等腰三角形;(2)①S△ABC=12×5x×4x=40cm2,而x>0,∴x=2cm,则BD=4cm,AD=6cm,CD=8cm,AC=10cm.当MN∥BC时,AM=AN,即10−t=t,此时t=5,当DN∥BC时,AD=AN,此时t=6,综上所述,若△DMN的边与BC平行时,t值为5或6;②ΔADN能成为等腰三角形,分三种情况:(ⅰ)若AD =AN =6,如图:则t =61=6s ; (ⅱ)若DA =DN ,如图:过点D 作DH AC ⊥于点H ,则AH =NH ,由1122ACD S AD CD AC DH =⋅=⋅,得11681022DH ⨯⨯=⨯⨯, 解得245DH =, 在Rt ADH 中,222224186()55AH AD DH =-=-=, 3625AN AH ∴==, 3615AN t s ∴==; (ⅲ)若ND =NA ,如图:过点N 作NQ AB ⊥于点Q ,则AQ =DQ =3,142NQ CD ==,5AN ∴==,51AN t s ∴==; 综上,点N 运动的时间为6s ,365s ,或5s 时,ΔADN 为等腰三角形. 【点睛】此题主要考查了等腰三角形的性质,平行线的性质,三角形的面积公式,勾股定理,解本题的关键是熟练掌握方程的思想方法和分类讨论思想.。
人教版八年级数学下册期末试卷(培优篇)(Word版含解析)

人教版八年级数学下册期末试卷(培优篇)(Word 版含解析)一、选择题1.函数11y x =-的自变量x 的取值范围是( ) A .0x >B .1≥xC .0x >且1x ≠D .1x >2.如图,正方形网格中的ABC ,若小方格边长为1,则ABC 的形状为( )A .直角三角形B .锐角三角形C .钝角三角形D .以上答案都不对3.如图,以ABC 的顶点A 为圆心,以BC 长为半径作弧;再以顶点C 为圆心,以AB 长为半径作弧,两弧交于点D ,则四边形ABCD 是平行四边形的理由是( )A .两组对边分别平行的四边形是平行四边形B .两组对边分别相等的四边形是平行四边形C .对角线互相平分的四边形是平行四边形D .一组对边平行且相等的四边形是平行四边形4.甲、乙两个同学在四次数学模拟测试中,平均成绩都是112分,方差分别是25S =甲,212S =乙,则甲、乙两个同学的数学成绩比较稳定的是( )A .甲B .乙C .甲和乙一样D .无法确定5.如图,平行四边形ABCD 的对角线AC 与BD 相交于点O .CE ⊥AD 于点E ,AB =23,AC =4,BD =8,则CE =( )A .72B .2217C .4217D .76.如图是两个全等的三角形纸片,其三边长之比为3: 4: 5,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为,A B S S ,已知15A B S S -=,则纸片的面积是( )A .102B .104C .106D .1087.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形.如图所示,若AF =5,CE =12,则该三角形的面积为( )A .60B .65C .120D .1308.甲、乙两车分别从A ,B 两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为23︰,甲、乙两车离AB 中点C 的路程(y 千米)与甲车出发时间(t 时)的关系图象如图所示,则下列说法错误的是( )A .A ,B 两地之间的距离为180千米 B .乙车的速度为36千米/时C .a 的值为3.75D .当乙车到达终点时,甲车距离终点还有30千米二、填空题9.已知,x y 是实数,且满足2212y x x =--,则xy 的平方根是____________. 10.已知菱形的边长与一条对角线的长分别为5和6,则它的面积是______.11.《九章算术》是我国古代重要的数学著作之一,其中记载了一道“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?译为:如图所示,ABC 中,90,ACB ∠=︒10,3,AC AB BC +==求AC 的长.在这个问题中,可求得的长为_________.12.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 _______. 13.若一次函数2y x b =+(b 为常数)的图象经过点(b ,9),则b =____.14.如图,已知矩形ABCD 中(AD >AB),EF 经过对角线的交点O ,且分别交AD ,BC 于E ,F ,请你添加一个条件:______,使四边形EBFD 是菱形.15.如图所示,直线2y x =+与两坐标轴分别交于A 、B 两点,点C 是OB 的中点,D 、E 分别是直线AB 、y 轴上的动点,当CDE ∆周长最小时,点D 的坐标为_____.16.已知矩形ABCD ,点E 在AD 边上,DE AE >,连接BE ,将ABE △沿着BE 翻折得到BFE △,射线EF 交BC 于G ,若点G 为BC 的中点,1FG =,6DE =,则BE 长为________.三、解答题17.(1)148312242÷+⨯- (2)(32126)2352--⨯+18.如图,牧童在离河边3km 的A 处牧马,小屋位于他南6km 东9km 的B 处,他想把他的马牵到河边饮水,然后回小屋.他要完成此过程所走的最短路程是多少?并在图中画出饮水C 所在在位置(保留作图痕迹).19.如图,是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作:(1)请在网格中建立直角坐标系,使A 点坐标为(4,2)-,B 点坐标为(2,4)-; (2)在网格上,找一格点C ,使点C 与线段AB 组成等腰三角形,这样的C 点共有 个;(3)在(1)(2)的前提下,在第四象限中,当ABC 是以AB 为底的等腰三角形,且腰长为无理数时,ABC 的周长是 ,面积是 .20.如图,矩形ABCD 的对角线相交于点O ,DE ∥AC ,CE ∥BD ,求证:四边形OCED 是菱形.21.阅读,并回答下列问题:公元322ra r a a+≈+2的近似值. (12211+1321212≈+=⨯2看23124⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭2≈___________≈______________;依次算法,所得2的近似值会越来越精确.(2)按照上述取近似值的方法,当2取近似值577408时,求近似公式中的a和r的值.22.清明期间,某校计划组织八年级学生去树湘纪念馆参观,与某公交公司洽谈后,得知该公司有A,B两种不同型号客车,它们的载客量和租金如下表所示:类别A型客车B型客车载客量(人/辆)5030租金(元/辆)300180经计算,租用A,B型客车共15辆较为合理,设租用A型客车x辆,根据要求回答下列问题:(1)用含x的代数式填写下表:类别车辆数(辆)载客量(人)租金(元)A型客车x50x300xB型客车15﹣x(2)若租用A型客车的数量不小于B型客车数量的2倍,采用怎样的方案可以使租车总费用y最少,最少是多少?23.如图1,在平面直角坐标系xOy中,直线l1:y=x+6交x轴于点A,交y轴于点B,经过点B的直线l2:y=kx+b交x轴于点C,且l2与l1关于y轴对称.(1)求直线l2的函数表达式;(2)点D,E分别是线段AB,AC上的点,将线段DE绕点D逆时针α度后得到线段DF.①如图2,当点D的坐标为(﹣2,m),α=45°,且点F恰好落在线段BC上时,求线段AE 的长;②如图3,当点D的坐标为(﹣1,n),α=90°,且点E恰好和原点O重合时,在直线y=3﹣13上是否存在一点G,使得∠DGF=∠DGO?若存在,直接写出点G的坐标;若不存在,请说明理由.24.已知:直线364y x=+与x轴、y轴分别相交于点A和点B,点C在线段AO上.将BCO∆沿BC折叠后,点O恰好落在AB边上点D处.(1)直接写出点A、点B的坐标:(2)求AC的长;(3)点P为平面内一动点,且满足以A、B、C、P为顶点的四边形为平行四边形,请直接回答:①符合要求的P 点有几个? ②写出一个符合要求的P 点坐标.25.在正方形AMFN 中,以AM 为BC 边上的高作等边三角形ABC ,将AB 绕点A 逆时针旋转90°至点D ,D 点恰好落在NF 上,连接BD ,AC 与BD 交于点E ,连接CD , (1)如图1,求证:△AMC ≌△AND ; (2)如图1,若DF=3,求AE 的长;(3)如图2,将△CDF 绕点D 顺时针旋转α(090α<<),点C,F 的对应点分别为1C 、1F ,连接1AF 、1BC ,点G 是1BC 的中点,连接AG ,试探索1AGAF 是否为定值,若是定值,则求出该值;若不是,请说明理由.26.在正方形ABCD 中,AB =4,点E 是边AD 上一动点,以CE 为边,在CE 的右侧作正方形CEFG ,连结BF .(1)如图1,当点E 与点A 重合时,则BF 的长为 . (2)如图2,当AE =1时,求点F 到AD 的距离和BF 的长.(3)当BF最短时,请直接写出此时AE的长.【参考答案】一、选择题1.D解析:D【分析】根据二次根式有意义的条件:被开方数大于等于零,以及分式有意义的条件分母不等于零可得结果.【详解】y=解:∵函数x->,∴10x>,解得:1故选:D.【点睛】本题考查了函数自变量的取值范围,熟知二次根式有意义的条件以及分式有意义的条件是解本题的关键.2.A解析:A【分析】根据勾股定理求得△ABC各边的长,再利用勾股定理的逆定理进行判定,从而不难得到其形状.【详解】解:∵正方形小方格边长为1,∴BC 22442,AC=AB=在△ABC中,∵BC2+AC2=32+18=50,AB2=50,∴BC2+AC2=AB2,∴△ABC是直角三角形.故选:A.【点睛】考查了勾股定理的逆定理,解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.3.B解析:B【解析】【分析】根据平行四边形的判定解答即可. 【详解】解:由题意可知,AB =CD ,AD =BC ,∴四边形ABCD 是平行四边形(两组对边分别相等的四边形是平行四边形), 故选:B . 【点睛】此题主要考查了平行四边形的判定,正确把握两组对边分别相等的四边形是平行四边形是解题关键.4.A解析:A 【解析】 【分析】平均成绩相同情况下,方差越小越稳定即可求解. 【详解】解:∵甲、乙两个同学在四次数学模拟测试中,平均成绩都是112分,方差分别是25S =甲,212S =乙,2S 甲<2S 乙,∴甲同学的数学成绩比较稳定. 故选择A . 【点睛】本题考查用平均数,方差进行决策,掌握平均数是集中趋势的物理量,方差是离散程度的物理量,方差越小波动越小,方差越大波动越大越不稳定是解题关键.5.C解析:C 【分析】先根据平行四边形的性质可得2,4CD AB OC OD ====,再根据勾股定理的逆定理可得AC CD ⊥,然后利用勾股定理可得AD 的长,最后利用三角形的面积公式即可得. 【详解】解:四边形ABCD 是平行四边形,4,8AB AC BD ===, 112,422CD AB OC AC OD BD ====∴==, 22241216OC CD OD ∴+=+==,COD ∴是直角三角形,AC CD ⊥,在Rt ACD △中,AD == 1122RtACDS AD CE AC CD =⋅=⋅, 11422∴⨯=⨯⨯解得4217CE =, 故选:C . 【点睛】本题考查了平行四边形的性质、勾股定理、勾股定理的逆定理等知识点,熟练掌握勾股定理的逆定理是解题关键.6.D解析:D 【解析】 【分析】设3AC FH x ==,则4BC GH x ==,5AB GF x ==,根据勾股定理即可求得CD 的长,利用x 表示出A S ,同理表示出B S ,根据15A B S S -=,即可求得x 的值,进而求得三角形的面积. 【详解】解:设3AC FH x ==,则4BC GH x ==,5AB GF x ==. 设CD y =,则4BD x y =-,DE CD y ==, 在直角BDE ∆中,532BE x x x =-=, 根据勾股定理可得:2224(4)x y x y +=-, 解得:32y x =, 则2113322222A S BE DE x x x ==⨯=, 同理可得:223B S x =,15A B S S -=,∴22321523x x -=, 解得:32x =,∴纸片的面积是:213461082x x x ⨯==,故选:D ..【点睛】本题主要考查了翻折变换(折叠问题),三角形面积的计算,根据勾股定理求得CD 的长是解题的关键.7.A解析:A【解析】 【分析】设小正方形的边长为x ,则AB =5+x ,BC =12+x ,由全等三角形的性质可求AC 得长,由勾股定理可求解小正方形的边长,进而可求解. 【详解】解:设小正方形的边长为x ,∵AF =5,CE =12, ∴AB =5+x ,BC =12+x ,∵△AFM ≌△ADM ,△CDM ≌△CEM , ∴AD =AF =5,CD =CE =12, ∴AC =AD +CD =5+12=17, 在Rt △ABC 中,AC 2=AB 2+BC 2, ∴172=(5+x )2+(12+x )2, 解得x =3(负值已舍), ∴AB =8,BC =15,∴△ABC 的面积为:12×8×15=60,故选:A . 【点睛】本题主要考查了勾股定理,解一元二次方程,利用勾股定理求解小正方形的边长是解题的关键.8.D解析:D 【分析】根据两车相遇时甲、乙所走路程的比为2:3及两车相遇所用时间,即可求出A 、B 两地之间的距离;根据乙车的速度=相遇时乙车行驶的路程÷两车相遇所用时间,进而求出乙车的速度;根据甲车的速度=相遇时甲车行驶的路程÷两车相遇所用时间即可求出甲车的速度,然后根据时间=两地之间路程的一半÷甲车的速度,进而求出a 值;根据时间=两地之间路程÷乙车的速度求出乙车到达终点所用时间,再求出该时间内甲车行驶的路程,用两地间的距离与甲车行驶的路程之差即可得出结论. 【详解】解:A 、A 、B 两地之间的距离为18×2÷32()2323-++=180(千米),所以A 正确;B 、乙车的速度为180323⨯+÷3=36(千米/小时),所以B 正确; C 、甲车的速度为1802323⨯÷+=24(千米/小时), a 的值为180÷2÷24=3.75,所以C 正确;D 、乙车到达终点的时间为180÷36=5(小时),甲车行驶5小时的路程为24×5=120(千米),当乙车到达终点时,甲车距离终点距离为180﹣120=60(千米),所以D 错误. 故选:D【点睛】本题考查了一次函数的实际应用,结合函数的图象并逐一求出选项的内容判断正误是解题的关键二、填空题9.±【解析】【分析】根据二次根式有意义的条件可求得x ,然后求得y ,最后求平方根即可.【详解】解:∵,x y 是实数,且满足12y =,∴20x -≥并且20x -≥,解得2x =,此时12y =,∴24xy =,其平方根是±故答案为:±【点睛】本题考查二次根式有意义的条件,求一个数的平方根,二次根式的化简,理解二次根式有意义被开方数非负是解题关键.10.24【解析】【分析】根据题意,勾股定理求得另一条对角线的长度,根据菱形的面积等于对角线乘积的一半即可求解.【详解】如图,四边形ABCD 的菱形,连接,AC BD 交于点O ,依题意设5AB =,6BD =,则11,322AO AC BO BD===,2222534 AO AB BO∴=--=,8AC∴=,S∴菱形ABCD118624 22AC BD=⋅=⨯⨯=.故答案为:24.【点睛】本题考查了根据菱形的性质求菱形的面积,勾股定理,作出图形求得另外一条对角线的长是解题的关键.11.A解析:55【解析】【分析】设AC=x,可知AB=10-x,再根据勾股定理即可得出结论.【详解】解:设AC=x,∵AC+AB=10,∴AB=10-x.在Rt△ABC中,∠ACB=90°,∴AC2+BC2=AB2,即x2+32=(10-x)2解得:x=4.55,即AC=4.55.故答案为:4.55.【点睛】本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.12.5【分析】先根据勾股定理计算出斜边,再根据在直角三角形中,斜边上的中线等于斜边的一半即可求解.【详解】解:因为直角三角形的两条直角边分别5和12,由勾股定理可得:斜边13=,因为斜边上的中线等于斜边的一半,所以斜边中线=13÷2=6.5,故答案为:6.5.【点睛】本题主要考查勾股定理和直角三角形斜边上的中线等于斜边的一半,解决本题的关键是要熟练掌握勾股定理和直角三角形斜边上的中线等于斜边的一半.13.3【分析】把点(b ,9)代入函数解析式,即可求解.【详解】∵一次函数2y x b =+(b 为常数)的图象经过点(b ,9),∴92b b =+,解得:b=3,故答案是:3.【点睛】本题主要考查一次函数图象上的点的坐标特征,掌握待定系数法,是解题的关键. 14.E解析:EF ⊥BD【分析】通过证明△OBF ≌△ODE ,可证四边形EBFD 是平行四边形,若四边形EBFD 是菱形,则对角线互相垂直,因而可添加条件:EF ⊥BD .【详解】当EF ⊥BD 时,四边形EBFD 是菱形.理由:∵四边形ABCD 是矩形,∴AD ∥BC ,OB=OD ,∴∠FBO=∠EDO ,在△OBF 和△ODE 中EDO FBO BO DOEOD FOB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△OBF ≌△ODE (ASA ),∴OE=OF,∴四边形EBFD是平行四边形,∵EF⊥BD,∴四边形EBFD是菱形.故答案为:EF⊥BD.【点睛】本题考查了矩形的性质,平行四边形的判定,菱形的判定,以及全等三角形的判定方法,熟练掌握性质及判定方法是解答本题的关键.15.【分析】作点C关于AB的对称点F,关于AO的对称点G,连接DF,EG,由轴对称的性质,可得DF=DC,EC=EG,故当点F,D,E,G在同一直线上时,△CDE的周长=CD+DE+CE=DF+DE解析:53 (,)44【分析】作点C关于AB的对称点F,关于AO的对称点G,连接DF,EG,由轴对称的性质,可得DF=DC,EC=EG,故当点F,D,E,G在同一直线上时,△CDE的周长=CD+DE+CE=DF +DE+EG=FG,此时△DEC周长最小,然后求出F、G的坐标从而求出直线FG的解析式,再求出直线AB和直线FG的交点坐标即可得到答案.【详解】解:如图,作点C关于AB的对称点F,关于AO的对称点G,连接FG分别交AB、OA于点D、E,由轴对称的性质可知,CD=DF,CE=GE,BF=BC,∠FBD=∠CBD,∴△CDE的周长=CD+CE+DE=FD+DE+EG,∴要使三角形CDE的周长最小,即FD+DE+EG最小,∴当F、D、E、G四点共线时,FD+DE+EG最小,∵直线y=x+2与两坐标轴分别交于A、B两点,∴B(-2,0),∴OA=OB,∴∠ABC=∠ABD=45°,∴∠FBC=90°,∵点C 是OB 的中点,∴C (1-,0),∴G 点坐标为(1,0),1BF BC ==,∴F 点坐标为(-2,1),设直线GF 的解析式为y kx b =+,∴021k b k b +=⎧⎨-+=⎩, ∴1313k b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴直线GF 的解析式为1133y x =-+, 联立11332y x y x ⎧=-+⎪⎨⎪=+⎩, 解得5434x y ⎧=-⎪⎪⎨⎪=⎪⎩, ∴D 点坐标为(54-,34) 故答案为:(54-,34). 【点睛】本题主要考查了轴对称-最短路线问题,一次函数与几何综合,解题的关键是利用对称性在找到△CDE 周长的最小时点D 、点E 位置,凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.16.【分析】先设,根据,,可得,,再根据,可得,进而得出方程,即可得到的长,可求得,再利用勾股定理可以,再用一次勾股定理即可算出.【详解】解:设,,,,,又为的中点,,由折叠可得,,解析:先设AE EF x ==,根据6DE =,1FG =,可得6AD x BC =+=,1EG x =+,再根据GEB GBE ∠=∠,可得EG BG =,进而得出方程612x x ++=,即可得到AE 的长,可求得EG BG =,再利用勾股定理可以BF ,再用一次勾股定理即可算出BE .【详解】解:设AE EF x ==,6DE =,1FG =,6AD x BC ∴=+=,1EG x =+,又G 为BC 的中点,1622x BG BC +∴==, 由折叠可得,AEB GEB ∠=∠,由//AD BC ,可得AEB GBE ∠=∠,GEB GBE ∴∠=∠,EG BG ∴=,612x x +∴+=, 解得4x =,即4AE =,5EG BG EF FG ∴==+=,90BAE BFE ∠=∠=︒,BF ∴BE ∴=故答案是:【点睛】本题主要考查了折叠问题,勾股定理、三角全等、解题的关键是折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.三、解答题17.(1);(2)【分析】(1)先计算二次根式的除法和乘法,再进行二次根式的加减运算;(2)先化简最简二次根式,然后进行二次根式的乘法,最后合并同类二次根式即可.【详解】(1)原式;解析:(1)4;(2)18-(1)先计算二次根式的除法和乘法,再进行二次根式的加减运算;(2)先化简最简二次根式,然后进行二次根式的乘法,最后合并同类二次根式即可.【详解】(1)原式=4=4=(2)原式=⨯624=--18=-【点睛】本题考查了二次根式的混合运算,掌握二次根式的运算法则并能正确进行运算是关键. 18.最短路程是;画图见解析.【分析】先作关于的对称点,连接,构建直角三角形,利用勾股定理即可得出答案.【详解】解:如图,作出点关于的对称点,连接交于点,则点是马饮水的位置, 根据对称性可得,,解析:最短路程是15km ;画图见解析.【分析】先作A 关于MN 的对称点,连接A B ',构建直角三角形,利用勾股定理即可得出答案.【详解】解:如图,作出A 点关于MN 的对称点A ',连接A B '交MN 于点C ,则点C 是马饮水的位置,根据对称性可得AC A C '=,326km AA '=⨯=,则A B A C BC ''=+,∴A B AC BC '=+,由已知得6km OA =,9km OB =,6612km A O A A AO ''=+=+=,在Rt A OB '△中,由勾股定理求得15km A B ',即15km AC BC +=,答:他要完成这件事情所走的最短路程是15km ,饮水C 所在位置.【点睛】本题考查的是勾股定理和轴对称在实际生活中的运用,需要同学们联系实际,题目是一道比较典型的题目,难度适中.19.(1)见解析;(2)10;(3),4.【解析】【分析】(1)根据A 点坐标为,B 点坐标为特点,建立直角坐标系;(2)分三种情况讨论,若AB=AC 或AB=BC ,或BC=AC ,此时的点C 在线段AB 解析:(1)见解析;(2)10;(3)10224.【解析】【分析】(1)根据A 点坐标为(4,2)-,B 点坐标为(2,4)-特点,建立直角坐标系;(2)分三种情况讨论,若AB =AC 或AB =BC ,或BC =AC ,此时的点C 在线段AB 的垂直平分线上,据此画图;(3)根据题意,符合条件的点是点8(1,1)C -,结合勾股定理解得221310AC BC =+122ABC SS S S =--正方形解得其面积.【详解】解:(1)如图建立直角坐标系,(2)分三种情况讨论,如图,若AB=AC或AB=BC,或BC=AC,此时的点C在线段AB的垂直平分线上,符合条件的点C共有10个,故答案为:10;(3)在(1)(2)的前提下,在第四象限中,当ABC是以AB为底的等腰三角形,且腰长为无理数时,符合条件的点是点8(1,1)C -ABAC BC =ABC C121123321322932422ABC S S S S =--=⨯-⨯⨯⨯-⨯⨯=--=正方形故答案为:4.【点睛】本题考查网格与勾股定理、网格中画等腰三角形、等腰三角形的性质等知识,是重要考点,掌握相关知识是解题关键.20.见解析【分析】首先根据两对边互相平行的四边形是平行四边形证明四边形OCED 是平行四边形,再根据矩形的性质可得OC=OD ,即可利用一组邻边相等的平行四边形是菱形判定出结论.【详解】证明:∵DE解析:见解析【分析】首先根据两对边互相平行的四边形是平行四边形证明四边形OCED 是平行四边形,再根据矩形的性质可得OC=OD ,即可利用一组邻边相等的平行四边形是菱形判定出结论.【详解】证明:∵DE ∥AC ,CE ∥BD ,∴四边形OCED 是平行四边形.∵四边形ABCD 是矩形,∴OC=OD=12AC=12BD∴四边形OCED 是菱形. 21.(1);(2)或 ;或【解析】【分析】根据近似公式计算出近似值的过程和方法计算的近似值和确定a 和r 的值.【详解】(1)根据近似公式可知:≈故答案为;(2)∵∴∴∴整理,解析:(1)1343222-+⨯;1712(2)1712a =或2417;1144r =-或2289 【解析】【分析】的近似值和确定a 和r 的值.【详解】(1≈1343222-+⨯≈1712故答案为1343222-+⨯;1712(2)∵2r a a≈≈+ ∴225772408a r r a a ⎧+=⎪⎨+=⎪⎩∴5772()408r a a =⨯- ∴25772()2408a a a +⨯-= 整理,22045774080a a -+= 解得:1712a =或2417a = ∴1144r =-或2289r = 故答案为1712a =或2417 ;1144r =-或2289 【点睛】本题考查二次根式的估算,审清题意,根据题目所给的近似公式计算是解题关键. 22.(1)30(15﹣x ),180(15﹣x );(2)租A 型客车10辆,B 型客车5辆,可使租车总费用y 最少,最少为3900元【分析】(1)根据“B 型车的载客量=租的辆数×满载人数”以及“租B 型车应付解析:(1)30(15﹣x ),180(15﹣x );(2)租A 型客车10辆,B 型客车5辆,可使租车总费用y 最少,最少为3900元【分析】(1)根据“B 型车的载客量=租的辆数×满载人数”以及“租B 型车应付租金=每辆的租金×租的辆数”即可得出结论;(2)设租车的总费用为y 元,根据“总租金=租A 型车的租金+租B 型车的租金”即可得出y 关于x 的函数关系式,再根据A 型客车的数量不小于B 型客车数量的2倍,列出关于x 的一元一次不等式,解不等式即可得出x 的取值范围,根据一次函数的性质即可解决最值问题.【详解】解:(1)设租用A 型客车x 辆,则租用B 型客车(15﹣x )辆,B 型车的载客量30(15﹣x ),租金为180(15﹣x ).故答案为:30(15﹣x ),180(15﹣x );(2)根据题意得:x ≥2(15﹣x ),解得:x ≥10,∵y =300x +180(15﹣x )=120x +2700,又∵120>0,∴y 随x 的增大而增大,∵x 是正整数,∴当x 取最小值10时,y 有最小值3900,答:租A 型客车10辆,B 型客车5辆,可使租车总费用y 最少,最少为3900元.【点睛】本题考查了列代数式,一元一次不等式的应用,一次函数的应用,理解题意,根据一次函数的的性质求最值是解题的关键.23.(1)y=-x+6;(2)①;②,或或,【分析】(1)先求出点A ,B 的坐标,再运用待定系数法求出直线直线l2的函数解析式;(2)①将点D (-2,m )代入y=x+6中,求出D (-2,4),如图2解析:(1)y =-x +6;(2)①4+②1(2G ,3-或2(2,3G 或3(2G ,3 【分析】(1)先求出点A ,B 的坐标,再运用待定系数法求出直线直线l 2的函数解析式;(2)①将点D (-2,m )代入y =x +6中,求出D (-2,4),如图2,作∠DHF =45°,利用AAS 证明△ADE ≌△HFD ,再运用等腰直角三角形性质即可求出答案;②将D (-1,n )代入y =x +6中,得D (-1,5),过D 作DM ⊥x 轴于M ,作FN ⊥DM 于N ,如图3,利用AAS 可证得△FDN ≌△DEM ,进而得出F (4,6),再根据∠DGF =∠DGO 分类讨论即可.【详解】解:(1)6y x =+交x 轴于点A ,交y 轴于点B ,(6,0)A ∴-,(0,6)B ,2l 与1l 关于y 轴对称,)0(6,C ∴,设直线2l 为:y kx b =+,将B 、C 坐标代入得606k b b +=⎧⎨=⎩,解得16k b =-⎧⎨=⎩, ∴直线2l 的函数解析式为:6y x =-+;(2)①将点(2,)D m -代入6y x =+中,得:26m -+=,解得:4m =,(2,4)D ∴-,如图2,作45DHF ∠=︒,6OA OB ==,45EAD EDF DHF ∴∠=∠=∠=︒,135AED ADE ∴∠+∠=︒,135ADE HDF ∠+∠=︒,AED HDF ∴∠=∠,在ADE ∆和HFD ∆中,EAD DHF AED HDF DE FD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ADE HFD AAS ∴∆≅∆,22(62)442HF AD ∴=-++=AE HD =,又6OA OB OC ===,90AOB COB ∠=∠=︒,ABO ∴∆和COB ∆均为等腰直角三角形,45ABO CBO ∴∠=∠=︒,90ABC ∴∠=︒,18090HBF ABC ∴∠=︒-∠=︒,BFH ∴∆是等腰直角三角形,24BH ∴=, 62AB =62442422AE HD AB BH AD ∴==+-=-+②将(1,)D n -代入6y x =+中,得:165n =-+=,(1,5)D ∴-,则5DM =,1EM =,过D 作DM x ⊥轴于M ,作FN DM ⊥于N ,如图3,DE DF =,90EDF DME FND ∠=∠=∠=︒,90MDE FDN ∴∠+∠=︒,90MDE DEM ∠+∠=︒,FDN DEM ∴∠=∠,在FDN ∆和DEM ∆中,FND DME FDN DEM DF ED ∠=∠⎧⎪∠=∠⎨⎪=⎩, FDN DEM ∴∆≅∆()AAS ,5FN DM ∴==,1DN EM ==,514BF FN BN ∴=-=-=,516EB MN DM DN ====+=,(4,6)F ∴,当点F 、O 、1G 三点共线时,如图3,11DG O DG F ∠=∠,设直线EF 的解析式为y mx =,(4,6)F ,46m ∴=, 解得:32m =, ∴直线EF 的解析式为32y x =, 当33132x =2132x = 1213(2G ∴313); 如图4,连接DG 2,FG 2,过点D 作DM ⊥OG 2,DN ⊥FG 2,∵22DG F DG O ∠=∠,∴DM =DN ,又DO =DF ,∴2Rt DG M Rt DFN ≅△△(HL ),∴∠ODM =∠FDN ,又∠ODN +∠FDN =90°,∴∠ODM +∠ODN =90°,即∠MDN =90°,∴四边形DMG 2N 是正方形,∴∠OG 2F =90°,设2(,313)G a -,22290FG O DG O DG F ∠=∠+∠=︒,22222G O G F OF ∴+=,222222(313)(4)(3136)46a a ∴+-+-+--=+,解得:122a a ==,2(2,313)G ∴-;当3DG 平分3OG F ∠时,如图5,DO DF =,33DG O DG F ∠=∠,33OG FG ∴=,又33DG DG =, 33()DOG DFG SSS ∴∆≅∆,设OF 与3DG 交于点H ,OH FH ∴=,(0,0)O ,(4,6)F ,(2,3)H ∴,设直线DG 解析式为11y k x b =+,(1,5)D -,()2,3H ,∴1111523k b k b -+=⎧⎨+=⎩, 解得:1123133k b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴直线DG 解析式为21333y x =-+,联立方程组213333y x y ⎧=-+⎪⎨⎪=⎩,解得:23x y ⎧=⎪⎨⎪=⎩3(2G ∴,3; 综上所述,符合条件的G的坐标为1(2G,3或2(2,3G或3(2G,3.【点睛】本题是一次函数综合题,考查了运用待定系数法求一次函数解析式,求一次函数图象与坐标轴交点坐标,利用解方程组求两直线交点坐标,等腰直角三角形判定和性质,全等三角形判定和性质,勾股定理等,添加辅助线构造全等三角形,运用分类讨论思想和数形结合思想是解题关键.24.(1)A (-8,0)、B (0,6);(2)5;(3)①3个;②(-5,6)或(-11,-6)或(5,6).【解析】【分析】(1)利用待定系数法解决问题即可.(2)由翻折不变性可知,OC=CD解析:(1)A (-8,0)、B (0,6);(2)5;(3)①3个;②(-5,6)或(-11,-6)或(5,6).【解析】【分析】(1)利用待定系数法解决问题即可.(2)由翻折不变性可知,OC=CD ,OB=BD=6,∠ODB=∠BOC=90°,推出AD=AB-BD=4,设CD=OC=x ,在Rt △ADC 中,根据AD 2+CD 2=AC 2,构建方程即可解决问题.(3)①根据平行四边形的定义画出图形即可判断.②利用平行四边形的性质求解即可解决问题.【详解】解:(1)对于直线364y x =+,令x=0,得到y=6, ∴B (0,6),令y=0,得到x=8-,∴A (8-,0);(2)∵A (8-,0),B (0,6),∴OA=8,OB=6,∵∠AOB=90°,∴228610AB =+=,由翻折不变性可知,OC=CD ,OB=BD=6,∠ODB=∠BOC=90°,∴AD=AB-BD=4,设CD=OC=x ,在Rt △ADC 中,∵∠ADC=90°,∴AD 2+CD 2=AC 2,∴42+x 2=(8-x )2,解得:x=3,∴OC=3,AC=OA -OC=8-3=5.(3)①符合条件的点P 有3个,如图所示:②∵A (-8,0),C (-3,0),B (0,6),当AB 为对角线时,1//BP AC ,由平行四边形的性质,得15BP AC ==,∴P 1(-5,6);当AB 为边时,//AB CP ,点P 在第三象限时,有点B 向下平移6个单位,向左平移3个单位得到点C ,∴点A 向下平移6个单位,向左平移3个单位得到点P 2,∴P 2(-11,-6);点P 在第二象限时,有35BP AC ==,∴P 3(5,6);∴点P 的坐标为:(-5,6)或(-11,-6)或(5,6).【点睛】本题属于一次函数综合题,考查了待定系数法,解直角三角形,平行四边形的判定和性质等知识,解题的关键是熟练掌握基本知识,学会用分类讨论的思想思考问题,属于中考常考题型.25.(1)见解析;(2)AE =;(3)(3),理由见解析.【分析】(1)运用四边形AMFN 是正方形得到判断△AMC,△AND 是Rt △,进一步说明△ABC 是等边三角形,在结合旋转的性质,即可证明.(解析:(1)见解析;(2)AE =23;(3)(3)122AG AF =,理由见解析. 【分析】(1)运用四边形AMFN 是正方形得到判断△AMC,△AND 是Rt △,进一步说明△ABC 是等边三角形,在结合旋转的性质,即可证明.(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x ,则AE=2x GE=3x ,得到△GBE 是等腰直角三角形和∠DHF=30°,再结合直角三角形的性质,判定Rt △AMC ≌Rt △AND ,最后通过计算求得AE 的长;(3)延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM FG =,可得GMB ∆≌11GFC ∆,从而得到111BM FC DF == 1BMG GFN ∠=,可知BM ∥1F N , 再根据题意证明ABM ∆≌1ADF ∆,进一步说明1AMF ∆是等腰直角三角形,然后再使用勾股定理求解即可. 【详解】(1)证明:∵四边形AMFN 是正方形,∴AM=AN ∠AMC=∠N=90°∴△AMC,△AND 是Rt △∵△ABC 是等边三角形∴AB=AC∵旋转后AB=AD∴AC=AD∴Rt △AMC ≌Rt △AND(HL)(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x则AE=2x 3x易得△GBE 是等腰直角三角形∴BG=EG 3x∴AB=BC=(31)x易得∠DHF=30°∴HD=2DF=23 ,HF=3 ∴BF=BH+HF=233+∵Rt △AMC ≌Rt △AND(HL)∴易得CF=DF=3∴BC=BF-CF=233333+-=+∴(31)33x +=+∴3x =∴AE =223x =(3)122AG AF =; 理由:如图2中,延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM F G =,则GMB ∆≌11GFC ∆,∴111BM FC DF == 1BMG GFN ∠=, ∴BM ∥1F N ,∴MBA N ∠=∠∵0190NAO OF D ∠=∠= 1AON DOF ∠=∠∴1N ADF ∠=∠∴1ABM ADF ∠=∠,∵AB AD =∴ABM ∆≌1ADF ∆(SAS )∴1AM AF = 1MAB DAF ∠=∠∴0190MAF BAD ∠=∠=∴1AMF ∆是等腰直角三角形∴1AG MF ⊥ 1AG GF =∴12AF AG =∴12AG AF =【点睛】本题考查正方形的性质、三角形全等、以及勾股定理等知识点,综合性强,难度较大,但解答的关键是正确做出辅助线.26.(1);(2)点F 到AD 的距离为3,BF=;(3)2【分析】(1)连接DF ,证明△ADF ≌△CDA ,得出CDF 共线,然后用勾股定理即可; (2)过点F 作FH ⊥AD 交AD 的延长线于点H ,FH ⊥BC解析:(1)45;(2)点F 到AD 的距离为3,BF =74;(3)2【分析】(1)连接DF ,证明△ADF ≌△CDA ,得出CDF 共线,然后用勾股定理即可;(2)过点F 作FH ⊥AD 交AD 的延长线于点H ,FH ⊥BC 交BC 的延长线于K ,证明△EHF ≌△CDE ,再用勾股定理即可;(3)当B ,D ,F 共线时,此时BF 取最小值,求出此时AE 的值即可.【详解】解:(1)如图,连接DF ,∵∠CAF =90°,∠CAD =45°,∴∠DAF =45°,在△CAD 和△FAD 中,AF AC CAD FAD AD AD =⎧⎪∠=∠⎨⎪=⎩, ∴△CAD ≌△FAD (SAS ),∴DF =CD ,∴∠ADC =∠ADF =90°,∴C ,D ,F 共线,∴BF 2=BC 2+CF 2=42+82=80,∴BF =5故答案为:45(2)如图,过点F 作FH ⊥AD 交AD 的延长线于点H ,FH ⊥BC 交BC 的延长线于K ,。
人教版八年级下册数学期末试卷(培优篇)(Word版含解析)
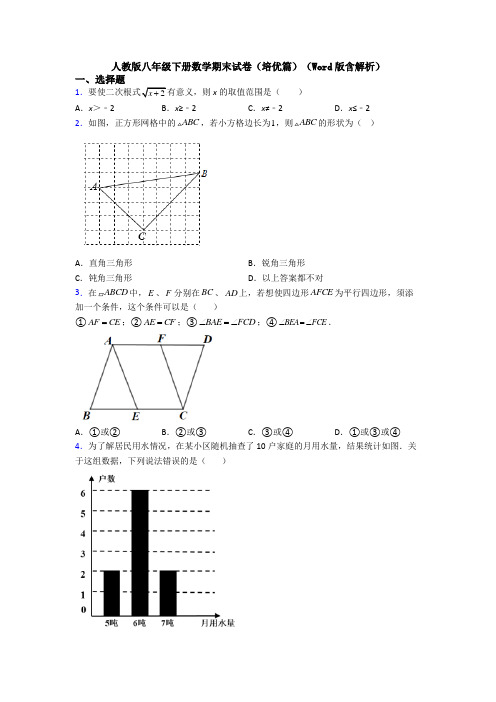
人教版八年级下册数学期末试卷(培优篇)(Word 版含解析)一、选择题1.要使二次根式2x +有意义,则x 的取值范围是( )A .x >﹣2B .x ≥﹣2C .x ≠﹣2D .x ≤﹣2 2.如图,正方形网格中的ABC ,若小方格边长为1,则ABC 的形状为( )A .直角三角形B .锐角三角形C .钝角三角形D .以上答案都不对 3.在ABCD 中,E 、F 分别在BC 、AD 上,若想使四边形AFCE 为平行四边形,须添加一个条件,这个条件可以是( ) ①AF CE =;②AE CF =;③BAE FCD ∠=∠;④BEA FCE ∠=∠.A .①或②B .②或③C .③或④D .①或③或④ 4.为了解居民用水情况,在某小区随机抽查了10户家庭的月用水量,结果统计如图.关于这组数据,下列说法错误的是( )A .众数是6B .中位数是6C .平均数是6D .方差是4 5.如图,四边形ABCD 的对角线AC ,BD 相交于点O ,AC ⊥BD ,E ,F 分别是AB ,CD 的中点,若AC =BD =2,则EF 的长是( )A .2B .3C .62D .26.如图,在菱形ABCD 中,∠A =110°,E ,F 分别是边AB 和BC 的中点,EP ⊥CD 于点P ,则∠FPC =( )A .35°B .45°C .50°D .55°7.如图,在长方形ABCD 中,分别按图中方式放入同样大小的直角三角形纸片.如果按图①方式摆放,刚好放下4个;如果按图②方式摆放,刚好放下3个.若BC =4a ,则按图③方式摆放时,剩余部分CF 的长为( )A .23aB .32aC .53aD .35a8.如图所示,已知点C (1,0),直线7y x =-+与两坐标轴分别交于A ,B 两点,D ,E 分别是线段AB ,OA 上的动点,则△CDE 的周长的最小值是( )A .42B .10C.424+D.12二、填空题9.若二次根式210x+有意义,则x的取值范围是 ___.10.如图,在菱形ABCD中,E,F,G分别是AD,AB,CD的中点,且10cmFG=,6cmEF=,则菱形ABCD的面积是___2cm.11.在平面直角坐标系中,若点(),4M x到原点的距离是5,则x的值是________.12.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为___.13.一个水库的水位在最近5h内持续上涨.下表记录了这5h内6个时间点的水位高度,其中x表示时间,y表示水位高度.x/h012345y/m3 3.2 3.4 3.6 3.84根据表格中水位的变化规律,则y与x的函数表达式为____.14.在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=___________.(结果保留根号)15.已知直线33y x=x轴,y轴分别交于点A,B,点C是射线AB上的动点,点D在第一象限,四边形OACD是平行四边形.若点D关于直线OC的对称点D恰好落在y 轴上,则点C的坐标为______.16.如图,∠ABD =∠BDC =90°,AB =12,BC =8,CD =210,按如图方式折叠,使得点A 与点D 重合,折痕为HG ,则线段BH 的长为___.三、解答题17.计算:①33118(3)2⨯+-; ②2(32)24-+.18.春节期间,乐乐帮妈妈挂灯笼时,发现,如图长2.5米的梯子AB 斜靠在一竖直的墙AC 上,这时BC 为1.5米,当梯子的底端B 向右移动0.5米到D 处时,你能帮乐乐算算梯子顶端A 下滑多少米吗?(E 处).19.如图,在4×3正方形网格中,每个小正方形的边长都是1,正方形顶点叫格点,连接两个网格格点的线段叫网格线段,点A 固定在格点上.(1)若a 是图中能用网格线段表示的最小无理数,b 是图中能用网格线段表示的最大无理数,则a = ,b = ;(2)请你画出顶点在格点上且边长为5的所有菱形ABCD ,你画出的菱形面积为 ; 20.如图,在平行四边形ABCD 中,点E 是边AB 的中点,连接CE 并延长CE 交DA 的延长线于点F ,连接AC ,BF .(1)求证:四边形AFBC 是平行四边形(2)当AEC ∠的度数为______度时,四边形AFBC 是菱形;(3)若52D ∠=︒,则当AEC ∠的度数为______度时,四边形AFBC 是矩形. 21.阅读下列解题过程:54+1(54)(54)(54)⨯-+-2254(5)(4)--5452 65+1(65)(65)(65)⨯-+-2265(6)(5)--65请回答下列问题:(1)观察上面的解题过程,请直接写出结果. 1n n ++= .(2)利用上面提供的信息请化简: (21324320132014)+++++的值. 22.甲、乙两组工人同时加工某种零件,甲组在工作中有一段时间停产更新设备,更新设备后,甲组的工作效率是原来的2倍.乙组工作2小时后,由于部分工人离开,工作效率有所降低.两组各自加工零件的数量y (件)与时间x (小时)之间的函数图象如图所示.(1)直接写出线段DE的函数关系式,并写出自变量的取值范围;(2)求甲乙两组何时加工的零件数相同;(3)若甲、乙两组加工的零件合在一起装箱,每320件装成一箱,零件装箱的时间忽略不计,直接写出经过多长时间恰好装满2箱.23.如图,在平面直角坐标系中,已知▱OABC的顶点A(10,0)、C(2,4),点D是OA 的中点,点P在BC上由点B向点C运动.(1)求点B的坐标;(2)若点P运动速度为每秒2个单位长度,点P运动的时间为t秒,当四边形PCDA是平行四边形时,求t的值;(3)当△ODP是等腰三角形时,直接写出点P的坐标.24.如图1,直线y=kx+b经过第一象限内的定点P(3,4).(1)若b=7,则k=_______;(2)如图2,直线y=kx+b与y轴交于点C,已知点A(6,t),过点A作AB//y轴交第一象限内的直线y=kx+b于点B,连接OB,若BP平分∠OBA.①证明OBC是等腰三角形;②求k的值;(3)如图3,点M是x轴正半轴上的一个动点,连接PM,把线段PM绕点M顺时针旋转90°至线段NM(∠PMN=90°且PM=MN),连接OP,ON,PN,当OPN周长最小时,求点N的坐标;25.综合与实践:如图1,在正方形ABCD 中,连接对角线AC ,点O 是AC 的中点,点E 是线段OA 上任意一点(不与点A ,O 重合),连接DE ,BE .过点E 作EF DE ⊥交直线BC 于点F .(1)试猜想线段DE 与EF 的数量关系,并说明理由;(2)试猜想线段,,CE CD CF 之间的数量关系,并说明理由;(3)如图2,当E 在线段CO 上时(不与点C ,O 重合),EF 交BC 延长线于点F ,保持其余条件不变,直接写出线段,,CE CD CF 之间的数量关系.26.如图,在等腰Rt ABC 中,90ACB ∠=︒,AC BC =,点D 为BC 边中点,点E 在线段AD 上,BED CAD α∠=∠=,过点C 作CF BE ⊥于F ,CF 交AD 于点G .(1)求GCD ∠的大小(用含α的式子表示)(2)①求证:BE BC =;②写出AE AD=______的值. 【参考答案】一、选择题1.B解析:B【分析】根据二次根式有意义的条件进行求解即可.【详解】∵x+≥,∴20x≥-.∴2故选:B.【点睛】本题考查了二次根式,解一元一次不等式,明确二次根式有意义的条件是解题的关键.2.A解析:A【分析】根据勾股定理求得△ABC各边的长,再利用勾股定理的逆定理进行判定,从而不难得到其形状.【详解】解:∵正方形小方格边长为1,∴BC 22442,AC=AB=在△ABC中,∵BC2+AC2=32+18=50,AB2=50,∴BC2+AC2=AB2,∴△ABC是直角三角形.故选:A.【点睛】考查了勾股定理的逆定理,解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.3.D解析:D【解析】【分析】由平行四边形的判定定理依次判断即可解答.【详解】解:∵四边形ABCD是平行四边形,∴AB//CD,AB=CD,∠B=∠D,AD//BC,AD=BC,∴AF//EC∵AF=EC,∴四边形AFCE是平行四边形,故①符合题意;∵AF //EC ,AE CF =,∴四边形AFCE 可能是平行四边形、也可能是等腰梯形,故②不符合题意;如果∠BAE =∠FCD ,则△ABE ≌△DFC (ASA )∴BE =DF ,∴AD -DF =BC -BE ,即AF =CE ,∵AF //CE ,∴四边形AFCE 是平行四边形,故③符合题意;如果∠BEA =∠FCE ,∴AE //CF ,∵AF //CE ,∴四边形AFCE 是平行四边形、故④符合题意.故选D .【点睛】本题主要考查了平行四边形的性质与判定.灵活运用平行四边形的性质与判定定理是解答本题的关键.4.D解析:D【解析】【分析】根据统计图得出10户家庭的用水量数据,求得众数,中位数,平均数,方差,进而逐项判断即可【详解】根据统计图可得这10户家庭的用水量分别为:5,5,6,6,6,6,6,6,7,7其中6出现了6次,次数最多,故众数是6,故A 选项正确,不符合题意;这组数据的中位数为:6,故B 选项正确,不符合题意; 这组数据的平均数为1(256672)610⨯+⨯+⨯=,故C 选项正确,不符合题意; 这组数据的方差为:()()()222212566662760.410S ⎡⎤=⨯-+⨯-+⨯-=⎣⎦,故D 选项不正确,符合题意.故选D .【点睛】本题考查了求众数,中位数,平均数,方差,掌握方差的计算公式是解题的关键.方差的计算公式:2222121[()()()]n s x x x x x x n=-+-++-…. 5.D解析:D【分析】分别取,AD BC 的中点为,G H ,连接,,,EG HE HF FG ,利用中点四边形的性质可以推出1111//,//,//,//2222EG BD HF BD HE AC FG AC ,再根据AC BD ⊥,可以推导出四边形EGFH 是正方形即可求解.【详解】解:分别取,AD BC 的中点为,G H ,连接,,,EG HE HF FG ,,E F 分别是,AB CD 的中点,1111//,//,//,//2222EG BD HF BD HE AC FG AC ∴, 又,2AC BD AC BD ⊥==,1,HE EG GF HF HF FG ∴====⊥,∴四边形EGFH 是正方形,22EF FG ∴=故选:D .【点睛】本题考查了中点四边形的性质、正方形的判定及性质,解题的关键是作出适当的辅助线,利用题意证明出四边形EGFH 是正方形.6.D解析:D【解析】【分析】延长PF 交AB 的延长线于点G .根据已知可得∠B ,∠BEF ,∠BFE 的度数,再根据余角的性质可得到∠EPF 的度数,从而不难求得∠FPC 的度数.【详解】解:延长PF 交AB 的延长线于点G .在△BGF 与△CPF 中,,GBF PCF BF CFBFG CFP ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BGF ≌△CPF (ASA ),∴GF =PF ,∴F 为PG 中点.又∵由题可知,∠BEP =90°,∴12EF PG =(直角三角形斜边上的中线等于斜边的一半), ∵12PF PG =(中点定义), ∴EF =PF ,∴∠FEP =∠EPF , ∵∠BEP =∠EPC =90°,∴∠BEP ﹣∠FEP =∠EPC ﹣∠EPF ,即∠BEF =∠FPC ,∵四边形ABCD 为菱形,∴AB =BC ,∠ABC =180°﹣∠A =70°,∵E ,F 分别为AB ,BC 的中点,∴BE =BF ,()118070552BEF BFE ∠=∠=︒-︒=︒, 易证FE =FG ,∴∠FGE =∠FEG =55°,∵AG ∥CD ,∴∠FPC =∠EGF =55°故选D .【点睛】此题主要考查了菱形的性质的理解及运用,灵活应用菱形的性质是解决问题的关键. 7.A解析:A【解析】【分析】由题意得出图①中,BE =a ,图②中,BE =43a ,由勾股定理求出小直角三角形的斜边长为53a ,进而得出答案. 【详解】解:∵BC =4a ,∴图①中,BE =a ,图②中,BE =43a , ∴2245()33a a a +,∴图③中纸盒底部剩余部分CF的长为4a-2×53a=23a;故选:A.【点睛】本题考查了矩形的性质以及勾股定理;熟练掌握矩形的性质和勾股定理是解题的关键.8.B解析:B【解析】【分析】点C关于OA的对称点C′(-1,0),点C关于直线AB的对称点C″(7,6),连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,可以证明这个最小值就是线段C′C″.【详解】解:如图,点C(1,0)关于y轴的对称点C′(-1,0),点C关于直线AB的对称点C″,∵直线AB的解析式为y=-x+7,∴直线CC″的解析式为y=x-1,由71 y xy x-+⎧⎨-⎩==解得43xy==⎧⎨⎩,∴直线AB与直线CC″的交点坐标为K(4,3),∵K是CC″中点,C(1,0),设C″坐标为(m,n),∴14232mn+⎧=⎪⎪⎨+⎪=⎪⎩,解得:76mn=⎧⎨=⎩∴C″(7,6).连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,△DEC的周长=DE+EC+CD=EC′+ED+DC″=C′C22(71)(60)10++-故答案为10.【点睛】本题考查轴对称-最短问题、两点之间距离公式等知识,解题的关键是利用对称性在找到点D 、点E 位置,将三角形的周长转化为线段的长.二、填空题9.5x ≥-【解析】【分析】根据二次根式有意义的条件可直接进行列式求解.【详解】解:∵二次根式210x +有意义,∴2100x +≥,解得:5x ≥-;故答案为5x ≥-.【点睛】本题主要考查二次根式有意义的条件,熟练掌握二次根式有意义的条件是解题的关键. 10.A解析:96【解析】【分析】连接AC ,BD ,交点为O ,EF 与AC 交于点M ,EG 与BD 交于点N ,由三角形中位线定理得出//EF BD ,12EF BD =,//EG AC ,12EG AC =,得出90FEG ∠=︒,由勾股定理求出EG 的长,根据菱形的面积公式可得出答案.【详解】解:如图,连接AC ,BD ,交点为O ,EF 与AC 交于点M ,EG 与BD 交于点N ,四边形ABCD 是菱形,AC BD ∴⊥,E ,F ,G 分别是AD ,AB ,CD 的中点,//EF BD ∴,12EF BD =,//EG AC ,12EG AC =, ∴四边形OMEN 是矩形,90FEG ∴∠=︒,10FG cm =,6EF cm =,22221068EG FG EF cm ∴=--=,16AC cm ∴=,12BD cm =,∴菱形ABCD 的面积是211161296()22AC BD cm ⋅=⨯⨯=. 故答案为96.【点睛】本题考查了菱形的性质,三角形中位线定理,勾股定理,菱形的面积,根据三角形的中位线定理求出AC 和BD 的长是解题的关键.11.3或-3【解析】【分析】根据点(),4M x 到原点的距离是5,可列出方程,从而可以求得x 的值.【详解】解:∵点(),4M x 到原点的距离是5, ∴5=,解得:x=3或-3,故答案为:3或-3.【点睛】本题考查了坐标系中两点之间的距离,解题的关键是利用勾股定理列出方程求解. 12.D解析:5【分析】设DE =x ,则AE =8-x .先根据折叠的性质和平行线的性质,得∠EBD =∠CBD =∠EDB ,则BE =DE =x ,然后在直角三角形ABE 中根据勾股定理即可求解.【详解】解:设DE =x ,则AE =8-x .根据折叠的性质,得∠EBD =∠CBD .∵AD ∥BC ,∴∠CBD =∠ADB ,∴∠EBD =∠EDB ,∴BE =DE =x .在直角三角形ABE 中,根据勾股定理,得x 2=(8-x )2+16,解得x =5.故答案为:5.【点睛】本题主要考查了矩形与折叠问题、平行线的性质、等角对等边的性质和勾股定理,难度适中.13.y =0.2x +3【分析】根据记录表由待定系数法就可以求出y 与x 的函数表达式.【详解】解:根据表格信息可知,每小时水位上升0.2m ,y 是x 的的一次函数,设y 与x 的函数表达式为y =kx +b ,把(0,3)和(1,3.2)代入得:33.2b k b =⎧⎨+=⎩, 解得:0.23k b =⎧⎨=⎩. 故y 与x 的函数表达式为y =0.2x +3.故答案为:y =0.2x +3.【点睛】考查了待定系数法求一次函数解析式,在解答时确定两个变量是一次函数函数关系是解题关键.14.E 解析:3【分析】先延长EF 和BC ,交于点G ,再根据条件可以判断三角形ABE 为等腰直角三角形,并求得其斜边BE 的长,然后根据条件判断三角形BEG 为等腰三角形,最后根据△EFD ∽△GFC 得出CG 与DE 的倍数关系,并根据BG=BC+CG 进行计算即可.【详解】延长EF 和BC ,交于点G .∵矩形ABCD 中,∠B 的角平分线BE 与AD 交于点E ,∴∠ABE=∠AEB=45°,∴AB=AE=9,∴直角三角形ABE 中,又∵∠BED 的角平分线EF 与DC 交于点F ,∴∠BEG=∠DEF .∵AD ∥BC ,∴∠G=∠DEF ,∴∠BEG=∠G ,∴.由∠G=∠DEF ,∠EFD=∠GFC ,可得△EFD ∽△GFC , ∴122CG CF CF DE DF CF ===. 设CG=x ,DE=2x ,则AD=9+2x=BC .∵BG=BC+CG ,∴,解得,∴BC=9+2(-3).故答案为.考点:矩形的性质;等腰三角形的判定;相似三角形的判定与性质.15.或.【分析】先根据题意求得,,,分点在第二象限和第一象限两种情况讨论,根据点关于直线的对称点恰好落在轴上,根据含30度角的直角三角形的性质,在第一象限时候,证明是等边三角形,在第二象限时候证明是 解析:3332⎛ ⎝⎭或332⎛- ⎝⎭. 【分析】先根据题意求得30BAO ∠=︒,60ABO ∠=︒,12OB AB =,分C 点在第二象限和第一象限两种情况讨论,根据点D 关于直线OC 的对称点D 恰好落在y 轴上,根据含30度角的直角三角形的性质,在第一象限时候,证明BCO 是等边三角形,在第二象限时候证明ODD '是等边三角形,利用等边三角形的性质,分别求得C 点的坐标.【详解】33y =与x 轴,y 轴分别交于点A ,B , 令0y =,3x =-,∴(3,0)A -,令0x =,3y =3)B ∴,3,3OA OB ∴==90AOB ∠=︒,2223AB AO BO ∴=+30BAO ∴∠=︒,60ABO ∠=︒,12OB AB ∴=, ①如图,当C 点在第二象限时,设DD '交x 轴于点E ,交AO 于点F ,CD 交y 轴于点G ,四边形OACD 是平行四边形,//AC OD ∴,//CD AO ,AC OD OD '==,30CAO ∠=︒,30DOE CAO ∴∠=∠=︒,30ODG DOE ∴∠=∠=︒,//CD AO ,AO OB ⊥,90DGD '∴∠=︒,9060DOG DOE ∴∠=︒-∠=︒,OD OD '=,30ODD OD D ''∴∠=∠=︒,点D 关于直线OC 的对称点为D 点,CO DD '∴⊥,60COB FOD '∴∠=∠=︒,60ABO ∠=︒,BCO ∴△是等边三角形,BO CO BC ∴==, 12BO AB =, 12BC AB =∴, C ∴点为AB 的中点,(3,0)A -,3)B ,33(2C ∴-, ②如图,当C 点在第二象限时,延长DC 交y 轴于点H ,则CH OD '⊥,点D 关于直线OC 的对称点为D 点,CD CD OD OD ''∴==,DOC D OC '∠=∠,60ABO BOD ∠=∠=︒,ODD '∴△是等边三角形,60DOD '∴∠=︒,30DOC D OC '∴∠=∠=︒,12CH OC ∴=, 30BAO ∠=︒,90AOB ∠=︒,3CO AO ∴==, ∴32CH =, 222233(2)3OH OC CH CH CH CH ∴=-=-=333()2C ∴. 综合①②可知C 的坐标为3332⎛ ⎝⎭或332⎛- ⎝⎭. 故答案为: 3332⎛ ⎝⎭或332⎛- ⎝⎭. 【点睛】本题考查了一次函数图像的性质,平行四边形的性质,等边三角形的性质,含30度角的直角三角形的性质,勾股定理,轴对称的性质,此题方法比较多,利用等边三角形的性质是解题的关键.16.5【分析】在Rt △BDC 中由勾股定理可求出BD ,根据翻折变换可得AH =HD ,在Rt △BDH中由勾股定理可得答案.【详解】解:在Rt△BDC中,∵BC=8,CD=2,∴BD=,由题意,得解析:5【分析】在Rt△BDC中由勾股定理可求出BD,根据翻折变换可得AH=HD,在Rt△BDH中由勾股定理可得答案.【详解】解:在Rt△BDC中,∵BC=8,CD=∴BD=由题意,得AH=HD,设BH=x,则AH=12﹣x=HD,在Rt△BDH中,由勾股定理得,HB2+BD2=HD2,即x2)2=(12﹣x)2,解得x=5,即HB=5,故答案为:5.【点睛】本题考查了翻折变换,勾股定理.掌握翻折变换的性质及勾股定理是解题的关键.三、解答题17.①0;②5【分析】(1)先运用二次根式或立方根的性质化简各个根式,再计算即可;(2)先运用完全平方公式计算,再合并同类二次根式计算即可.【详解】解:①原式=0;②原式=5.【解析:①0;②5【分析】(1)先运用二次根式或立方根的性质化简各个根式,再计算即可;(2)先运用完全平方公式计算,再合并同类二次根式计算即可.【详解】解:原式3=- 33=-=0;②2原式32=+-=5.【点睛】本题考查了二次根式的混合运算,熟练掌握二次根式的运算法则和运算顺序是解题的关键.18.5米【分析】在中,由勾股定理可求出AC 的值,在中,由勾股定理可求出CE 的值,最后根据线段的和差关系即可得出答案.【详解】解:∵,在中,由勾股定理得,,∴米,(负值已舍去)∵米,∴在中,解析:5米【分析】在Rt ABC ∆中,由勾股定理可求出AC 的值,在Rt ECD ∆中,由勾股定理可求出CE 的值,最后根据线段的和差关系即可得出答案.【详解】解:∵90C ∠=︒,在Rt ABC ∆中,由勾股定理得,222222.5 1.54AC AB BC =-=-=, ∴2AC =米,(负值已舍去)∵0.5BD =米,∴在Rt ECD ∆中,()2222222.5 1.5CE DE CD CB BD =-=-+=, ∴ 1.5CE =米∴2 1.50.5AE AC CE =-=-=(米)答:梯子顶端A 下滑0.5米.【点睛】本题考查勾股定理的应用,在直角三角形里根据勾股定理,知道其中两边就可求出第三边,从而可求解.19.(1);(2)见解析,菱形面积为4或5.【解析】【分析】(1)根据题意,画出图形,即可求解;(2)先画出边长为的所有菱形ABCD,,然后求出面积即可.【详解】解:如图,(1)∵a是图解析:(1)2,25;(2)见解析,菱形面积为4或5.【解析】【分析】(1)根据题意,画出图形,即可求解;(2)先画出边长为5的所有菱形ABCD,,然后求出面积即可.【详解】解:如图,(1)∵a是图中能用网格线段表示的最小无理数,∴22112a=+=,∵b是图中能用网格线段表示的最大无理数,224225b=+=;(2)∵22215+=,即可画出图形,如图,菱形ABC1D1和菱形ABC2D2即为所求;菱形ABC1D1的面积为12442⨯⨯=;菱形ABC2D2223110+=,故菱形ABC 2D 2的面积为152;ABCD 的面积为4或5.【点睛】本题主要考查了应用设计与作图以及勾股定理等知识,熟练掌握菱形的性质是解题关键. 20.(1)见解析;(2)90;(3)104【分析】(1)根据题意,可以先证明和全等,然后即可得到,然后对角线互相平分的四边形是平行四边形可以证明结论成立;(2)根据菱形的性质,可以得到的度数;(解析:(1)见解析;(2)90;(3)104【分析】(1)根据题意,可以先证明AEF ∆和BEC ∆全等,然后即可得到EC EF =,然后对角线互相平分的四边形是平行四边形可以证明结论成立;(2)根据菱形的性质,可以得到AEC ∠的度数;(3)根据矩形的性质,可以得到AEC ∠的度数.【详解】(1)证明:四边形ABCD 是平行四边形,//DA CB ∴,EAF EBC ∴∠=∠,点E 是边AB 的中点,AE BE ∴=,在AEF ∆和BEC ∆中,EAF ECB AE BE AEF BEC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()AEF BEC ASA ∴∆≅∆,EF EC ∴=,又AE BE =,∴四边形AFBC 是平行四边形;(2)当AEC ∠的度数为90︒时,四边形AFBC 是菱形, 理由:四边形AFBC 是菱形,AB CF ∴⊥,90AEC ∴∠=︒,故答案为:90;(3)当AEC ∠的度数为104度时,四边形AFBC 是矩形, 理由:四边形AFBC 是矩形,AB CF ∴=,EC EB ∴=,ECB EBC ∴∠=∠,四边形ABCD 是平行四边形,52D ∠=︒,52D EBC ∴∠=∠=︒,52ECB ∴∠=︒,5252104AEC ECB EBC ∴∠=∠+∠=︒+︒=︒,故答案为:104.【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、矩形的性质、菱形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答. 21.(1)(3)【解析】【分析】(1)利用已知数据变化规律直接得出答案;(2)利用分母有理化的规律将原式化简进而求出即可.【详解】解:(1)(2)利用上面提供的信息请化简:﹣1.【点解析:(1=31 【解析】【分析】(1)利用已知数据变化规律直接得出答案;(2)利用分母有理化的规律将原式化简进而求出即可.【详解】解:(1(2)利用上面提供的信息请化简:2013++1==﹣1.【点睛】考核知识点:实数运算.22.(1)y =40x+20(2≤x≤9);(2)5.5小时;(3)8小时【分析】(1)利用待定系数法求一次函数解析式即可;(2)求出C 点坐标,利用待定系数法求线段BC 的函数关系式,根据线段DE ,B解析:(1)y =40x +20(2≤x ≤9);(2)5.5小时;(3)8小时【分析】(1)利用待定系数法求一次函数解析式即可;(2)求出C 点坐标,利用待定系数法求线段BC 的函数关系式,根据线段DE ,BC 的函数解析式即可求解;(3)假设经过x 小时恰好装满2箱,甲组6.5小时加工的零件为300件,此时乙组加工的零件为40×6.5+20=280,两组生产的不够两箱,甲组一共加工了6.5小时,要想装满两箱,乙应加工320×2﹣300=340,进而列方程40x +20=340求解即可.【详解】解:(1)由图象得:D (2,100),E (9,380),设线段DE 的解析式为:y =kx +b ,∴21009380k b k b +=⎧⎨+=⎩, 解得:4020k b =⎧⎨=⎩, ∴y =40x +20(2≤x ≤9);(2)∵甲组的工作效率是原来的2倍,∴C 点纵坐标是:60÷2×2×(6.5﹣2.5)+60=300,∴C (6.5,300),设线段BC 的解析式为:11y k x b =+,∴11112.5606.5300k b k b +=⎧⎨+=⎩, 解得:116090k b =⎧⎨=-⎩, ∴y =60x ﹣90(2.5≤x ≤6.5),由题意得:40x +20=60x ﹣90,解得:x =5.5,答:甲乙两组5.5小时,加工的零件数相同;(3)设经过x 小时恰好装满二箱,由图象得:甲组6.5小时加工的零件为300件,乙组6.5小时加工的零件为40×6.5+20=280(件),∴此时不够装满2箱.恰好装满2箱乙应加工320×2﹣300=340(件),40x +20=340,解得:x =8,答:经过8小时恰好装满2箱.【点睛】本题考查一次函数的应用,正确获取图象信息,根据题意得出函数关系式以及数形结合是解题的关键.23.(1)B(12,4);(2);(3)【分析】(1)由四边形是平行四边形,得到,,于是得到,,可求出点的坐标;(2)根据四边形是平行四边形,得到,即,解方程即可得到结论;(3)如图2,可分三解析:(1)B(12,4);(2);(3)【分析】(1)由四边形是平行四边形,得到,,于是得到,,可求出点B的坐标;(2)根据四边形是平行四边形,得到,即,解方程即可得到结论;(3)如图2,可分三种情况:①当时,②当时,③当时分别讨论计算即可.【详解】解:如图1,过C作于E,过B作于F,四边形是平行四边形,,,,C的坐标分别为,,,,,;(2)设点P运动秒时,四边形是平行四边形,由题意得:,点D是的中点,,四边形是平行四边形,,即,,∴当秒时,四边形是平行四边形;(3)如图2,①当时,过作于E,则,,,又,C的坐标分别为,,∴,即有,当点P与点C重合时,,;②当时,过作于G,则,,;③当时,过作于F,则,,,;综上所述:当是等腰三角形时,点P的坐标为,,,,.【点睛】本题是四边形综合题,考查了平行四边形的性质,等腰三角形的性质,勾股定理,熟练掌握平行四边形的性质和等腰三角形的性质是解题的关键.24.(1)-1;(2)①证明见详解;②;(3)(,)【解析】【分析】(1)把P(3,4),b=7代入y=kx+b中,可得k=-1(2)①根据平行的性质:内错角相等,证明∠OCB=∠OBC,由等角解析:(1)-1;(2)①证明见详解;②34-;(3)(7715,2815-)【解析】【分析】(1)把P(3,4),b=7代入y=kx+b中,可得k=-1(2)①根据平行的性质:内错角相等,证明∠OCB=∠OBC,由等角对等边得到OBC是等腰三角形②根据坐标证明P是BC的中点,由等腰三角形三线合一性质得OP⊥BC,求出OP函数关系式中k的值,根据两个一次函数图像互相垂直时k的关系,求解出直线BC的表达式中的k=3 4 -(3)根据动点M的运动情况分析出N的轨迹函数,然后证明△OHG是等腰直角三角形,根据中点坐标公式求得直线O’P的表达式,联立方程求出N点坐标【详解】(1)把P(3,4),b=7代入y=kx+b中,可得4=3k+7解得k=-1故答案为-1(2)①∵AB∥y轴∴∠ABC=∠OCB∵BP平分∠OBA∴∠OBC=∠ABC∴∠OCB=∠OBC∴OBC是等腰三角形②如图4所示,连接OP∵AB//y轴,A(6,t)∴B点横坐标是6∵P横坐标是3∴P是BC的中点∴OP⊥BC设直线OP的表达式为y=kx将P(3,4)代入得4=3k解得k= 43,则设直线BC的表达式中的k=3 4 -.故答案为34-. (3)①如图5-1,当点M 与O 重合时,作PE ⊥y 轴于点E ,作NF ⊥y 轴于点F∵PM ⊥NM∴∠PMN=90°∴∠PME+∠NMF=90°∵∠FMN+∠FNM=90°∴∠PME=∠MNF在△PEM △MFN 中=PME MNF PEM MFN PM MN ∠=∠⎧⎪∠∠⎨⎪=⎩∴△PEO ≌△OFN (AAS )∴MF=PE=3,FN=ME=4则N 点的坐标为(4,-3)②如图5-2所示,,当PM ⊥x 轴时,N 点在x 轴上,则MN=PM=3,ON=OM+MN=7,∴N 的坐标为(7,0)综上所述得点N 在直线y=x-7的直线上运动设直线y=x-7与坐标轴分别交于点G 、H ,作O 关于直线HG 的对称点O`,连接O`P 交直线HG 于点N ,此时ON+PN 有最小值,最小值为线段O`P 的长度.如图5-3所示.当直线y=x-7可得H(0,-7),G(7,0),OG=OH,△OHG是等腰直角三角形,当OQ⊥HG时,Q是HG的中点,由中点坐标公式可得Q(72,-72),∵O`与O对称∴Q是OO`的中点由中点坐标公式可得O’(7,-7),∴可得直线O’P的表达式为1149y x44=-+联立方程1149447x xy x⎧=+⎪⎨⎪=-⎩﹣,解得77152815 xy⎧=⎪⎪⎨⎪=-⎪⎩∴N点坐标为(7715,2815-)∴当△OPN周长最小时,点N的坐标为(7715,2815-)故答案为(7715,2815-)【点睛】本题考查的是一次函数综合运用,涉及到三角形全等、角平分线的性质,平行的性质等,熟练掌握数形结合的解题方法是解决此题目的关键,综合性强,难度较大.25.(1),理由见解析;(2),理由见解析;(3),理由见解析【分析】(1)先根据正方形的性质可证得,由此可得,,再根据同角的补角相等证得,等量代换可得,由此可得,再等量代换即可得证;(2)过点E解析:(1)DE EF=,理由见解析;(2CD CF=+,理由见解析;(3)CD CF=-,理由见解析【分析】(1)先根据正方形的性质可证得BCE DCE≌,由此可得CBE CDE∠=∠,BE DE=,再根据同角的补角相等证得CDE EFB∠=∠,等量代换可得CBE EFB∠=∠,由此可得BE EF=,再等量代换即可得证;(2)过点E作EG EC⊥交CB的延长线于点G,先证明EG EC=,利用勾股定理可得CG,再证明EGF ECB△≌△,由此可得GF CB CD==,最后再等量代换即可得证;(3)仿照(1)和(2CD CF=-.【详解】解:(1)DE EF=,理由如下:∵四边形ABCD是正方形,∴BC CD AD==,90BCD ADC∠=∠=︒,∴180452ADCDAC DCA︒-∠∠=∠==︒,∴45BCE BCD DCA∠=∠-∠=︒,∴BCE DCE∠=∠,在BCE与DCE中,BC DCBCE DCECE CE=⎧⎪∠=∠⎨⎪=⎩∴()BCE DCE SAS≌,∴CBE CDE∠=∠,BE DE=,∵EF DE⊥,∴90FED∠=︒,∵360EFC BCD CDE FED∠+∠+∠+∠=︒,∴180CDE EFC∠+∠=︒,∵180EFC EFB∠+∠=︒,∴CDE EFB∠=∠,∴CBE EFB∠=∠,∴BE EF=,∴DE EF=;(2CD CF=+,理由如下:如图,过点E作EG EC⊥交CB的延长线于点G,∴90CEG ∠=︒,由(1)知:45BCE ∠=︒,∴45EGC BCE ∠=∠=︒,∴EG EC =,∴在Rt GEC △中,222CG CE EG CE =+=,在EGF △与ECB 中,EGF ECB EFG EBC EF EB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()EGF ECB AAS △≌△,∴GF CB CD ==,又∵CG GF CF CD CF =+=+,∴2CE CD CF =+;(3)2CE CD CF =-,理由如下:如图,过点E 作EG EC ⊥交BC 于点G ,设CD 与EF 的交点为点P ,∴90CEG ∠=︒,由(1)可知:45BCE ∠=︒,∴45EGC BCE ∠=∠=︒,∴EG EC =,∴在Rt GEC △中,222CG CE EG CE +,∵EF DE ⊥,∴90FED ∠=︒,∴90CDE EPD ∠+∠=︒,∵18090DCF BCD ∠=︒-∠=︒,∴90CFE CPF ∠+∠=︒,又∵EPD CPF ∠=∠,∴CDE CFE ∠=∠,由(1)可知:CBE CDE ∠=∠,∴CBE CFE ∠=∠,在EGF △与ECB 中,EGF ECB EFG EBC EG EC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()EGF ECB AAS △≌△,∴GF CB CD ==,又∵CG GF CF CD CF =-=-,∴CD CF =-.【点睛】本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形的判定与性质以及勾股定理的应用,作出正确的辅助线并能灵活运用相关图形的性质是解决本题的关键. 26.(1)见解析;(2)①见解析;②【分析】(1)根据直角三角形中两锐角互余以及三角形外角的性质可得结果;(2)①延长AD 至Q ,使得,连接BQ ,可证,根据已知以及等腰三角形的性质可得结论;②作,解析:(1)见解析;(2)①见解析;②25AE AD = 【分析】(1)根据直角三角形中两锐角互余以及三角形外角的性质可得结果;(2)①延长AD 至Q ,使得AD QD =,连接BQ ,可证()ACD QBD SAS ≌,根据已知以及等腰三角形的性质可得结论;②作,BP EQ CK AD ⊥⊥,连接CE ,证明CK EK =,设CD x =,则2BC AC x ==,根据勾股定理求得AE 、AD 的长度,求比值即可.【详解】解:(1)在Rt ABC 中,90ACB ∠=︒,∴90CAD ADC ∠+∠=︒∵CAD α∠=,∴90ADC α∠=︒-,∵CF BE ⊥,∴90EFG ∠=︒∵BED α∠=,∴90EGC BED EFG α∠=∠+∠=︒+,∵EGC ADC GCD ∠=∠+∠,∴()()90902GCD EGC ADC ααα∠=∠-∠=︒+-︒-=;(2)①延长AD 至Q ,使得AD QD =,连接BQ ,∵点D 为BC 边中点,∴CD BD =,又∵ADC QDB ∠=∠,∴()ACD QBD SAS ≌,∴CAD Q ∠=∠,AC QB =∵BED CAD α∠=∠=,∴Q BED α∠=∠=,∴EB QB =,∴AC EB =,∵AC BC =,∴BE BC =;②作,BP EQ CK AD ⊥⊥,连接CE ,∴90CKA DPB ∠=∠=︒,由(2)知,AC QB CAD Q =∠=∠,∴()ACK QBP AAS ≌∴CK BP =,∵90,90CAD ADC DCA ADC ∠+∠=︒∠+∠=︒,又∵BED CAD α∠=∠=,2GCD α∠=,∴902CBE α∠=︒-,∵BC BE =,∴45BCE BEC α∠=∠=︒+,∴45ECK CEK ∠=∠=︒,∴CK EK =,设CD x =,则2BC AC x ==,∴AD =, ∵1122CK AD AC CD =, ∴52CKx x x =, ∴CK x EK==,∴DK ==,∴DE DK EK x =+=,∴AE AD DE =-==,∴25AE AD ==, 故答案为:25. 【点睛】本题主要考查三角形综合问题,涉及到全等三角形判定与性质,等腰三角形的判定与性质,勾股定理等知识点,作出合理辅助线构造全等三角形以及应用勾股定理表示出各线段的长度是解题的关键.。
人教版八年级下册数学期末试卷(培优篇)(Word版含解析)
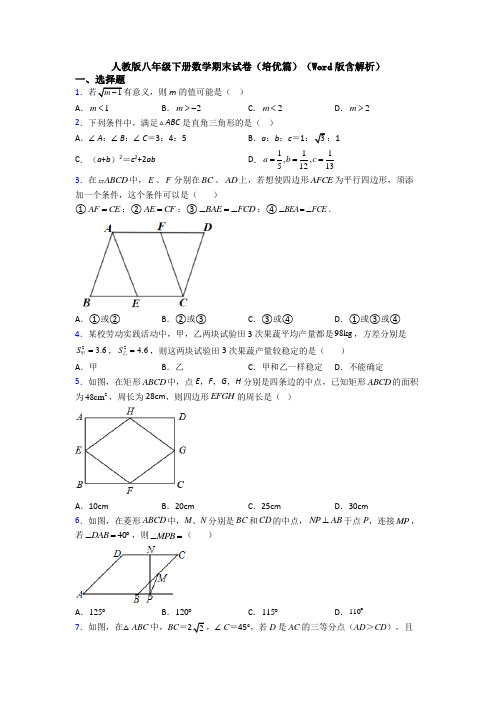
人教版八年级下册数学期末试卷(培优篇)(Word 版含解析) 一、选择题 1.若1m -有意义,则m 的值可能是( )A .1m <B .2m >-C .2m <D .2m > 2.下列条件中,满足ABC 是直角三角形的是( )A .∠A :∠B :∠C =3:4:5B .a :b :c =1:3:1C .(a +b )2=c 2+2abD .111,,51213a b c === 3.在ABCD 中,E 、F 分别在BC 、AD 上,若想使四边形AFCE 为平行四边形,须添加一个条件,这个条件可以是( )①AF CE =;②AE CF =;③BAE FCD ∠=∠;④BEA FCE ∠=∠.A .①或②B .②或③C .③或④D .①或③或④ 4.某校劳动实践活动中,甲,乙两块试验田3次果蔬平均产量都是98kg ,方差分别是2 3.6S =甲,2 4.6S =乙,则这两块试验田3次果蔬产量较稳定的是( )A .甲B .乙C .甲和乙一样稳定D .不能确定 5.如图,在矩形ABCD 中,点E ,F ,G ,H 分别是四条边的中点,已知矩形ABCD 的面积为248cm ,周长为28cm ,则四边形EFGH 的周长是( )A .10cmB .20cmC .25cmD .30cm6.如图,在菱形ABCD 中,M 、N 分别是BC 和CD 的中点,NP AB ⊥于点P ,连接MP ,若40DAB ∠=︒,则MPB ∠=( )A .125︒B .120︒C .115︒D .110︒7.如图,在△ABC 中,BC =2∠C =45°,若D 是AC 的三等分点(AD >CD ),且AB =BD ,则AB 的长为( )A .2B .5C .3D .528.如图1,动点P 从菱形ABCD 的顶点A 出发,沿A →C →D 以1cm /s 的速度运动到点D .设点P 的运动时间为(s ),△PAB 的面积为y (cm 2).表示y 与x 的函数关系的图象如图2所示,则a 的值为( )A .5B .52C .2D .25二、填空题9.式子3x +在实数范围内有意义,则实数x 的取值范围是________.10.已知菱形的边长与一条对角线的长分别为5和6,则它的面积是______.11.如图,在△ABC 中,∠ACB =90°,以它的三边为边分别向外作正方形,面积分别为S 1,S 2,S 3,已知S 1=5,S 2=12,则S 3=_____.12.如图,矩形ABCD 的对角线AC 与BD 相交点O ,6AB =,8BC =,P ,Q 分别为AO ,AD 的中点,则PQ 的长度为______.13.在平面直角坐标系,(2,0)A -,(0,3)B ,点M 在直线12y x =上,M 在第一象限,且6MAB S =△,则点M 的坐标为____.14.如图,两个完全相同的三角尺ABC 和DEF 在直线l 上滑动.要使四边形CBFE 为菱形,还需添加的一个条件是____(写出一个即可).15.如图,直线:4AB y x =+与直线:22BC y x =--相交于点B ,直线AB 与y 轴交于点A ,直线BC 与x 轴交于点D 与y 轴交于点C ,AE BC ∥交x 轴于点E .直线AB 上有一点P (P 在x 轴上方)且DEP ABC S S =,则点P 的坐标为_______.16.如图,正方形ABCD 的面积为144,点H 是边DC 上的一个动点,将正方形沿过点H 的直线GH 折叠(点G 在边AB 上),使顶点D 的对应点E 恰好落在BC 边上的三等分点处,则线段DH 的长是___.三、解答题17.计算:(1)2340100.15-+; (2)()()()201515112283π-⎛⎫-+--+---+ ⎪⎝⎭ 18.一个25米长的梯子AB ,斜靠在一竖直的墙AO 上,这时的AO 距离为24米,如果梯子的顶端A 沿墙下滑4米,那么梯子底端B 外移多少米?19.如图,正方形网格中的△ABC ,若小方格边长为1(1)判断△ABC 是什么形状?并说明理由.(2)求AC 边上的高.20.如图,在ABCD 中,两条对角线AC 和BD 相交于点O ,并且6BD =,8AC =,5BC =.(1)AC 与BD 有什么位置关系?为什么?(2)四边形ABCD 是菱形吗?为什么?21.阅读下列解题过程:21+21(21)(21)-+-2;1 32 +=32(32)(32)-+-=3-2;1 43 +=434343-+-()()=4-3=2-3;…解答下列各题:(1)1109+=;(2)观察下面的解题过程,请直接写出式子11n n--=.(3)利用这一规律计算:(111213243++++++…+120212020+)×(2021+1).22.某电影院普通票价20元/张,暑假为了促销,新推出两种优惠卡:①金卡售价600元/张,每次凭卡不再收费.②银卡售价150元/张,每次凭卡另收10元.暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设看电影x次时,所需总费用为y元.(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A,B,C的坐标;(3)请根据函数图象,提出1条合算的消费建议.23.如图,矩形ABCD中,AB=4,AD=3,∠A的角平分线交边CD于点E.点P从点A出发沿射线AE以每秒2个单位长度的速度运动,Q为AP的中点,过点Q作QH⊥AB于点H,在射线AE的下方作平行四边形PQHM(点M在点H的右侧),设P点运动时间为秒.(1)直接写出的面积(用含的代数式表示).(2)当点M 落在BC 边上时,求的值.(3)在运动过程中,整个图形中形成的三角形是否存在全等三角形?若存在,请写出所有全等三角形,并求出对应的的值;若不存在请说明理由(不能添加辅助线). 24.如图,在平面直角坐标系中,直线28y x =+与x 轴交于点A,与y 轴交于点B,过点B 的直线x 轴于点C ,且AB=BC .(1)求直线BC 的表达式(2)点P 为线段AB 上一点,点Q 为线段BC 延长线上一点,且AP=CQ,PQ 交x 轴于点P ,设点Q 的横坐标为m ,求PBQ ∆的面积(用含m 的代数式表示)(3)在(2)的条件下,点M 在y 轴的负半轴上,且MP=MQ ,若45BQM ︒∠=求点P 的坐标.25.如图1,在OAB 中,OAB 90∠=,30AOB ∠=,8OB =,以OB 为边,在OAB Λ外作等边OBC Λ,D 是OB 的中点,连接AD 并延长交OC 于E .(1)求证:四边形ABCE 是平行四边形;(2)连接AC ,BE 交于点P ,求AP 的长及AP 边上的高BH ;(3)在(2)的条件下,将四边形OABC 置于如图所示的平面直角坐标系中,以E 为坐标原点,其余条件不变,以AP 为边向右上方作正方形APMN :①M 点的坐标为 .②直接写出正方形APMN 与四边形OABC 重叠部分的面积(图中阴影部分).26.某数学活动小组在一次活动中,对一个数学问题作如下研究:(1)如图1,△ABC中分别以AB,AC为边向外作等腰△ABE和等腰△ACD使AE=AB,AD =AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.(2)如图2,△ABC中分别以AB,AC为边向外作等腰Rt△ABE和等腰Rt△ACD,∠EAB=∠CAD=90°,连接BD,CE,若AB=4,BC=2,∠ABC=45゜,求BD的长.(3)如图3,四边形ABCD中,连接AC,CD=BC,∠BCD=60°,∠BAD=30°,AB=15,AC=25,求AD的长.【参考答案】一、选择题1.D解析:D【分析】根据二次根式有意义的条件列出不等式,根据题意解答即可.【详解】解:由题意得,10m-,解得,1m,则m能取的为大于等于1的数,符合条件的为2m>故选:D .【点睛】本题考查的是二次根式有意义的条件,掌握二次根式的被开方数是非负数是解题的关键.2.C解析:C【分析】由直角三角形的定义,只要验证最大角是否是90︒;由勾股定理的逆定理,只要验证两较短边的平方和是否等于最长边的平方即可.【详解】解:A、∵::3:4:5A B C∠∠=,518075 345C∴∠=⨯︒=︒++,故不能判定ABC是直角三角形;B、22211(3)+≠,故不能判定ABC是直角三角形;C 、由22()2a b c ab +=+,可得:222+=a b c ,故能判定ABC 是直角三角形;D 、222111()()()12135+≠,故不能判定ABC 是直角三角形;故选:C .【点睛】本题主要考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可,也考查了三角形的内角和定理的应用. 3.D解析:D【解析】【分析】由平行四边形的判定定理依次判断即可解答.【详解】解:∵四边形ABCD 是平行四边形,∴AB //CD ,AB =CD ,∠B =∠D ,AD //BC ,AD =BC ,∴AF //EC∵AF =EC ,∴四边形AFCE 是平行四边形,故①符合题意;∵AF //EC ,AE CF =,∴四边形AFCE 可能是平行四边形、也可能是等腰梯形,故②不符合题意;如果∠BAE =∠FCD ,则△ABE ≌△DFC (ASA )∴BE =DF ,∴AD -DF =BC -BE ,即AF =CE ,∵AF //CE ,∴四边形AFCE 是平行四边形,故③符合题意;如果∠BEA =∠FCE ,∴AE //CF ,∵AF //CE ,∴四边形AFCE 是平行四边形、故④符合题意.故选D .【点睛】本题主要考查了平行四边形的性质与判定.灵活运用平行四边形的性质与判定定理是解答本题的关键.4.A解析:A【解析】【分析】根据两组数据的平均数相同,则方差小的更稳定即可求解.【详解】甲,乙两块试验田3次果蔬平均产量都是98kg ,方差分别是2 3.6S =甲,2 4.6S =乙,3.64.6<∴这两块试验田3次果蔬产量较稳定的是:甲.故选A【点睛】本题考查了方差的意义,若两组数据的平均数相同,则方差小的更稳定,理解方差的意义是解题的关键.5.B解析:B【分析】连接BD ,AC ,如图,先求出矩形的边长,再根据矩形的性质和勾股定理得到A C =BD =10cm ,再利用三角形中位线性质得到HG =EF =EH =GF =5cm ,,然后计算四边形EFGH 的周长.【详解】解:连接AC 、BD ,∵矩形ABCD 的面积为248cm ,周长为28cm ,∴AB =6cm ,AD =8cm ,AC =BD 226810+=cm ,∵点E ,F ,G ,H 分别是四条边的中点,∴HG 为△ACD 为中位线,EF 为△BAC 的中位线,∴HG =EF =12×10=5cm ,同理可得EH =GF =5cm ,∴四边形EFGH 的周长为4×5=20cm .故选:B .【点睛】本题考查了中点四边形:顺次连接任意四边形各边中点所得的四边形为平行四边形.也考查了矩形的性质和勾股定理以及中位线的性质. 6.D解析:D【解析】【分析】如图,连接,,DB NM 延长NM 交AB 于,H 先求解70DBA ∠=︒,再证明//,70,NM DB NHP ∠=︒ 再利用直角三角形的斜边上的中线等于斜边的一半证明,MP MH = 可得70,MPH ∠=︒ 从而可得答案.【详解】解:如图,连接,,DB NM 延长NM 交AB 于,H菱形ABCD ,40DAB ∠=︒,()1,18070,//,2AB AD DBA BDA A AB CD ∴=∠=∠=︒-∠=︒,N M 分别为,CD CB 的中点,//,70,NM DB NHA DBA ∴∠=∠=︒ ,CM BM =//,AB CD,,C CBH CNM MHB ∴∠=∠∠=∠,CNM BHM ∴≌,NM HM ∴=,NP AB ⊥,70,MP MH MPH MHP ∴=∠=∠=︒18070110.MPB ∴∠=︒-︒=︒故选:.D【点睛】本题考查的是直角三角形斜边上的中线等于斜边的一半,等腰三角形的性质,菱形的性质,灵活应用以上知识解题是解题的关键.7.B解析:B【解析】【分析】作BE ⊥AC 于E ,根据等腰三角形三线合一性质可得AE =DE ,根据∠C =45°,得出∠EBC =180°-∠C -∠BEC =180°-45°-90°=45°,可得BE =CE ,利用勾股定理求出CE =BE =2,根据D 是AC 的三等分点得出AE =DE =121233AC AC ⨯==CD ,求出CD =1,利用勾股定理2222215AB BE AE +=+即可.【详解】解:作BE ⊥AC 于E ,∵AB =BD ,∴AE =DE ,∵∠C =45°,∴∠EBC =180°-∠C -∠BEC =180°-45°-90°=45°,∴BE =CE ,在Rt △BEC 中, ∴()22222+222BE CE CE BC ===, ∴CE =BE =2,∵D 是AC 的三等分点,∴CD =13AC ,AD =AC -CD =1233AC AC AC -=, ∴AE =DE =121233AC AC ⨯==CD , ∴CE =CD +DE =2CD =2,∴CD =1,∴AE =1,在Rt △ABE 中,根据勾股定理2222215AB BE AE =+=+=.故选B .【点睛】本题考查等腰三角形的性质,等腰直角三角形判定与性质,勾股定理,三等分线段,掌握等腰三角形的性质,等腰直角三角形判定与性质,勾股定理,三等分线段是解题关键. 8.B解析:B【分析】由图2知,菱形的边长为a ,对角线5BD 为225()2a -254a -当点P 在线段AC 上运动时,y 12=AP 12⨯BD 21524a =-,即可求解. 【详解】解:由图2知,菱形的边长为a ,对角线AC 5=则对角线BD 为225()2a -=254a - 当点P 在线段AC 上运动时,y 12=AP 12⨯BD 12=,由图2知,当x =y =a ,即a 12= 解得:a 52=, 故选:B .【点睛】本题考查的是动点图象问题,涉及到函数、解直角三角形等知识,此类问题关键是:弄清楚不同时间段,图象和图形的对应关系,进而求解.二、填空题9.x ≥﹣3【解析】【分析】根据二次根式有意义的条件,根号内的式子必需大于等于0,即可求出答案.【详解】在实数范围内有意义,则3+x ≥0,解得:x ≥﹣3.故答案为:x ≥﹣3.【点睛】本题主要考查了二次根式有意义,熟练其要求是解决本题的关键.10.24【解析】【分析】根据题意,勾股定理求得另一条对角线的长度,根据菱形的面积等于对角线乘积的一半即可求解.【详解】如图,四边形ABCD 的菱形,连接,AC BD 交于点O ,依题意设5AB =,6BD =,则11,322AO AC BO BD ===, 2222534AO AB BO ∴=--=,8AC ∴=,S ∴菱形ABCD 11862422AC BD =⋅=⨯⨯=. 故答案为:24.【点睛】本题考查了根据菱形的性质求菱形的面积,勾股定理,作出图形求得另外一条对角线的长是解题的关键.11.A解析:17【解析】【分析】根据勾股定理即可得到结论.【详解】解:∵∠ACB =90°,S 1=5,S 2=12,∴AC 2=5,BC 2=12,∴AB 2=AC 2+BC 2=5+12=17,∴S 3=17,故答案为:17.【点睛】本题考查了勾股定理,正方形的面积,正确的识别图形是解题的关键.12.5【分析】先利用勾股定理求解,BD 再利用矩形的性质求解,OD 从而根据中位线的性质可得答案.【详解】解: 矩形ABCD ,6AB =,8BC =,18,90,,2AD BAD OB OD BD ∴=∠=︒== 226810,5,BD OD ∴=+==P ,Q 分别为AO ,AD 的中点,1 2.5.2PQ OD ∴== 故答案为:2.5.【点睛】本题考查的是矩形的性质,勾股定理的应用,三角形的中位线的性质,灵活应用以上知识是解题的关键.13.33,2⎛⎫ ⎪⎝⎭ 【分析】过点M 作MN y ⊥ 于点P 交直线AB 于点N ,可求出直线AB 的解析式为332y x =+ ,然后设点M 的坐标为1,2a a ⎛⎫ ⎪⎝⎭,其中0a > ,则11a 2,32N a ⎛⎫- ⎪⎝⎭ ,从而得到223MN a =+,最后根据6MAB S =△,可得到1223623a ⎛⎫+⨯= ⎪⎝⎭,解出a ,即可求解. 【详解】解:如图,过点M 作MN y ⊥ 于点P 交直线AB 于点N ,设直线AB 的解析式为()0y kx b k =+≠ ,把(2,0)A -,(0,3)B ,代入得:203k b b ⎧-+=⎨=⎩ ,解得:323k b ⎧=⎪⎨⎪=⎩ , ∴直线AB 的解析式为332y x =+ , ∵点M 在直线12y x =上,M 在第一象限, 设点M 的坐标为1,2a a ⎛⎫ ⎪⎝⎭,其中0a > , 当12y a = 时,1a 23x =- ,∴11a 2,32N a ⎛⎫- ⎪⎝⎭ , ∴122233MN a a a ⎛⎫=--=+ ⎪⎝⎭, ∵6MAB S =△, ∴162MAB BMN AMN S S S MN BO =+=⨯= , ∵(0,3)B ,∴3BO = ,∴1223623a ⎛⎫+⨯= ⎪⎝⎭, 解得:3a = ,∴33,2⎛⎫ ⎪⎝⎭M . 故答案为:33,2⎛⎫ ⎪⎝⎭. 【点睛】本题主要考查了一次函数图象上点的坐标特征,求一次函数解析式,运用数形结合思想,通过设点的坐标利用三角形的面积构造方程是解题的关键.14.C解析:CB=BF ;BE ⊥CF ;∠EBF=60°;BD=BF 等(写出一个即可).【分析】根据邻边相等的平行四边形是菱形或对角线互相垂直的平行四边形是菱形进而判断即可.【详解】解:根据题意可得出:四边形CBFE 是平行四边形,当CB=BF 时,平行四边形CBFE 是菱形,当CB=BF ;BE ⊥CF ;∠EBF=60°;BD=BF 时,都可以得出四边形CBFE 为菱形.故答案为:如:CB=BF ;BE ⊥CF ;∠EBF=60°;BD=BF 等.【点睛】此题主要考查了菱形的判定,关键是熟练掌握菱形的判定方法:①菱形定义:一组邻边相等的平行四边形是菱形;②四条边都相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形.15.(-3,4)【分析】先求出A (0,4),D (-1,0),C (0,-2),得到AC=6,再求出B 点坐标,从而求出△ABC 的面积;然后求出直线AE 的解析式得到E 点坐标即可求出DE 的长,再由进行求解即解析:(-3,4)【分析】先求出A (0,4),D (-1,0),C (0,-2),得到AC =6,再求出B 点坐标,从而求出△ABC 的面积;然后求出直线AE 的解析式得到E 点坐标即可求出DE 的长,再由162DEP P ABC S DE y S △进行求解即可.【详解】解:∵A 是直线4y x =+与y 轴的交点,C 、D 是直线22y x =--与y 轴、x 轴的交点, ∴A (0,4),D (-1,0),C (0,-2),∴AC =6;联立422y x y x =+⎧⎨=--⎩, 解得22x y =-⎧⎨=⎩, ∴点B 的坐标为(-2,2),∴()1==62ABC B S AC x ⋅-△, ∵AE BC ∥,∴可设直线AE 的解析式为2y x b =-+,∴4b =,∴直线AE 的解析式为24y x =-+,∵E 是直线AE 与x 轴的交点,∴点E 坐标为(2,0),∴DE =3,∴162DEP P ABC S DE y S △,∴=4P y ,∴=3P x ,∴点P 的坐标为(-3,4),故答案为:(-3,4).【点睛】本题主要考查了一次函数综合,求一次函数与坐标轴的交点,两直线的交点坐标,三角形面积,解题的关键在于能够熟练掌握一次函数的相关知识.16.或【分析】由已知可知CE=4或CE=8,由折叠可知DH=EH,则CH=12﹣DH,分两种情况求,在Rt△ECH中,利用勾股定理求解.【详解】解:∵正方形ABCD的面积为144,∴正方形的边解析:263或203【分析】由已知可知CE=4或CE=8,由折叠可知DH=EH,则CH=12﹣DH,分两种情况求,在Rt△ECH中,利用勾股定理求解.【详解】解:∵正方形ABCD的面积为144,∴正方形的边长为12,∵E为BC的三等分点,∴BE=4或BE=8,由折叠可知DH=EH,∴CH=12﹣DH,当CE=8时,在Rt△ECH中,EH2=EC2+CH2,∴DH2=64+(12﹣DH)2,∴DH=263;当CE=4时,在Rt△ECH中,EH2=EC2+CH2,∴DH2=16+(12﹣DH)2,∴DH=203;综上所述:DH的长为263或203,故答案为263或203.【点睛】本题考查了正方形的性质,折叠的性质,勾股定理,以及分类讨论的数学思想,分类讨论是解答本题的关键.三、解答题17.(1);(2)−7+3【分析】(1)先把各二次根式化为最特意二次根式,再合并即可得到答案;(2)分别根据平方差公式、负整数指数幂的运算法则,绝对值的代数意义,零指数幂的运算法则以及二次根式的性解析:(1);(2)− 【分析】(1)先把各二次根式化为最特意二次根式,再合并即可得到答案;(2)分别根据平方差公式、负整数指数幂的运算法则,绝对值的代数意义,零指数幂的运算法则以及二次根式的性质代简各项后再合并即可得到答案.【详解】解:(1=(2))()20111123π-⎛⎫--+- ⎪⎝⎭=51911---+=7-+【点睛】本题主要考查了二次根式的加减以及实数的混合运算,熟练掌握运算法则是解答本题的关键.18.8米.【分析】梯子下滑4米,梯子的长度不变始终为25米,利用勾股定理分别求出OB 、OB '的长度,进而求出BB '的长度即可.【详解】解:如图,依题意可知AB =25(米),AO =24(米),∠解析:8米.【分析】梯子下滑4米,梯子的长度不变始终为25米,利用勾股定理分别求出OB 、OB '的长度,进而求出BB '的长度即可.【详解】解:如图,依题意可知AB =25(米),AO =24(米),∠O =90°,∴ BO 2=AB 2﹣AO 2=252-242,∴ BO =7(米),移动后,A O '=20(米),222222()25205(1)B O A B A O ''''--===∴ 15B O '= (米),∴ =1578BB B O BO ''-=-=(米).答:梯子底端B 外移8米.【点睛】本题考查的是勾股定理的应用及勾股定理在直角三角形中的正确运用,本题中求B O '的长度是解题的关键.19.(1)△ABC 是直角三角形.理由见解析;(2)【解析】【分析】(1)根据勾股定理和勾股定理的逆定理可直接判断;(2)根据三角形的面积公式可求解.【详解】解:(1)△ABC 是直角三角形.理解析:(1)△ABC 是直角三角形.理由见解析;(2【解析】【分析】(1)根据勾股定理和勾股定理的逆定理可直接判断;(2)根据三角形的面积公式可求解.【详解】解:(1)△ABC 是直角三角形.理由如下:由题意可得,AB BCAC =∴AB 2+BC 2=AC 2,∴∠B =90°,∴△ABC 是直角三角形;(2)设AC 边上的高为h .∵S △ABC =12AC •h =12AB •BC ,∴h =13AB BC AC == 【点睛】本题主要考查了勾股定理和勾股定理的逆定理,解题的关键在于能够熟练掌握相关知识进行求解.20.(1)AC ⊥BD ,证明见解析;(2)四边形ABCD 是菱形,见解析【分析】(1)首先根据平行四边形的性质得出OC, OB的长,再利用勾股定理逆定理求出∠BOC=90,可得AC与BD的位置关系;(解析:(1)AC⊥BD,证明见解析;(2)四边形ABCD是菱形,见解析【分析】(1)首先根据平行四边形的性质得出OC,OB的长,再利用勾股定理逆定理求出∠BOC=90︒,可得AC与BD的位置关系;(2)菱形的判定方法:对角线互相垂直平分的四边形是菱形,可得答案.【详解】解:(1)AC⊥BD;理由如下:在ABCD中,132==OB BD,142OC AC==∵22291625+=+==OB OC BC∴∠BOC=90︒∴AC⊥BD.(2)四边形ABCD是菱形∵四边形ABCD是平行四边形(已知),AC⊥BD(已证)∴四边形ABCD是菱形.【点睛】此题主要考查了菱形的判定,平行四边形的性质,以及勾股定理的逆定理的运用,解题的关键是根据条件证出BO2+CO2=CB2.21.(1);(2);(3)2020【解析】【分析】(1)把分子分母都乘以,然后利用平方差公式和二次根式的性质计算,即可得到答案;(2)把分子分母都乘以,然后利用平方差公式和二次根式的性质计算,即解析:(13;(23)2020【解析】【分析】(1,然后利用平方差公式和二次根式的性质计算,即可得到答案;(2到答案;(3)根据(1)和(2)的结论,先分母有理化,经加减运算后,再利用平方差公式计算,即可得到答案.【详解】(133;(2==×)(31+×)1)×)=20211-=2020.【点睛】本题考查了二次根式和数字规律的知识:解题的关键是熟练掌握二次根式混合运算、数字规律、平方差公式的性质,从而完成求解.22.(1)y=10x+150,y=20x;(2)A(0,150),B(15,300),C(45,600);(3)当0<x<15时,选择普通消费更划算;当x=15时,银卡,普通票总费用相同,均比金卡划算;解析:(1)y=10x+150,y=20x;(2)A(0,150),B(15,300),C(45,600);(3)当0<x<15时,选择普通消费更划算;当x=15时,银卡,普通票总费用相同,均比金卡划算;当15<x<45时,银卡消费更划算;当x=45时,金卡,银卡的总费用相同,均比普通票划算;当x>45时,金卡消费更划算.【分析】(1)弄清题意,结合图象易知普通票为正比例函数图象,银卡为一次函数图象,依题意写出即可;(2)银卡函数关系式y=10x+150,令x=0时即可求出A点坐标,令银卡函数与普通卡函数关系式相等即可找到B点坐标,令银卡函数关系式y=600,即可找到C点坐标;(3)结合图象分当0<x<15时,x=15时,15<x<45时,x=45时,x>45时五段,依次分析出最合算的消费建议即可.【详解】解:(1)由题意得,选择银卡时,y与x之间的函数关系式为:y=10x+150;选择普通票时,y与x之间的函数关系式为:y=20x;(2)由题意可得:当y=10x+150,x=0时,y=150,故A(0,150),当10x+150=20x,解得:x=15,则y=300,故B(15,300),当y=10x+150=600时,解得:x=45,故C(45,600);(3)如图所示,由A、B、C三点坐标可得:当0<x<15时,选择普通消费更划算;当x=15时,银卡,普通票总费用相同,均比金卡划算;当15<x<45时,银卡消费更划算;当x=45时,金卡,银卡的总费用相同,均比普通票划算;当x>45时,金卡消费更划算.【点睛】本题考查一次函数应用,重点掌握一次函数的基本性质熟练应用,能结合实际灵活运用是解题的关键.23.(1);(2);(3)存在,如图2(见解析),当时,;如图3(见解析),当时,;如图4(见解析),当时,.【分析】(1)先根据线段中点的定义可得,再根据矩形的性质、角平分线的定义可得,从而可得是解析:(1);(2);(3)存在,如图2(见解析),当时,;如图3(见解析),当时,;如图4(见解析),当时,.【分析】(1)先根据线段中点的定义可得,再根据矩形的性质、角平分线的定义可得,从而可得是等腰直角三角形,然后根据等腰直角三角形的性质可得AH的长,最后根据等腰直角三角形的面积公式即可得;(2)先根据平行四边形的性质可得,从而可得,再根据三角形中位线定理可得是的中位线,从而可得,然后与(1)所求的建立等式求解即可得;(3)分①当点H是AB的中点时,;②当点Q与点E重合时,;③当时,三种情况,分别求解即可得.【详解】(1)由题意得:,点Q为AP的中点,,四边形ABCD是矩形,,是BAD的角平分线,,,是等腰直角三角形,,则的面积为;(2)如图1,四边形PQHM是平行四边形,,点M在BC边上,,点Q为AP的中点,是的中位线,,由(1)知,,则,解得;(3)由题意,有以下三种情况:①如图2,当点H是AB的中点时,则,四边形PQHM是平行四边形,,,在和中,,,由(2)可知,此时;②如图3,当点Q与点E重合时,在和中,,,,则,解得;③如图4,当时,四边形ABCD是矩形,四边形PQHM是平行四边形,,,在和中,,,,,在中,,是等腰直角三角形,,,在中,,是等腰直角三角形,,则由得:,解得;综上,如图2,当时,;如图3,当时,;如图4,当时,.【点睛】本题考查了矩形的性质、三角形中位线定理、三角形全等的判定定理与性质、等腰直角三角形的判定与性质等知识点,较难的是题(3),依据题意,正确分三种情况讨论并画出图形是解题关键.24.(1)y=-2x+8;(2)S=16m-2m2;(3)(-2,4)【解析】【分析】(1)先求出点A,点B坐标,由等腰三角形的性质可求点C坐标,由待定系数法可求BC 的解析式;(2)过点P作PG解析:(1)y=-2x+8;(2)S=16m-2m2;(3)(-2,4)【解析】【分析】(1)先求出点A,点B坐标,由等腰三角形的性质可求点C坐标,由待定系数法可求BC 的解析式;(2)过点P作PG⊥AC,PE∥BC交AC于E,过点Q作HQ⊥AC,由“AAS”可证△AGP≌△CHQ,可得AG=HC=m-4,PG=HQ=2m-8,由“AAS”可证△PEF≌△QCF,可得S△PEF=S△QCF,即可求解;(3)如图2,连接AM,CM,过点P作PE⊥AC,由“SSS”可证△APM≌△CQM,△ABM≌△CBM,可得∠PAM=∠MCQ,∠BQM=∠APM=45°,∠BAM=∠BCM,由“AAS”可证△APE≌△MAO,可得AE=OM,PE=AO=4,可求m的值,可得点P的坐标.【详解】解:(1)∵直线y=2x+8与x轴交于点A,与y轴交于点B,∴点B(0,8),点A(-4,0)∴AO=4,BO=8,∵AB=BC,BO⊥AC,∴AO=CO=4,∴点C(4,0),设直线BC解析式为:y=kx+b,由题意可得:804bk b=⎧⎨=+⎩,解得:28kb=-⎧⎨=⎩,∴直线BC解析式为:y=-2x+8;(2)如图1,过点P作PG⊥AC,PE∥BC交AC于E,过点Q作HQ⊥AC,设△PBQ的面积为S,∵AB=CB,∴∠BAC=∠BCA,∵点Q横坐标为m,∴点Q(m,-2m+8)∴HQ=2m-8,CH=m-4,∵AP=CQ,∠BAC=∠BCA=∠QCH,∠AGP=∠QHC=90°,∴△AGP≌△CHQ(AAS),∴AG=HC=m-4,PG=HQ=2m-8,∵PE∥BC,∴∠PEA=∠ACB,∠EPF=∠CQF,∴∠PEA=∠PAE,∴AP=PE,且AP=CQ,∴PE=CQ,且∠EPF=∠CQF,∠PFE=∠CFQ,∴△PEF≌△QCF(AAS)∴S△PEF=S△QCF,∴△PBQ的面积=四边形BCFP的面积+△CFQ的面积=四边形BCFP的面积+△PEF的面积=四边形PECB的面积,∴S=S△ABC-S△PAE=12×8×8-12×(2m-8)×(2m-8)=16m-2m2;(3)如图2,连接AM,CM,过点P作PE⊥AC,∵AB=BC,BO⊥AC,∴BO是AC的垂直平分线,∴AM=CM,且AP=CQ,PM=MQ,∴△APM≌△CQM(SSS)∴∠PAM=∠MCQ,∠BQM=∠APM=45°,∵AM=CM,AB=BC,BM=BM,∴△ABM≌△CBM(SSS)∴∠BAM=∠BCM,∴∠BCM=∠MCQ,且∠BCM+∠MCQ=180°,∴∠BCM=∠MCQ=∠PAM=90°,且∠APM=45°,∴∠APM=∠AMP=45°,∴AP=AM,∵∠PAO+∠MAO=90°,∠MAO+∠AMO=90°,∴∠PAO=∠AMO,且∠PEA=∠AOM=90°,AM=AP,∴△APE≌△MAO(AAS)∴AE=OM,PE=AO=4,∴2m-8=4,∴m=6,∴P(-2,4).【点睛】本题是一次函数综合题,考查了待定系数法求解析式,全等三角形的判定和性质,等腰三角形的性质,添加恰当辅助线构造全等三角形是本题的关键.25.(1)见解析;(2),;(3)①;②【分析】(1)利用直角三角形斜边中线的性质可得DO=DA,推出∠AEO=60°,进一步得出BC ∥AE ,CO ∥AB ,可得结论; (2)先计算出OA=,推出PB=解析:(1)见解析;(2)PA =BH 3)①(4M +;【分析】(1)利用直角三角形斜边中线的性质可得DO=DA ,推出∠AEO=60°,进一步得出BC ∥AE ,CO ∥AB ,可得结论;(2)先计算出OA=PB=AP=BH 即可;(3)①求出直线PM 的解析式为,再利用两点间的距离公式计算即可;②易得直线BC 的解析式为y=,联立直线BC 和直线PM 的解析式成方程组,求得点G 的坐标,再利用三角形面积公式计算. 【详解】(1)证明:∵Rt △OAB 中,D 为OB 的中点, ∴AD=12OB ,OD=BD=12OB ,∴DO=DA ,∴∠DAO=∠DOA=30°,∠EOA=90°, ∴∠AEO=60°,又∵△OBC 为等边三角形, ∴∠BCO=∠AEO=60°, ∴BC ∥AE ,∵∠BAO=∠COA=90°, ∴CO ∥AB ,∴四边形ABCE 是平行四边形;(2)解:在Rt △AOB 中,∠AOB=30°,OB=8, ∴AB=4, ∴OA=∵四边形ABCE 是平行四边形, ∴PB=PE ,PC=PA , ∴PB=∴PC PA == ∴1122ABC S AC BH AB BE ∆=⋅⋅=⋅⋅,即11422BH ⨯=⨯⨯ ∴BH(3)①∵C (0,4), 设直线AC 的解析式为y=kx+4, ∵P(0), ∴0=, 解得,k=, ∴y=, ∵∠APM=90°, ∴直线PM 的解析式为, ∵P(0), ∴, 解得,m=-3,∴直线PM 的解析式为, 设M (x), ∵AP= ∴(x-2+)2=(2, 化简得,x 2,解得,x 1=4,x 2=4(不合题意舍去), 当x=4时,(4)-3= ∴M(4,故答案为:(4, ②∵(0,4),C B ∴直线BC的解析式为:4y =+,联立34y y x ⎧=-⎪⎪⎨⎪=+⎪⎩,解得65x y ⎧=⎪⎪⎨⎪=⎪⎩,∴6)5G ,161=4252PBG PBA S S S ∆∆∴+=⨯+⨯阴【点睛】本题考查的是平行四边形的判定,等边三角形的性质,两点间的距离,正方形的性质,矩形的性质,一次函数的图象和性质,掌握相关的判定定理和性质定理是解题的关键. 26.(1)CE=BD ,见解析;(2)6;(3)20【分析】(1)证△EAC ≌△BAD 即可;(2)证△EAC ≌△BAD ,得BD=CE ,易得∠EBC=90゜,从而在Rt △EBC 中运用勾股定理即可求得结解析:(1)CE =BD ,见解析;(2)6;(3)20【分析】(1)证△EAC ≌△BAD 即可;(2)证△EAC ≌△BAD ,得BD =CE ,易得∠EBC =90゜,从而在Rt △EBC 中运用勾股定理即可求得结果;(3)连接BD ,把△ACD 绕点D 顺时针旋转60゜得到△EBD ,连接AE ,则可得BE =AC ,△ADE 是等边三角形,从而易得AB ⊥AE ,在Rt △BAE 中由勾股定理可求得AE ,也即AD 的长.【详解】(1)∵∠EAB =∠CAD∴∠BAC +∠EAB =∠BAC +∠CAD即∠EAC =∠BAD在△EAC 和△BAD 中AE AB EAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩∴△EAC ≌△BAD (SAS )∴CE =BD(2)∵∠EAB =∠CAD =90゜∴∠BAC +∠EAB =∠BAC +∠CAD即∠EAC =∠BAD∵△EAB 、△CAD 都是等腰直角三角形,且∠EAB =∠CAD =90゜∴AE =AB =4,∠EBA =45゜,AC =AD∴由勾股定理得:BE ==在△EAC 和△BAD 中AE AB EAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩∴△EAC ≌△BAD (SAS )∴CE =BD∵∠EBC =∠EBA +∠ABC =45゜+45゜=90゜∴在Rt△EBC中,由勾股定理得:2222=+=+=(42)26CE BE BC∴BD=6(3)如图,连接BD∵CD=BC,∠BCD=60゜∴△BCD是等边三角形把△ACD绕点D顺时针旋转60゜得到△EBD,点E与点A对应,连接AE则BE=AC=25,△ADE是等边三角形∴∠DAE=60゜,AD=AE∴∠BAE=∠BAD+∠DAE=30゜+60゜=90゜即AB⊥AE在Rt△BAE中,由勾股定理得:2222AE BE AB=-=-=251520∴AD=20【点睛】本题是三角形的综合题,考查了三角形全等的判定与性质,等腰三角形的性质,等边三角形的判定与性质,勾股定理,旋转变换,第三问作旋转变换是关键,也是难点.本质上来说,前两问也可看成把△EAC绕A点逆时针旋转的角度一定角度而得到△BAD.。
人教版数学八年级下册数学期末试卷(培优篇)(Word版含解析)

人教版数学八年级下册数学期末试卷(培优篇)(Word 版含解析) 一、选择题 1.如果72x x +-在实数范围内有意义,则x 的取值范围是( ) A .x ≠2 B .x ≥﹣7 C .x ≥2 D .x ≥﹣7且x ≠2 2.下列由线段a ,b ,c 组成的三角形不是直角三角形的是( )A .a :b :c =1:2:3B .a =54,b =1,c =34C .a =4,b =5,c =41D .a =3,b =4,c =5 3.给出下列命题,其中错误命题的个数是( ) ①四条边相等的四边形是正方形;②四边形具有不稳定性;③有两个锐角对应相等的两个直角三角形全等;④一组对边平行的四边形是平行四边形.A .1B .2C .3D .44.在脱贫攻坚工作中,为比较甲、乙两村扶贫攻坚工作的成效,从这两村中,各随机抽取20户对其年收入情况进行调查.统计结果是两村年人均收入的平均数相同,方差分别是S 甲2=6000,S 乙2=480,则年人均收入比较均衡的村是( )A .甲村B .乙村C .甲、乙两村一样D .无法确定 5.如图,在正方形ABCD 和正方形CEFG 中,点D 在CG 上,BC =1,CE =3,H 是AF 的中点,那么CH 的长是( )A .25B .5C .35D .26.如图,把—个长方形纸片对折两次,然后剪下—个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为( )A .60°B .30°C .45°D .90°7.如图,四边形ABCD 是矩形,点E 在线段CB 的延长线上,连接DE 交AB 于点F ,2AED CED ∠=∠,点G 是DF 的中点,若1BE =,3CD =,则DF 的长为( )A .8B .9C .42D .210 8.一个容器内有进水管和出水管,开始4min 内只进水不出水,在随后的8min 内既进水又出水,第12min 后只出水不进水.进水管每分钟的进水量和出水量每分钟的出水量始终不变,容器内水量y (单位:L )与时间x (单位:min )之间的关系如图所示.根据图象有下列说法:①进水管每分钟的进水量为5L ;②412x ≤≤时,5154y x =+;③当12x =时,30y =;④当15y =时,3x =,或17x =.其中正确说法的个数是( ) A .1个 B .2个 C .3个 D .4个二、填空题9.二次根式9x +在实数范围内有意义,则x 的取值范围是__.10.已知菱形的周长等于8,一条对角线长为2,则此菱形的面积为___.11.若直角三角形的两边长分别为2,6,那么第三边长是______.12.如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,E 为AB 的中点,连接OE .若10CD =,则OE 的长为________.13.若函数y=kx+3的图象经过点(3,6),则k=_____.14.如图所示,在四边形ABCD 中,顺次连接四边中点E 、F 、G 、H ,构成一个新的四边形,请你对四边形ABCD添加一个条件,使四边形EFGH成一个菱形,这个条件是__________.15.如图,在平面直角坐标系中,点A1,A2,A3,…,都在x轴正半轴上,点B1,B2,B3,…,都在直线y=kx上,∠B1OA1=30°,△A1B1A2,△A2B2A3,△A3B3A4,…,都是等边三角形,且OA1=1,则点B6的纵坐标是_________.16.如图,直角三角形纸片的两直角边长分别为6,8,按如图那样折叠,使点A与点B重合,折痕为DE,则:BCE BDES S等于____________.三、解答题17.计算题(1)32712+48(221233(321233+(130;(451512718.笔直的河流一侧有一旅游地C,河边有两个漂流点A,B.其中AB=AC,由于某种原因,由C到A的路现在已经不通,为方便游客决定在河边新建一个漂流点H(A,H,B在同一直线上),并新修一条路CH,测得BC=5千米,CH=4千米,BH=3千米.(1)判断△BCH的形状,并说明理由;(2)求原路线AC的长.19.如图,网格中的ABC,若小方格边长为1,请你根据所学的知识,(1)判断ABC是什么形状?并说明理由;(2)求ABC的面积.20.如图,在△ABC中,D,E分别是AB,BC的中点,连接DE并延长至点F,使得DE=EF,连接CF.(1)求证:四边形ADFC是平行四边形;(2)若∠A=∠B,连接CD,BF.求证:四边形BFCD是矩形.21.先阅读下列的解答过程,然后再解答:±a、b,使a+b=m,ab=n,使得2m n22+=a b na b m()()=2±±=a>b)m n a b a b2=()7+437+437+212m=7,n=12,由于4+3=7,4×3=12即22+=3412(4)(3)7=∴7+432+=7+212=(43)23(1423-=,9+45=;(219415-22.已知某列货车挂有A,B两种不同规格的货车厢共60节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元,设使用该列车全部车厢的总费用为y万元,这列货车挂A型车厢x节.(1)试写出y与x之间的函数关系式;(2)若使用该列车全部车厢的总费用少于45万元,则至少挂A 型车厢多少节? 23.如图.正方形ABCD 的边长为4,点E 从点A 出发,以每秒1个单位长度的速度沿射线AD 运动,运动时间为t 秒(t >0),以AE 为一条边,在正方形ABCD 左侧作正方形AEFG ,连接BF .(1)当t =1时,求BF 的长度;(2)在点E 运动的过程中,求D 、F 两点之间距离的最小值;(3)连接AF 、DF ,当△ADF 是等腰三角形时,求t 的值.24.如图,在平面直角坐标系xOy 中,直线384y x =-+分别交x 、y 轴于点A 、B ,将正比例函数2y x =的图像沿y 轴向下平移3个单位长度得到直线l ,直线l 分别交x 、y 轴于点C 、D ,交直线AB 于点E .(1)直线l 对应的函数表达式是__________,点E 的坐标是__________;(2)在直线AB 上存在点F (不与点E 重合),使BF BE =,求点F 的坐标;(3)在x 轴上是否存在点P ,使2PDO PBO ∠=∠?若存在,求点P 的坐标;若不存在,请说明理由.25.如图,在四边形OABC 是边长为4的正方形点P 为OA 边上任意一点(与点O A 、不重合),连接CP ,过点P 作PM CP ⊥,且PM CP =,过点M 作MN AO ∥,交BO 于点,N 联结BM CN 、,设OP x =.(1)当1x =时,点M 的坐标为( , )(2)设CNMB S y =四形边,求出y 与x 的函数关系式,写出函数的自变量的取值范围.(3)在x 轴正半轴上存在点Q ,使得QMN 是等腰三角形,请直接写出不少于4个符合条件的点Q 的坐标(用x 的式子表示)26.如图,两个全等的等边三角形△ABC与△ACD,拼成的四边形ABCD中,AC=6,点E、F分别为AB、AD边上的动点,满足BE=AF,连接EF交AC于点G,连接BD与CE、AC、CF分别交于点M、O、N,且AC⊥BD.(1)求证:△CEF是等边三角形.(2)△AEF的周长最小值是.(3)若BE=3,求证:BM=MN=DN.【参考答案】一、选择题1.D解析:D【分析】由已知可得x﹣2≠0,x+7≥0,求出x的范围即可.【详解】解:∵7 x+∴x﹣2≠0,x+7≥0,∴x≠2,x≥﹣7,∴x≥﹣7且x≠2,故选:D.【点睛】此题主要考查二次根式与分式有意义的条件,解题的关键是熟知其各自的特点.2.A解析:A【分析】运用勾股定理的逆定理进行计算求解即可判断.【详解】解:A 、∵::1:2:3a b c =,设a k =,2b k =,3c k =(其中k >0)∴2222259a b k k c +=≠=,故选项A 中的三条线段不能构成直角三角形;B 、12+(34)2=(54)2,故选项B 中的三条线段能构成直角三角形;C 、42+522,故选项C 中的三条线段能构成直角三角形;D 、32+42=52,故选项D 中的三条线段能构成直角三角形;故选A .【点睛】本题主要考查了勾股定理的逆定理,解题的关键在于能够熟练掌握勾股定理的逆定理. 3.C解析:C【解析】【分析】利用正方形的判定、直角三角形全等的判定、平行四边形的判定定理对每个选项依次判定解答.【详解】①四条边相等的四边形是菱形,故①错误;②四边形具有不稳定性,故②正确;③两直角三角形隐含一个条件是两直角相等,两个锐角对应相等,因此构成了AAA ,不能判定全等,故③错误;④一组对边平行且相等的四边形是平行四边形,故④错误;综上,错误的命题有①③④共3个.故选:C .【点睛】本题考查了命题与定理的知识,解题的关键是了解正方形的判定、平行四边形的判定及直角三角形全等的判定.4.B解析:B【解析】【分析】根据方差的意义求解即可,方差是反映一组数据的波动大小的一个量,方差越大,则平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.【详解】S 甲2=6000,S 乙2=480,∴ S 乙2< S 甲2,∴年人均收入比较均衡的村是乙,故选:B .【点睛】本题主要考查方差的意义,属于基础题,比较简单,熟练掌握方差的意义是解题的关键. 5.B解析:B【分析】连接AC 、CF ,如图,根据正方形的性质得∠ACD =45°,∠FCG =45°,AC =2,CF =32,则∠ACF =90°,再利用勾股定理计算出AF =25,然后根据直角三角形斜边上的中线求CH 的长.【详解】连接AC 、CF ,如图,∵四边形ABCD 和四边形CEFG 都是正方形,∴∠ACD =45°,FCG =45°,AC =2BC =2,CF =2CE =32,∴∠ACF =45°+45°=90°,在Rt △ACF 中,AF =()()22232=25+, ∵H 是AF 的中点,∴CH =12AF =5 .故选B .【点睛】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.两条对角线将正方形分成四个全等的等腰直角三角形.也考查了直角三角形斜边上的中线性质及勾股定理.6.C解析:C【解析】【分析】根据翻折变换的性质及正方形的判定进行分析从而得到答案.【详解】解:一张长方形纸片对折两次后,剪下一个角,是菱形,而出现的四边形的两条对角线分别是两组对角的平分线,剪下的直角三角形是由两条对角线分割成的4个直角三角形中的一个,若该直角三角形是等腰直角三角形,则剪出的菱形为正方形,所以当剪口线与折痕成45°角,菱形就变成了正方形.故选C.【点睛】本题考查了剪纸问题、通过折叠变换考查正方形的有关知识及学生的逻辑思维能力,解答此类题最好动手操作,易得出答案.7.D解析:D【解析】【分析】由矩形性质及G为中点,可得∠AGE=2∠ADE=2∠CED=∠AED,从而可得AE=AG,由矩形性质AB=CD=3,由勾股定理可得AE,再根据直角形的性质从而可求得DF的长.【详解】∵四边形ABCD是矩形∴∠DAB=∠ABC=∠ABE=90゜,AB=CD=3,AD∥BC∵G点是DF的中点∴AG是Rt△DAF斜边DF上的中线∴AG=DG=1DF2∴∠GAD=∠ADE∴∠AGE=2∠ADE∵AD∥BC∴∠CED=∠ADE∴∠AGE=2∠CED∵∠AED=2∠CED∴∠AED=∠AGE∴AE=AG在Rt△ABE中,由勾股定理得:AE∴AG=∴2==DF AG故选:D.【点睛】本题考查了等腰三角形的判定,勾股定理,矩形的性质,直角三角形斜边上中线的性质等知识,关键是得出∠AED=∠AGE.8.C解析:C【分析】根据图象可知进水的速度为5(L/min),再根据第10分钟时容器内水量为27.5L可得出水的速度,从而求出第12min时容器内水量,利用待定系数法求出4≤x≤12时,y与x之间的函数关系式,再对各个选项逐一判断即可.【详解】解:由图象可知,进水的速度为:20÷4=5(L/min),故①说法正确;出水的速度为:5−(27.5−20)÷(10−4)=3.75(L/min),第12min时容器内水量为:20+(12−4)×(5−3.75)=30(L),故③说法正确;15÷3=3(min),12+(30−15)÷3.75=16(min),故当y=15时,x=3或x=16,故说法④错误;设4≤x≤12时,y与x之间的函数关系式为y=kx+b,根据题意,得420 1027.5k bk b+=⎧⎨+=⎩,解得5415kb⎧=⎪⎨⎪=⎩,所以4≤x≤12时,y=54x+15,故说法②正确.所以正确说法的个数是3个.故选:C.【点睛】此题考查了一次函数的应用,解题时首先正确理解题意,利用数形结合的方法即可解决问题.二、填空题9.x≥﹣9【解析】【分析】由二次根式的非负性可得x+9≥0,即可求解.【详解】解:∵∴x+9≥0,∴x≥﹣9,故答案为x≥﹣9.【点睛】)0a≥的式子叫二次根式,熟练掌握二次根式成立的条件是解答本题的关键.10.A解析:2.【解析】【分析】根据周长先求出边长,由菱形的对角线平分且垂直求出它的另一条对角线的长,再根据面积公式求得面积.【详解】解:如图:∵菱形ABCD 的周长等于8cm ,∴AB =8÷4=2cm ,AC ⊥BD ,AO =CO ,BO =DO ,∵AC=2,∴AO =1,∴BO 3∴菱形的面积为332. 故答案为:232.【点睛】本题考查了菱形的四条边相等的性质,以及对角线互相垂直平分的性质,还考查了菱形面积的计算,对角线乘积的一半.11.2或22【解析】【分析】 2626边的长.【详解】 26第三边的长()()22622-=,26第三边的长()()226222+=故答案为:2或22【点睛】本题考查了勾股定理,由于已知的两边是直角边还是斜边并不明确,所以一定要分类讨论.12.A解析:5【分析】根据直角三角形斜边上的中线等于斜边的一半计算即可;【详解】∵四边形ABCD 时菱形,∴AC BD ⊥,∴90AOB ∠=︒,∵E 为AB 的中点,10CD AB ==, ∴152OE AB ==; 故答案是5.【点睛】本题主要考查了菱形的性质和直角三角形的性质,准确分析计算是解题的关键. 13.1【解析】∵函数y=kx+3的图象经过点(3,6),∴336k +=,解得:k=1.故答案为:1.14.A解析:答案不唯一,例AC=BD 等【分析】连接AC 、BD ,先证明四边形ABCD 是平行四边形,再根据菱形的特点添加条件即可.【详解】连接AC ,∵点E 、F 分别是AB 、BC 的中点,∴EF 是△ABC 的中位线,∴EF ∥AC ,EF=12AC , 同理HG ∥AC ,HG=12AC, ∴EF ∥HG ,EF=HG ,∴四边形EFGH 是平行四边形,连接BD,同理EH=FG,EF ∥FG ,当AC=BD 时,四边形EFGH 是平行四边形,故答案为:答案不唯一,例AC=BD 等.此题考查三角形中位线性质,平行四边形的判定及性质,菱形的判定.15.【分析】设△BnAnAn+1的边长为an,根据勾股定理求出点M坐标,求出直线的解析式,得出∠AnOBn=30°,再结合等边三角形的性质及外角的性质即可得出∠OBnAn=30°,从而得出AnBn=解析:3【分析】设△B n A n A n+1的边长为a n,根据勾股定理求出点M坐标,求出直线的解析式,得出∠A n OB n=30°,再结合等边三角形的性质及外角的性质即可得出∠OB n A n=30°,从而得出A n B n=OA n,列出部分a n的值,发现规律a n+1=2a n,依此规律结合等边三角形的性质即可得出结论.【详解】设△B n A n A n+1的边长为a n,点B1,B2,B3,…是直线y= kx上的第一象限内的点,过A1作A1M⊥x轴交直线OB1于M点,∵OA1=1,∴点M的横坐标为1,∵∠MOA1=30°,∴OM=2A1M在Rt△OMA1中,由勾股定理(2A1M)2=A1M2+13解得A1M∴点M的坐标为(13点M在y= kx上,∴k3∵∠A1OB1 = 30°,又△B n A n A n+1为等边三角形,∴∠B n A n A n+1 = 60°,∴∠OB n A n = ∠B n A n A n+1 -∠B n OA n=30°,∴A n B n = OA n,∴a 1 =1,a 2=1+1=2= 2a 1,a 3= 1+a 1 +a 2=4= 2a 2,a 4 = 1+a 1 +a 2十a 3 =8= 2a 3,a n+1 = 2a n ,a 5 =2a 4= 16, a 6 = 2a 5 = 32,a 7= 2a 6= 64,∵△A 6B 6A 7为等边三角形,∴点B 6的坐标为(a 7-12a 6a 7- 12a 6)), ∴点B6的坐标为(48,故答案为:【点睛】本题考查了一次函数的性质、等边三角形的性质以及三角形外角的性质,勾股定理,解题的关键是找出规律:a n+1=2a n 本题属于灵活题,难度较大,解决该题型题目时,根据等边三角形边的特征找出边的变化规律是关键.16.14:25【分析】在中利用勾股定理计算出,根据折叠的性质得到,,设,则,,在中根据勾股定理计算出,则,利用三角形面积公式计算出,在中利用勾股定理计算出,利用三角形面积公式计算出,然后求出两面积的解析:14:25【分析】在Rt BEC △中利用勾股定理计算出10AB =,根据折叠的性质得到5AD BD ==,EA EB =,设AE x =,则BE x =,8EC x =-,在Rt BEC △中根据勾股定理计算出254x =,则257844EC ,利用三角形面积公式计算出1172162244BCE SBC CE ,在Rt BED △中利用勾股定理计算出222515()544ED ,利用三角形面积公式计算出11157552248BDE S BD DE ∆==⨯⨯=,然后求出两面积的比. 【详解】 解:在Rt BAC 中,6BC =,8AC =,10AB ∴=,把ABC ∆沿DE 使A 与B 重合,AD BD ∴=,EA EB =,152BD AB ∴==, 设AE x =,则BE x =,8EC x =-,在Rt BEC △中,222BE EC BC ,即222(8)6x x =-+, 254x ∴=, 2578844EC x , 1172162244BCE S BC CE , 在Rt BED △中,222BE ED BD ,222515()544ED , 11157552248BDE S BD DE ∆∴==⨯⨯=, 2175::14:2548BCE BDE S S ∆∆∴==. 故答案为:14:25.【点睛】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等,对应角相等.也考查了勾股定理.三、解答题17.(1);(2);(3);(4)【分析】(1)根据立方根以及二次根式的加减运算求解即可;(2)根据二次根式的四则运算求解即可;(3)根据二次根式的除法以及零指数幂的运算求解即可;(4)根据平解析:(1)3-+2)63)6;(4)4-【分析】(1)根据立方根以及二次根式的加减运算求解即可;(2)根据二次根式的四则运算求解即可;(3)根据二次根式的除法以及零指数幂的运算求解即可;(4)根据平方差公式以及二次根式的加减运算,求解即可. 【详解】解:(1)313=-+=-+(2)6==;(30(122116=⨯++=;(4)1)514=---【点睛】此题考查了二次根式的四则运算,涉及了零指数幂、立方根以及平方差公式,解题的关键是熟练掌握二次根式的有关运算.18.(1)直角三角形,理由见解析;(2)原来的路线AC的长为千米.【分析】(1)根据勾股定理的逆定理解答即可;(2)根据勾股定理解答即可.【详解】解:(1)△HBC是直角三角形,理由是:在△解析:(1)直角三角形,理由见解析;(2)原来的路线AC的长为256千米.【分析】(1)根据勾股定理的逆定理解答即可;(2)根据勾股定理解答即可.【详解】解:(1)△HBC是直角三角形,理由是:在△CHB中,∵CH2+BH2=42+32=25,BC2=25,∴CH2+BH2=BC2,∴△HBC是直角三角形且∠CHB=90°;(2)设AC=AB=x千米,则AH=AB-BH=(x-3)千米,在Rt△ACH中,由已知得AC=x,AH=x-3,CH=4,由勾股定理得:AC2=AH2+CH2,∴x2=(x-3)2+42,解这个方程,得x=256,答:原来的路线AC的长为256千米.【点睛】本题考查勾股定理的应用,解决本题的关键是掌握勾股定理的逆定理和定理.19.(1)直角三角形,理由见解析;(2)5【解析】【分析】(1)根据网格及勾股定理分别求出AB2、BC2、AC2的长,得出,再根据勾股定理的逆定理判断出三角形ABC的形状;(2)判断出AB和AC解析:(1)直角三角形,理由见解析;(2)5【解析】【分析】(1)根据网格及勾股定理分别求出AB 2、BC 2、AC 2的长,得出222AB AC BC +=,再根据勾股定理的逆定理判断出三角形ABC 的形状;(2)判断出AB 和AC 分别为底和高,利用公式直接计算出面积.【详解】解:(1)∵222125AB =+=,2222420AC =+=,2223425BC =+=,222AB AC BC ∴+=,ABC ∴为直角三角形;(2)由(1)可知:AB AC ==12ABC SAB AC = 12= 5=;ABC ∴的面积为5.【点睛】本题考查了勾股定理,勾股定理逆定理,三角形的面积,充分利用网格是解题关键. 20.(1)见解析;(2)见解析【分析】(1)根据三角形中位线定理可得,结合已知条件,根据一组对边平行且相等即可证明四边形ADFC 是平行四边形;(2)先证明是平行四边形,进而根据等角对等边可得,由(解析:(1)见解析;(2)见解析【分析】(1)根据三角形中位线定理可得12DE AC =,结合已知条件,根据一组对边平行且相等即可证明四边形ADFC 是平行四边形;(2)先证明CDBF 是平行四边形,进而根据等角对等边可得AC BC =,由(1)可知AC DF =,根据对角线相等的平行四边形是矩形即可得证.【详解】(1)∵D ,E 分别是AB ,BC 的中点,∴DE //AC 且12DE AC =, ∵DE FE =,∴DF //AC 且DF AC =,∴四边形ADFC 为平行四边形.(2)连接BF ,CD ,如图,由(1)知四边形ADFC为平行四边形,=,∴CF//AB且CF ADD是AB的中点,所以AD BD=,∴CF//DB且=CF BD,∴四边形BFCD为平行四边形,∵∠A=∠B,∴AC=BC,由(1)知,DF=AC,∴DF=BC,∴四边形BFCD为矩形.【点睛】本题考查了三角形中位线定理,平行四边形的性质与判定,矩形的判定定理,掌握以上性质与定理是解题的关键.21.(1),;(2)【解析】【分析】(1)化简时,根据范例确定a,b值为3和1,化简时,根据范例确定a,b值为4和5,再根据范例求解.(2)化简时,根据范例确定a,b值为15和4,再根据范例求解析:(131,2+5;(2152【解析】【分析】(1423-时,根据范例确定a,b值为3和19+45a,b值为4和5,再根据范例求解.(219415-a,b值为15和4,再根据范例求解.【详解】解:(1423-m=4,n=3,由于3+1=4,3×1=3即22+=313(3)(1)4=∴11;m=9,n=20,由于4+5=9,4×5=20即229+==∴2=(2m=19,n=60,由于15+4=19,15×4=60即2219+==∴22=【点睛】本题考查了二次根式的化简,根据题中的范例把根号内的式子整理成完全平方的形式是解答此题的关键.22.(1)y=﹣0.2x+48;(2)该列车全部车厢的总费用少于45万元,则至少挂A型车厢16节.【分析】(1)先变换单位,设用A型车厢x节,则用B型车厢(60﹣x)节,总运费为y万元,根据题意列出解析:(1)y=﹣0.2x+48;(2)该列车全部车厢的总费用少于45万元,则至少挂A型车厢16节.【分析】(1)先变换单位,设用A型车厢x节,则用B型车厢(60﹣x)节,总运费为y万元,根据题意列出函数关系式;(2)根据用该列车全部车厢的总费用少于45万元列出不等式求解即可.【详解】解:(1)6000元=0.6万元,8000元=0.8万元,设用A型车厢x节,则用B型车厢(60﹣x)节,总运费为y万元,依题意,得y=0.6x+0.8(60﹣x)=﹣0.2x+48;(2)由题意,得﹣0.2x+48<45,解得:x>15,∵x为正整数,∴x的最小值为16,答:该列车全部车厢的总费用少于45万元,则至少挂A型车厢16节.【点睛】本题考查一次函数的应用,关键是根据题意列出函数关系式.23.(1)(2)(3)2或或4【分析】(1)由勾股定理可求出答案;(2)延长AF,过点D作射线AF的垂线,垂足为H,设AH=DH=x,在Rt△AHD中,得出x2+x2=42,解方程解析:(1)(2)(3)2或或4【分析】(1)由勾股定理可求出答案;(2)延长AF,过点D作射线AF的垂线,垂足为H,设AH=DH=x,在Rt△AHD中,得出x2+x2=42,解方程求出x即可得出答案;(3)分AF=DF,AF=AD,AD=DF三种情况,由正方形的性质及直角三角形的性质可得出答案.【详解】解:(1)当t=1时,AE=1,∵四边形AEFG是正方形,∴AG=FG=AE=1,∠G=90°,∴BF===,(2)如图1,延长AF,过点D作射线AF的垂线,垂足为H,∵四边形AGFE是正方形,∴AE=EF,∠AEF=90°,∴∠EAF=45°,∵DH⊥AH,∴∠AHD=90°,∠ADH=45°=∠EAF,∴AH=DH,设AH=DH=x,∵在Rt△AHD中,∠AHD=90°,∴x2+x2=42,解得x1=﹣2(舍去),x2=2,∴D、F两点之间的最小距离为2;(3)当AF=DF时,由(2)知,点F与点H重合,过H作HK⊥AD于K,如图2,∵AH =DH ,HK ⊥AD ,∴AK ==2, ∴t =2.当AF =AD =4时,设AE =EF =x ,∵在Rt △AEF 中,∠AEF =90°,∴x 2+x 2=42,解得x 1=﹣2(舍去),x 2=2, ∴AE =2, 即t =2.当AD =DF =4时,点E 与D 重合,t =4, 综上所述,t 为2或2或4. 【点睛】本题是四边形综合题,考查了勾股定理,正方形的性质,等腰三角形的性质等知识,解题的关键是熟练掌握正方形的性质,学会用分类讨论的思想思考问题.24.(1),;(2)存在,;(3)或【解析】【分析】(1)根据一次函数平移的方法求出直线l 对应的函数表达式,再联立两个直线解析式求出交点坐标;(2)作轴于M ,轴于N ,利用,得到F 点的横坐标,再代解析:(1)23y x =-,()4,5;(2)存在,()4,11F -;(3)()4,0P 或()4,0-【解析】【分析】(1)根据一次函数平移的方法求出直线l 对应的函数表达式,再联立两个直线解析式求出交点坐标;(2)作EM y ⊥轴于M ,FN y ⊥轴于N ,利用()EBM FBN AAS ≌,得到F 点的横坐标,再代入解析式求出F 点纵坐标即可;(3)在y 轴正半轴上取一点Q ,使3OQ OD ==,利用等腰三角形的性质得PBO BPQ ∠=∠,即可求出5PQ BQ ==,再由勾股定理求出OP 的长,得到点P 坐标.【详解】解:(1)正比例函数2y x =的图像沿y 轴向下平移3个单位长度,得23y x =-, 联立两个直线解析式,得38423y x y x ⎧=-+⎪⎨⎪=-⎩,解得45x y =⎧⎨=⎩, ∴()4,5E ,故答案是:23y x =-,()4,5;(2)如图,作EM y ⊥轴于M ,FN y ⊥轴于N ,∴4EM =,90EMB FNB ∠=∠=︒,∵BE BF =,EBM FBN ∠=∠,∴()EBM FBN AAS ≌,∴4FN EM ==,在384y x =-+中,当4x =-时,11y =, ∴()4,11F -;(3)易知()0,8B ,()0,3D -,∴8OB =,3OD =,如图,在y 轴正半轴上取一点Q ,使3OQ OD ==,∵90POB ∠=︒,OQ OD =,∴PQ PD =,∴PDO PQO PBO BPQ ∠=∠=∠+∠,∵2PDO PBO ∠=∠,∴PBO BPQ ∠=∠,∴5PQ BQ ==,∴由勾股定理得:4OP =,∴()4,0P 或()4,0-.【点睛】本题考查一次函数综合,解题的关键是掌握一次函数解析式的求法,以及利用数形结合思想解决一次函数与几何综合问题.25.(1)点的坐标为;(2);(3),,,【分析】(1)过点作,由“”可证,可得,,即可求点坐标;(2)由(1)可知,设OP=x ,则可得M 点坐标为(4+x ,x ),由直线OB 解析式可得N (x ,解析:(1)点M 的坐标为(51),;(2)()44y x =-()04x <<;(3)()224160Q x x ++-,, ()234160Q x x +--, ,()24160Q x x +-,, ()25160(224)Q x x x --<<,【分析】(1)过点M 作ME OA ⊥,由“AAS ”可证COP PEM ∆≅∆,可得4CO PE ==,1OP ME ==,即可求点M 坐标;(2)由(1)可知COP PEM ∆≅∆,设OP=x ,则可得M 点坐标为(4+x ,x ),由直线OB 解析式可得N (x ,x ),即可知MN=4,由一组对边平行而且相等的四边形是平行四边形即可证明四边形BCNM 是平行四边形,进而可求y 与x 的函数关系式;(3)首先画出符合要求的点Q 的图形,共分三种情况,第一种情况:当MN 为底边时,第二种情况:当M 为顶点MN 为腰时,第三种情况:当N 为顶点MN 为腰时,然后根据图形特征结合勾股定理求出各种情况点的坐标即可解答.【详解】解:(1)如图,过点M 作ME OA ⊥,CP PM ⊥90CPO MPE ∴∠+∠=︒,且90CPO PCO ∠+∠=︒PCO MPE ∴∠=∠,且CP PM =,90COP PEM ∠=∠=︒()COP PEM AAS ∴∆≅∆4CO PE ∴==,1OP ME ==5OE ∴=∴点M 坐标为(5,1)故答案为(5,1)(2)由(1)可知COP PEM ∆≅∆4CO PE ∴==,OP ME x ==∴点M 坐标为(4,)x x +四边形OABC 是边长为4的正方形,∴点(4,4)B∴直线BO 的解析式为:y x =//MN AO ,交BO 于点N ,∴点N 坐标为(,)x x4MN BC ∴==,且//BC MN∴四边形BCNM 是平行四边形4(4)y x ∴=- (04)x <<(3)在x 轴正半轴上存在点Q ,使得QMN ∆是等腰三角形,此时点Q 的坐标为:1(2,0)Q x +,22(416Q x x +--,0),23(416Q x x ++-,240)(16Q x x +-,250)(16Q x x --,0)其中(04)x <<,理由:当(2)可知,(04)OP x x =<<,4MN PE ==,//MN x 轴,所以共分为以下几种请:第一种情况:当MN 为底边时,作MN 的垂直平分线,与x 轴的交点为1Q ,如图2所示111222PQ PE MN ===, 12OQ x ∴=+,1(2,0)Q x ∴+第二种情况:如图3所示,当M 为顶点MN 为腰时,以M 为圆心,MN 的长为半径画弧交x 轴于点2Q 、3Q ,连接2MQ 、3MQ ,则234MQ MQ ==, 2222Q E MQ ME ∴=-, 222416OQ OE Q E x x ∴=-=+--,22(416Q x x ∴+--,0),32Q E Q E =,233416OQ OE Q E x x =+=++-,23(416Q x x ∴++-,0);第三种情况,当以N 为顶点、MN 为腰时,以N 为圆心,MN 长为半径画圆弧交x 轴正半轴于点4Q ,当022x <<时,如图4所示,则2224416PQ NQ NP x --24416OQ OP PQ x x ∴=+=-即24(16Q x x -0).当2x =则4ON =,此时Q 点与O 点重合,舍去;当224x <时,如图5,以N 为圆心,MN 为半径画弧,与x 轴的交点为4Q ,5Q .4Q 的坐标为:24(16Q x x -0).2516OQ x x =- 25(16Q x x ∴-0)所以,综上所述,1(2,0)Q x +,22(416Q x x +-0),23(416Q x x +-,240)(16Q x x -250)(16Q x x -0)使QMN ∆是等腰三角形.【点睛】本题考查四边形综合题,解题的关键是明确题意,画出相应的图象,找出所求问题需要的条件,利用数形结合的思想解答问题.26.(1)见解析;(2)6+3;(3)见解析【分析】(1)证明△BEC ≌△AFC (SAS ),可得结论.(2)△AEF 的周长=AE+AF+EF =AE+BE+EF =AB+EF =6+EF ,推出EF 的值最 解析:(1)见解析;(2)33)见解析【分析】(1)证明△BEC ≌△AFC (SAS ),可得结论.(2)△AEF 的周长=AE +AF +EF =AE +BE +EF =AB +EF =6+EF ,推出EF 的值最小时,△AEF 的周长最小,因为△ECF 是等边三角形,推出EF =CE ,推出当CE ⊥AB 时,CE 的值最小. (3)求出BD =3BM =DN =3BM =MN =DN =3【详解】(1)证明:∵△ABC ,△ACD 是全等的等边三角形,∴AC =BC ,∠ABC =∠DAC =∠BCA =60°,∵AF =BE ,在△CBE 和△CAF 中,CB CA CBE CAF BE AF =⎧⎪∠=∠⎨⎪=⎩, ∴△BEC ≌△AFC (SAS ),∴CE =CF ,∠BCE =∠ACF ,∴∠BCE +∠ACE =∠ACF +∠ACE ,∴∠ECF =∠BCA =60°,∴△CEF 是等边三角形.(2)解:∵△AEF 的周长=AE +AF +EF =AE +BE +EF =AB +EF =6+EF ,∴EF 的值最小时,△AEF 的周长最小,∵△ECF 是等边三角形,∴EF =CE ,∴当CE ⊥AB 时,CE 的值最小,∵三角形ABC 是等边三角形,∴∠ABC =60°,∴∠BCE =30°,∴BE =132BC =, ∴CE=∴△AEF 的周长的最小值为故答案为:(3)证明:∵△ABC ,△ACD 是全等的等边三角形,AC ⊥BD∴AO =CO ,BO =DO ,∠ABO =12∠ABC =30°∵BE =3,AB =AC =6,∴点E 为AB 中点,点F 为AD 中点,∴AO =12AB =3,∴BO=∴BD =∵△ABC 是等边三角形,BE =AE =3,∴CE ⊥AB ,∴BM =2EM , ∴222132BM BM ⎛⎫+= ⎪⎝⎭ ∴BM =同理可得DN =∴MN =BD ﹣BM ﹣DN =∴BM =MN =DN .【点睛】此题考查了三角形全等,勾股定理,线段最值问题,解题的关键是根据题意找到题目中边角之间的关系.。
人教版数学八年级下册数学期末试卷(培优篇)(Word版含解析)

人教版数学八年级下册数学期末试卷(培优篇)(Word 版含解析) 一、选择题1.要使12021x-有意义,x 的取值范围是( ).A .2021x ≥B .2021x ≤C .2021x >D .2021x < 2.由线段a ,b ,c 组成的三角形不能..构成直角三角形的是( ) A .0.6,0.8,1B .4,5,6C .5,12,13D .20,21,293.小红同学周末在家做家务,不慎把家里的一块平行四边形玻璃打碎成如图所示的四块,为了能从玻璃店配到一块与原来相同的玻璃,他应该带其中( )两块去玻璃店.A .①②B .②④C .②③D .①③4.某次数学趣味竞赛共有10组题目,某班得分情况如下表.全班40名学生成绩的众数是( )人数 2 5 13107 3成绩(分)5060 70 8090 100A .75B .70C .80D .90 5.ABC ∆的周长为60,三条边之比为13:12:5,则这个三角形的面积为( )A .30B .90C .60D .1206.如图是两个全等的三角形纸片,其三边长之比为3: 4: 5,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为,A B S S ,已知15A B S S -=,则纸片的面积是( )A .102B .104C .106D .1087.如图,在直角三角形ABC 中,∠C=90°,AB=10,AC=8,点E ,F 分别为AC 和AB 的中点,则EF= ( )A .3B .4C .5D .68.如图,若正比例函数y =kx 图象与四条直线x =1,x =2,y =1,y =2相交围成的正方形有公共点,则k 的取值范围是( )A .k ≤2B .k ≥12C .0<k <12D .12≤k ≤2二、填空题9.若式子11x x +-有意义,则x 的取值范围是______________. 10.如图,菱形ABCD 的对角线AC 、BD 相交于点O ,点M 、N 分别为边AB 、BC 的中点,连接MN ,若1MN =,23BD =,则菱形的面积为______.11.如图,在Rt △ABC 中,∠C =90°,AD 平分∠CAB ,BC =12cm ,AC =9cm ,那么BD 的长是_____.12.如图,在矩形ABCD 中,对角线AC 、BD 交于点O ,已知5OD =,6AD =,则该矩形的周长是______.13.已知一次函数的图象经过(2,0),(0,4)-两点,则该一次函数解析式是______. 14.在矩形ABCD 中,3AB =,ABC ∠的平分线BE 交AD 所在的直线于点E ,若2DE =,则AD 的长为__________.15.如图,将一块等腰直角三角板ABC 放置在平面直角坐标系中,90,ACB AC BC ∠=︒=,点A 在y 轴的正半轴上,点C 在x 轴的负半轴上,点B 在第二象限,AC 所在直线的函数表达式是22y x =+,若保持AC 的长不变,当点A 在y 轴的正半轴滑动,点C 随之在x 轴的负半轴上滑动,则在滑动过程中,点B 与原点O 的最大距离是_______.16.如图,折叠矩形纸片ABCD ,先折出折痕(对角线)BD ,再折叠使AD 边与BD 重合,得折痕DG .(1)若AG =1,∠ABD =30°,求AD 的长; (2)若AB =4,BC =3,求AG 的长.三、解答题17.(1)计算:112273⎛⎫-⨯ ⎪ ⎪⎝⎭; (2)计算:()()351518+---.18.一个25米长的梯子AB ,斜靠在一竖直的墙AO 上,这时的AO 距离为24米,如果梯子的顶端A 沿墙下滑4米,那么梯子底端B 外移多少米?19.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图形.(1)在图1中,画一个等腰三角形(不含直角),使它的面积为8; (2)在图2中,画一个直角三角形,使它的三边长都是有理数; (3)在图3中,画一个正方形,使它的面积为10.20.已知:如图,在四边形ABCD 中,AB 与CD 不平行,E ,F ,G ,H 分别是AD ,BC ,BD ,AC 的中点.(1)求证:四边形EGFH 是平行四边形;(2)当AB CD ,四边形EGFH 是怎样的四边形?证明你的结论. 21.先观察下列等式,再回答问题: 2211+2+()1 =1+1=2;2212+2+()212=2 12;2213+2+()3=3+13=313;…(1)根据上面三个等式提供的信息,请猜想第四个等式;(2)请按照上面各等式规律,试写出用 n (n 为正整数)表示的等式,并用所学知识证明.22.暑期将至,某游泳馆面向学生推出暑期优惠活动,活动方案如下. 方案一:购买一张学生暑期专享卡,每次游泳费用按六折优惠; 方案二:不购买学生暑期专享卡,每次游泳费用按八折优惠.设某学生暑期游泳x (次),按照方案一所需费用为y 1(元),且y 1=k 1x +b ;按照方案二所需费用为y 2(元),且y 2=k 2x .其函数图象如图所示. (1)求k 1和b 的值;(2)八年级学生小华计划暑期前往该游泳馆游泳8次,应选择哪种方案所需费用更少?请说明理由.23.如图①,C为线段BD上的一点,BC≠CD,分别以BC,BD为边在BD的上方作等边△ABC和等边△CDE,连接AE,F,G,H分别是BC,AE,CD的中点,连接FG,GH,FH.(1)△FGH的形状是;(2)将图①中的△CDE绕点C顺时针旋转,其他条件不变,(1)的结论是否成立?结合图②说明理由;(3)若BC=,CD=4,将△CDE绕点C旋转一周,当A,E,D三点共线时,直接写出△FGH的周长.24.如图所示,在平面直角坐标系中,点B的坐标为(4,8),过点B分别作BA⊥y轴,BC⊥x轴,得到一个长方形OABC,D为y轴上的一点,将长方形OABC沿着直线DM折叠,使得点A与点C重合,点B落在点F处,直线DM交BC于点E.(1)直接写出点D的坐标;(2)若点P 为x 轴上一点,是否存在点P 使△PDE 的周长最小?若存在,请求出△PDE 的最小周长;若不存在,请说明理由.(3)在(2)的条件下,若Q 点是线段DE 上一点(不含端点),连接PQ .有一动点H 从P 点出发,沿线段PQ 以每秒1个单位的速度运动到点Q ,再沿着线段QE 以每秒5个单位长度的速度运动到点E 后停止.请直接写出点H 在整个运动过程中所用的最少时间t ,以及此时点Q 的坐标.25.如图,在平面直角坐标系中,点A (1,4),点B (3,2),连接OA ,OB .(1)求直线OB 与AB 的解析式; (2)求△AOB 的面积.(3)下面两道小题,任选一道作答.作答时,请注明题号,若多做,则按首做题计入总分.①在y 轴上是否存在一点P ,使△PAB 周长最小.若存在,请直接写出....点P 坐标;若不存在,请说明理由.②在平面内是否存在一点C ,使以A ,O ,C ,B 为顶点的四边形是平行四边形.若存在,请直接写出....点C 坐标;若不存在,请说明理由. 26.如图所示,四边形ABCD 是正方形, M 是AB 延长线上一点.直角三角尺的一条直角边经过点D ,且直角顶点E 在AB 边上滑动(点E 不与点AB 、重合),另一直角边与CBM ∠的平分线BF 相交于点F . (1)求证: ADE FEM ∠=∠;(2)如图(1),当点E 在AB 边的中点位置时,猜想DE 与EF 的数量关系,并证明你的猜想; (3)如图(2),当点E 在AB 边(除两端点)上的任意位置时,猜想此时DE 与EF 有怎样的数量关系,并证明你的猜想.【参考答案】一、选择题 1.D 解析:D【分析】根据二次根式有意义的条件:被开方数要大于等于0和分式有意义的条件:分母不能为0,进行求解即可得到答案. 【详解】 解:∵有意义,∴00≥≠,∴2021x <, 故选D . 【点睛】本题主要考查了二次根式和分式有意义的条件,解题的关键在于能够熟练掌握相关知识进行求解.2.B解析:B 【分析】利用勾股定理的逆定理进行逐一判断即可. 【详解】解:A 、∵2220.60.81+=,∴能构成直角三角形,不符合题意; B 、∵222456+≠,∴不能构成直角三角形,符合题意; C 、∵22251213+=,∴能构成直角三角形,不符合题意; D 、∵222202129+=,∴能构成直角三角形,不符合题意; 故选B . 【点睛】本题主要考查了勾股定理的逆定理,解题的关键在于能够熟练掌握:如果三角形的三边a 、b 、c 的三边满足222+=a b c ,那么这个三角形是直角三角形.3.B解析:B 【解析】 【分析】为了能从玻璃店配到一块与原来相同的玻璃,必须能够确定平行四边形的大小和形状,根据平行四边形的判定即可判断. 【详解】A 、①②只能确定平行四边形的形状,还能确定一组对边的大小,但另一组对边的大小无法确定,故不合题意;B 、②④两块两个角的两边互相平行,且中间部分相连,角的两边延长线的交点就是平行四边形的顶点,所以能确定平行四边形的四个顶点,因而能确定其大小和形状,故符合题意;C 、②③只能确定平行四边形的形状,还能确定一组对边的大小,但另一组对边的大小无法确定,故不合题意;D 、①③只能确定平行四边形的形状,无法确定两组对边的大小,故不合题意; 故选:B . 【点睛】本题考查了平行四边形的判定,关键是理解确定一个平行四边形,既要考虑形状,又要考虑大小,两者同时确定了才可确定一个平行四边形.4.B解析:B 【解析】 【分析】根据众数的定义进行解答即可. 【详解】解:70出现了13次,出现的次数最多,则众数是70; 故选:B . 【点睛】此题考查了众数,掌握众数的定义:众数是一组数据中出现次数最多的数是解题的关键.5.D解析:D 【分析】根据已知条件可求得三边的长,再判断这个三角形是直角三角形,即可求得面积. 【详解】∵三条边之比为13:12:5, ∴122+52=132, ∴△ABC 是直角三角形, ∵△ABC 的周长为60, ∴三边长分别是:26,24,10, ∴这个三角形的面积是:24×10÷2=120, 故选D . 【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.6.D解析:D 【解析】 【分析】设3AC FH x ==,则4BC GH x ==,5AB GF x ==,根据勾股定理即可求得CD 的长,利用x 表示出A S ,同理表示出B S ,根据15A B S S -=,即可求得x 的值,进而求得三角形的面积. 【详解】解:设3AC FH x ==,则4BC GH x ==,5AB GF x ==.设CD y =,则4BD x y =-,DE CD y ==, 在直角BDE ∆中,532BE x x x =-=, 根据勾股定理可得:2224(4)x y x y +=-, 解得:32y x =, 则2113322222A S BE DE x x x ==⨯=, 同理可得:223B S x =,15A B S S -=,∴22321523x x -=, 解得:32x =,∴纸片的面积是:213461082x x x ⨯==,故选:D ..【点睛】本题主要考查了翻折变换(折叠问题),三角形面积的计算,根据勾股定理求得CD 的长是解题的关键.7.A解析:A 【解析】 【详解】∵直角三角形ABC 中,∠C =90°,AB =10,AC =8, ∴221086BC =-=.∵点E 、F 分别为AC 、AB 的中点, ∴EF 是△ABC 的中位线, ∴116322EF BC ==⨯=. 故选A .8.D解析:D 【分析】如图,可知当直线y kx =在过点A 和点C 两点之间的时候满足条件,把A 、B 两点分别代入可求得k 的最小值和最大值,可求得答案. 【详解】解:直线y kx =与正方形ABCD 有公共点,∴直线y kx =在过点A 和点C 两直线之间之间,如图,可知(2,1)A ,(1,2)C ,当直线y kx =过A 点时,代入可得12k =,解得12k =, 当直线y kx =过C 点时,代入可得2k =,解得2k =,k ∴的取值范围为:122k , 故选D . 【点睛】本题主要考查一次函数图象点的坐标,由条件得出直线在过A 和C 两点间的直线是解题的关键,注意数形结合思想的应用.二、填空题9.0x ≥且1x ≠ 【解析】 【分析】根据分式有意义可得10x -≠,根据二次根式有意义的条件可得0x ≥,再解即可. 【详解】由题意得:10x -≠,且0x ≥, 解得:0x ≥且1x ≠, 故答案为:0x ≥且1x ≠. 【点睛】本题主要考查了分式有意义和二次根式有意义的条件,关键是掌握分式有意义的条件是分母不等于零,二次根式中的被开方数是非负数.10.A 解析:23【解析】 【分析】根据MN 是△ABC 的中位线,根据三角形中位线定理求的AC 的长,然后根据菱形的性质求解. 【详解】解:∵M、N是AB和BC的中点,即MN是△ABC的中位线,∴AC=2MN=2,∵23BD=,所以菱形的面积为1122323 22BD AC=⨯⨯=,故答案为:23【点睛】本题考查了三角形的中位线定理和菱形的性质,理解中位线定理求的AC的长是关键.11.D解析:152cm【解析】【分析】作DE⊥AB于E,根据勾股定理求出AB,证明△ACD≌△AED,根据全等三角形的性质得到CD=ED,AE=AC=9,根据角平分线的性质、勾股定理列式计算即可.【详解】解:作DE⊥AB于E,由勾股定理得,AB22A BC C+22912+15,在△ACD和△AED中,CAD EADACD AED90 AD AD ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩,∴△ACD≌△AED(AAS)∴CD=ED,AE=AC=9,∴BE=AB﹣AE=6,在Rt△BED中,BD2=DE2+BE2,即BD2=(12﹣BD)2+62,解得,BD=152,故答案为:152cm.【点睛】此题考查的是勾股定理和全等三角形的判定及性质,掌握利用勾股定理解直角三角形和全等三角形的判定及性质是解决此题的关键.12.B解析:28【分析】先求出BD ,再根据勾股定理求出AB ,即可求矩形的周长.【详解】解:∵四边形ABCD 是矩形,∴∠BAD=90°,OD =OB =5,即BD =10, ∴22221068AB BD AD =-=-=,矩形的周长为()28628⨯+=,故答案为:28.【点睛】本题考查了矩形的性质和勾股定理,解题关键是熟练运用勾股定理求出矩形的边长. 13.y =2x -4【分析】由一次函数的图象经过(2,0),(0,-4)两点,可设一次函数解析式为y =kx +b(k ≠0).然后将点的坐标代入解析式,故得2k +b =0,b =-4.进而推导出函数解析式为y =2x -4.【详解】解:设该一次函数的解析式为:y =kx +b (k ≠0).由题意得:2004k b k b +=⎧⎨⋅+=-⎩, 解得:24k b =⎧⎨=-⎩, ∴该一次函数的解析式为y =2x -4.故答案为:y =2x -4.【点睛】本题主要考查用待定系数法求一次函数解析式,熟练掌握用待定系数法求一次函数解析式是解决本题的关键.14.5或1【分析】当点E 在AD 上时,根据平行线的性质和角平分线的定义可得3AE AB ==,可得AD 的长;当点E 在AD 的延长线上时,同理可求出AD 的长.【详解】解:如图1,当点E 在AD 上时,四边形ABCD是矩形,∴∠=︒,//A90AD BC,∴∠=∠,AEB CBE∠,BE平分ABC∴∠=∠,ABE CBE∴∠=∠,ABE AEB3∴==,AE ABDE=,2∴=+=+=;325AD AE DEAE=,如图2,当点E在AD的延长线上时,同理3∴=-=-=.321AD AE DE故答案为:5或1.【点睛】本题主要考查了矩形的性质,等腰直角三角形的性质等知识,解题的关键是正确画出两种图形.15.【分析】根据自变量与函数值得对应关系,可得A,C点坐标,根据勾股定理,可得AC 的长度;根据全等三角形的判定与性质,可得CD,BD的长,可得B点坐标;首先取AC的中点E,连接BE,OE,OB,可求+55【分析】根据自变量与函数值得对应关系,可得A,C点坐标,根据勾股定理,可得AC的长度;根据全等三角形的判定与性质,可得CD,BD的长,可得B点坐标;首先取AC的中点E,连接BE,OE,OB,可求得OE与BE的长,然后由三角形三边关系,求得点B到原点的最大距离.【详解】解:当x=0时,y=2x+2=2,∴A(0,2);当y=2x+2=0时,x=-1,∴C(-1,0).∴OA=2,OC=1,∴AC =22OA OC +=5,如图所示,过点B 作BD ⊥x 轴于点D .∵∠ACO +∠ACB +∠BCD =180°,∠ACO +∠CAO =90°,∠ACB =90°,∴∠CAO =∠BC D .在△AOC 和△CDB 中,AOC CDB CAO BCD AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AOC ≌△CDB (AAS ),∴CD =AO =2,DB =OC =1,OD =OC +CD =3,∴点B 的坐标为(-3,1).如图所示.取AC 的中点E ,连接BE ,OE ,OB ,∵∠AOC =90°,AC =5,∴OE =CE =12AC =52, ∵BC ⊥AC ,BC =5,∴BE =22BC CE +=52, 若点O ,E ,B 不在一条直线上,则OB <OE +BE =5522, 若点O ,E ,B 在一条直线上,则OB =OE +BE =5522, ∴当O ,E ,B 三点在一条直线上时,OB 取得最大值,最大值为552+, 故答案为:552+.【点睛】此题考查了一次函数综合题,利用自变量与函数值的对应关系是求AC 长度的关键,又利用了勾股定理;求点B 的坐标的关键是利用全等三角形的判定与性质得出CD ,BD 的长;求点B 与原点O 的最大距离的关键是直角三角形斜边上的中线的性质以及三角形三边关系.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.16.(1);(2)【分析】(1)由折叠的性质可以得到∠ADG=∠BDG=30°,再根据含30°直角三角形的性质即可求得AD的长;(2)过点G作GE⊥BD交BD于E,由折叠的性质可以得到AG=GE,解析:(1)AD=2)32 AG=【分析】(1)由折叠的性质可以得到∠ADG=∠BDG=30°,再根据含30°直角三角形的性质即可求得AD的长;(2)过点G作GE⊥BD交BD于E,由折叠的性质可以得到AG=GE,AD=DE,从而得到BE 的长,在三角形BGE中运用勾股定理求解即可得到答案.【详解】解:(1)由折叠的性质可知∠ADG=∠BDG∵四边形ABCD是矩形,∠ABD=30°∴∠A=90°∴∠ADB=60°∴∠ADG=∠BDG=30°∴DG=2AG=2AD(2)如图所示,过点G作GE⊥BD交BD于E由折叠的性质可知∠ADG=∠BDG∵∠DAG=90°,∠DEG=90°∴△DAG≌△DEG∴AD=DE,AG=GE∵BC=3,AB=4∴AD=BC=DE=3∴5BD==∴BE=BD-DE=2,BG=AB-AG=AB-GE=4-GE设AG=GE=x,则BG=4-x∵222GE BE BG+=∴()22224x x+=-解得32 x=∴AG的长为32.【点睛】本题主要考查了折叠的性质,矩形的性质,全等三角形的性质与判定,勾股定理和含30°的直角三角形的性质,解题的关键在于能够熟练掌握相关知识进行求解计算.三、解答题17.(1)15;(2)6【分析】(1)先化简为最简二次根式,先计算括号里的,再计算二次根式乘法即可, (2)先利用平方差公式简算,和立方根,然后再算加减法即可.【详解】解:(1),,,;解析:(1)15;(2)6【分析】(1)先化简为最简二次根式,先计算括号里的,再计算二次根式乘法即可,(2)先利用平方差公式简算,和立方根,然后再算加减法即可.【详解】解:(1)112273 3333⎛=⨯ ⎝⎭5333= 15=; (2))351518- =()22512---, 512=-+,=6.【点睛】本题考查二次根式混合运算,最简二次根式,平方差公式,同类二次根式,掌握二次根式混合运算法则,最简二次根式,平方差公式巧用,同类二次根式及合并法则是解题关键. 18.8米.【分析】梯子下滑4米,梯子的长度不变始终为25米,利用勾股定理分别求出OB 、OB '的长度,进而求出BB '的长度即可.【详解】解:如图,依题意可知AB =25(米),AO =24(米),∠解析:8米.【分析】梯子下滑4米,梯子的长度不变始终为25米,利用勾股定理分别求出OB 、OB '的长度,进而求出BB '的长度即可.【详解】解:如图,依题意可知AB =25(米),AO =24(米),∠O =90°,∴ BO 2=AB 2﹣AO 2=252-242,∴ BO =7(米),移动后,A O '=20(米),222222()25205(1)B O A B A O ''''--===∴ 15B O '= (米),∴ =1578BB B O BO ''-=-=(米).答:梯子底端B 外移8米.【点睛】本题考查的是勾股定理的应用及勾股定理在直角三角形中的正确运用,本题中求B O '的长度是解题的关键.19.(1)作图见详解;(2)作图见详解;(3)作图见详解.【解析】【分析】(1)根据题意找出三角形底为4,高为4的三角形即可;(2)根据题意可画出直角边分别为3,4的直角三角形,斜边通过勾股定理 解析:(1)作图见详解;(2)作图见详解;(3)作图见详解.【解析】【分析】(1)根据题意找出三角形底为4,高为4的三角形即可;(2)根据题意可画出直角边分别为3,4的直角三角形,斜边通过勾股定理计算为5,符合题意;(3的正方形.【详解】(1)如图所示,三角形底为4,高为4,面积为8,符合题意,即为所求;(2)如图所示,三角形为所求,直角边分别为3,4,根据勾股定理,斜边为5,符合题意;(3)如图所示,正方形为所求,正方形变长为223110+=,面积为:101010⨯=,符合题意.【点睛】此题主要考查网格与图形,解题的关键是熟练运用勾股定理.20.(1)见解析;(2)菱形,见解析【分析】(1)根据三角形中位线定理得到EG=AB,EG∥AB,FH=AB,FH∥AB,根据平行四边形的判定定理证明结论;(2)依据四边形ABCD是平行四边形,再解析:(1)见解析;(2)菱形,见解析【分析】(1)根据三角形中位线定理得到EG=12AB,EG∥AB,FH=12AB,FH∥AB,根据平行四边形的判定定理证明结论;(2)依据四边形ABCD是平行四边形,再运用三角形中位线定理证明邻边相等,从而证明它是菱形.【详解】(1)证明:∵E,G分别是AD,BD的中点,∴EG是△DAB的中位线,∴EG=12AB,EG∥AB,同理,FH =12AB ,FH ∥AB ,∴EG =FH ,EG ∥FH ,∴四边形EGFH 是平行四边形;(2)菱形.理由:∵F ,G 分别是BC ,BD 的中点,∴FG 是△DCB 的中位线,∴FG =12CD ,FG ∥CD ,又∵EG =12AB ,∴当AB =CD 时,EG =FG ,∴平行四边形EGFH 是菱形.【点睛】本题考查的是中点四边形,掌握三角形中位线定理、矩形、菱形的判定定理是解题的关键.解题时要注意三角形的中位线平行于第三边,并且等于第三边的一半. 21.(1);(2),证明见解析.【解析】【分析】(1)根据“第一个等式内数字为1,第二个等式内数字为2,第三个等式内数字为3”,即可猜想出第四个等式为44;(2)根据等式的变化,找出变化规律“n解析:(1144+=144;(2211n n n n ++=,证明见解析.【解析】【分析】(1)根据“第一个等式内数字为1,第二个等式内数字为2,第三个等式内数字为3”,即=414+=414;(2)根据等式的变化,找出变化规律=n 211n n n ++=”,再利用222112n n n n++=+()()开方即可证出结论成立. 【详解】(1)∵1+1=2;=212+=212;=313+=313;里面的数字分别为1、2、3,∴ 144+= 144.(21+1=2,212+=212313+=313=414+=414,…,∴= 211n n n n ++=.证明:等式左边==n 211n n n++==右边.=n 211n n n ++=成立. 【点睛】本题考查了二次根式的性质与化简以及规律型中数的变化类,解题的关键是:(1)猜测出第四个等式中变化的数字为4;(2)找出变化规律n 211n n n ++=”.解决该题型题目时,根据数值的变化找出变化规律是关键.22.(1)y1=15x+30;(2)选择方案一所需费用更少,理由见解析【分析】(1)利用待定系数法求解即可;(2)求出y2与x 之间的函数关系式,将x=8分别代入y1、y2关于x 的函数解析式,比较即解析:(1)y 1=15x +30;(2)选择方案一所需费用更少,理由见解析【分析】(1)利用待定系数法求解即可;(2)求出y 2与x 之间的函数关系式,将x =8分别代入y 1、y 2关于x 的函数解析式,比较即可.【详解】解:(1)根据题意,得:138430k b b +=⎧⎨=⎩,解得:11830k b =⎧⎨=⎩, ∴方案一所需费用y 1与x 之间的函数关系式为y 1=18x +30,∴k 1=18,b =30;(2)∵打折前的每次游泳费用为18÷0.6=30(元),∴k 2=30×0.8=24;∴y 2=24x ,当游泳8次时,选择方案一所需费用:y 1=18×8+30=174(元),选择方案二所需费用:y 2=24×8=192(元),∵174<192,∴选择方案一所需费用更少.【点睛】本题考查了一次函数的应用,解题的关键是理解两种优惠活动方案,求出y1、y2关于x的函数解析式.23.(1)等边三角形;(2)成立,理由见解析;(3)或.【分析】(1)根据题意先判断出四边形ABCE和四边形ACDE都是梯形.得出FG为梯形ABCE的中位线,GH为梯形ACDE的中位线.从而得出,.解析:(1)等边三角形;(2)成立,理由见解析;(3)或.【分析】(1)根据题意先判断出四边形ABCE和四边形ACDE都是梯形.得出FG为梯形ABCE的中位线,GH为梯形ACDE的中位线.从而得出,.即证明为等边三角形.(2)先判断出PF,PG是△ABC和△CDE的中位线,再判断出∠FPG=∠FCH,进而证明△FPG≌△FCH,得出结论FG=FH,∠PFG=∠CFH,最后证明出∠GFH=,即证明△FGH 为等边三角形.(3)①当点E在AE上时,先求出CM,进而求出AM,即可求出AD,再判断出,进而求出BE=AD=2,,即可判断出,再求出BN、EN,进而求出BD,最后即可求出FH,即可得出结果;②当点D在AE的延长线上时同①的方法即可得出结果.【详解】(1)∵ABC和都为等边三角形,且边长不相等.∴,.∴四边形ABCE和四边形ACDE都是梯形.又∵F、G、H分别是BC、AE、CD中点,∴FG为梯形ABCE的中位线,GH为梯形ACDE的中位线.∴,.∴,.∴为等边三角形.故答案为:等边三角形.(2)取AC的中点P,连接PF,PG,∵△ABC和△CDE都是等边三角形,∴AB=BC,CE=CD,∠BAC=∠ACB=∠ECD=∠B=60°.又F,G,H分别是BC,AE,CD的中点,∴FP=12AB,FC=12BC,CH=12CD,PG=12CE,PG∥CE,PF∥AB.∴FP=FC,PG=CH,∠GPC+∠PCE=180°,∠FPC=∠BAC=60°,∠PFC=∠B=60°.∴∠FPG=∠FPC+∠GPC=60°+∠GPC,∠GPC=180°-∠PCE.∴∠FCH=360°-∠ACB-∠ECD-∠PCE=360°-60°-60°-(180°-∠GPC)=60°+∠GPC.∴∠FPG=∠FCH.∴△FPG≌△FCH(SAS).∴FG=FH,∠PFG=∠CFH.∴∠GFH=∠GFC+∠CFH=∠GFC+∠PFG=∠PFC=60°.∴△FGH为等边三角形.所以成立.(3)①当点D在AE上时,如图,∵ABC是等边三角形,∴,.∵是等边三角形,∴,,过点C作于M,∴,在中,根据勾股定理得,,在中,根据勾股定理得,, ∴,∵,∴,∴,连接BE,在和中,,∴(SAS),∴BE=AD=2, ,∵,∴,∴,过点B作于N,∴,在中,,∴,∴,DN=DE-EN=3,连接BD,根据勾股定理得:,∵点H是CD中点,点F是BC中点,∴FH是的中位线,∴,由(2)可知,△FGH为等边三角形.∴△FGH的周长.②当点D在AE的延长线上时,如图,同理可求,所以△FGH的周长.即满足条件的△FGH的周长位或.【点睛】本题考查等边三角形的判定和性质,全等三角形的判定和性质,勾股定理,含30角的直角三角形的性质,三角形的中位线定理.属于几何变换综合题,综合性强,较难.24.(1)D(0,3);(2)存在,6;(3)5秒,Q(,)【解析】【分析】(1)设D(0,m),且m>0,运用矩形性质和折叠性质可得:OD=m,OA=8,CD=8﹣m,再利用勾股定理建立方程求解解析:(1)D(0,3);(2)存在,3)5秒,Q(32,154)【解析】【分析】(1)设D(0,m),且m>0,运用矩形性质和折叠性质可得:OD=m,OA=8,CD=8﹣m,再利用勾股定理建立方程求解即可;(2)如图1,作点D关于x轴的对称点D′,连接D′E,交x轴于点P,则点P即为所求,此时△PDE的周长最小,运用勾股定理可得CE=5,BE=3,作EG⊥OA,在Rt△DEG中,可得DE=Rt△D′EG中,可得'D E(3)运用待定系数法求得直线D′E的解析式为y=2x﹣3,进而求得P(32,0),过点E作EG⊥y轴于点G,过点Q、P分别作y轴的平行线,分别交EG于点H、H′,H′P交DE于点Q′,利用待定系数法可得直线DE的解析式为y=12x+3,设Q(t,12t+3),则H(t,5),再运用勾股定理即可求出答案.【详解】解:(1)设D(0,m),且m>0,∴OD=m,∵四边形OABC是矩形,∴OA=BC=8,AB=OC=4,∠AOC=90°,∵将长方形OABC沿着直线DM折叠,使得点A与点C重合,∴CD=AD=OA﹣OD=8﹣m,在Rt△CDO中,OD2+OC2=CD2,∴m2+42=(8﹣m)2,解得:m=3,∴点D的坐标为(0,3);(2)存在.如图1,作点D关于x轴的对称点D′,连接D′E,交x轴于点P,则点P即为所求,此时△PDE的周长最小,在Rt△CEF中,BE=EF=BC﹣CE,EF2+CF2=CE2,BC=8,CF=4,∴CE=5,BE=3,作EG⊥OA,∵OD=AG=BE=3,OA=8,∴DG=2,在Rt△DEG中,EG2+DG2=DE2,EG=4,∴DE=25在Rt△D′EG中,EG2+D′G2=D′E2,EG=4,D′G=8,∴D′E=45∴△PDE周长的最小值为DE+D′E=5(3)由(2)得,E(4,5),D′(0,﹣3),设直线D′E的解析式为y=kx+b,则453k bb+=⎧⎨=-⎩,解得:23kb=⎧⎨=-⎩,∴直线D′E的解析式为y=2x﹣3,令y=0,得2x﹣3=0,解得:x=32,∴P(32,0),过点E作EG⊥y轴于点G,过点Q、P分别作y轴的平行线,分别交EG于点H、H′,H′P 交DE于点Q′,设直线DE 的解析式为y =k ′x +b ′,则345b k b =⎧⎨+='''⎩,解得:123k b ⎧=⎪⎨⎪='⎩', ∴直线DE 的解析式为y =12x +3, 设Q (t ,12t +3),则H (t ,5), ∴QH =5﹣(12t +3)=2﹣12t ,EH =4﹣t ,由勾股定理得:DE 22221(2)(4)2QH EH t t +-+-52﹣12t 5,∴点H 在整个运动过程中所用时间=15PQ PQ +QH , 当P 、Q 、H 在一条直线上时,PQ +QH 最小,即为PH ′=5,点Q 坐标(32,154),故:点H 在整个运动过程中所用最少时间为5秒,此时点Q 的坐标(32,154).【点睛】本题考查了矩形的性质,折叠的性质,勾股定理,一次函数的性质,线段的动点问题,以及最短路径问题,解题的关键是熟练掌握所学的知识,正确的作出辅助线,从而进行分析.25.(1)直线OB 的解析式为,直线AB 的解析式为y= -x+5(2)5;(3)①存在,(0,);②存在,(2,-2)或(4,6)或(-2,2) 【分析】(1)根据题意分别设出两直线的解析式,代入直线上解析:(1)直线OB 的解析式为23y x =,直线AB 的解析式为y = -x +5(2)5;(3)①存在,(0,72);②存在,(2,-2)或(4,6)或(-2,2)【分析】(1)根据题意分别设出两直线的解析式,代入直线上两点坐标即可求出直线OB 与AB 的解析式;(2)延长线段AB 交x 轴于点D ,求出D 的坐标,分别求出AOD S ∆、BOD S ∆由AOB AOD BOD S S S ∆∆∆=-即可求得;(3)①根据两点之间线段最短,A 、B 在y 轴同侧,作出点A 关于y 的对称点A ',连接A 'B 与y 轴的交点即为所求点P ;②使以A ,O ,C ,B 为顶点的四边形是平行四边形,则分三种情况分析,分别以OA 、AB 、OB 为对角线作出平行四边形,利用中点坐标公式代入求解即可. 【详解】解:(1)设直线OB 的解析式为y =mx , ∵点B (3,2),∴2223,,33m m y x === ,∴直线OB 的解析式为23y x =, 设直线AB 的解析式为y =kx +b ,根据题意可得:432k b k b +=⎧⎨+=⎩解之得15k b =-⎧⎨=⎩∴直线AB 的解析式为y = -x +5. 故答案为:直线OB 的解析式为23y x =,直线AB 的解析式为y = -x +5; (2)如图,延长线段AB 交x 轴于点D , 当y =0时,-x +5=0,x =5, ∴点D 横坐标为5,OD =5,∴11541022AOD A S OD y ∆=⨯⨯=⨯⨯=,11525,22BOD B S OD y ∆=⨯⨯=⨯⨯=∴5AOB AOD BOD S S S ∆∆∆=-=, 故答案为:5.(3)①存在,(0,72);过点A 作y 轴的对称点A ',连接A 'B ,交y 轴与点P ,则点P 即为使△PAB 周长最小的点, 由作图可知,点A '坐标为(1,4)-,又点B (3,2)则直线A 'B 的解析式为:1722y x =-+,∴点P 坐标为7(0,)2,故答案为:7(0,)2;②存在. (2,2)- 或(4,6)或(2,2)-. 有三种情况,如图所示:设点C 坐标为(,)x y , 当平行四边形以AO 为对角线时,由中点坐标公式可知,AO 的中点坐标和BC 中点坐标相同,∴310240x y +=+⎧⎨+=+⎩解得22x y =-⎧⎨=⎩∴点1C 坐标为(2,2)-,当平行四边形以AB 为对角线时,AB 的中点坐标和OC 的中点坐标相同,则031024x y +=+⎧⎨+=+⎩ 46x y =⎧⎨=⎩∴点2C 的坐标为(4,6),当平行四边形以BO 为对角线时,BO 的中点坐标和AC 的中点坐标相同,则130420x y +=+⎧⎨+=+⎩解得22x y =⎧⎨=-⎩∴点3C 坐标为(2,2)-,故答案为:存在,(2,2)-或(4,6)或(2,2)-.【点睛】本题考查了直线解析式的求法,列二元一次方程组求解问题,割补法求三角形的面积,两点之间线段最短,“将军饮马”模型的应用,添加点构造平行四边形,利用中点坐标公式求点坐标题型.26.(1)详见解析;(2),理由详见解析;(3),理由详见解析 【分析】(1)根据,等量代换即可证明;(2)DE=EF ,连接NE ,在DA 边上截取DN=EB ,证出△DNE ≌△EBF 即可得出答案;(3)在解析:(1)详见解析;(2)DE EF =,理由详见解析;(3)DE EF =,理由详见解析 【分析】(1)根据90,90AED FEB ADE AED ∠+∠=︒∠+∠=︒,等量代换即可证明;(2)DE=EF ,连接NE ,在DA 边上截取DN=EB ,证出△DNE ≌△EBF 即可得出答案;(3)在DA 边上截取DN EB =,连接NE ,证出()DNE EBF ASA ≌即可得出答案.【详解】(1)证明:∵90DAB DEF ∠=∠=︒,。
人教版八年级下册数学期末试卷(培优篇)(Word版含解析)

人教版八年级下册数学期末试卷(培优篇)(Word 版含解析) 一、选择题 1.式子10x -在实数范围内有意义,则x 的取值范围是( )A .x ≥10B .x ≠10C .x ≤10D .x >10 2.下列几组数中,能作为直角三角形三边长度的是( ) A .2,3,4 B .4,5,6 C .6,8,11 D .5,12,13 3.在四边形ABCD 中,对角线AC 与BD 交于点O ,下列条件一定能判定四边形ABCD 为平行四边形的是( )A .AD ∥BC ,AB =CDB .AO =OC ,BO =OD C .AD =CB ,AB ∥CD D .∠A =∠B ,∠C =∠D4.期间,红星中学门卫对周末提前返校的5名学生进行体温检测,记录如下:36.1℃,36.5℃,36.9℃,36.5℃,36.6℃,则这5名学生体温的众数是( )A .36.1℃B .36.6℃C .36.5℃D .36.9℃ 5.如图所示,正方形ABCD 的边长为4,点E 为线段BC 上一动点,连结AE ,将AE 绕点E 顺时针旋转90°至EF ,连结BF ,取BF 的中点M ,若点E 从点B 运动至点C ,则点M 经过的路径长为( )A .2B .22C .23D .46.在菱形ABCD 中,80ABC ∠=︒,BA BE =,则DAE =∠( )A .20︒B .30C .40︒D .50︒7.如图,作Rt ABC ,90C ∠=︒,2BC AC =;以A 为圆心,以AC 长为半径画弧,交斜边AB 与点D ;以B 为圆心,以BD 长为半径画弧,交BC 与点E .若6BC =,则CE =( )A .935-B .356-C .353-D .351- 8.如图,直线 y 1 与 y 2 相交于点C , y 1 与 x 轴交于点 D ,与 y 轴交于点(0,1), y 2 与 x 轴 交于点 B (3,0),与 y 轴交于点 A ,下列说法正确的个数有( )①y 1的 解 析 式 为12y x =+;② OA = OB ;③22AC BC =;④12y y ⊥;⑤ ∆AOB ≅ ∆BCD . A .2 个 B .3个 C .4 个 D .5 个二、填空题9.要使式子28x +有意义,则x 的取值范围是________.10.已知菱形的边长与一条对角线的长分别为5和6,则它的面积是______.11.如图,在△ABC 中,∠ACB =90°,AC =6cm ,BC=8cm ,分别以三角形的三条边为边作正方形,则三个正方形的面 S 1+S 2+S 3 的值为_______.12.如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,E 为AB 的中点,连接OE .若10CD =,则OE 的长为________.13.已知一次函数y=kx +b 图像过点(0,5)与(2,3),则该一次函数的表达式为_____. 14.如图,在四边形ABCD 中,AB CD ≠,E ,F ,G ,H 分别是AB ,BD ,CD ,AC 的中点,要使四边形EFGH 是菱形,四边形ABCD 还应满足的一个条件是______.15.正方形111A B C O ,2221A B C C ,3332A B C C ,…,按如图所示的方式放置,点1A ,2A ,3A ,…和点1C ,2C ,3C ,…分别在直线1y x =+和x 轴上,已知点()11,1B ,()23,2B ,则n B 的横坐标是_____.16.如图,对折矩形纸片ABCD ,使AD 与BC 重合得到折痕EF ,将纸片展平,再一次折叠,使点A 落到EF 上的点G 处,并使折痕经过点B ,交EF 于点H ,交AD 于点M .已知2AB =,则线段HG 的长度为________.三、解答题17.(1)124183-⨯(2)()()236322-+- 18.如图,在甲村到乙村的公路一旁有一块山地正在开发.现A 处需要爆破,已知点A 与公路上的停靠站B ,C 的距离分别为400 m 和300 m ,且AC ⊥AB .为了安全起见,如果爆破点A 周围半径260 m 的区域内不能有车辆和行人,问在进行爆破时,公路BC 段是否需要暂时封闭?为什么?19.图(a )、图(b )是三张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1请在图a )、图(b )中,分别画出符合要求的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合具体要求如下:(1)画一个面积为10的等腰直角三角形;(2)画一个面积为12的平行四边形20.如图,在ABC 中,AB AC =,AH BC ⊥于点H ,E 是A 上一点,过点B 作//BF EC ,交EH 的延长线于点F ,连接BE ,CF .(1)求证:四边形BECF 是菱形;(2)若BAC ECF ∠=∠,求ACF ∠的度数.21.[阅读材料]我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,为三角形和多边形的面积计算提供了新的方法和思路,在知道三角形三边的长而不知道高的情况下使用秦九韶公式可以更简便地求出面积,比如说在测量土地的面积的时候,不用测三角形的高,只需测两点间的距离,就可以方便地求出答案,即三角形的三边长分别为a 、b 、c ,则其面积S 2222221()42a b c a b ⎡⎤+--⎢⎥⎣⎦出一辙,即三角形的三边长分别为a 、b 、c ,记p =2a b c ++,则其面积S =()()()p p a p b p c ---价的,计算各有优劣,它填补了中国数学史中的一个空白,从中可以看出中国古代已经具有很高的数学水平.[解决问题](1)当三角形的三边a =7,b =8,c =9时,请你从上面两个公式里,选择合适的公式计算出三角形的面积.(2)当三角形的三边a 7,b =2c =3时,请你从上面两个公式里,选择合适的公式计算出三角形的面积.22.互联网时代,一部手机就可搞定午餐是新零售时代的重要表现形式,打包是最早出现的外卖形式,虽然古老,却延续至今,随着电话、手机、网络的普及,外卖行业得到迅速的发展.某知名外卖平台招聘外卖骑手,并提供了如下两种日工资方案:方案一:每日底薪50元,每完成一单外卖业务再提成3元;方案二:每日底薪80元,外卖业务的前30单没有提成,超过30单的部分,每完成一单提成5元.设骑手每日完成的外卖业务量为x 单(x 为正整数),方案一、方案二中骑手的日工资分别为y 1、y 2(单位:元).(1)分别写出y 1、y 2关于x 的函数关系式;(2)若小强是该外卖平台的一名骑手,从日工资收入的角度考虑,他应该选择哪种日工资方案?并说明理由.23.定义:有一组对边相等且这一组对边所在直线互相垂直的凸四边形叫做“等垂四边形”.(提出问题)(1)如图①,四边形ABCD 与四边形AEFG 都是正方形,135180AEB ︒<∠<︒,求证:四边形BEGD 是“等垂四边形”;(类比探究)(2)如图②,四边形ABCD 是“等垂四边形”,AD BC ≠,连接BD ,点E ,F ,G 分别是AD ,BC ,BD 的中点,连接1EG ,FG ,EF .试判定EFG 的形状,并证明; (综合运用)(3)如图③,四边形ABCD 是“等垂四边形”,4=AD ,10BC =,则边AB 长的最小值为________.24.如图,已知点()4,0A 、()0,2B ,线段OA OC =且点C 在y 轴负半轴上,连接AC .(1)如图1,求直线AB 的解析式;(2)如图1,点P 是直线CA 上一点,若3ABC ABP SS =,求满足条件的点P 坐标; (3)如图2,点M 为直线5:2l x =上一点,将点M 水平向右平移6个单位至点N ,连接BM 、MN 、NC ,求BM MN NC ++的最小值及此时点N 的坐标.25.如图,在四边形OABC 是边长为4的正方形点P 为OA 边上任意一点(与点O A 、不重合),连接CP ,过点P 作PM CP ⊥,且PM CP =,过点M 作MN AO ∥,交BO 于点,N 联结BM CN 、,设OP x =.(1)当1x =时,点M 的坐标为( , )(2)设CNMB S y =四形边,求出y 与x 的函数关系式,写出函数的自变量的取值范围.(3)在x 轴正半轴上存在点Q ,使得QMN 是等腰三角形,请直接写出不少于4个符合条件的点Q 的坐标(用x 的式子表示)26.在正方形AMFN 中,以AM 为BC 边上的高作等边三角形ABC ,将AB 绕点A 逆时针旋转90°至点D ,D 点恰好落在NF 上,连接BD ,AC 与BD 交于点E ,连接CD ,(1)如图1,求证:△AMC ≌△AND ;(2)如图1,若DF=3,求AE 的长;(3)如图2,将△CDF 绕点D 顺时针旋转α(090α<<),点C,F 的对应点分别为1C 、1F ,连接1AF 、1BC ,点G 是1BC 的中点,连接AG ,试探索1AG AF 是否为定值,若是定值,则求出该值;若不是,请说明理由.【参考答案】一、选择题1.A解析:A【分析】二次根式中的被开方数是非负数.根据二次根式有意义的条件列出不等式,解不等式即可.【详解】解:由题意得,x﹣10≥0,解得x≥10,故选:A.【点睛】本题考查的是二次根式有意义的条件,掌握二次根式中的被开方数是非负数是解题的关键.2.D解析:D【分析】利用勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.【详解】解:A、22+32≠42,故不是直角三角形,故错误;B、42+52≠62,故不是直角三角形,故错误;C、62+82≠112,故不是直角三角形,故错误;D、52+122=132,故是直角三角形,故正确.故选D.【点睛】本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.3.B解析:B【解析】【分析】由平行四边形的判定方法分别对各个选项进行判断即可.【详解】A、由AD∥BC,AB=CD,不能判定四边形ABCD为平行四边形,故选项A不符合题意;B、∵AO=OC,BO=OD,∴四边形ABCD为平行四边形,故选项B符合题意;C、由AD=CB,AB∥CD,不能判定四边形ABCD为平行四边形,故选项C不符合题意;D、由∠A=∠B,∠C=∠D,不能判定四边形ABCD为平行四边形,故选项D不符合题意;故选:B .【点睛】本题考查了平行四边形的判定,关键是掌握平行四边形的各种判定方法.4.C解析:C【解析】【分析】根据众数的定义:一组数据中出现次数最多的数据,进行求解即可.【详解】解:∵36.5℃出现了两次,出现的次数最多,∴这组数据的众数为36.5℃,故选C .【点睛】本题主要考查了众数的定义,解题的关键在于能够熟知众数的定义.5.B解析:B【分析】已知EF ⊥AE ,当E 点在线段BC 上运动到两端时,正好是M 点运动的两个端点,由此可以判断M 点的运动轨迹是BC 、CD 中点的连线长.【详解】解:取BC 、CD 的中点G 、H ,连接GH ,连接BD∴GH 为△BCD 的中位线,即12GH BD = ∵将AE 绕点E 顺时针旋转90°至EF ,∴EF ⊥AE ,当E 点在B 处时,M 点在BC 的中点G 处,当E 点在C 点处时,M 点在CD 中点处, ∴点M 经过的路径长为GH 的长,∵正方形ABCD 的边长为4,∴2242BD BC CD =+=∴1222GH BD ==, 故选B .【点睛】本题主要考查了正方形的性质,勾股定理和中位线定理,解题的关键在于找到M 点的运动轨迹.6.B解析:B【解析】【分析】利用菱形的性质和等腰三角形的性质即可求解.【详解】解:在菱形ABCD 中,80ABC ∠=︒,∴18080100BAD ∠=︒-︒=︒,40ABE ∠=︒,∵BA BE =, ∴18040702BAE BEA ︒-︒∠=∠==︒, ∴1007030DAE BAD BAE ∠=∠-∠=︒-︒=︒,故选:B .【点睛】本题考查了菱形的性质和等腰三角形的性质,运用知识准确计算是解题的关键. 7.A解析:A【解析】【分析】根据勾股定理求出AB ,再根据圆的定义可求得AD=AC ,BE=BD 即可求解.【详解】解:∵2BC AC =,6BC =,∴AC =3,在Rt ABC 中,90C ∠=︒,由勾股定理得:AB由题意,AD=AC=3,BE=BD=AB -AD =-3,∴CE=BC -BE =6-(3)=9-故选:A .【点睛】本题考查圆的定义、勾股定理,熟练掌握勾股定理是解答的关键.8.A解析:A【分析】通过待定系数法,求出直线y 1的解析式,于是可对①进行判断;利用待定系数法求出y 2的解析式为y =﹣x +3,则可确定A (0,3),所以OA =OB ,于是可对②进行判断;通过两点间的距离公式求出AC 、BC 的长,从而对③进行判断;计算∠EDO 和∠ABO 的度数,再通过三角形的内角和定理得出∠DCB 的度数,即可对④进行判断;通过计算BD 和AB 的长可对⑤进行判断.【详解】由图可知:直线y 1过点(0,1),(1,2),∴直线y 1的解析式为11y x =+,所以①错误;设y 2的解析式为y =kx +b ,把C (1,2),B (3,0)代入得:230k b k b +=⎧⎨+=⎩,解得:13k b =-⎧⎨=⎩,所以y 2的解析式为y =﹣x +3,当x =0时,y =﹣x +3=3,则A (0,3),则OA =OB ,所以②正确;∵A (0,3),C (1,2),B (3,0),∴AC =221(32)2+-=,BC =22(13)222-+=,∴21222AC BC ==,所以③错误; 在11y x =+中,令y 1=0,得x =-1,∴D (-1,0),∴OD =1.∵OE =1,∴OD =OE ,∴∠EDO =45°.∵OA =OB =3,∴∠ABO =45°,∴∠DCB =180°-45°-45°=90°,∴DC ⊥AB ,∴12y y ⊥,故④正确;因为BD =3+1=4,而AB =32,所以△AOB 与△BCD 不全等,所以⑤错误.故正确的有②④.故选A .【点睛】本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;也考查了全等三角形的判定.二、填空题9.x ≥﹣4【解析】【分析】直接利用二次根式中被开方数的取值范围即二次根式中的被开方数是非负数,即可得出答案.【详解】28x +则2x +8≥0,解得:x ≥﹣4;故答案为:x ≥﹣4.【点睛】本题主要考查了二次根式有意义的条件,准确计算是解题的关键.10.24【解析】【分析】根据题意,勾股定理求得另一条对角线的长度,根据菱形的面积等于对角线乘积的一半即可求解.【详解】如图,四边形ABCD 的菱形,连接,AC BD 交于点O ,依题意设5AB =,6BD =,则11,322AO AC BO BD ===, 2222534AO AB BO ∴=--=,8AC ∴=,S ∴菱形ABCD 11862422AC BD =⋅=⨯⨯=. 故答案为:24.【点睛】本题考查了根据菱形的性质求菱形的面积,勾股定理,作出图形求得另外一条对角线的长是解题的关键.11.A解析:200【解析】【分析】根据正方形的面积公式和勾股定理,即可得到阴影部分的面积S 1+S 2+S 3的值.解:∵∠ACB =90°,AC =6,BC =8,∴AB 2=AC 2+BC 2=62+82=100∴S 1+S 2+S 3=AC 2+BC 2 +AB 2=62+82+100=200故答案为:200【点睛】本题考查勾股定理,解题关键是将勾股定理和正方形的面积公式进行结合应用. 12.A解析:5【分析】根据直角三角形斜边上的中线等于斜边的一半计算即可;【详解】∵四边形ABCD 时菱形,∴AC BD ⊥,∴90AOB ∠=︒,∵E 为AB 的中点,10CD AB ==, ∴152OE AB ==; 故答案是5.【点睛】本题主要考查了菱形的性质和直角三角形的性质,准确分析计算是解题的关键. 13.y =-x +5【分析】由直线y =kx +b 经过(0,5)、(2,3)两点,代入可求出函数关系式.【详解】解:把点(0,5)和点(2,3)代入y =kx +b 得532b k b =⎧⎨=+⎩,解得:15k b =-⎧⎨=⎩, 所以一次函数的表达式为y =-x +5,故答案为:y =-x +5.【点睛】此题主要考查了待定系数法求一次函数解析式,注意利用一次函数的特点,来列出方程组求解是解题关键.14.AD BC =【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得//EF AD 且12EF AD =,同理可得//GH AD 且12GH AD =,//EH BC 且12EH BC =,然后证明四边形EFGH 是平行四边形,再根据邻边相等的平行四边形是菱形解答.解:还应满足AD BC =.理由如下:E ,F 分别是AB ,BD 的中点,//EF AD ∴且12EF AD =, 同理可得://GH AD 且12GH AD =,//EH BC 且12EH BC =, //EF GH ∴且EF GH =,∴四边形EFGH 是平行四边形,AD BC =, ∴1122AD BC =, 即EF EH =,EFGH ∴是菱形.故答案是:AD BC =.【点睛】本题考查了中点四边形,其中涉及到了菱形的判定,平行四边形的判定,三角形的中位线定理,根据三角形的中位线平行于第三边并且等于第三边的一半得到四边形EFGH 的对边平行且相等从而判定出平行四边形是解题的关键,也是本题的突破口.15.【分析】根据,,,,……,即可归纳出的横坐标.【详解】解:∵点,,,…和点,,,…分别在直线和轴上,已知点,,∴(0,1),(1,2),(3,4),……,∴,(7,8),,∴,故答案解析:12n -【分析】根据()11,1B ,()23,2B ,()37,4B ,()415,8B ,……,即可归纳出n B 的横坐标.【详解】解:∵点1A ,2A ,3A ,…和点1C ,2C ,3C ,…分别在直线1y x =+和x 轴上,已知点()11,1B ,()23,2B ,∴1A (0,1),2A (1,2),3A (3,4),……,∴()37,4B ,4A (7,8),()415,8B ,∴()121,2n n n B --,故答案是:12n -.本题主要考查一次函数图像和正方形的性质,根据点()11,1B ,()23,2B ,()37,4B ,()415,8B ,找出n B 横坐标的变化规律,是解题的关键.16.【分析】根据折叠的性质,,,,结合题意得出,则,进而得到,于是证明是等边三角形,得到,,最后在中,由勾股定理求解即可.【详解】解:由折叠可得,,,,,由题意得,点E 是AB 的中点,且,∴,【分析】根据折叠的性质,AM MG =,AB BG =,AMH BMG ∠=∠,结合题意得出1122EB AB BG ==,则30EGB ∠=︒,进而得到60MGH ∠=︒,于是证明MHG △是等边三角形,得到60GMH MHG ∠=∠=︒,AM HG HM ==,最后在AMB 中,由勾股定理求解即可.【详解】解:由折叠可得,AM MG =,AB BG =,AMH BMG ∠=∠,90A MGB ∠=∠=︒, 由题意得,点E 是AB 的中点,且AB EF ⊥, ∴1122EB AB BG ==,且//AD EF , ∴30EGB ∠=︒,∴60MGH ∠=︒,∵//AD EF ,∴AMH MHG ∠=∠,∴GMH MHG ∠=∠∴MHG △是等边三角形,∴60GMH MHG ∠=∠=︒,AM HG HM ==∴30MBG ∠=︒,在AMB 中,设HG x =,则HM HB AM x ===,根据勾股定理得:222AM AB BM +=,即()22222x x +=,解得:1x 2x =.本题考查矩形的性质,折叠的性质,等边三角形的判定及性质,以及勾股定理,清楚图形的边角关系是解题关键.三、解答题17.(1);(2)【分析】(1)先算二次根式的乘法,再合并同类二次根式即可求解;(2)先利用分配律和完全平方公式化简二次根式,再合并同类二次根式,即可求解.【详解】解:(1)原式===;解析:(12)3【分析】(1)先算二次根式的乘法,再合并同类二次根式即可求解;(2)先利用分配律和完全平方公式化简二次根式,再合并同类二次根式,即可求解.【详解】解:(1)原式==(2)原式324++-=3-=3.【点睛】本题主要考查二次根式的混合运算,掌握二次根式的运算法则和乘法公式,是解题的关键.18.需要封闭,理由见解析【分析】过作于先求解再利用等面积法求解再与260比较,可得答案.【详解】解:过作于所以进行爆破时,公路BC 段需要暂时封闭.【点睛】解析:需要封闭,理由见解析【分析】过A 作AK BC ⊥于,K 先求解,BC 再利用等面积法求解,AK 再与260比较,可得答案.【详解】解:过A 作AK BC ⊥于,K,400,300,AB AC AB AC 22500,BC AB AC 11,22AB AC BC AK 300400500,AK240,AK240260,所以进行爆破时,公路BC 段需要暂时封闭.【点睛】本题考查的是勾股定理的应用,利用等面积法求解直角三角形斜边上的高,掌握“等面积法求解直角三角形斜边上的高”是解题的关键.19.(1)见解析;(2)见解析【解析】【分析】(1)根据等腰直角三角形的性质求出边长分别为、、,再网格中找到相应的格点,作图即可;(2)根据平行四边形的面积为12,确定底边长为4、高为3,在网格 解析:(1)见解析;(2)见解析【解析】【分析】(1)根据等腰直角三角形的性质求出边长分别为25、25、210,再网格中找到相应的格点,作图即可;(2)根据平行四边形的面积为12,确定底边长为4、高为3,在网格中找到相应的格点,作图即可.【详解】解:(1)根据等腰直角三角形的面积为为10,设两个直角边为x ,则21102x = 解得25x =,由勾股定理得,斜边长为22(25)(25)210+=222524=+,在网格中找到到相应的格点使得两条直角边为25,连线即可,其中25是以2,4为直角边的直角三角形的斜边,如图(a )(2)根据平行四边形的面积为12,可以作底边长为4、高为3的平行四边形,在图中选取相应的格点,使得平行四边形的边长为为4、高为3,如图(b )【点睛】此题考查了等腰直角三角形的性质,勾股定理,平行四边形的性质,熟练掌握相关基本性质是解题的关键.20.(1)见解析;(2)90°【分析】(1)由题意利用全等三角形的判定证得,得出,进而利用菱形的判定定理进行证明即可;(2)由题意利用菱形的性质可得,进而进行角的等量替换得出即的度数.【详解】解析:(1)见解析;(2)90°【分析】(1)由题意利用全等三角形的判定证得BHF CEE ASA △≌△(),得出EH FH =,进而利用菱形的判定定理进行证明即可;(2)由题意利用菱形的性质可得12ECB FCB ECF ∠=∠=∠,进而进行角的等量替换得出90FCB ACH ∠+∠=︒即ACF ∠的度数.【详解】解:(1)证明:∵AB AC =,AH BC ⊥,∴BH HC =,90BHF CHE ∠=∠=︒,∵//BF EC ,∴FBH ECH ∠=∠,∴BHF CEE ASA △≌△(), ∴EH FH =,∴四边形BECF 是平行四边形.又∵EF BC ⊥,∴四边形BECF 是菱形;(2)∵四边形BECF 是菱形, ∴12ECB FCB ECF ∠=∠=∠. ∵AB AC =,AH BC ⊥, ∴12CAH BAC ∠=∠. ∵BAC ECF ∠=∠,∴CAH FCB ∠=∠,∵90CAH ACH ∠+∠=︒,∴90FCB ACH ∠+∠=︒.即90ACF ∠=︒.【点睛】本题考查菱形的判定与性质,熟练掌握全等三角形的判定和性质以及菱形的判定与性质是解题的关键.21.(1)S=12;(2)S =【解析】【分析】(1)利用三角形的三边均为整数,可选择海伦公式进行计算;(2)利用三角形的三边中有无理数,可选择秦九韶公式进行计算.【详解】解:(1),由海伦解析:(1)S 2)S 【解析】【分析】(1)利用三角形的三边均为整数,可选择海伦公式进行计算;(2)利用三角形的三边中有无理数,可选择秦九韶公式进行计算.【详解】解:(1)789122p++==,∴由海伦公式得:S===(2)由秦九韶公式得:S==【点睛】本题主要考查了数学常识,三角形的面积,二次根式的应用,根据三角形三边数字的特征选择恰当的公式是解题的关键.22.(1)y1=50+3x;当0<x<30且n为整数时,y2=80;当x≥30时且n为整数时,y2=5x-70;(2)见解析【分析】(1)根据题意,可以写出y1,y2关于x的函数解析式;(2)在0解析:(1)y1=50+3x;当0<x<30且n为整数时,y2=80;当x≥30时且n为整数时,y2=5x-70;(2)见解析【分析】(1)根据题意,可以写出y1,y2关于x的函数解析式;(2)在0<x<30范围内,令y1=y2,求x的值,可得y1>y2时x的取值范围,在x≥30时,令y1=y2可得x的值,即可得y1>y2时可得x的取值范围.【详解】解:(1)由题意得:y1=50+3x,当0<x<30且x为整数时,y2=80,当x≥30时且x为整数时,y2=80+5(x-30)=5x-70;(2)当0<x<30且x为整数时,当50+3x=80时,解得x=10,即10<x<30时,y1>y2,0<x<10时,y1<y2,当x≥30且x为整数时,50+3x=5x-70时,解得x=60,即x>60时,y2>y1,30≤x<60时,y2<y1,∴从日工资收入的角度考虑,①当0<x <10或x >60时,y 2>y 1,他应该选择方案二;②当10<x <60时,y 1>y 2,他应该选择方案一;③当x =10或x =60时,y 1=y 2,他选择两个方案均可.【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质解答. 23.(1)见解析;(2)△EFG 是等腰直角三角形,理由见解析(3)【分析】(1)延长,交于点,先证,得,.结合,知,即可得.从而得证; (2)延长,交于点,由四边形是“等垂四边形”, 知,,从而得, 解析:(1)见解析;(2)△EFG 是等腰直角三角形,理由见解析(3)32 【分析】 (1)延长BE ,DG 交于点H ,先证ABE ADG ∆≅∆,得BE DG =,ABE ADG ∠=∠.结合90ABD ADB ∠+∠=︒,知90ABE EBD ADB DBE ADB ADG ∠+∠+∠=∠+∠+∠=︒,即可得90BHD ∠=︒.从而得证;(2)延长BA ,CD 交于点H ,由四边形ABCD 是“等垂四边形”, AD BC ≠知AB CD ⊥,AB CD =,从而得90HBC HCB ∠+∠=︒,根据三个中点知12EG AB =,12GF CD =,,//EG AB ,//GF DC ,据此得BFG C ∠=∠,EGD HBD ∠=∠,EG GF =.由90EGF EGD FGD ABD DBC GFB ABD DBC C HBC HCB ∠=∠+∠=∠+∠+∠=∠+∠+∠=∠+∠=︒可得答案;(3)延长BA ,CD 交于点H ,分别取AD ,BC 的中点E ,F .连接HE ,EF ,HF ,由1152322EF HF HE BC AD ≥-=-=-=及232AB EF =≥.可得答案.【详解】解:(1)如图①,延长BE ,DG 交于点H ,四边形ABCD 与四边形AEFG 都为正方形,AB AD ∴=,AE AG =,90BAD EAG ∠=∠=︒.BAE DAG ∴∠=∠.()ABE ADG SAS ∴∆≅∆.BE DG ∴=,ABE ADG ∠=∠.90ABD ADB ∠+∠=︒,90ABE EBD ADB DBE ADB ADG ∴∠+∠+∠=∠+∠+∠=︒,即90EBD BDG ∠+∠=︒,90BHD =∴∠︒.BE DG ∴⊥.又=BE DG ,∴四边形BEGD 是“等垂四边形”.(2)EFG ∆是等腰直角三角形.理由如下:如图②,延长BA ,CD 交于点H ,四边形ABCD 是“等垂四边形”, AD BC ≠,AB CD ∴⊥,AB CD =,90HBC HCB ∴∠+∠=︒点E ,F ,G 分别是AD ,BC ,BD 的中点, 12EG AB ∴=,12GF CD =,//EG AB ,//GF DC , BFG C ∴∠=∠,EGD HBD ∠=∠,EG GF =.90EGF EGD FGD ABD DBC GFB ABD DBC C HBC HCB ∴∠=∠+∠=∠+∠+∠=∠+∠+∠=∠+∠=︒.EFG ∴∆是等腰直角三角形.(3)延长BA ,CD 交于点H ,分别取AD ,BC 的中点E ,F .连接HE ,EF ,HF ,则1152322EF HF HE BC AD ≥-=-=-=,由(2)可知232AB EF ≥AB ∴最小值为32 故答案为:32【点睛】本题是四边形的综合问题,解题的关键是掌握正方形的性质,全等三角形的判定与性质,三角形中位线定理及等腰直角三角形的性质等知识点.24.(1);(2)点P 的坐标为(,)或(,);(3)的最小值为;点N 的坐标为(,).【解析】【分析】(1)直接利用待定系数法,即可求出直线的解析式;(2)根据题意,先求出点C 的坐标,然后求出直线解析:(1)122y x =-+;(2)点P 的坐标为(163,43)或(83,43-);(3)BM MN NC ++的最小值为6N 的坐标为(172,711). 【解析】【分析】(1)直接利用待定系数法,即可求出直线的解析式;(2)根据题意,先求出点C 的坐标,然后求出直线AC 的解析式,由3ABC ABP S S =,得到3AC AP =,再分别求出AC 和AP 的长度,即可求出点P 的坐标;(3)根据题意,6MN =为定值,在图中找出一点B ',使得B N BM '=,即点B '、N 、C 三点共线时,使得BM MN NC ++有最小值,此时求出B C B N NC BM NC ''=+=+,即可得到答案.【详解】解:(1)设直线AB 为y kx b =+,把点()4,0A 、()0,2B ,代入,则402k b b +=⎧⎨=⎩,解得:122k b ⎧=-⎪⎨⎪=⎩, ∴122y x =-+; (2)∵线段4OA OC ==,且点C 在y 轴负半轴上,∴点C 的坐标为(0,-4),∵点A 为(4,0),∴直线AC 的解析式为:4y x =-;∵点B 到直线AC 的距离就是△ABC 和△ABP 的高,∴△ABC 和△ABP 的高相同,∵3ABC ABP SS =, ∴11322AC h AP h ••=⨯••, ∴3AC AP =,∵AC ==∴13AP =⨯ ∵点P 在直线AC 上,则设点P 为(x ,x -4),∴2242(4)(4)243AP x x x =-+-=•-=, ∴443x -=, ∴163x =或83x =, ∴点P 的坐标为(163,43)或(83,43-); (3)根据题意,∵点B 与点M 的水平距离为52, ∴在点N 的右边水平距离为52处作直线11x =,如图:令点B '为(11,2),此时有B N BM '=,∵6MN =, ∴66BM MN NC BM NC B N NC '++=++=++,∴当点B '、N 、C 三点共线时,使得BM MN NC ++有最小值,最小值为:66BM MN NC B N NC B C ''++=++=+;∵点B '(11,2),点C 为(0,-4),∴直线B C '的解析式为:6411y x =-, 2211(24)157B C '++∴BM MN NC ++有最小值为:66157B C '+=+∵点N 的横坐标为:517622+=, ∴点N 的纵坐标为:6177411211y =⨯-=, ∴点N 的坐标为:(172,711). 【点睛】 本题考查了一次函数的性质,利用勾股定理求两点之间的距离,最短路径问题,坐标与图形,解题的关键是熟练掌握一次函数的图形和性质,正确找出使得线段之和最小时的临界点,注意运用数形结合的思想进行解题.25.(1)点的坐标为;(2);(3),,,【分析】(1)过点作,由“”可证,可得,,即可求点坐标;(2)由(1)可知,设OP=x ,则可得M 点坐标为(4+x ,x ),由直线OB 解析式可得N (x ,解析:(1)点M 的坐标为(51),;(2)()44y x =-()04x <<;(3)()224160Q x x ++-,, ()234160Q x x +--, ,()24160Q x x +-,, ()25160(224)Q x x x --<<,【分析】(1)过点M 作ME OA ⊥,由“AAS ”可证COP PEM ∆≅∆,可得4CO PE ==,1OP ME ==,即可求点M 坐标;(2)由(1)可知COP PEM ∆≅∆,设OP=x ,则可得M 点坐标为(4+x ,x ),由直线OB 解析式可得N (x ,x ),即可知MN=4,由一组对边平行而且相等的四边形是平行四边形即可证明四边形BCNM 是平行四边形,进而可求y 与x 的函数关系式;(3)首先画出符合要求的点Q 的图形,共分三种情况,第一种情况:当MN 为底边时,第二种情况:当M 为顶点MN 为腰时,第三种情况:当N 为顶点MN 为腰时,然后根据图形特征结合勾股定理求出各种情况点的坐标即可解答.【详解】解:(1)如图,过点M 作ME OA ⊥,CP PM ⊥90CPO MPE ∴∠+∠=︒,且90CPO PCO ∠+∠=︒PCO MPE ∴∠=∠,且CP PM =,90COP PEM ∠=∠=︒()COP PEM AAS ∴∆≅∆4CO PE ∴==,1OP ME ==5OE ∴=∴点M 坐标为(5,1)故答案为(5,1)(2)由(1)可知COP PEM ∆≅∆4CO PE ∴==,OP ME x ==∴点M 坐标为(4,)x x +四边形OABC 是边长为4的正方形,∴点(4,4)B∴直线BO 的解析式为:y x =//MN AO ,交BO 于点N ,∴点N 坐标为(,)x x4MN BC ∴==,且//BC MN∴四边形BCNM 是平行四边形4(4)y x ∴=- (04)x <<(3)在x 轴正半轴上存在点Q ,使得QMN ∆是等腰三角形,此时点Q 的坐标为:1(2,0)Q x +,22(416Q x x +--,0),23(416Q x x ++-,240)(16Q x x +-,250)(16Q x x --,0)其中(04)x <<,理由:当(2)可知,(04)OP x x =<<,4MN PE ==,//MN x 轴,所以共分为以下几种请:第一种情况:当MN 为底边时,作MN 的垂直平分线,与x 轴的交点为1Q ,如图2所示111222PQ PE MN ===, 12OQ x ∴=+,1(2,0)Q x ∴+第二种情况:如图3所示,当M 为顶点MN 为腰时,以M 为圆心,MN 的长为半径画弧交x 轴于点2Q 、3Q ,连接2MQ 、3MQ ,则234MQ MQ ==, 2222Q E MQ ME ∴=-, 222416OQ OE Q E x x ∴=-=+--,22(416Q x x ∴+--,0),32Q E Q E =,233416OQ OE Q E x x =+=++-,23(416Q x x ∴++-,0);第三种情况,当以N 为顶点、MN 为腰时,以N 为圆心,MN 长为半径画圆弧交x 轴正半轴于点4Q ,当022x <<时,如图4所示,则2224416PQ NQ NP x --24416OQ OP PQ x x ∴=+=-即24(16Q x x -0).当2x =则4ON =,此时Q 点与O 点重合,舍去;当224x <时,如图5,以N 为圆心,MN 为半径画弧,与x 轴的交点为4Q ,5Q .4Q 的坐标为:24(16Q x x -0).2516OQ x x =- 25(16Q x x ∴-0)所以,综上所述,1(2,0)Q x +,22(416Q x x +-0),23(416Q x x +-,240)(16Q x x -250)(16Q x x -0)使QMN ∆是等腰三角形.【点睛】本题考查四边形综合题,解题的关键是明确题意,画出相应的图象,找出所求问题需要的条件,利用数形结合的思想解答问题.26.(1)见解析;(2)AE =;(3)(3),理由见解析.【分析】(1)运用四边形AMFN 是正方形得到判断△AMC,△AND 是Rt △,进一步说明△ABC 是等边三角形,在结合旋转的性质,即可证明.(解析:(1)见解析;(2)AE =233)(3)122AG AF =,理由见解析. 【分析】(1)运用四边形AMFN 是正方形得到判断△AMC,△AND 是Rt △,进一步说明△ABC 是等边三角形,在结合旋转的性质,即可证明.(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x ,则AE=2x 3x ,得到△GBE 是等腰直角三角形和∠DHF=30°,再结合直角三角形的性质,判定Rt △AMC ≌Rt △AND ,最后通过计算求得AE 的长;(3)延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM FG =,可得GMB ∆≌11GFC ∆,从而得到111BM FC DF == 1BMG GFN ∠=,可知BM ∥1F N , 再根据题意证明ABM ∆≌1ADF ∆,进一步说明1AMF ∆是等腰直角三角形,然后再使用勾股定理求解即可. 【详解】(1)证明:∵四边形AMFN 是正方形,∴AM=AN ∠AMC=∠N=90°∴△AMC,△AND 是Rt △∵△ABC 是等边三角形∴AB=AC∵旋转后AB=AD∴AC=AD∴Rt △AMC ≌Rt △AND(HL)(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x则AE=2x 3x易得△GBE 是等腰直角三角形∴BG=EG 3x∴AB=BC=(31)x易得∠DHF=30°∴HD=2DF=23,HF=3∴BF=BH+HF=233∵Rt △AMC ≌Rt △AND(HL)∴易得3∴BC=BF-CF=233333∴(31)33x =∴3x =∴AE =23x =(3)12AG AF = 理由:如图2中,延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM FG =,则GMB ∆≌11GFC ∆,。
