【数学建模 参考文献】第五章非平稳时间序列分析的程序
非平稳时间序列建模步骤

非平稳时间序列建模步骤介绍非平稳时间序列是指其统计特性在时间上发生变化的序列。
在实际应用中,我们经常面临非平稳时间序列的建模问题,如股票价格、气温变化等。
本文将探讨非平稳时间序列建模的步骤和方法。
为什么要建立模型非平稳时间序列在其统计特性的变化中存在一定的规律性,因此建立模型可以帮助我们理解和预测序列的行为。
模型可以从数据中提取有用的信息,揭示序列的规律和动态特征。
步骤一:观察时间序列的特性在建立模型之前,我们首先需要观察时间序列的特性,包括趋势、周期性、季节性和随机性等。
这些特性是决定时间序列模型选择的重要因素。
步骤二:平稳化处理由于非平稳时间序列的统计特性随时间变化,不利于建模和分析。
因此,我们需要对时间序列进行平稳化处理。
常用的平稳化方法包括差分法和变换法。
2.1 差分法差分法是通过计算相邻两个观测值的差异来实现序列的平稳化。
一阶差分是指相邻观测值之间的差异,二阶差分是指一阶差分的差异,以此类推。
差分法可以有效地去除序列的趋势和季节性,使序列平稳。
2.2 变换法变换法是通过对时间序列进行数学变换,将非平稳序列转化为平稳序列。
常用的变换方法包括对数变换、平方根变换和 Box-Cox 变换等。
变换法可以改变序列的分布特性,使序列满足平稳性的要求。
步骤三:选择模型平稳化处理后,我们需要选择合适的模型进行建模。
常用的时间序列模型包括自回归移动平均模型(ARMA)、自回归积分移动平均模型(ARIMA)、季节性自回归移动平均模型(SARIMA)和指数平滑模型等。
3.1 自回归移动平均模型(ARMA)ARMA 模型是描述时间序列随机变动的经典模型,其包括自回归和移动平均两个部分。
自回归部分考虑了序列的历史值对当前值的影响,移动平均部分考虑了序列的误差对当前值的影响。
ARMA 模型适用于没有趋势和季节性的平稳序列。
3.2 自回归积分移动平均模型(ARIMA)ARIMA 模型是在 ARMA 模型基础上引入了积分项,用于处理非平稳序列。
时间序列分析第五章非平稳序列的随机分析

考察差分运算对该序列线性趋势信息的提 取作用
2020/3/12
时间序列分析
差分前后时序图
原序列时序图
差分后序列时序图
2020/3/12
时间序列分析
例5.2
尝试提取1950年——1999年北京市民用 车辆拥有量序列的确定性信息
2020/3/12
时间序列分析
Green函数递推公式
1 1 1 2 1 1 2 2
j 1 j1 pd j pd j
t
2
,
E(
t
s
)
0,
s
t
Exs t 0,s t
2020/3/12
时间序列分析
ARIMA 模型族
d=0 ARIMA(p,d,q)=ARMA(p,q)
P=0 ARIMA(P,d,q)=IMA(d,q)
q=0 ARIMA(P,d,q)=ARI(p,d)
d=1,P=q=0 ARIMA(P,d,q)=random walk model
差分后序列时序图
一阶差分
二阶差分
2020/3/12
时间序列分析
例5.3
差分运算提取1962年1月——1975年12月平均 每头奶牛的月产奶量序列中的确定性信息
2020/3/12
时间序列分析
差分后差分
2020/3/12
时间序列分析
过差分
足够多次的差分运算可以充分地提取原 序列中的非平稳确定性信息
2020/3/12
时间序列分析
随机游走模型( random walk)
模型结构
时间序列分析 第五章-非平稳序列的随机分析
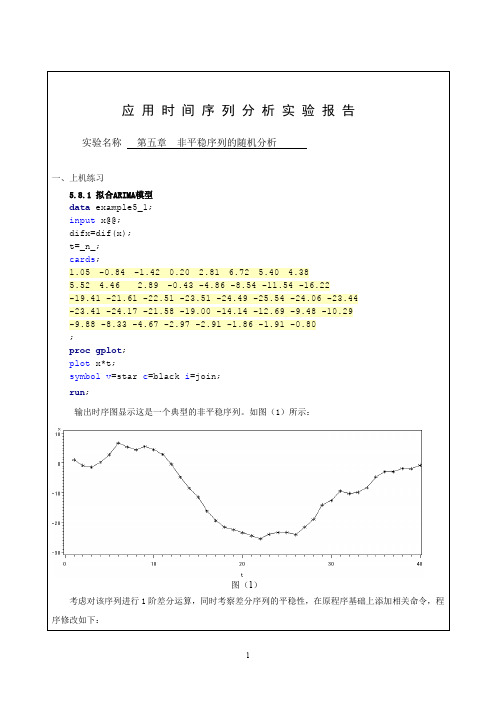
图(1)考虑对该序列进行1阶差分运算,同时考察差分序列的平稳性,在原程序基础上添加相关命令,程序修改如下:图(2)时序图显示差分后序列difx没有明显的非平稳特征。
(2)“identify var=x(1);”,使用该命令可以识别差分后序列的平稳性。
纯随机性和适当的拟合图(6)普通最小二乘估计结果图(8)最终拟合模型输出结果图(9)拟合效果图图(12)带有延迟因变量的回归模型拟合效果图5.8.3拟合GARCH模型SAS系统中AUTOREG过程功能非常强大,不仅可以提供上述的分析功能,还可以提供异方差性检验乃至条件异方差模型建模。
以临时数据集example5_3数据为例,介绍GARCH模型的拟合,相关命令如下:data example5_3;input x@@;t=_n_;cards;10.77 13.30 16.64 19.54 18.97 20.52 24.3623.51 27.16 30.80 31.84 31.63 32.68 34.9033.85 33.09 35.46 35.32 39.94 37.47 35.2433.03 32.67 35.20 32.36 32.34 38.45 38.1732.14 39.70 49.42 47.86 48.34 62.50 63.5667.61 64.59 66.17 67.50 76.12 79.31 78.8581.34 87.06 86.41 93.20 82.95 72.96 61.1061.27 71.58 88.34 98.70 97.31 97.17 91.1780.20 85.12 81.40 70.87 57.75 52.35 67.5087.95 85.46 84.55 98.16 102.42 113.02 119.95122.37 126.96 122.79 127.96 139.20 141.05 140.87137.08 145.53 145.59 134.36 122.54 106.92 97.23110.39 132.40 152.30 154.91 152.69 162.67 160.31142.57 146.54 153.83 141.81 157.83 161.79 142.07139.43 140.92 154.61 172.33 191.78 199.27 197.57189.29 181.49 166.84 154.28 150.12 165.17 170.32;proc gplot data=example5_3;plot x*t=1;symbol1c=black i=join v=start;proc autoreg data=example5_3;model x=t/nlag=5dwprob archtest;model x=t/nlag=2noint garch=(p=1,q=1);output out=out p=p residual=residual lcl=lcl ucl=ucl cev=cev;data out;set out;l95=-1.96*sqrt(51.42515);u95=1.96*sqrt(51.42515);Lcl_GARCH=-1.96*sqrt(cev);Ucl_GARCH=1.96*sqrt(cev);Lcl_p=p-1.96*sqrt(cev);Ucl_p=p+1.96*sqrt(cev);proc gplot data=out;plot residual*t=2 l95*t=3 Lcl_GARCH*t=4 u95*t=3 Ucl_GARCH*t=4/overlay; plot x*t=5 lcl*t=3 LCL_p*t=4 ucl*t=3 UCL_p*t=4/overlay;symbol2c=green i=needle v=none;symbol3v=black i=join c=none w=2l=2;symbol4c=red i=join v=none;symbol5c=green i=join v=none;run;该序列输出时序图如图(13)所示。
时间序列分析中的非平稳信号分析方法研究

时间序列分析中的非平稳信号分析方法研究时间序列分析是统计学中的领域,用来研究一组与时间有关的数据。
时间序列分析非常重要,因为它可以帮助研究者预测机器人,股市和其他急于观察的数据。
但是,有时候我们会遇到一些非平稳的信号,导致预测分析非常困难。
在这种情况下,对非平稳信号的分析方法成为了非常重要的研究领域。
I. 什么是非平稳信号?平稳信号是指时间序列中平均值和方差都不随时间而变化的信号。
在这种情况下,我们可以使用平稳信号的统计模型进行分析和预测。
但是,在现实生活中,出现非平稳信号的情况是普遍存在的。
例如,物价、股票价格等往往都呈现出随时间变化的趋势性和季节性。
II. 非平稳信号的特点非平稳信号是指时间序列中均值,方差或者两者都在变化的信号。
与平稳信号不同,非平稳信号的各种统计量都会随时间的推移而变化,因此在真实的数据应用过程中非常常见。
1. 缺乏稳定性:不同时间点的数据存在着不同的特征,可以说非平稳序列在统计特征上表现出的一种不稳定性。
2. 时间相关性:非平稳时间序列中的不同时间点可能不是独立的,也就是说以前的一个时间点可能会对后续的时间点产生影响,这种影响通常以趋势的形式呈现。
3. 不存在平稳的统计模型:由于非平稳信号缺乏稳定性,所以不存在平稳的统计模型,要研究非平稳信号需要寻找其他方法。
III. 非平稳信号分析方法在研究非平稳信号的过程中,最常用的方法包括:时间序列分解、差分方法、ARIMA和ARCH模型等。
1. 时间序列分解时间序列分解是将非平稳信号分解为一些成分,例如趋势、周期和随机元素。
这种方法可以使我们更好地理解信号的变化过程和对不同成分的影响。
时间序列分解同时也对信号的去除趋势和季节成分非常有用。
2. 差分方法差分方法是通过对时间序列之间差异的计算,将其转化为平稳时间序列,从而避免非平稳信号带来的影响,使得时间序列分析得以进行。
这种方法适用于不太具有周期性的时序数据。
3. ARIMA模型ARIMA模型是最常用的时间序列分析方法之一。
时间序列分析--第五章非平稳序列的随机分析

50
乘积季节模型
使用场合
序列的季节效应、长期趋势效应和随机波动之间有着复 杂地相互关联性,简单的季节模型不能充分地提取其中 的相关关系
构造原理
短期相关性用低阶ARMA(p,q)模型提取
季节相关性用以周期步长S为单位的ARMA(P,Q)模型提取
假设短期相关和季节效应之间具有乘积关系,模型结构
3
差分运算的实质
差分方法是一种非常简便、有效的确定 性信息提取方法
Cramer分解定理在理论上保证了适当阶 数的差分一定可以充分提取确定性信息
差分运算的实质是使用自回归的方式提 取确定性信息
d
d xt (1 B)d xt (1)i Cdi xti i0
5/10/2019
模型中有部分系数省缺了,那么该模型 称为疏系数模型。
5/10/2019
课件
34
疏系数模型类型
如果只是自相关部分有省缺系数,那么该疏系 数模型可以简记为ARIMA(( p1,, pm ), d, q)
p1,, pm 为非零自相关系数的阶数
如果只是移动平滑部分有省缺系数,那么该疏 系数模型可以简记为 ARIMA( p, d, (q1,, qn ))
26
建模
定阶
ARIMA(0,1,1)
参数估计
(1 B)xt 4.99661 (1 0.70766 B) t
Var(t ) 56.48763
模型检验
模型显著 参数显著
5/10/2019
课件
27
ARIMA模型预测
原则
最小均方误差预测原理
Green函数递推公式
一阶差分
第五章非平稳时间序列分析的程序

input year sha;dif=dif(sha);cards;1964 971965 1301966 156.51967 135.21968 137.71969 180.51970 205.21971 1901972 188.61973 196.71974 180.31975 210.81976 1961977 2231978 238.21979 263.51980 292.61981 3171982 335.41983 3271984 321.91985 353.51986 397.81987 436.81988 465.71989 476.71990 462.61991 460.81992 501.81993 501.51994 489.51995 542.31996 512.21997 559.81998 5421999 567;proc gplot;plot sha*year dif*year; symbol v=star c=red i=join;data a;input year x;dif1=dif(x);dif2=dif(dif1); cards;1950 5.43 1951 6.19 1952 6.63 1953 7.18 1954 8.95 1955 10.14 1956 11.74 1957 12.6 1958 17.26 1959 21.07 1960 22.38 1961 24 1962 24.8 1963 26.13 1964 27.61 1965 29.95 1966 33.92 1967 33.21 1968 34.8 1969 37.16 1970 42.41 1971 49.44 1972 57.74 1973 67.27 1974 78.57 1975 91.71 1976 106.7 1977 119.93 1978 135.84 1979 155.49 1980 178.29 1981 199.14 1982 215.75 1983 232.63 1984 260.41 1985 321.121986 361.951987 408.071988 464.381989 511.321990 551.361991 606.111992 691.741993 817.581994 941.951995 10401996 1100.081997 1219.091998 1319.31999 1452.94;proc gplot;plot x*year dif1*year dif2*year;symbol v=star c=red i=join;run;data a;input milk@@;time=intnx('month','1jan1962'd,_n_-1);format time year4.;dif1=dif(milk);dif1_12=dif12(dif1);cards;589 561 640 656 727 697 640 599 568 577 553 582 600 566 653 673 742 716 660 617 583 587 565 598 628 618 688 705 770 736 678 639 604 611 594 634 658 622 709 722 782 756 702 653 615 621 602 635 677 635 736 755 811 798 735 697 661 667 645 688 713 667 762 784 837 817 767 722 681 687 660 698 717 696 775 796 858 826 783 740 701 706 677 711 734 690 785 805 871 845 801 764 725 723 690 734 750 707 807 824 886 859 819 783 740 747 711 751 804 756 860 878 942 913 869 834 790 800 763 800 826 799 890 900 961 935 894 855809 810 766 805 821 773 883 898 957 924 881 837 784 791 760 802 828 778 889 902 969 947 908 867 815 812 773 813 834 782 892 903 966 937 896 858 817 827 797 843 ;proc gplot;plot milk*time dif1*time dif1_12*time;symbol v=star c=red i=join;run;data a;x0=0;do t=-10 to 1000;rand=10*rannor(12345);x=x0+rand;x0=x;if t>0 then output;end;proc gplot;plot x*t;symbol v=none c=black i=join;run;data a;x0=0;do t=-10 to 1000;rand=10*rannor(12345);x=x0+rand;x0=x;if t>0 then output;end;proc gplot;plot x*t;symbol v=none c=black i=join;run;goptions vsize=7cm hsize=10cm;data na_in;t=_n_;time=intnx('year','1jan1952'd,_n_-1);format time year4.;input agric indus cons trans commer;dif=dif(agric) ;keep time agric dif;cards;100 100 100 100 100 101.6 133.6 138.1 12 133 103.3 159.1 133.3 136 136.4 111.5 169.1 152.4 140 137.5 116.5 219.1 261.9 164 146.6 120.1 244.5 242.9 176 146.6 120.3 383.5 367 270.8 155.9 100.6 501.5 388.6 356.5 170.383.6 541.4 394 383.6 164.184.7 315.9 129.5 221.1 130.1 88.7 267.4 161.9 171.5 117.7 98.9 300.7 205.1 176 120.8 111.9 374.9 259 198.6 123.9 122.9 477.7 286 261.7 128 131.9 598.5 313 297.8 155.9 134.2 504.3 296.8 239.2 164.1 131.6 458.6 237.5 225.6 151.8 132.2 622.3 323.8 284.3 179.6 139.8 863 421 343 199.2 142 979 468.3 370.8 201.2 140.5 1043.5 452.5 389.3 208 153.1 1134.3 457.8 412.5 224.5 159.2 1128.9 484.1 394 220.6 162.3 1297.3 542 444.9 220.6 159.1 1249.2 568.3 426.4 214.8 155.1 1434 578.8 491.3 242 161.2 1679.1 573.5 546.9 296.4 171.5 1814.7 584.1 560.8 316.8 168.4 2012.7 757.7 584 318.8 180.4 2046.8 770 607.2 379.4 201.6 2170.1 806.9 681.3 397.5 218.7 2383.7 954.3 755.5 449.1 247 2738.8 1056.7 852.8 499.5 253.7 3275.2 1310.6 1024.3 593.7 261.4 3590.6 1540 1140.2 636.3 273.2 4058.8 1744.8 1269.9 715 279.4 4765 1884 1413.6 760.8 ;proc print;proc gplot;plot agric*time=1 dif*time=1;symbol1 c=red i=join v=square;proc arima;identify var=agric(1) stationarity=(adf) nlag=18;estimate q=1;forecast lead=10 id=time interval=year out=out;proc print data=out;proc gplot;where time>='1jan1955'd;plot agric*time=2 forecast*time=3 (l95 u95)*time=4/overlay; symbol2 c=black i=none v=star;symbol3 c=red i=join v=none;symbol4 c=green i=join v=none l=3 w=1;proc autoreg data=na_in;model agric=t/nlag=2 method=ml dwprob;output out=p p=a1 pm=a2 lcl=lcl ucl=ucl;proc gplot data=p;where time>='1jan1955'd;plot agric*time=2 a1*time=3 lcl*time=4 ucl*time=4/overlay; proc autoreg data=na_in;model agric=dif/LAGDEP=DIF nlag=1 method=ml noint; output out=p p=b1 pm=b2 lcl=lcl ucl=ucl;proc gplot data=p;where time>='1jan1955'd;plot agric*time=2 b1*time=3 lcl*time=4 ucl*time=4/overlay; run;goptions vsize=7cm hsize=10cm;data a;input year x@@;dif=dif(x);cards;1917 183.11918 183.91919 163.11920 179.51921 181.41922 173.41923 167.61924 177.41925 171.71926 170.11927 163.71928 151.91929 145.41930 1451931 138.91932 131.51933 125.7 1934 129.5 1935 129.6 1936 129.5 1937 132.2 1938 134.1 1939 132.1 1940 137.4 1941 148.1 1942 174.1 1943 174.7 1944 156.7 1945 143.3 1946 189.7 1947 212 1948 200.4 1949 201.8 1950 200.7 1951 215.6 1952 222.5 1953 231.5 1954 237.9 1955 244 1956 259.4 1957 268.8 1958 264.3 1959 264.5 1960 268.1 1961 264 1962 252.8 1963 240 1964 229.1 1965 204.8 1966 193.3 1967 179 1968 178.1 1969 181.1 1970 165.6 1971 159.8 1972 136.1 1973 126.3 1974 123.3 1975 118.5 ;proc gplot;plot x*year dif*year;symbol c=black i=join v=square;proc arima;identify var=x(1);estimate p=(1 4) noint;forecast lead=5 id=year out=out;proc gplot data=out;plot x*year=1 forecast*year=2 l95*year=3 u95*year=3/overlay; symbol1 c=black i=none v=star;symbol2 c=red i=join v=none;symbol3 c=green i=join v=none;run;goptions vsize=7cm hsize=10cm;data a;input x@@;dif1_4=dif4(dif(x));time=intnx('quarter','1jan1962'd,_n_-1);format time year4.;cards;1.1 0.5 0.4 0.7 1.6 0.6 0.5 0.7 1.3 0.6 0.5 0.7 1.2 0.5 0.4 0.6 0.9 0.5 0.5 1.12.9 2.1 1.7 2 2.7 1.3 0.9 1 1.6 0.6 0.5 0.7 1.1 0.5 0.5 0.6 1.2 0.7 0.7 11.5 1 0.9 1.1 1.5 1 1 1.62.6 2.1 2.33.6 54.5 4.5 4.95.7 4.3 4 4.4 5.2 4.3 4.2 4.5 5.2 4.1 3.9 4.1 4.8 3.5 3.4 3.5 4.2 3.4 3.6 4.3 5.5 4.8 5.46.5 8 77.48.5 10.1 8.9 8.8 9 10 8.7 8.8 8.9 10.4 8.9 8.9 9 10.2 8.6 8.4 8.49.9 8.5 8.6 8.7 9.8 8.6 8.4 8.2 8.8 7.6 7.5 7.6 8.1 7.1 6.9 6.6 6.8 6 6.2 6.2 ;proc gplot;plot x*time dif1_4*time;symbol c=black i=join v=star;proc arima;identify var=x(1,4);estimate p=2 noint;forecast lead=0 id=time out=out;proc gplot data=out;plot x*time=1 forecast*time=2 /overlay;symbol1 c=black i=none v=star;symbol2 c=red i=join v=none;run;data a;input x@@;dif1_12=dif12(dif(x));time=intnx('month','1jan1948'd,_n_-1);format time year4.;cards;446 650 592 561 491 592 604 635 580 510 553 554 628 708 629 724 820 865 1007 1025 955 889 965 878 1103 1092 978 823 827 928 838 720 756 658 838 684 779 754 794 681 658 644 622 588 720 670 746 616 646 678 552 560 578 514 541 576 522 530 564 442 520 484 538 454 404 424 432 458 556 506 633 708 1013 1031 1101 1061 1048 1005 987 1006 1075 854 1008 777 982 894 795 799 781 776 761 839 842 811 843 753 848 756 848 828 857 838 986 847 801 739 865 767 941 846 768 709 798 831 833 798 806 771 951 799 1156 1332 1276 1373 1325 1326 1314 1343 1225 1133 1075 1023 1266 1237 1180 1046 1010 1010 1046 985 971 1037 1026 947 1097 1018 1054 978 955 1067 1132 1092 1019 1110 1262 1174 1391 1533 1479 1411 1370 1486 1451 1309 1316 1319 1233 1113 1363 1245 1205 1084 1048 1131 1138 1271 1244 1139 1205 1030 1300 1319 1198 1147 1140 1216 1200 1271 1254 1203 1272 1073 1375 1400 1322 1214 1096 1198 1132 1193 1163 1120 1164 966 1154 1306 1123 1033 940 1151 1013 1105 1011 963 1040 838 1012 963 888 840 880 939 868 1001 956 966 896 843 1180 1103 1044 972 897 1103 1056 1055 1287 1231 1076 929 1105 1127 988 903 845 1020 994 1036 1050 977 956 818 1031 1061 964 967 867 1058 987 1119 1202 1097 994 840 1086 1238 1264 1171 1206 13031393 1463 1601 1495 1561 1404 1705 1739 1667 1599 1516 1625 1629 1809 1831 1665 1659 1457 1707 1607 1616 1522 1585 1657 1717 1789 1814 1698 1481 1330 1646 1596 1496 1386 1302 1524 1547 1632 1668 1421 1475 1396 1706 1715 1586 1477 1500 1648 1745 1856 2067 1856 2104 2061 2809 2783 2748 2642 2628 2714 2699 2776 2795 2673 2558 2394 2784 2751 2521 2372 2202 2469 2686 2815 2831 2661 2590 2383 2670 2771 2628 2381 2224 2556 2512 2690 2726 2493 2544 2232 2494 2315 2217 2100 2116 2319 2491 2432 2470 2191 2241 2117 2370 2392 2255 2077 2047 2255 2233 2539 2394 2341 2231 2171 2487 2449 2300 2387 2474 2667 2791 2904 2737 2849 2723 2613 2950 2825 2717 2593 2703 2836 2938 2975 3064 3092 3063 2991;proc gplot;plot x*time dif1_12*time;symbol c=black i=join v=none;proc arima;identify var=x(1,12);estimate p=1 q=(1)(12) noint;forecast lead=0 id=time out=out;proc gplot data=out;plot x*time=1 forecast*time=2 /overlay;symbol1 c=black i=none v=dot h=0.2;symbol2 c=red i=join v=none;run;data a;input returns@@;dif=dif(returns);r2=dif**2;y=log(returns);dify=dif(y);time=intnx('month','1apr1963'd,_n_-1);format time year4.;cards;0.00238 0.00238 0.00236 0.0025 0.00254 0.0026 0.00285 0.002810.00241 0.00288 0.00287 0.00292 0.00294 0.00273 0.00271 0.002820.00267 0.00273 0.00293 0.00285 0.00296 0.00281 0.00326 0.003210.00315 0.00319 0.00313 0.00313 0.00319 0.00313 0.0033 0.003190.00315 0.00355 0.0037 0.00371 0.00364 0.00381 0.00372 0.003680.00374 0.00389 0.00415 0.00389 0.00343 0.00377 0.00368 0.003640.00338 0.00283 0.00271 0.003 0.00309 0.00317 0.00343 0.003470.00355 0.0036 0.00398 0.00385 0.00389 0.00444 0.00453 0.004440.00432 0.00406 0.00432 0.00461 0.00398 0.005 0.00487 0.00470.00432 0.00508 0.00478 0.00508 0.00593 0.0055 0.00593 0.005420.0054 0.0054 0.00631 0.00534 0.00546 0.00542 0.00546 0.004950.005 0.00508 0.00483 0.00444 0.00377 0.00355 0.00338 0.002640.00283 0.00305 0.00338 0.00406;proc gplot;plot returns*time dif*time r2*time y*time dify*time;symbol c=black i=join v=none;proc arima;identify var=returns ;identify var=y(1);estimate p=0 q=0 noint;forecast lead=0 id=time out=out;data out;merge a out;by time;estimate=exp(y);proc gplot;plot returns*time=1 estimate*time=2 /overlay;symbol1 c=black i=none v=star h=0.5;symbol2 c=red i=join v=none;run;data a;input a@@;laga=lag(a);t=_n_;cards;143.1 140.3 139.4 140.7 139.6 140.4 141.2 140.9 141.3 141.7 142.8 144.7 144.4 140.9 139.5 140.8 138.7 139 140 140.4 141.6 142.3 143.4 145.7 145.7 142.8 141.8 143.5 141.8 142.4 142.8 142.7 144.3 145.7 147.6 150.5 150.2 146.9 146 148 145.8 146.2 146.4 145.8 146.9 148.4 150.2 153.3 153.6 150.1 149.3 151.5 149.3 151.4 151.3 150.9 152.5 154.4 156.7 159 159.4 155.4 154.6 156.8 154.2 155.5 157.1 157 159.4 161.3 163.1 166.4 166.9 161.9 161.5 164.2 160.3 162.2 163.5 162.8 165.6 168.2 169.9 174.4 175.6 170.3 170.4 174.1 169.6 171.7 171 170 172.7 173.4 174.6 178.6 178.4 173.4 174.6 176.6 174.1 177.4 179.1 179 181.7 183.9 185.7 190.3 189 184.9 185.4 189.3 186.5 190.2 191.9 191.4 193.9 196.3 199.6 204.8 205.9 199.3 199.8 203.6 199.4 202.3 203.3 201.5 203.2 205 207 211.4212.9 204 205.5 210.1 206.2 208.9 210.1 210 212.8 214.4 216.7 222.2 222.6 216.6 218.6 223.7 221.1 225.2 227.5 225.9 227.7 229.1 231.2 236.9 237.5 231.4 234.2 239.5 234.7 238.8 241.8 241.3 244.5 247 250.5 258.9 259.4 251.2 251.6 257 253.6 259.3 261.1 258.6 259.5 261.4 265.6 273.3 271.8 264.1 266.5 271.6 266.3 271.5 273.5 271 272.6 274.8 278.8 285.2 281.8 273.3 276.4 281.4 278.1 286 288 286.3 287.8 288.5 293.5 299 296.8 289 291.4 299.9 295.1 299.4 302.3 301 302.5 307 309.7 318.6 317.7 309 312.2 322.7 315.6 321.7 326.3 324.3 327.7 332 335.4 344.1 343.4 332 334.9 347.5 342.4 349.4 353.9 351.7 357 359.4 362.9 372.5 367.8 356.4 360.8 376.2 367.1 376.7 383.3 381.9 385.6 387.7 389.8 398.6 390.7 380.9 382.4 387.1 377.8 387.6 394.8 398.5 404.9 411 416.1 419.8 416.5 405.7 412.5 431.3 418.6 423 427.9 426.1 427.3 429.8 435.2 447.2 448.7 432.6 435.8 451.3 441.1 446.5 449.6 450 456.4 466 474.5 486 483 474.2 482.9 498.7 494.1 503.7 510.7 508.5 511.5 517.4 522.1 533.4 530.4 517.6 524.2 539.2 530.8 541.4 543.3 539 542.5 542.1 549.6 564.5 561.1 551.9 558.3 575 569.4 585.2 592 594.8 602.2 605.5 615.1 633.5 626.8 613.1 624.6 647.2 645.7 663.5 674 679.1 685.2 692.8 709.5 740.6 737.5 717.1 723.5 752.5 739.9 744.4 746.8 745 745.2 753.7 756 765.9 764.7 745 752.1 778.3 763.8 778.8 785.6 781.3 780 780.8 787.1 803.2 793 772.3 775.2 791.3 767.2 773.8 781.7 777.4 778.5 784.5 791.4 811.9 802.4 788.3 796.2 818 797.3 810.8 812.9 814.5 818.9 817.6 826.1 844.3 833.2 823.4 835 852.9 841.9 857.8 861.9 864.2 867.3 875 893.4 916.8 918.1 916.5;proc gplot;plot a*T;symbol v=none i=join c=black;proc autoreg;model a=laga/lagdep=laga nlag=2 garch=(p=1,q=1);output out=out p=forecast ;proc gplot;plot a*t=1 forecast*t=2 /overlay;symbol1 c=black v=star i=none h=0.1;symbol2 c=red v=none i=join;run;data example5_1;input x@@;difx=dif(x);t=_n_;cards;1.05 -0.84 -1.42 0.202.81 6.72 5.40 4.385.52 4.46 2.89 -0.43 -4.86 -8.54 -11.54 -16.22-19.41 -21.61 -22.51 -23.51 -24.49 -25.54 -24.06 -23.44-23.41 -24.17 -21.58 -19.00 -14.14 -12.69 -9.48 -10.29-9.88 -8.33 -4.67 -2.97 -2.91 -1.86 -1.91 -0.80 ;proc gplot;plot x*t difx*t;symbol v=star c=black i=join;proc arima;identify var=x(1);estimate p=1;forecast lead=5 id=t out=out;proc gplot data=out;plot x*t=1 forecast*t=2 l95*t=3 u95*t=3/overlay;symbol1 c=black i=none v=star;symbol2 c=red i=join v=none;symbol3 c=green I=join v=none;run;goptions vsize=7cm hsize=10cm;data example5_2;input x@@;lagx=lag(x);t=_n_;cards;3.03 8.46 10.22 9.80 11.96 2.838.43 13.77 16.18 16.84 19.57 13.2614.78 24.48 28.16 28.27 32.62 18.4425.25 38.36 43.70 44.46 50.66 33.0139.97 60.17 68.12 68.84 78.15 49.8462.23 91.49 103.20 104.53 118.18 77.8894.75 138.36 155.68 157.46 177.69 117.15;proc gplot data=example5_2;plot x*t=1;symbol1 c=black i=join v=star;proc autoreg data=example5_2;model x=t/ dwprob ;proc autoreg data=example5_2;model x=t/nlag=5 backstep method=ml noint ;output out=out p=xp pm=trend;proc gplot data=out;plot x*t=2 xp*t=3 trend*t=4 / overlay ;symbol2 v=star i=none c=black;symbol3 v=none i=join c=red w=2;symbol4 v=none i=join c=green w=2;proc autoreg data=example5_2;model x=lagx/lagdep=lagx;model x=lagx/lagdep=lagx noint;output out=out p=xp;proc gplot data=out;plot x*t=2 xp*t=3 / overlay ;run;data example5_3;input x@@;t=_n_;cards;10.77 13.30 16.64 19.54 18.97 20.52 24.36 23.51 27.16 30.80 31.84 31.63 32.68 34.90 33.85 33.09 35.46 35.32 39.94 37.47 35.24 33.03 32.67 35.20 32.36 32.34 38.45 38.17 32.14 39.70 49.42 47.86 48.34 62.50 63.56 67.61 64.59 66.17 67.50 76.12 79.31 78.85 81.34 87.06 86.41 93.20 82.95 72.96 61.10 61.27 71.58 88.34 98.70 97.31 97.17 91.17 80.20 85.12 81.40 70.87 57.75 52.35 67.50 87.95 85.46 84.55 98.16 102.42 113.02 119.95 122.37 126.96 122.79 127.96 139.20 141.05 140.87 137.08 145.53 145.59 134.36 122.54 106.92 97.23 110.39 132.40 152.30 154.91 152.69 162.67 160.31 142.57 146.54 153.83 141.81 157.83 161.79 142.07 139.43 140.92 154.61 172.33 191.78 199.27 197.57 189.29 181.49 166.84 154.28 150.12 165.17 170.32 £»proc gplot data=example5_3;plot x*t=1;symbol1 c=black i=join v=star;proc autoreg data=example5_3;model x=t/nlag=5 dwprob archtest;model x=t/nlag=2 noint garch=(p=1,q=1);output out=out p=xp;proc gplot data=out;plot x*t=2 xp*t=3/overlay;symbol2 v=star i=none c=black;symbol3 v=none i=join c=red w=2;run;。
非平稳时间序列的随机分析

第二节 差分运算
对于随机非平稳序列来说,我们难以直接找 到其变化发展规律,主要是因为非平稳序列通常 都具有某种不稳定的趋势。所以,分析非平稳序 列的第一步是采取有效的手段提取其趋势使序列 变为平稳序列,然后利用平稳序列分析方法来处 理。提取序列趋势的工具主要是差分运算。
kt
t
例如,若
xt a bt t
则对序列 xt 做一阶差分
xt b t
就提取了序列中的确定性趋势信息。
若 xt a bt ct2 t ,则对 xt 做二阶差分
2 x 2c 2
t
t
即可提取序列中的确定性趋势信息。
yt 01yt q 2yt q1 vt
式中,vt 为残差序列。如果我们基于历史信息: ytq , ytq1, 预测 yt 的值,则 vt 可以理解为预测
误差,记 Var(v ) 2(q) ,显然有 2(q) Var( y ) ,
t
v
v
t
且滞后期 q 越大,意味着预测的步长越长,预测
的误差就越大,即2v(q) 越大。
实际上,时间序列中的差分运算类似于函数的 求导运算,如果一个时间序列的确定性趋势是时间 的 d 次多项式,则 d 阶差分后的序列的确定性趋势 就一定是常数,将不会再蕴含时间趋势,从而实现 序列的平稳化。
d
d
tj
j k,
( k 为常数)
j0
而由Cramer分解定理知,方差齐性非平稳序 列都可以分解为如下形式:
y
)t
,说明序列发展的
随机性强,历史信息对现值估计效果差,这时称
序列 yt是随机序列。
例如,对于平稳的ARMA(p,q) 模型:
非平稳和季节时间序列模型分析方法

非平稳和季节时间序列模型分析方法时间序列分析是指对时间序列数据进行建模和预测的统计方法。
根据数据的特点,时间序列可以分为平稳序列和非平稳序列。
在实际应用中,很多时间序列数据并不满足平稳性的假设,因此需要对非平稳序列进行处理和分析。
非平稳序列分析的方法之一是差分法。
差分法的基本思想是通过对原始序列进行差分,得到一个新的序列,使其成为平稳序列。
差分法可以通过一阶差分、二阶差分等方法来实现。
一般来说,一阶差分可以用来处理线性趋势,而二阶差分可以用来处理二次趋势。
另一种非平稳序列分析的方法是趋势-季节分解法。
这种方法首先对时间序列进行趋势分解,将原始序列拆分为趋势、季节和残差三个部分。
然后对残差序列进行平稳性检验,判断是否需要进一步进行差分。
最后,可以利用拆分后的趋势和季节序列进行预测。
对于带有季节性的时间序列数据,还可以采用季节时间序列模型进行分析。
常见的季节时间序列模型包括季节自回归移动平均模型(SARIMA)和季节指数平滑模型。
这些模型可以对季节性进行建模,并利用历史数据进行预测。
总结起来,非平稳和季节时间序列的分析方法可以包括差分法、趋势-季节分解法和季节时间序列模型。
这些方法能够有效地处理和分析非平稳和带有季节性的时间序列数据,为实际应用提供了重要的参考。
时间序列分析是一种广泛应用于金融、经济、气象、销售、股票市场等领域的数据分析方法,它的目标是根据过去的数据模式,预测未来的趋势和行为。
在时间序列分析中,平稳性是一个重要的概念,指的是在时间序列的整个时间范围内,序列的统计特性不会随着时间的推移而发生显著的变化。
然而,在实际应用中,很多时间序列数据并不满足平稳性的假设,因此需要对非平稳序列进行处理和分析。
非平稳序列的特点是随着时间的推移,其均值、方差和协方差等统计特性会发生显著的变化。
这使得对其进行建模和预测变得困难。
因此,我们需要采取一些方法来处理非平稳序列,使其满足平稳性的假设。
差分法是一种常用的处理非平稳序列的方法。
非平稳时间序列分析
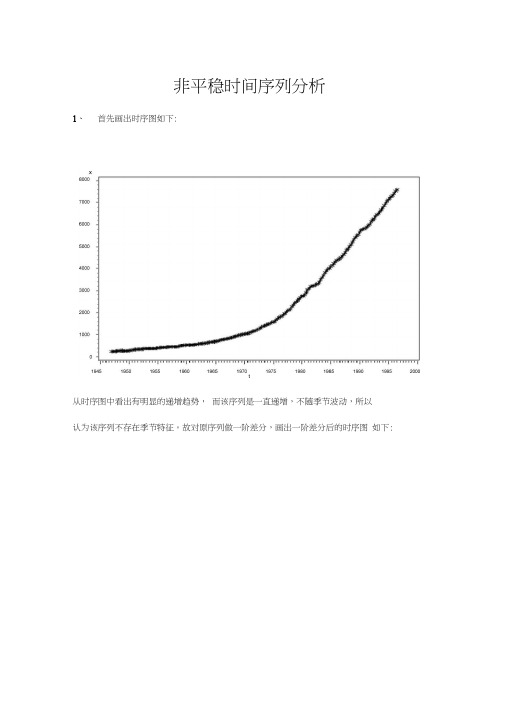
非平稳时间序列分析1、首先画出时序图如下:t从时序图中看出有明显的递增趋势,而该序列是一直递增,不随季节波动,所以认为该序列不存在季节特征。
故对原序列做一阶差分,画出一阶差分后的时序图如下:difx140 130 120 110 100 90 80 70 60 50 40 30 20 10 0 -10从中可以看到一阶差分后序列仍然带有明显的增长趋势,再做二阶差分:dif2x90 80 70 60 50 40 30 20 10 0 -10 -20 -30 -40 -50 -60 -70 -80 -90 -100 -110做完二阶差分可以看到,数据的趋势已经消除,接下来对二阶差分后的序列进行194519501945 19551960196519701975198019851990199520001950 1955 1960 1965 1970 1975 1980 1985 1990 1995 2000检验:AutocorrelationsLag Covariance Correlation -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1 Std Error0 577.333 1.00000 | |********************| 01 -209.345 -.36261 | *******| . | 0.0712472 -52.915660 -.09166 | .**| . | 0.0800693 9.139195 0.01583 | . | . | 0.0806004 15.375892 0.02663 . |* . | 0.0806155 -59.441547 -.10296 .**| . | 0.0806606 -23.834489 -.04128 | . *| . | 0.0813247 100.285 0.17370 | . |*** | 0.0814318 -146.329 -.25346 | *****| . | 0.0832909 52.228658 0.09047 | . |**. | 0.08711810 21.008575 0.03639 | . |* . | 0.08759311 134.018 0.23213 | . |***** | 0.08767012 -181.531 -.31443 | ******| . | 0.09073613 23.268470 0.04030 | . |* . | 0.09610814 71.112195 0.12317 | . |** . | 0.09619415 -105.621 -.18295 | ****| . | 0.09699116 37.591996 0.06511 . |* . | 0.09872717 23.031506 0.03989 | . |* . | 0.09894518 45.654745 0.07908 | . |** . | 0.09902719 -101.320 -.17550 | ****| . | 0.09934720 127.607 0.22103 | . |**** | 0.10090821 -61.519663 -.10656 | . **| . | 0.10333722 35.825317 0.06205 | . |* . | 0.10389323 -93.627333 -.16217 | .***| . | 0.10408124 55.451208 0.09605 | . |** . |从其自相关图中可以看出二阶差分后的序列自相关系数很快衰减为零,且都在两倍标准差范围之内,所以认为平稳,白噪声检验结果:Autocorrelation Check for White NoiseTo Chi- Pr >Lag Square DF ChiSq------------------- Autocorrelations -------------------6 30.70 6 <.0001 -0.363 -0.092 0.016 0.027 -0.103 -0.04112 84.54 12 <.0001 0.174 -0.253 0.090 0.036 0.232 -0.31418 97.98 18 <.0001 0.040 0.123 -0.183 0.065 0.040 0.07924 126.99 24 <.0001 -0.175 0.221 -0.107 0.062 -0.162 0.096P 值都小于 0.05 ,认为不是白噪声。
非平稳时序数据时间序列分析方法研究

非平稳时序数据时间序列分析方法研究时间序列分析是一种重要的数据分析方法,它可以对时间序列数据进行建模、预测和分析。
然而在实际应用中,我们往往会遇到非平稳的时间序列数据。
非平稳时间序列数据的特点是其均值、方差等统计特征会随时间变化而变化,这给分析和预测带来了一定的困难。
本文将介绍非平稳时间序列数据的常见特征、分析方法和预测方法。
一、非平稳时间序列数据的常见特征1. 长期趋势:非平稳时间序列数据在较长时间范围内往往具有明显的上升或下降趋势。
2. 季节性变化:非平稳时间序列数据往往具有周期性的季节性变化,如气温、雨量等。
3. 波动性变化:非平稳时间序列数据在短期内往往呈现出较大的波动性,如股票价格、汇率等。
二、非平稳时间序列数据的分析方法1. 差分法:差分法是最常用的处理非平稳时间序列数据的方法,其思想在于将时间序列数据的差分转换为平稳时间序列数据再进行建模和分析。
差分法有一阶差分法、二阶差分法等多种,根据具体问题选择不同的差分方法。
2. 增长率法:增长率法是将时间序列数据的增长率序列作为新的时间序列数据来建模和分析,常用于处理长期趋势明显的非平稳时间序列数据。
3. 滑动平均法:滑动平均法是通过计算一定时间范围内数据的平均值来平滑时间序列数据并去除噪声干扰,常用于处理周期性和波动性明显的非平稳时间序列数据。
三、非平稳时间序列数据的预测方法1. ARIMA模型:ARIMA模型是传统的时间序列建模技术之一,其通过差分法将非平稳时间序列数据转化为平稳时间序列数据后建立自回归模型、移动平均模型和差分模型,用于进行预测。
2. GARCH模型:GARCH模型是通过对时间序列数据的方差进行建模并考虑异方差性差异来进行预测的一种方法,常用于处理波动性明显的非平稳时间序列数据。
3. ARCH模型:ARCH模型是GARCH模型的前身,其只考虑时间序列数据的方差进行建模,适用于处理时间序列数据的波动性变化。
总而言之,非平稳时间序列数据分析方法和预测方法的选择需要根据具体问题来确定。
平稳性和非平稳时间序列分析

β1 + β 3 Xt 如果我们作下列变换 ecmt = Yt − 1− β2 α = β2 − 1 ,那么模型变为:
,
∆Yt = β 0 + β1∆X t + αecmt −1 + ε t
误差修正模型的自动调整机制类似于适应性预 期模型。如果误差修正项的系数 α 在统计上 是显著的,它将告诉我们 Y 在一个时期里的失 衡,有多大一个比例部分可在下一期得到纠正。 或者更应该说“失衡”对下一期 水平变化的 Y 影响的大小)。
6
1、基本的DF检验方法 (1)检验时间序列{ Yt }是否属于最基本的 单位根过程,也就是随机游走过程 Yt = Yt −1 + ε t ,其中 ε t 为白噪声过程。 (2)检验思路 首先 Yt 服从如下的自回归模型 Yt = δYt −1 + ε t
7
如果其中 δ = 1 ,或者变换成如下的回归 模型 ∆Yt = λYt −1 + ε t 中的 λ = 0 ,那么时间序列{ Yt }就是最基 本的单位根过程 Yt = Yt −1 + ε t ,肯定是非平 稳的。 对上述差分模型中的显著性检验,就是 检验时间序列是否存在上述单位根问题。
25
ˆ 3、把 ut −1 作为误差修正项,代入前述ECM 模型。因为 Yt 和 X t 有协整关系,ECM模 型各项都平稳,因此可直接用OLS法估计 参数。最后再进行相关检验和进行应用 分析等。
26
15
四、时间序列的协积性 (一)定义 如果一组时间序列都 X 1 ,L, X n 是同阶单积 的( I (d ) ),并且存在向量 ( β1 ,L, β n ) 使加权组合 β1 X 1 + L + β n X n 为平稳序列 (I (0)),则称这组时间序列为“协积的 协积的” 协积的 (Cointegrated),其中 ( β1 ,L, β n ) 称为 “协积向量”。
9_第五章_非平稳时间序列的随机分析_残差自回归模型

9_第五章_非平稳时间序列的随机分析_残差自回归模型在时间序列分析中,我们常常遇到非平稳时间序列的问题,这些时间序列的均值和方差都是随着时间变化而变化的。
对于这样的时间序列,我们可以通过使用残差自回归模型来对其进行建模和分析。
残差自回归模型是指将时间序列的残差作为目标变量,将其滞后值作为自变量进行回归分析。
通过构建残差自回归模型,我们可以研究和预测非平稳时间序列中的随机变动。
在构建残差自回归模型之前,我们首先需要对非平稳时间序列进行平稳化处理。
常见的平稳化方法包括差分法和对数差分法。
差分法是指对时间序列进行一阶或高阶差分,使其成为平稳的时间序列。
对数差分法是指先对时间序列取对数,然后对取对数后的序列进行差分。
平稳化之后,我们可以将时间序列表示为自回归模型的形式,即ARMA(p,q)模型。
ARMA(p,q)模型可表示为:Y_t=c+φ_1*Y_(t-1)+φ_2*Y_(t-2)+...+φ_p*Y_(t-p)+ε_t-θ_1*ε_(t-1)-θ_2*ε_(t-2)-...-θ_q*ε_(t-q)其中,Y_t为时间序列的观测值,c为常数项,φ_1,φ_2,...,φ_p为自回归系数,ε_t为残差项,θ_1,θ_2,...,θ_q为残差自回归系数。
当我们构建完残差自回归模型后,我们可以对模型的拟合程度进行评估,常用的方法包括残差序列的自相关图和偏自相关图。
如果残差序列呈现出随机的特征,且自相关系数和偏自相关系数都接近于零,则说明残差自回归模型拟合得较好。
此外,我们也可以使用残差自回归模型进行预测。
预测方法一般包括点预测和区间预测。
点预测是指对未来一期的观测值进行预测,区间预测是指对未来多期的观测值进行预测,并给出一个置信区间。
需要注意的是,在进行残差自回归模型分析时,我们需要确保残差序列是一个白噪声序列,即残差项之间是独立且具有相同的分布。
如果残差序列不满足白噪声假设,我们需要对模型进行修正。
总结起来,通过使用残差自回归模型,我们可以对非平稳时间序列进行建模和分析。
非平稳和季节时间序列模型分析方法

非平稳和季节时间序列模型分析方法非平稳时间序列是指在时间序列数据中,均值、方差、自相关函数等统计性质随时间变化的数据。
这种时间序列模型常常由于其自身的特性而较难进行分析和预测。
不过,季节时间序列是非平稳时间序列的一种特殊类型,其特点是在数据中存在明显的季节性变化。
对于这种时间序列,可以采用不同的分析方法进行预测和建模。
一、非平稳时间序列分析方法:1.差分法:差分法是通过对序列数据进行相邻时间点的差分,使得序列转变为平稳时间序列。
差分法有一阶差分、二阶差分等。
通过差分法可以使得序列的单位根等统计性质得到稳定。
2.滑动平均法:滑动平均法基于序列的平均值,将序列转化为平稳时间序列。
该方法通过计算序列的滑动平均值来消除序列的变化趋势。
3.指数平滑法:指数平滑法是一种通过加权平均的方法来消除序列的变化趋势。
指数平滑法可以根据实际情况选择不同的权重系数来进行计算。
4.回归分析:对于非平稳时间序列,通过引入自变量,建立回归模型来描述序列的变化。
回归分析可以通过多个变量的关系来解释序列的变动。
二、季节时间序列分析方法:1.季节分解法:季节分解法是将季节时间序列分解为长期趋势、季节性和随机成分的组合。
这种方法可以将季节性的变动独立出来,从而更好地进行建模和预测。
2.季节移动平均法:季节移动平均法通过计算时间序列在相邻季节的平均值,消除序列的季节性变动。
这种方法可以降低季节时间序列的变化趋势。
3.季节差分法:季节差分法是将季节时间序列转化为其相邻时间点的差分。
通过差分法可以去除序列的季节性变化,使得序列更为平稳。
4.季节ARIMA模型:季节ARIMA模型是一种结合了季节差分和ARIMA 模型的方法。
该方法可以同时考虑序列的季节性变化和非平稳性,通过建立ARIMA模型来进行预测和分析。
以上所述是常用的非平稳和季节时间序列模型分析方法。
根据实际情况,我们可以选择合适的方法来分析和预测时间序列数据,以提高分析的准确性。
第五章 非平稳序列的随机分析_11.10

g 3、转换函数的确定:要使得Var[g(xt)]等于常数, (⋅) 与 h(⋅) 、转换函数的确定: 等于常数, 1 具有倒函数关系, 具有倒函数关系,即 g ′( µ t ) = h( µ t )
常用转换函数的确定
实践中,许多金融时序都呈现出异方差性质, 实践中,许多金融时序都呈现出异方差性质,通 常序列的标准差与其均值具有某种正比关系。 常序列的标准差与其均值具有某种正比关系。
1、零均值 、
E (ε t ) = 0
2、纯随机 Cov (ε t , ε t −i ) = 0, ∀i ≥ 1 、 3、方差齐性 、
Var (ε t ) = σ ε
2
5.4 异方差的性质
异方差的定义
如果随机误差序列的方差会随着时间的变化而 如果随机误差序列的方差会 随着时间的变化而 变化, 变化,这种情况被称作为异方差
拟合模型口径及拟合效果图
∇ log( xt ) = ε t ⇔ log( xt ) − log( xt −1 ) = ε t
注:图中星号为序列观察值;红色曲线为序列拟合值 图中星号为序列观察值;
例5.11的SAS过程 的 过程
data a; input returns@@; dif=dif(returns); /*构建残差序列 构建残差序列*/ 构建残差序列 r2=dif**2; /*构建残差平方和序列 构建残差平方和序列*/ 构建残差平方和序列 y=log(returns); /*原序列对数变换 原序列对数变换*/ 原序列对数变换 dify=dif(y); /*对数变换后序列差分 对数变换后序列差分*/ 对数变换后序列差分 time=intnx('month','1apr1963'd,_n_-1); format time year4.; cards; 原始数据 ; proc gplot; plot returns*time dif*time r2*time y*time dify*time; /*对应书上的图 对应书上的图5-37~图5-41*/ 对应书上的图 图 symbol c=black i=join v=none;
非平稳时间序列分析与预测技术

非平稳时间序列分析与预测技术随着科技的不断发展和数据需求的增加,时间序列分析与预测技术在各行各业中扮演着重要的角色。
在现实生活中,很多数据都呈现出非平稳的特性,这使得传统的平稳时间序列分析方法可能不再适用。
因此,研究非平稳时间序列的分析与预测技术显得尤为重要。
### 非平稳时间序列的特点非平稳时间序列与平稳时间序列不同,它的均值、方差或自相关性随时间变化而变化。
这使得非平稳时间序列更具挑战性,也更具有实际意义。
在实际数据中,非平稳时间序列更为常见,因此我们需要一些特定的技术来处理这类数据。
### 非平稳时间序列分析方法常见的非平稳时间序列分析方法包括趋势分解、差分法、移动平均法等。
趋势分解是将非平稳时间序列分解为趋势项、季节项和随机项,以便更好地分析其规律性。
差分法是通过对数据进行差分操作,将非平稳时间序列转化为平稳时间序列,再应用传统的时间序列分析方法。
移动平均法则是通过计算数据的移动平均值来减小数据的变异性,从而更好地揭示数据的规律。
### 非平稳时间序列预测技术在面对非平稳时间序列的预测问题时,我们可以借助传统的时间序列预测技术,如ARIMA模型、指数平滑法等。
ARIMA模型是一种常用的时间序列预测模型,可以有效地处理具有自回归和滞后项的数据。
指数平滑法则通过指数加权的方法,对数据进行平滑处理,从而得到预测结果。
这些方法在处理非平稳时间序列时都具有一定的效果,可以为我们提供准确的预测结果。
### 应用案例以股市数据为例,股市价格表现出明显的非平稳特性,但投资者又需要准确的价格预测来做出决策。
通过对股市数据进行趋势分解、差分和移动平均处理,再应用ARIMA模型或指数平滑法进行预测,投资者可以更好地把握市场趋势,做出明智的投资选择。
### 总结非平稳时间序列分析与预测技术在实际应用中具有广泛的应用前景,可以帮助我们更好地理解数据的本质,做出准确的预测。
通过不断研究和探索,我们可以不断完善非平稳时间序列分析与预测技术,为各行各业的数据分析提供更可靠的支持。
非平稳时间序列预测建模研究

非平稳时间序列预测建模研究随着经济、金融等领域非平稳时间序列数据的增多,非平稳时间序列建模的研究也越来越成为关注的热点。
本文将从预测建模的角度,介绍最近几年来国内外学者们在这一领域的探索和发展。
1. 背景介绍非平稳时间序列数据是指随时间推移而变化的数据,其均值、方差、自相关等统计特征随着时间的变化而发生改变。
因此,对于非平稳时间序列的预测建模,传统的时间序列方法往往不能很好地适应数据动态变化的特点。
因此,如何处理非平稳时间序列数据,成为了建模研究中一个重要的问题。
2. 研究现状目前,非平稳时间序列建模研究主要包括以下几个方面:(1)差分法差分法是一种最常用的非平稳时间序列预测方法。
其基本思想是将非平稳时间序列转化为平稳时间序列,再进行预测建模。
差分法的优点是简便易行,但其也存在一些缺陷,如变异系数不同情况下预测精度有较大差异,选择滞后期时若选择不当将导致差分信号滞后。
(2)单变量模型单变量模型是一种将过去的观测值作为当前值,基于ARIMA模型的预测方法。
单变量模型可以利用过去的观测值,来预测未来一个时间点的值,但是其受限于过去观测值的作用,无法考虑到其他因素对观测值的影响。
(3)向量自回归模型向量自回归模型是一种考虑多个变量之间相互影响的模型,可以容易地处理非平稳时间序列,具有强的可拓展性和柔性,但是由于模型参数较多,训练时间较长,对于大规模数据的建模存在困难。
(4)深度学习模型近年来,深度学习模型中的循环神经网络已经成为一种热门的预测方法。
LSTM模型作为一种深度学习模型,在处理非平稳时间序列的预测建模方面,具有良好的性能。
但是,LSTM模型的参数较多,训练时间较长,同时,其也受初值选取的影响。
3. 发展趋势在近年来的研究中,非平稳时间序列预测建模的方向主要包括以下两个方面:(1)多源信息融合不同数据来源之间的信息具有互补性,可以为非平稳时间序列的预测模型提供更多的特征。
因此,近年来,研究者开始尝试将不同数据源的信息进行融合,进而提高预测精度。
非平稳的时间序列平稳化的方法

非平稳的时间序列平稳化的方法
时间序列是指在时间上按一定间隔排列的一组数据,它是许多实际问题中经常遇到的一类数据。
在实际应用中,我们经常遇到非平稳的时间序列,即数据具有随时间变化的趋势、季节性或周期性等特征,这导致时间序列的随机性较弱,难以进行有效的分析和预测。
为了解决这个问题,需要对非平稳的时间序列进行平稳化处理,使其满足平稳性条件,从而提高分析和预测的准确性。
平稳性是指时间序列在时间上的统计性质不随时间而改变,即均值、方差和自相关系数不随时间变化。
在实际应用中,我们通常采用差分法、对数变换法、移动平均法和指数平滑法等方法对非平稳的时间序列进行平稳化处理。
差分法是指对时间序列进行一阶或高阶差分运算,使其满足平稳性条件。
对数变换法是指对时间序列取对数,从而将其变成线性关系,进而使其满足平稳性条件。
移动平均法是指对时间序列进行平均处理,消除季节性和周期性的影响,使其满足平稳性条件。
指数平滑法是指根据过去的数据,通过加权平均的方法对未来数据进行预测,从而使时间序列平稳。
总之,选择何种方法进行时间序列平稳化需要根据具体情况而定,需要结合数据的特征和应用场景进行选择。
- 1 -。
实验五非平稳序列的确定性分析

路漫漫其修远兮,吾将上下而求索 - 百度文库实验五 非平稳序列的确定性分析【实验目的】对非平稳时间序列的确定性分析 【实验内容】1.趋势分析; 2.季节效应分析; 3.综合分析; 4. X-12过程。
【实验指导】 一、ARMA 模型分解二、确定性因素分解 ⏹ 传统的因素分解⏹ 长期趋势 ⏹ 循环波动 ⏹ 季节性变化 ⏹ 随机波动⏹ 现在的因素分解⏹ 长期趋势波动 ⏹ 季节性变化 ⏹ 随机波动(一)趋势分析有些时间序列具有非常显著的趋势,我们分析的目的就是要找到序列中的这种趋势,并利用这种趋势对序列的发展作出合理的预测方法: 1.趋势拟合法趋势拟合法就是把时间作为自变量,相应的序列观察值作为因变量,建立序列值随时间变化的回归模型的方法。
(1)线性拟合例1:拟合澳大利亚政府1981——1990年每季度的消费支出序列,数据见下表。
tt B B x εμ)()(ΦΘ+=确定性序列随机序列8444 9215 8879 8990 8115 9457 8590 9294 8997 9574 9051 9724 9120 10143 9746 10074 9578 10817 10116 10779 9901 11266 10686 10961 10121 11333 10677 11325 10698 11624 11052 11393 10609 12077 11376 11777 11225 12231 11884 12109800090001000011000120001300081828384858687888990GOV_CONS长期趋势呈现出非常的线性递增趋势,于是考虑使用线性模型2,1,2, (40)()0,()t t t t x a bt I t E I Var I σ=++=⎧⎨==⎩拟合该序列的发展。
使用最小二乘法得到未知参数的估计值为:ˆˆ8498.69,89.12ab ==. 对拟合模型进行检验,检验结果显示方程显著成立,且参数非常显著。
