湖南省长沙市雅礼中学2019届高三上学期月考(一)数学理试题 扫描版
湖南省长沙市雅礼中学2019届高5月考数学(理)试题 Word版含解析

湖南省长沙市雅礼中学2019届高5月月考试题数学(理)全卷满分150分,考试时间120分钟。
★祝考试顺利★注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题作答用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试卷和草稿纸上无效。
3.非选择题作答用0.5毫米黑色墨水签字笔直接答在答题卡上对应的答题区域内。
答在试卷和草稿纸上无效。
考生必须保持答题卡的整洁。
考试结束后,只需上交答题卡。
第I卷一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集I是实数集R,都是I的子集(如图所示),则阴影部分所表示的集合为A. B.C. D.【答案】B【解析】由题意,由图知阴影部分所表示的集合为故选B.【点睛】本题考查Venn图表达集合的关系及运算,解题的关键是根据图象得出再由集合的运算求出阴影部分所表示的集合.2.设,其中x,y是实数,则A. 1B.C.D. 2【答案】B【解析】试题分析:因为所以故选B.【考点】复数运算【名师点睛】复数题也是每年高考的必考内容,一般以客观题的形式出现,属得分题.高考中考查频率较高的内容有:复数相等、复数的几何意义、共轭复数、复数的模及复数的乘除运算.这类问题一般难度不大,但容易出现运算错误,特别是中的负号易忽略,所以做复数题时要注意运算的准确性.3.已知命题:函数的图象恒过定点;命题:若函数为偶函数,则函数的图象关于直线对称,则下列命题为真命题的是()A. B. C. D.【答案】D【解析】试题分析:因为函数的图象恒过定点,所以命题为假命题,若函数为偶函数,则函数的图象关于直线对称,所以命题也为假命题,所以为真命题.故选D.考点:复合命题的真假.【方法点睛】由函数的奇偶性,对称轴和平移得到命题假,则为真命题. 复合命题的真假判断的方法:(1)非复合命题判断真假:当为真时,非为假;当为假时,非为真,即“非”形式的复合命题的真假与的真假相反;(2)“且”形式的复合命题真假判断:当、为真时,且为真;当、中至少有一个为假时,且为假,即“且”形式的复合命题,当与同为真时为真;(3)“或”形式的复合命题真假判断:当,中至少有一个为真时,“或”为真;当,都为假时,“或”为假,即“或”形式的复合命题,当与同为假时为假.本题考查命题的真假判断解题时要认真审题,注意复合命题的性质的合理应用,属于中档题.4.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是A. 56B. 60C. 120D. 140【答案】D【解析】【分析】根据已知中的频率分布直方图,先计算出自习时间不少于22.5小时的频率,进而可得自习时间不少于22.5小时的频数.【详解】根据频率分布直方图,200名学生中每周的自习时间不少于22.5小时的频率为(0.16+0.08+0.04)×2.5=0.7,故200名学生中每周的自习时间不少于22.5小时的人数为200×0.7=140.故选:D.【点睛】本题考查的知识点是频率分布直方图,难度不大,属于基础题目.5.执行如图所示的程序框图,若输入如下四个函数:①;②;③;④.则输出的函数是()A. B.C. D.【答案】A【解析】试题分析:对①,显然满足,且存在零点.故选A.考点:程序框图及函数的性质.6.若变量x,y满足则x2+y2的最大值是A. 4B. 9C. 10D. 12【答案】C【解析】试题分析:画出可行域如图所示,点A(3,1)到原点距离最大,所以,选C.【考点】简单线性规划【名师点睛】本题主要考查简单线性规划的应用,是一道基础题目.从历年高考题目看,简单线性规划问题是不等式中的基本问题,往往围绕目标函数最值的确定,涉及直线的斜率、两点间的距离等,考查考生的绘图、用图能力,以及应用数学知识解决实际问题的能力.视频7.在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关。
2019-2019学年度湖南省长沙市雅礼中学高三上学期月考(三)数学(理)试题含答案

2019-2019学年度湖南省长沙市雅礼中学高三上学期月考(三)数学(理科)全卷满分150分,考试时间120分钟。
★祝考试顺利★注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题作答用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试卷和草稿纸上无效。
3.非选择题作答用0.5毫米黑色墨水签字笔直接答在答题卡上对应的答题区域内。
答在试卷和草稿纸上无效。
考生必须保持答题卡的整洁。
考试结束后,只需上交答题卡。
第I 卷 (选择题, 共60分)一、选择题(共12小题,每小题5分,共60分,每小题只有一个正确答案)在每小题给出的四个选项中,只有一项是最符合题目要求的,选出正确的选项并将该选项在答题卡上涂黑。
1.已知{}{}(31)222log ,1x A x y B y x y -===+=,则A B =A .1(0,)3B .1[2,)3-C .1(,2]3D .1(,2)32.若2210()cos 2x a dx xdx π-=⎰⎰,则a 等于 A .1- B .1 C .2 D .43.命题“*x R n N ∀∈∃∈,,使得2n x ≥”的否定形式是( )A . *x R n N ∀∈∃∈,,使得2n x <B . *x R n N ∀∈∀∈,,使得2n x <C . *x R n N ∃∈∃∈,,使得2n x <D . *x R n N ∃∈∀∈,,使得2n x <4.函数()2ln f x x =的图象与函数()245g x x x =-+的图象的交点个数为( ) A . 3 B . 2 C . 1 D . 05.设D 为ABC ∆所在平面内一点,若3BC CD =,则下列关系中正确的是( )A . 1433AD AB AC =-+ B . 1433AD AB AC =- C . 4133AD AB AC =+ D . 431-3AD A AC B = 6.已知,,,则a ,b ,c 的大小关系为( )A .B .C .D .7.甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老实说:你们四人中有位优秀,位良好,我现在给甲看看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则()A.乙可以知道四人的成绩 B.丁可以知道四人的成绩C.乙、丁可以知道对方的成绩 D.乙、丁可以知道自己的成绩8.设函数的图象为,下面结论中正确的是()A.函数的最小正周期是B.图象关于点对称C.图象可由函数的图象向右平移个单位得到D.函数在区间上是增函数9.执行如图所示的程序框图,输出的s值为()A. B. C. D.10.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A. B. C. D.11.若a,b是函数f(x)=x2-px+q(p>0,q>0)的两个不同的零点,且a,b,-2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于( )A.6 B.7 C.8 D.912.已知函数.若g(x)存在2个零点,则a的取值范围是()A. [–1,0) B. [0,+∞) C. [–1,+∞) D. [1,+∞)二、填空题:本题共4小题,每小题5分,共20分.13.曲线在点处的切线的斜率为,则________.14.已知,x y 满足30350 30x y x y x -+≤⎧⎪++≤⎨⎪+≥⎩,则2z x y =+的最大值是__________.15.若,则____________.16.已知三棱锥S ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S ABC 的体积为9,则球O 的表面积为________.三、解答题:共70分.解答题应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.17.(本小题满分12分)在△ABC 中,a=7,b=8,cosB= – .(1)求∠A ;(2)求AC 边上的高.18.(本小题满分12分)已知函数()()2cos sin cos 1f x x x x x R =-+∈,.(1)求函数()f x 的最小正周期;(2)求函数()f x 在区间π3π84⎡⎤⎢⎥⎣⎦,上的最小值和最大值. 19.(本小题满分12分)已知为等差数列的前项和,且,.(1)求数列的通项公式;(2)设,求数列的前项和.20.(本小题满分12分)如图,在三棱柱ABC −中,平面ABC ,D ,E ,F ,G 分别为,AC ,,的中点,AB=BC=,AC==2.(1)求证:AC ⊥平面BEF ;(2)求二面角B −CD −C 1的余弦值;21.(本小题满分12分)设函数()1ln x xbe f x ae x x -=+,曲线y=f(x)在点(1, f(1))处的切线方程为y=e(x-1)+2.(1)求,a b ;(2)证明: ()1f x >.选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线l 1的参数方程为(t 为参数),直线l 2的参数方程为.设l 1与l 2的交点为P ,当k 变化时,P 的轨迹为曲线C .(1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设,M 为l 3与C 的交点,求M的极径.23(本小题满分10分).已知.(1)当时,求不等式的解集;(2)若时不等式成立,求的取值范围.高三年级数学(理科)答案一、选择题(12x5)二、填空题(4x5)13. -3 14. 514. 16. 36π三、解答题(70分)17(12分).解:(1)在△ABC 中,∵cos B =–,∴B ∈(,π),∴sin B =.由正弦定(2)在△ABC 中,∵sin C =sin (A +B )=sin A cos B +sin B cos A ==.如图所示,在△ABC 中,∵sin C =,∴h ==,∴AC 边上的高为.18(12分).(Ⅰ)解: ()()π2cos sin cos 1sin2cos224f x x x x x x x ⎛⎫=-+=-=- ⎪⎝⎭. 因此,函数()f x 的最小正周期为π.(Ⅱ)因为()π24f x x ⎛⎫=- ⎪⎝⎭在区间π3π88⎡⎤⎢⎥⎣⎦,上为增函数, 在区间3π3π84⎡⎤⎢⎥⎣⎦,上为减函数,又π08f ⎛⎫= ⎪⎝⎭, 3π8f ⎛⎫= ⎪⎝⎭, 3π3πππ14244f ⎛⎫⎛⎫=-==- ⎪ ⎪⎝⎭⎝⎭,故函数()f x 在区间π3π84⎡⎤⎢⎥⎣⎦,1-.19(12分).(1)设等差数列的公差为,则由已知,得,解得,故;(2)由已知可得,.20.(本小题满分12分)如图,在三棱柱ABC−中,平面ABC,D,E,F,G分别为,AC,,的中点,AB=BC=,AC==2.(1)求证:AC⊥平面BEF;(2)求二面角B−CD−C1的余弦值;解:(Ⅰ)在三棱柱ABC-A1B1C1中,∵CC1⊥平面ABC,∴四边形A1ACC1为矩形.又E, F分别为AC,A1C1的中点,∴AC⊥EF.∵AB=BC.∴AC⊥BE,∴AC⊥平面BEF.(Ⅱ)由(I)知AC⊥EF,AC⊥BE,EF∥CC1.又CC1⊥平面ABC,∴EF⊥平面ABC.∵BE平面ABC,∴EF⊥BE.如图建立空间直角坐称系E-xyz.由题意得B(0,2,0),C(-1,0,0),D(1,0,1),F(0,0,2),G(0,2,1).∴,设平面BCD 的法向量为,∴,∴,令a =2,则b =-1,c =-4,∴平面BCD 的法向量,又∵平面CDC 1的法向量为,∴.由图可得二面角B -CD -C 1为钝角,所以二面角B -CD -C 1的余弦值为.21.(12分)试题解析:(1)函数()f x 的定义域为()0,+∞,()112'ln x x x x a b b f x ae x e e e x x x--=+-+. 由题意可得()12f =, ()'1f e =.故1a =, 2b =.(2)证明:由(1)知, ()12ln x x f x e x e x -=+, 从而()1f x >等价于2ln x x x xe e->-. 设函数()ln g x x x =,则()'1ln g x x =+. 所以当10,x e ⎛⎫∈ ⎪⎝⎭, ()'0g x <;当1,x e⎛⎫∈+∞ ⎪⎝⎭时, ()'0g x >. 故()g x 在10,e ⎛⎫ ⎪⎝⎭上单调递减, 1,e⎛⎫+∞ ⎪⎝⎭上单调递增,从而()g x 在()0,+∞上的最小值为11g e e ⎛⎫=- ⎪⎝⎭. 设函数()2x h x xe e-=-,则()()'1x h x e x -=-. 所以当()0,1x ∈时, ()'0h x >;当()1,x ∈+∞时, ()'0h x <.故()h x 在()0,1上单调递增,在()1,+∞上单调递减,从而()h x 在()0,+∞上的最大值为()11h e=-. 综上,当0x >时, ()()g x h x >,即()1f x >.22(10分).(1)消去参数得的普通方程;消去参数m 得l 2的普通方程.设,由题设得,消去k 得.所以C的普通方程为.(2)C的极坐标方程为.联立得.故,从而.代入得,所以交点M的极径为. 23.(10分)解:(1)当时,,即故不等式的解集为.(2)当时成立等价于当时成立.若,则当时;若,的解集为,所以,故.综上,的取值范围为.。
湖南省长沙市雅礼中学2022-2023学年高三上学期第一次月考数学试卷含答案

注意事项:1.答题前,先将自己的姓名、考号填写在试卷和答题卡上,并将考号条形码粘贴在答 题卡上的指定位置。
2.请在答题卡上各题号对应的答题区域内答题,写在试卷、草稿纸和答题卡上的非答 题区域均无效。
3.选择题用 2B 铅笔把所选答案的标号涂黑,非选择题用黑色签字笔作答。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合=+<∈=P x x x N Q |log (1)1,,1,3,56}{}{,M =P ∪Q ,则集合M 中的元素共有( ) A .4个B .6个C .8个D .无数个2.设函数f x mx mx =−−2()1,命题“x ∃∈1,3][,f x m ≤−+()2是假命题”,则实数m 的取值范围是( )A .,37−∞⎛⎝⎤⎦⎥ B .−∞,3]( C .37,+∞⎛⎝ ⎫⎭⎪ D .3,+∞)(3.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章有弧田面积计算问题, 计算术曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面积的计算公式为:弧田面积=21(弦×矢+矢×矢).弧田是由圆弧(简称为弧田弧)和以圆弧的端点为端点的线段(简称为弧田弦)围成的平面图形,公式中“弦”指的是弧田弦的长,“矢”等于弧田弧所在圆的半径与圆心到弧田弦的距离之差.现有一弧田,其弦长AB 等于6m ,其弧所在圆为圆O ,若用上述弧田面积计算公式算得该弧田的面积为2m 72,则∠=AOB cos ( )A .251 B .−257C .51D .257 4.已知⎝⎭ ⎪+=⎛⎫απ32sin 1,则⎝⎭ ⎪+⎛⎫απ6sin 2的值为( )A .21B .−21CD5.如图,在棱长为2的正方体−ABCD A B C D 1111中,E ,F 分别是棱AA 1,CC 1的中点,过BE 的平面α与直线A F 1平行,则平面α截该正方体所得截面的面积为( ) AB.C .4D .56.已知函数f (x )=x 3+ax 2-x 的图象在点A (1,f (1))处的切线方程为y =4x -3,则函数y =f (x)湖南省雅礼中学高三年级第一次月考 数学试卷的极大值为( ) A .1B .527−C .−2527D .-17. 20222022202232022322022212022020202222C C C C C +−+−的值为A .0B .1C .-1D .202228.已知函数()f x 是定义在R 上的奇函数,对任意的x ∈R ,均有(2)()f x f x +=且(1)0f =,当[0,1)x ∈时,()21x f x =−,则方程()1||0f x g x −=的实根个数为( ) A .6B .8C .10D .12二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知由样本数据点集合{}(,)123,i i x y i n =,,,,求得的回归直线方程为 1.50.5y x =+,且3x =,现发现两个数据点12,2(2)..和4.8,(7)8.误差较大,去除后重新求得的回归直线l 的斜率为1.2,则( )A .变量x 与y 具有正相关关系B .去除后y 的估计值增加速度变快C .去除后与去除前均值x ,y 不变D .去除后的回归方程为 1.2 1.4y x =+10.如图所示,是一个3×3九宫格,现从这9个数字中随机挑出3个不同的数字,记事件A 1:恰好挑出的是1、2、3;记事件A 2:恰好挑出的是1、4、7;记事件A 3:挑出的数字里含有数字1.下列说法正确的是( )12 B .事件A 1,A 2是独立事件 C .P (A 1|A 3)=P (A 2|A 3)D .P (A 3)=P (A 1)+P (A 2)11.在正四面体ABCD 中,若AB = ) A .该四面体外接球的表面积为3πB .直线与平面BCDC .如果点M 在CD 上,则AM BM +D .过线段一个三等分点且与 12.若存在实常数k 和b ,使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足:()F x kx b ≥+和()G x kx b ≤+恒成立,则称此直线y kx b =+为()F x 和()G x 的“隔离直线”,已知函数()2f x x =(R x ∈),()1g x x=(0x <),()2eln h x x =(e 为自然对数的底数),则( )A .()()()m x f x g x =−在x ⎛⎫∈ ⎪⎝⎭内单调递增B .()f x 和()g x 间存在“隔离直线”,且k 的取值范围是[]4,1−C .()f x 和()g x 之间存在“隔离直线”,且b 的最小值为1−三、填空题:本题共4小题,每小题5分,共20分.13.已知随机变量X 服从正态分布()28,X N σ~,(10)P x m ≥=,(68)P x n ≤≤=,则182m n+的最小值为____________.14.某中学元旦晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在节目乙的前面,节目丙不能排在最后一位,则该晚会节目演出顺序的编排方案共有_________. 15.=−−20cos 6420cos 120sin 3222_________. 16.已知函数()eln 2x f x x =,()22x g x x m=−,若函数()()()h x g f x m =+有3个不同的零点x 1,x 2,x 3(x 1<x 2<x 3),则()()()1232f x f x f x ++的取值范围是_________.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知.2,4,53)4sin(,4,0,553cos sin ⎪⎭⎫⎝⎛∈=−⎪⎭⎫ ⎝⎛∈=+ππβπβπααα (1)求α2sin 和α2tan 的值; (2)求()βα2cos +的值.18.已知2mx⎛⎝的展开式中,第4项的系数与倒数第4项的系数之比为.(1)求m 的值;(2)求展开式中所有项的系数和与二项式系数和; (3)将展开式中所有项重新排列,求有理项不相邻的概率.19.已知函数2()(,)f x x bx c b c R =++∈,且()0f x ≤的解集为[1,2]−. (1)求函数()f x 的解析式;(2)解关于x 的不等式mf(x)>2(x −m −1);(3)设g(x)=2f(x)+3x−1,若对于任意的x 1,x 2∈[−2,1]都有()()12g x g x M −≤,求M 的最小值.20.某学校共有2000名学生,其中女生1200人,为了解该校学生在学校的月消费情况,采取分层抽样随机抽取了200名学生进行调查,月消费金额分布在550~1050元之间.根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示,将月消费金额不低于850元的学生称为“高消费群”.(1)求a 的值,并估计该校学生月消费金额的平均数;(同一组中的数据用该组区间的中点值作代表)(2)若样本中属于“高消费群”的男生有10人,完成下列2×2列联表,并判断是否有99.9%以上的把握认为该校学生属于“高消费群”与“性别”有关.(()()()()()2n ad bc K a b c d a c b d −=++++,其中n =a +b +c +d )21.在多面体ABCDE 中,平面ACDE ⊥平面ABC ,四边形ACDE 为直角梯形,CD ∥AE ,AC ⊥AE ,AB ⊥BC ,CD =1,AE =AC =2,F 为DE 的中点,且点E 满足4EB EG =.(1)证明:GF ∥平面ABC ;(2)当多面体ABCDE 的体积最大时,求二面角A -BE -D 的余弦值.22.已知函数()e cos x f x x x =+.(1)判断函数()f x 在[0,)+∞上的单调性,并说明理由;(2)对任意的0x ≥,e sin cos 2x x x x ax ++≥+,求实数a 的取值范围.湖南省雅礼中学高三年级第一次月考数学试卷参考答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.B 2.B 3.D 4.B 5.B 6.A 7.B 8.D二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.ACD 10.AC 11.ACD 12.AD三、填空题:本题共4小题,每小题5分,共20分.13.25 14.300种 15.-32 16.()11002⎛⎫−⋃ ⎪⎝⎭,,四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.18.(1)展开式的通项为()152222122rrm m rrr r r mm T C x x C x −−−+⎛⎫=⋅⋅=⋅⋅ ⎪⎝⎭, ∴展开式中第4项的系数为332m C ⋅,倒数第4项的系数为332m m m C −−⋅,33332122m m m m C C −−⋅∴=⋅,即611,722m m −=∴=. (2)令1x =可得展开式中所有项的系数和为732187=,展开式中所有项的二项式系数和为72128=.(3)展开式共有8项,由(1)可得当522rm −为整数,即0,2,4,6r =时为有理项,共4项, ∴由插空法可得有理项不相邻的概率为484485 114A A A =. 19.(1)因为()0f x ≤的解集为[1,2]−,所以20x bx c ++=的根为1−,2, 所以1b −=,2c =−,即1b =−,2c =−;所以2()2f x x x =−−;(2)mf(x)>2(x −m −1),化简有()222(1)m x x x m −−>−−,整理得(2)(1)0mx x −−>,所以当0m =时,不等式的解集为(,1)−∞,当02m <<时,不等式的解集为2(,1),⎛⎫−∞+∞ ⎪⎝⎭m ,当2m =时,不等式的解集为(,1)(1,)−∞+∞, 当2m >时,不等式的解集为()2(,)1,−∞+∞m,(3)因为[2,1]x ∈−时2()3123f x x x x +−=+−,根据二次函数的图像性质,有2()3123[4,0]f x x x x +−=+−∈−, 则有2()3123()22f x x xx g x +−+−==,所以,1(),116⎡⎤∈⎢⎥⎣⎦g x ,因为对于任意的x 1,x 2∈[−2,1]都有()()12g x g x M −≤, 即求()()12max g x g x M −≤,转化为()()−≤max min g x g x M , 而()(1)1==max g x g , 1()(1)16min g x g =−=, 所以,此时可得1516M ≥, 所以M 的最小值为1516. 20.(1)由频率分布直方图中所有小矩形的面积之和为1得到方程,解得a ,再根据频率分布直方图中平均数计算公式计算可得;(2)按照分层抽样求出样本中男生、女生的人数,再由频率分布直方图求出“高消费群”的人数,即可完善列联表,计算出卡方,即可判断; (1)解:由频率分布直方图可得()1000.00150.00350.00150.0011a ⨯++++=,解得0.0025a =, 所以样本的平均数为()6000.00157000.00358000.00259000.001510000.001100770⨯+⨯+⨯+⨯+⨯⨯=(元)(2)解:依题意知,样本中男生20001200200802000−⨯=人,女生12002001202000⨯=人,属于“高消费群”的有()0.00150.00110020050+⨯⨯=人,列出下列22⨯列联表:所以22001080407011.1110.828 5015080120K⨯−⨯=≈>⨯⨯⨯,所以有99.9%以上的把握认为该校学生属于“高消费群”与“性别”有关.21.(1)取AB,EB中点M,N,连接CM,MN,ND.在梯形ACDE中,DC∥EA且DC=12EA,且M,N分别为BA,BE中点,∴MN//EA,MN=12EA,∴MN//CD,MN=CD,即四边形CDNM是平行四边形,∴CM//DN,又14EG EB=,N为EB中点,∴G为EN中点,又F为ED中点,∴GF//DN,即GF//CM,又CM⊂平面ABC,GF⊄平面ABC,∴GF∥平面ABC.(2)在平面ABC内,过B作BH⊥AC交AC于H.∴平面ACDE⊥平面ABC,平面ACDE平面ABC=AC,BH⊂平面ABC,BH⊥AC,∴BH⊥平面ACDE,则BH为四棱锥B-ACDE的高,又底面ACDE 面积确定,要使多面体ABCDE 体积最大,即BH 最大,此时AB =BC过点H 作HP ∥AE ,易知HB ,HC ,HP 两两垂直,以{HB ,HC ,HP }为正交基底建立如图所示的平面直角坐标系H -xyz ,∴A (0,−1,0),B (1,0,0),E (0,−1,2),D (0,1,1),则AB =(1,1,0),BE =(−1,−1,2),DE =(0,−2,1).设n 1⃗⃗⃗⃗ =(x 1,y 1,x 1)为平面ABE 的一个法向量,则1100n AB n BE ⎧⋅=⎪⎨⋅=⎪⎩,即11111020x y x y z +=⎧⎨−−+=⎩,取n 1⃗⃗⃗⃗ =(1,−1,0),设n 2⃗⃗⃗⃗ =(x 2,y 2,z 2)为平面DBE 的一个法向量,则220n DE n BE ⎧⋅=⎪⎨⋅=⎪⎩,即222222020y z x y z −+=⎧⎨−−+=⎩,取n 2⃗⃗⃗⃗ =(3,1,2), ∴1212127cos ,7n n n n n n ⋅<>==⋅,由图知:二面角A −BE −D 为钝二面角,∴二面角A −BE −D 的余弦值为. 22.(1)解:函数()f x 在[0,)+∞上是单调增函数,理由如下: 因为()e cos x f x x x =+,所以()e cos (sin )x f x x x x =+−'+. 记()e 1x g x x =−−,则()e 1x g x '=−,令()0g x '=,得0x =. 当0x >时,()0,()'>g x g x 为单调增函数; 当0x <时,()0,()g x g x '<为单调减涵数,所以min ()(0)0g x g ==,所以()e 10x g x x =−−≥,即e 1x x ≥+. 又sin 1,cos 1x x ≤≥−,所以()1cos (sin )(1sin )(1cos )0f x x x x x x x x ≥+++−=−++≥', 所以函数()f x 在[0,)+∞上是单调增函数. (2)解:记()e sin cos 2(0)x p x x x ax x =++−−≥,是()e cos x p x x x a =+−'. 由(1)知,()e cos x p x x x a =+−'为[0,)+∞上的单调增函数.1°当10a −≥时,(0)10p a =−≥',所以()(0)0p x p ''≥≥,所以()p x 为[0,)+∞上的单调增函数,所以()(0)0p x p ≥=,即e sin cos 2x x x x ax ++≥+.所以1a ≤符合题意. 2°当10a −<时,(0)10p a =−<',又()e cos e 2a a p a a a a a =−≥'+−. 记()e 2(1)x q x x x =−>,则()e 2e 20x q x =−>−>',所以()q x 为(1,)+∞上的单调增函数,所以()(1)e 20q x q >=−>, 所以e 20(1)x x x −>>,所以()e 20a p a a ≥−>'.又()p x 在[0,)+∞上的图象不间断,且()p x 为[0,)+∞上的单调增函数, 根据零点存在性定理知,存在唯一的零点0(0,)x ∈+∞,使得()00p x =. 所以当00x x ≤≤时,()0p x '≤,()p x 单调递减,所以()0(0)0p x p <=, 这与任意的0x ≥,e sin cos 2x x x x ax ++≥+矛盾, 所以1a >不符合题意 综上可得1a ≤.。
湖南省长沙市雅礼中学2018-2019学年高三上学期第三次月考试卷数学含答案

增,所以1
h(x)
Hale Waihona Puke e2.当k
1
时,
g
'( x)
0
,
g(x)
在 [0,
]上递增,
g(x)
g (0)
0
,符合题意;当
2
k
e2
时,
g
'( x)
0
,
g(x)
在 [0,
] 上递减,
g(x)
g (0)
0
,与题意不合;当1
k
e2
时,
g ( x)
为一
2
个递增函数,而
g
'(0)
1
k
0
,
g
'( )
2
e2
k
0
,由零点存在性定理,必存在一个零点
2. 【答案】D 【解析】
考 点:函数导数与不等式.1
【思路点晴】本题主要考查导数的运用,涉及划归与转化的数学思想方法.首先令 f x 0 将函数变为两个函 数 g x ex 2x 1 , h x ax a ,将题意中的“存在唯一整数,使得 g t 在直线 h x 的下方”,转化为 存在唯一的整数,使得 g t 在直线 h x ax a 的下方.利用导数可求得函数的极值,由此可求得 m 的取值
湖南省长沙市雅礼中学 2018-2019 学年高三上学期第三次月考试卷数学含答案(参考答案) 一、选择题(本大题共 12 小题,每小题 5 分,共 60 分.每小题给出的四个选项中,只有一项是 符合题目要求的.)
1. 【答案】C
【解析】由已知等式,得 c 3b cos C 3c cos B ,由正弦定理,得 sin C 3(sin B cos C sin C cos B) ,则 sin C 3sin(B C) 3sin A ,所以 sin C : sin A 3 :1 ,故选 C.
湖南省长沙市一中·雅礼中学2019届高三三月联考(数学理)

长沙市一中、雅礼中学高三联考试卷理科数学一、选择题(本大题共8小题,每小题5分,共40分;在每小题所给的四个选项中,只有一项是符合题目要求的)1.设U 为全集,M 、P 是U 的两个非空子集,且(),U M P P M P =则ð等于( )A .MB .PC .U P ðD .∅2.A =2{||1|1,},{|log 1,},x x x B x x x -≥∈=>∈R R 则“x ∈A ”是“x ∈B ”的( )A .充分非必要条件B .必要非充分条件C .充分必要条件D .既非充分也非必要条件3.如图是将二进制数11111(2)化为十进制数的一个程序框图,判断框内应填入的条件是( ) A .i ≤5B .i ≤4C .i >5D .i >44.如图表示甲、乙两名篮球运动员每场比赛得分情况的茎叶图,则甲和乙得分的中位数的和是( ) A .56分B .57分C .58分D .59分5.如左图,在平面内两两等距离的一簇平行直线,任意相邻两平行直线间的距离为d (d >0),向平面内任意抛掷一枚长为l (l <d )的小针,已知小针与平行线相交的概率P 等于右图中阴影部分面积与矩形的面积之比,则P 的值为( ) A .2ld πB .2d l πC .4l dπ D .3l d π6.若函数||3([,])x y x a b =∈的值域为[1,9],则a 2 + b 2 – 2a 的取值范围是( )甲 乙 40 8 44 1 258 54 2 365 9566213 234 9541A .[8,12]B .C .[4,12]D .[2,7.已知m ,n ,s ,t ∈R +,m + n = 2,9m n s t +=,其中m 、n 是常数,当s + t 取最小值49时,m 、n 对应的点(m ,n )是双曲线22142x y -=一条弦的中点,则此弦所在的直线方程为( )A .210x y -+=B .210x y --=C .230x y +-=D .230x y +-=8.在△ABC 中,若I 是△ABC 的内心,AI 的延长线交BC 于D ,则AB : AC = BD : DC ,称为三角形的角平分线定理,已知AC = 2,BC = 3,AB = 4.且AI xAB yAC =+,利用三角形的角平分线定理可求得x + y 的值为( ) A .13B .49C .23D .59二、填空题(本大题共7小题;每小题5分,共35分,将每小题的答案填在题中的横线上.)9.直线l 过点2)-及圆2220x y y +-=的圆心,则直线l 的倾斜角大小为 .10.若12z =i ,且443201234(),x z a x a x a x a x a -=++++则a 2等于 .11.下图是一个物体的三视图,已知俯视图中的圆与三角形内切,根据图中尺寸(单位:cm ),可求得a 的值为 cm ,该物体的体积为 cm 3.12.如图,AC 为⊙O 的直径,BD ⊥AC 于P ,PC = 2,PA = 8,则CD 的长为 ,cos ∠ACB = .(用数字表示) 13.已知点A (1,0),P 是曲线1x >上任一点,设P 到直线l :12y =-的距离为d ,则|PA | + d 的最小值是 .14.已知函数()f x 的定义域为{|,1}x x R x ∈≠且,(1)f x +为奇函数,当1x <时,2()21f x x x =-+,则当1x >时,()f x 的递减区间是 .15.下面的数组均由三个数组成,它们是:(1,2,3),(2,4,6),(3,8,11),(4,16,20),(5,32,37),…,(a n ,b n ,c n ).(1)请写出c n的一个表达式,c n = ;(2)若数列{c n}的前n项和为M n,则M10 = .(用数字作答)三、解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)16.(本小题满分12分)在△ABC中,角A、B、C的对边分别为a,b,c,已知向量且.⊥(2,),(cos,cos),p c a b q B C=-=p q(1)求角B的大小;(2)若b =ABC面积的最大值.17.(本小题满分12分)如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC =,M为BC的中点.(1)证明AM⊥PM;并求二面角P—AM—D的大小;(2)求点D到平面AMP的距离.18.(本小题满分12分)一只口袋中装有标号为1、2、3、4的大小与重量相同的4个小球,从该口袋中每次取出1球,记下标号后再放回口袋,连续取三次.(1)求三次取出的小球的标号之和为5的概率;(2)设三次取出的小球的标号中最大的数字为X,求随机变量X的布分列和数学期望.19.(本小题满分13分)某市电信宽带网用户收费标准如下表:(假定每月初均可以和电信部门约定上网方案)有限包月制(限(1)若某用户某月上网时间为T小时,当T在什么范围内时,选择甲方案最合算?请说明理由(2)王先生因工作需要需在家上网,他一年内每月的上网时间T(小时)与月份n的函数关系为T = f (n) =3237(112,)4nn n+≤≤∈N.若公司能报销王先生全年的上网费用,问公司最少为此花费多少元?20.(本小题满分13分)如图,设椭圆22221(0)x ya ba b+=>>的左、右焦点分别为F1、F2,上顶点为A ,过点A 且与A F 1垂直的直线分别交椭圆和x 轴正半轴于P 、Q 两点,满足85AP PQ =.(1)求椭圆的离心率;(2)若过A 、Q 、F 1三点的圆恰好与直线l :30x +=相切,求椭圆方程.(3)在(2)的条件下,过F 2的直线l 与椭圆相交于异于椭圆左、右顶点的M ,N 两点,B 为椭圆的左顶点,求BM BN 的取值范围.21.(本小题满分13分)已知函数f (x ) = ln (2 + 3x ) 23.2x -(1)求f (x )在[0,1]上的最大值;(2)若对11[,],|ln|ln[()3]062x a x f x x'∀∈-++>不等式恒成立,求实数a的取值范围;(3)若关于x的方程f (x) = –2x + b在[0,1]上恰有两个不同的实根,求实数b的取值范围.长沙市一中、雅礼中学高三联考试卷理科数学答案一、选择题(本大题共8小题,每小题5分,共40分;在每小题所给的四个选项中,只有一项是符合题目要求的)1.设U 为全集,M 、P 是U 的两个非空子集,且(),U M P P M P =则ð等于( )A .MB .PC .U P ðD .∅【解析】D 由(),.U UM P P P M P P =⊆=∅知,所以痧故选D .2.A =2{||1|1,},{|log 1,},x x x B x x x -≥∈=>∈R R 则“x ∈A ”是“x ∈B ”的( )A .充分非必要条件B .必要非充分条件C .充分必要条件D .既非充分也非必要条件【解析】B 由已知得(,0][2,),(2,),A B =-∞+∞=+∞若“x ∈B ”则必有“x ∈A ”,反之不成立,即得“x ∈A ”是“x ∈B ”的必要不充分条件,故选B . 3.如图是将二进制数11111(2)化为十进制数的一个程序框图,判断框内应填入的条件是( ) A .i ≤5B .i ≤4C .i >5D .i >4【解析】D ;(11111)(2) = 1 + 2 + 22 + 23 + 24,(*) 在程序框图中,当i = 1时,S = 1 + 2×1 = 1 + 2,当i = 2时,S = 1 + 2 (1 + 2) = 1 + 2 + 22,…,由(*)式知i = 4时已完成计算,∴应填入条件i >4.∴故选D .4.如图表示甲、乙两名篮球运动员每场比赛得分情况的茎叶图,则甲和乙得分的中位数的和是( ) A .56分B .57分C .58分D .59分【解析】B 由图可知甲的中位数为32,乙的中位数为25,故和为57.故选B .5.如图,在平面内两两等距离的一簇平行直线,任意相邻两平行直线间的距离为d (d >0),向平面内任意抛掷一枚长为l (l <d )的小针,已知小针与平行线相交的概率P 等于阴影面积与矩形的面积之比,则P 的值为( )甲 乙 40 8 44 1 258 54 2 365 9566213 234 9541A .2l d πB .2d l πC .4l dπ D .3l d π【解析】A 先求阴影部分的面积,22022sin (cos ),.2224ll l l l S d P d d ππαααππ==-===⎰所以故选A .6.若||3([,])x y x a b =∈的值域为[1,9],则a 2 + b 2 – 2a 的取值范围是( )A .[8,12]B.C .[4,12]D .[2,【解析】C 由于||3([,])x y x a b =∈的值域是[1,9],由指数函数的单调性.所以0≤|x |≤2,若a = –2,则b ∈[0,2]从而a 2 + b 2 – 2a ∈[8,12],若b = 2,则a ∈[–2,0].从而a 2 + b 2 – 2a ∈[4,12].因此a 2 + b 2 – 2a ∈[4,12].故选C . 7.已知m ,n ,s ,t ∈R +,m + n = 2,9m n s t +=,其中m 、n 是常数,当s + t 取最小值49时,m 、n 对应点(m ,n )是双曲线22142x y -=一弦的中点,则此弦所在的直线方程为( )A .210x y -+=B .210x y --=C .230x y +-=D .230x y +-=【解析】A由已知得111()()(999m n mt ns s t s t m n m n s t s t ⎛⎫+=++=+++≥++= ⎪⎝⎭21,9由于s + t 的最小值是4,9因此214289=,又m + n = 2,所以m = n = 1.设以点(m ,n )为中点的弦的两个端点的坐标分别是1122(,),(,)x y x y ,则有121212121,222x x y y x x y y ++==+=+=即①.又该两点在双曲线上,则有22111,42x y -= 22221,42x y -=两式相减得12121212()()()()042x x x x y y y y +-+--=②,把①代入②得121212y y x x -=-,即所求直线的斜率是12,所求直线的方程是11(1),2y x -=-210x y -+=即.故选A .8.在△ABC 中,若I 是△ABC 的内心,AI 的延长线交BC 于D ,则AB : AC = BD : DC ,称为三角形的角平分线定理,已知AC = 2,BC = 3,AB = 4.且A I xA B yA C =+,利用三角形的角平分线定理可求得x + y 的值为( ) A .13B .49C .23D .59【解析】C 在△ABC 中,I 为内心,联结AI 并延长交BC 于点D .则BD ABDC AC=4122..233AD AB AC ===+故又BC = 3,则BD = 2,DC = 1.在△ABC 中,422422,..23993A I AB A I A D A B AC x y ID B D =====++=即故故选C . 二、填空题(本大题共7小题;每小题5分,共35分,将每小题的答案填在题中的横线上.) 9.直线l过点2)-及圆2220x y y +-=的圆心,则直线l 的倾斜角大小为 . 【解析】120° 依题意得,圆2220x y y +-=的圆心为(0,1),过点2)(0,1)-与的直线的斜率k =∴直线l 的倾斜角大小为120°.10.若12z =i ,且443201234(),x z a x a x a x a x a -=++++则a 2等于 .【解析】3-+i414(),r rr r T C x z -+=-依题意4 – r = 2,即r = 2,222241()632a C z ⎛⎫∴=-=⨯-=-+ ⎪ ⎪⎝⎭11.下图是一个物体的三视图,根据图中尺寸(单位:cm ),可求得实数a 的值为 ,该物体的体积为 cm 3.6π+ 该物体为正三棱柱与球的组合体,可知324123326a v ππ⎛⎫===+ ⎪⎝⎭12.如图,AC 为⊙O 的直径,BD ⊥AC 于P ,PC = 2,PA = 8,则CD 的长为 ,cos ∠ACB =.(用数字表示) 【解析】 由射影定理得CD 2= CP ·CA = 2×10, ∴CDcos ∠ACB= sin ∠D =CP CD == 13.已知点A (1,0),P 是曲线2cos ()1cos 2x y θθθ=⎧∈⎨=+⎩R 上任一点,设P 到直线l :12y =-的距离为d ,则|PA | +d 的最小值是 .a221cos 22cos ,2(02).y x y y θθθ=+==≤≤消去得其图象是一段抛物线,F 10,2⎛⎫⎪⎝⎭是其的焦点,l 是其准线,d = |PF |当A 、P 、F 三点共线时,|PA | + d 最小,其值是||AF =14.已知函数()f x 的定义域为{|,1}x x R x ∈≠且,(1)f x +为奇函数,当1x <时,2()21f x x x =-+,则当1x >时,()f x 的递减区间是 7[,)4+∞ .15.下面的数组均由三个数组成,它们是:(1,2,3),(2,4,6),(3,8,11),(4,16,20),(5,32,37),…,(a n ,b n ,c n ).(1)请写出c n 的一个表达式,c n = ;(2)若数列{c n }的前n 项和为M n ,则M 10 = .(用数字作答)【解析】c n = n + 2n ;2101 由1,2,3,4,5,……猜想a n = n ;由2,4,8,16,32,……猜想b n = 2n ;由每组数都是“前两个之和等于第三个”猜想c n = n + 2n .从而M 10 = (1 + 2 + … + 10) + (2 + 22+ … + 210) =1010(101)2(21)2101.221⨯+-+=-三、解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤) 16.(本小题满分12分)在△ABC 中,角A 、B 、C 的对边分别为a ,b ,c ,已知向量(2,),(cos ,cos ),p c a b q B C =-=p q ⊥且.(1)求角B 的大小;(2)若b =ABC 面积的最大值.【解析】(1)p q ⊥由,可得(2)cos cos 0p q c a B b c =-+=,由正弦定理:sin cos 2sin cos sin cos 0,sin()2sin cos .C B A B B C C B A B -+=+=从而(3分) 又B + C =π– A ,sin(C + B ) = sin A ,且sin A >0,故1cos ,(0,),23B B B ππ=∈∴=又(6分)(2)由余弦定理b 2 = a 2 + c 2 – 2ac cos B = a 2 + c 2 – ac ≥ac ,又b =ac ≤12 (9分)故11sin 1222ABCSac B =≤⨯=,因此当a = c =ABC 的面积最大且最大值为 (12分)17.(本小题满分12分)如图,边长为2的等边△PCD 所在的平面垂直于矩形ABCD 所在的平面,BC =,M 为BC 的中点.(1)证明AM ⊥PM ;并求二面角P —AM —D 的大小; (2)求点D 到平面AMP 的距离.【解析】(1)取CD 的中点E ,连接PE 、EM 、EA ,∵△PCD 为正三角形,∴PE ⊥CD ,∵平面PCD ⊥平面ABCD ,∴PE ⊥平面ABCD∴PE ⊥AM(3分)∵四边形ABCD 是矩形,∴△ADE 、△ECM 、△ABM 均为直角三角形,由勾股定理可求得2223,,90,EM AM AE EM AM AE AME ===∴+=∴∠=︒AM EM ∴⊥ (4分)∴AM ⊥平面PME ,∴PM ⊥AM ,∴∠PME 是二面角P —AM —D 的平面角, (6分)PE = PD sin60°,∴tan 1,45,PE PME PME EM ∠===∴∠=︒ ∴二面角P —AM —D 为45°. (8分)(2)设点D 到平面PAM 的距离为d ,连接DM ,则V P —ADM = V D —PAM ,111,2 2.332ADMPAMADMS PE Sd SAD CD ∴===而在Rt △PEM 中,由勾股定理可求得PM =1113(10)3,233PAMSAM PM d d ∴==∴⨯⨯⨯=分即点D 到平面PAM (12分)另解(1)以D 点为原点,分别以直线DA 、DC 为x 轴、y 轴,建立如图所示的这空间直角坐标系D —xyz ,依题意,得D (0,0,0),P (0,1,C (0,2,0),A 0,0),M 2,0)(2分)(2,2,0)(0,1,3,)(2,1,3),(2,2,0)(PM AM ∴=-=-=-=(2,1,3)(2,2,0)0,,.PM AM PM AM AM PM ∴=--=⊥∴⊥即(4分)设n = (x ,y ,z ),且n ⊥平面PAM ,则0,(,,)(2,1,3)0,0,(,,)(2,2,0)0PM x y z AM x y z ⎧⎧=-=⎪⎪⎨⎨=-=⎪⎪⎩⎩即n n0,,20,,y z y x ⎧+==⎪∴⎨+=⎪⎪⎩⎩取y = 1,=得n (7分)取P = (0,0,1),∵P ⊥平面ABCD ,∴cos<n ,p >=3||||6==n Pn P 结合图形可知,二面角P —AM —D 为45° (9分)(2)设点D 到平面PAM 的距离为d ,由(1)可知=n ,与平面PAM 垂直,则d =|||(22,0,0)(2,1,3)|2||DA n n ==(12分)18.(本小题满分12分)一只口袋中装有标号为1、2、3、4的大小相同的4个小球,从该口袋中每次取出1球,记下标号后再放回口袋,连续取三次. (1)求三次取出的小球的三个标号之和为5的概率;(2)设三次取出的小球的标号中最大的数字为X ,求随机变量X 的布分列和数学期望. 【解析】由题设每次取出的小球的标号为i (i = 1、2、3、4)其概率14P =(1分)(1)记取出的小球的标号组合为(1,1,3)和(1,2,2)为事件A ,B 且A 、B 互斥,(2分)则所求事件的概率P 1 = P (A + B ) = P (A ) + P (B ) = 22113311113444432C C ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭ (4分) (2)X 的可知取值为1、2、3、4(5分) 311(1)464P X ⎛⎫=== ⎪⎝⎭(6分) 33312331117(2)44464P X C C ⎛⎫⎛⎫⎛⎫==++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(7分) 333333111133333311111119(3).44444464P X C C C C A ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫==+++++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(9分)333133311137(4)63.44464P X C A ⎛⎫⎛⎫⎛⎫==++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(10分)则X 的分布列如下表EX = 1×164+ 2×764+ 3×1964+ 4×3764= 5516. (12分)19.(本小题满分13分)某市电信宽带网用户收费标准如下表:(假定每月初均可以和电信部门约定上网方案)有限包月制(限(1)若某用户某月上网时间为T 小时,当T 在什么范围内时,选择甲方案最合算?并说明理由(2)王先生因工作需要需在家上网,他一年内每月的上网时间T (小时)与月份n 的函数关系为T = f (n ) =3237(112,)4n n n +≤≤∈N .若公司能报销王先生全年的上网费用,问公司最少会为此花多少元?【解析】(1)当T ≤30时,选择丙方案合算;当T >30时,由30 + 3 (T – 30)≤50,得30<T ≤2363,此时选择丙方案合算;(2分)当2363≤T ≤60时,选择乙方案合算;(4分)当T >60时,由50 + 3 (T – 60)≤70,得60<T ≤2663,此时选择乙方案合算;当T ≥2663,选择甲方案合算.(6分) 综上可得,当T 2(66,)3∈+∞时,选择甲方案合算.(7分)(2)因为3(1)(),4f n f n +-=所以{f (n )}为首项f (1) = 60,公差d =34的等差数列,且每月上网时间逐月递增.令32372866,9439n T n +=≥≥得,可知前9个月选择乙方案,最后3个月选择甲方案上网花费最少.(9分)此时,一年的上网总费用为991132379[503(60)]370450(1)44n n n n ==++-+⨯=+-+∑∑ 21045081210741(=++=元)即一年内公司最少会为王先生花费上网费741元(13分)20.(本小题满分13分)如图设椭圆22221(0)x y a b a b+=>>的左、右焦点分别为F 1、F 2,上顶点为A ,过点A 与A F 1垂直的直线分别交椭圆和x 轴正半轴于P 、Q 两点,且85AP PQ =.(1)求椭圆的离心率;(2)若过A 、Q 、F 1三点的圆恰好与直线l :30x +=相切,求椭圆方程.(3)过F 2的直线l 与椭圆相交于异于椭圆左、右顶点的M ,N 两点,B 为椭圆的左顶点,求BM BN 的取值范围.【解析】(1)设点Q (x 0,0),F 1(–c ,0), 其中c(0,).A b 85AP PQ =,得222000285853,,1.131313132x P x b x a a ⎛⎫⎛⎫⎛⎫∴+=⇒= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭①而22000(,),(,),,0,0,.b FA c b AQ x b FA AQ FA AQ cx b x c==-⊥∴=∴-==②由①②知2b 2 = 3ac ,∴2c 2 + 3ac – 2a 2 = 0.∴2e 2 + 3e – 2 = 0,∴1.2e =(4分)(2)满足条件的圆心2222222,0,,(,0)222b c b c a c c O c O c c c c ⎛⎫----''==∴ ⎪⎝⎭ 圆半径222.22b a c r a c+=== 由圆与直线l:|3|30,,2c x a ++==相切得又a = 2c , ∴c = 1,a = 2,b221.43x y +=(8分)(3)(i )当MN ⊥x 轴时()33331,,1,,2,0,3,,3,,2222M N B BM BN ⎛⎫⎛⎫⎛⎫⎛⎫--∴==- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭27.4BM BN ∴=(ii )当MN 与x 轴不垂直时,设M (x 1,y 1),N (x 2,y 2)l 的方程为y = k (x – 1) (k ≠0)代入椭圆方程得()22222212122284124384120,,,4343k k k x k x k x x x x k k -+-+-=+==++则 12y y =2221212121122(1)(1)(),(2,),(2,),x k x x k x x k x x k BM x y BN x y --=-++=+=+此时BM BN = 222212121212122272()4(1)(2)()443k x x x x y y k x x k x x k k ++++=++-+++==+22727344k<+.从而2704BM BN <≤ (13分)21.(本小题满分13分)已知函数f (x ) = ln (2 + 3x ) 23.2x -(1)求f (x )在[0,1]上的最大值;(2)若对11[,],|ln |ln[()3]062x a x f x x '∀∈-++>不等式恒成立,求实数a 的取值范围;(3)若关于x 的方程f (x ) = –2x + b 在[0,1]上恰有两个不同的实根,求实数b 的取值范围.【解析】(1)33(1)(31)1()3,()01().23323x x f x x f x x x x x -+-''=-====-++令得或舍去(1分) ∴当110,()0,()1,()0,()33x f x f x x f x f x ''≤<><≤<时单调递增;当时单调递减. (3分)11ln336f ⎛⎫∴=- ⎪⎝⎭为函数f (x )在[0,1]上的最大值.(4分) (2)由33|ln |ln[()3]0ln lnln ln ,2323a x f x x a x a x x x'-++>>-<+++得或① (5分)设232333()ln ln ln ,()ln ln ln ,2332323x x xh x x g x x x x x+=-==+=+++依题意知a >h (x )或a <g (x )在x ∈11,62⎡⎤⎢⎥⎣⎦上恒成立,222233(23)3323126()0,()(26)0,3(23)3(23)2323x x x xg x h x x x x x x x x x x ++-+''==>=+=>++++(6分) ∴g (x )与h (x )都在11,62⎡⎤⎢⎥⎣⎦上递增,要使不等式①成立,当且仅当1171,ln ln .26125a h a g a a ⎛⎫⎛⎫><>< ⎪ ⎪⎝⎭⎝⎭或即或(9分)(3)由2233()2ln(23)20.()ln(23)2,22f x x b x x x b x x x x b ϕ=-+⇒+-+-==+-+-令2379()32,,()0,()2323x x x x x x x x ϕϕϕ⎡-''=-+=∈>⎢++⎣⎦令当时于是在上递增; ,()0,()x x x ϕϕ⎤⎤'∈<⎥⎥⎣⎦⎣⎦当时于是在上递减.(11分)而(0),(1),()2()0[0,1]f x x b x ϕϕϕϕϕ>>∴=-+=⎝⎭⎝⎭即在上恰有两个不同实根等价于(0)ln 20717ln(20,ln 5ln(26261(1)ln 502b b b b ϕϕϕ⎧⎪=-≤⎪⎪=+->∴+≤<-⎨⎪⎝⎭⎪⎪=+-≤⎩ (13分)。
湖南省长沙市雅礼中学2019届高三上学期11月份月考数学(理)试题(解析版)

2019届湖南雅礼中学高三上学期11月份月考试题第I卷一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集I是实数集R,都是I的子集(如图所示),则阴影部分所表示的集合为A. B.C. D.【答案】B【解析】由题意,由图知阴影部分所表示的集合为故选B.【点睛】本题考查Venn图表达集合的关系及运算,解题的关键是根据图象得出再由集合的运算求出阴影部分所表示的集合.2.设,其中x,y是实数,则A. 1B.C.D. 2【答案】B【解析】试题分析:因为所以故选B.【考点】复数运算【名师点睛】复数题也是每年高考的必考内容,一般以客观题的形式出现,属得分题.高考中考查频率较高的内容有:复数相等、复数的几何意义、共轭复数、复数的模及复数的乘除运算.这类问题一般难度不大,但容易出现运算错误,特别是中的负号易忽略,所以做复数题时要注意运算的准确性.3.已知命题:函数的图象恒过定点;命题:若函数为偶函数,则函数的图象关于直线对称,则下列命题为真命题的是()A. B. C. D.【答案】D【解析】试题分析:当时,,所以命题为假命题;若函数为偶函数,即函数的图象向右平移1个单位后关于轴对称,所以的图象关于直线对称,所以命题为假命题。
由此可判断选项A为真命题. 考点:逻辑联结词与命题。
4.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是A. 56B. 60C. 120D. 140【答案】D【解析】【分析】根据已知中的频率分布直方图,先计算出自习时间不少于22.5小时的频率,进而可得自习时间不少于22.5小时的频数.【详解】根据频率分布直方图,200名学生中每周的自习时间不少于22.5小时的频率为(0.16+0.08+0.04)×2.5=0.7,故200名学生中每周的自习时间不少于22.5小时的人数为200×0.7=140.故选:D.【点睛】本题考查的知识点是频率分布直方图,难度不大,属于基础题目.5.执行如图所示的程序框图,若输入如下四个函数:①;②;③;④.则输出的函数是()A. B.C. D.【答案】A【解析】试题分析:对①,显然满足,且存在零点.故选A.考点:程序框图及函数的性质.6.若变量x,y满足则x2+y2的最大值是A. 4B. 9C. 10D. 12【答案】C【解析】试题分析:画出可行域如图所示,点A(3,1)到原点距离最大,所以,选C.【考点】简单线性规划【名师点睛】本题主要考查简单线性规划的应用,是一道基础题目.从历年高考题目看,简单线性规划问题是不等式中的基本问题,往往围绕目标函数最值的确定,涉及直线的斜率、两点间的距离等,考查考生的绘图、用图能力,以及应用数学知识解决实际问题的能力.【此处有视频,请去附件查看】7.在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关。
【数学】湖南省长沙市雅礼中学2019届高三上学期月考(一)试题(文)(解析版)-副本

,
∴ 故选: A
2.在复平面内,复数
的共轭复数对应的点位于(
)
A. 第一象限 【答案】 B
B. 第二象限
C. 第三象限
【解析】利用两个复数代数形式的除法,虚数单位
复数,从而得到答案 .
D. 第四象限 i 的幂运算性质化简复数 z,求出其共轭
∵复数
=
= =﹣1﹣ 3i,
∴
,它在复平面内对应点的坐标为(﹣ 1, 3),
word 文档,可自行编辑,欢迎下载使用
,
由
,解得: A( 2, 1),
由 z=2x+y 得: y=﹣ 2x+z, 显然直线 y=﹣2x+z 过( 2, 1)时, z 最大, 故 z 的最大值是: z=4+1=5 , 故选: D. 5.已知回归直线的斜率的估计值是 1.23,样本点的中心为 ( 4,5),则回归直线的方程是 ( )
word 文档,可自行编辑,欢迎下载使用
湖南省长沙市雅礼中学 2019 届高三上学期月考(一)
数学试题(文)
第 I卷 一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中, 只有一个选项是符合题目要求的
1.已知集合
,则
()
A.
B.
C.
D.
【答案】 A
【解析】化简集合 A,根据交集的定义写出 A∩B.
A.
B.
C.
D.
【答案】 C
【解析】根据回归直线方程一定经过样本中心点这一信息,即可得到结果.
由条件知,
,
设回归直线方程为
,
则
.
∴回归直线的方程是
故选: C
6.在数列 中,
湖南省长沙市雅礼中学2019届高三上学期月考二理数答案

) # %$ %$ 槡 设& 则6 槡 假设存在点 6 满足条件 *分 63 & % $ " + + " " " ! $ # # ) # %$ 槡 则 设平面 3 $ 63 槡 $ 6 的法向量为3 * 5 4 # ! " " $ ! # #
雅礼中学# 二 $ " %届高三月考试卷
数学 理科 参考答案
一 选择题 题!号 答!案 " , # & ' . ( . ) * . + / % , " $ , " " . " # ,
# 解析 由0 ( ! . " $ $ 1 ! " # " " 20
" 1 1 ! 0 " #1 2槡 20 20 #" #
解析 由图像可得"3 % ! ,!
& & " " ! # 3 4 5 6 3! 则# ' #
# %$ %$ %$ %$ %$ %$ %$ 当 $ 取% 不含端点 解析 易知 $ 在弦% & 上 $ ' $ (3 $ )7)' $ )7) ( $ ) ! ' ! & 中点 ! 3 " $ ! ,!
其方程为43 由原点到9的距离为槡 假设存在符合题意的直线9 : *7. # &得
. # # )分 3槡 &#. 3 & " 7 : ! # " 7 : 槡 * # 7 3 " 4 ## # 得 联立方程,' " 7 ' : *7 + : . *7 ' . ! " 3 $ ! . : *7. 43
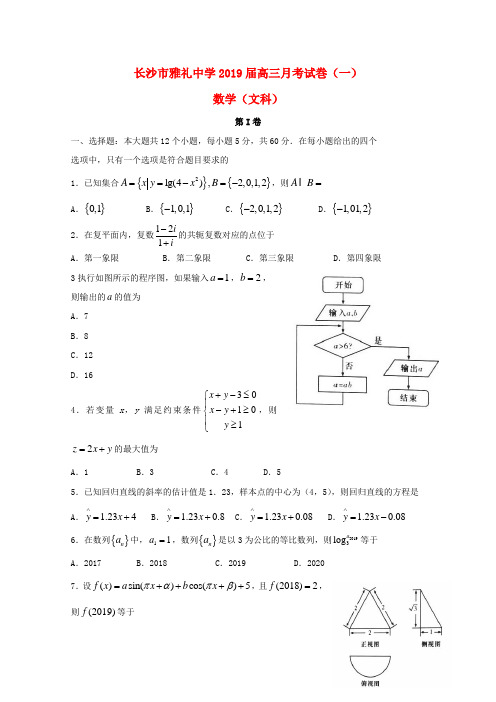
湖南省长沙市雅礼中学2019届高三数学上学期月考试题(一)文
长沙市雅礼中学2019届高三月考试巻(一)数学(文科)第I 卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个 选项中,只有一个选项是符合题目要求的1.已知集合{}{}2lg(4),2,0,1,2A x y x B ==-=-,则A B =A .{}0,1B .{}1,0,1-C .{}2,0,1,2-D .{}1,01,2-2.在复平面内,复数121i i-+的共轭复数对应的点位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限 3执行如图所示的程序图,如果输入1a =,2b =,则输出的a 的值为A .7B .8C .12D .164.若变量x ,y 满足约束条件30101x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩,则2z x y =+的最大值为A .1B .3C .4D .55.已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是A . 1.234y x ∧=+B . 1.230.8y x ∧=+C . 1.230.08y x ∧=+D . 1.230.08y x ∧=-6.在数列{}n a 中,11a =,数列{}n a 是以3为公比的等比数列,则20193log a 等于 A .2017 B .2018 C .2019 D .20207.设()s i n ()c o s ()5f x a x b x παπβ=++++,且(2018)2f =,则(2019)f 等于A .2B .2-C .8D .8-8.某几何体的三视图如图所示,其中俯视图是个半圆,则该几何体的表面积为A .32π B.π.52π+.32π+9.将函数sin 2y x =的图象向右平移16π个单位后得到的函数为()f x ,则函数()f x 的图象 A .关于点(12π,0)对称 B .关于直线12x π=对称 C .关于直线512x π=对称 D .关于点(5,012π)对称 10.若函数6,2()(03log ,2x a x x f x a x -+≤⎧=>⎨+>⎩且1a ≠)的值域是[4,+∞),则实数a 的取值范围是A .(1,2]B .(0,2]C .[2,)+∞ D.(111.已知点F 是双曲线22221(0,0)x y a b a b-=>>的左焦点,点E 是该双曲线的右顶点,过F 且垂直于x 轴的直线与双曲线交于A 、B 两点,若△ABE 是饨角三角形,则该双曲线的离心率e 的取值范围是A .(1,)+∞B .(1,2) C.[1,1 D .(2,)+∞12.已知△ABC 是边长为2的等边三角形,P 为△ABC 所在平面内一点,则()PA PB PC ⋅+的最小值是A .32-B .2-C .43- D .1- 第II 卷本卷包括必考题和选考题两部分.第13~21题为必考题,每个试題考生都必须作答.第22~23题为选考题,考生根据要求作答.二、填空题:本大题共4小題,每小题5分,共20分13.锐角△ABC 中,AB =4,AC =3,△ABC的面积为BC =_______。
炎德英才大联考2019届雅礼中学高三理数(试题)

!"!若&,$$),$$且当-+,$$ 时$恒有&$*)++!$则以&$)为坐标的点5!&$)"所形 /$*++!
成的平面区域的面积为!!!!! !3!对于函数0!!$"和0#!$"$设&0&$0 0!!$")$'$)0&$0 0#!$")$'$若存在
'&回答第卷时将答案写在答题卡上写在本试卷上无效 (&考试结束后将本试卷和答题卡一并交回
第卷
一选择题本题共!#小题每小题"分在每小题给出的四个选项中只有一项是符合 题目要求的!
!!在复平面内复数")!#*+*+#$!#则复数"的共轭复数"# 对应的点所在象限为
,!第一象限
/!!$2
(!若&)456#'))456'#*)456(3则下列结论正确的是
,!)&&&*
-!&&)&*
.!*&)&&
/!)&*&&
"!如图所示程序框图的算法思路源于我国古代数学名著九章算术中的一种运算方法
执行该程序框图若输入的&)分别为!2("则输出的&)
,!$
-!'
.!%
/!#1
:!
!!$
!#$
!1$
5
&
$!(
)
且:! 的期望/!:!")!#$万元,若投资乙项目一年后可获得的利润:#!万元"与该项 目建设材料的成本有关$在生产的过程中$公司将根据成本情况决定是否在第二和第
