量子力学第三章习题
量子力学课后习题答案

量子力学习题及解答第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv e chv d kThv v v 11833-⋅=πρ, (1)以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThc λλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ 把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
量子力学第三章作业及答案

第三章3.1 设ˆˆ,AB 均为厄米算符,试证: ()ˆˆˆˆ1 AB-BA是否为厄米算符; ()()ˆˆˆˆ2 i AB-BA 是否为厄米算符. 解: ()†††††ˆˆˆˆˆˆˆˆˆˆ AB-BA =B A -A B =BA-AB所以不是厄米算符()()()()()††††††ˆˆˆˆˆˆˆˆˆˆi AB-BA =-i AB-BA =-i B A -A B ˆˆˆˆˆˆˆˆ=-i BA-AB=i AB-BA ⎡⎤⎣⎦所以是厄米算符3.2 设体系的波函数为球谐函数(),lm Y θϕ,求其角动量矢量与z 轴的夹角 解: 由于z L cos L θ=,因为()()()22ˆ,1,lmlm L Y l l Y θϕθϕ=+ ()()ˆ,,z lm lm L Y m Y θϕθϕ=故可取)L =,z L m =,所以,cos z L mL θ==3.3 已知 ˆ[sin cot cos ]x L i φθφθφ∂∂=+∂∂,ˆ[cos cot sin ]y L i φθφθφ∂∂=--∂∂ 问(),1lm Y θϕ=是否为ˆx L ,ˆy L 的本征态;如果是,求其本征值.解: 由于()ˆ,0x lm L Y θϕ=, ()ˆ,0y lm L Y θϕ=所以为ˆx L ,ˆy L 的本征态, 其本征值为03.4 在经典情形,对称陀螺的能量算符为()22211ˆˆˆˆ22x y z x zH L L L I I =++ 1. 问(),lm Y θϕ是否为ˆH的本征态; 2. 如果是,求其本征值.解:()()2222222211ˆˆˆˆ2211ˆˆˆ22111ˆˆ222x y zx zz z x zz x z x H L L L I I L L L I I L L I I I =++=-+⎛⎫=+- ⎪⎝⎭所以, 其本征值为()2221111222xz x E l l m I I I ⎛⎫=++- ⎪⎝⎭3.5设粒子处于范围在[0,]a 的一维无限深势阱中,状态用波函数113()sin sinx xx a a ππψ=+描述,(1)该波函数是否归一,如不归一,请写出归一化波函数 (2)求粒子能量的可能值及相应概率。
量子力学第三章习题

3.2.氢原子处在基态 ,求:
(1) 的平均值;
(2)势能 的平均值;
(3)最可几半径;
(4)动能的平均值;
(5)动量的几率分布函数.
解:(1) 的平均值:
(2)求势能的平均值:
(3)求最可几半径:
电子在半径为 的球面上的几率为
求上式对 的导数
令上式等于零,则可求得最可几半径为:
(2)求粒子动量的平均值:
由上式 已经看出,粒子在状态 中取 和 几率相等,所以动量的平均值为零,实际上:
或
3.8.在一维无限深势阱中运动的粒子,势阱的宽度为 ,如果粒子状态的波函数为
,
A为归一化常数,求粒子能量的几率分布和能量的平均值.
解:首先将波函数归一化:
所以
将给定的波函数视为能量本征函数
的线性叠加,即
第三章量子力学中的力学量
3.1一维谐振子处在基态 ,求
(1)势能的平均值 ;
(2)动量的几率分布函数;
(3)动能的平均值 .
解:(1)势能的平均值:
(2)动量的几率分布函数
所以
(3)动能的平均值
计算可知,这一状态中的振子的势能和动能的平均值相等,都是零点能 的一半.
以上计算中,用到积分公式:
费曼方法介绍:
费曼方法求动能势能平均值.
动能平均值:
于是有:
这样根据费曼的方法,有
同样地,有
这样根据费曼的方法,有
当然有
是自洽的.
*3.3.证明氢原子中电子运动所产生的电流密度在球极坐标系中的分量是
解:电流密度
而 为电子的几率流密度
在球坐标系中电子运动状态函数为
其中 均为实数, 是实数,只有 是非实数,而
量子力学课后习题答案

量子力学习题及解答第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv e chv d kThv v v 11833-⋅=πρ, (1)以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThc λλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ 把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
量子力学习题解答

解:
( 1)先求归一化因子,由
∫ ∫ 1=
∞ ψ (x) 2 dx =
−∞
∞ 0
A2 x2e−2λxdx
=
1 4λ3
A2
à
A = 2λ3/ 2
故归一
化波函数为ψ
(
x)
=
2λ3 /
0,
2
xe−
λx
,
当x ≥ 0 当x < 0
∫∞ x en −ax dx 0
=
n! an+1
∫ ∫ ∞
c( p) = −∞
0
(r,θ ,ϕ ) 2r2
sin
θ
drdθ
dϕ
=
4
a
3 0
e − 2r / a0
r 2dr
w(r )
=
4 a03
e −2 r /
a0
r2
dw(r) dr
=
4 a03
2
−
2 a0
r re−2r / a0
令
dw(r) = 0,⇒ dr
r1 = 0,
r2 = ∞,
r3 = a0
当 r1 = 0, r2 = ∞时,w(r) = 0 为概率最小位置;
=
α π
h2 α2 2m
⋅
π α
−α
2
⋅
π 2α 3
1
=
α π
h2 α2 2m
π 2α
=
h2 α2 4m
=
h2 4m
⋅
mω h
=
1 hω 4
或 T = E −U = 1 hω − 1 hω = 1 hω
2
4
4
∫ (3) c( p) =
量子力学习题解答-第3章

第三章形式理论本章主要内容概要:1. 力学量算符与其本征函数量子力学中力学量(可观测量)用厄米算符表示,厄米算符满足()**ˆˆ()()()()f x Qg x dx Qf x g x dx =⎰⎰或者用狄拉克符号,ˆˆf QgQf g =,其中(),()f x g x 为任意满足平方可积条件的函数(在x →±∞,(),()f x g x 为零)。
厄米算符具有实本征值的本征函数(系),具有不同本征值的本征函数相互正交,若本征值为分离谱,本征函数可归一化,是物理上可实现的态。
若本征值为连续谱,本征函数可归一化为δ函数,这种本征函数不是物理上可实现的态,但是它们的叠加可以是物理上可实现的态。
一组相互对易的厄米算符有共同的本征函数系。
而两个不对易的厄米算符没有共同的本征函数系,它们称为不相容力学量。
对任意态测量不相容力学量ˆˆ,Q F ,不可能同时得到确定值,它们的标准差满足不确定原理2221ˆˆ,2QFQ F i σσ⎛⎫⎡⎤≥ ⎪⎣⎦⎝⎭2. 广义统计诠释设力学量ˆQ 具有分离谱的正交归一本征函数系{}()n f x 本征值为{}nq ,即 ()*ˆ()(), ()(), ,1,2,3,...n n n m n mnQf x q f x f x f x dx m n δ===⎰或ˆ, n n n m n mnQ f q f f f δ== 这个本征函数系是完备的,即1n n nf f =∑(恒等算符,封闭型),任意一个波函数可以用这个本征函数系展开 (,)(),nn nx t cf x ψ=∑ 或nn n n nnf f c f ψ=ψ=∑∑展开系数为*()()(,)n n nc t f fx x t dx =ψ=ψ⎰若(,)x t ψ是归一化的,n c 也是归一化的,21n nc =∑。
广义统计诠释指出,对(,)x t ψ态测量力学量Q ,得到的可能结果必是Q 本征值中的一个,得到n q 几率为2n c 。
曾谨言量子力学第3章

即
则O+和O-均是厄米算符。
定理: 在体系的任何状态下,厄米算符的平均值必为实数。 证明:
ˆ ( , A ˆ ) ( A ˆ , ) ( , A ˆ ) A ˆ A
ˆ A ˆ A
(41)
Note: 所有力学量的算符均是厄米算符 性质: (1) 两个厄米算符之和仍是厄米算符 (2)两个厄米算符之积不一定是厄米算符 (3)无论厄米算符A,B是否对易,算符
1 ˆ ˆ ˆˆ 1 ˆ ˆ ˆˆ ( AB BA), ( AB BA) 均是厄米算符 2 2i
(4)任何算符总可分解为两个厄米算符的线性组合
球坐标系下的角动量算符 r x 2 y 2 z 2 x r sin θ cosφ 2 2 y r sin θ sin φ , θ arctan( x y / z ) z r cosθ φ arctan(y / x ) ˆ l x i sin φ θ cotθ cosφ φ ˆ l y i cosφ θ cotθ sin φ φ ˆ l z i φ 2 1 1 ˆ2 2 l sin θ θ sin θ θ sin 2 θ φ 2
如 算符A 则
ˆ ˆ p (i) i p
的厄米共轭算符A+定义为
ˆ φ ) ( A ˆ ψ ,φ ) (ψ , A
(41)
~ ˆ φ ) (A ˆ ψ , φ ) (φ , A ˆ ψ ) (φ , A ˆ ψ ) (ψ , A ˆ φ) (ψ , A
量子力学 第三章习题与解答

第三章习题解答3.1 一维谐振子处在基态t i x e x ωαπαψ2222)(--=,求:(1)势能的平均值2221x U μω=; (2)动能的平均值μ22p T =;(3)动量的几率分布函数。
解:(1) ⎰∞∞--==dx e x x U x 2222222121απαμωμω μωμωππαμω ⋅==⋅=2222221111221ω 41= (2) ⎰∞∞-==dx x p x p T )(ˆ)(2122*2ψψμμ ⎰∞∞----=dx e dx d e x x 22222122221)(21ααμπα ⎰∞∞---=dx e x x 22)1(22222αααμπα][222222222⎰⎰∞∞--∞∞---=dx e x dx e x xααααμπα]2[23222απααπαμπα⋅-=μωμαμαπαμπα⋅===442222222 ω 41=或 ωωω 414121=-=-=U E T (3) ⎰=dx x x p c p )()()(*ψψ 212221⎰∞∞---=dx ee Px i xαπαπ⎰∞∞---=dx eePx i x222121απαπ⎰∞∞--+-=dx ep ip x 2222)(21 21αααπαπ ⎰∞∞-+--=dx ee ip x p 222222)(212 21αααπαπ παπαπα22122p e -=22221απαp e-=动量几率分布函数为 2221)()(2απαωp ep c p -==#3.2.氢原子处在基态0/301),,(a r e a r -=πϕθψ,求:(1)r 的平均值;(2)势能re 2-的平均值;(3)最可几半径; (4)动能的平均值;(5)动量的几率分布函数。
解:(1)ϕθθπτϕθψππd rd d r re a d r r r a r sin 1),,(0220/23020⎰⎰⎰⎰∞-==⎰∞-=0/233004dr a r a a r04030232!34a a a =⎪⎪⎭⎫⎝⎛=2203020/232020/232202/2322214 4 sin sin 1)()2(000a e a a e drr ea e d drd r e a e d drd r e ra e r e U a r a r a r -=⎪⎪⎭⎫ ⎝⎛-=-=-=-=-=⎰⎰⎰⎰⎰⎰⎰∞-∞-∞-ππππϕθθπϕθθπ(3)电子出现在r+dr 球壳内出现的几率为 ⎰⎰=ππϕθθϕθψω02022 sin )],,([)(d drd r r dr r dr r e a a r 2/23004-=2/23004)(r e a r a r -=ω 0/2030)22(4)(a r re r a a dr r d --=ω令 0321 , ,0 0)(a r r r drr d =∞==⇒=,ω 当0)( ,0 21=∞==r r r ω时,为几率最小位置/22203022)482(4)(a r e r a r a a dr r d -+-=ω08)(230220<-=-=e a dr r d a r ω ∴ 0a r =是最可几半径。
第三章 原子结构习题及答案

第三章原子结构习题1.是非判断题1-1基态氢原子的能量具有确定值,但它的核外电子的位置不确定。
1-2微观粒子的质量越小,运动速度越快,波动性就表现得越明显。
1-3原子中某电子的合理的波函数,代表了该电子可能存在的运动状态,该运动状态可视为一个原子轨道。
1-4对于氢原子的1s轨道,不应该理解为电子绕核作圆周运动,因为电子有波粒二象性,它的运动轨道是测不准的。
1-5因为氢原子只有一个电子,所以它只有一条原子轨道。
1-6 p轨道的空间构型为双球形,则每一个球形代表一条原子轨道。
1-7因为在s轨道中可以填充两个自旋方向相反的电子,因此s轨道必有两个不同的伸展方向,它们分别指向正和负。
1-8不同磁量子数m表示不同的原子轨道,因此它们所具有的能量也不相同。
1-9随着原子序数的增加,n、l相同的原子轨道的能量也随之不断增加。
1-10每一个原子中的原子轨道需要有3个量子数才能具体确定,而每一个电子则需要4个量子数才能具体确定。
1-11磁量子数m决定原子轨道在空间的取向。
1-12多电子原子中,电子的能量决定与主量子数n和角量子数l。
1-13主量子n相同,角量子数l不同,随l增大,屏蔽作用增加。
1-14 3个p轨道的能量,形状、大小都相同,不同的是在空间的取向。
1-15磁量子数m=0的轨道都是球形对称的轨道。
1-16氢原子的能级中,4s=4p=4d=4f,而多电子原子中,4s<4p<4d<4f。
1-17主量子数n为4时,有4s,4p,4d,4f四条轨道。
1-18电子云的黑点表示电子可能出现的位置,疏密程度表示电子出现在该范围的机会大小。
1-19描述原子核外电子运动状态的波函数Ψ需要用四个量子数来确定。
1-20一组n,l,m组合可以表达核外电子的一种运动状态。
1-21某原子的价电子构型为2s22p2,若用四个量子数表示2p2两个价电子的运动状态,则分别为2,2,0,-1/2和2,2,1,+1/2。
1-22 Na原子的3s能级与K原子的3s能级具有相同的能量。
量子力学曾谨言习题解答第三章

第三章: 一维定态问题[1]对于无限深势阱中运动的粒子(见图3-1)证明2a x =)()(22226112πn ax x -=- 并证明当∞→n 时上述结果与经典结论一致。
[解]写出归一化波函数: ()ax n ax n πsin2=ψ (1)先计算坐标平均值:xdx axn axdx ax n axdx x aaa)(⎰⎰⎰-==ψ=222cos11sin2ππ 利用公式:2sin cos sin ppx p pxx pxdx x +-=⎰(2)得2c o s s i n c o s ppx ppxx pxdx x +-=⎰(3)22cos 22sin 221022a a x n n a a x n x n a xa x a=⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛-=ππππ计算均方根值用()x x x x x ,)(222-=-以知,可计算2xdx axn x adx axn x adx x xaa)(⎰⎰⎰-==ψ=2222222cos11sin2ππ 利用公式px ppx x ppx x ppxdx x sin 1cos 2sin 1cos 3222-+=⎰(5)aa x n x n a a x n n a x n a x a x222222cos 222sin 22311πππππ⋅⎪⎭⎫ ⎝⎛-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--=222223πn aa-=()22222222223⎪⎭⎫ ⎝⎛--=-=-a n aaxx x x π)( 2222212πn aa-=(6)在经典力学的一维无限深势阱问题中,因粒子局限在(0,a )范围中运动,各点的几率密度看作相同,由于总几率是1,几率密度a1=ω。
210a xdx axdx x aa===⎰⎰ω31222adx x axa==⎰()22222222223⎪⎭⎫ ⎝⎛--=-=-a n aaxx x x π)( 故当∞→n 时二者相一致。
#[2]试求在不对称势力阱中粒子的能级。
量子力学第四版卷一(曾谨言著)习题集规范标准答案第3章-补充

补充3.5)设粒子处于半壁高的势场中⎪⎩⎪⎨⎧><<-<∞=ax a x V x V ,00,x ,)(0 (1) 求粒子的能量本征值。
求至少存在一条束缚能级的体积。
解:分区域写出eq s .:ax ,0)()(a x 0 ,0)()(22"212'"1>=-<<=+x k x x k x ψψψψ (2)其中 ()22022'2k ,2ηηE E V k μμ-=+=(3) 方程的解为kxkxx ik x ik DeCe x Be Ae x --+=+=)()(21''ψψ (4)根据对波函数的有限性要求,当∞→x 时,)(2x ψ有限,则0=C当0=x 时,0)(1=x ψ,则0=+B A 于是ax , )(x 0 ,sin )(2'1>=<<=-kxDe x a x k F x ψψ (5)在a x =处,波函数及其一级导数连续,得ka ka kDe a k F k De a k F ---=='''cos ,sin (6)上两方程相比,得 kk a k tg ''-= (7)即 ()E E V E V atg +--=⎥⎦⎤⎢⎣⎡+0022ημ(7’) 若令 ηξ==a a k k ,'(8)则由(7)和(3),我们将得到两个方程:⎪⎩⎪⎨⎧=+-=(10)9) ( 2220a V ctg ημηξξξη(10)式是以a V r 202ημ=为半径的圆。
对于束缚态来说,00<<-E V ,结合(3)、(8)式可知,ξ和η都大于零。
(10)式表达的圆与曲线ξξηctg -=在第一象限的交点可决定束缚态能级。
当2π≥r ,即222πμ≥a V η,亦即 82220ηπμ≥a V (11)时,至少存在一个束缚态能级。
量子力学第三章习题

而 比较上两式,我们得到:
当时,则 此时我们同时求得能量的本征值和本征函数.
(3)角动量分量 的本征值方程为 它是的一个因子。 的值取决于量子数,题给定的状态不是的本征态,而是本征态的线 性叠加。在态中,而在态中,故在所给的态中,的可能值为和,出现和 的几率分别为和,即和。 的平均值
3.10. 一粒子在硬壁球形空腔中运动,势能为 求粒子的能级和定态波函数。
解: 这是一个无限深方势阱的问题,它只存在束缚态解.当,. 设粒子的质量为,因此,系统的哈密顿算符为 考虑到的球对称性,采用球坐标系,此时,有
第三章 量子力学中的力学量
3.1 一维谐振子处在基态 ,求
(1) 势能的平均值 ;
(2) 动量的几率分布函数;
(3) 动能的平均值 .
解: (1) 势能的平均值:
(2) 动量的几率分布函数
所以
(3) 动能的平均值
计算可知,这一状态中的振子的势能和动能的平均值相等,都是零点
能的一半.
以上计算中,用到积分公式: 费曼方法介绍: 设某系统的能量本征值方程为 其中含有一参数, 那么, 便有 于是有 再根据, 得到
(5) 另解:氢原子基态波函数为
, 仅是的函数而
, 所以只考虑径向的“测不准关系”
氢原子的径向能量为 而 所以
因而
取
由上两式得
即
将上式代入氢原子的径向能量表示式中
得
基态能量是上面表达式使取极小值。满足这一条件的由求极值的方法求
量子力学 第四版 卷一 (曾谨言 著)习题答案第3章-补充

2
2
代入边界条件 (b) 0 ,得 2
(b) sin(kb ) 0,kb n 2
因而 kb n , 2 (x) C sin[k(x b) n ]
C sin k(x b)
或 2(x)
(2)
C sin k(x b)
和V0 情形相同,C=A ,偶宇称解是
1(x) Asin k(x b)
x 2 2m(m 1 ) m2 2 1
2
a2
(m 1 ) 2m(m 1 ) m2 2 (m 1 )
2
2
m 2
m(m 1) 2
测不准关系中的不准度是:
p 2
* m
(
i
)
2
d 2 m dx 2
dx
2mE
m2 2
x2
2m(m
1 ) 2
m2 2
1 a2
(m 1 ) 2m(m 1 ) m2 2 (m 1 )
ka n , kb n
相减得 k(b a) (n n) n
n 是整数,可作为能级编号.
kn
n ba
因此能级是
En
2 2 2m
( n )2 ba
是二度简并的
注: 在本题中因为左右两个势阱对称,粒子在两者中都能出现, 和实际上是同一个函数,只是的取值 范围不同.
考察V0 为有限值情形的解,先设 E<V0 设区间 (a, b) 中的解是
区间 (b,a) ,设波函数:Байду номын сангаас
再考虑
2 (x) b sin(kx ) (5) (x a)x b 在二点的连续条件得
代入
B sin(ka ) 0, B sin(kb ) 0
得: ka p , kb p ,但 p, p 整数,因此区间 (b,a) 的波函数:
苏汝铿量子力学课后习题及答案chapter3

ˆ, B ˆ ⎤ = 0 。对于有三个分量 x,y,z 的算符,在证明中往往只证明 ˆ 对易,就是说, ⎡ A 和B
⎣ ⎦
其中的任一个分量,其余分量类推。 证:
( p × l + l × p ) x = p y l z − pz l y + l y pz − lz p y
=⎡ ⎣ p y , lz ⎤ ⎦+⎡ ⎣l y , p z ⎤ ⎦
所以有
(3.1)
ˆ 2α ˆ ˆ ˆ 2 −β ˆ = 2β αβ
(2)如果
(3.2)
ˆ n −1α ˆ n−2 ˆ ˆ n −1 − β ˆ = nβ αβ
成立,利用数学归纳法可以证明第三式,实际上
(3.3)
ˆ n −1 α ˆ n−2 )β ˆ =ቤተ መጻሕፍቲ ባይዱ(β ˆ ˆ ˆ n = αβ ˆ ˆ n −1 β ˆ + (n − 1) β αβ ˆ n −1 (αβ ˆ n −1 ˆ ˆ ) +(n − 1) β =β ˆ n −1 ( βα ˆ n −1 ˆ ˆ + 1) +(n − 1) β =β ˆ =β
∫
∞
−∞
ˆ ( x)ψ ( x)dx 来算 ψ *n ( x ) F n
ˆ 写成 p ˆ 的对易形式 ˆx 和 H 其平均值,并巧妙的使用薛定谔方程而证得。而方法二是把 F 1 ˆ ⎤ ,进而证得命题。 ˆ = − d V ( x) = 1 [ p ˆx, H ˆ x , V ( x) ] = ⎡ p F ⎦ i= i= ⎣ dx
1 ˆ⎤ ˆ = − d V ( x) = 1 [ p ˆ x , V ( x)] = ⎡ p ˆx, H F ⎦ i= i= ⎣ dx ˆ 的期望值为 于是在体系束缚定态ψ n ( x) 中,此力 F F= 1 1 ∞ ˆ ⎤ψ ( x)dx ˆ x , V ( x ) ] = ∫ ψ n* ( x ) ⎡ p ˆx, H [p ⎣ ⎦ n −∞ i= i= 1 ∞ * * ˆ ψ ( x)dx − ∞ ( H ˆxH ˆ xψ n ( x)dx = ψ n ( x) p n ∫−∞ ˆψ n ( x)) p ∫ i= −∞ =0
量子力学导论第3节答案

第三章一维定态问题3.1)设粒子处在二维无限深势阱中,⎩⎨⎧∞<<<<=其余区域,0,0 ,0),(b y a x y x V 求粒子的能量本征值和本征波函数。
如b a = ,能级的简并度如何?解:能量的本征值和本征函数为mE yx n n 222π =)(2222b n a n yx +,2,1, ,sinsin2==y x y x n n n n byn axn abyxππψ若b a =,则 )(222222y x n n n n maE yx +=π ay n a x n a y x n n yxππψsin sin 2=这时,若y x n n =,则能级不简并;若y x n n ≠,则能级一般是二度简并的(有偶然简并情况,如5,10==y x n n 与2,11''==y x n n )3.2)设粒子限制在矩形匣子中运动,即⎩⎨⎧∞<<<<<<=其余区域 ,0,0,0 ,0),,(c z b y a x z y x V 求粒子的能量本征值和本征波函数。
如c b a ==,讨论能级的简并度。
解:能量本征值和本征波函数为)(222222222cn b n an m n n n E zyxzy x ++=π ,,3,2,1,, ,sin sin sin 8==z y x z y x n n n c z n b y n a x n abc n n n zy x πππψ当c b a ==时,)(2222222z y x n n n man n n E z y x ++=π a y n a y n a x n a n n n z y x z y x πππψsinsin sin 223⎪⎭⎫ ⎝⎛= z y x n n n ==时,能级不简并;z y x n n n ,,三者中有二者相等,而第三者不等时,能级一般为三重简并的。
量子力学第三章作业答案

1、指出下列算符哪个是厄米算符,说明其理由。
224 dxd dx d i dx d ,,,x p x ˆˆ, )ˆˆˆˆ(21x p p x x x + 解: 不是, 是, 是 不是 是 (1) ˆx p是厄米算符,又因为,ˆx d p i dx =- ,所以d i dx 也是厄米算符,ddx不是厄米算符。
(2) 2222ˆxd p dx =- 是厄米算符,所以224d dx是厄米算符。
(3) ()†††ˆˆˆˆˆˆˆˆx x x x xpp x p x xp ==≠,所以不是厄米算符。
(4)()()()††††††††11ˆˆˆˆˆˆˆˆ()()2211ˆˆˆˆ2211ˆˆˆˆ221ˆˆˆˆ2x x x x x x x x x x xp p x xp p x xp p x p x x p p x xp ⎛⎫+=+ ⎪⎝⎭=+=+=+所以是厄米算符 2、如果 Fˆ和 G ˆ都是厄米算符,但互不对易,试判断下列算符中哪些是厄米算符?(1)G F ˆˆ; (2)F G ˆˆ;(3)G F ˆˆ+F G ˆˆ; (4)G F ˆˆF G ˆˆ-; (5)i (G F ˆˆ+F G ˆˆ); (6)i (G F ˆˆF G ˆˆ-); (7)G Fˆˆ+; (8)G F ˆˆ-; (9))ˆˆ(G F i +; (10))ˆˆ(G F i -;解:(1)(2)不是。
(3)是,(4)不是,(5)不是,(6)是,(7)是(8)是,(9)不是,(10)不是3、下列函数哪些是算符22dx d 的本征函数,其本征值是什么?①2x , ② x e , ③x s i n, ④x c o s 3, ⑤x x c o s s i n + 解:22dxd 2x =2 不是22dxd xe =x e ,是,本征值为1.22dxd x sin =-x sin ,是,本征值为-1. 22dxd x cos 3=-x cos 3,是,本征值为-1. 22dxd (x x cos sin +)=-(x x cos sin +), 是,本征值为-14、证明:[Ô,[Û,Ê]] + [Û,[Ê, Ô]] + [Ê,[ Ô,Û]] = 0 证明:[Ô,[Û,Ê]] + [Û,[Ê, Ô]] + [Ê,[ Ô,Û]]= [Ô, ÛÊ-ÊÛ]+ [Û, ÊÔ -ÔÊ]+ [Ê, Ô Û -Û Ô]=[Ô, ÛÊ] -[Ô, ÊÛ]+ [Û, ÊÔ]- [Û, ÔÊ]+ [Ê, ÔÛ] -[Ê, ÛÔ]=ÔÛÊ- ÛÊÔ- ÔÊÛ+ÊÛÔ+ ÛÊÔ-ÊÔÛ- ÛÔÊ+ ÔÊÛ+ÊÔÛ- ÔÛÊ-ÊÛÔ+ ÛÔÊ=05、证明:处于1s 、2p 和3d 态的氢原子中的电子,当它处于距原子核的距离分别为00094a a a 、、的球壳处的几率最(0a 为第一玻尔轨道半径)。
量子力学课后习题

第一章 绪论1. 在0K 附近,钠的价电子能量约为3电子伏,求其德布洛意波长。
2. 氦原子的动能是32E kT =(k 为玻耳兹曼常数),求T =1K 时,氦原子的德布洛意波长。
3. 利用玻尔-索末菲的量子化条件,求 (1) 一维谐振子的能量;(2) 在均匀磁场中作圆周运动的电子轨道的可能半径。
4. 两个光子在一定条件下可发转化为正负电子对。
如果两光子的能量相等,问要实现这种转化,光子的波长最大是多少? 第二章 波函数和薛定谔方程1. 证明在定态中,几率密度和几率流密度与时间无关。
2. 由下列两定态波函数计算几率流密度:(1)11ikr e rψ=,(2)11ikr e rψ-=3. 求粒子在一维无限深势阱 中运动的能级和波函数。
4. 证明(2.6-14)式中的归一化常数是5. 求一维线性谐振子处于第一激发态时几率最大的位置。
6. 试求算符ˆix dFie dx=-的本征函数。
7. 如果把坐标原点取在一维无限深势阱的中心,求阱中粒子的波函数和能级的表达式。
0,2(),2a x U x a x ⎧≤⎪⎪=⎨⎪∞≥⎪⎩⎩⎨⎧≥≤∞<<=a x x ax x V 或0,0,0)(aA 1='第三章 量子力学中的力学量1. 一维线性谐振子处于基态,求: (1)势能的平均值; (2)动能的平均值; (3)动量的几率分布函数。
2. 氢原子处于基态()0,,ra r ψθϕ-=,求: (1)r 的平均值;(2)势能2e r-的平均值;(3)最可几半径; (4)动能的平均值; (5)动量的几率分布函数。
3. 一刚性转子转动惯量为I ,它的能量的经典表示式是22L H I=,L 为角动量。
求与此对应的量子体系在下列情况下的定态能量及波函数: (1)转子绕一固定轴转动; (2)转子绕一固定点转动。
4. 一维运动的粒子的状态是⎩⎨⎧=-0)(xAxe x λψ 00<≥x x 其中0>λ,求(1)粒子动量的几率分布函数; (2)粒子的平均动量。
《原子物理与量子力学》一至三章部分习题解答
2.7 有限深势阱(P52) 有限深势阱( )
(1)势场为 ) (2)定态 ) Schrödinger方程为 Schrödinger方程为 E<U0时
(3)方程的解为 )
HUST APPLIED PHYSICS 13
(4)利用标准条件定解(单值、有限、连续) 利用标准条件定解(单值、有限、连续) 单值条件满足。 单值条件满足。 再考虑连 续性, 续性,得 有限
必须 同时 成立
HUST APPLIED PHYSICS 14
或者
10
(5)体系的定态分两种情况 )
10
10
0
0
0
−10 0
0.5
E ((×10 ) E × 10
−8
−16 −8
1
能级均为分立能级
HUST
−10 0
0.5
E (× 10 )
1
−10 0
0.5
APPLIED PHYSICS
E ((× 10 ) E × 10
第一章 原子的基本状况
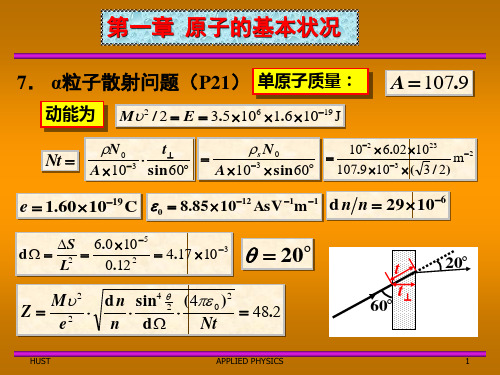
7. α粒子散射问题(P21) 单原子质量: . 粒子散射问题 粒子散射问题( ) 单原子质量:
动能为
60
t t⊥
20
HUST
APPLIED PHYSICS
1
第二章 原子的能级和辐射
8.对应原理(P77) .对应原理( )
转动频率为
HUST
APPLIED PHYSICS
2
9.类氢体系能级公式应用(P77) .类氢体系能级公式应用( )
1.4 量子化通则(P16) 量子化通则( )
(1)一维谐振子 ) 势能为
Bohr-Sommerfeld量子化条件Hale Waihona Puke 量子化条件令HUST
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
满足此点的 用 表示,则有
,
由此解得 把上式代入方程(3),得到氢原子中电子最小能量:
(5)
另解:氢原子基态波函数为
,
仅是 的函数而
,
所以只考虑径向的“测不准关系”
氢原子的径向能量为
而
所以
因而
取
由上两式得 即
将上式代入氢原子的径向能量表示式中
得
基态能量是上面表达式使 取极小值。满足这一条件的 由求极值的方法求得,即
则电流密度的径向分量 为:
电流密度 方向的 分量为
其实 是很显然的,因为 和 对 不起作用,所以状态函数与实函数的情况相同.
电流密度 方向的 分量为
综上所述:
3.4.由上题知,氢原子中的电流可以看作是由许多圆电流组成的.
(1)求一圆电流的磁矩;
(2)证明氢原子磁矩为
原子磁矩与角动量之比
这个比值,称为回转比磁比率.
(2)求粒子动量的平均值:
由上式 已经看出,粒子在状态 中取 和 几率相等,所以动量的平均值为零,实际上:
或
3.8.在一维无限深势阱中运动的粒子,势阱的宽度为 ,如果粒子状态的波函数为
,
A为归一化常数,求粒子能量的几率分布和能量的平均值.
解:首先将波函数归一化:
所以
将给定的波函数视为能量本征函数
的线性叠加,即
,(2)
动量值不能比它的值的不准确量更小是显而易见的。所以最小可能动量值是 。把核看作静止不动。电子绕核运动的能量等于它的动能( )和它的势能(处于距核 处, )的总和。为了进行估算。假定电子总能量的经典表达式仍然是有意义的。将方程 代入动能表达式,得到氢原子中电子的总能量
。(3)
图1表示电子能量对于 的依赖关系。由图可见曲线有一个最小值;从对应于最小值的点满足 。可以很容易地求出 的 值,记为 。换句话说,氢原子的电子在距核的距离 等于 处,出现的几率最大(能量最低状态)。将式(3)对 求导,并令其等于零,得到:
第三章量子力学中的力学量
3.1一维谐振子处在基态 ,求
(1)势能的平均值 ;
(2)动量的几率分布函数;
(3)动能的平均值 .
解:(1)势能的平均值:
(2)动量的几率分布函数
所以
(3)动能的平均值
计算可知,这一状态中的振子的势能和动能的平均值相等,都是零点能 的一半.
以上计算中,用到积分公式:
费曼方法介绍:
本征函数为根据有源自其中归一化系数为此时
3.11.求3.6题中粒子位置和动量的不确定性
解:根据3.6的结果以及对任何一个力学量 有
便有
由3.6题知:
动量的平均值:
动能的平均值:
因此有
此外,有
由于 是关于 的偶函数,因此
另外,我们有
故我们有
最终有
3.12.粒子处于状态
式中 为常量.求粒子的动量平均值,并计算测不准关系
解:(1)一个微分的园环中通过电流所产生的磁矩
在球极坐标中(核处于原点),某一 的圆环附近流过电流 面积的微分圆面积电流为
该圆电流的磁矩为
式中 是环子 的所围成的面积.将 代入得
是一圆周电流的磁矩.
(2)氢原子的磁矩为:
(SI)
若用CGS单位制, ,
则 (CGS)
注意到 ,则立即可以得到回转磁比率:
其中系数
其中
而
将两式结果代入 得
因此,能量的几率分布函数
粒子的能量平均值:
能量还可以方便的由平均值的积分公式求得
3.9.设氢原子处于状态
求氢原子的能量、角动量的平方及角动量 分量的可能值,这些可能值出现的几率和这些力学量的平均值.
解:(1)能量
能量的本征值方程为
其能量为
可见所给的波函数是能量的本征函数,本征值为 ,即
所以
将上式代入得
即:
此外,根据(1)与(3)两道小题,有
3.2.氢原子处在基态 ,求:
(1) 的平均值;
(2)势能 的平均值;
(3)最可几半径;
(4)动能的平均值;
(5)动量的几率分布函数.
解:(1) 的平均值:
(2)求势能的平均值:
(3)求最可几半径:
电子在半径为 的球面上的几率为
求上式对 的导数
令上式等于零,则可求得最可几半径为:
代入方程(1),便得到径向波函数 满足的方程
(2)
令
则 (3)
首先考虑, 态即 的状态波函数与角度无关,则薛定谔方程变为
(4)
它的解为
即
要求 在 时有限,所以 ,故
因为在 处是硬壁,粒子绝不可能透出外面,所以 于是有
即
即 与 联立求解得到粒子的能级为
(5)
这一量子化的能级与一维无限深势阱能级结果类似。波函数中常数 由归一条件求得
解: 是不归一的,因此令归一化常数为 ,则有
因此得:
最后得归一化波函数为
(1)求粒子动量的平均值
(2)计算测不准关系
因
另解:
所以
最后得:
3.13.利用测不准关系估计氢原子的基态能量。
解:假设氢原子中电子的运动出现在一个具有半径 的区域,电子位置的不准确量可取成 ,根据测不准关系式
。(1)
电子动量 的值的最小不准确量 ,为明确起见,假定
(4)动能的平均值
(5)动量的几率分布函数
欲求动量的几率分布,必须先将波函数按动量的本征函数展开.即
其中
将氢原子的基态波函数代入得:
因为在积分过程中 不变,我们 选沿 轴方向,即 对 的积分已经完成,以下作对 的积分:
将上式的结果代入 中,最后对 积分:
这就是当氢原子处在基态时,电子动量的绝对值取 的几率.电子动量的绝对值在 范围内的几率,等于 乘以动量空间的体积元 .此题中势能动能平均值可用费曼方法求解.
所以
最后得到一化的波函数为:
(6)
(7)
再考虑 的一般情况,径向方程(2)化为
(8)
边界条件为
令 ,则(8)式化为
这正是球贝塞尔方程,它的解可取为球贝塞尔函数 或球诺伊曼函数 .由于解要求在 有限,所以只取球贝塞尔函数 为本方程的解
由边界条件 确定.
由于 取有限值, 只能取一系列分立值.把 的根记为 ,其中 ,则粒子的本征值为
的平均值
3.10.一粒子在硬壁球形空腔中运动,势能为
求粒子的能级和定态波函数。
解:这是一个无限深方势阱的问题,它只存在束缚态解.当 , .
设粒子的质量为 ,因此,系统的哈密顿算符为
考虑到 的球对称性,采用球坐标系,此时,有
(1)
在中心势中,角动量 是守恒量.因此它的各分量都是守恒量.选体系的守恒量完全集为 ,本征值方程(1)的解为 的本征态.
(2)角动量的平方
角动量平方的本征值方程为
其
可见所给的波函数是角动量平方的本征函态,角动量平方有确定的值(对应于 )
(3)角动量 分量
的本征值方程为
它是 的一个因子。
的值取决于量子数 ,题给定的状态不是 的本征态,而是 本征态的线性叠加。在 态中, 而在 态中 ,故在所给的态 中, 的可能值为 和 ,出现 和 的几率分别为 和 ,即 和 。
费曼方法求动能势能平均值.
动能平均值:
于是有:
这样根据费曼的方法,有
同样地,有
这样根据费曼的方法,有
当然有
是自洽的.
*3.3.证明氢原子中电子运动所产生的电流密度在球极坐标系中的分量是
解:电流密度
而 为电子的几率流密度
在球坐标系中电子运动状态函数为
其中 均为实数, 是实数,只有 是非实数,而
另外球坐标中的梯度算符为
其中
其解
考虑单值条件,即 ,得
由此得
也可以将本征函数改写为
即
可归一化为:
最后得
因此本征值为
3.6.设 粒子的状态为
求此时的平均动量和平均动能.
解:方法I:
将上式代入 中得
可见动量可以取5个值,依次是: 和
由归一化条件: 得
所以归一化系数为
它们出现的几率分别为是: 和
动量的平均值:
动能的平均值:
方法II:
3.5.一刚性转子转动惯量为I,它的能量的经典表示式是 , 为角动量,求与此对应的量子体系在下列情况下的定态能量及波函数:
(1)转子绕一固定点转动;
(2)转子绕一固定轴转动.
解:空间转子是在中心力场中运动的特例,即它是被约束在球面上运动的体系.这种情况下,体系的哈密顿为
(1)对于定点转动,状态与 都有关,设能量的本征函数为 ,有
即
而
比较上两式,我们得到:
当 时,则
此时我们同时求得能量的本征值和本征函数.
(2)转子绕一固定轴转动.
对于定轴转动,即转子被约束在某个平面内的圆周上转动,我们可以假设 ,波函数与 无关.此时体系的哈密顿算符亦与 无关,写作
波函数与 无关,只取决于 中的
即
将哈密顿算符作用于上式得到能量的本征值为
或直接解本征值方程
设某系统的能量本征值方程为
其中 含有一参数 ,那么,便有
于是有
再根据 ,得到
.
这个公式对于求某些力学量本征态下的平均值问题会非常有用.具体到这里的(1)、(3)小题,有
(1) .
因而
.
这样便有
这里,用到了 ,因此,有
(3) .
因而
.
根据费曼方法,有
这样,便有
从以上两例,可以看到:利用费曼方法,可以非常简捷地得到所要的结果.这种方法,在后面还会用到.
上面利用欧拉公式直接展开,结果与方法I一样,以下运算与方法I完全相同.
3.7.一维运动粒子的状态是
