分析判断函数图像专题Word版
高考数学:专题10 函数图像的判断(解析版)

【高考地位】函数图像作为高中数学一个“重头戏”,是研究函数性质、方程、不等式重要武器,已经成为各省市高考命题一个热点。
在高考中经常以几类初等函数图像为基础,结合函数性质综合考查,多以选择、填空题形式出现。
【方法点评】方法一 特值法使用情景:函数()f x 解析式已知情况下解题模板:第一步 将自变量或者函数值赋以特殊值;第二步 分别一一验证选项是否符合要求; 第三步 得出结论.例1 函数x x x y sin cos +=图象大致为( )【答案】C考点:函数图像【点评】特值法是解决复杂函数图像问题方法之一,其将复杂问题简单化,且操作性简单可行。
【变式演练1】函数()2ln y x x =+图象大致为( )A .B .C .D .【答案】A【解析】试题分析:解:令()2ln y x x =+0=,解得1,1,2--=x ,∴该函数有三个零点,故排除B ;当2-<x 时,02<+x ,2>x ,02ln ln >>∴x ,∴当2-<x 时,()2ln y x x =+0<,排除C 、D .故选A .考点:函数图象.【变式演练2】函数()1cos f x x x x ⎛⎫=-⎪⎝⎭(x ππ-≤≤且0x ≠)图象可能为( )【答案】D 【解析】考点:1.函数基本性质;2.函数图象. 【变式演练3】现有四个函数:①②③④图象(部分)如下,则按照从左到右将图象对应函数序号安排正确一组是( )A .④①②③ B.①④③② C.①④②③ D.③④②① 【答案】C【解析】试题分析:因为,所以是偶函数,图象关于轴对称,即与左1图对应,故排除选项A 、D ,因为当时,,故函数图象与左3图对应,故排除选项B ;故选C .【方法点睛】本题考查通过函数解析式和性质确定函数图象,属于中档题;已知函数解析式确定函数图象,往往从以下几方面考虑:定义域(确定图象是否连续),奇偶性(确定图象对称性),单调性(确定图象变化趋势),最值(确定图象最高点或最低点),特殊点函数值(通过特殊函数值排除选项),其主要方法是排除法.考点:1.函数奇偶性;2.函数图象.【变式演练4】函数xe x y )1(2-=图象大致是( )【答案】C 【解析】考点:偶函数图象性质.方法二 利用函数基本性质判断其图像使用情景:函数()f x 解析式已知情况下解题模板:第一步 根据已知函数解析式分析其变化特征如单调性、奇偶性、定义域和值域等;第二步 结合简单基本初等函数图像特征如对称性、周期性等进行判断即可; 第三步 得出结论.例2 函数()(1)ln ||f x x x =-图象大致为( )【答案】A 【解析】考点:1、导数在研究函数单调性中应用;2、函数图像.【思路点睛】本题主要考查了导数在研究函数单调性中应用和函数图像,具有一定综合性,属中档题.其解题一般思路为:首先观察函数表达式特征如0)1(=f ,然后运用导数在研究函数单调性和极值中应用求出函数单调区间,进而判断选项,最后将所选选项进行验证得出答案即可.其解题关键是合理地分段求出函数单调性.【变式演练5】如图,周长为1圆圆心C 在y 轴上,顶点()01A ,,一动点M 从A 开始逆时针绕圆运动一周,记走过弧长AM x =,直线AM 与x 轴交于点()0N t ,,则函数()t f x =图象大致为( )A .B .C .D .【答案】D 【解析】试题分析:由圆对称性可知,动点N 轨迹关于原点对称,且在原点处,21=x ,0=y ;当点M 位于左半圆时,随着弧AM 长递增,t 值递增,且变化由快到慢,由给定图象可知选D . 考点:函数图象.【变式演练6】如图可能是下列哪个函数图象( )A .221xy x =-- B .2sin 41x xy x =+C .ln x y x=D .2(2)xy x x e =- 【答案】D 【解析】考点:函数图象和性质.【变式演练7】如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆,垂直于x 轴直线:(0)l x t t a =≤≤经过原点O 向右平行移动,l 在移动过程中扫过平面图形面积为y (图中阴影部分),若函数()y f x =大致图像如图,那么平面图形形状不可能是( )【答案】C【解析】试题分析:由函数图象可知,几何体具有对称性,选项A ,B ,D ,l 在移动过程中扫过平面图形面积为y ,在中线位置前,都是先慢后快,然后相反.选项C ,后面是直线增加,不满足题意. 考点:函数图象与图形面积变换关系. 【变式演练8】函数()21x f x e-=(e 是自然对数底数)部分图象大致是( )【答案】C 【解析】【变式演练9】函数2ln x x y x=图象大致是( )A .B .C .D .【答案】D 【解析】试题分析:从题设中提供解析式中可以看出1,0±≠x ,且当0>x 时, x x y ln =,由于x y ln 1/+=,故函数x x y ln =在区间)1,0(e 单调递减;在区间),1(+∞e单调递增.由函数图象对称性可知应选D. 考点:函数图象性质及运用.【变式演练10】函数()21cos 1e xf x x ⎛⎫=-⎪+⎝⎭图象大致形状是( ) A . B .C .D .【答案】B 【解析】考点:函数奇偶性及函数图象. 【变式演练11】若函数()2(2)m xf x x m-=+图象如图所示,则m 范围为( )A .(),1-∞-B .()1,2-C .()0,2D .()1,2 【答案】D考点:1.函数奇偶性;2.函数单调性;3.导数应用.【高考再现】1. 【2016高考新课标1卷】函数22xy x e =-在[]2,2-图像大致为(A )(B )(C )(D )【答案】D考点:函数图像与性质【名师点睛】函数中识图题多次出现在高考试题中,也可以说是高考热点问题,这类题目一般比较灵活,对解题能力要求较高,故也是高考中难点,解决这类问题方法一般是利用间接法,即由函数性质排除不符合条件选项.2.【2015高考安徽,理9】函数()()2ax bf x x c +=+图象如图所示,则下列结论成立是( )(A )0a >,0b >,0c < (B )0a <,0b >,0c >(C )0a <,0b >,0c < (D )0a <,0b <,0c <【答案】 C【考点定位】1.函数图象与应用.【名师点睛】函数图象分析判断主要依据两点:一是根据函数性质,如函数奇偶性、单调性、值域、定义域等;二是根据特殊点函数值,采用排除方法得出正确选项.本题主要是通过函数解析式判断其定义域,并在图形中判断出来,另外,根据特殊点位置能够判断,,a b c 正负关系.3.【2015高考新课标2,理10】如图,长方形ABCD 边2AB =,1BC =,O 是AB 中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠=.将动P 到A 、B 两点距离之和表示为x 函数()f x ,则()y f x =图像大致为( )(D)(C)(B)(A)yπ4π23π4ππ3π4π2π4yyπ4π23π4ππ3π4π2π4yDPCOAx【答案】B【考点定位】函数图象和性质.【名师点睛】本题考查函数图像与性质,表面看觉得很难,但是如果认真审题,读懂题意,通过点P 运动轨迹来判断图像对称性以及特殊点函数值比较,也可较容易找到答案,属于中档题.4.【2015高考北京,理7】如图,函数()f x 图象为折线ACB ,则不等式()()2log 1f x x +≥解集是( )A .{}|10x x -<≤B .{}|11x x -≤≤C .{}|11x x -<≤D .{}|12x x -<≤【答案】C【解析】如图所示,把函数2log y x =图象向左平移一个单位得到2log (1)y x =+图象1x =时两图象相交,不等式解为11x -<≤,用集合表示解集选C【考点定位】本题考查作基本函数图象和函数图象变换及利用函数图象解不等式等有关知识,体现了数形结合思想.【名师点睛】本题考查作基本函数图象和函数图象变换及利用函数图象解不等式等有关知识,本题属于基础题,首先是函数图象平移变换,把2log y x =沿x 轴向左平移2个单位,得到2log (y x =+2)图象,要求正确画出画出图象,利用数形结合写出不等式解集.5.【2014年.浙江卷.理7】在同意直角坐标系中,函数x x g x x x f a alog )(),0()(=≥=图像可能是( )答案: D考点:函数图像.【名师点睛】本题主要考查了函数指数与对数函数图像和性质,属于常见题目,难度不大;识图常用方法:(1)定性分析法:通过对问题进行定性分析,从而得出图象上升(或下降)趋势,利用这一特征分析解决问题;(2)定量计算法:通过定量计算来分析解决问题;(3)函数模型法:由所提供图象特征,联想相关函数模型,利用这一函数模型来分析解决问题.6. 【2014福建,理4】若函数log (0,1)a y x a a =>≠且图像如右图所示,则下列函数图像正确是( )13OxyDC BAy=log a (-x)y=(-x)ay=x ay=a -x-1-3113OO OO1y x1xy1xyxy【答案】B 【解析】考点:函数图象.【名师点睛】本题主要考查函数图像识别问题及分析问题解决问题能力,求解此题首先要根据图像经过特殊点,确定参数值,然后利用函数单调性确定正确选项,解决此类问题要重视特殊点及单调性应用.【反馈练习】1. 【2017届河北武邑中学高三上周考8.14数学试卷,文5】函数111y x =--图象是( )【答案】B 【解析】试题分析:将1y x =-图象沿x 轴向右平移1个单位得到11y x =--图象,再沿y 轴向上平移1个单位得到111y x =--图象.故选B . 考点:函数图象平移变换.2. 【2017届广东华南师大附中高三综合测试一数学试卷,文10】函数2ln xy x=图象大致为( )A .B .C .D .【答案】B3. 【2017届广东佛山一中高三上学期月考一数学试卷,理6】函数22x y x -=图象大致是( )【答案】A 【解析】试题分析:当1x <-时,22x x <,即220x x -<,排除C 、D ,当3x =时,322310y =-=-<,排除B ,故选A .考点:函数图象.4. 【2016-2017学年山西榆社中学高一10月月考数学试卷,理7】已知函数()f x 定义域为[],a b ,函数()y f x =图象如图甲所示,则函数(||)f x 图象是图乙中( )【答案】B 【解析】考点:函数图象与性质.5. 【2016-2017学年河北徐水县一中高一上月考一数学试卷,理5】下列图中,画在同一坐标系中,函数2y ax bx =+与y ax b =+(0a ≠,0b ≠)函数图象只可能是( )【答案】B【解析】试题分析:()2f x ax bx =+图象是抛物线,()g x ax b =+图象是直线.A 选项()f x 开口向上,说明0a >,直线应斜向上,故A 错误.D 选项()f x 开口向下,说明0a <,直线应斜向下,故D 错误. C 选项()f x 图象不过原点,错误.故选B. 考点:函数图象与性质.6. 【2017届河北武邑中学高三上周考8.14数学试卷,理9】已知函数()y f x =大致图象如图所示,则函数()y f x =解析式应为( )A .()ln x f x e x =B .()ln(||)xf x ex -=C .()ln(||)xf x e x = D .||()ln(||)x f x e x = 【答案】C 【解析】考点:函数性质.7. 【2017届湖南长沙长郡中学高三上周测十二数学试卷,文8】函数22()(44)log x x f x x -=-图象大致为( )【答案】A 【解析】试题分析:因为22()(44)log x x f x x -=-,()2222()(44)log (44)log x x x x f x x x f x ---=-=--=-,所以22()(44)log x x f x x -=-是奇函数,排除B 、C ,又因为0x →时,0y →,所以排除D ,故选A.考点:1、函数图象;2、函数奇偶性.8. 【2017届重庆市第八中学高三上适应性考试一数学试卷,理10】如图1,圆O 半径为1,A 是圆上定点,P 是圆上动点,角x 始边为射线OA ,终边为射线OP ,过点P 作直线OA 垂线,垂足为M ,将点M 到直线OP 距离与O 到M 距离之和表示成x 函数()f x ,则()y f x =在[]0,π上图象大致是( )A .B .C .D .【答案】B 【解析】考点:函数实际应用.9.【 2017届河南新乡一中高三9月月考数学试卷,文7】设曲线2()1f x x =+在点(,())x f x 处切线斜率为()g x ,则函数()cos y g x x =部分图象可以为( )【答案】A 【解析】试题分析:()()()()()2,cos 2cos ,,cos cos g x x g x x x x g x g x x x ==-=--=,()cos y g x x ∴=为奇函数,排除B ,D ,令0.1x =时0y >,故选A .考点:1、函数图象及性质;2、选择题“特殊值”法.10. 【2017届湖北襄阳五中高三上学期开学考数学试卷,文6】已知函数)(x f 是定义在R 上增函数,则函数1|)1(|--=x f y 图象可能是( )A .B .C .D .【答案】B 【解析】考点:函数图象,图象变换.。
分析判断函数图象

分析判断函数图象类型一分析函数图象★1.随着移动互联网的快速发展,OFO、摩拜等互联网共享单车应运而生并快速发展.小冬骑的摩拜单车,爸爸骑的摩托车,沿相同路线由A地到B地,行驶过程中路程y和时间x的函数关系的图象如图,根据图象分析,何时俩人相遇,谁先到达B地()第1题图A. 4分钟时相遇,爸爸先到B. 20分钟时相遇,爸爸先到C. 4分钟时相遇,小冬先到D. 20分钟时相遇,小冬先到B【解析】观察函数图象可以知道,两函数图象的交点为(20,4),且爸爸先到,∴俩人20分钟时相遇.★2.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是()A. 凌晨4时气温最低为-3 ℃B. 14时气温最高为8 ℃C. 从0时至14时,气温随时间增长而上升D. 从14时至24时,气温随时间增长而下降第2题图C【解析】A.由图象可知,在凌晨4点函数图象在最低点为-3,∴凌晨4时气温最低为-3℃,正确;B.由图象可知,在14点函数图象在最高点为8,∴14时气温最高为8℃,正确;C.由图象可知,从4时至14时,气温随时间增长而上升,不是从0时,故本选项错误;D.由图象可知,从14时至24时,气温随时间增长而下降,正确,故选C.★3.我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的函数关系如图所示,则下列说法中,正确的个数有()个.①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③当x=4 时,甲、乙两队所挖管道长度相同;④甲队比乙队提前2天完成任务.A. 1B. 2C. 3D. 4第3题图D【解析】由图象可得,甲队每天挖:600÷6=100米,故①正确,乙队开挖两天后,每天挖:(500-300)÷(6-2)=50米,故②正确,当甲乙挖的管道长度相等时,100x=300+(x-2)×50,得x=4,故③正确,甲队比乙队提前完成的天数为:(600-300)÷50+2-6=2(天),故④正确.★4.某仓库调拨一批物资,调进物资共用8小时.调进物资4小时后同时开始调出物资(调进与调出物资的速度均保持不变).该仓库库存物资w(吨)与时间t(小时)之间的函数关系如图.则这批物资调出的速度(吨/小时)及从开始调进到全部调出所需要的时间(小时)分别是()A. 10, 10B. 25, 8.8C. 10, 8.8D. 25, 9第4题图B【解析】调进物资的速度是60÷4=15(吨/时),当在第4小时时,库存物资应该有60吨,在第8小时时库存20吨,所以调出速度是60-20+15×44=25(吨/时),所以剩余的20吨完全调出需要20÷25=0.8(小时).故这批物资从开始调进到全部调出需要的时间是8+0.8=8.8(小时).★5. 如图,在Rt △ABC 中,∠ACB =90°,D 为斜边AB 的中点,动点P 从B 点出发,沿B →C →A 运动.如图①所示,设S △DPB =y ,点P 运动的路程为x ,若y 与x 之间的函数图象如图②所示,则图②中Q 点的坐标是( )第5题图A. (4,4)B. (4,3)C. (4,6)D. (4,12)B 【解析】根据题意和图象可得,BC =4,AC =7-4=3,∵∠ACB =90°,点D 为AB 的中点,点x =4时,S △DPB =S △ACB 2,∴y =S △DPB =12S △ACB =12×3×42=3,即点Q 的坐标是(4,3).★6. 设圆、等腰直角三角形、正方形和等边三角形边界上的一个定点为Q (如四个选项中的图形),动点P 从点Q 出发,在其边界上按顺时针方向匀速运动一周后又回到起点Q .设点P 运动的时间是t ,点P 和点Q 之间的距离是d ,如图是d 与t 之间函数关系的大致图象,则该图形可能是( )第6题图D【解析】A.圆,随着点P运动,d的长度先变速增加至PQ 为直径,然后再变速减小至点P回到点Q,题干图象不符合;B.等腰直角三角形,点P在一开始沿直角边运动时,d的长度为直线变化增大,沿另一条直角边运动时,设直角边长为a,则d=a2+(t-a)2(a<t<2a),在斜边运动时,d的长度为直线变化减小,且长度与直角边不相等,题干图象不符合;C.正方形,点P在开始与结束的两边上直线变化,在另两边上,先变速增加至∠Q的对角顶点,再变速减小至另一顶点,题干图象不符合;D.等边三角形,点P在开始与结束的两边上直线变化,在点Q的对边上时,设等边三角形的边长为a,则y=(32+(32a-t)2(a<x<2a),2a)符合题干图象.类型二判断函数图象★1.如图,直角边长为 2 的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S 关于t的图象大致为()第1题图B【解析】根据题意可得,等腰直角三角形斜边为2,斜边上的高为1,而等边三角形的边长为3,高为33,故等腰直角三角形2沿水平线从左向右匀速穿过等边三角形时,出现等腰直角三角形完全处于等边三角形内部的情况,故两图形重合部分的面积先增大,然后不变,再减小,S关于t的图象的中间部分为水平的线段,故A,D选项错误;当t=0时,S=0,故C选项错误,B选项正确.★2.如图,正方形ABCD的边长为2 cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是()第2题图A 【解析】当P 点由A 运动到B 点时,即0≤x ≤2时,y =12×2x =x ,当P 点由B 运动到C 点时,即2<x <4时,即y =12×2×2=2,∴符合题意的函数关系的图象是A.★3.李明骑车上学,一开始以某一速度行进,途中车子发生故障,只好停下修车,车修好后,因怕耽误时间,于是加快了车速.如用s 表示李明离家的距离,t 为时间.在下面给出的表示s 与t 的关系图中,符合上述情况的是( )C 【解析】∵停下修车时,路程没变化,观察图象,A 、B 、D 的路程始终都在变化,故错误;C 、修车时的路程没变化,所以C 选项是正确的.★4. 小强将一个球竖直向上抛起,球升到最高点,垂直下落,直到地面.在此过程中,球的高度(h)与时间(t)的关系可以用图中的哪一幅来近似地刻画( )C 【解析】因为是小强将一个球竖直向上抛,小强有一定的身高,故D 一定不符合;小强抛出小球后,小球开始是向上运动的,故高度在增加,故A一定错误;小球升到一定高度后,会自由落下,高度就会降低,故B错误,C正确.★5.小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是()D【解析】由题意可知,当先向空玻璃杯注水时,玻璃杯内水位迅速上升,注满玻璃杯后,鱼缸水位开始上升,此时最高水位h 不变,当鱼缸水位与玻璃杯水位相等后在继续注水,鱼缸内水位h 缓慢上升,由此可判断D选项符合题意.★6.某市煤气公司计划在地下修建一个容积为104 m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是()A【解析】根据题意可知:S=104d(S>0,d>0),依据反比例函数的图象和性质可知,图象为反比例函数在第一象限内的部分.故选A.★7.如图,将一个边长为6的正方形纸片(如图①),在四个角上分别剪去边长为x的同样大小的小正方形,翻折粘合成一个无盖的长方体(如图②),设无盖的长方体的侧面积为S,则反映S与x之间的函数关系的大致图象是()第7题图D【解析】因为正方形纸片的边长为6,所以0<x<3,长方体的底面边长为6-2x,高为x,则侧面积S=4(6-2x)x=-8x2+24x =-8(x-32)2+18,所以对应的图象为选项D.★8.小明每天早上沿着矩形公园ABCD跑步,爸爸站在AC的某一个固定点处负责进行计时指导.假设小明在矩形公园ABCD的边上沿着A→B→C→D→A的方向跑步一周,小明跑步的路程为x米,小明与爸爸之间的距离为y米.y与x之间的函数关系如图②所示,则爸爸所在的位置可能为图①的()第8题图A. A点B. M点C. O点D. N点B【解析】矩形ABCD关于点O成中心对称,若爸爸在点O 处,函数图形应为中心对称图形,图象与已知实际不符,故C错;若爸爸在A处,当小明在A处时,小明和爸爸的距离是0,图象与实际不符合,故A错;若爸爸在点M处,如解图,点S,点D,点R,点C,点U,点B,点W,点A代表小明在矩形的不同位置,通过观察MA,MW,MB,MV,MC,MR,MD,MS的大小可以知道,图形与实际符合,所以B选项是正确的;若小明在点N处,开始时刻小明与爸爸的距离最远,图象与实际不符,故D错.第8题解图。
函数图象的分析与判断

A.C→B→A→E
B.C→D→E→A
C.A→E→C→B
图1
图2
D.A→E→D→C
选择填空题突破
10.如图1,点E为矩形ABCD的边AD上的一点,点P从点B出发沿 折线BE→ED→DC运动到点C时停止.点Q从点B出发沿BC运动到点C时 停止,它们运动的速度都是2 cm/s.若P,Q两点同时开始运动,设运动 时间为t(s),△BPQ的面积为y(cm2),y与t的函数关系图象如图2所示,则
选择填空题突破
类型 函数图象的分析 例2 如图1,四边形ABCD是菱形,对角线AC,BD相交于点O,
P,Q两点同时从点O出发,以1 cm/s的速度在菱形的对角线及边上运 动 . 点 P 的 运 动 路 线 为 O→A→D→O , 点 Q 的 运 动 路 线 为 O→C→B→ O.设运动的时间为x s,P,Q之间的距离为y cm,y与x的函数关系的大 致图象如图2所示,
BD=8,点P是对角线BD上任意一点,过点P作EF∥AC,与平行四边形
的两条边分别相交于点E,F.设BP=x,EF=y,则能大致表示y与x之
间函数关系的图象为
( D)
选择填空题突破
3.如图,等边三角形BC和等边三角形
ECD的边BC,CD在同一条直线上,将△ABC
向右平移,直到点B与点D重合为止,设点B
选择填空题突破
训练 6.如图1,在矩形ABCD中,动点P从点B出发,沿折线
B→C→D→B运动,设点P经过的路程为x,△APB的面积为y.若y关于x
的函数图象如图2所示,则图2中的a等于
( C)
A.3
B.2 5
C.6
D.8
图1
图2
选择填空题突破
7.如图1,在△ABC中,点P从点A出发向点C运动,在运动过程
专题01 函数图像的识别与辨析(解析版)

专题01 函数图像的识别与辨析一、题型选讲题型一 、由函数的解析式识别图像函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项 例1、【2020年天津卷】.函数241xy x =+的图象大致为( ) AC.【答案】A【解析】由函数的解析式可得:()()241xf x f x x --==-+,则函数()f x 为奇函数,其图象关于坐标原点对称,选项CD 错误; 当1x =时,42011y ==>+,选项B 错误. 故选:A.例2、【浙江卷】.函数y =x cos x +sin x 在区间[–π,+π]的图象大致为( )A. B..C. D.【答案】A【解析】因为()cos sin f x x x x =+,则()()cos sin f x x x x f x -=--=-, 即题中所给的函数为奇函数,函数图象关于坐标原点对称, 据此可知选项CD 错误;且x π=时,cos sin 0y ππππ=+=-<,据此可知选项B 错误. 故选:A.例3、【2019年高考全国Ⅰ卷理数】函数f (x )=在[,]-ππ的图像大致为 A .B .C .D .【答案】D 【解析】由22sin()()sin ()()cos()()cos x x x xf x f x x x x x -+----===--+-+,得()f x 是奇函数,其图象关于原点对称.又22π1π42π2()1,π2π()2f ++==>2π(π)01πf =>-+,可知应为D 选项中的图象. 故选D .题型二、由函数的图像辨析函数的解析式由函数的图像确定解析式,首先要观察函数的图像,可以从以下几个方面入手:(1)观察函数的对称性,判断函数的奇偶性;(2)观察图像所在象限,判断函数的定义域和值域;(3)从图像中观察一些特殊位置以及图像的发展趋势;结合上面的信息进行对函数解析式的排除。
(完整word版)高中数学函数图像总结,推荐文档

编制者;石嘉炜
①k>0时,y的值随x值的增大而增大;
②k﹤O时,y的值随x值的增大而减小.
|k|越大,直线与x轴相交的锐角度数越大(直线陡),|k|越小,直线与x轴相交的锐角度数越小(直线缓);
①当b>0时,直线与y轴交于正半轴上;②当b<0时,直线与y轴交于负半轴上;③当b=0时,直线经过原点,是正比例函数.
①当k>0,b>0时,直线经过第一、二、三象限(直线不经过第四象限);②当k>0,b﹥O时,直线经过第一、三、四象限(直线不经过第二象限);③当k﹤O,b>0时,直线经过第一、二、四象限(直线不经过第三象限);④当k﹤O,b﹤O时,直线经过第二、三、四象限(直线不经过第一象限)
(1)正比例函数y=kx的图象必经过原点;
(2)当k>0时,图象经过第一、三象限,y随x的增大而增大;(3)当k<0时,图象经过第二、四象限,y随x的增大而减小.。
九年级判断函数图像知识点

九年级判断函数图像知识点函数图像是数学中的重要概念,它通过给定的输入值得到相应的输出值,并将这种关系用图形的方式展示出来。
对于九年级的学生来说,学习如何判断函数图像是非常关键的。
本文将为大家介绍一些判断函数图像的重要知识点。
首先,我们需要了解如何根据函数的表达式来判断函数图像的形状。
以一次函数为例,一次函数的一般形式为y=ax+b,其中a 和b为常数。
当a为正数时,图像是一个从左下方向右上方倾斜的直线;当a为负数时,图像则是一个从左上方向右下方倾斜的直线。
而b则决定了直线与y轴的交点位置。
根据函数表达式的系数,我们可以判断函数图像在平面直角坐标系中的大致形状。
其次,函数的二次函数形式也是九年级需要掌握的重要内容。
二次函数的一般形式为y=ax²+bx+c,其中a、b和c为常数,且a 不为零。
二次函数的图像形状是一个拱形,被称为抛物线。
根据二次函数的系数,我们可以判断抛物线的开口方向以及在平面直角坐标系中的位置。
当a为正数时,抛物线开口向上;当a为负数时,抛物线开口向下。
而b和c则决定了抛物线的位置,例如顶点坐标和与x轴交点的位置等。
除了一次函数和二次函数,九年级还需要了解其他常见的函数类型,如绝对值函数、分段函数等。
绝对值函数的一般形式为y=|x|,其图像是一个以原点为对称中心的V字形曲线。
而分段函数由多个不同部分的函数组成,每个部分遵循特定的条件。
对于分段函数,我们可以根据不同的条件判断函数图像在不同的部分如何呈现。
在判断函数图像的过程中,我们还需要注意一些特殊情况。
例如,当函数表达式中存在有理数指数时,我们需要特殊对待。
对于有理数指数的相关知识,我们需要通过数值计算或利用图象软件来得到准确的结果。
此外,我们还需要注意函数图像中的对称性。
例如,奇函数的图像关于原点对称,而偶函数的图像关于y轴对称。
了解这些特殊情况可以帮助我们更准确地判断函数图像。
最后,判断函数图像是一个需要多方面能力的任务。
函数 图像的分析与判断

专题一:函数图像的分析与判断1. 如图,一只蚂蚁从点O出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁的运动时间为t 时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是()2. (2016许昌一模)如图①,四边形ABCD中,BC∥AD,∠A=90°,点P从A点出发,沿折线AB→BC→CD运动,到点D时停止,已知△PAD的面积s与点P运动的路程x的函数图象如图②所示,则点P从开始到停止运动的总路程为()A.4 B.2+13C.5 D.4+133. (2016重庆A卷)甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发。
在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示。
则乙到终点时,甲距终点的距离是__________米。
4.(2016新乡一模)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发以1cm/s的速度沿着边BA向A点运动,到达A点停止运动. 设P点运动时间为x(s),△BPQ的面积为y(cm²),则关于x的函数图象是()5. (2016安阳二模)如图,在Rt△ABC中,∠ACB=90°,BC=2,AC=4.点D是AC边的中点.点E在线段AD上,过点E作EF∥AB交BD于点F,连接AF,设AE=x,△AEF的面积为y,则能表示y与x函数关系的大致图象是()6.(2016开封一模)如图,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A-B-C的方向运动,到达点C时停止。
设点M运动的路程为x,MN²=y,则y关于x的函数图象大致为( )A. B. C. D.7.(2014年北京中考、2015新乡一模)已知点A为某封闭图形边界上一定点,动点P从点A 出发,沿其边界顺时针匀速运动一周。
最全一次函数图像专题(带解析)完整版.doc

最全一次函数图像专题(带解析)完整版.doc最全一次函数图像专题(带解析)完整版一次函数也称为一次方程或线性方程,是数学中的重要概念。
在本专题中,我们将详细讨论一次函数的图像及相关概念和性质。
一、一次函数的定义与性质一次函数是指形如y = kx + b的函数,其中k和b为常数,k 称为斜率,b称为截距。
一次函数的图像是一条直线,其斜率决定了直线的倾斜程度,截距决定了直线与y轴的交点位置。
二、一次函数的图像特征1. 斜率k的正负决定了直线的倾斜方向。
当k为正数时,直线向右上方倾斜;当k为负数时,直线向右下方倾斜。
2. 斜率k的绝对值决定了直线的倾斜程度。
绝对值越大,倾斜程度越大。
3. 当k为0时,直线为水平线;当k不存在时,直线为竖直线。
三、一次函数图像的基本形状1. 当k>0时,直线从左下方向右上方倾斜。
2. 当k=1时,直线为45°斜线。
3. 当k=-1时,直线为水平斜线。
4. 当k=0时,直线为水平线。
5. 当k不存在时,直线为竖直线。
四、一次函数的图像平移1. 沿x轴平移的结果:将y = kx + b中的b替换为b',则得到的函数为y = kx + b'。
平移后的直线与原直线平行,斜率不变,但截距发生了变化。
2. 沿y轴平移的结果:将y = kx + b中的k替换为k',则得到的函数为y = k'x + b。
平移后的直线与原直线平行,截距不变,但斜率发生了变化。
五、一次函数的图像伸缩1. 垂直伸缩的结果:将y = kx + b中的k替换为ak,其中a 为正数。
当a>1时,直线变得更陡峭;当0<a<1时,直线变得更平缓。
2. 水平伸缩的结果:将y = kx + b中的x替换为x/a,其中a为正数。
当a>1时,直线变得更平缓;当0<a<1时,直线变得更陡峭。
六、一次函数的解析法与图像的关系1. 斜率k的正负决定了图像的倾斜方向。
专题:函数图像的分析和判断问题

专题:函数图像的分析和判断问题类型一、与实际问题结合的函数图像1. (2019∙随州)“龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终贏得比赛,下列函数图象可以体现这一故事过程的是( )2. (2019∙武汉)“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度。
人们根据壶中水面的位置计算时间,用t 表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是( )3. (2019∙黄冈)已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x 表示时间,y表示林茂离家的距离.依据图中的信息,下列说法错误的是()A.体育场离林茂家2.5kmB.体育场离文具店1kmC.林茂从体育场出发到文具店的平均速度是50m/minD.林茂从文具店回家的平均速度是60m/min4. (2019∙随州)第一次“龟兔赛跑”,兔子因为在途中睡觉而输掉比赛,很不服气,决定与乌龟再比一次,并且骄傲地说,这次我一定不睡觉,让乌龟先跑一段距离我再去追都可以赢。
结果兔子又一次输掉了比赛,则下列函数图象可以体现这次比赛过程的是( )5. (2017∙东营)小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,小明从家到学校行驶路程s(m)与时间t(min)的大致图象是( )6. (2019∙赤峰)如图是九年级某考生做的水滴入一个玻璃容器的示意图(滴水速度保持不变),能正确反映容器中水的高度(h)与时间(t)之间对应关系的大致图象是()7. (2019∙无锡)“低碳生活,绿色出行”是一种环保,健康的生活方式,小丽从甲地出发沿一条笔直的公路骑行前往乙地,她与乙地之间的距离y(km)与出发时间之间的函数关系式如图1中线段AB所示。
判断函数的好方法Word版
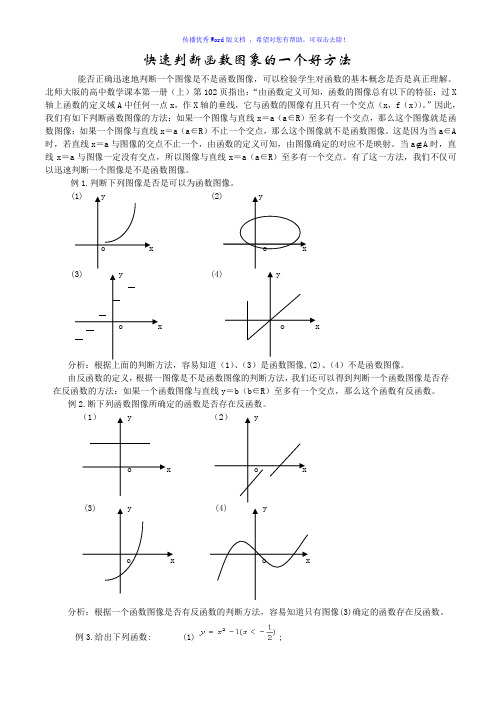
快速判断函数图象的一个好方法能否正确迅速地判断一个图像是不是函数图像,可以检验学生对函数的基本概念是否是真正理解。
北师大版的高中数学课本第一册(上)第102页指出:“由函数定义可知,函数的图像总有以下的特征:过X 轴上函数的定义域A中任何一点x,作X轴的垂线,它与函数的图像有且只有一个交点(x,f(x))。
”因此,我们有如下判断函数图像的方法:如果一个图像与直线x=a(a∈R)至多有一个交点,那么这个图像就是函数图像;如果一个图像与直线x=a(a∈R)不止一个交点,那么这个图像就不是函数图像。
这是因为当a∈A 时,若直线x=a与图像的交点不止一个,由函数的定义可知,由图像确定的对应不是映射。
当a A时,直线x=a与图像一定没有交点,所以图像与直线x=a(a∈R)至多有一个交点。
有了这一方法,我们不仅可以迅速判断一个图像是不是函数图像。
例1.判断下列图像是否是可以为函数图像。
(1) y (2) yo x o x(3) y (4) yo x o x分析:根据上面的判断方法,容易知道(1)、(3)是函数图像,(2)、(4)不是函数图像。
由反函数的定义,根据一图像是不是函数图像的判断方法,我们还可以得到判断一个函数图像是否存在反函数的方法:如果一个函数图像与直线y=b(b∈R)至多有一个交点,那么这个函数有反函数。
例2.断下列函数图像所确定的函数是否存在反函数。
(1) y (2) yo x o x(3) y (4) yo x o x分析:根据一个函数图像是否有反函数的判断方法,容易知道只有图像(3)确定的函数存在反函数。
例3.给出下列函数: (1);(2); (3);(4); (5).其中不存在反函数的是__________________.分析:判断一个函数是否有反函数,从概念上讲即看对函数值域内任意一个y,依照函数的对应法则,自变量总有唯一确定的值与之对应,由于这种判断难度较大,故通常可对给出的函数的图像运用上面介绍的方法进行观察,断定是否具有反函数.不难看(3),(4),(5)均不存在反函数.运用上述方法我们不仅可以判断一个图像是否是函数图像及从一个函数图像去判断这个函数是否有反函数,还可以帮助学生迅速判断自己所作函数图像是否正确,发现错误,及时纠正。
第6炼函数的图像Word版含解析

第6炼函数的图像Word版含解析函数的图像是指将函数的输入和输出转化为一个坐标系中的点,并将这些点连线得到的曲线。
函数的图像能够帮助我们更直观地了解函数的性质和特点。
要绘制函数的图像,首先需要确定坐标系的范围,即确定x坐标和y坐标的取值范围。
然后,我们需要根据函数的定义,计算出一组输入和输出的对应值,并将它们转换为坐标系中的点。
举例来说,我们以一次函数y=2x为例来解析函数的图像。
首先,确定坐标系的范围,假设x的取值范围是-5到5,y的取值范围是-10到10。
然后,我们可以选择一组x的值,比如x=-5,-4,-3,-2,-1,0,1,2,3,4,5、将这些x的值代入函数中,计算得到对应的y的值,再将这些点绘制在坐标系中,并用直线连接。
对于y=2x来说,当x=-5时,y=2*(-5)=-10;当x=-4时,y=2*(-4)=-8;当x=-3时,y=2*(-3)=-6......依次类推。
我们可以得到一组对应的点(-5,-10),(-4,-8),(-3,-6)......将这些点连线,我们就得到了y=2x函数的图像。
函数的图像能够帮助我们更直观地理解函数的性质和特点。
在上述例子中,我们可以看到y=2x的图像是一条斜率为2的直线。
从图像上我们可以看出,当x增加时,y也增加,且y的增加速度是x的两倍。
这样的信息可以帮助我们更好地理解函数的性质和特点,比如确定函数的增减性、变化趋势等。
除了一次函数,还有其他类型的函数的图像。
对于二次函数而言,它的图像是一条抛物线。
对于三次函数、四次函数等拐点较多的函数,其图像可能更为复杂。
此外,还有指数函数、对数函数、三角函数等特殊函数。
绘制这些函数的图像需要更多的计算和技巧。
绘制函数的图像可以通过手工的方式,也可以借助计算机和数学软件来实现。
在计算机和数学软件上,我们可以输入函数的表达式,并设置坐标系的范围,软件将自动计算并绘制出函数的图像。
这样可以更方便地观察和研究函数的特点。
专题10:高考数学中函数图像的判断(解析版)-备战高考数学(文)三轮复习查缺补漏特色专题

专题10:高考数学中函数图像的判断知识点和精选提升题(解析版)【高考地位】函数图像作为高中数学的一个“重头戏”,是研究函数性质、方程、不等式的重要武器,已经成为各省市高考命题的一个热点。
在高考中经常以几类初等函数的图像为基础,结合函数的性质综合考查,多以选择、填空题的形式出现。
给定函数找图像,可以从以下几个方面入手:1)奇偶性或对称性,奇函数关于原点对称,偶函数关于y轴对称。
2)单调性,可以是整个定义域中的单调性,也可以是某个小区间或某一点附近的单调性。
3)某些点处的函数值的符号或大小关系等,一些不在函数图像上点的极限,比如x趋近于正负无穷或开区间端点时的函数值【方法点评】方法一特值法使用情景:函数的解析式已知的情况下解题模板:第一步将自变量或者函数值赋以特殊值;第二步分别一一验证选项是否符合要求;第三步得出结论 .方法二利用函数的基本性质判断其图像使用情景:函数的解析式已知的情况下解题模板:第一步根据已知函数解析式分析其变化特征如单调性、奇偶性、定义域和值域等;第二步结合简单的基本初等函数的图像特征如对称性、周期性极值等进行判断即可;第三步得出结论 .一、单选题1.函数1()ln1f xx x=+-的图象大致为()A .B .C .D .【答案】B【分析】根据1x >,01x <<时函数值的符号,利用排除法即可得答案.【详解】1x >时,ln 010x x >⎧⇒⎨->⎩1()0ln 1f x x x =>+-,可排除D ;01x <<时,ln 010x x <⎧⇒⎨-<⎩1()0ln 1f x x x =<+-,可排除AC.故选:B.2.已知函数()y f x =的部分图象如图所示,则函数()y f x =的解析式可能为()A .()()()sin 222x x f x x -=⋅+B .()()()sin 222x x f x x -=⋅-C .()()()cos 222x x f x x -=⋅+D .()()()cos 222x x f x x -=⋅- 【答案】B【分析】根据奇偶性排除AD ,根据图象过原点排除C ,从而可得答案.【详解】由图可知函数图象关于y 轴对称,且图象过原点,对于A , ()()()()()()sin 222sin 222x x x x f x x x f x ---=-⋅+=-⋅+=-,()y f x =是奇函数,图象关于原点对称,不合题意,排除A ;对于C ,()()000cos 02220f =⋅+=≠,不合题意,排除C ;对于D ,()()()()()()cos 222cos 222x x x x f x x x f x ---=-⋅-=-⋅-=-,()y f x =是奇函数,图象关于原点对称,不合题意,排除D ;故选:B.【点睛】方法点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的特征点,排除不合要求的图象.3.函数3x y -=的大致图像是( )A .B .C .D .【答案】C【分析】根据函数的最大值排除A B D 可得答案.【详解】因为||0x -≤,所以||0331x y -=≤=,排除A B D.故选:C4.函数21()f x x x =-的图象大致形状是( ) A . B .C .D .【答案】D【分析】利用排除法,先判断函数的奇偶性,再取特殊值即可判断【详解】解:函数的定义域为{}0x x ≠, 因为2211()()()f x x x f x x x -=--=-=-, 所以()f x 为偶函数,所以其图像关于y 轴对称,所以排除A ,B ,因为2117(2)220244f =-=-=>,所以排除C , 故选:D5.函数()sin ln ||f x x x =⋅的部分图象大致为( ) A . B . C . D .【答案】D【分析】先根据函数的奇偶性,可排除A ,C ,根据当01x <<时,()0f x <即可排除B .得出答案.【详解】因为()sin ln ||(0)f x x x x =⋅≠,所以()sin()ln ||sin ln ||()f x x x x x f x -=-⋅-=-=-,所以()f x 为奇函数,故排除A ,C .当01x <<时,sin 0x >,ln ||0x <,则()0f x <,故排除B ,故选:D .【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的特征点,排除不合要求的图象.6.函数1()ln 1x f x x+=-的图象大致为( )A .B .C .D .【答案】B【分析】根据奇偶性的定义可判断函数为奇函数,故可排除C,D ,令12x =,可得函数值并判断正负,进而可得答案.【详解】 由1()ln ln(1)ln(1)1x f x x x x+==+---, 可得函数的定义域为()1,1-,关于坐标原点对称,且()ln(1)ln(1)()f x x x f x -=--+=-,故函数()f x 为奇函数,进而可排除C,D , 又令12x =,可知1112()ln ln301212f +==>-,故可排除A. 故选:B.【点睛】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.7.函数sin sin x y e x =的图象大致为( )A .B .C .D .【答案】C【分析】首先判断函数的奇偶性,再利用特殊值,即可判断;【详解】解:因为()sin sin x y f x e x ==,定义域为R ,()()()sin sin sin sin x x f x ex e x ---=-=-,即()()f x f x -≠且()()f x f x -≠-,即()sin sin x f x ex =为非奇非偶函数,故排除A ,D ;又()sin00sin00f e==,故排除B ;故选:C 8.函数()cos ,11ln ,1x e x f x x x x π⎧≤⎪=⎨⎛⎫-> ⎪⎪⎝⎭⎩的图像大致是( ) A . B .C . D .【答案】A【分析】根据题意,由函数的解析式分析可得x →+∞时,有1()ln()f x x x=-→+∞,排除,B C ,求出(1)f 的值,排除D 项,即可得到答案.【详解】根据题意,函数()cos ,11ln ,1x e x f x x x x π⎧≤⎪=⎨⎛⎫-> ⎪⎪⎝⎭⎩, 当1x >时,有1()ln()f x x x=-,x →+∞时,1x x -→+∞有1()ln()f x x x=-→+∞,排除,B C , 当1x =时,cos 1(1)f e e π==,排除D 项, 故选:A.【点睛】方法点睛:该题考查的是有关函数图象识别问题,常见解题方法如下:(1)从定义域入手,排除不合条件的选项;(2)根据函数图象的对称性、单调性、函数值的符号、函数值的变化趋势排除选项; (3)根据某个自变量对应函数值的大小排除不合题意的选项.9.已知0a >,且1a ≠,函数x y a =与()log a y x =-的图象只能是下图中的( ) A . B . C . D .【答案】B【分析】根据函数()log a y x =-的图象与log a y x =的图象关于y 轴对称,函数x y a =的图象与log a y x =的图象关于直线y x =对称,即可判断.【详解】当1a >时,函数x y a =与()log a y x =-的大致图象如图所示:当01a <<时,函数x y a =与()log a y x =-的大致图象如图所示:根据题意,所以正确的是B .故选:B .【点睛】本题主要考查指数函数与对数函数的图象的理解和应用,属于容易题.10.已知函数()f x 133,1log ,1x x x x ⎧≤⎪=⎨>⎪⎩,则函数()1y f x =-的大致图象是( ) A . B .C .D .【答案】D【分析】由()f x 得到()1f x -的解析式,根据函数的单调性和特殊点判断.【详解】因为函数()f x 133,1log ,1x x x x ⎧≤⎪=⎨>⎪⎩, 所以函数()1f x -()1133,0log 1,0x x x x -⎧≥⎪=⎨-<⎪⎩, 当0x ≥时,函数()1y f x =-递减,当0x <时,函数()1y f x =-递增,且过()1,1点,故选:D11.若01a <<,则函数()log 1a y x =-的图象可能是( ) A . B .C .D .【答案】D【分析】根据函数的定义域和函数的奇偶性、结合图象变换和对数函数的单调性,即可求解.【详解】因为01a <<,函数()()log 1a g x x =-满足10x ->,解答1x <-或1x >, 即函数()()log 1a g x x =-的定义域为()(),11,-∞-+∞,排除A 、B , 又由()()()()log 1log 1a a g x x x g x -=--=-=,所以函数()g x 为偶函数, 所以函数()g x 的图象关于y 对称的偶函数,当1x >时,函数()()log 1a g x x =-是函数log ay x =的图像向右平移一个单位得到的,可排除C.故选:D.12.如图是函数()f x 的图像,()f x 的解析式可能是( )A .1()ln 1+=-x f x xB .1()ln 1-=+x f x x C .11()11=++-f x x x D .11()11=-+-f x x x【答案】C 【分析】利用赋值法代入0x =,2x =,12x =-,用排除法即可得到答案.【详解】由图象可知(0)0f =,若11()11=-+-f x x x ,11(0)20101f =-=+-,故可排除D ; 当2x =时,(2)0f >,若1()ln1-=+x f x x ,211(2)lnln 0213f -==<+,故可排除B ; 当12x =-时,1()02f ->,若1()ln 1+=-x f x x ,11112()ln ln 012312f -+-==<-,故可排除A ; 故选:C. 【点睛】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.13.函数()3313xx f x =-的图象大致为( ) A . B .C .D .【答案】D 【分析】求函数的定义域为{}|0x x ≠,分别计算0x >和0x <时函数值的符号,利用排除法即可得正确选项. 【详解】由130x -≠可得0x ≠,所以函数()f x 的定义域为{}|0x x ≠,当0x >时,31x>,所以130x -<,330x >,可得()33013xx f x =<-,故排除选项AC ,当0x <时,031x<<,所以103x ->,330x <,可得()33013xx f x =<-,故排除选项B, 故选:D 【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象. 14.在同直角坐标系中,1y a x b=-+与log ()a y x b =-的图象可能是( ) A . B .C . D .【答案】A 【分析】 利用函数1y a x b=-+的单调性排除选项,以及根据函数()log a y x b =-的图象判断0b ->,再利用函数1y a x b=-+的对称性排除选项.【详解】 函数1y a x b =-+的单调性与1y x=-的单调性一致,两段区间都是单调递增,故排除BC ,AD 选项中,()log a y x b =-,当0x =时,()log 0a b -<,即0b ->,而1y a x b=-+关于点(),b a -对称,因为0b ->,故排除D. 故选:A 【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.15.函数()31ln ||x f x x =+的大致图象为( )A .B .C .D .【答案】A 【分析】首先判断函数的奇偶性,排除选项,再判断10,e x ⎛⎫∈ ⎪⎝⎭时,函数值的正负,排除选项. 【详解】显然,01ln 0x x ≠⎧⎨+≠⎩,解得:0x ≠且1x e ≠±,函数的定义域关于原点对称,且()()f x f x -=-,函数是奇函数,关于原点对称,排除CD ;当10,e x ⎛⎫∈ ⎪⎝⎭,30x >,1ln 0x +<,所以()0f x <,排除B故选:A .16.函数()21ln f x x x =+的图像大致为( ) A .B .C .D .【答案】B 【分析】先判断函数奇偶性,可排除D ,再取特殊值判断正负可排除AC. 【详解】()f x 的定义域为{}0x x ≠,且()()()2211ln ln f x x x f x xx -=-+=+=-,则()f x 是偶函数,图象关于y 轴对称,故D 错误;()1ln1110f =+=>,故A 错误;()12ln 204f =+>,故C 错误. 故选:B. 【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.17.设实数a b <,函数2()()y a x a x b =--的图象可能是( ).A .B .C .D .【答案】D 【分析】就0a >、0a =、0a <结合函数的导数分类讨论后可得正确的选项. 【详解】若0a >,则0b a >>,故2()()y a x a x b =--的零点均为正数,ABCD 均不符合. 若0a =,则0y =,ABCD 均不符合. 若0a <,则当x b >时,0y <,故排除AC.又()()()2()(22)3y a x b a x a x b a x b x b a '=---=---+,当x b =时,0y '=,故函数在较大零点处的导数为零,故B 不符合,D 符合, 故选:D.18.已知幂函数1234,,,abcdy x y x y x y x ==== 在第一象限的图象如图所示,则( )A .a b c d >>>B .>>>b c d aC .>>>d b c aD .>>>c b d a【答案】B 【分析】取2x =,结合图象得出2222d a c b <<<,最后由指数函数的性质得出大小关系. 【详解】由图象可知,当2x =时,2222d a c b <<<,则a d c b <<< 故选:B19.已知函数()f x 的图象如图,则()f x 的解析式可能是( )A .()21f x x x =-B .()21f x x=-C .()21x f x x=-D .()21x f x x-= 【答案】B 【分析】由()f x 的零点可排除选项A ;由0x <时,()0f x <,可排除选项C ,由()00f =可排除选项D ,即可得正确选项. 【详解】对于A :()21f x x x =-令()0f x =,可得1x =±,由()f x 图象知只有()00f =,故选项A 不正确; 对于选项C :()201x f x x=>-,由()f x 的图象知当0x <时,()0f x <,故选项C 不正确;对于选项D :()21x f x -=在0x =处没有定义,由()f x 的图象可知()00f =,故选项D 不正确; 由排除法可知选项B 正确, 故选:B 【点睛】思路点睛:由函数图象选择解析式:根据图象的定义域,单调性、奇偶性、特殊点的函数值、极限思想等利用排除法可求解.20.设a 与b 均为实数,0a >且1a ≠,已知函数log ()a y x b =+的图象如图所示,则2+a b 的值为( )A .6B .8C .10D .12【答案】C 【分析】根据函数过的点即可求出,a b ,进而求出2+a b 的值. 【详解】解:令()log ()a f x y x b ==+,由图可知:()0log 2a f b ==,()()3log 30a f b -=-+=,即2310a b b a ⎧=⎪-+=⎨⎪>⎩, 解得:{24a b ==,故224210a b +=+⨯=, 故选:C.。
专题二 函数图象的判断

2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
人生诚然有许多烦恼,但在满怀 信心,意志坚定的人看来,无难不可 摧,乐观努力,就是秘诀。
谢谢大家
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
谢谢大家
再见
再见
谢谢大家,再会!
2017年中考数学命题研究(贵专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
2017年中考数学命题研究(贵阳专版)
函数及其函数图象的分析判断

√
【思维点拨】.由①可得,甲走了_ ______小时到了 <m></m> 地,由②可得,甲在 <m></m> 地休息了半小时,由③可得,甲从 <m></m> 地走了_ ________小时到达 <m></m> 地,共用了2小时;由④可得,乙用了_______小时到了 <m></m> 地,在 <m></m> 地休息了 <m></m> 小时.
3
6
6
【即学即练】如图, 和 都是边长为2的等边三角形,它们的边 , 在同一条直线 上,点 , 重合.现将 沿着直线 向右移动,直至点 与点 重合时停止移动.在此过程中,设点 移动的距离为 ,两个三角形重叠部分的面积为 ,则 随 变化的函数图象大致为( )
即学即练题图
第三章 函数
命题点2 函数及其函数图象的分析判断(必考)
2023年安徽中考:数学
ห้องสมุดไป่ตู้022版课标要求
1. 探索简单实例中的数量关系和变化规律,了解常量、变量的意义;了解函数的概念和表示法,能举出函数的实例;
2. 能确定简单实际问题中函数自变量的取值范围,会求函数值;
3. 能结合图象对简单实际问题中的函数关系进行分析;
>
,
<
一、三、四
【即学即练】若 ,则正比例函数 与反比例函数 在同一平面直角坐标系中的大致图象可能是( )
A. B. C. D.
√
4. 分析实际问题判断函数图象(2016.9)
例②:(2016安徽9题4分)一段笔直的公路 长20千米,途中有一处休息点 , 长15千米,甲、乙两名长跑爱好者同时从点 出发,①甲以15千米/时的速度匀速跑至点 ,②原地休息半小时后,③再以10千米/时的速度匀速跑至终点 ;④乙以12千米/时的速度匀速跑至终点 ,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程 (千米)与时间 (小时)函数关系的图象是( )
中考复习篇之《专题一 分析判断函数图象》

专题一 分析判断函数图象类型一 分析函数性质判断函数图象(2017·安徽)已知抛物线y =ax 2+bx +c与反比例函数y =bx 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y =bx +ac 的图象可能是( )【分析】由抛物线与反比例函数的图象在第一象限有一个公共点可判断b>0,a≠0,由公共点的横坐标为1可得交点为(1,b),代入抛物线方程可得a,c的关系,然后判断一次函数的图象.【自主解答】【方法点拨】1.抓住题干中的重要信息,本题中注意隐含条件(由抛物线说明a≠0)和交点位置(由公共点在第一象限说明b>0);2.坐标代入法,本题中已知公共点的横坐标,分别代入两个函数表达式后建立等式找出a,c的关系是解决本题的关键.【难点突破】通过公共点(1,b)找出a=-c是解答本题的突破口.1.(2019·杭州)已知一次函数y 1=ax +b 和y 2=bx +a(a≠b),函数y 1和y 2的图象可能是( )2.(2019·合肥行知中学一模)已知二次函数y =a(x -m)2-n 的图象如图所示,则一次函数y =mx +a 与反比例函数y =-mnx在同一坐标系内的图象可能是( )3.(2019·合肥38中一模)二次函数y =ax 2+bx +c 的图象如图所示,则一次函数y =bx +b 2-4ac 与反比例函数y =a +b +cx在同一坐标系内的图象大致为( )4.(2019·宁夏)函数y =kx 和y =kx +2(k≠0)在同一直角坐标系中的大致图象是( )5.(2019·呼和浩特)二次函数y =ax 2与一次函数y =ax +a 在同一坐标系中的大致图象可能是( )6.(2019·合肥庐阳区一模)如图,反比例函数y 1=kx 的图象与以 y 轴为对称轴的二次函数y 2=ax 2+bx +c 的图象交于点 A ,则函数y =ax 2+(b -k)x +c 的图象可能是( )类型二分析实际问题判断函数图象(2016·安徽)一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米.甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C.下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )【分析】 由甲跑1小时后休息半小时,可知1~32小时的图象与x 轴平行;直接求出乙跑步所用的时间.结合各选项即可得出答案. 【自主解答】【方法点拨】在解答与实际问题有关的函数图象题时,应从以下几个方面入手:①找起点:结合题干中所给自变量及因变量的取值范围,在图象中找出相对应的点;②找特殊点(交点或转折点):说明图象在此点处将发生变化;③判断图象趋势:判断出函数的增减性;④看是否与坐标轴相交.【难点突破】本题的突破口是抓住甲在1~32小时的图象与x 轴平行,同时乙在第53小时到达终点.1.小明看到了一首诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”,读完后,他想用图象描述这首诗的内容.如果用纵轴表示父亲与儿子行进中离家的距离,横轴表示父亲离家的时间,那么下列图象中大致符合这首诗含义的是( )2.已知A、B两个旅游景点相距120千米,甲同学骑自行车以20千米/时的速度由景点A出发前往景点B,乙同学骑摩托车以40千米/时的速度由景点B出发前往景点A,甲出发3小时后乙开始出发,各自到达目的地后停止前进.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下列图象中能正确反映s 与t之间函数关系的是( )3.(2019·赤峰)如图是九年级某考生做的水滴入一个玻璃容器的示意图(滴水速度保持不变),能正确反映容器中水的高度(h)与时间(t)之间对应关系的大致图象是( )类型三分析几何动态问题判断函数图象(2018·安徽)如图,直线l1,l2都与直线l 垂直,垂足分别为M,N,MN=1.正方形ABCD的边长为2,对角线AC在直线l 上,且点C位于点M处.将正方形ABCD沿l向右平移,直到点A与点N重合为止.记点C平移的距离为x,正方形ABCD的边位于l1,l2之间部分的长度和为y,则y关于x的函数图象大致为( )【自主解答】【方法点拨】此类函数是由分段函数组成,解题的关键是认真分析题意,弄清每一段上的函数值是如何随自变量的变化而变化的,在解决此类问题时,有时需要先求出函数的关系式再进行判断.【难点突破】解答本题的突破口是通过分类讨论表示每段函数关系式.1.(2019·铜仁)如图,平行四边形ABCD中,对角线AC、BD相交于点O,且AC =6,BD=8,P是对角线BD上任意一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F.设BP=x,EF=y,则能大致表示y与x之间关系的图象为( )2.(2019·天水)已知点P为某个封闭图形边界上一定点,动点M从点P出发,沿其边界顺时针匀速运动一周.设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )3.(2019·衢州)如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C.设P点经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是( )4.(2019·合肥42中一模)如图,正方形ABCD的边长为3 cm,动点P从B点出发以3 cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动,另一动点Q 同时从B点出发,以1 cm/s的速度沿着边BA向A点运动,到达A点停止运动,设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )5.(2019·本溪)如图,点P是以AB为直径的半圆上的动点,CA⊥AB,PD⊥AC 于点D,连接AP,设AP=x,PA-PD=y,则下列函数图象能反映y与x之间关系的是( )6.(2019·芜湖一模)如图,在等腰三角形ABC中,AB=AC=4 cm,∠B=30°,点P从点B出发,以 3cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA→AC方向运动到点C停止.若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )类型四分析函数图象判断结论正误(2013·安徽)图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )A.当x=3时,EC<EMB.当y=9时,EC>EMC.当x增大时,EC·CF的值增大D.当y增大时,BE·DF的值不变【分析】首先由待定系数法求出反比例函数的表达式,从而可得xy=9,由△AEF 是等腰直角三角形可推出△BEC、△DCF也是等腰直角三角形,因而EC·CF,BE·DF都可以用x,y来表示,从而可判断正误.【自主解答】【方法点拨】1.图象过定点,常用待定系数法求出函数表达式;2.对于两条线段长乘积值的变化,往往找出乘积值与变量之间的关系进行判断,有时需要转化为二次函数,利用二次函数的性质进行判断.【难点突破】利用待定系数法求出反比例函数表达式,从而得出xy=9是解答本题的突破口.1.(2019·黄冈)已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后走回家.图中x表示时间,y表示林茂离家的距离.依据图中的信息,下列说法错误的是( )A.体育场离林茂家2.5 kmB.体育场离文具店1 kmC.林茂从体育场出发到文具店的平均速度是50 m/minD.林茂从文具店回家的平均速度是60 m/min2.(2019·合肥二模)甲、乙两车从A地出发,沿同一路线驶向B地.甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地.甲、乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的是( )A .①②③B .①②④C .②③④D .①②③④3.(2019·霍邱县二模)如图1,已知平行四边形ABCD 中,点E 是AB 边上一动点(与点A 不重合),设AE =x ,DE 的延长线交CB 的延长线于点F ,设BF =y ,且y 与x 之间的函数关系图象如图2所示,则下面结论中不正确的是( )A .AD =2B .当x =1时,y =6C .若AD =DE ,则BF =EF =1 D .若BF =2BC ,则AE =43参考答案【专题类型突破】 类型一【例1】 ∵抛物线与反比例函数的图象在第一象限有一个公共点, ∴b>0,a≠0,且公共点的坐标为(1,b),代入抛物线方程可得b =a +b +c. ∴a=-c.∴一次函数为y =bx -a 2.故选B. 跟踪训练1.A 2.B 3.D 4.B5.D 【解析】由一次函数y =ax +a 可知,一次函数的图象与x 轴交于点(-1,0),排除A 、B ;当a >0时,二次函数y =ax 2开口向上,一次函数y =ax +a 经过一、二、三象限;当a <0时,二次函数开口向下,一次函数经过二、三、四象限,排除C ,故选D. 6.A 类型二【例2】 由题意可知,甲所跑路程分为3个时段:开始1小时,以15千米/时的速度匀速由点A 跑至点B ,所跑路程为15千米;第1小时至第32小时休息,所跑路程不变;第32小时至第2小时,以10千米/时的速度匀速跑至终点C ,所跑路程为5千米,即甲累计所跑路程为20千米,所用时间为2小时,并且甲开始1小时内的速度大于第32小时至第2小时之间的速度.因此选项A 、C 符合甲的情况.乙从点A 出发,以12千米/时的速度匀速跑至终点C ,所跑路程为20千米,所用时间为53小时,并且乙的速度小于甲开始的速度但大于甲第3时段的速度.∴选项A 、B 符合乙的情况.故选A. 跟踪训练 1.C 2.A 3.D 类型三【例3】 由正方形ABCD 的边长为2,易求得其对角线长为2,对角线的一半是1.分三种情况:①当0≤x≤1时,y =22x ,函数图象为直线的一部分(线段),且y 随x 的增大而增大;②当1<x≤2时,y =22,函数图象是平行于x 轴的一条线段;③当2<x≤3时,y =-22x +62,函数图象为直线的一部分(线段),且y 随x 的增大而减小.只有选项A 符合条件,故选A. 跟踪训练1.D 2.D 3.C 4.C5.C 【解析】设圆的半径为R ,如解图,连接PB ,则sin∠ABP=AP 2R =12R x ,∵CA⊥AB,即AC 是圆的切线,∴∠PAD=∠PBA,则PD =APsin∠PAD=x×12R x=12R x 2,则y =PA -PD =-12Rx 2+x ,图象为开口向下的抛物线.故选C.6.D类型四【例4】 ∵反比例函数图象过点(3,3),∴y=9x.∵△AEF 是等腰直角三角形,∴△EBC、△CDF 都是等腰直角三角形.A 项:在矩形ABCD 中,当BC =3时,CD =3,此时矩形ABCD 是边长为3的正方形.∴当x =3时,EC =EM =32,故本选项错误.B 项:当y =9时,x =1.∴EC=2,CF =92,∴EM=52,∴EC<EM ,故本选项错误.C 项:∵EC·CF=2x·2y =2xy =18,值不变,故本选项错误.D 项:∵BE·DF=xy =9,值不变,故本选项正确.故选D.跟踪训练1.C2.D 【解析】由题意可得,a =4+0.5=4.5,故①正确,甲的速度是460÷(7+4060)=60(km/h),故②正确,设乙刚开始的速度为x km/h ,则4x +(7-4.5)×(x -50)=460,得x =90,设经过b min ,乙追上甲,90×b 60=60×40+b 60,解得b =80,故③正确,乙刚到达货站时,甲距B 地:60×(7-4)=180(km),故④正确,故选D.3.C 【解析】∵ABCD 为平行四边形,∴AD∥BC,AB∥DC.∴∠F=∠ADF,∠FBE=∠A.∴△BFE∽△ADE.∴BF AD =BE AE .设AB =a ,AD =b ,则BE =AB -AE =a -x.∴y b=a -x x .∴y =ab x-b.∵图象过点(2,2),(4,0),∴a=4,b =2.故A 正确.∵a =4,b =2,∴y=8x-2,∴当x =1时,y =6,故B 正确.若AD =DE ,则∠A=∠AED ,∵∠A=∠FBE ,∠AED=∠FEB ,∴∠FBE=∠FEB.∴BF=EF.∴若AD =DE ,则总有BF =EF ,它们并不总等于1,故C 不正确.若BF =2BC ,∵BF AD =BE AE ,∴2BC BC=4-AE AE .解得AE =43.故D 正确.故选C.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分析判断函数图像题题型一:分析动点(直线、面)问题的函数图像例、(2014•安徽)如图,矩形ABCD 中,9,4,AB BC ==动点P 从A 点出发,按A B C →→的方向在AB 和BC 上移动,记,PA x =点D 到直线PA 的距离为y ,则y 关于x 的函数关系图像大致是 ( )分析:本题需分两段讨论,即点P 在AB 段和BC 段,按照面积公式分别列出面积y 与x 的函数关系.当点P 在边AB 上运动时,即03x ≤≤时,4y =,其图象为一线段; 当点P 在边BC 上运动时,即35x <≤时,连接AC 、DP , 根据ADPABPCDPSSSS=--ABCD得到:113434622xy =⨯-⨯⨯=,即12y x =,其图象为一段双曲线. 故选B.总结:(1)根据题意确定出动点在不同的线段上运动时的范围,得到自变量x (或t )的取值范围;(2)在某一个确定的范围内,用含自变量x (或t )的代数式表示出所需的线段D CBA 4 3 54 35 4 3 553 4 O OOOy xy xy xxy y x PDC BA长,利用面积公式或三角形相似的性质,表示出所需求图形的面积或线段比,化简得出y (或s )关于x (或t )的关系式;(3)根据关系式,结合自变量取值范围,判断出函数图像。
练习:1、(2012•安徽)如图,A 点在半径为2的⊙O 上,过线段OA 上的一点P 作直线ℓ,与⊙O 过A 点的切线交于点B ,且∠APB=60°,设OP=x ,则△PAB 的面积y 关于x 的函数图象大致是( )A .B .C .D .2、(2011•安徽)如图,点P 是菱形ABCD 的对角线AC 上的一个动点,过点P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点.设AC =2,BD =1,AP =x ,△AMN的面积为y ,则y 关于x 的函数图象大致形状是 ( )3、(2014•黄冈市)在ΔABC 中,BC=10,BC 边上的高h=5,点E 在AB 上,过点E 作EF ∥BC ,交AC 于F ,D 为BC 上的一点,连DE 、DF .设E 到BC 的距离为x ,则ΔDEF 的面积为S 关于x 的函数图象大致为( )OOOOxx x x y y y y 1 2 1 2 1 2 1 2DB AABCDEF第8题图2.552542.552542.5525425452.5SxO Sx OSxOO xS4、(2014•玉林)如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x ,两个三角形重叠面积为y ,则y 关于x 的函数图象是( )A .B .C .D .5、(2014•河南)如图,在Rt △ABC 中,∠C=900,AC=1cm ,BC=2cm ,点P 从A 出发,以1cm/s 的速沿折线AC CB BA →→运动,最终回到A 点。
设点P 的运动时间为x (s ),线段AP 的长度为y (cm ),则能反映y 与x 之间函数关系的图像大致是 ( )6、(2014•龙东)如图,在平面直角坐标系中,边长为1的正方形ABCD 中,AD 边的中点处有一动点P ,动点P 沿P →D →C →B →A →P 运动一周,则P 点的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是 ( )A B C DA DPC B 2 1120 x y 2 2 2 21 01 2 3 4ys10 1 2 3 4ys10 1 2 3 4ys10 1 2 3 4ys7、(2014•兰州)如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是()A.B.C.D.题型二:分析函数图像判断结论正误例、(2013•安徽)图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是()A.当x=3时,EC<EMB.当y=9时,EC>EMC.当x增大时,EC•CF的值增大D.当y增大时,BE•DF的值不变分析:因为等腰直角三角形AEF的斜边EF过C点,M为EF的中点,所以△BEC 和△DCF都是直角三角形;观察反比例函数图象得x=3,y=3,则反比例解析式为9yx;当x=3时,y=3,即BC=CD=3,所以CE=2BC=322CD=32C点与M 点重合,则EC=EM,所以A选项错误;当y=9时,x=1,即BC=1,CD=9,所以EC=2,而EM=32,所以B 选项错误;因为EC•CF=2x (62-2x )=-2(x-3)2+18,所以当0<x <3时,EC•CF 的值随x 的增大而增大,所以C 选项错误;因为BE•DF=BC•CD=xy=9,即BE•DF 的值不变,所以D 选项正确. 故选D .总结:对于这类问题,首先要从题干出发,将几何图形与函数图像对比着看,结合起来求解,注意,对于每个选项,可以将选项里面的条件作为已知,结合题干中所给的条件,综合起来进行分析。
练习:1、(2014•连云港)如图,△ABC 的三个顶点分别为A (1,2),B (2,5),C (6,1).若函数ky x=在第一象限内的图像与△ABC 有交点,则k 的取值范围是( )A .2≤k ≤494B .6≤k ≤10C .2≤k ≤6D .2≤k ≤2522、(2014•温州)如图,矩形ABCD 的顶点A 在第一象限,AB ∥x 轴,AD ∥y 轴,且对角线的交点与原点重合,在边AB 从小于AD 到大于AD 的变化过程中,若矩形ABCD 的周长始终 保持不变,则经过动点A 的反比例函数(0)ky k x=≠中,k 的值的变化情况是 ( )A. 一直增大B. 一直减小C. 先增大后减小D. 先减小后增大 题型三:分析实际问题判断函数图像例、(2010•安徽)甲、乙两个准备在一段长为1200米的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s 和6m/s ,起跑前乙在起点,甲在乙前面y x (第8题图)246–2246–2O100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两之间的距离y (m )与时间t (s )的函数图象是( )A .B .C .D .分析:甲在乙前面,而乙的速度大于甲,则此过程为乙先追上甲后再超过甲,全程时间以乙跑的时间计算,算出相遇时间判断图象.此过程可看作追及过程,由相遇到越来越远,按照等量关系“甲在相遇前跑的路程+100=乙在相遇前跑的路程”列出等式100v t v t ⋅=⋅+乙甲,根据甲、乙跑步的速度分别为4m/s 和6m/s ,起跑前乙在起点,甲在乙前面100米处, 则乙要追上甲,所需时间为t=50, 全程乙跑完后计时结束t 总=12006=200, 则计时结束后甲乙的距离()()300s v v t t m ∆=--=乙甲总 由上述分析可看出,C 选项函数图象符合 故选C .总结:(1)找起点:结合题干中所给自变量及因变量的取值范围,对应到图像中找相对应点;(2)找特殊点:即交点或转折点,说明图像在此点处发生变化; (3)判断图像趋势:判断出函数的增减性; (4)看是否与坐标轴相交:即此时另外一个量为0. 练习:1、(2014•哈尔滨)早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回.两人相遇后,小刚立即赶往学校,妈妈回家,l5分钟妈妈到家,再经过3分钟小刚到达学校.小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间函数关系如图所示.下列四种说法:①打电话时.小刚和妈妈的距离为1 250米;②打完电话后,经过23分钟小刚到达学校;③小刚与妈妈相遇后,妈妈回家的速度为l50米/分:④小刚家与学校的距离为2 550米.其中正确的个数是( ).(A)1个 (B)2个 (C)3个 (D)4个2、(2014•武汉)为了解某一路口某一时刻的汽车流量,小明同学10天中在同一时段统计该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图:由此估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为()A.9 B.10 C.12 D.153、(2014•常州)甲,乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲, l乙分别表示甲,乙两人前往目的地所走的路程s km随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )A、4个B、3个C、2个D、1个4、(2014•抚州)一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍,其主视图如图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h 与注水时间t 之间关系的大致图象是( )A. B. C. D. 题型四:分析二次函数图像判断其系数类问题例、(2014•南充)二次函数y =2ax bx c ++(a ≠0)图象如图所示,下列结论:①abc >0;②2a b +=0;③当m ≠1时,a b +>2am bm +;④a b c -+>0;⑤若211ax bx +=222ax bx +,且1x ≠2x ,则12x x +=2.其中正确的有( )A .①②③B .②④C .②⑤D .②③⑤分析:∵抛物线开口向下,∴a <0. ∵抛物线对称轴为性质12bx a=-= ,∴b=﹣2a >0,即20a b +=. 所以②正确. ∵抛物线与y 轴的交点在x 轴上方, ∴c >0,∴abc <0. 所以①错误.∵抛物线对称轴为性质x=1,∴函数的最大值为a b c ++.∴当m≠1时,a b c ++>2am bm +,即a b +>2am bm +. 所以③正确. ∵抛物线与x 轴的一个交点在(3,0)的左侧,而对称轴为性质x=1, ∴抛物线与x 轴的另一个交点在(﹣1,0)的右侧. ∴当x=﹣1时,y <0,∴a b c -+<0. 所以④错误.∵211ax bx +=222ax bx +,∴2211220ax bx ax bx +--= ∴()120a x x b ++=,∴12x x +=2,所以⑤正确故选D 。
