高二数学下学期期末复习
高中高二数学下学期期末复习试卷(含解析)-人教版高二全册数学试题

2014-2015学年某某省某某市东海县石榴高中高二(下)期末数学复习试卷一、填空题:1.已知集合P={﹣4,﹣2,0,2,4},Q={x|﹣1<x<3},则P∩Q=.2.若复数z1=3+4i,z2=1+2i(i是虚数单位),则z1﹣z2=.3.命题:∀x∈R,sinx<2的否定是.4.复数z=(1+3i)i(i是虚数单位),则z的实部是.5.已知函数y=f(x),x∈[0,2π]的导函数y=f′(x)的图象,如图所示,则y=f(x)的单调增区间为.6.已知则满足的x值为.7.函数在[2,4]上是增函数的充要条件是m的取值X围为.8.已知函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,则实数a的取值X 围是.9.设x,y满足约束条件,若目标函数z=abx+y(a>0,b>0)的最大值为35,则a+b的最小值为.10.曲线在点(4,e2)处的切线与坐标轴所围三角形的面积为.11.在平面直角坐标系xOy中,若直线y=2a与函数y=|x﹣a|﹣1的图象只有一个交点,则a的值为.12.已知实数a,b,c满足a+b+c=9,ab+bc+ca=24,则b的取值X围是.13.设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是.14.观察下面的数阵,第20行第20个数是.12 3 45 6 7 8 910 11 12 13 14 15 1617 18 19 20 21 22 23 24 25…二、解答题(共6小题,满分0分)15.给定两个命题:p:对任意实数x都有ax2+ax+1>0恒成立;q:关于x的方程x2﹣x+a=0有实数根,如果p和q中至少有一个为真命题,某某数a的取值X围.16.已知复数z1满足(z1﹣2)(1+i)=1﹣i(i为虚数单位),复数z2的虚部为2,且z1•z2是实数,求z2.17.已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求:(Ⅰ)x0的值;(Ⅱ)a,b,c的值.18.因发生意外交通事故,一辆货车上的某种液体泄漏到一渔塘中.为了治污,根据环保部门的建议,现决定在渔塘中投放一种可与污染液体发生化学反应的药剂.已知每投放a(1≤a≤4,且a∈R)个单位的药剂,它在水中释放的浓度y(克/升)随着时间x(天)变化的函数关系式近似为y=a•f(x),其中f(x)=.若多次投放,则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.(Ⅰ)若一次投放4个单位的药剂,则有效治污时间可达几天?(Ⅱ)若第一次投放2个单位的药剂,6天后再投放a个单位的药剂,要使接下来的4天中能够持续有效治污,试求a的最小值(精确到0.1,参考数据:取1.4).19.试比较n n+1与(n+1)n(n∈N*)的大小,分别取n=1,2,3,4,5加以试验,根据试验结果猜测一个一般性结论.20.对于定义在区间D上的函数f(x)和g(x),如果对于任意x∈D,都有|f(x)﹣g(x)|≤1成立,那么称函数f(x)在区间D上可被函数g(x)替代.(1)若,试判断在区间[[1,e]]上f(x)能否被g(x)替代?(2)记f(x)=x,g(x)=lnx,证明f(x)在上不能被g(x)替代;(3)设,若f(x)在区间[1,e]上能被g(x)替代,某某数a的X围.2014-2015学年某某省某某市东海县石榴高中高二(下)期末数学复习试卷参考答案与试题解析一、填空题:1.已知集合P={﹣4,﹣2,0,2,4},Q={x|﹣1<x<3},则P∩Q={0,2} .考点:交集及其运算.专题:计算题.分析:通过理解集合的表示法化简集合P和集合Q,两集合的交集是集合P和Q中的共同的数.解答:解:∵P={﹣4,﹣2,0,2,4},Q={x|﹣1<x<3},∴P∩Q={0,2}故答案为:{0,2}点评:本题考查集合的表示法、集合交集的求法.2.若复数z1=3+4i,z2=1+2i(i是虚数单位),则z1﹣z2= 2+2i .考点:复数代数形式的加减运算.专题:计算题.分析:根据复数减法的运算法则,当且仅当实部与虚部分别相减可求.解答:解:Z1﹣Z2=(3+4i)﹣(1+2i)=2+2i故答案为:2+2i点评:本题主要考查了复数减法的基本运算,运算法则:当且仅当实部与虚部分别相减,属于基础试题.3.命题:∀x∈R,sinx<2的否定是“∃x∈R,sinx≥2”.考点:命题的否定.分析:根据命题“∀x∈R,sinx<2”是全称命题,其否定为特称命题,即“∃x∈R,sinx≥2”.从而得到本题答案.解答:解:∵命题“∀x∈R,sinx<2”是全称命题.∴命题的否定是存在x值,使sinx<2不成立,即“∃x∈R,sinx≥2”.故答案为:“∃x∈R,sinx≥2”.点评:本题给出全称命题,求该命题的否定形式.着重考查了含有量词的命题的否定、全称命题和特称命题等知识点,属于基础题.4.复数z=(1+3i)i(i是虚数单位),则z的实部是﹣3 .考点:复数的基本概念.专题:计算题.分析:利用两个复数代数形式的乘法,虚数单位i的幂运算性质,化简=(1+3i)i,依据使不得定义求得z的实部.解答:解:复数z=(1+3i)i=﹣3+i,故实部为﹣3,故答案为﹣3.点评:本题考查两个复数代数形式的乘法,虚数单位i的幂运算性质,以及复数为实数的条件.5.已知函数y=f(x),x∈[0,2π]的导函数y=f′(x)的图象,如图所示,则y=f(x)的单调增区间为[0,π].考点:函数的单调性与导数的关系.专题:数形结合.分析:根据据f′(x)≥0,函数f(x)单调递增;f′(x)≤0时,f(x)单调递减;从图中找到f′(x)≥0的区间即可.解答:解:据f′(x)≥0,函数f(x)单调递增;f′(x)≤0时,f(x)单调递减由图得到x∈[0,π]时,f′(x)≥0故y=f (x)的单调增区间为[0,π]故答案为[0,π]点评:本题考查函数的单调性与导函数符号的关系:f′(x)≥0时,函数f(x)单调递增;f′(x)≤0时,f(x)单调递减6.已知则满足的x值为 3 .考点:分段函数的解析式求法及其图象的作法;函数的值.分析:分x≤1和x>1两段讨论,x≤1时,得,x>1时,得,分别求解.解答:解:x≤1时,f(x)=,x=2,不合题意,舍去;x>1时,,=3综上所示,x=3故答案为:3点评:本题考查分段函数求值问题,属基本题.7.函数在[2,4]上是增函数的充要条件是m的取值X围为.考点:利用导数研究函数的单调性;必要条件、充分条件与充要条件的判断.专题:计算题.分析:先求导函数,要使函数在[2,4]上是增函数,则﹣x2+mx+2≥0在[2,4]上恒成立,故可建立不等式,解之即可求得m的取值X围.解答:解:求导函数要使函数在[2,4]上是增函数,则﹣x2+mx+2≥0在[2,4]上恒成立,构建函数g(x)=﹣x2+mx+2,因为函数图象恒过点(0,2),所以﹣x2+mx+2≥0在[2,4]上恒成立,只需m根据函数的单调递增,解得,即所求m的X围为故答案为:点评:本题考查利用导数研究函数的单调性,解题的关键是求导函数,将问题转化为﹣x2+mx+2≥0在[2,4]上恒成立.8.已知函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,则实数a的取值X 围是﹣1≤a<7 .考点:函数在某点取得极值的条件.专题:计算题.分析:首先利用函数的导数与极值的关系求出a的值,由于函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,所以f′(﹣1)f′(1)<0,进而验证a=﹣1与a=7时是否符合题意,即可求答案.解答:解:由题意,f′(x)=3x2+4x﹣a,当f′(﹣1)f′(1)<0时,函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,解得﹣1<a<7,当a=﹣1时,f′(x)=3x2+4x+1=0,在(﹣1,1)上恰有一根x=﹣,当a=7时,f′(x)=3x2+4x﹣7=0在(﹣1,1)上无实根,则a的取值X围是﹣1≤a<7,故答案为﹣1≤a<7.点评:考查利用导数研究函数的极值问题,体现了数形结合和转化的思想方法.9.设x,y满足约束条件,若目标函数z=abx+y(a>0,b>0)的最大值为35,则a+b的最小值为8 .考点:简单线性规划.专题:计算题;压轴题;数形结合.分析:本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件,画出满足约束条件的可行域,再根据目标函数z=abx+y(a>0,b>0)的最大值为35,求出a,b的关系式,再利用基本不等式求出a+b的最小值.解答:解:满足约束条件的区域是一个四边形,如图4个顶点是(0,0),(0,1),(,0),(2,3),由图易得目标函数在(2,3)取最大值35,即35=2ab+3∴ab=16,∴a+b≥2 =8,在a=b=8时是等号成立,∴a+b的最小值为8.故答案为:8点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.10.曲线在点(4,e2)处的切线与坐标轴所围三角形的面积为e2.考点:定积分在求面积中的应用.专题:计算题.分析:先利用复合函数求导法则求已知函数的导函数,再利用导数的几何意义求切线斜率,进而利用直线的点斜式写出切线方程,最后求直线与坐标轴的交点,计算直角三角形的面积即可解答:解:y′=,y′|x=4=e2∴曲线在点(4,e2)处的切线方程为y﹣e2=e2(x﹣4)即y=e2x﹣e2令x=0,得y=﹣e2,令y=0,得x=2∴此切线与坐标轴所围三角形的面积为×2×e2=e2故答案为e2点评:本题主要考查了导数的几何意义,求曲线在某点出的切线方程的方法,利用导数求切线方程是解决本题的关键11.在平面直角坐标系xOy中,若直线y=2a与函数y=|x﹣a|﹣1的图象只有一个交点,则a的值为.考点:函数的零点与方程根的关系.专题:函数的性质及应用.分析:由已知直线y=2a与函数y=|x﹣a|﹣1的图象特点分析一个交点时,两个图象的位置,确定a.解答:解:由已知直线y=2a是平行于x轴的直线,函数y=|x﹣a|﹣1的图象是折线,所以直线y=2a过折线顶点时满足题意,所以2a=﹣1,解得a=﹣;故答案为:.点评:本题考查了函数的图象;考查利用数形结合求参数.12.已知实数a,b,c满足a+b+c=9,ab+bc+ca=24,则b的取值X围是[1,5].考点:函数最值的应用.专题:计算题;综合题.分析:根据a+b+c=9,ab+bc+ca=24,得到a+c=9﹣b,并代入ab+bc+ca=24,得到ac=24﹣(a+c)b,然后利用基本不等式ac,即可求得b的取值X围.解答:解:∵a+b+c=9,∴a+c=9﹣b,∵ab+ac+bc=(a+c)b+ac=24,得ac=24﹣(a+c)b;又∵ac,∴24﹣(a+c)b,即24﹣(9﹣b)b,整理得b2﹣6b+5≤0,∴1≤b≤5;故答案为[1,5].点评:此题考查了利用基本不等式求最值的问题,注意基本不等式成立的条件为一正、二定、三等,以及消元思想的应用,属中档题.13.设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是(﹣∞,﹣3)∪(0,3).考点:利用导数研究函数的单调性;函数奇偶性的性质.专题:导数的概念及应用.分析:构造函数h(x)=f(x)g(x),利用已知可判断出其奇偶性和单调性,进而即可得出不等式的解集.解答:解:令h(x)=f(x)g(x),则h(﹣x)=f(﹣x)g(﹣x)=﹣f(x)g(x)=﹣h(x),因此函数h(x)在R上是奇函数.①∵当x<0时,h′(x)=f′(x)g(x)+f(x)g′(x)>0,∴h(x)在x<0时单调递增,故函数h(x)在R上单调递增.∵h(﹣3)=f(﹣3)g(﹣3)=0,∴h(x)=f(x)g(x)<0=h(﹣3),∴x<﹣3.②当x>0时,函数h(x)在R上是奇函数,可知:h(x)在(0,+∞)上单调递增,且h (3)=﹣h(﹣3)=0,∴h(x)<0,的解集为(0,3).∴不等式f(x)g(x)<0的解集是(﹣∞,﹣3)∪(0,3).故答案为(﹣∞,﹣3)∪(0,3).点评:恰当构造函数,熟练掌握函数的奇偶性单调性是解题的关键.14.观察下面的数阵,第20行第20个数是381 .12 3 45 6 7 8 910 11 12 13 14 15 1617 18 19 20 21 22 23 24 25…考点:归纳推理.专题:综合题;推理和证明.分析:观察这个数列知,第n行的最后一个数是n2,第19行的最后一个数是192=361,由此可求出第20行第20个数.解答:解:观察这个数列知,第n行的最后一个数是n2,第19行的最后一个数是192=361,∴第20行第20个数是361+20=381.故答案为:381.点评:本题给出三角形数阵,求第20行第20个数,着重考查了递归数列和归纳推理等知识点,属于基础题.二、解答题(共6小题,满分0分)15.给定两个命题:p:对任意实数x都有ax2+ax+1>0恒成立;q:关于x的方程x2﹣x+a=0有实数根,如果p和q中至少有一个为真命题,某某数a的取值X围.考点:复合命题的真假.专题:简易逻辑.分析:根据二次函数恒成立的充要条件,我们可以求出命题p为真时,实数a的取值X围,根据二次函数有实根的充要条件,我们可以求出命题q为真时,实数a的取值X围,则命题p,q中一个为真,分类讨论后,即可得到实数a的取值X围.解答:解:对任意实数x都有ax2+ax+1>0恒成立⇔a=0或⇔0≤a<4;关于x的方程x2﹣x+a=0有实数根⇔△=1﹣4a≥0⇔a≤;p和q中至少有一个为真命题如果p真q假,则有0≤a<4,且a>,∴<a<4;如果p假q真,则有a<0,或a≥4,且a≤∴a<0;如果p真q真,则有0≤a<4,且a≤,∴0≤a≤;所以实数a的取值X围为(﹣∞,4)点评:本题考查的知识点是命题的真假判断与应用,复合命题的真假,函数恒成立问题,其中判断出命题p与命题q为真时,实数a的取值X围,是解答本题的关键.16.已知复数z1满足(z1﹣2)(1+i)=1﹣i(i为虚数单位),复数z2的虚部为2,且z1•z2是实数,求z2.考点:复数代数形式的混合运算.专题:计算题.分析:利用复数的除法运算法则求出z1,设出复数z2;利用复数的乘法运算法则求出z1•z2;利用当虚部为0时复数为实数,求出z2.解答:解:∴z1=2﹣i设z2=a+2i(a∈R)∴z1•z2=(2﹣i)(a+2i)=(2a+2)+(4﹣a)i∵z1•z2是实数∴4﹣a=0解得a=4所以z2=4+2i点评:本题考查复数的除法、乘法运算法则、考查复数为实数的充要条件是虚部为0.17.已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求:(Ⅰ)x0的值;(Ⅱ)a,b,c的值.考点:利用导数研究函数的极值.专题:计算题.分析:(1)观察图象满足f′(x)=0的点附近的导数的符号的变化情况,来确定极大值,求出x0的值;(2)根据图象可得f'(1)=0,f'(2)=0,f(1)=5,建立三个方程,联立方程组求解即可.解答:解:(Ⅰ)由图象可知,在(﹣∝,1)上f'(x)>0,在(1,2)上f'(x)<0.在(2,+∝)上f'(x)>0.故f(x)在(﹣∝,1),(2,+∝)上递增,在(1,2)上递减.因此f(x)在x=1处取得极大值,所以x0=1.(Ⅱ)f'(x)=3ax2+2bx+c,由f'(1)=0,f'(2)=0,f(1)=5,得解得a=2,b=﹣9,c=12.点评:本题主要考查了利用导数研究函数的极值,以及观察图形的能力,属于基础题.18.因发生意外交通事故,一辆货车上的某种液体泄漏到一渔塘中.为了治污,根据环保部门的建议,现决定在渔塘中投放一种可与污染液体发生化学反应的药剂.已知每投放a(1≤a≤4,且a∈R)个单位的药剂,它在水中释放的浓度y(克/升)随着时间x(天)变化的函数关系式近似为y=a•f(x),其中f(x)=.若多次投放,则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.(Ⅰ)若一次投放4个单位的药剂,则有效治污时间可达几天?(Ⅱ)若第一次投放2个单位的药剂,6天后再投放a个单位的药剂,要使接下来的4天中能够持续有效治污,试求a的最小值(精确到0.1,参考数据:取1.4).考点:函数模型的选择与应用.专题:函数的性质及应用.分析:(Ⅰ)通过a=4可知y=,分别令每段对应函数值大于等于4,计算即得结论;(Ⅱ)通过化简、利用基本不等式可知y=2•(5﹣x)+a[﹣1]=(14﹣x)+﹣a﹣4≥﹣a﹣4,再令﹣a﹣4≥4,计算即得结论.解答:解:(Ⅰ)∵a=4,∴y=,当0≤x≤4时,由﹣4≥4,解得x≥0,∴此时0≤x≤4;当4<x≤10时,由20﹣2x≥4,解得x≤8,∴此时4<x≤8;综上所述,0≤x≤8,即若一次投放4个单位的制剂,则有效治污时间可达8天;(Ⅱ)当6≤x≤10时,y=2•(5﹣x)+a[﹣1]=10﹣x+﹣a=(14﹣x)+﹣a﹣4,∵14﹣x∈[4,8],而1≤a≤4,∴∈[4,8],∴y=(14﹣x)+﹣a﹣4≥2﹣a﹣4=﹣a﹣4,当且仅当14﹣x=即x=14﹣4时,y有最小值为﹣a﹣4,令﹣a﹣4≥4,解得24﹣16≤a≤4,∴a的最小值为24﹣16≈1.6.点评:本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.19.试比较n n+1与(n+1)n(n∈N*)的大小,分别取n=1,2,3,4,5加以试验,根据试验结果猜测一个一般性结论.考点:数学归纳法.专题:点列、递归数列与数学归纳法.分析:本题考查的知识点是归纳推理与数学归纳法,我们可以列出n n+1与(n+1)n(n∈N*)的前若干项,然后分别比较其大小,然后由归纳推理猜想出一个一般性的结论,然后利用数学归纳法进行证明.解答:解:当n=1时,n n+1=1,(n+1)n=2,此时,n n+1<(n+1)n,当n=2时,n n+1=8,(n+1)n=9,此时,n n+1<(n+1)n,当n=3时,n n+1=81,(n+1)n=64,此时,n n+1>(n+1)n,当n=4时,n n+1=1024,(n+1)n=625,此时,n n+1>(n+1)n,根据上述结论,我们猜想:当n≥3时,n n+1>(n+1)n(n∈N*)恒成立.证明:①当n=3时,n n+1=34=81>(n+1)n=43=64即n n+1>(n+1)n成立.②假设当n=k时,k k+1>(k+1)k成立,即:>1则当n=k+1时,=(k+1)()k+1>(k+1)()k+1=>1即(k+1)k+2>(k+2)k+1成立,即当n=k+1时也成立,∴当n≥3时,n n+1>(n+1)n(n∈N*)恒成立.点评:本题考查了数学归纳法的应用,证明步骤的应用,归纳推理,考查计算能力,属于中档题.20.对于定义在区间D上的函数f(x)和g(x),如果对于任意x∈D,都有|f(x)﹣g(x)|≤1成立,那么称函数f(x)在区间D上可被函数g(x)替代.(1)若,试判断在区间[[1,e]]上f(x)能否被g(x)替代?(2)记f(x)=x,g(x)=lnx,证明f(x)在上不能被g(x)替代;(3)设,若f(x)在区间[1,e]上能被g(x)替代,某某数a的X围.考点:函数恒成立问题;函数单调性的性质.专题:证明题;综合题;压轴题.分析:(1)构造函数,通过研究h(x)的导数得出其单调性,从而得出其在区间[[1,e]上的值域,可以证出f(x)能被g(x)替代;(2)构造函数k(x)=f(x)﹣g(x)=x﹣lnx,可得在区间上函数k(x)为减函数,在区间(1,m)上为增函数,因此函数k(x)在区间的最小值为k(1)=1,最大值是k(m)大于1,所以不满足对于任意x∈D,都有|f(x)﹣g(x)|≤1成立,故f(x)在上不能被g(x)替代;(3)根据题意得出不等式,去掉绝对值,再根据x﹣lnx的正负转化为或,通过讨论右边函数的最值,得出实数a的X围解答:解:(1)∵,令,∵,∴h(x)在[1,e]上单调增,∴.∴|f(x)﹣g(x)|≤1,即在区间[[1,e]]上f(x)能被g(x)替代.(2)记k(x)=f(x)﹣g(x)=x﹣lnx,可得当时,k′(x)<0,在区间上函数k(x)为减函数,当1<x<m时,k′(x)>0,在区间(1,m)上函数k(x)为增函数∴函数k(x)在区间的最小值为k(1)=1,最大值是k(m)>1,所以不满足对于任意x∈D,都有|f(x)﹣g(x)|≤1成立,故f(x)在上不能被g(x)替代;(3)∵f(x)在区间[1,e]上能被g(x)替代,即|f(x)﹣g(x)|≤1对于x∈[1,e]恒成立.∴.,由(2)知,当x∈[1,e]时,x﹣lnx>0恒成立,∴有,令,∵=,由(1)的结果可知,∴F'(x)恒大于零,∴.②,令,∵=,∵,∴G'(x)恒大于零,∴,即实数a的X围为点评:本题考查了利用导数研究函数的单调性,通过分类讨论解决了不等式恒成立的问题,属于难题.。
高二下学期期末数学考试复习 优质常考题型
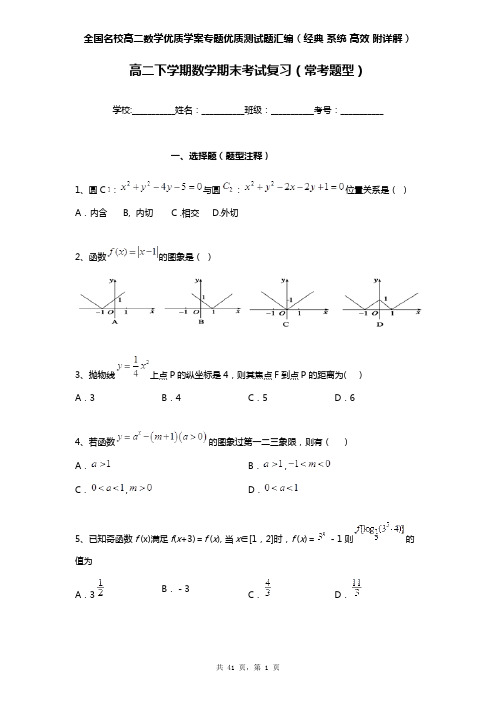
高二下学期数学期末考试复习(常考题型)学校:___________姓名:___________班级:___________考号:___________一、选择题(题型注释)1、圆C:与圆:位置关系是()A.内含 B, 内切 C .相交 D.外切2、函数的图象是()3、抛物线上点P的纵坐标是4,则其焦点F到点P的距离为( )A.3B.4C.5D.64、若函数的图象过第一二三象限,则有()A.B.,C.,D.5、已知奇函数f (x)满足f(x+3)=f (x), 当x∈[1,2]时,f (x)=-1则的值为A.3B.-3C.D.6、设成等比数列,其公比为2,则的值为()D.1A.B.C.7、数列{a n}的通项公式是,若前n项和为10,则项数n为()A.120B.99C.110D.1218、若,则=()A.B.C.D.9、有5名同学被安排在周一至周五值日,已知同学甲只能在周一值日,那么5名同学值日顺序的编排方案共有A.12种B.24种C.48种D.120种10、为不重合的直线,为不重合的平面,则下列说法正确的是()A.,则B.,则C.,则D.,则11、已知函数,,当时,方程的根的个数是()A.8B.6C.4D.212、抛物线的准线方程是()A.B.C.D.13、已知对任意恒成立,则a的最大值为()A.0B.1C.2D.3二、填空题(题型注释)14、已知函数,若时恒成立,则实数的取值范围是.15、已知直线与曲线相切于点,则实数的值为______.16、展开式中的常数项是.17、若函数有三个零点,则正数的范围是 .三、解答题(题型注释)18、(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分)已知向量,且.(Ⅰ)若,求的值;(Ⅱ)设的内角的对边分别为,,且,求函数的值域.19、(本小题满分14分)如图,已知四棱锥的底面是矩形,、分别是、的中点,底面,,(1)求证:平面(2)求二面角的余弦值。
高二下学期期末复习数学练习五

高二下学期期末复习数学练习五1.用数学归纳法证明33n n ≥(n ≥3,n ∈N )第一步应验证( )A. n =1B. n =2C. n =3D. n =42.如果复数2()(1)m i m i ++是实数,则实数m =( )A .1B .1- C.3.二项式12)2(xx +展开式中的常数项是( )A .第7项B .第8项C .第9项D .第10项4.抛掷红、黄两颗骰子,当红色骰子的点数为4或6时,两颗骰子的点数之积大于20的概率是A.14B.13C.12D.355.函数()()()221f x x x =-+在区间[]0,2上的值域为( )A. [-2,0 ]B. [-4,1]C. [-4,0 ]D. [-2, 9]6.空间四边形O A B C 中,O B O C =,3A OB A OC π∠=∠=,则cos <,O A BC >的值是( )A .21 B .22 C .-21 D .07.三个元件123,,T T T 正常工作的概率分别为,43,43,21且是互相独立的.将它们中某两个元件并联后再和第三元件串联接入电路,在如图的电路中,电路不发生故障的概率是( ) A .3215 B .329 C . 327 D .32178.抛一枚均匀硬币,正反每面出现的概率都是12,反复这样抛掷,数列{}a n 定义如下:⎩⎨⎧-=次投掷出现反面,第次投掷出现正面,第n n a n 11,若S a a a n N n n =+++∈12 ()*,则事件“S 82=”的概率,事件“S 2≠0,S 8=2”的概率分别是( ) A .125613128,B .73213128,C .12815327, D .256112815, 9.正三棱柱111C B A ABC -的底面边长为3,侧棱3231=AA ,D 是CB 延长线上一点,且BC BD =,则二面角B AD B --1的大小( )A .3πB .6πC .65π D .32π10.我们知道1-⎰的几何意义是以(0,0)为圆心,1为半径的单位圆在x 轴上方部分(半圆)的面积,则将该半圆绕x 轴旋转一周,所得几何体的体积可以表示为( ) A .120(1)x dx -⎰ B .121(1)x dx π--⎰C .11π-⎰ D .121(1)x dx --⎰11.在4次独立重复试验中,随机事件A 恰好发生1次的概率不大于其恰好发生两次的概率,则事件A 在一次试验中发生的概率P 的取值范围是 .12.将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表.从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n 次全行的数都为1的是第 行;第61行中1的个数是 . 第1行 1 1 第2行 1 0 1 第3行 1 1 1 1 第4行 1 0 0 0 1 第5行 1 1 0 0 1 1 …… ………………………………………13.若,n m 为正整数, 2m ≥, n 除以m 的余数为r , 记作mod(,)r n m =. 如15除以6的余数为3, 则3mod(15,6)=. 数列{}n a 满足1m o d (2,3)a =, 22m od(2,3)a =, ,m od(2,3)kk a =, . n S 为数列{}n a 的前n 项和, 则2012a =____________,n S =______________.14.设a ∈R ,函数233)(x ax x f -=.(Ⅰ)若2=x 是函数)(x f y =的极值点,求实数a 的值;(Ⅱ)若函数()()xg x e f x =在[02],上是单调减函数,求实数a 的取值范围.15.2012年伦敦奥运会伦敦站的火炬传递中邀请了5位奥运冠军和3位歌手参加传递, (Ⅰ) 若3位歌手互不相邻,求伦敦站的不同传递方案的种数. (直接用数字作答) (Ⅱ)在这8位参加传递的人中选3人参加一项奥运宣传活动, 用X 表示参加此次宣传活动的歌手的人数. ①列出X 的所有可能的取值结果; ②求随机变量X 的分布列; ③求参加此次活动的人中歌手至少有2名的概率.16.如图所示,在直三棱柱111ABC A B C -中,90ACB ∠=,2A B =,1B C =,1AA =,点D 是棱1C C 的中点.(Ⅰ)证明:1A D ⊥平面11AB C ; (Ⅱ)求二面角11B AB C --的余弦值.17.已知函数1()2ln f x a x x x=-+,(,0a R a ∈≠且);2()g x x x =--()b R +∈.(Ⅰ)若()f x 是在定义域上有极值,求实数a 的取值范围;(Ⅱ)当a =[]11,x e ∀∈,总[]21,x e ∃∈,使得12()()f x g x <,求实数b 的取值范围.( 其中e 为自然对数的底数)(Ⅲ)对,2n N n ∀∈≥且,证明: 4ln(!)(1)(2)n n n <-+高二下学期期末复习数学练习五答案CBCBC DABAB 11. 215⎡⎤⎢⎥⎣⎦,;12. 32,12n-;13. 1; 31;23;2n n n S n n +⎧⎪⎪=⎨⎪⎪⎩为奇数为偶数14.解:(Ⅰ)2()363(2)f x ax x x ax '=-=-.因为2x =是函数()y f x =的极值点,所以(2)0f '=,即6(22)0a -=, 所以1a =.经检验,当1a =时,2x =是函数()y f x =的极值点. 即1a =.(Ⅱ)由题设,'322()(336)x g x e ax x ax x =-+-,又0x e >, 所以,(0,2]x ∀∈,3223360ax x ax x -+-≤,这等价于,不等式2322363633x x x a x xx x++≤=++对(0,2]x ∈恒成立.令236()3x h x x x+=+((0,2]x ∈),则22'22223(46)3[(2)2]()0(3)(3)x x x h x x x x x ++++=-=-<++,所以()h x 在区间0,2](上是减函数, 所以()h x 的最小值为6(2)5h =.所以65a ≤.即实数a 的取值范围为6(,]5-∞.15.解: (1)14400 ……………………………(2分) (2)①X 的所有可能的取值结果为: 0, 1, 2, 3. ……………………………(3分)②353385(0)28C C P X C===, 21533815(1)28C C P X C===12533815(2)56C C P X C ===, 0353381(0)56C C P X C ===所以随机变量X 的分布列为:……………………..(10分) ③ 参加此次活动的人中歌手至少有2名的概率为:1512(2)(2)(3)==56567P X P X P X ≥==+=+16.解:解法一:(Ⅰ)∵90ACB ∠= ,∴B C A C ⊥. ∵三棱柱111ABC A B C -为直三棱柱,∴1BC C C ⊥. ∵1AC C C C = ,∴B C ⊥平面11AC C A . 解法二:∵90ACB ∠= ,∴B C A C ⊥.∵三棱柱111ABC A B C -为直三棱柱,∴1BC C C ⊥.∵1AC C C C = ,∴B C ⊥平面11AC C A . ……2分以C 为坐标原点,C B 、1C C 、C A 所在的直线分别为x 轴、y 轴、z轴建立如图所示的空间直角坐标系,则()0,0,0C ,()1,0,0B ,(0,0,A ,()10C,()10B ,(1A ,0,02D ⎛⎫⎪ ⎪⎝⎭. ……4分 (Ⅰ)10,2A D ⎛=- ⎝⎭,()111,0,0B C =- ,(1AB = ,∵1110A D B C = ,110A D AB = ,∴111AD BC ⊥ ,11A D AB ⊥,即111AD BC ⊥,11A D AB⊥. ∵1111B C AB B = ,∴1A D ⊥平面11AB C .(Ⅱ)设(),,x y z =n 是平面1A B B 的法向量,由110,0.A B B B ⎧=⎪⎨=⎪⎩n n 得0,0.x ⎧+-=⎪=取1z =,则)0,1=n 是平面1A B B 的一个法向量.又10,,2A D ⎛=- ⎝⎭是平面11AB C 的一个法向量,且1,AD<n >与二面角11B AB C --的大小相等.由)1110,0,12cos ,=62AD AD AD ⎛- ==-⋅n <n >n.故二面角11B AB C --的余弦值为6-.17.解:(Ⅰ)()f x 的定义域为()0,+∞,要()f x 在定义域内有极值,则 22221()0210x ax f x x ax x-+-'==⇔-+-=有两不等正根,2201210a a a a >⎧∴⇒>⎨-+->⎩(Ⅱ)1()f x x x x=-+,要对[]11,x e ∀∈,总[]21,x e ∃∈,使得12()()f x g x <则只需m ax m ax ()()f x g x <,由221()01x f x x x-+-'=>⇒-<<得函数()f x在1)1)e 上递增,在,上递减,所以函数()f x 在25x =处有最大值;max ()1)1)2f x f ==-;又()g x 在(1,)e 上递减,故max ()(1)2g x g ==-故有21)21)b ->-⇒>(Ⅲ)当1a =时,1()2ln f x x x x=-+,2221()0x x f x x-+-'=≤恒成立,故()f x 在定义域()0,+∞上单调递减,故当1x ≥时,1()2ln (1)0f x x x f x=-+≤=即12ln x x x≤-所以对,2n N n ∀∈≥且,总有12ln n n n n≤-<,故有4(2)(1)2(ln 2ln 3ln )232ln(!)ln(!)(1)(2)2n n n n n n n n +-+++<+++⇔<⇔<-+。
高二下学期期末复习卷(数学)

高二(下)数学期末复习试卷班级____________学号____________姓名_____________一.选择题:1.“12x >且22x >”是“124x x +>且124x x >”的 ( A ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 2.在各项都为正数的等比数列{}n a 中,若569,a a =则3132310log log log a a a +++= ( B ) A . 12 B .10 C .8 D .32log 5+3.抛物线281x y -=的准线方程是 ( B ) A . 321=x B. 2=y C . 321=y D. 2-=y4. (x -31x12)展开式中的常数项为 ( D )A . 1320B .-1320C .220D .- 2205.设,,αβγ是平面,,,m n l 是直线,使m β⊥成立的条件可以是 ( D )A .=,l l m αβαβ⊥⊥I ,B .,,m αγαγβγ=⊥⊥IC .,,m αγβγα⊥⊥⊥D .,,n n m αβα⊥⊥⊥6.若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为( C )A .[B .(C .[D .( 7.要得到一个奇函数,只需将函数x x x f cos 3sin )(-=的图象 ( D )A .向右平移π6个单位 B .向右平移π3个单位 C .向左平移π6个单位D .向左平移π3个单位8.若函数ln y x ax =-的增区间为(0,1),则a 的值是 ( D )A .01a <<B .01<<-aC .1a =-D .1a = 9.已知等差数列{}n a 的前n 项和为n S ,且3100(12)S x dx =+⎰,2017,S =则30S 为 ( A )A .15B .20C .25D .30 10.如图,过抛物线y 2=2px (p >0)的焦点F 的直线l 交抛物线于点A 、B ,交其准线于点C ,若|BC|=2|BF|,且|AF|=3, 则此抛物线的方程为 ( A ) A .y 2=3xB .y 2=6xC .y 2=9xD .y 2=x 3二、填空题: 11.若a=,则a =___________.12.计算311log 224()lg539---+=______________.0 13.在如下程序框图中,已知:x xe x f =)(,则输出的是_________ . ()(2008)x f x x e =+14.加工某一零件需经过三道工序,设第一、二、三道工序的次品率分别为170、 169、168,且各道工序互不影响,则加工出来的零件的次品率为______. 6968673170696870p =-⨯⨯=15.圆柱形容器内盛有高度为3cm 的水,若放入三个相同的珠(球的半么与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是____cm .1.516.已知平面区域⎪⎩⎪⎨⎧≤-≥≥+-02052x x a y y x 的面积为5,则实数=a _______.7217.以下五个关于圆锥曲线的命题中:①双曲线221169x y -=与椭圆2214924x y +=有相同的焦点; ②方程22310x x -+=的两根可分别作为椭圆和双曲线的离心率;③设A 、B 为两个定点,k 为常数,若||||PA PB k -=,则动点P 的轨迹为双曲线;④过抛物线24y x =的焦点作直线与抛物线相交于A 、B 两点,则使它们的横坐标之和 等于5的直线有且只有两条。
日照实验高中高二下学期期末复习数学练习二十二(选修2-2和2-3)

日照实验高中高二下学期期末复习数学练习二十二(选修2-2和2-3)1.复数z 满足:()(2)5z i i --=;则z = ()A 22i -- ()B 22i -+ ()C i 2-2 ()D i 2+22.若曲线ax x y +=3在坐标原点处的切线方程是02=-y x ,则实数=aA. 1B. 1-C. 2D.2-3.设a ∈Z ,且0≤a ≤13,若512012+a 能被13整除,则a =A.0B.1C.11D.124.袋子里有3颗白球,4颗黑球,5颗红球.由甲、乙、丙三人依次各抽取一个球,抽取后不放回.若每颗球被抽到的 机会均等,则甲、乙、丙三人所得之球颜色互异的概率是 (A )14 (B )13 (C )27 (D )3115.曲线2y x =与直线2x y +=围成的图形的面积为 A .72 B .4 C .92D .5 6.已知x 与y 之间的一组数据:已求得关于y 与x 的线性回归方程y =2.1x +0.85,则m 的值为A .1B .0.85C .0.7D .0.57.如图,四边形ABCD 被两条对角线分成四个小三角形,现有4种不同颜色将它染色,使相邻三角形均不同色,求使△AOB 与△COD 同色且△BOC 与△AOD 也同色的概率 A 51 B 61 C 71 D 218.若函数()2x f x e x a =--在R 上有两个零点,则实数a 的取值范围是A.12ln 2,2⎡⎫-+∞⎪⎢⎣⎭ B.1,2ln 22⎛⎤-∞-⎥⎝⎦C.[)22ln 2,-+∞D.(],22ln 2-∞- 9.函数()4x ex f -=π的部分图象大致是10.跳格游戏:如图,人从格子外只能进入第1个格子,在格子中每次可向前跳1格或2格,那么人从格外跳到第8个格子的方法种数为A .8种B .13种C .21种D .34种11.(x +a x )(2x -1x)5的展开式中各项系数的和为2,则该展开式中常数项为__________12.已知20211205232323C C C C C C C =++;303122130844444444C C C C C C C C C =+++;404132231936363636C C C C C C C C C =+++ 观察以上等式的规律, 在横线处填写一个合适的式子使得下列等式成立,3031046________________C C C =+.13.在共有2 013项的等差数列{a n }中,有等式(a 1+a 3+…+a 2 013)-(a 2+a 4+…+a 2 012)=a 1 007成立;类比上述性质,在共有2 011项的等比数列{b n }中,相应的有等式________成立.14.把圆周4等分,A 是其中一个分点,动点P 在四个分点上按逆时针方向前进,掷一个各面分别写有数字1,2,3,4且质地均匀的正四面体,P 从点A 出发按照正四面体底面上所掷的点数前进(数字为n 就前进n 步),转一周之前继续投掷,转一周或超过一周即停止投掷。
日照实验高中高二下学期期末复习数学练习四(选修2-2和2-3)

日照实验高中高二下学期期末复习数学练习四(选修2-2和2-3)1.复数⎝ ⎛⎭⎪⎫3-i 1+i 2=( )A .-3-4iB .-3+4iC .3-4iD .3+4i2.二项式30的展开式的常数项为第( )项 A . 17 B .18 C .19 D .20 3.设2921101211(1)(21)(2)(2)(2)x x a a x a x a x ++=+++++++,则01211a a a a ++++的值为A .2-B .1-C .1D .2 4.设回归直线方程为ˆ2 1.5y x =-,则变量x 增加一个单位时,( )A .y 平均增加1.5个单位 B.y 平均增加2个单位 C .y 平均减少1.5个单位 D.y 平均减少2个单位 5.用数学归纳法证明不等式“)2(2413212111>>+++++n n n n ”时的过程中,由k n =到1+=k n 时,不等式的左边( )(A )增加了一项)1(21+k (B )增加了两项)1(21121+++k k (C )增加了两项)1(21121+++k k ,又减少了11+k ;(D )增加了一项)1(21+k ,又减少了一项11+k6,由1,2,3,4,5,6组成无重复数字且1,3都不与5相邻的六位偶数的个数是( )A .72B .96C .108D .1447.抛掷甲、乙两颗骰子,若事件A :“甲骰子的点数大于4”;事件B :“甲、乙两骰子的点数之和等于7”,则(|)P B A 的值等于( )A.13 B.118 C.16 D.198,设随机变量X~N (2,4),则D (21X )的值等于 ( )A.1B.2C.21D.4 9,曲线3x y =在点)1,1(处的切线与x 轴、直线2=x 所围成的三角形的面积为( )(A )38 (B )37 (C )35 (D )34 10、已知直线kx y =是x y ln =的切线,则k 的值为( )(A )e 1 (B )e 1- (C )e 2 (D )e2-11、函数13)(3+-=x x x f 在闭区间]0,3[-上的最大值与最小值分别为:12.设随机变量ξ的概率分布列为()1cP k k ξ==+,0123k =,,,,则(2)P ξ== . 13、用火柴棒按下图的方法搭三角形:按图示的规律搭下去,则所用火柴棒数n a 与所搭三角形的个数n 之间的关系式可以是 .14. 函数g (x )=ax 3+2(1-a )x 2-3ax 在区间⎝⎛⎭⎫-∞,a3内单调递减,则a 的取值范围是________. 第0行 1 第1行 1 1第2行 1 2 1第3行 1 3 3 1 第4行 1 4 6 4 1 第5行 1 5 10 10 5 1 …… …… ……15. 如图,在由二项式系数所构成的杨辉三角形中,第_____行中从左至右第14与第15个数的比为3:2.16,假设关于某设备使用年限x若由资料知,y 对x (1)回归直线方程;(2)估计使用年限为1017,已知二次函数2()3f x ax bx =+-在1x =处取得极值,且在(0,3)-点处的切线与直线20x y +=平行. (1)求()f x 的解析式;(2)求函数()()4g x xf x x =+的单调递增区间及极值。
高二下学期文科数学期末复习试题含答案

高二文科数学期末复习一、填空题:1.若复数z 满足()12i 34i z +=-+(i 是虚数单位),则=z . 答案:i 21+.2.设全集=U Z ,集合2{|20=--≥A x x x ,}∈x Z ,则U=A (用列举法表示).答案:{0,1}.3.若复数z 满足i iz 31+-=(i 是虚数单位),则=z .i +4.已知A ,B 均为集合{=U 2,4,6,8,10}的子集,且}4{=⋂B A ,}10{)(=⋂A B C U ,则=A .答案:{4,10}5.已知全集R U =,集合=A {32|≤≤-x x },=B {1|-<x x 或4>x },那么集合⋂A (UB )等于 .答案:{x|-1≤x≤3}解析:主要考查集合运算.由题意可得,UB ={x|-1≤x≤4},A ={x|-2≤x≤3},所以(⋂A U)B ={x|-1≤x≤3}.6.已知集合},3,1{m A =,}4,3{=B ,且}4,3,2,1{=B A ,则实数m = . 答案:27.命题“若b a >,则b a 22>”的否命题为 . 答案:若b a ≤,则ba22≤8.设函数()⎩⎨⎧=x xx f 2log 2 11>≤x x ,则()[]=2f f .答案:2 9.函数)23(log 5.0-=x y 的定义域是 .答案:]1,32(10.已知9.01.17.01.1,7.0log ,9.0log ===c b a ,则c b a ,,按从小到大依次为 .答案:c a b <<11.设函数)(x f 是定义在R 上的奇函数.若当),0(∞+∈x 时,x x f lg )(=,则满足0)(>x f 的x 的取值范围是 .答案:),1()0,1(∞+-12.曲线C :x x y ln =在点M (e ,e )处的切线方程为 . 答案:e x y -=213.已知函数211)(xx f -=的定义域为M ,)1(log )(2x x g -=(1-≤x )的值域为N ,则(RM )N ⋂等于 .答案:{x|x≥1}解析:考查定义域求解.可求得集合M ={x|-1<x<1},集合N ={g (x )|g (x )≥1},则RM ={x|x≤-1或x≥1},∴(RM )N ⋂={x|x≥1}.14.设⎪⎩⎪⎨⎧+--=,11,2|1|)(2x x x f 1||1||>≤x x ,则)]21([f f 等于 .答案:134解析:本题主要考查分段函数运算. ∵232|121|)21(-=--=f ,∴134)23(11)23()]21([2=-+=-=f f f .15.已知函数)1ln()(2++=x x x f ,若实数a ,b 满足0)1()(=-+b f a f ,则b a +等于 .答案:1解析:考查函数奇偶性.观察得)(x f 在定义域内是增函数, 而)1ln()(2++-=-x x x f )(11ln2x f x x -=++=,∴)(x f 是奇函数,则)1()1()(b f b f a f -=--=,∴b a -=1,即1=+b a .16.若函数)(log )(3ax x x f a -=(0>a ,1≠a )在区间(21-,0)上单调递增,则a 的范围是 .答案:143<≤a解析:本题考查复合函数单调性,要注意分类讨论.设ax x x u -=3)(,由复合函数的单调性,可分10<<a 和1>a 两种情况讨论:①当10<<a 时,ax x x u -=3)(在(21-,0)上单调递减,即03)('2≤-=a x x u 在(21-,0)上恒成立,∴43≥a ,∴143<≤a ;②当1>a 时,ax x x u -=3)(在(21-,0)上单调递增,即03)('2≥-=a x x u 在(21-,0)上恒成立,∴0≤a ,∴a 无解.综上,可知143<≤a .17.已知()f x 为偶函数,且)3()1(x f x f -=+,当02≤≤-x 时,xx f 3)(=,则=)2011(f . 答案:3118.函数221x xy =+的值域为 .答案:)1,0(19.已知函数)(x f 的定义域为A ,若其值域也为A ,则称区间A 为)(x f 的保值区间.若()ln g x x m x =++的保值区间是[,)e +∞ ,则实数m 的值为 .答案:1-20.若不等式0122<-+-m x mx 对任意]2,2[-∈m 恒成立,则实数x 的取值范围是 .答案:)213,217(+-21.直线1=y 与曲线a x x y +-=2有四个交点,则实数a 的取值范围是 . 答案:)45,1(22.已知函数0)(3(log 2≠-=a ax y a 且)1±≠a 在]2,0[上是减函数,则实数a 的取值范围是 . 答案:)23,1()0,1( -二、解答题: 1.已知函数132)(++-=x x x f 的定义域为A ,函数)1()]2)(1lg[()(<---=a x a a x x g 的定义域为B . (1)求A ;(2)若A B ⊆,求实数a 的取值范围. 解:(1)由0132≥++-x x ,得011≥+-x x ,∴1-<x 或1≥x , ……4分即),1[)1,(+∞--∞= A ; ……6分 (2)由0)2)(1(>---x a a x ,得0)2)(1(<---a x a x .∵1<a ,∴a a 21>+.∴)1,2(+=a a B . ……8分 ∵A B ⊆,∴12≥a 或11-≤+a ,即21≥a 或2-≤a . ……12分而1<a ,∴121<≤a 或2-≤a .故当A B ⊆时,实数a 的取值范围是)1,21[]2,( --∞. ……14分2.已知命题p :函数)2(log 25.0a x x y ++=的值域为R ,命题q :函数x a y )25(--= 是减函数.若p 或q 为真命题,p 且q 为假命题,求实数a 的取值范围.解:对命题p :∵函数)2(log 25.0a x x y ++=的值域为R ,∴1)1(222-++=++a x a x x 可以取到),0(+∞上的每一个值,∴01≤-a ,即1≤a ; ……4分命题q :∵函数xa y )25(--=是减函数,∴125>-a ,即2<a . ……8分 ∵p 或q 为真命题,p 且q 为假命题,∴命题p 与命题q 一真一假,若p 真q 假,则1≤a 且2≥a ,无解, ……10分 若p 假q 真,则21<<a , ……12分 ∴实数a 的取值范围是)2,1( ……14分3.某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为2.1万元/辆,年销售量为1000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为)10(<<x x ,则出厂价相应提高的比例为x 75.0,同时预计年销售量增加的比例为x 6.0.已知年利润=(出厂价–投入成本)⨯年销售量.(1)写出本年度预计的年利润y 与投入成本增加的比例x 的关系式;(2)为使本年度的年利润比上年有所增加,问投入成本增加的比例x 应在什么范围内? 解:(1)由题意得)10)(6.01(1000)]1(1)75.01(2.1[<<+⨯⨯+⨯-+⨯=x x x x y ,…5分 整理得 )10( 20020602<<++-=x x x y ;……7分(2)要保证本年度的利润比上年度有所增加,当且仅当⎩⎨⎧<<>⨯--.10,01000)12.1(x y …10分即⎩⎨⎧<<>+-.10,020602x x x 解不等式得 310<<x . ……13分答:为保证本年度的年利润比上年度有所增加,投入成本增加的比例x 应满足33.00<<x .…14分 4.已知命题p :指数函数xa x f )62()(-=在R 上单调递减,命题Q :关于x 的方程012322=++-a ax x 的两个实根均大于3.若p 或q 为真,p 且q 为假,求实数a 的取值范围.解:若p 真,则f (x )=(2a -6)x在R 上单调递减,∴0<2a -6<1,∴3<a<72,若q 真,令f (x )=x 2-3ax +2a 2+1,则应满足⎩⎪⎨⎪⎧Δ= -3a 2-4 2a 2+1 ≥0--3a2>3f 3 =9-9a +2a 2+1>0,∴⎩⎪⎨⎪⎧a ≥2或a ≤-2a>2a<2或a>52,故a>52,又由题意应有p 真q 假或p 假q 真.①若p 真q 假,则⎩⎪⎨⎪⎧3<a<72a ≤52,a 无解.②若p 假q 真,则⎩⎪⎨⎪⎧a ≤3或a ≥72a>52,∴52<a ≤3或a ≥72.故a 的取值范围是{a|52<a ≤3或a ≥72}.5.已知函数)(x f 满足对任意实数y x ,都有1)()()(+++=+xy y f x f y x f ,且2)2(-=-f .(1)求)1(f 的值;(2)证明:对一切大于1的正整数t ,恒有t t f >)(;(3)试求满足t t f =)(的所有的整数t ,并说明理由.解:(1)令0==y x ,得1)0(-=f ;令1-==y x ,得2)1()1()2(+-+-=-f f f ,又2)2(-=-f ,∴2)1(-=-f ; 令1,1-==y x ,得)1()1()0(-+=f f f ,∴1)1(=f . ……4分 (2)令1=x ,得2)()1(+=-+y y f y f ①∴当N y ∈时,有0)()1(>-+y f y f ,由1)1(),()1(=>+f y f y f 知对*N y ∈有0)(>y f ,∴当*N y ∈时,111)(2)()1(+>+++=++=+y y y f y y f y f ,于是对于一切大于1的正整数t ,恒有t t f >)(. ……9分 (3)由①及(1)可知1)4(,1)3(=--=-f f ; ……11分下面证明当整数4-≤t 时,t t f >)(,∵4-≤t ,∴02)2(>≥+-t 由① 得0)2()1()(>+-=+-t t f t f ,即 0)4()5(>---f f ,同理0)5()6(>---f f , ……,0)2()1(>+-+t f t f ,0)1()(>+-t f t f , 将以上不等式相加得41)4()(->=->f t f ,∴当4-≤t 时,t t f >)(, ……15分 综上,满足条件的整数只有2,1-=t . ……16分6.如下图所示,图1是定义在R 上的二次函数)(x f 的部分图象,图2是函数)(log )(b x x g a +=的部分图象.(1)分别求出函数)(x f 和)(x g 的解析式;(2)如果函数)]([x f g y =在区间[1,m )上单调递减,求实数m 的取值范围. 解:(1)由题图1得,二次函数)(x f 的顶点坐标为(1,2), 故可设函数2)1()(2+-=x a x f ,又函数)(x f 的图象过点(0,0),故2-=a , 整理得x x x f 42)(2+-=.由题图2得,函数)(log )(b x x g a +=的图象过点(0,0)和(1,1),故有⎩⎨⎧=+=1)1(log 0log b b aa ,∴⎩⎨⎧==12b a ,∴)1(log )(2+=x x g (1->x ).(2)由(1)得)142(l og )]([22++-==x x x f g y 是由t y 2log =和1422++-=x x t 复合而成的函数,而t y 2log =在定义域上单调递增,要使函数)]([x f g y =在区间[1,m )上单调递减,必须1422++-=x x t 在区间[1,m )上单调递减,且有0>t 恒成立.由0=t 得262±=x ,又因为t 的图象的对称轴为1=x .所以满足条件的m 的取值范围为2621±<<m .7.已知1212)3(4)(234+-++-=x x m x x x f ,R m ∈.(1)若f 0)1('=,求m 的值,并求)(x f 的单调区间;(2)若对于任意实数x ,0)(≥x f 恒成立,求m 的取值范围.解:(1)由f ′(x )=4x 3-12x 2+2(3+m )x -12,得f ′(1)=4-12+2(3+m )-12=0,解得m =7.………2分所以 f ′(x )=4 x 3-12x 2+20x -12=4(x -1)(x 2-2x +3) .方程x 2-2x +3=0的判别式Δ=22-3×4=-8<0,所以x 2-2x +3>0. 所以f ′(x )=0,解得x =1.……………………………4分由此可得f (x )的单调减区间是(-∞,1),f (x )的单调增区间是(1,+∞).…8分(2)f (x )=x 4-4x 3+(3+m )x 2-12x +12=(x 2+3)(x -2)2+(m -4)x 2. 当m <4时,f (2)=4(m -4)<0,不合题意;……………12分当m≥4时,f (x )=(x 2+3)(x -2)2+(m -4)x 2≥0,对一切实数x 恒成立. 所以,m 的取值范围是[4,+∞).……………16分。
日照实验高中高二下学期期末复习数学练习六(选修2-2和2-3)

- 1 -日照实验高中高二下学期期末复习数学练习六(选修2-2和2-3)1.复数13)31(2-+i i 的值是A .2B .21C .21-D .2-2.已知(pxx -22)的展开式中,不含x 的项是2720,那么正数p 的值是 ( )A . 1B .2C .3D .43.将一骰子连续抛掷三次,它落地时向上的点数依次..成等差数列的概率为( ) A.19B.112C.115D.1184.今天为星期四,则今天后的第20062天是A .星期一B .星期二C .星期四D .星期日 5.函数22()()x a y x a b+=++的图象如右图所示,则 A .(0,1),(0,1)a b ∈∈ B .(0,1),(1,)a b ∈∈+∞C .(1,0),(1,)a b ∈-∈+∞D .(1,0),(0,1)a b ∈-∈6.10个球中有一个红球,有放回的抽取,每次取出一球,直到第n 次才取得()k k n ≤次红球的概率为( )AC7.设随机变量~(0,1)N ξ,记)()(x P x <=Φξ,则(11)P ξ-<<等于 A .2(1)1Φ-B .2(1)1Φ--C .(1)(1)2Φ+Φ-D .(1)(1)Φ+Φ-8.把语文、数学、物理、历史、外语这五门课程安排在一天的五节课里,如果数学必须比历史先上,则不同的排法有 A .48 B .24 C .60 D .120 9.口袋里放有大小相同的2个红球和1个白球,有 放回的每次模取一个球,定义数列{}n a :⎩⎨⎧-=次摸取白球第次摸取红球第n n a n 11 如果n S 为数列{}n a 的前n 项之和,那么37=S 的概率为 A .729224B .72928C .238735D .7528 10.有A .B .C .D .E .F6个集装箱,准备用甲.乙.丙三辆卡车运送,每台卡车一次运两个.若卡车甲不能运A 箱, 卡车乙不能运B 箱,此外无其它任何限制;要把这6个集装箱分配给这3台卡车运送,则不同的分配方案的种数为 A .168 B .84 C .56 D .42- 2 -11. (2x+x )4的展开式中x 3的系数是12.曲线1,0,2===y x x y ,所围成的图形的面积可用定积分表示为__________.13.已知不等式23x x ->的解集与不等式20x ax b ++>的解集相等,则实数a b += . 14.从1=1,1-4=-(1+2),1-4+9=1+2+3,1-4+9-16=-(1+2+3+4),…,推广到第n 个等式为_________.15.已知函数)0(1)1(3)(223>+-+-=k k x k kx x f ,若)(x f 的单调减区间是 (0,4),则在曲线)(x f y =的切线 中,斜率最小的切线方程是_________________.16.已知(41x +3x 2)n 展开式中的倒数第三项的系数为45,求:(1)含x 3的项;(2)系数最大的项.17.某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积. (Ⅰ)记“函数x x x f ξ+=2)(为R 上的偶函数”为事件A ,求事件A 的概率; (Ⅱ)求ξ的分布列和数学期望. 18.已知函数3()3f x x x =-(1)求函数()f x 在3[3,]2-上的最大值和最小值(2)过点(2,6)P -作曲线()y f x =的切线,求此切线的方程 19.函数数列{})(x f n 满足:)0(1)(21>+=x xx x f ,)]([)(11x f f x f n n =+(1)求)(),(32x f x f ;(2)猜想)(x f n 的表达式,并证明你的结论. 20.设函数()|2|2.f x x a a =-+(I )若不等式()6f x ≤的解集为{|64}x x -≤≤,求实数a 的值;(II )在(I )的条件下,若不等式2()(1)5f x k x ≤--的解集非空,求实数k 的取值范围。
高二下学期期末复习数学练习四

高二下学期期末复习数学练习四1.若i 是虚数单位,设()()11 2ia b i a b R i+=++∈-,,则复数Z a bi =+在复平面内对应的点位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限2.在n xx )1(3+的展开式中,只有第13项的二项式系数最大,那么x 的指数是整数的项共有A . 3项B . 4项C . 5项D .6项 3.给出下列命题:①直线l 的方向向量为a=(1,-1,2),直线m 的方向向量为12b=(2,1,-)则l m ⊥ ②直线l 的方向向量为a=(0,1,-1),平面α的法向量为n=(1,-1,-1),l ⊂α≠则l ⊥α. ③平面,αβ的法向量分别为12n =(0,1,3),n =(1,0,2),则 //αβ.④平面α经过三点A(1,0,-1),B(0,1,0),C(-1,2,0),向量n=(1,u,t)是平面α的法向量,则u +t =1.其中真命题的序号是( )A .②③B .①④C .③④D .①②4.某种种子每粒发芽的概率都是0.9,现播种了1,000粒种子,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X ,则X 的数学期望为( )A .100B .180C .200D .205.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了下表:则根据表中的数据,计算随机变量K 的值,并参考有关公式,你认为性别与是否喜爱打篮球之间有关系的把握有( )A .0B . 95%C .99%D .100%6.曲线1+=x xy 在点)0,0(处的切线方程为( ) A .x y -= B .x y 21= C .x y = D .x y 2=7.曲线xy 2=与直线1-=x y 及4=x 所围成的封闭图形的面积为( )A .2ln 2-B . 2ln 24-C . 2ln 28-D . 2ln 28.某校高三年级举行一次演讲赛共有10位同学参赛,其中一班有3位,二班有2位,其它班有 5位,若采用抽签的方式确定他们的演讲顺序,则一班3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学没有被排在一起的概率为( )A .110B .120C .140D .11209.正三棱柱111ABC A B C -的棱长都为2,,,E F G 为111,,AB AA AC 的中点,则1B F 与面GEF 成角的正弦值是( )A .53 B .65 C .1033 D .1063 10.将“日、照、市”填入如图所示的44⨯小方格内,每格内只填入一个汉字,且任意两个汉字既不同行也不同列,则不同的填写方法有( )A.288B.144C.576D.9611.某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续..正确回答出两个问题,即停止答题,晋级下一轮.假设某选手正确回答每个问题的概率都是0.8,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一轮的概率等于 . 12.若函数x x x f ln 8)(2-=在其定义域内的一个子区间)1,1(+-k k 内是单调函数,则实数k 的取值范围是________ ____13.已知经过计算和验证有下列正确的不等式:,<,,根据以上不等式的规律,请写出对正实数mn ,成立的条件不等式__________.14. 已知S 是△ABC 所在平面外一点,D 是SC 的中点,若BD =xAB yAC zAS ++,则x +y +z = .15.用总长14.8m 的钢条做一个长方体容器的框架,如果所做容器的底面的一边长比另一边长多0.5m ,那么高是多少时容器的容积最大?并求出它的最大容积.A B C A 1B 1C 1GF E16.编号为1,2,3,4,5的五位学生随意入座编号为1,2,3,4,5的五个座位,每位学生坐一个座位。
高二(下)期末数学复习试卷三(文科)

高二(下)期末数学复习试卷三(文科)一、选择题(每小题5分,共60.0分)1.设复数z满足(1+i)z=2i,则|z|=()A. 12B. √22C. √2D. 22.用反证法证明“三角形中最多只有一个内角是钝角”的结论的否定是( )A. 有两个内角是钝角B. 有三个内角是钝角C. 至少有两个内角是钝角D. 没有一个内角是钝角3.设函数y=√4−x2的定义域为A,函数y=ln(1-x)的定义域为B,则A∩B=()A. (1,2)B. (1,2]C. (−2,1)D. [−2,1)4.设i为虚数单位,m∈R,“复数m(m−1)+i是纯虚数”是“m=1”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件5.执行如图所示的程序框图,如果运行结果为720,那么判断框中可以填入( )A. k<6?B. k<7?C. k>6?D. k>7?6.设某中学的高中女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(x i,y i)(i=1,2,3,…,n),用最小二乘法近似得到回归直线方程为,则下列结论中不正确的是()A. y与x具有正线性相关关系B. 回归直线过样本的中心点(x,y)C. 若该中学某高中女生身高增加1cm,则其体重约增加0.85kgD. 若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg7.函数f(x)=ln|x+1|x+1的大致图象为()A. B.C. D.8.用二分法求方程近似解的过程中,已知在区间[a,b]上,f(a)>0,f(b)<0,并计算得到f(a+b2)<0,那么下一步要计算的函数值为()A. f(3a+b4) B. f(a+3b4) C. f(a+b4) D. f(3a+3b4)9.随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,图2是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级,一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( )①1月至8月空气合格天数超过20天的月份有5个②第二季度与第一季度相比,空气达标天数的比重下降了 ③8月是空气质量最好的一个月 ④6月份的空气质量最差.A. ①②③B. ①②④C. ①③④D. ②③④10. 下列说法错误的是()A. 在统计学中,独立性检验是检验两个分类变量是否有关系的一种统计方法B. 在残差图中,残差分布的带状区域的宽度越狭窄,其模拟的效果越好C. 线性回归方程对应的直线y ̂=b ̂x +a ̂至少经过其样本数据点中的一个点D. 在回归分析中,相关指数R 2越大,模拟的效果越好 11. 若函数f (x )=12x 2-9ln x 在区间[a -1,a +1]上单调递减,则实数a 的取值范围是( )A. 1<a ≤2B. a ≥4C. a ≤2D. 0<a ≤312. 已知定义在R 上的函数y =f (x )对任意的x 满足f (x +1)=−f (x ),当−1≤x <1,f (x )=x 3.函数g(x)={|log a x|,x >0−1x,x <0,若函数h (x )=f (x )-g (x )在[-6,+∞)上恰有6个零点,实数a 的取值范围是( )A. (0,17)⋃(7,+∞)B. [19,17)⋃(7,9]C. (19,17]⋃[7,9)D. [19,1)⋃(1,9]二、填空题(本大题共4小题,每题5分,共20.0分)13. 函数f (x )=ax 3+3x 2+2,若f ′(-1)=6,则a 的值等于______ . 14. ln1=0,ln (2+3+4)=2ln3,ln (3+4+5+6+7)=2ln5,ln (4+5+6+7+8+9+10)=2ln7,……则根据以上四个等式,猜想第n 个等式是______.(n ∈N *) 15. 已知函数f(x)={3x −1,x >0−2x 2−4x,x ≤0,若方程f(x)=m 有3个不等的实根,则实数m 的取值范围是________.16. 已知函数f (x )的定义域为[-1,5],部分对应值如下表,f (x )的导函数y =f ˈ(x )图象如图所示.下列关于f (x )的命题:X -1 0 4 5 f (x )1221①函数f(x)的极大值点为0,4;②函数f(x)在[0,2]上是减函数;③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;④当1<a<2时,函数y=f(x)-a有4个零点.其中正确命题的序号是__________.三、解答题(本大题共7小题,共84.0分)17.已知命题p:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立,命题q:函数y=log a(1-2x)在定义域上单调递增,若“p∨q”为真命题且“p∧q”为假命题,求实数a的取值范围.18.已知函数f(x)=(a2-3a+3)a x是指数函数.(1)求f(x)的表达式;(2)判断F(x)=f(x)-f(-x)的奇偶性,并加以证明;(3)解不等式:log a(1-x)>log a(x+2).19.为了解某地区观众对大型综艺活动《中国好声音》的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众收看该节目的场数与所对应的人数表:场数91011121314人数10182225205将收看该节目场次不低于13场的观众称为“歌迷”,已知“歌迷”中有10名女性.(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料我们能否有95%的把握认为“歌迷”与性别有关?非歌迷歌迷合计男女合计(Ⅱ)将收看该节目所有场次(14场)的观众称为“超级歌迷”,已知“超级歌迷”中有2名女性,若从“超级歌迷”中任意选取2人,求至少有1名女性观众的概率.P(K2≥k)0.050.01k 3.841 6.635.附:K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)20. 中国"一带一路"战略构思提出后,某科技企业为抓住"一带一路"带来的机遇,决定开发生产一款大型电子设备.生产这种设备的年固定成本为500万元,每生产x台,需另投入成本c (x )(万元),当年产量不足80台时,c (x )=12x 2+40x(万元);当年产量不小于80台时,c (x )=101x +8100x−2180(万元).若每台设备售价为100万元,通过市场分析,该企业生产的电子设备能全部售完.(1)求年利润y(万元)关于年产量x(台)的函数关系式;(2)年产量为多少台时,该企业在这一电子设备的生产中所获利润最大?21. 已知函数f (x )=x •ln x .(Ⅰ)求曲线y =f (x )在点(1,f (1))处的切线方程; (Ⅱ)求f (x )的单调区间;(Ⅲ)若对于任意x ∈[1e ,e],都有f (x )≤ax -1,求实数a 的取值范围.四、选考题(本题满分10,请在22题23题任选一题作答,多答则以22题计分,解答应写出文字说明、证明过程或演算步骤.)[选修4-4:坐标系与参数方程]22. 已知曲线C 1在平面直角坐标系中的参数方程为{x =√55ty =2√55t −1(t 为参数),以坐标原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,有曲线C 2:ρ=2cosθ-4sinθ (1)将C 1的方程化为普通方程,并求出C 2的平面直角坐标方程 (2)求曲线C 1和C 2两交点之间的距离.23. 已知函数f (x )=|2x +1|-|x -m |(m ∈R ).(1)当m =1时,解不等式f (x )≥2;(2)若关于x 的不等式f (x )≥|x -3|的解集包含[3,4],求m 的取值范围.答案和解析1.【答案】C2.【答案】C3.【答案】D4.【答案】B5.【答案】C6.【答案】D7.【答案】A8.【答案】A9.【答案】A 10.【答案】C 11.【答案】A 12.【答案】B【解析】解:∵对任意的x 满足f (x+1)=-f (x ),∴f (x+2)=-f (x+1)=f (x ),即函数f (x )是以2为周期的函数,画出函数f (x )、g (x )在[-6,+∞)的图象,由图象可知:在y 轴的左侧有2个交点,只要在右侧有4个交点即可,则即有,故7<a≤9或≤a <.13.【答案】4 14.【答案】15.【答案】(0,2) 16.【答案】①②【解析】由导函数的图象可知:当x ∈(-1,0),(2,4)时,f′(x )>0, 函数f (x )增区间为(-1,0),(2,4); 当x ∈(0,2),(4,5)时,f′(x )<0, 函数f (x )减区间为(0,2),(4,5). 由此可知函数f (x )的极大值点为0,4,命题①正确; ∵函数在x=0,2处有意义,∴函数f (x )在[0,2]上是减函数,命题②正确; 当x ∈[-1,t]时,f (x )的最大值是2,那么t 的最大值为5,命题③不正确; 2是函数的极小值点,若f (2)>1,则函数y=f (x )-a 不一定有4个零点,命题④不正确. ∴正确命题的序号是①②. 故答案为:①②.17.【答案】解:不等式(a -2)x 2+2(a -2)x -4<0对任意实数x 恒成立.当a =2时不等式等价为-4<0成立,当a ≠2时,可得{a −2<0∆=4(a −2)2+16(a −2)<0,解得-2<a <2,综上-2<a ≤2.即p :-2<a ≤2,函数y =log a (1-2x )在定义域上单调递增,可得0<a <1,即q :0<a <1,若“p ∨q ”为真命题且“p ∧q ”为假命题,则p ,q 为一真一假,若p 真q 假,则{−2<a ≤2a ≥1或a ≤0即1≤a ≤2或-2<a ≤0,若p 假q 真,则{a >2或a ≤−20<a <1,此时无解,故实数a 的取值范围是1≤a ≤2或-2<a ≤0. 18.【答案】解:(1)∵函数f(x)=(a 2−3a +3)a x 是指数函数,a >0且a ≠1, ∴a 2-3a +3=1,可得a =2或a =1(舍去),∴f (x )=2x ;(2)由(1)得F (x )=2x -2-x ,∴F (-x )=2-x -2x ,∴F (-x )=-F (x ), ∴F (x )是奇函数;(3)不等式:log 2(1-x )>log 2(x +2),以2为底单调递增, 即1-x >x +2>0,∴-2<x <-12,解集为{x |-2<x <-12}.19.【答案】解:(Ⅰ)由统计表可知,在抽取的100人中,“歌迷”有25人,从而完2×2…(分)将列联表中的数据代入公式计算,得: K 2=100×(30×10−45×15)275×25×45×55=10033≈3.030 因为3.030<3.841,所以我们没有95%的把握认为“歌迷”与性别有关.…(6分)(Ⅱ)由统计表可知,“超级歌迷”有5人,从而一切可能结果所组成的基本事件空间为Ω={(a 1,a 2),(a 1,a 3),(a 2,a 3),(a 1,b 1),(a 1,b 2),(a 2,b 1),(a 2,b 2),(a 3,b 1),(a 3,b 2),(b 1,b 2)}其中a i 表示男性,i =1,2,3,b i 表示女性,i =1,2.Ω由10个等可能的基本事件组成.…(9分)用A 表示“任选2人中,至少有1个是女性”这一事件,则A ={(a 1,b 1),(a 1,b 2),(a 2,b 1),(a 2,b 2),(a 3,b 1),(a 3,b 2),(b 1,b 2) },事件A 由7个基本事件组成.∴P (A )=710 (12)20.【答案】解:(1)∵当0<x <80时,∴y =100x −(12x 2+40x)−500=−12x 2+60x −500,∵当x ≥80时,∴y =100x −(101x +8100x−2180)−500=1680−(x +8100x),∴y ={−12x 2+60x −500,0<x <801680−(x +8100x),x ≥80; (2)∵由(1)可知当0<x <80时,y =−12(x −60)2+1300,∴此时当x =60时y 取得最大值为1300(万元),∵当x ≥80时,y =1680−(x +8100x)≤1680−2√x ·8100x=1500,∴当且仅当x =8100x,即x =90时,y 取最大值为1500(万元),∴综上所述,当年产量为90台时,该企业在这一电子设备的生产中所获利润最大,最大利润为1500万元.21.【答案】解:(Ⅰ)因为函数f (x )=x lnx ,所以f′(x)=lnx +x ⋅1x =lnx +1,f '(1)=ln1+1=1.又因为f (1)=0,所以曲线y =f (x )在点(1,f (1))处的切线方程为y =x -1.(Ⅱ)函数f (x )=x lnx 定义域为(0,+∞),由(Ⅰ)可知,f '(x )=ln x +1. 令f ′(x )=0,解得x =1e .所以,f (x )的单调递增区间是(1e ,+∞),f (x )的单调递减区间是(0,1e ). (Ⅲ)当1e ≤x ≤e 时,“f (x )≤ax -1”等价于“a ≥lnx +1x ”.令g(x)=lnx +1x ,x ∈[1e,e],g′(x)=1x−1x 2=x−1x 2,x ∈[1e ,e].当x ∈(1e ,1)时,g '(x )<0,所以以g (x )在区间(1e ,1)单调递减.当x ∈(1,e )时,g '(x )>0,所以g (x )在区间(1,e )单调递增.而g(1e )=−lne +e =e −1>1.5,g(e)=lne +1e =1+1e <1.5.所以g (x )在区间[1e ,e]上的最大值为g(1e )=e −1.所以当a ≥e -1时,对于任意x ∈[1e ,e],都有f (x )≤ax -1.22.【答案】解:(1)曲线C 1在平面直角坐标系中的参数方程为{x =√55ty =2√55t −1(t 为参数),消去参数t 可得普通方程:y =2x -1.由曲线C 2:ρ=2cosθ-4sinθ,即ρ2=ρ(2cosθ-4sinθ),可得直角坐标方程:x 2+y 2=2x -4y .(2)x 2+y 2=2x -4y .化为(x -1)2+(y +2)2=5.可得圆心C 2(1,-2),半径r =√5. 圆心C 2(1,-2)到直线y =2x -1的距离为d =√12+22∴曲线C 1和C 2两交点之间的距离=2√5−(√12+22)2=8√55. 23.【答案】解:(1)当x ≤−12时,f (x )=-2x -1+(x -1)=-x -2,由f (x )≥2解得x ≤-4,综合得x ≤-4;当−12<x <1时,f (x )=(2x +1)+(x -1)=3x ,由f (x )≥2解得x ≥23,综合得23≤x <1;当x ≥1时,f (x )=(2x +1)-(x -1)=x +2,由f (x )≥2解得x ≥0,综合得x ≥1.所以f (x )≥2的解集是(−∞,−4]∪[23,+∞).(2)∵f (x )=|2x +1|-|x -m |≥|x -3|的解集包含[3,4],∴当x ∈[3,4]时,|2x +1|-|x -m |≥|x -3|恒成立原式可变为2x +1-|x -m |≥x -3,即|x -m |≤x +4,∴-x -4≤x -m ≤x +4即-4≤m ≤2x +4在x ∈[3,4]上恒成立,显然当x =3时,2x +4取得最小值10,即m 的取值范围是[-4,10].。
高二数学期末考哪些知识点

高二数学期末考哪些知识点高二数学期末考知识点数学是一门学科,对学生来说,无论是在基础教育阶段还是高中阶段,都是必修的科目。
针对高二数学期末考试,下面列举了一些较为重要的知识点供大家学习和复习参考。
一、函数与方程1. 函数的概念与性质- 函数的定义及表示方法- 奇偶函数的判断及性质- 函数的单调性及最值2. 一次函数和二次函数- 一次函数的性质、图像及应用- 二次函数的性质、图像及应用- 二次函数与一元二次方程的关系3. 三角函数- 基本概念与性质- 三角函数的图像、周期性及性质- 三角函数的和差化积、倍角公式等运算方法二、空间与向量1. 空间几何- 点、线、面的性质与判定- 空间中的平面与直线的位置关系- 空间几何问题的应用2. 向量的基本概念与运算- 向量的定义、性质及表示方法- 向量的加减、数量积及应用- 向量的线性相关性与线性无关性3. 空间中直线和平面的方程- 直线的向量方程、参数方程及一般方程 - 平面的点法式方程及一般方程- 直线和平面的位置关系与应用三、概率与统计1. 概率基础- 随机事件及其运算- 事件的概率及性质- 古典概型与几何概型2. 排列与组合- 排列与组合的基本概念- 排列与组合的计算公式- 排列组合问题的应用3. 统计与抽样调查- 数据的收集与整理- 描述统计与统计图表- 抽样调查与推断统计四、导数与微分1. 导数的概念与性质- 导数的定义与计算方法- 导数的几何意义与物理应用- 导数与函数的关系2. 微分的概念与应用- 微分的定义及计算方法- 微分中值定理的应用- 高阶导数与函数的性质以上列出的知识点只是高二数学期末考试的一部分内容,学生在复习时还需综合教材、教师的指导以及平时的学习情况进行全面复习。
通过归纳总结每个知识点的要点,合理安排复习时间,并进行大量的练习和习题训练,相信可以在期末考试中取得好成绩。
祝愿所有参加考试的学生都能充分发挥自己的优势和潜力,取得令人满意的成绩!加油!。
2020-2021学年高二数学下学期期末专项复习2.1 坐标平面上的直线解析版

专题2.1 坐标平面上的直线【章节复习专项训练】【考点1】 :直线的方程例题1.(2020·上海师大附中高二期末)直线方程20x y m -+=的一个方向向量d 可以是( ) A .(2,1)- B .(2,1) C .(1,2)- D .(1,2)【答案】D【分析】先根据直线方程得直线的一个法向量,再根据法向量可得直线的方向向量. 【详解】解:依题意,()2,1-为直线的一个法向量,∴方向向量为()1,2, 故选:D .【变式1】(2021·上海市奉贤中学高二期末)如图,平面上过点P (1,2)的直线与x 轴正半轴交于点A ,与y 轴正半轴交于点B .过点P 分别作直线垂直于x 轴与y 轴,垂足分别为M ,N .则满足2020PAMPBNS S-=的直线有( )条A .0B .1C .2D .3【答案】B【分析】设直线AB 为y =k (x -1)+2()0k <,分别令x =0,y =0,求得点A ,B 的坐标, 然后由2020PAMPBNSS-=求解.【详解】因为过点P (1,2),且斜率存在, 设直线AB 为y =k (x -1)+2()0k <, 令x =0,y =2-k ; 令y =0,x =2k k- 2(,0),(0,2)k A B k k-∴-, 2,2,AM PM BN k k∴=-==-,2020PAMPBNSS-=,121()21()202022k k ∴⨯-⨯-⨯⨯-=, 即2404040k k --=,0k <,所以k 的取值只有一个, 故这样的直线有一条. 故选:B【变式2】(2021·上海高二期末)直线1123x y l -+=:的一个方向向量可以是( ) A .(2,3) B .(2-,3)C .(3,2)D .(3-,2)【答案】A【分析】将直线方程转化为()3112y x +=-,求得斜率即可. 【详解】直线1123x y l -+=:可化为:()3112y x +=-,所以直线的斜率为32k, 所以直线的一个方向向量可以是(2,3) 故选:A【变式3】(2020·上海曹杨二中高二期末)已知直角坐标系xOy 平面上的直线1x ya b+=经过第一、第二和第四象限,则,a b 满足( ) A .0,0a b >> B .0a >,0b < C .0a <,0b < D .0a <,0b <【答案】A【分析】求出直线与坐标轴的交点,即可得出答案. 【详解】令0x =,则y b =;令0y =,则x a = 所以(0,),(,0)b a 在直线1x ya b+=上因为直线1x ya b+=经过第一、第二和第四象限 所以0,0a b >> 故选:A【点睛】本题主要考查了由直线所过象限求参数范围,属于基础题.例题2.(2020·上海市建平中学高二期末)过点()1,2C ,且与直线20x y --=垂直的直线方程为______. 【答案】30x y +-=【分析】先由垂直关系求出所求直线的斜率,再利用点斜式可求出直线方程 【详解】解:因为所求直线与直线20x y --=垂直, 所以所求直线的斜率为1-, 因为所求直线过点()1,2C ,所以所求直线方程为2(1)y x -=--,即30x y +-=, 故答案为:30x y +-=【点睛】此题考查两直线的位置关系,考查直线方程的求法,属于基础题【变式1】(2020·上海曹杨二中高二期末)过点()3,2P -且与直线210x y ++=垂直的直线方程是______. 【答案】270x y --=【分析】根据直线的垂直关系,设出所求直线方程,将()3,2P -代入方程,即可求解. 【详解】所求直线与直线210x y ++=垂直, 设该直线方程为20x y c -+=,()3,2P -代入上式方程得7c =-,所以所求的直线方程为270x y --=. 故答案为:270x y --=.【点睛】本题考查直线的位置关系求方程,利用直线的位置关系合理设方程是解题的关键,属于容易题. 【变式2】(2020·上海市控江中学高二期末)经过点()1,0,且以()2,5d =为一个方向向量的直线l 的方程为_____.【答案】5250x y --=【分析】求出直线l 的斜率,可得出直线l 的点斜式方程,化为一般式即可. 【详解】直线l 的斜率为52k =,所以,直线l 的方程为()512y x =-,即5250x y --=. 故答案为:5250x y --=.【点睛】本题考查直线的方程,考查直线的方向向量与斜率的关系,考查计算能力,属于基础题. 【变式3】(2020·上海高二期末)已知点()1,2A ,()3,0B ,则线段AB 的垂直平分线的方程是_____. 【答案】10x y --=【分析】先求出AB 的中点M 的坐标,再求出直线AB 的斜率,根据两直线垂直时斜率乘积为1-得到垂直平分线的斜率,最后用点斜式公式即可求出直线方程. 【详解】解:设M 的坐标为(),x y , 则1322x,2012y,所以()2,1M . 因为直线AB 的斜率为120113k , 所以线段AB 垂直平分线的斜率2111k , 则线段AB 的垂直平分线的方程为112y x 化简得10x y --=. 故答案为:10x y --=【点睛】本题考查求线段AB 的垂直平分线:即要求垂直平分线线上一点与直线的斜率,根据中点坐标公式求出AB 的中点M 的坐标利用A 与B 的坐标求出直线AB 的斜率根据两直线垂直时斜率乘积为1-得到垂直平分线的斜率根据M 的坐标和求出的斜率写出AB 的垂直平分线的方程即可.【变式4】(2020·上海高二期末)若直线l 过点3(2,)A -且平行于向量(6,5)d =,则直线l 的点方向式方程是___________. 【答案】2365x y -+= 【分析】利用直线l 的点方向式方程即可得出. 【详解】由已知可得:直线l 的点方向式方程是2365x y -+=.故答案为:2365x y -+=. 【点睛】本题考查直线的点方向式方程,考查推理能力与计算能力,属于基础题.【变式5】(2021·上海市松江二中高二期末)若关于x 、y 的二元一次方程组42mx y m x my m +=+⎧⎨+=⎩无解,则实数m =________ 【答案】2-【分析】根据方程组无解,得到直线42+=+mx y m 与直线+=x my m 平行,根据两直线平行的充要条件,即可求出结果.【详解】因为关于x 、y 的二元一次方程组42mx y m x my m +=+⎧⎨+=⎩无解,所以直线42+=+mx y m 与直线+=x my m 平行,所以24024m m m m ⎧-=⎪⎨+≠⎪⎩,解得:2m =-.故答案为:2-【点睛】本题主要考查由方程组无解求参数,熟记直线与直线平行的判定条件,灵活运用转化与化归的思想即可,属于常考题型.【变式6】(2020·上海师大附中高二期末)直线10x y -+= 上一点P 的横坐标是3,若该直线绕点P 逆时针旋转90°得直线l ,则直线l 的方程是____________. 【答案】70x y +-=【详解】(,3,4)P l 的倾斜角为4590135,tan1351k ︒-︒=︒=︒=-, 则其方程为43y x -=-+,即70x y +-=. 故答案为:70x y +-=.【变式7】(2021·上海市奉贤中学高二期末)数学家欧拉在1765年提出定理;三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称之为三角形的欧拉线.已知ABC 的顶点A (4,0),B (0,2),AC BC =,则ABC 的欧拉线所在直线方程为___________.【答案】2x -y -3=0【分析】根据题意求出线段AB 的垂直平分线即可求解. 【详解】线段AB 的中点为(2,1),201042AB k -==--, 线段AB 的垂直平分线为:y =2(x -2)+1,即2x -y -3=0 AC =BC ,∴三角形的外心、重心、垂心依次位于AB 的垂直平分线上,因此ABC 的欧拉线方程为2x -y -3=0. 故答案为:2x -y -3=0.【变式8】(2020·华东师范大学附属周浦中学高二期末)直线l 经过点(3,5)P -,且(1,2)n =是直线l 的一个法向量,则直线l 的一般式方程是________. 【答案】270x y ++=【分析】由直线的法向量可得直线的方向向量,进而可得直线的斜率,由直线方程的点斜式即可得出结果. 【详解】直线的法向量为(1,2)n =,则直线的方向向量为(2,1)m =-,直线的斜率为12k =- 由点斜式可得:1(5)(3)2y x --=--,即270x y ++= 故答案为:270x y ++=【变式9】(2020·上海市三林中学高二期末)过点()1,0且与直线20x y +=垂直的直线的方程______. 【答案】210x y --=【分析】方法一,利用两条直线互相垂直,斜率之积等于-1,求出垂线的斜率,再求垂线的方程; 方法二,根据两条直线互相垂直的关系,设出垂线的方程,利用垂线过某点,求出垂线的方程. 【详解】方法一,直线20x y +=的斜率是-2, 则与这条直线垂直的直线方程的斜率是12, ∴过点()1,0且与直线20x y +=垂直的直线方程为()1012y x -=-, 即210x y --=;方法二,设与直线20x y +=垂直的直线方程为20x y a -+=, 且该垂线过过点()1,0,∴11200a ⨯-⨯+=,解得1a =-,∴这条垂线的直线方程为210x y --=. 故答案为:210x y --=.【点睛】本题考查了直线方程的求法与应用问题,也考查了直线垂直的应用问题,是基础题目.例题3.(2021·上海高二期末)已知直线l 与直线250x y +-=平行,并且直线l 与两坐标轴围成的三角形的面积为4,求直线l 的一般式方程. 【答案】240x y ++=或240x y +-=【分析】设所求直线方程为()205x y C C ++=≠-,求出直线l 与两坐标轴的交点坐标,结合已知条件可得出关于C 的方程,进而可求得直线l 的方程.【详解】由于直线l 与直线250x y +-=平行,设直线l 的方程为()205x y C C ++=≠-, 在直线l 的方程中,令0x =,可得y C =-;令0y =,可得2Cx =-. 所以,直线l 交x 轴于点,02C ⎛⎫-⎪⎝⎭,交y 轴于点()0,C -. 由于直线l 与两坐标轴围成的三角形的面积为4,则214224C C C ⨯-⨯-==,解得4C =±. 因此,直线l 的方程为240x y ++=或240x y +-=.【变式1】(2020·上海高二期末)已知直线1:220l x y +-=和2:10l mx y -+=. (1)当12l l //时,求m 的值; (2)当1l 与2l 的夹角为4π时,求m 的值. 【答案】(1)2-;(2)3或13-. 【分析】(1)直接利用线线平行的充要条件的应用求出结果. (2)直接利用夹角公式的应用求出结果.【详解】(1)直线1:220l x y +-=和2:10l mx y -+=. 所以20m --=,解得:2m =-.(2)由于1:220l x y +-=的斜率12k =-,2:10l mx y -+=的斜率2=k m .所以2112tan||141k kk kπ-==+,解得3m=或13-.【点睛】本题考查的知识要点:线线平行的充要条件的应用,夹角公式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.【考点2】:直线的倾斜角和斜率例题1.(2020·上海市杨浦高级中学高二期末)直线210x y+-=的倾斜角为().A.arctan2B.arctan2-C.()arctan2π--D.arctan2π-【答案】D【分析】先根据所给直线的斜率-2,直线的斜率是倾斜角的正切,得到[)tan=20ααπ-∈,,,根据倾斜角的范围和正切的反三角函数的值域确定结果.【详解】因为直线210x y+-=的斜率2k=-,所以[)tan=20ααπ-∈,,,所以=arctan2απ-.所以直线210x y+-=的倾斜角为arctan2π-.故选:D【点睛】求斜率的方法:①定义法:()tan90kαα=≠;②两点法求斜率:()212121y yk x xx x-=≠-;③由直线方程求斜率;④由直线的方向向量求斜率.【变式1】(2020·上海高二期末)下图中的直线1l、2l、3l的斜率分别为1k、2k、3k,则()A.123k k k<<B.312k k k<<C.321k k k<<D.132k k k<<【答案】D【分析】根据斜率与直线倾斜角的关系判断即可.【详解】由图可知:10k <,20k >,30k >,且直线3l 的倾斜角小于直线2l 的倾斜角,所以32k k <,综上可知:132k k k <<.故选:D .【点睛】本题主要考查了直线斜率与倾斜角的关系,属于基础题.【变式2】(2020·上海高二期末)已知l 过定点()4,5的直线的一个方向向量是()2,3d =-,则直线l 的点方向式方程可以为( ) A .()()3425x y -=- B .45=23x y --- C .()()34250x y -+-= D .45=32x y -- 【答案】B【分析】利用直线的点向式方程可以直接得到所求的方程. 【详解】因为直线l 的方向向量为()2,3d =-且经过点()4,5, 故直线l 的点向式方程为45=23x y ---. 故选:B .【点睛】本题考查直线的点向式方程,注意点向式方程的标准形式,此题属于基础题.【变式3】.(2021·上海市建平中学高二期末)直线l 的倾斜角为θ,则直线l 关于直线y =x 对称的直线l '的倾斜角不可能为( ) A .θ B .2θπ- C .πθ-D .32πθ- 【答案】C【分析】可分类讨论求出对称直线l '的倾斜角,然后判断. 【详解】当[0,]2πθ∈时,直线l '的倾斜角为2θπ-,当,2πθπ⎛⎫∈ ⎪⎝⎭时,直线l '的倾斜角为32πθ-,当4πθ=时,直线l '的倾斜角为4πθ=,因此ABD 均可能,只有C 不可能.实际上当直线l '倾斜角为πθ-时,直线l '与直线l 关于和x 轴垂直的直线对称. 故选:C .【变式4】.(2020·上海市洋泾中学高二期末)若直线0ax by c 的一个法向量()3,1n =-,则该直线的倾斜角为( ) A .6πB .3πC .23π D .56π 【答案】B【分析】根据直线的方程可得直线的法向量,结合题设条件可得,a b 的关系,从而可求直线的斜率进而得到直线的倾斜角.【详解】由直线的方程为0ax by c可得直线的法向量为(),m a b =,故,m n 共线,所以()1b a ⨯-=,即ab-=,设直线的倾斜角为[)()0,θθπ∈,则tan θ=3πθ=.故选:B.例题2.(2020·上海市进才中学高二期末)直线210x y -+=的倾斜角为________. 【答案】1arctan2【分析】根据直线方程求出直线的斜率,从而求出倾斜角. 【详解】直线210x y -+=的斜率12k =, 所以直线的倾斜角是1arctan 2. 故答案为:1arctan2. 【变式1】(2020·上海高二期末)直线40x my 的倾斜角为4π,则m 的值是_____. 【答案】1【分析】由直线的倾斜角求出斜率,再由斜率列式求得m 值. 【详解】解:直线40x my 的倾斜角为4π. 所以该直线的斜率为tan 14π=,所以11m=,解得:1m =. 故答案为:1.【点睛】本题考查直线的斜率与倾斜角的关系,是基础题.【变式2】(2020·上海市七宝中学)直线l 的倾斜角范围是__________; 【答案】0,【分析】由直线的倾斜角定义来确定. 【详解】由直线倾斜角的定义:x 轴正向与直线向上方向之间所成的角叫直线的倾斜角.特别地,当直线与x 轴平行或重合时,我们规定它的倾斜角为0度. 范围:倾斜角的取值范围是0°≤α<180°. 故答案为:0,【点睛】本题主要考查了直线倾斜角的定义及范围,还考查了理解辨析的能力,属于基础题. 【变式3】(2020·上海高二期末)若直线l 的倾斜角的范围为,43ππ⎡⎫⎪⎢⎣⎭,则l 的斜率的取值范围是__________.【答案】【分析】利用直线斜率与倾斜角的关系、三角函数的单调性即可得出. 【详解】直线l 的倾斜角,43θππ⎡⎫⎪⎢∈⎣⎭,则l 的斜率tan [1θ∈.故答案为:.【点睛】本题考查直线斜率与倾斜角的关系、三角函数的单调性,考查推理能力与计算能力,属于基础题. 【变式4】(2020·上海复旦附中高二期末)一个方向向量为(1,3d =的直线的倾斜角的大小是__________. 【答案】60︒【分析】根据直线的方向向量可得直线的斜率,然后可求直线的倾斜角.【详解】因为直线的方向向量为(1,3d =,所以直线的斜率为k = 所以直线的倾斜角的大小是60︒. 故答案为:60︒.【点睛】本题主要考查直线的倾斜角,明确直线的方向向量与直线的斜率间的关系是求解的关键,侧重考查数学运算的核心素养.【变式5】(2020·上海市金山中学高二期末)直线l :4y =+的倾斜角的大小为______.【答案】3π;【分析】由直线的斜率与倾斜角的关系可得tan θ=. 【详解】解:设直线的倾斜角为θ,由直线l 的方程为:4y =+可得tan θ= 又[)0,θπ∈, 所以3πθ=,故答案为:3π.【点睛】本题考查了直线的斜率与倾斜角的关系,属基础题.【变式6】(2021·上海市松江二中高二期末)若直线l 的参数方程是2,()12x t t y t =+⎧∈⎨=--⎩R ,则l 的斜率为________. 【答案】-2【分析】把参数方程消参化为斜截式方程即可求出斜率.【详解】由2,()12x t t y t =+⎧∈⎨=--⎩R ,消去参数t 可得23y x =-+, 所以直线的斜率2k =- 故答案为2-【点睛】本题考查直线的参数方程与一般方程的互化,属于基础题.【变式7】(2021·上海市奉贤中学高二期末)直线23y x =-+的倾斜角是___________(结果用反三角表示). 【答案】arctan 2π-【分析】根据斜率公式tan k α=化简即可.【详解】解:由题意得tan 2,arctan 2k ααπ==-∴=- 故答案为:arctan 2π-.【变式8】(2021·上海高二期末)直线1:10l x y +-=与直线2:20l x y -+=夹角的大小为___________. 【答案】2π 【分析】根据直线方程求得两直线的斜率,进而可求得倾斜角,即可求得答案.【详解】直线1:10l x y +-=的斜率为-1,因为倾斜角[0,)απ∈,即tan 1α=-,所以1l 的倾斜角为34π, 同理直线2:20l x y -+=的斜率为1,所以2l 的倾斜角为4π, 所以直线1l 与2l 的夹角为3442πππ-=. 故答案为:2π 【变式9】(2021·上海曹杨二中高二期末)若直线l 的倾斜角为34π,则l 的一个方向向量d 可以是______.(只需填写一个) 【答案】()1,1-【分析】利用直线倾斜角确定直线斜率,进而确定方向向量的横纵坐标之比,写出方向向量. 【详解】直线l 的倾斜角为34π,故直线的斜率3tan 14k π==-, 故方向向量的横纵坐标之比为1-, 故d 可以是()1,1-, 故答案为:()1,1-.【变式10】(2020·上海曹杨二中高二期末)设()1,2A ,()3,1B -,若直线2y kx =-与线段AB 有公共点,则实数k 的取值范围是______. 【答案】(][),14,-∞-+∞【分析】画出图象求出定点与A 、B 两点连线的斜率,即可求出实数k 的取值范围.【详解】解:直线2y kx =-恒过定点()0,2-,由题意平面内两点()1,2A ,()3,1B -,直线2y kx =-与线段AB 恒有公共点,如图求出定点与A 、B 两点连线的斜率,()122410k --==-.()212130k --==---,所以直线2y kx =-与线段AB 恒有公共点,则实数k 的取值范围是(][),14,-∞-+∞,故答案为:(][),14,-∞-+∞【点睛】本题考查直线斜率的求法,考查数形结合的思想的应用,考查计算能力.【变式11】(2020·上海高二期末)已知直线l 的一个方向向量是(1,2),则它的斜率为______________. 【答案】2【分析】根据直线方向向量与直线斜率关系求斜率即可. 【详解】直线l 的一个方向向量是(1,2),则直线的斜率为:2=21故答案为:2【点睛】本题考查直线方向向量以及直线斜率,考查基本分析求解能力,属基础题. 【变式12】(2020·上海高二期末)直线210x y +-=的倾斜角为________. 【答案】arctan 2π-【分析】先求直线210x y +-=的斜率,进而用反三角函数转化为倾斜角即可. 【详解】直线210x y +-=的斜率为2k =-,设倾斜角为α,所以tan 2α,则arctan 2απ-= 故答案为:arctan 2π-【点睛】本题关键是倾斜角以及反三角函数的问题,考查计算能力.【变式13】(2020·上海市控江中学高二期末)若不垂直于x 轴的直线10kx y -+=与直线20x y -=所成的角的大小为25,则实数k 的值为_____.【答案】34【分析】设直线20x y -=的倾斜角为α,记β=k 的方程,进而可求得实数k 的值.【详解】设直线20x y -=的倾斜角为α,记β=,则tan 2α=,cos 5β=,sin 5β=,1tan 2β=,由题意可得tan 21tan 1tan 122k k k k αβα--===++,解得34k =.故答案为:34. 【点睛】本题主要考查直线夹角公式的应用,涉及两角差的正切公式的应用,考查计算能力,属于基础题. 【变式14】.(2020·上海交大附中高二期末)直线223x ty t =+⎧⎨=+⎩(参数t R ∈)的倾斜角为_________.【答案】12arctan【分析】代入消参,将参数方程化为普通方程,再根据斜率求得倾斜角. 【详解】由3y t =+可得3t y =-,代入22x t =+,可得()223x y =+- 整理得:直线的一般式方程为240x y -+= 则直线的斜率为12k =,设其倾斜角为θ,[)0,θπ∈ 故12arctanθ=. 故答案为:12arctan. 【点睛】本题考查将直线的参数方程化为普通方程,以及由直线斜率求解倾斜角,属基础题.例3.(2019·上海高二期末)已经直线:1l y kx =-与两点()()1,5,4,2.A B - (1)若l 与直线AB 平行,求它们之间的距离以及l 的倾斜角;(2)若l 与线段AB 无公共点,求k 的取值范围. 【答案】(1)d =;3arctan 5θπ=-;(2)36,4⎛⎫- ⎪⎝⎭【分析】(1)由两点连线斜率公式可求得AB k ,即k ,从而得到直线l 方程及tan θ、直线AB 方程;根据反三角函数可求得倾斜角θ,利用平行直线间距离公式可求得所求距离d ;(2)首先确定直线恒过定点()0,1C -,可知临界状态为,AC BC ,利用两点连线斜率公式求得,AC AB k k ,可知(),AC AB k k k ∈,从而得到结果. 【详解】(1)由,A B 坐标可得:523145AB k -==--- ∴直线AB 方程为:()3245y x -=--,即35220x y +-= l 与直线AB 平行 35AB k k ∴==- 3:15l y x ∴=--,即3550x y ++=设直线l 倾斜角为θ 3tan 5θ∴=- 3arctan 5θπ∴=-直线l 与直线AB之间距离34d ==(2)由题意知,直线l 恒过点()0,1C -51610AC k +∴==---,213404BC k +==- l 与线段AB 无公共点 (),AC AB k k k ∴∈,即36,4k ⎛⎫∈- ⎪⎝⎭【点睛】本题是对直线部分知识的综合考查,涉及到直线斜率与倾斜角的关系、两条直线平行的位置关系的应用、平行直线间距离公式、根据直线与线段交点情况求解斜率范围的问题,属于基础题. 【考点3】 :两条直线的位置关系例题1.(2020·上海高二期末)直线210x y ++=与直线36100x y 的位置关系是( ) A .相交 B .重合C .平行D .垂直【答案】C【分析】根据直线的一般方程满足111222A B C A B C =≠,则两直线平行. 【详解】解: 直线210x y ++=与直线36100x y ,满足1213610, 故直线210x y ++=与直线36100x y 平行. 故选:C【点睛】本题考查直线与直线的位置关系,若两直线满足111222A B C A B C =≠,则两直线平行. 【变式1】.(2020·上海市金山中学高二期末)已知两条直线1l 与2l 不重合,则“1l 与2l 的斜率相等”是“1l 与2l 的平行”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】A【分析】“1l 与2l 的平行”则有“1l 与2l 的斜率相等”或“1l 与2l 的斜率均不存在”两种情况,再判断即可得解. 【详解】解:因为两条直线1l 与2l 不重合,由“1l 与2l 的斜率相等”可得“1l 与2l 的平行”; 由“1l 与2l 的平行”则可得“1l 与2l 的斜率相等”或“1l 与2l 的斜率均不存在”, 即“1l 与2l 的斜率相等”是“1l 与2l 的平行”的充分不必要条件, 故选:A.【点睛】本题考查了两直线平行的充分必要条件,重点考查了直线的斜率,属基础题. 【变式2】.(2020·上海市嘉定区封浜高级中学高二期末)14a =是“直线(1)310a x ay +++=与直线(1)(1)30a x a y -++-=相互垂直”的( ).A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】A【分析】对a 分类讨论,利用两条相互垂直的直线与斜率之间的关系即可得出. 【详解】解:对于:直线(1)310a x ay +++=与直线(1)(1)30a x a y -++-=, 当0a =时,分别化为:10x +=,30x y -+-=,此时两条直线不垂直,舍去;当1a =-时,分别化为:310y -+=,230x --=,此时两条直线相互垂直,因此1a =-满足条件; 当1a ≠-,0时,两条直线的斜率分别为:13a a +-,11a a -+,由于两条直线垂直,可得11131a aa a +--⨯=-+,解得14a =或1-(舍去). 综上可得:两条直线相互垂直的充要条件为:14a =或1-. ∴14a =是“直线(1)310a x ay +++=与直线(1)(1)30a x a y -++-=相互垂直”的充分而不必要条件. 故选:A .【点睛】本题考查了两条相互垂直的直线与斜率之间的关系,考查了分类讨论思想、推理能力与计算能力,属于中档题.例题2.(2021·上海闵行中学高二期末)过点()3,5与直线y x m =+垂直的直线方程是___________. 【答案】80x y +-=【分析】设与y x m =+垂直的直线方程为y x n =-+,利用过的点,求出n 即可. 【详解】设所求直线为y x n =-+ 过点()3,5,故8n = 直线方程为80x y +-= 故答案为:80x y +-=【变式1】.(2021·上海位育中学高二期末)已知直线1:230l ax y a ++=与直线2:3(1)70l x a y a +-+-=互相垂直,则a =________ 【答案】25【分析】利用两条直线垂直的等价条件可得()3210a a +-=,解方程即可求a 的值. 【详解】因为直线1:230l ax y a ++=与直线2:3(1)70l x a y a +-+-=互相垂直, 所以()3210a a +-=,解得:25a =, 故答案为:25.【变式2】.(2021·上海市进才中学高二期末)若直线1:210l ax y ++=与2:(1)10l x a y +++=互相垂直,则a 的值为_________. 【答案】23-【分析】根据两个直线垂直的公式代入计算. 【详解】因为12l l ⊥,所以2(1)0a a ++=,得23a =-. 故答案为:23-【变式3】.(2021·上海市复兴高级中学高二期末)已知直线220x y +-=和10x y -+=的夹角为______. 【答案】arctan 3【分析】求出两直线的斜率,利用相交两直线的夹角公式求解而得. 【详解】直线220x y +-=和10x y -+=的斜率分别为k 1=-2,k 2=1, 设直线220x y +-=和10x y -+=的夹角为(0)2πθθ<≤,而两直线不垂直,由夹角公式得:121221tan ||||311(2)1k k k k θ---===++-⋅,所以arctan 3θ=. 答案为:arctan 3【变式4】.(2020·上海闵行中学高二期末)已知直线1:10l ax y -+=,2:10l x ay --=,且12l l ⊥,则实数a =_________. 【答案】0【分析】依据两条直线垂直充要条件12120A A B B +=直接计算即可. 【详解】因为12l l ⊥,所以()()1100a a a ⨯+-⨯-=⇒= 故答案为:0【变式5】..(2020·上海高二期末)已知直线1:42l mx y m +=+,2:l x my m +=,若12//l l ,则实数m =________.【答案】2-【分析】根据直线互相平行的判定公式得到结果. 【详解】直线1:42l mx y m +=+,2:l x my m +=, 若12//l l ,则24102m m -⨯=⇒=±,当2m =时,1l 和2l 化简为:1:22l x y +=,2:22l x y +=,此时,1l 与2l 重合,故2m =时不符合题意当2m =-时,1l 和2l 化简为:1:20l x y -=,2:220l x y -+=,此时,1l 与2l 不重合且平行,故2m =-时符合题意 故答案为:2-.【点睛】这个题目考查了已知两直线的位置关系求参数的应用,属于基础题.【变式6】.(2020·上海高二期末)直线10x y ++=与直线30x y -+=的夹角大小等于___________. 【答案】2π【分析】算出两条直线的斜率,根据它们的乘积为1-可得它们的夹角. 【详解】设两条直线的夹角为θ,直线10x y ++=的斜率为11k =-,直线30x y -+=的斜率为21k =, 因为121k k =-,所以两条直线垂直,所以2πθ=.故答案为:2π. 【点睛】本题考查直线的夹角,注意先判断它们是否垂直,如果不垂直,则利用夹角公式1212tan 1k k k k θ-=+来计算,本题属于容易题.【变式7】.(2020·上海市洋泾中学高二期末)已知直线1:220++=l x ay 与直线2:(1)310l a x y -++=平行,则实数a 的值为__________ 【答案】2-或3【分析】根据两直线平行,直接列式求解. 【详解】12//l l ,22131a a ∴=≠-,解得:2a =-或3a =. 故答案为:2-或3【变式8】.(2020·上海高二期末)直线1:210l x y -+=与直线2:210l x y ++=的夹角为______________. 【答案】90︒【分析】先利用斜率之积为1-,判定两直线垂直,即可得解.【详解】由直线1:210l x y -+=与直线2:210l x y ++=的方程可知,两直线的斜率分别为:1212,2k k ==-,∴121k k =-,∴12l l ⊥,∴两直线的夹角为90︒. 故答案为:90︒.【点睛】本题考查两直线的夹角的求法,关键根据两直线的方程求得斜率,根据斜率是否乘积为1-,从而判定两直线是否垂直是关键点.【变式9】.(2020·上海格致中学高二期末)若直线1:2310l x y +-=的方向向量是直线2:20l ax y a -+=的法向量,则实数a 的值等于__________. 【答案】32【分析】由题意结合直线方向向量、法向量的概念可得12l l ⊥,再由直线垂直的性质即可得解. 【详解】直线1l 的方向向量是直线2l 的法向量,∴12l l ⊥,∴230a -=,解得32a =. 故答案为:32. 【点睛】本题考查了直线方向向量、法向量概念的应用,考查了直线垂直的性质,属于基础题.【变式10】.(2020·上海高二期末)已知直线1l :210ax y -+=、2l :()130x a a y ++-=,若12l l ⊥,则实数a =_________.【答案】0或12- 【分析】若直线1l :1110A x B y C ++=与直线2l :2220A x B y C ++=垂直,则12120A A B B +=,代入数据计算即得. 【详解】直线1l :210ax y -+=、2l :()130x a a y ++-=,且12l l ⊥,()()1+210a a a ∴⨯-⨯+=,即220a a +=,解得0a =或12a =-. 故答案为:0a =或12a =-. 【点睛】本题考查直线的位置关系,属于基础题.【变式11】.(2020·上海市三林中学高二期末)已知直线1l :()6180x t y +--=,直线2l :()()46160t x t y +++-=,若1l 与2l 平行,则t =______.【答案】-5【分析】由平行关系可得()()()6641t t t ⨯+=+-,解方程验证排除重合可得.【详解】由题意可得()()()6641t t t ⨯+=+-,解方程可得5t =-或8t =,经验证8t =时直线重合,应舍去故当5t =-时,两直线平行.故答案为:-5.【点睛】本题考查直线的一般式方程和平行关系,属基础题.【变式12】.(2021·上海市奉贤中学高二期末)已知直线()()1:3410l k x k y -+-+=与()2:23230l k x y --+=平行,则k 的值是____.【答案】3或5【分析】由两直线平行得出()()()23243k k k --=--,解出k 的值,然后代入两直线方程进行验证. 【详解】直线()()1:3410l k x k x y -+-++=与()2:23230l k x y --+=平行,()()()23243k k k ∴--=--,整理得()()350k k --=,解得3k =或5.当3k =时,直线1:10l y +=,23:02l y -=,两直线平行; 当5k =时,直线1:210l x y -+=,23:202l x y -+=,两直线平行. 因此,3k =或5.故答案为3或5.【点睛】本题考查直线的一般方程与平行关系,在求出参数后还应代入两直线方程进行验证,考查运算求解能力,属于基础题.例题3.(2020·上海高二期末)已知二元一次方程组()()32232120k x y k x k y k ⎧--=⎪⎨++++=⎪⎩无解,求k 的值: 【答案】32k 【分析】根据题意知两直线平行,根据直线与直线平行的关系建立方程,求解验证即可.【详解】解:因为二元一次方程组()()32232120k x y k x k y k ⎧--=⎪⎨++++=⎪⎩无解, 则()322k x y k --=与()32120x k y k ++++=平行, 由3223212k k k k ---=≠++,解得:32k . 经过验证满足题意. 32k ∴=时方程组无解. 【点睛】本题考查两直线平行,求参数,是基础题.【考点4】 :点到直线的距离例题1.(2020·上海市七宝中学)直线l 经过点()2,1P -,且点()1,2--A 到l 的距离为1,则直线l 的方程为______.【答案】2x =-或4350x y ++=【分析】当直线l 斜率存在时,设出点斜式并利用点到直线的距离公式算出l 的方程为4350x y ++=;当直线与x 轴垂直时,l 方程为2x =-也符合题意.由此即可得到此直线l 的方程.【详解】设直线l 的方程为()12y k x -=+,即210kx y k -++=∵点()1,2--A 到l 的距离为1,1=,解之得43k =-, 得l 的方程为4350x y ++=.当直线与x 轴垂直时,方程为2x =-,点()1,2--A 到l 的距离为1,∴直线l 的方程为2x =-或4350x y ++=.故答案为:2x =-或4350x y ++=【点睛】本题主要考查求经过定点,且到定点的距离等于定长的直线l 方程,着重考查了直线的方程、点到直线的距离公式等知识,属于基础题.【变式1】.(2020·上海高二期末)若O 为坐标原点,P 是直线20x y -+=上的动点,则||OP 的最小值为______________.【分析】线段OP 的最小值,就是原点到已知直线的距离,根据点到直线的距离公式即可得出.【详解】解:原点到直线的距离d==故||OP【点睛】本题考查了点到直线的距离公式、转化方法,属于基础题.【变式2】.(2020·上海高二期末)已知点()4,1P,点Q的坐标(),x y满足212x y=,则点P与点Q距离的最小值为_____.【分析】先将212x y=转化为直线220x y--=,再求点P到直线220x y--=的距离即可.【详解】解: 点Q的坐标(),x y满足212x y=,则点Q在直线220x y--=上,则点P与点Q距离的最小值即为点P到直线220x y--=的距离:d===故点P与点Q故答案为:【点睛】本题考查二阶行列式的运算,考查点到直线的距离公式,是基础题.【变式3】.(2019·上海市进才中学高二期末)圆22240x y x y+-+=的圆心到直线3450x y+-=的距离等于________。
专题07 随机变量及其分布【专项训练】高二数学下学期期末专项复习(新人教A版2019)

专题07 随机变量及其分布【专项训练】一、单选题1.若随机变量~(,)B n p ξ,且()2E ξ=,8()5D ξ=,则p =( ) A .15B .25C .35D .45【答案】A 【详解】解:因为随机变量~(,)B n p ξ,且()2E ξ=,8()5D ξ=, 所以28(1)5np np p =⎧⎪⎨-=⎪⎩,解得1015n p =⎧⎪⎨=⎪⎩,故选:A2.学校从高一、高二、高三中各选派10名同学参加“建党100周年党史宣讲”系列报告会,其中三个年级参会同学中女生人数分别为5、6、7,学习后学校随机选取一名同学汇报学习心得,结果选出一名女同学,则该名女同学来自高三年级的概率为( ) A .718B .730C .915D .13【答案】A 【详解】设事件A 为“30人中抽出一名女同学”,事件B 为“30人中抽出一名高三同学”, 则56718()3030P A ++==,7()30P AB =, 所以()()7()18P AB P B A P A ==,故选:A.3.已知离散型随机变量X 的分布列为则X 的数学期望E (X )=( ) A .1 B .1.5 C .2.5D .1.7【详解】()10.420.530.1 1.7E X=⨯+⨯+⨯=.故选:D.4.某次市教学质量检测,甲、乙、丙三科考试成绩服从正态分布,相应的正态曲线如图所示,则下列说法中正确的是()A.三科总体的标准差相同B.甲、乙、丙三科的总体的平均数不相同C.丙科总体的平均数最小D.甲科总体的标准差最小【答案】D【详解】解:由图象知甲、乙、丙三科的平均分一样,但标准差不同,σ甲<σ乙<σ丙.故选:D.5.已知P(B|A)=13,P(A)=25,则P(AB)等于()A.56B.910C.215D.115【答案】C 【详解】由题意,知()()(122315 )5P AB P B A P A==⨯=故选:C6.随机变量X所有可能取值是-2,0,3,5,且P(X=-2)=14,P(X=3)=12,P(X=5)=112,则P(X=0)的值为()A.0 B.14C.16D.18【详解】由各个变量概率和为1可得:P (X =-2)+P (X =0)+P (X =3)+P (X =5)=1, 所以111(0)14212P X +=++=,解得1(0)6P X == 故选:C7.袋中有大小相同的红球6个,白球5个,从袋中每次任意取出1个球且不放回,直到取出的球是白球为止,所需要的取球次数为随机变量X ,则X 的可能取值为( )A .1,2,3,…,6B .1,2,3,…,7C .0,1,2,…,5D .1,2,…,5 【答案】B 【详解】由于取到白球时停止,所以最少取球次数为1,即第一次就取到了白球; 最多次数是7次,即把所有的黑球取完之后再取到白球. 所以取球次数可以是1,2,3,…,7. 故选:B8.若离散型随机变量2~4,3X B ⎛⎫ ⎪⎝⎭,则()E X 和()D X 分别为( ) A .83,169 B .83,89C .89,83D .169,83【答案】B 【详解】因为离散型随机变量2~4,3X B ⎛⎫ ⎪⎝⎭, 所以()28433E X =⨯=, ()22841339D X ⎛⎫=⨯⨯-= ⎪⎝⎭.9.设随机变量()24,N ζδ,若()10.4P a ζ>+=,则()7P a ζ>-=( )A .0.4B .0.5C .0.6D .0.7【答案】C随机变量2~(4,8)N ζ,对称轴为:4μ= 因为(1)0.40.5P a ζ>+=<,所以14a +>, 根据对称性可得(1)(7)0.4P a P a ζζ>+=<-=, 则(7)0.6P a ζ>-=. 故选:C.10.设()()221122,,,X N Y N μσμσ~~,这两个正态分布密度曲线如图所示.下列结论中正确的是( )A .()()21P Y P Y μμ≥≥≥B .()()21P X P X σσ≤≤≤C .函数()()F t P X t =>在R 上单调递增D .()()111122222222P X P Y μσμσμσμσ-<<+=-<<+ 【答案】D 【详解】由正态分布密度曲线的性质得:X ,Y 的正态分布密度曲线分别关于直线12,x x μμ==对称, 对于A :由图象得12μμ<,所以()()21P Y P Y μμ≥<≥,故A 不正确;对于B :由图象得X 的正态分布密度曲线较Y 的正态分布密度曲线“廋高”,所以12σσ<,所以()()21>P X P X σσ≤≤,故B 不正确;对于C :由图象得:当1>t μ时,函数()()F t P X t =>在()t +∞,上单调递减,故C 不正确; 对于D :根据3σ原则:()111168.3%P X μσμσ-<<+=,()11112295.4%P X μσμσ-<<+=,()11113399.7%P X μσμσ-<<+=,无论σ 取何值时,有()()111122222222P X P Y μσμσμσμσ-<<+=-<<+,故D 正确,故选:D.二、多选题11.近年来中国进入一个鲜花消费的增长期,某农户利用精准扶贫政策,贷款承包了一个新型温室鲜花大棚,种植销售红玫瑰和白玫瑰.若这个大棚的红玫瑰和白玫瑰的日销量分别服从正态分布()2,30N μ和()2280,40N ,则下列选项正确的是( )附:若随机变量X 服从正态分布()2,N μσ,则()0.6826P X μσμσ-<<+≈.A .若红玫瑰日销售量范围在(30,280)μ-的概率是0.6826,则红玫瑰日销售量的平均数约为250B .红玫瑰日销售量比白玫瑰日销售量更集中C .白玫瑰日销售量比红玫瑰日销售量更集中D .白玫瑰日销售量范围在()280,320的概率约为0.3413 【答案】ABD 【详解】对于A ,因为红玫瑰日销售量范围在(30,280)μ-的概率是0.6826, 故30280μ+≈即250μ≈,故A 正确.对于B ,因为3040<,故红玫瑰日销售量比白玫瑰日销售量更集中,故B 对,C 错. 白玫瑰日销售量范围在()280,320的概率约为0.68260.34132=,故D 正确. 故选:ABD.12.已知三个正态分布密度函数()()()222,1,2,3i i x i f x x R i μσ--=∈=的图象如图所示,则下列结论正确的是( )A .123σσσ==B .123σσσ=<C .123μμμ=>D .123μμμ<=【答案】BD 【详解】正态密度曲线关于直线x μ=对称,且μ越大图象越靠近右边,σ越小图象越瘦长. 因此,123μμμ<=,123σσσ=<.13.甲、乙两人练习射击,命中目标的概率分别为12和13,甲、乙两人各射击一次,下列说法正确的是( )A .目标恰好被命中一次的概率为1123+ B .目标恰好被命中两次的概率为1123⨯C .目标被命中的概率为12112323⨯+⨯D .目标被命中的概率为12123-⨯【答案】BD 【详解】甲、乙两人练习射击,命中目标的概率分别为12和13,甲、乙两人各射击一次, 在A 中,目标恰好被命中一次的概率为1112123232⨯+⨯=,故A 错误; 在B 中,由相互独立事件概率乘法公式得:目标恰好被命中两次的概率为111236⨯=,故B 正确; 在CD 中,目标被命中的概率为112111233⎛⎫⎛⎫--⨯-= ⎪ ⎪⎝⎭⎝⎭,故C 错误,D 正确. 故选:BD .14.袋子中有2个黑球,1个白球,现从袋子中有放回地随机取球4次,取到白球记0分,黑球记1分,记4次取球的总分数为X ,则( ) A .2~4,3XB ⎛⎫ ⎪⎝⎭B .8(2)81P X ==C .X 的期望8()3E X =D .X 的方差8()9D X =【答案】ACD 【详解】从袋子中有放回地随机取球4次,则每次取球互不影响, 并且每次取到的黑球概率相等,又取到黑球记1分, 取4次球的总分数,即为取到黑球的个数,所以随机变量X 服从二项分布2~4,3X B ⎛⎫ ⎪⎝⎭,故A 正确;2X =,记其概率为22242124(2)3381P X C ⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭,故B 错误;因为2~4,3X B ⎛⎫ ⎪⎝⎭,所以X 的期望28()433E X =⨯=,故C 正确; 因为2~4,3X B ⎛⎫ ⎪⎝⎭,所以X 的方差218()4339D X =⨯⨯=,故D 正确. 故选:ACD . 15.已知()2~,X N μσ,22()2()x f x μσ--=,x ∈R ,则( )A .曲线()y f x =与x 轴围成的几何图形的面积小于1B .函数()f x 图象关于直线=x μ对称C .()2()()P X P X P X μσμμσμσ>-=<<++≥+D .函数()()F x P X x =>在R 上单调递增 【答案】BC 【详解】选项A. 曲线()y f x =与x 轴围成的几何图形的面积等于1, 所以A 不正确.选项B. 222()x f x σμ-+=,222()x f x σμ--=所以()()f x f x μμ+=-,所以函数()f x 图象关于直线x μ=对称,所以选项B 正确.选项C. 因为()()P X P X μμσμμσ>>-=<>+所以()()()P X P X P X μσμσμσμσ>-=-<<++≥+2()()P X P X μμσμσ=<<++≥+ 所以选项C 正确.选项D. 由正态分布曲线可知,当x 越大时,其概率越小.即函数()()F x P X x =>随x 的增大而减小,是减函数,所以选项D 不正确. 故选:BC三、解答题16.设离散型随机变量X 的分布列为求:(1)21X +的分布列; (2)求(14)P X <≤的值. 【详解】由分布列的性质知:0.20.10.10.31m ++++=,解得0.3m = (1)由题意可知(211)(0)0.2P X P X +====,(213)(1)0.1P X P X +====,(215)(2)0.1P X P X +==== (217)(3)0.3P X P X +====,(219)(4)0.3P X P X +====所以21X +的分布列为:(2)(14)(2)(3)(4)0.10.30.30.7P X P X P X P X <≤==+=+==++=17.为降低雾霾等恶劣气候对居民的影响,某公司研发了一种新型防雾霾产品.每一台新产品在进入市场前都必须进行两种不同的检测,只有两种检测都合格才能进行销售,否则不能销售.已知该新型防雾霾产品第一种检测不合格的概率为16,第二种检测不合格的概率为110,两种检测是否合格相互独立.(1)求每台新型防雾霾产品不能销售的概率;(2)如果产品可以销售,则每台产品可获利40元;如果产品不能销售,则每台产品亏损80元(即获利80-元).现有该新型防雾霾产品3台,随机变量X 表示这3台产品的获利,求X 的分布列及数学期望. 【详解】(1)设事件A 表示“每台新型防雾霾产品不能销售” 事件A 表示“每台新型防雾霾产品能销售” 所以()113116104P A ⎛⎫⎛⎫=--= ⎪⎪⎝⎭⎝⎭ 所以()()114P A P A =-= (2)根据(1)可知,“每台新型防雾霾产品能销售”的概率为34 “每台新型防雾霾产品不能销售”的概率为14X 所有的可能取值为:240-,120-,0,120则()30311240464P X C ⎛⎫=-== ⎪⎝⎭ ()2131391204464P X C ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭()1223132704464P X C ⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭ ()333327120464P X C ⎛⎫=== ⎪⎝⎭所以X 的分布列为所以()()1927240120120646464EX =-⨯+-⨯+⨯ 则30EX =18.为落实中央“坚持五育并举,全面发展素质教育,强化体育锻炼”的精神,某高中学校鼓励学生自发组织各项体育比赛活动,甲、乙两名同学利用课余时间进行乒乓球比赛,规定:每一局比赛中获胜方记1分,失败方记0分,没有平局,首先获得5分者获胜,比赛结束.假设每局比赛甲获胜的概率都是35. (1)求比赛结束时恰好打了6局的概率;(2)若甲以3:1的比分领先时,记X 表示到结束比赛时还需要比赛的局数,求X 的分布列及期望. 【详解】解:(1)比赛结束时恰好打了6局,甲获胜的概率为44153234865553125P C ⎛⎫⎛⎫=⨯⨯⨯=⎪ ⎪⎝⎭⎝⎭,恰好打了6局,乙获胜的概率为14125322965553125P C ⎛⎫⎛⎫=⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭, 所以比赛结束时恰好打了6局的概率为1248696582312531253125P P P =+=+=. (2)X 的可能取值为2,3,4,5,()2392525P X ⎛⎫===⎪⎝⎭, ()12233363555125P X C ==⨯⨯⨯=,()2413323212445555625P X C ⎛⎫⎛⎫==⨯⨯⨯+=⎪ ⎪⎝⎭⎝⎭, ()331344323232965555555625P X C C ⎛⎫⎛⎫==⨯⨯⨯+⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭. 所以X 的分布列如下:故()936124961966234525125625625625E X =⨯+⨯+⨯+⨯=.。
高二数学期末复习计划

监利县实验高中高二数学下学期期末复习计划高二数学组一、指导思想(1)使所学知识系统化、结构化、让学生将一学年来的数学知识连成一个有机整体,更利于学生理解;(2)精讲多练,巩固基本技能;(3)抓好方法教学,归纳、总结解题方法;(4)做好中档题训练,提高学生运用知识分析问题的能力。
(5)可适当突破综合题,注意尖子生的培养(6)搞好核心知识点的梳理与训练,宏志班可以适当提高试题难度,有针对性训练。
二、复习措施1.切实抓好”双基”的训练高二数学的基础知识、基本技能,是学生进行数学运算、数学推理的基本材料,是形成数学能力的基石。
因此在每一个章节复习中,为了有效地使学生弄清知识的结构,宜先用一定的时间让学生按照自己的实际查漏补缺,有目的地自由复习,教师可根据学生情况,整理专门的单元复习卷对学生的基础知识进行补缺补漏。
这块内容由各备课小组自行讨论合作整理。
(1)文科考试内容:高二数学必修5第3.3节线性规划、必修2第3章直线与方程选,必修2第4章圆与方程,必修3,选修1-1,1-2(2)理科考试内容:高二数学必修5第3.3节线性规划、必修2第3章直线与方程选,必修2第4章圆与方程,必修3,选修2-1,2-2,2-3,(3)高二数学统考时间,7月2号下午2:10--4:102.统一复习备课,积极备考,形成合力。
利用每周2的教研组会统一备考复习思路。
精心准备期末复习材料,备课组统一统筹的期末复习卷,一定要确保每周六考试的效果。
3.用好往年统考卷,模拟期末考试难度,找准方向,把握好期望难度。
4.考前指导,注意对学生的常错、易错题型进行强调纠正,同时教学中可渗透一些题型的解题技巧。
5.复习期间,每周六周练卷照常进行,内容全覆盖,与复习试卷互不干扰。
三具体安排高考过后,尽快结束新授,尽快转入复习,保质保量做好期末复习备考工作,具体安排如下。
专题1 线性规划,直线,圆一套复习训练卷和一套标准考试卷(欧阳竹)专题2 框图,统计,概率(古典,几何)一套复习训练卷和一套标准考试卷(孙中瑾)专题3选修2-3 计数原理,分布列(几种分布,独立重复试验,条件概率),统计案例,一套复习训练卷和一套标准考试卷(刘冰莲)专题4选修2-1 逻辑用语,圆锥曲线,空间向量与立几,一套复习训练卷和一套标准考试卷(蔡应发)专题5选修2-2 导数,推理与证明,复数一套复习训练卷和一套标准考试卷(姚雪梅)专题6 小题训练5套(欧阳竹)以上安排只是一个粗线条的大致安排,具体的复习中,鼓励老师们自己编写有特色的复习训练卷,印出来大家共享,从分发挥大家的智慧,大家的智慧才是最好的智慧。
日照实验高中高二下学期期末复习数学练习一(选修2-2和2-3)

日照实验高中高二下学期期末复习数学练习一(选修2-2和2-3)1.设复数z 满足(1)2i z i -=,则=z A . i +-1 B . i --1 C .i +1 D .i -12.设随机变量ξ服从正态分布),(92N ,若)1()1(-<=+>c P c P ξξ,则c =A.1B.2C.3D.43.由直线12x =,x=2,曲线1y x =及x 轴所围成图形的面积为 A .154 B .174 C .1ln 22D .2ln 24.根据上表可得回归方程ˆˆˆybx a =+中的ˆb 为9.4,据此模型预报广告费用为6万元时销售额为 A .63.6万元B .65.5万元C .67.7万元D .72.0万元5.将三颗骰子各掷一次,设事件A=“三个点数都不相同”,B=“至少出现一个6点”,则 概率)(B A P 等于A.9160 B. 21 C. 185 D. 216916.我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点A (-3,4),且法向量为n =(1,-2)的直线(点法式)方程为:1×(x +3)+(-2)×(y -4)=0,化简得x -2y +11=0.类比以上方法,在空间直角坐标系中,经过点A (1,2,3),且法向量为n =(-1,-2,1)的平面的方程为A .x +2y -z -2=0B .x -2y -z -2=0C .x +2y +z -2=0D .x +2y +z +2=0 7.在38(1)(1)x x -+的展开式中,含2x 项的系数是n ,若n n n x a x a x a a nx +⋅⋅⋅+++=-2210)8(,则=+⋅⋅⋅++n a a a a 210 A.0 B.1 C.-1 D.715 8.已知函数x e a x x x f )()1()(2+-=在1=x 处取得极大值,则实数a 的取值范围为(A ))1,(--∞ (B )R (C )),1(∞+ (D ))0,(-∞9.形如45132这样的数叫做“五位波浪数”,即十位数字、千位数字均比它们各自相邻的数字大,则由1,2, 3, 4, 5可构成不重复的“五位波浪数”的概率为 A.110 B.15 C.320 D. 21510.在9(1)x +的二项展开式中任取2项,i p 表示取出的2项中有i 项系数为奇数的概率. 若用随机变量ξ表示取出的2项中系数为奇数的项数i ,则随机变量ξ的数学期望E ξ=A. 815 B.23 C .1315 D. 4511.若不等式3x a -<的解集是{}06x x <<,则实数a 等于_______ 12.函数1()xf x x e-=+的最小值等于________13.设][x 表示不超过x 的最大整数,如)(][ ,3][ ,2]5[ *N k k k ∈===π.我们发现:3]3[]2[]1[=++;10]8[]7[]6[]5[]4[=++++;21]15[]14[]13[]12[]11[]10[]9[=++++++;.......通过合情推理,写出一般性的结论 _____________ (用含n 的式子表示) 14. 已知x 、y 的取值如下表:从所得的散点图分析,y 与x 线性相关,且y ^=0.95x +a ^,则a ^=_______.15.已知集合{}1,2,3,4,5I =,选择I 的两个非空集合A 和B ,满足A 中最大的数小于B 中最小的数,则不同的选择方法总数等于_________ 16..17.已知22)nx 的展开式中,第5项的系数与第3项的系数之比是10:1,求展开式中: (1)含1-x 的项;(2)系数最大的项. 18.已知函数()ln ()f x x a x a R =-∈(1)当2a =时,求曲线()y f x =在点(1,(1))A f 处的切线方程;(2)求函数()f x 的极值.19.已知函数()()x f x x k e =-(I )若1k =,求()f x 在1x =处的切线方程;(II )求()f x 在区间]0,1⎡⎣上的最小值。
高二数学下学期期末复习(7)--抛物线方程及性质

期末复习(7)----- 抛物线方程及性质一、建构知识网络(1)抛物线的定义:_________________________________________________的轨迹(2)抛物线y 2=2px(p>0)的焦点_______;顶点________;准线________;抛物线y 2= -2px(p>0)的焦点_______;顶点________;准线________;抛物线y 2=2px(p ≠0)的焦点_______;顶点________;准线________;抛物线y 2=ax(a ≠0)的焦点_______;顶点________;准线________;(3) 抛物线x 2=2py(p>0)的焦点_______;顶点________;准线________;抛物线x 2= -2py(p>0)的焦点_______;顶点________;准线________;抛物线x 2=2py(p ≠0)的焦点_______;顶点________;准线________;抛物线y=a x 2 (a ≠0)的焦点_______;顶点________;准线________;(4)比较抛物线与双曲线在性质上的不同二、双基题目1.在抛物线y 2=2px 上,横坐标为4的点到焦点的距离为5,则p 的值为 A.21 B.1 C.2 D.42.设a ≠0,a ∈R ,则抛物线y =4ax 2的焦点坐标为A.(a ,0)B.(0,a )C.(0,a161) D.随a 符号而定 3.以抛物线y 2=2px (p >0)的焦半径|PF |为直径的圆与y 轴位置关系为A.相交B.相离C.相切D.不确定答案:4.以椭圆252x +162y =1的中心为顶点,以椭圆的左准线为准线的抛物线与椭圆右准线交于A 、B 两点,则|AB |的值为___________.5. 对于顶点在原点的抛物线,给出下列条件:①焦点在y 轴上;②焦点在x 轴上;③抛物线上横坐标为1的点到焦点的距离等于6;④抛物线的通径的长为5;⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1).能使这抛物线方程为y 2=10x 的条件是______.(要求填写合适条件的序号)答案:C ;C ;C ;3100;②⑤ 三、经典例题【例1】 求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程:(1)过点(-3,2);(2)焦点在直线x -2y -4=0上.(3)焦点在y 轴上,抛物线上一点M(m,-3)到焦点距离为5,求m 的值。
高二数学第二学期期末复习

高二数学第二学期期末复习主要内容:概率统计(随机变量的分布列、统计)、立体几何、函数极限与导数、复数概率统计随机变量的分布列归根结底还是要考察概率的计算,高中阶段常见概率主要就是两类:等可能事件的概率和独立重复试验的概率,注意识别概率模型,灵活应用独立事件同时发生和互斥事件有一个发生的概率计算公式.期望与方差是反应随机变量的两个常用的数字特征,需要记住其定义式和二项分布、几何分布的相关结论.1、甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分。
假设甲队中每人答对的概率均为,乙队中3人答对的概率分别为且各人正确与否相互之间没有影响.用表示甲队的总得分.(Ⅰ)求随机变量分布列和数学期望;(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).(Ⅰ)解法一:由题意知,的可能取值为0,1,2,3,且所以的分布列为的数学期望为解法二:根据题设可知因此的分布列为(Ⅱ)解法一:用C表示“甲得2分乙得1分”这一事件,用D表示“甲得3分乙得0分”这一事件,所以AB=C+D,且C、D互斥,又由互斥事件的概率公式得解法二:用Ak表示“甲队得k分”这一事件,用Bk表示“乙队得k分”这一事件,k=0,1,2,3由于事件A3B0,A2B1为互斥事件,故P(AB)=P(A3B0∪A2B1)=P(A3B0)+P(A2B1).=2、随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为.(1)求的分布列;(2)求1件产品的平均利润(即的数学期望);(3)经技术革新后,仍有四个等级的产品,但次品率降为,一等品率提高为.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?解析:(1)的所有可能取值有6,2,1,-2;,,故的分布列为(2)(3)设技术革新后的三等品率为,则此时1件产品的平均利润为依题意,,即,解得所以三等品率最多为.立体几何立体几何主要研究了空间的点、线、面的两个问题:位置关系和数量关系.其中位置关系中,要注意特殊位置关系(垂直与平行)的判定和性质,对于数量关系,主要集中在角和距离,需要弄清楚定义和常用解决问题的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年第二学期周练(1)试题卷高二数学(理科)2017.4.27一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上......... 1.复数1ii-的虚部是 . 2.有三对师徒共6个人,站成一排照相,每对师徒相邻的站法共有 .(填数字) 3. 用反证法证明命题:“已知,a b N ∈,若ab 不能被7整除,则a ,b 都不能被7整除”时,假设的内容应为 .4.函数xy e =在2x =处的切线的斜率为 .5.用0到9这十个数字组成没有重复数字且能被5整除的三位数的个数为 .6. 在二项式的展开式中,前3项的二项式系数之和等于79,则展开式中的系数为 .7. (x -y )(x +y )8的展开式中x 2y 7的系数为 .8.如果复数z 满足2z i -=,那么1+z 的最小值是 .9. 同时抛掷两枚质地均匀的硬币,当至少有一枚硬币正面向上时,就说这次试验成功,则在2次试验中成功次数X 的均值是 .10.集合{1,2,3,,}(3)n n ⋅⋅⋅≥中,每两个相异数作乘积,将所有这些乘积的和记为n T ,如:222231121323[6(123)]112T =⨯+⨯+⨯=-++=;2222241121314232434[10(1234)]352T =⨯+⨯+⨯+⨯+⨯+⨯=-+++=;22222251121314153545[15(12345)]852T =⨯+⨯+⨯+⨯+⋅⋅⋅+⨯+⨯=-++++=,则7T = .(写出计算结果)11. 将3个男同学和3个女同学排成一列,若男同学甲与另外两个男同学不相邻,则不同的排法种数为 .(填数字)12.已知椭圆C :x 225 + y 29=1的左焦点为F ,点M 是椭圆C 上一点,点N 是MF 的中点,O 是椭圆的中心,ON =4,则点M 到椭圆C 的左准线的距离为 .13.若函数f (x )=x - 13sin 2x + a sin x 在(-∞,+∞)单调递增,则a 的取值范围是 .122nx ⎛⎫+ ⎪⎝⎭4x14.已知函数x xax f -=)(,且对于任意)1,0(∈x 都有1)1()(≥-x f x f 恒成立.则实数a 的取值范围是 .二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字说明、证明过程或演算步骤.15.(本题14分)一个盒子装有六张卡片,上面分别写着如下六个定义域为R 的函数: f 1(x )=x ,f 2(x )=x 2,f 3(x )=x 3,f 4(x )=sin x ,f 5(x )=cos x ,f 6(x )=2.(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.16.(本题14分)如图,在四棱锥P ﹣ABCD 中,底面ABCD 为直角梯形,AD ∥BC ,∠ADC =90°,平面PAD ⊥底面ABCD ,Q 为AD 的中点,M 是棱PC 上的点,PA =PD =2,BC = 12,AD =1,CD =3.(1)求证:平面PQB ⊥平面PAD ;(2)设PM =t MC ,若二面角M ﹣BQ ﹣C 的平面角的大小为30°,试确定t 的值.17. (本题14分)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X ,求X 的分布列和数学期望.18. (本题16分) 已知n n x x f )1()(+=,n ∈N *.(1) 若)(3)(2)()(654x f x f x f x g ++=,求)(x g 中含2x 项的系数;(2) 若n p 是)(x f n 展开式中所有无理项的系数和,数列}{n a 是各项都大于1的数组成的数列,试用数学归纳法证明:n p 12(1)n a a a ⋅⋅⋅+≥(1+1a )(1+2a )⋅⋅⋅(1+n a ).19.(本题16分)设椭圆C : x 2a 2 + y 2b2 =1(a >b >0)的左、右焦点分别为F 1、F 2,上顶点为A ,过A 与AF 2垂直的直线交x 轴负半轴于Q 点,且F 1恰好是线段QF 2的中点. (1)若过A 、Q 、F 2三点的圆恰好与直线3x -4y -7=0相切,求椭圆C 的方程;(2)在(1)的条件下,B 是椭圆C 的左顶点,过点R (32,0)作与x 轴不重合的直线l 交椭圆C 于E 、F 两点,直线BE 、BF 分别交直线x = 83于M 、N 两点,若直线MR 、NR 的斜率分别为k 1,k 2,试问:k 1k 2是否为定值?若是,求出该定值;若不是,请说明理由.20.(本题16分)已知函数2()()e xf x x a =-在2x =时取得极小值.(1)求实数a 的值;(2)是否存在区间[],m n ,使得()f x 在该区间上的值域为44[e ,e ]m n ?若存在,求出m ,的值;若不存在,说明理由.1.122.48 3. ,a b 至少有一个能被7整除 4. 2e . 5.136 6.7. 解析:(x +y )8中,T r +1=C r 8x 8-r y r ,令r =7,再令r =6,得x 2y 7的系数为C 78-C 68=8-28=-20. 答案:-20 8.2 9. 32 10.322 11.【答案】288 【解析】【考点】排列、组合的实际应用.【分析】根据题意,分2种情况讨论:①、3个男同学均不相邻,用插空法分析可得此时的排法数目,②、另外两个男同学相邻,将这两个男同学看成一个整体,用捆绑法分析可得此时的排法数目,进而由分类计数原理计算可得答案. 【解答】解:根据题意,分2种情况讨论: ①、3个男同学均不相邻,将三名女同学全排列,有A 33=6种排法,排好后有4个空位, 在4个空位中,任选3个,安排3个男同学,有A 43=24种安排方法,此时共有6×24=144种不同的排法; ②、另外两个男同学相邻,将这两个男同学看成一个整体,考虑2人的顺序,有A 22=2种情况,将三名女同学全排列,有A 33=6种排法,排好后有4个空位,在4个空位中,任选2个,安排甲和这2个男同学,有A 42=12种安排方法,此时共有2×6×12=144种不同的排法; 则共有144+144=288种不同的排法; 故答案为:288.【标题】浙江省绍兴市2017届高考一模数学试题 12. 5213.解析:选C f ′(x )=1-23cos 2x +acos x =1-23(2cos 2x -1)+acos x =-43cos 2x +acos49516x +53,f (x )在R 上单调递增,则f ′(x )≥0在R 上恒成立,令cos x =t ,t ∈-1,1],则-43t 2+at +53≥0在-1,1]上恒成立,即4t 2-3at -5≤0在-1,1]上恒成立,令g (t )=4t 2-3at -5,则⎩⎪⎨⎪⎧g (1)=4-3a -5≤0,g (-1)=4+3a -5≤0,解得-13≤a ≤13 14 41-≤a 或1≥a15. 【解析】【考点】离散型随机变量及其分布列;奇函数.【分析】(1)由任意两个奇函数的和为奇函数,而原来的六个函数中奇函数有三个,故可用古典概型求解;(2)ξ可取1,2,3,4,ξ=k 的含义为前k ﹣1次取出的均为奇函数,第k 次取出的是偶函数,分别求概率,列出分布列,再求期望即可.【解答】解:(1)记事件A 为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,由题意知.(2)ξ可取1,2,3,4,;故ξ的分布列为.答:ξ的数学期望为.16. 解:(1)记事件A 1={从甲箱中摸出的1个球是红球}, A 2={从乙箱中摸出的1个球是红球},B 1={顾客抽奖1次获一等奖},B 2={顾客抽奖1次获二等奖},C ={顾客抽奖1次能获奖}.由题意知A 1与A 2相互独立,A 1A 2与A 1A 2互斥,B 1与B 2互斥,且B 1=A 1A 2,B 2=A 1A 2+A 1A 2,C =B 1+B 2.因为P (A 1)=410=25,P (A 2)=510=12, 所以P (B 1)=P (A 1A 2)=P (A 1)P (A 2)=25×12=15,P (B 2)=P (A 1A 2+A 1A 2)=P (A 1A 2)+P (A 1A 2) =P (A 1)P (A 2)+P (A 1)P (A 2) =P (A 1)(1-P (A 2))+(1-P (A 1))P (A 2) =25×⎝⎛⎭⎫1-12+⎝⎛⎭⎫1-25×12=12. 故所求概率为P (C )=P (B 1+B 2)=P (B 1)+P (B 2)=15+12=710.即顾客抽奖1次能获奖的概率是710. (2)顾客抽奖3次可视为3次独立重复试验, 由(1)知,顾客抽奖1次获一等奖的概率为15,所以X ~B ⎝⎛⎭⎫3,15. 于是P (X =0)=C 03⎝⎛⎭⎫150⎝⎛⎭⎫453=64125, P (X =1)=C 13⎝⎛⎭⎫151⎝⎛⎭⎫452=48125, P (X =2)=C 23⎝⎛⎭⎫152⎝⎛⎭⎫451=12125, P (X =3)=C 33⎝⎛⎭⎫153⎝⎛⎭⎫450=1125. 故X 的分布列为X 的数学期望为E (X )=3×15=35.17.【答案】(1) 解:g(x)中含x2项的系数为C44+2C45+3C46=1+10+45=56.(3分)(2) 证明:由题意,p n=2n-1.(5分)①当n=1时,p1(a1+1)=a1+1,成立;②假设当n=k时,p k(a1a2…a k+1)≥(1+a1)(1+a2)…(1+a k)成立,当n=k+1时,(1+a1)(1+a2)…(1+a k)(1+a k+1)≤2k-1(a1a2…a k+1)(1+a k+1)=2k-1(a1a2…a k a k+1+a1a2…a k+a k+1+1).(*)∵ a k>1,a1a2…a k(a k+1-1)≥a k+1-1,即a1a2…a k a k+1+1≥a1a2…a k+a k+1,代入(*)式得(1+a1)(1+a2)…(1+a k)(1+a k+1)≤2k(a1a2…a k a k+1+1)成立.综合①②可知,p n(a1a2…a n+1)≥(1+a1)(1+a2)…(1+a n)对任意n∈N*成立.(10分)18.【考点】二面角的平面角及求法;平面与平面垂直的判定.【分析】(1)由AD∥BC,BC=AD,Q为AD的中点,可得四边形BCDQ为平行四边形,得到CD∥BQ.结合∠ADC=90°,得QB⊥AD.然后利用面面垂直的性质得BQ⊥平面PAD.再由线面垂直的判定得平面PQB⊥平面PAD;(2)由PA=PD,Q为AD的中点,得PQ⊥AD.结合(1)可得PQ⊥平面ABCD.以Q 为原点建立空间直角坐标系.然后求出平面BQC的一个法向量,再由PM=tMC把平面MBQ 的一个法向量用含有t的代数式表示,结合二面角M﹣BQ﹣C的平面角的大小为30°求得t 的值.【解答】(1)求证:∵AD∥BC,BC=AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD∥BQ.∵∠ADC=90°,∴∠AQB=90°,即QB⊥AD.又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴BQ⊥平面PAD.∵BQ⊂平面PQB,∴平面PQB⊥平面PAD;(2)解:∵PA=PD,Q为AD的中点,∴PQ⊥AD.∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PQ⊥平面ABCD.如图,以Q为原点建立空间直角坐标系.则面BQC的法向量为;Q(0,0,0),P(0,0,),B(0,,0),C(﹣1,).设M(x,y,z),则,,∵PM=tMC,∴,则,即,在平面MBQ中,,,设平面MBQ的一个法向量,由,,取z=t,得x=.∴平面MBQ法向量为.∵二面角M﹣BQ﹣C为30°,∴,解得t=3.【点评】本题考查平面与平面垂直的判定,考查了空间想象能力和思维能力,训练了利用空间向量求解二面角的平面角,是中档题.19.【考点】直线与椭圆的位置关系.【分析】(1)由题意可知b2=3c2,根据点到直线的距离公式,即可求得c的值,求得a和b的值,求得椭圆方程;(2)设直线PQ方程,代入椭圆方程,利用韦达定理及直线的斜率公式,求得M和N点的纵坐标,利用斜率公式求得k1,k2,利用韦达定理即可求得k1k2.【解答】解:(1)由题意可知A(0,b),F1是线段QF1的中点,设F1(﹣c,0),F2(c,0),则Q(﹣3c,0),∵∠QAF1=90°,∴b2=3c2,由题意Rt△QAF1外接圆圆心为斜边的QF1中点F1(﹣c,0),半径等于2c,由A,Q,F2,三点恰好与直线3x﹣4y﹣7=0相切,∴F1(﹣c,0)到直线的距离等于半径2c,即=2c,解得:c=1,b2=3,a2=4,∴椭圆的标准方程:;(2)设E(x1,y1),F(x2,y2),直线PQ的方程为x=my+,代入椭圆方程,4(4+3m2)y2+36my﹣21=0,y1+y2=﹣,y1y2=﹣,由B,E,M,三点共线,可知:=,即y M=,同理可得:y N=,∴k1k2=×==,由4(x1+2)(x2+2)=(2my1+7)(2my2+7)=4m2y1y2+14m(y1+y2)+49,∴k 1k 2==﹣,∴k 1k 2是否为定值﹣.【点评】本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,属于中档题.20. (1)()e ()(2)x f x x a x a '=--+,由题意知(2)0f '=,解得2a =或4a =.当2a =时,()e (2)x f x x x '=-,易知()f x 在(0,2)上为减函数,在(2,)+∞上为增函数,符合题意;当4a =时,()e (2)(4)x f x x x '=--,易知()f x 在(0,2)上为增函数,在(2,4),(4,)+∞上为减函数,不符合题意.所以,满足条件的2a =.(2)因为()0f x ≥,所以0m ≥.① 若0m =,则2n ≥,因为4(0)4e f n =<,所以24(2)e e n n n -=. 设2(2)()e (2)x x g x x x -=≥,则2224(2)()e 0x x x g x x x ⎡⎤--'=+⎢⎥⎣⎦≥, 所以()g x 在[2,)+∞上为增函数.由于4(4)e g =,即方程24(2)e e n n n -=有唯一解为4n =.② 若0m >,则[]2,m n ∉,即2n m >>或02m n <<<.(Ⅰ)2n m >>时,2424()(2)e e ()(2)e e m n f m m m f n n n ⎧=-=⎨=-=⎩, 由①可知不存在满足条件的,m n .(Ⅱ)02m n <<<时,2424(2)e e (2)e e m n m n n m⎧-=⎨-=⎩,两式相除得22(2)e (2)e m n m m n n -=-.设2()(2)e (02)x h x x x x =-<<,则32()(44)e (2)(1)(2)e x x h x x x x x x x '=--+=+--,()h x 在(0,1)递增,在(1,2)递减,由()()h m h n =得01m <<,12n <<,此时24(2)e 4e e m m n -<<,矛盾.综上所述,满足条件的,m n 值只有一组,且0,4m n ==.。
