2016九年级数学锐角三角函数导学案
濠知教育初三数学锐角三角函数导学案
学 生教 师 吴老师 日 期 2013/12/22 年 级 初三学 科数学时 段10:10-11:40学 情 分 析 锐角三角函数在中考试题中时常与四边形、圆的知识相结合构成高分值的综合题,题型常以填空、选择、简答或综合出现,分值一般在20%左右,有时也单独成题,形成创新与探索型试题;有利于培养学生的综合素质。
课 题 锐角三角函数学习目标与 考点分析 本节知识的考查一般以填空题和选择题的形式出现,主要考查锐角三角函数的意义,即运用sin a 、cos a 、tan a 、cot a 准确表示出直角三角形中两边的比(a 为锐角),考查锐角三角函数的增减性,特殊角的三角函数值以及互为余角、同角三角函数间的关系。
学习重点 难 点让学生熟练掌握解题的方法,会运用知识灵活计算,并能正确地进行相关题目的运算教学方法 讲练结合、互动启发教学过程【例1】在Rt △ABC 中,∠C =900,AC =12,BC =15。
(1)求AB 的长;(2)求sinA 、cosA 的值; (3)求A A 22cos sin +的值; (4)比较sinA 、cosB 的大小。
变式:(1)在Rt △ABC 中,∠C =900,5=a ,2=b ,则sinA = 。
(2)在Rt △ABC 中,∠A =900,如果BC =10,sinB =0.6,那么AC = 。
濠知教育学科导学案【例2】计算:020045sin 30cot 60sin +⋅【例3】已知,在Rt △ABC 中,∠C =900,25tan =B ,那么cosA ( ) A 、25 B 、35C 、552 D 、32变式:已知α为锐角,且54cos =α,则ααcot sin += 。
【例4】已知3cot tan =+αα,α为锐角,则αα22cot tan += 。
评注:由锐角三角函数定义不难推出1cos sin 22=+A A ,1cot tan =⋅αα,它们是中考中常用的“等式”。
最新人教版九年级数学下册《用计算器求锐角三角函数值及锐角》精品导学案
第二十八章 锐角三角函数28.1 锐角三角函数第4课时 用计算器求锐角三角函数值及锐角学习目标:1. 会使用科学计算器求锐角的三角函数值.2. 会根据锐角的三角函数值,借助科学计算器求锐角的大小.3. 熟练运用计算器解决锐角三角函数中的问题. 重点:1.会使用科学计算器求锐角的三角函数值.2.会根据锐角的三角函数值,借助科学计算器求锐角的大小. 难点:熟练运用计算器解决锐角三角函数中的问题.一、知识链接 1.填写下表: 2. sin 30° cos60°, cos 30° sin 60°,sin 230° + cos 230° = .一、要点探究探究点1:用计算器求锐角的三角函数值或角的度数 【典例精析】(1) 用计算器求sin18°的值;(2) 用计算器求tan30°36′的值;(3) 已知sin A = 0.501 8,用计算器求∠A的度数.练一练 1. 用计算器求下列各式的值(精确到0.000 1):(1) sin47°;(2) sin12°30′;(3) cos25°18′;(4) sin18°+cos55°-tan59°.2. 已知下列锐角三角函数值,用计算器求锐角∠A,∠B的度数(结果精确到0.1°):(1) sin A=0.7,sin B=0.01;(2) cos A=0.15,cos B=0.8;(3) tan A=2.4,tan B=0.5.探究点2:利用计算器探索三角函数的性质(1)通过计算(可用计算器),比较下列各对数的大小,并提出你的猜想:①sin30°____2sin15°cos15°;②sin36°____2sin18°cos18°;③sin45°____2sin22.5°cos22.5°;④sin60°____2sin30°cos30°;⑤sin80°____2sin40°cos40°.猜想:已知0°<α<45°,则sin2α___2sinαcosα.(2) 如图,在△ABC中,AB=AC=1,∠BAC=2α,请利用面积方法验证(1) 中的结论.练一练(1) 利用计算器求值,并提出你的猜想(结果保留四位小数):sin25°≈ ,cos65°≈ ,cos58°≈ ,sin32°≈ ,sin67°≈ ,cos23°≈ ,cos17°≈ ,sin73°≈ ;猜想:已知0°<α<90°,则sin αcos(90°-α),cos αsin(90°-α).(2) 利用计算器求值,并提出你的猜想(结果保留四位小数):sin20°≈ ,cos20°≈ ,sin220°≈ ,cos220°≈ ;sin35°≈ ,cos35°≈ ,sin235°≈ ,cos235°≈ ;猜想:已知0°<α<90°,则sin2α + cos2α = .二、课堂小结1. 用计算器求sin24°37′18″的值,以下按键顺序正确的是 ( )2. 下列式子中,不成立的是( )A.sin35°= cos55°B.sin30°+ sin45°= sin75°C.cos30°= sin60°D.sin260°+ cos260°=13. 利用计算器求值:(1) sin40°≈ (精确到0.0001);(2) sin15°30′≈ (精确到0.0001);(3) 若sin α = 0.5225,则α ≈ (精确到0.1°);(4) 若sin α = 0.8090,则α ≈ (精确到0.1°).4. 已知:sin232°+ cos2α =1,则锐角α = .5.用计算器比较大小:sin87°tan87°.6.在Rt△ABC中,∠C = 90°,∠BAC = 42°24′,∠BAC的平分线AT = 14.7 cm,用计算器求AC的长(精确到0.001cm).参考答案自主学习一、知识链接1.2.= = 1课堂探究一、要点探究探究点1:用计算器求锐角的三角函数值或角的度数【典例精析】例1解:(1)第一步:按计算器键;第二步:输入角度值18;屏幕显示答案:0.309 016 994.(2)方法①:第一步:按计算器键;第二步:输入角度值30.6 (因为30°36′= 30.6°);屏幕显示答案:0.591 398 351.方法②:第一步:按计算器键;第二步:输入角度值30,分值36 (使用键);屏幕显示答案:0.591 398 351.(3)第一步:按计算器键;第二步:然后输入函数值0. 501 8;屏幕显示答案:30.119 158 67°(按实际需要进行精确).还可以利用键,进一步得到∠A= 30°07′08.97 ″(这说明锐角A精确到1′的结果为30°7′,精确到1″的结果为30°7′9″).练一练 1. 解:(1)0.7314 (2)0.2164 (3)0.9041 (4)-0.78172.解:(1) ∠A ≈ 44.4°;∠B ≈ 0.6°.(2) ∠A ≈ 81.4°;∠B ≈ 36.9°. (3) ∠A ≈ 67.4°;∠B ≈ 26.6°.探究点2:利用计算器探索三角函数的性质例2 解:(1)① = ② = ③ = ④ = ⑤ = =(2)∵ S ∠ABC =12AB · sin2α · AC =12sin2α,S ∠ABC =12×2AB ·sin α · AC ·cos α =sin α ·cos α,∠sin2α=2sin αcos α. 此方法也是高中才会研究的求面积的计算公式,建议初中阶段不要深挖.练一练 解:(1)0.4226 0.4226 0.5299 0.5299 0.9205 0.9205 0.9563 0.9563 = =(2)0.3420 0.9397 0.1170 0.8830 0.5736 0.8192 0.3290 0.6710 1 当堂检测1. A2. B3.(1) 0.6428(2) 0.2672(3) 31.5 (4)54.04. 32°5. <6.解:∵ AT 平分∠BAC ,且∠BAC = 42°24′, ∴ ∠CAT =21∠BAC = 21°12′. 在Rt △ACT 中 ,cos ∠CAT =ACAT , ∴ AC = AT · cos ∠CAT = 14.7×cos21°12′ ≈13.705(cm).学生励志寄语:人生,想要闯出一片广阔的天地,就要你们努力去为自己的目标奋斗、勤奋刻苦、充满自信的过好每一天,雏鹰总会凌空翱翔。
九年级数学《锐角三角函数的应用》导学案(共2课时)

**九年制学校(初中部)导学案
年级:九科目:数学主备人:审核:
内容:《锐角三角函数的简单应用(1)》课型:新授时间: 2月14日
2.升国旗时,某同学站在离旗杆底部
20m处行注目礼,当国旗升至旗杆端时,
从甲楼顶部测得乙楼顶部的仰角为30°,
两个村庄抢险,飞机在距地面450
60︒(如图).求A、B
**九年制学校(初中部)导学案
年级: 九 科目: 数学 主备人: 审核:
内容:《锐角三角函数的简单应用(2)》 课 型: 新授 时间: 2月15日 二、课中导学:
例1. 小明为了测量停留在空中的气球的高度,他先在地面上找一点,站在这
点测得气球的仰角为27°,然后向气球方向走了50米,测得气球的仰角为40°。
这时他就能算出气球的高度了。
他是如何求得气球的高度呢?(小明的身高是1.6米)
(tan27°=0.51,tan40°=0.84,结果精确到0.1米)
例2.如图所示,已知:在△ABC 中,∠A=60°,∠B=45°,AB=8. 求:△ABC 的面积(结果可保留根号).
热气球的探测器显示,270 400 G F E
D
B
A
C。
人教版九年级数学下册《锐角三角函数(一)》导学案

28.1锐角三角函数(一)导学案
一、教学目标
知识与技能初步了解锐角三角函数的意义,初步理
解在直角三角形中一个锐角的对边与斜边的
比值就是这个锐角的正弦的定义,并会根据
已知直角三角形的边长求一个锐角的正弦
值。
过程与方法从实际问题入手研究,经历从发现到解决
直角三角形中的一个锐角所对应的对边与斜
边之间的关系的过程,体会研究数学问题的
一般方法以及所采用的思考问题的方法。
情感态度与价值观在解决问题的过程中体验求索的科
学精神以及严谨的科学态度,进一步激发学
习需求。
二、教学重难点
重点锐角的正弦的定义
难点理解直角三角形中一个锐角与其对边与斜边比值的对应关系。
三、学习过程
1、验证正弦函数
2、正弦函数的定义
3、例题示范
4、巩固训练。
锐角三角函数的定义 导学案
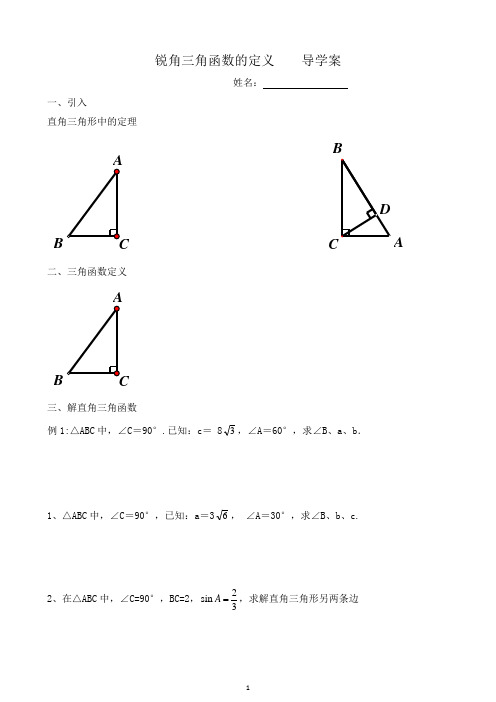
锐角三角函数的定义导学案姓名:一、引入直角三角形中的定理BD CBA二、三角函数定义B三、解直角三角函数例1:△ABC中,∠C=90°.已知:c= 83,∠A=60°,求∠B、a、b.1、△ABC中,∠C=90°,已知:a=36,∠A=30°,求∠B、b、c.2、在△ABC中,∠C=90°,BC=2,2sin3A ,求解直角三角形另两条边3、在△ABC 中,∠ACB =90°,cosA=33,AB =8cm ,则△ABC 的面积为4、由下列条件解直角三角形:在Rt △ABC 中,∠C=90°:(1)已知a=4,c=24, (2)已知b=10,∠B=60°.例2:在Rt △ABC 中,∠C =90°,a =2,b =3,则cosA = ,sinB = ,tanB = 。
1、直角三角形ABC 的面积为24cm 2,直角边AB 为6cm ,∠A 是锐角,则sinA = 。
2、如图,在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD =2,AC =3,则sinB 的值是( )3、在△ABC 中,∠C=90°,AB=5,AC=4,则cosB = ,sinA = ,tanA = 。
cosA = ,sinB = ,tanB = 。
4、如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB ,tan ∠BCD=,AC=12,则BC= .5、在Rt△ABC 中,∠C=90°,AB=3,BC=1,则sinA="______," tanA=" _______," cosA=_______ SinB="______," tanB=" _______," cosB=_______6、如图,在菱形ABCD 中,DE ⊥AB , 垂足为E , DE =8cm , , 则菱形ABCD 的面积是__________.7、如图,正方形网格中,每一个小正方形的边长都是 , 四边形的四个顶点都在格点上,为边的中点,若把四边形绕着点顺时针旋转.【小题1】画出四边形旋转后的图形;【小题2】设点旋转后的对应点为 , 则;【小题3】求点在旋转过程中所经过的路径长.例3:已知tan α=125,α是锐角,则sin α= 。
新人教版九年级数学下册《用计算器求锐角三角函数值及锐角》精品导学案

28.1锐角三角函数第4课时 用计算器求锐角三角函数值及锐角【学习目标】让学生熟识计算器一些功能键的使用【学习重点】运用计算器处理三角函数中的值或角的问题【学习难点】知道值求角的处理【导学过程】求下列各式的值.(1)sin30°·cos45°+cos60°; (2)2sin60°-2cos30°·sin45°(3); (4)-sin60°(1-sin30°). (5)tan45°·sin60°-4sin30°·cos45°·tan30°(6)+cos45°·cos30°合作交流:学生去完成课本68页 练习1、2题学生展示:用计算器求锐角的正弦、余弦、正切值学生去完成课本69页的第4、5题 .自我反思:本节课我的收获: 。
学生励志寄语:2cos602sin 302︒︒-sin 45cos3032cos 60︒+︒-︒sin 45tan 30tan 60︒︒-︒人生,想要闯出一片广阔的天地,就要你们努力去为自己的目标奋斗、勤奋刻苦、充满自信的过好每一天,雏鹰总会凌空翱翔。
只有一个的知识、阅历、素质、修养达到足够的积淀时,オ能真正做到不说张扬之语,不干张扬之事,处于低谷不颓废,過到困难不退缩,一帆风顺不得意,成绩面前不炫耀,永远保持着踏踏实实,平平常常的生活态度和格调。
以成熟,豁达,自信,睿智处世做事。
就가定会拥有属于自己的一片广阔的天地。
人教版九年级下册28.1《锐角三角函数》教案

(五)总结回顾(用时5分钟)
今天的学习,我们了解了锐角三角函数的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对锐角三角函数的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
-锐角三角函数关系的理解:正弦、余弦、正切之间的关系较为复杂,学生难以理解和记忆。
-锐角三角函数图像的掌握:学生可能无法将图像与函数的性质有效联系起来。
举例解释:
-通过对比和实际操作,帮助学生区分正弦、余弦、正切的定义,例如通过直角三角形的模型进行直观展示。
-设计具体的计算题目,指导学生如何根据角度求函数值,强调记忆特殊角度的函数值,如30°、45°、60°等。
3.重点难点解析:在讲授过程中,我会特别强调正弦、余弦、正切函数的定义和应用这两个重点。对于难点部分,我会通过举分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与锐角三角函数相关的实际问题,如测量旗杆的高度。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。通过测量角度和距离,演示锐角三角函数的基本原理。
人教版九年级下册28.1《锐角三角函数》教案
一、教学内容
人教版九年级下册第28章《锐角三角函数》第1节,主要包括以下内容:
1.锐角三角函数的定义:正弦、余弦、正切的概念及其在直角三角形中的应用。
2.锐角三角函数的值:通过具体例子,让学生学会如何求锐角三角函数的值。
3.锐角三角函数的关系:掌握正弦、余弦、正切之间的基本关系,并能运用这些关系解决实际问题。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
精品人教版数学9年级下. 特殊角的锐角三角函数(教案与导学案)

第二十八章锐角三角函数28.1锐角三角函第3课时特殊角的锐角三角函数【知识与技能】1.理解并掌握30°,45°,60°的三角函数值,能用它们进展有关计算;2.能依据30°,45°,60°的三角函数值,说出相应锐角的度数.【过程与方法】经历探索30°,45°,60°角的三角函数值的过程,进一步体会三角函数的意义.【情感态度】在探索特殊角的三角函数值的过程中,增强学生的推理能力和计算能力. 【教学重点】熟记30°,45°,60°的三角函数值,并用它们进展计算.【教学难点】探索30°,45°,60°的三角函数值的指导过程.一、情境导入,初步认识问题在前面我们已经得到sin3o°= 12,sin45°=2,你能得到30°,45°角的其它三角函数值吗?不妨试试看.【教学说明】 教师可引导学生从所给结论sinA = sin30°=12出发,设 BC = 1,那么 AB = 2,由勾股定理可得30°的其它三角函数值,同样在图〔2)中,仍可设BC = 1, 那么AC = 1,45°的其它三角函数值.这里设BC = 1是为了方便计算.二、思考探究,获取新知通过对上述问题的思考,可以得到:sin30°=12,cos30°= 2,tan30°= 3,sin45°= 2,cos45°= 2, tan45°= 1.【想一想】 60°角的三角函数值各是多少?你是如何得到的?在学生的相互交流中可得出结论:sin60°= 2,cos60°= 12 ,tan60°教师再将上述所有结论整理,制成下表.三、典例精析,掌握新知例1 求以下各式的值.(1)cos260°+ sin260°;〔2〕cos45tan45sin45︒-︒︒.解〔1〕原式 =12()2 +32()2 =14+34= 1;〔2〕原式 =2222- 1 = 0.例2 〔1〕如图〔1〕,在Rt△ABC中,∠C=90°,AB = 6,BC = 3,求∠A的度数;〔2〕如图〔2〕,圆锥的高AO等于圆锥的底面半径OB的3倍,求α.解〔1〕∵sinA = BC32AB26==,∴∠A = 45°;〔2〕∵tanα = OA33OBOBOB==,∴α = 60°.【教学说明】以上两例均可先由学生自主完成,然后教师在展示解答过程,加深学生对本节知识的理解,并指明两例题的侧重点不一样,例1侧重于运用特殊角的三角函数值来参与计算,而例2那么是通过计算一个角的某一三角函数值后,利用锐角的三角函数值与锐角之间的一一对应关系,从而确定锐角的度数.这样处理,可让学生熟记特殊角的三角函数值.四、运用新知,深化理解1.在△ABC中,∠A,∠B都是锐角,且tanA = 12,cosB =32,那么△ABC的形状是〔〕A.直角三角形B.钝角三角形C.锐角三角形D.不能确定2.计算:〔1〕3tan30°- tan45°+ 12sin60°= ___________ .〔2〕60160sincos︒-︒+130tan︒- sin45°= ___________ .3.在Rt△ABC中,∠C=90°,BC = 7,AC = 21,试求∠A、∠B的度数.4.边长为2的正方形ABCD在平面直角坐标系中的位置如下图,且∠OBC=30°,试求A、D两点坐标.【教学说明】四道题均可让学生自主探究,也可小组内讨论,到达解决问题的目的.教师巡视,发现问题给予指导,对优秀者和积极参与者给予鼓励,增强学生的学习信心.在完成上述题目后,教师引导学生完成创优作业中本课时的“名师导学〞局部.【答案】 1.B 【解析】∵cosB =32,∴∠B = 30°,又∵tanA =12<3 2= tan30°,∴∠A < 30°,∠A + ∠B < 60°,∴∠C = 180°- (∠A + ∠B)> 120°.即△ABC 是钝角三角形,应选B.2.〔1〕5314-〔2〕2232【解析】〔1〕原式 =31331322⨯-+⨯3314+ =5314-〔2〕原式 =3221312-233222323.由题意易得:tanA =73213BCAC===,tanB = 3ACBC=,∴∠A= 30°,∠B = 60°.4.解:∵ OB = BC·cosB =323⨯=, OC = BC·sinB =1212⨯=,∴B 点的坐标是〔3,0-〕.过D点作DE 垂直于y轴,交y轴于E点,易证△OBC≅△ECD,∴∠DCE = ∠CBO =30°.∴CE = cos∠DCE ·CD =3232⨯=,∴OE = OC + CE = 13+,DE = 112CD=,∴D 点的坐标是〔1,13-+〕.五、师生互动,课堂小结1.如何理解并熟记特殊角的三角函数值?同学间相互交流.2.运用特殊角的三角函数值可解决哪两类问题?【教学说明】师生共同回忆,对于问题1,可引导学生利用图形进展推理计算,也可通过表格中横排的数的变化规律来记忆.1.布置作业:从教材P68〜70习题28. 1中选取.2.完成创优作业中本课时的“课时作业〞局部.本课时教学以“自主探究〞为主体形式,所以应先给学生自主动手的时间,给学生提供创新的空间与可能,再给不同层次的学生提供一个交流合作的时机,培养学生独立探究和合作学习的能力.28.1 锐角三角函数第3课时特殊角的锐角三角函数一、新课导入1.课题导入情景:出示一副三角尺,教师手中的两块三角尺中有几个不同的锐角?问题:分别求出这几个锐角的正弦值、余弦值和正切值.本节课我们学习30°,45°,60°角的三角函数值.〔板书课题〕2.学习目标〔1〕推导并熟记30°,45°,60°角的三角函数值.〔2〕能运用30°,45°,60°角的三角函数值进展简单的计算.〔3〕能由30°,45°,60°角的三角函数值求对应的锐角.〔4〕会运用计算器求锐角三角函数的三角函数值和由三角函数值求锐角.3.学习重、难点重点:推导并熟记30°,45°,60°角的三角函数值.难点:相关运算.二、分层学习1.自学指导〔1〕自学内容:教材P65探究~P66例3上面的内容.〔2〕自学时间:8分钟.〔3〕自学方法:完成探究提纲.②通过计算,得到30°,45°,60°角的正弦值、余弦值、正切值如下表:③观察上表,sin30°,sin45°,sin60°的值有什么规律?cos30°,cos45°,cos60°呢?tan30°,tan45°,tan60°呢?2.自学:学生可参考自学指导进展自学.3.助学〔1〕师助生:①明了学情:明了学生能否推导30°,45°,60°角的三角函数值.②差异指导:根据学情进展针对性指导.〔2〕生助生:小组内相互交流、研讨、纠正错误.4.强化:特殊角的三角函数值的推导和记忆以及30°,45°,60°角的正弦值、余弦值、正切值的变化规律.1.自学指导〔1〕自学内容:教材P66例3~P67练习上面的内容.〔2〕自学时间:10分钟.〔3〕自学方法:先自主学习,再同桌之间讨论交流,互相纠错.〔4〕自学参考提纲:①含30°,45°,60°角的三角函数值的计算题的解题要点是什么?熟练掌握特殊锐角的三角函数值.②求直角三角形中某锐角的解题要点是什么?先求该锐角的正弦值或余弦值或正切值,然后根据特殊锐角的三角函数值求该锐角的度数.③求以下各式的值:1-2sin30°cos30°;=1-2×12×3223-3tan30°-tan45°+2sin60°;=3×3-1+2×3=231.(cos230°+sin230°)×tan60°.=[3〕2+〔12〕2]×3 3④在Rt△ABC中,∠C=90°,BC7AC21,求∠A、∠B的度数.∵tan A=73321==BCAC,∴∠A=30°,∠B=60°.2.自学:学生可结合自学指导进展自学.3.助学〔1〕师助生:①明了学情:明了学生对特殊角的三角函数值表的掌握情况.②差异指导:根据学情指导学生记忆或推导特殊角的三角函数值.〔2〕生助生:小组交流、研讨.4.强化〔1〕求特殊锐角的三角函数值的关键是先把它转化为实数的运算,再根据实数的运算法那么计算.〔2〕求锐角的度数的关键是先求其正弦值或余弦值或正切值,然后对应特殊锐角的三角函数值求角的度数.〔3〕当A、B为锐角时,假设A≠B,那么sin A≠sin B,cos A≠cos B,tan A≠tanB.1.自学指导〔1〕自学内容:教材P67~P68.〔2〕自学时间:10分钟.〔3〕自学指导:完成探究提纲.〔4〕探究提纲:①用计算器求sin18°的值.sin18°=0.309016994.②用计算器求tan30°36′的值.tan30°36′=0.591398351.③sin A=0.5018,用计算器求锐角A的度数.∠A=30.11915867°或∠A=30°7′8.97″.④∠A是锐角,用计算器探索sin A与cos A的数量关系.sin2A+cos2A=1.⑤∠A 是锐角,用计算器探索sin A 、cos A 与tan A 的数量关系.sin tan cos.AA A⑥当一个锐角逐渐增大时,这个角的各三角函数值会发生怎样的变化呢?请用计算器探索其中的规律.正弦值逐渐增大,余弦值逐渐减小,正切值逐渐增大. ⑦用计算器求以下各锐角三角函数的值: sin35° 0.573576436 cos55° 0.573576436 tan80°25′43″ 5.93036308⑧以下锐角三角函数值,用计算器求相应锐角的度数: sin A =0.6275∠A =38.86591697° cos A =0.6252∠A =51.30313157° tan A =4.8425∠A =78.3321511°三、评价1.学生自我评价:这节课你学到了什么?还有什么疑惑?2.教师对学生的评价:〔1〕表现性评价:根据学生的情感态度和学习效果等方面进展评价. 〔2〕纸笔评价:课堂评价检测. 3.教师的自我评价〔教学反思〕.本课时中的特殊角是指30°,45°,60°的角,课堂上采用“自主探究〞的形式,给学生自主动手的时间并提供创新的空间与可能,再给不同层次的学生提供一个交流合作的时机,培养学生独立探究和合作的能力.本节课的最终教学目的是让学生理解并掌握30°,45°,60°角的三角函数值,并且能够熟记其函数值,然后利用它们进展计算.一、根底稳固〔70分〕1.(5分)2cos(α-10°)=1,那么锐角α= 70° .2.(5分) α为锐角,tanα3cosα等于〔A〕A.12B.22C.32D.333.(5分)用计算器计算cos44°的结果〔准确到0.01〕是〔B〕4.(5分)tanα=0.3249,那么α约为〔B〕A.17°B.18°C.19°D.20°5.(40分)求以下各式的值.〔1〕sin45°+cos45°;22=2.〔2〕sin45°cos60°-cos45°;=22×12-22=-2 4.〔3〕cos245°+tan60°cos30°;=2〕23×3=12+32=2.(4〕1-cos30°sin60°+tan30°.=3123+33=3-1.6.(10分)在△ABC中,∠A,∠B都是锐角,且sin A=3,tan B=1,求∠C的度数.解:∵∠A是锐角且sin A=32,∴∠A=60°.∵∠B是锐角且tan B=1,∴∠B=45°.∴∠C=180°-∠A-∠B=75°.二、综合应用〔20分〕7.(10分)在△ABC中,锐角A,B满足〔sin A-3〕2+|cos B-3|=0,那么△ABC是〔D〕A.等腰三角形B.等边三角形C.等腰直角三角形D.直角三角形8.(10分)如图,△ABC内接于⊙O,AB,CD为⊙O的直径,D E⊥AB于点E,BC=1,AC=3,那么∠D的度数为30° .三、拓展延伸〔10分〕9.(10分)对于钝角α,定义它的三角函数值如下:sinα=sin〔180°-α〕,cosα=-cos〔180°-α〕.〔1〕求sin 120°,cos 120°,sin 150°的值;解:sin120°=sin(180°-120°)=sin60°=3 .Cos120°=-cos(180°-120°)=-cos60°=-1 2 .sin150°=sin(180°-150°)=sin30°=1 2 .〔2〕假设一个三角形的三个内角的比是1∶1∶4,A ,B 是这个三角形的两个顶点,sin A ,cos B 是方程4x 2-mx-1=0的两个不相等的实数根,求m 的值及∠A 和∠B 的大小.解:∵三角形的三个内角的比是1∶1∶4,∴三角形三个内角度数分别为30°,30°,120°.∴∠A =30°或120°,∠B =30°或120°.∴sin A =sin30°=12或sin A =sin120°=,cos B =cos30°=或cos B =cos120°=-12. 又∵sin A ,cos B 是方程4x 2-mx-1=0的两个不相等的实数根, ∴sin A +cos B =4m ,sin A ·cos B =-14. ∴sin A =12,cos B =-12,∴∠A =30°,∠B =120°,m=0.。
苏科版九下数学 第7章《锐角三角函数》导学案(共10课时)

第七章锐角三角函数(1)正切函数班级_________姓名_________学习目标1、认识锐角的正切的概念。
2、会求一个锐角的正切值。
3、经历操作观察思考求解等过程,感受数形结合的数学思想方法。
学习重点:锐角的正切的概念学习难点:锐角的正切的概念,感受数形结合的数学思想方法知识要点在Rt△ABC中,∠C=90°,∠A的对边与邻边的比值是∠A的正切,记作一、情境创设问题1. 我们从家到学校,免不了要爬坡,有些坡好爬,有些坡爬起来很累,这是为什么?观察斜坡的倾斜程度,你有什么发现?如何刻画斜坡的倾斜程度?如上图,这两个直角三角形中,∠C=∠C′=90°,且有一条直角边相等,但斜边不相等,哪个坡更陡?①本节课我们研究两直角边的比值与锐角的关系,因此同学们首先应思考:当锐角固定时,两直角边的比值是否也固定?tan.②给出正切概念:如图,在Rt△ABC中,,把∠A的对边与邻边的比叫做∠A的正切,记作:ABCA二、典型例题例1.根据下列图中所给条件分别求出下列图中∠A、∠B的正切值。
BCA113A2C1BB AC35通过上述计算,你有什么发现?互余两角的正切值.例2.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,AB=5,求∠ACD 、∠BCD的正切值。
结论:等角的正切值.例3.如图(1),∠A=30°,∠C=90°,根据三角函数定义求出30°、45°、60°的正切值.BCA(1)(2)(3)例4.如图,∠A=15°,∠C=90°,求出15°正切值.例5、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若BD:AD=1:4,试求tan∠BCD的值。
例6、如图,△ABC中,AE⊥BC于E,D是AC边上的一点,DH⊥BC于H,BD交AE于F。
已知DH:BD=3:4,求∠BFE的正切值.分析求tan∠BFE,在△BFE任何一边长都不知的情况下,很是困难。
九年级数学锐角三角函数导学案

二、自主学习。(5 分钟)
1.cos30°=____; tan45°=
.
2.如图,在 Rt△ABC 中,∠ C=90°,
BC=?6,sinA= 3 ,求 cosA、tanB 的值.
5
B
6
A
C
关计算。
【导学过程】
三.学以致用。(15 分钟)
13
OD;(2)根据需要, 水面要以每小 时 0.5 m 的速度下降,则经过多长
4.已知 为锐角, 且 sin( 10 ) 3 ,则
2
C
等于( )
A
时间才能将水排干?
E
D
B O
学习好资料
欢迎下载
课题: 28. 1 锐角三角函数( 2) 【学习目标】 (1) 理解余弦、正切的概念。
(2) 熟练运用锐角三角函数的概念进
∠A的邻边 b
C. 3 ; D. 4
5
5
则 sin ∠BAC= ; sin ∠ADC= .
A
D
B
学习好资料
欢迎下载
5.在
中,∠C=90°,a,b,c 分别 ( ) A . sin A 3
2
是∠ A、∠B、∠C 的对边,则有( )
B . tan A 1
2
A.
B.
C. cos B 3
2
D. tan B 3
=5,AC=4,则 sinA =( )
3
4
3
A.5 B .5 C .4
4 D .3
2.在 Rt△ABC 中,∠C=9 00,AC=
2BC,则 sinA =_________
3.在 Rt△ABC 中,∠ C 为直角, ∠
《锐角三角函数》 导学案

《锐角三角函数》导学案一、学习目标1、理解锐角三角函数的定义,能够准确说出正弦、余弦、正切的概念。
2、掌握锐角三角函数的求值方法,会利用已知条件求出锐角的三角函数值。
3、能够运用锐角三角函数解决与直角三角形相关的实际问题。
二、学习重难点1、重点(1)锐角三角函数的概念,包括正弦、余弦、正切的定义。
(2)特殊锐角(30°、45°、60°)的三角函数值及其应用。
2、难点(1)理解锐角三角函数的本质,以及如何在直角三角形中准确地表示出三角函数值。
(2)运用锐角三角函数解决实际问题时,如何将实际问题转化为数学模型。
三、知识回顾1、直角三角形的性质(1)直角三角形的两个锐角互余。
(2)直角三角形斜边的平方等于两直角边的平方和(勾股定理)。
2、相似三角形的性质(1)对应角相等,对应边成比例。
(2)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比。
四、新课导入在生活中,我们常常会遇到需要测量高度、距离等问题,比如测量大树的高度、河流的宽度等。
而这些问题往往可以通过直角三角形的知识来解决。
今天,我们就来学习一种新的数学工具——锐角三角函数,它将帮助我们更方便、更准确地解决这类问题。
五、知识讲解1、锐角三角函数的定义在直角三角形中,如果一个锐角的对边与斜边的比值是一个固定值,那么这个比值就叫做这个锐角的正弦,记作 sinA。
即 sinA =对边/斜边。
同理,如果一个锐角的邻边与斜边的比值是一个固定值,那么这个比值就叫做这个锐角的余弦,记作 cosA。
即 cosA =邻边/斜边。
如果一个锐角的对边与邻边的比值是一个固定值,那么这个比值就叫做这个锐角的正切,记作 tanA。
即 tanA =对边/邻边。
例如,在直角三角形 ABC 中,∠C = 90°,∠A 为锐角,BC 为∠A 的对边,AC 为∠A 的邻边,AB 为斜边。
则 sinA = BC / AB,cosA = AC / AB,tanA = BC / AC。
锐角三角函数(第一课时)导学案

年级:九年级 班级: 学生姓名: 制作人: 不知名 编号:2023-1228.1.1锐角三角函数(第一课时)【学习目标】1.初步了解锐角三角函数的意义,理解一个锐角的正弦的定义.2.会根据已知条件求一个锐角的正弦值.【预学案】1.如图在Rt △ABC 中,∠C=90°,∠A=30°,BC=10m ,求AB.2.如图在Rt △ABC 中,∠C=90°,∠A=30°,AB=20m ,求BC.【探究案】请你认真阅读课本61的内容,边学边思考下列问题:思考1:如果使出水口的高度为50m ,那么需要准备多长的水管?____________ 如果使出水口的高度为a m ,那么需要准备多长的水管? ; 结论:直角三角形中,30°角的对边与斜边的比值是 思考2:在Rt △ABC 中,∠C=90°,∠A=45°,∠A 的对边与斜边的比值是一个定值吗? 如果是,是多少?结论:直角三角形中,45°角的对边与斜边的比值思考3:Rt △ABC 和Rt △A′B′C′中,∠C=∠C=90°,∠A=∠A′=a ,那么有什么关系?为什么?结论:在直角三角形中,当锐角A 的度数一定时,不管三角形的大小如何, ∠A 的对边与斜边的比值 .【归纳】在Rt △ABC 中,∠C=90°,我们把锐角A 的对边与斜边的比叫做∠A 的____________,记作________,即_______ __.4.如图(1),在Rt △ABC 中,∠C=90°,求sinA=_____sinB=______.5.如图(2),在Rt △ABC 中,∠C=90°,求sinA=_____ ,图2图1134C A C BsinB=_____ .【检测案】1.在Rt△ABC中,∠C=900,sinA=,求sinB的值________.2.如图,已知点P的坐标是(a,b),则sinα等于()A.B.C.3.已知圆锥的底面半径为5cm,侧面积为65πcm2,设圆锥的母线与高的夹角为θ(如图所示),则sinθ的值为()A.B.C.D.4.如图,Rt△ABC中,∠C=900,CD⊥AB于D点,AC=3,BC=4,求sinA,sin∠BCD 的值.5.如图,菱形ABCD的边长为10 cm,DE⊥AB,sinA=35,求DE的长和菱形ABCD的面积.6.如图,在△ABC中,∠C=90°,sinA=14,BC=2,求AC,AB的长.。
《锐角三角函数》导学案

锐角三角函数一:【课前预习】(一):【知识梳理】1.直角三角形的边角关系(如图)(1)边的关系(勾股定理):AC 2+BC 2=AB 2;(2)角的关系:∠A+∠B=∠C=900;(3)边角关系: ①:00901230C BC AB A ⎫∠=⎪⇒=⎬∠=⎪⎭②:锐角三角函数:∠A 的正弦=A a sin A=c∠的对边,即斜边; ∠A 的余弦=A b cos A=c∠的邻边,即斜边 , ∠A 的正切=A a tan=A b∠的对边,即∠的邻边 注:三角函数值是一个比值.2.特殊角的三角函数值.3.三角函数的关系(1) 互为余角的三角函数关系.sin (90○-A )=cosA , cos (90○-A )=sin A tan (90○-A )= cotA(2) 同角的三角函数关系.平方关系:sin 2 A+cos 2A=l4.三角函数的大小比较①正弦、正切是增函数.三角函数值随角的增大而增大,随角的减小而减小. ②余弦是减函数.三角函数值随角的增大而减小,随角的减小而增大。
(二):【课前练习】1.等腰直角三角形一个锐角的余弦为( )A .12 3. 2B 2.2C D .l2.点M(tan 60°,-cos60°)关于x 轴的对称点M′的坐标是( )3.在 △ABC 中,已知∠C=90°,sinB=0.6,则cosA 的值是( )3443. . . .4355A B C D4.已知∠A 为锐角,且cosA≤0.5,那么( )A .0°<∠A≤60° B.60°≤∠A<90° C .0°<∠A≤30° D.30°≤∠A <90°二:【经典考题剖析】1.如图,在Rt△ABC 中,∠C=90°,∠A=45°,点D 在AC 上,∠BDC=60°,AD=l ,求BD 、DC 的长.2.先化简,再求其值,213(2)22xxxx x+÷-+++-其中x=tan45-cos30°3. 计算:①sin248○+ sin242○-tan44○×tan45○×tan 46○②cos 255○+ cos235○4.比较大小(在空格处填写“<”或“>”或“=”)若α=45○,则sinα________cosα;若α<45○,则sinα cosα;若α>45°,则 sinα cosα.5.⑴如图①、②锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律;⑵根据你探索到的规律,试比较18○、34○、50○、61○、88○这些锐角的正弦值的大小和余弦值的大小.三:【课后训练】1. 2sin60°-cos30°·tan45°的结果为()A.33.2B3.2C- D.02.在△ABC中,∠A为锐角,已知 cos(90°-A)=32,sin(90°-B)=32,则△ABC一定是()A.锐角三角形;B.直角三角形;C.钝角三角形;D.等腰三角形3.如图,在平面直角坐标系中,已知A(3,0)点B(0,-4),则cos∠OAB等于__________4.cos2α+sin242○ =1,则锐角α=______.5.在下列不等式中,错误的是()A.sin45○>sin30○;B.cos60○<oos30○;C.tan45○>tan30○;D.cot30○<cot60○6.如图,在△ABC中,AC=3,BC=4,AB=5,则tanB的值是()3434A...4355B C D7.如图所示,在菱形ABCD中,AE⊥BC于 E点,EC=1,∠B=30°,求菱形ABCD的周长.8.如图所示,在△ABC中,∠ACB=90°,BC=6,AC=8 ,CD⊥AB,求:①sin∠ACD 的值;②tan∠BCD的值CB9.如图,某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A/B之间的距离,他从湖边的C处测得A在北偏西45°方向上,测得B在北偏东32°方向上,且量得B、C之间的距离为100米,根据上述测量结果,请你帮小明计算A山之间的距离是多少?(结果精确至1米.参考数据:sin32○≈0.5299,cos32○≈0.8480)10.某住宅小区修了一个塔形建筑物AB,如图所示,在与建筑物底部同一水平线的C处,测得点A的仰角为45°,然后向塔方向前进8米到达D处,在D处测得点A的仰角为60°,求建筑物的高度.(精确0.1米)四:【课后小结】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)1353CBA(1)34CB A 课题:28.1锐角三角函数(1)【学习目标】1、理解正弦(sinA )概念,2、能根据正弦概念正确的进行计算3、高效度过课堂的每一分钟。
【学习重点】能根据正弦概念正确进行计算【学习难点】正弦概念的理解【学习过程】一、自主学习及检测(10分钟) 自学课本指定的内容,完成预习笔记后,完成下列题目1.如图,在Rt △ABC 中,∠C=90°,求sinA 和sinB 的值.2.识记下列锐角三角函数值:sin30o= . sin45o= . sin60o=由此归纳:正弦值随角度的增大而二.学以致用。
(20分钟)1、在Rt △ABC 中,∠C =900,AC=4,BC=3,则sinA ( )A .43B .34 C .53 D .542.如图,角α的顶点为O ,它的一边在x 轴的正半轴上,另一边OA 上有一点P (3,4),则 sin α= . 2题图 3题图 3.如图,在Rt ABC △中,CD 是斜边AB 上的中线,已知2CD =,3AC =,则s i n B的值是( )A .23B .32C .34D .434题图 6题图4.如图,在Rt △ABC 中,∠AC B=900,CD ⊥AB 于D ,已知AC=3,AB=5,则sin ∠ACD 等于( )DCABA .43B .34C .53D .54 5.在△ABC 中,∠C =90°, BC =6 cm ,53sin =A ,则AB 的长是 cm . 6.如图,菱形ABCD 的边长为10cm ,DE ⊥AB ,3sin 5A =,则这个菱形的面积= cm 2.7.当锐角A>450时,sinA 的值( ) A .小于22B .大于22C .小于23 D .大于23 8.计算:2sin4502sin300三.反馈检测.(15分钟)1.在直角△ABC 中,∠C =90o ,若AB =5,AC =4,则sinA =( ) A .35 B .45 C .34 D .43 2.在Rt △ABC 中,∠C =900,AC=2BC,则sinA =_________ 3.在Rt △ABC 中,∠C 为直角, ∠A=300,则sinA+sinB=( )A .1;B .231+;C .221+; D .414.已知α为锐角,且23)10sin(=︒-α,则αA.︒D.︒80 5. 在△ABC 中,∠C=90°,BC=2,sinA=23,则边AC 的长是( )A .13B .3C .43 D . 56.把Rt △ABC 的各边扩大n倍(n为正整数),那么锐角A的对边与斜边的比( )A.扩大2n倍 B.扩大n倍C.缩小n倍 D.保持不变 7.在△ABC 中,∠C 为直角,直角边a=5cm ,b=12cm ,求sinA+sinB中考真题:1. 如图是一个半圆形桥洞截面示意图,圆心为O ,直径AB 是河底线,弦CD 是水位线,CD ∥AB ,且CD = 24 m ,OE ⊥CD 于点E .已测得sin ∠DOE =1213.(1)求半径OD ;(2)根据需要,水面要以每小时0.5 m 的速度下降,则经过多长时间才能将水排干?6CB A课题:28.1锐角三角函数(2) 【学习目标】(1)理解余弦、正切的概念。
(2)熟练运用锐角三角函数的概念进行有关计算。
【学习重.难点】熟练运用锐角三角函数的概念进行有关计算。
【导学过程】一.课前小测.(5分钟)1.在Rt △ABC 中,∠C 为直角,AC=4,BC=3,则sinA=A . 43B . 34C . 53D . 542、如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D 。
已知AC= 5 , BC=2,那么sin ∠ACD =( )AB .23CD3、如图,已知AB 是⊙O 的直径,点 C 、D 在⊙O 上, 且AB =5,BC=3.则sin ∠BAC= ; sin ∠ADC= .二、自主学习。
(5分钟)1.cos30°=____; tan45°= . 2.如图,在Rt △ABC 中,∠C=90°,BC=•6,sinA=35,求cosA 、tanB 的值.三.学以致用。
(15分钟) 1.在Rt △ABC 中,∠C 为直角,a=1,b=2,则cosA=________ tanA=______. 2.在Rt △ABC 中,∠C 为直角,若sinA=53,则cosB=_________ 3.在中,∠C =90°,如果cos A=45 那么的值为() A .35B .54C .34D .434.如图,在Rt △ABC 中,∠C 为直角,CD ⊥AB 于D ,已知AC=3,AB=5,则tan∠BCD 等于( )A .43; B .34; C .53; D .54BCDAB∠A的邻边b∠A的对边a 斜边c CBAC5.在中,∠C =90°,a ,b ,c 分别是∠A 、∠B 、∠C 的对边,则有() A .B .C .D .四.反馈检测。
(15分钟)1.在Rt △ABC 中,∠C 为直角,sinA=22,则cosB 的值是( )A .21B .23C .1D .222.三角形在方格纸中的位置如图所示,则tan α的值是( )A .35B .43C .34D .452题图 4题图3.在△ABC 中,∠C =90°,tan A =13,则sin B =( )A.10B .23C .34D .104.如图,在Rt ABC △中,90ACB ∠=,1BC =,2AB =,则下列结论正确的是( )A.sin 2A = B .1tan 2A = C.cos 2B =D.tan B = 5.如图,在ABC △中,90ACB ∠=,CD AB ⊥于D,若AC =AB =则tan BCD ∠的值为( )5题图 7题图6.在△ABC 中,∠C 为直角,cosa=135,求sinA 、tanA 的值中考真题:(5分钟)(2008·宁夏中考)如图7,在△ABC中,∠C =90°,sin A =54,AB =15,求△ABC 的周长和tan A 的值.ACBD课题:28.1锐角三角函数(3) 【学习目标】⑴: 能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数。
⑵: 能熟练计算含有30°、45°、60°角的三角函数的运算式 【学习重.难点】熟记30°、45°、60°角的三角函数值,能熟练计算含有30°、45°、60°角的三角函数的运算式 【导学过程】一、课前小测.(5分钟) 1.Rt △ABC 中,∠C 为直角,AC=5,BC=12,那么下列∠A 的四个三角函数中正确的是( )A . sinA=135;B .cosA=1312;C . tanA=1213; D . cotA=1252.如图,在Rt △ABC 中,∠C 为直角,CD ⊥AB 于D ,已知AC=3,AB=5,则tan ∠BCD 等于( )A .43; B .34; C .53; D .54cos303602cos 458-+3.已知∠A 为锐角,且cosA ≤12,那么( )A .0°<∠A ≤60°B .60°≤∠A<90C .0°<∠A ≤30°D .30°≤∠A<90°4.在△ABC 中,∠A 、∠B 都是锐角,且sinA=12 ,cosB= 32 ,则△ABC 的形状是( )A .直角三角形B .钝角三角形C .锐角三角形D .不能确定 5.下列各式中不正确的是( ). A .sin260°+cos260°=1 B .sin30°+cos30°=1 C .sin35°=cos55° D .tan45°>sin45°6.(1)计算2sin30°-2cos60°+tan45°(2)104cos30sin 60(2)2008)-︒︒+--四.反馈检测。
(15分钟)1.如果α是锐角,且135cos sin 22=︒+α,那么=α_______.2.在△ABC 中,三边之比为a :b :c=1::2,则sinA+tanA 等于( ).1.2B C D3.sin272°+sin218°=_______. 4.若( 3 tanA-3)2+│2cosB- 3 │=0,则△ABC 是( ).A .直角三角形B .等边三角形C .含有60°的任意三角形D .顶角为钝角的等腰三角形 5、设α、β均为锐角,且sin α-cos β=0,则α+β=_______.6.计算:2cos 45tan 60cos30+=_____.7.计算1sin 60cos302-=_____8.计算(1)sin 60tan 45cos30︒-︒︒(2)3-1+(2π-1)0-33tan30°-tan45°(3)104cos30sin 60(2)2008)-︒︒+--中考真题:(5分钟)1.计算:0200912sin 603tan 30(1)3⎛⎫-++- ⎪⎝⎭°°课题:28.2解直角三角形(1)【学习目标】使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形 【学习重.难点】三角函数在解直角三角形中的灵活运用【导学过程】 一、课前小测.(5分钟)计算:104cos30sin 60(2)2008)-︒︒+--计算:3-1+(2π-1)0-33tan30°-tan45°二、自主学习 1.在△ABC 中,∠C=90°,∠A 、∠B 、∠C 所对的边分别为a 、b 、c ,且,,解这个三角形2.在Rt △ABC 中, ∠B =30o ,b=20,解这个三角形.三.学以致用。
(15分钟) 1、在△ABC 中,∠C=90°,AC=6,BC=8,么sinA=________. 2、在△ABC 中,∠C=90°,sinA=35,则cosA 的值是( ) A .35 B .45 C .916.2525D 3、Rt △ABC 中,若sinA=45,AB=10,那么BC=_____,tanB=______. 4.在Rt △ABC 中,CD 为斜边AB 上的高,已知AD=8,BD=4,那么tanA 等 于( ).A.2 B.3C..48D5.如图,菱形ABCD 的周长为40cm ,DE AB ⊥,垂足为E,3sin 5A =,则下列结论正确的有________ ①6cm = ②2cm BE = ③菱形面积为260cm④BD =6、已知:如图,在ΔABC 中,∠ACB =CD ⊥AB ,垂足为D ,若∠B =30°,CD 求ΔABC 的其它元素.课题:28.2解直角三角形(21、在△ABC 中,∠C=90°,BC=5,则sinA 的值是( )A.135B.1312C.125 D.5122.如图,CD 是Rt △ABC 33sin =A ,BD=1,则AD=________. 3.在△ABC 中,∠C=90°,且∠B 平分线的长为26,则a=_______ b=______,c=_____. 5、等腰三角形底边长为10㎝,周长为36cm ,那么底角的余弦等于( ).A 、513B 、1213C 、1013D 、5126.如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,则AB=( ) A.4 B.5 C.32D.3387、如图,已知正方形ABCD 的边长为2,如果将线段BD 绕着点B 旋转后,点D 落在CB 的延长线上的D ′处,那么tan ∠BAD ′=4、在矩形ABCD 中,DE ⊥AC 于E ,设∠且53cos =α,AB = 4, 则AD 的长为(A .3 B .316 C .320 D .5168、 在△ABC 中,∠C 为直角,AC=6,BAC ∠的平分线AD=43,解此直角三角形。
