【竞赛题】人教版小学五年级下册数学第09讲《立体几何》竞赛试题(含详解)
【教培专用】人教版数学小学五年级下册第九讲《图形的运动》基础版(含答案、学生版)

第9讲图形的运动知识点一:旋转1.旋转的意义把一个图形绕着某一点转动一定的角度的图形变换叫做旋转。
2.旋转的三要素(1)旋转点(或旋转中心):物体旋转时所绕的点就是旋转点(或旋转中心)。
(2)旋转方向:钟表中指针运动的方向为顺时针方向;与钟表中指针运动的方向相反的方向为逆时针方向。
(3)旋转角度:对应线段的夹角或对应点与旋转中心所连线段的夹角就是旋转角度。
3.图形旋转的特征:图形旋转后,形状和大小都没有发生变化,只是方向和位置变化了。
4.图形旋转的性质:旋转时,旋转中心的位置不变,图形的每个点、每条线段、每个角都绕旋转点按旋转方向转动了大小等于旋转角度的角。
旋转前后,对应点到旋转点的距离相等,对应线段和对应角分别相等。
5.在方格纸上画简单图形旋转90°后的图形的方法(1)找出原图形的关键点;(2)明确是顺时针旋转还是逆时针旋转。
(3)根据旋转方向,借助三角尺或量角器画原图形关键点与旋转中心所连线段的垂线;(4)在所画垂线上量出或数出与原线段相等的长度(即找到原图形关键点的对应点);(5)顺次连接所找到的对应点,即可得到原图形旋转90°后的图形。
知识点二:利用平移或旋转等变换方式拼图先观察变换后的图形,然后思路分析其中的每部分可以由原始图案经过什么样的变换得到,灵活运用平移和旋转可以有不同的变换方法。
考点一:确定轴对称图形的对称轴数及位置【典例1】.(2020秋•德江县期末)下面四个图形只能画出两条对称轴的是()A.B.C.D.【分析】根据轴对称图形定义:如果一个图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,即可画出每个图形对称轴.据此解答即可。
【解答】解:能画出无数条对称轴;能画出两条对称轴;能画出三条对称轴;能画出六条对称轴。
故选:B。
【点评】此题考查了根据轴对称图形定义画出轴对称图形的对称轴的方法。
【典例2】(2020秋•深圳期末)在等腰三角形、长方形、正方形、圆、扇形中,有一条对称轴的图形有()种.A.1B.2C.3【分析】依据轴对称图形的概念,及在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,由此即可判断出给出图形的对称轴的条数.【解答】解:在等腰三角形、长方形、正方形、圆、扇形中,其中有一条对称轴的图形有等腰三角形和扇形2种.故选:B.【点评】解答此题的主要依据是:轴对称图形的概念及其特征.考点2:旋转【典例1】(2020•长沙模拟)如图,三角形ABC怎样旋转可以得到三角形A′BC′下面说法正确的是()A.绕B点逆时针旋转90°B.绕B点顺时针旋转90°C.绕C点顺时针旋转90°D.绕C点逆时针旋转180°【分析】根据旋转的特征,三角形ABC绕点B顺时针旋转90°,点B的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的三角形A′BC′。
2020—2021年最新人教版五年级数学下册竞赛试题(精品试题).docx

2020—2021年最新人教版五年级数学下册竞赛试题(精品试题).docx2020—2021年新人教版五年级数学竞赛试题一、填空。
1、如果口04是3的倍数,那么口里可能是()。
2、10以内的质数有(),合数有(),既不是质数也不是合数的有(),这些数中,既是奇数又是质数的有(),既是偶数又是质数的有()。
3、a是偶数(a>0),与它相邻的两个偶数是( )和( ).4、4立方分米200立方厘米=( )立方分米3700立方厘米=( )立方分米( )立方厘米5、把一个棱长为10分米的正方体切成1厘米的小正方体,然后一个挨一个排成一行,长()米。
6、把三个棱长为a厘米的正方体拼成一个长方体,拼成的长方体的表面积是()平方厘米。
7、一本《新华字典》的体积约是()。
8、一个两位数能同时被2、3、5整除,这个两位数最大是(),最小是()。
9、一个正方体的表面积是24立方分米,它的棱长是()分米,它的体积是()立方分米。
10、24的因数有才()个,其中有()个质数。
11、一个长方体的体积是54立方分米,宽和高都是3分米,这个长方体六个面中最大面的面积是()立方分米。
二、判断。
1、两个质数的和一定是质数。
()2、因为21÷3=7,所以21是3和7的倍数。
()3、两个奇数的和一定合数。
()4、体积相等的两个正方体的表面积也一定相等。
()5、用4个同样大小的正方体就可以拼成一个大正方体。
()6、一个长方体(不含正方体)最多有两个面相等。
()7、棱长为1m的大正方体可以切成1000个棱长1dm的小正方体。
()8、两个体积单位间的进率是1000. ()9、棱长为6dm的正方体的体积和表面积相等。
()10、如果a÷b=6( b≠0),则a是b的倍数,b是a的因数。
()三、选择题。
1、12的因数中,质数有()个。
A. 2B.3C.62、一个合数至少有()个因数。
A. 1B.2C.3D.3个以上3、一个木料长(),一间客厅的面积是(),一个墨水画的体积是()。
【经典】小学五年级数学下册名校竞赛卷含答案word百度文库

【经典】小学五年级数学下册名校竞赛卷含答案word百度文库一、拓展提优试题1.(15分)一个自然数恰有9个互不相同的约数,其中3个约数A,B,C满足:①A+B+C=79②A×A=B×C那么,这个自然数是.2.(7分)后羿朝三个箭靶分别射了三支箭,如图:他在第一个箭靶上得了29分,第二个箭靶上得了43分.请问他在第三个箭靶上得了分.3.有一行数:1,1,2,3,5,8,13,21,…,从第三个数开始,每个数都是前两个数的和,问在前2007个数中,有是偶数.4.先将从1开始的自然数排成一列:123456789101112131415…然后按一定规律分组:1,23,456,7891,01112,131415,…在分组后的数中,有一个十位数,这个十位数是.5.如图,从A到B,有条不同的路线.(不能重复经过同一个点)6.已知一个五位回文数等于45与一个四位回文数的乘积(即=45×),那么这个五位回文数最大的可能值是59895.7.如图,正方形的边长是6厘米,AE=8厘米,求OB=厘米.8.三位偶数A、B、C、D、E满足A<B<C<D<E,若A+B+C+D+E=4306,则A最小.9.某数学竞赛有10道题,规定每答对一题得5分,答错或不答扣2分.A、B 两人各自答题,得分之和是58分,A比B多得14分,则A答对道题.10.如图,将一个等腰三角形ABC沿EF对折,顶点A与底边的中点D重合,若△ABC的周长是16厘米,四边形BCEF的周长是10厘米,则BC=厘米.11.解放军战士在洪水不断冲毁大坝的过程中要修好大坝,若10人需45分钟,20人需要20分钟,则14人修好大坝需分钟.12.用1、2、3、5、6、7、8、9这8个数字最多可以组成个质数(每个数字只能使用一次,且必须使用).13.用一根34米长的绳子围成一个矩形,且矩形边长都是整数米,共有种不同的围法(边长相同的矩形算同一种围法).14.(15分)甲、乙两船顺流每小时行8千米,逆流每小时行4千米,若甲船顺流而下,然后返回;乙船逆流而上,然后返回,两船同时出发,经过3小时同时回到各自的出发点,在这3小时中有多长时间甲、乙两船同向航行?15.(7分)对于a、b,定义运算“@”为:a@b=(a+5)×b,若x@1.3=11.05,则x=.【参考答案】一、拓展提优试题1.解:一个自然数N恰有9个互不相同的约数,则可得N=x2y2,或者N=x8,(1)当N=x8,则九个约数分别是:1,x,x2,x3,x4,x5,x6,x7,x8,其中有3个约数A、B、C且满足A×A=B×C,不可能.(2)当N=x2y2,则九个约数分别是:1,x,y,x2,xy,y2,x2y,xy2,x2y2,其中有3个约数A、B、C且满足A×A=B×C,①A=x,B=1,C=x2,则x+1+x2=79,无解.②A=xy,B=1,C=x2y2,则xy+1+x2y2=79,无解.③A=xy,B=x,C=xy2,则xy+x+xy2=79,无解.④A=xy,B=x2,C=y2,则xy+x2+y2=79,解得:,则N=32×72=441.⑤A=x2y,B=x2y2,C=x2,则x2y+x2y2+x2=79,无解.故答案为441.2.【分析】这个箭靶共三个环,设最小的环为a分,中间环为b分,最外环为c分,得:第一个靶得分为:2b+c=29①第二个靶得分为:2a+c=43②第三个靶得分为:a+b+c③通过等量代换,解决问题.解:设最小的环为a分,中间环为b分,最外环为c分,得:第一个靶得分为:2b+c=29①第二个靶得分为:2a+c=43②第三个靶得分为:a+b+c③由①+②得:2a+2b+2c=29+43=72即a+b+c=36即第三个靶的得分为36分.答:他在第三个箭靶上得了36分故答案为:36.3.【分析】因为前两个数相加得偶数,即奇数+奇数=偶数;同理,第四个数是:奇数+偶数=奇数,以此类推,总是奇数、奇数、偶数、奇数、奇数、偶数…;每三个数一个循环周期,然后确定2007个数里面有几个循环周期,再结合余数,即可得出偶数的个数.解:2007÷3=669,又因为,每一个循环周期中有2个奇数,1个偶数,所以前2007个数中偶数的个数是:1×669=669;答:前2007个数中,有699是偶数.故答案为:699.4.解:方法一:据分组律可得:从131415向后为1617181,92021222,324252627,2829303132(十位数),…;方法二:位数之前应该有1+2+3+…+9=45位.1位数有9位,10﹣19有20位,20﹣27有16位,所以十位数的开头应为28,为2829303132.故填:2829303132.5.解:如图,因为,从A到B有5条直连线路,每条直连线路均有5种不同的路线可以到达B点,所以,共有不同线路:5×5=25(条),答:从A到B,有25条不同的路线,故答案为:25.6.解:根据分析,得知,=45=5×9既能被5整除,又能被9整除,故a的最大值为5,b=9,45被59□95整除,则□=8,五位数最大为59895故答案为:598957.解:6×6÷2=18(平方厘米),18×2÷8=4.5(厘米);答:OB长4.5厘米.故答案为:4.5.8.解:最大的三位偶数是998,要满足A最小且A<B<C<D<E,则E最大是998,D最大是996,C最大是994,B最大是992,4306﹣(998+996+994+992)=4306﹣3980=326,所以此时A最小是326.故答案为:326.9.解:(58+14)÷2=72÷2=36(分)答错:(5×10﹣36)÷(2+5)=14÷7=2(道)答对:10﹣2=8道.故答案为:8.10.解:△ABC的周长是16厘米,可得△AEF的周长为:16÷2=8 (厘米),△AEF和四边形BCEF周长和为:8+10=18(厘米),所以BC=18﹣16=2(厘米),答:BC=2厘米.故答案为:2.11.解:假设每人每分钟修大坝1份洪水冲毁大坝速度:(10×45﹣20×20)÷(45﹣20)=(450﹣400)÷25=50÷25=2(份)大坝原有的份数45×10﹣2×45=450﹣90=360(份)14人修好大坝需要的时间360÷(14﹣2)=360÷12=30(分钟)答:14人修好大坝需30分钟.故答案为:30.12.解:可以组成下列质数:2、3、5、7、61、89,一共有6个.答:用1、2、3、5、6、7、8、9这8个数字最多可以组成 6个质数.故答案为:6.13.解:设矩形的长为am,宽为bm,且a≥b,根据题意,a+b=17,由于a,b均为整数,因此(a,b)的取值有以下8种:(16,1),(15,2),(14,3),(13,4),(12,5),(11,6),(10,7),(9,8),故答案为8.14.解:设3小时顺流行驶单趟用时间为x小时,则逆流行驶单趟用的时间为(3﹣x)小时,故:x:(3﹣x)=4:88x=4×(3﹣x)8x=12﹣4x12x=12x=1逆流行驶单趟用的时间:3﹣1=2(小时),两船航行方向相同的时间为:2﹣1=1(小时),答:在3个小时中,有1小时两船同向都在逆向航行.15.解:由定义可知:x@1.3=11.05,(x+5)1.3=11.05,x+5=8.5,x=8.5﹣5=3.5故答案为:3.5。
五年级下册数学智力竞赛试题(附参考答案)

一、填一填。
(每空1分,后3题每空2分,共26分。
) 1. 能同时被2、3、5整除的最大两位数是( )。
2. 60有( )个因数,91有( )个因数。
3.已知a =2×3×7,b =2×5,a 和b 的最小公倍数是( ),最大公因数是( )。
4.把两个棱长是5分米的正方体粘合成一个长方体,这个长方体的表面积是( ),体积是( )。
5.把4米长的绳子平均分成7段,每段长是全长的)()(,每段长( )米。
6.在a5里,当a 是( )时,这个分数值是1;当a 是( )时,这个分数值是5。
7.)()(35)(2116)(87==÷==←填小数。
8.三个连续奇数的和是219,这三个数的平均数是( ),其中最大的数是( )。
9.把37化成小数,小数点后面第2017位的数字是( )。
10.分子是7的最小假分数是( ),分母是7的最大真分数是( )。
11. 比较大小。
77777777777955555555555712.一个长、宽、高分别为21厘米、15厘米和12厘米的的长方体,现从它的上面尽可能大的切下一个正方体,然后从剩余的部分再尽可能大的切下一个正方体,最后再从第二次剩余的部分尽可能大的切下一个正方体,剩下的体积是( )立方厘米。
13. 下图中有( )个三角形。
二、判一判。
(对的打“√”,错的打“×”)(共12分)1. 长方体的6个面一定都是长方形。
( )2. 两个质数的积一定是合数。
( )3. 两个数的乘积一定的它们的公倍数。
( )4.五角星是轴对称图形,它只有1条对称轴。
( )5.做一个零件,甲用了12 小时,乙用了13 小时,甲的效率高。
( )6.大于120 而小于720 的分数有5个。
( )7. 分子和分母的公因数只有1的分数是最简分数。
( )8.一个正方体的棱长之和是36厘米,体积是27立方厘米。
( ) 三、选一选。
小学五年级下学期数学竞赛试题(含答案)一图文百度文库

小学五年级下学期数学竞赛试题(含答案)一图文百度文库一、拓展提优试题1.(15分)一个自然数恰有9个互不相同的约数,其中3个约数A,B,C满足:①A+B+C=79②A×A=B×C那么,这个自然数是.2.如图所示,P为平行四边形ABDC外一点。
已知PCD∆的面积等于5平方厘米,PAB∆的面积等于11平方厘米。
则平行四边形ABCD的面积是CADBP3.一个除法算式中,被除数、除数、商与余数都是自然数,并且商与余数相等.若被除数是47,则除数是,余数是.4.如图:平行四边形ABCD中,OE=EF=FD.平行四边形面积是240平方厘米,阴影部分的面积是平方厘米.5.(8分)有一种细胞,每隔1小时死亡2个细胞,余下的每个细胞分裂成2个.若经过5小时后细胞的个数记为164.最开始的时候有个细胞.6.(8分)有四个人甲、乙、丙、丁,乙欠甲1元,丙欠乙2元,丁欠丙3元,甲欠丁4元.要想把他们之间的欠款结清,只因要甲拿出元.7.小猫咪A、B、C、D、E、F排队依次从猫妈妈手中领鱼干,每只小猫咪每次领一条,领完后在道队尾继续排队领,直到鱼干发完.若猫妈妈有278条鱼干,则最后一个领到鱼干的小猫咪是.8.三位偶数A、B、C、D、E满足A<B<C<D<E,若A+B+C+D+E=4306,则A最小.9.用1、2、3、5、6、7、8、9这8个数字最多可以组成个质数(每个数字只能使用一次,且必须使用).10.某长方体的长、宽、高(长、宽、高均大于1)是三个彼此互质的自然数,若这个长方体的体积是665,则它的表面积是.11.用一根34米长的绳子围成一个矩形,且矩形边长都是整数米,共有种不同的围法(边长相同的矩形算同一种围法).12.(8分)小胖把这个月的工资都用来买了一支股票.第一天该股票价格上涨,第二天下跌,第三天上涨,第四天下跌,此时他的股票价值刚好5000元,那么小胖这个月的工资是元.13.(7分)如图,按此规律,图4中的小方块应为个.14.(7分)对于a、b,定义运算“@”为:a@b=(a+5)×b,若x@1.3=11.05,则x=.15.若2副网球拍和7个网球一共220元,且1副网球拍比1个网球贵83元.求网球的单价.【参考答案】一、拓展提优试题1.解:一个自然数N恰有9个互不相同的约数,则可得N=x2y2,或者N=x8,(1)当N=x8,则九个约数分别是:1,x,x2,x3,x4,x5,x6,x7,x8,其中有3个约数A、B、C且满足A×A=B×C,不可能.(2)当N=x2y2,则九个约数分别是:1,x,y,x2,xy,y2,x2y,xy2,x2y2,其中有3个约数A、B、C且满足A×A=B×C,①A=x,B=1,C=x2,则x+1+x2=79,无解.②A =xy ,B =1,C =x 2y 2,则xy +1+x 2y 2=79,无解.③A =xy ,B =x ,C =xy 2,则xy +x +xy 2=79,无解.④A =xy ,B =x 2,C =y 2,则xy +x 2+y 2=79,解得:,则N =32×72=441.⑤A =x 2y ,B =x 2y 2,C =x 2,则x 2y +x 2y 2+x 2=79,无解.故答案为441.2.12[解答]作PF AB ⊥,由于//AB DC ,所以PF CD ⊥。
【精选】小学五年级下学期数学竞赛试题(含答案)图文百度文库

【精选】小学五年级下学期数学竞赛试题(含答案)图文百度文库一、拓展提优试题1.数一数,图中有多少个正方形?2.数学家维纳是控制论的创始人.在他获得哈佛大学博士学位的授予仪式上,有人看他一脸稚气的样子,好奇地询问他的年龄.维纳的回答很有趣,他说:“我的年龄的立方是一个四位数,年龄的四次方是一个六位数,这两个数刚好把0﹣9这10个数字全都用上了,不重也不漏,”那么,维纳这一年岁,(注:数a的立方等于a×a×a,数a的四次方等于a×a×a×a)3.请从1、2、3、…、9、10中选出若干个数,使得1、2、3、…、19、20这20个数中的每个数都等于某个选出的数或某两个选出的数(可以相等)的和.那么,至少需要选出个数.4.如图,正方形的边长是6厘米,AE=8厘米,求OB=厘米.5.定义新运算:a&b=(a+1)÷b,求:2&(3&4)的值为.6.解放军战士在洪水不断冲毁大坝的过程中要修好大坝,若10人需45分钟,20人需要20分钟,则14人修好大坝需分钟.7.四位数的所有因数中,有3个是质数,其它39个不是质数.那么,四位数有个因数.8.如图,魔术师在一个转盘上的16个位置写下来了1﹣16共16个数,四名观众甲、乙、丙、丁参与魔术表演.魔术师闭上眼,然后甲从转盘中选一个数,乙、丙、丁按照顺时针方向依次选取下一个数,图示是一种可能的选取方式,魔术师睁开眼,说:“选到偶数的观众请举手.”,这时候,只有甲和丁举手,这时候魔术师就大喝一声:“我知道你们选的数了!”.你认为甲和丁选的数的乘积是.9.(8分)一个大于1的正整数加1能被2整除,加2能被3整除,加3能被4整除,加4能被5整除,这个正整数最小是.10.(8分)在如图每个方框中填入一个数字,使得乘法竖式成立.那么,两个乘数的和是.11.如图六角星的6个顶点恰好是一个正六边形的6个顶点,那么阴影部分面积是空白部分面积的倍.12.小明准备和面包饺子,他在1.5千克面粉中加入了5千克的水,发现面和得太稀了,奶奶告诉他,包饺子的面需要按照3份面,2份水和面,于是小明分三次加入相同分量的面粉,终于将面按按要求和好了,那么他每次加入了千克面粉.13.(8分)小胖把这个月的工资都用来买了一支股票.第一天该股票价格上涨,第二天下跌,第三天上涨,第四天下跌,此时他的股票价值刚好5000元,那么小胖这个月的工资是元.14.如图是一个由26个相同的小正方体堆成的几何体,它的底层由5×4个小正方体构成,如果把它的外表面(包括底面)全部涂成红色,那么当这个几何体被拆开后,有3个面是红色的小正方体有块.15.(7分)对于a、b,定义运算“@”为:a@b=(a+5)×b,若x@1.3=11.05,则x=.【参考答案】一、拓展提优试题1.解:通过有规律的数,得出:(1)边长为1的正方形有4×3=12(个);(2)边长为2的正方形有6个;(3)边长为3的正方形有2个.(4)以小正方形的对角线为边的正方形有8个;(5)以对角线的一半为边长的正方形是17个;(6)以3个对角线的一半为边长的正方形有1个.所以图中共有正方形:12+6+2+8+17+1=46(个).答:图中有46个正方形.2.解:先用估值的方法大概确定一下维纳的年龄范围.根据174=83521,184=104976,194=130321,根据题意可得:他的年龄大于或等于18岁;再看,183=5832,193=6859,213=9261,223=10648,说明维纳的年龄小于22岁.根据这两个范围可知可能是18、19、20、21的一个数.又因为20、21无论是三次方还是四次方,它们的尾数分别都是:0、1,与“10个数字全都用上了,不重也不漏”不符,所以不用考虑了.只剩下18、19这两个数了.一个一个试,18×18×18=5832,18×18×18×18=104976;19×19×19=6859,19×19×19×19=130321;符合要求是18.故答案为:18.3.解:列举如下:1=1;2=2;3=1+2;4=2+2;5=5;6=1+5;7=2+5;8=8;9=9;10=10;11=1+10;12=2+10;13=5+8;14=7+7;15=5+10;16=8+8;17=8+9;18=8+10;19=9+10;通过观察,可看出从1、2、3、…、9、10中选出若干个数分别为{1,2,5,8,9,10};就能使得1、2、3、…、19、20这20个数中的每个数都等于某个选出的数或某两个选出的数(可以相等)的和.故至少需要选出6个数.故答案为6.4.解:6×6÷2=18(平方厘米),18×2÷8=4.5(厘米);答:OB长4.5厘米.故答案为:4.5.5.解:2&(3&4),=(2+1)÷[(3+1)÷4],=3÷1,=3;故答案为:3.6.解:假设每人每分钟修大坝1份洪水冲毁大坝速度:(10×45﹣20×20)÷(45﹣20)=(450﹣400)÷25=50÷25=2(份)大坝原有的份数45×10﹣2×45=450﹣90=360(份)14人修好大坝需要的时间360÷(14﹣2)=360÷12=30(分钟)答:14人修好大坝需30分钟.故答案为:30.7.解:首先根据奇偶位数和相等一定是11的倍数.因数一共的个数是3+39=42(个),将42分解成3个数字相乘42=2×3×7.=a×b2×c6.如果是11×52×26=17600(不是四位数不满足条件).再看一下如果这个数字最小是=11×32×26=6336.=3663=11×37×32.因数的个数共2×2×3=12(个).故答案为:12个.8.解:依题意可知:2个偶数中间间隔是2个奇数.发现只有数字10,11,9,12是符合条件的数字.乘积为10×12=120.故答案为:1209.解:根据分析:这个数除以2,3,4,5均余1,那么这个数减去1后就能同时被2,3,4,5整除;2,3,4,5的最小公倍数是60,则这个数为60的倍数加1.又因为这个数大于1,所以这个数最小是61.故答案为:61.10.解:依题意可知:结果的首位是2,那么在第二个结果中的首位还是2.再根据第一个结果中有一个1,那么就是有和数字5相乘以后数字1的进位同时十位数字是偶数才能满足条件,第一个乘数的个位数字只能是2或者3才能满足进位是1.当第一个乘数尾数是2时,首位数字无论是哪一个偶数都不能得到200多的结果.不满足题意.当第一个乘数尾数是3时,来看看偶数的情况.23×9=207.43,63,83无论乘以数字几都不能构成百位十位是20的结果.故是23×95=2185,那么23+95=118.故答案为:11811.解:根据分析,如图所示,将图进行分割成面积相等的三角形,阴影部分由18个小三角形组成,而空白部分有6个小三角形,故阴影部分面积是空白部分面积的18÷6=3倍.故答案是:3.12.解:根据分析,因面和水的比为3:2,即每一份水需要:3÷2=1.5份面粉,现在有5千克水,则需要面粉:5×1.5=7.5千克,而现有面粉量为:1.5千克,故还须加:7.5﹣1.5=6千克,分三次加入,则每次须加入:6÷3=2千克.故答案是:2.13.解:5000÷(1﹣)÷(1+)÷(1﹣)÷(1+)=5000××××=5000(元)答:小胖这个月的工资是5000元.故答案为:5000.14.解:依题意可知:第一层的共有4个角满足条件.第二层的4个角是4面红色,去掉所有的角块其余的符合条件.分别是3+2+3+2=10(个);共10+4=14(个);故答案为:1415.解:由定义可知:x@1.3=11.05,(x+5)1.3=11.05,x+5=8.5,x=8.5﹣5=3.5故答案为:3.5。
小学五年级下学期数学竞赛试题(含答案)图文百度文库

小学五年级下学期数学竞赛试题(含答案)图文百度文库一、拓展提优试题1.由120个棱长为1的正方体,拼成一个长方体,表面全部涂色,只有一面染色的小正方体,最多有块2.(7分)将偶数按下图进行排列,问:2008排在第列.2 4681614121018 20 22 2432 30 28 26…3.数一数,图中有多少个正方形?4.如果一个自然数的约数的个数是奇数,我们称这个自然数为“希望数”,那么,1000以内最大的“希望数”是.5.有白球和红球共300个,纸盒100个.每个纸盒里都放3个球,其中放1个白球的纸盒有27个,放2个或3个红球的纸盒共有42个,放3个白球和3个红球的纸盒数量相同.那么,白球共有个.6.用长是5厘米、宽是4厘米、高是3厘米的长方体木块叠成一个正方体,至少需要这种长方体木块块.7.(8分)在长方形ABCD中,BE=5,EC=4,CF=4,FD=1,如图所示,那么△AEF的面积是;8.小胖和小亚两人在生日都是在五月份,而且都是星期三.小胖的生日晚,又知两人的生日日期之和是38,小胖的生日是5月日.9.(1)数一数图1中有个三角形.(2)数一数图2中有个正方形.10.(8分)有一种细胞,每隔1小时死亡2个细胞,余下的每个细胞分裂成2个.若经过5小时后细胞的个数记为164.最开始的时候有 个细胞.11.某商店的同种点心有大小两种包装礼盒,大盒85.6元一盒,内有点心32块,小盒46.8元一盒,内有点心15块,若王雷用654元买了9盒点心,则他可得点心 块.12.某数学竞赛有10道题,规定每答对一题得5分,答错或不答扣2分.A 、B 两人各自答题,得分之和是58分,A 比B 多得14分,则A 答对 道题.13.同时掷4个相同的小正方体(小正方体的六个面上分别写有数字1、2、3、4、5、6,则朝上一面的4个数字的和有 种.14.某长方体的长、宽、高(长、宽、高均大于1)是三个彼此互质的自然数,若这个长方体的体积是665,则它的表面积是 .15.如图是一个正方体的平面展开图,若该正方体相对的两个面上的数值相等,则a ﹣b ×c 的值是 .【参考答案】一、拓展提优试题1.64 [解答]设长方体的长、宽、高分别为,,l m n (不妨设l m n ≥≥),容易知道只有一面染色的小正方体只有每个面上可能有一些。
五年下学期数学竞赛试题及答案【各地真题】

五年下学期数学竞赛试题一.选择题(共10题,共20分)1.如果a、b都是质数,那么他们的和是()。
A.奇数B.偶数C.奇数或偶数2.既是奇数又是质数的数是()。
A.9B.21C.293.在旋转过程中,确定一个图形旋转后的位置,除了需要知道此图形原来的位置外,还需要知道()。
A.图形的形状、旋转中心B.图形的形状、旋转角C.旋转中心、旋转角D.以上答案都不对4.一个两位数,既是5的倍数,又是偶数,这个数最小是()。
A.15B.10C.905.钟面指针做的是()运动的。
A.平移B.旋转C.既是平移又是旋转6.自然数中,凡是17的倍数()。
A.都是偶数B.有偶数有奇数C.都是奇数7.将下图直角三角形绕O点逆时针旋转90°可以得到图形()。
A. B. C. D.8.图是一个平面纸板图,下面有几个立体图形,其中有一个是左边的纸板折合而成的,请你找出来。
( )A. B. C. D.9.如图:从阴影三角形A到B的运动是()。
A.平移B.旋转C.不确定10.为公村计划种2公顷大白菜,实际比计划多种了公顷,实际种了()公顷大白菜。
A.2B.C.D.二.判断题(共10题,共20分)1.在自然数中,除了质数就是合数。
()2.所有的偶数都是合数,所有的奇数都是质数。
()3.任何一个非0自然数的约数至少有两个。
()4.正方体的棱长扩大为原来的5倍,表面积就扩大为原来的25倍。
()5.用4个小正方体摆几何体,从正面看是的图形,可以摆出2种几何体。
()6.如果a是奇数,a+1必定是偶数。
()7.如果一个数个位上的数字是3的倍数,这个数就是3的倍数。
()8.线段AB长3厘米,绕着它的端点A旋转180度后,这条线段变成了6厘米。
()9.3的倍数一定都是奇数。
()10.个位上是369的数,都是3的倍数。
()三.填空题(共10题,共31分)1.陀螺的转动属于()现象,缆车的运动属于()现象。
2.填一填。
(1)指针从A开始,绕点O顺时针旋转90°到()。
小学五年级下学期数学竞赛试题(含答案)一

小学五年级下学期数学竞赛试题(含答案)一一、拓展提优试题∆的面积等于5平方厘1.如图所示,P为平行四边形ABDC外一点。
已知PCD米,PAB∆的面积等于11平方厘米。
则平行四边形ABCD的面积是2.甲乙两人分别从AB两地同时出发相向而行,当甲走到一半时,乙将速度提1200米处相遇,并且最后同时到达,那么两地相高一倍,结果两人在距离B地3.由120个棱长为1的正方体,拼成一个长方体,表面全部涂色,只有一面染4.星期天早晨,哥哥和弟弟去练习跑步,哥哥每分钟跑110米,弟弟每分钟跑80米,弟弟比哥哥多跑了半小时,结果比哥哥多跑了900米,那么,哥哥跑了米.5.鸡与兔共100只,鸡的脚比兔的脚多26只.那么,鸡有只.6.小胖和小亚两人在生日都是在五月份,而且都是星期三.小胖的生日晚,又知两人的生日日期之和是38,小胖的生日是5月日.7.将100按“加15,减12,加3,加15,减12,加3,…”的顺序不断重复运算,运算26步后,得到的结果是.(1步指每“加”或“减”一个数)8.某商店的同种点心有大小两种包装礼盒,大盒85.6元一盒,内有点心32块,小盒46.8元一盒,内有点心15块,若王雷用654元买了9盒点心,则他可得点心块.9.李双骑车以320米分钟的速度从A地驶向B地,途中因自行车故障推车继续向前步行5分钟到距B地1800米的某地修车,15分钟后以原来骑车速度的1.5倍继续向前驶向B地,到达B地时,比预计时间多用17分钟,则李双推车步行的速度是米/分钟.10.解放军战士在洪水不断冲毁大坝的过程中要修好大坝,若10人需45分钟,20人需要20分钟,则14人修好大坝需分钟.11.对于自然数N ,如果1﹣9这九个自然数中至少有六个数可以整除N ,则称N 是一个“六合数”,则在大于2000的自然数中,最小的“六合数”是 .12.用一根34米长的绳子围成一个矩形,且矩形边长都是整数米,共有 种不同的围法(边长相同的矩形算同一种围法).13.(8分)有一个特殊的计算器,当输入一个数后,计算器先将这个数乘以3,然后将其结果是数字逆序排列,接着再加2后显示最后的结果,小明输入了一个四位数后,显示结果是2015,那么小明输入的四位数是 .14.定义新运算:θa =,则(θ3)+(θ5)+(θ7)(+θ9)+(θ11)的计算结果化成最简真分数后,分子与分母的和是 .15.同学们去春游,带水壶的有80人,带水果的有70人,两样都没带的有6人.若既带水壶又带水果的人数是所有参加春游人数的一半,则参加春游的同学共有 人.【参考答案】一、拓展提优试题1.12[解答]作PF AB ⊥,由于//AB DC ,所以PF CD ⊥。
人教版五年级数学下册 专项分类必刷卷——立体与几何(试卷)(含答案)

专项分类必刷卷 (三) 立体与几何(基础卷)建议用时:40分钟满分:50+10分一、填空题。
(每空1分,共16分)1.在括号里填上合适的体积或容积单位。
(1)一瓶胶水 310( ) (2)一个苹果的体积约是300( )2. 3200cm³=( )dm³5m³=( )dm³5.8 L=( )mL 8.6L=( )dm³=( )mL3.一个长方体相交于同一个顶点的三条棱长度分别是8cm,6cm和5cm,这个长方体的棱长总和是( ) cm,表面积是( )cm²,体积是( )cm³。
4.在透明的封闭长方体盒子内放置棱长为1 cm的小正方体,如图。
这个透明的长方体盒子的表面积是( )cm²。
5.如图所示,长方体水箱的底面积是2dm²,,石块的体积是( )dm³。
6.从前面看到的形状是,从左面看到的形状是,搭这样的立体图形,最多要用( )个小正方体,最少要用( )个小正方体。
(不考虑只有棱相接的情况)7.易错题一个长方体箱子,从里面量长、宽、高分别是9 dm、8 dm、6 dm,这个箱子的容积是()dm³。
如果在这个箱子里放棱长是2d m的正方体木块,最多可以放( )个。
二、选择题。
(每题2分,共6分)1.下面图形中,能围成正方体的是( )。
2.根据右面从三个方向看到的图形,摆出的几何体是( )。
3.一个长方体盒子,底面是一个边长6cm的正方形,高10cm,如果在盒子四周贴一圈包装纸,贴包装纸的面积至少是( )cm²。
A.240B.60C. 600D. 3600三、求下列图形的表面积和体积。
(8分)四、连一连。
(6分)五、解决问题。
(共14分)1.教材改编如图是一个长方体的孔明灯,它的底面是边长30cm的正方形,高50cm。
(8分)(1)制作这个孔明灯,至少需要多少厘米的竹条搭框架?(接头处不计)(4分)(2)除了下底面外,其他面都要糊上透光性较好的阻燃棉纸,制作这个孔明灯至少需要多少平方分米的阻燃棉纸?(4分)2.有一个长10cm,宽8cm,高12cm的长方体玻璃容器。
五年级下学期数学竞赛试题(含答案)一图文百度文库

五年级下学期数学竞赛试题(含答案)一图文百度文库一、拓展提优试题1.如图,在等腰直角三角形ABC中,斜边AB上有一点D,已知CD=5,BD 比AD长2,那么三角形ABC的面积是.2.(15分)如图,正六边形ABCDEF的面积为1222,K、M、N分别AB,CD,EF的中点,那么三角形PQR的边长是.3.(7分)爱尔兰作家刘易斯曾写过一篇反讽寓言,文中描述了一个名为尼亚特泊的野蛮国家.在这个国家里使用西巴巴数字.西巴巴数字的形状与通用的阿拉伯数字相同,但含义相反.如“0”表示“9”,“1”表示“8”,以次类推.他们写数字是从左到右,使用的运算符号也与我们使用的一样.例如,他们用62代表我们所写的37.按照尼亚特泊人的习惯,应怎样写837+742的和是419.【分析】“0”表示“9”,0+9=9,“1”表示“8”,1+8=9,由此可知西巴巴数字,表示的数字与正常数字的和都是9;由此找出837、742表示的数字,然后相加即可.4.(7分)后羿朝三个箭靶分别射了三支箭,如图:他在第一个箭靶上得了29分,第二个箭靶上得了43分.请问他在第三个箭靶上得了分.5.有一行数:1,1,2,3,5,8,13,21,…,从第三个数开始,每个数都是前两个数的和,问在前2007个数中,有是偶数.6.数一数,图中有多少个正方形?7.某次入学考试有1000人参加,平均分是55分,录取了200人,录取者的平均分与未录取的平均分相差60分,录取分数线比录取者的平均分少4分.录取分数线是分.8.对于自然数N,如果在1﹣9这九个自然数中至少有七个数是N的因数,则称N是一个“七星数”,则在大于2000的自然数中,最小的“七星数”是.9.大于0的自然数n是3的倍数,3n是5的倍数,则n的最小值是.10.从1、2、3、4、5中任取3个组成一个三位数,其中不能被3整除的三位数有个.11.如果2头牛可以换42只羊,3只羊可以换26只兔,2只兔可以换3只鸡,则3头牛可以换多少只鸡?12.(15分)甲、乙两船顺流每小时行8千米,逆流每小时行4千米,若甲船顺流而下,然后返回;乙船逆流而上,然后返回,两船同时出发,经过3小时同时回到各自的出发点,在这3小时中有多长时间甲、乙两船同向航行?13.(8分)在如图每个方框中填入一个数字,使得乘法竖式成立.那么,两个乘数的和是.14.同学们去春游,带水壶的有80人,带水果的有70人,两样都没带的有6人.若既带水壶又带水果的人数是所有参加春游人数的一半,则参加春游的同学共有人.15.(7分)如图,按此规律,图4中的小方块应为个.【参考答案】一、拓展提优试题1.解:作CE⊥AB于E.∵CA=CB,CE⊥AB,∴CE=AE=BE,∵BD﹣AD=2,∴BE+DE﹣(AE﹣DE)=2,∴DE=1,在Rt△CDE中,CE2=CD2﹣DE2=24,∴S=•AB•CE=CE2=24,△ABC故答案为242.解:如图延长BA和EF交于点O,并连接AE,由正六边形的性质,我们可知S ABCM=S CDEN=S EF AK=六边形面积,根据容斥原理,重叠部分三个三角形面积和等于阴影部分面积,且因为对称,△AKP,△CMQ,△ENR三个三角形是一样的,有KP=RN,AP=ER,RP=PQ,=,则=,=,由鸟头定理可知道3×KP×AP=RP×PQ,综上可得:PR=2KP=RE,那么由三角形AEK是六边形面积的,且S△APK ,=S△AKES△APK=S ABCDEF=47,所以阴影面积为47×3=141故答案为141.3.解:西巴巴数字8表示阿拉伯数字9﹣8=1,西巴巴数字3表示阿拉伯数字9﹣3=6,西巴巴数字7表示阿拉伯数字9﹣7=2,西巴巴数字4表示阿拉伯数字9﹣4=5,西巴巴数字2表示阿拉伯数字9﹣2=7,所以837+742表示的正常算式为:162+257=419.故答案为:419.4.【分析】这个箭靶共三个环,设最小的环为a分,中间环为b分,最外环为c分,得:第一个靶得分为:2b+c=29①第二个靶得分为:2a+c=43②第三个靶得分为:a+b+c③通过等量代换,解决问题.解:设最小的环为a分,中间环为b分,最外环为c分,得:第一个靶得分为:2b+c=29①第二个靶得分为:2a+c=43②第三个靶得分为:a+b+c③由①+②得:2a+2b+2c=29+43=72即a+b+c=36即第三个靶的得分为36分.答:他在第三个箭靶上得了36分故答案为:36.5.【分析】因为前两个数相加得偶数,即奇数+奇数=偶数;同理,第四个数是:奇数+偶数=奇数,以此类推,总是奇数、奇数、偶数、奇数、奇数、偶数…;每三个数一个循环周期,然后确定2007个数里面有几个循环周期,再结合余数,即可得出偶数的个数.解:2007÷3=669,又因为,每一个循环周期中有2个奇数,1个偶数,所以前2007个数中偶数的个数是:1×669=669;答:前2007个数中,有699是偶数.故答案为:699.6.解:通过有规律的数,得出:(1)边长为1的正方形有4×3=12(个);(2)边长为2的正方形有6个;(3)边长为3的正方形有2个.(4)以小正方形的对角线为边的正方形有8个;(5)以对角线的一半为边长的正方形是17个;(6)以3个对角线的一半为边长的正方形有1个.所以图中共有正方形:12+6+2+8+17+1=46(个).答:图中有46个正方形.7.解:设录取者的平均成绩为X分,我们可以得到方程,200X+(1000﹣200)×(X﹣60)=55×1000,200X+800(X﹣60)=55000,1000X﹣48000=55000,1000X=103000,X=103;所以录取分数线是103﹣4=99(分).答:录取分数线是99分.故答案为:99.8.解:根据分析,在2000~2020之间排除掉奇数,剩下的偶数还可以排除掉不能被3整除的偶数,最后只剩下:2004、2010、2016,再将三个数分别分解质因数得:2004=2×2×3×167;2010=2×3×5×67;2016=2×2×2×2×2×3×3×7,显然2014和2010的质因数在1~9中不到7个,不符合题意,排除,符合题意的只有2016,此时2016的因数分别是:2、3、4、6、7、8、9.故答案是:2016.9.解:3n是5的倍数,3n的个数一定是0或5又因为大于0的自然数n是3的倍数,所以3n最小是453n=45n=15所以n最小取15时,n是3的倍数,3n是5的倍数.答:n的最小值是15.故答案为:15.10.解:1+2+3=6,1+2+4=7,1+2+5=8,2+3+4=9,2+3+5=10,3+4+5=12,其中不能被3整除的数的和是7、8、10,即有三组(1、2、4),(1、2、5)(2、3、5),每一组可以组成3×2×1=6个,三组共可以组成6×3=18个,即不能被3整除的数共有18个.故答案为:18.11.解:42÷2=21(只)21÷3×26=7×26=182(只)182÷2×3=91×3=273(只)273×3=819(只)答:3头牛可以换819只鸡.12.解:设3小时顺流行驶单趟用时间为x小时,则逆流行驶单趟用的时间为(3﹣x)小时,故:x:(3﹣x)=4:88x=4×(3﹣x)8x=12﹣4x12x=12x=1逆流行驶单趟用的时间:3﹣1=2(小时),两船航行方向相同的时间为:2﹣1=1(小时),答:在3个小时中,有1小时两船同向都在逆向航行.13.解:依题意可知:结果的首位是2,那么在第二个结果中的首位还是2.再根据第一个结果中有一个1,那么就是有和数字5相乘以后数字1的进位同时十位数字是偶数才能满足条件,第一个乘数的个位数字只能是2或者3才能满足进位是1.当第一个乘数尾数是2时,首位数字无论是哪一个偶数都不能得到200多的结果.不满足题意.当第一个乘数尾数是3时,来看看偶数的情况.23×9=207.43,63,83无论乘以数字几都不能构成百位十位是20的结果.故是23×95=2185,那么23+95=118.故答案为:11814.解:设既带水壶又带水果的为x人,则参加春游的同学共有2x人,由题意可得:80+70﹣x+6=2x156﹣x=2x3x=156x=52则2x=2×52=104答:则参加春游的同学共有104人.故答案为:104.15.解:因为图1中小方块的个数为1+2×3=7个,图2中小方块的个数为1+(1+2)+3×4=16个,图3中小方块的个数为1+(1+2)+(1+2+3)+4×5=30个,所以图4中小方块的个数为1+(1+2)+(1+2+3)+(1+2+3+4)+5×6=50个,故答案为:50.。
【竞赛题】人教版小学五年级下册数学第09讲《立体几何》竞赛试题(含详解)

第九讲立体几何- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -首先,我们来学习一下长方体、正方体的体积与表面积的计算方法.练一练.1.一个正方体的棱长总和是72厘米,它的一个面是边长_______厘米的正方形,它的表面积是_______平方厘米,体积是_______立方厘米.2.一个长方体的长是5分米,宽是45厘米,高是24厘米,它的表面积是_______平方厘米,体积是_______立方厘米.3.做一个长8分米,宽4分米,高6分米的长方体玻璃鱼缸,至少需要_______平方分米的玻璃.4.有一块棱长是10厘米的正方体的铁块,现在要把它熔铸成一个横截面积是20平方厘米的长方体,这个长方体的长是_______厘米.如果要求这个长方体每条棱的长度都是整数厘米,它的表面积最小是_______平方厘米.相信同学们对于这些公式都很熟悉,但是对于较复杂的立体图形,往往我们并不能直接应用公式进行计算,这个时候又该怎么办呢?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题1.有30个边长为1米的正方体,如图所示堆成一个四层的立体图形.请问:该立体图形的表面积等于多少平方米?分析:所谓表面积,就是立体图形露在外面的总面积.我们可以从上、下、左、右、前、后6个不同的方向去考虑这个立体图形,把每个方向露出的面积加在一起就行了.练习1.用14个棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?在观察物体的时候,我们往往可以从不同的角度进行观察.角度不同,看到的风景就会不同.比如:我们可以从正面看,上面看,左面看,看到的图形分别称为正视图,俯视图和左视图.并且容易发现:正面看和后面看,上面看和下面看,左面看和右面看得到的图形是相同的.对于较复杂的立体图形,通过三视图法往往可以很方便地计算出表面积.例题2.一个正方体被切成24个大小形状相同的小长方体(见下图),这些小长方体的表面积之和为162平方厘米,那么原正方体的体积是多少立方厘米?分析:我们先来分析一下切成小块的过程中,图形的表面积是如何变化的.同学们请看下图:一刀下去,正方体被一分为二.表面积和原来比,正好多出了A,B两个面.不难看出,这两个面的面积都等于原正方体6个面中1个面的面积.按这种方法,每切一刀,增加的都是两个面的面积.同学们可以计算一下,按如图的方式切了6刀后,表面积究竟增加了多少?练习2.一个正方体被切成36个大小形状相同的小长方体(见下图),这些小长方体的表面积之和为500平方厘米,那么原正方体的体积是多少立方厘米?例题3.如图,有一个边长为30厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小正方体后,表面积变为5496平方厘米,那么挖掉的小正方体的棱长是多少厘米?分析:挖去小正方体后,表面积会发生变化.如果挖的位置,最终结果会有区别吗?练习3.一个正方体棱长10厘米,在它的表面上挖去一个棱长3厘米的小正方体.请求出剩下立体图形表面积的所有可能.除了长方体、正方体之外,圆柱和圆锥在我们的生活中也特别常见.如图,圆柱的两个圆面叫做底面;周围的面叫做侧面;两个底面之间的距离叫做高. 圆锥的圆面叫做底面;尖点叫做顶点;顶点到底面的距离叫做高,顶点到底面圆周上任意一点的连线叫做母线.关于圆锥的内容,我们不作深入的学习,同学们只需要学会如何计算它的体积即可.大家可以把圆柱想象成一个底面是圆形的柱子,那其他柱体也就是底面是其他图形的柱子.如图,所有“上下一般粗”的图形都称为柱体,图中的两个图形分别叫做三棱柱和四棱柱,它们的体积计算公式都是:V =⨯底面积高例题4.(1)如下左图,是长为8,宽为4的长方形,以长方形的长为轴旋转一周,求所形成的立体图形的体积和表面积是多少. (2)如下右图,是直角边分别为3和4的直角三角形,以边长为4的直角边为轴旋转一周,求所形成的立体图形的体积.分析:圆柱体的底面半径和高与长方形的长和高有什么关系?圆锥体呢?练习4.有一个圆柱和一个圆锥,它们的高和底面直径如图所示.圆柱体积及表面积分别是多少?圆锥的体积是多少?(π取3.14)6例题5.下图是一个棱长为4厘米的正方体,分别在前、后、左、右、上、下各面的中心位置挖去一个棱长1厘米的正方体,做成一种玩具.该玩具的表面积是多少平方厘米?如果把这些洞都打穿,表面积又变成了多少平方厘米?分析:打穿以后,表面积的计算有点复杂.想想都有哪些面是露在外面的?例题6.如图,一个底面长20分米,宽8分米,高15分米的长方形水池,存有三分之二池水.将一个高50分米,体积400立方分米的长方体竖直放入池中,那么长方体被水浸湿的部分有几分米高?分析:很明显长方体没有被水浸没,还有一部分在外面.水的体积没有变化过,但是形状发生了变化.原来是一个长方体,后来是什么样的形状?-正多面体正多面体,指各面都是全等的正多边形且每一个顶点所接的面数都是一样的凸多面体.一共有五种正多面体,分别是正四面体、正六面体(正方体)、正八面体、正十二面体和正二十面体.这些正多面体的作法都收录在了《几何原本》的第13卷中.柏拉图认为世界万物都是由火、气、水、土四元素构成的,其形状如正多面体中的四个.➢火的热令人感到尖锐和刺痛,好像小小的正四面体.➢空气是用正八面体制的,可以粗略感受到,它极细小的结合体十分顺滑.➢当水放到人的手上,它会自然流出,那它就应该是由很多小球所组成,好像正二十面体.➢土与其他的元素相异,因为它可以被堆栈,正如立方体.剩下没有用的正多面体——正十二面体,柏拉图以不清晰的语调写道:“神使用正十二面体以整理整个天空旳星座.”柏拉图的学生亚里士多德添加了第五个元素——以太,并认为天空是用此组成,但他没有将以太和正十二面体联系起来.约翰内斯·开普勒依随文艺复兴建立数学对应的传统,将五个正多面体对应五个行星——水星、金星、火星、木星和土星,同时它们本身亦对应了五个古典元素.在立体图形中,正多面体非常对称.除了正多面体之外,还有很多图形也具有非常漂亮的对称性.下面就是一些例子,不过要注意,它们可不是正多面体哦.作业1.如图所示,一个正方体被切成16个大小形状相同的小长方体,这些小长方体的表面积之和为256平方厘米,那么原正方体的体积是多少?作业2.一个正方体棱长8厘米,在它的表面上挖去一个棱长为2厘米的小正方体.则剩下的立体图形表面积可能是多少?作业3.如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小正方体后,表面积变为2454平方厘米,那么挖掉的小正方体的边长是多少?作业4.图中的立体图形中,每个小正方形的边长都是1.那么这个立体图形的表面积和体积分别是多少?作业5.正方形的边长为4,按照图中所示的方式旋转,那么得到的旋转体的体积和表面积分别是多少?(π取3)俗话说,兴趣是最好的老师。
五年级下册数学竞赛试题-第十节单立体图形的认识寒假专版 全国通用
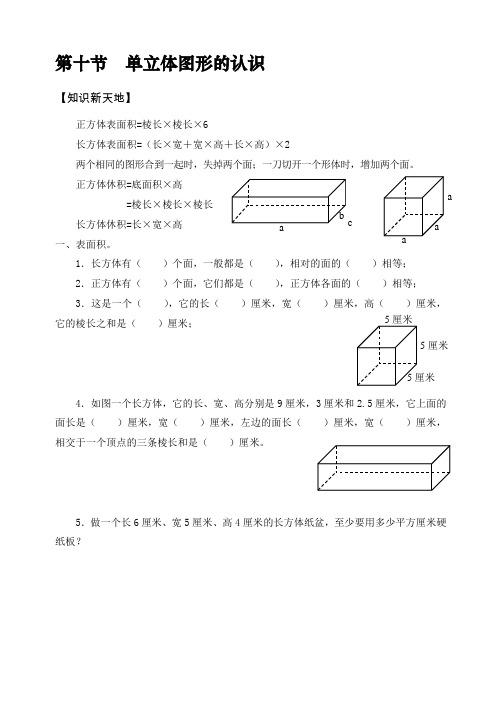
第十节 单立体图形的认识【知识新天地】正方体表面积=棱长×棱长×6长方体表面积=(长×宽+宽×高+长×高)×2两个相同的图形合到一起时,失掉两个面;一刀切开一个形体时,增加两个面。
正方体休积=底面积×高 =棱长×棱长×棱长 长方体休积=长×宽×高 一、表面积。
1.长方体有( )个面,一般都是( ),相对的面的( )相等; 2.正方体有( )个面,它们都是( ),正方体各面的( )相等; 3.这是一个( ),它的长( )厘米,宽( )厘米,高( )厘米,它的棱长之和是( )厘米;4.如图一个长方体,它的长、宽、高分别是9厘米,3厘米和2.5厘米,它上面的面长是( )厘米,宽( )厘米,左边的面长( )厘米,宽( )厘米,相交于一个顶点的三条棱长和是( )厘米。
5.做一个长6厘米、宽5厘米、高4厘米的长方体纸盆,至少要用多少平方厘米硬纸板?5厘米5厘米 5厘米aaa bc6.一个正方体纸盒,棱长3厘米,求它的表面积。
如果这个盒子没有盖子,做这个盒子要用多少纸板,该如何列式* 7.两个完全一样的长方形,长为5厘米,宽为4厘米,高为3厘米;把它们拼在一起组成新的长方形,在这些新的长方形中,表面积最小的是多少?二、体积。
1.下面的图形都是棱长1厘米的小正方体拼成的,它们的体积分别是:2.一个正方体水箱棱长总和是36米,表面积是( ),容积是( ),占地面积是( )。
3.一个正方体棱长是a ,表面积是( ),体积是( )。
4.下图,两个物体的表面积是( ),两个物体的体积是( )。
A .甲>乙B .甲<乙C .甲=乙5.一个长方体,长5厘米,宽4厘米,高2厘米,它的体积是( )。
A .40厘米B .40平方厘米C .40立方厘米6.把若干个1立方分米的正方体木块摆成一个最小的正方体(不包括1块),这个正方体的体积是( )。
【详解】5年级下册第09讲_立体几何

第九讲 立体几何例题1. 答案:72详解:用三视图法.从上往下看,面积为16平方米;从左往右看,面积为10平方米;从前往后看,面积也是10平方米.所以这个立体图形的表面积是()161010272++⨯=平方米.例题2. 答案:27详解:一共切了6刀,会增加12个大正方形的面积.加上原来的6个大正方形,一共有18个大正方形.162189÷=,每个大正方形的面积是9平方厘米,边长就应该是3厘米.正方体的体积是33327⨯⨯=立方厘米.例题3. 答案:4详解:在角上挖一个正方体,表面积不会增加.在棱上挖一个正方体,会增加2个小正方形的面积.在面上挖一个正方体,会增加4个小正方形的面积.一共增加了6个小正方形的面积.说明一个小正方形的面积是()25496630616-⨯÷=平方厘米,边长是4厘米.即小正方体的棱长是4厘米.例题4. 答案:(1)401.92,301.44;(2)37.68详解:(1)得到的旋转体为圆柱体,圆柱体的底面半径为4,高为8,则体积为2π48128π=401.92⨯⨯=,表面积为222π2π2π482π496π301.44r h r ⨯+=⨯⨯⨯+⨯⨯==.(2)以边长为4的直角边为轴旋转一周,所得立体图形为底面半径为3,高为4的圆锥体,体积为21π3412π37.683⨯⨯⨯==.例题5. 答案:120,126详解:从一个面中心位置挖去一个棱长1厘米的正方体,比原来增加4个面,增加了4平方厘米.共挖去6个正方体,增加24个面,增加了24平方厘米.加上原来的面积96平方厘米,共120平方厘米.如果把这些洞打穿,每个洞的表面积为31412⨯⨯=平方厘米,3个洞的表面积为36平方厘米.总的表面积变为96366126+-=平方厘米.例题6. 答案:101019详解:首先可算出这个长方体的底面积是8平方分米.将这个长方体竖直放入水中,该长方体一定不会被浸没.水池中水的体积为22081516003⨯⨯⨯=立方分米.放入长方体后水面的高度为()2001016002088101919÷⨯-==分米.长方体被水浸湿部分的高度也就是101019分米.练习1. 答案:46简答:()977246++⨯=.练习2.答案:125简答:切了7刀,会增加14个大正方形,加上原来的6个一共20个.由此可知每个大正方形的面积是5002025÷=平方厘米,边长是5厘米.原正方体的体积是125立方厘米.练习3.答案:600平方厘米,618平方厘米,636平方厘米简答:如果从角上挖,表面积不变,仍为600平方厘米;如果从棱上挖,表面积增加2个小正方体的面,表面积变为60092618+⨯=平方厘米;如果从面上挖,表面积增加4个小正方体的面,表面积变为60094636+⨯=平方厘米.练习4.答案:696,768简答:如果只挖6个小正方体,表面积会增加24个小正方形,变成22⨯+⨯=平方厘米.如610242696果打穿,表面积为22⨯-⨯+⨯⨯=平方厘米.610622424768作业1.答案:300简答:切了3刀,增加了6个面.切开后,立体图形的表面积为5512300⨯⨯=.作业2.答案:384、392或400平方厘米简答:有挖角上、棱上与面上三种可能.作业3.答案:3简答:各挖掉一个小正方体后,表面积会增加6个小正方形的面积.那么一个正方形的面积是()-÷=平方厘米,小正方体的棱长为3厘米.2454240069作业4.答案:46,14简答:从上面可以看到9个正方形;从左边可以看到7个正方形,还有一个看不到的,一共8个;从前面可以看到6个正方形.所以表面积为()++⨯=.体积为14.986246作业5.答案:48,72简答:旋转得到的圆柱底面半径为2,高为4.441648=⨯+⨯==.Sπππ=⨯==,42442472Vππ。
通用版小学五年级数学下册【竞赛类题型】专项训练卷及解析

小学五年级数学下册【竞赛类题型】专项训练卷第一讲立体图形及展开例题选讲例1:图1所示的是一个正方体纸盒拆开后平摊在桌面上的形状。
如果将这个展开图恢复成原来的正方体,图中的点F、点G分别与哪个点重合?【分析与解答】为了研究方便,我们将正方体六个面分别标上序号1、2、3、4、5、6,如果将l作为底面,那么4就是后面,5为右面,6为前面,2则是左面,3就是上面,(如图2)。
从图中不难看出点F与点N,重合,点G与点S重合。
还有一种方法就是动手制作一张展开图,折一折,结果就一目了然了,同学们不妨试试吧!例2:一只小虫从图l所示的长方体上的A点出发,沿长方体的表面爬行,依次经过前面、上面、后面、底面,最后到达P点。
请你为它设计一条最短的爬行路线。
【分析与解答】因为小虫在长方体的表面爬行,所以我们可以将长方体的前、后、上、下西个面展开成平面图形(如图2)。
又因为在平面上“两点之间的线段长度最短”,所以连接AP,则线段AP为小虫爬行的最短路线。
练习与思考1.如图所示的是一个正方体纸盒拆开后平摊在桌面上的形状。
如果将这个展开图恢复成原来的正方体,图中的点B、点D分别与哪个点重合?2.如图所示的是一个棱长3厘米的正方体木块,一只蚂蚁从A点沿表面爬向B点。
请画出蚂蚁爬行的最短路线。
问:这样的路线共有几条?3.将一张长方形硬纸片,剪去多余部分后,折叠成一个棱长为l厘米的正方体。
这张长方形硬纸片的面积最小是多少平方厘米?4.一块长方形的铁皮,长28厘米,在这块铁皮的四角各剪下一个边长为4厘米的小正方形,然后通过折叠、焊接做成一个无盖的长方体盒子。
已知这个盒子的容积是960立方厘米,求原来长方形铁皮的面积。
5.如图所示的是一个正方体木块的表面展开图,若在正方体的各面填上数,使其对面两数之和为7,则A、B、c处填的数各是多少?6.如图所示的10个展开图中,哪些可以做成完整的正方体?7.如图所示的是一个长方体,四边形APQC、是长方体的一个截面(即过长方体上4点A、P、Q、C的平面与长方体相交所得到的图形),P、Q分别为棱A1B1、B1C1,的中点,请在此长方体的平面展开图上,标出线段AC、cQ、QP、PA。
小学五年级奥数立体几何(二)习题

【例2】(★★★★)(《小数报》数学竞赛决赛) 一个长方体的宽和高相等, 并且都等于长的一半. 将这个长方体切成12 个小长方体, 这些小长方体的表面之和为600平方分米. 求这个大长方体 的体积.
【例3】(★★★) 一个盖着瓶盖的瓶子里面装着一些水, 瓶底面积为10平方厘米, (如下图 所示), 请你根据图中标明的数据, 计算瓶子的容积是___.
2
知识大总结 1. 柱体,体积=底面积×高.
⑴ 正方体,长方体,圆柱体 ⑵ 容积,水、酒精等液体 2. 体积考点 ⑴ 切割改变的是表面积,总体积不变. ⑵ 阿基米德老头
完全侵入,液体升高部分=侵入物体体积 不完全侵入,液体底面积发生变化.
完全侵入
【今日讲题】 例2,例4,超常大挑战
【讲题心得】
__________________________________________________________________ ___________________. 【家长评价】
本讲主线 1.柱体体积公式 2. 阿基米德的浴盆.
立体几何(二)
1. 体积, 物体占有空间的多少. 2. 柱体, 体积=底面积×高
⑴ 长方体=长×宽×高 ⑵ 正方体=边长×边长×边长 3. 单位, 立方米, 立方分米, 立方厘米(千进制)
【例1】(★★★) 把一根长2.4米的长方体木料锯成5段(如图), 表面积比原来增加了96平 方厘米. 这根木料原来的体积是_____立方厘米. 2.4米
7cm
5cm4cm1源自【例4】(★★★★) 有n个同样大小的正方体, 将它们堆成一个长方体, 这个长方体的底面就 是原正方体的底面. 如果这个长方体的表面积是3096平方厘米, 当从这 个长方体的顶部拿去一个正方体后, 新的长方体的表面积比原长方体的 表面积减少144平方厘米, 那么n为多少?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九讲立体几何
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
首先,我们来学习一下长方体、正方体的体积与表面积的计算方法.
练一练.
1.一个正方体的棱长总和是72厘米,它的一个面是边长_______厘米的正方形,它的表面积是_______平方厘米,体积是_______立方厘米.
2.一个长方体的长是5分米,宽是45厘米,高是24厘米,它的表面积是_______平方厘米,体积是_______立方厘米.
3.做一个长8分米,宽4分米,高6分米的长方体玻璃鱼缸,至少需要_______平方分米的玻璃.
4.有一块棱长是10厘米的正方体的铁块,现在要把它熔铸成一个横截面积是20平方厘米的长方体,这个长方体的长是_______厘米.如果要求这个长方体每条棱的长度都是整数厘米,它的表面积最小是_______平方厘米.
相信同学们对于这些公式都很熟悉,但是对于较复杂的立体图形,往往我们并不能直接
应用公式进行计算,这个时候又该怎么办呢?
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
例题1.
有30个边长为1米的正方体,如图所示堆成一个四层的立体图形.请问:该立体图形的表面积等于多少平方米?
分析:所谓表面积,就是立体图形露在外面的总面积.我们可以从上、下、左、右、前、后6个不同的方向去考虑这个立体图形,把每个方向露出的面积加在一起就行了.
练习1.
用14个棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?
在观察物体的时候,我们往往可以从不同的角度进行观察.角度不同,看到的风景就会
不同.比如:我们可以从正面看,上面看,左面看,看到的图形分别称为正视图,俯视图和左视图.并且容易发现:正面看和后面看,上面看和下面看,左面看和右面看得到的图形是相同的.对于较复杂的立体图形,通过三视图法往往可以很方便地计算出表面积.
例题2.
一个正方体被切成24个大小形状相同的小长方体(见下图),这些小长方体的表面积之和为162平方厘米,那么原正方体的体积是多少立方厘米?
分析:我们先来分析一下切成小块的过程中,图形的表面积是如何变化的.同学们请看下图:
一刀下去,正方体被一分为二.表面积和原来比,正好多出了A,B两个面.不难看出,这两个面的面积都等于原正方体6个面中1个面的面积.按这种方法,每切一刀,增加的都是两个面的面积.同学们可以计算一下,按如图的方式切了6刀后,表面积究竟增加了多少?
练习2.
一个正方体被切成36个大小形状相同的小长方体(见下图),这些小长方体的表面积之和为500平方厘米,那么原正方体的体积是多少立方厘米?
例题3.
如图,有一个边长为30厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小正方体后,表面积变为5496平方厘米,那么挖掉的小正方体的棱长是多少厘米?分析:挖去小正方体后,表面积会发生变化.如果挖的位置,最终结果会有区别吗?
练习3.
一个正方体棱长10厘米,在它的表面上挖去一个棱长3厘米的小正方体.请求出剩下立体图形表面积的所有可能.
除了长方体、正方体之外,圆柱和圆锥在我们的生活中也特别常见.
如图,圆柱的两个圆面叫做底面;周围的面叫做侧面;两个底面之间的距离叫做高. 圆锥的圆面叫做底面;尖点叫做顶点;顶点到底面的距离叫做高,顶点到底面圆周上任意一点的连线叫做母线.关于圆锥的内容,我们不作深入的学习,同学们只需要学会如何计算它的体积即可.
大家可以把圆柱想象成一个底面是圆形的柱子,那其他柱体也就是底面是其他图形的柱子.如图,所有“上下一般粗”的图形都称为柱体,图中的两个图形分别叫做三棱柱和四棱柱,它们的体积计算公式都是:
V =⨯底面积高
例题4.
(1)如下左图,是长为8,宽为4的长方形,以长方形的长为轴旋转一周,求所形成的立体图形的体积和表面积是多少. (2)如下右图,是直角边分别为3和4的直角三角形,以边长为4的直角边为轴旋转一周,求所形成的立体图形的体积.
分析:圆柱体的底面半径和高与长方形的长和高有什么关系?圆锥体呢?
练习4.
有一个圆柱和一个圆锥,它们的高和底面直径如图所示.圆柱体积及表面积分别是多少?圆锥的体积是多少?(π取3.14)
6
例题5.
下图是一个棱长为4厘米的正方体,分别在前、后、左、右、上、下各面的中心位置挖去一个棱长1厘米的正方体,做成一种玩具.该玩具的表面积是多少平方厘米?如果把这些洞都打穿,表面积又变成了多少平方厘米?
分析:打穿以后,表面积的计算有点复杂.想想都有哪些面是露在外面的?
例题6.
如图,一个底面长20分米,宽8分米,高15分米的长方形水池,存有三分之二池水.将一个高50分米,体积400立方分米的长方体竖直放入池中,那么长方体被水浸湿的部分有几分米高?
分析:很明显长方体没有被水浸没,还有一部分在外面.水的体积没有变化过,但是形状发生了变化.原来是一个长方体,后来是什么样的形状?
-
正多面体
正多面体,指各面都是全等的正多边形且每一个顶点所接的面数都是一样的凸多面体.一共有五种正多面体,分别是正四面体、正六面体(正方体)、正八面体、正十二面体和正二十面体.这些正多面体的作法都收录在了《几何原本》的第13卷中.
柏拉图认为世界万物都是由火、气、水、土四元素构成的,其形状如正多面体中的四个.➢火的热令人感到尖锐和刺痛,好像小小的正四面体.
➢空气是用正八面体制的,可以粗略感受到,它极细小的结合体十分顺滑.
➢当水放到人的手上,它会自然流出,那它就应该是由很多小球所组成,好像正二十面体.
➢土与其他的元素相异,因为它可以被堆栈,正如立方体.
剩下没有用的正多面体——正十二面体,柏拉图以不清晰的语调写道:“神使用正十二面体以整理整个天空旳星座.”柏拉图的学生亚里士多德添加了第五个元素——以太,并认为天空是用此组成,但他没有将以太和正十二面体联系起来.
约翰内斯·开普勒依随文艺复兴建立数学对应的传统,将五个正多面体对应五个行星——水星、金星、火星、木星和土星,同时它们本身亦对应了五个古典元素.在立体图形中,正多面体非常对称.除了正多面体之外,还有很多图形也具有非常漂亮的对称性.下面就是一些例子,不过要注意,它们可不是正多面体哦.
作业1.如图所示,一个正方体被切成16个大小形状相同的小长方体,这些小长方体的表面积之和为256平方厘米,那么原正方体的体积是多少?
作业2.一个正方体棱长8厘米,在它的表面上挖去一个棱长为2厘米的小正方体.则剩下的立体图形表面积可能是多少?
作业3.如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小正方体后,表面积变为2454平方厘米,那么挖掉的小正方体的边长是多少?
作业4.图中的立体图形中,每个小正方形的边长都是1.那么这个立体图形的表面积和体积分别是多少?
作业5.正方形的边长为4,按照图中所示的方式旋转,那么得到的旋转体的体积和表面积分别是多少?(π取3)
学习与生活的苦,每一个人必须选择一个。
不管你选择了哪一个,都应该尽最大的努力做到最好,只有做到最好,人生才会在不留遗憾。
老一辈教育我们,书山有路勤为径,学海无涯苦作舟;吃得人中苦,方为人上人;吃亏是福,在学习的年龄不要贪图享乐;认认真真听课,勤勤恳恳学习,美好的未来可以值得可期。
知识在当今社会知识就是财富就是能量,愿在知识的海洋里你我成为良书益友,结伴同行,共同迈向美好生活,迈向未来。
