《优化探究》2016届高三数学人教A版文科一轮复习课件 第二章 函数、导数及其应用 2-11
2016届高三数学人教A版文科一轮复习课件 第二章 函数、导数及其应用 2-2

B.f(x)=|x-1|
山
C.f(x)=1x-x
D.f(x)=ln(x+1)
东 金 太
(2)函数 y=xx+ +21在(-1,+∞)上是________(填“增函数”或“减函
阳 书 业
有
数”).
限
公
司
菜 单 隐藏
第十二页,编辑于星期五:二十点 十七分。
高考总复习 A 数学
抓主干
知识 回扣
解析 (1)由(x1-x2)[f(x1)-f(x2)]<0 可知,f(x)在(0,+∞)是减函数,
解析:要使 y=log5(2x+1)有意义,则 2x+1>0,即 x>-12,而 y=log5u
为(0,+∞)上的增函数,当 x>-12时,u=2x+1 也为增函数,故原函数
山
的单调增区间是-21,+∞.
东 金
太
答案:-12,+∞
阳 书 业
有
限
公
司
菜 单 隐藏
第九页,编辑于星期五:二十点 十七分。
高考总复习 A 数学
求导 → 判断f ′x正、负 → 单调性区间
(4)定义法
山
取值 → 作差 → 变形 → 定号 → 单调性区间
东
金
求函数的单调区间,一定要注意定义域优先原则.
太 阳
书
业
有
限
公
司
菜 单 隐藏
第十五页,编辑于星期五:二十点 十七分。
抓主干 知识 回扣
求函数的单调区间(师生共研)
研考向
考点
探究
例 2 求下列函数的单调区间:
阳
书
(4)利用函数的单调性求解最值(或恒成立)问题.
2016届高三数学人教A版文科一轮复习课件 第二章 函数、导数及其应用 2-4
高效
训练
x2+3xx≤-3或x≥0
解析 f(x)=-x2-3x-3<x<0.
令 g(x)=a|x-1|,
如图所示,
山
东
金
太
阳
书
业
有
限
公
司
菜 单 隐藏
第十三页,编辑于星期五:二十点 十七分。
高考总复习 A 数学
抓主干 知识 回扣
研考向
考点 探究
当 g(x)=a|x-1|(x≤1)与 y=f(x)有四个交点时,f(x)与 g(x)有四个交
域为[0,+∞)知 n 为奇数,m 为偶数.在幂函数 y=xα 中,当 α>1 时,
图象在第一象限的部分下凸,当 0<α<1 时,图象在第一象限的部分上凸, 山
故选 C.
东 金
太
答案:C
阳
书
业
有
限
公
司
菜 单 隐藏
第二十三页,编辑于星期五:二十点 十七分。
抓主干 知识 回扣 研考向 考点 探究 提素能 高效 训练
点, 提素能
高效 训练
联立yy==-a1x-2-x3 x 得 x2+(3-a)x+a=0,
Δ=(3-a)2-4a>0
得 a<1 或 a>9,由图可知 0<a<1.
山 东
当 g(x)=a|x-1|(x>1)与 y=f(x)=x2+3x(x>0)有两个交点时,又 y=a(x
金 太
-1)(x<1)与 y=f(x)一定有两个交点,故 y=f(x)与 y=g(x)一定有四个交点.
太 阳
(3)两根式:
.
书 业
f(x)=a(x-x1)(x-x2)(a≠0)
2016届高三数学人教A版文科一轮复习课件 第二章 函数、导数及其应用 2-12
山
(2)利用导数解决优化问题的步骤:
东
①审题,设未知数.②结合题意列出函数关系式.③确定函数的定
金 太
义域.④在定义域内求极值、最值.⑤下结论.
阳 书
业
有
限
公
司
菜 单 隐藏
第二十页,编辑于星期五:二十点 十七分。
抓主干 知识 回扣
研考向 考点 探究
提素能 高效 训练
高考总复习 A 数学
2.(2014 年泰安模拟)某种产品每件成本为 6 元,每件售价为 x 元
0,不符合题意.
③当-2a>4,即 a<-8 时,f(x)在[1,4]上的最小值可能在 x=1 或 x=4
山 东
处取得,而 f(1)≠8,由 f(4)=2(64+16a+a2)=8 得 a=-10 或 a=-6(舍
金 太
去),当 a=-10 时,f(x)在(1,4)上单调递减,f(x)在[1,4]上的最小值为 f(4)
所以当x=40时,y有最小值.
阳
书
答案:40
业
有
限
公
司
菜 单 隐藏
第七页,编辑于星期五:二十点 十七分。
抓主干 知识 回扣
研考向 考点 探究
提素能 高效 训练
高考总复习 A 数学 函数的最值与导数(师生共研)
例 1 (2014 年高考江西卷)已知函数 f(x)=(4x2+4ax+a2) x,其中
a<0.
抓主干 知识 回扣
研考向 考点 探究
提素能 高效 训练
高考总复习 A 数学
第十二节 导数的综合应用
最新考纲展示
1.会求闭区间上函数的最大值、最小值(其中多项式函数一般不超
2016届高三数学人教A版文科一轮复习课件 第二章 函数、导数及其应用 2-5
抓主干 知识 回扣
研考向
考点 探究
提素能
解析:在同一平面直角坐标系中分别作出 y=x,y=12x,y=2x 的图
高效
训练
象(如图),显然 x<0 时,x<2x<12x.
即 c<0 时,c<2c<12c.故选 C. 答案:C
菜 单 隐藏
山 东 金 太 阳 书 业 有 限 公 司
第十七页,编辑于星期五:二十点 十八分。
抓主干
知识
回扣
研考向 考点
3.函数 y=x|xa|x(0<a<1)的图象的大致形状是(
)
探究
提素能 高效 训练
解析:函数定义域为{x|x∈R,x≠0},且 y=x|xa|x=a-x,ax,x>x0<,0.
当 x>0
山 东 金
太
时,函数是一个指数函数,其底数 0<a<1,所以函数递减;当 x<0 时, 阳 书
规律方法 y=ax,y=|ax|,y=a|x|(a>0且a≠1)三者之间的关系:
y=ax与y=|ax|是同一函数的不同表现形式.
函数y=a|x|与y=ax不同,前者是一个偶函数,其图象关于y轴对称,
当x≥0时两函数图象相同.
山 东
金
太
阳
书
业
有
限
公
司
菜 单 隐藏
第十五页,编辑于星期五:二十点 十八分。
提素能 高效 训练
1
1
2
33=2×33-2×3×3-3
1
1
=2×33-2×33=0;
(2)原式=29512+0.112+6247-23-3+3478
2016届高三数学人教A版文科一轮复习课件 第二章 函数、导数及其应用 2巧突破
高考总复习 A 数学
(2)由(1)知,f(x)=x2+8ln x,令 F(x)=f(x)-2x=x2-2x+8ln x.
因为 F(1)=-1<0,f(2)=8ln 2>0,所以 F(x)=0 在(0,+∞)至少有
一个根.
又因为 F′(x)=2x-2+8x≥2 16-2=6>0,
山
所以 F(x)在(0,+∞)上递增,
解析:(1)因为 f(x)=a2ln x-x2+ax,
其中 x>0,
所以 f′(x)=ax2-2x+a=-x-ax2x+a.
山 东
金
由于 a>0,所以 f(x)的递增区间为(0,a),递减区间为(a,+∞). 太
阳
(2)要使 e-1≤f(x)≤e2 对 x∈[1,e]恒成立,则 f(1)≥e-1,得 a-1≥e 书
菜 单 隐藏
高考总复习 A 数学
山 东 金 太 阳 书 业 有 限 公 司
第十三页,编辑于星期五:二十点 十八分。
高考总复习 A 数学
2.设函数f(x)=a2ln x-x2+ax,a>0. (1)求f(x)的单调区间; (2)求所有的实数a,使e-1≤f(x)≤e2对x∈[1,e]恒成立.(注:e为自 然对数的底数)
而 g′(x)=2ax-a+1x=2ax2-xax+1,
当 a=0 时,g′(x)=1x>0,此时 g(x)在(0,+∞)上单调递增;
当 a≠0 时,只需 g′(x)≥0 在(0,+∞)上恒成立,因为 x∈(0,+
山
∞),只要 2ax2-ax+1≥0,则需要 a>0,
东
金
对于函数 y=2ax2-ax+1,过定点(0,1),对称轴 x=14>0,只需 Δ=
2016届高三数学人教A版文科一轮复习课件 第二章 函数、导数及其应用 2-1

抓主干 知识 回扣
高考总复习 A 数学
研考向 考点 探究
提素能
高效
训练
规律方法 简单函数定义域的类型及求法
(1)已知函数的解析式,则构造使解析式有意义的不等式(组)求解.
(2)对实际问题:由实际意义及使解析式有意义构成的不等式(组)求
解.
(3)若已知函数f(x)的定义域为[a,b],则函数f(g(x))的定义域由不等
5,
太 阳 书 业
有
∴所求函数的定义域为1- 2
Байду номын сангаас5,0∪1,1+2
5.
限 公 司
菜 单 隐藏
第十九页,编辑于星期五:二十点 十七分。
抓主干 知识 回扣
研考向 考点 探究
提素能 高效 训练
角度三 已知定义域确定参数问题
高考总复习 A 数学
3.若函数 f(x)= 2x2+2ax-a-1的定义域为 R,则 a 的取值范围
析式;
(3)已知 f(x)+2f1x=x(x≠0),求 f(x)的解析式.
山
解析 (1)f(1-cos x)=sin2x=1-cos2x,
东 金
令t=1-cos x,则cos x=1-t,t∈[0,2],
太 阳
∴f(t)=1-(1-t)2=2t-t2,t∈[0,2],
书 业
即f(x)=2x-x2,x∈[0,2].
菜 单 隐藏
第六页,编辑于星期五:二十点 十七分。
抓主干 知识 回扣
研考向 考点 探究
提素能 高效 训练
高考总复习 A 数学
1.解决函数的一些问题时,易忽视“定义域优先”的原则.
2.易混“函数”与“映射”的概念:函数是特殊的映射,映射不一定是函
2016届高三数学人教A版文科一轮复习课件 第二章 函数、导数及其应用 2-7
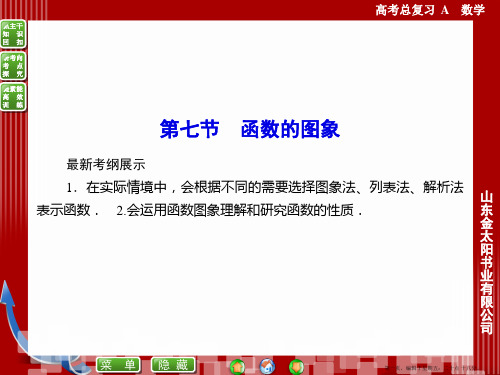
(1)y=|x-2|(x+1);(2)y=|x2-2|x|-3|.
解析:(1)函数化为
y=-x-x12-221-2+94x49≥x<22,,
图象如图.
菜 单 隐藏
高考总复习 A 数学
山 东 金 太 阳 书 业 有 限 公 司
第十九页,编辑于星期五:二十点 十八分。
高考总复习 A 数学
抓主干 知识 回扣
山 东 金 太 阳 书 业 有 限 公 司
菜 单 隐藏
第二十五页,编辑于星期五:二十点 十八分。
抓主干 知识 回扣
研考向 考点 探究
考点
探究
①函数的定义域、值域.
提素能
高效 训练
②函数的性质(单调性、奇偶性、周期性等).
③函数图象上的特殊点(与坐标轴的交点、经过的定点等).
(2)对于给定函数的图象,要能从象的左右、上下分布范围、变化趋
势、对称性等方面研究函数的定义域、值域(最值)、单调性、奇偶性、周
期性,注意图象与函数解析式中参数的关系,常用的方法有:
研考向 考点 探究
提素能 高效 训练
高考总复习 A 数学
角度一 确定方程根的个数等有关问题
1.函数 y=1-1 x的图象与函数 y=2sin πx(-2≤x≤4)的图象所有交
点的横坐标之和等于( )
山 东
A.2
B.4
金 太
C.6
D.8
阳 书
业
有
限
公
司
菜 单 隐藏
第二十二页,编辑于星期五:二十点 十八分。
提素能
高效 训练
4.设函数f(x)=|x+1|+|x-a|的图象关于直线x=1对称,则a的值为
()
A.3
2016届人教A版高考数学大一轮复习课件 探究课2

【训练1】 已知函数f(x)=(a-1)ln x+ax2+1,求函数f(x)的单调 区间.
解
f(x)
的
定
义
域
为
(0
,
+
∞)
,
f′(x)
=
a-1 x
+
2ax
=
2ax2+x a-1.
(1)当 a≥1 时,f′(x)>0,故 f(x)在(0,+∞)上单调递增;
(2)当 a≤0 时,f′(x)<0,故 f(x)在(0,+∞)上单调递减;
第十三页,编辑于星期五:十八点 四十一分。
【例 3】 已知函数 f(x)=ax+xln x 的图象在点 x=e(e 为自然对 数的底数)处的切线斜率为 3. (1)求实数 a 的值; (2)若 k∈Z,且 k<xf-x1对任意 x>1 恒成立,求 k 的最大值. 解 (1)因为f(x)=ax+xln x, 所以f′(x)=a+ln x+1. 因为函数f(x)=ax+xln x的图象在点x=e处的切线斜率为3, 所以f′(e)=3,即a+ln e+1=3,所以a=1.
第十二页,编辑于星期五:十八点 四十一分。
热点二 利用导数求解函数的极值、最值 用导数研究函数的极值或最值是高考命题的重要题型之 一.对于此类问题的求解,首先,要理解函数极值的概 念,需要清楚导数为零的点不一定是极值点,只有在该点 两侧导数的符号相反,即函数在该点两侧的单调性相反 时,该点才是函数的极值点;其次,要区分极值与最值, 函数的极值是一个局部概念,而最值是某个区间的整体性 概念.
第一页,编辑于星期五:十八点 四十一分。
热点一 利用导数解决函数的单调性问题 函数的单调性是函数在定义域内的局部性质,因此利用导 数讨论函数的单调性时,要先研究函数的定义域,再利用 导数f′(x)在定义域内的符号来判断函数的单调性.这类问题 主要有两种考查方式:(1)判断函数f(x)的单调性或求单调区 间.(2)利用函数的单调性或单调区间,求参数的范围.
2016届高三数学人教A版文科一轮复习课件 第二章 函数、导数及其应用 2-3
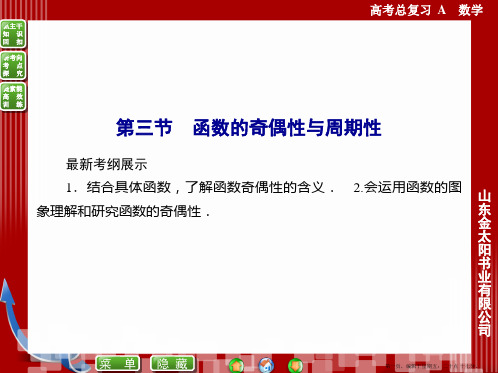
C.1
D.3
解析:解法一 ∵f(x)-g(x)=x3+x2+1,∴f(-x)-g(-x)=-x3+
x2+1,又由题意可知f(-x)=f(x),g(-x)=-g(x),∴f(x)+g(x)=-x3
山 东
+x2+1,则f(1)+g(1)=1,故选C.
金 太
解法二 令f(x)=x2+1,g(x)=-x3,显然符合题意,
阳
书
∴f(1)+g(1)=12+1-13=1.选C.
业
答案:C
有 限
公
司
菜 单 隐藏
第八页,编辑于星期五:二十点 十七分。
高考总复习 A 数学
抓主干 知识 回扣
研考向 考点 探究
提素能
高效 训练
3.函数 f(x)对于任意实数 x 满足条件 f(x+2)=f1x,若 f(1)=-5,
则 f(f(5))=________.
是偶;
c.“奇·偶”是奇,“奇÷偶”是奇.
(2)判断函数奇偶性时应注意问题:
①分段函数奇偶性的判断,要注意定义域内x取值的任意性,应分
山 东
段讨论,讨论时可依据x的范围取相应的解析式,判断f(x)与f(-x)的关 金
太
系,得出结论,也可以利用图象作判断.
阳
②“性质法”中的结论是在两个函数的公共定义域内才成立的.
C.f(x)|g(x)|是奇函数
D.|f(x)g(x)|是奇函数
解析:由题意可知f(-x)=-f(x),g(-x)=g(x),对于选项A,f(-
x)·g(-x)=-f(x)·g(x),所以f(x)g(x)是奇函数,故A项错误;对于选项B,
山 东
|f(-x)|g(-x)=|-f(x)|g(x)=|f(x)|g(x),所以|f(x)|g(x)是偶函数,故B项错 金
2016届高三数学人教A版文科一轮复习课件 第二章 函数、导数及其应用 2-11
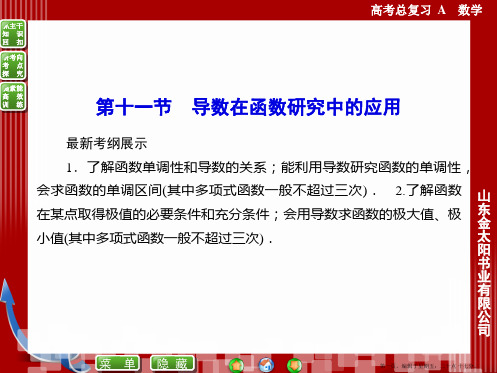
A.[-1,+∞)
B.(-1,+∞)
C.(-∞,-1]
D.(-∞,-1)
山
解析:f
′(x)=-x+x+b 2≤0 在(-1,+∞)上恒成立,即 b≤x(x
东 金 太
+2)在(-1,+∞)上恒成立.又 x(x+2)=(x+1)2-1>-1,∴b≤-1,
阳 书
故选 C.
业 有
答案:C
限 公
司
菜 单 隐藏
当 a<0 时,令 g(x)=ax2+(2a+2)x+a,
由于 Δ=(2a+2)2-4a2=4(2a+1).
①当 a=-12时,Δ=0,
山 东
f ′(x)=-x21x+x-1122≤0,函数 f(x)在(0,+∞)上单调递减.
金 太 阳 书
业
②当 a<-21时,Δ<0,g(x)<0,
有 限 公
f ′(x)<0,函数 f(x)在(0,+∞)上单调递减.
高考总复习 A 数学
研考向 考点 探究
提素能 高效 训练
解析 (1)由题意知 a=0 时,f(x)=xx- +11,x∈(0,+∞),
此时 f ′(x)=x+212.
可得 f ′(1)=12,又 f(1)=0,
山 东 金
所以曲线 y=f(x)在(1,f(1))处的切线方程为 x-2y-1=0.
太 阳
司
菜 单 隐藏
第十一页,编辑于星期五:二十点 十七分。
抓主干 知识 回扣
研考向
考点
探究
提素能 高效
③当-21<a<0 时,Δ>0,
训练
设 x1,x2(x1<x2)是函数 g(x)的两个零点,
2016届高考数学理新课标A版一轮总复习课件 第2章 函数、导数及其应用-2
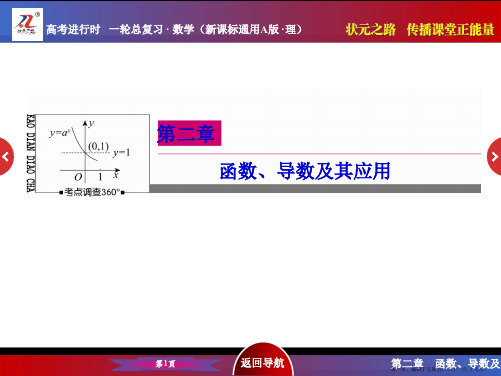
而 y=log1 u 在(0,+∞)上是单调递减函数,
2
∴y=log1 (x2-3x+2)的单调递减区间为(2,+∞),单调递增
2
区间为(-∞,1).
第25页
返回导航
第二章 第二节 第二十五页,编辑于星期五:二十一点 十七分。
第12页
返回导航
第二章 第二节 第十二页,编辑于星期五:二十一点 十七分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
2 条结论——函数最值的有关结论 (1)闭区间上的连续函数一定存在最大值和最小值.当函数在闭 区间上单调时最值一定在端点取到. (2)开区间上的“单峰”函数一定存在最大值(最小值).
返回导航
第二章 第二节 第二十三页,编辑于星期五:二十一点 十七分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
画出函数图像如图所示,单调递增区间为(-∞,-1]和[0,1), 单调递减区间为[-1,0]和[1,+∞).
(2)令 u=x2-3x+2,则原函数可以看作 y=log1 u 与 u=x2-3x
2
+2 的复合函数. 令 u=x2-3x+2>0,则 x<1 或 x>2. ∴函数 y=log1 (x2-3x+2)的定义域为(-∞,1)∪(2,+∞).
2
又 u=x2-3x+2 的对称轴 x=32,且开口向上.
第24页
返回导航
第二章 第二节 第二十四页,编辑于星期五:二十一点 十七分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
第16页
返回导航
第二章 第二节 第十六页,编辑于星期五:二十一点 十七分。
优化探究高考数学一轮复习 第二章 第八节 函数与方程课件 理 新人教A版

=ex+12x-2 的零点所在的
区间是( B )
A.0,12 C.(1,2)
B.12,1 D.(2,3)
试题
解析
∵f′(x)=ex+12>0,∴f(x)
在 R 上单调递增,又 f12=
e-74< 3-74<0,f(1)=e
-
3 2
>
0
,
∴
零
点
在
区
间
12,1上.
的零点所在的区
间为( )
A.(0,1) B.(1,2)
C.(2,3)
D.(3,4)
法二:函数 f(x)的零点所在的区间转化为函数 g(x)= ln x,h(x)=-x+2 图象交点的横坐标所在的范围, 如图所示, 可知 f(x)的零点所在的区间为(1,2).
考点一
题组训练
确定函数 f(x)的零点所在区间的两种常用方法 (1)利用函数零点的存在性定理:首先看函数 y=f(x) 在区间[a,b]上的图象是否连续,再看是否有 f(a)·f(b) <0.若有,则函数 y=f(x)在区间(a,b)内必有零点. (2)数形结合法:通过画函数图象,观察图象与 x 轴 在给定区间上是否有交点来判断.
必记结论 有关函数零点的结论
(1)若连续不断的函数 f(x)在定义域上是单调函数,则 f(x) 至多有一个零点. (2)连续不断的函数,其相邻两个零点之间的所有函数值 保持同号. (3)连续不断的函数图象通过零点时,函数值可能变号, 也可能不变号.
知识点一
知识点一 知识点二
[自测练习]
试题
解析
1.函数 y=|log2x|-12x 的零
用.令 f(x)=ex-x-2,
则由表中数据可得 f(1)
《优化探究》高考数学总复习(人教A文)配套课件2-13

1.已知 a 为实数,且函数 f(x)=(x2-4)· (x-a). (1)求导函数 f′(x); (2)若 f′(-1)=0,求函数 f(x)在[-2,2]上的最大值和最小值.
解析:(1)由 f(x)=x3-ax2-4x+4a, ∴f′(x)=3x2-2ax-4. 1 (2)因为 f′(-1)=0,所以 a= , 2 1 2 有 f(x)= x - x - 4x+2,f′(x)=3x2-x-4. 2
• 解析:y′=-x2+81,令y′=0,解得x=9(x =-9舍去). • 当0<x<9时,y′>0; • 当 x>9 时, y′<0 ,则当 x = 9 时, y 取得最大 值. • 答案:C
• 3 .(课本习题改编 ) 函数f(x) =12x-x3在区 间[-3,3]上的最小值是( ) • A.-9 B.-16 • C.-12 D.-11 • 解析:由f′(x)=12-3x2=0,得x=-2或 x=2. • 又f(-3)=-9,f(-2)=-16,f(2)= 16, f(3)=9, • ∴函数f(x)在[-3,3]上的最小值为-16. • 答案:B
• 5.(2013年广州模拟)设函数f(x)=ax3-3x +1(x∈R),若对于任意x∈[-1,1],都有 (构造法 )若 x=0,则不论 a 取何值, f(x)≥0 显然成立; f解析: (x )≥ 0 成立,则实数 a的值为 ________ .
3 1 当 x>0, 即 x∈ (0,1]时, f(x)=ax -3x+1≥0 可化为 a≥ 2 - 3.设 g(x) x x
答案:4
• 考向一 函数的最值问题 • [例1] (2012年高考江西卷)已知函数f(x)= (ax2+bx+c)ex在[0,1]上单调递减且满足f(0) =1,f(1)=0. • (1)求a的取值范围; • (2)设g(x)=f(x)-f′(x),求g(x)在[0,1]上的最 大值和最小值.
优化探究高三一轮人教A文科数学复习第二章函数、导数

A 组 考点基础演练一、选择题1.(2015年大同模拟)幂函数y =f (x )的图象经过点⎝⎛⎭⎫4,12,则f ⎝⎛⎭⎫14的值为( ) A .1 B .2 C .3D .4解析:设幂函数为y =x α,∵幂函数的图象经过点⎝⎛⎭⎫4,12,∴4α=12,∴α=-12,∴y =x -12,则f ⎝⎛⎭⎫14=⎝⎛⎭⎫14-12=2.答案:B2.幂函数f (x )的图象在第一、三象限,且f (3)<f (2),则下列各式中一定成立的是( ) A .f (-3)<f (-2) B .f (-3)>f (-2) C .f (-3)>f (2)D .f (3)<f (-2)解析:幂函数f (x )的图象在第一、三象限,则f (x )为奇函数,∵f (3)<f (2),∴-f (3)>-f (2),即f (-3)>f (-2).答案:B3.设a =⎝⎛⎭⎫3525,b =⎝⎛⎭⎫2535,c =⎝⎛⎭⎫2525,则a ,b ,c 的大小关系是( ) A .a >c >b B .a >b >c C .c >a >bD .b >c >a解析:由y =x 25在(0,+∞)上递增知a >c ,由y =⎝⎛⎭⎫25x 在R 上递减知c >b . 答案:A4.已知函数y =ax 2+bx +c ,如果a >b >c ,且a +b +c =0,则它的图象是( )解析:∵a >b >c ,a +b +c =0, ∴a >0,c <0,∴y =ax 2+bx +c 的开口向上,且与y 轴的交点(0,c )在负半轴上. 答案:D5.“a ≤0”是“函数f (x )=|(ax -1)x |在区间(0,+∞)内单调递增”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件解析:由二次函数的图象和性质知f (x )=|(ax -1)x |在(0,+∞)内单调递增,只需f (x )的图象在(0,+∞)上与x 轴无交点,即a =0或1a <0,整理得a ≤0,而当a ≤0时,结合图象可知f (x )在(0,+∞)上为增函数.故a ≤0是f (x )在(0,+∞)上单调递增的充要条件,故选C.答案:C 二、填空题6.(2015年海口模拟)二次函数f (x )的二次项系数为正,且对任意x 恒有f (2+x )=f (2-x ),若f (1-2x 2)<f (1+2x -x 2),则x 的取值范围是________.解析:由f (2+x )=f (2-x ),知x =2为对称轴,由于二次项系数为正的二次函数中距对称轴较近的点的纵坐标较小,∴|1-2x 2-2|<|1+2x -x 2-2|,即|2x 2+1|<|x 2-2x +1|,∴2x 2+1<x 2-2x +1,∴-2<x <0.答案:(-2,0)7.(2014年高考江苏卷)已知函数f (x )=x 2+mx -1,若对于任意x ∈[m ,m +1],都有f (x )<0成立,则实数m 的取值范围是________.解析:据题意,⎩⎪⎨⎪⎧f (m )=m 2+m 2-1<0f (m +1)=(m +1)2+m (m +1)-1<0解得-22<m <0. 答案:⎝⎛⎭⎫-22,0 8.已知函数f (x )=-x 2+2ax +1-a 在x ∈[0,1]时有最大值2,则a 的值为________. 解析:f (x )=-(x -a )2+a 2-a +1, 当a >1时,y max =a ;当0≤a ≤1时,y max =a 2-a +1; 当a <0时,y max =1-a .根据已知条件:⎩⎪⎨⎪⎧ a >1,a =2,或⎩⎪⎨⎪⎧ 0≤a ≤1,a 2-a +1=2或⎩⎪⎨⎪⎧a <0,1-a =2,解得a =2,或a =-1. 答案:2或-1三、解答题9.已知二次函数f (x )=ax 2+bx +1为偶函数,且f (-1)=-1. (1)求函数f (x )的解析式;(2)若函数g (x )=f (x )+(2-k )x 在区间[-2,2]上单调递减,求实数k 的取值范围. 解析:(1)∵二次函数f (x )=ax 2+bx +1为偶函数, ∴对称轴x =-b2a =0,得b =0,由f (-1)=a +1=-1,得a =-2, ∴f (x )=-2x 2+1.(2)g (x )=-2x 2+(2-k )x +1∵抛物线g (x )的开口向下,对称轴x =2-k4,∴函数g (x )在⎣⎢⎡⎭⎪⎫2-k 4,+∞上单调递减. 依题意可得2-k4≤-2,解得k ≥10,∴实数k 的取值范围为[10,+∞).10.已知二次函数y =f (x )=x 2+bx +c 的图象过点(1,13),且函数y =f ⎝⎛⎭⎫x -12是偶函数. (1)求f (x )的解析式;(2)已知t <2,g (x )=[f (x )-x 2-13]·|x |,求函数g (x )在[t,2]上的最大值和最小值.解析:(1)因为函数y =f ⎝⎛⎭⎫x -12是偶函数,所以二次函数f (x )=x 2+bx +c 的对称轴方程为x =-12,故b =1.又因为二次函数f (x )=x 2+bx +c 的图象过点(1,13),所以1+b +c =13,故c =11,因此,f (x )的解析式为f (x )=x 2+x +11.(2)g (x )=(x -2)·|x |,当x ≤0时,g (x )=-(x -1)2+1,当x >0时,g (x )=(x -1)2-1, 由此可知g (x )max =0,当1≤t <2,g (x )min =t 2-2t ; 当1-2≤t <1,g (x )min =-1; 当t <1-2,g (x )min =-t 2+2t .B 组 高考题型专练1.(2014年揭阳测试)已知f (x )=2x 2+px +q ,g (x )=x +4x 是定义在集合M =⎩⎨⎧⎭⎬⎫x ⎪⎪1≤x ≤52上的两个函数.对任意的x ∈M ,存在常数x 0∈M ,使得f (x )≥f (x 0),g (x )≥g (x 0),且f (x 0)=g (x 0).则函数f (x )在集合M 上的最大值为( )A.92 B .4 C .6D.892解析:利用导数可知函数g (x )=x +4x 在区间⎣⎡⎦⎤1,52上的最小值为4,最大值为5,对任意的x ∈M ,存在常数x 0∈M ,使得g (x )≥g (x 0),则g (x 0)=g (x )min =4,此时x 0=2,根据题意知,f (x )min =f (x 0)=4,根据题意知f (x )min =f (2)=4,即二次函数f (x )=2x 2+px +q 的顶点坐标为(2,4),因此-p4=2⇒p=-8,∴f (x )=2x 2-8x +q ,f (2)=2×22-2×8+q =q -8=4⇒q =12,∴f (x )=2x 2-8x +12=2(x -2)2+4,因此函数f (x )在集合M 上的最大值为f (x )max =f (1)=6,故选C.答案:C2.(2015年潍坊模拟)对任意实数a ,b 定义运算“⊗”:a ⊗b =⎩⎪⎨⎪⎧b ,a -b ≥1,a ,a -b <1.设f (x )=(x 2-1)⊗(4+x ),若函数y =f (x )+k 的图象与x 轴恰有三个不同交点,则k 的取值范围是( )A .(-2,1)B .[0,1]C .[-2,0)D .[-2,1)解析:当x 2-1-(4+x )≥1时,x ≥3或x ≤-2;当x 2-1-(4+x )<1时-2<x <3,故f (x )=⎩⎪⎨⎪⎧4+x ,x ≥3或x ≤-2x 2-1,-2<x <3,f (x )的图象如下图所示,y =f (x ) +k 的图象与x 轴有三个不同交点转化为y =f (x )与y =-k 有三个不同交点,由图可知-1<-k ≤2,故-2≤k <1.答案:D3.已知函数f (x )=x 2+ax +b (a ,b ∈R )的值域为[0,+∞),若关于x 的不等式f (x )<c 的解集为(m ,m +6),则实数c 的值为________.解析:∵f (x )=x 2+ax +b 的值域为[0,+∞),∴b -a 24=0,∴f (x )=x 2+ax +14a 2=⎝⎛⎭⎫x +12a 2.又∵f (x )<c 的解集为(m ,m +6), ∴m +m +6=-a ,∴m =-12a -3,∴c =f (m )=⎝⎛⎭⎫-12a -32+a ⎝⎛⎭⎫-12a -3+14a 2=9.答案:94.若二次函数f (x )=ax 2+bx +c (a ≠0)的图象和直线y =x 无交点,现有下列结论: ①方程f [f (x )]=x 一定没有实数根;②若a >0,则不等式f [f (x )]>x 对一切实数x 都成立; ③若a <0,则必存在实数x 0,使f [f (x 0)]>x 0;④函数g (x )=ax 2-bx +c (a ≠0)的图象与直线y =-x 一定没有交点, 其中正确的结论是________(写出所有正确结论的编号).解析:因为函数f (x )的图象与直线y =x 没有交点,所以f (x )>x (a >0)或f (x )<x (a <0)恒成立. 因为f [f (x )]>f (x )>x 或f [f (x )]<f (x )<x 恒成立,所以f [f (x )]=x 没有实数根,故①正确; 若a >0,则不等式f [f (x )]>f (x )>x 对一切实数x 都成立,故②正确;若a <0,则不等式f [f (x )]<x 对一切实数x 都成立,所以不存在实数x 0,使f [f (x 0)]>x 0,故③错误; 由函数g (x )=f (-x ),与f (x )的图象关于y 轴对称,所以g (x )和直线y =-x 也一定没有交点,故④正确.答案为①②④.答案:①②④5.(2015年聊城模拟)设二次函数f (x )=ax 2+bx (a ≠0)满足条件:①f (-1+x )=f (-1-x );②函数f (x )的图象与直线y =x 只有一个公共点.(1)求f (x )的解析式;(2)若不等式πf (x )>⎝⎛⎭⎫1π2-tx在t ∈[-2,2]时恒成立,求实数x 的取值范围. 解析:(1)∵由①知f (x )=ax 2+bx (a ≠0)的对称轴是直线x =-1,∴b =2a .∵函数f (x )的图象与直线y =x 只有一个公共点,∴方程组⎩⎪⎨⎪⎧y =ax 2+bx ,y =x 有且只有一个解,即ax 2+(b -1)x =0有两个相同的实根,∴Δ=(b -1)2=0,即b =1,∴a =12.∴f (x )=12x 2+x .(2)∵π>1,∴πf (x )>⎝⎛⎭⎫1π2-tx 等价于f (x )>tx -2,即12x 2+x >tx -2在t ∈[-2,2]时恒成立⇔函数g (t )=xt -⎝⎛⎭⎫12x 2+x +2<0在t ∈[-2,2]时恒成立, ∴⎩⎪⎨⎪⎧ g (2)<0,g (-2)<0,即⎩⎪⎨⎪⎧x 2-2x +4>0,x 2+6x +4>0,解得x <-3-5或x >-3+5,故实数x 的取值范围是(-∞,-3-5)∪(-3+5,+∞).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则f(x)在这个区间上为常数函数;若f
调函数.
2.若函数y=f(x)在区间(a,b)上单调递增,则f 山 东 减,则f ′(x)≤0,且在(a,b)的任意子区间,等号不恒成立. 金 太 3.使f ′(x)=0的离散的点不影响函数的单调性. 阳 4.f′(x0)=0是x0为f(x)的极值点的非充分非必要条件.例如,f(x)= 书 业 x3,f′(0)=0,但x=0不是极值点;又如 f(x)=|x|,x=0是它的极小值点, 有 限 但f′(0)不存在. 公 司 b)的任意子区间,等号不恒成立;若函数y=f(x)在区间(a,b)上单调递
例1 x-1 (2014 年高考山东卷)设函数 f(x)=aln x+ , 其中 a 为常数. x+1
(1)若 a=0,求曲线 y=f(x)在点(1,f(1))处的切线方程; (2)讨论函数 f(x)的单调性.
山 东 金 太 阳 书 业 有 限 公 司
菜 单
隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
山 东 金 太 阳 书 业 有 限 公 司
菜 单
隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
已知函数的单调性求参数的取值范围(高频研析) 考情分析 利用导数根据函数的单调性 (区间) 求参数的取值范围, 山 东 金 太 阳 书 业 有 限 公 司
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
二、利用导数研究函数的极值 1.函数的极大值 在包含x0的一个区间(a,b)内,函数y=f(x)在任何一点的函数值都 小于 x0点的函数值,称点x0为函数y=f(x)的极大值点,其函数值f(x0) _______ 为函数的极大值. 2.函数的极小值 在包含x0的一个区间(a,b)内,函数y=f(x)在任何一点的函数值都 大于 x0点的函数值,称点x0为函数y=f(x)的极小值点,其函数值f(x0) _______ 为函数的极小值.极大值与极小值统称为 极值 ,极大值点与极小值 点统称为极值点. 山 东 金 太 阳 书 业 有 限 公 司
菜 单 隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
1 1.函数 y=2x2-ln x 的单调递减区间为( A.(-1,1] C.[1,+∞) B.(0,1]
)
D.(0,+∞)
山 1 2 1 解析: 函数 y = 2 x - ln x 的定义域为 (0 ,+ ∞) , y′ = x - x = 东 金 太 x-1x+1 阳 ,令 y ′≤ 0 ,可得 0< x ≤ 1. x 书 业 答案:B 有 限 公 司
山 东 金 太 阳 书 业 有 限 公 司
菜 单
隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
规律方法
(1) 当f(x) 不含参数时,可以通过解不等式 f
′(x)>0(或 f
′(x)<0)直接得到单调递增(或递减)区间.
(2)导数法证明函数f(x)在(a,b)内的单调性的步骤: ①求f ′(x).
菜 单
隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
1.在某个区间(a,b)上,若f
增;若f
′(x)>0,则f(x)在这个区间上单调递
′(x)=0恒成立, ′(x)的符号不确定,则f(x)不是单 ′(x)≥0,且在(a,
′(x)<0,则f(x)在这个区间上单调递减;若f
(1)讨论f(x)的单调性; (2)若f(x)在区间(1,2)是增函数,求a的取值范围.
解析:(1)f ′(x)=3ax2+6x+3,f ′(x)=0的判别式Δ=36(1-a).
①若a≥1,则Δ≤0,因此f ′(x)≥0,且f ′(x)=0当且仅当a=1,x= -1.故此时f(x)在R上是增函数.
山 东 金 太 阳 书 业 有 限 公 司
是高考考查函数单调性的一个重要考向,常与函数、不等式、最值等
知识综合以解答题的形式出现,考查根据函数在某区间上单调递增(减) 或存在单调区间或为单调函数求参数的取值范围等问题.
菜 单
隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
角度一 已知函数在某区间上的单调递增(减),求参数的取值范围 1 1.若 f(x)=-2x2+bln(x+2)在(-1,+∞)上是减函数,则 b 的取值 范围是( ) B.(-1,+∞) D.(-∞,-1)
右侧图象在x轴上方的只有一个,故选A.
山 东 金 太 阳 书 业 有 限 公 司
菜 单
隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
4 .若函数 f(x) = x3 + ax2 + 3x - 9 在 x =- 3 时取得极值,则 a 等于 ( )
A.2
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
第十一节
最新考纲展示
导数在函数研究中的应用
1.了解函数单调性和导数的关系;能利用导数研究函数的单调性,
会求函数的单调区间(其中多项式函数一般不超过三次).
极小值(其中多项式函数一般不超过三次).
2.了解函数
在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、
f
1 ②当 a<-2时,Δ<0,g(x)<0, f ′(x)<0,函数 f(x)在(0,+∞)上单调递减.
菜 单 隐 藏
山 东 金 太 阳 书 业 有 限 公 司
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
1 ③当-2<a<0 时,Δ>0, 设 x1,x2(x1<x2)是函数 g(x)的两个零点, -a+1+ 2a+1 -a+1- 2a+1 则 x1= ,x2= . a a a+1- 2a+1 a2+2a+1- 2a+1 由于 x1= = >0, -a -a 所以 x∈(0,x1)时,g(x)<0,f ′(x)<0,函数 f(x)单调递减, x∈(x1,x2)时,g(x)>0,f ′(x)>0,函数 f(x)单调递增, x∈(x2,+∞)时,g(x)<0,f ′(x)<0,函数 f(x)单调递减.
菜 单 隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
2.函数y=f(x)的图象如图所示,则y=f ′(x)的图象可能是(
)
研考向 考 点 探 究 提素能 高 效 训 练
解析:据函数的图象易知,x<0时恒有 f ′(x)<0. 答案:D
菜 单 隐 藏
′(x)>0,当x>0时,恒有 f
山 东 金 太 阳 书 业 有 限 公 司
菜 单
隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
②由于 a≠0,故当 a<1 时,f ′(x)=0 有两个根 -1+ 1-a -1- 1-a x1= ,x2= . a a 若 0<a<1,则当 x∈(-∞,x2)或 x∈(x1,+∞)时,f ′(x)>0, 故 f(x)分别在(-∞,x2),(x1,+∞)是增函数;
②确认f ′(x)在(a,b)内的符号.
③得出结论:f ′(x)>0时为增函数;f ′(x)<0时为减函数.
山 东 金 太 阳 书 业 有 限 公 司
菜 单
隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
1.(2014年高考全国大纲卷)函数f(x)=ax3+3x2+3x(a≠0).
C.4 解析:f 答案:D
B.3
D.5 ′(x)=3x2+2ax+3,由题意知f ′(-3)=0,即3×(-3)2 山 东 金 太 阳 书 业 有 限 公 司
+2×(-3)a+3=0,解得a=5.
菜 单
隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
利用导数研究函数的单调性(师生共研)
山 东 金 太 阳 书 业 有 限 公 司
菜 单
隐 藏
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
综上可得: 当 a≥0 时,函数 f(x)在(0,+∞)上单调递增; 1 当 a≤-2时,函数 f(x)在(0,+∞)上单调递减;
1 -a+1+ 2a+1 , 当-2<a<0 时,f(x)在0, a -a+1- 2a+1 ,+∞上单调递减, a -a+1+ 2a+1 -a+1- 2a+1 上单调递增. 在 , a a
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
3.函数f(x)的定义域为开区间(a,b),导函数f
′(x)在(a,b)内的图
象如图所示,则函数f(x)在开区间(a,b)内有极小值点(
)
A .1 个 C.3个 解析:导函数f 答案:A
B.2个 D.4个 ′(x)的图象与x轴的交点中,左侧图象在x轴下方,
高考总复习 A 数学
抓主干 知 识 回 扣
研考向 考 点 探 究 提素能 高 效 训 练
(2)当 a>0,x>0 时,f ′(x)=3ax2+6x+3>0,故当 a>0 时,f(x) 在区间(1,2)是增函数. 当 a<0 时, f(x)在区间(1,2)是增函数当且仅当 f′(1)≥0 且 f′(2)≥0, 5 解得-4≤a<0. 5 综上,a 的取值范围是 -4,0 ∪(0,+∞).
