任务二十七单跨超静定梁的内力计算及内力图绘制
快速准确绘制单跨静定梁内力图

快速准确绘制单跨静定梁内力图摘要:单跨静定梁的内力图是弯曲杆件强度、刚度计算及做超静定结构内力图的基础。
本文作者从四方面阐述,提出快速准确绘制单跨静定梁内力图的方法。
关键词:内力图;校核;截面内力;图线类型;叠加法一、引言弯曲变形是工程中常见的一种基本变形,以弯曲变形为主要变形的杆件称为梁。
例如房屋建筑中,梁受到楼面荷载和梁自重的作用,将发生弯曲变形;其它如阳台挑梁、梁式桥的主梁等,都是以弯曲变形为主的构件。
在对梁进行强度和刚度计算时,通常要先画出剪力图和弯矩图,以便清楚地看出梁的各个截面上剪力和弯矩的大小、正负以及最值所在截面的位置。
而单跨静定梁的内力图是弯曲杆件强度、刚度计算及做超静定结构内力图的基础,如果这一部分没有学好,弯曲杆件的强度、刚度就无从计算,超静定结构的内力图也就很难做出。
在多年的教学实践中,根据学生信息反馈,本人探索、研究、试行,提出快速准确绘制单跨静定梁内力图的方法以供学生和同行商榷。
二、支座反力计算一定要校核能否正确画出单跨静定梁的内力图,支座反力的对错是关键。
怎样求支座反力是静力学的主要内容,这里不再赘述。
总的来说,支座反力由静力平衡方程解出,求解过程中,在正确的受力图上,列出独立并包含最少未知量的方程,尽量避免解方程组,求出支座反力后一定要用同解方程校核。
例如图1所示简支梁:反力计算正确。
在这个例子中,大多数学生在第二步计算RB 时就用方程,即RB=10+10×2-RA,如果RA 算错了,则RB 肯定也会跟着出错,所以在教学中建议学生尽量用力矩方程求支座反力,用投影方程校核,保证计算正确。
三、熟练掌握截面法求指定截面内力要做出结构的内力图,还必须能正确计算出控制截面的内力。
所谓控制截面指的是:杆端截面、集中力、集中力偶作用面、分布荷载集度变化处。
用截面法求这些截面的内力是做内力图的基础。
这一部分比较容易掌握,许多教材介绍的也比较少,但大部分学生在做内力图时又算不出特定截面的内力,因此,这一部分应投入比较多的精力。
《建筑力学与结构》课件——第十章 超静定结构的内力计算

力法计算超静定结构
(2) 建立力法方程
11X 1 12X 2 1F 0 21X 1 22X 2 2F 0
建筑力学与结构
(3) 计算系数和自由项
δ11 4a3 / 3EI
1F 5qa4 / 8EI
2024/11/13
δ22 a3 / 3EI δ12 δ21 a3 / 2EI 2F qa4 / 4EI
M AB
M1X1
MF
l 3 ql 8
1 ql 2 2
1 ql 2 8
取多余未知力作为基本未知量,通过基本结构,利用
计算静定结构的位移,达到求解超静定结构的方法,称为力
法。
2024/11/13
13
力法计算超静定结构
2.力法的典型方程
建筑力学与结构
1 11 X1 12 X 2 1F 0 2 21 X1 22 X 2 2F 0
2024/11/13
14
力法计算超静定结构
建筑力学与结构 n次超静定结构
δ11 X 1 δ12 X 2 δ1i X i δ1n X n 1F 0 δ21 X1 δ22 X 2 δ2i X i δ2n X n 2F 0
…………………………………………..……
δn1 X1 δn2 X 2 δni X i δnn X n nF 0
2024/11/13
7超静定次数的确定来自建筑力学与结构 3.去掉一个固定支座或切断一根梁式杆,相当于去掉三个约束,用 三个约束反力代替该约束作用。
2024/11/13
8
超静定次数的确定
建筑力学与结构 4.将一刚结点改为单铰联结或将一个固定支座改为固定铰支座,相 当于去掉一个约束,用一个约束反力代替该约束作用。
各杆的杆端弯矩表达式
任务二十七单跨超静定梁的内力计算及内力图绘制

… nn X n nP 0 n n1 X 1 n2 X 2 … n3 X 3 根据位移互等定理可知副系数
五、 力法典型方程
该方程称为力法的典型方程 按前面求静定结构位移的方法求得典型方程中的系数和自由 项后,即可解得多余力Xi。
然后可按照静定结构的分析方法求得原结构的全部反力和内力。 …
M 3是反对称图形。
由图形相乘可知:
13 31
23 32
M 1 M 3 ds 0 EI
M 2 M 3 ds 0 EI
七、对称性的利用
故力法典型方程简化为
11 x1 12 x2 1P 0 21 x1 22 x2 2 P 0
图的相应纵标叠加,即可绘出
静定结构无异。它可用来分析任何类型的超静定结构。
四、 超静定次数的确定与基本结构
超静定次数(degree of static indeterminacy ):多余联系的 数目或多余力的数目 确定超静定次数最直接的方法就是在原结构上去掉多余联系, 直至超静定结构变成静定结构,所去掉的多余联系的数目,就是原 结构的超静定次数。
结构力学基本知识
超静定结构的内力计算
项目十
任务二十七 单跨超静定梁的内力计算及内力图绘制
教学内容 一、超静定结构的概念 二、力法的基本原理 三、力法的基本方程 四、超静定次数的确定与基本结构 五、 力法典型方程 六、力法的计算步骤和举例 七、对称性的利用
一、超静定结构的概念
静定结构 (statically determinate structure) 支座反力和各截面的内力都可以用静力平衡条件唯一确定,是没 有多余联系的几何不变体系。 超静定结构 (statically indeterminate structure )
本章主要介绍了单跨静定梁和多跨静定梁的内力分析计算1

图10
图11
图12
3.3.2
多跨静定梁的内力计算
由层次图可见,作用于基本部分上的荷载,并不 影响附属部分,而作用于附属部分上的荷载,会以支 座反力的形式影响基本部分,因此在多跨静定梁的内 力计算时,应先计算高层次的附属部分,后计算低层 次的附属部分,然后将附属部分的支座反力反向作用 于基本部分,计算其内力,最后将各单跨梁的内力图 联成一体,即为多跨静定梁的内力图。
例6 试作出如图13(a)所示的四跨静定梁的弯矩图和剪 力图。
解:(1) 绘制层次图,如图13(b)所示。
(2) 计算支座反力,先从高层次的附属部分开 始,逐层向下计算:
① EF段:由静力平衡条件得
∑ME=0: ∑Y=0: YF×4-10×2=0 YF=5kN YE=20+10-YF=25kN
解:(1)求支座反力 先假设反力方向如图所示,以 整梁为研究对象: ∑X=0: XA-P=0 XA=P=4kN ∑MB=0: YA*l-q*l*0.5*l=0 YA=0.5ql =0.5×3×4kN=6kN ∑Y=0: YA+YB=ql YB=ql-VA =(3×4-6) kN=6kN
即:
q′l′=ql q=q′l′/l=q′/cosα
下面以承受沿水平向分布的均布荷载的斜梁为例进 行内力分析,如图(b)所示。 根据平衡条件,可以求出支座反力为: XA=0, YA=YB=1/2ql
则距A支座距离为x的截面上的内力可由取隔离体求出。 如图(c)所示,荷载qx、YA,在梁轴方向(t方向)的分 力分别为qxsinα、YAsinα;在梁法线方向(n方向) 的分力分别为:qxcosα、YAcosα。则由平衡条件得: ∑T=0: YAsinα-qxsinα+NX=0 NX=(qx-1/2ql)sinα ∑N=0: YAcosα-qxcosα-QX=0 QX=(1/2ql-qx)cosα ∑MX=0: YAx-qx· x/2-MX=0 MX=1/2qx(1-x)
超静定结构自内力的计算

A
B
l
以上两过程的叠加
B
MBA
A
1 3i
M
AB
1 6i
M BA
l
A B
我们的任务是要由杆端位移求 杆端力,变换上面的式子可得:
B
1 6i
M AB
1 3i
M BA
l
M M
AB BA
4i A 2i A
2i B 4i B
6i 6i
l l
(1)
QAB
QBA
6i l
A
6i l
B
12i l2
θB
X2
Δ
X1=1
1
M1
1/l
1
M2
X2=1 1/l
X1
4i
A
2i B
6i l
X2
2i
A
4i B
6i l
可以将上式写成矩阵形式
M AB
4i
M
BA
2i
2i 4i
6i
l 6i
l
A B
QAB
6i l
6i l
12i l 2
1
4
2
3
几种不同远端支座的刚度方程
1
1
X2 1
0
0
X3 1
0 2C a
3C
0
支座移动时,结构中的位移以及 位移条件的校核公式如下:
i
Mi Mds EI
iC
Mi Mds EI
Ri ci
制造误差引起的内力计算: AB杆造长了1cm,如何作弯矩图?
A
10m 10m
X3 X1 X2
五.温度变化时超静定结构的计算
土木工程力学(本)综合练习2

说明:为了帮助大家复习,这份辅导材料一共有两部分内容。
第一部分为课程的考核说明,大家看完以后能明确考试重点和要求。
第二部分为综合练习和答案,供大家复习自测用。
土木工程力学(本)课程考核说明一、课程的性质土木工程力学(本)是中央广播电视大学土木工程专业的一门必修课,课程为5学分,开设一学期。
通过本课程的学习,使学生了解各类杆件结构的受力性能,掌握分析计算杆件结构的基本概念、基本原理和基本方法,为后续有关专业课程的学习及进行结构设计打下坚实的力学基础。
二、关于课程考核的有关说明1.考核对象中央广播电视大学土木工程(专科起点本科)专业的学生。
2.考核方式本课程采用形成性考核与终结性考试相结合的方式。
总成绩为100分,及格为60分。
形成性考核占总成绩的30%;终结性考试占总成绩的70%。
形成性考核由中央电大统一组织编写形成性考核册。
形成性考核册由4次形成性考核作业组成。
学员应按照教学进度及时完成各次计分作业。
每次形成性考核作业满分为100分,由教师按照学员完成作业的情况评定成绩,并按4次作业的平均成绩计算学员的形成性考核成绩。
学员形成性考核完成情况由中央电大和省电大分阶段检查。
终结性考试为半开卷笔试,由中央电大统一命题,统一组织考试。
3.命题依据本考核说明是依据2007年7月审定的土木工程力学(本)课程教学大纲编写的。
本课程所采用的文字教材为贾影主编,中央广播电视大学出版社出版的《土木工程力学(本)》教材。
本考核说明及本课程所采用的文字教材是课程命题的依据。
4.考试要求本课程考试重点是考核学员对结构分析的基本概念,基本理论和基本方法的掌握情况。
本考核说明对各章都规定了考核要求,按了解、理解和掌握三个层次说明学员应达到的考核标准。
了解是最低层次的要求,凡是属于了解的部分内容,要求对它们的概念、理论及计算方法有基本的认识。
理解是较高层次的要求,凡是属于理解的部分内容,要求在理解的基础上,能运用这一部分知识对结构的受力和变形有一正确的分析和判断。
单跨静定梁的内力计算

单跨静定梁的内力计算单跨静定梁的内力计算是结构工程中重要的计算内容之一。
静定梁是指在受力状态下,其内力可以通过静力学原理直接计算得出的梁结构。
而单跨静定梁是指只有一个支座的静定梁,是静力学中最简单的结构之一。
在计算单跨静定梁的内力时,首先需要明确梁的受力情况。
在单跨静定梁中,通常会受到集中力、均布载荷或者集中力和均布载荷的组合作用。
根据力的平衡条件和梁的几何特性,可以计算出梁的内力,包括弯矩和剪力。
在计算单跨静定梁的内力时,可以采用梁的截面法。
根据力的平衡条件,可以先计算出支座的水平力和垂直力,然后通过力和力矩的平衡条件计算出梁的内力。
在计算弯矩和剪力时,需要根据梁的几何形状和受力情况,采用力的平衡和力矩平衡的原理进行计算。
在计算单跨静定梁的内力时,需要注意以下几点:1. 确定梁的受力情况:包括集中力、均布载荷的大小和作用位置等。
2. 绘制梁的受力图:根据受力情况,绘制出梁的受力图,明确受力的方向和大小。
3. 采用力的平衡和力矩平衡的原理计算内力:根据力的平衡和力矩平衡的原理,计算出梁的内力,包括弯矩和剪力。
4. 考虑梁的内力图:根据计算出的内力,绘制出梁的内力图,明确各处的内力分布情况。
通过以上步骤,可以准确计算出单跨静定梁的内力,为梁的设计和施工提供重要的参考依据。
在实际工程中,计算出的内力可以用来确定梁的截面尺寸和材料的选择,确保梁的受力性能符合设计要求,保证梁的安全性和稳定性。
同时,计算出的内力也可以用来指导梁的施工和监测,确保梁的受力状态符合设计要求,提高梁的使用性能和寿命。
总的来说,单跨静定梁的内力计算是结构工程中的基础计算内容,通过合理的计算方法和步骤,可以准确计算出梁的内力,为梁的设计和施工提供重要的参考依据,确保梁的受力性能符合设计要求,提高梁的使用性能和寿命。
希望以上内容能够对您的工作和学习有所帮助。
简捷法绘制单跨静定梁的内力图分析.pdf

简捷法绘制单跨静定梁的内力图分析摘要:正确计算截面内力,快速绘制静定梁内力图十分重要,阐述了用简捷法作单跨静定梁的内力图的基本条件,并举例说明了内力图在集中力、集中力偶处的特点和规律,还强调了弯矩图中抛物线的开口方向以及控制截面的选择方法。
关键词:简捷法;剪力;剪力图;弯矩;弯矩图 梁的内力图绘制的目的是用图示方法形象地表示出剪力Q、弯矩M 沿梁长变化的情况,绘制梁的内力图是材料力学教材中的一个重点和难点内容,熟练、正确地绘制内力图是材料力学的一项基本功,也是后续课程结构力学的基础。
绘制梁内力图的方法有静力法、简捷法和叠加法,其中简捷法是利用剪力、弯矩和荷载集度之间的微分关系作图的一种简便方法,通常是用来确定梁的危险截面作为强度计算的依据,因此熟练掌握简捷法作梁的内力图是十分必要的。
1 简捷法绘制单跨静定梁的内力图的基本要求 (1)能快速准确地计算单跨梁的支座反力(悬臂梁除外) 支座反力的正确与否直接影响内力的计算,因此在静力学的学习过程中要打好基础。
(2)能用简便方法求解指定截面的内力 1.1 求剪力的简便方法 某截面的剪力等于该截面一侧所有外力在截面上投影的代数和,即Q= Y 左侧外力 (或) Y 右侧外力 代数和中的符号为截面左侧向上的外力(或右侧向下的外力)使截面产生正的剪力,反之产生负剪力。
(即外力左上右下为正) 1.2 求弯矩的简便方法 某截面的弯矩等于该截面一侧所有外力对截面形心力矩的代数和,即M= M c 左侧外力 (或 M c 右侧外力 ) 代数和中的符号为截面的左边绕截面顺时针转的力矩或力偶矩(或右边绕截面逆时针转的力矩或力偶矩)使截面产生正的弯矩,反之产生负弯矩。
(即外力矩或力偶矩左顺右逆为正) 1.3 举例说明:求图1 中1-1 截面的剪力和弯矩 解:取左侧为研究对象,根据简便方法有: Q 1=25-5×4=5k N M 1=25×2-5×4×2=10kN•m 验证:取右侧为研究对象,根据简便方法有: Q=15-10=5kN M 1=10×4-15×2=10kN•m 1.4 能将梁正确分段,根据各段梁上的荷载情况,判断剪力图和弯矩图的形状,寻找控制面,算出各控制面的Q 和M 弯矩、剪力与荷载集度之间的微分关系如下: dM(x)dx=Q(x) dQ(x)dx=q(x) d 2M(x)dx 2=q(x) 利用弯矩、剪力与荷载集度之间的微分关系及其几何意义,可总结出下列一些规律,用来校核或绘制梁的剪力图和弯矩图,其规律如下表所示: 注意:根据函数图线的几何意义,当q>0(向上)时,弯矩图为开口向下的二次抛物线;反之q<0(向下)一时,弯矩图为开口向上的二次抛物线,即抛物线的凹性和凸性和均布荷载的方向保持一致。
建筑力学基础知识—单跨静定梁内力求解

q
A FAy
C
3m
B
3m
FB
解(1)计算支座反力(以整个梁为研究对象)
MAF 0 MBF 0
FB
6 46
6 2
0
FA y 6
4 62 2
0
(2)计算截面C处的剪力FQC、弯矩MC
Y 0 MC F 0
FQC FAy 43 0
MC
FA y
3
43
3 2
0
FQC 0KN M C 18KN m
2.探索研究——单跨静定梁的内力求解
利用截面法计算指定截面的剪力和弯矩的步骤
01 计算支座反力
用假想的截面在欲 求内力处将梁截成 两段,取其中一段 为研究对象。
02
03
画出研究对象的内力 图。截面上的剪力和 弯矩均按正方向假设
建立平衡方程, 求解剪力和弯矩
04
2.探索研究——单跨静定梁的内力求解
例1 简支梁如图所示,
a
F b
已知F =30kN,a=2m,b=3m,
A
试求截面1—1(距A支座1.5m)上的剪力和弯矩。
1 1C
B FB
FAy
解 (1)计算支座反力(以整个梁为研究对象)
MAF 0
FB 12 KN
l
MBF 0
FAy 18 KN
(2)计算截面的内力(取左段为研究对象)
Y 0 M1F 0
FAy FQ1 0 M1 FAy 1.5 0
P=4KN
Y 0 P FQ1 0
FQ1 4KN
M1(Fi ) 0 P 1 M1 0
M1 4KN m
M1 1 FQ1
图(b)
2.探索研究——单跨静定梁的内力求解
弯曲内力—单跨静定梁的内力图(材料力学课件)

FA
FB
ql 2
()
(2)列剪力方程和弯矩方程
FS (x)
FA
qx
1 2
ql
qx
(0< x l)
M (x)
FA x
1 2
qx 2
1 2
qlx
1 2
qx 2
(0 x l)
(3) 绘制剪力图和弯矩图
两端支座处: 梁跨中:
ql FSmax 2
M max
ql 2 8
q
A C
x
FA
l
1 ql
2
1 ql 2 8
剪力为常数,FS图为
平直线;弯矩为一次
FaFS图FS图(b) (b) 函数,M图为斜直线。
l
Fa
M图
l (c)
M图 (c)
集中力F处,剪力图 发生突变,弯矩图
有尖角。
单跨静定梁的内力图
2.单一荷载下静定梁的内力图
A
解:(1)求支座约束力
FA
由梁的整体平衡条件可求得:
M l
e
()
FA
(2)列剪力方程和弯矩方程
单跨静定梁的内力图
1. 剪力方程和弯矩方程 为了形象地表示剪力和弯矩沿梁轴线变化的规律,以沿梁轴线的横坐标x表示梁横
截面的位置,以纵坐标表示相应横截面上的剪力或弯矩,按剪力方程和弯矩方程绘出 图形,这种图形分别称为剪力图和弯矩图,即梁的内力图。
剪力方程
FS FS (x)
正剪力画在x轴上方负 剪力画在x轴下方,并在
图中标明“ ”、x轴下方负 剪力画在x轴上方,并在
图中标明“ ”、“ ”。
单跨静定梁的内力图
2.单一荷载下静定梁的内力图
单跨静定梁的内力图(1)PPT课件

.
3
单跨静定梁的内力图
❖ 2.剪力图和弯矩图
❖ 为了能直观地观察出梁各截面上的剪力 和弯矩随截面位置变化的规律,可仿照轴力 图的作法绘出剪力图和弯矩图。绘图时以平 行梁轴线的x为横坐标,表示各横截面的位置, 以FQ或M为纵坐标,表示相应横截面上的剪 力和弯矩,规定FQ轴向上为正,M轴向下为 正。
.
.
7
例4.8 试作图示简支梁在集中荷载
a 1 Fb 2
作用下的剪力图和弯矩图。
解:1. 求支座反力 FA=b/l FP FB=a/l FP
A x
C l
B
1 F2
2.用截面法计算x确定的截 面的内力
A FA
x
x
B FB
AC:
FQ(x)
= FA (0<
= X
FPb/l
< a)
M(X) = FAX= FPb/l x
FA
(0< X < l ) 0.5ql
x M(X)
FQ FQ(x)
3.作内力图
(剪力图)
剪力图:一条斜直线
B FB
x 0.5ql
x
弯矩图:二次抛物线
M
ql 2/8 (弯矩图)
.
6
写出梁的内力方程,作内力图。并指出最大内力值以及
q
解
它们所在的截面。
Ax l
B 1.用截面法计算x确定的截面
q MB
Ax
.
10
M
FB
CB
M(X) M
M(X)
FA
FQ(x)
FQ
FQ(x) x
BC: FQ(x) =(L-<FAX+F<B=30/2 l )
M/l
学习任务4 多跨静定梁的内力计算与内力图绘制

5.2 多跨静定梁的内力计算与内力图绘制
• 在任意荷载作用下,用静力学平衡方程可以 求出全部约束力和内力的结构称为静定结构 ;仅用静力学平衡方程不能求出全部约束力 和内力的结构称为超静定结构。
• 从几何组成方面来讲:没有多余联系(约束 )的几何不变体系称为静定结构;具有多余 联系(约束)的几何不变体系称为超静定结 构。
F1 A
F2
B
C
F1 A
F1 A
F1 A
F2 C B
F2
C F2 C
F3 E
D
F3 E D
F4
F F4
F
层 G次
图
G
F3 E
F4 G
F
F3
E
F4
G F
二、多跨静定梁的内力计算
10kN
10kN
A
BC
60° D
2m 4m
F1 A
2m 2m
B C
2m
F2 D
4kN/m
4kN
A
DE
F
4m C 2mBiblioteka 2m 2mq ABA
q
B
C
D
一、 多跨静定梁的组成
(由两段及以上构件组成的梁称为多跨梁)
• 基本部分:直接与地基构成 几何不变体系,能够单独承 担荷载的部分。
• 附属部分:须依靠基本部分 才能成为几何不变的部分
• 层次图:基本部分画在第一 层,附属部分画在第二层
……
F1
F2
A
BC
D
F1 A
F2
C B
D
层次图
作图示多跨梁 的内力图。
大谢家谢辛欣苦赏!了!
Thanks
国家开放大学电大《力学》题库
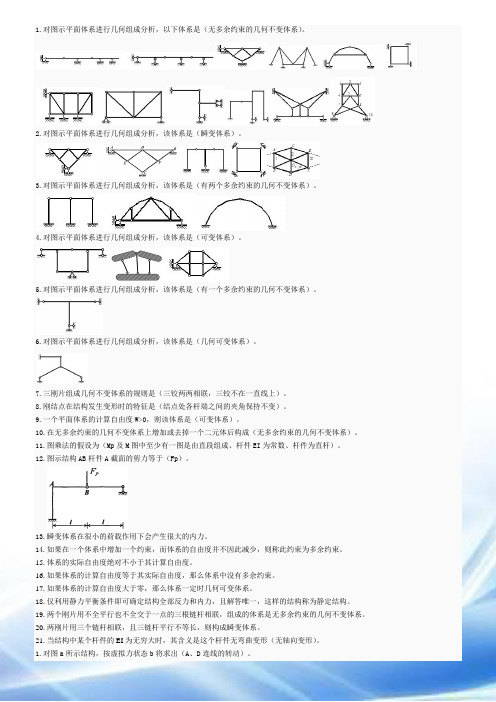
1.对图示平面体系进行几何组成分析,以下体系是(无多余约束的几何不变体系)。
2.对图示平面体系进行几何组成分析,该体系是(瞬变体系)。
3.对图示平面体系进行几何组成分析,该体系是(有两个多余约束的几何不变体系)。
4.对图示平面体系进行几何组成分析,该体系是(可变体系)。
5.对图示平面体系进行几何组成分析,该体系是(有一个多余约束的几何不变体系)。
6.对图示平面体系进行几何组成分析,该体系是(几何可变体系)。
7.三刚片组成几何不变体系的规则是(三铰两两相联,三铰不在一直线上)。
8.刚结点在结构发生变形时的特征是(结点处各杆端之间的夹角保持不变)。
9.一个平面体系的计算自由度W>0,则该体系是(可变体系)。
10.在无多余约束的几何不变体系上增加或去掉一个二元体后构成(无多余约束的几何不变体系)。
11.图乘法的假设为(Mp及M图中至少有一图是由直段组成、杆件EI为常数、杆件为直杆)。
12.图示结构AB杆件A截面的剪力等于(Fp)。
13.瞬变体系在很小的荷载作用下会产生很大的内力。
14.如果在一个体系中增加一个约束,而体系的自由度并不因此减少,则称此约束为多余约束。
15.体系的实际自由度绝对不小于其计算自由度。
16.如果体系的计算自由度等于其实际自由度,那么体系中没有多余约束。
17.如果体系的计算自由度大于零,那么体系一定时几何可变体系。
18.仅利用静力平衡条件即可确定结构全部反力和内力,且解答唯一,这样的结构称为静定结构。
19.两个刚片用不全平行也不全交于一点的三根链杆相联,组成的体系是无多余约束的几何不变体系。
20.两刚片用三个链杆相联,且三链杆平行不等长,则构成瞬变体系。
21.当结构中某个杆件的EI为无穷大时,其含义是这个杆件无弯曲变形(无轴向变形)。
1.对图a所示结构,按虚拟力状态b将求出(A、D连线的转动)。
2.图示虚拟状态是为了求(A截面转角)。
3.图示为刚架的虚设力状态,按此力状态及位移计算公式可求出()。
杆件内力及内力图的绘制(梁的内力)(1)

(2) 计算1-1截面的内力
利用计算剪力和弯矩的规律,由1-1截面左侧外力计 算 Q1=RA=-2000N(负剪力) M1=RA×200=-400N· m(负弯矩) (3) 计算2-2截面的内力 利用计算剪力和弯矩的规律,由2-2截面的右侧外力 计算
Q2=q×0.4-RB=-4000N(负剪力)
【例 2】外伸梁受载荷作用如图12(a)所示。图中截面1-1 是指从右侧无限接近于支座B。试求截面1-1和截面2-2的 剪力和弯矩。 【解】(1) 求支座反力
以整梁为研究对象,受力图如图12(a)。由平衡方程 求解支座反力。 ∑mB(F)=0,RC· a-P×2a-Me=0 RC=(2Pa+Me)/a=(2Pa+Pa)/a=3P ∑mC(F)=0,-RB· a-Pa-Me=0 RB=(-Pa-Me)/a=(-Pa-Pa)/a=-2P
(1) 梁内任一截面上的剪力,其大小等于该截面 左侧(或右侧)梁上所有外力的代数和;梁内任一截面 的弯矩,其大小等于该截面左侧(右侧)梁上所有外 力对于该截面形心之矩的代数和。
(2) 外力对内力的符号规则 左上右下,剪力为正;左顺右逆,弯矩为正。 (3) 代数和的正负,就是剪力或弯矩的正负。
截面m-m上剪力Q的大小和方向以及弯矩M的 大小和转向,可由右段梁的平衡方程确定
∑Fy=0,NB-Q=0 Q=NB ∑mC(F)= 0,NB· x-M=0
M=NB· x
根据作用力和反作用力的关系,分别以梁的左 段和右段为研究对象求出的Q和M,大小是相等的, 而方向或转向是相反的(图8(b)、(c))。
(3) 求截面2-2的内力
用2-2截面将梁假想地截开,取右段为研究对象,受 力图如图12(c)。由平衡方程求Q2和M2 ∑Fy=0,Q2-P=0 Q2=P(正剪力) ∑m2(F)= 0,-M2-P· a/2=0 M2=-Pa/2 (负弯矩)
浅谈单跨静定梁内力图的绘制要点

浅谈单跨静定梁内力图的绘制要点作者:殷礼君程龙来源:《卷宗》2015年第06期摘要:静定梁由于其设计简单,施工方便而在实际工程中被广泛应用。
同时它也是组成各种结构的基本构件之一,它的受力分析是各种结构受力分析的基础。
设计静定梁的前提是知道它的内力分布情况,而内力图则可以直观明了的显示出梁的内力分布情况,为梁的设计施工提供依据。
本文对静定梁的内力图绘制方法和注意事项进行了探讨,希望能给读者带来帮助。
关键词:静定梁;内力计算;内力图绘制1 单跨静定梁的内力计算求出梁的内力是绘制其内力图的前提,而求出静定梁的支座反力是求其内力的基础。
所有单跨静定梁都是由梁和地基按两刚片规则组成的静定结构,所以其支座反力都只有三个,取整个梁为隔离体由梁在何在作用下,任一截面上一般有内力分量:轴力,剪力和弯矩。
在计算内力前对内力正负号作以下规定:轴力拉为正压为负;剪力以使该截面所在隔离体有顺时针转动趋势为正,反之为负;弯矩以使梁的下册纤维受拉为正,反之为负。
截面法是计算内力的基本方法,将结构沿拟求内力的截面截开,取截面任一侧为隔离体利用平衡条件(1.1),计算所求内力。
由截面法的运算可知:轴力等于截面一侧所有外力(包括荷载、反力)沿截面法线方向的投影代数和。
剪力等于截面一侧所有外力沿截面方向的投影代数和。
弯矩等于截面一侧所有外力对截面形心的力矩代数和。
2 内力图的绘制2.1 内力图的绘制方法内力图是表示各截面内力分布状况的图形,通常以平行于杆轴线的坐标表示截面的位置,以垂直于轴线的坐标表示内力的大小。
内力图绘制的基本方法:先求出结构的内力方程式,即用截面法写出内力与截面位置坐标x之间的关系式,然后根据内力方程式沿着杆轴画出内力图。
对于结构或外荷载比较复杂的情况,在内力图绘制过程中还可利用叠加法进行绘制。
作图时,应标明图名、单位、数值;对轴力图和剪力图还应标明正负,弯矩图可不标正负,但必须画在杆件受拉一侧。
2.2 荷载与内力间的微关系在荷载均匀分布的直梁中,取出一微段dx为隔离体,如下图所示,由平衡条件并略去高阶微量,可得:在集中荷载作用处,取微段dx为隔离体,如下图所示,可得:从这些关系式可以知道:轴力图上某点处切线斜率等于该点处轴向荷载大小,但符号相反;剪力图上某点处切线斜率等于该点处横向荷载大小,但符号相反;弯矩图上某点处切线斜率等于该点处的剪力。
《单跨超静定梁》PPT课件

作用所产生的杆端弯矩称为固端弯矩,相应的剪力称
为固端剪力。用MAB、MBA、QAB、QBA表示。2Biblioteka 、讨论几种情况 例1:解:
3
11 X1 12 X 2 1P 0 21 X1 22 X 2 2P 0
4
5
6
7
超静定结构与静定结构的对比:
8
例2: 解:
9
11 X1 12 X 2 1C 0 21 X1 22 X 2 2C 0
1
二、杆端力的表示方法和正负号的规定
1、弯矩:MAB表示AB杆A端的弯矩。对杆端而言,顺 时针为正,逆时针为负;对结点而言,顺时针为负, 逆时针为正。
2、剪力:QAB表示AB杆A端的剪力。正负号规定同 “材力”。
A MAB0
P
B MBA0
P A
QAB0
B QBA0
3、固端弯矩、固端剪力:单跨超静定梁仅由于荷载
10
皮肌炎图片——皮肌炎的症状表现
• 皮肌炎是一种引起皮肤、肌肉、 心、肺、肾等多脏器严重损害的, 全身性疾病,而且不少患者同时 伴有恶性肿瘤。它的1症状表现如 下:
• 1、早期皮肌炎患者,还往往伴 有全身不适症状,如-全身肌肉酸 痛,软弱无力,上楼梯时感觉两 腿费力;举手梳理头发时,举高 手臂很吃力;抬头转头缓慢而费 力。
12
当 A时 1,
M BA
2
EI l
2i
M AB
4
EI l
4i
i---线刚度.
13
见P111表
例3:
14
见P111表
例4:
15
见P111表
例5:
16
17
例6:
18
例7:
等截面单跨超静定梁的内力计算

B M图 B
X1=1
M图 11 X1 A
1 1 2 l 11 l 1 EI 2 3 3EI
FQ图
3EI X1 A 3i A ( ) l
2) A l A
i l
B
Δ
A 3i M AB l
B M图
M图
11 X1
l3 11 3EI
l Fl 2 X1 0 3EI 16 EI
X1
3Fl 16
M M1 X 1 M p
3 Fl 16
F
B
5 Fl 32
11 F 16
A
A
+
B
5 F 16
M 图
FQ 图
载常数图:
3l 16
1
B
5l 32 5 16
A
11 16
q
2)
A
B
A
X1
基本体系
B
l
基本方程: A 1
11 X 1 1 p 0
Fl 8
F
A
Fl 8
1 F 2
B
A
+
B
1 F 2
Fl 8
载常数图:
M 图
l 8
FQ 图
1
l 8
A
1 2
B
l 8
1 2
M 图
q
4)
A
B
A
X1
基本体系 A X1=1
X2
B
l
基本方程: 11 X 1 12 X 2 1 p 0
B
21 X 1 22 X 2 2 p 0
Mp图
1 l 1 l ql 2 ql 2 2l ql 3 11 1 l 1 1 p EI EI EI 2 2 8 3 3EI
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因此可解出多余力X1
X1
1P
11
ql 4 8 EI
l3 3EI
3ql 8
三、 力法的基本方程
多余力X1 求出后,其余所有反力和内力都可用静力平衡条件确定。超 静定结构的最后弯矩图M,可利用已经绘出的 M 1 和 M 图按叠加原理绘出, P 即
四、 超静定次数的确定与基本结构
从超静定结构上去掉多余联系的方式有以下几种:
1. 去掉支座处的支杆或切断一根链杆,相当下去掉一个联系,
如图 (a) (b) 所示;
四、 超静定次数的确定与基本结构
2. 撤去一个铰支座或撤去一个单铰,相当于去掉二个联系,如 图 (c) (d) 所示;
四、 超静定次数的确定与基本结构
用来确定X1的条件是:基本结构在原有荷载和多余力共同
作用下,在去掉多余联系处的位移应与原结构中相应的位移相 等。 为了唯一确定超静定结构的反力和内力,必须同时考虑静 力平衡条件和变形协调条件
1 11 1P 0
三、 力法的基本方程
若以 11表示X1为单位力(即 成
用点沿X1方向产生的位移,则有 11=
M M 1 X1 M P
X1 M 以 M 倍,再与 P
图如图 (c)所示。 综上所述可知,力法是以多余力作为基本未知量,取去掉多 余联系后的静定结构为基本结构,并根据去掉多余联系处的已知 位移条件建立基本方程,将多余力首先求出,而以后的计算即与 应用上式绘制弯矩图时,可将 M 1 图的纵标乘
X 1=1)时,基本结构在X1作
11X1,于是上式可写
11 X 1 1P 0
X1 - 1P
11
式(a)就是根据原结构的变形条件建立的用以确定X1的变 形协调方程,即为力法基本方程。
三、 力法的基本方程
为了具体计算位移 δ11和△
1p,分别绘出基本结构的单
位弯矩图M1和荷载弯矩图Mp(由荷载q产生),分别如图 (a)、 (b) 所示 :
支座反力和各截面的内力不能完全由静力平衡条件唯一确定,是有
多余联系的几何不变体系。
一、超静定结构的概念
静定刚架
超静定刚架
有多余联系是超静定结构区别于静定结构的基本特性
二、力法的基本原理
1. 力法(force method)的基本结构
去掉多余联系用多余未知力来代替后得到的静定结构 称为按力法计算的基本结构。
二、
力法的基本原理
现在要设法解出基本结构的多余力X1,一旦求得多余
力X1,就可在基本结构上用静力平衡条件求出原结构的所 有反力和内力。因此多余力是最基本的未知力,又可称为
力法的基本未知量。但是这个基本未知量X1不能用静力平
衡条件求出,而必须根据基本结构的受力和变形与原结构 相同的原则来确定。
三、 力法的基本方程
模块三结构力学Leabharlann 本知识超静定结构的内力计算
项目十
任务二十七 单跨超静定梁的内力计算及内力图绘制
教学重点 超静定结构的概念、力法的基本原理、力法的基本方程、超静定 次数的确定与基本结构、力法典型方程、力法的计算步骤
教学难点 力法的基本方程、超静定次数的确定与基本结构、力法典型 方程、力法的计算
模块三
3. 切断一根梁式杆或去掉一个固定支座,相当于去掉
三个联系,如图 (e) 所示;
四、 超静定次数的确定与基本结构
4. 将一刚结点改为单铰联结成或将一个固定支座改为固定铰支 座,相当于去掉一个联系,如图 (f) 所示。
对于同一个超静定结构,可用各种不同的方式去掉多余联 系而得到不同的静定结构。因此在力法计算中,同一结构的基 本结构可有各种不同的形式。但应注意,去掉多余联系后基本 结构必须是几何不变的。为了保证基本结构的几何不变性,结 构中的某些联系是不能去掉的。
四、 超静定次数的确定与基本结构
图 (a)所示超静定结构属内部超静定结构,因此,只能在结 构内部去掉多余联系得基本结构,如 (b)所示。
四、 超静定次数的确定与基本结构
对于具有多个框格的结构,按框格的数目来确定超静定的次数 是较方便的。一个封闭的无铰框格,其超静定次数等于3,故当一个 结构有n个封闭无铰框格时,其超静定次数等于3n。如图 (a)所示结 构的超静定次数等于3x8=24。当结构的某些结点为铰接时,则一个 单铰减少一个超静定次数。图 (b)所示结构的超静定次数等于 3x8-5=19。
四、 超静定次数的确定与基本结构
如图 (a)所示刚架,具有一个多余联系。若将横梁某处改为铰 接,即相当于去掉一个联系得到图 (b)所示静定结构;当去掉 B支
座的水平链杆则得到图 (c)所示静定结构,它们都可作为基本结构。
但是,若去掉 A支座的竖向链杆或 B支座的竖向链杆,即成瞬变体 系[图 (d)]所示,显然是不允许的,当然也就不能作为基本结构。
M
三、 力法的基本方程
用图乘法计算这些位移
11
1P
M1M1 1 l 2 2l l3 dx EI EI 2 3 3EI
M 1M P 1 1 ql 2 3l ql 4 dx l EI EI 3 2 4 8EI
结构力学基本知识
超静定结构的内力计算
项目十
任务二十七 单跨超静定梁的内力计算及内力图绘制
教学内容 一、超静定结构的概念 二、力法的基本原理 三、力法的基本方程 四、超静定次数的确定与基本结构 五、 力法典型方程 六、力法的计算步骤和举例 七、对称性的利用
一、超静定结构的概念
静定结构 (statically determinate structure) 支座反力和各截面的内力都可以用静力平衡条件唯一确定,是没 有多余联系的几何不变体系。 超静定结构 (statically indeterminate structure )
图的相应纵标叠加,即可绘出
静定结构无异。它可用来分析任何类型的超静定结构。
四、 超静定次数的确定与基本结构
超静定次数(degree of static indeterminacy ):多余联系的 数目或多余力的数目 确定超静定次数最直接的方法就是在原结构上去掉多余联系, 直至超静定结构变成静定结构,所去掉的多余联系的数目,就是原 结构的超静定次数。
