浅谈如何求几何体异面上两点间最短距离(1)

立体图形中的距离最短问题

立体图形中的距离最短问题根据新课程标准，培养学生的空间观念主要表现在：“能由实物的形状想像出几何图形，由几何图形想像出实物的形状，进行几何体与其三视图、展开图之间的转化；能根据条件做出立体模型或画出图形；……”。

空间图形的建立需要有一个循序渐进的过程，从小学到初中，再到高中，渐渐加强，作为一个初、高中的知识衔接模块，让学生在初中阶段能理解空间图形，特别是空间图形的展开图，夯实基础，显得尤为重要。

立体图形上点点之间的距离最短问题，通过把立体图形转化为平面图形，然后再运用“两点之间，线段最短”来解决。

解决这一类距离最短的问题，可以利用轴对称或平移或旋转等几何图形的变换，把两条或多条线段和最短的问题转化为平面上两点之间的距离最短的问题来解决。

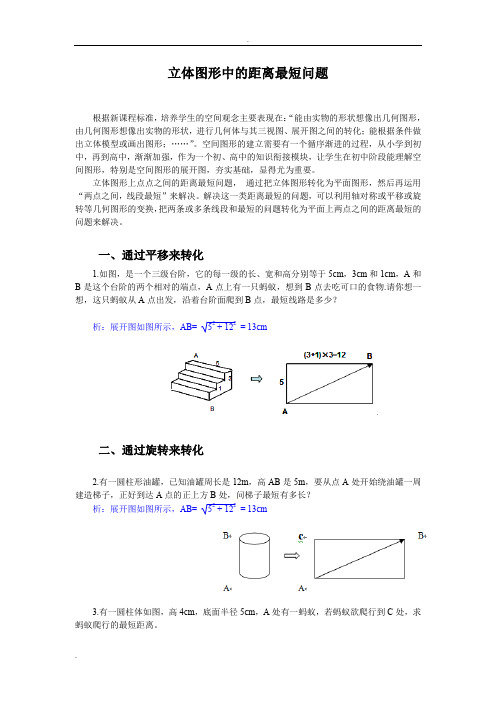
一、通过平移来转化1.如图，是一个三级台阶，它的每一级的长、宽和高分别等于5cm，3cm和1cm，A和B是这个台阶的两个相对的端点，A点上有一只蚂蚁，想到B点去吃可口的食物.请你想一想，这只蚂蚁从A点出发，沿着台阶面爬到B点，最短线路是多少？析：展开图如图所示，AB= 52 + 122= 13cm二、通过旋转来转化2.有一圆柱形油罐，已知油罐周长是12m，高AB是5m，要从点A处开始绕油罐一周建造梯子，正好到达A点的正上方B处，问梯子最短有多长？析：展开图如图所示，AB= 52 + 122= 13cm3.有一圆柱体如图，高4cm，底面半径5cm，A处有一蚂蚁，若蚂蚁欲爬行到C处，求蚂蚁爬行的最短距离。

AB = 4，BC 为底面周长的一半即BC = 5πAC = AB 2 + BC 2 = 42 + (5π)2= 16 + 25π24.葛藤是一种刁钻的植物，它的腰杆不硬，为了争夺雨露阳光，常常绕着树干盘旋而上，它还有一手绝招，就是它绕树盘升的路线总是沿最短路线--螺旋前进的，难道植物也懂数学？通过阅读以上信息，解决下列问题：（1）如果树干的周长（即图中圆柱体的底面周长）为30cm ，绕一圈升高（即圆柱的高）40cm ，则它爬行一圈的路程是多少？（2）如果树干的周长为80cm ，绕一圈爬行100cm ，它爬行10圈到达树顶，则树干高多少？（1）如图，⊙O 的周长为30cm ，即AC=30cm ，高是40cm ，则BC=40cm ，由勾股定理得AB =50cm ．故爬行一圈的路程是50cm ；（2）⊙O 的周长为80cm ，即AC=80cm ，绕一圈爬行100cm ，则AB = 100cm ，高BC = 60cm ．∴树干高=60×10=600cm=6m ．故树干高6m5.已知O 为圆锥顶点，OA 、OB 为圆锥的母线，C 为OB 中点，一只小蚂蚁从点C 开始沿圆锥侧面爬行到点A ，另一只小蚂蚁绕着圆锥侧面爬行到点B ，它们所爬行的最短路线的痕迹如右图所示．若沿OA 剪开，则得到的圆锥侧面展开图为（）要求蚂蚁爬行的最短距离，需将圆锥的侧面展开，进而根据“两点之间线段最短”得出结果，再利用做对称点作出另一只小蚂蚁绕着圆锥侧面爬行到点B ，它们所爬行的最短路线．A .B .C .D .故选C6.如图，一直圆锥的母线长为QA=8，底面圆的半径r=2，若一只小蚂蚁从A点出发，绕圆锥的侧面爬行一周后又回到A点，则蚂蚁爬行的最短路线长是______（结果保留根式）。

立体几何中的求距离问题

**立体几何中的求距离问题**1. **定义与公式**在立体几何中，距离是一个重要的概念。

它表示点与点之间、线与线之间、面与面之间的最短距离。

对于两点A和B，它们之间的距离称为AB的距离，用公式表示为：AB = sqrt[(x2 - x1)² + (y2 - y1)² + (z2 - z1)²]。

2. **求解方法**求两点间的距离主要依赖于坐标变换和勾股定理。

首先，需要确定两点的三维坐标，然后通过计算两坐标之间的差的平方，再开方得到距离。

3. **实际应用**在实际生活中，距离的概念广泛应用于各种场景，如地理学中的地球距离、物理学中的物体间距离、工程学中的结构尺寸等。

在科学研究和工程实践中，计算距离是一个必不可少的步骤。

4. **易错点**在计算距离时，容易出现错误的地方包括单位不一致、坐标表示错误或计算错误等。

为了避免这些问题，需要仔细检查并确保所有的单位和坐标都是正确的。

5. **真题演练**给定两点A(1,2,3)和B(4,5,6)，求AB的距离。

解：根据公式，AB的距离为：sqrt[(4-1)² + (5-2)² + (6-3)²] = sqrt(9+9+9) = 3*sqrt(3)6. **知识点总结**求两点间的距离主要依赖于坐标变换和勾股定理。

在实际应用中，计算距离是一个重要的步骤。

为了避免错误，需要仔细检查坐标和单位。

7. **未来学习建议**在未来的学习中，可以进一步探索距离在不同领域的应用，如医学影像分析、地理信息系统等。

同时，可以尝试解决更复杂的几何问题，如多维空间中的距离计算、曲面上的最短路径等。

此外，可以学习更多关于向量和矩阵的知识，这些工具对于解决复杂的几何问题非常有帮助。

高中数学：几何体表面两点间的最短距离

高中数学：几何体表面两点间的最短距离正方体木块AC1的棱长为1，蜘蛛位于A1B1的中点M 处，苍蝇停留在D点，问蜘蛛应采用怎样的最短路线，才能最迅速地抓住苍蝇？利用正方体的平面展开图形进行分析，问题十分简单。

在展开图中，由于平面上两点间以直线距离为最短，故M至D应取直线段。

因为MND长＝MgD长＝MefD长＝MPD长＝故MPD长为应采取的最短线路结论：借助平面几何的知识来解决立体几何中的问题，是处理立体几何问题的最佳方法。

要计算空间图形表面两点间的最短距离，只要利用了几何体的展开图形，就能把学生所熟悉的平面图形与立几图形有机地结合起来，使问题化难为易。

空间图形求表面上折线段最小值时，关键是弄清几何体中的有关点、线在展开图中的相应位置关系。

解决的方法就是把各侧面展开铺在平面上，根据“平面内连结两点的线段最短”的方法来解决。

例1、圆锥S—AB的底面半径为R，母线长SA＝3R，D为SA的中点，一个动点自底面圆周上的A点，沿圆锥侧面移动到D点，求这点移动的最短距离。

解：如图，沿圆锥母线SA剪开展成平面图形，则AD最短。

因为∠ASD＝。

所以由余弦定理，得例2、圆台的上底半径为6 cm，下底半径为12 cm，高为。

下底面内两条半径OA与OB互相垂直，M是母线B1B上一点，且BM：MB1＝2：1，求圆台侧面上A、M两点间的最短行程。

解：如图，在直角梯形OO1B1B中，由公式，求得如图，设圆台的侧面展开扇环的中心角∠＝θ，，则θ＝，解得x＝9 cm，θ＝240°。

依题意得，PM＝＝12cm，∠APB＝。

PA＝PB＝18cm。

在△PAM中运用余弦定理得：故圆台侧面上A、M两点间的最短行程为例3、设正三棱柱的侧棱长为3，底面边长是1，沿侧面从A 点到A1点，当路径AM—MN—NA1最短时，求AM与A1N 所成的角。

解：如图5（甲），过A作AP//A1N交B1B于P，则AM与AP所夹锐角（或直角），就是所求的角。

两异面直线的最短距离

两异面直线的最短距离两异面直线的最短距离是指两条不在同一平面内的直线之间的最短距离。

这个问题在数学和物理学中都有广泛的应用，例如在计算机图形学中，我们需要计算两个不相交的物体之间的最短距离，这就需要计算它们所在的两个异面直线的最短距离。

首先，我们需要知道两个异面直线之间的距离是如何定义的。

假设我们有两个直线L1和L2，它们的方向向量分别为v1和v2，那么它们之间的距离d可以通过以下公式计算：d = |(P2 - P1) · n|其中，P1和P2分别是L1和L2上的任意两个点，n是v1和v2的叉积，表示L1和L2所在平面的法向量，·表示向量的点积，|·|表示向量的模长。

这个公式的意义是，我们先找到L1和L2所在平面，然后计算从L1上任意一点到L2所在平面的距离，这个距离就是L1和L2之间的最短距离。

接下来，我们来看一下如何计算n。

由于v1和v2不在同一平面内，它们的叉积n一定不为零向量。

我们可以通过以下公式计算n：n = v1 × v2其中，×表示向量的叉积。

最后，我们来看一下如何计算d。

假设我们已经知道了L1和L2上的任意两个点P1和P2，那么我们可以通过以下公式计算d：d = |(P2 - P1) · n| / |n|其中，·表示向量的点积，|·|表示向量的模长。

这个公式的意义是，我们先计算从P1到P2的向量，然后将它投影到n上，得到它在n方向上的长度，最后除以n的模长，得到L1和L2之间的最短距离。

综上所述，计算两异面直线的最短距离需要先计算它们所在平面的法向量，然后计算从一条直线上的任意一点到另一条直线所在平面的距离，最后除以法向量的模长。

这个问题在计算机图形学、机器人学、物理学等领域都有广泛的应用，是一个非常重要的数学问题。

2019贵州国考行测点睛：如何求解几何问题中的最短距离

2019贵州国考行测点睛：如何求解几何问题中的最短距离在几何问题的考查中，会遇到求解最短距离的题目，其中最短距离指的是：两点之间线段最短。

但是有时候所求是立体图形不在一个平面上的两点，那么怎么来求两点之间的最短距离呢?中公教育专家认为，此时就需要我们运用空间想象的能力，将立体图形展开成为平面图形进行求解。

1.方法：利用空间想象力，把立体图形展开成一个平面图形，利用最短或最远距离解题。

2.关键：在求解过程中，会涉及到最短或最远距离，要能找到这些距离。

平时在生活中，可以多画一画立体图的展开图，培养自己的空间想象力。

1.有一个长方体如图所示，上下两个面是正方形，边长为a，高为2a，若从A点到B点的表面最短距离的连线与边CD相交与F点，已知BF长为10，求这个长方体的体积?A.90B.90C.540D.【中公解析】由题意可将A点和B点最短距离的连线划出，交CD于F点，得到图形如图，由相似三角形知道，BD：BE=BF：AB=1：3，所以知道AB连线为30，由三角形ABE勾股定理得到，，选择选项D。

平面如图：2.颗气象卫星与地心距离相等，并可同时覆盖全球地表，现假设地球半径为R，这3颗卫星距地球最短距离为()。

A. RB. RC.RD.2R【中公解析】3颗卫星组成的平面与地球相切时距离最短且可覆盖全球表面。

如图所示，等边三角形顶点到其内接圆圆心距离为2R，卫星距离地球最短距离为R。

故选择C选项。

3.如图，正四面体ABCD，P、Q分别是棱AB、CD的三等分点和四等分点(AB=3AP=4CQ)，棱AC上有一点M，要使M到P、Q距离之和最小，则MC∶MA=( )。

A.1∶2B.4∶5C.3∶4D.5∶6【中公解析】如图展开，PQ为最短距离。

△APM与△CQM相似，MC∶MA=CQ∶AP=3∶4。

故选择C选项。

立体几何中最短距离的求解策略

立体几何中最短距离的求解策略
在立体几何中，最短距离指的是从一点到另一点之间最短可到达的距离，也叫最短链接距离。

面对复杂的立体几何问题，如何求解最短距离，给出解决策略是非常有必要的。

解决立体几何中最短距离的求解策略主要分为三个步骤：
首先，我们需要分析最短距离的特点，也就是所谓的“直线最短”原则，也就是几何图形中的任意两点之间的最短距离必须是直线距离。

其次，根据几何图形的形状和特性，求解具体问题中的最短距离。

例如，分析棱柱之间的最短距离是什么，棱柱之间最短距离为棱柱的直径；分析球面上任意两点之间的最短距离是什么，球面任意两点之间的最短距离是一个弧线的弦长。

最后，运用数学原理求解最短距离的问题，按照古典几何计算思路，计算出最短距离的标准式；其次，运用现代几何理论，使用科学计算方法给出解决最短距离问题的数值解。

以上是解决立体几何中最短距离的求解策略，主要有分析最短距离特点、根据形状和特性求解具体最短距离、运用数学原理求解最短距离三个步骤。

做好最短距离求解既是立体几何研究的重点，也是解决实际工程问题的重要基础。

立体几何的最小距离

立体几何的最小距离
立体几何中的最小距离问题是一个比较复杂的问题，它涉及到空间中点、线、面之间的最短距离的计算。

在解决立体几何的最小距离问题时，通常需要利用空间几何的基本定理和公式，如勾股定理、点到线的距离公式、点到平面的距离公式等。

对于不同的几何元素之间的最小距离问题，需要选择适当的公式进行计算。

例如，两点之间的最短距离可以通过勾股定理计算，点到线的最短距离可以通过将点与线段的两个端点分别连接，然后比较连接线段和平行于线段且经过点的直线的长度来计算。

此外，最小距离的计算可能涉及到非常复杂的数学运算和几何形状，因此在实际应用中，可能需要借助计算机编程和数学软件来辅助计算。

这些工具可以提供高效的数值计算和图形可视化功能，有助于更准确和直观地理解和分析最小距离的问题。

综上所述，立体几何的最小距离问题需要利用空间几何的基本定理和公式进行计算，同时可能需要借助计算机编程和数学软件来辅助计算。

两异面直线的最短距离

两异面直线的最短距离两异面直线的最短距离是指在三维空间中，两条不相交的直线之间的最短距离。

这个问题在几何学和计算几何学中具有重要的意义，它与空间中的点、直线、平面的位置关系紧密相关。

本文将围绕这一主题展开讨论，探究两异面直线的最短距离的计算方法以及其应用。

为了更好地理解两异面直线的最短距离，我们首先需要了解异面直线的特点。

异面直线是指在三维空间中，两条直线既不平行也不相交的情况。

由于异面直线的特殊性，计算它们之间的最短距离并不像计算平面上两条直线的最短距离那样简单。

为了计算两异面直线的最短距离，我们可以利用向量的知识。

设两异面直线分别为L1和L2，它们的方向向量分别为v1和v2，而过L1上一点P到L2的垂足为Q。

由于v1和v2分别垂直于L1和L2，所以向量v1和v2的内积为0。

因此，我们可以得到以下方程：(v1·v2) = 0，其中·表示向量的内积运算。

通过解这个方程组，我们可以求得L1和L2的最短距离。

具体的计算过程在本文中省略，读者可以通过阅读相关的数学教材来了解详细的计算方法。

除了数学计算，两异面直线的最短距离还有一些实际应用。

在计算机图形学中，这个问题经常出现在三维建模和渲染中。

例如，在虚拟现实和电影制作中，我们需要计算人物或物体与环境的交互，这时两异面直线的最短距离就能帮助我们判断物体是否与环境发生碰撞。

在工程领域中，两异面直线的最短距离也有广泛的应用。

例如，在机械设计中，我们需要计算机械零件之间的最小安全间隙，以确保它们能够正常运行而不会发生摩擦、碰撞等问题。

这时，两异面直线的最短距离就可以为我们提供重要的参考。

在实际应用中，我们可能会遇到一些特殊情况，例如两异面直线平行或者相交。

对于平行的情况，两异面直线的最短距离为它们之间的垂直距离。

而对于相交的情况，两异面直线的最短距离为0，因为它们有一个公共点。

总结起来，两异面直线的最短距离是计算几何学中一个重要的问题。

通过利用向量的知识，我们可以求解两异面直线的最短距离，并将其应用到实际问题中。

异面直线距离的求法

异面直线距离的求法“哎呀，这异面直线距离可真是个让人头疼的问题啊！”异面直线距离的求法呢，主要有这么几种常见的方法。

一种是直接法，就是找出或作出异面直线的公垂线段，然后计算其长度。

比如说，在一个正方体中，面对角线和体对角线就是异面直线，我们可以通过一些几何关系找到它们的公垂线段。

再比如，看这个例子，有一个三棱锥，其中两条异面直线，我们可以通过仔细观察和分析，找到与这两条异面直线都垂直的线段，这就是公垂线段啦，然后利用一些已知条件去算出它的长度。

还有定义法，根据异面直线距离的定义，转化成求两平行平面之间的距离。

就好像有两个平行的平面，异面直线分别在这两个平面上，那这两个平面之间的距离就是异面直线的距离。

另外，还有一种叫转化法。

可以把异面直线的距离问题转化为线面距离或面面距离问题来求解。

比如把异面直线中的一条放到一个平面内，另一条直线和这个平面平行，那就把求异面直线距离转化成了求线面距离。

向量法也是常用的。

通过建立空间直角坐标系，利用向量的方法来求异面直线的距离。

这个方法对于一些复杂的图形很有效。

总之呢，求异面直线距离的方法要根据具体的题目情况来选择，灵活运用这些方法，多做一些题目，就能更好地掌握啦。

“嘿，小王啊，你看这个图形，用哪种方法求异面直线距离比较好呢？”“我觉得可以用直接法先试试。

”“对，先观察一下，看看能不能找到公垂线段。

”在实际解题过程中，一定要认真分析图形的特点和条件，选择最合适的方法来求解异面直线距离，这样才能又快又准确地得出答案。

就像上次给学生们讲的那道题，乍一看好像挺复杂，但仔细分析后，发现用定义法就能很轻松地解决。

所以啊，遇到问题不要慌，静下心来好好分析，肯定能找到解决办法的。

希望这些解释能让你对异面直线距离的求法有更清楚的认识和理解，以后遇到这类问题就不会再犯难啦！。

利用展开法求几何体表面上两点间的最短距离

利用展开法求几何体表面上两点间的最短距离陕西省汉中市405学校侯有岐 723312简单几何体的侧面展开图,除用以计算几何体的面积外,还有一个很重要的作用,教材上很少涉及.但对学生来说却很有趣,这就是用以解决几何体上两点间的最短距离问题.这类问题乍看起来无从下手,但作适当的转化,就可找到问题的突破口,使问题变得简单明了.本文通过教学中的例子对这个问题进行探讨.一、对于多面体上两点间的最短距离,直接求解往往有困难,可采取把立体图形展开成平面图形,通过“化折为直”的途径予以解决.例1（2005年江西高考题）分析: 引导学生观察直观图,进行分析、探索.根据对称性,从E 到F 走“近道”绕过棱11111B B A B AC 、、有三种走法：1E B B 1（）——F ； 1E A F B 1（2）——；1E A F C 1 （3）——.要求最短距离,怎么办?在三棱柱表面上弯来拐去的不好确定.若能把每一条路线所经过的两个平面“拉平”就好办了，因此，把表面展开，在展开图中进行比较、计算. 解: 对于三种走法(1)、（2）、（3），作三棱柱的表面展开图（如图示），连接EF ，得到三条线段，设它们的长分别为123 l l l 、、，则12l == 2l ==32l ==. 因为 321l l l <<,所以沿棱柱表面从E 到F 两点的最短路径的长度为 2. 点评: 由上例可以看出,在多面体中,要求几何体表面上两点之间的最短距离,可利用展开图.由平面上“两点之间线段最短” 即可求得,如果路径有多条,可通过比较,选取最短者.例2(2006年江西高考题)分析: 在例1的基础上,学生可很快得到本题的解题思路:沿侧棱1AA 展开并重复一次得展开图(如图示),图中矩形对角线1AA 的长即为所求的最短距离.显然1AA 10==.二、对于旋转体表面上两点间的最短距离，直接求解学生可能感到束手无策，若能将空间曲面转化为平面，就可通过“化曲为直”的途径予以解决.。

求异面直线之间距离的四个技巧

异面直线是既不平行也不相交的两条直线.这组直线的空间位置关系较为特殊，我们往往很难直接求得异面直线之间的距离，需采用一些方法和技巧，如平移法、向量法、等体积法、构造函数法等，才能使问题获解.下面结合实例，谈一谈求异面直线之间距离的四个技巧.一、平移法求异面直线之间的距离，要首先把握异面直线之间距离的定义和两直线之间的位置关系.异面直线之间的距离是指这两直线之间的公垂线的长，而公垂线必须同时垂直于两条异面直线.可采用平移法，通过平移其中的一条直线a ，使其与另一条直线b 相交，这样便构造出一个平面，过直线a 上的一点作这个平面的垂线，该线即为两条异面直线的公垂线，求得公垂线的长即可求得两条异面直线之间的距离.例1.如图1所示，正方体ABCD -A 1B 1C 1D 1的棱长为a ，求异面直线A 1D 和AC 之间的距离.解：连接BD 1、BD 、AD 1，设BD 与AC 的交点为M ，AN 与A 1D 的交点为F ，根据三垂线定理可知：BD 1⊥A 1D ，BD 1⊥AC ，因为N 为DD 1的中点，由三角形中位线的性质可知BD 1∥MN ,MN ∥EF ,即BD 1∥EF ，可知EF 即为异面直线A 1D 和AC 的公垂线，因为BD 1=3a ，所以MN.又因为N 为DD 1的中点，且AA 1∥DN ，则△AA 1F ∽△NDF ，所以AF NF =AA 1ND=2，AF NF =23.因为EF ∥MN ，则EF MN =AF AN =23，可知EF =23MN=，因此异面直线A 1D 和AC之间的距离为.采用平移法解题，需仔细观察立体几何图形中的点、线、面之间的位置关系，尤其要关注线和面之间的垂直、平行关系，通过平移直线将原本看起来毫无联系的两条异面直线关联起来，再利用平面几何知识，如勾股定理、正余弦定理、两点间的距离公式、三角形中位线的性质等来求公垂线的长.图1图2二、向量法对于易于建立空间直角坐标系的立体几何问题，可采用向量法来求解.在求异面直线之间的距离时，可分别求得两条直线的方向向量a 、b ，并设出两条异面的公垂线，然后根据向量之间的垂直关系建立方程组，通过解方程求得公垂线的方向向量，最后求其模长，即可求得异面直线之间的距离.例2.如图2所示，正方体ABCD -A ′B ′C ′D ′的棱长为1，其对角线为AC ′，点M 、N 分别为棱BB ′和B ′C ′的中点，MN 的中点为P ，求异面直线DP 与AC ′之间的距离.解：如图2所示，以D ′为原点，D ′C ′为x 轴、D ′A ′为y 轴、D ′D 为z 轴建立空间直角坐标系，设DP 与AC ′的公垂线为QR ，分别与DP 、AC ′相交于点Q 、R ，根据定比分点公式可得 OR =sOA +(1-s ) OC ′， OQ =t OP +(1-s ) OD ，0<s <1，0<t <1，则A (0,1,1)，C ′(1,0,0)，P (1,34,14)，D (0,0,1)，则R (1-s ,s ,s )，Q (t ,34t ,1-34t ).因为 RQ ⊥AC ′且 RQ ⊥ DP ，所以ìíîïï3s +t -2=0,178t +s -74=0,解得ìíîïïs =4086,s =5286,可得R (4686,4086,4086)，Q (5286,3986,4786)，则RQ 的模长为，即异面直线DP 与AC ′之间的距离为.相较于常规方法，向量法更加简单.在运用向量法解题时，同学们需熟记一些向量的运算法则，如向量的加法、减法，向量的数量积公式、模的公式.探索探索与与研研究究49三、等体积法等体积法一般适用于求解三棱锥问题，是指转换三棱锥的底面和高，根据同一个三棱锥或两个三棱锥的体积相等建立关系式，求得问题的答案.在求异面直线之间的距离时，可将异面直线置于三棱锥中，采用等体积法求三棱锥的高，进而求得两条异面的公垂线的长.在解题时，同学们要善于寻找体积相等的三棱锥，或易于计算体积的三棱锥的底面和高，建立等价关系式.例3.如图3所示，正方体ABCD -A 1B 1C 1D 1的棱长为2，点E 为BC 的中点，求直线ED 1与直线CC1之间的距离.图3图4解：如图4所示，过点E 作EE 1∥CC 1，连接D 1E 1.已知点E 为BC 的中点，则点E 1为B 1C 1的中点，所以B 1E 1=E 1C 1.因为EE 1⊂平面D 1EE 1，EE 1∥CC 1，则CC 1∥平面D 1EE 1，则异面直线ED 1与CC 1之间的距离即为直线CC 1到平面D 1EE 1的距离，也就是点C 1到平面D 1EE 1的距离.设点C 1到平面D 1EE 1的距离为a ，由V C 1-D 1EE 1=V E -C 1D 1E 1可得：13S △D 1EE 1·a =13S △C 1D 1E1·EE 1.因为CC 1⊥A 1B 1C 1D 1，EE 1⊥A 1B 1C 1D 1，且D 1E 1⊂平面A 1B 1C 1D 1，则EE 1⊥D 1E 1，S △D 1EE 1=12×EE 1×D 1E 1=5.因为正方体的棱长为2，则S △C 1D 1E 1=1，EE 1=2，故C 1到平面D 1EE 1的距离a =S △C 1D 1E 1·EE 1S △D 1EE1=1×25=则直线ED 1与直线CC1之间的距离为.运用该等体积法求异面直线之间的距离，可省去找公垂线的麻烦，且简化了运算的过程.四、函数构造法我们知道，公垂线是两条异面直线之间的最小距离.若很容易找到异面之间的公垂线，但无法快速求得公垂线的长，或无法找到公垂线，可根据勾股定理、正余弦定理、两点间的距离公式等求得公垂线的表达式，或两异面直线上任意两点之间的距离的表达式，然后将其构造成函数模型，通过研究函数的单调性，求得函数的最小值，即可求得异面直线之间的距离.例4.如图5所示，正方体ABCD -A 1B 1C 1D 1的棱长为a ，A 1B 和D 1B 1为正方形ABA 1B 1和正方形A 1B 1C 1D 1的对角线，求异面直线A 1B 和D 1B 1之间的距离.解：在A 1B 上任取一点M ，作MP ⊥A 1B 1于点P ，作NP ⊥A 1B 1于点P ，与D 1B 1交于点N .根据三垂线定理可知MN ⊥D 1B 1.设A 1M =x ，在等腰△A 1PM 中，MP =A 1P ，因为A 1B 1=a ，PB 1=a -，PN =(a )sin 45°=12(2a -x )，由于平面ABA 1B 1⊥平面A 1B 1C 1D 1，所以PN ⊥PM ，在Rt△PMN 中，MN =PM 2+PN 2=函数y =为复合函数，与二次函数y =3(x -)2+43a 2的单调性一致，由二次函数的性质可知当x 时，函数的最小值为，所以异面直线A 1B 和D 1B 1之间的距离为.通过添加辅助线，构造出垂直于D 1B 1的平面PNM ，只要在平面PNM 中找到一条直线垂直于A 1B ，那么该直线即是异面直线A 1B 和D 1B 1的公垂线.在Rt△PMN 中，根据勾股定理建立关于x 的关系式，求得公垂线的表达式，然后将其看作关于x 的函数式，通过分析函数的单调性求得函数的最小值，即可解题.可见，求异面直线之间的距离，关键是根据几何图形的特点和性质，以及点、线、面的位置关系找到异面直线的公垂线，并求得其长度.同学们可根据题目的条件，灵活选用上述四种方法.（作者单位：江苏省昆山文峰高级中学）图5探索探索与与研研究究50。

浅谈立体几何异面直线的距离

浅谈立体几何异面直线的距离
立体几何异面直线的距离是一个关于立体几何的重要概念，在数学和工程领域应用广泛。

它是两条异面直线之间的最短距离，这条最短距离称为异面直线距离。

在三维空间中，异面直线可以从一系列不同的角度来定义，例如异面直线、共面直线、线段之间的距离等等。

异面直线距离可以用两种不同的方式来表示：一种是以投影的方式表示，另一种是以方向向量的方式表示。

投影是把一个向量或者一条直线从一种坐标系统映射到另一种坐标系统的过程，它可以让我们非常清晰的观察到直线的距离。

方向向量的方式则是表示两条异面直线通过一个方向向量来表示，这个方向向量表示了两条异面直线之间的最短距离。

异面直线距离是在计算机图形学中非常重要的一类算法，它可以用来测量物体的距离，也可以用来确定物体的位置。

例如，在三维空间的一个大场景中，我们需要确定一个物体的位置，就需要用异面直线距离来测量两个物体之间的最短距离，然后再根据这个最短距离来确定物体的位置。

异面直线距离也可以用来求解一些几何问题，例如求解空间中两个平面之间的最短距离、两条曲线之间的最短距离等等。

此外，异面直线距离也被广泛应用于计算机图像处理，比如图像的灰度匹配、边缘检测等等。

它也可以用来计算一些高级的几何结构，比如平面交叉检测、曲面交叉检测等等。

总而言之，异面直线距离是一个重要的几何概念，它在数学和工
程领域有着广泛的应用。

它可以用来解决各种问题，比如计算物体之间的最短距离、计算空间几何结构、图像处理等等。

因此，异面直线距离是一个重要的几何概念，研究它有重要的意义，在工程领域的应用能够提高工程的质量和效率。

利用展开法求几何体表面上两点间的最短距离

利用展开法求几何体表面上两点间的最短距离陕西省汉中市405学校侯有岐 723312简单几何体的侧面展开图,除用以计算几何体的面积外,还有一个很重要的作用,教材上很少涉及.但对学生来说却很有趣,这就是用以解决几何体上两点间的最短距离问题.这类问题乍看起来无从下手,但作适当的转化,就可找到问题的突破口,使问题变得简单明了.本文通过教学中的例子对这个问题进行探讨.一、对于多面体上两点间的最短距离,直接求解往往有困难,可采取把立体图形展开成平面图形,通过“化折为直”的途径予以解决.例1（2005年江西高考题）分析: 引导学生观察直观图,进行分析、探索.根据对称性,从E 到F 走“近道”绕过棱11111B B A B AC 、、有三种走法：1E B B 1（）——F ； 1E A F B 1（2）——；1E A F C 1 （3）——.要求最短距离,怎么办?在三棱柱表面上弯来拐去的不好确定.若能把每一条路线所经过的两个平面“拉平”就好办了，因此，把表面展开，在展开图中进行比较、计算. 解: 对于三种走法(1)、（2）、（3），作三棱柱的表面展开图（如图示），连接EF ，得到三条线段，设它们的长分别为123 l l l 、、，则12l == 2l ==32l ==. 因为 321l l l <<,所以沿棱柱表面从E 到F 两点的最短路径的长度为 2. 点评: 由上例可以看出,在多面体中,要求几何体表面上两点之间的最短距离,可利用展开图.由平面上“两点之间线段最短” 即可求得,如果路径有多条,可通过比较,选取最短者.例2(2006年江西高考题)分析: 在例1的基础上,学生可很快得到本题的解题思路:沿侧棱1AA 展开并重复一次得展开图(如图示),图中矩形对角线1AA 的长即为所求的最短距离.显然1AA 10==.二、对于旋转体表面上两点间的最短距离，直接求解学生可能感到束手无策，若能将空间曲面转化为平面，就可通过“化曲为直”的途径予以解决.。

求两条异面直线之间距离的两个公式

求两条异面直线之间距离的两个公式在三维几何中，两条异面直线之间的距离是指两条直线之间的最短距离。

在解决实际问题时，我们经常需要计算两条直线之间的距离，因此找到计算直线之间距离的公式对于解决问题非常重要。

下面将介绍两个计算异面直线之间距离的公式：点法式和向量法式。

1.点法式：假设有两条直线L1和L2，分别由点A1(x1,y1,z1)和A2(x2,y2,z2)以及方向向量v1(a1,b1,c1)和v2(a2,b2,c2)所确定。

步骤如下：1)选择L1上的任意一点P1，使用向量v1连接P1和A1、可以得到向量P1A12)在同一平面上，选择L2上的任意一点P2，使用向量v2连接P2和A2、可以得到向量P2A23)计算向量P1A1和向量P2A2的叉积，得到向量N。

叉积公式为：N=P1A1×P2A24)计算向量N的长度，即向量N的模长。

向量N的模长为：，N，=√(a3^2+b3^2+c3^2)。

5)计算点P1到直线L2的距离。

距离公式为：d=，[P2P1×N]，/，N，其中[P2P1×N]表示向量P2P1和向量N的叉积。

2.向量法式：假设有两条直线L1和L2，分别由点A1(x1,y1,z1)和A2(x2,y2,z2)以及方向向量v1(a1,b1,c1)和v2(a2,b2,c2)所确定。

步骤如下：1)计算两条直线的方向向量叉积，得到向量N。

叉积公式为：N=v1×v22)计算向量N的长度，即向量N的模长。

向量N的模长为：，N，=√(a3^2+b3^2+c3^2)。

3)选择L1上的任意一点P1和L2上的任意一点P2，计算向量P2P14)计算向量P2P1与向量N的点积，得到距离d。

点积公式为：d=，P2P1·N，/，N，其中[P2P1·N]表示向量P2P1和向量N的点积。

这两个公式可以用于计算两条异面直线之间的最短距离。

如果结果为正值，则表示直线L1与直线L2不相交，并且距离为计算结果；如果结果为零，则表示直线L1与直线L2相交；如果结果为负值，则表示直线L1与直线L2相交，但距离为零。

异面直线上两点间的距离公式

异面直线上两点间的距离公式在三维空间中，我们经常需要计算两个点之间的距离。

当这两个点在同一平面上时，我们可以使用平面上两点间的距离公式来计算它们之间的距离。

但是，当这两个点不在同一平面上时，我们需要使用异面直线上两点间的距离公式来计算它们之间的距离。

异面直线上两点间的距离公式如下：d = |(ax1 + by1 + cz1 + d) - (ax2 + by2 + cz2 + d)| / √(a^2 + b^2 + c^2)其中，(x1, y1, z1)和(x2, y2, z2)是两个点的坐标，a、b、c和d是直线的方程系数，d是直线的截距，| |表示绝对值，√表示平方根。

这个公式的推导过程比较复杂，我们不在这里详细讲解。

但是，我们可以通过一个简单的例子来理解这个公式的应用。

假设我们有两个点A(1, 2, 3)和B(4, 5, 6)，它们分别在以下两个平面上：平面1：2x + 3y - z = 4平面2：x - 2y + 3z = 5我们需要计算点A和点B之间的距离。

由于这两个点不在同一平面上，我们不能使用平面上两点间的距离公式来计算它们之间的距离。

相反，我们需要使用异面直线上两点间的距离公式。

我们需要找到这两个平面的法向量。

平面1的法向量为(2, 3, -1)，平面2的法向量为(1, -2, 3)。

这两个法向量可以通过平面的方程系数得到。

接下来，我们需要找到这两个平面的交点，也就是它们所在的直线。

我们可以通过将这两个平面的方程联立，解出它们的交点坐标。

这个过程比较繁琐，我们不在这里详细讲解。

最终，我们得到这两个平面的交点坐标为(-1, 1, 0)。

现在，我们可以得到这两个平面所在的直线的方程。

我们可以选择其中一个平面的方程作为直线的方程，例如平面1的方程2x + 3y - z = 4。

我们可以将这个方程转化为参数方程的形式：x = ty = (4 - 2t) / 3z = (2t - 4) / 3这个参数方程表示了这条直线上的所有点。

浅谈如何求几何体异面上两点间最短距离(1)

浅谈如何求几何体异面上两点间最短距离湖北省十堰市房县上龛中学付彬我们知道，在同一平面上，两点之间线段最短。

但如果两点不在同一平面上，而是在几何体的两个不同面上，问题又会如何呢？众所周知，一个立体图形沿着某些棱剪开并铺平，能够展开成平面图形，如长方体，三棱锥，圆柱等。

这里，我们不妨利用平面展开图把几何体异面上两点之间最短距离问题化归为同一平面上两点之间最短距离问题：先将所需几何体表面展开得到平面图形，连结两点，求出两点间线段的长，从而得到几何体异面上两点之间的最短距离。

下面我们结合实例来说明侧面展开图的方法.一、几何体为棱柱问题1 如图1所示，已知长方体蛋糕上A 点有只蜘蛛在寻找实物，B 点有只苍蝇正在进食。

若这块长方体蛋糕的长、宽、高分别为7 cm ，5cm 和5 cm ，那么这只蜘蛛在A 点发现苍蝇后，到B 点逮到苍蝇的最短爬行路线有多长？分析：①如图1-1，把长方体的上表面和正面展开成平面图形，连结AB ；②如图1-2，把长方体的正面和右侧面展开成平面图形，连结AB 。

两者中较小的AB 值就是所求。

解：①如图1-1，由题意，得∠ACB ＝90。

，AC ＝7，BC ＝5＋5＝10，∴ AB ＝1491072222=+=+BC AC②如图1-2，由题意，得∠ACB ＝90。

，AC ＝7＋5＝12，BC ＝5，∴ AB ＝135122222=+=+BC AC∵ 13149< ∴ 所求最短爬行路线长149cm 。

二、几何体为棱锥问题２如图２，课桌上放着一个正三棱锥S-ABC ，SA=1,∠ASB=30°, 蚂蚁从点A 沿三棱锥的侧面爬行（必须经过三棱锥的三个侧面）再回到A ，它按怎样的路线爬行，才使其行迹最短.解：根据图２，沿SA 剪开得展开图２.在⊿SAE 中，,,SE=－1.利用尺规作图可以找到E 和F ，从而确定蚂蚁的最佳行迹AEFA.图1-1图1-2 图1三、几何体为圆锥问题３如图３，课桌上放着一个圆锥，点Ａ为圆锥底面圆周上一点，SA=3,OA=1蚂蚁从点A沿圆锥的侧面爬行再回到A，它按怎样的路线爬行，才使其行迹最短.分析：有趣的是蚂蚁的最佳行迹不是底面的圆周，而是向上爬，到达一个最高点后向下爬行.解：根据图３，沿SA剪开得展开图３.在⊿SAB中，∠ASB＝，AB=3.取SC的中点D，其最佳行迹是曲线段ADB,在侧面展开图上是直线段ADB.四、几何体为圆柱问题４如图４，课桌上放着一个圆柱，蚂蚁从点A沿圆柱的侧面爬行到另一点B，它按怎样的路线爬行，才使其行迹最短.解：根据图４，沿AE剪开得展开图4.若点B落在展开图的中位线EF上,则蚂蚁应按AB1或MB１两条线段在圆柱上的对应曲线爬行.若点B落在展开图的中位线EF的左侧,则蚂蚁应按MB2两条线段在圆柱上的对应曲线爬行.若点B落在展开图的中位线EF的右侧,则蚂蚁应按AB2两条线段在圆柱上的对应曲线爬行.五、几何体为球问题５如图５，球O的表面上有两点A、B，∠AOB＝60 。

异面直线上两点间距离公式应用

异面直线上两点间距离公式应用假设有两个异面直线，分别可以用两个参数方程表示为：L1:x=x1+a*t1y=y1+b*t1z=z1+c*t1L2:x=x2+d*t2y=y2+e*t2z=z2+f*t2其中，(x1,y1,z1)和(x2,y2,z2)分别是两条直线上的已知点，而(a,b,c)和(d,e,f)是两个方向向量。

参数t1和t2是实数。

首先，我们可以使用点向式来表达两个直线上的任意一点P1和P2: P1=(x1+a*t1,y1+b*t1,z1+c*t1)P2=(x2+d*t2,y2+e*t2,z2+f*t2)然后，我们可以使用向量形式计算P1P2的模长，即最短距离。

首先求得向量P1P2的坐标差P1P2=(x2+d*t2-x1-a*t1,y2+e*t2-y1-b*t1,z2+f*t2-z1-c*t1)然后，求得向量P1P2的模长：P1P2，=√((x2+d*t2-x1-a*t1)^2+(y2+e*t2-y1-b*t1)^2+(z2+f*t2-z1-c*t1)^2)接下来，我们需要找到最短距离。

由于题目给出的是两个向量，我们需要找到两个直线上最近的两个点。

具体做法是将向量P1P2与方向向量(a,b,c)和(d,e,f)分别进行垂直化处理。

当向量P1P2垂直于两个方向向量时，即点P1P2与直线L1和L2垂直。

我们可以得到以下两个方程：((x2+d*t2-x1-a*t1)*a)+((y2+e*t2-y1-b*t1)*b)+((z2+f*t2-z1-c*t1)*c)=0((x2+d*t2-x1-a*t1)*d)+((y2+e*t2-y1-b*t1)*e)+((z2+f*t2-z1-c*t1)*f)=0我们可以交叉相乘并整理以上两个方程，得到一个关于t1和t2的二次方程。

解这个方程，我们可以求出最短距离。

这个二次方程形式如下：((a*d)+(b*e)+(c*f))*t1*t2+((a*(x2-x1)+b*(y2-y1)+c*(z2-z1))*d+(a*d+b*e+c*f)*(x1-x2)+(x2-x1)*(d*f-a*f)-(d*b-a*e)*(z2-z1)+(z2-z1)*(a*e-d*c))*t1+((a*(y2-y1)-b*(x2-x1))*e+(c*(x2-x1)-a*(z2-z1))*f+(b*(z2-z1)-c*(y2-y1))*d)=0我们使用Δ来表示这个二次方程的判别式，即Δ = b^2 - 4ac。

两条异面直线的距离公式

两条异面直线的距离公式概述：两条异面直线的距离公式是解决空间几何问题中的一个非常重要的工具，它可以用来计算两条不共面的直线之间的最短距离。

这个公式是基于向量和点的概念建立的，但是理解起来相对简单，只需要一些基本的向量和几何知识即可掌握它的应用。

正文：在平面几何中，我们可以轻松地计算两条直线之间的距离。

但是在三维空间中，情况要复杂得多。

这是因为两条不共面的直线之间有许多可能的距离，因此，我们需要找到一种方法来计算它们之间的最短距离，这就是两条异面直线的距离公式。

首先，我们需要了解什么是异面直线。

如果两条直线不在同一个平面内，那么它们就是异面直线。

这就意味着没有办法通过平移或旋转使得它们重合。

因此，在三维空间中，异面直线的距离是唯一确定的，并且是两条不共面直线之间的最短距离。

为了计算两条异面直线之间的距离，我们需要首先找到它们的交点。

这个交点可以通过求解两个方程来得到，每个方程描述一条直线的位置。

然后，我们需要找到一个点位于第一条直线上，另一个点位于第二条直线上，并且它们之间的距离是我们要求的最短距离。

这可以通过以下公式来计算：d = |(P1 – P2) · n| / |n|其中d是两条直线之间的最短距离，P1和P2分别是两条直线上的点，n是垂直于两条直线的向量。

现在，让我们逐步地理解这个公式。

首先，我们需要找到两个点，它们分别在两条直线上。

为了找到这些点，我们可以用以下公式：P1 = A1 + t1D1P2 = A2 + t2D2其中，A1和A2是第一条直线和第二条直线上的一个已知点，D1和D2是它们的方向向量，t1和t2是直线参数。

通过求解以上两个方程，我们可以找到两条直线的一个公共点P。

如果这两条直线共面，则它们的交点无限多，我们就需要选择其中一个。

接下来，我们需要找到n向量，它垂直于两条直线。

n 可以通过向量积来计算：n = D1 x D2然后，我们可以通过点积计算P1和P2之间的向量与n之间的夹角的余弦值：cosθ = (P1 –P2) · n / (|P1 –P2| × |n|)由于n是垂直于两个向量的向量，因此它们的点积等于0。

异面直线的距离求法

异面直线的距离求法咱们聊聊异面直线的那点事儿，特别是它们之间距离的那些小秘密。

在数学的浩瀚宇宙里，异面直线就像是两条永远不会交汇的银河，各自闪耀在各自的天际。

虽然它们看起来遥不可及，但咱们数学界的朋友们，总爱琢磨这些看似不可能的事儿，比如怎么计算它们之间的距离。

想象一下，你手里有两根笔直的铅笔，它们不在同一个平面上，就像是夜空中最亮的两颗星，遥遥相望。

这时候，你可能就纳闷了：这俩家伙到底隔了多远呢？别急，咱们有妙招。

首先，咱们得找个“桥梁”，让这两条直线能间接地“握手言和”。

这个桥梁，就是咱们常说的“公垂线段”。

你可以把它想象成一座连接两个星球的隐形桥梁，它垂直于这两条直线所在的平面，就像一根定海神针，稳稳地立在那儿。

要找这个公垂线段，咱们得先用点技巧。

假设这两条直线分别是A和B，咱们可以在A上随便找个点P，然后向B所在的方向投射一条光线，就像手电筒照亮夜空一样。

这条光线会与B有一个交点Q，但Q不一定是咱们要找的公垂线段的端点。

不过别急，咱们可以沿着这条光线，找到一个与B平行且与A垂直的平面。

在这个平面上，A会有一个“影子”，咱们称它为A'。

现在，A'和B就在同一个平面上了，它们之间的距离，就是咱们要找的异面直线的距离。

而A'到B的最短距离，就是咱们之前说的公垂线段的长度。

这个长度，就像是你和心仪的人之间的距离，虽然不能直接到达，但可以通过一些巧妙的方法，测量出那份微妙而确切的“远”。

计算这个距离的时候，咱们得用到一些三角函数和几何知识，就像是解谜游戏一样，一步步揭开谜底。

不过别担心，只要你跟着步骤走，就像跟着导航找路一样，总能找到那个答案。

说到这里，你是不是觉得异面直线的距离求法也没那么神秘了呢？其实，数学就像是一座宝藏岛，里面藏着无数的秘密和惊喜。

只要咱们用心去挖掘，总能发现那些隐藏在数字和公式背后的美丽和奥秘。

所以，下次当你再看到那些看似复杂的数学问题时，不妨换个角度，用一颗好奇和探索的心去面对它们。

异面直线之间距离公式

异面直线之间距离公式异面直线之间的距离公式是一个重要的几何定理，在几何学和物理学中有广泛的应用。

它可以用来计算两条不相交的直线之间的最短距离，而不需要求解两条直线的交点。

本文将简要介绍异面直线之间距离公式的概念和推导方法，并通过实际例子展示其应用。

异面直线指的是不在同一个平面上的直线。

在三维空间中，我们可以用参数方程或者点向式方程来表示一条直线。

假设我们有两条异面直线，分别用参数方程表示为：L1: x = x1 + a1t, y = y1 + b1t, z = z1 + c1tL2: x = x2 + a2s, y = y2 + b2s, z = z2 + c2s其中(x1, y1, z1)和(x2, y2, z2)是两条直线上的已知点，(a1, b1, c1)和(a2, b2, c2)是两条直线的方向向量，t和s是参数。

异面直线之间的距离可以通过求解它们的最近点来得到。

最近点是指两条直线上的点，它们的距离最短。

假设最近点分别为P和Q，它们分别在L1和L2上。

那么向量PQ就是两条直线之间的最短距离的方向向量。

我们可以通过以下步骤来推导异面直线之间距离的公式。

1. 首先，我们可以得到向量PQ的方向向量为：d = PQ = (x2 - x1, y2 - y1, z2 - z1)2. 由于向量d是与两条直线的方向向量正交的向量，即与(a1, b1,c1)和(a2, b2, c2)垂直。

因此，我们可以得到以下两个方程：(a1, b1, c1) · d = 0(a2, b2, c2) · d = 0其中·表示向量的点乘运算。

3. 将d的分量代入以上两个方程，我们可以得到一个关于t和s的线性方程组：(a1(x2 - x1) + b1(y2 - y1) + c1(z2 - z1))t = -a1(x1 - x2) - b1(y1 - y2) - c1(z1 - z2)(a2(x2 - x1) + b2(y2 - y1) + c2(z2 - z1))s = -a2(x1 - x2) - b2(y1 - y2) - c2(z1 - z2)4. 解这个线性方程组，我们可以得到t和s的值。