第八节--方程的近似解复习课程
新北师大版第2章第8节方程解的存在性及方程的近似解课件(48张)

对点强化 1 (1)(2022·江西高三模考)已知函数
f(x)=|fl(n xx|--3s)in ,x,x>03<x≤3 ,则 f(x)在(0,10)上的零点个数为(
)
A.6
B.7
C.8
D.9
B 由题意,当 0<x≤3 时,作出函数 y=|ln x|与 y=sin x 的图象.
由图可知,函数 y=|ln x|与 y=sin x 在(0,1)和[1,3]内各有一个交点,
返回导航
解析 方程 f(x)-kx=0⇔f(x)-2-(kx-2)=0. 画出 y=f(x)-2 与 y=kx-2 的函数图象如图所示:
返回导航
2.(多选题)已知函数 f(x)的图象是连续不断的,且有如下对应值表:
x 1 2 345 6 7
f(x) -4 -2 1 4 2 -1 -3
在下列区间中,函数 f(x)必有零点的区间为( )
A.(1,2)
B.(2,3)
C.(5,6)
D.(5,7)
BCD 由所给的函数值表知,
f(1)f(2)>0,f(2)f(3)<0,f(5)f(6)<0,f(5)f(7)<0,
返回导航
2.二分法 对于一般的函数 y=f(x),x∈[a,b],若函数 y=f(x)的图象是一条连__续__ 的曲线,_____f_(_a_)·_f_(b_)_<__0________,则每次取区间的中点,将区间一分为 二,再经比较,按需要留下其中一个小区间的求方程近似解的方法称为二 分法.
返回导航
返回导航
考点三 函数零点的应用 命题点 1 根据函数零点个数求参数
(2022·全国模拟)已知函数 f(x)=x|l2n+(2,x-x≤1)1,|+2,x>1. ,若关 于 x 的方程 f(x)-kx=0 有且只有一个实数根,则实数 k 的取值范围是 ________________.
方程的近似解ppt课件高品质版

通过试值,得到方程的解在2和3之间, 并且接近2. 取x=2.1进行试值,2.13=9.261>9
2< x <2.1
再取x=2.08, x=2.09继续试值,
2.08< x <2.09
作业
同步练习
随着年岁的叠加,我们会渐渐发现:越是有智慧的人,越是谦虚,因为昂头的只是稗子,低头的才是稻子;越是富有的人,越是高贵,因为真正的富裕是灵魂上的高贵以 及精神世界的富足;越是优秀的人,越是努力,因为优秀从来不是与生俱来,从来不是一蹴而就。随着沧桑的累积,我们也会慢慢懂得:成功的路,其实并不拥挤,因为 能够坚持到底的人实在太少;所有优秀的人,其实就是活得很努力的人,所谓的胜利,其实最后就是自身价值观的胜利。人到中年,突然间醒悟许多,总算明白:人生, 只有将世间的路一一走遍,才能到尽头;生活,只有将尘世况味种种尝遍,才能熬出头。这世间,从来没有最好,只有更好。每天,总想要努力醒得比太阳还早,因为总 觉得世间万物,太阳是最能赐人力量和能量的。每当面对喷薄的日出,心中的太阳随之冉冉腾起,生命之火熊熊燃烧,生活的热情就会光芒四射。我真的难以想象,那些 从来不早起的人,一生到底能够看到几回日升?那些从来没有良好习惯的人,活到最后到底该是多么的遗憾与愧疚?曾国藩说:早晨不起,误一天的事;幼时不学,误一 生的事。尼采也说:每一个不曾起舞的日子,都是对生命的辜负。光阴易逝,岂容我待?越是努力的人,越是没有时间抱怨,越是没有工夫颓丧。每当走在黎明的曙光里, 看到那些兢兢业业清洁城市的“美容师”,我就会由衷地欣赏并在心底赞叹他们,因为他们活得很努力很认真。每当看见那些奔跑在朝霞绚烂里的晨练者,我就会从心里 为他们竖起大拇指,因为他们给自己力量的同时,也赠予他人能量。我总觉得:你可以不优秀,但你必须有认真的态度;你可以不成功,但你必须努力。这个世界上,从 来没有谁比谁更优秀,只有谁比谁更努力。我也始终认为:一个活得很努力的人,自带光芒万丈;一个人认真的样子,比任何时候都要美好;一个能够自律自控的人,他 的人生也就成功了大半。世间每一种的好,从来都只为懂得努力的人盛装而来。有时候,我真的感觉,人生的另一个名字应该叫做努力,努力了就会无悔,努力了就会无 愧;生活的另一种说法应该叫做煎熬,熬过了漫漫黑夜,天就亮了,熬过了萧萧冬日,春天就来了。人生不易,越努力越幸运;余生不长,越珍惜越精彩。人生,是一本 太仓促的书,越认真越深刻;生命,是一条无名的河,越往前越深邃。愿你不要为已逝的年华叹息,不要为前路的茫茫而裹足不前愿你相信所有的坚持总能奏响黎明的号 角,所有的努力总能孕育硕果的盛驾光临。愿你坚信越是成功的人越是不允许自己颓废散漫,越是优秀的人越是努力……生活中很多时候,我们遇到一些复杂的情况,会 很容易被眼前的障碍所蒙蔽,找不到解决问题的方法。这时候,如果能从当前的环境脱离出来,从一个新角度去解决问题,也许就会柳暗花明。一个土豪,每次出门都担 心家中被盗,想买只狼狗栓门前护院,但又不想雇人喂狗浪费银两。苦思良久后终得一法:每次出门前把WiFi修改成无密码,然后放心出门每次回来都能看到十几个人捧 着手机蹲在自家门口,从此无忧。护院,未必一定要养狗换个角度想问题,结果大不同。一位大爷到菜市场买菜,挑了3个西红柿到到秤盘,摊主秤了下:“一斤半3块 7。”大爷:“做汤不用那么多。”去掉了最大的西红柿。摊主:“一斤二两,3块。”正当身边人想提醒大爷注意秤时,大爷从容的掏出了七毛钱,拿起刚刚去掉的那个大 的西红柿,潇洒地换种算法,独辟蹊径,你会发现解决问题的另一个方法。生活中,我们特别容易陷入非A即B的思维死角,但其实,遭遇两难困境时换个角度思考,也许 就会明白:路的旁边还有路。一个鱼塘新开张,钓费100块。钓了一整天没钓到鱼,老板说凡是没钓到的就送一只鸡。很多人都去了,回来的时候每人拎着一只鸡,大家 都很高兴!觉得老板很够意思。后来,钓鱼场看门大爷告诉大家,老板本来就是个养鸡专业户,这鱼塘本来就没鱼。巧妙的去库存,还让顾客心甘情愿买单。新时代,做 营销,必须打破传统思维。孩子不愿意做爸爸留的课外作业,于是爸爸灵机一动说:儿子,我来做作业,你来检查如何?孩子高兴的答应了,并且把爸爸的“作业”认真 的检查了一遍,还列出算式给爸爸讲解了一遍不过他可能怎么也不明白为什么爸爸所有作业都做错了。巧妙转换角色,后退一步,有时候是另一种前进。一个博士群里有 人提问:一滴水从很高很高的地方自由落体下来,砸到人会不会砸伤?或砸死?群里一下就热闹起来,各种公式,各种假设,各种阻力,重力,加速度的计算,足足讨论 了近一个小时 后来,一个不小心进错群的人默默问了一句:你们没有淋过雨吗 人们常常容易被日常思维所禁锢,而忘却了最简单也是最直接的路有两个年轻人,大学毕
数学必修一用二分法求方程的近似解课件

点?
提示:不能.看一个函数能否用二分法求其零点的依据是函数 图象在零点附近是连续不断的,且在该零点左右函数值异号.
人教A版必修一· 新课标· 数学
2.二分法的步骤 给定精确度ε,用二分法求f(x)零点近似值的步骤如下: (1)确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε; (2)求区间(a,b)的中点c;
答案:B
人教A版必修一· 新课标· 数学
2.设f(x)=3x+2x-8,用二分法求方程3x+2x-8=0在x∈(1,2) 内近似解的过程中得 f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根在区间 ( ) A.(1.25,1.5) B.(1,1.25)
C.(1.5,2)
D.不能确定
解析:∵f(1.5)>0,f(1.25)<0,∴方程根在区间 (1.25,1.5)内. 答案:A
3 在? 如果沿线路一小段一小段查找,困难很多.每查一个点要爬一 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电
话线路发生了故障.这是一条10 km长的线路,如何迅速查出故障所
次电线杆子,10 km,大约有200多根电线杆子呢.想一想,维修线
路的工人师傅怎样工作最合理?
人教A版必修一· 新课标· 数学
(0.6875,0.75) 0.71875 0.0625
∵0.0625<0.1,∴方程的近似解为 0.6875.
人教A版必修一· 新课标· 数学
类型三 【例 3】 二分法的实际应用 中央电视台有一档娱乐节目“幸运 52”,主持人李
咏会给选手在限定时间内猜某一物品的售价的机会,如果猜中,就把 物品奖励给选手,同时获得一枚商标.某次猜一种品牌的手机,手机
(3.8) 第八节 方程的近似解(少学时简约型)

0.4
O
1
x
2 y 1.1 x 0.4 1.6
• 用二分法逐次逼近方程实根
取 1 = 1/2( 0 + 1 )= 0.5,计算得 f( 1)= -0.55 < 0; 因为 f( 0 )= -1.4,f( 1 )= 1.6,故取 a1 = 1 = 0.5,b1= 1,隔离区间[ 0.5,1].
根的隔离工作可通过函数作图来实现,即先较准确
地作出曲线 y = f( x )的图形,从图形上定出曲线与 x 轴
的交点的大致位置。
y
b2
y f x
a4 b3 b4
a2 a1
1
b1
2 a3 O 3
4
x
完成了根的隔离这一步工作,第二步就是在各隔离
区间内确定实根的近似值。
确定实根的近似值可以以隔离区间的端点作为根的 初始近似值,通过逐步改善根的近似值的精确度,直至
来说明牛顿切线法的实施步骤。 此时 f( a )与 f ( x )同号,取 x0 = a,并在端点 ( x0, f( x0 ))作切线。这切线的方程为 y - f( x0 )= f ( x0 )( x - x0 ). y y f x 令 y = 0,从上式解出 x, x 0 x1 得切线与 x 轴交点的横坐标
过曲线的图形来寻求和建立求方程近似实根的方法。 y y f x f x 0
1
2
O
3
4
x
为求出方程的全部实根,首先须确定实根的个数及
各实根的大致范围,这一步工作称为根的隔离。
具体讲,根的隔离就是确定若干隔离区间[ ai,bi ], 使得每个区间[ ai,bi ]内方程 f( x )= 0 有唯一的实根。
4.5.2用二分法求方程的近似解课件(人教版)

)
答案:×,×,×.
辨析2:用二分法研究函数() = 3 + 3 − 1的零点时,第一次经计算(0) <
0,(0.5) > 0,可得其中一个零点0 ∈________,第二次计算________,以上横线
上应填的内容为( ).
A.(0,0.5),(0.25)
B.(0,1),(0.25)
2.5390625
0.010
(2.53125,2.5390625) 2.53515625
0.001
新知探索
零点所在区间
中点的值
中点函数近似
值
(2,3)
2.5
−0.084
(2.5,3)
2.75
0.512
(2.5,2.75)
2.625
0.215
(2.5,2.625)
2.5625
0.066
(2.5,2.5625)
0,所以0 ∈ (1,1.5).
再取区间(1,1.5)的中点2 = 1.25,用信息技术算得(1.25) ≈ −0.87.因为
(1.25)(1.5) < 0,所以0 ∈ (1.25,1.5).
同理可得,0 ∈ (1.375,1.5),0 ∈ (1.375,1.4375).
由于|1.375 − 1.4375| = 0.0625 < 0.1,所以,原方程的近似解可取为1.375.
间中点的方法,逐步缩小零点所在的范围.
新知探索
取(2,3)的中点2.5,用计算工具算得(2.5) ≈ −0.084.因为(2.5)(3) < 0,所以零
点在区间(2.5,3)内.
再取区间(2.5,3)的中点2.75,用计算工具算得(2.75) ≈ 0.512.因为(2.5)(2.75) <
第8节 函数与方程--2025年高考数学复习讲义及练习解析

第八节函数与方程课标解读考向预测1.理解函数的零点与方程解的联系,掌握函数的零点、方程的根、图象交点(横坐标)三者之间的灵活转化.2.理解函数零点存在定理,并能简单应用.3.会用二分法求方程的近似解.从近三年高考情况来看,函数零点(方程的根)个数的判断、由零点存在定理判断零点(方程的根)是否存在、利用函数零点(方程的根)确定参数的取值范围等是考查的热点.本节内容也可与导数结合考查,难度较大.预计2025年高考函数与方程仍会出题,可能以选择题或填空题考查三种形式的灵活转化,也可能与导数结合考查,难度较大.必备知识——强基础1.函数的零点对于函数y =f (x ),我们把使f (x )=0的实数x 叫做函数y =f (x )的零点.2.方程的根与函数零点的关系方程f (x )=0有实数解⇔函数y =f (x )有零点⇔函数y =f (x )的图象与x 轴有公共点.3.函数零点存在定理如果函数y =f (x )在区间[a ,b ]上的图象是一条连续不断的曲线,且有01f (a )f (b )<0,那么,函数y =f (x )在区间(a ,b )内至少有一个零点,即存在c ∈(a ,b ),使得f (c )=0,c 也就是方程f (x )=0的解.4.二分法对于在区间[a ,b ]上连续不断且02f (a )f (b )<0的函数y =f (x ),通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点的近似值的方法叫做二分法.求方程f (x )=0的近似解就是求函数y =f (x )零点的近似值.函数零点的相关技巧:(1)若连续函数f (x )在定义域上是单调函数,则f (x )至多有一个零点.(2)连续不断的函数f (x ),其相邻的两个零点之间的所有函数值同号.(3)连续不断的函数f (x )通过零点时,函数值不一定变号.(4)连续不断的函数f (x )在闭区间[a ,b ]上有零点,不一定能推出f (a )f (b )<0.1.概念辨析(正确的打“√”,错误的打“×”)(1)函数的零点就是函数的图象与x轴的交点.()(2)连续函数y=f(x)在区间(a,b)内有零点,则f(a)f(b)<0.()(3)函数y=f(x)为R上的单调函数,则f(x)有且仅有一个零点.()(4)二次函数y=ax2+bx+c(a≠0),若b2-4ac<0,则f(x)无零点.()答案(1)×(2)×(3)×(4)√2.小题热身(1)(人教A必修第一册4.5.1例1改编)已知函数f(x)=23x+1+a的零点为1,则实数a的值为()A.-2B.-12D.2C.12答案B(2)下列函数图象与x轴都有公共点,其中不能用二分法求图中函数零点近似值的是()答案A解析根据题意,利用二分法求函数零点的条件是函数在零点的左、右两侧的函数值符号相反,即图象穿过x轴,据此分析,知选项A中的函数不能用二分法求零点.故选A. (3)(人教A必修第一册习题4.5T2改编)已知函数y=f(x)的图象是一条连续不断的曲线,部分对应关系如表所示,则该函数的零点个数至少为()x123456y126.115.15-3.9216.78-45.6-232.64A.2B.3C.4D.5解析由表可知,f (2)f (3)<0,f (3)f (4)<0,f (4)f (5)<0,所以函数f (x )在区间[1,6]上至少有3个零点.故选B.(4)若函数f (x )=kx +1在[1,2]上有零点,则实数k 的取值范围是________.答案-1,-12考点探究——提素养考点一函数零点所在区间的判断例1(1)(2024·湖南长沙长郡中学高三月考)函数f (x )=5-2x -lg (2x +1)的零点所在的区间是()A .(0,1)B .(1,2)C .(2,3)D .(3,4)答案C解析因为函数f (x )=5-2x -lg (2x +1)-12,+,所以函数f (x )最多只有一个零点,因为f (0)f (1)=5(3-lg 3)>0,f (1)f (2)=(3-lg 3)(1-lg 5)>0,f (2)f (3)=(1-lg 5)(-1-lg 7)<0,f (3)f (4)=(-1-lg 7)×(-3-lg 9)>0,所以函数f (x )=5-2x -lg (2x +1)的零点所在的区间是(2,3).故选C.(2)用二分法求函数f (x )=3x -x -4的一个零点,其参考数据如下:f (1.6000)≈0.200f (1.5875)≈0.133f (1.5750)≈0.067f (1.5625)≈0.003f (1.5562)≈-0.029f (1.5500)≈-0.060据此数据,可得方程3x -x -4=0的一个近似解为________(精确度为0.01).答案 1.56(答案不唯一,在[1.5562,1.5625]上即可)解析注意到f (1.5562)≈-0.029和f (1.5625)≈0.003,显然f (1.5562)f (1.5625)<0,又|1.5562-1.5625|=0.0063<0.01,所以近似解可取1.56.【通性通法】确定函数零点所在区间的常用方法(1)利用函数零点存在定理:首先看函数y =f (x )在区间[a ,b ]上的图象是否连续,再看是否有f (a )f (b )<0.若有,则函数y =f (x )在区间(a ,b )内必有零点.(2)数形结合法:通过画函数图象,观察图象与x 轴在给定区间上是否有交点来判断.【巩固迁移】1.(2023·广东梅州高三二模)用二分法求方程log 4x -12x=0的近似解时,所取的第一个区间可A.(0,1)B.(1,2) C.(2,3)D.(3,4)答案B解析令f(x)=log4x-12x,因为函数y=log4x,y=-12x在(0,+∞)上都是增函数,所以函数f(x)=log4x-12x在(0,+∞)上是增函数,f(1)=-12<0,f(2)=log42-14=12-14=14>0,所以函数f(x)=log4x-12x在区间(1,2)上有唯一零点,所以用二分法求方程log4x-12x=0的近似解时,所取的第一个区间可以是(1,2).故选B.2.已知2<a<3<b<4,函数y=log a x与y=-x+b的交点为(x0,y0),且x0∈(n,n+1),n∈N*,则n=________.答案2解析依题意,x0为方程log a x=-x+b的解,即为函数f(x)=log a x+x-b的零点,∵2<a<3<b<4,∴f(x)在(0,+∞)上单调递增,又f(2)=log a2+2-b<0,f(3)=log a3+3-b>0,∴x0∈(2,3),即n=2.考点二函数零点个数的判断例2(1)已知函数f(x)2-4,x≤1,2(x-1),x>1,则函数y=f(x)零点的个数为________.答案2解析当x≤1时,由f(x)=x2-4=0,可得x=2(舍去)或x=-2;当x>1时,由f(x)=log2(x -1)=0,可得x=2.综上所述,函数y=f(x)零点的个数为2.(2)方程ln x+cos x=13在(0,1)上的实数根的个数为________.答案1解析解法一:ln x+cos x=13,即cos x-13=-ln x,在同一平面直角坐标系中,分别作出函数y=cos x-13和y=-ln x的大致图象,如图所示,在(0,1)上两函数的图象只有一个交点,即方程ln x+cos x=13在(0,1)上的实数根的个数为1.解法二:令f(x)=ln x+cos x-13,则f′(x)=1x-sin x,显然在(0,1)上f′(x)>0,所以函数f(x)在(0,1)上单调递增,又ln 1e +cos 1e -13=-1-13+cos 1e <0,f (1)=ln 1+cos1-13=0+cos1-13>cos π3-13=12-13>0,所以在(0,1)上函数f (x )的图象和x 轴有且只有一个交点,即方程ln x +cos x =13在(0,1)上的实数根的个数为1.【通性通法】求解函数零点个数的基本方法(1)直接法:令f (x )=0,方程有多少个解,则f (x )有多少个零点.(2)构造函数法:判断函数的性质,并结合零点存在定理判断.(3)图象法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后观察求解,此时需要根据零点个数合理寻找“临界”情况,特别注意边界值的取舍.【巩固迁移】3.(2024·江苏无锡模拟)函数f (x )2-2,x ≤0,x -6+lg x ,x >0的零点的个数为________.答案2解析当x ≤0时,f (x )=x 2-2,根据二次函数的性质可知,此时f (x )单调递减,零点为x =-2;当x >0时,f (x )=2x -6+lg x ,∵y =2x -6单调递增,y =lg x 单调递增,∴f (x )=2x -6+lg x 单调递增.f (1)=-4<0,f (3)=lg 3>0,由零点存在定理知,在区间(1,3)必有唯一零点.综上所述,函数f (x )的零点的个数为2.4.函数f (x )|-|log 2x |的零点有________个.答案2解析f (x )|-|log 2x ||=|log 2x |的根的个数,即为y |与y =|log 2x |图象交点的个数,画出大致图象如图所示,则由图象可知交点有2个,即函数f (x )的零点有2个.考点三函数零点的应用(多考向探究)考向1利用零点比较大小例3已知函数f (x )=3x +x ,g (x )=log 2x +x ,h (x )=x 3+x 的零点分别为a ,b ,c ,则a ,b ,c 的大小顺序为()A .a <c <bB .a <b <cC.b<a<c D.b<c<a答案A解析解法一:因为函数y=3x,y=x均为R上的增函数,故函数f(x)=3x+x为R上的增函数,因为f(-1)=13-1<0,f(0)=1>0,所以-1<a<0.因为函数y=log2x,y=x在(0,+∞)上均为增函数,故函数g(x)=log2x+x在(0,+∞)上为增函数,因为1+12<0,g(1)=1>0,所以12<b<1.由h(c)=c(c2+1)=0可得c=0,因此a<c<b.故选A.解法二:由题设,3a=-a,log2b=-b,c3=-c,所以问题可转化为直线y=-x与y=3x,y=log2x,y=x3的图象的交点问题,函数图象如图所示,由图可知a<c=0<b.故选A.【通性通法】(1)直接利用方程研究零点.(2)利用图象交点研究零点.(3)利用零点存在定理研究零点.【巩固迁移】5.(2023·江西南昌模拟预测)已知函数f(x)=2x+x-4,g(x)=e x+x-4,h(x)=ln x+x-4的零点分别是a,b,c,则a,b,c的大小顺序是()A.a<b<c B.c<b<aC.b<a<c D.c<a<b答案C解析由已知条件得f(x)的零点可以看成y=2x的图象与直线y=4-x的交点的横坐标,g(x)的零点可以看成y=e x的图象与直线y=4-x的交点的横坐标,h(x)的零点可以看成y=ln x 的图象与直线y=4-x的交点的横坐标,在同一坐标系内分别画出函数y=2x,y=e x,y=ln x,y=4-x的图象,如图所示,由图可知b<a<c.故选C.考向2根据零点个数求参数例4(2023·山东济南高三三模)已知函数f (x )x +1)2,x ≤0,x |,x >0,若函数g (x )=f (x )-b 有四个不同的零点,则实数b 的取值范围为()A .(0,1]B .[0,1]C .(0,1)D .(1,+∞)答案A解析依题意,函数g (x )=f (x )-b 有四个不同的零点,即f (x )=b 有四个解,转化为函数y =f (x )与y =b 的图象有四个交点,由函数y =f (x )可知,当x ∈(-∞,-1]时,函数单调递减,y ∈[0,+∞);当x ∈(-1,0]时,函数单调递增,y ∈(0,1];当x ∈(0,1)时,函数单调递减,y ∈(0,+∞);当x ∈[1,+∞)时,函数单调递增,y ∈[0,+∞).结合图象,可知实数b 的取值范围为(0,1].故选A.【通性通法】根据零点个数求参数的方法(1)直接法:直接根据题设条件构建关于参数的不等式(组),再通过解不等式(组)确定参数范围.(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决.(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.一是转化为两个函数y =g (x ),y =h (x )的图象的交点个数问题,画出两个函数的图象,其交点的个数就是函数零点的个数,二是转化为y =a ,y =g (x )的图象的交点个数问题.【巩固迁移】6.(2024·安徽蚌埠高三摸底)已知函数f (x )=2|x |+x 2+a 有唯一的零点,则实数a 的值为()A .1B .-1C .0D .-2答案B解析函数f (x )=2|x |+x 2+a 的定义域为R ,f (-x )=2|-x |+(-x )2+a =f (x ),即函数f (x )为偶函数,当x ≥0时,f (x )=2x +x 2+a ,则f (x )在[0,+∞)上单调递增,在(-∞,0)上单调递减,则当x =0时,f (x )min =a +1,由函数f (x )=2|x |+x 2+a 有唯一的零点,得a +1=0,解得a =-1,所以实数a 的值为-1.故选B.7.设a ∈R ,对任意实数x ,记f (x )=min{|x |-2,x 2-ax +3a -5}.若f (x )至少有3个零点,则实数a 的取值范围为________.答案[10,+∞)解析设g (x )=x 2-ax +3a -5,h (x )=|x |-2,由|x |-2=0可得x =±2.要使得函数f (x )至少有3个零点,则函数g (x )至少有一个零点,则Δ=a 2-12a +20≥0,解得a ≤2或a ≥10.①当a =2时,g (x )=x 2-2x +1,作出函数g (x ),h (x )的图象如图所示,此时函数f (x )只有2个零点,不符合题意;②当a <2时,设函数g (x )的2个零点分别为x 1,x 2(x 1<x 2),要使得函数f (x )至少有3个零点,则x 2≤-2,-2,-2)=4+5a -5≥0,无解;③当a =10时,g (x )=x 2-10x +25,作出函数g (x ),h (x )的图象如图所示,由图可知,函数f (x )的零点个数为3,符合题意;④当a >10时,设函数g (x )的2个零点分别为x 3,x 4(x 3<x 4),要使得函数f (x )至少有3个零点,则x 3≥2,,=4+a -5≥0,解得a >4,所以a >10.综上所述,实数a 的取值范围是[10,+∞).考向3根据零点范围求参数例5已知函数f (x )=log 2(x +1)-1x +m 在区间(1,3]上有零点,则实数m 的取值范围为________.答案-53,解析由于函数y =log 2(x +1),y =m -1x在区间(1,3]上单调递增,所以函数f (x )在(1,3]上单调递增,由于函数f (x )=log 2(x +1)-1x +m 在区间(1,3]上有零点,,≥0,<0,+53≥0,解得-53≤m <0.因此实数m 的取值范围是-53,【通性通法】根据零点范围求参数的方法(1)利用零点存在定理构建不等式(组)求解.(2)分离参数后转化为函数的值域(最值)问题求解.(3)转化为两个熟悉的函数图象的上下关系问题,从而构建不等式(组)求解.【巩固迁移】8.(2024·湖北荆州中学高三月考)已知f (x )是定义在R 上且周期为3的函数,当x ∈[0,3)时,f (x )=|x 2-2x +12|,若函数y =f (x )-a 在区间[-3,4]上有10个零点(互不相同),则实数a 的取值范围是________.答案解析作出函数f (x )=|x 2-2x +12|,x ∈[0,3)的图象,可见f (0)=12,当x =1时,f (x )极大值=12,方程f (x )-a =0在[-3,4]上有10个零点,即函数y =f (x )的图象与直线y =a 在[-3,4]上有10个交点,由于函数f (x )的周期为3,因此直线y =a 与函数f (x )=|x 2-2x +12|,x ∈[0,3)的图象有4个交点,则有a课时作业一、单项选择题1.(2024·江苏扬中第二高级中学高三期初检测)函数f (x )=2x +3x 的零点所在的一个区间是()A .(-2,-1)B .(-1,0)C .(0,1)D .(1,2)答案B解析因为函数f (x )=2x +3x 在定义域内单调递增,f (-1)=12-3=-52<0,f (0)=1+0=1>0,所以由函数零点存在定理可知,函数f (x )的零点所在的区间为(-1,0).故选B.2.已知函数f (x )x -1,x ≤1,+log 2x ,x >1,则函数f (x )的零点为()A .2B .-2,0C.12D .0答案D解析当x ≤1时,令f (x )=2x -1=0,解得x =0;当x >1时,令f (x )=1+log 2x =0,解得x=12(舍去).综上所述,函数f (x )的零点为0.故选D.3.函数f (x )=e x |ln x |-1的零点个数是()A .1B .2C .3D .4答案B解析令f (x )=e x |ln x |-1=0,即|ln x |=e -x ,则函数f (x )=e x |ln x |-1的零点个数等价于两个函数y =e -x 与y =|ln x |图象的交点个数,y =e -x 与y =|ln x |的图象如图所示,由图可知,两个函数的图象有2个交点,故函数f (x )=e x |ln x |-1的零点个数是2.故选B.4.(2023·河南扶沟期末)若关于x 的方程log 12x =m1-m在区间m 的取值范围是()(1,+∞)答案B解析y =log 12x,则1<y <2,即1<m 1-m<2,解得12<m <23.故选B.5.已知三个函数f (x )=2x -1+x -1,g (x )=e x -1-1,h (x )=log 2(x -1)+x -1的零点依次为a ,b ,c ,则a ,b ,c 的大小关系是()A .a >b >c B .a >c >b C .c >a >b D .c >b >a答案D解析∵函数f (x )=2x -1+x -1为增函数,又f (0)=2-1-1=-12<0,f (1)=1>0,∴a ∈(0,1),由g (x )=e x -1-1=0,得x =1,即b =1,∵h (x )=log 2(x -1)+x -1在(1,+∞)上单调递增,又log +32-1=-12<0,h (2)=log 2(2-1)+2-1=1>0,∴32<c <2,∴c >b >a .故选D.6.若方程m x -x -m =0(m >0,且m ≠1)有两个不同的实数根,则实数m 的取值范围是()A .(0,1)B .(2,+∞)C .(0,1)∪(2,+∞)D .(1,+∞)答案D解析方程m x -x -m =0有两个不同的实数根等价于函数y =m x 与y =x +m 的图象有两个不同的交点,当m >1时,如图1所示,由图可知,当m >1时,函数y =m x 与y =x +m 的图象有两个不同的交点,满足题意;当0<m <1时,如图2所示,由图可知,当0<m <1时,函数y =m x 与y =x +m 的图象有且仅有一个交点,不满足题意.综上所述,实数m的取值范围为(1,+∞).故选D.7.已知函数f (x )x ,x ≤0,x ,x >0,若函数g (x )=f (x )+x -m 恰有两个不同的零点,则实数m 的取值范围是()A .[0,1]B .(-1,1)C .[0,1)D .(-∞,1]答案D解析由题意,函数f (x )x ,x ≤0,x ,x >0,当x ≤0时,函数f (x )=e x 为增函数,其中f (0)=1,当x >0时,函数f (x )=ln x 为增函数,且f (1)=0,又由函数g (x )=f (x )+x -m 恰有两个不同的零点,即为g (x )=0有两个不等的实数根,即y =f (x )与y =-x +m 的图象有两个不同的交点,如图所示,当y =-x +m 恰好过点(1,0),(0,1)时,两函数的图象有两个不同的交点,结合图象,要使得函数g (x )=f (x )+x -m 恰有两个不同的零点,实数m 的取值范围是(-∞,1].故选D.8.已知函数f (x )x |,0<x ≤10,-12x +6,x >10,若a ,b ,c 均不相等,且f (a )=f (b )=f (c ),则abc 的取值范围是()A .(1,10)B .(5,6)C .(10,12)D .(20,24)答案C解析函数f (x )的图象如图所示,不妨设a <b <c ,则-lg a =lg b =-12c +6∈(0,1),所以ab=1,0<-12c +6<1,所以ab =1,10<c <12,所以10<abc <12.故选C.二、多项选择题9.下列说法正确的是()A .函数y =x 2-3x -4的零点是(4,0),(-1,0)B .方程e x =3+x 有两个解C .函数y =3x ,y =log 3x 的图象关于直线y =x 对称D .用二分法求方程3x +3x -8=0在x ∈(1,2)内的近似解的过程中得到f (1)<0,f (1.5)>0,f (1.25)<0,则方程的根落在区间(1.25,1.5)上答案BCD解析对于A ,令y =x 2-3x -4=0,解得x =-1或x =4,所以函数y =x 2-3x -4的零点是-1和4,故A错误;对于B,分别作出y=e x,y=3+x的图象,y=e x与y=3+x的图象有两个交点,即方程e x=3+x有两个解,故B正确;对于C,因为同底数的指数函数和对数函数的图象关于直线y=x对称,所以函数y=3x,y=log3x的图象关于直线y=x对称,故C正确;对于D,因为y=3x+3x-8单调递增,由零点存在定理知,因为f(1)<0,f(1.5)>0,f(1.25)<0,所以方程的根落在区间(1.25,1.5)上,故D正确.故选BCD.10.若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1<x2,则下列结论正确的是()A.当m=0时,x1=2,x2=3B.m>-14C.当m>0时,2<x1<x2<3D.二次函数y=(x-x1)(x-x2)+m的零点为2和3答案ABD解析对于A,易知当m=0时,(x-2)(x-3)=0的根为2,3,故A正确;对于B,设y=(x-2)(x-3)=x2-5x+6-14≥-14,因为y=(x-2)(x-3)的图象与直线y=m有两个交点,所以m>-14,故B正确;对于C,当m>0时,y=(x-2)(x-3)-m的图象由y=(x-2)(x-3)的图象向下平移m个单位长度得到,x1<2<3<x2,故C错误;对于D,由(x-2)(x-3)=m 展开得,x2-5x+6-m=0,利用根与系数的关系求出x1+x2=5,x1x2=6-m,代入y=(x-x1)(x-x2)+m可得y=(x-x1)(x-x2)+m=(x-2)(x-3)-m+m=(x-2)(x-3),所以二次函数y=(x-x1)(x-x2)+m的零点为2和3,故D正确.故选ABD.11.已知函数f(x)x-1|,x<1,4x2+16x-13,x≥1,函数g(x)=f(x)-a,则下列结论正确的是()A.若g(x)有3个不同的零点,则a的取值范围是[1,2)B.若g(x)有4个不同的零点,则a的取值范围是(0,1)C.若g(x)有4个不同的零点x1,x2,x3,x4(x1<x2<x3<x4),则x3+x4=4D.若g(x)有4个不同的零点x1,x2,x3,x4(x1<x2<x3<x4),则x3x4答案BCD解析令g(x)=f(x)-a=0,得f(x)=a,所以g(x)的零点个数即为函数y=f(x)与y=a图象的交点个数,故作出函数y =f (x )的图象如图,由图可知,若g (x )有3个不同的零点,则a 的取值范围是[1,2)∪{0},故A 错误;若g (x )有4个不同的零点,则a 的取值范围是(0,1),故B 正确;若g (x )有4个不同的零点x 1,x 2,x 3,x 4(x 1<x 2<x 3<x 4),此时x 3,x 4关于直线x =2对称,所以x 3+x 4=4,故C 正确;由C 项可知x 3=4-x 4,所以x 3x 4=(4-x 4)x 4=-x 24+4x 4,由于g (x )有4个不同的零点,a 的取值范围是(0,1),故0<-4x 24+16x 4-13<1,所以134<-x 24+4x 4<72,故D 正确.故选BCD.三、填空题12.已知函数f (x )=log 2(x -1)+a 在区间(2,3)上有且仅有一个零点,则实数a 的取值范围为________.答案(-1,0)解析由对数函数的性质,可得f (x )为增函数,又函数f (x )在(2,3)上有且仅有一个零点,所以f (2)f (3)<0,即a (a +1)<0,解得-1<a <0,所以实数a 的取值范围是(-1,0).13.已知函数f (x )x -1|+1,x >0,x 2-2x ,x ≤0,若函数y =f (x )-kx -1有m 个零点,函数y =f (x )-1k x-1有n 个零点,且m +n =7,则非零实数k 的取值范围是________.答案,13∪[3,+∞)解析f (x )的图象与直线y =kx +1和y =1kx +1共7个交点,f (x )的图象如图所示,所以①k <3,3,解得0<k ≤13;0<1k <3,≥3,解得k ≥3.综上,非零实数k ,13∪[3,+∞).14.(2024·河北衡水中学高三月考)已知函数f (x )=x -1x -2与g (x )=1-sinπx ,则函数F (x )=f (x )-g (x )在区间[-2,6]内所有零点的和为________.答案16解析令F (x )=f (x )-g (x )=0,得f (x )=g (x ),在同一平面直角坐标系中分别画出函数f (x )=1+1x -2与g (x )=1-sinπx 的图象,如图所示,又f (x ),g (x )的图象都关于点(2,1)对称,结合图象可知f (x )与g (x )的图象在[-2,6]上共有8个交点,交点的横坐标即F (x )=f (x )-g (x )的零点,由对称性可得,所有零点的和为4×2×2=16.15.已知函数f (x )+1x ,x <0,x ,x >0,则方程f (f (x ))+3=0的解的个数为()A .3B .4C .5D .6答案C解析已知函数f (x )+1x ,x <0,x ,x >0,∴令f (x )=-3,则当x >0时,ln x =-3,解得x =1e 3;当x <0时,x +1x =-3,解得x =-3±52.∵f (f (x ))+3=0,即f (f (x ))=-3,则f (x )=1e 3或f (x )=-3±52.由f (x )=1e 3,得ln x =1e 3,此方程只有一个根,∵当x <0时,f (x )=x +1x ≤-2,当且仅当x =-1时,等号成立,∴f (x )=-3+52仅在x >0时有一个根,f (x )=-3-52在x <0时有两个根,在x >0时有一个根.综上,方程f (f (x ))+3=0的解的个数为5.故选C.16.(多选)(2024·湖北荆州模拟)已知函数f (x )|log 12x |,0<x<4,4≤x ≤14,若方程f (x )=m 有四个不等的实根x 1,x 2,x 3,x 4,且x 1<x 2<x 3<x 4,则下列结论正确的是()A .0<m <2B .x 1x 2=12C .x 3x 4∈(48,55)D .x 1x 3∈(1,5)答案ACD解析对于A ,当0<x <1时,log 12x >0,则f (x )=log 12x ,易得f (x )在(0,1)上单调递减,且f (x )>f (1)=0,当1≤x <4时,log 12x ≤0,则f (x )=-log 1x ,易得f (x )在[1,4)上单调递增,且f (1)≤f (x )<f (4),即0≤f (x )<2,当4≤x ≤14时,f (x )=则由f (x )=x ∈[4,14]的图象,可知f (x )在[4,8)上单调递减,在[8,14]上单调递增,且f (4)=2,f (5)=0,f (8)=4,f (11)=0,f (14)==4,从而利用对数函数与正弦函数的性质,画出f (x )的图象,如图所示,因为方程f (x )=m 有四个不等实根,所以f (x )与y =m 的图象有四个交点,所以0<m <2,故A 正确;对于B ,结合A 项分析可得log 12x 1=-log 12x 2,所以log 12(x 1x 2)=0,则x 1x 2=1,故B 错误;对于C ,D ,由正弦函数的性质及结合图象可知(x 3,m )与(x 4,m )关于直线x =8对称,所以x 3+x 4=16,又当0<x <1时,f (x )=log 12x ,令f (x )=2,得x =14,所以14<x 1<1,4<x 3<5,所以x 1x 3∈(1,5),x3x 4=x 3(16-x 3)=-x 23+16x 3=-(x 3-8)2+64,因为x 3∈(4,5),所以x 3x 4∈(48,55),故C ,D 正确.故选ACD.17.已知定义在R 上的奇函数y =f (x )满足f (1+x )=f (1-x ),当-1≤x <0时,f (x )=x 2,则方程f (x )+12=0在[-2,6]内的所有根之和为________.答案12解析因为f (1+x )=f (1-x ),所以y =f (x )的图象关于直线x =1对称,又函数y =f (x )在R 上为奇函数,且当-1≤x <0时,f (x )=x 2,由此画出f (x )在区间[-2,6]上的图象如图所示.f (x )+12=0⇒f (x )=-12,由图可知,y =-12与f (x )的图象有4个交点,其中两个关于直线x =1对称,两个关于直线x =5对称,所以方程f (x )+12=0在[-2,6]内的所有根之和为2×1+2×5=12.18.(2024·山东泰安高三期末)已知函数f (x )2(x +1),x >3,x +3|,-9≤x ≤3,若x 1<x 2,x 1<x 3,且f (x 1)=f (x 2),f (x 1)+f (x 3)=4,则x 3x 1+x 2的取值范围是________.答案-52,-12解析对于f (x )2(x +1),x >3,+3|,-9≤x ≤3,当x >3时,f (x )>2,当-9≤x ≤3时,0≤f (x )≤2,并且图象关于直线x =-3对称,函数f (x )的图象如下图所示,如果x 1>3,则f (x 1)=f (x 2)不成立,∴x 1∈[-9,3],x 2∈[-9,3],并且有x 1+x 2=-6,0<f (x 1)≤2.由f (x 1)+f (x 3)=4可知,2≤f (x 3)<4,∴2≤log 2(x 3+1)<4,3≤x 3<15.∴x 3x 1+x 2=-16x 3-52,-12.。
苏教版必修第一册812用二分法求方程的近似解课件_3

令f(x)=2x3+3x-3,经计算, f(0)=-3<0,f(1)=2>0,f(0)·f(1)<0, 所以函数f(x)在(0,1)内存在零点, 即方程2x3+3x-3=0在(0,1)内有解. 取(0,1)的中点,经计算f(0.5)<0, 又f(1)>0,所以方程2x3+3x-3=0在(0.5,1)内有解.
(2)用二分法求方程2x+3x-7=0在区间(1,3)内的近似解,取区间的中点 为x0=2,那么下一个有根的区间是__(_1_,2_)__.
设f(x)=2x+3x-7, f(1)=2+3-7<0, f(3)=10>0,f(2)=3>0, ∵f(1)·f(2)<0, ∴f(x)零点所在的区间为(1,2), ∴方程2x+3x-7=0下一个有根的区间是(1,2).
2.设f(x)=lg x+x-3,用二分法求方程lg x+x-3=0在(2,3)内近似解的过
程中得f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,则方程的根落在区间
A.(2,2.25)
√C.(2.5,2.75)
B.(2.25,2.5) D.(2.75,3)
因为f(2.5)<0,f(2.75)>0,由函数零点存在定理知,方程的根在区间 (2.5,2.75).
问题3 如何求方程x3-3=0的近似解呢? 提示 可以转化为求对应函数f(x)=x3-3的近似零点.
知识梳理
用二分法求方程的一个近似解的操作流程
步骤1 步骤2 步骤3
方程f(x)=0的解 ↓转化为
函数f(x)的零点 ↓f(a)f(b)<0
确定f(x)的零点x0∈_(_a_,__b_) ↓
第八节 方程的近似解

例如,对于方程 f (x) = x3 – x – 1 = 0,作图如下:
因为 f (1) = -1 < 0,
y
(x) = x + 1
f (2) = 5 > 0, 在 (1 , 2) 内 f (x) > 0, 所以 [1 , 2] 为隔离区间.
(x) = x3
O
x
f (x) = x3 – x – 1
第八节 方程的近似解 第二步在隔离区间上求满足精度要求的根.
nL
M
R
f(L) f(M) f(R)
1 1 1.5
2
-1 0.87
5
2 1 1.25 1.5
-1 -0.2969 0.87
3 1.25 1.375 1.5 -0.2969 0.2246 0.87
4 1.25 1.3125 1.375 -0.2969 -0.0515 0.2246
5 1.3125 1.3437 1.375 -0.0515 0.08239 0.2246
6 1.3125 1.3281 1.3437 -0.0515 0.01447 0.08239
第八节 方程的近似解
nL
M
R
f(L) f(M) f(R)
6 1.3125 1.3281 1.3437 -0.0515 0.01447 0.08239
7 1.3125 1.3201 1.3281 -0.0515 -0.01961 0.01447
所以近似根为 x 1.3246 .
第八节 方程的近似解
三、切线法
设 f (x) 在 [a , b] 上具有二阶导数,f (a) f (b) < 0 且 f (x) 及 f (x) 在 [a , b] 上保持定号. 则 [a , b] 为根的一 个隔离区间.
3-7曲率3-8方程的近似解

主要内容: 一、 弧微分 二、 曲率及其计算公式 三、 曲率圆与曲率半径
第三章
1
一.弧长函数及其微分
1.光滑曲线:若 f ( x) 在(a, b) 内具有一阶连续导数(连续
转动的切线),则称曲线 y f为( x光) 滑曲线 .
2.弧长函数
(1)光滑曲线上有向弧 M0 M 的值s规定如下y :
y
K
(1
y
2
)
3 2
显然, 当x b 时, k最大. 2a
又( b , b2 4ac)为抛物线的顶点, 2a 4a
抛物线在顶点处的曲率最大.
14
了解:我国铁路常用立方抛物线
y
1 6Rl
x3
作缓和曲线,
6
2.定义:
(1)平均曲率:单位弧段上切线转角 y
C
的大小. 即
M.
弧段MM的平均曲率为 K . s
M
S
0
(2)曲线 y f ( x)在点M处的曲率: o
M.
)
S
x
当s 0时,平均曲率的极限叫做该曲线在点M处的曲率.
即K lim , s0 s
若 lim d 存在,则 K d .
则y
R2 y3
,
x y
,
R2
y
K
3
(1 y2 )2
y3 R3
1. R
y3
注意: 圆上各点处的曲率等于半径的倒数,且半径
越小曲率越大.
12
解法二
x
若圆方程为
y
R cos ,( R sin
为参) 数
y dy R cosd cot, dy csc2 d dx R sin d
28.4方程的近似解教案(冀教版九年级上)教学设计
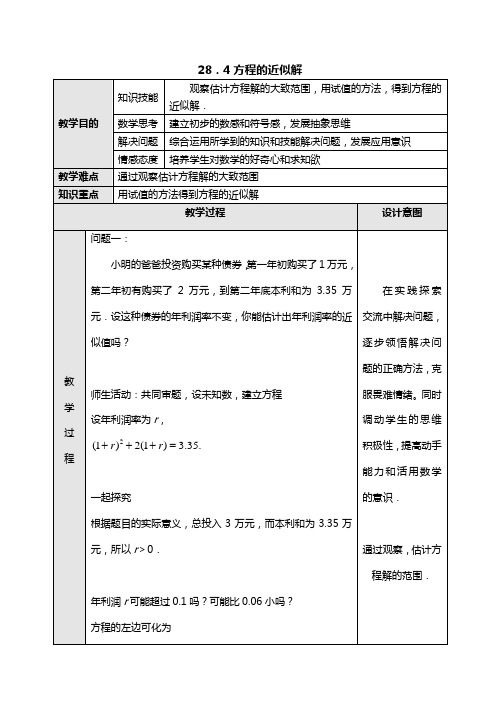
方程的左边可化为
当r=0.1时,方程的左边=1.1×3.1=3.41>3.35
0<r<0.1
当r=0.06时,方程的左边=1.06×3. 06=3.3.2436<3.35
0.06<r<0.1
课堂练习
一架长为10m的梯子斜靠在墙上,梯子的顶端A除到地面的距离为8m.如果梯子的顶端沿墙面下滑1m,那么梯子的底端在地面上滑动的距离也是1m吗?请列出方程,并估计方程解的大致范围(误差不超过0.1m).
28.4方程的近似解
教学目的
知识技能
观察估计方程解的大致范围,用试值的方法,得到方程的近似解.
数学思考
建立初步的数感和符号感,发展抽象思维
解决问题
综合运用所学到的知识和技能解决问题,发展应用意识
情感态度
培养学生对数学的好奇心和求知欲
教学难点
通过观察估计方程解的大致范围
知识重点
用试值的方法得到方程的近似解
问题二:估计方程x3-9=0的解.
解:将方程化成x3=9
由于23=8<9,33=27>9
通过试值,得到方程的解在2和3之间,并且接近2.
取x=2.1进行试值,2.13=9.261>9
2<x<2.1
再取x=2.08,x=2.09继续试值,
2.08<x<2.09
在实践探索交流中解决问题,逐步领悟解决问题的正确方法,克服畏难情绪。同时调动学生的思维积极性,提高动手能力和活用数学的意识.
通过观察,估计方程解的范围.
用试值的方法得到方程的近似解
通过估计方程的近似解,解决实际问题.
对高次方程进行估算,求其近似解.
小结与作业
课堂小结
学生讨论总结,本节课的所得和估算要点
人教A版数学必修一用二分法求方程的近似解配套教学课件

人教A版数学必修一3.1.2 用二分法求方程的近似解 配套教学课件(共19张PPT)
三、自行探究
利用计算器,求方程 lgx=3- x的近似解.(精确到0.1)
解:画出y=lg x及y=3 -x的图象,观察图象得,方程lgx=3 - x 有唯一解,记为x,且这个解在区间(2,3)内。
设 f (x)=lgx+x -3
用二分法求方程的近似解
教学过程:
一、提出问题: 1.能否求解以下几个方程 (1) 2x=4-x (2) x2-2x-1=0 (3) x3+3x-1=0
2.能否求出它们的近似解?
3.什么方法?
y=2x
y
4
1 0 12
y=4-x
x
4
4.能否找到其它的方法,使解更精确?
探究解法
(1)不解方程,如何求方程x2-2x-1=0 的一个正的近似解(精确到0.1)?
3
-+
2
2.375 2.475
f(2.375)<0,f(2.4375)>0 2.375<x1<2.4375
3
二、方法探究
(2)能否简述上述求方程近似解的过程?
(3)二分法(bisection method):象上面这种求方程 近似解的方法称为二分法,它是求一元方程近似解的常用 方法。 定义如下:
对于区间[a,b]上连续不断、且f(a)f(b)<0的函数y=f(x),通过 不断地把函数f(x)的零点所在的区间一分为二,使区间的 两个端点逐步逼近零点,进而得到零点近似值的方法叫做 二分法(bisection)
No Image
人教A版数学必修一3.1.2 用二分法求方程的近似解 配套教学课件(共19张PPT)
08 第八节 方程的近似解

第八节方程的近似解高次代数方程或其余范例的方程求准确根普通比拟艰苦盼望追求方程近似根的无效盘算办法.散布图示★咨询题的提出★二分法★切线法★例1★例2★内容小结★习题3-8★前往内容要点一、求近似实根的步调:〔1〕断定根的年夜抵范畴 根的断绝〔2〕以根的断绝区间的端点作为根的初始近似值,逐渐改良根的近似值的准确度,直至求得满意准确度请求的近似实根.二、二分法跟切线法(牛顿法).例题选讲例1用二分法求方程的实根的近似值,使偏差不超越解令显然在内延续.故在内枯燥添加,至少有一个实根.在内有独一的实根.取等于一个断绝区间.故故故故故故故假设0.670作为根的缺乏近似值,0.671作为根的多余近似值,那么其偏差都小于例2用切线法求方程的实根的近似值,使偏差不超越解令因故是一个断绝区间.在上,与同号,令用切线法盘算得:盘算停顿.所得根的近似值为0.671,其偏差都小于牛顿(Newton,lsaac,1643~1727)天然跟天然法则暗藏在黑夜里,天主说“落生牛顿〞.因而天下就充溢黑暗.Newtan墓志铭数学跟迷信中的宏年夜停顿,简直老是树破在作出一点一点滴奉献的很多人的任务之上.需求一团体来走那最高跟最初的一步,那团体要可以灵敏地从缭乱的猜想跟阐明中清算出后人的有代价的办法,有充足的设想利巴这些碎片从新构造起来,同时充足勇敢地制订一个雄伟的方案.在微积分中,那团体确实是牛顿.牛顿(1642-1727)生于英格兰乌尔斯托帕的一个小村落里,父亲是在他诞生前两个月逝世的,母亲治理着夫君留下的农庄,母亲再醮后,是由外祖母把他抚育年夜.并供他上学.他从小在低规范的地点黉舍承受教导,除对机器计划有兴味外,是个不什么特别的青年人,1661年他进入剑桥年夜学的三一学院进修,年夜学时代除了巴罗(Barrow)外,他从他的教师那儿只失掉了非常少的一点鼓励,他本人做试验同时研讨事先一些数学家的著述,如Descartes的《多少何》,Galileo,Kepler等的著述。
【数学】用二分法求方程的近似解教学课件 高一数学必修第一册同步课堂(人教A版2019)

若f(a)·f(c)<0,则令b=c(此时零点x0∈(a,c));若f(b)·f(c)<0,则令a=c(此时零点x0∈(c,b); 4. 判断是否达到精度ε,若|a-b|<ε,则得到零点近似值a(或b),否则重复步骤2~4;
总结新知
用二分法求函数零点近似值的步骤
1. 确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
2. 求区间(a,b)的中点c; 3. 计算f(c) ;
若f(c)=0,则c就是函数的零点c ; 若f(a)·f(c)<0,此时零点x0∈(a,c),则令b=c;若f(b)·f(c)<0,此时零点x0∈(c,b), 则令a=c;
因为(2,3)⊇(2.5,3)⊇(2.5,2.75),所以零点所在的范围变小了.如果重复上述的 步骤,那么零点所在的范围会越来越小.
这样,我们就可以通过有限次重复相同的步骤,将零点所在的范围缩小到满足一 定精度的区间,区间内的任意一点都可以作为函数零点的近似值.为了方便,我 们把区间的一个端点作为零点的近似值.
解:因为函数f(x)=2x+3x-6在R上单调递增,且f(1)=2+3-6=-1<0,f(2)=4 + 6 - 6 = 4>0 , 即 f(1)f(2)<0 , 所 以 函 数 f(x) 在 R 上 存 在 唯 一 的 零 点 , 设 为 x0 , 则 x0∈(1,2).利用二分法,可以得到下表:
能力提升 题型二 用二分法求方程的近似解(或函数零点的近似值)
方程的近似解 教案

方程的近似解教案教案标题:方程的近似解教案目标:1. 了解方程的概念及其在数学中的重要性。
2. 理解近似解的概念,并能够使用适当的方法求解方程的近似解。
3. 学会评估近似解的准确性,并能够解释近似解的实际意义。
教学准备:1. 教师准备:教师需要掌握方程的基本概念和求解方法,并熟悉近似解的计算方法。
2. 学生准备:学生需要掌握基本的代数运算和方程的基本知识。
教学过程:引入活动:1. 教师可以通过一个实际问题引入方程的概念,例如:小明和小红一起去购物,他们一共花费了120元,小明花费的钱数是小红的2倍,那么小明和小红各自花费了多少钱?请学生思考并列出方程。
知识讲解:2. 教师讲解方程的定义,并解释方程与实际问题之间的联系。
强调方程在数学中的应用和重要性。
3. 教师介绍近似解的概念,解释近似解在实际问题中的实际意义。
示范演示:4. 教师通过一个简单的方程求解示例,引导学生了解如何使用适当的方法求解方程的近似解。
示例:解方程2x + 3 = 7,求其近似解。
练习活动:5. 学生分组进行练习活动,解决一系列方程求近似解的问题。
教师可以提供一些实际问题,让学生应用所学知识进行求解。
讨论与总结:6. 教师组织学生进行讨论,比较不同方法求解方程的近似解的优缺点,并让学生总结求解方程近似解的方法和步骤。
评估:7. 教师布置一些练习题,让学生独立完成,并进行评估。
评估内容可以包括求解方程的近似解和评估近似解的准确性。
拓展活动:8. 对于掌握较好的学生,教师可以引导他们进行更复杂的方程近似解求解问题,拓展学生的思维能力和应用能力。
教学反思:9. 教师对本节课的教学进行总结和反思,针对学生的学习情况做出调整,并准备下一步的教学内容。
教案扩展:1. 可以引入更多实际问题,让学生应用方程的近似解求解方法。
2. 可以引入更多求解方程的近似解的方法,如牛顿法等。
3. 可以通过实际案例,让学生了解方程近似解在科学研究和工程领域的应用。
28.4方程的近似解教案(冀教版九年级上)教学设计

数学思考
建立初步的数感和符号感,发展抽象思维
解决问题
综合运用所学到的知识和技能解决问题,发展应用意识
情感态度
培养学生对数学的好奇心和求知欲
教学难点
通过观察估计方程解的大致范围
知识重点
用试值的方法得到方程的近似解
教学过程
设计意图
教
学
过
程
问题一:
小明的爸爸投资购买某种债券,第一年初购买了1万元,第二年初有购买了2万元,到第二年底本利和为3.35万元.设这种债券的年利润率不变,你能估计出年利润率的近似值吗?
师生活动:共同审题,设未知数,建立方程
设年利润率为r,
一起探究
根据题目的实际意义,总投入3万元,而本利和为3.35万元,所以r>0.
通过观察,估计方程解的范围.
用试值的方法得到方程的近似解
通过估计方程的近似解,解决实际问题.
对高次方程进行估算,求其近似解.
小结与作业
课堂小结
学生讨论总结,本节课的所得和估算要点
本课作业
课本第48页 习题1、2、3
课后随笔(课堂设计理念,实际教学效果及改进设想)
问题二:估计方程x3-9=0 的解.
解:将方程化成x3=9
由于23=8<9,33=27>9
通过试值,得到方程的解在2和3之间,并且接近2.
取x=2.1进行试值,2.13=9.261>9
2<x<2.1
再取x=2.08,x=2.09继续试值,
2.08<x<2.09
在实践探索交流中解决问题,逐步领悟解决问题的正确方法,克服畏难情绪。同时调动学生的思维积极性,提高动手能力和活用数学的意识.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八节方程的近似解
教材习题3-8答案(上册P209)
5
1•解:令 f (x) x 5x 1,则 f (x)在 1,0 连续,又 f( 1)
1,0上单调递增,因而f(x)在 1,0内有唯一实根•
以下用切线法求
的近似值:
f '(x) 3x 2 3 0,则f(x)单调递增.所以f(x) 0至多有
1 0, f (1) 3 0知:f(x) 0在(0,1)内有唯一实根•取
点定理知:至少存在一点
(1,0),使得 f( )
0.又 f (X )
5x 4
0,则f(x)在
个隔离区间•列表如下:
5 0, f(0)
1 0,由零 f (x)
20x 3 0,取 x 0
1,( f(x °) f (x)
0),代入递推公式 X n 1
X n
f (X n ) f '(x n )'
x 1
1
— 0.5, x 2 5 5 0.21,
X 3
0.21
f(
°21)
f ( 0.21)
0.20, x 4
0.20 30)
0.20.
f ( 0.20)
0.20.
2.解:令 f (x) x 3x 1
一个实根.又由f (0)
a 0,b
1, 0,1 就是
于是0.32 0.33,即0.32作为根的不足近似值,0.33作为根的过剩近似值,其误差都
小于0.001.
3.解:令f(x) xlnx 1 (x 0) f (x) Inx,令f (x) In x 0,得f (x)的零点为e.
当x (0,e)时,f'(x) 0;当x (e,)时,f'(x) 0.所以f(x)在(0,e)内单调减少,f (x)在(e,)上单调增加.又Q lim f (x) lim xln x 1 1,在(0, e)内
x 0 x 0
f (x) 0, f (x) 0 至多有一个实根.又由f(1) 1 0, f(e) e 1 0 知:f (x) 0 在(0,e)内有唯一实根.取a 0,b e, 0,e是根的一个隔离区间.因为当x (0, e)时,
1 ' 1
f(X)— 0, f (x) — 0,相对应课本P207图3-32(C),以下用迭代公式做(略).
x x。
