(优选)第二讲向量与矩阵运算
线性代数中的矩阵与向量之运算技巧

线性代数中的矩阵与向量之运算技巧矩阵和向量是线性代数中最基础的概念之一。
了解它们的运算技巧是学好线性代数的前提。
本文将介绍一些常用的矩阵和向量运算技巧。
一、矩阵基本运算1. 加减法运算对于两个相同大小的矩阵A和B,它们的和(A+B)和差(A-B)分别对应位置上的元素相加减得到。
例如:A = [[1,2],[3,4]]B = [[-1,3],[4,-2]]则 A+B = [[0,5],[7,2]],A-B = [[2,-1],[-1,6]]2. 数乘运算对于数k和一个矩阵A,它们的积(kA)就是把A的每个元素都乘以k得到。
例如:A = [[1,2],[3,4]]k = 2则 kA = [[2,4],[6,8]]3. 矩阵乘法对于两个矩阵A和B,若A的列数等于B的行数,则它们可以相乘得到一个新的矩阵C。
C的每个元素都是A的一行与B的一列对应元素的乘积之和。
例如:A = [[1,2,3],[4,5,6]]B = [[-1,3],[2,-4],[5,1]]则 AB = [[18,-8],[39,9]]注意:矩阵乘法不满足交换律,即A×B ≠ B×A。
二、向量基本运算1. 加减法运算对于两个相同长度的向量v和w,它们的和(v+w)和差(v-w)分别对应位上的元素相加减得到。
例如:v = [1,2,3]w = [-1,4,2]则 v+w = [0,6,5],v-w = [2,-2,1]2. 数乘运算对于数k和一个向量v,它们的积(kv)就是把v的每个元素都乘以k得到。
例如:v = [1,2,3]k = 2则 kv = [2,4,6]3. 点积运算对于两个长度相同的向量v和w,它们的点积(v·w)是将两个向量对应位置元素的乘积相加得到的一个数。
例如:v = [1,2,3]w = [-1,4,2]则 v·w = 9本文介绍的是矩阵和向量的基本运算技巧,仅是线性代数的冰山一角,线性代数是一门内涵丰富的课程,需要大家认真研究,深入理解。
向量与矩阵运算

向量与矩阵运算在高中数学学科中,向量与矩阵运算是一项重要的内容。
向量与矩阵的概念与运算规则不仅在数学中有广泛的应用,而且在物理、工程、计算机科学等领域也有着重要的地位。
本文将详细介绍向量与矩阵的定义、基本运算以及一些常见应用。
一、向量的定义与基本运算向量是有方向和大小的量,通常用箭头表示。
向量可表示为一个有序的数字组成的列,也可以视为从原点指向某一点的箭头。
例如,向量A可以表示为(A1, A2, ..., An)。
向量的基本运算包括加法和数乘。
向量的加法是对应元素相加,即A +B = (A1 + B1, A2 + B2, ..., An + Bn),其中A和B为同维数的向量。
数乘是将向量的每个元素都乘以一个实数,即kA = (kA1, kA2, ..., kAn),其中k为实数。
二、矩阵的定义与基本运算矩阵是一个按照矩形排列的数表,通常用大写字母表示。
矩阵有行与列组成,用m×n表示,其中m表示矩阵的行数,n表示矩阵的列数。
矩阵的基本运算包括矩阵加法、矩阵数乘和矩阵乘法。
矩阵的加法是对应元素相加,即A + B = [aij + bij],其中A和B为同维数的矩阵。
矩阵的数乘是将矩阵的每个元素都乘以一个实数,即kA = [kaij]。
矩阵的乘法是一种复合运算,需要满足乘法的规则。
若A为m×n 的矩阵,B为n×p的矩阵,则AB为m×p的矩阵。
矩阵AB的第i行第j列元素可以表示为:ABij = aij * bij,其中aij表示A矩阵的第i行第j 列元素,bij表示B矩阵的第i行第j列元素。
三、向量与矩阵的应用向量与矩阵运算在许多实际问题中有着广泛的应用。
以下是一些常见的应用领域:1. 物理学:在物理学中,向量和矩阵可以用来描述物体的运动和力的作用。
例如,位移向量可以用来描述物体的位置变化,力矩矩阵可以用来描述物体受到的力的作用。
2. 工程学:向量和矩阵可以用来描述工程中的各种变量和关系。
向量矩阵概念与运算
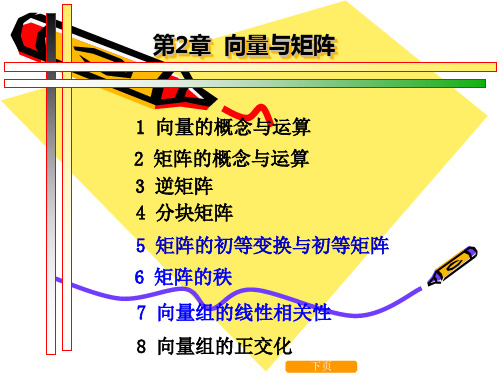
1 向量的概念与运算 2 矩阵的概念与运算 3 逆矩阵 4 分块矩阵 5 矩阵的初等变换与初等矩阵 6 矩阵的秩 7 向量组的线性相关性 8 向量组的正交化
下页
第1节 向量的概念与运算
1.1 向量的概念
定义1 n个数a1,a2, ,an组成的有序数组 (a1, a2, , an), 称为n维向量,记为a,其中a i (i=1,2,…,n)叫做向量的第i个分量.
i =1
例如,设a=(-1, 1, 0, 2)T,b=(2, 0, -1, 3)T , 则a与b
的内积为 (a , b ) =(-1)2+10+0(-1)+23 =4 .
下页
内积的性质
设a,b,g为Rn中的任意向量,k为常数. (1) ( a,b ) =(b,a ) ; (2) (ka,b ) = k ( a,b ) ; (3) (a+b,g ) = ( a,g ) + ( b, g ) ; (4) ( a,a ) 0,当且仅当a=o时,有( a,a ) =0 .
下页
负矩阵
称矩阵
-a11 -a12 -a1n -a21 -a22 -a2n
为A的负矩阵,记作 –A.
零矩阵
-am1 -am2 -amn
所有元素均为0的矩阵称为零矩阵,记为O.
行矩阵与列矩阵
只有一行的矩阵称为行矩阵,只有一列的矩阵称为列矩阵.常用小
例4.n维单位向量组e1,e2,,en,是两两 正交的:(ei ,ej ) =0 (ij) .
下页
标准正交向量组
定义6 如果m个非零向量组 a1,a2,,am两两正交, 即 (ai ,aj )=0(ij),则称该向量组为正交向量组.
向量与矩阵计算

向量与矩阵计算在数学中,向量和矩阵是非常重要的概念和工具。
它们在各种领域的数学和物理问题中都扮演着重要的角色。
本文将详细介绍向量和矩阵的计算方法以及其应用。
1. 向量的表示和计算向量是具有大小和方向的量,可以用箭头表示。
在坐标系中,向量可以用有序数对表示。
例如,对于一个二维空间中的向量v,可以表示为v=(x, y),其中x和y分别是向量v在x轴和y轴上的分量。
向量的计算包括加法、减法和数量乘法。
向量的加法是将两个向量相应分量相加,即v1+v2=(x1+x2, y1+y2)。
向量的减法是将被减向量的分量分别减去减向量的分量,即v1-v2=(x1-x2, y1-y2)。
数量乘法是将向量的每个分量乘以一个实数,即k*v=(k*x, k*y),其中k是实数。
2. 矩阵的表示和计算矩阵是一个矩形的数表,由行和列组成。
一个m×n的矩阵有m行和n列。
矩阵中的元素可以是实数或复数。
矩阵可以用方括号表示。
例如,一个2×3矩阵A可以表示为:A = [a11, a12, a13;a21, a22, a23]矩阵的加法是将对应元素相加,即A+B=[a11+b11, a12+b12,a13+b13; a21+b21, a22+b22, a23+b23]。
矩阵的数量乘法是将矩阵的每个元素乘以一个实数,即kA=[ka11, ka12, ka13; ka21, ka22, ka23],其中k是实数。
矩阵的乘法是两个矩阵相乘的操作。
如果矩阵A是一个m×n的矩阵,矩阵B是一个n×p的矩阵,那么它们的乘积矩阵C是一个m×p的矩阵。
矩阵的乘法遵循分配律和结合律。
3. 向量的点积和叉积向量的点积也称为内积,计算方法是将两个向量对应分量相乘,并将结果相加。
对于二维向量v=(x1, y1)和w=(x2, y2),它们的点积为v·w=x1*x2+y1*y2。
向量的点积有很多应用,例如计算向量间的夹角、计算向量在某个方向上的投影等。
矩阵和向量的应用

线性组合在矩阵和向量运算中具有广泛的应用,如求解线性方程组、计算向量空间中的向 量和等。
矩阵和向量的线性变换
线性变换定义
线性变换是向量空间中一种特殊的映射,它将向量空间中的每个向量 映射到另一个向量,且满足加法变换和标量乘法变换的线性性质。
线性变换性质
线性变换具有可加性和标量乘法性质,即对于任意标量$k$和向量$mathbf{a}, mathbf{b}$,有$T(kmathbf{a} + mathbf{b}) = kT(mathbf{a}) + T(mathbf{b})$。
未来矩阵和向量的发展方向
算法优化
并行计算
随着大数据和云计算技术的发展,矩阵和 向量的算法优化将成为一个重要方向,以 提高计算效率和精度。
利用并行计算技术加速矩阵和向量的计算 过程,提高大规模数值计算的效率。
应用拓展
理论完善
随着各领域的不断发展,矩阵和向量的应 用场景将不断拓展,如人工智能、机器学 习、量子计算等领域。
矩阵的算法实现
矩阵乘法
通过分块处理、分步计算等方式实现矩阵乘法,提高 计算效率。
矩阵转置
通过交换矩阵的行和列得到转置矩阵,实现矩阵的行 列互换。
矩阵求逆
通过高斯消元法、LU分解等算法求解矩阵的逆矩阵。
向量的算法实现
向量加法
对应元素相加得到新的向量。
向量数乘
一个标量与一个向量相乘得到新的向量。
向量点积
线性映射应用
线性映射在许多领域都有应用,如物理学中的刚体运动、控制系统中的状态方程等。
03
矩阵和向量的应用
在几何学中的应用
线性变换
01
矩阵可以表示平面上或空间中的线性变换,如旋转、缩放、平
矩阵与向量的运算

矩阵与向量的运算矩阵与向量是线性代数中的重要概念,它们的运算涉及到了许多实际问题的解决。
在本文中,我们将探讨矩阵与向量的运算规则,并以实际应用为例,展示它们在不同领域的重要性。
一、矩阵与向量的基本概念矩阵是由m行n列的数按照一定顺序排列而成的矩形数表,用大写字母表示,如A。
向量是由n个数按照一定顺序排列而成的数表,用小写字母表示,如x。
矩阵中的每个数称为元素,向量中的每个数称为分量。
矩阵与向量的运算包括加法、减法和数乘三种基本运算。
二、矩阵与向量的加法矩阵与向量的加法是指将同型矩阵或向量的对应元素相加得到一个新的矩阵或向量。
例如,对于两个同型矩阵A和B,它们的加法规则为:A + B = (a_ij + b_ij),其中a_ij和b_ij分别表示A和B的第i行第j列的元素。
同样地,对于两个同型向量x和y,它们的加法规则为:x + y = (x_i + y_i),其中x_i和y_i分别表示x和y的第i个分量。
三、矩阵与向量的减法矩阵与向量的减法是指将同型矩阵或向量的对应元素相减得到一个新的矩阵或向量。
例如,对于两个同型矩阵A和B,它们的减法规则为:A - B = (a_ij - b_ij),其中a_ij和b_ij分别表示A和B的第i行第j列的元素。
同样地,对于两个同型向量x和y,它们的减法规则为:x - y = (x_i - y_i),其中x_i和y_i分别表示x和y的第i个分量。
四、矩阵与向量的数乘矩阵与向量的数乘是指将矩阵或向量的每个元素乘以一个常数得到一个新的矩阵或向量。
例如,对于一个矩阵A和一个常数k,它们的数乘规则为:kA = (ka_ij),其中a_ij表示A的第i行第j列的元素。
同样地,对于一个向量x和一个常数k,它们的数乘规则为:kx = (kx_i),其中x_i表示x的第i个分量。
五、矩阵与向量的乘法矩阵与向量的乘法是指将一个矩阵的每一行与一个向量进行点乘得到一个新的向量。
例如,对于一个矩阵A和一个向量x,它们的乘法规则为:Ax = (a_i1x_1 +a_i2x_2 + ... + a_inx_n),其中a_ij表示A的第i行第j列的元素,x_i表示x的第i个分量。
矩阵与向量的运算

矩阵与向量的运算在线性代数中,矩阵与向量是基本的概念之一,并且在数学和应用领域中具有广泛的应用。
矩阵可以看作是一个由数字组成的矩形数组,而向量则可以看作是一个具有一维的矩阵。
本文将介绍关于矩阵与向量的运算,包括加法、减法、数乘以及矩阵乘法等。
1. 加法和减法矩阵和向量的加法和减法操作是一种逐个元素相加或相减的操作。
假设有两个相同大小的矩阵A和B,它们的加法和减法可以表示如下:A +B = CA -B = D其中C和D分别为结果矩阵,其每个元素的数值等于相加或相减之后的结果。
同样,向量的加法和减法也是类似的操作。
2. 数乘数乘是指一个数与矩阵或向量的每个元素相乘的操作。
假设有一个矩阵A和一个标量α,其数乘操作可以表示如下:αA = B其中B为结果矩阵,其每个元素的数值等于该元素与标量的乘积。
同样,向量的数乘操作也是类似的。
3. 矩阵乘法矩阵乘法是指两个矩阵相乘的操作。
假设有一个m×n的矩阵A和一个n×p的矩阵B,其乘法操作可以表示如下:A ×B = C其中C为结果矩阵,其大小为m×p。
矩阵乘法的计算规则是,A的每一行与B的每一列对应元素相乘后求和,得到结果矩阵C的对应位置的元素。
需要注意的是,矩阵乘法满足结合律,但不满足交换律。
即AB ≠ BA。
同时,矩阵乘法的定义要求前一个矩阵的列数等于后一个矩阵的行数,才能进行乘法操作。
4. 矩阵与向量的乘法矩阵与向量的乘法是指矩阵与列向量相乘的操作。
假设有一个m×n 的矩阵A和一个n维的列向量x,其乘法操作可以表示如下:A × x = y其中y为结果向量,其维度与A的行数m相同。
矩阵与向量的乘法实际上是矩阵乘法的特殊情况,可以视为每一行与列向量的对应元素相乘后求和得到结果向量y的对应位置的元素。
总结:矩阵与向量的运算包括加法、减法、数乘以及矩阵乘法等。
加法和减法是逐个元素相加或相减的操作,数乘是将矩阵或向量的每个元素与标量相乘的操作,矩阵乘法是两个矩阵相乘的操作,而矩阵与向量的乘法是指矩阵与列向量相乘的操作。
向量与矩阵的运算与性质

向量与矩阵的运算与性质向量和矩阵是线性代数中两个重要的概念,它们在各个领域的数学和科学问题中起着至关重要的作用。
本文将探讨向量与矩阵的运算与性质,包括向量的加法、乘法和性质,矩阵的加法、乘法和性质等方面。
向量的运算与性质向量是有方向和大小的量,通常用箭头表示。
在二维空间中,向量可以用坐标形式表示为 (x, y),其中 x 和 y 分别代表向量在 x 轴和 y 轴上的分量。
向量的加法是将两个向量相加得到一个新的向量。
如果向量 A 的坐标表示为 (x1, y1),向量 B 的坐标表示为 (x2, y2),则它们的和向量 C的坐标可以表示为 (x1 + x2, y1 + y2)。
这体现了向量加法的几何意义,即将一个向量平移后与另一个向量的末端相连接得到一个新向量。
向量的乘法有两种情况,分别是数量乘法和点乘法。
数量乘法是将向量的每个分量都与一个标量相乘,得到的结果仍然是一个向量。
例如,如果向量 A 的坐标表示为 (x, y),标量为 k,则数量乘法运算的结果为 kA = (kx, ky)。
点乘法是将两个向量进行点乘,得到一个标量。
点乘法的结果可以表示为A·B = |A||B|cosθ,其中 |A| 和 |B| 分别代表向量的模长,θ 表示两个向量之间的夹角。
向量具有许多重要的性质。
例如,向量的加法满足交换律和结合律,即 A + B = B + A,(A + B) + C = A + (B + C)。
向量的数量乘法满足结合律,即 k(lA) = (kl)A。
此外,向量的数量乘法还满足分配律,即 k(A + B) = kA + kB。
矩阵的运算与性质矩阵是一个按照行和列排列的矩形数组,它由 m 行 n 列的元素组成,记作 A = [a_ij],其中 a_ij 表示矩阵 A 中第 i 行第 j 列的元素。
矩阵的加法是将两个矩阵对应位置的元素相加得到一个新的矩阵。
例如,如果矩阵 A 的第 i 行第 j 列的元素表示为 a_ij,矩阵 B 的第 i 行第 j 列的元素表示为 b_ij,则它们的和矩阵 C 的第 i 行第 j 列的元素可以表示为 c_ij = a_ij + b_ij。
向量矩阵的概念与运算

ቤተ መጻሕፍቲ ባይዱ 02
向量矩阵的基本运算
向量的加法、数乘运算
向量加法
向量加法是指将两个同维度的向量对 应分量相加,得到一个新的向量。
数乘运算
数乘运算是将一个标量与一个向量相 乘,得到一个新的向量,其每个分量 都是原向量对应分量与标量的乘积。
向量的点乘、叉乘运算
点乘
点乘是指两个向量的对应分量相乘后 求和,得到一个标量。
总结词
向量的几何意义是表示有向线段,而矩阵的几何意义则与其维度和具体应用场景相关。
详细描述
向量的几何意义是有向线段,其起点和终点分别对应向量的起始点和终止点。在二维坐 标系中,向量的大小(或长度)可以通过勾股定理计算得到。矩阵的几何意义则与其维 度和应用场景相关。例如,一个2x2的矩阵可以表示一个平面上的线性变换,通过矩阵
向量矩阵在控制系统中的应用
01
02
03
线性时不变系统
向量矩阵可以用来描述线 性时不变系统的状态空间 模型。
控制律设计
向量矩阵可以用来设计和 分析控制律,如PID控制 器等。
系统稳定性分析
向量矩阵可以用来分析系 统的稳定性,如 Lyapunov稳定性等。
感谢您的观看
THANKS
弹性力学
向量矩阵可以用来描述弹性力学中的应变和应力等物 理量。
电磁学
向量矩阵可以用来描述电磁场中的矢量,如电场和磁 场。
向量矩阵在计算机图形学中的应用
3D模型变换
向量矩阵可以用来表示和实现3D模型的旋转 、缩放和平移等变换。
光照模型
向量矩阵可以用来表示光照模型中的光照方 向和强度等信息。
动画制作
向量矩阵可以用来实现动画中的关键帧插值 和运动合成等效果。
线性代数中的向量与矩阵运算

线性代数中的向量与矩阵运算线性代数是数学中的一个重要分支,研究向量、向量空间和线性变换等概念及其性质。
在线性代数中,向量和矩阵是最基本的概念之一,其运算规则和性质对于解决实际问题和理论研究都具有重要意义。
一、向量的定义与运算向量是线性代数中最基本的概念之一。
向量可以用有序数组表示,也可以用箭头表示,箭头的方向表示向量的方向,箭头的长度表示向量的大小。
向量的运算包括加法和数乘两种运算。
向量的加法满足交换律和结合律,即对于任意两个向量a和b,有a+b=b+a和(a+b)+c=a+(b+c)。
向量的数乘是指将向量的每个分量与一个实数相乘,得到一个新的向量。
数乘满足结合律和分配律,即对于任意向量a和实数k,有k(a+b)=ka+kb 和(k+l)a=ka+la。
二、矩阵的定义与运算矩阵是由m行n列的数排成的一个矩形数表,用大写字母表示。
矩阵的运算包括加法、数乘和乘法三种运算。
矩阵的加法是指将两个相同大小的矩阵对应位置的元素相加,得到一个新的矩阵。
矩阵的数乘是指将矩阵的每个元素与一个实数相乘,得到一个新的矩阵。
矩阵的乘法是指将一个m行n列的矩阵与一个n行p列的矩阵相乘,得到一个m行p 列的矩阵。
矩阵的乘法不满足交换律,即AB≠BA,但满足结合律,即(AB)C=A(BC)。
矩阵的乘法还满足分配律,即A(B+C)=AB+AC和(A+B)C=AC+BC。
三、向量与矩阵的关系向量可以看作是只有一列的矩阵,矩阵可以看作是多个向量的组合。
向量与矩阵之间的运算也是线性代数中的重要内容。
对于一个m行n列的矩阵A和一个n维的列向量x,矩阵A与向量x的乘积Ax是一个m维的列向量,其中的每个元素是矩阵A的每一行与向量x的对应位置元素的乘积之和。
这种运算可以看作是将矩阵的每一行与向量的每一列进行对应位置的乘积,并将结果相加得到一个新的向量。
矩阵的转置是指将矩阵的行与列对调得到的新矩阵。
对于一个m行n列的矩阵A,其转置矩阵记作A^T,其中的元素a_ij变为a_ji。
2024高考数学向量与矩阵运算

2024高考数学向量与矩阵运算在2024年的高考中,数学科目依然是考生们备战的重中之重。
而在数学中,向量与矩阵运算是一个重要的知识点。
本文将围绕向量与矩阵运算展开,帮助考生们理解和掌握相关的知识。
一、向量的基本概念与表示方法向量是数学中的一个重要概念,它常常用来表示方向和大小。
在三维空间中,向量通常由三个有序实数组成。
例如,向量A可以表示为A = (a₁,a₂,a₃)。
其中,a₁、a₂和a₃分别表示A在x轴、y轴和z轴上的分量。
二、向量的运算法则1. 向量的加法向量的加法是指将两个向量A和B相加得到一个新的向量C,表示为C = A + B。
向量的加法满足交换律和结合律,即A + B = B + A,(A + B) + C = A + (B + C)。
2. 向量的数乘向量的数乘是指将一个向量A与一个实数k相乘得到一个新的向量C,表示为C = kA。
数乘可以改变向量的大小和方向,当k > 0时,C 与A的方向相同;当k < 0时,C与A的方向相反。
3. 向量的数量积向量的数量积又称为内积或点乘,表示为A · B。
其中,A · B = |A| |B| cosθ,其中|A|和|B|分别表示向量A和B的模,θ表示A和B之间的夹角。
三、矩阵的基本概念与表示方法矩阵是数学中的另一个重要概念,它由一组数按照矩形排列而成。
矩阵可以表示为一个m行n列的矩形数组。
例如,一个矩阵A可以表示为:```A = [a₁₁ a₁₂ a₁₃a₂₁ a₂₂ a₂₃a₃₁ a₃₂ a₃₃]```在矩阵中,aᵢⱼ表示位于第i行第j列的元素。
四、矩阵的运算法则1. 矩阵的加法矩阵的加法是指将两个相同的m行n列的矩阵A和B相加得到一个新的矩阵C,表示为C = A + B。
矩阵的加法满足交换律和结合律,即A + B = B + A,(A + B) + C = A + (B + C)。
2. 矩阵的数乘矩阵的数乘是指将一个矩阵A中的每个元素都乘以一个实数k得到一个新的矩阵C,表示为C = kA。
向量与矩阵在高等数学中的代数运算与应用

向量与矩阵在高等数学中的代数运算与应用1. 向量与矩阵的基本概念与性质向量是高等数学中的基本概念之一。
它可以理解为有方向和大小的量,常用箭头表示。
向量可以加减、与标量乘除,还可以进行内积和外积等运算。
在代数运算中,向量可以进行加减运算和数乘运算。
向量的代数运算具有交换律和结合律。
矩阵是一个矩形的数表,由行(横向元素)和列(纵向元素)组成。
矩阵也可以是一个二维数组,每个元素都有明确的位置。
矩阵的运算包括加法、减法、数乘、转置和乘法等。
2. 向量与矩阵的代数运算a. 向量的加法与减法:向量的加法是对应位置上的元素相加,得到一个新的向量;向量的减法是对应位置上的元素相减,得到一个新的向量。
b. 向量的数乘:数乘即将向量的每个元素乘以一个标量。
数乘之后,向量的方向不变,但大小会发生变化。
c. 矩阵的加法与减法:矩阵加法与减法是将对应位置上的元素相加或相减,得到一个新的矩阵。
要求进行加法或减法的两个矩阵必须具有相同的行数和列数。
d. 矩阵的数乘:数乘即将矩阵的每个元素乘以一个标量。
e. 矩阵的乘法:矩阵的乘法是指将一个矩阵的每个元素与另一个矩阵的对应元素相乘,并将结果相加。
要进行乘法运算,前一个矩阵的列数必须等于后一个矩阵的行数。
f. 矩阵的转置:矩阵的转置是指将矩阵的行与列对换得到的新矩阵。
3. 向量与矩阵的应用a. 线性代数:线性代数是现代数学的一个分支,广泛应用于物理学、工程学和计算机科学等领域。
向量和矩阵是线性代数的基础,在解决方程组和矩阵变换等问题中起到重要作用。
b. 几何学:向量在几何学中用于表示方向和大小。
通过向量的加法、减法和数乘运算,可以进行几何变换,如平移、旋转和缩放等。
c. 物理学:向量在物理学中广泛应用于描述物体的运动和力的作用。
例如,速度和加速度可以用矢量表示,这样可以更方便地进行分析和计算。
d. 经济学:向量和矩阵在经济学中用于描述经济关系和模型。
例如,用向量表示不同商品的价格和数量,用矩阵表示市场的供给和需求关系。
向量与矩阵的运算与应用

奇异值分解是将矩阵表示为三个矩阵相乘 的形式。具有一些特性和计算方法,在统 计分析、图像处理、推荐系统等领域广泛 应用。
奇异值分解
分解形式 应用领域
表示为三个矩阵相乘的形式 在统计分析、图像处理、推荐系统等领域的应用
性质与计算
奇异值分解的性质和计算方法
● 04
第4章 矩阵的运算与应用
矩阵求逆与矩阵 方程
矩阵求逆是通过与幺元矩阵相乘得到逆元 矩阵的运算。而矩阵方程是线性方程组的 一种表示形式,通常为AXB。掌握矩阵求 逆与矩阵方程对于解决线性方程组、应用 于工程计算等具有重要意义。
矩阵求逆与矩阵方 程的重要性
逆元矩阵 工程计算
线性方程组
矩阵求逆的关键 实际场景中的运用
矩阵方程的应用
对角化与相似矩阵
可对角化矩阵
可以由对角矩阵表示的矩阵
01
相似矩阵
具有相同特征值但不一定相同特征向量的矩阵
02
04 03
Unified fonts make reading more fluent.
Theme color makes PPT more convenient to change.
Adjust the spacing to adapt to Chinese typesetting, use the reference line in PPT.
知识回顾
在向量与矩阵的知识回顾中,我们重新审 视了它们的基本定义、运算规则和应用领 域。向量与矩阵在数学、计算机科学、工 程等领域扮演着重要角色,是许多问题求 解的关键工具。
发展趋势
机器学习应用
向量与矩阵在模式识别、数据分析等机器学习领域得到 广泛应用
第二讲 向量与矩阵运算

a=[1 2 3; 4 5 6; 2 3 5]; 》b=i 0.3333 -2.0000 -0.6667 -0.3333 1.0000
x1 x2 x3 2 x4 1 x x 2x x 1 1 2 3 4 2 x1 x2 x3 x1 x3 x4 1
例:a=[1:1:4]
==> a=[1, 2, 3, 4]
b=[0:pi/3:pi] ==> b=[0, 1.0472, 2.0944, 3.1416] c=[6:-2:0] ==> c = [6, 4, 2, 0]
(3)用linspace函数产生行向量。 其调用格式为: >> linspace(a,b,n) 其中a和b是生成向量的第一个和最后一个元素, n是元素总数( 采用等分)。 >>a= linspace(1,3,3) a=[1,2,3]
对于奇异矩阵或长方阵b,把同时满足xbx=b和bxb=x (penrose第一,第二方程)的矩阵x 称为b的伪矩阵,matlab中求伪矩阵x的命令为pinv(b); 是方阵逆阵的推广。
矩阵的乘方
A 是方阵,p 是正整数 A^p 表示 A 的 p 次幂,即 p 个 A 相乘。
三、矩阵的数组运算
数组运算:对应元素进行运算
数组运算包括:点乘、点除、点幂
相应的数组运算符为: “.* ” , “./ ” , “.\ ” 和 “ .^ ” 点与算术运算符之间不能有空格!
例:>> A=[1 2 3; 4 5 6]; B=[3 2 1; 6 5 4];
>> C=A+B; D=A-B;
矩阵的普通乘法
要求参与运算的矩阵满足线性代数中矩阵相乘的原则
向量与矩阵

向量与矩阵是线性代数中非常重要的概念,在数学、物理、计算机科学等领域都有广泛的应用。
它们不仅是描述和处理复杂数据的有效工具,还能帮助我们理解线性空间和线性变换的本质。
首先,让我们来看看向量。
向量是一个有方向和大小的量,可以用箭头表示。
在二维平面上,一个向量可以用一个有序的数对 (x, y) 表示。
其中,x 和 y 分别表示向量在 x 和 y 轴上的分量。
在三维空间中,一个向量可以用一个有序的数组 (x, y, z) 表示。
向量还可以表示为一列或一行的矩阵。
向量之间可以做加法和数乘运算。
向量的加法是把两个向量相应分量相加并得到一个新的向量。
向量的数乘是将向量的每个分量乘以一个标量。
这些运算满足交换律、结合律和分配律,因此向量空间具有良好的代数结构。
另一方面,矩阵是一个有序的二维数组,可以看作是一组向量的排列。
矩阵的大小由行数和列数决定。
矩阵的每个元素可以是实数或复数。
我们可以把矩阵看作是多个向量组成的集合,其中每个向量对应矩阵中的一列或一行。
矩阵的加法和数乘运算与向量类似,也满足交换律、结合律和分配律。
此外,矩阵还有乘法运算,即将两个矩阵相乘得到一个新的矩阵。
矩阵乘法的定义比较复杂,但它有很多重要的性质,例如结合律、分配律和乘法单位元的存在性。
矩阵乘法在线性代数中有广泛的应用,例如解线性方程组、线性变换等。
向量和矩阵之间也可以进行相互转换。
一个 n 维向量可以看作是一个1×n 的矩阵,它的列数为 n。
而一个m×n 的矩阵可以看作是一个 m 维向量的集合,其中每个向量有 n 个分量。
这种转换使得我们可以用向量的观点来分析和处理矩阵,也可以用矩阵的观点来处理向量。
向量和矩阵的概念在许多领域中都有广泛的应用。
在物理学中,向量表示力、速度、加速度等物理量,矩阵表示转动、变换等物理过程。
在计算机科学中,向量和矩阵是图形处理、机器学习和数据分析等领域中的基础工具。
在工程学中,向量和矩阵用于建模和求解复杂系统。
向量矩阵运算原理

向量矩阵运算原理向量矩阵运算是线性代数中的重要概念,它描述了向量和矩阵在数学上的运算规则和性质。
在机器学习、统计学、物理学等领域中,向量矩阵运算被广泛应用于数据处理、模型建立和问题求解等方面。
下面将介绍向量矩阵运算的原理和相关参考内容。
一、向量向量是有序的一组数值,可以用于表示空间中的点、方向和大小等。
假设向量v有n个元素,可以表示为v=(v1,v2,...,vn),其中每个元素均为实数。
向量的运算包括加法、标量乘法和内积三类。
1. 向量加法:向量加法是指将两个向量逐个对应元素相加,得到一个新的向量。
假设有两个向量a=(a1,a2,...,an)和b=(b1,b2,...,bn),它们的加法表示为c=a+b=(a1+b1,a2+b2,...,an+bn)。
2. 标量乘法:标量乘法是指将一个标量与向量的每个元素相乘,得到一个新的向量。
假设有一个向量a=(a1,a2,...,an)和一个标量k,它们的标量乘法表示为c=k*a=(k*a1,k*a2,...,k*an)。
3. 内积:内积是指两个向量对应元素相乘后再求和的结果。
假设有两个向量a=(a1,a2,...,an)和b=(b1,b2,...,bn),它们的内积表示为c=a·b=a1*b1+a2*b2+...+an*bn。
二、矩阵矩阵是由若干个数排成的矩形阵列,是向量的推广形式。
矩阵可以用于表示多个向量或者多个方程所组成的线性系统。
假设矩阵A有m行n列,可以表示为A=[a_ij],其中a_ij表示第i行第j列的元素。
矩阵的运算包括加法、标量乘法和矩阵乘法三类。
1. 矩阵加法:矩阵加法是指将两个矩阵的对应元素相加,得到一个新的矩阵。
假设有两个矩阵A=[a_ij]和B=[b_ij],它们的加法表示为C=A+B=[a_ij+b_ij]。
2. 标量乘法:标量乘法是指将一个标量与矩阵的每个元素相乘,得到一个新的矩阵。
假设有一个矩阵A=[a_ij]和一个标量k,它们的标量乘法表示为C=k*A=[k*a_ij]。
向量和矩阵

向量和矩阵向量和矩阵在数学、物理和科学研究中有着广泛的应用。
它们可以用来描述实体的空间位置,力的方向,场的影响,甚至社会调研等。
因此,了解向量、矩阵的概念和它们之间的关系对于学习数学和物理有着非常重要的作用。
首先,让我们来了解一下向量。
向量是一种线性数据结构,用来表示具有方向和大小的量,它由两个或多个分量构成,比如,$v=(a,b,c)$就是一个三维向量。
向量运算包括加法和乘法操作,其中,加法操作可以定义为将两个向量组合起来,得到的是一个新的向量,称为向量的和,乘法操作可以定义为一个向量乘以一个数得到一个新的向量,而这个新的向量就是原向量的一个乘数倍。
其次,是矩阵。
矩阵是一种数据结构,它由一系列列表构成,列表中的元素可以是数字,也可以是向量或其他矩阵。
矩阵可以进行加法和乘法操作,其中,加法操作是指将两个矩阵相加,得到的矩阵元素就是两个矩阵元素相加;乘法操作是指将一个矩阵乘以另一个矩阵,得到的矩阵元素是两个矩阵元素的乘积,这就是矩阵的乘法。
此外,矩阵和向量也有其他相互之间的联系,如,一个矩阵可以由一组向量组成;一个向量可以由一行或一列的矩阵元素组成;一个矩阵可以被一个数乘以,称为矩阵的数乘。
现在,我们来谈谈矩阵和向量之间的应用。
矩阵可以用来求解线性方程组,我们可以用向量加法和乘法来解决空间问题,比如,可以用向量来表示一个物体的运动,用矩阵来描述物体的变形等。
同样,我们可以用矩阵和向量来计算空间中坐标变换,比如,可以用矩阵来表示一个旋转,利用向量可以描述这种旋转。
此外,在数字信号处理和机器学习中,向量和矩阵也都有着重要的作用。
在数字信号处理中,矩阵用来表示滤波器,向量用来表示信号;在机器学习中,向量和矩阵用来表示特征,以及训练模型时的权重。
总之,向量和矩阵是一种非常有用的数学工具,可以用来描述和表示各种物理现象和空间问题,它们也有着广泛的应用,可以用来解决数学和物理问题,广泛应用于数字信号处理和机器学习等。
向量与矩阵的运算

运用矩阵构造符[ ]包含所创建矩阵的所有元素;
使用逗号“ ,”或者空格“ ”分隔矩阵的列;
使用分号“ ;”或者回车键分隔矩阵的行。
向量与矩阵运算
向量与矩阵的生成(续)
矩阵的生成 直接输入: A=[1, 2, 3; 4, 5, 6; 7, 8, 9] 由向量生成 通过编写m文件生成 由函数生成
矩阵的旋转
fliplr(A) 垂直方向为轴翻转矩阵 flipud(A) 水平方向为轴翻转矩阵
rot90(A) 逆时针旋转 90 度; rot90(A,k) 逆时针旋转 k×90 度 >> B=fliplr(A) >> C=flipud(A) >> D=rot90(A), E=rot90(A,-1)
tril(A) triu(A)
rand(m,n) 产生 0~1 间均匀分布的随机矩阵 m=n 时简写为 rand(n)
randn(m,n) 产生均值为0,方差为1的标准正态分布随机矩阵 m=n 时简写为 randn(n)
【练习1】分别建立3×3、3×2和与矩阵A同样大小的 零矩阵。
(1) 建立一个3×3零矩阵。
【例】删除4阶随机矩阵的第3列 本例目的:理解缩小矩阵尺寸的方法
Matlab中常见数学函数
sin、cos、tan、cot、sec、csc、…
asin、acos、atan、acot、asec、acsc、… exp、log、log2、log10、sqrt
abs、conj、real、imag、sign fix、floor、ceil、round、mod、rem max、min、sum、mean、sort、fft norm、rank、det、inv、eig、lu、qr、svd …… ① log 是自然对数,即以 e 为底数 ② mod(x,y) 结果与 y 同号,rem(x,y) 则与 x 同号 ③ max 等函数的参数是矩阵时,是作用在矩阵各列上
矩阵向量及其运算

矩阵向量及其运算介绍矩阵和向量是线性代数中的重要概念,它们在数学和计算领域中有广泛的应用。
本文将介绍矩阵和向量的定义以及它们的运算。
矩阵矩阵是一个由数值排列成的矩形阵列。
一个矩阵通常用大写字母表示,例如A。
矩阵的行数和列数分别称为矩阵的行数和列数。
一个m × n的矩阵A有m行n列,即A是一个m × n矩阵。
矩阵的元素用小写字母表示,例如a<sub>ij</sub>表示A的第i行第j列的元素。
矩阵也可以用矩阵元素的行向量表示,例如[A]表示矩阵A,其中向量a<sub>i</sub>是A的第i行元素。
向量向量是一个有序的数值集合,可以表示为一个列矩阵或者行矩阵。
一个n维列向量表示为x = [x₁, x₂, ..., xₙ],其中xᵢ是向量的第i个元素。
同样,一个n维行向量表示为x = [x₁, x₂, ..., xₙ]。
矩阵和向量的运算矩阵和向量可以进行各种运算。
以下是一些常见的矩阵和向量运算:1. 加法:矩阵和向量的加法是逐个元素相加。
如果A和B是同样大小的矩阵或向量,它们的和表示为C = A + B,其中C的每个元素是A和B对应元素之和。
2. 减法:矩阵和向量的减法是逐个元素相减。
如果A和B是同样大小的矩阵或向量,它们的差表示为C = A - B,其中C的每个元素是A和B对应元素之差。
3. 数乘:矩阵和向量的数乘是将矩阵或向量的每个元素乘以一个标量。
如果A是一个矩阵或向量,k是一个标量,数乘的结果表示为B = kA,其中B的每个元素是A对应元素乘以k的结果。
4. 矩阵乘法:矩阵乘法是指两个矩阵相乘的操作。
如果A是一个m × n矩阵,B是一个n × p矩阵,它们的乘积表示为C = AB,其中C是一个m × p矩阵,C的第i行第j列的元素等于A的第i行与B的第j列的乘积之和。
5. 向量乘法:向量乘法是指一个矩阵和一个向量相乘的操作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
data.mat文件中。 save data a b ——将工作空间中a和b变量存
到data.mat文件中。 下次运行matlab时即可用load指令调用已生成 的mat文件。
load —— load data —— load data a b ——
自己动手
A(:) 与 A(:,:) 的区别 ? 如何获得由 A 的第一、三行和第一、二列组成的子矩阵?
b=[a(1,1:2);a(3,1:2)]
矩阵操作
矩阵的旋转
fliplr(A) 左右旋转 flipud(A) 上下旋转 rot90(A) 逆时针旋转 90 度;
rot90(A,k) 逆时针旋转 k×90 度
例如 a=[1 2 0;3 0 5;7 8 9] a =1 2 0
305 789 a(3,3)=0 a =1 2 0 305 780
数据的保存与获取
把matlab工作空间中一些有用的数据 长久保存下来的方法是生成mat数据文 件。 save —— 将工作空间中所有的变量 存到matlab.mat文件中。
矩阵操作
改变矩阵的形状:reshape
reshape(A,m,n): 将矩阵元素按 列方向 重组成m*n的矩阵 重组后得到的新矩阵的元素个数 必须与原矩阵元素个数相等!
矩阵操作
查看矩阵的大小:size
size(A) 列出矩阵 A 的行数和列数 size(A,1) 返回矩阵 A 的行数 size(A,2) 返回矩阵 A 的列数
(优选)第二讲向量与矩阵 运算
向量的生成 ✓ 直接输入: ✓ 冒号运算符:形式x=x0:step:xn
例:a=[1:4] ==> a=[1, 2, 3, 4]
b=[0:pi/3:pi] ==> b=[0, 1.0472, 2.0944, 3.1416] c=[6:-2:0] ==> c = [6, 4, 2, 0]
✓ 用matlab函数
A=linspace(1,5) %产生1~5的100个线性等间隔 的数 注意:与冒号运算符方法的区别
A=logspace(1,5) %产生10^1~10^5的50个对数 等间隔的数
注意:matlab严格区分大小写字母,因此a与A 是两个不同的变量。
matlab函数名必须小写。
矩阵的生成
注意:此时[ ]可不用。 冒号的作用:用于生成等间隔的向量, 默认间隔为1。
向量的生成 ✓ 直接输入: ✓ 冒号运算符 ✓ 从矩阵中抽取行或列
A=[1 2 3; 4 5 6;7 8 9];
B=A(1,:)
B=
123
冒号的作用:用于用于选出矩阵指定 行、列及元素。
向量的生成 ✓ 直接输入: ✓ 冒号运算符 ✓ 从矩阵中抽取行或列
例:>> A=[1 2 3; 4 5 6]
>> size(A) >> size(A,1) >> size(A,2)
length(x) 返回向量 X 的长度 length(A) 等价于 max(size(A))
矩阵基本运算
矩阵的加减:对应分量进行运算
要求: 1.参与加减运算的矩阵具有相同的维数 2.允许参与运算的两矩阵之一是标量。标量与矩阵的 所有元素分别进行加减操作。
c=cross(A,B,dim)
矩阵操作
提取矩阵的部分元素: 冒号运算符
A(:) A的所有元素 A(:,:) 二维矩阵A的所有元素 A(:,k) A的第 k 列, A(k,:) A的第 k 行 A(k:m) A的第 k 到第 m 个元素 A(:,k:m) A的第 k 到第 m 列组成的子矩阵
提取一个矩阵的上三角部分 产生 0~1 间均匀分布的随机矩阵 m=n 时简写为 rand(n)
randn(m,n) 产生均值为0,方差为1的标准正态分布随机矩阵 m=n 时简写为 randn(n)
矩阵的修改
直接修改
可用键找到所要修改的矩阵,用键移动到要修改的 矩阵元素上即可修改。
指令修改 可以用A(,)= 来修改。
✓ 直接输入: A=[1, 2, 3; 4, 5, 6; 7, 8, 9] ✓ 由向量生成 ✓ 通过编写m文件生成 ✓ 通过外部数据文件加载 ✓ 由函数生成
例:>> x=[1,2,3];y=[2,3,4]; >> A=[x,y], B=[x;y]
例:>> load A.mat 例:>> C=magic(3)
常见矩阵生成函数
zeros(m,n) ones(m,n)
eye(m,n)
diag(X)
tril(A) triu(A) rand(m,n)
生成一个 m 行 n 列的零矩阵,m=n 时可简写为 zeros(n)
生成一个 m 行 n 列的元素全为 1 的矩阵, m=n 时可写为 ones(n) 生成一个主对角线全为 1 的 m 行 n 列矩阵, m=n 时可简写为 eye(n),即为 n 维单位矩阵 若 X 是矩阵,则 diag(X) 为 X 的主对角线向量 若 X 是向量,diag(X) 产生以 X 为主对角线的对角矩阵 提取一个矩阵的下三角部分
例:>> A=[1 2 3; 4 5 6]; B=[3 2 1; 6 5 4]
>> C=A+B; D=A-B;
矩阵的普通乘法
要求参与运算的矩阵满足线性代数中矩阵相乘的原则, 标量可与任何矩阵相乘
即可恢复保 存过的所有 变量
mat文件是标准的二进制文件, 还可以ASCII码形式保存。
向量的运算
向量的加减(数加减): 向量的数乘 向量的点积: 格式:c=dot(A,B)%返回向量A、B的标量积。 A、B必须长度相等,与sum(a.*b)等效)
c=dot(A,B,dim) 向量的叉积: 格式:c=cross(A,B)%返回向量A、B的叉 积向量。 A、B必须3个元素的向量
例:>> A=[1 2 3;4 5 6]
>> B=fliplr(A) >> C=flipud(A) >> D=rot90(A), E=rot90(A,-1)
矩阵操作
矩阵的转置与共轭转置
’ 共轭转置 .’ 转置,矩阵元素不取共轭
点与单引号之间不能有空格!
例:>> A=[1 2;2i 3i]
>> B=A’ >> C=A.’
