2009年初二数学竞赛模拟题

合集下载

2009年八年级数学竞赛试卷.doc

八年级数学竞赛试卷1一、填空题（共8小题，每小题5分，满分40分）1、已知数轴上有A，B两点，它们的距离为2，点A与原点O的距离为3，那么所有满足条件的点B与原点O的距离和等于.2、若ab＞0，则的值等于.3、如图，点O在直线AB上，OC，OD，OE，OF是位于AB同一侧的射线，那么在这个图形中，不大于平角的角共有.4、已知关于x，y的方程组为，若x+y=-1，则m= .5、根据指令[s，A]（s≥0，0°＜A＜180°），机器人在平面上能完成下列动作：先原地逆时针旋转角度A，再朝其面对的方向沿直线行走距离s，现机器人在直角坐标系的坐标原点，且面对x轴正方向，若下指令[4，90°]，则机器人应移动到点.6、有数组（1，1，1），（2，4，8），（3，9，27），…，则第100组的三个数之和为 .7、完成某项工程，甲、乙合做要2天，乙、丙合做要4天，丙、甲合做要2.4天，则甲单独完成此项工程要天.8、如图，在等腰△ABC中，AB=AC，∠A=120°，D点在边BC上，且BD=1，DC=2，则AD= .二、选择题（共8小题，每小题5分，满分40分）9、已知x≠0，则的值是（）A、0B、-2C、0或-2D、0或210、已知三角形三边的长均为整数，其中某两条边长之差为5，若此三角形周长为奇数，则第三边长的最小值为（）A、8B、7C、6D、511、方程组的解的个数为（）A、1B、2C、3D、412、已知一次函数y=ax+b的图象经过一、二、三象限，且与x轴交于点（-2，0），则不等式ax＞b的解集为（）A、x＞-2B、x＜-2C、x＞2D、x＜213、已知x是实数，则的值是（）A、B、C、D、无法确定的14、下列条件中，不能判定两个直角三角形全等的是（）A、两条直角边对应相等B、斜边和一锐角对应相等C、斜边和一条直角边对应相等D、面积相等15、已知函数f（x）=x5+ax3+bx-8，且f（-2）=10，那么f（2）等于（）A、-26B、-18C、-10D、1016、设[x]表示不大于x的最大整数，如[3.4]=3，[2]=2，[-3.4]=-4，则下列结论中，不成立的有几个（）①[x]≤x＜[x]+l；②x-1＜[x]≤x；③[-x]=-[x]；④[2x]=2[x]；⑤[x]+[l-x]=1．A、4B、3C、2D、1三、解答题（共4小题，满分40分）17、两个八位数11111111和99999999的乘积有几个数字是奇数？18、定义新运算“⊕”，对任意实数a，b有，求解方程4⊕x=5．19、如图，在四边形ABCD中，AC平分∠BAD，过C作CE⊥AB于E，并且，求∠ABC+∠ADC的度数．20、已知：在△ABC中，∠A=90°，AB=AC，D为AC中点，AE ⊥BD于E，延长AE交BC于F，求证：∠ADB=∠CDF．。

初二数学竞赛试题7套整理版(含答案)电子教案

初二数学竞赛试题7套整理版(含答案)2009年初中数学（初二组）初赛试卷 01一、选择题（本大题满分42分，每小题7分）1、下列名人中：①比尔·盖茨 ②高斯 ③袁隆平 ④诺贝尔 ⑤陈景润 ⑥华罗庚 ⑦高尔基⑧爱因斯坦，其中是数学家的是（）A ．①④⑦ B.③④⑧ C.②⑥⑧ D.②⑤⑥2、已知111,,b c aa b c a b c +=+=+≠≠则a 2b 2c 2=( ) A.5 B.3.5 C.1 D.0.53、在直角坐标系中，若一点的纵横坐标都是整数，则称该点为整点。

设k 为整数，当直线2y x =-与y kx k =+的交点为整点时，k 的值可以取（）A ．4个 B.5个 C.6个 D.7个4、如图，边长为1的正方形ABCD 绕A 逆时针旋转300到正方形AB ‘C ’D ‘，图中阴影部分的面积为（）A.11 D.125、已知()421M p p q =+，其中,p q 为质数，且满足29q p -=，则M =（） A.2009 B.2005 C.2003 D.2000（第4题图）（第6题图）6、四边形ABCD 中0060,90,DAB B D ∠=∠=∠=1,2BC CD ==,则对角线AC 的长为（）二、填空题（本大题满分28分，每小题7分）1、如果有2009名学生排成一列，按1、2、3、4、5、4、3、2、1、2、3、4、5、4、3、2、 1•••的规律报数，那么第2009名学生所报的数是。

2、已知,,a b c 满足2224222a b a c ac -++++=+，则a b c -+的值为______ 3、已知如图，在矩形ABCD 中，AE BD ⊥，垂足为E ，030ADB∠=且BC =ECD 的面积为_____（第4、有一等腰钝角三角形纸片，若能从一个顶点出发，将其剪成两个等腰三角形纸片，则等腰三角形纸片的顶角为_______度。

三、简答题（本大题满分20分）1.如图，直线OB 是一次函数2y x =-的图象，点A 使得ACO 为等腰三角形，点C 坐标。

2009年第20届全国希望杯数学邀请赛数学初二第1试试卷

第二十届“希望杯”全国数学邀请赛(2009年)初二第一试一、选择题（每小题4分，共40分）1．在一次视力检查中，初二（1）班的50人中只有8人的视力达标．用扇形图表示视力检查结果，则表示视力达标的扇形的圆心角是（）A．64.8ºB．57.6ºC．48ºD．16º2．如图，已知点B在反比例函数y＝kx的图象上．从点B分别作x轴和y轴的垂线，垂足分别为A、C．若△ABC的面积是4，则反比例函数的解析式是（）A．y＝－8x B．y＝8x C．y＝－4x D．y＝4x3．如果a＋2ab＋b＝2，且b是有理数，那么（）A．a是整数B．a是有理数C．a是无理数D．a可能是有理数，也可能是无理数4．复印纸的型号有A0、A1、A2、A3、A4等，它们有如下的关系：将上一个型号（例如A3）的复印纸在长的方向对折后得到两张下一型号（A4）的复印纸，且各种型号的复印纸的长与宽的比相等，那么这些型号的复印纸的长与宽的比约为（）A．1.141∶1 B．1∶1 C．1∶0.618 D．1.732∶15．The number of integer solutions for the syetem of inequalities⎩⎨⎧x－2a≥0，3－2x＞－1about x is just 6，then the range of value for real number a is （）A．－2.5＜a≤－2 B．－2.5≤a≤－2 C．－5＜a≤－4 D．－5≤a≤－4(integer solutions 整数解syetem of inequalities 不等式组the range of value 取值范围)6．若分式|x|－23x－2的值是负数，则x的取值范围是（）A．23＜x＜2 B．x＞23或x＜－2C．－2＜x＜2且x≠23D．23＜x＜2或x＜－27．在100到1000的整数中(含100和1000)，既不是完全平方数，也不是完全立方数的有（）A．890个B．884个C．874个D．864个8．如图，在正方形ABCD中，E是CD边的中点，点F在BC上，∠EAF＝∠DAE，则下列结论中正确的是（）A．∠EAF＝∠F AB B．BC＝3FCC．AF＝AE＋FC D．AF＝BC＋FC9．计算：33)7411()7411(-++，结果等于（）A．58 B．387C．247D．32710．已知在代数式a＋bx＋cx2中，a、b、c都是整数，当x＝3时，该式的值是2008；当x＝7时，该式的值是2009，这样的代数式有（）A CBD A ．0个 B ．1个 C ．10个 D ．无穷多个二、A 组填空题（每小题4分，共40分）11．某地区有20000户居民，从中随机抽取200户，调查是否已安装电话，结果如右表所示，则该地区已安装电话的户数大约是．12．若14x ＋5－21x 2＝－2，则6x 2－4x ＋5＝．13．不等式x －1＞2 x 的最大整数解是．14．已知m 是整数，以4m ＋5、2m －1、20－m 这三个数作为同一个三角形三边的长，则这样的三角形有个．15．当x 依次取1，2，3， (2009)1 2， 1 3， 1 4，…， 1 2009时，代数式 x 21＋x 2的值的和等于．16．由直线y ＝x ＋2、y ＝－x ＋2和x 轴围成的三角形与圆心在点(1，1)、半径为1的圆构成的图形覆盖的面积等于． 17．在Rt △ABC 中，∠C ＝90º，斜边AB 边上的高为h ，则两直角边的和a ＋b 与斜边及其高的和c ＋h 的大小关系是a ＋b c ＋h （填“＞”、“＝”、“＜”）． 18．The figure on the right is composed of square ABCD and triangle BCE ，where ∠BEC is right angle ．Supposethe length of CE is a ，and the length of BE is b ，then the distance between point A and line CE equals to ．(be composed of 由…组成 right angle 直角 length 长度 distance 距离)19．如图，在△ABC 中，AB ＞BC ，BD 平分∠ABC ，若BD 将△ABC 的周长分为4∶3的两部分，则△ABD与△BCD 的面积比等于．20．如果将n 个棋子放入10个盒子内，可以找到一种放法，使每个盒子内都有棋子，且这10个盒子内的棋子数都不同；若将(n ＋1)个棋子放入11个盒子内，却找不到一种放法，能使每个盒子内都有棋子，并且这11个盒子内的棋子数都不同，那么整数n 的最大值等于，最小值等于．三、B 组填空题（每小题8分，共40分）21．如果自然数a 与b (a ＞b )的和、差、积、商相加得27，那么a ＝，b ＝． 22．若 a b ＋c ＝ b c ＋a ＝ ca ＋b ，则2a ＋2b ＋c a ＋b －3c＝或．23．若关于x 的方程 1 x －1－ a2－x ＝ 2(a ＋1) x 2－3x ＋2无解，则a ＝或或．24．对于正整数k ，记直线y ＝－k k ＋1x ＋ 1k ＋1与坐标轴所围成的直角三角形的面积为S k ，则S k ＝，S 1＋S 2＋S 3＋S 4＝．25．将 1 2， 1 3， 1 4，…， 1100这99个分数化成小数，则其中的有限小数有个，纯循环小数有个(纯循环小数是指从小数点后第一位开始循环的小数)．【部分详解】1、解：扇形的圆心角=8÷50×360°=57.6°．故选B．2、解：由题意得：三角形的面积等于1/ 2 |k|，∴|k|=8，又∵反比例函数图象在四象限．∴k＜0，∴k=-8，∴反比例函数的解析式是y=-8/ x ．故选A．3、4、5、这六个整数解为1,0，-1，-2，-3，-4-5<2a<=-4,故选A6、7、解：在100到1000中（包括100和1000），完全平方的有100、121、144、169、196、225、256、289、324、361、400、441、484、529、576、625、676 729、784、841、900、961，共22个，完全立方的有125、216、343、512、729、1000，共6个，729既是完全平方数，又是立方数，∴既不是完全平方数，也不是完全立方数个数为901-22-6+1=874．故选C．8、9、10、解：根据题意，得a+3b+9c=2008，①a+7b+49c=2009，②，由②-①，得4b+40c=1，③∵a、b、c都是整数，∴③的左边是4的倍数，与右边不等，所以，这样的代数式不存在；故选A．11、解：安装的频率=95/ 200 ，∴该地区已安装电话的户数大约=20000×95 /200 =9500．故答案为：9500．12、13、14、解：根据三角形两边之和大于第三边，可得（4m+5）+（2m-1）＞20-m，7m＞16①；（4m+5）+（20-m）＞2m-1，m＞-26②；（2m-1）+（20-m）＞4m+5，3m＜14③．整理16/7 ＜m＜14/ 3 ．∵m取整数∴m=3或4．故这样的三角形有2个．故答案为：2．15、16、17、18、19、20、解：①对于n值为最大的情况，从已知n值最小为出发点，在增加一个盒子之后若出现使得各个盒子中的棋子数不相同，则应该有1、2、3、4、5、6、7、8、9、10、11．而1+2+3+4+5+6+7+8+9+10+11=66，如果n=65，n+1=66，就能够找到11个不重复且不为0的方法了，所以最大值是64个②对于n值最小的情况，必有一盒子中放有1棋子，而其它的也都各不相同，为使总棋子数最小则其它应依次为2、3、4、5、6、7、8、9、10，共有55 颗，若再添一颗棋子则找不到各个不同的方法，所以n值最小为55．故答案为：64、55．21、22、23、24、25、解：分母中只含有质因数2的数是：2，4，8，16，32，64；分母中只含有质因数5的数是：5，25；分母中只含有质因数2和5的数是：10，20，40，50，80，100；一共有：6+2+6=14（个）；答：能化成有限小数的分数有14个．故答案为：14．1/2,1/4,1/5,1/8,1/10.1/16.1/20,1/25,1/32,1/40,1/50,1/64,1/80,1/100分母分解的质因数中不含2或5，则该分数为纯循环小数100以内的质数为25个，去掉2和5还有13个还有9,21,33,39,49,51,57,63,69,77,87,91,93,99共14个所以共有39个。

2009-2010学年上学期八年级竞赛数赛数学试题(含答案)97

2009--2010学年上学期八年级竞赛数学试题（总分100分）一、选择题（每小题5分，共30分）1、已知三点A （2,3),B(5，4)，C （-4，1）依次连接这三点，则（） A.构成等边三角形 B.构成直角三角形 C.构成锐角三角形 D.三点在同一直线上2、边长为整数，周长为20的三角形个数是（） **个 B.6个 C.8个 D.123．已知a+b+c≠0，且a+b c =b+c a =a+cb =p ，则直线y=px+p 不经过（）A.第一象限B.第二象限C.第三象限D.第四象限4．若交换代数式中的任意两个字母，代数式不变，则称这个代数式为完全对称式，如a+b+c 就是一个完全对称式.已知三个代数式：①a(b+c)+b(a+c)+c(a+b)；②ab c ac b bc a 222++；③ac bc ab c b a ---++222．其中是完全对称式的( ) A ．只有①② B ．只有①③C ．只有②③D ．有①②③5．已知=++++++++2009200913312211112222 （） A.1 B.20092008 C ．20102009 D ．200920106．下图是韩老师早晨出门散步时,离家的距离y 与时间x 之间的函数图象,若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是（）二、填空题（每小题5分，共30分）7．已知正数a,b,c, 满足ab+a+b=bc+b+c=ca+c+a=99,则(a+1)(b+1)(c+1)= . 8．当x ＝3时，函数y=33++qx px 的值是2005，则当x ＝－3时，函数y=33++qx px 的值为 .9．已知62-+x x 是多项式12234-+++-+b a bx ax x x 的因式，则=a ，=b .10．如图，已知Rt △ABC ，∠C ＝90°，∠A ＝30°，在直线BC 或AC 上取一点P ，使得△PAB 是等腰三角形，则符合条件的P 点有 . 11．一次函数111+++-=k x k k y （k 为正整数）的图像与x 轴、y 轴的交点是O B A ,,为原点.设Rt △ABO 的面积是k S ，则2009321S S S S ++++ = .12．如图，△ABC 是边长为3的等边三角形，△BDC 是等腰三角形，且∠BDC ＝120°．以D 为顶点作一个60°角，使其两边分别交AB 于点M ，交AC 于点N ，连接MN ，则△AMN 的周长为 .三、解答题（每小题10分，共40分）13．阅读下列解题过程：2545)4()5()45()45()45()45(145122-=-=--=-⨯+-⨯=+；56)5()6(56)56()56()56(156122-=--=-⨯+-⨯=+．请回答下列问题：（1）观察上面的解题过程，请直接写出式子=-+11n n ；（2）利用上面所提供的解法，请化简9101451341231121++++++++++ 的值．第6题图C BA14．已知△ABC 是等边三角形，E 是AC 延长线上一点，选择一点D ，使得△CDE 是等边三角形，如果M 是线段AD 的中点，N 是线段BE 的中点. 求证：△CMN 是等边三角形.15．设关于x 的一次函数11b x a y +=与22b x a y +=，则称函数)()(2211b x a n b x a m y +++=（其中1=+n m ）为此两个函数的生成函数．（1）当x=1时，求函数1y x =+与y=2x 的生成函数的值；（2）若函数11b x a y +=与22b x a y +=的图象的交点为P ，判断点P 是否在此两个函数的生成函数的图象上，并说明理由．16．我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售。

【免费下载】初中八年级数学竞赛试题八

16．若 abc 0 ，则 a b c abc 的最大值是
最小值是
．
a b c abc
cm2．
17．已知 F (x) 表示关于 x 的运算规律： F (x) x3 ，（例如 F (2) 23 8, F (3) 33 27, ）．又规定
F (x) F (x 1) F (x) ，则 F (a b)
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

2009年慈溪上林中学八年级第二学期数学竞赛题

2009年上林中学八年级第二学期数学竞赛题时间：２小时满分：１２０分命题者：胡伟君班级学号姓名一、选择题（每小题3分，共30分）1. 计算12－22＋32－42＋52－62＋…＋19992的值是（）A ．199000B ．－199000C ．1999D ．－1999 2．已知|a|= 5，2b = 3，且ab ＜0，则a －b =（）A. 8B. —2C. 8或—8D. 2或—2 3. 如图，数轴上A B ，两点表示的数分别是1A 关于点B 的对称点是点C ，则点C 所表示的数是（） A1 B．1 C．2 D．14．同时抛掷两枚均匀的骰子1次，两枚骰子面朝上的点数之和大于8的概率是（）A ．12B ．13C ．518D ．4115. 已知A （—2，—3）、B （1，1），将线段AB 绕B 点顺时针旋转90度，则点A 对应的像A ˊ 的坐标为（）A.（－3，４）B.（１，－５）C.（５，－２）D.（－２，３） 6．同学们喜欢足球吗？足球一般是用黑白两种颜色的皮块缝制而成，如图所示黑色皮块是正五边形，白色皮块是正六边形．若一个球上共有黑白皮块32块，请你计算一下，黑色皮块和白色皮块的块数依次为（）．A ．16块、16块B ．8块、24块C ．20块、12块D ．12块、20块7．如图，正方形DECF 内接于Rt △ABC 中，D 在斜边AB 上，且AD=4㎝, BD=3㎝,则图中阴影部分的面积为（）㎝2． A ．5 B ．６Ｃ．７Ｄ．８ 8．方程2 (2 y －x ＋ 7) = x y 的自然数解有（）个A. 2B. 3C. 4D.无数9．“龟兔赛跑”讲述了这样的故事：龟兔同时出发，沿直线向同一目标奔跑，领先的兔子看着缓慢爬行的乌龟，骄傲起来，停下来睡了一觉．当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到了终点，……. 用s 1，s 2分别表示乌龟和兔子所行的路程，t 为时间，则下列图象中与故事情节相吻合的是（）．10.下面四个图形是标出了长宽之比的台球桌的俯视图，一个球从一个角落以45°角击出，在桌子边沿回弹若干次后，最终必将落入角落的一个球囊。

2009年南昌市数学竞赛_初二_

2010 年第 4 期
25Biblioteka 求 x 和 y.参考答案
一、 1 D. 易知直线 AB 的解析式为 y = 1 x + 7 . 3 3 当 x = - 4 时, y = 1 . 于是, 点 C 在直线 AB 上. 2 C. 设三角形三边长为 a、 b、 c( a #b #c). 由 a + b + c= 20 a #7 . 又 a + b > a, 2a < 20 a < 10 ,则 7∃a ∃9 . 故可列出 ( a, b, c) = (9 , 9 , 2 ), ( 9 , 8 , 3 ), ( 9 , 7 , 4), ( 9 , 6 , 5), (8 , 8 , 4 ), ( 8 , 7 , 5 ), ( 8 , 6 , 6), ( 7 , 7 , 6), 共八组 . 3 C. 1 001 1 002 因为 3 的个位数字为 3 , 7 的个位 1 003 数字为 9 , 13 的个位数字为 7 , 所以 , N 的个位数字为 9 . 4 B. 如图 3, 过点 B 作 BP % BP, 使 BP % = BP, 联结 P % A. 易得
P% A = PC. 设 PA = k. 则 PB = 2k, PC = P % A = 3k. 联结 PP % . 在 Rt∀PBP % 中, 有 P% PB = 45 且 PP % = 2 2k. 2 2 2 在 ∀P % AP 中 , 有 P % A = P% P + PA . 所以, P% PA = 90 APB = 135 . 5 C. 2 因为 - ( a + 1 ) < 0, 所以, 在每个象限中 , y 随 x 的增大而增大 . 因此, y 1 < y 2. 1 又 ( - 1, y 1 ) 在第二象限中 , 而 , y 在 2 3

08-09学年度第二学期数学竞赛试题

城郊初中数学竞赛试卷（时间;90分钟满分 150分）一．选择题（每小题2分，共30分）1. 设[a ]是有理数，用[a ]表示不超过a 的最大整数，如[1.7]＝1，[－1]＝－1，[0]＝0，[－1.2]＝－2，则在以下四个结论中，正确的是（） A 、[a ]＋[－a ]＝0B 、[a ]＋[－a ]等于0或－1C 、[a ]＋[－a ]≠0D 、[a ]＋[－a ]等于0或1 2. 如右图所示,a 、b 是有理数，则式子a b b a b a -++++化简的结果为（）A 、3a+bB 、C 、3b+aD 、3b-a 3．如果a 是有理数，则112007a +的值不可能为（）A 、1B 、－1C 、0D 、－2007 4. 设“●，▲，■”分别表示三种不同的物体，如下图所示，前两架天平保持平衡，如果要使第三架天平也平衡，那么“？”处应放“■”的个数为 ( )密封线内不得答题●● ▲■ ●■ ▲ ●▲?123A 、 5B 、 4C 、3D 、 25. 已知a 的绝对值是它的本身；b 的相反数是它的本身；c 的倒数是它的本身。

则结果不唯一的是（） A 、ab B 、ac C 、bc D 、abc 6、[(－b)2]3的计算结果为（）A 、－b 5B 、b 5C 、－b 6D 、b 67、若三角形三个内角A 、B 、C 满足A ＞3B ，C ＜2B, 则这个三角形是（）A 、钝角三角形B 、直角三角形C 、锐角三角形但不等边D 、等边三角形 8、要使分式xx -11有意义，则x 的取值范围是（）A 、≠x 0B 、≠x 1且≠x 0C 、≠x 0或≠x ±1D 、≠x 0且≠x ±19、如x 2+mx －4能在整数范围内分解因式，则m 的可能值为（）A 、±2B 、±3C 、±2，0D 、±3，010、已知a –b=3，那么a 3–b 3–9ab 的值是（）A 、3B 、9C 、27D 、8111.若方程的二根为,则代数式的值为( ) A 、 B 、C 、D 、12.已知中，为直角，设，,则的大小关系为 ( ) A 、B 、C 、D 、以上情况都有可能13.下列几何图形中，既是轴对称图形又是中心对称图形的是（）A 、等边三角形B 、等腰梯形C 、平行四边形D 、菱形14.已知那么代数式的值是( )A 、2000B 、-2000C 、2001D 、-2001 15.如图1,梯形中，，平分，且，厘米，厘米，则的面积是( )A 、平方厘米B 、9平方厘米C 、6平方厘米（D ）3平方厘米二、填空题（每小题2分，共30分）16. 按规律填数：1741035221--，，，_________。

奥数-2009-2010年度八年级(上)学科竞赛数学试题(含答案)-卷

2009~2010年度八年级上学期学科竞赛数学试卷题号一二三四五总分 21 22 23 24 25 26 27 28 29 得分（说明：全卷共8页，满分120分）一、选择题（本题共10小题，每小题3分，共30分，每小题给的四个答案中，有且只有一个是正确的，将你认为正确的选项填在题后的括号内）1．在227，8，–3.1416 ，π，25，0.61161116……，39中无理数有（）A ．2个B ．3个C ．4个D ．5个 2．下列说法不正确的是（）A 、51251±的平方根是；B 、0.2的算术平方根是0.02；C 、的一个平方根是819- ；D 、3273-=-3．如图在所示的象棋盘上，建立适当的平面直角坐标系，使帅位于点（-1，0）上、相位于点（1，0）上，则炮位于点（） A 、（-3，3） B 、（0，3） C 、（-4，3）D 、（4，3）4．将一张矩形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是（） A 、矩形 B 、三角形 C 、梯形 D 、菱形5. 函数y =-2x-5的图象不经过（）A 、第一象限B 、第二象限C 、第三象限D 、第四象限 6．下列图形中，是中心．．对称图形的是（）学校：班级：座号：姓名：密封线内不要答题○帅 ○相 ○炮12-3-210-13A7．若532+y x b a 与x y b a 2425-是同类项，则（） A 、⎩⎨⎧==2,1y x B 、⎩⎨⎧-==1,2y x C 、⎩⎨⎧==2,0y x D 、⎩⎨⎧==1,3y x8．下列各组条件中，能判定四边形ABCD 为矩形的是（）A 、∠A+∠B=900B 、AB ∥CD ，AB=CD ，AC=BDC 、AB ∥CD ，AD=BC ，AC=BD D 、AC=BD ，∠A=9009．已知正比例函数kx y =（0≠k ）的函数值y 随x 的增大而减小，则一次函数k x y +=的图象大致是（）．xyxyxyxyOOOOA B C D 10．如图，在菱形ABCD 中，∠BAD=700，AB 的垂直平分线交对角线AC于点F ，E 为垂足，连结DF ，则∠CDF 等于（） A. 600B. 700C. 750D. 85二、填空题（本题共10小题，每小题3分，共30分，请把你认为正确的答案写在横线上）11．比较实数的大小：————.12．计算：3123-＝．13．已知⎩⎨⎧==1,2y x 方程2x －ay=5的一个解，则a ＝ ,14．如图所示：数轴上点A 所表示的数为a ，则a 的值是______. （14题图） 15. 一个正数的两个平方根分别是2m-1和 4-3m,则这个正数是_____________.F ED CBA16. 若点A （-2，3）先向右平移3个单位，在向下平移1个单位，得到的点的坐标为_______. 17．正方形切去一角后，所得多边形的内角和为． 18．将平面直角坐标系内某个图形各个点的横坐标不变，纵坐标都乘以-1，所得图形与原图形关于_______对称。

2009年全国初中数学联赛(含答案)

12009年全国初中数学联合竞赛试题参考答案第一试一、选择题（本题满分42分，每小题7分）1．设71a =，则32312612a a a +--=（）A ．24B ．25C ．4710D ．4712【解析】 A ．由()217a +=，有2226,62a a a a +==-．于是32312612a a a +--()()3621262612a a a a =-+---()2261212621224a a a a =+-=+-=2．在ABC △中，最大角A ∠是最小角C ∠的两倍，且7AB =，8AC =，则BC =（）A ．2B ．10C 105D ．73【解析】 C ．做A ∠的角平分线交BC 边于D ．于是78AB BD AC DC ==．不妨设7,8BD x DC x ==，由BAD BAC △∽△，有BD AB AB BC =，即77715x x =，于是715x ，15105BC x =3．用[]x 表示不大于x 的最大整数，则方程[]2230x x --=的解的个数为（）2A ．1B ．2C ．3D ．4【解析】 C ．原问题等价于函数23y x =-与函数[]2y x =的图像的交点个数问题．观察出交点个数为3个．方程的解分别为2,3x x =-=，另一个位于2，3之间．4．设正方形ABCD 的中点为点O ，在以五个数A 、B 、C 、D 、O 为顶点所构成的所有三角形中任意取出两个，它们的面积相等的概率为（）A ．314B ．37C ．12D ．47【解析】 B ．不妨设三角形边长为1，则三角形的面积有两种，一种是14，形如ABO △，有4个；一种是12，形如ABD △，有4个．于是对于这8个三角形，先选出任意一个，再选出其余7个三角形中面积和它相等的三角形（共3个）中的一个，概率为37．5．如图，在矩形ABCD 中，3AB =，2BC =，以BC 为直径在矩形内作半圆，自点A 作半圆的切线AE ，则sin CBE ∠=（）A 6B ．23C ．13D 103ECBDA【解析】 D ．取BC 中点F ，连接AF ，则CBE BAF ∠=∠，于是2210sin sin 13CBE BAF ∠=∠==+6．设n 是大于1909的正整数，使得19092009n n--为完全平方数的n 的个数是（）A ．3B ．4C ．5D ．6【解析】 B ．由1909100120092009n n n -=-+--，而1002009n-可能取整数2,5,4,10,25,50,100．若10012009n --为完全平方数，则有1002,5,10,502009n=-．于是这样的n 有4个．二、填空题（本题满分28分，每小题7分）1．已知t 是实数，若a ，b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根，则()()2211a b --的最小值是．【解析】3-．2,1a b ab t +==-，又由0∆≥知2t 1≤≤．于是()()()222222111a b a b a b --=+-+424t =-．于是当1t =时代数式有最小值3-．2．设D 是ABC △ 的边AB 上的一点，作DE BC ∥交AC 于点E ，作DF AC ∥交BC 于点F ，已知ADE △、DBF △的面积分别为m 和n ，则四边形DECF 的面积为．【解析】 2mn ADE BDF △∽△，相似比为ADDB．观察到DEF △的面积等于m 和n 的等比中项，所以所求答案为2mn3．如果实数a ，b 满足条件221a b +=，221221a b a b a -+++=-，则a b += ．【解析】 1-．分情况讨论，可得221221a b a b a -+++=-或22(12)21a b a b a --+++=-．如果是第一种，则222b b a +=-，消去a 可得2230b b --=，可得1b =-或32．经检验，1,0b a =-=符合，所求结果为1-；如果是第二种，则224a b b a -=-．因为去绝对值符号的时候有120a b -+≤，即21a b +≥，而10b +≥，则设法凑出含有1b +的形式．因为2240a a b b +--=，所以2222114()22a ab b a b +--++=，即22238(1)4a a b a +=+≤，所以8a ≥或0a ≤，因此只能有0a =，和第一种情况是同一个解．4．已知a ，b 是正整数，且满足15152a b 是整数，则这样的有序数对()a b ，共有对．5【解析】 7．显然两个根式的值都是有理数（否则把它平方即可发现）．穷举，可能是1+1，112+， 1122+，1144+，1136+，考虑顺序，共7种．第二试（A ）一、（本题满分20分）已知二次函数()20y x bx c c =++<的图象与x 轴的交点分别为A 、B ，与y 轴的交点为C ．设ABC △的外接圆的圆心为点P ．⑴ 证明：P ⊙与y 轴的另一个交点为定点．⑵ 如果AB 恰好为P ⊙的直径且2ABC S =△，求b 和c 的值．【解析】 ⑴ 易求得点C 的坐标为()0c ，，设()10A x ，，()20B x ，，则12x x b +=-，12x x c =．设P ⊙与y 轴的另一个交点为D ，由于AB 、CD 是P ⊙的两条相交弦，它们的交点为点O ，所以OA OB OC OD ⨯=⨯则121x x c OA OB OD OC c c⨯====．因为0c <，所以点C 在y 轴的负半轴上，从而点D 在y 轴的正半轴上，旗开得胜6所以点D 为定点，它的坐标为()01，． ⑵ 因为AB CD ⊥，如果AB 恰好为P ⊙的直径，则C 、D 关于点O 对称，所以点C 的坐标为()01-，，即1c =-．又()()222121212444AB x x x x x x b c b =-+---+所以21141222ABC S AB OC b =⋅+⋅△，解得23b =±．二、（本题满分25分）设CD 是直角三角形ABC 的斜边AD 上的高，1I 、2I 分别是ADC △、BDC △的内心，3AC =，4BC =，求12I I ．I 2I 1CABBACE DFI 1I 2【解析】作1I E AB ⊥于E ，2I F AB ⊥于F ．旗开得胜7在直角三角形ABC 中，3AC =，4BC =，225AB AC BC +=．又CD AB ⊥，由射影定理可得295AC AD AB ==，故165BD AB AD =-=，22125CD AC AD -．因为1I E 为直角三角形ACD 的内切圆的半径，所以()11325I E AD CD AC =+-=．连接1DI 、2DI ，则1DI 、2DI 分别是ADC ∠和BDC ∠的平分线，所以112245I DC I DA I DC I DB ∠=∠=∠=∠=o，故1290I DI ∠=o，所以12I D I D ⊥，1113325sin sin 45I E DI ADI ===∠o ．同量，可求得245I F =，242DI ．所以2212122I I DI DI +三、（本题满分25分）已知a ，b ，c 为正数，满足如下两个条件：32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②旗开得胜8a b c【解析】证法1：将①②两式相乘，得()8b c a c a b a b c a b c bcca ab +-+-+-⎛⎫++++= ⎪⎝⎭，即()()()2222228b c a c a b a b c bccaab+-+-+-++=，即()()()222222440b c a c a b a b c bccaab+-+-+--+-+=，即()()()2222220b c a c a b a b c bccaab----+-++=，即()()()()()()0b c a b c a c a b c a b a b c a b c bccaab-+---+--+++-++=，即()()()()0b c a ab c a b c a b c a b c abc-+----++++=⎡⎤⎣⎦，即()22220b c a ab a b c abc-+⎡⎤--+=⎣⎦，即()()220b c a c a b abc-+⎡⎤--=⎣⎦，即()()()0b c a c a b c a b abc-++--+=，所以0b c a -+=或0c a b +-=或0c a b -+=，即b a c +=或c a b +=或c b a +=．a b c9证法2：结合①式，由②式可得32232232214a b c bc ca ab ---++=，变形，得()2221102424a b c abc -++=③又由①式得()21024a b c ++=，即()22210242a b c ab bc ca ++=-++，代入③式，得()110242102424ab bc ca abc --++=⎡⎤⎣⎦，即()164096abc ab bc ca =++-．()()()()()331616161625616409625632160a b c abc ab bc ca a b c ---=-+++++-=-+⨯-=，所以16a =或16b =或16c =．结合①式可得b a c +=或c a b +=或c b a +=．a b c第二试（B ）一、（本题满分20分）已知二次函数()20y x bx c c =++<的图象与x 轴的交点分别为A 、B ，与y 轴的交点为C ．设ABC △的外接圆的圆心为点P ．10⑴ 证明：P ⊙与y 轴的另一个交点为定点．⑵ 如果AB 恰好为P ⊙的直径且2ABC S =△，求b 和c 的值．【解析】 ⑴ 易求得点C 的坐标为()0c ，，设()10A x ，，()20B x ，，则12x x b +=-，12x x c =．设P ⊙与y 轴的另一个交点为D ，由于AB 、CD 是P ⊙的两条相交弦，它们的交点为点O ，所以OA OB OC OD ⨯=⨯则121x x c OA OB OD OC c c⨯====．因为0c <，所以点C 在y 轴的负半轴上，从而点D 在y 轴的正半轴上，所以点D 为定点，它的坐标为()01，． ⑵ 因为AB CD ⊥，如果AB 恰好为P ⊙的直径，则C 、D 关于点O 对称，所以点C 的坐标为()01-，，即1c =-．又()()222121212444AB x x x x x x b c b =-+---+所以21141222ABC S AB OC b =⋅+⋅△，解得23b =±．旗开得胜11二、（本题满分25分）已知ABC △中，90ACB ∠=o ，AB 边上的高线CH 与ABC △的两条内角平分线AM 、BN 分别交于P 、Q 两点PM 、QN 的中点分别为E 、F ．求证：DE AB ∥．ACBHNMF P EQQEP F MNHBCA【解析】因为BN 是ABC ∠的平分线，所以ABN CBN ∠=∠．又因为CH AB ⊥，所以9090CQN BQH ABN CBN CNB ∠=∠=-∠=-∠=∠o o ，因此CQ NC =．又F 是QN 的中点，所以CF QN ⊥，所以90CFB CHB ∠==∠o ，因此C 、F 、H 、B 四点共圆．又FBH FBC ∠=∠，所以FC FH =，故点F 在CH 的中垂线上．、同理可证，点E 在CH 的中垂线上．旗开得胜12因此EF CH ⊥，又AB CH ⊥，所以EF AB ∥．三、（本题满分25分）已知a ，b ，c 为正数，满足如下两个条件：32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②a b c【解析】证法1：将①②两式相乘，得()8b c a c a b a b c a b c bc ca ab +-+-+-⎛⎫++++= ⎪⎝⎭，即()()()2222228b c a c a b a b c bccaab+-+-+-++=，即()()()222222440b c a c a b a b c bccaab+-+-+--+-+=，即()()()2222220b c a c a b a b c bccaab----+-++=，即()()()()()()0b c a b c a c a b c a b a b c a b c bccaab-+---+--+++-++=，13即()()()()0b c a ab c a b c a b c a b c abc-+----++++=⎡⎤⎣⎦，即()22220b c a ab a b c abc-+⎡⎤--+=⎣⎦，即()()220b c a c a b abc-+⎡⎤--=⎣⎦，即()()()0b c a c a b c a b abc-++--+=，所以0b c a -+=或0c a b +-=或0c a b -+=，即b a c +=或c a b +=或c b a +=．a b c证法2：结合①式，由②式可得32232232214a b c bc ca ab ---++=，变形，得()2221102424a b c abc -++=③又由①式得()21024a b c ++=，即()22210242a b c ab bc ca ++=-++，代入③式，得()110242102424ab bc ca abc --++=⎡⎤⎣⎦，即()164096abc ab bc ca =++-．()()()()()331616161625616409625632160a b c abc ab bc ca a b c ---=-+++++-=-+⨯-=，所以16a =或16b =或16c =．结合①式可得b a c +=或c a b +=或c b a +=．a b c第二试（C）一、（本题满分20分）△的已知二次函数()20y x bx c c=++<的图象与x轴的交点分别为A、B，与y轴的交点为C．设ABC 外接圆的圆心为点P．⊙与y轴的另一个交点为定点．⑴ 证明：P1415⑵ 如果AB 恰好为P ⊙的直径且2ABC S =△，求b 和c 的值．【解析】 ⑴ 易求得点C 的坐标为()0c ，，设()10A x ，，()20B x ，，则12x x b +=-，12x x c =．设P ⊙与y 轴的另一个交点为D ，由于AB 、CD 是P ⊙的两条相交弦，它们的交点为点O ，所以OA OB OC OD ⨯=⨯则121x x c OA OB OD OC c c⨯====．因为0c <，所以点C 在y 轴的负半轴上，从而点D 在y 轴的正半轴上，所以点D 为定点，它的坐标为()01，． ⑵ 因为AB CD ⊥，如果AB 恰好为P ⊙的直径，则C 、D 关于点O 对称，所以点C 的坐标为()01-，，即1c =-．又()()222121212444AB x x x x x x b c b =-+---+所以21141222ABC S AB OC b =⋅+⋅△，解得23b =±．16二、（本题满分25分）已知ABC △中，90ACB ∠=o ，AB 边上的高线CH 与ABC △的两条内角平分线AM 、BN 分别交于P 、Q 两点PM 、QN 的中点分别为E 、F ．求证：DE AB ∥．ACBHNMF P EQQEP F MNHBCA【解析】因为BN 是ABC ∠的平分线，所以ABN CBN ∠=∠．又因为CH AB ⊥，所以9090CQN BQH ABN CBN CNB ∠=∠=-∠=-∠=∠o o ，因此CQ NC =．又F 是QN 的中点，所以CF QN ⊥，所以90CFB CHB ∠==∠o ，因此C 、F 、H 、B 四点共圆．又FBH FBC ∠=∠，所以FC FH =，故点F 在CH 的中垂线上．、同理可证，点E 在CH 的中垂线上．因此EF CH ⊥，又AB CH ⊥，所以EF AB ∥．17三、（本题满分25分）已知a ，b ，c 为正数，满足如下两个条件：32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②a b c【解析】解法1：将①②两式相乘，得()8b c a c a b a b c a b c bc ca ab +-+-+-⎛⎫++++= ⎪⎝⎭，即()()()2222228b c a c a b a b c bccaab+-+-+-++=，即()()()222222440b c a c a b a b c bccaab+-+-+--+-+=，即()()()2222220b c a c a b a b c bccaab----+-++=，即()()()()()()0b c a b c a c a b c a b a b c a b c bccaab-+---+--+++-++=，即()()()()0b c a ab c a b c a b c a b c abc-+----++++=⎡⎤⎣⎦，18即()22220b c a ab a b c abc-+⎡⎤--+=⎣⎦，即()()220b c a c a b abc-+⎡⎤--=⎣⎦，即()()()0b c a c a b c a b abc-++--+=，所以0b c a -+=或0c a b +-=或0c a b -+=，即b a c +=或c a b +=或c b a +=．a b c 90o ．解法2：结合①式，由②式可得32232232214a b c bc ca ab ---++=，变形，得()2221102424a b c abc -++=③又由①式得()21024a b c ++=，即()22210242a b c ab bc ca ++=-++，代入③式，得()110242102424ab bc ca abc --++=⎡⎤⎣⎦，即()164096abc ab bc ca =++-．()()()()()331616161625616409625632160a b c abc ab bc ca a b c ---=-+++++-=-+⨯-=，所以16a =或16b =或16c =．结合①式可得b a c +=或c a b +=或c b a +=．a b c 90o ．19。

2009年北京市中学生数学竞赛初二年级竞赛试1

2009年北京市中学生数学竞赛初二年级竞赛试题一、选择题（满分25分，每小题只有一个正确答案，答对得5分）1.当16m =-时，代数式2221539933m m m m m m m m ---÷---++的值是（）A.－1B.12-C.12D.1 2.一个正八边形中最长的对角线等于a ，最短的对角线等b ，则这个正八边形的面积为（）A.22a b +B. 22a b -C.a b +D.ab 3.11111161111161621212626313136+++++⨯⨯⨯⨯⨯⨯的值是（）. A.118 B.136 C.133 D.1664.若n 是正整数，记1×2×3×…×n =n !，比如1！=1，4！=1×2×3×4=24，等等，若M =1!×2！×3！×4！×5！×6！×7！×8！×9！，则M 的约数中是完全平方数的共有（）A.504个B.672个C.864个D.936个5.将2009表示成两个整数的平方差的形式，则不同的表示方法有（）A.16种B.14种C.12种D.10种二、填空题（满分35分，每小题7分） 1. 2245.113.945.113.931.2-+⨯的值等于 . 2.平行四边形ABCD 中，AD=a ，CD=b ，过点B 分别作AD 边上的高a h 和CD 边上的高b h ，已知a h a ≥，b h b ≥，对角线AC=20厘米，平行四边形ABCD的面积为平方厘米.3.已知01a <<，并且1232829183030303030a a a a a ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤++++++⋅⋅⋅++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦，则[]10a 等于 .（其中[]x 表示不超过x 的最大整数）4.已知△ABC 中，∠A ，∠B ，∠C 的外角度数之比为α∶β∶γ（α，β，γ均为正数），则∠A ∶∠B ∶∠C 等于 .（用含α，β，γ的式子之比表示）5.当12x ≤≤等于 .三、（满分10分）已知0a b c ++=，2221a b c ++=.（1）求ab bc ca ++的值（2）求444a b c ++的值四、（满分15分）如图所示，六边形ABCDEF 中，AB=BC=CD=DE=EF=FA ，并且∠A+∠C+∠E=∠B ＋∠D ＋∠F ，求证∠A ＝∠D ，∠B=∠E ，∠C=∠F.五、（满分15分）（1）证明：由2009个1和任意个0组成的自然数不是完全平方数；（2）试说明，存在最左边2009位都是1的形如200911111***个的自然数（其中*代表阿拉伯数码）是完全平方数.F E DC B A。

2009年全国初中数学竞赛武汉赛区预赛试题

Ｊ
２
一
竞赛全国初中数学
）
武汉赛区预赛试题
７．如图３所示，ＡＡＥ是以正方形ＡＤ的对角线为边的等ＣＢＣ
边三角形，上Ａ曰交且曰的延长线于点Ｆ，则８瑚
、
选择题（小题６，吩）每分共３
１一个正数．的两个平方根分别是叶ｌ与，的值为（则ｎ
Ａ＞２Ｂ＜２．Ｃ．＞２－
）
１已知方程＋础一ｌＯｍ是整数）两个不相等的正Ｑ：，ｍ＋－（有整数根，则ｍ＝．
Ｄ．ｘ－＜２
二、空题（填每小题６，０）分共３分
６对于任意实数。，，，，ｃｄ规定了一种运算
则｛５ｌ２时，＝当３＿＝５Ｉ４２
５８
重蕊
编者语：亲爱的同学们本刊 2 0 0 9 年第 1 1 期数独游
，
戏正在火热进行中速速挑战有精美礼品等着你哦 !
，，
数独
3
(s u d 0 ㈨
．
第
，
A B
，
-
90
F
，
它的内切圆分别
，
( 1 ) 求s 的最小值
与边B
C CA A B
，
，
一
相切于点D E
，，
，
连结A D 且 A D 与内
，
( 2 ) 若对任何实数z y都有 s
，
≥

2009年初中数学竞赛选拔模拟试卷

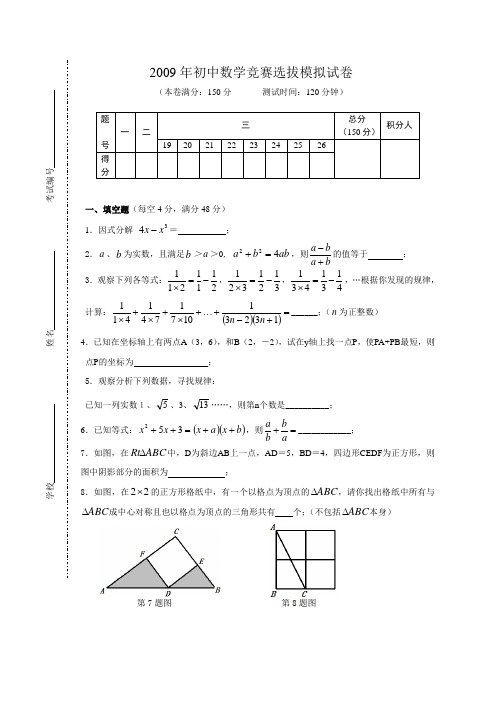
2009年初中数学竞赛选拔模拟试卷（本卷满分：150分测试时间：120分钟）一、填空题（每空4分，满分48分）1．因式分解34xx-＝；2．a、b为实数，且满足b＞a＞0, abba422=+，则baba+-的值等于；3．观察下列各等式：2111211-=⨯，3121321-=⨯，4131431-=⨯，…根据你发现的规律，计算：()()=+-+⋯+⨯+⨯+⨯132311071741411nn______；（n为正整数）4．已知在坐标轴上有两点A（3，6），和B（2，－2），试在y轴上找一点P，使PA+PB最短，则点P的坐标为；5．观察分析下列数据，寻找规律：已知一列实数１、5、3、13……，则第n个数是__________；6．已知等式：()()bxaxxx++=++352，则=+abba____________；7．如图，在ABCRt∆中，D为斜边AB上一点，AD＝5，BD＝4，四边形CEDF为正方形，则图中阴影部分的面积为；8．如图，在22⨯的正方形格纸中，有一个以格点为顶点的ABC∆，请你找出格纸中所有与ABC∆成中心对称且也以格点为顶点的三角形共有个；（不包括ABC∆本身）学校姓名考试编号第7题图第8题图9．已知不等式组⎩⎨⎧<-≥+0123a x x 无解，则a 的取值范围是；10．以O 为圆心的两个同心圆的半径分别为()223+cm 和()223-cm ，⊙O 1与这两个圆都相切，则⊙O 1的半径是； 11．若不论x 取何值时，分式3212-+-m x x总有意义，则m 的取值范围是_________；12．如图所示，在ABC Rt ∆中，已知︒=∠90B ，6=AB ，8=BC ，F E D ,,分别是三边CA BC AB ,,上的点，则FD EF DE ++的最小值为。

二．选择题（每小题4分，满分24分）13．若（x －1）2的算术平方根是x －1，则x 的取值范围是（） A ．x ＜1B ．x≤1C ．x ＞1D ．x≥114．已知0<⋅n m 且1101m n n m ->->>++，那么n ，m ，1n，1n m+的大小关系是（）A ．11m n n n m<<+< B ．11m n n m n <+<< C ．11n m n mn+<<<D ．11m n n m n<+<<15．下列五个命题：（1）若直角三角形的两条边长为3和4，则第三边长是5；（2）()2a＝a （a ≥0）；（3）若点P （a ，b ）在第三象限，则点P ＇（－a ，－b ＋1）在第一象限；（4）顺次连结对角线互相垂直且相等的四边形各边中点的四边形是正方形；（5）两边及第三边上的中线对应相等的两个三角形全等。

2009年八年级三科联赛数学试题

7．若3 x3－ kx2 ＋4被3 x －1除后余5，则k 的值为（）
(A)－10 (B)10 (C)－8 (D)8
8．已知 A ＝＋＋＋……＋＋，则A的整数部分是（）
(A)2007 (B)2008 (C)2009 (D)2010
八年级数学参考答案
一、填空
1．3 2． ≤ a ≤1 3．4－2 4．60o 5．64o 6．18
二、选择题
7．C 8．D 9．D 10．C 11．A 12．B
三、解答题
13．解：⑴设甲队单独做需要 x 天完成，乙队单独做需要 y 天完成
意力保持较为理想的稳定状态，随后学生的注意力开始分散，经过实验分析可
知，学生的注意力指标数 y 随时间 x (min)的变化规律如下图所示(其中AB、BC 分
别为线段，CD 为双曲线的一部分)．
⑴开始上课后第五分钟时与第三十分钟相比较，何时
学生的注意力更集中？
⑵一道数学竞赛题，须要讲19 min，为了效果较好，
B 两县的运费（元/吨）如下表所示：
⑴设 C 县运到 A 县的化肥为 x 吨，求总运费 w (元)与 x (吨)的函数解析式，并写出自变量 x 的取值范围．
⑵求最低总运费，并说明总运费最低时的运送方案．
C D
A 35 40
B 30 45
18．求使 m2＋ m ＋8是完全平方数的所有整数 m 的积是多少？
16．
17．⑴由题意，得 w ＝35 x ＋40(90－ x )＋30(100－ x )＋45( x －40)
＝10 x ＋4800(40≤ x ≤90)………………………………………………………………… （4分）

2009年全国初中数学竞赛试题

报出来若报出来的数如图所示则报
．
，
3
的人
一
心里想的数是
参考答案
、
．
选择题
，
1 10
1
2 3
．
由题设知口 ≥ 3
=
所以题设的等式可化为
于是
a
=
／ f b + 2 f + 、瓦二巧矿
a +
o
，
3 ，6 —
2
，
从而
9
b 1
=
．
选C
I~
}
．
8
、
6
r
4 5
-
：
,
2 64
9
；
=
㈣
，
；
fx 3
心里想的数应是 8 吨
．
=
2 544
，
fx 4
；
-
2 364
于是报 7 的人心里想的
【3 6 0 1 7 2 0 9 y
=
【4 6 0 1 7 2 0 9 y
=
．
数是
16
一
12
一
(8 吨 ) 4 帆
=
=
，
报
9
的人心里想的数是
20
一
(4 慨 )
2
．
A B OC
—
A ABC
，
所以
器器即
=
，
上
=
』
，
所以扛
0
—
1= 0
．
第1 0 题图
副

2009年初中数学竞赛选拔模拟试卷(含答案)

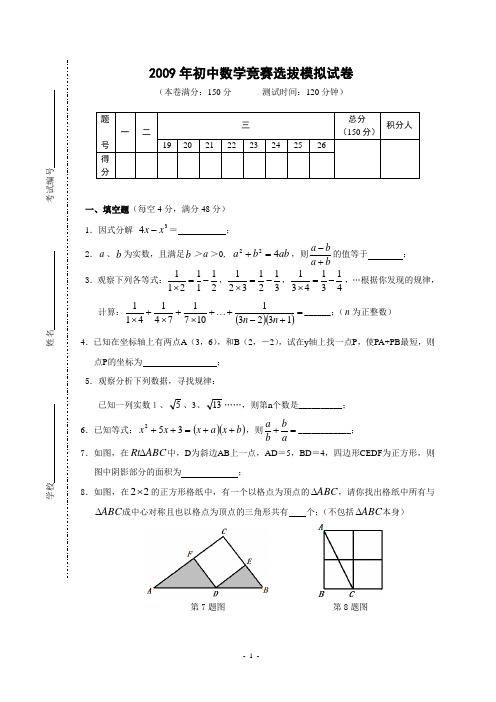
2009年初中数学竞赛选拔模拟试卷（本卷满分：150分测试时间：120分钟）一、填空题（每空4分，满分48分）1．因式分解34xx-＝；2．a、b为实数，且满足b＞a＞0, abba422=+，则baba+-的值等于；3．观察下列各等式：2111211-=⨯，3121321-=⨯，4131431-=⨯，…根据你发现的规律，计算：()()=+-+⋯+⨯+⨯+⨯132311071741411nn______；（n为正整数）4．已知在坐标轴上有两点A（3，6），和B（2，－2），试在y轴上找一点P，使PA+PB最短，则点P的坐标为；5．观察分析下列数据，寻找规律：已知一列实数１、5、3、13……，则第n个数是__________；6．已知等式：()()bxaxxx++=++352，则=+abba____________；7．如图，在ABCRt∆中，D为斜边AB上一点，AD＝5，BD＝4，四边形CEDF为正方形，则图中阴影部分的面积为；8．如图，在22⨯的正方形格纸中，有一个以格点为顶点的ABC∆，请你找出格纸中所有与ABC∆成中心对称且也以格点为顶点的三角形共有个；（不包括ABC∆本身）学校姓名考试编号第7题图第8题图9．已知不等式组⎩⎨⎧<-≥+0123a x x 无解，则a 的取值范围是；10．以O 为圆心的两个同心圆的半径分别为()223+cm 和()223-cm ，⊙O 1与这两个圆都相切，则⊙O 1的半径是； 11．若不论x 取何值时，分式3212-+-m x x 总有意义，则m 的取值范围是_________； 12．如图所示，在ABC Rt ∆中，已知︒=∠90B ，6=AB ，8=BC ，F E D ,,分别是三边CA BC AB ,,上的点，则FD EF DE ++的最小值为。

二、选择题（每小题4分，满分24分）13．若（x －1）2的算术平方根是x －1，则x 的取值范围是（） A ．x ＜1B ．x≤1C ．x ＞1D ．x≥114．已知0<⋅n m 且1101m n n m ->->>++，那么n ，m ，1n ，1n m+的大小关系是（）A ．11m n n n m <<+<B ．11m n n m n <+<<C ．11n m n m n +<<<D ．11m n n m n<+<<15．下列五个命题：（1）若直角三角形的两条边长为3和4，则第三边长是5；（2）()2a ＝a （a ≥0）；（3）若点P （a ，b ）在第三象限，则点P ＇（－a ，－b ＋1）在第一象限；（4）顺次连结对角线互相垂直且相等的四边形各边中点的四边形是正方形；（5）两边及第三边上的中线对应相等的两个三角形全等。

2009年路桥实验中学八年级数学竞赛试题

（第6题）（第5题）2008学年路桥实验中学八年级数学竞赛试题（考试时间：120分钟，总分共120分）命题人：王万丰亲爱的同学们，欢迎参加路桥实验中学文化周数学活动！在这里，重要的不是为了胜人一筹，而是由此更上一层楼。

进一步明白学好数学需要多方面的知识和素养，同时再一次展现你的灵性和潜能，品味数学的博大精深。

一、选择题（本题共8小题，每小题5分,共40分。

）1、若有m 个数的平均数是a , 另有n 个数的平均数是b ,则这m n +个数的平均数是( )（A ）2b a + （B ）n m b a ++ （C ）n m b a ++ （D ）n m nb ma ++2、若440-=m ，则估计m 的值所在的范围是（） (A)21<<m (B)32<<m(C)43<<m (D)54<<m3、函数1y x x=+的图象如图所示，下列对该函数性质的论断正确．．的是（） (A)该函数的图象是轴对称图形(B)在每个象限内，y 的值随x 值的增大而减小(C)当0x >时，该函数在1x =时取得最小值2 (D)y 的值可能为14．如图是一个切去了一个角的正方体纸盒，切面与棱的交点A 、B 、C 均是棱的中点，现将纸盒剪开展成平面，则展开图不可能是（）A B C D5、如图，在三角形ABC 中，AB ＞AC ，D 、E 分别是AB 、AC 上的点，△ADE 沿线段DE 翻折，使点A 落在边BC 上，记为A '．若四边形ADA E '是菱形，则下列说法正确的是( )A . DE 是△ABC 的中位线B . AA '是BC 边上的中线 C . AA '是BC 边上的高D . AA '是△ABC 的角平分线 6、在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点，观察图中每正方形（实线）四条边上的整点的个数，请你猜测由里向外第10个正方形（实线）四条边上的整点的个数共有（）yxO1-2 2-1 (第3题)ABCDEA 'A450BCMN （第12题）x123 -11 2 3 y （第11题）（第13题）A 、35个B 、40个C 、41个D 、45个7、直角三角形纸片的两直角边长分别为6，8，现将ABC △如图那样折叠，使点A 与点B 重合，折痕为DE ，则CE 的长为（） A ．1 B ． 2C ．47D ．238、7条长度均为整数厘米的线段：a 1，a 2，a 3，a 4，a 5，a 6，a 7，满足a 1＜a 2＜a 3＜a 4＜a 5＜a 6＜a 7，且这7条线段中的任意3条都不能构成三角形．若a 1=1厘米，a 2=2厘米，则a 7 的最小值为（） (A) 21厘米(B) 18厘米(C) 15厘米(D) 12厘米二、填空题（本题共6小题，每小题5分，共30分）9、若实数b a 、满足0444522=+++-a b ab a ，则=ab ；10、观察下列各等式：2111211-=⨯，3121321-=⨯，4131431-=⨯，…根据你发现的规律计算：当()()3110132311071741411=+-+⋯+⨯+⨯+⨯n n 时（n 为正整数），=n ；11、我们知道，数形结合是数学重要的思想方法，如把方程x －2＝1—x 的解看成函数y ＝x －2的图象与函数y ＝1－x 的图象的交点的横坐标。

2009-2012年湖州市(期望杯)初二数学竞赛试题和答案

2009年湖州市初二数学竞赛试题（考试时间：2008年5月10日上午9：00—11：00）答题时注意；1．用圆珠笔或钢笔作答．2．解答书写时不要超过装订线．3．可以用计算器一、选择题（共8小题，每小题5分，满分40分．以下每小题均给出了代号为A，B，C，D的四个选项，其中有且只有一个选项是正确的．请将正确选项的代号填入题后的括号里．不填、多填或错填均得零分）1．如图，三个图形的周长相等，则（）（A）a<b<c （B）c<a<b （C）a<c<b （D）c<b<a2a2aa abc c2.设1a=，则32312612a a a+--=（）A.24.B. 25.C. 10.D. 12.3.桌上放着6张扑克牌，全部正面朝下。

你已被告知其中有两张且只有两张是老K，但是你不知道老K在哪个位置。

你随便取了两张并把它们翻开，会出现下面两种情况：(1)两张牌中至少有l张是老K；(2)两张牌中没有l张是老K。

比较这两种情况的可能性，可知( )A．(1)的可能性大 B．(2)的可能性大 C．两者一样． D．无法比较4.要使多项式(1)(3)(4)(8)x x x x m-+--+为一个完全平方式，则m等于（）A．12 B．24 C．98 D．1965.数学大师陈省身于2004年12月3日在天津逝世．陈省身教授在微分几何等领域做出了杰出贡献，是获得沃尔夫奖的惟一华人．他曾经指出,平面几何中有两个重要定理，一个是勾股定理，另一个是三角形内角和定理，后者表明平面三角形可以千变万化，但是三个内角的和是不变量．下列几个关于不变量的叙述：(1)边长确定的平行四边形ABCD ，当∠A 变化时，其任意一组对角之和不变； (2)当多边形的边数不断增加时，它的外角和不变； (3)当△ABC 绕顶点A 旋转时，△ABC 各内角的大小不变； (4)在放大镜下观察，含角a 的图形放大时，角a 的大小不变； (5)当圆的半径变化时，圆的周长与半径的比值不变； (6)当圆的半径变化时，圆的周长与面积的比值不变，其中，错误的叙述有 ( )(A)2个 (B)3个 (C)4个 (D)5个6.在直角坐标系中，若一点的纵横坐标都是整数，则称该点为整点。

2009年株洲市初中数学竞赛初二试卷和答案

-3-2012332 A B C D E FG 2009年株洲市初中数学竞赛试卷（初二年级）时量：120分钟总分：100分注意事项：1、用黑色、蓝色钢笔或圆珠笔作答；2、在密封线内答题，答题内容不要超过密封线；3、不准使用计算器。

1．下列计算错误的是A ．236()a a = B ．22x +32x =52x C ．（a-b ）（-a-b ）=b 2-a 2 D ．3=-2．不相等的有理数a,b,c 在数轴上的对应点分别是A 、B 、C ，如果|a b ||b c ||a c |-+-=-那么点B ：A ．在A 、C 点之间B ．在A 、C 两点的右边 C ．在A 、C 两点的左边D ．上述三种均可能 3．一个长方形的周长是14，面积是12，则长方形的一条对角线长为A ．4B ．5C ．7D ．4．在平面直角坐标系y o x 内，已知A (3，3)，点P 是x 轴上一点，则使△AOP 为等腰三角形的点P 共有A ．2个B ．3个C ．4个D . 5个5、某种商品若按标价的八折出售，可获利20%，若按原标价出售，可获利A ．25%B ．40%C ．50%D ．66.7%6．如图，图①是某城市十二月份1至10日的最低气温随时间变化的图象；图②是这十天中最低气温天数的条形统计图； ① （第６题图）（第７题图）则下列说法错误的是：A ．图②中0℃的条形框高度应为2B ．这十天最低气温的众数是2℃C ．这十天最低气温的平均数是0℃D ．这十天最低气温的中位数是-1℃ 7．如图为某公司的产品标志图案，图中∠A+∠B+∠C+∠D+∠E+∠F+∠G= A ．360° B ．540° C ．630° D ．720°CBE8．某人从一鱼摊上买了3条鱼，平均每条 a 元，又从另一个鱼摊上买了2 条鱼，平均每条b 元，而后以每条a b2+元的价格售出，结果发现赔了钱，原因是： A ．a > b B ．a < b C ． a b ≠ D ．与a ，b 间的大小无关二、填空题（每题 5分，共30分）9．计算222008803610042009-⨯+的值是_________________．10．如果关于x 的不等式组3x-m 02x-n 0≥⎧⎨<⎩的整数解仅为1，2，3，那么适合这个不等式组的整数对(m ，n)共有___________________对.11．直线y=3x-k 与直线y=-2x+6交于第一象限，则k 的取值范围是______________________． 12．如图为由一些边长为1cm 正方体堆积在桌面形成的几何体的三视图，则该几何体露在外面部分的表面积是_________ cm 2．正视图左视图俯视图（第１２题图）（第１３题图） 13．等腰直角三角形ABC ∆中，AC=BC=3，E 在BC 上，BE=2，P 为AB 上一个动点，则 PC+PE 的最小值是 __________________________．14．如图，将一个边长为1的正三角形的每条边三等分，以中间一段为边向形外作正三角形，并擦去中间一段，得图（2），如此继续下去，得图（3）……这样得到的图案叫雪花曲线，雪花曲线有一个奇妙的性质：其周长可以无限增加，但其围成的图形的面积总是有限的．如图可得，第1个图有3条边，周长为3；第2个图有12条边，周长为4；则第4个图形周长是_______________；第n 个图形的周长是___________________．三、解答题（本大题共4个小题，共38分，解答应写出必要的文字说明，证明过程或演算步骤）+15．（本题满分8分）已知a-b= 4,ab+c2+4=0,求a c16．（本题满分10分）某个学生参加军训，进行打靶训练，必须射击10次，在第6，7，8，9 次射击中，分别得了9.0环,8.4环,8.1环,9.3环,他的前9次射击所得的平均环数高于前5次射击所得的平均环数。