广东省惠州市2015届高三第三次调研考试数学(文)试题及答案

广东省惠州市高三数学第三次调研试卷文(含解析)

广东省惠州市2015届高三第三次调研数学试卷（文科）一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.1．（5分）若集合A={0，1，2，3}，B={1，2，4}，则集合A∪B=（）A．{0，1，2，3，4} B．{1，2，3，4} C．{1，2} D．{0}2．（5分）已知0＜a＜2，复数z=a+i（i是虚数单位），则|z|的取值范围是（）A．B．（1，5）C．（1，3）D．3．（5分）函数f（x）=+ln（x+1）的定义域为（）A．（2，+∞）B．（﹣1，2）∪（2，+∞）C．（﹣1，2）D．（﹣1，2]4．（5分）等差数列{a n}的前n项和为S n，且S3=6，a1=4，则公差d等于（）A．1 B．C．﹣2 D．35．（5分）已知a∈R，则“a2＜2a”是“a＜2”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件6．（5分）圆（x+2）2+y2=4与圆（x﹣2）2+（y﹣1）2=9的位置关系为（）A．内切B．相交C．外切D．相离7．（5分）下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行8．（5分）设变量x，y满足约束条件，则的最大值为（）A．3 B．6 C．D．19．（5分）如图是某个四面体的三视图，该四面体的体积为（）A．72 B．36 C．24 D．1210．（5分）已知函数f（x﹣1）是定义在R上的奇函数，若对于任意两个实数x1≠x2，不等式恒成立，则不等式f（x+3）＜0的解集为（）A．（﹣∞，﹣3）B．（4，+∞）C．（﹣∞，1）D．（﹣∞，﹣4）二、填空题：（本大题共3小题，分为必做题和选做题两部分．每小题5分，满分15分）（一）必做题：第11至13题为必做题，每道试题考生都必须作答．11．（5分）已知向量，且，则x=．12．（5分）在△ABC中，内角A，B，C对边的边长分别是a，b，c，若a=15，b=10，A=，则cosB=．13．（5分）A，B，C是平面内不共线的三点，点P在该平面内且有，现将一粒黄豆随机撒在△ABC内，则这粒黄豆落在△PBC内的概率为．（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答，按第一题记分【坐标系与参数方程选做题】（共1小题，满分5分）14．（5分）在极坐标系中，直线，被圆ρ=4截得的弦长为．【几何证明选做题】15．如图，已知△ABC内接于圆O，点D在OC的延长线上，AD切圆O于A，若∠ABC=30°，AC=2，则AD的长为．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（12分）已知向量=（cosx+sinx，2sinx），=（cosx﹣sinx，﹣cosx），f（x）=•，（1）求f（x）的最小正周期；（2）当x∈时，求f（x）的最小值以及取得最小值时x的值．17．（12分）惠州市某县区共有甲、乙、丙三所高中的2015届高三文科学生共有800人，各学校男、女生人数如表：甲高中乙高中丙高中女生153 x y男生97 90 z已知在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2．（1）求表中x的值；（2）惠州市第三次调研考试后，该县区决定从三所高中的所有2015届高三文科学生中利用随机数表法抽取100人进行成绩统计分析，先将800人按001，002，…，800进行编号．如果从第8行第7列的数开始向右读，请你依次写出最先检测的3个人的编号；（下面摘取了随机数表中第7行至第9行）8442 1753 3157 2455 0688 7704 7447 6721 7633 5026 83926301 5316 5916 9275 3862 9821 5071 7512 8673 5807 44391326 3321 1342 7864 1607 8252 0744 3815 0324 4299 7931（3）已知y≥145，z≥145，求丙高中学校中的女生比男生人数多的概率．18．（14分）如图，在直三棱柱A1B1C1﹣ABC中，AB⊥BC，E、F分别是A1B，AC1的中点．（1）求证：EF∥平面ABC；（2）求证：平面AEF⊥平面AA1B1B；（3）若AB=BC=a，A1A=2a，求三棱锥F﹣ABC的体积．19．（14分）已知递增等差数列{a n}中的a2，a5是函数f（x）=x2﹣7x+10的两个零点．数列{b n}满足，点（b n，S n）在直线y=﹣x+1上，其中S n是数列{b n}的前n项和．（1）求数列{a n}和{b n}的通项公式；（2）令c n=a n•b n，求数列{c n}的前n项和T n．20．（14分）已知直线y=﹣2上有一个动点Q，过点Q作直线l1垂直于x轴，动点P在l1上，且满足OP⊥OQ（O为坐标原点），记点P的轨迹为C．（1）求曲线C的方程；（2）若直线l2是曲线C的一条切线，当点（0，2）到直线l2的距离最短时，求直线l2的方程．21．（14分）已知函数f（x）=x2+2ax+1（a∈R），f′（x）是f（x）的导函数．（1）若x∈，不等式f（x）≤f′（x）恒成立，求a的取值范围；（2）解关于x的方程f（x）=|f′（x）|；（3）设函数，求g（x）在x∈时的最小值．广东省惠州市2015届高三第三次调研数学试卷（文科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.1．（5分）若集合A={0，1，2，3}，B={1，2，4}，则集合A∪B=（）A．{0，1，2，3，4} B．{1，2，3，4} C．{1，2} D．{0}考点：并集及其运算．专题：集合．分析：按照并集的定义直接写出A∪B即可．解答：解：∵A={0，1，2，3}，B={1，2，4}，∴A∪B={0，1，2，3，4}故答案为：A点评：本题考查集合的运算，求并集及运算．属于基础题．2．（5分）已知0＜a＜2，复数z=a+i（i是虚数单位），则|z|的取值范围是（）A．B．（1，5）C．（1，3）D．考点：复数求模．专题：数系的扩充和复数．分析：直接由复数模的公式写出|z|=，再由0＜a＜2求得1＜a2+1＜5，则答案可求．解答：解：∵复数z=a+i，则|z|=，由0＜a＜2，得1＜a2+1＜5，∴|z|∈（1，）．故选：D．点评：本题考查了复数模的求法，考查了函数的值域，是基础的计算题．3．（5分）函数f（x）=+ln（x+1）的定义域为（）A．（2，+∞）B．（﹣1，2）∪（2，+∞）C．（﹣1，2）D．（﹣1，2]考点：对数函数的定义域．专题：函数的性质及应用．分析：根据二次根式的性质结合对数函数的性质得到不等式组，解出即可．解答：解：由题意得：，解得：﹣1＜x＜2，故选：C．点评：本题考查了二次根式的性质，考查了对数函数的性质，是一道基础题．4．（5分）等差数列{a n}的前n项和为S n，且S3=6，a1=4，则公差d等于（）A．1 B．C．﹣2 D．3考点：等差数列的性质．专题：计算题．分析：由题意可得 S3=6=（a1+a3），且 a3=a1+2d，a1=4，解方程求得公差d的值．解答：解：∵S3=6=（a1+a3），且 a3=a1+2d，a1=4，∴d=﹣2，故选C．点评：本题考查等差数列的定义和性质，通项公式，前n项和公式的应用，属于基础题．5．（5分）已知a∈R，则“a2＜2a”是“a＜2”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：先解出a2＜2a，再进行判断即可解答：解：因为a2＜2a，所以0＜a＜2，则“a2＜2a”是“a＜2”的充分而不必要条件；故选：A．点评：本题考查了充分必要条件，考查了集合之间的关系，是一道基础题．6．（5分）圆（x+2）2+y2=4与圆（x﹣2）2+（y﹣1）2=9的位置关系为（）A．内切B．相交C．外切D．相离考点：圆与圆的位置关系及其判定．专题：直线与圆．分析：求出两圆的圆心和半径，计算两圆的圆心距，将圆心距和两圆的半径之和或半径之差作对比，判断两圆的位置关系．解答：解：圆（x+2）2+y2=4的圆心C1（﹣2，0），半径r=2．圆（x﹣2）2+（y﹣1）2=9的圆心C2（2，1），半径R=3，两圆的圆心距d==，R+r=5，R﹣r=1，R+r＞d＞R﹣r，所以两圆相交，故选B．点评：本题考查圆与圆的位置关系及其判定的方法，关键是求圆心距和两圆的半径．7．（5分）下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行考点：命题的真假判断与应用；空间中直线与平面之间的位置关系．专题：简易逻辑．分析：利用直线与平面所成的角的定义，可排除A；利用面面平行的位置关系与点到平面的距离关系可排除B；利用线面平行的判定定理和性质定理可判断C正确；利用面面垂直的性质可排除D．解答：解：A、若两条直线和同一个平面所成的角相等，则这两条直线平行、相交或异面，故A错误；B、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行或相交，故B错误；C、设平面α∩β=a，l∥α，l∥β，由线面平行的性质定理，在平面α内存在直线b∥l，在平面β内存在直线c∥l，所以由平行公理知b∥c，从而由线面平行的判定定理可证明b∥β，进而由线面平行的性质定理证明得b∥a，从而l∥a，故C正确；D，若两个平面都垂直于第三个平面，则这两个平面平行或相交，排除D．故选C．点评：本题主要考查了空间线面平行和垂直的位置关系，线面平行的判定和性质，面面垂直的性质和判定，空间想象能力，属基础题．8．（5分）设变量x，y满足约束条件，则的最大值为（）A．3 B．6 C．D．1考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对应的平面区域，利用数形结合即可得到结论．解答：解：作出不等式组对应的平面区域如图：设k=，则k的几何意义为区域内的点P（x，y）到圆点O的斜率，由图象可知，OA的斜率最大，由，解得其中A（1，6），则OA的斜率k=6，故的最大值为6，故选：B点评：本题主要考查线性规划的应用，利用数形结合以及直线的斜率公式是解决本题的关键．9．（5分）如图是某个四面体的三视图，该四面体的体积为（）A．72 B．36 C．24 D．12考点：由三视图求面积、体积．专题：计算题．分析：通过三视图，判断几何体的形状，利用三视图的数据，求解几何体的体积即可．解答：解：由题意可知，几何体是三棱锥，底面三角形的一边长为6，底面三角形的高为：4，棱锥的一条侧棱垂直底面的三角形的一个顶点，棱锥的高为：3．所以几何体的体积：=12．故选D．点评：本题考查三视图视图能力与几何体的判断，几何体的体积的求法，考查计算能力．10．（5分）已知函数f（x﹣1）是定义在R上的奇函数，若对于任意两个实数x1≠x2，不等式恒成立，则不等式f（x+3）＜0的解集为（）A．（﹣∞，﹣3）B．（4，+∞）C．（﹣∞，1）D．（﹣∞，﹣4）考点：函数奇偶性的性质．专题：函数的性质及应用．分析：对于任意两个实数x1≠x2，不等式恒成立，可得函数f（x）在R上单调递增．由函数f（x﹣1）是定义在R上的奇函数，可得f（﹣1）=0，即可解出．解答：解：∵对于任意两个实数x1≠x2，不等式恒成立，∴函数f（x）在R上单调递增．∵函数f（x﹣1）是定义在R上的奇函数，∴f（﹣1）=0，∴不等式f（x+3）＜0=f（﹣1）化为x+3＜﹣1，解得x＜﹣4，∴不等式的解集为：（﹣∞，﹣4）．故选：D．点评：本题考查了抽象函数的奇偶性与单调性，考查了推理能力，属于中档题．二、填空题：（本大题共3小题，分为必做题和选做题两部分．每小题5分，满分15分）（一）必做题：第11至13题为必做题，每道试题考生都必须作答．11．（5分）已知向量，且，则x=0．考点：平面向量的坐标运算；平行向量与共线向量．专题：平面向量及应用．分析：根据题意，得•=0，求出x的值即可．解答：解：∵，且，∴，解得x=0．故答案为：0．点评：本题考查了的知识点是利用平面向量的数量积判断两个平面向量的垂直关系，是基础题．12．（5分）在△ABC中，内角A，B，C对边的边长分别是a，b，c，若a=15，b=10，A=，则cosB=．考点：正弦定理．专题：解三角形．分析：利用正弦定理列出关系式，把a，b，sinA的值代入求出sinB的值，即可求出cosB 的值即可．解答：解：∵△ABC中，a=15，b=10，sinA=，∴由正弦定理=得：sinB===，∵b＜a，∴B＜A，即B为锐角，则cosB==，故答案为：点评：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．13．（5分）A，B，C是平面内不共线的三点，点P在该平面内且有，现将一粒黄豆随机撒在△ABC内，则这粒黄豆落在△PBC内的概率为．考点：几何概型．专题：概率与统计．分析：由P在该平面内且有，得到PB=PA且P在线段AB上，所以△PBC的面积是△ABC的，由几何概型的概率公式可求．解答：解：由P在该平面内且有，得到PB=PA且P在线段AB上，所以△PBC的面积是△ABC的，由几何概型的概率公式这粒黄豆落在△PBC内的概率为；故答案为：．点评：本题给出点P满足的条件，求P点落在△PBC内的概率，着重考查了平面向量共线的充要条件和几何概型等知识，属于基础题．（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答，按第一题记分【坐标系与参数方程选做题】（共1小题，满分5分）14．（5分）在极坐标系中，直线，被圆ρ=4截得的弦长为4．考点：直线的参数方程．专题：坐标系和参数方程．分析：把直线与圆的极坐标方程化为直角坐标方程，再利用弦长公式弦长=2（d 为圆心到直线的距离）即可得出．解答：解：直线，化为=2，∴x+y﹣2=0，圆ρ=4化为x2+y2=16．∴圆心O（0，0）到直线的距离d==2．∴直线被圆截得的弦长=2==4．故答案为：4．点评：本题考查了把极坐标方程化为直角坐标方程、弦长公式、点到直线的距离公式，考查了计算能力，属于基础题．【几何证明选做题】15．如图，已知△ABC内接于圆O，点D在OC的延长线上，AD切圆O于A，若∠ABC=30°，AC=2，则AD的长为．考点：与圆有关的比例线段．专题：直线与圆．分析：作CE⊥AD于点E，由已知结合三角形中角的关系得到AE的长度，再由AD=2AE得答案．解答：解：如图，作CE⊥AD于点E，∵∠ABC=30°，∴∠CDA=30°，则∠COA=60°，∴△AOC为正三角形，∴∠CAO=60°，AC=OC，∴∠CAE=30°，AC=CD，又∵CE⊥AD，∴AE=，则AD=2AE=．故答案为：．点评：本题考查了与圆有关的比例线段，考查了直角三角形的解法，是中档题．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（12分）已知向量=（cosx+sinx，2sinx），=（cosx﹣sinx，﹣cosx），f（x）=•，（1）求f（x）的最小正周期；（2）当x∈时，求f（x）的最小值以及取得最小值时x的值．考点：三角函数中的恒等变换应用；平面向量数量积的运算．专题：三角函数的图像与性质．分析：（1）先求得f（x）=cos（2x+），根据周期公式可得f（x）的最小正周期；（2）先求得2x+∈，由函数的单调性质可得当2x+=π即x=时，取到f（x）的最小值﹣．解答：解：f（x）=•=（cosx+sinx）（cosx﹣sinx）+2sinx（﹣cosx）=cos2x﹣sin2x﹣2sinxcosx=cos2x﹣sin2x=cos（2x+）（1）T==π（2）x∈时，2x+∈∴当2x+=π即x=时，取到f（x）的最小值﹣．点评：本题主要考察了三角函数中的恒等变换应用，平面向量数量积的运算，三角函数的图象与性质，属于基础题．17．（12分）惠州市某县区共有甲、乙、丙三所高中的2015届高三文科学生共有800人，各学校男、女生人数如表：甲高中乙高中丙高中女生153 x y男生97 90 z已知在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2．（1）求表中x的值；（2）惠州市第三次调研考试后，该县区决定从三所高中的所有2015届高三文科学生中利用随机数表法抽取100人进行成绩统计分析，先将800人按001，002，…，800进行编号．如果从第8行第7列的数开始向右读，请你依次写出最先检测的3个人的编号；（下面摘取了随机数表中第7行至第9行）8442 1753 3157 2455 0688 7704 7447 6721 7633 5026 83926301 5316 5916 9275 3862 9821 5071 7512 8673 5807 44391326 3321 1342 7864 1607 8252 0744 3815 0324 4299 7931（3）已知y≥145，z≥145，求丙高中学校中的女生比男生人数多的概率．考点：概率的应用．专题：综合题；概率与统计．分析：（1）利用在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2，求出表中x的值；（2）根据从第8行第7列的数开始向右读，即可写出最先检测的3个人的编号；（3）y+z=800﹣153﹣97﹣160﹣90=300，y≥145，z≥145，图象为线段y+z=300（145≤y≤155），即可求丙高中学校中的女生比男生人数多的概率．解答：解：（1）∵在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2，∴x=800×0.2=160；（2）从第8行第7列的数开始向右读，最先检测的3个人的编号为165、538、629；（3）y+z=800﹣153﹣97﹣160﹣90=300，y≥145，z≥145，图象为线段y+z=300（145≤y≤155）∵丙高中学校中的女生比男生人数多，∴y＞z，∴丙高中学校中的女生比男生人数多的概率为．点评：本题考查概率的应用，考查学生分析解决问题的能力，正确计算是关键．18．（14分）如图，在直三棱柱A1B1C1﹣ABC中，AB⊥BC，E、F分别是A1B，AC1的中点．（1）求证：EF∥平面ABC；（2）求证：平面AEF⊥平面AA1B1B；（3）若AB=BC=a，A1A=2a，求三棱锥F﹣ABC的体积．考点：平面与平面垂直的判定；直线与平面平行的判定．专题：证明题；空间位置关系与距离．分析：（1）连结A1C，可证EF是△A1BC的中位线，即EF∥BC，从而可证EF∥平面ABC．（2）易知BC⊥B1B，又由BC⊥BA，即BC垂直平面ABB1A1，又EF∥BC，即EF⊥平面ABB1A1，即可证明平面AEF⊥平面AA1B1B，（3）由直三棱柱可知V三棱锥F﹣ABC=S△ABC×h=S△ABC××CC1，代入即可求值．解答：证明：（1）连结A1C，由A1C1CA 是矩形，则A1C必过AC1的中点F，即F是A1C的中点，同理E是A1B的中点，则EF是△A1BC的中位线，即EF∥BC，又由BC在平面ABC中，EF在平面ABC外，则EF∥平面ABC．（2）由A1B1C1﹣ABC是直棱柱，则B1B⊥BC，即BC⊥B1B，又由BC⊥BA，即BC垂直平面ABB1A1，又由（1）知EF∥BC，即EF⊥平面ABB1A1，而EF在平面AEF中，则平面AEF⊥平面AA1B1B，（3）∵三棱柱A1B1C1﹣ABC是直三棱柱．∴V三棱锥F﹣ABC=S△ABC×h=S△ABC××CC1=×a×a×a=．点评：本题主要考查了平面与平面垂直的判定，直线与平面平行的判定，考查了空间想象能力，属于中档题．19．（14分）已知递增等差数列{a n}中的a2，a5是函数f（x）=x2﹣7x+10的两个零点．数列{b n}满足，点（b n，S n）在直线y=﹣x+1上，其中S n是数列{b n}的前n项和．（1）求数列{a n}和{b n}的通项公式；（2）令c n=a n•b n，求数列{c n}的前n项和T n．考点：数列的求和．专题：等差数列与等比数列．分析：（1）先解出两个零点，再利用等差、等比数列的通项公式即可；（2）直接使用错位相减法求之即可．解答：解：（1）因为a2，a5是函数f（x）=x2﹣7x+10的两个零点，则，解得：或．又等差数列{a n}递增，则，所以…3分因为点（b n，S n）在直线y=﹣x+1上，则S n=﹣b n+1．当n=1时，b1=S1=﹣b1+1，即．当n≥2时，b n=S n﹣S n﹣1=（﹣b n+1）﹣（﹣b n﹣1+1），即．所以数列{b n}为首项为，公比为的等比数列，即．…6分（2）由（1）知：且，则所以①②．①﹣②得：．所以．…12分点评：本题考查知识点等差、等比数列的通项公式；错位相减法求数列的和，考查分析问题解决问题的能力，20．（14分）已知直线y=﹣2上有一个动点Q，过点Q作直线l1垂直于x轴，动点P在l1上，且满足OP⊥OQ（O为坐标原点），记点P的轨迹为C．（1）求曲线C的方程；（2）若直线l2是曲线C的一条切线，当点（0，2）到直线l2的距离最短时，求直线l2的方程．考点：抛物线的标准方程；直线的一般式方程．专题：计算题．分析：（1）先设P点坐标，进而得出Q点坐标，再根据OP⊥OQ⇒k OP•k OQ=﹣1，求出曲线方程；（2）设出直线直线l2的方程，然后与曲线方程联立，由于直线l2与曲线C相切，得出二次函数有两个相等实根，求出，再由点到直线距离公式表示出d，根据a+b≥2，求得b的值，即可得到直线方程．解答：解：（1）设点P的坐标为（x，y），则点Q的坐标为（x，﹣2）．∵OP⊥OQ，∴k OP•k OQ=﹣1．当x≠0时，得，化简得x2=2y．（2分）当x=0时，P、O、Q三点共线，不符合题意，故x≠0．∴曲线C的方程为x2=2y（x≠0）．（4分）（2）∵直线l2与曲线C相切，∴直线l2的斜率存在．设直线l2的方程为y=kx+b，（5分）由得x2﹣2kx﹣2b=0．∵直线l2与曲线C相切，∴△=4k2+8b=0，即．（6分）点（0，2）到直线l2的距离=（7分）=（8分）（9分）=．（10分）当且仅当，即时，等号成立．此时b=﹣1．（12分）∴直线l2的方程为或．（14分）点评：本题考查了抛物线和直线的方程以及二次函数的根的个数，对于（2）问关键是利用了a+b≥2，求出b的值．属于中档题．21．（14分）已知函数f（x）=x2+2ax+1（a∈R），f′（x）是f（x）的导函数．（1）若x∈，不等式f（x）≤f′（x）恒成立，求a的取值范围；（2）解关于x的方程f（x）=|f′（x）|；（3）设函数，求g（x）在x∈时的最小值．考点：利用导数求闭区间上函数的最值；函数恒成立问题．专题：综合题；导数的综合应用．分析：（1）根据f（x）≤f′（x），可得x2﹣2x+1≤2a（1﹣x），分离参数，确定右边函数的最大值，即可求a的取值范围；（2）由f（x）=|f′（x）|，可得|x+a|=1+a或|x+a|=1﹣a，再分类讨论，即可得到结论；（3）由f（x）﹣f′（x）=（x﹣1），，对a进行分类讨论，即可确定g（x）在x∈时的最小值．解答：解：（1）因为f（x）≤f′（x），所以x2﹣2x+1≤2a（1﹣x），又因为﹣2≤x≤﹣1，所以在x∈时恒成立，因为，所以．（2）因为f（x）=|f′（x）|，所以x2+2ax+1=2|x+a|，所以（x+a）2﹣2|x+a|+1﹣a2=0，则|x+a|=1+a或|x+a|=1﹣a．①当a＜﹣1时，|x+a|=1﹣a，所以x=﹣1或x=1﹣2a；②当﹣1≤a≤1时，|x+a|=1﹣a或|x+a|=1+a，所以x=±1或x=1﹣2a或x=﹣（1+2a）；③当a＞1时，|x+a|=1+a，所以x=1或x=﹣（1+2a）．（3）因为f（x）﹣f′（x）=（x﹣1），①若，则x∈时，f（x）≥f′（x），所以g（x）=f′（x）=2x+2a，从而g（x）的最小值为g（2）=2a+4；②若，则x∈时，f（x）＜f′（x），所以g（x）=f（x）=x2+2ax+1，当时，g（x）的最小值为g（2）=4a+5，当﹣4＜a＜﹣2时，g（x）的最小值为g（﹣a）=1﹣a2，当a≤﹣4时，g（x）的最小值为g（4）=8a+17．③若，则x∈时，当x∈时，g（x）最小值为g（1﹣2a）=2﹣2a．因为，（4a+5）﹣（2﹣2a）=6a+3＜0，所以g（x）最小值为4a+5．综上所述，．点评：本题考查导数知识的运用，考查函数的最值，考查恒成立问题，考查分类讨论的数学思想，正确分类是关键．。

广东省惠州市高三数学第三次调研考试试题文(扫描版)

广东省惠州市2013届高三第三次调研考试数学（文）试题扫描版含答案新人教A版惠州市2013届高三第三次调研考试数学文科数学答案一.选择题（本大题共10小题，每小题5分，共50分）题号 1 2 3 4 5 6 7 8 9 10 答案CDADBBCDAC1. 【解析】i i(1-i)1i 1(i 1)(1)2iz i +===++-，2z =选C2.【解析】0a =时，{}10B x A ===∅⊆，0a ≠时，1B x x A a ⎧⎫==-⊆⎨⎬⎩⎭，111,1a a-=--=，故选0a =或1a =或-1，选D ． 3. 【解析】2239,93,a a a a =⇒==⇔=±故为充分非必要条件，选A 。

4. 【解析】y sinx =，3y x =为奇函数，xy e =为非奇非偶函数，2ln 1y x =+为偶函数，选D5.【解析】26304(23)(46)(23)13x x p q ⨯+=⇒=-⇒+=-+-=-=，，，．故选B ．6.【解析】1232155a a a a ++=⇒=，()()21231380552516a a a a a d d d =⇒=-+⇒-=，132d a ⇒=⇒=，1112131333699105a a a a d ++=+=+=．故选B ．7.【解析】抛线线2410y x =的焦点222(10),10c a b ∴=+=，0．1010e ==． 3,1a b ∴==，2219x y -=．选C8.【解析】m n ，平行α，m n ，可以相交也可以异面，故A 不正确；“墙角”三面互相垂直，说明B 错误；l αβ⋂=，只需//m l ，便有//,//m m αβ，故C 错误；m α⊥，n α⊥则同垂直于一个平面的两条直线平行，D 正确。

9.【解析】由设()f x x α=，图象过点12()2，得121211()()222αα==⇒=， 11244441log (2)log 2log 44f ===．故选A ． d210. 【解析】点P 是单位圆上的动点，点P 所转过的角度设为α，则α=l ，当2πα=，弦AP 的长度21d => ，由选项的图可知，选C 。

惠州市2015届高三第二次调研考试数学(文科)试题及参考答案

惠州市2015届高三第二次调研考试数学试题 (文科） 2014.10本试卷共4页，21小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

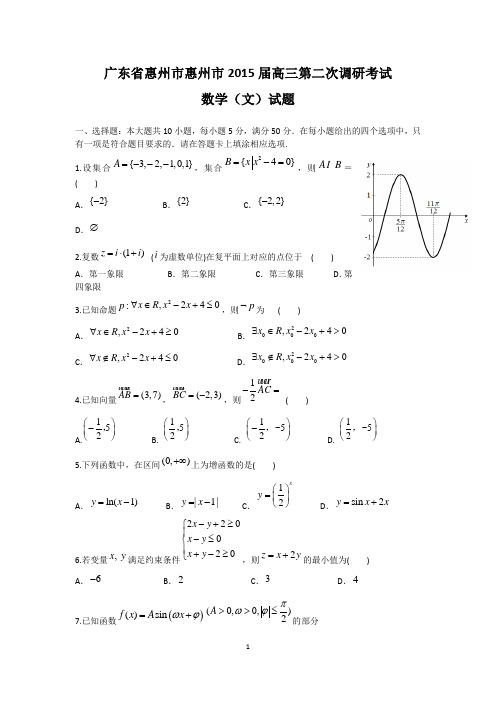
4．考生必须保持答题卡的整洁．考试结束后，将答题卡一并交回．参考公式：锥体的体积公式13V Sh =，其中S 为锥体的底面积，h 为锥体的高. 一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.1.设集合{3,2,1,0,1}A =---，集合2{40}B x x =-=，则AB ＝ ( )A ．{2}-B ．{2}C ．{2,2}-D ．∅2.复数(1)z i i =⋅+ (i 为虚数单位)在复平面上对应的点位于 ( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限3.已知命题:p 2,240x R x x ∀∈-+≤，则¬p 为 ( )A ．2,240x R x x ∀∈-+≥B ．2000,240x R x x ∃∈-+> C ．2,240x R x x ∀∉-+≤ D ．2000,240x R x x ∃∉-+> 4.已知向量(3,7)AB =，(2,3)BC =-，则12AC -= ( ) A.152⎛⎫- ⎪⎝⎭， B. 152⎛⎫ ⎪⎝⎭， C. 152⎛⎫- ⎪⎝⎭，- D. 152⎛⎫ ⎪⎝⎭，- 5.下列函数中，在区间(0,)+∞上为增函数的是( )A ．ln(1)y x =-B ．|1|y x =-C ．12xy ⎛⎫= ⎪⎝⎭D ．sin 2y x x =+6.若变量,x y 满足约束条件220020x y x y x y -+≥⎧⎪-≤⎨⎪+-≥⎩，则2z x y =+的最小值为( )A ．6-B ．2C ．3D ．4 7.已知函数()()sin f x A x ωϕ=+(0,0,)2A πωϕ>>≤的部分图象如图所示,则函数()y f x =的表达式是( ) A.()2sin(2)3f x x π=- B. ()2sin(2)3f x x π=+C.2()2sin(2)3f x x π=+D. ()2sin()12f x x π=+8.方程20([0,1])x x n n ++=∈有实根的概率为（） A ．12 B ．13 C ．14 D ．349.圆心在(1,2)-，半径为x 轴上截得的弦长等于 ( )A． B ．6 C． D ．810.某学校要召开学生代表大会，规定各班每10人推选一名代表，当各班人数除以10的余数大于6时再增选一名代表．那么，各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数[]y x = ([]x 表示不大于x 的最大整数）可以表示为 ( ) A ．[]10x y = B ．3[]10x y += C ．4[]10x y += D ．5[]10x y += 二、填空题：（本大题共5小题，分为必做题和选做题两部分．每小题5分，满分20分）（一）必做题：第11至13题为必做题，每道试题考生都必须作答． 11.抛物线240x y +=的准线方程是 .12.在等比数列{}n a 中，54a =，78a =，则9a = _________. 13.在△ABC 中，3A π∠=，3BC =，AB =，则C ∠=_________.（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答的，只计前一题的得分。

广东省惠州市2015届高三第一次调研考试数学文试题 Wor

广东省惠州市2015届高三第一次调研考试数学试题(文科）【试卷综评】本试卷特点（1）注重基础知识，基本技能的考查，符合新课程标准和命题的意图及宗旨。

考查的都是基本概念和基本方法，关注学生基本能力的考查的同时，仍然紧扣双基。

总体感觉试题对学生双基的考查既全面又突出重点，对教师的教和学生的学检测到位，同时对后续的教与学又起到了良好的导向和激励。

（2）注重能力考查，更注重数学思想的考查。

试卷对数学思想和数学能力的考查较为突出。

（3）在考查基本知识、基本技能的条件下，适当兼顾了对学生综合能力的考查。

一、选择题（本大题共10小题，每小题5分，满分50分.每小题给出的四个选项中，只有一项是符合题目要求.）1．复数1iZ i =+（其中i 为虚数单位）的虚部是（） A.12-B.12iC.12D.12i -【知识点】虚数的概念;虚数除法的运算法则.【答案解析】C 解析：解：化简得iz 2121+=，则虚部为21，故选C .【思路点拨】分式上下同时乘以分子的共轭复数再化简整理即可. 2．已知集合(){}lg 3A x y x ==+，{}2B x x =≥，则AB =（）A. (3,2]-B.(3,)-+∞C.[2,)+∞D.[3,)-+∞ 【知识点】对数不等式的解法；交集的概念. 【答案解析】C 解析：解： (){}{}lg 33A x y x x x ==+=>-，{}2B x x =≥，所以[2,)AB =+∞,故选C.【思路点拨】先通过解对数不等式求出集合A ，再求交集即可. 3．下列函数在定义域内为奇函数的是（）A.1y x x =+B. sin y x x =C. 1y x =-D. cos y x =【知识点】奇函数的定义.奇偶性的判断方法.【答案解析】 A 解析：解：根据奇函数的定义可知：11(),()(),f x x f x x f x x x =+-=-+=--故选A.【思路点拨】利用奇偶性的判断方法直接判断即可得出结论.4.命题“21,11x x <<<若则-”的逆否命题是（） A.21,1,1x x x ≥≥≤-若则或 B.若11<<-x ，则12<xC.若1x >或1x <-，则12>xD.若1x ≥或1x ≤-，则12≥x 【知识点】四种命题；逆否命题.【答案解析】D 解析：解：由逆否命题的变换可知，命题“若12<x ，则11<<-x ” 的逆否命题是“若1x ≥或1x ≤-，则12≥x ”，故选D. 【思路点拨】根据逆否命题的变换可得选项. 5．若向量(1,2),BA =(4,5),CA =则BC =A.(5,7)B.(3,3)--C.(3,3)D.(5,7)-- 【知识点】相反向量；向量的四则运算. 【答案解析】B解析：解：因为(4,5CA =(4,5AC =--,所以()3,3BC BA AC =+=--，故选B.【思路点拨】由相反向量的定义得(4,5)AC =--，再结合向量的加法运算即可.6．若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法计算，得数据如下：那么方程32220x x x +--=的一个最接近的近似根为（）A ．1.2B ．1.3C ．1.4D ．1.5 【知识点】零点的判断方法. 【答案解析】C 解析：解：因为()1.40625 0.0540f =<－，()1.4375 0.1620f =>，由零点存在定理知，最接近的近似根为1.4. 【思路点拨】由表格找出最大的零点区间即可．7．执行如图所示的程序框图,若输入n 的值为7,则输出的s 的值为（） A ．22 B ．16 C ．15 D ．11（7题）（8题）【知识点】循环结构的程序框图.【答案解析】B 解析：解：程序执行过程中，,i s 的值依次为1,1i s ==；1,2s i ==；11,3s i =+=； 112,4s i =++=； 1123,5s i =+++=； 11234,6s i =++++=；112345,7s i =+++++=，输出s 的值为16.【典型总结】依次取i,s 的值，可知当i=7时可得结果.8．函数())(,0,)2f x x x R πωϕωϕ=+∈><的部分图象如图所示，则,ωϕ的值分别是（）A ．2,3π-B.2,6π-C.4,6π-D.4,3π【知识点】函数y=Asin （ωx+φ）的图象变换．【答案解析】A 解析：解：由图知()f x在5π12x =且最小正周期T 满足35ππ+.4123T =故A 32π3π,2,4ωω⨯==5π)12θ⨯+=，5πsin()1,6θ+=5πππ2π,2π,623k k k θθ+=+=-∈Z .所以π()(2).3x f x -=或由5(π)12f =π()(2).3x f x -= 【典型总结】根据图象的两个点A 、B 的横坐标，得到四分之三个周期的值，得到周期的值，做出ω的值，把图象所过的一个点的坐标代入方程做出初相，写出解析式，代入数值得到结果．9．若双曲线22221x y a b -=）A.2±B. C.12±D.2±【知识点】双曲线的离心率的概念；渐近线方程.【答案解析】B 解析：解：双曲线的离心率c e a a ====，所以b a =by x a =±，其斜率为 B.【典型总结】先由双曲线的离心率转化出ba =，然后去求渐进线的斜率即可.10．已知函数222,0()()()2(1),2,0x x x f x f a f a f x x x ⎧+≥⎪=-+≤⎨-<⎪⎩,若则实数a 的取值范围是A.[)1,0- B.[]0,1 C.[]1,1- D.[]2,2-【知识点】函数的奇偶性；函数的单调性；绝对值不等式的解法.【答案解析】C 解析：解：由偶函数定义可得()f x 是偶函数，故()()f a f a -=，原不等式等价于()(1)f a f ≤，又根据偶函数定义，()()f a f a =(1)f ≤，函数()f x 在(0,)+∞单调递增，1a ≤，[1,1]a ∈-．或利用图象求a 范围．选C.【思路点拨】由函数()f x 是偶函数可得()||1f a £,进而解1a ≤即可.二、填空题：（本大题共5小题，考生作答4小题，每小题5分，满分20分.）（一）必做题（11～13题） 11. 计算33log 18log 2-= ．【知识点】对数的运算性质．【答案解析】2 解析：解：333318log 18log 2log log 922-===【思路点拨】利用对数的换底公式和运算法则直接求解．12．变量x、y满足线性约束条件2222x yx yxy+≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩，则目标函数z x y=+的最大值为.【知识点】简单的线性规划.【答案解析】43解析：解：作出不等式组2222x yx yxy+≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩所表示的可行域如图所示，联立2222x yx y+=⎧⎨+=⎩得22,33A⎛⎫⎪⎝⎭，作直线:l z x y=+，则z为直线l在x轴上的截距，当直线l经过可行域上的点A时，直线l在x轴上的截距最大，此时z取最大值，即max 224 333z=+=.【思路点拨】先根据约束条件画出可行域，再利用几何意义求最值，只需求出直线z=x+y过点22,33A⎛⎫⎪⎝⎭时，z最大值即可．13．若某几何体的三视图如图所示，则此几何体的体积等于【知识点】由三视图求体积．【答案解析】24 解析：解：由三视图可知，原几何体是一个三棱柱被截去了一小三棱锥得到的，如图111345(34)324 232V=⨯⨯⨯-⨯⨯⨯=【思路点拨】先根据三视图判断几何体的形状，再利用体积公式计算即可．（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答的，只计前一题的得分。

广东省惠州市2015届高三第二次调研考试数学(文)试题及解析

广东省惠州市惠州市2015届高三第二次调研考试数学（文）试题一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.1.设集合{3,2,1,0,1}A=---，集合2{40}B x x=-=，则A B＝( )A．{2}-B．{2}C．{2,2}-D．∅2.复数(1)z i i=⋅+(i为虚数单位)在复平面上对应的点位于( )A．第一象限B．第二象限C．第三象限D．第四象限3.已知命题:p2,240x R x x∀∈-+≤，则¬p为( )A．2,240x R x x∀∈-+≥B．2000,240x R x x∃∈-+>C．2,240x R x x∀∉-+≤D．2000,240x R x x∃∉-+>4.已知向量(3,7)AB =，(2,3)BC=-，则12AC-=( )A.152⎛⎫-⎪⎝⎭，B.152⎛⎫⎪⎝⎭，C.152⎛⎫-⎪⎝⎭，-D.152⎛⎫⎪⎝⎭，-5.下列函数中，在区间(0,)+∞上为增函数的是( )A．ln(1)y x=-B．|1|y x=-C．12xy⎛⎫= ⎪⎝⎭D．sin2y x x=+6.若变量,x y满足约束条件22020x yx yx y-+≥⎧⎪-≤⎨⎪+-≥⎩，则2z x y=+的最小值为( )A．6-B．2C．3D．47.已知函数()()sinf x A xωϕ=+(0,0,)2Aπωϕ>>≤的部分图象如图所示,则函数()y f x =的表达式是( )A.()2sin(2)3f x x π=-B. ()2sin(2)3f x x π=+C.2()2sin(2)3f x x π=+D. ()2sin()12f x x π=+8.方程20([0,1])x x n n ++=∈有实根的概率为（）A ．12B ．13C ．14D ．349.圆心在(1,2)-，半径为x 轴上截得的弦长等于 ( ) A． B ．6 C． D ．810.某学校要召开学生代表大会，规定各班每10人推选一名代表，当各班人数除以10的余数大于6时再增选一名代表．那么，各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数[]y x = ([]x 表示不大于x 的最大整数）可以表示为 ( )A ．[]10x y =B ．3[]10x y +=C ．4[]10x y +=D ．5[]10x y +=二、填空题：（本大题共5小题，分为必做题和选做题两部分．每小题5分，满分20分）（一）必做题：第11至13题为必做题，每道试题考生都必须作答．11.抛物线240x y +=的准线方程是 .12.在等比数列{}n a 中，54a =，78a =，则9a = _________.13.在△ABC 中，3A π∠=，3BC =，AB =，则C ∠=_________.（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答的，只计前一题的得分。

广东省惠州市2015届高三第二次调研考试-数学文-Word版含答案

广东省惠州市2015届高三第二次调研考试-数学文-Word版含答案惠州市2015届高三第二次调研考试数学试题 (文科） 2014.10本试卷共4页，21小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡的整洁．考试结束后，将答题卡一并交回．参考公式：锥体的体积公式13V Sh ，其中S 为锥体的底面积，h 为锥体的高.一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.1.设集合{3,2,1,0,1}A =---，集合2{40}B x x =-=，则A B I ＝( )A ．{2}-B ．{2}C ．{2,2}-D ．∅2.复数(1)z i i =⋅+ (i 为虚数单位)在复平面上对应的点位于 ( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3.已知命题:p 2,240x R xx ∀∈-+≤，则¬p 为 ( )A ．2,240x R x x ∀∈-+≥B ．200,240x R xx ∃∈-+>C ．2,240x R x x ∀∉-+≤D ．200,240x R xx ∃∉-+> 4.已知向量(3,7)AB =u u u r，(2,3)BC =-u u u r，则12AC -=u u u r ( )A.152⎛⎫- ⎪⎝⎭， B. 152⎛⎫⎪⎝⎭， C. 152⎛⎫- ⎪⎝⎭，-D.152⎛⎫ ⎪⎝⎭，-5.下列函数中，在区间(0,)+∞上为增函数的是( )A ．ln(1)y x =-B ．|1|y x =-C ．12xy ⎛⎫= ⎪⎝⎭D ．sin 2y x x =+6.若变量,x y 满足约束条件220020x y x y x y -+≥⎧⎪-≤⎨⎪+-≥⎩，则2z x y =+的最小值为( )A ．6- B ．2C ．3D ．47.已知函数()()sin f x A x ωϕ=+(0,0,)2A πωϕ>>≤的部分图象如图所示,则函数()y f x =的表达式是( )A.()2sin(2)3f x x π=- B. ()2sin(2)3f x x π=+ C.2()2sin(2)3f x x π=+ D.()2sin()12f x x π=+8.方程20([0,1])xx n n ++=∈有实根的概率为（）A ．12B ．13C ．14D ．349.圆心在(1,2)-，半径为25x 轴上截得的弦长等于 ( )A ．3B ．6C ．62 D ．810.某学校要召开学生代表大会，规定各班每10人推选一名代表，恒谦网当各班人数除以10的余数大于6时再增选一名代表．那么，各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数[]y x = ([]x 表示不大于x 的最大整数）可以表示为 ( )A ．[]10x y =B ．3[]10x y +=C ．4[]10x y += D ．5[]10x y +=二、填空题：（本大题共5小题，分为必做题和选做题两部分．每小题5分，满分20分）（一）必做题：第11至13题为必做题，每道试题考生都必须作答．11.抛物线240x y +=的准线方程是 .12.在等比数列{}na 中，54a=，78a=，则9a = _________.13.在△ABC 中，3A π∠=，3BC =，AB =，则C ∠=_________.（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答的，只计前一题的得分。

广东省惠州市2015届高三第三次调研

2015届惠州市高三第三次调研考试一、单选题13. 如图所示，物体m 与斜面体M 一起静止在水平面上，若将斜面的倾角θ减小一些，下列说法正确的是 A. 斜面体对物体的支持力减小 B ．斜面体对物体的摩擦力减小C ．水平面对斜面体的支持力减小D ．水平面对斜面体的摩擦力减小14．一个物体沿直线运动，从0=t 时刻开始，物体的t v -的图像如图所示，图线与纵横坐标轴的交点分别为s m /5.0和s 1-，由此可知A. 物体做匀速直线运动B. 物体做变加速直线运动C. 物体的初速度大小为s m /5.0D. 物体的初速度大小为s m /115. 阻值不计的矩形线圈在匀强磁场中，绕垂直于磁感线的轴匀速转动，线圈两端的电压随时间的变化规律如图所示．则下列说法中正确的是A ．线圈两端电压的平均值为V 10B．电压表连接在线圈两端时，其示数为V 20C ．在s 01.0时，线圈平面与磁场垂直D ．当接外电路时，线圈内的电流方向s 1内改变50次16. 质量为m 的通电细杆置于倾角为θ的光滑导轨上,导轨的宽度为d ,有垂直于纸面向里的电流I 通过细杆, 在如图所示的A 、B 、C 、D 四个图中,能使细杆沿导轨向上运动的最小磁感应强度是二、双选题17. 北斗卫星系统由地球同步轨道卫星与低轨道卫星两种卫星组成，这两种卫星正常运行时A. 低轨卫星和地球同步卫星的轨道平面一定重合B. 低轨卫星的环绕速率不可能大于s km /9.7C. 地球同步卫星比低轨卫星的转动周期大D. 低轨卫星和地球同步卫星，可能具有相同的角速度18. 竖直悬挂的轻弹簧下连接一个小球，用手托起小球，使弹簧处于压缩状态，如图所示．则迅速放手后A ．小球开始向下做匀加速运动B ．弹簧恢复原长时小球速度达到最大C ．弹簧恢复原长时小球加速度等于gD ．小球运动过程中最大加速度大于gm MθθθθθA B C D2020-st /V U /001.002.019. 如图是密立根油滴实验的示意图.油滴从喷雾器的喷嘴喷出，落到图中的匀强电场中，调节两板间的电压，通过显微镜观察到某一油滴静止在电场中.下列说法正确的是A ．油滴带正电B ．油滴带负电C ．只要测出两板间的距离和电压就能求出油滴的电量D ．该实验测得油滴所带电荷量等于元电荷的整数倍 20．闭合回路由电阻R 与导线组成,其内部磁场大小按t B -图变化,方向如图所示,则回路中A. 电流方向为顺时针方向B. 电流强度越来越大C. 磁通量的变化率恒定不变D. 产生的感应电动势越来越大21.光滑水平面上静止的物体，受到一个水平拉力F 作用开始运动，拉力随时间变化如图所示，用K E 、v 、x ∆、P 分别表示物体的动能、速度、位移和水平拉力的功率，下列四个图像中分别定性描述了这些物理量随时间变化的情况，正确的是三、非选择题34.（18分）（1）（8分）某实验小组利用电磁打点计时器和如图的其他器材开展多项实验探究，选择了一条符合实验要求的纸带，数据如图（相邻计数点的时间为T ）,回答下列问题：① 按装置安装器材时，纸带应穿过电磁打点计时器的限位孔从复写纸的 (填“上”或“下”)表面通过.第19题图第34（1）题图② 若是探究重力做功和物体动能的变化的关系.需求出重锤运动到各计数点的瞬时速度，试写出在E 点时重锤运动的瞬时速度=E v （用题中字母表示）. ③ 若是测量重力加速度g . 为减少实验的偶然误差，采用逐差法处理数据，则加速度大小可以表示为=g （用题中字母表示）. ④ 如果研究重锤在AE 运动过程中机械能守恒时，重锤增加的动能总是小于减小的重力势能,造成实验误差的主要原因是 (只写一条).（2）（10分）某实验小组要精确测定额定电压为V 3的LED 灯正常工作时的电阻，已知该灯正常工作时电阻大约Ω100，电学符号与小灯泡电学符号相同.现有的器材规格如下：A ．待测LED 灯X RB ．直流毫安表1A （量程mA 10~0，内阻约为Ω100）C ．直流毫安表2A （量程mA 40~0，内阻约为Ω40）D ．直流电压表1V （量程V 3~0，内阻约为Ωk 5）E ．直流电压表2V （量程V 15~0，内阻约为Ωk 15）F ．直流电源（输出电压V 5.4，内阻很小）G ．滑动变阻器1R 1（阻值范围Ω50~0，允许最大电流A 1） H ．滑动变阻器2R （阻值范围Ωk 10~0，允许最大电流A 1） I ．开关一个、导线若干① 为了尽可能精确测定LED 灯正常工作时的电阻，所选电流表为___（填“1A ”或“2A ”），所选电压表为____（填“1V ”或“2V ”）；滑动变阻器应选（填“1R ”或“2R ”）② 请根据实验原理图甲，完成图乙未完成的实物连接；③ 闭合开关S 后，某次测量时电压表的示数如丙所示，该示数为_________V . 甲ErsR x R V丙35.（18分）如图所示，光滑的水平导轨MN 右端N 处与水平传送带理想连接，传送带长度L=0.8m ，皮带以恒定速率v=3.0m/s 向右匀速运动。

广东省惠州市高三数学第三次调研考试题文(扫描版)新人教A版

惠州市2014届高三第三次调研考试试题数学（文科）答案一、选择题题号1 2 3 4 5 6 7 8 9 10 答案B A B B DC A CD A【解析】 1.{35}A B x x =<<I ，选B.2. ∵1(2)a i +-是实数，∴2a =,则212a i i i i i++==-，选A. 3. ∵a r ∥b r ，∴22(4)10x ⨯--⨯=，解得1x =-，选B.4. 当1sin 2x =时，2,6x k k Z ππ=+∈，或52,6x k k Z ππ=+∈,故不是充分条件；反之成立，选B.5.由圆心(,0)a =1a =±,故选D.6.抽样比为150********=，则从高二年级学生中应抽取330910⨯=人，选C. 7. 252816a a a =⋅=，又0n a >，故54a =，选A.8. (12345)520S =+++++=，故选C.9. 222123922221239123410100a a a a -⋅⋅⋅⋅=⨯⨯⨯⨯=----……，故选D. 10．可知函数0)x 1x ln()x ()x 1x ln(x )x (f )x (f 2323=++--+-+-=-+，所以函数为奇函数,同时，3()f x x =-=)1ln(23x x x +++，是增函数，注意到)b (a )b (f )a (f b a )b (f )a (f ----=++，所以0ba )b (f )a (f >++，选A. 二、填空题11. 2 12.413.10 15. 32 【解析】11.设此正三棱柱的高为h ，则其主视图面积为ah ，所以2h a =，左视图是边长分别为2a ，h的矩形，所以面积为22ah =. 12. 由正弦定理，sin sin a c A C =，解得sin A = 13.不等式组表示的可行域如图所示，直线2y x z =-+过直线1x y -=-和直线22x y -=交点(3,4)时， z 有最大值10.14. 曲线C 的直角坐标方程为x y +=224，直线l 的直角坐标方程为10x y +-=，圆心到直线的距离为d =，故弦长AB ==15.设圆O 的半径为r ，由222AO AE OE =+得22(1)r r +=+，解得1OE OD OB r ====；依题意知Rt ABC Rt AOE ∆:V , 故BC AB OE AO=，解得32BC =. 三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16.解：（1）∵函数()sin()6f x x πω=+的周期是π且0ω>T ππω∴==2，解得2ω= … ……………………………………………………2分 ∴()sin(2)6f x x π=+…………………………3分∴()sin(2)sin 1212632f ππππ=⨯+==………………………………………5分（2）()()()sin[2()]sin[2()]61266126g x f x f x x x ππππππ=++-=+++-+……………6分sin(2)sin 2cos2sin 2)24x x x x x ππ=++=++…………………8分当22,42x k k z πππ+=+∈即8x k ππ=+时， ()g x…………………10分此时x 的集合为{,}8x x k k Z ππ=+∈……………………………………12分ED CB A O17.解：（1）……………………3分（2）由表可知：用分层抽样的方法从甲班抽取的人数为86=412⨯人，……………4分从乙班抽取的人数为46=212⨯人……………………………………………5分（3）设从甲班抽取的人为d c b a ,,,，从乙班抽取的人为1，2；“抽到的两个人恰好都来自甲班”为事件A .………………………………………6分所得基本事件共有15种，即：12,2,1,2,1,,2,1,,,2,1,,,d d c c cd b b bd bc a a ad ac ab ……………………………8分其中事件A 包含基本事件,,,,,ab ac ad bc bd cd ，共6种，……………………10分由古典概型可得62()155P A == ……………………………………………………12分 18.解：（1）连接ED EF 、， ∵ABCD 是正方形，E 是AC 的中点， ∴ED AC ⊥……………………………………1分又∵E F 、分别是AC PC 、的中点∴ EF ∥PA ……………………………………2分又∵PA ABCD ⊥平面， ∴EF ABCD ⊥平面，……3分∵AC ABCD ⊂平面, ∴EF AC ⊥…………………4分又∵ED EF=E I ∴AC DEF ⊥平面…………5分又∵DF DEF ⊂平面故AC DF ⊥…………………………………………………7分（2）∵PA ABCD ⊥平面，∴是PA 三棱锥P CED -的高，2PA =∵ABCD 是正方形，E 是AC 的中点，∴CED V 是等腰直角三角形………9分 1AB =，故CE ED ==,111224CED S CE ED =⋅==V ………………………12分故111123346C PED P CED CED V V S PA --==⋅⋅=⋅⋅=V ………………………14分19.解：（1）∵n n a S -=12 1n ∴=时，a a S a -==∴=11111123………………………1分 2n ≥时，n n a S -=12，n n a S ---=1112………………………2分两式相减得：n n n n n a a a s s ----=-=-111122，n n a a -∴=113，………3分 {}n a ∴是以a =113为首项，13为公比的等比数列 n n a ∴=13……………………4分 ∴1(27)(27)3n n nb n a n =-=-………………………………………5分 (2) 23531273333n nn T ----=+++……+……① 234115312733333n n n T +----=+++……+②………………………………7分 ①-②得：234125111272(333333n n n T +-=-++++n 1……+)-3……………8分 111(1)5227332133313n n n +--=--+⨯-- 142433n n +-=-- …………9分 223n nn T -∴=--…………………10分 11112252(2)333n n n n n n n n T T +++----=-----=Q ………………11分 ∴当2n ≤时，12503n n +-<，1n n T T +<，即321T T T << 当3n ≥时，1n n T T +>,此时3n T T >， ∴35527n T T ≥=-………………………………12分又当3n ≥时，203nn ->，此时2n T <- 而21523T T -=<=-，∴153n T T ≤=-………………………13分∴555273n T -≤≤-………………………………………14分 20．（1）解：依题意设抛物线C 的方程为：22y px =，…………………1分∵点E 在抛物线上，∴222p =⨯解得2p =，． ………………………………3分∴抛物线C 的方程为24y x =． ………………………4分（2）证明：由（1）知 (1,0)F ，则可设直线AB 的方程为：1x ky =+………………5分由214x ky y x=+⎧⎨=⎩消去y 得：2440y y --=则22(4)41(4)16160k k =-⨯⨯-=+>V 设1122(,),(,)A x y B x y ，则12124,4y y k y y +==-………………………7分1212AOB S OF y y =⋅-==V 9分 ∵点M 在线段AB 上运动，原点O 关于点M 的对称点为D ∴AOB ADB S S =V V ………………………11分故2AOB S S ==V 四边形OADB ∴当0k =时，有S 四边形OADB 最小值4………………………13分∴四边形OADB 的面积的最小值为4. ………………………14分21.解：（1）()ln f x x x =的定义域为(0,)+∞………………………………………………1分()1f x lnx '=+，…………………………………………2分（2）由2()2f x x ax ≤-+得：22xlnx x ax ≤-+，当x ∈(0,2)时，g x '<()0,g x ()单调递减；当x ∈+∞(2,)时，g x '>()0,g x ()单调递增；[()](2)3ln 2min g x g ∴==-………………………………………………7分当x ∈(0,1)时，h x '>()0,h x ()单调递增；当x ∈+∞(1,)时，h x '<()0,h x ()单调递减；分 ∴对一切(0,)x ∈+∞，()()f x h x >，即12ln 0x x e ex-+> ∴函数12ln x y x e ex=-+没有零点。

广东省惠州市高三数学第三次调研试卷文(含解析)

广东省惠州市2015届高三第三次调研数学试卷（文科）一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.1．（5分）若集合A={0，1，2，3}，B={1，2，4}，则集合A∪B=（）A．{0，1，2，3，4} B．{1，2，3，4} C．{1，2} D．{0}2．（5分）已知0＜a＜2，复数z=a+i（i是虚数单位），则|z|的取值范围是（）A．B．（1，5）C．（1，3）D．3．（5分）函数f（x）=+ln（x+1）的定义域为（）A．（2，+∞）B．（﹣1，2）∪（2，+∞）C．（﹣1，2）D．（﹣1，2]4．（5分）等差数列{a n}的前n项和为S n，且S3=6，a1=4，则公差d等于（）A．1 B．C．﹣2 D．35．（5分）已知a∈R，则“a2＜2a”是“a＜2”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件6．（5分）圆（x+2）2+y2=4与圆（x﹣2）2+（y﹣1）2=9的位置关系为（）A．内切B．相交C．外切D．相离7．（5分）下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行8．（5分）设变量x，y满足约束条件，则的最大值为（）A．3 B．6 C．D．19．（5分）如图是某个四面体的三视图，该四面体的体积为（）A．72 B．36 C．24 D．1210．（5分）已知函数f（x﹣1）是定义在R上的奇函数，若对于任意两个实数x1≠x2，不等式恒成立，则不等式f（x+3）＜0的解集为（）A．（﹣∞，﹣3）B．（4，+∞）C．（﹣∞，1）D．（﹣∞，﹣4）二、填空题：（本大题共3小题，分为必做题和选做题两部分．每小题5分，满分15分）（一）必做题：第11至13题为必做题，每道试题考生都必须作答．11．（5分）已知向量，且，则x=．12．（5分）在△ABC中，内角A，B，C对边的边长分别是a，b，c，若a=15，b=10，A=，则cosB=．13．（5分）A，B，C是平面内不共线的三点，点P在该平面内且有，现将一粒黄豆随机撒在△ABC内，则这粒黄豆落在△PBC内的概率为．（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答，按第一题记分【坐标系与参数方程选做题】（共1小题，满分5分）14．（5分）在极坐标系中，直线，被圆ρ=4截得的弦长为．【几何证明选做题】15．如图，已知△ABC内接于圆O，点D在OC的延长线上，AD切圆O于A，若∠ABC=30°，AC=2，则AD的长为．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（12分）已知向量=（cosx+sinx，2sinx），=（cosx﹣sinx，﹣cosx），f（x）=•，（1）求f（x）的最小正周期；（2）当x∈时，求f（x）的最小值以及取得最小值时x的值．17．（12分）惠州市某县区共有甲、乙、丙三所高中的2015届高三文科学生共有800人，各学校男、女生人数如表：甲高中乙高中丙高中女生153 x y男生97 90 z已知在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2．（1）求表中x的值；（2）惠州市第三次调研考试后，该县区决定从三所高中的所有2015届高三文科学生中利用随机数表法抽取100人进行成绩统计分析，先将800人按001，002，…，800进行编号．如果从第8行第7列的数开始向右读，请你依次写出最先检测的3个人的编号；（下面摘取了随机数表中第7行至第9行）8442 1753 3157 2455 0688 7704 7447 6721 7633 5026 83926301 5316 5916 9275 3862 9821 5071 7512 8673 5807 44391326 3321 1342 7864 1607 8252 0744 3815 0324 4299 7931（3）已知y≥145，z≥145，求丙高中学校中的女生比男生人数多的概率．18．（14分）如图，在直三棱柱A1B1C1﹣ABC中，AB⊥BC，E、F分别是A1B，AC1的中点．（1）求证：EF∥平面ABC；（2）求证：平面AEF⊥平面AA1B1B；（3）若AB=BC=a，A1A=2a，求三棱锥F﹣ABC的体积．19．（14分）已知递增等差数列{a n}中的a2，a5是函数f（x）=x2﹣7x+10的两个零点．数列{b n}满足，点（b n，S n）在直线y=﹣x+1上，其中S n是数列{b n}的前n项和．（1）求数列{a n}和{b n}的通项公式；（2）令c n=a n•b n，求数列{c n}的前n项和T n．20．（14分）已知直线y=﹣2上有一个动点Q，过点Q作直线l1垂直于x轴，动点P在l1上，且满足OP⊥OQ（O为坐标原点），记点P的轨迹为C．（1）求曲线C的方程；（2）若直线l2是曲线C的一条切线，当点（0，2）到直线l2的距离最短时，求直线l2的方程．21．（14分）已知函数f（x）=x2+2ax+1（a∈R），f′（x）是f（x）的导函数．（1）若x∈，不等式f（x）≤f′（x）恒成立，求a的取值范围；（2）解关于x的方程f（x）=|f′（x）|；（3）设函数，求g（x）在x∈时的最小值．广东省惠州市2015届高三第三次调研数学试卷（文科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.1．（5分）若集合A={0，1，2，3}，B={1，2，4}，则集合A∪B=（）A．{0，1，2，3，4} B．{1，2，3，4} C．{1，2} D．{0}考点：并集及其运算．专题：集合．分析：按照并集的定义直接写出A∪B即可．解答：解：∵A={0，1，2，3}，B={1，2，4}，∴A∪B={0，1，2，3，4}故答案为：A点评：本题考查集合的运算，求并集及运算．属于基础题．2．（5分）已知0＜a＜2，复数z=a+i（i是虚数单位），则|z|的取值范围是（）A．B．（1，5）C．（1，3）D．考点：复数求模．专题：数系的扩充和复数．分析：直接由复数模的公式写出|z|=，再由0＜a＜2求得1＜a2+1＜5，则答案可求．解答：解：∵复数z=a+i，则|z|=，由0＜a＜2，得1＜a2+1＜5，∴|z|∈（1，）．故选：D．点评：本题考查了复数模的求法，考查了函数的值域，是基础的计算题．3．（5分）函数f（x）=+ln（x+1）的定义域为（）A．（2，+∞）B．（﹣1，2）∪（2，+∞）C．（﹣1，2）D．（﹣1，2]考点：对数函数的定义域．专题：函数的性质及应用．分析：根据二次根式的性质结合对数函数的性质得到不等式组，解出即可．解答：解：由题意得：，解得：﹣1＜x＜2，故选：C．点评：本题考查了二次根式的性质，考查了对数函数的性质，是一道基础题．4．（5分）等差数列{a n}的前n项和为S n，且S3=6，a1=4，则公差d等于（）A．1 B．C．﹣2 D．3考点：等差数列的性质．专题：计算题．分析：由题意可得 S3=6=（a1+a3），且 a3=a1+2d，a1=4，解方程求得公差d的值．解答：解：∵S3=6=（a1+a3），且 a3=a1+2d，a1=4，∴d=﹣2，故选C．点评：本题考查等差数列的定义和性质，通项公式，前n项和公式的应用，属于基础题．5．（5分）已知a∈R，则“a2＜2a”是“a＜2”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：先解出a2＜2a，再进行判断即可解答：解：因为a2＜2a，所以0＜a＜2，则“a2＜2a”是“a＜2”的充分而不必要条件；故选：A．点评：本题考查了充分必要条件，考查了集合之间的关系，是一道基础题．6．（5分）圆（x+2）2+y2=4与圆（x﹣2）2+（y﹣1）2=9的位置关系为（）A．内切B．相交C．外切D．相离考点：圆与圆的位置关系及其判定．专题：直线与圆．分析：求出两圆的圆心和半径，计算两圆的圆心距，将圆心距和两圆的半径之和或半径之差作对比，判断两圆的位置关系．解答：解：圆（x+2）2+y2=4的圆心C1（﹣2，0），半径r=2．圆（x﹣2）2+（y﹣1）2=9的圆心C2（2，1），半径R=3，两圆的圆心距d==，R+r=5，R﹣r=1，R+r＞d＞R﹣r，所以两圆相交，故选B．点评：本题考查圆与圆的位置关系及其判定的方法，关键是求圆心距和两圆的半径．7．（5分）下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行考点：命题的真假判断与应用；空间中直线与平面之间的位置关系．专题：简易逻辑．分析：利用直线与平面所成的角的定义，可排除A；利用面面平行的位置关系与点到平面的距离关系可排除B；利用线面平行的判定定理和性质定理可判断C正确；利用面面垂直的性质可排除D．解答：解：A、若两条直线和同一个平面所成的角相等，则这两条直线平行、相交或异面，故A错误；B、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行或相交，故B错误；C、设平面α∩β=a，l∥α，l∥β，由线面平行的性质定理，在平面α内存在直线b∥l，在平面β内存在直线c∥l，所以由平行公理知b∥c，从而由线面平行的判定定理可证明b∥β，进而由线面平行的性质定理证明得b∥a，从而l∥a，故C正确；D，若两个平面都垂直于第三个平面，则这两个平面平行或相交，排除D．故选C．点评：本题主要考查了空间线面平行和垂直的位置关系，线面平行的判定和性质，面面垂直的性质和判定，空间想象能力，属基础题．8．（5分）设变量x，y满足约束条件，则的最大值为（）A．3 B．6 C．D．1考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对应的平面区域，利用数形结合即可得到结论．解答：解：作出不等式组对应的平面区域如图：设k=，则k的几何意义为区域内的点P（x，y）到圆点O的斜率，由图象可知，OA的斜率最大，由，解得其中A（1，6），则OA的斜率k=6，故的最大值为6，故选：B点评：本题主要考查线性规划的应用，利用数形结合以及直线的斜率公式是解决本题的关键．9．（5分）如图是某个四面体的三视图，该四面体的体积为（）A．72 B．36 C．24 D．12考点：由三视图求面积、体积．专题：计算题．分析：通过三视图，判断几何体的形状，利用三视图的数据，求解几何体的体积即可．解答：解：由题意可知，几何体是三棱锥，底面三角形的一边长为6，底面三角形的高为：4，棱锥的一条侧棱垂直底面的三角形的一个顶点，棱锥的高为：3．所以几何体的体积：=12．故选D．点评：本题考查三视图视图能力与几何体的判断，几何体的体积的求法，考查计算能力．10．（5分）已知函数f（x﹣1）是定义在R上的奇函数，若对于任意两个实数x1≠x2，不等式恒成立，则不等式f（x+3）＜0的解集为（）A．（﹣∞，﹣3）B．（4，+∞）C．（﹣∞，1）D．（﹣∞，﹣4）考点：函数奇偶性的性质．专题：函数的性质及应用．分析：对于任意两个实数x1≠x2，不等式恒成立，可得函数f（x）在R上单调递增．由函数f（x﹣1）是定义在R上的奇函数，可得f（﹣1）=0，即可解出．解答：解：∵对于任意两个实数x1≠x2，不等式恒成立，∴函数f（x）在R上单调递增．∵函数f（x﹣1）是定义在R上的奇函数，∴f（﹣1）=0，∴不等式f（x+3）＜0=f（﹣1）化为x+3＜﹣1，解得x＜﹣4，∴不等式的解集为：（﹣∞，﹣4）．故选：D．点评：本题考查了抽象函数的奇偶性与单调性，考查了推理能力，属于中档题．二、填空题：（本大题共3小题，分为必做题和选做题两部分．每小题5分，满分15分）（一）必做题：第11至13题为必做题，每道试题考生都必须作答．11．（5分）已知向量，且，则x=0．考点：平面向量的坐标运算；平行向量与共线向量．专题：平面向量及应用．分析：根据题意，得•=0，求出x的值即可．解答：解：∵，且，∴，解得x=0．故答案为：0．点评：本题考查了的知识点是利用平面向量的数量积判断两个平面向量的垂直关系，是基础题．12．（5分）在△ABC中，内角A，B，C对边的边长分别是a，b，c，若a=15，b=10，A=，则cosB=．考点：正弦定理．专题：解三角形．分析：利用正弦定理列出关系式，把a，b，sinA的值代入求出sinB的值，即可求出cosB 的值即可．解答：解：∵△ABC中，a=15，b=10，sinA=，∴由正弦定理=得：sinB===，∵b＜a，∴B＜A，即B为锐角，则cosB==，故答案为：点评：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．13．（5分）A，B，C是平面内不共线的三点，点P在该平面内且有，现将一粒黄豆随机撒在△ABC内，则这粒黄豆落在△PBC内的概率为．考点：几何概型．专题：概率与统计．分析：由P在该平面内且有，得到PB=PA且P在线段AB上，所以△PBC的面积是△ABC的，由几何概型的概率公式可求．解答：解：由P在该平面内且有，得到PB=PA且P在线段AB上，所以△PBC的面积是△ABC的，由几何概型的概率公式这粒黄豆落在△PBC内的概率为；故答案为：．点评：本题给出点P满足的条件，求P点落在△PBC内的概率，着重考查了平面向量共线的充要条件和几何概型等知识，属于基础题．（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答，按第一题记分【坐标系与参数方程选做题】（共1小题，满分5分）14．（5分）在极坐标系中，直线，被圆ρ=4截得的弦长为4．考点：直线的参数方程．专题：坐标系和参数方程．分析：把直线与圆的极坐标方程化为直角坐标方程，再利用弦长公式弦长=2（d 为圆心到直线的距离）即可得出．解答：解：直线，化为=2，∴x+y﹣2=0，圆ρ=4化为x2+y2=16．∴圆心O（0，0）到直线的距离d==2．∴直线被圆截得的弦长=2==4．故答案为：4．点评：本题考查了把极坐标方程化为直角坐标方程、弦长公式、点到直线的距离公式，考查了计算能力，属于基础题．【几何证明选做题】15．如图，已知△ABC内接于圆O，点D在OC的延长线上，AD切圆O于A，若∠ABC=30°，AC=2，则AD的长为．考点：与圆有关的比例线段．专题：直线与圆．分析：作CE⊥AD于点E，由已知结合三角形中角的关系得到AE的长度，再由AD=2AE得答案．解答：解：如图，作CE⊥AD于点E，∵∠ABC=30°，∴∠CDA=30°，则∠COA=60°，∴△AOC为正三角形，∴∠CAO=60°，AC=OC，∴∠CAE=30°，AC=CD，又∵CE⊥AD，∴AE=，则AD=2AE=．故答案为：．点评：本题考查了与圆有关的比例线段，考查了直角三角形的解法，是中档题．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（12分）已知向量=（cosx+sinx，2sinx），=（cosx﹣sinx，﹣cosx），f（x）=•，（1）求f（x）的最小正周期；（2）当x∈时，求f（x）的最小值以及取得最小值时x的值．考点：三角函数中的恒等变换应用；平面向量数量积的运算．专题：三角函数的图像与性质．分析：（1）先求得f（x）=cos（2x+），根据周期公式可得f（x）的最小正周期；（2）先求得2x+∈，由函数的单调性质可得当2x+=π即x=时，取到f（x）的最小值﹣．解答：解：f（x）=•=（cosx+sinx）（cosx﹣sinx）+2sinx（﹣cosx）=cos2x﹣sin2x﹣2sinxcosx=cos2x﹣sin2x=cos（2x+）（1）T==π（2）x∈时，2x+∈∴当2x+=π即x=时，取到f（x）的最小值﹣．点评：本题主要考察了三角函数中的恒等变换应用，平面向量数量积的运算，三角函数的图象与性质，属于基础题．17．（12分）惠州市某县区共有甲、乙、丙三所高中的2015届高三文科学生共有800人，各学校男、女生人数如表：甲高中乙高中丙高中女生153 x y男生97 90 z已知在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2．（1）求表中x的值；（2）惠州市第三次调研考试后，该县区决定从三所高中的所有2015届高三文科学生中利用随机数表法抽取100人进行成绩统计分析，先将800人按001，002，…，800进行编号．如果从第8行第7列的数开始向右读，请你依次写出最先检测的3个人的编号；（下面摘取了随机数表中第7行至第9行）8442 1753 3157 2455 0688 7704 7447 6721 7633 5026 83926301 5316 5916 9275 3862 9821 5071 7512 8673 5807 44391326 3321 1342 7864 1607 8252 0744 3815 0324 4299 7931（3）已知y≥145，z≥145，求丙高中学校中的女生比男生人数多的概率．考点：概率的应用．专题：综合题；概率与统计．分析：（1）利用在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2，求出表中x的值；（2）根据从第8行第7列的数开始向右读，即可写出最先检测的3个人的编号；（3）y+z=800﹣153﹣97﹣160﹣90=300，y≥145，z≥145，图象为线段y+z=300（145≤y≤155），即可求丙高中学校中的女生比男生人数多的概率．解答：解：（1）∵在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2，∴x=800×0.2=160；（2）从第8行第7列的数开始向右读，最先检测的3个人的编号为165、538、629；（3）y+z=800﹣153﹣97﹣160﹣90=300，y≥145，z≥145，图象为线段y+z=300（145≤y≤155）∵丙高中学校中的女生比男生人数多，∴y＞z，∴丙高中学校中的女生比男生人数多的概率为．点评：本题考查概率的应用，考查学生分析解决问题的能力，正确计算是关键．18．（14分）如图，在直三棱柱A1B1C1﹣ABC中，AB⊥BC，E、F分别是A1B，AC1的中点．（1）求证：EF∥平面ABC；（2）求证：平面AEF⊥平面AA1B1B；（3）若AB=BC=a，A1A=2a，求三棱锥F﹣ABC的体积．考点：平面与平面垂直的判定；直线与平面平行的判定．专题：证明题；空间位置关系与距离．分析：（1）连结A1C，可证EF是△A1BC的中位线，即EF∥BC，从而可证EF∥平面ABC．（2）易知BC⊥B1B，又由BC⊥BA，即BC垂直平面ABB1A1，又EF∥BC，即EF⊥平面ABB1A1，即可证明平面AEF⊥平面AA1B1B，（3）由直三棱柱可知V三棱锥F﹣ABC=S△ABC×h=S△ABC××CC1，代入即可求值．解答：证明：（1）连结A1C，由A1C1CA 是矩形，则A1C必过AC1的中点F，即F是A1C的中点，同理E是A1B的中点，则EF是△A1BC的中位线，即EF∥BC，又由BC在平面ABC中，EF在平面ABC外，则EF∥平面ABC．（2）由A1B1C1﹣ABC是直棱柱，则B1B⊥BC，即BC⊥B1B，又由BC⊥BA，即BC垂直平面ABB1A1，又由（1）知EF∥BC，即EF⊥平面ABB1A1，而EF在平面AEF中，则平面AEF⊥平面AA1B1B，（3）∵三棱柱A1B1C1﹣ABC是直三棱柱．∴V三棱锥F﹣ABC=S△ABC×h=S△ABC××CC1=×a×a×a=．点评：本题主要考查了平面与平面垂直的判定，直线与平面平行的判定，考查了空间想象能力，属于中档题．19．（14分）已知递增等差数列{a n}中的a2，a5是函数f（x）=x2﹣7x+10的两个零点．数列{b n}满足，点（b n，S n）在直线y=﹣x+1上，其中S n是数列{b n}的前n项和．（1）求数列{a n}和{b n}的通项公式；（2）令c n=a n•b n，求数列{c n}的前n项和T n．考点：数列的求和．专题：等差数列与等比数列．分析：（1）先解出两个零点，再利用等差、等比数列的通项公式即可；（2）直接使用错位相减法求之即可．解答：解：（1）因为a2，a5是函数f（x）=x2﹣7x+10的两个零点，则，解得：或．又等差数列{a n}递增，则，所以…3分因为点（b n，S n）在直线y=﹣x+1上，则S n=﹣b n+1．当n=1时，b1=S1=﹣b1+1，即．当n≥2时，b n=S n﹣S n﹣1=（﹣b n+1）﹣（﹣b n﹣1+1），即．所以数列{b n}为首项为，公比为的等比数列，即．…6分（2）由（1）知：且，则所以①②．①﹣②得：．所以．…12分点评：本题考查知识点等差、等比数列的通项公式；错位相减法求数列的和，考查分析问题解决问题的能力，20．（14分）已知直线y=﹣2上有一个动点Q，过点Q作直线l1垂直于x轴，动点P在l1上，且满足OP⊥OQ（O为坐标原点），记点P的轨迹为C．（1）求曲线C的方程；（2）若直线l2是曲线C的一条切线，当点（0，2）到直线l2的距离最短时，求直线l2的方程．考点：抛物线的标准方程；直线的一般式方程．专题：计算题．分析：（1）先设P点坐标，进而得出Q点坐标，再根据OP⊥OQ⇒k OP•k OQ=﹣1，求出曲线方程；（2）设出直线直线l2的方程，然后与曲线方程联立，由于直线l2与曲线C相切，得出二次函数有两个相等实根，求出，再由点到直线距离公式表示出d，根据a+b≥2，求得b的值，即可得到直线方程．解答：解：（1）设点P的坐标为（x，y），则点Q的坐标为（x，﹣2）．∵OP⊥OQ，∴k OP•k OQ=﹣1．当x≠0时，得，化简得x2=2y．（2分）当x=0时，P、O、Q三点共线，不符合题意，故x≠0．∴曲线C的方程为x2=2y（x≠0）．（4分）（2）∵直线l2与曲线C相切，∴直线l2的斜率存在．设直线l2的方程为y=kx+b，（5分）由得x2﹣2kx﹣2b=0．∵直线l2与曲线C相切，∴△=4k2+8b=0，即．（6分）点（0，2）到直线l2的距离=（7分）=（8分）（9分）=．（10分）当且仅当，即时，等号成立．此时b=﹣1．（12分）∴直线l2的方程为或．（14分）点评：本题考查了抛物线和直线的方程以及二次函数的根的个数，对于（2）问关键是利用了a+b≥2，求出b的值．属于中档题．21．（14分）已知函数f（x）=x2+2ax+1（a∈R），f′（x）是f（x）的导函数．（1）若x∈，不等式f（x）≤f′（x）恒成立，求a的取值范围；（2）解关于x的方程f（x）=|f′（x）|；（3）设函数，求g（x）在x∈时的最小值．考点：利用导数求闭区间上函数的最值；函数恒成立问题．专题：综合题；导数的综合应用．分析：（1）根据f（x）≤f′（x），可得x2﹣2x+1≤2a（1﹣x），分离参数，确定右边函数的最大值，即可求a的取值范围；（2）由f（x）=|f′（x）|，可得|x+a|=1+a或|x+a|=1﹣a，再分类讨论，即可得到结论；（3）由f（x）﹣f′（x）=（x﹣1），，对a进行分类讨论，即可确定g（x）在x∈时的最小值．解答：解：（1）因为f（x）≤f′（x），所以x2﹣2x+1≤2a（1﹣x），又因为﹣2≤x≤﹣1，所以在x∈时恒成立，因为，所以．（2）因为f（x）=|f′（x）|，所以x2+2ax+1=2|x+a|，所以（x+a）2﹣2|x+a|+1﹣a2=0，则|x+a|=1+a或|x+a|=1﹣a．①当a＜﹣1时，|x+a|=1﹣a，所以x=﹣1或x=1﹣2a；②当﹣1≤a≤1时，|x+a|=1﹣a或|x+a|=1+a，所以x=±1或x=1﹣2a或x=﹣（1+2a）；③当a＞1时，|x+a|=1+a，所以x=1或x=﹣（1+2a）．（3）因为f（x）﹣f′（x）=（x﹣1），①若，则x∈时，f（x）≥f′（x），所以g（x）=f′（x）=2x+2a，从而g（x）的最小值为g（2）=2a+4；②若，则x∈时，f（x）＜f′（x），所以g（x）=f（x）=x2+2ax+1，当时，g（x）的最小值为g（2）=4a+5，当﹣4＜a＜﹣2时，g（x）的最小值为g（﹣a）=1﹣a2，当a≤﹣4时，g（x）的最小值为g（4）=8a+17．③若，则x∈时，当x∈时，g（x）最小值为g（1﹣2a）=2﹣2a．因为，（4a+5）﹣（2﹣2a）=6a+3＜0，所以g（x）最小值为4a+5．综上所述，．点评：本题考查导数知识的运用，考查函数的最值，考查恒成立问题，考查分类讨论的数学思想，正确分类是关键．。

2015惠州市第三次调研考试(惠三调)课件完美版

惠州市2015届高三第三次调研考试
语文试卷答案
1*B．
A．qī/xī、lì 、nào/chuò； B．fǔ/pú、nǔ/nú、jùn/juàn； C．què、guàn、chàng/chāng； D．zhù、lí ng、bì /pì
2*A． A．“风生水起”比喻事情做得特别好，一定的时间里就发展得特别快，迅速壮大起来或是产生意料之外的效果。 B．“栩栩如生”形容逼真得像是活的一样。 C．“触目惊心”是指看到某种严重的情况引起内心的震动。此处不合语境。 D．身无长物：形容贫穷。此处属望文生义。
3．*D
A．缺主语，去掉“由于”或“使”； B．“印度空间研究组织（ISRO）…… 成为……国家”搭配不当； C．成分赘余，应删掉“因为”。 4．*B 5．*A【性：真心，真实意图】 6．*D．均意为“把，拿”。 A．①比得上/②好像，如同。 B．① “为……所”表被动/②与“赐”结合，构成名词性结构。 C．①表被动/②造成） 7．*B 8．*B 【不是向李宗谔借钱，是拿不少钱帮助李宗谔。】
22、字数不同的不给分。版面宗旨与版面名称不相关，或不知所云者不给分。结构相似即可。示例：第二版：敞开心扉，剖析内心，书写人生轨迹第四版：抒发情感，描摹梦想。
23、答对一项给1分，答对三项给4 分，全对给6分。顺序不论，意思对即可。 ①尊重自由（自由表达） ②开放宽容 ③坚持操守（理想） ④坚持原创（原创思考）。
10、这首诗写僧人惠衷的修行生活。一、二句是说僧人云游四方，走遍天涯海角依然是意犹未尽。他四处传教，普渡众生，以四海为家，漂泊不定，可是只要能够心安，天涯海角哪里不是家呢？这是僧人惠衷生活的一个重要的生活内容。三、四句意思是：平日里惠衷经常与山中老宿谈诗论禅，已很少看《楞严经》了。对于为什么“案上楞严已不看”，诗的五、六两句作了回答，原来，诗人已从清静闲适的生活之中体悟到禅的妙趣。倚枕看花，闭门对竹。大自然优美、静谧的环境对于僧人有一定的移情作用，可以让他们更好地参佛坐禅；另外，花开花落、竹木生长的自然现象又让僧人感悟到万物生生灭灭的佛理。末尾两句写僧人生活拮据，客人来了，只有清茶相待，别无他物，卢桔、杨梅都没有成熟，尚有酸味，不能供客。生活虽然贫困，僧人却不为所动，甘守清贫，心中平实、祥和，因为他已经从修禅

数学文卷·2015届广东省惠州市第一中学(惠州市)高三第一次调研考试

广东省惠州市2015届高三第一次调研考试数学试题(文科）【试卷综评】本试卷特点（1）注重基础知识，基本技能的考查，符合新课程标准和命题的意图及宗旨。

考查的都是基本概念和基本方法，关注学生基本能力的考查的同时，仍然紧扣双基。

总体感觉试题对学生双基的考查既全面又突出重点，对教师的教和学生的学检测到位，同时对后续的教与学又起到了良好的导向和激励。

（2）注重能力考查，更注重数学思想的考查。

试卷对数学思想和数学能力的考查较为突出。

（3）在考查基本知识、基本技能的条件下，适当兼顾了对学生综合能力的考查。

一、选择题（本大题共10小题，每小题5分，满分50分.每小题给出的四个选项中，只有一项是符合题目要求.）1．复数1iZ i =+（其中i 为虚数单位）的虚部是（） A.12-B.12iC.12D.12i -【知识点】虚数的概念;虚数除法的运算法则.【答案解析】C 解析：解：化简得iz 2121+=，则虚部为21，故选C .【思路点拨】分式上下同时乘以分子的共轭复数再化简整理即可. 2．已知集合(){}lg 3A x y x ==+，{}2B x x =≥，则AB =（）A. (3,2]-B.(3,)-+∞C.[2,)+∞D.[3,)-+∞ 【知识点】对数不等式的解法；交集的概念. 【答案解析】C 解析：解： (){}{}lg 33A x y x x x ==+=>-，{}2B x x =≥，所以[2,)AB =+∞,故选C.【思路点拨】先通过解对数不等式求出集合A ，再求交集即可. 3．下列函数在定义域内为奇函数的是（）A.1y x x =+B. sin y x x =C. 1y x =-D. cos y x =【知识点】奇函数的定义.奇偶性的判断方法.【答案解析】 A 解析：解：根据奇函数的定义可知：11(),()(),f x x f x x f x x x =+-=-+=--故选A.【思路点拨】利用奇偶性的判断方法直接判断即可得出结论.4.命题“21,11x x <<<若则-”的逆否命题是（） A.21,1,1x x x ≥≥≤-若则或 B.若11<<-x ，则12<xC.若1x >或1x <-，则12>xD.若1x ≥或1x ≤-，则12≥x 【知识点】四种命题；逆否命题.【答案解析】D 解析：解：由逆否命题的变换可知，命题“若12<x ，则11<<-x ” 的逆否命题是“若1x ≥或1x ≤-，则12≥x ”，故选D. 【思路点拨】根据逆否命题的变换可得选项. 5．若向量(1,2),BA =(4,5),CA =则BC =A.(5,7)B.(3,3)--C.(3,3)D.(5,7)-- 【知识点】相反向量；向量的四则运算. 【答案解析】B解析：解：因为(4,5CA =(4,5AC =--,所以()3,3B C B A A C =+=--，故选B.【思路点拨】由相反向量的定义得(4,5)AC =--，再结合向量的加法运算即可.6．若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法计算，得数据如下：那么方程32220x x x +--=的一个最接近的近似根为（）A ．1.2B ．1.3C ．1.4D ．1.5 【知识点】零点的判断方法. 【答案解析】C 解析：解：因为()1.40625 0.0540f =<－，()1.4375 0.1620f =>，由零点存在定理知，最接近的近似根为1.4. 【思路点拨】由表格找出最大的零点区间即可．7．执行如图所示的程序框图,若输入n 的值为7,则输出的s 的值为（） A ．22 B ．16 C ．15 D ．11（7题）（8题）【知识点】循环结构的程序框图.【答案解析】B 解析：解：程序执行过程中，,i s 的值依次为1,1i s ==；1,2s i ==；11,3s i =+=； 112,4s i =++=； 1123,5s i =+++=； 11234,6s i =++++=；112345,7s i =+++++=，输出s 的值为16.【典型总结】依次取i,s的值，可知当i=7时可得结果.8．函数())(,0,)2f x x x R πωϕωϕ=+∈><的部分图象如图所示，则,ωϕ的值分别是（）A ．2,3π-B.2,6π-C.4,6π-D.4,3π【知识点】函数y=Asin （ωx+φ）的图象变换．【答案解析】A 解析：解：由图知()f x在5π12x =且最小正周期T 满足35ππ+.4123T =故A 32π3π,2,4ωω⨯==5π)12θ⨯+=，5πsin()1,6θ+=5πππ2π,2π,623k k k θθ+=+=-∈Z .所以π()(2).3x f x -=或由5(π)12f =π()(2).3x f x -= 【典型总结】根据图象的两个点A 、B 的横坐标，得到四分之三个周期的值，得到周期的值，做出ω的值，把图象所过的一个点的坐标代入方程做出初相，写出解析式，代入数值得到结果．9．若双曲线22221x y a b -=）A.2±B. C.12±D.±【知识点】双曲线的离心率的概念；渐近线方程.【答案解析】B 解析：解：双曲线的离心率c e a a ====，所以b a =，其渐近线的方程为by x a =±，其斜率为 B.【典型总结】先由双曲线的离心率转化出ba =，然后去求渐进线的斜率即可.10．已知函数222,0()()()2(1),2,0x x x f x f a f a f x x x ⎧+≥⎪=-+≤⎨-<⎪⎩,若则实数a 的取值范围是A.[)1,0- B.[]0,1 C.[]1,1- D.[]2,2-【知识点】函数的奇偶性；函数的单调性；绝对值不等式的解法.【答案解析】C 解析：解：由偶函数定义可得()f x 是偶函数，故()()f a f a -=，原不等式等价于()(1)f a f ≤，又根据偶函数定义，()()f a f a =(1)f ≤，函数()f x 在(0,)+∞单调递增，1a ≤，[1,1]a ∈-．或利用图象求a 范围．选C.【思路点拨】由函数()f x 是偶函数可得()||1f a £,进而解1a ≤即可.二、填空题：（本大题共5小题，考生作答4小题，每小题5分，满分20分.）（一）必做题（11～13题） 11. 计算33log 18log 2-= ．【知识点】对数的运算性质．【答案解析】2 解析：解：333318log 18log 2log log 922-===【思路点拨】利用对数的换底公式和运算法则直接求解．12．变量x 、y 满足线性约束条件222200x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩，则目标函数z x y =+的最大值为 .【知识点】简单的线性规划.【答案解析】43 解析：解：作出不等式组22220x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩所表示的可行域如图所示，联立2222x y x y +=⎧⎨+=⎩得22,33A ⎛⎫⎪⎝⎭，作直线:l z x y =+，则z 为直线l 在x 轴上的截距，当直线l 经过可行域上的点A 时，直线l 在x 轴上的截距最大，此时z 取最大值，即max 224333z =+=.【思路点拨】先根据约束条件画出可行域，再利用几何意义求最值，只需求出直线z=x+y过点22,33A ⎛⎫ ⎪⎝⎭时，z 最大值即可．13．若某几何体的三视图如图所示，则此几何体的体积等于【知识点】由三视图求体积．【答案解析】24 解析：解：由三视图可知，到的，如图111345(34)324232V =⨯⨯⨯-⨯⨯⨯=【思路点拨】先根据三视图判断几何体的形状，再利用体积公式计算即可．（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答的，只计前一题的得分。

惠州市2015届高三第二次调研考试数学(文科)试题及参考答案

惠州市2015届高三第二次调研考试数学试题 (文科） 2014.10本试卷共4页，21小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡的整洁．考试结束后，将答题卡一并交回．参考公式：锥体的体积公式13V Sh =，其中S 为锥体的底面积，h 为锥体的高. 一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.1.设集合{3,2,1,0,1}A =---，集合2{40}B x x =-=，则AB ＝ ( )A ．{2}-B ．{2}C ．{2,2}-D ．∅2.复数(1)z i i =⋅+ (i 为虚数单位)在复平面上对应的点位于 ( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限3.已知命题:p 2,240x R x x ∀∈-+≤，则¬p 为 ( )A ．2,240x R x x ∀∈-+≥B ．2000,240x R x x ∃∈-+> C ．2,240x R x x ∀∉-+≤ D ．2000,240x R x x ∃∉-+> 4.已知向量(3,7)AB =，(2,3)BC =-，则12AC -= ( ) A.152⎛⎫- ⎪⎝⎭， B. 152⎛⎫ ⎪⎝⎭， C. 152⎛⎫- ⎪⎝⎭，- D. 152⎛⎫ ⎪⎝⎭，- 5.下列函数中，在区间(0,)+∞上为增函数的是( )A ．ln(1)y x =-B ．|1|y x =-C ．12xy ⎛⎫= ⎪⎝⎭D ．sin 2y x x =+6.若变量,x y 满足约束条件220020x y x y x y -+≥⎧⎪-≤⎨⎪+-≥⎩，则2z x y =+的最小值为( )A ．6-B ．2C ．3D ．4 7.已知函数()()sin f x A x ωϕ=+(0,0,)2A πωϕ>>≤的部分图象如图所示,则函数()y f x =的表达式是( ) A.()2sin(2)3f x x π=- B. ()2sin(2)3f x x π=+C.2()2sin(2)3f x x π=+D. ()2sin()12f x x π=+8.方程20([0,1])x x n n ++=∈有实根的概率为（） A ．12 B ．13 C ．14 D ．349.圆心在(1,2)-，半径为x 轴上截得的弦长等于 ( )A． B ．6 C． D ．810.某学校要召开学生代表大会，规定各班每10人推选一名代表，当各班人数除以10的余数大于6时再增选一名代表．那么，各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数[]y x = ([]x 表示不大于x 的最大整数）可以表示为 ( ) A ．[]10x y = B ．3[]10x y += C ．4[]10x y += D ．5[]10x y += 二、填空题：（本大题共5小题，分为必做题和选做题两部分．每小题5分，满分20分）（一）必做题：第11至13题为必做题，每道试题考生都必须作答． 11.抛物线240x y +=的准线方程是 .12.在等比数列{}n a 中，54a =，78a =，则9a = _________. 13.在△ABC 中，3A π∠=，3BC =，AB =，则C ∠=_________.（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答的，只计前一题的得分。

广东省惠州市高三数学第三次调研试卷文(含解析)

广东省惠州市2015届高三第三次调研数学试卷（文科）一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.1．（5分）若集合A={0，1，2，3}，B={1，2，4}，则集合A∪B=（）A．{0，1，2，3，4} B．{1，2，3，4} C．{1，2} D．{0}2．（5分）已知0＜a＜2，复数z=a+i（i是虚数单位），则|z|的取值范围是（）A．B．（1，5）C．（1，3）D．3．（5分）函数f（x）=+ln（x+1）的定义域为（）A．（2，+∞）B．（﹣1，2）∪（2，+∞）C．（﹣1，2）D．（﹣1，2]4．（5分）等差数列{a n}的前n项和为S n，且S3=6，a1=4，则公差d等于（）A．1 B．C．﹣2 D．35．（5分）已知a∈R，则“a2＜2a”是“a＜2”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件6．（5分）圆（x+2）2+y2=4与圆（x﹣2）2+（y﹣1）2=9的位置关系为（）A．内切B．相交C．外切D．相离7．（5分）下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行8．（5分）设变量x，y满足约束条件，则的最大值为（）A．3 B．6 C．D．19．（5分）如图是某个四面体的三视图，该四面体的体积为（）A．72 B．36 C．24 D．1210．（5分）已知函数f（x﹣1）是定义在R上的奇函数，若对于任意两个实数x1≠x2，不等式恒成立，则不等式f（x+3）＜0的解集为（）A．（﹣∞，﹣3）B．（4，+∞）C．（﹣∞，1）D．（﹣∞，﹣4）二、填空题：（本大题共3小题，分为必做题和选做题两部分．每小题5分，满分15分）（一）必做题：第11至13题为必做题，每道试题考生都必须作答．11．（5分）已知向量，且，则x=．12．（5分）在△ABC中，内角A，B，C对边的边长分别是a，b，c，若a=15，b=10，A=，则cosB=．13．（5分）A，B，C是平面内不共线的三点，点P在该平面内且有，现将一粒黄豆随机撒在△ABC内，则这粒黄豆落在△PBC内的概率为．（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答，按第一题记分【坐标系与参数方程选做题】（共1小题，满分5分）14．（5分）在极坐标系中，直线，被圆ρ=4截得的弦长为．【几何证明选做题】15．如图，已知△ABC内接于圆O，点D在OC的延长线上，AD切圆O于A，若∠ABC=30°，AC=2，则AD的长为．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（12分）已知向量=（cosx+sinx，2sinx），=（cosx﹣sinx，﹣cosx），f（x）=•，（1）求f（x）的最小正周期；（2）当x∈时，求f（x）的最小值以及取得最小值时x的值．17．（12分）惠州市某县区共有甲、乙、丙三所高中的2015届高三文科学生共有800人，各学校男、女生人数如表：甲高中乙高中丙高中女生153 x y男生97 90 z已知在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2．（1）求表中x的值；（2）惠州市第三次调研考试后，该县区决定从三所高中的所有2015届高三文科学生中利用随机数表法抽取100人进行成绩统计分析，先将800人按001，002，…，800进行编号．如果从第8行第7列的数开始向右读，请你依次写出最先检测的3个人的编号；（下面摘取了随机数表中第7行至第9行）8442 1753 3157 2455 0688 7704 7447 6721 7633 5026 83926301 5316 5916 9275 3862 9821 5071 7512 8673 5807 44391326 3321 1342 7864 1607 8252 0744 3815 0324 4299 7931（3）已知y≥145，z≥145，求丙高中学校中的女生比男生人数多的概率．18．（14分）如图，在直三棱柱A1B1C1﹣ABC中，AB⊥BC，E、F分别是A1B，AC1的中点．（1）求证：EF∥平面ABC；（2）求证：平面AEF⊥平面AA1B1B；（3）若AB=BC=a，A1A=2a，求三棱锥F﹣ABC的体积．19．（14分）已知递增等差数列{a n}中的a2，a5是函数f（x）=x2﹣7x+10的两个零点．数列{b n}满足，点（b n，S n）在直线y=﹣x+1上，其中S n是数列{b n}的前n项和．（1）求数列{a n}和{b n}的通项公式；（2）令c n=a n•b n，求数列{c n}的前n项和T n．20．（14分）已知直线y=﹣2上有一个动点Q，过点Q作直线l1垂直于x轴，动点P在l1上，且满足OP⊥OQ（O为坐标原点），记点P的轨迹为C．（1）求曲线C的方程；（2）若直线l2是曲线C的一条切线，当点（0，2）到直线l2的距离最短时，求直线l2的方程．21．（14分）已知函数f（x）=x2+2ax+1（a∈R），f′（x）是f（x）的导函数．（1）若x∈，不等式f（x）≤f′（x）恒成立，求a的取值范围；（2）解关于x的方程f（x）=|f′（x）|；（3）设函数，求g（x）在x∈时的最小值．广东省惠州市2015届高三第三次调研数学试卷（文科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.1．（5分）若集合A={0，1，2，3}，B={1，2，4}，则集合A∪B=（）A．{0，1，2，3，4} B．{1，2，3，4} C．{1，2} D．{0}考点：并集及其运算．专题：集合．分析：按照并集的定义直接写出A∪B即可．解答：解：∵A={0，1，2，3}，B={1，2，4}，∴A∪B={0，1，2，3，4}故答案为：A点评：本题考查集合的运算，求并集及运算．属于基础题．2．（5分）已知0＜a＜2，复数z=a+i（i是虚数单位），则|z|的取值范围是（）A．B．（1，5）C．（1，3）D．考点：复数求模．专题：数系的扩充和复数．分析：直接由复数模的公式写出|z|=，再由0＜a＜2求得1＜a2+1＜5，则答案可求．解答：解：∵复数z=a+i，则|z|=，由0＜a＜2，得1＜a2+1＜5，∴|z|∈（1，）．故选：D．点评：本题考查了复数模的求法，考查了函数的值域，是基础的计算题．3．（5分）函数f（x）=+ln（x+1）的定义域为（）A．（2，+∞）B．（﹣1，2）∪（2，+∞）C．（﹣1，2）D．（﹣1，2]考点：对数函数的定义域．专题：函数的性质及应用．分析：根据二次根式的性质结合对数函数的性质得到不等式组，解出即可．解答：解：由题意得：，解得：﹣1＜x＜2，故选：C．点评：本题考查了二次根式的性质，考查了对数函数的性质，是一道基础题．4．（5分）等差数列{a n}的前n项和为S n，且S3=6，a1=4，则公差d等于（）A．1 B．C．﹣2 D．3考点：等差数列的性质．专题：计算题．分析：由题意可得 S3=6=（a1+a3），且 a3=a1+2d，a1=4，解方程求得公差d的值．解答：解：∵S3=6=（a1+a3），且 a3=a1+2d，a1=4，∴d=﹣2，故选C．点评：本题考查等差数列的定义和性质，通项公式，前n项和公式的应用，属于基础题．5．（5分）已知a∈R，则“a2＜2a”是“a＜2”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：先解出a2＜2a，再进行判断即可解答：解：因为a2＜2a，所以0＜a＜2，则“a2＜2a”是“a＜2”的充分而不必要条件；故选：A．点评：本题考查了充分必要条件，考查了集合之间的关系，是一道基础题．6．（5分）圆（x+2）2+y2=4与圆（x﹣2）2+（y﹣1）2=9的位置关系为（）A．内切B．相交C．外切D．相离考点：圆与圆的位置关系及其判定．专题：直线与圆．分析：求出两圆的圆心和半径，计算两圆的圆心距，将圆心距和两圆的半径之和或半径之差作对比，判断两圆的位置关系．解答：解：圆（x+2）2+y2=4的圆心C1（﹣2，0），半径r=2．圆（x﹣2）2+（y﹣1）2=9的圆心C2（2，1），半径R=3，两圆的圆心距d==，R+r=5，R﹣r=1，R+r＞d＞R﹣r，所以两圆相交，故选B．点评：本题考查圆与圆的位置关系及其判定的方法，关键是求圆心距和两圆的半径．7．（5分）下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行考点：命题的真假判断与应用；空间中直线与平面之间的位置关系．专题：简易逻辑．分析：利用直线与平面所成的角的定义，可排除A；利用面面平行的位置关系与点到平面的距离关系可排除B；利用线面平行的判定定理和性质定理可判断C正确；利用面面垂直的性质可排除D．解答：解：A、若两条直线和同一个平面所成的角相等，则这两条直线平行、相交或异面，故A错误；B、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行或相交，故B错误；C、设平面α∩β=a，l∥α，l∥β，由线面平行的性质定理，在平面α内存在直线b∥l，在平面β内存在直线c∥l，所以由平行公理知b∥c，从而由线面平行的判定定理可证明b∥β，进而由线面平行的性质定理证明得b∥a，从而l∥a，故C正确；D，若两个平面都垂直于第三个平面，则这两个平面平行或相交，排除D．故选C．点评：本题主要考查了空间线面平行和垂直的位置关系，线面平行的判定和性质，面面垂直的性质和判定，空间想象能力，属基础题．8．（5分）设变量x，y满足约束条件，则的最大值为（）A．3 B．6 C．D．1考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对应的平面区域，利用数形结合即可得到结论．解答：解：作出不等式组对应的平面区域如图：设k=，则k的几何意义为区域内的点P（x，y）到圆点O的斜率，由图象可知，OA的斜率最大，由，解得其中A（1，6），则OA的斜率k=6，故的最大值为6，故选：B点评：本题主要考查线性规划的应用，利用数形结合以及直线的斜率公式是解决本题的关键．9．（5分）如图是某个四面体的三视图，该四面体的体积为（）A．72 B．36 C．24 D．12考点：由三视图求面积、体积．专题：计算题．分析：通过三视图，判断几何体的形状，利用三视图的数据，求解几何体的体积即可．解答：解：由题意可知，几何体是三棱锥，底面三角形的一边长为6，底面三角形的高为：4，棱锥的一条侧棱垂直底面的三角形的一个顶点，棱锥的高为：3．所以几何体的体积：=12．故选D．点评：本题考查三视图视图能力与几何体的判断，几何体的体积的求法，考查计算能力．10．（5分）已知函数f（x﹣1）是定义在R上的奇函数，若对于任意两个实数x1≠x2，不等式恒成立，则不等式f（x+3）＜0的解集为（）A．（﹣∞，﹣3）B．（4，+∞）C．（﹣∞，1）D．（﹣∞，﹣4）考点：函数奇偶性的性质．专题：函数的性质及应用．分析：对于任意两个实数x1≠x2，不等式恒成立，可得函数f（x）在R上单调递增．由函数f（x﹣1）是定义在R上的奇函数，可得f（﹣1）=0，即可解出．解答：解：∵对于任意两个实数x1≠x2，不等式恒成立，∴函数f（x）在R上单调递增．∵函数f（x﹣1）是定义在R上的奇函数，∴f（﹣1）=0，∴不等式f（x+3）＜0=f（﹣1）化为x+3＜﹣1，解得x＜﹣4，∴不等式的解集为：（﹣∞，﹣4）．故选：D．点评：本题考查了抽象函数的奇偶性与单调性，考查了推理能力，属于中档题．二、填空题：（本大题共3小题，分为必做题和选做题两部分．每小题5分，满分15分）（一）必做题：第11至13题为必做题，每道试题考生都必须作答．11．（5分）已知向量，且，则x=0．考点：平面向量的坐标运算；平行向量与共线向量．专题：平面向量及应用．分析：根据题意，得•=0，求出x的值即可．解答：解：∵，且，∴，解得x=0．故答案为：0．点评：本题考查了的知识点是利用平面向量的数量积判断两个平面向量的垂直关系，是基础题．12．（5分）在△ABC中，内角A，B，C对边的边长分别是a，b，c，若a=15，b=10，A=，则cosB=．考点：正弦定理．专题：解三角形．分析：利用正弦定理列出关系式，把a，b，sinA的值代入求出sinB的值，即可求出cosB 的值即可．解答：解：∵△ABC中，a=15，b=10，sinA=，∴由正弦定理=得：sinB===，∵b＜a，∴B＜A，即B为锐角，则cosB==，故答案为：点评：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．13．（5分）A，B，C是平面内不共线的三点，点P在该平面内且有，现将一粒黄豆随机撒在△ABC内，则这粒黄豆落在△PBC内的概率为．考点：几何概型．专题：概率与统计．分析：由P在该平面内且有，得到PB=PA且P在线段AB上，所以△PBC的面积是△ABC的，由几何概型的概率公式可求．解答：解：由P在该平面内且有，得到PB=PA且P在线段AB上，所以△PBC的面积是△ABC的，由几何概型的概率公式这粒黄豆落在△PBC内的概率为；故答案为：．点评：本题给出点P满足的条件，求P点落在△PBC内的概率，着重考查了平面向量共线的充要条件和几何概型等知识，属于基础题．（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答，按第一题记分【坐标系与参数方程选做题】（共1小题，满分5分）14．（5分）在极坐标系中，直线，被圆ρ=4截得的弦长为4．考点：直线的参数方程．专题：坐标系和参数方程．分析：把直线与圆的极坐标方程化为直角坐标方程，再利用弦长公式弦长=2（d 为圆心到直线的距离）即可得出．解答：解：直线，化为=2，∴x+y﹣2=0，圆ρ=4化为x2+y2=16．∴圆心O（0，0）到直线的距离d==2．∴直线被圆截得的弦长=2==4．故答案为：4．点评：本题考查了把极坐标方程化为直角坐标方程、弦长公式、点到直线的距离公式，考查了计算能力，属于基础题．【几何证明选做题】15．如图，已知△ABC内接于圆O，点D在OC的延长线上，AD切圆O于A，若∠ABC=30°，AC=2，则AD的长为．考点：与圆有关的比例线段．专题：直线与圆．分析：作CE⊥AD于点E，由已知结合三角形中角的关系得到AE的长度，再由AD=2AE得答案．解答：解：如图，作CE⊥AD于点E，∵∠ABC=30°，∴∠CDA=30°，则∠COA=60°，∴△AOC为正三角形，∴∠CAO=60°，AC=OC，∴∠CAE=30°，AC=CD，又∵CE⊥AD，∴AE=，则AD=2AE=．故答案为：．点评：本题考查了与圆有关的比例线段，考查了直角三角形的解法，是中档题．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（12分）已知向量=（cosx+sinx，2sinx），=（cosx﹣sinx，﹣cosx），f（x）=•，（1）求f（x）的最小正周期；（2）当x∈时，求f（x）的最小值以及取得最小值时x的值．考点：三角函数中的恒等变换应用；平面向量数量积的运算．专题：三角函数的图像与性质．分析：（1）先求得f（x）=cos（2x+），根据周期公式可得f（x）的最小正周期；（2）先求得2x+∈，由函数的单调性质可得当2x+=π即x=时，取到f（x）的最小值﹣．解答：解：f（x）=•=（cosx+sinx）（cosx﹣sinx）+2sinx（﹣cosx）=cos2x﹣sin2x﹣2sinxcosx=cos2x﹣sin2x=cos（2x+）（1）T==π（2）x∈时，2x+∈∴当2x+=π即x=时，取到f（x）的最小值﹣．点评：本题主要考察了三角函数中的恒等变换应用，平面向量数量积的运算，三角函数的图象与性质，属于基础题．17．（12分）惠州市某县区共有甲、乙、丙三所高中的2015届高三文科学生共有800人，各学校男、女生人数如表：甲高中乙高中丙高中女生153 x y男生97 90 z已知在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2．（1）求表中x的值；（2）惠州市第三次调研考试后，该县区决定从三所高中的所有2015届高三文科学生中利用随机数表法抽取100人进行成绩统计分析，先将800人按001，002，…，800进行编号．如果从第8行第7列的数开始向右读，请你依次写出最先检测的3个人的编号；（下面摘取了随机数表中第7行至第9行）8442 1753 3157 2455 0688 7704 7447 6721 7633 5026 83926301 5316 5916 9275 3862 9821 5071 7512 8673 5807 44391326 3321 1342 7864 1607 8252 0744 3815 0324 4299 7931（3）已知y≥145，z≥145，求丙高中学校中的女生比男生人数多的概率．考点：概率的应用．专题：综合题；概率与统计．分析：（1）利用在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2，求出表中x的值；（2）根据从第8行第7列的数开始向右读，即可写出最先检测的3个人的编号；（3）y+z=800﹣153﹣97﹣160﹣90=300，y≥145，z≥145，图象为线段y+z=300（145≤y≤155），即可求丙高中学校中的女生比男生人数多的概率．解答：解：（1）∵在三所高中的所有2015届高三文科学生中随机抽取1人，抽到乙高中女生的概率为0.2，∴x=800×0.2=160；（2）从第8行第7列的数开始向右读，最先检测的3个人的编号为165、538、629；（3）y+z=800﹣153﹣97﹣160﹣90=300，y≥145，z≥145，图象为线段y+z=300（145≤y≤155）∵丙高中学校中的女生比男生人数多，∴y＞z，∴丙高中学校中的女生比男生人数多的概率为．点评：本题考查概率的应用，考查学生分析解决问题的能力，正确计算是关键．18．（14分）如图，在直三棱柱A1B1C1﹣ABC中，AB⊥BC，E、F分别是A1B，AC1的中点．（1）求证：EF∥平面ABC；（2）求证：平面AEF⊥平面AA1B1B；（3）若AB=BC=a，A1A=2a，求三棱锥F﹣ABC的体积．考点：平面与平面垂直的判定；直线与平面平行的判定．专题：证明题；空间位置关系与距离．分析：（1）连结A1C，可证EF是△A1BC的中位线，即EF∥BC，从而可证EF∥平面ABC．（2）易知BC⊥B1B，又由BC⊥BA，即BC垂直平面ABB1A1，又EF∥BC，即EF⊥平面ABB1A1，即可证明平面AEF⊥平面AA1B1B，（3）由直三棱柱可知V三棱锥F﹣ABC=S△ABC×h=S△ABC××CC1，代入即可求值．解答：证明：（1）连结A1C，由A1C1CA 是矩形，则A1C必过AC1的中点F，即F是A1C的中点，同理E是A1B的中点，则EF是△A1BC的中位线，即EF∥BC，又由BC在平面ABC中，EF在平面ABC外，则EF∥平面ABC．（2）由A1B1C1﹣ABC是直棱柱，则B1B⊥BC，即BC⊥B1B，又由BC⊥BA，即BC垂直平面ABB1A1，又由（1）知EF∥BC，即EF⊥平面ABB1A1，而EF在平面AEF中，则平面AEF⊥平面AA1B1B，（3）∵三棱柱A1B1C1﹣ABC是直三棱柱．∴V三棱锥F﹣ABC=S△ABC×h=S△ABC××CC1=×a×a×a=．点评：本题主要考查了平面与平面垂直的判定，直线与平面平行的判定，考查了空间想象能力，属于中档题．19．（14分）已知递增等差数列{a n}中的a2，a5是函数f（x）=x2﹣7x+10的两个零点．数列{b n}满足，点（b n，S n）在直线y=﹣x+1上，其中S n是数列{b n}的前n项和．（1）求数列{a n}和{b n}的通项公式；（2）令c n=a n•b n，求数列{c n}的前n项和T n．考点：数列的求和．专题：等差数列与等比数列．分析：（1）先解出两个零点，再利用等差、等比数列的通项公式即可；（2）直接使用错位相减法求之即可．解答：解：（1）因为a2，a5是函数f（x）=x2﹣7x+10的两个零点，则，解得：或．又等差数列{a n}递增，则，所以…3分因为点（b n，S n）在直线y=﹣x+1上，则S n=﹣b n+1．当n=1时，b1=S1=﹣b1+1，即．当n≥2时，b n=S n﹣S n﹣1=（﹣b n+1）﹣（﹣b n﹣1+1），即．所以数列{b n}为首项为，公比为的等比数列，即．…6分（2）由（1）知：且，则所以①②．①﹣②得：．所以．…12分点评：本题考查知识点等差、等比数列的通项公式；错位相减法求数列的和，考查分析问题解决问题的能力，20．（14分）已知直线y=﹣2上有一个动点Q，过点Q作直线l1垂直于x轴，动点P在l1上，且满足OP⊥OQ（O为坐标原点），记点P的轨迹为C．（1）求曲线C的方程；（2）若直线l2是曲线C的一条切线，当点（0，2）到直线l2的距离最短时，求直线l2的方程．考点：抛物线的标准方程；直线的一般式方程．专题：计算题．分析：（1）先设P点坐标，进而得出Q点坐标，再根据OP⊥OQ⇒k OP•k OQ=﹣1，求出曲线方程；（2）设出直线直线l2的方程，然后与曲线方程联立，由于直线l2与曲线C相切，得出二次函数有两个相等实根，求出，再由点到直线距离公式表示出d，根据a+b≥2，求得b的值，即可得到直线方程．解答：解：（1）设点P的坐标为（x，y），则点Q的坐标为（x，﹣2）．∵OP⊥OQ，∴k OP•k OQ=﹣1．当x≠0时，得，化简得x2=2y．（2分）当x=0时，P、O、Q三点共线，不符合题意，故x≠0．∴曲线C的方程为x2=2y（x≠0）．（4分）（2）∵直线l2与曲线C相切，∴直线l2的斜率存在．设直线l2的方程为y=kx+b，（5分）由得x2﹣2kx﹣2b=0．∵直线l2与曲线C相切，∴△=4k2+8b=0，即．（6分）点（0，2）到直线l2的距离=（7分）=（8分）（9分）=．（10分）当且仅当，即时，等号成立．此时b=﹣1．（12分）∴直线l2的方程为或．（14分）点评：本题考查了抛物线和直线的方程以及二次函数的根的个数，对于（2）问关键是利用了a+b≥2，求出b的值．属于中档题．21．（14分）已知函数f（x）=x2+2ax+1（a∈R），f′（x）是f（x）的导函数．（1）若x∈，不等式f（x）≤f′（x）恒成立，求a的取值范围；（2）解关于x的方程f（x）=|f′（x）|；（3）设函数，求g（x）在x∈时的最小值．考点：利用导数求闭区间上函数的最值；函数恒成立问题．专题：综合题；导数的综合应用．分析：（1）根据f（x）≤f′（x），可得x2﹣2x+1≤2a（1﹣x），分离参数，确定右边函数的最大值，即可求a的取值范围；（2）由f（x）=|f′（x）|，可得|x+a|=1+a或|x+a|=1﹣a，再分类讨论，即可得到结论；（3）由f（x）﹣f′（x）=（x﹣1），，对a进行分类讨论，即可确定g（x）在x∈时的最小值．解答：解：（1）因为f（x）≤f′（x），所以x2﹣2x+1≤2a（1﹣x），又因为﹣2≤x≤﹣1，所以在x∈时恒成立，因为，所以．（2）因为f（x）=|f′（x）|，所以x2+2ax+1=2|x+a|，所以（x+a）2﹣2|x+a|+1﹣a2=0，则|x+a|=1+a或|x+a|=1﹣a．①当a＜﹣1时，|x+a|=1﹣a，所以x=﹣1或x=1﹣2a；②当﹣1≤a≤1时，|x+a|=1﹣a或|x+a|=1+a，所以x=±1或x=1﹣2a或x=﹣（1+2a）；③当a＞1时，|x+a|=1+a，所以x=1或x=﹣（1+2a）．（3）因为f（x）﹣f′（x）=（x﹣1），①若，则x∈时，f（x）≥f′（x），所以g（x）=f′（x）=2x+2a，从而g（x）的最小值为g（2）=2a+4；②若，则x∈时，f（x）＜f′（x），所以g（x）=f（x）=x2+2ax+1，当时，g（x）的最小值为g（2）=4a+5，当﹣4＜a＜﹣2时，g（x）的最小值为g（﹣a）=1﹣a2，当a≤﹣4时，g（x）的最小值为g（4）=8a+17．③若，则x∈时，当x∈时，g（x）最小值为g（1﹣2a）=2﹣2a．因为，（4a+5）﹣（2﹣2a）=6a+3＜0，所以g（x）最小值为4a+5．综上所述，．点评：本题考查导数知识的运用，考查函数的最值，考查恒成立问题，考查分类讨论的数学思想，正确分类是关键．。

2015惠州三调数学(理科)试题(终审稿)参考答案与评分标准

惠州市2015届高三第三次调研考试数学 (理科）参考答案与评分标准一．选择题：共8小题，每小题5分，满分40分题号 1 2 3 4 5 6 7 8 答案ACBADBBD1．【解析】由1x ≤得11x -≤≤，{}11|A x x ∴=-≤≤；由y x =得0x ≥，{}0|B x x ∴=≥。

{}01A B x x ∴=≤≤|。

故选A.2．【解析】首先cos y x =是偶函数，且在()0,π上单减，而()0,1⊂()0,π，故cos y x =满足条件。

故选C.3．【解析】由不等式的性质知，当0a b >>时，22a b >成立；反之，例如取31,a b =-=，显然22a b >，而0a b >>不成立。

故选B. 4．【解析】由已知知13,b c ==，所以2a =，所以62c e a ==。

选A. 5．【解析】当m α⊂，//n α时，必有//m n 或m 与n 异面直线，而m 与n 是共面的两条直线，所以//m n 。

故选D.6．【解析】分两类。

第一类：甲、乙两人中恰有一人参加，方法种数为134254480C C A ⋅⋅= 种，第二类：甲、乙两人同时参加，方法种数为2454240C A ⋅=种，根据分类计数原理，满足条件的方法种数为480+240=720种。

故选B. 7．【解析】对任意的n N +∈，均有12n n n a a a ++++为定值，123120()()n n n n n n a a a a a a +++++∴++-++=，故3n n a a +=，{}n a ∴是以3为周期的数列，故172a a ==，2984a a ==，393a a ==， 100123979899100133243299()()()S a a a a a a a a ∴=+++++++=+++=。

选B.8．【解析】对于（1），12324dPQπααα⎛⎫=-+-=-+ ⎪⎝⎭(,)sin cos sin ，,(,)R d P Q α∈∴的最大值为32+，故（1）不正确。

广东省惠州市2015届高三第三次调研考试数学(文)试题及答案

广东省惠州市高三数学第三次调研试卷文(含解析)

广东省惠州市高三数学第三次调研考试试题 文(扫描版)

惠州市2015届高三第二次调研考试数学(文科)试题及参考答案

广东省惠州市2015届高三第一次调研考试数学文试题 Wor

广东省惠州市2015届高三第二次调研考试数学(文)试题及解析

广东省惠州市2015届高三第二次调研考试-数学文-Word版含答案

广东省惠州市2015届高三第三次调研

广东省惠州市高三数学第三次调研考试题 文(扫描版)新人教A版

广东省惠州市高三数学第三次调研试卷 文(含解析)

2015惠州市第三次调研考试(惠三调)课件完美版

数学文卷·2015届广东省惠州市第一中学(惠州市)高三第一次调研考试

惠州市2015届高三第二次调研考试数学(文科)试题及参考答案

广东省惠州市高三数学第三次调研试卷 文(含解析)

2015惠州三调数学(理科)试题(终审稿)参考答案与评分标准

广东省惠州市高三数学第三次调研考试试题文(扫描版)

广东省惠州市高三数学第三次调研考试题文(扫描版)新人教A版

广东省惠州市高三数学第三次调研试卷文(含解析)

广东省惠州市高三数学第三次调研试卷文(含解析)