平面法向量在立体几何中的应用
立体几何中的利器——平面法向量
子 里形 成 正 确 概念 有 极大 的帮 助 。但 是 还 有 部 分 同学 对 波 的叠 实 验应 使 现 象 明显 。让 每 一 个 学 生 , 别 是 最 后 一 排 学 生都 看 特 加 原 理难 以理解 , 又缺 乏 想 象力 , 此笔 者 又 用 计 算 机 模 拟 制 作 得 清楚 。 因此 , 师 应想 办法 把 一 些 细微 的现 象 进 行 放 大 , 一 为 教 把 了一 条直 线 上 两传 播 方 向相 反 的 两 列 波 的叠 加 , 十 分 形 象 直 些 在水 平 面 上 进 行 的演 示 “ 格 ” 转 化 成 竖 直 平 面 上 让 学 生 观 可 定 ,
r
评述 : 利用 法 向量 解立 体 几何 题 , 以克 服平 面 的 垂 线难 作 、 可
:
,
‘ , j I 叫 :
角难 找 、 难 画等 难 点 , 要 评 估 综 合 几 何 法 与 向量 法 在 解 决 立 图 但 几综 合 问题 时 的优 劣 , 根据 题 目特点 灵 活 使 用 . 而恰 当 的 建 系 是
由:
L n 1 3・
一
o 求 出满足 方 程组 的 可
一
线面 垂直 : 以法 向量 为 载 体 , 化 为 求平 面法 向量 与 直 线 所 转
个 解 , 而求 出平 面 的 在 的向量 平行 从
个 法 向量 .
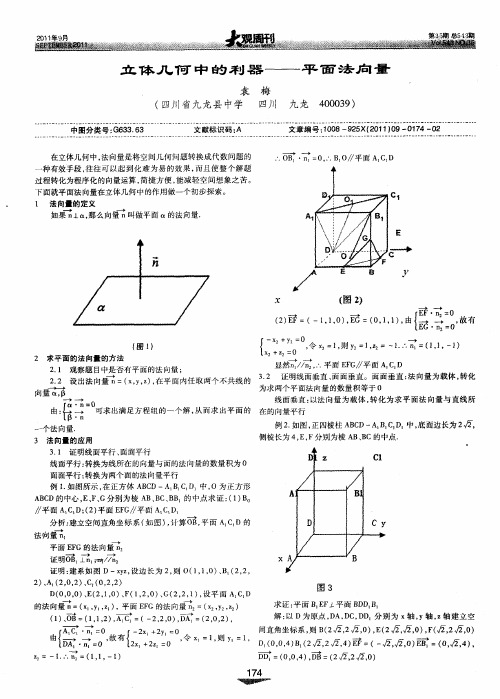
例 2 如 图 , 四棱 柱 A C A B CD 中 , 面边 长为 2 , . 正 B D— 。。 . . 底 侧 棱 长为 4 E, , F分别 为棱 A B B、C的中点 .
意 创 设有 悖 “ 理 ” 常 的奇 妙 情 景 来 激 发 学 生 求 知 的 内 驱 力 。⑧ 实 验 要险 . 当学 生 想象 中的 实 验结 果 会 引 起 不 良后 果 ( 损 坏 东 如 参 考 文 献
法向量在立体几何中的应用分类解析

法向量在立体几何中的应用分类解析一、法向量在解决立体几何问题方面用着广泛的应用,下面我们就来详细总结下法向量在立体几何方面的各种应用吧。
1.用法向量证明空间几何中的平行关系⑴线线平行。
设直线12,l l 的方向向量分别是a b 、,则要证明1l ∥2l ,只需证明a ∥b ,即()a kb k R =∈.⑵线面平行。
设直线l 的方向向量是a ,平面α的法向量是u ,则要证明l ∥α,只需证明a u ⊥,即0a u ⋅=.⑶面面平行。
若平面α的法向量为u ,平面β的法向量为v ,要证α∥β,只需证u ∥v ,即证u v λ=.2. 用向量方法判定空间的垂直关系⑴线线垂直。
设直线12,l l 的方向向量分别是a b 、,则要证明12l l ⊥,只需证明a b ⊥,即0a b ⋅=. ⑵线面垂直设直线l 的方向向量是a ,平面α内的两个相交向量分别为m n 、,若0,.0a m l a n α⎧⋅=⎪⊥⎨⋅=⎪⎩则 ⑶面面垂直若平面α的法向量为u ,平面β的法向量为v ,要证αβ⊥,只需证u v ⊥,即证0u v ⋅=.3. 利用向量求空间角。
⑴求异面直线所成的角已知,a b 为两异面直线,A ,C 与B ,D 分别是,a b 上的任意两点,,a b 所成的角为θ,则cos .AC BD AC BDθ⋅=⑵求直线和平面所成的角求法:设直线l 的方向向量为a ,平面α的法向量为u ,直线与平面所成的角为θ,a 与u 的夹角为ϕ, 则θ为ϕ的余角或ϕ的补角的余角.即有:cos s .in a u a uϕθ⋅==⑶求二面角二面角的平面角是指在二面角βα--l 的棱上任取一点O ,分别在两个半平面内作射线l BO l AO ⊥⊥,,则AOB ∠为二面角βα--l 的平面角.如图:求法:设二面角l αβ--的两个半平面的法向量分别为m n 、,再设m n 、的夹角为ϕ,二面角l αβ--的平面角为θ,则二面角θ为m n 、的夹角ϕ或其补角.πϕ- 根据具体图形确定θ是锐角或是钝角: 如果θ是锐角,则cos cos m n m nθϕ⋅==, 即arccosm n m nθ⋅=;如果θ是钝角,则cos cos m nm nθϕ⋅=-=-, 即arccos m n m n θ⎛⎫⋅ ⎪=-⎪⎝⎭. 4. 利用向量求空间距离点A 到平面α的距离(1).若点P 为平面α外一点,点M 为平面α内任一点,平面α的法向量为n ,则P 到平面α的距离就等于MP 在法向量n 方向上的投影的绝对值.即cos ,d MP n MP=n MP MP n MP⋅=⋅n MP n⋅=(2). 直线a 与平面α之间的距离当一条直线和一个平面平行时,直线上的各点到平面的距离相等。
法向量在立体几何中的应用总

法向量在立体几何中的应用(一)
1.向量法求夹角
直线a 与直线b 所成的角就是直线a 与b 的方向向量的夹角或补角。
2.向量法求线面角
如图,PA 是平面α的斜线,n
为平面α的法向量,设PA 与平面α所成的角是θ,
则sin AP n
AP n
θ=
3.法向量证明线面平行、面面平行和面面垂直
(1)已知n 为平面α的法向量,a 为平面α外直线a 的方向向量,若a n ⊥
,则//a α; (2)已知1n 、2n 分别为平面α、β的法向量,若12//n n ,则//αβ;若12n n ⊥
,则αβ⊥
法向量在立几中的应用(三)——求二面角的平面角
1.法向量求二面角的平面角
如图,平面α、β的法向量分别为1n 、2n
,则二面角的平面角θ与两个法向量的夹角12,n n α=<>
之间的关系为θα=或θπα=-
法向量在立体几何中的应用(二)
1.法向量求点面距
如图,PA 为平面α的一条斜线,n
为平面α的法向量,则 ()
cos 0AP n AO OP n OP n OP n OP n =+===
⇒ A P n OP n =
即点P 到平面α的距离公式为AP n d n
=
θ
3.异面直线的距离
如图,异面直线a 、b 的距离可以转化为两平行平面α、β的距离,n
为同时与a 、
b 的方向向量垂直的向量(即法向量)
,因此异面直线a 、b 的距离为 EF n d n =
其中,E 、F 分别为异面直线a 、b 上的任意点。
法向量的应用

法向量在立几中的应用随着新教材中向量工具的引入,立体几何的解题更加灵活多样,这为那些空间想象能力较差的同学提供了机遇。
利用平面的法向量几乎可以解决所有的立几计算问题,尤其在求二面角和点到面的距离时,法向量有着它独有的优势−−不用作图而直接计算。
以下举例说明法向量在立几中的一些应用。
一 法向量的有关概念如果一个向量所在直线垂直于平面,则该向量是平面的一个法向量。
二 法向量的主要作用 1 证明线面平行取和直线平行的向量,验证该向量和法向量的点积是否为零。
2 证明面面垂直验证两个平面的法向量的点积是否为零。
3 求直线和直线所成的角利用两条直线的方向向量的夹角的余弦的绝对值为两直线的夹角的余弦而得。
4 求直线和平面所成的角如图,已知PA 为平面α的一条斜线,n 为平面α的一个法向量,过P 作平面α的垂线PO ,连结OA 则∠PAO 为斜线PA 和平面α所成的角,记为θ易得|2sin(|sin -=πθ|cos ||cos ||cos |====5 求点到平面的距离如图点P 为平面外一点,点A一点,平面的法向量为n,过点P 作平面线PO ,记PA 和平面α所成的角为θ到平面的距离||||||sin ||||PA n PA n PA PA PO d ∙=∙===θ6 求二面角的大小如图在二面角βα--l 中n 1和n 2分别为 平面α和β的法向量若二面角βα--l记二面角βα--l 的大小为θ,若该二面角为锐二面角则=θ或-=πθ(依据两平面法向量的方向而定),但总有|cos ||cos |=θ=||2121n n ∙所以此时||arccos 2121n n ∙=θ若二面角βα--l 为钝二面角则=θ或-=πθ(依据两平面法向量的方向而定),但总有|||cos |=θ=2121所以此时||arccos2121n n ∙-=πθ三 法向量的求法如图,在正方体ABCD-A 1B !C 1D 1中G 、E 、F 分别为AA 1、AB 、BC 的中点,求平面GEF 的法向量。
空间向量在立体几何中的应用-立体几何

点,A是α内任一点,则点P到α的距离d= | PA·m | .
|m|
考点一 用向量证明平行、垂直问题
如图,在四棱锥P—ABCD 中,PA⊥平面ABCD,底面 ABCD为矩形,且PA=AD, E,F分别为线段AB,PD的中 点.求证:
(1) AF∥平面PEC;
相等或互补 .
5.空间的距离
(1)一个点到它在一个平面内 正射影 的距离,叫做 点到这个平面的距离.
(2)已知直线l平行平面α,则l上任一点到α的距离 都 相等 ,且叫做l到α的距离.
返回目录
(3)和两个平行平面同时 垂直 的直线,叫做两 个平面的公垂线.公垂线夹在平行平面间的部分,叫做两 个平面的 公垂线段 .两平行平面的任两条公垂线段的长 都相等,公垂线段的 长度 叫做两平行平面的距离, 也是一个平面内任一点到另一个平面的距离.
EC=(
a
22 ,1,0),∴AF=
1
2 EP+
1 EC,
2
2
2
又AF⊂ 平面PEC,∴AF∥平面PEC.
(2)PD=(0,1,-1),CD=(-a,0,0), 11
∴AF·PD=(0, 2, 2)·(0,1,-1)=0, AF·CD=(0, 1 , 1 )·(-a,0,0)=0,
22 ∴AF⊥PD,AF⊥CD,又PD∩CD=D,
∴m⊥n.
∴平面ADE⊥平面A1D1F.
返回目录
考点二 用向量求线线角与线面角 如图所示,已知点P在正方体ABCDA′B′C′D′的对角线BD′上,∠PDA=60°. (1)求DP与CC′所成角的大小; (2)求DP与平面AA ′ D′D所成角的大小
【分析】建立空间直角坐标系,利用空间向量方法求解. 返回目录
平面几何中的向量与立体几何体的位置关系

平面几何中的向量与立体几何体的位置关系在平面几何中,向量与立体几何体的位置关系是一个重要的研究领域。
向量是平面几何的基础概念,而立体几何体则是空间中的实体物体。
在这篇文章中,我们将探讨向量与立体几何体之间的关系,并探索它们在几何学中的应用。
一、向量的定义与性质向量是由大小和方向决定的量,用有向线段表示。
在二维平面中,向量通常由两个坐标表示,分别为横坐标和纵坐标。
例如,向量AB可以表示为(1,2)。
向量的性质包括加法、减法、数量乘法、数量除法等。
二、向量的运算在平面几何中,向量的运算是基本操作之一。
向量的加法是指将两个向量按照一定的规则相加,得到一个新的向量。
向量的减法和数量乘法也是类似的操作。
通过向量的运算,我们可以获得两个向量之间的关系,例如平行、垂直等。
三、向量的模与方向角向量的模表示向量的大小,而方向角表示向量与横轴之间的夹角。
向量的模可以使用勾股定理计算,方向角可以使用三角函数计算。
通过向量的模与方向角,我们可以准确地描述向量在平面中的位置与方向。
四、向量的应用在几何学中,向量有着广泛的应用。
例如,我们可以使用向量来表示线段,通过线段的向量运算可以得到线段的长度、方向等信息。
此外,向量还可以用来表示平面中的直线和曲线,通过向量的性质可以判断直线的平行、垂直关系,计算曲线的斜率等。
五、向量与立体几何体的位置关系在立体几何中,向量与几何体的位置关系是一个研究的重点。
通过向量的表示,我们可以描述几何体在空间中的方位与位置。
例如,我们可以通过指定一个点和一个向量来表示一条直线,通过两个向量来表示一个平面。
通过向量的运算,可以判断几何体之间的相对位置,例如平面与平面的交角、直线与平面的垂直关系等。
六、应用实例例如,我们可以通过向量的运算来计算一个立方体的体积。
假设立方体的一条边长为a,我们可以将其表示为向量OA,其中O是立方体的一个顶点。
那么立方体的体积可以表示为V=a^3,其中a是向量的模。
再例如,我们可以通过向量的运算来判断一个平面是否位于一个平行六面体的底面上。
数学与应用数学专业毕业论文-向量在立体几何中的应用

向量在立体几何中的应用摘要作为现代数学的重要标志之一的向量已进入了中学数学教学,为用代数方法研究几何问题提供了强有力的工具,促进了高中几何的代数化.而在高中数学体系中,几何占有很重要的地位,有些几何问题用常规方法去解决往往比较复杂,运用向量作行与数的转化,则使过程得到大大的简化.向量法应用于平面几何中时,它能将平面几何许多问题代数化、程序化从而得到有效的解决,体现了数学中数与形的完美结合.立体几何常常涉及到的两大问题:证明与计算,用空间向量解决立体几何中的这些问题,其独到之处,在于用向量来处理空间问题,淡化了传统方法的有“形”到“形”的推理过程,使解题变得程序化.装关键词:向量;立体几何;证明;计算;运用订线ABSTRACTAs one of the important signs of modern mathematics the vector has entered middle school mathematics teaching, using algebraic method research geometry problems provides powerful tools, promoted the high school of the geometry of algebra. And in the high school mathematics system, geometric occupies a very important position, some geometry problems with conventional method to solve tend to be complex, using vector for the number of rows and transformation, makes the process is greatly simplified. Vector method was used the plane geometry, it will be when the plane geometry many problems algebra effectively, programmed to solve, reflected in mathematics, the perfect combination of Numbers and forms. Three-dimensional geometry often involved the two big problems: proof and calculation, with space vector solve three-dimensional geometry in these problems, its unique, is using vector to deal with the problem of space, fade the traditional methods are "form" to "form" reasoning process, causes the problem-solving become programmed.Keywords:Vector; solid geometry; proof; calculation; use目录摘要 (Ⅰ)ABSTRACT (Ⅰ)1 向量方法在研究几何问题中的作用 (1)2 向量方法解决证明问题的直接应用 (2)2.1平行问题 (2)2.1.1证明两直线平行 (2)2.1.2证明线面平行 (3)2.2垂直问题 (4)2.2.1证明两直线垂直 (4)2.2.2证明线面垂直 (4)2.2.3证明面面垂直 (5)2.3处理角的问题 (6)2.3.1求异面直线所成的角 (6)2.3.2求线面角 (7)2.3.3求二面角 (8)3 向量方法解决度量问题的直接应用 (10)3.1两点间的距离 (10)3.2点与直线距离 (10)3.3点到面的距离 (11)3.4求两异面直线的距离 (11)3.5求面积 (12)3.6求体积 (13)4 向量方法解决证明与计算问题有关的综合应用 (14)5 向量在立体几何中应用的教学反思 (21)5.1对比综合法与向量法的利弊 (21)5.2向量法解决立体几何问题的步骤 (22)5.3向量法能解决所有立体几何问题吗 (22)参考文献 (23)1 向量方法在研究几何问题中的作用]1[向量是高中数学新增加的内容,在作用上它取代了以往复数在高中数学教材中的地位,但从目前的使用情况来看,向量的作用要远远大于复数.一个复数所对应的点只能在平面上,而向量却有平面向量和空间向量之分,这一点在与几何(尤其是立体几何)的联系上表现得更加突出.向量知识、向量观点在数学、物理等学科的很多分支上都有着广泛的应用,它具有代数形式和几何形式的“双重身份”,能融数形于一体,能与中学数学教学内容中的许多主干知识相结合,形成知识交汇点.向量进入高中数学教材,为用代数方法研究几何问题提供了强有力的工具,促进了高中几何的代数化.而在高中数学体系中,几何占有很重要的地位,有些几何问题用常规方法去解决往往比较繁杂,而运用向量作形与数的转化,则能使过程得到大大的简化.用向量法解决几何问题有着思路清晰、过程简洁的优点,往往会产生意想不到的神奇效果.著名教育家布鲁纳说过:“学习的最好刺激是对所学材料的兴趣,简单的重复将会引起学生大脑疲劳,学习兴趣衰退.”这充分揭示了方法求变的重要性,如果我们能重视向量的教学,重视学生在学习向量过程中产生的障碍并且提供相应的教学对策,必然能引导学生拓展思路,减轻他们的学习负担.向量方法在解决几何问题时充分体现了它的优越性,平面向量就具有较强的工具性作用,向量方法不仅可以用来解决不等式、三角、复数、物理、测量等某些问题,还可以简捷明快地解决平面几何许多常见证明(平行、垂直、共线、相切、角相等)与求值(距离、角、比值等)问题.不难看出向量法应用于平面几何中时,它能将平面几何许多问题代数化、程序化从而得到有效的解决,体现了数学中数与形的完美结合.向量法是将几何问题代数化,用代数方法研究几何问题.立体几何的证明与计算常常涉及到两大问题:一是位置关系,它主要包括线线垂直、线面垂直、线线平行、线面平行;二是度量问题,它主要包括点到线、点到面的距离,线线、线面所成的角,面面所成角等.用空间向量解决立体几何中的这些问题,其独到之处,在于用向量来处理空间问题,淡化了传统方法的有“形”到“形”的推理过程,使解题变得程序化.那么解立体几何题时就可以用向量方法,对某些传统性较大,随机性较强的立体几何问题,引入向量工具之后,可提供一些通法.2 向量方法解决证明问题的直接应用2.1平行问题]2[2.1.1证明两直线平行b a CD AB b D C a B A //,,;,⇒=∈∈λ. 知),(),,(2211y x CD y x AB ==,则有b a y x y x //1221⇒=. 例 1 已知直线OA ⊥平面α,直线BD ⊥平面α,O 、B 为垂足,求证:OA//BD.证明:如上图,以点O 为原点,以射线OA 为z 轴,建立空间直角坐标系xyz O -,k j i ,,为沿x 轴,y 轴,z 轴的坐标向量,且设),,(z y x BD =,∵α⊥BD ,∴j BD i BD ⊥⊥,∴0)0,0,1(),,(==⋅=⋅x z y x i BD ,0)0,1,0(),,(==⋅=⋅y z y x ,∴),0,0(z =∴k z BD =,又知O 、B 为两个不同的点,∴OA BD //.方法思路:在两条直线上分别取不同的两点得到两向量,转化为证明两向量平行.2.1.2证明线面平行1、线∉a 面α,a B A ∈,,面α的法向量为n ,α//0AB n AB n AB ⇔⊥⇔=⋅. 方法思路:求面的法向量,在直线找不同两点得一向量,证明这一向量与法向量垂直(即证明数量积为0),则可得线面平行.2、已知面α外的直线a 的方向向量为a ,21,e e 是平面α的一组基底(不共线的向量),若αλλ//2211a e e a ⇔+=.例2 如上图,正方形ABCD 所在平面与正方形ABEF 所在平面互相垂直,P 、Q 分别是对角线AC 、BF 上的一点,且AP = FQ,求证:PQ ∥平面BCE.证明:设λ=,∵AP = FQ, ∴λ=,∴FQ AF PA PQ ++==λλ++-=λλλλ+-+--=)1(λλ-+∴//PQ 平面BCE.方法思路:证明直线的方向向量可用平面的一组基底线性表示(即在平面内存在一向量与方向相等),则可得面内一直线与面外的线平行,从而证明线面平行.2.1.3面面平行1、不重合的两平面α与β的法向量分别是m 和n ,βαλ//⇔=.方法思路:求平面的法向量,转化为证明两法向量平行,则两平面平行.2、不重合的两平面α与β,面α的法向量为,若βαβ//⇔⊥.方法思路:求出其中一平面的法向量,再证该法向量与另一面的不共线的两向量数量积为0(即垂直),则可得两平面平行.2.2垂直问题]3[2.2.1证明两直线垂直不重合的直线a 和直线b 的方向向量分别为a 和b ,则有b a b a ⊥⇒=⋅0. 例3 如图,已知四棱锥P-ABCD 的底面为等腰梯形,AB //CD,AC ⊥BD ,垂足为H ,PH 是四棱锥的高 ,E 为AD 中点.证明:PE ⊥BC证明:以H 为原点,,,HA HB HP 分别为,,x y z 轴,线段HA 的长为单位长, 建立空间直角坐标系如图, 则(1,0,0),(0,1,0)A B设 (,0,0),(0,0,)(0,0)C m P n m n <>,则 )0,2,21(),0,,0(m E m D , 可得)0,1,(),,2,21(-=-=m n m , 因为0022m m PE BC ⋅=-+=, 所以 PE BC ⊥.2.2.2证明线面垂直直线l 的方向向量为]4[,平面α的方向向量为,则有αλ⊥⇒⋅=l . 例4,如图,m, n 是平面α内的两条相交直线.如果n l m l ⊥⊥,,求证:α⊥l .证明:在α内作任一直线g ,分别在g n m l ,,,上取非零向量g n m l ,,,. 因为m 与n 相交,所以向量n m ,不平行.由向量共面的充要条件知,存在唯一的有序实数对(x,y ),使n y m x g +=将上式两边与向量l 作数量积,得n l y m l x g l ⋅+⋅=⋅,因为 0,0=⊥=⊥n l m l ,所以0=⋅g l ,所以g l ⊥即g l ⊥.这就证明了直线l 垂直于平面α内的任意一条直线,所以α⊥l .方法思路:找直线的方向向量(在两直线上取两点得一向量)及平面的法向量,只需证明两向量平行,则可证线面垂直. 2.2.3证明面面垂直1、不重合的平面α与β的法向量分别为m 和n ,则有βα⊥⇔=⋅0n m . 方法思路:找平面的法向量,只需证明两向量数量积为0,则可证明两平面垂直.2、平面β的法向量为n ,21,e e 是平面α的一组基底(不共线的向量),则有βαλλ⊥⇔+=2211e e n .例5 在正方体ABCD-A 1B 1C 1D 1中,E 、F 分别是BB 1,CD 的中点(1)求证:AD ⊥D 1F ;(2)证明平面AED ⊥平面A 1FD 1分析:涉及正方体中一些特殊的点、线、面的问题,建立空间直角坐标系来解,不仅容易找到解题方向,而且坐标也简单,此时“垂直”问题转化为“两向量数量积为“0”的问题,当然也可用其它的证法.证明:建立空间直角坐标系如图,并设AB=2,则A(0,0,0), D(0,2,0), A 1(0,0,2)D 1(0,2,2),E(2,0,1), F(1,2,0)(1)(0,2,0),AD = 1(1,0,2)D F =-m n gα l AB C DA 1B 1C 1D 1z y∴ 1AD D F ⋅=0×1+2×1+0×(-2)=0, ∴AD ⊥D 1F(2)AE =(2,0,1) 1D F =(1,0,-2),||5AE = ,|1|5D F = 设AE 与D 1F 的夹角为θ,则θcos =055)2(10012|F D ||AE |FD AE 11=-⨯+⨯+⨯=⋅所以D 1F ⊥AE ,由(1)知D 1F ⊥AD ,又AD ∩AE=A ,∴D 1F ⊥平面AED ,∵D 1F ⊂平面A 1FD 1M∴平面AED ⊥平面A 1FD 1方法思路:找其中以平面的法向量,证明法向量与另一平面平行,即法向量可以用另一平面的一组基底(不共线的向量)线性表示.2.3处理角的问题]5[2.3.1求异面直线所成的角a,b 是两异面直线,b D C a B A ∈∈,,,,a ,b 所成的角为θ,则有CD AB CDAB CD AB ⋅⋅=〉〈=,cos cos θ.例6 如图所示,三棱锥A-BCD,AB ,,CD BD BCD ⊥⊥平面若AB=BC=2BD,求二面角B-AC-D 的大小.解: 如图建立空间直角坐标系O-xyz,∵AB=BC=2BD,设BD=1则AB=BC=2,DC=3A(1,0,2),B(1,0,0),C(0,3,0),D(0,0,0))2,0,1(),0,3,0(),0,3,1(),2,0,0(==-=-=→→→→DA DCBC AB设平面ABC 的法向量为),,(1111z y x n =→, 则00.11=⇒=→→z n AB030.111=+-⇒=→→y x n BC取平面ABC 的法向量)0,1,3(1=→n 设平面ACD 的法向量为),,(2222z y x n =→则00.22=⇒=→→y n DC020.222=+⇒=→→z x n DA取法向量)1,0,2(-=→n cos<→→21,n n >=5151040131001)2(32221-=++⨯++⨯+⨯+-⨯=⋅→→→→n n n n 515arccos,21->=∴<→→πn n 互补平面角与二面角><--∴→→21,n n D AC B , 515arccos的大小的所求二面角D AC B --∴. 方法思路:找两异面直线的方向向量,转化为向量的夹角问题,套公式(但要理解异面直线所成的夹角与向量的夹角相等或互补).2.3.2求线面角设平面α的斜线l 与面α所成的角为β,若,,l B A ∈m 是面α的法向量,则有〉〈=m AB ,cos sin β.例7如图,直三棱柱ABC —A 1B 1C 1中,底面是等腰直角三角形,∠ACB =90,侧棱AA 1=2,D 、E分别是CC 1与A 1B 的中点,点E 在平面ABD 上的射影是△ABD 的重心G.求A 1B 与平面ABD 所成角的大小(结果用余弦值表示);D D A 1C 1B 1z E解析:如图所示,建立坐标系,坐标原点为C ,设a CA 2=,则)0,0,2(a A ,)0,2,0(a B ,)1,0,0(D ,)2,0,2(1a A ,)1,,(a a E ,)31,32,32(a a G , ∵ ()2,,333a a GE =---,()0,2,1BD a =-,032322=-=⋅a , ∴1=a ,()112,,333GE =---,()12,2,2A B =--∵ GE 为平面ABD的法向量,且32,cos 1==〉〈GE B A . ∴ A 1B 与平面ABD 所成角的余弦值是32. 方法思路:找直线的方向向量与平面的法向量,转化为向量的夹角问题,再套公式(注意线面角与两向量所在直线夹角互余).2.3.3求二面角方法一:构造二面角βα--l 的两个半平面βα、的法向量21n n 、(都取向上的方向,如右图所示),则 ① 若二面角βα--l 是“钝角型”的如图3甲所示,那么其大小等于两法向量21n n 、的夹角的补角,即||||cos 2121n n ⋅=θ.② 若二面角βα--l 是“锐角型”的如右图所示,那么其大小等于两法向量21n n 、的夹角,即||||cos 2121n n ⋅=θ方法二:在二面角的棱l 上确定两个点B A 、,过B A 、分别在平面βα、内求出与l 垂直的向量21n n 、,则二面角βα--l 的大小等于向量21n n 、的夹角,即 ||||cos 2121n n ⋅=θ.例8 在长方体ABCD —A 1B 1C 1D 1中,AB=2,BC=4,AA 1=2,点Q 是BC 的中点,求此时二面角A —A 1D —Q 的大小.解 如图所示,建立空间直角坐标系xyz O -, 依题意:A 1(0,0,2),D (0,a ,0). ∴Q (2,2,0),D (0,4,0), ∴)20,2(),2,2,2(1-=-=A , 面AA 1D 的法向量)0,0,1(1=n , 设面A 1DQ 的法向量),,(3212a a a n =,则⎪⎩⎪⎨⎧=+-=⋅=-+=⋅,022,022*********a a QD n a a a Q A n ⎩⎨⎧==⇒,2,1312a a a a ∴)2,,(1112a a a n =, 令a 1=1,则)2,1,1(2=n ,∴66611,cos 21=⨯=>=<n n , 二面角的平面角为锐角,∴二面角A —A 1D —Q 的大小为66arccos. 此法在处理二面角问题时,可能会遇到二面角的具体大小问题,如本题中若令11-=a ,则)2,1,1(2---=n ,∴66,cos 21->=<n n ,∴二面角A —A 1D —Q 的大小 是><21,n n 66arccos-=π的补角66arccos .所以在计算之前不妨先依题意直观判断一下所求二面角的大小,然后根据计算取“相等角”或取“补角”.O (A 1z3 向量方法解决度量问题的直接应用3.1两点间的距离]6[两点间距离重在“转化”,即将空间两点间距离转化为向量的长度问题.利用向量的模,可以推导出空间两点的距离公式,即空间两点()()11112222,,,,,P x y z P x y z ,则()()()22212212121d PP x x y y z z ==-+-+-例1 在三棱锥S ABC -中,面SAC ⊥面ABC ,SA AC ⊥,BC AC ⊥6SA =,21,8AC BC ==,求SB 的长. 分析 如图,本题可以用几何法求出SB , 但需要证明若用向量法,注意到SA ,AC ,BC 之间的关系.建立以A 点为原点的空间直角坐标系.则无须证明就有如下巧解.解 如图,建立以A 为原点的空间直角坐标系,则()()()0,0,0,21,0,0,0,6A B S ,所以()()()222080216011SB SB ==-+-+-=.本题用向量法巧妙地把与SB 有关元素的位置关系转化为相应向量是SB 的数量关系,构造向量的空间距离模型,然后通过数值计算将问题加以解决.3.2点与直线距离]7[如图 求得向量AP 在向量AB 的射影长为d , 则点P 到直线AB 22AP d -例2 设P 为矩形ABCD 所在平面外的一点,直线PA 垂直平面外的一点, 直线PA 垂直平面ABCD ,AB =3,BC =4,PA =1 求点P 到直线BP 的距离. 解()()29BP BD BA AP BC BA AB ⋅=+⋅+==BD5所以BP 在BD 上的射影长为95,又10BP =,所以点P 到直线BD 的距离3.3点到面的距离任取一点α∈Q 得m PQ ,是平面α的法向量,则有:点P 到平面α的距离mm PQ d ⋅=(向量PQ 在法向量m 的投影的长度).方法思路:求出平面的任一法向量m (方程组可求),在平面内任取一点Q 与点P 得一向量转化为PQ 在法向量的投影长度,套公式.3.4求两异面直线的距离知b a ,是两异面直线,b D C a B A ∈∈,,,,找一向量与两异面直线都垂直的向量m ,则两异面直线的距离mm AC d ⋅=例3如图,三棱柱中,已知A BCD 是边长为1的正方形,四边形 B B A A ''是矩形,。
法向量在立体几何中的应用.

法向量在立体几何中的应用查宝才(扬州市新华中学,江苏 225002)向量在数学和物理学中的应用很广泛,在解析几何与立体几何里的应用更为直接,用向量的方法特别便于研究空间里涉及直线和平面的各种问题。
将向量引入中学数学后,既丰富了中学数学内容,拓宽了中学生的视野;也为我们解决数学问题带来了一套全新的思想方法——向量法。
下面就向量中的一种特殊向量——法向量,结合近几年的高考题,谈谈其在立体几何有关问题中的应用。
1 法向量的定义1.1 定义1 如果一个非零向量n 与平面α垂直,则称向量n 为平面α的法向量。
1.2 定义2 任意一个三元一次方程:0=+++D Cz By Ax ,222(C B A ++)0≠都表示空间直角坐标系内的一个平面,其中),,(C B A n =为其一个法向量。
]1[事实上,设点),,(0000z y x P 是平面α上的一个定点,),,(C B A n =是平面α的法向量,设点),,(z y x P 是平面α上任一点,则总有n P P ⊥0。
∴ 00=⋅n P P , 故 0),,(),,(000=---⋅z z y y x x C B A , 即 0)()()(000=-+-+-z z C y y B x x A , ∴ 0000=---++Cz By Ax Cz By Ax ,……① 设 000Cz By Ax D ---=,则 ① 式可化为0=+++D Cz By Ax )0(222≠++C B A ,即为点P 的轨迹方程。
从而,任意一个三元一次方程:0=+++D Cz By Ax )0(222≠++C B A , 都表示一个平面的方程,其法向量为),,(C B A =。
2 法向量在立体几何中的应用 2.1 利用法向量可处理线面角问题 设θ为直线l 与平面α所成的角,ϕ为直线l 的方向向量v 与平面α的法向量n 之间的夹角,则有θπϕ-=2(图1)或θπϕ+=2(图2)图1 图2特别地 0=ϕ时,2πθ=,α⊥l ;2πϕ=时,0=θ,α⊆l 或α//l例1(2003年, 新课程 、江苏 、辽宁卷高考题)如图3,在直三棱柱111C B A ABC -中,底面是等腰直角三角形,ο90=∠ACB ,侧棱21=AA ,D ,E 分别是1CC 与B A 1的中点,点E 在平面上的射影是ABD ∆的重心G 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面法向量在立体几何中的应用
作者:张凤丽
来源:《新课程·中学》2014年第04期
高中数学提出了法向量的概念,它在立体几何研究中有着重要应用。
法向量从另一个角度描述了平面的具体位置关系,因而一部分与平面有关的问题,若能借助于法向量来解决,往往能避开传统方法中的诸多不便。
下面就具体来谈一谈法向量的应用。
一、法向量在直线与平面所成的角中的应用
如图,平面α与平面α的一条斜线AB,n为平面α的法向量,■为直线AB的方向向量,易得:直线AB与平面α所成的角等于■-或等于-■。
■
例1.在棱长为a的正方体ABCD-A1B1C1D1中,E,F分别是AB与C1D1的中点,求
A1B1与截面A1ECF所成角的正弦值。
解:如图,以A为原点,分别以AB,AD,AA1为x,y,z轴,建立空间直角坐标系,则有E(■,0,0),A1(0,0,a),F(■,a,a),B1(a,0,a),
■
设截面A1ECF的法向量为n=(x,y,z)
因为■=(■,0,-a),■=(■,a,0),
■=(a,0,0),
所以:■·n=(■,0,-a)·(x,y,z)=0,
■·n=(■,a,0)·(x,y,z)=0
即:■x-az=0且■x+ay=0,解得x=2z,y=-z,
令z=1,则n=(2,-1,1),
∵cos=■=■=■,
设A1B1与截面A1ECF所成角为θ,易知θ=■,
∴sinθ=cos=■。
二、法向量在有关平面与平面所成角问题中的应用
如图,设n1,n2分别为二面角α-l-β的两个半平面α、β的法向量,易知:与二面角α-l-β的平面角θ之间的关系为:θ=π-或者θ=,因此只要确定了两平面的法向量,即可求出二面角的大小。
■
例2.如图在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
SA=AB=BC=2AD,求平面SCD与平面SBA所成的二面角θ的正切值。
■
分析:此题若用传统的“一作,二证,三计算”的方法去解,过程很繁杂,利用向量来解就较简单。
解:如图,以A为原点,分别以AD,AB,AS为x,y,z轴,建立空间直角坐标系,并设AD=1,则有:
D(1,0,0),S(0,0,2),C(2,2,0),
易知平面SAB的法向量n1=■=(1,0,0),
设平面SCD的法向量n2=(x,y,z)因为■=(1,0,-2),■=(1,2,0),
由n2·■=n2·■=0,得x-2z=0,即x+2y=0即:x=2z,y=-z,
令z=1,则n2=(2,-1,1),
所以cosθ=■=■,易得:tanθ=■。
立体几何,因其要求学生具有较高的空间想象能力、逻辑思维能力以及解题过程中的技巧性、随机性,让学生感到头疼,而向量的引入就恰恰解决了这一点。
采用向量代数的观点,使很多过去难以处理的问题有了统一的处理方法,因此,加强高中教学中对向量的研究与应用是十分必要的。
(作者单位山东省滕州市第一中学)
?誗编辑王团兰。
