整式的混合运算专项训练(二)(北师版)(含答案)

合集下载

整式的混合运算(北师版)(含答案)

学生做题前请先回答以下问题问题1：①单项式×单项式：_____乘以_____，______乘以_____．②单项式÷单项式：_____除以_____，_____除以_____．问题2：①单项式×多项式：根据________________，转化为_________．②多项式×多项式：根据________________，转化为_________．③多项式÷单项式：借用____________，转化为_________．问题3：平方差公式：_____________________；完全平方公式：①_________________；②__________________．我们记完全平方公式的口诀是什么？整式的混合运算（北师版）一、单选题(共16道，每道6分)1.通过世界各国卫生组织的协作和努力，甲型H1N1流感疫情得到了有效的控制，到目前为止，全球感染人数约为人左右，占全球人口的百分比约为，将数字用科学记数法表示为( )A. B.C. D.答案：B解题思路：把写成的形式为．科学记数法需要注意两点：①小数点位置，②单位．其中小数点向右平移6个单位，因此指数为“-6”，此题无单位问题．故选B．试题难度：三颗星知识点：科学记数法2.绿色植物靠吸收光量子来进行光合作用，已知每个光量子的波长约为毫米，则每个光量子的波长可用科学记数法表示为( )米．A. B.C. D.答案：B解题思路：把毫米写成毫米的形式为毫米，再换算单位1毫米=米，因此毫米米．故选B．试题难度：三颗星知识点：科学记数法3.如图，在边长为的正方形中央剪去一边长为的小正方形，将剩余部分剪开密铺成一个平行四边形，则该平行四边形的面积为( )A. B.C. D.答案：C解题思路：由题意知，平行四边形的面积即是大正方形的面积减去小正方形的面积．故选C．试题难度：三颗星知识点：整式的乘除4.已知，那么的值为( )A.0B.1C.-1D.2答案：D解题思路：观察可知底数不同，但是都可以化成以2为底数的幂的形式，因此先转化，再进行计算．由题意知，即，，故选D．试题难度：三颗星知识点：同底数幂乘除5.若的展开式中不含的二次项，则与的关系是( )A.相等B.互为相反数C.互为倒数D.乘积为-1答案：A解题思路：观察式子结构，可以通过握手原则展开．∵上式中不含的二次项∴∴故选A．试题难度：三颗星知识点：整式的乘法6.若，，则的值为( )A.5B.9C.18D.24答案：D解题思路：根据“同底数幂相乘，底数不变，指数相加”的逆用进行计算．∵，故选D．试题难度：三颗星知识点：同底数幂的乘法7.已知，那么的值为( )A.5B.4C.1D.0答案：A解题思路：，，由题意知，即，．故选A．试题难度：三颗星知识点：积的乘方、幂的乘方8.计算的结果是( )A. B.C. D.2答案：A解题思路：观察结构，分为两个部分；先乘方，再乘除，最后算加减，如果有括号先算括号里面的．故选A．试题难度：三颗星知识点：幂的运算法则9.计算的结果是( )A. B.C. D.答案：C解题思路：故选C．试题难度：三颗星知识点：整式的乘除10.计算的结果是( )A. B.C. D.答案：B解题思路：故选B．试题难度：三颗星知识点：整式的乘除11.计算的结果是( )A. B.C. D.答案：B解题思路：故选B．试题难度：三颗星知识点：整式的乘除12.计算的结果为( )A. B.C. D.答案：D解题思路：故选D．试题难度：三颗星知识点：整式的混合运算13.计算的结果是( )A. B.C. D.答案：B解题思路：故选B．试题难度：三颗星知识点：整式的乘除14.当，时，代数式的值为( )A. B.C. D.答案：B解题思路：当，时，故选B．试题难度：三颗星知识点：化简求值15.的个位数字是( )A.1B.3C.7D.9答案：A解题思路：观察式子结构，直接算比较麻烦，对可以乘上构成平方差公式，为保证值不变，再乘．个位数字是3，个位数字是9，个位数字是7，个位数字是1个位数字是3，因此的个位数字是以3，9，7，1为循环节，循环周期为4，因为16能够被4整除，所以的个位数字为1．故选A．试题难度：三颗星知识点：整式的乘法16.已知是完全平方式，则的值为( )A.1B.3C.-3D.±3答案：D解题思路：观察式子特征，是完全平方式，所以应该由首平方，尾平方，二倍乘积组成，据此可判断为二倍乘积项，∴，又因为完全平方公式有两个，故，对比可得，故选D．试题难度：三颗星知识点：完全平方公式学生做题后建议通过以下问题总结反思问题1：若的展开式中不含项，求a的值．你是怎么思考的？（请说出两种思路）问题2：若，，则________．你是怎么思考的？。

北师大版数学六年级上册 2.4分数混合运算(二)(2) 同步练习(含答案)

第4课时分数混合运算(二)(2)(教材P 25)一、(新知导练)填一填。

幸福花园总占地面积60公顷，其中绿化面积占总占地面积的38，建筑的占地面积有多少公顷？60×38求的是( )面积，60－60×38求的是()面积。

1－38求的是( )，60×(1－38)求的是()。

二、先想想运算顺序，再用你喜欢的方法计算。

(56＋49)×18 78×7×3243×65＋43×45 23÷8＋13×18三、看图列式计算。

1.2.四、妈妈的支付宝里有24000元，第一次转出总数的16，第二次转出总数的38，妈妈从支付宝中一共转出多少元？五、养殖场有家禽600只，其中鸡占14，鸭占35，其余是鹅。

1．鸭比鸡多多少只？2．如果明年养殖场的家禽增加14，明年养殖场一共需要养家禽多少只？六、刘叔叔今年承包了45km 2荒山，其中13栽种杉树，余下部分的35栽种油茶。

刘叔叔今年栽种油茶的面积是多少平方千米？第4课时分数混合运算(二)(2)一、绿化建筑的占地建筑的占地面积占总占地面积的几分之几建筑的占地面积二、23 196 83 18三、1.90×(1－56)＝15(t) 2.52×(1－14)＋52＝91(人)四、24000×(16＋38)＝13000(元)五、1.600×(35－14)＝210(只) 2.600×(1＋14)＝750(只)六、45×(1－13)×35＝18(km 2)。

北师大版七年级下册第一章整式的运算全章同步训练以及答案

北师大版七年级下册第一章整式的运算全章同步训练以及答案(总41页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除- 2 - 第一章整式的运算同步练习1.1 整式一、精心选一选⒈ 下列说法正确的个数是【】① 单项式a 的系数为0，次数为0； ②21-ab 是单项式； ③ －xyz 的系数是－1，次数是1； ④ π是单项式，而2不是单项式．A ．0个B ．1个C ．2个D ．3个 ⒉若单项式1232--x n m 和c b a 245的次数相同，则代数式322+-x x 的值为【】A ．14B ．20C ．27D ．35二、耐心填一填：⒈ 3a 2b 3c 系数是次数是；πR 2系数是次数是． ⒉ n ＝时，单项式231+n xy 的次数是6．三、用心做一做：⒈ 下列各代数式是不是单项式？如果是，请指出它们的系数和次数． ⑴ a 52 ⑵ b a 2- ⑶32b a - ⑷ 0.1532y x ⑸ 2x ＋1 ⑹ y ⑺ －m⒉ 小明认为既然单项式322y x 的次数是5，那么多项式322y x +的次数也是5．他的想法对吗为什么由此，你能谈谈单项式和多项式次数的确定有什么不同吗相信你能完成一、精心选一选⒈ 下列说法正确的个数是【】- 3 - ① 单项式是整式；② 单项式也是多项式；③ 单项式和多项式都是整式．A ．0个B ．1个C ．2个D ．3个⒉ 把3a 3－5和a 2b ＋ab 2＋1按某种标准进行分类时属于同一类，则下列哪一个多项式也属于此类【】A ．－a 5－b 5B ．4x 2－7C ．xyz －1D ．a 2＋2ab ＋b 2⒊ 若多项式(m ＋4)x 3＋2x 2＋x －1的次数是2，则m 2－m 的值为【】A ．10B ．12C ．16D ．20二、耐心填一填⒈ 多项式x 3y ＋5xy －6－4xy 2是的和．⒉ 5x 2＋4x －3是次项式，其中常数项是．⒊ 如图1-1-1则这个平面图形的面积是。

北师大版数学七年级下册《整式的运算》单元测试卷及答案

第一章整式及其运算单元测试一、选择题：（每题3分，共36分）1．下列计算正确的是 ( )347.235A x x x ⋅= 3331243.x x x B =⋅ 336.235C x x x += 325.428D x x x ⋅=2．下列多项式乘法，能用平方差公式计算的是 ( ))23)(23(+--⋅x x A ))((a b b a B +---⋅ (32)(23C x x ⋅-+- )32)(23(-+⋅x xD 3．下列各式正确的是 ( )222)(b a b a A +=+⋅ 2(6)(6)6B x x x ⋅+-=-22)()(x y y x C -=-⋅⋅ 42)2(22++=+⋅x x x D4．下列计算正确的是 ( )1052.(10)(5)2A a a a ÷= 2321.n n n B x x x +-+÷=2()()C a b b a a b ⋅-÷-=- 43331.(5)(10)2D a b c a b ac -÷=- )45)(45.(52222y x y x +--运算的结果是 ( )441625.y x A -- 4224164025.y y x x B -+-⋅44.2516C x y - 4224164025.y y x x D +-6．下列计算正确的是 ( );:4)2(:6)3(;872222221055y y y b a b a q p pq x x x =⋅-=-==+④③②①6322242:();b b b p q p q ÷=-=-⑤⑥A. ①②④B.②③⑤C.③④D.④⑥7．运算结果是 42221b a ab +-的是 ( )22.(1)A ab -+ 22)1.(ab B +222.(1)C a b -+ 222.)1.(b a D --8．若)1)(2(-+-x a x 中不含x 的一次项，则 ( )1.=a A 1.-=a B .2C a =-2.=a D9．若,2,32==x x b a 则232)()(x x b a -的值为 ( )A. 0B. 1C. 3D. 510.长方形一边长为,2b a +另一边比它小a b -则长方形面积为 ( )222.b ab a A -+ ab a B +22.2244.b ab a C ++ 22.252D a ab b ++11.下列多项式的积，计算结果为3372234+--+x x x x 的是 ( ))3)(12)(1(2++-⋅x x x A )1)(12)(3(2++-⋅x x x B2(1)(21)(3)C x x x ⋅+-- )3)(1)(12(2---⋅x x x D12．若2449x mx -+是一个完全平方式，则聊的值为 ( ).14 .14 .28 .28A B C D ±± 二、填空题：（每空2分，共46分）23.132y x -的系数是，次数是． 14．若2512m x y --与122+n xy 是同类项，则_______ m n +=⋅ 23522315()()()_______;()()()_____b b b x x x ⋅---=---=⋅23232316.(2)_____.(2)(4)_____xy a b a b -=÷-=⋅2217(2)(2)______;(35)(_______)259.a b a b x y y x ⋅---=+=-221218(2)______,()_______.43x y a b ⋅-=--= 19．计算：4026911162()()_______(710)(410)________33--⨯⨯---=⋅⨯⨯=⋅ 220082009120.200920082010_______;(3)()_______3-⨯=-⨯-=⋅ 2221(32)(32)(94)________(1)(1)________.a b a b a b m n m n ⋅+-+=⋅----=22.已知：3m 2,5,_________m n n a a a +===⋅则23.若,2632-=--x x 则2266_______.x x -+=24.若,0323=--y x 则84_______.x y ÷=25.若,51=-x x 则21()________x x+=⋅ 26．已知：,0136422=++-+y x y x 则_______x y +=⋅27.若x ，y 为正整数，且,3222=⋅y x 则x ，y 的值共有对．三、解答题：（共68分）28．计算：（每小题4分，共40分）;)()1(33a a a s ÷-⋅23235223(2)2()2.(2)x x x x x x -⋅-⋅+(3)(2)(3);a a +-);12(6)2)(4(23-+-x x x x2(5)()(2)(2);x y x x +-+-)3)(3()23)(32)(6(x y y x x y y x +---+2)2(2)4)(2)(7(y x y x y x ++-+.)2()4824)(8(2223223xy y x y x y x -+-+-2211(9)(2)(2)22x y x y -+ 2111(10)(3)(9)(3)242a a a --+ 29．先化简，再求值：（每小题5分，共10分）2(1)(2)(21)5(1)(1)3(1)m m m m m +--+-++其中.1-=m),21(:)](2)())[(2(222y y x y y x y x ---+--+其中.1,21-==y x 30．（5分）解方程：.)2(3223)1)(1(2-+-=--+x x x x x 31．（8分）若,2,52-==-xy y x 求下列各式的值：.)2)(2(;4)1(222y x y x ++32.（5分）菜单位为响应政府发出的全民健身的号召，打算在长宽分别为20米和11米的长方形大厅内修建一长方形健身房ABCD，该健身房的四面墙壁中有两侧沿用大厅的旧墙壁（如图为平面示意图），已知装修旧墙壁的费用为口元，平方米，比新建（含装修）墙壁的费用每平方米少50元，设健身房的高为3米，一面旧墙壁AB的长为x米，BC为)5x米，则修建健身房墙壁的总投入(为多少元？（用含口、x的代数式表示）参考答案一、DBCDB DACBD CD二、13.32- ,3 14.5 15.10b ,7x 16.3648,2x y a --17.224,53a b y x -+- 18.222211444,1639x xy y a ab b -+++ 19.168,2.810-⨯ 20. 12008,3-- 21.44228116,21a b n m m --+- 22.4023.14 24.825.29 26.略 27.4三、28.(1)835a a a =-÷=-(2)6282688882().282284x x x x x x x x x =--+=--+=(3)222366a a a a a =+--=--(4)333233228(6126)861262126x x x x x x x x x x x =-+-=--+=-+(5)22222424x xy y x xy y =++-+=++(6)222222943391278y x xy x y xy y x xy =---++=-+(7)222222828836x xy y x xy y x xy =--+++=+(8)32232222(2484)(4)621x y x y x y x y x y =-+-÷=-+-(9)=2222224224111[(2)()](4)1622416x y x y x x y y -=-=-+ (10)=22224211191(9)(9)(9)81444216a a a a a --=-=-+ 29. (1)2222325(1)3(21)96;1m m m m m m m =+---+++=+=-当时;原式=-3(2)=211(42)()84;22xy y y x y -÷-=-+当x=,y=-1时;原式=-8 30.222222321442366924624246692244246 13x=26x=2x x x x x x x x x x x x x x x ---=+-+--=-+-+---+=-++31.22222222(1)(2)444()425,2425817x y x xy y x xy x y xyx y xy x y -=-+∴+=++-==-∴+=-= 222222(2)(2)44417,2(2)1789x y x xy y x y xy x y +=+++==∴+=-= 且32.[3(5)3][3(5)3](50)12303007503(25)(250)()x x a x x a ax a x x a +-⨯⨯++-⨯⨯+=-+-=-+元。

专题1.4 幂的运算与整式混合运算专项训练(北师大版)(原卷版)

专题1.4 幂的运算与整式混合运算专项训练【北师大版】考卷信息：本套训练卷共40题，题型针对性较高，覆盖面广，选题有深度，可加强学生对幂的运算与整式混合运算的理解！1．（2023春·四川达州·七年级校考期末）计算：(1)a3⋅a4⋅a+(a2)4−(−2a4)2．(2)a⋅a7−(−3a4)2+a10÷a2(3)−3x2(2x−4y)+2x x2−xy．2．（2023春·陕西西安·七年级校考期中）计算ab2b−2ab2+1(1)−12(2)(2x−y)(x+y)−(x−y)23．（2023春·山东菏泽·七年级统考期中）计算：a2b3；(1)(−2a2b)3÷(−2ab)⋅13(2)(27x3+18x2−3x)÷(−3x)．4．（2023春·山西晋中·七年级统考期中）计算．(1)−3x2y2⋅6xy3÷9x3y4(2)(a+3)(4a−1)−2(3+a)(2a+0.5)5．（2023春·安徽宣城·七年级校考期中）计算：(2x+y)(x−y)+y2⋅(2x)2．6．（2023春·湖南永州·七年级校考期中）计算：(1)1042；(2)(a+b)2−(a−b)2．7．（2023春·山东枣庄·七年级统考期中）计算:(1)a3·a5+(3a4)2÷a2．(2)计算: (x+2y)2+(x−2y)(x+2y)+x(x−4y)．8．（2023春·安徽滁州·七年级校考期中）（1）若3×9n－1×32n＋1=316，求n的值；（2）若2x＋2+2x＋1=24，求x的值．9．（2023春·广西北海·七年级统考期中）用简便方法计算：(1)100.2×99.8(2)103210．（2023春·湖南益阳·七年级校考期中）计算：(1)a2⋅a6−(−2a4)2；(2)(1+a)(1−a)+(a+3)2．11．（2023春·河北石家庄·七年级校考期中）计算：(1)(−2a2b)3⋅(ab2c)÷a4(2)2xy2−3xy2+5xy3(−xy)(3)(3x+2)(x+1)+2(x−3)(x+2)12．（2023春·江苏常州·七年级统考期中）用简便方法计算：(1)101×99(2)32×22+14×23+10×2413．（2023春·上海·七年级统考期末）计算：a2b+1ab−1⋅2ab−2a⋅(−ab)2．214．（2023春·福建莆田·七年级校考期中）（1）已知2m=a，32n=b，m，n为正整数，求23m+10n的值；（2）已知x n=3，y n=2，求xy22n的值．a2b)3⋅(−4ab2)÷(−2a2b)；15．（2023春·福建福州·七年级校考期中）（1）计算：(−12（2）用整式乘法公式计算：20222−2021×2023．16．（2023春·安徽宣城·七年级校考期中）先化简，再求值：(3x−2y)(3x+y)−3(x−y)(x+y)−(−y+2x)2÷x，其中x=1，y=2．17．（2023春·河南驻马店·七年级驻马店市第二初级中学校考期中）先化简，后求值：(x−y)(x+2y)−(x+y)2÷y，其中(x−2)2+|1+y|=0．18．（2023春·河北保定·七年级校考期中）先化简，再求值：(x+y)(x−y)+(x+y)2−6x2y+4xy2÷2y，其中x=−2，y=1．319．（2023春·安徽宿州·七年级校考期中）计算∶(1)(a2b)2÷(a2b2)(2)99×101+1(用乘法公式计算)(3)x2y(x2+2y)−2x2y2(4)化简求值(x+2y)2+(x+2y)(x−2y)−4xy，其中x=1，y=2100．20．（2023春·湖南永州·七年级校考期中）（1）已知a+1a =3，求a2+1a2的值；（2）已知(a−b)2=9，ab=18，求a2+b2的值．21．（2023春·湖南永州·七年级校考期中）先化简、再求值：12x2⋅16xy−4y2−4x3y+4x2y2，其中x=2，y=−1．22．（2023春·陕西西安·七年级校考期中）已知m满足(3m−2015)2+(2014−3m)2=5．(1)求(2015−3m)(2014−3m)的值．(2)求6m−4029的值．23．（2023春·陕西西安·七年级校考期中）先化简，再求值(1)(3a+b)2−(b+3a)(3a−b)−6b2÷(−2b)，其中a=−13,b=−2．(2)已知x2−x+1=0，求代数式(x+1)2−(x+1)(2x−1)的值．24．（2023春·陕西西安·七年级校考期中）求值，若(x+3p)x2−x+13q的积中不含x的一次项与x的二次项，(1)求p,q的值；(2)求代数式6p−q的值．25．（2023春·湖南娄底·七年级校考期中）（1）计算：(−2m)2⋅2−2m−3；（2）用简便方法计算：186.72−2×186.7×86.7+86.72．26．（2023春·河北保定·七年级校考期中）（1）(−a)2⋅(a2)2÷a3（2）(2x−3y)2−(y+3x)(3x−y)（3）(2x−y+1)(2x+y−1)（4）用简便方法计算：1232−121×11927．（2023春·上海闵行·七年级上海市民办文绮中学校考期中）因式分解(x2+x)2+4(x2+x)−12．28．（2023春·上海·七年级统考期末）计算：x⋅(−x)5⋅x6+(−x5)2⋅x2+(−x)43．29．（2023春·上海·七年级统考期末）化简求值：(x−y)(y−x)−−y2+2x(x−y)，其中x=12，y=−2．30．（2023春·福建宁德·七年级统考期末）计算：(1)(a−b)2+2a(a+b)；(2)[(4x+y)(x−y)+y(x+y)]÷2x，其中x=2，y=−1．31．（2023春·山东淄博·六年级统考期中）计算：(1)x(x+2y)−(x−2y)2；(2)(a2b−4ab2+b)÷b−(a+b)(a−b)．32．（2023春·山东烟台·六年级统考期中）计算：(1)(m2n)4⋅(−m2n)3÷(m2n)5；(2)a(a+2)−(a+b)(a−b)−b(b−3)．33．（2023春·黑龙江哈尔滨·七年级哈尔滨市萧红中学校考期中）计算(1)(−a2)5⋅(b4)2÷(ab)3(2)982+98×4+4（用简便算法计算）34．（2023春·江苏淮安·七年级统考期末）计算(1)已知2x=5，2y=3，求：2x−2y的值．(2)x−2y+3=0，求：2x÷4y×8的值．35．（2023春·江苏扬州·七年级统考期中）运用乘法公式计算：(1)(3−4y)(3+4y)+(3+4y)2(2)(2a−b+3)(2a−b−3)36．（2023春·广西北海·七年级统考期中）计算：(1)3x4⋅x2+(2x2)3(2)3a(9a+3)−4a(2a−1)37．（2023春·山东泰安·六年级统考期中）计算：(1)a4⋅a2−(−a2)3a5b3÷(−a3b)⋅(−3a)2(2)19(3)(a−2b)(a2+2ab+4b2)(4)(a−2b+c)(a+2b+c)38．（2023春·安徽六安·七年级统考期中）计算：(1)(x+1)(x−2)−(x−2)2；(2)(a+2b−3c)(a−2b+3c)．39．（2023春·广东深圳·七年级统考期末）计算：(1)a2⋅a4+(2a3)2−3a7÷a；(2)m(2m−3)−(m−4)(m+1)．40．（2023春·河南南阳·七年级统考期末）先化简，再计算：。

北师大版三年级数学上册混合运算专项练习及答案(必考题)

北师大版三年级数学上册混合运算专项练习及答案（必考题）一、口算1、口算．49÷7×3＝ 63÷9×5＝ 4×6÷3＝ 45÷（54÷6）＝32÷8×5＝ 16＋16÷8＝ 81÷9÷9＝ 28÷（42÷6）＝2、口算．500×3= 25×4= 0×450= 7×8+9= 110×4= 3×220= 4×500= 0×10+90= 200×8= 800×9= 5×700= 28—40×0= 102×2= 101×7= 42÷7= 72÷9=3、想一想，算一算。

90÷3＝ 20÷5＝ 40÷8＝900÷3＝ 200÷5＝ 400÷8＝9000÷3＝ 2000÷5＝ 4000÷8＝4、口算题。

60÷2＝ 500÷5＝ 140﹣70＝ 33÷3＝300÷5＝ 360÷3＝ 29×3＝ 550÷5＝30×30＝ 24÷4＝ 30×4＝ 240÷8＝5、直接写得数48÷4= 30×14= 25×4= 72÷9×5= 0÷15= 56×0= 360÷9= 10×15÷5= 10×20= 50×11= 54÷3= 88÷4×2=二、竖式计算1、用竖式计算，带△的要验算。

北师大版七年级数学上册整式计算题专项练习(附答案)

北师大版七年级数学上册整式计算题专项练习(附答案)1.将表达式化简：$-a-b+2a-b=-b+a$2.将表达式化简：$(x+2)(y+3)-(x+1)(y-2)=xy+3x+2y+6-xy+x-2y+2=x+3x+2+6+x-2y+2=4x-2y+10$3.将表达式化简：$(2x-y)(2x+y)+2y2=4x2-y2+2y2=4x2$4.将表达式化简：$\frac{x(x-y)}{x-2}+\frac{2y}{x-2}=\frac{x(x-y)+2y}{x-2}=\frac{x^{2}-xy+2y}{x-2}$6.将表达式化简：$(2a+1)^{2}-2(2a+1)+3=4a^{2}+8a+4-4a-2+3=4a^{2}+4a+5$8.将表达式化简：$-(x-5)(x+5)-\frac{(3x-2y)(-2y-3x)}{x+1}=\frac{-(x^{2}-25)(x+1)+(9x^{2}-12xy+4y^{2})}{x+1}=\frac{-x^{3}-10x^{2}-21x+4y^{2}}{x+1}$10.将表达式化简：$3(x+1)(x-1)-(2x-1)(x+y)2(x-y)2=3(x^{2}-1)-2x^{3}+x^{2}y+xy^{2}-2xy^{2}+2y^{3}=3x^{2}-3-2x^{3}+x^{2}y-y^{2}$15.将表达式化简：$-\frac{1}{2}-(-1)^{2006}+\frac{2^{11}\times(-3)^{432}}{2}= -\frac{1}{2}-1+2^{10}\times3^{432}=2^{10}\times3^{432}-\frac{3}{2}$20.将表达式化简：$(2a-1)^{2}+(2a-1)(a+4)=4a^{2}-4a+1+2a^{2}+7a-4=6a^{2}+3a-3$21.将表达式化简：$(x+2y)^{2}-2(x-y)(x+y)+2y(x-3y)=x^{2}+4xy+4y^{2}-2(x^{2}-y^{2})+2xy-6y^{2}=x^{2}+6xy-8y^{2}$22.将表达式化简：$5(x-1)(x+3)-2(x-5)(x-2)=5(x^{2}+2x-3)-2(x^{2}-3x+10)=3x^{2}+16x-40$23.将表达式化简：$(a-b)(a^{2}+ab+b^{2})=a^{3}-b^{3}$24.将表达式化简：$(3y+2)(y-4)-3(y-2)(y-3)=3y^{2}-5y-18$25.将表达式化简：$a(b-c)+b(c-a)+c(a-b)=ab-ac+bc-bc+ac-ab=0$26.将表达式化简：$(-2mn^{2})^{2}-4mn^{3}(mn+1)=4m^{2}n^{4}-4m^{2}n^{4}-4mn^{3}= -4mn^{3}$28.将表达式化简：$-(x+2)(x-2)=-(x^{2}-4)=-x^{2}+4$30.将表达式化简：$(x-3y)(x+3y)-(x-3y)=x^{2}-9y^{2}-x+3y$1.原式=2.原式=-400+4=9604；原式=-+1=13.原式=900×219；原式=-(2009+1)(2009-1)=2xxxxxxxxxxxx=-xxxxxxx4.原式=6a^2+3a-3，当a=2时，原式=6×(-2)^2+3×(-2)-3=24-6-3=155.原式=-x^2+6xy，当x=2，y=2时，原式=-(-2)^2+6×(-2)×2=-4-24=-286.原式=-3x^2+24x-357.原式=a^3-b3=(a-b)(a^2+ab+b^2)8.原式=5y-269.原式=6xy-18y210.原式=(a-c+b)^2-b^2=a^2-2ac+2bc+c^2-b^211.原式=15×10^912.原式=2a+2解答题：1.①原式=12-(-8)+(-7)-15=38②原式=-1+2×(-5)-(-3)÷(-1)=-1+(-10)-3=-14③原式=2x-3y+5x+4y=7x+y④原式=5a+2a^-1-4(3-8a+2a)=5a+2a^-1-12+32a-8a=34a+2a^-1-122.1) 原式=4-2×2-(-36)÷4=4-4+9=92) 原式=9a-6b-2a+6b=7a3.①原式=7x+4(x-2)-2(2x-x+3)=7x+4x-8-2x+2=9x-6②原式=4ab-3b-[(a+b)-(a-b)]=4ab-3b-a-b+a+b=4ab-3b-a③原式=3mn-5m-3m+5mn=8mn-8m④原式=2a+2(a+1)-3(a-1)=2a+2a+2-3a+3=4a+54.①原式=4a+18b-15a-12b=4a-15a+18b-12b=-11a+6b②原式=3x+6x^-1-3x-4x^-1=2x+2x^-15.原式=3(x-1)-(x-5)=3x-3-x+5=2x+26.原式=3(x+y)+4(x+y)-6(x+y)=7(x+y)=7(5+3)=567.原式=2(x-3y)-(x-y)=2x-6y-x+y=x-5y8.由6M=2N-4得M=N/3-2/3，代入M=x+3x-5和N=3x+5中得到：x+3x-5=N/3-2/3+3x-5解得x=7/69.原式=A+B=5a-2ab-4a+4ab=a先化简，再求值：3（A+B）﹣2（2A﹣B），其中A=﹣2，B=1．分析：先代入数值，再按照整式的加减运算顺序进行计算．解答：代入A=﹣2，B=1得：3（A+B）﹣2（2A﹣B）=3（﹣2+1）﹣2（2（﹣2）﹣1）=3﹣4﹣（﹣5）=9．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握整式的加减运算顺序及代入数值的方法．10．设a=14x﹣6，b=﹣7x+3，c=21x﹣1．1）求a﹣（b﹣c）的值；2）当x=时，求a﹣（b﹣c）的值．分析：先代入数值，再按照整式的加减运算顺序进行计算．解答：代入a=14x﹣6，b=﹣7x+3，c=21x﹣1得：1）a﹣（b﹣c）=14x﹣6﹣（﹣7x+3﹣21x+1）=14x﹣6﹣﹣7x+3﹣21x﹣1=6x﹣4；2）当x=时，a﹣（b﹣c）=6×﹣4﹣4=﹣28．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握整式的加减运算顺序及代入数值的方法．11．化简求值：已知a、b满足：|a﹣2|+（b+1）=0，求代数式2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）的值．分析：先化简|a﹣2|+（b+1）=0得a=2，b=﹣1，再代入求值．解答：代入a=2，b=﹣1得：2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）=2（2×2﹣3（﹣1））﹣（2﹣4（﹣1））+2（﹣3×2+2（﹣1））=4+9+6=19．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握绝对值的性质及代入求值的方法．12．已知（x+1）+|y﹣1|=0，求2（xy﹣5xy）﹣（3xy﹣xy）的值．分析：先解方程|x﹣1|+（y+1）=0，得x=﹣1，y=﹣2，再代入求值．解答：解方程得x=﹣1，y=﹣2，代入得：2（xy﹣5xy）﹣（3xy﹣xy）=2（﹣1×﹣2﹣5﹣1×﹣2）﹣（3﹣1×﹣2）=4﹣（3+2）=﹣1．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握绝对值的性质及代入求值的方法．解答：将3（x+y）+4（x+y）﹣6（x+y）化简得：(3+4-6)(x+y)=x+y=-2代入x=5，y=3，得到3（5+3）+4（5+3）﹣6（5+3）=24 所以，代数式3（x+y）+4（x+y）﹣6（x+y）的值为24.点评：本题考查了整式的加减、化简和求值，需要熟练掌握去括号、合并同类项和代入数值的方法。

专题1.4 幂的运算与整式混合运算专项训练(北师大版)(解析版)

专题 1.4 幂的运算与整式混合运算专项训练
考卷信息：
【北师大版】
本套训练卷共 40 题，题型针对性较高，覆盖面广，选题有深度，可加强学生对幂的运算与整式混合运算的理解！
1．（2023 春·四川达州·七年级校考期末）计算：
(1)�3 ⋅ �4 ⋅ � + (�2)4 − ( − 2�4)2．
(2)� ⋅ �7 − ( − 3�4)2 + �10 ÷ �2 (3)−3�2 2� − 4� + 2� �2 − �� ．【答案】(1)−2�8
(2)−7�8
(3)−4�3 + 10�2�
【分析】（1）分别根据同底数幂的乘法法则，幂的乘方与积的乘方运算法则化简即可；（2）分别根据同底数幂的乘除法法则以及积的乘方运算法则计算即可；（3）根据单项式乘多项式的运算法则计算即可．【详解】（1）�3 ⋅ �4 ⋅ � + (�2)4 − ( − 2�4)2
【分析】（1）根据单项式乘以多项式运算法则，进行计算即可；
（2）根据多项式乘以多项式，完全平方公式，进行计算即可．
【详解】（1）解：−
1 2
�
2 �2 − 2� 2 + 1
3
=−
1 3
�3
2 + �2
3 −1�
2
；
（2）解： 2� − � � + � − � − � 2
= 2�2 + �� − �2 − �2 − 2�� + �2
第3页共 29页
= 54�4�5 ÷ 9�3�4 = 6��；（2）解：原式= 4�2 − � + 12� − 3 − 4�2 − 12� − � − 3 =− 2� − 6．【点睛】本题考查整式的混合运算，熟练掌握选积的乘方、单项式相乘除、多项式乘以多项式运算法则是解题的关键． 5．（2023 春·安徽宣城·七年级校考期中）计算： 2� + � � − � + �2 ⋅ 2� 2．【答案】8�4 − 4�3� 【分析】先对括号内的整式乘法进行计算，括号外利用积的乘方进行计算，再将括号内的各项合并同类项，最后和括号外的单项式相乘即可．【详解】解： 2� + � � − � + �2 × 2� 2 = 2�2 − 2�� + �� − �2 + �2 × 4�2 = 2�2 − �� × 4�2 = 8�4 − 4�3� 【点睛】本题考查整式乘法的混合运算，积的乘方，多项式乘多项式等，掌握相关的运算法则和运算顺序是解题的关键． 6．（2023 春·湖南永州·七年级校考期中）计算： (1)1042； (2) � + 2 − � − 2．【答案】(1)10816 (2)4�

整式的混合运算专练习题附答案

整式的混合运算专练学校:___________姓名：___________班级：___________考号：___________一、解答题1．先化简，再求值：（1）()()33232222y y y y -÷，其中1y =；（2）()()()()()222222x y x y x y x xy x ⎡⎤-+-+-+÷-⎣⎦，其中x =4y =．【答案】（1）72y -，2-；（2）4x y -+，19．【分析】（1）原式利用幂的乘方与积的乘方运算法则计算，再利用单项式乘除单项式法则计算得到最简结果，把y 的值代入计算即可求出值；（2）原式利用平方差公式，完全平方公式，以及多项式除以单项式法则计算得到最简结果，把x 与y 的值代入计算即可求出值．【详解】解：（1）()()33232222y y y y -÷ 792282y y y =-÷ 7724y y =-72y =-，当1y =时，原式7212=-⨯=-；（2）()()()()()222222x y x y x y x xy x ⎡⎤-+-+-+÷-⎣⎦()()222222442x xy y x y x xy x =-++---÷-()()24x xy x =-÷- 4x y =-+，当x =4y =时，原式4419=⨯=．【点睛】本题考查了整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键． m n 2m n +（2）先化简，再求值：22(3)(24)(2)x y x x y x y ⎡⎤---+÷-⎣⎦，其中1x =，2y =．【答案】（1）18；（2）92x y -，-8 【分析】（1）逆用同底数幂的乘法法则和幂的乘方法则计算；（2）先把中括号里去括号合并同类项，再算除法，然后把1x =，2y =代入计算；【详解】解：（1）因为=2m x ，=3n x ，所以=2m x ，29n x =，所以218m n x x ⋅=，所以218m n x +=；（2）原式()22226924(2)x xy y x xy x y =-+-++÷-()229(2)xy y y =-+÷-22(2)9(2)xy y y y =-÷-+÷- 92x y =-，当1x =，2y =时，原式9122=-⨯19=-8=-．【点睛】本题考查了整式的混合运算，熟练掌握运算顺序及乘法公式是解答本题的关键．混合运算的顺序是先算乘方，再算乘除，最后算加减；同级运算，按从左到右的顺序计算；如果有括号，先算括号里面的，并按小括号、中括号、大括号的顺序进行；有时也可以根据运算定律改变运算的顺序． 3．计算：()()()222x y x y x y x +++-- 【答案】2xy 【分析】先根据完全平方公式计算，再合并同类项即可【详解】=2222222x xy y x y x +++-- =2xy ．【点睛】本题考查了整式的混合运算，熟练掌握运算顺序及乘法公式是解答本题的关键．完全平方公式是(a ±b )2=a 2±2ab +b 2；平方差公式是(a +b )(a -b )=a 2-b 2． 4．计算下列各题（1）()222(2)x y xy -⋅- （2）24(1)(25)(25)x x x +-+-【答案】（1）538x y -；（2）8x 29+．【分析】（1）先进行积的乘方计算，再计算乘法即可；（2）先分别利用完全平方公式公式和平方差公式计算，在进行合并同类项即可．【详解】解：（1）()222(2)x y xy -⋅-42=4(2)x y xy ⋅- 53=8x y -；（2）24(1)(25)(25)x x x +-+- 22=4(1)(4225)x x x +--+22=444825x x x -+++=829x +．【点睛】本题考查整式的运算，解题的关键是熟练运用整式的运算法则，本题属于基础题型．5．先化简，再求值：(()3m m m m --，其中1m =．【答案】32m -；1. 【分析】根据题意利用平方差公式和整式乘法运算进行化简，进而代入1m =利用实数的运算法则进行计算即可. 【详解】22=--+m m m23=-32m把1m-=-=.m=代入可得：321)21【点睛】本题考查含算术平方根的整式化简，熟练掌握平方差公式和整式乘法运算法则以及算术平方根性质是解题的关键.6．计算：（1）x（x﹣2）﹣（x＋2）（x﹣2），其中x＝12（2）（2x＋y）（2x﹣y）＋4（x＋y）2（3）（a﹣3）2﹣a（a＋8）（4）（x﹣2）2﹣x（x＋4）【答案】（1）﹣2x+4，3（2）8x2+8xy+3y2（3）﹣14a+9（4）﹣8x+4【分析】（1）先计算乘法，再合并即可求解；（2）先利用平方差公式和完全平方公式计算，再合并即可求解；（3）先计算乘法，再合并即可求解；（4）先计算乘法，再合并即可求解．（1）解：原式＝x2﹣2x﹣（x2﹣4）＝x2﹣2x﹣x2+4＝﹣2x+4，时，原式＝﹣1+4＝3．当x＝12解：(2x+y）（2x﹣y）+4（x+y）2＝4x2﹣y2+4（x2+2xy+y2）＝4x2﹣y2+4x2+8xy+4y2＝8x2+8xy+3y2．（3）（a﹣3）2﹣a（a+8）=a2﹣6a+9﹣a2﹣8a＝﹣14a+9．（4）（x﹣2）2﹣x（x+4）．（x﹣2）2﹣x（x+4）＝x2+4﹣4x﹣x2﹣4x＝﹣8x+4．【点睛】本题主要考查了整式的混合运算，熟练掌握平方差公式和完全平方公式，整式的混合运算法则是解题的关键．7．先化简，再求值：（a+2）2+（1+a）（1﹣a），其中12a=-．【答案】45,3a 【分析】先利用完全平方公式与平方差公式进行整式的乘法运算，再合并同类项，最后把12 a=-代入化简后的代数式求值即可. 【详解】解：（a+2）2+（1+a）（1﹣a）原式22441a a a=+++-45a=+当12a=-时，原式14525 3.2【点睛】本题考查的是整式的乘法运算，完全平方公式与平方差公式的应用，熟练的利用两个公8．计算：()()()222x y y x y x +-+-．【答案】252x xy + 【分析】先运用乘法公式进行计算，再合并同类项即可．【详解】解：()()()222x y y x y x +-+-，=()222224x xy y y x ++--，=222224x xy y y x ++-+， =252x xy +．【点睛】本题考查了整式的乘法，解题关键是熟记乘法公式，准确进行计算． 9．计算（1）（﹣3ab 2）（﹣a 2c ）2÷6ab 2；（2）（x ＋2y ）（x ﹣2y ）﹣（x ＋y ）2 【答案】（1）﹣12a 4c 2；（2）﹣5y 2﹣2xy ．【分析】（1）先计算积的乘方，然后根据正式的乘除计算法则进行求解即可；（2）利用完全平方公式和平方差公式先去括号，然后根据整式的加减计算法则求解即可．【详解】解：（1）()()222236ab a c ab --÷242236ab a c ab =-⋅÷ 522236a b c ab =-÷4212a c =-；（2）()()()222x y x y x y +--+ ()222242x y x xy y =--++ 222242x y x xy y =----【点睛】本题主要考查了积的乘方，整式的乘除运算，乘法公式，以及整式的四则混合运算，解题的关键在于能够熟练掌握相关计算法则．10．①先化简，再求值：（a 2b －2ab 2－b 3）÷b －（a －b ）（a ＋b ），其中a ＝－2，12b =． ②若x 2＋ax ＋8和多项式x 2－3x ＋b 相乘的积中不含x 3、x 2项，求ab 的值．【答案】①-2ab ，2；②3．【分析】①先算乘法和除法，再合并同类项，最后代入求出即可．②多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加．结果中不含二次项和三次项，则说明这两项的系数为0，建立关于a ，b 等式，求出后再求代数式值，即可求得ab 的值．．【详解】解：①（a 2b -2ab 2-b 3）÷b -（a -b ）（a +b ） =a 2-2ab -b 2-a 2+b 2 =-2ab ，当a =-2，12b =时，原式=12(2)22；②∵（x 2+ax +8）（x 2-3x +b ）=x 4+（-3+a ）x 3+（b -3a +8）x 2+（ab-24）x +8b ，又∵不含x 2、x 3项， ∴-3+a =0，b -3a +8=0，解得a =3，b =1， ∴ab =3×1=3．【点睛】本题考查整式的混合运算，多项式乘多项式．①中主要考查学生的化简能力和计算能力；②中根据不含某一项就是这一项的系数等于0列式求解a 、b 的值是解题的关键．11．（1）化简：22(2)(2)(2)8a b a b a b b -+--+；（2）先化简，再求值：2(21)(2)(2)2(2)--+---x x x x x ，其中3x =-．【答案】（1）4ab ；（2）25x +；14．（1）利用完全平方公式和平方差公式展开，合并同类项即可得到结果．（2）利用完全平方公式和平方差公式进行乘法运算展开，再合并同类项即可化简，然后将3x =-代入计算即可得到结果．【详解】（1）解：原式222224448a b a ab b b =--+-+ 4ab =．（2）解：原式()222441424=-+---+x x x x x222441424=-+-+-+x x x x x25x =+．当3x =-时，原式2(3)5=-+14=．【点睛】此题考查了整式的混合运算，涉及的知识有：平方差公式，完全平方公式，去括号法则以及合并同类项法则，熟练掌握公式及法则是解本题的关键．平方差公式：22()()a b a b a b +-=+，完全平方公式：222()2a b a ab b ±=±+． 12．计算（1）23375(3)(2)(9)x y xy z x y -÷-；（2）（21x 4y 3－35x 3y 2+7x 2y 2）÷（－7x 2y ）（3）()()2282x y y x y x x ⎡⎤++÷⎣⎦－－【答案】（1）6yz ；（2）2235x y xy y -+-；（3）42x-．【分析】（1）直接根据整式的乘除混合运算法则计算即可；（2）根据整式的混合运算法则计算即可；（3）根据整式的混合运算法则计算即可．【详解】解：（1）原式＝6337527(2)(9)x y xy z x y -÷- ＝7675(54)(9)x y z x y -÷-（2）原式＝43232222221(7)35(7)7(7)x y x y x y x y x y x y ÷--÷-+÷- ＝2235x y xy y -+-；（3）原式＝2221(228)2x xy y xy y x x++---⨯ ＝21(8)2x x x-⨯ ＝211822x x x x⨯-⨯ ＝42x -．【点睛】本题考查了整式混合运算，熟练掌握运算法则是解本题的关键． 13．化简：a 2•（﹣a ）4﹣（3a 3）2＋（﹣2a 2）3 【答案】-16a 6 【分析】先算积的乘方，然后进行同底数幂的乘法运算，最后合并同类项化简即可．【详解】解：()()()234232·32a a a a --+-2466·98a a a a =--，66698a a a =--， 616a =-．【点睛】题目主要考查整式的混合运算，包括积的乘方，幂的乘方，同底数幂的乘法，整式的加减法等，熟练掌握各个运算法则是解题关键．14．先化简，再求值：2(21)4(1)(1)a a a --+-，其中14a =-．【答案】45,a 6 【分析】先按照完全平方公式与平方差公式计算整式的乘法运算，再合并同类项，把14a =-代入化简后的代数式即可得到答案. 【详解】解：2(21)4(1)(1)a a a --+-22当14a =-时，原式14515 6.4【点睛】本题考查的是整式的乘法运算，化简求值，掌握“利用完全平方公式与平方差公式进行简便运算”是解题的关键.15．化简：m （m +2）﹣（m ﹣1）2．【答案】4m ﹣1 【分析】利用单项式乘以多项式法则运算，利用完全平方公式展开，去括号．合并同类项即可．【详解】解：m （m +2）﹣（m ﹣1）2，＝m 2+2m ﹣（m 2﹣2m +1），＝m 2+2m ﹣m 2+2m ﹣1，＝4m ﹣1．【点睛】本题考查乘法公式化简，掌握单项式乘以多项式法则，完全平方公式是解题关键． 16．先化简，再求值：（1）22()()a a b a b +-+，其中a =b =（2）已知10224ba ==，化简211111454545b a a b a b ⎛⎫⎛⎫⎛⎫+⋅--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，并求值．【答案】（1）22a b -，−2；（2）2121025ab b --，−18或14 【分析】（1）利用单项式乘多项式及完全平方公式展开，合并同类项即可；最后代入即可求得值；（2）分别用平方差公式和完全平方公式展开，合并同类项即可；再由已知条件求出a 与b 的值，并代入化简后的算式中求得值．【详解】（1）222222222()()2a ab a b a a b b a b a a b =+--=+--+-当a =b =22222a b -=-=-；22222111111625161025a b a ab b =---- 212=1025ab b -- ∵10224b a ==∴252(2)a =，21022b =∴32a =±，b =5当a =32，b =5时，22121232551810251025ab b --=-⨯⨯-⨯=-；当a =−32，b =5时，221212(32)551410251025ab b --=-⨯-⨯-⨯=；即代数式的值为−18或14【点睛】本题是整式乘法的混合运算，主要考查了多项式的乘法，乘法公式，幂和乘方的逆用，二次根式的乘法运算，掌握多项式的乘法法则及乘法公式的特点，并能正确运算是关键．17．计算（1）x （x －2y ）＋（x ＋y ）2；（2）（－a 3b ）2÷（－3a 5b 2）（3）（－2a ）6－（－2a 3）2－[（－2a ）2]3（4）（2a －3b ）（3a ＋2b ）【答案】（1）222x y +；（2）13a -；（3）64a -；（4）22656a ab b -- 【分析】（1）根据单项式乘多项式以及完全平方公式去括号，然后根据合并同类项计算法则进行求解即可；（2）先计算积的乘方，然后根据单项式除以单项式的计算法则进行求解即可；（3）先计算积的乘方，然后合并同类项即可；（4）根据多项式乘以多项式的计算法则进行求解即可．【详解】解：（1）()()22x x y x y -++22222x xy x xy y =-+++ 222x y =+；（2）()()23523a b a b -÷-()62523a b a b =÷-13a =-；（3）()()()32623222a a a ⎡⎤-----⎣⎦ ()36626444a a a =-- 66664464a a a =--64a =-；（4）()()2332a b a b -+226946a ab ab b =-+-22656a ab b =--．【点睛】本题主要考查了整式的混合计算，积的乘方，合并同类项，单项式除以单项式，多项式乘以多项式，解题的关键在于能够熟练掌握相关计算法则．18．某同学化简a (a +2b )-(a +b )(a -b )出现了错误，解答过程如下：原式=()2222a ab a b +--(第一步) =2222a ab a b +--(第二步)=2ab 2b -(第三步)（1）该同学解答过程从第_____步开始出错．（2）写出此题的正确解答过程．【答案】（1）二；（2）见解析【分析】（1）解答过程去括号没有变化，故第二步出错；（2）根据整式的乘法的与运算进行计算即可，注意去括号要变号【详解】（1）()2222a ab a b +--2222a ab a b =+-+，所以，改同学解答过程从第二步开始出错故答案为：二（2）原式=()2222a ab a b +-- =2222a ab a b +-+=2ab 2b +【点睛】本题考查了整式的混合运算，平方差公式，正确的计算是解题的关键．19．先化简，再求值：()21242x y y x y ⎛⎫+-+ ⎪⎝⎭，其中2x =-，12y =．【答案】222x y +，92【分析】先利用完全平方公式和单项式乘多项式的运算法则去括号，然后再合并同类项，求出化简结果，将字母的值代入化简结果，求出整个代数式的值．【详解】解：原式2224442x xy y xy y =++--222x y =+，将2x =-，12y =代入得：2222192(2)2()22x y +=-+⨯=．【点睛】本题主要是考查了整式的化简求值，熟练掌握完全平方公式以及单项式乘多项式的法则，是求解本题的关键．20．先化简，再求值（1）(3)(2)(4)x x x x +-+-，其中2x =．（2）22()()()2m n m n m n m -+++-．其中m =2，n =1【答案】（1）56x -；4；（2）2mn ；4．【分析】（1）先计算整式的乘法，然后合并同类项化简，最后代入求值即可；（2）利用平方差及完全平方公式展开，然后合并同类项，最后将已知值代入求解即可．【详解】解：（1）()()()324x x x x +-+-222364x x x x x =-+-+-，56x =-；当2x =时，原式526=⨯-4=；（2）()()()222m n m n m n m -+++-2222222m n m mn n m =-+++-，2mn =；当2m =，1n =时，原式221=⨯⨯4=．【点睛】题目主要考查整式的乘法及加减混合运算，平方差公式，完全平方公式，整式的化简求值，熟练掌握两个公式及运算法则是解题关键．21．先化简，再求值：[（x ﹣3y ）2+（x +y ）（x ﹣y ）﹣x （2x ﹣4y ）]÷（﹣2y ），其中x ＝2，y ＝1．【答案】x ﹣4y ；﹣2．【分析】先根据完全平方公式，平方差公式，单项式乘多项式进行计算，再合并同类项，再根据多项式除以单项式进行计算，最后代入求出答案即可．【详解】解：[（x ﹣3y ）2+（x +y ）（x ﹣y ）﹣x （2x ﹣4y ）]÷（﹣2y ）=（x 2-6xy +9y 2+x 2-y 2-2x 2+4xy ）÷（-2y ）=（-2xy +8y 2）÷（-2y ）=x -4y ，当x =2，y =1时，原式=2-4×1=2-4=-2．【点睛】本题考查了整式的化简与求值，能正确根据整式的运算法则进行化简是解此题的关键，注意运算顺序．22．先化简，再求值：（2ab 3﹣4a 2b 2）÷2ab +（2a +b ）（2a ﹣b ），其中a ＝2，b ＝1．【答案】4a 2-2ab ，12．【分析】原式先算乘除，然后再算加减，最后代入求值．【详解】解：（2ab 3﹣4a 2b 2）÷2ab +（2a +b ）（2a ﹣b ）=b 2-2ab +4a 2-b 2=4a 2-2ab ，当a =2，b =1时，原式=4×22-2×2×1=16-4=12．【点睛】本题考查了整式的混合运算—化简求值，掌握多项式除以单项式的运算法则和平方差公式（a +b ）（a -b ）=a 2-b 2的结构是解题关键．23．先化简，再求值：（2x ﹣3y ）2﹣（2x +y ）（2x ﹣y ）+5y （x ﹣2y ），其中x ，y 满足15x -+|y +3|＝0．【答案】﹣7xy ，215【分析】首先利用完全平方公式及平方差公式对原式进行去括号，并合并同类项进行化简，之后利用算数平方根及绝对值的非负性进行求解x 、y ，代入化简结果即可．【详解】解：原式＝4x 2﹣12xy +9y 2﹣（4x 2﹣y 2）+5xy ﹣10y 2＝4x 2﹣12xy +9y 2﹣4x 2+y 2+5xy ﹣10y 2＝﹣7xy ，∵15x -+|y +3|＝0， ∴x ﹣15＝0，y +3＝0， ∴x ＝15，y ＝﹣3， ∴原式＝﹣7×15×（﹣3）＝215．【点睛】本题考查的是利用整式乘法进行化简，同时利用非负性进行求解，熟练掌握公式法是解本题的关键．24．一个工件的体积V = a (a + 1)(5a + 1) + (3a + 2)(3a - 2) - a + 4．其形状和部分尺寸如图所示．（1）化简体积V ；（2）求工件的长x （用含a 的式子表示）．【答案】（1）5a 3 + 15a 2；（2）a + 3【分析】（1）根据整式的乘法和平方差公式，化简求解即可；（2）根据图形可以写出该工件的体积，然后根据所求出的体积与题目中的体积相等，即可求解；【详解】解：（1）()()(15134)()232V a a a a a a =++++--+22()(51)(94)4a a a a a =+++--+322255944a a a a a a =++++--+32515a a =+故答案为32515a a +（2）由图形可得，该工件的体积为2235V a a x a a x a x =⨯⨯-⨯⨯=由题意可得：2325515a x a a =+ 解得32251535a a x a a+==+ 故答案为3a +【点睛】此题考查了整式的四则运算，涉及了平方差公式，解题的额关键是掌握整式四则运算法则，正确去式子进行化简．25．先化简，再求值：2(2)(2)(2)x y x y x y +-+-，其中12x =-，2y =．【答案】224y xy +，4【分析】先提取公因式，再整理即可化简．将12x =-，2y =代入化简后的式子求值即可．【详解】2(2)(2)(2)x y x y x y +-+- [](2)(2)(2)x y x y x y =++--2(2)y x y =+224y xy =+，将12x =-，2y =代入，得：22124224()242y xy +=⨯+⨯-⨯=．本题考查整式的化简求值．掌握整式的混合运算法则是解答本题的关键．26．计算：（1）2b （2a +3b ）+（a ﹣2b ）2（2）22441x x x -+÷-（x 221x x ---）．【答案】（1）a 2+10b 2；（2）21x x -+．【分析】（1）根据单项式乘多项式以及完全平方公式展开，再合并即可；（2）原式括号中通分并利用同分母分式的减法法则计算，约分即可得到结果．【详解】解：（1）2b （2a +3b ）+（a ﹣2b ）2=4a b +6b 2+a 2-4ab+4b 2=a 2+10b 2；（2）22441x x x -+÷-（x 221x x ---） 222(2)2()11(1)(1)x x x x x x x x ---=÷---+- 2((2)2()1)(1)1x x x x x --+-=÷-- 2(1)(2)2(11)x x x x x --=⋅+--- 21x x -=+．【点睛】本题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．还考查了整式的混合运算．27．计算：（1）3a 3b •（﹣2b ）2﹣（ab ）3（2）（x ＋2y ﹣1）（x ＋2y ＋1）【答案】（1）11a 3b 3；（2）x 2＋4y 2＋4xy －1【分析】（1）先算积的乘方，再合并同类项，即可；（2）先利用平方差公式，再完全平方公式，即可求解．【详解】解：（1）原式=3a 3b •4b 2﹣a 3b 3=12a 3b 3﹣a 3b 3（2）原式=（x ＋2y ）2﹣12= x 2＋4y 2＋4xy －1．【点睛】本题主要考查整式的混合运算，熟练掌握乘法公式，整式的运算法则，是解题的关键．28．计算下列各题（1）20201-（2）2422311()(2)24a b ab a ab ⋅-+⋅-（3）21[()())2(]x y x y x y x --+÷＋（4）()(1221)()1a a a a -++-【答案】（1）3；（2）4674a b -；（3）44x y -；（4）2a - 【分析】（1）根据实数与二次根式的混合运算法则即可求解；（2）根据幂的运算法则即可化简求解；（3）根据整式的混合运算法则求解；（4）根据整式的乘法运算法则求解．【详解】（1）原式=3331255+⨯-=+（2）原式()2422364646461117824444a b a b a a b a b a b a b =⋅+⋅-=-=-；（3）()()()212x y x y x y x ⎡⎤-+-+÷⎣⎦ 2222122x xy y x y x ⎡⎤=-++-÷⎣⎦()21222x xy x =-÷44x y =- （4）()()()12211a a a a ++－－ 22222a a a =-+-2a =-．【点睛】此题主要考查实数、二次根式、整式乘除混合运算，解题的关键是熟知各自的运算法则．29．计算：（1）（x +2y ）（3x ﹣2y ）．（2）（x +1）2﹣（2x +5）（2x ﹣5）．【答案】（1）22344x xy y +-；（2）23226x x -++．【分析】（1）根据多项式乘以多项式的法则即可得；（2）先计算完全平方公式和平方差公式，再计算整式的加减即可得．【详解】解：（1）原式223264x xy xy y =-+-，22344x xy y =+-；（2）原式2221(425)x x x =++--，2221425x x x =++-+，23226x x =-++．【点睛】本题考查了乘法公式、整式的乘法与加减法，熟练掌握公式和运算法则是解题关键． 30．计算：（1）()()22x y y y x ---；（2）22431211a a a a -⎛⎫÷- ⎪+++⎝⎭．【答案】（1）2x ；（2）21a a ++．【分析】（1）利用完全平方公式、单项式乘以多项式法则解题；（2）利用平方差公式、完全平方公式原式化为2(2)(2)1(1)2a a a a a +-+⨯+-，再结合整式的乘除法解题即可．【详解】解：（1）()()22x y y y x ---222=22x xy y y xy -+-+ 2x =（2）22431211a a a a -⎛⎫÷- ⎪+++⎝⎭ 2(2)(2)13=(1)1a a a a a +-+-⎛⎫÷ ⎪++⎝⎭ 2(2)(2)1(1)2a a a a a +-+=⨯+- 21a a +=+．【点睛】本题考查整式的乘除，涉及平方差公式、完全平方公式等知识，是重要考点，难度一般，掌握相关知识是解题关键．。

北师大版七年级数学下册第一章整式的运算复习及其整理(带练习)

第一章整式的运算第一节整式1．整式的有关概念：（1）单项式的定义：像1.5V ，28n π，h r 231π等，都是数与字母的乘积，这样的代数式叫做单项式．（2）单项式的次数：一个单项式中，所有字母的指数和叫做这个单项式的次数．（3）多项式的概念：几个单项式的和叫做多项式．（4）多项式的次数：一个多项式中，次数最高项的次数，叫做这个多项式的次数．（5）整式的概念：单项式和多项式统称为整式．2．定义的补充：（1）单项式的系数：单项式中的数字因数叫做单项式的系数．（2）多项式的项数：多项式中单项式的个数叫做多项式的项数．（3）区别是否是整式：关键：分母中是否含有字母？分母有字母的为分式，如a 分之3是分式。

3．例题讲解：例1：下列代数式中，哪些是整式？单项式？多项式？并指出它们的系数和次数？（！）ab ＋c （2）ax 2＋bx ＋c （3）－5（4)π.2y x － (5)12－x x 例2：求多项式363222+--b ab a 的各项系数之和？第二节整式的加减一、知识点复习：1、填空：整式包括单项式和多项式.2、整式的加减实质上就是去括号后,合并同类项,运算结果是一个多项式或是单项式.3、所含字母相同，并且相同字母的指数也分别相同的项叫做同类项。

4、括号前面是“－”号,去括号时,括号内各项要变号,一个数与多项式相乘时,这个数与括号内各项都要相乘。

二、练习：例1：下列各式，是同类项的一组是（）（A ）y x 222与231yx （B ）n m 22与22m n 例2、计算：（1）)134()73(22+-++k k k k （2）)2()2123(22x xy x x xy x +---+例3：先化简，再求值：()[],673235222x x x x x x +++--其中x=21 例4、已知：A=x 3－x 2－1，B=x 2－2，计算：（1）B －A （2）A －3B第三节同底数幂的乘法一、复习提问2.指出下列各式的底数与指数：(1)34；(2)a 3；(3)(a+b)2；(4)(-2)3；(5)-23．3、同底数幂的乘法法则: m n m n a a a += （,m n 都是正数）是幂的运算中最基本的法则,在应用法则运算时,要注意以下几点:①法则使用的前提条件是：幂的底数相同而且是相乘时，底数a 可以是一个具体的数字式字母，也可以是一个单项或多项式；②指数是1时，不要误以为没有指数；③不要将同底数幂的乘法与整式的加法相混淆，对乘法，只要底数相同指数就可以相加；而对于加法，不仅底数相同，还要求指数相同才能相加；④当三个或三个以上同底数幂相乘时，法则可推广为 m n p m n p a a a a++=（其中m 、n 、p 均为正数）；⑤公式还可以逆用： m n m n aa a +=（m 、n 均为正整数）二、巩固练习(1)107×104； (2)x 2·x 5；(3)10·102·104；(4)-a ·(-a)3；(5）(-a)2·(-a)3三、小结1．同底数幂相乘，底数不变，指数相加，对这个法则要注重理解“同底、相乘、不变、相加”这八个字．2．解题时要注意a 的指数是1．3．解题时，是什么运算就应用什么法则．同底数幂相乘，就应用同底数幂的乘法法则；整式加减就要合并同类项，不能混淆．4．-a 2的底数a ，不是-a ．计算-a 2·a 2的结果是-(a 2·a 2)=-a 4，而不是(-a)2+2=a 4．5．若底数是多项式时，要把底数看成一个整体进行计算第四节幂的乘方与积的乘方一、知识点复习：1. 幂的乘方法则：()m n mn a a =(,m n 都是正整数)幂的乘方,底数不变，指数相乘。

(完整版)整式的混合运算专项练习99题(有答案有过程)

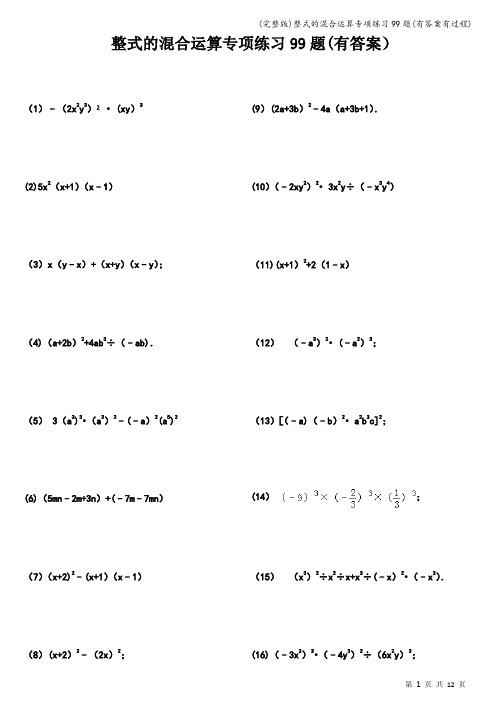
(完整版)整式的混合运算专项练习99题(有答案有过程) 整式的混合运算专项练习99题(有答案）（1）﹣（2x2y3）²•(xy）3(2)5x2（x+1）（x﹣1）（3）x（y﹣x）+（x+y）（x﹣y）；（4)（a+2b）2+4ab3÷（﹣ab)．（5） 3（a2)3•（a3）2﹣(﹣a）2(a5)2 (6)（5mn﹣2m+3n）+(﹣7m﹣7mn）（7）（x+2)2﹣(x+1）（x﹣1）（8）(x+2）2﹣（2x）2；(9）(2a+3b）2﹣4a（a+3b+1）．(10）（﹣2xy2）2•3x2y÷（﹣x3y4）（11)(x+1）2+2（1﹣x）（12）（﹣a3）2•(﹣a2）3；（13）［（﹣a)（﹣b）2•a2b3c]2；(14）；（15）（x3）2÷x2÷x+x3÷(﹣x）2•（﹣x2）．(16)（﹣3x2）3•（﹣4y3）2÷（6x2y）3；(完整版)整式的混合运算专项练习99题(有答案有过程)(17）（﹣x﹣y）2﹣（2y﹣x）(x+2y)（18)(19）（a+b)(﹣b+a）+(a+b）2﹣2a(a+b）（20)；（21）x（x+1）﹣（2x+1）（2x﹣3）；(22）（2a+3b)2﹣（2a﹣3b）2．（23）2a2﹣a8÷a6；（24)(2﹣x）(2+x)+（x+4）（x﹣1）（25）（﹣2ab3)2+ab4•（﹣3ab2）；（26）(2a+3)（2a﹣3）+（a﹣3）2．（27）12ab2（abc）4÷（﹣3a2b3c）÷[2(abc）3]．(28)（﹣2x2）3÷（﹣x）2（29)（﹣2m﹣1)（3m﹣2)（30）2x•（﹣x2+3x）﹣3x2•（x+1）．（31)3a•（﹣ab2）﹣（﹣3ab)2．（32）﹣3x•（2x2﹣x+4)(完整版)整式的混合运算专项练习99题(有答案有过程)（33）2x3•（﹣2xy）(﹣xy) 3．（34)3（x2﹣2x+3）﹣3x(x+1)=0．（35)（3x+2)(3x+1）﹣(3x+1）2．（36）2a（a+b)﹣（a+b)2．（37）x（2x﹣7）+（3﹣2x）2．（38）（﹣3x2y）2÷(﹣3x3y2）（39）（a+2）2﹣（a+1)（a﹣1)（40）（a2)4÷a2（41）．（42）a（ab2﹣4b）+4a3b÷a2；(43)（x﹣8y）（x﹣y）．(44）（3x2y)3•(﹣5y）;（45）［(x+y）2﹣y（2x+y）﹣4x］÷2x．（46）（2x+a)2﹣（2x﹣a)2（47）［（2x2)3﹣6x3（x3+2x2）]÷(﹣2x2）（48）(x﹣2)（x+2)﹣(x+1)(x﹣3）(完整版)整式的混合运算专项练习99题(有答案有过程)（49）（2a)3•b4÷12a3b2（50）(3x﹣1)(2x+3)﹣6x2．（51）（﹣6x2）2+（﹣3x2）•x﹣27x5÷（﹣9x2）（52）（﹣2y2）3+y•y5(53）（x+2）2﹣（x+1)（x﹣1）（54）（a+b）（a﹣b）+(a+b）2﹣a（2a+b) (55）（﹣a）2•（a2)2÷a3（56）(15x2y﹣10xy2）÷5xy．（57)［（2x2)3﹣6x3（x3+2x2+x）］÷（﹣x）4．(58)（x+1)2+2(1﹣x）﹣x2（59）（12a3﹣6a2+3a）÷3a（60)5x2(x+1)（x﹣1）(61）（b﹣2a）2﹣4a（a﹣b）（62)（﹣3ab2)3（﹣4ab2）(63）（3a﹣2）（a﹣6)(64)（3a3b﹣9a2b2﹣21a2b3）÷（﹣3a2b）(完整版)整式的混合运算专项练习99题(有答案有过程)（65）（x+3)（x﹣2)﹣(x﹣2）2（66）（3x+4y）（3x﹣4y)（67）（x+3y）(2x﹣y）﹣y（5x+3y)（68）3（a5）2•（﹣a3)2﹣（2a3)2•（a2）5；（69)4xy+(x﹣2y）2+(x+3y)（3y﹣x)（70）﹣3x2y2•（﹣2xy）2．（71）（a﹣2b）2+(a+2b）（a﹣2b）（72）．（73）．（74）（﹣2xy2)3+（﹣3xy4）（﹣2x2y2）(75）（2x)3×(﹣3xy2）(76）（a+3b）（a﹣2b）﹣（2a﹣b）2．（77）（﹣2x2y）3+(3x2）2•(﹣x2）•y3．（78）(m2n）3•（﹣m4n）÷（﹣mn）2（79）（2a﹣1）2（2a+1）2（80）（x4y+6x3y2﹣x2y3）÷（3x2y）(完整版)整式的混合运算专项练习99题(有答案有过程)(81）(2x﹣3y+1）（2x+3y﹣1）（82)（﹣2x）（4x2﹣2x+1）(83）(6a3﹣4a2+2a）÷2a（84）(2x﹣y）（2x+y)﹣(x﹣3y）2（85）(4x2﹣2x3+6x）÷（﹣2x）﹣（2x﹣1）2．(86）．（87）[x（xy2+2xy）﹣y（x2y﹣6x2y2）］÷2x2y．(88）x6÷（﹣x）2﹣(x）2•27x2．（89）（2x+y）（2x﹣3y）+4y（2x+y) (90）（m+2）（m﹣2)+（m﹣1）（m+5）（91)［（x+y）2﹣y（2x+y)﹣8x］÷2x．（92)（2xy2﹣6xy）÷2x+y（y+2）（93）(27a3﹣15a2+6a）÷(3a）（94）x(x+2y)﹣(x+1)2+2x．（95)（x2y3)2÷(x3y4）•(﹣4xy）（96）a3•a3+（﹣2a3）2﹣（﹣a2）3．(完整版)整式的混合运算专项练习99题(有答案有过程)（99）［(2x+y）2﹣y（y+2x）﹣4x]÷2x．（97）（2x+1)（x+3）﹣6（x2+x﹣1）；（98）[x（x2y2﹣xy)﹣y（x2﹣x3y）]+3x2y．(完整版)整式的混合运算专项练习99题(有答案有过程) 整式混合运算99题参考答案:（1)﹣（2x2y3）²•（xy）3=﹣4x4y6•x3y3=﹣4x7y9；(2）5x2（x+1)(x﹣1),=5x2(x2﹣1）,=5x4﹣5x2．（3）x（y﹣x）+（x+y）（x﹣y），=xy﹣x2+x2﹣y2，=xy﹣y2；（4）（a+2b)2+4ab3÷（﹣ab），=a2+4ab+4b2﹣4b2，=a2+4ab(5)3（a2）3•（a3）2﹣(﹣a）2（a5）2，=3a6•a6﹣a2•a10,=3a12﹣a12，=2a12．（6）（5mn﹣2m+3n）+(﹣7m﹣7mn）, =5mn﹣2m+3n﹣7m﹣7mn，=(5﹣7）mn+（﹣2+7）m+3n，=3n﹣9m﹣2mn；(7）（x+2）2﹣(x+1）（x﹣1)，=x2+4x+4﹣x2+x﹣x+1，=4x+5．（8）（x+2）2﹣（2x）2，=x2+4x+4﹣4x2，=﹣3x2+4x+4;（9）(2a+3b）2﹣4a（a+3b+1），=4a2+12ab+9b2﹣4a2﹣12ab﹣4a，=9b2﹣4a．（10)（﹣2xy2）2•3x2y÷（﹣x3y4），=4x2y4•3x2y÷（﹣x3y4），=12x4y5÷（﹣x3y4），=﹣12xy（11）（x+1)2+2（1﹣x），=（x+1）2+2（1﹣x），=x2+2x+1+2﹣2x，=x2+3．（12）（﹣a3)2•（﹣a2）3,=a6•(﹣a6）,=﹣a12；（13）[(﹣a）（﹣b）2•a2b3c］2,=（﹣a3b5c）2，=a6b10c2;(14）, =（9××）3，=23，=8；(15）（x3）2÷x2÷x+x3÷(﹣x）2•（﹣x2），=x6÷x2÷x+x3÷x2•（﹣x2),=x3﹣x3,(完整版)整式的混合运算专项练习99题(有答案有过程)=0．（16）原式=﹣27x6•（16y6)÷（216x6y3)=﹣2y3；(17）原式=(﹣x﹣y）2﹣（2y﹣x）（x+2y），=x2+2xy+y2﹣(4y2﹣x2），=x2+2xy+y2﹣4y2+x2,=2xy﹣3y2（18）=[3x2y÷(﹣xy)］+[﹣xy2÷（﹣xy）]+［xy÷(﹣xy）］，=﹣6x+2y﹣1;（19）(a+b）（﹣b+a）+(a+b）2﹣2a（a+b)，=（a+b）(a﹣b+a+b﹣2a）,=0（20）原式=［2x(3x6y6）•y2]÷9x7y8，=（6x7y6•y2）÷9x7y8，=2x7y8÷9x7y8，=；(21）原式=x2+x﹣（4x2﹣6x+2x﹣3)，=x2+x﹣4x2+6x﹣2x+3，=﹣3x2+5x+3；（22）原式=（2a+3b+2a﹣3b)（2a+3b﹣2a+3b），=4a•9b，=36ab(23)2a2﹣a8÷a6,=2a2﹣a2，=a2；(24）(2﹣x）（2+x)+(x+4)（x﹣1），=4﹣x2+x2+3x﹣4,=3x．（25）（﹣2ab3)2+ab4•（﹣3ab2），=4a2b6﹣3a2b6，=a2b6；（26)（2a+3)(2a﹣3）+（a﹣3)2，=4a2﹣9+a2﹣6a+9,=5a2﹣6a（27）原式=12a5b6c4÷(﹣3a2b3c）÷2a3b3c3 =﹣4a3b3c3÷2a3b3c3=﹣2（28）原式=﹣8x6÷x2=﹣8x4；（29）原式=﹣6m2+4m﹣3m+2=﹣6m2+m+2 (30)原式=﹣2x3+6x2﹣3x3﹣3x2=﹣5x3+3x2．（31）3a•（﹣ab2）﹣（﹣3ab）2﹣12a2b2，=﹣3a2b2﹣9a2b2﹣12a2b2,=﹣24a2b2（32)原式=﹣6x3+3x2﹣12x；（33)原式=2x3•（﹣2xy）（﹣x3y3)=x7y4（34)3（x2﹣2x+3）﹣3x（x+1）=0,∴3x2﹣6x+9﹣3x2﹣3x=0，∴﹣9x=﹣9,∴x=1(35）原式=9x2+3x+6x+2﹣9x2﹣6x﹣1=3x﹣1．(36）2a(a+b）﹣（a+b）2．=（a+b）(2a﹣a﹣b）=（a+b）（a﹣b）(完整版)整式的混合运算专项练习99题(有答案有过程)（37）．原式=2x2﹣7x+9﹣12x+4x2=6x2﹣19x+9．（38）(﹣3x2y）2÷（﹣3x3y2)，=9x4y2÷（﹣3x3y2）,=﹣3x；（39）（a+2）2﹣（a+1)（a﹣1），=a2+4a+4﹣（a2﹣1），=a2+4a+4﹣a2+1，=4a+5（40)原式=a8÷a2=a6；(41）原式=a2b﹣6ab2+6ab2=a2b．（42）原式=a2b2﹣4ab+4ab=a2b2；(43)原式=x2﹣xy﹣8xy+8y2=x2﹣9xy+8y2（44）原式=27x6y3•（﹣5y）=﹣135x6y4；（45）原式=（x2+y2+2xy﹣2xy﹣y2﹣4x）÷2x=（x2﹣4x）÷2x=x﹣2（46)原式=[（2x+a）+（2x﹣a）]［（2x+a)﹣（2x ﹣a）]=（2x+a+2x﹣a)（2x+a﹣2x+a)=4x•2a=8ax；（47）原式=（8x6﹣6x6﹣12x5）÷（﹣2x2）=2（x6﹣6x5）÷（﹣2x2）=﹣x4+6x3=6x3﹣x4；（48)原式=x2﹣4﹣（x2﹣2x﹣3)=x2﹣4﹣x2+2x+3=2x﹣1(49）原式=8a3•b4÷12a3b2，=b2．（50）原式=(6x2+9x﹣2x﹣3)﹣6x2=6x2+9x﹣2x﹣3﹣6x2=7x﹣3（51）（﹣6x2)2+（﹣3x2)•x﹣27x5÷(﹣9x2)=36x4﹣3x3+3x3=36x4（52）（﹣2y2）3+y•y5=﹣8y6+y6=﹣7y6；(53)（x+2）2﹣（x+1）（x﹣1）=x2+4x+4﹣x2+1=4x+5．（54）原式=a2﹣b2+a2+2ab+b2﹣2a2﹣ab=ab．（55）（﹣a）2•（a2）2÷a3=a2•a4÷a3=a6÷a3=a3；（56）（15x2y﹣10xy2）÷5xy=3x﹣2y（57）原式=［8x6﹣6x6﹣12x5﹣6x4］÷x4=[2x6﹣12x5﹣6x4]÷x4=2x2﹣12x﹣6（58）原式=(x+1）2+2（1﹣x）﹣x2=x2+2x+1+2﹣2x﹣x2=3．(完整版)整式的混合运算专项练习99题(有答案有过程)（59）（12a3﹣6a2+3a）÷3a=4a2﹣2a+1；（60）5x2（x+1）（x﹣1)=5x2（x2﹣1)=5x4﹣5x2．（61）原式=b2﹣4ab+4a2﹣4a2+4ab=b2（62)原式=（﹣27a3b6）(﹣4ab2)=108a4b8（63）原式=3a2﹣18a﹣2a+12=3a2﹣20a+12（64）化成单项式除以单项式﹣a+3b+7b2（65）原式=x2﹣2x+3x﹣6﹣（x2﹣4x+4)=x2+x﹣6﹣x2+4x﹣4=5x﹣10;(66)原式=9x2﹣16y2；（67）原式=2x2﹣xy+6xy﹣3y2﹣5xy﹣3y2=2x2﹣6y2．(68）原式=3a10•a6﹣4a6•a10=3a16﹣4a16=﹣a16;（69）原式=4xy+x2﹣4xy+4y4+9y2﹣x2=4y4+9y2．（70)原式=﹣3x2y2•4x2y2=﹣12x4y4；（71）原式=a2﹣4ab+4b2+a2﹣4b2=2a2﹣4ab （72）原式=a2﹣4b2﹣2ab+4b2=a2﹣2ab（73)原式=10x3﹣2x3=8x3(74）原式=﹣8x3y6+6x3y6=﹣2x3y6．(75）原式=8x3×（﹣3xy2）=﹣24x4y2;(76)原式=a2﹣2ab+3ab﹣6b2﹣(4a2﹣4ab+b2）=a2﹣2ab+3ab﹣6b2﹣4a2+4ab﹣b2=﹣3a2+5ab﹣7b2（77)原式=﹣8x6y3+9x4•（﹣x2)•y3=﹣8x6y3﹣9x6y3=﹣17x6y3（78）原式=﹣m10n4÷m2n2=﹣m8n2;（79）原式=[（2a﹣1）（2a+1）]2=16a4﹣8a2+1；（80)原式=x2+2xy ﹣y2；（81）原式=[2x﹣(3y﹣1）]［2x+（3y﹣1）]=4x2﹣9y2+6y﹣1（82）（﹣2x)（4x2﹣2x+1），=﹣8x3+4x2﹣2x；（83)(6a3﹣4a2+2a）÷2a，=3a2﹣2a+1．（84)（2x﹣y）（2x+y）﹣(x﹣3y）2，=4x2﹣y2﹣x2+6xy﹣9y2，=3x2+6xy﹣10y2．（85）原式=﹣2x+x2﹣3﹣（2x﹣1）2=﹣2x+x2﹣3﹣（4x2﹣4x+1）=﹣2x+x2﹣3﹣4x2+4x﹣1=x2﹣4x2﹣2x+4x﹣3﹣1=﹣3x2+2x﹣4（86)原式=（9m2+6mn+n2﹣6mn﹣n2）÷2m=9m2÷2m(完整版)整式的混合运算专项练习99题(有答案有过程)=m（87)原式=(x2y2+2x2y﹣x2y2+6x2y3）÷2x2y=（2x2y+6x2y3)÷2x2y=1+3y2（88)原式=x6÷x2﹣x2•27x2=x4﹣3x4=﹣2x4．(89）原式=(2x+y)（2x﹣3y+4y）=（2x+y）（2x+y）=（2x+y）2（90）原式=m2﹣4+m2+5m﹣m﹣5=2m2+4m﹣9；(91）原式=［x2+2xy+y2﹣（2xy+y2）﹣8x］÷2x=（x2+2xy+y2﹣2xy﹣y2﹣8x）÷2x=(x2﹣8x）÷2x=x﹣4．(92）．原式=2xy2÷2x﹣6xy÷2x+y2+2y=y2﹣3y+y2+2y=2y2﹣y(93）原式=9a2﹣5a+2；（94）原式=x2+2xy﹣x2﹣2x﹣1+2x=2xy﹣1；（95)原式=x4y6÷（x3y4）•(﹣4xy）=x4y6××（﹣4xy）=×（﹣4xy）=﹣；（96）原式=a3+3+4a6+a6=a6+4a6+a6=6a6（97）（2x+1）（x+3)﹣6（x2+x﹣1）=2x2+6x+x+3﹣6x2﹣6x+6=﹣4x2+x+9;(98)［x（x2y2﹣xy）﹣y（x2﹣x3y)］+3x2y =［x3y2﹣x2y﹣x2y+x3y2]+3x2y=2x3y2﹣2x2y+3x2y=2x3y2+x2y（99）原式=[(2x+y）（2x+y﹣y）﹣4x］÷2x =[（2x+y)×2x﹣4x］÷2x=2x(2x+y﹣2）÷2x=2x+y﹣2．。

北师大版二年级数学上册混合运算专项练习(及答案)

北师大版二年级数学上册混合运算专项练习（及答案）一、口算1、直接写出得数．87-7= 90+10= 20+5= 7+9= 85-5= 76-6= 17-8= 88-8= 3+70+5= 78-8+3= 64-4+9= 73-3+6=2、直接写出得数。

463-= 8215+= 5930-= 87264-+=6023+= 949+= 7924-= 45920++= 928-= 4332+= 8742-= ()542419--=3、直接写出得数．21÷6= 19÷4= 67÷9= 38÷5= 52÷7= 71÷8= 17÷2= 25÷3=4、直接写出得数．1×2＝ 6×3＝ 5×8＝ 4×4＋4＝ 9×8＝ 5＋21＝ 37－13＝ 6×6－6＝ 18＋40＝ 42－9＝ 26＋29＝ 3×7＋14＝5、口算．5×6= 72÷8= 9×9= 22+36= 3×3×3＝ 4×7= 18÷6= 8×6= 98-46= 24÷4×9＝ 3×8= 24÷6= 54-6= 72-35= 8×4－22＝ 9×5= 21÷3= 56-7= 47+35= 18－4÷2＝二、竖式计算1、用竖式计算，带★的要验算．62÷9＝ 592＋103＝ ★238＋254＝ ★907－265＝2、列竖式计算。

36＋57－45＝ 82－33－29＝ 40＋19＋8＝ 53＋（46－16）＝3、用竖式计算。

（1）28＋25＋17＝（2）84－40－27＝（3）72－47＋16＝4、用竖式计算。

48＋32＋10＝ 45－26－18＝ 78＋16－17＝5、．用竖式计算。

专题1.5 整式的混合运算与化简求值专项训练(30道)(举一反三)(北师大版)(解析版)

专题1.5 整式的混合运算与化简求值专项训练（30道）【北师大版】1．（2021秋•万州区期末）计算：（1）（5x4﹣6x3）÷（﹣x）+3x•（x﹣x2）；（2）（x+2y）（x﹣3y）﹣x（x+4y）+9xy．【分析】（1）根据多项式除以单项式和单项式乘多项式可以将题目中的式子展开，然后合并同类项即可；（2）根据多项式乘多项式、单项式乘多项式可以将题目中的式子展开，然后合并同类项即可．【解答】解：（1）（5x4﹣6x3）÷（﹣x）+3x•（x﹣x2）＝﹣5x3+6x2+3x2﹣3x3＝﹣8x3+9x2；（2）（x+2y）（x﹣3y）﹣x（x+4y）+9xy＝x2﹣3xy+2xy﹣6y2﹣x2﹣4xy+9xy＝4xy﹣6y2．2．（2021秋•云阳县期末）计算：（1）（x+5）2﹣（x+3）（x﹣3）；（2）（x+y）（x﹣3y）+（2x2y+6xy2）÷2x．【分析】（1）根据完全平方公式和平方差公式可以将题目中的式子展开，然后合并同类项即可；（2）根据多项式乘多项式和多项式除以单项式可以将题目中的式子展开，然后合并同类项即可．【解答】解：（1）（x+5）2﹣（x+3）（x﹣3）＝x2+10x+25﹣x2+9＝10x+34；（2）（x+y）（x﹣3y）+（2x2y+6xy2）÷2x＝x2﹣3xy+xy﹣3y2+xy+3y2＝x2﹣xy．3．（2021秋•泗水县期末）计算：（1）2（x3）2•x3﹣（3x3）3+（5x）2•x7；（2）（x﹣2y）（x+2y）﹣（x﹣y）2．【分析】（1）先利用幂的乘方与积的乘方运算法则计算乘方，然后根据单项式乘单项式的运算法则计算乘法，最后算加减；（2）利用完全平方公式和平方差公式计算乘方和乘法，然后去括号，合并同类项进行化简．【解答】解：（1）原式＝2x6•x3﹣27x9+25x2•x7＝2x9﹣27x9+25x9＝0；（2）原式＝x2﹣4y2﹣（x2﹣2xy+y2）＝x2﹣4y2﹣x2+2xy﹣y2＝2xy﹣5y2．4．（2021秋•鞍山期末）按照要求进行计算：（1）计算：[x（x2y2﹣xy）﹣（xy2﹣y）（x2﹣xy）]÷3xy2；（2）利用乘法公式进行计算：（2x+y+z）（2x﹣y﹣z）．【分析】（1）利用单项式乘多项式，多项式乘多项式的运算法则先计算括号内的乘法，然后将括号内的式子去括号，合并同类项进行化简，最后根据多项式除以单项式的运算法则计算除法；（2）利用平方差公式和完全平方公式进行计算．【解答】解：（1）原式＝[x3y2﹣x2y﹣（x3y2﹣x2y3﹣x2y+xy2）]÷3xy2＝（x3y2﹣x2y﹣x3y2+x2y3+x2y﹣xy2）÷3xy2＝（x2y3﹣xy2）÷3xy2=13xy―13；（2）原式＝[2x+（y+z）][2x﹣（y+z）]＝（2x）2﹣（y+z）2＝4x2﹣（y2+2yz+z2）＝4x2﹣y2﹣2yz﹣z2．5．（2021秋•大石桥市期末）计算题（1）（2x+3）（2x﹣3）﹣4x（x﹣1）+（x﹣2）2；（2）[（m+n）（m﹣n）+（m﹣n）2﹣4m（m﹣n）]÷2m．【分析】（1）直接利用平方差公式、完全平方公式以及单项式乘多项式，进而合并同类项进而得出答案；（2）直接利用平方差公式、完全平方公式以及单项式乘多项式，进而合并同类项，再利用整式的除法运算法则进而得出答案．【解答】解：（1）原式＝4x2﹣9﹣4x2+4x+x2﹣4x+4＝x2﹣5；（2）原式＝（m2﹣n2+m2﹣2mn+n2﹣4m2+4mn）÷2m ＝（﹣2m2+2mn）÷2m＝﹣2m2÷2m+2mn÷2m＝﹣m+n．6．（2021秋•沙市区校级期中）计算．①（﹣4x3y+xy3―13xy）÷（―13xy）．②（x﹣2）（x﹣3）﹣（2x﹣1）（2x+1）．【分析】①根据多项式除以单项式法则进行计算即可；②先根据多项式乘多项式和平方差公式进行计算，再合并同类项即可．【解答】解：①原式＝﹣4x3y÷（―13xy）+xy3÷（―13xy）―13xy÷（―13xy）＝12x2﹣3y2+1；②原式＝（x2﹣3x﹣2x+6）﹣（4x2﹣1）＝x2﹣3x﹣2x+6﹣4x2+1＝﹣3x2﹣5x+7．7．（2021秋•淅川县期中）计算：（1）6a（a﹣2）﹣（2﹣3a）2；（2）（2x2﹣3y）（2x2+3y）﹣2x•（﹣3x3）．【分析】（1）原式利用单项式乘多项式法则，以及完全平方公式化简，去括号合并即可得到结果；（2）原式利用平方差公式，以及单项式乘单项式法则计算，合并即可得到结果．【解答】解：（1）原式＝6a2﹣12a﹣（9a2﹣12a+4）＝6a2﹣12a﹣9a2+12a﹣4＝﹣3a2﹣4；（2）原式＝4x4﹣9y2+6x4＝10x4﹣9y2．8．（2021秋•双台子区校级期中）化简：（1）（x+y）（x﹣y）﹣（2x﹣y）（x+3y）；（2）（x﹣2y+4）（x﹣2y﹣4）．【分析】（1）先根据平方差公式和多项式乘以多项式计算乘法，再去括号合并同类项即可得答案；（2）先用平方差公式，再用完全平方公式计算即可．【解答】解：（1）原式＝x2﹣y2﹣（2x2+6xy﹣xy﹣3y2）＝x2﹣y2﹣2x2﹣6xy+xy+3y2＝﹣x2﹣5xy+2y2；（2）原式＝（x﹣2y）2﹣16＝x2﹣4xy+4y2﹣16．9．（2021春•东昌府区期末）计算：（1）12x3y2•（―23x2y3z2）•34x2yz3；（2）（3a+2b）（a+2b+1）﹣2b（2b+1）．【分析】（1）利用单项式乘单项式的运算法则对式子进行运算即可；（2）利用多项式乘多项式与单项式乘多项式的运算法则进行去括号运算，再进行合并同类项即可．【解答】解：（1）12x3y2•（―23x2y3z2）•34x2yz3=[12×(―23)×34]⋅x3+2+2y2+3+1z2+3=―14x7y6z5；（2）（3a+2b）（a+2b+1）﹣2b（2b+1）＝3a2+6ab+3a+2ab+4b2+2b﹣4b2﹣2b＝3a2+8ab+3a．10．（2021春•沙坪坝区校级期末）计算：（1）（x﹣y）（x﹣2y）﹣3x（13x﹣2y）+（2x+y）（2x﹣y）．（2）[43ab(―12a)2+(a2b)2÷3ab]÷(―2a)3．【分析】（1）直接利用多项式乘多项式以及单项式乘多项式分别计算得出答案；（2）直接利用积的乘方运算法则以及整式的加减运算、整式的除法运算法则分别计算得出答案．【解答】解：（1）原式＝x2﹣3xy+2y2﹣x2+6xy+4x2﹣y2＝4x2+y2+3xy；（2）原式＝（43ab•14a2+a4b2÷3ab）÷（﹣8a3）＝（13a 3b +13a 3b ）÷（﹣8a 3）=23a 3b ÷（﹣8a 3）=―112b ．11．（2021春•沈河区校级月考）运用乘法公式计算：（1）[（x +2y ）2﹣（3x +y ）（3x ﹣y ）﹣5y 2]÷（12x ）；（2）（m ﹣2n +3）（m +2n ﹣3）．【分析】（1）根据完全平方公式、平方差公式、多项式除以单项式可以解答本题；（2）根据完全平方公式、平方差公式可以解答本题．【解答】解：（1）[（x +2y ）2﹣（3x +y ）（3x ﹣y ）﹣5y 2]÷（12x ）＝（x 2+4xy +4y 2﹣9x 2+y 2﹣5y 2）÷（12x ）＝（﹣8x 2+4xy ）÷（12x ）＝﹣16x +8y ；（2）（m ﹣2n +3）（m +2n ﹣3）＝[m ﹣（2n ﹣3）][m +（2n ﹣3）]＝m 2﹣（2n ﹣3）2＝m 2﹣4n 2+12n ﹣9．12．（2020秋•腾冲市期末）计算：（1）（5x ）2•x 7﹣（3x 3）3+2（x 3）2+x 3；（2）（x +2y ）（x ﹣2y ）﹣2x （x +3y ）+（x +y ）2．【分析】（1）根据积的乘方、同底数幂的乘法和合并同类项可以解答本题；（2）根据平方差公式、单项式乘多项式和完全平方公式可以解答本题．【解答】解：（1）（5x ）2•x 7﹣（3x 3）3+2（x 3）2+x 3＝25x 2•x 7﹣27x 9+2x 6+x 3＝25x 9﹣27x 9+2x 6+x 3＝﹣2x 9+2x 6+x 3；（2）（x +2y ）（x ﹣2y ）﹣2x （x +3y ）+（x +y ）2＝x 2﹣4y 2﹣2x 2﹣6xy +x 2+2xy +y 2＝﹣3y2﹣4xy．13．（2021秋•淇县期末）化简求值：（2a﹣b）2﹣（a﹣2b）（a+2b）+（6a2b+8ab2）÷2b，其中a＝2，b＝﹣1．【分析】根据完全平方公式、平方差公式和多项式除以单项式可以将题目中的式子化简，然后将a、b的值代入化简后的式子即可．【解答】解：（2a﹣b）2﹣（a﹣2b）（a+2b）+（6a2b+8ab2）÷2b＝4a2﹣4ab+b2﹣a2+4b2+3a2+4ab＝6a2+5b2，当a＝2，b＝﹣1时，原式＝6a2+5b2＝6×22+5×（﹣1）2＝6×4+5×1＝24+5＝29．14．（2021秋•澄海区期末）化简求值：[（x﹣2y）（x+y）﹣（x+2y）（x﹣2y）]÷（﹣2y），其中x=2 3，y＝﹣1．【分析】原式中括号里利用多项式乘多项式法则，以及平方差公式计算，去括号合并后利用多项式除以单项式法则计算得到最简结果，把x与y的值代入计算即可求出值．【解答】解：原式＝[（x2+xy﹣2xy﹣2y2）﹣（x2﹣4y2）]÷（﹣2y）＝（x2+xy﹣2xy﹣2y2﹣x2+4y2）÷（﹣2y）＝（﹣xy+2y2）÷（﹣2y）=12x﹣y，当x=23，y＝﹣1时，原式=12×23+1=13+1=4 3．15．（2021秋•漳州期末）先化简，再求值：[（x﹣2y）2+（x+2y）（x﹣2y）]÷2x，其中x＝﹣2，y=1 2．【分析】根据整式的加减运算法则进行化简，然后将x与y的值代入原式即可求出答案．【解答】解：原式＝（x2﹣4xy+4y2+x2﹣4y2）÷2x ＝（2x2﹣4xy）÷2x＝x﹣2y，当x＝﹣2，y=12时，原式＝﹣2﹣2×1 2＝﹣2﹣1＝﹣3．16．（2021秋•泰兴市期末）先化简，再求值：已知2a2+5b（a﹣1）+3﹣2（a2﹣ab﹣1），其中a=―17，b＝1．【分析】直接去括号，进而合并同类项，再把已知数据代入得出答案．【解答】解：原式＝2a2+5ab﹣5b+3﹣2a2+2ab+2＝7ab﹣5b+5，当a=―17，b＝1时，原式＝7×（―17）×1﹣5×1+5＝﹣1﹣5+5＝﹣1．17．（2021秋•西峡县期末）先化简，再求值[（a﹣2b）2+（a﹣2b）（a+2b）﹣2a（2a﹣b）]÷2a，其中，a＝﹣1，b=(―23)2．【分析】先根据完全平方公式，平方差公式，单项式乘多项式算括号里面的，再合并同类项，算除法，最后代入求出答案即可．【解答】解：[（a﹣2b）2+（a﹣2b）（a+2b）﹣2a（2a﹣b）]÷2a＝（a2﹣4ab+4b2+a2﹣4b2﹣4a2+2ab）÷2a＝（﹣2a2﹣2ab）÷2a＝﹣a﹣b，当a＝﹣1，b=(―23)2=49时，原式＝﹣（﹣1）―49=1―49=59．18．（2021秋•东坡区期末）先化简，再求值：[（x﹣2y）2+（x﹣2y）（x+2y）﹣2x（2x﹣y）]÷（﹣2x），其中x=―12，y＝1．【分析】先根据完全平方公式，平方差公式和单项式乘多项式算括号里面的，再合并同类项，算除法，再代入求出答案即可．【解答】解：[（x﹣2y）2+（x﹣2y）（x+2y）﹣2x（2x﹣y）]÷（﹣2x）＝（x2﹣4xy+4y2+x2﹣4y2﹣4x2+2xy）÷（﹣2x）＝（﹣2x2﹣2xy）÷（﹣2x）＝x+y，当x=―12，y＝1时，原式=―12+1=12．19．（2021秋•长沙期末）已知x，y满足（x﹣2）2+|y﹣3|＝0．先化简，再求值：[（x﹣2y）（x+2y）﹣（x﹣y）2+y（y+2x）]÷（﹣2y）．【分析】先根据整式的加减运算法则以及乘除运算法则进行化简，然后将x与y的值求出，最后代入化简后的式子即可求出答案．【解答】解：原式＝[x2﹣4y2﹣（x2﹣2xy+y2）+y2+2xy]÷（﹣2y）＝（x2﹣4y2﹣x2+2xy﹣y2+y2+2xy）÷（﹣2y）＝（4xy﹣4y2）÷（﹣2y）＝2y﹣2x，∵（x﹣2）2+|y﹣3|＝0，∴x﹣2＝0，y﹣3＝0，∴x＝2，y＝3，当x＝2，y＝3时，原式＝2×3﹣2×2＝6﹣4＝2．20．（2021秋•南召县期末）先化简，再求值：（2m+1）（2m﹣1）﹣（m﹣1）2+（2m）3÷（﹣8m），其中m2+m﹣2＝0．【分析】先算乘方，再算乘法和除法，再合并同类项，最后代入求出即可．【解答】解：原式＝4m2﹣1﹣（m2﹣2m+1）+8m3÷（﹣8m）＝4m2﹣1﹣m2+2m﹣1﹣m2＝2m2+2m﹣2＝2（m2+m）﹣2，∵m2+m﹣2＝0，∴m2+m＝2，当m2+m＝2时，原式＝2×2﹣2＝2．21．（2021秋•克东县期末）先化简，再求值：[（―12x3y4）3+（―16xy2）2•3xy2]÷（―12xy2）3，其中x＝﹣2，y=12．【分析】原式中括号中利用幂的乘方与积的乘方运算法则计算，合并后利用多项式乘以单项式法则计算得到最简结果，把x与y的值代入计算即可求出值．【解答】解：原式＝（―18x9y12+112x3y6）÷（―18x3y6）＝x6y6―23，当x＝﹣2，y=12时，原式＝1―23=13．22．（2020秋•惠城区期末）已知实数a，b满足a+b＝2，ab=34，求（2a4﹣a2）÷（﹣a）2﹣（a+b）（a﹣b）的值．【分析】先根据积的乘方算乘方，再根据多项式除以单项式和平方差公式进行计算，再合并同类项，最后变形后代入，即可求出答案．【解答】解：（2a4﹣a2）÷（﹣a）2﹣（a+b）（a﹣b）＝（2a4﹣a2）÷a2﹣（a2﹣b2）＝2a2﹣1﹣a2+b2＝a2+b2﹣1，当a+b＝2，ab=34时，原式＝（a+b）2﹣2ab﹣1＝22﹣2×34―1＝4―32―1=3 2．23．（2021秋•原阳县月考）化简求值．（1）已知（x﹣1）（2x﹣1）﹣（x+1）2+1，其中x2﹣5x＝3；（2）已知[（x﹣2y）2+（x﹣2y）（x+2y）﹣2x（2x﹣y）]÷（﹣2x），其中x＝1，y＝﹣2．【分析】（1）先根据多项式乘多项式和完全平方公式进行计算，再合并同类项，最后代入求出答案即可；（2）先根据完全平方公式，平方差公式和单项式乘多项式进行计算，再合并同类项，再算除法，最后代入求出答案即可．【解答】解：（1）（x﹣1）（2x﹣1）﹣（x+1）2+1＝2x2﹣x﹣2x+1﹣x2﹣2x﹣1+1＝x2﹣5x+1，当x2﹣5x＝3时，原式＝3+1＝4；（2）[（x﹣2y）2+（x﹣2y）（x+2y）﹣2x（2x﹣y）]÷（﹣2x）＝（x2﹣4xy+4y2+x2﹣4y2﹣4x2+2xy）÷（﹣2x）＝（﹣2x2﹣2xy）÷（﹣2x）＝x+y，当x＝1，y＝﹣2时，原式＝1+（﹣2）＝﹣1．24．（2021秋•隆昌市校级月考）先化简，再求值：（1）（2x﹣1）2+（x+2）（x﹣2）﹣（x4﹣3x3）÷x2，其中x=―1 2；（2）（2x﹣1）2﹣x（x+4）+（x﹣3）（x+3），实数x满足x2﹣2x﹣2＝0．【分析】（1）先根据完全平方公式，平方差公式，多项式除以单项式进行计算，再合并同类项，最后代入求出答案即可；（2）先根据完全平方公式，平方差公式和单项式乘多项式进行计算，再合并同类项，最后代入求出答案即可．【解答】解：（1）（2x﹣1）2+（x+2）（x﹣2）﹣（x4﹣3x3）÷x2＝4x2﹣4x+1+x2﹣4﹣x2+3x＝4x2﹣x﹣3，当x=―12时，原式＝4×（―12）2﹣（―12）﹣3＝1+12―3＝﹣112；（2）（2x﹣1）2﹣x（x+4）+（x﹣3）（x+3）＝4x2﹣4x+1﹣x2﹣4x+x2﹣9＝4x2﹣8x﹣8，∵x2﹣2x﹣2＝0，∴x2﹣2x＝2，当x2﹣2x＝2时，原式＝4×2﹣8＝0．25．（2021•沙坪坝区校级开学）化简求值[（x+2y）（﹣2y+x）﹣（x+2y）（5y﹣2x）+14y2]÷（―12 x），+4y2﹣4y+1＝0．【分析】先算括号内的呃呃乘法，合并同类项，算除法，求出x、y的值，最后代入求出答案即可．【解答】解：[（x+2y）（﹣2y+x）﹣（x+2y）（5y﹣2x）+14y2]÷（―12 x）＝（x2﹣4y2﹣5xy+2x2﹣10y2+4xy+14y2）÷（―12 x）＝（3x2﹣xy）÷（―12 x）＝﹣6x+2y，4y2﹣4y+1＝0，（2y﹣1）2＝0，∴x﹣y＝0且2y﹣1＝0，解得：x＝y=1 2，当x＝y=12时，原式＝﹣6×12+2×12=―3+1＝﹣2．26．（2021春•龙岗区校级月考）先化简，再求值：（1）[（x+2y）2﹣（3x+y）（3x﹣y）﹣5y2]÷2x，其中x=―12，y＝3．（2）（2a﹣b）²﹣（a+1﹣b）（a+1+b）+（a+1）²，其中a=12，b＝﹣2．【分析】（1）直接利用乘法公式化简，合并同类项，再结合整式除法运算法则化简，最后把x、y的值代入得出答案；（2）直接利用乘法公式化简，再合并同类项，最后把a、b的值代入得出答案．【解答】解：（1）[（x+2y）2﹣（3x+y）（3x﹣y）﹣5y2]÷2x＝[x2+4xy+4y2﹣（9x2﹣y2）﹣5y2]÷2x＝（x2+4xy+4y2﹣9x2+y2﹣5y2）÷2x＝（﹣8x2+4xy）÷2x＝﹣4x+2y，当x=―12，y＝3时，原式＝﹣4×（―12）+2×3＝2+6＝8；（2）（2a﹣b）²﹣（a+1﹣b）（a+1+b）+（a+1）²，＝4a2﹣4ab+b2﹣[（a+1）2﹣b2]+（a+1）²＝4a2﹣4ab+b2﹣（a+1）2+b2+（a+1）²＝4a2﹣4ab+2b2当a=12，b＝﹣2时，原式＝4×（12）2﹣4×12×（﹣2）+2×（﹣2）2＝4×14+4+2×4＝1+4+8＝13．27．（2020秋•罗湖区校级期末）先化简，再求值：（1）已知a2﹣3a+1＝0，求代数式（3a﹣2）2﹣3a（2a﹣1）+5的值；（2）[（x+2y）2﹣（3x+y）（﹣y+3x）﹣5y2]÷（﹣4x），其中x=―12，y＝2．【分析】（1）先根据整式的混合运算顺序和运算法则化简原式，再将a2﹣3a+1＝0化成a2﹣3a＝﹣1整体代入计算可得；（2）先根据整式的混合运算顺序和运算法则化简原式，再代入解答即可．【解答】解：（1）原式＝9a2﹣12a+4﹣6a2+3a+5＝3a2﹣9a+9＝3（a2﹣3a）+9，当a2﹣3a+1＝0，即a2﹣3a＝﹣1时，原式＝3（a2﹣3a）+9＝3×（﹣1）+9＝﹣3+9＝6；（2）原式＝（x2+4xy+4y2﹣9x2+y2﹣5y2）÷（﹣4x）＝﹣y+2x把x=―12，y＝2代入﹣y+2x＝﹣2﹣1＝﹣3．28．（2020秋•饶平县校级期末）已知多项式x2﹣3x+n与多项式x2+mx的乘积中的展开式中，不含x2项和x3项，试化简求值：[（2m+n）2﹣（2m+n）（2m﹣n）﹣6n]÷（﹣2n）．【分析】两多项式相乘后，利用多项式乘多项式法则计算，由乘积中的展开式中，不含x2项和x3项，确定出m与n的值，原式化简后代入计算即可求出值．【解答】解：根据题意得：（x2﹣3x+n）（x2+mx）＝x4+mx3﹣3x3﹣3mx2+nx2+mnx＝x4+（m﹣3）x3+（﹣3m+n）x2+mnx，∵多项式x2﹣3x+n与多项式x2+mx的乘积中的展开式中，不含x2项和x3项，∴m﹣3＝0，﹣3m+n＝0，解得：m＝3，n＝9，则原式＝（4m2+4mn+n2﹣4m2+n2﹣6n）÷（﹣2n）＝（4mn+2n2﹣6n）÷（﹣2n）＝﹣2m﹣n+3，当m＝3，n＝9时，原式＝﹣6﹣9+3＝﹣12．29．（2021秋•德城区校级月考）先化简，再求值：（1）[2x（x2y﹣xy2）+xy（xy﹣x2）]÷（x2y），其中x＝2016，y＝2015．（2）32（x+y+z）2+32（x﹣y﹣z）（x﹣y+z）﹣3z（x+y），其中x+y＝5，xy＝4．【分析】（1）先算乘法，再合并同类项，算除法，最后代入求出即可；（2）先算乘法，再合并同类项，算除法，最后代入求出即可．【解答】解：（1）原式＝（2x3y﹣2x2y2+x2y2﹣x3y）÷（x2y）＝（x3y﹣x2y2）÷（x2y）＝x﹣y，当x＝2 016，y＝2 015时，原式＝2 016﹣2 015＝1；（2）原式=32[（x+y）+z]2+32[（x+y）2﹣z2]﹣3xz﹣3yz=32（x2+y2+z2+2xy+2xz+2yz）+32（x2﹣2xy+y2﹣z2）﹣3xz﹣3yz=32x2+32y2+32z2+3xy+3xz+3yz+32x2﹣3xy+32y2―32z2﹣3xz﹣3yz＝3x2+3y2＝3（x2+y2），因为x+y＝5，xy＝4 所以x2+y2＝（x+y）2﹣2xy＝52﹣2×4＝25﹣8＝17，所以原式＝3×17＝51．30．（2021春•项城市校级期末）（1）化简求值：[（a+12b）2﹣（a―12b）2]（2a―12b）（12b+2a）（14b2+4a2）（其中a＝﹣1，b＝2）；（2）已知y＝﹣x2+（a﹣1）x+2a﹣3，当x＝﹣1时，y＝0．①求a的值；②当x＝1时，求y的值．【分析】（1）首先化简，然后把a＝﹣1，b＝2代入化简后的算式，求出算式的值是多少即可．（2）①根据点的坐标满足函数解析式，可得关于a的方程，根据解方程，可得答案；②根据自变量与函数值的对应关系，可得答案．【解答】解：（1）[（a+12b）2﹣（a―12b）2]（2a―12b）（12b+2a）（14b2+4a2）＝（a+12b+a―12b）（a+12b﹣a+12b）（4a2―14b2）（14b2+4a2）＝2ab（16a4―116b4）∵当a＝﹣1，b＝2时，∴原式＝2×（﹣1）×2×[16×（﹣1）4―116×24]＝﹣4×（16﹣1）＝﹣60；（2）①y＝﹣x2+（a﹣1）x+2a﹣3，当x＝﹣1时，y＝0，得﹣1﹣（a﹣1）+2a﹣3＝0，解得a＝3；②函数解析式为y＝﹣x2+2x+3，当x＝1时，y＝﹣1+2+3＝4．。

整式乘除综合检测(二)(北师版)(含答案)

学生做题前请先回答以下问题问题1：整式混合运算处理方法：①观察结构划部分；②有序操作依法则；③每步推进一点点．其中，在合并同类项时，要________，同类项画相同的线．请利用上述方法计算：．问题2：由完全平方公式，可得（1）__________或__________；（2）__________或__________或__________．问题3：填空：问题4：已知，，求的值．思路分析：①观察题目特征，判断此类题目为“知二求二”问题；②“_______”即为公式中的a，“_________”即为公式中的b，根据他们之间的关系可得_________________________________；③将，代入求解即可．所以=__________．问题5：已知，求的值．你是怎么思考的？问题6：最值问题：①若关于x的二次多项式可以写成的形式，则由___________，可知___________，因此此多项式有最____值为____；②若关于x的二次多项式可以写成的形式，则由___________，可知___________，因此此多项式有最____值为____．整式乘除综合检测（二）（北师版）一、单选题(共10道，每道10分)1.计算的结果是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：整式的乘除混合运算2.计算的结果是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：负指数幂3.若，，则的值为( )A.-136B.-2C.-4D.-8答案：B解题思路：试题难度：三颗星知识点：完全平方公式的应用4.若，，则的结果为( )A.7B.13C.94D.106答案：D解题思路：试题难度：三颗星知识点：完全平方公式的应用5.若，则的值为( )A.256B.196C.194D.322答案：C解题思路：试题难度：三颗星知识点：完全平方公式的应用6.若，则的结果为( )A.40B.5C.10D.20答案：B解题思路：试题难度：三颗星知识点：完全平方公式的应用7.若是完全平方式，则的值为( )A.3B.-3C.±9D.±3答案：D解题思路：试题难度：三颗星知识点：完全平方公式8.若是完全平方式，则的值为( )A.-4B.4C.-16D.16答案：A解题思路：试题难度：三颗星知识点：完全平方公式9.多项式加上下列单项式后，不能成为一个整式的完全平方的是( )A. B.C. D.-1答案：C解题思路：试题难度：三颗星知识点：完全平方公式的应用10.多项式取得最小值时，与的值及多项式的最值分别为( )A.，最小值为16B.，最小值为13C.，最小值为10D.，最小值为10答案：C解题思路：试题难度：三颗星知识点：完全平方公式的应用。

专题05整式加减(计算题专项训练)(北师大版)(原卷版+解析)

专题05 整式加减1．（2022秋·福建厦门·七年级厦门一中校考期中）化简下列各式（1）2x−3y−4x+6y（2）3(b−a)+2(b−a)（3）2(xy+y2)−(xy+2y2−1)（4）3a2−12[a+2(a2−2a)]2．（2022秋·辽宁锦州·七年级统考期中）化简下列各式：（1）3x2y−2x2y+x2y；（2）5m+2n−m−3n；（3）(5a2+2a−1)−4(3−8a+2a2)；（4）3x2−[7x−2(4x−3)−2x2]．3．（2022秋·四川绵阳·七年级校考期中）化简：（1）3x−[x−2(x−y)]+y（2）2a2−[12(ab−4a2)+8ab]−12ab4．（2022秋·甘肃兰州·七年级校考期中）化简．（1）a2−2ab−5a2+12ac+3ab−c2−8ac−2a2．（2）(4ab−b2)−2(a2+2ab−b2)．5．（2022秋·四川成都·七年级校考期中）化简（1）x−5y+(−3x+6y)b)−2(4b−5a)（2）3a+4(a+326．（2022秋·全国·七年级期末）化简：（1）2x2−3x+4y2+5x−3x2−3y2−2x(2−8a−4a2)（2）(5a2−4a+3)−127．（2023春·四川达州·七年级四川省万源中学校考阶段练习）化简：（1）7a2b+(−4a2b+5ab2)−(2a2b−3ab2)；（2）5x2−[x2+(5x2−2x)−(x2−3x)]．8．（2022秋·浙江·七年级专题练习）化简：x+4y)；（1）(2x−3y)+(−52（2）5a2−[a2+(5a2−2a)−2(a2−3a)]9．（2022秋·四川绵阳·七年级东辰国际学校校考阶段练习）化简：（1）(2x−3y)−2(−5x−4y)（2）2(xy2+x2y)−[2xy2−3(1−x2y)]−210．（2022秋·江西南昌·七年级校联考期中）整式化简：（1）4a3−3a2b+5ab2+a2b−5ab2−3a3；（2）5x2−7x−[3x2+2(x2−4x−1)]．11．（2022秋·江苏南京·七年级统考期中）化简．（1）x3−3x2−2x3+5x2+2x；（2）5(x−2y)−3(x−2y)+4(x−2y)−(2y−x)．12．（2022秋·山西晋中·七年级统考期中）化简：（1）−4ab+14b2−5ab−12b2（2）(−x2+3xy−12y2)−2(−12x2+xy−32y2)13．（2022秋·天津·七年级天津市滨海新区塘沽第一中学校考期中）化简：（1）3a2−ab+7−4a2+2ab−7（2）(2x2−12+3x)−4(x−x2+12).14．（2023春·广东梅州·七年级校考开学考试）化简：（1）2(3x2y−2xy2)−(x2y−3xy2).（2）2(3a2−7a)−(4a2−2a−1)+3(−2a2−5a−4).15．（2022秋·四川遂宁·七年级射洪中学校考期中）化简（1）4x2+2(3xy−2x2)−(7xy−1)（2）5ab2−[2a2b−(4ab2−2a2b)]+4a2b+116．（2022秋·湖南永州·七年级校考期中）化简：（1）(8−x2y+7xy2−6xy)−[8xy−(x2y+y2x)]（2）3a2−2[2a2−(2ab−a2)+4ab]17．（2022秋·全国·七年级期末）化简：（1）3m2n−mn2−15mn+2n2m−0.8mn−3m2n；（2）2x2−[3x−2(−x2+2x−1)−4]．18．（2022秋·重庆江津·七年级校考期中）化简：（1）−a2b+(3ab2−a2b)−2(2ab2−a2b)．（2）8x2y−{−6x2y−[3(x2+x2y)−x2y+2]}−1．19．（2022秋·安徽滁州·七年级校考阶段练习）化简：（1）2x2−(−x2+3xy+2y2)−(x2−xy+2y2)（2）34x2y−[12xy+13(12x2y−9xy)]．20．（2022秋·全国·七年级期末）化简：（1）4x2+3y2+2xy−4x2−4y2；（2）−3(12x+y)−2[x−(2x+13y2)]+(−32x+13y2)．专题05 整式加减1．（2022秋·福建厦门·七年级厦门一中校考期中）化简下列各式（1）2x−3y−4x+6y（2）3(b−a)+2(b−a)（3）2(xy+y2)−(xy+2y2−1)（4）3a2−12[a+2(a2−2a)]【思路点拨】（1）根据整式的加减运算法则即可得；（2）先合并同类项，再去括号即可得；（3）先去括号，再计算整式的加减即可得；（4）先去括号，再计算整式的加减即可得．【解题过程】（1）解：原式=(2x−4x)+(6y−3y)=−2x+3y．（2）解：原式=5(b−a)=5b−5a．（3）解：原式=2xy+2y2−xy−2y2+1=xy+1．（4）解：原式=3a2−12(a+2a2−4a)=3a2−12(2a2−3a)=3a2−a2+3 2 a=2a2+32a．2．（2022秋·辽宁锦州·七年级统考期中）化简下列各式：（1）3x2y−2x2y+x2y；（2）5m+2n−m−3n；（3）(5a2+2a−1)−4(3−8a+2a2)；（4）3x2−[7x−2(4x−3)−2x2]．【思路点拨】（1）直接把同类项的系数相加减，字母与字母的指数不变，即可得到答案；（2）直接把同类项的系数相加减，字母与字母的指数不变，即可得到答案；（3）先去括号，再合并同类项即可；（4）先去小括号，再去中括号，再合并同类项即可．【解题过程】（1）解：3x2y−2x2y+x2y=(3−2+1)x2y=2x2y；（2）解：5m+2n−m−3n=(5−1)m+(2−3)n=4m−n；（3）(5a2+2a−1)−4(3−8a+2a2)=(5a2+2a−1)−(12−32a+8a2)=5a2+2a−1−12+32a−8a2=−3a2+34a−13；（4）3x2−[7x−2(4x−3)−2x2]=3x2−(7x−8x+6−2x2)=3x2−7x+8x−6+2x2=5x2+x−63．（2022秋·四川绵阳·七年级校考期中）化简：（1）3x−[x−2(x−y)]+y（2）2a2−[12(ab−4a2)+8ab]−12ab【思路点拨】（1）先去小括号，再去中括号，最后合并同类项即可；（2）先去小括号，再去中括号，最后合并同类项即可．【解题过程】（1）解：3x−[x−2(x−y)]+y=3x−[x−2x+2y]+y=3x−x+2x−2y+y =4x−y；（2）解：2a2−[12(ab−4a2)+8ab]−12ab=2a2−[12ab−2a2+8ab]−12ab=2a2−12ab+2a2−8ab−12ab=4a2−9ab．4．（2022秋·甘肃兰州·七年级校考期中）化简．（1）a2−2ab−5a2+12ac+3ab−c2−8ac−2a2．（2）(4ab−b2)−2(a2+2ab−b2)．【思路点拨】（1）合并同类项即可；（2）先去括号，再合并同类项即可．【解题过程】（1）解：a2−2ab−5a2+12ac+3ab−c2−8ac−2a2=−6a2+ab+4ac−c2；（2）解：(4ab−b2)−2(a2+2ab−b2)=4ab−b2−2a2−4ab+2b2 =−2a2+b2．5．（2022秋·四川成都·七年级校考期中）化简（1）x−5y+(−3x+6y)（2）3a+4(a+32b)−2(4b−5a)【思路点拨】（1）先去括号，再合并同类项即可；（2）先去括号，再合并同类项,根据整式的加减运算法则即可求解．【解题过程】（1）解：x−5y+(−3x+6y)=x−5y−3x+6y=y−2x；b)−2(4b−5a)（2）解：3a+4(a+32=3a+4a+6b−8b+10a=17a−2b．6．（2022秋·全国·七年级期末）化简：（1）2x2−3x+4y2+5x−3x2−3y2−2x(2−8a−4a2)（2）(5a2−4a+3)−12【思路点拨】（1）利用整式添括号和加减法运算即可得到答案，（2）利用整式去括号和加减法运算即可得到答案．【解题过程】（1）解：原式=2x2−3x2+(5x−3x−2x)+(4y2−3y2)=−x2+y2；（2）解：原式=5a2−4a+3−1+4a+2a2=7a2+2．7．（2023春·四川达州·七年级四川省万源中学校考阶段练习）化简：（1）7a2b+(−4a2b+5ab2)−(2a2b−3ab2)；（2）5x2−[x2+(5x2−2x)−(x2−3x)]．【思路点拨】（1）先去括号，再合并同类项即可；（2）去小括号后合并同类项，然后再去括号，合并同类项即可．【解题过程】（1）解：原式=7a2b−4a2b+5ab2−2a2b+3ab2=a2b+8ab2；（2）解：原式=5x2−(x2+5x2−2x−2x2+6x)=5x2−(4x2+4x)=5x2−4x2−4x=x2−4x．8．（2022秋·浙江·七年级专题练习）化简：x+4y)；（1）(2x−3y)+(−52（2）5a2−[a2+(5a2−2a)−2(a2−3a)]【思路点拨】（1）将原式去括号，然后合并同类项即可；（2）将原式去括号，然后合并同类项即可．【解题过程】x+4y)，（1）解：(2x−3y)+(−52x+4y，=2x−3y−52=-1x+y；2（2）解：5a2−[a2+(5a2−2a)−2(a2−3a)]，=5a2−[a2+5a2−2a−2a2+6a]，=5a2−a2-5a2+2a+2a2-6a，=a2-4a．9．（2022秋·四川绵阳·七年级东辰国际学校校考阶段练习）化简：（1）(2x−3y)−2(−5x−4y)（2）2(xy2+x2y)−[2xy2−3(1−x2y)]−2【思路点拨】（1）先去括号，然后找出同类型合并即可；（2）按照先去小括号，再去中括号，最后合并同类项即可．【解题过程】（1）(2x−3y)−2(−5x−4y)=2x−3y+10x+8y=12x+5y（2）2(xy2+x2y)−[2xy2−3(1−x2y)]−2=2xy2+2x2y−[2xy2−3+3x2y)]−2=2xy2+2x2y−2xy2+3−3x2y−2=2xy2−2xy2+2x2y−3x2y+3−2=−x2y+1 10．（2022秋·江西南昌·七年级校联考期中）整式化简：（1）4a3−3a2b+5ab2+a2b−5ab2−3a3；（2）5x2−7x−[3x2+2(x2−4x−1)]．【解题过程】（1）解：4a3−3a2b+5ab2+a2b−5ab2−3a3=4a3−3a3+a2b−3a2b+5ab2−5ab2=(4−3)a3+(1−3)a2b+(5−5)ab2=a3−2a2b；（2）解：5x2−7x−[3x2+2(x2−4x−1)]=5x2−7x−(3x2+2x2−8x−2)=5x2−7x−3x2−2x2+8x+2=5x2−3x2−2x2−7x+8x+2=x+2．11．（2022秋·江苏南京·七年级统考期中）化简．（1）x3−3x2−2x3+5x2+2x；（2）5(x−2y)−3(x−2y)+4(x−2y)−(2y−x)．【思路点拨】（1）合并同类项即可求解；（2）先去括号，然后合并同类项．【解题过程】（1）解：x3−3x2−2x3+5x2+2x=(1−2)x3+(−3+5)x2+2x=−x3+2x2+2x；（2）解：5（x−2y）−3（x−2y）+4（x−2y）−（2y−x）=5x−10y−3x+6y+4x−8y−2y+x=(5x−3x+4x+x)+(−10y+6y−8y−2y) =7x−14y．12．（2022秋·山西晋中·七年级统考期中）化简：（1）−4ab+14b2−5ab−12b2（2）(−x2+3xy−12y2)−2(−12x2+xy−32y2)【思路点拨】（1）移项，合并同类项即可；（2）去括号，移项，合并同类项即可．【解题过程】（1）解：−4ab+14b2−5ab−12b2=−4ab−5ab+14b2−12b2=(−4−5)ab+(14−12)b2=−9ab−14b2；（2）解：(−x2+3xy−12y2)−2(−12x2+xy−32y2)=−x2+3xy−12y2+x2−2xy+3y2=−x2+x2+3xy−2xy−12y2+3y2=xy+52y2．13．（2022秋·天津·七年级天津市滨海新区塘沽第一中学校考期中）化简：（1）3a2−ab+7−4a2+2ab−7（2）(2x2−12+3x)−4(x−x2+12).【思路点拨】（1）合并同类项即可；（2）先去括号，再根据整式的加减运算法则进行计算即可．【解题过程】（1）解：3a2−ab+7−4a2+2ab−7=−a2+ab（2）解：(2x2−12+3x)−4(x−x2+12)=2x2−12+3x−4x+4x2−2=6x2−x−5214．（2023春·广东梅州·七年级校考开学考试）化简：（1）2(3x2y−2xy2)−(x2y−3xy2).（2）2(3a2−7a)−(4a2−2a−1)+3(−2a2−5a−4).【思路点拨】（1）按照去括号、合并同类项的顺序进行计算即可；（2）按照去括号、合并同类项的顺序进行计算即可.【解题过程】（1）解：2(3x2y−2xy2)−(x2y−3xy2)=6x2y−4xy2−x2y+3xy2=5x2y−xy2（2）2(3a2−7a)−(4a2−2a−1)+3(−2a2−5a−4)=6a2−14a−4a2+2a+1−6a2−15a−12=−4a2−27a−1115．（2022秋·四川遂宁·七年级射洪中学校考期中）化简（1）4x2+2(3xy−2x2)−(7xy−1)（2）5ab2−[2a2b−(4ab2−2a2b)]+4a2b+1【思路点拨】（1）先去括号，再按照整式的加减混合运算法则进行化简即可；（2）先去小括号，再去中括号，再按照整式的加减混合运算法则进行化简即可．【解题过程】（1）解：原式=4x2+6xy−4x2−7xy+1=−xy+1．（2）解：原式=5ab2−(2a2b−4ab2+2a2b)+4a2b+1=5ab2−2a2b+4ab2−2a2b+4a2b+1=9ab2+1．16．（2022秋·湖南永州·七年级校考期中）化简：（1）(8−x2y+7xy2−6xy)−[8xy−(x2y+y2x)]（2）3a2−2[2a2−(2ab−a2)+4ab]【思路点拨】（1）先去括号，然后再合并同类项即可；（2）按照整式的混合运算法则计算即可．【解题过程】（1）解：(8−x2y+7xy2−6xy)−[8xy−(x2y+y2x)] =8−x2y+7xy2−6xy−8xy+x2y+y2x=(7xy2+y2x)+(−x2y+x2y)+(−6xy−8xy)+8=8xy2−14xy+8．（2）解：3a2−2[2a2−(2ab−a2)+4ab]=3a2−2[2a2−2ab+a2+4ab]=3a2−2[3a2+2ab]=3a2−6a2−4ab=−3a2−4ab．17．（2022秋·全国·七年级期末）化简：（1）3m2n−mn2−15mn+2n2m−0.8mn−3m2n；（2）2x2−[3x−2(−x2+2x−1)−4]．【思路点拨】（1）先找出同类项，然后合并同类项即可；（2）先去括号，然后合并同类项即可．【解题过程】（1）解：3m2n−mn2−15mn+2n2m−0.8mn−3m2n=3m2n−3m2n−mn2+2n2m−15mn−0.8mn=mn2−mn；（2）解：2x2−[3x−2(−x2+2x−1)−4]=2x2−3x+2(−x2+2x−1)+4=2x2−3x−2x2+4x−2+4=2x2−2x2−3x+4x−2+4=x+2 18．（2022秋·重庆江津·七年级校考期中）化简：（1）−a2b+(3ab2−a2b)−2(2ab2−a2b)．（2）8x2y−{−6x2y−[3(x2+x2y)−x2y+2]}−1．【思路点拨】（1）先去括号，再根据整式加减的法则进行计算即可；（2）先去括号，再根据整式加减的法则进行计算即可．【解题过程】（1）−a2b+(3ab2−a2b)−2(2ab2−a2b)=−a2b+3ab2−a2b−4ab2+2a2b=−ab2；（2）8x2y−{−6x2y−[3(x2+x2y)−x2y+2]}−1=8x2y−[−6x2y−(3x2+3x2y−x2y+2)]−1=8x2y−(−6x2y−3x2−3x2y+x2y−2)−1=8x2y+6x2y+3x2+3x2y−x2y+2−1=16x2y+3x2+119．（2022秋·安徽滁州·七年级校考阶段练习）化简：（1）2x2−(−x2+3xy+2y2)−(x2−xy+2y2)（2）34x2y−[12xy+13(12x2y−9xy)]．【思路点拨】（1）直接利用去括号法则，去掉括号后，合并同类项即可；（2）按照去括号法则，先去掉小括号，再去掉中括号，最后合并同类项即可．【解题过程】（1）解：2x2−(−x2+3xy+2y2)−(x2−xy+2y2)=2x2+x2−3xy−2y2−x2+xy−2y2=(2+1−1)x2+(−3+1)xy+(−2−2)y2=2x2−2xy−4y2．（2）解：34x2y−[12xy+13(12x2y−9xy)]=34x2y−(12xy+16x2y−3xy)=34x2y−12xy−16x2y+3xy=712x2y+52xy．20．（2022秋·全国·七年级期末）化简：（1）4x2+3y2+2xy−4x2−4y2；（2）−3(12x+y)−2[x−(2x+13y2)]+(−32x+13y2)．【思路点拨】（1）根据整式的加减运算法则，利用合并同类项运算直接求解即可得到答案；（2）根据整式的加减及乘法运算法则，利用去括号法则先去括号，再根据合并同类项运算计算即可得到答案．【解题过程】（1）解：4x2+3y2+2xy−4x2−4y2=(4x2−4x2)+(3y2−4y2)+2xy=(4−4)x2+(3−4)y2+2xy=−y2+2xy；（2）解：−3(12x+y)−2[x−(2x+13y2)]+(−32x+13y2)=−32x−3y−2x+2(2x+13y2)−32x+13y2=−32x−3y−2x+4x+23y2−32x+13y2=(−32x−2x+4x−32x)−3y+(23y2+13y2)=(−32×2−2+4)x−3y+(23+13)y2=−x−3y+y2．。