信道和信道容量
合集下载
第三章 信道模型和信道容量
这是可知疑义度H(X/Y)=0，平均交互信息量达到最大值 I(X,Y)=H(X)，C=logr。从平均意义上讲，这种信道可以把信源 的信息全部传递道信宿。这种每列只有一个非0元素的信道也 是一种无噪声信道，称为无噪声信道。
确定信道
这类信道的转移概率等于1或者等于0， 每一列的元素可有一个或多个1，可知其 噪声熵H(Y/X)=0，此时的平均交互信息 量达到最大值。
离散信道
X
P(Y/X)
Y
离散信道分类： 无干扰信道 有干扰无记忆信道 有干扰有记忆信道
离散信道三种表达方式
概率空间描述 X={a1,a2,……ar} P(Y/X)={p(bj/ai)}
j=1,2,……s) Y={b1,b2,……bs} 0≤p(bj/ai)≤1
(i=1,2,……r;
转移矩阵描述
信道组合
串联信道 并联信道
4.4 时间离散的无记忆连续 信道
可加噪声信道
P(y|x)=p(y-x)=p(z)
Hc (Y | X ) Hc (Z ) I (X ;Y ) Hc (Y ) Hc (Z )
可加噪声信道
高斯噪声信道
I
(X
;Y
)
H
(Y
)
Hc
(X
)
1 2
log(1
2 x 2 z
)
例已知一个二元信源连接一个二元信道， 如图给出。X={x1,x2}, [p(xi)]={1/2,1/2}
求I(X；Y)，H(X,Y)，H(X/Y)，和H(Y/X)。
信道容量
C max R max I (X ;Y )bit / 符号
PX
PX
1
Ct
max PX
Rt
信道及信道容量
信道及信道容量
研究信道容量的意义?
信道是信息传输的通道。由于干扰而丢失的信息为 H(X|Y ); 在接收端获取的关于发送端信源X的信息量是：
I(X;Y)＝H(X)-H(X|Y) 即：信道中平均每个符号传送的信息量。对于信道,所关心的问 题是平均每个符号传送的最大信息量。这就是信道容量C=max I(X;Y) bit/符号
4、根据信道中所受的噪声种类不同，分为随机差错信道和突发 差错信道。
随机差错信道：噪声独立地、随机地影响每个传输的码元。如加 性高斯白噪声(AGWN)信道。 突发差错信道：大的脉冲干扰或闪电对码元的影响是前后相关的。 错误成串出现，且是突发性的。如移动信道。
5、根据输入/输出信号的特点，分为离散信道、连续信道、半离 散半连续信道和波形信道。
根据信道的参数，将信道分为三大类：
1、无干扰信道 理想信道，信道中没有随机干扰
P(Y |X )1 Y fX ()
P(Y|X)0 YfX ()
或干扰很小。输出与输入之间有完全确定的对应关系。
2、有干扰无记忆信道
无记忆：任意时刻的输出符号，只统计依赖于对应时刻
的输入符号，而与其它时刻的输入符号、输出符号无关.
I(X;Y)＝I(Y;X)＝Hc(X)- Hc(X|Y) ＝Hc(X)＋Hc(Y)- Hc(XY) ＝Hc(Y)- Hc(Y|X)
Hc(XY)＝Hc(X)＋Hc(Y|X)＝Hc(Y) ＋Hc(X|Y)
二、波形信源的熵 理解讨论方法即可
H c(x()t )L l i m H c(X )
三、 连续信源最大熵定理
转移概率矩阵（传递阵矩）P :
P11 P12 P1m
P [
P ij
]
P21
P22
研究信道容量的意义?
信道是信息传输的通道。由于干扰而丢失的信息为 H(X|Y ); 在接收端获取的关于发送端信源X的信息量是：
I(X;Y)＝H(X)-H(X|Y) 即：信道中平均每个符号传送的信息量。对于信道,所关心的问 题是平均每个符号传送的最大信息量。这就是信道容量C=max I(X;Y) bit/符号
4、根据信道中所受的噪声种类不同，分为随机差错信道和突发 差错信道。
随机差错信道：噪声独立地、随机地影响每个传输的码元。如加 性高斯白噪声(AGWN)信道。 突发差错信道：大的脉冲干扰或闪电对码元的影响是前后相关的。 错误成串出现，且是突发性的。如移动信道。
5、根据输入/输出信号的特点，分为离散信道、连续信道、半离 散半连续信道和波形信道。
根据信道的参数，将信道分为三大类：
1、无干扰信道 理想信道，信道中没有随机干扰
P(Y |X )1 Y fX ()
P(Y|X)0 YfX ()
或干扰很小。输出与输入之间有完全确定的对应关系。
2、有干扰无记忆信道
无记忆：任意时刻的输出符号，只统计依赖于对应时刻
的输入符号，而与其它时刻的输入符号、输出符号无关.
I(X;Y)＝I(Y;X)＝Hc(X)- Hc(X|Y) ＝Hc(X)＋Hc(Y)- Hc(XY) ＝Hc(Y)- Hc(Y|X)
Hc(XY)＝Hc(X)＋Hc(Y|X)＝Hc(Y) ＋Hc(X|Y)
二、波形信源的熵 理解讨论方法即可
H c(x()t )L l i m H c(X )
三、 连续信源最大熵定理
转移概率矩阵（传递阵矩）P :
P11 P12 P1m
P [
P ij
]
P21
P22
信道与信道容量
1.6.2 信道容量
根据香农信息论，对于连续信道，如果信道带宽为B， 并且受到加性高斯白噪声的干扰，则信道容量的理论公式为
C=B㏒2（1+S/N）（b/s） 式中。 N为白噪声的平均功率； S是信号的平均功率； S/N 为信噪比。信道容量C是指信道可能传输的最大信息速率 （即信道能达到的最大传输能力）。虽然上式是在一定条件 下获得的（要求输入信号也为高斯信号才能实现上述可能 性），但对其他情况也可作为近似式使用。
例1 已知彩色电视图象由5ⅹ105个像素组成。设每个像素有 64种彩色度，每种彩色度有16个亮度等级。设所有彩色度和 亮度等级的组合机会均等，并统计独立。（1）试计算每秒 传送100个画面所需信道容量；（2）如果接受机信噪比为 30dB，为了传送彩色图象所需信道带宽为多少？
例2 设有一个图像要在电话线路中实现传真传输。大约要传输2.25ⅹ106个 像素，每个像素有12个亮度等级。假设所有亮度等级都是等概率的，电 话电路具有3kHz带宽和30dB信噪比。试求在该标准电话线路上传输一 张传真图片需要的最小时间。
在数字通信系统中，如果仅研究编码和解码问题， 可得到另一种广义信道---编码信道。编码信道的范围是 从编码器输出端至解码器输入端。这是因为从编码和解 码角度来看，编码器是把信源产生的消息信号转化为数 字信号。反之，解码器是将数字信号恢复原来的消息信 号；而编码器输出端至解码器输入端之间的一切环节只 是起了传输数字信号的作用，所以可以把它看成一个整 体---编码信道。当然，根据研究问题的不同，还可以定 义其他广义信道。
解： Rb = RBN㏒2N
RBN= Rb／×106 / 29.9 ×103=0.269 ×103s=4.5min
例3 已知八进制数字信号的传输速率为1600波 特。试问变换成二进制数字信号时的传输速率为多 少？ 解： Rb = RBN㏒2N = 1600× ㏒28 = 4800 b/s
信道、信道容量、数据传输速率
信道、信道容量、数据传输速率简介：信道、信道容量、数据传输速率（比特率）、电脑装置带宽列表一、信道的概念信道，是信号在通信系统中传输的通道，是信号从发射端传输到接收端所经过的传输媒质，这是狭义信道的定义。
广义信道的定义除了包括传输媒质，还包括信号传输的相关设备。
信道容量是在通信信道上可靠地传输信息时能够达到的最大速率。
根据有噪信道编码定理，给定信道的信道容量是其以任意小的差错概率传输信息的极限速率。
信道容量的单位为比特每秒、奈特每秒等等。
香农在第二次世界大战期间发展出信息论，并给出了信道容量的定义和计算信道容量的数学模型。
他指出，信道容量是信道的输入与输出的互信息量的最大值，这一最大取值由输入信号的概率分布决定。
二、信道的分类（一）狭义信道的分类狭义信道，按照传输媒质来划分，可以分为有线信道、无线信道和存储信道三类。
1. 有线信道有线信道以导线为传输媒质，信号沿导线进行传输，信号的能量集中在导线附近，因此传输效率高，但是部署不够灵活。
这一类信道使用的传输媒质包括用电线传输电信号的架空明线、电话线、双绞线、对称电缆和同轴电缆等等，还有传输经过调制的光脉冲信号的光导纤维。
2. 无线信道无线信道主要有以辐射无线电波为传输方式的无线电信道和在水下传播声波的水声信道等。
无线电信号由发射机的天线辐射到整个自由空间上进行传播。
不同频段的无线电波有不同的传播方式，主要有：地波传输：地球和电离层构成波导，中长波、长波和甚长波可以在这天然波导内沿着地面传播并绕过地面的障碍物。
长波可以应用于海事通信，中波调幅广播也利用了地波传输。
天波传输：短波、超短波可以通过电离层形成的反射信道和对流层形成的散射信道进行传播。
短波电台就利用了天波传输方式。
天波传输的距离最大可以达到400千米左右。
电离层和对流层的反射与散射，形成了从发射机到接收机的多条随时间变化的传播路径，电波信号经过这些路径在接收端形成相长或相消的叠加，使得接收信号的幅度和相位呈随机变化，这就是多径信道的衰落，这种信道被称作衰落信道。
信道、信道容量、数据传输速率
简介：信道、信道容量、数据传输速率（比特率）、电脑装置带宽列表一、信道的概念信道，是信号在通信系统中传输的通道，是信号从发射端传输到接收端所经过的传输媒质，这是狭义信道的定义。
广义信道的定义除了包括传输媒质，还包括信号传输的相关设备。
信道容量是在通信信道上可靠地传输信息时能够达到的最大速率。
根据有噪信道编码定理，给定信道的信道容量是其以任意小的差错概率传输信息的极限速率。
信道容量的单位为比特每秒、奈特每秒等等。
香农在第二次世界大战期间发展出信息论，并给出了信道容量的定义和计算信道容量的数学模型。
他指出，信道容量是信道的输入与输出的互信息量的最大值，这一最大取值由输入信号的概率分布决定。
二、信道的分类（一）狭义信道的分类狭义信道，按照传输媒质来划分，可以分为有线信道、无线信道和存储信道三类。
1. 有线信道有线信道以导线为传输媒质，信号沿导线进行传输，信号的能量集中在导线附近，因此传输效率高，但是部署不够灵活。
这一类信道使用的传输媒质包括用电线传输电信号的架空明线、电话线、双绞线、对称电缆和同轴电缆等等，还有传输经过调制的光脉冲信号的光导纤维。
2. 无线信道无线信道主要有以辐射无线电波为传输方式的无线电信道和在水下传播声波的水声信道等。
无线电信号由发射机的天线辐射到整个自由空间上进行传播。
不同频段的无线电波有不同的传播方式，主要有：地波传输：地球和电离层构成波导，中长波、长波和甚长波可以在这天然波导内沿着地面传播并绕过地面的障碍物。
长波可以应用于海事通信，中波调幅广播也利用了地波传输。
天波传输：短波、超短波可以通过电离层形成的反射信道和对流层形成的散射信道进行传播。
短波电台就利用了天波传输方式。
天波传输的距离最大可以达到400千米左右。
电离层和对流层的反射与散射，形成了从发射机到接收机的多条随时间变化的传播路径，电波信号经过这些路径在接收端形成相长或相消的叠加，使得接收信号的幅度和相位呈随机变化，这就是多径信道的衰落，这种信道被称作衰落信道。
信道、信道容量、数据传输速率
编码信道是指数字信号由编码器输出端传输到译码器输入端经过的部分。对于编译码的研究者来说，编码器输出的数字序列经过编码信道上的一系列变换之后，在译码器的输入端成为另一组数字序列，研究者只关系这两组数字序列之间的变换关系，而并不关心这一系列变换发生的具体物理过程，甚至并不关心信号在调制信道上的具体变化。编码器输出的数字序列与到译码器输入的数字序列之间的关系，通常用多端口网络的转移概率作为编码信道的数学模型进行描述。
二、信道的分类
（一）狭义信道的分类
狭义信道，按照传输媒质来划分，可以分为有线信道、无线信道和存储信道三类。
1. 有线信道
有线信道以导线为传输媒质，信号沿导线进行传输，信号的能量集中在导线附用电线传输电信号的架空明线、电话线、双绞线、对称电缆和同轴电缆等等，还有传输经过调制的光脉冲信号的光导纤维。
天波传输：短波、超短波可以通过电离层形成的反射信道和对流层形成的散射信道进行传播。短波电台就利用了天波传输方式。天波传输的距离最大可以达到400千米左右。电离层和对流层的反射与散射，形成了从发射机到接收机的多条随时间变化的传播路径，电波信号经过这些路径在接收端形成相长或相消的叠加，使得接收信号的幅度和相位呈随机变化，这就是多径信道的衰落，这种信道被称作衰落信道。
调制信道的数学模型为：
y(t) = x(t) * h(t;τ) + n(t)
其中x(t)是调制信道在时刻t的输入信号，即已调信号。y(t)是调制信道在时刻t的输出信号。h(t;τ)是信道的冲激响应，τ代表时延，h(t;τ)表示在时刻t、延时为τ时信道对冲激函数δ(t)的响应，描述了信道对输入信号的畸变和延时。*为卷积算子。n(t) 是调制信道上存在的加性噪声，与输入信号x(t)无关，又被称为"加性干扰"。由于信道的线性性质，并且考虑信道噪声，x(t) * h(t;τ) + n(t)就是x(t)通过由信道响应h(t;τ)描述的调制信道的输出。调制信道可以同时有多个输入信号和多个输出信号，这时的x(t)和y(t)是矢量信号。
二、信道的分类
（一）狭义信道的分类
狭义信道，按照传输媒质来划分，可以分为有线信道、无线信道和存储信道三类。
1. 有线信道
有线信道以导线为传输媒质，信号沿导线进行传输，信号的能量集中在导线附用电线传输电信号的架空明线、电话线、双绞线、对称电缆和同轴电缆等等，还有传输经过调制的光脉冲信号的光导纤维。
天波传输：短波、超短波可以通过电离层形成的反射信道和对流层形成的散射信道进行传播。短波电台就利用了天波传输方式。天波传输的距离最大可以达到400千米左右。电离层和对流层的反射与散射，形成了从发射机到接收机的多条随时间变化的传播路径，电波信号经过这些路径在接收端形成相长或相消的叠加，使得接收信号的幅度和相位呈随机变化，这就是多径信道的衰落，这种信道被称作衰落信道。
调制信道的数学模型为：
y(t) = x(t) * h(t;τ) + n(t)
其中x(t)是调制信道在时刻t的输入信号，即已调信号。y(t)是调制信道在时刻t的输出信号。h(t;τ)是信道的冲激响应，τ代表时延，h(t;τ)表示在时刻t、延时为τ时信道对冲激函数δ(t)的响应，描述了信道对输入信号的畸变和延时。*为卷积算子。n(t) 是调制信道上存在的加性噪声，与输入信号x(t)无关，又被称为"加性干扰"。由于信道的线性性质，并且考虑信道噪声，x(t) * h(t;τ) + n(t)就是x(t)通过由信道响应h(t;τ)描述的调制信道的输出。调制信道可以同时有多个输入信号和多个输出信号，这时的x(t)和y(t)是矢量信号。
第三章信道及信道容量PPT课件
第三章 信道及信道容量
第一节 信道分类及表示参数 第二节 单符号离散信道及其容量 第三节 离散序列信道及其容量 第四节 连续信道及其容量
05.12.2020
1
研究信道容量的意义?
信道是信息传输的通道。由于干扰而丢失的信息为 H(X|Y ); 在接收端获取的关于发送端信源X的信息量是：
I(X;Y)＝H(X)-H(X|Y) 即：信道中平均每个符号传送的信息量。对于信道,所关心的问 题是平均每个符号传送的最大信息量。这就是信道容量C=max I(X;Y) bit/符号
每个数字对应一种颜色（反之未必），数字已知，则颜色确 定，H(X|Y)=0。H(X,Y)=H(Y)=…..
6、2.21（3）信号放大问题。课上已经强调过，仍出错。
7、向孔祥品学习
05.12.2020
9
复习：第四节 连续信源的熵和互信息
一、单符号连续信源的熵 相对熵（差熵）
H c(X ) p X (x)lop X g (x)dx Hc(XY )p(xy)lopg(xy)dxdy Hc(Y/X )p(xy)lopg(y/x)dxdy
(2) 离散无记忆信道(DMC-Discrete Memoryless Channel)
仍是单符号离散信道，符号集中的符号数目大于2 。
05.12.2020
7
转移概率矩阵（传递阵矩）P :
P11 P12 P1m
P [
P ij
]
P21
P22
P2m
Pn1
Pn2
Pnm
m
m
转移概率矩 元阵 素中 之 1。 各 和 P(b 行 j等 |ai)的 于 Pij1
2 Pm2,通常m0,2 P,此时有：
H0C5.1(2X.202)0
第一节 信道分类及表示参数 第二节 单符号离散信道及其容量 第三节 离散序列信道及其容量 第四节 连续信道及其容量
05.12.2020
1
研究信道容量的意义?
信道是信息传输的通道。由于干扰而丢失的信息为 H(X|Y ); 在接收端获取的关于发送端信源X的信息量是：
I(X;Y)＝H(X)-H(X|Y) 即：信道中平均每个符号传送的信息量。对于信道,所关心的问 题是平均每个符号传送的最大信息量。这就是信道容量C=max I(X;Y) bit/符号
每个数字对应一种颜色（反之未必），数字已知，则颜色确 定，H(X|Y)=0。H(X,Y)=H(Y)=…..
6、2.21（3）信号放大问题。课上已经强调过，仍出错。
7、向孔祥品学习
05.12.2020
9
复习：第四节 连续信源的熵和互信息
一、单符号连续信源的熵 相对熵（差熵）
H c(X ) p X (x)lop X g (x)dx Hc(XY )p(xy)lopg(xy)dxdy Hc(Y/X )p(xy)lopg(y/x)dxdy
(2) 离散无记忆信道(DMC-Discrete Memoryless Channel)
仍是单符号离散信道，符号集中的符号数目大于2 。
05.12.2020
7
转移概率矩阵（传递阵矩）P :
P11 P12 P1m
P [
P ij
]
P21
P22
P2m
Pn1
Pn2
Pnm
m
m
转移概率矩 元阵 素中 之 1。 各 和 P(b 行 j等 |ai)的 于 Pij1
2 Pm2,通常m0,2 P,此时有：
H0C5.1(2X.202)0
信道及信道容量
P 1
信道1 p( j | k )
P2
信道2 P p( j | k )
若信道1和信道2级联，则要求信道1的输出集和信道2的输入集 相同。给定信道1和信道2的转移概率 p( j | k ) 和 p( j | k ) ， 则 级联信道的转移概率为 p ( j | k ) j p( j | k ) p( j | k j ) 这样就得到了一个新的离散信道，输入集为 X1 ，输出集为 Y2 ， 转移概率矩阵为 {P( j | k )}。
信息工程学院通信工程系
3.2 离散信道及数学模型
多符号离散信道数学模型 X=X1X2… Xk ….XN
P(Y|X)
Y=Y1Y2…Yk ….YN
{p(yj|xi)}
Xk取值: {x1, x2, …, xn}， 则X共有nN 种 i , i=1～nN Yk取值: {y1, y2, …, ym}， 则Y共有mN种 j , j=1～mN
在物理信道一定的情况下，总是希望传输的信息越 多越好。这不仅仅与物理信道本身特性有关，还与载荷
信息的信号形式和信源输出信号的统计特性有关。
本章讨论“什么条件下，通过信道的信息量最大”。
信息工程学院通信工程系
3.1 信道分类和描述
信道分类
1、根据信道两端输入和输出集合的个数，分为： 两端信道(单用户信道)--输入、输出均只有一个 多端信道(多用户信道)--输入、输出有多个 2、根据输入、输出随机变量的个数，分为： 单符号信道--输入、输出用随机变量表示 多符号信道--输入、输出用随机矢量表示 3、根据信道上有无噪声(干扰)，分为： 有噪(扰)信道 无噪(扰)信道
[ （1） 信道输入统计概率空间：X , p( X )] [ （2） 信道输出统计概率空间：Y , p (Y )] （3） 信道的统计特性，即信道转移概率矩阵：p( y | x)
信道1 p( j | k )
P2
信道2 P p( j | k )
若信道1和信道2级联，则要求信道1的输出集和信道2的输入集 相同。给定信道1和信道2的转移概率 p( j | k ) 和 p( j | k ) ， 则 级联信道的转移概率为 p ( j | k ) j p( j | k ) p( j | k j ) 这样就得到了一个新的离散信道，输入集为 X1 ，输出集为 Y2 ， 转移概率矩阵为 {P( j | k )}。
信息工程学院通信工程系
3.2 离散信道及数学模型
多符号离散信道数学模型 X=X1X2… Xk ….XN
P(Y|X)
Y=Y1Y2…Yk ….YN
{p(yj|xi)}
Xk取值: {x1, x2, …, xn}， 则X共有nN 种 i , i=1～nN Yk取值: {y1, y2, …, ym}， 则Y共有mN种 j , j=1～mN
在物理信道一定的情况下，总是希望传输的信息越 多越好。这不仅仅与物理信道本身特性有关，还与载荷
信息的信号形式和信源输出信号的统计特性有关。
本章讨论“什么条件下，通过信道的信息量最大”。
信息工程学院通信工程系
3.1 信道分类和描述
信道分类
1、根据信道两端输入和输出集合的个数，分为： 两端信道(单用户信道)--输入、输出均只有一个 多端信道(多用户信道)--输入、输出有多个 2、根据输入、输出随机变量的个数，分为： 单符号信道--输入、输出用随机变量表示 多符号信道--输入、输出用随机矢量表示 3、根据信道上有无噪声(干扰)，分为： 有噪(扰)信道 无噪(扰)信道
[ （1） 信道输入统计概率空间：X , p( X )] [ （2） 信道输出统计概率空间：Y , p (Y )] （3） 信道的统计特性，即信道转移概率矩阵：p( y | x)
第三章信道及信道容量
2但为有限值,即
p11
P
p2
1
p12 p22
,
p1m
p2m
pn1
pn2
pn
m
②二进制对称信道（BSC）：输入和输出信号的符号数都 是2，即X∈A={0,1}和Y∈B={0，1}的对称信道。
1-p
0 p
0
1p p
p
P
p
1p
1
1
1-p
16
《信息论与编码》
3）有干扰有记忆信道：每个信道输出不但与当前输入信号 之间有转移概率关系，而且与其它时刻的输入输出信号也 有关。
27
《信息论与编码》
2）信道容量的定义 对于某特定信道，可找到某种信源的概率分布p(ai)，使
得 I（X；Y）达到最大。
C m ax { I(X ;Y )} (b it/符 号 ) p(x)
注：对于特定的信道，信道容量是个定值，但是在传输信 息时信道能否提供其最大传输能力，则取决于输入端的概 率分布。一般相应的输入概率分布称为最佳输入分布。
28
若平均传输一个符号需要t秒钟，则信道单位时间内 平均传输的最大信息量为：
C T1 tm p(axx ){I(X;Y)}(bit/秒 )
即信道传输速率。
信道容量C已与输入信源的概率分布无关，它只是 信道传输概率的函数，只与信道的统计特性有关。 所以，信道容量是完全描述信道特性的参量，是信 道能够传输的最大信息量。
这样，波形信道化为多维连续信道，信道转移概率密度 函数为
其中：
19
《信息论与编码》
如果多维连续信道的转移概率密度函数满足
这样的信道称为连续无记忆信道即在任一时刻输出变 量只与对应时刻的输入变量有关，与以前时刻的输入输出 都无关。
信道及信道容量
• 恒参信道的性质不随时间变化：线性时不变系统。实 际信道的特性不随时间变化或基本不变，或变化极慢 。
ei（t） h(t)
eo(t)=ei(t)*h(t)+n(t)
n(t)
11
Center for Wireless Communications (CWC), BUPT
恒参信道特性（续）
• h(t) <=> H(ω)=∣H(ω)∣ejΨ(ω) • 幅频特性：∣H(ω)∣≠k(常数)，产生幅频畸变； • 相频特性：Ψ(ω) ≠ωtd ，产生相位畸变； • 用群迟延频率特性：τ(ω)=dΨ(ω)/dω来描述相频特性。 • 理想信道： H(ω)=k，衰减ei(t)、有时延； • τ(ω)= td，无相频畸变。 • 工程设计时，应使∣H(ω)∣的畸变范围及τ(ω)的误差范
j
2
(e
j
2
j
e 2)
V0e
j
et0
j
2
2 c os (
2
)
V0f(t-t0)+V0f(t-t0- )
H ()
2V0
cos( 2
)
2V0
f
01
3
5
2
2
2
18
Center for Wireless Communications (CWC), BUPT
• 扩频技术：尤其对窄带干扰非常有用，在扩频通信基本原理中介绍 。
20
Center for Wireless Communications (CWC), BUPT
分集接收技术
• 分集技术根据获得独立路径信号的方法： (1) 时间分集： (2) 频率分集： (3) 空间分集： (4)时频分集
ei（t） h(t)
eo(t)=ei(t)*h(t)+n(t)
n(t)
11
Center for Wireless Communications (CWC), BUPT
恒参信道特性（续）
• h(t) <=> H(ω)=∣H(ω)∣ejΨ(ω) • 幅频特性：∣H(ω)∣≠k(常数)，产生幅频畸变； • 相频特性：Ψ(ω) ≠ωtd ，产生相位畸变； • 用群迟延频率特性：τ(ω)=dΨ(ω)/dω来描述相频特性。 • 理想信道： H(ω)=k，衰减ei(t)、有时延； • τ(ω)= td，无相频畸变。 • 工程设计时，应使∣H(ω)∣的畸变范围及τ(ω)的误差范
j
2
(e
j
2
j
e 2)
V0e
j
et0
j
2
2 c os (
2
)
V0f(t-t0)+V0f(t-t0- )
H ()
2V0
cos( 2
)
2V0
f
01
3
5
2
2
2
18
Center for Wireless Communications (CWC), BUPT
• 扩频技术：尤其对窄带干扰非常有用，在扩频通信基本原理中介绍 。
20
Center for Wireless Communications (CWC), BUPT
分集接收技术
• 分集技术根据获得独立路径信号的方法： (1) 时间分集： (2) 频率分集： (3) 空间分集： (4)时频分集
第3章 信道与信道容量
max p(x)
H C (Y )
1 log
2
2e
2
pn(n)＝N(0, 2) 连续单符号信道
噪声是均值为零、方差为 2的加性高斯噪声
34
3.4 连续信道及其容量
连续单符号加性信道
pY (y) ＝N(0,P)，pn(n)＝N(0, 2)，y=x+n，所以 pX (x)＝N(0, S)
3
3.1 信道分类和表示参数
二进制对称信道(BSC)
P
1 p
p
p 1 p
4
3.1 信道分类和表示参数
离散无记忆信道
a1 a2
b1
p11 p12 p1m
b2 b3
P
p21
p22
p2m
an
bm
pn1
pn2
pnm
5
3.1 信道分类和表示参数
离散输入、连续输出信道
pY ( y / ai )
31
3.3 离散序列信道及其容量
扩展信道
(1 p)2 p(1 p) p(1 p) p2
1
P
p(1 p(1
p) p)
(1 p)2 p2
p2 (1 p)2
p(1
p)
p(1 p)
p2 p(1 p) p(1 p) (1 p)2
C2 log2 4 H[(1 p)2 , p(1 p), p(1 p), p 2 ]
1 1 1 1
13
3 1
6 1
6 1
6 6 3 3
1 1 1
2 1
3 1
6 1
6 2 3
1 1 1
3 6 2
12
3.2 离散单个符号信道及其容量
信道模型及信道容量
i 1 j 1 r s
p(ai b j ) p(ai ) p(b j ) I (Y ; X )
p(b j ai ) log
i 1 j 1
r
s
p(b j ai ) p(b j ) p(ai )
I ( X ; Y ) I (Y ; X )
结 论 平均互信息特性：
平均互信息量的非负性 平均互信息量的极值性（凸函数） 平均互信息量的交互性（对称性）
单符号信道的数学模型：
{ X , p( y / x),Y }
单维离散信道的数学模型
输入输出的联合概率为：
p(bj ai ) p(ai ) p(bj / ai ) p(bi ) p(a j / bi )
P(ai )
称作输入概率/先验概率
P(bj / ai ) 称作前向概率 P(ai / bj ) 称作后向概率/后验概率
平均互信息量
当信宿Y收到某一具体符号bj(Y=bj)后，推测信 源X发符号ai的概率，已由先验概率p(ai)转变为 后验概率p(ai/bj)，从bj中获取关于输入符号的信 息量，应是互信息量I(ai ; bj)在两个概率空间X 和Y中的统计平均值：
I ( X ; Y ) p(ai b j ) I (ai ; b j )
称为信宿熵
H(Y/X)——散布度，噪声熵。 表示由噪声引起的不确定性的增加。
(3)
I ( X ; Y ) p(ai b j ) log
i 1 j 1
r
s
p(ai b j ) p(ai ) p(b j )
联合熵
H ( X ) H (Y ) H ( XY )
I ( X ;Y ) H ( X ) H ( X / Y ) H (Y ) H (Y / X ) H ( X ) H (Y ) H ( XY )
p(ai b j ) p(ai ) p(b j ) I (Y ; X )
p(b j ai ) log
i 1 j 1
r
s
p(b j ai ) p(b j ) p(ai )
I ( X ; Y ) I (Y ; X )
结 论 平均互信息特性：
平均互信息量的非负性 平均互信息量的极值性（凸函数） 平均互信息量的交互性（对称性）
单符号信道的数学模型：
{ X , p( y / x),Y }
单维离散信道的数学模型
输入输出的联合概率为：
p(bj ai ) p(ai ) p(bj / ai ) p(bi ) p(a j / bi )
P(ai )
称作输入概率/先验概率
P(bj / ai ) 称作前向概率 P(ai / bj ) 称作后向概率/后验概率
平均互信息量
当信宿Y收到某一具体符号bj(Y=bj)后，推测信 源X发符号ai的概率，已由先验概率p(ai)转变为 后验概率p(ai/bj)，从bj中获取关于输入符号的信 息量，应是互信息量I(ai ; bj)在两个概率空间X 和Y中的统计平均值：
I ( X ; Y ) p(ai b j ) I (ai ; b j )
称为信宿熵
H(Y/X)——散布度，噪声熵。 表示由噪声引起的不确定性的增加。
(3)
I ( X ; Y ) p(ai b j ) log
i 1 j 1
r
s
p(ai b j ) p(ai ) p(b j )
联合熵
H ( X ) H (Y ) H ( XY )
I ( X ;Y ) H ( X ) H ( X / Y ) H (Y ) H (Y / X ) H ( X ) H (Y ) H ( XY )
信道及信道容量
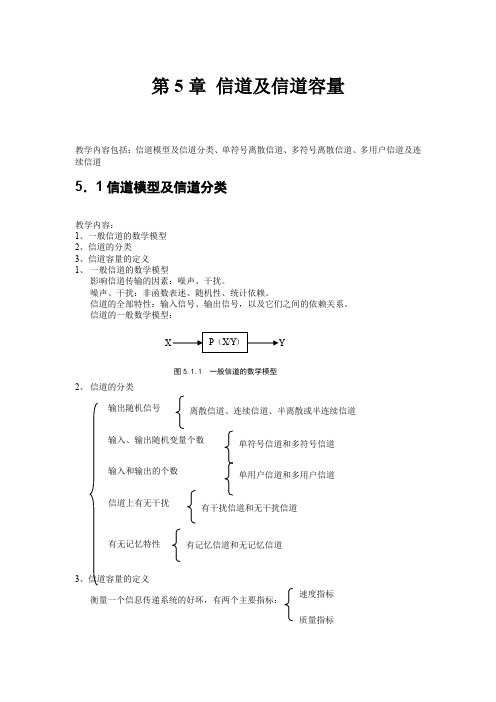
第5章 信道及信道容量教学内容包括：信道模型及信道分类、单符号离散信道、多符号离散信道、多用户信道及连续信道5．1信道模型及信道分类教学内容：1、一般信道的数学模型2、信道的分类3、信道容量的定义1、 一般信道的数学模型影响信道传输的因素：噪声、干扰。
噪声、干扰：非函数表述、随机性、统计依赖。
信道的全部特性：输入信号、输出信号，以及它们之间的依赖关系。
信道的一般数学模型：2、 信道的分类输出随机信号输入、输出随机变量个数输入和输出的个数信道上有无干扰有无记忆特性3、信道容量的定义衡量一个信息传递系统的好坏，有两个主要指标：图5.1.1 一般信道的数学模型离散信道、连续信道、半离散或半连续信道 单符号信道和多符号信道 有干扰信道和无干扰信道有记忆信道和无记忆信道单用户信道和多用户信道 速度指标质量指标速度指标：信息（传输）率R ，即信道中平均每个符号传递的信息量；质量指标：平均差错率e P ，即对信道输出符号进行译码的平均错误概率；目标：速度快、错误少，即R 尽量大而e P 尽量小。
信道容量：信息率R 能大到什么程度； )/()()/()();(X Y H Y H Y X H X H Y X I R -=-==若信道平均传送一个符号所需时间为t 秒，则);(1Y X I t R t =（bit/s ）称t R 为信息（传输）速率。
分析：对于给定的信道，总存在一个信源（其概率分布为*)(X P ），会使信道的信息率R 达到最大。
（);(Y X I 是输入概率)(X P 的上凸函数，这意味着);(Y X I 关于)(X P 存在最大值）每个给定的信道都存在一个最大的信息率，这个最大的信息率定义为该信道的信道容量，记为C ，即);(max max Y X I R C XXP P ==bit/符号 （5.1.3）信道容量也可以定义为信道的最大的信息速率，记为t C⎭⎬⎫⎩⎨⎧==);(1max max Y X I t R C XX P t P t （bit /s ） （5.1.4） 解释：(1)信道容量C 是信道信息率R 的上限，定量描述了信道（信息的）最大通过能力； (2)使得给定信道的);(Y X I 达到最大值（即信道容量C ）的输入分布，称为最佳输入（概率）分布，记为*)(X P ；(3)信道的);(Y X I 与输入概率分布)(X P 和转移概率分布)/(X Y P 两者有关，但信道容量C 是信道的固有参数，只与信道转移概率)/(X Y P 有关。
信道及信道容量
Page
3
第3章 信道及信道容量
相 关 知 识 复 习
在高斯信道下，信道的信息通过能力与
信道的频带宽度、信道的工作时间、信道的
噪声功率密度有关。
频带越宽，工作时间越长，信号、噪声 功率比越大，信道的通过能力就越强，信道 容量越大。
Information Theory and Coding
Page
4
a2 p(a 2 ) b2 p(b2 )
ar p(a r ) bs p(bs )
输入符号集合的元素个数为r，输出符号集合的元素个数为s。
Information Theory and Coding
Page 15
第3章 信道及信道容量
该类信道的特性可用条件转移概率进行描述。
随机差错信道：信道中传输码元所遭受的噪声 是随机的、独立的，这种噪声相互之间不具有 关联性，码元错误不会成串出现。 如：高斯白噪声信道。 突发差错信道：信道中噪声或干扰对传输码元 的影响具有关联性，相互之间不独立，使码元 错误成串出现。 如：衰落信道、码间干扰信道。移动通信的信 道、光盘存储属于该类信道。
端信道。
Information Theory and Coding
Page
10
第3章 信道及信道容量
4．离散信道、连续信道、半离散半连续信道和 波形信道 离散信道：又称数字信道，该类信道中输入空 间、输出空间均为离散时间集合，集合中事件 的数量是有限的，或者无限的，随机变量取值
3.1 信 道 分 类
Information Theory and Coding
Page
5
第3章 信道及信道容量
3.1信道分类
X={X0,X1,X2… Xr-1}含r个 元素的输入符号集
信道与信道容量
• 对于一般信道,信道容量计算相当复杂,我们只 讨论某些特殊类型的信道：
• 离散信道可分成： • 无干扰(无噪)信道
– 无噪无损信道 – 有噪无损信道 – 无噪有损信道
• 有干扰无记忆信道 • 有干扰有记忆信道
29
3.2 离散单个符号信道 及其容量
• 信道的输入和输出均以单个符号的形式， 或者以序列形式但符号之间不相关，即 无记忆。这类信道分析起来较为简单。
• p(ai|bj):后向概率
– 已知信道输出端接收到符号bj但发送的输 入符号为ai的概率。
19
二进制离散信道BSC
• 二进制离散信道BSC
– 该信道模型的输入和输出 信号的符号数都是2； – 输入符号X取值{0,1}； – 输出符号Y取值{0,1}
1-p 0 p 1 1-p 1 0 p
• 很重要的一种特殊信道 • 信道转移概率：
30
3.2.1 无干扰离散信道
• 设信道的输入X∈A={a1 … an},输出Y∈B={b1 … bm}
• 无噪无损信道
– 输入和输出符号之间有确定的一一对应关系
0 p(b j | ai ) p(ai | b j ) 1
X a1 1 b1
i j i j
(i, j 1,2,3)
32
无干扰离散信道
• 无嗓无损信道
• 由 H(X |Y)
p( x , y ) log p( x | y ) H (Y | X ) p( x , y ) log p( y | x )
i j i j ij i j j i ij
• 计算得：
• 噪声熵H(Y|X) = 0 损失熵H(X|Y) = 0
21
二元删除信道BEC
• 离散信道可分成： • 无干扰(无噪)信道
– 无噪无损信道 – 有噪无损信道 – 无噪有损信道
• 有干扰无记忆信道 • 有干扰有记忆信道
29
3.2 离散单个符号信道 及其容量
• 信道的输入和输出均以单个符号的形式， 或者以序列形式但符号之间不相关，即 无记忆。这类信道分析起来较为简单。
• p(ai|bj):后向概率
– 已知信道输出端接收到符号bj但发送的输 入符号为ai的概率。
19
二进制离散信道BSC
• 二进制离散信道BSC
– 该信道模型的输入和输出 信号的符号数都是2； – 输入符号X取值{0,1}； – 输出符号Y取值{0,1}
1-p 0 p 1 1-p 1 0 p
• 很重要的一种特殊信道 • 信道转移概率：
30
3.2.1 无干扰离散信道
• 设信道的输入X∈A={a1 … an},输出Y∈B={b1 … bm}
• 无噪无损信道
– 输入和输出符号之间有确定的一一对应关系
0 p(b j | ai ) p(ai | b j ) 1
X a1 1 b1
i j i j
(i, j 1,2,3)
32
无干扰离散信道
• 无嗓无损信道
• 由 H(X |Y)
p( x , y ) log p( x | y ) H (Y | X ) p( x , y ) log p( y | x )
i j i j ij i j j i ij
• 计算得：
• 噪声熵H(Y|X) = 0 损失熵H(X|Y) = 0
21
二元删除信道BEC
4-第四讲-信道容量及其计算
（3）、一般DMC容量的计算
一般信道容量的计算方法 （拉格朗日乘子法）
定理1：如果信道的输入随机序列为 通过信道传输，接收到的随机序列为 若信道是无记忆的，即满足 则
（4）、扩展信道的信道容量
证明：设信道输入输出序列X和Y的一个取值为
I（X；Y）是输入随机变量的概率分布的上凸函数，所以对于固定的信道，总存在一种信源分布，使传输每个符号平均获得的信息量最大，也就是说，每一个固定信道都有一个最大的信息传输率。 信道容量定义为信道中每个符号所能传递的最大信息量，也就是最大 I (X；Y)值。
此时输入的概率分布称为最佳输入分布。
例：
( P 95－例3. 5 )
输出符号集个数
（2）、准对称信道的容量
准对称信道：信道矩阵（列）的子阵是对称矩阵。
定理：达到准对称离散信道信道容量的输入分布为 等概分布。
r是输入个数，n是不相交子集数，Nk是行之和，Mk是列之和
解：达到信道容量的输入分布为等概分布。
此时输出分布为：
4－2 信道容量的计算
（1）、对称信道的容量
对称信道：信道矩阵的每一行都是由同一概率分布的 不同排列组成，并且每一列也是同一元素 集的不同的排列组成。
1/3
1/3
1/6
1/6
1/3
1/3
1/6
1/6
行
列
1/2
1/3
1/6
1/6
1/3
1/2
1/3
1/6
1/2
0
1
q
1-p
1-q
p
1
2
0
删除信道的必要性
2、 信道容量定义
信息传输率：信道中平均每个符号所能传送的信息量。 R = I(X;Y) = H(X)-H(X|Y) （bit/符号）
一般信道容量的计算方法 （拉格朗日乘子法）
定理1：如果信道的输入随机序列为 通过信道传输，接收到的随机序列为 若信道是无记忆的，即满足 则
（4）、扩展信道的信道容量
证明：设信道输入输出序列X和Y的一个取值为
I（X；Y）是输入随机变量的概率分布的上凸函数，所以对于固定的信道，总存在一种信源分布，使传输每个符号平均获得的信息量最大，也就是说，每一个固定信道都有一个最大的信息传输率。 信道容量定义为信道中每个符号所能传递的最大信息量，也就是最大 I (X；Y)值。
此时输入的概率分布称为最佳输入分布。
例：
( P 95－例3. 5 )
输出符号集个数
（2）、准对称信道的容量
准对称信道：信道矩阵（列）的子阵是对称矩阵。
定理：达到准对称离散信道信道容量的输入分布为 等概分布。
r是输入个数，n是不相交子集数，Nk是行之和，Mk是列之和
解：达到信道容量的输入分布为等概分布。
此时输出分布为：
4－2 信道容量的计算
（1）、对称信道的容量
对称信道：信道矩阵的每一行都是由同一概率分布的 不同排列组成，并且每一列也是同一元素 集的不同的排列组成。
1/3
1/3
1/6
1/6
1/3
1/3
1/6
1/6
行
列
1/2
1/3
1/6
1/6
1/3
1/2
1/3
1/6
1/2
0
1
q
1-p
1-q
p
1
2
0
删除信道的必要性
2、 信道容量定义
信息传输率：信道中平均每个符号所能传送的信息量。 R = I(X;Y) = H(X)-H(X|Y) （bit/符号）
与信道容量
Department of Communication China Ji Liang University
25
第 三 章 信 道 与 信 道 容 量
③ 具有归并性能的无噪信道
这种信道如下图所示。 这种信道如下图所示。 n>m，输入 的符号集个数大于输出 的符号集个数。 的符号集个数大于输出Y的符号集个数 ，输入X的符号集个数大于输出 的符号集个数。
2012-4-6
Department of Communication China Ji Liang University
24
第 三 章 信 道 与 信 道 容 量
信道疑义度 H(X/Y)=0， I(X;Y)= H(X) -H(X/Y)= H(X) 。 ，
信道容量为： 信道容量为：
2012-4-6
2012-4-6
Department of Communication China Ji Liang University
10
第 三 章 信 道 与 信 道 容 量
b）二进制对称信道 ） （简称为 BSC信道 ） 信道
0 输入 p 1-p 0 输出
p 1 1-p 1
二进制对称信道
2012-4-6
Department of Communication China Ji Liang University
2012-4-6
Department of Communication China Ji Liang University
26
第 三 章 信 道 与 信 道 容 量
信道噪声熵 H(Y/X)=0。 信道容量为：
2012-4-6
Department of Communication China Ji Liang University
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
I ( X ;Y )
9
信道容量的计算
• 对于一般信道,信道容量计算相当复杂,我们只 讨论某些特殊类型的信道：
• 离散信道可分成： • 无干扰(无噪)信道
– 无嗓无损信道 – 有噪无损信道 – 无噪有损信道
• 有干扰无记忆信道 • 有干扰有记忆信道
10
无干扰离散信道
• 无嗓无损信道
C
max
p(ai )
5
离散无记忆信道DMC
• 信道输入是n元符号X∈{a1, a2, …, an} • 信道输出是m元符号Y∈{b1, b2, …, bm} • 转移矩阵
– 已知X,输出Y统计特性
p11
b1
a1
p12
b1 b2 bm p11 p12 p1m a1
p21
a2
p22
:
b2
P
p21
p22
p2m
H (Y | ai ) i 1,2,n
H
(Y
|
X
)
H
(Y
|
ai
)
H
(
p1
,
p2
,
pm
)
15
对称DMC信道
• 对称DMC信道的容量：
C log m H ( p1, p2 pm )
m
log m pij log pij j 1
• 上式是对称离散信道能够传输的最大的平均信
息量,它只与对称信道矩阵中行矢量{p1, p2,…pm } 和输出符号集的个数m有关。
4
有干扰无记忆信道
• 有干扰无记忆信道
– 信道的输出信号Y与输入信号X之间没有确 定的关系,但转移概率满足:
p(Y | X ) p( y1 | x1) p( y2 | x2) p( yL | xL )
• 有干扰无记忆信道可分为: – 二进制离散信道 – 离散无记忆信道 – 离散输入、连续输出信道 – 波形信道
I (X ;Y ) H (Y ) H (Y | X ) H ( p p) H ( p)
1 H( p)
18
BSC信道容量
• BSC信道容量
C 1 H( p)
• 当p固定时,I (X,Y) 是ω的 型上凸函数。
• I (X,Y) 对ω存在一
I(XY)
个极大值。
1-H(p)
ω
19
BSC信道容量
– 信道矩阵中各列之和也等于1 14
对称DMC信道
• 对称离散信道的平均互信息为
I(X ,Y) H(X ) H(X |Y) H(Y) H(Y | X )
H (Y | X ) p(ai ) p(bj | ai ) log p(bj | ai )
i
j
p(bj | ai ) log p(bj | ai ) j
17
H(Y) ( p p)log 1 ( p p)log 1
p p
p p
H( p p)
H (Y | X ) p(ai ) p(bj | ai ) log p(bj | ai )
i
j
p(bj | ai ) log p(bj | ai )
j
[ p log p p log p] H ( p)
xi ) log
p(y j | xi ) p(y j )
n
p( y j ) p(xi ) p( y j | xi ) i1
• 信道的信息传输率就是平均互信息
8
信道容量
• 信道容量C：
– 最大的信息传输率
C max I(X ;Y ) p(ai )
• 单位时间的信道容量：
1
Ct
T
max
p(ai )
• 强对称信道的信道容量：
C
log
2
n
H
(1
p,
n
p 1
,,
n
p 16 ) 1
BSC信道容量
• •
设二进制对称信道的输入概率空间 信道矩阵：
X 0
P
1
P
1 p
p
p 1 p
p p
p p
1
p(b 0) p(ai ) p(b0 | ai ) p p i0
1
p(b 1) p(ai )p(b1 | ai ) p p i0
• 信道转移概率矩阵p(Y|X)：
– 描述输入/输出的统计依赖关系,反映信道统计关 系
p(Y|X)
X
Y
信道
3
无干扰(无噪声)信道
• 无干扰(无噪声)信道
– 信道的输出信号Y与输入信号X之间有确定 的关系Y=f (X),已知X后就确知Y
– 转移概率:
p(Y
|
X
)
1, 0,
Y f(X) Y f(X)
I
(
XLeabharlann ;Y)max
H
(
X
)
max
H
(Y
)
log
2
n
• 有嗓无损信道
C
max
p(ai )
I
(
X
;Y
)
max
H
(Y
)
log
2
m
• 无嗓有损信道
C
max
p(ai )
I
(
X
;Y
)
max
H
(
X
)
log
2
n
11
3.2.1 对称DMC信道
• 对称离散信道：
• 对称性:
– 每一行都是由同一集{p1, p2,…pm} 的诸元素 不同排列组成——输入对称
– 每一列都是由集{q1, q2,…qn}的诸元素不同 排列组成——输出对称
1 1 1 1
P
3
3
6
6
1 1 1 1
6 6 3 3
1
2
P
1 6
1
3
1 1
3
6
1 1
2 3
1
1
12
6 2
满足对称 性,所对应 的信道是 对称离散 信道。
对称DMC信道
• 信道矩阵
1 1 1 1 P 3 3 6 6
a2
: :
: : :
pn1
pn2
pnm
an
an
pnm
m
bm
p(bj | ai ) 1 i 1,2,n 6
j 1
3.2 离散单个符号信道 及其容量
7
信道容量
• 平均互信息I (X;Y)：
– 接收到符号Y后平均每个符号获得的关于X
的信息量。
I(X;Y)
i
j
p(xi ) p(y j
|
第三章
信道与信道容量
内容
3.1 信道分类和表示参数 3.2 离散单个符号信道及其容量 3.3 离散序列信道及其容量 3.4 连续信道及其容量
2
信道
• 设信道的输入X=(X1, X2 … Xi,… ), Xi ∈{a1 … an} 输出Y= (Y1, Y2 … Yj,…), Yj ∈{b1 … bm}
1 1 1 1 6 3 6 3
P
0.7 0.2
0.1 0.1
0.2 0.7
• 不具有对称性,因而所对应的信通不是对 称离散信道。
13
对称DMC信道
• 若输入符号和输出符号个数相同,都等于n,且信 道矩阵为
1 p
P
n
p 1
p n 1 1 p
p
n
p
1
n 1
p n 1
p n 1
1
p
• 此信道称为强对称信道 (均匀信道)
• BSC信道容量
C 1 H( p)
• 当固定信源的概率分布ω时,I (X,Y) 是p的 型 下
凸函数。 • 当p = 0,
C =1－0 = 1bit = H(X)
信道无噪声
C
信道强噪声
• 当p =1/2,
C 1 H(1,1) 0 22
20