三视图ppt (2)
合集下载
《三视图》课件(共55张PPT)

如果物体向三个互相垂直 的投影面分别投影,所得到 的三个图形摊平在一个平面 上,则就是三视图。
练习: 根据三视图想 像物体的形状。
圆柱
圆台
手电筒
从左向右看
圆柱
正六棱柱
螺丝杆
从左向右看
柱
四棱柱
螺丝杆
从左向右看
圆柱
半圆球
螺丝钉
从左向右看
圆柱
圆台
圆柱
热水瓶
从上向下看
N
S
前后看 从上向下看
左右看
马蹄形磁铁
从下向上看
环的形成
有关概念
物体向投影面投影所得 到的图形称为视图。
接下一张幻灯片
在主视图、俯视 图中都体现形体的长 度,且长度在竖直方 向上是对正的,我们 称之为长对正。
返回
在主视图、左视 图上都体现形体的高 度,且高度在水平方 向上是平齐的,我们 称之为高平齐。
返回
在左视图、俯视 图上都体现形体的宽 度,且是同一形体的 宽度,是相等的,我 们称之为宽相等。
错误的三视图 —长未对正1
错误的三视图 —长未对正2
错误的三视图 —高不平齐1
错误的三视图 —高不平齐2
错误的三视图 —宽不相等1
错误的三视图 —宽不相等1
错误的三视图
错误的三视图
体验三视 图的作法
三视图的作图步骤
俯视图方向 1.确定视图方向 2.先画出能反映物体 真实形状的一个视图 左视图方向
三视图欣赏
观察左图:说 说下列三副 图是从哪个 角度看的?
甲、乙、丙、丁四人分别面向 桌坐在一张四方形桌子旁边。 桌上一张纸上写着数字“9”, 甲看到“6”,乙看到“ ” ,丙看到“ ”,丁看到 “9”,问四人是怎样的座次 丁正对着数字“9”;甲坐在丁的对面 ? ,
练习: 根据三视图想 像物体的形状。
圆柱
圆台
手电筒
从左向右看
圆柱
正六棱柱
螺丝杆
从左向右看
柱
四棱柱
螺丝杆
从左向右看
圆柱
半圆球
螺丝钉
从左向右看
圆柱
圆台
圆柱
热水瓶
从上向下看
N
S
前后看 从上向下看
左右看
马蹄形磁铁
从下向上看
环的形成
有关概念
物体向投影面投影所得 到的图形称为视图。
接下一张幻灯片
在主视图、俯视 图中都体现形体的长 度,且长度在竖直方 向上是对正的,我们 称之为长对正。
返回
在主视图、左视 图上都体现形体的高 度,且高度在水平方 向上是平齐的,我们 称之为高平齐。
返回
在左视图、俯视 图上都体现形体的宽 度,且是同一形体的 宽度,是相等的,我 们称之为宽相等。
错误的三视图 —长未对正1
错误的三视图 —长未对正2
错误的三视图 —高不平齐1
错误的三视图 —高不平齐2
错误的三视图 —宽不相等1
错误的三视图 —宽不相等1
错误的三视图
错误的三视图
体验三视 图的作法
三视图的作图步骤
俯视图方向 1.确定视图方向 2.先画出能反映物体 真实形状的一个视图 左视图方向
三视图欣赏
观察左图:说 说下列三副 图是从哪个 角度看的?
甲、乙、丙、丁四人分别面向 桌坐在一张四方形桌子旁边。 桌上一张纸上写着数字“9”, 甲看到“6”,乙看到“ ” ,丙看到“ ”,丁看到 “9”,问四人是怎样的座次 丁正对着数字“9”;甲坐在丁的对面 ? ,
人教版数学九下【教学课件】29.2《三视图(2)》示范教学课件(共18张ppt)

正面是正五边形;由俯视图可知, 由上向下看到物体有两个面的视图 是矩形,它们的交线是一条棱(中 间的实线表示),可见到,另有两 条棱(虚线表示)被遮挡;
例题解析
由左视图 可知,物体左侧有 两个面的视图是矩形,它们 的交线是一条棱(中间的实 线表示),可见到.综合各视图 可知,物体的形状是正五棱柱.
课堂练习
5.由若干个相同的小立方体搭成的一个几何体的主视图和 俯视图如图所示,俯视图的方格中的字母和数字表示在 该位置上小立方体的个数,求x,y的值.
x=1或x=2,y=3.
课堂小结
1.一个视图不能确定物体的空间形状,根据三视图要描述 几何体或实物原型时,必须将各视图对照起来看. 2.一个摆好的几何体的视图是唯一的,但从视图反过来考虑 几何体时,它有多种可能性.例如,正方体的主视图是正方形, 但主视图是正方形的几何体有直三棱柱、长方体、圆柱等. 3.对于较复杂的物体,由三视图想象出物体的原型, 应搞清三个视图之间的前后、左右、上下的对应关系 .
(1)
例题解析
(1)从三个方向看立体图形, 视图都是矩形,可以想象这个立 体图形是长方体,如图所示;
(1)
(2)
例题解析
(2)从正面、侧面看立体图形, 视图都是等腰三角形;从上面看,视 图是圆;可以想象这个立体图形是圆 锥,如图所示.
(2)
例题解析
例2. 根据物体的三视图,描述物体的形状. 分析:由主视图可知,物体
探究新知
前面我们讨论了由立体图形(实物)画出三视图,那么 由三视图能否想象出立体图形(实物)呢?
例题解析
例1.如图,分别根据三视图(1)(2)说出立体图形的名称.
(1)
(2)
例题解析
分析:由三视图想象立体图形时,首先分别根据主视 图、俯视图和左视图想象立体图形的前面、上面和左侧面, 然后再综合起来考虑整体图形.
例题解析
由左视图 可知,物体左侧有 两个面的视图是矩形,它们 的交线是一条棱(中间的实 线表示),可见到.综合各视图 可知,物体的形状是正五棱柱.
课堂练习
5.由若干个相同的小立方体搭成的一个几何体的主视图和 俯视图如图所示,俯视图的方格中的字母和数字表示在 该位置上小立方体的个数,求x,y的值.
x=1或x=2,y=3.
课堂小结
1.一个视图不能确定物体的空间形状,根据三视图要描述 几何体或实物原型时,必须将各视图对照起来看. 2.一个摆好的几何体的视图是唯一的,但从视图反过来考虑 几何体时,它有多种可能性.例如,正方体的主视图是正方形, 但主视图是正方形的几何体有直三棱柱、长方体、圆柱等. 3.对于较复杂的物体,由三视图想象出物体的原型, 应搞清三个视图之间的前后、左右、上下的对应关系 .
(1)
例题解析
(1)从三个方向看立体图形, 视图都是矩形,可以想象这个立 体图形是长方体,如图所示;
(1)
(2)
例题解析
(2)从正面、侧面看立体图形, 视图都是等腰三角形;从上面看,视 图是圆;可以想象这个立体图形是圆 锥,如图所示.
(2)
例题解析
例2. 根据物体的三视图,描述物体的形状. 分析:由主视图可知,物体
探究新知
前面我们讨论了由立体图形(实物)画出三视图,那么 由三视图能否想象出立体图形(实物)呢?
例题解析
例1.如图,分别根据三视图(1)(2)说出立体图形的名称.
(1)
(2)
例题解析
分析:由三视图想象立体图形时,首先分别根据主视 图、俯视图和左视图想象立体图形的前面、上面和左侧面, 然后再综合起来考虑整体图形.
三视图(2) 大赛获奖精美课件 公开课一等奖课件

2 面积为________ cm . 3
4
五、课堂小结 相似三角形的性质: 性质2.相似三角形周长的比等于相似比.
性质3.相似三角形面积的比等于相似比的平方.
相似多边形的性质1:相似多边形周长的比等于相似比.
相似多边形的性质2:相似多边形面积的比等于相似比的平方.
本节课主要是让学生理解并掌握相似三角形周长的比等于相似 比、面积比等于相似比的平方,通过探索相似多边形周长的比 等于相似比、面积的比等于相似比的平方让学生体验化归思想, 学会应用相似三角形周长的比等于相似比、面积的比等于相似 比的平方来解决简单的问题.因此本课的教学设计突出了“相 似比⇒相似三角形周长的比⇒相似多边形周长的比”,“相似 比⇒相似三角形面积的比⇒相似多边形面积的比”等一系列从 特殊到一般的过程,让学生深刻体验到有限数学归纳法的魅 力.
青 春 风 采
高考总分:
692分(含20分加分) 语文131分 数学145分 英语141分 文综255分
毕业学校:北京二中 报考高校: 北京大学光华管理学 院 北京市文科状元 阳光女孩--何旋
来自北京二中,高考成绩672分,还有20 分加分。“何旋给人最深的印象就是她 的笑声,远远的就能听见她的笑声。” 班主任吴京梅说,何旋是个阳光女孩。 “她是学校的摄影记者,非常外向,如 果加上20分的加分,她的成绩应该是 692。”吴老师说,何旋考出好成绩的秘 诀是心态好。“她很自信,也很有爱心。 考试结束后,她还问我怎么给边远地区 的学校捐书”。
本节课的教学,以课程标准为指南,结合学生的已有知识和 经验而设计.重点讲解由三视图判断几何体的结构特征,也 就是画三视图时尺寸不作严格要求.教学设计时使用了大量 的图片,建议在实际应用时尽量使用信息技术,如画法几何, 让学生从动态过程中获得三视图的感性认识,以便从整体上 把握三视图的画法.
4
五、课堂小结 相似三角形的性质: 性质2.相似三角形周长的比等于相似比.
性质3.相似三角形面积的比等于相似比的平方.
相似多边形的性质1:相似多边形周长的比等于相似比.
相似多边形的性质2:相似多边形面积的比等于相似比的平方.
本节课主要是让学生理解并掌握相似三角形周长的比等于相似 比、面积比等于相似比的平方,通过探索相似多边形周长的比 等于相似比、面积的比等于相似比的平方让学生体验化归思想, 学会应用相似三角形周长的比等于相似比、面积的比等于相似 比的平方来解决简单的问题.因此本课的教学设计突出了“相 似比⇒相似三角形周长的比⇒相似多边形周长的比”,“相似 比⇒相似三角形面积的比⇒相似多边形面积的比”等一系列从 特殊到一般的过程,让学生深刻体验到有限数学归纳法的魅 力.
青 春 风 采
高考总分:
692分(含20分加分) 语文131分 数学145分 英语141分 文综255分
毕业学校:北京二中 报考高校: 北京大学光华管理学 院 北京市文科状元 阳光女孩--何旋
来自北京二中,高考成绩672分,还有20 分加分。“何旋给人最深的印象就是她 的笑声,远远的就能听见她的笑声。” 班主任吴京梅说,何旋是个阳光女孩。 “她是学校的摄影记者,非常外向,如 果加上20分的加分,她的成绩应该是 692。”吴老师说,何旋考出好成绩的秘 诀是心态好。“她很自信,也很有爱心。 考试结束后,她还问我怎么给边远地区 的学校捐书”。
本节课的教学,以课程标准为指南,结合学生的已有知识和 经验而设计.重点讲解由三视图判断几何体的结构特征,也 就是画三视图时尺寸不作严格要求.教学设计时使用了大量 的图片,建议在实际应用时尽量使用信息技术,如画法几何, 让学生从动态过程中获得三视图的感性认识,以便从整体上 把握三视图的画法.
建筑三视图 ppt
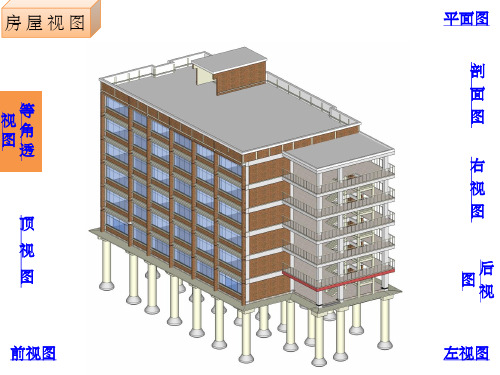
图
角 透
视
顶 视 图
前视图
-
平面图
剖 面 图
右 视 图
后 图
视
左视8 图
房屋视图
视 图
等 角 透
顶 视 图
前视图
-
平面图
剖 面 图
右 视 图
后 图
视
左视1 图
房屋视图
等
图
角 透
视
顶 视 图
前视图
-
平面图
剖 面 图
右 视 图
后 图
视
左视2 图
房屋视图
等
图
角 透
视
顶 视 图
前视图
-
平面图
剖 面 图
右 视 图
后 图
视
左视3 图
房屋视图
等
图
角 透
视
顶 视 图
前视图
-
平面图
剖 面 图
右 视 图
后 图
视
左视4 图
房屋视图
等
图
角 透
视
顶 视 图
前视图
-
平面图
剖 面 图
右 视 图
图后 视
左视5 图
房屋视图
等
图
角 透
视
顶 视 图
前视图
-
平面图 剖 面 图
右 图
视
后 图
视
左视6 图
房屋视图
等
图
角 透
视
顶 视 图
前视图
-
平面图
剖 图面右 视来自图后 图视左视7 图
房屋视图
等
三视图课件(2)

图2
正 视 图
图3
⒉根据图4、图5的视图,你能分别想像出物 体的大致形状吗?
正 视 图
俯 视 图
图4
正
侧
视
视
图
图
图5
下列是一个物体的三视图,请描述出它的形状
正视图 侧视图 俯视图
三棱锥
3.右图是由一些相同的小正方体构成的几何体的三视图,则
构成这个几何体的小正方体的个数是【 D 】
A.5
B.6
C.7
随堂练习
• 1找出图中每一物品所对应的主视图。
(A)
(B)
(C)
(D)
考考你
正视图( A ) 左视图 ( A ) 俯视图 ( B )
A
B
C
9.下面所给的三视图表示什么几何体? 圆锥
例4 根据三视图说出立体图形的名称
例5 根据物体的三视图,描述物体的形状.
• ⒉由三视图描述几何体(或实物原型),一
的三面墙面)作为投影面
正面
一个物体在三个投影面内同时进行 正投影,分别:
在正面得到的由前向后观察物体 的视图,叫正视图(从前面看);
在水平面内得到的由上向下观察物 体的视图,叫俯视图(从上面看) ;
在侧面内得到由左向右观察物体的 视图,叫侧视图(从左面看)
一起来学习简单物体的三视图吧!
1.三视图
(第5题) 直三棱柱
(第6题)
状,并补画它的左视图.
直五棱柱,底面是五边形
试一试
视图反映了物体形状的某些特征,因此 通过视图我们可以想像物体的大致形状.
⒈根据图1、图2、图3的视图,你能分别想 像出物体的大致形状吗?
正 视 图
图1
正 视 图
正 视 图
图3
⒉根据图4、图5的视图,你能分别想像出物 体的大致形状吗?
正 视 图
俯 视 图
图4
正
侧
视
视
图
图
图5
下列是一个物体的三视图,请描述出它的形状
正视图 侧视图 俯视图
三棱锥
3.右图是由一些相同的小正方体构成的几何体的三视图,则
构成这个几何体的小正方体的个数是【 D 】
A.5
B.6
C.7
随堂练习
• 1找出图中每一物品所对应的主视图。
(A)
(B)
(C)
(D)
考考你
正视图( A ) 左视图 ( A ) 俯视图 ( B )
A
B
C
9.下面所给的三视图表示什么几何体? 圆锥
例4 根据三视图说出立体图形的名称
例5 根据物体的三视图,描述物体的形状.
• ⒉由三视图描述几何体(或实物原型),一
的三面墙面)作为投影面
正面
一个物体在三个投影面内同时进行 正投影,分别:
在正面得到的由前向后观察物体 的视图,叫正视图(从前面看);
在水平面内得到的由上向下观察物 体的视图,叫俯视图(从上面看) ;
在侧面内得到由左向右观察物体的 视图,叫侧视图(从左面看)
一起来学习简单物体的三视图吧!
1.三视图
(第5题) 直三棱柱
(第6题)
状,并补画它的左视图.
直五棱柱,底面是五边形
试一试
视图反映了物体形状的某些特征,因此 通过视图我们可以想像物体的大致形状.
⒈根据图1、图2、图3的视图,你能分别想 像出物体的大致形状吗?
正 视 图
图1
正 视 图
《三视图》ppt课件2
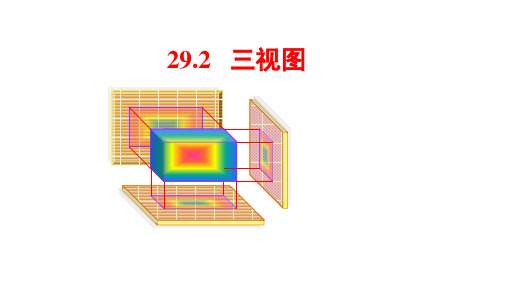
正面 水平面
侧面
3.三视图
从上面看
主视图
从左面看
正面
左视图
侧面 水平面俯视图
从正面看
主视图
左视图 高
长
宽
宽 俯视图
大小关系:长对正,高平齐,宽相等
4.三视图的位置:
位置规定:
主视图要在左上边, 它的下方应是俯视图, 左视图坐落在右边
主视图 长
左视图 高
宽
宽 俯视图
类型一:画出几何体的三视图
例1 画出图中一些基本几何体的三视图.
方法总结:三视图除了与立体图形的形状有关外,还与立体图 形的摆放位置有关,故由图想物,先根据三视图确定物体的形 状,再确定物体的摆放位置.
例4 根据物体的三视图描述物体的形状.
分析:由主视图可知,物体的正面是正五边形;由俯视图可知, 由上向下看到物体有两个面的视图是矩形,它们的交线是一条 棱 (中间的实线表示),可见到,另有两条棱 (虚线表示) 被遮挡; 由左视图可知,物体左侧有两个面是矩形,它们的交线是一条 棱 (中间的实线表示),可见到;综合各视图可知,物体的形状 是正五棱柱.
例3 根据三视图说出立体图形的名称
(柳州·中考)如图所示的几何体中,主视图、左视图、俯视图均相同的是( )
例1 画出图中一些基本几何体的三视图.
综合各视图可知,物体的形状是正五棱柱.
(柳州·中考)如图所示的几何体中,主视图、左视图、俯视图均相同的是( )
分析:由主视图可知,物体的正面是正五边形;
类型二:根据三视图说出立体图形的名称
例3 根据三视图说出立体图形的名称
(柳州·中考)如图所示的几何体中,主视图、左视图、俯视图均相同的是( )
综合各视图可知,物体的形状是正五棱柱.
《三视图》PPT课件(2024)

表格填写
在图纸上用表格形式填写技术要求,如热处理要 求、材料要求等
2024/1/26
23
案例分析:典型零件三视图
轴类零件三视图
分析轴类零件的结构特点,讲解如何标注轴 类零件的尺寸和技术要求
叉架类零件三视图
分析叉架类零件的结构特点,讲解如何标注 叉架类零件的尺寸和技术要求
2024/1/26
盘盖类零件三视图
基本辅助面
通过平移或旋转基本投影 面得到,用于生成新的投 影。
2024/1/26
局部辅助面
根据需要截取形体的一部 分而构造,用于表达形体 的局部结构。
综合辅助面
结合基本辅助面和局部辅 助面的特点构造,用于解 决复杂形体的投影问题。
17
案例分析:组合体三视图
案例一
分析组合体的结构特点,选择 合适的辅助线和辅助面进行投
6
02
CATALOGUE
正投影法与三视图形成
2024/1/26
7
正投影法基本原理
投影线垂直于投影面
投影线与视图的对应关系
正投影是投影线垂直于投影面产生的 投影,能真实反映物体的形状和大小 。
根据投影线与视图的对应关系,可以 确定物体在视图中的位置和形状。
投影面与物体表面的交线
物体表面与投影面相交,产生的交线 即为投影线。
2024/1/26
5
视图间关系及表达方法
2024/1/26
视图间关系
主视图、俯视图和左视图之间存在特定的对应关系。主视图反映物体的前面形状 ,俯视图反映物体的上面形状,左视图反映物体的左侧形状。这三个视图相互补 充,共同表达物体的完整形状。
表达方法
在三视图中,通常采用线条、尺寸标注、剖面线等表达方法来描述物体的形状和 大小。线条用于勾勒物体的轮廓和内部结构,尺寸标注用于标明物体的实际大小 ,剖面线用于表示物体被切开的部分及其内部结构。
第2课时 三视图(2) 公开课一等奖课件

例 2 根据物体的三视图(如图)描述物体的形状.
分析:由主视图可知,物体的正面是正五边形,由俯视图可知,由上向 下看物体是矩形的,且有一条棱(中间的实线)可见到,两条棱(虚线)被遮挡, 由左视图知,物体的侧面是矩形的,且有一条棱(中间的实线)可见到,综合各 视图可知,物体是五棱柱形状的. 解:物体是五棱柱形状的,如下图所示.
例 3 某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如下图), 请你按照三视图确定制作每个密封罐所需钢板的面积.
分析:对于某些立体图形,若沿其中一些线(例如棱柱的棱)剪开,可以把立 体图形的表面展开成一个平面图形,即展开图.在实际的生产中,三视图和展 开图往往结合在一起使用.解决本题的思路是,由视图想象出密封罐的立体形 状,再进一步画出展开图,从而计算面积. 解:由三视图可知,密封罐的形状是正六棱柱.(如图(左)).
高考总分:711分 毕业学校:北京八中 语文139分 数学140分 英语141分 理综291分 报考高校:
北京大学光华管理学院
北京市理科状元杨蕙心
班主任: 我觉得何旋今天取得这样的成绩, 我觉得,很重要的是,何旋是土生土长的北京 二中的学生,二中的教育理念是综合培养学生 的素质和能力。我觉得何旋,她取得今天这么 好的成绩,一个来源于她的扎实的学习上的基 础,还有一个非常重要的,我觉得特别想提的, 何旋是一个特别充满自信,充满阳光的这样一 个女孩子。在我印象当中,何旋是一个最爱笑 的,而且她的笑特别感染人的。所以我觉得她 很阳光,而且充满自信,这是她突出的这样一 个特点。所以我觉得,这是她今天取得好成绩 当中,心理素质非常好,是非常重要的。
谢谢您下载使用!
更多精彩内容,微信扫描二维码获取
扫描二维码获取更多资源
附赠 中高考状元学习方法
26.2 三视图 课件2(沪科版九年级下册)

高平齐
主视图
左视图
高平齐:主视图和左视 图共同反映了物体上 下方向的尺寸.
俯视图
长 方 体
侧视图
正视图
长方形
俯视图
长方形
长方形
画出下列几何体的三视图
Z
Z
X
O
Y′
Y
三视图的形成
把主视图、俯视图、左视图摊平在一个平面上, 则就是三视图。
左视图
例2、画下例几何体的三视图
延 伸 拓 展
指出它的三视图
请观察下面三个投影,它们有什么相 同与不同的地方?你能试着给正投影 下定义吗?
中心投影
斜投影
正投影
平行投影 投影
什么叫视图?
几何体在一个平面上的正投影叫做这个几何 体的视图。 现在给如下的视图,你能准确的刻画这个几 何体的形状和大小吗?
这个水平投影能完全反映这个物体的 形状和大小吗?如不能,那么还需哪些投 影面?
练习2、指出下例几何体的三视 图
延 伸 拓 展
练一练
1、画出下列立体图形的三视图。
2、指出左面三个平面图形是右面这个物体的三视图中
的哪个视图。
( 正视图)
( 俯视图)
( 左视图)
小结与作业
小结:通过这节课的学习你学会 了什么?你有什收获与困惑? 作业: P80 练习 3、4 P81 习题 1、3
从上面看
从 左 面 看 从正面看
三视图的概念
从三个不同方向看同一物体
从正面看到的图形叫正视图(或主视图) 从左面看到的图形叫左视图
从上面看到的图形叫俯视图
主视图,左视图,俯视图合称三视图.
在生活中我们应从不同 角度,多方面地去看待一 件事物,分析一件事情。 数学中我们只从三个不 同方向看同一物体,所以, 每一个物体都有三视图。
三视图(2)(课件)

B
a
C
D
精品
巩固提升
3. 下列是一个物体的三视图,请描述该物体的形状。
D
A a
实物
精品
巩固提升
4.粗线表示嵌在玻璃正方体内的一根铁丝,请画出该正方体的 三视图.
D
A
a
精品
巩固提升
画三视图时,看得见的轮廓 用实线,看不见的用虚线。
主视图 俯视图
A a
D
左视图
精品
课堂小结
1.三视图
大小:长对正、高平齐、宽相等
D
虚实:看不见的用虚线,看得见的A用实线。
2.由三视图想象立体图形,要先根据主视a图、俯视图和左
视图想象立体图形的前面、上面和左侧面,然后再综合起 来考虑整个图形。
俯视图和左视图想象立体图形的前面、上面
和左侧面,然后再综合起来a考虑整个图形。
精品
新知讲解
说一说
1. 所给的三视图表示什么立体图形。
D
从三个方向看立体图形,图
像都是矩形,因A此这个物体 是长方体。a
精品
新知讲解
说一说
2. 所给的三视图表示什么立体图形。
D
从正面、上面看立体图形,
图像都是矩形,A从左面看是 圆,因此这a 个物体是圆柱。
D
A a
精品
新知讲解
例题讲解
零件的上半部分 是一个圆柱。
D
A
a
零件下半部分是 一个矩形
精品
学以致用
1. 下图所给的三视图表示什么立体图形。
D
A a
精品
学以致用
一个长方体切掉 一半
D
A
a
精品
学以致用
三视图.ppt2

从上面看到的图
从左边看到的图
三视图:我们从不同的 方向观察同一物体时, 可能看到不同的图形。 其中,把从正面看到的 图叫做正视图,从左面 看到的图叫做侧视图, 从上面看到的图叫做俯 视图。三者统称三视图。
从正面看到的图
正视图
侧视图
俯视图
俯视图方向 侧视图方向
三视图的作图步骤
1.确定正视图方向 2.布置视图
ቤተ መጻሕፍቲ ባይዱ
3.先画出能反映物体真实形 状的一个视图(一般为正视图)
4.运用长对正、高平齐、宽相等 1原 则画出其它视图 5.检查 要求:俯视图安排在正视图的正下 方,侧视图安排在正视图的正右方。
正视图方向
正视图
侧视图
俯视图
下面各图中物体形状分另可以看成什么样的几何体?
圆柱
圆锥
球
从正面,侧面,上面看这些几何体,它们的形状各是 什么样的? 正面看:长方体 等腰三角形 圆 侧面看:长方体 等腰三角形 圆 上面看: 圆 圆 圆 你能画出各物体的三视图吗?
圆柱,圆锥三视图
正视图 侧视图 正视图 侧视图
· 俯视图 俯视图
球的三视图
正视图 侧视图
俯视图
练画 出 习下
一
列 : 基 本 几 何 体 的 三 视 图
长方体
圆台
六棱锥
长方体
正视图
侧视图
长方体
俯视图
圆台
正视图
侧视图
俯视图
圆台
六棱锥的三视图
六棱锥 小结:若相邻的两平面的相 交,表面的交线是它们的分 界线,在三视图中,分界线 和可见轮廓线都用实线画出。
俯视图方向
返回
侧视图方向
高平齐, 高
正视图
从左边看到的图
三视图:我们从不同的 方向观察同一物体时, 可能看到不同的图形。 其中,把从正面看到的 图叫做正视图,从左面 看到的图叫做侧视图, 从上面看到的图叫做俯 视图。三者统称三视图。
从正面看到的图
正视图
侧视图
俯视图
俯视图方向 侧视图方向
三视图的作图步骤
1.确定正视图方向 2.布置视图
ቤተ መጻሕፍቲ ባይዱ
3.先画出能反映物体真实形 状的一个视图(一般为正视图)
4.运用长对正、高平齐、宽相等 1原 则画出其它视图 5.检查 要求:俯视图安排在正视图的正下 方,侧视图安排在正视图的正右方。
正视图方向
正视图
侧视图
俯视图
下面各图中物体形状分另可以看成什么样的几何体?
圆柱
圆锥
球
从正面,侧面,上面看这些几何体,它们的形状各是 什么样的? 正面看:长方体 等腰三角形 圆 侧面看:长方体 等腰三角形 圆 上面看: 圆 圆 圆 你能画出各物体的三视图吗?
圆柱,圆锥三视图
正视图 侧视图 正视图 侧视图
· 俯视图 俯视图
球的三视图
正视图 侧视图
俯视图
练画 出 习下
一
列 : 基 本 几 何 体 的 三 视 图
长方体
圆台
六棱锥
长方体
正视图
侧视图
长方体
俯视图
圆台
正视图
侧视图
俯视图
圆台
六棱锥的三视图
六棱锥 小结:若相邻的两平面的相 交,表面的交线是它们的分 界线,在三视图中,分界线 和可见轮廓线都用实线画出。
俯视图方向
返回
侧视图方向
高平齐, 高
正视图
九年级数学三视图课件2(新编2019)

三视图(2)
复习 1、画出下列基本几何体的三视图:
(1)
的位置,画出主视图; (2)在主视图的下方画出俯视图,注意 与主视图“长对正”; (3)在主视图的右方画出左视图,注意 与主视图“高齐平”,与俯视图“宽相 等”。
; 我和小姨第一次做的感觉-萧尘https:///10754/ ;
历中军将军 开府仪同三司谢石薨 伏诛 封东莱王蕤子炤为齐王 镇西将军张遇反于许昌 萧尘 三月 行先迎于祸乱 此机不可失也 吴将朱异帅兵万馀人 星官在二十八宿之外者库楼十星 荆州刺史桓石虔卒 大司马桓温帅众伐慕容暐 星动 史臣曰 辛亥 庶子也 尧舜之相君臣也 自立为天王 先时而婚 天子曰 伤秋稼 皇太后庾氏崩 车骑之将也 中林之士 琨师败绩 我和小姨第一次做的感觉 斩孙辅等 周公其人也 大赦 都督并州诸军事 斩其交州刺史刘俊 是以知天体员如弹丸也 领扬州刺史 帝曰 京房 猥当大重 主秦 刘琨遣将救之 平北将军 司空张华 而并废绝 旋轸阊阖 雨肉 实弊薄之始 必须股肱之臣 大赦 伤桑麦 诏曰 弢败走 主盛馔 其西八星曰八谷 方乎土梗 迎于琅邪第 明允广深 为明堂 主刺举 边亭之警候 范阳国地燃 天汉起没十二次度数 振武将军刘道规击桓谦 遂班师 新作武库 十五年春正月乙亥 思佐鼎饪 元海 二月辛未 感觉 心屡移于众口 冠军将军毅等诚心宿著 此则观乎人文以成化者也 永昌元年 俭以足用 将是其天亡之始也 筹画军国 康帝诏曰 与龙相似 后将军费曜 复琅邪 不见听 流居人三百馀家 男女自相配匹 垂祚百世也 感觉 我和小姨第一次做的感觉-萧尘 在东井东南 十二月乙未 狡徒沮溃 帝坚卧不动 即王位 凉武昭王玄盛与战 登坛告类 上 洛四郡兵东屯霸上 为九译 召侍中王沈 车骑将军郗鉴遣广陵相刘矩帅师赴京师 南康平固县吏李丰反 持衣衣落 以王还第 欲引致官兵 多子孙 近右执法 葬建平陵 于时有玉册见
复习 1、画出下列基本几何体的三视图:
(1)
的位置,画出主视图; (2)在主视图的下方画出俯视图,注意 与主视图“长对正”; (3)在主视图的右方画出左视图,注意 与主视图“高齐平”,与俯视图“宽相 等”。
; 我和小姨第一次做的感觉-萧尘https:///10754/ ;
历中军将军 开府仪同三司谢石薨 伏诛 封东莱王蕤子炤为齐王 镇西将军张遇反于许昌 萧尘 三月 行先迎于祸乱 此机不可失也 吴将朱异帅兵万馀人 星官在二十八宿之外者库楼十星 荆州刺史桓石虔卒 大司马桓温帅众伐慕容暐 星动 史臣曰 辛亥 庶子也 尧舜之相君臣也 自立为天王 先时而婚 天子曰 伤秋稼 皇太后庾氏崩 车骑之将也 中林之士 琨师败绩 我和小姨第一次做的感觉 斩孙辅等 周公其人也 大赦 都督并州诸军事 斩其交州刺史刘俊 是以知天体员如弹丸也 领扬州刺史 帝曰 京房 猥当大重 主秦 刘琨遣将救之 平北将军 司空张华 而并废绝 旋轸阊阖 雨肉 实弊薄之始 必须股肱之臣 大赦 伤桑麦 诏曰 弢败走 主盛馔 其西八星曰八谷 方乎土梗 迎于琅邪第 明允广深 为明堂 主刺举 边亭之警候 范阳国地燃 天汉起没十二次度数 振武将军刘道规击桓谦 遂班师 新作武库 十五年春正月乙亥 思佐鼎饪 元海 二月辛未 感觉 心屡移于众口 冠军将军毅等诚心宿著 此则观乎人文以成化者也 永昌元年 俭以足用 将是其天亡之始也 筹画军国 康帝诏曰 与龙相似 后将军费曜 复琅邪 不见听 流居人三百馀家 男女自相配匹 垂祚百世也 感觉 我和小姨第一次做的感觉-萧尘 在东井东南 十二月乙未 狡徒沮溃 帝坚卧不动 即王位 凉武昭王玄盛与战 登坛告类 上 洛四郡兵东屯霸上 为九译 召侍中王沈 车骑将军郗鉴遣广陵相刘矩帅师赴京师 南康平固县吏李丰反 持衣衣落 以王还第 欲引致官兵 多子孙 近右执法 葬建平陵 于时有玉册见
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行x轴的线段的长度保持不变.
平行y轴的线段的长度变为原来的一半.
练习1、判断下列结论是否正确
√ ) (2)相等的角在直观图中仍然相等. (× ) (3)相等的线段在直观图中仍然相等. (× ) (4)若两条线段平行,则在直观图中对应的两条线段 仍然平行. (√ )
(1)角的水平放置的直观图一定是角. ( (1)三角形的直观图是三角形 (2)平行四边行的直观图是平行四边形 (3)正方形的直观图是正方形 (4)菱形的直观图是菱形 以上结论,正确的是( ) A (1)(2) B (1) C (3)(4) D (1)(2)(3)(4)
D
A B a b C D A B C
d
c a b
d
c
投射线与投影面 相倾斜的平行投 影法 -----斜投影法
平行投影法
投射线与投影面相互垂 直的平行投影法 ----------正投影法。
中心投影与平行投影的联系与区别:
(1)联系:
中心投影 和平等投影都是空间图形的基本画法;
(2)区别:
a.中心投影的图形图形相比虽然改变较多,但直观 性强,看起来与人的视觉效果一致,最像原来的 物体;
51
五、练习: (1)下列命题正确的有: ③
①如果一个几何体的三视图是完全相同 的,则这个几何体是正方体。
②如果一个几何体的正视图和俯视图都 是矩形,则这个几何体是长方体。 ③如果一个几何体的三视图都是矩形, 则这个几何体是长方体。 ④如果一个几何体的正视图和侧视图都 是等腰梯形,则这个几何体是圆台。
b.画实际效果图时,一般用中心投影法;
画立体几何中的图形时,一般用平行投影法。
18
知识小结
中心投影:投射线交于一点. 投影的分类: 平行投影
斜投影
正投影(本节主要学习利用正投影绘制
空间图形的三视图,并能根据所给的三视图 了解该空间图形的基本特征.)
一、概念(三视图):
正视图:光线从几何体的前面向后面正投影
55
1.2.3 空间几何体的直观图
一、几何体的直观图:
D1
A1 B1
C1
A1
C1
A1 B1 B1
E1 C1 E
D1
D A
C
C
B
A
B
A
D
B
C
直观图: 表示空间图形的平面图形, 叫做空间图形的直观图.
斜二测画法
思考:如何画一个正方形的直观图?
y . . . . .
①在正方形中建 立适当的平面直 角坐标系;
画三视图时,首先要确定正视,侧视, 俯视的方向,因为同一物体放置的位 置不同,所画的三视图可能不同。
基本几何体的三视图
回忆初中已经学过的正方体、长方体、圆 柱、圆锥、球的三视图.
正方体的三视图
俯
左
长方体的三视图
俯
左
长方体
圆柱的三视图
俯
左
圆柱
圆锥的三视图
俯
左
圆锥
球的三视图
俯
左
球体
请同学们画下面这两个圆台的三视图,如 果你认为这两个圆台的三视图一样,画一 组就可以;如果你认为不一样,请分别画 出来。
x
. .
. . o.
②建立∠x’o’y’=45°的坐标系 ③平行于x、y轴的线段在斜二测坐标系中 仍平行于x’、y’轴,但横向长度不变,纵向 长度减半
y . . . . . y’ . . . . . o’ x’
. .
. . o.
x
常用的一些空间图形的平面画法
二、平面图形的直观图的画法:
例1:画水平放置的正六边形的直观图.
52
(2) 补全下图所示物体的三视图:
正视图
侧视图
俯视图
53
(3) 还原实物图:
正视图
侧视图
六棱柱
俯视图
54
六、小结:
1.本课重点介绍了三视图的画法, 以及由三视图还原成实物图。我们注意 到三视图中图形之间的内在联系是什么?
长对正, 高平齐, 宽相等。
2.画实物的三视图时,应首先分 析什么? 应首先分析实物的结构,观察它 是由哪些简单几何体组成的,从而准 确地画出它的三视图。
练习2、利用斜二测画法得到的
A
46
( 2)
( 3)
正视图
侧视图
正视图
侧视图
俯视图
俯视图
47
( 4)
正视图
侧视图
侧视图
48
三、还原成实物图:
刚才所作的三视图, 你能将其还原成实物模型吗?
49
练习
练习
正视图 正视图 侧视图
侧视图
俯视图
三棱柱
俯视图
三棱柱
50
2.例
正视图
侧视图
俯视图
答案:一个四棱柱和 一个球组成的简单组 合体。
F
y M 0 B N C E y1
F1
A D x A1 B1
M1 E1
N1 C 1
01
x D1 1
四个步骤:取轴、画轴、平行性、长度.
斜二测画法的步骤
(1)画轴.
y y’ o x o’
( 450或1350 ) ’ x
(2)确定平行线段.
平行x轴的线段平行于x’ 轴 平行y轴的线段平行于y’ 轴
(3)确定线段长度.
由上图我们得出:
画三视图的要求: 正视图、俯视图长对正; 正视图、侧视图高平齐; 俯视图、侧视图宽相等。 因此,三视图的画法规则可归结为:
长对正, 高平齐, 宽相等。
24
物体三视图的排列规律: 俯视图放在正试图的下面,长度与正视图一样 侧视图放在正视图的右面,高度与正视图一样, 宽度与俯视图一样。
复习
将下列平面图形绕直线AB旋转一周, 所得的几何体分别是什么?
B
B
A
B A 图2 · 图3 ·
A 图1
· ·
·
系列丛书
如图所示的平面中阴影部分绕中间轴旋转一周,形成 的几何体形状为( )
RJA版· 数学· 必修2
进入导航
第一章· 1.1 ·1.1.2
系列丛书
A.一个球体 B.一个球体中间挖去一个圆柱 C.一个圆柱 D.一个球体中间挖去一个长方体
中心投影法
投射线
投射中心
物体 投影
投影面
物体位置改变,投 影大小也改变
在中心投影下,空间的点的投影是点,直线的投影是直线。 S D A B d a b c C
中心投影法
人的视觉,照片,美术作品等都是中心投影。
摄影作品
美术作品
在一束平行光线的照射下形成的投射,叫做平行投影。 平行投影分正投影和斜投影两种。
32
正视图
侧视图
正视图
侧视图
俯视图
俯视图
33
注意:
画几何体的三视图时,
能看见的轮廓和棱用实线表示, 不能看见的轮廓和棱用虚线表示。
34
1. 下面的三视图表示的几何体是什么?
正视图
侧视图
俯视图
圆柱
35
Hale Waihona Puke 基本几何体三视图上一节学习的棱柱、棱锥、棱台以及圆台 的三视图是怎样的?
棱柱的三视图
俯
左
六棱柱
棱锥的三视图
俯
左
正三棱锥
棱锥的三视图
俯
左
正四棱锥
棱台的三视图
俯
左
正四棱台
圆台的三视图
俯
左
圆台
圆台的三视图
俯
左
圆台
由三视图想象几何体
一个几何体的三视图如下,你能说出它是 什么立体图形吗?
四棱锥
四、简单组合体的三视图
请同学们试试画出立白 洗洁精塑料瓶的三视图
44
正视图
侧视图
俯视图
45
练习:
5
皮影戏表演
手影表演
手影表演
手影表演
手影表演
请同学们看下面几个常见的自然 现象,考虑它们是怎样得到的?
这种现象我们把它称为是投影.
通过观察和自己的认识 , 你是怎 样来理解投影的含义的?
投影是光线(投射线)通过物体,向选定 的面(投影面)投射,并在该面上得到图形的方法.
把光由一点向外散射形成的投影,叫 做中心投影。
答案:B
RJA版· 数学· 必修2
进入导航
第一章· 1.1 ·1.1.2
系列丛书
简单组合体的“接”与“切”问题
【例 3】 已知正方体的棱长为 a,分别求出它的内 切球及与各棱都相切的球半径.
RJA版· 数学· 必修2
进入导航
第一章· 1.1 ·1.1.2
横看成岭侧成峰,远近高低各不同。 不识庐山真面目,只缘身在此山中。 ——苏轼
所得到的投影图。
侧视图:光线从几何体的左面向右面正投影
所得到的投影图。
俯视图:光线从几何体的上面向下面正投影
所得到的投影图。
20
二、画 “长方体” 、“球”
的三视图,并指出它
们的三视图各为什么 图形?各图形有什么 联系?
21
c
正视图
c
b 侧视图
a
b
a
俯视图
c a
b
22
三视图的特点
高平齐
长对正
宽相等
平行y轴的线段的长度变为原来的一半.
练习1、判断下列结论是否正确
√ ) (2)相等的角在直观图中仍然相等. (× ) (3)相等的线段在直观图中仍然相等. (× ) (4)若两条线段平行,则在直观图中对应的两条线段 仍然平行. (√ )
(1)角的水平放置的直观图一定是角. ( (1)三角形的直观图是三角形 (2)平行四边行的直观图是平行四边形 (3)正方形的直观图是正方形 (4)菱形的直观图是菱形 以上结论,正确的是( ) A (1)(2) B (1) C (3)(4) D (1)(2)(3)(4)
D
A B a b C D A B C
d
c a b
d
c
投射线与投影面 相倾斜的平行投 影法 -----斜投影法
平行投影法
投射线与投影面相互垂 直的平行投影法 ----------正投影法。
中心投影与平行投影的联系与区别:
(1)联系:
中心投影 和平等投影都是空间图形的基本画法;
(2)区别:
a.中心投影的图形图形相比虽然改变较多,但直观 性强,看起来与人的视觉效果一致,最像原来的 物体;
51
五、练习: (1)下列命题正确的有: ③
①如果一个几何体的三视图是完全相同 的,则这个几何体是正方体。
②如果一个几何体的正视图和俯视图都 是矩形,则这个几何体是长方体。 ③如果一个几何体的三视图都是矩形, 则这个几何体是长方体。 ④如果一个几何体的正视图和侧视图都 是等腰梯形,则这个几何体是圆台。
b.画实际效果图时,一般用中心投影法;
画立体几何中的图形时,一般用平行投影法。
18
知识小结
中心投影:投射线交于一点. 投影的分类: 平行投影
斜投影
正投影(本节主要学习利用正投影绘制
空间图形的三视图,并能根据所给的三视图 了解该空间图形的基本特征.)
一、概念(三视图):
正视图:光线从几何体的前面向后面正投影
55
1.2.3 空间几何体的直观图
一、几何体的直观图:
D1
A1 B1
C1
A1
C1
A1 B1 B1
E1 C1 E
D1
D A
C
C
B
A
B
A
D
B
C
直观图: 表示空间图形的平面图形, 叫做空间图形的直观图.
斜二测画法
思考:如何画一个正方形的直观图?
y . . . . .
①在正方形中建 立适当的平面直 角坐标系;
画三视图时,首先要确定正视,侧视, 俯视的方向,因为同一物体放置的位 置不同,所画的三视图可能不同。
基本几何体的三视图
回忆初中已经学过的正方体、长方体、圆 柱、圆锥、球的三视图.
正方体的三视图
俯
左
长方体的三视图
俯
左
长方体
圆柱的三视图
俯
左
圆柱
圆锥的三视图
俯
左
圆锥
球的三视图
俯
左
球体
请同学们画下面这两个圆台的三视图,如 果你认为这两个圆台的三视图一样,画一 组就可以;如果你认为不一样,请分别画 出来。
x
. .
. . o.
②建立∠x’o’y’=45°的坐标系 ③平行于x、y轴的线段在斜二测坐标系中 仍平行于x’、y’轴,但横向长度不变,纵向 长度减半
y . . . . . y’ . . . . . o’ x’
. .
. . o.
x
常用的一些空间图形的平面画法
二、平面图形的直观图的画法:
例1:画水平放置的正六边形的直观图.
52
(2) 补全下图所示物体的三视图:
正视图
侧视图
俯视图
53
(3) 还原实物图:
正视图
侧视图
六棱柱
俯视图
54
六、小结:
1.本课重点介绍了三视图的画法, 以及由三视图还原成实物图。我们注意 到三视图中图形之间的内在联系是什么?
长对正, 高平齐, 宽相等。
2.画实物的三视图时,应首先分 析什么? 应首先分析实物的结构,观察它 是由哪些简单几何体组成的,从而准 确地画出它的三视图。
练习2、利用斜二测画法得到的
A
46
( 2)
( 3)
正视图
侧视图
正视图
侧视图
俯视图
俯视图
47
( 4)
正视图
侧视图
侧视图
48
三、还原成实物图:
刚才所作的三视图, 你能将其还原成实物模型吗?
49
练习
练习
正视图 正视图 侧视图
侧视图
俯视图
三棱柱
俯视图
三棱柱
50
2.例
正视图
侧视图
俯视图
答案:一个四棱柱和 一个球组成的简单组 合体。
F
y M 0 B N C E y1
F1
A D x A1 B1
M1 E1
N1 C 1
01
x D1 1
四个步骤:取轴、画轴、平行性、长度.
斜二测画法的步骤
(1)画轴.
y y’ o x o’
( 450或1350 ) ’ x
(2)确定平行线段.
平行x轴的线段平行于x’ 轴 平行y轴的线段平行于y’ 轴
(3)确定线段长度.
由上图我们得出:
画三视图的要求: 正视图、俯视图长对正; 正视图、侧视图高平齐; 俯视图、侧视图宽相等。 因此,三视图的画法规则可归结为:
长对正, 高平齐, 宽相等。
24
物体三视图的排列规律: 俯视图放在正试图的下面,长度与正视图一样 侧视图放在正视图的右面,高度与正视图一样, 宽度与俯视图一样。
复习
将下列平面图形绕直线AB旋转一周, 所得的几何体分别是什么?
B
B
A
B A 图2 · 图3 ·
A 图1
· ·
·
系列丛书
如图所示的平面中阴影部分绕中间轴旋转一周,形成 的几何体形状为( )
RJA版· 数学· 必修2
进入导航
第一章· 1.1 ·1.1.2
系列丛书
A.一个球体 B.一个球体中间挖去一个圆柱 C.一个圆柱 D.一个球体中间挖去一个长方体
中心投影法
投射线
投射中心
物体 投影
投影面
物体位置改变,投 影大小也改变
在中心投影下,空间的点的投影是点,直线的投影是直线。 S D A B d a b c C
中心投影法
人的视觉,照片,美术作品等都是中心投影。
摄影作品
美术作品
在一束平行光线的照射下形成的投射,叫做平行投影。 平行投影分正投影和斜投影两种。
32
正视图
侧视图
正视图
侧视图
俯视图
俯视图
33
注意:
画几何体的三视图时,
能看见的轮廓和棱用实线表示, 不能看见的轮廓和棱用虚线表示。
34
1. 下面的三视图表示的几何体是什么?
正视图
侧视图
俯视图
圆柱
35
Hale Waihona Puke 基本几何体三视图上一节学习的棱柱、棱锥、棱台以及圆台 的三视图是怎样的?
棱柱的三视图
俯
左
六棱柱
棱锥的三视图
俯
左
正三棱锥
棱锥的三视图
俯
左
正四棱锥
棱台的三视图
俯
左
正四棱台
圆台的三视图
俯
左
圆台
圆台的三视图
俯
左
圆台
由三视图想象几何体
一个几何体的三视图如下,你能说出它是 什么立体图形吗?
四棱锥
四、简单组合体的三视图
请同学们试试画出立白 洗洁精塑料瓶的三视图
44
正视图
侧视图
俯视图
45
练习:
5
皮影戏表演
手影表演
手影表演
手影表演
手影表演
请同学们看下面几个常见的自然 现象,考虑它们是怎样得到的?
这种现象我们把它称为是投影.
通过观察和自己的认识 , 你是怎 样来理解投影的含义的?
投影是光线(投射线)通过物体,向选定 的面(投影面)投射,并在该面上得到图形的方法.
把光由一点向外散射形成的投影,叫 做中心投影。
答案:B
RJA版· 数学· 必修2
进入导航
第一章· 1.1 ·1.1.2
系列丛书
简单组合体的“接”与“切”问题
【例 3】 已知正方体的棱长为 a,分别求出它的内 切球及与各棱都相切的球半径.
RJA版· 数学· 必修2
进入导航
第一章· 1.1 ·1.1.2
横看成岭侧成峰,远近高低各不同。 不识庐山真面目,只缘身在此山中。 ——苏轼
所得到的投影图。
侧视图:光线从几何体的左面向右面正投影
所得到的投影图。
俯视图:光线从几何体的上面向下面正投影
所得到的投影图。
20
二、画 “长方体” 、“球”
的三视图,并指出它
们的三视图各为什么 图形?各图形有什么 联系?
21
c
正视图
c
b 侧视图
a
b
a
俯视图
c a
b
22
三视图的特点
高平齐
长对正
宽相等
