2019-2020学年八年级数学上册 12.3 乘法公式 2《两数和(差)的平方》导学案(新版)华东师大版.doc

合集下载

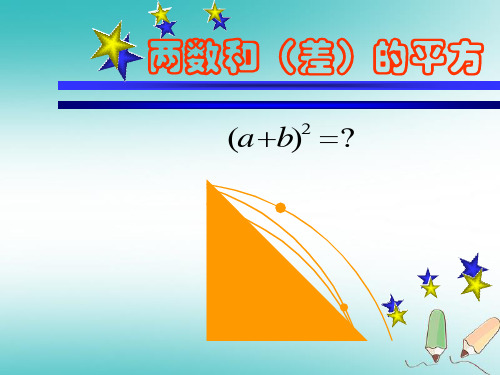
12.3.2乘法公式2两数和(或差)的平方

a ab ab b b）（ a a 2 2ab b 2
2 2
2
‖
图13.3.2
a 2ab b
2
2
（2）用等式表示下图中图形面积的运算.
图13.3.2
（a b)
2
______
＝
a2
+
2ab
+
b ___
2
第（2）题
小结
“两数和的平方”公式:
语言描述：
两数和的平方，等于它们的平方和加上积的2倍.
语言表述：两数和（差）的平方，等于它们的平方和加上（减去）它们乘积的两倍。
公式的结构特征：
（1）公式左边是两数和(差)的平方；
（2）公式右边是二次三项式，它是左边两数的平方和加上（减去）左边两数积的两倍。
即：首平方，尾平方，二倍在中央。
（三）达标练习
A组
（1） ( x 3)
2 2
2 2
1、计算：
x 2 x 3 3
2
2
(1)(x 3)
x 6x 9
（2） (2 x y ) 2 (2 x) 2 2 2 x y y 2 4 x 2 4 xy y 2
（2） (2 x y )
（三）达标练习
A组
（1） ( x 3)
2 2
2 2
a 2ab b 2ab
2 2
2
2 4 xy 4 ( x y) __________ _ ( x y) 2 2 2 2 x 2 xy y 4 xy x 2 xy y
(a＋b)2 = a2＋2ab＋b2 2 2 2 (a－b) = a －2ab＋b

12.3 乘法公式(第2课时)(课件)八年级数学上册(华东师大版)

A．10 B．13 C．16 D．19
【详解】解：设正方形A的边长为a，正方形B的边长为b，由图甲得：(a-b)2=3，即a2+b2-2ab=3，由图乙得：(a+b)2-a2-b2=16，整理得2ab=16，所以a2+b2=19．即正方形A、B的面积之和为19．故选：D．
当堂检测
5．如果x2-x+m是完全平方式，则m的值为（）
当堂检测
1.下面各式的计算是否正确？如果不正确，应当怎样改正？
（1）(x+y)2=x2 +y2 (2)(x －y)2 =x2 －y2 (3) (－x +y)2 =x2+2xy +y2 (4) (2x+y)2 =4x2 +2xy +y2
× x2+2xy +y2 × x2－2xy +y2 × x2 －2xy +y2 × 4x2+4xy +y2
讲授新课
补充例题已知x+y=4，xy=2，求（1）x2+y2；（2）3x2-xy+3y2；（3）x-y 解 (1)x2+y2=(x+y)2-2xy=42-2×2=16-4=12 (2)3x2-xy+3y2=3(x+y)2-7xy=3×42-7×4=3×16-28=20 (3)(x-y)2＝(x+y)2-4xy =42-4×2=8 所以 x-y= x2 - y2 = 8 2 2
22
=16a2+4ab+b42
讲授新课
试一试推导两数差的平方公式（a-b）2
(a b)2 [a (b)]2 a2 2a(b) (b)2 a2 2ab b2

八年级数学上册第12章整式的乘除 12.3 乘法公式 2 两数和(差)的平方教案 (新版)华东师

两数和(差)的平方利用完全平方公式，可以使一些计算简便．对于一些形式上不符合公式的可进行适当的转化，使之符合公式的应用．完全平方公式的变形如下表：于对公式进行变式使用．在解题中充分体现应用公式的思维灵活性，综合并灵活地解决有关的不同类型的问题.活动四：课堂总结反思当堂检测1.用完全平方公式计算(课本P35页练习)(1)(x＋3)2(2)(2x＋y)2(3)(x－3)2(4)(2m－3n)2(5)(－2m＋n)2(6)(－2m－n)22.一个正方形的边长为a cm.若边长减少6 cm，则这个正方形的面积减少了多少？3.纠错练习：下面的计算是否正确？如有错误，请改正：(1)(x＋y)2＝x2＋y2；(2)(－m＋n)2＝－m2＋n2；(3)(－a－1)2＝－a2－2a－1.4.计算：(a＋b＋c)25.小兵计算一个二项整式的平方式时，得到正确结果是4x2＋________＋25y2，但中间一项不慎被污染了，这一项应是( )A.10xy B．20xy C．±10xy D．±20xy6.运用乘法公式计算：(1)(x＋1)(x－1)(x2－1)；(2)(x＋3)(x－3)(x2－9)；，及时反馈学习效果．通过完成练习使学生进一步熟练掌握公式的结构特征.2.教师引导学生进行探索，必要时进行适当的启发和提示.(3)(x＋2)2－(x－2)2；(4)(x＋y＋z)(x－y－z)；(5)(a＋2b＋c)2；(6)(2a＋b＋1)(2a＋b－1)；7.已知a＋b＝－6，ab＝8，求(1)a2＋b2；(2)(a－b)2. 课堂总结谈谈你的收获吧！布置作业课本P37第2、3、4题．【知识网络】框架图式总结，加上生动记忆方法，使学生易于接受.【教学反思】①[授课流程反思]A．新课导入□B．情景导入□让学生带着原有的知识背景、生活体验和理解走进学习活动，并通过自己的主动探索，与同学合作交流、反思等，构建对知识的形成和运用．②[讲授效果反思]A．重点□B．难点□C．易错点□教师在此立足于强化新知识的同时，着眼于激发学生的思考兴趣和发现兴趣，培养学生的科学猜测能力．本节课在中学代数占据着非常重要的位置，一定要使学生熟悉这个公式及它的各种变形．③[师生互动反思]在整个教学过程中充分运用探究学习与合作学习．有学生之间的交流，也有师生之间的交流，在课堂中构建和谐，某某的气氛．对于反思，更进一步提升.。

八年级数学上册12.3乘法公式第2课时两数和差的平方习题课件(新版)华东师大版

.化简－2x4＋8x3＋32，值为3078
20．(9分)已知x＋y＝3，xy＝－12，求下列各式的值： (1)x2＋y2； (2)x2－xy＋y2.
20.∵x＋y＝3，xy＝－12.∴(x＋y)2＝x2＋y2＋2xy＝ 9，∴(1)x2＋y2＝9－2xy＝9＋2×12＝33 (2)x2－xy＋y2＝33－(－12)＝45
12．3 乘法(chéngfǎ)公式
第2课时(kèshí) 两数和(差)的平方
第一页，共14页。
两数和(差)的平方： ①两数和的平方：两数和的平方，等于(děngyú)它们的平_方__和_____加上这两数积的___2_____倍．即：(a＋b)2＝__________a_2＋__2_a_b_＋__b_2_____________．
A．x2－1
B．x2－2x＋1
C．x2－2x－1
D．x2＋1
2．(3分)计算(－2y＋x)2的结果是( )A
A．x2－4xy＋4y2
B．－x2－4xy－4y2
C．x2＋4xy＋4y2
D．－x2＋4xy－4y2
第三页，共14页。
3．(3分)运算结果为x2－2x＋1的是( B )
A．(x＋1)2
B．(－x＋1)2
②两数差的平方：两数差的平方，等于(děngyú)它们的平_方__和_____减去
这两数积的___2_____倍．即：(a－b)2＝_________a_2－__2_a_b_＋__b_2________________．
第二页，共14页。
1．(3分)下列各式中，与(x－1)2相等(xiāngděng)的B 是( )
(2)(－3m－2n)2；
9m2＋12mn＋4n2
(3)(－a＋2b)2；

12.3乘法公式(两数和差平方公式)

12.3平方公式目标解读：1.推导两数和、差的平方公式，理解两数和、差的平方公式的意义。

2.掌握乘法公式，用乘法公式进行有关计算。

重点：两数和、差的平方公式应用难点：推导两数和、差的平方公式知识点1两数和、差的平方用多项式乘法运算验证归纳总结：两数和或差的平方，等于这两数的平方和加上或减去它们的积的倍。

拓展一、利用乘法公式进行运算例9992-1002×998拓展二、巧用平方和、平方差公式计算拓展三、变化整式的形式求值拓展四、整体代入法化简求值拓展五、求图形的面积拓展六、灵活运用两数和差的平方公式拓展七判断三角形的形状五、拓展延伸1.利用完全平方公式进行计算（1）1022(2）1992(3）（x＋2）2－（x－2）22.下列可以用两数和乘以这两数差公式计算的是（）（A）（x-y）（x+y）（B）（x-y）（y-x）（C）（x-y）（-y+x）（D）（x-y）（-x+y）3、计算（1）（4a＋5b）2 （2）（-6a＋9b）2（3）（7a－3b）2（4）（-2x－3y）24、已知x+y=3，xy=-12，求下列各式的值。

（1）x2+y2 (2)x2-xy+y2(3)(x-y)2 (4) |x-y|5、已知x-y=4,xy=21,则x2+y2的算术平方根等于多少6、已知x+y=3,x2+y2=5,则xy的值等于多少？14.3.2 两数和的平方(A卷)(教材针对性训练题60分 30分钟)一、判断:下列等式是否成立,对的打“∨”,错的打“×”号(每小题1分,共6分)1.(x-y)2=x2-y2( );2.a2-b2=(a-b)2+2ab-2b2( )3.a2+b2=(a-b)2+2ab( );4.a2-b2=(a+b)2-2ab( )5.(0.5x-y)2=0.25x2-xy+y2( );6.(a+1)(-a-1)=a2-1( )二、填空题:(每小题3分,共24分)7.23___5x⎛⎫+⎪⎝⎭=925x2+6xy+25y2;8.5022=(______+______)2=____________________=___________.9.若a2+2a=1则(a+1)2=________.10.(______+b2)=9a2+_______+_________.11.若(x-3)2=x2+kx+9,则k=_________.12.若x2+y2=12,xy=4,则(x-y)2=_________.13.x2+y2=(x-y)2+_______=(x+y)2-_______.14.(_____-2)2=_____-12x+________.三、选择题:(每小题3分,共18分)15.乘法公式中a、b可表示( )A.数B.多项式C.单项式D.以上都可以16.下列各式计算正确的是( )A.(a-b)2=a2-b2;B.(2x-y)2=4x2-2xy+y2C.(a2+2b)2=a4+4b2;D.(12x+3)2=14x2+3x+917.下列各式中,计算结果是2mn-m2-n2的是( )A.(m-n)2B.-(m-n)2;C.-(m+n)2D.(m+n)218.若x2+ax=(x+12)2+b,则a、b的值是( )A.a=1,b=14B.a=1,b=-14; C.a=0,b=-12D.a=2,b=1219.(a+3b)2-(3a+b)2的计算结果是( )A.8(a-b)2B.8(a+b)2;C.8b2-8a2D.8a2-8b220.下列各式中,形如a2±2ab+b2的形式的多项式有( )①a2-a+14,②x2+xy+y2,③116m2+m+1,④x2-xy+14y2,⑤m2+4n2+2mn,⑥14a4b2-a2b+1.A.2个B.3个C.4个D.5个四、(每小题4分,共12分)21.化简:(9-a2)2-(3-a)(3+a)(9+a2);22.化简并求值:(x3+2)2-2(x+2)(x-2)(x2+4)-(x3-2)2,其中x=1 2 .23.已知A=1234567×1234569,B=12345682,试比较A 、B 的大小.答案:一、1.× 2.∨ 3.∨ 4.× 5.∨ 6.× 二、7.5y 8.500;2;250000+2000+4;252004.9.2 10.3a;6ab;b 211.- 6 12.4 13.2xy;2xy 14.211,,4864x x . 三、15.D 16.D 17.B 18.B 19.C 20.B 四、21.解:原式=81-18a 2+a 4-(9-a 2)(9+a 2) =81-18a 2+a4-(81-a 4) =81-18a 2+a 4-81+a 4 =2a 4-18a 222.解:原式=x 6+4x 3+4-2(x 2-4)(x 2+4)-(x 6-4x 3+4) =x 6+4x 3+4-2(x 4-16)-x 6+4x 3-4 =8x 3-2x 4+32当x=-12时,原式=3411111782328232132302281688⎛⎫⎛⎫⎛⎫⨯--⨯+=⨯--⨯+=--+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭23.解:设m=1234568,则1234567=m-1,1234569=m+1,则A=(m-1)(m+1)=m 2-1,B=m 2. 显然m 2-1<m 2,所以A<B.14.3.2 两数和的平方(B卷)(综合应用创新训练题 60分 40分钟)一、学科内综合题:(28分)1.(6分)解不等式:(x2-2)(-x2+2)>(2x-x2)(2x+x2)+4x.2.(6分)解方程组:222(x+3)(2)(7)(4)(4)12 1y y x xx y⎧+-=-++--⎨+=-⎩3.(6分)△ABC三边长a、b、c满足b+c=8,bc=a2-12a+52,试问△ABC 是什么三角形?4.(10分)(1)图是一个长为2a,宽为2b的矩形, 若把此图沿图中虚线用剪刀均分为四块小长方形,然后按图的形状拼成一个正方形,请问:这两个图形的什么量不变?所得的正方形的面积比原矩形的面积多出的阴影部分的面积用a、b 的代数式表示为_________.(2)由(1)的探索中,可得出的结论是:在周长一定的矩形中,_____________时,面积最大;(3)若一矩形的周长为36cm,则当边长为多少时,该图形的面积最大?最大面积是多少?二、应用题:(5分)5.已知一个正方形木板,它的边长是(a+3)cm,从中锯去一个边长是(a-1)cm 的正方形,求剩余木板的面积是多少?三、创新题:(共22分) (一)多解题(9分)6.已知:a+b=7,ab=-12,求下列各式的值. (1)a 2+b 2;(2)a 2-ab+b 2;(3)(a-b)2(二)多变题(8分) 7.已知:x 2-3x+1=0,求x 4+41x的值.bb aa一变:已知:(x2+1)(y2+1)=4xy,求代数式x2-5y+1的值.(三)新解法题(5分)8.设a、b、c、d都是整数且m=a2+b2,n=c2+d2,试说明：m、n可表示成两个整数的平方和的形式.四、新中考题:(共5分)9.(2003,海南省,2分)下列各式中,不一定成立的是( )A.(a+b)2=a2+2ab+b2;B.(b-a)2=a2-2ab+b2C.(a+b)(a-b)=a2-b2;D.(a-b)2=a2-b210.(2003,福州市,3分)观察下列各式:1×3=12+2×1,2×4=22+2×2,3×5= 32+2×3,……请你将猜想到的规律用自然数n(n≥1)表示出来:_____________.答案:一、1.解:-(x2-2)2>(2x)2-(x2)2+4x,-(x4-4x2+4)>4x2-x4+4x,-x4+4x2-4<4x2-x4+4x,-4<4x,∴x<-1.2.解:由①得:x2+6x+9+y2-4y+4=49-14y+y2+x2-16-12,6x-4y+14y=49-28-9-4,6x+10y=8,即3x+5y=4,③由③-②×③得:2y=7,∴y=3.5,把y=3.5代入②得:x=-3.5-1=-4.5,∴4.53.5 xy=-⎧⎨=⎩3.解:由b+c=8得c=8-b,代入bc=a 2-12a+52得 b(8-b)=a 2-12a+52,8b-b 2=a 2-12a+52,a 2-12a+36+b 2-8b+16=0,逆用完全平方公式得 (a-b)2+(b-4)2=0,所以a-6=0且b-4=0,即a=6,b=4, 把b=4代入c=8-b 得c=8-4=4. ∴c=b=4,因此△ABC 是等腰三角形.4.(1)这两个图形的周长不变 (a-b)2=a 2-2ab+b 2 (2)在周长一定的矩形中,长等于宽时面积最大. (3)9cm,81cm 2 二、5.解:剩余木板的面积是:(a+3)2-(a-1)2=(a+3+a-1)(a+3-a+1)=(2a+2)×4=8a+8(cm 2) 三、(一) 6.解法一:(1)a 2+b 2=(a+b)2-2ab=72-2×(-12)=49+24=73.(2)a 2-ab+b 2=(a 2+b 2)-ab=73-(-12)=73+12=85,(3)(a-b)2=a 2-2ab+b 2=(a 2+b 2)-2ab=73-2×(-12)=73+24=97. 解法二:(1)∵a+b=7,∴(a+b)2=49,又ab=-12,即a 2+2ab+b 2=49,∴a 2+b 2=49-2×(-12)= 49+24=73.(2)∵(a+b)2=49,又ab=-12,∴a 2+b 2+2ab=49,∴a 2+b 2-ab=49-3ab=49-3×(- 12)=49+36=85. (3)∵a+b=7,ab=-12,∴(a-b)2=(a+b)2-4ab=49-4×(-12)=49+48=97. (二) 7.解:由x 2-3x+1=0,知x ≠0,∴x-3+ =0,∴x+1x=3,∴x 2+21x=(x+1x )2-2x ×1x =32-2=7 ∴x 4+41x =(x 2+21x)2-2=72-2=47一变:∵(x 2+1)(y 2+1)=4xy,∴x 2y 2+x 2+y 2+1=4xy. ∴(x 2y 2-2xy+1)+(x 2-2xy+y 2)=0,(xy-1)2+(x-y)2=0,∴100xy x y -=⎧⎨-=⎩∴x=y,x 2=1,∴x=±1.当x=1时,y=1;当x=-1时.y=-1∴当x=1,y=1时,x 2-5y+1=12-5×1+1=1-5+1=-3.当x=-1,y=-1时,x 2-5y+1=(-1)2-5×(-1)+1=1+5+1=7.(三)8.解:∵m=a2+b2,n=c2+d2∴mn=(a2+b)(c2+d2)=a2c2+a2d2+b2c2+b2d2=a2c2+2abcd+b2d2+b2c2-2abcd+a2d2=(ac+bd)2+(bc-ad)2或=(ac-bd)2+(bc+ad)2四、9.D 10.n(n+2)=n2+2n14.3.2 两数和的平方 (C卷)(能力拔高训练题 20分 20分钟)探究题:(每小题10分,共20分)1.给出下列算式:32-12=8=8×1,52-32=16=8×2,72-52=24=8×3,92-72=32=8×4=32,…(1)观察上面一系列式子,你能发现什么规律?用含n的式子表示出来:_____________________( n为正整数)(2)根据你发现的规律:计算:20052-20032=________________,这时,n=______.2.观察下面各式规律:12+(1×2)2+22=(1×2+1)2,22+(2×3)2+32=(2×3+1)2,32+ (3×4)2+42=(3×4+1)2,…(1)写出第2001行式子:_____________________________________;(2)写出第n行式子:____________________________________________,并说明你的结论为什么是正确的.答案:1.(1)(2n+1)2-(2n-1)2=8n(2)8016,10022.(1)20012+(2001×2002)2+20022=(2001×2002+1)2(2)n2+[n(n+1)]2+(n+1)2=[n(n+1)+1]2∵左边=n2+n2(n+1)2+(n+1)2=n2+n2(n2+2n+1)+n2+2n+1=n2+n4+2n3+n2+n2+2n+1=n4+2n3+3n2+2n+1又∵右边=[n(n+1)+1]2=n2(n+1)2+2n(n+1)+1=n2(n2+2n+1)+2n2+2n+1=n4+2n3+n2+2n2+2n+1=n4+2n3+3n2+2n+1因为左边=右边,所以n2+[n(n+1)]2+(n+1)2=[n(n+1)+1]2是正确的.。

人教版2020八年级数学上册第12章整式的乘除 12.3 乘法公式 1 两数和乘以这两数的差学案

12.3 乘法公式1 两数和乘以这两数的差课前知识管理1、两数和与这两数差的积等于这两个数的平方差：(a+b)(a-b)=a 2-b 2所以，我们把这个公式叫作平方差公式.平方差公式可以形象记忆为：(□+△)(□—△)=□2—△2.几何背景：如图，阴影部分的面积可以看成是大正方形的面积减去小正方形的面积，即a 2－b 2.若把小长方形Ⅲ旋转到小长方形Ⅳ的位置，则此时的阴影部分的面积又可以看成S Ⅰ+S Ⅲ＝S Ⅰ+S Ⅳ＝（a+b ）（a －b ），从而验证了平方差公式（a+b ）（a －b ）＝a 2－b 2. 2、平方差公式的特征：（1）公式左边的两个因式都是二项式，必须是相同的两数的和与差.或者说两个二项式必须有一项完全相同，另一项只有符号不同.（2）公式中的a 与b 可以是数，也可以换成一个代数式.名师导学互动典例精析：知识点1：直接应用平方差公式例1、计算：)421)(214(22x x +-．【解题思路】此题是两个二项式相乘，且这两个二项式中各有一完全相同的项24x ，另外一项－21与21互为相反数，符合平方差公式的结构特点，因此，可直接套用平方差公式．【解】)421)(214(22x x +-=4116)21()4(4222-=-x x ．【方法归纳】将两个括号内的相同项24x 看作□，符号相反的项－21与21看作△，就可以直接运用平方差公式.对应练习：计算(y —2x)(—2x —y). 知识点2：连用平方差公式化简例2、化简：()()()()()224488x y x y x yxy x y -++++.【解题思路】本题的前两项能利用平方差公式得到()22x y -，它与第三项()22xy +又能构成平方差公式，依次类推，较轻松地得到结果. 【解】原式=()()()()22224488x y xy x y x y -+++=()()()444488x y x y x y -++=()()88881616.x yxy x y -+=-【方法归纳】连用平方差公式使运算量大大减小，实现简算目的. 对应练习：计算：))()()()((884422b a b a b a b a b a ++++-知识点3：分组后运用平方差公式例3、计算: (2a+3)(3a+5)(2a-3)(3a-5).【解题思路】若直接运算,则计算比较繁琐,如果运用乘法的交换律将第一、三结合，第二、四结合分组，就可以利用乘法公式计算.【解】(2a+3)(3a+5)(2a －3)(2a －5)=[(2a+3)(2a －3)][(3a+5)(3a －5)]=(4a 2-9)(9a 2－25)=36a 4－181a 2+225.【方法归纳】根据算式中各因式的特征，恰当分组后利用乘法公式可以简化计算，减少运算量.对应练习：计算：(x+2)(x 2+4)(x —2). 知识点4：添项后运用平方差公式例4．计算；1)12)(12)(12)(12(842+++++．【解题思路】本题若添上一个因式“２－１”后，则可以连续四次运用平方差公式计算．【解】原式＝=+++++-1)12)(12)(12)(12)(12(8421)12)(12)(12)(12(8422++++- ＝1)12)(12)(12(844+++-＝16168821121)12)(12(=+-=++-．【方法归纳】本题的解题关键是在不改变原式的值的前提下，将原式添上一个因式，使得它能运用乘法公式计算．对应练习：某同学在计算)14)(14(32++时，把3写成14-后，发现可以连续运用两数和乘以这两数差公式计算：2551161)4()14)(14()14)(14)(14()14)(14(32222222=-=-=+-=++-=++.请借鉴该同学的经验，计算：1584221)211)(211)(211)(211(+++++. 知识点5：逆用平方差公式例5．计算：22)43()32(a b ba --+【解题思路】若直接运用完全平方公式展开再相减，运算量大，若把式中的“32ba +”与“a b43-”分别视为平方差公式中的a 、b ，逆用平方差公式，则运算简便．解：22)43()32(a bb a --+ab a a b a a b b a a b b a 4126322433243322+-=⨯⎪⎭⎫ ⎝⎛+-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+=.【方法归纳】本题正向思考解题较为麻烦，若抓住题目的特征，逆用公式解题，往往显得简单．对应练习：计算：⎪⎭⎫ ⎝⎛-⋅⋅⋅⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-22221011411311211. 知识点6：变形后运用平方差公式例6.计算293.【解题思路】注意到93接近整百数100，二者相差7，若使用数字93、7巧构平方差公式便可实现简算.【解】()()864949860077937939322=+=+-+=.【方法归纳】公式()()22b a b a b a -=-+可以变形为()()22b b a b a a +-+=.对应练习：计算：298知识点7：拆项变形后使用例7、计算(x-y+1)(x+y-5).【解题思路】观察式子的特点,可以将两个多项式拆成两个数的和与这两个数的差的形式.然后利用平分差公式计算. 解：(x-y+1)(x+y-5)=(x-y-2+3)(x-y-2-3)=[(x-2)-(y-3)][(x-2)+(y-3)]=(x-2)2-(y-3)2=x 2-4x+4-y 2+6y-9=x 2-y 2-4x+6y-5.【方法归纳】拆项的关键在于将两个因式中的相同项、相反项正确分析出来，并恰当分组，使之符合平方差公式的结构特征. 对应练习：()()3232-++-b a b a易错警示例8、计算：(2x +3)(2y -3). 错解：(2x +3)(2y -3)=4xy -9.错解分析：(2x +3)(2y -3)中的两个因式不符合“两个数的和与这两个数的差的积”，因此不能用平方差公式做，只能按多项式乘以多项式的法则进行运算．正解：(2x +3)(2y -3)=4xy -6x +6y -9. 例9、(2x +9)(2x -9).错解：(2x +9)(2x -9)=4x 2-9.错解分析：(2x +9)(2x -9)应等于2x 与9的平方差，即(2x )2-92，错解中没有把第二项9平方，当第二项是完全平方数时，很容易犯这样的错误．正解：(2x +9)(2x -9)=(2x )2-92=4x 2-81.例10、(a 3-8)(a 3+8).错解：(a 3-8)(a 3+8)=a 9-64.错解分析：(a 3-8)(a 3+8)中(a 3)2=a 6，而(a 3)2≠a 9.正解：(a 3-8)(a 3+8)=(a 3)2-82=a 6-64. 例11、(-2a -7)(2a -7)．错解：(-2a -7)(2a -7)＝4a 2-49.错解分析：(-2a -7)(2a -7)符合平方差公式的特征，但到底是哪个数的平方减去哪个数的平方呢？错解中认为就是前面一个数的平方减去后面一个数的平方，但(-2a -7)(2a -7)≠(-2a )2-72，应该是两式中符号相同的数的平方减去符号相反的那个数的平方，即： (-2a -7)(2a -7)=(-7-2a )(-7+2a ) =(-7)2-(2a )2或(-2a -7)(2a -7)=－(2a +7)(2a -7) =－[(2a )2-72]．正解： (-2a -7)(2a -7) = (-7-2a )(-7+2a ) =(-7)2-(2a )2=49-4a 2．课堂练习评测知识点1：平方差公式1、在边长为a 的正方形纸片中剪去一个边长为b 的小正方形()a b >（如图1），把余下的部分沿虚线剪开，拼成一个矩形（如图2），分别计算这两个图形阴影部分的面积，可以验证的乘法公式是（用字母表示）．2、已知2a b +=，则224a b b -+的值是 3、下列计算中，错误的有（）①（3a+4）（3a －4）=9a 2－4；②（2a 2－b ）（2a 2+b ）=4a 2－b 2；③（3－x ）（x+3）=x 2－9；④（－x+y ）·（x+y ）=－（x －y ）（x+y ）=－x 2－y 2． A ．1个 B ．2个 C ．3个 D ．4个知识点2：平方差公式的实际应用4、一个长方形的面积是(x 2－9)平方米，其长为(x ＋3)米，用含有x 的整式表示它的宽为___________米.知识点3：平方差公式的运用5、计算：2221123443m n n m ⎛⎫⎛⎫-+-- ⎪⎪⎝⎭⎝⎭;6、计算：(3x-2y)(9x 2+4y 2)(-2y-3x)7、平方差公式的常见变形(1)位置变化:(a+b)(-b+a)=________; (2)符号变化:(-a-b)(a-b)=_______.(3)系数变化:(2a+3b)(2a-3b)=_______.(4)指数变化:(a 2+b 3)(a 2-b 3)=_____.(5)项数变化:(a+2b-c)(a-2b-c)=_________________;(6)连用公式:(a+b)(a-b)(a 2+b 2)= __________________.课后作业练习基础训练一、填空题1、=--+-)2)(2(y y _______.2、=-+)2)(2(y x y x ______.3、=-+)3121)(3121(b a b a ______. 4、=---))((22x a x a _______. 5、=++-))()((22b a b a b a _______. 6、=-+-))((y x y x _______. 7、=+-----+))(())((y x y x y x y x _______.8、+xy (_______）-xy (_______）81122-=y x .二、选择题9、下列各式中，能直接用平方差公式计算的是（） A )22)(2(b a b a +--; B )2)(2(a b b a +-; C )2)(2(b a b a +--; D )2)(2(b a a b ++-. 10、下列各式中，运算结果是223625y x -的是（） A )56)(56(x y x y --+- ; B )56)(65(x y y x +-; C )56)(56(x y x y ++- ; D )65)(65(y x y x +--.11、为了应用平方差公式计算(x+2y-1)(x-2y+1),下列变形正确的是( )A.[x-(2y+1)]2B.[x-(2y-1)][x+(2y-1)]C.[(x-2y)+1][(x-2y)-1]D.[x+(2y+1)]2三、解答题12、计算)2)(2())((n m n m n m n m -+-+-.13、先化简后求值2),2)(2()2)(2(22-=-+--+x x x x x .提高训练14、解方程4)2()1)(1(2=---+x x x x .15、已知代数式(-4x+3y)(-3y-4x)与多项式M 的差是(2x+3y)(8x-9y),求多项式M.16、一个长方形菜地,长为(2a+3)cm,宽为(2a-3)cm, 那么这块菜地的面积是多少?17、一个长方体的游泳池的长为(4a 2+9b 2)米,宽为(2a+3b)米,高为(2a-3b)米,那么这个游泳池的容积是多少?12.3.1对应练习答案：1.解：原式=[(—2x)+y][(—2x)—y]=(—2x)2—y 2=4x 2—y 2.2.解：原式＝))()(())()()((88444488442222b a b a b a b a b a b a b a ++-=+++-＝16168888))((b a b a b a -=+-．3.解：原式=(x+2)(x —2)(x 2+4)=(x 2—4)(x 2+4)=x 4—16. 4.答案：2 5.解：原式=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⋅⋅⋅⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+10111011411411311311211211 1091011434532342123⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⨯=2011=. 6.解：()()96044960022982989822=+=+-+=. 7.答案：96422-+-b b a . 课堂作业练习参考答案：1、答案：()()22a b a b a b +-=-2、答案：43、答案：D4、答案：（3x -）5、解:原式=22224211134916m n m n ⎛⎫⎛⎫--=- ⎪ ⎪⎝⎭⎝⎭.6、解:原式=[(3x-2y)(-3x-2y)](9x 2+4y 2) =(4y 2-9x 2)(9x 2+4y 2)=16y 4-81x 47、(1)a 2-b 2 (2)b 2-a 2 (3)4a 2-9b 2 (4)a 4-b 6 (5)(a-c)2-4b 2=a 2-2ac+c 2-4b 2(6)a 4-b 4课后作业练习参考答案：1～8：24y -；224y x -；229141b a -；24a x -；44b a -；22x y -；0；91,91. 9、D ；10、A ；11、D 12、23n ；13、化简结果为24x x -，求值结果为12；14、5.2=x15、解:由题意得: M=(-4x+3y)(-3y-4x)-(2x+3y)(8x-9y)=(-4x)2-(3y)2-(16x 2-18xy+24xy-27y 2)=16x 2-9y 2-16x 2-6xy+27y 2=18y 2-6xy.16、解:这块菜地的面积为: (2a+3)(2a-3)=(2a)2-9=4a 2-9(cm 2)17、解:游泳池的容积是:(4a 2+9b 2)(2a+3b)(2a-3b)=[(2a)2-(3b)2](4a 2+9b 2)=(4a 2-9b 2)(4a 2+9b 2)=(4a 2)2-(9b 2)2=16a 4-81b 4(米3)。

数学华师版八年级上第12章12.3乘法公式 2.两数和(差)的平方

13
12
6.观察下列各式的规律: 12+（1×2）2+22=（1×2+1）2； 22+（2×3）2+32=（2×3+1）2； 32+（3×4）2+42=（3×4+1）2； … （1）写出第2014行的式子；（2）写出第n行的式子，并说明你的结论是正确的.
解：（1）（2014）2+（2014×2015）2+（2015）2=（2014×2015+1）2
=1+4x+4x2 (2)(-2x+1)2 解：原式=(-2x)2+2× (-2x)×1+12
=4x2-4x+1
11
5.（1）已知a+b=3，ab=2，求a2+b2 解：a2+b2=（a+b）2-2ab.∵a+b=3， ab=2，∴a2+b2=32-2×2=5. （2）若已知a+b=10，a2+b2=4，ab的值呢？解：∵a+b=10，∴（a+b）2=102， a2+2ab+b2=100，∴2ab=100-（a2+b2）. 又∵a2+b2=4，∴2ab=100-4，ab=48.
7
随堂训练
1.填空题
8
2.下列各式中哪些可以运用完全平方公式计算（ C ） A.（a+b）（a+c） B.(x+y)（-y+x） C.(ab-3x)(-3x+ab) D.(-m+n)(m+n)
9
3.计算：
10
4.利用完全平方公式计算： (1)(-1-2x)2；解：原式=(-1)2-2×(-1)×(2x)+（2x)2

八年级数学上册 12.3 乘法公式 2《两数和(差)的平方》教案 (新版)华东师大版

12.3.2 两数和（差）的平方【教学目标】：1．能说出两数和的平方与两数差的平方公式的特点，并会用式子表示。

2．能正确地利用两数和的平方与两数差的平方公式进行多项式的乘法。

3．通过两数和的平方与两数差的平方公式的得出，使学生明白数形结合的思想。

重点：掌握公式的特点，牢记公式。

难点：具体问题具体分析，会用公式进行计算。

【教学建议】：(1)在教学中应在讨论的基础上，从代数运算的角度运用多项式乘法法则，推导出公式()2222b ab a b a ++=+。

(2)关于公式 ()2222b ab a b a ++=+的获得，要鼓励学生自己探索，鼓励学生算法的多样化，学生既要按多项式的乘法的法则计算；也可以利用公式()2222b ab a b a ++=+来获得结果。

【评价建议】：过程性：（1）公式推导过程中关注学生对多项式乘法法则的掌握程序；（2）公式得出后关注学生对公式的理解；（3）关注学生算法的合理性及其与同学们进行交流的积极性。

知识性：关注学生对符合完全平方式计算的多项式乘法观察的敏锐性，熟练运用完全平方公式进行简单的计算。

【教学过程】：1.知识与回顾：（1）两数和的公式是什么？（2）口述多项式乘以多项式法则。

（3）计算（2x －1）（3x －4）、（5x ＋3）（5x －3）2.设计活动，导入新课。

师：有一位老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果来招待他们。

来一个孩子，老人就给这个孩子一块糖，来两个孩子，老人就给每个孩子两块糖，来三个，就给每人三块……(1) 第一天有a 个男孩去了老人家，老人一共给了这些孩子多少块糖？〖设计说明〗从具有现实生活实际的情境设计问题，可以激发生学生学习兴趣，让学生乐于利用所学知识解决实际问题，也可以体现数学的实用性。

（2）第二天有b 个女孩一起去了老人家，老人一共给了这些孩子多少块糖？（3）第三天这（a ＋b ）个孩子一起去看老人，老人一共给了这些孩子多少块糖？（4）这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多？多多少？〖设计说明〗通过一系列的问题，不仅可以体现循序渐进的原则，也利于学生更有效地运用所学知识解决实际问题。

2019年秋数学华东师大版八年级上册习题课件：第12章 12.3 2.两数和(差)的平方

(2)试猜想 n(n＋1)(n＋2)(n＋3)＋1 是哪一个数的平方，并予以证明．
解：猜想：n(n＋1)(n＋2)(n＋3)＋1＝(n2＋3n＋1)2. 证明如下：等式左边＝[n(n＋3)][(n＋1)(n＋2)]＋1＝(n2＋3n)(n2＋3n＋2)＋1 ＝(n2＋3n)2＋2(n2＋3n)＋1＝(n2＋3n＋1)2＝等式右边，∴左边＝右边，∴n(n ＋1)(n＋2)(n＋3)＋1＝(n2＋3n＋1)2.
＋3a＋1；⑤a2＋4ab＋2b2.其中是完全平方式的是( A )
A．①③
B．②④
C．③④
D．①⑤
10．若(x＋y)2－M＝(x－y)2，则 M 为( C )
A．2xy
B．±2xy
C．4xy
D．±4xy
11．(乐山中考)已知 x＋x1＝3，则下列三个等式：①x2＋x12＝7；②x－1x＝ 5；
③2x2－6x＝－2.其中正确的个数有( C )
D．x2＋3x＋9
2．下列计算正确的是( C )
A．(x＋2)2＝x2＋4
B．(2x－2y)2＝4x2－4xy＋4y2
C．(y－4)2＝y2－8y＋16
D．(3－2x)2＝9－12x－4x2
3．已知 x2＋16x＋k 是完全平方式，则常数 k 等于( A )
A．64
B．48
C．32
D．16
4．已知 x＋y＝－5，xy＝6，则 x2＋y2 的值是( B )
数学八年级上册•HS
第12章整式的ห้องสมุดไป่ตู้除
12.3 乘法公式 2．两数和(差)的平方
两数和(差)的平方．【例 1】计算： (1)(2a＋b)2； (2)(－x＋2y)2. 【思路分析】第(1)题用“和”的完全平方式；第(2)题可以看成(2y－x)2. 【规范解答】(1)原式＝(2a)2＋2·2a·b＋b2＝4a2＋4ab＋b2； (2)原式＝(2y－x)2＝(2y)2－2·2y·x＋x2＝4y2－4xy＋x2. 【方法归纳】当二项式中两项符号相同时，一般选用“两数和”的平方，当二项式中两项符号相反时，一般选用“两数差”的平方．

八年级数学上册12.3乘法公式2两数和(差)的平方作业(新版)华东师大版

[12.3 2.两数和(差)的平方]一、选择题1．运用乘法公式计算(x＋3)2的结果是( )A．x2＋9 B．x2－6x＋9C．x2＋6x＋9 D．x2＋3x＋92．在下列各式中，与(－a＋2b)2相等的是( )A．a2－4ab＋4b2 B．a2－4b2C．a2＋4b2 D．a2－2ab＋4b23．2017·福建长泰一中、华安一中联考若(x－2y)2＝x2－xy＋4y2＋M，则M为( )A．xy B．－xy C．3xy D．－3xy4．将一张边长为a cm(a>2)的正方形图片各边都减小2 cm，则缩小后的图片面积减少了( )A．(4a－4)cm2 B．4 cm2C．(a2－4)cm2 D．(2a－4)cm25．若(a＋b)2加上一个单项式后等于(a－b)2，则这个单项式为( )A．2ab B．－2ab C．4ab D．－4ab6．已知(x＋m)2＝x2＋nx＋36，则n的值为( )A．±6 B．±12 C．±18 D．±727．计算(a＋2b)2＋(a－2b)2的结果是( )A．2a2 B．4b2C．2a2－8b2 D．2a2＋8b28．2017·淄博若a＋b＝3，a2＋b2＝7，则ab等于( )A．2 B．1 C．－2 D．－1二、填空题9．计算：(x ＋1)2＝________；(m －3n )2＝________. 10．计算：(x ＋4)(x －4)－(x －4)2＝________． 11．(1)x 2＋49＋________＝(x ＋7)2； (2)(x －y )2＋________＝(x ＋y )2.12．若(3x －1)2＝ax 2＋bx ＋c ，则a ＋b ＋c ＝________．13．4个数a ，b ，c ，d 排列成⎪⎪⎪⎪⎪⎪ac bd ，我们称之为二阶行列式．规定它的运算法则为⎪⎪⎪⎪⎪⎪ac bd ＝ad －bc .若⎪⎪⎪⎪⎪⎪x ＋3 x －3x －3 x ＋3＝12，则x ＝________．图K －14－114．请你观察图K －14－1所示的图形，依据图形面积的关系，不需要添加辅助线，便可得到一个你非常熟悉的公式，这个公式是_____________________.三、解答题 15．计算：(1)2017·重庆(1)x (x －2y )－(x ＋y )2；(2)(3－2x ＋y )(3＋2x －y )．16．用公式简化计算： (1)10032； (2)982. 链接听课例2归纳总结17．先化简，再求值：(1)(a ＋b )(a －b )＋(a ＋b )2，其中a ＝－1，b ＝12；(2)2017·眉山(a ＋3)2－2(3a ＋4)，其中a ＝－2.18．(1)已知(x ＋y )2＝3，xy ＝1，求x 2＋y 2的值；(2)已知x ＋y ＝12，x －y ＝4，不解出x ，y 的值，求xy 的值.19．观察下列各式：1×2×3×4＋1＝25＝52；2×3×4×5＋1＝121＝112；3×4×5×6＋1＝361＝192；…根据上述算式所反映出的规律，猜想“任意四个连续正整数的积与1的和一定是一个完全平方数”，你认为这个猜想正确吗？说说你的理由．20．学校有一个边长为a的正方形草坪，现将其各边增加b，扩大草坪面积，有的同学说：“扩建后比扩建前面积增大b2.”你认为这种说法正确吗？若正确，请说明理由；若不正确，请你计算出扩建后比扩建前草坪的面积增大了多少．(写出解答过程)21．如图K－14－2，把一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后拼成一个正方形．(1)请用两种不同的方法求图②中阴影部分的面积．(直接用含m，n的代数式表示)方法1：____________；方法2：____________．(2)根据(1)中的结论，请你写出下列三个代数式(m＋n)2，(m－n)2，mn之间的等量关系．(3)根据(2)题中的等量关系，解决问题：已知实数a，b满足a＋b＝3，ab＝2，求a－b 的值．图K－14－2材料阅读先仔细阅读材料，再尝试解决问题：两数和(差)的平方公式x2±2xy＋y2＝(x±y)2及(x±y)2的值恒为非负数的特点在数学学习中有着广泛的应用，比如探求多项式2x2＋12x－4的最小值时，我们可以这样处理：解：原式＝2(x2＋6x－2)＝2(x2＋6x＋9－9－2)＝2[(x＋3)2－11]＝2(x＋3)2－22.因为无论x取什么数，都有(x＋3)2的值为非负数，所以(x＋3)2的最小值为0，此时x＝－3，进而2(x＋3)2－22的最小值是2×0－22＝－22，所以当x＝－3时，原多项式的最小值是－22.解决问题：请根据上面的解题思路，探求多项式3x2－6x＋12的最小值是多少，并写出对应的x的取值．详解详析【课时作业】 [课堂达标] 1．C 2.A3．[解析] D (x －2y )2＝x 2－4xy ＋4y 2，所以x 2－4xy ＋4y 2＝x 2－xy ＋4y 2＋M ，所以M ＝－3xy .4．[解析] A 原图片的面积为a 2cm 2，缩小后的图片的面积为(a －2)2cm 2，所以减少的面积为a 2－(a －2)2＝a 2－(a 2－4a ＋4)＝(4a －4)cm 2.5．[解析] D 根据题意，得(a －b )2－(a ＋b )2＝(a 2－2ab ＋b 2)－(a 2＋2ab ＋b 2)＝－4ab . 6．B 7.D8．[解析] B 因为(a ＋b )2＝a 2＋2ab ＋b 2，所以ab ＝（a ＋b ）2－（a 2＋b 2）2＝32－72＝1.9．x 2＋2x ＋1 m 2－6mn ＋9n 210．8x －32 11.(1)14x (2)4xy 12．[答案] 4[解析] 方法一：取x ＝1，代入已知等式，得(3×1－1)2＝a ＋b ＋c ，所以a ＋b ＋c ＝4. 方法二：已知式可化为9x 2－6x ＋1＝ax 2＋bx ＋c ，比较两边系数，得a ＝9，b ＝－6，c ＝1，所以a ＋b ＋c ＝9－6＋1＝4.13．1 [解析] 因为⎪⎪⎪⎪⎪⎪x ＋3 x －3x －3 x ＋3＝12，所以(x ＋3)2－(x －3)2＝12.解得x ＝1.故答案为1. 14. (x －y )2＝x 2－2xy ＋y 215．解：(1)原式＝x 2－2xy －(x 2＋2xy ＋y 2)＝x 2－2xy －x 2－2xy －y 2＝－4xy －y 2. (2)原式＝9－(2x －y )2＝9－4x 2＋4xy －y 2.16．解：(1)原式＝(1000＋3)2＝10002＋2×1000×3＋32＝1006009. (2)原式＝(100－2)2＝1002－2×100×2＋22 ＝9604.17．解：(1)(a ＋b )(a －b )＋(a ＋b )2＝a 2－b 2＋a 2＋2ab ＋b 2＝2a 2＋2ab . 当a ＝－1，b ＝12时，原式＝2×(－1)2＋2×(－1)×12＝1.(2)原式＝a 2＋6a ＋9－6a －8＝a 2＋1. 当a ＝－2时，原式＝(－2)2＋1＝5.18．[解析] 如果要先求出x ，y 的值再代入，现阶段同学们是无能为力的，若应用乘法公式的变形就可使问题迎刃而解了．解：(1)x 2＋y 2＝(x ＋y )2－2xy ＝3－2×1＝1. (2)因为(x ＋y )2－(x －y )2＝4xy ，所以122－42＝4xy ，所以4xy ＝128，即xy ＝32. 19．解：正确．理由：设四个连续的正整数为n ，n ＋1，n ＋2，n ＋3，则n (n ＋1)(n ＋2)(n ＋3)＋1 ＝(n 2＋3n )(n 2＋3n ＋2)＋1 ＝(n 2＋3n )2＋2(n 2＋3n )＋1 ＝(n 2＋3n ＋1)2.20．解：不正确．扩建后正方形草坪的边长为a ＋b ，增大面积为(a ＋b )2－a 2＝a 2＋2ab ＋b 2－a 2＝2ab ＋b 2，所以扩建后比扩建前草坪的面积增大2ab ＋b 2.21．解：(1)方法1：阴影部分的面积为(m＋n)2－4mn；方法2：阴影部分的边长为m－n，故阴影部分的面积为(m－n)2.(2)(m－n)2＝(m＋n)2－4mn.(3)∵(a－b)2＝(a＋b)2－4ab＝1，∴a－b＝±1.[素养提升]解：原式＝3(x2－2x＋4)＝3(x2－2x＋1－1＋4)＝3(x－1)2＋9.∵无论x取什么数，都有(x－1)2的值为非负数，∴(x－1)2的最小值为0，此时x＝1，∴3(x－1)2＋9的最小值为3×0＋9＝9.则当x＝1时，原多项式的最小值是9.。

2019年秋八年级数学上册第12章整式的乘除 12.3 乘法公式第2课时两数和(差)的平方课件

（3） (-2x-y)2 ( 2 x ) 2 2 ( 2 x ) ( y ) ( y ) 2 4 x 2 4 x y y （4） (a-b)2= a 2 2 a ( b ) ( b )2 a 2 2 a b b 2
做一做
研究性学习
①填空：（
）2 =9a2―（）+16b2 ；
请说出题中哪部分相当于公式中的哪部分相当于
解：
（1） (a+3b)2 ＝ a 2 2 a 3 b ( 3 b )2 a 2 6 a b 9 b 2
(2) (2x+3y)2 ( 2 x ) 2 2 2 x 3 y ( 3 y ) 2 4 x 2 1 2 x y 9 y 2
(2) (3m−2n)2
做题时要边念边写：首项的平方,
加上第一数与第二数乘的2倍,
=(3m)2 −2•(3m) •(2n)+(2n)2加上尾项的平方.
=9m2 −12mn + 4n2
例2、利用两数和的平方公式计算:
（1） (a+3b)2 (2) (2x+3y)2 （3） (-2x-y)2 （4） (a-b)2
课堂小结
你来总结
本题课你有什么收获或感想？你还有什么疑问
？
②计算：（―a+b）2和（―a―b）2 ；
③与（a+b）2及（a―b）2比较，你发现了什么律？
探索发现:(a+b)2=(―a―b)2 , （a―b）2 = （―a+b）2
解题规律:
当所给的二项式的符号相同时，就用“和”的完全平方式；
当所给的二项式的符号不同时，就用“差”的完全平方式。
能力提升
1. (1) (2a-5b)2 (3) (-3x+y)2

2019八年级数学上册第12章整式的乘除 12.3 乘法公式 1 两数和乘以这两数的差教案

计算：
(1)(x＋Βιβλιοθήκη )(x＋3)(2)(x－1)(x＋2)；(3)(x＋2)(x－2)；
(4)(x＋5)(x＋5)；(5)(x－5)(x－5)(6)(x2＋2x＋3)(2x－5)
学生回忆并回答．学生计算练习问为本节课作知识储备
活动
一：
创设
情境
导入
新课
【课堂引入】
计算：
(1)(x＋2)(x－2)；(2)(1＋3a)(1－3a)；
(3)(x＋5y)(x－5y)；(4)(y＋3z)(y－3z)．
做完之后，观察以上算式及运算结果，你能发现什么规律？再举两个例子验证你的发现．
从学生的已有的知识出发，利用多媒体，激发学生的强烈的好奇心和求知欲.
活动
二：
实践
探究
交流
新知
【探究】平方差公式
【学生活动】分四人小组，合作学习，获得以下结果：
(3)(1＋2c)(1－2c)；(4)(－2x－y)(2x－y)．
注意公式的变化形式：
(1)(b＋a)(－b＋a)＝(a＋b)(a－b)＝a2－b2.
(2)(－a－b)(a－b)＝[(－b)－a][(－b)＋a]
＝(－b)2－a2＝b2－a2.
(3)(a＋b)(a－b)(a2＋b2)＝(a2－b2)(a2＋b2)
【学生活动】先独立完成上面的演练题，再与同伴交流．
4．计算：(1＋ )(1＋ )(1＋ )(1＋ )＋ .
课堂总结
本节课的内容是两数和与这两数差的积，公式指出了具有特殊关系的两个二项式积的性质．运用平方差公式应满足两点：一是找出公式中的第一个数a，第二个数b；二是两数和乘以这两数差，这也是判断能否运用平方差公式的方法．
通过合作学习，体会在解决具体问题过程中与他人合作的重合性，体验数学活动充满着探索性和创造性．

【精品推荐】2020年秋八年级数学上册第12章整式的乘除12.3乘法公式2两数和差的平方课件新版华东师大版

；
(2x－3y)2＝4x2－12xy＋9y2.
完全平方公式的应用
自我诊断2. 若a＋b＝3，a－b＝7，则ab＝－10 .
易错点：公式的运用不准确．
自我诊断3. 计算：(－2x－y)2＝ 4x2＋4xy＋y2 ；
(－x＋2y)(x－2y)＝－x2＋4xy－y2
.
1．下列运算正确的是( C ) A．(a＋3)2＝a2＋9
A．2mn C．(m－n)2
B．(m＋n)2 D．m2－n2
4．如果 a2＋b2＝12，ab＝－3，则(a＋b)2 的值是( A )
A．6
B．18
C．3
D．12
5．一个正方形的边长增加 3cm，它的面积就增加 39cm2，这个正方形的边
长是 5cm .
6．计算： (1)(2m＋3n)2；解：原式＝4m2＋12mn＋9n2； (2)(－3a＋4b)2；解：原式＝9a2－24ab＋16b2； (3)(a＋b)2＋(a－b)(a＋b)－2ab；解：原式＝2a2； (4)(2m－5n)2－(2m＋5n)2. 解：原式＝－40mn.
7．用简便方法计算：
(1)100.22；解：原式＝(100＋0.2)2＝1002＋2×100×0.2＋0.22＝10040.04； (2)4992. 解：原式＝(500－1)2＝5002－2×500×1＋12＝249001.
8．(泰安中考)下列运算正确的是( D )
A．a2·a2＝2a2
B．a2＋a2＝a4
16．(贵阳中考)下面是小颖化简整式的过程，仔细阅读后解答所提出的问
题．
解：x(x＋2y)－(x＋1)2＋2x
＝x2＋2xy－x2＋2x＋1＋2x 第一步
＝2xy＋4x＋1

八年级数学上册第12章整式的乘除12.3乘法公式12.3.1两数和乘以这两数的差习题课件

5. 计算：
4 2 9 2 3 2 2 3 (1)(4x＋3y)(3y－4x)＝ 9y －16x ；
2 2 4 y － 9 x (2)(－3x－2y)(3x－2y)＝．
6. 填写适当的式子： (1)(－6a＋ 2b )(2b＋ 6a )＝4b2－36a2； (2)(a＋b－c)(a－b＋c)＝[a＋( b－c )][a－( b－c )] ＝a2－( b－c )2.
4. 化简(3＋1)× (32＋1)× (34＋1)× (38＋1)得( D ) A．(38＋1)2 C．3 －1
16
B．(38－1)2 1 16 D. 2× (3 －1)
1 【解析】原式＝2× (3－1)(3＋1)× (32＋1)× (34＋1)× (38 1 2 1 4 2 4 8 ＋1)＝2(3 －1)(3 ＋1)(3 ＋1)(3 ＋1)＝2(3 －1)(34＋1)(38 1 8 1 16 8 ＋1)＝2(3 －1)(3 ＋1)＝2(3 －1)．
10. 如图所示，在边长为 a 的正方形中剪去一个边长为 b 的小正方形(a＞b)，把剩下部分拼成一个梯形．
(1)分别计算这两个图形阴影部分的面积； (2)这个题从几何角度验证了哪个公式？
解：(1)阴影部分的面积为 a2－b2 或(a＋b)(a－b)； (2)(a＋b)(a－b)＝a2－b2.
(2)设两个连续偶数为 2k＋2 和 2k(其中 k 取非负整数)，由这两个连续偶数构造的神秘数是 4 的倍数吗？为什么？
解：是 4 的倍数，理由：∵(2k＋2)2－(2k)2＝8k＋4 ＝4(2k＋1)．∵k 为非负数，∴4(2k＋1)是 4 的倍数．
7. 如果(a＋b＋1)(a＋b－1)＝63，那么 a＋b 的值为
± 8

【华师大版教材】初二八年级数学上册《12.3.2 两数和(差)的平方》课件

知3－讲
解：(1)依题意，得x2－10x＋25＝x2＋kx＋25.
所以k＝－10.
(2)原式＝1－a2＋a2－4a＋4＝－4a＋5，当a＝－3时，原式＝－4×(－3)＋5＝12＋5＝17. (3)原式＝4x2－12x＋9－x2＋y2－y2＝3x2－12x＋9 ＝3(x2－4x＋3)．
因为x2－4x＋1＝0，所以x2－4x＝－1，
①(b－4c)2＝b2－16c2； ②(a－2bc)2＝a2＋4abc＋4b2c2； ④(4m－n)2＝16m2－8mn＋n2. A．①②③ B．①②④ C．①③④ D．②③④
（来自《典中点》）
知2－导
知识点
2
完全平方公式
做一做
用多项式乘法法则计算:(a+b)2.
(a+b)2=(a+b)(a＋b)=____________________.
（来自《典中点》）
1.完全平方公式的特征：左边是二项式的平方，右边是二次三项式，其中两项分别是公式左边两项的平方，中间一项是左边二项式中两项乘积的2倍． 2.公式中的a，b可以是单项式，也可以是多项式．公式也可以逆用： a2±2ab＋b2＝(a±b)2. 3.利用完全平方公式化简求值时常利用整体思想，把a2＋b2 ，ab， a±b看成一个整体，利用完全平方公式的变形，整体代换求值，常见的变形公式有：(1)a2＋b2＝(a＋b)2－2ab＝(a－b)2＋2ab； (2) (a＋b)2－(a－b)2＝4ab.
所以，原式＝3×(－1＋3)＝3×2＝6.
（来自《点拨》）
知3－讲
例4
已知a2＋b2＝13，ab＝6，
求(a＋b)2，(a－b)2的值．
导引：利用两数和(差)的平方公式展开，得到两数的平方和与这两数积的两倍，再将条件代入求解．解：因为a2＋b2＝13，ab＝6，

2019-2020年初中数学华师版八年级上册12.3.1两数和乘以这两数的差课件.ppt

=502－12
=(2a+3)(2a-3) =(2a)2－32 =4a2－9；（4）(－2x2－y)(－2x2+y)；
=(-2x2 )2－y2
=2500-1
=4x4－y2;
=2499；（5）(3x+4)(3x-4)-(2x+3)(3x-2).
=(9x2－16)－(6x2+5x -6)
=3x2－5x－ 10.
解: (a 2)(a 2) a2 4
答：改造后的长方形草坪的面积是(a2-4)平方米.
当堂练习
1.下面各式的计算对不对？如果不对，应当怎样改正？
（1）(x+2)(x-2)=x2-2 不对
改正：（1）(x+2)(x-2)=x2-4
（2）(-3a-2)(3a-2)=9a2-4
不对
改正方法1：(-3a-2)(3a-2)=-[(3a+2)(3a-2)]
①（x ＋1)( x－1）=x2 － 1， ②（m＋ 2)( m－2）=m2－22
x2 － 12 m2－22
③（2x＋ 1)( 2x－1)=4m2 － 12 ④（5y ＋ z)(5y－z)= 25y2 － z2
(2m)2 － 12 (5y)2 － z2
想一想：这些计算结果有什么特点？
知识要点
平方差公式
a2(3)(-a-b)(-a+bb)2= ________. (4)(a-b)(-a-b)=a_2_- _______.
b2 b2a2
典例精析
例1 填一填： (a-b)(a+b) (1+x)(1-x) (-3+a)(-3-a)
(1+a)(-1+a) (0.3x-1)(1+0.3x)

华师大版数学八年级上册12.3 乘法公式 2课题两数和(差)的平方

课题两数和(差)的平方【学习目标】1．让学生学会推导完全平方公式，并能运用公式进展简单的运算；2．体验数学活动充满着探索性和创造性，培养概括能力，体会数形结合的思想．【学习重点】完全平方公式的推导及利用完全平方公式进展简单计算．【学习难点】理解公式中字母的广泛含义．自学互研生成能力知识模块一探究两数和的平方公式阅读教材P32～P34，完成下面的内容：1．观察温故知新中计算练习的规律，你能很快地写出：(a＋b)2＝(a＋b)(a＋b)＝a2＋2ab＋b2．2．思考：你能说明a2＋b2与(a＋b)2的大小关系吗？解：(a＋b)2＝a2＋2ab＋b2≥a2＋b2.即(a＋b)2≥a2＋b2.3．图形演示：直观感知：a2＋b2≠(a＋b)2.几何探究(整体考虑，分割思考)：试一试：先观察右图，你能用一个代数式来表示该大正方形的面积吗？(a＋b)2．还有其他不同的表示方法吗？a2＋2ab＋b2．再用等式表示下列图中图形面积的运算：(a＋b)2＝a2＋2ab＋b2．4．概括：我们得到了一个非常重要而且十分有用的结果：两数和的平方公式：(a＋b)2＝a2＋2ab＋b2．感悟规律：你发现公式有何特征吗？(1)左边是两数(项)和的平方，右边是两数的平方和加上两数积的2倍； (2)语言表述：两数和的平方，等于这两数的平方和加上它们积的2倍．范例：计算：(1)(4m ＋n)2；(2)⎝⎛⎭⎫y ＋122；(3)(－2x ＋3y)2. 解：(1)原式＝(4m)2＋2×4m·n ＋n 2＝16m 2＋8mn ＋n 2；(2)原式＝y 2＋2×y·12＋⎝⎛⎭⎫122＝y 2＋y ＋14； (3)原式＝(－2x)2＋2×(－2x)·3y ＋(3y)2＝4x 2－12xy ＋9y 2.变例：计算：(－3a －2b)2.解：原式＝[－(3a ＋2b)]2＝(3a ＋2b)2＝9a 2＋12ab ＋4b 2.知识模块二探究两数差的平方公式试一试：你一定也能发现：(a －b)2＝a 2－2ab ＋b 2．1．某学生写出了如下的算式(a －b)2＝[a ＋(－b)]2，他是怎么想的？你能继续做下去吗？解：他将－b 看作一个整体项，那么(a －b)2＝[a ＋(－b)]2＝a 2＋2a·(－b)＋(－b)2＝a 2－2ab ＋b 2.学法指导：1.两数差的平方与平方差是有区别的，它们分别表示为(a －b)2与a 2－b 2；两数和的平方与平方和是有区别的，它们分别表示为(a ＋b)2与a 2＋b 2；2．体会数形结合的思想并运用；3．完全平方公式：(a ＋b )2＝a 2＋2ab ＋b 2；(a －b)2＝a 2－2ab ＋b 2.口诀：首平方、尾平方，首尾二倍放中央，中间符号回头望．即：(a±b)2＝a 2±2ab ＋b 2.利用完全平方公式可进展简便运算，注意符号问题．行为提示：教会学生怎么交流．先对学，再群学．充分在小组内展示自己，分析答案，提出疑惑，共同解决(可按结对子学—帮扶学—组内群学来开展)．在群学后期教师可有意安排每组展示问题，并给学生板书题目和组内演练的时间．2．你能用教材图12.3.3中的面积关系来解释两数差的平方公式吗？根据图可得(a －b)2＝a 2－2ab ＋b 2.3．概括：两数差的平方公式：(a －b)2＝a 2－2ab ＋b 2．感悟规律：你发现公式有何特征吗？(1)左边是两数(项)差的平方，右边是两数的平方和减去两数积的2倍；(2)语言表述：两数差的平方，等于这两数的平方和减去它们积的2倍．范例1：计算：(1)(－2a －5)2；(2)⎝⎛⎭⎫－3a ＋13b 2. 解：(1)原式＝4a 2＋20a ＋25；(2)原式＝9a 2－2ab ＋19b 2. 范例2：利用完全平方公式计算：(1)2；(2)992.解：(1)2＝()2＝102＋2×10×2＝100＋6＋0.09＝106.09；(2)992＝(100－1)2＝1002－2×100×1＋12＝10000－200＋1＝9801.交流展示生成新知1．将阅读教材时“生成的问题〞和通过“自学互研〞得出的“结论〞展示在各小组的小黑板上，并将疑难问题也板演到黑板上，再一次通过小组间就上述疑难问题相互释疑．2．各小组由组长统一分配展示任务，由代表将“问题和结论〞展示在黑板上，通过交流“生成新知〞．知识模块一探究两数和的平方公式知识模块二探究两数差的平方公式检测反应达成目标【当堂检测】见所赠光盘和学生用书；【课后检测】见学生用书．课后反思查漏补缺1．收获：________________________________________________________________________2．存在困惑：________________________________________________________________________。