2014年图形拓展问题

合集下载

2014年XXX版七年级数学上册第一章《丰富的图形世界》导学案

2014年XXX版七年级数学上册第一章《丰富的图形世界》导学案第一章丰富的图形世界第一节生活中的立体图形研究目标】1.通过从现实世界中抽象出形象的过程，感受图形世界的丰富多彩。

2.在具体情境中，认识圆柱、圆锥、正方体、长方体、棱柱、球，并能用自己的语言描述它们的某些特征。

3.通过丰富的实例，进一步认识点、线、面，初步感受点、线、面之间的关系。

4.在对图形进行观察、操作等活动中，积累处理图形的经验，发展空间观念。

研究方法】自主探究与合作交流相结合研究重难点】重点：认识常见的几何体的基本元素，了解棱柱的一些基本概念及其某些特性。

难点：用语言描述常见几何体的某些特征及对几何体的分类。

研究过程】模块一预反馈一、研究准备1.在小学研究过的立体图形有哪些？2.长方体有几个面？每一个面都是什么形状？正方体有几个面？每一个面都是什么形状？长方体的表面积和体积分别是多少？正方体的表面积和体积分别是多少？3.阅读教材：p2—p6第1节《生活中的立体图形》，并完成随堂练和题。

二、教材精读4.写出以下几何体的名称：（1）长方体；（2）正方体；（3）圆锥；（4）圆柱；（5）棱柱；（6）球。

5.棱柱的有关概念及其重要特点：1）棱柱的有关概念：在棱柱中，相邻两个面的交线叫做棱，相邻两个侧面的交线叫做棱棱。

2）棱柱的三个特征：一是棱柱的所有侧棱长都相等；二是棱柱的上下底面的形状都是相同的多边形；三是侧面都是相同的形状。

3）棱柱的分类：根据底面多边形的边数将棱柱分为三角柱、四边形柱、五边形柱、六边形柱等等；它们的底面分别是三角形、四边形、五边形、六边形等等。

4）棱柱中的元素之间的关系：底面多边形的边数n，可确定该棱柱有n个顶点、n条棱、其中有n-2条侧棱，有2个面，n个侧面。

实践练：请你按适当的标准对下列几何体进行分类。

引导：1）按柱体、锥体、球体分（最常见的分法）。

2）按组成几何体的面的平曲分。

3）按有没有顶点分。

归纳：圆柱和棱柱的异同：相同点：圆柱和棱柱都有个底面，且底面的形状和大小完全相同。

1.4运动学图像专题

1.4运动学图像的分析与应用一、x-t图象与v-t图象的比较形状相同的图线，在不同的图象中所表示的物理规律不同，通过下图中的例子体会x-t图象和v-t图象中图线表示的物理规律.1.首先明确所给的图象是什么图象，即认清图象中横、纵轴所代表的物理量及它们的函数关系.特别是那些图形相似容易混淆的图象，更要注意区分.2.要清楚地理解图象中的“点”、“线”、“斜率”、“截距”、“面积”的物理意义：(1)点：图线上的每一个点对应研究对象的一个状态，特别要注意“起点”、“终点”、“拐点”，它们往往对应一个特殊状态.(2)线：表示研究对象的变化过程和规律，如v-t图象中图线若为倾斜直线，则表示物体做匀变速直线运动.(3)斜率：表示横、纵坐标上两物理量的比值，常有一个重要的物理量与之对应，用于求解定量计算对应物理量的大小和定性分析变化的快慢问题.如x-t图象的斜率表示速度的大小，v-t图象的斜率表示加速度的大小.(4)面积：图线与坐标轴围成的面积常与某一表示过程的物理量相对应.如v-t图象与横轴包围的“面积”大小表示位移大小.(5)截距：表示横、纵坐标两物理量在“边界”条件下的大小.题型一：根据图像分析物体的运动情况1．(2014·天津卷)质点做直线运动的速度—时间图象如图所示，该质点( )[拓展复习功能v 、a 、s 、] A ．在第1秒末速度方向发生了改变 B ．在第2秒末加速度方向发生了改变 C ．在前2秒内发生的位移为零 D ．第3秒末和第5秒末的位置相同2．(2015广东高考)甲乙两人同时同地出发骑自行车做直线运动,前1小时内的位移-时间图象如图所示.下列表述正确的是()A ． 0.2-.05小时内,甲的加速度比乙的大B ． 0.8小时内,甲、乙骑行的路程相等C ．0.6-0.8小时内,甲的位移比乙的小D ．0.2-0.5小时内,甲的速度比乙的大3．(多选) 一质点在外力作用下做直线运动，其速度v 随时间t 变化的图象如图所示。

2014年中考数学高分冲刺17-图形的分割与剪拼

关键点十七图形的分割与剪拼纵观近年来全国各地的中考试卷，图形操作型的问题渐多，而这些题又可分为两大类：一类是围绕“图形变换”展开的（我们已有专题论及），另一类是围绕图形的分割与剪拼展开的。

我们现在要研究的，就是这后边的一类，分割与剪拼的形式与依据主要有：Ⅰ、原图形基础上进行分割，而分割的要求又分为：（1）借助于“边、角”计算的分割；（2）依“面积等分”为要求的分割；Ⅱ、将原图形等面积地变化成新图形的“剪与拼”。

一、图形的分割1、借助于“边、角”计算的分割例1 （1）已知ABC ∆中，︒=∠︒=∠5.67,90B A ，请画一条直线，把这个三角形分割成两个等腰三角形。

（2）已知ABC ∆中，C ∠是其最小的内角，过顶点B 的一条直线把这个三角形分割成了两个等腰三角形，请探求ABC ∠与C ∠之间的关系。

【观察与思考】对于（1）只需“构造等角”；对于（2），（1）可从“等边”推演角之间的关系。

解：（1）如图①，图②，有两种不同的分割法。

（2）设ABC ∠y =，C ∠x =，过顶点B 的直线 ① 交边AC 于D 。

在等腰三角形DBC 中，①若C ∠是顶角，如图③，则︒>∠90ADB ，,2190)180(21x x CDB CBD -︒=-︒=∠=∠ y x A --︒=∠180。

②此时只能有ABD A ∠=∠，即)2190(180x y y x -︒-=--︒， ︒=+∴54043y x ，即ABC ∠与C ∠的关系是：C ABC ∠-︒=∠43135。

②若C∠是底角，则有两种情况。

③AC A BC︒5.67 ︒5.67 ︒5.22︒5.22AB C︒45 ︒5.22︒5.22︒45 ABC DABD ∆中，x y ABD x ADB -=∠=∠,2。

Ⅰ、由AD AB =，得x y x -=2，此时有x y 3=，即有关系C ABC ∠=∠3。

④ Ⅱ、由BD AB =，得x yx 2180=--︒，此时 ︒=+1803y x ，即C ABC ∠-︒=∠3180。

小学奥数思维训练-几何图形剪拼通用版

（2）本题主要考查了复杂作图，根据面积确定出从正方形的中心入手求解是解题的关键，难度中等，但不容易考虑．
8．（1）
（2）
【解析】
试题分析：（1）将大正方形方的边长平均分成3等份，则可将大正方形分割为9个相等的小正方形，其中4个相邻的组成1个，其余5个小的各成1个．
（2）将大正方形方的边长平均分成4等份，分成3个2×2，4个1×1即可．
（1）如果分别剪开这两个正方形，再拼接成一个大正方形，应该怎么办？
（2）如果只允许剪开一个正方形，再拼接成一个大正方形，应该怎么办？
10．如图是由若干个小正方形组成的图形，你能将其剪成两块，然后拼成一个正方形吗？
11．请在图中标出分割线，把下图沿格线分成形状、大小都相同的四个部分，（如果两个图形通过旋转或翻转后重合，就认为它们的形状、大小是相同的）
试题分析：因为共有24个三角形，沿格线分割成形状、大小都相同的四个部分，每部分包括6个三角形，由此进行划分即可．
解：
点评：此题考查了图形的拆拼，明确每部分包括6个三角形，是解答此题的关键．
13．
【解析】
试题分析：将图分割成形状、大小完全相同的四块，即每个图形的面积占整个图形面积的，结合图形，进行分割即可．
3．如图，在一块正方形纸片中有一个正方形的空洞．现在要求用一条经过大正方形中心点的线段，把纸片分成面积相等的两部分，应该怎么办？
4．请把图中的两个图形分别沿格线剪成四个形状、大小都相同的图形．
5．请把图沿格线分成形状、大小都相同的三部分，使得每部分都恰好含有一个“○”．
6．如图，三角形和六角星的每条边长都相等，那么用多少个三角形可以拼成六角星？请在图中表示出来．
11．作图如下
【解析】
试题分析：因为共有16个方格，分成形状、大小都相同的四个部分，那么每个部分就有4个方格，根据原图形状，可分成4个“L”形的图形，解决问题．

2014国考真题及答案逻辑推理-图形推理-类比推理-逻辑判断

一、图形推理。

请按每道题的答题要求作答。

请开始答题：76。

从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性.【答案】D【解析】本题考查位置类中的旋转,第一幅图形是沿逆时针平移,第二幅图形是顺时针平移，然后进行叠加得出第三幅图形。

在第二段图形中，按照上述的规律，因此,得出本题答案C【拓展】位置类一直是近期国考中的热点，但是在位置类的知识点中,不仅仅只有旋转一点，还会有平移和翻转，所以有可能在之后的考试中，很有可能会将这些知识点融合.77。

从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。

【答案】D【解析】本题考查是对图形中的俯视图和侧视图，第一段的图形中的第二幅图是第一幅的俯视图，第三幅是第一幅的侧视图，按照上述规律，因此，得出本题答案D 【拓展】从各个角度来看图形，不仅仅只有俯视图和侧视图，还会包括主视图、左视图、仰视图等等，这些知识点就需要考生多多的进行提高，以防之后还会从这几个角度做文章.78。

从所给的四个选项中，选择最合适的一个填入问号处,使之呈现一定的规律性。

【答案】C【解析】本题考查的是位置类中的其他位置，所出现的图形都是有两个部分构成，然后从每个图形的位置来看分别依次是相离、相交、相离、相交这种规律，因此，本题答案得出C【拓展】本题主要考查了图形中位置类的其他位置，并不是按照大家正常所学的平移、旋转、翻转这些平常所见的几类，这就会给考生提醒，我们不能仅仅局限于正常的位置推理，还要多多注意一个图形中多个图形的整体位置，如相交、相切等这种静态位置关系。

79. 从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。

【答案】A【解析】本题考查的是位置类，第一行第一个图形阴影部分顺时针旋转90°，然后将第二个图形以数轴翻转得到第三个图形，第二行检验规律，因此，得出本题答案A 【拓展】从这道题中看到实际是考查了两个元素的翻转和旋转,并且众多考生都会对很明显都是阴影部分作为考查对象，但是学生也要注意，随着国考题目中的难度增大，阴影也有可能成为一个陷阱。

2014年国家公务员考试备考技巧：图形题九宫格思考路线

2014年国家公务员考试备考技巧：图形题九宫格思考路线华图教育专家在前面的两部分我们对于九宫格的思考路线简单介绍了三种，第一种是“O”型思考路线，第二种是“先横后竖”，这两类是比较常见的，尤其是第二种。

第三种是对角线型思考路线，那么在国考考试中除了简单的横竖这样的思考路线外，还多考创新和扩展，对于九宫格还有那些的扩展和创新呢，我们继续来归纳九宫格的思考路线。

1、“S”型思考路线“S”型思考路线是指用“S”或者蛇形将题目中的九个图连起来，组成一定的规律。

这里要注意的是“S”的方向，可以顺时针写也可以逆时针写，同样也不论是正着的“S”还是倒着的“S”，这要找到起点，按照方向可以连接成“S”，就符合这一规律。

【例题】【华图解析】选B。

此题有明显出头数，超出图形之外的部分。

题干部分线头数：5 7 173 9 151 11 ?在此九宫格中，呈现蛇形思考路线，连接结果是：1-3-5-7-9-11-?-15-17，所以“?”部分应该填的是13，呈现的是依次递增2的规律，所以选13个出头数的选项B。

【华图解析】选B。

此题考查锐角的个数：1 6 72 5 83 4 ?在此九宫格中，呈现蛇形思考路线，连接结果是：1-2-3-4-5-6-7-8-?，所以“?”部分应该填的是8，呈现的是依次递增1的规律，所以选9个锐角的图形，即选项B。

2、“e”型思考路线“e”型思考路线是指用“e”将题目中的九个图连起来，组成一定的规律。

这里要注意的是“e”的方向，可以顺时针写也可以逆时针写，同样也不论是正着的“e”还是倒着的“e”，这要找到起点，按照方向可以连接成“e”，就符合这一规律。

此规律在国考考试中还未出现过，但是在南方某些省份出现过这样的题，我们也要提高重视。

总结：我们一直在讨论三乘三的九宫格的思考路线，九宫格可以考察这五种思考路线，那如果出现四乘四的十六宫格的题目，依旧是用一样的方法，还是按照我们提出的这五种思考路线去做题。

6.探索图形的奥秘

2014年温州市小学数学小课题评比学校：苍南县钱库小学成员姓名：陈浩然金子扬黄宇翔小课题题目：探索图形的奥秘指导教师：林尾维探索图形的奥秘一、问题的提出数学学习时，经常会碰到极具挑战的题目。

一次，我就碰到了一道关于正方体涂色的难题。

我苦思冥想，却依旧束手无策。

这道题让我们留下了深刻的印象。

我们的脑海里就突然冒出一些想法:这样的题目能不能很快就做对呢？如果让别的同学来做这道题又会出现什么情况呢？心血来潮，我对本校六年级的同学进行了调查。

我们发下的题目是：36个小正方体拼成一个长方体，表面涂色，把它们拆开。

三面涂色最多有（）个，最少有（）个。

我们共发下了318张题目单，回收318张，回收率100%。

不看不知道，一调查还真吓一跳。

有错误的是314张，而正确的居然仅仅只有4张，错误率达到98.74%，正确率只有1.26%。

如图1，这两组数据是多么鲜明的对比啊！另外，两个填空中，只有一个空格对的共有26个，第一个空格对的有16个，第二个填空对的有10个。

第一个空格填8的有151个，占六年级总人数的47.48%，近占一半。

第二个空格填的填8的也较多，有47个。

图1 调查结果为什么同学们喜欢填8呢？我们这样的正方体涂色有没有什么规律？为了不要再掉进数学的“陷阱”。

于是，我们小组开始了探究之旅。

二、研究过程（一）正方体的涂色问题和规律1、从简单入手，探索棱长是2、3、4各种涂色小正方体的个数用棱长1cm的小正方体拼大正方体后，把它们的表面分别涂上颜色。

三面、两面、一面以及没有涂色的小正方体各有多少块？我们三人拿来易切割的材料，如马铃薯、萝卜等做成小正方体，再拼成各种大正方体，并把整个正方体涂上自己喜欢的颜色。

棱长是2厘米的是显而易见的，8个面都是三面涂色的。

棱长是3厘米的，如下图2。

三面涂色的小正方体，在原正方体的顶点处一共有8个。

两面涂色的小正方体在原正方体的每条棱的中间位置处，一共有12个。

一面涂色的小正方体在原正方体的每个面的中间位置处，一共有6个。

2014寒假班三年级数学思维拓展训练

目录第一讲加减法巧算第二讲找简单数列规律第三讲算式谜第四讲数图形第五讲最大与最小第六讲简单的倍数问题第七讲妙解一般应用题第八讲巧求周长第九讲长方形（正方形）面积第十讲平均数问题第十一讲用还原法解题第十二讲时间与日期第十三讲简单的逻辑推理第十四讲考试第十五讲讲评第一讲加减法巧算专题解析：在进行加减运算时，为了又快又准确，需要掌握一些巧算的方法，运用一些计算技巧，比如：凑整的方等等，今天就让我们来学习一下加减的巧算吧；1、什么叫“补数”？两个数相加，若能恰好凑成整十、整百、整千、整万…，就把其中的一个数叫做另一个数的“补数”。

如：1+9=10，3+7=10，11+89=100，33＋67=100….2、什么是凑整：凑整就是凑成整数（利用补数和），比如凑成整十、整百、整千…典型例题：例题一：（1）53+18+47+82 （2）（54+66）+（46+34）思路导航：把能加在一起的整十、整百、整千….的凑起来；随堂练习一：1、42+71+24+29+582、43+（38+45）+（55+62+57）例题二：999+99+9思路导航：运用补数，凑成整十、整百、整千…1、1999+199+192、888+88+8例题三：（1）526-73-27 （2）1253-（253-158）思路导航:分组凑整…随堂练习三：1、875-364-2362、1121-（121+200）例题四：512-382思路导航：拆补凑整法；1、574+7982、956-597作业：1、128+68+32+722、9999+999+99+93、300-56-444、467－103第二讲找简单数列规律专题简析：在日常生活中，我们经常会碰到一定排列的数，比如：一列自然数：1，2，3，4，5，6，7，8，…年份：1980，1981，1982，1983，1984，1985，1986，…像上面的这些例子，都是按某种法则排列的一列数，这样的一列数就叫做数列。

2014年暑假三年级精英班第6讲和差问题教师版

第六讲和差问题知识要点：和差问题是已知大小两个数的和与这两个数的差，求大小两个数各是多少的应用题。

为了解答和差问题，首先要弄清两个数相差多少的不同叙述方式。

有些题目明确给了两个数的差，而有些应用题把两个数的差“暗藏”起来，我们管暗藏的差叫“暗差”。

知道两个数的和，以及它们的差，要求这两个数，解决这类和差问题需要我们画线段图来分析。

一、基础应用：【例1】宜家家具店一套课桌椅的售价是275元，桌子比椅子贵95元，桌子和椅子各多少钱？【解析】桌子和椅子和为275元，差为95元。

我们可画如下线段图:先求桌子的话，就把椅子补上95元，变得和桌子一样多，总价也增加95元，27595370+=(元)，就变成两个桌子的价格。

桌子：(27595)2185+÷=(元)。

先求椅子的话，就把桌子去掉95元，变成两个椅子的价格。

椅子：(27595)290-÷=(元)。

【例2】在一个减法算式中，已知被减数是62，差比减数大8，问减数与差各是多少？【解析】被减数是减数与差的和，即减数与差的和为62，减数与差的差为8。

我们可画如下线段图：差： 628235+÷=（）减数：628227-÷=（）或 35827-= 或 623527-=。

27595628差【例3】有大、小两个水桶，一共装水72千克，两个桶都倒出同样多的水后分别还剩20千克和10千克．原来大、小两个水桶各装水多少千克？【解析】大桶和小桶装的水的和为72千克，因为都倒出相同多的水，所以差不变，差为201010-=（千克）。

我们可以画出如下线段图：如图，如果把大桶的水倒掉10千克之后就和小桶一样多了，所以小桶原来的水量为：(7210)231-÷=（千克）。

或者先计算大桶，给小桶增加10千克就变得和大桶一样多，所以大桶：(7210)241+÷=（千克）。

大桶还可以这样计算：723141-=（千克），或311041+=（千克）。

四年级上册美术教案-15正负图形｜浙美版(2014秋) (3)

15、正负图形教学目标1．欣赏正负图形，提高整体、局部观察图形的能力。

2．初步了解正负图形在形的重复、多形组合、形的虚实表现以及图底反转等方面的构成方式，尝试设计简单的正负图形。

3．感受正负图形的特殊魅力，拓展创新思维，了解正负图形独特的艺术价值。

教学重、难点：重点：了解正负图形的特点和构成方式，尝试设计简单的正负图形。

难点：用剪贴的形式设计有独特创意的正负图形。

课前准备：（学生）铅笔、彩纸、剪刀、胶水。

（教师）课件、彩纸、剪刀等。

教学过程：课前游戏先玩一个心理测试小游戏：这张图能看到几张脸？比一比谁找出的脸最多（9张代表智商很高）1、师：同学们，你们喜欢做游戏吗？那我们就来做个小游戏吧！老师想考考大家的眼力，比比看哪位同学找到的脸做多出示图片2、学生回答，请上台来指一指师：小游戏做完了，你们能来说说这张图巧妙在哪里吗？生：人脸借用柱子、植物，这种相互借用一、出示鲁宾杯，感受正负图形师：小游戏结束了，我们开始上课！上课！（起立！）同学们好！（老师好！）欢迎来到神奇的美术世界。

刚才通过游戏，老师发现你们都有一双慧眼，现在，再请你们观察一幅图，看看，你看到了什么？生：杯子生：人脸两张人脸师追问：哪部分是人脸，上来比划一下。

生上来比划，教师指点：你是怎么看出来这是张脸的呢？生：从杯子的边缘看出来的，这里是嘴、这是鼻子……师：你的观察力真棒！发现了杯子的边沿线就是人脸侧面的轮廓线呢！师：说说看，刚才你们怎么看这幅图是个杯子，怎么看这幅图又是两张人脸呢？预设：一定要让学生举手回答。

（关注中间白色的部分，就是杯子，关注黑色的部分，就是脸）师：看来这真是一幅神奇的图画啊，从不同的角度观察，我们看到的结果不一样。

这就是著名的鲁宾杯，而这幅图就是典型的正负图形。

（板书：正负图形）其中这图案部分，也就是杯子部分叫正形，而这衬托图案部分的背景叫负形。

正形和负形共用一条轮廓线（手指轮廓线），并且互相转换，就成了神奇的正负图形了。

2014年北师大版五年级上学期第三单元《看图找关系》

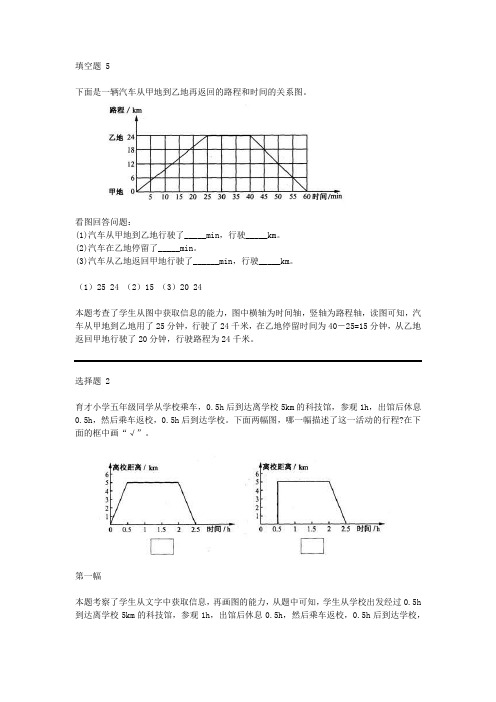
填空题 5下面是一辆汽车从甲地到乙地再返回的路程和时间的关系图。

看图回答问题：(1)汽车从甲地到乙地行驶了_____min，行驶_____km。

(2)汽车在乙地停留了_____min。

(3)汽车从乙地返回甲地行驶了______min，行驶_____km。

（1）25 24 （2）15 （3）20 24本题考查了学生从图中获取信息的能力，图中横轴为时间轴，竖轴为路程轴，读图可知，汽车从甲地到乙地用了25分钟，行驶了24千米，在乙地停留时间为40－25=15分钟，从乙地返回甲地行驶了20分钟，行驶路程为24千米。

选择题 2育才小学五年级同学从学校乘车，0.5h后到达离学校5km的科技馆，参观1h，出馆后休息0.5h，然后乘车返校，0.5h后到达学校。

下面两幅图，哪一幅描述了这一活动的行程?在下面的框中画“√”。

第一幅本题考察了学生从文字中获取信息，再画图的能力，从题中可知，学生从学校出发经过0.5h 到达离学校5km的科技馆，参观1h，出馆后休息0.5h，然后乘车返校，0.5h后到达学校，在比较两张图，第一张是从0开始行驶0.5h，然后开始停留的，第二张图是直接从0.5小时开始停留，没有行驶0.5小时的过程，所以选第一张。

解答题 5小明和小英一起上学。

小明觉得要迟到了，就跑步上学，跑累了，便走着到学校;小英开始走着，后来也跑了起来，直到校门口赶上了小明。

问：下列4幅图像，哪一幅描述了小英的行为?哪一幅描述了小明的行为?第②幅图描述了小明的行为第④幅图描述了小英的行为由题意可知，小明先是跑步，然后走着，小英先是走着，然后是跑步，根据题意可知，跑步所用的时间少，但是路程远，走着所用的时间多，但是路程近，比较图可知第2张图是小明的行为，第四张图是小英的行为。

填空题 4下图是小明和小红两人600米赛跑的行程图。

(1)跑完全程小明用了( )min。

(2)小明到达终点后，小红又跑了( )min才到终点。

(3)小明的平均速度是每分( )m，小红的平均速度是每分( )m。

2014年广东省乡镇考试图形推理练习题

2014年广东省乡镇考试图形推理练习题及解析一、根据下面的图表回答1～10题。

2001～2005年某市水环境情况表1.达标湖泊容量2005年比2001年( )。

A.上升了24.3%B.下降了24.3%C.上升了24.3个百分点D.下降了24.3个百分点【答案】D。

解析：由表可知，2005年达标湖泊容量由2001年的59.5%下降到了35.2%，下降了59.5-35.2=24.3个百分点，故选D。

2.尽管五年中降雨量大幅增加，但平原区地下水平均埋深仍逐年上升，这说明( )。

A.地下水开采量减少B.地下水开采量增加C.地下水量减少D.地下水量增加【答案】C。

解析：地下水平均埋深上升即可以挖到地下水的深度在上升，也就是说地下水量在减少，而“地下水开采量增加”是由“地下水量减少”推测出来的一种可能原因。

3.表中反映的是第几个五年计划期间的情况?A.“七五”B.“八五”C.“九五”D.“十五”【答案】D。

解析：常识题。

表中所示的2001-2005年属于“十五”计划年份。

4.从表中可以看出五年中治理最理想的项目是( )。

A.达标河段B.达标库容C.达标湖泊容量D.平原区地下水平均埋深【答案】A。

解析：由表格可知，2001-2005年，达标河段增加了45.2-41.6=3.6个百分点，达标库容增加了67.4-66.1=1.3个百分点;达标湖泊容量减少了，地下水平均埋深增加了，说明这两方面的情况恶化了。

综上所述，应选择A。

5.五年中达标河段同比治理最好的是哪一年?A.2002年B.2003年C.2004年D.2005年【答案】C。

解析：2002、2003年，达标河段占比下降了，同比为负;2004年达标河段增长了42.2-36.4=5.8个百分点，2005年增长45.2-42.2=3.0个百分点，比较可知，2004年达标河段占比增幅较大，即达标河段同比治理最好，故选C。

二、根据下列文字资料回答6～10题。

2003年6月份，“国房景气指数”达到107.04，比5月份上升0.76点，比去年同期上升2.39点。

2014年小升初数学总复习试题：组合图形

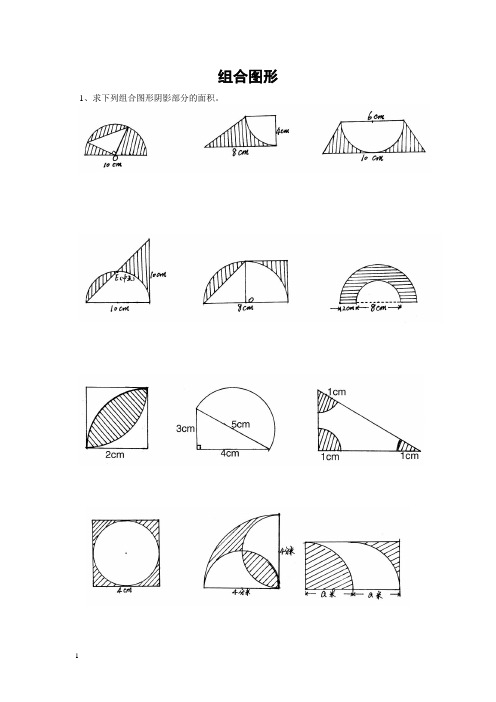
组合图形1、求下列组合图形阴影部分的面积。

2、①求它的周长和面积。

（单位：厘米）②圆的周长是18.84cm，求阴影部分面积。

③长方形的面积和圆的面积相等，已知圆④求直角三角形中阴影部分的面积。

的半径是3cm，求阴影部分的周长和面积。

（单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴影①比阴影②面积小48平方厘米，
①比阴影②面积少3cm2，求EC的长。

AB=40cm，求BC的长。

⑦平行四边形的面积是30cm2，⑧一个圆的半径是4cm，求阴影部分面积。

求阴影部分的面积。

⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，各占长方形ABCD的
1/3，求三角形AEF的面积。

⑩梯形上底8cm，下底16cm，阴影⑾求阴影部分面积。

（单位：cm）部分面积64cm2，求梯形面积。

⑿梯形面积是48平方厘米，阴影部分比空白⒀阴影部分比空白部分大6cm2，求S 阴。

部分12平方厘米，求阴影部分面积。

3、求下列图形的体积。

（单位：厘米）。

六年级数学试题-小升初专题训练-第6节：立体图形拓展人教课标版(2014秋)(含答案)

第6节：立体图形拓展【例1】用棱长为1的小正方体木块摆成一个长20，宽15，高10的长方体，然后将所摆成的长方体表面喷上颜色。

则没有喷到颜色的木块共有（）个。

【例2】一个长方体木块，锯掉5厘米后，得到一个正方体木块，表面积比原来减少100平方厘米，求原来长方体木块的表面积。

【例3】一个棱长是3厘米的正方体木块，各面中心凿出一孔面边长是1厘米的正方形柱孔，它余下的体积是多少立方厘米?表面积是多少平方厘米?1.将1立方米的大正方体锯成体积是1立方厘米的小正方体，然后将它们一个一个连成一排，其总长度是千米。

2. 一个正方体木块，棱长4 厘米，把它的外表涂成绿色，然后切割成棱长为1 厘米的小正方体。

小正方体中，只有一面是绿色的有（）块，没有一面是绿色的有（）块。

3.已知一个正方体的体积是729立方厘米，现在要在它的8个角上分别截去8个大小相同的小正方体，使得截去后余下的体积是665立方厘米，则截去的每个小正方体的棱长是。

形状不规则的物体可以用排水法求体积，形状规则的物体可以用公式直接求体积。

排水法的公式：V 物体＝V 现在－V 原来也可以 V 物体＝S 底面×(h 现在－ h 原来) V 物体＝S 底面×h 升高模块一：正方体题型举例模块二：液体浸物【例1】一个圆柱形容器中有足够量的水，在水中放入一个圆锥形铅锤后，水面上升了3厘米，已知容器内部底面的半径是铅锤底面半径的2倍，这个铅锤的高为多少厘米？【例2】一个圆柱形的容器的底部放着一块正方体铅块，现在向容器内匀速注水，20秒时水恰好没过铅块的上表面，又过了1.5分钟，水注满了容器。

若容器高度是24厘米，铅块高是6厘米，则容器底面积是多少平方厘米?【例3】如图，在底面是边长为60厘米的正方体容器里，直立放着一个高100厘米，底面边长为18厘米的正方形的铁块，这时容器里的水深是50厘米，现在把铁块提出容器之后，水面下降（）厘米1.一瓶装满的矿泉水，小亮喝了一些，把瓶盖拧紧后倒置放好在水平的桌面上，无水部分是高3cm，内直径是6cm的圆柱体，那么小亮喝了（）cm3水。

2014年六年级数学思维训练：几何综合一

2014年六年级数学思维训练：几何综合一一、兴趣篇1．图中八条边的长度正好分别是1、2、3、4、5、6、7、8厘米．已知a=2厘米，b=4厘米，c=5厘米，求图形的面积．2．如图所示，∠1+∠2+∠3+∠4+∠5+∠6等于度．3．平行四边形ABCD周长为75厘米，以BC为底时高是14厘米（如图）；以CD为底时高是16厘米．求：平行四边形ABCD的面积．4．如图，一个边长为1米的正方形被分成4个小长方形，它们的面积分别是平方米、平方米、平方米和平方米．已知图中的阴影部分是正方形，那么它的面积是多少平方米？5．如图，红、黄、绿三块大小一样的正方形纸片，放在一个正方形盒内，它们之间互相叠合．已知露在外面的部分中，红色的面积是20，黄色的面积是14，绿色的面积是lO．那么，正方形盒子的底面积是多少？6．如图，在三角形ABC中，IF和BC平行，GD和AB平行，HE和AC平行．已知AG：GF：FC=4：3：2，那么AH：HI：IB和BD：DE：EC分别是多少？7．如图，已知三角形ABC的面积为60平方厘米，D、E分别是AB、AC边的中点，求三角形OBC的面积．8．在如图的正方形中，A、B、C分别是ED、EG、GF的中点．请问：三角形CDO的面积是三角形ABO面积的几倍？9．如图，ABCD是平行四边形，面积为72平方厘米，E，F分别为AB，BC的中点，则图中阴影部分的面积为平方厘米．10．如图，在三角形ABC中，CE=2AE，F是AD的中点，三角形ABC的面积是1，那么阴影部分的面积是多少？二、拓展篇11．如图，A、B是两个大小完全一样的长方形，已知这两个长方形的长比宽长8厘米，图中的字母表示相应部分的长度．问：A、B中阴影部分的周长哪个长？长多少？12．如图，ABCDE是正五边形，CDF是正三角形，∠BFE等于多少度？13．一个各条边分别为5厘米、12厘米、13厘米的直角三角形，将它的短直角边对折到斜边上去和斜边相重合，如图所示．问：图中的阴影部分（即折叠的部分）的面积是多少平方厘米？14．图中大长方形被分成四个小长方形，面积分别为12、24、36、48．请问：图中阴影部分的面积是多少？15．三个面积都是12的正方形放在一个长方形的盒子里面，如图，盒中空白部分的面积已经标出，求图中大长方形的面积．16．如图，三角形ABC的面积为1，D、E分别为AB、AC的中点，F、G是BC边上的三等分点．求三角形DEF和三角形DOE的面积．17．如图，梯形ABCD的上底AD长10厘米，下底BC长15厘米．如果EF和上、下底平行，那么EF的长度为多少？18．如图，正六边形的面积为6，那么阴影部分的面积是多少？19．两盏4米高的路灯相距10米，有一个身高1.5米的同学行走在这两盏路灯之间，那么他的两个影子总长度是多少米？20．如图，D是长方形ABCD一条对角线的中点，图中已经标出两个三角形的面积为3和4，那么阴影直角三角形的面积是多少？21．如图，在三角形ABC中，AE=ED，D点是BC的四等分点，阴影部分的面积占三角形ABC面积的几分之几？22．如图，在三角形ABC中，三角形AEO的面积是1，三角形ABO的面积是2，三角形BOD的面积是3，则四边形DCEO的面积是多少？三、超越篇23．如图，长方形的面积是60平方厘米，其内3条长度相等且两两夹角为120°的线段将长方形分成了两个梯形和一个三角形．请问：一个梯形的面积是多少平方厘米？24．如图，P是三角形ABC内一点，DE平行于AB，FG平行于BC，HI平行于CA，四边形AIPD的面积是12，四边形PGCH的面积是15，四边形BEPF的面积是20．请问：三角形ABC的面积是多少？25．如图所示，正方形ABCD的面积为1．E、F分别是BC和DC的中点，DE和BF交于M点，DE和AF交于N点，那么阴影三角形MFN的面积为多少？26．如图，三角形ABC的面积为1，D、E、F分别是三条边上的三等分点，求阴影三角形的面积．27．如图，小悦测出家里瓷砖的长为24厘米，宽为10厘米，而且还测出了边上的中间线段均为4厘米，那么中间菱形的面积是多少平方厘米？28．如图，ED垂直于等腰梯形ABCD的上底AD，并交BC于G，AE平行于BD，∠DCB=45°，且三角形ABD和三角形EDC的面积分别为75、45，那么三角形AED的面积是多少？29．在长方形ABCD中，E、F、G、H分别是边AB、BC、CD、DA上的点，将长方形的四个角分别沿着HE、EF、FG、GH对折后，A点和B点重合，C点和D点重合．已知EH=3，EF=4，求线段AD和AB的长度比．30．如图，在长方形ABCD中，AE：ED=AF：AB=BG：GC．已知△EFC的面积为20，△FGD 的面积为16，那么长方形ABCD的面积是多少？2014年六年级数学思维训练：几何综合一参考答案和试题分析一、兴趣篇1．图中八条边的长度正好分别是1、2、3、4、5、6、7、8厘米．已知a=2厘米，b=4厘米，c=5厘米，求图形的面积．【分析】应先根据题目条件确定出每条边的长度，再进行等积变形，然后可据图形形状进行计算．【解答】解：如图所示，图形的面积为：7×2+5×（7﹣4）+6×1=14+15+6=35（平方厘米）答：图形的面积是35平方厘米．2．如图所示，∠1+∠2+∠3+∠4+∠5+∠6等于360度．【分析】如图，∠3=∠7，所以∠2+∠3=180°﹣∠A；同理，∠6=∠8，所以∠1+∠6=180°﹣∠C；∠4+∠5=180°﹣∠B；由此把这三个式子加起来即可得出，∠1+∠2+∠3+∠4+∠5+∠6=180°×3﹣（∠A+∠B+∠C），又因为∠A+∠B+∠C=180°，所以，∠1+∠2+∠3+∠4+∠5+∠6=360°．【解答】解：∠3=∠7，所以∠2+∠3=180°﹣∠A；同理，∠6=∠8，所以∠1+∠6=180°﹣∠C；∠4+∠5=180°﹣∠B；则∠1+∠2+∠3+∠4+∠5+∠6，=180°×3﹣（∠A+∠B+∠C），=540°﹣180°，=360°，答：∠1+∠2+∠3+∠4+∠5+∠6=360°．故答案为：360．3．平行四边形ABCD周长为75厘米，以BC为底时高是14厘米（如图）；以CD为底时高是16厘米．求：平行四边形ABCD的面积．【分析】用平行四边形的面积公式先求出邻边的关系，再由平行四边形的周长得到邻边的和，从而求得平行四边形的一条边长，进而求得其面积．【解答】解：由平行四边形面积公式知14×BC=16×CD，即14BC=16CD，则BC：CD=16：14=8：7，BC=CD，又2×（BC+CD）=75，则BC+CD=37.5（厘米），CD+CD=37.5（厘米），CD=17.5（厘米），因此，平行四边形ABCD的面积为：16×17.5=280（平方厘米）；答：平行四边形ABCD的面积为280平方厘米．4．如图，一个边长为1米的正方形被分成4个小长方形，它们的面积分别是平方米、平方米、平方米和平方米．已知图中的阴影部分是正方形，那么它的面积是多少平方米？【分析】大正方形的面积是：+++=1（平方米）；大正方形的边长就是1米；面积是平方米的长方形和面积是平方米的长方形的长相同，根据长方形的面积公式可知：它们的面积比是（FE×AE）：（FE×EB）=：，即：AE：EB=3：4；AE就是大正方形边长的；同理：面积是平方米的长方形的宽和面积是平方米长方形的长相等，所以CH：HD=2：1，CH就是大正方形边长的；小正方形的边长GH=BE﹣AF，由此求出求出它的边长，进而求出面积．【解答】解：如图所示：+++=1（平方米）；大正方形的边长就是1米；（FE×AE）：（FE×EB）=：，即：AE：EB=3：4；AE就是大正方形边长的；1×=（米）；（CH×HG）：（HG×HD）=：；BE：EC=2：1；CH是大正方形边长的；1×=（米）；FG=﹣=（米）；×=（平方米）；答：阴影部分的面积是平方米．5．如图，红、黄、绿三块大小一样的正方形纸片，放在一个正方形盒内，它们之间互相叠合．已知露在外面的部分中，红色的面积是20，黄色的面积是14，绿色的面积是lO．那么，正方形盒子的底面积是多少？【分析】如图，把黄块向左移动就会发现，黄色减少的面积等于绿色增加的面积，从而得出黄+绿=24，黄和绿各是24÷2=12，设红块边长是b，和红色并排的绿边是a，根据正方形的面积公式，得大正方形面积b2=20，两个长方形的面积ab=12，小正方形的面积a2=（ab）2÷b2，则正方形盒子的底面积就是两个正方形面积加上两个长方形面积．【解答】解：把黄块向左移动就会发现，黄色减少的面积等于绿色增加的面积，从而得出黄+绿=24，黄和绿各是24÷2=12，即两个长方形的面积都是12，设红块边长是b，和红色并排的绿边是a，则根据正方形的面积公式，得大正方形面积b2=20，两个长方形的面积ab=12，小正方形的面积a2=（ab）2÷b2=12×12÷20=144÷20，=7.2；底面积：20+12×2+7.2=51.2；答：正方形盒子的底面积是51.2．6．如图，在三角形ABC中，IF和BC平行，GD和AB平行，HE和AC平行．已知AG：GF：FC=4：3：2，那么AH：HI：IB和BD：DE：EC分别是多少？【分析】先求AH：HI：IB的比值，由AG：GF：FC=4：3：2，得出AF：FC=7：2；由△AIF∽△ABC，则AI：IB=AF：FC=7：2；由△FGO∽△FAI，则FO：OI=FG：GA=3：4；由△IHO∽△IAF，则HI：AH=OI：FO=4：3；所以AH：HI：IB=3：4：2．同理可证：BD：DE：EC=4：2：3．【解答】解：AG：GF：FC=4：3：2，则（AG+GF）：FC=（4+3）：2，即AF：FC=7：2；因为IF和BC平行，所以△AIF∽△ABC，则AI：IB=AF：FC=7：2；因为GD和AB平行，所以△FGO∽△FAI，则FO：OI=FG：GA=3：4；因为HE和AC平行，所以△IHO∽△IAF，则HI：AH=OI：FO=4：3；所以AH：HI：IB=3：4：2同理可证：BD：DE：EC=4：2：3答：AH：HI：IB=3：4：2；BD：DE：EC=4：2：3．7．如图，已知三角形ABC的面积为60平方厘米，D、E分别是AB、AC边的中点，求三角形OBC的面积．【分析】连接OA，如下图由题意等底同高的三角形的面积相等可知△CAD和△ABE的面积都等于△ABC的一半，即60÷2=30（平方厘米），这两个△的面积都减去四边形的ADOE 的面积得到S△BOD=S△COE，再根据等底同高的三角形的面积相等可知S△AOE=S△COE，S△AOD=S△BOD，所以S△AOE=S△COE=S△AOD，S△ADC=S△AOE+S△COE+S△AOD=30平方厘米，所以S△COE=30÷3=10平方厘米，由此可推出阴影部分的面积．【解答】解：由题意可知AE=CE，AD=BD，根据等底同高的三角形的面积相等得：S△ADC=S△BDC=60÷2=30平方厘米，S△AEB=S△CBE=30（平方厘米），所以S△ADC=S△AEB=30（平方厘米），则S△BOD=S△COE再根据等底同高的三角形的面积相等得：S△AOE=S△COE，S△AOD=S△BOD，所以S△AOE=S△COE=S△AOD=S△BOD，S△ADC=S△AOE+S△COE+S△AOD=30（平方厘米），所以S△COE=30÷3=10（平方厘米），所以S△BOC是：30﹣10=20（平方厘米），答：S△BOC是20平方厘米．8．在如图的正方形中，A、B、C分别是ED、EG、GF的中点．请问：三角形CDO的面积是三角形ABO面积的几倍？【分析】该四边形是正方形，所以四条边都相等，而A、B、C分别是ED、EG、GF的中点，所以不难得到：S△BED=S△CAD，而=，所以S△ADO=S△BED=S△CAD，因为三角形CDA 和三角形BAD是等第的三角形，且三角形CAD的高是三角形BAD高的2倍，所以S△ABD=S△CAD，再利用S△COD=S△CAD﹣S△AOD，S△COD=S△CAD﹣S△AOD，进而求出三角形CDO的面积和三角形ABO面积和三角形CAD面积的关系，据此解决即可．【解答】解：因为四边形是正方形且A、B、C分别是ED、EG、GF的中点．所以：AD=DE=CE=BE=DE，线段AO=BE所以：S△BED=S△CAD，S△AOD=S△BED=S△CAD，S△ABD=S△CAD所以：S△AOB=S△BAD﹣S△AOD=S△CAD﹣S△CAD=S△CADS△COD=S△CAD﹣S△AOD=S△CAD﹣S△CAD=S△CADS△CDO÷S△ABO=S△CAD÷S△CAD=3答：三角形CDO的面积是三角形ABO面积的3倍．9．如图，ABCD是平行四边形，面积为72平方厘米，E，F分别为AB，BC的中点，则图中阴影部分的面积为48平方厘米．【分析】如图所示，DE、DF分别于AC交于点M、N，则S△ADM=S△DMN=S△DNC，而S△AEM=S△NFC=S△ADM，平行四边形的面积已知，则可以求出三角形ADM的面积，阴影部分的面积=平行四边形的面积﹣3个空白三角形的面积．【解答】解：DE、DF分别于AC交于点M、N，M、N是AC的三等分点因为平行四边形的面积=72平方厘米，则S△ADC=72÷2=36（平方厘米），S△ADM=S△DMN=S△DNC=S△ADC=×36=12（平方厘米），S△AEM=S△NFC=S△ADM=×12=6（平方厘米），所以阴影部分的面积=72﹣12﹣6﹣6=60﹣12，=48（平方厘米）；答：阴影部分的面积是48平方厘米．故答案为：48．10．如图，在三角形ABC中，CE=2AE，F是AD的中点，三角形ABC的面积是1，那么阴影部分的面积是多少？【分析】连接CF，因为CE=2AE，所以==，同理，=，设S△AEF=1份，那么S△CEF=2份，因为F是AD的中点，S△CFD=S△ACF=S△AEF+S△CEF=1+2=3份，同理，，又因为==，所以，所以S△BDF=S△ABF=3份，这样S△ABC=1+2+3+3+3=9份；然后根据阴影部分的份数是2+3=5份，在解答即可．【解答】解：连接CF，因为CE=2AE，根据燕尾定理，所以==，同理，=，设S△AEF=1份，那么S△CEF=2份，因为F是AD的中点，S△CFD=S△ACF=S△AEF+S△CEF=1+2=3份，同理，，又因为==，所以，所以S△BDF=S△ABF=3份，这样S△ABC=1+2+3+3+3=9份，阴影部分的份数是：2+3=5份，5÷12=，即1×=．二、拓展篇11．如图，A、B是两个大小完全一样的长方形，已知这两个长方形的长比宽长8厘米，图中的字母表示相应部分的长度．问：A、B中阴影部分的周长哪个长？长多少？【分析】观察图形可知图形A中，阴影部分的周长分成两部分计算，分别是长a、宽a﹣b，和长2b、宽b的长方形的周长；图形B中，阴影部分的左上方的小线段向上、向左平移后，阴影部分的周长正好等于这个大长方形的周长，由图可知，大长方形的长是a+2b，宽是a+b，即可求出它们各自的周长，再根据大长方形的长比宽长8厘米，即a+2b﹣（a+b）=8厘米，推出b=8厘米，据此即可解答．【解答】解：图形A中阴影部分的周长是：2（a+a﹣b）+2（b+2b）=4a+4b，图形B中阴影部分的周长是：2（a+2b+a+b）=4a+6b，4a+6b﹣（4a+4b）=2b，又因为大长方形的长比宽长8厘米，即a+2b﹣（a+b）=8，可得b=8厘米，所以2b=2×8=16（厘米），答：图形B中的阴影部分的周长较长，比图形A中的阴影部分的周长长16厘米．12．如图，ABCDE是正五边形，CDF是正三角形，∠BFE等于多少度？【分析】根据正五边形的每个内角的度数是108°，正三角形的每个内角的度数是60°，可求∠BCF，∠EDF的度数，根据等腰三角形的性质，可求∠BFC，∠EFD的度数，再根据周角的定义可求∠BFE的度数．【解答】解：∠BCF=∠EDF=108°﹣60°=48°，因为BC=CF，DF=DE，所以∠BFC=∠EFD=（180°﹣48°）÷2=66°，因此∠BFE=360°﹣66°×2﹣60°=168°．答：∠BFE等于168度．13．一个各条边分别为5厘米、12厘米、13厘米的直角三角形，将它的短直角边对折到斜边上去和斜边相重合，如图所示．问：图中的阴影部分（即折叠的部分）的面积是多少平方厘米？【分析】根据“将它的短直角边对折到斜边上去和斜边相重合”，可知DC是AB的高，图中阴影部分（即折叠的部分）的面积和△ADC的面积相等；据此只要求出△ADC的底边CD的长，再乘高除以2即可得解；进而根据△ABC的面积=×AB×DC=×BC×AE，代入数据即可求出DC的长度，进而得解．【解答】解：见下图：×13×DC=×（12﹣DC）×5，13×DC=60﹣DC×5，DC=（厘米）；△ADC=△AEC=××5=（平方厘米）．答：图中的阴影部分（即折叠的部分）的面积是平方厘米．14．图中大长方形被分成四个小长方形，面积分别为12、24、36、48．请问：图中阴影部分的面积是多少？【分析】如图，由于阴影部分是两个同底，高之和等于大长方形宽的三角形，其面积是EF×AJ，我们可以设大长方形长AC=a，宽AJ=b，则EF的长为a﹣a=a，则阴影部分面积为×（a×b），由于a×b是大长方形的面积，其面积是四个小长方形面积之和，从而使问题得解．【解答】解：如图，阴影部分面积为：是EF×AJ，设大长方形的长为a，宽为b，则EF=a﹣ a=a，因此，阴影部分面积为×a×b，=×（a×b）=×（12+24+36+48）=×120=答：图中阴影部分的面积．故答案为：．15．三个面积都是12的正方形放在一个长方形的盒子里面，如图，盒中空白部分的面积已经标出，求图中大长方形的面积．【分析】白色小长方形3、4、5的宽都是大长方形的宽减去正方形边长，小长方形3的面积=（大长方形的底边﹣2倍的正方形边长）×（大长方形宽﹣正方形边长）=3，小长方形4+小长方形5的面积=（大长方形底边﹣正方形边长）×（大长方形宽﹣正方形边长）=9，所以（大长方形底边﹣正方形边长）是（大长方形的底边﹣2倍的正方形边长）的3倍，所以大长方形面积=大长方形的底边×大长方形的宽=2.5倍正方形边长×1.5倍正方形边长=2.5×1.5倍的正方形面积=2.5×1.5×12=45．【解答】解：由分析可知，小长方形3的面积=（大长方形的底边﹣2倍的正方形边长）×（大长方形宽﹣正方形边长）=3，小长方形4+小长方形5的面积=（大长方形底边﹣正方形边长）×（大长方形宽﹣正方形边长）=9，（大长方形底边﹣正方形边长）÷（大长方形的底边﹣2倍的正方形边长）=3，大长方形底边﹣正方形边长=3倍大长方形的底边﹣6倍的正方形边长，2倍大长方形的底边=5倍的正方形边长，大长方形的底边=2.5倍的正方形边长，则大长方形的宽=1.5倍正方形边长，大长方形面积=大长方形的底边×大长方形的宽=2.5倍正方形边长×1.5倍正方形边长=2.5×1.5倍的正方形面积=2.5×1.5×12=45．答：大长方形的面积是45．16．如图，三角形ABC的面积为1，D、E分别为AB、AC的中点，F、G是BC边上的三等分点．求三角形DEF和三角形DOE的面积．【分析】根据条件可知：三角形DEF的底DE=BC的一半，高也是一半，即可求得；利用DE和FG的倍数关系，在梯形DEGF中求出三角形DOE的面积．三角形BDF面积=（1÷2）×（1÷3）=，三角形CEF面积=（1÷2）×（2÷3）=，三角形ADE面积=（1÷2）×（1÷2）=，所以三角形DEF面积=1﹣﹣﹣=，又因为DE=，FG=，所以=，所以三角形DOE面积=三角形DEF面积×3÷（3+2）=×3÷5=．【解答】解：①过点A作线段BC的垂线，垂足为Q，过点D作线段BC的垂线，垂足为M，所以线段DM=AQ那么三角形ABC的面积是：BC×AQ÷2=1所以：BC×AQ=2因为D、E分别为AB、AC的中点，所以线段DE=BC，所以三角形DEF的面积：DE×DM÷2=×BC××AQ÷2=×2÷2=②又因为DE=，FG=，所以=，所以三角形DOE面积为：三角形DEF面积×3÷（3+2）=×3÷5=．答：三角形DEF的面积是，三角形DOE的面积．17．如图，梯形ABCD的上底AD长10厘米，下底BC长15厘米．如果EF和上、下底平行，那么EF的长度为多少？【分析】由平行线的性质可得===，得出OE和BC，OF和AD的关系，进而即可求解EF的长．【解答】解：∵AD∥BC，EF∥BC，∴===，又==，==∴OE=BC=×15=6（厘米），OF=AD=×10=6（厘米）∴EF=OE+OF=6+6=12（厘米）答：EF的长度为12厘米．18．如图，正六边形的面积为6，那么阴影部分的面积是多少？【分析】如图，连结AC、BF、CE、DF，根据正六边形的特征及梯形的蝴蝶定理，各三角形有如下关系，a：b：c：d=1：4：2：2，因此，阴影部分占六边形面积的，进而求出阴影部分面积．【解答】解：如图，连结AC、BF、CE、DF，根据六正边形的特征及蝴蝶定理，阴影部分面积：×6=×6=答：阴影部分的面积是．故答案为：．19．两盏4米高的路灯相距10米，有一个身高1.5米的同学行走在这两盏路灯之间，那么他的两个影子总长度是多少米？【分析】根据题意作出图象，利用相似三角形的性质说明即可．【解答】解：如图所示：CD、EF为路灯高度，AB为该人高度，BM、BN为该人前后的两个影子．由题意得：b=4米，a=1.5米，DF=10米，∵AB∥CD，∴==，∴==即MB=DB同理BN=FB∴MB+BN=（DB+FB）=0.6×10=6（米）答：他的两个影子总长度是6米．20．如图，D是长方形ABCD一条对角线的中点，图中已经标出两个三角形的面积为3和4，那么阴影直角三角形的面积是多少？【分析】根据题意可知长方形的面积是4×4=16，所以三角形BQW的面积就是5，然后根据面积是5和3的三角形，得到WQ和DC的比即可知道：BQ：BC的值，进而求得阴影三角形的面积即可，如下图即可．【解答】解：如图：设BC=x，阴影部分三角形的高为h，DC=y因为四边形ABCD是长方形，点O是对角线的中点，所以S△ABC=2×4=8，S△BCD=8所以：S△BWC=8﹣3=5即为：xh÷2=5xh=10所以S长方形ABCD=xy=4×4=16xh：xy=10：16即为：h：y=5：8所以：==所以：=S△BQW=×5=答：阴影直角三角形的面积是．21．如图，在三角形ABC中，AE=ED，D点是BC的四等分点，阴影部分的面积占三角形ABC面积的几分之几？【分析】连接CE，设S△CDE=1，S△BDE=S△ABE=3，则，所以，S△AEF=，，据此解答．【解答】解：连接CE，设S△CDE=1，因为AE=ED，S△ACE=1，D点是BC的四等分点，根据燕尾模型可得：S△BDE=S△ABE=3，则，所以，S△AEF=，．22．如图，在三角形ABC中，三角形AEO的面积是1，三角形ABO的面积是2，三角形BOD的面积是3，则四边形DCEO的面积是多少？【分析】根据题意可得所以==，==，所以所以：S△EOF：S△EBC=，S△AOF：S△ADC=，据此解决即可．【解答】解：如图：过点O作线段OF∥BC交AC于点F，因为三角形AEO的面积是1，三角形ABO的面积是2，三角形BOD的面积是3，所以==，==所以：S△EOF：S△EBC=，S△AOF：S△ADC=设S△EOF=x，S四边形EODF=y所以x：（3+y+x）=1：9①（1+x）：（1+x+y）=4：25②由①②解得：x=3，y=21所以四边形DCEO的面积是：3+21=24答：四边形DCEO的面积是24．三、超越篇23．如图，长方形的面积是60平方厘米，其内3条长度相等且两两夹角为120°的线段将长方形分成了两个梯形和一个三角形．请问：一个梯形的面积是多少平方厘米？【分析】过F点作FG⊥BC于G，根据含30°的三角形的性质得到EF=BF=2FG，依此可得△BFC=长方形的面积×，再根据图意得到一个梯形的面积．【解答】解：过F点作FG⊥BC于G．因为∠BFC=120°，BF=CF=EF，所以∠FBG=30°，所以EF=BF=2FG，所以FG=EG，所以△BFC=长方形的面积×=10（平方厘米）（60﹣10）÷2=50÷2=25（平方厘米）．答：一个梯形的面积是25平方厘米．24．如图，P是三角形ABC内一点，DE平行于AB，FG平行于BC，HI平行于CA，四边形AIPD的面积是12，四边形PGCH的面积是15，四边形BEPF的面积是20．请问：三角形ABC的面积是多少？【分析】观察图形可知，DE平行于AB，FG平行于BC，HI平行于CA，四边形AIPD的面积是12，四边形PGCH的面积是15，四边形BEPF的面积是20．又因为四边形AIPD和四边形BEPF的高相等，所以它们的底的比就等于它们的面积之比，即DP：PE=12：20=3：5；则DG：GC=3：5，又因为三角形PDG和四边形PHCG高相等，所以三角形PDG的面积和四边形PHCG的面积的一半的比是3：5，据此即可求出三角形PDG的面积，同理，再求出三角形PEH和三角形PIF的面积，据此把三个平行四边形和三个三角形的面积都加起来即可求出三角形ABC的面积．【解答】解：DE平行于AB，FG平行于BC，HI平行于CA，四边形AIPD的面积是12，四边形PGCH的面积是15，四边形BEPF的面积是20．又因为四边形AIPD和四边形BEPF的高相等，所以DP：PE=12：20=3：5；则DG：GC=3：5，又因为三角形PDG和平行四边形PHCG高相等，所以三角形PDG的面积和四边形PHCG的面积的一半的比是3：5，所以三角形PDG的面积是：（15÷2）×3÷5=4.5，同理：三角形PEH的面积和平行四边形PFBE的面积的一半的比是：5：4，所以三角形PEH的面积是：（20÷2）×5÷4=12.5，同理三角形PIF的面积和四边形PEBF的面积的一半的比是4：5，所以三角形PIF的面积是：（20÷2）×4÷5=8，12+20+15+4.5+12.5+8=72．答：三角形ABC的面积是72．25．如图所示，正方形ABCD的面积为1．E、F分别是BC和DC的中点，DE和BF交于M点，DE和AF交于N点，那么阴影三角形MFN的面积为多少？【分析】连接CM、EF和AE，根据中点的定义可知S△BEM=，S△DEF=，根据AN：FN=S△ADE：S△DEF=1：4，得到S△DFN=，再根据S△MFN=S△DEC﹣S△CME﹣S△CMF﹣S△DFN即可求解．【解答】解：连接CM、EF和AE，因为E、F是中点，所以S△BEM=S△CEM=S△CMF=1÷4÷3=，因为F是CD的中点，所以S△DEF=1÷4÷2=，AN：FN=S△ADE：S△DEF=（1÷2）：=1：4所以S△DFN=1÷4÷（1+4）=，所以S△MFN=S△DEC﹣S△CME﹣S△CMF﹣S△DFN=﹣﹣﹣=．答：阴影三角形MFN的面积为．26．如图，三角形ABC的面积为1，D、E、F分别是三条边上的三等分点，求阴影三角形的面积．【分析】因为D是BC的三等分点，根据高一定时，三角形的面积和底成正比例的性质可得，三角形ABC的面积：三角形ABD的面积=3：2，所以可得三角形ABD的面积是：1×=，同理可得，三角形ABD的面积：三角形BED的面积=3：2，则三角形BED的面积=×=；三角形EFD的面积：三角形BEG的面积=3：2，则阴影三角形的面积=×=．【解答】解：1×××=××=×=．答：阴影三角形的面积是．27．如图，小悦测出家里瓷砖的长为24厘米，宽为10厘米，而且还测出了边上的中间线段均为4厘米，那么中间菱形的面积是多少平方厘米？【分析】根据三角形全等和长方形知识，可知边上的小三角形都是等腰三角形；根据三角形相似的性质可求得左右两边三角形的高为：（10+4）×2÷7=4厘米，上下两个三角形的高为：（3+4）×2÷14=1厘米．从而可求四个小三角形的面积和为（4×4÷2+4×1÷2）=20平方厘米，每个大直角三角形的面积为7×14÷2=49平方厘米．故空白部分面积=49×4﹣20=176平方厘米，中间大菱形面积=24×10﹣176=64平方厘米．【解答】解：左右两边三角形的高为：（10+4）×2÷7=4（厘米）上下两个三角形的高为：（3+4）×2÷14=1（厘米）四个小三角形的面积和为：（4×4÷2+4×1÷2）=20（平方厘米）大直角三角形的面积为：7×14÷2=49（平方厘米）空白部分面积为：49×4﹣20=176（平方厘米）中间大菱形面积为：24×10﹣176=64（平方厘米）答：中间菱形的面积为64平方厘米．28．如图，ED垂直于等腰梯形ABCD的上底AD，并交BC于G，AE平行于BD，∠DCB=45°，且三角形ABD和三角形EDC的面积分别为75、45，那么三角形AED的面积是多少？【分析】过A作AH⊥BC，垂足为H，AH交BD于F．根据等腰梯形和平行四边形的性质，以及S△AED=S△ABD﹣S△AFB即可求解．【解答】解：过A作AH⊥BC，垂足为H，AH交BD于F，则AH∥EG．因为四边形ABCD是等腰梯形，AD∥BC，∠DCB=45°，所以∠ABC=45°，AH=DG=GC=BH，又因为AE∥BD，所以四边形AFDE是平行四边形，DE=AF，S△AED=S△AFD，因为S△DEC=DE•GC=45，S△ABD=S△AFD+S△AFB=75，其中S△AFD=S△AED，S△AFB=AF•BH=DE•GC=S△DEC=45，这样S△AED=S△ABD﹣S△AFB=75﹣45=30．答：三角形AED的面积是30．29．在长方形ABCD中，E、F、G、H分别是边AB、BC、CD、DA上的点，将长方形的四个角分别沿着HE、EF、FG、GH对折后，A点和B点重合，C点和D点重合．已知EH=3，EF=4，求线段AD和AB的长度比．【分析】本题主要考查的是相似三角形的性质，利用相似三角形的性质和对称性解答即可．【解答】解：由对称性得：∠AEH=∠A'EH，∠BEF=∠B'EF，∠AEH+∠A'EH+∠BEF+∠B'EF=180°，∠A'EH+∠B'EF=90°，∠HEF=90°．根据勾股定理得：HF=5，HF×EA'=HE×EF=3×4=12，EA'=2.4．由对称性得：AE=A'E BE=B'E A'E=B'E 所以AE=BE AE=BE=2.4，AB=4.8．由对称性得：AH=A'H BF=B'F DH=D'H CF=C'F A'H+B'F+D'H+C'F=2HF=10AH+BF+DH+CF=10AD+BC=10AD=5AD：AB=5：4.8=25：24答：线段AD和AB的长度比为25：24．30．如图，在长方形ABCD中，AE：ED=AF：AB=BG：GC．已知△EFC的面积为20，△FGD 的面积为16，那么长方形ABCD的面积是多少？【分析】利用比例性质和图形中比较得出和差问题．三角形EFD和三角形CFG的面积之差是4．面积之和等于长方形CDEG的一半．通过比例的内项积等于外项积得到GC*AF=AB*BG，观察一下发现三角形EFD等于四边形ABGE的一半．而四边形EDGF恰好等于四边形ABGE的一半夹上四边形EDCG的一半，所以三角形FDG恰好等于四边形EDCG的一半．【解答】解：设矩形ABCD的对边AB=CD=a，AD=BC=b，再设题中的比例常数AE：ED=AF：AB=BG：GC=k，把这个表达式变换成k和矩形ABCD边长a、b的表达式，则有：AE=BG=kb：（k+1）ED=GC=AF=ka，FB=（1﹣k）aS（矩形ABCD）=ab=S（Rt△AFE）+S（△FEC）+S（Rt△EDC）+S（Rt△FBC）=×AF×AE+20+×ED×CD+×FB×BC=×ka×kb：（k+1）+20+×b：（k+1）×a+×（1﹣k）a×b=×ab+20解ab，得：ab=（1）同理S（矩形ABCD）=ab=S（Rt△FBG）+S（△FGD）+S（Rt△GDC）+S（Rt△AFD）=FB×BG+16+GC×CD+AF×AD=（1﹣k）a×+16++b×a+ka×b=×ab+16解ab，得：ab=32（k+1）（2）根据（1）（2），解得k=，代入（1）或（2），得到S（矩形ABCD）=ab=52cm参和本试卷答题和审题的老师有：rdhx；xiaosh；TGT；duaizh；guangh；pysxzly；xuetao；pyl123；WX321；旭日芳草；chenyr；ycfml12082；kd274826（排名不分先后）菁优网2016年5月22日考点卡片1．角的度量【知识点归纳】1．角的度量：角度的测量是最基本的测量，最常用的工具是量角器．2．角的度量单位通常有两种，一种是角度制，另一种就是弧度制．角度制，就是用角的大小来度量角的大小的方法．在角度制中，我们把周角的看作1度，那么，半周就是180度，一周就是360度．由于1度的大小不因为圆的大小而改变，所以角度大小是一个和圆的半径无关的量．弧度制，顾名思义，就是用弧的长度来度量角的大小的方法．单位弧度定义为圆周上长度等于半径的圆弧和圆心构成的角．由于圆弧长短和圆半径之比，不因为圆的大小而改变，所以弧度数也是一个和圆的半径无关的量．角度以弧度给出时，通常不写弧度单位，有时记为rad或R．3．度量方法：量角要注意两对齐：量角器的中心和角的顶点对齐．量角器的0刻度线和角的一条边对齐．做到两对齐后看角的另一条边对着刻度线几，这个角就是几度．看刻度要分清内外圈．【命题方向】常考题型：例1：用一个放大10倍的放大镜看一个50°的角，看到的角是（）A、50°B、500°C、100°分析：用放大镜看角时，放大的是角的边，不改变角的形状，根据角的大小和边长无关可知角的度数不会改变．解：用放大镜看角时，放大的是角的边，不改变角的形状，根据角的大小和边长无关可知角的度数不会改变．所以用放大10倍的放大镜看一个50度的角，看到的度数仍是50度．故选：A．点评：用放大镜看角，很容易错误认为角的度数会被放大相同倍数，关键要学生理解角的大小和边的长短无关．也要认识到一个普遍规律：放大镜只改变物体大小，不改变物体形状，对角而言只是一种图形，既然形状不变，角度也不会改变．例2：下面每对时刻中，时钟的时针和分针所成的角不一样的有（）。

2014年广东省乡镇考试图形推理练习题及解析

2014年广东省乡镇考试图形推理练习题及解析1.请从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性：【答案】D。

解析：从每行来看，小图形的种类和数量都相同，也可简单看成每行中的黑色图形和白色图形的个数均为3，第三行中已有3个白色图形和2个黑色图形，所以应选择D。

2.请从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性：【答案】D。

解析：每行的前两个图形叠加去同存异得到第3个图形。

3.请从所给的四个选项中，选出最符合上边五个图形一致性规律的选项：【答案】D。

解析：题干中每个图形的封闭区域数均为1，选项中只有D满足。

4.请从所给的四个选项中，选出最符合上边五个图形一致性规律的选项：【答案】C。

解析：题干中各图形线段露头数依次为3、5、1、2、0、(4)，加入4构成连续的自然数。

5.下面四个所给的选项中，哪一选项的盒子不能由左边给定的图形做成?增城中公教育【答案】C。

解析：A、B、D三项均能由左边给定的图形折叠而成，C项两个含三角形的面是相对的，不会相邻，所以C项不能由左边给定的图形折叠而成。

6.【答案】D。

解析：每组图形中，前两个图形相加得到第3个图形，并遵循黑+黑=白，白+白=白，白+黑=黑的规律。

7.【答案】D。

解析：第一组图形中，各图形的直线段数分别为3、4、5;第二组图形中，各图形的直线段数分别为6、7、(8)。

增城中公教育8.【答案】D。

解析：第二组图形完全依照第一组图形的规律变化，且第二组图形里的白色方块相当于第一组图形里的白色椭圆，第二组图形里的白色圆圈相当于第一组图形里的白色三角，第二组图形里的黑色方块相当于第一组图形里的黑色椭圆。

9.【答案】B。

解析：每组图形的第三个图形都是先把第一个图形中的四个小图形逆时针旋转90度，再把第二个图形中的四个小图形顺时针旋转90度，然后再叠加得到的。

10.增城中公教育【答案】A。

解析：开口数量规律，第一组图形分别为2、1、0;第二组图形分别为3、2、(1)。

小学数学苏教版(2014秋)四年级上册第九单元整理与复习图形王国-章节测试习题(1)

章节测试题1.【答题】一个立体图形是由若干个相同的小正方体摆成的，从前面看到的图形是，从左面看到的图形是，摆这个图形最少要用（）个这样的小正方体．A.3B.4C.5【答案】A【分析】如图，一个立体图形是由若干个相同的小正方体摆成的，从前面看到的图形是，从左面看到的图形是，摆这个图形最少要用3块，最多要用6块．【解答】如图，摆这个图形最少要用3块，最多要用6块．故选A.2.【答题】从左面看是的有（）.A.①②⑤B.②③④C.③④⑤【答案】B【分析】此题考查的是观察物体.【解答】由图可知，从左面看①是，看②是，看③是，看④是，看⑤是，所以从左面看是的有②③④.选B.3.【答题】从正面看到的图形是的是（）.A.B.C.【答案】C【分析】此题考查的是从同一方向观察物体.【解答】由图可知，分别从正面观察这三个物体，只有才能在正面看到.故选C.4.【综合题文】看图回答问题.5.【综合题文】看图回答问题.6.【答题】一个由若干个同样大小的小正方体搭成的立体图形，从三个不同的方向看到的图形如下图，那么这个立体图形是由______个小正方体搭成的.【答案】5【分析】此题考查的是根据从三个方向看到的图形，拼摆相应的几何体.【解答】一个立体图形从上面看到的是，则第一层有3个小正方体；从正面看到的是，左面看到的是，则第二层有2个小正方体，立体图形如下：.求这个立体图形是由多少个小正方体搭成，列式计算为：3+2＝5（个）.故答案为5.7.【答题】小明用相同的正方体木块摆出了一个模型，这个模型从三个不同的方向看，符合下图的要求.搭建这个模型需要______个正方体木块.【答案】7【分析】根据从三个不同方向观察到的图形还原几何体，先从一个方向观察到的图形分析，推测可能出现的各种情况；再结合从其他两个方向观察到的图形综合分析；最后确定几何体.【解答】根据从三个不同方向观察到的图形，可以画出几何体，这个模型需要7个正方体木块.8.【答题】如下图，再添上一个同样大小的正方体，使它从左面和正面两个不同位置观察时，所得图形相同，有______种添加方法.【答案】3【分析】先分别画出添加正方体之前几何体从左面和正面看到的图形，再寻找添加一个正方体后使它从左面和正面看到的图形相同时的方法.【解答】由题可知，在添加正方体之前，几何体从左面和正面看到的图形如图所示：添加一个正方体后，使它从左面和正面看到的图形相同，几何体可以变为如图所示：此时从左面和正面看到的图形都为.所以有3种添加方法.9.【答题】丽丽用几个完全一样的小正方体摆了一个图形，从上面看是，从左面看是，从前面看是，这个图形由______个小正方体组成.【答案】4【分析】从不同位置观察由小正方体拼摆的物体，辨认观察到的物体的形状的方法：在哪一位置观察物体，就从哪一面数出小正方体的数量，并确定摆出的形状.【解答】丽丽用几个完全一样的小正方体摆了一个图形，从上面看是，从左面看是，从前面看是，则这个图形最下面一层有3个小正方体，第二层有1个小正方体，所以这个图形由4个小正方体组成.10.【答题】用若干个小正方体堆成一个立体图形，下面是从正面和上面看到的平面图形，这个立体图形最多有______个小正方体，最少有______个.【答案】16 10【分析】从正面和上面看到的图形出发还原立体图形即可.【解答】用若干个小正方体堆成一个立体图形，题中的图形是从正面和上面看到的平面图形，当这个立体图形有最多的小正方体时，如图所示：，其中数字表示该位置小正方体的个数，此时一共有小正方体：3×5+1=16（个）；当这个立体图形有最少的小正方体时，如图所示：，此时一共有小正方体：3×2+1×4=10（个），所以这个立体图形最多有16个小正方体，最少有10个. 11.【答题】一个由正方体组成的图形，从正面、左面、上面观察分别是：这是由______个正方体组成的立体图形.【答案】5【分析】此题考查的是根据三视图拼摆物体.【解答】根据从正面、左面、上面观察得到的图形可知，正方体拼摆物体图示如下：所以这是由5个正方体组成的立体图形.故答案为5.12.【答题】一个图形是由小正方体搭成的，从不同方向看到的形状如下，这个图形一共用了______个小正方体.【答案】7【分析】根据从三个不同方向观察到的图形还原几何体，先从一个方向观察到的图形分析，推测可能出现的各种情况；再结合从其他两个方向观察到的图形综合分析；最后确定几何体.【解答】从左面看，一共有2层小正方体，第1层有2排小正方体，第2层有1排小正方体；从上面看，第1排有1个小正方体，第2排有4个小正方体；从正面看，第1层有4个小正方体，第2层有2个小正方体.因此第1层第1排有1个小正方体，第1层第2排有4个小正方体，第2层有2个小正方体，因此这个图形一共用了小正方体：1+4+2=7（个）.故如图所示：13.【答题】下面的立体图形，从左面能看到______个正方形，从上面能看到______个正方形，从正面能看到______个正方形.【答案】2 4 3【分析】本题考查从不同的方向观察物体.【解答】由图可知，从左面能看到2个正方形，从上面能看到4个正方形，从正面能看到3个正方形.故此题的答案是2,4,3.14.【答题】下图是由若干个小正方体搭成的立体图形，它共有______个这样的小正方体.【答案】10【分析】此题考查的是观察物体.【解答】由图可以看出，前排有2个小正方体，中间一排有4个小正方体，后排有4个小正方体，则小正方体的个数总计为：2+4+4＝10（个）.故本题的答案是10.15.【答题】仓库里有一堆存放货物的正方体纸箱，从三个不同的方向看到的图形如下：这堆货物至少有______箱.【答案】9【分析】从不同方向观察组合立体图形，先结合三个方向看到的图形，再判断总共的层数，以及每一层纸箱的数量，综合分析一共有纸箱的数量.【解答】根据从上面看到的图形可知，这堆纸箱至少有5箱，再从正面和左面的图形看，共有3层，从上往下数，第一层有1箱，第二层有3箱，第三层有5箱，则这堆货物有：1+3+5＝9（箱）.立体图形如下：，故此题的答案是9.。

2014年学而思综合能力测评(学而思杯)数学试卷详解(一年级)

所代表的三位数是
．
【答案】369 【题目解析】由第一个式子，“而”和两个“学”一样大，所以由第二个式子，三个“学”和 9 一样大，那么“学”就
是 3，“而”就是 6，由第三个式子，“思”是 9 【考察知识】数字谜【知识体系】一年级寒假（二级上）——加、减竖式我会算
9. 春天到了，艳子老师带着一群小朋友排成“一”字队形去植树．从前向后数，艳子老师排第 8 个；从后向
以中国是第一【考察知识】逻辑推理【知识体系】一年级春季（二级下）——智趣推理
三、超常挑战（每题 12 分，共 60 分）
11. 小翠妈妈买了两块大正三角形（即三条边一样长的三角形）披萨，并把它们叠放在一起（如下图），妈妈告诉小翠，每个小正三角形一样大并且都是 1 元钱，那么这两块大正三角形披萨总共是元钱．
美国运动员说：俄国运动员紧跟在我后面；
俄国运动员说：我才不是最后一名；
中国运动员说：我比日本国人和美国人都快；
韩国运动员说：有三个人比我先到达终点．
那么，
国运动员是第一名．（填写国家名）
【答案】中【题目解析】中国比日本、美国快，美国比俄国快，所以日本、美国、俄国都不是第一，而韩国也不是第一个到的，所
6. 小俊去快餐店买汉堡套餐，每种套餐包括一个汉堡和一包薯条，现在快餐店有 3 种汉堡和两种薯条（如图），
那一共有
种不同的搭配方法．
【答案】6
【题目解析】搭配方式如图
【考察知识】搭配组合【知识体系】一年级春季（二级下）——我会排一排
7. 在下面算式的“□”中填入合适的“＋”或“－”符号，使得结果尽可能大，那么，结果最大是
1
1
1
那么“好”只能是 8 或 9，逐一尝试

六年级上册数学同步拓展-空间与图形趣味数学含解析-人教新课标(2014秋)

趣味数学数学小故事：靶上的爬虫某班战士进展打靶训练，靶上的那些圆环如下图，由间距相等的同心圆构成。

训练完毕后，战士们就地休息。

班长发现两只小虫在靶上慢悠悠地爬行，他灵机一动，向战士们说：“我们不但要学军事，而且还要学文化。

大家看，靶上的这些圆环宽度都是一样的。

假设上面这2只小虫都是匀速地爬行，并且两者速度一样。

如果1只沿最外层环的外缘爬行l周与沿内缘爬行l周所需时间的差为T1，而另1只沿最内层环的外缘、内缘各爬行1周所需时间的差为T2。

请问，T1和T2哪个大些？〞“外层的环比内层的大多了，当然T1比T2大。

〞有几个战士不假思索地答道。

他们的答复对吗？答案：我们假设最外层外缘距离靶心的距离是R1，最外层边缘距离靶心的距离是R2，那么小虫沿最外层外缘爬行一周的长度是：2πR1，沿最外层内缘爬行一周的长度是：2πR2。

内外缘爬行的距离差是2πR1－2πR2＝2π〔R1－R2〕。

同样，我们再假设最内层外缘距离靶心的距离是r1，最内层边缘距离靶心的距离是r2，那么小虫沿最内层外缘爬行一周的长度是：2πr1，沿最内层内缘爬行一周的长度是：2πr2。

内外缘爬行的距离差是2πr1－2πr2＝2π〔r1－r2〕。

因为小虫的爬行速度一样，比拟内、外两层的爬行时间差，只要比拟内、外层的爬行距离差就可以了。

而我们知道内层和外层的内、外缘与靶心的距离差一样，也就是R1－R2＝r1－r2。

所以，战士的答复是错误的，T1和T2应该是一样大。

生活中的圆圆在日常生活中可以说是随处可见。

我们这里仅仅举两个小例子。

例一，为什么下水道的盖子是圆形的？如果留意一下，会发现街上下水道的盖子几乎都是圆的，可是，为什么要做成圆的呢？做成其他形状的，比方正方形不好吗？这个问题最早是微软公司招聘员工时的面试题，并且很可能是微软最有名的面试问题。

事实上，由于曝光率太高，微软公司在面试中已经停顿使用这一问题了。

对这个问题的最好答复是：其他形状的盖子会有一个角度让井盖掉下去，但如果井盖做成圆形的，只要直径大于井口一点，那么无论从哪个角度都不会掉下去！比方正方形，因为正方形的对角线比它的边长要长，所以如果把一个正方形盖子立起来，稍微一转，它就会很容易掉到下水道里去。