第四章投入产出模型应用
第四章投入产出系数和模型
我们最终得到完全消耗系数矩阵应为:
B A A2 A3 Ak
B I I A A2 A3 Ak
而(I A)(I A A2 Ak )
I Ak (k ) I
因此,我们得到
B I (I A)1 B (I A)1 I
0.1737
0.3475 0.1969 0.1931
0.5019 0.6178 0.3900
根据 Q (I A)1Y计算得:
Q1 1.3127 Q2 0.0722 Q3 0.1737
0.3475 1.1969 0.1931
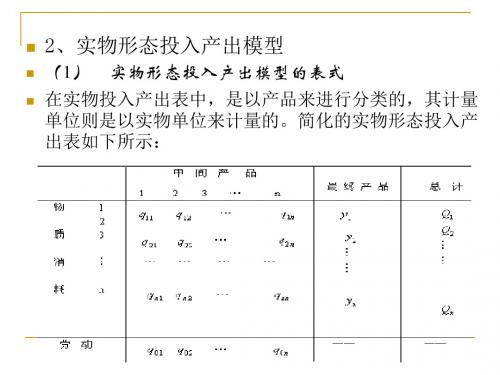
2、实物形态投入产出模型
(1) 实物形态投入产出模型的表式
在实物投入产出表中,是以产品来进行分类的,其计量 单位则是以实物单位来计量的。简化的实物形态投入产 出表如下所示:
上表的简要解释:
从行向看,反映的是各类产品的分配使用情况,其
中一部分作为中间产品供其它产品生产中使用(消 耗),另一部分则作为最终产品供投资和消费使用, 两部分相加就是一定时期内各类产品的生产总量。从 列向看,反映了各类产品生产中要消耗其它产品(包 括自身)的数量。但应指出的是,由于列向各类产品 的计量单位不一致,故不能进行运算,因此,实物投 入产出模型只有行模型没有列模型。
出来,则对了解和分析国民经济各部门间、产品间的内
在联系,搞好宏观经济结构的分析和预测是有很大帮助
的。
下面通过一图形来具体解释一下各种间接消耗关系 的含义。
完全消耗系数的定义——每生产单位j种(部门)最终
产品要直接、各种间接消耗(即完全消耗)i种(部门)
产品的数量。一般用来表示 数矩阵。
第4章 投入产出核算

中
产间 出投 部入
门
(
部门1 部门2
部门n
x11 x12 x1n ∑x1j f1
q1
x21 x22 x2n ∑x2j f2
q2
xn1 xn2 xnn ∑xnj fn
qn
)
小 计 ∑xi1 ∑xi2 ∑xin ∑∑xij ∑fi ∑qi
实物型投入产出表
中
产间 出投 部入
门
(
部门1 部门2
部门n
投 入 部 门 (中 间 产 品) 最终 总产出
部门 1 部门 2 部门 n 小 计 产品
x*11 x*12 x*1n ∑x*1j f*1
q*1
x*21 x*22 x*2n ∑x*2j f*2
q*2
x*n1 x*n2 x*nn ∑x*nj f*n
q*n
)
小 计 ∑xi1 ∑xi2 ∑xin ∑∑xij ∑fi ∑qi
固 定 资 产 折 旧 d1 d2 dn ∑dj
最 劳 动 者 报 酬 v1 v2 vn ∑vj
初
投 生 产 税 净 额 s1
s2
sn
∑sj
入 营 业 盈 余 m1 m2 mn ∑mj
增 加 值 y1 y2 yn ∑yj
(二)投入产出表的四大象限 暂不考虑作为合计数的“总投入”行与“总产出”列以
及生产部门的“小计”栏,可将投入产出表划分为四 大象限,分别表达特定的经济内容。
Ⅰ.中间流量
Ⅱ.最 终产品
Ⅲ.最初投入
(Ⅳ)
10
第Ⅰ象限(中间产品或中间消耗):核心。反映各部
投入产出模型应用

投入产出模型应用
一、投入产出分析的主要内容
• 投入产出表是进行结构分析的一种有力工具。 利用投入产出量化分析工具,分析产业关联中有关产
业间比例、产业内的投入结构、分配或销售结构, 以及产业间联系广度、深度等有关“结构分析”的 主要问题和内容。 (一)各产业部门的产出结构和投入结构 在投入产出表中,横行表示每个产业的总产出或总产 品是由中间产品和最终产品组成;也就是说每个行 业的产品需求,都可以分为所有产业对该产业的需 求(中间需求)以及由积累、消费以及净出口组成 的最终需求。所以,中间需求和最终需求的构成比 例反映了经济结构的一个重要特征。
重要的地位,这也是制定产业政策时确定主导产业的主 要依据之一 • 产业关联度基准的指标是产业关联度,它是产业的影响 力系数和感应度系数之和 。影响其他产业的波及作用 称作影响力系数,受到其他产业波及作用的叫做感应19度。
• 感应度系数=
该产业横行逆阵系数的 平均值
全部产业横行逆阵系数 的平均值的平均
按照中间需求率和中间投入率划分的产业群如果把中间需求率作为横轴把中间投入率作如果把中间需求率作为横轴把中间投入率作为纵轴建立平面直角坐标系并依据投入产出表为纵轴建立平面直角坐标系并依据投入产出表中的数据分别计算各产业的中间需求率和中间投入中的数据分别计算各产业的中间需求率和中间投入率然后把他们归类于四个象限中就可以形成一率然后把他们归类于四个象限中就可以形成一个产业立体结构图
4-4投入产出模型(I0)

产出 投入 农业 制造业 服务业 劳动 总投入
中间产品 农业 40 40 0 120 200 制造业 80 40 80 200 400 服务业 0 20 20 160 200
最终产品 总产品 80 300 100 20 500 200 400 200 500 1300
投入产出模型(I/O)
农业 0.2 0.1 0.0 0.15
最终产品 160 300 50 10
总产品 400 400 100 250
80
制造业 0.4 0.1 0.1 0.25
表3 直接消耗系数 服务业 0.0 0.2 0.1 0.8
投入产出模型(I/O)
2、投入产出表中的基本关系
完全消耗系数
完全消耗矩阵包含了直接消耗与全部间接消耗。
投入产出模型(I/O)
2、投入产出表中的基本关系
产出分配方程:
在投入分配表中,每一行满足以下关系:
xi xij yi
j 1
n
i 1,2,, n
(式1)
每一部门的总产出,等于该部门流向各部门作为中间消 耗用的产品(包括自身消耗)与提供给社会的最终产品之和。
投入产出模型(I/O)
等式两边消去相同项xij,则得
x
j 1 j i
n
ij
yi x ji zi
j 1 j i
n
i 1,2,, n
投入产出模型(I/O)
2、投入产出表中的基本关系
直接消耗系数 由表1可知,生产400单位的农业产品需要投入80单位农产品、 40单位制造业产品以及60单位的劳动。现在要问,如果要生产 500单位的农产品,需要各种投入量将是多少?在投入产出法中 采用了线性假设:当产出的水平变动幅度不大时,所需要的各种 投入量按比例变动。这种假设是我们能够根据一个给定的投入产 出表来计算各种产出水平时需要的投入量。 Eg:要生产500单位农产品,其投入需要量就可以将表中第1列数据 乘以1.25得到,即需要投入100单位农产品,50单位制造业产品 以及75单位的劳动。 表示第j部门生 为了计算与分析的方便,我们引入直接消耗系数aij: 产单位产品所需
投入产出分析论文 投入产出模型应用与分析
投入产出模型应用与分析一、投入产出分析简介投入产出分析,是研究经济系统各个部分间表现为投入与产出的相互依存关系的经济数量方法。
投入是进行一项活动的消耗。
如生产过程的消耗包括本系统内各部门产品的消耗(中间投入)和初始投入要素的消耗(最初投入)。
产出是指进行一项活动的结果。
如生产活动的结果是为本系统各部分生产的产品(物质产品和劳务)。
瓦西里·列昂剔夫(Wassily W.Leontief,1906—1999)是投入产出账户的创始人。
投入产出表同时表现了社会产品的实物分配和价值构成,全面反映了社会再生产中各部门的经济联系。
利用投入产出表及其数学模型,通过确定一些十分重要的经济参数,可以深入分析国民经济的各种重大比例和经济结构,这就对社会再生产过程进行系统的经济分析提供了非常有用的工具。
价值型投入产出表是根据国民经济各产品部门本期生产活动的产品与服务的分配去向和消耗来源排列而成的一张棋盘式平衡表。
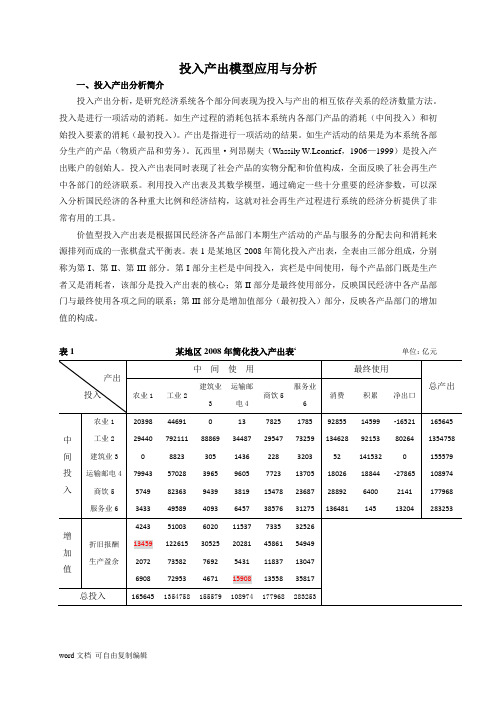
表1是某地区2008年简化投入产出表,全表由三部分组成,分别称为第I、第II、第III部分。
第I部分主栏是中间投入,宾栏是中间使用,每个产品部门既是生产者又是消耗者,该部分是投入产出表的核心;第II部分是最终使用部分,反映国民经济中各产品部门与最终使用各项之间的联系;第III部分是增加值部分(最初投入)部分,反映各产品部门的增加值的构成。
表1 某地区2008年简化投入产出表i单位:亿元二、投入产出模型(一)建立模型 1.行模型(1)建立行模型:i i X y nj ij x =+∑=1 (i =1,2,...,n) 引入直接消耗系数 ij a ,即:ij a =ij x /j X可得:i i X y jX nj ij a =+∑=1即用矩阵表示为: AX+Y=X化简后可得价值型行数学模型: X=(I-A)-1Y 或 X=B Y (2)计算相关矩阵A ,B=(I-A)-1-I ,B =(I-A)-1 =B+I直接消耗系数矩阵:A=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.1104 0.21680.05930.0263 0.0366 0.0207 0.0836 0.0870 0.0350 0.0607 0.0608 0.0347 0.0484 0.0434 0.0881 0.0255 0.0421 0.4826 0.0113 0.00130.0132 0.0020 0.0065 0.0000 0.2586 0.1660 0.3165 0.5712 0.5847 0.1777 0.0063 0.04400.0001 0.0000 0.03301231.0完全消耗系数矩阵:B=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.22350.34120.16110.1660 0.1902 0.1696 0.1885 0.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 0.1908 0.1689 0.2174 0.7095 0.02270.0133 0.0250 0.0178 0.0240 0.0197 1.00730.87641.11911.7485 1.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12040.1976完全需要系数矩阵:B =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12041.1976(3)价值型行数学模型 X=(I-A)-1Y=B Y⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.17310.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.1204 1.1976⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321Y Y Y Y Y Y2列模型 (1)建立列模型j j j j j X s t v d ni ij x =++++∑=1 (j =1,2,...,n)引入直接消耗系数 ij a 可得:j j j j j X s t v d j X ni ij a =++++∑=1即用矩阵表示为:AcX+N=X化简后可得价值型列数学模型: X=(I-Ac)-1N (2)计算相关矩阵A C ,(I-Ac)-1物耗系数矩阵:Ac=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.5187000000 0.5584000000 0.5122000000 0.6856000000 0.76370000000.8389增加值系数矩阵:(I-Ac)-1=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 2.0775*******.26440000002.0500000003.181********.231590000006.2081(3)价值型列数学模型 X=(I-Ac)-1N⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ 2.0775*******.26440000002.05000000003.181********.231590000006.2081⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321N N N N N N ij x :第i 部门(行部门)生产的产品或服务分配给第j 部门(列部门)用于生产消耗的产品产值;第j 部门(列部门)生产过程中直接消耗第i 部门的产品或服务的产品产值;i y :第i 部门在本期产品中提供的最终使用额,包括消费和积累;j d 、j v 、j t 、j s :分别为第j 部门的折旧,劳动报酬,生产税净额,和营业盈余; j m :为第j 部门的社会纯收入,等于j t +j s ; j N :为第j 部门的增加值,等于j d +j v +j t +j s ;i X :第i 部门总产出 ;j X :第j 部门总投入;A :直接消耗系数矩阵(ij a )n n ⨯X=(X 1 X 2.......X N )T —总产出的列向量;Y=(y 1 y 2.......y N )T —最终使用的列向量;j i ,=1,2,3,4,5,6分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门;n =6。
投入产出模型的应用

投入产出分析在XX中的应用投入产出分析在xx的应用一、投入产出简介投入产出是国民经济各部门间投入原材料和产出产品的平衡关系。
投入产出分析是由俄罗斯裔美国经济学家瓦西里·列昂惕夫(Wassily Leontief 1905-1999)创立的。
主要应用数学方法和电子计算机,研究各部门间这种平衡关系的一种现代管理方法。
其理论基础是瓦尔拉的一般均衡理论。
投入产出分析主要通过编制投入产出表来实现的。
投入产出表是由投入表与产出表交叉而成的。
前者反映各种产品的价值,包括物质消耗、劳动报酬和剩余产品;后者反映各种产品的分配使用情况。
在投入产出表的基础上,可以建立相应的数学模型。
例如,产品平衡模型、价值构成模型等,用以进行经济分析、政策模拟、计划论证和经济预测。
应用最早的是美国劳工部劳动统计局,于1942- 1944年编制了美国1939年投入产出表,利用这张表来研究美国的经济结构,预测战后美国的钢铁工业的生产和美国的就业情况,制定战时军备生产计划,研究裁军对美国经济的影响,收到了良好的效果。
由此,得到了美国政府和经济学界的重视,引起了世界各国的关注。
由于投入产出表的科学性、先进性和实用性,自50年代以来世界各国纷纷研究投入产出分析、编制和应用投入产出表。
到1990年,除个别国家外,世界上绝大多数国家都编制了投入产出表。
投入产出原理也得到了发展,由静态模型向优化模型发展,并应用到各个方面来研究宏观经济问题。
投入产出分析在我国的应用主要经历了以下几个阶段:1、初步研究及引入阶段。
五十年代末六十年代初,在著名经济学家孙冶方和著名科学家钱学森倡导下,经济理论界和一些高等院校开始研究投入产出理论。
"文革"期间,此项工作几乎中断。
2、快速发展阶段。
1974年,为研究宏观经济发展情况的需要,在国家统计局和国家计委的组织下,由国家统计局、国家计委、中国科学院、中国人民大学等单位联合编制了1973年全国61种产品的实物型投入产出表。
投入产出分析的应用

投入产出分析的应用1. 简介投入产出分析是一个用于评估经济活动影响的方法。
它用于衡量投入与产出之间的关系,并揭示出资资源如何在一个经济系统中被配置和分配。
投入产出分析可以帮助政府、企业和其他机构制定合理的经济政策,开展可行的项目,并评估各种决策的经济效益。
2. 概念和原理投入产出分析的基本概念包括投入、产出、中间需求和最终需求。
•投入:指用于生产物品和提供服务的资金、劳动力和资源。
•产出:指在一个经济系统中生产的物品和服务。
产出可以分为直接产出和间接产出。
直接产出是指生产者直接生产出的物品和服务,而间接产出是指通过中间需求和最终需求引发的其他行业的产出。
•中间需求:指一个行业为了生产其最终产出而需要购买的来自其他行业的产品和服务。
•最终需求:指最终用户需求的产品和服务,包括个人消费、政府采购、出口和固定资本投资等。
投入产出分析的核心原理是通过构建一个投入产出模型来描述投入和产出之间的关系。
投入产出模型采用一个矩阵来表示不同产业之间的相互关系。
通过矩阵运算可以得到各个产业的投入和产出之间的关系系数,如产出弹性、投入密度和技术变迁指数等。
3. 投入产出分析的应用领域3.1 经济政策制定投入产出分析可以帮助政府制定合理的经济政策。
通过该分析,政府可以了解不同行业之间的相互依赖度,以及对外依赖度。
政府可以根据这些信息来确定优先发展的产业,调整税收政策,促进经济发展和结构优化。
3.2 项目可行性评估投入产出分析可以用于评估项目的可行性。
通过分析项目的投入产出关系,可以预测项目的经济效益和潜在风险。
这有助于企业和投资者做出明智的决策,选择具有良好经济前景的项目。
3.3 决策支持投入产出分析可以为决策提供支持。
通过分析不同决策的影响,可以评估其对经济的影响。
这有助于决策者制定合理的决策方案,最大限度地提高经济效益。
3.4 区域经济分析投入产出分析可以用于区域经济分析。
通过分析不同行业和地区之间的投入和产出关系,可以了解不同地区的经济特点和优势。
投入产出-CGE模型及其应用

农业
4637
10168
16339
1105
-207
714
28579
中 间 投 入
工业
第Ⅰ 象限 5043
2269
100613
23493
129149
18936
41858
第Ⅱ象限 -458
第 Ⅱ象限 -458 1074
4667 -1187
190559
服务业
24677
19138
46084
42127
2602
94293
合计
135458
44166
305491
71691
45565
4002
601
313431
劳动者报酬
13316
22519
23116
77571
0
生产税净额 增 加 值
545
10249
Part
2
Part 1
Part 2
01
Part 3
Part 4
我们做过什么研究
02
“十一五”环保投入对经济拉动贡献研究
03
“大气行动计划”的社会经济、资源环境影响
04
“十二五”期间减排目标可达性分析
05
中国区域间虚拟大气污染物转移与环境公平
10
Part 1
Part 2
Part 3
Part 4
旅游规划实施的区域经济影响分析
旅游规划方案
解
基础设施 其它用品 其他服务
休闲娱乐设施
旅游规划区域经济影响评价软件框架
投入产出分析原理及应用

投入产出分析原理及应用投入产出分析是一种衡量经济活动效率的方法,主要用于度量一个经济体的产出与投入之间的关系。
它可以帮助决策者了解经济活动的效率水平,以及优化资源配置。
本文将介绍投入产出分析的原理、计算方法和应用。
投入产出分析的核心原理是通过建立产出与投入的关系模型,来衡量经济体所需的投入资源与其产出之间的关系。
一般来说,投入产出模型包括产出矩阵和投入矩阵。
产出矩阵以列向量的形式表示一个经济体所产出的各种产品或服务。
而投入矩阵则以行向量的形式表示经济体所使用的各种资源或要素。
这些矩阵之间的乘积将得出一个产出向量,它表示了经济体所能产出的各种产品或服务。
投入产出分析的关键在于计算投入产出矩阵。
一般情况下,投入产出矩阵可以通过调查和统计数据获得。
在计算投入产出矩阵时,我们需要注意考虑到投入产出关系的复杂性,例如资源之间的相互依赖关系和技术进步的影响。
利用投入产出矩阵,我们可以计算出一系列有关经济体效率的指标。
其中最重要的指标是生产率。
生产率是指单位投入资源所产出的产出量。
在投入产出分析中,我们可以通过计算产出矩阵与投入矩阵的乘积,再与投入矩阵相除得到一个生产率矩阵,从而衡量各种经济活动的效率水平。
投入产出分析的应用非常广泛。
首先,它可以用于优化资源配置。
通过衡量各种经济活动的效率,我们可以发现资源配置中的问题,并调整产业结构,实现资源的最佳利用。
例如,当某一部门的生产率较低时,我们可以考虑增加该部门的资源投入,以提高其产出。
而当某一部门的生产率过高时,我们可以减少其资源投入,以优化整体资源利用效率。
其次,投入产出分析可以用于预测和规划经济活动。
通过对历史数据的分析和对未来的预测,我们可以建立模型来预测某一经济体在特定条件下的产出和投入状况。
这对经济决策者来说非常重要,因为他们可以根据这些预测结果来制定合理的经济政策和规划。
此外,投入产出分析还可以用于评估政策和项目的影响。
通过建立一个投入产出模型,我们可以评估某一政策或项目对经济体的影响。
投入产出模型

投入产出模型
投入产出模型是一种经济分析工具,用于衡量一个产业或
经济体所产出的产品或服务与输入的资源之间的关系。
它
旨在测量和评估经济发展、资源利用和产业结构的效率和
影响。
投入产出模型的核心假设是经济体中各个产业之间存在着
相互依赖的关系。
模型以一个输入输出表的形式展现,其
中列出了各个产业的生产量和使用量。
这个矩阵描述了每
个产业之间的原始输入和最终产品流动的关系。
在投入产出模型中,产出是指一个经济体或产业所生产的
最终产品或服务的总量。
这些产出可以是消费品、投资品、政府服务等。
投入是指用于生产这些产出所需要的各种资源,如劳动力、资本、原材料等。
通过分析投入产出表,可以计算出不同产业之间的直接效
应和间接效应。
直接效应是指一个产业的产出对其他产业
的需求所产生的影响。
间接效应则是指这些产业间的相互依赖关系所带来的效应。
投入产出模型还可以计算出各个产业的乘数效应,即每一单位的最终需求对总产出的影响程度。
投入产出模型可以很好地衡量不同产业之间的相互关系,并为政府制定政策、企业进行决策提供指导。
它可以帮助分析经济体的结构和变化趋势,评估政策的影响和效果,以及预测经济增长和资源利用的潜在影响。
投入产出模型

系统控制方法——投入产出分析模型及其应用投入产出分析是将研究对象视为黑箱,通过系统的输入与输出分析研究,来判断和了解系统的状态、行为和功能。
具体地讲,它是研究管理系统各个部分间表现为投入与产出相互关系的经济数量分析方法。
在微观管理系统, 所谓投入是指产品生产所需原材料、辅助材料、燃料动力、固定资产折旧和劳动等等;所谓产出是指产品生产的总量及其分配使用方面的数量,如生产消费、外销量及增加储备等等,其中生产消费称为中间产品,外销产品和增加储备称为最终产品。
投入产出分析法最初是由国民经济各个产业部门(工业,农业等)间的联系发展起来的,故称其为部门联系平衡法或产业关联法,但它的应用十分广泛,不仅可应用于国民经济、地区经济的综合平衡,也可以有效地应用于企业内部的综合平衡,尤其适用于产品种类繁多,产品间联系复杂的企业。
在企业中应用投入产出分析通常包括三个步骤:一是编制投入产出表,二是建立投入产出数学模型;三是应用模型进行经济分析或实施优化分析。
一、企业投入产出表企业投入产出表按其用途不同和计量单位分为实物型投入产出表和价值型投入产出表两类。
现分述于下(一)实物型投入产出表企业实物型投入产出表的基本格式如表1所示。
实物型表包括四个象限(部分)。
Ⅰ象限是本企业自产产品用于本企业生产消耗的数量(以产量表示,)是反映企业内部中间产品间的技术联系,现以X ij代表本企业第i种自产产品用作第j种产品生产的消耗数量,称之为流量,表的这一部分称之为自产产品流量矩阵,以符号[X ij]表示,是一个方阵,表内i,j=1,2,…,n;Ⅱ象限(部分)是本企业自产产品的最终产品数量,包括外销产品、增加库存的数量及其他用途的数量,以Y i表示;Ⅲ象限(部分)是本企业生产中外购产品用作中间产品消耗的数量,以符号U ij表示外购产品i用于本企业第j种产品的生产消耗数量,表的这一部分称为外购产品流量矩阵,以[U ij]表示,基中的i=1,2,…,m为外购产品的品种数。
投入产出模型在产业结构调整中的应用

投入产出模型在产业结构调整中的应用摘要:随着经济全球化和市场竞争不断加剧,产业结构调整成为不可避免的趋势。
投入产出模型作为一种经济分析工具,可以帮助我们更好地理解和应对产业结构调整过程中的挑战和机遇。
本文将介绍投入产出模型的基本概念和原理,并探讨其在产业结构调整中的应用。
1. 引言产业结构调整是指在一定时间和空间范围内,不同产业之间的比重和地位发生变化的过程。
这种调整是经济发展中的必然现象,既是经济增长的推动力,也是适应外部环境变化的必要需求。
在产业结构调整中,投入产出模型可以提供有力的支持和指导。
2. 投入产出模型的概念和原理投入产出模型是一种用于描述一个经济系统内部各个部门之间相互依存关系的模型。
它基于产出与产业间的投入关系,通过建立一系列的线性方程组来描述投入和产出之间的关系。
投入产出模型的核心是投入产出表,该表将各个产业之间的投入和产出进行了全面而系统的记录和统计。
投入产出模型的原理是基于两个核心假设:一是所有生产要素市场完全竞争;二是经济体内的资源配置效率较高。
在这个模型中,有两种类型的投入:内部投入和外部投入。
内部投入指的是一个行业用于生产自身产品所需的投入,而外部投入则是指一个行业用于生产其他行业产品所需的投入。
3. 投入产出模型在产业结构调整中的应用(1)产业结构分析:投入产出模型可以通过分析投入和产出之间的关系,帮助我们了解不同产业之间的联系和依存关系。
通过计算不同产业的关联度系数和投入引力指标,我们可以评估产业结构的合理性,识别出各个产业的关键驱动因素,从而指导产业结构的调整和优化。
(2)产业链推演:投入产出模型还可以通过对产品和服务供应链的分析,揭示出产业之间的上下游关系和产业链的结构。
通过对产业链的推演,我们可以找到具有潜力的新兴产业和关键环节,为产业结构的调整和升级提供重要依据。
(3)就业和收入分析:投入产出模型可以帮助我们分析产业结构调整对就业和收入的影响。
通过考虑不同产业之间的劳动力投入和收入分配,我们可以评估产业结构调整对就业机会和社会福利的影响,从而制定相应的劳动力政策和社会保障措施。
投入产出模型的分析应用

钢材
水泥 水
利
电力
建
筑
劳务
业
┇ 居民
• 后向部门
防洪除涝 工业及居民供水 灌溉 水电 内河航运 淡水养殖
┇
前向部门
• 通过后向部门所产生的效应即水利基建投 资的后向效应(后向效益)
• 通过前向部门所产生的效应即水利基建投 资的前向效应(前向效益)。
• 投入产出技术与前向联系和后向联系 • 60年代
润部分的增加值比率
• 那么投入产出系统中的产出决定可以表示
为:
X 1 F 1
1
I
1 a 1 a 1 (c1d1 c2d2 )
1
1
I
1 a 1 c1v1 c2v2
1 a
• 现在将上面的这一投入产出乘数再恢复到 含多部门的矩阵形式。
• 为此,将把上面表1中的中间流量划分为n 个部门,同时把第三象限的收入划分为r个 收入群体,这样使第一象限成为一个n*n矩 阵,第三象限成为一个r*n矩阵。
• 以 Ai 表示前向联系
i A • T 表示后向联系
• 70年代
• 以表示 iT (I A)1 后向联系 • 以 (I A)1i 表示前向联系
• 如, iT (I A)1 表示单位最终产品对国
民经济各部门的拉动作用之和。
• 标准化:*影响力系数(后向系数),令 B~ (I A)1
•
Fj
局部闭模型
• 通常把居民作为内生部门,也就是把最终需求的 一部分放到中间流量中,加以内生化,称为局部 闭模型
• 原因:
– 第一、劳动报酬与材料、动力等相似,与生产大致上 具有线性关系。
– 第二、居民劳动报酬对各部门生产具有连锁反应,即 劳动报酬增加后,居民对各部门产品和劳务的需求必 然随之而扩大,从而刺激各部门生产的发展,这种连 锁反应在通常的投入产出开模型中反映不出来,利用 局部闭模型可以反映出来。
投入产出模型的应用

投入产出分析在XX中的应用投入产出分析在xx的应用一、投入产出简介投入产出是国民经济各部门间投入原材料和产出产品的平衡关系。
投入产出分析是由俄罗斯裔美国经济学家瓦西里·列昂惕夫(Wassily Leontief 1905-1999)创立的。
主要应用数学方法和电子计算机,研究各部门间这种平衡关系的一种现代管理方法。
其理论基础是瓦尔拉的一般均衡理论。
投入产出分析主要通过编制投入产出表来实现的。
投入产出表是由投入表与产出表交叉而成的。
前者反映各种产品的价值,包括物质消耗、劳动报酬和剩余产品;后者反映各种产品的分配使用情况。
在投入产出表的基础上,可以建立相应的数学模型。
例如,产品平衡模型、价值构成模型等,用以进行经济分析、政策模拟、计划论证和经济预测。
应用最早的是美国劳工部劳动统计局,于1942- 1944年编制了美国1939年投入产出表,利用这张表来研究美国的经济结构,预测战后美国的钢铁工业的生产和美国的就业情况,制定战时军备生产计划,研究裁军对美国经济的影响,收到了良好的效果。
由此,得到了美国政府和经济学界的重视,引起了世界各国的关注。
由于投入产出表的科学性、先进性和实用性,自50年代以来世界各国纷纷研究投入产出分析、编制和应用投入产出表。
到1990年,除个别国家外,世界上绝大多数国家都编制了投入产出表。
投入产出原理也得到了发展,由静态模型向优化模型发展,并应用到各个方面来研究宏观经济问题。
投入产出分析在我国的应用主要经历了以下几个阶段:1、初步研究及引入阶段。
五十年代末六十年代初,在著名经济学家孙冶方和著名科学家钱学森倡导下,经济理论界和一些高等院校开始研究投入产出理论。
"文革"期间,此项工作几乎中断。
2、快速发展阶段。
1974年,为研究宏观经济发展情况的需要,在国家统计局和国家计委的组织下,由国家统计局、国家计委、中国科学院、中国人民大学等单位联合编制了1973年全国61种产品的实物型投入产出表。
4-4投入产出模型(I0)

0.2 0.4 0 A 0.1 0.1 0.2 0 0.1 0.1
0.326 0.604 0.134 B ( I A) 1 I 0.151 0.208 0.268 0.017 0.134 0.141
0.8 - 0.4 0 I A 0.1 0.9 0.2 - 0.1 0.9 0 1.326 0.604 0.134 ( I A) 1 0.151 1.208 0.268 0.017 0.134 1.141
总产 出 x1 x2
Ⅰ
Ⅱ
n xn1 xn2 合计 折旧
xnn
ynxn新创Fra bibliotek 的价值工资 利润等
合计
d1 d2 dn v1 v2 Ⅲ vn
m1 m2 mn
Ⅳ
投入产出模型(I/O)
1、投入产出表
投入产出表中的部门,既不是通常在经济管理中按隶属关系划分的行 政部门,也不是一般在计划统计中按同类生产企业组成的经济部门, 而是由所用材料相同、工艺技术相同、经济用途相同的同类产品组成 的生产部门,即产品部门,又叫“纯部门”。 部门划分的多少,须根据计划工作和经济分析工作的需要而定。 部门分的较少,将许多部门归并成一个部门,影响资料的准确性;如 果分得太细,则收集资料和编制表格的工作量很大,而且投入产出表 中等于零的xij机会就多,填满率会较低。美国曾经计算过填满率 根据国外经验,部门划分的数目一般在20~200之间为宜。 划分的部门(部门个数) 不等于零的格子数 填满率/% 17 31 85 188 279 804 3846 10245 96.5 83.6 53.5 28.9
投入产出模型(I/O)
投入产出模型的推广及其应用

投入产出模型的推广及其应用投入产出模型是一种经济分析工具,用于评估一个经济体中不同部门之间的相互依赖关系和资源流动。
它可以帮助政府、企业和研究机构了解各个部门的贡献和影响,从而制定合理的政策和决策。
本文将介绍投入产出模型的基本原理、推广方式以及其在实际应用中的一些案例。
一、投入产出模型的基本原理投入产出模型是由经济学家沃森·勒奇(Wassily Leontief)在20世纪30年代提出的。
它基于一个简化假设,即一个经济体可以被划分为若干个部门,每个部门都需要一定数量的投入才能生产出相应的产出。
这些投入和产出之间存在着复杂的相互依赖关系,通过建立一个输入输出矩阵来描述这种关系。
输入输出矩阵是一个n行n列的方阵,其中n表示经济体中部门的数量。
矩阵中第i行第j列的元素表示第i个部门向第j个部门提供了多少单位的投入。
通过对输入输出矩阵进行数学运算,可以计算出每个部门的产出、就业和价值创造等指标。
二、投入产出模型的推广方式1. 数据收集:投入产出模型需要大量的数据支持,因此在推广应用之前,需要进行全面而准确的数据收集。
这包括各个部门的生产数据、投入数据以及经济体整体的经济指标等。
2. 模型构建:根据收集到的数据,可以构建输入输出矩阵,并计算各个部门的产出和就业情况。
这一步需要借助计量经济学方法和软件工具进行分析和计算。
3. 效果评估:通过比较不同部门之间的相互依赖关系和资源流动情况,可以评估不同政策或决策对整体经济效果的影响。
这有助于政府和企业制定更合理的发展战略和政策。
4. 推广应用:投入产出模型可以应用于各个领域,包括宏观经济政策制定、区域发展规划、环境影响评估等。
通过将模型推广到不同领域中,可以更好地理解各个部门之间的相互作用,并为决策者提供科学依据。
三、投入产出模型的应用案例1. 宏观经济政策制定:投入产出模型可以帮助政府评估不同政策对经济的影响。
政府可以通过模型计算出增加某个部门的投入会对整体就业和产出造成怎样的影响,从而制定合理的产业政策。
投入产出模型在经济增长分析中的应用研究

投入产出模型在经济增长分析中的应用研究投入产出模型是一种经济学家在分析经济增长时经常使用的工具。
它可以帮助我们理解不同产业之间的关系以及经济活动对经济增长的影响。
本文将探讨投入产出模型的基本概念和运用,并讨论其在经济增长分析中的应用。
首先,我们来介绍一下投入产出模型的基本原理。
投入产出模型是一种输入-产出分析法,它用来衡量不同产业之间的相互依赖性。
该模型将经济体系划分为不同的产业部门,并通过研究这些部门之间的关系来分析经济增长。
模型的核心是一个投入产出表,它记录了各个产业之间的关系。
表中的每个元素表示一种产品或服务的产出量,如钢铁、电力、教育等。
通过分析表格中的数值,我们可以了解到每个产业的总产出以及经济体系的总产出。
投入产出模型的一个关键概念是投入产出系数。
这些系数表示某个产业中每一单位产出所需的输入。
通过计算这些系数,我们可以了解每个产业对其他产业的重要性。
例如,如果某个产业的投入产出系数较高,说明这个产业对其他产业的需求较大。
这可以帮助我们预测经济体系中的连锁反应和潜在的脆弱性。
投入产出模型的一个重要应用是用于经济政策的评估。
通过分析产业之间的关系,我们可以评估各种政策对特定产业、区域或整个经济体系的影响。
例如,政府可以使用该模型来评估某项政策对就业率、产出和经济增长的影响。
此外,投入产出模型还可以用于制定战略规划。
通过研究产业之间的联系,企业或政府可以制定更有效的发展战略。
例如,如果某个产业的产出对其他产业的关联度较高,政府可以鼓励该产业的发展,从而推动整个经济体系的增长。
投入产出模型还可以用于预测经济增长。
通过分析历史数据和当前趋势,我们可以预测产业的未来发展方向和相对重要性。
这有助于企业和政府制定长期发展战略,从而为未来的经济增长做好准备。
然而,投入产出模型也有其局限性。
首先,该模型假设经济体系的结构稳定,不考虑结构的变化。
然而,在现实世界中,产业之间的联系是动态变化的,这可能导致模型的预测不准确。
投入产出模型在生态经济发展中的应用

投入产出模型在生态经济发展中的应用一、引言生态经济的发展不仅需要考虑经济效益,还需要兼顾社会和环境的可持续性发展。
投入产出模型是一种经济学模型,可以分析一个国家或地区的生产和消费以及经济与生态相互作用的关系。
本文将介绍投入产出模型在生态经济发展中的应用,并分析其优点与局限性。
二、投入产出模型的概念及原理投入产出模型是一种矩阵分析方法,用于研究一个经济系统的内部结构。
它可以揭示一个国家或地区的生产结构,衡量不同部门之间的联系,同时分析各部门对劳动力、资源和能源的需求量,以及它们对环境的影响。
该模型将经济体分成若干个部门,每个部门之间有购买、销售的关系,每个部门在生产过程中需要消耗投入以产出产品,而产出的产品又可以成为其他部门消耗的投入。
整个模型可以用一个矩阵来表示,其中的元素描述了一个部门采用自身的利润购买其他部门产品、向其他部门出售自身产品、消耗生产要素(如劳动力、资源、能源)的数量。
三、投入产出模型在生态经济发展中的应用1.衡量能源消耗和碳排放。
通过投入产出模型,可以分析哪些产业对能源和碳排放的需求最大,以及它们对环境的影响。
这些分析结果可以帮助政策制定者制定更加精准、具体的政策,推进低碳经济的发展。
2.评估生态损失。
投入产出模型可以追溯整个生产过程,包括所需的资源、原材料、能源和劳动力。
因此,通过该模型,可以评估生态损失,即针对生态系统的不必要伤害。
这对于政策制定者和企业管理者来说,是制定生态友好型经济政策和生产管理方案的重要依据。
3.预测生产结构的变化。
投入产出模型可以追踪生产过程中的每一个阶段,因此可以预测生产结构的变化,推测未来的变化趋势。
这对政策制定者来说,是通过改变生产结构来实现转型升级的重要手段。
4.促进地方经济和生态经济的有机结合。
投入产出模型可以分析一个地区的生产和消费结构,帮助政策制定者制定能更好地促进地方经济和生态环境的有机结合的策略。
4.投入产出模型的局限性1.忽略时间因素。
投入产出模型在全球价值链中的应用

投入产出模型在全球价值链中的应用一、投入产出模型的概念投入产出模型是一种经济分析工具,用于描述一个经济系统中各个部门之间的相互依赖关系。
它通过考虑各个部门之间的投入和产出关系,来分析经济系统中的产出变化对各个部门的影响。
二、全球价值链的特点全球价值链是指在全球范围内,不同国家和地区的企业和机构通过分工合作,共同参与产品或服务的生产和供应过程。
全球价值链的特点包括以下几个方面:1. 分工合作:不同国家和地区的企业和机构通过分工合作,各自承担特定环节的生产任务。
2. 跨国流动:生产要素和产品在全球范围内的流动,包括劳动力、资本、技术和原材料等。
3. 附加值分配:不同环节的附加值分配不均,不同国家和地区的企业和机构在全球价值链中承担不同的经济利益。
4. 知识密集型:全球价值链中的高附加值环节往往是知识密集型的,涉及到创新、研发和设计等。
投入产出模型可以用于分析全球价值链中各个环节之间的相互依赖关系、生产要素的流动以及附加值的分配等问题,具体应用包括以下几个方面:1. 产业结构调整:通过投入产出模型,可以分析全球价值链中各个产业的相互关系,帮助国家和地区优化产业结构,提高产业附加值水平。
例如,通过分析某个国家在全球价值链中的地位,可以确定该国应该加强哪些产业的发展,以提高经济效益。
2. 贸易政策分析:投入产出模型可以帮助分析贸易政策对全球价值链的影响。
例如,通过模拟不同贸易政策下的产出变化,可以评估贸易政策对各个产业和国家的影响,从而指导制定更有效的贸易政策。
3. 供应链风险管理:全球价值链中的供应链风险是一个重要问题。
通过投入产出模型,可以分析不同环节的供应链关系,评估供应链中的风险和脆弱性,并提出相应的风险管理策略。
4. 环境影响评估:投入产出模型可以用于评估全球价值链中的环境影响。
通过分析不同环节的能源消耗和排放情况,可以评估全球价值链对环境的影响,并为环境政策的制定提供科学依据。
投入产出模型在全球价值链中具有广泛的应用前景。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主要通过价值形态产品投入产出模型的实例,来说明投入产出模型在宏观经济分析和政策制订中的应用。
第一节 投入产出模型在宏观经济分析中的应用1、深入分析国民经济中的基本比例(结构)关系宏观经济中的重要比例关系有:两大部类的比例、农轻重的比例、产业结构、投资与消费比例等。
在经济分析中,投入产出法的主要优势是在结构分析上,这是其它分析方法难以做到的。
下面来分别介绍: (1)分析两大部类的比例关系马克思主义再生产原理明确指出,要使社会再生产顺利进行,就必须使两大部类产品在生产与分配使用之间保持一定的比例,这里不仅是指两大部类产品在实物形态上要顺利地实现交换,而且在价值形态上也要能得到补偿。
但这个原理在实际应用中,遇到困难最大的是,有关两大部类总量及结构数据难以得到。
而利用投入产出表,则可以较好地克服这个困难,即能够较精确地计算出整个社会产品中,两大部类产品各自的总量及其价值构成。
其具体计算过程如下: 计算生产生产资料部门(第一部类)和生产消费资料部门(第二部类)的总量 实际上,在简化投入产出表中,最终产品中的消费部分的和就是第二部类产品的总量,而全部中间产品加投资的和就是第一部类产品的总量。
亦即 每一部门的产品分为两大部类为:∑∑===+++nj ii i ijinj iijX w z xw z x11),,1(n i =因此,整个经济两大部类的总量为:∑∑∑∑=====+=ni in i n j ni iij w W z x W 121111计算各部门的部门物资消耗系数(cja )劳动报酬系数(vja )和社会纯收入系数(mja )即cja =∑=ni ija1j j vj X v a =jj mj X m a =),,2,1(n j = 计算第二部类产品(消费资料)的价值构成物资消耗:∑==nj jcj w a C 12劳动报酬:∑==nj jvj w a V 12社会纯收入:∑==nj jmj w a M 12即 2222M V C W ++= 计算第一部类产品的价值构成物资消耗:∑∑==-=n i nj ij C x C 1121劳动报酬:∑=-=nj j V v V 121社会纯收入:211M m M nj j -=∑=即 1111M V C W ++=由此我们就得到了分析两大部类比例所需要的有关数据。
同样如果需要,利用投入产出模型,还可以更具体计算出表中各部门产品中两大部类的数量,以及它们各自的价值构成。
(2)分析农业、轻工业、重工业的比例关系农业、轻工业、重工业是实际中的组织生产部门,一般认为,农业和轻工业生产的主要是消费品,重工业生产的主要是生产资料,所以它们之间的比例是两大部类比例的具体化,研究它们可以更好地应用马克思的再生产理论。
通过投入产出表(前表)则不仅可以分析农业、轻工业、重工业的内部结构,了解它们各自的具体部门构成,而且可以计算出这三个部门产品的价值构成,从社会再生产的角度来研究分析它们之间的内在必然联系。
首先,利用投入产出表可以计算出这三个部门产品的分配使用情况,借以了解它们产品满足各种社会需要的状况,以及农产品、轻工业品、重工业品组成两大部类产品的情况。
具体计算结果如下:表中展示了这三个部门产品用于社会产品生产消耗所占的比例,及作为最终产品用于消费和生产性投资的比例(例子)。
其次,利用投入产出表所提供的直接消耗系数与完全消耗系数,可以了解农、轻、重部门的内在联系(例子)。
各部门产品分配使用比重表再次,可以使农、轻、重比例具体化,进一步分析组成这三个部门的各细分部门之间的相互联系。
一般实际的投入产出表的部门分类更加细致,这一点是完全能够做到的。
最后,可以利用投入产出模型来探索反映农、轻、重比例是否协调的数量标志。
(3)分析积累与消费的比例关系利用投入产出模型,能够直接了解到构成积累和消费的物质内容。
一般投入产出表的分类较细,可以清楚地了解到一定生产结构下,积累和消费究竟是由那些部门的产品来提供的。
这样就能在积累安排与所需各类生产资料供应、消费资料需求与消费资料供给之间建立平衡。
下面我们来建立积累和消费的实物构成与社会总产品或最终产品之间的联系。
首先,定义一个新的系数——最终产品实物构成系数il d ,其计算公式为:l ilil Y y d =),,2,1,,,2,1(r l n i ==式中,l Y 为l 项最终产品的总量(例如表示为积累和消费的总量);il y 为i 部门所能提供给l 项最终产品的数量。
由此,可以得到∑∑====rl rl lil il i Y d y y 11),,2,1(n i =写成矩阵的形式则为L DY Y =式中⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=r nl n n r r n Y Y Y Y d d d d d d d d d D y y y Y2121222211121121,,Y ——i 部门提供给最终产品的数量;D ——最终产品实物构成系数矩阵;l Y ——为l 项最终产品数量的列向量。
如果将l DY A I Y )(-=代入上式,则有l l DY A I X DY X A I 1)()(--==-上式表明,在已知各部门最终产品实物构成系数和l Y 的条件下,就可计算出各部门的生产总量。
(4)分析各部门之间的比例关系利用投入产出表所提供的数据,可以更好地分析各部门之间的比例关系:首先,通过计算直接消耗系数和完全消耗系数,可以较深入地了解每一个部门与其它部门之间的内在联系和相互依存关系。
特别是通过完全消耗系数,可以揭示出部门之间的种种间接联系,因为有的部门之间只有很小的直接联系,却有很重要的间接联系。
其次,通过投入产出表中第一部分内各物资消耗(中间产品)的数量进行分析,可以了解各部门在生产中的相互依赖程度,并由此判断它们在国民经济中的地位和作用。
2、分析各部门产品价格的形成和各种产品价格之间的相互影响 各部门产品价格的形成模型我们已知投入产出表各列形成的关系,反映了各部门产品的价值形成过程,亦即是实际中产品价格的形成及组成,其计算公式为:∑=++=ni mjvj i ij j a a p a p 1 ),,2,1(n j =式中,ij p p ,分别为i j ,部门产品的价格;而ij a这里应为实物形态的直接消耗系数,亦即∑=ni iijp a1为生产单位j 产品的价格中,以价值形态表示的全部物资消耗;而mjvj a a +表示生产单位j 产品的净产值。
值得指出地是,如果ija 采用价值形态,则上式的计算结果jp 是价格指数(证明省略)。
上式写成矩阵的形式则为:)()(1M V A I P MV P A P T T +-=++=- 上式中的符号意义这里省略。
上式表明,在已知直接消耗系数矩阵、劳动消耗系数和社会纯收入列向量的条件下,就可以计算出各部门产品的价格。
(2)分析某个部门或某些部门产品价格变动对其它部门产品价格的影响模型 投入产出法的基本结论告诉我们,实际中各部门产品之间存在着错综复杂的联系,显然某一部门或某些部门的产品价格变动,必然会使其它部门产品的生产成本发生变化,从而引起其价格的变化。
我们首先来考虑最简单的情况:即假设第n 个部门产品的价格发生变化为n p ∆(不失一般性),并且假设不考虑市场供求关系的变化对产品价格的影响,同时假设其它(n-1)个部门产品的mjvj a a ,不发生变化。
那么有:∑=++=ni mjvj i ij j a a p a p 1 )1,,2,1(-=n j根据假设仍然还有∑=++∆+=∆+ni mjvj i i ij j j a a p p a p p 1)( ),,2,1(n j =由此又有∑∑-==∆+∆=∆∆=∆111n i nnj i ij j ni iij j p a p a p p a p ),,2,1(n j =若写成矩阵形式则为n nn n n n Tn n n n n n n p a a a p p p a a a a a a a a a p p p ∆⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∆∆∆⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∆∆∆---------121121111211122221*********[]n nn n n n T n p a a a A I p p p ∆⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∆∆∆∴----12111121上式的经济解释:n nn n n p a a a ∆⎪⎪⎪⎪⎪⎭⎫⎝⎛-121 表示第n 部门产品的价格提高n p ∆后,通过直接消耗系数计算出对其它(n-1)个部门产品价格的直接影响;如果再乘以()11---T n A I ,则表示对(n-1)个部门产品价格所有直接和间接影响,即全部影响。
值得指出的是,在实际计算过程中,其直接消耗系数矩阵往往是价值形态的,同时n p ∆为价格变化的百分比,因此,这时计算的结果则是其它(n-1)个部门产品价格变化的百分比。
同理,按照类似的过程,我们也可推出多部门产品价格变动的影响模型(省略)。
分析某些部门工资提高或利润、税金提高时对各部门产品价格的影响 这里仍利用前面投入产出表的数据,假设其它条件不变(即劳动生产率、生产结构等不变)的情况下,那么设轻工业和重工业部门的工资各提高5%,求对各部门产品价格带来的影响。
根据有关的数据及计算结果有:因此,如果轻工业和重工业部门的工资平均提高5%,则轻工业的直接劳动报酬系数由0.12提高至0.126;重工业的直接劳动报酬系数由0.18提高至0.186。
然后用公式1)()(--=+=A I A B I B A B v v v v 或者是进行计算,可得各部门的完全劳动报酬系数分别为农业0.7661;轻工业为0.5155;重工业为0.5194;其它为0.5356。
再与上表中的各部门完全社会纯收入系数相加,两者的合计数为:农业1.004;轻工业1.014;重工业1.0171;其它1.0058。
由此说明,农业的产品价格要提高0.4%;轻工业提高1.4%;重工业提高1.71%;其它部门提高0.58%。
如果假定某些部门的税收或利润提高,用同样的方式也可以计算出对各部门产品价格的影响。
上面的计算过程实际上是建立在投入产出法的一个重要结果基础上的,即)1,,1,1())((1=-+=+-A I A A B B m v m v 如果我们把净产值完全看成是活劳动创造的价值,则上式结论表明所有的产品价值是完全由劳动创造的,同时我们也可对比前面得到的一个类似结果1=++m j vj cj a a a ),,2,1(n j =这两个结论实际上是一致的。
另外,需要说明的是,上面的计算方法或过程,也可以用另一种方法来完成,即用产品价格的形成模型的变形公式()[])((1mj vjTa aA I p ∆+∆-=∆-同样能够完全类似的结果(省略计算过程)。
