黑龙江省肇源县第四中学2019---2020第一次月考试题初三数学试题
黑龙江省大庆市肇源县第四中学2018-2019初四数学月考
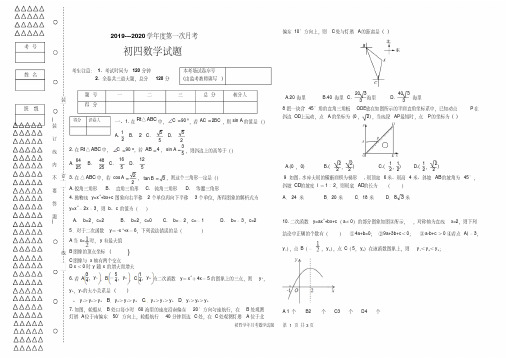
A.20 海里
20 3 B.40 海里 C. 3 海里
40 3 D. 3 海里
8 把一块含 45°角的直角三角板 ODE放在如图所示的平面直角坐标系中,已知动点
P在
斜边 OD上运动,点 A 的坐标为 (0 , 2) ,当线段 AP最短时,点 P 的坐标为 ( )
A.(0 , 0)
2019---2020 学年度第一次月考
考号
初四数学试题
偏东 10°方向上,则 C 处与灯塔 A 的距离是 ( )
姓名 班级
考生注意: 1、考试时间为 120 分钟 2、全卷共三道大题,总分 120 分
本考场试卷序号 (由监考教师填写 )
题号
一
二
装
得分
三
总分
核分人
(
得分 评卷人
一、1. 在 Rt△ ABC 中, C 90 ,若 AC 2BC ,则 sin A 的值是 ()
要
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
4. 抛物线 y=x 2+bx+c 图象向右平移 2 个单位再向下平移 3 个单位,所得图象的解析式为
答 y=x 2﹣ 2x﹣3,则 b、c 的值为( )
题
)
A. b=2, c=2
B. b=2, c=0 C. b=﹣ 2, c=﹣ 1
________ .
16. 已知抛物线 y=2x 2 -2mx+ m2+n 的顶点坐标为( 2, -5 )则 m+n=_______,
17. 某商场,服装进价的单价是 20 元,销售单价是 30 元时,月销售量是 230 件,而销
售单价每上涨一元,月销量就减少 10 件,设每件玩具的销售单价上涨 x,【 x 为正整数】
黑龙江省肇源县第四中学学年第一学期初四数学第一次月考(无答案)

2019---2019学年度第二学期第一次月考初四数学试题考生注意:1、考试时间为120分钟 2、全卷共三道大题,总分120分 题 号一二三总 分核分人得 分一、1.在Rt ABC △中,90C ∠=︒,若2AC BC =,则sin A 的值是() A.12 B.2 C.55 D.522.在Rt ABC △中,90C ∠=︒,若4AB =,3sin 5A =,则斜边上的高等于() A.6425 B.4825 C.165 D.125 3.在ABC △中,若2cos 2A =,tan 3B =,则这个三角形一定是() A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形4.抛物线y=x 2+bx+c 图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x 2﹣2x ﹣3,则b 、c 的值为( )A. b=2,c=2B. b=2,c=0C. b=﹣2,c=﹣1D. b=﹣3,c=2 5.对于二次函数y =-x 2+x -6,下列说法错误的是( ) A 当x=时,y 有最大值 B 图像的顶点坐标( ) C 图像与x 轴有两个交点D x <0时y 随x 的增大而增大6.若A ⎝ ⎛⎭⎪⎫34,y 1,B ⎝ ⎛⎭⎪⎫-54,y 2,C ⎝ ⎛⎭⎪⎫14,y 3为二次函数y =x 2+4x -5的图象上的三点,则y 1,y 2,y 3的大小关系是( )A .y 1>y 2>y 3 B .y 2>y 1>y 3 C .y 3>y 1>y 2 D .y 1>y 3>y 27. 如图,小岛在港口P 的北偏西60°方向,距港口56海里的A 处,货船从港口P 出发,沿北偏东45°方向匀速驶离港口P ,4小时后货船在小岛的正东方向,则货船的航行速度是( )A.72海里/时B.73海里/时C.76海里/时D.282海里/时8把一块含45°角的直角三角板ODE 放在如图所示的平面直角坐标系中,已知动点P 在斜边OD 上运动,点A 的坐标为(0,2),当线段AP 最短时,点P 的坐标为( ) A.(0,0) B.(22,22) C.(12,12) D.(12,22) 9如图,水库大坝的横断面积为梯形,坝顶宽6米、坝高4米、斜坡AB 的坡角为45°,斜坡CD 的坡度i =1∶2,则坝底AD 的长为 ( ) A . 24米B .20米C .18米D .38米10.二次函数y=ax 2+bx+c (a ≠0)的部分图象如图③所示,,对称轴为直线x=2,则下列结论中正确的个数有( ) ①4a+b=0; ②9a+3b+c <0; ③a-b+c >0 ④若点A(﹣3,y 1),点B (﹣ ,y 2),点C (5,y 3)在该函数图象上,则y 1<y 3<y 2;A 1个 B2个 C3个 D4个 二、填空11 12 13 14 15 16 17 18 19 2011.1)3(232++-=+-kx x k y k k,是二次函数,则k 的值是_________12. 如图,在Rt △ABC 中,AC =BC ,将Rt △ABC 沿过点B 的直线折叠,使点C 落在AB边上点F 处,折痕为BE ,这样可以求出22.5°的正切值是______13.周长为20的等腰三角形,一边长为6,则底角的余弦值为______.考 号姓 名装订线 (装订线内 不要 答 题 )班 级本考场试卷序号(由监考教师填写)得分 评卷人14.已知锐角A 满足表达式2sin 2A-7sinA+3=0则sinA 的值_________15.二次函数y =x 2-x -6的图象交x 轴于A ,B 两点,交y 轴于C 点,则△ABC 的面积为________. 16.已知抛物线y=2x 2-2mx+m 2+n 的顶点坐标为(2,-5)则m+n=_______,17. 某商场,每天可以售出 300 套服装.每套盈利10元,据市场调查发现,这种服装每提高 1 元售价,销量就减少 5 套,如果商场将售价定为 x 元/套,请你得出每天销售利润 y 与售价x 的函数表达式: .18.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A 滑行至B ,已知AB =500米,则这名滑雪运动员的高度下降了________米.(参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)19.如图,从热气球C 上测得建筑物A ,B 底部的俯角分别为30°和60°,如果这时气球的高度CD 为150米,且点A ,D ,B 在同一直线上,那么建筑物A ,B 间的距离为________20.抛物线y=ax 2 +c 与y=2x 2形状相同,其顶点坐标是(0,1)则其表达式_________ 三、计算 1. 2cos45°-16+(-14)-1+(π-3.14)0. 2.230116(2)(πtan60)33-⎛⎫--÷-+-︒-︒ ⎪⎝⎭ 22.(6分)如图,在△ABC 中,∠B =45°,AC =132,BC =10,求sinA 和AB . 23.有长为24 m 的篱笆,围成中间隔有一道篱笆的长方形的花圃,花圃的长可借用一段墙体(墙体的最大可用长度a=10)设花圃的宽AB 为x m,花圃ABCD 的面积为S m 2(1) 求S 与x 的函数关系式;(2) 如果要围成面积为45 m 2的花圃,AB 的长是多少米?24.如图,一艘油轮以240/min m 的速度向正北方向航行,行驶到A 处测得一灯塔C 在它的北偏西30小岛上,油轮继续向北航行,5min 后到达B 点,又测得灯塔C 在它的北偏西45方向,根据有关资记载,在距灯塔C 为中心1500m 范围内有暗礁.试问:这艘油轮不改变前进方向继续行驶是否有触 的危险?为什么? 25. 如图,某人在山坡坡脚C 处测得一座建筑物顶点A 的仰角为60°,沿山坡向上走到P 处再测得该建筑物顶点A 的仰角为45°.已知BC =90米,且B 、C 、D 在同一条直线上,山坡坡度为21(即tan ∠PCD =21). (1)求该建筑物的高度(即AB 的长).(2)求此人所在位置点P 的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)26.如图,AD 是△ABC 的中线,tan B =13,cos C =22,AC = 2.求:(1)BC 的长;(2)sin ∠ADC 的值.27如图抛物线y 1=x 2与直线y 2=x+b 的交点为A (-1,a )和点B (1) 求a,b 的值及点B 的坐标(2) 根据图像判断当x 为何值时,y 1 < y 2 28. 已知抛物线y= -41X 2+bx+4 与x 轴相交于A ,B 两点,与Y 轴相交于C , 若已知A 点的坐标(-2,0)(1)求抛物线的解析式及它的对称轴;(2)求点C 的坐标,连接AC 、BC 并求线段BC 所在直线的解析式;得分 评卷人考 号姓 名 装订线( 装订 线 内 不 要答题 )。
黑龙江省大庆市肇源县第四中学2019-2020学年中考数学模拟学业水平测试试题

黑龙江省大庆市肇源县第四中学2019-2020学年中考数学模拟学业水平测试试题一、选择题1.下列命题中,是假命题的是( )A .任意多边形的外角和为360°B .在△ABC 和△A′B′C′中,若AB =A′B′,BC =B′C′,∠C =∠C′=90°,则△ABC ≌△A′B′C′C .在一个三角形中,任意两边之差小于第三边D .同弧所对的圆周角和圆心角相等2.若数a 使关于x 的不等式组2122274x x x a-⎧≤-+⎪⎨⎪+-⎩>有且只有4个整数解,且使关于y 的分式方程211a y y+--=3的解为正数,则符合条件的所有整数a 的和为( ) A.﹣2 B.0 C.3 D.63.如图,正方形ABCD 的对角线AC 与BD 相交于点O ,∠ACB 的平分线分别交AB ,BD 于M ,N 两点.若AM =ON 的长为( )A .2 BC .D .4.菱形ABCD 中,605B AB ∠=︒=,,则以AC 为边长的正方形ACEF 的周长为( )A .15B .16C .17D .205.如图,在矩形ABCD 中,点E 、F 、G 、H 分别是边AD 、AB 、BC 、CD 的中点,连接EF 、FG 、GH 和HE .若2=AD AB ,用下列结论正确的是( )A .EF AB = B.2EF AB = C.EF = D.2EF AB = 6.如图,在平面直角坐标系中,已知点(3,6)A -,(9,3)B --,以原点O 为位似中心,相似比为13,把ABO ∆缩小,则点B 的对应点B '的坐标是( )A .(9,1)-或(9,1)-B .(3,1)--C .(1,2)-D .(3,1)--或(3,1) 7.如图是根据我市某天七个整点时的气温绘制成的统计图,则这七个整点时气温的中位数和众数分别是( )A .中位数31,众数是22B .中位数是22,众数是31C .中位数是26,众数是22D .中位数是22,众数是268.如图,DE ∥BC ,CD 平分∠ACB ,∠AED =50°,则∠EDC 的度数是( )A .50°B .40°C .30°D .25° 9.如图,菱形ABCD 的边AB=5,面积为20,∠BAD <90°,⊙O 与边AB 、AD 都相切,AO=2,则⊙O 的半径长等于( )A B C D 10.正比例函数y =kx(k≠0)的图象上一点A 到x 轴的距离与到y 轴的距离之比为2 : 3,且y 随x 的增大而减小,则k 的值是 ( )A .23B .32C .32-D .23- 11.定义:a 是不为1的有理数,我们把11a-称为a 的差倒数,如:2的差倒数是112-=﹣1,﹣1的差倒数是()111--=12,已知a 1=﹣13,a 2是a 1的差倒数,a 3是a 2的差倒数,a 4是a 3的差倒数,…,以此类推,a 2009的值为( )A .﹣13B .34C .4D .4312.如图,在ABCD 中, 对角线AC 、BD 相交于点O. E 、F 是对角线AC 上的两个不同点,当E 、F 两点满足下列条件时,四边形DEBF 不一定是平行四边形( ).A .AE =CFB .DE =BFC .ADE CBF ∠=∠D .AED CFB ∠=∠ 二、填空题13.函数y =中,自变量________的取值范围是________. 14.不等式组112(3)33x x x+⎧⎨+->⎩…的解集是_____. 15.因式分解ab 3-4ab= .16.n 边形的内角和等于540°,则n=_____.17.如图,已知直线AB ∥CD ,∠GEB 的平分线EF 交CD 于点F ,∠1=46°,则∠2=______.18.如图,AB 是圆O 的直径,弦CD ⊥AB ,∠BCD =30°,CD =S 阴影=_____.三、解答题19.如图,□ABCD 中,E 为BC 边上一点,连接DE ,若DE AD =,∠AFD+∠B=180°.求证:AB AF =.20.校园安全受到全社会的广泛关注,某市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:(1)在这次活动中抽查了多少名中学生?(2)若该中学共有学生1600人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”程度的人数.(3)若从对校园安全知识达到“了解程度的2个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.21.如图,AB ,AD 是⊙O 的弦,AO 平分BAD ∠.过点B 作⊙O 的切线交AO 的延长线于点C ,连接CD ,BO.延长BO 交⊙O 于点E ,交AD 于点F ,连接AE ,DE.(1)求证:CD 是⊙O 的切线;(2)若3AE DE ==,求AF 的长.22.先化简再求值:22211221x x x x x x x ++--÷++-,其中x=()011260-20162π--︒++- 23.如图1,在平面直角坐标系中,O 是坐标原点.点A 在x 轴的正半轴上,点A 的坐标为(10,0).一条抛物线214y x bx c =++经过O ,A ,B 三点,直线AB 的表达式为152y x =+,且与抛物线的对称轴交于点Q .(1)求抛物线的表达式;(2)如图2,在A ,B 两点之间的抛物线上有一动点P ,连结AP ,BP ,设点P 的横坐标为m ,△ABP 的面积S ,求出面积S 取得最大值时点P 的坐标;(3)如图3,将△OAB 沿射线BA 方向平移得到△DEF ,在平移过程中,以A ,D ,Q 为顶点的三角形能否成为等腰三角形?如果能,请直接写出此时点E 的坐标(点O 除外);如果不能,请说明理由.24.图①、图②均为3×3的正方形网格,每个小正方形的边长都为1,请在图①、图②中各画一个顶点在格点的三角形.要求:(1)所画的三角形为钝角三角形;(2倍;(3)图①、图②中所画的三角形不全等.25.请阅读下列材料,并完成相应的任务.三等分任意角问题是数学史上一个著名的问题,直到1837年,数学家才证明了“三等分任意角”是不能用尺规完成的.在探索中,出现了不同的解决问题的方法方法一:如图(1),四边形ABCD 是矩形,F 是DA 延长线上一点,G 是CF 上一点,CF 与AB 交于点E ,且∠ACG =∠AGC ,∠GAF =∠F ,此时∠ECB =13∠ACB . 方法二:数学家帕普斯借助函数给出一种“三等分锐角”的方法(如图(2)):将给定的锐角∠AOB 置于平面直角坐标系中,边OB 在x 轴上,边OA 与函数y =1x的图象交于点P ,以点P 为圆心,以2OP 长为半径作弧交图象于点R .过点P 作x 轴的平行线,过点R 作y 轴的平行线,两直线相交于点M ,连接OM 得到∠AOB ,过点P 作PH ⊥x 轴于点H ,过点R 作RQ ⊥PH 于点Q ,则∠MOB =13∠AOB . (1)在“方法一”中,若∠ACF =40°,GF =4,求BC 的长.(2)完成“方法二”的证明.【参考答案】***一、选择题13.2x ≥-且1x ≠14.0≤x<315.ab (b+2)(b-2).16.517.157°18.83π 三、解答题19.见解析.【解析】【分析】根据平行四边形的性质可证明ADF ∆≌DEC ∆,从而可得结论.【详解】在□ABCD 中,AB CD =,AB ∥CD ,AD ∥BC ,∴180B C ∠+∠=︒,ADF CED ∠=∠∵180AFD B ∠+∠=︒,∴C AFD ∠=∠又∵DE AD =,∴ADF ∆≌DEC ∆,∴AF CD =,∴AF AB =.【点睛】本题考查了平行四边形的性质以及全等三角形的判定与性质,掌握判定与性质是解题的关键.20.(1)80(2)400(3)23 【解析】【分析】(1)用“基本了解”的人数除以它所占的百分比得到调查的总人数;(2)计算出样本中“了解”程度的人数,然后用1600乘以基本中“了解”程度的人数的百分比可估计该中学学生中对校园安全知识达到“了解”程度的人数.(3)画树状图展示所有12种等可能的结果数,找出恰好抽到1个男生和1个女生的结果数,然后利用概率公式求解.【详解】解:(1)32÷40%=80(名),所以在这次活动中抽查了80名中学生;(2)“了解”的人数为80﹣32﹣18﹣10=20, 1600×2080=400, 所以估计该中学学生中对校园安全知识达到“了解”程度的人数为400人;(3)由题意列树状图:由树状图可知,在 4 名同学中随机抽取 2 名同学的所有等可能的结果有12 种,恰好抽到一男一女(记为事件A )的结果有8种,所以P (A )=82123=. 【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n ,再从中选出符合事件A 或B 的结果数目m ,然后利用概率公式计算事件A 或事件B 的概率.也考查了统计图.21.(1)详见解析;【解析】【分析】(1)欲证明CD 是⊙O 的切线,只要证明∠CDO =∠CBO =90°,由△COB ≌△COD 即可解决问题.(2)先证明∠BAO =∠OAD =∠DAE =∠ABO =30°,在Rt △AEF 中利用30度性质以及勾股定理即可解决【详解】解:(1)如图,连接OD .∵BC 为圆O 的切线,∴∠CBO =90°.∵AO 平分∠BAD ,∴∠OAB =∠OAF .∵OA =OB =OD ,∴∠OAB =∠ABO =∠OAF =∠ODA ,∵∠BOC =∠OAB +∠OBA ,∠DOC =∠OAD +∠ODA ,∴∠BOC =∠DOC ,在△COB 和△COD 中,CO CO COB COD OB OD ⎧⎪∠∠⎨⎪⎩===,∴BOC ≌△DOC ,∴∠CBO =∠CDO =90°,∴CD 是⊙O 的切线;(2)∵AE =DE ,∴AE DE =,∴∠DAE =∠ABO ,∴∠BAO =∠OAD =∠ABO∴∠BAO =∠OAD =∠DAE ,∵BE 是直径,∴∠BAE =90°,∴∠BAO =∠OAD =∠DAE =∠ABO =30°,∴∠AFE =90°,在Rt △AFE 中,∵AE =3,∠DAE =30°,∴EF =12AE =32, ∴AF2=.【点睛】本题考查切线的判定和性质、全等三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,发现特殊角30°,属于中考常考题型.22.12x -+,-1 【解析】先把除法转化为乘法,并把分子、分母分解因式约分,再按分式的加减法化简,然后把x 化简后代入计算即可.【详解】22211221x x x x x x x ++--÷++- =()()()2112211x x x x x x x +--⨯++-+ =122x x x x +-++ =12x x x --+ =12x -+,x=()011260-20162π--︒++-=11122+ =-1,当x=-1时,原式=1=112---+. 【点睛】本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的;最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了实数的混合运算.23.(1)21542y x x =-+;(2)当S 取得最大值16时,点P 的坐标为(6,6);(3)以A ,D ,Q 为顶点的三角形能成为等腰三角形,点E 坐标为:E 1(21,12-),E 2(15,52-),E 3(311124,-),E 4(16,﹣3). 【解析】【分析】(1)将点A 的坐标(10,0).O (0,0)代入抛物线214y x bx c =++,解出b ,c ,再代回,即可得抛物线的解析式;(2)先将直线与抛物线解析式联立,解出点B 坐标,再设出点P 和点G 坐标,用相关点的横纵坐标表示线段长河高,从而可得面积的表达式,再从函数角度即可得解;(3)利用勾股定理分别表示出AD 2,AQ 2,QD 2,再分AD =AQ ,AD =QD ,AQ =QD ,分别来求解,从而得点D 坐标,再将其横坐标加10,纵坐标不变即可得点E 的坐标.【详解】解:(1)∵抛物线214y x bx c =++经过O ,A ,B 三点,点A 的坐标为(10,0).O (0,0), ∴210101040b c c⎧=-⨯++⎪⎨⎪=⎩ ∴520b c ⎧=⎪⎨⎪=⎩,∴抛物线的表达式为:y =﹣14x 2+52x . (2)由21542152y x x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩得﹣14x 2+52x =152x -+, ∴x =2或x =10,∴点B (2,4).如图2,作PC ⊥x 轴于C 点,交AB 于点G ,∵动点P 在抛物线上,直线AB 的表达式为152y x =-+, ∴设P (m ,﹣14m 2+52m ),G (m ,152m -+), ∴PG =﹣14m 2+3m ﹣5, ∴S =12PG (x A ﹣x G )+12PG (x G ﹣x B )=12(﹣14m 2+3m ﹣5)(10﹣2)=﹣m 2+12m ﹣20=﹣(m ﹣6)2+16,∴当m =6时,S 最大=16,∴P (6,6)答:当S 取得最大值时点P 的坐标为(6,6).(3)∵抛物线的对称轴为x =5,点Q 在直线152y x =-+上, ∴Q 点坐标为(5,52),D 点在过O 点且平行于AB 的直线y =12x 上,设D (a ,12a -), ∴AD 2=(10﹣a )2+14a 2,AQ 2=25+254=1254,QD 2=(a ﹣5)2+215()22a -- ①当AD =AQ 时,(10﹣a )2+14a 2=1254,解得a 1=11,a 2=5, ∴D 1(11,12-),D 2(5,﹣52); ∴E 1(21,12-),E 2(15,-52); ②当AD =QD 时,(10﹣a )2+14a 2=(a ﹣5)2+215()22a --,解得a =112,∴D 3(112,114-),E 3(312,114-); ③当AQ =QD 时,1254=(a ﹣5)2+215()22a --,解得a =6, ∴D 4(6,﹣3),E 4(16,﹣3) 综上所述,以A ,D ,Q 为顶点的三角形能成为等腰三角形,点E 坐标为:E 1(21,12-),E 2(15,52-),E 3(312,114-),E 4(16,﹣3).【点睛】本题属于二次函数的综合题,主要考查了待定系数法求解析式、直线与抛物线所形成的三角形面积的最大值问题、图形平移形成等腰三角形后相关点的坐标等问题,综合性比较强,难度较大.24.见解析【解析】【分析】利用勾股定理作出符合条件的三角形三边,将原三角形扩大两倍即可【详解】解:如图所示;【点睛】此题考查勾股定理和作图-相似变换,解题关键在于掌握作图法则25.(1)2;(2)证明见解析.【解析】【分析】(1)先求出AC 的值再求出∠ACB ,利用三角函数即可解答(2)设点P 的坐标为(a ,1a ),点R 的坐标为(b ,1b ),则点Q 的坐标为(a ,1b ),点M 的坐标为(b ,1a ),求出直线OM 的解析式,得出四边形PQRM 为矩形,设PR 交MQ 于点S ,根据SP =SQ =SR =SM =12PR ,即可解答 【详解】(1)解:∵∠ACG =∠AGC ,∠GAF =∠F ,∴AC =AG =GF =4.∵∠ECB=13∠ACB,∠ACF=40°,∴∠ACB=32∠ACF=60°,∴BC=AC•cos∠ACB=4×12=2.(2)证明:设点P的坐标为(a,1a),点R的坐标为(b,1b),则点Q的坐标为(a,1b),点M的坐标为(b,1a).设直线OM的解析式为y=kx(k≠0),将M(b,1a)代入y=kx,得:1a=kb,∴k=1ab,∴直线OM的解析式为y=1abx.∵当x=a时,y=1b,∴点Q在直线OM上.∵PH⊥x轴,RQ⊥PH,MP∥x轴,MR∥y轴,∴四边形PQRM为矩形.设PR交MQ于点S,如图(2)所示.则SP=SQ=SR=SM=12 PR,∴∠SQR=∠SRQ.∵PR=2OP,∴PS=OP=12 PR,∴∠POS=∠PSO.∵∠PSQ=2∠SQR,∴∠POS=2∠SQR.∵RQ∥OB,∴∠MOB=∠SQR,∴∠POS=2∠MOB,∴∠MOB=13∠AOB.【点睛】此题考查三角函数值的应用,矩形的判定与性质,解题关键在于利三角函数进行计算。
黑龙江大庆肇源超等学校2019-2020学年度九年级上学期第一次月考数学试题答案

2019-2020初四数学第一次月考试题答案 一、A 、B 、B 、C 、C 、D 、B 、B 、D 、B 二、11、22 12、(1,1)13、4314、a=1,b=2,c=4 15、512 16、-1 17、7 18、-3<X<1 19、 y=-2(x-1)2 -6或y=-2X 2+4X-8都可以 20、(1)(2)(4) 21、(1) 2 (2)12 -2322.解:原式=122313a a a a +⨯=+++ ······················································· 2分 当32sin 6032333a =-=⨯-=-° ··················································· 1分 原式=233333=-+ 23、43+424、 解:如图所示:AB=3621⨯=18(海里)∠CBD=600 ∴∠ACB=300 ⇒AB=AC=18(海里)>16∴B 不在暗礁区内 在RT ∆CBD 中 .CD=CBSin600=1823⨯=93<16∴继续向东有危险.25、解:过点C 作CE ⊥BD 于E ,∵AB = 40米∴CE = 40米 ∵阳光入射角为︒30 ∴∠DCE =︒30 在Rt ⊿DCE 中 CD=2DECD 2=DE 2+CE 2 ∴233340≈⨯=DE , 而AC = BE = 1米 ∴DB = BE + ED =24231=+米答:新建楼房最高约24米。
黑龙江省肇源县第四中学2020届九年级上学期第一次月考数学试题

2019—2020学年度第一学期第一次质量检测初三 (数学)试题一、选择题:(每小题3分,共计30分)1.如果b a >,那么下列各式中正确的是()A .b a ->-B .33-<-b aC .b a 22-<-D .33ba < 2.等腰三角形的一个角是80°,则它的顶角的度数是()A .80°B .20°C .80°或50°D .80°或20°3.如图所示,OP 平分∠MON ,PA ⊥ON 于点A ,点Q 是射线OM 上的一个动点,若PA=2,则PQ 的最小值为()A .1B .2C .3D .4-3 -2 1第3题图第4题图4.用不等式表示图中的解集,其中正确的是( )A. x ≥-2B. x >-2C. x <-2D. x ≤-25.△ABC 中,∠A :∠B :∠C=1:2:3,最小边BC=4cm ,最长边AB 的长是( )6.若关于x 的不等式2)1(>-x a 可化为ax -<1,则a 的取值范围是( ) A .a>0 B .a<0 C .a>1 D .a<17.如图,在等腰△ABC 中,AB=AC ,∠A=40°,P 是△ABC 内一点,且∠1=∠2,则∠BPC 等于( )A .110°B .120°C .130°D .140°第7题图第8题图8.如图,在△ABC 中,∠ACB=90°,D,E 分别为AC,AB 的中点,连DE,CE.下列结论中不一定正确的 ( )A .B .C .D .9.如图,在等边ABC ∆中,,D E 分别是,BC AC 上的点,且BD CE =,AD 与BE 相交于点P ,则12∠+∠的度数是().A .045B .055C .060D .075ED BC ∥ED AC ⊥ACE BCE ∠=∠AE CE =第9题图第10题图10. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是()①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC :S△ABC=1:3.二、填空题:(每小题3分,共30分)11. 用不等式表示:x与5的差不大于x的2倍:。
黑龙江省大庆市肇源县第四中学2019--2020期中测试题
2019——2020学年度第一学期期中初四物理试题一、选择题(4分×10共40分)1、用毛皮摩擦过的橡胶棒接触验电器的金属球(如图所示),发现验电器的两个金属箔片张开。
以下说法正确的是( )A .毛皮和橡胶棒摩擦的过程中创造了电子B .毛皮和橡胶棒摩擦的过程中橡胶棒得到电子C .验电器的金属箔片张开是因为带了异种电荷D .橡胶棒接触验电器的金属球时,电子向橡胶棒转移 2、某型号家用全自动豆浆机,可以把它简化为电动机M 和加热管R 两部分,在下图中能实现这两部分各自独立工作的电路图是( )3、如图所示电路,当开关S 闭合后,两表均有示数,过一会儿发现电压表示数突然变小,电流表示数突然变大。
下列故障判断可能的是( )A .L 1灯短路B .L 2灯短路C .L 1灯丝断开D .L 2灯丝断开4、如图所示,当滑动变阻器的滑片向右滑动时,电流表和电压表的示数变化情况是( )A .电流表示数不变,电压表示数变大B .电流表示数变大,电压表示数不变C .电流表示数变小,电压表示数变小D .电流表示数变小,电压表示数变大5、某型号天燃气泄漏检测仪器的电路如图甲所示,图甲中R 为气敏电阻,其阻值R 与天然气浓度β的变化关系如图乙所示,已知R 0为定值电阻,电源电压恒定不变,用此仪器检测天然气是否泄漏,则下列判断正确的是( ) A . 天然气浓度增大时,电压表示数变小 B .天然气浓度减小时,电流表示数变大 C .天然气浓度增大时,电路中电流变小D .无论天然气浓度怎样变化,电压表与电流表示数的 比值不变6. 如图是电阻甲和乙的 U-I 图象,小明对图象信息作出的判断,正确的是( ) A . 当甲两端电压为0.5V 时,通过它的电流为0.3A B . 当乙两端电压为1V ,其电阻值为0.4ΩC . 将甲和乙串联,若电流为0.4A ,则它们两端的电压为3VD . 若甲和乙并联,若电压为2.5V ,则它们的干路电流为0.5A7.如图所示的电路中,电源两端的电压保持不变。
黑龙江省大庆市肇源县九年级数学上学期第一次月考(10月)试题

九年级数学上学期第一次月考试卷一、填空题(本大题共10小题,共30分)1.不等式x+1<5的正整数解是 ______ .2.若a>b,且c为有理数,则ac2 ______ bc2.3.当x ______ 时,代数式的值是正数.4.若不等式ax|a-1|>2是一元一次不等式,则a=____________.5.一种药品的说明书上写着:“每日用量60~120mg,分4次服用”,一次服用这种药量x(mg)范围为 _____________________ mg.6.如果一个等腰三角形的一个角等于80°,则底角的度数是 __________ .7.如图,在△ABC中,∠C=90°,AD是角平分线,AC=5,DC=3,则点D到AB的距离是 ______ .8.在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,且∠ADC=100°,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是 ______ .9.在△ABC中,AB=AC,AB的中垂线与AC所在直线相交所得的锐角为50°,则底角∠B= ______ .10.在R t△ABC中,∠C=90°,∠A=30°,若要在直线BC或直线AC上取一点P,使△ABP是等腰三角形,符合条件的点P有____________个点.二、选择题(本大题共10小题,共30分)11.不等式-3x≥6的解集在数轴上表示为()A. B. C. D.12.已知等腰三角形一腰上的高线与另一腰的夹角为50°,那么这个等腰三角形的顶角等于()A.15°或75°B.140°C.40°D.140°或40°13.己知AB=6cm,P是到A,B两点距离相等的点,则AP的长为()A.3cmB.4cmC.5cmD.不能确定14.在联欢晚会上,有A、B、C三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在△ABC的( )A.三边中线的交点B.三条角平分线的交点C.三边上高的交点D.三边中垂线的交点15.如图,直线l、l′、l″表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有()A.一处B.二处C.三处D.四处16.在R t△ABC中,∠ACB=90°,∠A=30°,BC=1,则AB边上的中线长为()A.1B.2C.1.5D.17.如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABE,DE⊥BC,若△DEC的周长是10cm,则BC=()A.8cmB.10cmC.11cmD.12cm18.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤S BDE:S△ACD=BD:AC,其中正确的个数为()A.5个B.4个C.3个D.2个19.不等式去分母后正确的是()A.3(1-x)≤2x+1B.3(1-x)≤2x+6C.3-x≤2x+1D.3-x≤2x+620.已知不等式4x-a≤0的正整数解是1,2,则a的取值范围是()A.8<a<12B.8≤a<12C.8<a≤12D.8≤a≤12三、解答题(本大题共8小题,共60分)21.解不等式x-2(x-1)>0,并将它的解集在数轴上表示出来.(6分)22.如图,在等边三角形ABC中,BD⊥AC于D,延长BC到E,使CE=CD,AB=6cm.(6分)(1)求BE的长;(2)判断△BDE的形状,并说明理由.23.铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽的比为3:2,则该行李箱的长的最大值为多少厘米? (6分)24.如图所示:B、C、D三点在一条直线上,△ABC和△ECD是等边三角形.求证:BE=AD.(6分)25.解答下列各题:(12分)(1)x取何值时,代数式3x+2的值不大于代数式4x+3的值?(2)当m为何值时,关于x的方程x-1=m的解不小于3?(3)已知不等式2(x+3)-4<0,化简:︳4x+1︱-︱2-4x︱26.△ABC中,AD为角平分线,DE⊥AB于E,DF⊥AC于F,AB=10cm,AC=8cm,△ABC的面积为54cm2,求DE的长.(7分)27.已知:如图,P、Q是△ABC边BC上两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.(7分)28.在△ABC中,AB=AC,P是BC上任意一点.(10分)(1)如图①,若P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,试探求PE,PF与BD之间的数量关系;(2)如图②,若P是BC延长线上一点,PF⊥AB于点F,PE⊥AC于点E,CD为△ABC的高线,试探求PE,PF与CD之间的数量关系.初三数学上学期第一次月考试卷答案一.填空(每空3分,共30分)1. 1,2,32. ≥3. >24. 25. 15mg<x<306. 50°或80°7. 38. 40°9. 70°或20°10. 6二.选择(每空3分,共30分)11.C 12.D 13.D 14.D 15.D 16.A 17.B 18.C 19.B 20.B三.解答(共60分)21.(6分)解:去括号得,x-2x+2>0,移项得,x-2x>-2,合并得,-x>-2,系数化为1,得x<2. .........4分解集在数轴上表示为:............6分22(6分).解:(1)∵△ABC为等边三角形,∴BC=AB=6cm,∵BD⊥AC,∴AD=CD=AC=3cm,∵CD=CE=3cm,∴BE=BC+CE=6cm+3cm=9cm; ..........3分(2)△BDE为等腰三角形.理由如下:∵△ABC为等边三角形,∴∠ABC=∠ACB=60°,∵BD⊥AC,∴∠CBD=∠ABC=30°,∵CD=CE,∴∠CDE=∠E,而∠CDE+∠E=∠ACB=60°,∴∠E=30°,∴∠CBD=∠E,∴△BDE为等腰三角形..........6分23.(6分)解:设长为3x厘米,则宽为2x厘米, .......1分由题意,得:5x+30≤160, ............3分解得:x≤26, ............4分故行李箱的长的最大值为:3x=78, ........5分答:行李箱的长的最大值为78厘米.........6分24.(7分)证明:∵△ABC和△ECD是等边三角形,∴∠ACB=∠ECD=60°,BC=AC,EC=CD.∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD.在△BCE和△ACD中,∴△BCE≌△ACD(SAS).∴BE=AD.(全等三角形的对应边相等)25.(12分)解:(1)∵代数式3x+2的值不大于代数式4x+3的值,∴3x+2≤4x+3,解得x≥-1. .........4分(2)解方程得,x=2m+2,∵方程的解不小于3,∴2m+2≥3,即2m≥1,解得m≥; .........4分(3)解: 2x+6-4﹤02x﹤-2x﹤-1 ......2分原式=-4x-1-(2-4x)=-4x-1-2+4x=-3...........4分26.(7分)解:∵AD为角平分线,DE⊥AB于E,DF⊥AC于F,∴DE=DF,∵△ABC的面积为54cm2,∴AB•DE+AC•DF=54,∵AB=10cm,AC=8cm,∴×10×DE+×8×DE=54,解得DE=6cm.27.(7分)解:∵BP=PQ=QC=AP=AQ,∴∠PAQ=∠APQ=∠AQP=60°,∠B=∠BAP,∠C=∠CAQ.又∵∠BAP+∠ABP=∠APQ,∠C+∠CAQ=∠AQP,∴∠BAP=∠CAQ=30°.∴∠BAC=120°.故∠BAC的度数是120°.28. (10分)解:(1)如图,连接AP,则S△ABC=S△ABP+S△ACP,所以,AC•BD=AB•PF+AC•PE,∵AB=AC,∴BD=PE+PF;(2)连接AP,则S△ABC=S△ABP-S△ACP,所以,AB•CD=AB•PF-AC•PE,∵AB=AC,∴CD=PF-PE.。
黑龙江省大庆市肇源县四校联考2024-2025学年九年级上学期10月月考数学试题

黑龙江省大庆市肇源县四校联考2024-2025学年九年级上学期10月月考数学试题一、单选题1.在百度上搜索“一带一路”,显示找到相关结果约52 900 000个,将数字52 900 000用科学记数法表示为( )A .752.910⨯B .80.52910⨯C .85.2910⨯D .75.2910⨯ 2.下列运算正确的是( )A .428a a a ⋅=B .()326a a -=C .()22ab ab =D .3222a a a ÷= 3.下列四边形:①平行四边形;②矩形;③菱形;④正方形.其中,是中心对称图形,而不是轴对称图形的有( )个A .0B .1C .2D .34.已知α为等腰直角三角形的一个锐角,则cosα等于( )A .12B .22C .32D .335.在下列四个函数中,当0x >时,y 随x 的增大而减小的函数是( )A .2y x =B .3y x = C .32y x =- D .2y x =6.若某人沿坡角为α的斜坡前进100m ,则他上升的最大高度是( )A .100sinαmB .100sin αmC .100cos αmD .100cosαm 7.若抛物线2y x 2x c =-+与y 轴的交点为(0,﹣3),则下列说法不正确的是【 】 A .抛物线开口向上B .抛物线的对称轴是x=1C .当x=1时,y 的最大值为﹣4D .抛物线与x 轴的交点为(-1,0),(3,0)8.已知抛物线2y mx nx =+和直线y mx n =+在同一坐标系内的图象如图,其中正确的是( )A .B .C .D .9.如图,菱形ABCD 中,60DAB ∠=︒,点P 是对角线AC 上的动点,点M 在边AB 上,且4AM =,则点P 到点M 与到边AB 的距离之和的最小值是( )A.4 B .C .2D 10.二次函数2y ax bx c =++(0a ≠)的图像如图,给出下列四个结论:①240ac b -<;②42a c b +<;③320b c +<;④()m am b b a ++<,⑤点()14,y -,()21,y 都在抛物线上,则有12y y <.其中正确的结论其中正确结论的个数是( )A .①③④B .②④⑤C .①③⑤D .②③④二、填空题11.函数y =x 的取值范围为. 12.已知23ab a b =+,则11a b +=. 13.分解因式:()2x x 38--=.14.让胡路区某校九(1)班举办“古诗词大赛”活动,全班48名同学推选16名同学组成红、黄、蓝、绿四个战队,每队参赛选手4人.若林昊和王宁都是比赛选手,则他们分到同一个战队的概率为.15.如图,矩形ABCD ,2AB =,1BC =,将矩形ABCD 绕点A 顺时针旋转90°得矩形AEFG ,连接CG 、EG ,则tan CGE ∠=.16.如图,已知抛物线y =x 2+bx +c 的对称轴为x =2,点A ,B 在抛物线上,且AB 与x 轴平行,其中点A 的坐标为(0,3),则点B 的坐标为.17.如图,平台AB 高为12m ,在B 处测得楼房CD 顶部点D 的仰角为45°,底部点C 的俯角为30°,则楼房CD 的高度为m .(结果精确到1m1.73≈)18.在同一平面直角坐标系内,将函数2243y x x =+-的图像向右平移2个单位,再向下平移1个单位得到图像函数的解析式是.三、解答题19.计算:0222tan 60-+-+︒20.(1)解不等式组11223x x ⎧≤⎪⎨⎪-<⎩;(2)先化简,再求值:211(1)2x x x x-+÷-,其中2x =. 21.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC 的三个顶点均在格点(网格线的交点)上.以原点O 为位似中心,画△A 1B 1C 1,使它与△ABC 的相似比为2,并写出点B 的对应点B 1的坐标.22.已知关于x 的一元二次方程23210x x a -++=有两个不相等的实数根.(1)求实数a 的取值范围;(2)若a 为符合条件的最大整数,且一元二次方程23210x x a -++=的两个根为1x ,2x,求221212x x x x +的值.23.今年,教育局大力推动“中华优秀传统文化进校园”活动,某校组织全校2000名学生参与了“爱我中华知识竞赛”活动,为了了解本次知识竞赛的成绩分布情况,随机抽取了部分学生的得分进行统计,请你根据统计图,回答下列问题:(1)求被抽取的学生人数;(2)求扇形统计图中,“90~100”分数段所在扇形的圆心角的度数;(3)补全频数分布直方图;(4)试估计该校此次竞赛的平均成绩.24.如图,平行四边形ABCD 中,过点A 作AE ⊥BC 于E ,连接DE ,F 为DE 中点,且∠BAE =∠DEC ,∠B =60°.(1)判断△AEF 的形状并说明理由;(2)若AB =2,求DE 的长.25.下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN ,DM ,CB 为三根垂直于AB 的支柱,垂足分别为N ,M ,B ,∠EAB=31°,DF ⊥BC 于点F ,∠CDF=45°,求DM 和BC 的水平距离BM 的长度.(结果精确到0.1 m .参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)26.如图,直线y x =与反双曲线(0)k y k x =>在第一象限交于点A ,AB x ⊥轴于()2,0B ,点C 是双曲线(0)k y k x=>图象上一动点.(1)求反比例函数的解析式;(2)①若OBC △的面积为1,求AOC △的面积.②在①的条件下,根据图象直接写出在第一象限内当x 满足什么条件时,经过点A 、C 的一次函数的函数值小于反比例函数k y x=的函数值. 27.爱贝玩具厂开发了一款新型益智玩具,一期计划生产200万件,预计20天后投入市场.该厂有甲、乙、丙三条生产线,由于丙生产线在技术创新升级中,则由甲、乙两条生产线先开始生产加工玩具.甲、乙两条生产线一起生产加工玩具4天后,乙生产线发生故障停止生产,只剩甲生产线单独加工玩具.为了能在规定时间完成任务,丙生产线加快了技术升级,6天后也投入生产.由于丙生产线技术升级后提高了效率,所以提前一天完成加工任务.已知甲、乙两条生产线生产玩具总量1y (万件)与时间x (天)的关系如图折线段OAB 所示,丙生产线生产玩具总量2y (万件)与时间x (天)的关系如图线段CD 所示.(1)求第5天结束时,生产玩具总量.(2)求玩具生产总量y (万件)与时间x (天)的函数关系式(注明x 的取值范围). (3)直接写出生产第几天时,甲、乙两条生产线生产玩具总量与丙生产线生产玩具总量差为20万件.28.如图,抛物线2y x bx c =-+交x 轴于点()1,0A ,交y 轴于点B ,对称轴是2x =.(1)求抛物线的解析式;(2)点P 是抛物线对称轴上的一个动点,是否存在点P ,使PAB V 的周长最小?若存在,求出点P 的坐标;若不存在,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边
所在的直线成 30°角, 则此三角板的最大边的长为
。
三、解答题:(共 60 分) 21.(1) (本题 5 分)解不等式 3x+5≥ x-1 ,并把解集在数轴上表示出来。
(2)(本题 5 分):已知 x=3 是方程 x=-a+1 的解,试求不等式( -5+a )x<-14 的解集。
E
28 .(本题 10 分)如图,在平面直角坐标系中,点 A 的坐标为( 1,0 ),以 线段 OA为边在第四象限内作等边三角形 AOB,点 C 为 X 轴的正半轴上一动点, ( OC大于 1)连接 BC,以线段 BC为边在第四象限内作等边三角形 CBD,连接 DA并延长,交 Y 轴于点 E。
18. 等腰三角形一腰上的高与另一腰的夹角为 50°,则该等腰三角形的底角
的度数为
。
19. 如图,在△ ABC中, BI 、CI 分别平分∠ ABC、∠ ACF,DE过点 I ,且 DE∥
BC.BD=8cm,CE=5cm,则 DE等于 _________ .
22. (本题 6 分)如图,△ ABC中, AB=AC,∠ BAC和∠ ACB的平分线相交于点 D,∠ ADC=12°5 ,求∠ ACB和∠ BAC的度数.
第 15 题图
第 16 题图
16. 如图 ,D,E 分别为 AB,AC的中点 , 将△ ABC沿线段 DE折叠 , 使点 A落在 BC边
上的点 F 处, 若∠ B=50°, 则∠ BDF=
。
17. 一个三角形的三边长度为 5cm,12cm,13cm,那么这个三角形三条角平分线
的交点到三边的距离是 _________ cm。
。
初三学年第一次检测数学试卷
第 2 页 共3页
24. (本题 6 分)如图,△ ABC中,E 是 BC边上的中点, DE⊥BC于 E,交∠ BAC 的平分线 AD于 D,过 D 作 DM⊥ AB于 M,作 DN⊥AC于 N,试证明: BM=CN.
A
27. (本题 8 分) 如图所示,在四边形 ABCD中,AD∥ BC,E 为 CD的中点,连
23. (本题 8 分)如图,已知 AC⊥BC,BD⊥ AD,AC与 BD交于 O,AC=BD. 求证:( 1) BC=AD;
( 2)△ OAB是等腰三角形.
第 19 题图
第 20 题图
20. 如图所示,△ ABC是等腰直角三角形∠ BAC=9°0 , AC=4,直线 l 垂直平分
AC交 AC于点 D,点 P 在直线 l 上,则△ APB的周长的最小值
A.a>0 B . a<0 C .a>1 D .a<1
10. 如图,在△ ABC中,∠C=90°,∠ B=30°,以 A 为圆心,任意长为半径画 弧分别交 AB、AC于点 M和 N,再分别以 M、N 为圆心,大于 MN的长为半径画
弧,两弧交于点 P,连结 AP并延长交 BC于点 D,则下列说法中正确的个数是
班级
2019—2020 学年度第一学期第一次质量检测
初 三 ( 数学 ) 试题
7. 如图,在等腰△ ABC中,AB=AC,∠ A=40°,P是△ ABC内一点,且∠ 1=∠ 2,
则∠ BPC等于(
)
A.110° B.120° C.130° D.140°
姓名
题号
一
二
三
总分
得分
装
一、选择题:(每小题 3 分,共计 30 分)
(
)
① AD是∠ BAC的平分线; ②∠ ADC=6°0 ;
③点 D 在 AB的中垂线上; ④ S△ : DAC S△ABC=1:3.
A. 1
B. 2
C. 3
D.4
初三学年第一次检测数学试卷
第 1 页 共3页
二、填空题:(每小题 3 分,共 30 分)
11. 用不等式表示: x 与 5 的差不大于 x 的 2 倍:
不订
若 PA=2,则 PQ的最小值为(
)
要
A.1BBiblioteka .2C.3
D
.4
答
第 7 题图
第 8 题图
8. 如图,在△ ABC中,∠ ACB=90°,D,E 分别为 AC,AB的中点,连 DE,CE.下列
结论中不一定正确的 (
)
A. ED ∥ BC
B . ED ⊥ AC C . ACE BCE
D . AE CE
(
1. 如果 a b ,那么下列各式中正确的是(
)
装
订
A . a b B . a 3 b 3 C . 2a 2b D . a b 33
线 2. 等腰三角形的一个角是 80°,则它的顶角的度数是(
)
内
A.80° B . 20° C .80°或 50° D .80°或 20°
3. 如图所示, OP平分∠ MON,PA⊥ON于点 A,点 Q是射线 OM上的一个动点,
9. 如图,在等边 ABC 中, D, E 分别是 BC, AC 上的点,且 BD CE , AD 与
BE相交于点 P,则 1 2 的度数是(
A. 450
B
. 550
C . 600
). D
. 750
题
)
-3 -2 -1 0 1
第 9 题图
第 10 题图
线
第 3 题图
第 4 题图
4. 用不等式表示图中的解集 , 其中正确的是 (
)
A. x ≥- 2 B. x >- 2 C. x <- 2 D. x ≤- 2
5. △ ABC中,∠A:∠B:∠ C=1:2:3,最小边 BC=4cm,最长边 AB的长是(
)
A. 5cm
B. 6cm
C.7cm
D. 8cm
6. 若关于 x 的不等式 (1 a) x 2 可化为 x 2 ,则 a 的取值范围是 ( ) 1a
接 AE,BE,且 BE⊥AE,延长 AE交 BC的延长线于点 F.已知 AD=2cm,BC=5cm. ( 1)求证: FC=AD;( 2)求 AB的长。
M
E
C
B
N
D
25. (本题 6 分)如图,某船向正东方向航行, 在 A 处测得岛 C 在北偏东 60° 方向,前进 6 海里到点 B 处,测得岛 C在北偏东 30°方向,已知海岛 C 周围 6 海里内有暗礁,若该船继续向东航行,有无触礁危险?请说明理由.
。
12. 等腰三角形一边长为 4cm,另一边长为 8cm,那么这个等腰三角形的周长
是 ________。
13. 关于 x 的不等式 2x-a< - 1 的解集是 x<2,则 a 的值是 ________。
14.满足- 4x≥- 12 的非负整数是 _____________。
15. 如图,将一个有 45°角的三角板的直角顶点放在一张宽为 3cm的纸带边沿
