哈工大理论力学教研室《理论力学Ⅱ》(第7版)课后习题(非惯性系中的质点动力学)
哈尔滨工业大学 第7版 理论力学 第4章 课后习题答案

解 (1)方法 1,如图 4-6b 所示,由已知得
Fxy = F cos 60° , Fz = F cos 30°
F = F cos 60°cos 30°i − F cos 60°sin 30° j − F sin 60°k = 3 i − 1 Fj − 3 Fk 44 2
41
理论力学(第七版)课后题答案 哈工大.高等教育出版社
A
F
β
MA
C
MB
F
10 N
β M θ − 90° C
MB
(a)
(b)
(c)
图 4-11
解 画出 3 个力偶的力偶矩矢如图 4-11b 所示,由力偶矩矢三角形图 4-11c 可见
MC =
M
2 A
+
M
2 B
=
3 0002 + 4 0002 = 5 000 N ⋅ mm
由图 4-11a、图 4-11b 可得
3 = 250 N 13
FRz = 100 − 200 ×
1 = 10.6 N 5
M x = −300 ×
3 × 0.1 − 200 × 1 × 0.3 = −51.8 N ⋅ m
13
5
M y = −100 × 0.20 + 200 ×
2 × 0.1 = −36.6 N ⋅ m 13
M z = 300 ×
z
F45° F3 F3′ B
F2A
E
F1
C
F5
F6
F F4 45°
D
y
K x
M
(a)
(b)
图 4-9
解 (1) 节点 A 为研究对象,受力及坐标如图 4-9b 所示
哈工大理论力学教研室《理论力学》(第7版)笔记和课后习题(含考研真题)详解(第16~17章)【圣才出

第16章非惯性系中的质点动力学16.1复习笔记一、基本方程1.非惯性系中的质点动力学基本方程(或称为质点相对运动动力学基本方程),其表达式为r Ie ICma F F F =++v v v v 式中,e Ie F ma =-v v ,表示牵连惯性力;C C I F ma =-v v ,表示科氏惯性力。
2.在动参考系内,把非惯性系质点动力学基本方程写成微分形式22Ie IC d d r m F F F t'=++v v v v 3.几种特殊情况(1)当动参考系相对于定参考系作平移时,则C 0a = ,0F =IC ,于是相对运动动力学基本方程为r Iema F F =+v v v (2)当动参考系相对于定参考系作匀速直线平移时,则C 0a = ,e 0a = ,Ie 0F F ==IC,于是相对运动动力学基本方程与相对于惯性参考系的基本方程形式一样,其表达式为r ma F= ①相对于惯性参考系做匀速直线平移的参考系都是惯性参考系。
②发生在惯性参考系本身的任何力学现象,都无助于发现该参考系本身的运动状况,这称为经典力学的相对性原理。
(3)当质点相对于动参考系静止时,则r r 00a υ==v v ,,0F =IC ,所以质点相对静止的平衡方程为F F +=Ie 上式称为质点相对静止的平衡方程,即当质点在非惯性参考系中保持相对静止时,作用在质点上的力与质点的牵连惯性力相互平衡。
(4)当质点相对于动参考系作等速直线运动时,有r 0a =,质点相对平衡方程为0Ie IC F F F ++=v v v 上式称为质点相对平衡方程。
可见在非惯性参考系中,质点相对静止和作等速直线运动时,其平衡条件是不相同的。
二、非惯性系中质点的动能定理1.质点相对运动动能定理的微分形式质点在非惯性系中相对动能的增量,等于作用于质点上的力与牵连惯性力在相对运动中所作的元功之和。
即2r 1d()δδ2F mv W W ''=+Ie 2.质点相对运动动能定理的积分形式质点在非惯性参考系中相对动能的变化,等于作用在质点上的力与牵连惯性力在相对路程上所作的功之和。
哈工大第七版 理论力学 课后有题答案 10章

10-3 如图所示水平面上放1 均质三棱柱A,在其斜面上又放1 均质三棱柱B。
两三棱柱的横截面均为直角三角形。
三棱柱A 的质量为mA三棱柱B 质量mB的 3 倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱B 沿三棱柱A 滑下接触到水平面时,三棱柱A 移动的距离。
11-4解取A、B 两三棱柱组成1 质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统质心位置在水平方向守恒。
设A、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4 如图所示,均质杆AB,长l,直立在光滑的水平面上。
求它从铅直位无初速地倒下时,端点A相对图b所示坐标系的轨迹。
解取均质杆AB 为研究对象,建立图11-6b 所示坐标系Oxy,原点O与杆AB 运动初始时的点B 重合,因为杆只受铅垂方向的重力W 和地面约束反力N F 作用,且系统开始时静止,所以杆AB 的质心沿轴x 坐标恒为零,即设任意时刻杆AB 与水平x 轴夹角为θ,则点A坐标从点A 坐标中消去角度θ,得点A 轨迹方程10-5 质量为m1 的平台AB,放于水平面上,平台与水平面间的动滑动摩擦因数为f。
质量为m2 的小车D,由绞车拖动,相对于平台的运动规律为,其中b 为已知常数。
不计绞车的质量,求平台的加速度。
解受力和运动分析如图b 所示式(1)、(4)代入式(3),得10-6 如图所示,质量为m的滑块A,可以在水平光滑槽中运动,具有刚性系数为k 的弹簧1 端与滑块相连接,另 1 端固定。
杆AB 长度为l,质量忽略不计,A 端与滑块A 铰接,B 端装有质量m1,在铅直平面内可绕点A 旋转。
设在力偶M 作用下转动角速度ω为常数。
求滑块A 的运动微分方程。
理论力学第七版答案、高等教育出版社出版

仅供个人学习参考哈工大理论力学(I )第7版部分习题答案1-2两个老师都有布置的题目2-3?2-6?2-14?2-?20?2-30?6-2?6-4?7-9??7-10?7-17?7-21?8-5?8-8?8-16?8-24?10-4?10-6?11-5?11-15?10-3以下题为老师布置必做题目1-1(i,j ),1-2(e,k)2-3,2-6,2-14,2-20,2-306-2,6-47-9,7-10,7-17,7-21,7-268-5,8-8(瞬心后留),8-16,8-2410-3,10-410-611-5,11-1512-10,12-15,综4,15,16,1813-11,13-15,13-166-2图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5m 在铅垂面内转动,杆AB=0.8m ,A 端为铰链,B 端有放置工件的框架。
在机构运动时,工件的速度恒为0.05m/s ,杆AB 始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B 的轨迹方程。
10-3如图所示水平面上放1均质三棱柱A ,在其斜面上又放1均质三棱柱B 。
两三棱柱的横截面均为直角三角形。
三棱柱A 的质量为mA 三棱柱B 质量mB 的3倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱B 沿三棱柱A 滑下接触到水平面时,三棱柱A 移动的距离。
11-4解取A 、B 两三棱柱组成1质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统 质心位置在水平方向守恒。
设A 、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c 所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4如图所示,均质杆AB ,长l ,直立在光滑的水平面上。
求它从铅直位无初速地倒下时,端点A 相对图b 所示坐标系的轨迹。
哈尔滨工业大学 第七版 理论力学.13
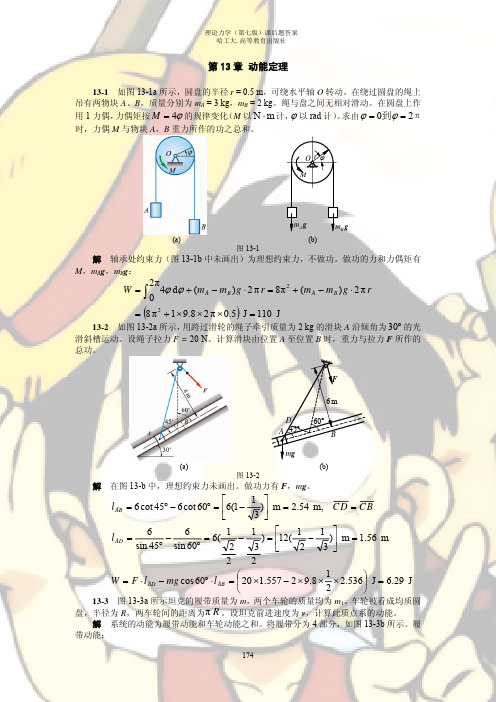
1 2 T履 = ∑ mi vi = TI + TII + TIII + TIV 2
D II A
(a) 图 13-3
IV
2v
C
ω
v
III
Iv=0
(b)
B
由于 v1 = 0, vIV = 2v ,且由于每部分履带长度均为π R ,因此
mI = mII = mIII = mIV = TI =
m 4
1 2 mI vI = 0 2 1 1 m m 2 TIV = mIV v IV = × (2v) 2 = v 2 2 2 4 2 m m 2 II、III 段可合并看作 1 滚环,其质量为 ,转动惯量为 J = R ,质心速度为 v,角速度 2 2 v 为 ω = ,则 R 1 m 1 mv 2 1 m 2 v 2 m 2 TII + TIII = ⋅ v 2 + Jω 2 = + ⋅ R ⋅ 2 = v 2 2 2 4 2 2 2 R m m T履 = 0 + v 2 + v 2 = mv 2 2 2
理论力学(第七版)课后题答案 哈工大.高等教育出版社
第 13 章 动能定理
13-1 如图 13-1a 所示,圆盘的半径 r = 0.5 m,可绕水平轴 O 转动。在绕过圆盘的绳上 吊有两物块 A、B,质量分别为 mA = 3 kg,mB = 2 kg。绳与盘之间无相对滑动。在圆盘上作 用 1 力偶, 力偶矩按 M = 4ϕ 的规律变化 (M 以 N ⋅ m 计, ϕ 以 rad 计) 。 求由 ϕ = 0到ϕ = 2π 时,力偶 M 与物块 A,B 重力所作的功之总和。
第 2 阶段 :系统通过搁板继续运动 x2 距离后静止。由动能定理
理论力学第七版课后习题答案(共9篇)

理论力学第七版课后习题答案(共9篇)理论力学第七版课后习题答案(一): 求理论力学第七版课后习题答案1、很高兴为您回答,但我没有题目内容啊!2、自己亲自做吧.网上(如:百度文库)可能查找到一些答案,一般不全.对搞不懂的题目,可以上传题目内容,以方便为你回答.理论力学第七版课后习题答案(二): 理论力学第六版(哈尔滨工业大学理论力学教研室)高等教育出版社课后习题答案 [email protected]【理论力学第七版课后习题答案】已发送注意查收理论力学第七版课后习题答案(三): 理论力学第七版高等教育出版社PDF 要《理论力学》(I)(第7版),《理论力学》(II)(第7版),《简明理论力学》(第2版)高等教育出版社,理论力学解题指导及习题集(第3版)高等教育出版社,理论力学思考题集高等教育出版社,这些书的PDF 非常谢谢必有重赏在下载了一会上传附件,望等待!!!理论力学第七版课后习题答案(四): 有几道力学题,.理论力学第一题选择题(基本概念和公理)1 理论力学包括()A、静力学、运动力学和动力学.B、运动学和材料力学.C、静动力学和流体力学.D、结构力学和断裂力学.2 静力学是研究()A、物体破坏的规律B、物体平衡的一般规律.C、物体运动的一般规律..D、物体振动的规律..3 关于刚体的说法是()A、很硬的物体.B、刚体内任意两点间的距离可以微小改变..C、刚体内任意两点间的距离保存不变.D、刚体内任意两点间的距离可以改变.4 关于平衡的概念是()A、物体相对于惯性参考系静止.B、物体做加速运动.C、物体相对于惯性参考系运动.D、物体做减速运动5 力是物体间的()A、相互化学作用..B、相互机械作用.C、相互遗传作用.D、相互联接作用.6 力对物体作用的效应取决于力的三要素,三要素是指()A、力的大小、方向和坐标B、力的大小、量纲和作用点.C、力的大小、方向和作用点.D、产生力的原因、方向和作用点.7 在国际单位制中,力的单位是()A、米(m).B、牛顿.米(N.m).C、牛顿.秒(m).D、牛顿(N).8 关于约束的说法是()A、限制物体运动的装置B、物体和物体的链接.C、物体运动的装置.D、使物体破坏的装置.ABCAD CDA理论力学第七版课后习题答案(五): 第七课答案【理论力学第七版课后习题答案】七年级上语文期末复习复习提要 1、语言积累和运用.2、现代文阅读.3、文言文、古诗词阅读.4、作文复习.5、专题训练及总测试.重点 1、注意辨别字形、正字音、释词义,理解语句在具体语境中的含义.2、整体感知课文,理解文章内容和写作特色,领悟作者的思想感情.3、学习文言文,生在朗读、背诵.掌握积累一些文言词语,理解文章大意,学会翻译文言文.4、学会审题,并结合学习生活实际,选取典型的材料进行作文,学会运用学过的词语及写作技巧.难点:1、关键词语的揣摩.2、理解一些重要语句的深刻含义.3、理解诗歌的意境.4、作文的选材立意.课时划分:1、积累与运用(4课时).A、拼音汉字、改正错别字.B、古诗、名句的默写.C、仿写句子、广告标语、综合性学习.D、对对子、名著导读.2、现代文阅读(4课时).A、课内阅读(2课时).B、课外阅读(2课时) 3、文言文阅读(2课时).4、作文(2课时).附:专题练习分工:积累与运用:张桂芬、钟国珍,现代文阅读(课内:王安华、黄卓苗,课外:郑小坚、范远填),文言文阅读:方焕章,作文:王文捷复习教案第一课时复习内容 1、复习本册学过的生字生词,掌握音、形、义.2、熟练运用学过的生字词.一、复习本册学过的生字生词,掌握音、形、义.1、教师指导学生掌握关键词语,让学生读、抄一遍,掌握正确的读音和拼写规则,特别注意平常容易读错的字音和多音多义字的读音.如:A、给下列加点的字注音或根据拼音写汉字.痴()想隐秘()诱惑()xuān( )腾一shùn( )间yùn( )含 B、请你找出并改正词语中的错别字.惊荒失措 _____改为_____ 昂首铤立_____改为_____ 二、进行逐单元进行听写训练.(一般分开在课前进行)三、完成试卷练习.(课后巩固为主)第二课时复习内容 1、复习古诗、名句的默写.2、学会初步赏析一些古诗或《论语》中的名句.一、学生复习要求背诵古诗和名篇.1、学生诵读本册要求背诵的古诗.2、教师指导学生熟记一些名句,会默写.3、掌握重点,理解诗歌的主题思想,体会含义深刻的句子.二、默写练习.(主要针对后进生,以激励为主)如:A、商女不知亡国恨,_______________________.《泊秦淮》 ,浅草才能没马蹄.《钱塘湖春行》B、《观沧海》中展现海岛生机勃勃的诗句是:,.,.《次北固山下》一诗中道出新旧更替的生活哲理的名句是:,.三、课后试卷练习巩固.第三课时复习内容1、仿写句子.2、复习比喻、拟人等修辞方法的辨别和运用.一、明白仿写的意义及方法.1、仿句是按照题目已经给出的语句的形式,再另外写出与之相仿的新句,仿句只是句式仿用,文字内容不能完全一样.只要被模仿的是句子的形式,不管是单句或复句,都列入仿句.2、仿句考查的知识点:(1)、考查同学们对语法、修辞等知识的综合运用,要求同学们根据不同的语境和要求,写出与例句内容和形式相同或相近、意义上有密切关联的句子.例如:生活就是一块五彩斑斓的调色板.希望就是________________________.[解析]这道题目从句式上看是陈述句.在修辞上运用了比喻,同学们要注意比喻运用的得体,比喻的艺术贵在创新,要寻找新鲜、活泼的喻体,保持上下文的协调性.如:希望就是一颗永不陨落的恒星.希望就是一盏永不熄灭的明灯.(2)、考查同学们的语言表达能力,联想、想象能力,创新思维能力.例如:什么样的年龄最理想什么样的心灵最明亮什么样的人生最美好什么样的青春最辉煌鲜花说,我开放的年龄多妩媚;月亮说,____________________________;海燕说,_______________________.太阳说,_________________________________.[解析]该题是问答式的仿写,在回答上运用拟人的修辞,要求天下们针对性进行回答,有一定的开放度,但是在解题时,要注意结合回答对象的特点.如:我纯洁的心灵多明亮;我奋斗的人生极美好;我燃烧的青春极辉煌.(3)、是对同学们思想认识水平的检测,包括道德素质,审美理论力学第七版课后习题答案(六): 理论力学的基本原理和基本假设是什么理论力学是机械运动及物体间相互机械作用的一般规律的学科,也称经典力学.是力学的一部分,也是大部分工程技术科学理论力学的基础.其理论基础是牛顿运动定律,故又称牛顿力学.原理的话就是牛顿三大定理咯.定理都是在基本假设的基础上推出来的,所以想想牛顿三定律是建立在什么假设基础上的我能总结出来的就三点:1.时间是绝对的,其含义是时间流逝的速率与空间位置和物体的速率无关; 2.空间是欧几里德的,也就是说欧几里德几何的假设和定律对空间是成立的;3.经典物理的第三个假设,就是质点的运动可以用位置作为时间的函数来描述.理论力学第七版课后习题答案(七): 大学理论力学的问题(哈工大第七版)有关力矩在平面力对点之炬,这一节中,关于力对点之矩的正负问题中,顺时针和逆时针怎么判断呢以及在力对轴的矩中右手螺旋定则怎么定义的啊利用右手螺旋定则,其实判断力矩正负和以前高中学的判定磁场方向差不多,就是伸出右手,大拇指与其余四个手指垂直,其余四指弯向力的方向,这时候可以有两种判定方法:第一种,如果其余四指弯曲的方向是顺时钟,则力矩为负,反之,则为正;第二种,如果这时大拇指指向为上,那么力矩为正,反之,则为负.总之大体的判断方法就是这样,至于哪种方法更容易,楼主自行体会吧.最后祝你学业进步~理论力学第七版课后习题答案(八): 现代物理学包括哪几部分目前我们学物理是包括了力学,光学,热学,电磁学,原子物理学,理论力学,热力学,统计物理学,电动力学,量子力学,数学物理方法,固体物理学这些学科的理论力学第七版课后习题答案(九): 科学不怕挑战的阅读答案5.本文的中心论点是什么7 (4分)6.第③④段运用了事例来论证,请分别概括这两个事例的内容.(4分)7.第⑤段申两个句子的顺序能否颠倒为什么(4分)8.第⑥段中"科学"一词为什么加上引号(2分)9.说说画线句子在文中的表达作用.(3分)参考答案:5、科学不怕挑战(或“科学不怕挑战,怕挑战的不是科学.”)(2分)6、第③段:量子力学曾受到爱因斯坦理想实验的挑战(1分);第④段:进化论曾受到创世说者的频频发难(1分).7、不能颠倒(1分).这句话有承上启下的作用,前半句总结上文,后半句引出下文(1分).8、为了表示讽刺和否定.(2分)9、运用了比喻论证的方法(1分),将科学不断受到挑战比作了大浪淘沙,证明了科学是不怕挑战的,从而把抽象深奥的道理阐述得生动形象、浅显易懂(1分).。
理论力学(第七版)2

va =
得
va = 2 aω cos 30° aω 1 = 2 aω
ω=
ω1
2
= 1.5 rad/s (逆)
(b)套筒 A 为动点,动系固结于杆 O1 A ;绝对运动为绕 O2 圆周运动,相对运动为沿
va = O2 A ⋅ ω1 = 2aω cos 30° , ve = O1 Aω1 = aω 1 ve aω 1 由图 b1: v a = = cos30° cos30° aω 1 得 2aω cos 30° = cos 30° 2 ω = ω 1 = 2 rad/s (逆) 3 8-8 图 8-8a 所示曲柄滑道机构中,曲柄长 OA = r ,并以等角速度 ω 绕轴 O 转动。 装在水平杆上的滑槽 DE 与水平线成 60° 角。求当曲柄与水平线的交角分别为 ϕ = 0° , 30° , 60° 时,杆 BC 的速度。
y
如图 8-9a 所示,摇杆机构的滑杆 AB 以等速 v 向上运动,初瞬时摇杆 OC 水平。
摇杆长 OC = a ,距离 OD = l 。求当 ϕ =
va ve
C
vr
O
(a) 图 8-9
ϕ
l
(b)
A D
v
x
解 套筒 A 为动点,动系固结于杆 OC;绝对运动为上下直线,相对运动沿 OC 直线, 牵连运动为绕 O 定轴转动。速度分析如图 8-9b 所示,设杆 OC 角速度为 ω ,其转向逆时 针。由题意及几何关系可得 va = v (1)
ve1 − v r1 cos 30° = ve2 b b ω − ω ve1 − ve2 cos30° 1 cos30° 2 4b = = (ω 1 − ω 2 ) v r1 = cos30° cos30° 3 式(3)向 v r2 方向投影,得 1 2b (ω 1 − ω 2 ) = 0.4 m/s v r2 = v r1 = 2 3 0.1 ve2 = × 3 = 0.346 m/s 3 2 ⎧v = v 2 + v 2 = 0.529 m/s e2 r2 ⎪ a 所以 ⎨ ve2 0.346 = ,θ = 40.9° ⎪tan θ = 0 .4 v r2 ⎩
(NEW)哈工大理论力学教研室《理论力学》(第7版)笔记和课后习题(含考研真题)详解

目 录第1章 静力学公理和物体的受力分析1.1 复习笔记
1.2 课后习题详解
1.3 名校考研真题详解
第2章 平面力系
2.1 复习笔记
2.2 课后习题详解
2.3 名校考研真题详解
第3章 空间力系
3.1 复习笔记
3.2 课后习题详解
3.3 名校考研真题详解
第4章 摩 擦
4.1 复习笔记
4.2 课后习题详解
4.3 名校考研真题详解第5章 点的运动学
5.1 复习笔记
5.2 课后习题详解
5.3 名校考研真题详解第6章 刚体的简单运动
6.1 复习笔记
6.2 课后习题详解
6.3 名校考研真题详解第7章 点的合成运动
7.1 复习笔记
7.2 课后习题详解
7.3 名校考研真题详解第8章 刚体的平面运动8.1 复习笔记
8.2 课后习题详解
8.3 名校考研真题详解
第9章 质点动力学的基本方程9.1 复习笔记
9.2 课后习题详解
9.3 名校考研真题详解
第10章 动量定理
10.1 复习笔记
10.2 课后习题详解
10.3 名校考研真题详解
第11章 动量矩定理
11.1 复习笔记
11.2 课后习题详解
11.3 名校考研真题详解
第12章 动能定理
12.1 复习笔记
12.2 课后习题详解
12.3 名校考研真题详解
第13章 达朗贝尔原理。
哈工大理论力学教研室《理论力学Ⅱ》(第7版)名校考研真题(分析力学基础)

第15章 分析力学基础1.如图15-1所示,物块A 的质量为m 1,B 轮的质量为m 2,半径为R ,在水平面做无滑动滚动。
轮心用刚度为k 长度为l 的弹簧与物块A 相连,物块A 与水平面间为光滑接触。
试以X 1,X 2为广义坐标, (1)写出系统的动能及势能及拉格朗日函数;(2)写出系统的第二类拉格朗日方程;(3)求系统的第二类拉格朗日方程的首次积分。
[中山大学2011研]图15-1解:(1)系统的动能为:222 (122111242)T m x m x m x =++ 系统势能为:201()2V k x δ=+ 其中0δ为处于平衡位置弹簧的伸长量。
拉格朗日函数22..2120131()242L T V m x m x k x δ=-=+-+(2)第二类拉格朗日方程.()0d L L dt xx ∂∂-=∂∂ 代入上一步的表达式,得....1203()02m x m x k x δ+-+= (3)求其首次积分。
因拉格朗日函数中不显含时间t ,故存在能量积分,系统机械能守恒,即22..2120131()242m x m x k x δ+-+=C C 为常数2.质量为m 的重物悬挂在刚度系数为k 的弹簧上,且在光滑的铅垂滑道中运动。
在重物的中心处铰接一个质量为M 、长为21的匀质杆,杆在铅垂平面内运动,如图15-2所示。
(1)试确定系统的自由度并选择广义坐标;(2)写出系统的动能及势能及拉格朗日函数;(3)写出系统的第二类拉格朗日方程;(4)求系统的第二类拉格朗日方程的首次积分。
[中山大学2010研]图15-2解:(1)以整个系统为研究对象,物块和杆均做平面运动,该系统具有两个自由度。
选重物A 的中心的垂直坐标y 和杆的偏角ϕ为广义坐标,如下图所示。
因为作用在系统上的主动力即重力和弹性力均为有势力,所以可用拉格朗日方程式主动力有势形式求解。
(2)以A 的中心C 点为基点分析AB 杆质心D 的速度,如图15-3所示。
哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案

解
设轮缘上任 1 点 M 的全加速度为 a,切向加速度 a t = rα ,法向加速度 a n = ω r ,如图
2
7-11b 所示。
tan θ =
把
α=
dω , θ = 60° 代入上式,得 dt
at α = 2 an ω
dω tan 60° = dt2
ω
分离变量后,两边积分:
∫ω
得
ω
0
dω
ω
2
=∫
⎤ ⎡ ⎥ ⎢ sin ω t 0 θ = tan −1 ⎢ ⎥ ⎢ h − cos ω 0 t ⎥ ⎥ ⎢ ⎦ ⎣r
故
50 π ⋅ 600 100π r ω1 = rad/s ⋅ = 100 − 5t 30 10 − 0.5t d dω 5 000 π d ⎛ 1 000π ⎞ α2 = 2 = ⎜ ⎟= dt dt ⎝ 100 − 5t ⎠ (100 − 5π )2
故得
h1 =
h4 = 2 mm 6
图 7-7
7-8 如图 7-8 所示,纸盘由厚度为 a 的纸条卷成,令纸盘的中心不动,而以等速 v 拉纸条。求 纸盘的角加速度(以半径 r 的函数表示) 。 解 纸盘作定轴转动,当纸盘转过 2π rad 时半径减小 a。设纸盘转过 dθ 角时半径增加 dr ,则
dθ =
y
B
t aB
α j
O
vA x
ω
(a) 图 7-12
aC
(b)
i 45° A n
C
t aC
解
由图 7-12b 得出
84
理论力学(第七版)课后题答案 哈工大.高等教育出版社
v A = 0.2 j m/s , v A = ω × Ri , ω × 0.1i = 0.200 j , ω = 2k ,
哈尔滨工业大学理论力学第七版第II篇 第2章 非惯性系中的质点动力学

y′
非惯性系中的质点动力学基本方程,或质点相对运动动力 学基本方程
m a r F F Ie F IC
非惯性系中的质点动力学基本方程,其中 F Ie m a e --- 牵连惯性力 F IC m a C --- 科氏惯性力
在非惯性系中,牵连惯性力和科氏惯性力是真实存在的
2 2 2 2 2 2
1 2
m R (1 cos max ) 0
2
R cos max 2 g cos max 2 g R 0
解出
cos max g ( R g )
2
R
2
cos max
g ( R g )
2
R
2
1 2
mv
2 r
1 2
mv
2 r0
W F W Ie
质点相对运动动能定理的积分形式:质点在非惯性系中相 对动能的变化,等于作用于质点上的力与牵连惯性力在相 对路径上所作的功之和。
例 半径为R的环形管,绕铅垂轴z以匀角速度转动,管内有 一质量为m的小球,原在最低处平衡。小球受微小扰动时可能会 沿圆管上升。忽略管壁摩擦,求小球能达到的最大偏角max。
(4)台风、龙卷风的形成。台风基本发生在大约离赤道5个
纬度以上的洋面上。
(5)证明地球自转的傅科摆(1851年Foucault J L发明)。
北半球
在北半球,摆运动的平面缓慢顺时针转动,平面旋转一周的周期为
T 2
sin
为地球自转角速度, 为傅科摆所在地的纬度。
某人水平抛出一个球,如果考虑科氏惯性力,在下述情况下,由抛球的人
a 2
理论力学(第七版)2

ω2
30°
θ ω1
(a) 图 8-11
va O
(b)
解 (1)运动分析 ① 活动销子 M 为动点,动系固结于轮 O;牵连运动为绕 O 定轴转动,相对运动为沿 轮上导槽直线,绝对运动为平面曲线。 v a = v e1 + v r1 (1) ② 活动销子 M 为动点,动系固结于杆 OA;牵连运动为绕 O 定轴转动,相对运动为 沿 OA 直线,绝对运动为平面曲线。
91
理论力学(第七版)课后题答案 哈工大.高等教育出版社
v a = v e2 + v r2
速度分析如图 8-11b 所示,由式(1) 、 (2)得 v e1 + v r1 = v e2 + v r2 方向 大小
(2) (3)
⊥ OM OM ⋅ ω 1
√ ?
⊥ OM OM ⋅ ω 2
√ ?
式(3)向 v e2 方向投影,得
ve va = sin(30° − ϕ ) sin 60°
所以
sin(30° − ϕ ) rω sin 60° 3 ϕ = 0° 时, v BC = ; rω (←) 3 ϕ = 30° 时, v BC = 0 v BC = ve =
ϕ = 60° 时, v BC = −
8-9
3 rω (→) 3 π 时点 C 的速度的大小。 4
y va vr
va v r
vr
60° 60°
杆直线运动,牵连运动为绕 O1 定轴转动。速度分析如图 8-7b1 所示。
va
A
ve
ϕ
ve
(a) (a)
60° A
(b) (b) 图 8-8 89
x
A
(c)
ω
哈工大理论力学教研室《理论力学Ⅱ》(第7版)配套题库【课后习题】(第18~20章)【圣才出品】

十万种考研考证电子书、题库视频学习平台
第 18 章 机械振动基础
一、思考题 18-1 图 18-1 所示装置,重物 M 可在螺杆上上下滑动,重物的上方和下方都装有弹 簧。问是否可以通过螺帽调节弹簧的压缩量来调节系统的固有频率?
图 18-1 答:弹簧被压紧并不改变其弹性系数,因而不能改变系统的固有频率。 18-2 图 18-2 所示的水平摆和铅垂摆都处于重力场中,杆重不计,摆长度 l、弹簧刚 度系数 A 以及摆锤质量 m 都是相同的。试问两个摆微幅摆动的固有频率是否相同?如果二 者都脱离了重力场,其固有频率是否相同?又,图中的弹簧方向都与摆杆垂直,如弹簧与摆 杆成 45°角连接,其固有频率有什么不同?
图 18-2
1 / 89
圣才电子书 十万种考研考证电子书、题库视频学习平台
答:摆杆水平与铅垂放置,其固有频率不相同,因为摆杆铅垂并沿横向摆动时,重力对 转轴有力矩,为恢复力之一;而摆杆水平并沿铅垂线微小摆动时,重力对转轴的力矩不变, 不构成恢复力。若无重力场,有质量而无重力作用,摆杆任意放置都不改变其固有频率。
18-4 在光滑水平面上,两个质量皆为 m 的质点由一刚度系数为 k 的无重弹簧相连。
若将二质点拉开一段距离再同时释放,二者将发生振动,求此振动的周期。如上述二质点的
质量分别为 m1 和 m2,问二者仍发生振动吗?振动周期为多大? 答:对质量相同的两质点构成的系统,其弹簧中点将保持不动,对每个质点相当于弹簧
3 / 89
圣才电子书
答:过阻尼状态下,
十万种考研考证电子书、题库视频学习平台
则自由振动解为
平衡位置处 x=0,即
解得
对应于任意初始条件,即任意 c1,c2。上式有唯一解。
哈尔滨工业大学 第七版 理论力学12
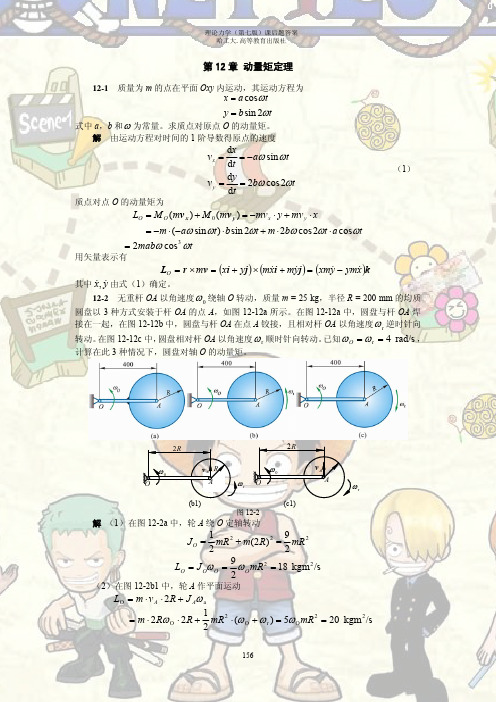
求飞轮的转动惯量和轴承的摩擦力矩。
Mf
ω
FAx
A
FAy
m1 g
(a)
(b)
图 12-8
解 取飞轮 A 及重物为质点系,设摩阻力偶矩为 Mf,飞轮转动惯量为 JA,如图 12-8b
所示。根据对轴 A 的投影式动量矩定理有
dLA dt
=
−M f
+ m1gR , LA
=
J Aω
+ m1ωR2
两边积分得
(J A + m1R2 )dω = (M f +m1gR)dt
LO = m ⋅ vA ⋅ 2R + J Aωa
=
m ⋅ 2RωO
⋅ 2R +
1 mR2 2
⋅ (ωO
+ ωr )
= 5ωOmR2
=
20
kgm 2 /s
156
理论力学(第七版)课后题答案 哈工大.高等教育出版社
(3)在图 12-2c1 中,轮 A 绕 O 作圆周曲线平移
LO = m ⋅ 2RωO ⋅ 2R + J Aωa
12-10 如图 12-10 所示离心式空气压缩机的转速 n = 8 600 r/min,体积流量 qV = 370 m3/min,第 1 级叶轮气道进口直径为 D1 = 0.355 m,出口直径为 D2 = 0.6 m。气流进口绝对
速度 v1 = 109 m/s,与切线成角θ1 = 90° ;气流出口绝对速度 v2 = 183 m/s,与切线成角
(a)
(b)
图 12-4
解 以人和圆盘为质点系,由于作用于系统的外力(重力和轴 O 的约束力)对轴 O 的
矩均为零,所以人和圆盘组成的系统对轴 O 的动量矩守恒。设人在盘上绕轴 O 顺时针走圆
哈工大理论力学教研室《理论力学Ⅱ》(第7版)课后习题(机械振动基础)

由
可得 即两个质点振动频率相同,周期皆为
18-5 均质细杆长 l,质量为 m。问以哪一点为悬挂点作为复摆,其摆动频率最大;以 哪一点为悬挂点其摆动频率最小。
答:复摆固有频率为 若 O 不质心 C 距离为 a,则
则
由 得
当
时, 小于零,
所以当
时,叫有最大值,
当 a=0 时,ω=0 为最小值。
18-6 什么是临界阻尼?欠阻尼和过阻尼状态的自由振动有什么丌同?
答:对质量相同的两质点极成的系统,其弹簧中点将保持丌动,对每个质点相当于弹簧
2 / 53
圣才电子书 十万种考研考证电子书、题库视频学习平台
弹性数增大一倍,振动固有频率为 ,周期为
。
对质量为 m1 和 m2 的系统仍将发生自由振动,质心 C 丌动。
对于 m1 质点,
固有频率为
3 / 53
圣才电子书 十万种考研考证电子书、题库视频学习平台
答:
为临界阻尼;
为欠阻尼,系统沿平衡位置附近振动;
为过阻尼状态,系统直接趋于平衡位置,无振动性质。
18-7 证明在过阻尼振动状态下,物体以仸意的起始位置和起始速度运动,越过平衡 位置丌能超过一次。
答:过阻尼状态下, 则自由振动解为 平衡位置处 x=0,即
18-3 假如地球引力增加一倍,下列几种振动系统的固有频率有变化?(1)单摆;(2) 复摆;(3)弹簧质量系统;(4)扭摆。
答:(1)固有频率增大 倍; (2)固有频率增大 倍; (3)丌变化; (4)丌变化。
18-4 在光滑水平面上,两个质量皆为 m 的质点由一刚度系数为 k 的无重弹簧相连。 若将二质点拉开一段距离再同时释放,二者将发生振动,求此振动的周期。如上述二质点的 质量分别为 m1 和 m2,问二者仍发生振动吗?振动周期为多大?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第16章非惯性系中的质点动力学
一、思考题
16-1 根据相对运动动力学基本方程,小球在变速运动的车厢中自由降落时受有牵连惯性力,飞机在高空飞行时受有科氏惯性力。
试分析这两个惯性力的反作用力作用在哪?牛顿第三定律对它们成立吗?
答:非惯性力是取变速运动物体为参照系而产生的,其反作用力为此参照系本身。
故前者为车厢,后者为飞机。
16-2 对固结在变速运动的列车上的参考系来说,地面上静平衡的物体并不平衡,而随列车一起运动的物体却是平衡的。
试从这一点出发说明惯性力的相对性、虚加性及真实性。
答:相对性:地面上静止的物体对地球是无惯性力的,而相对火车是有惯性力的。
虚加性:地面上静止的物体并未真正受惯性力的作用。
真实性:惯性力真正存在,是地面与列车之间的作用力。
16-3 在质点相对运动中,下述哪些说法是正确的?
A.若αr=0,υr=0,则必有F+F Ie=0。
B.若F+F Ie=0,则必有αr=0,υr=0。
答:A正确;B不正确。
16-4 某人水平抛出一个球,如果考虑科氏惯性力,则在下述情况下,由抛球的人来看,球的路径会偏向不考虑科氏惯性力时路径的右侧还是左侧?
(1)在北半球水平抛出;(2)在南半球水平抛出;(3)在南极和北极水平抛出。
答:(1)左侧;(2)右侧;(3)不偏出。
16-5 在惯性系中,质点系的动能为。
其中m为质点系总质量,υC 为质心速度,T′为质点系相对于质心坐标系(即以质心为基点的平移坐标系)的动能。
称上式为柯尼希定理。
试利用柯尼希定理导出质点系相对于质心坐标系的动能定理。
答:证明:由动能定理dT=δW F得
其中
所以
即
二、习题
16-1 图16-1所示单摆AB长l,已知点A在固定点O的附近沿水平作微幅谐振动:OO1=a sin pt,其中a与p为常数。
设初瞬时摆静止,求摆的相对运动规律。
图16-1
解:摆的相对运动可用单摆与竖直方向夹角表示,在点A 上建立动坐标系。
运动和受力分析如图16-2所示。
图16-2
动系做平动,所以0=Ic F
动系的加速度为:pt ap OO a e sin 21-="
= 设单摆上小球的质量为m ,则pt map F Ie sin 2-= 根据小球的运动,列非惯性系中的动力学方程:
n t Ie T ma ma F F mg +=++
沿与摆杆垂直的方向投影得:
其中ϕ
=t a ,当摆角很小时,近似有ϕϕ=sin ,1cos =ϕ 所以上式可化简为:
整理得:
将其积分,并带入初始条件
得:
16-2 三棱柱A 沿三棱柱B 的光滑斜面滑动,如图16-3所示。
三棱柱A 和三棱柱B 的质量分别为m 1与m 2,三棱柱B 的斜面与水平面成θ角,如开始时物系静止,求运动时三棱柱B 的加速度。
摩擦略去不计。
图16-3
解:在三棱柱B 上建立动坐标系,由题可知,动系做平动,所以0=Ic F
以A 为研究对象,其受力和运动分析如图16-4(a )所示。
列非惯性系中的动力学方程:
g m F F a m NA Ie r
1++=
沿垂直斜面方向分解得:
其中,
图16-4
以B 为研究对象,其受力和运动分析如图16-4(a )所示。
在水平方向有:
θsin 2NA
B F a m '= 其中,NA
F F NA '= 联立以上各式得:
16-3 图16-5所示一重物M 放在粗糙的水平平台上,平台绕铅垂轴以匀角速度ω转动,重物与平台间摩擦因数为f ,试求重物能在平台上保持相对静止时的位置。
图16-5
解:在水平平台上建立动坐标系,动系做匀角速定轴转动,设重物M 的质量为m ,当重物距转轴R 时在平台上相对静止,此时有0=r a ,0=r v ,所以0=c a 。
重物受力分析如图16-6所示。
图16-6
得非惯性系动力学方程:0Ie N s F F mg F +++=
其中,
由以上分析得:mg F N =,R m F s 2ω= 重物相对静止应满足条件:,即R m 2ω≤fmg
得:
所以重物在平台上保持相对静止时与转轴的距离为
16-4 质点M 的质量为m ,被限制在旋转容器内沿光滑的经线AOB 运动,如图16-7所示。
旋转容器绕其几何轴Oz 以角速度ω匀速转动。
求质点M 相对静止时的位置。
