机械原理答案第十一章齿轮系及其设计(学校教学)

机械原理公式

机械原理公式:第十一章:齿轮系及其设计1.行星轮系公式，齿轮数关系2.定轴轮系公式3.差动轮系求nH第七章:机械的转动及波动调节1.驱动工＝阻力工公式2.最大转速公式，标能量最大3.最大盈亏工公式4.飞轮转动惯量公式第十章:齿轮机构及其设计1.基圆半径，渐开线展角，压力角，展角与压力角公式，渐开线曲率半径，向径2.齿顶圆压力角，分度园压力角，分度园压力角与啮合角关系3.四半径大小关系4.齿顶圆曲率半径公式，分度圆曲率半径公式5.齿顶圆压力角公式，展开线压力角公式6.基圆半径与分度圆半径关系公式7.分度圆齿厚公式，齿槽公式，齿距公式8.齿顶圆半径公式，齿根圆半径公式9.分度圆半径公式10.啮合角公式11.重合度公式第八章:连杆机构及其设计1.周转副条件2.双曲柄条件3.曲柄摇杆条件4.极位夹角，摆角，行程速比系数，传动比，设计四杆机构的极位夹角第五章:机械传动的效率和自锁1.总效率第九章：凸轮机构及其设计（反转发）1.作大圆小圆内切2.由大圆作压力角3.大圆小圆差值作推杆位移4.推杆相切圆作反转推杆升高s的解法1.s圆与理论轮廓线的交点2.理论基圆求转角第三章：平面机构的运动分析瞬心法：1.构件1，3瞬心为p13，若1为机架，则p13是3的绝对速度2.求杆1上的m点速度，须知杆1角速度，须知杆1与动力杆的瞬心或者杆1与机架的瞬心3.无穷远的瞬心可以平行4.计算单位矢量方程图解法1.取重合点B（B1,B2,B3）VB2＝VB12.VB3＝VB2+VB3B23.作图第四章：平面机构的力的分析1.判断压缩还是拉升2.与夹角变化方向相反第二章：机构的结构分析1.自由度公式。

西工大教材-机械原理各章习题及答案

η = η1 •η 22 •η3 = 0.95 × 0.972 × 0.92 = 0.822
电动机所需的功率为
p = ρ • v /η = 5500 ×1.2 ×10−3 / 0.822 = 8.029(KW )
5-8 在图示斜面机构中，设已知摩擦面间的摩擦系数 f=0.2。求在 G 力作用下（反行程），此斜面机构的临界自锁条件和在此条件下正行程（在 F 力作用下）的效率。解 1）反行程的自锁条件在外行程（图 a），根据滑块的平衡条件：
解 1 ）取比例尺 μ 1 ＝ 1mm/mm 绘制机构运动简图（图 b ）
(a)
2 ）计算该机构的自由度
n=7
pι=9
ph=2（算齿轮副，因为凸轮与齿轮为一体） p’=
F’= F=3n-2pe-ph
=3x7-2x8-2 =1
G7
D 64 C
EF
3
9
B
2
8
A
ω1
b)
2-6 试计算如图所示各机构的自由度。图 a、d 为齿轮一连杆组合机构；图 b 为凸轮一连杆组合机构（图中在 D 处为铰连在一起的两个滑块）；图 c 为一精压机机构。并问在图 d 所示机构中，齿轮 3 与 5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目是否相同？为什么？
C3 重合点继续求解。
解 1）速度分析（图 b）取重合点 B2 与 B3，有
方向大小？
v vv vB3 = vB2 + vB3B2 ⊥ BD ⊥ AB // CD ω1lAB ?
D
C
3 d3
ω3
4
ω3 90°
2
B（B1、B2、B3）
ω1
A1 ϕ = 90°

《机械原理》第八版课后习题答案

第2章机构的结构分析(P29)2-12：图a 所示为一小型压力机。

图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O 连续转动。

在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C 轴上下摆动。

同时，又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。

最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。

试绘制其机构运动简图，并计算自由度。

解：分析机构的组成：此机构由偏心轮1’（与齿轮1固结）、连杆2、滑杆3、摆杆4、齿轮5、滚子6、滑块7、冲头8和机架9组成。

偏心轮1’与机架9、连杆2与滑杆3、滑杆3与摆杆4、摆杆4与滚子6、齿轮5与机架9、滑块7与冲头8均组成转动副，滑杆3与机架9、摆杆4与滑块7、冲头8与机架9均组成移动副，齿轮1与齿轮5、凸轮(槽)5与滚子6组成高副。

故解法一：7=n 9=l p 2=h p12927323=-⨯-⨯=--=h l p p n F解法二：8=n 10=l p 2=h p 局部自由度1='F11210283)2(3=--⨯-⨯='-'-+-=F p p p n F h l(P30) 2-17：试计算如图所示各机构的自由度。

图a 、d 为齿轮-连杆组合机构；图b 为凸轮-连杆组合机构（图中在D 处为铰接在一起的两个滑块）；图c 为一精压机机构。

并问在图d 所示机构中，齿轮3与5和齿条7与齿轮5的啮合高副所提供的约束数目是否相同？为什么？解： a) 4=n 5=l p 1=h p11524323=-⨯-⨯=--=h l p p n Fb) 5=n 6=l p 2=h p12625323=-⨯-⨯=--=h l p p n F12625323=-⨯-⨯=--=h l p p n Fc) 5=n 7=l p 0=h p10725323=-⨯-⨯=--=h l p p n Fd) 6=n 7=l p 3=h p13726323=-⨯-⨯=--=h l p p n F(C 可看做是转块和导块,有1个移动副和1个转动副)齿轮3与齿轮5的啮合为高副（因两齿轮中心距己被约束，故应为单侧接触）将提供1个约束。

机械原理11-本科)-轮系

ω
H 3
ω1 i1H = = 1 + 1.875= + 2.875 ωH
ω
H 1
例２：
在图示的周转轮系中，在图示的周转轮系中，设已知 z1=100, z2=101, z2’=100, z3 = 99. 试求传动比 iH1。
2 2′
解：为固定轮(即轮3为固定轮即n3=0) 为固定轮
n1 − nH n1 − nH i = = n3 − nH 0− nH
齿轮４对传动比没有影响，齿轮４对传动比没有影响，但能改变从动轮的转向，称为过轮或中介轮。轮的转向，称为过轮或中介轮。
§11—3 周转轮系传动比的计算一、周转轮系的分类按周转轮系所具有的自由度数目的不同分类：按周转轮系所具有的自由度数目的不同分类： 1) 行星轮系
F = 3× 3 − 2 × 3 − 2 = 1
i AB
从 A → B 从动轮齿数的连乘积 = 从 A → B 主动轮齿数的连乘积
二、首、末轮转向的确定 1、用“＋” “－”表示
ω1 ω1 1 ω2
1
2
ω2
p
vp
转向相反
2
转向相同
i 12
ω1 = = ω2
z2 − z1 z2 + z1
外啮合内啮合
对于平面定轴轮系，对于平面定轴轮系，设轮系中有 m对外啮合齿轮，则末轮转向为(-1) 对外啮合齿轮，则末轮转向为对外啮合齿轮
关键是先要把其中的周转轮系部分划分出来。周转轮系的找法：周转轮系的找法：先找出行星轮，然后找出系杆，先找出行星轮，然后找出系杆，以及与行星轮相啮合的所有中心轮。行星轮相啮合的所有中心轮。每一系杆，每一系杆，连同系杆上的行星轮和与行星轮相啮合的中心轮就组成一个周转轮系在将周转轮系一一找出之后，在将周转轮系一一找出之后，剩下的便是定轴轮系部分。定轴轮系部分。

机械原理课后习题答案部分

第二章2-1 何谓构件何谓运动副及运动副元素运动副是如何进行分类的答：参考教材5~7页;2-2 机构运动简图有何用处它能表示出原机构哪些方面的特征答：机构运动简图可以表示机构的组成和运动传递情况,可进行运动分析,也可用来进行动力分析;2-3 机构具有确定运动的条件是什么当机构的原动件数少于或多于机构的自由度时,机构的运动将发生什么情况答：参考教材12~13页;2-5 在计算平面机构的自由度时,应注意哪些事项答：参考教材15~17页;2-6 在图2-22所示的机构中,在铰链C、B、D处,被连接的两构件上连接点的轨迹都是重合的,那么能说该机构有三个虚约束吗为什么答：不能,因为在铰链C、B、D中任何一处,被连接的两构件上连接点的轨迹重合是由于其他两处的作用,所以只能算一处;2-7 何谓机构的组成原理何谓基本杆组它具有什么特性如何确定基本杆组的级别及机构的级别答：参考教材18~19页;2-8 为何要对平面高副机构进行“高副低代"“高副低代”应满足的条件是什么答：参考教材20~21页;2-11 如图所示为一简易冲床的初拟设计方案;设计者的思路是：动力由齿轮1输入,使轴 A连续回转；而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头上下运动以达到冲压目的;试绘出其机构运动简图,分析其是否能实现设计意图并提出修改方案;解：1取比例尺绘制机构运动简图;2分析其是否可实现设计意图;F=3n- 2P l +P h –p’ -F’=3×3-2×4+1-0-0=0此简易冲床不能运动,无法实现设计意图;3修改方案;为了使此机构运动,应增加一个自由度;办法是：增加一个活动构件,一个低副;修改方案很多,现提供两种;※2-13图示为一新型偏心轮滑阎式真空泵;其偏心轮1绕固定轴心A转动,与外环2固连在一起的滑阀3在可绕固定轴心C转动的圆柱4中滑动;当偏心轮按图示方向连续回转时可将设备中的空气吸入,并将空气从阀5中排出,从而形成真空;1试绘制其机构运动简图；2计算其自由度;解：1取比例尺作机构运动简图如图所示;2 F=3n-2p1+p h-p’-F’=3×4-2×4+0-0-1=12-14 解：1绘制机构运动简图1）绘制机构运动简图F=3n-2P l +P h –p’-F’=3×5-2×7+0-0-0=12）弯曲90o 时的机构运动简图※2-15试绘制所示仿人手型机械手的食指机构的机构运动简图以手掌8作为相对固定的机架,井计算自由度;解：1取比倒尺肌作机构运动简图；2计算自由度1⨯=-F210⨯73=2-17 计算如图所示各机构的自由度;aF=3n- 2P l +P h–p’-F’=3×4-2×5+1 -0-0=1A处为复合铰链bF=3n-2P l +P h–p’-F’=3×7-2×8+2-0-2=12、4处存在局部自由度cp’= 2P l ’+P h ’-3n’=2×10+0-3×6=2,F=3n-2P l +P h–p’-F’=3×11-2×17+0-2-0=1C、F、K 处存在复合铰链,重复部分引入虚约束※2-21图示为一收放式折叠支架机构;该支架中的件1和5分别用木螺钉连接于固定台板1’和括动台板5’上．两者在D处铰接,使活动台板能相对于固定台极转动;又通过件1,2,3,4组成的铰链四杆机构及连杆3上E点处的销子与件5上的连杆曲线槽组成的销槽连接使活动台板实现收放动作;在图示位置时,虽在活动台板上放有较重的重物．活动台板也不会自动收起,必须沿箭头方向推动件2,使铰链B,D重合时．活动台板才可收起如图中双点划线所示;现已知机构尺寸l AB=l AD=90 mm；l BC=l CD=25 mm,其余尺寸见图;试绘制该机构的运动简图,并计算其自由度;解：F=3n-2p1+p b-p’-F’=3×5-2×6+1-0-1=12-23 图示为一内燃机的机构简图,试计算其自由度,并分析组成此机构的基本杆组;有如在该机构中改选EG为原动件,试问组成此机构的基本杆组是否与前有所不同;解：1计算自由度F=3n-2P l +P h–p’-F’=3×7-2×10+0-0-0=12拆组3EG 为原动件,拆组2-24 试计算如图所示平面高副机构的自由度,并在高副低代后分析组成该机构的基本杆组;1、解：1计算自由度F=3n-2P l +P h –p ’-F ’=3×5-2×6+1-0-1=12从结构上去除局部自由度、虚约束、多余的移动副、转动副如图2所示 3高副低代如图3所示 4拆组如图4所示 2、解：1计算自由度F=3n-2P l +P h –p ’-F ’=3×-2×9+1-0-1=12从结构上去除局部自由度、虚约束、多余的移动副、转动副如图b 所示 3高副低代如图c 所示 4拆组如图d 所示第三章3—1 何谓速度瞬心相对瞬心与绝对瞬心有何异同点答：参考教材30~31页;3—2 何谓三心定理何种情况下的瞬心需用三心定理来确定答：参考教材31页;※3-3机构中,设已知构件的尺寸及点B 的速度v B 即速度矢量pb,试作出各机构在图示位置时的速度多边形;※3-4 试判断在图示的两机构中．B 点足否都存在哥氏加速度又在何位置哥氏加速度为零怍出相应的III 级组II 级组II 级组II 级组机构位置图;并思考下列问题;1什么条件下存在氏加速度2根椐上一条．请检查一下所有哥氏加速度为零的位置是否已全部找出;3图 a 中,a kB2B3=2ω2v B2B3对吗为什么;解：1图 a 存在哥氏加速度,图 b 不存在;2由于a kB2B3==2ω2v B2B3故ω3,v B2B3中只要有一项为零,则哥氏加速度为零;图 a 中B 点到达最高和最低点时构件1,3．4重合,此时v B2B3=0,当构件1与构件3相互垂直．即_f=；点到达最左及最右位置时ω2=ω3=0．故在此四个位置无哥氏加速度;图 b 中无论在什么位置都有ω2=ω3=0,故该机构在任何位置哥矢加速度都为零; 3对;因为ω3≡ω2;3-5 在图示的曲柄滑块机构中,已知mm l mm l mm l mm l DE BD A AB 40,50,100,30C ====,曲柄以等角速度s rad /101=ω回转,试用图解法求机构在︒=451ϕ位置时,点D 、E 的速度和加速度以及构件2的角速度和角加速度;解：1以选定的比例尺l μ作机构运动简图（2）速度分析AB)(m/s 3.01⊥==AB B l v ωBCBCv v v v v C C C B C B C //32322⊥∨∨+=+=？方向：？0？大小：？根据速度影像原理,作BC BD bc bd //2=求得点d,连接pd;根据速度影像原理,作BDE bde ∆≈∆求得点e,连接pe,由图可知)(/r 2/m/s,175.0m/s,173.0,m/s 23.0223232顺时针s ad l bc c c v pe v pd v BC v v C C v E v D ========μωμμμ （3）加速度分析A)(B m/s 3221→==AB B l a ω根据速度影像原理作BC BD c b d b /''/''2=求得点'd ,连接''d p ;根据速度影像原理,作BDE e d b ∆≈'''∆求得点e ',连接e p '',由图可知)(/36.8//,m/s 8.2'',m/s 64.2''2'2'22222顺时针s rad l c n l a e p a d p a BC a BC B C a E a D =======μαμμτ 3-6 在图示机构中,设已知各构件的尺寸,原动件1以等角速度1ω顺时针方向转动,试用图解法求机构在图示位置时构件3上C 点速度和加速度比例尺任选;abc3-7 在图示机构中,已知mm l mm l mm l mm l mm l BC CD EF A AE 50,75,35,40,70B =====,曲柄以等角速度s rad /101=ω回转,试用图解法求机构在︒=501ϕ位置时,C 点的速度c v 和加速度c a ; 解：1以选定的比例尺l μ作机构运动简图;速度分析m/s 72.0m/s,4.01111====AF F AB B l v l v ωω AFAF EFv v v v F F F F F //15145⊥⊥∨+==方向：大小：v d 用速度影响法求2速度分析CD ED v v v CDD C ⊥⊥∨+=方向：大小： BC AB v v v CBB C ⊥⊥∨+=方向：大小：3加速度分析)(m/s 2.7A),(B m/s 42211221A F l a l a AF F AB B →==→==ωω AFA F v a a a a a F F rF F k F F F F F ///21511515145→→∨++==方向：大小：ω EFEF l a a a a a EFEF n E F E F F ⊥→++==方向：大小：2444450ωτa d 用加速度影像法求CD D C l a a a a CDCDnCD D C ⊥→∨∨++=方向：大小：23ωτ CBB C l a a a a CB CBnCB B C ⊥→∨∨++=方向：大小：22ωτ 2m/s 3''=⋅=a C c p a μ3-8 在图示凸轮机构中,已知凸轮1以等角速度s rad /101=ω转动,凸轮为一偏心圆,其半径︒====90,50,15,251B ϕmm l mm l mm R AD A ;试用图解法求构件2的角速度2ω和角加速度2α; 解：1以选定的比例尺l μ作机构运动简图;2速度分析：将机构进行高副低代,其替代机构如图b 所示;m/s 15.0141===AB B B l v v ωCDAB BD v v v B B B B //4242⊥⊥∨+=方向：大小：？？)(/3.2//222逆时针s rad l pb l v BD v BD B ===μω3加速度分析A)m/s(B 5.12141→===AB B B l a a ω其中,）（顺时针222222222242242rad/s 9.143/''/,m/s 286.0,m/s 746.02=======BD a BD D B BD n D B B B k B B l b n l a l a v a μαωωτ 3-11 试求图示机构在图示位置时的全部瞬心; 解：a 总瞬心数：4×3/2=6对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上 d 总瞬心数：4×3/2=6对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上※3-12 标出图示的齿轮一连杆组合机构中所有瞬心,并用瞬心法求齿轮1与齿轮3的传动比ω1/ω3; 解：1瞬新的数目：K=NN-1/2=66-1/2=152)为求ω1/ω3需求3个瞬心P 16、P 36、P 13的位置,3)ω1/ω3= P 36P 13/P 16P 13=DK/AK,由构件1、3在K 点的速度方向相同,可知ω3与ω1同向;3-13 在图示四杆机构中,s rad mm l mm l CD AB /10,90,602===ω,试用瞬心法求：1当︒=165ϕ时点C 的速度C v ；当︒=165ϕ时构件3的BC 线上或其延长线上速度最小的一点E 的位置及其速度大小；3当0=C v 时ϕ角之值有两解;解：1以选定的比例尺l μ作机构运动简图（2）因P 24为构件2、4的顺心,则m/s 4.0rad/s 5.4424242242424=⋅==⋅=⋅=CD C D P A P l v DP AP l l ωωωω，对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上（3）因构件3的BC 线上速度最小的点到绝对瞬心P 13的距离最近,故从P 13作BC 线的垂线交于E 点; 对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上,故m/s 357.0131321313133313=⋅⋅=⋅⋅⋅=⋅⋅=⋅=E P B P l E P u B P v E P l v ABl l B l E P E ωμμωω（4）若0=C v ,则04=ω,DP AP l l DP A P 24242242424⋅=⋅=ωωω若024=A P ,则P 24与P 12重合,对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上若024=A P ,则A 、B 、C 三点共线;︒=⋅-++︒=︒=⋅-+=6.226)2arccos(1804.26)2arccos(22222221212211ADAC D C AD AC AD AC D C AD AC ϕϕ， ※3-15 在图示的牛头刨机构中,l AB =200 mnl,l CD =960 mm,l DE =160 mm, h=800mm,h 1=360mm,h 2=120mm;设曲柄以等角速度ω1=5 rad ／s ．逆时针方向回转．试以图解法求机构在φ1=135o 位置时．刨头点的速度v C ;sm AP v v P P P l p c l /24.1,,)2(151********===μωμ出瞬心利用顺心多边形依次定所示作机构运动简图，如图（1）以:解。

机械原理,孙恒,西北工业大学版第11齿轮系及其设计

所有从动轮齿数连乘积
定轴轮系的传动比 =
所有主动轮齿数连乘积
规定:首、末两轮转向相同时，其传动比为“+” ，反之为“— ”。当有空间齿轮时，转向关系的确定，只能画箭头
本例中，轮2为惰轮（或程过桥轮、中介轮）
§11-3 周转轮系的传动比 11给整个周转轮系加上一个公共角速度“ωH” ωH -ωH=0 ，即行星架“静止不动”，周转轮系转化为定轴轮系（转化轮系） ω1H=ω1-ωH ω2H=ω2-ωH ω3H=ω3-ωH ωHH=ωH-ωH=0
特别注意：“±” ，须由转化轮系中m、n两轮的转向关系来确定
§11—4 复合轮系的传动比 11 4
注意几点: 1.必须正确地将轮系中的各组成部分加以划分（找出行星架，并注意行星架往往是由轮系中具有其他功用的构件所兼任) 2.列出各组成轮系的传动比计算公式。 3.联解方程
例1. 图示的轮系，设已知各轮齿数，试求其传动比 i1H
,
（3）联解方程
ω1 −ωH z2 z3 = ω3 −ωH z1z2
200 −ωH 40 ⋅ 24 = −100 −ωH 30 ⋅ 20
nH = −600
§11—5 轮系的功用
1．实现分路传动 2．获得较大的传动比 3. 实现变速传动 4．实现换向传动 5．用作运动的合成和分解 6．在尺寸及重量较小的条件下，实现大功率传动
解: （1）区分轮系
2’—3 — 4 — H 周转轮系 1 — 2 定轴轮系
（2）列方程
n1 z2 40 i12 = = − = − = −2 n2 z1 20
i2′H = 1 − i2′4 = 1 − (−z4 / z2′ ) = 1 + 80 / 20 = 5

机械原理习题及答案

机械原理习题及答案-CAL-FENGHAI.-(YICAI)-Company One1兰州2017年7月4日于家属院复习资料第2章平面机构的结构分析1.组成机构的要素是和；构件是机构中的单元体。

2.具有、、等三个特征的构件组合体称为机器。

3.从机构结构观点来看，任何机构是由三部分组成。

4.运动副元素是指。

5.构件的自由度是指；机构的自由度是指。

6.两构件之间以线接触所组成的平面运动副，称为副，它产生个约束，而保留个自由度。

7.机构具有确定的相对运动条件是原动件数机构的自由度。

8.在平面机构中若引入一个高副将引入______个约束，而引入一个低副将引入_____个约束，构件数、约束数与机构自由度的关系是。

9.平面运动副的最大约束数为，最小约束数为。

10.当两构件构成运动副后，仍需保证能产生一定的相对运动，故在平面机构中，每个运动副引入的约束至多为，至少为。

11.计算机机构自由度的目的是______。

12.在平面机构中，具有两个约束的运动副是副，具有一个约束的运动副是副。

13.计算平面机构自由度的公式为Ｆ=，应用此公式时应注意判断：(A)铰链，(B)自由度，(C)约束。

14.机构中的复合铰链是指；局部自由度是指；虚约束是指。

15.划分机构的杆组时应先按的杆组级别考虑，机构的级别按杆组中的级别确定。

16.图示为一机构的初拟设计方案。

试：(1〕计算其自由度，分析其设计是否合理如有复合铰链，局部自由度和虚约束需说明。

(2)如此初拟方案不合理，请修改并用简图表示。

23题16图题17图17.在图示机构中，若以构件1为主动件，试：(1)计算自由度，说明是否有确定运动。

(2)如要使构件6有确定运动，并作连续转动，则可如何修改说明修改的要点，并用简图表示。

18.计算图示机构的自由度，将高副用低副代替，并选择原动件。

19.试画出图示机构的运动简图，并计算其自由度。

对图示机构作出仅含低副的替代机构，进行结构分析并确定机构的级别。

机械原理习题答案新

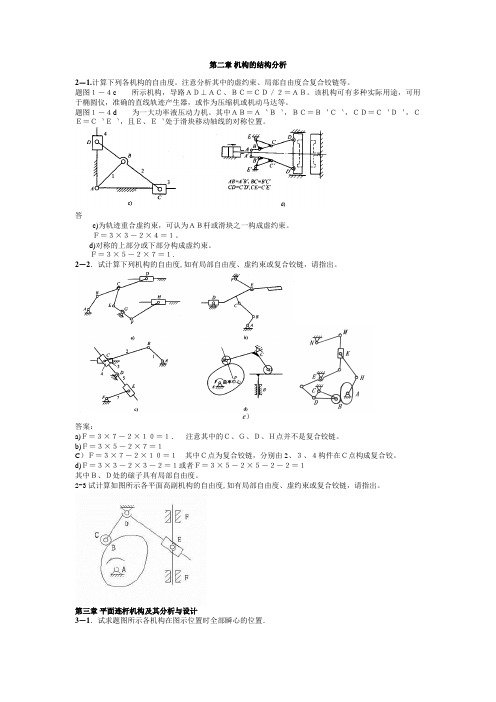
第二章机构的结构分析2－1.计算下列各机构的自由度。

注意分析其中的虚约束、局部自由度合复合铰链等。

题图１－４c所示机构，导路ＡＤ⊥ＡＣ、ＢＣ＝ＣＤ／２＝ＡＢ。

该机构可有多种实际用途，可用于椭圆仪，准确的直线轨迹产生器，或作为压缩机或机动马达等。

题图１－４d为一大功率液压动力机。

其中ＡＢ＝Ａ｀Ｂ｀，ＢＣ＝Ｂ｀Ｃ｀，ＣＤ＝Ｃ｀Ｄ｀，ＣＥ＝Ｃ｀Ｅ｀，且Ｅ、Ｅ｀处于滑块移动轴线的对称位置。

答c)为轨迹重合虚约束，可认为ＡＢ杆或滑块之一构成虚约束。

Ｆ＝３×３－２×４＝１。

d)对称的上部分或下部分构成虚约束。

Ｆ＝３×５－２×７＝１.2－2．试计算下列机构的自由度,如有局部自由度、虚约束或复合铰链，请指出。

e）答案：a)Ｆ＝３×７－２×１０＝１．注意其中的Ｃ、Ｇ、Ｄ、Ｈ点并不是复合铰链。

b)Ｆ＝３×５－２×７＝１C）Ｆ＝３×７－２×１０＝１其中Ｃ点为复合铰链，分别由2、３、４构件在Ｃ点构成复合铰。

d)Ｆ＝３×３－２×３－２＝１或者Ｆ＝３×５－２×５－２－２＝１其中Ｂ、Ｄ处的磙子具有局部自由度。

2-3试计算如图所示各平面高副机构的自由度,如有局部自由度、虚约束或复合铰链，请指出。

第三章平面连杆机构及其分析与设计3－1．试求题图所示各机构在图示位置时全部瞬心的位置．答案：瞬心P 12在A 点瞬心P 23、 P 24均在B 点瞬心P 34在C 点P 14、 P 13均在垂直导路的无瞬心P 23、 P 13均在B 点穷远处瞬心P 14、 P 24均在D 点3-5在图示的齿轮-连杆组合机构中，试用瞬心法求齿轮1与齿轮3的传动比31/ωω。

答案：此题关键是找到相对瞬心Ｐ13． 3-6在图示凸轮机构中，已知mm r 50=，mm l OA 22=，mm l AC 80=，οϕ901=，凸轮，凸轮以角速度s rad /101=ω逆时针方向转动。

机械原理课后习题答案

《机械原理》课后习题答案第2章（P27）2-2 计算下列机构的自由度，如遇有复合铰链、局部自由度、虚约束等加以说明。

（a）n=3，p l=3 F=3*3-2*3=3（b）n=3，p l=3，p h=2 F=3*3-2*3-2=1 （B处有局部自由度）（c）n=7，p l=10 F=3*7-2*10=1（d）n=4，p l=4，p h=2 F=3*4-2*4-2=2 （A处有复合铰链）（e）n=3，p l=4 F=3*3-2*4=1 （A或D处有虚约束）（f）n=3，p l=4 F=3*3-2*4=1 （构件4和转动副E、F引入虚约束）（g）n=3，p l=5 F=(3-1)*3-(2-1)*5=1 （有公共约束）（h）n=9，p l=12，p h=2 F=3*9-2*12-2=1 （M处有复合铰链，C处有局部自由度）2-3 计算下列机构的自由度，拆杆组并确定机构的级别。

（a）n=5，p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组，故此机构为Ⅱ级机构。

（b）n=5，p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。

（c）n=5，p l=7 F=3*5-2*7=1拆分时只须将主动件拆下，其它构件组成一个Ⅲ级杆组，故此机构为Ⅲ级机构。

2-4 验算下列运动链的运动是否确定，并提出具有确定运动的修改方案。

（a）n=3，p l=4，p h=1 F=3*3-2*4-1=0 该运动链不能运动。

修改方案如下图所示：（b）n=4，p l=6 F=3*4-2*6=0 该运动链不能运动。

修改方案如下图所示：或第3章（P42）3-2 下列机构中，已知机构尺寸，求在图示位置时的所有瞬心。

（a）（b）（c）(a) v3=v P13=ω1P14P13μl3-6 在图示齿轮连杆机构中，三个圆互作纯滚，试利用相对瞬心P13来讨论轮1与轮3的传动比i13。

第5章（P80）5-2 一铰接四杆机构（2）机构的两极限位置如下图：（3）传动角最大和最小位置如下图：5-3题略解：若使其成为曲柄摇杆机构，则最短杆必为连架杆，即a 为最短杆。

机械原理第11章_齿轮系及其设计

8.2.3 混合轮系的传动比
返回
2混合轮系传动比计算的基本思路 2混合轮系传动比计算的方法 2混合轮系传动比计算举例
混合轮系传动比计算的基本思路
返回
问题：能否通过对整个轮系加上一个公共的角速度（-ωH）来轮系的传动比？ 5由定轴轮系和周转轮系组成的混合轮系 5由多个周转轮系组成的混合轮系 5结论当给整个机构加上了一个公共的角速度（-ωH）后，虽然右半部分的周转轮系转化成了定轴轮系，但同时却使左半部分的定轴轮系转化成了周转轮系。
按基本构件的不同，周转轮系可分为两类：按基本构件的不同，周转轮系可分为两类：返回
2K-H型周转轮系：型周转轮系：型周转轮系 K表示太阳轮， H表示行星架。
3K型周转轮系：型周转轮系：型周转轮系基本构件是1、2、3三个太阳轮，而行星架H只起支撑作用，所以在轮系的型号中不含“H”。
z 2 z3 z5 z 2 z3 z5 3 z 2 z3 z5 i15 = (1) = (1) = z1 z 2′ z 3′ z1 z 2′ z 3′ z1 z 2′ z 3′
m
m为外啮合的对数负号表示主、从动轮转向相反。
各轮几何轴线不都平行，各轮几何轴线不都平行，但首尾两轮轴线互相平行的情况
ω1 = = ? ω5
返回
z 2 z3 z 4 z5 ω1 ω 1 ω 2 ω 3 ω 4 z 2 z 3 z 4 z 5 = = i15 = = z1 z 2′ z 3′ z 4 ω 5 ω 2 ω 3 ω 4 ω 5 z1 z 2′ z 3′ z 4
所有主动轮齿数的连乘积
结论：定轴轮系的传动比 = 所有从动轮齿数的连乘积按空格键继续
1H
z 2 z3 ω1 ω H i = = ω3 ω H z1 z 2′

机械原理_课后习题答案免费(全面)高教版西北工大

2) 求vC2
v C 2 = v B + v C 2 B = v C 3 + vC 2 C 3
方向：大小： ⊥AB
√
⊥BC ?
0 0
∥BC ?
取
μv = 0.005
m/s mm
作速度图
b
题3-10 解(续2)
[解] （2）速度分析
v B → vC 2 → v D , v E → ω 2
1) 求vB 2) 求vC2 3) 求vD 和求vE 用速度影像法
C
E
vC = v B + vCB v D = v B + v DB
(2) 求vE
D p(a, f )
v E = vC + v EC = v D + v ED
b d e c
题3-5 解
b) 解: 顺序 (1) 求vC
v B → vC → v E → v F
D B vB A E G F C
vC = v B + vCB
√
0 0
∥CD ?
b2 (b1) (b3)
其中 a B3B2 = 2ω2 v B3B2 = 0(∵ v B3B2 = 0)
a B1 ⎛ m / s 2 ⎞ 取 μa = ⎜ ⎟ 作加速度图 p ' b '1 ⎝ mm ⎠
题3-8 c) 解(续2)
[解] （3）加速度分析 a B 2 ( = a B1 ) → a B 3 → a C 3 1) 求aB2 A 1 ω1 2) 求aB3
取
√ v ⎛m/s⎞ μ v = B1 ⎜ ⎟ 作速度图 pb1 ⎝ mm ⎠
3) 求vC3 : 用速度影像法
v C 3 = 0 同时可求得 ω3 =

机械原理课后答案第11章

第11章作业11-1在给定轮系主动轮的转向后，可用什么方法来确定定轴轮系从动轮的转向？周转轮系中主、从动件的转向关系又用什么方法来确定?答：参考教材216~218页。

11-2如何划分一个复合轮系的定轴轮系部分和各基本周转轮系部分?在图示的轮系中，既然构件5作为行星架被划归在周转轮系部分中，在计算周转轮系部分的传动比时，是否应把齿轮5的齿数,Z5计入?答：划分一个复合轮系的定轴轮系部分和各基本周转轮系部分关键是要把其中的周转轮系部分划出来，周转轮糸的特点是具有行星轮和行星架，所以要先找到轮系中的行星轮，然后找出行星架。

每一行星架，连同行星架上的行星轮和与行星轮相啮合的太阳轮就组成一个基本周转轮糸。

在一个复合轮系中可能包括有几个基本周转轮系（一般每一个行星架就对应一个基本周转轮系)，当将这些周转轮一一找出之后．剩下的便是定轴轮糸部分了。

在图示的轮系中．虽然构件5作为行星架被划归在周转轮系部分中，但在计算周转轮系部分的传动比时．不应把齿轮5的齿数计入。

11-3在计算行星轮系的传动比时，式i mH=1-i H mn只有在什么情况下才是正确的?答在行星轮系，设固定轮为n, 即ωn=0时, i mH=1-i H mn公式才是正确的。

11-4在计算周转轮系的传动比时，式i H mn=(n m-n H)／(n n-n H)中的i H mn是什么传动比，如何确定其大小和“±”号?答: i H mn是在根据相对运动原理，设给原周转轮系加上一个公共角速度“-ωH”。

使之绕行星架的固定轴线回转，这时各构件之间的相对运动仍将保持不变，而行星架的角速度为0，即行星架“静止不动”了．于是周转轮系转化成了定轴轮系，这个转化轮系的传动比，其大小可以用i H mn=(n m-n H)／(n n-n H)中的i H mn公式计算；方向由“±”号确定，但注意，它由在转化轮系中m. n两轮的转向关系来确定。

11-5用转化轮系法计算行星轮系效率的理论基础是什么?为什么说当行星轮系为高速时，用它来计算行星轮系的效率会带来较大的误差?答: 用转化轮系法计算行星轮系效率的理论基础是行星轮系的转化轮系和原行星轮系的差别，仅在于给整个行星轮系附加了一个公共角速度“-ωH”。

湖南大学机械原理 ch11齿轮系及其设计

第11章
齿轮系及其设计
行星搅拌器
第11章
齿轮系及其设计
某涡轮螺旋桨发动机主减速器
第11章
齿轮系及其设计
湖南大学机械与汽车工程学院 Hunan University
College of Mechanical and Automobile Engineering
第十一章
齿轮系及其设计 (Gear Trains)
第11章
齿轮系及其设计
H i21 =
ω2 − ω H 成立否？ ω1 − ω H
H
p
z2
o
ωH
2
≠ω2－ωH
z1
ωH2 z3 ωH ω2
角速度ω2是一个向量它与牵连角速度ωH和相对角速度ωH2之间的关系为：
ω2 = ω H + ω2
r
r
rH
转化轮系中两齿轮轴线不平行时，不能直接计算
第11章
齿轮系及其设计
第11章例四：图示圆锥齿轮组成的轮系中，已知： z1＝33，z2＝12, z2’＝33, 求i3H 解:判别转向: 齿轮1、3方向相反
H i31 =
齿轮系及其设计 z2
o
z3
H
z1
ω3 − ω H ω3 − ω H = ω1 − ω H 0 − ωH
z1 +1 = − z3
= −i3 H
=－1
i3H =2
下面举例说明定轴轮系的传动比计算
第11章
齿轮系及其设计
i2'3
i45
ω1 z 2 i12 = ω1= i15 =ω 2 =1? z
i3′4
ω3 z 4 = = ω 4 z 3′
ω5
ω 2 z3 = = ω3 z 2'

孙桓《机械原理》笔记和课后习题(含考研真题)详解-第十一章至第十四章【圣才出品】

第11章齿轮系及其设计11.1复习笔记一、齿轮系及其分类1．定义由一系列的齿轮所组成的齿轮传动系统称为齿轮系，简称轮系。

2．分类根据轮系运转时各个齿轮的轴线相对于机架的位置是否固定，将轮系分为三大类：（1）定轴轮系运转时各个齿轮的轴线相对于机架的位置都是固定的轮系称为定轴轮系。

（2）周转轮系①定义如图11-1-1所示，运转时至少有一个齿轮轴线的位置不固定，而是绕着其他齿轮的固定轴线回转的轮系称为周转轮系。

图11-1-1周转轮系②基本构件在周转轮系中，一般都以太阳轮和行星架作为输入和输出构件，称为周转轮系的基本构件。

a．太阳轮轮系中绕固定轴回转的齿轮称为太阳轮。

如图11-1-1中齿轮l和内齿轮3都围绕着固定轴线OO回转，则齿轮1和内齿轮3为太阳轮；b．行星轮不仅绕自身轴线作自转，还随着行星架一起绕固定轴线做公转的齿轮称为行星轮。

如图11-1-1中齿轮2，其中构件H为行星架，又称转臂或系杆。

③分类a．根据其自由度的数目分类第一，差动轮系自由度为2的周转轮系称为差动轮系；第二，行星轮系自由度为1的周转轮系称为行星轮系。

b．根据基本构件的不同分类若轮系中的太阳轮以K表示，行星架以H表示，则如图11-1-1所示的轮系称为2K-H 型周转轮系。

（3）复合轮系既包含定轴轮系部分，又包含周转轮系部分，或者是由几部分周转轮系组成的轮系称为复合轮系。

二、定轴轮系的传动比1．轮系传动比的定义轮系的传动比是指轮系中首、末两构件的角速度之比。

2．传动比计算（1）定轴轮系的传动比等于组成该轮系的各对啮合齿轮传动比的连乘积；（2）传动比又等于各对啮合齿轮中所有从动轮齿数的连乘积与所有主动轮齿数的连乘积之比，即：定轴轮系的传动比＝所有从动轮齿数的连乘积/所有主动轮齿数的连乘积3．首、末轮转向关系的确定（1）转向的确定①齿轮的转向可用箭头表示，箭头方向表示齿轮可见侧的圆周速度的方向；②标志一对啮合传动的齿轮转向的箭头为同时指向节点或同时背离节点；③当首、末两轮的轴线彼此平行时，两轮的转向不是相同就是相反；当两者的转向相同时，规定其传动比为“＋”，反之为“－”；④若首、末两轮的轴线不平行，其间的转向关系只能在图上用箭头来表示。

机械原理复习题(第11章)答案Microsoft Word 文档

第11章齿轮系及其设计一、简答题： 1、（1）轮系按轴线在空间位置是否变动可以分为普通轮系（或定轴轮系）、周转轮系、复合轮系。

（2）普通轮系所有的轴线位置在运动过程中均固定不动的轮系。

周转轮系是在运动过程中至少有一个齿轮的几何轴线的位置不固定。

复合轮系由定轴轮系和周转轮系或者由两个以上的周转轮系组成。

二、分析、计算题： 1、解题要点：区分基本轮系，由齿轮1、2-2'、3及系杆4组成差动轮系；由齿轮1、2、5 及系杆4组成差动轮系；齿轮5、2-2'、3 及系杆4组成差动轮系；由齿轮1'、6、3 组成定轴轮系。

其中三个周转轮系并不是独立的，任取两个周转轮系求解，结果是一样的。

解： 1）求齿数1z 和3z 。

因为齿轮1和齿轮5同轴线所以有：2521r r r r +=- 由于各齿轮模数相同，则有：75252252251=⨯+=+=z z z因为齿轮3和齿轮5同轴线，所以有：3225r r r r +=+' 由于各齿轮模数相同，则有302025252253=-+=-+='z z z z 2）由齿轮1、2-2'、3及系杆4组成差动轮系有212075302521324341413-=⨯⨯-=-=--='z z z z n n n n i (1)3）由齿轮1、2、5及系杆4组成差动轮系有317525154541415-=-=-=--=z z n n n n i (2)4）齿轮1'、6、3组成定轴轮系，齿轮1'和3'轴线重合，且齿数相同有： 113313131-=-===''''''z z n n n n i13n n -= (3) (采用画箭头法判别31''i 的“+”、“－”号)将式(3)代入式(1)： )(214141n n n n ---=-解得 413n n = (4)将式(4)代入式(2)：)(3134544n n n n --=-解得 54554-==n n i ；齿轮5和系杆4转向相反。

机械原理课后答案——第十一章机械的运转及其速度波动的调节

机械的运转及其速度波动的调节
习题7-7 习题7-12
7-7 图示为一机床工作台的传动系统。设已知各齿轮的齿数，齿轮3 的分度圆半径r3，各齿轮的转动惯量J1 、 J2 、 J2’ 、 J3 ，齿轮1直接装在电动机轴上，故J1 中包含了电动机转子的转动惯量；工作台和被加工零件的重量之和为G。当取齿轮1为等效构件时，求该机械系统的等效转动惯量Je。
z1 2 z1 z 2 ' 2 G 2 z1 z 2 ' 2 J e J 1 ( J 2 J 2 ' )( ) J 3 ( ) r3 ( ) z2 z2 z3 g z2 z3
7-12 某内燃机曲柄轴上的驱动力矩随曲柄转角的变化曲线如图所示，其运动周期T=，曲柄的平均转速为nm=620 r/min。若用该内燃机驱动一阻抗力为常数的机械，要求机械运转的不均匀系数 =0.01，试求 1) 曲轴最大转速nmax 和相应的曲柄转角位置max； 2) 装在曲柄轴上的飞轮的转动惯量。
解：求等效转动惯量
1 1 1 1 1 1 G 2 2 2 2 2 J e 1 J 1 1 J 2 2 J 2 ' 2 J 3 3 ( 3 r3 ) 2 2 2 2 2 2 2 g 3 2 G 3 r3 2 2 2 2 2 J e J1 J 2 ( ) J 2 '( ) J3( ) ( ) 1 1 1 g 1 3 3 2 z 2 ' z1 2 z1 1 z2 1 2 1 z3 z2
解：确定阻抗力矩 W d W r
Wd 200

Wr M r
9

1 13 1 1050 200 200 2 6 18 2 9

第11章课后习题答案 .doc

第11章课后习题答案11-1 解1）由公式可知：轮齿的工作应力不变，则则，若，该齿轮传动能传递的功率11-2解由公式可知，由抗疲劳点蚀允许的最大扭矩有关系：设提高后的转矩和许用应力分别为、当转速不变时，转矩和功率可提高69%。

11-3解软齿面闭式齿轮传动应分别验算其接触强度和弯曲强度。

（1）许用应力查教材表11-1小齿轮45钢调质硬度：210～230HBS取220HBS；大齿轮ZG270-500正火硬度：140～170HBS，取155HBS。

查教材图11-7，查教材图11-10 ,查教材表11-4取，故：（2）验算接触强度，验算公式为：其中：小齿轮转矩载荷系数查教材表11-3得齿宽中心距齿数比则：、，能满足接触强度。

（3）验算弯曲强度，验算公式：其中：齿形系数：查教材图11-9得、则：满足弯曲强度。

11-4解开式齿轮传动的主要失效形式是磨损，目前的设计方法是按弯曲强度设计，并将许用应力降低以弥补磨损对齿轮的影响。

（1）许用弯曲应力查教材表11-1小齿轮45钢调质硬度：210～230HBS取220HBS；大齿轮45钢正火硬度：170～210HBS，取190HBS。

查教材图11-10得,查教材表11-4 ，并将许用应用降低30%故（2）其弯曲强度设计公式：其中：小齿轮转矩载荷系数查教材表11-3得取齿宽系数齿数，取齿数比齿形系数查教材图11-9得、因故将代入设计公式因此取模数中心距齿宽11-5解硬齿面闭式齿轮传动的主要失效形式是折断，设计方法是按弯曲强度设计，并验算其齿面接触强度。

（1）许用弯曲应力查教材表11-1，大小齿轮材料40Cr 表面淬火硬度：52～56HRC，取54HRC。

查教材图11-10得，查材料图11-7得。

查教材表11-4 ，因齿轮传动是双向工作，弯曲应力为对称循环，应将极限值乘70%。

故（2）按弯曲强度设计，设计公式：其中：小齿轮转矩载荷系数查教材表11-3得取齿宽系数齿数，取齿数比齿形系数应将齿形系数较大值代入公式，而齿形系数值与齿数成反比，将小齿轮的齿形系数代入设计公式，查教材图11-9得因此取模数（3）验算接触强度，验算公式：其中：中心距齿宽，取满足接触强度。

机械原理第七版习题解答(第4、7、11章)

8
《机械原理》习题课
解根据等效转动惯量的等效原则，有
1 2 J e 1
2
1 2
J 1 1
2
1 2
( J 2 J 2 ) 2
2
1 2
J 3 3
2
1 G 2 g
v
2
则：
J e J1 1 2 ( J 2 J 2 )(
2 1
2
) J3(
2
3 1

G rB 4 r A 1 1 2 1
10 40
2

G rB r A 1 2 i1 4
2
1 6 0 0 .9 8 0 .9 7 9
2 9 8 .1 8 ( N )
故提升10kN的重物，必须施加于链轮A上的圆周力 F为298．18N。
24
《机械原理》习题课
11-19 图示为纺织机中的差动轮系，设
20
《机械原理》习题课
解此轮系为一个3K型行星轮系，即有三个中心轮(1，3及4)。若任取两个中心轮和与其相啮合的行星轮及系杆H便组成一个2K-H 型的行星轮系。且有三种情况： 1-2-3-H行星轮系、4-2’(2)-3H行星轮系及1-2’(2)-4-H差动轮系。而仅有两个轮系是独立的，为了求解简单，常选两个行星轮系进行求解。即
1
5
《机械原理》习题课
解
arctan f
总反力 F R 1 2 及 F R 3 2 的方位如图
F F
题4-14
6
机械原理习题解答
(第7章-机械的运转及其速度波动的调节)
7
《机械原理》习题课
7-7图示为一机床工作台的传动系统。设已知各齿轮的齿数，齿轮3的分度圆半径r3，各齿轮的转动惯量 J 1 , J 2 , J 2 , J 3 ，齿轮1直接装在电动机轴上，故J1中包含了电动机转子的转动惯量；工作台和被加工零件的重量之和为G。当取齿轮1为等效构件时，试求该机械系统的等效转动惯量Je。