24.4弧长及扇形面积(第1课时)课件(好)
合集下载
24.4弧长及扇形面积(第1课时)课件

r
例1 如图,圆心角为60°的扇形的半径为10厘 米,求这个扇形的面积和周长.(π≈3.14) 解:因为n=60°,r=10厘米,所以扇形面积为
nr 2 60 3.14 10 2 S ≈52.33(平方厘米); 360 360
扇形的周长为
l nr 60 3.14 10 2r 20 180 180
90 图 23.3.2 360
图 23.3.2
45 360 n 360
图 23.3.2
n r 2 360
图 23.3.2
结论:
如果扇形面积为s,圆心角度数为n,圆半径 是r,那么扇形面积计算公式为
Q l n° r O
扇形面 积S
n 2 s r 360 nr r 1
180
lr 2 2
D
有水部分的面积 = S扇+ S△
A
E
B
0
0.24 0.09 3
C
4、如图所示,分别以n边形的顶点为圆心, 以单位1为半径画圆,则图中阴影部分的面积之 和为 个平方单位.
一、弧长的计算公式
n nr l 2r 360 180
二、扇形面积计算公式
n 1 2 s r 或s lr 360 2
n nr 50 l 2r = 3 cm 360 180
50 答:此圆弧的长度为 cm 3
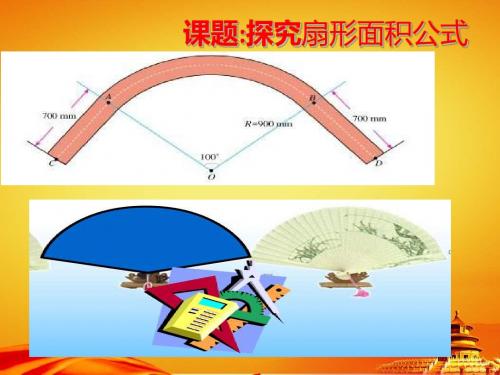
例2制造弯形管道时,要先按中心线计算“展直长 度”,再下料,试计算图所示管道的展直长度 L(单 位:mm,精确到1mm)
解:由弧长公式,可得弧AB
180
的长
L 100 900 500 1570(mm)
3
2
3
cm
九年级数学人教版(上册)第1课时 弧长和扇形面积

(2)若弦 BC=2 3 cm,求图中阴影部分的面积.
解:∵BC=2 3 cm, ∴CE=12BC= 3 cm. ∵∠AOC=60°,∴∠C=30°. 设 OE=x cm,则 OC=2x cm. ∵OE2+EC2=OC2, ∴x2+( 3)2=(2x)2,解得 x=1. ∴∴OS E阴影==1Scm扇形,OBOC-C=S△2OcBmC=. 1203×6π0×22-12×2 3×1=(43π- 3)cm2.
7.(2021·盘锦)如图,⊙A,⊙B,⊙C 两两不相交,且半径都等 于 2,则图中三个扇形(即阴影部分)的面积之和为 2π (结果保留 π).
8.如图,某数学兴趣小组将边长为 5 的正方形铁丝框 ABCD 变 形为以点 A 为圆心,AB 为半径的扇形(忽略铁丝的粗细),则所得的 扇形 ABD 的面积为 25 .
第二十四章 圆
24.4 弧长和扇形面积 第1课时 弧长和扇形面积
知识点 1 弧长公式及其应用
1.(2021·梧州)若扇形的半径为 3,圆心角为 60°,则此扇形的
弧长是(B )
1 A.2π
B.π
3 C.2π
D.2π
【变式】 已知一个扇形的半径为 6,弧长为 4π,则这个扇形 的圆心角为 120° .
在 Rt△AOF 中,OA=2 3,∠OAF=30°,
∴OF=12OA= 3,AF=3. ∴AB=2AF=2×3=6.∴BD=2. ∴S 阴影=S△AOD+S 扇形 OBC-S△BDO=2 23×2+30×π×3(602 3)2-
2× 2
3=
3+π.
15.(2020·淄博)如图,放置在直线 l 上的扇形 OAB 由图①滚动(无
10.如图,在菱形 ABCD 中,∠B=70°,AB=3,以 AD 为直
人教版九年级数学上册《24章 圆 24.4 弧长和扇形面积 实验与探究 设计跑道》优质课课件_27

2.已知扇形的半径为2cm,弧长为 4 cm ,
则扇形的面积为___4__c_m__2__.
S扇形
1 lR 2
小结
A
B
O
O
l nR
180
S扇形
nR 2
360
比较扇形面积与弧长公式, 用弧长表示扇形面积:
S扇形
1 lR 2
已知扇形的圆心角为1500,弧长为 20 cm,则扇
形的面积为__2_4_0___c_m__2.
1.一块等边三角形木块,边长为1,如图,现 将木块沿水平线翻滚。
(1)画出B点从开始至结束所经过的路径; (2)求此路径长;
(3)求此路径与水平线所围成的图形的面积。
B B●
2.如图,水平放置的一个圆柱形排水管道的 横截面半径为6m,其中水高3m,求截面上 有水部分的面积。
3. 如图,在2×2的网格中,每个小正方形的边长
1 个圆面积
2
1
个圆面积
4
S扇形
n R2
360
例2.已知扇形的圆心角为120°,半径为2, 求这个扇形的面积
1.已知扇形的圆心角为300,面积为 3 cm,2 则 这个扇形的半径R=__6__c_m__.
2.已知扇形的半径为5,面积为 10 ,则这个 扇形的圆心角是__1_4__4_°_.
在田径二百米的比赛中, 每位运动员的起跑位置相同吗?
圆心角是
1个圆周长
1396800000 的弧长是多少?
1 个圆周长
2
1
个圆周长
4
l nR
180
n表示1°的圆心角的倍数
例1.已知圆弧的半径为50厘米,圆心角为60°, 求此圆弧的长度.
2014年秋人教版九年级数学上册:24.4《弧长及扇形的面积》ppt课件
则450
S 的圆心角所对的扇形面积表示为 扇 形
S 扇形
45 R 360
1 R 2 360
2
则 10的圆心角所对的扇形面积表示为
则n0圆心角是所对的扇形面积表示为
S 扇形
nR 2 360
O n° A
B
即:n0圆心角的扇形面积公式表示为
O n°
A
B
注意: 1.扇形面积的大小由圆的大小(半径)、圆心角的度 数决定. 2. 公式中 n 的意义. n 表示 1 °圆心角的倍数,它是不 带单位的;
四 课堂程序
6 π (1)半径为3的圆,周长是_________
1.学生回答
固旧知,为后面 (2)半径为R的圆,周长是_________ C=2πR 巩 学习作铺垫 4π (3)半径为2的圆,面积是_________ (4)半径为R的圆,面积是_________ S=πR2 设计意图 2.学生自主学习, 通过学生 自主学习从 学生自主阅读数学九年上册课本第二 提问方式进 行小结,让 十四章 圆 第112页 扇形面积部分 学生养成学 —总结— 在小学我们已经学习过有关圆的面积公 习 培养自主学 式,扇形与圆有怎样的关系,那么扇形面 习的良好学 习习惯,确 积应怎样计算?它与圆的面积之间有怎样 定本节课的 学习目标。 的关系呢?本节课我们将进行探索.
本节知识在中招考试中所占的分值:
2012年 2013年 4分 4分
一、教材分析
2.学情分析
在学习这节课知识之前,学生已经学习了与圆相关的概念,垂径定理,圆心 角,圆周角定理及扇形的弧长公式等内容,是有一定的学科基础,同时学生 也想继续探究新的知识.
3.学习目标:
(一) 知识目标 1). 了解扇形的概念 2) 理解n°的圆心角所对的扇形面积的计算公式 3) 会运用公式求扇形面积. (二) 能力目标 1).经历探索扇形面积计算公式的过程,培养学生的探索能 力. 2).了解扇形面积公式后,能用公式解决问题,训练学生的 数学运用能力. (三)情感与价值观目标 1).经历探索扇形面积计算公式,让学生体验教学活动充满 着探索与创造,感受数学的严谨性以及数学结论的确定 性. 2).通过用扇形面积公式解决实际问题,让学生体验数学与 人类生活的密切联系,激发学生学习数学的兴趣,提高他 们的学习积极性,同时提高大家的运用能力.
S 的圆心角所对的扇形面积表示为 扇 形
S 扇形
45 R 360
1 R 2 360
2
则 10的圆心角所对的扇形面积表示为
则n0圆心角是所对的扇形面积表示为
S 扇形
nR 2 360
O n° A
B
即:n0圆心角的扇形面积公式表示为
O n°
A
B
注意: 1.扇形面积的大小由圆的大小(半径)、圆心角的度 数决定. 2. 公式中 n 的意义. n 表示 1 °圆心角的倍数,它是不 带单位的;
四 课堂程序
6 π (1)半径为3的圆,周长是_________
1.学生回答
固旧知,为后面 (2)半径为R的圆,周长是_________ C=2πR 巩 学习作铺垫 4π (3)半径为2的圆,面积是_________ (4)半径为R的圆,面积是_________ S=πR2 设计意图 2.学生自主学习, 通过学生 自主学习从 学生自主阅读数学九年上册课本第二 提问方式进 行小结,让 十四章 圆 第112页 扇形面积部分 学生养成学 —总结— 在小学我们已经学习过有关圆的面积公 习 培养自主学 式,扇形与圆有怎样的关系,那么扇形面 习的良好学 习习惯,确 积应怎样计算?它与圆的面积之间有怎样 定本节课的 学习目标。 的关系呢?本节课我们将进行探索.
本节知识在中招考试中所占的分值:
2012年 2013年 4分 4分
一、教材分析
2.学情分析
在学习这节课知识之前,学生已经学习了与圆相关的概念,垂径定理,圆心 角,圆周角定理及扇形的弧长公式等内容,是有一定的学科基础,同时学生 也想继续探究新的知识.
3.学习目标:
(一) 知识目标 1). 了解扇形的概念 2) 理解n°的圆心角所对的扇形面积的计算公式 3) 会运用公式求扇形面积. (二) 能力目标 1).经历探索扇形面积计算公式的过程,培养学生的探索能 力. 2).了解扇形面积公式后,能用公式解决问题,训练学生的 数学运用能力. (三)情感与价值观目标 1).经历探索扇形面积计算公式,让学生体验教学活动充满 着探索与创造,感受数学的严谨性以及数学结论的确定 性. 2).通过用扇形面积公式解决实际问题,让学生体验数学与 人类生活的密切联系,激发学生学习数学的兴趣,提高他 们的学习积极性,同时提高大家的运用能力.
学考优化指导九年级人教版数学教学课件:24.4

42-12 = 15,
∴用这个扇形卷成的圆锥的高为 15厘米,圆锥的侧面积为 4π
厘米 2.
拓展点一 拓展点二 拓展点三
解决此类问题时要紧紧抓住两者之间的两个对应关系:(1) 圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面 周长等于侧面展开图的扇形弧长.正确记忆这两个关系是 解题的关键.
拓展点一 拓展点二 拓展点三
知识点一 知识点二 知识点三
解:(1)∵圆锥的高为 4 2,底面半径为 2, ∴圆锥的母线长为 6,底面周长是 2×2π=4π,
则侧面积是12×4π×6=12π,底面积是 π×22=4π,则全面积是 12π+4π=16π.
(2)∵圆锥底面半径是 2, ∴圆锥的底面周长为 4π,设圆锥的侧面展开图的扇形圆心角为
=
12lr.
名师解读:根据扇形的面积公式和弧长公式,已知S扇形,l,n,r四个量 中的任意两个,都可以求出另外的两个量.
知识点一 知识点二 知识点三
例2 如果扇形所含的圆心角为150°,弧长为5π,那么扇形的面积 是( )
A.5π B.10π C.15πD.30π 解析:设该扇形的半径为 r,则 5π=115800π������,解得 r=6,则该扇形的面 积 S=1503π6×0 62=15π. 答案:C
,解得r=12.
答案:B
知识点一 知识点二 知识点三
解答这类问题时,一般根据弧长公式直接求解或根据公 式变形求解.
知识点一 知识点二 知识点三
知识点二扇形的面积公式
半径为r的圆中,圆心角为n°的扇形的面积为
S=���3���π6���0���2
=
���������� 180
×
������ 2
∴用这个扇形卷成的圆锥的高为 15厘米,圆锥的侧面积为 4π
厘米 2.
拓展点一 拓展点二 拓展点三
解决此类问题时要紧紧抓住两者之间的两个对应关系:(1) 圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面 周长等于侧面展开图的扇形弧长.正确记忆这两个关系是 解题的关键.
拓展点一 拓展点二 拓展点三
知识点一 知识点二 知识点三
解:(1)∵圆锥的高为 4 2,底面半径为 2, ∴圆锥的母线长为 6,底面周长是 2×2π=4π,
则侧面积是12×4π×6=12π,底面积是 π×22=4π,则全面积是 12π+4π=16π.
(2)∵圆锥底面半径是 2, ∴圆锥的底面周长为 4π,设圆锥的侧面展开图的扇形圆心角为
=
12lr.
名师解读:根据扇形的面积公式和弧长公式,已知S扇形,l,n,r四个量 中的任意两个,都可以求出另外的两个量.
知识点一 知识点二 知识点三
例2 如果扇形所含的圆心角为150°,弧长为5π,那么扇形的面积 是( )
A.5π B.10π C.15πD.30π 解析:设该扇形的半径为 r,则 5π=115800π������,解得 r=6,则该扇形的面 积 S=1503π6×0 62=15π. 答案:C
,解得r=12.
答案:B
知识点一 知识点二 知识点三
解答这类问题时,一般根据弧长公式直接求解或根据公 式变形求解.
知识点一 知识点二 知识点三
知识点二扇形的面积公式
半径为r的圆中,圆心角为n°的扇形的面积为
S=���3���π6���0���2
=
���������� 180
×
������ 2
人教版九年级数学上册课件:24.4弧长和扇形面积(共19张PPT)

-
1353π6×0 152=375π(cm2).
9
能力提升
11.如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分.图2中, 图形的相关数据:半径OA=2 cm,∠AOB=120°,则图2的周长为 83π ________cm.(结果保留π)
10
12.如图,在△ABC中,AC=4,将△ABC绕点C逆时针旋 转30°得到△FGC,则图43中π 阴影部分的面积为________.
第二十四章 圆
弧长和扇形面积
第一课时
知识展示
知识点 1 弧长公式 n°的圆心角所对的弧长 l 的计算公式为 l=n1π8R0 ,其中 R 为半径. 核心提示:在弧长公式中,已知 l、n、R 中的任意两个量,都可以求出第三个 量. 知识点 2 扇形的定义 由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
分析:先用扇形OAB的面积-三角形OAB的面积求出上面空白部分面积,再用扇形OCD的面积-三角形OCD的面积-上面空白部分的面
积7.,如即图可,求5分出.别阴以影【五部边分黑形的A龙面BC积D江.E的顶哈点尔为圆滨心,中以1考为半】径作一五个个圆,扇则图形中的阴影弧部分长的面是积之1和1为π__c___m___.,半径是18
2
知识点 3 扇形面积公式 (1)n°圆心角的扇形面积公式:S 扇形=n3π6R02 ,其中 R 为半径. (2)弧长为 l 的扇形面积公式:S 扇形=12lR,其中 R 为半径. 【典例】如图,半径为 12 的圆中,两圆心角∠AOB=60°、∠COD=120°,连接 AB、CD,求图中阴影部分的面积.
cm,则此扇形的圆心角是__________度. 71.2.如如图图,,分在别△以AB五C中边,形AACB=CD4E,的将顶△点AB为C圆绕心点,C逆以时11为针1半旋0 径转作30五°得个到圆△,FG则C,图则中图阴中影阴部影分部的分面的积面之积和为为________________.. 一列火车以6每.小时【28 江km的苏速度泰经州过10中秒通考过弯】道.如那么图弯,道所分对的别圆心以角为正___三_____角__度形.(π的取3.3个顶点为圆心, 98..一已段知铁扇边路形弯所长道在成圆为圆半弧 径半形为,4径,圆弧弧画长的为弧半6径π,,是则2三扇km形.段面积弧为_围_____成____.的图形称为莱洛三角形.若正三角 分 积析,:即先 可用 求形扇 出形 阴边影OA部长B的分面为的积面6-积三.c角m形,OAB则的面该积求莱出上洛面三空白角部分形6面π积的,再周用扇长形为OCD_的_面__积_-__三_角c形mOC. D的面积-上面空白部分的面
【课件】24.4弧长和扇形面积

∴AF= AB2+BF2= 22+12= 5.由平行四边形的性质,△FEC≌
△CGF,∴S△FEC=S△CGF,∴S 阴影=S 扇形 BAC+S△ABF+S△FGC-S 扇形 FAG
=90×3π60×22+12×2×1+12×(1+2)×1-90×π
×( 360
5)2=52-π4
16.(2014·昆明)如图,在△ABC 中,∠ABC=90°,D 是边 AC 上的一点,连接 BD,使∠A=2∠1,E 是 BC 上的一点,以 BE 为直径的⊙O 经过点 D.
(1)求证:AC 是⊙O 的切线; (2)若∠A=60°,⊙O 的半径为 2,求阴影部分的面积.(结果
保留根号和π)
解:(1)连接 OD,∵OB=OD,∴∠1=∠BDO,∴∠DOC=2 ∠1=∠A.在 Rt△ABC 中,∠A+∠C=90°,即∠DOC+∠C=90 °,∴∠ODC=90°,即 OD⊥DC,∴AC 为圆 O 的切线
3.已知扇形的圆心角为 45°,弧长等于π2 ,则该扇形的半径是 ___2__.
4.(2014·兰州)如图,在△ABC 中,∠ACB=90°,∠ABC=30
°,AB=2.将△ABC 绕直角顶点 C 逆时针旋转 60°得△A′B′C,则点
B 转过的路径长为(B )
π A. 3
3π B. 3
2π C. 3
∠FAB=90°.∵线段 AF 绕点 F 顺时针旋转 90°得线段 FG,∴∠
AFB+∠CFG=∠AFG=90°,∴∠CFG=∠FAB=∠ECB,∴EC
∥FG.∵AF=EC,AF=FG,∴EC=FG,∴四边形 EFGC 是平行四
边形,∴EF∥CG
(2)∵AB=2,E 是 AB 的中点,∴FB=BE=12AB=12×2=1,
初三九年级数学ppt课件弧长和扇形面积公式

5.方法小结: 问题1:求一个图形的面积,而这个图形是未知图形时,我 们应该把未知图形化为什么图形呢? 问题2:通过以前的学习,我们又是通过什么方式把未知图 形化为已知图形的呢?
活动6 达标检测2
1 . 120°的圆心角所对的弧长是 12π cm , 则此弧所在的圆的半径是
________. 2 . 如图, 在4×4 的方格中 (共有16 个方格 ) , 每个小方格都是边长为 1
活动5 反馈新知
1 . 已知扇形的半径为 3 cm , 面积为 3π cm2 , 则扇形的圆心角是 ________°,扇形的弧长是________cm.(结果保留π)(答案:120,2π) 2.师生共同完成教材第112页例2. 3.完成教材第113页练习第3题. 4.如图,已知扇形的圆心角是直角 ,半径是2,则图中阴影部分的 面积是________.(结果不计算近似值)(答案:π-2)
的正方形. O , A , B 分别是小正方形的顶点 , 则扇形 OAB 的弧长等于
________.(结果保留根号及π)
3.如图,矩形ABCD中,AB=1,AD=,以AD的长为半径的⊙A 交BC边于点E,则图中阴影部分的面积为________.
活动7 课堂小结与作业布置 课堂小结 1.弧长公式是什么?扇形的面积公式呢?是怎样推导出来的? 如何理解这两个公式?这两个公式有什么作用?这两个公式有 什么联系? 2.在解决部分与整体关系的问题时,我们应学会用什么方法 去解决? 3.解决不规则图形的面积问题时,我们应用什么数学思想去 添加辅助线? 作业布置 教材第115页 习题24.4第1题的(1),(2)题,第2~8题.
24.4
弧长和扇形面积
第1课时 弧长和扇形面积公式
1.理解弧长与圆周长的关系 ,能用比例的方法推导弧长公式 , 并能利用弧长公式进行相关计算. 2.类比推导弧长公式的方法推导扇形面积公式 ,并能利用扇形 面积公式进行相关计算.
新人教版九年级数学上册《24章 圆 24.4 弧长和扇形面积 实验与探究 设计跑道》公开课课件_27

用弧长来表示扇形的面积吗?
A
B
O
A
B
O
S 扇形 形
nR 22
360
l nR
180
1
S 扇形
lR 2
(1)当已知弧长L和半径R, 求扇形面
积时,应选用
S扇形
1 2
LR
(2)当已知半径和圆心角的度数,求扇
形面积时,应选用
S 扇形
nR 2
360
例2:如图、水平放置的圆柱形排水管道的截面半径
B●
B
B1
B1
B2
F'
BA
60°
1
BC
DE
B FB2
2
在一块空旷的草地上有一根柱 子,柱子上栓着一条长3m的绳 子,绳子的一端栓着一只狗。
(1)这只狗的最大活动区域有 多大? S圆=9πm2
(2)如果这只狗只能绕柱 子转过no 的角,那么它的最 大活动区域是一个什么图形 呢?
no
3m
如下图,由组成圆心角的___两__条__半__径___和圆
(5) 半 角n.°.所径.的对为.圆.的R.,心弧n角°长所的公对圆式的心是弧:长是l __l __3n6_n10__28_R_0R__n1_8R0_
试一试,看看谁最棒!
(6)半径为 4,90°圆心角所对的弧长是多少?
l 90 4 2
180
例题剖析:
例1:制造弯形管道时,要先按中心线计算“展直长
是6cm,其中水面高3cm,求截面上有水部分的面积。
(结果取整数)。
分析:有水部分的面积 = S扇- S△ 解:连接OA、OB,过点O作OC垂直AB,
垂足为D, 交 AB 于点C,则
A
B
O
A
B
O
S 扇形 形
nR 22
360
l nR
180
1
S 扇形
lR 2
(1)当已知弧长L和半径R, 求扇形面
积时,应选用
S扇形
1 2
LR
(2)当已知半径和圆心角的度数,求扇
形面积时,应选用
S 扇形
nR 2
360
例2:如图、水平放置的圆柱形排水管道的截面半径
B●
B
B1
B1
B2
F'
BA
60°
1
BC
DE
B FB2
2
在一块空旷的草地上有一根柱 子,柱子上栓着一条长3m的绳 子,绳子的一端栓着一只狗。
(1)这只狗的最大活动区域有 多大? S圆=9πm2
(2)如果这只狗只能绕柱 子转过no 的角,那么它的最 大活动区域是一个什么图形 呢?
no
3m
如下图,由组成圆心角的___两__条__半__径___和圆
(5) 半 角n.°.所径.的对为.圆.的R.,心弧n角°长所的公对圆式的心是弧:长是l __l __3n6_n10__28_R_0R__n1_8R0_
试一试,看看谁最棒!
(6)半径为 4,90°圆心角所对的弧长是多少?
l 90 4 2
180
例题剖析:
例1:制造弯形管道时,要先按中心线计算“展直长
是6cm,其中水面高3cm,求截面上有水部分的面积。
(结果取整数)。
分析:有水部分的面积 = S扇- S△ 解:连接OA、OB,过点O作OC垂直AB,
垂足为D, 交 AB 于点C,则
人教版九年级数学上册《弧长和扇形面积》圆PPT课件(第1课时)

(2)弧长单位和半径单位一致.
创设情境
探究新知
应用新知
巩固新知
做一做
弧长公式
:
l=
π
180
1.在半径为24 cm的圆中,30°的圆心角所对的弧长为 4π cm,
60°的圆心角所对的弧长为 8π cm,120°的圆心角所对的弧
长为
16π cm.
2.半径为6 cm的圆中,75°的圆心角所对的弧长是 2.5π cm;
D.80°
,扇形OAB的面积为15π,则
(
巩固新知
π,半径是6,那么此扇形的
AB 所对的圆心角是( B )
课堂小结
布置作业
A.120°
B.72°
C.36°
D.60°
创设情境
随堂练习
3.如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水
探究新知
面高0.9 m,求截面上有水部分的面积(结果保留小数点后两位).
线,垂足为D,交
于点C,连接
O●
巩固新知
课堂小结
布置作业
AC.
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m).
∴OD=DC.
又AD⊥DC,
∴AD是线段OC的垂直平分线.
∴AC=AO=OC.
A
D
C
B
创设情境
典型例题
【例2】如图,水平放置的圆柱形排水管道的截面半径是0.6m,
探究新知
圆心角
有关,
创设情境
典型例题
【例1】制造弯形管道时,要先按中心线计算“展直长度”,
探究新知
再下料,试计算图所示管道的展直长度L (结果取整数) .
A
创设情境
探究新知
应用新知
巩固新知
做一做
弧长公式
:
l=
π
180
1.在半径为24 cm的圆中,30°的圆心角所对的弧长为 4π cm,
60°的圆心角所对的弧长为 8π cm,120°的圆心角所对的弧
长为
16π cm.
2.半径为6 cm的圆中,75°的圆心角所对的弧长是 2.5π cm;
D.80°
,扇形OAB的面积为15π,则
(
巩固新知
π,半径是6,那么此扇形的
AB 所对的圆心角是( B )
课堂小结
布置作业
A.120°
B.72°
C.36°
D.60°
创设情境
随堂练习
3.如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水
探究新知
面高0.9 m,求截面上有水部分的面积(结果保留小数点后两位).
线,垂足为D,交
于点C,连接
O●
巩固新知
课堂小结
布置作业
AC.
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m).
∴OD=DC.
又AD⊥DC,
∴AD是线段OC的垂直平分线.
∴AC=AO=OC.
A
D
C
B
创设情境
典型例题
【例2】如图,水平放置的圆柱形排水管道的截面半径是0.6m,
探究新知
圆心角
有关,
创设情境
典型例题
【例1】制造弯形管道时,要先按中心线计算“展直长度”,
探究新知
再下料,试计算图所示管道的展直长度L (结果取整数) .
A
第二十四章圆 24.4 第1课时

2
课前预习
1. 圆心角为60°,半径为2 cm的扇形的弧长是 __________cm. 2. 已知扇形的半径为3 cm,面积为6π cm2,则该扇形 的弧长等于___4_π___c_m__ .
3
课堂讲练
典型例题
知识点1:弧长的计算 【例1】 在半径为6 cm的圆中,求120°的圆心角所对 的弧长.
解:(1)∵弧长l=
=20ቤተ መጻሕፍቲ ባይዱ,
∴r=
=24(cm).
(2)扇形面积= lr= ×20π×24=240π(cm2).
10
课堂讲练
3. 如图24-4-3,半圆O的直径AB=2,弦CD∥AB, ∠CAD=30°,求阴影部分的面积. (结果保留π) 解:如答图24-4-2所示,连接OC,OD. ∵∠CAD=30°,∴∠COD=60°. ∵AB∥CD,∴S△ACD=S△COD ∴阴影部分的面积=S弓形CD+S△ACD=扇形OCD的面积=
第二十四章 圆
24.4 弧长和扇形面积
第1课时 弧长和扇形面积(一)
1
课前预习
A. 弧长及扇形面积公式: (1)弧长公式:__________(其中n为弧所对的圆心角 的度数); (2)扇形面积公式:______________或_____=____l_R__ (其中n为弧长所对的圆心角的度数,l为扇形的弧长, R为半径).
A. 175π cm2
C.
cm2
B. 350π cm2 D. 150π cm2
13
分层训练
3. 如图24-4-6,已知扇形AOB的半径为2,圆心角为 90°,连接AB,则图中阴影部分的面积是( A ) A. π-2 B. π-4 C. 4π-2 D. 4π-4 4. (2017菏泽)一个扇形的圆心角为100°,面积为 15πcm2,则此扇形的半径长为__________.
课前预习
1. 圆心角为60°,半径为2 cm的扇形的弧长是 __________cm. 2. 已知扇形的半径为3 cm,面积为6π cm2,则该扇形 的弧长等于___4_π___c_m__ .
3
课堂讲练
典型例题
知识点1:弧长的计算 【例1】 在半径为6 cm的圆中,求120°的圆心角所对 的弧长.
解:(1)∵弧长l=
=20ቤተ መጻሕፍቲ ባይዱ,
∴r=
=24(cm).
(2)扇形面积= lr= ×20π×24=240π(cm2).
10
课堂讲练
3. 如图24-4-3,半圆O的直径AB=2,弦CD∥AB, ∠CAD=30°,求阴影部分的面积. (结果保留π) 解:如答图24-4-2所示,连接OC,OD. ∵∠CAD=30°,∴∠COD=60°. ∵AB∥CD,∴S△ACD=S△COD ∴阴影部分的面积=S弓形CD+S△ACD=扇形OCD的面积=
第二十四章 圆
24.4 弧长和扇形面积
第1课时 弧长和扇形面积(一)
1
课前预习
A. 弧长及扇形面积公式: (1)弧长公式:__________(其中n为弧所对的圆心角 的度数); (2)扇形面积公式:______________或_____=____l_R__ (其中n为弧长所对的圆心角的度数,l为扇形的弧长, R为半径).
A. 175π cm2
C.
cm2
B. 350π cm2 D. 150π cm2
13
分层训练
3. 如图24-4-6,已知扇形AOB的半径为2,圆心角为 90°,连接AB,则图中阴影部分的面积是( A ) A. π-2 B. π-4 C. 4π-2 D. 4π-4 4. (2017菏泽)一个扇形的圆心角为100°,面积为 15πcm2,则此扇形的半径长为__________.
人教版九年级数学上册第24章《 圆:弧长和扇形面积》

第二十四章 圆
1.如图,四边形ABCD中,AD∥BC,∠B=∠C,以点C为圆
心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB
=6,则扇形CDE(阴影部分)的面积D是( )
A. 3 π 2
C.π
B. π 2
D.6π
2.如图,已知扇形AOB的半径为2,圆心角为90°,连接AB,
则图中阴影部分的面积是( A )
角有关.
比较扇形面积公式与弧长公式,可以用弧长表示扇 形面积:
1 S扇形 2 lR
其中l为扇形的弧长,R为半径.
第二十四章 圆
【例2】如图1,水平放置的圆柱形排水管道的截
面半径是0.6 m,其中水面高 0.3 m,
求截面上有水部分的面积(结果保留小
数点后两位).
解:如图2,连接OA,OB,作弦AB的垂直平 分线,垂足为D,交A⌒B于点C,连接AC.
第二十四章 圆
24.4 弧长和扇形面积 第1课时 弧长和扇形面积
第二十四章 圆
思知考点:
我们知道,弧是圆的一部分,弧长就是圆周长的一 部分,想一想,如何计算圆周长?圆的周长可以看作是 多少度的圆心角所对的弧长?由此出发,1°的圆心角 所对的弧长是多少?n°的圆心角呢?
第二十四章 圆
(1)半径为R的圆,周长是多少? (2)圆的周长可以看作是多少度的圆心角所对的弧? (3)1°圆心角所对的弧长是多少? (4)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍? (5)n°圆心角所对的弧长是多少? (1)C=2πR
(2)360°
(3)
n°
(4)n 倍
o
(5) 也可以用A⌒Bl表示A⌒B的长.
第二十四章 圆
【例1】制造弯形管道时,经常要先按中心线计算“展直长度”, 再下料,试计算如图所示的管道的展直长度L(结果取整数).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扇 形 面 积 S
n 2 s r 360 nr r 1
180
lr 2 2
n 1 2 s r 或s lr 360 2
练习:
1、如果扇形的圆心角是230°,那么这个扇 23 形的面积等于这个扇形所在圆的面积的 36
2 2、扇形的面积是它所在圆的面积的 ,这个 扇形的圆心角的度数是_________ 240° °.3
90 2r 360
图 23.3.2
45 360 n 360
45 2r 360
n 2r 360
图 23.3.2
结论:
如果弧长为l,圆心角度数为n,圆的半径为r, 那么,弧长的计算公式为:
n nr l 2r 360 180
练一练: 已知圆弧的半径为50厘米,圆心角为60°,求 此圆弧的长度。 解:
3、扇形的面积是S,它的半径是r,这个扇形 2s 的弧长是
r
例1 如图,圆心角为60°的扇形的半径为10厘 米,求这个扇形的面积和周长.(π≈3.14) 解:因为n=60°,r=10厘米,所以扇形面积为
nr 2 60 3.14102 S ≈52.33(平方厘米); 360 360
扇形的周长为
l nr 60 3.14 10 2r 20 180 180
图 23.3.5
≈ 30.47(厘米)。
一、弧长的计算公式
n nr l 2r 360 180
二、扇形面积计算公式
n 1 2 s r 或s lr 360 2
180 r 2 360 90 r 2 360
45 r 2 360
90 图 23.3.2 360
图 23.3.2
45 360 n 360
图 23.3.2
n r 2 360
图 23.3.2
结论:
如果扇形面积为s,圆心角度数为n,圆半径 是r,那么扇形面积计算公式为
Q l n° r O
问题探究:
上面求的是的圆心角900所对的弧长,若 圆心角为n0,如何计算它所对的弧长呢?
思考:
请同学们计算半径为 r,圆心角分别为 1800、900、450、n0所对的弧长。
图 23.3.2
圆心角占整个周角的
180
所对弧长是
180 2r 360
90 图 23.3.2 360
图 23.3.2
24.4弧长和扇形面积
知识回顾
圆的周长公式 o
r
p
C=2πr
圆的面积公式
2 S=πr
问题情景:
如图是圆弧形状的铁轨示意图,其中铁轨 的半径为100米,圆心角为90°.你能求 出这段铁轨的长度吗?
解:∵圆心角900
1 ∴铁轨长度是圆周长的 4 则铁轨长是
图 23.3.1
1 2 100 50米 4
n nr 50 l 2r = 3 cm 360 180
50 答:此圆弧的长度为 cm 3
扇形:
如图,由组成圆心角的两条半径 和圆心角所对的弧所围成的图形 叫扇形.
Q
l n° r O
扇 形 面 积 S
怎样计算圆心角是n0 的扇形面积?
圆心角占整个周角的
180 360
所对扇形面积是
n 2 s r 360 nr r 1
180
lr 2 2
n 1 2 s r 或s lr 360 2
练习:
1、如果扇形的圆心角是230°,那么这个扇 23 形的面积等于这个扇形所在圆的面积的 36
2 2、扇形的面积是它所在圆的面积的 ,这个 扇形的圆心角的度数是_________ 240° °.3
90 2r 360
图 23.3.2
45 360 n 360
45 2r 360
n 2r 360
图 23.3.2
结论:
如果弧长为l,圆心角度数为n,圆的半径为r, 那么,弧长的计算公式为:
n nr l 2r 360 180
练一练: 已知圆弧的半径为50厘米,圆心角为60°,求 此圆弧的长度。 解:
3、扇形的面积是S,它的半径是r,这个扇形 2s 的弧长是
r
例1 如图,圆心角为60°的扇形的半径为10厘 米,求这个扇形的面积和周长.(π≈3.14) 解:因为n=60°,r=10厘米,所以扇形面积为
nr 2 60 3.14102 S ≈52.33(平方厘米); 360 360
扇形的周长为
l nr 60 3.14 10 2r 20 180 180
图 23.3.5
≈ 30.47(厘米)。
一、弧长的计算公式
n nr l 2r 360 180
二、扇形面积计算公式
n 1 2 s r 或s lr 360 2
180 r 2 360 90 r 2 360
45 r 2 360
90 图 23.3.2 360
图 23.3.2
45 360 n 360
图 23.3.2
n r 2 360
图 23.3.2
结论:
如果扇形面积为s,圆心角度数为n,圆半径 是r,那么扇形面积计算公式为
Q l n° r O
问题探究:
上面求的是的圆心角900所对的弧长,若 圆心角为n0,如何计算它所对的弧长呢?
思考:
请同学们计算半径为 r,圆心角分别为 1800、900、450、n0所对的弧长。
图 23.3.2
圆心角占整个周角的
180
所对弧长是
180 2r 360
90 图 23.3.2 360
图 23.3.2
24.4弧长和扇形面积
知识回顾
圆的周长公式 o
r
p
C=2πr
圆的面积公式
2 S=πr
问题情景:
如图是圆弧形状的铁轨示意图,其中铁轨 的半径为100米,圆心角为90°.你能求 出这段铁轨的长度吗?
解:∵圆心角900
1 ∴铁轨长度是圆周长的 4 则铁轨长是
图 23.3.1
1 2 100 50米 4
n nr 50 l 2r = 3 cm 360 180
50 答:此圆弧的长度为 cm 3
扇形:
如图,由组成圆心角的两条半径 和圆心角所对的弧所围成的图形 叫扇形.
Q
l n° r O
扇 形 面 积 S
怎样计算圆心角是n0 的扇形面积?
圆心角占整个周角的
180 360
所对扇形面积是
