Lecture Note for Computational Geometry-Geometric Sampling and Center Points Lectured by Pr
Lecture notes for ESSLLI-97

begin
let r be any rule in Q remove r from Q if c(r) 2 Cn(S ) then =
begin end
S := S fc(r)g for every rule s such that p(s) 2 Cn(S ) do add s to Q;
end
Figure 1: Algorithm to compute a basis for CnB (W )
Then, for every set of formulas W there is a least set T closed under PC + B and containing W .
Proposition 2.1 Let B be a set of inference rules (defaults without justi cations).
1
2 Introduction to Default Logic
Default logic is a knowledge representation mechanism allowing for reasoning in the presence of incomplete information. It handles the logical aspects of modalities such as \normally", \usually", etc. Syntactically, default logic extends the rst order logic (we will be treating propositional case almost exclusively) by introducing new entities called default rules or, simply, defaults. A default rule is a construct of the form : r = ' : M 1 ;# : : ; M m where '; 1; : : : ; k ; # are formulas of the language. The formula ' is called the premise or prerequisite of r and is denoted by p(r). The set f 1 ; : : : ; k g is called the set of justi cation of r and is denoted by j (r). The formula # is called the conclusion or consequent of r and is denoted c(r). Justi cations are used in default logic to explicitly represent conditions blocking applicability of defaults. That is, application of a rule of proof is quali ed by the absence of explicit information that would implying inconsistency of one of the justi cations of the rule. Put in yet another way, a default is applicable if its premise has been already established and all its justi cations are consistent, that is, their negations are not provable. It is precisely that presence of justi cations that allows us to model modalities such as \normally" and \usually" within default logic. In our format, a default rule has just one premise. This is an immaterial restriction since we will be assuming the usual rules of logic anyway. Default logic deals with default theories, that is, pairs (D; W ), where D is a collection of defaults and W is a collection of formulas. Default logic subsumes standard proof systems. It turns out that usual inference rules of the form ' # can simply be considered as defaults with empty set of justi cations. All major approaches to semantics of default logic are based on the natural semantics for a proof system in which propositional logic (PC) is extended by a collection of such standard inference rules (say B ). We will denote such systems by PC + B . We will now describe some properties of systems PC + B . A set of formulas T is closed under an inference rule r if the fact that ' 2 T implies that # 2 T . Similarly, T is closed under a set of rules B is it is closed under all rules in B . A set of formulas T is closed under inference in PC + B if T is closed under B and under propositional provability. We have the following fact. 2
北京大学ACM暑期课讲义-计算几何教程

计算几何教程
计算几何的恶心之处
代码长,难写。
需要讨论各种边界情况。后面所介绍的算
法,有些对于边界情况的处理很完美,不 需要再做讨论;有些则不然,需要自行处 理边界情况。
精度误差
二维矢量
2-Dimension Vector
矢量
既有大小又有方向的量。
算法演示
2 被弹出栈,3 进栈。
算法演示
没有点被弹出栈,4 进栈。
算法演示
4 被弹出栈,5 进栈。
算法演示
5 被弹出栈,6 进栈。
算法演示
6 被弹出栈,7 进栈。
算法演示
如此直到下凸壳被找到。
算法演示
倒序进行扫描找到上凸壳。
Graham 扫描的时间复杂度
这太傻缺了。算法的瓶颈在排序,所以时
总时间复杂度 O(N2 log N)。
算法扩展
SPOJ CIRUT
求恰好被覆盖 1 次、2 次、„、N 次的面积。
算法的本质在于对“裸露”部分进行处理。
这种方法也可以用于求很多圆与很多凸多 边形的面积并——但是情况复杂得多,要 讨论的情况也多得多。
三维矢量
3-Dimension Vector
总体来说讨论比较辛苦,写起来不算很难。
精度存在比较大的问题,而且半平面交的
题目一般都容许 O(N2) 算法,所以并不是 很常用。
半平面交练习题
POJ 1279 POJ 3525 POJ 2451 POJ 3384
求多边形的核。核中的点满足其到多边形边 界上任一点之间的线段只与多边形在那一点相交。 求凸多边形最大内切圆半径。 裸的半平面交。朱泽园专门为他的算法出的 题,要求 O(N log N) 算法。 求在凸多边形内部放两个半径为 r 的圆所能 覆盖的最大面积。两圆可以重叠,但不能与多边形相交。 需要用到旋转卡壳。
共形几何代数的国际反响

“共形几何代数”的国际反响李洪波研究员主创(第一作者)的共形几何代数,现已成为国际几何代数研究的主流,获得高度评价。
现将google 网搜索到的有关材料整理如下。
一. 网站的爆炸性新闻2003 年计算机图形学年会(SIGGRAPH )于2003 年7 月下旬在美国洛杉矶举行。
这是计算机图形学领域的全球盛会,约有二万五千人到会。
多家媒体对此会进行了报道,其中一家网站() 公布了一条“爆炸性新闻”(BREAKING NEWS )。
这条新闻报道,在本届年会的基调演讲(Keynote Address ),即唯一的全体大会报告中,宣布了一件令与会者极为惊喜的研究成果:天文学数据、计算机图形学和新兴的“共形几何代数”领域,正在为研究人员提供宇宙形态的清晰图片。
这个大会报告题为:宇宙模型-- 宇宙的形态。
报告人萊森毕( A. Lasenby )教授,是英国剑桥大学著名的卡文迪什(Cavendish )实验室的副主任。
他宣称,期望通过本报告,与大家共享最近两项激动人心的进展,一项是宇宙学的新进展,另一项是有关几何表述的新进展,其可用于计算机图形学和机器人。
关于宇宙学的新进展,报告中讲道:(1) 可能现已接近理解宇宙的几何;(2) 现已相当肯定它的年龄及其命运(fate )。
关于几何表述的新进展,报告中讲述的要点是:(1)提供了一种统一的语言,其以简明的方式统一表述所有的初等几何,包括欧氏几何、双曲(非欧)几何、球几何、投影几何、仿射几何等。
(2)无间隙地连接到许多其它的数学、物理和工程的领域,包括计算机图形学。
(3)这个新技术称为“共形几何代数” (CGA) 。
关于两项新进展之间的联系,报告作了如下的解释:上述的几何表述,可用于任意的维数,自然可用于四维时空,而我们正在研究这一类空间的几何,即所谓的德西特(de Sitter )空间,它是一种常曲率的时空,在宇宙学中是非常重要的。
报告中极力推崇的“共形几何代数” , 其主创者, 是中国科学院数学与系统科学研究院的李洪波研究员。
MIT基础数学讲义(计算机系)lecture15

For example, suppose A is a set of students, B is a set of recitations, and f de nes the assignment
f f;1( x1x2 : : : xn]) = (x1 x2 x3 : : : xn)
(xn x1 x2 : : : xn;1)
(xn;1 xn x1 : : : xn;2)
: : :x1 appears (x2 x3 x4 : : :
in n di
x1)g
erent
places : : :
By the Division Rule, jAj = njBj. This gives:
de in
nition, however, f A to some element
;b12(bB) c,atnhebne
a set,
f ;1(b)
not just a single value. For exampe, if f
is actually the empty set. In the special
4
Lecture 15: Lecture Notes
1 The Division Rule
We will state the Division Rule twice, once informally and then again with more precise notation.
Theorem 1.1 (Division Rule) If B is a nite set and f : A 7! B maps precisely k items of A to
Computational Geometry Theory and Applications

Max-Planck-lnstitut fiir Informatik, Im Stadtwald, 66123 Saarbriicken, Germany b RIB Bausoftware GmbH, Vaihinger Str. 151, 70507 Stuttgart, Germany c Fachbereich Mathematik und lnformatik, Martin-Luther Universitiit Halle-Wittenberg, 06120 Halle, Germany
Communicated by C.M. Hoffmann;submitted 15 August 1997; accepted 6 January 1998
Abstract
In this paper we describe and discuss a kernel for higher-dimensional computational geometry and we present its application in the calculation of convex hulls and Delaunay triangulations. The kernel is available in form of a software library module programmed in C++ extending LEDA. We introduce the basic data types like points, vectors, directions, hyperplanes, segments, rays, lines, spheres, affine transformations, and operations connecting these types. The description consists of a motivation for the basic class layout as well as topics like layered software design, runtime correctness via checking routines and documentation issues. Finally we shortly describe the usage of the kernel in the application domain. © 1998 Elsevier Science B.V.
信息技术在几何直观中的应用

信息技术在几何直观中的应用英文回答:In today's digital age, information technology (IT) has become an essential tool for enhancing our understanding of various subjects, including geometry. The integration of IT in geometry education offers numerous benefits, such as improved visualization, interactive learning experiences, and enhanced problem-solving abilities.One significant contribution of IT to geometry is the ability to create dynamic and interactive visualizations. Geometry is a subject that heavily relies on spatial reasoning and the ability to visualize complex shapes and relationships. Traditional methods of teaching geometry often involve static diagrams and textbooks, which canlimit students' understanding. However, IT tools such as 3D modeling software and virtual reality (VR) allow students to manipulate and explore geometric objects in an immersive and interactive manner. This enhanced visualization helpsstudents develop a deeper understanding of geometric concepts and enables them to see how different parts of a shape relate to each other.Another advantage of IT in geometry education is its ability to facilitate interactive learning experiences. Online platforms and software provide students with access to interactive simulations, games, and quizzes that make learning geometry more engaging and enjoyable. These interactive activities allow students to explore concepts at their own pace, experiment with different variables, and receive immediate feedback on their progress. By actively participating in these interactive learning experiences, students develop a more profound understanding of geometry and retain information more effectively.Furthermore, IT can enhance students' problem-solving abilities in geometry. Traditional methods of solving geometry problems often involve rote memorization of formulas and theorems. However, IT tools such as dynamic geometry software (DGS) allow students to construct geometric figures and manipulate their propertiesinteractively. This hands-on approach to problem-solving encourages students to experiment with different strategies and develop a more intuitive understanding of geometric relationships. By using DGS, students can explore the effects of changing variables and parameters, which helps them develop critical thinking skills and the ability to solve problems creatively.In summary, the integration of IT in geometry education offers numerous advantages, including improved visualization, interactive learning experiences, and enhanced problem-solving abilities. Dynamic visualizations, interactive simulations, and DGS empower students to engage with geometry in a more immersive and meaningful way, fostering a deeper understanding of spatial relationships and problem-solving strategies.中文回答:信息技术在几何直观中的应用。
MIT基础数学讲义(计算机系)lecture16

n
+
r r
;
1!:
2
Lecture 16: Lecture Notes
In the example above, we found six ways to choose two elements from the set S = fA B Cg with
rseept eistit;i3o+n22;a1llo=we6d.. Sure enough, the theorem says that the number of 2-combinations of a 3-element
swthaircshainsd;nb+arrr;s1.
This .
is
the
number
of
ordinary
r-combinations
of
a
set
with
n
+
r
;
1
elements,
1.2 Triple-Scoop Ice Cream Cones
Baskin-Robbins is an ice cream store that has 31 di erent avors. How many di erent triple-scoop ice cream cones are possible at Baskin-Robbins? Two ice cream cones are considered the same if one can be obtained from the other by reordering the scoops. Of course, we are permitted to have two or even three scoops of the same avor.
CGAL – THE COMPUTATIONAL GEOMETRY ALGORITHM LIBRARY

CGAL–THE COMPUTATIONAL GEOMETRYALGORITHM LIBRARYAndreas FabriINRIA2004,Route des Lucioles06903Sophia-Antipolis,FranceAndreas.Fabri@sophia.inria.frABSTRACTThe Cgal project()is a collaborative effort of several research institutes in Europe.The mission of the project is to make the most important of the solutions and methods developed in computational geometry available to users in industry and academia.Keywords:Computational geometry,C++,generic programming,exact computation paradigmINTRODUCTION Computational geometry is a research area in data structures and algorithm design which is a branch of theoretical computer science.In the seventies the term was coined,Preparata/Shamos wrote thefirst text book[20],the eighties brought theoretically op-timal,but unimplementable algorithms,the nineties saw a renaissance of simple algorithms,partially due to new complexitiy analysis methods1.The Cgal project was started in1995,by a group of European research institutes.The goal was to develop a computational geometry library,that is a homoge-neous and coherent collection of algorithms.The de-sign goals were robustness,efficiency,andflexibility. We content ourselves with an extended abstract be-cause several overview papers,library design papers, as well as papers about individual modules were pub-lished in the past.Instead we take excerpts from some of these publications and refer to further readings.1Obviously,this short“history of computational geom-etry”is an oversimplification.1.THE LIBRARYThe“product”of the Cgal project is Cgal,the Computational Geometry Algorithm Library,a highly modular C++library of data structures and algo-rithms.The data structures and algorithms were developed in academia,that is they are state of the art.The imple-mentations are not only academic proofs of concept, but they are robust,that is they can deal with degen-erate input,and they are time and space efficient. The library contains1000classes,300kloc,docu-mented on1000manual pages,that is it contains a critical mass of algorithms to be useful,and it is de-composed in reasonably sized classes that are well doc-umented.Cgal is currently supported on(although not technically limited to)Solaris,Linux,Irix,and Windows,in combination with the appropriate C++ compiler from Microsoft,Borland,Sgi,Kai and Gnu. We currently have release cycles of about9months, and about1500downloads per release.The library consists of a kernel,the basic library,a col-lection of algorithms and data structures,and a sup-port library.1.1KernelThe geometric kernel contains simple(constant-size) geometric objects like points,lines,segments,trian-gles,tetrahedra.There are geometric predicates on those objects.Furthermore,there are operations such as computing intersection and distance of objects and affine transformations.In fact Cgal offers several kernels.They differ in the representation of coordinates(Cartesian and homoge-neous coordinates),in the memory management(refer-ence counted or copying).There are even kernels that allow to execute two other kernels in parallel,and to check whether the geometric predicates give the same result.This is particularly useful tofind out where an algorithm that usesfloating point arithmetic has nu-merical problems,by executing it in parallel with an exact arithmetic.1.2Basic LibraryThe basic library contains more complex geometric objects and data structures:2D/3D convex hulls, 2D/3D triangulations,boolean operations on poly-gons,polygon decomposition in monotone or convex parts,a generic half-edge data structure,geometric optimisation algorithms based on a quadratic solver for computing minimum enclosing sphere or ellipses in arbitrary dimension,arrangements of curves in the plane,multidimensional search structures for window queries,etc.The basic library is independent from the kernel.Ev-ery algorithm defines in a very precise way which prim-itives it uses.For example,a2D convex hull algorithm can take points as input and must be able to decide if one point lies to the left of another point,and to decide when you go from one point via a second point to a third point,if you make a left or a right turn.In this case the algorithm is parameterized by the point type and the two predicates that work on the point type.The algorithm is implemented in terms of the types and operations of the interface only.Generally, the Cgal kernel provides these types and predicates. For ease of use the algorithm has default arguments for these parameters,that is the user has not to worry about this,but has means of changing it,if necessary. Among the data structures of the library,triangula-tions are probably the most relevant ones for mesh gen-eration.All triangulation data structures have pow-erful Api s,and they are fully dynamic,that is they offer methods to insert and to remove points and con-straints.Cgal offers a Delaunay and a regular Delaunay trian-gulation.In2D it offers additionally constrained and constrained Delaunay triangulation.A Delaunay triangulation of a set of points fulfills the following empty circle property:the circumscribing circle of any facet of the triangulation contains no data point in its interior.For a point set with no subset of four cocircular points the Delaunay triangulation is unique,it is the dual of the Voronoi diagram of the points.A constrained triangulation is a triangulation of a set of points that has to include among its edges a given set of segments joining the points.The corresponding edges are called constrained edges.A constrained Delaunay triangulation is a triangula-tion with constrained edges which tries to be as much Delaunay as possible.As constrained edges are not necessarily Delaunay edges,the triangles of a con-strained Delaunay triangulation do not necessarily ful-fill the empty circle property but they fulfill a weaker constrained empty circle property.To state this prop-erty,it is convenient to think of constrained edges as blocking the view.Then,a triangulation is con-strained Delaunay,iffthe circumscribing circle of any facets encloses no vertex visible from the interior of the facet.Cgal has a triangulation class that efficiently answers point location queries.Internally,the data structure is a hierarchy of triangulations.The triangulation at the lowest level is the original triangulation where opera-tions and point location are to be performed.Then at each succedding level,the data structure stores a triangulation of a small random sample of the vertices of the triangulation at the preceeding level.Point lo-cation is done through a top down nearest neighbor query.The nearest neighbor query isfirst performed naively in the top level triangulation.Then,at each following level,the nearest neighbor at that level is found through a linear walk performed from the near-est neighbor found at the preceeding level.Because the number of vertices in each triangulation is only a small fraction of the number of vertices of the preceed-ing triangulation,the data structure remains small and achieves fast point location queries on real data.This structure has an optimal behaviour when it is built for 2D/3D Delaunay triangulations[7].Because in prac-tice it also works well for other types of triangulations, it is parameterized with a triangulation class.Efficiency is a must in order to be of practical rele-vance.For example the construction of a3D Delau-nay triangulation of2million points in a surface re-construction application takes340sec and650MB of memory,on a Pentium III at550MHz.We currently work on constrained3D as well as on conformal Delaunay triangulation.The latter means that Steiner points are added,so that the Delaunay triangulation of the points automatically respects the constraints.1.3Support LibraryThe support library contains non-geometric data structures,and interfaces to other libraries providing visualization and numberetypes.2.TECHNOLOGYThe Cgal library represents cutting edge technology. This holds for the geometric algorithms,as well as for the software design,where we did not reinvent the wheel,but followed best practice.2.1C++Cgal is implemented in C++[15].There were sim-ilar efforts for making geometry libraries:the Xyz Geobench[21]was written in Pascal and the Geome-try Workbench[17]was written in Smalltalk.Because these language disappeared or were never widely ac-cepted these efforts were deemed to fail.Being as mainstream as possible was not the only rea-son for choosing C++.It is object-oriented,that is it allows a clean separation of specification and imple-mentation.It supports polymorphism,and most im-portantly for Cgal,it supports the generic program-ming paradigm.2.2Generic ProgrammingGeneric programming[18]gives a tremendousflexi-bility during development,and efficient code at run time of a program.Its power became apparent with the Stl,the Standard Template Library,which is now part of the Iso C++standard,and shipped with every C++compiler.As the Stl,Cgal makes use of the concept of iterators to decouple data structures from algorithms operating on them.Iterators are an abstraction of pointers,that is everything that implements a dereference and incre-ment operator is an iterator2For example,a set of points can be inserted into a triangulation with a function that has the same sig-nature independently from the implementation of the set.This avoids copying to one canonical container, or an inflation of functions with“the most common containers”as argument.typedef Cartesian<double>K;typedef K::Point_2Point;typedef Istream_iterator<Point,istream>Iter; Triangulation_2<K>T;vector<Point>v;//points taken from a vector of pointsT.insert(v.begin(),v.end());//points taken from standard inputT.insert(Iter(cin),Iter());Because a triangulation is a container of vertices and faces,it provides iterators that allow to enumerate them.class Delaunay_triangulation_2{Face_iterator faces_begin();Face_iterator faces_end();};Because the faces adjacent to a vertex are in a cir-cular order with no natural beginning or end,Cgal introduces the concept of circulators.class Delaunay_triangulation_2::Vertex{Face_circulator incident_faces();};Similar to Stl containers being parameterized with the type of objects they contain,the geometric ker-nels provided by Cgal are parameterised with a num-ber type,e.g.,floating point,rational,or real exact numbers.This offers a trade-offbetween robustness and efficiency.Best results are obtained by combining them,what we will explain in the next section.2A simplification again.In fact there is a complete hi-erarchy of iterators with different requirements on the set of operations.Cartesian<double>//floating point Homogeneous<Gmpz>//rationalsCartesian<leda_real>//real numbers Cartesian<Filtered_exact<double,leda_real>>This parameterization is only the tip of the iceberg concerning the adaptability and extensibility of the kernel[13].As stated earlier the basic library is independent from the kernel.All data structures in the basic library are parameterised with a class that provides all the geometric primitives the data structure uses. template<class Geometry>class Delaunay_triangulation_2{void insert(Geometry::Point_2t){if(Geometry::orientation(p,q,t)==..)if(Geometry::incircle(p,q,r,t))}};For most data structures any Cgal kernel can be cho-sen as template argument.Exceptions are data struc-tures that need very particular predicates,which are not expected to be useful in other contexts.This mechanism further allows to use projection classes.For example,3D points,together with pred-icates that compute on the projection of the points, without explicitely constructing2D points.This al-lows to triangulate the points of a Gis terrain model, or the face of a polyhedron,without changing a line of code in the triangulation data structure.Finally,this allows to seamlessly integrate a Cgal tri-angulation in an already existing application,and to let it operate on the application point type.In fact,the triangulation classes have a second tem-plate argument besides the geometry,namely the com-binatorics.Triangulations can be represented by ver-tices and faces,where each face has a pointer to its three incident faces and three incident vertices,and where each vertex has a pointer to an incident face. Alternatively,it can be represented by vertices and halfedges,where each halfedge knows its successor,its reverse halfedge,and a vertex,and where each vertex knows an incident halfedge.Although a face based representation is more compact,it may be interesting for an application to use the halfedge data structure, as the triangulation may be a single step in an ap-plication pipeline,or in an application loop,so that converting forth and back between different represen-tations is no option.Stroustrup[26]provides a general introduction to C++ template programming.Austern[1]provides a good reference for generic programming and the Stl,and a good reference for the C++Standard Library is the book of Josuttis[14].Cgal is not the only library which has adopted this paradigm.It is used by the Matrix Template Library [22],by the Boost Graph Library[23],by the Grid Algorithm Library[3],in the oonumerics[19],and the Blitz++project[27].Note that it is an explicit goal of the two scientific computing projects to offer solutions that are as fast as Fortran code.They know that their community cannot make any compromise on speed for only getting aesthetically or software engineering wise better code.2.3Exact ComputingThe established approach for robust geometric al-gorithms following the exact computation paradigm [28]requires the exact evaluation of geometric predi-cates,i.e.,decisions derived from geometric computa-tions have to be correct.While this can be achieved straightforwardly by relying on an exact number type, this is not the most efficient approach,and the idea of so-calledfilters has been developed to speed up the exact evaluation of predicates[4,11,24].The basic idea is to use afiltering step before the costly computation with an exact number type.Thefilter step evaluates quickly and approximately the result of the predicate,but is also able to decide if the answer it gives is certified to be true or if there is a risk for a false answer,in which case the exact number type is used tofind the correct answer.Cgal implements such afiltering technic using inter-val arithmetic,via the Interval nt number type[4]. This number type stores an interval of values which bounds are double s,and propagates the round-offer-rors that occur duringfloating point computations. The comparison operators on this number type have the property that they throw a C++exception in the case that the two intervals to be compared overlap. When this occurs,it means that thefilter can not cer-tify the exactness of the result using its approximate computation.Then we have tofind a different method to evaluate exactly the predicate,by using an exact but slower number type.As this failure is supposed to happen rarely on average,the overall performance of the algorithm is about the same as the evaluation of the predicate over the intervals,which is pretty fast.Note that Cgal offers only few exact number types. We concentrate on our core competence,namely ge-ometric algorithms,including geometric predicates. The generic programming approach allows to plug in arbitrary precision number types for integers and ra-tionals(Gmp[12]),and approximations of reals(Core [16],and Leda[5]).3.APPLICATION AREASCgal is enabling technology,that is it does not pro-vide a vertical solution in one application area,but provides geometric primitives for many very different application areas.Here are some examples for how Cgal data structures get used:3D regular triangulation for transition mesh generation in geological modelling[2],3D Delaunay triangulation for coarse grained molecular dynamics [10],and for surface reconstruction[8],2D Delaunay triangulations for cell decomposition in air traffic con-trol,polyhedral surfaces for surface extraction from Mri s,smallest enclosing spheres for fast collision de-tection in games,boolean operations on polygons for segmentation algorithms in imaging,arrangements of arcs of circles and polylines for controlling processing tools as laser and mill.4.CONCLUSION AND OUTLOOKIn itsfirst years the Cgal project was seen scepti-cally as we used very advanced C++techniques,that nowadays are widely accepted as best practice,and supported by almost all C++compilers.A more philosophically discussion,entitled“gems vs. libraries”,is about whether libraries force to make compromises leading to inefficiencies.Our experience is that only the design process is slower,as everything has tofit in the big picture.On the other hand it is often obvious how something has to be done,if one is familiar with the overall design ideas of the library. Also,by many the library is perceived as monolithic. However,this is not a technical,but a packaging and documentation problem,which we plan to overcome. Cgal is used in teaching,in computational geome-try research and by people that have a clear end-user perspective as they work outside of computational ge-ometry and computer science.Although Cgal is distributed as source code,it is not open source,which is currently under discussion.It makes sense to do it now,because the design of the library is stable,we start having a critical mass of algorithms and data structures to further build on, and the next step is broadening the base,a task that needs a community effort.So far we have not reached the goal to be widely used by industry.This is partially due to the fact that no company offers support for it,something that is about to change as we work towards a Cgal company.ACKNOWLEDGMENTSThis work has been supported by Esprit Ltr projects No.21957(Cgal)and No.28155(Galia).Thanks to all those colleagues from the Cgal project from whom I scavenged a paragraph or code sniplet.REFERENCES[1]M.H.Austern Generic Programming and theSTL.Addison-Wesley,1998.[2]S.Balaven,C.Bennis,J-D.Boissonnat&S.Sarda.Generation of hybrid grids using power diagrams.In Proc.Numerical Grid Gen-eration in Field Simulations,2000.[3]G.Berti A Generic Toolbox for the Grid Crafts-man.17th GAMM-Seminar Leipzig on“Con-struction of Grid Generation Algorithms”,2001.[4]H.Br¨o nnimann,C.Burnikel&S.Pion.In-terval arithmetic yields efficient dynamicfilters for computational geometry.Proc.14th Annu.ACM put.Geom.(1998),pp.165–174.[5] C.Burnikel,K.Mehlhorn&S.SchirraThe LEDA class real number.Technical Re-port MPI-I-96-1-001,Max-Planck Institut In-form.,Saarbr¨u cken,Germany,Jan.1996.[6]CGAL,the Computational Geometry Algo-rithms Library./.[7]O.Devillers Improved incremental random-ized Delaunay triangulation.In Proc.14th Annu.ACM put.Geom.,pages106-115, 1998.[8]T.K.Dey,J.Giesen&J.Hudson.Delau-nay based shape reconstruction from large data.Proc.IEEE Symposium in Parallel and Large Data Visualization and Graphics,2001.[9] A.Fabri,G.-J.Giezeman,L.Kettner,S.Schirra&S.Sch¨o nherr On the design of Cgal,the computational geometry algorithms li-brary,Software-Practice and Experience,2000, Vol.30,1167-1202.[10]G.De Fabritiis,P.V.Coveney&E.G.Flekkoy Multiscale modelling of complexfluids,Proceedings of5th European SGI/Cray MPP Workshop,Bologna(Italy)(1999)[11]S.Fortune&C.J.Van Wyk.Static analysisyields efficient exact integer arithmetic for com-putational geometry.ACM Trans.Graph.15,3 (July1996),223–248.[12]Gmp–Arithmetic without limitations./gmp/[13]S.Hert,M.Hoffmann,L.Kettner,S.Pion&M.Seel An Adaptable and Extensible Geom-etry Kernel.5th Workshop on Algorithm Engi-neering,BRICS,University of Aarhus,Denmark, August28-30,2001.[14]N.M.Josuttis The C++Standard Library,ATutorial and Reference.Addison-Wesley,1999.[15]International standard ISO/IEC14882:Pro-gramming languages–C++.American National Standards Institute,11West42nd Street,New York10036,1998.[16]V.Karamcheti,C.Li,I.Pechtchanski&C.Yap.The CORE Library Project,1.2ed.,1999./exact/core/.[17] A.Knight,J.May,J.McAffer,T.Nguyen&J.-R.Sack A Computational Geometry Workbench.ACM Symposium on Comutational Geometry,1990.[18] D.R.Musser&A.A.Stepanov Generic pro-gramming.In1st Intl.Joint Conf.of ISSAC-88 and AAEC-6(1989),Springer LNCS358,pp.13–25.[19]Scientific Computing in Object-Oriented Lan-guages[20] F.Preparata,M.I.Shamos ComputationalGeometry–An Introduction.Springer Verlag, New York,1985.[21]P.Schorn The XYZ GeoBench for the ex-perimental evaluation of geometric algorithms, Series in Discrete Mathematics and Theoretical Computer Science,Volume15,137-151,1994. [22]J.G.Siek& A.Lumsdaine The MatrixTemplate Library:Generic Components for High perfromance scientific puting in Science and Engineering,1999./research/mtl/[23]J.G.Siek,A.Lumsdaine&L.-Q.Lee TheBoost Graph Library./libs/libraries.htm[24]Shewchuk,J.R.Adaptive precisionfloating-point arithmetic and fast robust geometric pred-icates.Discrete Comput.Geom.18,3(1997), 305–363.[25]Standard Template Library programmer’sguide./tech/stl/.[26] B.Stroustrup The C++Programming Lan-guage,3rd Edition.Addison-Wesley,1997. [27]T.Veldhuizen Techniques for scientific C++.Technical Report542,Department of Computer Science,Indiana University,2000./~tveldhui/papers/techniques/.[28] C.K.Yap&T.Dub´e The exact computationparadigm.In Computing in Euclidean Geometry,D.-Z.Du and F.K.Hwang,Eds.,2nd ed.,vol.4of Lecture Notes Series on Computing.World Sci-entific,Singapore,1995,pp.452–492.。
斯坦福大学公开课:机器学习课程note1翻译

斯坦福大学公开课:机器学习课程note1翻译第一篇:斯坦福大学公开课:机器学习课程note1翻译CS229 Lecture notesAndrew Ng 监督式学习让我们开始先讨论几个关于监督式学习的问题。
假设我们有一组数据集是波特兰,俄勒冈州的47所房子的面积以及对应的价格我们可以在坐标图中画出这些数据:给出这些数据,怎么样我们才能用一个关于房子面积的函数预测出其他波特兰的房子的价格。
为了将来使用的方便,我们使用x表示“输入变量”(在这个例子中就是房子的面积),也叫做“输入特征”,y表示“输出变量”也叫做“目标变量”就是我们要预测的那个变量(这个例子中就是价格)。
一对(x,y)叫做一组训练样本,并且我们用来学习的---一列训练样本{(x,y);i=1,…,m}--叫做一个训练集。
注意:这个上标“(i)”在这个符号iiiiii表示法中就是训练集中的索引项,并不是表示次幂的概念。
我们会使用χ表示输入变量的定义域,使用表示输出变量的值域。
在这个例子中χ=Y=R为了更正式的描述我们这个预测问题,我们的目标是给出一个训练集,去学习产生一个函数h:X→ Y 因此h(x)是一个好的预测对于近似的y。
由于历史性的原因,这个函数h被叫做“假设”。
预测过程的顺序图示如下:当我们预测的目标变量是连续的,就像在我们例子中的房子的价格,我们叫这一类的学习问题为“回归问题”,当我们预测的目标变量仅仅只能取到一部分的离散的值(就像如果给出一个居住面积,让你去预测这个是房子还是公寓,等等),我们叫这一类的问题是“分类问题”PART I Linear Reression 为了使我们的房子问题更加有趣,我们假设我们知道每个房子中有几间卧室:在这里,x是一个二维的向量属于R。
例如,x1i就是训练集中第i个房子的居住面积,i是训练集中第i个房子的卧室数量。
(通常情况下,当设计一个学习问题的时候,这些输x22入变量是由你决定去选择哪些,因此如果你是在Portland收集房子的数据,你可能会决定包含其他的特征,比如房子是否带有壁炉,这个洗澡间的数量等等。
Lecture Notes in Computer Science 1

Lecture Notes in Computer Science 1 Multiscale feature extraction from the visualenvironment in an active vision systemY.Machrouh1, J.-S.Liénard1, P.Tarroux1,2Abstract. This paper presents a visual architecture able to identify salient re-gions in a visual scene and to use them to focus on interesting locations. It is in-spired by the ability of natural vision systems to perform a differential process-ing of spatial frequencies both in time and space and to focus their attention ona very local part of the visual scene. The present paper analyzes how this dif-ferential processing of spatial frequencies is able to provide an artificial systemwith the information required to perform an exploration of its visual worldbased on a center-surround distinction of the external scene. It shows how thesalient locations can be gathered on the basis of their similarities to form a highlevel representation of the visual scene.IntroductionThe use of active mechanisms seems to be a way to improve the abilities of machine vision systems. Active systems search salient features in the visual scene through a dynamic exploration. They can direct their search toward the most meaningful stimuli using attentional mechanisms leading to a reduction of the computational load [1,2].Thus, natural vision is a behavioral task, not a passive filtering process. An explora-tion of the visual world that relates perception and action allows to label the external space with natural landmarks associated with the exploratory behavior. In this re-spect, the relationships between agents and natural systems suggest that certain as-pects of natural perception can be successfully incorporated in artificial agents.Otherwise, during the past few years, several studies have been devoted to the under-standing of the essence of vision considered as an information processing mechanism[4]. This approach is grounded on Barlow’s proposal [5] which stated that the mainorganizational principle in visual systems is the reduction of the redundancy of the incoming stimuli.These considerations, issued form information theory, led several authors to analyze the statistical organization of natural images. They demonstrated that natural images (those which do not exhibit any specific bias in their pixel distribution) have a sta-tionary statistics and an auto-similar structure. As a consequence of these characteris-tics, their power spectra fall off as 1/f2 [8].In this context, different authors [6,14] demonstrated that a way to transform the initial redundancy was to improve the statistical independence of the image descrip-1LIMSI-CNRS BP 133 F-91403 Orsay Cedex2ENS 45 rue d’Ulm F-75230 Paris cedex 05Lecture Notes in Computer Science 2tors. According to this hypothesis, an image can be viewed as a linear superposition of several underlying independent sources.The filters that provide this statistical independence can be computed through the application of the source separation adequate algorithms (Infomax, BSS, ICA).One can show [6,14] that the optimal filters computed according to these principles are multiscale local orientation detectors similar to a Gabor wavelet basis [7]. However, although a lot of work has been devoted to the understanding of these theo-retical bases of information processing in natural visual system, few attempts have been made thus far to use these principles in artificial vision systems. Practical im-plementations impose some limitations that require to analyze what is really obtained with simplified models based on these general principles. On the other hand, no arti-ficial vision system has been designed to include both multiscale wavelet analysis and differential spatial and temporal processing of spatial frequencies. A prerequisite to the design of such a system is to be able to characterize the information obtained from a bank of wavelet filters in different frequency channels.We thus analyzed here the information issued from various combinations of high and low frequencies of statistically uncorrelated signals. Our aim was to determine how to build a multivariate representation of the scene that allows a dynamic grouping of image points on the basis of their similarities in a given context and for a given task.System overviewImage dataA set of 11 natural images selected from a larger database was used in the present study. Pictures that include too many traces of human activity (buildings, roads…) were avoided. Only images with similar initial resolution (around 256x512 pixels) were retained.Figure 1. Sample image from the set of natural images used in the present work.(original size 512x256)The images were discarded when their power spectrum did not fit the 1/f2 characteris-tics [8]. Figure 1 shows one typical example of an image used in the present study.Lecture Notes in Computer Science 3 Initial filtersA guideline for this work was to retain among the filtering characteristics of the pri-mate visual system those which can be useful for the elaboration of an artificial sys-tem of situated and active vision.Two characteristics have attracted our attention: the elimination of image redundancy in the processing steps designed to maximize the statistical independence of the scene descriptors and the differences in the processing of spatial frequencies between the center and the surround of the visual field.The visual scene was filtered by a first bank of Gabor wavelets in four spatial orienta-tions and four spatial frequencies (1/8, 1/16, 1/32, 1/64). For each initial image we got 32 resulting images (two for each quadrature pair of each of the 16 Gabor filter). This multiscale processing was implemented using a Burt pyramid according to the method proposed by Guérin-Dugué [10].For the purpose of this study and in order to obtain a complete view of what informa-tion is obtained from a detector during a systematic exploration of the visual scene, the whole scene was filtered by the entire bank of filters. In an operational system with a focal vision only a small part of these computations are needed.Simple cells – Complex cellsAn important distinction between the use of wavelets in image processing and the filtering steps in the visual system is the presence of strong non-linearities in the latter. Primary visual cortex shows several cell types according to the non linearities they implement. Simple cells (SC) perform an additive combination of their inputs. They respond to an oriented stimulus localized at the center of their receptive field. The so-called complex cells (CC), on the contrary, exhibit a kind of translational invariance and respond to a stimulus whatever its position in the receptive field of the cell.Figure 2. Effects of filtering of the statistical independance criterion. Init: Initial image, SC: Simple Cells, CC: Complex cellsLecture Notes in Computer Science 4 Other cell types (mainly in extrastriate cortex) combine these outputs in order to be sensitive to curvature and terminations (end-stop cells).To model simple cells we used additive units with a zero threshold ramp transfer function which amounts to take into account only the positive part of Gabor filters. The inhibitory part is indeed not transmitted by these cells.According to Field [5], we modeled complex cells output as the norm of quadrature pair Gabor filters. We verified that this implementation effectively leads to a reduc-tion of the redundancy for both cell types by a comparison of the kurtosis before and after filtering (Figure 2). Kurtosis is indeed a good measurement of the statistical independence of a set of detectors [9].A third type of detector with large receptive fields and designed to provide a contex-tual information will be considered in the following section.In order to build a set of higher level detectors suitable for the extraction of complex features we performed a Karhunen-Loeve transform of the outputs. A set of 1744 image patches (5x5) extracted randomly from the initial 11 natural images was used to build these spaces. We thus obtained 8 eigen-vectors at the output of simple cells and 4 eigen-vectors at the output of complex cells for each frequency band. These computations amount to a non-linear principal component projection of the initial image performed with two different types of non linearities.Global energy – Local contextAs stated above, we assumed the existence of detectors sensitive to the global energy in the different orientations. In an image region corresponding to the fovea, the sys-tem computes a global energy vector for each of the four orientations. This vector is used to build a signature that can be used to classify the region. Such an analysis provides us with contextual information [11,13]. We consider the identification of these contexts as a prerequisite for the recognition of objects. The importance of contextual information in natural systems can be deduced from the experimental observation that object recognition is effectively facilitated if the objects are viewed in congruent contexts [13].Thus, the system computes three output sets on each image: (i) an output directly issued from the Gabor filters filtered by a ramp function (SC), (ii) an output giving the local energy at the output of these filters analogous to the output of complex cells (CC) and (iii) a large field output providing contextual information.ResultsSimple cellsFor each image point the system provides a high dimensional vector made of 32 ori-entation components spread over 4 frequency bands for SC detectors and 16 orienta-tion components in 4 frequency bands for CC detectors.Although Gabor detectors maximize the statistical independence of their outputs, in practice they are not strictly independent. The analysis of these outputs through aLecture Notes in Computer Science 5 Karhunen-Loeve transform leads to a data representation basis that sorts the represen-tations according to their greatest statistical significance.The first axis corresponding to the highest eigen-value shows highly variable details from one scene to another (figure 3 left). It emphasizes details related to the structures present in the scene. This probably results from the fact that these structures are cor-related in a given scene due to the correlation induced by the presence of objects. They are uncorrelated from one scene to another because each scene has a different organization.Figure 3. Output of SC filters: projection of the output along the first (top) and the last (botttom) eigen-vector of the output spaceOn the contrary, details filtered by the axes corresponding to the lowest eigen-values (figure 3 right) are expected to weakly contribute to the total variance. They corre-spond to features most frequently observed from one image to another.Figure 4. Eigen-images from CC filters. The images are computed as the projection of the CC outputs on the eigen-vectors defining the output space of these filters. Columns range from high to low frequencies (from left to right: 1/8 to 1/64). Lines show the filter outputs along the principal components (top: highest variance, bottom : lowest variance).The same region revealed by the first projection axis (Figure 3 left)(% initial vari-ance : 29.4%) of the KL transform and the last projection axis (Figure 3 right)(% initial variance : 2.47%) shows that, while the first axis tends to reveal long edges thatLecture Notes in Computer Science 6 contribute significantly to the general structure of the objects, the last axis tends to reveal termination and curvature points that are not characteristic of the image struc-ture.We obtain a complex set of features along the different axes. The most representative of the presence of objects correspond to the first axes. On the others, features repre-senting complex combinations of stimuli frequently observed in natural images seem to be sorted according to their level of abstractness.Complex cellsThe same transform can be applied to the output of complex cells. Figure 4 shows the main axes of the KL transform following the computation of the Gabor norm for different spatial frequency bands.The projection axes (rows in the figure) extract distinct features from the initial image as well within the same frequency band (rows) as between different frequency bands (columns)(note that for instance the building vanishes in axis 3 projection. Figure 4 3rd row). These features are entirely different from those extracted by the output transform of SC.One can observe that high frequency details disappear in low frequency channels except for objects which exhibit frequency similarities (high frequency details re-peated over a large area like the building).Objects in the foreground, which are apparently characterized by low frequencies, appear in low frequency channels while they are not represented in high frequency band. Low frequency channels are able to distinguish features that have some spatial extension (the building or the foreground bushes).A comparison of the lowest frequency channels (Figure 4 right column) shows that the locations revealed on the different axes are largely uncorrelated, thus correspond-ing to different points of view on the scene.The lesser number of low frequency features (figure 4 right column) defines a small set of landmarks able to characterize the visual space and to guide exploratory sac-cades. This low-frequency information is the only one available in the periphery of the visual field.Correlation between channelsOne of the important questions raised by this analysis is how different are the indices obtained from the different frequency channels. If two channels correspond to the same combination of basic features, the corresponding eigen-vectors should be simi-lar. Thus, a measure of the similarity between the eigen-vectors in different frequency bands is given by the product of the eigen-matrices in these frequency bands. Using this method we compared the output spaces of respectively simple and complex cells for different frequency bands. We obtained strongly different results for the compari-son of output spaces in SC channels and in CC channels.For simple cells, the correlation between the axes of the spaces corresponding to different frequencies are low and distributed over the different axes (data not shown) while in complex cells the respectively high and low frequency bands exhibit simi-larities (table 1).Lecture Notes in Computer Science 7 Table 1. Analysis of the output space for CC detectors. The eigen-vectors corresponding to the same axes show a very high correlation between respectively high and low frequency channels. The cross-correlation between eigen vectors corresponding to different axes is usually low (not reprinted here)FrequenciesAxes f0/f1 f0/f2 f0/f3 f1/f2 f1/f3 f2/f3F1 0.990 0.442 0.410 0,365 0,330 0,996F2 0.997 0.517 0.501 0.507 0.486 0.997F3 0.991 0.363 0.370 0.425 0.424 0.995F4 0.994 0.656 0,653 0.641 0.630 0.996These results lead to the conclusion that the combination of simple cells outputs across the frequency bands underline uncorrelated details, whereas the outputs in high (resp. low) frequency bands correspond most frequently to similar stimuli.A pyramidal decomposition of the scene allows to combine these characteristics to identify spatial positions characterized by spectral compositions as diverse as possi-ble.This diversity seems to lead to a greater separability of these spatial positions and seems to be able to facilitate objet discrimination.Identification of global contextsCells sensitive to low frequencies have large receptive fields. However in higher layers of the visual system cell types that encode intermediate representations also exhibit larger receptive fields. They combine the output of the cells in the preceding layers and gather the information coming from brighter regions of the visual field.A vector that combines the global energy components associated with each frequency channel provides a suitable code for representing the whole fovea. It has been shown that such vectors can be used to classify visual scenes according to the context they belong to [11,13]. In the present study, we build such detectors in computing the mean energy provided by the output of CC cells in the four frequency bands already mentioned.To determine how spatial indices provided by the channels previously described can be used for the identification of interesting locations in the scene, we performed the following experiment:A set of salient locations are computed from the eigen-images defined previously. Points in the image are selected at random or on the basis of these salient locations. At each point the mean energies of the CC outputs in an image window correspond-ing to the fovea were computed for each frequency. We thus obtained an energy vec-tor for each of the selected point. A PCA analysis was performed on this set of vec-tors. One should keep in mind that this use of PCA differs from its use in the previous sections. The Karhunen-Loeve transform was previously used as a self-organization tool leading to a set of linear combination defining complex features frequently oc-curring in natural images. In this section, PCA should be considered as a mean to analyze the structure of the space at the output of the SC and CC filters.Lecture Notes in Computer Science 8acFigure 5. Clustering of fixation points corresponding to different regions of the visual scene. Clusters were identified on the first three principal components and the fixation points corre-sponding to each cluster plotted on the diagrams at their position in the initial image (a). (b) fixation points obtained from the second eigen-image and the second frequency channel shown Fig. 4. The other diagrams show the location of some clusters gathering salient points on the basis of their spatial frequencies and orientation properties: (c) trees and bushes, (d) building, (e) strong curvature at the border between hill and sky (f) another region of interest at the same limitWhen the locations in the image are selected at random no obvious structure were observed in the PCA space. On the contrary, when they are selected on the basis of their saliencies, clusters were identified in the PCA space. Figure 5 show the loca-tions of some of these clusters on the original image. Points corresponding to a simi-lar context are grouped into the same cluster. The example shows for instance the ability of the method to separate fixation points on the basis of their natural or artifi-cial nature (Figure 5 c and d).It should be noted that Figure 5 shows only a small sample of the structures that can be identified. Only 1/16 of the available dimensions is presented here. Thus, the method transforms the initial image into a huge set of clusters each characterized by similar spectral signatures.Discussion and conclusionThe visual filter system proposed in the present work produces a set of features that can be used to guide the exploration of the external scene. The features extracted by the non linear combination of SC channels seem rather suitable for object recognition. Features obtained from the computation of local energy (CC channels) allow a parti-tion of the image into salient regions arranged according to their frequency composi-tion. The computation of the global energy provides local context information and can be used to segment the scene on the basis of its spectral characteristics.Lecture Notes in Computer Science 9 Thus, the output of this filtering system provides on one hand locations of interest able to guide an attentional system and on the other hand clusters of locations ar-ranged according to their spectral signature.This approach can be considered as an extension of textures segmentation methods [3] to the question of the identification of contexts and an extension of the method proposed by Hérault [11] to the analysis of local contexts. However it emphasizes the relativity of the context notion; the segmentation of the visual scene in (i) a global context and (ii) objects is an oversimplificationThe visual scene is thus scattered into a set of projections on several disjoint sub-spaces. In each of these subspaces, salient points form clusters according to their similarities. These salient points are projected into disjoint sets of clusters and the corresponding objects can thus be grouped according to different points of view.An object class is not characterized by a unique high level representation, but by the transient association of a subset of properties. This association can thus dynamically depend on the current task. Objects are not considered as similar and grouped on the basis of their intrinsic properties but according to those of their properties linked to a given goal.A further step in this work will be to demonstrate how such coding abilities could indeed facilitate object classification. This requires to incorporate the present algo-rithms in the control architecture of a perceptive agent such that it can build a hierar-chy of perception-action links based on the dynamic grouping of the perceived fea-tures.ACKNOWLEDGMENTSThis work was supported by a grant from the “GIS Sciences de la cognition” CNRS.REFERENCES[1] Allport, A., Visual attention. In M.I. Posner (Ed.), Foundations of cognitive science,The MIT Press, 1989.[2] Aloimonos, Y. (Ed.), Active Perception, Lawrence Erlbaum, Hillsdale,NJ, 1993.[3] Andrey, P. and Tarroux, P., Unsupervised segmentation of Markov Random Fieldmodeled textured images using selectionist relaxation, IEEE Transactions on PatternAnalysis and Machine Intelligence, 20 (1996) 252-263.[4] Atick, J.J. and Redlich, A.N., Towards a Theory of Early Visual Processing, NeuralComputation, 2 (1990) 308-320.[5] Barlow, H.B., Possible principles underlying the transformation of sensory messages.In W. Rosenblith (Ed.), Sensory Communication, The MIT Press, cambridge, MA,1961, pp. 217-234.[6] Bell, A.J. and Sejnowski, T.J., The ''independent components'' of natural scenes areedge filters, Vision Research, 37 (1997) 3327-3338.[7] Daugman, J. and Downing, C., Gabor wavelets for statistical pattern recognition. InM.A. Arbib (Ed.), The Handbook of Brain Theory and Neural Networks, The MITPress, Cambridge, MA, 1995, pp. 414-420.Lecture Notes in Computer Science 10 [8] Field, D.J., Relations between the statistics of natural images and the response prop-erties of cortical cells, Journal of the Optical Society of America A, 4 (1987) 2379-2394.[9] Field, D.J., What is the goal of sensory coding?, Neural Computation, 6 (1994) 559-601.[10] Guérin-Dugué, A. and Palagi, P.M., Implantations de filtres de Gabor par pyramided'images passe-bas, Traitement du signal, 13 (1996) 1-11.[11] Hérault, J., Oliva, A. and Guérin-Dugué, A., Scene categorisation by curvilinearcomponent analysis of low frequency spectra. , ESANN'97, Bruges, 1997, pp. 91-96.[12] Linsker, R., Self-organization in a perceptual network, Computer Magazine, 21(1988) 105-117.[13] Oliva, A. and Schyns, P.G., Coarse blobs or fine edges? Evidence that informationdiagnosticity changes the perception of complex visual stimuli, Cognitive Psychol-ogy, 34 (1997) 72-107.[14] Olshausen, B.A. and Field, D.J., Emergence of simple-cell receptive field propertiesby learning a sparse code for natural images, Nature, 381 (1996) 607-609.。
Computational Geometry

Interval b is [ br, (b+1)r ] x lies in b = floor (x/r)
{
r 0
Solution using bucketing
Only n buckets of B might get occupied at most. How do we convert this infinite array into a finite one: Use hashing In O(1) time, we can determine which bucket a point falls in. In O(1) expected time, we can look the bucket up in the hash table Total time for bucketing is expected O(n) The total running time can be made O(n) with high probability using multiple hash functions ( essentially using more than one hash function and choosing one at run time to fool the adversary ).
Similar?
Similarity measure
Other similarity Measures
d ( p, q) cos( p, q)
d ( p, q ) e
|| p q||2 2 r 2
d i 1
pi qi
| p || q |
The dimension
Lets assume that our points are in one dimensional space. ( d = 1 ). We will generalize to higher dimension ( Where d = some constant ).
csc学习计划 英文

csc学习计划英文IntroductionComputer Science (CSC) is a highly dynamic and evolving field that encompasses a wide range of topics including programming, algorithms, data structures, computer systems, and artificial intelligence. As a student pursuing a degree in CSC, it is important to develop a comprehensive study plan that covers all these areas and ensures a thorough understanding of the subject matter. This study plan will outline the key areas of study, resources, and strategies for success in the field of Computer Science.Year 1: Foundation CoursesDuring the first year of study, it is important to focus on building a solid foundation in the key concepts of Computer Science. This will include a strong emphasis on mathematics, programming, and basic algorithms.1. Mathematics: A solid understanding of mathematics is crucial for success in Computer Science. Therefore, it is essential to take courses in calculus, discrete mathematics, and linear algebra. These courses will provide the foundational knowledge and skills necessary for understanding complex algorithms and computational processes.2. Programming: The ability to write and understand code is a fundamental skill for any computer scientist. Therefore, it is essential to take programming courses in languages such as Python, Java, or C++. These courses will provide the skills necessary to develop algorithms, data structures, and other foundational concepts in Computer Science.3. Data Structures and Algorithms: This course will provide a comprehensive understanding of fundamental data structures such as arrays, linked lists, stacks, queues, and trees. It will also cover the analysis and design of algorithms, with a focus on time and space complexity.Year 2: Intermediate CoursesIn the second year of study, it is important to deepen your understanding of Computer Science by delving into more complex topics such as computer systems, software engineering, and artificial intelligence.1. Computer Systems: This course will provide an in-depth understanding of computer architecture, operating systems, and networks. It will cover the design and organization of computer systems, as well as the principles of operating systems and networking.2. Software Engineering: This course will provide a comprehensive understanding of software development processes, methodologies, and tools. It will cover topics such as requirements engineering, software design, testing, and maintenance.3. Artificial Intelligence: This course will provide an introduction to the principles and techniques of artificial intelligence, including machine learning, neural networks, andnatural language processing. It will cover the design and implementation of intelligent systems and applications.Year 3: Advanced CoursesIn the final year of study, it is important to focus on advanced topics in Computer Science, such as advanced algorithms, data mining, and computer vision.1. Advanced Algorithms: This course will cover advanced topics in algorithm design and analysis, such as dynamic programming, graph algorithms, and computational geometry. It will focus on developing efficient algorithms for solving complex computational problems.2. Data Mining: This course will provide an in-depth understanding of data mining techniques and applications, including clustering, classification, and association rule mining. It will cover the use of machine learning algorithms to extract valuable insights from large datasets.3. Computer Vision: This course will provide an introduction to the principles and techniques of computer vision, including image processing, object recognition, and scene understanding. It will cover the design and implementation of computer vision systems and applications.Extra-Curricular ActivitiesIn addition to the core curriculum, it is important to engage in extra-curricular activities that will enhance your skills and knowledge in Computer Science. This may include participating in programming competitions, hackathons, and research projects. These activities will provide valuable hands-on experience and practical skills that will complement your academic studies.ResourcesThere are a wide range of resources available for studying Computer Science, including textbooks, online courses, and open-source software. Some recommended resources include:- Textbooks: "Introduction to the Theory of Computation" by Michael Sipser, "Introduction to Algorithms" by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and "Computer Systems: A Programmer's Perspective" by Randal E. Bryant and David R. O'Hallaron.- Online Courses: Coursera, edX, and Udacity offer a variety of online courses in Computer Science, including programming, algorithms, and artificial intelligence.- Open-Source Software: GitHub and SourceForge are valuable resources for finding and contributing to open-source software projects, which can provide practical experience and contribute to the open-source community.Strategies for SuccessIn order to succeed in studying Computer Science, it is important to adopt several strategies that will maximize your learning and understanding of the subject matter. These strategies include:- Active Learning: Engage in active learning by working on programming projects, solving algorithmic problems, and participating in group discussions. This will reinforce your understanding of key concepts and foster a deeper level of understanding.- Time Management: Manage your time effectively by prioritizing your studies, setting achievable goals, and maintaining a healthy balance between academics and other activities.- Collaboration: Collaborate with your peers, mentors, and professors to exchange ideas, seek assistance, and build a supportive network within the field of Computer Science.ConclusionStudying Computer Science requires a comprehensive study plan that covers a wide range of topics and emphasizes hands-on experience, practical skills, and collaboration. By following this study plan and utilizing the recommended resources and strategies, you can achieve success in the field of Computer Science and pursue a rewarding and fulfilling career in technology.。
MIT基础数学讲义(计算机系)lecture 25

1.1 Markov's Inequality
We can obtain a weak bound on the probability that at least one of the events A1 A2 : : : AN occurs using Markov's Theorem:
2 Ex(T ) 1
1.2 An Alternate Proof
We can obtain Fact 1 in another way. Recall Boole's Inequality, which says that for any events A1 A2 : : : AN , we have: Pr(A1 A2 : : : AN ) Pr(A1 ) + Pr(A2) + : : : + Pr(AN )
Massachusetts Institute of Technology 6.042J/18.062J: Mathematics for Computer Science Professor Tom Leighton
Lecture 25 4 Dec 97
Lecture Notes
This lecture is devoted to one rather general probability question. Let A1 A2 : : : AN be mutually independent events over the same sample space. Let the random variable T be the number of these events that occur. What is the probability that at least k events occur? That is, what is Pr(T k)? This question comes up often. For example, suppose we want to know the probability that at least k heads come up in N tosses of a coin. Here Ai is the event that that the coin is heads on the i-th toss, T is the total number of heads, and Pr(T k) is the probability that at least k heads come up. As a second example, suppose that we want the probability of a student answering at least k questions correctly on an exam with N questions. In this case, Ai is the event that the student answers the i-th question correctly, T is the total number of questions answered correctly, and Pr(T k) is the probability that the student answers at least k questions correctly. There is an important di erence between these two examples. The rst example is a special case in that all events Ai have equal probability that is, the coin is as likely to come up heads on one ip as on another. In particular, suppose that the coin comes up heads with probability p. Then all events Ai have probability p, and T has the now-familiar binomial distribution: ! n pk (1 ; p)n;k = f (k) Pr(T = k) = k np We studied the binomial distribution extensively two weeks ago. Therefore, we already have an answer to the question posed above in the special case where all events Ai have equal probability. In the second example, however, some exam questions might be more di cult than others. If question 1 is easier than question 2, then the probability of event A1 is greater than the probability of event A2. This lecture focuses on questions of this more general type in which the events Ai may have di erent probabilities.
国际的数学的类核心期刊表中英文全文
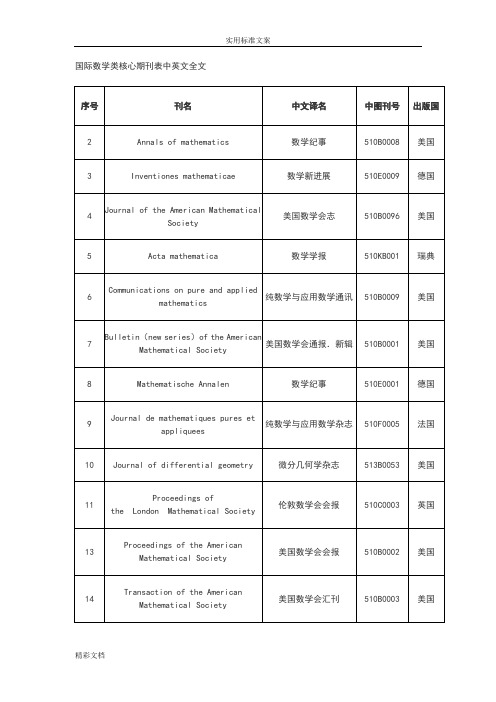
519LB010
德国
100
Topology and its applications
拓扑学及其应用
513LB003
荷兰
101
Scandinavian Journal of statistics
斯堪的纳维亚统计学杂志
299C0062
荷兰
102
Archive for mathematical logic
落基山数学杂志
510B0Q68
英国
91
Mathematical Intelligencer
数学益智
510E0010
美国
92
Journal of geometry and physics
几何学与物理学杂志
513LB017
德国
93
Topology
拓扑学
513C0001
荷兰
94
TheMichiganmathematical Journal
Acta arithmetica
299C0053
荷兰
97
Theory of probability and its applications
概率论及其应用
513B0063
英国
98
Probability theory and related fields
概率论及相关领域杂志
510E0008
美国
99
Computational optimization and applications
国际数学类核心期刊表中英文全文
序号
刊名
中文译名
中图刊号
出版国
2
Annals of mathematics
Lecture Notes in Computer Science, Volume 936)

{ Kahn semantics applies to static networks, whereas the pi{calculus can
encode dynamic networks. The solution to this problem is motivated by tools used in the study of computation in Linear Logic 8], in particular the Geometry of Interaction program 9, 1]. For the purposes of this paper, the key relevant idea is to mimic dynamic networks (of the lambda calculus) by ow of structured tokens in a static network. { The second complication that arises is the non-determinism in pi{calculus processes. The approach we adopt here is to use a variant of the generalization of the determinate data- ow semantics to a semantics for indeterminate data ow networks 22, 2].
By changing the structure of the tokens, the resulting semantics applies uniformly to the Calculus of Communicating Systems 19] and the pi{calculus. This change of structure of tokens is suggested by the nature of computation in the pi{calculus. The de nitions of the process combinators essentially stand unchanged. In particular, the de nition of parallel composition is unchanged. Thus our treatment of interaction is \generic", an essential criterion for any good description of parallel composition. Furthermore, for all of these calculi, our semantics distinguishes the processes a k b and ab + ba. More generally, for CCS, we show that our semantics induces the same process equivalence as a pomset-based semannger-Verlag Berlin Heidelberg 1995. This work is subject to copyright. All rights are reserved, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, re-use of illustrations, recitation, broadcasting, reproduction on microfilms or in any other way, and storage in data banks. Duplication of this publication or parts thereof is permitted only under the provisions of the German Copyright Law of September 9, 1965, in its current version, and permission for use must always be obtained from Springer-Verlag. Violations are liable for prosecution under the German Copyright Law.
MIT基础数学讲义(计算机系)24

These two examples show that Markov's Theorem gives weak results for well-behaved random variables however, the theorem is actually tight for some nasty examples. Suppose we ip 100 fair coins and use Markov's Theorem to compute the probability of getting all heads: Pr(heads 100) Ex(heads) = 50 = 1 100 100 2
Massachusetts Institute of Technology 6.042J/18.062J: Mathematics for Computer Science Professor Tom Leighton
Lecture 24 2 Dec 97
Lecture Notes 1 Deviation from the Mean
If the coins in are mutually independent, then the actual probability of getting all heads is a miniscule 1 in 2100. In this case, Markov's Theorem looks very weak. However, in applying Markov's Theorem, we made no independence assumptions. In fact, if all the coins are glued together, then probability of throwing all heads is exactly 1 . In this nasty case, Markov's Theorem is actually 2 tight!
海天讲座(四)最优传输理论

海天讲座(四)最优传输理论图1.纽约暴雪(崔丽摄)。
公元2016年2⽉11⽇上午,加州理⼯学院,⿇省理⼯学院以及“激光⼲涉引⼒波天⽂台(LIGO)”的研究⼈员在华盛顿宣布⼈类⾸次听到了宇宙的涟漪-引⼒波,从⽽从实验⾓度再度证实了爱因斯坦⼴义相对论。
当时,⽼顾正在飞往加州的飞机上,获知消息后异常激动。
从历史上看,爱因斯坦⼴义相对论的理论⾃洽性的证明是“正质量猜测”,由丘成桐先⽣和其学⽣Schoen于1979年共同完成。
后来丘成桐先⽣所证明的卡拉⽐-丘流形成为现代超弦理论的基⽯,丘成桐先⽣所⽤的⼿法是复蒙⽇-安培⽅程。
⽼顾此⾏的⽬的就是向国际学界同⾏介绍我们在蒙⽇-安培⽅程计算⽅⾯的理论进展。
从暴雪肆虐的纽约来到阳光明媚的洛杉矶,⽼顾顿觉⾃然的慷慨和⼈⽣的美好。
洛杉矶的天空⼀如既往,蓝得令⼈发晕。
UCLA 校园内的学⼦早已夏装打扮,不知是因为奥巴马的来访还是何故,许多⼥⽣都⼿持⼀柄长径玫瑰,青春靓丽,笑容灿烂。
会议名称是'Shape Analysis and Learning by Geometry and Machine'【1】,在纯粹和应⽤数学学院(IPAM)召开。
与会者是世界知名专家学者,有⽔平集⽅法(Level Set Method)之⽗UCLA的Stanley Osher教授,计算⼏何之⽗Stanford的Leo Guibas教授,历史上⾸位 International Mathematical Union (IMU)⼥主席,Duke的Ingrid Daubechies教授,机器学习的先驱Ohio State 的Mikhail Belkin教授等等。
同时有许多来⾃以⾊列,法国的知名科学家。
与许多合作伙伴和⽼朋友再度相逢,切磋思想,重温友情。
在法国巴黎有⼀个地铁车站-蒙⽇⼴场,在⾥昂旧城有⼀条⽼街-安培⼤街。
最优传输理论由法国学者开创,传统悠久,硕果累累。
法国现代的数学家Yann brenier, Cédric Villani都为最优传输理论做出了杰出贡献。
利用对称性求最小值问题

利用对称性求最小值问题唐乐红【摘要】Secure multi-party computation has been more and more widely used in many fields.It has become one of the hot issues in information security field.Privacy-Preserving Computational Geometry ( PPCG) is a spe-cial kind of secure multi-party computation problem.By using existing scalar product protocol, we propose a new protocol by using symmetry to solve the minimum value problem, and furthermore analyze the correctness, secur-ity and complexity performance of the protocol.%安全多方计算问题,在很多领域得到了越来越广泛的应用,已成为信息安全领域的研究热点之一。
保护私有信息的计算几何问题,是一类特殊的安全多方计算问题。
利用点积协议,提出了关于利用对称性求最小值问题的保密协议,并分析了协议的正确性、安全性和复杂性。
【期刊名称】《兰州工业学院学报》【年(卷),期】2015(000)001【总页数】3页(P56-58)【关键词】安全多方计算;计算几何;点积协议;最小值问题【作者】唐乐红【作者单位】福州大学阳光学院,福建福州 350015【正文语种】中文【中图分类】TP309所谓的安全多方计算(Secure Multi-party Computation,SMC),是指在一个分布式网络中,在各参与方互相不信任的情况下,能够在保护各参与方输入信息隐私的同时,协同合作完成一定的任务.SMC在很多领域得到了越来越广泛的应用.保护私有信息的计算几何问题(Privacy-Preserving Computational Geometry,PPCG)是指在分布式网络环境中,对参与者各自输入信息保密的前提下,使得所有参与者通过合作完成某项计算几何问题.例如:A、B两个开发商想共同合作开发某个区域,但又不希望在施工前向对方泄露自己的计划,如何在保护各自计划的条件下,求出A的两个施工地点与B的施工路线之间的最小距离.此时,我们可以把施工地点抽象成1 个点,施工线路抽象成1 条线[1].这个问题可以转化为求一条直线上的动点与两定点之间的最小值问题.本文所设计的协议,前提是假定双方的计算环境是安全的,通过利用已有的点积协议,提出了利用对称性保密求一条直线上的动点与两定点之间的最小值问题.整个计算过程要求双方严格执行协议规程,这就是通常所说的半诚实.安全点积协议[2]现已成为安全多方计算SMC中的一个重要基础协议,在SMC中有着广泛的应用.安全点积协议可以形式化地描述为:Alice拥有一个私有向量X=(x 1,x2,…,xn),Bob 则拥有另一个私有向量Y=(y1,y2,…,yn),双方希望在不向对方透露各自私有数据的情况下,通过协作计算获得点积结果xiyi.不经意传输协议(Oblivious Transfer,OT)[3],是一种可以保护双方隐私的通信协议.此协议是一个由发送方A和接收方B共同参与的双方通信协议.基本思路为:发送方A发出m1,m2,...,mn的n条消息,执行协议后接收方B将得到其中的一条或几条消息.发送方A不能控制接收方B的选择,也不知道接收方B收到的是哪一条或哪几条消息,而接收方B不能得到其选择之外的信息.输入:Alice拥有数据X=(x1,x2,…,xn),Bob拥有数据Y=(y1,y2,…,yn).输出:Alice获得X·Y+v,其中v是Bob选取的随机数.执行过程:1) Alice和Bob事先协商好两个数p和m,能使得pm足够大.2) Alice生成任意m个随机向量V1,…,Vm,并且满足.3) Bob生成任意m个数r1,…,rm,使其满足4) 对每个j=1,…,m,执行以下步骤:(1) Alice秘密选取一个随机数k,1≤k≤p.(2) Alice将(H1,…,Hp)传递给Bob,其中Hk=Vj,其余都是随机生成.因为k是只有Alice知道的秘密数,所以Bob并不会知道Vj的位置.(3) Bob计算Zj,i=Hi·Y+rj,i=1,…,p.(4) Alice利用不经意传输协议得到Zj=Zj,k=Vj·Y+rj,而Bob并不知道k的值.5) Alice计算Zj=X·Y+v.此协议的通信代价为p·m·n·d,这里d表示为每个数据的二进制位数,p、m为安全参数,计算代价为m次协议.若已知直线L1:a1x+b1y=c1和直线外一个点P1(x1,y1),则求出点P1(x1,y1)关于此直线的对称点).对称点的坐标计算公式为已知点P1(x1,y1)、P2(x2,y2),以及一条直线L:ax+by=c,在直线L上找出一个点m,使得的值最小,最后求出此最小值.直线上有一个动点,要求出动点与两定点间距离的最小值,可以利用对称性来解决.根据定理:平面内两点间直线段最短,就可以求出距离的最小值.本题求的是两条线段长度之和的最小值.当两个定点在直线的不同侧时,最小值就是两个定点之间的距离.当两个定点在直线的同侧时,则以直线为对称轴,作其中一个点的对称点,最小值则为另一个点与此对称点间的距离[5].如图1所示.我们在此假设两个点在直线的同侧.输入:Alice拥有点P1(x1,y1)、P2(x2,y2),Bob拥有一条直线L:ax+by=c.输出|+|mp2|的最小值.(m是直线L上的一个动点)执行过程:1) Alice在本地独立生成一个向量X=(x2,x1,y1,1),Bob同样也在本地生成一个向量和Bob通过共同利用共享点积协议得到获得u1的值,Bob获得u2的值.2) Alice在本地独立生成一个向量M=(y2,y1,x1,1),Bob也在本地独立生成一个向量和Bob通过共同利用共享点积协议得到获得v1的值,Bob获得v2的值.3) Alice 将得到的u1、v1的值传给Bob,Bob 将得到的u2、v2的值传给Alice.接着Alice和Bob各自在本地利用得到的数据计算出的值.协议结束.1) 正确性分析. 要计算出最小值,必须先求出其中一个点关于直线L的对称点.因此,我们先计算出点P1(x1,y1)关于直线L的对称点).最小值d即为点P1(x1,y1)与点)之间的距离.根据距离公式可以得到通过以上的分析,可以得知该协议是正确的.2) 安全性分析.协议在步骤(1)(2)(3)中均有信息交互,所以分别对这三步进行安全性分析.步骤(1)中,Alice、Bob只调用了点积协议,Alice得到了u1,Bob得到了u2,基于点积协议的安全性,Alice不能从u1推导出Y,Bob也不能从u2推导出X.步骤(2)与步骤(1)同样分析.步骤(3)中,Alice、Bob均得到u1、u2、v1、v2.Alice通过所得到的这4个值,可以分析得出下面的2个方程.但是总共有a、b、c3个未知数.所以方程组有无穷多解.因此,Alice无法推出Bob 的私有信息.同理,Bob也无法推出Alice的私有信息.综上所述,参与者Alice和Bob的私有信息均不会泄露,协议是安全的.3) 复杂性分析.本协议中调用了2次的点积协议.根据协议内容以及基于不经意传输协议(OT)的点积协议的复杂性可知,本协议的通信复杂度为2·p·m·n·d+2,计算复杂度为O(2mp).保护私有信息的计算几何(PPCG)问题在对私有信息高度敏感的领域有着重要的应用前景.本文通过利用点积协议,设计出了利用对称性保密求一条直线上的动点与两定点之间的最小值问题,并分析了该协议的正确性、安全性和复杂性.[1] 刘文,罗守山,陈萍. 保护私有信息的点线关系判定协议及其应用[J]. 北京邮电大学学报, 2008,31(2):72-75.[2] Atallah M J, Du W.Secure multi-party computationalgeometry[C]//Lecture Notes in Computer Science 2125. Berlin:Springer ,2001:165-179.[3] 邱卫东,黄征,李祥学,等. 密码协议基础[M].北京:高等教育出版社,2009:120-121.[4] Mikhail J Atallah, Wenliang Du. Secure multi-party computational geometry[C]//In 7th Int. Workshop on Algorithms and DataStructures(WAD-S 2001), Lecture Note in Computer Sciences 2125, Springer-Verlag, New York:Springer-verlag,2001:165-179.[5] 王珽,罗文俊. 基于阈值的点线距离与位置关系保密判定协议[J].计算机工程与应用,2010,46(13):87-89.Key words: secure multi-party; computational geometry; scalar product protocol; the minimum value。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
sets in C have a common point. For example, in 1-D, assume 3 intervals I1, I2, I3 and I i ∩ I j ≠ φ (i≠j, i,j = 1,2,3), then
I1 ∩ I 2 ∩ I 3 ≠ φ Proof: Assume
So Pr[s is a δ-median] = 1-2( −3δ 3 + 2δ 2 ) . When δ = ¼, Pr[s is a δ-median] = 1-2x5/32 = 11/16 >1/2. It shows this method improves the estimation of δ-median.
and
i i P_
P − = {Pi | ai < 0} .
j j
From the equations P•a = 0, or
Theorem 3: If P⊂ Rd has n points, then its set of δ-center is the intersection of a family of closed halfspaces whose member each contains at least n•(1-δ) points of P and has at least d points of P in its boundary hyperplanes.
Theorem 1: (Helly) Suppose C={C1,C2,…Cn,..C∞} is a family of convex sets in Rd and +1 for every d+1 of them (Ci1,…Cid+1), if there exist a common point ( ∩idj = i1 C j ≠ φ ), then all
Center point is the extension of median in 1-D to high dimension Rd.
Definition 3: c is a δ-center point of P if taking any projecting to 1D, c’s projection is still a δ-median in that projection direction.
let’s define Γ = {H + | H + ∩ P >
d n} , now we only need to prove: for all H1+, …, d +1 d +1 1 n and ∩ H i+ = R d − ∪ H i− , it infers Hd+1+ ⊂ Γ , ∩ H i+ ≠ φ . Recall | H i + ∩ P |> d +1 i =1 d +1 1 ( P ∩ H i− ) < (d + 1) ⋅ ⋅n = n, that P ∩ H i + = P ∩ ( R d − ∪ H i− ) . Now we have: ∪ d +1 i =1
Theorem 4: (Radon’s theorem) Let Let P = {p1,…pn} ⊂ Rd such that n ≥ d+2, then P can be partitioned into two sets P1 and P2 such that P1 ∪ P 2 = P and the Convex Hulls CH ( P 1 ) ∩ CH ( P 2) ≠ φ P1 ∩ P 2 = φ
I1 ∩ I 2 = S3 ≠ φ I1 ∩ I 3 = S2 ≠ φ
I 2 ∩ I 3 = S1 ≠ φ Without of generality, assume S1 is in the middle of S2 and S3. Recall that S 2 ⊂ I1 and S3 ⊂ I1 , so obviously, we have S1 ⊂ I1 . Also S1 ⊂ I 2 ∩ I 3 , now we have I1 ∩ I 2 ∩ I 3 = S1 ≠ φ
Definition 2: A center point of a set P of n points in Rd is a point c of Rd such that every hyperplance passing through c partitions P into two subsets each of size at most n•d/(d+1).
Theorem 2: Let P = {P1,…Pn} ⊂ Rd, there will exist a point c ∈ Rd such that c is a
1 d +1
center point.
Proof: For any half plane H, let | H + ∩ P |≥| H − ∩ P | . If | H + ∩ P |> d n , then c ∈ H + . d +1
Lecture Note for Computational Geometry -Geometred by Prof. Shang-Hua Teng on Nov. 29 Scribed by Zhuangli Liang (sliang@) Boston University
Here when we talk about halfspace, we mean significant halfspace defined by the hyperplane containing at least d points of P. Now the linear programming algorithm is to n find a point in the common intersection of a family of no more than < n d halfspaces. d In other words, the linear programming problem in d dimension is subject to no more than nd inequality constrains. From Helly’s theorem, it can be solved in O(nd) time.
n
11×n P a = 0( d +1)×1 Since n >d+1, there exists a non-trivial solution a ≠ 0 . From 11×n ⋅ a = 0 , we have
∑a
i
= 0 . Now we define the partitions P + = {Pi | ai ≥ 0}
which means there must exist at least a point c out of
∪ ( P ∩ H i− ) and c ∈ ∩ H i+ ≠ φ .
i =1 i =1
d +1
d +1
We can apply this theorem in the linear programming problem.
Definition 1: Given a set P of n points in Rd and c ∈ P, if | P ≥ c |> δ and | P < c |> δ , then c is a δ-median of P.
If we randomly choose an element s from the set P, then the probability Pr[s is a δ-median] = 1-2δ. This is a not bad approximation when δ is small. To improve this probability, we can test it in a t elements sample T⊂P. This procedure is described as below (1) After s is picked, t element T⊂P are randomly picked min(| T < s |,| T ≥ s |) (2) φ = is computed |T | (3) if φ ≤ δ − ε , then s is a good estimation of δ-median, with error ε . Otherwise, s is a bad estimation and another s need to be picked and test again. This is a useful tool to estimate a δ-median with small error. Given a sample number of t~800, the probability Pr[testing is wrong] < 4%. Also, this testing procedure doesn’t depend on n, which can be a very large number. Now, we give another way to estimate the δ-median. In k randomly picked elements S⊂P and let s be the median of S, what will be Pr[s is a δ-median of P] ? First, we examine a simple example. when k=3 and S={s1,s2,s3}, s=median{ s1,s2,s3}, since we only care about the relative rank in P, without generality, we assume 1 2 n −1 P= {0, , ,..., } . Obviously, Pr[s is a δ-median] = 1-Pr[ s<δ, or s>δ ] = 1-2Pr[ s<δ ]. n n n 3 Recall Pr[ s<δ ] = Pr[ at least two of { s1,s2,s3 } ≤ δ ] = δ 2 (1 − δ ) + δ 3 = −3δ 3 + 2δ 2 2
