【数学】江苏省南通市高级中学2015届高三一模
江苏省南通市2015届高三第一次调研考试语文试题

江苏省南通市2015届高三第一次调研考试语文试题高三2011-01-31 11:19江苏省南通市2015届高三第一次调研考试语文试题一、语言文字运用(15分)1.下列词语中加点的字,每对读音都不相同的一组是(3分)A.脊椎/椎心泣血着落/着手成春抹脸/厉兵秣马B.闪烁/众口铄金积攒/人头攒动脉络/脉脉含情C.场院/逢场作戏盘桓/烜赫一时切削/削价处理D.肄业/肆无忌惮绰约/踔厉风发给与/供应给养2.下列各句中,没有语病的一句是(3分)A.与早已流行的互联网论坛和博客相比,微博以140字的限制、便捷的转发机制以及对终端设备的简单要求降低了民众表达言论的门槛。
B.苏州河淤泥疏浚工程正式全线启动,显示了上海市政府部门彻底治理苏州河长期存在的污染问题、打造东方“莱茵河”的决心。
C.“新生代农民工”自从被列入政府重点关注的对象之后,各级政府积极行动,将关心新生代农民工成长作为新一年度工作重点。
D.2010年的国产大片《孔子》《赵氏孤儿》等都善于从本土文化土壤中吸纳养分,呈现出本土特色鲜明、原创力充沛、文化厚度不断增加。
3.下面的文字说明了利用等离子体杀死细菌的过程,请依次概括这个过程的三个阶段。
(每点不超过6个字)(4分)等离子体是一种离子化气体,一般温度高达数千摄氏度。
科学家在一个大气压环境下让等离子体的温度平稳保持在35℃到40℃之间;再利用低温等离子体破坏细菌的DNA结构,杀死生长在伤口处的由生物膜保护的细菌。
由于低温等离子体直接瞄准了小面积的特定感染区域,因此在治疗过程中周围组织不会受损。
4.仿照示例,从“橡皮人”“考碗族”“奈特尔家庭”三种职场现象中选择一个,作劝勉或警醒式的点评。
(不超过40个字)(5分)【示例】软实力:软实力,是相对于知识、文凭等“硬实力”而言的,是指一个人在职场中会唱歌、字漂亮、有气质等各种影响自身发展潜力和感召力的因素。
点评:软实力是一个人综合素质的体现,全面提升软、硬实力才能在职场立于不败之地。
三角函数模型
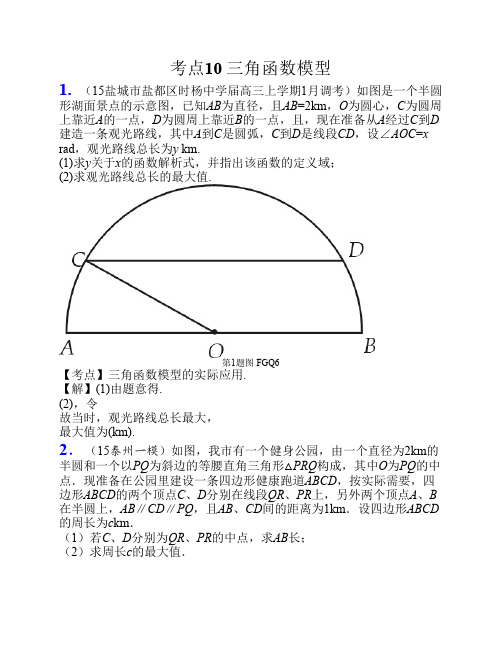
考点10 三角函数模型1.(15盐城市盐都区时杨中学届高三上学期1月调考)如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且,现在准备从A经过C到D 建造一条观光路线,其中A到C是圆弧,C到D是线段CD,设∠AOC=x rad,观光路线总长为y km.(1)求y关于x的函数解析式,并指出该函数的定义域;(2)求观光路线总长的最大值.第1题图 FGQ6【考点】三角函数模型的实际应用.【解】(1)由题意得.(2),令故当时,观光路线总长最大,最大值为(km).2.(15泰州一模)如图,我市有一个健身公园,由一个直径为2km的半圆和一个以PQ为斜边的等腰直角三角形△PRQ构成,其中O为PQ的中点.现准备在公园里建设一条四边形健康跑道ABCD,按实际需要,四边形ABCD的两个顶点C、D分别在线段QR、PR上,另外两个顶点A、B 在半圆上,AB∥CD∥PQ,且AB、CD间的距离为1km.设四边形ABCD 的周长为c km.(1)若C、D分别为QR、PR的中点,求AB长;(2)求周长c的最大值.第2题图 JSY27【考点】三角函数的最值;在实际问题中建立三角函数模型.【解】(1)连结RO并延长分别交AB、CD于M、N,连结OB,∵C、D分别为QR、PR的中点,PQ=2,∴,∵△PRQ为等腰直角三角形,PQ为斜边,∴,.∵MN=1,∴.在Rt△BMO中,BO=1,∴,∴. (2)设∠BOM=θ,<<在Rt△BMO中,BO=1,∴BM=sinθ,OM=cosθ.∵MN=1,∴CN=RN=1-ON=OM=cosθ,∴,,当sinθ+cosθ=即有sin2θ=,即或时取等号.∴当或时,周长c的最大值为km.第2题图 JSY283.(15连云港赣榆海头9月调研)如图所示,某人想制造一个支架,它由四根金属杆PH,HA,HB,HC构成,其底端三点A,B,C均匀地固定在半径为3m的圆O上(圆O在地面上),P,H,O三点相异且共线,PO与地面垂直.现要求点P到地面的距离恰为3m,记用料总长为L=PH+HA+HB+HC,设∠HAO=.(1)试将L表示为的函数,并注明定义域;(2)当的正弦值是多少时,用料最省?第3题图 cqn003【考点】球的体积和表面积.【解】(1)因PO与地面垂直,且三点A,B,C均匀地固定在半径为3m 的圆O上,则△AOH,△BOH,△CO H是全等的直角三角形,又圆O的半径为3,所以OH=3tan,AH=BH=CH=,…(3分)又,所以,…(6分)若点P,H重合,则,即,所以,从而,.…(8分)(2)由(1)知,所以,当=0时,,…(12分)令,,当时,>0;当时,<0;所以函数L在(0,)上单调递减,在上单调递增,…(15分)所以当,即时,L有最小值,此时用料最省.…(16分)4.(15江苏模拟(三))如图,有一景区的平面图是一半圆形,其中AB长为2km,C、D两点在半圆弧上,满足BC=CD.设.(1)现要在景区内铺设一条观光道路,由线段AB、BC、CD和DA组成,则当θ为何值时,观光道路的总长l最长,并求l的最大值.(2)若要在景区内种植鲜花,其中在△AOD和△BOC内种满鲜花,在扇形COD内种一半面积的鲜花,则当θ为何值时,鲜花种植面积S最大.第4题图 cqn4【解】(1)由题,,取BC中点M,连结OM.则,.∴.同理可得,.∴.即.∴当,即时,有.第4题图 cqn10(2),,.∴.∴∵,∴解得,列表得+0-递增极大值递减∴当时,有.答:(1)当时,观光道路的总长l最长,最长为5km;(2)当时,鲜花种植面积S最大.5.(江苏省南京市2015届高三上学期9月调考数学试卷)如图,公路AM、AN围成的是一块顶角为a的角形耕地,其中tan a=.在该块土地中P 处有一小型建筑,经测量,它到公路AM,AN的距离分别为km,km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.第5题图 FGQ19【考点】解三角形的实际应用.【解】过点P作PE⊥AM,PF⊥AN,垂足为E、F,连接PA.设AB=x,AC=y.因为P到AM,AN的距离分别为3,,即PE=3,PF=.由①因为tan a=,所以sin a=.所以②由①②可得. ③因为.当且仅当取“=”,结合③解得x=5,y=.所以有最小值15.答:当AB=5km时,该工业园区的面积最小,最小面积为.第5题图 FGQ206.(江苏省南通市2015届高三第一次模拟考试数学试题)在长为20m,宽为16m的长方形展厅正中央有一圆盘形展台(圆心为点C),展厅入口位于长方形的长边的中间,在展厅一角B点处安装监控摄像头,使点B与圆C在同一水平面上,且展台与入口都在摄像头水平监控范围内(如图阴影所示 ).第6题图 FGQ50(1 )若圆盘半径为m,求监控摄像头最小水平视角的正切值;(2 )过监控摄像头最大水平视角为60°,求圆盘半径的最大值.(注:水平摄像视角指镜头中心点水平观察物体边缘的实现的夹角 )【考点】直线与圆的位置关系.【解】(1 )过B作圆C的切线BE,切点为E,设圆C所在平面上入口中点为A,连接CA,CE,CB,则CE⊥BE,CA⊥AB第6题图 FGQ15∴监控摄像头水平视角为∠ABE时,水平视角最小.在直角三角形ABC中,AB=10,AC=8,tan∠ABC=,在直角三角形BCE中,CE=,,tan∠CBE= ,∴tan∠ABE=tan(∠ABC+∠CBE ),∴监控摄像头最小水平视角的正切值为.(2 )当∠ABE=60°时,若直线BE与圆C相切,则圆C的半径最大.在平面ABC内,以B为坐标原点,BA为x轴建立平面直角坐标系,则直线BE方程为y=x,∴,∴圆C的半径最大为(m ).7.(15南通市如东县栟茶高级中学高三上学期第二次学情调研)某小区想利用一矩形空地ABCD建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一条直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场.(1)假设DN=x(m),试将五边形MBCDN的面积y表示为x的函数,并注明函数的定义域;(2)问:应如何设计,可使市民健身广场的面积最大?并求出健身广场的最大面积.第7题图 FGQ59【考点】解三角形的实际应用.【解】 (1)作GH⊥EF,垂足为H∵DN=x,所以NH=40-x,NA=60-x,∵,∴,∴过M作交CD于T,则有,可解得,由于N与F重合时,AM=AF=30适合条件,故x∈(0,30].第7题图 FGQ60(2),所以当且仅当,即x=20∈(0,30]时,y取得最大值2000,答:当DN=20m时,得到的市民健身广场面积最大,最大面积为2000m2.8.(15宿迁市沭阳县银河学校高三上学期开学试卷)某固定在墙上的广告金属支架如图所示,根据要求,AB至少长3米,C为AB的中点,B 到D的距离比CD的长小0.5米,∠BCD=60°(1)若CD=x,BC=y,将支架的总长度表示为y的函数,并写出函数的定义域.(注:支架的总长度为图中线段AB、BD和CD长度之和)(2)如何设计AB,CD的长,可使支架总长度最短.第8题 Abc13【考点】解三角形的实际应用.【解】(1)由CD=x,则BD=x-0.5,BC=y,则支架的总长度为AC+BC+BD+CD,在△BCD中,由余弦定理+-2xy cos60°=,化简得-xy+x-0.25=0,即x= ①记l=y+y+x-0.5+x=2y+2x-0.5=-0.5(y≥1.5).(2)由题中条件得2y≥3,即y≥1.5,设y-1=t(t≥0.5)则原式l=4t++5.5∵t≥0.5,∴由基本不等式4t+当且仅当4t=,即t=时成立,∴y=+1,∴x=,∴当AB=,CD=时,金属支架总长度最短.9.(15无锡市高三上学期期中试卷)如图,ABC为一直角三角形草坪,其中∠C=90°,BC=2米,AB=4米,为了重建草坪,设计师准备了两套方案:方案一RNN-01 方案二RNN-02第9题图方案一:扩大为一个直角三角形,其中斜边DE过点B,且与AC平行,DF过点A,EF过点C;方案二:扩大为一个等边三角形,其中DE过点B,DF过点A,EF过点C.(1)求方案一中三角形DEF面积的最小值;(2)求方案二中三角形DEF面积的最大值.【考点】基本不等式在最值问题中的应用.【答案】(1)在方案一:在三角形AFC中,设∠ACF=α,α∈,则,…(2分)因为DE∥AC,所以∠E=α,,且,即,…(4分)°解得,…(6分)所以,所以当=1,即=45°时,有最小值.(2)在方案二:在三角形DBA中,设∠DBA=,∈,则,解得,三角形CBE中,有,解得,…则等边三角形的边长为,…(14分)所以边长的最大值为,所以面积的最大值为.…(16分)10.(15南京一中等五校联考)如图,某广场为一半径为80米的半圆形区域,现准备在其一扇形区域OAB内建两个圆形花坛,该扇形的圆心角为变量2(0<2<π),其中半径较大的花坛⊙P内切于该扇形,半径较小的花坛⊙Q与⊙P外切,且与OA、OB相切.(1)求⊙P的半径(用表示);(2)求⊙Q的半径的最大值.第10题图 RNN-12【考点】三角函数的最值;三角函数中的恒等变换应用.【解】(1)设⊙P切OA于M,连PM,⊙Q切OA于N,连QN,记⊙P、⊙Q的半径分别为、.∵⊙P与⊙O内切,∴|OP|=80,∴,∴.(2)∵∴,∴令t=1+sin∈(1,2),∴=,令m=∈(,1),=80(),∴m=时,有最大值10.第10题图 RNN-0711.如图,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A 地侦察发现,在南偏东方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民.此时,C地位于中国海监船的南偏东方向的10海里处,中国海监船以每小时30海里的距离赶往C地救援我国渔民,能不能及时赶到?(≈1.41,≈1.73,≈2.45)第17题图 FGQ79【解】 如图,过点A作AD⊥BC,交BC的延长线于点D.因为∠CAD=,AC=10海里,所以△ACD是等腰直角三角形.所以AD=CD=AC=×10= (海里).在中,因为∠DAB=,所以BD=AD×tan= (海里).所以BC=BD-CD=(-)海里.因为中国海监船以每小时30海里的速度航行,某国军舰正以每小时13海里的速度航行,所以中国海监船到达C点所用的时间(小时),某国军舰到达C点所用的时间 (小时).因为,所以中国海监船能及时赶到.。
江苏省南通市通州区2025届高三上学期第一次质量监测数学试卷(含答案)

江苏省南通市通州区2025届高三上学期第一次质量监测数学试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A ={1,3,5,7},B ={x|−x 2+4x ≥0},则A ∩B =( )A. [1,3]B. [5,7]C. {1,3}D. {5,7}2.设函数f(x)={log 2 (2−x),x <1,2x−1,x⩾1,则f(−2)+f(log 210)=( )A. 4B. 5C. 6D. 73.“ln x >ln y ”是“ x >y ”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.当阳光射入海水后,海水中的光照强度随着深度增加而减弱,可用I D =I 0e −KD 表示其总衰减规律,其中K 是消光系数,D(单位:米)是海水深度,I D (单位:坎德拉)和I 0(单位:坎德拉)分别表示在深度D 处和海面的光强.已知某海域5米深处的光强是海面光强的40%,则该海域消光系数K 的值约为( ) (参考数据:ln 2≈0.7,ln5≈1.6)A. 0.2B. 0.18C. 0.1D. 0.145.函数y =f(x)的图象如图1所示,则如图2所示的函数图象所对应的函数解析式可能为( )A. y =f(1−12x)B. y =−f(1−12x)C. y =f(4−2x)D. y =−f(4−2x)6.今年暑期档,全国各大院线推出多部精彩影片,其中比较热门的有《异形:夺命舰》,《名侦探柯南》,《抓娃娃》,《逆行人生》,《姥姥的外孙》这5部,小明和小华两位同学准备从这5部影片中各选2部观看,若两人所选的影片至多有一部相同,且小明一定选看《名侦探柯南》,则两位同学不同的观影方案种数为( )A. 12B. 24C. 28D. 367.已知x >0,y >0,x +y =1,则12x +xy +1的最小值为( )A. 54B. 43C. 1D.228.若函数f(x)=e 2x4−axe x 有两个极值点,则实数a 的取值范围是( )A. (−∞,−12)B. (−12,0)C. (12,+∞)D. (0,12)二、多选题:本题共3小题,共15分。
2024年江苏省南通市部分学校中考数学一模试卷及答案解析

2024年江苏省南通市部分学校中考数学一模试卷一、选择题(本大题共10小题,每小题3分,共30分.)1.(3分)下列结果中,是负数的是()A.﹣(﹣2)B.﹣|﹣1|C.3×2D.0×(﹣4)2.(3分)风能是一种清洁能源,我国风能储量很大,仅陆地上风能储量就有253000兆瓦,将数据253000用科学记数法表示为()A.25.3×104B.2.53×104C.2.53×105D.0.253×106 3.(3分)如图是由四个小正方体叠成的一个立体图形,那么它的主视图是()A.B.C.D.4.(3分)下列各图中,可看作轴对称图形的是()A.B.C.D.5.(3分)如图,四边形ABCD的对角线AC,BD相交于点O,OA=OC,且AB∥CD,则添加下列一个条件能判定四边形ABCD是菱形的是()A.AC=BD B.∠ADB=∠CDB C.∠ABC=∠DCB D.AD=BC6.(3分)如图,直线l1∥l2,含有30°的直角三角板的一个顶点C落在l2上,直角边交l1于点D,连接BD,使得BD⊥l2,若∠1=72°,则∠2的度数是()A.48°B.58°C.42°D.18°7.(3分)我国古代数学名著《九章算术》中记载:“粟米之法:粟率五十;粝米三十.今有米在十斗桶中,不知其数.满中添粟而舂之,得米七斗.问故米几何?”意思为:50斗谷子能出30斗米,即出米率为.今有米在容量为10斗的桶中,但不知道数量是多少.再向桶中加满谷子,再舂成米,共得米7斗.问原来有米多少斗?如果设原来有米x 斗,向桶中加谷子y斗,那么可列方程组为()A.B.C.D.8.(3分)若关于x的不等式组有且只有3个整数解,则a的取值范围是()A.﹣1≤a<0B.﹣1<a≤0C.﹣4<a≤﹣3D.﹣4≤a<﹣3 9.(3分)如图,四边形ABCD是边长为2cm的正方形,点E,点F分别为边AD,CD中点,点O为正方形的中心,连接OE,OF,点P从点E出发沿E﹣O﹣F运动,同时点Q 从点B出发沿BC运动,两点运动速度均为1cm/s,当点P运动到点F时,两点同时停止运动,设运动时间为t s,连接BP,PQ,△BPQ的面积为S cm2,下列图象能正确反映出S与t的函数关系的是()A.B.C.D.10.(3分)已知实数a,b满足4a2+b=n,b2+2a=n,b≠2a.其中n为自然数,则n的最小值是()A.4B.5C.6D.7二、填空题(本大题共8小题,第11~12题每小题3分,第13~18题每小题3分,共30分.)11.(3分)代数式在实数范围内有意义,则x的取值范围是.12.(3分)因式分解:2x﹣8x3=.13.(4分)底面圆半径为10cm、高为的圆锥的侧面展开图的面积为cm2.14.(4分)某种型号的小型无人机着陆后滑行的距离S(米)关于滑行的时间t(秒)的函数解析式是S=﹣0.25t2+10t,无人机着陆后滑行秒才能停下来.15.(4分)如图,社小山的东侧炼A处有一个热气球,由于受西风的影响,以30m/min的速度沿与地面成75°角的方向飞行,20min后到达点C处,此时热气球上的人测得小山西侧点B处的俯角为30°,则小山东西两侧A,B两点间的距离为.16.(4分)如图,在矩形ABCD中,AB=3,BC=10,点E在边BC上,DF⊥AE,垂足为F.若DF=6,则线段EF的长为.17.(4分)若a,b是一元二次方程x2﹣5x﹣2=0的两个实数根,则的值为.18.(4分)如图,点A,B在反比例函数y=(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是.三、解答题(本大题共8小题,共90分.解答时应写出文字说明、证明过程或演算步骤)19.(10分)(1)计算:;(2)先化简,再求值:,其中x=3.20.(8分)如图,已知A,D,C,E在同一直线上,BC和DF相交于点O,AD=CE,AB ∥DF,AB=DF.(1)求证:△ABC≌△DFE;(2)连接CF,若∠BCF=54°,∠DFC=20°,求∠DFE的度数.21.(10分)某市今年初中物理、化学实验技能学业水平考查,采用学生抽签方式决定各自的考查内容.规定:每位考生必须在4个物理实验考查内容(用A、B、C、D表示)和4个化学实验考查内容(用E、F、G、H表示)中各抽取一个进行实验技能考查.小刚在看不到签的情况下,从中各随机抽取一个.(1)小刚抽到物理实验A的概率是;(2)用列表法或画树状图法中的一种方法,求小刚抽到物理实验B和化学实验F的概率.22.(10分)青年大学习是共青团中央为组织引导广大青年深入学习宣传贯彻习近平新时代中国特色社会主义思想和党的十九大精神持续引向深人组织的青年学习行动.某校举办了相关知识竞赛(百分制),并分别在七、八年级中各随机抽取20名学生的成绩进行统计、整理与分析,绘制成如图两幅统计图.成绩用x表示,并且分为A、B、C、D、E五个等级,并且分别是:A:50≤x<60;B:60≤x<70;C:70≤x<80;D:80≤x<90;E:90≤x≤100.七、八年级成绩的平均数、中位数众数如下表:平均数中位数众数七年级76m75八年级777678其中,七年级成绩在C等级的数据为77、75、75、78、79、75、73、75;八年级成绩在E等级的有3人.根据以上信息,解答下列问题:(1)扇形统计图中B等级所占圆心角的度数是,表中m的值为;(2)通过以上数据分析,你认为哪个年级对青年大学习知识掌握得更好?请说明理由;(3)请对该校学生“青年大学习”的掌握情况作出合理的评价.23.(12分)如图,AB是⊙O的直径,点C在⊙O上,∠ABC=60°,⊙O的切线CD与AB的延长线相交于点D.(1)求证:BD=BC;(2)若⊙O的半径为6,求图中阴影部分的面积.24.(13分)随着“双减”政策的逐步落实,其中增加中学生体育锻炼时间的政策引发社会的广泛关注,体育用品需求增加,某商店决定购进A、B两种羽毛球拍进行销售,已知每副A种球拍的进价比每副B种球拍贵20元,用2800元购进A种球拍的数量与用2000元购进B种球拍的数量相同.(1)求A、B两种羽毛球拍每副的进价;(2)若该商店决定购进这两种羽毛球拍共100副,考虑市场需求和资金周转,用于购买这100副羽毛球拍的资金不超过5900元,那么该商店最多可购进A种羽毛球拍多少副?(3)若销售A种羽毛球拍每副可获利润25元,B种羽毛球拍每副可获利润20元,在第(2)问条件下,如何进货获利最大?最大利润是多少元?25.(13分)如图1,P是正方形ABCD边BC上一点,线段AE与AD关于直线AP对称,连接EB并延长交直线AP于点F,连接CF.(1)补全图形,求∠AFE的大小;(2)用等式表示线段CF,BE之间的数量关系,并证明;(3)连接CE,G是CE的中点,AB=2,若点P从点B运动到点C,直接写出DG的最大值.26.(14分)定义:若一个函数的图象上存在横、纵坐标之和为零的点,则称该点为这个函数图象的“平衡点”.例如,点(﹣1,1)是函数y=x+2的图象的“平衡点”.(1)在函数①y=﹣x+3,②y=,③y=﹣x2+2x+1,④y=x2+x+7的图象上,存在“平衡点”的函数是;(填序号)(2)设函数y=﹣(x>0)与y=2x+b的图象的“平衡点”分别为点A、B,过点A作AC⊥y轴,垂足为C.当△ABC为等腰三角形时,求b的值;(3)若将函数y=x2+2x的图象绕y轴上一点M旋转180°,M在(0,﹣1)下方,旋转后的图象上恰有1个“平衡点”时,求M的坐标.2024年江苏省南通市部分学校中考数学一模试卷参考答案与试题解析一、选择题(本大题共10小题,每小题3分,共30分.)1.【分析】利用相反数的意义及绝对值的性质化简A、B,再利用乘法法则计算即可得到C、D.【解答】解:∵A、﹣(﹣2)=2,∴A项不符合题意;∵B、﹣|﹣1|=﹣1,∴B项符合题意;∵C、3×2=6,∴C项不符合题意;∵D、0×(﹣4)=0,∴D项不符合题意.故选:B.【点评】本题考查了相反数的意义,绝对值的性质,有理数的乘法法则,掌握绝对值的性质是解题的关键.2.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:253000=2.53×105.故选:C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【解答】解:从正面看易得第一层有3个正方形,第二层中间有1个正方形.故选:C.【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.4.【分析】根据轴对称图形的概念进行判断即可.【解答】解:A、不是轴对称图形,不符合题意;B、是轴对称图形,符合题意;C、不是轴对称图形,不符合题意;D、不是轴对称图形,不符合题意;故选:B.【点评】本题考查了轴对称图形,解题关键是抓住轴对称图形是指将一个图形沿着某条直线折叠,直线两旁的部分能够完全重合.5.【分析】根据菱形的判定方法分别对各个选项进行判定,即可得出结论.【解答】解:∵AB∥CD,∴∠BAO=∠DCO,∠ABO=∠CDO,∵OA=OC,∴△AOB≌△COD(AAS),∴AB=CD,∴四边形ABCD是平行四边形,A、当AC=BD时,四边形ABCD是矩形;故选项A不符合题意;B、∵AB∥CD,∴∠ABD=∠CDB,∵∠ADB=∠CDB,∴∠ADB=∠ABD,∴AD=AB,∴四边形ABCD为菱形,故选项B符合题意;C、∵AB∥CD,∴∠ABC+∠BCD=180°,∵∠ABC=∠DCB∴∠ABC=∠DCB=90°,∴四边形ABCD是矩形;故选项C不符合题意;D、当AD=BC时,不能判定四边形ABCD为菱形;故选项D不符合题意.故选:B.【点评】本题考查了菱形的判定,平行四边形的判定和性质,等腰三角形的判定和性质,熟练掌握菱形的判定定理是解题的关键.6.【分析】根据平行的性质可得∠DEB=∠1=72°,根据三角形的外角的定义可得∠ADC=42°,再根据平角进行计算即可得到答案.【解答】解:如图,设AB与l1相交于点E,∵l1∥l2,∠1=72°,∴∠DEB=∠1=72°,∵∠A+∠ADC=∠DEB=72°,∠A=30°,∴∠ADE=42°,∵∠ADC+∠BDE+∠2=180°,BD⊥l2,∴∠2=48°.故选:A.【点评】本题主要考查了平行线的性质、三角形外角的定义,平角的定义,熟练掌握平行线的性质、三角形外角的定义,平角的定义是解题的关键.7.【分析】根据原来的米+向桶中加的谷子=10,原来的米+桶中的谷子舂成米=7即可得出答案.【解答】解:根据题意得:,故选:A.【点评】本题考查了由实际问题抽象出二元一次方程组,找到等量关系:原来的米+向桶中加的谷子=10,原来的米+桶中的谷子舂成米=7是解题的关键.8.【分析】先解出每个不等式的解集,即可得到不等式组的解集,然后根据不等式组有且只有3个整数解,即可得到a的取值范围.【解答】解:,解不等式①,得:x≤2,解不等式②,得:x>a,∴该不等式组的解集是a<x≤2,∵关于x的不等式组有且只有3个整数解,∴这三个整数解是0,1,2,∴﹣1≤a<0,故选:A.【点评】本题考查一元一次不等式组的整数解,解答本题的关键是明确解一元一次不等式的方法.9.【分析】当0<t≤1时,点P在OE上,当1<t≤2时,点P在OF上,分别求出S与t 的函数关系,即可解答.【解答】解:如图,当0<t≤1时,由题得,PE=BQ=t cm,∵正方向ABCD是边长为2cm,∴P到BC的距离为(2﹣t)cm,∴S=t•(2﹣t)=﹣t2+t,如图,当1<t≤2时,由题得,PF=CQ=(2﹣t)cm,∴四边形CFPQ为矩形,∴PQ=CF=1cm,∴S=t•1=t,故选:D.【点评】本题考查了动点问题的函数图象应用,三角形面积的计算是解题关键.10.【分析】由原式知,(4a2+b)﹣(b2+2a)=0,进一步变形得(2a﹣b)(2a+b﹣)=0,因为b≠2a,所以2a+b﹣=0,得b=﹣2a,代入b2+2a=n得,(﹣2a)+2a=n,配方法求极值.【解答】解:由原式知,(4a2+b)﹣(b2+2a)=0,∴(4a2﹣b2)﹣(2a﹣b)=0∴(2a﹣b)(2a+b)﹣(2a﹣b)=0∴(2a﹣b)(2a+b﹣)=0∵b≠2a∴2a+b﹣=0,∴b=﹣2a,代入b2+2a=n得,(﹣2a)2+2a=n,整理,得n=4a2﹣2a+7=(2a﹣)2+5≥5,∴自然数n的最小值为6故选C.【点评】本题考查等式的基本性质,平方差公式、完全平方公式、配方法求极值;根据式子的具体特征,结合乘法公式对代数式作恒等变形是解题的关键.二、填空题(本大题共8小题,第11~12题每小题3分,第13~18题每小题3分,共30分.)11.【分析】根据二次根式有意义的条件列出不等式,解不等式得到答案.【解答】解:由题意得,x﹣5≥0,解得x≥5,故答案为:x≥5.【点评】本题考查的是二次根式有意义的条件,掌握二次根式的被开方数是非负数是解题的关键.12.【分析】先提公因式,再利用平方差公式继续分解即可解答.【解答】解:2x﹣8x3=2x(1﹣4x2)=2x(1+2x)(1﹣2x),故答案为:2x(1+2x)(1﹣2x).【点评】本题考查了提公因式法与公式法的综合运用,一定要注意如果多项式的各项含有公因式,必须先提公因式.13.【分析】先求出圆锥的母线长,再根据扇形的面积公式计算即可.【解答】解:∵圆锥的底面半径为10cm,高为10cm,∴圆锥的母线为=20(cm),∴圆锥的侧面展开图的面积为×(2π×10)×20=200π(cm2).故答案为:200π.【点评】本题考查圆锥的计算,解题的关键是求出圆锥的母线和掌握圆锥的侧面展开图的面积公式.14.【分析】飞机停下时,也就是滑行距离最远时,即在本题中需求出s最大时对应的t值.【解答】解:由题意得,S=﹣0.25t2+10t=﹣0.25(t2﹣40t+400﹣400)=﹣0.25(t﹣20)2+100,∵﹣0.25<0,∴t=20时,飞机滑行的距离最大,即当t=20秒时,飞机才能停下来.故答案为:20.【点评】本题考查了二次函数的应用,能熟练的应用配方法得到顶点式是解题关键.15.【分析】作AD⊥BC于D,根据速度和时间先求得AC的长,在Rt△ACD中,求得∠ACD 的度数,再求得AD的长度,然后根据∠B=30°求出AB的长.【解答】解:如图,过点A作AD⊥BC,垂足为D,在Rt△ACD中,∠ACD=75°﹣30°=45°,AC=30×20=600(米),∴AD=AC•sin45°=300(米).在Rt△ABD中,∵∠B=30°,∴AB=2AD=600(米).故答案为:600.【点评】本题考查了解直角三角形的应用,解答本题的关键是根据仰角和俯角构造直角三角形并解直角三角形,难度适中.16.【分析】证明△AFD∽△EBA,得到,求出AF,即可求出AE,从而可得EF.【解答】解:∵四边形ABCD为矩形,∴AB=CD=3,BC=AD=10,AD∥BC,∴∠AEB=∠DAF,∴△AFD∽△EBA,∴,∵DF=6,∴AF===8,∴,∴AE=5,∴EF=AF﹣AE=8﹣5=3,故答案为:3.【点评】本题考查了相似三角形的判定和性质,矩形的性质,勾股定理,解题的关键是掌握相似三角形的判定方法.17.【分析】先根据一元二次方程的解的定义及根与系数的关系得出a +b =5,a 2=5a +2,再将其代入整理后的代数式计算即可.【解答】解:∵a ,b 是一元二次方程x 2﹣5x ﹣2=0的两个实数根,∴a +b =5,a 2﹣5a ﹣2=0,即:a 2=5a +2,∴,故答案为:5.【点评】本题考查了根与系数的关系:若x 1,x 2是一元二次方程ax 2+bx +c =0(a ≠0)的两根时,,x 1•x 2=.也考查了一元二次方程的解.18.【分析】过点B 作直线AC 的垂线交直线AC 于点F ,由△BCE 的面积是△ADE 的面积的2倍以及E 是AB 的中点即可得出S △ABC =2S △ABD ,结合CD =k 即可得出点A 、B 的坐标,再根据AB =2AC 、AF =AC +BD 即可求出AB 、AF 的长度,根据勾股定理即可算出k 的值,此题得解.【解答】解:过点B 作直线AC 的垂线交直线AC 于点F ,如图所示.∵△BCE 的面积是△ADE 的面积的2倍,E 是AB 的中点,∴S △ABC =2S △BCE ,S △ABD =2S △ADE ,∴S △ABC =2S △ABD ,且△ABC 和△ABD 的高均为BF ,∴AC =2BD ,又∵OC •AC =OD •BD ,∴OD =2OC .∵CD =k ,∴点A 的坐标为(,3),点B 的坐标为(﹣,﹣),∴AC =3,BD =,∴AB =2AC =6,AF =AC +BD =,∴CD =k ===.故答案为:.【点评】本题考查了反比例函数图象上点的坐标特征、三角形的面积公式以及勾股定理,构造直角三角形利用勾股定理巧妙得出k值是解题的关键.三、解答题(本大题共8小题,共90分.解答时应写出文字说明、证明过程或演算步骤)19.【分析】(1)先化简,然后算加减法即可;(2)先算括号内的式子,再算括号外的除法,然后将x的值代入化简后的式子计算即可.【解答】解:(1)=3+﹣1﹣=+;(2)=•===,当x=3时,原式==﹣5.【点评】本题考查实数的运算、分式的化简求值,熟练掌握运算法则是解答本题的关键.20.【分析】(1)由平行线的性质得∠A=∠FDE,根据等式的性质可得AC=DE,再由SAS 证明△ABC≌△DFE即可;(2)先根据三角形的外角可得∠DOC=74°,由平行线的性质可得∠B=∠DOC,最后由全等三角形的性质可得结论.【解答】(1)证明:∵AB∥DF,∴∠A=∠EDF,∵AD=CE,∴AD+CD=CE+CD,即AC=DE,在△ABC和△DFE中,,∴△ABC≌△DFE(SAS);(2)解:∵∠BCF=54°,∠DFC=20°,∴∠DOC=∠BCF+∠DFC=54°+20°=74°,∵AB∥DF,∴∠B=∠DOC=74°,∵△ABC≌△DFE,∴∠DFE=∠B=74°.【点评】本题考查了全等三角形的判定与性质,平行线的性质,证明三角形全等是解题的关键.21.【分析】(1)直接利用概率公式计算;(2)画树状图展示所有16种等可能的结果,再找出抽到B和F的结果数,然后根据概率公式计算.【解答】解:(1)小刚抽到物理实验A的概率是;故答案为:;(2)画树状图为:共有16种等可能的结果,其中抽到B和F的结果数为1,所以小刚抽到物理实验B和化学实验F的概率=.【点评】本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或事件B的概率.22.【分析】(1)求出调查人数以及B等级的学生人数所占的百分比即可求出相应的圆心角度数,根据中位数的定义求出中位数即可得出m的值;(2)通过平均数、中位数、众数的大小比较得出答案;(3)根据平均数、中位数、众数综合进行判断即可.【解答】解:(1)由条形统计图可得,调查人数为2+5+8+2+3=20(人),扇形统计图中B等级所占圆心角的度数是360=90°,将七年级这20名学生的成绩从小到大排列,处在中间位置的两个数的平均数为=75,因此中位数是75分,即m=75,故答案为:90°,75;(2)八年级学生的成绩较好,理由:八年级学生成绩的平均数、中位数、众数均比七年级学生的平均数、中位数、众数大,所以八年级学生成绩较好;(3)青年学生对深入学习宣传贯彻习近平新时代中国特色社会主义思想和党的十九大精神掌握情况一般,还需要进一步加强学习和宣传.【点评】本题考查条形统计图、扇形统计图,平均数、中位数、众数,理解两个统计图中数量之间的关系以及中位数、众数、平均数的意义是正确解答的前提.23.【分析】(1)连接OC,可证明△BOC是等边三角形,则∠BOC=∠BCO=60°,由CD 与⊙O相切于点C,得∠OCD=90°,即可求得∠D=90°﹣∠BOC=30°,∠BCD=90°﹣∠BCO=30°,所以∠BCD=∠D,则BD=BC;(2)作CE⊥OB于点E,则CE=OC•sin60°=3,可求得S阴影=S扇形BOC﹣S△BOC=6π﹣9.【解答】(1)证明:连接OC,则OC=OB,∵∠ABC=60°,∴△BOC是等边三角形,∴∠BOC=∠BCO=60°,∵CD与⊙O相切于点C,∴CD⊥OC,∴∠OCD=90°,∴∠D=90°﹣∠BOC=30°,∠BCD=90°﹣∠BCO=30°,∴∠BCD=∠D,∴BD=BC.(2)解:作CE⊥OB于点E,则∠OEC=90°,∵OC=OB=6,∴CE=OC•sin60°=6×=3,∴S阴影=S扇形BOC﹣S△BOC=﹣×6×3=6π﹣9,∴阴影部分的面积是6π﹣9.【点评】此题重点考查切线的性质、等边三角形的判定与性质、等腰三角形的判定、锐角三角函数与解直角三角形、三角形的面积公式、扇形的面积公式等知识,正确地作出所需要的辅助线是解题的关键.24.【分析】(1)设A种羽毛球拍每副的进价为x元,根据用2800元购进A种球拍的数量与用2000元购进B种球拍的数量相同,列分式方程,求解即可;(2)设该商店购进A种羽毛球拍m副,根据购买这100副羽毛球拍的资金不超过5900元,列一元一次不等式,求解即可;(3)设总利润为w元,表示出w与m的函数关系式,根据一次函数的性质即可确定如何进货总利润最大,并进一步求出最大利润即可.【解答】解:(1)设A种羽毛球拍每副的进价为x元,根据题意,得,解得x=70,经检验,x=70是原分式方程的根,且符合题意,70﹣20=50(元),答:A种羽毛球拍每副的进价为70元,B种羽毛球拍每副的进价为50元;(2)设该商店购进A种羽毛球拍m副,根据题意,得70m+50(100﹣m)≤5900,解得m≤45,m为正整数,答:该商店最多购进A种羽毛球拍45副;(3)设总利润为w元,w=25m+20(100﹣m)=5m+2000,∵5>0,∴w随着m的增大而增大,当m=45时,w取得最大值,最大利润为5×45+2000=2225(元),此时购进A种羽毛球拍45副,B种羽毛球拍100﹣45=55(副),答:购进A种羽毛球拍45副,B种羽毛球拍55副时,总获利最大,最大利润为2225元.【点评】本题考查了分式方程的应用,一元一次不等式的应用,一次函数的应用,理解题意并根据题意建立相应的关系式是解题的关键.25.【分析】(1)由轴对称的性质可得∠DAP=∠EAP=70°,AD=AE,由等腰三角形的性质和三角形内角和定理可求解;(2)先求出∠AFE=45°,通过证明△CDF∽△BDE,可得BE=CF;(3)先确定点G在以O为圆心,1为半径的圆上运动,再根据等腰直角三角形的性质求解即可.【解答】解:(1)补全图形如图1所示;设∠BAP=x,∴∠DAP=90°﹣x,∵线段AE与AD关于直线AP对称,∴∠DAP=∠EAP=90°﹣x,AD=AE,∴∠BAE=90°﹣2x,AB=AE,∴∠E=∠ABE=45°+x,∴∠AFE=180°﹣(90°﹣x)﹣(45°+x)=45°;(2)BE=CF;证明:如图2,连接DF,DE,BD,∵四边形ABCD是正方形,∴BD=CD,∠CDB=45°,∵线段AE与AD关于直线AP对称,∴DF=EF,∠DFA=∠AFE=45°,∴∠DFE=90°,∴∠FDE=45°=∠CDB,DE=DF,∴∠CDF=∠BDE,,∴△CDF∽△BDE,∴,∴BE=CF;(3)如图3,连接AC,BD交于点O,连接OG,∵四边形ABCD是正方形,∴AO=CO,又∵G是CE中点,∴OG=AE=AD=1,∴点G在以O为圆心,1为半径的圆上运动,∴点P从点B运动到点C,点G的运动到BD上时DG的值最大,且DG的最大值为DO+OG,∵OD=AD=,∴DG的最大值为1.【点评】本题是四边形综合题,考查了正方形的性质,轴对称的性质,相似三角形的判断和性质,三角形中位线定理等知识,灵活运用这些性质解决问题是本题的关键.26.【分析】(1)在y=﹣x+3中,令y=﹣x得﹣x=﹣x+3,方程无解,可知y=﹣x+3的图象上不存在“平衡点”;同理可得y=,y=x2+x+7的图象上不存在“平衡点”,y=﹣x2+2x+1的图象上存在“平衡点”;(2)在y=﹣中,令y=﹣x得A(2,﹣2)或(﹣2,2);在y=2x+b中,令y=﹣x 得B(﹣,),当A(2,﹣2)时,C(0,﹣2),可得AB2=2(2+)2,BC2=+(2+)2,AC2=4,分三种情况列方程可得答案;(3)设M(0,m),m<﹣1,求出抛物线y=x2+2x的顶点为(﹣1,﹣1),而点(﹣1,﹣1)关于M(0,m)的对称点为(1,2m+1),可得旋转后的抛物线解析式为y=﹣(x ﹣1)2+2m+1=﹣x2+2x+2m,令y=﹣x得x2﹣3x﹣2m=0,根据旋转后的图象上恰有1个“平衡点”,知x2﹣3x﹣2m=0有两个相等实数根,故9+8m=0,m=﹣,从而得M的坐标为(0,﹣).【解答】解:(1)根据“平衡点”的定义,“平衡点”的横、纵坐标互为相反数,在y=﹣x+3中,令y=﹣x得﹣x=﹣x+3,方程无解,∴y=﹣x+3的图象上不存在“平衡点”;同理可得y=,y=x2+x+7的图象上不存在“平衡点”,y=﹣x2+2x+1的图象上存在“平衡点”;故答案为:③;(2)在y=﹣中,令y=﹣x得﹣x=﹣,解得x=2或x=﹣2,∵x>0,∴A(2,﹣2);在y=2x+b中,令y=﹣x得﹣x=2x+b,解得x=﹣,∴B(﹣,),当A(2,﹣2)时,C(0,﹣2),∴AB2=2(2+)2,BC2=+(2+)2,AC2=4,若AB=BC,则2(2+)2=+(2+)2,解得b=﹣3;若AB=AC,则2(2+)2=4,解得b=﹣3﹣6或b=3﹣6;若BC=AC,则+(2+)2=4,解得b=0或b=﹣6(此时A,B重合,舍去);∴b的值为﹣3或﹣3﹣6或3﹣6或0;(3)设M(0,m),m<﹣1,∵y=x2+2x=(x+1)2﹣1,∴抛物线y=x2+2x的顶点为(﹣1,﹣1),点(﹣1,﹣1)关于M(0,m)的对称点为(1,2m+1),∴旋转后的抛物线解析式为y=﹣(x﹣1)2+2m+1=﹣x2+2x+2m,在y=﹣x2+2x+2m中,令y=﹣x得:﹣x=﹣x2+2x+2m,∴x2﹣3x﹣2m=0,∵旋转后的图象上恰有1个“平衡点”,∴x2﹣3x﹣2m=0有两个相等实数根,∴Δ=0,即9+8m=0,∴m=﹣,∴M的坐标为(0,﹣).【点评】本题考查二次函数的综合应用,涉及新定义,等腰三角形,一元二次方程根的判别式,旋转变换等知识,解题的关键是读懂新定义,利用二次函数与一元二次方程的关系解决问题。
高三数学一轮复习备考试题:函数(含答案解析)

江苏省2015年高考一轮复习备考试题函数一、填空题1、(2014年江苏高考)已知函数1)(2-+=mx x x f ,若对于任意]1,[+∈m m x ,都有0)(<x f 成立,则实数m 的取值范围是 ▲ .2、(2014年江苏高考)已知)(f x 是定义在R 上且周期为3的函数,当)3,0[x 时,|212|)(2+-=x x x f a x f -=)(y 在区间]4,3[-上有10个零点(互不相同),则实数a 的取值范围是 ▲ . 3、(2013年江苏高考)已知)(x f 是定义在R 上的奇函数。
当0>x 时,x x x f 4)(2-=,则不等式x x f >)(的解集用区间表示为 。
4、(2012年江苏高考)函数x x f 6log 21)(-=的定义域为 ▲ .5、(2012年江苏省高考)设()f x 是定义在R 上且周期为2的函数,在区间[11]-,上,0111()201x x ax f x bx x <+-⎧⎪=+⎨⎪+⎩≤≤≤,,,,其中a b ∈R ,.若1322f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,则3a b +的值为 ▲ . 6、(2012年江苏省5分)已知函数2()()f x x ax b a b =++∈R ,的值域为[0)+∞,,若关于x 的不等式()f x c <的解集为(6)m m +,,则实数c 的值为 ▲ .7、(2015届江苏南京高三9月调研)设f (x )=x 2-3x +a .若函数f (x )在区间(1,3)内有零点,则实数a 的取值范围为 ▲8、(2015届江苏南通市直中学高三9月调研)已知函数23 1 ()x a x f x x a x ⎧+>⎪=⎨+⎪⎩≤,,,1,若()f x 在R 上为增函数,则实数a 的取值范围是 ▲9、(2015届江苏苏州高三9月调研)已知函数()2log 1a x f x x-=+为奇函数,则实数a 的值为 ▲ 10、(南京市2014届高三第三次模拟)已知函数f (x )=⎩⎨⎧x ,x ≥0,x 2,x <0, ,则关于x 的不等式f (x 2)>f (3-2x )的解集是 ▲11、(南通市2014届高三第三次调研)已知函数()f x 对任意的x ∈R 满足()()f x f x -=,且当0x ≥时,2()1f x x ax =-+.若()f x 有4个零点,则实数a 的取值范围是 ▲ .112、(苏锡常镇四市2014届高三5月调研(二))函数y =A ,函数()lg 2y x =-的定义域为B ,则A I B = ▲13、(苏锡常镇四市2014届高三5月调研(二))已知奇函数()f x 是R 上的单调函数,若函数2()()y f x f k x =+-只有一个零点,则实数k 的值是 ▲ .14、(徐州市2014届高三第三次模拟)已知函数()f x 是定义在R 上的奇函数,且当0x ≤时,2()3f x x x =--,则不等式(1)4f x x ->-+的解集是 ▲15、(徐州市2014届高三第三次模拟)已知函数1()()e x af x a x=-∈R .若存在实数m ,n , 使得()0f x ≥的解集恰为[],m n ,则a 的取值范围是 ▲16、(南京、盐城市2014届高三第二次模拟(淮安三模))函数f (x )=ln x +1-x 的定义域为 ▲ 17、(南京、盐城市2014届高三第二次模拟(淮安三模))已知f (x )是定义在R 上的奇函数,当0≤x≤1时,f (x )=x 2,当x >0时,f (x +1)=f (x )+f (1).若直线y =kx 与函数y =f (x )的图象恰有5个不同的公共点,则实数k 的值为 ▲ 18、(2014江苏百校联考一)函数1()2sin(),[2,4]1f x x x xπ=-∈--的所有零点之和为 .19、(南京、盐城市2014高三第一次模拟)若函数()f x 是定义在R 上的偶函数,且在区间[0.)+∞上是单调增函数.如果实数t 满足1(ln )(ln )2(1)f t f f t+<时,那么t 的取值范围是 20、(苏锡常镇四市2014届高三3月调研(一))已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+,若函数()g x 恰有两个不同的零点,则实数k 的取值范围为 ▲ 21、(南通市2014届高三上学期期末考试)设函数()y f x =是定义域为R ,周期为2的周期函数,且当[)11x ∈-,时,2()1f x x =-;已知函数lg ||0()10x x g x x ≠⎧⎪=⎨=⎪⎩,,,. 则函数()f x 和()g x 的图象在区间[]510-,内公共点的个数为 . 22、(苏州市2014届高三1月第一次调研)已知22(0),()(0)x x x f x x x x ⎧+⎪=⎨-+<⎪⎩≥,则不等式2(1)12f x x -+<的解集是 ▲23、(泰州市2014届高三上学期期末考试)设函数()()f x x a x a b =--+(,a b 都是实数).则下列叙述中,正确的序号是 ▲ .(请把所有叙述正确的序号都填上) ①对任意实数,a b ,函数()y f x =在R 上是单调函数; ②存在实数,a b ,函数()y f x =在R 上不是单调函数; ③对任意实数,a b ,函数()y f x =的图像都是中心对称图形; ④存在实数,a b ,使得函数()y f x =的图像不是中心对称图形. 24、(江苏省扬州中学2014届高三上学期12月月考)设12()1f x x=+,11()[()]n n f x f f x +=,且(0)1(0)2n n n f a f -=+,则2014a = ▲25、、(江苏省诚贤中学2014届高三12月月考)在用二分法...求方程3210x x --=的一个近似解时,现在已经将一根锁定在区间(1,2),则下一步可断定该根所在的区间为 ▲ . 26、(江苏省东海县第二中学2014届高三第三次学情调研)已知函数ln (),()xf x kxg x x==,如果关于x 的方程()()f x g x =在区间1[,]e e内有两个实数解,那么实数k 的取值范围是 ▲ .27、(江苏省阜宁中学2014届高三第三次调研)已知函数()()2log ,12,01x x f x f x x ⎧⎪=⎨<<⎪⎩≥,则()3212f ⎡⎤⎢⎥⎢⎥⎣⎦= ▲28、(无锡市2014届高三上学期期中)定义在R 上的奇函数()f x ,当0x ≥时,2log (1)(01)()|3|1(1)x x f x x x +≤<⎧=⎨--≥⎩,则函数1()()2g x f x =-的所有零点之和为_____。
江苏省南通市2015届高三期中调研测试

江苏省南通市2015届高三期中调研测试语文试题Ⅰ一、语言文字运用(15分)1.在下面一段话空缺处依次填入词语,最恰当的一组是(3分)中国艺术也是一种心灵的艺术。
艺术家抚弄艺术,在乎其“市场价值”,用它来搭建心灵之“庐”。
明代末年的戏剧家祁彪佳说其寓园为之所,可寄寓心灵。
A.放任不是而是安贫乐道B.放置不仅是而且是安身立命C.放任不仅是而且是安贫乐道D.放置不是而是安身立命2.下列诗句与“雨昏青草湖边过”对仗工整的一项是(3分)A.薄罗轻剪越溪纹B.山家烟火春日晴C.花落黄陵庙里啼D.饮马长城窟更寒3.下列交际用语使用得体的一项是(3分)A.打扰您了!我想垂询一下如何解压并尽快消除心理阴影的问题!B.明日搬新家,为答谢您的祝贺,特于家中备下薄酒,恭请光临!C.贵书店即将开张大吉,无论是多忙,到时我都一定会拨冗出席!D.天气日渐寒冷,侄儿在校是否需要叔父寄送御寒物品?望钧裁!4.在下面一段文字横线处填入语句,衔接最恰当的一项是(3分)诗籍店铺真是只有米粒大小,在一道小街上。
有时也遇见克莱曼答斯基女士,匆匆地来匆匆地去。
①犄角儿上还有一张桌子,坐着一个戴近视眼镜的,和蔼可亲的,圆脸的中年妇人。
②屋子有点黑,四壁是书架,中间桌上放着些诗歌篇子,木刻画。
③桌前装着火炉,炉旁蹲着一只大白狮子猫,和女人一样安静无言。
④铺子在一楼,只一间,可是和读诗那座楼远隔着一条甬道。
⑤篇子有宽长两种,印着诗歌,加上些零星的彩画,是给大人和孩子玩儿的。
A.①②④⑤③B.④②⑤①③C.④①③②⑤D.①④⑤③②5.阅读右边这幅漫画,对它的寓意理解最贴切的一项是(3分)A.传统如陷阱,陷入便不能自拔。
B.只有走出传统,才能推陈出新。
C.面对传统,应当学会自我救赎。
D.泥古不化,易被传统捆住手脚。
二、文言文阅读(18分)阅读下面的文言文,完成6~9题。
送方希则序欧阳修庄子以绅笏为柴栅,班固以名声为缰锁。
夫官位爵禄,人之所甚欲,彼岂恶之邪?盖将有感云尔。
江苏省南通市2015届高三第一次调研考试语文试题 Word版含答案

南通市2015届高三第一次调研测试语文一、语言文字运用(15分)1.在下面一段话空缺处依次填入词语,最恰当的一组是(3分)我们在继承音乐传统的时候,应持▲的态度。
自古以来少数民族音乐与汉族音乐的交流从未间断,少数民族的音乐早已成为中华民族音乐中▲的重要组成部分,中华民族音乐也在各民族音乐融合的基础上▲,在世界音乐文化大舞台上绽放光彩。
A. 开放密不可分百花齐放B.开阔亲密无间百花齐放C. 开阔亲密无间渐臻佳境D.开放密不可分渐臻佳境2.下列各句中,没有语病的一项是(3分)A.华为智能手机出货量稳居全球第三,不仅成功树立起中国智能手机的良好形象,而且改变了运营商和消费者对华为手机的认识。
B.政府部门既要明确其与慈善组织的关系,也要加强对慈善组织和慈善活动的管理,这样才能为慈善事业发展注入不竭的动力。
C.李娜在网球场上的坚韧表现以及所取得的成就,在为中国体育赢得全世界瞩目的同时,也有效传达了关于力与美的正能量。
D.汉赋虽然呈现出堆砌词藻以至好用生词僻字,但在丰富文学作品的词汇、锤炼语言辞句等方面,都取得了一定的突破。
3.下列标语表述不得体的一项是(3分)A.小草有生命,足下多留“青”。
(草坪标语)B.轻轻地我走了,正如我轻轻地来。
(图书馆标语)C.扬起希望的风帆,走上新生的坦途。
(医院标语)D.司机一杯酒,亲人几多愁。
(公路标语)4.依次填入下面一段文字画横线处的语句,最恰当的一组是(3分)这时节,我感到了寂寞。
在这寂寞中我意识到了我自己的存在——片刻的孤立的存在。
这种境界并不易得,与环境有关,更与心境有关。
▲,只要内心清净,随便在市廛里,陋巷里,都可以感觉到一种空灵悠逸的境界,▲。
在这种境界中,我们可以在想象中翱翔,跳出尘世的渣滓,与古人同游。
所以我说,▲。
①寂寞是一种清福②所谓“心远地自偏”是也③寂寞不一定要到深山大泽里去寻求A.①②③B.③②①C.③①②D.②①③5.对下列材料主旨理解最恰当的一项是(3分)清代著名戏曲理论家李渔对写作有形象的比喻:“基址初平,间架未定,先筹何处建厅,何处开户,栋需何木,梁用何材,必俟成局了然,始可挥斤运斧。
江苏省南通市2023-2024学年高三第一次调研测试数学(解析版)

南通市2024届高三第一次调研测试数学2024.01.24注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上指定位置上,在其他位置作答一律无效。
3.本卷满分为150分,考试时间为120分钟。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x|-2<x<3},B={0,1,2,3},则A∩B=A.{-2,-1} B.{0,1} C.{0,1,2} D.{0,1,2,3}2.已知z+z=8,z-z=6i,则z z=A.25 B.16 C.9 D.53.若向量a=(λ,4),b=(2,μ),则“λμ=8”是“a∥b”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.设{a n}为等比数列,a2=2a4+3a6,则a4-a7 a2-a5=A.19B.13C.3 D.95.从正方体的八个顶点中选择四个顶点构成空间四面体,则该四面体不可能A.每个面都是等边三角形B.每个面都是直角三角形C.有一个面是等边三角形,另外三个面都是直角三角形D.有两个面是等边三角形,另外两个面是直角三角形6.已知直线y=x-1与抛物线C:x2=2py(p>0)相切于M点,则M到C的焦点距离为A.1 B.2 C.3 D.4直线与抛物线相切,则4p2-8p=0,7.已知函数f(x)及其导函数f′(x)的定义域均为(0,+∞),若xf′(x)<2f(x),则A.4e2f(2)<16f(e)<e2f(4) B.e2f(4)<4e2f(2)<16f(e)C.e2f(4)<16f(e)<4e2f(2) D.16f(e)<e2f(4)<4e2f(2)8.某中学开展劳动实习,学生制作一个矩形框架的工艺品.要求将一个边长分别为10cm 和20cm的矩形零件的四个顶点分别焊接在矩形框架的四条边上,则矩形框架周长的最小值为A.202cm B.305cm C.405cm D.602cm二、选择题:本题共4小题,每小题5分,共20分。
江苏省南通市第一中学2014-2015学年高三上学期10月阶段测试(月考) 数学(理) Word版含解析(苏教版)

2014—2015学年度第一学期江苏省南通第一中学高三阶段考试数学试题注意事项:本试卷分试题和答卷两部分,共160分,考试时间为120分钟.一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上......... 1. 已知集合U ={2,3,6,8},A ={2,3},B ={2,6,8},则(∁U A )∩B = ▲ . 2. 命题“若x ,y 都是偶数,则x +y 也是偶数”的逆否命题是 ▲ . 3.函数()f x =的定义域是 ▲ .4. 若a =30.6,b =log 30.2,c =0.63,则a 、b 、c 的大小关系为 ▲ .(从大到小排列) 5. 函数y =x e x 的最小值是 ▲ .6. 已知U =R ,集合A ={x |x 2-x -2=0},B ={x |mx +1=0},B ∩(∁U A )=∅,则m = ▲ . 7. 已知命题p :“∃x ∈R ,使得x 2+2ax +1<0成立”为真命题,则实数a 的取值范围是 ▲ . 8.已知函数()f x =的值域是[)0+∞,则实数m 的取值范围是 ▲ .9. 已知函数f (x )=ax 3+b sin x +4(a ,b ∈R ),f (lg(log 210))=5,则f (lg(lg 2))= ▲ .10.已知函数f (x )=⎩⎪⎨⎪⎧(1-3a )x +10a ,x ≤7,a x -7,x >7是定义域R 上的递减函数,则实数a 的取值范围是 ▲ .11.函数f (x )是定义在[-4,4]上的偶函数,其在[0,4]上的图象如图所示,那么不等式f (x )cos x <0的解集为 ▲ .12.已知函数y =f (x )(x ∈R )满足f (x +2)=f (x ),且当x ∈[-1,1]时,f (x )=|x |,函数g (x )=⎩⎪⎨⎪⎧sin (πx ),x >0,-1x,x <0,则函数h (x )=f (x )-g (x )在区间[-5,5]上的零点的个数为 ▲ .13.将一个长宽分别是a ,b (0<b <a )的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,若这个长方体的外接球的体积存在最小值,则ab的取值范围是 ▲ .14.设a >0,函数2(),()ln a f x x g x x x x=+=-,若对任意的x 1,x 2∈[1,e ],都有12()()f x g x ≥成立,则实数a 的取值范围是 ▲ .二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字说明、证明过程或演算步骤.15.(本小题14分)已知集合A ={y |y =2x -1,0<x ≤1},B ={x |(x -a )[x -(a +3)]<0}.分别根据下列条件,求实数a 的取值范围. (1)A ∩B =A ;(2)A ∩B ≠∅. 16.(本小题14分)已知二次函数f (x )=ax 2+bx +1(a >0),F (x )=⎩⎪⎨⎪⎧f (x ),x >0,-f (x ),x <0.若f (-1)=0,且对任意实数x 均有f (x )≥0成立. (1)求F (x )的表达式;(2)当x ∈[-2,2]时,g (x )=f (x )-k x 是单调函数,求k 的取值范围.17.A,B 两地相距S 千米,要将A 地所产汽油运往B 地.已知甲、乙二型运油车行驶S 千米的耗油量(不妨设空载时,满载时相同)分别为各自满载油量的11,1514,且甲型车的满载油量是乙型车的56,今拟在A,B 之间设一运油中转站C ,由从A 出发,往返于A,C 之间的甲型车将A 处的汽油运至C 处,再由从C 出发,往返于C,B 之间的乙型车将C 处收到的汽油运至B 处.若C 处收到的汽油应一次性运走,且各辆车的往返耗油从各自所载汽油中扣除,问C 地设在何处,可使运油率最大?此时,甲、乙二型汽车应如何配备?(运油率精确到1%,运油率=B 处收到的汽油A 处运出的汽油×100%) 18.(本小题16分)已知定义域为R 的函数()122x x af x b+-+=+是奇函数,(1)求,a b 的值;( 2) 判断并证明函数()f x 的单调性;(3)若对任意的t ∈R ,不等式()()22220f t f t k -+-<恒成立,求k 的取值范围.19.(本小题16分)已知函数()2f x x x a x =-+.(1)若函数()f x 在R 上是增函数,求实数a 的取值范围;(2)求所有的实数a ,使得对任意[1,2]x ∈时,函数()f x 的图象恒在函数()21g x x =+图象的下方;(3)若存在[4,4]a ∈-,使得关于x 的方程()()f x t f a =有三个不相等的实数根,求实数t 的取值范围.20.(本小题16分)已知函数f (x )=sin x -x cos x 的导函数为f ′(x ). (1)求证:f (x )在(0,π)上为增函数;(2)若存在x ∈(0,π),使得f ′(x )>12x 2+λx 成立,求实数λ的取值范围;(3)设F (x )=f ′(x )+2cos x ,曲线y =F (x )上存在不同的三点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3), x 1<x 2<x 3,且x 1,x 2,x 3∈(0,π),比较直线AB 的斜率与直线BC 的斜率的大小,并证明._____________________________________________________________________________________命题、校对、制卷: 吴勇贫 审核:吴勇贫江苏省南通第一中学2015届高三阶段考试理科数学答案1. 解析 由集合的运算,可得(∁U A )∩B ={6,8}∩{2,6,8}={6,8}.答案 {6,8}2.解析 由于“x ,y 都是偶数”的否定表达是“x ,y 不都是偶数”,“x +y 是偶数”的否定表达是“x +y 不是偶数”,故原命题的逆否命题为“若x +y 不是偶数,则x ,y 不都是偶数”. 答案 若x +y 不是偶数,则x 、y 不都是偶数 3. {0}∪[1,+∞);4. 解析 30.6>1,log 30.2<0,0<0.63<1,所以a >c >b .答案 a >c >b5. 解析 y ′=e x +x e x =(1+x )e x ,令y ′=0,则x =-1,因为x <-1时,y ′<0,x >-1时,y ′>0,所以x =-1时,y min =-1e .答案 -1e6.答案0,1,-12;7. 解析 “∃x ∈R ,x 2+2ax +1<0”是真命题,即不等式x 2+2ax +1<0有解,∴Δ=(2a )2-4>0,得a 2>1,即a >1或a <-1. 答案 (-∞,-1)∪(1,+∞)8.[][)0,19,+∞,试题分析:由题意得:函数2(3)1y mx m x =+-+的值域包含[)0,+∞, 当m =0时,31[0,),y x =-+∈⊃+∞R 满足题意;当0m ≠时,要满足值域包含[)0,+∞,需使得0,0.m >∆≥即9m ≥或01m <≤, 综合得:实数m 的取值范围是[][)0,19,+∞.9.解析 ∵f (x )=ax 3+b sin x +4,①∴f (-x )=a (-x )3+b sin(-x )+4, 即f (-x )=-ax 3-b sin x +4,② ①+②得f (x )+f (-x )=8,③又∵lg(log 210)=lg ⎝⎛⎭⎫1lg 2=lg(lg 2)-1=-lg(lg 2), ∴f (lg(log 210))=f (-lg(lg 2))=5,又由③式知f (-lg(lg 2))+f (lg(lg 2))=8, ∴5+f (lg(lg 2))=8,∴f (lg(lg 2))=3. 答案 310.解析 ∵函数f (x )=⎩⎪⎨⎪⎧(1-3a )x +10a ,x ≤7,a x -7,x >7是定义域上的递减函数,∴⎩⎪⎨⎪⎧1-3a <0,0<a <1,(1-3a )×7+10a ≥a 0,即⎩⎪⎨⎪⎧1-3a <0,0<a <1,7-11a ≥1,解得13<a ≤611.答案 ⎝⎛⎦⎤13,61111.解析 当x ∈(0,1)时,cos x >0,f (x )>0;当x ∈⎝⎛⎭⎫1,π2时,cos x >0,f (x )<0; 当x ∈⎝⎛⎭⎫π2,4时,cos x <0,f (x )<0,当x ∈(-1,0)时,cos x >0,f (x )>0;当x ∈⎝⎛⎭⎫-π2,-1时,cos x >0,f (x )<0; 当x ∈⎝⎛⎭⎫-4,-π2时,cos x <0,f (x )<0. 故不等式f (x )cos x <0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪-π2<x <-1,或1<x <π2. 答案 ⎩⎨⎧⎭⎬⎫x |-π2<x <-1,或1<x <π212.解析 函数y =f (x )(x ∈R )满足f (x +1)=-f (x ),故f (x +2)=-f (x +1)=-[-f (x )]=f (x ),即函数f (x )的周期为2,作出x ∈[-1,1]时,f (x )=|x |的图象,并利用周期性作出函数f (x )在[-5,5]上的图象,在同一坐标系内再作出g (x )在[-5,5]上的图象,由图象可知,函数f (x )与g (x )的图象有9个交点,所以函数h (x )=f (x )-g (x )在区间[-5,5]上的零点的个数为9.答案 913.解析 设切去正方形的边长为x ,x ∈⎝⎛⎭⎫0,b 2,则该长方体外接球的半径为r 2=14[(a -2x )2+(b -2x )2+x 2]=14[9x 2-4(a +b )x +a 2+b 2],在x ∈⎝⎛⎭⎫0,b 2存在最小值时,必有0<2(a +b )9<b 2,解得a b <54,又0<b <a ⇒a b >1,故ab 的取值范围是⎝⎛⎭⎫1,54. 14.答案)+∞.15.解 因为集合A 是函数y =2x -1(0<x ≤1)的值域,所以A =(-1,1],B =(a ,a +3).…………………………4分(1)A ∩B =A ⇔A ⊆B ⇔⎩⎪⎨⎪⎧a ≤-1,a +3>1,即-2<a ≤-1,故当A ∩B =A 时,a 的取值范围是(-2,-1].……………………7分 (2)当A ∩B =∅时,结合数轴知,a ≥1或a +3≤-1,即a ≥1或a ≤-4. …………12分 故当A ∩B ≠∅时,a 的取值范围是(-4,1). …………………14分16.解 (1)∵f (-1)=0,∴a -b +1=0,∴b =a +1,……………………2分 ∴f (x )=ax 2+(a +1)x +1.∵对任意实数x 均有f (x )≥0恒成立, ∴⎩⎪⎨⎪⎧ a >0,Δ=(a +1)2-4a ≤0,∴⎩⎪⎨⎪⎧a >0,(a -1)2≤0.………………4分 ∴a =1,从而b =2,∴f (x )=x 2+2x +1, ………………6分∴F (x )=⎩⎪⎨⎪⎧x 2+2x +1,x >0,-x 2-2x -1,x <0. ………………8分(2)g (x )=x 2+2x +1-k x =x 2+(2-k )x +1. ∵g (x )在[-2,2]上是单调函数, ∴k -22≤-2或k -22≥2,………………12分解得k ≤-2或k ≥6. ………………14分 故k 的取值范围是(-∞,-2]∪[6,+∞). 17.解:设AC =l (千米),0<l <S ,则CB =S -l (千米),设甲型车满车载油量为a 吨,则乙型车满车载油量为65a 吨.…………2分一辆甲型车往返一次,C 地收到的汽油为12(1)15la S -⋅吨,一辆乙型车往返一次,B 地收到的汽油为1212()(1)[1]1514l S l a S S--⋅⨯-⋅吨.………6分故运油率21(1)(1)261157(1)()1577l S l a l l S S y a S S--⋅⨯-⋅==-⋅+⋅ 2216()105357l l S S =-+⋅+. …………8分 当1335242()105l S =-=-时,y 有最大值,max 24387%280y =≈. …………10分 此时一辆甲型车运到C 处的汽油量为910a 吨,设甲、乙二型车各x 、y 辆,则有96105a x a y ⋅=⋅,所以43x y =. …………12分答:C 地设在靠近B 地的四分之一处,可使运油率最大,此时甲、乙二型车数量之比为4:3.………………………………………………14分18.解:(1)()(),f x f x -=-112222x x x x a ab b--++-+-∴=++,()()()()112222x x x x b a b a -+-∴+-=+-,42222222x x x x ab b a a b --∴-+⋅-⋅=⋅-⋅4201222ab a b ab a b-=⎧=⎧⎪=⇒⎨⎨=⎩⎪=⎩. 4分 (2)因为()11212xf x =-++,所以()y f x =是单调递减的.证明:设12,x x <()()()()211212221212x x x x f x f x --=++,因为12,x x <所以21220,x x ->从而()()12f x f x >,所以()y f x =在R 上是单调递减的. 10分(3)()()2222,f t f t k -<--又()f x 是奇函数,∴()()2222,f t f k t -<-又()f x 是减函数,∴2222t k t ->-,即232,k t <-∴ 2.k <- 16分19.解:(1)22(2),,()2(2),,x a x x a f x x x a x x a x x a ⎧+-⎪=-+=⎨-++<⎪⎩≥由()f x 在R 上是增函数,则2,22,2a a a a -⎧-⎪⎪⎨+⎪⎪⎩≥≤即22a -≤≤,则a 范围为22a -≤≤;…4分 (2)由题意得对任意的实数[1,2]x ∈,()()f x g x <恒成立,即1x x a -<,当[1,2]x ∈恒成立,即1x a x -<,11x a x x-<-<,11x a x x x -<<+,故只要1x a x-<且1a x x <+在[1,2]x ∈上恒成立即可,在[1,2]x ∈时,只要1x x -的最大值小于a 且1x x+的最小值大于a 即可,而当[1,2]x ∈时,21110x x x '⎛⎫-=+> ⎪⎝⎭,1x x -为增函数,max 132x x ⎛⎫-= ⎪⎝⎭;当[1,2]x ∈时,21110x x x '⎛⎫+=-> ⎪⎝⎭,1x x +为增函数,min 12x x ⎛⎫+= ⎪⎝⎭,所以322a <<;(3)当22a -≤≤时,()f x 在R 上是增函数,则关于x 的方程()()f x t f a =不可能有三个不等的实数根; 则当(2,4]a ∈时,由22(2),,()(2),x a x x a f x x a x x a⎧+-⎪=⎨-++<⎪⎩≥得x a ≥时,2()(2)f x x a x =+-对称轴22a x a -=<,则()f x 在[,)x a ∈+∞为增函数,此时()f x 的值域为[(),)[2,)f a a +∞=+∞,x a <时,2()(2)f x x a x =-++对称轴22a x a +=<,则()f x 在2,2a x +⎛⎤∈-∞ ⎥⎝⎦为增函数,此时()f x 的值域为2(2),4a ⎛⎤+-∞ ⎥⎝⎦, ()f x 在2,2a x a +⎡⎫∈⎪⎢⎣⎭为减函数,此时()f x 的值域为2(2)2,4a a ⎛⎤+ ⎥⎝⎦;由存在(2,4]a ∈,方程()()2f x t f a ta ==有三个不相等的实根,则2(2)22,4a ta a ⎛⎫+∈ ⎪⎝⎭,即存在(2,4]a ∈,使得2(2)1,8a t a ⎛⎫+∈ ⎪⎝⎭即可,令2(2)14()488a g a a a a +⎛⎫==++⎪⎝⎭, 只要使()max ()t g a <即可,而()g a 在(2,4]a ∈上是增函数,()max 9()(4)8g a g ==, 故实数t 的取值范围为91,8⎛⎫ ⎪⎝⎭; 同理可求当[4,2)a ∈--时,t 的取值范围为91,8⎛⎫⎪⎝⎭;综上所述,实数t 的取值范围为91,8⎛⎫⎪⎝⎭.20.解 (1)证明:f′(x )=x sin x ,当x ∈(0,π)时,sin x >0,所以f′(x )>0恒成立,所以f (x ) 在(0,π)上单调递增.………………………………4分(2)因为f′(x )>12x 2+λx ,所以x sin x >12x 2+λx .当0<x <π时,λ<sin x -12x . ………………………………6分设φ(x )=sin x -12x ,x ∈(0,π),则φ′(x )=cos x -12.当0<x <π3时,φ′(x )>0;当π3<x <π时,φ′(x )<0.于是φ (x )在(0,π3)上单调递增,在 (π3,π)上单调递减,…………………………8分所以当0<x <π时,φ(x )max =g (π3)=32-π6因此λ<32-π6. ………………………………10分(3)由题意知只要判断F (x 3)-F (x 2)x 3-x 2<F (x 2)-F (x 1)x 2-x 1的大小.首先证明:F (x 3)-F (x 2)x 3-x 2<F′(x 2).由于x 2<x 3,因此只要证:F (x 3)-F (x 2)<(x 3-x 2) F′(x 2).………………………………12分 设函数G (x )=F (x )-F (x 2)-(x -x 2) F′(x 2)( x 2<x <π),因为F ′(x )=x cos x -sin x =-f (x ),所以G′(x )=F′(x )-F′(x 2)=f (x 2)-f (x ), 由(1)知f (x )在(0,π)上为增函数,所以G′(x )<0. 则G (x )在(x 2,π)上单调递减,又x >x 2,故G (x )<G (x 2)=0.而x 2<x 3<π,则G (x 3)<0,即F (x 3)-F (x 2)-(x 3-x 2) F′(x 2)<0,即F (x 3)-F (x 2)<(x 3-x 2) F′(x 2).从而F (x 3)-F (x 2)x 3-x 2<F′(x 2)得证. ………………………………14分同理可以证明:F′(x 2)<F (x 2)-F (x 1)x 2-x 1.因此有F (x 3)-F (x 2)x 3-x 2<F (x 2)-F (x 1)x 2-x 1,即直线AB 的斜率大于直线BC 的斜率.……………16分。
2015年江苏省南通市高考一模数学试卷【解析版】

2015年江苏省南通市高考数学一模试卷一、填空题1.(5分)已知集合A={﹣2,﹣1},B={﹣1,2,3},则A∩B=.2.(5分)已知复数z满足(3+4i)z=1(i为虚数单位),则z的模为.3.(5分)某中学共有学生2800人,其中高一年级970人,高二年级930人,高三年级900人,现采用分层抽样的方法,抽取280人进行体育达标检测,则抽取高二年级学生人数为.4.(5分)函数f(x)=lg(﹣x2+2x+3)的定义域为.5.(5分)如图是一个算法流程图,则输出的x的值为.6.(5分)同时抛掷两枚质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具),观察向上的点数,则两个点数之积不小于4的概率为.7.(5分)底面边长为2,高为1的正四棱锥的侧面积为.8.(5分)在平面直角坐标系xOy中,以直线y=±2x为渐近线,且经过抛物线y2=4x焦点的双曲线的方程是.9.(5分)在平面直角坐标系xOy中,记曲线y=2x﹣.(m∈R,m≠﹣2)在x =1处的切线为直线l,若直线l在两坐标轴上的截距之和为12,则m的值为.10.(5分)已知函数f(x)=sin(2x+)若y=f(x﹣φ)(0<φ<)是偶函数则φ=.11.(5分)在等差数列{a n}中,已知首项a1>0,公差d>0.若a1+a2≤60,a2+a3≤100,则5a1+a5的最大值为.12.(5分)已知函数y=a x+b(b>0)的图象经过点P(1,3),如图所示,则+的最小值为.13.(5分)如图,⊙O内接△ABC中,M是BC的中点,AC=3.若•=4,则AB=.14.(5分)已知f(x)是定义在[1,+∞]上的函数,且f(x)=,则函数y=2xf(x)﹣3在区间(1,2015)上零点的个数为.二、解答题15.(16分)在△ABC中,角A,B,C的对边分别为a,b,c.已知b cos C+c cos B =2a cos A.(1)求角A的大小;(2)若•=,求△ABC的面积.16.(13分)如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.(1)求证:BC⊥AM;(2)若N是AB的中点,且CN∥平面AB1M,求CM的长.17.(12分)如图,在平面直角坐标系xOy中,F1,F2分别是椭圆+=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),且△BF1F2是边长为2的等边三角形.(1)求椭圆的方程;(2)过右焦点F2的直线l与椭圆交于A,C两点,记△ABF2,△BCF2的面积分别为S1,S2.若S1=2S2,求直线l的斜率.18.(12分)在长为20m,宽为16m的长方形展厅正中央有一圆盘形展台(圆心为点C),展厅入口位于长方形的长边的中间,在展厅一角B点处安装监控摄像头,使点B与圆C在同一水平面上,且展台与入口都在摄像头水平监控范围内(如图阴影所示).(1)若圆盘半径为2m,求监控摄像头最小水平视角的正切值;(2)过监控摄像头最大水平视角为60°,求圆盘半径的最大值.(注:水平摄像视角指镜头中心点水平观察物体边缘的实现的夹角.)19.(14分)若函数y=f(x)在x=x0处取得极大值或极小值,则称x0为函数y =f(x)的极值点.已知函数f(x)=ax3+3xlnx﹣1(a∈R).(1)当a=0时,求f(x)的极值;(2)若f(x)在区间(,e)上有且只有一个极值点,求实数a的取值范围.20.(13分)设数列{a n}的前n项和为S n.若≤2(n∈N*),则称{a n}是“紧密数列”(1)若数列{a n}的前n项和S n=(n2+3n)(n∈N*),证明:{a n}是“紧密数列”;(2)设数列{a n}是公比为q的等比数列,若数列{a n}与{S n}都是“紧密数列”,求q的取值范围.2015年江苏省南通市高考数学一模试卷参考答案与试题解析一、填空题1.(5分)已知集合A={﹣2,﹣1},B={﹣1,2,3},则A∩B={﹣1}.【解答】解:∵集合A={﹣2,﹣1},B={﹣1,2,3},∴A∩B={﹣1}.故答案为:{﹣1}.2.(5分)已知复数z满足(3+4i)z=1(i为虚数单位),则z的模为.【解答】解:复数z满足(3+4i)z=1(i为虚数单位),可得:|(3+4i)z|=1,即|3+4i||z|=1,可得5|z|=1.∴z的模为:.故答案为:.3.(5分)某中学共有学生2800人,其中高一年级970人,高二年级930人,高三年级900人,现采用分层抽样的方法,抽取280人进行体育达标检测,则抽取高二年级学生人数为93.【解答】解:抽取280人进行体育达标检测,则抽取高二年级学生人数为人,故答案为:934.(5分)函数f(x)=lg(﹣x2+2x+3)的定义域为(﹣1,3).【解答】解:要使函数有意义,则需﹣x2+2x+3>0,解得,﹣1<x<3.则定义域为(﹣1,3).故答案为:(﹣1,3).5.(5分)如图是一个算法流程图,则输出的x的值为.【解答】解:模拟执行算法流程,可得n=1,x=1执行循环体,x=,n=2不满足条件n>6,执行循环体,x=,n=3不满足条件n>6,执行循环体,x=,n=4不满足条件n>6,执行循环体,x=,n=5不满足条件n>6,执行循环体,x=,n=6不满足条件n>6,执行循环体,x=,n=7满足条件n>6,退出循环,输出x的值为.故答案为:.6.(5分)同时抛掷两枚质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具),观察向上的点数,则两个点数之积不小于4的概率为.【解答】解:列表得:∴一共有36种情况,向上的点数之积不小于4共有31个.因此出现向上面的点数之积不小于4的概率P=.故答案为:.7.(5分)底面边长为2,高为1的正四棱锥的侧面积为4.【解答】解:正四棱锥底面边长为2,高为1,则侧面的高h==,故此正四棱锥的侧面积S=4•×2×=4.故答案为:4.8.(5分)在平面直角坐标系xOy中,以直线y=±2x为渐近线,且经过抛物线y2=4x焦点的双曲线的方程是.【解答】解:设以直线y=±2x为渐近线的双曲线的方程为(λ≠0),∵双曲线经过抛物线y2=4x焦点F(1,0),∴1=λ,∴双曲线方程为:.故答案为:.9.(5分)在平面直角坐标系xOy中,记曲线y=2x﹣.(m∈R,m≠﹣2)在x=1处的切线为直线l,若直线l在两坐标轴上的截距之和为12,则m的值为﹣3或﹣4.【解答】解:∵y=2x﹣,∴y′=2+;故当x=1时,y=2﹣m,y′=2+m;故直线l的方程为y=(2+m)(x﹣1)+2﹣m;令x=0得,y=﹣(2+m)+2﹣m=﹣2m;令y=0得,x=+1=;故﹣2m+=12,解得,m=﹣3或m=﹣4.故答案为:﹣3或﹣4.10.(5分)已知函数f(x)=sin(2x+)若y=f(x﹣φ)(0<φ<)是偶函数则φ=.【解答】解:∵f(x)=sin(2x+)∴y=f(x﹣φ)=sin[2(x﹣φ)+]=sin(2x﹣2φ+)∵y=f(x﹣φ)是偶函数∴﹣2φ+=k,k∈Z从而解得:φ=﹣,k∈Z∵0<φ<∴可解得:φ=.故答案为:.11.(5分)在等差数列{a n}中,已知首项a1>0,公差d>0.若a1+a2≤60,a2+a3≤100,则5a1+a5的最大值为200.【解答】解:∵在等差数列{a n}中,已知首项a1>0,公差d>0,又a1+a2≤60,a2+a3≤100,∴2a1+d≤60,2a1+3d≤100,∴5a1+a5=6a1+4d=x(2a1+d)+y(2a1+3d)=(2x+2y)a1+(x+3y)d,∴2x+2y=6,x+3y=4,解得x=,y=,∴5a1+a5=(2a1+d)+(2a1+3d)≤=200故答案为:20012.(5分)已知函数y=a x+b(b>0)的图象经过点P(1,3),如图所示,则+的最小值为.【解答】解:∵函数y=a x+b(b>0)的图象经过点P(1,3),∴3=a+b,a>1,b>0.∴(a﹣1)+b=2.∴+===,当且仅当a﹣1=2b=时取等号.故答案为:.13.(5分)如图,⊙O内接△ABC中,M是BC的中点,AC=3.若•=4,则AB=.【解答】解:因为O是△ABC的外心,∴O在AB、AC边的射影分别是AB、AC的中点,=,同理,得到,∵,∴=,∴||=.故答案为:.14.(5分)已知f(x)是定义在[1,+∞]上的函数,且f(x)=,则函数y=2xf(x)﹣3在区间(1,2015)上零点的个数为11.【解答】解:令函数y=2xf(x)﹣3=0,得到方程f(x)=,当x∈[1,2)时,函数f(x)先增后减,在x=时取得最大值1,而y=在x=时也有y=1;当x∈[2,22)时,f(x)=f(),在x=3处函数f(x)取得最大值,而y=在x=3时也有y=;当x∈[22,23)时,f(x)=f(),在x=6处函数f(x)取得最大值,而y=在x=6时也有y=;…,当x∈[210,211)时,f(x)=f(),在x=1536处函数f(x)取得最大值,而y=在x=1536时也有y=;综合以上分析,将区间(1,2015)分成11段,每段恰有一个交点,所以共有11个交点,即有11个零点.故答案为:11.二、解答题15.(16分)在△ABC中,角A,B,C的对边分别为a,b,c.已知b cos C+c cos B =2a cos A.(1)求角A的大小;(2)若•=,求△ABC的面积.【解答】解:(1)由正弦定理得sin B cos C+sin C cos B=2sin A cos A,即sin(B+C)=2sin A cos A,则sin A=2sin A cos A,在三角形中,sin A≠0,∴cos A=,即A=;(2)若•=,则AB•AC cos A=AB•AC=,即AB•AC=2,则△ABC的面积S=AB•AC sin A==.16.(13分)如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.(1)求证:BC⊥AM;(2)若N是AB的中点,且CN∥平面AB1M,求CM的长.【解答】(1)证明:∵ABC﹣A1B1C1为直三棱柱,∴C1C⊥平面ABC,∴BC⊥C1C,又BC⊥AC,∴BC⊥平面ACC1A1,∵AM在平面ACC1A1上,∴BC⊥AM.(2)解:取AB1的中点P,连接MP,NP,∵P为AB1中点,N为AB中点,∴NP为△ABB1的中位线,∴NP∥BB1,又∵C1C,B1B都是直三棱柱的棱,∴C1C∥B1B,∴MC∥B1B,∴NP∥CM,∴NPCM共面,又∵CN∥平面AB 1M,∴CN MP,∴PNCM是平行四边形,∴CM=NP=BB1=CC1=.17.(12分)如图,在平面直角坐标系xOy中,F1,F2分别是椭圆+=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),且△BF1F2是边长为2的等边三角形.(1)求椭圆的方程;(2)过右焦点F2的直线l与椭圆交于A,C两点,记△ABF2,△BCF2的面积分别为S1,S2.若S1=2S2,求直线l的斜率.【解答】解:(1)∵△BF1F2是边长为2的等边三角形,∴a=2c=2,则c=1,b==,则椭圆的方程为.(2)设B到直线AC的距离为h,由S1=2S2,则,即AF2=2F2C,∴,设A(x1,y1),C(x2,y2),∵F2(1,0),∴(1﹣x1,﹣y1)=2(x2﹣1,y2),即,由,解得,∴直线l的斜率为k=.18.(12分)在长为20m,宽为16m的长方形展厅正中央有一圆盘形展台(圆心为点C),展厅入口位于长方形的长边的中间,在展厅一角B点处安装监控摄像头,使点B与圆C在同一水平面上,且展台与入口都在摄像头水平监控范围内(如图阴影所示).(1)若圆盘半径为2m,求监控摄像头最小水平视角的正切值;(2)过监控摄像头最大水平视角为60°,求圆盘半径的最大值.(注:水平摄像视角指镜头中心点水平观察物体边缘的实现的夹角.)【解答】解:(1)过B作圆C的切线BE,切点为E,设圆C所在平面上入口中点为A,连接CA,CE,CB,则CE⊥BE,⊥CA⊥AB∴监控摄像头水平视角为∠ABE时,水平视角最小.在直角三角形ABC中,AB=10,AC=8,tan∠ABC=,在直角三角形BCE中,CE=2,BE==12,tan∠CBE=,∴tan∠ABE=tan(∠ABC+∠CBE)=1+,∴监控摄像头最小水平视角的正切值为1+;(2)当∠ABE=60°时,若直线BE与圆C相切,则圆C的半径最大.在平面ABC内,以B为坐标原点,BA为x轴建立平面直角坐标系,则直线BE 方程为y=x,∴CE==5﹣4,∴圆C的半径最大为5﹣4(m).19.(14分)若函数y=f(x)在x=x0处取得极大值或极小值,则称x0为函数y =f(x)的极值点.已知函数f(x)=ax3+3xlnx﹣1(a∈R).(1)当a=0时,求f(x)的极值;(2)若f(x)在区间(,e)上有且只有一个极值点,求实数a的取值范围.【解答】解:(1)当a=0时,f(x)=3xlnx﹣1的定义域为(0,+∞),f′(x)=3lnx+3=3(lnx+1),故f(x)=3xlnx﹣1在(0,)上是减函数,在(,+∞)上是增函数;故f(x)在x=时取得极小值f()=﹣3﹣1;(2)函数f(x)=ax3+3xlnx﹣1的定义域为(0,+∞),f′(x)=3(ax2+lnx+1),令g(x)=ax2+lnx+1,则g′(x)=2ax+=,当a>0时,g′(x)>0在(0,+∞)恒成立,故f′(x)=3(ax2+lnx+1)在(0,+∞)上是增函数,而f′()=3[a()2+ln+1]=3a()2>0,故当x∈(,e)时,f′(x)>0恒成立,故f(x)在区间(,e)上单调递增,故f(x)在区间(,e)上没有极值点;当a=0时,由(1)知,f(x)在区间(,e)上没有极值点;当a<0时,令=0解得,x=;故g(x)=ax2+lnx+1在(0,)上是增函数,在(,+∞)上是减函数,①当g(e)•g()<0,即﹣<a<0时,g(x)在(,e)上有且只有一个零点,且在该零点两侧异号,②令g()=0得=0,不可能;③令g(e)=0得a=﹣,所以∈(,e),而g()=g()=+ln>0,又g()<0,所以g(x)在(,e)上有且只有一个零点,且在该零点两侧异号,综上所述,实数a的取值范围是[﹣,0).20.(13分)设数列{a n}的前n项和为S n.若≤2(n∈N*),则称{a n}是“紧密数列”(1)若数列{a n}的前n项和S n=(n2+3n)(n∈N*),证明:{a n}是“紧密数列”;(2)设数列{a n}是公比为q的等比数列,若数列{a n}与{S n}都是“紧密数列”,求q的取值范围.【解答】证明:(1)由S n=(n2+3n)(n∈N*)得,S n﹣1=[(n﹣1)2+3(n﹣1)](n≥2),两式相减得,a n=(n2+3n﹣n2+2n﹣1﹣3n+3)=(2n+2)=(n+1),当n=1时,a1=S1=(1+3)=1,也适合上式,所以a n=(n+1),则==1+>1,所以显然成立,因为=1+随着n的增大而减小,所以当n=1时取到最大值,则≤1+=<2,则≤2成立,所以数列{a n}是“紧密数列”;解:(2)由题意得,等比数列{a n}的公比q当q≠1时,所以,,则==q,==,因为数列{a n}与{S n}都是“紧密数列”,所以,解得,当q=1时,a n=a1,S n=na1,则,=1+,则,满足“紧密数列”的条件,故q的取值范围是[,1]。
江苏省南通市2015届高三第三次调研测试

江苏省南通市2015届高三第三次调研测试高三2013-06-04 22:15江苏省南通市2015届高三第三次调研测试语文试题一、语言文字运用(15分)1.下列词语中加点的字,每对读音都不相同的一组是(3分)A.轶事/卷帙浩繁旖旎/倚马可待贮藏/凝神伫立B.狭隘/挟山超海拾掇/缀文成篇契约/锲而不舍C.赡养/瞻前顾后龃龉/含英咀华脉络/恪尽职守D.案牍/买椟还珠栈桥/践约守诺酝酿/琳琅满目2.下列各句子中,没有语病的一项是(3分)A.3月份,中央电视台等主流媒体先后对苹果公司售后服务的“双重标准”提出质疑,这让苹果公司陷入了入华以来最大的舆论危机。
B.专家提醒,人感染H7N9禽流感起病的48小时内可以服用达菲进行治疗是有效的,而以为服用板蓝根能预防禽流感的观点存在误区。
C.青歌赛经过多年的实践和不断创新,已成为普及音乐知识、发现和推出声乐人才、引领和推动中国声乐事业发展繁荣的重要舞台。
D.对于“五一”小长假期间全国各地旅游景点门票是否涨价的问题,国家旅游局新闻发言人在近期召开的信息发布会上已予以确认。
3.下面这段文字是从哪三个方面指出儒、道“离异而对立”的?请简要概括,不超过20个字。
(4分)儒、道是离异而对立的。
一个入世,乐观进取;一个出世,消极退避。
如果说荀子强调的是“性无伪则不能自美”,那么庄子强调的却是“天地有大美而不言”;前者强调艺术的人工制作和外在功利,后者突出的是自然,即美和艺术的独立。
如果前者由于以其狭隘实用的功利框架,经常造成对艺术和审美的束缚、损害和破坏;那么后者则恰恰给予这种框架和束缚以强有力的冲击、解脱和否定。
4.下面是一位高三学生毕业时写给自己老师的一封信。
请从语言的简明、连贯、得体等角度加以修改。
(5分)敬爱的老师:您好!您渊博的知识启迪我的智慧,您关怀的目光滋润我的心田,我的人生一直受到您亲切话语的激励。
我的成长离不开您无微不至的悉心培养。
……虽然我毕业了,但您永远是我的老师,您的教导将永远铭刻在我的心里。
集合的概念课件-2025届高三数学一轮复习

然数,∴ B =
6
{1,2,3,6}.(集合B的代表元素是 ,注意与A区分)
6−x
例2-5 用描述法表示下列集合:
1
3
2
4
3
5
4
6
5
7
(1){ , , , , };
【解析】可表示为{x|x =
n
,n
n+2
∈ + 且n ≤ 5}.
(2)偶数集;
【解析】可表示为{x|x = 2n,n ∈ }.(奇数集可表示为{x|x = 2n + 1,n ∈ })
列集合和运算:
①G = {x|x是非负整数},⊕ 为整数的加法;
②G = {x|x是偶数},⊕ 为整数的乘法;
③G = {x|x是二次三项式},⊕ 为多项式的加法.
①
其中G关于运算⊕ 为“融洽集”的是____.(写出所有满足条件的序号)
【解析】①G = {x|x是非负整数},⊕ 为整数的加法,满足对任意a,b ∈ G,都有
是( AD
)
A.0 ∈
2
B.
7
∈
C.−3 ∉ Z
D.π ∉ Q
【解析】0是自然数(0是最小的自然数),即有0 ∈ ,故A正确;
2
2
不是整数,即有
7
7
∉ Z,故B错误;
−3是负整数,即有−3 ∈ ,故C错误;
π 是无理数,即有π ∉ Q,故D正确.
例2-4 用列举法表示下列集合:
(1)A = {x ∈
且k + 1 ∉ A,那么k是A的一个“孤立元”.给定S = {1,2,3,4,5,6,7,8},由S
的3个元素构成的所有集合中,不含“孤立元”的集合个数为( D
2015新作文:新材料“ 鲤鱼们都想跃过龙门变为龙”作文导写及优秀作文( 2015届高三南通市一模优秀

2015新作文:新材料“鲤鱼们都想跃过龙门变为龙”作文导写及优秀作文( 2015届高三南通市一模优秀2015新作文新材料“鲤鱼们都想跃过龙门变为龙”作文导写及优秀作文( 2015届高三南通市一模优秀作文)阅读下面的材料,根据要求写一篇不少于800字的文章。
鲤鱼们都想跃过龙门变为龙。
可是龙门太高,只能望而兴叹。
于是祈求佛祖降低龙门高度。
佛祖被感动,降低了高度,每条鲤鱼都顺利跃过,实现了梦想。
但它们很快发现自己没有了做龙的感觉。
要求:选好角度,确定立意,明确文体,自拟标题;不要脱离材料内容及含意的范围作文,不要套作,不得抄袭。
一、审题1.对本次“材料作文”的基本认识材料是多义的,角度、立意有多种。
但考生在“自选”“自定”时不能超越“材料”能指、所指的“固定范围”,不能任意发挥、无边无际。
2.对“鲤鱼跃龙门”材料的基本理解。
从“鲤鱼”角度,可这样理解:鲤鱼“向佛祖祈求”,有如下表述:成功无捷径(做事不可一蹴而就,或“欲速则不达”);实现理想需自身努力鲤鱼终“无做龙的感觉”,有如下表述:没有高标准的梦想价值低下;拼搏成就精彩,凭借切实努力实现梦想更有成就感(梦想因汗水而美丽),追求卓越(坚持高标准)才能真正成为龙(取得真正的成功);理想的实现应追求实质。
从过程与结果的关系看,有如下表述:夯实过程方可收获丰硕成果。
从“佛祖”的角度,可这样理解:不能因个人情感而改变评价标准,不能随意降低评价标准,选拔人才要坚守尺度。
从“龙门”的角度,可这样理解:降低了高度的龙门价值低下,真正的成功之门(人才选拔)不可能降低标准。
要注意的是,有些作文的题目乍一看似乎过于宽泛或扣题不紧,但文中有具体阐述。
如文章题目为“梅花香自苦寒来”,不太准确,但作文中写的是“为梦想切实努力”。
这样的主题、行文符合题意。
反之,题目看似很准,但行文中却有游离材料的明显表现。
二、优秀作文为梦想加冕如东高级中学高三班梁天晴当马丁路德振臂高呼“我有一个梦想”之时,这世纪的最强音已然为梦想构筑了辉煌的黄金台。
江苏省南通市2024-2025学年高三上学期10月调研考试 数学含答案

2024/2025学年度高三第一次调研测试数学(答案在最后)2025.09一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.命题“N x ∀∈,20x >”的否定为()A.N x ∀∈,20x ≤B.N x ∃∈,20x ≤C.N x ∃∈,20x > D.N x ∀∈,20x <2.已知集合{}2,Z A x x x =<∈,(){}2ln 3B x y x x ==-,则A B = ()A.{}02x x << B.{}23x x -<< C.{1}D.{0,1,2}3.已知点(3,4)P -是角α终边上一点,则cos2α=()A.725B.725-C.2425D.2425-4.已知函数()1,121,12xa x f x x x⎧⎛⎫+≤⎪ ⎪⎪⎝⎭=⎨⎪>⎪⎩在R 上单调递减,则实数a 的取值范围为()A.0a < B.12a >-C.102a -<< D.102a ≤<5.已知函数()f x 部分图象如图所示,则其解析式可能为()A.()()2ee xxf x x-=- B.()2()ee xxf x x-=+C.()()e exxf x x -=- D.()()e exxf x x -=+6.过点(3,1)作曲线ln(1)y x =-的切线,则这样的切线共有()A.0条B.1条C.2条D.3条7.锐角α、β满足sin cos()sin βαβα=+,若1tan 2α=,则cos()αβ+=()A.12B.2C.2D.2-8.若函数())2sin 20f x x x ωωω=->在π0,2⎛⎫⎪⎝⎭上只有一个零点,则ω的取值范围为()A.14,33⎛⎤ ⎥⎝⎦B.14,33⎡⎫⎪⎢⎣⎭C.17,66⎛⎤⎥⎝⎦D.17,66⎡⎫⎪⎢⎣⎭二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知011a b <<-<,则()A .01b << B.a b> C.1a b -< D.14ab <10.已知1x ,2x ,3x 是函数32()1f x x a x =-+的三个零点(0a >,123x x x <<),则()A.32a >B.120x x <<C .()()13f x f x ''= D.()()()1231110f x f x f x ''++='11.若定义在R 上的函数()f x 的图象关于点(2,2)成中心对称,且(1)f x +是偶函数,则()A.()f x 图象关于0x =轴对称B.(2)2f x +-为奇函数C.(2)()f x f x += D.20()42i f i ==∑三、填空题:本题共3小题,每小题5分,共15分.12.若函数()2sin cos 2x af x x +=-是奇函数,则π2f ⎛⎫= ⎪⎝⎭______.13.“1x y <<”是“ln ln x x y y <”的________条件.(选填“充分不必要、必要不充分、充要、既不充分也不必要”)14.班上共有45名学生,其中40人会打乒乓球,30人会骑自行车,25人会打羽毛球,则三个运动项目都会的同学至少有________人.四、解答题:本题共5小题,共77分.解答时应写出文字说明、证明过程或演算步骤.15.已知α、β为锐角,sin 10α=,1tan 3β=.(1)求tan 2α的值;(2)求2αβ+的大小.16.已知函数()e e 22x x f x x -=--+.(e 2.71828=⋅⋅⋅)(1)判断函数()2y f x =-的奇偶性并证明,据此说明()f x 图象的对称性;(2)若任意(1,)x ∈+∞,(ln )()4f m x f x +>,求实数m 的取值范围.17.若函数()()πcos 0,2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭图象的相邻对称轴距离为π2,且π162f ⎛⎫=- ⎪⎝⎭.(1)求()f x 的解析式;(2)将()f x 的图象向右平移5π12个单位,再将所得图象上每个点的横坐标变为原来的2倍(纵坐标不变)得到函数=的图象.当∈0,π时,求不等式()24g x g x ⎛⎫≤+ ⎪⎝⎭π的解.18.绿色、环保是新时代健康生活的理念,某一运动场馆投放空气净化剂净化场馆,已知每瓶空气净化剂含量为a ,投放后该空气净化剂以每小时10%的速度减少,根据经验,当场馆内空气净化剂含量不低于3a 时有净化效果,且至少需要持续净化12小时才能达到净化目的.现有9瓶该空气净化剂.(1)如果一次性投放该空气净化剂9瓶,能否达到净化的目的?如果能,说明理由;如果不能,最多可净化多长时间?(精确到0.1小时)(2)如果9瓶空气净化剂分两次投放,在第一次投放后间隔6小时进行第二次投放,为达到净化目的,试给出两次投放的所有可能方案?(每次投放的瓶数为整数,投放用时忽略不计)(参考数据:lg 30.477≈,60.90.53≈).19.已知函数2()2ln 1f x x ax =-+,0a ≥.(1)若()f x 的最大值为0,求a 的值;(2)若存在(,)k m n ∈,使得()()()()f n f m f k n m '-=-,则称k 为()f x 在区间(,)m n 上的“巧点”.(ⅰ)当0a =时,若1为()f x 在区间(,)m n 上的“巧点””,证明:2m n +>;(ⅱ)求证:任意0a >,()f x 在区间(,)m n 上存在唯一“巧点”k .2024/2025学年度高三第一次调研测试数学2025.09一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.【1题答案】【答案】B【2题答案】【答案】C【3题答案】【答案】B【4题答案】【答案】D【5题答案】【答案】A【6题答案】【答案】C【7题答案】【答案】B【8题答案】【答案】A二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.【9题答案】【答案】ACD【10题答案】【答案】ABD【11题答案】【答案】BD三、填空题:本题共3小题,每小题5分,共15分.【12题答案】【答案】1-【13题答案】【答案】充分不必要【14题答案】【答案】5四、解答题:本题共5小题,共77分.解答时应写出文字说明、证明过程或演算步骤.【15题答案】【答案】(1)724(2)π4.【16题答案】【答案】(1)奇函数,理由见解析,()f x 图像关于(0,2)中心对称(2)e m >-.【17题答案】【答案】(1)()πcos 23f x x ⎛⎫=+ ⎪⎝⎭(2)11π012x <≤【18题答案】【答案】(1)不能达到净化目的,最多可净化10.4小时;(2)第一次投放6瓶,第二次投放3瓶;或在第一次投放7瓶,第二次投放2瓶.【19题答案】【答案】(1)1a =(2)(ⅰ)证明见解析;(ⅱ)证明见解析。
专题:基本不等式常见题型归纳

专题函数常见题型归纳三个不等式关系:(1)a ,b ∈R ,a 2+b 2≥2ab ,当且仅当a =b 时取等号. (2)a ,b ∈R +,a +b ≥2ab ,当且仅当a =b 时取等号. (3)a ,b ∈R ,a 2+b 22≤(a +b2)2,当且仅当a =b 时取等号.上述三个不等关系揭示了a 2+b 2,ab ,a +b 三者间的不等关系. 其中,基本不等式及其变形:a ,b ∈R +,a +b ≥2ab (或ab ≤(a +b2)2),当且仅当a=b 时取等号,所以当和为定值时,可求积的最值;当积为定值是,可求和的最值.利用基本不等式求最值:一正、二定、三等号. 【题型一】利用拼凑法构造不等关系【典例1】(扬州市2015—2016学年度第一学期期末·11)已知1>>b a 且7log 3log 2=+a b b a ,则112-+b a 的最小值为 .【解析】∵1>>b a 且7log 3log 2=+a b b a ∴32log 7log a a b b +=,解得1log 2a b =或log 3a b =,∵1>>b a ∴1log 2a b =,即2a b =.2111111a ab a +=-++--13≥=. 练习:1.(南京市、盐城市2015届高三年级第一次模拟·10)若实数满足,且,则的最小值为 .解析:由log 2x+log 2y=1可得log 2xy=1=log 22,则有xy=2,那么==(x -y )+≥2=4,当且仅当(x -y )=,即x=+1,y=-1时等号成立,故的最小值为4.2.(苏北四市(徐州、淮安、连云港、宿迁)2017届高三上学期期末)若实数,x y 满足133(0)2xy x x +=<<,则313x y +-的最小值为 .3.(无锡市2017届高三上学期期末)已知0,0,2a b c >>>,且2a b +=,则2ac c c b ab +-+的最小值为 . 【典例2】(南京市2015届高三年级第三次模拟·12)已知x ,y 为正实数,则4x 4x +y +yx +y 的最大值为 .解析:由于4x 4x +y +y x +y =))(4()4()(4y x y x y x y y x x +++++=22225484y xy x yxy x ++++ =1+22543y xy x xy ++=1+345x y y x ⋅++≤1+5423+⋅xy y x =43,当且仅当4y x =xy,即y=2x 时等号成立. 【典例3】若正数a 、b 满足3ab a b =++,则a b +的最小值为__________. 解析:由,a b R +∈,得223(),()4()1202a b ab a b a b a b +=++≤+-+-≥,解得6a b +≥(当且仅当a b =且3ab a b =++,即3a b ==时,取等号).变式:1.若,a b R +∈,且满足22a b a b +=+,则a b +的最大值为_________.解析:因为,a b R +∈,所以由22222()2a b a b a b a b a b ++=+⇒+=+≥,2()a b +-2()0a b +≤,解得02a b <+≤(当且仅当a b =且22a b a b +=+,即1a b ==时,取等号).2.设0,0>>y x ,822=++xy y x ,则y x 2+的最小值为_______ 43.设R y x ∈,,1422=++xy y x ,则y x +2的最大值为_________10524.(苏北四市(淮安、宿迁、连云港、徐州)2017届高三上学期期中)已知正数a ,b 满足195a b+=,则ab 的最小值为 【题型二】含条件的最值求法【典例4】(苏州市2017届高三上期末调研测试)已知正数y x ,满足1=+y x ,则1124+++y x 的最小值为 练习1.(江苏省镇江市高三数学期末·14)已知正数y x ,满足111=+yx ,则1914-+-y yx x 的最小值为 . 解析:对于正数x ,y ,由于x 1+y 1=1,则知x>1,y>1,那么14-x x +14-y y =(14-x x +14-y y )(1+1-x 1-y 1)=(14-x x +14-y y )(xx 1-+y y 1-)≥(x x x x 114-⋅-+yy y y 114-⋅-)2=25,当且仅当14-x x ·y y 1-=14-y y ·xx 1-时等号成立.2.(2013~2014学年度苏锡常镇四市高三教学情况调查(一)·11)已知正数满足,则的最小值为 .解析:,当且仅当时,取等号.故答案为:9.3.(南通市2015届高三第一次调研测试·12)已知函数(0)xy a b b =+>的图像经过点(1,3)P ,如下图所示,则411a b+-的最小值为 .解析:由题可得a+b=3,且a>1,那么14-a +b 1=21(a -1+b )(14-a +b 1)=21(4+b a 1-+14-a b +1)≥21(2141-⋅-a b b a +5)=29,当且仅当b a 1-=14-a b 时等号成立. 4.(江苏省苏北四市2015届高三第一次模拟考试·12)己知a ,b 为正数,且直线 与直线 互相平行,则2a+3b 的最小值为________.【解析】由于直线ax+by -6=0与直线2x+(b -3)y+5=0互相平行,则有=,即3a+2b=ab ,那么2a+3b=(2a+3b )·=(2a+3b )(+)=++13≥2+13=25,当且仅当=,即a=b 时等号成立.5.常数a ,b 和正变量x ,y 满足ab =16,a x +2b y =12.若x +2y 的最小值为64,则a b=________.答案:64;(考查基本不等式的应用).6.已知正实数,a b 满足()()12122a b b b a a +=++,则ab 的最大值为 .答案:【题型三】代入消元法【典例5】(苏州市2016届高三调研测试·14)已知14ab =,,(0,1)a b ∈,则1211ab+--的最小值为 .解析:由14ab =得14a b = ,2221211424122711411451451a b b b b b b b b b b b +---+--=+==+---+--+- 令71b t -=则22714949111418451427183427b t b b t t t t-+=+=-≥+-+--+-+-当且仅当2t =即214等号成立.练习1.(江苏省扬州市2015届高三上学期期末·12)设实数x ,y 满足x 2+2xy -1=0,则x 2+y 2的最小值是 .解析:由x 2+2xy -1=0可得y=212x x -,那么x 2+y 2= x 2+222(1)4x x -=54x 2+214x -12≥21212,当且仅当54x 2=214x ,即x 4=15时等号成立.2.(苏州市2014届高三调研测试·13)已知正实数x ,y 满足,则x + y 的最小值为 . 解析:∵正实数x ,y 满足xy+2x+y=4,∴(0<x <2).∴x+y=x+==(x+1)+﹣3,当且仅当时取等号.∴x+y 的最小值为.故答案为:.3.(南通市2014届高三第三次调研测试·9)已知正实数,x y 满足(1)(1)16x y -+=,则x y +的最小值为 .解析:∵正实数x ,y 满足(x ﹣1)(y+1)=16,∴1116++=y x ,∴x+y=()8116121116=+⋅+≥+++y y y y ,当且仅当y=3,(x=5)时取等号.∴x+y 的最小值为8.故答案为:8.4.(扬州市2017届高三上学期期中)若2,0>>b a ,且3=+b a ,则使得214-+b a 取得最小值的实数a = 。
集合的基本运算

考点2 集合的基本运算1. (15泰州一模)已知{}1,3,4A =,{}3,4,5B =,则A B =. 【考点】交集及其运算.【答案】{}3,4【分析】{}1,3,4A =,{}3,4,5B =, {}3,4A B ∴= .2. (江苏2015高考冲刺压轴卷二)已知集合{}2|20A x x x =--<,(){}|ln 1B x y x ==-,则A B = .【考点】本题考查集合、一元二次不等式的计算及对数函数的性质.【答案】{}|11x x -<<【分析】∵{}{}2|20|12A x x x x x =--=-<<<,(){}{}|ln 1|1B x y x x x ==-=<, ∴{}|11A B x x =- <<.3. (2015江苏高考冲刺压轴卷(三))设集合S ={x ∈N |0<x <6},T ={4,5,6},则S ∩T =.【考点】集合的交集运算.【答案】{}4,5【分析】S ={1,2,3,4,5},所以S ∩T ={}4,5. 4. (2015高考冲刺压轴卷(江苏)试卷一)已知集合{}{}1,2,4,,4A B a ==,若{}1,2,3,4A B = ,则A B = ________.【考点】集合的并集、交集运算.【答案】{}4【分析】根据{}1,2,4A =,{},4B a =,{}{}1,2,3,434A B a A B =⇒=⇒= . 5. (江苏省淮安市淮阴区南陈集中学2015届高三上学期10月调考数学试卷)已知集合2{|320}A x x x =-+≤,{}|1B x x =>,则集合A B = ________.【考点】集合的交集运算.【答案】{|12}x x <≤【分析】由A 中方程变形得:(1)(2)0x x --≤,解得:12x ≤≤,即{|12}A x x =≤≤; 由B 中方程解得:1x -<或1x >,即{|1B x x =-<或1}x >,则{|12}A B x x =< ≤. 6. (江苏省淮安市淮阴区南陈集中学2015届高三上学期10月调考数学试卷)已知[]2,2,4x y x =∈的值域为集合A ,22log (3)2(1)y x m x m ⎡⎤=-++-+⎣⎦定义域为集合B ,其中1m ≠.(1)当m =4,求A B ;(2)设全集为R ,若A B ⊆R ð,求实数m 的取值范围.【考点】交集及其运算,集合的包含关系判断及应用,对数函数的定义域.【解】(1)∵[]2,2,4xy x =∈的值域为[]4,16A =, 当m =4,27100x x -+->,解得(2,5)B =,∴[)4,5A B = .(2)若m >1,则{|2B x x =R ≤ð或1}x m +≥∴1413m m +⇒<≤≤.若m <1,则{|1B x x m =+R ≤ð或2}x ≥,此时A B ⊆R ð成立.综上所述,实数m 的取值范围为(,1)(1,3)-∞ . 7. (江苏省南通市2015届高三第一次模拟考试数学试题)已知集合{21}A =--,,{123}B =-,,,则A B = ________.【考点】集合的交集运算.【答案】{}1-【分析】∵集合{21}A =--,,{123}B =-,,,∴{}1A B =- . 8. (淮安都梁中学2015届高三10月调研)已知集合{}1,3,A m =,{}3,4B =,{}1,2,3,4A B = ,则m = .【考点】并集及其运算【答案】2【分析】因为{}1,2,3,4A B = ,因为B 中元素为3,4,所以A 中必然要有2,所以得到m 的值为2.9. (2015江苏省盐城市响水中学高三上调研)已知集合A ={y |y =12x,x ∈R };B ={y |2log 1y x=(-),x ∈R },则A ∩B = . 【考点】交集及其运算.【答案】(0,+∞) 【分析】由集合A ={y | y =12x ,x ∈R },可得A ={y |y >0},由B ={y|2log 1y x =(-),x ∈R },可得B ={y |y ∈R },∴A ∩B ={y |y >0},故答案为:(0,+∞). 10. (15江苏模拟(三))已知集合A ={1,2,3,4,5},集合B ={x |x <a },其中a ∈Z ,若A B={1,2},则a = .【答案】3 【分析】由A ={1,2,3,4,5},A B={1,2}可得{1,2}⊆B ,又因为a ∈Z ,所以a =3. 11.(15江苏高考压轴)已知集合{}1,0,3A =-,集合{}2B x y x ==-,则A B = .【答案】{}1,0-【分析】{}{}{}2202B x y x x x x x ==-=-=≥≤,又{}103A =-,,所以{}10A B =- ,12. (15南通海门包场9月调研)已知集合A ={-1,3,2m -1},B ={3,2m },且A ∩B =B ,那么实数m = .【考点】交集及其运算.【答案】1【分析】由A ∩B =B ,得B ⊆A .又A ={-1,3,2m -1},B ={3,2m },∴2m =2m -1,解得m =1.此时集合A 有意义. 13. (15南通海门包场9月调研)设全集U =R ,f (x )=2x +3x +2,g (x )=2x +(m +1)x +m ,m ∈R .(1)设集合A={x|f(x)=0},B={x|g(x)=0}.若(U Að)∩B=∅,求m的值.(2)设集合P={y|y=f(x)},Q={m|g(x)在区间[-1,+∞)上是增函数},求P∩Q.【考点】交、并、补集的混合运算.【解】(1)∵集合A={x|f(x)=0},B={x|g(x)=0}.∴A={-1,-2},-1∈B,-m∈B,若(U Að)∩B=∅,则-m∈A,即m=1或m=2,(2)∵集合P={y|y=f(x)}=[-14,+∞),Q={m|g(x)在区间[-1,+∞)上是增函数}={m|112m+--≤}=[1,+∞),∴P∩Q=[1,+∞).14. (15南通市直调考)已知集合A={-2,-1},B={-1,2,3},则A∪B= .【考点】并集及其运算.【答案】{-2,-1,2,3}【分析】集合A={-2,-1},B={-1,2,3},则A∪B={-2,-1,2,3}.15. (15连云港赣榆海头9月调研)已知集合A={-2,-1,0,1,2},集合B={x|2x<1},则A∩B= .【考点】交集及其运算.【答案】{0}【分析】∵集合A={-2,-1,0,1,2},集合B={x|2x<1}={x|-1<x<1},∴A∩B={0}.16. 设函数f(x)=2x-2ax-82a(a>0),记不等式f(x)≤0的解集为A.(1)当a=1时,求集合A;(2)若(-1,1)⊆A,求实数a的取值范围.【考点】集合的包含关系判断及应用.【解】(1)当a=1时,f(x)=2x-2x-8,由不等式2x-2x-8≤0,化为(x-4)(x+2)≤0,解得﹣2≤x≤4,∴集合A={x|-2≤x≤4}.(2)∵2x-2ax-82a≤0,∴(x-4a)(x+2a)≤0,又∵a>0,∴-2a≤x≤4a,∴A=[-2a,4a].又∵(-1,1)⊆A,∴1214a a--⎧⎨⎩≥≤,解得12a ≥, ∴实数a 的取值范围是1+2⎡⎫∞⎪⎢⎣⎭,.17.(15淮安市金湖中学高三上学期第一次学情检测数学试卷)若集合A ={x |y =1x -},B ={y |22y x =+},则A ∩B = .【考点】交集及其运算.【答案】[2,+∞)【分析】因为A ={x |y =1x -},B ={y |22y x =+},则A ={x |x ≥1},B ={y |y ≥2} 所以A ∩B =B ;故答案为:[2,+∞).18. (15江阴市高三上学期月考数学试卷)已知全集U ={1,2,3,4},集合A ={l ,2,3},B ={2,3,4},则U AB (∩)ð= . 【考点】交、并、补集的混合运算.【答案】{1,4}【分析】∵全集U ={1,2,3,4},集合A ={l ,2,3},B ={2,3,4},∴A ∩B ={2,3},则U AB (∩)ð={1,4}. 故答案为:{1,4}.19.(15南京市湖滨中学高三上学期10月学情检测数学试卷)已知集合A ={1},B ={1,9},则A ∪B = .【考点】并集及其运算.【答案】{1,9}【分析】∵A ={1},B ={1,9},∴A ∪B ={1,9}.20.(15南通市如东县栟茶高级中学高三上学期第二次学情调研)若集合A ={0,1},集合B ={0,-1},则A B = ________.【考点】并集及其运算.【答案】{-1,0,1}【分析】A B = {-1,0,1}.21. (15宿迁市沭阳县银河学校高三上学期开学试卷)若A ={x ∈Z |2≤2x ≤16},B ={3,4,5},则A ∩B = .【考点】指数函数单调性的应用;交集及其运算.【答案】{3,4}【分析】∵A={x∈Z|2≤2x≤16}={x∈Z|1≤x≤4}={1,2,3,4},B={3,4,5},∴A∩B={3,4}.22.(15无锡市高三上学期期中试卷)已知全集U={1,3,5,7,9},A={1,5,9},B={3,C(A∪B)的子集个数为______.5,9},则U【考点】交、并、补集的混合运算;子集.【答案】2【分析】∵A={1,5,9},B={3,5,9},∴A∪B={1,3,5,9},C(A∪B)={7},∵全集U={1,3,5,7,9}∴UC(A∪B)的子集个数为2个.则U23.(15南京一中等五校联考)已知集合M={x|x<1},N={x|lg(2x+1)>0},则M∩N=______.【考点】交集及其运算.【答案】(0,1)【分析】N={x|lg(2x+1)>0}={x|2x+1>1}={x|x>0},∵M={x|x<1},∴M∩N={x|0<x<1}=(0,1),故答案为:(0,1)。
江苏省南通市高级中学2014-2015学年高三一模 数学试卷

江苏省南通市高级中学2014-2015学年高三一模数学试卷 试题Ⅰ注 意 事 项一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上. 1. 已知集合{}1 3 5 9U =,,,,{}1 3 9A =,,,{}1 9B =,,则()U C A B = ▲ .2. 若9z z ⋅=(其中z 表示复数z 的共轭复数),则复数z 的模为 ▲ . 3. 已知函数()af x x =在1x =处的导数为2-,则实数a 的值是 ▲ . 4. 根据国家质量监督检验检疫局发布的《车辆驾驶人员血液、呼气酒精含量阈值与检验》 (GB19522—2004)中规定车辆驾驶人员血液酒精含量:“饮酒驾车”的临界值为20mg/100ml ;“醉酒驾车”的临界值为80mg/100ml .某地区交通执法部门统计了5月份的执法记录数据:根据此数据,可估计该地区5月份“饮酒驾车” 发生的频率等于 ▲ .5. 要得到函数sin 2y x =的函数图象,可将函数()πsin 23y x =+的图象向右至少平移 ▲ 个单位.6.在平面直角坐标系xOy 中,“直线y x b=+,b ∈R与曲线x =”的充要条件是“ ▲ ”.7. 如图,i N 表示第i 个学生的学号,i G 表示第i 个学生的成绩,已知学号在1~10的学生的成绩依次为401、392、385、359、 372、327、354、361、345、337,则打印出的第5组数据是 ▲ .8. 在△ABC 中,若tan :A tan :tan 1:2:3B C =,则A = ▲ . 9. 已知()y f x =是R 上的奇函数,且0x >时,()1f x =,则不等式2()(0)f x x f -<的解集为 ▲ . 10.设正四棱锥的侧棱长为1,则其体积的最大值为 ▲ . 11.已知平面向量a ,b ,c 满足1=a ,2=b ,a ,b 的夹角等于π,且()()0-⋅-=a c b c ,则c的取值范围是 ▲ .12.在平面直角坐标系xOy 中,过点11( 0)A x ,、22( 0)A x ,分别作x 轴的垂线与抛物线22x y =分别交于点12A A ''、,直线12A A ''与 x 轴交于点33( 0)A x ,,这样就称12x x 、确定了3x .同样,可由23x x 、确定4x ,…,若12x =,23x =,则5x = ▲ .13.定义:min {x ,y}为实数x ,y 中较小的数.已知{}22min 4b h a a b =+,,其中a ,b 均为正实数,则h 的最大值是 ▲ .14.在平面直角坐标系xOy 中,直角三角形ABC 的三个顶点都在椭圆2221 (1)x y a a +=>上,其中0 1A (,)为直角顶点.若该三角形的面积的最大值为278,则实数a 的值为 ▲ .二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本题满分14分)已知函数()()2ππ()sin cos sin sin f x x x x x x x =+++-∈R,. (1)求()f x 的最小正周期和值域;(2)若x x =()0π2x ≤≤为()f x 的一个零点,求0sin 2x 的值.16.(本题满分14分)如图,在边长为1的菱形ABCD 中,将正三角形BCD 沿BD 向上折起,折起后的点C(第7题)记为C ',且CC a '=(0a <<).(1)若a ,求二面角C —BD —C '的大小; (2)当a 变化时,线段CC '上是否总存在一点 E ,使得A C '//平面BED ?请说明理由.17.(本题满分15分)在平面直角坐标系xOy 中,设A 、B 是双曲线2212y x -=上的两点,(12)M ,是线段AB 的中点,线段AB 的垂直平分线与双曲线相交于C 、D 两点. (1)求直线AB 与CD 的方程;(2)判断A 、B 、C 、D 四点是否共圆?若共圆,请求出圆的方程;若不共圆,请说明理由. 18.(本题满分15分)某省高考数学阅卷点共有400名阅卷老师,为了高效地完成文、理科数学卷的阅卷任务,需将400名阅卷老师分成两组同时展开阅卷工作,一组完成269捆文科卷,另一组完成475捆理科卷.根据历年阅卷经验,文科每捆卷需要一位阅卷老师工作3天完成,理科每捆卷需要一位阅卷老师工作4天完成.(假定每位阅卷老师工作一天的阅卷量相同,每捆卷的份数也相同)(1)如何安排文、理科阅卷老师的人数,使得全省数学阅卷时间最省?(2)由于今年理科阅卷任务较重,理科实际每捆卷需要一位阅卷老师工作4.5天完成,在按(1)分配的人数阅卷4天后,阅卷领导小组决定从文科组抽调20名阅卷老师去阅理科卷,试问完成全省数学阅卷任务至少需要多少天?(天数精确到小数点后第3位)(参考数据:807 6.782119≈,95 6.78614≈,331 3.34399≈,1013.5 3.367301≈)19.(本题满分16分) 已知函数()f x 的导函数()f x '是二次函数,且()0f x '=的两根为1±.若()f x 的极大值与极小值 之和为0,(2)2f -=.(1)求函数()f x 的解析式;(第16题)D C 'A BC(2)若函数在开区间(99)m m --,上存在最大值与最小值,求实数m 的取值范围. (3)设函数()()f x x g x =⋅,正实数a ,b ,c 满足()()()0ag b bg c cg a ==>,证明:a b c ==.20.(本题满分16分) 设首项为1的正项数列{}n a的前n 项和为n S ,数列{}2na 的前n 项和为n T ,且24()3n n S p T --=,其中p 为常数.(1)求p 的值;(2)求证:数列{}n a为等比数列;(3)证明:“数列n a ,12x n a +,22y n a +成等差数列,其中x 、y 均为整数”的充要条件是“1x =,且2y =”.试题Ⅱ(附加题) 21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A .(几何证明选讲)如图,AB 是半圆的直径,C 是AB 延长线上一点,CD 切 半圆于点D ,CD=2,DE ⊥AB ,垂足为E ,且E 是OB 的 中点,求BC 的长. B .(矩阵与变换)已知矩阵122a ⎡⎤⎢⎥⎣⎦的属于特征值b 的一个特征向量为11⎡⎤⎢⎥⎣⎦,求实数a 、b 的值.C .(极坐标与参数方程)在平面直角坐标系xOy 中,已知点(1 2)A -,在曲线22 2 x pt y pt ⎧=⎪⎨=⎪⎩,(t 为参数,p 为正常数),求p 的值.D .(不等式选讲)设123 a a a ,,均为正数,且1231a a a ++=,求证:1231119.a a a ++≥【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.22.已知函数2()2(1)ln(1)2f x x x x x =++--,[)0x ∈+∞,,求()f x 的最大值.23.(1)已知*k n ∈N 、,且k n ≤,求证:11C C k k n n k n --=;(2)设数列0a ,1a ,2a ,…满足01a a ≠,112i i i a a a -++=(i =1,2,3,…).证明:对任意的正整数n ,011222012()C (1)C (1)C (1)C n n n n nn n n n n p x a x a x x a x x a x --=-+-+-+⋅⋅⋅+是 关于x 的一次式.南通市数学一模试卷 参考答案1.{}5; 2. 3; 3. 2; 4. 0.09; 5.π6; 6. b =; 7. 8361,;8. π4;9. (01),; 10. ; 11. ⎣⎦; 12. 1; 13. 1; 14. 3. 答案解析 1.易得{}1 3 9A B A ==,,U ,则()U A B =U ð{}5;2.3z =;3. 易得2()af x x '=-,则(1)2f a '=-=-,即2a =; 4. “饮酒驾车” 发生的频率等于11520.09200++=;5. 将()()πsin 2sin 23y x x π=+=+6向右至少平移π6个单位得sin 2y x =;6. 1=,且0b <,即b =7. 打印出的第5组数据是学号为8号,且成绩为361,故结果是8361,; 8. 设tan A k=,则t a n B k=,tan 3C k=,且k >,利用t an t a n t a n t a n ()1t a n t a nA B C A B A B +=-+=--可 求得1k =,所以A π=;9. 易得(0)0f =,20x x -<,故所求解集为(0 1),; 10. 法 1 设正四棱锥的底面边长为x ,则体积13V x =,记()22y t t =-,0t >,利用导数可求得当43t =时,max 3227y=,此时max V =; 法2 设正四棱锥的侧棱与底面所成角为θ,则()22122cos sin 1sin sin 33V θθθθ=⨯⨯=-⨯,0<θπ<,记()21 01y t t t =-<<,,利用导数可求得当t =时,max y =,此时max V ;15.命题立意:本题主要考查三角函数的图像与性质、两角和与差的正、余弦公式,考查运算求解 能力.(1)易得()2221()sin 2sin cos 2f x x x x x =+-1cos212cos222x x x -=+- 1s i n 2c o s 22x x =-+=()π12sin 262x -+,(5分)所以()f x 周期π,值域为35 ⎡⎤-⎢⎥⎣⎦,;(7分)(2)由()00π1()2sin 2062f x x =-+=得()0π1sin 2064x -=-<,(9分) 又由0π02x ≤≤得02ππ5π666x ≤≤--,所以02ππ0 66x ≤≤--,故()0πcos 26x -=,(11分)此时,()00ππsin 2sin 266x x ⎡⎤=-+⎢⎥⎣⎦()()00ππππsin 2cos cos 2sin 6666x x =-+-1142=-.(14分)O AB2CM 1C(第11题图)16.命题立意:本题主要考查直线与平面、平面与平面的位置关系,考查空间想象、推理论证能力.解:(1)连结AC ,交BD 于点O ,连结OC ', 菱形ABCD 中,CO BD ⊥,因三角形BCD 沿BD 折起,所以C O BD '⊥, 故C OC '∠为二面角C —BD —C '的平面角,(5分)易得C O CO '==CC '= 所以C OC π'∠=3,二面角C —BD —C '的大小为π3;(7分)(2)当a 变化时,线段CC '的中点E 总满足A C '//平面BED ,下证之:(9分) 因为E ,O 分别为线段CC ',AC 的中点, 所以//OE AC ',(11分) 又AC '⊄平面BED ,OE ⊂平面BED , 所以A C '//平面BED. (14分) 17.命题立意:本题主要考查求双曲线、直线、圆等基础知识,考查运算求解与探究能力.解:(1)设A 11()x y ,,则11(24)B x y --,, 代入双曲线2212y x -=得2211221112(4)(2)12y x y x ⎧-=⎪⎪⎨-⎪--=⎪⎩,,解得110x y ⎧⎨=⎩=-1,或1134x y =⎧⎨=⎩,, 即A B 、的坐标为10-(,)、34(,),所以AB :1y x =+,CD :3y x =-+;(7分)(2)A 、B 、C 、D 四点共圆,下证之:(9分)证明:由3y x =-+与221y x -=联立方程组可得C D 、的坐标为(36--+、(36-+-,(11分)由三点A 、B 、C 可先确定一个圆22(3)(6)40x y ++-=①,(13分)经检验(36D -+-适合①式,所以A 、B 、C 、D 四点共圆.(15分)(注:本题亦可以利用圆的几何性质判断四点共圆)(第16题图)DC 'ABCOE18.命题立意:本题主要考查数学建模和解决实际问题的能力,考查运算求解能力. 解:(1)设文科阅卷人数为x ,且x ∈*N ,则阅卷时间为2693119.246()4754119.246400x x f x x x ⨯⎧⎪=⎨⨯⎪>-⎩≤,,,,(5分) 而(119) 6.782f =,(120) 6.786f =,故(119)(120)f f <,答:当文、理科阅卷人数分别是119,281时,全省阅卷时间最省;(8分)(2)文科阅卷时间为:1269311943347.34399⨯-⨯⨯⨯+=,(11分) 理科阅卷时间为:1475 4.52814 4.54.547.367301⨯-⨯⨯⨯+=,(14分) 答:全省阅卷时间最短为7.367天.(15分)19.命题立意:本题主要考查利用导数研究三次函数的图像与性质等基础知识,考查灵活运用数形解:(1)设()(1)(1)f x a x x '=+-,则可设()3()3x f x a x c=-+,其中c 因为()f x 的极大值与极小值之和为0, 所以(1)(1)0f f -+=,即0c =,由(2)2f -=得3a =-,所以3()3f x x x =-;(5分)(2)由(1)得3()3f x x x =-,且()3(1)(1)f x x x '=-+-列表:由题意得,三次函数在开区间上存在的最大值与最小值必为极值(如图),(7分) 又(2)2f -=,故(2)2f =-, 所以192m <-≤,且291m --<-≤,x (21)--,1- (11)-, 1 (12),y '- 0 + 0 - y ↘ 极小值2- ↗ 极大值2 ↘解得78m <≤;(10分)(3)题设等价与222(3)(3)(3)a b b c c a -=-=-,且a ,b ,c >0,所以a ,b ,c假设在a ,b ,c 中有两个不等,不妨设a ≠b ,则a >b 或a <b .若a >b ,则由22(3)(3)a b b c -=-得2233b c -<-即b c >, 又由22(3)(3)b c c a -=-得c >a . 于是a >b >c >a ,出现矛盾.同理,若a <b ,也必出现出矛盾. 故假设不成立,所以a b c ==.(16分)20.命题立意:本题主要考查等差、等比数列的定义与通项公式、求和公式等基础知识,考查灵活运用基本量进行探索求解、推理分析能力.解:(1)n = 1时,由24(1)13p --=得p = 0或2,(2分) 若p = 0时,243n n S T -=, 当2n =时,22224(1)13a a -++=,解得20a =或212a =-, 而0n a >,所以p = 0不符合题意,故p = 2;(5分)(2)当p = 2时,241(2)33n n T S =-- ①,则21141(2)33n n T S ++=--②,②-①并化简得1134n n n a S S ++=-- ③,则22134n n n a S S +++=-- ④, ④-③得2112n n a a ++=(n *∈N ),又易得2112a a =, 所以数列{an}是等比数列,且112n na -=;(10分) (3)充分性:若x = 1,y = 2,由112n n a -=知n a ,12x n a +,22yn a +依次为112n -,22n ,142n +,满足112142222n nn -+⨯=+,即an ,2xan +1,2yan +2成等差数列;(12分)必要性:假设n a ,12xn a +,22yn a +成等差数列,其中x 、y 均为整数,又112n na -=,所以11111222222x y n nn -+⋅⋅=+⋅, 化简得2221x y --=显然2x y >-,设(2)k x y =--,因为x 、y 均为整数,所以当2k ≥时,2221x y -->或2221x y --<,故当1k =,且当1x =,且20y -=时上式成立,即证. (16分)21.A .命题立意:本题主要考查三角形、圆的有关知识,考查推理论证、运算求解能力. 解:连接OD ,则OD ⊥DC , 在Rt △OED 中,12OE =OB 12=OD , 所以∠ODE =30°,(5分)在Rt △ODC 中,∠DCO =30°,由DC =2得OD =DCtan30°=,所以BC =.(10分)B .命题立意:本题主要考查二阶矩阵的特征值与特征向量,考查运算求解能力.解:由二阶矩阵的特征值与特征向量的概念知122a ⎡⎤⎢⎥⎣⎦11⎡⎤⎢⎥⎣⎦=11b ⎡⎤⎢⎥⎣⎦,(5分)所以3 2 b b a =⎧⎨=+⎩,,解得1 3a b ==,.(10分) C .命题立意:本题主要考查参数方程,考查运算求解能力.解:由22 2 x pt y pt ⎧=⎪⎨=⎪⎩,,(t 为参数,p 为正常数),消去参数t 得22y px =,(8分)将点(1 2)A -,代入22y px =得2p =.(10分)D .命题立意:本题主要考查证明不等式的基本方法,考查推理论证能力. 证明:因为a1,a2,a3均为正数,且12310a a a ++=>,所以123111a a a ++()123123111()a a a =++++()()11123123111339a a a a a a ⋅=≥,(8分)当且仅当12313a a a ===时等号成立,所以1239111a a a ++≥.(10分)22.命题立意:本题主要考查复合函数求导等知识,考查运算求解、推理论证能力.证明:由2()2(1)ln(1)2f x x x x x =++--得()2ln(1)2f x x x '=+-,(2分)令()2ln(1)2g x x x =+-,则22()211x g x x x -'=-=++, 当10x -<<时,()0g x '>,()g x 在(1 0)-,上为增函数; 当x >0时,()0g x '<,()g x 在(0)+∞,上为减函数, 所以()g x 在x=0处取得极大值,且(0)0g =,(6分)故()0f x '≤(当且仅当0x =时取等号),所以函数()f x 为[)0+∞,上的减函数,(8分)则()(0)0f x f =≤,即()f x 的最大值为0.(10分)23.命题立意:本题主要考查组合数的性质、二项式定理,考查推理论证能力.(1)证明:左边!!C !()!(1)!()!k n n n k k k n k k n k ==⋅=---, 右边(1)!!(1)!()!(1)!()!n n n k n k k n k -=⋅=----,所以11C C k k n n k n --=;(3分)(2)证明:由题意得数列0a ,1a ,2a ,…为等差数列,且公差为100a a -≠.(5分)则011222012()C (1)C (1)C (1)C n n n n n n n n n n p x a x a x x a x x a x --=-+-+-+⋅⋅⋅+[][]0110010010C (1)+()C (1)+()Cn n n n n n n a x a a a x x a n a a x -=-+--+⋅⋅⋅+- 01111222010C (1)C (1)C ()C (1)+2C (1)C n n n n n n n n n n n n n n a x x x x a a x x x x n x ---⎡⎤⎡⎤=-+-+⋅⋅⋅++---+⋅⋅⋅+⎣⎦⎣⎦[]011211010111(1)()C (1)+C (1)C n n n n n n n n a x x a a n x x x x x -------⎡⎤=-++---+⋅⋅⋅+⎣⎦ []1010()(1)n a a a n x x x -=+-+-010()a a a nx =+-, 所以对任意的正整数n ,()p x 是关于x 的一次式.(10分)。
江苏省南通市2015届高三第一次调研考试物理试题 Word版含答案

南通市2015届高三第一次调研测试物 理一、单项选择题.本题共5小题,每小题3分,共计15分.每小题只有一个选项符合题意. 1.如图所示的电路中,电源内阻不可忽略,R 为半导体热敏电阻,其阻值随温度的升高而减小.当R 所在位置温度升高时A .灯泡L 1变亮B .灯泡L 2变亮C .电压表读数增大D .电源内阻消耗功率减小 2.如图所示,小船沿直线AB 过河,船头始终垂直于河岸.若水流速度增大,为保持航线不变,下列措施与结论正确的是A .增大船速,过河时间不变B .增大船速,过河时间缩短C .减小船速,过河时间变长D .减小船速,过河时间不变3.如图所示,a 、b 都是较轻的铝环,a 环闭合,b 环断开,横梁可以绕中间支点自由转动,开始时整个装置静止.下列说法中正确的是 A .条形磁铁插入a 环时,横梁不会发生转动B .只有当条形磁铁N 极拔出铝环时,横梁才会转动C .条形磁铁用相同方式分别插入a 、b 环时,两环转动情况相同D .铝环a 产生的感应电流总是阻碍铝环与磁铁间的相对运动4.如图所示,两个带等量正电荷的相同小球,固定在绝缘、粗糙的水平面上A 、B 两点,O 是AB 的中点.带正电的小滑块从C 点由静止释放,在电场力作用下向右点运动,则滑块从C 点运动到O 点的过程中A .电势能不断增大B .电场力先做正功后做负功C .加速度不断减小D .速度先增大后减小5.如图所示,AB 、AC 两光滑细杆组成的直角支架固定在竖直平面内,AB 与水平面的夹角为30°,两细杆上分别套有带孔的a 、b 两小球,在细线作用下处于静止状态,细线恰好水平.某时刻剪断细线,在两球下滑到底端的过程中,下列结论中正确的是 A .a 、b 两球到底端时速度相同B .a 、b 两球重力做功相同C .小球a 下滑的时间大于小球b 下滑的时间D .小球a 受到的弹力小于小球b 受到的弹力二、多项选择题.本题共4小题,每小题4分,共计16分.每小题有多个选项符合题意.全部选对的得4分,选对但不全的得2分,错选或不答的得0分.6.某兴趣小组自制一小型发电机,使线圈在匀强磁场中绕垂直于磁场方向的固定轴转动,穿过线圈的磁通量Φ随时间t 按正弦规律变化的图象如图所示,线圈转动周期为T ,线圈产生的电动势的最大值为E m .则A .在4Tt 时,磁场方向与线圈平面垂直第3题图 第1题图第2题图第4题图 B C第5题图 第6题图ΦB .在2Tt =时,线圈中的磁通量变化率最大 C .线圈中电动势的瞬时值2sin()m te E Tπ= D .若线圈转速增大为原来的2倍,则线圈中电动势变为原来的4倍7.我国研制并成功发射了“嫦娥二号”探月卫星.若卫星在距月球表面高度为h 的轨道上以速度v 做匀速圆周运动,月球的半径为R ,则A .卫星运行时的向心加速度为hR v +2 B .卫星运行时的角速度为h R v+C .月球表面的重力加速度为Rh R v )(2+ D .卫星绕月球表面飞行的速度为R hR v +8.一汽车以速度v 0在平直路面上匀速行驶,在t =0时刻将汽车发动机的输出功率调为另一个恒定值,设汽车行驶过程中受到的阻力恒定不变.从t =0时刻开始,汽车运动的v -t 图象可能正确的有9.如图所示,直角坐标系xOy 位于竖直平面内,y 轴竖直向上.第Ⅲ、Ⅳ象限内有垂直于坐标面向外的匀强磁场,第Ⅳ象限同时存在方向平行于y 轴的匀强电场(图中未画出).一带电小球从x 轴上的A 点由静止释放,恰好从P 点垂直于y 轴进入第Ⅳ象限,然后做圆周运动,从Q 点垂直于x 轴进入第Ⅰ象限,Q 点距O 点的距离为d ,重力加速度为g .根据以上信息,可以求出的物理量有 A .圆周运动的速度大小 B .电场强度的大小和方向 C .小球在第Ⅳ象限运动的时间D .磁感应强度大小三、简答题:本题分必做题(第lO 、11题)和选做题(第12题)两部分,共计42分.请将解答填写在答题卡相应的位置. 必做题 10.(8分)小张和小明测绘标有“3.8 V 0.4 A ”小灯泡的伏安特性曲线,提供的实验器材有:A .电源E (4 V ,内阻约0.4 Ω)B .电压表V (2 V ,内阻为2 kΩ)C .电流表A (0.6 A ,内阻约0.3 Ω)D .滑动变阻器R (0~10Ω)E .三个定值电阻(R 1 =1kΩ,R 2=2kΩ,R 3=5kΩ)F .开关及导线若干(1)小明研究后发现,电压表的量程不能满足实验要求,为了完成测量,他将电压表进行了改装.在给定的定值电阻中选用 ▲ (选填“R 1”、“R 2”或“R 3”)与电压表 ▲ (选填 “串联”或“并联”),完成改装.v vv ABCDv第9题图(2)小张选好器材后,按照该实验要求连接电路,如图所示(图中电压表已经过改装).闭合开关前,小明发现电路中存在两处不恰当的地方,分别是: ① ▲ ;② ▲ .(3)正确连接电路后,闭合开关,移动滑动变阻器的滑片P ,电压表和电流表的示数改变,但均不能变为零.由此可以推断电路中发生的故障可能是导线 ▲ (选填图中表示导线的序号)出现了 ▲ (选填“短路”或“断路”).11.(10分)为了测量小滑块与水平桌面间的动摩擦因数,某小组设计了如图甲所示的实验装置,其中挡板可固定在桌面上,轻弹簧左端与挡板相连,图中桌面高为h ,O 1、O 2、A 、B 、C 点在同一水平直线上.已知重力加速度为g ,空气阻力可忽略不计.实验过程一:挡板固定在O 1点,推动滑块压缩弹簧,滑块移到A 处,测量O 1A 的距离,如图甲所示.滑块由静止释放,落在水平面上的P 点,测出P 点到桌面右端的水平距离为x 1;实验过程二:将挡板的固定点移到距O 1点距离为d 的O 2点,如图乙所示,推动滑块压缩弹簧,滑块移到C 处,使O 2C 的距离与O 1A 的距离相等.滑块由静止释放,落在水平面上的Q 点,测出Q 点到桌面右端的水平距离为x 2.(1)为完成本实验,下列说法中正确的是 ▲ .A .必须测出小滑块的质量B .必须测出弹簧的劲度系数C .弹簧的压缩量不能太小D .必须测出弹簧的原长(2)写出动摩擦因数的表达式μ= ▲ (用题中所给物理量的符号表示).(3)小红在进行实验过程二时,发现滑块未能滑出桌面.为了测量小滑块与水平桌面间的动摩擦因数,还需测量的物理量是 ▲ .(4)某同学认为,不测量桌面高度,改用秒表测出小滑块从飞离桌面到落地的时间,也可测出小滑块与水平桌面间的动摩擦因数.此实验方案 ▲ (选填“可行”或“不可行”),理由是 ▲ .第10题图第11题图12.选做题(请从A 、B 和C 三小题中选定两小题作答,并在答题卡上把所选题目对应字母后的方框涂满涂黑.如都作答,则按A 、B 两小题评分.) A .(选修模块3-3)(12分) (1)一定质量的理想气体分别在T 1、T 2温度下发生等温 变化,相应的两条等温线如图所示,T 2对应的图线上有A 、B 两点,表示气体的两个状态.则 ▲ .A .温度为T 1时气体分子的平均动能比T 2时大B .A 到B 的过程中,气体内能增加C .A 到B 的过程中,气体从外界吸收热量D .A 到B 的过程中,气体分子单位时间内对器壁单位面积上的碰撞次数减少(2)在用油膜法测分子大小的实验中,取体积为V 1的纯油酸用酒精稀释,配成体积为V 2的油酸酒精溶液.现将体积为V 0的一滴油酸酒精溶液滴在水面上,稳定后油膜的面积为S ,已知油酸的摩尔质量为M ,密度为 ,阿伏伽德罗常数为N A ,则油酸分子的直径为 ▲ ,这一滴溶液中所含的油酸分子数为 ▲ .(3)某同学估测室温的装置如图所示,气缸导热性能良好,用绝热的活塞封闭一定质量的理想气体.室温时气体的体积V 1=66mL ,将气缸竖直放置于冰水混合物中,稳定后封闭气体的体积V 2=60mL .不计活塞重力及活塞与缸壁间的摩擦,室内大气压p 0=1.0×105Pa . ①室温是多少? ②上述过程中,外界对气体做的功是多少?B .(选修模块3-4)(12分)(1)下列说法中正确的是 ▲ .A .在光的双缝干涉实验中,条纹间距与缝的宽度成正比B .真空中的光速在不同的惯性参考系中都是相同的,与光源、观察者间的相对运动无关C .只有障碍物的尺寸比波长小得多时才会发生衍射现象D .红光在玻璃砖中的传播速度比紫光在玻璃砖中的传播速度大(2)一列简谐横波沿x 轴传播,图甲是t =1s 时的波形图,图乙是x =3m 处质点的振动图象,则该波的传播速度为 ▲ m/s ,传播方向为 ▲ .第12A (1)题图第12A(3)题图(3)如图所示,一根长直棒AB 竖直地插入水平池底,水深a =0.8m ,棒露出水面部分的长度b =0.6m ,太阳光斜射到水面上,与水面夹角α=37°,已知水的折射率n =43,sin37°=0.6,cos37°=0.8.求: ①太阳光射入水中的折射角β; ②棒在池底的影长l .C .(选修模块3-5)(12分)(1)钍23490Th 具有放射性,它能放出一个新的粒子而变为镤23491Pa ,同时伴随有γ射线产生,其方程为2342349091Th Pa x →+,钍的半衰期为24天.则下列说法中正确的是 ▲ .A .x 为质子B .x 是钍核中的一个中子转化成一个质子时产生的C .γ射线是镤原子核放出的D .1g 钍23490Th 经过120天后还剩0.2g 钍(2)某金属的截止极限频率恰好等于氢原子量子数n =4能级跃迁到n =2能级所发出光的频率.氢原子辐射光子后能量 ▲ (选填“增大”、“不变”或“减小”).现用氢原子由n =2能级跃迁到n =1能级所发出的光照射该金属,则逸出光电子的最大初动能是 ▲ (已知氢原子n =1、2、4能级的能量值分别为E 1、E 2、E 4).(3)如图所示,A 和B 两小车静止在光滑的水平面上,质量分别为m 1、m 2,A 车上有一质量为m 0的人,以速度v 0向右跳上B 车,并与B 车相对静止.求: ①人跳离A 车后,A 车的速度大小和方向; ②人跳上B 车后,A 、B 两车的速度大小之比.四、计算题:本题共3小题,共计47分.解答时请写出必要的文字说明、方程式和重要的演算步骤,只写出最后答案的不能得分,有数值计算的题,答案中必须明确写出数值和单位. 13.(15分)如图所示,水平面上两平行光滑金属导轨间距为L ,左端用导线连接阻值为R的电阻.在间距为d 的虚线MN 、PQ 之间,存在方向垂直导轨平面向下的磁场,磁感应强度大小只随着与MN 的距离变化而变化.质量为m 、电阻为r 的导体棒ab 垂直导轨放置,在大小为F 的水平恒力作用下由静止开始向右运动,到达虚线MN 时的速度为v 0.此后恰能以加速度a 在磁场中做匀加速运动.导轨电阻不计,始终与导体棒电接触良好.求:(1)导体棒开始运动的位置到MN 的距离x ; (2)磁场左边缘MN 处的磁感应强度大小B ;(3)导体棒通过磁场区域过程中,电阻R 上产生的焦耳热Q R .第12C (3)题图第12B (3)题图R 第13题图14.(16分)某电视台的娱乐节目中,有一个拉板块的双人游戏,考验两人的默契度.如图所示,一长L =0.60m 、质量M =0.40kg 的木板靠在光滑竖直墙面上,木板右下方有一质量m =0.80kg 的小滑块(可视为质点),滑块与木板间的动摩擦因数为μ=0.20,滑块与木板间的最大静摩擦力等于滑动摩擦力,取g =10m/s 2.一人用水平恒力F 1向左作用在滑块上,另一人用竖直恒力F 2向上拉动滑块,使滑块从地面由静止开始向上运动. (1)为使木板能向上运动,求F 1必须满足什么条件?(2)若F 1=22N ,为使滑块与木板能发生相对滑动,求F 2必须满足什么条件?(3)游戏中,如果滑块上移h =1.5m 时,滑块与木板没有分离,才算两人配合默契,游戏成功.现F 1=24N ,F 2=16N ,请通过计算判断游戏能否成功?15.(16分)如图所示,足够大的荧光屏ON 垂直xOy 坐标面,与x 轴夹角为30°,当y 轴与ON 间有沿+y 方向、场强为E 的匀强电场时,一质量为m 、电荷量为-q 的离子从y 轴上的P 点,以速度v 0、沿+x 轴方向射入电场,恰好垂直打到荧光屏上的M 点(图中未标出).现撤去电场,在y 轴与ON 间加上垂直坐标面向里的匀强磁场,相同的离子仍以速度v 0从y 轴上的Q 点沿+x 轴方向射入磁场,恰好也垂直打到荧光屏上的M 点,离子的重力不计.求:(1)离子在电场中运动的时间t 1;(2)P 点距O 点的距离y 1和离子在磁场中运动的加速度大小a ;(3)若相同的离子分别从y 轴上的不同位置以速度v ky =(0y >,k 为常数)、沿+x轴方向射入磁场,离子都能打到荧光屏上,k 应满足的条件.第15题图第14题图南通市2015届高三第一次调研测试物理参考答案及评分标准一、单项选择题:本题共5小题,每小题3分,共计15分.每小题只有一个选项符合题意.1.A 2.B 3.D 4.D 5.C二、多项选择题:本题共4小题,每小题4分,共计16分.每小题有多个选项符合题意.全部选对的得4分,选对但不全的得2分,错选或不答的得O 分. 6.AB 7.ABD 8.BD 9.AC三、简答题:本题共3小题,共计42分.请将解答填写在答题卡相应的位置. 10.(8分)(1)R 2(1分) 串联(1分)(2)电流表内接(2分) 滑片P 置于b 处(2分) (3)8(1分) 断路(1分)11.(10分)(1)C (3分) (2)22124x x dh-(3分)(3)滑块停止滑动的位置到B 点的距离(2分)(4)不可行(1分) 滑块在空中飞行时间很短,难以把握计时起点和终点,秒表测时间误差较大(1分) 12.A (选修模块3-3)(12分) (1)CD (3分) (2)102VV V S(2分) 102A VV N V M ρ(2分)(用分子的立方体和球模型分别估测得出2322201V S V V 、23222016V S V V π均给分) (3)解:①设室温为T 1,则 2211T VT V =(2分)代入数据解得 o1300.3K =27.3C T = (1分) ②外界对气体做的功 0W p V =⋅∆ (1分) 解得 0.60J W =(1分)B (选修模块3- 4)(12分)(1)BD (3分) (2)2(2分) -x 轴方向(2分)(3)①设折射角为β,则 os i n (90)s i n n αβ-=(2分)代入数据解得o37β=(1分) ②影长 otan(90)tan l b a αβ=-+ (1分) 代入数据解得 1.4m l =(1分)C (选修模块3-5)(12分)(1)BC (3分) (2)减小(2分) 2142E E E --(2分)第12B (3)题答图(3)①设人跳离A 车后,A 车的速度为v A ,研究A 车和人组成的系统,以向右为正方向,由动量守恒定律有 0001=+v m v m A (1分) 解得 01v m m v A -=(1分) 负号表示A 车的速度方向向左 (1分) ②研究人和B 车,由动量守恒定律有 B v m m v m )(2000+= (1分) 解得021A Bv m m v m +=(1分)四、计算题:本题共3小题,共计47分.解答时请写出必要的文字说明、方程式和重要的演算步骤,只写出最后答案的不能得分,有数值计算的题,答案中必须明确写出数值和单位. 13.(15分)解:(1)导体棒在磁场外,由动能定理有 2012F x m v =(2分) 解得 22mv x F=(1分) (2)导体棒刚进磁场时产生的电动势 0E B L v =(1分) 由闭合电路欧姆定律有 rR EI += (1分) 又 F I L B =安(1分) 由牛顿第二定律有 ma F F =-安 (1分) 解得)B =(2分) (3)导体棒穿过磁场过程,由牛顿第二定律有 ma F F =-安(1分) 导体棒克服安培力做功 d F W 安= (1分) 电路中产生的焦耳热 W Q =(1分) 电阻R 上产生的焦耳热 R RQ Q R r=+ (1分) 解得 )(ma F rR RdQ R -+=(2分) 14.(16分)解:(1)滑块与木板间的滑动摩擦力 1f F μ=(1分) 对木板应有 f M g >(1分) 代入数据得 N 201>F(2分) (2)对木板由牛顿第二定律有11Ma Mg F =-μ(1分) 对滑块由牛顿第二定律有 212ma mg F F =--μ (2分) 要能发生相对滑动应有 12a a > (1分) 代入数据可得 F 2>13.2N(2分)(3)对滑块由牛顿第二定律有 213F F m g m a μ--= (1分) 设滑块上升h 的时间为t ,则 2312h a t =(1分) 对木板由牛顿第二定律有14F Mg Ma μ-=(1分) 设木板在t 时间上升的高度为H ,则 2412H a t =(1分)代入数据可得 0.75m H = (1分)由于h L H <+,滑块在上升到 1.5m 之前已经脱离了木板,游戏不能成功. (1分)15.(16分)解:(1)设离子垂直打到荧光屏上的M 点时,沿y 方向的分速度大小为v y ,在电场中运动的加速度为a 1,则o tan 30y v v = (1分)1qE ma =(1分) 11y v a t =(1分) 解得1t qE = (1分)(2)由几何关系可知2o 111011tan 302y a t v t =+ (2分) 解得 20152mv y qE=(1分) 设离子在磁场中做圆周运动半径为y 2,则 o201c o s 30y v t = (1分) 而 202v a y =(1分)解得 2qEa m=(1分)(3)如图所示,设从纵坐标为y 处射入磁场的离子,恰好能打到荧光屏上,对应的圆周运动半径为r 0,则0ocos30r r y += (1分)此离子进入磁场时的速度v ky =,设运动半径为r ,则2v qBv m r=(1分) 为使离子能打到荧光屏上应满足 0r r ≥ (1分)而 0q B v m a =(1分) 解得k ≥(2分)第15题(1)(2)答图O 第15题(3)答图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南通市高级中学2014-2015年高三数学一模试卷、填空题:本大题共14小题,每小题5分,共70分•请把答案直接填写在答题卡相应位置上.1 已知集合U =幺,3, 5 9}, A =tl, 3, 9} , B = tl, 9},则C u (AU B)=2 •若z z =9(其中z表示复数z的共轭复数),则复数z的模为 __________________ •f(X)=旦“3 •已知函数x在xi处的导数为-2,则实数a的值是 __________________ •2 *4已知函数y=a n x ( a.式0, n^N )的图象在x = 1处的切线斜率为2a nJ+1(n >2,n^N*),且当n =1时,其图象经过(2,8 ),贝V a? = _____________________ .y = sin 2x —5 •要得到函数y=sin2x的函数图象,可将函数3的图象向右至少平移__________ 个单位.6•在平面直角坐标系xOy中,直线y =x b,b• R与曲线^~y2相切”的充要条件是a ??7•如图,Ni表示第i个学生的学号,的成绩依次为401、392、385、359、组数据是____________ •在厶ABC中,若tan A:tan B: tan C 2:3,则A =Gi表示第i个学生的成绩,已知学号在1~10的学生372、327、354、361、345、337,则打印出的第5正实数,则h的最大值是27其中(0,)为直角顶点.若该三角形的面积的最大值为8二、解答题:本大题共6小题,共90分•请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15. (本题满分14分)f (x) =sin2x +2^3sin xcosx +sin(x + n)sin(x-兀),R已知函数 4 4,.(1 )求f(x)的最小正周期和值域;(0< X0<」)彳 / \ • c9.已知y=f(x)是R上的奇函数,且x 0时,2f(x)/,则不等式f(x -x):::f(0)集为10 •设正四棱锥的侧棱长为1,则其体积的最大值为11.已知平面向量a, b, c满足n二1, b =2 , a , b 的夹角等于3,且(a -c) (b —c) =0 ,则c的取值范围是12.在平面直角坐标系xOy中,过点0)、2 AX , 0)分别作x轴的垂线与抛物线X =2y分别交于点A1、A2,直线A A2与x轴交于点A(X3,0),这样就称为、X2确定了X3 .同样, 可由X2、X3确定X4 ,...若卄为=2 X2 =3 则X5 二13•定义:min{x, y}为实数X, y中较小的数.h = min 7a , 2b2已知a- 4b},其中a, b均为14 •在平面直角坐标系xOy中,直角三角形ABC的三个顶点都在椭圆2X2ay2=1 (a 1)上,则实数a的值为(2)若x =x°2为f(x)的一个零点,求sin2x0的值.16. (本题满分14分)如图,在边长为1的菱形ABCD中,将正三角形BCD沿BD向上折起,折起后的点C记为C,且CC =a( 0::: a .;:•叮3).a _ —(1 )若"T,求二面角C—BD-L的大小;(2 )当a变化时,线段CC •上是否总存在一点E,使得A C //平面BED?请说明理由.17. (本题满分15分)22 _y_在平面直角坐标系xOy中,设A、B是双曲线X __2 "上的两点,M(1,2)是线段AB 的中点,线段AB的垂直平分线与双曲线相交于C、D两点.(1)求直线AB与CD的方程;(2)判断A、B、C、D四点是否共圆?若共圆,请求出圆的方程;若不共圆,请说明理由.18. (本题满分15分)某省高考数学阅卷点共有400名阅卷老师,为了高效地完成文、理科数学卷的阅卷任务,需将400名阅卷老师分成两组同时展开阅卷工作,一组完成269捆文科卷,另一组完成475捆理科卷.根据历年阅卷经验,文科每捆卷需要一位阅卷老师工作3天完成,理科每捆卷需要一位阅卷老师工作4天完成.(假定每位阅卷老师工作一天的阅卷量相同,每捆卷的份数也相同)(1)如何安排文、理科阅卷老师的人数,使得全省数学阅卷时间最省?(2)由于今年理科阅卷任务较重,理科实际每捆卷需要一位阅卷老师工作 4.5天完成,在按(1 )分配的人数阅卷4天后,阅卷领导小组决定从文科组抽调20名阅卷老师去阅理科卷,试问完成全省数学阅卷任务至少需要多少天?(天数精确到小数点后第3位)8076.782 95 : 6.786 絮:3.343 ^c^5:3.367(参考数据:119, 14 , 99,30119. (本题满分16分)已知函数f(x)的导函数f °)是二次函数,且f(x)=0的两根为二1 .若f(x)的极大值与极小值之和为0,f(—2)=2.(1)求函数f (x)的解析式;(2)若函数在开区间(山一9,9一m)上存在最大值与最小值,求实数m的取值范围.(3)设函数f(x)二xg(x),正实数a, b, c满足ag(b^bg(c) =cg(a) 0,证明:a 二b=c.20. (本题满分16分)4-0 -pfTn = 3其中p为常数•(1 )求p的值;(2)求证:数列3 '为等比数列;(3)证明:数列a n , ^3n 1, 2a n 2成等差数列,其中X、、均为整数”的充要条件是’x =1,且y二2设首项为1的正项数列4昇的前n项和为S n,数列‘為’的前n项和为T n,且试题n (附加题)21. 【选做题】本题包括 A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作 答•若多做,则按作答的前两题评分•解答时应写出文字说明、证明过程或演算步骤. A. (几何证明选讲)如图,AB 是半圆的直径,C 是AB 延长线上一点,CD 切半圆于点 D , CD=2, DE 丄AB,垂足 为E ,且E 是0B 的中点,求BC 的长.(第21-A 题)B. (矩阵与变换)1 2已知矩阵-2 a的属于特征值b的一个特征向量为C. (极坐标与参数方程)x =2pt 2,在平面直角坐标系xOy 中,已知点A (1,-2)在曲线y =2p t( t 为参数,p 为正常数),求p的值.D. (不等式选讲)【必做题】第22、23题,每小题10分,共计20分•请在答题卡指定区域内作答,解答时 应写出文字说明、证明过程或演算步骤.22 .已知函数 伦)=2(15n (1+x )-x 2-2x , x “P ),求 f (x )的最大值.11,求实数a、b 的值.设A, a 2,比均为正数,且a1 a2 a3 =1,求证: a 1 a 2 a 323. (1)已知 k 、n w N *,且 k < n ,求证: © = n C<7证明:对任意的正整数 n , P(x)二a °C 0(1—x)n+a i C n x(1—x)2+a 2d x 2(1—x)n,+ …+a n C :x n是 关于x 的一次式.(2)设数列a。
, a i,a2, ••满足a oS,ai J. a i 1= 2ai(i=1, 2, 3,…).8.10. 12.13.1.{5}.23;3. 2. 9. (°,1);4.3 "27 •答案解析 易得 AU B =A = 11, 3, 2. 3. 易得 f(xT ,则4. 5;5. 6. 易得7.8. 参考答案4. 5 ; 7t711. ILe (AU B ) - .初G 匸向右至少平移打印出的第 7.=个单位得y 二sin2x.5组数据是学号为8号,且成绩为设 tan A =k , 贝y t as =n k361,故结果是tan C =3ktanC - -tan(A B) 口tan A tan B1 - tan Atan B 可A"求得k =1,所以 -. 9.易得 f(0)=° 2,X -x :::°,故所求解集为 (0,1)•10.法1 设正四棱锥的底面边长为 x ,则体积y =t 22 - t t o ,利用导数可求得当"3时, y max法2设正四棱锥的侧棱与底面所成角为二,则V8,361 . ;1-舟= Jx 2 34 2「记32 27,此时"max27 ;=1 2cos 2 v sin T 1 - - 1「sin 2v sin v33Vmaxi 3 2 ‘3迁,记y = 1 -忙t, 0 ::: t ::: 1,利用导数可求得当t 二可时,ymax 二-,此时V =%3 max 一 27 ;15•命题立意:本题主要考查三角函数的图像与性质、两角和与差的正、余弦公式,考查运 算求解能力.(1)易得 f (x )=sin 2x •歸 2x 1sin 2x —cos x 2二呼歸 2x —如s2x严x o-『0,故cos2x 0-汀-f ,(11 分)此时,sin2x 0=sin F2x-尹扌]_ 1 3 . ~5 1 _ 15-' 3 "_4 2 4 28 • (14 分)16 •命题立意:本题主要考查直线与平面、平面与平面的位置关系,考查空间想象、推理论 证能力. 解: (1)连结AC ,交BD 于点0 ,连结OC ,菱形 ABCD 中,CO— BD ,因三角形BCD 沿BD 折起,所以C°—BD ,故•C 0C为二面角C-BD —C'的平面角,(5 分).3 s i nx2 cos 2 2sin 2x Ji 亠1N2 = 6 f 2:3 51 I 2,2」; (5分)(2 )由 又由所以f(x )周期n,值域为f (x 0) =2sin 2x ()-卫严1=0 sin 2x ) 6 2 得0< x 0<n- n < 2x °- n5n,0 2 得 6 06 6,(7分)一訂 4::0,(9 分) 所以= sin 2x o -n cos - ■ cos 2x ° -nsin —6 6 6 6DCfA)B所以,CD : y = —X 3 ;( 7 分) D 四点共圆,下证之:(9分)2丄X 2 H证明:由y =—x 与 2 一联立方程组可得(2) A 、B 、CC 、D的坐标为 、,(11 分)2 2由三点A 、B 、C 可先确定一个圆(x 3)(^6)二40①,(13 分)经检验D 3 2 5, 5适合①式,所以A 、B 、C D 四点共圆.(15 分)(注:本题亦可以利用圆的几何性质判断四点共圆)18•命题立意:本题主要考查数学建模和解决实际问题的能力,考查运算求解能力.解:(1 )设文科阅卷人数为 X ,且x ・N * ,则阅卷时间为f(x)=OC x <119"6,ilOOhx , x 〉119,246.(5分)而 f (119) =6.782, f (120) =6.786,故 f(119) :: f(120), 答:当文、理科阅卷人数分别是119,281时,全省阅卷时间最省;(8 分)C ° =co =也 cc '=逅 易得 2 ,而 2 ,所以.COC二】,二面角C — BD- C 的大小为';(7 分)(2)当a变化时,线段CC 的中点E 总满足A C //平面BED,下证之:(9 分)因为E , O 分别为线段CC , AC 的中点, 所以°E 〃AC , (11分) 又AC ,二平面BED 0E 平面BED 所以A C //平面BED. ( 14分)17.命题立意:本题主要考查求双曲线、直线、圆等基础知识,考查运算求解与探究能力.71解:(1 )设 A(X1,2x 2y 11x 1,y1),则B(2-为,4-yj ,代入双曲22y 彳 x1 /口2 得(2 _x 1)2 (4 ~^1) 解得 x 1=-1,x 1护=o 或y 1二 3,=4,即 A B 的坐标为(—1 0)、(3, 4),269 3-119 丄 4 34 37.343(2)文科阅卷时间为:99, (11 分)1475 4.5 —281 丄 4 4.54 7.367理科阅卷时间为:301 , ( 14 分)答:全省阅卷时间最短为几367天.(15分)19.命题立意:本题主要考查利用导数研究三次函数的图像与性质等基础知识,考查灵活运用数形结合、化归与转化思想进行运算求解、推理论证的综合能力.解:(i)设f(x)mx "(xj,x3f(x) =a x i亠c则可设3,其中c为常数•因为f(x)的极大值与极小值之和为0,所以f("厂 f(1)=0,即c=03所以f (x) =3x -X ;( 5 分)由(门得f(x)=3x—x3,且「(x) = —3(x+1)(x—1)列表:x (—2, —1) -1 (—1, 1) 1 (1, 2)y - 0 + 0 -y' 极小值一2/极大值2'(如图),(7分)11。
