一次函数与行程问题
第18讲 一次函数专题(一)

第18讲 一次函数专题(一)---利用图像解决实际问题一、一次函数与行程问题1.如图,折线ABC 是在某市乘出租车所付车费y (元)与行车里程x (km )之间的函数关系图像.(1)根据图像,写出当3 x 时该图像的函数关系式; (2)某人乘坐2.5km ,应付多少钱?(3)某人乘坐13km ,应付多少钱? (4)若某人付车费30.8元,出租车行驶了多少千米?2.甲、乙二人骑自行车同时从张庄出发,沿同一路线去李庄.甲行驶20分钟因事耽误一会儿,事后继续按原速行驶.如图表示甲、乙二人骑自行车行驶的路程y (千米)随时间x (分)变化的图象(全程),根据图象回答下列问题:(1)乙比甲晚多长时间到达李庄? (2)甲因事耽误了多长时间?(3)x 为何值时,乙行驶的路程比甲行驶的路程多1千米?3.甲、乙两人沿相同的路线同时有A 地B 地匀速前进,他们距离B 地的路程S (千米)与前进的时间x (小时)的函数图像如图所示,则乙追上甲是距离B 地______千米.4.甲、乙两人从A 地出发前往B 地,甲、乙(实线为甲,虚线为乙)两人距离A 地的路程S (百米)与行走时间t (分)的函数关系图像如图所示,则甲与乙相遇的时间为乙出发后第_______分.第3题图 第4题图二、行程中的往返5.甲、乙两车要从A 地沿同一公路到B 地,乙车比甲车先行1小时,设甲车与乙车之间的路程为y (km ),甲车行驶时间为t (h ),y (km )与t (h )之间函数关系的图象如图所示(假设甲、乙两车的速度始终保持不变).则a 的值是____________6.一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,设行驶的时间为x (时),两车之间的距离为y (千米),图中的折线表示从两车出发至快车到达乙地过程中y 与x 之间的函数关系,已知两车相遇时快车比慢车多行驶40千米,若快车从甲地达到乙地所需时间为t 时,则t =__________。
一次函数之行程问题

一次函数——行程问题例:甲、乙两车分别从A 、B 两地沿同一路线同时出发,以各自的速度 匀速行驶,相向而行,甲到B 地,乙到A 地,各自到达目的地停止.设甲、乙两车与A 地的路程分别为y 甲(km )、y 乙(km ),乙车行驶的时间为(h)x ,y 甲、y 乙与x 之间的函数图象如图所示.(1)甲车的速度是 km /h ,乙车的速度是 k m /h . (2)求y 甲、y 乙与x 之间的函数解析式. (3)求甲、乙两车相遇的时间.(4)设两车之间的路程为 z (km) (z≥0) ,求z 与x 之间的函数关系式. (5)在图②中画出z 与x 的函数图象. (6)直接写出两车相距200km 时x 的值.图①图②变式训练:甲、乙两车分别从A 、B 两地同时出发相向而行,甲到B 地后立即返回,y z (km)两车距离各自出发地的路程(km)y与各自行驶时间(h)x之间的函数图象如图所示.(1)请直接写出甲、乙两车离各自出发地的距离y与x之间的函数关系式,并写出自变量x的取值范围.(2)两车在途中相遇了次.(3)求每次相遇的时间.(h)课后作业:1.在一条直线上依次有A、B、C三个港口,甲、乙两船分别从A、B港口同时出发,沿直线匀速行驶到C港后停止.设甲、乙两船与B港的路程分别为y 甲(km )、y 乙(km ),乙船行驶的时间为x (h ),y 甲、y 乙与x 之间的函数图象如图所示.(1)A 、C 两港口之间的路程为 km , a . (2)写出y 甲与x 之间的函数解析式. (3)直接写出两船相距10km 时x 的值.(第1题)2.一列长为120m 的火车匀速行驶,经过一条长为160m 的隧道.从车头驶 入隧道入口到车尾离开隧道出口共用14s .设车头驶入隧道入口x (s)时,火车在隧道内的长度.......为y (m).y/km(1)求火车行驶的速度.(2)当014x ≤≤时,求y 与x 的函数关系式.(3)在给出的平面直角坐标系中画出y 与x 的函数图象.(第2题)y /m。
一次函数与行程问题

一次函数与行程问题1.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,求a,b,c的值2.高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,乐乐和颖颖相约到杭州市的某游乐园游玩,乐乐乘私家车从衢州出发1小时后,颖颖乘坐高铁从衢州出发,先到杭州火车站,然后再转车出租车取游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.请结合图象解决下面问题:(1)高铁的平均速度是每小时多少千米?(2)当颖颖达到杭州火车东站时,乐乐距离游乐园还有多少千米?(3)若乐乐要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/小时?3.某天早晨,张强从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离(米)与张强出发的时间(分)之间的函数图象.根据图象信息解答下列问题:(1)求张强返回时的速度.(2)妈妈比按原速返回提前多少分钟到家?(3)请直接写出张强与妈妈何时相距1000米?4.小慧和小聪沿图1中的景区公路游览,小慧乘坐车速为30km/h的电动汽车,早上7:00从宾馆出发,游玩后中午12:00回到宾馆现. 小聪骑自行车从飞瀑出发前往宾馆,速度为20km/h,途中遇见小慧时,小慧恰好游完一景点后乘车前往下一景点,上午10:00小聪到达宾馆. 图2中的图象分别表示两人离宾馆的路程s(km)与时间t(h)的函数关系. 试结合图中信息回答:(1)小聪上午几点钟从飞瀑出发?(2)试求线段AB,GH的交叉点B的坐标,并说明它的实际意义;(3)如果小聪到达宾馆后,立即以30km/h的速度按原路返回,那么返回途中他几点钟遇见小慧?5.“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班.王叔叔某天骑自行车上班从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T (t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).(1)①当t=2分钟时,速度v=米/分钟,路程s=米;②当t=15分钟时,速度v=米/分钟,路程s=米.(2)当0≤t≤3和3<t≤15时,分别求出路程s(米)关于时间t(分钟)的函数解析式;(3)求王叔叔该天上班从家出发行进了750米时所用的时间t.。
(完整版)一次函数与行程问题
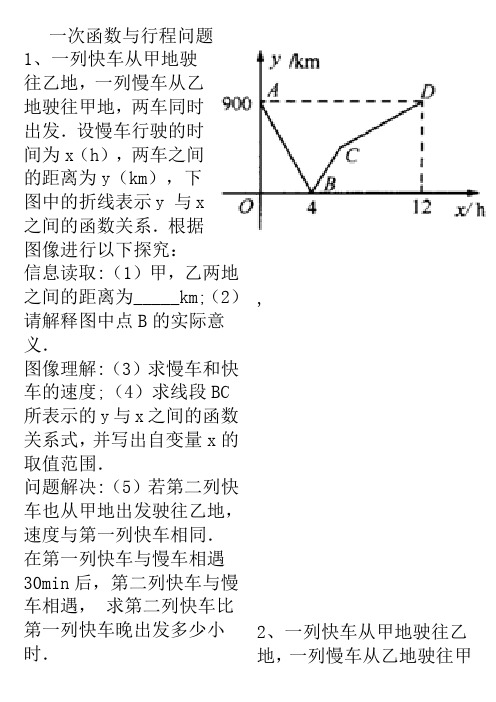
一次函数与行程问题1、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),下图中的折线表示y•与x之间的函数关系.根据图像进行以下探究:信息读取:(1)甲,乙两地之间的距离为_____km;(2)请解释图中点B的实际意义.图像理解:(3)求慢车和快车的速度;(4)求线段BC 所表示的y与x之间的函数关系式,并写出自变量x的取值范围.问题解决:(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.•在第一列快车与慢车相遇30min后,第二列快车与慢车相遇,•求第二列快车比第一列快车晚出发多少小时.,2、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(小时),两车之间的距离为y (千米),图中的折线表示从两车出发至快车到达乙地过程中y与x的函数关系.根据图象解决下列问题:(1)求直线AB的解析式:(2)求甲、乙两地之间的距离;(3)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t小时,求t的值3、一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程y1(km)与行使的时间x(h )之间的函数关系,如图中AB所示;慢车离乙地的路程y2(km)与行使的时间x(h)之间的函数关系,如图中线段OC所示,根据图象进行以下研究.解读信息:(1)甲,乙两地之间的距离为km;(2)线段AB的解析式为;线段OC的解析式为问题解决:(3)设快,慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数图象4、在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:(1)写出A、B两地之间的距离;(2)求出点M的坐标,并解释该点坐标所表示的实际意义;(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围./’J、、5、黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.(2)求渔船和渔政船相遇时,两船与黄岩岛的距离.(3)在渔政船驶往黄岩岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?6、甲、乙两车分别从A、B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶.(1)A、B两地的距离千米;乙车速度是;a= .(2)乙出发多长时间后两车相距330千米?7、有一天,龟、兔进行了600m赛跑.如图表示龟兔赛跑的路程S(m)与时间t(min)的关系,根据图象回答以下问题:(1)赛跑中,兔子共睡了多长时间?(2)写出乌龟跑的路程S (m)与时间t(min)的函数关系式;(3)赛跑开始后,乌龟在第几分钟时从睡觉的兔子旁经过?8、2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:(1)由于汽车发生故障,甲组在途中停留了小时;(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定?9、周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.(1)求小明骑车的速度和在甲地游玩的时间;(2)小明从家出发多少小时后被妈妈追上?此时离家多远?(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.10、周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟后,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.(1)求小明骑车的速度和在南亚所游玩的时间;(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.11、甲.乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:(1)线段CD表示轿车在途中停留了_________ h;(2)求线段DE对应的函数解析式;(3)求轿车从甲地出发后经过多长时间追上货车.12、甲、乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置,我们用数轴表示这条公路,原点为零千米路标,如图1所示,并作如下约定:(1)速度v>0,表示汽车向数轴正方向行驶;速度v<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止;(2)纵坐标s >0,表示汽车位于原点右侧;纵坐标s<0,表示汽车位于原点左侧;纵坐标s=0,表示汽车位于原点,遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数的图象的形式画在了同一直角坐标系中,如图2所示.①由图象确定甲、乙两车的行驶方向,速度的大小及出发前两车的位置.②甲、乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置,如不能相遇,请说明理由.13、设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示。
一次函数与行程问题(word文档良心出品)
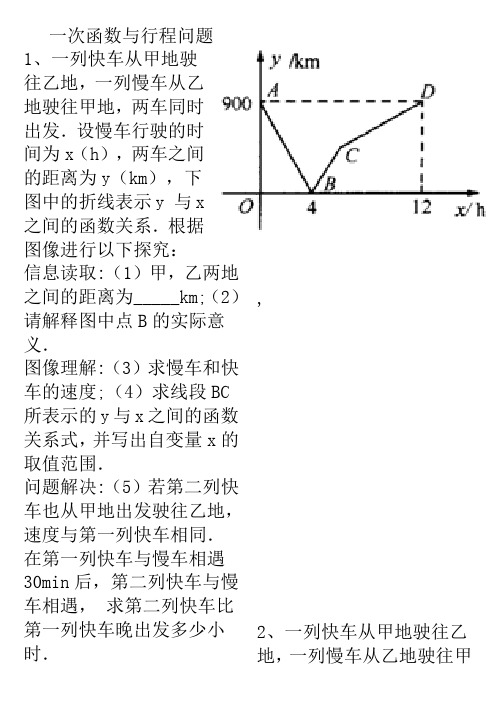
一次函数与行程问题1、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),下图中的折线表示y•与x之间的函数关系.根据图像进行以下探究:信息读取:(1)甲,乙两地之间的距离为_____km;(2)请解释图中点B的实际意义.图像理解:(3)求慢车和快车的速度;(4)求线段BC 所表示的y与x之间的函数关系式,并写出自变量x的取值范围.问题解决:(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.•在第一列快车与慢车相遇30min后,第二列快车与慢车相遇,•求第二列快车比第一列快车晚出发多少小时., 2、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(小时),两车之间的距离为y (千米),图中的折线表示从两车出发至快车到达乙地过程中y与x的函数关系.根据图象解决下列问题:(1)求直线AB的解析式:(2)求甲、乙两地之间的距离;(3)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t小时,求t的值3、一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程y1(km)与行使的时间x(h)之间的函数关系,如图中AB所示;慢车离乙地的路程y2(km)与行使的时间x(h)之间的函数关系,如图中线段OC所示,根据图象进行以下研究.解读信息:(1)甲,乙两地之间的距离为km;(2)线段AB的解析式为;线段OC的解析式为问题解决:(3)设快,慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数图象4、在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A 地,到达A 地后立即按原路返回,如图是甲、乙两人离B 地的距离y (km )与行驶时x (h )之间的函数图象,根据图象解答以下问题:(1)写出A 、B 两地之间的距离;(2)求出点M 的坐标,并解释该点坐标所表示的实际意义;(3)若两人之间保持的距离不超过3km 时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x 的取值范围./’J、、5、黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.(2)求渔船和渔政船相遇时,两船与黄岩岛的距离.(3)在渔政船驶往黄岩岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?6、甲、乙两车分别从A、B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S (千米)与甲车出发时间t (小时)之间的函数图象,其中D 点表示甲车到达B 地,停止行驶. (1)A 、B 两地的距离 千米;乙车速度是;a= . (2)乙出发多长时间后两车相距330千米? 7、有一天,龟、兔进行了600m 赛跑.如图表示龟兔赛跑的路程S (m )与时间t (min )的关系,根据图象回答以下问题: (1)赛跑中,兔子共睡了多长时间? (2)写出乌龟跑的路程S (m )与时间t (min )的函数关系式; (3)赛跑开始后,乌龟在第几分钟时从睡觉的兔子旁经过?8、2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:(1)由于汽车发生故障,甲组在途中停留了小时;(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定?9、周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.(1)求小明骑车的速度和在甲地游玩的时间;(2)小明从家出发多少小时后被妈妈追上?此时离家多远?(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.10、周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟后,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.(1)求小明骑车的速度和在南亚所游玩的时间;(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.11、甲.乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:(1)线段CD表示轿车在途中停留了_________ h;(2)求线段DE对应的函数解析式;(3)求轿车从甲地出发后经过多长时间追上货车.12、甲、乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置,我们用数轴表示这条公路,原点为零千米路标,如图1所示,并作如下约定:(1)速度v>0,表示汽车向数轴正方向行驶;速度v<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止;(2)纵坐标s >0,表示汽车位于原点右侧;纵坐标s<0,表示汽车位于原点左侧;纵坐标s=0,表示汽车位于原点,遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数的图象的形式画在了同一直角坐标系中,如图2所示.①由图象确定甲、乙两车的行驶方向,速度的大小及出发前两车的位置.②甲、乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置,如不能相遇,请说明理由.13、设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示。
(完整版)一次函数与行程问题

一次函数与行程问题1、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),下图中的折线表示y?与x之间的函数关系.根据图像进行以下探究:信息读取:(1)甲,乙两地之间的距离为_____km;(2)请解释图中点B的实际意义.图像理解:(3)求慢车和快车的速度;(4)求线段BC 所表示的y与x之间的函数关系式,并写出自变量x的取值范围.问题解决:(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.?在第一列快车与慢车相遇30min后,第二列快车与慢车相遇,?求第二列快车比第一列快车晚出发多少小时.,2、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(小时),两车之间的距离为y (千米),图中的折线表示从两车出发至快车到达乙地过程中y与x的函数关系.根据图象解决下列问题:(1)求直线AB的解析式:(2)求甲、乙两地之间的距离;(3)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t小时,求t的值3、一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程y1(km)与行使的时间x(h)之间的函数关系,如图中AB所示;慢车离乙地的路程y2(km)与行使的时间x(h)之间的函数关系,如图中线段OC所示,根据图象进行以下研究.解读信息:(1)甲,乙两地之间的距离为km;(2)线段AB的解析式为;线段OC的解析式为问题解决:(3)设快,慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数图象4、在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:(1)写出A、B两地之间的距离;(2)求出点M的坐标,并解释该点坐标所表示的实际意义;(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围./’J、、5、黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.(2)求渔船和渔政船相遇时,两船与黄岩岛的距离.(3)在渔政船驶往黄岩岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?6、甲、乙两车分别从A、B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶.(1)A、B两地的距离千米;乙车速度是;a= .(2)乙出发多长时间后两车相距330千米?7、有一天,龟、兔进行了600m赛跑.如图表示龟兔赛跑的路程S(m)与时间t(min)的关系,根据图象回答以下问题:(1)赛跑中,兔子共睡了多长时间?(2)写出乌龟跑的路程S (m)与时间t(min)的函数关系式;(3)赛跑开始后,乌龟在第几分钟时从睡觉的兔子旁经过?8、2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发 1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y 乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:(1)由于汽车发生故障,甲组在途中停留了小时;(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定?9、周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.(1)求小明骑车的速度和在甲地游玩的时间;(2)小明从家出发多少小时后被妈妈追上?此时离家多远?(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.10、周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟后,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.(1)求小明骑车的速度和在南亚所游玩的时间;(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.11、甲.乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:(1)线段CD表示轿车在途中停留了_________ h;(2)求线段DE对应的函数解析式;(3)求轿车从甲地出发后经过多长时间追上货车.12、甲、乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置,我们用数轴表示这条公路,原点为零千米路标,如图1所示,并作如下约定:(1)速度v>0,表示汽车向数轴正方向行驶;速度v<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止;(2)纵坐标s >0,表示汽车位于原点右侧;纵坐标s<0,表示汽车位于原点左侧;纵坐标s=0,表示汽车位于原点,遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数的图象的形式画在了同一直角坐标系中,如图2所示.①由图象确定甲、乙两车的行驶方向,速度的大小及出发前两车的位置.②甲、乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置,如不能相遇,请说明理由.13、设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示。
8年级-上册-数学-第5章《一次函数》专题-方案最优、行程问题-每日好题分享

浙教版-8年级-上册-数学-第5章《一元函数》《一次函数》专题-方案最优、行程问题-每日好题挑选一、一次函数的应用—方案最优化问题【例1】为促进青少年体育运动的发展,某教育集团需要购买一批篮球和足球,已知一个篮球比一个足球的单价高30元,买两个篮球和三个足球一共需要510元.(1)求篮球和足球的单价;(2)根据实际需要,集团决定购买篮球和足球共100个,其中篮球购买的数量不少于40个,若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),求y与x之间的函数关系式;(3)在(2)的条件下,由于集团可用于购买这批篮球和足球的资金最多为10500元,求购买篮球和足球各多少个时,能使总费用y最小,并求出y的最小值.【练1-1】学校需要购买一批篮球和足球,已知一个篮球比一个足球的单价高30元,买两个篮球和三个足球一共需要510元.(1)求篮球和足球的单价分别为多少元?(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?(3)若学校购买这批篮球和足球的总费用为W(元),在(2)的条件下,求哪种方案能使总费用W最小,并求出W的最小值.【练1-2】某商场筹集资金12.8万元,一次性购进空调,彩电共30台,根据市场需要,这些空调,彩电可以全部销售,全部销售后利润不低于1.5万元,其中空调、彩电的进价和售价如下表所示:设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.(1)试出y与x之间的函数关系式;(2)商场有哪几种进货方案可以选择?(3)根据你所学的有关函数知识选择哪种方案获利最大,最大利润为多少?项目空调彩电进价(月/台)54003500售价(月/台)61003900【练1-3】湖南洞庭湖区盛产稻谷和棉花,销往全国各地,湖边某货运码头,有稻谷和棉花共3000吨,其中稻谷比棉花多500吨.(1)求稻谷和棉花各是多少吨;(2)现有甲、乙两种不同型号的集装箱共58个,将这批稻谷和棉花运往外地,已知稻谷35吨和棉花15吨可装满一个甲型集装箱;稻谷25吨和棉花35吨可装满一个乙型集装箱.在58个集装箱全部使用的情况下,共有几种方案安排使用甲、乙两种集装箱?(3)在(2)的情况下,甲种集装箱每箱收费1000元,乙种集装箱每箱收费1200元,乙种集装箱老板想扩大市场,提出惠民措施:每箱可优惠m 元(m<250).问怎么安排集装箱这批货物总运输费最少?二、一次函数的应用—行程问题【例2】甲车从A 地出发匀速驶向B 地,到达B 地后,立即按原路原速返回A 地;乙车从B 地出发沿相同路线匀速驶向A 地,出发1小时后,乙车因故障在途中停车1小时,然后继续按原速驶向A 地,乙车在行驶过程中的速度是80千米/时,甲车比乙车早1小时到达A 地,两车距各自出发地的路程y 千米与甲车行驶时间x 小时之间的函数关系如图所示,请结合图象信息解答下列问题:(1)写出甲车行驶的速度,并直接写出图中括号内正确的数;(2)求甲车从B 地返回A 地的过程中,y 与x 的函数关系式(不需要写出自变量x 的取值范围);(3)直接写出乙车出发多少小时,两车恰好相距80千米。
一次函数的行程问题

一次函数(也称为线性函数)描述了一个直线的数学模型,其一般形式为y = mx + b,其中m 是斜率(表示直线的倾斜程度),b 是y 轴截距(表示直线与y 轴的交点)。
如果我们把一次函数的自变量(x)解释为时间,因变量(y)解释为位置或距离,那么可以将行程问题与一次函数相联系。
行程问题通常涉及计算物体在一段时间内的位置或距离。
例如,设想一个汽车以恒定的速度行驶。
如果我们知道汽车的速度是v,行驶的时间是t,那么汽车行驶的距离可以表示为y = vt + b,其中 b 是汽车的初始位置(起点)。
在这个例子中,斜率m 就是速度v,而截距b 是起点位置。
通过解析这个一次函数,我们可以根据已知的速度和时间来计算汽车在某个时间点的位置,或者根据已知的位置和速度来推断汽车在某个时间点的时间。
这种方法可以用于解决各种行程问题,包括运动的物体、旅行的距离等等。
一次函数与行程问题例析

一次函数在初中数学中有很重要的应用,许多行程问题常常通过一次函数的形式出现,要解答此类问题,关键是要能够看懂图像,从中获取有用的信息,只有这样才能正确的求解.下面举例分析,相信对提高同学们的解题能力肯定会有所帮助.例 1. 一次函数y = kx + b(k ≠ 0)的图像是一条直线,它可以表示许多实际意义.如图1所示,x代表时间(小时),y代表路程(千米),那么从图像上可以看出,某人出发时(x = 0)离某地(原点)2千米.出发1小时后,由x = 1得到y = 5,即某人离开某地5千米,他实际走了3千米.在图2中,AC、BC分别表示甲、乙两人的运动图像,请结合图像回答下述问题:(1) 图2中,点A(0, 2)、B(1, 0)各表示什么实际意义?(2) 求甲、乙两人各自的运动速度.(3) 求甲出发3小时后,甲、乙两人各自距原地(原点)多远?解析:(1) 点A(0, 2)表示甲出发时离某地2千米;点B(1, 0)表示甲出发1小时后,已从某地(原点)出发.(2) 由A(0, 2)、C(2, 4)可知甲2小时走2千米,由B(1, 0)、C(2, 4)可知,乙1小时走4千米,所以甲的速度为1千米/时,乙的速度为4千米/时.(3) 3小时后,甲离原地为1 × 3 + 2 = 5(千米),乙离原地为2 × 4 = 8(千米).例2. A、B两地相距50千米,甲于某日下午1点骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图3中的折线PQR和线段MN分别表示甲、乙所行驶的路程s与该日下午时间t之间的关系.试根据图形填空:(1) 甲出发_____小时,乙才出发.(2) 乙行驶_____小时可追上甲,此时两人距B地还有_____千米.解析:(1)由M(2, 0)可知,乙是在甲出发1小时后于下午2点出发的.(2)设乙行驶t小时追上甲,由M(2, 0)、N(3, 50)可知乙的速度为50千米/时.由Q(2, 20)、R(5, 50)可知,甲从下午2点开始速度为10千米/时.∴50t?10t = 20,∴t =■,则50t = 25.即乙行驶■小时就追上甲,此时两人距B地还有25千米.例3. 假定甲、乙在一次赛跑中,路程s与时间t的关系如图4所示.那么可以知道:(1) 这是一次_____米的赛跑;(2) 甲、乙两人中先到达终点的是______;(3) 乙在这次赛跑中的速度为_____米、秒.解析:从图像上容易看出:(1) 这是一次100米的赛跑.(2) 甲经12秒到达终点,乙经12.5秒到达终点,显然是甲先到达终点.(3) 乙这次赛跑的速度为■= 8米/秒.例 4. 某同学骑自行车上学,开始以正常速度匀速行驶,行至中途因车出了毛病,需要修理,但修车铺已过,他只好推着车返回修车铺.车修好后,因为怕迟到,他比修车前加快了骑车速度,继续匀速行驶,图5是他与出发地的距离s关于行驶时间t的函数关系图像,那么符合这个同学行驶过程情况的图像大致是()解析:由于该同学有返回的过程,在这个过程中随着时间的增加,路程要减小,同时车修好后,他提高了骑行的速度,则图像与正常速度骑行的图像要陡一些,故应选B.练习:如图6所示,表示一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图像(分别为正比例函数和一次函数).两地间的距离是80千米.请你根据图像回答或解决下列问题:(1)谁出发较早?早多长时间?谁到达乙地较早?早到多长时间?(2)两人在途中行驶的速度分别是多少?(3)请你分别求出表示自行车和摩托车行驶过程中的函数解析式(不要求写出自变量的取值范围).(4)指出在什么时间段内两车均行驶在途中(不包括端点);在这一时间段内,请你分别按下列条件列出关于时间x的方程或不等式(不要化简,也不要求解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面.参考答案:(1)自行车出发早3小时,摩托车到达乙地早2小时;(2)自行车:10千米/时,摩托车:■千米/时;(3)自行车:y = 10x,摩托车:y = ■x-80;(4)当3 ■x-80;当x = 4.8时,10x =■x-80;③当4.8 < x < 6时,10x <■x-80.(作者单位:安徽省灵璧县黄湾中学)。
一次函数与行程问题解题技巧

一次函数与行程问题解题技巧
一次函数是初中数学中比较基础的概念,也是高中数学中不可避免的内容。
在解题过程中,我们可以通过对一次函数的特征和性质的掌握,来应用到实际问题中,例如行程问题。
行程问题是一类常见的实际问题,在解题中需要运用一次函数的知识和技巧。
具体来说,我们可以通过以下步骤来解决一般的行程问题:
1.明确问题:明确问题中的已知条件和未知量,确定问题的求解目标。
2.建立模型:通过观察题目,找出行程问题中的关键因素,建立与之相应的一次函数模型。
3.求解问题:根据模型,使用一次函数的性质和运算法则,求出未知量的值。
举个例子,如果一辆汽车以每小时60公里的速度行驶,那么在2小时内能行驶多少公里?这个问题中,已知条件是汽车的速度和行驶时间,未知量是行驶的距离。
我们可以建立以下的一次函数模型:
行驶距离 = 速度×时间
行驶距离 = 60 × 2 = 120 公里
通过这个模型,我们可以很快地求出汽车在2小时内能行驶的距离。
除了这种基本的行程问题,还有一些更为复杂的行程问题,例如两车相向而行问题、两车追及问题等。
这些问题需要我们进一步掌握一次函数的性质和运算法则,才能解决。
总之,掌握一次函数和行程问题的基本知识和技巧,将有助于我们解决更多实际问题,提高数学应用能力。
一次函数行程问题

一次函数行程问题
一次函数是指函数的形式为y = kx + b,其中k和b都是常数,x和y分别代表自变量和因变量。
对于行程问题,我们可以将行驶距离作为x轴,时间作为y轴,那么这个函数的斜率k就代表了车辆的行驶速度,截距b则代表了起点的初始时间。
假设一辆车从起点A出发,以60km/h的速度向终点B行驶,途中没有任何停留,假设两地之间的距离为120km,那么这辆车到达终点所需的时间t可以通过一次函数来表示:
y = kx + b
其中,k为行驶速度,即60km/h;b为起点的初始时间,即0;x 为行驶距离,即从起点到当前位置的距离;y为已经行驶的时间,即从起点到当前位置所花费的时间。
因此,该函数可以表示为:
y = 60/120 x + 0
化简可得:
y = 1/2 x
即,当行驶距离为x时,所需的时间为y = 1/2x小时。
例如,当车辆行驶了60km时,所需的时间就是y = 1/2 * 60 = 30分钟。
需要注意的是,在实际问题中,由于路况、交通信号等因素的影响,车辆的速度可能会有所波动,因此我们需要对行驶速度进行实测或者平均值计算,以获得更加准确的结果。
一次函数行程问题解题技巧(一)

一次函数行程问题解题技巧(一)一次函数行程问题解题数学中的一次函数,也称为一元一次方程,是我们在中学时期就要学习的基本内容。
行程问题则是一类常见的实际问题,如何将其转化为一元一次方程进行解析呢?下面是几个重要技巧:抽象化首先要做的是抽象化问题。
行程问题往往伴随着时间和速度的变化,我们需要将其分块并进行符号化。
例如:王明从A地出发,经过60km/h的速度行驶t小时后到达B地,然后返回A地,同样以60km/h的速度行驶t+1小时后到达A地,问王明这次行程的总路程是多少?我们可以将其分为四个部分:1.从A地到B地,用时为t小时,速度为60 km/h。
2.从B地返回A地,用时为t+1小时,速度为60 km/h。
3.从A地到B地,用时为t+1小时,速度为60 km/h。
4.从B地返回A地,用时为t小时,速度为60 km/h。
建立方程我们可以将每一部分的路程用符号表示出来,并建立方程:1.AB路程:60t2.BA路程:60(t+1)3.AB路程:60(t+1)4.BA路程:60t则总路程为:60t+60(t+1)+60(t+1)+60t=240t+120解方程最后一步是解一元一次方程,这里的解法略。
不过需要注意的是,在得到答案之后,要根据实际意义进行检验,特别是负数或零的情况。
结论以上就是一次函数行程问题解题的主要技巧,下次遇到行程问题,我们可以尝试使用这些方法进行解析。
注意事项除了上述的技巧,在解决一次函数行程问题时,还需要注意以下几点:1.计算路程时,要注意单位的统一,保持一致可以减少错误的发生。
2.所有的数据要保持符号一致,例如速度和时间的正负方向。
3.在计算路程的时候,不要将速度和时间混淆。
速度是距离单位时间的变化率,可用公式:路程=速度×时间计算得出。
总结一次函数行程问题是一种实际生活中常见的问题类型,对于学习了一次函数的同学来说,应该将其作为练习的内容。
具体而言,我们需要对问题进行符号化处理,建立起一元一次方程,最后再进行计算求解。
一次函数图象与路程问题

多解情况
在某些路程问题中,由于起始点、终 点和速度的不同,可能导致多种解法。 例如,同一段路程,可以选择不同的 路径或使用不同的交通工具。
变种问题
路程问题可以经过变形,如增加限制 条件(如时间限制、费用限制等)或 改变距离的计算方式(如按面积计算 而不是按直线距离计算)。
路程问题的实际应用价值
日常生活中的运用
01
02
03
确定斜率和截距
根据一次函数的解析式, 确定函数的斜率和截距。
描点
在坐标系中选取适当的点, 并标出对应的x和y值。
连线
根据描出的点,用平滑的 曲线连接各点,得到一次 函数的图象。
02 路程问题的基本概念
路程的定义与计算
路程
物体运动轨迹的长度,计 算公式为 $s = text{速度} times text{时间}$。
匀加速运动的路程问题
总结词
匀加速运动中,路程、速度和时间之间存在非线性关系,但可以用一次函数近似 表示。
详细描述
在匀加速运动中,速度随时间线性增加,但加速度保持恒定。设初速度为v0,加速 度为a,时间为t,则末速度v=v0+at。由于速度的增加是线性的,路程s可以用一次 函数近似表示为s=kt+b(k=(v0+v)/2)。
04 结合实例解析路程问题
实际生活中的路程问题
出租车计费
出租车的费用与行驶里程数成正 比,这是典型的线性关系,可以
通过一次函数来表示。
速度与时间
速度是距离和时间的比值,当距离 一定时,时间与速度成反比,可以 用一次函数来表示这种关系。
匀速运动
物体在直线上做匀速运动时,其位 移与时间成正比,可以用一次函数 来表示这种关系。
一次函数中的行程问题

一次函数中的行程问题Linear equations and the concept of slope are fundamental ideas in mathematics that have practical applications in our daily lives. When we encounter a problem involving a linear function, such as a travel distance problem, we can use the equation \( y = mx + b \) to model the relationship between the variables. In the context of a travel problem, the slope \( m \) represents the speed of travel, while the y-intercept \( b \) can indicate the starting point of the journey.在数学中,一次函数和斜率的概念是基础性的思想,它们在我们日常生活中具有实际应用。
当我们遇到涉及线性函数的问题,比如一次函数中的行程问题,我们可以使用方程 \( y = mx + b \) 来建模变量之间的关系。
在行程问题中,斜率 \( m \) 代表着行程的速度,而y-截距 \( b \) 可以表示旅程的起点。
When solving a travel distance problem using a linear equation, we can identify the slope of the equation to determine the speed of travel. For example, if the slope of the equation is 60 mph, it indicates that the person is traveling at a speed of 60 miles per hour. By knowing the speed, we can calculate the distance traveled in agiven time interval by substituting the values into the equation \( y = mx + b \).当使用一次函数解决行程问题时,我们可以识别方程的斜率来确定行程的速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数与行程问题1、一列快车从甲地驶
往乙地,一列慢车从乙
地驶往甲地,两车同时
出发.设慢车行驶的时
间为x(h),两车之间
的距离为y(km),下
图中的折线表示y•与x
之间的函数关系.根据
图像进行以下探究:
信息读取:(1)甲,乙两地
之间的距离为_____km;(2)请解释图中点B的实际意义.
图像理解:(3)求慢车和快车的速度;(4)求线段BC
所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
问题解决:(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.•在第一列快车与慢车相遇30min后,第二列快车与慢车相遇,•求第二列快车比第一列快车晚出发多少小时.,
2、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲
地,两车同时出发,匀速行驶.设行驶的时间为x(小时),两车之间的距离为y (千米),图中的折线表示从两车出发至快车到达乙
地过程中y与x的函数关系.根据图象解决下列问题:
(1)求直线AB的解析式:(2)求甲、乙两地之间的距离;
(3)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t小时,求t的值
3、一列快车由甲
地开往乙地,一
列慢车由乙地开
往甲地,两车同
时出发,匀速运
动,快车离乙地
的路程y1(km)
与行使的时间x
(h
)之间的函数关系,
如图中AB所示;慢车离乙地的路程y2(km)与行使的时间x(h)之间的函数关系,如图中线段OC 所示,根据图象进行以下研究.
解读信息:(1)甲,乙两地之间的距离为
km;
(2)线段AB的解析式为
;线段OC的解析式为
问题解决:(3)设快,慢车之间的距离为y (km),求y与慢车行驶
时间x(h)的函数关系式,并画出函数图象4、在一条笔直的公路上有
A、B两地,甲骑自行车从A 地到B地;乙骑自行车从B 地到A地,到达A地后立即
按原路返回,如图是甲、乙两人离B 地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:?
(1)写出A、B两地之间的距离;?
(2)求出点M的坐标,并
解释该点坐标所表示的实际意义;?
(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围./’J
、、
5、黄岩岛是我国南沙
群岛的一个小岛,渔产
丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰
艇进入我国水域向黄岩岛
驶来,渔船向渔政部门报
告,并立即返航,渔政船接
到报告后,立即从该港口出
发赶往黄岩岛.下图是渔政
船及渔船与港口的距离s和
渔船离开港口的时间t之间
的函数图象.(假设渔船与
渔政船沿同一航线航行)
(1)直接写出渔船离港口
的距离s和它离开港口的时
间t的函数关系式.
(2)求渔船和渔政船相遇
时,两船与黄岩岛的距离.
(3)在渔政船驶往黄岩岛
的过程中,求渔船从港口出
发经过多长时间与渔政船
相距30海里
6、甲、乙两车分别从A、
B两地相向
而行,甲车
出发1小时
后乙车出
发,并以各
自速度匀
速行驶,两
车相遇后
依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)
与甲车出发时间t(小时)之间的函数图象,其中D 点表示甲车到达B地,停止行驶.
(1)A、B两地的距离
千米;乙车速度
是;
a= .
(2)乙出发多长时间后两车相距330千米7、有一天,龟、兔进行了600m赛跑.如图表示龟兔赛跑的路程S(m)与时间t
(min)的
关系,根据
图象回答
以下问题:
(1)赛跑中,兔子共睡了多长时间?
(2)写出乌龟跑的路程S (m)与时间t(min)的函数关系式;
(3)赛跑开始后,乌龟在第几分钟时从睡觉的兔子旁经过
8、2008年5月12日14时28分四川汶川发生里氏级强力地震.某市接到上级通知,立即派
出甲、乙两个抗震
救灾小组乘车沿同
一路线赶赴距出发
点480千米的灾
区.乙组由于要携
带一些救灾物资,
比甲组迟出发小时
(从甲组出发时开
始计时).图中的
折线、线段分别表
示甲、乙两组的所
走路程y甲(千米)、
y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:(1)由于汽车发生故障,甲组在途中停留了
小时;
(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙两组在第一次相遇
时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定
9、周末,小明骑自行车从家里出发到野外郊游.从家出发小时后到达甲地,游玩一段时间后按原速前往乙
地.小明离家
1小时20分钟
后,妈妈驾车
沿相同路线前往乙地,如图是他们离家的路程y (km)与小明离家时间x (h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;(2)小明从家出发多少小时后被妈妈追上此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.
10、周末,小
明骑自行车从
家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟后,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.(1)求小明骑车的速度和在南亚所游玩的时间;
(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.11、甲.乙两地距离300km,一辆货车和一辆轿车先后
从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x (h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了_________h;(2)求线段DE对应的函数解析式;
(3)求轿车从甲地出发后经过多长时间追上货车.
12、甲、乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置,我们用数轴表示这条公路,原点为零千米路标,如图1所示,并作如下约定:(1)速度v>0,表示汽车向数轴正方向行驶;速度v<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止;(2)纵坐标s >0,表示汽车位于原点右侧;纵坐标s<0,表示汽车位于原点左侧;纵坐标s=0,表示汽车位于原点,遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数的图象的形式画在
了同一直角坐标系中,如图2所示.
①由图象确定甲、乙两车的行驶方向,速度的大小及出发前两车的位置.
②甲、乙两车能否相遇如能相遇,求相遇时的时刻及在公路上的位置,如不能相遇,请说明理由.
13、设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示。
(1)A点的实际意义是
B点的实际意义是
(2)线段BC的实际意义是(3)求甲、乙两车的速度。
14、在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原
路返回,第二组由甲地匀速步行经乙地继续前行到丙
地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为
S1(km)和S2(km),图中的折线分别表示S1、S2与t之间的函数关系.
(1)甲、乙两地之间的距离为km,乙、丙两地之间的距离为
km;
(2)求第二组由甲地出发首次到达乙地及由乙地
到达丙地所用的时间分别
是多少
(3)求
图中线段AB 所表示的S 2与t
间的函数关系式,并
写出自变量t 的取值范围.
16、甲、乙两车同时从地出发,以各自的速度匀速向地行驶.甲车先到达地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离(千米)与乙车行驶时间x (小时)之间的函数图象. (1)请将图中的
( )内填上正确的值,并直接写出甲车从到的行驶速度; (2)求从甲车返回到与乙车相遇过程中与x 之间的函数关系式,并写出自变量x 的取范围.
(3)求2· 4·
6·
8·
S(km)
2 0
t(h)
A B
出甲车返回时行驶速度及、两地的距离.。
