三角形综合训练
解三角形小题综合 原卷版--高一下学期备战期末专题训练

期末专题04 解三角形小题综合一、单选题1.(2022春·江苏常州·高一校联考期末)在ABC 中,5AB =,6BC =,8AC =,则ABC的形状是( ) A .锐角三角形B .直角三角形C .钝角三角形D .无法判断2.(2022春·江苏连云港·高一统考期末)在锐角三角形ABC 中,2sin a b A =,则B =( )A .6πB .4π C .3πD .712π 3.(2022春·江苏泰州·高一统考期末)在ABC 中,角A ,B ,C 所对的边分别为a ,b ,csin A =,则sin B =( )A B C D .134.(2022春·江苏淮安·高一统考期末)在ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,若cos a c B =,则ABC 的形状( ) A .锐角三角形B .直角三角形C .钝角三角形D .不能确定5.(2022春·江苏淮安·高一统考期末)在ABC 中,45B =°,点D 是边BC 上一点,5AD =,7AC =,3DC =,则边AB 的长是( )A .BCD .6.(2022秋·江苏南京·高一南京市第九中学校考期末)中国早在八千多年前就有了玉器,古人视玉为宝,玉佩不再是简单的装饰,而有着表达身份、感情、风度以及语言交流的作用.不同形状、不同图案的玉佩又代表不同的寓意.如图1所示的扇形玉佩,其形状具体说来应该是扇形的一部分(如图2),经测量知4ABCD ==,3BC =,7AD =,则该玉佩的面积为( )A .496πB .493πC .496πD .493π7.(2022秋·江苏南通·高一统考期末)图1是南北方向、水平放置的圭表(一种度量日影长的天文仪器,由“圭”和“表”两个部件组成)示意图,其中表高为h ,日影长为l .图2是地球轴截面的示意图,虚线表示点A 处的水平面.已知某测绘兴趣小组在冬至日正午时刻(太阳直射点的纬度为南纬2326′°)在某地利用一表高为2dm 的圭表按图1方式放置后,测得日影长为2.98dm ,则该地的纬度约为北纬( )(参考数据:tan 340.67°≈,tan 56 1.49°≈)A .2326′°B .3234′°C .34°D .56°8.(2022春·江苏镇江·高一扬中市第二高级中学校考期末)设()2πsin cos cos 4f x x x x =−+,在锐角ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若02A f=,1a =,则ABC 面积的最大值为( )A BC D 9.(2022春·江苏扬州·在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,下列各组条件中,使得ABC 恰有一个解的是( )A .π2,4,3ab A == B .π4,3a b A=C .2π4,3a b A === D .2π4,3a b A === 10.(2022春·江苏南通·高一统考期末)已知ABC 为锐角三角形,2AC =,π6A =,则BC 的取值范围为( )A .()1,+∞B .()1,2C .D .211.(2022春·江苏镇江·高一统考期末)已知A ,B 两地的距离为10km ,B ,C 两地的距离为20km ,且测得点B 对点A 和点C 的张角为120°,则点B 到AC 的距离为( )km .A B C D 12.(2022春·江苏无锡·高一统考期末)设ABC 内角A ,B ,C 所对的边分别为a ,b ,c .若2b =,2sin 6sin a C A =,则ABC 面积的最大值为( )AB C D .313.(2022春·江苏南通·高一金沙中学校考期末)ABC 中,,,A B C 的对边分别为a b c ,,,则( )A .若a b c <<,则cos sinBC < B .,A B ∃使得sin()sin sin A B A B +=+ C .,B C ∀都有tan tan tan()1tan tan B CB C B C++=−⋅D .若sin cos A A +A 是钝角 14.(2022春·江苏南通·高一统考期末)在ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,若8,sin 2sin cos 0ac B C A =+=,则ABC 面积的最大值为( ) A .1 B .3 C .2 D .415.(2022春·江苏扬州·高一期末)△ABC 的三内角A 、B 、C 所对边的长分别是a 、b 、c ,设向量()()p a c b q b a c a =+=−−,,,,若p q ∥,则角C 的大小为( )A .π6B .π3C .π2D .2π316.(2022春·江苏苏州·高一校考期末)如图所示,为了测量A ,B 处岛屿的距离,小明在D 处观测,A ,B 分别在D 处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C 处,观测B 在C A 在C 处的北偏西60°方向,则A ,B 两处岛屿间的距离为 ( )A .B .C .20(1+海里D .40海里17.(2022春·江苏苏州·高一统考期末)已知锐角三角形ABC 中,角,,A B C 所对的边分别为,,,a b c ABC 的面积为S ,且()22sin 2b c B S −⋅=,若a kc =,则k 的取值范围是( ) A .()1,2 B .()0,3 C .()1,3 D .()0,2二、多选题18.(2022春·江苏南京·高一南京市中华中学校考期末)在ABC 中,下列结论中,正确的是( )A .若cos2cos2AB =,则ABC 是等腰三角形B .若sin sin A B >,则A B >C .若222AB AC BC +<,则ABC 为钝角三角形D .若60A = ,4AC =,且结合BC 的长解三角形,有两解,则BC 长的取值范围是)+∞19.(2022春·江苏南京·高一统考期末)在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知45,2A c =°=,下列说法正确的是( )A .若a ABC = 有两解B .若3,a ABC = 有两解C .若ABC 为锐角三角形,则b 的取值范围是D .若ABC 为钝角三角形,则b 的取值范围是20.(2022春·江苏宿迁·高一沭阳县修远中学校考期末)在三角形ABC 中,π3A ∠=,若三角形有两解,则ca的可能取值为( )A B .1.1 C D .1.0121.(2022春·江苏南通·高一统考期末)设ABC 的内角A ,B ,C 的对边分别为a ,b ,.c若c =,30B = ,则角A 可能为( )A .135B .105C .45D .1522.(2022春·江苏苏州·高一校联考期末)在ABC 中,角,,A B C 对边分别为,,a b c ,设向量()(),,,m c a b n a c =+= ,且//m n,则下列选项正确的是( ) A .2A B =B .2C A =C .12ca<<D .若ABC 的面积为24c ,则2C π=23.(2022春·江苏泰州·高一统考期末)在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c .若b =2c =cos 2cos 33A AC +=,则下列说法正确的有( )A .3A C π+=B .sinC =C .2a =D .ABC S =24.(2022春·江苏扬州·高一统考期末)如图所示,ABC 中,324AB AC BC ===,,,点M 为线段AB 中点,P 为线段CM 的中点,延长AP 交边BC 于点N ,则下列结论正确的有( ).A .1142AP AB AC =+ B .3BN NC =C .||AN =D .AP 与AC 25.(2022春·江苏徐州·高一统考期末)已知ABC 内角A ,B ,C 所对的边分别为a ,b ,c ,以下结论中正确的是( )A .若AB >,则sin sin A B >B .若2a =,b =3B π=,则该三角形有两解 C .若cos cos a A b B =,则ABC 一定为等腰三角形 D .若222sin sin sin C A B >+,则ABC 一定为钝角三角形26.(2022春·江苏无锡·高一统考期末)ABC 的内角A ,B ,C 所对边分别为a ,b ,c ,下列说法中正确的是( )A .若sin sin AB >,则A B >B .若2220a b c +−>,则ABC 是锐角三角形 C .若cos cos a B b A a +=,则ABC 是等腰三角形D .若sin cos cos a b c A B C==,则ABC 是等边三角形27.(2022春·江苏苏州·高一江苏省昆山中学校考期末)在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,则下列说法正确的是( ) A .cos cos ca Bb A +B .若cos cos a A b B =,则ABC 为等腰或直角三角形 C .若22tan tan a B b A =,则a b =D .若333a b c +=,则ABC 为锐角三角形28.(2022春·江苏苏州·高一校考期末)在△ABC 中,角,,A B C 所对的边分别是,,a b c ,下列说法正确的是( )A .若acosA=bcosB ,则ABC 是等腰三角形B .若45,3AB B AC °==,则满足条件的三角形有且只有一个C .若ABC 不是直角三角形,则tan tan tan tan tan tan A B C A B C ++=D .若0BC AB ⋅<,则ABC 为钝角三角形三、填空题29.(2022春·江苏连云港·高一统考期末)曲柄连杆机构的示意图如图所示,当曲柄OA 在水平位置OB 时,连杆端点P 在Q 的位置,当OA 自OB 按顺时针方向旋转角α时,P 和Q 之间的距离是cm x ,若3cm OA =,7cm AP =,120α°=,则x 的值是_________.30.(2022春·江苏南京·高一江苏省江浦高级中学校联考期末)已知轮船A 和轮船B 同时离开C 岛,A 船沿北偏东30°的方向航行,B 船沿正北方向航行(如图).若A 船的航行速度为40n mile /h ,1小时后,B 船测得A 船位于B 船的北偏东45°的方向上,则此时A ,B 两船相距_______________n mile .31.(2022春·江苏无锡·高一统考期末)ABC 的内角A ,B ,C 所对边分别为a ,b ,c,已知60C =°,1a =,c =b =___________.32.(2022春·江苏扬州·高一期末)《后汉书·张衡传》:“阳嘉元年,复造候风地动仪.以精铜铸成,员径八尺,合盖隆起,形似酒尊,饰以篆文山龟鸟兽之形.中有都柱,傍行八道,施关发机.外有八龙,首衔铜丸,下有蟾蜍,张口承之.其牙机巧制,皆隐在尊中,覆盖周密无际.如有地动,尊则振龙,机发吐丸,而蟾蜍衔之.振声激扬,伺者因此觉知.虽一龙发机,而七首不动,寻其方面,乃知震之所在.验之以事,合契若神.”如图为张衡地动仪的结构图,现在相距120km 的A ,B 两地各放置一个地动仪,B 在A 的东偏北75°方向,若A 地地动仪正东方向的铜丸落下,B 地地动仪东南方向的铜丸落下,则地震的位置距离B 地______km33.(2022春·江苏泰州·高一统考期末)如图所示,该图由三个全等的BAD 、ACF △、CBE △构成,其中DEF 和ABC 都为等边三角形.若2DF =,12DAB π∠=,则AB =_______.34.(2022春·江苏常州·高一统考期末)在ABC 中,AB =3BC =,45B =°,点D 在边BC 上,且cos ADC ∠tan DAC ∠的值为___________.35.(2022春·江苏南通·高一统考期末)设ABC 的内角A ,B ,C 的对边分别为a ,b ,.c 已知6a =,2b =,要使ABC 则c 的大小可取__________(取整数值,答案不唯一).36.(2022春·江苏南京·高一南京市中华中学校考期末)拿破仑是十九世纪法国伟大的军事家、政治家,对数学也很有兴趣,他发现并证明了著名的拿破仑定理:“以任意三角形的三条边为边向外构造三个等边三角形,则这三个等边三角形的中心恰为另一个等边三角形的顶点”,在△ABC 中,以AB ,BC ,CA 为边向外构造的三个等边三角形的中心依次为D ,E ,F ,若30,4BACDF ∠== ,利用拿破仑定理可求得AB +AC 的最大值为___.。
2023年中考九年级数学高频考点专题训练--三角形综合

2023年中考九年级数学高频考点专题训练--三角形综合1.如图,在△ABC中,AB=AC,DE垂直平分AC,CE△AB,AF△BC,(1)求证:CF=EF;(2)求△EFB的度数.2.如图,在△ABC中,∠B=60°,AB=8,BC=10,动点P从点A出发以每秒1个单位的速度沿AB匀速运动,同时动点Q从点B出发,以每秒2个单位的速度沿BC匀速运动,点Q到达点C后,立即以每秒4个单位的速度沿CB返回,当点Q返回到点B时,P、Q两点都停止运动,设点Q运动时间为t秒.(1)当t=3时,BQ=,当t=7时,BQ=.(2)如图,当点P运动到AB的中点时,猜想PQ与AB的位置关系,并证明你的结论.(3)在点P、Q运动过程中,若△BPQ是等边三角形时,求t的值.3.如图,在△ABC中,AB=AC=18cm,BC=10cm,AD=2BD.动点P以2cm/s的速度沿射线BC运动,同时,点Q从点C出发,以acm/s的速度向终点A运动,当Q点停止运动时,P点也随之停止运动,设点P的运动时间为t(s)(t>0).(1)用含t的代数式表示PC的长;(2)若点Q的运动速度为1cm/s,当△CQP是以△C为顶角的等腰三角形时,求t的值;(3)当点Q的运动速度为多少时,能使△BPD与△CQP在某一时刻全等.4.如图,在ΔABC中,∠C=90°,将ΔACE沿着AE折叠以后C点正好落在AB边上的点D处.(1)当∠B=28°时,求∠CAE的度数;(2)当AC=6,AB=10时,求线段DE的长.5.如图,△ABC由两个全等的含45°的直角板拼成,其中,∠ACB=90°,AC=BC,AB= 8,点D是AB边长的中点,点E时AB边上一动点(点E不与点A、B重合),连接CE,过点B作BF⊥CE于F,交射线CD于点G.(1)当点E在点D的左侧运动时,(图).求证:△ACE≌△CBG;(2)当点E在点D的右侧运动时(图)(1)中的结论是否成立?请说明理由:(3)当点E运动到何处时,BG=5,试求出此时AE的长.6.如图1,在等腰三角形ABC中,∠A=120°,AB=AC,点D、E分别在边AB、AC上,AD= AE,连接BE,点M、N、P分别为DE、BE、BC的中点.(1)观察猜想:图1中,线段NM、NP的数量关系是,∠MNP的大小为;(2)探究证明:把△ADE绕点A顺时针方向旋转到如图2所示的位置,连接MP、BD、CE,判断△MNP的形状,并说明理由.7.如图,△ABC 中,AB=AC,△BAC <60°,将线段AB 绕点A逆时针旋转60°得到点D,点 E 与点D 关于直线BC 对称,连接CD,CE,DE.(1)依题意补全图形;(2)判断△CDE 的形状,并证明;(3)请问在直线CE上是否存在点P,使得PA - PB =CD 成立?若存在,请用文字描述出点P 的准确位置,并画图证明;若不存在,请说明理由.8.如图,点M是△ABC的边AB上一点,连接CM,过A作AD⊥CM于点D,过B作BE⊥CM于点E.(1)如图①,若点M为AB的中点时,连接AE,BD,求证:四边形ADBE是平行四边形;(2)如图②,若点M不是AB的中点,点O是AB上不与M重合的一点,连接DO,EO,已知点O在DE的垂直平分线上,求证:AO=BO.9.(1)阅读理解:如图①,在△ABC中,若AB=8,AC=4,求BC边上的中线AD的取值范围是(2)问题解决:如图②,在△ABC中D是BC边上的中点,DE△DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;(3)问题拓展:如图③,在四边形ABCD中,△B+△D=180°,CB=CD,△BCD=140°,以C为顶点作一个70角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.10.在平面直角坐标系中,O为坐标原点,直线y=mx+m交x轴于点A,交y轴的正半轴于点B,点C在x轴的正半轴上,连接BC,tan∠BAO=3tan∠BCO.(1)求点A,C的坐标;(2)如图1,点P在第一象限内,横坐标为t.PD⊥y轴于点D,PA⊥BC于点E,AP= BC,求m与t之间的函数关系式(不必写出自变量t的取值范围)(3)如图2,在(2)的条件下,设BC交DP于点F,当BF=PE时,求m的值.11.综合与实践问题情境:在数学课上老师出了这样一道题:如图1,在△ABC中AB=AC=6,∠BAC=30°,求BC的长.(1)探究发现:如图2,勤奋小组经过思考后,发现:把△ABC绕点A顺时针旋转90°得到△ADE,连接BD,BE,利用直角三角形的性质即可求解,请你根据勤奋小组的思路,求BC的长;(2)探究拓展:如图3,缜密小组的同学在勤奋小组的启发下,把△ABC绕点A顺时针旋转120°后得到△ADE,连接BD,CE交于点F,交AB于点G,请你判断四边形ADFC的形状并证明;(3)奇异小组的同学把图3中的△BGF绕点B顺时针旋转,在旋转过程中,连接AF,发现AF的长度在不断变化,直接写出AF的最大值和最小值.12.综合与实践.特例感知.两块三角板△ADB与△EFC全等,△ADB=△EFC=90°,△B=45°,AB=6.(1)将直角边AD和EF重合摆放.点P、Q分别为BE、AF的中点,连接PQ,如图1.则△APQ的形状为.(2)操作探究若将△EFC绕点C顺时针旋转45°,点P恰好落在AD上,BE与AC交于点G,连接PF,如图2.①FG:GA=▲ ;②PF与DC的位置关系为▲ ;③求PQ的长;(3)开放拓展若△EFC绕点C旋转一周,当AC△CF时,△AEC为.13.在Rt△ABC中,△ACB=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB 上,连接BD,过点D作DF△AC于点F.(1)如图1,当点F与点A重合时,求△ABC的度数;(2)若△DAF=△DBA,①如图2,当点F在线段CA上时,求△ABC的度数;②当点F在线段CA的延长线上,且BC=7时,请直接写出△ABD的面积.14.在△ABC中,AB=AC,△BAC=90,BD平分△ABC交AC于点D.(1)如图1,点F为BC上一点,连接AF交BD于点E.若AB=BF,求证:BD垂直平分AF.(2)如图2,CE△BD,垂足E在BD的延长线上.试判断线段CE和BD的数量关系,并说明理由.(3)如图3,点F为BC上一点,△EFC= 12△ABC,CE△EF,垂足为E,EF与AC交于点M.直接写出线段CE与线段FM的数量关系.15.如图,在菱形ABCD中,△ABC是锐角,E是BC边上的动点,将射线AE绕点A按逆时针方向旋转,交直线CD于点F.(1)当AE△BC,△EAF=△ABC时,①求证:AE=AF;②连结BD,EF,若EFBD=25,求S△AEFS菱形ABCD的值;(2)当△EAF=12△BAD时,延长BC交射线AF于点M,延长DC交射线AE于点N,连结AC,MN,若AB=4,AC=2,则当CE为何值时,△AMN是等腰三角形.16.已知点O是线段AB的中点,点P是直线l上的任意一点,分别过点A和点B作直线l的垂线,垂足分别为点C和点D.我们定义垂足与中点之间的距离为“足中距”.(1)[猜想验证]如图1,当点P与点O重合时,请你猜想、验证后直接写出“足中距”OC和OD 的数量关系是.(2)[探究证明]如图2,当点P是线段AB上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.(3)[拓展延伸]如图3,①当点P是线段BA延长线上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;②若∠COD=60°,请直接写出线段AC、BD、OC之间的数量关系.答案解析部分1.【答案】(1)证明:∵DE垂直平分AC,∴AE=CE,∵CE△AB,∴△ACE是等腰直角三角形,△BEC=90°,∵AB=AC,AF△BC,∴BF=CF,即F是BC的中点,∴Rt△BCE中,EF= 12BC=CF;(2)解:由(1)得:△ACE是等腰直角三角形,∴△BAC=△ACE=45°,又∵AB=AC,∴△ABC=△ACB= 12(180°−45°)=67.5°,∴△BCE=△ACB-△ACE=67.5°-45°=22.5°,∵CF=EF,∴△CEF=△BCE=22.5°,∵△EFB是△CEF的外角,∴△EFB=△CEF+△BCE=22.5°+22.5°=45°. 2.【答案】(1)6;2(2)解:PQ⊥AB,理由如下:在BQ上截取BE=BP,∵点P运动到AB的中点,∴AP=PB=4,∴t=41=4s,∴BQ=4×2=8,∵PB=BE=4,∠B=60°,∴△PEB是等边三角形,∴PE=BE=4,∠EPB=∠PEB=60°,∴QE=PE=4,∴∠EPQ=∠EQP,∵∠EPQ+∠EQP=∠PEB=60°,∴∠QPE=30°,∴∠QPE+∠EPB=90°=∠QPB,∴PQ⊥AB;(3)解:当0≤t≤5,BQ=2t,当5<t≤152,BQ=10−4(t−5)=30−4t,∵△BPQ是等边三角形,∴BP=BQ,∴8−t=2t或8−t=30−4t,∴t=83或t=223.3.【答案】(1)解:∵点P的运动速度为2cm/s,∴BP=2t,∴PC=10−2t;(2)解:△CQP以∠C为顶角的等腰三角形,则PC=CQ,PC=10−2t,CQ=t,即10−2t=t,解得:t=10 3,∴当t=103s时,△CQP是以∠C为顶角的等腰三角形;(3)解:①当BP=CQ时,BD=CP,此时△BPD≅△CQP,根据题意可得:BP=2t,CQ=at,BD=13AB=6,PC=10−2t,∴2t=at,6=10−2t,解得:a =2,t =2, ②当BP ≠CQ 时,∵△BPD 与△CQP 全等,∠B =∠C ,∴BP =CP =12BC =5,BD =CQ =6,∴t =52s ,∴a =CQ t =125cm/s , 综上可得:当Q 的速度为2cm/s 或125cm/s 时,△BPD 与△CQP 在某一时刻全等.4.【答案】(1)∵∠C =90° , ∠B =28°∴∠CAB =90−∠B =90°−28°=62°由折叠的性质可知 ∠CAE =∠EAB∴∠CAE =12∠CAB =31° (2)∵∠C =90° , AC =6 , AB =10 ∴BC =√AB 2−AC 2=√102−62=8由折叠的性质可知 AC =AD,CE =DE,∠EDA =∠C =90°∴∠EDB =180°−∠EDA =180°−90°=90°设 DE =x ,则 BE =8−x,DB =10−6=4 在 Rt △EDB 中, ED 2+DB 2=EB 2 ∴x 2+42=(8−x)2 解得 x =3 ∴DE =35.【答案】(1)证明:在 Rt △ABC 中,∵AC =BC ,∴∠A =∠ABC =45° .∵点 D 是 AB 的中点,∴∠BCG =12∠ACB =45° ,∴∠A =∠BCG .∵BF ⊥CE ,∴∠CBG +∠BCF =90° . ∵∠ACE +∠BCF =90° , ∴∠CBG =∠ACE , 在 △ACE 和 △CBG 中,{∠ACE =∠CBGAC =BC ∠A =∠BCG,∴△ACE ≌△CBG (ASA) (2)解:结论仍然成立,即△ACE△△CBG . 理由如下:在Rt△ABC 中, ∵AC=BC ,∴△A=△ABC=45°.∵点D 是AB 的中点,∴△BCG= 12 △ACB=45°,∴△A=△BCG .∵BF△CE ,∴△CBG+△BCF=90°. ∵△ACE+△BCF=90°, ∴△CBG=△ACE , 在 △ACE 和 △CBG 中,{∠ACE =∠CBGAC =BC ∠A =∠BCG,∴△ACE ≌△CBG (ASA) (3)解:在Rt△ABC 中, ∵AC=BC ,点D 是AB 的中点, ∴CD△AB ,CD=AD=BD= 12AB=4,在Rt△BDG 中, DG =√BG 2−BD 2=√52−42=3 , 点E 在运动的过程中,分两种情况讨论: ①当点E 在点D 的左侧运动时,CG=CD-DG=1, ∵△ACE△△CBG , ∴AE=CG=1;②当点E 在点D 的右侧运动时,CG=CD+DG=7, ∵△ACE△△CBG , ∴AE=CG=7. 故答案为:1或7.6.【答案】(1)NM =NP ;60°(2)解:△MNP 是等边三角形.理由如下:由旋转可得,△BAD =△CAE ,又∵AB =AC ,AD =AE ,∴△ABD△△ACE (SAS ),∴BD =CE ,△ABD =△ACE ,∵点M 、N 、P 分别为DE 、BE 、BC 的中点.∴MN =12BD ,PN =12CE ,MN△BD ,PN△CE ,∴MN =PN ,△ENM =△EBD ,△BPN =△BCE,∴△ENP=△NBP+△NPB=△NBP+△ECB,∵△EBD=△ABD+△ABE=△ACE+△ABE,∴△MNP=△MNE+△ENP=△ACE+△ABE+△EBC+△EBC+△ECB=180°−△BAC=60°,∴△MNP是等边三角形.7.【答案】(1)解:如图即为所求,(2)解:△CDE是等边三角形.如图,连接BD、CE,由点D与点E关于直线BC对称可知BF垂直平分DE,∴CD=CE,BD=BE由旋转可知AB=AD,∠BAD=60°,∴△ABD为等边三角形∴AB=BD=AD,∠BAD=∠ABD=60°∴∠CAD=60°−∠BAC∵AB=AC∴∠ABC=180°−∠BAC2=90°−∠BAC2,BE=BD=AB=AC∴∠FBD=∠ABC−∠ABD=90°−∠BAC2−60°=30°−∠BAC2∴∠EBD=2∠FBD=60°−∠BAC∴∠CAD=∠FBD在△ACD和△BED中,{AD=BD ∠CAD=∠EBD AC=BE∴△ACD≅△BED(SAS)∴CD=ED∴CD=ED=CE∴△CDE是等边三角形;(3)解:存在,如图,将△BCD绕点B逆时针旋转60°得到△ABC′,延长AC′交直线CE于点P,连接BP,由(2)得△CDE是等边三角形,∴∠DCE=60°∴∠DCF=∠ECF=30°∴∠BCD=150°由旋转可得CD=C′A,∠C′BC=60°,∠BC′A=∠BCD=150°,∴∠BC′P=30°∵PA−PB=CD,PA−PC′=C′A=CD∴PB=PC′∴∠C′BP=∠BC′P=30°∴∠PBC=30°∵∠BCP=∠ECF=30°∴∠PBC=∠BCP∴BP=CP所以直线CE上存在点P,使得PA - PB =CD 成立,点P在点C左边距离为CE长的位置. 8.【答案】(1)证明:证法一:∵AD⊥CM,BE⊥CM.∴AD∥BE,∴∠ADM=∠BEM=90°(或∠DAM=∠EBM)∵点M为AB的中点,∴AM=BM∵∠AMD=∠BME,∴△ADM≌△BEM∴AD=BE∴四边形ADBE是平行四边形证法二:∵AD⊥CM,BE⊥CM.∴∠ADM=∠BEM=90°∵点M为AB的中点,∴AM=BM∵∠AMD=∠BME,∴△ADM≌△BEM∴DM=EM∴四边形ADBE是平行四边形(2)证明:延长DO交BE于F,∵AD⊥CM,BE⊥CM.∴AD∥BE,∠BEM=90°∴∠DAO=∠EBO,∠ODE+∠OFE=∠DEO+∠FEO=90°∵点O在DE的垂直平分线上,∴DO=EO∴∠ODE=∠DEO∴∠OFE=∠FEO∴FO=EO∴DO=FO∵∠AOD=∠BOF∴△ADO≌△BFO∴AO=BO.9.【答案】(1)2<AD<6(2)解:如图2,延长FD至点M,使DM=DF,连接BM、EM同(1)得:△BMD≅△CFD(SAS)∴BM=CF∵DE⊥DF,DM=DF∴DE是MF的垂直平分线∴EM=EF在△BME中,由三角形的三边关系得:BE+BM>EM∴BE+CF>EF;(3)解:BE+DF=EF;证明如下:如图3,延长AB至点N,使BN=DF,连接CN∵∠ABC+∠D=180°,∠NBC+∠ABC=180°∴∠NBC=∠D在△NBC和△FDC中,{BN=DF ∠NBC=∠D CB=CD∴△NBC≅△FDC(SAS)∴CN=CF,∠NCB=∠FCD ∵∠BCD=140°,∠ECF=70°∴∠BCE+∠FCD=70°∴∠BCE+∠NCB=70°∴∠ECN=70°=∠ECF在△NCE和△FCE中,{CN=CF ∠ECN=∠ECF CE=CE∴△NCE≌△FCE(SAS)∴EN=EF∵BE+BN=EN∴BE+DF=EF.10.【答案】(1)解:∵直线y=mx+m交x轴于点A,交y轴的正半轴于点B,当x=0时,y=m,∴B(0,m)当y=0时,mx+m=0,解得x=-1∴A(-1,0)∴OA=1,OB=m∵tan∠BAO=OBOA=m1=m,tan∠BCO=OBOC=mOC又tan∠BAO=3tan∠BCO∴3mOC=m∴OC=3∴C(3,0)(2)解:过点P作PH△x轴于点H,则△PHA=90°=△BOC∴△PAH+△APH=90°∵AP△BC∴△AEC=90°∴△PAH+△BCO=90°∴△APH =△BCO∵AP=BC∴△APH△△BCO,∴PH=OC=3,AH=BO,∴t-(-1)=m,则m=t+1;(3)解:过点E作EM△x轴于点M,延长ME交BD于N,则△NMO=90°∵△APH△△BCO,PH=3=OC,BD=m-3∴△DBF =△PAH,∵PD△y轴∴△PDO =△PHO=△DOH =△NMO=90°∴△NPE =△PAH=△DBF∵BF=PE∴△BDF△△PNE,∴BD=NP= m-3=MH,∵OH=t∴OM=OH-MH=OH-MH=t-(m-3)=t-m+3又OC=3∴CM=OC-OM=3-(t-m+3)=m-t∵m=t+1∴CM=m-t=1∴AM=AH-MH=(1+t)- (m-3)=1+t-m+3=3∵△CEM =△EAM∴1EM=EM3故EM= √3∴tan△EAM= tan△CBO∴EM AM=√33=3m,∴m=3 √3.11.【答案】(1)解:如图4,延长CB、DE交于点H.∵△ABC绕点A顺时针旋转90°得到△ADE∴△ABC≌△ADE,∠CAE=∠BAD=90°,△H=90°,∴AB=AD=6,AC=AE=6,∠DAE=∠BAC,DE=BC ∵AB=AC=6,∠BAC=30°∴△ABC是等腰三角形,∠BAE=∠CAE−∠BAC=60°∴∠ABC=180°−∠BAC2=75°,∵AE=AB=6∴△AEB是等边三角形∴BE=AB=6,∠ABE=60°∴∠EBH=180°−∠ABE−∠ABC=45°∴△EBH是等腰直角三角形∴HE=HB.∵AD=AB,∠DAB=90°.∴△ABD是等腰直角三角形,∠BDA=45°.在Rt△EBH中,由勾股定理,得HE2+HB2=BE2.∴HE2+HB2=62=36.∴HE2=HB2=18∴HE=HB=√18=3√2.在△BDH中,∠H=90°,∠BDH=∠EDA−∠BDA=∠ABC−∠BDA=30°.在Rt△BDH中,BH=12BD=3√2.∴BD=6√2.在Rt△BDH中,tan∠BDH=BH DH,∴3√2 DH=√3 3,∴DH=3√6.∴DE=DH−EH=3√6−3√2.∵DE=BC,∴BC的长是3√6−3√2.(2)解:四边形ADFC是菱形.理由如下:∵△ABC绕点A顺时针旋转120°得到△ADE,AB=AC,∠BAC=30°,∴△ABC≌△ADE,∠BAD=∠CAE=120°.∴AC=AE,AB=AD,∠BAC=∠DAE=30°.∴AC=AE=AB=AD.∴△ACE是等腰三角形∴∠ACE=∠AEC=180°−∠CAE2=30°.同理可得:∠ABD=∠ADB=30°.∵∠ACB=180°−∠BAC2=75°.∴∠BCG=∠ACB−∠ACE=45°,∠FBC=∠ABC+∠ABF=105°.∴在△BFC中,∠BFG=180°−∠FBC−∠BCG=30°.∴∠BFG=∠ACF,∠BFG=∠ADB.∴DB∥AC,FC∥AD.∴四边形ADFC是平行四边形.∵AD=AC,∴四边形ADFC是菱形.(3)解:如图5,作AH△BD于点H,则∠AHB=90°∵△ABC绕点A顺时针旋转120°得到△ADE,∴△ABC≌△ADE,∠BAD=120°∴AB=AD=6∴△ABD是等腰三角形∴BH=DH=12BD∴∠ABD=∠ADB=180°−∠BAD2=30°.在Rt△ABH中,△AHB=90°,△ABH=30°,AB=6∵BHAB=cos∠ABH=cos30°∴BH=3√3∴BD=2 BH=6√3由(2)知四边形ADFC是菱形∴DF=AD=6∴BF=BD-DF=6√3-6当△BGF绕点B顺时针旋转,在旋转过程中,当旋转到A、B、F第一次三点共线时,如图6,△BGF≌△BG″F″,∴BF=BF″此时AF有最小值,此时AF=AF″=AB-BF″=AB-BF=6-(6√3-6)=12-6√3当旋转到A、B、F第二次三点共线时,如图7,△BGF≌△BG′F′,∴BF=BF′此时AF有最大值,此时AF=AB+BF′=AB+BF=6+6√3-6=6√3故AF的最大值是6√3,AF的最小值是12−6√3 12.【答案】(1)等腰直角三角形(2)①∵AB=6,△B=45°,△ADB=90°,∴√AD2+BD2=AB,∴AD=BD= 3√2,∴EF= 3√2,∵△BFC=△BAC=90°,∴△GFE=△BAG,∵△AGP=△EGF,∴△ABQ=△GBF,∴△EGF△△BGA,∴FGAG=EFAB,∴FGAG=EFAB=3√26=√22=1√2故答案为:1:√2;②如图,过P作PM//BC交CE与点M,∴EMCM=EPBP=11,∴EM=CM∴FM//BC,∴F在PM上,∴PF△CD,故答案为:平行;③∵BP=PE,BD=CD,∴DP为△BCE的中位线,∴PD//CE,∵CE△BC,∴PD△BC,又∵AD△BC,∴P在AD上,△APF=△ADC=90°,∵Q 为AF 的中点, ∴PQ= 12AF ,又∵△B=45°,△ADB=90°,∴EF =√22AB =3√2 ,∴FC=EF= 3√2 , ∴AF=AC-CF=6- 3√2 ,∴PQ= 12AF = 3−3√22;(3)22.5°或67.5°13.【答案】(1)解:由旋转的性质可得△ABC△△ADE∴△BAC=△DAE∵DF△AC ,点F 与点A 重合, ∴△CAD=90° ∴△BAC=△DAE=45° ∵△ACB=90°∴△ABC=90°-△CAB=45°;(2)①∵△ABC△△ADE ,则△BAC=△DAE=12△DAF∵△DAF=△DBA , ∴△DAE=12△DAF=12△DBA∵△ABC△△ADE ∴AB=AD∴△DBA=△BDA ,设△BAC=△BAD-x ,则△DBA=△BDA-2x ∵△BAD+△ABD+△ADB=180° ∴x+2x+2x=180°解得:x=36° ∴△BAC=36°∴△ABC=90°-△BAC=54°; ②493√3 14.【答案】(1)证明:∵BD 平分△ABC ,∵BA=BF,BE=BE,∴△ABE△△FBE(SAS),∴AE=FE,△AEB=△FEB= 12× 180°=90°,∴BD垂直平分AF.(2)解:BD=2CE,理由如下:延长CE,交BA的延长线于G,∵CE△BD,△ABE=△FBE,∴GE=2CE=2GE,∵△CED=90°=△BAD,△ADB=△EDC,∴△ABD=△GCA,又AB=AC,△BAD=△CAG,∴△BAD△△CAG(ASA),∴BD=CG=2CE,(3)解:FM=2 CE,理由如下:作FM的中垂线NH交CF于N,交FM于H,∴FN=MN,MH=FH= 12FM,∴△NMH=△NBH,∵△EFC= 12△ABC=22.5°,∴△MNC=2△NFH=2× 12△ABC=△ABC,∵AB=AC,△BAC=90,∴△ABC=△ACB=△MNC=45°,∵△EMC=△MFC+△MCF=22.5°+45°=67.5°,∴△ECM=90°-△EMC=22.5°,∴△NFH=△MCE,又∵△FHN=△E=90°,∴△FNH△△CME(AAS),∴FH=CE,∴FM=2FH=2CE.15.【答案】(1)解:①∵菱形ABCD,∴AB=AD,△ABC=△ADC,AD△BC,∵AE△BC,∴AE△AD,∴△EAF+△DAF=△BAE+△ABE=90°,∵△EAF=△ABC,∴△DAF=△BAE,在△ABE和△ADF中{∠ABC=∠ADC AB=AD ∠DAF=∠BAE∴△ABE△△ADF(ASA)∴AE=AF.②连接AC,∵菱形ABCD,∴AB=BC=CD,AC△BD,∵△ABE△△ADF,∴BE=CF , ∴CE=CF ∵AE=AF ∴AC△EF ∴BD△FE , ∴△CEF△△CBD , ∴EC BC =EF BD =25设EC=2a ,则AB=BC=5x ,BE=3a , ∴AE =√25a 2−9a 2=4a , ∵AE AB =AF BC ,△EAF=△ABC , ∴△AEF△△BAC ,S △AEF S △ABC =(AEAB)2=(4a 5a)2=1625S △AEFS 菱形ABCD=S △AEF 2S △ABC=12×1625=825.(2)解:∵菱形ABCD , ∴△BAC=12△BAD ,∵△EAF=12△BAD ,∴△BAC=△EAF , ∴△BAE=△CAM , ∵AB△CD , ∴△BAE=△ANC ,同理可知:△AMC=△NAC , ∴△MAC△△ANC , ∴AC CN =AM NA; 当△AMN 时等腰三角形, 当AM=AN 时,在△ANC和△MAC中{∠ANC=∠CAM AM=AN ∠AMC=∠NAC∴△ANC△△MAC(ASA)∴CN=AC=2,∵AB△CN,∴△CEN△△BEA,∴CEBE=CNAB=24=12∵AB=BC=4∴CE4−CE=12解之:CE=43;当NA=MN时△NMA=△NAM,∵AB=BC,∴△BAC=△BCA,∵△BAC=△EAF,∴△NMA=△NAM=△BAC=△BCA,∴△ANM△△ABC,∴AMAN=ACAB=12∴AC CN =AM NA =12 ∴CN=2AC=4=AB 解之:AC=2∵△CEN△△BEA (AAS ) ∴CE=BE=2; 当MA=MN 时,易证△MNA=△MAN=△BAC=△BCA , ∴△AMN△△ABC ∴AM AN =AB AC =42=2 ∴CN=12AC=1∵△CEN△△BEA , ∴CE BE =CN AB =14 ∴CE 4−CE =14 解之:CE =45;∴当CE 为43或2或45时,△AMN 是等腰三角形.16.【答案】(1)OC =OD(2)解:数量关系依然成立.证明(方法一):过点O 作直线 EF//CD ,交BD 于点F ,延长AC 交EF 于点E .∵EF//CD∴∠DCE=∠E=∠CDF=90°∴四边形CEFD为矩形.∴∠OFD=90°,CE=DF由(1)知,OE=OF∴△COE≌△DOF(SAS),∴OC=OD.证明(方法二):延长CO交BD于点E,∵AC⊥CD,BD⊥CD,∴AC//BD,∴∠A=∠B,∵点O为AB的中点,∴AO=BO,又∵∠AOC=∠BOE,∴△AOC≌△BOE(ASA),∴OC=OE,∵∠CDE=90°,∴OD=OC.(3)解:①数量关系依然成立.证明(方法一):过点O作直线EF//CD,交BD于点F,延长CA交EF于点E.∵EF//CD∴∠DCE=∠E=∠CDF=90°∴四边形CEFD为矩形.∴∠OFD=90°,CE=DF由(1)知,OE=OF∴△COE≌△DOF(SAS),∴OC=OD.10分证明(方法二):延长CO交DB的延长线于点E,∵AC⊥CD,BD⊥CD,∴AC//BD,∴∠ACO=∠E,∴点O为AB的中点,∴AO=BO,又∵∠AOC=∠BOE,∴△AOC≌△BOE(AAS),∴OC=OE,∵∠CDE=90°,∴OD=OC.②AC+BD=√3OC。
三角形全等专题训练

三角形全等综合练习一1、如图(1):AD ⊥BC ,垂足为D ,BD=CD 。
求证:△ABD ≌△ACD 。
2、如图(2):AC ∥EF ,AC=EF ,AE=BD 。
求证:△ABC ≌△EDF 。
3、如图(3):DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
4、 如图(4):AB=AC ,AD=AE ,AB ⊥AC ,AD ⊥AE 。
求证:(1)∠B=∠C ,(2)BD=CE5、如图(5):AB ⊥BD ,ED ⊥BD ,AB=CD ,BC=DE 。
求证:AC ⊥CE 。
6、如图(6):CG=CF ,BC=DC ,AB=ED ,点A 、B 、C 、D 、E 在同一直线上。
求证:(1)AF=EG ,(2)BF ∥DG 。
(图1)DC B A F E (图2)D C B A FE (图3)D C B A E(图4)D C B A GF E (图6)D C B A E (图5)D B A7、如图(7):AC ⊥BC ,BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN=BC 。
求证:(1)MN 平分∠AMB ,(2)∠A=∠CBM 。
8、如图(8):A 、B 、C 、D 四点在同一直线上,AC=DB ,BE ∥CF ,AE ∥DF 。
求证:△ABE ≌△DCF 。
9、如图(9)AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
10、如图(10)∠BAC=∠DAE ,∠ABD=∠ACE ,BD=CE 。
求证:AB=AC 。
11、如图(11)∠1=∠2,∠3=∠4,P 是BC 上任一点。
求证:PA=PD 。
34、如图:AD 是△ABC 中∠BAC 的平分线,过AD 的中点E 作EF ⊥AD 交BC 的延长线于F ,连结AF 。
求证:∠B=∠CAF 。
图12N M (图7)C B A FE (图8)D C B A MF E (图9)C B A E (图10)D C B A P 4321(图11)D B A FE D C B A三角形全等综合练习二13、如图(13)△ABC ≌△EDC 。
四年级三角形专题训练

四年级三角形专题训练一、三角形的认识基础题。
1. 由三条()围成的图形(每相邻两条线段的端点相连)叫做三角形。
- 答案:线段。
- 解析:三角形的定义就是由三条线段首尾顺次相接围成的封闭图形。
2. 三角形有()条边,()个角,()个顶点。
- 答案:3,3,3。
- 解析:这是三角形的基本特征,三条边、三个角和三个顶点。
3. 从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的()。
- 答案:高。
- 解析:这是三角形高的定义,三角形的高是从一个顶点向对边作的垂线段。
4. 一个三角形有()条高。
- 答案:3。
- 解析:因为三角形有三个顶点,过每个顶点都可以作对边的高,所以一个三角形有3条高。
二、三角形的分类题。
5. 三角形按角分类可以分为()三角形、()三角形和()三角形。
- 答案:锐角、直角、钝角。
- 解析:锐角三角形是三个角都是锐角(小于90°)的三角形;直角三角形是有一个角是直角(等于90°)的三角形;钝角三角形是有一个角是钝角(大于90°小于180°)的三角形。
6. 一个三角形中最大的角是89°,这个三角形是()三角形。
- 答案:锐角。
- 解析:因为最大角是89°,小于90°,所以三个角都是锐角,这个三角形是锐角三角形。
7. 一个三角形中至少有()个锐角。
- 答案:2。
- 解析:直角三角形有2个锐角,钝角三角形也有2个锐角,锐角三角形有3个锐角,所以一个三角形至少有2个锐角。
8. 等腰三角形的两腰(),两个底角()。
- 答案:相等,相等。
- 解析:这是等腰三角形的重要特征,两腰长度相等,两底角的度数相等。
9. 等边三角形的三条边(),三个角也(),每个角都是()度。
- 答案:相等,相等,60。
- 解析:等边三角形是特殊的等腰三角形,它的三条边都相等,根据三角形内角和是180°,三个角相等,所以每个角都是180°÷3 = 60°。
全等三角形基本模型综合训练(二)(解析版)(北师大版)

全等三角形基本模型综合训练(二)1.如图,将△ABC 沿DE ,EF 翻折,顶点A ,B 均落在点O 处,且EA 与EB 重合于线段EO ,若△CDO +△CFO =98︒,则△C 的度数为( )A .40°B .41°C .42°D .43°【答案】B 【详解】解:如图,连接AO 、BO .由折叠的性质可得EA =EB =EO ,△△AOB =90°,△OAB +△OBA =90°,△DO =DA ,FO =FB ,△△DAO =△DOA ,△FOB =△FBO ,△△CDO =2△DAO ,△CFO =2△FBO ,又△△CDO +△CFO =98°,△2△DAO +2△FBO =98°,△△DAO +△FBO =49°,△△CAB +△CBA =△DAO +△OAB +△OBA +△FBO =139°,△△C =180°﹣(△CAB +△CBA )=180°﹣139°=41°,故选B .2.如图,已知正方形ABCD 的边长为3,点E 是AB 边上一动点,连接ED ,将ED 绕点E 顺时针旋转90︒到EF ,连接,DF CF ,则当DF CF +之和取最小值时,DCF 的周长为( )A.353B.433C.523D.133【答案】A【详解】解:连接BF,过点F作FG△AB交AB延长线于点G,△将ED绕点E顺时针旋转90°到EF,△EF△DE,且EF=DE,△△AED△△GFE(AAS),△FG=AE,△F点在BF的射线上运动,作点C关于BF的对称点C',△EG=DA,FG=AE,△AE=BG,△BG=FG,△△FBG=45°,△△CBF=45°,△BF是△CBC′的角平分线,即F点在△CBC′的角平分线上运动,△C'点在AB的延长线上,当D、F、C'三点共线时,DF+CF=DC'最小,在Rt△ADC'中,AD=3,AC'=6,△DC5△DF+CF的最小值为5△此时DCF的周长为353.故选:A.3.如图,△ABC 中,△A =30°,BC =3,△ABC 的面积9,点D 、E 、F 分别是三边AB 、BC 、CA 上的动点,则△DEF周长的最小值为( )A .5B .6C .8D .10【答案】B 【详解】解:作E 点关于AB 的对称点G ,作E 点关于AC 的对称点H ,连接GH ,交AB 于D 点,交AC 于F 点,连接AG ,AH ,AE ,如图所示:∴由对称性可知GD DE =,EF FH =,AG AE AH ==,DEF ∴∆的周长DE DF EF GD DF FH GH =++=++=,GAD DAE ∠=∠,EAC HAC ∠=∠,2GAH BAC ∴∠=∠,30BAC ∠=︒,60GAH ∴∠=︒,GH AE ∴=,∴当AE BC ⊥时,GH 最短,此时DEF ∆的周长最小,3BC =,ABC ∆的面积9,6AE ∴=,DEF ∴∆的周长最小值为6,故选:B .4.如图,等边三角形ABC的边长为4,点D是AB边的中点,点E是BC边上的一个动点,以DE为边作等边三角形DEF,连接AF,则AF的最小值为()A.2B3C.2D.3【答案】B【详解】解:当AF△AB时,AF的值最小,过D作DG△BC,△DG△BC,AF△AB△△DGB=△DGE=△DAF=90°△△B+△BDG=90°,△GDE+△DEG=90°△△ABC和△DEF都是等边三角形△DF=EF,△B=△FDE=60°,△BDG=30°△△ADF+△GDE=180°-△BDG-△FDE=180°-60°-30°=90°△△ADF=△DEG又△△DGE=△DAF=90°,DE=DF△△DEG△△FDA(AAS)△AF=DG331BD43 222故选:B.5.如图,P为等边△ABC内一点,△APC=150°,且△APD=30°,AP=6,CP=3,DP=7,则BD的长为______.【答案】34【详解】将△CP A绕点C逆时针旋转60°得到△CEB,连接EP,△CE=CP,△ECB=△PCA,△CEB=△CP A=150°,BE=AP=6,△等边△ABC,△△ACP+△PCB=60°,△△ECB+△PCB=60°,即△ECP=60°,△△ECP为等边三角形,△△CPE=△CEP=60°,PE=6,△△DEB=90°,△△APC=150°,△APD=30°,△△DPC=120°,△△DPE=180°,即D、P、E三点共线,△ED=3+7=10,△BD22DE BE34故答案为346.如图,以Rt△ABC的斜边AB为一边在△ABC同侧作正方形ABEF.点O为AE与BF的交点,连接CO.若CA=2,CO=3CB的长为________.【答案】26【详解】如图,在BC上截取BD=AC=2,连接OD,△四边形AFEB 是正方形,△AO =BO ,△AOB =△ACB =90°,△△CAO =90°-△ACH ,△DBO =90°-△BHO ,△△ACH =△BHO ,△△CAO =△DBO ,△△ACO △△BDO ,△DO =CO =23△AOC =△BOD ,△△BOD +△AOD =90°,△△AOD +△AOC =90°,即△COD =90°,△CD 22(23)(23)26+△BC =BD +CD =26+故答案为:26+7.已知:如图,BD 为△ABC 的角平分线,且BD=BC ,E 为BD 延长线上的一点,BE=BA ,过E 作EF△AB ,F 为垂足,下列结论:①△ABD△△EBC ;②△BCE+△BCD=180°;③AD=EF=EC ;④BA+BC=2BF ,其中正确的结论有________(填序号).【答案】①②④【详解】解:①△BD 为△ABC 的角平分线,△△ABD=△CBD ,在△ABD 和△EBC 中,BD BC ABD CBD BE BA =⎧⎪∠=∠⎨⎪=⎩,△△ABD△△EBC (SAS ), △①正确;②△BD 为△ABC的角平分线,BD=BC ,BE=BA ,△△BCD=△BDC=△BAE=△BEA ,△△ABD△△EBC,△△BCE=△BDA,△△BCE+△BCD=△BDA+△BDC=180°,△②正确;③△△BCE=△BDA,△BCE=△BCD+△DCE,△BDA=△DAE+△BEA,△BCD=△BEA,△△DCE=△DAE,△△ACE为等腰三角形,△AE=EC,△△ABD△△EBC,△AD=EC,△AD=AE=EC,△BD为△ABC的角平分线,EF△AB,而EC不垂直与BC,△EF≠EC,△③错误;④过E作EG△BC于G点,△E是BD上的点,△EF=EG,在Rt△BEG和Rt△BEF中,BE BEBE EG=⎧⎨=⎩,△Rt△BEG△Rt△BEF(HL),△BG=BF,在Rt△CEG和Rt△AFE中,EF FG AE CE=⎧⎨=⎩,△Rt△CEG△Rt△AFE(HL),△AF=CG,△BA+BC=BF+FA+BG-CG=BF+BG=2BF,△④正确.故答案为①②④.8.如图,已知四边形ABCD中,AC平分△BAD,CE△AB于点E,且AE=12(AB+AD),若△D=115°,则△B=________.【答案】65°【详解】试题分析:如图,在AB上截取AF=AD,连接CF,△AC平分△BAD,AC为公共边,△△AFC△△ADC,△△ADC=△AFC,△AE=12(AB+AD),AF=AD,△AF+EF=12(AF+BF+AF),△EF=12BF,△EF=BE,△CE△AB,△△ABC=△BFC,△△ADC+△ABC=180°,△△D=115°,△△B=65°.9.已知在Rt ABC 中,90C ∠=︒,75ABC ∠=︒,5AB =.点E 为边AC 上的动点,点F 为边AB 上的动点,则线段FE EB +的最小值是__________.【答案】52【详解】解:如图作F 点关于AC 的对称点F ',连接A F '并延长交BC 延长线于点B ′,作BD △AB ′于点D ,由对称性可得EF =E F ',由垂线段的性质可得B 到AB ′的最短距离为BD ,△EF +EB =E F '+EB =B F '≥BD ,Rt △ABC 中,△BAC =90°-△ABC =15°,△△BAD =2△BAC =30°,Rt △ABD 中,AB =5,△BDA =90°,△BAD =30°,△BD =52,△线段FE EB +的最小值是52, 故答案为:52; 10.在矩形ABCD 中,AD ,CD 边的中点分别为E ,F ,连接BF ,CE 交于点G ,若2AB =,CG CF =,则BG 的长为______.410 【详解】解:如图,延长AD 交BF 的延长线于M .△AD ,CD 边的中点分别为E ,F ,2AB =,△11122CF DF AB CD ====,AE DE =. △CG CF =,△1CG =.△四边形ABCD 是矩形,△BC AM ∥,BC AD =,△CBF DMF ∠=∠,90BCF MDF ∠=∠=︒. 在BCF △与MDF △中90CBF DMF BCF MDF CF DF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,△()BCF MDF AAS ≌,△=BC DM AD =. 设AE DE x ==,则2AD DM BC x ===.△BC EM ,△CBG M ∠=∠,BCG GEM ∠=, △BCG MEG ∽,△CG BC BG EG EM GM==. △1CG =,AE DE x ==,2AD DM BC x ===,△122x EG x x =+,△32EG =, △35122CE EG CG =+=+=,△222253222ED CE CD ⎛⎫=--= ⎪⎝⎭, △23AD BC DM ===,39322EM =+=,△3462AM AE DE DM =++=⨯=, △222226210BM AB AM++△210GM BM BG BG =-=.△BC BG EM GM =,△392102BG -,△410BG = 410 11.如图,已知△AED =△ACB =90°,AC =BC =3,AE =DE =1,点D 在AB 上,连接CE ,点M ,点N 分别为BD ,CE 的中点,则MN 的长为_____.10【详解】解:连接DN 并延长DN 交AC 于F ,连接BF ,如图,△△AED =△ACB =90°,AC =BC =3,AE =DE =1,45EAD EDA BAC ∴∠=∠=∠=︒,DE AC ∴∥,DEN FCN ∴∠=∠,△点N 为CE 的中点,EN NC ∴=,在DEN 和FCN △中,DNE FNC EN NCDEN FCN ∠=∠⎧⎪=⎨⎪∠=∠⎩()DEN FCN ASA ∴△≌△,DE FC DN NF ∴==,,AE FC ∴=,△点M 为BD 的中点,MN ∴是BDF 的中位线,12MN BF ∴=, 45EAD BAC ∠=∠=︒,90EACFCB ∴∠=∠=︒,在CAE 和BCF △中,EAC FCB AE FC ⎪∠=∠⎨⎪=⎩()CAE BCF SAS ∴△≌△,BF CE ∴=,22221111013222MN CE AE AC ∴==++=. 12.如图,已知△ABC 中,AB=AC ,△BAC=90°,分别过B ,C 向经过点A 的直线EF 作垂线,垂足为E ,F .(1)如图1,当EF 与斜边BC 不相交时,请证明EF=BE+CF ;(2)如图2,当EF 与斜边BC 相交时,其他条件不变,写出EF 、BE 、CF 之间的数量关系,并说明理由; (3)如图3,猜想EF 、BE 、CF 之间又存在怎样的数量关系,写出猜想,不必说明理由.【答案】(1)证明见解析;(2) EF= BE -CF ,理由见解析;(3)EF=CF -BE ,理由见解析.【详解】(1)证明:△BE△EA ,CF△AF ,△△BAC=△BEA=△CFE=90°,△△EAB+△CAF=90°,△EBA+△EAB=90°,△△CAF=△EBA ,在△ABE 和△CAF 中,BEA AFC EBA FAC AB AC ===∠∠⎧⎪∠∠⎨⎪⎩△△BEA△△AFC (AAS ), △EA=FC ,BE=AF ,△EF=EA+AF=BE+CF .(2)证明:△BE△EA ,CF△AF ,△△BAC=△BEA=△CFE=90°,△△EAB+△CAF=90°,△ABE+△EAB=90°,△△CAF=△ABE ,在△ABE 和△ACF 中,EBA FAC BEA CFA AB AC ∠∠⎧⎪∠∠⎨⎪⎩===,△△BEA△△AFC (AAS ),△EA=FC ,BE=AF ,△EF=AF -AE ,△EF=BE -CF .(3)EF=CF -BE ,理由是:△BE△EA ,CF△AF ,△△BAC=△BEA=△CFA=90°,△△EAB+△CAF=90°,△ABE+△EAB=90°,△△CAF=△ABE ,在△ABE 和△ACF 中,BEA CFA AB AC ⎪∠∠⎨⎪⎩==,△△BEA△△AFC (AAS ),△EA=FC ,BE=CF ,△EF=EA -AF ,△EF=CF -BE .13.如图①,在四边形ABCD 中,5AB AD ==,53BC CD ==,90B ∠=︒.点M 在边AD 上,2AM =,点N 是边BC 上一动点.以MN 为斜边作Rt MNP △,若点P 在四边形ABCD 的边上,则称点P 是线段MN 的“勾股点”.(1)如图①,线段MN 的中点O 到BC 的距离是______.A 3B .52C .3D .23(2)如图②,当2AP =时,求BN 的长度.(3)是否存在点N ,使线段MN 恰好有两个“勾股点”?若存在,请直接写出BN 的长度或取值范围;若不存在,请说明理由.【答案】(1)C ;(2)33(3)33318【解析】(1)如图1,过点M 作 MQ △AB 交BA 的延长线于点Q ,过点O 作 OE △BC ,垂足为E ,过点M 作MF △BC ,垂足为F ,连接AC ,△AB =AD ,CB =CD ,AC =AC ,5AB AD ==,53BC CD ==90B ∠=︒,AM =2,△△ABC △△ADC ,△△D =△B =90°,AC 225(53)10+=,△△DAC =△BAC =△QAM =60°,△DCA =BCA =△QMA =30°,△△DAC =△BAC =60°,△DCA =BCA =30°,△QA =1,QM 3△MQ △AB ,OE △BC ,90B ∠=︒,△四边形MQBF 是矩形,△MF =QB =AB +QA =5+1=6,,△MF △CB ,OE △BC ,△OE ∥MF ,△NO NE OM EF =, △OM =ON ,△NE =EF ,△OE =12MF =3,故选C .(2)过点M 作MQ △AB 交BA 的延长线于点Q ,△点P 是线段MN 的“勾股点”.△△MPN =90°,△△QPM =△BNP ,△△QPM △△BNP ,△QP QM BN BP =, △33BN =△BN =33 (3)根据(2)得,BN =33P 是线段MN 的“勾股点”.过点N 作NG △DC ,垂足为G ,当DM =DP =3时, 点P 是线段MN 的“勾股点”.△点P 是线段MN 的“勾股点”.△△MPN =90°,△PG =GN ,设BN =x ,则NC =(53x ),根据(2),得△NCG =60°,△PG =GN 3(53)x ,GC =1(53)2x ,3(53)x +1(53)2x =(533),解得x =318, 故当BN =318或33MN 恰好有两个“勾股点”.14.已知ABC ,90,6cm ACB AC BC ∠==︒=,点P 从点A 出发,沿AB 2cm 的速度向终点B 运动,同时,动点Q 从点B 出发沿BC 方向以每秒1cm 的速度向终点C 运动,设运动的时间为t 秒.(1)如上左图,若PQ BC ⊥,求t 的值;(2)如上中图,若PQ PC =,求t 的值;(3)如上右图,将PQC △沿BC 翻折至P QC '处,当t 为何值时,四边形QPCP '为菱形?【答案】(1)3t =;(2)2t =;(3)2t = 【解析】(1)解:由题意可得:2AP t =,226662AB +cm BQ t =, 则(622)cm BP AB AP t =-=,△90,ACB PQ BC ︒∠=⊥,△PQ AC ∥, △PQB ACB ∽,△BP BQ BA BC=, 622662t t -=, △3t =.(2)过点P 作PE BC ⊥交BC 于E 点,如图,BQ t =,6CQ t =-, △PQ PC =,△622CQ t QE EC -===, △PE AC ∥,△PEB ACB ∽,△BP BE AB BC=, 66222662t t t -+-=,解得:2t =.(3)如图,连接PP '交CQ 于D ,△四边形QPCP '为菱形,△PP CQ '⊥,CD DQ =,△点Q 的速度是每秒1cm ,△11(8)cm 22CD CQ t ==-, 过点P 作PO AC ⊥于O ,则四边形CDPO 是矩形,△CD OP =,△90,C AC BC ∠=︒=,△ABC 是等腰直角三角形,△45A ∠=︒,△点P 2cm , △22cm PO t t ==, △1(6)2t t -=,解得:2t =.15.图1是边长分别为a 和()b a b >的两个等边三角形纸片ABC 和CDE △叠放在一起(C 与C '重合)的图形.(1)操作:固定ABC ,将CDE △绕点C 按顺时针方向旋转20°,连结AD ,BE ,如图2,则ECA ∠=______度,并直接写出线段BE 与AD 的数量关系____.(2)操作:若将图1中的CDE △,绕点C 按顺时针方向旋转120°,使点B 、C 、D 在同一条直线上,连结AD 、BE ,如图3.①线段BE 与AD 之间是否仍存在(1)中的结论?若是,请证明;若不是,请直接写出BE 与AD 之间的数量关系;②求APB ∠的度数.(3)若将图1中的CDE △,绕点C 按逆时针方向旋转一个角()0360αα<<︒,当α等于多少度时,BCD △的面积最大?请直接写出答案.【答案】(1)40,BE =AD ;(2)①存在,理由见详解;②60°(3)当α=150°或330°时,BCD △的面积最大【解析】(1)△△ABC 和△CDE 是等边三角形,△BC =AC ,CE =CD ,△BCA =60°,△旋转20°△△BCE =△ACD =20°,△△CBE △△CAD (SAS ),△BE =AD (全等三角形的对应边相等),△ECA ∠=△BCA -△BCE△ECA ∠=60°-20°=40°故答案为:40,BE =AD(2)如图1,①(1)中结论仍然成立,理由如下:△△ABC和△CDE是等边三角形,BC=AC,CE=CD,△△BCE=△ACD=120°,△△CBE△△CAD(SAS),△BE=AD;②△△CBE△△CAD,△△CBE=△CAD,又△AOP=△BOC,△△APB=△ACB=60°;(3)如图2,当D运动到D1或D2,即BC△D1D2S△BCD最大12BC CD=⋅12=ab,此时旋转角是60°+90°=150°,或360°﹣30°=330°,△当α=150°或330°.16.知识再现:已知,如图1,四边形ABCD 是正方形,点M 、N 分别在边BC 、CD 上,连接AM 、AN 、MN ,且45MAN ∠=︒,延长CB 至G 使BG DN =,连接AG ,根据三角形全等的知识,我们可以证明MN BM DN =+.(1)知识探究:如图1中,作AH MN ⊥,垂足为点H ,猜想AH 与AB 有什么数量关系?并进行证明.(2)知识运用:如图2,四边形ABCD 是正方形,E 是边BC 的中点,F 为边CD 上一点,2FEC BAE ∠=∠,24AB =,求DF 的长.(3)知识拓展:已知45BAC ∠=︒,AD BC ⊥于点D ,且2BD =,6AD =,求CD 的长.【答案】(1)=AH AB ,证明见解析;(2)8;(3)3CD =【解析】(1)解:=AH AB ,理由如下:△四边形ABCD 是正方形,△AD AB =,=90ABG ADN ∠∠=︒,在ADN △和ABG 中,AD AB ADN ABG DN BG =⎧⎪∠=∠⎨⎪=⎩△()ADN ABG SAS ≌△△,△AG AN =,GAB NAD ∠=∠,△45MAN ∠=︒,90DAB ∠=︒,△45BAM NAD ∠+∠=︒,△45BAM GAB ∠+∠=︒,即45GAM MAN ∠=∠=︒,在GAM △和NAM △中,AG NG GAM MAN AM AM =⎧⎪∠=∠⎨⎪=⎩△()GAM NAM SAS ≌△△,△MN GM =,△GAM NAM =S △△S ,即1122AB GM AH MN =, △=AH AB ,(2)解:作AM EF ⊥交EF 与点M ,连接EF ,如图,设=BAE α∠,则2FEC α∠=,△=90B ∠︒,△=90BEA α∠︒-,△2FEC α∠=,△=90AEM α∠︒-,在ABE △和AME △中,ABE AME AEB AEM AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩△()ABE AME AAS ≌△△,△=BE ME ,=A AB M ,△24AB =,ABCD 为正方形,E 为BC 中点, △==12BE M E ,在Rt AMF △和Rt ADF 中,AD AM AF AF =⎧⎨=⎩△()AMF ADF HL ≌△△,△DF MF =,设DF x =,则24CF x =-,12EF x =+,△222EF CF EC =+,即()()222122412x x +=-+,解之得:8x =, △8DF =,(3)方法1、解:由题意可知:22210AB AD BD =+=作CE AB ⊥交AB 于点E ,如图,设CD a =,则236AC a =+△45BAC ∠=︒,236AC a =+△2362a AE EC += △()2113662=210222a a +⨯⨯+=12a -(舍去),=3a ,△3CD = 方法2、解:对比图1和图3可以发现当6AH AD ==,2BD MH ==,45BAC MAN ∠=∠=︒,CD NH =, 由(1)可知:AH AB =, 在Rt ABM 和Rt AHM 中,AM AM AB AH =⎧⎨=⎩△()ABM AHM HL △≌△, △2BM MH ==,△624MC =-=,同理可得:()AHN ADN HL △≌△, △DN HN =,设=DN HN x =,则6NC x =-,2MN x =+,△222NC MC MN +=,即()()222642x x -+=+,解之得3x =△=3CD NH。
人教版 八年级数学 上册第11章 三角形 综合巩固训练(含答案)

人教版八年级数学第11章三角形综合巩固训练一、选择题(本大题共10道小题)1. 如图,在△ABC中,AC边上的高是()图A.线段DA B.线段BAC.线段BC D.线段BD2. 在△ABC中,∠A=95°,∠B=40°,则∠C的度数是()A. 35°B. 40°C. 45°D. 50°3. 如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为()A. 40°B. 50°C. 60°D. 70°4. 下列各组数中,不可能成为一个三角形三边长的是()A. 2,3,4B. 5,7,7C. 5,6,12D. 6,8,105. 在△ABC中,∠A,∠C与∠B处的外角的度数如图所示,则x的值是()A.80 B.70 C.65 D.606. 若一个正多边形的每一个外角都等于40°,则它是()A.正九边形B.正十边形C.正十一边形D.正十二边形7. 把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是()A.六边形B.五边形C.四边形D.三角形8. 若在n边形内部任意取一点P,将点P与各顶点连接起来,可以把n边形分成n个三角形,利用这个事实,可以探索到n边形的内角和为()A.180°×n B.180°×n-180°C.180°×n+180°D.180°×n-360°9. (2019•大庆)如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM 的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是A.15°B.30°C.45°D.60°10. 如图,在△ABC中,∠ACB=70°,∠1=∠2,则∠BPC的度数为()A.70°B.108°C.110°D.125°二、填空题(本大题共8道小题)11. 如图,已知AB,CD相交于点O,且∠A=38°,∠B=58°,∠C=44°,则∠D =________°.12. 如图所示,x的值为________.13. 如图,若A表示四边形,B表示正多边形,则阴影部分表示________.14. 若一个等腰三角形两边的长分别为2 cm,5 cm,则它的周长为________cm.15. 如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就可以说明一个几何定理.请你写出这个定理的内容:______________________.16. 如图,在△ABC中,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别是D,E,F.若AC=4,AD=3,BE=2,则BC=________.17. 如图,在四边形ABCD中,AB∥CD,将四边形ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B=________°.18. 如图,在△ABC中,点D在BC的延长线上,∠A=m°,∠ABC和∠ACD 的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…;∠A2019BC和∠A2019CD的平分线交于点A2020,则∠A2020=________°.三、解答题(本大题共4道小题)19. 某单位修建正多边形花台,已知正多边形花台的一个外角的度数比一个内角度数的多12°.(1)求出这个正多边形的一个内角的度数;(2)求这个正多边形的边数.20. 如图,AE,BO,CO分别平分∠BAC,∠ABC,∠ACB,OD⊥BC于点D. 求证:∠1=∠2.21. 探究与证明如图①,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.(1)猜测∠1与∠2的关系,并说明理由;(2)如果∠ABC是钝角,如图②,(1)中的结论是否还成立?22. 已知:多边形的外角∠CBE和∠CDF的平分线分别为BM,DN.(1)若多边形为四边形ABCD.①如图 (a ),∠A =50°,∠C =100°,BM 与DN 交于点P ,求∠BPD 的度数; ②如图(b ),猜测当∠A 和∠C 满足什么数量关系时,BM ∥DN ,并证明你的猜想. (2)如图(c ),若多边形是五边形ABCDG ,已知∠A =140°,∠G =100°,∠BCD =120°,BM 与DN 交于点P ,求∠BPD 的度数.人教版 八年级数学 第11章 三角形 综合巩固训练-答案一、选择题(本大题共10道小题)1. 【答案】D2. 【答案】C【解析】根据三角形内角和为180°,∠C =180°-∠A -∠B =45°.3. 【答案】B【解析】∵AB ∥CD ,∴∠A =∠ACD =40°,∵∠ACB =90°,∴∠B =90°-∠A =90°-40°=50°.4. 【答案】C 【解析】若三条线段的长满足三角形的三边,则这三条线段长满足最小的两边之和大于地三边,由题意,A ,B ,D 都能构成三角形,C 中5+6=11<12,不能构成三角形.5. 【答案】B6. 【答案】A[解析] 由于正多边形的外角和为360°,且每一个外角都相等,因此边数=360°40°=9.7. 【答案】A[解析] 剪去一个角的方法有三种:经过两个顶点,则少了一条边;经过一个顶点和一边,边数不变;经过两条邻边,边数增加一条.所以一个n 边形剪去一个角后,剩下的形状可能是n 边形或(n +1)边形或(n -1)边形.8. 【答案】D9. 【答案】B【解析】∵BE是∠ABC的平分线,∴∠EBM=12∠ABC,∵CE是外角∠ACM的平分线,∴∠ECM=12∠ACM,则∠BEC=∠ECM–∠EBM=12×(∠ACM–∠ABC)=12∠A=30°,故选B.10. 【答案】C[解析] ∵在△ABC中,∠ACB=70°,∠1=∠2,∴∠2+∠BCP=∠1+∠BCP=∠ACB=70°.∴∠BPC=180°-∠2-∠BCP=180°-70°=110°.二、填空题(本大题共8道小题)11. 【答案】64[解析] 由三角形内角和定理可知∠A+∠D+∠AOD=180°,∠B +∠C+∠BOC=180°.∵∠AOD=∠BOC,∴∠A+∠D=∠B+∠C.∴∠D=64°.12. 【答案】55°[解析] 由多边形的外角和等于360°,得360°-105°-60°+x+2x=360°,解得x=55°.13. 【答案】正方形14. 【答案】12[解析] 分两种情况讨论:①当腰长为5 cm时,三边长分别为5 cm,5 cm,2 cm,满足三角形三边关系,周长=5+5+2=12(cm).②当腰长为2 cm时,三边长分别为5 cm,2 cm,2 cm.∵2+2=4<5,∴5 cm,2 cm,2 cm不满足三角形的三边关系.综上,它的周长为12 cm.15. 【答案】三角形三个内角的和等于180°16. 【答案】83 [解析] ∵S △ABC =12AC·BE =12BC·AD ,∴BC =AC·BE AD =4×23=83.17. 【答案】114[解析] 因为AB ∥CD ,所以∠BAB′=∠1=44°.由折叠的性质知∠BAC =12∠BAB′=22°.在△ABC 中,∠B =180°-(∠BAC +∠2)=114°.18. 【答案】(m22020)三、解答题(本大题共4道小题)19. 【答案】解:(1)设这个多边形的一个内角的度数是x °,则与其相邻的外角度数是x °+12°. 由题意,得x+x+12=180,解得x=140. 即这个正多边形的一个内角的度数是140°.(2)这个正多边形的每一个外角的度数为180°-140°=40°,所以这个正多边形的边数是=9.20. 【答案】证明:∵AE ,BO ,CO 分别平分∠BAC ,∠ABC ,∠ACB , ∴∠ABO =12∠ABC ,∠BAE =12∠BAC ,∠OCD =12∠ACB. ∵∠1=∠ABO +∠BAE ,∴∠1=12∠ABC +12∠BAC =12(180°-∠ACB)=90°-12∠ACB. 又∵∠2=90°-∠OCD =90°-12∠ACB ,∴∠1=∠2.21. 【答案】解:(1)∠1=∠2.理由如下: ∵AD ⊥BC ,CE ⊥AB ,∴△ABD 和△BCE 都是直角三角形.∴∠1+∠B =90°,∠2+∠B =90°. ∴∠1=∠2.(2)(1)中的结论仍然成立.理由如下: ∵AD ⊥BC ,CE ⊥AB , ∴∠D =∠E =90°.∴∠2+∠ABD =90°,∠1+∠CBE =90°. 又∵∠ABD =∠CBE , ∴∠1=∠2.22. 【答案】解:(1)①∵∠A =50°,∠C =100°, ∴在四边形ABCD 中,∠ABC +∠ADC =360°-∠A -∠C =210°. ∴∠CBE +∠CDF =150°.∵外角∠CBE 和∠CDF 的平分线分别为BM ,DN , ∴∠PBC +∠PDC =12∠CBE +12∠CDF =75°. ∴∠BPD =360°-50°-210°-75°=25°. ②当∠A =∠C 时,BM ∥DN. 证明:如图(a),连接BD.∵BM ∥DN ,∴∠BDN +∠DBM =180°.∴∠FDN +∠ADB +∠ABD +∠MBE =360°-180°=180°, 即12(∠FDC +∠CBE)+(∠ADB +∠ABD)=180°. ∴12(360°-∠ADC -∠CBA)+(180°-∠A)=180°. ∴12(360°-360°+∠A +∠C)+(180°-∠A)=180°. ∴∠A =∠C.(2)∵∠A =140°,∠G =100°,∠BCD =120°,∠A+∠ABC+∠BCD+∠CDG+∠G=540°,∴∠ABC+∠CDG=180°.∴∠CBE+∠CDF=180°.∵BP平分∠CBE,DP平分∠CDF,∴∠CBP+∠CDP=12(∠CBE+∠CDF)=90°.如图(b),延长DC交BP于点Q.∵∠BCD=∠CBP+∠CQB,∠CQB=∠QDP+∠BPD,∴∠BCD=∠CBP+∠QDP+∠BPD.∴∠BPD=120°-90°=30°.。
三角形综合训练(构造等腰)(人教版)(含答案)

三角形综合训练(构造等腰)(人教版)一、单选题(共7道,每道12分)1.如图,线段AB,BC的垂直平分线CD,DE相交于点D,∠ADC=50°,则∠ABC=( )A.10°B.30°C.25°D.40°答案:C解题思路:试题难度:三颗星知识点:垂直平分线的性质2.如图,在长方形ABCD中,AD∥BC,AD=BC,将△BCD沿对角线BD翻折,点C落在点处,交AD于点E,若BC=6,CD=3,则线段DE的长为( )A.3B.C.5D.答案:B解题思路:试题难度:三颗星知识点:折叠问题3.如图,在△ABC中,BG,CG分别平分∠ABC,∠ACF,DE过点G,且DE∥BC,若BD=8cm,CE=5cm,则DE=( )A.2cmB.3cmC.4cmD.5cm答案:B解题思路:试题难度:三颗星知识点:角平分线加平行会出现等腰三角形4.如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE,若AC=5,BC=3,则BD的长为( )A.2.5B.1.5C.2D.1答案:D解题思路:试题难度:三颗星知识点:三线合一5.如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠ABE=54°,则∠BED的度数为( )A.108°B.120°C.126°D.144°答案:C解题思路:试题难度:三颗星知识点:由“三线合一”想到构造等腰三角形6.如图,在△ABC中,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D.有下列结论:①AC-BE=AE;②∠BAD-∠C=∠DAE;③∠DAE=∠C.其中正确的是( )A.①②B.②③C.①③D.①②③答案:A解题思路:试题难度:三颗星知识点:由“三线合一”想到构造等腰三角形7.如图,BD,CE分别是∠ABC和∠ACB的角平分线,已知AG⊥BD,AF⊥CE,若BF=1,FG=3,GC=2,则△ABC的周长为( )A.10B.12C.14D.15答案:D解题思路:试题难度:三颗星知识点:两线重合想等腰二、填空题(共1道,每道16分)8.如图,△ABC中,AP垂直∠ABC的平分线BP于点P.若△PBC的面积为6,且△APB的面积是△APC的面积的2倍,则△APB的面积=____.答案:4解题思路:试题难度:知识点:角平分线加垂直出现等腰三角形。
三角形综合训练(两圆一线) (人教版)(含答案)

三角形综合训练(两圆一线)(人教版)一、单选题(共8道,每道12分)1.已知:如图,线段AB的端点A在直线上,AB与的夹角为60°,请在直线上另找一点C,使△ABC是等腰三角形.这样的点有( )A.1个B.2个C.3个D.4个答案:B解题思路:试题难度:三颗星知识点:等腰三角形的存在性2.在平面直角坐标系中,O为坐标原点,A(2,2),在x轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P共有( )A.4个B.3个C.2个D.1个答案:A解题思路:试题难度:三颗星知识点:两圆一线构造等腰三角形3.如图,已知直线PQ⊥MN于点O,点A,B分别在MN,PQ上,OA=1,OB=2,在直线MN 或直线PQ上找一点C,使△ABC是等腰三角形,则这样的点C有( )个.A.3B.4C.7D.8答案:D解题思路:试题难度:三颗星知识点:两圆一线构造等腰三角形4.如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有( )A.4个B.5个C.6个D.7个答案:C解题思路:试题难度:三颗星知识点:两圆一线构造等腰三角形5.如图,边长为6的正方形ABCD内部有一点P,BP=4,∠PBC=60°,点Q为正方形边上一动点,且△PBQ是等腰三角形,则符合条件的Q点有( )个.A.3B.4C.5D.6答案:C解题思路:试题难度:三颗星知识点:两圆一线构造等腰三角形6.如图,在正方形网格的格点(即最小正方形的顶点)中找一点C,使得△ABC是等腰三角形,且AB为其中一腰.这样的C点有( )个.A.8B.9C.10D.11答案:B解题思路:试题难度:三颗星知识点:两圆一线构造等腰三角形7.如图,在长方形ABCD中,∠ABC=90°,AB=3,BC=4.如果BC边上存在点P,使△APD为等腰三角形,则BP的长为( )A.或B.或2C.或2D.,或2答案:D解题思路:试题难度:三颗星知识点:两圆一线构造等腰三角形8.如图,已知平面直角坐标系中有点A(3,0)和点B(0,-4),在x轴上存在一点C,使得△ABC 为等腰三角形,则点C的坐标为( )A.(-4,0),(-1,0),(9,0)或B.(0,-4),(0,-1),(0,9)或C.(8,0),(-2,0),(-3,0)或D.(0,8),(0,-2),(0,-3)或答案:C解题思路:试题难度:三颗星知识点:两圆一线构造等腰三角形。
全等三角形综合练习
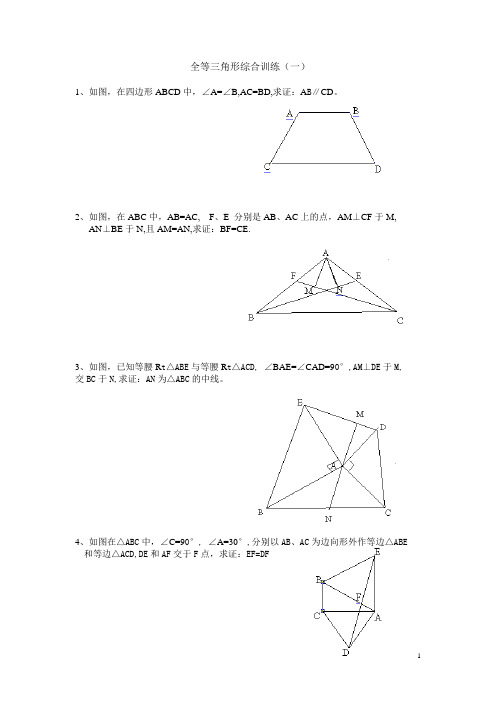
全等三角形综合训练(一)1、如图,在四边形ABCD中,∠A=∠B,AC=BD,求证:A B∥CD。
2、如图,在ABC中,AB=AC, F、E 分别是AB、AC上的点,AM⊥CF于M,AN⊥BE于N,且AM=AN,求证:BF=CE.3、如图,已知等腰R t△ABE与等腰R t△ACD,∠BAE=∠CAD=90°,AM⊥DE于M, 交BC于N,求证:AN为△ABC的中线。
4、如图在△ABC中,∠C=90°,∠A=30°,分别以AB、AC为边向形外作等边△ABE和等边△ACD,DE和AF交于F点,求证:EF=DF5、如图、已知等边△ABC和等边△BDE,点A、B、D在一条直线上,连AE、CD交于点P.(1)AE=CD;(2)求∠DPE的度数;(3)若△BDE绕B点旋转任意角度,其它条件不变,则(1)、(2)的结论是否仍成立?试证明。
6、如图、已知等腰Rt△ABC和等腰Rt△CDE,AC=BC,CD=CE,M、N分别为AE、BD的中点,连CM、CN.(1)判断CM与CN的位置关系和数量关系;(2)若Rt△CDE绕C点旋转任意角度,其它条件不变,则(1)的结论是否仍成立?试证明。
7、如图,已知等腰Rt△ABC的直角顶点C在X轴上,B在Y轴上。
(1)若点C的坐标为(2,0),A的坐标为(-2,-2),求点B的坐标;(2)在(1)的条件下,AB交X轴于F,边AC交Y轴于E,连EF,①求证:CE=AE;②求证:∠CEB=∠AEF。
(3)如图,直角边BC在坐标轴上运动,使点A在第四象限内,过点A作AD⊥y轴y于点D,求的值。
8、如图,在平面直角坐标系中,点B的坐标是(-1,0),点C的坐标是(1, 0),点D 为y轴上一点,点A为第二象限内一动点,且∠BAC=2∠BDO;过D作DM⊥AC于M.(1)求证:∠ABD=∠ACD;(2)若点E在BA的延长线上,求证:AD平分∠CAE;(3)当A点运动时,的值是否发生变化?若不变,求其值,若变化,请说明理由。
2023年九年级中考数学重难点训练——三角形的综合

2023年中考数学重难点训练——三角形的综合一、综合题1.如图,AC 为矩形ABCD 的对角线,将边AB 沿AE 折叠,使点B 落在AC 上的点M 处,将边CD 沿CF折叠,使点D 落在AC 上的点N 处。
(1)求证:四边形AECF 是平行四边形; (2)若AB=6,AC=10,求四边形AECF 的面积。
2.如图,已知菱形中 ABCD ,且 60BAD ∠=︒ 延长 AB 至点 E ,使 BE AB = ,连接 BD 和CE .(1)求证:DAB CBE ≌ ; (2)求证:四边形 DBEC 是菱形.3.已知:如图,四边形ABCD 是正方形,点E 、F 分别在BC 、CD 上,连接AE 、EF 、AF ,且∠DAE =∠AEF .(1)求证:EF =BE+DF ;(2)线段AF 的垂直平分线交AD 于点G ,连接FG ,求证:∠EFG =90°; (3)在(2)的条件下,若tan∠DFG =34 ,EF = 203,求S ∠AEF . 4.如图所示,已知∠ABC 中,BC=30cm ,AD=10cm .AD 是高,矩形EFGH 内接于∠ABC 中,且长边FG 在BC 边上.设EF=x , FG=y .(1)求y 与x 的函数关系式.并求自变量x 的取值范围. (2)若x :y=1:2,求矩形EFGH 的面积.(3)当EF 为何值时,矩形EFGH 的面积最大?最大面积是多少?5.如图,Rt∠ABC 中,分别以AB 、AC 为斜边,向∠ABC 的内侧作等腰Rt∠ABE 、Rt∠ACD ,点M 是BC 的中点,连接MD 、ME .(1)若AB =8,AC =4,求DE 的长;(2)求证:AB ﹣AC =2DM .6.如图,菱形ABCD 中,∠B =60°,AB =3cm ,过点A 作∠EAF =60°,分别交DC ,BC 的延长线于点E ,F ,连接EF.(1)如图1,当CE =CF 时,判断∠AEF 的形状,并说明理由;(2)若∠AEF 是直角三角形,求CE ,CF 的长度;(3)当CE ,CF 的长度发生变化时,∠CEF 的面积是否会发生变化,请说明理由.7.已知等边∠ABC 和射线AP ,作AC 边关于射线AP 的对称线段AD ,连接BD ,CD .(1)如图1,当射线AP 在∠BAC 内部时, ①请依题意补全图形;②若∠PAC =15°,则∠BDC = ▲ 度; ③若∠PAC =x°,试求∠BDC 的度数;(2)如图2,当射线AP 在∠BAC 外部的AC 右侧时,设BD 交AP 于点E , ①∠BDC = ▲ 度;②线段AE ,BE ,DE 之间有何数量关系?试说明理由.8.如图,正方形OABC 的边OA ,OC 在坐标轴上,点B 的坐标为(﹣2,2).点P 从点A 出发,以每秒1个单位长度的速度沿x 轴向点O 运动;点Q 从点O 同时出发,以相同的速度沿x 轴正方向运动,过点Q 作直线l 垂直x 轴.当点P 到达点O 时,点Q 也停止运动.连接BP ,作PD∠BP 交直线l 于点D.连结BD 交y 轴于点E ,连接PE.设点P 的运动时间为t (s ).(1)①点D 的坐标为 (用含t 的代数式表示). ②当0<t≤2时,∠PED 的大小范围是 .(2)当0<t <2时,∠POE 的周长C 是否随t 的变化而变化?若变化,求出C 关于t 的关系式;若不变,求出C 的值.(3)当t = 秒时,∠PBE 为等腰三角形(直接给出答案).9.如图,已知正方形OEFG 的顶点O 与正方形ABCD 的中心O 重合,若正方形OEFG 绕O 点旋转.(1)探究:在旋转的过程中线段BE 与线段CG 有什么数量关系及位置关系?证明你的结论; (2)若正方形ABCD 的边长为a ,探究:在旋转过程中四边形OMCN 的面积是否发生变化?若不变化求其面积,若变化指出变化过程.10.(1)问题发现:如图(1),在∠OAB 和∠OCD 中,OA =OB ,OC =OD ,∠AOB =∠COD =36°,连接AC ,BD 交于点M .①ACBD的值为 ;②∠AMB 的度数为 ; (2)类比探究 :如图(2),在∠OAB 和∠OCD 中,∠AOB =∠COD =90°,∠OAB =∠OCD =30°,连接AC ,交BD 的延长线于点M .请计算ACBD的值及∠AMB 的度数. (3)拓展延伸:在(2)的条件下,将∠OCD 绕点O 在平面内旋转,AC ,BD 所在直线交于点M .若OD=1,OB 13C 与点M 重合时AC 的长.11.如图,以BC 为边分别作菱形BCDE 和菱形BCFG (点C ,D ,F 共线),动点A 在以BC 为直径且处于菱形BCFG 内的圆弧上,连接EF 交BC 于点O .设θG ∠=.(1)求证:无论θ为何值,EF 与BC 相互平分;并请直接写出使EF BC ⊥成立的θ值. (2)当θ90=︒时,试给出tan ABC ∠的值,使得EF 垂直平分AC ,请说明理由.12.如图①,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.(1)写出点C,D的坐标并求出四边形ABDC的面积;(2)在y轴上是否存在一点Q,连接QA,QB,使∠AQB的面积等于四边形ABDC的面积的一半?若存在这样的点,求出点Q的坐标;若不存在,请说明理由;(3)如图②,点P是线段BD上一个动点,连接PC,PO,当点P在线段BD上运动时,试探究∠OPC与∠PCD,∠POB的数量关系,并证明你的结论.13.如图1,菱形ABCD中,DE∠AB,垂足为E,DE=3cm,AE=4cm,把四边形BCDE沿DE所在直线折叠,使点B落在AE上的点M处,点C落在点N处,MN交AD于点F.(1)证明:FA=FM;(2)求四边形DEMF面积;(3)如图2,点P从点D出发,沿D→N→F路径以每秒1cm的速度匀速运动,设运动时间为t秒,当t 为何值时,∠DPF的面积与四边形DEMF的面积相等.14.如图,平面直角坐标系中,点A在第一象限,AB∠x轴于B,AC∠y轴于C,A(4m,3m),且四边形ABOC的面积为48.(1)如图①,求A点的坐标;(2)如图②,点D从O出发以每秒1个单位的速度沿y轴正半轴运动,同时点E从A出发,以每秒2个单位的速度沿射线BA运动,DE交线段AC于F,设运动的时间为t,当S∠AEF<S∠CDF时,求t的取值范围.15.如图1,在等腰直角三角形ADC中,904ADC AD∠==,.点E是AD的中点,以DE为边作正方形DEFG,连接AG CE,.将正方形DEFG绕点D顺时针旋转,旋转角为(090)αα<<.(1)如图2,在旋转过程中,①判断AGD∆与CED∆是否全等,并说明理由;②当CE CD=时,AG与EF交于点H,求GH的长.(2)如图3,延长CE交直线AG于点P.①求证:AG CP⊥;②在旋转过程中,线段PC的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.16.如图1,菱形ABCD的对角线AC、BD相交于点O,且AC=6cm,BD=8cm,分别过点B、C作AC与BD的平行线相交于点E.(1)判断四边形BOCE的形状并证明;(2)点G从点A沿射线AC的方向以2cm/s的速度移动了t秒,连接BG,当S∠ABG=2S∠OBG时,求t的值.(3)如图2,长度为3cm的线段GH在射线AC上运动,求BG+BH的最小值.17.如图1,已知点A,B,C,D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.(1)求证:∠ACE∠∠DBF;(2)如果把∠DBF沿AD折翻折使点F落在点G,如图2,连接BE和CG.求证:四边形BGCE是平行四边形.18.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)如图1,连接AF、CE求证:四边形AFCE为菱形;(2)如图1,求AF的长;(3)如图2,动点P、Q分别从A、C两点同时出发,沿∠AFB和∠CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t 秒.若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.答案解析部分1.【答案】(1)证明:∵折叠,∴AM=AB ,CN=CD ,∠FNC=∠D=90°,∠AME=∠B=90°,∴∠ANF=90°,∠CME=90°,∵四边形ABCD 为矩形,∴AB=CD ,AD∠BC , ∴AM=CN ,∴AM ﹣MN=CN ﹣MN ,即AN=CM , 在∠ANF 和∠CME 中,∴∠ANF∠∠CME (ASA ),∴AF=CE ,又∵AF∠CE ,∴四边形AECF 是平行四边形;(2)解:∵AB=6,AC=10,∴BC=8,设CE=x ,则EM=8﹣x ,CM=10﹣6=4,在Rt∠CEM 中,(8﹣x )2+42=x 2,解得:x=5,∴四边形AECF 的面积的面积为:EC•AB=5×6=30.2.【答案】(1)解:∵菱形 ABCD∴AD BC , AD BC = ∴CBE DAB ∠=∠ ∵BE AB =∴()DAB CBE SAS ≌ (2)解:∵菱形 ABCD , ∴DC BE , ==DC AD AB BE = , ∴四边形 DBEC 是平行四边形, ∵60DAB ∠=︒ ∴∠ABD 是等边三角形 ∴AB BD BE == . ∴四边形 DBEC 是菱形.3.【答案】(1)证明:过点A 作AH∠EF 于点H ,∵四边形ABCD 是正方形,∴AB =AD ,∠B =∠D =90°,AD∠BC , ∴∠BEA =∠DAE , ∵∠DAE =∠AEF , ∴∠BEA =∠AEF , 在∠ABE 和∠AHE 中,∵B AHEBEA AEH AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴∠ABE∠∠AHE (AAS ), ∴AB =AH ,BE =HE , ∴AH =AD ,∴Rt∠AHF∠Rt∠ADF (HL ), ∴DF =HF , ∵EF =HE+HF , ∴EF =BE+DF(2)解:如图2,由题意知GA =GF ,∴∠GAF =∠GFA , 由(1)知∠AFE =∠AFD , ∵∠FAD+∠AFD =90°, ∴∠GFA+∠AFE =90°,∴∠EFG =90°(3)解:由tan∠DFG = DG DF = 34可设DG =3x ,DF =4x , 则AG =GF =22DG DF +=()()2234x x +=5x ,EH =DF =4x ,∴BC =CD =AD =8x ,∴CF=CD﹣DF=4x,∵EF=203,∴BE=EH=EF﹣FH=203﹣4x,则EC=BC﹣BE=8x﹣(203﹣4x)=12x﹣203,在Rt∠ECF中,由EF2=EC2+CF2得(203)2=(12x﹣203)2+(4x)2,解得:x1=0(舍),x2=1,即AH=AD=8x=8,∴S∠AEF=12EF•AH=12×203×8=8034.【答案】(1)解:如图,∵EF=x,FG=y,∴DM=EF=x,AM=AD-DM=10-x,∵EH//BC,∴EH AMBC AD=,即1030y x-=,∴y=30-3x;∵y>0,∴30-3x>0,即x<10,∵x>0,∴x取值范围为0<x<10;(2)解:∵x:y=1:2,∴y=2x,∵y=30-3x,∴2x=30-3x,∴x=6,∴y=12,∴矩形EFGH的面积=6×12=72;(3)解:设四边形EFGH的面积为S,则S=x(30-3x)=-3x2+30x=-3(x-5)2+75,∴当x=5时,即EF=5时,S有最大值为75.5.【答案】(1)解:直角∠ABE中,AE=22AB=4 2,在直角∠ACD中,AD=22AC=2 2,则DE=AE﹣AD=4 2﹣2 2=2 2;(2)解:延长CD交AB于点F.在∠ADF和∠ADC中,{∠FAD=∠CADAD=AD∠ADF=∠ADC,∴∠ADF∠∠ADC(ASA),∴AC=AF,CD=DF,又∵M是BC的中点,∴DM是∠CBF的中位线,∴DM=12BF=12(AB﹣AF)=12(AB﹣AC),∴AB﹣AC=2DM.6.【答案】(1)解:∠AEF是等边三角形,理由如下:连接BE、DF,如图1所示:∵四边形ABCD是菱形,∴AB=BC=DC=AD,∠ABC=∠ADC,在∠BCE和∠DCF中,BD DCBCE DCFCE CF=⎧⎪∠=∠⎨⎪=⎩,∴∠BCE∠∠DCF(SAS),∴∠BE=DF,CBE=∠CDF,∴∠ABC+∠CBE=∠ADC+∠CDF,即∠ABE=∠ADF,在∠ABE和∠ADF中,AB ADABE ADFBE DF=⎧⎪∠=∠⎨⎪=⎩,∴∠ABE∠∠ADF(SAS),∴AE=AF,又∵∠EAF=60°,∴∠AEF是等边三角形;(2)解:分两种情况:①∠AFE=90°时,连接AC、MN,如图2所示:∵四边形ABCD是菱形,∴AB=BC=DC=AD=3,∠D=∠B=60°,AD∠BC,AB∠CD,∴∠ABC和∠ADC是等边三角形,∴AC=AD,∠ACM=∠D=∠CAD=60°=∠EAF,∴∠MAC=∠NAD,在∠MAC和∠NAD中,MAC NADAC ADACM D∠=∠⎧⎪=⎨⎪∠=∠⎩,∴∠MAC∠∠NAD(ASA),∴AM=AN,CM=DN,∵∠EAF=60°,∴∠AMN是等边三角形,∴AM=MN=AN,设AM=AN=MN=m,DN=CM=b,BM=CN=a,∵CF∠AD,∴∠CFN∠∠DAN,∴CF FN CN aAD AN DN b===,∴FN=amb,∴AF=m+amb,同理:AE=m+bma,在Rt∠AEF中,∵∠EAF=60°,∴∠AEF=30°,∴AE=2AF,∴m+bma=2(m+amb),整理得:b2﹣ab﹣2a2=0,(b﹣2a)(b+a)=0,∵b+a≠0,∴b﹣2a=0,∴b=2a,∴CFAD=12,∴CF =12 AD = 32, 同理:CE =2AB =6;②∠AEF =90°时,连接AC 、MN ,如图3所示:同①得:CE =12 AD = 32,CF =2AB =6; (3)解:当CE ,CF 的长度发生变化时,∠CEF 的面积不发生变化;理由如下:作FH∠CD 于H ,如图4所示:由(2)得:BM =CN =a ,CM =DN =b , ∵AD∠CF , ∴∠ADN∠∠FCN ,∴AD DN bCF CN a== , ∵CE∠AB ,∴∠FCH =∠B =60°,∠CEM∠∠BAM ,∴CE CM bAB BM a == , ∴AD CECF AB= , ∴CF×CE =AD×AB =3×3=9, ∵CH =CF×sin∠FCH =CF×sin60°=32CF , ∠CEF 的面积= 12 CE×FH = 12 CE× 3CF = 12 ×9× 3 = 93,∴∠CEF 的面积是定值,不发生变化.7.【答案】(1)解:①解:如图,补全图形:;②150°;③由对称可知,∠PAC=∠PAD=x°, ∵AD=AB=AC ,∠BAD=60°-2x°, ∴∠ADC=1802902x x ︒-︒=︒-︒ ,∠ADB= ()180602602x x ︒-︒-︒=︒+︒ , ∴∠BDC=∠ADC+∠ADB= 90x ︒-︒ + 60x ︒+︒ =150°; ∠BDC 的度数为150°;(2)解:①30°;②BD=2DE+AE ,理由如下: 如图,在BD 上截取EG=EC ,由(2)①知:∠BDC=30°,∠ADB=∠ABD=60°-α, 由对称可知,∠EDC=∠ECD=30°,∠AED=90°+30°=120°, ∴∠BEC=∠EDC+∠ECD=60°, ∴∠CGE 是等边三角形, ∴∠BGC=∠AED=120°,∵∠CBG=60°-∠ABD=60°-(60°-α)=α, ∵∠CBG=∠DAE=α, ∴∠CBG∠∠DAE (AAS ),∴AE=BG,∵EG=CE=DE,∴BD=2DE+BG,即BD=2DE+AE.8.【答案】(1)(t,t);90°≤∠PED<135°(2)解:结论:∠POE的周长C=4,是定值.理由:延长OA到K,使得AK=CE,连接BK,∵BC=BA,∠BCE=∠BAK=90°,CE=AK,∴∠KAB∠∠ECB(SAS),∴KB=EB,∠KBA=∠EBC,∵∠EBP=45°,∠ABC=90°,∴∠ABP+∠EBC=45°,∴∠KBP=∠KBA+∠ABP=∠EBC+∠ABP=45°,∴∠KBP=∠EBP,∴∠KBP∠∠EBP(SAS),∴KP=EP,∴EP=KP=KA+AP=CE+AP,∴∠POE的周长C=PE+OP+OE=PA+OP+OE+EC=2OA=4,是定值.(3)2或(22﹣2)9.【答案】(1)解:BE=CG,BE∠CG,理由如下:连接OB、OC,延长GC交BE于T点,交OE于H点,∵O是正方形的中心,∴OB=OC.∵∠BOE+∠MOC=90°,∠COG+∠MOC=90°,∴∠BOE=∠COG.又OE=OG,∴∠OBE∠∠OCG(SAS).∴BE=CG,∠BEO=∠CGO.∵∠OHG+∠CGO=90°,∠OHG=∠EHT,∴∠EHT+∠BEO=90°,即∠HTE=90°,所以GC∠BE(2)解:在旋转过程中四边形OMCN的面积不发生变化,理由如下:在∠OBM和∠OCN中45BOM CONOB OCOBM OCN∠=∠⎧⎪=⎨⎪∠=∠=⎩∴∠OBM∠∠OCN(ASA)∴四边形OMCN的面积=∠OMC面积+∠OCN面积=∠OMC面积+∠OBM面积=∠OBC面积.∵∠OBC面积=14a2.所以在旋转过程中四边形OMCN的面积不发生变化.10.【答案】(1)1;36°(2)解:在∠OAB 和∠OCD 中,∵∠AOB=∠COD=90°,∠OAB=∠OCD=30°, ∴tan30°=3OD OB OC OA ==, ∵∠AOB+∠DOA=∠COD+∠DOA , 即∠DOB=∠COA , ∴∠DOB∠∠COA , ∴3AC OC BD OD== ∠DBO=∠CAO ,∵∠DBO+∠OEB=90°,∠OEB=∠MEA , ∴∠CAO+∠MEA=90°, ∴∠AMB=90°, ∴ACBD3,∠AMB=90°; (3)3311.【答案】(1)证明:如图所示:连接BF 、CE ,∵菱形BCDE 和菱形BCFG (点C ,D ,F 共线), ∴点G 、B 、E 共线,FC BG FC BC BE ∴==, ,FC BE FC BE ∴=, ,∴四边形BFCE 是平行四边形,∴EF 与BC 相互平分,即:无论θ为何值,EF 与BC 相互平分; 又∵EF BC ⊥, ∴四边形BFCE 是菱形,∴BE=BF ,又∵菱形BCDE 和菱形BCFG ,GF BG BF BE ∴=== , GFB ∴ 为等边三角形, θ60G ∴∠==︒;(2)解:如图所示:连接AF ,AO ,设EF 与AC 交于点H ,∵EF 垂直平分AC90AF FC AO CO AHO ∴==∠=︒,, ,由(1)知,O 为BC 的中点,∴动点A 在以O 为圆心,BC 为直径且处于菱形BCFG 内的圆弧上,90BAC AO BO CO ∴∠=︒==, ,OBA OAB ∴∠=∠ ,90OAB OAC AOH OAC ∠+∠=∠+∠=︒ , AOH OAB OBA ∴∠=∠=∠ ,在AOF 和COF 中,AF CF AO CO FO FO =⎧⎪=⎨⎪=⎩, AOF COF ∴≌ , FAO FCO ∴∠=∠ ,∵θ90=︒,菱形BCFG , ∴四边形BCFG 为正方形,90FCO FC BC ∴∠=︒=, , 90FAO FCO ∴∠=∠=︒,设FC BC x ==,则AF CF x == ,1122AO OC BC x === ,在Rt FAO 中,212AF xtan FOA AO x ∠===, AOH OBA ∠=∠, 2tan ABC tan FOA ∴∠=∠=.12.【答案】(1)解:由题意,点C 的坐标为(0,2),D 点坐标为(4,2),∵AC∠BD ,∴四边形ABCD 为平行四边形, ∴四边形ABDC 的面积=2×4=8. (2)解:存在.设Q 点坐标为(0,t ),∵S ∠QAB = 12S 四边形ABCD ,∴12•4•|t|=4,解得t =±2, ∴Q 点坐标为(0,2)或(0,﹣2). (3)解:结论:∠OPC =∠PCD +∠POB . 理由:过点P 作PE∠CD .∵AB∠CD , ∴PE∠AB∠CD ,∴∠EPC =∠PCD ,∠EPO =∠POB , ∴∠OPC =∠EPC +∠EPO =∠PCD +∠POB .13.【答案】(1)证明:∵四边形ABCD 是菱形,∴AD∠BC , ∴∠A+∠B =180°,由折叠可知∠NMB =∠B ,且∠NMA+∠NMB =180°, ∴∠A =∠NMA , ∴FA =FM ;(2)解:过点F 作FG∠AM 于G ,由(1)可知AG =GM =1AM 2, Rt∠ADE 中,AE =4cm ,DE =3cm , ∴AD =5cm ,∵四边形ABCD 是菱形, ∴AB =AD =5cm , ∴EB =AB ﹣AE =1cm , ∴EM =EB =1cm , ∴AM =AE ﹣EM =3cm ,∴13AG AM 22== cm ,又∵3tan 4FG DE A AG AE ∠=== cm , ∴9FG 8=cm , ∴2ADE AFM 1111927S AE DE 346cm ,S AB FG 32222816∆=⋅=⨯⨯==⋅=⨯⨯=cm 2, ∴S 四边形DEMF =S ∠ADE ﹣S ∠AFM =6﹣27691616= cm 2 ; (3)解:分两种情况:①0<t≤5时,如图2,此时P 在边DN 上,过点F 作FH∠ND 于H ,∵DN∠AM , ∴53DN FN AM FM == , ∵MN =BC =5,∴FN =525588⨯= , sin∠N =FH DE 3FN AD 5== , ∴FH = 32515588⨯= , S ∠DPF = 11151522816DP FH t ⋅=⋅⋅= ,令 1569t 1616= 解得: 6915t = ; ②∵DN+FN =5+ 256588= , 当 6558t << 时,P 在FN 上,如图3,过P 作PK∠DN 于K ,∵PN =t ﹣5, ∴PK =3(5)5t - , S ∠DPF =S ∠NFD ﹣S ∠NPD =11513319555(5)2825216t t ⨯⨯-⨯⨯-=-+ , 令﹣ 319569t 21616+= ,解得:t = 214, 所以,综上,当t = 6915 或t = 214时,∠DPF 面积与四边形DEMF 面积相等. 14.【答案】(1)解:∵ AB∠x 轴, AC∠y 轴,∴四边形ABOC 是矩形,∵AC =4m ,AB=3m ,四边形ABOC 的面积为48, ∴4m×3m=48, ∴m=2或-2,∵点A 在第一象限, ∴m=2,∴A (8,6);(2)解:由题意知,OD=t ,AE=2t , ∵S ∠AEF <S ∠CDF ,∴S ∠CDF +S 五边形ABODF >S ∠AEF +S 五边形ABODF ,即S 四边形ABOC >S 梯形DOBE , ∴148(62)82t t >++⨯ , ∴2t < ,∴t 的取值范围是 02t << .15.【答案】(1)①全等,理由如下:在等腰直角三角形 ADC 中,AD=CD , 90ADC ∠= , 在正方形 DEFG 中,GD=ED , 90GDE ∠= , 又∵90ADE EDC ∠+∠=︒ , 90ADE ADG ∠+∠=︒ , ∴ADG CDE ∠=∠ 在AGD 和 CED 中,AD CD ADG CDE GD ED =⎧⎪∠=∠⎨⎪=⎩, ∴AGD CED ≅ (SAS );②如解图2,过A 点作AM∠GD ,垂足为M ,交FE 与N ,∵点 E 是 AD 的中点,∴在正方形 DEFG 中,DE=GD=GF=EF=2, 由①得AGD CED ≅ ,∴AG CE = , 又∵CE CD = , ∴4AG AD CD === , ∵AM∠GD , ∴112GM GD == , 又∵90D F ∠=∠=︒ , ∴四边形GMNF 是矩形, ∴2MN GF == , 在 Rt AGM 中, 22224115AM AG GM =-=-=,∴15cos AM GAM AG ∠==∵//FG AM , ∴GAM AGF ∠=∠ ∴15cos 4FG AGF GH ∠==, ∴815cos 15FG GH AGF ===∠. (2)①由①得 AGD CED ≅ ,∴GAD ECD ∠=∠ ,又∵90ECD ECA DAC ∠+∠+∠=︒ ,∴90GAD ECA DAC ∠+∠+∠=︒ , ∴90APC ∠=︒ ,即: AG CP ⊥ ;②∵90APC ∠=︒ , ∴sin PC AC PAC =⋅∠ , ∴当 PAC ∠ 最大时,PC 最大, ∵∠DAC=45°,是定值,∴GAD ∠ 最大时, PAC ∠ 最大,PC 最大, ∵AD=4,GD=2,∴当GD∠AG , 30GAD ∠=︒ 最大,如解图3,此时 22224223AG AD GD =-=-=,又∵AG CP ⊥ , EF FG ⊥ ,∴F 点与P 点重合, ∴CEFP 四点共线,∴CP=CE+EF=AG+EF= 232 , ∴线段 PC 得最大值为: 232 .16.【答案】(1)结论:四边形BOCE 是矩形.理由:∵BE∠OC ,EC∠OB , ∴四边形OBEC 是平行四边形, ∵四边形ABCD 是菱形, ∴AC∠BD , ∴∠BOC =90°,∴四边形BOCE 是矩形.(2)如图2中,∵四边形ABCD 是菱形,∴OA =OC =3cm ,OB =OD =4cm , ∵S ∠ABG =2S ∠OBG , ∴AG =2OG ,∴2t =2(3﹣2t )或2t =2(2t ﹣3), 解得t =1或t =3,∴满足条件的t 的值为1或3.(3)如图2中,设OG =x ,则BG +BH =224x ++22(3)4x -+ ,欲求BG +BH 的最小值,相当于在x 轴上找一点P(x ,0),使得点P(x ,0)到A(0,4)和B(3,4)的距离最小,如图3中,作点B 关于x 轴的对称点 B ' ,连接 AB ' 交x 轴于P ,连接BP ,此时PA +PB 的值最小, ∵A(0,4), B ' (3,﹣4), ∴当B 点在y 轴右侧时, AP +PB =AP + PB ' = AB ' =2283+=73,当B 点在y 轴左侧时,由于线段整体移动,同理,得 AP +PB =AP + PB ' = AB ' = 73,∴BG +BH 的最小值为73.17.【答案】(1)证明:如图1,∵OB =OC ,∴∠ACE =∠DBF , 在∠ACE 和∠DBF 中,ACE DBFE FAE FD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴∠ACE∠∠DBF (AAS ) (2)证明:如图2,∵∠ACE =∠DBF ,∠DBG =∠DBF , ∴∠ACE =∠DBG ,∴CE∠BG ,∵CE =BF ,BG =BF , ∴CE =BG ,∴四边形BGCE 是平行四边形.18.【答案】(1)证明:∵四边形ABCD 是矩形, ∴AD∠BC , ∴∠EAO=∠FCO ,∵EF 是AC 的垂直平分线, ∴OA=OC , ∵∠AOE=∠COF , ∴ΔAOE∠ΔCOF (ASA ), ∴OE=OF , ∵OA=OC ,∴四边形AFCE 是平行四边形, ∵EF∠AC ,∴平行四边形AFCE 是菱形; (2)解:∵四边形AFCE 是菱形, ∴AF=FC ,设AF=xcm ,则CF=xcm ,BF=(8-x)cm , ∵四边形ABCD 是矩形,∴∠B=90°,则在RtΔABF 中,由勾股定理得: ()22248x x +-=, 解得:x=5,即AF=5cm ; (3)解:分为三种情况:①P 在AF 上,∵P 的速度是1cm/s ,而Q 的速度是0.8cm/s ,∴Q 只能在CD 上,此时以A 、P 、C 、Q 四点为顶点的四边形不是平行四边形;②当P 在BF 上时,Q 在CD 或DE 上,其中只有当Q 在DE 上时,以A 、P 、C 、Q 四点为顶点的四边形才有可能是平行四边形,如图,∵AQ=8-(0.8t -4),CP=5+(t -5), ∴8-(0.8t -4)=5+(t -5),解得: 203t =; ③当P 在AB 上时,Q 在DE 或CE 上,此时以A 、P 、C 、Q 四点为顶点的四边形不是平行四边形; 综上所述,当203t =时,以A 、P 、C 、Q 四点为顶点的四边形是平行四边形.。
三角形综合训练

三角形综合训练(2013.12.5)1.(2013山东德州,4,3分)如图,AB∥CD,点E在BC上,且CD=CE,∠D=740,,则∠B的度数为()A、680B、320C、220D、1602.(2013河北省,8,3分)如图1,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( ) A.40海里B.60海里C.70海里D.80海里3.(2013湖北荆门,14,3分)若等腰三角形的一个内角为50°,则它的顶角为______.4.(2013广东广州,11,3分)点P在线段AB的垂直平分线上,P A=7,则PB=______.5.(2013白银,13,4分)等腰三角形的周长为16,其一边长为6,则另两边为.6.(2013贵州毕节,7,3分)已知等腰三角形的一边长为4,另一边长为8,则这个等腰三角形的周长为_________ 7.(2013贵州省黔西南州,20,3分)如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=度.8(2013四川内江,18,8分)已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB 边上一点.求证:BD=AE.9.(2013湖北荆门,19,9分)如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.(1)求证:BE=CE;(2)若BE的延长线交AC于点F,且BF⊥AC,垂足为F,如图2,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.AB CDEF(图2)AB CDE(图1)整式运算练习(2013.12.5)1.(2012安徽)计算32)2(x -的结果是( )A.52x - B. 68x - C.62x - D.58x - 2.(2012陕西)计算23)5(a -的结果是( )A .510a - B .610aC .525a -D .625a3.( 2012年浙江省宁波市)(-2)0的值为 ( ) A.-2 B.0 C.1 D.2 4.(2012连云港,3,3分)下列格式计算正确的是( )A. (a+1)2=a 2+1B. a 2+ a 3= a 5C. a 8÷ a 2= a 6D. 3a 2-2 a 2= 15.(2012湖北襄阳2,3分)下列计算正确的是( )A .a 3-a =a 2 B .(-2a)2=4a 2 C .x 3·x -2=x -6D .x 6÷x 3=x 26.(2012山东东营,8,3分)若43=x,79=y ,则yx 23-的值为( )A .74 B .47 C .3- D .727.(2012云南省,8 ,3分)若2214a b -=,12a b -= ,则a b +的值为( )A .12- B. 12 C. 1 D. 28.(2012山东德州中考,10,4,)化简:6363a a ÷= .9.(2012,黔东南州,13)二次三项式29x kx -+是一个完全平方式,则k 的值是 10.(2012贵州遵义,13,4分)已知x+y=﹣5,xy=6,则x 2+y 2= .11.(2012安徽8分)计算:)2()1)(3(-+-+a a a a 12.(2012江苏盐城4分)化简:(a-b)2+b(2a+b) .13.(2012福州)化简:()()2111a a a -++- 14. (2012贵州贵阳8分)先化简,再求值:2b 2+(a+b)(a-b)- (a-b)2,其中a=-3,b=21.15.(2012广东汕头,15,7分)先化简,再求值:(x+3)(x ﹣3)﹣x (x ﹣2),其中x=4.16.(2012浙江丽水6分,18题)(本题6分)已知A=2x+y ,B=2x-y ,计算A 2-B 2.。
第十一章三角形综合训练题及答案
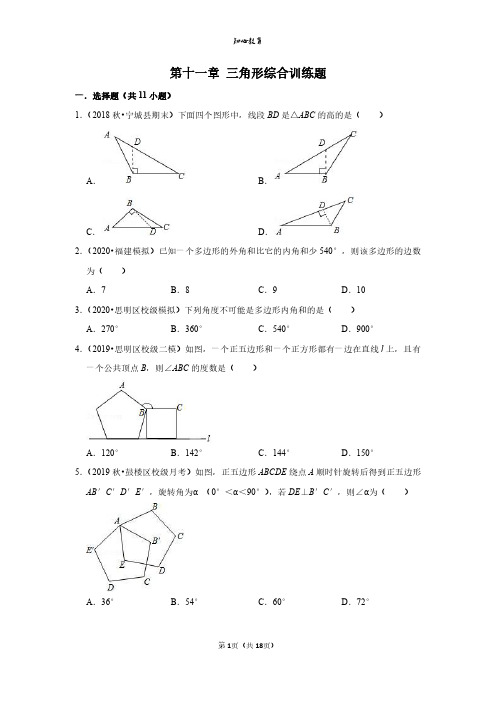
△ACD 的周长差为( )
A.6
B.3
C.2
D.不确定
9.(2017 秋•满洲里市期末)如图所示,将△ABC 沿着 DE 折叠,使点 A 与点 N 重合,若∠
A=65°,则∠1+∠2=( )
A.25°
B.65°
C.115°
D.130°
10.(2018 秋•伍家岗区期末)如图,七边形 ABCDEFG 中,AB、ED 的延长线交于点 O,
∴∠B=∠BAE=∠E=
=108°,
D.72°
∵正五边形 ABCDE 绕点 A 顺时针旋转后得到正五边形 AB′C′D′E′,旋转角为α(0° ≤α≤90°), ∴∠BAB′=α,∠B′=∠B=108°, ∵DE⊥B′C′, ∴∠B′OE=90°, ∴∠B′AE=360°﹣∠B′﹣∠E﹣∠B′OE=360°﹣108°﹣108°﹣90°=54°, ∴∠BAB′=∠BAE﹣∠B′AE=108°﹣54°=54°, 即∠α=54°.
第 7页(共 18页)
知心教育
一个公共顶点 B,则∠ABC 的度数是( )
A.120°50°
【解答】解:如图:
由题意:∠ABE=108°,∠CBF=90°,∠BEF=72°,∠BFE=90°,
∴∠EBF=180°﹣72°﹣90°=18°,
∴∠ABC=360°﹣108°﹣18°﹣90°=144°,
23.(2019 春•丰泽区期末)如图 1,线段 AB、CD 相交于点 O,连接 AD、CB. (1)请说明:∠A+∠D=∠B+∠C; (2)点 M 在 OD 上,点 N 在 OB 上,AM 与 CN 相交于点 P,且∠DAP= ∠DAB.∠ DCP= ∠DCB,其中 n 为大于 1 的自然数(如图 2). ①当 n=2 时,试探索∠P 与∠D、∠B 之间的数量关系,并请说明理由; ②对于大于 1 的任意自然数 n,∠P 与∠D、∠B 之间存在着怎样的数量关系?请直接写 出你的探索结果,不必说明理由.
(必修5)解三角形 综合提高训练题(含详细答案)Microsoft Word 文档 (3)

(数学5必修)第一章:解三角形综合提高训练题一、选择题1.A 为△ABC 的内角,则A A cos sin +的取值范围是( )A .)2,2(B .)2,2(-C .]2,1(-D .]2,2[-2.在△ABC 中,若,900=C 则三边的比c b a +等于( ) A .2cos 2B A + B .2cos 2B A - C .2sin 2B A + D .2sin 2B A - 3.在△ABC 中,若8,3,7===c b a ,则其面积等于( )A .12B .221 C .28 D .364.在△ABC 中,090C ∠=,00450<<A ,则下列各式中正确的是( ) A .sin cos A A > B .sin cos B A >C .sin cos A B >D .sin cos B B >5.在△ABC 中,若)())((c b b c a c a +=-+,则A ∠=( )A .090B .060C .0120D .0150 6.在△ABC 中,若22tan tan ba B A =,则△ABC 的形状是( ) A .直角三角形 B .等腰或直角三角形C .不能确定D .等腰三角形二、填空题1.在△ABC 中,若,sin sin B A >则A 一定大于B ,对吗?填_________(对或错)2.在△ABC 中,若,1cos cos cos 222=++C B A 则△ABC 的形状是______________。
3.在△ABC 中,∠C 是钝角,设,cos cos ,sin sin ,sin B A z B A y C x +=+== 则z y x ,,的大小关系是___________________________。
4.在△ABC 中,若b c a 2=+,则=+-+C A C A C A sin sin 31cos cos cos cos ______。
三角形相似综合训练-2023年中考数学拉分专题(教师版含解析)
专题02 三角形相似综合训练1.如图,在矩形ABCD 中,将ADC △绕点D 逆时针旋转90︒得到FDE B F E ,、、三点恰好在同一直线上,AC 与BE 相交于点G ,连接DG .以下结论正确的是( )①AC BE ⊥;BCG GAD ~②;③点F 是线段CD 的黄金分割点;④CG EG = A .①②③ B .①③C .①②③D .①③④【答案】D 【详解】证明:FDE ADC ≌,∴AD DF DC DE ==,又∴四边形ABCD 是矩形,∴90ADC ∠=︒, ∴90DAC DCA ∠+∠=即DAG DEF ∠+∠=即BGC 是直角三角形,而AGD 不是直角三角形,∴②错误;Rt FCB 和Rt 中, BFC EFC ∠=∠Rt FCB Rt FDE ∽, FC BCDF DE=, BC AD DF DE DC ===,FC DFDF DC=, F 是线段CD 的黄金分割点,和DEG '中,∴SAS DCG DEG '≌(DG DG CDG ='∠=,90CDG GDA ∠+∠=︒90EDG GDA ∠'+∠=90GDG ∠'=︒,∴GDG '是等腰直角三角形,2GG DG '=EG CG '=EG EG ='故选:D .【我思故我在】2.如图,在ABC 中,D 、E 分别在AB 边和AC 边上,//DE BC ,M 为BC 边上一点(不与B 、C 重合),连结AM 交DE 于点N ,则( )A .ADANANAEB .BD MNMN CEC .DN NEBM MCD .DN NEMC BM,AN ANNE DN NEAM AMMCBMMC,故选相似三角形的判定和性质,解题的关键是熟练掌握3.如图,在ABC ∆中,2AC =,4BC =,D 为BC 边上的一点,且CAD B ∠=∠.若ADC ∆的面积为a ,则ABD ∆的面积为( )A .2aB .52aC .3aD .72aACD BCA ∆,再由相似三角形的性质得到答案ACD BCA ∆,2AC BC ⎛⎫= ⎪⎝⎭,即BCA ∆的面积为的面积为:.4.如图,在矩形ABCD 中,E,F分别为边BC 、CD 中点,线段AE ,AF 与对角线BD 分别交于点G ,H .设矩形ABCD 的面积为S ,则以下4个结论中:①AG :GE =2:1 ②BG :GH :HD =1:1:1;③12325S S S S ++=;④ 246124S S S =::::正确的结论有( )A .1个B .2个C .3个D .4个【答案】C∴,BGE DGA ∽ 2,AG AD BGGE BE DG===②∴AG AD BGGE BE DG==13BG BD =,1所以本题的3个结论符合题意; 故选:C .【我思故我在】本题考查了矩形的性质,三角形相似的性质和判定,三角形面积等知识,解题的关键是理解题意,等底同高三角形面积相等,相似三角形面积的比等于相似比的平方. 5.如图,在正方形ABCD 中,BPC △是等边三角形,BP 、CP 的延长线分别交AD 于E 、F ,连接BD 、DP ,BD 与CF 相交于点H .给出以下结论:①3BE AE =;②DFP BPH ;③2DP PH PC =⋅;④若2AB =,则1BPD S △.其中正确结论的是( )A .①②③④B .②③④C .①②④D .①③④从而证明DFP BPH ,正确;利用DPH CPD ~,得DP PC ,将ΔBPD S 转化为S 四边形解:BPC ∆是等边三角形,BC ,60PBC PCB BPC ∠=∠=∠=ABCD 中,AB BC CD =,A ∠30ABE DCF ∴∠==︒2BE AE ∴=故①错误PC CD =PDC ∴∠=FDP ∴∠=DBA =∠DFP ∠=DFP BPH ∴~,故②正确;30PDH PCD ∠=∠=︒DPH CPD ∴~,∴DP PHPC DP=, 2DP PH PC ∴=⋅,故③正确;如图,过点P 作PM正方形的边长6.如图, 在平行四边形ABCD 中, 点,M N 分别是AD BC 、上的点, 且22AM DM BN CN ==,, 点O 是CM , DN 的交点, 直线AB 分别与CM DN ,的延长线交于点,P Q . 若平行四边形ABCD 的面积为144 , 则POQ △的面积为( )A .72B .216C .268D .300∴AMP DMC ∽, AP AMDC DM=, 2AM DM = 2AP AMDC DM==, 2AP CD =, ∴COD POQ ∽, 1215h CD h PQ ==, ∴∴POQ 的高为56h ,144ABCDS CD h =⋅=151POQS=故选:D 【我思故我在】的性质及平行四边形的性质是解题的关键.7.如图,在正方形ABCD 中,点G 是BC 上一点,且12GC BG =,连接DG 交对角线AC 于F 点,过D 点作DE DG ⊥交CA 的延长线于点E ,若5AE =,则DF 的长为( )A .BC .92D ,证明DEH DGC ∽,推出,求出5EH HA ==延长线于H ,DE DG ⊥EDG ∠∴21∴∠+∠1∠∠∴=DEH DGC ∴∽,∴EH DHGC DC =, 12GC BG =, ∴设GC x =,则BG =∴3EH DHGC x=, AC 是正方形DAC ∴∠EAH ∠=HEA ∴∠=EH HA ∴=2EH HA ∴+EH HA ∴=在正方形8.已知,如图,平行四边形ABCD 中,:1:3=CE BE ,且1EFC S =△,那么ABCS=_____.ACD ABC SS =,证明1:4AD =,则CE AD =. 9.P 是ABC 边上的任一点(P 不与A 、B 、C 重合),过点P 的一条直线截ABC ,如果截得的三角形与ABC 相似,我们称这条直线为过点P 的∴ABC 的“相似线”.Rt ABC △中,90C ∠=︒,30B ∠=︒,当点P 是边BC 上一个三等分点时(PB PC >),过点P 的ABC 的“相似线”最多有___________条.【答案】4【分析】根据相似线的定义,可知截得的三角形与ABC 有一个公共角,分①公共角为A ∠时;②公共角为B ∠时;③公共角为C ∠时;三种情况进行讨论,即可得出答案.【详解】解:①当公共角为A ∠时,不存在;②公共角为B ∠时,过点P 作PD BC ⊥,交AB 于点D ,如图所示:∴90DPB C ∠=∠=︒,B B ∠=∠,∴BPD BCA ∽;过点P 作PD AB ⊥于点D ,如图所示:∴90PDB C ∠=∠=︒,B B ∠=∠,∴BPD BAC ∽△△;③公共角为C ∠时,连接AP ,如图所示:∴30B ∠=︒,∴2AB AC =,设AC a =,则2AB a =,∴ACP BCA∽;过点P作PD AB∥,交∴CDP CAB∽;综上分析可知,过点的ABC的“相似线故答案为:4.【我思故我在】本题主要考查了相似三角形的判定,平行线的性质,勾股定理,解题的关键是熟练掌握三角形相似的判定方法.10.如图,在ABC中,6BC=,AE AFEB FC=,动点P在射线EF上,BP交CE于点D,CBP∠的平分线交CE于点Q,当14CQ CE=时,EP BP+的值为______.【答案】18【分析】如图,延长EF交BQ的延长线于G.首先证明PB PG=,EP PB EG+=,由EG BC∥,11.如图,在矩形ABCD中,点E,F分别是,==∠=︒∠=︒,则BC的长度是___________.3,6,30,45BE CD FED FDE【答案】3##3+【分析】作FN DE ⊥于点N ,延长DE 交CB 的延长线于点M ,先证FND ∆是等腰直角三角形,设FN x =,利用勾股定理、含30度角的直角三角形的性质求出DN ,EF ,NE 的长度,FDE ∠=DFN ∴∠FND ∴∆是等腰直角三角形.由题意得:设FN x =FED ∠=2EF FN ∴=NE ∴=DE DN ∴=3BE =,AE BE ∴=又EAD ∠=EAD ∴∆∆≌AD BM ∴=EBM ∠=EBM ∴∆∽BM BE MN NF ∴=解得:BM 12.如图,在ABC 中,146AB AC ==,,在AC 上取一点D ,使2AD =,如果在AB 上取点E ,使ADE 和ABC 相似,则AE =___________.①ABC AED ;②ABC ADE ;可根据各四条线段的比例关系式求出AE 的长.此时ADE ACB ,::AC AE AD =,146AC AD ==,,此时ADE ABC ,::AC AD AE =,146AC AD ==,,67=, 故答案为:143或67.13.如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M 在旋转中心O 的正下方,某一时刻,太阳光线恰好垂直照射叶片OA 、OB ,此时各叶片影子在点M 右侧成线段CD .测得8.5m MC =,13m CD =,垂直于地面的木棒EF 与影子FG 的比为23:.则点O 、M 之间的距离等于___________m ;【答案】10【分析】连接OM 交AC 于点H ,过点C 作CN BD ⊥,通过证明HMC EFG HAO ∽∽△△△,通过相似三角形对应边成比例即可解答.【详解】解:连接OM 交AC 于点H ,过点C 作CN BD ⊥,14.如图,在平行四边形ABCD 中,点E 在边BC 上,连结AE 并延长,交对角线BD 于点F 、DC 的延长线于点G .如果23CE BE =,求FE EG的值.15.矩形ABCD 中,AC BD ,为对角线,6cm 8cm AB BC ==,,E 为DC 中点,动点P 从点A 出发沿AB 方向,向点B 运动,动点Q 同时以相同速度,从点B 出发沿BC 方向向点C 运动,P 、Q 的速度都是1cm/秒,其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为x 秒.()06t <<(1)PQ AC ∥时,求运动时间t ;(2)PQ BD ⊥时,求运动时间t ;(3)当t 为何值时,以点P ,B ,Q 为顶点的三角形与QCE 相似?(4)连接PE PQE ,△的面积能否达到矩形ABCD 面积的三分之一,若能求出t 的值;若不能,说明理由.7BP BQBP BQ为顶点的三角形与QCE相似216.解答题=;(1)如图1,ABC和ADE都是等边三角形,连接BD、CE,求证,BD CE[类比探究](2)如图2,ABC 和ADE 都是等腰直角三角形,90ABC ADE ∠=∠=︒,连接BD CE ,.求BD CE的值.[拓展提升](3)如图3,ABC 和ADE 都是直角三角形,90ABC ADE ∠=∠=︒,2AC AE AB AD==.连接BD CE 、,延长CE 交BD 于点F ,连接AF .若AFC ∠恰好等于90︒,请直接写出此时AF BF CF ,,之间的数量关系.证明BAD CAE ∽,从而得出结果;B 作BH CF ⊥,垂足为点AOF BOH ∆∽,根据对应边成比例,【详解】(1)解:∴ABC 和ADE 都是等边三角形,AC ,AD AE =,∠∠DAE BAC =BAC BAE ∠-∠,即:在BAD 和CAE 中,AB AC DAB EAC AD AE =∠=∠=,(SAS BAD CAE ≌△△BD CE =.∴ABC 和ADE 都是等腰直角三角形,45BAC =∠=︒,ADE ∠ADE △∽,AE AC ,则AD AB AE AC=,BAE BAC -∠=∠-∠在BAD 和CAE 中,DAB EAC =∠,AD AE ∴BAD CAE ∽,BD AB CE AC =, 令AB x =,根据勾股定理可得:2BD AB x CE AC x===(3)∴BAD CAE ∽,ACE ABD ∠=∠,在FOB ∆和AOC ∆中,ACE ABD ∠=∠,∠60OFB OAC ∠=∠=设FH x =,OH y =,则17.在△ABC 中,90ACB ∠=,BE 是AC 边上的中线,点D 在射线BC 上.(1)如图1,点D 在BC 边上,:1:2CD BD =,AD 与BE 相交于点P ,过点A 作AF BC ,交BE 的延长线于点F ,易得AP PD的值为 ; (2)如图2,在△ABC 中,90ACB ∠=,点D 在BC 的延长线上,AD 与AC 边上的中线BE 的延长线交于点P ,:1:2DC BC =,求AP PD的值; (3)在(2)的条件下,若CD=2,AC=6,则BP= .18.在∴ABC 中,CA CB =,ACB α∠=,点P 在平面内不与点A ,C 重合,连接AP ,将线段AP 绕点P 逆时针旋转α得到线段DP ,连接,,AD BD CP .(1)如图①,当60α=︒,BD CP的值是 ,直线BD 与直线CP 相交所成的较小角的度数是 . (2)如图②,当90α=︒时,请写出BD CP的值及直线BD 与直线CP 相交所成的较小角的度数,并说明理由. (3)当90α=︒时,若点E ,F 分别是,CA CB 中点,点P 在直线EF 上,请直接写出当C ,P ,D 在同一直线上时,求AD CP 的值. ,ABC 是等腰直角三角形,根据等腰直角三角形的性质证明,利用相似的性质即可得解;上,和P 在线段解:如图,延长CP 交60︒,∴ABC 是等边三角形,由题意可知∴PAD 是等边三角形,PAD ∠=∠CAP ∠+∠在CAP 和BAD 中,CA BA CAP BAD AP AD =⎧⎪∠=∠⎨⎪=⎩,CAP BAD △≌△ (SAS),PC BD ACP =∠=∠在AOC 和△1BD PC=,直线BD ∴ABC 是等腰直角三角形,CAB ∠=∠∴ AB AC =AB AD AC AP∴=CAB ∠+∠AD是ABC的中位线,2219.如图,点E是矩形ABCD的边AB的中点,F是BC边上一动点(点F与点B,点C不重合),线段DE和:AF相交于点P,连接PC.(1)若在线段DP 上取一点Q ,使得2DP EQ =,连接AQ ,猜想PC 与AQ 的关系并证明;(2)若AF DE ⊥时,8,10AB AD ==,求BF 的长;(3)当点F 为BC 的中点时,求AP PF 的值. AEQCDP ∆,即可得出结论;,再判断出DAE ABF ,即可得出结论;,先判断出(AAS)ADE BGE ∆≅∆,再判断出2,2AD BF BG BF ==,进而判断出,即可得出结论.∴90BAF AED .90BAF AFB ∠+∠=︒,AED AFB ∠=∠,90DAE ABF ∠=∠=︒,∴DAEABF , AD AE AB BF =,即1083.2BF =;(3)解:如图,延长AD GC ,APD FPG ∆,23AD GF ==.【我思故我在】此题查了矩形的性质,构造出相似三角形是解本题的关键.。
全等三角形的性质与判定综合训练

双休日作业(全等三角形的性质与判定)【知识梳理】 1、全等三角形的性质全等三角形的对应角 ;全等三角形的对应边 . 2、全等三角形的判定方法⑴____________⑵_____________⑶______________⑷____ ______ 题型1——小试牛刀练一练1、已知图中的两个三角形全等,则∠α度数是( )A.72°B.60°C.58°D.50°2、如图,给出下列四组条件:( )①AB DE BC EF AC DF ===,,; ②AB DE B E BC EF =∠=∠=,,; ③B E BC EF C F ∠=∠=∠=∠,,; ④AB DE AC DF B E ==∠=∠,,. 其中,能使ABC DEF △≌△的条件共有( ) A .1组 B .2组 C .3组 D .4组3、如图,已知AB=AD 那么添加下列一个条件后,仍无法判定△ABC ≌△ADC 的是 A .CB CD = B .BAC DAC =∠∠ C .BCA DCA =∠∠ D .90B D ==︒∠∠4、如图所示,在△ABC 中,D 、E 分别是边AC 、BC 上的点,若△ADB ≌△EDB ≌△EDC ,则∠C 的度数为( )A. 15°B. 20°C.25° D. 30°5、如图所示,△ABC ≌△AEF ,AB =AE ,∠B =∠E ,则下列结论:( )①AC =AF ;②∠FAB =∠EAB ;③EF =BC ;④∠EAB =∠FAC. 其中正确的个数是 A. 1个 B. 2个 C. 3个 D. 4个6、某同学把一块三角形的玻璃打碎了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的第2题第1题AB CD第3题第4题第5题方法是( ) A .带①去 B .带②去 C .带③ D .带①②③去7.(2012•柳州)如图,小强利用全等三角形的知识测量池塘两端M 、N 的距离,如果△PQO ≌△NMO ,则只需测出其长度的线段是( )A .POB .PQ 吧C .MOD .MQ8.(2012中考)如图,已知点A ,D ,C ,F 在同一条直线上,AB =DE ,BC =EF ,要使△ABC ≌△DEF ,还需要添加一个条件是( )A.∠BCA =∠F B . ∠B =∠E C . BC ∥EFD .∠A =∠EDF(2011•江苏宿迁)如图,已知9.∠1=∠2,则不一定能使△ABD ≌△ACD 的条件是( )A 、AB=A B 、BD=CD C 、∠B=∠CD 、∠BDA=∠CDA10、(2011南昌)如图,在下列条件中,不能证明△ABD ≌△ACD 的是( ) A.BD =DC ,AB =ACB.∠ADB =∠ADC ,BD =DCC.∠B =∠C ,∠BAD =∠CADD.∠B =∠C ,BD =DC11.(2011湖北十堰)工人师傅常用角尺平分一个任意角。
2023学年八年级数学上册高分突破必练专题(人教版) 三角形综合能力提升训练(解析版)
三角形综合能力提升训练一.选择题(共17小题)1.某零件的形状如图所示按照要求∠B=20°∠BCD=110°∠D=30°那么∠A 的度数是()A.50°B.60°C.70°D.80°【答案】B【解答】解:延长DC交AB于E∵∠BCD=∠B+∠CEB∠BCD=110°∠B=20°∴∠CEB=110°﹣20°=90°∵∠CEB=∠A+∠D∠D=30°∴∠A=90°﹣30°=60°故选:B.2.如图在△ABC中∠ACB=80°点D在AB上将△ABC沿CD折叠点B落在边AC的点E处.若∠ADE=24°则∠A的度数为()A.24°B.32°C.38°D.48°【答案】C【解答】解:∵∠ADE=24°∴∠BDE=180°﹣∠ADE=156°∵将△ABC沿CD折叠点B落在边AC的点E处∴∠BCD=∠ACD∠BDC=∠EDC=∠BDE==78°∵∠ACB=80°∴∠ACD=∠BCD=ACB=40°∴∠A=180°﹣∠ACD﹣∠ADE﹣∠CDE=180°﹣40°﹣78°﹣24°=38°故选:C.3.如图BP平分∠ABC交CD于点F DP平分∠ADC交AB于点E若∠A=45°∠P =40°则∠C的度数为()A.30°B.35°C.40°D.45°【答案】B【解答】解:∵∠A+∠ADG+∠AGD=180°∠ABC+∠C+∠BGC=180°∴∠A+∠ADG+∠AGD=∠ABC+∠C+∠BGC.又∵∠AGD=∠BGC∴∠A+∠ADG=∠C+∠GBC.∴∠A﹣∠C=∠GBC﹣∠ADG.同理可得∠A+∠ADE=∠P+∠PBE.∴∠A﹣∠P=∠PBE﹣∠ADE.∵BP平分∠ABC交CD于点F DP平分∠ADC交AB于点E∴∠GBC=2∠PBE∠ADG=2∠ADE.∴∠A﹣∠C=2(∠A﹣∠P).∴∠A+∠C=2∠P.又∵∠A=45°∠P=40°∴∠C=35°.故选:B.4.如图已知AB∥DC Rt△FEG直角顶点在CD上已知∠FEC=35°则∠GHB=()A.35°B.45°C.55°D.65°【答案】C【解答】解:∵∠FEG=90°∴∠GED+∠CEF=90°∵∠CEF=35°∴∠GED=55°∵AB∥CD∴∠GHB=∠GED=55°.故选:C.5.如图△ABC中CD平分∠ACB点M在线段CD上且MN⊥CD交BA的延长线于点N.若∠B=30°∠CAN=96°则∠N的度数为()A.22°B.27°C.30°D.37°【答案】B【解答】解:如图所示∠NAC是三角形ABC的一个外角∴∠NAC=∠B+∠ACB即∠ACB=∠NAC﹣∠B;∵CD平分∠ACB∴∠ACD=∠DCB=∠ACB∵∠B=30°∠CAN=96°∴∠ACD=∠ACB=(96°﹣30°)=33°∵MN⊥CD∴在直角三角形OMC中∠COM=90°﹣33°=57°∵∠NOA与∠COM互为对顶角∴∠NOA=∠COM=57°∴∠N=180°﹣57°﹣96°=27°.故选:B.6.如图①、②中∠A=42°∠1=∠2 ∠3=∠4 则∠O1+∠O2的度数为()A.111B.174C.153D.132【答案】D【解答】解:∵∠A+∠ABC+∠ACB=180°∴∠ABC+∠ACB=180°﹣42°=138°.∵∠1=∠2=∠ABC∠3=∠4=∠ACB∴∠2+∠4=69°.∵∠2+∠4+∠O1=180°∴∠O1=180°﹣69°=111°.∵∠ACD=∠A+∠ABC=42°+∠ABC又∵∠1=∠2=∠ABC∠3=∠4=∠ACD∴∠4=(42°+∠ABC)=21°+∠ABC.∵∠4=∠2+∠O2.∴∠O2=∠4﹣∠2=21°+∠ABC﹣ABC=21°∴∠O1+∠O2=111°+21°=132°.故选:D.7.如图∠AOB=60°点M、N分别在OA、OB上运动(不与点O重合)ME平分∠AMN ME的反向延长线与∠MNO的平分线交于点F在M、N的运动过程中∠F的度数()A.变大B.变小C.等于45°D.等于30°【答案】D【解答】解:∵∠AMN是△OMN的外角∴∠AMN=∠O+∠ONM∵∠EMN是△FMN的外角∴∠EMN=∠F+∠FNM∵ME平分∠AMN FN平分∠MNO∴∠AMN=2∠EMN∠ONM=2∠FNM∴∠O=2∠F∴∠F=30°.故选:D.8.如图BE、CF都是△ABC的角平分线且∠BDC=115°则∠A=()A.50°B.45°C.65°D.70°【答案】A【解答】解:∵BE、CF都是△ABC的角平分线∴∠EBC=∠ABC∠BCF=∠ACB.∵∠EBC+∠FCB+∠BDC=180°∠BDC=115°∴∠EBC+∠FCB=65°.∴∠ABC+∠ACB=130°.∵∠ABC+∠ACB+∠A=180°∴∠A=50°.故选:A.9.如图在△ABC中AD是BC边上的高AE BF分别是∠BAC∠ABC的平分线.∠BAC=50°∠ABC=60°.则∠DAE+∠ACD等于()A.75°B.80°C.85°D.90°【答案】A【解答】解:∵AD是BC边上的高∠ABC=60°∴∠BAD=30°∵∠BAC=50°AE平分∠BAC∴∠BAE=25°∴∠DAE=30°﹣25°=5°∵△ABC中∠C=180°﹣∠ABC﹣∠BAC=70°∴∠EAD+∠ACD=5°+70°=75°.故选:A.10.如图在△ABC中设∠A=x°∠ABC与∠ACD的平分线交于点A1得∠A1;∠A1BC与∠A1CD的平分线相交于点A2得∠A2;…;∠A2021BC与∠A2021CD的平分线相交于点A2022得∠A2022则∠A2022是()度.A.x B.x C.x D.x【答案】C【解答】解:∵∠ACD是△ABC三角形的外角∠A1CD是△A1BC的外角∴∠A=∠ACD﹣∠ABC∠A1=∠A1CD﹣∠A1BC∵BA1和CA1分别是∠ABC和∠ACD的角平分线∴∠A1BC=∠ABC∠A1CD=∠ACD∴∠A1=∠ACD﹣∠ABC=∠A=x°同理可得∠A2=∠A1=×x°∠A3=∠A2=××x°…∴∠A2022=x°故选:C.11.如图在△ABC中∠C=90°∠B=70°点D、E分别在AB、AC上将△ADE 沿DE折叠使点A落在点F处.则∠BDF﹣∠CEF=()A.20°B.30°C.40°D.50°【答案】C【解答】解:∵∠A+∠B+∠C=180°∠C=90°∠B=70°∴∠A=20°.∵△DEF是由△DEA折叠成的∴∠1=∠2 ∠3=∠DEF.∵∠BDF+∠1+∠2=180°∴∠BDF=180°﹣2∠1.∵∠CEF+∠CED=∠DEF=∠3 ∠CED=∠1+∠A∠3+∠1+∠A=180°∴∠3=180°﹣∠1﹣∠A.∴∠CEF=∠3﹣∠CED.=180°﹣∠1﹣∠A﹣∠1﹣∠A=180°﹣2∠1﹣2∠A=140°﹣2∠1.∴∠BDF﹣∠CEF=180°﹣2∠1﹣(140°﹣2∠1)=180°﹣2∠1﹣140°+2∠1=40°.故选:C.12.如图在△ABC中∠A=60°∠B=70°CD是∠ACB的平分线CH⊥AB于点H 则∠DCH的度数是()A.5°B.10°C.15°D.20°【答案】A【解答】解:在△ABC中∵∠A=60°∠B=70°∴∠ACB=180°﹣∠A﹣∠B=50°.∵CD是∠ACB的平分线∴∠ACD=∠ACB=25°.∵CH⊥AB于点H∴∠CHB=90°.∴∠ACH=∠CHB﹣∠A=30°.∴∠DCH=∠ACH﹣∠ACD=30°﹣25°=5°.故选:A.13.如图在Rt△ABC中∠ACB=90°∠A=30°点D是AC上一点将△ABD沿线段BD翻折使得点A落在A'处若∠A'BC=30°则∠CBD=()A.5°B.10°C.15°D.20°【答案】C【解答】解:∵∠ACB=90°∠A=30°∴∠ABC=180°﹣∠ACB﹣∠A=60°由折叠性质得:∠ABD=∠A'BD∴∠ABC﹣∠CBD=∠A'BC+∠CBD∴60°﹣∠CBD=30°+∠CBD解得:∠CBD=15°.故选:C.14.如图图①是四边形纸条ABCD其中AB∥CD E F分别为AB、CD上的两个点将纸条ABCD沿EF折叠得到图②再将图②沿DF折叠得到图③若在图③中∠FEM =24°则∠EFC为()A.48°B.72°C.108°D.132°【答案】C【解答】解:如图②由折叠得:∠B'EF=∠FEM=24°∵AE∥DF∴∠EFM=24°∠BMF=∠DME=48°∵BM∥CF∴∠CFM+∠BMF=180°∴∠CFM=180°﹣48°=132°由折叠得:如图③∠MFC=132°∴∠EFC=∠MFC﹣∠EFM=132°﹣24°=108°故选:C.15.如图在△ABC中E为BC延长线上一点∠ABC与∠ACE的平分线相交于点D∠D=15°则∠A的度数为()A.30°B.45°C.20°D.22.5°【答案】A【解答】解:∵∠ABC的平分线与∠ACE的平分线交于点D∴∠ABD=∠CBD∠ACD=∠ECD∵∠ACE=∠A+∠ABC即∠ACD+∠ECD=∠ABD+∠CBD+∠A∴2∠ECD=2∠CBD+∠A∴∠A=2(∠ECD﹣∠CBD)∵∠ECD=∠CBD+∠D∠D=15°∴∠D=∠ECD﹣∠CBD=15°∴∠A=2×15°=30°.故选:A.16.如图点D在△ABC内且∠BDC=120°∠1+∠2=55°则∠A的度数为()A.50°B.60°C.65°D.75°【答案】C【解答】解:∵∠D=120°∴∠DBC+∠DCB=60°∵∠1+∠2=55°∴∠ABC+∠ACB=60°+55°=115°∴∠A=180°﹣115°=65°故选:C.17.如图∠ABD∠ACD的角平分线交于点P若∠A=50°∠D=10°则∠P的度数为()A.15°B.20°C.25°D.30°【答案】B【解答】解:延长DC与AB交于点E.∵∠ACD是△ACE的外角∠A=50°∴∠ACD=∠A+∠AEC=50°+∠AEC.∵∠AEC是△BDE的外角∴∠AEC=∠ABD+∠D=∠ABD+10°∴∠ACD=50°+∠AEC=50°+∠ABD+10°整理得∠ACD﹣∠ABD=60°.设AC与BP相交于O则∠AOB=∠POC∴∠P+∠ACD=∠A+∠ABD即∠P=50°﹣(∠ACD﹣∠ABD)=20°.故选:B.二.填空题(共5小题)18.如图将△ABC纸片沿DE折叠使点A落在点A'处且A'B平分∠ABC A'C平分∠ACB若∠BA'C=120°则∠1+∠2的度数为.【答案】120°【解答】解:如图连接AA'∵A'B平分∠ABC A'C平分∠ACB∴∠A'BC=∠ABC∠A'CB=∠ACB∵∠BA'C=120°∴∠A'BC+∠A'CB=180°﹣120°=60°∴∠ABC+∠ACB=120°∴∠BAC=180°﹣120°=60°∵沿DE折叠∴∠DAA'=∠DA'A∠EAA'=∠EA'A∵∠1=∠DAA'+∠DA'A=2∠DAA' ∠2=∠EAA'+∠EA'A=2∠EAA'∴∠1+∠2=2∠DAA'+2∠EAA'=2∠BAC=2×60°=120°故答案为:120°.19.如图BP是△ABC中∠ABC的平分线CP是∠ACB的外角的平分线如果∠ABP=20°∠ACP=50°则∠P=°.【答案】30【解答】解:∵BP是△ABC中∠ABC的平分线CP是∠ACB的外角的平分线∴∠ABP=∠CBP=20°∠ACP=∠MCP=50°∵∠PCM是△BCP的外角∴∠P=∠PCM﹣∠CBP=50°﹣20°=30°故答案为:30°.20.在△ABC中∠ABC∠ACB的平分线交于点O∠ACB的外角平分线所在直线与∠ABC的平分线相交于点D与∠ABC的外角平分线相交于点E则下列结论一定正确的是.(填写所有正确结论的序号)①;②;③∠E=∠A;④∠E+∠DCF=90°+∠ABD.【答案】①②④【解答】解:∵∠ABC∠ACB的平分线交于点O∴∠ABD=∠OBC=∠ABC∠OCB=∠ACO=∠ACB∴∠OBC+∠OCB=(∠ABC+∠ACB)∵∠A+∠ABC+∠ACB=180°∴∠ABC+∠ACB=180°﹣∠A∵∠BOC+∠OBC+∠OCB=180°∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣×(180°﹣∠A)=90°+∠A故①正确∵CD平分∠ACF∴∠DCF=∠ACF∵∠ACF=∠ABC+∠A∠DCF=∠OBC+∠D∴∠D=∠A故②正确;∵∠MBC=∠A+∠ACB∠BCN=∠A+∠ABC∠ACB+∠A+∠ABC=180°∴∠MBC+∠BCN=∠A+∠ACB+∠A+∠ABC=180°+∠A∵BE平分∠MBC CE平分∠BCN∴∠MBC=2∠EBC∠BCN=2∠BCE∴∠EBC+∠BCE=90°+∠A∵∠E+∠EBC++BCE=180°∴∠E=180°﹣(∠EBC++BCE)=180°﹣(90°+∠A)=90°﹣∠A故③错误;∵∠DCF=∠DBC+∠D∴∠E+∠DCF=90°﹣∠A+∠DBC+∠A=90°+∠DBC∵∠ABD=∠DBC∴∠E+∠DCF=90°+∠ABD.故④正确综上正确的有:①②④.21.用一条宽度相等的足够长的纸条打一个结(如图1所示)然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图中∠BAC=度.【答案】36【解答】解:∵∠ABC==108°△ABC是等腰三角形∴∠BAC=∠BCA=36度.22.如图所示把同样大小的黑色棋子摆放在正多边形的边上按照这样的规律摆下去则第n个图形需要黑色棋子的个数是.【答案】n2+2n【解答】解:第一个是1×3第二个是2×4第三个是3×5…第n个是n•(n+2)=n2+2n故答案为:n2+2n.三.解答题(共8小题)23.如图所示D是△ABC边BC的中点E是AD上一点满足AE=BD=DC F A=FE.求∠ADC的度数.【解答】解:延长AD至G使AD=DG连接BG在DG上截取DH=DC在△ADC和△GDB中∴△ADC≌△GDB(SAS)∴AC=BG∠G=∠CAD∵F A=FE∴∠CAD=∠AEF∴∠G=∠CAD=∠AEF=∠BED∴BG=BE=AC∵AE=DC=BD∴AE+ED=DH+ED∴AD=EH在△DAC和△HEB中∴△DAC≌△HEB(SAS)∴CD=BH∴BD=BH=DH∴△BDH为等边三角形∴∠C=∠BDH=60°=∠ADC.故答案为:60°.24.在△ABC中AE平分∠BAC∠C>∠B.(1)课本原题再现:如图1 若AD⊥BC于点D∠ABC=40°∠ACB=60°求∠EAD的度数.(写出解答过程)(2)如图1 根据(1)的解答过程猜想并写出∠B、∠C、∠EAD之间的数量关系.(3)小明继续探究如图2在线段AE上任取一点P过点P作PD⊥BC于点D请尝试写出∠B、∠C、∠EPD之间的数量关系并说明理由.【解答】(1)先求出∠BAC根据角平分线定义求出∠CAE根据三角形内角和定理求出∠CAD代入∠DAE=∠CAE﹣∠CAD求出即可;(2)先利用三角形的内角和及角平分线的定义求得∠CAE=90°﹣(∠ABC+∠ACB)再根据直角三角形的性质可得∠CAD=90°﹣∠ACB然后由∠EAD=∠CAE﹣∠CAD 代入计算可求解;(3)过A作AG⊥BC于G由三角形的内角和定理及角平分线的定义可求得∠EAC=90°﹣∠ABC﹣∠ACB再根据直角三角形的性质可得∠GAC=90°﹣∠ACB进而可求解.25.如图在△ABC中点D是BC边上的一点∠B=50°∠BAD=30°将△ABD沿AD折叠得到△AED AE与BC交于点F.(1)求∠AFC的度数;(2)求∠EDF的度数.【解答】解:(1)∵△ABD沿AD折叠得到△AED∴∠BAD=∠DAF∵∠B=50°∠BAD=30°∴∠AFC=∠B+∠BAD+∠DAF=110°;(2)∵∠B=50°∠BAD=30°∴∠ADB=180°﹣50°﹣30°=100°∠ADC=50°+30°=80°∵△ABD沿AD折叠得到△AED∴∠ADE=∠ADB=100°∴∠EDF=∠ADE﹣∠ADC=100°﹣80°=20°.26.如图将长方形纸片ABCD(四个内角均为直角两组对边分别平行)沿EF折叠后点C、D分别落在点M、N的位置EN的延长线交BC于点G.(1)若∠EFG=68°求∠AEN、∠BGN的度数;(2)若点P是射线BA上一点(点P不与点A重合)过点P作PH⊥EG于H PQ平分∠APH PQ与EF有怎样的位置关系?为什么?【解答】解:(1)由折叠可知∠DEF=∠GEF∵AD∥BC∴∠EFG=∠DEF=68°∴∠AEN=180°﹣∠DEN=44°∴∠BGN=∠DEG=136°;(2)PQ⊥EF或PQ∥EF;①点P在线段AB上PQ⊥EF如图设PQ交EF于点T∵PQ平分∠APH∴∠APQ=∠HPQ设∠APQ=∠HPQ=α∠DEF=∠GEF=β由题意可知∠A=90°∵PH⊥EG∴∠PHE=90°在四边形APHE中∠A+∠APH+∠PHE+∠AEH=360°∴∠APH+∠AEG=180°∵∠AEG=180°﹣∠GED=180°﹣2β∴2α+180°﹣2β=180°∴α=β∵∠TEA=βα+∠AKP=90°∠AKP=∠TKE∴∠TKE+∠KET=90°∴∠KTE=90°∴PQ⊥EF;②点P在线段BA的延长线上PQ∥EF如图设PQ交EF于点T∵PQ平分∠APH∴∠APQ=∠HPQ设∠APQ=∠HPQ=α∠DEF=∠GEF=β由题意可知∠ABC=90°在四边形APHE中∠A+∠BPH+∠PHG+∠BGH=360°∴∠BGE+∠BFH=180°∵长方形纸片ABCD中AD∥BC∴∠BGE=∠GED=2β∴2α+2β=180°∴α+β=90°∵α+∠PTE=90°∴β=∠ETP即∠GEF=∠ETP∴PQ∥EF综上所述:点P在线段AB上PQ⊥EF;点P在线段BA的延长线上PQ∥EF.27.(1)阅读并填空:如图①BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线.试说明∠D=90°+∠A的理由.解:因为BD平分∠ABC(已知)所以∠1=(角平分线定义).同理:∠2=.因为∠A+∠ABC+∠ACB=180°∠1+∠2+∠D=180°()所以∠D=(等式性质).即:∠D=90°+∠A.(2)探究请直接写出结果并任选一种情况说明理由:(i)如图②BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线.试探究∠D 与∠A之间的等量关系.答:∠D与∠A之间的等量关系是.(ii)如图③BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线.试探究∠D与∠A之间的等量关系.答:∠D与∠A之间的等量关系是.【解答】解:(1)解:因为BD平分∠ABC(已知)所以∠1=∠ABC(角平分线定义).同理:∠2=∠ACB.因为∠A+∠ABC+∠ACB=180°∠1+∠2+∠D=180°(三角形的内角和等于180°)所以∠D=180°﹣(∠ABC+∠ACB)(等式性质).即:∠D=90°+∠A.故答案为:ABC ACB三角形的内角和等于180°180°﹣(∠ABC+∠ACB).(2)解:(i)∠D与∠A之间的等量关系是:∠D=90°﹣∠A.理由:∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线∴∠EBD=∠DBC∠BCD=∠DCF∴∠DBC+∠DCB+∠D=180°∴∠A+∠ABC+∠ACB=180°而∠ABC=180°﹣2∠DBC∠ACB=180°﹣2∠DCB∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°∴∠A﹣2(∠DBC+∠DCB)=﹣180°∴∠A﹣2(180°﹣∠D)=﹣180°∴∠A+2∠D=180°∴∠D=90°﹣∠A故答案为:∠D=90°﹣∠A;(ii)∠D与∠A之间的等量关系是:∠D=∠A.理由:∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线∴∠DCE=∠DBC+∠D∵∠A+2∠DBC=2∠DCE∴∠A+2∠DBC=2∠DBC+2∠D∴∠A=2∠D即:∠D=∠A.故答案为:∠D=∠A.28.如图①△ABC中BD平分∠ABC且与△ABC的外角∠ACE的角平分线交于点D.(1)若∠ABC=75°∠ACB=45°求∠D的度数;(2)若把∠A截去得到四边形MNCB如图②猜想∠D、∠M、∠N的关系并说明理由.【解答】解:∵∠ACE=∠A+∠ABC∴∠ACD+∠ECD=∠A+∠ABD+∠DBE∠DCE=∠D+∠DBC又BD平分∠ABC CD平分∠ACE∴∠ABD=∠DBE∠ACD=∠ECD∴∠A=2(∠DCE﹣∠DBC)∠D=∠DCE﹣∠DBC∴∠A=2∠D∵∠ABC=75°∠ACB=45°∴∠A=60°∴∠D=30°;(2)∠D=(∠M+∠N﹣180°);理由:延长BM、CN交于点A则∠A=∠BMN+∠CNM﹣180°由(1)知∠D=A∴∠D=(∠M+∠N﹣180°).29.a b c分别为△ABC的三边且满足a+b=3c﹣2 a﹣b=2c﹣6.(1)求c的取值范围;(2)若△ABC的周长为18 求c的值.【解答】解:(1)∵a b c分别为△ABC的三边a+b=3c﹣2 a﹣b=2c﹣6∴解得:1<c<6;(2)∵△ABC的周长为18 a+b=3c﹣2∴a+b+c=4c﹣2=18解得c=5.30.问题情景如图1 △ABC中有一块直角三角板PMN放置在△ABC上(P点在△ABC 内)使三角板PMN的两条直角边PM、PN恰好分别经过点B和点C.试问∠ABP与∠ACP是否存在某种确定的数量关系?(1)特殊探究:若∠A=50°则∠ABC+∠ACB=度∠PBC+∠PCB=度∠ABP+∠ACP=度;(2)类比探索:请探究∠ABP+∠ACP与∠A的关系.(3)类比延伸:如图2 改变直角三角板PMN的位置;使P点在△ABC外三角板PMN 的两条直角边PM、PN仍然分别经过点B和点C(2)中的结论是否仍然成立?若不成立请直接写出你的结论.【解答】解:(1)∵∠A=50°∴∠ABC+∠ACB=180°﹣50°=130°∵∠P=90°∴∠PBC+∠PCB=90°∴∠ABP+∠ACP=130°﹣90°=40°.故答案为:130 90 40;(2)结论:∠ABP+∠ACP=90°﹣∠A.证明:∵90°+(∠ABP+∠ACP)+∠A=180°∴∠ABP+∠ACP+∠A=90°∴∠ABP+∠ACP=90°﹣∠A.(3)不成立;存在∠ACP﹣∠ABP=90°﹣∠A.理由:△ABC中∠ABC+∠ACB=180°﹣∠A∵∠MPN=90°∴∠PBC+∠PCB=90°∴(∠ABC+∠ACB)﹣(∠PBC+∠PCB)=180°﹣∠A﹣90°即∠ABC+∠ACP+∠PCB﹣∠ABP﹣∠ABC﹣∠PCB=90°﹣∠A ∴∠ACP﹣∠ABP=90°﹣∠A.。
全等三角形综合压轴题训练(详细介绍“关系”共8张)

▪ 充分利用全等三角形、角平分线的性 质及判定证边相等、角相等
例3:如图,四边形ABDC中,∠D=∠ABD=90° ,点. O为BD的中点,且OA平分∠BAC. (1)求证:OC平分∠ACD; (2)求证:OA⊥OC; (3)求证:AB+CD=AC.
第6页,共8页。
▪ 例3、如图,正方形ABCD中,∠1=∠2,Q在DC上,P在BC上。求 证:PA=PB+DQ。
第7页,共8页。
▪ 一题多变:万变不离其宗
(1)如图,将三角形ABC纸片沿DE折叠成图①,此时点A落在四边形 BCED内部, 则∠ A与∠ 1, ∠ 2之间有一种数量关系保持不变, 找出这种数量关系并说明理由;
(2)若折成图②或图③,即点A落在BE或CD上时,分别写出∠ A与 ∠ 2, ∠ A与∠ 1之间的关系,并说明理由;
全等三角形综合压轴题训练
第1页,共8页。
▪ 一题多变:万变不离其宗
1.如图1,在△ABC中,∠A=α,OB、OC分别平分 ∠ABC、∠ACB,则∠O的度数是___________.
2.如图2,在四边形ABCD中,∠A+∠D=α,OB、OC 分别平分∠ABC、∠BCD,则∠O的度数是_____________.
(3)若折成图④,写出∠A与∠ 1, ∠ 2之间的关系式,说明理由. (4)若折成图5,写出∠A与∠ 1, ∠ 2之间的关系边形ABCDE中,∠A+∠B+∠E=α,DP、 CP分别平分∠EDC、∠BCD,则∠P的度数是__________.
图1
12
图2
第2页,共8页。
图3
▪ 一题多变:万变不离其宗
例1:在△ABC中,∠BAC=90°,AB=AC,L是过A的一条直
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形综合训练课前预习1. 回顾下列定理的内容,并完成下列各题.垂直平分线性质定理: 垂直平分线上的点___________________________________.角平分线性质定理: 角平分线上的点_____________________________________. 等腰三角形性质:等腰三角形两底角_______,三线______.等边三角形:①判定:____________________的等腰三角形是等边三角形._______________________的三角形是等边三角形. ②性质:等边三角形_______________、_________________.2. 已知:如图,线段AB 的端点A 在直线l 上,AB 与l 的夹角为30º,请在直线l 上另找一点C ,使△ABC 是等腰三角形.这样的点能找几个?求出每个等腰三角形顶角的度数.知识点睛1. 几何综合题的思考流程(1)标注条件,合理转化;(2)组合特征,分析结构;(3)由因导果,执果索因.2. 常见几何结构举例等腰三角形结构分析(1)边和角:___________________、___________________.(2)特殊的线:(顶角的平分线,底边上的中线,底边上的高)____________________.(3)面积:h 1+h 2_____h (填“>”、“<”或“=”) (4)构造: ①两线重合②平行线+角平分线③倍角(或半角) ∠ABC =2∠ACB作∠ABC 的平分线 延长CB 至D ,使BD =BAEA B DCAB C 作AC 的垂直平分线 作∠DCB =∠ABC ,补成等腰三角形④几何变换(旋转、折叠)旋转变换:对应点到旋转中心的距离相等,即会出现等腰三角形;折叠变换:对称轴上的点到对应点的距离相等,即会出现等腰三角形.⑤两圆一线两圆:以点A 或点B 为圆心,线段AB 长为半径的圆;一线:线段AB 的垂直平分线.M A C B h h 2h 1C A D A D A精讲精练1. 如图,在△ABC 中,AB =AC ,DE 垂直平分AB ,BE ⊥AC ,AF ⊥BC ,则∠EFC =_______.第1题图 第2题图 第3题图 第4题图2. 如图,在△ABC 中,AB =AC ,D ,E 是△ABC 内两点,AD 平分∠BAC ,∠EBC =∠E =60°.若BE =6cm ,DE =2cm ,则BC =________.3. 如图,在等腰三角形ABC 中,AB =AC ,∠BAC =50°,∠BAC 的平分线与AB 的中垂线交于点O ,点C 沿EF 折叠后与点O 重合,连接OC ,则∠CEF 的度数为__________.4. 如图,将长方形ABCD 对折,得折痕PQ ,再沿MN 翻折,使点C 恰好落在折痕PQ 上的点C′处,点D 落在点D′处,其中M 是BC 的中点,连接AC′,BC′.有下列三角形:①△ABC′;②△BMC′;③△MFC′.其中一定是等腰三角形的是______(填写序号).第6题图 第7题图5. 如图,∠C =2∠B ,12ACBC =,AD 为△ABC 中BC 边上的中线.若AE ⊥BC 于点E ,则DE =______BC . 6. 在等腰直角三角形ABC 中,∠A =90°,点D 在线段BC 上,∠EDB 12=∠C ,BE ⊥DE ,垂足为E ,DE 与AB 相交于点F ,则BE FD =_________. 7. 如图,在△ABC 中,∠ACB =90°,∠BAC =30°,将△ABC 绕点C 按逆时针方向旋转α角(0°<α<90°)得到△DEC ,8.第9题图 第10题图9. 如图,在正方形网格中,网格线的交点称为格点.已知A ,B 是两格点,若点C 也是图中的格点,且使得△ABC为等腰三角形,则符合题意的点C 有( )A .6个B .7个C .8个D .9个10. 如图,在长方形ABCD 中,AB =4,BC =E 是折线段AD -DC 上的一个动点(点E 不与点A 重合),点P 是点A 关于BE 的对称点,则使△PCB 为等腰三角形的点E 的位置共有( )A .2个B .3个C .4个D .5个C'B'B C A D F C E B A A E D B C B E C F O A D Q P D'C'N C E B D F A A B C D E E A C F B αA F E B D C A B C D E P三角形综合训练(习题)例题示范例1:如图,在△ABC 中,AB =AC ,∠A =120°,EF 垂直平分AB ,垂足为点E ,EF 交BC 于点F .若BC =12cm ,则EF =________.思路分析: 1. 标注条件,合理转化(如AB =AC 转为∠B =∠C ) 2. 分析结构,整合信息 ①垂直平分,连AF ,转移边和角②在Rt △ACF 中,∠C =30°,得142AF BF CF === ③在Rt △BEF 中,∠B =30°,得EF =2巩固练习1. 如图,在Rt △ABC 中,∠BAC =90°,AC =6,BC =10,过点A 作DE ∥BC ,交∠ABC 的平分线于点E ,交∠ACB的平分线于点D ,则DE 的长为( )A .18B .16C .14D .8第1题图 第2题图 第3题图 第4题图2. 如图,△ABC 和△ADE 都是等腰直角三角形,∠BAC =∠DAE =90°,AE ∥CD ,且AE =CD .连接CE ,交AD 于点F ,连接BD ,交CE 于点G ,连接BE .则下列结论:①BD =CE ;②△ACD 是等腰直角三角形;③∠ADB =∠AEB ;④CD =EF .其中一定正确的是( )A .①②③B .①②④C .①③④D .②③④3. 如图,等边三角形ABC 的三条角平分线相交于点O ,过点O 作EF ∥BC ,交AB 于点E ,交AC 于点F ,则图中的等腰三角形有_________个.4. 如图,在△ABC 中,AB =AC ,∠A =120°,BC =6cm ,AB 的垂直平分线交BC 于点M ,交AB 于点E ,AC 的垂直平分线交BC 于点N ,交AC 于点F ,则MN 的长为( )A .4cmB .3cmC .2cmD .1cm5. 如图,△ABC 的面积为4cm 2,BP 平分∠ABC ,且AP ⊥BP 于点P ,则△PBC 的面积为_____________. 7. 如图,已知∠AOB =60°,点P 在边OA 上,OP =10,点M ,N 在边OB 上,PM =PN ,若MN =2,则OM 的长___.8. 如图,D 为∠BAC 的平分线上一点,过点D 作DE ∥AB ,交AC 于点E ,作DF ⊥AB 于点F ,若∠DAE =15°,AE =8,则DF 的长为___________.9. 如图,在△ABC 中,AC =BC ,∠ACB =90°,AE 平分∠BAC ,交BC 于点E ,BD ⊥AE ,交AE 的延长线于点D ,连接CD .下列结论:①AC +CE =AB ;②CD 12=AE ;③∠ADC =45°.其中正确结论的序号是_______________.2120°30°1284F E C B A E D C A G F A D B C E A C O F E N M A B E C F思考小结请按照等腰三角形结构分析的方法,完成等边三角形和等腰直角三角形的结构分析:等边三角形结构分析:(1)边和角:__________________,__________________.(2)特殊的线:(顶角的平分线,底边上的中线,底边上的高)____________________.等边三角形有_______条对称轴,把它分为两个含有30°角的直角三角形.(3)面积:边长为a 的等边三角形的面积为____________.(4)构造:几何变换(旋转、折叠)旋转变换:对应点到旋转中心的距离相等,即会出现等腰三角形,当旋转60°时,会出现等边三角形;折叠变换:对称轴上的点到对应点的距离相等,即会出现等腰三角形,将含有30°角的直角三角形沿长直角边翻折,会出现等边三角形.等腰直角三角形结构分析:(1)边和角:__________________,__________________.(2)特殊的线:(顶角的平分线,底边上的中线,底边上的高)____________________.等腰直角三角形有_______条对称轴,把它分为两个含有45°角的直角三角形. (3)面积:直角边为a 的等腰直角三角形的面积为________.(4)构造:几何变换(旋转、折叠)旋转变换:对应点到旋转中心的距离相等,即会出现等腰三角形,当旋转90°时,会出现等腰直角三角形; 折叠变换:对称轴上的点到对应点的距离相等,即会出现等腰三角形,将含有45°角的直角三角形沿直角边翻折,会出现等腰直角三角形.【参考答案】课前预习1. 到这条线段两个端点的距离相等 到这个角的两边的距离相等 相等,合一①有一个角是60°,有两个角是60°②三边都相等,三个角都是60°2. 这样的点能找4个,每个等腰三角形的顶角度数分别为150°,30°,120°, 120°知识点睛2. (1)等边对等角,等角对等边(2)三线合一(3)=精讲精练1、 45°2、8 cm3、50°4、①②③5、146、127、40°或20° 81 9、C 10、C 【参考答案】巩固练习1、 C2、A3、74、C5、2 cm 26、47、48、49、①②③思考小结等边三角形结构分析:(1)三边都相等,三个角都是60°(2)三线合一,3(3)24等腰三角形结构分析: (1)两腰相等,两底角都是45°(2)三线合一,1(3)22aa 45°a 30°。
