函数的连续性
第六节 函数的连续性

如果函数 f ( x )在开区间 (a , b)内连续 , 且在 左端点x a处右连续 , 在右端点 x b处左连续 , 则称函数f ( x )在闭区间 [a, b]上连续 .
连续函数的图形是一条连续而不间断的曲线.
6
例3 证明函数y sinx在区间 (,)内连续 .
证 x (,),
x 0 x 0
f ( x ) lim f ( x ) f ( x ).
故 f ( x)在( , )上连续 .
12
例5 设f ( x )在( 0, )上连续,且满足x (0, ), f ( x ) f ( x ). 证明 f ( x )在 (0, ) 上为常数.
1 当 x 0 时, lim f ( x ) 2, l i m f ( x ) f (0). x 0 x 0 a 1 所以当 a 时 ,f ( x )在 ( , ) 内 是 连 续 的 ; 2 1 当a 时 ,f ( x )在 ( , 0) (0, ) 内 连 续 2 23 且x 0 是 第 一 类 跳 跃 型 间 断.点
y sin 1 x
1 解 因 为 f ( x )在x 0 处 没 定 义 , 且limsin 不 存 在 , x 0 x 所以 x 0 为第二类间断点 .
这种情形称为振荡型间断点.
19
第 一 类 间 断 点 第 二 类 间 断 点
y
y 可去型
y 跳跃型
o
x0
x
o y
x0
x
o
x0
x
o
x 振荡型
lim f [ ( x )] f [ lim ( x )] f [ ( x0 )] f ( u0 ).
函数的连续性

第九节 函数的连续性和间断点有了极限的概念,我们就可以来讨论函数的一种重要特性——连续性。
首先,我们应注意到连续性也是客观现实的反映,是从许多自然现象的观察中抽象出来的一种共同特性。
如气温T 随时间t 的变化而连续变化,铁棒长度l 随着温度u 的变化而连续变化等。
它们的共同特性是:一方面在变化,另一方面是在逐渐变化的。
可在很短一段时间内,T 的变化很小;同样当温度u 变化很小时,l 的变化也很小。
这些现象反映在数学上就是自变量有一个微小的变化时,函数的变化也是微小的。
下面我们就专门来讨论这种概念。
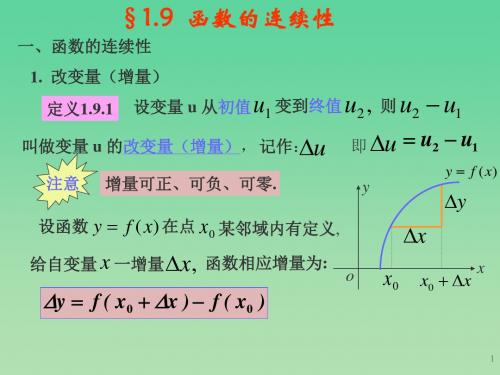
一、函数的连续性1. 预备知识改变量:设变量u 从它的一个初值1u 变到终值2u ,终值与初值的差21u u -,就叫u 的改变量,记作21u u u ∆=-。
改变量也叫增量。
注意:①1u ,2u 并不是u 可取值的起点和终点,而是u 变化过程中从1u 变到2u 。
②u ∆可正可负。
③u ∆是一个整体记号,不是某个量∆与变量u 的乘积。
2. 函数()y f x =在0x x =定义1 当自变量x 在点0x 的改变量x ∆为无穷小时,相应函数的改变量()()()()000y f x x f x f x f x ∆=+∆-=- 也是同一过程中的无穷小量,即0lim x y ∆→∆则称()f x 在0x 处连续,见图1-37.定理1 ()f x 在0x 处连续的充要条 件是()()00lim x x f x f x →=。
证明 由定义1,()()()()()000000lim 0lim lim lim 0lim .x x x x x x x x x y f x f x f x f x f x ∆→→→→→∆=⇔⎡⎣⇔-=⇔=由定理1,我们可将定义1改写为以下定义2.定义2 如果0ε∀>,0δ∃>,当0x x δ-<时,有()()0f x f x ε-<,则()f x 在0x 处连续。
函数的连续性与间断点

设函数 f (x) 在点 x0 的某去心邻域内有定义,如果 函数 f (x) 在点 x0 满足下列三种情况之一,则点 x0 为
f (x) 的间断点:
①、在 x0 处没有定义;
②、在 x0 处有定义,但 lim f (x) 不存在;
xx0
③、在 x0 处有定义,且 lim f (x) 存在,但
xx0
例3 证明函数 y sin x 在 (, ) 内连续 .
证 x (, )
y sin(x x) sin x
2sin
x 2
cos(x
x 2
)
y
2
sin
x 2
cos(x
x 2
)
2
x 2
1
x
0
(x 0)
即
lim y 0
x0
这说明 y sin x 在 (, ) 内连续 .
同样可证:函数 y cos x 在 (, ) 内连续 .
五、函数的间断点
定义5 如果函数 f (x) 在点 x0 不连续, 则称 f (x)
在点 x0 处间断, 并称点 x0为函数 f (x) 的间断点或
不连续点 .
1
o
x
1
解 因为 lim f (x) lim(x 1) 1 f (0 0)
x0
x0
lim f (x) lim (x 1) 1 f (0 0)
x0
x0
但
f (0 0) f (0 0)
所以是跳跃间断点 .
第二类间断点
如果函数 f (x) 在 x0 的左、 右极限至少有一个 不存在, 则称 x0 为 f (x) 的第二类间断点 .
函数的连续性

函数的连续性
函数的连续性是指函数在定义域上的变化情况,其主要内容是有限性、连续性和可导性。
有限性的概念是指函数的解析可以是有限的,它可以用有限的表示法来描述。
例如,函数y = x^2 + 2x - 4的解析表示式就是一个有限的表达式。
有限性是理解函数特征的基础,而连续性是更进一步理解函数特征的手段。
连续性定义为:存在任意位置x0处,它的函数值y0(即
y=f(x0)=y0)与其附近的函数值的差别不会超过一定的正定值,当此附近的自变量值在x0处的改变量趋近于零时,此函数值
的改变量也趋近于零,我们就称该函数在x0处是连续的,写
成数学形式就是:lim (x→x0) f(x) = y0
可导性是连续性的强化,也就是说它综合考虑了函数的变化和变化量之间的关系,它是指函数在定义域上任意一点x处,只要自变量x存在可导的微分,就说明函数y有可导的前提。
可导性的表述方式就是不等式:|f(x1)-f(x2)| ≤ M|x1-x2|,即自变
量x1和x2之间的变化量应小于某个正常数M,函数值在x1
和x2之间的变化量应小于M |x1-x2|。
函数的连续性是数学分析中的基本概念,它与微积分的应用紧密相连。
它的概念很容易理解,但在实际应用中却要求解答者拥有较强的抽象意识和概括能力,因此学习和研究它的概念是非常重要的。
《高等数学》第三节 函数的连续性

如果 x0 是函数 第一类间断点 可去间断点
f ( x) 的间断点,可将其分成两类:
f ( x) 在点 x0 处的左右极限存在;
其它
f ( x) 在点 x0 处的左右极限至少有
第二类间断点
一个不存在. 无穷间断点 振荡间断点 其它
例2 考察函数
2 x 0 x 1 f ( x) 1 x 1 在 x 1处的连续性. 1 x x 1
解 该函数在点x 1 处没有定义,所以函数在x 1 处间断;又因为
1 x 1 x 1 lim
,极限
x 1
不存在,趋于无穷,所以 是函数
f ( x)
1 x 1 的第二类间断点,
且为无穷间断点.
例4 考察函数
解 该函数在
1 f (x) sin 在 x 0 处的连续性. x
lim y lim f ( x0 x) f ( x0 ) 0 函数增量 y 也趋于零,即 x0 x0
,则称函数
y f ( x) 在点 x0
处连续,x0 称为函数 f ( x)
的连续点.
若记 x x0 x ,则 y f ( x) f ( x0 ) ,且当
x 0 处没有定义,
所以函数在 x 0 处间断,又因为当
x0
时,极限不存在,函数值在1与-1之间无
限次地振荡,所以 x 0 是
f ( x ) sin 1 x
的第二
类间断点,且为振荡间断点.
二、初等函数的连续性
g ( x) 均 定理1(连续函数的四则运算) 如果 f ( x)、
在点
f (b) ,
为介于 f (a) 与 f (b) 之间的任一实
高等数学:第一讲 函数的连续性

y f (x)
f (x0 )
0
x0
x
2.函数在一点的连续性同极限一样,都是函数的局部性质.
3. 判别函数y=f (x)在点x0连续的步骤:
(1) y = f (x)在点x0的某个邻域内有定义, y = f (x0) 存在;
(2) 极限
存在;
(3) 函数在 x0 处极限值等于函数值,即
例1 讨论函数 f (x)=x+1在x=2处的连续性.
且
lim
x x0
f (x)
f ( x0 ) , 称y = f (x) 在x0处左连续.
设函数y = f (x) 在[x0, x0+ ) 有定义,
且
lim
x x0
f (x)
f ( x0 ) , 称y = f (x) 在x0处右连续.
定理1
函数 y f ( x)在点 x0处连续的充要条件
是函数 y f ( x)在点 x0处既左连续又右连续,即
定义 2 设函数y=f (x)在点x0的某邻域内有定义,如
果x→x0时,相应的函数值f(x)→f(x0)
,即
lim
x x0
f (x)
f ( x0 ),
则称函数 y=f (x)在点x0连续,点x0为函数y=f (x)的连续点.
说明:
1. 函数 y=f (x)在点x0连续的几何意义:函数图形在x0不断开, 图像是连续不断的.
函数的连续性
函数的连续性
1、函数y=f (x) 在点 x0处的连续性
定义1 设y=f (x)在点x0的某邻域内有定义,如果当x在
x0处的增量x趋于零时,相应的函数增量y=f (x0+ x)- f(x0)也
函数的连续性
y y f x
a o
x b
17
例1.证明方程 x3 3x2 1 在(0,1)内至少有一个根. 证. 设 f (x) x3 3x2 1, f (x) C[0,1],
f (0) 1, f (1) 1, f (0) f (1) 0,
由零点定理知,在(0,1)内至少有一点 ,使得 f ( ) 0.
间断点的分类:
第一类间断点 ( 特点:左、右极限都存在 )
f f
( (
x0 x0
0) 0)
f ( x0 f ( x0
0 ), 0 ),
可去间断点; 跳跃间断点;
第二类间断点 (特点:左、右极限至少有一个不存在)
7
例4. 函数 f (x) 1 在x 0处无定义, 从而间断.
所以 f (x)在 x 0 处连续.
6
二、函数的间断点及其分类
f
(x) 在点x0
处连续.
12))..fli(mx0
) f
; (x)
;
3)
.
x x0
lim
x x0
f (x)
f ( x0 ).
以上三个条件只要有一条不满足,函数f (x) 在点 x0 处不连续. 即 f (x) 在点 x0 处间断, 并称 x0为函数f (x)的间断点.
10
定理1.9.2 (复合函数的连续性)
设函数 u g( x ) 在点 x x0 处连续, 函数 y f (u)在点u u0处连续, 则 函数 y f ( g( x )) 在点 x x0 处连续
g( x0 ) u0
lim f ( g( x )) f ( lim g( x ))
数学知识点:函数的连续性_知识点总结

数学知识点:函数的连续性_知识点总结
(1)如果函数y=f(x)在点x=x0处及其附近有定义,并且满足,则称函数y=f(x)在点x=x0处连续;否则称y=f(x)在点x=x0处不连续,或间断点。
(2)如果函数f(x)在某一开区间(a,b)内每一点处都连续,就说函数f(x)在开区间(a,b)内连续,对于闭区间[a,b]上的函数f(x),高考语文,如果在开区间(a,b)内连续,在左端点x=a处有,在右端点x=b处有,就说函数f(x)在闭区间[a,b]上连续。
3、如果f(x)是闭区间[a,b]上的连续函数,那么在闭区间[a,b]上f(x)一定有最大值和最小值。
函数的连续性的特点:
(1)f(x)在x0处有定义;
(2)f(x)在x0处的极限存在;
(3)f(x)在点x0处的极限等于函数值。
三大特点,缺一不可。
常用结论:
如果f(x)是闭区间[a,b]上的连续函数,那么在闭区间[a,b]上f(x)一定有最大值和最小值。
函数的连续性

函数的连续性函数的连续性是数学中重要的一个概念,它描述了函数在某个点附近的表现。
连续性可以用来刻画函数的光滑程度和连贯性,对于分析和解决实际问题具有重要的意义。
本文将详细介绍函数的连续性以及相关的性质和定理。
1. 连续函数的定义与性质连续函数是指在定义域上的每一个点都具有连续性的函数。
具体而言,若函数f(x)在某一点x=a处的极限存在且与f(a)的函数值相等,那么函数f(x)在点x=a处连续。
连续函数具有以下重要性质:- 连续函数的和、差、积仍为连续函数;- 连续函数的复合函数仍为连续函数;- 有界闭区间上的连续函数一定存在最大值和最小值。
2. 初等函数的连续性初等函数是由常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数等通过有限次的代数运算与函数复合得到的函数。
初等函数在其定义域上都是连续函数。
初等函数的连续性可以通过初等函数的定义和性质来证明。
以指数函数为例,指数函数f(x) = exp(x)在整个实数域上都是连续函数,因为它是由幂函数与以基数e为底的指数函数复合得到的。
3. 间断点与连续点函数可以在某些点上具有间断现象,这些点称为间断点。
间断点分为可去间断点、跳跃间断点和无穷间断点。
相应地,函数在某些点上具有连续性,这些点称为连续点。
可去间断点是指在该点处存在左极限和右极限,但极限值不相等。
通过修正函数在该点处的定义可以使其连续。
跳跃间断点是指在该点处左右极限存在且不相等,函数在该点处无法修正。
4. 连续函数的中值定理中值定理是连续函数的重要定理之一,它刻画了连续函数在某个区间上的平均增长率等于其两个端点处斜率之间某个值的关系。
根据中值定理,如果函数f(x)在闭区间[a,b]上连续,且可导于开区间(a,b)内,则存在一个点c∈(a,b),满足f(b)-f(a)=(b-a)f'(c)。
这个定理在微积分和实际问题的分析中有广泛的应用。
5. 连续函数的一致连续性一致连续性是连续函数的另一个重要性质,它描述了函数在整个定义域上的连续性。
函数的连续性

16
可 f ( x0 )无定义 去 lim lim 间 x x f ( x) x x f ( x) 第 0 0 断 f ( x0 )有定义,但 lim f ( x) f ( x0 ) 一 x x0 点 类 间 跳 断 跃 f ( x0 )有定义,但 lim f ( x) lim f ( x) 点 间 x x0 x x0 断 点 第 二 lim lim 类 x x0 f ( x)与 x x0 f ( x) 间 至少有一个不存在 断 点
无 穷 非 无 穷
x x0
lim f ( x)与 lim f ( x)
x x0
至少有一个为无穷
17
三、连续函数的性质
1、连续函数的四则运算 若函数 f (x), g (x) 在点 x0 连续,则
f ( x) f ( x)g ( x), f ( x) g ( x), ( g ( x0 ) 0) g ( x)
x 0
lim y 0
则称函数y f ( x)在 x0 点连续。
注:x x x0 , y f ( x) f ( x0 )或者y f ( x0 x) f ( x0 )
定义1 设函数y f ( x)在点 x0 的某领域内有定义, 若有
x x0
lim f ( x) f ( x0 )
8
解 (2)函数f(x)在x=1处有定义,且 f(1)=1
x 1
lim f ( x ) lim ( 2 x ) 1 ,
x 1
x 1
lim f ( x ) lim x 1 ,
x 1
因为当x→0时,f(x)的左﹑右极限存在且相等, 所以极限存在
lim f ( x ) 1 f (1)
函 数 的 连 续 性

高等数学应用教程 1.4.3 闭区间上连续函数的性质
定理1(最大值和最小值定理) 在闭区间上连续 的函数一定有最大值和最小值.
若 f ( x) C[a, b], y
则 1 ,2 [a, b],
y f (x)
高等数学应用教程 1.4.3 闭区间上连续函数的性质
几何解释:
y
连续曲线弧 y f ( x)的两个 端点位于x轴的不同侧,则曲 a o
线弧与 x轴至少有一个交点.
y f (x) 1 2 3 b x
高等数学应用教程 1.4.3 闭区间上连续函数的性质
y
几 连续曲线弧 y f ( x)的两个
何 解
22
故 y arcsin x 在[1,1]上也是单调增加且连续.
同理 y arccos x 在[1,1]上单调减少且连续;
y arctan x, y arccot x 在[,]上单调且连续.
高等数学应用教程
1.4.1 函数连续性的概念
初等函数的连续性
定理1.7 一切初等函数在其定义区间上都是连续的.
x0
x
1
解 原式 lim ln(1 x)x x0
1
ln[lim(1 x)x ] x0
ln e
1.
高等数学应用教程
1.4.2 函数的间断点及分类
1.4.2 函数的间断点及分类
函数 f ( x)在点 x0处连续必须满足的三个条件 : (1) f ( x)在点x0处有定义;
(2) lim f ( x)存在; x x0
解 f (1) 1,
f (1 0) 2, f (1 0) 2,
lim f ( x) 2 f (1), x1
高等数学 第6节 函数的连续性

因为
,所以此函数不连续.
定义4 设在x0的任何邻域内总有异于x0而属于函数
f (x)的定义域的点,而 f (x) 在x0处不连续,
则称x0是函数
f (x)
的一个间断点.
• 若 lim f ( x) 存在,且 lim f ( x) A ,而函数 y f (x) 在点 x 0 x x x x 处无定义,或者虽然有定义,但 f ( x0 ) A,则点x 0 是函数 y f (x)的一个间断点,称此类间断点为函数
一切初等函数 在定义区间内 连续
例如,
y 1 x 的连续区间为
2
(端点为单侧连续)
y ln sin x 的连续区间为
而 y
cos x 1 的定义域为
因此它无连续点
机动 目录 上页 下页 返回 结束
例7. 设
x 1 x, ( x) x 4 , x 1
讨论复合函数 解:
例1. 证明函数
在
内连续 .
证: x ( , )
y sin( x x) sin x
y 2 sin
x 2
cos( x
x 2
)
x
x 0
0
即 这说明 在 在
机动
内连续 .
同样可证: 函数
内连续 .
目录 上页 下页 返回 结束
例2. 设函数
y
又如,
1
o
1
x
y
也无最大值和最小值
2
1
o
1
2
x
机动
目录
上页
下页
返回
结束
有界性: 在闭区间上连续的函数在该区间上有界.
第三章函数的连续性

第三章 函数的连续性第二章我们研究的是函数随自变量变化的趋势,因而不考虑函数在自变量的极限点的值.这一章我们要专门研究函数在自变量一点的值及其附近的变化情况.自然界中有许多现象,如气温的变化、河水的流动、植物的生长等等,都是连续变化着的.若将这些现象反映在函数关系上,就是指函数的连续性.直观地看,函数的连续性指的是自变量x 的微小变化只能引起因变量()y f x =的微小变化.比如当时间变动很微小时,气温的变化也很微小.我们在生活中常常遇见的都是这样性态的函数. 比如,我们到超市去买水果,水果的售价是重量的函数. 当重量的误差很小时,所引起的应付款的差异是很小的.因此,商家与顾客也不在乎重量少或多了一两钱.但是,自然界有些现象也是突变的.比如,在正常情况下,地壳震动的振幅随时间的变化是渐变的,但在发生强烈地震的很短时间内,地壳振动的振幅会发生突变,造成地壳的断裂和下陷、建筑物的倒塌. 电路开关在闭合时的电压也会陡然增加大很大. 这类函数具有一种突变的性质,即自变量的微小变化可引起函数值的很大跨度的变化.为了描述变量在变化过程中的这两种不同状态,数学上就抽象出函数的连续与间断这两个相互对立的概念.研究这两种函数都必须从分析自变量与函数的增量开始.§3.1 函数的增量与连续概念一、 增量定义3.1 设变量u 从它的一个初值1u 变化到终值2u ,终值与初值的差21u u -被称为变量u 的增量,也称为改变量,记作u ∆,即21u u u ∆=-.增量u ∆可以是正的,也可以是负的. 在u ∆为正的情况下,变量u 从1u 变化到21u u u =+∆时是增大的;当u ∆为负的情况下,变量u 是减少的.现在假定函数()y f x =在点0x 的某一个邻域内是有定义的(图3-1). 自变量x 从0x 变化到0x x +∆时,称x ∆为自变量x 的增量. 在0x 的邻域内当自变量x 从0x 变化到0x x +∆时,函数()y f x =相应的从0()f x 变化到0()f x x +∆,因此函数()y f x =的对应增量为00()()f x x f x +∆-记作y ∆,即00()()y f x x f x ∆=+∆-,这就是函数()y f x =的增量.假如保持0x 不变而让自变量的增量x ∆变动,一般说来,函数()y f x =的增量y ∆也要随着变动.例1半径为r 的均匀圆形铁片,加热后半径增大r ∆,问面积改变了多少? 解 设S 为圆形铁片的面积. 半径为r 的圆形铁片面积函数为2()S r r π=.当加热后半径的改变量为r ∆时,其面积改变量222()()()2()S S r r S r r r r r r r ππππ∆=+∆-=+∆-=∆+∆.二、 函数的连续性直观的看,函数连续性的概念可以这样来描述:如果当x ∆趋于零时,函数()y f x =的对应增量y ∆也趋于零,即0lim 0x y ∆→∆=或是000lim[()()]0x f x x f x ∆→+∆-=,那么就称函数()y f x =在点0x 处是连续的. 因此有下述定义:定义3.2 设函数()y f x =在0x 的某一邻域()0U x 内有定义.如果0lim x y ∆→∆=000lim[()()]0x f x x f x ∆→+∆-= (1) 那么就称函数()y f x =在点0x 连续.若令0x x x =+∆,则当0x ∆→时有0x x →,于是函数()y f x =在点0x 连续的定义也可以改写为:()x f x x 0lim →=()0x f (2)由函数()y f x =当0x x →时的极限的定义可知,上述定义也可用""εδ-语言来表述:()y f x =在点0x 连续0ε⇔∀>,0δ∃>,当δ<-0x x 时有()()ε<-0x f x f (为什么不是00x x δ<-<?).下面说明左连续与右连续的概念.如果()00lim ()x x f x f x --→=存在且等于0()f x ,即00()()f x f x -=,则称函数()y f x =在点0x 左连续.如果()00lim ()x x f x f x ++→=存在且等于0()f x ,即00()()f x f x +=,则称函数()y f x =在点0x 右连续.由极限与左、右极限的关系,不难知道函数()f x 在点0x 连续()f x ⇔在点0x 既左连续又右连续.思考:怎样用函数极限的归结原则表述函数在一点连续?(提示:函数()f x 在点0x 右连续的充分必要条件是:对任何从0x 的右边趋于0x 的点列n x (0n x x →且0n x x ≥) ,都有0lim ()()n n f x f x →∞=.) 例 2 讨论函数 ()21,00,01,0x x f x x x x ⎧+<⎪==⎨⎪->⎩在点0=x 的连续性.解 因为()()00lim lim 11x x f x x ++→→=-=-, ()()200lim lim 11x x f x x -+→→=+=,而()00f =,所以()f x 在点0=x 既不右连续,也不左连续,从而它在点0=x 不连续(见图3-2).区间上的连续函数:在区间上每一点都连续的函数,叫做在该区间上的连续函数,或者说函数在该区间上连续. 如果区间包括端点,那么函数在右端点连续是指左连续,在左端点连续是指右连续.连续函数的图形是一条连续而不间断的曲线.思考:函数在区间上不连续是什么意思?例3 证明 00lim sin sin x x x x →=,0x R ∀∈. 证 利用三角函数的和差化积公式sin sin 2cos sin 22x y x y x y +--= 以及不等式sin x x ≤ 得到000sin sin 2cos sin 22x x x x x x +--=0002sin 222x x x x x x --≤≤=- , 所以由夹逼准则知道00lim sin sin 0x x x x →-=,即00lim sin sin x x x x →=. 因此sin y x =在点0x 连续,由于0x 是R 中任意一点,故sin y x =在它的定义域(,)-∞+∞内连续. 类似,还可以说明余弦函数cos y x =在定义域(,)-∞+∞内是连续的.三、 函数的间断点函数()y f x =在点0x 连续的定义包含着下列三点含义:(1)()y f x =在点0x 有定义;(2)()y f x =在点0x 有极限,也就是说()f x 在0x 的左、右极限均存在而且相等;(3)()y f x =在点0x 的极限值等于()f x 在0x 的函数值.上述三条中只要有一条不满足,就称函数()f x 在0x 处间断,使得函数()f x 不连续的点0x 称为此函数的不连续点或间断点.下面举例来说明函数间断点的几种常见类型.例4 正切函数tan y x =在2x π=处没有定义,所以点2x π=是函数tan x 的间断点.又因 2lim tan x x π→=∞, 我们称2x π=为函数tan x 的无穷间断点.例5 函数1sin y x =在点0x =没有定义,所以点0x =是函数1sin x的间断点.函数xy 1sin =的图象如图3-3所示.可见,当0→x 时,其函数值无限次地在-1与1的范围内振荡,而不趋于任何确定的数.我们称点0x =是函数1sin x的振荡间断点.例6 函数,1,()1, 1.2x x y f x x ≠⎧⎪==⎨=⎪⎩ 这里11lim ()lim 1x x f x x →→==,但是1(1)2f =,所以()1lim x f x →()1f ≠. 因此点1x =是函数的间断点. 但是如果改变函数()f x 在点1x =的定义:令(1)1f =,则函数()f x 在点1x =成为连续的。
2.7函数的连续性

函数f(x)在点x0处连续,应该满足下列三点: (1) f(x)在点x0及其某邻域U(x0)内有定义;
( 2 ) lim f ( x )=a 存在; x® x0
(3) a=f(x0).
lim
x x0
f
x
f
x0 ,
例1 证明函数f(x)=3x2-1在x=1处连续.
证 因为f(1)=3×1-1=2,
则有 lim f [(x)] f (a) f [ lim (x)].
x x0
x x0
例9 求 lim ln(1 x) .
x0
x
1
解 原式 lim ln(1 x)x
x0
1
ln[lim(1 x)x ] x0
ln e 1.
例10 求 lim e x 1 . x0 x
解 令 e x 1 y, 则 x ln(1 y),
连续函数的几何意义:
若函数y= f(x)在(a,b)内连续,则y= f(x)在(a,b)上的函数图 形是一条连续而不间断的曲线,反之也对.
下面给出函数连续性的等价定义:
1.函数的增量 Increment of a function
设函数 f (x)在U (x0, )内有定义, x U (x0, ), 记
由定义1知 函数 f ( x)在 x 0处连续.
例3
讨论函数
f (x)
x
x
2, 2,
x 0, 在 x 0处的 x 0,
连续性.
解 lim f ( x) lim( x 2) 2 f (0),
x0
x0
lim f ( x) lim( x 2) 2 f (0),
x0
x0
右连续但不左连续 ,
函数连续的三个条件

函数连续的三个条件
函数连续性的定义:“连续”是相对于“间断”而言的,顾名思义就是接连不断的。
设函数f()在点0的一些邻域内有定义,若极限
lim(→0)f()=f(0), 则称f()在点0处连续。
如果函数f()在区间D的每一点都是连续的,则称f()在区间D上连续。
判断函数连续性的第一种方法:图形直观判断法。
可以观察函数的二维图形,可以判定函数的曲线是连续的还是间断的。
判断函数连续性的第一种方法:函数定义法。
用函数连续性的定义判断函数是否连续。
若极限lim(→0)f()=f(0), 则称f()在点0处连续。
判断函数连续性的第三种方法:导数法。
若函数f()在点0可导,则函数f()在点0连续。
所以可以通过求一个函数的导数,来判断函数是否连续。
函数在一个区间内可导,则这个函数一定连续。
函数的连续性

在闭区间上连续的函数必取得介于最大值M与最小值m 之间的任何值 >>>
作业:
P43 习题1—6 2、(2) 3、(4) 4、 5、
下页
❖最大值与最小值
对于在区间I上有定义的函数f(x) 如果有x0I 使得对于 任一xI都有
f(x)f(x0) (f(x)f(x0)) 则称f(x0)是函数f(x)在区间I上的最大值(最小值)
应注意的问题:
并非任何函数都有最大值和 最小值
例 如 , 函 数 f(x)=x在 开 区 间 (a b)内既无最大值又无最小值
•间断点的定义
设函数 f(x)在点x0的某去心邻域内有定义 在此前提 下 如果函数 f(x)有下列三种情形之一
(1)在x0没有定义
(2)虽然在x0有定义 但 lim f(x) 不存在
x x0
(3)虽然在x0有定义且lim f(x)存在 但 lim f(x)f(x0)
x x0
x x0
则函数 f(x)在点x0不连续 而点x0称为函数 f(x)的不连续点
lim
x x0
P(
x)
=
P(x0
)
注: 如果区间包括端点 那么函数在右端点连续是指左连续
在左端点连续是指右连续
下页
❖连续函数
在区间上每一点都连续的函数 叫做在该区间上的 连续函数 或者说函数在该区间上连续
•连续函数举例 2 函数 y=sin x 在区间(- +)内是连续的
这是因为 函数y=sin x在(- +)内任意一点x处有 定义 并且
lim Dy =0
Dx0
lim [
x x0
f
(x)-
f
(x0)]= 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九节 函数的连续性和间断点有了极限的概念,我们就可以来讨论函数的一种重要特性——连续性。
首先,我们应注意到连续性也是客观现实的反映,是从许多自然现象的观察中抽象出来的一种共同特性。
如气温T 随时间t 的变化而连续变化,铁棒长度l 随着温度u 的变化而连续变化等。
它们的共同特性是:一方面在变化,另一方面是在逐渐变化的。
可在很短一段时间内,T 的变化很小;同样当温度u 变化很小时,l 的变化也很小。
这些现象反映在数学上就是自变量有一个微小的变化时,函数的变化也是微小的。
下面我们就专门来讨论这种概念。
一、函数的连续性1. 预备知识改变量:设变量u 从它的一个初值1u 变到终值2u ,终值与初值的差21u u -,就叫u 的改变量,记作21u u u ∆=-。
改变量也叫增量。
注意:①1u ,2u 并不是u 可取值的起点和终点,而是u 变化过程中从1u 变到2u 。
②u ∆可正可负。
③u ∆是一个整体记号,不是某个量∆与变量u 的乘积。
2. 函数()y f x =在0x x =定义1 当自变量x 在点0x 的改变量x ∆为无穷小时,相应函数的改变量()()()()000y f x x f x f x f x ∆=+∆-=- 也是同一过程中的无穷小量,即0lim x y ∆→∆则称()f x 在0x 处连续,见图1-37.定理1 ()f x 在0x 处连续的充要条件是()()00lim x x f x f x →=。
证明 由定义1,()()()()()000000lim 0lim lim lim 0lim .x x x x x x x x x y f x f x f x f x f x ∆→→→→→∆=⇔⎡⎣⇔-=⇔=由定理1,我们可将定义1改写为以下定义2.定义2 如果0ε∀>,0δ∃>,当0x x δ-<时,有()()0f x f x ε-<,则()f x 在0x 处连续。
3. 函数()y f x =在点0x 连续的要求⑴()f x 在点0x 有意义,即有确定的函数值()0f x ; ⑵()0lim x x f x →存在;⑶极限值=函数值,即()()00lim x x f x f x →=。
这三要素缺一不可。
4. 连续与极限的区别当()f x 在0x 处有极限时,()f x 在0x 处可无定义,也可有()()00lim x x f x f x →≠。
而当()f x 在0x 处连续时,()f x 在0x 一定有意义并且()()00lim x x f x f x →=必成立。
所以,函数()y f x =在点0x 处连续,则函数()y f x =在0x 点处必有极限,反之不成立。
5. 左右连续定义3 如果()()()000lim 0x x f x f x f x +→=+=,则称()f x 在0x 处右连续;如果()()()000lim 0x x f x f x f x -→=-=,则称()f x 在0x 处左连续。
所以()f x 在0x 处连续亦可用以下定义描述。
定义4 若()()()00000f x f x f x +=-=,即函数()y f x =在点0x 处左极限等于右极限等于函数值,则函数()y f x =在点0x 处连续。
6. ()f x 在某区间连续⑴()f x 在(),a b 内连续是指()0,x a b ∀∈,()f x 在0x 处连续。
⑵()f x 在[],a b 上连续是指()f x 在(),a b 内连续,在x a =点右连续,在x b =点左连续。
注意:证明分断点处的连续性时一定要用定义4.若()f x 在(),a b 内连续,则称(),a b 为()f x 的连续区间。
7. 连续函数的几何意义连续函数()y f x =的图形是一条不断开的曲线。
例1 证明()31y f x x ==+在1x =处连续。
证明 注意()()()113113113y f x f x x ∆=+∆-=+∆+-⨯-=∆⎡⎤⎣⎦,所以lim lim 3x x y x ∆→∆→∆=∆从而y 在1x =处连续。
例2 讨论()1,01,01,0x x f x x x x ->⎧⎪==⎨⎪+<⎩在0x =处的 连续性。
解 因为()()()000lim lim 11x x f f x x ++→→+==-=, ()()()000lim lim 11x x f f x x --→→-==+=, ()01f =,所以()()()00000f f f +=-=。
由定义4,()f x 在0x =处连续,见图1-38.例3 证明多项式函数在(,)-∞+∞内连续。
证明 设()1011n n n n P x a x a x a x a --=++++。
由极限运算法则知0(,)x ∀∈-∞+∞,()()101110010100lim (lim )(lim )lim n n n nx x x x x x x x n n n n P x a x a x a x a a x a xa x a P x --→→→→--=++++=++++=由0x 的任意性知()P x 在(,)-∞+∞内连续。
例4 证明有理函数()()()P x F x Q x =(P 为m 次多项式,Q 为n 次多项式),在 ()0Q x ≠点处处连续。
证明 0(,)x ∀∈-∞+∞,且()00Q x ≠,有()()()()()()()()00000lim lim lim x x x x x x P x P x P x F x F x Q x Q x Q x →→→====,所以()F x 在其定义域内处处连续。
例5 求证sin y x =在(,)-∞+∞内连续。
证明 (,)x ∀∈-∞+∞,给x 一个增量()x x x x ∆=+∆-,则2sin()sin 2sin cos22x x xy x x x ∆+∆∆=+∆-=, 从而000lim lim 2sin cos lim 2cos 02222x x x x x x x y x x ∆→∆→∆→∆∆∆∆⎛⎫⎛⎫∆=+=+= ⎪ ⎪⎝⎭⎝⎭,所以sin y x =在x 点连续。
由x 的任意性知sin x 在(,)-∞+∞内连续。
例6 证明cos y x =在(,)-∞+∞内连续。
证明 (,)x ∀∈-∞+∞,()x x x x ∆=+∆-,有cos()cos 2sin sin 22x x y x x x x ∆∆⎛⎫∆=+∆-=-+ ⎪⎝⎭, 所以000lim 2lim sin sin 2lim sin 02222x x x x x x x y x x ∆→∆→∆→∆∆∆∆⎛⎫⎛⎫∆=-+=-+= ⎪ ⎪⎝⎭⎝⎭,所以cos x 在(,)-∞+∞内连续。
二、函数的间断点与函数的连续性相对的概念是函数的间断性。
1. 间断点的定义若()f x 在点0x 处不连续,则称0x 为()f x 的一个间断点。
函数间断的几何解释是()f x 的图形在0x x =处断开。
例7 讨论()2,00,02,0x x y f x x x x -<⎧⎪===⎨⎪+>⎩的间断点。
解 注意 ()()()()()()()000,00lim lim 22,00lim lim 2xx x x f f f x x f f x x +-→→→→=+==+=-==- 可见()()()00000f f f +≠-≠,所以()f x 在0x =处不连续,即0x =为()y f x =的间断点。
这种()()0000f x f x +≠-的间断点,我们称其为跳跃间断点,见图1-39. 2. 间断点的分类函数()f x 在0x ⑴()f x 在0x 点无意义,即()0f x 不存在; ⑵()f x 在0x 点极限不存在,即()0lim x x f x →不存在;⑶极限值≠函数值,即()()00lim x x f x f x →≠。
我们称左右极限都存在的间断点为第一类间断点;其余间断点统称为第二类间断点。
进而,设0x 为()f x 的第一类间断点,如果还有()()0000f x f x +=-,则称0x 为()f x 的可去间断点;如果有()()0000f x f x +≠-,则称0x 为()f x 的跳跃间断点。
下表给出了间断点的分类情况。
()()()()()()()()()00000000000lim 0000x x f x f x f x f x f x f x f x f x f x →⎧⎧⎧⎪⎪⎪+=-⎨⎪≠⎪⎪⎩⎪+-⎪⎪⎨⎨⎪⎪+≠-⎪⎪⎪⎩⎪⎪⎩无意义:可补充定义可去间断点第一类间断点:可修改定义和间断点均存在不可去间断点(跳跃间断点)第二类间断点:除去第一类均为第二类间断点3. 函数的连续区间讨论函数的连续区间,就是在其定义域内排除间断点,主要在分段点、端点来考虑是否为间断点。
例8 研究tan y x =在2x π=处的连续性。
解 因为tan y x =在2x π=处无意义,所以2x π=是间断点。
又因为2lim tan x x π→=∞,即极限不存在,所以2x π=属第二类间断点,通常称其为无穷间断点,见图1-40.例9 讨论1sin y x=在0x =点的连续性。
解 因为1sin y x =在0x =处无意义,且01limsin x x →不存在,所以0x =为y 的第二类间断点。
这时,1sin y x =在-1和1通常称其为振荡间断点,见图1-41. 例10讨论211x y x -=-在点1x =解 因为y 在1x =处无意义,故1x =为间断点。
但111(1)(1)lim lim lim(1)1x x x x x y x x →→→-+==+-(1)2y =函数21,112,1x x y x x ⎧-≠⎪=-⎨⎪=⎩在定义域内处处连续。
例11 讨论,11,12x x y x ≠⎧⎪=⎨=⎪⎩在点1x =处的连续性,见图1-42.解 注意1(1)2y =而11lim lim 1(1)x x y x y →→==≠所以1x =为第一类可去间断点,修改定义(1)y 1=后,则函数,11,1x x z x ≠⎧=⎨=⎩处处连续,称函数z 为函数,11,12x x y x ≠⎧⎪=⎨=⎪⎩的连续延拓函数。
习题1.91.设函数()2,012,12x x f x x x ⎧≤≤=⎨-<≤⎩,试讨论()f x 在1x =处的连续性。
2.指出下列函数的间断点,并指明是哪一类间断点。
(1)()22132x f x x x -=-+; (2)()211f x x =-;(3)()1x f x e =; (4)()1cos f x x =3.设()()11xf x x =+,问怎样补充定义()0f ,才能使()f x 在0x =处连续。
