《命题及关系》课件19页
合集下载
命题及其关系ppt课件
注意正确理解否命题
14
小结:
1、如何判断一个语句是否是命题？ 2、如何判断一个命题的真假？ 3、怎样把命题改写成“若p, 则q”的形式？ 4、四种命题的如何写？（注意否命题）
15
16
原命题 若p 则q 互
否 否命题
若p 则 q
互逆 互逆
逆命题 若q 则p
互
否 逆否命题
若q 则p
17
思考
原命题的真假与其它三种 命题的真假有什么关系？
19
(2)两个三角形全等,则它们的面积相等.
. 逆命题:两个三角形的面积相等,则它们全等.
否命题:两个三角形不全等,则它们的面积不 相等.
逆否命题:两个三角形的面积不相等,则它们 不全等.
原命题 (真) 否命题 (假)
逆命题 (假) 逆否命题 (真)
20
(3)相等的角是对顶角 逆命题: 对顶角相等. 否命题: 不相等的角不是对顶角. 逆否命题: 不是对顶角就不相等.
23
例5：等价命题的应用
证明：已知函数f(x)是(- ,+ )上的增函数，
a,b∈R，若f(a)+f(b)≥f(-a)+f(-b)，则a+b≥0.
证明：原命题的逆否命题为“已知函数f(x)是
(- ,+ )上的增函数，a,b∈R，若a+b＜0，
则f(a)+f(b)＜f(-a)+f(-b)”. 若a+b＜0,则a＜-b，b＜-a.
1
下面的语句的表述形式有什么特点？你能判断 它们的真假吗？ (1)若xy＝1，则x、y互为倒数 ; (2)相似三角形的周长相等； (3)2+4=5 ; (4)如果b≤－1，那么x2-2bx+b2+b=0方程有实根；
14
小结:
1、如何判断一个语句是否是命题？ 2、如何判断一个命题的真假？ 3、怎样把命题改写成“若p, 则q”的形式？ 4、四种命题的如何写？（注意否命题）
15
16
原命题 若p 则q 互
否 否命题
若p 则 q
互逆 互逆
逆命题 若q 则p
互
否 逆否命题
若q 则p
17
思考
原命题的真假与其它三种 命题的真假有什么关系？
19
(2)两个三角形全等,则它们的面积相等.
. 逆命题:两个三角形的面积相等,则它们全等.
否命题:两个三角形不全等,则它们的面积不 相等.
逆否命题:两个三角形的面积不相等,则它们 不全等.
原命题 (真) 否命题 (假)
逆命题 (假) 逆否命题 (真)
20
(3)相等的角是对顶角 逆命题: 对顶角相等. 否命题: 不相等的角不是对顶角. 逆否命题: 不是对顶角就不相等.
23
例5：等价命题的应用
证明：已知函数f(x)是(- ,+ )上的增函数，
a,b∈R，若f(a)+f(b)≥f(-a)+f(-b)，则a+b≥0.
证明：原命题的逆否命题为“已知函数f(x)是
(- ,+ )上的增函数，a,b∈R，若a+b＜0，
则f(a)+f(b)＜f(-a)+f(-b)”. 若a+b＜0,则a＜-b，b＜-a.
1
下面的语句的表述形式有什么特点？你能判断 它们的真假吗？ (1)若xy＝1，则x、y互为倒数 ; (2)相似三角形的周长相等； (3)2+4=5 ; (4)如果b≤－1，那么x2-2bx+b2+b=0方程有实根；
1.1 命题及其关系ppt课件
都 是 质 数 ， 费尔马 于 是 他 用 归 纳 推 理 提 出猜 想(费马猜想)
任 何 形 如22n 1(n N * )的 数 都 是 质 数
例1 已知数列{an}中，a1=1,an+1=an/(an+1), 试求出a2,a3,a4并猜想{an}的通项公式
类比：
骨牌倒下
命题成立
第1张骨牌倒下
这种证明方法叫做 数学归纳法
例2 用数学归纳法证明
12 22 32 n2 n(n 1)(2n 1) 6
重点：两个步骤、一个结论； 注意：递推基础不可少，
归纳假设要用到， 结论写明莫忘掉。
数学归纳法的核心思想
数学归纳法是一种完全归纳法 ，它是在可 靠的基础上，利用命题自身具有的传递性，运 用“有限”的手段，来解决“无限”的问题。 它克服了完全归纳法的繁杂、不可行的缺点， 又克服了不完全归纳法结论不可靠的不足，使 我们认识到事情由简到繁、由特殊到一般、由 有限到无穷。
Hale Waihona Puke 例3：用数学归纳法证明 1+3+5+…+(2n1)=n2
2.3 数学归纳法
两个猜想：
已知数列{an}中，a1=1,an+1=an/(an+1),试 求出a2,a3,a4并猜想{an}的通项公式
猜想： an=__1_/_n____
21
2 1 5 222 1 17 223 1 257
结论是错误的。
n 5时，22n 是一个合数：
224 1 65537 225 1 4294967297 641 6700417
数学归纳法
对于由不完全归纳法得到的某些与正整数n有关 的数学命题我们常采用下面的方法来证明它们的正 确性：
命题及其关系(公开课)(课堂PPT)
高二数学 选修2-1 第一章 常用逻辑用语
1.1 命题及其关系
2
材料探究
歌德是18世纪德国的一位著名文艺大师， 一天，他与一位批评家“狭路相逢”，这位 文艺批评家生性古怪，遇到歌德走来，不仅 没有相让，反而卖弄聪明，一边趾高气扬地 往前走。一边大声说道：“我从来不给傻子 让路！”而对如此的尴尬的局面，歌德只是 笑容可掏，谦恭的闪在一旁，一边有礼貌回 答道“呵呵，我可恰恰相反。”结果故作聪 明的批评家，反倒自讨没趣。
（2）若四边形是菱形，则它的对角线 互相垂直且平分．
解：(1)条件p：整数a能被2整除， 结论q：整数a是偶数。
(2)条件p：四边形是菱形， 结论q：四边形的对角线互相垂直且平分。
11
学以致用
“若p则q”形式的命题的书写
数学中有一些命题虽然表面上不是“若p， 则q”的形式,例如“垂直于同一条直线的两 个平面平行”，但是把它的形式作适当改变， 就可以写成“若p，则q”的形式：
若两个平面垂直于同一条直线， 则这两个平面平行． 这样，它的条件和结论就很清楚了．
12
学以致用
例3 将下列命题改写成“若p,则q”的形式,并判断真假:
（1）垂直于同一条直线的两条直线平行； 若两条直线垂直于同一直线， 则这两条直线平行。
（2）负数的立方是负数; 若一个数是负数， 则这个数的立方是负数。
②都可以判断真假.
6
自主探究
命题的概念：
一般地,在数学中,我们把用语言、符号 或式子表达的,可以判断真假的陈述句。
真命题：判断为真的语句。 假命题：判断为假的语句。
命题① ②能 陈判 述断 句真假
7
学以致用
以下语句是命题么？ (1)7是23的约数吗?（ ） (2)x>5. （ ）
1.1 命题及其关系
2
材料探究
歌德是18世纪德国的一位著名文艺大师， 一天，他与一位批评家“狭路相逢”，这位 文艺批评家生性古怪，遇到歌德走来，不仅 没有相让，反而卖弄聪明，一边趾高气扬地 往前走。一边大声说道：“我从来不给傻子 让路！”而对如此的尴尬的局面，歌德只是 笑容可掏，谦恭的闪在一旁，一边有礼貌回 答道“呵呵，我可恰恰相反。”结果故作聪 明的批评家，反倒自讨没趣。
（2）若四边形是菱形，则它的对角线 互相垂直且平分．
解：(1)条件p：整数a能被2整除， 结论q：整数a是偶数。
(2)条件p：四边形是菱形， 结论q：四边形的对角线互相垂直且平分。
11
学以致用
“若p则q”形式的命题的书写
数学中有一些命题虽然表面上不是“若p， 则q”的形式,例如“垂直于同一条直线的两 个平面平行”，但是把它的形式作适当改变， 就可以写成“若p，则q”的形式：
若两个平面垂直于同一条直线， 则这两个平面平行． 这样，它的条件和结论就很清楚了．
12
学以致用
例3 将下列命题改写成“若p,则q”的形式,并判断真假:
（1）垂直于同一条直线的两条直线平行； 若两条直线垂直于同一直线， 则这两条直线平行。
（2）负数的立方是负数; 若一个数是负数， 则这个数的立方是负数。
②都可以判断真假.
6
自主探究
命题的概念：
一般地,在数学中,我们把用语言、符号 或式子表达的,可以判断真假的陈述句。
真命题：判断为真的语句。 假命题：判断为假的语句。
命题① ②能 陈判 述断 句真假
7
学以致用
以下语句是命题么？ (1)7是23的约数吗?（ ） (2)x>5. （ ）
命题及其关系课件(新人教选修2-1).
1 ■知识回顾（1）同位角相等，两直线平行。
原命题（2）两直线平行,同位角相等。
逆命题（3）同位角不相等，两直线不平行否命题（4）两直线不平行，同位角不相等逆否命题请观察上面命题中条件和结论与命题（1）中的和结论有什么区别?2.V 什么叫互逆命题？一个命题的条件和结论，分别是另一个命题的结论和条件，这两个命题就叫做互逆侖题。
扌巴其中一个叫做原命题，则另一个叫做原命题的逆命题。
V 什么叫互否命题？一个命题的条件和结论，分另JJ是另一个命题的条件的否定和结论的否定，这两个命题就叫做互否命题。
扌巴其中一个叫做原命题，则另一个叫做原命题的否命题。
:区分否命题和命题的否定（非P ）OV 什么叫互为逆否命题？一个命题的条件和纟吉论，分另！J是另一个命题的纟吉论的否定和条件的否定，这两个命题就叫做互为逆否侖题。
把其中一个叫做原命题，则另一2.个叫做原命题的逆否命题。
3 ■知识巩固分别写出下列命题。
B 原命题：若四边形是正方形，则四边形两对角线垂直。
逆命题： 若四边形两对角线垂直，则四边形是正方形。
否命题： 若四边形不是正方形，则四边形两对角线不垂直。
逆否命题： 若四边形两对角线不垂直，则四边形不是正方形。
ks5u 精品课件 o A 原命题：若o>b,则a+c>b+c. C 原命题：若”则§逆命题： 若a+ob+c,则 否命题： 若日sb,则a+c<b+c. 逆命题:否命题:逆否命题： 若a+csb+c,贝临勺）. 逆否命题： 若「q 则卩3 ■知识巩固把下列命题改写成“若p 则孑滋形式并写出逆命题、否命题、逆否命题。
仁负数的平方是正数 原命题： 逆命题：否命题：逆否命题：若一个数是负数，则它的平方是正数。
若一个数的平方是正数，则它是负数。
若一个数不是负数，则它的平方不是正数。
若一个数的平方不是正数，则它不是负数。
2 •正方形的四条边相等 原命题： 逆命题：否命题：逆否命题： 若一个四边形是正方形，则它的四条边相等。
四种命题及其关系完整(精品)ppt课件
完整版ppt课件
20
例 证明：若p2＋q2＝2，则p＋q≤2.
证明: 假设 p q 2 ,
假设原命题结 论的反面成立
则 ( p q)2 4 , ∴ p2 q2 2 pq 4 ,
看能否推出原命题 条件的反面成立
∵ p2 q2 ≥2 pq ,
∴ 2( p2 q2 ) 4 , ∴ p2 q2 2 , 尝试成功
其中p叫做命题的条件,q叫做命题的结论.
完整版ppt课件
2
下列四个命题中,命题(1)与命题(2)(3)(4)的条件 和结论之间分别有什么关系?
(1)若f(x)是正弦函数,则f(x)是周期函数; (2)若f(x)是周期函数,则f(x)是正弦函数; (3)若f(x)不是正弦函数,则f(x)不是周期函数; (4)若f(x)不是周期函数,则f(x)不是正弦函数;
2、四种命题间的相互关系及其真假性的关系：
作业：习题1.1 A组 2-4题
∴ p2 q2 2 .
得证
这表明原命题的逆否命题为真命题,从而原命
题也为真命题.
完整版ppt课件
21
练习 用反证法证明：
如果a>b>0，那么 a b .
证明: 假设 a 不大于 b 则 a< b 或 a= b 因为 a>0,b>0 所以
a <b aaba
abbb a<b
a= ba=b
这些条件都与已知ab0矛盾
──这是一种很好的尝试,它往往具有 正难则反,出奇制胜的效果.
──它其实是反证法的一种特殊表现:从命
题结论的反面出发, 引出矛盾(如证明结论的条
件不成立),从而证明命题成立的推理方法.
完整版ppt课件
17
命题及其关系PPT教学课件
(1)必要不充分 (2)充分不必要 (3)充分不必要 解析： (1)等价转化为判断，q：a＝0且b＝0是p ：ab＝0的 什么条件． ∵a＝0且b＝0，则ab＝0成立，∴ q⇒ p， 而ab＝0推不出a＝0且b＝0，如a＝0，b＝8， ∴p⇒ q， ∴ q是p 的充分不必要条件，即p是q的充分不必要 条件．
【例1】 以下列命题为原命题，分别写出 它们的逆命题、否命题和逆否命题， 并判断它们的真假． (1)内接于圆的四边形的对角互补； (2)已知a、b、c、d是实数， 若a＝b，c＝d，则a＋c＝b＋d.
解： (1)原命题： “若四边形内接于圆，则它的对角互补”； 逆命题： “若四边形对角互补，则它必内接于某圆”； 否命题： “若四边形不内接于圆，则它的对角不互补”； 逆否命题： “若四边形的对角不互补，则它不内接于圆”. 四种命题都正确．
否命题：“已知a、b、c、d是实数， 若a≠b或c≠d，则a＋c≠b＋d” (注意“a＝b，c＝d”的否定是“a≠b或c≠d”， 只需要至少有一个不等即可)， 此命题不正确，a＝1，c＝1，b＝1.5，d＝0.5， a≠b或c≠d，但a＋c＝b＋d.
逆否命题：“已知a、b、c、d是实数， 若a＋c≠b＋d，则a≠b或c≠d”. 逆否命题还可以写成：“已知a、b、c、d是实数，若a ＋c≠b＋d， 则a＝b，c＝d两个等式至少有一个不成立”， 由原命题为真得此命题显然为真．
变式2－1
用“充分不必要”、“必要不充分”、“充要”、 “既不充分也不必要”填空．
(1) “ p:ab 0”是“q:a 0或b 0”的________条件；
(2)若非空集合A，B，C满足A∪B＝C， 且B不是A的子集，则“p：x∈C ”是 “q：x∈A ”的________条件； (3)“p：x>0”是“q：x≠0”的________条件．
1.1命题及其关系PPT优秀课件
点拨：正难则反，看逆否命题
正面叙述的词语及其否定
正面词语 等于 否定 大于＞ 小于＜ 是 都是
不等于 不大于 不小于 不是 不都是
或
且
至多有一个 至少有一个 任意的 所有的 至少有两个 一个也没有 存在 某些
三、反证法
☆用反证法证明命题的一般步骤： （1）假设命题的结论不成立，即假设结论的反面成立； （2）从这个假设出发，经过推理论证，得出矛盾； （3）由矛盾判定假设不正确，从而肯定命题的结论正确. ☆理论根据：原命题与其逆否命题的等价性.
互逆
说明：四种命题的关系相对的
例 6 、写出下列原命题的其他三种命题， 并判断真假 （1）若 x＝2且 y 3，则 x y 5 （2）设 x , y N ，若 x y是偶数， 则 x , y都是偶数 （3）若 a b，则 ac bc
2 2
变形：若 x y 0，则x 0或y 0
例1 判断下列语句中哪些是命题？是真命题还是 假命题？ (1)空集是任何集合的子集; (2)若整数a是素数，则a是奇数; (3)指数函数是增函数吗？ (4)若空间中两条直线不相交，则这两条直线平行; (5)
22 2 ;
(6)x>15. 上面(2)(4)具有“若p,则q”的形式.在数学中，这种形式的命 题是常见的.
(4)若x2=1,则x=1;
(5)两个全等三角形的面积相等; (6)3能被2整除.
以上均为陈述句,(1)(3)(5)为真,(2)(4)(6)为假.
命题的概念
一般地,在数学中,我们把用语言、符 号或式子表达的,可以判断真假的陈述句 叫做命题. 其中判断为真的语句叫做真命题,判 断为假的语句叫做假命题.
让我想一 想
逆命题： 若q则p.
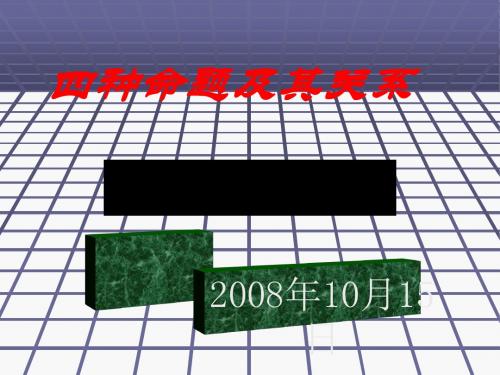
正面叙述的词语及其否定
正面词语 等于 否定 大于＞ 小于＜ 是 都是
不等于 不大于 不小于 不是 不都是
或
且
至多有一个 至少有一个 任意的 所有的 至少有两个 一个也没有 存在 某些
三、反证法
☆用反证法证明命题的一般步骤： （1）假设命题的结论不成立，即假设结论的反面成立； （2）从这个假设出发，经过推理论证，得出矛盾； （3）由矛盾判定假设不正确，从而肯定命题的结论正确. ☆理论根据：原命题与其逆否命题的等价性.
互逆
说明：四种命题的关系相对的
例 6 、写出下列原命题的其他三种命题， 并判断真假 （1）若 x＝2且 y 3，则 x y 5 （2）设 x , y N ，若 x y是偶数， 则 x , y都是偶数 （3）若 a b，则 ac bc
2 2
变形：若 x y 0，则x 0或y 0
例1 判断下列语句中哪些是命题？是真命题还是 假命题？ (1)空集是任何集合的子集; (2)若整数a是素数，则a是奇数; (3)指数函数是增函数吗？ (4)若空间中两条直线不相交，则这两条直线平行; (5)
22 2 ;
(6)x>15. 上面(2)(4)具有“若p,则q”的形式.在数学中，这种形式的命 题是常见的.
(4)若x2=1,则x=1;
(5)两个全等三角形的面积相等; (6)3能被2整除.
以上均为陈述句,(1)(3)(5)为真,(2)(4)(6)为假.
命题的概念
一般地,在数学中,我们把用语言、符 号或式子表达的,可以判断真假的陈述句 叫做命题. 其中判断为真的语句叫做真命题,判 断为假的语句叫做假命题.
让我想一 想
逆命题： 若q则p.
《命题及其关系》课件
巩固新知
写出下面逆命题、否命题、
逆否命题，并判断真假。
原命题：若a=0, (真则) ab=0。 逆命题：若ab=0, (假则)a=0。 否命题：若a≠ 0, 则(a假b)≠0。 逆否命题：若ab≠(0真,则) a≠0。
课堂小结 1.命题的概念 2.四种命题 3.四种命题的关系
1.我们 四个全 都是骗 子
假 假假 假
原命题：
若四边形对角线相等， 则四边形是平行四边形 逆命题：否命题： 逆否命题：
若若四四边边形形不是对是平角平行线行四不四边相边形等形，， 则则四四边边形形对对不角角是线线平不相行相等四等。边。形。
一般地,四种命题的真假性, 有而且仅有下面四种情况:
原命题 逆命题 否命题 逆否命 题
3.体会运用常用逻辑用语表述数学 内容的准确性、简捷性.
1.1.1命题
下形（（（123列式） ） ）语有130.是25句什>是152整的么;的语数句约表特;都数是述点;陈并且可述?句
你（4能）对判顶断角它相等们; 的以判
真（（56假） ）若3吗能x?2被=12,整则除x=; 1.
断 真 假
命题的概念
是 你们是
老实人 还是骗 子？
3.我们
四个人
2.我们当中 中有两 只有一个人 个人是 是骗子 骗子
4.我 是老 实人
（(2)2若）两垂个直平于面同垂一直个于平同面一的平两面个，平则面 平这行两。个平面互相平行。 假命题
1.1.2四种命题
思考
（（（（别这把一题别和叫做题一是条做一做请1234一（一是 两 其 个观是结做原的个另件互个原））））1个察个另 个 中 叫同两同两另论命否命一的叫命互为）上命位直位直命中一命一做一的题命题个否做题逆否面角线角线的题题个 题 个 原个否，题的命定原的否命命相平不不条的的命就叫命命定则。条题，命逆命题题等 行相 平件条条中题叫做题行等题，另件的这题否题。和， ，条件，，件的做原的结的这一和结两，命把。件两 同同两和论和结命逆互条两个结论个则题其把和直 位位直有结结论题命逆件个 叫 论的 命 另 。中其结线 角角线什论论和，题命论的命做，否题一一中平相不不么，与，行等平相条则题否题原分定就个个区命。。行等分分别件另。定就命别和叫叫叫？，
1.1命题及其关系PPT课件
m2
(2 ) 当 q 是 真 命 题 且 p 是 假 命 题 时 m1 1m2
2021
9
观察与思考
①如果两个三角形全等，那么它们的面积相等；
②如果两个三角形的面积相等，那么它们全等；
③如果两个三角形不全等，那么它们的面积不相 等；
④如果两个三角形的面积不相等，那么它们不全 等. 试问:命题②，③，④与命题①有何关系？
逆 否 命 题 为 ： 若 a b 1 , 则 a 2 b 2 2 a 4 b 3 0 .
证明：若a-b=1，则
a2-b2+2a-4b-3
=(a+b)(a-b)+2a-4b-3
=a+b+2a-4b-3
=3a-3b-3=3(a-b)-3
=3×1-3=0
所以原命题的逆否命题为真命题，
所以原命题也2为021 真命题。
则x2＞0，所以
x2+y2 ＞0，
也就是说x2+y2 ≠0.
因此，原命题的逆否命题为真命题，
从而原命题为真命2021题.
25
证明命题的方法
方法一：直接法，从命题的条件p出发，经 推理直接得出结论p，证明其为真命题；
方法二：等价法，证明命题（若p，则q） 的等价命题——逆否命题（若┐q，则┐q） 为真，则原命题也为真；
1. 将命题“a>0时，函数y=ax+b的值随x值的增加而增加” 改写成“若p，则q”的形式，并判断命题的真假。
解: a>0时，若x增加，则函数y=ax+b 的值也随之增加，它是真命题．
在本题中，a>0是大前提，应单独给出， 不能把大前提也放在命题的条件部分内．
2021
8
命题及其关系公开课ppt课件
例2 下列命题： ①“若xy＝1，则x、y互为倒数”的逆命题 ②“四边相等的四边形是正方形”的否命题； ③“梯形不是平行四边形”的逆否命题； ④“若ac2>bc2，则a>b”的逆命题. 其中的真命题是__①__②__③____.
跟踪训练2 有下列四个命题：
①"若x＋y＝0,则x、y互为相反数"的否命题;
∴f(a)<f(－b),f(b)<f(－a). ∴f(a)＋f(b)<f(－a)＋f(－b). 这与已知条件f(a)＋f(b)≥f(－a)＋f(－b)相矛盾. 因此假设不成立，故a＋b≥0.
小结 在解答命题的过程中很容易把逆否命题的证法与 反证法混淆,导致错误的原因是忽视了这两种证法的本质 区别.
跟踪训练3证明:若a2－4b2－2a＋1≠0,则a≠2b＋1.
(4)若两个角不相等, 则它们不是对顶角 逆否命题： 若 ┐q ,则┐p
原命题,逆命题,否命题,逆否命题
四种命题形式: 原命题: 若p,则q 逆命题: 若q,则p 否命题: 若¬p,则¬q
逆否命题: 若¬q,则¬p
四种命题之间的关系
原命题 若p则q
互逆
逆命题 若q则p
互 否
否命题 若﹁p则﹁q 互逆
由原命题与逆否命题具有相同的真假性可知，结论正确.
1.命题“若 f(x)是奇函数，则 f(－x)是奇函数”的否命题是
(B )
A.若 f(x)是偶函数，则 f(－x)是偶函数 B.若 f(x)不是奇函数，则 f(－x)不是奇函数 C.若 f(－x)是奇函数，则 f(x)是奇函数 D.若 f(－x)不是奇函数，则 f(x)不是奇函数
例3证明:已知函数f ( x)是(, )上的增函数, a, b R, 若f (a) f (b) f (a) f (b),则a b 0.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
练习中的命题(2)(4)(9),具有 “若P, 则q” 的形式
也可写成 “如果P,那么q” 的形式
也可写成 “只要P,就有q” 的形式
通常,我们把这种形式的命题中的P叫做命 题的条件,q叫做结论.
记做: p q
例2 指出下列命题中的条件p和结论q; (1)若整数a能被2整除,则a是偶数; (2)若四边形是菱形,则它的对角线互相垂直且平分. 解：(1)条件p:整数a能被2整除,结论q：整数a是偶数;
逆命题为：若q，则p，即交换原命题的条件和 结论即得其逆命题.
否命题为：若┐p，则┐q，即同时否定原命题的 条件和结论，即得其否命题.
逆否命题为：若┐q，则┐p，即交换原命题的 条件和结论，并且同时否定，则得其逆否命题.
（2）四种命题的真假关系：
谢谢！
19
练习 判断下面的语句是否为命题?若是命题， 指出它的真假。
(1) 空集是任何集合的子集.
(2)若整数a是素数,则a是奇数. (3)对于任意的实数a,都有a2+1>0.
(4)若平面上两条直线不相交,则这两条直线平行. (5)x2+x>0. (6)91是素数. (7)指数函数是增函数吗?
( (2)2 2 (9)若|x-8y)|=|a-b|,则x-y=a-b.
以上均为陈述句,(1)(2)为真,(3)(4) 为假, (5) (6)的真 假需要根据实际情况确定，总是可以确定真假.
思考:下面的语句的表述形式有什么 特点？你能判断它们的真假吗？ (1)若直线a∥b，则a和b无公共点. (2)２＋４＝７. (3)垂直于同一条直线的两个平面平行． (4)若x2=1，则x=1.
(2)条件p:四边形是菱形,结论q：四边形的对角线互 相垂直且平分.
有一些命题表面上不是“若p,则q”的形式,但 可以改写成“若p,则q”的形式,例如:
垂直于同一条直线的两个平面平行. 若两个平面垂直于同一条直线,则这两个平面平行.
例3 将下列命题改写成“若p,则q”的形式,并判断 真假; (1)垂直于同一条直线的两条直线平行; (2)负数的立方是负数; (3)对顶角相等; (4)等腰三角形两腰的中线相等; (5)偶函数的图像关于y轴对称; (6)垂直于同一个平面的两个平面平行.
２、互否命题：如果第一个命题的条件和结论 是第二个命题的条件和结论的否定，那么这两个命 题叫做互否命题。如果把其中一个命题叫做原命题， 那么另一个叫做原命题的否命题。
３、互为逆否命题：如果第一个命题的条件和 结论分别是第二个命题的结论的否定和条件的否定， 那么这两个命题叫做互为逆否命题。
一个符号
条件Ｐ的否定，记作“Ｐ”。读作“非
（1）全等三角形的对应边相等；
（2）四条边相等的四边形是正方形。
思考：原命题、逆命题、否命题、逆否命 题的真假有什么关系呢？
一般地,四种命题的真假性,有而且仅有 下面四种情况:
原命题 逆命题 否命题 逆否命题
真
真
真
真
真
假
假
真
假
假
假
假
假
真
真
假
小结
（1）四种命题的概念与表示形式，即如
果原命题为：若p，则q，则它的：
(5)两个全等三角形的面积相等. (６)３能被２整除.
我们把用语言、符号或式子表达的， 可以判断真假的陈述句称为命题．
其中判断为真的语句称为真命题，判断为 假的语句称为假命题．
1.1.1命题的概念
一般地,在数学中,我们把用语言、符 号或式子表达的,可以判断真假的陈述句 叫做命题.
其中判断为真的语句叫做真命题,判 断为假的语句叫做假命题.
？ 观察与思考
如果两个三角形全等，那么它们的面积相等；① 如果两个三角形的面积相等，那么它们全等；② 如果两个三角形不全等，那么它们的面积不相等；③ 如果两个三角形的面积不相等，那么它们不全等；④
试问：命题②，③，④与命题①有何关系？
三个概念
１、互逆命题：如果第一个命题的条件（或题
设）是第二个命题的结论，且第一个命题的结论是 第二个命题的条件，那么这两个命题叫互逆命题。 如果把其中一个命题叫做原命题，那么另一个叫做 原命题的逆命题。
1.1《命题及关系》
下列语句的表述形式有什么特点?你能判断它们 的真假吗?
(1)三角形的 三 内角之和等于1 8 0 ;
(2)如果a,b是任意两个正实数，那么 ab; 2 ab
(3) sin 60
2; 2
(4)如果实数a满足a2=9,则a=3;
(5)中学生目前的学业负担过重;
(6)中国将在本世纪中叶达到中等发达国家的水平 .
原命题
互逆 逆命题
命 题
题 若p则q
若q则p的ຫໍສະໝຸດ 与逆逆否互
命
互
题
命否
题
否
与 否
同 真
否命题
逆否命题
命 题
假 。
若﹁p则﹁q
互逆
若﹁q则﹁p
同 真
假。
三.典型例题分析：
例1：写出命题“若a=0，则ab=0”的逆命 题、否命题与逆否命题，并判断其真假。
例2：把下列命题改写成“若则”的形式， 并写出它的逆命题、否命题与逆否命题，同 时指出它们的真假：
例1 判断下列语句中哪些是命题？是真命题还是
假命题？
(1)空集是任何集合的子集;
真命题
(2)若整数a是素数，则a是奇数;
假命题
(3)指数函数是增函数吗？
(4)若空间中两条直线不相交，则这两条直线平行; 假命题
(5) 22 2;
真命题
(6)x>15.
判断 一个语句是不是命题，关键判断：（1）是否为陈 述句；（2）能否判断真假。
Ｐ”。
原命题：若p 则q 逆命题：若q 则p
否命题：若 p 则 q
逆否命题：若 q 则 p
课堂小结
1、命题的概念
让我想一 想
2、能指出命题的条件和结论
3、四种命题形式：
原命题：若p则q. 否命题： 若¬p则¬q.
逆命题： 若q则p. 逆否命题： 若¬q则¬p.
四种命题之间的 关系
原
原 命