2011年揭阳市高考一模数学试题文
2011年高考全国数学试卷(新课标)-文科(含详解答案)

绝密★启用前2011年普通高等学校招生全国统一考试文科数学(必修+选修I)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页。
第Ⅱ卷3至4页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题...卷上作答无效....... 3.第Ⅰ卷共l2小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的. 一、选择题(1)设集合U={}1,2,3,4,{}1,2,3,M ={}2,3,4,N =则U=(M N )I ð (A ){}12,(B ){}23, (C ){}2,4 (D ){}1,4 【答案】D【命题意图】本题主要考查集合交并补运算. 【解析】{2,3},(){1,4}U M N M N =∴=ðQ I I(2)函数0)y x =≥的反函数为(A )2()4xy x R =∈ (B )2(0)4xy x =≥(C )24y x =()x R ∈ (D )24(0)y x x =≥ 【答案】B【命题意图】本题主要考查反函数的求法.【解析】由原函数反解得24yx =,又原函数的值域为0y ≥,所以函数0)y x =≥的反函数为2(0)4xy x =≥.(3)设向量,a b 满足||||1a b == ,12a b ⋅=-r r ,则2a b +=(A (B (C (D【答案】B【命题意图】本题主要考查平面向量的数量积与长度的计算方法.【解析】2221|2|||44||14()432a b a a b b +=+⋅+=+⨯-+=r r r r r u r ,所以2a b +=r r (4)若变量x ,y 满足约束条件63-21x y x y x +≤⎧⎪-≤⎨⎪≥⎩,则=23z x y +的最小值为(A )17 (B )14 (C )5 (D )3 【答案】C【命题意图】本题主要考查简单的线性规划.【解析】作出不等式组表示的可行域,从图中不难观察当直线=23z x y +过直线x=1与x-3y=-2的交点(1,1)时取得最小值,所以最小值为5.(5)下面四个条件中,使a b >成立的充分而不必要的条件是(A )1a b +> (B )1a b -> (C )22a b > (D )33a b > 【答案】A【命题意图】本题主要考查充要条件及不等式的性质.【解析】即寻找命题P ,使P a b ⇒>,且a b >推不出P ,逐项验证知可选A.(6)设n S 为等差数列{}n a 的前n 项和,若11a =,公差2d =,224k k S S +-=,则k = (A )8 (B )7 (C )6 (D )5 【答案】D【命题意图】本题主要考查等差数列的基本公式的应用. 【解析】解法一2(2)(1)(1)[(2)12][12]442422k k k k k k S S k k k +++--=+⨯+⨯-⨯+⨯=+=,解得5k =.解法二: 221[1(1)2](12)4424k k k k S S a a k k k +++-=+=++⨯++⨯=+=,解得5k =.(7)设函数()cos (0)f x x ωω=>,将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,则ω的最小值等于(A )13(B )3 (C )6 (D )9【答案】C【命题意图】本题主要考查三角函数的周期性与三角函数图像变换的关系.【解析】由题意将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,说明了3π是此函数周期的整数倍,得2()3k k Z ππω⨯=∈,解得6k ω=,又0ω>,令1k =,得min 6ω=.(8)已知直二面角l αβ--,点A α∈,A C l ⊥,C 为垂足,B β∈,B D l ⊥,D 为垂 足,若2,1AB AC BD ===,则C D = (A ) 2 (B(C (D )1 【答案】C【命题意图】本题主要考查二面角的平面角及解三角形.【解析】因为l αβ--是直二面角, A C l ⊥,∴AC ⊥平面β,A C B C ∴⊥BC ∴=又B D l ⊥,CD ∴=(9) 4位同学每人从甲、乙、丙3门课程中选修1门,则恰有2人选修课程甲的不同选法共有 (A) 12种 (B) 24种 (C) 30种 (D)36种 【答案】B【命题意图】本题主要考查两个原理与排列组合知识,考察考生分析问题的能力.【解析】第一步选出2人选修课程甲有246C =种方法,第二步安排剩余两人从乙、丙中各选1门课程有22⨯种选法,根据分步计数原理,有6424⨯=种选法.(10) 设()f x 是周期为2的奇函数,当01x ≤≤时,()f x =2(1)x x -,则5()2f -=(A) -12(B)1 4- (C)14(D)12【答案】A【命题意图】本题主要考查利用函数的周期性和奇偶性求函数值的方法. 关键是把通过周期性和奇偶性把自变量52-转化到区间[0,1]上进行求值.【解析】由()f x 是周期为2的奇函数,利用周期性和奇偶性得:5511111((2)()()2(12222222f f f f -=-+=-=-=-⨯⨯-=-(11)设两圆1C 、2C 都和两坐标轴相切,且都过点(4,1),则两圆心的距离12C C = (A)4 (B)【答案】C【命题意图】本题主要考查圆的方程与两点间的距离公式.【解析】由题意知圆心在直线y=x 上并且在第一象限,设圆心坐标为(,)(0)a a a >,则a =,即210170a a -+=,所以由两点间的距离公式可求出128C C ===.(12)已知平面α截一球面得圆M ,过圆心M 且与α成060二面角的平面β截该球面得圆N .若该球面的半径为4,圆M 的面积为4π,则圆N 的面积为(A)7π (B)9π (C)11π (D)13π 【答案】D【命题意图】本题主要考查二面角的概念与球的性质.【解析】如图所示,由圆M 的面积为4π知球心O 到圆M 的距离O M =,在R t O M N ∆中,30OMN ︒∠=, ∴12O N O M ==故圆N 的半径r ==,∴圆N的面积为213S r ππ==.第Ⅱ卷注意事项:1答题前,考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考 证号填写清楚,然后贴好条形码。
广东省揭阳市2011—2012学年度高三学业水平考试文科数学,PPT版

n
α
4.已知f ( x )是定义在R上的奇函数,当x ≥ 0时f ( x ) = 3 x + m ( m为常数 ),则函数f ( x )的大致图像为( B )
f ( x )为奇函数,图像关于原点对称,f (0) = 0, 且在(0, +∞ )上为增函数 .
5.已知倾斜角为α的直线l 与直线x − 2 y + 2 = 0平行,则 tan 2α的值为( C ) 4 A. 5 3 B. 4 4 C. 3 2 D. 3
pm2.5(毫毫/立立立)
24小时平均浓度 小时平均浓度 (毫克 立方米 毫克/立方米 毫克 立方米)
13.在△ABC中,已知A = 60o , b = 4, c = 5, 则 sin B =
.
a = 4 + 5 − 2 ⋅ 4 ⋅ 5cos 60 = 21,
2 2 0
bc sin A 2 2 7 ∴ sin B = = = ac 7 7
( A, D ),( A, E ),( A, F ),( B , C ),( B , D ),( B , E ),( B , F ),(C , D ),(C , E ), (C , F ),( D, E ),( D, F ),( E , F ).
(D 其中2件等级系数都是 8的事件有: , E ),( D, F ),( E , F )故所 3 1 求的概率P = = 15 5
频频/组组 160/3 120/3 100/0 160 120 60 20 ( + + + + + ) × 0.005 × 30 = 27 3 3 3 3 3 3
20/3 0 0.065 0.070 0.075 0.0800.0850.0900.0950.1000.105
揭阳市2011年高中毕业班高考第一次模拟考(文科综合)参考答案及评分说明

揭阳市年高中毕业班高考第一次模拟考文科综合参考答案及评分说明一、选择题:本大题共35小题,每小题4分,共140分。
在每题给出的四个选项中,只有一项是符合题目要求的。
二、非选择题:本大题共6个小题,满分160分。
(政治科部分参考答案,共52分)36.(26分)答案要点:(1)自2006年以来,我国居民消费价格指数和食品价格指数波动较大,有通货膨胀压力。
(2分)其中食品价格指数的涨幅高于同期的CPI涨幅,说明食品价格指数是影响CPI指数变化的主要因素。
(2分)(2)省政府在2010年为稳定物价、改善民生,采取了一系列措施,这符合:①市场调节具有自发性、盲目性和滞后性等固有弊端,国家运用宏观调控的有关手段稳定物价水平。
(3分)②宏观调控的主要手段有经济手段、法律手段和必要的行政手段等,省政府通过财政补贴稳定物价,增加城乡低保价格临时补贴的做法体现了运用财政政策加强宏观调控。
(3分)③科学发展观的第一要义是发展,核心是以人为本,基本要求是全面协调可持续发展,根本方法是统筹兼顾,政省府采取多种手段稳定消费价格,发放临时价格补贴,坚持以人为本,维护群众利益,促进经济社会全面发展。
体现了科学发展观的要求。
(5分)(评分说明:学生若能从其他角度如“国家财政是促进社会公平、保障人民生活的物质保障”作答,言之有理者可酌情给2-3分,本小题总分不超过11分。
)(3)①人民为《纲要》出谋划策,提交全国人大审议体现了国家的一切权力属于人民。
(3分)②坚持党的领导、人民当家作主和依法治国的有机统一,党审议通过制定“十二五”规划的建议,人民为《纲要》出谋划策,制定要依照一定的过程;(3分)③坚持民主内容与形式的统一,政府依据《建议》和民意编制规划等;(2分)④坚持人民代表大会制度等一系列政治制度,提交全国人大审议等,体现了保障人民当家作主,充分发挥我国社会主义民主政治的优势。
(3分)(评分说明:学生若能从其他角度如“充分发扬人民民主;坚持国家的专政职能;坚持民主集中制;坚持中国共产党领导的多党合作和政治协商制度;民族区域自治制度;基层群众自治制度等”作答,言之有理者可酌情给2-3分,本小题总分不超过11分。
广东省揭阳市高考一模数学文科试卷

当 时,方程表示双曲线.-------------------------------------------6分
(2)由(1)知,当 时,轨迹T的方程为: .
连结OE,易知轨迹T上有两个点A ,B 满足 ,
A.甲先到达B地 B.乙先到达B地
C.甲乙同时到达B地 D.无法确定谁先到达B地
二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.
(一)必做题(11-13题)
11.命题“ ”的否定为.
12.椭圆 上一点P到右焦点的距离是长轴两端点到右焦点距离的等差中项,则P点的坐标为.
13.随机抽取某中学甲、乙两个班各10名同学,测量他们的身高(单位:cm)获得身高数据的茎叶图如下图甲,在样本的20人中,记身高在 , 的人数依次为 、 、 、 .图乙是统计样本中身高在一定范围内的人数的算法流程图,由图甲可知甲、乙两班中平均身高较高的是班;图乙输出的 .(用数字作答)
得 即 ------------------------------------2分
当 时,方程表示两条与x轴平行的直线;(答方程表示两条直线不扣分)----------------------------3分
当 时,方程表示以原点为圆心,4为半径的圆;(答方程表示圆不扣分)-----------------------4分
由 得
∴ 的单调减区间 .-------------------------12分
17.解:(1)该组合体的主视图和侧视图如右图示:-----3分
(2)∵ 平面 , 平面
∴平面 平面ABCD
∵ ∴BC 平面 ----------5分
广东省揭阳市高中数学毕业班第二次高考模拟考试 理

广东省揭阳市2011年高中毕业班第二次高考模拟考数学(理科)本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.2.选择题将答案代号填在答题卡的选择题答案栏中,不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须填写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:锥体的体积公式:13V Sh =,其中S 表示底面积,h 表示高. 乘法公式:2233()()a b a ab b a b +-+=+.一.选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|11,}M x x x Z =-≤≤∈,{|02}N x x =≤≤,则MN 为A. {1}B. {0,1,2}C. {|01}x x ≤≤D. {0,1} 2.设(12)34i z i -=+,则||z 为A B C .5 3. 为了解某商品销售量y (件)与销售价格x (元/件)的关系,统计了(x,y)的10组值,并画成散点图如图1,则其回归方程可能是 A . 10198y x ∧=-- B. 10198y x ∧=-+ C. 10198y x ∧=+ D.10198y x ∧=-图14.要得到函数sin(2)4y x π=+的图象,只要将函数sin 2y x =的图象A.向左平移4π单位 B.向右平移4π单位 C.向右平移8π单位 D.向左平移8π单位DECBA图2主视图C 1B 1A 1CB A5.已知命题p :x R ∃∈,5cos 4x =;命题q :2,10x R x x ∀∈-+>.则下列结论正确的是 A .命题p q ∧是真命题 B .命题p q ∧⌝是真命题 C .命题p q ⌝∧是真命题 D .命题p q ⌝∨⌝是假命题6.如图2,三棱柱111ABC A B C -的侧棱长和底面边长均为4,且侧棱1AA ⊥底面ABC ,其主视图(又称正视图)是边长为4的正方形,则此三棱柱的侧视图(又称左视图)的面积为A .16 B. C..7.已知点(,)M x y 满足1,10,220.x x y x y ≥⎧⎪-+≥⎨⎪--≤⎩若ax y +的最小值为3,则a 的值为A .1B .2C .3D .48.已知平面区域0{(,)|y x y y ≥⎧⎪Ω=⎨≤⎪⎩,直线2y mx m =+和曲线y =有两个不同的交点,它们围成的平面区域为M ,向区域Ω上随机投一点A ,点A 落在区域M 内的概率为()P M ,若01m ≤≤,则()P M 的取值范围为 A .2(0,]2ππ- B .2(0,]2ππ+ C .2[,1]2ππ+ D .2[,1]2ππ- 二.填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13题) 9.函数()ln(2)xf x x =- 的定义域为 .10.双曲线29x -216y =1的离心率e = ;焦点到渐近线的距离为 .11.在Rt ABC ∆中,0C=90∠,AB AC ⋅= .12.根据图3所示的程序框图,若0514231,5,10,a a a a a a ======3则输出的V 值为 .13.在平面直角坐标系中,定义点11(,)P x y 、22(,)Q x y 之间的直角距离为1212(,)||||d P Q x x y y =-+-若点(,1),(1,2),(2,5)A x B C ,且(,)(,)d A B d A C >,则x 的取值范围为 .(二)选做题(14、15题,考生只能从中选做一题, 两题全答的,只计前一题的得分)DCBAP男女6432性别人数科别甲科室乙科室14.(几何证明选做题)如图4,BD ⊥AE ,90C?o ,AB =4, BC =2,AD =3,则DE = ;CE = . 图4 15.(坐标系与参数方程选做题) 设M 、N 分别是曲线2sin 0ρθ+=和s ()42in πρθ+=上的动点,则M 与N 的最小距离是 .三.解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16. (本小题满分12分)在ABC ∆中,a b c 、、分别为角A B C 、、的对边,△ABC 的面积S满足cos 2S A =. (1)求角A 的值;(2)若a =B 的大小为,x 用x 表示c ,并求c 的取值范围. 17.(本小题满分12分)某单位甲乙两个科室人数及男女工作人员分布情况见右表.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两个科室中共抽取3名工作人员进行一项关于“低碳生活”的调查. (1)求从甲、乙两科室各抽取的人数; (2)求从甲科室抽取的工作人员中至少有1名女性的概率;(3)记ξ表示抽取的3名工作人员中男性的人数,求ξ的分布列及数学期望18. (本小题满分14分)已知数列{}n a 是首项11a =,公差大于0的等差数列,其前n项和为n S ,数列{}n b 是首项12b =的等比数列,且2216b S =,3372b S =. (1) 求n a 和n b ;(2) 令11c =,221k k c a -=,212k k k c a kb +=+(⋅⋅⋅=,3,2,1k ),求数列{}n c 的前12+n 项和12+n T .19.(本小题满分14分)已知如图5,四棱锥P -ABCD 的底面ABCD 为矩形,且PA=AD=1,AB=2,120PAB ∠=,90PBC ∠=.(1)求证:平面PAD ⊥平面PAB ;(2)求三棱锥D -PAC 的体积;(3)求直线PC 与平面ABCD 所成角的正弦值. 图x520.(本小题满分14分)已知:向量(3,0)OA =,O 为坐标原点,动点M 满足:||||4OM OA OM OA ++-=. (1) 求动点 M 的轨迹 C 的方程;(2)已知直线1l 、2l 都过点(0,1)B ,且12l l ⊥,1l 、2l 与轨迹C 分别交于点D 、E ,试探究是否存在这样的直线?使得△BDE 是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由. 21.(本小题满分14分) 已知:函数2()21f x ax x =-+. (1) 若113a ≤≤,且()f x 在[1,3]上的最大值为()M a ,最小值为()N a ,令()()()g a M a N a =-,求()g a 的表达式;(2) 在(1)的条件下,求证:1()2g a ≥; (3)设0a >,证明对任意的121,[,)x x a∈+∞,1212|()()|||f x f x a x x -≥-.揭阳市2011年高中毕业班第二次高考模拟考 数学(理科)参考答案及评分说明一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数. 一.选择题:DCBD CDCD解析:5.因命题p 假,命题q 真,所以答案选C. 6.该三棱柱的侧视图是长为4,宽为 D.7. 由各选项知a 取正值,设ax y z +=,结合图形易得当直线y ax z =-+ 过点(1,0)时,ax y +取得最小值,故3a =,选C. 8.已知直线2y mx m =+过半圆y =上一点(-2,0), 当m=0时直线与x轴重合,这时()1P M =,故可排除A,B,若m=1,如图可求得当2()2P M ππ-=,故选D. 二.填空题:9. {|23x x <<或3}x >;10.53、4; 11. 3;12.32;13. 0x <或3x >;14.5、解析:10.因3,45a b c ==⇒=,所以53e =,焦点(5,0)到渐近线43y x =的距离为4545d ⨯== 11. ()2AB AC AC+CB AC AC 3⋅=⋅==,或AB AC |AB||AC|cos A ⋅=⋅|||AB ||AC ||AB |AC =⋅2||3AC ==. 12.该框图是求多项式5432543210a x a x a x a x a x a +++++当01x x ==时的值,依题意知5432543210a x a x a x a x a x a +++++5(1)x =+,故输出的v值为5(11)32+=.13.由定义得|1|1|2|4|1||2|3x x x x -+>-+⇒--->,解得0x <或3x >. 14.依题意得△ADB∽△ACB AD ABAD AE AC AB AC AE ⇒=⇒⋅=⋅()AD AD DE AC AB ⇒+=⋅64953DE ⨯-⇒==,DB =由DB AD DB ACEC EC AC AD⋅=⇒==15.将方程2sin 0ρθ+=和s ()42in πρθ+=化为普通方程得2220x y y ++=1x y +=结合图形易得M 与N 1.三.解答题:16.解:(1)在ABC ∆中,由cos 2S A =1sin 2bc A =得tan A =-------------------------------------------------------------------------------3分∵0A π<< ∴3A π=-------------------------------------------5分(2)由3a A π==及正弦定理得2sin sin a c A C===,------------7分 ∴22sin 2sin()2sin()3c C A B x ππ==--=---------------------------9分∵3A π= ∴203x π<< ∴22033x ππ<-<--------------------10分∴20sin()13x π<-≤, 202sin()23x π<-≤ 即(0,2]c ∈ ------------------------------------------------------------12分17.解:(1)从甲组应抽取的人数为310215⨯=,从乙组中应抽取的人数为35115⨯=;--------2分(2)从甲组抽取的工作人员中至少有1名女性的概率26210213C P C =-=(或11246421023C C C P C +==)----------------------------------------------------5分(3)ξ的可能取值为0,1,2,3-----------------------------------------------------6分2142211054(0)75C C P C C ξ==⋅=,------------------------------------------------------------7分1111246324212110510522(1)75C C C C C P C C C C ξ==⋅+⋅=,---------------------------------------------8分2163211051(3)5C C P C C ξ==⋅=,---------------------------------------------------------------9分34(2)1(0)(1)(3)75P P P P ξξξξ==-=-=-==(或 2111166432212110510534(2)75C C C C C P C C C C ξ==⋅+⋅=)-------10分∴ξ的分布列如右4223419012375757555E ξ=⨯+⨯+⨯+⨯=---------------------------------12分 18.解:(1)设数列{}n a 的公差为d (0d >)数列{}n b 的公比为q ,则1(1),n a n d =+- 12n n b q -=.------------------1分 依题意得222(2)16b S q d =+=,2332(33)72b S q d =+=由此得2(2)8(1)12q d q d +=⎧⎨+=⎩ ∵0d >,解得22d q =⎧⎨=⎩.----------------------5分∴21n a n =-,2n n b =.----------------------------------------------6分 (2) ∵()211121342()2n T c a a b a a b +=++++++⋅ +⋅⋅⋅212()n n n a a nb -+++=2121(2)n n S b b nb ++++⋅⋅⋅+---------------------------------------9分令122n A b b nb =+++则22222n A n =+⋅++⋅2312222(1)22n n A n n +=+⋅++-+⋅212222n n A n +-=+++-⋅,∴11222n n A n ++=⋅-+-----------------12分又2222(1)42n n n a S n +==,∴2112114222n n n T n n +++=++⋅-+2134(1)2n n n +=++-.-------------------14分19. (1)证明:∵ABCD 为矩形∴AD AB ⊥且//AD BC --------------------------------------1分 ∵BC PB ⊥ ∴DA PB ⊥且AB PB B = --------------------2分∴DA ⊥平面PAB ,又∵DA ⊂平面PAD∴平面PAD ⊥平面PAB -----------------------------------------5分(2) ∵D PAC P DAC P ABC C PAB V V V V ----===----------------------------------7分P ABCDE 由(1)知DA ⊥平面PAB ,且//AD BC ∴BC ⊥平面PAB -------------8分 ∴111sin 332C PAB PAB V S BC PA AB PAB BC -∆=⋅=⋅⋅⋅∠⋅11216=⨯⨯=----10分 (3)解法1:以点A 为坐标原点,AB 右图示,则依题意可得(0,0,1)D ,(0,2,1)C,1(,0)22P - 可得35(,1)22CP =--, ----------------------------12分 平面ABCD 的单位法向量为(1,0,0)m =,设直线PC 与平面ABCD 所成角为θ,则cos()2||||m CP m CP πθ⋅-===⋅∴sin 8θ=,即直线PC 与平面ABCD 所成角的正弦值8分解法2:由(1)知DA ⊥平面PAB ,∵AD ⊂面ABCD∴平面ABCD⊥平面PAB, 在平面PAB 内,过点P 作PE ⊥AB ,垂足为E ,则PE ⊥平面ABCD,连结EC ,则∠PCE 为直线PC 与平面ABCD 所成的角-------------12分 在Rt△PEA中,∵∠PAE=60°,PA=1,∴PE =,又2222cos1207PB PA AB PA AB =+-⋅=∴PC==在Rt△PEC 中sinPE PC θ===.即直线PC 与平面ABCD 所成角的正弦值8分20.(1)解法1:设'()A ------------------------------ 1分 则|||||'|||OM OA OM OA OMOA OM OA ++-=-+-=|'|||4MA MA +=>分∴动点M 的轨迹为以A 、'A 为焦点,长轴长为 4的椭圆-----------------5分 由42c a a =⇒= ∴ 1b ==----------------------------- 6分∴ 动点M 的轨迹 C 的方程为2214x y += ---------------------------------7分 [解法2:设点(,)M x y ,则(3,),()OM OA x y OM OA x y +=+-=------------------------2分 ∵||||4OM OA OM OA ++-=4=>------------------------------ 4分∴点 M 的轨迹C 是以(为焦点,长轴长为 4 的椭圆------------5分∴2,a c == ∴ 1b == --------------------------6分∴ 动点M 的轨迹 C 的方程为2214x y += ------------------7分] (2)由(1)知,轨迹C 是椭圆2214x y +=,点(0,1)B 是它的上顶点, 设满足条件的直线1l 、2l 存在,直线1l 的方程为1(0)y kx k =+>----① 则直线2l 的方程为11y x k=-+,-------------②--------------------------------------------------------------8分将①代入椭圆方程并整理得:22(14)80k x kx ++=,可得2814D kx k -=+,则228114D k y k -=++.--9分将②代入椭圆方程并整理得:22(4)80k x kx +-=,可得284E kx k =+,则2814E y k -=++.---10分 由△BDE 是等腰直角三角形得||||BD BE =⇒=2422222222264646464(14)(14)(4)(4)k k k k k k k ⇒+=+++++222222222222(1)11(14)(4)(14)(4)k k k k k k k k ++⇒=⇒=++++221144k k k ⇒=++3232414144k k k k k k ⇒+=+⇒-=-2(1)(1)4(1)k k k k k ⇒-++=-----③--------12分∴1k =或2310k k -+=-----④-----------------------------------------------------------------------13分 ∵方程④的根判别式50∆=>,即方程④有两个不相等的实根,且不为1. ∴方程③有三个互不相等的实根. 即满足条件的直线1l 、2l 存在,共有3组.-----------------------------------------------------------14分 (注:只答存在1组,给2分) 21.解:(1)∵211()()1f x a x aa=-+-由113a ≤≤得113a ≤≤ ∴11()()1N a f a a ==-.-----------------------2分 当112a ≤<,即112a <≤时,()M a (3)95f a ==-,故1()96g a a a=+-;-----------3分当123a ≤≤,即1132a ≤≤时,()M a (1)1f a ==-,故1()2g a a a=+-.-------------4分∴1112,[,];32()1196,(,1].2a a a g a a a a ⎧+-∈⎪⎪=⎨⎪+-∈⎪⎩-------------------------------------------------5分(2)∵当11[,]32a ∈时,21'()1g a a =-0<,∴函数()g a 在11[,]32上为减函数;---------6分当1(,1]2a ∈时,21'()90g a a =->,∴函数()g a 在1(,1]2上为增函数,-------------7分 ∴当12a =时,()g a 取最小值,min 11()()22g a g ==,-------------------------------8分 故1()2g a ≥.------------------------------------------------------------------9分 (3)∵当0a >时,抛物线2()21f x ax x =-+开口向上,对称轴为1x a=,∴函数()f x 在1[,)a +∞上为增函数,-----------------------------------------------------------10分(或由'()220f x ax =-≥得1x a ≥,∴函数()f x 在1[,)a+∞上为增函数) 不妨设12x x ≤,由121,[,)x x a ∈+∞得12()()f x f x ≤∴1212|()()|||f x f x a x x -≥-2121()()()f x f x a x x ⇔-≥-2211()()f x ax f x ax ⇔-≥- 令2()()(2)1x f x ax ax a x ϕ=-=-++,x ∈1[,)a +∞----------------------------------12分∵抛物线()y x ϕ=开口向上,对称轴为22a x a +=,且211122a a a a +=+>∴函数()x ϕ在1[,)a +∞上单调递增,∴对任意的121,[,)x x a ∈+∞,21x x ≥有21()()x x ϕϕ≥,即2()()f x a x f -≥-1|()(f x f ⇔-≥-----------14分。
揭阳市2011年高中毕业班高考第一次模拟考试语文试卷

揭阳市2011年高中毕业班高考第一次模拟考试语文本试卷共8页,满分为150分。
考试时间150分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卡上。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔或涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回。
一、本大题4小题,每小题3分,共12分。
1.下列词语中加点的字,每对的读音完全相同的一组是:A.揪心/啾唧纰漏/脱坯奴颜婢膝/刚愎自用B.散步/散记空当/空闲否极泰来/臧否人物C.碣石/竭诚地壳/甲壳间不容发/黑白相间D.新鲜/鲜有喝彩/负荷弱不禁风/忍俊不禁2.下列各句中,加点的熟语使用恰当的一项是A.卡尔扎伊不仅要会见中国领导人,他还会与中国的媒体见面,毕竟日程太紧,像故宫等名胜只好忍痛割爱,而长城是不能不去的。
B.出口侵权的原因,在于企业知识产权法律意识淡薄,有侥幸心理,企图“打擦边球”,坐收渔利;而经济利益的驱动,则是此类侵权事件频发的深层原因。
C.他们最初创业时手无寸铁,穷得叮当响,然而仅仅经过两年的奋斗,现在已经成了拥有千万资产的实业家。
D.民营企业的发展总要遇到出生难、融资难、准入市场难等难题,这些难题的根子在思想上。
观念不转变,有好政策,也只能是歪嘴和尚念经——老跑调。
3 下列各句中,没有语病的一项是A.有关部门要查明事故原因,严肃追究责任者,但是也要吸取事故教训,举一反三,严防类似事故再次发生。
B.中国知识产权人起诉日本电视台侵权播放中国电视剧一案启动赔偿诉讼程序,这是中国对日发起知识产权诉讼的第一起案件。
C.美国空军正在研发一种高超音速导弹,力求能在数分钟内完成对恐怖组织首领等美军方认定的“高价值”个人目标进行远程打击。
揭阳市高三一模试题数学(文)参考答案

x 揭阳市2011—2012学年度高中三年级学业水平考试数学试题(文科)参考答案及评分说明一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数.一.选择题:B C B B C A D B C C解析:1.∵{1,0,1}A =-,210i A +=∈,故选B.4.由该函数的图象过原点且关于原点对称可排除A 、C ,由()f x 在[0,)+∞为增函数,可排除D ,故选B.5.依题意知:1tan 2α=,从而22tan 4tan 21tan 3ααα==-,选C. 6.由22,13c b a ==⇒=3c e a ⇒===,选A. 7.()BA BC AF ⋅+u u u r u u u r u u u r =()BA BC CD BA BD ⋅+=⋅u u u r u u u r u u u r u u u r u u u r=0,选D.8. 由三视图知,该几何体为圆锥,其底面的半径为1,r =高h =母线3l ==, 故24S rl r πππ=+=表,故选B.9.∵a b ⊥r r∴2()02x z y z z x y -++=⇒=+,点(,)x y 的可行域如图示,当直线2z x y =+过点(1,1)时,Z 取得最大值,max 213z =+=,选C.10.依题意得111213212223313233a a a a a a a a a ++++++++12223222333936a a a a =++==,选C. 二.填空题:11. {|12}x x x >≠且(或{|122}x x x <<>或;12. 27; 13.772. 14.15.解析: 11.由101211x x x x ->⎧⇒>≠⎨-≠⎩且.12.该市当月“pm2.5”含量不达标有801001601206020()0.0053027333333+++++⨯⨯=(天); 13.====⋅⋅-+=72sin sin ,2160cos 54254022ac A bc B a 77214.把直线和圆的参数方程化为普通方程得,01=++y x 22(3)(1)25x y -++=,于是弦心距,223=d 弦长l ==15.∵,PCB PAC CPB APC ∠=∠∠=∠ ∴PBC ∆∽PCA ∆∴12PB BC BC AC PC AC AC =⇒=⇒=三.解答题:16.解:(1)∵()sin cos ),4f x x x x x R π=-=-∈----------------------------2分∴函数()f x 的最小正周期2T π=------------------------------------3分(2)函数()f x .--------------------------------5分 (3)由1()4f α=得1sin cos 4αα-= ∴21(sin cos )16αα-=,----------------------------------------------------6分1151sin 2,sin 21616αα-==--------------------------------------------------7分∴21531(sin cos )1sin 211616ααα+=+=+=-------------------------------------9分∵(0,)2πα∈,∴sin cos 0αα+>∴sin cos αα+=.----------------------------------------------------12分 17.解:(1)由样本数据知,30件产品中等级系数7ξ≥有6件,即一等品有6件,二等品有9件,三等品有15件-------------------------------------------------------3分∴样本中一等品的频率为60.230=,故估计该厂生产的产品的一等品率为0.2;-----4分 二等品的频率为90.330=,故估计该厂生产的产品的二等品率为0.3;-------------5分 三等品的频率为150.530=,故估计该厂生产的产品的三等品的频率为0.5.---------6分 (2)样本中一等品有6件,其中等级系数为7的有3件,等级系数为8的也有3件,-7分 记等级系数为7的3件产品分别为1C 、2C 、3C ,等级系数为8的3件产品分别为1P 、2P 、3P .则从样本的一等品中随机抽取2件的所有可能为:FEDPPDEFM121323(,),(,),(,),C C C C C C 12(,),P P 1323(,),(,)P P P P ,11121321(,),(,),(,),(,),C P C P C P C P 2223(,),(,)C P C P ,3132(,),(,),C P C P 33(,)C P .共15种,-------------------------------10分记从“一等品中随机抽取2件,2件等级系数都是8”为事件A ,则A 包含的基本事件有 12(,),P P 1323(,),(,)P P P P 共3种,-------------------------11分 故所求的概率31()155P A ==.-------------------------------------------------12分 18.(1)证明:依题意知图①折前,AD AE CD CF ⊥⊥,-------------------------------1分 ∴,PD PE PF PD ⊥⊥,-------------------------------------------------------2分 ∵PE PF P =I ∴PD ⊥平面PEF -----------------------------------4分 又∵EF ⊂平面PEF ∴PD EF ⊥----------------------------------------5分 (2)解法1:依题意知图①中AE=CF=12 ∴PE= PF=12, 在△BEF中2EF ==,-----6分 在PEF ∆中,222PE PF EF PE PF +=∴⊥∴8121212121=⋅⋅=⋅⋅=∆PF PE S PEF -------------------8分 ∴13P DEF D PEF PEF V V S PD --∆==⋅11113824=⨯⨯=.-----10分【(2)解法2:依题意知图①中AE=CF=12 ∴PE= PF=12,在△BEF中2EF ==,-----------------------6分 取EF 的中点M ,连结PM则PMEF ⊥,∴4PM =-------------7分∴111228PEF S EF PM ∆=⋅==---------------8分 ∴13P DEF D PEF PEF V V S PD --∆==⋅11113824=⨯⨯=.------------------------------10分】 (3) 由(2)知PE PF ⊥,又PE PD ⊥ ∴⊥PE 平面PDF ---------------------12分 ∴线段PE 的长就是点E 到平面PDF 的距离--------------------------------------13分∵12PE =, ∴点E 到平面PDF 的距离为1219.解(1)解法1.依题意得点P 的坐标为(,0)m -.-------1分∵以点()2,1M -为圆心的圆与直线l 相切与点P ,∴MP l ⊥.0(1)112MP l k k m --⋅=⋅=---,解得1m =-.----3分∴点P 的坐标为()1,0.设所求圆的半径r ,则22||112r PM ==+=,------------------------------------5分 ∴所求圆的方程为()222(1)2x y -++=.--------------------------------------6分 【解法2.设所求圆的方程为()2222(1)x y r -++=,--------------------------------1分依题意知点P 的坐标为(,0)m -.----------------------------------------------2分 ∵以点()2,1M -为圆心的圆与直线l 相切于点(),0P m -,∴222(2)1,.m r r ⎧++=⎪⎨=⎪⎩解得1,m r =-⎧⎪⎨=⎪⎩-------------------------------------------5分∴所求的圆的方程为()222(1)2x y -++=.------------------------------------6分】(2)解法1.将直线方程y x m =+中的y 换成y -,可得直线l '的方程为y x m =--.--------------------------------------------7分由21,.x y m y x m ⎧=⎪⎨⎪=--⎩得20mx x m ++=,(0)m ≠-----------------------------------9分 2Δ14m =-,--------------------------------------------------------------10分∵直线l '与抛物线21:C x y m=相切 ∴0∆=,解得12m =±.----------------------------------------------------12分 当12m =时,直线l 的方程为12y x =+,抛物线C 的方程为22x y =,-------------13分当12m =-时,直线l 的方程为12y x =-,抛物线C 的方程为22x y =-.----------14分【解法2.将直线方程y x m =+中的y 换成y -,可得直线l '的方程为y x m =--.-----7分设直线l '与抛物线21:C x y m=相切的切点为()00,x y ,---------------------------8分 由2y mx =得2y mx '=,则021mx =----①-----------------------------------10分00y x m =--------②200y mx =.---------③①②③联立得1142m m m =-21142m m ⇒=⇒=±,----------------------------12分 当12m =时,直线l 的方程为12y x =+,抛物线C 的方程为22x y =,-------------13分当12m =-时,直线l 的方程为12y x =-,抛物线C 的方程为22x y =-.----------14分】20.解:(1)解法1:∵1240a a +=,12256,a a =且1q >解得12832a a =⎧⎨=⎩---------------2分∴214a q a == ∴11211842n n n n a a q --+==⨯=---------------------------------4分 ∴ 2log n n b a ==212log 221n n +=+--------------------------------------------6分【解法2:由1240a a +=,12256,a a =且1q >得12832a a =⎧⎨=⎩ ∴214a q a ==---------------------------------------------------2分∴112122log log loglog 42,n n n n n na b b a a a +++-=-===----------------------------3分 又1212log log 83,b a ===-------------------------------------------------------4分 ∴{}n b 是以3为首项,2为公差的等差数列,----------------------------------------5分 ∴3(1)221n b n n =+-⨯=+;----------------------------------------------------6分】 (2)当2n ≥时,1121,n n n T T b n ---==-∴()()()()11232211n n n n n T T T T T T T T T T ---=-+-+-+-+L =()()()()12132123532n n n n --+-+-+++=L ()()11;n n =-+---------------8分∵当2n ≥时,()()1111111211n T n n n n ⎛⎫==- ⎪-+-+⎝⎭,----------------------------10分 ∴21ni iT =∑=2341111n T T T T ++++L111111111111123243531211n n n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+-+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥----+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦L =111131111.221421n n n n ⎛⎫⎛⎫+--=-+ ⎪ ⎪++⎝⎭⎝⎭--------------------------------------12分 ∵2n ≥,∴111151236n n +≤+=+ ∴31113151.4214263n n ⎛⎫-+≥-⋅= ⎪+⎝⎭ 又1101n n +>+ ∴311134214n n ⎛⎫-+< ⎪+⎝⎭ 即对,2n N n *∀∈≥,211334n i i T =≤<∑.----------------------------------------------14分21.解:(1)当1=a 时,32()2f x x x x =--+2'()321f x x x =--=(1)(31)x x -+,------------------------------------------2分 令'()0f x =,解得121,13x x =-=. 当'()0f x >时,得1x >或13x <-; 当'()0f x <时,得113x -<<. 当x 变化时,'()f x ,()f x 的变化情况如下表:-------------------------------------------------------------------------------4分 ∴当13x =-时,函数()f x 有极大值,15()=()2,327f x f -=极大-----------------------5分 当1x =时函数()f x 有极小值,()(1)1f x f ==极小---------------------------------6分 (2)∵2'()321f x x ax =--,∴对x R ∀∈,4'()||3f x x ≥-成立,即24321||3x ax x --≥-对x R ∀∈成立,--------------------------------------7分 ①当0x >时,有213(21)03x a x -++≥,即12133a x x+≤+,对(0,)x ∀∈+∞恒成立,----------------------------------9分∵1323x x +≥=,当且仅当13x =时等号成立, ∴212a +≤12a ⇒≤------------------------------------------------------11分 ②当0x <时,有213(12)03x a x +-+≥,即1123||3||a x x -≤+,对(,0)x ∀∈-∞恒成立,∵13||23||x x +≥=,当且仅当13x =-时等号成立,∴11222a a -≤⇒≥-----------------------------------------------------13分 ③当0x =时,a R ∈综上得实数a 的取值范围为11[,]22-.-------------------------------------------14分。
揭阳一中届高三上学期摸底考试文数word版本

揭阳一中2011—2012学年高三上学期摸底考试数 学(文科)本试卷共21页,三大题,满分150分。
考试用时120分钟。
第I 卷(选择题)(50分)一、选择题:本大题共10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合}3{<=x x M ,)086|(2<+-=x x x N ,则M ∩N=( ) A.φ B.}30|{<<x x C.}31|{<<x x D.}32|{<<x x 2.复数ii--13等于( ) A.1+2i B.1-2i C.2+i D.2-i3.“1±=a ”是函数y=cos 2ax-sin 2ax 的最小正周期为“π”的( ) A .充分不必要条件 B .必要不充分条件C.充要条件 D .既不充分条件也不必要条件4.定义在R 上的函数f(x)满足⎩⎨⎧>---≤-=0),2()1(0),4(log )(2x x f x f x x x f ,则f(3)的值为( ) A.-1 B. -2 C.1 D. 2 5.一个算法的程序框图如下图所示,若该程序输出的结果为65,则判断框中应填入的条件是( )A.i<4B.i<5C.i ≥5D.i<6 6.如果一空间几何体的正视图与侧视图均为等边三角形,俯视图是半径为3的圆及其圆心,则这个几何体的体积为( )A .π3 B.3π C .π33 D .π39 7.已知向量b a ,的夹角为600,且1||,2||==b a ,则向量a 与b a 2+的夹角为( ) A.1500B.1200C.600D.3008.设斜率为2的直线l 过抛物线y 2=ax(a ≠0)的焦点F ,且和y 轴交于点A ,若△OAF(O 为坐标原点)的面积为4,则抛物线方程为( ).A .x y 42±= B.x y 82±= C.y 2=4x D.y 2=8x9.已知命题]2,1[:∈∀x p,x 2-a ≥0,命题R x q ∈∃:,x 2+2ax+2-a=0.若命题p 且q 是真命题,则实数a 的取值范围为( )A .a ≤-2或a=1 B.a ≤-2或1≤a ≤2 C .a ≥1 D .-2≤a ≤110.已知O 为直角坐标系原点,P ,Q 坐标均满足不等式组⎪⎩⎪⎨⎧≥-≤+-≤-+010*******x y x y x ,则使cos ∠POQ取最小值时的∠POQ 的大小为( ) A .2πB .πC .2πD .4π 第II 卷(非选择题)(100分)二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11-13题)11.设S n 是等差数列{a n }的前n 项和,若a 4=9,S 3=15,则数列{a n }的通项为________ 12.若直线2ax-by+2=0(a>0,b>0)被圆x 2+y 2+2x-4y+1=0截得的弦长为4,则ba 31+的最小值为________13.某企业三月中旬生产,A 、B 、C 三种产品共3000件,根据分层抽样的结果;企业统计员制作了如下的统计表格;由于不小心,表格中A 、C 产品的有关数据已被污染看不清楚,统计员记得A 产品的样本容量比C 产品的样本容量多10,根据以上信息,可得C 的产品数量是____件。
广东揭阳市高三第一次模拟考试数学文试题含答案

揭阳市2016年高中毕业班高考第一次模拟考试数学(文科)参考答案及评分说明一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数.一、选择题:BBCDBA CADBDA解析:12解法一:设(,)M x y ,由||2||AM BM ≤得22222()()33x y +-≥,即点M 恒在圆22222()()33x y +-=的外部(含圆周)上,故当线段AD 与圆相切时,t 取最小值,∵:12x yAD t +=2|2|23t t t -=⇒=答案A. 解法二:由||2||AM BM ≤可得sin ||2,sin ||ABM AM BAD BM ∠=≤∠sin 2sin 24ABM BAD t ∴∠≤∠=+恒成立,故12≤,解得3t ≥解法三:设,(,12),AM AD BM AM AB t λλλ=∴=-=-由||2||AM BM ≤恒成立可得2222||4||,(4)4[A MB M t t λλλ≤∴+≤+-化简得22(312)1640t λλ+-+≥221616(312)0t ∴∆=-+≤,解得3t ≥二、填空题:13.6;14.934x ≤<;15.48;16.2. 解析:16.∵A 、B 、C 成等差数列,∴2A C B +=,又A B C π++=,∴3B π=,由1sin 2ABC S ac B ∆==4ac =,∵2222cos b a c ac B =+-22a c ac =+-,及222a c ac +≥,∴24b ac ≥=,2b ≥,∴b 的最小值为2.三、解答题:17.解:(1)当1n =时,111232S a =-,即111232a a =-,112a =;------------------1分当2n ≥时,由1232n n S a =-,得111232n n S a --=-,两式相减, 得1233n n n a a a -=-,即13nn a a -=,-------------------------------------------------4分 数列{}n a 是以112a =为首项,3为公比的等比数列,1132n n a -=⋅;---------------------6分(2)证明:∵312log 221n n b a n =+=-,-----------------------------------------8分 ∴()()111111212122121n n b b n n n n +⎛⎫==- ⎪-+-+⎝⎭, ∴12231111111111123352121n n b b b b b b n n +⎛⎫+++=-+-++- ⎪-+⎝⎭-------------------10分11112212n ⎛⎫=-< ⎪+⎝⎭.----------------------------------12分 18.解:(Ⅰ)-----------------------------2分∵23.7781K ≈<3.84 1,∴在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关。
全国2011年高考全国数学试卷1及答案
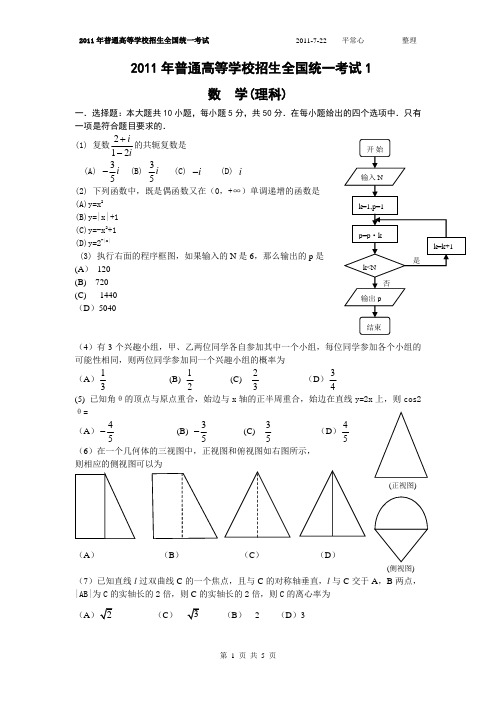
2011年普通高等学校招生全国统一考试1数 学(理科)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中.只有一项是符合题目要求的.(1) 复数212ii +-的共轭复数是 (A) 35i - (B) 35i (C) i - (D) i(2) 下列函数中,既是偶函数又在(0,+∞)单调递增的函数是(A)y=x 2(B)y=|x|+1(C)y=-x 2+1 (D)y=2-|x|(3) 执行右面的程序框图,如果输入的N 是6,那么输出的p 是 (A ) 120(B) 720 (C) 1440 (D )5040(4)有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则两位同学参加同一个兴趣小组的概率为 (A )13 (B) 12 (C) 23 (D )34(5) 已知角θ的顶点与原点重合,始边与x 轴的正半周重合,始边在直线y=2x 上,则cos2θ= (A )45-(B) 35- (C) 35 (D )45(6)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为(A ) (B ) (C ) (D )(7)已知直线l 过双曲线C 的一个焦点,且与C 的对称轴垂直,l 与C 交于A ,B 两点,|AB|为C 的实轴长的2倍,则C 的实轴长的2倍,则C 的离心率为 (A (C )(B ) 2 (D )3(8)51()(2)a x x x x+-的展开式中各项系数的和为2,则该展开式中常数项为 (A )-40 (C ) -20 (B ) 20 (D )40(9)由曲线y ,直线y=x-2及y 轴所围成的图形的面积为(A )310 (B )4 (C )163(D )6 (10)已知a与b 均为单位向量,其夹角为θ,有下列四个命题12:||10,3p a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:||1,3p a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:||10,3p a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:||1,3p a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是(A )14,p p (B )13,p p (C )23,p p (D )24,p p (11)设函数()sin()cos()f x x x ωϕωϕ=+++(0,||)2πωϕ><的最小正周期为π,且()()f x f x -=,则(A )()f x 在(0,)2π单调递减 (B )()f x 在3(,)44ππ单调递减(C )()f x 在(0,)2π单调递增 (D )()f x 在3(,)44ππ单调递增 (12)函数11y x=-的图象与函数2sin (24)y x x π=-≤≤的图象所有交点的横坐标之和等于(A) 2 (B)4 (C)6 (D)8第Ⅱ卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答,第(22)题~第(24)题为选考题,考生根据要求作答。
2011年揭阳市高中毕业班高考第一次模拟考 文-推荐下载

x
1234
f (x) 1 3 1 3
13. 某市新年第一个月前 10 天监测到空气污染指数如下表
(主要污染物为可吸入颗粒物):(第 i 天监测得到的数据记为 ai )
i 1 2 3 4 5 6 7 8 9 10
D. {8,10}
D. (1, )
D. 26
6.
A. y 3 x 2
已知函数 y
图象大致是
o
A.
y
f (x), x g(x), x
x
B. y
0 0.
7. 已知 为锐角,且 cos( ) 4 , 则 cos 的值为. 65
43 3
A.
10
8. 一个正方体截去两个角后所得几何体的正视图 (又称主视图)、侧视图(又称左视图)如右图 所示,则其俯视图为.
A. (, 2]
B.{0,8,10} C.{6,8,10}
B. (2, )
3. 已知复数 z (tan 3)i 1 ,则“ ”是“ z 是纯虚数”的
i
3
C. (1, 2]
A.充要条件 B.必要不充分条件 C.充分不必要条件 D.既不充分也不必要条件
4. 设向量 a (1, 2),b (2, y),若a则/ /b, | 3a b | 等于
一. 选择题:本大题共 10 小题,每小题 5 分,满分 50 分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1. 已知集合U {0, 2, 4,6,8,10} , A {2, 4,6} ,则 CU A
揭阳市2011年高中毕业班高考第一次模拟考

揭阳市2011年高中毕业班高考第一次模拟考文科综合本试卷分选择题和非选择题两部分,共41题,共10页,满分300分。
考试用时150分钟。
注意事项:1、答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卡上。
2B铅笔将考生号填涂在答题卡相应位置上。
2、选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3、非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各小题指定的位置上如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4、考生必须保持试卷和答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本大题共35小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
24、2010年3月24日,国务院常务会议明确指出,要鼓励和引导民间投资健康发展,从经济学角度看,说明了①坚持和完善以公有制为主体,多种所有制经济共同发展的基本经济制度②坚持鼓励、支持和引导非公有制经济发展的方针③民间资本是社会主义经济的重要组成部分④民间资本是社会主义初级阶段的一种重要的集体所有制经济A、①②B、③④C、②③D、②④25、下图是我国相关企业在芭比娃娃生产链中所处的位置,这对生产经营者的启示是A、要及时把握市场需求,生产适销对路的产品B、要努力提高劳动生产率,给产品提供降价空间C、要不断扩大生产规模,提高市场竞争力D、要坚持技术创新,开发自主知识产权的产品26、20l0年度国家公务员考试于12月5日进行,有141万人通过报名审核,最热职位创下4961:l的纪录。
公务员考试“高烧不退”,再次引发了全社会对当前就业问题的关注。
为此政府应该①加强职业技能培训,使每个人都具备报考公务员的条件②鼓励劳动者自主创业、自谋职业.以创业带动就业③完善就业服务体系,保证每个劳动者都能找到称心的岗位④加强政策支持和就业指导,建立健全公共投资带动就业的机制A、①③B、③④C、②④D、①②27、假如你有幸成为一位2010年广州亚运会的志愿者,你认为在服务过程中应当①维护国家安全、荣誉和利益②遵守宪法和法律、维护社会稳定③直接管理有关国家事务④增强民族自豪感、自尊心和自信心A、①②③B、②③④C、①③④D、①②④28、胡锦涛主席在新疆考察时强调,新疆要紧紧抓住机遇,坚持一手抓改革发展,一手抓团结稳定,之所以强调“抓团结稳定”,其原因在于①民族凝聚力是衡量一个国家综合国力的重要标志之一②坚持民族团结稳定是实现各民族共同繁荣的物质保证③民族团结进步事业的发展符合各族人民的根本利益④保持社会稳定能为民族地区发展创造良好社会环境A、①②③B、①③④C、①②④D、②③④29、2010年9月,美国众议院通过《汇率改革促进公平贸易法案》,旨在向中国施加压力令人民币升值。
广东省揭阳市高三数学第二次模拟考试 理

揭阳市2011年高中毕业班第二次高考模拟考数学(理科)本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.2.选择题将答案代号填在答题卡的选择题答案栏中,不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须填写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:锥体的体积公式:13V Sh =,其中S 表示底面积,h 表示高. 乘法公式:2233()()a b a ab b a b +-+=+.一.选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|11,}M x x x Z =-≤≤∈,{|02}N x x =≤≤,则MN 为A. {1}B. {0,1,2}C. {|01}x x ≤≤D. {0,1} 2.设(12)34i z i -=+,则||z 为A .3 B .5C .5 3. 为了解某商品销售量y (件)与销售价格x (元/件)的关系,统计了(x,y)的10组值,并画成散点图如图1,则其回归方程可能是 A . 10198y x ∧=-- B. 10198y x ∧=-+ C. 10198y x ∧=+ D.10198y x ∧=-图1图2主视图C 1B 1A 1CB A4.要得到函数sin(2)4y x π=+的图象,只要将函数sin 2y x =的图象A.向左平移4π单位 B.向右平移4π单位 C.向右平移8π单位 D.向左平移8π单位5.已知命题p :x R ∃∈,5cos 4x =;命题q :2,10x R x x ∀∈-+>.则下列结论正确的是A .命题p q ∧是真命题B .命题p q ∧⌝是真命题C .命题p q ⌝∧是真命题D .命题p q ⌝∨⌝是假命题 6.如图2,三棱柱111ABC A B C -的侧棱长和底面边长均为4,且侧棱1AA ⊥底面ABC ,其主视图(又称正视图)是边长为4的正方形,则此三棱柱的侧视图(又称左视图)的面积为A .16 B. C..7.已知点(,)M x y 满足1,10,220.x x y x y ≥⎧⎪-+≥⎨⎪--≤⎩若ax y +的最小值为3,则a 的值为A .1B .2C .3D .48.已知平面区域0{(,)|y x y y ≥⎧⎪Ω=⎨≤⎪⎩,直线2y mx m =+和曲线y =有两个不同的交点,它们围成的平面区域为M ,向区域Ω上随机投一点A ,点A 落在区域M 内的概率为()P M ,若01m ≤≤,则()P M 的取值范围为 A .2(0,]2ππ- B .2(0,]2ππ+ C .2[,1]2ππ+ D .2[,1]2ππ- 二.填空题:本大题共7小题,考生作答6小题,每小题5分,满分30(一)必做题(9~13题) 9.函数()ln(2)xf x x =- 的定义域为 .10.双曲线29x -216y =1的离心率e = ;焦点到渐近线的距离为 . 11.在Rt ABC ∆中,0C=90∠,AB AC ⋅= .12.根据图3所示的程序框图,若0514231,5,10,a a a a a a ======3DEB A男女6432性别人数科别甲科室乙科室则输出的V 值为 .13.在平面直角坐标系中,定义点11(,)P x y 、22(,)Q x y 之间的直角距离为1212(,)||||d P Q x x y y =-+-若点(,1),(1,2),(2,5)A x B C ,且(,)(,)d A B d A C >,则x 的取值范围为 .(二)选做题(14、15题,考生只能从中选做一题, 两题全答的,只计前一题的得分)14.(几何证明选做题)如图4,BD ⊥AE ,90C?o ,AB =4, BC =2,AD =3,则DE = ;CE = . 图415.(坐标系与参数方程选做题) 设M 、N 分别是曲线2sin 0ρθ+=和s ()42in πρθ+=上的动点,则M 与N 的最小距离是 .三.解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16. (本小题满分12分)在ABC ∆中,a b c 、、分别为角A B C 、、的对边,△ABC 的面积S满足cos S A =. (1)求角A 的值;(2)若a =B 的大小为,x 用x 表示c ,并求c 的取值范围.17.(本小题满分12分)某单位甲乙两个科室人数及男女工作人员分布情况见右表.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两个 科室中共抽取3名工作人员进行一项关于“低碳生活”的调查.(1)求从甲、乙两科室各抽取的人数;(2)求从甲科室抽取的工作人员中至少有1名女性的概率; (3)记ξ表示抽取的3名工作人员中男性的人数,求ξ的分布列及数学期望.18. (本小题满分14分)已知数列{}n a 是首项11a =,公差大于0的等差数列,其前n项和为n S ,数列{}n b 是首项12b =的等比数列,且2216b S =,3372b S =.DCBA(1) 求n a 和n b ;(2) 令11c =,221k k c a -=,212k k k c a kb +=+(⋅⋅⋅=,3,2,1k ),求数列{}n c 的前12+n 项和12+n T .19.(本小题满分14分)已知如图5,四棱锥P -ABCD 的底面ABCD 为矩形,且PA=AD=1,AB=2,120PAB ∠=,90PBC ∠=.(1)求证:平面PAD ⊥平面PAB ;(2)求三棱锥D -PAC 的体积;(3)求直线PC 与平面ABCD 所成角的正弦值. 图520.(本小题满分14分)已知:向量(3,0)OA =,O 为坐标原点,动点M 满足:||||4OM OA OM OA ++-=. (1) 求动点 M 的轨迹 C 的方程;(2)已知直线1l 、2l 都过点(0,1)B ,且12l l ⊥,1l 、2l 与轨迹C 分别交于点D 、E ,试探究是否存在这样的直线?使得△BDE 是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.21.(本小题满分14分)已知:函数2()21f x ax x =-+. (1) 若113a ≤≤,且()f x 在[1,3]上的最大值为()M a ,最小值为()N a ,令()()()g a M a N a =-,求()g a 的表达式;(2) 在(1)的条件下,求证:1()2g a ≥; (3)设0a >,证明对任意的121,[,)x x a∈+∞,1212|()()|||f x f x a x x -≥-.y=2x-2x揭阳市2011年高中毕业班第二次高考模拟考数学(理科)参考答案及评分说明一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数. 一.选择题:DCBD CDCD 解析:5.因命题p 假,命题q 真,所以答案选C. 6.该三棱柱的侧视图是长为4,宽为 D.7. 由各选项知a 取正值,设ax y z +=,结合图形易得当直线y ax z =-+ 过点(1,0)时,ax y +取得最小值,故3a =,选C. 8.已知直线2y mx m =+过半圆y =上一点(-2,0), 当m=0时直线与x轴重合,这时()1P M =,故可排除A,B,若m=1,如图可求得当2()2P M ππ-=,故选D. 二.填空题:9. {|23x x <<或3}x >;10.53、4; 11. 3;12.32;13. 0x <或3x >;14.5、1 . 解析:10.因3,45a b c ==⇒=,所以53e =,焦点(5,0)到渐近线43y x =的距离为4545d ⨯== 11. ()2AB AC AC+CB AC AC 3⋅=⋅==,或AB AC |AB||AC|cos A ⋅=⋅|||AB ||AC ||AB |AC =⋅2||3AC ==. 12.该框图是求多项式5432543210a x a x a x a x a x a +++++当01x x ==时的值,依题意知5432543210a x a x a x a x a x a +++++5(1)x =+,故输出的v值为5(11)32+=.13.由定义得|1|1|2|4|1||2|3x x x x -+>-+⇒--->,解得0x <或3x >.14.依题意得△ADB ∽△ACB AD ABAD AE AC AB AC AE ⇒=⇒⋅=⋅()AD AD DE AC AB ⇒+=⋅ 64953DE ⨯-⇒==,DB =由DB AD DB ACEC EC AC AD⋅=⇒==15.将方程2sin 0ρθ+=和s ()4in πρθ+=化为普通方程得2220x y y ++=1x y +=结合图形易得M 与N1.三.解答题:16.解:(1)在ABC ∆中,由cos S A =1sin 2bc A =得tan A =-------------------------------------------------------------------------------3分∵0A π<< ∴3A π=-------------------------------------------5分(2)由3a A π==及正弦定理得2sin sin a c A C===,------------7分 ∴22sin 2sin()2sin()3c C A B x ππ==--=---------------------------9分∵3A π= ∴203x π<< ∴22033x ππ<-<--------------------10分∴20sin()13x π<-≤, 202sin()23x π<-≤ 即(0,2]c ∈ ------------------------------------------------------------12分17.解:(1)从甲组应抽取的人数为310215⨯=,从乙组中应抽取的人数为35115⨯=;--------2分(2)从甲组抽取的工作人员中至少有1名女性的概率26210213C P C =-=(或11246421023C C C P C +==)----------------------------------------------------5分(3)ξ的可能取值为0,1,2,3-----------------------------------------------------6分2142211054(0)75C C P C C ξ==⋅=,------------------------------------------------------------7分1111246324212110510522(1)75C C C C C P C C C C ξ==⋅+⋅=,---------------------------------------------8分2163211051(3)5C C P C C ξ==⋅=,---------------------------------------------------------------9分34(2)1(0)(1)(3)75P P P P ξξξξ==-=-=-==(或 2111166432212110510534(2)75C C C C C P C C C C ξ==⋅+⋅=)-------10分∴ξ的分布列如右4223419012375757555E ξ=⨯+⨯+⨯+⨯=---------------------------------12分 18.解:(1)设数列{}n a 的公差为d (0d >)数列{}n b 的公比为q ,则1(1),n a n d =+- 12n n b q -=.------------------1分 依题意得222(2)16b S q d =+=,2332(33)72b S q d =+=由此得2(2)8(1)12q d q d +=⎧⎨+=⎩ ∵0d >,解得22d q =⎧⎨=⎩.----------------------5分∴21n a n =-,2n n b =.----------------------------------------------6分 (2) ∵()211121342()2n T c a a b a a b +=++++++⋅ +⋅⋅⋅212()n n n a a nb -+++=2121(2)n n S b b nb ++++⋅⋅⋅+---------------------------------------9分令122n A b b nb =+++则22222n A n =+⋅++⋅2312222(1)22n n A n n +=+⋅++-+⋅P ABCDE 212222n n A n +-=+++-⋅,∴11222n n A n ++=⋅-+-----------------12分又2222(1)42n n n a S n +==,∴2112114222n n n T n n +++=++⋅-+2134(1)2n n n +=++-.-------------------14分 19. (1)证明:∵ABCD 为矩形∴AD AB ⊥且//AD BC --------------------------------------1分 ∵BC PB ⊥ ∴DA PB ⊥且AB PB B = --------------------2分∴DA ⊥平面PAB ,又∵DA ⊂平面PAD∴平面PAD ⊥平面PAB -----------------------------------------5分(2) ∵D PAC P DAC P ABC C PAB V V V V ----===----------------------------------7分由(1)知DA ⊥平面PAB ,且//AD BC ∴BC ⊥平面PAB -------------8分 ∴111sin 332C PAB PAB V S BC PA AB PAB BC -∆=⋅=⋅⋅⋅∠⋅11216=⨯⨯=----10分 (3)解法1:以点A 为坐标原点,AB 右图示,则依题意可得(0,0,1)D ,(0,2,1)C,1(,0)22P - 可得35(,1)2CP =--, ----------------------------12分 平面ABCD 的单位法向量为(1,0,0)m =,设直线PC 与平面ABCD所成角为θ,则cos()2||||m CP m CP πθ⋅-===⋅∴sin θ=,即直线PC 与平面ABCD 分 解法2:由(1)知DA ⊥平面PAB ,∵AD ⊂面ABCD∴平面ABCD⊥平面PAB, 在平面PAB 内,过点P 作PE ⊥AB ,垂足为E ,则PE ⊥平面ABCD,连结EC ,则∠PCE 为直线PC 与平面ABCD 所成的角-------------12分 在Rt△PEA中,∵∠PAE=60°,PA=1,∴PE=,又2222cos1207PB PA AB PA AB =+-⋅=∴PC ==在Rt△PEC中sinPEPCθ===.即直线PC与平面ABCD所成角的正弦值分20.(1)解法1:设'()A------------------------------ 1分则|||||'|||OM OA OM OA OM OA OM OA++-=-+-=|'|||4MA MA+=>分∴动点M的轨迹为以A、'A为焦点,长轴长为 4的椭圆-----------------5分由42c a a=⇒=∴1b==----------------------------- 6分∴动点M的轨迹C的方程为2214xy+=---------------------------------7分[解法2:设点(,)M x y,则(3,),()OM OA x y OM OA x y+=+-=------------------------2分∵||||4OM OAOM OA++-=4=>------------------------------ 4分∴点M的轨迹C是以(为焦点,长轴长为 4 的椭圆------------5分∴2,a c==∴1b== --------------------------6分∴动点M的轨迹C的方程为2214xy+=------------------7分](2)由(1)知,轨迹C是椭圆2214xy+=,点(0,1)B是它的上顶点,设满足条件的直线1l、2l存在,直线1l的方程为1(0)y kx k=+>----①则直线2l的方程为11y xk=-+,-------------②--------------------------------------------------------------8分将①代入椭圆方程并整理得:22(14)80k x kx++=,可得2814Dkxk-=+,则228114Dkyk-=++.--9分将②代入椭圆方程并整理得:22(4)80k x kx +-=,可得284E kx k =+,则2814E y k-=++.---10分 由△BDE 是等腰直角三角形得||||BD BE=⇒=2422222222264646464(14)(14)(4)(4)k k k k k k k ⇒+=+++++222222222222(1)11(14)(4)(14)(4)k k k k k k k k ++⇒=⇒=++++221144k k k ⇒=++ 3232414144k k k k k k ⇒+=+⇒-=-2(1)(1)4(1)k k k k k ⇒-++=-----③--------12分∴1k =或2310k k -+=-----④-----------------------------------------------------------------------13分 ∵方程④的根判别式50∆=>,即方程④有两个不相等的实根,且不为1. ∴方程③有三个互不相等的实根.即满足条件的直线1l 、2l 存在,共有3组.-----------------------------------------------------------14分 (注:只答存在1组,给2分) 21.解:(1)∵211()()1f x a x aa=-+-由113a ≤≤得113a ≤≤ ∴11()()1N a f a a ==-.-----------------------2分 当112a ≤<,即112a <≤时,()M a (3)95f a ==-,故1()96g a a a=+-;-----------3分当123a ≤≤,即1132a ≤≤时,()M a (1)1f a ==-,故1()2g a a a=+-.-------------4分∴1112,[,];32()1196,(,1].2a a a g a a a a ⎧+-∈⎪⎪=⎨⎪+-∈⎪⎩-------------------------------------------------5分(2)∵当11[,]32a ∈时,21'()1g a a =-0<,∴函数()g a 在11[,]32上为减函数;---------6分 当1(,1]2a ∈时,21'()90g a a =->,∴函数()g a 在1(,1]2上为增函数,-------------7分 ∴当12a =时,()g a 取最小值,min 11()()22g a g ==,-------------------------------8分 故1()2g a ≥.------------------------------------------------------------------9分 (3)∵当0a >时,抛物线2()21f x ax x =-+开口向上,对称轴为1x a=, ∴函数()f x 在1[,)a +∞上为增函数,-----------------------------------------------------------10分(或由'()220f x ax =-≥得1x a ≥,∴函数()f x 在1[,)a+∞上为增函数) 不妨设12x x ≤,由121,[,)x x a ∈+∞得12()()f x f x ≤∴1212|()()|||f x f x a x x -≥-2121()()()f x f x a x x ⇔-≥-2211()()f x ax f x ax ⇔-≥- 令2()()(2)1x f x ax ax a x ϕ=-=-++,x ∈1[,)a+∞----------------------------------12分 ∵抛物线()y x ϕ=开口向上,对称轴为22a x a +=,且211122a a a a+=+> ∴函数()x ϕ在1[,)a +∞上单调递增,∴对任意的121,[,)x x a∈+∞,21x x ≥ 有21()()x x ϕϕ≥,即2()()f x a x f -≥-1|()(f x f ⇔-≥-----------14分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
揭阳市2011年高中毕业班高考第一次模拟考数 学 (文科)本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须填写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.参考公式:锥体的体积公式13V Sh =,其中S 表示底面积,h 表示高. 一. 选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知集合{0,2,4,6,8,10}U =,{2,4,6}A =,则U C A = A .{2,4,6}B .{0,8,10}C .{6,8,10}D .{8,10}2.函数()lg(1)f x x =-的定义域是A .(, 2]-∞ B.(2,)+∞ C.(1,2] D.(1,)+∞3.已知复数z =则“3πθ=”是“z 是纯虚数”的A .充要条件B .必要不充分条件C .充分不必要条件D .既不充分也不必要条件 4. 设向量(1,2),(2,),//,|3|a b y a b a b ==-+若则等于 A .5B .6CD .265. 已知双曲线22221x y a b-=(a >0, b >0)的离心率为2,一个焦点与抛物线216y x =的焦点相同,则双曲线的渐近线方程为 A. 32y x =±B. y x =C. y x =D. y =x侧视图正视图DCBA6. 已知函数(),0(),0.f x xyg x x>⎧=⎨<⎩是偶函数,()logaf x x=的图象过点(2,1),则()y g x=对应的图象大致是A. B. C. D.7.已知α为锐角,且4cos(),65πα+=则cosα的值为.A. B.C.D.8.一个正方体截去两个角后所得几何体的正视图(又称主视图)、侧视图(又称左视图)如右图所示,则其俯视图为.9.已知函数()sin(0)f x x xωωω=>的图象与x轴的两个相邻交点的距离等于2π,则为得到函数()y f x=的图象可以把函数siny xω=的图象上所有的点.A.向右平移6π,再将所得图象上所有的点的纵坐标变为原来的2倍;B.向右平移3π,再将所得图象上所有的点的纵坐标变为原来的2倍;C.向左平移12π,再将所得图象上所有的点的纵坐标变为原来的12倍;DEAC BD .向左平移12π,再将所得图象上所有的点的纵坐标变为原来的2倍. 10. 直线3y kx =+与圆22(2)(3)4x y -+-=相交于M 、N 两点,若MN ≤k 的取值范围是A .[B .C .3(,[,)-∞+∞D .[二. 填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11~13题)11. 已知1{1,,1,2}2α∈-,则使函数y x α=在[0,)+∞上单调递增的所有α值为 . 12. 已知函数(),()f x g x 分别由下表给出:则满足(())(())f g x g f x =的x 值为 .13. 某市新年第一个月前10天监测到空气污染指数如下表(主要污染物为可吸入颗粒物):(第i 天监测得到的数据记为i a )在对上述数据的分析中,一部分计算见右图所示的算法流程图, 则这10个数据的平均数a = ,输出的S 值是_ , (二)选做题(14、15题,考生只能从中选做一题)14.(几何证明选做题)如图所示,圆的内接三角形ABC 的角平分线BD 与AC 交于点D ,与圆交于点E,连结AE ,已知ED=3,BD=6 , 则线段AE 的长= . 15. (坐标系与参数方程选做题) 已知直线112,:()2.x t l t y kt =-⎧⎨=+⎩为参数,2,:12.x s l y s =⎧⎨=-⎩(s 为参数),若1l //2l ,则k = ;若12l l ⊥,则k = . 第13题图第14题图0.08/克)0.050.040.020.03频率/组距0.010.07产品重量(克)频数(490,495](495,500](500,505](505,510](510,515]481486三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤。
16.(本小题满分12分)已知数列{}n a 是首项为2,公比为12的等比数列,n S 为{}n a 的前n 项和. (1)求数列{}n a 的通项n a 及n S ;(2)设数列{}n n b a +是首项为-2,公差为2的等差数列,求数列{}n b 的通项公式及其前n 项和n T .17. (本小题满分12分)某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;(3)由以上统计数据完成下面22⨯列联表,并回答有多大的把握认为“产品的包装质量与附:下面的临界值表供参考:HGDEFABC(参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++)18.(本小题满分14分)已知如图:平行四边形ABCD 中,6BC =,正方形ADEF 所在平面与平面ABCD 垂直,G ,H 分别是DF ,BE 的中点. (1)求证:GH ∥平面CDE ;(2)若2,CD DB ==F-ABCD 的体积. 19. (本小题满分14分)如图,某人在塔的正东方向上的C 处在与塔垂直的水 平面内沿南偏西60°的方向以每分钟100米的速度步行了 1分钟以后,在点D 处望见塔的底端B 在东北方向上,已知沿途塔的仰角AEB ∠=α,α的最大值为60.(1)求该人沿南偏西60°的方向走到仰角α最大时,走了几分钟; (2)求塔的高AB.20.(本小题满分14分)在直角坐标系xoy 上取两个定点12(2,0),(2,0)A A -,再取两个动点1(0,),N m 2(0,)N n , 且3mn =.(1)求直线11A N 与22A N 交点的轨迹M 的方程;(2)已知点G (1,0)和'(1,0)G -,点P 在轨迹M 上运动,现以P 为圆心,PG 为半径作圆P,试探究是否存在一个以点'(1,0)G -为圆心的定圆,总与圆P 内切?若存在,求出该定圆的方程;若不存在,请说明理由. 21.(本小题满分14分)已知函数 321()(21)3(2)13f x x a x a a x =-++++,a R ∈. (1)当0a =时,求曲线()y f x =在点(3,(3)f )处的切线方程; (2)当1a =-时,求函数()y f x =在[0,4]上的最大值和最小值;(3)当函数'()y f x =在0,4()上有唯一的零点时,求实数a 的取值范围.揭阳市2011年高中毕业班高考第一次模拟考数学(文科)参考答案及评分说明一. 解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二. 计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部 分的解答有较严重的错误,就不再给分.三. 答右端所注分数,表示考生正确做到这一步应得的累加分数. 四. 给整数分数. 一.选择题:BCCADBDCAC解析: 3. (tan z i θ==+,当3πθ=时,z i =是纯虚数,反之当z 是纯虚数时,θ未必为3π,故选C. 4. 4(1,2)a b y a b ⇒=-⇒=//3+||5a b ⇒=3+,选A. 5. 依题意得双曲线的半焦距4c =,由22ce a a==⇒=,∴b ==的焦点在x 轴,∴双曲线的渐近线方程为y =.选D.6. 依题意易得2()log f x x =(0x >)因函数的图象关于y 轴对称,可得2()log ()g x x =- (0x <),选B.7. cos cos 66ππαα⎡⎤⎛⎫=+-==⎪⎢⎥⎝⎭⎣⎦310.选D. 8. 依题意可知该几何体的直观图如右,其俯视图应选C. 9. 依题意知2ω=,故()2sin(2)3f x x π=-2sin 2()6x π=-,故选A. 10.当|MN |=1,可求出k =,再结合图形可得答案C. 或设圆心到直线3y kx =+的距离为d ,则d =22||()42MN d =-且MN≤231k k≥⇒≥k≤二. 填空题:11.1,1,22;12. 2, 4、; 13. 60、3.4、;14.15. 4、-1解析:12. 将1,2,3,4x=依次代入方程(())(())f g x g f x=检验,易得2,4x=14. ∵,E E EAD EBA∠=∠∠=∠∴EDA∆∽EAB∆AE EDBE AE⇒=2AE ED BE⇒=⋅39=⨯AE⇒=.15. 将1l、2l的方程化为直角坐标方程得:1:240l kx y k+--=,2:210l x y+-=,由1l//2l得24211k k+=≠⇒4k=,由12l l⊥得220k+=1k⇒=-三.解答题:16. 解:(1)∵数列{}n a是首项12a=,公比12q=的等比数列∴1212()22n nna--=⋅=,---------------------------------------3分12(1)124(1)1212nn nS-==--.-------------------------------------6分(2)依题意得:22(1)24n nb a n n+=-+-=--------------------------------7分∴224242nn nb n a n-=--=-----------------------------------------9分设数列{}n nb a+的前n项和为nP则(224)(3)2nn nP n n-+-==--------------------------------------10分∴221(3)4(1)3422nn n n nT P S n n n n-=-=---=--+.------------------12分H G DEFAC 17. 解:(1)甲流水线样本的频率分布直方图如下:----------------------4分(2)由表1知甲样本中合格品数为814830++=,由图1知乙样本中合格品数为(0.060.090.03)54036++⨯⨯=,故甲样本合格品的频率为300.7540= 乙样本合格品的频率为360.940=, 据此可估计从甲流水线任取1件产品,该产品恰好是合格品的概率为0.75从乙流水线任取1件产品,该产品恰好是合格品的概率为0.9.----------------6分(3)22⨯列联表如下:------10分∵22()()()()()n ad bc K a b c d a c b d -=++++=280(120360) 3.11766144040⨯-≈⨯⨯⨯ 2.706> ∴有90%的把握认为产品的包装质量与两条自动包装流水线的选择有关.---------12分18.(1)证法1:∵//EF AD ,//AD BC ∴//EF BC 且EF AD BC ==∴四边形EFBC 是平行四边形 ∴H 为FC 的中点--------2分 又∵G 是FD 的中点∴//HG CD ----------------------------------------4分∵HG ⊄平面CDE ,CD ⊂平面CDE∴GH ∥平面CDE -------------------------------------------------------7分 证法2:连结EA ,∵ADEF 是正方形 ∴G 是AE 的中点-------------------------1分∴在⊿EAB 中,//GH AB -----------------------------------------------3分 又∵AB ∥CD ,∴GH ∥CD ,----------------------------------------------4分 ∵HG ⊄平面CDE ,CD ⊂平面CDE∴GH ∥平面CDE -------------------------------------------------------7分(2)∵平面ADEF ⊥平面ABCD ,交线为AD且F A ⊥AD ,∴F A ⊥平面ABCD . ----------------------------------------------------9分∵6BC =, ∴6FA =又∵2,CD DB == ,222CD DB BC +=∴BD ⊥CD -----------------------------------------------------------11分 ∴ ABCDSCD BD =⋅=∴ F ABCD V -=13ABCDS FA ⋅=163⨯=14分 19.解:(1)依题意知在△DBC 中30BCD ∠=,18045135DBC ∠=-=CD =100(m),1801353015D ∠=--=,------------3分由正弦定理得sin sin CD BCDBC D=∠∠∴sin 100sin15sin sin135CD D BC⋅∠⨯==1001)2==(m)-----------------6分 在Rt △ABE 中,tan ABBEα=∵AB 为定长 ∴当BE 的长最小时,α取最大值60°,这时BE CD ⊥--------8分当BE CD ⊥时,在Rt △BEC 中cosEC BC BCE =⋅∠1)25(32=⋅=(m), ----------------9分设该人沿南偏西60°的方向走到仰角α最大时,走了t 分钟,则100EC t ===-------------------------------10分 (2)由(1)知当α取得最大值60°时, BE CD ⊥,在Rt △BEC 中,sin BE BC BCD =⋅∠ -----------------------------------12分∴tan 60sin tan 60ABBE BC BCD =⋅=⋅∠⋅=11)25(32⋅=(m )即所求塔高为25(3m. --------------------------------------------14分 20.解:(1)依题意知直线11A N 的方程为:(2)2my x =+----------------①--------2分 直线22A N 的方程为:(2)2ny x =-----------------------------②-------4分设(,)Q x y 是直线11A N 与22A N 交点,①×②得22(4)4mn y x =-- 由3mn = 整理得22143x y +=--------------------------------------6分 ∵12,N N 不与原点重合 ∴点12(2,0),(2,0)A A -不在轨迹M 上--------------7分∴轨迹M 的方程为22143x y +=(2x ≠±)--------------------------------8分 (2)由(1)知,点G (1,0)和'(1,0)G -为椭圆22143x y +=的两焦点,----------9分 由椭圆的定义得|'|||4PG PG +=,即|'|4||PG PG =------------------11分∴以'G 为圆心,以4为半径的圆与P 内切,即存在定圆'G ,该定圆与P 恒内切,其方程为:22(1)16x y ++=-----14分21.解:(1)当0a =时, 321()13f x x x =-+, ∴(3)1f =, ∵2'()2f x x x =----------------------------------------2分曲线在点(3,1)处的切线的斜率'(3)3k f ==∴所求的切线方程为13(3)y x -=-,即38y x =--------------------------3分 (2)当1a =-时,函数321()313f x x x x =+-+ ∵2'()23f x x x =+-,令'()0f x =得121,3x x ==------------------------5分2[0,4]x ∉,当(0,1)x ∈时,'()0f x <,即函数()y f x =在(0,1)上单调递减,当(1,4)x ∈时,'()0f x >,即函数()y f x =在(1,4)上单调递增 ∴函数()y f x =在[0,4]上有最小值,2()(1)3f x f ==-最小值,---------------7分 又1(0)1,(4)263f f == ∴当1a =-时,函数()y f x =在[0,4]上的最大值和最小值分别为1226,33-.-----8分(3) ∵2'()2(21)3(2)f x x a x a a =-+++(3)(2)x a x a =---∴123,2x a x a ==+-----------------------------------------------------10分 ①当12x x =时,32a a =+,解得1a =,这时123x x ==,函数'()y f x =在(0,4)上有 唯一的零点,故1a =为所求;-------------------------------------------11分 ②当12x x >时,即32a a >+1a ⇒>,这时12x x >3>,又函数'()y f x =在(0,4)上有唯一的零点, ∴2134,324,424.3 4.3x a a x a <<<+<⎧⎧⇒⇒≤<⎨⎨≥≥⎩⎩,------------------------------12分 ③当12x x <时,即1a <,这时12x x <3<又函数'()y f x =在(0,4)上有唯一的零点,∴120,30,200 3.02 3.x a a x a ≤≤⎧⎧⇒⇒-<≤⎨⎨<<<+<⎩⎩-------------------------------13分 综上得当函数'()y f x =在(0,4)上有唯一的零点时,20a -<≤或423a ≤<或1a =.-------------------------------------------14分。
