课时2 反比例函数的综合题
九年级数学上册第六章反比例函数2反比例函数的图象与性质第2课时反比例函数的性质作业课件新版北师大版

解:(2)∵A,B两点在函数y=kx(x>0)的图象上, ∴A(1,k),B(k,1), ∴AO= 12+k2.延长CA,DB交于点E,则E(k,k), ∴AE=k-1,BE=k-1,∠AEB=90°, ∴AB= (k-1)2+(k-1)2. ∵AO=AB, ∴ 12+k2= (k-1)2+(k-1)2,解得k=2+ 3或k=2- 3. ∵k>1,∴k=2+ 3
∴S=m(n-3)=mn-3m=92,解得m=32,∴n=6,
∴点P的坐标是(32,6);
②当点P在点B的右侧时,∵P(m,n)在函数y=kx的图象上, ∴mn=9,∴S=n(m-3)=mn-3n=92,解得n=32,∴m=6, ∴点P的坐标是(6,32).综上所述,点P的坐标为(6,32)或(32,6) (3)当0<m<3时,点P在点B的左边,此时S=9-3m; 当m=3时,点P与点B重合,S=0;当m>3时,点P在点B的右边,
15.如图,一次函数y=kx+b的图象与x轴交于点A,
与反比例函数y=mx (x>0)的图象交于点B(2,n), 过点B作BC⊥x轴于点C,点P(3n-4,1)是该反比例函数图象上的一点, 且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
解:将B(2,n),P(3n-4,1)代入反比例函数y=mx 中,
第六章 反比例函数
6.2 反比例函数的图象与性质
第2课时 反比例函数性质
1.(2018·衡阳)对于反比例函数y=-2x,下列说法不正确的是( D ) A.图象分布在第二、四象限 B.当x>0时,y随x的增大而增大 C.图象经过点(1,-2) D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
反比例函数复习(第2课时)

点C在一次函数图象上,当时,,即
m C(-4,1).y x
y
4 x
如图,已知反比例函数y=-
8 一次函数y=kx+b x
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是- 2. 求:(1)一次函数的解析式; (2)△AOB的面积. 解:(1)由已知易得A(-2,4), B(4,-2),代入y=kx+b中,求得y=-x+2; (2)当y=0时,x=2,则y=-x+2与x轴的交点
y y y yy
0 ①
x ②
0
x
0 ③
x
0 0
x x
④
练一练
2
20 一、三 象限, y 的图象在第________ x
函数
减小 在每一象限内,y 随x 的增大而_________. 函数
30 二、四 象限, y 的图象在第________ x
增大 在每一象限内,y 随x 的增大而_________. y 函数 x ,当x>0时,图象在第____ 一 象限, 减小 y随x 的增大而_________.
随堂练习
k 若 y (k 0) 当 x= -3,-2,-1时值为 y1 , y2 , y3 , x 小刚说 y1 y2 y3 . y
你同意他的观点吗?试说明理由
0
x
问题探讨
要动动脑筋吆!
函数
的图象上有三点
(-3,y1), (-1,y2), (2,y3),则函数值y1、y2、y3的
y y y y
0 ①
x ②
0
x
0 ③
x
0 ④
x
随堂练习
k — 已知反比例函数y= x 的图象在第一、
三象限, 则一次函数y= -kx+4经过第
中考数学 考点系统复习 第三章 函数 第四节 反比例函数 课时2 反比例函数的综合题

∴EF=3OH=12.,∴EM=8,
即点 E 的横坐标为-8.
1 ∵点 E 在直线 y=-2x-2 上,
∴点 E 的坐标为(-8,2).
1 (2)把 x=-2 代入 y=2x+2, 得 y=-2×12+2=1, ∴点 P(-2,1)在一次函数 y=k1x+b 的图象上.
(3)由图象得 x≥2 或-6≤x<0 时,k1x+b≥kx2.
8.(2021·温州)如图,点 A,B 在反比例函数 y
=kx(k>0,x>0)的图象上,AC⊥x 轴于点 C,BD⊥x
7.(2021·新疆)如图,一次函数 y=k1x+b(k1≠0)与反比例函数 y=kx2(k2 ≠0)的图象交于点 A(2,3),B(n,-1). (1)求反比例函数和一次函数的解析式; (2)判断点 P(-2,1)是否在一次函数 y= k1x+b 的图象上,并说明理由; (3)直接写出不等式 k1x+b≥kx2的解集.
k ∵点 A 在反比例函数 y=x(x>0)的图象上,∴k=1.
(2)作 AD⊥x 轴于点 D,BE⊥x 轴于点 E, ∵A(1,1),C(-2,0),∴AD=1,CD=3, 由题意,易得△BCE≌△CAD(AAS),
∴CE=AD=1,BE=CD=3,∴B(-3,3). 13
易得直线 AB 的解析式为 y=-2x+2.
11.(2021·聊城)如图,过 C 点的直线 y =-12x-2 与 x 轴,y 轴分别交于 A,B 两 点,且 BC=AB,过点 C 作 CH⊥x 轴,垂 足为点 H,交反比例函数 y=kx(x>0)的图 象于点 D,连接 OD,△ODH 的面积为 6.
(1)求 k 值和点 D 的坐标; (2)如图,连接 BD,OC,点 E 在直线 y=-12x-2 上,且位于第二象限内, 若△BDE 的面积是△OCD 面积的 2 倍,求点 E 的坐标.
实际问题与反比例函数(第2课时)

17.2 实际问题与反比例函数(2)
学习目标 我的目标 我实现
1.能找出实际问题中的等量关系;2. 熟练利用反比例函数解决实际问题
学习过程 我的学习 我作主
题1(书本51页):码头工人以每天30吨的速度往一所轮船上装载货物,装载完毕恰好用了8天时间。
(说明总货物是多少?)
(1)轮船到达目的地后开始卸货,卸货速度天)(单位:吨/v 与卸货时间t (单位:天)
之间有怎样的函数关系?
解:根据已知条件可知:轮船上的货物总量为 ,再根据公
式卸货速度= 可知:
(2)由于遇到紧急情况,船上的货物必须在不超过5天内卸载完毕,那么平均每天至少要卸多少吨货物?
思考:本小题已知什么条件? 解:
题2:一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用6小时到达目的地。
(说明甲地到乙地的距离是多少?)
(1)当他从原路匀速返回时,汽车的的速度v 与时间t 有怎样的函数关系?
(2)如果该司机必须在4小时之内回到甲地,则返程时的速度不能低于多少?
题3:小艳家用购电卡购买了1000度电。
(1)那么这些电所够使用的天数m与小艳家平均每天的用电度数n有怎样的函数关系?(2)如果平均每天用电4度,这些电可以用多长时间?
题4:已知经过闭合电路的电流I与电路的电阻R是反比例函数关系。
(1)你能结合下表中的已知条件,写出电流I与电阻R是的函数关系式吗?
(2)根据你(1)的结论,完成下表(精确到0.01):。
11.2+反比例函数的图像及性质(例)2课时

11.2 反比例函数的图像及性质(例)2课时一.选择题(共4小题)1.(2019•相城区一模)已知反比例函数3(k y k x-=为常数),当0x <时,y 随x 的增大而减小,k 的取值范围是( ) A .0k <B .0k >C .3k <D .3k >2.(2019春•姑苏区校级期末)已知点(1,2)A 在反比例函数ky x=的图象上,则该反比例函数的解析式是( ) A .1y x=B .4y x=C .2y x=D .2y x =3.(2019春•吴中区期中)已知11(P x ,1)y 、22(P x ,2)y 是反比例函数2y x=的图象上的两点,且120x x <<,则1y ,2y 的大小关系是( ) A .120y y <<B .210y y <<C .210y y <<D .120y y <<4.(2019•河西区一模)已知反比例函数6y x=,当13x <<时,y 的取值范围是( ) A .0y l <<B .12y <<C .6y >D .26y <<二.填空题(共4小题)5.(2019春•邗江区校级期末)图1所示矩形ABCD 中,BC x =,CD y =,y 与x 满足的反比例函数关系如图2所示,等腰直角三角形AEF 的斜边EF 过C 点,M 为EF 的中点,则下列结论正确的序号是 .①当3x =时,EC EM <; ②当9y =时,EC EM >③当x 增大时,EC CF 的值增大 ④当y 增大时,BE DF 的值不变.6.(2019春•太仓市期中)图象经过点(1,1)-的反比例函数的表达式是 . 7.(2019秋•市中区期中)反比例函数2m y x-=的图象在第二、四象限,那么实数m 的取值范围是 .8.(2019春•相城区期末)如图,在平面直角坐标系中,菱形OABC 的边OA 在x 轴上,AC 与OB 交于点(4,2)D ,反比例函数ky x=的图象经过点D .若将菱形OABC 向左平移n 个单位,使点C 落在该反比例函数图象上,则n 的值为 .三.解答题(共4小题)9.(2015春•张家港市校级期中)已知y 是x 的反比例函数,且当4x =,1y =-. (1)函数y 与x 之间的函数表达式为 ; (2)当132x --剟时,y 的取值范围是 ; (3)若1x >时,y 的取值范围是 ; (4)若2y <时,x 的取值范围是 .10.(2019•相城区一模)如图,边长为2的正方形ABCD 的顶点A ,B 在x 轴正半轴上,反比例函数ky x=在第一象限的图象经过点D ,交BC 于E . (1)当点E 的坐标为(3,)n 时,求n 和k 的值; (2)若点E 是BC 的中点,求OD 的长.11.(2014春•张家港市校级期末)已知函数23(2)k y k x -=-为反比例函数. (1)求k 的值;(2)它的图象在第 象限内,在各象限内,y 随x 增大而 ;(3)当30.5x --剟时,此函数的最大值为 ,最小值为 . 12.(2019•镇平县一模)如图,在矩形OABC 中,3OA =,2OC =,点F 是AB 上的一个动点(F不与A,B重合),过点F的反比例函数kyx=的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;(2)当k为何值时,EFA∆的面积最大,最大面积是多少?11.2 反比例函数的图像及性质(例)2课时参考答案与试题解析一.选择题(共4小题)1.(2019•相城区一模)已知反比例函数3(k y k x-=为常数),当0x <时,y 随x 的增大而减小,k 的取值范围是( ) A .0k <B .0k >C .3k <D .3k >【分析】利用反比例的性质得到30k ->,然后解不等式即可. 【解答】解:当0x <时,y 随x 的增大而减小, 30k ∴->, 3k ∴>.故选:D .2.(2019春•姑苏区校级期末)已知点(1,2)A 在反比例函数ky x=的图象上,则该反比例函数的解析式是( ) A .1y x=B .4y x=C .2y x=D .2y x =【分析】把(1,2)A 代入解析式就得到k 的值,从而求出解析式. 【解答】解:点(1,2)A 在反比例函数ky x=的图象上, 21k ∴=, 2k ∴=,则这个反比例函数的解析式是2y x=. 故选:C .3.(2019春•吴中区期中)已知11(P x ,1)y 、22(P x ,2)y 是反比例函数2y x=的图象上的两点,且120x x <<,则1y ,2y 的大小关系是( ) A .120y y <<B .210y y <<C .210y y <<D .120y y <<【分析】根据反比例函数的性质和增减性,结合横坐标的大小和正负,即可得到答案. 【解答】解:反比例函数2y x=,0k >,0x ∴<时,0y <,y 随着x 的增大而减小,又120x x <<,210y y ∴<<,故选:B .4.(2019•河西区一模)已知反比例函数6y x=,当13x <<时,y 的取值范围是( ) A .0y l <<B .12y <<C .6y >D .26y <<【分析】利用反比例函数的性质,由x 的取值范围并结合反比例函数的图象解答即可. 【解答】解:60k =>,∴在每个象限内y 随x 的增大而减小,又当1x =时,6y =, 当3x =时,2y =,∴当13x <<时,26y <<.故选:D .二.填空题(共4小题)5.(2019春•邗江区校级期末)图1所示矩形ABCD 中,BC x =,CD y =,y 与x 满足的反比例函数关系如图2所示,等腰直角三角形AEF 的斜边EF 过C 点,M 为EF 的中点,则下列结论正确的序号是 ④ .①当3x =时,EC EM <; ②当9y =时,EC EM >③当x 增大时,EC CF 的值增大 ④当y 增大时,BE DF 的值不变.【分析】由于等腰直角三角形AEF 的斜边EF 过C 点,则BEC ∆和DCF ∆都是直角三角形;观察反比例函数图象得反比例解析式为9y x=;当3x =时,3y =,即3BC CD ==,根据等腰直角三角形的性质得CE =CF =,则C 点与M 点重合;当9y =时,根据反比例函数的解析式得1x =,即1BC =,9CD =,所以EF =EM =;由于2EC CF x =;利用等腰直角三角形的性质BE DF BC CD xy ==,然后再根据反比例函数的性质得9BE DF =,其值为定值.【解答】解:因为等腰直角三角形AEF 的斜边EF 过C 点,M 为EF 的中点,所以BEC ∆和DCF ∆都是直角三角形;观察反比例函数图象得3x =,3y =,则反比例解析式为9y x=;①、当3x =时,3y =,即3B C C D ==,所以CE =,CF ==C 点与M 点重合,则EC EM =,所以①错误;②、当9y =时,1x =,即1BC =,9CD =,所以EC =EF =EM =,所以②错误; ③、因为22218EC CF xy xy ==⨯=,所以,EC CF 为定值,所以③错误;④、因为9BE DF BC CD xy ===,即BE DF 的值不变,所以④正确. 故答案为:④.6.(2019春•太仓市期中)图象经过点(1,1)-的反比例函数的表达式是 1y x =- .【分析】设此反比例函数的解析式为(0)ky k x=≠,再把点(1,1)-代入此函数解析式求出k 的值即可.【解答】解:设此反比例函数的解析式为(0)ky k x=≠,反比例函数的图象经过点(1,1)-, 111k ∴=⨯-=-,∴反比例函数的解析式为:1y x=-. 故答案为:1y x=-.7.(2019秋•市中区期中)反比例函数2m y x-=的图象在第二、四象限,那么实数m 的取值范围是 2m < . 【分析】由于反比例函数2m y x-=的图象在二、四限内,则20m -<,解得m 的取值范围即可.【解答】解:由题意得,反比例函数2m y x-=的图象在二、四象限内,则20m -<, 解得2m <. 故答案为:2m <.8.(2019春•相城区期末)如图,在平面直角坐标系中,菱形OABC 的边OA 在x 轴上,AC 与OB 交于点(4,2)D ,反比例函数ky x=的图象经过点D .若将菱形OABC 向左平移n 个单位,使点C 落在该反比例函数图象上,则n 的值为 1 .【分析】要求n 的值,求出CG 即可,根据菱形OABC ,AC 与OB 交于点(4,2)D ,可求出点B 坐标和反比例函数的关系式,借助勾股定理可求菱形的边长,进而求出点C 、G 的坐标,根据横坐标的变化得出平移距离.【解答】解:过点D 、B 分别作DE x ⊥轴,BF x ⊥轴,垂足为E 、F ,延长BC 交反比例函数图象于点G ,交y 轴于点H , (4,2)D2DE ∴=,4OE =,反比例函数的关系式为:8y x=, OABC 是菱形,OA AB BC CO ∴===,DO CD =,又//DE BF , ∴12DE DO OE BF OC OF ===, 8OF ∴=,4BF =,(8,4)B ∴,设菱形边长AB a =,则8AF a =-,在Rt ABF ∆中,由勾股定理得:222(8)4a a =-+,解得5a =, 853CE BH BC ∴=-=-=,(3,4)C ∴把4y=代入8yx=得,2x=,(2,4)G∴321CG∴=-=,即点C向左平移1个单位到点G.故答案为:1三.解答题(共4小题)9.(2015春•张家港市校级期中)已知y是x的反比例函数,且当4x=,1y=-.(1)函数y与x之间的函数表达式为4yx=-;(2)当132x--剟时,y的取值范围是;(3)若1x>时,y的取值范围是;(4)若2y<时,x的取值范围是.【分析】(1)利用待定系数法确定反比例函数的解析式即可;(2)根据自变量的取值范围确定函数值的取值范围即可;(3)根据自变量的取值范围确定函数值的取值范围即可;(4)根据函数值的取值范围确定自变量的取值范围即可.【解答】解:(1)设反比例函数的解析式为kyx =,当4x=,1y=-,144k∴=-⨯=-,∴反比例函数的解析式为4yx=-;(2)当132x--剟时,4yx=-连续递增又当3x=-时,43y=,当12x=-时,8y=,∴当132x --剟时,y 的取值范围是483y 剟;(3)当1x =时,4y =-,4k =-,在每一象限内y 随着x 的增大而增大,∴当1x >时,y 的取值范围是40y -<<;(4)当2y =时,2x =-,4k =-,在每一象限内y 随着x 的增大而增大,∴当2y <时,y 的取值范围是0x >或2x <-;故答案为:4y x =-;483x 剟;40y -<<;0x >或2x <-.10.(2019•相城区一模)如图,边长为2的正方形ABCD 的顶点A ,B 在x 轴正半轴上,反比例函数ky x=在第一象限的图象经过点D ,交BC 于E . (1)当点E 的坐标为(3,)n 时,求n 和k 的值; (2)若点E 是BC 的中点,求OD 的长.【分析】(1)由题意表示出点D 的坐标,由反比例函数经过点D 、E 列出关于n 的方程,求得n 的值,进而求得k 的值.(2)设(,2)D x 则(2,1)E x +,由反比例函数经过点D 、E 列出关于x 的方程,求得x 的值即可得出答案.【解答】解:(1)正方形ABCD 的边长为2,点E 的坐标为(3,)n , 3OB ∴=,2AB AD ==,(1,2)D ∴,反比例函数ky x=在第一象限的图象经过点D , 122k ∴=⨯=,∴反比例为:2y x=, 反比例函数ky x=在第一象限的图象交BC 于E , 23n ∴=; (2)设(,2)D x 则(2,1)E x +, 反比例函数ky x=在第一象限的图象经过点D 、点E , 22x x ∴=+,解得2x =, (2,2)D ∴, 2OA AD ∴==,OD ∴==11.(2014春•张家港市校级期末)已知函数23(2)k y k x -=-为反比例函数. (1)求k 的值;(2)它的图象在第 二、四 象限内,在各象限内,y 随x 增大而 ; (3)当30.5x --剟时,此函数的最大值为 ,最小值为 .【分析】(1)根据反比例函数的定义确定k 的取值即可,注意比例系数不能为0; (2)根据反比例函数的性质描述其图象的位置和增减性即可; (3)根据反比例函数的增减性确定其最值即可. 【解答】解:(1)23(2)k y k x -=-为反比例函数,231k ∴-=-,20k -≠,解得:2k =-;(2)由(1)得反比例函数的解析式为4y x=-,40k =-<,∴它的图象在第二、四象限内,在各象限内,y 随x 增大而增大;(3)当30.5x --剟,∴483y 剟, ∴此函数的最大值为8,最小值为43. 12.(2019•镇平县一模)如图,在矩形OABC 中,3OA =,2OC =,点F 是AB 上的一个动点(F 不与A ,B 重合),过点F 的反比例函数k y x=的图象与BC 边交于点E . (1)当F 为AB 的中点时,求该函数的解析式;(2)当k 为何值时,EFA ∆的面积最大,最大面积是多少?【分析】(1)当F 为AB 的中点时,点F 的坐标为(3,1),由此代入求得函数解析式即可;(2)根据图中的点的坐标表示出三角形的面积,得到关于k 的二次函数,利用二次函数求出最值即可.【解答】解:(1)在矩形OABC 中,3OA =,2OC =,(3,2)B ∴, F 为AB 的中点,(3,1)F ∴,点F 在反比例函数k y x =的图象上, 3k ∴=,∴该函数的解析式为3y x=;(2)由题意知E ,F 两点坐标分别为(2k E ,2),(3,)3k F , 1111(3)2232EFA S AF BE k k ∆∴==⨯-, 211212k k =- 21(699)12k k =--+-213(3)124k =--+ 当3k =时,S 有最大值.34S =最大值.考点卡片1.反比例函数的定义(1)反比例函数的概念形如y(k为常数,k≠0)的函数称为反比例函数.其中x是自变量,y是函数,自变量x 的取值范围是不等于0的一切实数.(2)反比例函数的判断判断一个函数是否是反比例函数,首先看看两个变量是否具有反比例关系,然后根据反比例函数的意义去判断,其形式为y(k为常数,k≠0)或y=kx﹣1(k为常数,k≠0).2.反比例函数的图象用描点法画反比例函数的图象,步骤:列表﹣﹣﹣描点﹣﹣﹣连线.(1)列表取值时,x≠0,因为x=0函数无意义,为了使描出的点具有代表性,可以以“0”为中心,向两边对称式取值,即正、负数各一半,且互为相反数,这样也便于求y值.(2)由于函数图象的特征还不清楚,所以要尽量多取一些数值,多描一些点,这样便于连线,使画出的图象更精确.(3)连线时要用平滑的曲线按照自变量从小到大的顺序连接,切忌画成折线.(4)由于x≠0,k≠0,所以y≠0,函数图象永远不会与x轴、y轴相交,只是无限靠近两坐标轴.3.反比例函数的性质反比例函数的性质(1)反比例函数y(k≠0)的图象是双曲线;(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.注意:反比例函数的图象与坐标轴没有交点.4.反比例函数系数k的几何意义比例系数k的几何意义在反比例函数y图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.5.反比例函数图象上点的坐标特征反比例函数y=k/x(k为常数,k≠0)的图象是双曲线,①图象上的点(x,y)的横纵坐标的积是定值k,即xy=k;②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;③在y=k/x图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.6.待定系数法求反比例函数解析式用待定系数法求反比例函数的解析式要注意:(1)设出含有待定系数的反比例函数解析式y(k为常数,k≠0);(2)把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.7.菱形的性质(1)菱形的定义:有一组邻边相等的平行四边形叫做菱形.(2)菱形的性质①菱形具有平行四边形的一切性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.(3)菱形的面积计算①利用平行四边形的面积公式.②菱形面积ab.(a、b是两条对角线的长度)8.坐标与图形变化-平移(1)平移变换与坐标变化①向右平移a个单位,坐标P(x,y)⇒P(x+a,y)①向左平移a个单位,坐标P(x,y)⇒P(x﹣a,y)①向上平移b个单位,坐标P(x,y)⇒P(x,y+b)①向下平移b个单位,坐标P(x,y)⇒P(x,y﹣b)(2)在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.(即:横坐标,右移加,左移减;纵坐标,上移加,下移减.)。
浙教版八年级下测试题6.2 第2课时 反比例函数的性质

第2课时 反比例函数的性质1.有下列函数:①y =-3x ;②y =x -1;③y =-1x (x <0);④y =1x (x >0).其中当x 在各自的自变量取值范围内取值时,y 随x 的增大而增大的函数有( C ) A .①② B .①④ C .②③D .③④2.[2013·义乌]已知两点P 1(x 1,y 1),P 2(x 2,y 2)在反比例函数y =3x 的图象上,当x 1>x 2>0时,下列结论正确的是( A )A .0<y 1<y 2B .0<y 2<y 1C .y 1<y 2<0D .y 2<y 1<03.[2013·株洲]已知点A (1,y 1),B (2,y 2),C (-3,y 3)都在反比例函数y =6x 的图象上,则y 1,y 2,y 3的大小关系是( D )A .y 3<y 1<y 2B .y 1<y 2<y 3C .y 2<y 1<y 3D .y 3<y 2<y 14.[2013·衢州]若函数y =m +2x 的图象在其所在的每一象限内,函数值y 随自变量x 的增大而增大,则m 的取值范围是( A )A .m <-2B .m <0C .m >-2D .m >05.[2013·南充]如图6-2-9,函数y 1=k 1x 与y 2=k 2x 的图象相交于点A (1,2)图6-2-9和点B .当y 1<y 2时,自变量x 的取值范围是( C )A .x >1B .-1<x <0C .-1<x <0或x >1D .x <-1或0<x <16.[2013·海南]点(2,y 1),(3,y 2)在函数y =-2x 的图象上,则y 1__<__y 2(填“>”或“=”或“<”).7.[2011·淮安]如图6-2-10,反比例函数y =k x 的图象经过点A (-1,-2),则当x >1时,函数值y 的取值范围是( D )图6-2-10A .y >1B .0<y <1C .y >2D .0<y <2【解析】 ∵反比例函数的图象过点A (-1,-2),∴由函数图象可知,x <-1时,-2<y <0,∴当x >1时,0<y <2.8.[2013·陕西]如果一个正比例函数的图象与反比例函数y =6x 的图象交于A (x 1,y 1),B (x 2,y 2)两点,那么(x 2-x 1)(y 2-y 1)的值为__24__.9.汽车匀速行驶在相距S 千米的甲、乙两地之间,图6-2-11是行驶时间t (h)与行驶速度v (km/h)函数图象的一部分.图6-2-11(1)求行驶时间t (h)与行驶速度v (km/h)之间的函数关系;(2)若该函数图象的两个端点为A (40,1)和B (m ,0.5),求m 的值;(3)若规定在该段公路上汽车的行驶速度不得超过50 km/h ,则汽车通过该路段最少需要多少时间?解:(1)把(40,1)的坐标代入t =kv ,得k =40,∴行驶时间t (h)与行驶速度v (km/h)之间的函数关系是t =40v ,故答案为t =40v . (2)由(1)知函数的解析式为t =40v ,把B (m ,0.5)的坐标代入t =40v ,得0.5=40m , 解得m =80;(3)把v =50代入t =40v ,得t =0.8. 由题意知v ≤50, ∴t ≥0.8.答:汽车通过该路段最少需要0.8小时.10.若直线y =kx +b 经过第一、二、四象限,则函数y =kbx 的图象在 ( B ) A .第一、三象限 B .第二、四象限C.第三、四象限D.第一、二象限【解析】由直线y=kx+b经过第一、二、四象限,可得k<0,b>0,所以kb<0,则函数y=kbx的图象在第二、四象限.11.[2012·张家界]当a≠0时,函数y=ax+1与函数y=ax在同一坐标系中的图象可能是(C)A BC D图6-2-12【解析】分a>0和a<0两种情况讨论,分析出两函数图象所在象限,再在四个选项中找到正确选项.当a>0时,函数y=ax+1的图象过第一、二、三象限,函数y=ax的图象在第一、三象限;当a<0时,函数y=ax+1的图象过第一、二、四象限,函数y=ax的图象在第二、四象限.故选C.12.[2012·天津]已知反比例函数y=k-1x(k为常数,k≠1).(1)其图象与正比例函数y=x的图象的一个交点为P.若点P的纵坐标是2,求k的值;(2)若在其图象的每一分支上,y都随x的增大而减小,求k的取值范围;(3)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1),B(x2,y2),当y1>y2时,试比较x1与x2的大小.解:(1)由题意,设点P 的坐标为(m ,2). ∵点P 在正比例函数y =x 的图象上, ∴2=m ,即m =2. ∴点P 的坐标为(2,2).∵点P 在反比例函数y =k -1x 的图象上, ∴2=k -12,解得k =5. (2)∵在反比例函数y =k -1x图象的每一分支上,y 都随x 的增大而减小, ∴k -1>0,解得k >1.(3)∵反比例函数y =k -1x 图象的一支位于第二象限, ∴在该函数图象的每一分支上y 都随x 的增大而增大.∵点A (x 1,y 1)与点B (x 2,y 2)在该函数的第二象限的图象上,且y 1>y 2,∴x 1>x 213.[2013·嘉兴]如图6-2-13,一次函数y =kx +1(k ≠0)与反比例函数y =mx (m ≠0)的图象有公共点A (1,2).直线l ⊥x 轴于点N (3,0),与一次函数和反比例函数的图象分别交于点B ,C .图6-2-13(1)求一次函数与反比例函数的解析式; (2)求△ABC 的面积.解:(1)∵点A (1,2)在一次函数y =kx +1的图象上,∴k =1, ∴一次函数的解析式为y =x +1.∵点A (1,2)在反比例函数y =mx 的图象上, ∴m =2,∴反比例函数的解析式为y =2x .(2)∵对于一次函数y =x +1,当x =3时,y =4. ∴点B 的坐标为(3,4),∵对于反比例函数y =2x ,当x =3时,y =23, ∴点C 的坐标为⎝ ⎛⎭⎪⎫3,23.则BC =4-23=103,以BC 为底,BC 边上的高为3-1=2, ∴S △ABC =12×2×103=103.。
2022-2022学年九年级数学上册 1.2.2 反比例函数y=k÷x(k<0)的图象与性质习题课件

【综合运用】 17.(14 分)已知反比例函数 y=kx(k 为常数,且 k≠0)的图象 经过点 A(-2,3). (1)求这个函数的表达式,并说明当 x>0 时,随着 x 的增大, y 的值如何变化; (2)若矩形 ABCD 关于坐标轴对称,且对角线的交点为原点 O,已知点 B 在第三象限,求 B,C,D 三点的坐标; (3)在(2)的条件下,另一反比例函数的图象经过 D 点,试说 明这两个函数图象之间有何位置关系.
x -3
-1
y
124
123
(1)写出这个函数的表达式; (2)根据函数表示式完成上表; (3)依上表在平面直角坐标系内描点,并作出函数的图象.
解:(1)y=-2x; (2)表中依次填:23 -2 -12 -4 -2 1 -23;(3)图略.
6.知(识3 点分)2(201反4·比阜例新函)数反比y=例xk函(k<数0)y的=性m+x质1在每个象限内的 函数值 y 随 x 的增大而增大,则 m 的取值范围是( D ) A.m<0 B.m>0
•
11、人总是珍惜为得到。2022/5/92022/5/92022/5/9M ay-229-May-22
•
12、人乱于心,不宽余请。2022/5/92022/5/92022/5/9Monday, May 09, 2022
12.(2014·天水)已知函数 y=mx 的图象如图,以下结论: ①m<0;②在每个分支上 y 随 x 的增大而增大;③若点 A(- 1,a),点 B(2,b)在图象上,则 a<b;④若点 P(x,y)在图
反比例函数的图像和性质(第2课时)(作业)(夯实基础+能力提升)(原卷版)

18.3反比例函数的图像和性质(第2课时)(作业)(夯实基础+能力提升)【夯实基础】一、单选题1.(2022·上海浦东新·八年级期末)在反比例函数y =2x的图像上有三点A 1(x 1,y 1)、A 2(x 2,y 2)、A 3(x 3,y 3),已知x 1< x 2<0<x 3则下列各式中,正确的是( ) A .y 1<y 2<y 3B .y 3< y 2< y 1C .、y 2< y 1< y 3D .y 3< y 1< y 22.(2022·上海·八年级期末)已知三点(),a m 、(),b n 和(),c t 都在反比例函数2021y x=的图像上,若0a b c <<<,则m 、n 和t 的大小关系是( )A .t n m <<B .t m n <<C .m t nD .m n t <<3.(2022·上海·八年级单元测试)已知函数y =kx (k ≠0)中y 随x 的增大而增大,那么它和函数(0)ky k x=≠在同一直角坐标平面内的大致图象可能是( )A .B .C .D .4.(2022·上海·八年级单元测试)已知反比例函数y =kx(k ≠0),且在各自象限内,y 随x 的增大而增大,则下列点可能在这个函数图象上的为( ) A .(2,3) B .(-2,3)C .(3,0)D .(-3,0)5.(2022·上海·八年级单元测试)关于函数2y x=-,下列说法中正确的是( )A .图像位于第一、三象限B .图像与坐标轴没有交点C .图像是一条直线D .y 的值随x 的值增大而减小6.(2022·上海·八年级单元测试)已知点2,1在反比例函数(0)ky k x=≠的图象上,则这个函数图象一定经过点( ) A .(2,1)-- B .(2,2)C .16,2⎛⎫- ⎪⎝⎭D .(3,1)--二、填空题7.(2022·上海·八年级单元测试)若1(1,)M y -、21(,)2N y -两点都在函数ky x=的图像上,且1y <2y ,则k的取值范围是______.8.(2022·上海·八年级单元测试)已知反比例函数3ay x-=,如果在每个象限内,y 随自变量x 的增大而增大,那么a 的取值范围为__________.9.(2022·上海·八年级开学考试)反比例函数y=3k x-的图象,当x >0时,y 随x 的增大而增大,则k 的取值范围是_____.10.(2022·上海·八年级单元测试)如果函数2ky x的图像与直线y x =无交点,那么k 的取值范围为_______.11.(2022·上海·八年级期末)已知函数5k y x-=的图象在每个象限内,y 的值随x 的值增大而减小,则k 的取值范围是_________.12.(2022·上海·八年级期末)已知反比例函数1k y x-=(k 是常数,1k ≠)的图像有一支在第四象限,那么k 的取值范围是__________.13.(2022·上海·八年级期末)已知反比例函数(0)ay a x=>的图像上有两点()11,A y ,()22,B y ,那么1y ______2y .(填“>”或“<”)14.(2022·上海松江·八年级期末)已知反比例函数3k y x-=的图象位于第二、四象限,则k 的取值范围是_____.15.(2022·上海市南洋模范中学八年级期末)1l 是反比例函数ky x=在第一象限内的图像,且过点()2,5A ,2l 与1l 关于x 轴对称,那么图像2l 的函数解析式为______.16.(2022·上海·八年级单元测试)已知三点(a ,m )、(b ,n )和(c ,t )在反比例函数y =kx(k >0)的图像上,若a <0<b <c ,则m 、n 和t 的大小关系是 ___.(用“<”连接)17.(2022·上海·八年级单元测试)已知: y 与x 成反比例,且x =1时,y =3,则x =12-时,y =______.三、解答题18.(2022·上海·上外附中八年级期末)已知函数 12y y y =-,且 1y 为 x 的反比例函数, 2y 为 x 的正比例函数,且 32x =- 和 1x = 时,y 的值都是1,求y 关于x 的函数关系式.19.(2022·上海·八年级单元测试)已知y =y 1+y 2,y 1与x 成正比例,y 2与x 成反比例,且当x =﹣1时,y =﹣4;当x =3时,203y =,求y 关于x 的函数解析式.20.(2022·上海·八年级单元测试)参照反比例函数研究的内容与方法,研究下列函数:(1)研究函数11yx=+:①画出它的图像;②它的图像是什么图形?可看作怎样的图形经过怎样的平移得到?③说明它所具有的性质.(2)研究函数13yx=+的图像与性质;(3)由(1)(2)的图像经过平移,你还能得出怎样的函数图像与性质,请举例说明;(4)研究函数452xyx+=-的图像与性质.21.(2022·上海·八年级单元测试)已知反比例函数的图象经过点A(-2,-3).(1)求该反比例函数的表达式;(2)判断点3(2)B是否在该反比例函数的图象上,并说明理由.22.(2022·上海·八年级单元测试)已知反比例函数y=kx(k为常数,k≠0)的图象经过点A(2,3)(1)求k 的值;(2)此函数图象在 象限,在每个象限内,y 随x 的增大而 ;(填“增大”或“减小”) (3)判断点B (﹣1,6)是否在这个函数的图象上,并说明理由; (4)当﹣3<x <﹣1时,则y 的取值范围为 .【能力提升】一、单选题1.(2022·上海·八年级单元测试)关于某个函数表达式,甲、乙、丙三位同学都正确地说出了该函数的一个特征.甲:函数图像经过点(1,1)-;乙:函数图像经过第四象限;丙:当0x >时,y 随x 的增大而增大.则这个函数表达式可能是( ) A .y x =-B .1y x=C .y x =D .1y x=-2.(2022·上海·八年级期末)下列函数中,函数值y 随x 的增大而增大的是( ) A .3x y =-;B .3x y =; C .1y x=;D .1y x=-.3.(2022·上海浦东新·八年级期末)已知函数()0ky k x=≠中,在每个象限内,y 的值随x 的值增大而增大,那么它和函数()0y kx k =-≠在同一直角坐标平面内的大致图像是( ).A .B .C .D .4.(2022·上海·八年级期末)已知点11(,)x y ,22(,)x y 均在双曲线1y x=-上,下列说法中错误的是( )A .若12x x =,则12y y =B .若12x x =-,则12y y =-C .若120x x <<,则12y y <D .若120x x <<,则12y y >5.(2022·上海市南洋模范中学八年级期末)下列函数中,y 随x 的增大而减小的是( ) A .2y x = B .2y x=C .2y x =-D .2y x=-6.(2022·上海市崇明区横沙中学八年级期末)反比例函数my x=的图像在第二、四象限内,则点(,1)m -在( ) A .第一象限 B .第二象限C .第三象限D .第四象限二、填空题7.(2022·上海·八年级单元测试)在描述某一个反比例函数的性质时,甲同学说:“从这个反比例函数图像上任意一点向x 轴、y 轴作垂线,与两坐标轴所围成的长方形的面积为2022.”乙同学说:“这个反比例函数在同一个象限内,y 的值随着x 的值增大而增大.”根据这两位同学所描述,此反比例函数的解析式是_______. 8.(2022·上海·八年级单元测试)已知点P 位于第三象限内,且点P 到两坐标轴的距离分别为3和2.若反比例函数图象经过点P ,则该反比例函数的解析式为______.9.(2022·上海·八年级期末)若三个点(-2,1y ),(-1,2y ),(2,3y )都在反比例函数6y x=-的图像上,则1y 、2y 、3y 的大小关系是________.10.(2022·上海·八年级单元测试)在同一平面直角坐标系中,正比例函数y =k 1x 的图像与反比例函数2k y x=的图像一个交点的坐标是(-1,3),则它们另一个交点的坐标是_______.三、解答题11.(2022·上海·八年级单元测试)如图,点A ,B 在反比例函数ky x=的图像上,A 点坐标(1,6),B 点坐标(,)(1)m n m >.(1)求反比例函数的解析式;(2)过点B 作BC y ⊥轴,垂足为点C ,联结AC ,当6ABCS=时,求点B 的坐标.。
湘教版数学九年级上册_课时作业:第2课时_反比例函数y=k÷x(k<0)的图象与性质

1.2 第2课时 反比例函数y =kx (k <0)的图象与性质一、选择题1.若点A (-2,3)在反比例函数y =kx 的图象上,则k 的值是( )A .-6B .-2C .2D .62.对于反比例函数y =-2x ,下列说法不正确的是( )A .图象分布在第二、四象限B .当x >0时,y 随x 的增大而增大C .图象经过点(1,-2)D .若点A (x 1,y 1),B (x 2,y 2),都在图象上,且x 1<x 2,则y 1<y 23.已知反比例函数y =kbx (kb ≠0)的图象如图K -3-1所示,则一次函数y =kx +b 的图象可能是( )图K -3-1 图K -3-24.反比例函数y =-2x 的图象上有两点P 1(x 1,y 1),P 2(x 2,y 2).若x 1<0<x 2,则下列结论正确的是( )A .y 1<y 2<0B .y 1<0<y 2C .y 1>y 2>0D .y 1>0>y 25.反比例函数y =-3x(x <0)的图象如图K -3-3所示,则矩形OAPB 的面积是( )图K -3-3A .3B .-3 C.32 D .-326.如图K -3-4,A 为反比例函数y =kx 的图象上的一点,AB ⊥y 轴于点B ,点P 在x 轴上,S △ABP =2,则这个反比例函数的表达式为( )图K -3-4A .y =2xB .y =-2xC .y =4xD .y =-4x二、填空题7.若反比例函数y =2-kx 的图象位于第二、四象限,则k 的取值范围是________.8.如图K -3-5,在平面直角坐标系中,O 为坐标原点,P 是反比例函数y =2x 图象上的一点,P A ⊥x 轴于点A ,则△POA 的面积为________.9.已知反比例函数y =kx 的图象经过点(3,-1),则当1<y <3时,自变量x 的取值范围是________.图K -3-5 图K -3-610.如图K -3-6,D 为矩形OABC 的边AB 的中点,反比例函数y =kx (x >0)的图象经过点D ,交BC 边于点E .若△BDE 的面积为1,则k =________.三、解答题11.已知y 是x 的反比例函数,且当x =2时,y =-3. (1)求反比例函数的表达式;(2)在图K -3-7中画出这个函数的图象; (3)试判断点P (-2,3)是否在这个函数的图象上.图K -3-712.已知函数y =(k -2)xk 2-5为反比例函数. (1)求k 的值;(2)它的图象在第________象限内,在各象限内,y 随x 的增大而________(填变化情况); (3)求出-2≤x ≤-12时,y 的取值范围.13.已知反比例函数y =k -1x(k 为常数,k ≠1).(1)若该反比例函数的图象在每个象限内,y 随x 的增大而增大,求k 的取值范围; (2)若其图象的一支位于第二象限,在这一支上任取两点A (x 1,y 1),B (x 2,y 2),当y 1>y 2时,试比较x 1,x 2的大小.14.如图K -3-8,点A 在反比例函数y =kx 的图象在第二象限内的分支上,AB ⊥x 轴于点B ,O 是原点,且△AOB 的面积为1.试解答下列问题:(1)比例系数k =________;(2)在图K -3-8的平面直角坐标系中,画出这个函数图象的另一个分支; (3)当x >1时,写出y 的取值范围.图K -3-8分类讨论思想如图K -3-9,四边形ABCD 为正方形,点A 的坐标为(0,2),点B 的坐标为(0,-3),反比例函数y =kx(k ≠0)的图象经过点C .(1)求反比例函数的表达式;(2)若P 是反比例函数图象上的一点,△P AD 的面积恰好等于正方形ABCD 的面积,求点P 的坐标.图K -3-9详解详析[课堂达标] 1.[答案] A 2.[答案] D 3.[答案] C4.[解析] D ∵反比例函数y =-2x 中k =-2<0,∴此函数图象在第二、四象限.∵x 1<0<x 2,∴点P 1(x 1,y 1)在第二象限,点P 2(x 2,y 2)在第四象限,∴y 1>0>y 2. 5.[解析] A ∵点P 在反比例函数y =-3x (x <0)的图象上,∴可设P(x ,-3x ),∴OA =-x ,PA =-3x ,∴S 矩形OAPB =OA·PA =-x·(-3x)=3.故选A .6.[解析] D 连接OA.∵△AOB 的面积=△ABP 的面积=2,△AOB 的面积=12|k|,∴12|k|=2,∴k =±4.又∵反比例函数的图象位于第二、四象限,∴k <0,∴k =-4,∴这个反比例函数的表达式为y =-4x.故选D .7.[答案] k >2 8.[答案] 19.[答案] -3<x <-1[解析] ∵反比例函数y =kx 的图象经过点(3,-1),∴k =3×(-1)=-3,∴反比例函数的表达式为y =-3x .∵反比例函数y =-3x 中k =-3<0,∴该反比例函数的图象在第二、四象限,且在每个象限内y 随x 的增大而增大.当y =1时,x =-3;当y =3时,x =-1.∴当1<y <3时,自变量x 的取值范围是-3<x <-1. 10.[答案] 4[解析] 设D(a ,ka).∵D 为矩形OABC 中AB 边的中点, ∴B(2a ,k a ),∴C(2a ,0),∴E(2a ,k2a ).∵△BDE 的面积为1, ∴12·a·(k a -k2a )=1, 解得k =4. 故答案为4.11.解:(1)设反比例函数的表达式为y =kx ,把x =2,y =-3代入,得k =2×(-3)=-6,所以反比例函数的表达式为y =-6x.(2)如图所示:(3)当x =-2时,y =-6x =3,所以点P(-2,3)在这个函数的图象上.12.解:(1)由题意得k 2-5=-1,解得k =±2. ∵k -2≠0,∴k =-2.(2)∵k -2=-4<0,∴反比例函数的图象在第二、四象限,在各象限内,y 随着x 的增大而增大.故答案为二、四 增大.(3)∵反比例函数的表达式为y =-4x ,∴当x =-2时,y =2;当x =-12时,y =8.由(2)得,当-2≤x≤-12时,2≤y≤8.13.解:(1)由题意,得k -1<0,解得k <1.(2)由反比例函数y =k -1x 的图象的一支位于第二象限,得k -1<0,∴在第二象限内,y随x 的增大而增大,∴当y 1>y 2时,x 1>x 2.14.解:(1)-2 (2)如图所示:(3)利用函数图象,可得当x >1时,-2<y <0. [素养提升]解:(1)∵点A 的坐标为(0,2),点B 的坐标为(0,-3),∴AB =5. ∵四边形ABCD 为正方形, ∴点C 的坐标为(5,-3).∵反比例函数y =kx的图象经过点C ,∴-3=k 5,解得k =-15,∴反比例函数的表达式为y =-15x.(2)设点P 到AD 的距离为h.∵△PAD 的面积恰好等于正方形ABCD 的面积, ∴12×5×h =52.解得h =10. ①当点P 在第二象限时,y P =h +2=12.此时,x P =-1512=-54.∴点P 的坐标为⎝⎛⎭⎫-54,12. ②当点P 在第四象限时,y P =-(h -2)=-8.此时,x P =-15-8=158,∴点P 的坐标为⎝⎛⎭⎫158,-8. 综上所述,点P 的坐标为(-54,12) (158,-8).。
11.2+反比例函数的图像及性质(练)2课时

11.2 反比例函数的图像及性质(练)2课时一.选择题(共4小题)1.已知反比例函数6y x=-,下列结论中不正确的是( )A .图象必经过点(3,2)-B .图象位于第二、四象限C .若2x <-,则03y <<D .在每一个象限内,y 随x 值的增大而减小2.已知点A 与点B 关于原点对称,A 的坐标是(2,3)-,那么经过点B 的反比例函数的解析式是( ) A .2y x=-B .3y x=-C .6y x=-D .32y x=-3.点(1,4)-在反比例函数ky x=的图象上,则下列各点在此函数图象上的是( ) A .(4,1)- B .1(4-,1)C .(4,1)--D .1(4,2)4.关于反比例函数2y x=,下列说法不正确的是( ) A .函数图象分别位于第一、第三象限B .当0x >时,y 随x 的增大而减小C .函数图象经过点(1,2)D .若点1(A x ,1)y ,2(B x ,2)y 都在函数图象上,且12x x <,则12y y > 二.填空题(共4小题) 5.已知反比例函数1(k y k x-=是常数,1)k ≠的图象有一支在第二象限,那么k 的取值范围是 .6.已知y 与2x +成反比例,当4x =时,2y =,当0x =时,y = . 7.若反比例函数13ky x-=的图象经过第一、三象限,则k 的取值范围是 . 8.如图,在平面直角坐标系中,菱形OABC 的边OA 在x 轴上,AC 与OB 交于点D (8,4),反比例函数ky x=的图象经过点D .若将菱形OABC 向左平移n 个单位,使点C 落在该反比例函数图象上,则n 的值为 .三.解答题(共4小题)9.定义:如图,若双曲线(0)ky k x =>与它的其中一条对称轴y x =相交于两点A ,B ,则线段AB 的长称为双曲线(0)ky k x=>的对径.(1)求双曲线1y x=的对径;(2)若某双曲线(0)ky k x=>的对径是k 的值.10.如图,PA x ⊥轴于点A ,连接OP ,PA ,PO 分别与反比例函数(0)ky k x=>的图象交于点B ,C .(1)求证:22AB OC AP OP=; (2)已知(4,3)P ,PB PC =,求k 的值.11.已知y 是x 的反比例函数,且当2x =时,3y =-,请你确定该反比例函数的解析式,并求当6y =时,自变量x 的值. 12.如图,P 是反比例函数ky x=图象上一点,//PM x 轴交y 轴于点M ,2M P =,点Q 的坐标为(4,0),连接PO、PQ,OPM∆的∆的面积为3,求该反比例函数的表达式是OPQ面积.11.2 反比例函数的图像及性质(练)2课时参考答案与试题解析一.选择题(共4小题)1.已知反比例函数6y x=-,下列结论中不正确的是( )A .图象必经过点(3,2)-B .图象位于第二、四象限C .若2x <-,则03y <<D .在每一个象限内,y 随x 值的增大而减小 【分析】根据反比例函数的性质进行选择即可. 【解答】解:A 、图象必经过点(3,2)-,故A 正确;B 、图象位于第二、四象限,故B 正确;C 、若2x <-,则03y <<,故C 正确;D 、在每一个象限内,y 随x 值的增大而增大,故D 错误;故选:D .2.已知点A 与点B 关于原点对称,A 的坐标是(2,3)-,那么经过点B 的反比例函数的解析式是( ) A .2y x=-B .3y x=-C .6y x=-D .32y x=-【分析】先根据中心对称的点的横坐标互为相反数,纵坐标互为相反数,求得B 为(2,3)-,然后把(2,3)-代入函数ky x=中可先求出k 的值,那么就可求出函数解析式. 【解答】解:点(2,3)A -,∴点A 关于原点对称的点B 的坐标(2,3)-,反比例函数ky x=经过B 点, 236k ∴=-⨯=-,∴反比例函数的解析式是6y x=-. 故选:C .3.点(1,4)-在反比例函数ky x=的图象上,则下列各点在此函数图象上的是( )A .(4,1)-B .1(4-,1)C .(4,1)--D .1(4,2)【分析】将点(1,4)-代入ky x=,求出函数解析式即可解题; 【解答】解:将点(1,4)-代入k y x=, 4k ∴=-, 4y x-∴=, ∴点(4,1)-在函数图象上,故选:A .4.关于反比例函数2y x=,下列说法不正确的是( ) A .函数图象分别位于第一、第三象限B .当0x >时,y 随x 的增大而减小C .函数图象经过点(1,2)D .若点1(A x ,1)y ,2(B x ,2)y 都在函数图象上,且12x x <,则12y y >【分析】根据反比例函数图象上点的坐标特征对C 进行判断;根据反比例函数的性质对A 、B 、D 进行判断.【解答】解:A 、20k =>,则双曲线2y x=的两支分别位于第一、第三象限,所以A 选项的说法正确;B 、当0x >时,y 随着x 的增大而减小,所以B 选项的说法正确;C 、把1x =代入2y x =得2y =,则点(1,2)在2y x=的图象上,所以C 选项的说法正确; D 、点1(A x ,1)y 、2(B x 、2)y 都在反比例函数2y x=的图象上,若120x x <<,则12y y >,所以D 选项的说法错误. 故选:D .二.填空题(共4小题) 5.已知反比例函数1(k y k x-=是常数,1)k ≠的图象有一支在第二象限,那么k 的取值范围是 1k < .【分析】由于反比例函数1k y x-=的图象有一支在第二象限,可得10k -<,求出k 的取值范围即可.【解答】解:反比例函数1k y x-=的图象有一支在第二象限, 10k ∴-<,解得1k <. 故答案为:1k <.6.已知y 与2x +成反比例,当4x =时,2y =,当0x =时,y = 6 . 【分析】设(0)2ky k x =≠+,利用待定系数法求反比例函数解析式求出k 的值,再求解即可. 【解答】解:y 与2x +成反比例,∴设(0)2ky k x =≠+, 4x =时,2y =,∴242k=+, 解得12k =, 122y x ∴=+, ∴当0x =时,12602y ==+. 故答案为:6. 7.若反比例函数13k y x -=的图象经过第一、三象限,则k 的取值范围是 13k < . 【分析】先根据反比例函数的性质列出关于k 的不等式,求出k 的取值范围即可. 【解答】解:反比例函数13ky x-=的图象经过第一、三象限, 130k ∴-…,解得13k <.故答案为:13k <. 8.如图,在平面直角坐标系中,菱形OABC 的边OA 在x 轴上,AC 与OB 交于点D (8,4),反比例函数ky x=的图象经过点D .若将菱形OABC 向左平移n 个单位,使点C 落在该反比例函数图象上,则n 的值为 2 .【分析】根据菱形的性质得出CD AD =,//BC OA ,根据D (8,4)和反比例函数ky x=的图象经过点D 求出32k =,C 点的纵坐标是248⨯=,求出C 的坐标,即可得出答案. 【解答】解:四边形ABCO 是菱形, CD AD ∴=,//BC OA ,D (8,4),反比例函数ky x=的图象经过点D , 84210OA ∴=+÷=,B 点坐标为(16,8),32k =,C 点的纵坐标是248⨯=, C ∴点坐标为(6,8),32y x=, 把8y =代入得:4x =, 642n ∴=-=,∴向左平移2个单位长度,反比例函数能过C 点.故答案为:2.三.解答题(共4小题)9.定义:如图,若双曲线(0)ky k x =>与它的其中一条对称轴y x =相交于两点A ,B ,则线段AB 的长称为双曲线(0)ky k x=>的对径.(1)求双曲线1y x=的对径;(2)若某双曲线(0)ky k x=>的对径是k 的值.【分析】过A 点作AC x ⊥轴于C .(1)先解方程组1y x y x⎧=⎪⎨⎪=⎩,可得到A 点坐标为(1,1),B 点坐标为(1,1)--,即1OC AC ==,则OAC ∆为等腰直角三角形,得到OA ==2AB OA ==曲线1y x=的对径; (2)根据双曲线的对径的定义得到当双曲线的对径为AB =OA =,根据OA ,则5OC AC ==,得到点A 坐标为(5,5),把(5,5)A 代入双曲线(0)ky k x=>即可得到k 的值.【解答】解:过A 点作AC x ⊥轴于C ,如图. (1)解方程组1y x y x⎧=⎪⎨⎪=⎩,得1111x y =⎧⎨=⎩,2211x y =-⎧⎨=-⎩, A ∴点坐标为(1,1),B 点坐标为(1,1)--,1OC AC ∴==,OA ∴=2AB OA ∴==,∴双曲线1y x=的对径是(2)双曲线的对径为AB =OA =OA ∴,5OC AC ∴==,∴点A 坐标为(5,5),把(5,5)A 代入双曲线(0)ky k x=>得5525k =⨯=,即k 的值为25.10.如图,PA x ⊥轴于点A ,连接OP ,PA ,PO 分别与反比例函数(0)ky k x=>的图象交于点B ,C .(1)求证:22AB OC AP OP =; (2)已知(4,3)P ,PB PC =,求k 的值.【分析】(1)作CD x ⊥轴于点D ,连接OB ,可得//CD AB ,由相似三角形的性质可得22OCD OPA S OC S OP ∆∆=,即可证22AB OC AP OP =; (2)设PB PC m ==,则3AB m =-,5OC m =-,代入(1)的结论中可求m 的值,即可求k 的值.【解答】(1)作CD x ⊥轴于点D ,连接OB ,//CD AB ∴,12OCD AOB S S k ∆∆==,OCD OPA ∴∆∆∽∴22OCD OPA S OC S OP ∆∆=∴221212AOB OCD AOP OAP AB OAS S AB OC AP S S OP AP OA ∆∆∆∆⨯====⨯ (2)(4,3)P , 3AP ∴=,4OA =,5OP ∴=设PB PC m ==,则3AB m =-,5OC m =-,由(1)得:223(5)35m m --=解得:0m =(舍去),53m =5164(3)33k ∴=⨯-=11.已知y 是x 的反比例函数,且当2x =时,3y =-,请你确定该反比例函数的解析式,并求当6y =时,自变量x 的值.【分析】由题意y 是x 的反比例函数,可设(0)ky k x=≠,然后利用待定系数法进行求解;把6y =代入函数解析式求得相应的x 的值即可. 【解答】解:设反比例函数(0)ky k x=≠,当2x =时,3y =-, 2(3)6k xy ∴==⨯-=-,y ∴与x 之间的函数关系式6y x =-.把6y =代入6y x=-,则1x =-.12.如图,P 是反比例函数ky x=图象上一点,//PM x 轴交y 轴于点M ,2M P =,点Q 的坐标为(4,0),连接PO 、PQ ,OPM ∆的面积为3,求该反比例函数的表达式是OPQ ∆的面积.第11页(共11页)【分析】(1)此题只需根据反比例函数系数k 的几何意义,由OPM ∆的面积确定出比例系数k 的值即可;(2)由2PM =得出点P 的纵坐标,即OPQ ∆在OQ 上的高,结合点Q 的坐标为(4,0)可得答案.【解答】解:设(,)P a b ,0a >,0b >, //PM x 轴,132OPM S ab ∆∴==, 6ab ∴=, P 是反比例函数k y x =图象上一点, k b a∴=,即6k ab ==, ∴反比例函数的表达式为6y x =, 2MP =,即P 点的横坐标为2,632y ∴==, 14362OPQ S ∆∴=⨯⨯=.。
人教版九年级数学下册第26章《实际问题与反比例函数》课时练习题(含答案)

人教版九年级数学下册第26章《2.实际问题与反比例函数》课时练习题(含答案)一、单选题1.已知蓄电池的电压为定值,使用蓄电池时,电流I (单位:A )与电阻R (单位:Ω)是反比例函数关系,它的图象如图所示.则这个反比例函数的解析式为( )A .24I R =B .36I R =C .48I R =D .64I R= 2.港珠澳大桥桥隧全长55千米,其中主桥长29.6千米,一辆汽车从主桥通过时,汽车的平均速度 v (千米/时)与时间 t (小时)的函数关系式为( )A .55t v =B .25.4v t =C .v =29.6tD .29.6v t= 3.研究发现,近视镜的度数y (度)与镜片焦距x (米)成反比例函数关系,小明佩戴的400度近视镜片的焦距为0.25米,经过一段时间的矫正治疗加之注意用眼健康,现在镜片焦距为0.4米,则小明的近视镜度数可以调整为( )A .300度B .500度C .250度D .200度 4.在显示汽车油箱内油量的装置模拟示意图中,电压U 一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积V 与电路中总电阻0R R R R =+总总()是反比例关系,电流I 与R 总也是反比例关系,则I 与V 的函数关系是( )A .反比例函数B .正比例函数C .二次函数D .以上答案都不对 5.在压力不变的情况下,某物体所受到的压强P (Pa )与它的受力面积S (2m )之间成反比例函数关系,且当S =0.1时,P =1000.下列说法中,错误..的是( ) A .P 与S 之间的函数表达式为100P S =B .当S =0.4时,P =250C .当受力面积小于20.2m 时,压强大于500PaD .该物体所受到的压强随着它的受力面积的增大而增大6.学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温y (℃)与通电时间(min)x 成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y 与通电时间x 之间的关系如图所示,则下列说法中正确的是( )A .水温从20℃加热到100℃,需要7minB .水温下降过程中,y 与x 的函数关系式是400y x= C .上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水D .水温不低于30℃的时间为77min 37.春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过5min 的集中药物喷洒,再封闭宿舍10min ,然后打开门窗进行通风,室内每立方米空气中含药量()3mg /m y 与药物在空气中的持续时间(min)x 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )A .经过5min 集中喷洒药物,室内空气中的含药量最高达到310mg /mB .室内空气中的含药量不低于38mg /m 的持续时间达到了11minC .当室内空气中的含药量不低于35mg /m 且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效D .当室内空气中的含药量低于32mg /m 时,对人体才是安全的,所以从室内空气中的含药量达到32mg /m 开始,需经过59min 后,学生才能进入室内8.如图,点C 在反比例函数y=k x(x>0)的图象上,过点C 的直线与x 轴,y 轴分别交于点A ,B ,且AB=BC ,△AOB 的面积为1,则k 的值为( )A .1B .2C .3D .4二、填空题9.列车从甲地驶往乙地.行完全程所需的时间()h t 与行驶的平均速度()km/h v 之间的反比例函数关系如图所示.若列车要在2.5h 内到达,则速度至少需要提高到__________km/h .10.如图,一块长方体大理石板的A 、B 、C 三个面上的边长如图所示,如果大理石板的A 面向下放在地上时地面所受压强为m 帕,则把大理石板B 面向下放在地上时,地面所受压强是________m 帕.11.某蓄水池的排水管的平均排水量为每小时8立方米,6小时可以将满池水全部排空.现在排水量为平均每小时Q立方米,那么将满池水排空所需要的时间为t(小时),写出时间t (小时)与Q之间的函数表达式_____.12.对于函数2yx=,当函数值y<﹣1时,自变量x的取值范围是_______________.13.随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当10x≥时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是________.三、解答题14.某市政府计划建设一项水利工程,工程需要运送的土石方总量为610立方米,某运输公司承担了运送土石方的任务.(1)设该公司平均每天运送土石方总量为y立方米,完成运送任务所需时间为t天.①求y关于t的函数表达式.②若080t<≤时,求y的取值范围.(2)若1辆卡车每天可运送土石方210立方米,工期要求在80天内完成,公司至少要安排多少辆相同型号卡车运输?15.心理学家研究发现,一般情况下,一节课40分钟,学生的注意力随教师讲课时间的变化而变化.学生的注意力指数y随时间x(分)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).(1)上课后的第5分钟与第30分钟相比较,_______分钟时学生的注意力更集中.(2)分别求出线段AB和双曲线CD的函数关系式.(3)一道数学题,需要讲18分钟,为了学生听课效果较好,要求学生的注意力指数不低于40,那么经过适当的时间安排,教师能否在学生注意力达到所需状态下讲完这道题?16.为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:时间x(天) 3 5 6 9 ……硫化物的浓度y(mg/L) 4.5 2.7 2.25 1.5 ……(1)在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;(2)在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L ?为什么?17.设函数y 1=k x ,y 2=﹣k x(k >0). (1)当2≤x ≤3时,函数y 1的最大值是a ,函数y 2的最小值是a ﹣4,求a 和k 的值.(2)设m ≠0,且m ≠﹣1,当x =m 时,y 1=p ;当x =m +1时,y 1=q .圆圆说:“p 一定大于q ”.你认为圆圆的说法正确吗?为什么?18.当下教育主管部门提倡加强高效课堂建设,要求教师课堂上要精讲,把时间、思考、课堂还给学生.通过实验发现:学生在课堂上听课注意力指标随上课时间的变化而变化,上课开始后,学生的学习兴趣递增,中间一段时间,学生的兴趣保持平稳高效状态,后阶段注意力开始分散.学生注意力指标y 随时间x (分钟)变化的函数图象如图所示,当010x ≤<和1020x ≤<时,图象是线段,当2045x ≤≤时,图象是反比例函数的一部分.(1)求点A 对应的指标值.(2)如果学生在课堂上的注意力指标不低于30属于学习高效阶段,请你求出学生在课堂上的学习高效时间段。
中考数学 精讲篇 考点系统复习 第三章 函数 第三节 反比例函数

1 (2)由(1)得:△BCH 的面积为2×4×4=8.
9.(2016·重庆 A 卷第 22 题 10 分)如图,在平面直角坐标系中,一次函 数 y=ax+b(a≠0)的图象与反比例函数 y=kx(k≠0)的图象交于第二、第 四象限内的 A,B 两点,与 y 轴交于 C 点.过 A 作 AH⊥y 轴,垂足为点 H,
8
8 32
∴BE=3.∴k=4×3= 3 .故选:D.
命题点 2:反比例函数与一次函数、三角函数、几何图形的综合(近 6 年考查 4 次) 7.(2017·重庆 A 卷第 22 题 10 分)如图,在平面直角坐 标系中,一次函数 y=mx+n(m≠0)的图象与反比例函数 y =kx(k≠0)的图象交于第一、三象限内的 A,B 两点,与 y 轴交于点 C.过点 B 作 BM⊥x 轴,垂足为 M,BM=OM,OB= 2 2,点 A 的纵坐标为 4.
4 OH=3,tan∠AOH=3,点 B 的坐标为(m,-2). (1)求△AHO 的周长; (2)求该反比例函数和一次函数的解析式.
解:(1)∵AH⊥y 轴于点 H,∴∠AHO=90°. AH 4
∵tan∠AOH=OH=3,OH=3, ∴AH=4. OA= AH2+OH2= 42+32=5. ∴△AHO 的周长为 3+4+5=12.
∴一次函数的解析式为 y=-x-1.
令 y=0,得 x=-1,∴点 C 的坐标为(-1,0).
1
(2)由(1)知,点 A 的坐标为(-4,3), 点 A 在反比例函数 y=kx(k≠0)的图象上, ∴∵∴反点3比=B(例-mk,函4.-数∴2的k)=在解-反析1比式2,例为函y=数-y=1x2-. 1x2的图象上,
2021秋九上第1章反比例函数1、2反比例函数的图像与性质2反比例函数y=kxk<0的图象与性质习题

解:由题意知点 B 的坐标为-2,32. 把点 B-2,32的坐标代入 y=kx,得 k=-3. ∴反比例函数的表达式为 y=-3x.
(2)若P(x1,y1),Q(x2,y2)是该反比例函数图象上
的两点,且x1<x2时,y1>y2,指出点P,Q各
位于哪个象限,并简要说明理由. 解:结论:点 P 在第二象限,点 Q 在第四象限.
第1章 反比例函数
1.2 反比例函数的图象与性质 第2课时 反比例函数y= (k<0)的图象
与性质
提示:点击 进入习题
1D 2B 3A 4B
5A 6D 7B 8C
答案显示
提示:点击 进入习题
9C 10 见习题 11 见习题 12 见习题 13 见习题
答案显示
1.【中考·营口】反比例函数 y=-4x(x>0)的图象 位于( D )
【答案】B
*3.【中考·河北】如图,函数 y=1x-(1xx(>x0<)0,)的
图象所在坐标系的原点是( A )
A.点 M B.点 N C.点 P D.点 Q 【点拨】易知函数 y=1x-(1x(x>x<0)0, )的图象关于 y 轴对 称,且图象位于 x 轴上方,所以点 M 是原点.
4.【中考·泸州】如图,一次函数 y1=ax+b 和反比例函 数 y2=kx的图象相交于 A,B 两点,则使 y1>y2 成立的 x 的取值范围是( B ) A.-2<x<0 或 0<x<4 B.x<-2 或 0<x<4 C.x<-2 或 x>4 D.-2<x<0 或 x>4
【答案】A
6.【中考·天门】反比例函数 y=-3x,下列说法不正确 的是( ) A.图象经过点(1,-3) B.图象位于第二、四象限 C.图象关于直线 y=x 对称 D.y 随 x 的增大而增大
人教版数学九年级下册26.1.2第2课时+反比例函数的图象和性质的的综合运用课件

y k 1、若点P(2,3)在反比例函数
的图像上,则k= 6 _
x
2、若点P(m,n)在反比例函数 y 6 图像上,则mn= 6_
x
3、如图,S矩形ABCD= 6 S△ABD=__3_
A
D
S矩形ABCD与S△ABD有何关系?
2
S△ABD=
1 2
S矩形ABCD
B3
C
4、如图,点P是反比例函数图象上的一点,过点P分别向x轴
∴ 当 x < 0 时,y 随 x 的增大而减小, ∴ 当 -3 < x < -1 时,-6 < y < -2.
二 反比例函数图象和性质的综合
例2 如图,是反比例函数 y m 5 图象的一支. 根
据图象,回答下列问题:
x
(1) 图象的另一支位于哪个象限?常数 m 的取值范围
是什么?
y
解:因为这个反比例函数图象的一
函数的图象上? 解:设这个反比例函数的解析式为 y k ,因为点
x A (2,6)在其图象上,所以有 6 k ,解得 k =12.
2 所以反比例函数的解析式为 y 12 .
x
因为点 B,C 的坐标都满足该解析式,而点 D 的坐标不满足,所以点 B,C 在这个函数的图 象上,点 D 不在这个函数的图象上.
y
设点 P 的坐标为 (a,b)
∵点
P
(a,b)
在函数
y
k x
的图
象上,∴ b k ,即 ab=k. a
PB
SA
AO
x
BP
若点 P 在第二象限,则 a<0,b>0,
∴ S矩形 AOBP=PB·PA=-a·b=-ab=-k;
中考数学《反比例函数的实际应用》专项练习题及答案

中考数学《反比例函数的实际应用》专项练习题及答案一、单选题1.某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对(m,n),在坐标系中进行描点,则正确的是()A.B.C.D.2.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m 3)的反比例函数,其图象如图所示.当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体体积应()A.不大于2435m3B.不小于2435m3C.不大于3524m 3D.不小于3524m 33.根据图1所示的程序,得到了y与x的函数图象,如图2.若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.则以下结论:①x<0时,y=2x②∥OPQ的面积为定值.③x>0时,y随x的增大而增大.④MQ=2PM.⑤∥POQ可以等于90°.其中正确结论是()A.①②④B.②④⑤C.③④⑤D.②③⑤4.小明乘车从县城到怀化,行车的速度v(km/ℎ)和行车时间t(ℎ)之间函数图是()A.B.C.D.5.矩形的长为x,宽为y,面积为12,则y与x之间的函数关系用图象表示大致为()A.B.C.D.6.已知甲,乙两地相距s(单位:km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(单位:h)关于行驶速度v(单位:kmℎ⁄)的函数图象是()A.B.C.D.7.一个面积为20的矩形,若长与宽分别为x,y,则y与x之间的关系用图象可表示为()A.B.C.D.8.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10∥,加热到100∥,停止加热,水温开始下降,此时水温(∥)与开机后用时(min)成反比例关系.直至水温降至30∥,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30∥时,接通电源后,水温y (∥)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50∥的水,则接通电源的时间可以是当天上午的()A.7:20B.7:30C.7:45D.7:509.已知力F所作的功是15焦,则力F与物体在力的方向上通过的距离S的图象大致是如图中的()A.B.C.D.10.如图,点P(3a,a)是反比例函y=(k>0)与∥O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为()A.y=3x B.y=10x C.y=12x D.y=27x11.如图,在直角坐标系中,矩形ABCD的顶点A坐标为(﹣1,0),顶点B的坐标为(0,﹣2),经过顶点C的双曲线y=kx(k>0)与线段AD交于点E,且AE:DE=2:1,则k的值为()A.4B.6C.8D.1212.阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1200N和0.5m,则这一杠杆的动力F和动力臂l之间的函数图象大致是()A.B.C.D.二、填空题13.在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V=.14.如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为(用含n的代数式表示)15.如图,点A在双曲线y= k x的第一象限的那一支上,AB∥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若∥ADE的面积为32,则k的值为.16.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示.点P(4,3)在图象上,则当力达到10N时,物体在力的方向上移动的距离是m.17.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.如果以此蓄电池为电源的用电器的限制不能超过12A,那么用电器的可变电阻应控制的范围是.18.若12x m﹣1y2与3xy n+1是同类项,点P(m,n)在双曲线y=a−1x上,则a的值为.三、综合题19.在平面直角坐标系中,反比例函数y= mx(x>0)的图象上有一点A(a,3),过点A作AB∥x轴于点B,将点B沿x轴正方向平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数于点D,CD= 32,直线AD与x轴交于点M,与y轴交于点N.(1)用含a的式子表示点D的横坐标为:;(2)求a的值和直线AD的函数表达式;(3)请判断线段AN与MD的数量关系,并说明理由;(4)若一次函数y1=k1x+b1经过点(10,9),与双曲线y= mx(x>0)交于点P,且该一次函数y1的值随x的增大而增大,请确定P点横坐标n的取值范围(不必写出过程)20.如图,在∥ABCD中,设BC边的长为x(cm),BC边上的高线AE长为y(cm),已知∥ABCD 的面积等于24cm2.(1)求y关于x的函数表达式;(2)求当3<y<6时x的取值范围.21.如图,在平面直角坐标系xOy中,∥ABC的边AC在x轴上,边BC∥x轴,双曲线y= k x(x>0)与边BC交于点D(4,m),与边AB交于点E(2,n).(1)求n关于m的函数关系式;(2)若BD=2,tan∥BAC= 12,求k的值和点B的坐标.22.某养猪场对猪舍进行喷药消毒.在消毒的过程中,先经过5min的药物集中喷洒,再封闭猪舍10min,然后再打开窗户进行通风.已知室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)之间的函数图象如图所示,其中在打开窗户通风前y与x分别满足两个一次函数,在通风后y与x满足反比例函数.(1)求反比例函数的关系式;(2)当猪舍内空气中含药量不低于5mg m3⁄且持续时间不少于21min,才能有效杀死病毒,问此次消毒是否有效?23.某机床加工一批机器零件,如果每小时加工30个,那么12小时可以完成.(1)设每小时加工x个零件,所需时间为y小时,写出y与x之间的函数关系式,画出图象;(2)若要在一个工作日(8小时)内完成,每小时要比原来多加工几个?24.如图1,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如表x(cm)1015202530y(g)3020151210(1)把表中(x,y)的各组对应值作为点的坐标,在图2的坐标系中描出相应的点,用平滑曲线连接这些点;(2)观察所画的图象,猜测y与x之间的函数关系,求出函数关系式;(3)当砝码的质量为24g时,活动托盘B与点O的距离是多少?参考答案1.【答案】C 2.【答案】B 3.【答案】B 4.【答案】B 5.【答案】C 6.【答案】B 7.【答案】C 8.【答案】A 9.【答案】B 10.【答案】C 11.【答案】B 12.【答案】A 13.【答案】40014.【答案】145n(n+1)或 65n(n+1 15.【答案】8316.【答案】1.2 17.【答案】R≥3W 18.【答案】3 19.【答案】(1)a+2(2)解:∵CD∥y 轴,且CD= 32∴D (a+2, 32 )∵A 、D 都在反比例函数图象上∴{m =3am =32(a +2) ,解得 {a =2m =6 ,即a 的值为2 ∴A (2,3),D (4, 32 )设直线AD 的函数表达式为y=kx+b把A 、D 的坐标代入可得 {2k +b =34k +b =32,解得 {k =−34b =92∴直线AD 的函数表达式为y=﹣ 34 x+ 92 ;(3)解:结论:AN=MD理由:在y=﹣ 34 x+ 92 中,令y=0可得x=6,令x=0可得y= 92∴M (6,0),N (0, 92)∵A (2,3),D (4, 32)∴AN= √(2−0)2+(3−92)2 = 52 ,MD= √(6−4)2+(0−32)2= 52∴AN=MD ;(4)解:如图,当直线与x 垂直时n 的值最大,当直线与x 轴平行时n 的值最小当直线垂直x 轴时,则可知E 点横坐标为10,即此时n 的值为10当直线平行x 轴时,则F 点的纵坐标为9,由(1)可得反比例函数解析式为y= 6x,当y=9时,可解得x= 23 ,即P 点的横坐标为 23 ,即此时n 的值为 23∵一次函数y 1的值随x 的增大而增大 ∴直线在直线P 1E 和直线P 2F 之间∴n 的取值范围为 23<n <10.20.【答案】(1)解:∵BC 边的长为x (cm ),BC 边上的高线AE 长为y (cm ),已知∥ABCD 的面积等于24cm 2.∴根据平行四边形的面积计算方法得:xy =24 ∴y =24x(x >0);(2)解:当y =3时x =8,当y =6时x =4 所以当3<y <6时x 的取值范围为4<x <8.21.【答案】(1)解:∵点D (4,m ),点E (2,n )在双曲线y= k x(x >0) 上∴4m=2n ,解得n=2m ;(2)解:过点E 作EF∥BC 于点F∵由(1)可知n=2m∴DF=m∵BD=2∴BF=2﹣m∵点D(4,m),点E(2,n)∴EF=4﹣2=2∵EF∥x轴∴tan∥BAC=tan∥BEF= BFEF=2−m2=12,解得m=1∴D(4,1)∴k=4×1=4,B(4,3).22.【答案】(1)解:设反比例函数关系式为y=k x. ∵反比例函数的图象过点(15,8)∴k=120.∴y=120 x.(2)解:设正比例函数关系式为y=kx. 把x=5,y=10代入上式,得k=2 .∴y=2x.当y=5时,x=52.把y=5代入y=120x,得x=24.∴24−52=21.5>21.答:此次消毒能有效杀死该病毒.23.【答案】(1)解:由题意可得y= 30×12x=360 x即y与x的函数关系式是y= 360x,函数图象如右图所示(2)解:由题意可得3608−30=45−30=15答:每小时要比原来多加工15个24.【答案】(1)解:如图所示:(2)解:由图象猜测y与x之间的函数关系为反比例函数∴设y= kx(k≠0)把x=10,y=30代入得:k=300∴y= 300 x将其余各点代入验证均适合∴y与x的函数关系式为:y= 300 x(3)解:把y=24代入y= 300x得:x=12.5∴当砝码的质量为24g时,活动托盘B与点O的距离是12.5cm。
人教版初三数学9年级下册 第26章(反比例函数)复习讲义及例题和习题(含答案)
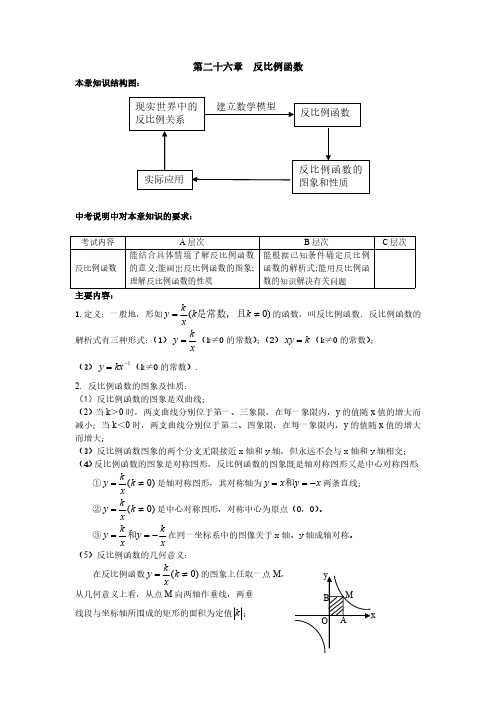
第二十六章 反比例函数本章知识结构图:中考说明中对本章知识的要求:考试内容A 层次B 层次C 层次反比例函数能结合具体情境了解反比例函数的意义;能画出反比例函数的图象;理解反比例函数的性质能根据已知条件确定反比例函数的解析式;能用反比例函数的知识解决有关问题主要内容:1.定义:一般地,形如)0(≠=k k x ky 是常数,且的函数,叫反比例函数. 反比例函数的解析式有三种形式:(1)xky =(k ≠0的常数);(2)k xy =(k ≠0的常数);(3)1-=kx y (k ≠0的常数).2. 反比例函数的图象及性质:(1)反比例函数的图象是双曲线;(2)当k >0时,两支曲线分别位于第一、三象限,在每一象限内,y 的值随x 值的增大而减小;当k <0时,两支曲线分别位于第二、四象限,在每一象限内,y 的值随x 值的增大而增大;(3)反比例函数图象的两个分支无限接近x 轴和y 轴,但永远不会与x 轴和y 轴相交;(4)反比例函数的图象是对称图形,反比例函数的图象既是轴对称图形又是中心对称图形:①)0(≠=k x ky 是轴对称图形,其对称轴为x y x y -==和两条直线;②)0(≠=k x ky 是中心对称图形,对称中心为原点(0,0)。
③xky x k y -==和在同一坐标系中的图像关于x 轴、y 轴成轴对称。
(5)反比例函数的几何意义:在反比例函数)0(≠=k xky 的图象上任取一点M ,从几何意义上看,从点M 向两轴作垂线,两垂线段与坐标轴所围成的矩形的面积为定值k ;(6)k 越大,双曲线越远离原点。
3.反比例函数在代数、几何及实际问题中的应用。
四、例题与习题:1.下面的函数是反比例函数的是 ( )A . 13+=x yB .x x y 22+= C . 2xy =D .xy 2=2.用电器的输出功率与通过的电流、用电器的电阻之间的关系是,下面说法正确的是()A .为定值,与成反比例B .为定值,与成反比例C .为定值,与成正比例D .为定值,与成正比例3.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m 3)是体积V (单位:m 3)的反比例函数,它的图象如图3所示,当310m V =时,气体的密度是( )A .5kg/m 3B .2kg/m 3C .100kg/m 3D .1kg/m 34. 已知三角形的面积一定,则它底边上的高与底边之间的函数关系的图象大致是( )B .C .D .5.某物体对地面的压力为定值,物体对地面的压强p (Pa )与受力面积S (m 2)之间的函数关系如图所示,这一函数表达式为p = .6.点在反比例函数的图象上,则 .7.点(3,-4)在反比例函数ky x=的图象上,则下列各点中,在此图象上的是( )A.(3,4)B. (-2,-6)C.(-2,6)D.(-3,-4)P I R 2P I R =P I R P 2I R P I R P 2I R a h a (231)P m -,1y x=m =8.已知某反比例函数的图象经过点()m n ,,则它一定也经过点( )A .()m n -,B .()n m ,C .()m n -,D .()m n ,9.已知反比例函数的图象经过点(m ,2)和(-2,3)则m 的值为 .10.已知n 是正整数,n P (n x ,n y )是反比例函数xky =图象上的一列点,其中1x 1=,2x 2=,…,n x n =,记211y x T =,322y x T =,…,1099y x T =;若1T 1=,则921T T T ⋅⋅⋅⋅⋅⋅的值是_________.11.在平面直角坐标系中,将点(53)P ,向左平移6个单位,再向下平移1个单位,恰好在函数ky x=的图象上,则此函数的图象分布在第 象限.12.对于反比例函数(),下列说法不正确的是( )A. 它的图象分布在第一、三象限B. 点(,)在它的图象上C. 它的图象是中心对称图形D. 每个象限内,随的增大而增大13. 一个函数具有下列性质:①它的图像经过点(-1,1);②它的图像在二、四象限内; ③在每个象限内,函数值y 随自变量x 的增大而增大.则这个函数的解析式可以为 .14.已知反比例函数y =x2k -的图象位于第一、第三象限,则k 的取值范围是( ).(A )k >2 (B ) k ≥2(C )k ≤2(D ) k <215.若反比例函数的图象经过点,其中,则此反比例函数的图象在( )A .第一、二象限B .第一、三象限C .第二、四象限D .第三、四象限16.若反比例函数1k y x-=的图象在其每个象限内,y 随x 的增大而减小,则k 的值可以是( )A.-1B.3C.0D.-317.若点00()x y ,在函数ky x=(0x <)的图象上,且002x y =-,则它的图象大致是( )18.设反比例函数中,在每一象限内,随的增大而增大,则一次函数的图象不经过()xk y 2=0≠k k k y x ky x=(3)m m ,0m ≠)0(≠-=k xky y x k kx y -=A .B .C .D .(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限19.如果点11()A x y ,和点22()B x y ,是直线y kx b =-上的两点,且当12x x <时,12y y <,那么函数ky x=的图象大致是( )20.若()A a b ,,(2)B a c -,两点均在函数1y x=的图象上,且0a <,则b 与c 的大小关系为( )A .b c>B .b c<C .b c=D .无法判断21.已知点A (3,y 1),B (-2,y 2),C (-6,y 3)分别为函数xky =(k<0)的图象上的三个点.则y 1 、y 2 、y 3的大小关系为 (用“<”连接).22.在反比例函数的图象上有两点A ,B ,当时,有,则的取值范围是( )A 、B 、C 、D 、23.若A (,)、B (,)在函数的图象上,则当、满足______________________________________时,>.24. 已知直线与双曲线的一个交点A 的坐标为(-1,-2).则=_____;=____;它们的另一个交点坐标是______.25.在平面直角坐标系xoy 中,直线yx =向上平移1个单位长度得到直线l .直线l 与反比例函数ky x=的图象的一个交点为(2)A a ,,则k 的值等于 .26.如果函数x y 2=的图象与双曲线)0(≠=k xky 相交,则当0<x 时,该交点位于A .第一象限B .第二象限C .第三象限D .第四象限27.在同一平面直角坐标系中,函数xy 1=与函数x y =的图象交点个数是( )A 、0个B 、1个C 、2个D 、3个28.函数1ky x-=的图象与直线y x =没有交点,那么k 的取值范围是( ) A .1k > B .1k < C .1k >- D .1k <-12my x-=()11,x y ()22,x y 120x x <<12y y <m 0m <0m >12m <12m >1x 1y 2x 2y 12y x=1x 2x 1y 2y mx y =xky =m k xxxx.D .29.在同一坐标系中,一次函数(1)21y k x k =-++与反比例函数ky x=的图象没有交点,则常数k 的取值范围是.30.如图,直线)0(>=k kx y 与双曲线xy 2=交于A 、B 两点,若A 、B 两点的坐标分别为A ()11,y x ,B ()22,y x ,则1221y x y x +的值为()A . -8B .4C . -4D . 031.已知反比例函数2y x=,下列结论中,不正确的是( ) A .图象必经过点(12),B .y 随x 的增大而减少C .图象在第一、三象限内D .若1x >,则2y <32.已知函数1y x=的图象如下,当1x ≥-时,y 的取值范围是( ) A .1y <- B .1y ≤- C .1y ≤- 或0y > D .1y <-或0y ≥33.如图,一次函数与反比例函数的图象相交于A、B 两点,则图中使反比例函数的值小于一次函数的值的x 的取值范围是_____________.34.如图,正方形ABOC 的边长为2,反比例函数xky =过点A ,则K 的值是( )A .2B .-2C .4D .-435.过反比例函数(0)ky k x=>的图象上的一点分别作x 、y 轴的垂线段,如果垂线段与x 、y 轴所围成的矩形面积是6,那么该函数的表达式是______;若点A(-3,m)在这个反比例函数的图象上,则m=______.36.如图,若点A 在反比例函数(0)ky k x=≠的图象上,AM x ⊥轴于点M ,AMO △的面积为3,则k =.37.在反比例函数4y x=的图象中,_4-1-1yx第32题图第34题图第33题图第36题图阴影部分的面积不等于4的是( )A .B .C .D .38.两个反比例函数k y x =和1y x =在第一象限内的图象如图所示,点P 在ky x =的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x=的图象于点B ,当点P在ky x=的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形PAOB 的面积不会发生变化;③PA 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 .(把你认为正确结论的序号都填上,少填或错填不给分).39.如图,第四象限的角平分线OM 与反比例函数()0≠=k xky 的图象交于点A ,已知OA=23,则该函数的解析式为( )A .xy 3=B .xy 3-= C .xy 9=D .xy 9-=40.如图,一次函数122y x =-的图象分别交x 轴、y 轴于A 、B ,P 为AB 上一点且PC 为△AOB 的中位线,PC 的延长线交反比例函数(0)k y k x =>的图象于Q ,32OQC S ∆=,则k的值和Q 点的坐标分别为______________.ky x =1y x=(第38题图)第39题图41.当m 取什么数时,函数2)1(--=m xm y 为反比例函数式?42.已知反比例函数102)2(--=m x m y 的图象,在每一象限内y 随x 的增大而减小,求反比例函数的解析式.43.平行于直线y x =的直线l 不经过第四象限,且与函数3(0)y x x=>和图象交于点A ,过点A 作AB y ⊥轴于点B ,AC x ⊥轴于点C四边形ABOC 的周长为8.求直线l 的解析式.44.已知正比例函数的图象与反比例函数(为常数,)的图象有一个交点的横坐标是2.(1)求两个函数图象的交点坐标;(2)若点,是反比例函数图象上的两点,且,试比较的大小.45.已知一次函数y kx b =+的图象与反比例函数my x=的图象相交于A (-6,-2)、B (4,3)两点.(1)求出两函数解析式;(2)画出这两个函数的图象;(3)根据图象回答:当x 为何值时,一次函数的函数值大于反比例函数的函数值?46.如图,直线y =x +1与双曲线x2y =交于A 、B 两点,其中A 点在第一象限.C 为x 轴正半轴上一点,且S △ABC =3.(1)求A 、B 、C 三点的坐标;(2)在坐标平面内,是否存在点P ,使以A 、B 、C 、P 为顶点的四边形为平行四边形?若存在,请直接写出点P 的坐标,若不存在,请说明理由.47.为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y (毫克)与时间t (小时)成正比;药物释放完毕后,y 与y kx =5ky x-=k 0k ≠11()A x y ,22()B x y ,5ky x-=12x x <12y y ,3(0)x x>(第47题)t 的函数关系式为tay =(a 为常数),如图所示.据图中提供的信息,解答下列问题: (1)写出从药物释放开始,y 与t 之间的两个函数关系式及相应的自变量的取值范围; (2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?48.我们学习了利用函数图象求方程的近似解,例如:把方程的解看成函数的图象与函数的图象交点的横坐标.如图,已画出反比例函数在第一象限内的图象,请你按照上述方法,利用此图象求方程的正数解.(要求画出相应函数的图象;求出的解精确到0.1)49.如图,帆船A 和帆船B 在太湖湖面上训练,O 为湖面上的一个定点,教练船静候于O点.训练时要求A 、B 两船始终关于O 点对称.以O 为原点.建立如图所示的坐标系,轴、y 轴的正方向分别表示正东、正北方向.设A 、B 两船可近似看成在双曲线上运动,湖面风平浪静,双帆远影优美.训练中当教练船与A 、B 两船恰好在直线上时,三船同时发现湖面上有一遇险的C 船,此时教练船测得C 船在东南45°方向上,A 船测得AC 与AB 的夹角为60°,B 船也同时测得C 船的位置(假设C 船位置213x x -=-21y x =-3y x =-1y x=210x x --=x 4y x=y x=不再改变,A 、B 、C 三船可分别用A 、B 、C 三点表示).(1)发现C 船时,A 、B 、C 三船所在位置的坐标分别为 A( , )、B( ,)和C(,);(2)发现C 船,三船立即停止训练,并分别从A 、O 、B 三点出发沿最短路线同时前往救援,设A 、B 两船 的速度相等,教练船与A 船的速度之比为3:4,问教练船是否最先赶到?请说明理由。
反比例函数的图象和性质(第2课时)

综上,反比例函数在其定义域内的两个区间 上均为单调递减。
利用性质求最值问题
对于形如 $y = ax + frac{b}{x}$ (a > 0, b > 0) 的函数,可以利用反比例函数的 性质求最值。由于 a、b 同号,函数在 x > 0 时有最小值,在 x < 0 时有最大值 。
通过将原函数转化为 $y = a(x + frac{b}{ax})$,进而利用反比例函数的性质,可 以求得函数的最小值为 $2sqrt{ab}$,当且仅当 $x = sqrt{frac{b}{a}}$ 时取到。
06
课后作业及拓展延伸
完成课后作业题目
题目1
已知反比例函数 $y = frac{k}{x}$($k neq 0$),当 $x = 2$ 时,$y = 3$,求该反
比例函数的解析式。
题目2
已知点 $A(x_1, y_1)$ 和 $B(x_2, y_2)$ 在反比例函数 $y = frac{k}{x}$($k > 0$)的图 象上,且 $x_1 < x_2$,比较
图象在各象限的分布情况
当$k > 0$时,反比例函数的图象分布在第一象限和第三象限。在每个象限内,随着$x$的增大,$y$的值逐渐 减小,但永远不会等于0。
当$k < 0$时,反比例函数的图象分布在第二象限和第四象限。在每个象限内,随着$x$的增大,$y$的值逐渐 增大,但同样永远不会等于0。
03
利用性质解决实际应用问题
在经济学中,反比例函数常被用来描述成本、收益等经济量 之间的关系。例如,当某一商品的需求量 x 增加时,其价格 y 会相应下降,这时可以用反比例函数来描述这种关系。
在工程学中,反比例函数也可以用来描述某些物理量之间的 关系。例如,电路中的电阻 R 与电流 I 成反比关系,即 $R = frac{U}{I}$,其中 U 为电压。这时可以利用反比例函数的 性质来分析电路的特性。
第2课时 反比例函数的图象与性质的综合应用

象是 __D__ .
y
Ox A
y
O
x
B
y
O
x
C
y x
o
D
课堂小结
1、反比例函数的性质: 反比例函数y=k/x的图象,当 k>0时,图象位于第一、三象限,在每一象限内,y的值 随x的增大而减小; 当k<0时,图象位于第二、四象限, y的值随x的增大而增大。 2、双曲线的两条分支逼近坐标轴但不可能与坐标轴相交。 3、反比例函数的图象是一个以原点为对称中心的中心对 称图形。 4、在反比例函数y=k/x的图象上任取一点,分别作坐标 轴的垂线(或平行线),与坐标轴所围成的S矩形=▕k▏
2 反比例函数的图象与性质
第2课时 反比例函数的图象与性质的综合 应用
新课引入
1.下列函数中,哪些是反比例函数?
(1)
y 1 x 1
y 3
(2) x
(3)
y
1 x2
(5) y 1
3x
(4)
y
2 x
答案:(2)(4)(5)
新课引入
2.写出反比例函数的表达式:_y___kx__(_k_是 __常 ___数__, _. k 0)
3.反比例函数的图象是__双__曲_线_______.
4.反比例函数
y2 x
5.反比例函数
y
4 x
的图象在第_二__、__四____象限内. 经过点(m,2),则m的值2______.
6.反比例函数
y
k x
的图象经过点(2,-3), 则它的表
达式为______y_____6x____.
新课讲解
观察反比例函数的图象,回答下列问题:
解:依题意得:
第2课时反比例函数图象上点的增减变化规律

第 2 课时反比率函数图象上点的增减变化规律【学习目标】1.进一步稳固作反比率函数的图象的方法.2.联合反比率函数的图象,认识反比率函数的值随自变量的变化的规律.3.逐渐提升从函数的图象中获守信息的能力,研究并掌握反比率函数的主要性质.【学习要点】研究反比率函数的主要性质.【学习难点】理解反比率函数性质的研究过程,从“数” 和“形” 双方面综合考虑问题.情形导入生成问题1.已知反比率函数y=m-1的图象的一支位于第一象限,则常数m 的取值范围是m> 1.x2.当x>0时,函数5的图象在 ( A ) y=-xA.第四象限B.第三象限C.第二象限D.第一象限k的一个交点的坐标为(2,4) ,则它们的另一个交点的坐标为 ( B ) 3.如图,直线y=2x与双曲线y=xA. (-2, 4) B.(- 2,- 4) C. (- 4,- 2)D. (2,- 4)自学互研生成能力知识模块研究反比率函数图象上点的增减变化规律先阅读教材 P154-155页的内容,而后达成下边的填空:k的图象:1.对于反比率函数y=x(1)当 k>0 时,图象的两支曲线分别位于第一、三象限,在每一象限内,y 的值随 x 的增大而减小;(2)当 k<0 时,图象的两支曲线分别位于第二、四象限,在每一象限内,y 的值随 x 的增大而增大.kP 分别作 x 轴和 y 轴的垂线,与坐标轴围成的矩形面积为2.若P是反比率函数y=x图象上随意一点,过点S,则 S=|k|.试一试:观察反比例函数y =2x, y =4x, y =6x的图象,你能发现它们的共同特征吗?(1)函数图象分别位于哪几个象限内?(2) 在每一个象限内,跟着x 值的增大,y 的值是如何变化的?能说明这是为何吗?(3) 反比率函数的图象可能与x 轴订交吗?可能与y 轴订交吗?为何?让学生经过对三个反比率函数的图象进行仔细的察看、类比、剖析、沟通,归纳归纳出反比率函数(k> 0)的主要性质.议一议:观察当k=- 2,- 4,- 6 时,反比率函数y= kx的图象,它们有哪些共同特点?让学生经过类比,剖析、归纳、归纳出k<0 时图象的共同特点.说一说:你能试试着谈谈反比率函数y=k的图象有哪些共同特点吗?x归纳:对于反比率函数y= k的图象,当xk>0 时,在每一象限内,y 的值随x 值的增大而减小;当k< 0 时,在每一个象限内,y 的值随 x 的增大而增大.想想:在一个反比率函数图象上任取两点P、Q,过点 P 分别作面积为 S1;过点 Q 分别作 x 轴、 y 轴的平行线,与坐标轴围成的矩形面积为x 轴、 y 轴的平行线,与坐标轴围成的矩形S2, S1与 S2有什么关系?为何?2(1)让我们从详细的反比率函数y=x开始考虑:此时, S1与 S2有什么关系?为何?k(2)对于一般的反比率函数y=x呢?给出详细的反比率函数y=2,让学生按题目要求,取点、结构矩形S 、S ,自主研究 S与 S 之间的关系,x1212而后由学生解说,教师进行方法的总结和点拨.变一变:在一个反比率函数图象上任取两点P、Q,过点 P 作 x 轴的垂线,连结PO(O 为原点 ),与坐标轴围成的三角形面积为 S1;过点 Q 作 x 轴的垂线,连结 QO ,与坐标轴围成的三角形面积为S2, S1与 S2有什么关系?对应练习:21.对于反比率函数y=x的图象,以下说法正确的选项是( D )A.图象经过点 (1, 1)B.两个分支散布在第二、四象限C.两个分支对于x 轴成轴对称 D.当 x< 0 时, y 随 x 的增大而减小52.已知两点P1(x1,y1),P2(x2,y2)在函数y=x的图象上,当x1> x2> 0 时,以下结论正确的选项是( A )A. 0< y1< y2B. 0<y2< y1C. y1< y2< 0D. y2< y1< 023.如图,点 B 在反比率函数y=x(x >0) 的图象上,横坐标为1,过 B 分别向x 轴, y 轴作垂线,垂足分别为A , C,则矩形OABC 的面积为 ( B )A.1B.2C.3D.4沟通展现生成新知1.将阅读教材时“生成的问题”和经过“自主研究、合作研究”得出的“结论”展现在各小组的小黑板上.并将疑难问题也板演到黑板上,再一次经过小组间就上述疑难问题互相释疑.2.各小组由组长一致分派展现任务,由代表将“问题和结论”展现在黑板上,经过沟通“生成新知”.知识模块研究反比率函数图象上点的增减变化规律检测反应达成目标k1.如图,正方形ABOC 的边长为2,反比率函数y=x的图象经过点 A ,则 k 的值是 ( D )A.2B.-2C.4 D.- 4k 2.如图,菱形OABC的极点C的坐标为(3,4),极点A在x轴的正半轴上.反比率函数y=x(x>0)的图象经过极点 B,则 k 的值为 ( D)A. 12B. 20C. 24 D .321图象上,则y1与 y2的大小关系是:y1> y2( 选填3 .若点A(1 , y1) 和点B(2 , y2) 在反比率函数y =x“>”“<”或“=”).k4.如图,M为反比率函数y=x的图象上的一点,MA 垂直 y 轴,垂足为 A ,△ MAO 的面积为2,则 k 的值为 4.5.如图,点A是反比率函数6的图象上一点,过点 A 作 AB ⊥ x 轴,垂足为点B,线段 AB 交反比率函数y=x2的图象于点 C,则△ OAC 的面积为2.y=x课后反省查漏补缺1.收获:________________________________________________________________________2.存在疑惑:________________________________________________________________________。
