结构化学基础习题答案分子的对称性培训资料
结构化学基础习题答案分子的对称性

04分子的对称性【】和都是直线型分子,写出该分子的对称元素。
解:HCN:; CS2:【】写出分子中的对称元素。
解:【】写出三重映轴和三重反轴的全部对称操作。
解:依据三重映轴S3所进行的全部对称操作为:,,,,依据三重反轴进行的全部对称操作为:,,,,【】写出四重映轴和四重反轴的全部对称操作。
解:依据S4进行的全部对称操作为:依据进行的全部对称操作为:【】写出和通过原点并与轴重合的轴的对称操作的表示矩阵。
解:,【】用对称操作的表示矩阵证明:(a)(b)(c)解:(a),推广之,有,即:一个偶次旋转轴与一个垂直于它的镜面组合,必定在垂足上出现对称中心。
(b)这说明,若分子中存在两个互相垂直的C2轴,则其交点上必定出现垂直于这两个C2轴的第三个C2轴。
推广之,交角为的两个轴组合,在其交点上必定出现一个垂直于这两个C2轴轴,在垂直于轴且过交点的平面内必有n个C2 轴。
进而可推得,一个轴与垂直于它的C2 轴组合,在垂直于的平面内有n个C2 轴,相邻两轴的夹角为。
(c)这说明,两个互相垂直的镜面组合,可得一个轴,此轴正是两镜面的交线。
推而广之,若两个镜面相交且交角为,则其交线必为一个n次旋转轴。
同理,轴和通过该轴的镜面组合,可得n个镜面,相邻镜面之交角为。
【】写出(反式)分子全部对称操作及其乘法表。
解:反式C2H2C l2分子的全部对称操作为:对称操作群的乘法为:【】写出下列分子所归属的点群:,,氯苯,苯,萘。
【】判断下列结论是否正确,说明理由。
(a)凡直线型分子一定有轴;(b)甲烷分子有对称中心;(c)分子中最高轴次与点群记号中的相同(例如中最高轴次为轴);(d)分子本身有镜面,它的镜像和它本身相同。
解:(a)正确。
直线形分子可能具有对称中心(点群),也可能不具有对称中心(点群)。
但无论是否具有对称中心,当将它们绕着连接个原子的直线转动任意角度时,都能复原。
因此,所有直线形分子都有轴,该轴与连接个原子的直线重合。
结构化学第四章分子的对称性习题及答案

一、填空题
1.群的表示可分为可约表示和不可约表示。
2.判断分子有无旋光性的标准是是否具有反轴。
3. 分子有无偶极矩与分子对称性有密切关系,只有属于C n和C nv这两类点群的分子才具有偶极矩,而其它点群的分子偶极矩为0。
二、选择题
1. CO2分子没有偶极矩,表明该分子是【D 】
A. 以共价键结合的
B. 以离子键结合的
C. V形的
D. 线形的,并且有对称中心
2. 根据分子的对称性,可知CCl4分子的偶极矩等于【A 】
A. 0
B. 1.03
C. 1.85
D. 1.67
3. 组成点群的群元素是什么【A 】
A. 对称操作
B. 对称元素
C. 对称中心
D. 对称面
4. CH4属于下列哪类分子点群【A 】
A. T d
B. D h
C. C3v
D. C s
5. H2O属于下列哪类分子点群【 A 】
A. C2v
B. C3v
C. C2h
D. O h
三、回答问题
1. 找出H2O分子和NH3分子的对称元素和对称操作及其所属点群,并建立其对称操作的乘积表。
课本第125页:表4.2.1和表4.2.2
课本第142页:表4.6.3。
分子对称性习题答案

分子对称性习题答案分子对称性习题答案分子对称性是化学中一个重要的概念,它可以帮助我们理解分子的性质和反应。
在学习分子对称性的过程中,我们常常会遇到一些习题,下面我将为大家提供一些分子对称性习题的答案,希望对大家的学习有所帮助。
1. 对称性的定义是什么?对称性是指分子在空间中存在的对称操作,使得分子的外观在经过这些操作后保持不变。
常见的对称操作包括旋转、镜面反射和反转。
2. 如何确定分子的对称中心?分子的对称中心是指分子中存在一个点,经过该点进行旋转180度后,分子的外观保持不变。
确定分子的对称中心的方法是找出分子中所有的旋转轴,然后判断是否存在旋转180度后保持不变的点。
3. 如何确定分子的对称元素?分子的对称元素是指分子中存在的对称操作,使得分子在经过这些操作后保持不变。
常见的对称元素包括旋转轴、镜面反射面和反转中心。
4. 如何确定分子的点群?分子的点群是指分子在空间中具有的所有对称操作的集合。
确定分子的点群的方法是找出分子中所有的对称元素,并根据这些对称元素的组合关系确定分子的点群。
5. 如何确定分子的对称轴?分子的对称轴是指分子中存在的一个轴,经过该轴进行旋转后,分子的外观保持不变。
确定分子的对称轴的方法是找出分子中所有的旋转轴,并判断是否存在旋转后保持不变的轴。
6. 如何确定分子的镜面反射面?分子的镜面反射面是指分子中存在的一个平面,经过该平面进行镜面反射后,分子的外观保持不变。
确定分子的镜面反射面的方法是找出分子中所有的镜面反射面,并判断是否存在镜面反射后保持不变的平面。
7. 如何确定分子的反转中心?分子的反转中心是指分子中存在的一个点,经过该点进行反转后,分子的外观保持不变。
确定分子的反转中心的方法是找出分子中所有的反转中心,并判断是否存在反转后保持不变的点。
8. 请给出一些常见的分子的对称性描述。
- 水分子(H2O)具有C2v点群,其中包含一个C2轴和一个垂直于C2轴的镜面反射面。
安徽高中化学竞赛结构化学第四章分子的对称性习题-教学文档

安徽高中化学竞赛结构化学第四章分子的对称性习题-教学文档1. 下列哪种对称操作是真操作(B)A.反映 B.旋转 C.反演2. 下列哪种分子与立方烷具有完全相同的对称性:(C)A.C60 B.金刚烷 C.SF63. 设想从乙烷分子的重叠构象出发,经过非重叠非交叉构象,最后变为交叉构象. 点群的变化是:(B)A. D3→D3h→D3dB. D3h→D3→D3dC. C3h→C3→C3V4. S在室温下稳定存在的形式为正交硫, 其中的分子是S8环, 分子点群为(B)A.C4vB. D4dC. D8h5. 对s、p、d、f 原子轨道分别进行反演操作,可以看出它们的对称性分别是(B)A.u, g, u, g B. g, u, g, u C. g, g, g, g 6. CH4分子中具有映轴S4 (B )A.但旋转轴C4和与之垂直的镜面都不独立存在B.旋转轴C4和与之垂直的镜面也都独立存在C.旋转轴C4也存在,而与之垂直的镜面不存在7. 对映异构体的旋光大小相等、方向相反(B )A. 其中偏振面顺、逆时针旋转者分别称为右旋体和左旋体,记作(+)和(-)B. 其中偏振面顺、逆时针旋转者分别称为左旋体和右旋体,记作(-)和(+)C. 对映异构体的等量混合物称为内消旋体,用(±)标记.8. CH4分子中具有映轴S4 ( A)A.但旋转轴C4和与之垂直的镜面都不独立存在B.旋转轴C4和与之垂直的镜面也都独立存在C.旋转轴C4也存在,而与之垂直的镜面不存在9. 对映异构体的旋光大小相等、方向相反( A )A. 其中偏振面顺、逆时针旋转者分别称为右旋体和左旋体,记作(+)和(-)B. 其中偏振面顺、逆时针旋转者分别称为左旋体和右旋体,记作(-)和(+)C. 对映异构体的等量混合物称为内消旋体,用(±)标记.10. 丙二烯分子属于D 2d 点群. 由此推测 ( C ) A. 分子中只有σ键B. 分子中有一个大π键Π33C. 分子中有两个互相垂直的小π键11. 己三烯电环化反应, 在加热条件下保持什么对称性不变?( B )A .C 2B.mC. m 和C 212. 旋光性分子的对映异构体可用R 与S 区分, 分别取自拉丁词右和左的首字母;旋光方向用(+)与(-)区分, 分别代表右旋和左旋( C) A .R 型分子的旋光方向必定是(+),S 型分子必定是(-)B .R 型分子的旋光方向必定是(-),S 型分子必定是(+)C .一般地说,由R 、S 构型不能断定分子的旋光方向 13. 一个分子的分子点群是指:( A ) A .全部对称操作的集合 B .全部对称元素的集合 C .全部实对称操作的集合14. 对于CO 2和H 2O ,下列哪种说法是正确的:( A )A. CO 2振动的红外与拉曼活性是互斥的,而H 2O 则否B. SO 2振动的红外与拉曼活性是互斥的,而H 2O 则否C. 它们都属于C 2v 点群15. 群中的某些元素若可以通过相似变换联系起来,它们就共同组成( A ) A.一个类 B. 一个子群 C.一个不可约表示 16. 对一个可约表示进行约化得到几个不可约表示。
第2章分子对称性与分子结构-习题

第二章分子的对称性与分子结构【习题】2.1 确定下列分子或物体所属的点群:(1)SiHDBr2 (四面体)(2)SiFClBrI (四面体)(3)SiH2Br2(四面体)(4)PCl3 (三角锥体)(5)OPCl3(三角锥体)(6)CO2(直线形)(7)P4O6(四面体)(8)Mn(CO)5I (八面体)(9)字母T和Z(10)一支粉笔2.2 找出下列各分子中的最高次旋转轴,并指出其中哪些分子还含有不与主轴重合的其他对称轴:(1)C10H6F2;(2)C6H6;(3)C6H3Br3 三溴苯(所有异构体)2.3 指出下列分子或离子所属的点群,并写出它们所含有的对称元素。
(1)CoCl42-;(2)Ni(CN)42-;(3)cis-CoCl4(NH3)2-(可忽略H原子);(4)C6H12(椅式);(5)PF3;(6)(CH3)2B(μ-H)2B(CH3)2;(7)[Cl-I-Cl]-;(8)cis-Pt(NH3)Cl2;(9)trans-Pt(NH3)2Cl2;(10)交错式-C2H6;(11)二茂铁(交错式)。
22.4 化学式为MCl42-的配离子,D2d点群结构和T d点群结构时所含对称元素有何不同?2.5 配离子[MA2B2]2-当分别采取D2h和C2v结构时所含对称元素有何不同?2.6 对比D4h点群与C4h点群,指出在后一点群中缺少哪一关键性元素?各举一分子(离子)实例。
2.7 三亚乙基二胺(也叫1,4-二氮杂环(2,2,2)辛烷)属于什么点群?2.8 PtCl42-属于什么点群?画出它的结构,标出各类操作元素(每类只标一个)。
2.9 已知下列分子(离子)所属的点群,画出它们的结构:(1)B(OH)3(C3h);(2)Cr(en)33+(D3);(3)Co(gly)3(C3);(4)Mn2(CO)10(D4d);(5)(H2C=C=CH2)(D2d)。
2.10画出MA2B2C2类型的八面体配合物的所有几何异构体的结构式;指出每种异构体所属的点群;辨别出不对称的异构体。
无机化学答案 第2章分子对称性与分子结构-习题答案

aA2 =1/24 [1×1×4+8×1×1+3×1×0+6×(-1)×0+ 6×(-1)×2]=0
aE =1/24 [1×2×4+8×(-1)×1+3×2×0+6×0×0+6×0×2]=0
aT1 =1/24 [1×3×4+8×0×1+3×(-1)×0+6×1×0+6×(-1)×2]=0
4
aT2 =1/4 [1×3×4+8×0×1+3×(-1)×0+6×(-1)×0+6×1×2]=1 得Γ=A1 ⊕ T2
T2
3
0
-1 -1
1
(x , y , z)
(xy , xz , yz)
以CH4的 4 条杂化轨道为基(分别记为r1、r2、r 3、r 4),依据Td点群的对称元素对其进行
操作,得可约表示Γ:
Td
E
8C3
3C2
6S4
6σd
Γ
4
1
0
0
2
r 1、r2、r 3、r 4
用群分解公式将Γ约化:
aA1 =1/24(1×1×4+8×1×1+3×1×0+6×1×0+6×1×2)=1
2.5 [MA2B2]2-呈平面四边形构型时属D2h点群,含有对称元素:C2、2C2'、σh、i、2σv。[MA2B2]2 -呈四面体构型时属C2v点群,含有对称元素:C2、2σv。
2.6 C4h点群比D4h点群缺少 4 条垂直于主轴的C2'旋转轴。D4h点群的例子有配离子PtCl42-,C4h 点群例子有:
B
C
A
C
A
B
C2v
C
B
A
B
A
C
C2v
C
B
A
A
B
C
D2h
结构化学练习题带答案

结构化学复习题一、选择填空题第一章量子力学基础知识1.实物微粒和光一样,既有性,又有性,这种性质称为性。
2.光的微粒性由实验证实,电子波动性由实验证实。
3。
电子具有波动性,其波长与下列哪种电磁波同数量级?(A)X射线 (B)紫外线(C)可见光(D)红外线4。
电子自旋的假设是被下列何人的实验证明的?(A)Zeeman (B)Gouy (C)Stark (D)Stern-Gerlach5。
如果f和g是算符,则(f+g)(f—g)等于下列的哪一个?(A)f2-g2;(B)f2—g2-fg+gf; (C)f2+g2; (D)(f—g)(f+g)6.在能量的本征态下,下列哪种说法是正确的?(A)只有能量有确定值;(B)所有力学量都有确定值;(C)动量一定有确定值; (D)几个力学量可同时有确定值;7.试将指数函数e±ix表示成三角函数的形式——--——8.微观粒子的任何一个状态都可以用来描述; 表示粒子出现的概率密度。
9。
Planck常数h的值为下列的哪一个?(A)1.38×10-30J/s (B)1.38×10—16J/s (C)6。
02×10—27J·s (D)6.62×10—34J·s 10。
一维势箱中粒子的零点能是答案: 1.略。
2。
略. 3。
A 4。
D 5.B 6。
D 7.略 8.略 9。
D 10。
略第二章原子的结构性质1。
用来表示核外某电子的运动状态的下列各组量子数(n, 1, m, m s)中,哪一组是合理的?(A)2,1,—1,—1/2;(B)0,0,0,1/2; (C)3,1,2,1/2; (D)2,1,0,0。
2。
若氢原子中的电子处于主量子数n=100的能级上,其能量是下列的哪一个: (A)13。
6Ev;(B)13。
6/10000eV; (C)-13。
6/100eV;(D)—13.6/10000eV;3.氢原子的p x状态,其磁量子数为下列的哪一个?(A)m=+1;(B)m=—1;(C)|m|=1; (D)m=0;4.若将N原子的基电子组态写成1s22s22p x22p y1违背了下列哪一条?(A)Pauli原理;(B)Hund规则;(C)对称性一致的原则;(D)Bohr理论5。
结构化学 第四章习题(周公度)

第四章分子的对称性1、HCN和CS2都是线性分子。
写出该分子的对称元素解:HCN分子构型为线性不对称构型,具有的对称元素有:C∞,nσV; CS2分子为线性对称性分子构型,具有对称元素有:C∞,nC2, nσV ,σh 2、写出H3CCl分子的对称元素解:H3CCl 的对称元素有:C3,3σV3、写出三重映轴S3和三重反轴I3的全部对称操作解:S31=C3σ; S32=C32 ; S33=σ; S34= C3 ; S35 = C32σI31= C3i ; I32=C32 ; I33= i; I34= C3 ; I35 = C32i4、写出四重映轴S4和四重反轴I4的全部对称操作解:S41=C4σ; S42=C2 ; S43=C43σ; S44= EI41= C4i ; I42=C2 ; I43=C43 i; I44= E5、写出σxz和通过原点并与x轴重合的C2轴的对称操作C21的表示矩阵解:σxz和C2轴所在位置如图所示(基函数为坐标)σxz(x,y,z)’=(x,-y,z)σxz的变换矩阵为C21(x,y,z)’=(x,-y,-z)C21的变换矩阵为6、用对称操作的表示矩阵证明(1) C2(z) σxy = i(2) C2(x)C2(y) =C2(z)(3) σyzσxz=C2(z)解:C2(x),C2(y),C2(z),σxy,σyz,σxz,i对称操作的变换矩阵分别为,,,,,(1) C2(z) σxy = i=(2) C2(x)C2(y) =C2(z)=(3) σyzσxz=C2(z)=7、写出ClCH=CHCl(反式)分子的全部对称操作及其乘法表解:反式1,2-二氯乙烯的结构为:具有的对称元素为C2, I ; σh,σh即为分子平面,i位于C-C键中心C2与σh垂直。
分子为C2h群8、写出下列分子所隶属的点群:HCN,SO3,氯苯(C6H5)Cl,苯(C6H5),萘(C10H8)解HCN(属于C∞V),SO3(D3h),氯苯(C6H5)Cl(C2v),苯(C6H5)(D6h),萘(C10H8)(D2h)9、判断下列结论是否正确,说明理由(1) 凡线性分子一定有C∞轴(2) 甲烷分子有对称中心(3) 分子中最高轴次(n)与点群记号中的n相同(4) 分子本身有镜面,它的镜像和它本身全同解 (1) 正确线性分子的分子轴为一个C∞轴(2) 错甲烷分子没有对称中心(3) 错在只含一根主旋转轴的分子点群记号中n与主轴次相同,而在T,I,O类群中不相同(4) 正确分子含镜面,镜面前后部分成镜像关系,整个分子与它的镜像等同。
第四章-分子的对称性

第四章分子对称性一、概念及问答题1、对称操作与点操作能不改变物体内部任何两点间的距离而使物体复原的操作叫对称操作,对于分子等有限物体,在进行操作时,分子中至少有一点是不动的,叫做点操作2、旋转轴和旋转操作旋转操作是将分子绕通过其中心轴旋转一定的角度使分子复原的操作,旋转依据的对称元素为旋转轴,n次旋转轴用C n表示。
3、对称中心和反演操作当分子有对称中心i时,从分子中任一原子至对称中心连一直线,将此线延长,必可在和对称中心等距离的另一侧找到另一相同原子。
和对称中心相应的操作。
叫做反演操作。
4、镜面和反映操作镜面是平分分子的平面,在分子中除位于镜面上的原子外,其他成对地排在镜面两侧,它们通过反映操作可以复原。
反映操作是使分子的每一点都反映到该点到镜面垂线的延长线上,在镜面另一侧等距离处。
5、C n群属于这类点群的分子,它的对称元素只有一个n次旋转轴。
6、C nh群属于这类点群的分子,它的对称元素只有一个n次旋转轴和垂直于此轴的镜σ。
面h7、C nv群属于这类点群的分子,它的对称元素只有一个n次旋转轴和通过此轴的镜面σ。
v8、D nh群在C n群中加入一垂直于C n轴的C2轴,则在垂直于C n轴的平面内必有n个σ,得D nh群。
C2轴得D n群,在此基础上有一个垂直于C n轴的镜面hσ能得到另外的什么群?9、在C3V点群中增加h得到D3h群。
根据组合原理两个夹角为α的对称面的交线必为一其转角为2α的对称轴,C 3V 中有三个v σ面,v σ与h σ之间为90度,所以必有三个C 2轴垂直于C 3轴,构成了D 3h 群。
10、假定-24CuCl 原来属于T d 群,四个氯原子的标记如图所示,当出现下列情况时,它所属点群如何变化? a. 1Cl Cu -键长缩短b. 1Cl Cu -和2Cl Cu -缩短同样长度c. 12Cl Cl -间距离缩短 答:a. C 3V b. C 2V c. C 2V11、一立方体,在8个项角上放8个相同的球,如图所示,那么: a. 去掉1,2号球分子是什么点群? b. 去掉1,3号球分子是什么点群?答:a. C 2V b. C 2V12、写出偶极矩的概念、物理意义及计算公式。
分子的对称性及分子结构习题及答案

第二章分子的对称性与分子结构【补充习题及答案】1.HCN和CS2都是直线形分子,请写出它们具有的对称元素的种类。
答案:HCN:C∞、σv。
CS2:C∞、C2'、σh、σv、i、S∞。
2.指出下列分子存在的对称元素:(1)AsCl3;(2)BHFBr;(3)SiH4答案:(1)AsCl3分子为三角锥形,存在对称元素C3和3σv。
(2)BHFBr分子为三角形,存在对称元素1个σ。
(3)SiH4分子为四面体形,存在对称元素4C3、3C2、3S4、6σd。
3.SF5Cl分子的形状和SF6相似,试指出它的点群。
答案:SF5Cl分子仍为八面体,但1条键与其他键不同,分子点群为C4v。
4.正八面体6个顶点上的原子有3个被另一种原子取代,有几种可能的方式?取代产物各属于什么点群?取代产物是否具有旋光性和偶极矩?答案:只有经式(mer-)和面式(fac-)两种取代方式。
经式产物属于C2v点群,面式产物属于C3v点群。
均有偶极矩,均无旋光性。
5.指出下列各对分子的点群。
(1)CO2和 SO2 (2)二茂铁(交错式)和二茂钌(重叠式)(3)[IF6]+八面体)和[IF6]-(五角锥)(4) SnClF(角形)和XeClF(线形)(5)mer-WCl3F3和fac-WCl3F3(6)顺式和反式Mo(CO)4Cl2答案:(1)CO2:D∞h点群;SO2:C2v点群。
(2)二茂铁(交错式):D5h点群;二茂钌(重叠式):D5d点群。
(3) [IF6]+(八面体):O h点群;[IF6]-(五角锥):C5v点群。
(4)SnClF(角形):C s点群;XeClF(线形):C∞v点群。
(5)mer-WCl3F3:C2v点群;fac-WCl3F3:C3v点群。
(6)顺式Mo(CO)4Cl2:C2v;反式Mo(CO)4Cl2 :D4h点群6.如何判断一个分子有无永久偶极矩和有无旋光性?答案:对称元素不是交于一点的分子具有永久偶极矩。
结构化学习题答案

结构化学习题答案结构化学是化学学科中的一个重要分支,它研究原子、分子和晶体的结构以及它们的性质。
以下是一些结构化学习题的答案示例:1. 原子轨道的能级顺序:- 根据量子力学理论,原子轨道的能级顺序通常遵循以下顺序:1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f。
2. 分子的几何构型:- 例如,水分子(H2O)的几何构型是弯曲的,因为氧原子与两个氢原子形成共价键,并且氧原子上有两对孤对电子。
3. 分子的极性:- 一个分子是否具有极性取决于其分子内电荷分布的对称性。
如果电荷分布不均匀,分子就是极性的。
例如,二氧化碳(CO2)分子是非极性的,因为它是线性的,电荷分布对称。
4. 晶体的点群对称性:- 晶体的点群对称性是指晶体结构中原子排列的对称性。
例如,立方晶体具有高对称性,其点群为O_h。
5. 分子轨道理论:- 分子轨道理论用于描述分子中电子的分布。
根据这一理论,原子轨道可以组合形成分子轨道,这些分子轨道可以是成键的、非键的或反键的。
6. X射线衍射分析:- X射线衍射是一种用于确定晶体结构的技术。
当X射线与晶体相互作用时,它们会被晶体中的原子散射,产生衍射图案,这个图案可以用来推断晶体的原子排列。
7. 化学键的类型:- 化学键主要包括共价键、离子键和金属键。
共价键是由两个原子共享电子对形成的,离子键是由电子从一个原子转移到另一个原子形成的,而金属键是由金属原子之间的电子云形成的。
8. 分子间力:- 分子间力包括范德华力、氢键和偶极-偶极相互作用。
这些力影响分子的物理性质,如沸点和溶解性。
9. 晶体缺陷:- 晶体缺陷包括点缺陷、线缺陷(如位错)和面缺陷(如晶界)。
这些缺陷可以影响晶体的物理和化学性质。
10. 配位化合物的结构:- 配位化合物是由中心金属原子或离子与配体通过配位键连接形成的。
第四章 分子的对称性
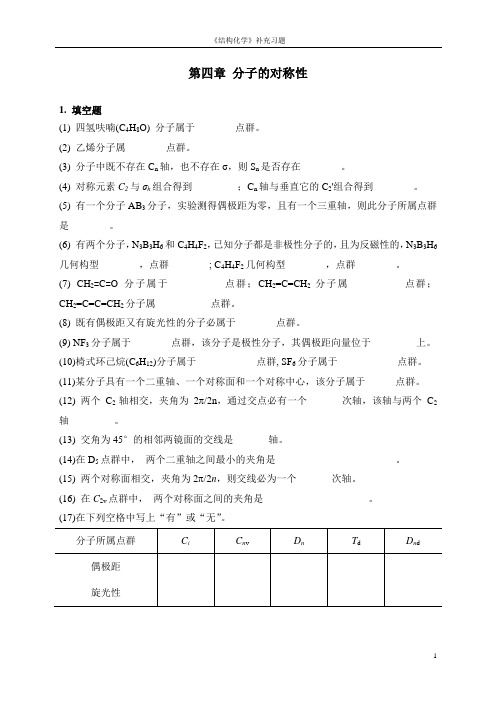
第四章分子的对称性1. 填空题(1) 四氢呋喃(C4H8O) 分子属于________点群。
(2) 乙烯分子属________点群。
(3) 分子中既不存在C n轴,也不存在σ,则S n是否存在________。
(4) 对称元素C2与σh组合得到_________;C n轴与垂直它的C2'组合得到________。
(5) 有一个分子AB3分子,实验测得偶极距为零,且有一个三重轴,则此分子所属点群是________。
(6) 有两个分子,N3B3H6和C4H4F2,已知分子都是非极性分子的,且为反磁性的,N3B3H6几何构型________,点群________; C4H4F2几何构型________,点群________。
(7) CH2=C=O 分子属于___________点群;CH2=C=CH2分子属___________点群;CH2=C=C=CH2分子属___________点群。
(8) 既有偶极距又有旋光性的分子必属于________点群。
(9) NF3分子属于________点群,该分子是极性分子,其偶极距向量位于_________上。
(10)椅式环己烷(C6H12)分子属于____________点群, SF6分子属于____________点群。
(11)某分子具有一个二重轴、一个对称面和一个对称中心,该分子属于______点群。
(12) 两个C2轴相交,夹角为2π/2n,通过交点必有一个_______次轴,该轴与两个C2轴_________。
(13) 交角为45°的相邻两镜面的交线是_______轴。
(14)在D5点群中,两个二重轴之间最小的夹角是________________________。
(15) 两个对称面相交,夹角为2π/2n,则交线必为一个_______次轴。
(16) 在C2v点群中,两个对称面之间的夹角是_____________________。
(17)在下列空格中写上“有”或“无”。
结构化学习题答案第4章

2组长:070601314 组员:070601313070601315 070601344 070601345070601352第四章 双原子分子结构与性质1.简述 LCAO-MO 的三个基本原则,其依据是什么?由此可推出共价键应具有什么样的特征?答:1.(1)对称性一致(匹配)原则: φa = φs 而φb = φ pz 时, φs 和φ pz 在σˆ yz 的操作下对称性一致。
故 σˆ yz ⎰φs H ˆφ pz d τ = β s , pz ,所以, β s , pz ≠ 0 ,可以组合成分子轨道(2)最大重叠原则:在 α a 和α b 确定的条件下,要求 β 值越大越好,即要求 S ab 应尽可能的大(3)能量相近原则: 当α a = α b 时,可得 h = β ,c 1a = c 1b , c 1a =- c 1b ,能有效组合成分子轨道;2.共价键具有方向性。
2、以 H 2+为例,讨论共价键的本质。
答:下图给出了原子轨道等值线图。
在二核之间有较大几率振幅,没有节面,而在核间值则较小且存在节面。
从该图还可以看出,分子轨道不是原子轨道电 子云的简单的加和,而是发生了波的叠加和强烈的干涉作用。
图 4.1 H +的 ψ 1(a)和 ψ 2(b)的等值线图研究表明,采用 LCAO-MO 法处理 H 2+是成功的,反映了原子间形成共价键的本质。
但由计算的得到的Re=132pm,De=170.8kJ/mol,与实验测定值Re=106pm、De=269.0 kJ/mol 还有较大差别,要求精确解,还需改进。
所以上处理方法被称为简单分子轨道法。
当更精确的进行线性变分法处理,得到的最佳结果为Re=105.8pm、De=268.8 kJ/mol,十分接近H2+的实际状态。
成键后电子云向核和核间集中,被形象的称为电子桥。
通过以上讨论,我们看到,当二个原子相互接近时,由于原子轨道间的叠加,产生强烈的干涉作用,使核间电子密度增大。
分子的对称性习题解答

乐山师范学院 化学学院
本章习题解答
【4.1】HCN 和 CS2 都是直线型分子,写出该分子的对称元素。 解:HCN:直线型分子,左右不对称,分子所在的直线为 C∞ ,包含 对称轴的平面为对称面: ∞σv ;
CS2:直线型分子,左右对称,分子所在的直线为 C∞ ,包含对称 轴的平面为对称面: ∞σv ;C 原子为对称中心 i ,经过 C 原子垂直于对 称轴的面为σv 。
面,也没有包含主轴且平分垂直于主轴二重轴的对称面,故为: D2
【4.15】由下列分子的偶极矩数据,推测分子立体构型及其点群。 (a) C3O2 ( µ = 0 ) 解:由于偶极矩为 0,因此具有较高的对称性,若三个 C 原子等价, 则为正三角形,两个氧原子必须对称地分布于正三角形中心的垂直线
上,即为三角双锥形,但这种结果不符合 C 四价,氧二价。
(c) 用矩阵的方法证明:
⎛ −1 0 0⎞
⎛1 0 0⎞
⎛ −1 0 0⎞
σ yz
=
⎜ ⎜
0
1
0
⎟ ⎟
,
σ
xz
=
⎜ ⎜
0
−1
0
⎟ ⎟
, C1 2(z)
=
⎜ ⎜
0
−1
0
⎟ ⎟
⎜⎝ 0 0 1 ⎟⎠
⎜⎝ 0 0 1 ⎟⎠
⎜⎝ 0 0 1 ⎟⎠
⎛ −1 0 0⎞⎛ 1 0 0⎞ ⎛ −1 0 0⎞
∵⎜⎜ 0 ⎜⎝ 0
用作用的结果证明:
⎡x⎤
⎡ x ⎤ ⎡−x⎤
C21(z)σ xy
⎢ ⎢
y ⎥⎥
=
C21( z )
⎢ ⎢
y
⎥ ⎥
=
⎢⎢− y⎥⎥
第2章分子对称性与分子结构-习题

第2章分子对称性与分子结构-习题第二章分子的对称性与分子结构【习题】2.1 确定下列分子或物体所属的点群:(1)SiHDBr2 (四面体)(2)SiFClBrI (四面体)(3)SiH2Br2(四面体)(4)PCl3 (三角锥体)(5)OPCl3(三角锥体)(6)CO2(直线形)(7)P4O6(四面体)(8)Mn(CO)5I (八面体)(9)字母T和Z(10)一支粉笔2.2 找出下列各分子中的最高次旋转轴,并指出其中哪些分子还含有不与主轴重合的其他对称轴:(1)C10H6F2;(2)C6H6;(3)C6H3Br3 三溴苯(所有异构体)2.3 指出下列分子或离子所属的点群,并写出它们所含有的对称元素。
(1)CoCl42-;(2)Ni(CN)42-;(3)cis-CoCl4(NH3)2-(可忽略H原子);(4)C6H12(椅式);(5)PF3;(6)(CH3)2B(μ-H)2B(CH3)2;(7)[Cl-I-Cl]-;(8)cis-Pt(NH3)Cl2;(9)trans-Pt(NH3)2Cl2;(10)交错式-C2H6;(11)二茂铁(交错式)。
22.4 化学式为MCl42-的配离子,D2d点群结构和T d点群结构时所含对称元素有何不同?2.5 配离子[MA2B2]2-当分别采取D2h和C2v结构时所含对称元素有何不同?2.6 对比D4h点群与C4h点群,指出在后一点群中缺少哪一关键性元素?各举一分子(离子)实例。
2.7 三亚乙基二胺(也叫1,4-二氮杂环(2,2,2)辛烷)属于什么点群?2.8 PtCl42-属于什么点群?画出它的结构,标出各类操作元素(每类只标一个)。
2.9 已知下列分子(离子)所属的点群,画出它们的结构:(1)B(OH)3(C3h);(2)Cr(en)33+(D3);(3)Co(gly)3(C3);(4)Mn2(CO)10(D4d);(5)(H2C=C=CH2)(D2d)。
2.10画出MA2B2C2类型的八面体配合物的所有几何异构体的结构式;指出每种异构体所属的点群;辨别出不对称的异构体。
第三章分子的对称性和点群 基础训练

符号
对称元素 对称操作
对 称 轴 ( 真 旋转操作
轴)
对称面
反映操作
符号
对称元素 对称中心
对称操作 反演操作
放映轴(非真轴) 旋转反映操作
(2)写出气相分子 分子全部独立的对称元素。
答:属于 点群,独立的对称元素有
。
(3)分子的对称元素仅有7种,即 这种说法对吗?
及轴次为1、2、3、4、6的旋转煮、放映轴和反轴,
和
,已知分子都是非极性的,且为反磁性的,
几 何 构 型 _________ , 点 群 ________ , ______________。
几 何 构 型 _________ , 点 群
(7)
分子属_____________点群。
(8)
杂化的几何构型属于________________点群。
(9)既有偶极矩又有旋光性的分子必属于______________点群。
答:
点群
旋光性 无
有
无
无
无
有
无
无
无
无
偶极矩 无
有
无
有
无
无
无
无
无
无
(6)写出下列分子所属点群及有无偶极矩。
(a) ;( b) ;( c)
答 :( a) , ,有偶极矩;
(b) , ,有偶极矩;
(c)
, ,无偶极矩。
第三章 分子的对称性和点群 自测题
1、选择题 (1)下列说法正确的是( ) A 凡是八面体配合物一定属于 点群 B 凡是四面体构型的分子一定属于 点群 C 异核双远祖分子一定没有对称中心
(3)对称元素 与 组合得到______________; 轴与垂直它的 组合得到__________。
第四章、分子对称性习题及解答

第四章、分子对称性习题一、填空题4101、I 3和I 6不是独立的对称元素,因为I 3= ,I 6= 。
4102、对称元素C 2与σh 组合,得到___________________;C n 次轴与垂直它的C 2组合,得到______________。
4103、d 3(2d z ,d xy ,d 22y x -)sp(p z )杂化的几何构型属于_________点群。
4104、有一个 AB 3分子,实验测得其偶极矩为零且有一个三重轴,则此分子所属点群是_______________________。
4105、有两个分子,N 3B 3H 6和 C 4H 4F 2,它们都为非极性,且为反磁性,则N 3B 3H 6几何构型___________,点群___________。
C 4H 4F 2几何构型_________,点群__________。
4106、NF 3分子属于_____________点群。
该分子是极性分子, 其偶极矩向量位于__________上。
4107、下列分子所属的点群:SO 3 , SO 32- , CH 3+ , CH 3- , BF 3 。
4108、写出下列分子所属的点群:CHCl 3, B 2H 6, SF 6, NF 3, SO 32-4109、CH 2═C ═O 分子属于________点群,其大π键是________。
4110、环形 S 8分子属 D 4d 点群,分子中包含轴次最高的对称轴为_______。
4111、分子具有旋光性,则可能属于___________等点群。
4112、判别分子有无旋光性的标准是__________。
4113、既具有偶极矩,又具有旋光性的分子必属于_________点群。
4114、偶极矩μ=0,而可能有旋光性的分子所属的点群为____________;偶极矩μ≠0,而一定没有旋光性的分子所属的点群为___________。
4115、乙烷分子的重迭式、全交叉式和任意角度时所属的点群分别为: , , 。
无机化学答案 第2章分子对称性与分子结构-习题答案

B
C
A
C
A
B
C2v
C
B
A
B
A
C
C2v
C
B
A
A
B
C
D2h
2.11 降为D2d对称性。
2.12 Td点群的阶为 24,共有E、C3、C2、S4、σd 5 类操作,相应每类操作的阶分别为 1、8、 3、6、6,不可约表示A1、A2、E、T1、T2的维数分别为一维、一维、二维、三维、三维。
3
2.13 (1)C3v点群的阶为 6; (2)对称操作类数为 3; (3)不可约表示数为 3; (4)NH3分子中偶极矩按照不可约表示A1方式变换; (5)绕z轴的旋转Rz所属的不可约表示为A2; (6)x,y 坐标所属的不可约表示为 E。
1,2,4 取代:最高次轴:C1,其他轴:无 1,3,5 取代:最高次轴:C3,3 个C2⊥C3
2.3(1)属Td点群,含对称元素:4C3、3C2、3S4、6σd
(2)属D4h点群,含对称元素C4、C2、2 C2' 、 2C2'' 、i、2S4、σh、2σv、2σd
(3)若忽略H原子,属C2v点群,含对称元素C2、2σv (4)属D3d点群,含对称元素C3、3C2'⊥C3、i、2S6、3σd (5)属C3v点群,含对称元素C3、3σv (6)属D2h点群,含对称元素C2、2C2'⊥C2、i、2σv、σh (7)属D∞h点群,含对称元素C∞、∞C2'、σh、∞σv、i、S∞ (8)属C2v点群,含对称元素C2、2σv
aA2 =1/24 [1×1×4+8×1×1+3×1×0+6×(-1)×0+ 6×(-1)×2]=0
aE =1/24 [1×2×4+8×(-1)×1+3×2×0+6×0×0+6×0×2]=0
北师大 结构化学 第4章 分子对称性和群论

北师大 结构化学 课后习题第4章 分子对称性和群论习题与思考题解析1. 以H 2O 为例说明对称操作和对称元素的含义。
解:H 2O 分子为V 型结构,若将该分子经过O 原子且平分H-O-H 键角的直线旋转1800便可得到其等价图形,该直线称为对称元素-对称轴,其轴次为2,即为二重轴,用2C 表示。
绕2C 轴的对称操作叫旋转,用2ˆC 表示。
2. 写出HCN ,CO 2,H 2O 2,CH 2==CH 2和C 6H 6分子的对称元素,并指出所属对称元素系。
答:HCN 分子的对称元素:1个C ∞轴、∞个v σ面,属于'v C ∞对称元素系。
CO 2分子的对称元素:1个C ∞轴、∞个2C 轴、1个h σ、∞个v σ面和i 对称中心;属于'h D ∞对称元素系。
H 2O 2分子的对称元素:只有1个2C 轴,属于'2C 对称元素系。
CH 2==CH 2分子的对称元素:3个相互垂直的2C 轴、3个对称面(1个h σ、2个v σ),对称中心i ;属于'2h D 对称元素系。
C 6H 6分子的对称元素:1个6C 轴、6个垂直于6C 轴的2C 轴、1个h σ面、6个v σ面、和对称中心i ,属于'6hD 对称元素系。
3. 试证明某图形若兼有2C 轴和与它垂直的h σ对称面,则必定存在对称中心i 。
证明:假设该图形的2C 轴与z 轴重合,则与它垂直的h σ对称面为xy 平面。
则对称元素2()C z 和()h xy σ对应的对称操作2ˆˆ(),()h C z xy σ的矩阵表示为: 2100ˆ()010001C z -=- 和 100ˆ()010001h xy σ=- 则 210010100ˆˆˆ()()010010010010011h C z xy i σ--=-=-=--由此得证。
4. 写出xy σ和通过原点并与x 轴重合的2()C x 轴的对称操作的表示矩阵。
解:空间有一点(x , y , z ),经过对称面xy σ作用后得到点(x , y , -z ),经过2()C x 对称轴作用后得到点(x , -y , -z ),所以xy σ和2()C x 对应对称操作2ˆˆ,()xy C x σ的矩阵为: 100ˆ010001xy σ=- 和 21ˆ010001C =-- 5. 用对称操作的表示矩阵证明:(1) 2ˆˆˆ()xy C z i σ= (2) 222ˆˆˆ()()()C x C y C z = (3) 2ˆˆˆ()yz xz C z σσ= 证明:(1) 因为对称操作2ˆˆ(),xy C z σ的矩阵为: 21ˆ()010001C z -=- 和 10ˆ010001xy σ=- 所以210010100ˆˆˆ()010010010010011xy C z i σ--=-=-=--,由此得证。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
谢谢10 解:若忽略分子中键和键之间的各种相互作用(共轭效应、空间阻碍效应和诱导效应等),则整个分子的偶极距近似等于个键距的矢量和。按矢量加和规则,C6H4ClCH3三种异构体的偶极距推算如下: ClCH3 3312222cos60CClCCHCClCCHo 2230305.17101.3410CmCm 123030125.17101.34102CmCm 304.6510Cm ClCH3 3312222cos60CClCCHCClCCHm 2230305.17101.3410CmCm 123030125.17101.34102CmCm 305.9510Cm ClCH3 3CClCCHp 30305.17101.3410CmCm 306.5110Cm 由结果可见,C6H4ClCH3 间位异构体偶极距的推算值和实验值很吻合,而对位异构体和邻位异构体,特别是邻位异构体两者差别较大。这既与共轭效应有关,更与紧邻的Cl原子和-CH3之间的空间阻碍效应有关。事实上,两基团夹角大于60。 【4.19】水分子的偶极矩为306.1810Cm,而2FO只有300.9010Cm,它们的键角值很近,试说明为什么2FO的偶极矩要比2HO小很多。 解:2HO分子和2FO均属于2vC点群。前者的键角为104.5,后者的键角为103.2。由于O和H两元素的电负性差1.24远大于O和F两元素的电负性差0.54,因而键矩OH大于键矩OF。多原子分子的偶极矩近似等于各键矩的矢量和,H2O分子和F2O分子的偶极距可分别表达为: 22104.52cos2103.22cos2HOOH称性
谢谢2 04分子的对称性 【4.1】HCN和2CS都是直线型分子,写出该分子的对称元素。 解:HCN:,C; CS2:2,,,,hCCi 【4.2】写出3HCCl分子中的对称元素。 解:3,3C 【4.3】写出三重映轴3S和三重反轴3I的全部对称操作。 解:依据三重映轴S3所进行的全部对称操作为: 1133hSC,2233SC,33hS 4133SC,5233hSC,63SE 依据三重反轴3I进行的全部对称操作为: 1133IiC,2233IC,33Ii 4133IC,5233IiC,63IE 【4.4】写出四重映轴4S和四重反轴4I的全部对称操作。 解:依据S4进行的全部对称操作为: 11213344442444,,,hhSCSCSCSE 依据4I进行的全部对称操作为: 11213344442444,,,IiCICIiCIE 【4.5】写出xz和通过原点并与轴重合的2C轴的对称操作12C的表示矩阵。 解:100010001xz, 12100010001xC 【4.6】用对称操作的表示矩阵证明: (a) 2xyCzi (b) 222CxCyCz (c) 2yzxzCz 解: (a)1122xyzzxxxCyCyyzzz, xxiyyzz
谢谢5 轴为3C或3I,轴次与点群记号中的n相同。当n为偶数时,最高对称轴为2nI,其轴次是点群记号中n的2倍。例如,丙二烯分子属2dD点群,最高对称轴为4I。轴次是点群记号中的n的2倍。 (d)正确。可以证明,若一个分子具有反轴对称性,即拥有对称中心,镜面或4m(m为正整数)次反轴,则它就能被任何第二类对称操作(反演,反映,旋转-反演或旋转-反映)复原。若一个分子能被任何第二类对称操作复原,则它就一定和它的镜像叠合,即全同。因此,分子本身有镜面时,其镜像与它本身全同。 【4.10】联苯6565CHCH有三种不同构象,两苯环的二面角分别为:(a)0,(b)090,(c)0090,试判断这三种构象的点群。 解: 【4.11】5SFCl分子的形状和6SF相似,试指出它的点群。 解:SF6分子呈正八面体构型,属hO点群。当其中一个F原子被Cl原子取代后,所得分子SF5Cl的形状与SF6 分子的形状相似(见图4.11),但对称性降低了。SF5Cl分子的点群为4vC。 图4.11 SF5Cl的结构
谢谢9 解:在C2H2分子中,C原子以sp杂化轨道分别与另一C原子的sp杂化轨道和H原子的1s轨道重叠形成的两个键;两个C原子的xp轨道相互重叠形成x键,yp轨道相互重叠形成y键,分子呈直线形,属hD点群,因而偶极距为0。而在H2O2分子中,O原子以3sp杂化轨道(也有人认为以纯p轨道)分别与另一个O原子的3sp杂化轨道和H原子的1s轨道重叠形成的两个夹角为9652的键;两OH键分布在以过氧键OO为交线、交角为9351的两个平面内,分子呈弯曲形(见4.15题答案附图),属2C点群,因而有偶极距。 在C2H4分子中,C原子以2sp杂化轨道分别与另一C原子的2sp杂化轨道及两个H原子的1s轨道重叠形成共面的3个键;两C原子剩余的p轨道互相重叠形成键,分子呈平面构型,属2hD点群(121.3,117.4CCHHCH)。对于N2H4分子,既然偶极距不为0 ,则其几何构型既不可能是平面的: NNHHHH 也不可能是反式的: NNHHHH 它应是顺式构型: NNHHHH 属2nC点群[见4.15题(f)],或介于顺式和反式构型之间,属2C点群。 反式-C2H2Cl2和顺式-C2H2Cl2 化学式相同,分子内成键情况相似,皆为平面构型。但两者对称性不同,前者属2hC点群,后者属2C点群。因此,前者偶极距为0,后者偶极距不为0。 分子的偶极距为0 ,表明它呈平面构型,N原子以2sp杂化轨道与C原子成键,分子属2hC点群。 分子的偶极距不为0,表明S原子连接的两苯环不共面。可以推测,S原子以3sp杂化轨道成键,分子沿着SS连线折叠成蝴蝶形,具有2C点群的对称性。 【4.18】已知连接苯环上CCl键矩为305.1510Cm,3CCH键矩为301.3410Cm。试推算邻位、间位和对位的643CHClCH的偶极矩,并与实验值4.15,5.94,306.3410Cm相比较。 SSNN
谢谢8 解: 注:由于N原子中有孤对电子存在,使它和相邻3个原子形成的化学键呈三角锥形分布。 【4.16】指出下列分子的点群、旋光性和偶极矩情况: (a) 33HCOCH (b) 32HCCHCH (c) 5IF (d) 8S(环形) (e) 22ClHCCHCl(交叉式) (f)BrN (g)NH2CH3Cl 解:兹将各分子的序号,点群,旋光性和偶极距等情况列表如下: 序号 点群 旋光性 偶极距 *a 2C 无 有 *b sC 无 有 c 4C 无 有 d 4dD 无 无 e 2hC 无 无 f sC 无 有 g 1C 有 有 注:在判断分子的点群时,除特别注明外总是将—CH3看作圆球对称性的基团。 【4.17】请阐明表4.4.3中4对化学式相似的化合物,偶极矩不同,分子构型主要差异是什么?
谢谢3 12xyzCi 推广之,有,1122xyxynznzCCi 即:一个偶次旋转轴与一个垂直于它的镜面组合,必定在垂足上出现对称中心。 (b) 12zxxCyyzz 这说明,若分子中存在两个互相垂直的C2轴,则其交点上必定出现垂直于这两个C2轴的第三个C2轴。推广之,交角为2/2n的两个轴组合,在其交点上必定出现一个垂直于这两个C2轴nC轴,在垂直于nC轴且过交点的平面内必有n个C2 轴。进而可推得,一个nC轴与垂直于它的C2 轴组合,在垂直于nC的平面内有n个C2 轴,相邻两轴的夹角为2/2n。 (c)yzxzyzxxxyyyzzz 12zxxCyyzz 12yzxzxC 这说明,两个互相垂直的镜面组合,可得一个2C轴,此2C轴正是两镜面的交线。推而广之,若两个镜面相交且交角为2/2n,则其交线必为一个n次旋转轴。同理,nC轴和通过该轴的镜面组合,可得n个镜面,相邻镜面之交角为2/2n。 【4.7】写出ClHCCHCl(反式)分子全部对称操作及其乘法表。 解:反式C2H2Cl2分子的全部对称操作为: 12,,,hECi 对称操作群的乘法为: 2hC E 12C h i E E 12C h i 12C 12C E i h h h i E 12C i i h 12C E 【4.8】写出下列分子所归属的点群:HCN,3SO,氯苯65CHCl,苯66CH,萘108CH。 解:
谢谢6 【4.12】画一立方体,在8个顶角上放8个相同的球,写明编号。若:(a)去掉2个球,(b)去掉3个球。分别列表指出所去掉的球的号数,指出剩余的球的构成的图形属于什么点群? 解:图4.12示出8个相同求的位置及其编号。 (a) 去掉2个球: 去掉的球的号数 所剩球构成的图形所属的点群 图形记号 1和2,或任意两个共棱的球 2C A 1和3,或任意两个面对角线上的球 2C B 1和7,或任意两个体对角线上的球 3dD C (b) 去掉3个球 去掉的球的号数 所剩球构成的图形所属的点群 图形记号 1,2,4或任意两条相交的棱上的三个球 5C D 1,3,7或任意两条平行的棱上的三个球 5C E 1,3,8或任意由3C轴联系起来的三个球 3C F 123456781234567812345678ABC 123456781234567812345678DEF 【4.13】判断一个分子有无永久偶极矩和有无旋光性的标准分别是什么?
谢谢4 分子 HCN SO3 C6H5Cl C6H6 C10H8 点群 C 3hD 2uC 6hD 2hD 【4.9】判断下列结论是否正确,说明理由。 (a) 凡直线型分子一定有C轴; (b) 甲烷分子有对称中心; (c) 分子中最高轴次n与点群记号中的n相同(例如3hC中最高轴次为3C轴); (d) 分子本身有镜面,它的镜像和它本身相同。 解: (a) 正确。直线形分子可能具有对称中心(hD点群),也可能不具有对称中心(vC点群)。但无论是否具有对称中心,当将它们绕着连接个原子的直线转动任意角度时,都能复原。因此,所有直线形分子都有C轴,该轴与连接个原子的直线重合。 (b) 不正确。因为,若分子有对称中心,则必可在从任一原子至对称中心连线的延长线上等距离处找到另一相当原子。甲烷分子(dT点群)呈正四面体构型,显然不符合此条件。因此,它无对称中心。按分子中的四重反轴进行旋转-反演操作时,反演所依据的“反轴上的一个点”是分子的中心,但不是对称中心。事实上,属于dT点群的分子皆无对称中心。 (c) 就具体情况而言,应该说(c)不全错,但作为一个命题,它就错了。 这里的对称轴包括旋转轴和反轴(或映轴)。在某些情况中,分子最高对称轴的轴次(n)与点群记号中的n相同,而在另一些情况中,两者不同。这两种情况可以在属于nhC,nhD和ndD等点群的分子中找到。 在nhC点群的分子中,当n为偶数时,最高对称轴是nC轴或nI轴。其轴次与点群记号中的n相同。例如,反式C2H2Cl2分子属2hC点群,其最高对称轴为2C轴,轴次与点群记号的n相同。当n为基数时,最高对称轴为2hI,即最高对称轴的轴次是分子点群记号中的n的2倍。例如,H3BO3分子属2hC点群,而最高对称轴为6I。 在nhD点群的分子中,当n为基数时,最高对称轴为nC轴或nI轴,其轴次(n)与点群记号中的n相同。例如,C6H6分子属6hD点群,在最高对称轴为6C或6I,轴次与点群记号中的n相同。而当n为奇数时,最高对称轴为2nI,轴次为点群记号中的n的2倍。例如,CO3-属3hD点群,最高对称轴为6I,轴次是点群记号中的n的2倍。 在ndD点群的分子中,当n为奇数时,最高对称轴为nC轴或nI轴,其轴次与分子点群记号中的n相同。例如,椅式环己烷分子属3dD点群,其最高对称
