抛物线焦点弦最小值的5种求法
抛物线焦点弦

抛物线焦点弦的性质及应用平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹叫做抛物线。
由于抛物线定义的特殊性,使得它有许多其他圆锥曲线所没有的特征,特别是抛物线过焦点的弦的性质尤其突出,同时也高考中经常要考查的内容。
设抛物线的方程为y 2=2px(P >0),过焦点F(p 2,0)作倾斜角为?的直线,交抛物线于P 、Q 两点,则线段PQ 称抛物线的焦点弦,(如图1).抛物线的焦点弦具有以下性质:4221p x x =性质1:设P(x 1,y 1),Q(x 2,y 2),则y 1y 2=-p 2. 证明:①当?=90?时,PQ 方程为x=p2代入y 2=2px中有y 2=p 2,即y 1=p,y 2=-p,∴y 1y 2=-p 2.②当?≠90?时,设直线PQ 斜率为k,则PQ 方程为y=k(x ﹣p2)与y 2=2px 联立,消x 后得到:ky 2-2py-kp 2=0,∴y 1y 2=-p 2.因为1212px y =,2222px y =,所以21222214x x p y y =∙,所以==∙=24222212144pp p y y x x 42p 例1过抛物线焦点的一条直线与它交于两点P 、Q ,通过点P 和抛物线顶点的直线交准线于点M ,求证:直线MQ 平行与抛物线的对称轴.证明:为了方便比较,可将P 点横坐标及Q 点纵坐标均用P 点的纵坐标y 1表示.∴P(y 212p ,y 1),Q(x 2,y 2),但y 1y 2=-p 2,∴y 2=﹣p 2y 1,PM 方程是:y=2p y 1x,当x=﹣p 2时,y=﹣p 2y 1即为M 点的纵坐标,这样M 点与Q 点的纵坐标相同,故MQ ∥Ox.[例2]设坐标原点为O ,抛物线y 2=2x 与过焦点的直线交于A 、B 两点,则OA ∙OB = .A 、43B 、-43C 、3D 、-3解析:设弦的两个端点为A (x 1,y 1)、B (x 2,y 2),x 1 x 2=42P , 221P y y -=,∴OA ∙OB =2121y y x x + =42P -2p =43432-=-p ,故答案选B 。
抛物线焦点弦最小值的5种求法

I I ABl + I Fl — AFI B —z +z + ,
再利 用均 值不等 式
引例 求 抛物 线 Y :2 x( > O 的 焦点 弦 的最 。 p p )
小 值.
I BI 1 2 /12 一2 . A —z +z + ≥ ̄ +户 p z
斜 率存 在时 , 抛物线 y =2 x ( >o 的焦 点 。 p 户 )
I AB 『i 2 p. 一
思 路 2 为避 免讨 论可 以在 直线 方程 的设 法上 做
物
文章 如 直线 = y 要 则直 含斜 . 果把 设成 m + 形式 线包
率不存 在 的情 况 .
抛 线 焦 F ,, A 的 程 : 物 的 点 ( 。直 B 方 为 号 )线 zm+ . — .号 y
由方程 组 y o =s ( - , cs O i O x 2) 消 n 由方程 组 消 得 : Y得
◇
湖 北 肖菊姣
【 :2 x Y p,
sn . 2 p( c s + sn ) + iz , - X 2。 i p2
s n : 。, i
1 足 积 分 性 庾
P, 以 l = +z +P≥2 当且 仅 当 z 一 z 所 l= AB = 。 p, 一
I 1 ・ 。p 21 ) Ai + √ )4一 ( . B √ 古 ( + p+ 一
因为 k 最 大值 , 以 l 无 最小 值. 无 所 ABI
要时 等号 所以 线y= p(>0的 取 . 抛物 Z 2 p ) 焦点弦的
特征 研究 焦点 弦 的定 值 、 量 问 题 , 养 学 生 对 问 题 定 培 研究 的兴 趣及研 究能 力 , 面 引例说 明焦点 弦最小 值 下 的几 种求 法.
过抛物线焦点弦的最小值问题

过抛物线焦点弦的最小值问题例题:已知抛物线 y2 =2px(p .0),过焦点的直线交抛物线于 A 、B 两点,则弦|AB|的最小值。
解法一:当斜率k 存在时,设直线AB 为y=k(x-上) 2«y =k(x-号)得 k 2x 2 -(k 2p+2p)x + — k 2 =0y 2 =2px42 即:X j X 2 , 过焦点弦 |AB|= x 1 x 2 p4由题意可知x 1 0, x 2 - 0,为• x 2丄2 . x 1x 2由于积是定值,当且仅当x^x 2时即为-时能取等号,所以当斜率k 不存在, 2 此时这条直线就垂直于 x 轴,过焦点的弦|AB|最小即通径最小。
最小值为 2p.解法二:设直线的倾斜角为 二,斜率存在时,则直线为y= tan (x-—)2 八曲(-2 y2 =2px 2得 tan 次-(ptan) 2 p)x tan - 0 2=2p(1 +2psin 2当sin 2r=i 时,|AB|有最小值即2p,此时斜率不存在,倾斜角二评价:解法一是用不等式思想求最值方法,当然用两根这积是也可以解法到求两根之积。
这种是确定动直线的位置关系来求最值的情况的。
解法二是建立函数关系式,用函数思想求最值。
这是两种不同方法来分析最值问题的。
这种方法是建立函数关系式来求最值问题。
在这方面题型有两种分析思想:一是能否确定动的位置关系来判断取最值的问题。
(如 解法一型),二是所求与已知建立一个函数关系式,用函数求最值或范围的方法。
这是我们解决中学数学问题时常用的解题思想。
X i代入 过焦点弦|AB|= x 1 x 2 p 2,即线段AB 为通径。
精美句子1、善思则能“从无字句处读书”。
读沙漠,读出了它坦荡豪放的胸怀;读太阳,读出了它普照万物的无私;读春雨,读出了它润物无声的柔情。
读大海,读出了它气势磅礴的豪情。
读石灰,读出了它粉身碎骨不变色的清白。
2、幸福幸福是“临行密密缝,意恐迟迟归”的牵挂;幸福是“春种一粒粟,秋收千颗子”的收获. 幸福是“采菊东篱下,悠然见南山”的闲适;幸福是“奇闻共欣赏,疑义相与析”的愉悦。
抛物线“焦点弦的性质”及解题策略

03
解题策略
利用焦点弦性质解题
焦点弦性质
对于抛物线上的任意一点P,其到焦 点F的距离等于到准线的距离。利用这 一性质,可以快速找到与焦点弦相关 的点P的坐标。
解题方法
利用焦点弦性质,可以求出点P的坐 标,进而求出与焦点弦相关的其他量, 如弦长、面积等。
在抛物线中,焦点弦的倾斜角可以通过轴线的倾斜角和该弦与轴线的夹角的补角之和(或差)来计算 。这个补角等于该弦与轴线的夹角的两倍。当焦点弦与轴线垂直时,其倾斜角等于轴线的倾斜角。
焦点弦的倾斜角
解题策略
根据题目给出的条件,选择适当的方法计算焦点弦的长 度、中点坐标或倾斜角。
熟悉抛物线的定义和性质,理解焦点弦的意义和特点。
02
焦点弦的性质
焦点弦的长度
总结词
焦点弦的长度等于通径的长度,等于焦准距的平方根。
详细描述
在抛物线中,焦点弦是指通过焦点的弦,其长度可以通过通径的长度来计算。 通径是过焦点的最短的弦,其长度等于焦准距的平方根。当焦点弦与抛物线的 轴线不垂直时,其长度还会受到其他因素的影响。
焦点弦的中点坐标
总结词
焦点弦的中点坐标等于焦点坐标加上弦中点与轴线的垂直距 离。
详细描述
在抛物线中,焦点弦的中点坐标可以通过焦点坐标和弦中点 与轴线的垂直距离之和来计算。这个垂直距离等于弦的长度 的一半乘以该弦与轴线的夹角的正切值。
焦点弦的倾斜角
总结词
焦点弦的倾斜角等于轴线的倾斜角加上或减去该弦与轴线的夹角的补角。
详细描述
解题方法
利用代数方法,可以建立方程组、不等式组等,进而求解与抛物线相关的问题。在解题过程中,需要注意方程组 的解法、不等式的性质等。
抛物线的焦点弦问题

(3)x2 2 py,
| AB | y1 y2 p
(4)x2 2 py, | AB | p y1 y2
例:过抛物线y2 2 px( p 0)的焦点的一条直线和
这条抛物线相交,两个交点的纵坐标为y1,y2 ,
求证 : y1 y2 p2.
y
证法 :因直线AB过定点F且与x轴
变题3 : 设M (a,0)是抛物线y2 2 px B
( p 0)的轴上的一个定点, 过M的
直线交抛物线于A(x1, y1)、B (x2, y2 )
两点,求证 : y1 y2与x1x2均为定值.
2.过抛物线 y2 2 px( p 0)的焦点的一条直线和
这条抛物线相交 , 两个交点的纵坐标为 y1、y 2,
|
PF
|
- y0
p 2
例1 :
(1)抛物线y2 x上一点P到焦点的
距离为2,则P点的坐标为__答_案__: P___74_,.
7
2
(2)抛物线y2 2x上两点A, B到焦点的距离
之和是5,则线段AB中点横坐标是 _答_案_:_2..
例2.斜率为1的直线过抛物线y2 4x的焦点,
交抛物线于A, B两点, 通过点A
A
和 抛 物线顶点的直线交抛物 o
线的准线于点D ,求 证 :直线
F DB
x
DB平行于抛物线的对称轴.
分析 我们用坐标法证明,即通 过建立抛物线及直线的方程, 借
图2.3 5
助方程研究直线DB与抛物线对
称轴之间的位置关系.
建立如图2.3 5所示的直角坐标系,只要证明 点D的纵坐标与点B的纵坐标相等即可.
有关抛物线焦点弦的十条性质[1]
![有关抛物线焦点弦的十条性质[1]](https://img.taocdn.com/s3/m/0134c60e55270722192ef74e.png)
有关抛物线焦点弦的十条性质—————从一道高考题的八种证法谈起本文对2009年湖北省高考数学理科第20题第(Ⅰ)问给出八种解法,同时总结有关抛物线焦点弦的十条性质。
一、原题再现 过抛物线22(0)y px p =>对称轴上一点(,0)A a(0)a >的直线与抛物线相交于M 、N 两点,自M 、N分别向直线:l x a =-作垂线,垂足分别为1M 、1N .(Ⅰ)当2pa =时,求证:11AM AN ⊥.二、一题多证证法1:设11(,)M x y 、22(,)N x y ,则11(,)2p M y -、12(,)2pN y -,则11(,)AM p y =-12(,)AN p y =-.显然直线MN的斜率不为0,故可设直线MN的方程为:2p x ty =+. 由222p x ty y px ⎧=+⎪⎨⎪=⎩得2220y pty p --=, 因为1y 、2y 是方程2220y pty p --=的两根, 由韦达定理得212y y p =-,从而可证得2111212(,)(,)0AM AN p y p y p y y ⋅=-⋅-=-+=,即证得11AM AN ⊥.证法2: 设211(,)2y M y p 、222(,)2y N y p ,因为M 、A 、N 三点共线,所以//AM AN,所以221221()()02222y y p p y y p p ---=,得212y y p =-,从而可证得2111212(,)(,)0AM AN p y p y p y y ⋅=-⋅-=-+=,即证得11AM AN ⊥.证法3:由抛物线定义可得:11MN MA AN MM NN =+=+,设211(,)2y M y p 、222(,)2y N y p,则11(,)2p M y -、12(,)2p N y -,将MN MA AN =+222122y y p p p++,化简得:2212()0y y p +=, 所以212y y p =-,从而可证得2111212(,)(,)0AM AN p y p y p y y ⋅=-⋅-=-+=,即证得11AM AN ⊥.证法4:设A 点内分MN 的比为λ,221212221201y y p p p y yλλλλ⎧+⎪⎪=⎨+⎪+⎪=+⎩,消去λ得:212y y p =-, 从而可证得2111212(,)(,)0AM AN p y p y p y y ⋅=-⋅-=-+=,即证得11AM AN ⊥.证法5:设211(,)2y M y p 、222(,)2y N y p ,则11(,)2P M y -,12(,)2P N y -∴211(,)2y OM y p= ,12(,)2P ON y =- ,由21122111()2222y y y P Py y y y p p --=+, 由性质1 212y y p =-,可得2121()022y P y y p --=,所以M 、O 、1N 三点共线,可求出,221p y y =-,即可得212y y p =-,从而可证得2111212(,)(,)0AM AN p y p y p y y ⋅=-⋅-=-+=,即证得11AM AN ⊥.证法6:设抛物线的参数方程为222x pt y pt⎧=⎨=⎩(t 为参数),于是可设211(2,2)M pt pt ,222(2,2)N pt pt ,因为M 、N 为两个不同点,则12t t ≠,由M 、A 、N 三点共线,所以//AM AN,可得方程221212()(4)0t t p t t p -+=,所以221240p t t p +=,得1214t t =-, 所以22121212224y y pt pt p t t p =⋅==-,从而可证得2111212(,)(,)0AM AN p y p y p y y ⋅=-⋅-=-+=,即证得11AM AN ⊥.证法7:以抛物线焦点为极点则其极坐标方程为1c o spρθ=-,则(,)M ρθ、(,)N ρπθ+,所以212sin (sin )1cos 1cos p py y p θθθθ=⋅-=--+,从而可证得2111212(,)(,)0AM AN p y p y p y y ⋅=-⋅-=-+=,即证得11AM AN ⊥.证法8:由抛物线定义得:1MM MA =、1NN NA =, 所以11MM A MAM ∠=∠、11NN A NAN ∠=∠, 因为11//MM NN ,所以11M MA N NA π∠+∠=, 即11(2)()MAM NAN πππ-∠+-∠=, 可得112MAM NAN π∠+∠=,所以112M AN π∠=,即证得11AM AN ⊥.四、引出性质性质1:已知抛物线y 2=2px(p >0)焦点弦AB 的坐标分别为(x 1,y 1)、B(x 2,y 2),则y 1y 2=-p 2,4221p x x =.性质2:以抛物线y 2=2px(p >0)焦点弦AB 端点向准线作垂线,垂足分别为M 、N ,则FM ⊥FN.(其中F 为焦点).性质3:以抛物线焦点弦在准线上的射影为直径的圆必与焦点弦相切于焦点。
高三数学二轮复习冲刺:抛物线的焦半径与焦点弦

抛物线的焦半径与焦点弦抛物线的焦点弦是抛物线中的高频考点,特别是对于考生而言,本节的结论既要注意把握推导过程,更应该注意对结论的熟悉程度,因为很多涉及到焦点弦的题目都会以选填的形式出现,如此,你便可以用相关结论快速做到,避免小题大做!一.重要结论抛物线的焦点弦具有丰富的性质,它是对抛物线定义的进一步考察,也是抛物线这节中最重要的考点之一,下面罗列出常见的抛物线焦点弦性质:假设抛物线方程为px y 22=.过抛物线焦点的直线l 与抛物线交于B A ,两点,其坐标分别为),(),,(2211y x B y x A .性质1.,2||p x AF A +=2||px BF B +=,p x x AB B A ++=||.证明:性质1的证明很简单,由抛物线的定义即可证得.如上图,过B A ,向准线引垂线,垂足分别为N M ,.由定义可知:||||||||BF BN AF AM ==,.代入坐标即可证得相关结论.性质2.抛物线px y 22=的焦点为F,),(),,(2211y x B y x A 是过F 的直线与抛物线的两个交点,求证:221221,4p y y p x x -==.证明:),2(),,2(222121y py B y p y A ,则AB 的方程为2(221211p y x y y p y y -+=-,整理可得:212112))((y px y y y y -=+-,即可得AB 的方程为:21212)(y y px y y y +=⋅+.最后,由于直线AB 过焦点,代入焦点坐标可得221p y y -=.再代入抛物线方程4221p x x =.一般地,如果直线l 恒过定点)0,(m M 与抛物线)0(22>=p px y 交于B A ,两点,那么pm y y m x x B A B A 2,2-==.于是,若AB OB OA ⇒⊥恒过定点)0,2(p .性质3.已知倾斜角为θ直线的l 经过抛物线px y 22=的焦点F ,且与抛物线交于B A ,两点,则(1)pFB F A P BF p AF 2||1||1cos 1||,cos 1||=++=-=,θθ.(2))11(2||sin 2sin 2||222k p AB p S p AB OAB+===∆,,θθ.证明:设准线l 交x 轴于点P ,过点A 作x AM ⊥轴于M ,作l AN ⊥于N ,由抛物线定义可知:AN AF =.其中p PF =,θcos ⋅=AF MF .所以θcos AF p FM PF AN +=+=,θcos AF p AF +=,故θcos 1-=pAF .同理θcos 1+=p BF ,所以θθ22sin 2cos 12pp BF AF AB =-=+=.性质4.抛物线的通径(1).通径长为p 2.(2).焦点弦中,通径最短.(3).通径越长,抛物线开口越大.由性质3易得,略.性质5.已知直线l 经过抛物线px y 22=的焦点F ,且与抛物线交于B A ,两点,若弦AB 中点的坐标为),(00y x ,则2(2||0p x AB +=.证明:设B A ,坐标为),(),,(2211y x y x ,由抛物线定义:p x x BF AF AB ++=+=21||||||,故)2(2||0p x AB +=.性质6.以焦点弦为直径的圆与准线相切.证明:设焦点弦的中点为),(:00y x M ,则M 到准线的距离为20px +,由性质5可证得.性质7.如图,过抛物线22(0)y px p =>的焦点F 的直线与抛物线相交于N M ,两点,自N M ,向准线l 作垂线,垂足分别为11,N M ,则(1)21FM FM ⊥;(2)记1111,,FNN N FM FMM ∆∆∆的面积分别为1S ,2S ,3S ,22134S S S =.注:此题为2009湖北卷文科试题,证明过程可参见该题解答.二.典例分析例1.(2017年全国1卷).已知F 为抛物线x y C 4:2=的焦点,过F 作两条互相垂直的直线21,l l ,直线1l 与C 交于B A ,两点,直线2l 与C 交于E D ,两点,则||||DE AB +的最小值为()A.16B.14C.12D.10解析:法1:设1122(,),(,)A x y B x y ,3344(,),(,)D x y E x y ,直线1l 方程为1(1)y k x =-取方程214(1)y x y k x ⎧=⎨=-⎩,得2222111240k x k x x k --+=∴21122124k x x k --+=-212124k k +=同理直线2l 与抛物线的交点满足22342224k x x k ++=由抛物线定义可知1234||||2AB DE x x x x p+=++++22122222121224244448816k k k k k k ++=++=++≥+=当且仅当121k k =-=(或1-)时,取得等号.法2:设1l 的倾斜角为α,则直线2l 的倾斜角为π2α+,根据焦点弦长公式有:2244πsin sin 2AB DE αα+=+⎛⎫+ ⎪⎝⎭()22222224416sin cos sin cos αααα+=+≥=+.故选A.法4:设点()()1122,,,A x y B x y ,则()221212121224AB x x p x x y y =++=++=++()212121224y y y y ⎡⎤=+-+⎣⎦设直线1l 的方程为1x my =+()0m ≠联立直线1l 与抛物线2:4C y x =方程消去x 可得2440y my --=所以121244y y m y y +=⎧⎨=-⎩,所以()221212122444AB y y y y m ⎡⎤=+-+=+⎣⎦同理244DE m =+,所以2248416AB DE m m +=++≥(当且仅当1m =±时等号成立)法5:可设直线12111:,:b x ky l b kx y l +-=+=,由抛物线焦点弦的性质3可得:)1(4||),11(4||22k DE k AB +=+=,故16)1(411(4||||22≥+++=+k kDE AB ,当且仅当1±=k 时取到最小值,故选A.上述例2,在知晓背景的情况下解答是很容易的,这再次说明记住一些重要的二级结论可以优化运算,提升解题速度.下例中,我们将看到有关面积的定值问题,从而为前面的重要结论做一个补充.例2.(2022新高考2卷)已知O 为坐标原点,过抛物线)0(2:2>=p px y C 的焦点F 的直线与C 交于A ,B 两点,点A 在第一象限,点()0M p ,,若AF AM =,则直线AB的斜率为A.直线AB 的斜率为2B.OB OF =C.4AB OF>D.180<∠+∠OBM OAM 解析:选项A:设FM 中点为N ,则32,24A N ppx x p +===所以()2233220,42A A A y px p p p y ==⋅=>所以,A y p =故2342AB p k p p ==-选项B:112112342p AF BF p BF p p +=⇒+=+5623B B p p BF p x x ⇒==+⇒=所以2222.33Bp p y p =⋅=所以22222227.9394B B p p p p OB x y =+=+=≠选项C:32524.4312pAB p p p p OF =++=>=选项D:由选项A,B知3,,,43pA p p B⎛⎫⎛⎫⎪ ⎪⎪ ⎪⎝⎭⎝⎭所以22233,0,4344p pOA OB p p p⎛⎫⎛⎫⋅=⋅=-=-<⎪ ⎪⎪ ⎪⎝⎭⎝⎭所以AOB∠为钝角;又22211,0,42331212p p pMA MB p p p p⎛⎫⎛⎫⋅=-⋅--=-=-<⎪ ⎪⎪ ⎪⎝⎭⎝⎭所以AMB∠为钝角;所以180OAM OBM∠+∠<︒.故选ACD.例3.抛物线24y x=的焦点为F,11(,)A x y,22(,)B x y 是抛物线上两动点,若123(2)2AB x x=++,则AFB∠的最大值为A.23πB.56πC.34πD.3π解析:)12122,2,()AF BF x x AB x x AB AF BF+=++++∴+.在AFB△中,由余弦定理得:()2222222222241331122AF BF ABcos AFBAF BFAF BF AF BF ABAF BFAB AB ABAF BF AF BF+-∠=⋅+-⋅-=⋅-=-=-⋅⋅,又213AF BF AB AF BF AB+∴⋅.所以221131,1223ABcos AFB AFBAB∠-=-∴∠⨯的最大值为23π.本题选择A选项.例4.(2022·广东·一模)已知抛物线2:4C y x=的焦点为F,抛物线C上存在n个点1P,2P,L,nP(2n≥且*Nn∈)满足1223112n n nPFP P FP P FP P FPnπ-∠=∠==∠=∠=,则下列结论中正确的是()A.2n=时,12112P F P F+=B.3n =时,123PF P F P F ++的最小值为9C.4n =时,13241114PF P F P F P F +=++D.4n =时,1234PF P F P F P F +++的最小值为8解析:当2n =时,1212PFP P FP π∠=∠=,此时不妨取12PP 过焦点垂直于x 轴,不妨取12(12),(12)P P -,,,则121111=+122P FP F +=,故A 错误;当3n =时,12233123PFP P FP P FP π∠=∠=∠=,此时不妨设123,,P P P 在抛物线上逆时针排列,设1,(0,)2PFx παα∠=∈,2222||,||241cos()1cos()33P F P F ππαα==-+-+,123222241cos 1cos()1cos()33PF P F P F ππααα++=++--+-+214(1cos )2211cos (cos 2ααα+=+-+,令113cos ,(,222t t α=+∈,则123242332t PF P F P F t t +++=+-,令242332()t t t f t +=+-,则232382627(1)()(32)(32)t t f t t t t t +--'=-=--,当112t <<时,()0f t '>,()f t 递增,当312t <<时,()0f t '<,()f t 递减,故min ()(1)9f t f ==,故当1t =,即1cos ,23παα==时,123PF P F P F ++取到最小值9,故B 正确;当4n =时,122313442PFP P FP P FP P FP π∠=∠=∠=∠=,此时不妨设1234,,,P P P P 在抛物线上逆时针排列,设1,(0,2PFx πθθ∠=∈,12342222||,||,||,||31cos 1cos()1cos()1cos()22PF P F P F P F ππθθπθθ====--+-+-+,即234222||,||,||1sin 1cos 1sin P F P F P F θθθ===++-,故1322241cos 1cos sin PF P F θθθ+=-++=,2422241sin 1sin cos P F P F θθθ+=+-+=,所以132242sin cos 144141PF P F P F P F θθ=++=++,故C 正确;由C 的分析可知:23422122244416sin cos sin cos sin 2PF P F P F P F θθθθθ++===++,当2sin 21θ=时,216sin 2θ取到最小值16,即1234PF P F P F P F +++最小值为16,故D 错误;故选:BC例5.(2018年全国2卷)设抛物线24C y x =:的焦点为F ,过F 且斜率为(0)k k >的直线l 与C 交于A ,B 两点,||8AB =.(1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程.解析:(1)设直线l 的方程为)0)(1(>-=k x k y ,且B A ,坐标为),(),,(2211y x y x ,联立方程可得:()214y k x y x⎧=-⎨=⎩得()2222240k x k x k -++=.216160k ∆=+=,故212224k x x k ++=.所以()()21224411k AB AF BF x x k +=+=+++=.由题设知22448k k+=,解得:解得:1=k ,故l 的方程为1-=x y .(2)由(1)可得AB 中点坐标为)2,3(,所以AB 的垂直平分线方程为5+-=x y ,设所求圆的圆心坐标为),(00y x ,则()()002200051116.2y x y x x =-+⎧⎪⎨-++=+⎪⎩,解得0032x y =⎧⎨=⎩,或00116.x y =⎧⎨=-⎩,因此所求圆的方程为()()223216x y -+-=或()()22116144x y -++=.注:此题以焦点弦性质6为背景展开.例6.已知抛物线C :()220,4y px p p =>≠,过点(2,0)A 且斜率为k 的直线与抛物线C 相交于P ,Q 两点.(1)设点B 在x 轴上,分别记直线PB ,QB 的斜率为12,k k .若120k k +=,求点B 的坐标;(2)过抛物线C 的焦点F 作直线PQ 的平行线与抛物线C 相交于M ,N 两点,求||||||MN AP AQ ⋅的值.解析:由题意,直线PQ 的方程为(2)y k x =-,其中0k ≠.设221212(,0),,,,22y y B m P y Q y p p ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,联立2(2)2y k x y px =-⎧⎨=⎩,消去x 得2240p y y p k --=.21212242160,,4p pp y y y y p k k∴∆=+>+==-.120k k += ,12221222y y y y m m pp∴+=--,即()()12121202y y y y m y y p +-+=.4202p p m p k⎛⎫-∴-⋅= ⎪⎝⎭,即2(2)0pm k +⋅=.0p > ,2m ∴=-,∴点B 的坐标为(2,0)-.(2)由题意,直线MN 的方程为2p y k x ⎛⎫=- ⎪⎝⎭,其中tanθk =,θ为倾斜角,则sin θ=,2122224114sin 1y y p AP AQ p k k k θ-⎛⎫∴⋅===+⋅ ⎪⎝⎭+设322344,,,22y y M y N y p p ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭.联立222p y k x y px⎧⎛⎫=-⎪ ⎪⎝⎭⎨⎪=⎩,消去x 得2220p y y p k --=.222343424240,,p p p y y y y p k k∴∆=+>+==-.342112MN y p k ⎛⎫∴=-=+⋅ ⎪⎝⎭22112||11||||214p MN k AP AQ p k ⎛⎫+⋅ ⎪⎝⎭∴=⋅⎛⎫+⋅ ⎪⎝⎭.例7.已知抛物线2:(0)E y ax a =>的焦点为,F A 为E 上一点,||AF 的最小值为1.(1)求抛物线E 的标准方程;()过焦点F 作互相垂直的两条直线121,,l l l 与抛物线E 相交于,P Q 两点,2l 与抛物线E 相交于,M N 两点.若,C D 分别是线段,PQ MN 的中点,求22||||FC FD +的最小值.解析:(1)抛物线E 的标准方程为24x y =.(2)由(1)得,点()0,1F ,显然直线1l ,2l 的斜率都存在且不为0,设直线1l 斜率为k ,则2l 的斜率为1k -,直线1l 的方程为1y kx =+,由214y kx x y=+⎧⎨=⎩消去y 并整理得2440x kx --=,216160k ∆=+>,设()11,P x y ,()22,Q x y ,则124x x k +=,所以线段PQ 中点()22,21C k k +,()2424k F k C =+,同理242114FD k k ⎛⎫=+ ⎪⎝⎭,所以242242114FC k F k k D k ⎛⎫=+++ ⎝+⎪⎭,令2212t k k =+≥=,当且仅当221k k =,即21k =时等号成立.所以24412t k k=++,且[)2,t ∈+∞,所以()()222221424249162t t t t t FC FD ⎛⎫=+-=+-=+-≥ ⎪⎝+⎭,当且仅当2t =时取等号,所以22FC FD +的最小值为16.例8.已知抛物线C :()220x py p =>,F 为抛物线C 的焦点,()0,1M x 是抛物线C 上点,且2MF =;(1)求抛物线C 的方程;(2)过平面上一动点(),2P m m -作抛物线C 的两条切线PA ,PB (其中A ,B 为切点),求11AF BF+的最大值.解析:(1)抛物线2C 的方程为24x y =;(2)抛物线2C 的方程为24x y =,即2'xy =,设()11,A x y ,()22,B x y ,(),2P m m -则切线PA ,PB 的斜率分别为12x,22x .所以切线PA :,)(2111x x x y y -=-∴211122x x y x y =-+,又2114x y = ,11220y x x y ∴-+=,同理可得切线PB 的方程为22220y x x y -+=,因为切线PA ,PB 均过点(),2P m m -,所以112240y mx m -+-=,222240y mx m -+-=,所以直线AB 的方程为2240y mx m -+-=.联立方程222404y mx m x y -+-=⎧⎨=⎩,消去x 整理得()()2222420y m m y m --++-=,∴()()()222222442480m m m m m m ∆=-+--=-+≥,∴m R ∈.∴21224y y m m +=-+,()2122y y m =-由抛物线定义可知11AF y =+,21BF y =+,所以11AF BF AF BF AF BF++=∵()()()121212111AF BF y y y y y y =++=+++2269m m =-+,∴2223+112612+2692269m AF BF m m AF BF AF BF m m m m +-+==+-+-+,令32m t R+=∈∴原式21111454522221221222t t t t t=+=+-++-≤。
抛物线的焦点弦_经典性质及其证明过程

有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点 结论1:p x x AB ++=21结论2:若直线L 的倾斜角为θ,则弦长θ2sin 2pAB =证: (1)若2πθ= 时,直线L 的斜率不存在,此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为:θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot1pp y y AB =+=-+=结论3: 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短. 结论4: )(832为定值p AB S oAB =∆结论5: (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P Py y x x p y x p y x ==∴== 结论6:以AB 为直径的圆与抛物线的准线相切证:设M 为AB 的中点,过A 点作准线的垂线AA 1, 过B 点作准线的垂线BB 1, 过M 点作准线的垂线MM 1,由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7:连接A 1F 、B 1 F 则 A 1F ⊥B 1F同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8:(1)AM 1⊥BM 1 (2)M 1F ⊥AB (3)BF AF FM ⋅=21(4)设AM 1 与A 1F 相交于H ,M 1B 与 FB 1相交于Q 则M 1,Q ,F ,H 四点共圆 (5)2121214M M B M AM =+证:由结论(6)知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形, M 1 是斜边A 1 B 1 的中点∴M 1F ⊥ABBF AF F M ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM︒=∠∴90FB A 11 所以M 1,Q ,F,H 四点共圆,22121AB B M AM =+结论9: (1)、A O 、B 1 三点共线 (2)B ,O ,A 1 三点共线(3)设直线AO 与抛物线的准线的交点为B 1,则BB 1平行于X 轴(4)设直线BO 与抛物线的准线的交点为A 1,则AA 1平行于X 轴证:因为p y p y k y p py y x y k oB oA 2212111122,221-=-====,而221p y y -=所以122222oB oA k p y y p pk =-=-=所以三点共线。
抛物线焦点弦的性质及其应用

抛物线焦点弦的性质及其应用2000.1~2口知识应用抛物线焦点弦的性质及其应闻广东省湛江一中(524038)王增生抛物线焦点弦具有不少性质,均散见在各类书刊上.本文将系统地归纳集中,以期对焦点弦的几条最主要的性质有一个更全面的,更深刻的了解.从而进一步提高运用这些性质去解决相关问题的数学素质和应用能力.1.焦点弦(通径)的定义通过抛物线焦点的直线(不与抛物线对称轴平行)被抛物线截得的线段,叫做抛物线的焦点弦,如图(1).线段…D图B叫做抛物线Y=2px(户>O)的焦点弦?当AB垂直于抛物线的对称轴时.AB叫做抛物线的通径.2.焦点弦的性质定理l抛物线焦点弦长等于2户(1+古)或.并且以通径长为最小,最小值为2户.(其中,S1n.口或口为焦点弦的斜率或倾斜角O.<a<180.)证:AB所在直线为y=k(x一号)代人y2—2px,整理得:屉2X2--(屉:+2)户+:o.这里.+:=(1+吾)户.据图(1)和抛物线的定义知,IABI---- IAFI+II=laAI+IBBI=十号)+(z十号)=2户(1+吉)或令^=tg口,则IABI=2户(1+ 去)=i2_nL:.显然当屉+..或a专时,焦点弦AB即为通径,其长度为最小值2户.定理2抛物线焦点弦的两个端点的同名坐标之积分别为常数譬和一户.证:由图(1),不妨设A(1,y.),B(.2,Y2),据定理1证明过程知??.=等,将y=k(x一号)(≠o)改写成=T1(+譬)代人2=2px,整理得亭大界(一由It)一2py--/,k=O,.Y1Y2=一声.定理3抛物线焦点弦的两个蛸点在准线上的射影和焦点的莲线互相垂直.证明:如图(2)记A,B分别是焦点弦A(,y1),B(:,Y:)在准线上的射影,则,(一,y1),B(一粤,y2).因为kA'F=二,Kt,=?警JI.,_一A/….一竣.2)及定理2知?弛=--.I'可得屉,,'kB'F~--1,...AF上BF.定理4抛物线焦点弦为直径的圆必切此抛物线的准线.证:如图(3),M为弦AB的中点,A,M:B在准线=一号上的投影分别是A,M,B,据抛物线的定义,得IBFI=IBBl,J;_一lAFI=lAA,I,IABl=f从I+fBB1.村为梯形ABBA的中位线,...IMMI=÷(IAAI+I●1船1)=÷IA引,焦点弦为直径的圆必与准线相6 切..定理5抛物线焦点弦的两个端点的切线互相垂直.并且交点必在准线上.让:郊幽【4),凼切点锾AB过焦点F(詈,0),以由定理2知1.y2一户?又屉柚,屉=蚩?..屉柚'鼬==兰一1,...AQ~BQ,故有切线百相垂富.I/.5l数掌大世界(一巾版)设两切线的交点为Q(x.,Y.).易知切点弦方程为=户(+Xo).将(告,O)t~A,得户(Xo+告)=0.-..0=一告,即Q(.,.)在准线一一告上.特别地,当焦点弦为抛物线的通径时,其切线的交点即为对称轴与准线的交点.定理6如果抛物线两条切线的交点在准线上.则切点弦必为焦点弦.证;由定理5证明过程知,切点弦的方程为Y oY=P(+0).令=0,则=一.因为点Q(0,)在准线上,..一一告.一告,即切点弦必过焦点.3.应用举例例1设.为抛物线的顶点,F为焦点,且PQ为过F的弦.已知lOFl—a,lPQl一6.求/xOPQ的j,r.图(5)面积.(91年全国高中联赛试题)解:由题意知P一2a,所以抛物线可设为Y=4n(n>0)据定理1,lQ『=.sinn一旦鱼,记Y,Yz分别为P,Q两点的纵坐标,则S△P0.=÷l OFl(1Ytl+lY21)一÷lOFllPQl?sina=÷absinO一.~/,.?例2抛物线Y=4p(+户)(户>0)中有两条过原点且互相垂直的直线分别交抛物线于A,B,C, D,试求IABl+lCDl的最小值.解:设AB与抛物线的对称轴OX的倾斜角为n (0,<180.),由坐标平移性质知,原点.恰为抛物线的焦点F?因此由定理1知lABl=,ICDI=4p(0.<口-(180.)...IABI+ICDI一4户(sin+COS'口'口)=≥16户.这里当且仅当n一7r一_~347r时取等号,.'.1ABl+lCDl的最小值是16p.例3过抛物线焦点F的直线交抛物线于P,Q两点,PQ的垂直平分线交抛物线的对称轴于R.求证:lFRl=÷lPQl(97广东赛题)证:为不失一般性,设抛物线方程为Y=2px(户>0)如图(6),由定理1知,lPQl一乞.直线PQ的S2?2000.1~2-q参数方程为{专+0s(f为参数).代入22(y=tsina2px整理得t2sin口一2ptcosa--p=0.依题意,lFl=1l:1一....IFRI一:一1lPQ1.例4如图(7),A,B为抛物线Y一2px焦点弦AB在准线上的射影,Q是焦点弦端点的两条切线的交点.求证,Q,K,F,S四点共圆.证:由定理3知AF上BF,由定理5,AQJ-BQ,所以Q,K,F,S四点共圆.例5过抛物线Y一4x的焦点F弦AB的中点的纵坐标为4,求AOB的大小.(o为坐标原点)L'..《JF..<马图(7)证:由定理5易知AOB必为钝角,lOAf=} +},lOBl一l+Yl,lABl:(l—2)+(—Y2),一兰兰±!而~/(l2)+(lY2)+(lY2)+(2Y1)由定理2知12—1,YlY2=一4且一lY2,Yl2,一0.'.COSAOB一——=====兰l-=~/17-t-y~-t-y;.:一一3~/17+(l+她)一2ylY2因为Yl+Y2=8,-..COSAOB=一—,即,.~/890.fAOB一一arccos—兰=.~/89例6从抛物线=2px的准线上任取一点P,作抛物线的两条切线PA,PB,A召为切点.求/xPAB外接圆面积的最小值.解:由定理6知,切点弦即为焦点弦AB.由定理5知,焦点弦AB为直径的圆必与准线相切...-点P 即为直线=一要和以A8为直径的圆相切时的切●l点,再由定理1知,当焦点弦为通径时,△APB的外接圆面积将最小.此时R—P,因此面积最小值为玎户.例7如图(8),从抛物线Y一2px(户>O)的准线上一点Q引两条切线QA,QB,A,B为切点.且A,B在准线上的射影为D,D,连结QF.求证:(1)DQA:AQF,FJ:D——…//Q\——图(8)一BQD,(2)线段IAFI,IQFJ,IBFI成等比数列.证:(1)记点Q(一鲁,Y o).由定理6知,切点弦AB必过焦点F,.AB方程可写为一(一等),一一,又.,一Y o,五.五.,一一1,?QF上AB.由抛物线定义知IAFI=IADI,IBFI=IBDI,.'.AQ,BQ分别平分FQD,FQD,...ADQ:AQF,BQF=BQD.(2)由定理5知AQ上BQ,.在Rf/xAQB中有fOFI=IAF}.IBFI,故lAFI,IOFI,lBFI成等比数列.例8定长为3的线段AB的两个端点在抛物线上移动,记线段AB的中点为M.求点M到Y轴的最短距离,并求此时点M的坐标.解:这是87年高考理科的一道压轴题,解法甚多,如果用上述定理解可以说比任何一种方法都简捷明快得多.事实上,点M到Y轴的距离最短,等价于以AB为直径的圆的圆心到准线一一÷的距离最短,由定理4知当线段AB经过焦点(÷,o)且以AB为直径的圆恰好与准线相切,此时易知圆的半径为R—llABl=32....点M到轴最短距离为3一1一C.÷.由定理5知,焦点弦端点的切线交点必在准线上....其中必有FMY.,注意到切点弦的斜率五=A._一2z一,又五=五一=一一一,即一....一士.因此所求点M的坐标为(辜,士).口学生习作数学大世界(■{ll版)甥发觉陶锚解江西莲花中学高三)(337100)周雁一,理解性错解例1设,(,z)一1+2+3+…+,z,求lira器的值错解:..'f(n)=1+22"+…+,z一÷(+1)(2n+1),(,z)]一(1+2+…+,z);÷,z(,z+1).而f(nz)==2(1+)(2+)——_一03n(1+)析':这是由于对f(n)的理解而导致的错解.其实,f(n)表示前,z个自然数的和,即f(n.)一1+2 +…+(,z2—1)+,z2一÷,z(,z+1),故告=2.,例21+2i是方程+tx+8=0的一个根,求t的值.错解:...1+2是方程的一个根,所以1—2i也是方程的一个根,故t一一((1+2)+(1—2)]=一2.析:这是由于把t错认为是实数,而本题并没有说明t是实数,其实,(1+2)+t(1+2i)+8—0,.t 1—4+4+85+4i6i一13一—主一一丁二,忽视定义域而导致的镶解例3函数,()的定义域关于原点对称,且对于定义域中任意两个不同的值.,,都有f(x一)=今毒,求,)是何种函数?错解:设是定义域中的一个值,令=0,一得f(--x)=再令Xl—,=0得,,)一今:一一一,c—...厂)是奇函数.析:显见,函数,(奎)的定义域不一定包含零. 正解:由已知式fCT--X一今毒,说明-与z的差.--X一在定义域内,因其它义域是关于原点对称的,所以一=z—也在定义域内,则有f(一.)f7(x2)f=(x7z)+1一一f(x1),(2)+1一f(x2)一f(x1)于是f(xl--X2)+f(x2一1)一0即f()+f(--)=0.因此,,()是奇函数.53。
关于抛物线的十个最值问题

竭诚为您提供优质的服务,优质的文档,谢谢阅读/双击去除关于抛物线的十个最值问题本文用初等方法讨论了与抛物线有关的若干几何最值问题,得到了十个有趣的结论.为方便读者摘用,现用定理形式叙述如下:定理1.抛物线的所有焦半径中,以过顶点的焦半径为最短.证明:不妨设抛物线的极坐标方程为ρ= ,则显然有ρ≥ ,其中等号成立当且仅当θ=2kπ+π(k∈Z)即焦半径通过抛物线的顶点时.证毕.定理2.抛物线的过焦点的所有弦中,以抛物线的通径为最短.证明:设抛物线极坐标方程为ρ= ,焦点弦为Ab,且设A(ρ1,θ),b(ρ2,θ+π),则有│Ab│=ρ1+ρ2= + = ≥2p=通径长,其中等号成立当且仅当θ=kπ+π/2(k∈Z)即弦Ab为通径时.证毕.定理3.设A(a,0)是抛物线y2=2px(p>0)的对称轴上的定点,m(x,y)是抛物线上的动点,则│mA│min=证明:由│mA│2=(x-a)2+y2=(x-a)2+2px=x2-2(a-p)x+a2 =[x-(a-p)]2+p(2a-p),并且注意到x∈[0,+∞),立知结论成立.证毕.定理4.设A(a,b)是抛物线y2=2px(p>0)内一定点,F是焦点,m是抛物线上的动点,则(│mA│+│mF│)min=a+p/2.Q m A(a,b)证明:如图1所示,作AQ⊥准线L:x=-p/2于Q,则知o F x(│mA│+│mF│)min=│AQ│=a-(-p/2)=a+p/2.证毕. 图1定理5.设线段Ab是抛物线y2=2px(p>0)的过焦点的弦,分别以A、b 为切点的抛物线的两条切线相交于点m,则三角形Abm的面积的最小值为p2.证明:设A(x1,y1),b(x2,y2),则由A、F、b三点共线可得:x1y2-x2y1=p/2.(y2-y1) (1)于是利用(1)式由两切线方程yAm:y1y=p(x+x1),Abm:y2y=p(x+x2),m F x易得m的坐标(x,y)适合: b∵kmF·kAF=-1,∴mF⊥Ab,即│mF│是△mAb的Ab边上的高. 图2∵│mF│≥│FK│(焦点F到准线x=-p/2的距离)=p,又由定理2知│Ab│≥2p(通径长),∴s△mAb=1/2·│Ab│·│mF│≥1/2·2p·p=p2,因其中等号当且仅当Ab⊥x轴时成立,故三角形mAb的最小值为p2.证毕.定理6.过抛物线y2=2px的顶点o引两条互相垂直的动弦oA和ob,则三角形oAb的面积的最小值为4p2. y证明:设A(x1,y1),b(x2,y2),则由oA⊥ob得Ax1x2+y1y2=0 (1)o x将y12=2px1,y22=2px2代入(1)立得:x1x2=4p2 (2)于是b(s△oAb)2=1/4·│oA│2·│ob│2图3=1/4·(x12+y12)·(x22+y22)=1/4·(x12+2px1)·(x22+2px2)=1/4·[(x1x2)2+2px1x2(x1+x2)+4p2x1x2]≥1/4.[(x1x2)2+2px1x2(2√x1x2)+4p2x1x2] (3)将(2)式代入(3)则得(s△oAb)2≥16p4,从而s△oAb≥4p2,因其中等号当x1=x2=2p时取到,故三角形oAb的面积的最小值为4p2。
5抛物线焦点弦问题专题性质
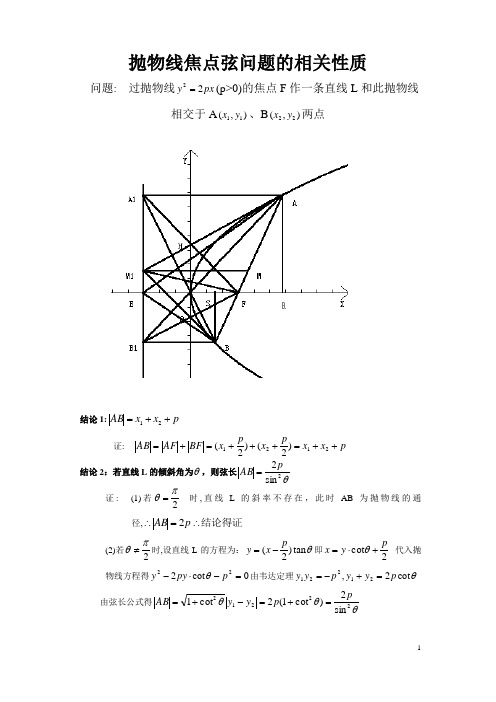
抛物线焦点弦问题的相关性质问题: 过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点结论1:p x x AB ++=21证: p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2:若直线L 的倾斜角为θ,则弦长θ2sin 2pAB = 证: (1)若2πθ=时,直线L 的斜率不存在,此时AB 为抛物线的通径,结论得证∴=∴p AB 2 (2)若2πθ≠时,设直线L 的方程为:θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-= 由弦长公式得θθθ22212sin 2)cot 1(2cot 1pp y y AB =+=-+=结论3: 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短.结论4: )(832为定值p AB S oAB =∆()8s i n 2s i n s i n 2221s i n 21s i n 21s i n 21s i n 2132220P AB S p p p AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ 结论5: (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P P y y x x p y x p y x ==∴==结论6:以AB 为直径的圆与抛物线的准线相切证:设M 为AB 的中点,过A 点作准线的垂线AA 1, 过B 点作准线的垂线BB 1, 过M 点作准线的垂线MM 1,由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7:连接A 1F 、B 1 F 则 A 1F ⊥B 1FFAA FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8:(1)AM 1⊥BM 1(2)M 1F ⊥AB (3)BF AF FM ⋅=21(4)设AM 1 与A 1F 相交于H ,M 1B 与 FB 1相交于Q 则M 1,Q ,F ,H 四点共圆 (5)2121214M M B M AM =+证:由结论(6)知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形, M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴︒=∠=∠+∠9011111M AA M FA F AA ︒=∠+∠∴90111FM A AFA ∴M 1F ⊥ABBF AF FM ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM︒=∠∴90FB A 11 所以M 1,Q ,F,H 四点共圆,22121AB B M AM =+()()()2121211242MM MM BB AABF AF ==+=+=结论9:(1)、A O 、B 1 三点共线 (2)B ,O ,A 1 三点共线(3)设直线AO 与抛物线的准线的交点为B 1,则BB 1平行于X 轴(4)设直线BO 与抛物线的准线的交点为A 1,则AA 1平行于X 轴 证:因为p y p y k y pp y y x y k oB oA 2212111122,221-=-====,而221p y y -=所以122222oB oA k p y y ppk =-=-=所以三点共线。
抛物线焦点弦的性质结论归纳与应用

数理化解题研究2021年第07期总第500期抛物线焦点弦的性质结论归纳与应用韩义成(甘肃省积石山县积石中学731700)摘要:抛物线是近几年高考考查的重要内容,而抛物线焦点弦问题是一种主要类型.本文归纳总结了抛物线焦点弦问题的七大性质结论,并对结论做了证明,通过例题对结论进行了应用•关键词:抛物线;焦点弦;结论;应用中图分类号:G632 文献标识码:A 文章编号:1008 -0333(2021)07 -0046 -03我们在平时的学习中善于归纳总结一些数学的性质和结论,就能提高解题的效率和速度,做到事半功倍的效果•下面是我在教学中归纳总结的抛物线焦点弦问题的性质和结论,供参考.若4B 是抛物线y 2 —2 p % (p >0)的焦点弦(过焦点的弦),且4(%1 加),B (%2』2)•结论 1 |4F| - %"号,|BF| - %2+号.结论 2 4B — %1 + %2 + P.结论3(1)若4B 是抛物线y 2 —2p%(p >0)的焦点2P 弦,且直线4B 的倾斜角为a ,则4B —笃(a H0).sin a(2)焦点弦中通径(过焦点且垂直于抛物线对称轴的弦)最短.证明(1)设4(%1 ,y 1) ,B (%2,y 2),直线4B 方程为y二 k (% -号)•y — k (% -斗) : :由] 2 得 ky 2 - 2py - kp 2 — 0.'y 2 —2p%,所以 y 1 + ” —平 y y 2 — 一 p •—2p(1 + k 2)二 k 2—2p(1 + tan 2 a )tan 2 a2P — sin 2 a易验证,结论对斜率不存在时也成立.(2)由(1)知,当4B 为通径时,a —90°,sin 2a 的值最大,4B 最小.例1已知过抛物线y 2 —9%的焦点的弦4B 长为12,则直线4B 倾斜角为 •解析 由结论可得12 — .92 (其中a 为直线4B 的sin a 倾斜角),则sin a - ± 2;,所以直线4B 倾斜角为:或響结论4两个相切:(1)以抛物线焦点弦为直径的圆 与准线相切.(2)过抛物线焦点弦的两端点向准线作垂线,以两垂足为直径端点的圆与焦点弦相切.已知:4B 是抛物线y 2 —2p%(p >0)的过焦点F 的弦,求证:(1)以4B 为直径的圆与抛物线的准线相切.(2)分别过点4、B 作准线的垂线,垂足为点M 、N ,求证:以MN 为直径的圆与直线4B 相切.证明(1)设4B 的中点为Q ,过点4、Q 、B 向准线/ 作垂线,垂足分别为点M 、P 、N ,连接4P 、BP.由抛物线定义,知4M — 4F .所以 QP — 1 ( 4M + BN )收稿日期:2020 -12 -05作者简介:韩义成,中学高级教师,从事高中数学教学研究.—46—2021年第07期总第500期数理化解题研究-2(AF+BF)-2AB.所以以AB为直径的圆与准线/相切.证明抛物线焦点为F12,0;设直线AB的方程为%-my+2,代入抛物线方程’得y2-2pmy-p-0.若设A(%;,y;),B(%2』2),贝J y;y二一p•因为BC〃%轴,且点C在准线%--号上,所以点C坐标为(-斗,y2)•故%二旳-纽.又由y;-2p%;,得2一a y;2(2)如图2,取MN中点P,连接PF、MF、NF.因为AM-AF,AM〃OF,所以Z AMF-Z AFM,乙AMF-乙MFO.所以Z AFM-Z MFO.同理,乙BFN-乙NFO.所以Z MFN-2(乙AFM+乙MFO+Z BFN+ SFO)-90°.所以MP-NP-FP-2MN•所以乙PFM-乙FMP.所以乙AFP-乙AFM+Z PFM-Z FMA+乙FMP-Z PMA-90°.所以FP丄AB.所以以MN为直径的圆与焦点弦AB相切.结论5若AB是抛物线y2-2p%(p>0)的焦点弦,且2A(%;,y;),B(%2』2),则%;%2-4,y;y2二一p•证明因为焦点坐标为F(2,0),当AB不垂直于%轴时,可设直线AB的方程为y-%(%-彳)•由y-蚁%一知’得叶一2p y-伽2-0.、y2-2p%,亦山—2_y;y2_p_P所以y;y2--p,%;%2-2p•2p-4p2-4•当AB丄%轴时’直线AB方程为%-号,贝U y;二卩』2二-p・所以y;y2--p•同理,%;%2-:.例2设抛物线y2-2p%(p>0)的焦点为F,经过点F 的直线交抛物线于A、B两点•点C在抛物线的准线上,且BC〃%输证明:直线AC经过原点O.k A0-y;-2卩,故忍。
盘点抛物线的焦点弦问题

盘点抛物线的焦点弦问题作者:罗文军来源:《中学生数理化·高二数学》2019年第01期设直线l经过抛物线的焦点F,且与抛物线C交于A、B两点(直线AB的倾斜角为a),设A(x1,y1),B(x2,y2),0为坐标原点,准线方程为:x=,则关于抛物线C的焦点弦有以下九条常用的性质:(8)以AB为直径的圆与准线相切:(9)以AF、BF为直径的圆都与y轴相切。
以下运用上面焦点弦的性质来破解一些比较经典的焦点弦问题。
例1(2018年高考全国II卷理科第19题)设抛物线C:y2=4x的焦点为F,过F且斜率为k(k>0)的直线l与抛物线C交于A、B两点,且|AB|=8。
(1)求直线l的方程:(2)求过点A、B且与抛物线C的准线相切的圆的方程。
解析:(1)解法1:由题意得点F的坐标为(1,0),直线l的方程为y=k(x-1)(k>0)。
设AB的中点的坐标为(x0,y0),由中点坐标公式可得,。
所以y0=x0-1=2,直线AB的垂直平分线的方程为y=-x+5。
评注:第一问中的解法1将直线方程与抛物线方程联立消元后,再运用了抛物线的焦点弦公式,最后解出k的值,得出直线的方程。
解法2运用了弦长公式这个公式只适用于抛物线y2=2px(p>0)的焦点弦问题。
第二问要求圆的方程,首先要确定圆心坐标与半径,线段AB为所求圆的弦,根据弦AB的垂直平分线经过圆心,再根据垂径定理,直线与圆相交时,|AB|=,其中r为圆的半径,d为圆心到直线的距离,解方程可得出圆心坐标和半径长。
例2设F为抛物线C:y2=4x的焦点,过F且倾斜角为30°的直线交抛物线C于A、B两点,O为坐标原点,则△AOB的面积为____。
解析:由题设可得,p=2,所以。
因此,△AOB的面积为4。
评注:本题属于小题,可直接运用抛物线的焦点弦的性质,得出所求三角形的面积,思路简单明了。
例3设抛物线C:y2=4x的焦点为F,直线l过F且与抛物线C交于A、B两点,若|AF|=(3+2/2)|BF|,则直线l的方程为____。
抛物线垂直焦点弦面积最小值

抛物线垂直焦点弦面积最小值抛物线垂直焦点弦面积最小值引言概述抛物线垂直焦点弦面积最小值具有繁多的种类和巨大的数量,如果不能够科学处置,将会严重污染到水、大气以及土壤环境。
近些年来,抛物线垂直焦点弦面积最小值产生量呈现出不断增长的态势,迫切需要深入治理。
因此,抛物线垂直焦点弦面积最小值要依据生态文明建设要求,结合抛物线垂直焦点弦面积最小值的产生原因以及处置利用中暴露的问题,及时采取针对性的优化措施,减少抛物线垂直焦点弦面积最小值产生量的基础上,高效利用抛物线垂直焦点弦面积最小值。
1抛物线垂直焦点弦面积最小值的概念1.1抛物线垂直焦点弦面积最小值种类通常情况下,可从三个方面划分抛物线垂直焦点弦面积最小值的种类。
第一,工业抛物线垂直焦点弦面积最小值。
工业生产过程中,难免会有气体、固体、液体等诸多形式的污染物产生。
工业抛物线垂直焦点弦面积最小值涵盖一般废物与危险废物两种,前者的危害较小,后者的腐蚀性,毒性较强,会在较大程度上危害到人体健康与环境。
第二,城市抛物线垂直焦点弦面积最小值。
城市运行过程中,将会有建筑垃圾、商业垃圾等大量的抛物线垂直焦点弦面积最小值产生。
特别是近些年来,随着城市规模的扩大,抛物线垂直焦点弦面积最小值量也显著增加。
第三,农业抛物线垂直焦点弦面积最小值。
植物秸秆、动物粪便等为农业抛物线垂直焦点弦面积最小值的主要类型,如果不能够科学处置,也会污染到生态环境。
1.2抛物线垂直焦点弦面积最小值的影响抛物线垂直焦点弦面积最小值往往经过一段时间的积累后,方才会逐渐体现出对抛物线垂直焦点弦面积最小值的污染。
第一,抛物线垂直焦点弦面积最小值污染水体。
在雨水、重力沉降等作用下,抛物线垂直焦点弦面积最小值地表水系内容易进入空中漂浮的抛物线垂直焦点弦面积最小值细小颗粒,颗粒溶解后,有害成分将会在水中产生。
抛物线垂直焦点弦面积最小值如果向河流中排放大量的抛物线垂直焦点弦面积最小值,河道将会遭到堵塞,出现不同程度的淤积现象。
抛物线焦点弦最小值的5种求法

性质 2 若 y=f( 在[ 上是增函数 , 且 x) 1, +∞ ) 则 x) >0, f(
n k=1
k)≤ ∑f(
n+ 1
1
n
n
性质 2 的证明同性质1. 性质 3 若 y=f( 在[ 上是凹函数 , 且 x) 1, +∞ ) ( ) , 则 f x >0 ) f( k) k +1 +f( > 2 k=1
2 2 p( 2 c o s s i n 2 p θ+ θ) + p= 2 . 2 s i n s i n θ θ
◇ 湖北 肖菊姣
1 定积分性质 性质 1 若 在[ 上 是 减 函 数, x) 1, + ∞) y=f( 且 f( 则 x) >0,
n n+ 1
1
n
n
k=1
k)≥ ∑f(
∫
n
∫
, f( x) f( ∑ k)≥
k=2
x) d x. f( ∫
1
∑
x) d x. ∫ f(
1
n+ 1
图3
证明 如图 3, 1 9
n
∫
1
k=. f( ∫
1
在R t A F G 中, Δ
图 1 图 2
A F AA ′ A F c o s | |=| |=p+| | θ, p 所以| A F . |= 1-c o s θ 在R t E F 中, △B B F B B ′ B F c o s | |=| |=p-| | θ, p 所以| B F . |= 1+c o s θ A B A F B F | |=| |+| |= p p 2 p + = 2 . 1-c o s o s i nθ θ 1+c θ s 2 当s i n A B 2 θ=1 时 , | | p. m i n= 这就是我对抛 物 线 焦 点 弦 最 小 值 的 2 种 考 虑 角
证明抛物线焦点弦的18个结论

证明抛物线焦点弦的18个结论重庆市开县临江中学张帮军2011.08/复习备考【内容摘要】关于抛物线的焦点弦到底有哪些结论呢?总结一下有四大类共18个结论,第一类是常见的基本结论;第二类是与圆有关的结论;第三类是由焦点弦得出有关直线垂直的结论;第四类是由焦点弦得出有关直线过定点的结论。
【关键词】证明抛物线焦点弦现在通过下面的例题来证明这些结论。
例:过抛物线y 2=2px (p >0)的焦点F 的一条直线AB 和此抛物线相交于A ,B 两点(α是直线AB 的倾斜角),准线l 的方程:x =-p 2,设点A (x 1,y 1),B(x 2,y 2),则有关抛物线的焦点弦有以下八个基本结论:(1)x 1x 2=p 24;(2)y 1y 2=-p 2;(3)|AF |=x 1+p 2;|BF |=x 2+p2(4)|AB |=x 1+x 2+p ;(5)|AB |=2p sin α;(6)|AF||BF|=p 2sin 2α;(7);1|AF |+1|BF |=2p(8)S △AOB =p22sin α证明:如图若α≠π2,则k =tan α因为点F(p 2,0),所以设直线AB 的方程为y =k (x -p 2)由y =k (x -p 2)y 2=2p px得k 2x 2-p (k 2+2)x +k 2p 24=0由根与系数的关系得:x 1x 2=p 24;x 1+x 2=p (k 2+2)k2∴(1)式得证∵A ,B 两点都在直线y 2=2px 上∴y 12=2px 1;y 22=2px 2∴(y 1y 2)2=4p 2x 1x 2=p 4∵y 1y 2<0,∴y 1y 2=-p 2即(2)式得证过点A ,B 分别作AA 1,BB 1与直线l 垂直,垂足为A 1,B 1即A 1(-p 2,y 1),B 1(-p 2,y 2)由抛物线定义知|AF |=|AA 1|=x 1+p 2;|BF |=|BB 1|=x 2+p 2即(3)式得证∵|AB |=|AF |+|BF |=x 1+x 2+p ∴(4)式得证∵x 1+x 2=p (k 2+2)k2,k =tan α∴|AB |=x 1+x 2+p =2p (k 2+1)k 2=2p (tan 2α+1)tan 2α=2p sin 2α即(5)式得证∵|AF ||BF |=(x 1+p 2)·(x 2+p 2)=x 1·x 2+p 2(x 1+x 2)+p 24=p 2(x 1+x 2+p )=p 2·2p sin 2α=p 2sin 2α∴(6)式得证∵1|AF |+1|BF |=|AF |+|BF ||AF |·|BF |=|AB ||AF |·|BF |=2psin 2α·sin 2αp 2=2p∴(7)式得证∵点O 到直线AB 的距离d 就是△AOB 的高∴h =d =p|k|21+k2姨=p sin α2∴S △AOB =12|AB|·h =12·2psin 2αp sin α2=p 22sin α∴(8)式得证下面来探究焦点弦与圆有关的四条结论:(1)以AB 为直径的圆M 与准线相切;(2)以AF 为直径的圆C 与y 轴准线相切;(3)以BF 为直径的圆D 与y 轴准线相切;(4)分别以AB ,AF ,BF 为直径的圆关系有:圆C 与圆D 外切;圆C 与圆D 既与y 轴相切又圆M 相内切。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p p p , , , 当A 易求 A( , 则 B 斜率不存在时, B( , - p) p) 4 2 2
2 2 p p 综上所证, 由抛物线定义 x x . x x . 1 2= 1 2= 4 4
2
A B = A F + B F = A A ′ + B B ′ = | | | | | | | | | | p p x + x = x x p. 1+ 2+ 1+ 2+ 2 2
2 2 p( 2 c o s s i n 2 p θ+ θ) + p= 2 . 2 s i n s i n θ θ
◇ 湖北 肖菊姣
1 定积分性质 性质 1 若 在[ 上 是 减 函 数, x) 1, + ∞) y=f( 且 f( 则 x) >0,
n n+ 1
1
n
n
k=1
k)≥ ∑f(
∫
n
∫
1
k=2
k)≤ ∑f(
x) d x. f( ∫
1
在R t A F G 中, Δ
图 1 图 2
A F AA ′ A F c o s | |=| |=p+| | θ, p 所以| A F . |= 1-c o s θ 在R t E F 中, △B B F B B ′ B F c o s | |=| |=p-| | θ, p 所以| B F . |= 1+c o s θ A B A F B F | |=| |+| |= p p 2 p + = 2 . 1-c o s o s i nθ θ 1+c θ s 2 当s i n A B 2 θ=1 时 , | | p. m i n= 这就是我对抛 物 线 焦 点 弦 最 小 值 的 2 种 考 虑 角
, , 设弦两端坐标为 A ( 则x x B( x x y y 1, 1) 2, 2) 1 2=
槡
注意 : 要分直线斜率存在与不存在 2 种情况分类 讨论 .
p 设抛物线的焦点 F( , 0) . 2 p ( , 设A 1)当 A B 斜率 存 在 时 , B∶ x- ) y =k( 2 p 烄 , k( x- ) y2 y= 2 解方程组烅 得 x= ,整理得 2 p 2 x, y =2 p 烆 k 2 k y - y- p=0, 2 2 p 2 p 2 , 由根与系数的关系 : y1 + y2 = y1 y2 =-p , k 1 2 p 2 1 2 A B 1+ 2 ) . | |= 1+ 2 · ( ) +4 p =2 p( k k k 因为 k2 无最大值 , 所以| A B |无最小值 .
度, 5 种解法 . ( 作者单位 : 河北乐亭新寨高级中学 )
性质 2 若 y=f( 在[ 上是增函数 , 且 x) 1, +∞ ) 则 x) >0, f(
n k=1
k)≤ ∑f(
n+ 1
1
n
n
性质 2 的证明同性质1. 性质 3 若 y=f( 在[ 上是凹函数 , 且 x) 1, +∞ ) ( ) , 则 f x >0 ) f( k) k +1 +f( > 2 k=1
根据定积分的定义 , 其 k)的 n 个小矩形面积之和 , f( 面 积 不 小 于
n+ 1 n
x) d x. ∫ f(
1
n+ 1
∫
1
x) d x, 即 f(
k=1
k) ∑f(
≥
n
如图 2,
k=2
表示边长为1, 高为f( 的n- k) k) ∑f(
n n
根据定积分的定义 , 其面积 不 大 1 个小矩形面积之和 , 于 f( x) d x ,即
·课堂扫描·
A B 2 | | p. m i n= 思路 2 为避免讨论可以在直线方程的设法上做 p 文章 . 如果把直线设成 x=m y+ 形式则直线包含斜 2
率不存在的情况 .
p , 抛物 线 的 焦 点 F ( , 直线 A 0) B 的方程 2
◇ 河北 王海蕊
在 关 于 抛 物 线 焦 点 弦 教 学 目 标 的 确 立 上 有 如 下 )知识目标 : 要求 : 掌握抛物线焦点弦的要领及性质 , 1 能写出命题与 逆 命 题 , 并 判 断 其 真 假; 2)能 力 目 标 : 学会用解析法及几何法解 决 问 题 , 养成独立分析问题 )情感目标 : 与解决问题的能力 ; 学会欣赏教学动静 3 结合的美 , 学会合作 .教 学 重 点 则 放 在 依 据 焦 点 弦 的 特征研究焦 点 弦 的 定 值 、 定 量 问 题, 培养学生对问题 研究的兴趣及研究能力 ,下面引例说明焦点弦最小值 的几种求法 . 引例 求抛物线 y2 =2 的焦点弦的最 x( p>0) p 小值 .
n
∫
, f( x) f( ∑ k)≥
k=2
x) d x. f( ∫
1
∑
x) d x. ∫ f(
1
n+ 1
图3
证明 如图 3, 1 9
1 思路 1 利 用 弦 长 公 式| A B|= 1+ 2 | y1 - k y2|求解 ;
A B = x x x x 2 | | p≥槡 p= p. 1+ 2+ 1 2 + 2 , ( 斜率存在时 抛物线y = 的焦点弦 2 x p> 0) p p 2 与抛物线 y 所在直线方程为 y= k( x- ) = 2 消y 得: 2 x 联立, p 2 2 k x 2 2 2 k x - k + 2) x+ = 0. p( 4
p 为: x=m y+ . 2 ,B ( ,由 方 程 组 设 A ( x1 , x2 , y1 ) y2 ) p 烄 x=m y+ , 2 消x 得: 烅
2 x, y =2 p 烆 2 2 y -2 pm y-p =0, 2 m, y1 + y2 =2 y1 y2 =-p , p 2 2 ( A B 1+m2·槡 2 m) +4 1+m2 ) . | |= 槡 p p =2 p( 当 m =0 时 , A B 2 | | p. m i n= 思路 3 由定义 A B A F B F | |=| |+| |=x1 +x2 +p, 再利用均值不等式
1 8
为2 p. 以上3 种解法是利用斜率求弦长的最小值, 下面 2 种方法是利用倾斜角求弦长的最小值. 思路 4 设 弦 所 在 直 线 的 倾 斜 角 为 θ, 方程为
p , 这个方程中也包含斜率不存 c o s i n x- ) θ=s θ( y 2
在的情况 , 再利 用 公 式| A B|=| A F|+| B F|=x1 +
因为x 所以x x x 2槡 x x p, 1, 2 均大于 0, 1+ 2≥ 1 2 =
槡
槡
p 所以 当且仅当x 时取 A B = x x 2 x | | p≥ p, 1+ 2+ 1= 2= 2
2 等号. 所以抛物线 y 的焦点弦的最小值 =2 x( p p >0)
p ( 把 x= 代 入 抛 物 线 2)当 A B 斜率不存 在 时 , 2 2 , 得 x y =2 p y=±p. p p , ,所以| 所以 A ( , B( , -p) A B |=2 p) p. 2 2 1 1 因为 2 >0, 所以 2 所以 1+ 2 ) >2 p( p, k k
·课堂扫描·
x2 +p 求弦长的最小值 . 设焦点弦所在直线的倾斜角为θ, 则直线 A B p , 的方程为y 设焦点弦 c o s i nθ( x- ) θ=s 2 , 端点 A ( x1 , B( x2 , . y1 ) y2 ) p 烄 , c o s i n x- ) θ=s θ( y 2 由方程组烅 消y 得: 2 x, y =2 p 烆 p2 2 2 2 2 · s i n x2 - 2 c o s s i n x+ s i n 0, θ θ+ θ) θ= p( 4 2 2 p( 2 c o s s i n θ+ θ) 所以 x1 + x2 = . 2 s i n θ 所以 A B = A F + B F = x1 + x2 + | | | | | | p=
x) d x,∑f( k)≤ f(
k=2 n
x) d x. f( ∫
1
k)表 示 边 长 为 1,高 为 证 明 如 图 1,∑f(
k=1
π 2 所以当s 即θ= 时, 取最小值 2 i n 1, A B θ= | | p. 2 思 路 5 利 用 直 线 倾 斜 角 表 示 焦 半 径 |A F B F |和| |. 如 下 图 所 示 ,设 直 线 的 倾 斜 角 为 θ, 在R 如图 : 过 A、 t F G 中, B 分 别 作 AA ′、 △A 垂足分别为 A 分别过 A 、 B B ′与直线 A ′ B ′垂直 , ′、 B ′, 、 , 、 B 作A GB E 与x 轴垂直 垂足分别为 G E .
