[很全]抛物线焦点弦的有关结论附答案
抛物线的焦点弦性质及其证明过程

有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点结论1:p x x AB ++=21p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2:若直线L 的倾斜角为θ,则弦长θ2sin 2pAB =证: (1)若2πθ= 时,直线L 的斜率不存在,此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为:θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot1pp y y AB =+=-+= 结论3: 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短. 结论4: )(832为定值p AB S oAB =∆()8sin 2sin sin 2221sin 21sin 21sin 21sin 2132220P AB S p p p AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ结论5: (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P Py y x x p y x p y x ==∴== 结论6:以AB 为直径的圆与抛物线的准线相切证:设M 为AB 的中点,过A 点作准线的垂线AA 1, 过B 点作准线的垂线BB 1, 过M 点作准线的垂线MM 1,由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7:连接A 1F 、B 1 F 则 A 1F ⊥B 1FFA A FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8:(1)AM 1⊥BM 1 (2)M 1F ⊥AB (3)BF AF FM ⋅=21(4)设AM 1 与A 1F 相交于H ,M 1B 与 FB 1相交于Q 则M 1,Q ,F ,H 四点共圆 (5)2121214M M B M AM =+证:由结论(6)知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形, M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴︒=∠=∠+∠9011111M AA M FA F AA ︒=∠+∠∴90111FM A AFA∴M 1F ⊥ABBF AF F M ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM︒=∠∴90FB A 11 所以M 1,Q ,F,H 四点共圆,22121AB B M AM =+()()()2121211242MM MM BB AABFAF ==+=+=结论9: (1)、A O 、B 1 三点共线 (2)B ,O ,A 1 三点共线(3)设直线AO 与抛物线的准线的交点为B 1,则BB 1平行于X 轴(4)设直线BO 与抛物线的准线的交点为A 1,则AA 1平行于X 轴证:因为p y p y k y p p y y x y k oB oA 2212111122,221-=-====,而221p y y -=所以122222oB oA k p y y ppk =-=-=所以三点共线。
抛物线焦点弦性质总结
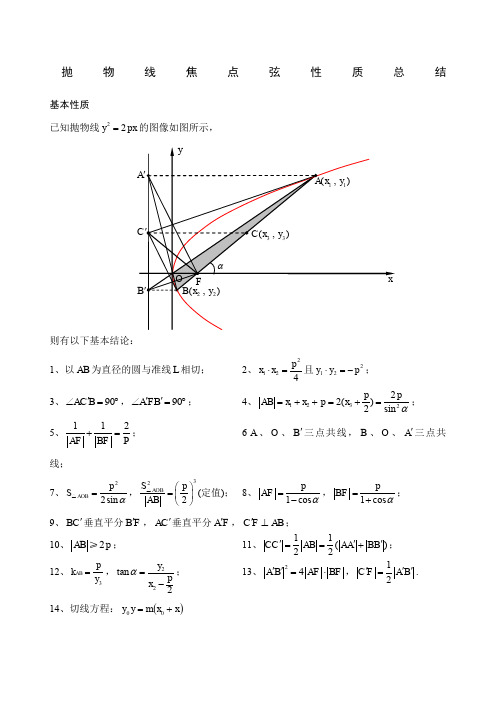
抛物线焦点弦性质总结基本性质 已知抛物线22y px =的图像如图所示,则有以下基本结论:1、以AB 为直径的圆与准线L 相切;2、2124p x x ⋅=且212y y p ⋅=-;3、90AC B '∠=︒,90A FB ''∠=︒;4、123222()2sin p p AB x x p x α=++=+=;5、112AF BF P +=; 6A 、O 、B '三点共线,B 、O 、A '三点共线;7、22sin AOB p S α=△,322AOB S p AB ⎛⎫= ⎪⎝⎭△(定值); 8、1cos p AF α=-,1cos p BF α=+; 9、BC '垂直平分B F ',AC '垂直平分A F ', C F AB '⊥;10、2AB p ≥;11、11()22CC AB AA BB '''==+; 12、3AB p k y =,22tan 2y p x α=-; 13、24A B AF BF ''=⋅,12C F A B '''=. 14、切线方程:()x x m y y +=00性质深究一、焦点弦与切线结论1、过抛物线焦点弦的两端点作抛物线的切线,两切线交点在准线上.特别地,当弦x AB ⊥轴时,则点P 的坐标为,02p ⎛⎫- ⎪⎝⎭. 结论2、切线交点与弦中点连线平行于对称轴结论3、弦AB 不过焦点即切线交点P 不在准线上时,切线交点与弦中点的连线也平行于对称轴.结论4、过抛物线准线上任一点作抛物线的切线,则过两切点的弦必过焦点.特别地,过准线与x 轴的交点作抛物线的切线,则过两切点AB 的弦必过焦点.结论5、过准线上任一点作抛物线的切线,过两切点的弦最短时,即为通径.AB 是抛物线px y 22=(p >0)焦点弦,Q 是AB 的中点,l 是抛物线的准线,l AA ⊥1,l BB ⊥1,过A ,B的切线相交于P ,PQ 与抛物线交于点M .则有结论6、PA ⊥PB .结论7、PF ⊥AB . 结论8、M 平分PQ . 结论9、PA 平分∠A 1AB ,PB 平分∠B 1BA .结论102=结论11、PAB S ∆2min p =二、非焦点弦与切线 当弦AB 不过焦点,切线交于P 点时,也有与上述结论类似结果:结论12、①p y y x p 221=,221y y y p += 结论13、PA 平分∠A 1AB ,同理PB 平分∠B 1BA .结论14、PFB PFA ∠=∠结论15、点M 平分PQ结论162PF =。
抛物线焦点弦问题(附答案解析)

(难度3星)1.(2019 •安徽高二期末(文))在平而直角坐标系中,抛物线关于轴对称,顶点为坐标原点,且经过点(2(1)求抛物线的标准方程:(2)过点 3的直线交抛物线于弘"两点,尸点是直线:=一2上任意一点.证明:直线、、的斜率依次成等差数列.【答案】(1)—2 : (2)证明见解析【解析】(1)因为抛物线关于轴对称,可设抛物线为亠2,而点(玄②在抛物线上,从而有另=2X2,得 =故抛物线方程为2=2 :(2)设点(―)是直线上任意一点,直线交抛物线于“、"两点,所以直线的斜率不等于0,可设直线:= +2交抛物线于(”』)、(?,?),由{可得:--2 - 2= 0从而有j + 2=2, 1 2= ~~ 2,1 ~ _ 2~= ------- •= ------ 9 =— --1^1 ?+/ 21且在直线上,所以有:1= 丄+Z 2= E+Z-2 —=―:=一'而2 =-,即证得证直线,,+ =2的斜率成等差数列.(难度2星)2. (2020 •河南高二期末(理))已知是抛物线: I (2,)是抛物线上一点,且| |=2(1)求抛物线的方程:(2)直线与抛物线交于,两点,若―'• 一 = -彳(否会过某个泄点若是,求出该立点坐标,若不是,说明理由.【答案】(1)2=4:⑵是,(2,6.【解析】(1)由抛物线的泄义知I | =』+三=2,.・.=2,•••抛物线的方程为:2=4(2)由题意知:可设的方程为:= + ,代入'=4有2— 4 — 4 = 0、(>。
的焦点,为坐标原点),则直线是设(b 1}>( 9 2)> 则r 2= -4、・・「(宀一么••1 2_ 托 _ 、S・・・•= 广?+ 厂2= 4 =_4 ・•・ =2••• 的方程为 = +Z恒过点(2,0).所以直线过左点(20・(难度2星)3.(2020 •江西高二期末(文))已知抛物线:亠2(2_ 2=谢圆心.(1)求抛物线Q的标准方程:(2)过抛物线的焦点尸的直线』与抛物线相交于两点,程.■【答案】(1)2=4(2)=2一戒=_2 +2【解析】(1)圆的标准方程为(一庁+ 2*圆心坐标为(20,>0的焦点尸为圆2 +| = £求直线』的方即焦点坐标为 g 则7= I =缩到抛物线的方程亠4(2)设直线的方程为: + /联立抛物线的方程2=4消整理得: 2- {4 2+2) +1=0:.』+ 尸 4 - + 2根据焦点弦的性质可知:| |= ;+ .+ =4 2+4又因为| | = 5 ..4 2+4=M得=±:所以所求直线的方程为:=2 = _2 +2(难度2星)4.(2019 •四川高二期末(文))已知点(一2。
抛物线焦点弦性质

抛物线焦点弦性质(1)过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点 且A 与B 在准线上的射影分别为A 1与B 1 结论1:p x x AB ++=21p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2:若直线L 的倾斜角为θ,则弦长θ2sin 2pAB = 证: (1)若2πθ=时, AB 为抛物线的通径,2,AB p =结论得证(2)若2πθ≠时,设直线L 的方程为:θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot 1pp y y AB =+=-+=结论3: 过焦点的弦中通径长最小,最小值为p 2.结论4:抛物线焦点弦的两个端点的同名坐标之积分别为常数42p 和2p -。
(证明见结论9)结论5: 焦点弦AB 被焦点F 分成m ,n 两部分,112m n p+= 即p FB FA 211=+ 证法1:过A 点作AR 垂直X 轴于点R ,过B 点作BS 垂直X 轴于点S ,设准线与x 轴交点为E,θ的倾斜角为因为直线L 则θθcos 1cos -=∴=+=+=P AF AF AF P FR EF ER PAF θcos 11-=∴同理可得P BF θcos 11+= ∴pFB FA 211=+证法2:12p m x =+ , 22pm x =+ 代入整理即可。
结论6:过抛物线的焦点作两条互相垂直的弦AB 、CD ,则1112AB CD p+=结论7:以AB 为直径的圆与抛物线的准线相切,切点即为11B A 的中点。
证:设M 为AB 的中点,过A 点作准线的垂线AA 1, 过B 点作准线的垂线BB 1,过M 点作准线的垂线 MM 1,由梯形的中位线性质和抛物线的定义知222111AB BFAF BB AA MM =+=+=结论得证。
(完整版)抛物线的焦点弦_经典性质及其证明过程
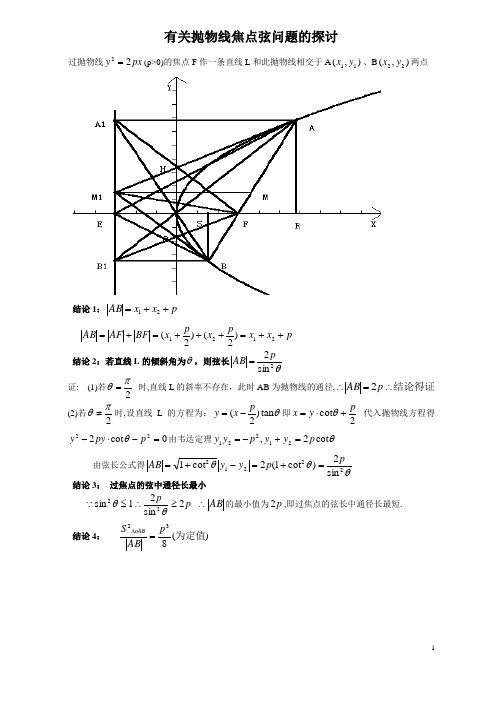
有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点结论1:p x x AB ++=21p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2:若直线L 的倾斜角为θ,则弦长θ2sin 2pAB =证: (1)若2πθ= 时,直线L 的斜率不存在,此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为:θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot1pp y y AB =+=-+= 结论3: 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短. 结论4: )(832为定值p AB S oAB =∆()8sin 2sin sin 2221sin 21sin 21sin 21sin 2132220P AB S p p p AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ结论5: (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P Py y x x p y x p y x ==∴== 结论6:以AB 为直径的圆与抛物线的准线相切证:设M 为AB 的中点,过A 点作准线的垂线AA 1, 过B 点作准线的垂线BB 1, 过M 点作准线的垂线MM 1,由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7:连接A 1F 、B 1 F 则 A 1F ⊥B 1FFA A FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8:(1)AM 1⊥BM 1 (2)M 1F ⊥AB (3)BF AF FM ⋅=21(4)设AM 1 与A 1F 相交于H ,M 1B 与 FB 1相交于Q 则M 1,Q ,F ,H 四点共圆 (5)2121214M M B M AM =+证:由结论(6)知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形, M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴︒=∠=∠+∠9011111M AA M FA F AA ︒=∠+∠∴90111FM A AFA∴M 1F ⊥ABBF AF F M ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM︒=∠∴90FB A 11 所以M 1,Q ,F,H 四点共圆,22121AB B M AM =+()()()2121211242MM MM BB AABFAF ==+=+=结论9: (1)、A O 、B 1 三点共线 (2)B ,O ,A 1 三点共线(3)设直线AO 与抛物线的准线的交点为B 1,则BB 1平行于X 轴(4)设直线BO 与抛物线的准线的交点为A 1,则AA 1平行于X 轴证:因为p y p y k y p p y y x y k oB oA 2212111122,221-=-====,而221p y y -=所以122222oB oA k p y y ppk =-=-=所以三点共线。
抛物线焦点弦22条结论

抛物线焦点弦22条结论抛物线是一种经典的数学曲线,被广泛应用于物理学、工程学、计算机图形学等领域。
在研究抛物线的性质和应用过程中,焦点和弦是两个重要的概念。
本文将介绍抛物线焦点弦的22条结论。
1. 抛物线的焦点是由平行于抛物线的直线反射后汇聚而成的点。
2. 抛物线的焦点是离抛物线顶点等距离的点。
3. 抛物线的焦点是所有平行于抛物线的直线的交点。
4. 抛物线的焦点是所有过抛物线的顶点的对称轴的交点。
5. 抛物线的焦点是所有与抛物线相切的直线的交点。
6. 抛物线的焦点是所有过抛物线的顶点并且与抛物线平行的直线的交点。
7. 抛物线的焦点是所有过抛物线的顶点并且与抛物线垂直的直线的交点。
8. 抛物线的焦点是所有经过抛物线的两个端点并且与抛物线垂直的直线的交点。
9. 抛物线的焦点是所有过抛物线的顶点且与抛物线切线垂直的直线的交点。
10. 抛物线的焦点是所有过抛物线的顶点且与抛物线切线平行的直线的交点。
11. 抛物线的焦点是所有与抛物线相交的直线的交点。
12. 抛物线的焦点是所有通过抛物线的两个端点且与抛物线相交的直线的交点。
13. 抛物线的焦点是所有过抛物线的顶点且与抛物线切线相交的直线的交点。
14. 抛物线的焦点是所有过抛物线的顶点且与抛物线切线平行且相交于抛物线的焦点的直线的交点。
15. 抛物线的焦点是所有过抛物线的顶点且与抛物线切线垂直且相交于抛物线的焦点的直线的交点。
16. 抛物线的焦点是所有过抛物线的顶点并且与抛物线切线平行于抛物线的对称轴的直线的交点。
17. 抛物线的焦点是所有过抛物线的顶点并且与抛物线切线垂直于抛物线的对称轴的直线的交点。
18. 抛物线的焦点是所有过抛物线的顶点且与抛物线对称轴平行的直线的交点。
19. 抛物线的焦点是所有过抛物线的顶点且与抛物线对称轴垂直的直线的交点。
20. 抛物线的焦点是所有通过抛物线的两个端点且与抛物线对称轴平行的直线的交点。
21. 抛物线的焦点是所有通过抛物线的两个端点且与抛物线对称轴垂直的直线的交点。
抛物线焦点弦问题(附答案解析)

(难度3星)1.(2019·安徽高二期末(文))在平面直角坐标系xxx 中,抛物线x 关于x 轴对称,顶点为坐标原点,且经过点(2,2).(1)求抛物线x 的标准方程;(2)过点x (1,0)的直线交抛物线于M 、N 两点,P 点是直线x :x =−1上任意一点.证明:直线xx、xx、xx 的斜率依次成等差数列.【答案】(1)x 2=2x ;(2)证明见解析【解析】(1)因为抛物线x 关于x 轴对称,可设抛物线为x 2=2xx ,而点(2,2)在抛物线上, 从而有22=2x ×2,得x =1,故抛物线方程为x 2=2x ;(2)设点x (−1,x )是直线x 上任意一点,—直线交抛物线于M 、N 两点,所以直线xx 的斜率不等于0,可设直线xx :x =xx +1交抛物线于x (x 1,x 1)、x (x 2,x 2),由{x =xx +1x 2=2x可得:x 2−2xx −2=0 从而有x 1+x 2=2x ,x 1x 2=−2,x xx =x 1−x x 1+1,x xx =x 2−x x 2+1,x xx =−x 2且在直线上,所以有:x 1=xx 1+1,x 2=xx 2+1x xx +x xx =x 1−x x 1+1+x 2−x x 2+1=2xx 1x 2+(2−xx )(x 1+x 2)−4x x 2x 1x 2+2x (x 1+x 2)+4 =−2xx 2−4x 2x +4=−x ,而2x xx =−x ,即证x xx +x xx =2x xx .得证直线xx ,xx ,xx 的斜率成等差数列.【(难度2星)2.(2020·河南高二期末(理))已知x 是抛物线x :x 2=2xx(x >0)的焦点,x (1,x )是抛物线上一点,且|xx |=2.(1)求抛物线x 的方程;(2)直线x 与抛物线x 交于x ,x 两点,若xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =−4(x为坐标原点),则直线x是否会过某个定点若是,求出该定点坐标,若不是,说明理由.【答案】(1)x 2=4x ;(2)是,x (2,0).【解析】(1)由抛物线的定义知|xx |=1+x 2=2,∴x =2,∴抛物线x 的方程为:x 2=4x*(2)由题意知:可设xx 的方程为:x =xx +x ,代入x 2=4x 有x 2−4xx −4x =0,设x (x 1,x 1),x (x 2,x 2),则x 1⋅x 2=−4x ,∴x 1⋅x 2=(x 1⋅x 2)216=x 2,∴xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =x 1⋅x 2+x 1⋅x 2=x 2−4x =−4∴x =2∴xx 的方程为x =xx +2,恒过点x (2,0).所以直线x 过定点(2,0).?(难度2星)3.(2020·江西高二期末(文))已知抛物线x :x 2=2xx (x >0)的焦点F 为圆x 2+x 2−2x =0的圆心.(1)求抛物线C 的标准方程;(2)过抛物线的焦点F 的直线l 与抛物线相交于xx 两点,且|xx |=5,求直线l 的方程.【答案】(1)x 2=4x (2)x =2x −2或x =−2x +2【解析】(1)圆的标准方程为(x −1)2+x 2=1,圆心坐标为(1,0),即焦点坐标为x (1,0),则x 2=1,x =2得到抛物线x 的方程x 2=4x(2)设直线x 的方程为:x =xx +1联立抛物线x 的方程x 2=4x 消x 整理得: 》x 2−(4x 2+2)x +1=0 ∴x 1+x 2=4x 2+2根据焦点弦的性质可知:|xx |=x 1+x 2+x =4x 2+4 又因为|xx |=5∴4x 2+4=5解得x =±12所以所求直线x 的方程为:x =2x −2或x =−2x +2(难度2星)4.(2019·四川高二期末(文))已知点x (−2,0),x (3,0),动点x (x ,x )满足: xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =x 2−6.(1)求动点P 的轨迹x ;-(2)已知点x (14,0),若曲线E 上一点M 到x 轴的距离为12,求|xx |的值.【答案】(1)焦点在x 轴,开口向右的抛物线x 2=x ;(2)12【解析】(1)x 点坐标为(x ,x ),则有:xx⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(−2−x ,−x ),xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(3−x ,−x ) ∴xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =x 2−x −6+x 2=x 2−6,即:x 2=x ,∴点P 的轨迹为焦点在x 轴,开口向右的抛物线.(2)由题意可得:x x =±12代入方程求得x x =14,所以x (14,±12),而x (14,0)∴|xx |=√(14−14)2+(±12−0)2=12 ,即|xx |=12.。
[很全]抛物线焦点弦的有关结论附答案
![[很全]抛物线焦点弦的有关结论附答案](https://img.taocdn.com/s3/m/4d4653f1ec3a87c24028c4c5.png)
[很全]抛物线焦点弦的有关结论知识点1:若是过抛物线的焦点的弦。
设,AB ()022>=p px y F (),,11y x A ()22,y x B 则(1);(2)4221p x x =221p y y -=证明:如图,(1)若的斜率不存在时,AB 依题意,221px x ==4221p x x =∴若的斜率存在时,设为则AB ,k ⎝⎛=:k y AB ()42222222222=++-⇒=⎪⎭⎫ ⎝⎛-p k px k x k px p x k 综上:.4221p x x =∴.4221p x x =(2),p y x p y x 2,2222211==Q ,22142221p y y p y y ±=⇒=∴但22121,0p y y y y -=∴<(2)另证:设与联立,得2:pmy x AB +=px y 22=22122,02p y y p pmy y -=∴=--知识点2:若是过抛物线的焦点的弦。
设,AB ()022>=p px y F (),,11y x A ()22,y x B 则(1)(2)设直线的倾斜角为;21p x x AB ++=AB α证明:(1)由抛物线的定义知,2,221px BF p x AF +=+=p x x BF AF AB ++=+=∴21(2)若由(1)知,2,90210p x x ===则α2p AB ==若联立,得px y p x k y AB 2,2:,9020=⎪⎭⎫ ⎝⎛-=≠与设α()42222222222=++-⇒=⎪⎭⎫ ⎝⎛-p k px k x k px p x k ,而,(),22221k k p x x +=+∴()222112k k p p x x AB +=++=∴αtan =k ()ααα222sin 2tan tan 12pp AB =+=∴知识点3:若是过抛物线的焦点的弦,则以为直径的圆与AB ()022>=p px y F AB 抛物线的准线相切。
抛物线焦点弦性质总结
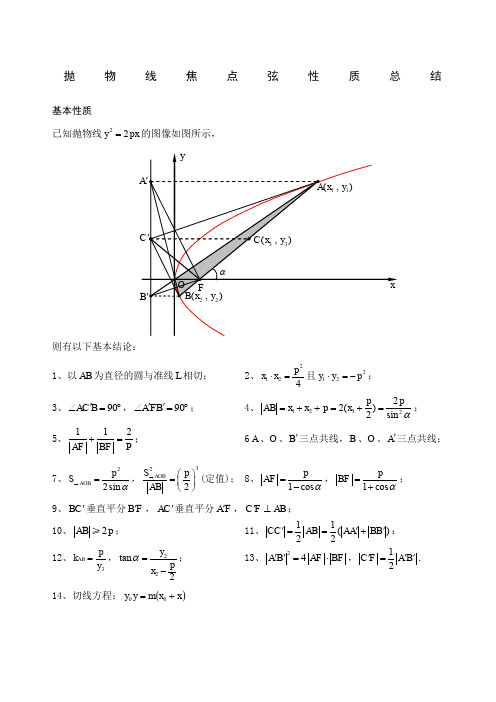
抛物线焦点弦性质总结基本性质 已知抛物线22y px =的图像如图所示,则有以下基本结论:1、以AB 为直径的圆与准线L 相切;2、2124p x x ⋅=且212y y p ⋅=-;3、90AC B '∠=︒,90A FB ''∠=︒;4、123222()2sin p p AB x x p x α=++=+=;5、112AF BF P +=;6A 、O 、B '三点共线,B 、O 、A '三点共线;7、22sin AOB p S α=△,322AOB S p AB ⎛⎫= ⎪⎝⎭△(定值); 8、1cos p AF α=-,1cos p BF α=+; 9、BC '垂直平分B F ',AC '垂直平分A F ', C F AB '⊥;10、2AB p ≥;11、11()22CC AB AA BB '''==+; 12、3AB p k y =,22tan 2y p x α=-; 13、24A B AF BF ''=⋅,12C F A B '''=. 14、切线方程:()x x m y y +=00性质深究一、焦点弦与切线结论1、过抛物线焦点弦的两端点作抛物线的切线,两切线交点在准线上.特别地,当弦x AB ⊥轴时,则点P 的坐标为,02p ⎛⎫- ⎪⎝⎭. 结论2、切线交点与弦中点连线平行于对称轴结论3、弦AB 不过焦点即切线交点P 不在准线上时,切线交点与弦中点的连线也平行于对称轴.结论4、过抛物线准线上任一点作抛物线的切线,则过两切点的弦必过焦点.特别地,过准线与x 轴的交点作抛物线的切线,则过两切点AB 的弦必过焦点.结论5、过准线上任一点作抛物线的切线,过两切点的弦最短时,即为通径.AB 是抛物线px y 22=(p >0)焦点弦,Q 是AB 的中点,l 是抛物线的准线,l AA ⊥1,l BB ⊥1,过A ,B 的切线相交于P ,PQ 与抛物线交于点M .则有结论6、PA ⊥PB .结论7、PF ⊥AB . 结论8、M 平分PQ . 结论9、PA 平分∠A 1AB ,PB 平分∠B 1BA .结论102PF =结论11、PAB S ∆2min p =二、非焦点弦与切线 当弦AB 不过焦点,切线交于P 点时,也有与上述结论类似结果:结论12、①p y y x p 221=,221y y y p += 结论13、PA 平分∠A 1AB ,同理PB 平分∠B 1BA .结论14、PFB PFA ∠=∠结论15、点M 平分PQ结论162=。
证明抛物线焦点弦的18个结论

证明抛物线焦点弦的18个结论1. 抛物线焦点弦的两个焦点与抛物线的焦点重合。
证明:根据抛物线的定义,焦点到定点和定点到直线的距离相等。
所以,焦点到直线的距离与直线到焦点的距离相等,因此两个焦点与焦点弦重合。
2. 抛物线焦点弦的两个端点与抛物线的准线的焦点重合。
证明:由于抛物线的准线与直线平行,所以准线到焦点的距离与焦点到直线的距离相等。
因此,抛物线焦点弦的两个端点与抛物线的准线的焦点重合。
3. 抛物线焦点弦与抛物线的法线平行。
证明:由于抛物线的定义,法线通过焦点并垂直于准线。
而抛物线焦点弦是抛物线的切线,与法线平行。
4. 抛物线焦点弦的中点位于抛物线的准线上。
证明:由于抛物线的准线与抛物线的焦点重合,所以抛物线焦点弦的中点与抛物线准线的焦点重合。
5. 抛物线焦点弦的两个焦点与抛物线焦点弦的中点共线。
证明:根据抛物线的定义,焦点到定点和定点到直线的距离相等。
所以焦点与抛物线焦点弦的中点共线。
6. 抛物线焦点弦与抛物线的切线平行。
证明:抛物线焦点弦是抛物线的切线,而抛物线的切线与准线平行。
7. 抛物线焦点弦在抛物线的对称轴上。
证明:由于抛物线的对称轴与准线重合,而抛物线焦点弦与准线重合,所以抛物线焦点弦在抛物线的对称轴上。
8. 抛物线焦点弦是抛物线的一个特殊弦,它经过焦点,并且与抛物线的对称轴垂直。
证明:由抛物线的定义可知,焦点到定点和定点到直线的距离相等。
所以抛物线焦点弦经过焦点。
另外,抛物线的对称轴与准线垂直,而抛物线焦点弦与准线重合,所以抛物线焦点弦与抛物线的对称轴垂直。
9. 抛物线焦点弦是抛物线的一条切线,且与抛物线的直径垂直。
证明:由抛物线的定义可知,抛物线的焦点到直线和焦点到定点的距离相等,所以抛物线焦点弦是抛物线的切线。
另外,根据抛物线的性质可知,直径与对称轴垂直,而抛物线焦点弦与对称轴重合,所以抛物线焦点弦与抛物线的直径垂直。
10. 抛物线焦点弦与抛物线的切线平行,并且经过抛物线的焦点。
(完整版)梳理抛物线焦点弦的有关结论

梳理抛物线焦点弦的有关结论知识点1:若AB 是过抛物线()022>=p px y 的焦点F 的弦。
设(),,11y x A ()22,y x B ,则(1)4221p x x =;(2)221p y y -=证明:如图,(1)若AB 的斜率不存在时,依题意,221px x ==4221p x x =∴若AB 的斜率存在时,设为,k 则⎭ ⎝⎛=2:k y AB()042222222222=++-⇒=⎪⎭⎫ ⎝⎛-p k px k x k px p x k.4221p x x =∴ 综上:.4221p x x =(2)p y x p y x 2,2222211== ,,22142221p y y p y y ±=⇒=∴但22121,0p y y y y -=∴< (2)另证:设2:pmy x AB +=与px y 22=联立,得 22122,02p y y p pmy y -=∴=--知识点2:若AB 是过抛物线()022>=p px y 的焦点F 的弦。
设(),,11y x A ()22,y x B ,则(1);21p x x AB ++=(2)设直线AB 证明:(1)由抛物线的定义知,2,221px BF p x AF +=+=p x x BF AF AB ++=+=∴21 (2)若,2,90210p x x ===则α由(1)知2p AB ==若px y p x k y AB 2,2:,9020=⎪⎭⎫ ⎝⎛-=≠与设α联立,得()042222222222=++-⇒=⎪⎭⎫ ⎝⎛-p k px k x k px p x k(),22221k k p x x +=+∴()222112k k p p x x AB +=++=∴,而αtan =k ,()ααα222sin 2tan tan 12pp AB =+=∴ 知识点3:若AB 是过抛物线()022>=p px y 的焦点F 的弦,则以AB 为直径的圆与抛物线的准线相切。
[很全]抛物线焦点弦的有关结论附答案.pdf
![[很全]抛物线焦点弦的有关结论附答案.pdf](https://img.taocdn.com/s3/m/bf18a9db27284b73f24250dd.png)
p 2
= 2 px k 2 x2
−
k2
+2
px +
k2 p2
=0
2
4
( ) x1
+ x2
=
p
k2 +2 k2
,
x1 x2
=
p2 4
.
由抛物线的定义知 m =
AF
= x1 +
p,n = 2
BF
= x2 +
p 2
3
一寸光阴不可轻
1 +1 = m+n = m n mn
x1 + x2 + p
x1 x2
AM
= m, BM
AA1 // KF // BB1
A1K B1K
=
AF FB
而 AF
=
A1 A, BF
=
B1 B
o
K
F
B
A1K = A1 A B1K B1B
A1 K A1 A
=
B1K B1B
,而 AA1K
=
BB1K
=
90 0
AA1K ∽ BB1K AKF = BKF
A1KA = B1KB
2
一寸光阴不可轻
知识点 6:若 AB 是过抛物线 y2 = 2 px(p 0)的焦点 F 的弦,o 为抛物线的顶点,连接
yC
=
−
p2 −p
2
= y2
y2
BC // OF
逆定理:若 AB 是过抛物线 y2 = 2 px(p 0)的焦点 F 的弦,过点 B 作 BC // OF 交抛物
线准线于点 C, 则 A、C、O 三点共线。
证明略
(完整版)抛物线的焦点弦_经典性质及其证明过程
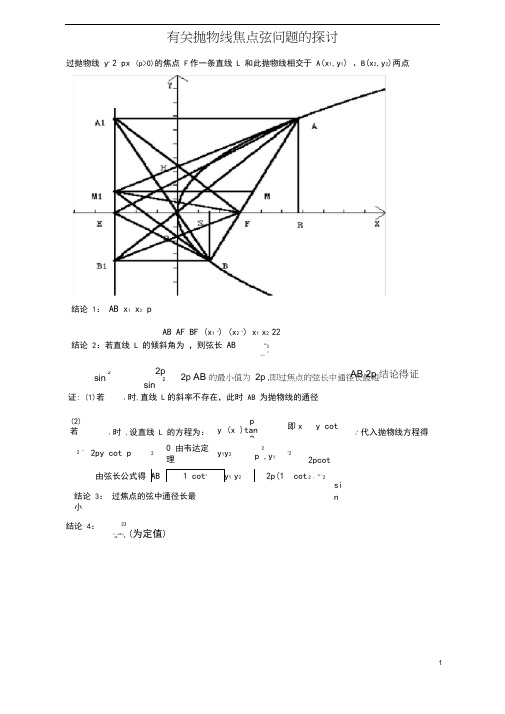
有关抛物线焦点弦问题的探讨过抛物线 y 22 px (p>0)的焦点 F 作一条直线 L 和此抛物线相交于 A (x 1,y 1) 、B (x 2,y 2)两点结论 1: AB x 1 x 2 pAB AF BF (x 1 p) (x 2 p) x 1 x 2 22结论 2:若直线 L 的倾斜角为 ,则弦长 AB 2p 2sin2结论 4:23S ABoAB p8(为定值)(2)若2时 ,设直线 L 的方程为: py (x )tan2 即xy cot2p代入抛物线方程得2 y2py cot p 2 0 由韦达定理y 1y 2 2 p ,y 1y22pcot2 )2p )2由弦长公式得 AB 1 cot 2y 1 y 2 2p(1 cot证: (1)若2时,直线 L 的斜率不存在,此时 AB 为抛物线的通径si n结论 3: 过焦点的弦中通径长最小 AB 2p 结论得证 2sin2p 2sin2p AB 的最小值为 2p ,即过焦点的弦长中通径长最短同理 B 1FOB 1FBA 1FB 1 90A 1FB 1 F2结论 8:(1)AM 1 BM 1 (2)M 1F AB (3) M 1F AF BF(4)设 AM 1 与 A 1F 相交于 H ,M 1B 与 FB 1相交于 Q 则M 1,Q ,F ,H 四点共圆 (5) AM 12M 1B 24M 1M 2证:由结论( 6)知 M 1 在以 AB 为直径的圆上 AM 1 BM 1A 1FB 1为直角三角形, M 1 是斜边 A 1 B 1 的中点A 1M 1 M 1F M1FA 1M1A 1FAA 1F AFA 1AA 1FFA 1MAA 1M190AFA 1A1FM190M 1FABM 1F2AFBFAM 1BM 1 AM1B 90又 A 1FB 1FA 1FB 1 90 所以 M 1,Q , F,H 四点共圆, AM 1 2M 1B 2AB 22 2 2 2AF BF 2AA 1 BB 1 22MM 1 24MM 1 2结论 9: (1) A 、O 、B 1 三点共线 ( 2)B ,O ,A 1 三点共线(3)设直线 AO 与抛物线的准线的交点为 B 1,则 BB 1平行于 X 轴( 4)设直线 BO 与抛物线的准线的交点为 A 1,则 AA 1平行于 X 轴S OAB SOBF1S 0AFOFBF 1sin 2OF AF sin OF 2S OABAB结论 5: (1) 证x 1AFP 3y 1y 22y1 2p ,x 2BF 2p 2sinOF AB sinp22psin2 sin 22 p2sin(2) x 1x 2=2 y22px 1x 2(y 1y 2)24P 2P 2结论 6:以 AB 证:设 M 为 AB 的中点,过 A 点作准线的垂线 过 M 点作准线的垂线 MM 1,由梯形的中位线性质和抛物线的定义知 为直径的圆与抛物线的准线相切AA 1, 过 B 点作准线的垂线 BB 1,MM 1结论 7:连接 A 1F 、 AA 1 AF,AA 1 BB 1 AF BF22B 1 F 则 A 1FAA 1F B 1FAB 2故结论得证AFA 1 AA 1 //OF AA 1FA 1FO A 1FO A 1FA41E,因为直线 L 的倾斜角为证:因为 k oAy1 x1y12 y12p,k oBoB 1y 11y2 p2y2,而 y 1y 2 p2 p2p2所以 k oA2p2 p y22y 2 pk oB 1所以三点共线。
抛物线焦点弦性质应用

2)
=
2
2 ;
2
3.焦半径: || + || = ; ||,||一个较长,一个较短.
不论开口向上还是向下,因为sinɑ > 0,
所以,较长 =
, 较短 =
;
1 − ɑ
1 + ɑ
d
2
4.面积:S∆OAB=2|ɑ| ; 若是到的距离,则
直平分线与x轴交于点T(5,0),O为坐标原点,则S△AOB
= 2 2 .
例 1 已知抛物线 C 的顶点是原点 O,焦点 F 在 x 轴的正半轴上,经过点 F 的
→ →
直线与抛物线 C 交于 A,B 两点,若OA·OB=-12,则抛物线 C 的方程为
A.x2=8y
例2
B.x2=4y
C.y2=8x
√
焦点弦的几个结论(AB是过焦点F的弦,A(x1,y1),
B(x2, y2)(ɑ为倾斜角)y2=±2px(p>0).
1.
2
坐标积:x1x2= ,12
4
= −2;
3 p2
OA OB
,AOB为钝角.
4
2.弦长公式: |AB|=|x1+x2|+p=2(1 +
3.焦半径:
1
||
1.过抛物线y2=4x的焦点F的直线l与抛物线交于
9
A,B两点,若|AF|=2|BF|,则|AB|= 2
,k= 2 2 .
2.过抛物线y2=12x的焦点F的直线l与抛物线交于
A,B两点,若|AB|=16,则直线斜率k=
|AF|=
12,或4
,|BF|= 4,或12
, பைடு நூலகம்AOB
与抛物线焦点弦有关的几个结论

与抛物线焦点弦有关的几个结论在抛物线与直线的关系中,过抛物线焦点的直线与抛物线的关系尤为重要,这是因为在这一关系中具有一些很有用的性质,这些性质常常是高考命题的切入点.不妨设抛物线方程为y2=2px(p>0),则焦点,准线l的方程:.过焦点F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,又作AA1⊥l, BB1⊥l,垂足分别为A1、B1.AB⊥x轴时,, , 此时弦A B叫抛物线的通径,它的长|AB|=2p.A B与x轴不垂直也不平行时,设弦A B所在直线的斜率为k(k≠0),则方程为(如图).由方程组消去y,得, 或消去x, 得.结论1:(定值),,结论2:y1y2=-p2(定值),.结论3:弦长.结论4:若此焦点弦A B被焦点F分成m,n两部分,则为定值.事实上,若AB⊥x轴,则m=n=p,.若A B与x轴不垂直,则..结论5:抛物线y2=2px(p>0)的焦点弦中通径最小.证法1:设弦AB所在的直线方程为.由方程组消去x,得y2-2pmy-p2=0.∴y1+y2=2pm,y1y2=-p2.当且仅当m=0,即弦A B为抛物线的通径时,它的长度最小且为2p.证法2:设过焦点F的弦A B所在直线的倾斜角为,则|AF|=|AA1|=p+|AF|cos, |BF|=|BB1|=p-|BF|cos,∴.,当且仅当=90°时,即弦A B为抛物线的通径时,它的长度最小且为2p.结论6:以焦点弦AB为直径的圆与抛物线的准线l相切(如图).事实上,取弦A B的中点C,作CC1⊥l,垂足为C1. 则.这表明圆心C到准线l的距离等于半径,故以焦点弦A B为直径的圆与抛物线的准线相切.结论7:以抛物线焦半径|AF|为直径的圆与y轴相切.事实上,.设A F的中点为D,则,∴D到y轴的距离.这表明圆心D到y轴的距离等于半径,故以抛物线焦半径|AF|为直径的圆与y轴相切.结论8:A1F⊥B1F(如图)事实上,设,则,。
高考数学抛物线焦点弦的性质

抛物线焦点弦的性质1、焦点弦定义:过焦点的直线割抛物线所成的相交弦。
2、焦点弦公式:设两交点),(),(2211y x B y x A ,可以通过两次焦半径公式得到: 当抛物线焦点在x 轴上时,焦点弦只与两焦点的横坐标有关:(0)p >若抛物线22y px =,)(21x x p AB ++=抛物线22y px =-,)(21x x p AB +-= 当抛物线焦点在y 轴上时,焦点弦只与两焦点的纵坐标有关:(0)p >若抛物线22x py =,)(21y y p AB ++=抛物线22x py =-,)(21y y p AB +-=3、通径:过焦点且垂直于对称轴的相交弦 直接应用抛物线定义,得到通径:p d 2=4、焦点弦常用结论:结论1:韦达定理⎪⎩⎪⎨⎧=-=pxy p x k y 2)2(20222=--⇒p y k p y 与04)2(22222=++-p k x p p k x k 221p y y -=⇒与421p x x = 结论2:p x x AB ++=21证:p x x p x p x BF AF AB ++=+++=+=2121)2()2( 结论3:假设直线L 的倾斜角为θ,那么弦长θ2sin 2p AB =证: (1)假设2πθ= 时,直线L 的斜率不存在,此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)假设2πθ≠时, 那么⎪⎩⎪⎨⎧=-=px y p x k y 2)2(20222=--⇒p y k p y ⎪⎩⎪⎨⎧-==+⇒221212p y y k p y y 结论4: 过焦点的弦中通径长最小p p 2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短. 结论4: )(832为定值p AB S oAB =∆ 结论5:以AB 为直径的圆与抛物线的准线相切 证:设M 为AB 的中点,过A 点作准线的垂线AA 1, 过B 点作准线的垂线BB 1,过M 点作准线的垂线MM 1,由梯形的中位线性质与抛物线的定义知 222111ABBFAF BB AA MM =+=+= 故结论得证结论6:连接A 1F 、B 1 F 那么 A 1F ⊥B 1F 同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F结论7:〔1〕AM 1⊥BM 1 〔2〕M 1F ⊥AB 〔3〕BF AF F M ⋅=21〔4〕设AM 1 与A 1F 相交于H ,M 1B 与 FB 1相交于Q 那么M 1,Q ,F ,H 四点共圆〔5〕2121214M M B M AM =+证:由结论〔6〕知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形, M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴ ︒=∠=∠+∠9011111M AA M FA F AA ︒=∠+∠∴90111FM A AFA ∴M 1F ⊥ABBF AF F M ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM ︒=∠∴90FB A 11 所以M 1,Q ,F,H 四点共圆,22121AB B M AM =+ 结论8: 〔1〕、A O 、B 1 三点共线 〔2〕B ,O ,A 1 三点共线〔3〕设直线AO 与抛物线的准线的交点为B 1,那么BB 1平行于X 轴〔4〕设直线BO 与抛物线的准线的交点为A 1,那么AA 1平行于X 轴 证:因为p y p y k y p py y x y k oB oA 2212111122,221-=-====,而221p y y -= 所以122222oB oA k p y y pp k =-=-=所以三点共线。
抛物线焦点弦性质很全
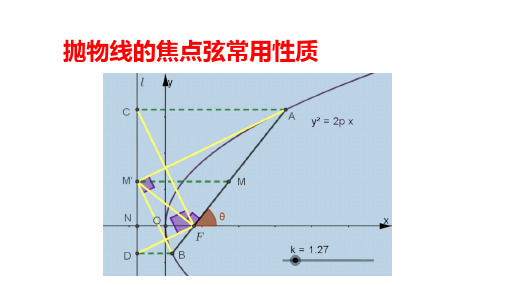
五、 CFD 900
CFO FCA AFC DFO FDB BFD CFO DFO AFC BFD 即有CFD AFC BFD
CFD 900
六、抛物线的焦点三角形的面积公式
S AOB
p2
2sin
S AOB
SAOF
SBOF
1 2
OF
y1
1 OF 2
y2
1 2 OF y1 y2
kMA kMB
2 py1 y12 p2
2 py2 y22 p2
kMA kMB
2 py1 y12 y1 y2
2 py2 y22 y1 y2
0
kMA kMB
MA, MB的倾斜角互补,即 AMF BMF
设:x my p ,代入y2 2 px可得
F
2
y1 y2 2 pm, y1 y2 p2
y1 y2 y1 y2 2 4 y1 y2 2 p m2 1
又k AB
tan
1 m
, 则m
1
tan
y1 y2 2 p
1
tan 2
1
2p
sin
SAOB
1 2
OF
y1 y2
1 p 2p
(1)若焦点在 x轴上,则 x1x2
p2 4
, y1 y2
p2
(2)若焦点在 y轴上,则 y1 y2
p2 4
, x1x2
p2
四、以抛物线的焦点弦为直径的圆与准线
证明:
MM1
1 2 ( AA1
BB1 )
1 ( AF BF ) 2
1 AB 2
即有:AM1B 900
引申:以焦半径为直径的圆与y轴相切(学生完成)
2 2 sin
很全 抛物线焦点弦的有关结论附答案

[很全]抛物线焦点弦的有关结论知识点1:若AB 是过抛物线()022>=p px y 的焦点F 的弦。
设(),,11y x A ()22,y x B ,则(1)4221p x x =;(2)221p y y -=证明:如图,(1)若AB 的斜率不存在时,依题意,221px x ==4221p x x =∴若AB 的斜率存在时,设为,k 则⎭ ⎝⎛=:k y AB.4221p x x =∴ 综上:.4221p x x =(2)p y x p y x 2,2222211==Θ,,22142221p y y p y y ±=⇒=∴但22121,0p y y y y -=∴< (2)另证:设2:pmy x AB +=与px y 22=联立,得22122,02p y y p pmy y -=∴=-- 知识点2:若AB 是过抛物线()022>=p px y 的焦点F 的弦。
设(),,11y x A ()22,y x B ,则(1);21p x x AB ++=(2)设直线AB 的倾斜角为α证明:(1)由抛物线的定义知(2)若,2,90210p x x ===则α由(1)知2p AB ==若px y p x k y AB 2,2:,9020=⎪⎭⎫ ⎝⎛-=≠与设α联立,得(),22221k k p x x +=+∴()222112kk p p x x AB +=++=∴知识点3:若AB 是过抛物线()022>=p px y 的焦点F 的弦,则以AB 为直径的圆与抛物线的准线相切。
证明:过点B A 、,11B A 、过AB 中点M 向准线引垂线,垂足为,N设以AB 为直径的圆的半径为,r∴以AB 为直径的圆与抛物线的准线相切。
知识点4:若AB 是过抛物线()022>=p px y 线的准线引垂线,垂足分别为,11B A 、则01190=∠FB A 。
证明借助于平行线和等腰三角形容易证明知识点5:若AB 是过抛物线()022>=p px y 的焦点x 轴相交于点K ,则.BKF AKF ∠=∠证明:过点B A 、分别作准线的垂线,垂足分别为B B A A K B K A 1111=∴BB KB A A K A 1111=∴,而11∠=∠BB K AA K AA 1∆∴∽K BB 1∆ KB B KA A 11∠=∠∴知识点6:若AB 是过抛物线()022>=p px y 的焦点F 的弦,o 为抛物线的顶点,连接AO 并延长交该抛物线的准线于点,C 则.//OF BC证明:设(),,11y x A ()22,y x B ,则由知识点1知221p y y -= 2222y y p p y C =--=∴逆定理:若AB 是过抛物线()022>=p px y 的焦点F 的弦,过点B 作OF BC //交抛物线准线于点,C 则O C A 、、三点共线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[很全]抛物线焦点弦的有关结论
知识点1:若AB 是过抛物线()022>=p px y 的焦点F 的弦。
设(),,11y x A ()22,y x B ,则
(1)4
2
21p x x =;(2)221p y y -=
证明:如图,
(1)若AB 的斜率不存在时,
依题意,2
21p
x x ==4221p x x =∴
若AB 的斜率存在时,设为,k 则⎭ ⎝
⎛
=2:k y AB
()
04222222
222
2=++-⇒=⎪⎭
⎫ ⎝⎛-p k px k x k px p x k
.4221p x x =∴ 综上:.4
2
21p x x =
(2)p y x p y x 2,22
22211== ,,22142
221p y y p y y ±=⇒=∴
但22121,0p y y y y -=∴< (2)另证:设2
:p
my x AB +
=与px y 22=联立,得22122,02p y y p pmy y -=∴=-- 知识点2:若AB 是过抛物线()022>=p px y 的焦点F 的弦。
设(),,11y x A ()22,y x B ,则(1);21p x x AB ++=(2)设直线AB 的倾斜角为α证明:(1)由抛物线的定义知
,2
,221p
x BF p x AF +=+=
p x x BF AF AB ++=+=∴21 (2)若,2,90210p x x =
==则α由(1)知2p AB ==若px y p x k y AB 2,2:,9020=⎪⎭⎫ ⎝
⎛
-=≠与设α联立,得
()
04222222
222
2
=++-⇒=⎪⎭⎫ ⎝
⎛-p k px k x k px p x k
(),22221k k p x x +=+∴()
22211
2k k p p x x AB +=++=∴,而αtan =k ,
()
α
αα2
22sin 2tan tan 12p
p AB =+=∴ 知识点3:若AB 是过抛物线()022>=p px y 的焦点F 的弦,则以AB 为直径的圆与抛物线的准线相切。
证明:过点B A 、,11B A 、过AB 中点M 向准线引垂线,垂足为,N 设以AB 为直径的圆的半径为,r
.
2211r MN MN BB AA BF AF AB r =∴=+=+==
∴以AB 为直径的圆与抛物线的准线相切。
知识点4:若AB 是过抛物线()022>=p px y 的焦点的准线引垂线,垂足分别为,11B A 、则0
1190=∠FB A 。
证明借助于平行线和等腰三角形容易证明
知识点5:若AB 是过抛物线()022>=p px y 的焦点x 轴相交于点K ,则.BKF AKF ∠=∠
证明:过点B A 、分别作准线的垂线,垂足分别为11////BB KF AA
B B BF A A AF FB AF K B K A 1111,===∴而 B B A A K B K A 1111=∴
B
B K
B A A K A 1111=∴,而01190=∠=∠K BB K AA K AA 1∆∴∽K BB 1∆ KB B KA A 11∠=∠∴ BKF AKF ∠=∠∴
知识点6:若AB 是过抛物线()022>=p px y 的焦点F 的弦,o 为抛物线的顶点,连接
AO 并延长交该抛物线的准线于点,C 则.//OF BC
证明:设(),,11y x A ()22,y x B ,则
⎪⎪⎭⎫ ⎝⎛--∴=1111
2,2,:x p y p C x x y y AB 1
2
2
1
111222y p p
y p y x p y y C -=⋅-=-=∴ 由知识点1知2
21p y y -= 22
22
y y p p y C =--=∴ OF BC //∴ 逆定理:若AB 是过抛物线()022>=p px y 的焦点F 的弦,过点B 作OF BC //交抛物线准线于点,C 则O C A 、、三点共线。
证明略
知识点7:若AB 是过抛物线()022>=p px y 的焦点F .2
11p
n m =+ 证法:(1)若x AB ⊥轴,则AB 为通径,而,2p AB =
p n m ==∴ ∴
.2
11p
n m =+ (2)若AB 与x 轴不垂直,设(),,11y x A ()22,y x B ,AB 的斜率为k ,则⎪⎭⎫ ⎝
⎛
-=2:p x k y l 与
px y 22=联立,得()
04222222
222
2=++-⇒=⎪⎭
⎫ ⎝⎛-p k px k x k px p x k
()
,22
221k
k p x x +=+∴.42
21p x x = 由抛物线的定义知2
,221p
x BF n p x AF m +==+
==
∴
()p p
x x p x x p x x mn
n m n m 2
4
2112
212121=+
++++=+=+ 知识点8:已知抛物线()022>=p px y 中,AB 为其过焦点F 的弦,,,n BF m AF ==则
⎪⎪⎭
⎫ ⎝⎛+=∆n m m n p S AOB
4
2
证明:设,θ=∠AFx 则
BOF AOF AOB S S S ∆∆∆+=
()()θθ
θπsin 4
sin 221sin 221n m p
p
m p +=⋅⋅+-⋅⋅=
而mn p p mn p n p m 2
2
2sin ,sin ,cos 1,cos 1=∴=∴+=-=θθ
θθ ().4422⎪⎪⎭
⎫
⎝⎛+=+=∴∆n m m n p mn p n m p S AOB
逆定理:已知抛物线()022>=p px y 中,AB 为其弦且与x 轴相交于点M ,若
,,n BM m AM ==且,4
2⎪⎪
⎭
⎫ ⎝⎛+=∆n m m n p S AOB
则弦AB 过焦点。
证明:设(),,11y x A ()22,y x B ,,θ=∠AMx ()0,t M ,则
BOM AOM AOB S S S ∆∆∆+==()()θθθπsin 2
1
sin 21sin 21t n m tn tm +=+-
而,sin ,sin 21n
y m
y =
=
θθ mn
y y 2
12sin -=
∴θ mn y y 21sin -=
∴θ ()()21212121
y y t mn n m mn y y t n m S AOB -+=-+=∴∆ 而()2214
22
p mn n m n m m n p S AOB
+=⎪⎪
⎭
⎫ ⎝⎛+=∆ 2221p y y t =-∴① 又可设
0222:2
2
=--⇒⎭
⎬⎫=+=pt pay y px y t ay x l pt y y 221-=∴②
(x 1,y 1)
(x 2,y 2)
x
y
B´
A´由①②得2p t =
AB ∴恒过焦点⎪⎭
⎫ ⎝⎛0,2p 例1、过抛物线24y x =的焦点做直线交抛物线于1122(,),(,)A x y B x y 两点,如果126x x +=,那么AB =_________. 8
变式:过抛物线24y x =的焦点做直线交抛物线于,A B 两点,如果8AB =,O 为坐标原点,则OAB ∆的重心的横坐标是_________. 2
例2、直线l 经过抛物线22(0)y px p =>的焦点F ,且与抛物线交于,A B 两点,由,A B 分别向准线引垂线
'',AA BB ,垂足分别为'',A B ,如果''A B a =,Q 为''A B 的中点,则QF = _________.(用a 表示)
2
a
变式:直线l 经过抛物线22(0)y px p =>的焦点F ,且与抛物线交于,A B 两点,由,A B 分别向准线引垂线'',AA BB ,垂足分别为'',A B ,如果,AR a BF b ==,Q 为''A B 的中点,
则QF =_________.(用,a b
例3、设坐标原点为O ,过焦点的直线l 交抛物线24y x =于,A B 两点,OA OB ⋅= -3 例4、过抛物线2
(0)y ax a =>的焦点F 作一直线交抛物线于,P Q 两点,若线段PF 与FQ 的长分别是,p q ,则
11p q +=_____. 4a
小结:
(1)抛物线中的焦点弦问题很多都可以转化为这个直角梯形中的问题,在解决这类问题时注意对这个梯形的运用;
(2)万变不离其宗,解决问题的关键仍然是抛物线定义.。
