高三数学周练4

合集下载

2019-2020年上海进才中学高三下数学周练四

3
3
众图像，且 f x 的解析式型如 ax b (a , b R) ，则有序实数对 a , b x
。
12．已知 f x ax2 bx c 在 0，1 上满足 f x 1 ，则 a b c 的最大值是
公二、选择题（本题满分 20 分，共有 4 题，每小题 5 分）信 13．过点 (1，2) 且与直线 x 1 y 1 有相同方向向量的直线的一般式方程是（
微13．过点 (1，2) 且与直线 x 1 y 1 有相同方向向量的直线的一般式方程是 5 3
（ A） x 1 y 2
（ B ） 5x 3y 11 0
（ D ）。
5 3
（ C ） 3(x 1) 5( y 2) 0
（ D ） 3x 5y 13 0
14．若函数 y x2 4x 2 的定义域为 0 ，m ，值域为 6 ， 2 ，则 m 的取值范围是（ B ）。
：平面 PCD 所成的角为 45 ， PB 与平面 ABD 成 30 角，求：
号（1）求 PB 与 CD 所成的角；
（2）求二面角 C PB D 的余弦值。
众
公
信
微
2
19．（本题满分 14 分）本题共有 2 个小题，第 1 小题满分 7 分，第 2 小题满分 7 分如图，已知 A , B , C 是长轴为 4 的椭圆上三点，点 A 是
SHXINGAOKAO 可能是单调函数？若可能，求出a 的取值范围；若不可能，请说明理由。：
号众公信微
4
上海市进才中学 2019 学年第二学期高三数学周练四
命题教师、审题教师
20200314
一、填空题（本题满分 54 分，共有 14 题，1~6 每小题 4 分，7~12 每小题 5 分）

高三数学上学期周练(四)理(2021学年)

河南省正阳县201８届高三数学上学期周练（四)理编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方,但是任然希望(河南省正阳县２0１８届高三数学上学期周练（四)理)的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为河南省正阳县20１８届高三数学上学期周练（四）理的全部内容。

侧（左）视图421俯视图22０１7—2018学年上期高三数学理科周练（四)一.选择题1.已知集合{|21},{|1}x A x B x x =>=<,则A B （)A ．{|01}x x <<B ．{|0}x x > C.{|1}x x > Ｄ．{|1}x x < 2．若复数31a ii++(a R ∈,ｉ为虚数单位）是纯虚数，则实数a 的值为（）Ａ．－３ ﻩ B ． —２ C. ４Ｄ.3 3． 3．某程序框图如图所示,现输入如下四个函数,则可以输出的函数是（ )A.f(x)=x 2ﻩ B.f(x ）=1xC ．ｆ（ｘ）=x e ﻩD ．f(x)=s ｉnx4。

已知正数x ，y 满足20350x y x y -≤⎧⎨-+≥⎩,则z=-2ｘ-y 的最小值为（）A ．2 Ｂ.0 C ．-2 D.—4 5. 等差数列{}n a 前n 项和为n S ,且20162015120162015S S -=,则数列{}n a 的公差为( ） A ．1 B ．2 Ｃ．２015 D.20１66。

已知|a ｜=1,|b |＝2，且()a a b ⊥-,则向量a 与向量b 的夹角为A. ３0°B.45°C. ６0° ﻩＤ．1２０° ７. 已知1021001210(1)(1)(1)...(1)x a a x a x a x +=+-+-++-,则8a 等于A.-５B.5 C ．９0 D.１80８. 某几何体的三视图如图所示，其俯视图是由一个半圆与其直径组成的图形,则此几何体的体积是( )Ａ．203πB ．6π Ｃ．103πﻩﻩ D ．163π9。

高考复习高三数学周练(四)(含详细答案)

高三代数综合测试四一．选择题：本大题共10小题：每小题6分：共60分.在每小题给出的四个选项中：只有一项是符合题目要求的. （1）复数9)11(ii +-的虚部是（）（A ）1 （B ）1- （C ）i （D ）i -（文）设{}{}22|40,|M x x N x x ax x a =-≥=-≥-：若MN M =：则a 的取值范围是（）（A ）[]0,2 （B ）[]1,2 （C ）[]2,1- （D ）[]2,2- （2）已知向量()()cos15,sin15,cos75,sin 75OA OB =︒︒=︒︒：则AB 为（）（A ）12（B）2 （C（D ）1（3）等比数列}{n a 中：5121=a ：公比21-=q ：用n ∏表示它的前n 项之积：n n a a a ⋅⋅⋅⋅=∏21：则12,,n∏∏∏中最大的是（）（A ）11∏ （B ）10∏ （C ） 9∏ （D ）8∏ （4）在△ABC 中：面积22()S a b c =--：则sin A = （）（A ）1715 （B ）178 （C ）1513 （D ）1713 （5）如图所示的电路：有c b a ,,三个开关：每个开关开或关的概率都是21：且是相互独立的：则灯泡甲亮的概率为（A ）81 （B ）41 （C ）21 （D ）161（6）随机变量ξ的概率分布规律为),4,3,2,1()1()(=+==n n n an P ξ其中a 是常数：则)2521(<<ξP 的值为（）（A ）32 （B ）43 （C ）54 （D ）65（7）设函数2)2(),0()4(,)0(2)0()(2-=-=-⎩⎨⎧>≤++=f f f x x c bx x x f 若：则关于x 的方程x x f =)(的解的个数为（）（A ）1个（B ）2个（C ）3个（D ）4个（8）若log b π<log a π<0, 则lim n nn nn a b a b →∞-+= （）（A ）1 （B ）－1 （C ） 0 （D ）3（文）已知O 为原点：()(),0,0,OA a OB a ==其中a 为常数且0,a AP t AB >= ()02t ≤≤：则OA OP 的最小值是（）（A ）0 （B ）2- （C ）2a - （D ）2a -（9）按一次电视机遥控器上的电源开关：电视机可能出现以下三种情况：①由原来的关机状态转为开机状态：②由原来的开机状态转为关机状态：③电视机保持原来的状态不变.由于电视机从关机状态转为开机状态要等待一段时间：一台电视机处于关机状态时：某人连续按了4次电源开关：结果使电视转为开机：则他所按的4次中可以发生的所有的情况种数为（）（A ）8 （B ）12 （C ）16 （D ）20 （10）实系数方程220x ax b ++=的一根大于0且小于1：另一个根大于1且小于2：则12--a b 的取值范围是（）（A ）)1,41( （B ）)1,21(（C ）)41,21(-（D ）)21,21(- 二、填空题：本大题共4小题：每小题5分：共20分.（11）某厂包装车间对包装质量进行检查时：采用这样的方法：在自动包装传送带上：每隔30分钟抽一包产品：进行质量检查：这样的抽样方法是抽样. （12）梯形的两对角线把梯形分成四部分, 有五种不同的颜色给这四部分涂色, 每一部分涂一种颜色, 任何相邻(具有公共边)的两部分涂不同的颜色, 则不同的涂色方法有种. （13）1023)21(x x -展开式中的常数项为 . （14）函数3()33f x x bx b =-+在（0：1）内有极小值：则实数b 的取值范围是____ ____.高三代数综合测试四答题卷班级姓名学号.（11）（12）（13）（14）三．解答题：本大题共4小题：共70分．解答应写出文字说明：证明过程或演算步骤.根据以上材料：解答下列问题：（Ⅰ）如果在该公司干10年：问选择第二方案比选择第一方案多加薪水多少元？（Ⅱ）如果第二方案中的每半年加300元改成每半年加a 元：问a 取何值时：总是选择第二方案比选择第一方案多加薪？（16）已知函数ax x x f +-=)2ln()(在)23,0(上是增函数：2||)(2a a e x g x+-=.当]3ln ,0[∈x 时：函数)(x g 的最大值M 与m 最小值的差为23：试求a 的值.（17）盒子中有大小相同的球10个：其中标号为1的球3个：标号为2的球4个：标号为5的球3个：第一次从盒中任意取1个球：放回后第二次再任意取一个球（假设取到每个球的可能性都相同）：记第一次与第二次取到球的标号之和为ξ. （Ⅰ）求随机变量ξ的分布列：（Ⅱ）求ξ的数学期望.（文）从4名男生和2名女生中任选3人参加演讲比赛：（Ⅰ）求所选3人都是男生的概率：（Ⅱ）求所选3人中恰有1名女生的概率：（Ⅲ）求所选3人中至少有一名女生的概率.（18）已知点集},|),{(n m y y x L ⋅==其中),1,1(),1,2(+=-=b n b x m 点列),(n n n b a P 在L 中：1P 为L 与y 轴的交点：等差数列}{n a 的公差为1：n N *∈.（Ⅰ）求数列}{n a ：}{n b 的通项公式：（Ⅱ）若),2(||51≥⋅=n P P n c n n 求23lim()n n c c c →∞+++：（Ⅲ）若),()2()12()(+∈⎩⎨⎧=-==N k k n b k n a n f n n 是否存在k N *∈使得),(2)11(k f k f =+若存在：求出k 的值：若不存在：请说明理由.代数综合测试四参考答案仅供参考）B/DDCBA 、DCB/DAA ：系统抽样、260、10532、01b << 15、解：（Ⅰ）在该公司干10年：第一种方案多加的薪水为：1000200030001000055000+++⋅⋅⋅+=第二种方案多加的薪水为：300600900600063000+++⋅⋅⋅+=（Ⅱ）设在该公司工作时间为()n n N *∈年：则第一方案多加的薪水为：(1)100010002n n S n -=+：第二方案多加的薪水为：2(21)'2n n S an a -=+：即'S S >对()n n N *∈恒成立：得：10003a >.16、解：解：a x x f +-=21)('： )(x f 在)23,0(上是增函数.021>+-∴a x 在∈x )23,0(上恒成立：21-->∴x a 恒成立：222121≥∴<--<a x . 设,xe t =则2||)()(2a a t x g t h +-==：31,3ln 0≤≤∴≤≤t x（ⅰ）当32<≤a 时：⎪⎪⎩⎪⎪⎨⎧≤≤+-<≤++-=3,21,2)(22t a a a t a t a a t t h2)(,21)1(22a a h m a a h M ==+-==∴：25231=∴=-=-∴a a m M（ⅱ）当3≥a 时：2)(2a a t t h ++-=23)3(,21)1(22a a h m a a h M +-==+-==∴：2=-∴m M 不符题意.综上：a 的取值为25=a . （对于不同的解法可根据本解法酌情给分）（Ⅱ）E ξ＝5.2（文）解：（Ⅰ）343615C P C ==：（Ⅱ）12243635C C P C ==：（Ⅲ）3436415C P C =-=. 18、解：（1）由⎪⎪⎩⎪⎪⎨⎧+=-=⋅=)1,1()1,2(b n b x m n m y ：得12+=x y)1,0(,12:1P x y L ∴+=∴：则,1,011==b a1(),21()n n a n n N b n n N **∴=-∈=-∈（2）当2≥n 时：：)1(5||),12,1(1-=--n P P n n P n nnn n n P P n c n n 111)1(1||51--=-==： 23lim()n n c c c →∞∴+++=1)11(lim )]111()3121()211[(lim =-=--+-+-∞→∞→nn n n n（3）假设存在符合条件的k 使命题成立当k 是偶数时：11+k 是奇数：则12)(,10)11(-=+=+k k f k k f 由),(2)11(k f k f =+得4=k ：当k 是奇数时：11+k 是偶数：则1)(,212)11(-=+=+k k f k k f ：由),(2)11(k f k f =+得k 无解：综上存在4=k ：使得)(2)11(k f k f =+. （对于不同的解法可根据本解法酌情给分）。

高三数学周练提升4

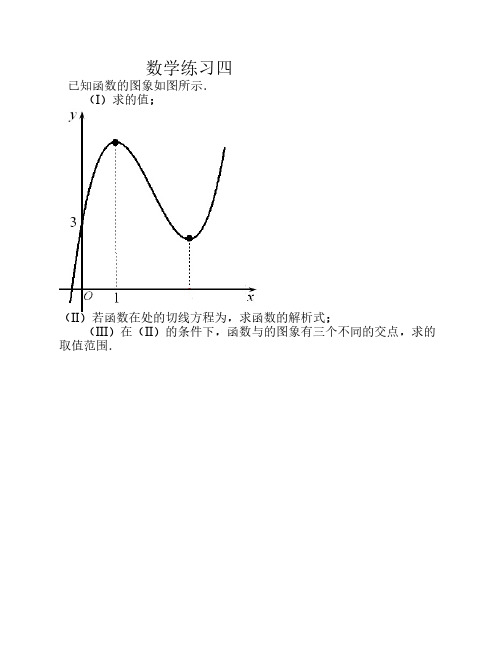
数学练习四1．已知函数的图象如图所示．（I）求的值；（II）若函数在处的切线方程为，求函数的解析式；（III）在（II）的条件下，函数与的图象有三个不同的交点，求的取值范围．2．已知函数．（I）求函数的单调区间；（II）函数的图象的在处切线的斜率为若函数在区间（1，3）上不是单调函数，求m的取值范围．3．已知函数的图象经过坐标原点，且在处取得极大值．（I）求实数的取值范围；（II）若方程恰好有两个不同的根，求的解析式；（III）对于（II）中的函数，对任意，求证：．4．已知常数，为自然对数的底数，函数，．（I）写出的单调递增区间，并证明；（II）讨论函数在区间上零点的个数．5．已知函数．（I）当时，求函数的最大值；（II）若函数没有零点，求实数的取值范围；6．已知是函数的一个极值点（）．（I）求实数的值；（II）求函数在的最大值和最小值．7．已知函数（I）当a=18时，求函数的单调区间；（II）求函数在区间上的最小值．8．已知函数在上不具有单调性．（I）求实数的取值范围；（II）若是的导函数，设，试证明：对任意两个不相等正数，不等式恒成立．9．已知函数（I）讨论函数的单调性；（II）证明：若10．已知函数．（I）若函数在区间上都是单调函数且它们的单调性相同，求实数的取值范围；（II）若，设，求证：当时，不等式成立．11．设曲线：（），表示导函数．（I）求函数的极值；（II）对于曲线上的不同两点，，，求证：存在唯一的，使直线的斜率等于．12．定义，（I）令函数，写出函数的定义域；（II）令函数的图象为曲线C，若存在实数b使得曲线C在处有斜率为－8的切线，求实数的取值范围；（III）当且时，求证．答案1．（本题满分12分）已知函数的图象如图所示．（I）求的值；（II）若函数在处的切线方程为，求函数的解析式；（III）在（II）的条件下，函数与的图象有三个不同的交点，求的取值范围．解：函数的导函数为 …………（2分）（I）由图可知函数的图象过点（0，3），且得 …………（4分）（II）依题意且解得所以 …………（8分）（III）．可转化为：有三个不等实根，即：与轴有三个交点；+0-0+增极大值减极小值增． …………（10分）当且仅当时，有三个交点，故而，为所求． …………（12分）2．（本小题满分12分）已知函数．（I）求函数的单调区间；（II）函数的图象的在处切线的斜率为若函数在区间（1，3）上不是单调函数，求m的取值范围．解：（I）（2分）当当当a=1时，不是单调函数（5分）（II）（6分）（8分）（10分）（12分）3．（本小题满分14分）已知函数的图象经过坐标原点，且在处取得极大值．（I）求实数的取值范围；（II）若方程恰好有两个不同的根，求的解析式；（III）对于（II）中的函数，对任意，求证：．解：（I）由，因为当时取得极大值，所以，所以；…………（4分）（II）由下表：+0-0-递增极大值递减极小值递增依题意得：，解得：所以函数的解析式是：…………（10分）（III）对任意的实数都有在区间[-2，2]有：函数上的最大值与最小值的差等于81，所以．…………（14分）4．（本小题满分12分）已知常数，为自然对数的底数，函数，．（I）写出的单调递增区间，并证明；（II）讨论函数在区间上零点的个数．解：（I），得的单调递增区间是， …………（2分）∵，∴，∴，即． …………（4分）（II），由，得，列表-0+单调递减极小值单调递增当时，函数取极小值，无极大值．…………（6分）由（I），∵，∴，∴， …………（8分）（i）当，即时，函数在区间不存在零点（ii）当，即时若，即时，函数在区间不存在零点若，即时，函数在区间存在一个零点；若，即时，函数在区间存在两个零点；综上所述，在上，我们有结论：当时，函数无零点；当时，函数有一个零点；当时，函数有两个零点．…………（12分）5．（本小题满分14分）已知函数．（I）当时，求函数的最大值；（II）若函数没有零点，求实数的取值范围；解：（I）当时，定义域为（1，+），令， ………………（2分）∵当，当，∴内是增函数，上是减函数∴当时，取最大值 ………………（4分）（II）①当，函数图象与函数图象有公共点，∴函数有零点，不合要求； ………………（8分）②当， ………………（6分）令，∵，∴内是增函数，上是减函数，∴的最大值是，∵函数没有零点，∴，，因此，若函数没有零点，则实数的取值范围．………………（10分）6．（本小题满分12分）已知是函数的一个极值点（）．（I）求实数的值；（II）求函数在的最大值和最小值．解：（I）由可得……（4分）∵是函数的一个极值点，∴∴，解得 ……………（6分）（II）由，得在递增，在递增，由，得在在递减∴是在的最小值； ……………（8分），∵∴在的最大值是． ……………（12分）7．（本小题满分14分）已知函数（I）当a=18时，求函数的单调区间；（II）求函数在区间上的最小值．解：（Ⅰ），2分由得，解得或注意到，所以函数的单调递增区间是（4，+∞）由得，解得-2＜＜4，注意到，所以函数的单调递减区间是.综上所述，函数的单调增区间是（4，+∞），单调减区间是 6分（Ⅱ）在时，所以，设当时，有△=16+4×2，此时，所以，在上单调递增，所以 8分当时，△=，令，即，解得或；令，即，解得.①若≥，即≥时，在区间单调递减，所以.②若，即时间，在区间上单调递减，在区间上单调递增，所以.③若≤，即≤2时，在区间单调递增，所以综上所述，当≥2时，；当时，；当≤时， 14分8．（本小题满分12分）已知函数在上不具有单调性．（I）求实数的取值范围；（II）若是的导函数，设，试证明：对任意两个不相等正数，不等式恒成立．解：（I）， ………………（2分）∵在上不具有单调性，∴在上有正也有负也有0，即二次函数在上有零点 ………………（4分）∵是对称轴是，开口向上的抛物线，∴的实数的取值范围 ………………（6分）（II）由（I），方法1：，∵，∴，…………（8分）设，在是减函数，在增函数，当时，取最小值∴从而，∴，函数是增函数，是两个不相等正数，不妨设，则∴，∵，∴∴，即 ………………（12分）方法2：、是曲线上任意两相异点，，，………（8分）设，令，，由，得由得在上是减函数，在上是增函数，在处取极小值，，∴所以即 ………………（12分）9．（本小题满分12分）（I）讨论函数的单调性；（II）证明：若（1）的定义域为，2分（i）若，则故在单调增加．（ii）若单调减少，在（0，a-1），单调增加．（iii）若单调增加．（II）考虑函数由由于，从而当时有故，当时，有10．（本小题满分14分）已知函数．（I）若函数在区间上都是单调函数且它们的单调性相同，求实数的取值范围；（II）若，设，求证：当时，不等式成立．解：（I）， ……………（2分）∵函数在区间上都是单调函数且它们的单调性相同，∴当时，恒成立， ……………（4分）即恒成立，∴在时恒成立，或在时恒成立，∵，∴或 ………………（6分）（II），∵定义域是，，即∴在是增函数，在实际减函数，在是增函数∴当时，取极大值，当时，取极小值， ………………（8分）∵，∴ ………………（10分）设，则，∴，∵，∴∴在是增函数，∴∴在也是增函数 ………………（12分）而，∴∴当时，不等式成立． ………………（14分）11．（本小题满分12分）设曲线：（），表示导函数．（I）求函数的极值；（II）对于曲线上的不同两点，，，求证：存在唯一的，使直线的斜率等于．解：（I），得当变化时，与变化情况如下表：＋0－单调递增极大值单调递减∴当时，取得极大值，没有极小值； …………（4分）（II）（方法1）∵，∴，∴即，设，，是的增函数，∵，∴；，，是的增函数，∵，∴，∴函数在内有零点， …………（10分）又∵，函数在是增函数，∴函数在内有唯一零点，命题成立…………（12分）（方法2）∵，∴，即，，且唯一设，则，再设，，∴∴在是增函数∴，同理∴方程在有解 …………（10分）∵一次函数在是增函数∴方程在有唯一解，命题成立………（12分）注：仅用函数单调性说明，没有去证明曲线不存在拐点，不给分．12.定义，（I）令函数，写出函数的定义域；（II）令函数的图象为曲线C，若存在实数b使得曲线C在处有斜率为－8的切线，求实数的取值范围；（III）当且时，求证．解：（I），即 ……………………（2分）得函数的定义域是， ……………………（4分）（II）设曲线处有斜率为－8的切线，又由题设∴存在实数b使得有解， ……………………（6分）①②③由①得代入③得，有解， ……………………（8分）方法1：，因为，所以，当时，存在实数，使得曲线C在处有斜率为－8的切线………………（10分）方法2：得，………………（10分）方法3：是的补集，即 ………………（10分）（III）令又令，单调递减. ……………………（12）分单调递减，，………………（14分）。

高三数学上学期第四次周测试题-人教版高三全册数学试题

f (x) cos x 0 的解集是（）
A． (3, ) (0,1) ( ,3)
2
2
C． (3, 1) (0,1) (1,3)
B． ( , 1) (0,1) ( ,3)
2
2
D． (3, ) (0,1) (1,3) 2
二．填空题 (本大题共 4 小题,每小题 5 分,共 20 分,请将答案填在答题卡的相应位置．)
word
{甲，乙}，{甲，丙}，{甲，丁}，{乙，丙}，{乙，丁}，{丙，丁} ,有 6 个基本事件
设“随机抽取两人进行访谈，这两人的两科成绩等级均为 A”为事件 B，所以事件 B 中包含的
基本事件有 1 个，则
. ……………………12 分
19．证明：作 FM∥CD 交 PC 于 M.
∵ 点 F 为 PD 中点， ∴ FM 1 CD .∵ k 1 ，
(1)若函数 y g(x) 图象恒过定点 P ，且点 P 关于直线 x 3 的对称点在 y f (x) 的图象上， 2
求 m 的值； (2)当 a 8 时，设 F (x) f '(x) g(x 1) ，讨论 F (x) 的单调性；
(3)在(1)的条件下，设
G(x)
f (x), x
g ( x),
∵ AE k ， AB 1， k 2 ，∴ AE 2 .
AB
2
2
又∵∠DAB＝45°，∴AB⊥DE.
又∵PD⊥平面 ABCD，∴PD⊥AB.
又∵ PD DE D ，∴AB⊥平面 PDE.
∵ AB 平面PAB ，∴平面 PED⊥平面 PAB. …………………………………12 分
20．解：（1）设
A． 3 B． 2 C． 4 D． 3 3.已知函数 f (x) 是定义在区间[a, a] (a 0) 上的奇函数，若 g(x) f (x) 2 ，则 g(x) 的

高三数学下学期第四次周考模拟试题

)32sin(π+=x y 塘栖中学2021届高三数学下学期第四次周考模拟试题制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日一、选择题〔本大题一一共8小题，每一小题5分，满分是40分。

在每一小题给出的四个选项里面，只有一项是哪一项符合题目要求的。

〕1．设全集U ＝R ，集合P {2}=>x x ，Q ＝2{20}--<x x x ，那么〔∁U P 〕 Q= A ．)21(，-B ．]21(，-C ．)12(，-D ．∅2．设a ，b 是实数，那么“||||a b a b -≥+〞是“0ab <〞的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件A ．0)(0)(==∈∀x g x f x 且R,B ．0)(0)(==∈∀x g x f x 或R,C ．0)(0)(000==∈∃x g x f x 且R,D ．0)(0)(000==∈∃x g x f x 或R,)0,12(π-中心对称A ．向右平移12πB ．向左平移12πC ．向右平移6πD ．向左平移6π6．实数a ，b 满足41)22()21(21>>>b a ，那么7．1F ，2F 分别为双曲线C ：12222=-by a x 的左、右焦点，假设存在过1F 的直线分别交双曲线C 的左、右支于A ，B 两点，使得122F BF BAF ∠=∠，那么双曲线C 的离心率e 的取值范围是 A ．()+∞,3B ．()521+, C ．()523+,D ．()31,8.在正三棱柱〔底面是正三角形的直棱柱〕111ABC A B C -中，12AB AA ==.假设点M 在ABC ∆ 所在平面上运动，且使得1AC M ∆的面积为1，那么动点M 的轨迹为二、填空题〔此题一共7小题，满分是36分，多空题每一小题6分，单空题每一小题4分。

〕 9．各项互不相等的等比数列{}n a 的公比为q ，前n 项和为n S ，假设3232S a a ,,成等差数列，且31=a ，那么q = ▲ ，n S = ▲ ．10．函数132log 1()21,x x f x x x x >⎧⎪=⎨⎪-+≤⎩,,,那么=))3((f f ▲ ，函数)(x f 的最大值是▲ ．11．实数x ，y 满足条件1,4,20,-≥-⎧⎪+≤⎨⎪-≤⎩x y x y x y 假设存在实数a 使得函数)0(<+=a y ax z 取到最大值)(a z 的解有无数个，那么=a ▲ ，)(a z = ▲ ． 12．)π2π(,∈α，)4πsin(2cos αα-=，那么α2sin = ▲ ，αsin = ▲ ． 13．正方形ABCD ，E 是边AB 的中点，将ADE △沿DE 折起至DE A '，如下图，假设A CD '为正三角形，那么ED 与平面DC A '所成角的余弦值是 ▲ ．〔第7题〕14．如图，点A 为圆O ：922=+y x 与圆C ：()16522=+-y x 在第一象限内的交点，过A的直线l 被圆O 和圆C 所截得的弦分别为NA ，MA 〔M ，N 不重合〕，假设MA NA =，那么直线l 的方程是 ▲15.ABC ∆中，||1BC =，2BA BC ⋅=，点P 为线段BC 上的动点，动点Q 满足PQ PA PB PC =++，那么PQ PB ⋅的最小值等于 ▲ ．三、解答题〔本大题一一共5小题，满分是74分。

2021年高三上学期周练(4)数学试题

2021年高三上学期周练（4）数学试题姓名班级一．填空题（5×14=70）1.已知A={1，2，3，4，5，6，7}，集合，则CM=2.若复数满足则3.已知命题p：∀x∈(1，＋∞)，log2x＞0，则非p为__________________4.已知sin(π－α)＝23，则cos(π－2α)＝_______5.已知函数，则的最小正周期是6.已知向量a，b满足，|b|＝2，a与b的夹角为60°，则|a－b|＝,则|a|＝7.如图，平行四边形ABCD的对角线AC和BD交于点M，设向量，则________ (用向量a,b表示)8.设是等差数列的前n项和，已知，，则=_____9.函数 y=x-lnx的单调递减区间为10.“a＝－14”是“函数f(x)＝ax2－x－1只有一个零点”的_______ _条件11.已知函数满足,且的最小值为,则正数的值为12.已知,,则的值为13.在△ABC中，，D是BC边上任意一点（D与B、C不重合），且，则等于14.设函数，记，若函数至少存在一个零点，则实数m的取值范围是二、解答题（14+14+14+16+16+16=90）15.(xx江苏T)在平面直角坐标系xOy中，点A(-1,-2),B(2,3),C(-2,-1)(1)求以线段AB、AC为邻边的平行四边形两条对角线的长(2)设实数t满足()·=0，求t的值16.中，，三内角成等差数列．（1）若，求长；（2）求的最大值17.已知向量a与向量b的夹角为，=2，=3，记向量m=3a-2b,n=2a+kb(1)若mn,求实数k的值（2）是否存在实数k，使得m//n?若存在，求出实数k；若不存在，请说明理由18. 已知函数．（1）求函数的单调递减区间；（2）若在上恒成立，求实数的取值范围．19.（本小题满分14分）某企业有两个生产车间分别在、两个位置，车间有100名员工，车间有400名员工。

新高三数学上学期周练试题(四)-人教版高三全册数学试题

河北定州中学2017届新高三数学周练（四）一、选择题：共12题每题5分共60分1．已知O 为坐标原点，双曲线2222:1(0,0)x y C a b a b -=>>的左焦点为(,0)(0)F c c ->，以OF 为直径的圆交双曲线C 的渐近线于A,B ，O 三点，且()0AO AF OF +⋅=．关于x 的方程2ax bx c +-=的两个实数根分别为1x 和2x ，则以12,,2x x 为边长的三角形的形状是（）A ．钝角三角形B ．直角三角形C ．锐角三角形D ．等腰直角三角形 2．已知(2,4),(3,)a b m =-=-，若a b a b +⋅=，则实数m =（）A ．32 B ．3 C ．6 D ．83．函数()f x 是定义在R 上的奇函数，当0x >时，()()2,0111,12x x f x f x x ⎧<≤⎪=⎨->⎪⎩则方程()1f x x =在[]-3,5上的所有实根之和为（）A ．0B ．2C ．4D ．64．已知直线1y x =-与双曲线221ax by +=（0,0a b ><）的渐近线交于,A B 两点，且过原点和线段AB 中点的直线的斜率为b a的值（）A ．．．． 5．已知抛物线C ：28y x =的焦点为F ，准线与x 轴的交点为K ，点A 在C 上且|||AK AF =，则AFK ∆的面积为（） A ．4 B ．8 C ．16 D ．32 6．已知()xf x x e =⋅，又2()()()g x f x t f x =+⋅()t R ∈若满足()1g x =-的x 有四个，则t 的取值范围为（）A ．21,e e ⎛⎫++∞ ⎪⎝⎭B ．21,e e ⎛⎫+-∞- ⎪⎝⎭ C ．21,2e e ⎛⎫+-- ⎪⎝⎭ D ．212,e e ⎛⎫+ ⎪⎝⎭ 7．设12,F F 是双曲线2214y x -=的左、右两个焦点，若双曲线右支上存在一点P ，使()220OP OF F P +⋅=（O 为坐标原点）且12PFPF λ=则λ的值为（）A ．2B ．12 C ．3 D ．138．已知函数2()2ln f x x x=-与()sin()g x x ωϕ=+有两个公共点，则在下列函数中满足条件的周期最大的()g x =（）A ．sin(2)2x ππ-B ．sin()22x ππ- C ．sin()2x ππ- D ．sin()2x ππ+ 9．已知函数()()()21131x f x e ax a +=++-，若存在()0,x ∈+∞，使得不等式()1f x <成立，则实数a 的取值范围为（）A ．()20,31e e ⎛⎫+ ⎪ ⎪+⎝⎭B ．20,1e ⎛⎫ ⎪+⎝⎭ C ．()2,31e e ⎛⎫+-∞ ⎪ ⎪+⎝⎭ D ．1,1e ⎛⎫-∞ ⎪+⎝⎭ 10．点A 是抛物线()21:20C y px p =>与双曲线()22222:10,0x y C a b a b -=>>的一条渐近线的交点，若点A 到抛物线1C 的准线的距离为p ，则双曲线2C的离心率等于（）AC11．已知函数()11,11x f x x x x -≤≤=-<->⎪⎩或，且函数()()2g x f x kx k =-+有两个不同的零点，则实数k 的取值范围是（）A．0k ≤≤ B ．103k -≤≤或k = C．k ≤或13k =-D．13k ≤≤-或0k = 12．过双曲线22221(0,0)x y a b a b -=>>左支上一点A 作相互垂直的两条直线分别经过两焦点12,F F ,其中一条与双曲线交于点B ，若()220AB AF BF +⋅=，则双曲线的离心率为（）ABD二、填空题：共4题每题5分共20分13．已知抛物线x y 42=与经过该抛物线焦点的直线l 在第一象限的交点为A A ,在y 轴和准线上的投影分别为点,B C ，2ABBC=，则直线l 的斜率为．14．已知1F 、2F 是椭圆C ：22221(0)x y a b a b +=>>的两个焦点，P 为椭圆C 上一点，且12PF PF ⊥.若12PF F ∆的面积为9，则b =____________.15．已知)2,1(A ,)2,1(-B ,动点P 满足BP AP ⊥,若双曲线)0,0(12222>>=-b a b y a x 的渐近线与动点P 的轨迹没有公共点，则双曲线离心率的取值范围是 .16．已知函数()()224,04log 22,46x x x f x x x ⎧-+≤<⎪=⎨-+≤≤⎪⎩，若存在1x ，2R x ∈，当12046x x ≤<≤≤时，()()12f x f x =，则()12x f x 的取值范围是．三、解答题：共8题共70分17．已知函数()()()ln 0x af x ax a x -=-≠．（Ⅰ）求此函数的单调区间及最值；（Ⅱ）求证：对于任意正整数n ，均有1＋12＋13…＋1n ≥ln!n e n （e 为自然对数的底数）．18．工作人员需进入核电站完成某项具有高辐射危险的任务，每次只派一个人进去，且每个人只派一次，工作时间不超过10分钟，如果前一个人10分钟内不能完成任务则撤出，再派下一个人。

高三数学第四次周练试卷试题

实验中学高三数学第四次周练试卷制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日命题人：聊秀平肖成荣第I 卷〔选择题，一共60分〕一、选择题：本大题一一共12小题，每一小题5分，一共60分。

以下各小题所给出的四个答案中只有一个是正确的。

1．全集I=R ，集合 A B x xy x A 则},4,3{},24|{=--==〔 U B 〕等于〔〕A ．〔2，3〕∪〔3，4〕B ．〔2，4〕C ．〔2，3〕∪〔3，4]D ．〔2，4]2．1．过点(1,2)P 引直线，使它与两点(2,3)A 、(4,5)B -间隔相等，那么此直线方程为〔〕 ()A 2370x y +-=或者460x y +-= ()B 460x y +-=()C 3270x y +-=或者460x y +-= ()D 46x y +=3．数列{a n }是等差数列，且a 3+a 11=50，a 4=13，那么a 2等于〔〕A ．1B ．4C ．5D ．64．当11≤≤-x 时，函数12)(++=a ax x f 的值有正有负，那么a 的取值范围是〔〕A ．31-≥a B ．1-≤a C ．311-<<-a D ．R5 如图，一个空间几何体的正视图、侧视图、俯视图为全等的等要直角三角形，假如直角三角形直角边长为1，那么这个几何体的体积为〔〕 A 1 B21 C 31D 61正视图侧视图俯视图6．以下说法正确的选项是〔〕 A ．定义在R 上的函数f(x)满足f(2)>f(1)，那么f(x)在R 上是增函数 B ．定义在R 上的函数f(x)满足f(2)>f(1)，那么f(x)在R 上不是减函数 C ．y=tanx 在定义域上是增函数D ．假设f(x+1)是奇函数，那么f(－x －1)=－f(x+1)7．盒中装着标有数字1，2，3，4的卡片各2张，从盒中任意任取3张，每张卡片被抽出的可能性都相等 ,那么抽出的3张卡片上最大的数字是4的概率；〔〕A 149 B 145 C 1411D14138 .设随即机变量§的概率分布列为P 〔§=k 〕=2kc,k=1,2,3,4,5,6。

晋江市养正中学高三数学周练(4)2013.4(教师版)

晋江市养正中学周练(4)2013.4(教师版)数学试题（理科）（命卷:郑明铿审卷:高三备课组考试时间：120分钟；满分：150分）第Ⅰ卷（选择题共50分）一、选择题：本大题共10小题,每小题5分，共50分.在每小题给出的四个选项中，只有一项是满足题目要求的.1. 下列命题中的假命题是( D )A. 0,2≥∈∀x R xB. 1log ,2=∈∃x R xC. 0)21(,>∈∀xR x D. 25sin ,=∈∃x R x2. 已知直线α平面⊥l ，直线β平面⊂m ，则“βα//”是“m l ⊥”的( A ) A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3. 已知某三棱锥的三视图（单位:C m)如图所示，则该三棱锥的体积是( A )A. 1cm 3B. 2cm 3C. 3 cm 3D. 6cm 34. 已知向量a ,b ，满足|a|=3,|b|=23且a 丄(a +b ),则a 与b 的夹角为( D ) A. 2πB.32π C.43π D.65π5. 某物体在变力F(x)=5-x 2 （x 的单位：m ，F 的单位：N)的作用下，沿着与F (x)成30°方向做直线运动，则从x=1处运动到x = 2处时变力F (x)所做的功为( C )A. J 23 B. J 3 C.J 334 D. 2J 36. 设复数iix -=12（i 是虚数单位），则20132013201333201322201312013xC x C x C x C +⋯+++=( C )A.iB. -iC. -1 +iD.1+i7.ΔABC 的内角A,B,C 的对边分别为a ，b,c ，已知c o s (A -C )+ cosB = 1,a =2c ，则C =( B )A.656ππ或B.6πC.323ππ或D.3π8. 某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A 原料1千克3原料2千克；生产乙产品1桶需耗A 原料2千克,B 原料1千克.每桶甲产品的利润是300元，每桶乙产品的利润是400元.公司在生产这两种产品的计划中，要求每天消耗A ，B 原料都不超过12千克.通过合理安排生产计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是( C )A. 1800 元B. 2400 元C. 2800 元D. 3100 元9. 已知F 1、F 2分别是双曲线12222=-by ax 的左、右焦点,P 为双曲线右支上的任意一点.若a PF PF 8||||221=，则双曲线离心率的取值范围是( C )A. (1,2]B. [2 +∞)C. (1,3]D. [3，+∞)10. 已知方程(1)(||2)4y x ++=,若对任意[,](,)x a b a b Z ∈∈，都存在唯一的[0,1]y ∈使方程成立；且对任意[0,1]y ∈，都有[,](,)x a b a b Z ∈∈使方程成立，则a b +的最大值等于（ D ） A ．-2B ． 0C ．1D ． 2第Ⅱ卷（非选择题共100分）二、填空题：本大题共5小题，每小题5分，共20分.11.右图是一个算法流程图，则输出的k 的值是________612.将甲、乙、丙3名志愿者安排在周一至周五的5天中参加某项志愿者活动，要求每人参加一天且每天至多安排一人，并要求甲安排在乙、丙的前面，则不同的安排方法共有______种.2013.在等比数列{a n }中，若r,s,t 是互不相等的正整数，则有等式成立.类比上述性质，相应地，在等差数列{b n }中,若r ，s ，t 是互不相等的正整数，则有等式____________________成立. (r-s)b t +(s-t)b r +(t-r)b s =014. 一袋中有红、黄、蓝三种颜色的小球各一个，每次从中取出一个，记下颜色后放回，当三种颜色的球全部取出时停止取球，则恰好取5次球时停止取球的概率为_______811415. 函数()f x 的导函数为()f x '，若对于定义域内任意1x 、2x 12()x x ≠，有121212()()()2f x f x x x f x x -+'=-恒成立，则称()f x 为恒均变函数．给出下列函数：①()=23f x x +；②2()23f x x x =-+；③1()=f x x；④()=x f x e ；⑤()=ln f x x ．其中为恒均变函数的序号是 .（写出所有满足条件的函数的序号）①②三、解答题：解答应写出文字说明、证明过程或演算步骤.16.(本小题满分13分）已知x 0, x 0+2π是函数f(x)=cos 2(ωx-6π)-sin 2ωx(ω>0)的两个相邻的零点.(I )求)12(πf 的值；(II)若对]0,127[π-∈∀x ，都有1|)(|≤-m x f ，求实数m 的取值范围.17. （本小题满分13分）为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图(如图)，已知图中从左到右的前3个小组的频率之比为1:2:3，其中第2小组的频数为12.（Ⅰ）求该校报考飞行员的总人数; （Ⅱ）以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中（人数很多）任选三人，设X 表示体重超过60公斤的学生人数，求X 的分布列和数学期望.18.(本小题满分13分）如图,在ΔAOB 中，已知,6,2ππ=∠=∠BAO AOB AB ＝4，D 为线段贴的中点. ΔAOC 是由绕直线AO 旋转而成，记二面角B-AO-C 的大小为θ 6.(I )当平面COD 丄平面AOB 时，求θ的值；（II ）当θ＝32π 求二面角B －OD －C 的余弦值19 (本小题满分13分）.如图,长为m +1(m>0)的线段A B 的两个端点A 和B 分别在x轴和y 轴上滑动,点M 是线段AB上一点,且MB m AM =(I)求点M 的轨迹Γ的方程,并判断轨迹Γ为何种圆锥曲线； (II)设过点Q(21,0)且斜率不为0的直线交轨迹Γ于C 、D 两点.试问在x轴上是否存在定点P ，使PQ 平分乙CPD ∠?若存在,求点P 的坐标；若不存在,请说明理由20. (本小题满分14分） (I)已知函数)1,0,0()()(2)(1>>+-+=-p a x a x a xx f pp pp ，求f(x)的最小值；(I I )证明：2)2(pppb a b a +≤+，其中a >0,b > O,P > 1；(III)证明na a a na a a pnp p pn+⋯++≤+⋯++21121)(其中a 1, a 2,…a n >0,p>1,*N n ∈21. 本题（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题做答，满分14分，如果多做，则按所做的前两题计分. 作答时，先用2B 铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中.（1）（本小题满分7分）选修4—2；矩阵与变换已知在一个二阶矩阵M 的变换作用下，点A(1,2)变成了点A′(4, 5)，点B(3，－1)变成了点B′(5,1)．（Ⅰ）求矩阵M ；（Ⅱ）若在矩阵M 的逆矩阵的变换作用下，点C(x,0)变成了点C′(4，y)，求x+y 的值. （2）（本小题满分7分）选修4—4：坐标系与参数方程在直角坐标系xOy 中，圆O 的参数方程为2cos 22sin 2x r y r θθ⎧=-+⎪⎨⎪=-+⎩，(θ为参数，0r >).以O 为极点，x 轴正半轴为极轴，并取相同的单位长度建立极坐标系，直线l 的极坐标方程为()2s i n 42πρθ+=. （Ⅰ）写出圆心的极坐标，（Ⅱ）求当r 为何值时，圆O 上的点到直线l 的最大距离为3.（3）（本小题满分7分）选修4—5：不等式选讲（Ⅰ）设2a a ∈≠-R 且，试比较222a a-+与的大小．（Ⅱ）求函数142y x x =-++的最大值．参考答案17解：（Ⅰ）设报考飞行员的人数为n ,前三小组的频率分别为321,,p p p ,则由条件可得:⎪⎩⎪⎨⎧=⨯++++==15)013.0037.0(323211312p p p p p p p解得375.0,25.0,125.0321===p p p ………………………………………………4分又因为np 1225.02==，故48=n ……………………………………………………6分（Ⅱ）由（Ⅰ）可得,一个报考学生体重超过60公斤的概率为855)013.0037.0(3=⨯++=p p ………………………………………………………8分所以x 服从二项分布,k k k C k x p -==33)83()85()(∴随机变量x 的分布列为：x 0123p51227512135512225512125…………………………………………………………………12分则815512125351222525121351512270=⨯+⨯+⨯+⨯=Ex ………………………………13分(或: 815853=⨯=Ex )18.21. 本题（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题做答，满分14分，如果多做，则按所做的前两题计分. 作答时，先用2B 铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中.（1）（本小题满分7分）选修4—2；矩阵与变换已知在一个二阶矩阵M 的变换作用下，点A(1,2)变成了点A′(4, 5)，点B(3，－1)变成了点B′(5,1)．（Ⅰ）求矩阵M ；（Ⅱ）若在矩阵M 的逆矩阵的变换作用下，点C(x,0)变成了点C′(4，y)，求x+y 的值.解：（Ⅰ）设该二阶矩阵为ab M cd ⎛⎫⎪⎝⎭＝，由题意得1425a b c d ⎛⎫⎛⎫⎛⎫=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,3511a b cd ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭,所以24253531a b c da bc d+=⎧⎪+=⎪⎨-=⎪⎪-=⎩解得2,1,1,2a b c d ====,故2112M ⎛⎫⎪⎝⎭＝…………………3分（Ⅱ）因为1212133det 30,121233M M-⎛⎫-⎪==≠=⎪- ⎪⎝⎭， 212044333,,6,2,12010333x x x y y x y ⎛⎫⎧-+=⎛⎫⎛⎫ ⎪⎪===-⎨⎪ ⎪ ⎪⎝⎭⎝⎭⎪--+= ⎪⎝⎭⎩解得4x y ∴+=.…………7分（2）（本小题满分7分）选修4—4：坐标系与参数方程在直角坐标系xOy 中，圆O 的参数方程为2cos 22sin 2x r y r θθ⎧=-+⎪⎨⎪=-+⎩，(θ为参数，0r >).以O为极点，x 轴正半轴为极轴，并取相同的单位长度建立极坐标系，直线l 的极坐标方程为()2sin 42πρθ+=. （Ⅰ）写出圆心的极坐标，（Ⅱ）求当r 为何值时，圆O 上的点到直线l 的最大距离为3.解：（Ⅰ）圆心的极坐标()51,4π.…………………………………………………………3分（Ⅱ）直线为10x y +-=，圆心22,22O ⎛⎫-- ⎪⎝⎭到直线的距离212d --=.圆O 上的点到直线的最大距离为2132r --+=，解得222r =-.……………7分（3）（本小题满分7分）选修4—5：不等式选讲（Ⅰ）设2a a ∈≠-R 且，试比较222a a -+与的大小．（Ⅱ）求函数142y x x =-++的最大值．解: （Ⅰ）()22222a a a a --=++, 20=22a a a=-+当时,； 22<22a a a <--+当时,；220>22a a a a >-≠-+当且时,.…………………………3分[]-2,1(II)函数定义域为， []()2(12)1x x x x +≥-+由柯西不等式得（1-）+（2+）4+2, 即()219,13x x x x -+≤-+≤4+2即4+2()m ax =013x x x -+=当且仅当时，等号成立，4+2.……………………7分。

河北省衡水中学高三数学下学期第四周周测试题理

衡水中学2016-2017学年度数学（理科）试卷周测4第Ⅰ卷(共60分）一、选择题：本大题共12个小题，每小题5分,共60分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

1.已知集合{1,3,4,5}A =，集合2{|450}B x Z x x =∈--<，则A B 的子集个数为（ ) A ．2 B ． 4 C ． 8 D ．162。

如图,复平面上的点1234,,,Z Z Z Z 到原点的距离都相等，若复数z 所对应的点为1Z ，则复数z i •（i 是虚数单位）的共轭复数所对应的点为（）A ．1ZB ．2ZC ．3ZD ．4Z3。

下列四个函数中，在0x =处取得极值的函数是( ) ①3y x =；②21y x =+;③||y x =;④2x y =A ．①②B ．①③C ．③④D ．②③4。

已知变量,x y 满足：202300x y x y x -≤⎧⎪-+≥⎨⎪≥⎩，则22)x y z +=的最大值为（）A 2B ．22。

2 D ．4 5.执行如图所示的程序框图，输出的结果是（）A ．5B ． 6 C.7 D ．86。

两个等差数列的前n 项和之比为51021n n +-，则它们的第7项之比为（）A ． 2B ． 3C 。

4513D ．70277.在某次联考数学测试中,学生成绩ξ服从正态分布2(100,)σ,(0)σ>，若ξ在(80,120)内的概率为0.8,则落在(0,80)内的概率为（ )A ．0。

05B ．0.1 C. 0。

15 D ．0.28。

函数()sin (0,0)f x A x A ωω=>>的部分图象如图所示，(1)(2)(3)(2015)f f f f ++++的值为（ )A ． 0B ．3262．2- 9。

若7280128(1)(12)x x a a x a x a x +-=++++，则127a a a +++的值是（ )A ．—2B ． -3 C. 125 D ．—13110。

精选高三数学下学期第四周周练试题文

江西省上饶市横峰县2017届高三数学下学期第四周周练试题文一.选择题(共6小题,每小题10分,共60分)1.若正方体的对角线长是4，则正方体的体积是（） A ．64 B ．216 C ．9364 D ．91282．若正三棱锥的斜高是高的332倍，则棱锥的侧面积是底面积的（） A ．32倍 B ．2倍 C ．38倍 D ．3倍3．一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B.4π+C.23π+D.43π+4．一球的体积和表面积在数值上相等，则该球的半径数值为（） A ．4 B ．3 C ．2 D ．15．将一个半径为R 的木球削成一个尽可能大的正方体，则此正方体的体积是（） A ．3323R B ．83R C ．3383R D ．9383R 6．设圆柱和圆锥的底面半径都是r ，高是,h 若要使圆柱侧面积小于圆锥侧面积，则（）A ．h <r 33 B ．r 33< h < r 3 C ．h >r 3 D ．不存在这种可能性二.填空题(共2小题,每小题10分,共20分)7.如图是一个几何体的三视图，若它的体积是=a _______侧(左)视图正(主)视图8.体积相等的球、正四面体和正方体，则它们的表面积间的大小关系为 .三.解答题9.(20分)斜三棱柱ABC —A ’B’C’中，底面是边长为a 的正三角形，侧棱长为 b ，侧棱AA ’与底面相邻两边AB 、AC 都成450角，求此三棱柱的侧面积和体积。

2017届高三下第4周周练数学(文)试题答案一.选择题(共6小题,每小题10分,共60分)1.若正方体的对角线长是4，则正方体的体积是（ C ） A ．64 B ．216 C ．9364 D ．91282．若正三棱锥的斜高是高的332倍，则棱锥的侧面积是底面积的（ B ） A ．32倍 B ．2倍 C ．38倍 D ．3倍3．一空间几何体的三视图如图所示,则该几何体的体积为( C ).A.2π+B.4π+C.2π+D.4π+4．一球的体积和表面积在数值上相等，则该球的半径数值为（ B ） A ．4 B ．3 C ．2 D ．15．将一个半径为R 的木球削成一个尽可能大的正方体，则此正方体的体积是（ D ） A ．3323R B ．83R C ．3383R D ．9383R 6．设圆柱和圆锥的底面半径都是r ，高是,h 若要使圆柱侧面积小于圆锥侧面积，则（ A ）A ．h <r 33 B ．r 33< h < r 3 C ．h >r 3 D ．不存在这种可能性二.填空题(共2小题,每小题10分,共20分)7.如图是一个几何体的三视图，若它的体积是=a 38.体积相等的球、正四面体和正方体，则它们的表面积间的大小关系为侧(左)视图正(主)视图球S < 正方体S < 正四面体S .三.解答题9.(20分)斜三棱柱ABC —A ’B’C’中，底面是边长为a 的正三角形，侧棱长为 b ，侧棱AA ’与底面相邻两边AB 、AC 都成450角，求此三棱柱的侧面积和体积。

高三数学周练(四)

高三数学周练（四）一．选择题1.（2011安徽理7）命题“所有能被2整聊的整数都是偶数”的否定是（A ）所有不能被2整除的数都是偶数（B ）所有能被2整除的整数都不是偶数（C ）存在一个不能被2整除的数都是偶数（D ）存在一个能被2整除的数都不是偶数2.(2010北京理数）（6）a 、b 为非零向量。

“ab ⊥”是“函数()()()f x xa b xb a =+-为一次函数”的（A ）充分而不必要条件（B ）必要不充分条件（C ）充分必要条件（D ）既不充分也不必要条件3.（2013年大纲版数学（理））若函数()21=f x x ax x++在1,+2⎛⎫∞⎪⎝⎭是增函数,则a 的取值范围是 (A)[-1,0] (B)[1,)-+∞ (C)[0,3] (D)[3,)+∞4.2012年高考（新课标理））已知函数1()ln(1)f x x x=+-;则()y f x =的图像大致为5.2013年安徽数学（理）试题）在平面直角坐标系中,O 是坐标原点,两定点,A B满足2,OA OB OA OB === 则点集{}|,1,,P O P O A O B Rλμλμλμ=++≤∈所表示的区域的面积是（）A ．B ．C ．D ．6.（2012年高考（江西理））观察下列各式:a+b=1.a ²+b 2=3,a 3+b 3=4 ,a 4+b 4=7,a 5+b 5=11,,则a 10+b 10=（）A ．28B ．76C ．123D ．1997.（2012年高考（四川理））设函数()2cos f x x x =-,{}n a 是公差为8π的等差数列,125()()()5f a f a f a π++⋅⋅⋅+=,则=-5123)]([a a a f（）A ．0B ．2116π C ．218π D ．21316π二．填空题：8.（2010福建理数）11．在等比数列{}n a 中,若公比q=4,且前3项之和等于21,则该数列的通项公式n a = ．9.（2013年高考新课标1（理））若函数()f x =22(1)()x x ax b -++的图像关于直线2x =-对称,则()f x的最大值是______. 10.（2013年福建数学（理）试题）如图ABC∆中,已知点D 在BC 边上,AD⊥AC,sin 3BAC AB AD ∠=== 则BD的长为_______________三．解答题：11.（2012年（湖北理））已知向量(cos sin ,sin )x x x ωωω=-a ,(cos sin ,)x x x ωωω=--b ,设函数()f x λ=⋅+a b ()x ∈R 的图象关于直线πx =对称,其中ω,λ为常数,且1(,1)2ω∈.(Ⅰ)求函数()f x 的最小正周期; (Ⅱ)若()y f x =的图象经过点π(,0)4,求函数()f x 在区间3π[0,]5上的取值范围.12.（2012年高考（山东理））已知函数ln ()xx kf x e+=(k 为常数, 2.71828e =⋅⋅⋅是自然对数的底数),曲线()y f x =在点(1,(1))f 处的切线与x 轴平行.(Ⅰ)求k 的值;(Ⅱ)求()f x 的单调区间;13.（2013年高考江西卷（理））正项数列{a n }的前项和{a n }满足:222(1)()0n n s n n s n n -+--+=(1)求数列{a n }的通项公式a n ; (2)令22)2(1nn a n n b ++=,数列{b n }的前n 项和为n T .证明:对于任意的*n N ∈,都有564nT <【答案】(1)解:由222(1)()0nn S n n S n n -+--+=,得2()(1)0n n S n n S ⎡⎤-++=⎣⎦.由于{}n a 是正项数列,所以20,n n S S n n >=+.于是112,2a S n ==≥时,221(1)(1)2n n n a S S n n n n n -=-=+----=.综上,数列{}n a 的通项2n a n =.(2)证明:由于2212,(2)nn nn a n b n a +==+.则222211114(2)16(2)nn b n n n n ⎡⎤+==-⎢⎥++⎣⎦. 222222222111111111111632435(1)(1)(2)n T n n n n ⎡⎤=-+-+-++-+-⎢⎥-++⎣⎦… 222211111151(1)162(1)(2)16264n n ⎡⎤=+--<+=⎢⎥++⎣⎦.。