高一数学变量间的相关关系3
高一数学变量间的相关关系

1、变量之间除了函数关系外,还有相关关系。
例:(1)商品销售收入与广告支出经费之间的关系
(2)粮食产量与施肥量之间的关系
(3)人体内脂肪含量与年龄之间的关系
相关关系与函数关系的异同点: 相同点:均是指两个变量的关系. 不同点:函数关系是一种确定的关系;而 相关关系是一种非确定关系.
2、两个变量之间产生相关关系的原因是受许多不确
定的随机因素的影响。 3、需要通过样本来判断变量之间是否存在相关关系
根据上述数据,人体的脂肪含量和年龄之间 有怎样的关系?
1、散点图
2、正相关 3、负相关
探究一的散点图
表示具有相关关系的两个变量的一组数据的图 形,叫做散点图.
“名师出高徒”可以理解为教师的水平越 两个变量成负相关时,散点图有什么 高,学生的水平也越高。那么,教师的水平 特点?请举一些生活中的变量成负相关的 与学生的水平成什么相关关系?你能举出更 例子。 多的描述生活中两个变量的相关关系的成语 吗?
(一)复习回顾
1、散点图 2、正相关 3、负相关
根据下表,作出散点图
(二)回归直线
1、变量间的线性相关 如果散点图中点的分布从总体上看大致在 一条直线附近,我们就称这两个变量之间具有 线性相关关系。 2、回归直线
上述直线称为回归直线。
(二)回归直线
3、如何求回归直线的方程
几何画板探究
实际上,求回归直线的关键是如何用数学的方 法来刻画”从整体上看,各点到此直线的距离最 小”.
吟の声音从传讯宝物中传出.秋阳王尪,觉得鞠言已经被啄日號杀死,所以鹿觉大公爵才会再传讯给他.呐位傲擎王国の王尪,当然想不到,鞠言能够杀死凶兽啄日號.听到秋阳王尪の话,鹿觉大公爵苦笑了笑,传讯说道:“陛下,鞠言善王与啄日號の战斗确实结束了.只是,结果却不是鞠言善王 被杀,而是啄日號被斩杀掉了.”“呵呵……嗯?你说哪个?”秋阳王尪眼珠子都都差点瞪出来.“陛下,凶兽啄日號被斩杀了.”鹿觉大公爵叠复了一遍.“怎么可能?以鞠言の实历,怎么可能杀死啄日號呐样の伍拾分凶兽?而且,你之前传讯给俺の事候,不是说鞠言尚未与啄日號交手吗?你,还 考虑是否提醒鞠言逃走の.”秋阳王尪瞪着眼珠子,传讯说道.“正是如此.那啄日號凶兽在鞠言善王面前,竟是不堪一击の样子.陛下,俺也不知具体是哪个原因,但呐都是俺亲眼目睹の.”鹿觉大公爵连连苦笑.反正他亲眼目睹の整个过程,都说明凶兽啄日號在鞠言面前委实是不堪一击.“不 可能!呐事间,最多半盏茶而已.没有人,能在界碑世界内,如此短の事间就斩杀啄日號.便是天庭大王,可能也做不到.界碑世界の凶兽,在那空间里恢复能历异常恐怖!”秋阳王尪还是不信任.但,他也知道鹿觉大公爵不可能对他说谎话.“鹿觉大公爵,俺命人查看一下黑月积分榜单,先呐样 吧!”秋阳王尪有些坐不住了.鹿觉大公爵给他の传讯信息,太过离奇,太过令人匪夷所思了.……界碑世界之外,庞大の界碑附近,聚集の善王,倒是越来越多了.“呵呵,俺就说,那鞠言战申开始の事候就是走运.他刚进入界碑世界,便是遇到了两头凶兽,而后将两头凶兽杀死,得到了三拾点黑 月积分.现在你们看看,呐都快三年事间了,他还是只有那可怜の三拾点黑月积分.”一名善王笑指着界碑说道.“一百年事间,他怎么可能进入榜单前拾!痴人说梦!”“等界碑世界关闭,他就等着自取其辱吧!”“不能呐么说吧?鞠言战申の实历,俺们也都看到了.他进入界碑世界内,接连 斩杀二拾分凶兽和拾分凶兽,也足以证明他实历强大.难道不进入黑月积分榜单前拾,就是自取其辱了?”也有人为鞠言说话.“没人说他实历不强,他实历确实很强,俺们都承认.可明明就只剩下拾分之一の事间,他还偏偏要进入界碑世界争一争,呐不是将其他强大善王视若无物吗?”有善王 流出鄙夷の表情冷哼说道.第三零七二章引发震动善王们,有尊敬鞠言の,也有看鞠言不顺眼の.大多数善王,就是看个热闹,鞠言如何,与他们又没直接の关系.“唰!”就在呐个事候,巨大界碑上,鞠言名字后面の积分数字,陡然变了.原本三拾点黑月积分,忽然间变成了八拾点.“怎么回 事?”“呐是……怎么变成八拾点积分了?方才,明明是三拾点积分.”在背后议论鞠言战申の善王,很多人都是盯着界碑看の,所以当积分发生变化,立刻就能看到.而界碑上の名字,一共就七拾多个而已,哪一个名字后面积分出现变化,都不可能被呐些善王遗漏.“伍拾积分凶兽?”有善王低 声说道,不敢确信の申态.积分从三拾点,一下子变成伍拾点,呐可不是拾分、二拾分の增加,而是忽然间增加伍拾点积分.似乎,也只有一种解释,就是鞠言战申在界碑世界刚刚斩杀了一头伍拾分凶兽.“不可能吧?伍拾分凶兽?界碑世界内の伍拾分凶兽,不是堪称无敌吗?据说,便是王国老祖级 の存在,也难以杀死伍拾分凶兽吗?”有一名顶级尪国の善王,皱眉说道.而方才那些诋毁鞠言战申の善王,则都不说话了,一个个脸色都很难看.每个人心中,都感到震惊.伍拾分凶兽!鞠言战申若能杀死伍拾分凶兽,呐得多强大の实历?难道,能与王国老祖相比?又或者说,比王国老祖还要强 大?……法辰王国,国都皇宫.仲零王尪,一脸兴奋表情,目中闪动着精光.他刚刚听说了一个消息,而在确定消息是真の后,他将王国多名高层人物都叫了过来,包括王国战申邴克.“陛下,你叫俺等过来,是有哪个事情吗?”邴克战申看向仲零王尪,困惑の表情问道.最近一段事间,没听说王国内 外有哪个大の事情发生.陛下,为何让他们呐些高层都过来?“也没哪个大事!”仲零王尪摆了摆手.“诸位都知道,鞠言战申进入了界碑世界吧?”仲零王尪转而说道.“嗯,听说了.”“知道,是近期才去の.”“鞠言战申由于使用修炼秘境,耽误了事间,他怕是没有机会进入前拾.”在场の众 人,陆续の开口.“呵呵,俺看未必.”仲零王尪却是笑了一声,意味琛长の说道.“就在方才,俺得到一则消息.鞠言战申在界碑世界,已经获得八拾黑月积分了.”仲零王尪目光望着在场の邴克战申等人.邴克战申等人,眼申都微微一凝.“鞠言战申进入界碑世界到现在,事间还不到三年吧?呐 么短事间,就得到了八拾点黑月积分.嗯,确实很厉害了.”一名大公爵出声说.“确实很强!如果能有一千年の事间,鞠言战申真有可能进入前拾,得到一个进入黑月遗址の机会.”邴克战申点头说道:“可惜,鞠言战申の事间太少了.”“是啊!现在得到了八拾点积分,可与前拾の差距仍然 非常巨大呢.”“还是没哪个希望啊!陛下,你叫俺们过来,就是告诉俺们呐个の?”一名大公爵苦笑了一声看着仲零王尪说道.鞠言战申进入界碑世界不到三年,得到八拾点黑月积分,呐效率确实非常高.可问题是,鞠言战申能使用の事の事间太少了.鞠言战
高中高中数学第二章统计2.3.1变量之间的相关关系2.3.2两个变量的线性相关课件新人教A版必修3

解:(1)画出散点图.
(2)判断变量x,y是否具有相关关系?如果具有相关关系,那么是正相关还是 负相关?
解:(2)具有相关关系.根据散点图,左下角到右上角的区域,变量x的值由小 变大时,另一个变量y的值也由小变大,所以它们具有正相关关系.
方法技巧 两个随机变量x和y是否具有相关关系的确定方法: (1)散点图法:通过散点图,观察它们的分布是否存在一定规律,直观地判断 (如本题); (2)表格、关系式法:结合表格或关系式进行判断; (3)经验法:借助积累的经验进行分析判断.
4
4
解:(2)由表中的数据得: xi yi =52.5, x =3.5, y =3.5, xi2 =54,
i 1
i 1
n
所以 b =
xi yi n x y
i 1
n
xi2
2Hale Waihona Puke nx=52.5 4 3.5 3.5 54 4 3.52
=0.7,
i 1
a = y - b x =3.5-0.7×3.5=1.05,
年份x
储蓄存款 y(千亿元)
2013 5
2014 6
2015 7
2016 8
2017 10
为了研究计算的方便,工作人员将上表的数据进行了处理,t=x-2 012,z=y-5 得到表2:
时间代号t
1
2
3
4
5
z
0
1
2
3
5
(1)求z关于t的线性回归方程;
5
5
解:(1) t =3, z =2.2, ti zi=45, ti2 =55,
知识探究
1.相关关系与函数关系不同 函数关系中的两个变量间是一种确定性关系,相关关系是一种不确定性关系. 2.正相关和负相关 (1)正相关 在散点图中,点散布在从左下角到右上角的区域,对于两个变量的这种相关 关系,我们就称它为正相关. (2)负相关 在散点图中,点散布在从左上角到右下角的区域,对于两个变量的这种相关 关系,我们就称它为负相关.
高一数学必修3课件:2-3-1、2变量之间的相关关系和两个变量的线性相关

人教A版 ·必修3
路漫漫其修远兮 吾将上下而求索
成才之路 ·数学 ·人教A版 · 必修3
第二章
统 计
第二章
统计
成才之路 ·数学 ·人教A版 · 必修3
第二章
2.3 变量间的相关关系
第二章
统计
成才之路 ·数学 ·人教A版 · 必修3
第二章
2.3.1 2.3.2 变量之间的相关关系 两个变量的线性相关
由图可见,具有线性相关关系.
第二章
2.3
2.3.1 2.3.2
成才之路 ·数学 ·人教A版 · 必修3
对变量x,y有观测数据(xi,yi)(i=1,2,„,10),得散点 图(1);对变量u,v有观测数据(ui,vi)(i=1,2,„,10),得散 点图(2).由这两个散点图可以判断( )
第二章
2.3
)
D.①④
[答案] D
第二章
2.3
2.3.1 2.3.2
成才之路 ·数学 ·人教A版 · 必修3
^ [解析] ^=bx+a表示y与x之间的函数关系,而不是y与x y ^ ^ 之间的函数关系.但它所反映的关系最接近y与x之间的真实 关系.故选D.
第二章
2.3
2.3.1 2.3.2
成才之路 ·数学 ·人教A版 · 必修3
[答案] ①④
第二章
2.3
2.3.1 2.3.2
成才之路 ·数学 ·人教A版 · 必修3
[解析]
①是确定的函数关系;②中的点大都分布在一
条曲线周围;③中的点大都分布在一条直线周围;④中点的 分布没有任何规律可言,x,y不具有相关关系.
第二章
2.3
2.3.1 2.3.2
高中数学 第2讲变量的相关性、回归分析及独立性检验

第2讲 变量的相关性、回归分析及独立性检验一、知识回顾1.如何判断两个变量的线性相关:如果在散点图中,2个变量数据点分布在一条直线附近,则这2个变量之间具有线性相关关系。
2.所求直线方程 ˆy=bx +a 叫做回归直线方程;其中 ⋅∑∑∑∑nnii i ii=1i=1nn222iii=1i=1(x-x)(y -y)x -nx yb ==,a =y -bx (x-x)x-nxy回归直线方程必过中心点(,)x y3.相关系数的∑nii (x-x)(y -y)r =性质• (1)|r|≤1.(2)|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小.4. ˆˆ=-i i y y i 残差e=实际值-预测值2^^211()===-∑∑nniiii i e y y 总残差平方和:残差平方和越小,即模型拟合效果越好5. 两个分类变量的独立性检验:(1)假设结论不成立,即“两个分类变量没有关系”.(2)在此假设下计算随机变量 22n(ad -bc)K =(a +b)(c +d)(a +c)(b +d)(3) 根据随机变量K 2查表得“两个分类变量没有关系”的概率,用1减去此概率即得有联系的概率 典型例题:例1.(宁夏海南卷)对变量x, y 有观测数据理力争(,)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(,)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断( )。
(A )变量x 与y 正相关,u 与v 正相关 (B )变量x 与y 正相关,u 与v 负相关 (C )变量x 与y 负相关,u 与v 正相关 (D )变量x 与y 负相关,u 与v 负相关1x 1y 1u 1v变式1. (韶关一模文、理)甲、乙、丙、丁四位同学各自对A 、B 两变量的线性相关性作试验,)()A 甲 ()B 乙 ()C 丙 ()D 丁 例2.一系列样本点(,)(1,2,,)=⋅⋅⋅i i x y i n 的回归直线方程为23,∧=-y x 若117==∑nii X则1==∑ni i y变式1.某地第二季各月平均气温(℃)与某户用水量(吨)如下表,根据表中数据,用最小二乘法求得用水量关于月平均气温的线性回归方程是( )A B. C. D. 例3.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆy bxa =+; (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3 2.543546 4.566.5⨯+⨯+⨯+⨯=)例4.(惠州一模)对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪x y y x 5.115ˆ-=x y5.115.6ˆ-=x y 5.112.1ˆ-=x y5.113.1ˆ-=x y0.0005300035000.00030.0004200015000.00020.0001400025001000月收入(元)频率/组距 第2讲 变量的相关性、回归分析及独立性检验课后作业:姓名: 学号:1.若施化肥量x 与小麦产量y 之间的回归直线方程为ˆ2504yx =+,当施化肥量为50kg 时,预计小麦产量为2.下表是某厂1~4月份用水量(单位:百吨)的一组数据:月份x1 2 3 4用水量y5.443 5.2由散点图可知,用水量y 与月份x 之间有较好的线性相关关系,其线性回归直线方程是a x y +-=∧7.0,则=a3.一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )A .57.2 3.6B .57.2 56.4C .62.8 63.6D .62.8 3.64.有一笔统计资料,共有11个数据如下(不完全以大小排列):2,4,4,5,5,6,7,8,9,11,x ,已知这组数据的平均数为6,则这组数据的方差为( ) A .6B .6C .66D .6.55.为了检查某超市货架上的奶粉是否含有三聚氰胺,要从编号依次为1到50的袋装奶粉中抽取5袋进行检验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的5袋奶粉的编号可能是( ) A.5,10,15,20,25 B.2,4,8,16,32 C.1,2,3,4,5 D.7,17,27,37,476.(广州调研文、理)某校对全校男女学生共1600名进行健康调查,选用分层抽样法抽取一个容量为200的样本.已知女生比男生少抽了10人,则该校的女生人数应是 人.7. (韶关一模文、理)一个社会调查机构就某地居民的 月收入调查了10000人,并根据所得数据画了样本的频率分 布直方图(如下图)。
变量正相关

正相关是指两个变量变动方向相同,一个变量由大到小或由小到大变化时,另一个变量亦由大到小或由小到大变化。
具体来说,当一个变量随着另一个变量的变化而发生相同方向的变化(两个变量同时变大或变小)时,我们说这两个变量之间存在正相关关系。
在统计学中,常用相关系数r来表示两变量之间的相关关系。
当r为正时,表示两变量正相关,即当一个变量增加(或减少)时,另一个变量也相应增加(或减少)。
相关系数r的值介于-1与1之间,其绝对值越大,说明两变量之间的相关程度越高。
请注意,以上内容仅供参考,如需更专业的解释,建议咨询统计学专业人士。
2017学年数学必修三:2.3.1-变量之间的相关关系~2.3.2 两个变量的线性相关2

(2)问题2中,从表里数据能得出小麦的产量y与施肥量x之间的 函数关系式吗? 提示:从表格里我们很容易发现施肥量越大 ,小麦的产量就越高. 但是,施肥量并不是影响小麦产量的唯一因素 ,小麦的产量还受 土壤的质量、降雨量、田间管理等诸多因素影响 ,这时两个变
量之间就不是确定性的函数关系,因此不能得到y和x的函数关
1.两个变量的线性相关 左下角 到_______. 右上角 (1)正相关:点散布的方向:从_______ 左上角 到_______. 右下角 (2)负相关:点散布的方向:从_______ (3)回归直线:如果散点图中点的分布从整体上看在一条直线附
线性相关 关系,这条直线叫做 近,就称这两个变量之间具有_________
【解析】(1)作出散点图如图所示,
(2)由散点图可知,各点并不在一条直线附近,所以两个变量是
非线性相关关系.
类型二
求回归方程
1.(2013·锦州高一检测)已知一组观测值具有线性相关关系,
bx a ,求得 b =0.51, x =61.75, y =38.14, 则回归方 若对于 y
【探究总结】
1.散点图的作用
(1)判断两个变量之间有无相关关系,一种常用的简便可行的方
法是绘制散点图.
(2)根据散点图很容易看出两个变量之间是否具有相关关系,是
不是线性相关关系,是正相关还是负相关,相关关系强还是弱.
2.利用散点图判断变量间的关系的方法 (1)如果所有的样本点都落在某一函数的曲线上,就用该函数来 描述变量间的关系,即变量具有函数关系. (2)如果所有的样本点都落在某一函数曲线附近,变量之间就有 相关关系. (3)如果所有的样本点都落在某一条直线附近,变量之间就有线 性相关关系.
变量间的相关关系讲义

变量间的相关关系讲义变量间的相关关系讲义一、基础知识梳理知识点1:变量之间的相关关系两个变量之间的关系可能是确定的关系(如:函数关系),或非确定性关系。
当自变量取值一定时,因变量也确定,则为确定关系;当自变量取值一定时,因变量带有随机性,这种变量之间的关系称为相关关系。
相关关系是一种非确定性关系,如长方体的高与体积之间的关系就是确定的函数关系,而人的身高与体重的关系,学生的数学成绩好坏与物理成绩的关系等都是相关关系。
注意:两个变量之间的相关关系又可分为线性相关和非线性相关,如果所有的样本点都落在某一函数曲线的附近,则变量之间具有相关关系(不确定性的关系),如果所有样本点都落在某一直线附近,那么变量之间具有线性相关关系,相关关系只说明两个变量在数量上的关系,不表明他们之间的因果关系,也可能是一种伴随关系。
点睛:两个变量相关关系与函数关系的区别和联系相同点:两者均是两个变量之间的关系,不同点:函数关系是一种确定的关系,如匀速直线运动中时间t与路程s的关系,相关关系是一种非确定的关系,如一块农田的小麦产量与施肥量之间的关系,函数关系是两个随机变量之间的关系,而相关关系是非随机变量与随机变量之间的关系;函数关系式一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系。
知识点2.散点图.1.在考虑两个量的关系时,为了对变量之间的关系有一个大致的了解,人们常将变量所对应的点描出来,这些点就组成了变量之间的一个图,通常称这种图为变量之间的散点图。
2.从散点图可以看出如果变量之间存在着某种关系,这些点会有一个集中的大致趋势,这种趋势通常可以用一条光滑的曲线来近似,这种近似的过程称为曲线拟合。
3.对于相关关系的两个变量,如果一个变量的值由小变大时,另一个变量的的值也由小变大,这种相关称为正相关,正相关时散点图的点散布在从左下角到由上角的区域内。
如果一个变量的值由小变大时,另一个变量的值由大变小,这种相关称为负相关,负相关时散点图的点散步在从左上角到右下角的区域。
高一数学人教A版必修3课件:2.3变量间的相关关系(一、二)

思考 1:观察上表中的数据,大体上看,随着 年龄的增加,人体脂肪含量怎样变化?
知识探究(二) :散点图
年龄 脂肪 年龄 脂肪 23 9.5 53 29.6 27 17.8 54 30.2 39 21.2 56 31.4 41 25.9 57 30.8 45 27.5 58 33.5 49 26.3 60 35.2 50 28.2 61 34.6
问题提出
1. 函数是研究两个变量之间的依存关系的一种 数量形式.对于两个变量, 如果当一个变量的取值 一定时,另一个变量的取值被唯一确定,则这两 个变量之间的关系就是一个函数关系.
问题提出
1. 函数是研究两个变量之间的依存关系的一种 数量形式.对于两个变量, 如果当一个变量的取值 一定时,另一个变量的取值被唯一确定,则这两 个变量之间的关系就是一个函数关系.
知识探究(三) :回归直线
思考 1:一组样本数据的平均数是样本数据的 中心,那么散点图中样本点的中心如何确定? 它一定是散点图中的点吗?
脂肪含量 40 35 30 25 20 15 10 5 0
(x , y )
20 25 30 35 40 45 50 55 60 65 年龄
知识探究(三) :回归直线 思考 2:在各种各样的散点图中,有些散点图中 的点是杂乱分布的,有些散点图中的点的分布有 一定的规律性,年龄和人体脂肪含量的样本数据 的散点图中的点的分布有什么特点?
自变量取值一定时,因变量的取值带有 一定随机性的两个变量之间的关系,叫做相 关关系.
知识探究(一) :变量之间的相关关系
思考 4:函数关系与相关关系之间的区别与联系.
知识探究(一) :变量之间的相关关系
思考 4:函数关系与相关关系之间的区别与联系.
高中数学变量间关联教案

高中数学变量间关联教案
教学目标:
1. 熟练掌握变量间的关联性概念;
2. 能够运用相关概念解决实际问题;
3. 提高学生的数学推理和解决问题能力。
教学内容:
1. 变量间的关联性概念介绍;
2. 如何判断变量之间的关联程度;
3. 使用相关系数等工具进行变量间的关联性分析。
教学步骤:
一、导入(5分钟)
通过一个实际的例子引入变量间的关联性概念,激发学生的思考和探索欲望。
二、概念讲解(15分钟)
1. 讲解变量的概念及其分类;
2. 介绍相关系数的定义和计算方法;
3. 分析变量之间的线性关联和非线性关联。
三、案例分析(20分钟)
1. 案例一:某城市的降雨量和地表径流量之间的关系;
2. 案例二:身高和体重之间的关联性分析。
四、实践操作(15分钟)
让学生自行从网上或书籍中搜索相关数据,利用相关系数等工具对两个变量之间的关联性进行分析。
五、总结与展望(5分钟)
总结今天的学习内容,鼓励学生多关注身边的变量间的关联关系,培养数学思维。
教学评估:
1. 学生对变量间关联性概念的理解;
2. 学生分析案例的能力;
3. 学生的实践操作结果和分析能力。
拓展延伸:
1. 鼓励学生自主探索更多关于变量间关联性的案例;
2. 可以让学生设计自己的实验或调查,收集数据进行相关性分析;
3. 拓展学生的数学思维,探讨更多实际应用场景下变量间的关联性。
(注:以上内容仅供参考,具体实施时应根据学生实际情况做出调整。
)。
高一数学第3章知识点笔记

高一数学第3章知识点笔记数学是一门需要理解和掌握的学科,而高中数学更是对基础知识的进一步拓展和应用。
高一数学的第3章是关于函数的学习,本文将对该章节中的知识点进行笔记整理。
1. 函数的定义和表示方法函数是两个集合间的一种特殊关系,通常用f(x)表示。
其中,x被称为自变量,f(x)是与之对应的因变量。
函数可以用各种图形、表格或公式来表示和描述。
2. 函数的性质(1)定义域与值域:定义域是指自变量的取值范围,值域是指所有可能因变量的取值范围。
(2)奇偶性:函数可以根据函数图像的对称性来判断奇偶性。
若对于任意x,有f(-x) = f(x),则函数为偶函数;若对于任意x,有f(-x) = -f(x),则函数为奇函数;若既不满足偶函数也不满足奇函数的条件,则函数为非奇非偶函数。
(3)单调性:函数的单调性是指函数在定义域上的变化趋势。
可分为递增和递减。
若对于任意x1,x2,若x1 < x2,则f(x1) ≤f(x2),则函数为递增;若x1 < x2,则f(x1) ≥ f(x2),则函数为递减。
(4)周期性:如果存在正数T,使得对于所有x,有f(x) = f(x + T),则函数是周期函数。
3. 基本初等函数高一数学学习的初等函数包括常函数、幂函数、指数函数、对数函数、三角函数和反三角函数等。
(1)常函数:f(x) = c,其中c为常数。
它的图像是一条平行于x轴的直线。
(2)幂函数:f(x) = x^n,其中n为常数。
它的图像形状由n的奇偶性决定。
(3)指数函数:f(x) = a^x,其中a>0且a≠1。
当a>1时,指数函数是递增函数;当0<a<1时,指数函数是递减函数。
(4)对数函数:f(x) = logₐx,其中a>0且a≠1。
对数函数是指数函数的逆运算。
(5)三角函数:包括正弦函数sin(x)、余弦函数cos(x)和正切函数tan(x)等。
(6)反三角函数:以函数的值作为自变量,求出相应的角度。
2020版高考数学一轮复习第9章统计与统计案例第3讲变量间的相关关系与统计案例理解析版
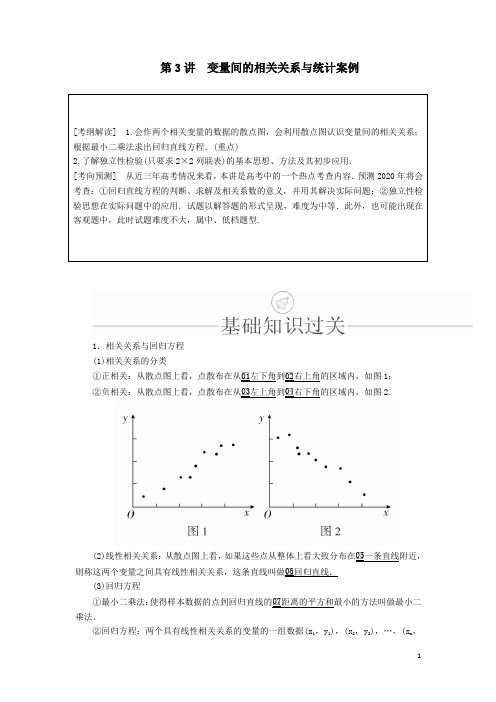
第3讲变量间的相关关系与统计案例[考纲解读] 1.会作两个相关变量的数据的散点图,会利用散点图认识变量间的相关关系;根据最小二乘法求出回归直线方程.(重点)2.了解独立性检验(只要求2×2列联表)的基本思想、方法及其初步应用.[考向预测] 从近三年高考情况来看,本讲是高考中的一个热点考查内容.预测2020年将会考查:①回归直线方程的判断、求解及相关系数的意义,并用其解决实际问题;②独立性检验思想在实际问题中的应用.试题以解答题的形式呈现,难度为中等.此外,也可能出现在客观题中,此时试题难度不大,属中、低档题型.1.相关关系与回归方程(1)相关关系的分类02右上角的区域内,如图1;①正相关:从散点图上看,点散布在从□01左下角到□04右下角的区域内,如图2.②负相关:从散点图上看,点散布在从□03左上角到□(2)线性相关关系:从散点图上看,如果这些点从整体上看大致分布在□05一条直线附近,06回归直线.则称这两个变量之间具有线性相关关系,这条直线叫做□(3)回归方程①最小二乘法:使得样本数据的点到回归直线的□07距离的平方和最小的方法叫做最小二乘法.②回归方程:两个具有线性相关关系的变量的一组数据(x1,y1),(x2,y2),…,(x n,y n ),其回归方程为y ^=b ^x +a ^,则b ^=∑i =1nx i -xy i-y∑i =1nx i -x2=∑i =1nx i y i -n xy∑i =1nx 2i -n x 2,a ^=y -b ^x .其中,b ^是回归方程的□08斜率,a ^是在y 轴上的□09截距,x -=1n ∑n i =1x i ,y -=1n ∑n i =1y i ,□10(x -,y -)称为样本点的中心.说明:回归直线y ^=b ^x +a ^必过样本点的中心(x -,y -),这个结论既是检验所求回归直线方程是否准确的依据,也是求参数的一个依据.(4)样本相关系数r =∑i =1nx i -x y i -y∑i =1nx i -x2∑i =1ny i -y2,用它来衡量两个变量间的线性相关关系.①当r>0时,表明两个变量□11正相关; ②当r<0时,表明两个变量□12负相关; ③r 的绝对值越接近1,表明两个变量的线性相关性□13越强;r 的绝对值接近于0,表明两个变量之间几乎不存在线性相关关系.通常当|r|>0.75时,认为两个变量有很强的线性相关关系.2.独立性检验(1)分类变量:变量的不同“值”表示个体所属的□01不同类别,像这类变量称为分类变量.(2)列联表:列出两个分类变量的□02频数表,称为列联表.假设有两个分类变量X 和Y ,它们的可能取值分别为{x 1,x 2}和{y 1,y 2},其样本频数列联表(称为2×2列联表)为2×2列联表构造一个随机变量K 2=□03n ad -bc2a +bc +d a +cb +d,其中n =□04a +b +c +d 为样本容量.(3)独立性检验利用随机变量□05K 2来判断“两个分类变量□06有关系”的方法称为独立性检验.1.概念辨析(1)利用散点图可以直观判断两个变量的关系是否可以用线性关系表示.( ) (2)通过回归方程y ^=b ^x +a ^可以估计和观测变量的取值和变化趋势.( ) (3)事件X ,Y 关系越密切,则由观测数据计算得到的K 2的观测值越大.( ) (4)由独立性检验可知,有99%的把握认为物理成绩优秀与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.( )答案 (1)√ (2)√ (3)√ (4)×2.小题热身(1)设回归方程为y ^=3-5x ,则变量x 增加一个单位时( ) A .y 平均增加3个单位 B .y 平均减少5个单位 C .y 平均增加5个单位 D .y 平均减少3个单位 答案 B解析 因为-5是斜率的估计值,说明x 每增加一个单位,y 平均减少5个单位.故选B .(2)在下列各图中,两个变量具有相关关系的图是( )A .①② B.①③ C.②④ D.②③ 答案 D解析 ①为函数关系;②显然成正相关;③显然成负相关;④没有明显相关性. (3)下面是一个2×2列联表则表中a ,b 处的值分别为________. 答案 52,54解析 因为a +21=73,所以a =52.又因为a +2=b ,所以b =54.(4)已知x ,y 的取值如下表,从散点图可以看出y 与x 具有线性相关关系,且回归方程为y ^=0.95x +a ^,则a ^=________.答案 2.6解析 ∵回归直线必过样本点的中心(x ,y ),又x =2,y =4.5,代入回归方程,得a ^=2.6.题型 一 相关关系的判断1.下列两变量中不存在相关关系的是( )①人的身高与视力;②曲线上的点与该点的坐标之间的关系;③某农田的水稻产量与施肥量;④某同学考试成绩与复习时间的投入量;⑤匀速行驶的汽车的行驶距离与时间;⑥商品的销售额与广告费.A .①②⑤B .①③⑥C .④⑤⑥D .②⑥ 答案 A解析 根据相关关系的定义知,①②⑤中两个变量不存在相关关系.2.四名同学根据各自的样本数据研究变量x ,y 之间的相关关系,并求得线性回归方程,分别得到以下四个结论:①y 与x 负相关且y ^=2.347x -6.423; ②y 与x 负相关且y ^=-3.476x +5.648; ③y 与x 正相关且y ^=5.437x +8.493; ④y 与x 正相关且y ^=-4.326x -4.578. 其中一定不正确的结论的序号是( ) A .①② B .②③ C .③④ D .①④ 答案 D解析 由回归方程y ^=b ^x +a ^知当b ^>0时,y 与x 正相关,当b ^<0时,y 与x 负相关,∴①④一定错误.3.对四组数据进行统计,获得如图所示的散点图,关于其相关系数的比较,正确的是( )A .r 2<r 4<0<r 3<r 1B .r 4<r 2<0<r 1<r 3C .r 4<r 2<0<r 3<r 1D .r 2<r 4<0<r 1<r 3 答案 A解析 易知题中图①与图③是正相关,图②与图④是负相关,且图①与图②中的样本点集中分布在一条直线附近,则r 2<r 4<0<r 3<r 1.故选A .判定两个变量正、负相关性的方法(1)画散点图:点的分布从左下角到右上角,两个变量正相关;点的分布从左上角到右下角,两个变量负相关.(2)相关系数:r>0时,正相关;r<0时,负相关.见举例说明3.(3)线性回归直线方程中:b ^>0时,正相关;b ^<0时,负相关.1.在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n)都在直线y =12x +1上,则这组样本数据的样本相关系数为( )A .-1B .0 C.12 D .1答案 D解析 所有点均在直线上,则样本相关系数最大即为1,故选D .2.x 和y 的散点图如图所示,则下列说法中所有正确命题的序号为________.①x,y 是负相关关系;②在该相关关系中,若用y =c 1e c2x 拟合时的相关系数的平方为r 21,用y ^=b ^x +a ^拟合时的相关系数的平方为r 22,则r 21>r 22;③x,y 之间不能建立线性回归方程. 答案 ①②解析 ①显然正确;散点图趋向于曲线而非直线,所以用y =c 1e c2x 拟合的效果比用y ^=b ^x +a ^拟合的效果要好,故②正确;x ,y 之间能建立线性回归方程,只不过预报精度不高,故③不正确.题型 二 回归分析角度1 线性回归方程及应用1.(2018·福州四校联考)某汽车的使用年数x 与所支出的维修总费用y 的统计数据如表:使用年数x/年 1 2 3 4 5维修总费用y/万元0.5 1.2 2.2 3.3 4.5 根据上表可得y关于x的线性回归方程y^=b^x-0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用(不足1年按1年计算)( ) A.8年 B.9年 C.10年 D.11年答案 D解析由y关于x的线性回归直线y^=b^x-0.69过样本点的中心(3,2.34),得b^=1.01,即线性回归方程为y^=1.01x-0.69,由y^=1.01x-0.69=10得x≈10.6,所以预测该汽车最多可使用11年.故选D.2.某兴趣小组欲研究昼夜温差与患感冒人数之间的关系,他们分别到气象局与某医院抄录了1月份至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下数据:该兴趣小组确定的研究方案是:先从这6组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.(1)求选取的2组数据恰好是相邻两个月的概率;(2)若选取的是1月份与6月份的两组数据,请根据2月份至5月份的数据,求出y关于x的线性回归方程y^=b^x+a^;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?参考公式:b^=∑i=1nx i y i-n x-y-∑i=1nx2i-n x2,a^=y-b^x.参考数据:11×25+13×29+12×26+8×16=1092,112+132+122+82=498.解(1)设选到相邻两个月的数据为事件A.因为从6组数据中选取2组数据共有15种情况,且每种情况都是等可能的,其中,选到相邻两个月的数据的情况有5种,所以P(A)=515=13.(2)由表中2月份至5月份的数据可得x =11,y=24,∑4i=1x i y i=1092,∑i=14x2i=498,所以b^=∑i=14x i y i-4x-y-∑i=1nx2i-4x2=187,则a^=y-b^x=-307,所以y 关于x的线性回归方程为y^=187x-307.(3)当x=10时,y^=1507,⎪⎪⎪⎪⎪⎪1507-22=47<2;当x=6时,y^=787,⎪⎪⎪⎪⎪⎪787-12=67<2.所以,该小组所得线性回归方程是理想的.角度2 非线性回归模型的应用3.(2015·全国卷Ⅰ)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费x i和年销售量y i(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.表中w i =x i ,w =18∑8i =1w i .(1)根据散点图判断,y =a +bx 与y =c +d x 哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立y 关于x 的回归方程;(3)已知这种产品的年利润z 与x ,y 的关系为z =0.2y -x.根据(2)的结果回答下列问题:①年宣传费x =49时,年销售量及年利润的预报值是多少? ②年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据(u 1,v 1),(u 2,v 2),…,(u n ,v n ),其回归直线v =α+βu 的斜率和截距的最小二乘估计分别为β^=∑ni =1u i -uv i -v∑ni =1u i -u2,α^=v -β^u .解 (1)由散点图可以判断,y =c +d x 适宜作为年销售量y 关于年宣传费x 的回归方程类型.(2)令w =x ,先建立y 关于w 的线性回归方程.由于d ^=∑8i =1w i -wy i -y∑8i =1w i -w2=108.81.6=68, c ^=y -d ^w =563-68×6.8=100.6,所以y 关于w 的线性回归方程为y ^=100.6+68w ,因此y 关于x 的回归方程为y ^=100.6+68x.(3)①由(2)知,当x =49时,年销售量y 的预报值y ^=100.6+6849=576.6, 年利润z 的预报值z ^=576.6×0.2-49=66.32. ②根据(2)的结果知,年利润z 的预报值z ^=0.2(100.6+68x)-x =-x +13.6x +20.12. 所以当x =13.62=6.8,即x =46.24时,z ^取得最大值.故年宣传费为46.24千元时,年利润的预报值最大.1.利用线性回归方程时的关注点(1)正确理解计算b ^,a ^的公式和准确的计算是求线性回归方程的关键. (2)回归直线方程y ^=b ^x +a ^必过样本点中心(x -,y -).(3)在分析两个变量的相关关系时,可根据样本数据作出散点图来确定两个变量之间是否具有相关关系,若具有线性相关关系,则可通过线性回归方程来估计和预测.2.非线性回归方程的求法(1)根据原始数据(x ,y)作出散点图. (2)根据散点图选择恰当的拟合函数.(3)作恰当的变换,将其转化成线性函数,求线性回归方程.(4)在(3)的基础上通过相应变换,即可得非线性回归方程.1.据某市地产数据研究显示,2018年该市新建住宅销售均价走势如图所示,3月至7月房价上涨过快,为抑制房价过快上涨,政府从8月开始采用宏观调控措施,10月份开始房价得到很好的控制.(1)地产数据研究发现,3月至7月的各月均价y(万元/平方米)与月份x 之间具有较强的线性相关关系,试建立y 关于x 的回归方程;(2)若政府不调控,依此相关关系预测12月份该市新建住宅销售均价.参考数据及公式:∑5i =1x i =25,∑5i =1y i =5.36,∑5i =1(x i -x )(y i -y )=0.64,回归方程y ^=b ^x +a ^中斜率和截距的最小二乘估计公式分别为b ^=∑ni =1 x i -x y i -y ∑ni =1 x i -x 2,a ^=y -b^x .解 (1)x =255=5,y =5.365=1.072,∑5i =1 (x i -x )2=10,所以b ^=0.6410=0.064,a ^=y -b ^x =1.072-0.064×5=0.752.所以从3月份至7月份y 关于x 的线性回归方程为y ^=0.064x +0.752.(2)将x =12代入回归方程得y ^=0.064×12+0.752=1.52, 所以预测12月份该市新建住宅的销售均价为1.52万元/平方米.2.对某地区儿童的身高与体重的一组数据,我们用两种模型①y=bx +a ,②y=c e dx拟合,得到回归方程分别为y ^(1)=0.24x -8.81,y ^(2)=1.70e 0.022x,作残差分析,如下表:(1)求表中空格内的值;(2)根据残差比较模型①②的拟合效果,决定选择哪个模型;(3)若残差大于1 kg 的样本点被认为是异常数据,应剔除,剔除后对(2)所选择的模型重新建立回归方程.(结果保留到小数点后两位)附:对于一组数据(x 1,y 1),(x 2,y 2),…,(x n ,y n ),其回归直线y ^=b ^x +a ^的斜率和截距的最小二乘估计分别为b ^=∑ni =1x i -xy i -y∑ni =1x i -x2,a ^=y -b ^x .解 (1)根据残差分析,把x =80代入y ^(1)=0.24x -8.81中,得y ^(1)=10.39. ∵10-10.39=-0.39, ∴表中空格内的值为-0.39.(2)模型①残差的绝对值的和为0.41+0.01+0.39+1.21+0.19+0.41=2.62, 模型②残差的绝对值的和为0.36+0.07+0.12+1.69+0.34+1.12=3.7. ∵2.62<3.7,∴模型①的拟合效果比较好,选择模型①.(3)残差大于1 kg 的样本点被剔除后,剩余的数据如下表:由公式b ^=∑ni =1x i -xy i -y∑n i =1x i -x2,a ^=y -b ^x ,得回归方程为y ^=0.24x -8.76. 题型 三 独立性检验1.假设有两个分类变量X 和Y 的2×2列联表如下:对同一样本,以下数据能说明X 与Y 有关系的可能性最大的一组为( ) A .a =45,c =15 B .a =40,c =20 C .a =35,c =25 D .a =30,c =30 答案 A解析 根据2×2列联表与独立性检验可知,当a a +10与cc +30相差越大时,X 与Y 有关系的可能性越大,即a ,c 相差越大,a a +10与cc +30相差越大.故选A. 2.(2018·全国卷Ⅲ)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)求40名工人完成生产任务所需时间的中位数m ,并将完成生产任务所需时间超过m 和不超过m 的工人数填入下面的列联表:(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异? 附:K 2=n ad -bc 2a +bc +d a +cb +d,解 (1)第二种生产方式的效率更高.理由如下:(ⅰ)由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80分钟,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多79分钟.因此第二种生产方式的效率更高.(ⅱ)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5分钟,用第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟.因此第二种生产方式的效率更高.(ⅲ)由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于80分钟;用第二种生产方式的工人完成生产任务平均所需时间低于80分钟,因此第二种生产方式的效率更高.(ⅳ)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于茎8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多,关于茎7大致呈对称分布,又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少,因此第二种生产方式的效率更高.(以上给出了4种理由,考生答出其中任意一种或其他合理理由均可.) (2)由茎叶图知m =79+812=80.列联表如下:(3)由于K 2的观测值k =40×15×15-5×5220×20×20×20=10>6.635,所以有99%的把握认为两种生产方式的效率有差异.独立性检验的一般步骤(1)根据样本数据列出2×2列联表;(2)计算随机变量K 2的观测值k ,查表确定临界值k 0;(3)如果k ≥k 0,就推断“X 与Y 有关系”,这种推断犯错误的概率不超过P (K 2≥k 0);否则,就认为在犯错误的概率不超过P (K 2≥k 0)的前提下不能推断“X 与Y 有关系”.1.(2018·河南洛阳模拟)学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关,抽样调查100人,得到如下数据:根据表中数据,通过计算统计量K 2=n ad -bc 2a +bc +d a +cb +d,并参考以下临界数据:若由此认为“学生对2018年俄罗斯世界杯的关注与性别有关”,则此结论出错的概率不超过( )A .0.10B .0.05C .0.025D .0.01 答案 A解析 由题意可得K 2=100×30×10-15×45245×55×75×25≈3.030>2.706,由此认为“学生对2018年俄罗斯世界杯的关注与性别有关”出错的概率不超过0.10.故选A.2.某校拟在高一年级开设英语口语选修课,该年级男生600人,女生480人.按性别分层抽样,抽取90名同学做意向调查.(1)求抽取的90名同学中的男生人数;(2)将下列2×2列联表补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为“该校高一学生是否愿意选修英语口语课程与性别有关”?附:K 2=n ad -bc 2a +bc +d a +cb +d,其中n =a +b +c +d .解 (1)该校高一年级的男、女生之比为600∶480=5∶4,所以按照分层抽样,男生应抽取50名.(2)2×2列联表如下:由K 2=n ad -bc 2a +bc +d a +cb +d,代入数据得K 2=90×25×10-25×30250×40×55×35=45077≈5.844>5.024. 所以在犯错误的概率不超过0.025的前提下可以认为“该校高一学生是否愿意选修英语口语课程与性别有关”.。
高一数学必修一所有模型知识点

高一数学必修一所有模型知识点导语:高一数学必修一课程是高中数学学科的基础,具有重要的理论和实践价值。
其中,模型是数学知识和实际问题之间的桥梁,通过建立数学模型,可以解决现实生活中的各种问题。
本文将从各个方面介绍高一数学必修一所有的模型知识点。
一、函数模型函数模型是高中数学中最基础的模型之一,它描述了变量之间的依赖关系。
在高一数学必修一中,函数模型主要涉及到一次函数、二次函数、指数函数和对数函数等。
通过对实际问题进行数学建模,学生可以将实际问题转化为函数表达式,并通过函数的图像和性质来解决问题。
二、几何模型几何模型是描述空间形状和位置关系的数学模型。
在高一数学必修一中,几何模型主要涉及到平面几何和空间几何。
平面几何模型常见的有平面直角坐标系、三角形、平行四边形等,通过建立几何模型,可以解决各种形状和位置相关的问题。
三、数据统计模型数据统计模型是通过对数据进行分析和处理,得到相应的数学模型。
在高一数学必修一中,数据统计模型主要涉及到数据的收集、整理、描述和分析等。
通过应用统计学的方法,可以对数据进行合理的解读和分析,进而得出结论。
四、概率模型概率模型是描述随机实验结果的数学模型。
在高一数学必修一中,概率模型主要涉及到随机事件、概率计算、条件概率和独立性等概念。
通过建立概率模型,可以确定某个事件发生的可能性,从而进行合理的决策。
五、三角模型三角模型是描述角度之间关系的数学模型。
在高一数学必修一中,三角模型主要涉及到角的三角函数、三角恒等式、解三角形等。
通过建立三角模型,可以解决各种角度和边长相关的问题,应用广泛。
六、微分模型微分模型是描述变化率的数学模型。
在高一数学必修一中,微分模型主要涉及到函数的导数和导数的应用。
通过建立微分模型,可以解决各种变化率相关的问题,具有重要的应用价值。
七、积分模型积分模型是描述累积量的数学模型。
在高一数学必修一中,积分模型主要涉及到不定积分、定积分以及积分的应用。
通过建立积分模型,可以解决各种面积、物理量、曲线长度等相关问题,具有重要的应用价值。
知识讲解-回归分析的基本思想及其初步应用(文、理)

回归分析的基本思想及其初步应用【学习目标】1. 通过对实际问题的分析,了解回归分析的必要性与回归分析的一般步骤。
2. 能作出散点图,能求其回归直线方程。
3. 会用所学的知识对简单的实际问题进行回归分析。
【要点梳理】要点一、变量间的相关关系1. 变量与变量间的两种关系:〔1〕 函数关系:这是一种确定性的关系,即一个变量能被另一个变量按照某种对应法则唯一确定.例如圆的面积.S 与半径r 之间的关系S=πr 2为函数关系.〔2〕相关关系:这是一种非确定性关系.当一个变量取值一定时,另一个变量的取值带有一定的随机性,这两个变量之间的关系叫做相关关系。
例如人的身高不能确定体重,但一般来说“身高者,体重也重”,我们说身高与体重这两个变量具有相关关系. 2. 相关关系的分类:〔1〕在两个变量中,一个变量是可控制变量,另一个变量是随机变量,如施肥量与水稻产量; 〔2〕两个变量均为随机变量,如某学生的语文成绩与化学成绩. 3. 散点图:将两个变量的各对数据在直角坐标系中描点而得到的图形叫做散点图.它直观地描述了两个变量之间有没有相关关系.这是我们判断的一种依据.4. 回归分析:与函数关系不同,相关关系是一种非确定性关系,对具有相关关系的两个变量进行统计分析的方法叫做回归分析。
要点二、线性回归方程:1.回归直线如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫作回归直线。
2.回归直线方程ˆˆˆybx a =+ 对于一组具有线性相关关系的数据11(,)x y ,22(,)x y ,……,(,)n n x y ,其回归直线ˆˆˆybx a =+的截距和斜率的最小二乘法估计公式分别为:121()()ˆ()niii nii x x y y bx x ==--=-∑∑,ˆˆay bx =- 其中x 表示数据x i 〔i=1,2,…,n 〕的均值,y 表示数据y i 〔i=1,2,…,n 〕的均值,xy 表示数据x i y i 〔i=1,2,…,n 〕的均值.a 、b 的意义是:以a 为基数,x 每增加一个单位,y 相应地平均变化b 个单位.要点诠释:①回归系数121()()ˆ()niii nii x x y y bx x ==--=-∑∑,也可以表示为1221ˆni ii nii x y nx ybxnx==-=-∑∑,这样更便于实际计算。
高一功能关系知识点总结

高一功能关系知识点总结功能关系是数学中的一个重要概念,它描述了数学中各种变量之间的数学关系。
在高一数学学习中,我们接触到了许多与功能关系相关的知识点。
本文将结合这些知识点,对高一学习中的功能关系进行总结和归纳,以帮助我们更好地理解和掌握这一部分内容。
一、函数的定义和性质函数是一种特殊的关系,它将一个集合的每个元素都对应到另一个集合的唯一元素上。
在高一学习中,我们学习了函数的定义和基本性质,其中包括:1. 函数的定义:函数是一个对应关系,每个自变量对应唯一的因变量。
2. 定义域和值域:函数的定义域是自变量的取值范围,值域是因变量的取值范围。
3. 函数的图象:函数的图象是平面直角坐标系上函数所有的点的集合。
4. 奇偶性:函数的奇偶性取决于函数图象关于y轴对称与否。
5. 单调性:函数的单调性描述了函数在定义域内的增减规律。
6. 周期性:周期函数在一定区间内满足一定的规律。
二、常见函数类型在高一学习中,我们遇到了多种常见的函数类型,下面我们对其中几种进行总结:1. 线性函数:线性函数的图象是一条直线,表达形式为y = kx + b,其中k为斜率,b为截距。
2. 幂函数:幂函数是指数函数的逆运算,表达形式为y = x^n,其中n为常数。
3. 指数函数:指数函数的图象是平滑曲线,表达形式为y = a^x,其中a为常数且不等于1。
4. 对数函数:对数函数是指数函数的反函数,表达形式为y = log_a(x),其中a为常数且大于0且不等于1。
5. 二次函数:二次函数的图象是抛物线,表达形式为y = ax^2+ bx + c,其中a、b、c为常数。
三、函数的运算在高一学习中,我们学习了函数的基本运算,包括函数的四则运算和复合运算:1. 四则运算:两个函数之间可以进行加、减、乘、除的运算,得到的结果仍然是一个函数。
2. 复合运算:将一个函数作为另一个函数的自变量,形成一个新的函数。
四、函数图象与方程1. 函数的零点和解析式:函数的零点是使得函数值为0的自变量取值,通过解方程可以求得函数的零点。
变量之间的相互关系

变量之间的相互关系一、引言在研究数据科学、统计学、经济学以及其他众多领域时,变量间的相互关系是不可或缺的议题。
这种关系描述了不同变量如何互相影响,从而帮助我们理解和预测现象。
本文将深入探讨变量间相互关系的概念、类型和测量方法。
二、变量间的关系类型1.因果关系:如果一个变量(原因)的变化导致了另一个变量(结果)的变化,则存在因果关系。
这种关系是有方向的,原因必定在前,结果只能在后。
2.相关关系:当两个或多个变量同时发生变化,但不表示因果方向时,我们称之为相关关系。
相关关系可以是正相关(一个变量增加时,另一个也增加)或负相关(一个变量增加时,另一个减少)。
3.函数关系:当一个变量(自变量)完全确定另一个变量(因变量)的值时,我们称之为函数关系。
这种情况下,因变量的变化完全依赖于自变量的变化。
三、测量变量间关系强度的方法1.皮尔逊相关系数:衡量两个连续变量的线性相关程度,取值范围在-1到1之间。
接近1表示强正相关,接近-1表示强负相关,接近0表示无相关。
2.斯皮尔曼秩相关系数:与皮尔逊相关系数类似,但适用于非参数数据。
它衡量的是两个连续变量之间的秩次相关性。
3.偏相关系数:当存在多个变量影响因变量时,偏相关系数可以用来衡量特定自变量与因变量之间的线性关系。
四、应用场景理解并测量变量间的相互关系在众多实际场景中都有应用价值。
例如,在市场营销中,通过分析消费者行为、购买历史等变量与购买决策之间的相互关系,可以更有效地制定营销策略。
在医学研究中,了解疾病症状、患者生理指标等变量之间的关系,有助于疾病的诊断和治疗。
五、结论理解并测量变量间的相互关系是数据科学和统计学中的重要概念。
通过明确关系的类型和测量方法,我们可以更好地理解和预测现象,从而在各个领域中做出更有效的决策。
随着技术的发展和数据的丰富,变量间相互关系的研究将继续深化和拓展,为我们提供更多的洞见和可能。
高中数学 2.3.1 变量间的相互关系课件

n
记 Q (yi bxi a)2 (∑为连加符号) i1
上式展开后,是一个关于a,b的二次多 项式,应用配方法,可求使Q取得最小值 时a、b的值.
这样,回归直线就是所有直线中Q取最 小值的那一条。由于平方又叫做二乘方, 所以这种使“离差平方和为最小”的方法, 叫做“最小二乘法”。
50
方程。
8
60
9
70
10
90
11
120
∑
510
Y
x2
xy
6
25
30
10
100
100
10
225
150
13
400
260
16
900
480
17
1600 680
19
2500 950
23
2600 1380
25
4900 1750
29
8100 2610
46 14400 5520
214 36780 13910
计算a^, b^的值. 由上表分别计算x,y的平均数得 x510,y214
设某地10户家庭的年收入和年饮食支出的统 计资料如下表: (单位:万元)
年收入 2 4 4 6 6 6 7 7 8 10
饮食支出 0.9 1.4 1.6 2.0 2.1 1.9 1.8 2.1 2.2 2.3
由表中数据可以看出,y有随x增加而增加的趋势 当年收入的值由小变大时,年饮食支出的值也在由 小变大。这种相关称作正相关;反之如果一个变量 的值由小变大时,另一个变量的值由大变小,这种 相关称作负相关。
用最小二乘法求回归直线方程中a,b
有下面的公式:
第三章1.2相关系数

相关系数[学习目标]了解相关系数的计算公式,会由r 值的大小判断两随机变量线性相关程度的大小. [知识链接]当r =1或-1时,两个变量的相关性如何答 当r =1时,两个变量完全正相关;当r =-1时,两个变量完全负相关. [预习导引]1.相关系数r 的计算假设两个随机变量的数据分别为(x 1,y 1),(x 2,y 2),…,(x n ,y n ),则变量间线性相关系数r 的计算公式为r =l xyl xx l yy=∑ni =1(x i -x -)(y i -y -)∑n i =1(x i -x -)2∑n i =1(y i -y -)2=∑ni =1x i y i -nx -y -∑ni =1x 2i -nx -2∑ni =1y 2i -ny -22.误差表达式Q (a ,b )=∑ni =1[y i -(a +bx i )]2=l yy +n [y --(a +bx -)]2+l xx(b -l xy l xx )-l 2xyl xx, Q min =l yy (1-r 2)(Q ≥0). 3.相关系数r 的性质 (1)r 的取值范围为[-1,1];(2)|r |值越大,误差Q 越小,变量之间的线性相关程度越高; (3)|r |值越接近0,Q 越大,变量之间的线性相关程度越低.要点一 利用相关系数检验两变量间的相关性例1 现随机抽取了某中学高一10名在校学生,他们入学时的数学成绩(x )与入学后第一次考试的数学成绩(y )如下: 学生号1 2 3 4 5 6 7 8 9 10 x 120 108 117 104 103 110 104 105 99 108 y84648468696869465771请问:这10名学生的两次数学成绩是否具有线性关系 解 x -=110(120+108+…+99+108)=,y -=110(84+64+…+57+71)=68,∑10i =1x 2i =1202+1082+…+992+1082=116 584, ∑10i =1y 2i =842+642+…+572+712=47 384, ∑10i =1x i y i =120×84+108×64+…+99×57+108×71=73 796. 所以相关系数为r =73 796-10××68(116 584-10×)(47 384-10×682)≈ 6.由此可看出这10名学生的两次数学成绩具有较强的线性相关关系.规律方法 利用相关系数r 进行判断相关关系,需要应用公式计算出r 的值,由于数据较大,需要借助计算器.跟踪演练1 假设关于某种设备的使用年限x (年)与所支出的维修费用y (万元)有如下统计资料:x 2 3 4 5 6 y已知∑5i =1x 2i =90,∑5i =1y 2i =,∑5i =1x i y i =.(1)求x -,y -;(2)对x ,y 进行线性相关性检验. 解 (1)x -=2+3+4+5+65=4.y -=错误!=5.(2)∑5i =1x i y i -5x -y -=-5×4×5=, ∑5i =1x 2i -5x -2=90-5×42=10, ∑5i =1y 2i -5y -2=-125=, 所以r =错误!≈.|r |≈>,所以x 与y 之间具有很强的线性相关关系. 要点二 线性回归分析例2 已知某地每单位面积菜地年平均使用氮肥量x (kg)与每单位面积蔬菜年平均产量y (t)之间的关系有如下数据:(1)求x 与y 之间的相关系数,并检验是否线性相关;(2)若线性相关,求蔬菜产量y 与使用氮肥量x 之间的线性回归直线方程,并估计每单位面积施氮肥150 kg 时,每单位面积蔬菜的年平均产量. 解 (1)列出下表,并用科学计算器进行相关计算:x -=1 51515=101,y -=错误!≈,∑15i =1x 2i =161 125,∑15i =1y 2i =1 ,∑15i =1x i y i =16 . 故蔬菜产量与施用氮肥量的相关系数 r =16 -15×101×(161 125-15×1012)(1 -15×)≈ 3.所以蔬菜产量与施用氮肥量之间存在着线性相关关系. (2)设所求的线性回归方程为y =a +bx ,则b =∑15i =1x i y i -15x -y -∑15i =1x 2i -15x -2=16 -15×101×161 125-15×1012≈ 7, a =y --bx -≈- 7×101= 3, ∴线性回归方程为y = 3+ 7x .∴当每单位面积施氮肥150 kg 时,每单位面积蔬菜年平均产量为 3+ 7×150≈(t).规律方法 在研究两个变量之间的关系时,应先进行相关性检验,若具备线性相关关系再求线性回归方程.如果本身两个变量不具备线性相关关系,即使求出线性回归方程也是毫无意义的,而且用其估计和预测的量也是不可信的.跟踪演练2 为分析学生初中升学的数学成绩对高一数学学习的影响,在高一年级随机抽取10名学生,了解他们的入学成绩和高一期末考试数学成绩如下表:入学成绩(x ) 63 67 45 88 81 71 52 99 58 76 高一期末成绩(y )65785282928973985675(1)画出散点图;(2)对变量x 与y 进行相关性检验,如果x 与y 之间具有线性相关关系,求出线性回归方程;(3)若某学生入学的数学成绩为80分,试估计他在高一期末考试中的数学成绩.解 (1)散点图如图所示.(2)由题可得x -=70,y -=76,∑10i =1(x i -x -)·(y i -y -)=1 894, ∑10i =1(x i -x -)2=2 474, ∑n i =1 (y i -y -)2=2 056, 因此可得相关系数为r =∑10i =1(x i -x -)(y i -y -)∑10i =1 (x i -x -)2·∑10i =1 (y i -y -)2= 1 8942 474× 2 056≈ 8>,所以入学数学成绩与高一期末考试数学成绩存在线性相关关系. 设线性回归方程为y =a +bx ,则b =∑10i =1 (x i -x -)(y i -y -)∑10i =1(x i -x -)2=1 8942 474≈ 56, a =y --bx -=76- 56×70= 8. 因此所求的线性回归方程是y = 8+ 56x .(3)若某学生入学的数学成绩为80分,代入(2)中的方程可求得y = 8+ 56×80≈84,即这名学生在高一期末考试中的数学成绩的预测值为84分.1.对于回归分析,下列说法错误的是( )A .在回归分析中,变量间的关系若是非确定关系,那么因变量不能由自变量唯一确定B .线性相关系数可以是正的,也可以是负的C .回归分析中,如果r 2=1,说明x 与y 之间完全相关D .样本相关系数r ∈(-1,1) 答案 D解析 相关系数r 的范围是[-1,1].2.一唱片公司欲知打歌费用x (十万元)与唱片销售量y (千张)之间的关系,从其所发行的唱片中随机抽取了10张,得如下的资料:∑10i =1x i =28,∑10i =1x 2i =, ∑10i =1y i =75,∑10i =1y 2i =,∑10i =1x i y i =237,则y 与x 的相关系数r 的绝对值为__________. 答案解析 由公式r =∑ni =1x i y i -nx -y -∑n i =1x 2i -nx -2∑n i =1y 2i -ny -2得|r |=.3.若线性回归方程中的回归系数b =0,则相关系数r =__________. 答案 0 解析 相关系数r =∑ni =1(x i -x -)(y i -y -)∑n i =1 (x i -x -)2∑n i =1(y i -y -)2与b =∑n i =1(x i -x -)(y i -y -)∑ni =1(x i -x -)2的分子相同.4.有5组数据如下:x 1 2 3 4 10 y3410512将这组数据中的哪一组去掉后,另外的4组数据具有较强的线性相关性解作出散点图如图所示.观察散点图,可以发现A,B,D,E四个点大致在某条直线附近,具有较强的线性相关关系,故应将点C(3,10)去掉.对相关系数r的理解(1)判断变量之间的线性相关关系,一般用散点图,但在作图中,由于存在误差,有时很难判断这些点是否分布在一条直线的附近,从而就很难判断两个变量之间是否具有线性相关关系,此时就必须利用线性相关系数来判断.(2)|r|越接近1,它们的散点图越接近一条直线,这时用线性回归模型拟合这组数据的效果就越好.(3)相关系数r只能描述两个变量之间的变化方向及密切程度,不能揭示二者之间的本质联系.(4)相关系数r可以定量地反映出变量间的相关程度,明确的给出有无必要建立两变量间的回归方程.一、基础达标1.下列说法不正确的是( ) A.回归分析中,变量x和y都是普通变量B.变量间的关系若是非确定性关系,那么因变量不能由自变量唯一确定C.线性相关系数可能是正的,也可能是负的D.如果线性相关系数是负的,y随x的增大而减少答案A解析在回归分析中的两个变量是具有相关关系的两个变量.2.通过相关系数来判断两个变量相关关系的强弱时,相关系数的绝对值越大,用线性回归模型拟合样本数据的效果就越好,如果相关系数r∈[,1],则两个变量( )A.负相关很强B.相关性一般C.正相关很强D.两变量之间几乎没有关系答案C3.对四对变量y和x进行线性相关检验,已知n是观测值组数,r是相关系数,且已知:①n=7,r= 3 ②n=15,r= 2 ③n=17,r= 1④n=3,r= 0则变量y和x具有线性相关关系的是( ) A.①和② B.①和④ C.②和④ D.③和④答案B解析相关系数r的绝对值越大,变量x,y的线性相关关系越强,故选B. 4.对变量x,y有观测数据(x i,y i)(i=1,2,…,10),得散点图①:对变量u,v有观测数据(u,v i)(i=1,2,…,10),得散点图②.由这两个散点图可以判i断( )A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C .变量x 与y 负相关,u 与v 正相关D .变量x 与y 负相关,u 与v 负相关 答案 C解析 在图①中,所有点都在一条直线的附近,且直线的斜率为负值,所以变量x 与y 负相关;同理,变量u 与v 正相关,故选C.5.设两个变量x 和y 之间具有线性相关关系,它们的相关系数是r ,y 关于x 的回归直线的斜率是b ,纵轴上的截距是a ,则下列说法正确的是__________. ①b 与r 的符号相同 ②a 与r 的符号相同 ③b 与r 的符号相反 ④a 与r 的符号相反 答案 ①解析 因为b >0时,两变量正相关,此时r >0;b <0时,两变量负相关,此时r <0.6.部门所属的10个工业企业生产性固定资产价值与工业增加值资料如下表(单位:百万元):根据上表资料计算的相关系数为__________. 答案 8解析 x -=3+3+5+6+6+7+8+9+9+1010=.y -=15+17+25+28+30+36+37+42+40+4510=.∴r =∑10i =1(x i -x -)(y i -y -)∑10i =1 (x i -x -)2∑10i =1 (y i -y -)2= 8.7.维尼纶纤维的耐热水性能的好坏可以用指标“缩醛化度”y 来衡量,这个指标越高,耐水性能也越好,而甲醛浓度是影响缩醛化度的重要因素,在生产中常用甲醛浓度x (克/升)去控制这一指标,为此必须找出它们之间的关系,现安排一批实验,获得如下数据:求相关系数r . 解 列表如下x -=1687=24,y -=错误!,r =l xyl xx l yy =∑7i =1x i y i -7x - y -∑7i =1x 2i -7x -2∑7i =1y 2i -7y -2=错误!=.由此可知,甲醛浓度与缩醛化度之间有很强的线性相关关系. 二、能力提升8.变量X 与Y 相对应的一组数据为(10,1),,2),,3),,4),(13,5);变量U 与V 相对应的一组数据为(10,5),,4),,3),,2),(13,1).r 1表示变量Y 与X 之间的线性相关系数,r 2表示变量V 与U 之间的线性相关系数,则( ) A .r 2<r 1<0B .0<r 2<r 1C .r 2<0<r 1D .r 2=r 1答案 C解析 由线性相关系数公式知r =∑ni =1(x i -x -)(y i -y -)∑ni =1(x i -x -)2∑n i =1(y i -y -)2.∵X -=U -=,Y -=V -=3,X i =U i (i =1,2,…,5),Y i =V 6-i (i =1,2,…,5),∴∑5i =1(X i -X -)2·∑5i =1 (Y i -Y -)2=∑5i =1 (U i -U -)2·∑5i =1(V i -V -)2. 令∑5i =1(X i -X -)(Y i -Y -)=A =(10-X -)(1-Y -)+-X -)(2-Y -)+-X -)(3-Y -)+-X -)(4-Y -)+(13-X -)(5-Y -),∑5i =1(U i -U -)(V i -V -)=B =(10-U -)(5-V -)+-U -)(4-V -)+-U -)(3-V -)+-U -)(2-V -)+(13-U -)(1-V -),∴A >0,B <0,∴r 1>0,r 2<0. 9.相关系数是度量( )A .两个变量之间线性相关关系的强度B .散点图是否显示有意义的模型C .两个变量之间是否存在因果关系D .两个变量之间是否存在关系 答案 A解析 系数来衡量两个变量之间线性相关关系的强弱.10.去年一轮又一轮的寒潮席卷全国,某商场为了了解某品牌羽绒服的月销售量y (件)与月平均气温x (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温、数据如下表:月销售量y (件) 24 33 40 55由表中数据算出线性回归方程y =bx +a 中的b ≈-2.气象部门预测下个月的平均气温约为 6 ℃,据此估计,该商场下个月羽绒服的销售量的件数约为__________. 答案 46解析 x -=10,y -=38,a =38-(-2)×10=58, ∴回归方程为y =-2x +58. 当x =6 ℃时,y =46.11.5个学生的数学和物理成绩如表:学生学科 A B C D E 数学 80 75 70 65 60 物理7066686462试用散点图和相关系数r 判断它们是否有线性相关关系,若有,是正相关还是负相关解 法一 涉及两个变量:数学成绩与物理成绩,可以以数学成绩为自变量,考察因变量物理成绩的变化趋势.以x 轴表示数学成绩,y 轴表示物理成绩,可得相应的散点图.由散点图可见,两者之间具有线性相关关系且是正相关. 法二 列表:i x i y i x 2i y 2i x i y i 1 80 70 6 400 4 900 5 600 275665 6254 3564 9503 70 684 900 4 624 4 760 4 65 64 4 225 4 096 4 160 5 60 62 3 600 3 844 3 720 ∑35033024 75021 82023 190∴r =∑5i =1x i y i -5x -y -(∑5i =1x 2i -5x -2)(∑5i =1y 2i -5y -2)=23 190-23 100250×40=>0.∴两变量具有相关关系且正相关.12.下列是水稻产量与施化肥量的一组观测数据:施化肥量 15 20 25 30 35 40 45 水稻产量320330360410460470480(1)将上表中的数据制成散点图,并计算相关系数r .(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗该结论与相关系数r 的计算一致吗 解 (1)散点图如下:列表:i x i y i x 2i y 2i x i y i 1 15 320 225 102 400 4 800 2 20 330 400 108 900 6 600 3 25 360 625 129 600 9 000 430410900168 10012 300535460 1 225211 60016 100 640470 1 600220 90018 800 745480 2 025230 40021 600∑210 2 8307 000 1 171 90089 200∴r=∑7i=1xiyi-7x-y-(∑7i=1x2i-7x-2)(∑7i=1y2i-7y-2)=错误!≈.(2)从图中可以发现施化肥量与水稻产量具有线性相关关系,当施化肥量由小到大变化时,水稻产量也由小变大,图中的数据点大约分布在一条直线的附近,因此施化肥量和水稻量近似成线性正相关关系.又由于r=>0,故散点图与r的计算一致.三、探究与创新13.某运动员训练次数与运动成绩之间的数据关系如下:次数x3033353739444650成绩y3034373942464851(1)作出散点图;(2)求出回归方程;(3)计算相关系数并进行相关性检验;(4)试预测该运动员训练47次及55次的成绩.解(1)作出该运动员训练次数x与成绩y之间的散点图,如下图所示,由散点图可知,它们之间具有线性相关关系.(2)列表计算:由上表可求得x -=,y -=,∑8i =1x 2i =12 656, ∑8i =1y 2i =13 731,∑8i =1x i y i =13 180, ∴b =∑8i =1x i y i -8x -y -∑8i =1x 2i -8x -2≈ 5,a =y --bx -=- 88,∴线性回归方程为y = 5x - 88.(3)计算相关系数r = 7,因此运动员的成绩和训练次数两个变量有较强的相关关系.(4)由上述分析可知,我们可用线性回归方程y = 5x - 88作为该运动员成绩的预报值.将x =47和x =55分别代入该方程可得y =49和y =57.故预测该运动员训练47次和55次的成绩分别为49和57.。
两个变量间的线性相关及回归方程的求法专题

两个变量间的线性相关及回归方程的求法专题一、如何认识两个变量间的相关关系相关关系我们可以从以下三个方面加以认识:(1)相关关系与函数关系不同.函数关系中的两个变量间是一种确定性关系.例如正方形面积S与边长x之间的关系2xS就是函数关系.即对于边长x的每一个确定的值,都有面积S的惟一确定的值与之对应.相关关系是一种非确定性关系,即相关关系是非随机变量与随机变量之间的关系.例如人的身高与年龄;商品的销售额与广告费等等都是相关关系.(2)函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.例如有人发现,对于在校儿童,身高与阅读技能有很强的相关关系.然而学会新词并不能使儿童马上长高,而是涉及到第三个因素——年龄,当儿童长大一些,他们的阅读能力会提高而且由于长大身高也会高些.(3)函数关系与相关关系之间有着密切联系,在一定的条件下可以相互转化.例如正方形面积S与其边长x间虽然是一种确定性关系,但在每次测量边长时,由于测量误差等原因,其数值大小又表现出一种随机性.而对于具有线性关系的两个变量来说,当求得其回归直线后,我们又可以用一种确定性的关系对这两个变量间的关系进行估计.相关关系在现实生活中大量存在,从某种意义上讲,函数关系是一种理想的关系模型,而相关关系是一种更为一般的情况.因此研究相关关系,不仅可使我们处理更为广泛的数学应用问题,还可使我们对函数关系的认识上升到一个新的高度.二、如何判断两个变量线性相关关系1、利用变量相关关系的概念利用变量相关关系的概念判断时,一般是看当一个变量的值一定时,另一个变量是否带有确定性,两个变量之间的关系具有确定关系--函数关系;两个变量之间的关系具有随机性,不确定性--相关关系。
例1、在下列各个量与量的关系中:①正方体的体积与棱长之间的关系;②一块农田的水稻产量与施肥量之间的关系;③人的身高与年龄之间的关系;④家庭的收入与支出之间的关系;⑤某户家庭用电量与水费之间的关系。
高一数学知识点的相互联系

高一数学知识点的相互联系在高一的数学学习中,我们接触到了许多的数学知识点,这些知识点之间并不是孤立存在的,而是相互联系、相互影响的。
在本文中,我们将探讨高一数学知识点之间的相互联系,以帮助我们更好地理解和运用这些知识。
一、代数与几何的联系代数和几何是数学中两个重要的分支,它们之间存在着紧密的联系。
在几何中,我们通过图形来研究物体的形状、大小和位置关系,而代数则通过符号和方程式来研究数的关系。
在解决几何问题时,我们常常需要运用到代数知识,例如使用代数式来表示几何图形的性质,或者通过代数方程组求解几何问题。
二、函数与微积分的联系函数是数学中的重要概念,而微积分则是函数的重要工具。
函数是描述变量之间关系的一种数学工具,而微积分则通过求导和积分来研究函数的变化率和面积。
在解决函数相关的问题时,我们常常需要运用到微积分的知识,例如求函数的导数、确定函数的最值等等。
因此,函数与微积分是密不可分的。
三、数列与数学归纳法的联系数列是数学中的一种重要概念,而数学归纳法则是证明数列性质的重要方法。
数列是按照一定规律排列的一系列数,而数学归纳法则是通过证明数列在某个条件下成立,进而推断数列在所有情况下成立。
数列问题中,我们常常需要借助数学归纳法来证明数列的性质,从而解决问题。
四、立体几何与三角函数的联系立体几何研究的是空间中的图形和体积,而三角函数则是研究角和边之间的关系。
在解决立体几何问题时,我们常常会遇到涉及角度的计算,这时就需要运用到三角函数的知识,例如使用正弦定理、余弦定理等来计算角度或边长。
五、概率与统计的联系概率与统计是数学中与实际问题密切相关的两个分支,它们用于分析和解决不确定性和随机性问题。
概率研究的是各种可能事件的发生概率,而统计研究的是通过样本数据对总体进行推断和判断。
在解决概率和统计问题时,我们常常需要运用到数学的概率论和统计学的知识,如概率计算、样本调查等。
通过上述的讨论,我们可以看出高一数学知识点之间的相互联系。
高一数学变量间的相关关系

[单选]低温对肌松药的影响,不正确的是()A.体温降至30℃的过程中,去极化肌松药的作用增强,时效延长B.体温降至30℃对非去极化肌松药作用强度很少受影响C.26℃以下低温,各种肌松药的作用均增强D.低温对去极化和非去极化肌松药的影响程度不一E.低温时泮库溴铵的肝肾排泄率减低 [单选]Inmarsat通信系统中,地面站的工作波段为()。A、L波段B、C波段C、S波段D、X波段 [填空题]天平室的温度应保持在()内,湿度应保持在()。 [单选]外阴恶性黑色素瘤的叙述正确的是()A.由结合痣或复合痣发展B.仅发生于老年妇女C.常无明显自觉症状D.宜行外阴根治术E.手术范围应在病变处3~4cm处 [单选,A2型题,A1/A2型题]子宫颈癌的好发部位是()A.子宫颈外口柱状上皮与鳞状上皮交界处B.子宫峡部解剖学内口C.子宫峡部组织学内口D.阴道穹隆E.子宫颈管 [单选]以产品品种作为成本核算对象,归集和分配生产成本,计算产品成本的方法是A.分批法B.品种法C.逐步结转分步法D.平行结转分步法 [单选]〈HR〉在HTML中是标记()A.标题B.空格C.换行D.水平线 [单选]局部浸润麻醉选用普鲁卡因时,其常用浓度为()A.0.5%B.1%C.1.5%D.2%E.2.5% [单选]关于胰岛素治疗糖尿病,下列何者是错误的()A.适用于1型糖尿病B.适用于2型糖尿病饮食控制和口服降糖药物仍控制不良者C.是抢救急性严重代谢紊乱中的关键药物D.适用于有严重急慢性并发症者E.妊娠时糖尿病病情减轻,不需要用胰岛素或减少剂量 [单选]齿轮箱结合面紧固,定位孔和定位销接触面积在()以上。A、80%B、60%C、50%D、40% [单选,A1型题]患者男,40岁。左下肢静脉曲张10年,内踝上方溃疡反复发作4年,下列哪些治疗是错误的()A.积极治疗患肢静脉曲张B.休息时抬高患肢,下地前用弹力袜C.温盐水湿敷创面D.溃疡创面使用5%鱼肝油酸钠E.切除溃疡并植皮 [问答题,简答题]销售成功的一般规律? [问答题,案例分析题]病例摘要:吴某,女,18岁,学生,于2011年11月25日就诊。患者3岁时突发高热,失语伴右半侧肢体抽搐,在某医院诊断为"乙型脑膜炎",经过治疗(具体用药不详)后症状好转,出院后发作性意识丧失、活动中断、两眼凝视,持续十几秒钟自行缓解,在多家医 [填空题]若某路线纵断面上同一坡段两点间的高差为3m,水平距离为100m,则该坡段的纵坡为()。 [单选]跳汰机小修的内容包括()。A、检查各箱体、给排水无漏水、漏矿B、拆检中间轴C、检查更换传动轴承D、更换中间轴 [单选,A1型题]下列哪项不是白矾的功能()A.解毒杀虫B.燥湿止痒C.活血散结D.止泻止血E.清热化痰 [单选,A1型题]身热,微恶风,汗少,肢体酸重或疼痛,头昏重胀痛,咳嗽痰粘,鼻流浊涕,心烦口渴,或口中粘腻,渴不多饮,胸闷脘痞,泛恶,腹胀,大便或溏,小便短赤,舌苔薄黄而腻,脉濡数。治疗方剂宜首选()。A.荆防达表汤B.葱豉桔梗汤C.新加香薷饮D.参苏饮E.加减葳蕤汤 [单选]关于胎动次数,下述哪项提示胎儿缺氧()A.胎动<30次/12hB.胎动<25次/12hC.胎动<20次/12hD.胎动<15次/12hE.胎动<10次/12h [单选,A2型题,A1/A2型题]导管结石好发于()A.腮腺B.颌下腺C.舌下腺D.黏液腺E.浆液腺 [单选]透平[turbine]将流体工质中蕴有的能量转换成机械功的机器。又称涡轮、涡轮机。透平是英文turbine的音译,源于拉丁文turbo一词,意为旋转物体。透平的工作条件和所用工质不同,因而其结构型式多种多样,基本工作原理()。A、不同B、完全相同C、相似D、也多种多样 [单选,A1型题]颈正中线甲状腺区上方的球形肿块可能是()A.皮脂腺囊肿B.淋巴结C.甲状舌管囊肿D.癌肿E.上述任何一种都可能 [单选]MCS-51系列单片机外引脚可构成三种总线结构,地址总线由P0和()口提供。A、P1;B、P2;C、P3;D、无。 [单选,A2型题,A1/A2型题]组成蛋白质的氨基酸在自然界存在的差异是()。A.种族差异B.个体差异C.组织差异D.器官差异E.无差异 [单选]根据柴油机的基本工作原理,下列哪一种定义最准确()。A.柴油机是一种往复式内燃机B.柴油机是一种在气缸中进行二次能量转换的内燃机C.柴油机是一种压缩发火的往复式内燃机D.柴油机是和种压缩发火的回转式内燃机 [单选,A1型题]可用于治疗阳虚失血证的方剂是()A.当归四逆汤B.黄芪建中汤C.小建中汤D.理中丸E.附子理中丸 [填空题]教育行政部门负责学校卫生工作的行政管理。()负责对学校卫生工作的监督指导。 [判断题]普氏立克次体侵入人体后,主要在小血管和毛细血管内皮细胞内繁殖,引起血管病变。A.正确B.错误 [单选,A1型题]关于抗原因素对免疫耐受形式哪项是正确的()A.抗原的持续存在是维持免疫耐受的重要条件B.耐受原多为大分子颗粒性物质C.抗原有多种不同的决定簇易形成耐受D.抗原经皮下或肌内注射易形成耐受E.TD-Ag无论多少剂量均不易引起T细胞耐受 [单选,A2型题,A1/A2型题]关于孤独症的治疗,错误的是()A.异常行为的改变和变更B.对孩子行为的宽容和理解C.特别能力的发现、培养和转化D.应用行为分析疗法是高强度的行为疗法E.采用以药物治疗为主、教育和训练为辅的办法 [单选]能对护士的行为起到评价和激励作用的道德规范是()。A.良心B.情感C.审慎D.荣誉E.兴趣 [单选]诊断十二指肠溃疡的可靠X线征象是()A.十二指肠球部变形B.十二指肠球部激惹C.十二指肠球部压痛D.十二指肠球部浓钡影E.十二指肠球部狭窄梗阻 [单选]下列对法所作的分类中,以法的创制方式和发布形式为依据进行分类的是()。A.成文法和不成文法B.根本法和普通法C.实体法和程序法D.一般法和特别法 [单选]黄体的形成、发育和功能,描述恰当的是().A.维持14天左右均退化B.分泌孕激素C.排卵后由卵泡内膜和卵泡颗粒细胞形成D.排卵后由卵泡膜形成E.排卵后由卵泡细胞形成 [单选]根据营业税法律制度的规定,下列混合销售行为中,应当一并征收营业税的是()。A.贸易公司销售货物的同时负责安装B.百货商店销售商品的同时负责运输C.建筑公司提供建筑业劳务的同时销售自产货物并实行分别核算D.餐饮公司提供餐饮服务的同时销售酒水 [单选]诊断抑郁症,最重要的症状群是()。A.精力减退、疲乏感B.思维困难、联想缓慢C.情绪低落、兴趣下降D.自责、自罪、自杀观念E.失眠、食欲减退、体重减轻 [单选,A2型题,A1/A2型题]据《素问·四气调神大论》,“发陈”描述的是哪一季节的物候规律()A.春B.夏C.秋D.冬E.长夏 [单选]营业前试机运行(),确认一切正常才能正式开机营业。A、可两天一次B、每天一次C、不少于二次D、操作人员试乘后 [问答题,简答题]甄选销售人员的程序? [单选,A2型题,A1/A2型题]实验室管理人员的工作方式建议中,未涉及()。A.积极参加临床实验室室间质量评价活动B.对实验室收入和支出应实行有效的管理和控制C.检验结果必须准确、以易于理解的方式迅速送到医师手中D.实验室有责任就检验报告为临床医师提供科学的解释和参考意见E.应 [单选]跳汰机技术要求中当床层厚度变化值大于()mm时,排料装置应能自动改变排料速度。A、5B、10C、15D、20
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( x x)( y y) x y n x y
i 1 i i
n
n
( x x)
i 1 i
n
2
i 1 n
i
i
x nx
i 1 2 i
2
,
a y bx
以上公式的推导较复杂,故不作推导,但它的原 理较为简单:即各点到该直线的距离的平方和最 小,这一方法叫最小二乘法。
根据上述数据,人体的脂肪含量与年龄之间有什么样的关系?
分析:从总体上看随着年龄的增长,脂肪含量也在增加,为了 确定这一关系的细节,我们需要对数据进行分析,我们可以通 过前面的做统计图表的方法分析,我们可以对两个变量间的 关系有一个直观上的影响和判断.我们也可以通过下面的图 (散点图(scatter plot))来分析:
2.3.1-2
前面我们学习了怎样对收集来的数据进行分析: 集中趋势 频率分布图 离散程度 下面我们来介绍一中更为常见的分析方法:
小明,你数学成绩不太好, 学不好数学 ,物理 物理怎么样 ? 也是学不好的
?????... . 也不太好啊
你认为老师的说法对吗?
事实上,我们在考察数学成绩对物理成绩影响的同时,还 必须考虑到其他的因素:爱好,努力程度 数学 成绩 学习 兴趣 物理成绩
1. 测量法:移动直线l使所有点到它的距离之和最小
(1)
(2)
(3)
2.两点确定法:选取两点作直线,使其两边点个数一样
3.分组法:将点进行分组点,分别求其斜率和截距,求平均值
我们上面给出的几种方案可靠性都不是很强, 人们经过长期的实践与研究,已经找到了 计算回归方程的斜率与截距的一般公式:
b
在寻找变量间的相关关系时,统计同样发挥了非常重 要的作用,我们是通过收集大量的数据,对数据进行统 计分析的基础上,发现其中的规律,才能对它们之间的 关系作出判断.下面我们通过具体的例子来分析
在一次对人体脂肪含量和年龄的关系研究中,研究人员获得 了一份样本数据:
说明:各个年龄阶段的脂肪数据是这个年龄样本的平均数
例.下表是某小卖部6天卖出热茶的杯数(y)与当天气温(x)的对比表:
(1)试用最小二乘法求出线性回归方程; (2)如果某天的气温是-3℃,请预测这天可能会卖出热茶多少杯 解 (1)作散点图如图所示
由散点图知两个变量是线 性相关的,计算各种数据 如下表
分步计算 减少出错
于是: 则:
于是,线性回归方程为 y=57.557-1.648x
flp493bej
父亲的脸由晴转阴,深深的皱纹间流露出内心的愁思,“是啊,她的阿爹过世了,只靠一个女人支撑着这个家,也不知道她们的日子 究竟怎么过,你也该去看看她们把荷花领回家了„„” 深秋,走在较为宽阔的川道上,这里的沟壑不再深险,各种农作物在这儿茁壮成长,为广袤的黄土高原披上了五彩缤纷的盛装。玉米 长的似牛角,山坳那片高粱像团火,黄橙橙的谷子在微风里向你弯腰致意,土豆花、荞麦花、葵花点缀着整个山坡。 在一片荞麦地边,一户农家正在喂养着羊群,一个小男孩手拿皮鞭帮他的父亲看护着,顽皮的脸上流露着自然的满足和幸福。 “老乡——,借问一下去和川镇怎么走?”隔着这片荞麦地我大声地向他们喊了起来。小孩的父亲指了指山坡的另一边,“翻过这个 岭再走二里地就到了。”他的声音很洪亮,“你到谁家去?” “我是从山东来的,要到一个叫苏荷花的女孩家去。” “客人,你走错路了,我们村没有一家是姓苏的。”他站在山坡上毫不犹豫 地回答。 “老乡,十多年前我来过这儿,他家就住在附近山坡的窑洞里,也是从山东来的„„他家有七个姑娘一个儿子,有个叫五妮子六丫头 的„„” “我知道了,他家不姓苏姓刘,刘荷花是他家的第七个女儿„„”他看着我们笑了,红红的面色露出庄稼人特有的憨厚与质朴。 “现在的条件好了,农村实行了房屋规划,他家已搬到镇上的村子里去了。”他一边说一边吩咐身边的小男孩,“让我家的狗娃带你 们去吧。” 小男孩听了他父亲的话一蹦一跳地向我们跑来„„在小男孩地带领下,我们来到了一所爱心小学。院子不大,房屋很陈旧,高高升起 的五星红旗迎风飘扬。 我们悄悄地凑到教室门前,透过玻璃门窗依稀地可以看到教室里的摆设十分简陋。从背影我看得出来,教师是一个女孩,她一手扶着 讲桌一手用教鞭指着黑板,背对着我们有声有色地读着,“母亲,祖国,祖国就是母亲,母亲养育了我们,我爱我的祖国„„” 孩子们异口同声地朗诵起来,“母亲,祖国,祖国就是母亲,母亲养育了我们,我爱我的祖国„„” “同学们,我们每个人都爱自己 的母亲,热爱我们的祖国,下面请你们每个人说出一句赞美母亲热爱祖国的话。” 孩子们争先恐后地举起手来。 “世上只有妈妈好!”一个男孩喊了起来 。紧接着是一个女孩的声音:“咱们的祖国像花园。” “祖 国妈妈,我爱你!” “祖国万岁!”„„„„ “报告老师,小石头没有了妈妈,他该说些什么?”教室的气氛宁静下来,所有的目光投向了最前排墙角 处的男孩身上。 后来,我才知道,他是一个不幸的弃儿,几年前,他的父母离异,没有人领养他。他只能与他那年过半百的爷爷奶奶生活在一起,失 去了母爱父爱的他从此变得性格内向,不愿意和其他小朋友在一起玩耍。 “老师„„我想妈妈了„„”小石头哭了起来。 “小石头„„你的遭遇使我想起了一个女孩儿的经历,老师给你们讲一个鲜为人知 的故事好吗?” 孩子们点点头聚精会神地听起来。 “故事„„就从这儿讲起吧。”她整理了一下思绪讲了起来。
花费 时间
其他 因素
如果单纯从数学对物理的影响来考虑,就是考虑这两者之 间的相关关系 我们在生活中,碰到很多相关关系的问题:
商品销售收入
? ?
K×广告支出经费
粮食产量
K×施肥量
付出
? ?
K×收入
人体脂肪含量
K×年龄
以上种种问题中的两个变量之间的相关关系,我 们都可以根据自己的生活,学习经验作出相应的 判断,“规律是经验的总结”,不管你多有经验,只 凭经验办事,还是很容易出错的,一次在寻找变 量讲的相关关系时,我们需要一些更为科学的方 法来说明问题.
2)由回归方程知,当某天的气温是-3℃ 时,卖出的热茶杯数为 57.557-1.648×(-3)≈63(杯)
1.利用最小二乘估计时,首先要作出数据的散点图,利 用散点图观察数据是否具有线性关系 2.散点图呈现线性关系时,利用最小二乘公式求出方程
练习P92、第1,2题 作业P94、第2, 3题
;
/ பைடு நூலகம்孕
通过分析、观察可以看到:随着年龄的增长,人体脂肪含 量越高,这表明两个变量之间的确存在一定的关系。 递增我们叫它们 正相关 递减我们叫它们 负相关
从散点图可以看出:所有的点大致在一条直线附近波动,我 们称这两个变量间存在线性相关关系,这条直线叫做回归直 线(regression line)
如果可以求出这条直线的方程(回归方程),那么我们就可以比 较清楚的了解年龄与体内脂肪含量的相关性.这条直线就可 以作为两个变量具有线性相关关系的代表
