最新七年级精品[中学联盟] 数学下册 平行线的性质 赛课课件 (8)
合集下载
平行线的性质ppt课件

(3) 移: 以关键点为起点作与移动方向平行且与移动距离相
等的线段,得到关键点的对应点;
(4) 连: 按原图顺次连结对应点 .
知4-讲
特别警示
确定一个图形平行移动后的位置需要三个条件:
(1)图形原来的位置;
(2)平行移动的方向;
(3)平行移动的距离.
这三个条件缺一不可.
知4-练
例4 如图 4.2-33,现要把方格纸(每个小正方形的边长均为
知1-讲
特别警示
1. 两条直线平行是前提,只有在这个前提下才
有同位角相等.
2. 按格式进行书写时,顺序不能颠倒,与判定
不能混淆.
知1-讲
3. 平行线的性质与平行线的判定的区别
(1) 平行线的判定是根据两角的数量关系得到两条直线的位
置关系,而平行线的性质是根据两条直线的位置关系得
到两角的数量关系;
又∵ EG 平分∠ BEF,∴∠ BEG=
∠
BEF=70° .
∵ AB ∥ CD, ∴∠ 2= ∠ BEG=70° .
答案:A
知2-练
2-1. [中 考·烟 台]一杆 古 秤 在 称 物 时 的状 态 如 图
所 示,已 知∠ 1=102°,则 ∠ 2 的度数为
78°
______.
感悟新知
知识点 3 平行线的性质3
若是,可直接求出;若不是,还需要
通过中间角进行转化 .
知1-练
1-1. [中考·台州]用一张等宽的纸条折成如图所示的图
140° .
案,若∠ 1=20 ° ,则 ∠ 2的度数为_______
感悟新知
知识点 2 平行线的性质2
知2-讲
1. 性质 2 两条平行直线被第三条直线所截,内错角相等 .
等的线段,得到关键点的对应点;
(4) 连: 按原图顺次连结对应点 .
知4-讲
特别警示
确定一个图形平行移动后的位置需要三个条件:
(1)图形原来的位置;
(2)平行移动的方向;
(3)平行移动的距离.
这三个条件缺一不可.
知4-练
例4 如图 4.2-33,现要把方格纸(每个小正方形的边长均为
知1-讲
特别警示
1. 两条直线平行是前提,只有在这个前提下才
有同位角相等.
2. 按格式进行书写时,顺序不能颠倒,与判定
不能混淆.
知1-讲
3. 平行线的性质与平行线的判定的区别
(1) 平行线的判定是根据两角的数量关系得到两条直线的位
置关系,而平行线的性质是根据两条直线的位置关系得
到两角的数量关系;
又∵ EG 平分∠ BEF,∴∠ BEG=
∠
BEF=70° .
∵ AB ∥ CD, ∴∠ 2= ∠ BEG=70° .
答案:A
知2-练
2-1. [中 考·烟 台]一杆 古 秤 在 称 物 时 的状 态 如 图
所 示,已 知∠ 1=102°,则 ∠ 2 的度数为
78°
______.
感悟新知
知识点 3 平行线的性质3
若是,可直接求出;若不是,还需要
通过中间角进行转化 .
知1-练
1-1. [中考·台州]用一张等宽的纸条折成如图所示的图
140° .
案,若∠ 1=20 ° ,则 ∠ 2的度数为_______
感悟新知
知识点 2 平行线的性质2
知2-讲
1. 性质 2 两条平行直线被第三条直线所截,内错角相等 .
人教版七年级数学下册教学平行线的性质精品课件PPT
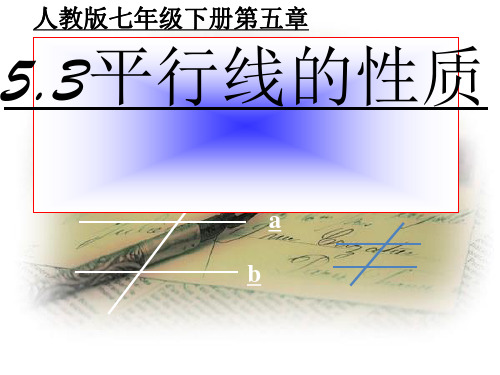
两条平行线被第三条直线所截,同旁内角互补.
简写为:两直线平行,同旁内角互补.
符号语言: ∵a∥b,
∴ 2+ 4=180°(两直线平行, 同旁内角互补).
人 教 版 七 年 级数学 下册教 学课件 -5.3.1 平行线 的性质
人 教 版 七 年 级数学 下册教 学课件 -5.3.1 平行线 的性质
人 教 版 七 年 级数学 下册教 学课件 -5.3.1 平行线 的性质
人 教 版 七 年 级数学 下册教 学课件 -5.3.1 平行线 的性质
练习二
2、已知∠1=60 °, ∠2=60 °,∠3=40° 证:(1)DE∥BC; (2) ∠C的度数
(1) 解: ∵∠1=60 °, ∠2=60 ° ∴∠1=∠2 ∴DE∥BC(同位角相等,两直线平行)
解: ∵a//b ∴ 1= 2(两直线平行,同位角相等). ∵ 1+ 4=180° (邻补角定义) ∴ 2+ 4=180°(等量代换)
人 教 版 七 年 级数学 下册教 学课件 -5.3.1 平行线 的性质
ቤተ መጻሕፍቲ ባይዱ
人 教 版 七 年 级数学 下册教 学课件 -5.3.1 平行线 的性质
平行线的性质3
解:∵四边形ABCD是梯形 ∴AB∥CD ∴∠A+∠D=180°,∠B+∠C=180°(两直线平行,同旁内角互补)
又∵ ∠A=100º, ∠B=115 ∴∠D=180°- ∠A=180°- 100º=80° ∴∠C=180°- ∠B=180°- 115º=65°
即 梯形的另外两个角分别为80°,65°
(2) 解: ∵DE∥BC ∴∠3=∠C(两直线平行,同位角相等)
又∵ ∠3=40° ∴∠C=40°(等量代换)
【最新】人教版七年级数学下册第五章《平行线的性质》优质公开课课件.ppt

10、人的志向通常和他们的能力成正比例。2021/1/112021/1/112021/1/111/11/2021 2:10:03 PM 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/1/112021/1/112021/1/11Jan-2111-Jan-21 12、越是无能的人,越喜欢挑剔别人的错儿。2021/1/112021/1/112021/1/11Monday, January 11, 2021 13、志不立,天下无可成之事。2021/1/112021/1/112021/1/112021/1/111/11/2021
又∵∠AED=40° (已知) ∴∠C=40 ° (等量代换)
小结:
已知
判定 得到
同位角相等 内错角相等 同旁内角互补
得到
两直线平行
性质
已知
小结 平行线的性质
图形
同 位
a
角b
1 2 c
内 错
a3
角b
2
c
同 旁
a
内
42
角b
c
已知 a//b
结果
理由
两直线平行 1 2 同位角相等
a//b 3 2 两直线平行 内错角相等
1 3
a
2 b
平行线的性质2
两条平行线被第三条直线所截,内错角相等 。 简单说成:两直线平行,内错角相等。
如图:已知a//b,那么2与 3有什么关系呢?
解: a//b (已知)
1= 2(两直线平行,同位角相等) c
1+ 3=180°(邻补角定义)
2+ 3=180°(等量代换)
a 同旁内角互补
作业:
• P22习题5.3第3、6题。
9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/1/112021/1/11Monday, January 11, 2021
又∵∠AED=40° (已知) ∴∠C=40 ° (等量代换)
小结:
已知
判定 得到
同位角相等 内错角相等 同旁内角互补
得到
两直线平行
性质
已知
小结 平行线的性质
图形
同 位
a
角b
1 2 c
内 错
a3
角b
2
c
同 旁
a
内
42
角b
c
已知 a//b
结果
理由
两直线平行 1 2 同位角相等
a//b 3 2 两直线平行 内错角相等
1 3
a
2 b
平行线的性质2
两条平行线被第三条直线所截,内错角相等 。 简单说成:两直线平行,内错角相等。
如图:已知a//b,那么2与 3有什么关系呢?
解: a//b (已知)
1= 2(两直线平行,同位角相等) c
1+ 3=180°(邻补角定义)
2+ 3=180°(等量代换)
a 同旁内角互补
作业:
• P22习题5.3第3、6题。
9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/1/112021/1/11Monday, January 11, 2021
《平行线的性质》七年级初一下册PPT课件

作用: (1)判定直线是否在平面内.
(2)判定点是否在平面内。
在生产、生活中,人们经
过长期观察与实践,总结出
关于平面的一些基本性质,
我们把它作为公理.这些公
理是进一步推理的基础.
新知探究
平面公理
生活中经常看到用三角架支撑照相机.
新知探究
平面公理
公理2 过不在一条直线上的三点,有且只有一个平面.
存在性
的交线为 OO1 ;
C
B
O
D
A
C1
D1
O1
正确
B1
A1
随堂练习
在正方体
ABCD A1B1C1D1 中,判断下列命题是否正确,并说明理由:
③由点A,O,C可以确定一个平面;
C
B
O
D
A
错误
C1
D1
B1
A1
随堂练习
例3:如图,直线AB、BC、CA两两相交,交点分别为A、B、C,证明:这三条直线共面。
点评:几何里的平面的特征:
1.无限延展
(没有边界)
2.不计大小
(无所谓面积)
3.不计厚薄
(没有质量)
新知探究
2. 平面的画法:
(1)通常用平行四边形表示,有时也可根据需要用其它平面图形表示,如:矩形;菱形;三角形;圆(椭圆)等等;
新知探究
(2) 通常画平行四边形表示平面,当平面是水平放置的时候,通常把平行四边形的锐角画成45°横
∠3
∠4
∠5
∠6
∠7
∠8
度数
角
度数
2
1
3
4
6
7
问题一:找出图中的角中,哪些是同位角?
(2)判定点是否在平面内。
在生产、生活中,人们经
过长期观察与实践,总结出
关于平面的一些基本性质,
我们把它作为公理.这些公
理是进一步推理的基础.
新知探究
平面公理
生活中经常看到用三角架支撑照相机.
新知探究
平面公理
公理2 过不在一条直线上的三点,有且只有一个平面.
存在性
的交线为 OO1 ;
C
B
O
D
A
C1
D1
O1
正确
B1
A1
随堂练习
在正方体
ABCD A1B1C1D1 中,判断下列命题是否正确,并说明理由:
③由点A,O,C可以确定一个平面;
C
B
O
D
A
错误
C1
D1
B1
A1
随堂练习
例3:如图,直线AB、BC、CA两两相交,交点分别为A、B、C,证明:这三条直线共面。
点评:几何里的平面的特征:
1.无限延展
(没有边界)
2.不计大小
(无所谓面积)
3.不计厚薄
(没有质量)
新知探究
2. 平面的画法:
(1)通常用平行四边形表示,有时也可根据需要用其它平面图形表示,如:矩形;菱形;三角形;圆(椭圆)等等;
新知探究
(2) 通常画平行四边形表示平面,当平面是水平放置的时候,通常把平行四边形的锐角画成45°横
∠3
∠4
∠5
∠6
∠7
∠8
度数
角
度数
2
1
3
4
6
7
问题一:找出图中的角中,哪些是同位角?
七年级数学下册《平行线的性质》PPT课件
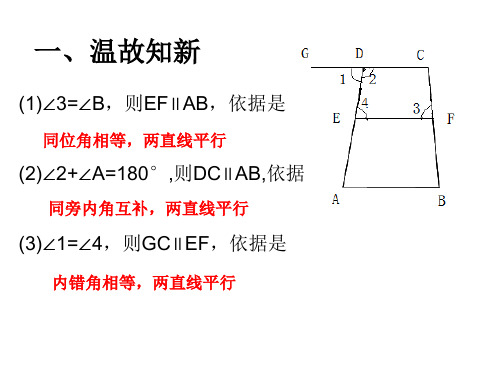
平行线的性质2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等。
2.如图:已知a//b,那么2与 3有什么关系呢?
解: a//b (已知)
1= 2(两直线平行,同位角相等) c
1+ 3=180°(邻补角的定义)
a
2+ 3=180°(等量代换)
42
3
b
1
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补. 简单说成:两直线平行,同旁内角互补.
三、范例点击
例1 如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度?
解:
∵ ∠2=∠1 (对顶角相等)
a
1
∴ ∠2=∠1 =54°
2
b
∵ a∥b(已知)
4
∴ ∠4=∠1=54°(两直线平行,同位角相等) 3
一、温故知新
(1)∠3=∠B,则EF∥AB,依据是
同位角相=180°,则DC∥AB,依据
同旁内角互补,两直线平行
(3)∠1=∠4,则GC∥EF,依据是
内错角相等,两直线平行
平行线的上述判定方法中,它 们是先知道什么……、 后知道什么?
同位角相等 内错角相等 同旁内角互补
两直线平行
5.3.1平行线的性质
二、新知探究
探究1 根据同位角相等可以判定两直线平行, 反过来如果两直线平行,同位角之间有 什么关系呢?
c a b
如果两直线不平行,上述结论还 成立吗?
平行线的性质1
两条平行线被第三条直线所截,同位 角相等.
简单说成:两直线平行,同位角相等.
探究2
1.如图,已知:a// b , 3与2有什么关系?
简单说成:两直线平行,内错角相等。
2.如图:已知a//b,那么2与 3有什么关系呢?
解: a//b (已知)
1= 2(两直线平行,同位角相等) c
1+ 3=180°(邻补角的定义)
a
2+ 3=180°(等量代换)
42
3
b
1
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补. 简单说成:两直线平行,同旁内角互补.
三、范例点击
例1 如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度?
解:
∵ ∠2=∠1 (对顶角相等)
a
1
∴ ∠2=∠1 =54°
2
b
∵ a∥b(已知)
4
∴ ∠4=∠1=54°(两直线平行,同位角相等) 3
一、温故知新
(1)∠3=∠B,则EF∥AB,依据是
同位角相=180°,则DC∥AB,依据
同旁内角互补,两直线平行
(3)∠1=∠4,则GC∥EF,依据是
内错角相等,两直线平行
平行线的上述判定方法中,它 们是先知道什么……、 后知道什么?
同位角相等 内错角相等 同旁内角互补
两直线平行
5.3.1平行线的性质
二、新知探究
探究1 根据同位角相等可以判定两直线平行, 反过来如果两直线平行,同位角之间有 什么关系呢?
c a b
如果两直线不平行,上述结论还 成立吗?
平行线的性质1
两条平行线被第三条直线所截,同位 角相等.
简单说成:两直线平行,同位角相等.
探究2
1.如图,已知:a// b , 3与2有什么关系?
最新人教版七年级数学下册《平行线的性质》优质ppt教学课件

C
∴ AB∥CD.
B F D
5.综合运用,巩固提高
练习2 已知:如图,∠AGD=∠ACB, ∠1=∠2,CD与EF平行吗?为什么?
A
G1D E
C
2 F
B
5.综合运用,巩固提高
理由如下: ∵ ∠AGD =∠ACB ,
∴ GD∥BC.
∵∠1和∠3是内错角, ∴∠1=∠3(两直线平行,内错角相等). C ∵∠1=∠2, ∴∠2=∠3. ∵∠2和∠3是同位角,
2
A 1
43 E
B
D
4.巩固新知,深化理解
例2 如图,已知AB∥CD,AE∥CF,∠A= 39°, ∠C是多少度?为什么?
E F
A
G
C
B D
4.巩固新知,深化理解
E F
A
G
1
B
C
D
解:∵AB∥CD, ∴ ∠C=∠1. ∵ AE∥CF, ∴ ∠A=∠1. ∴∠C=∠A. ∵∠A= 39º, ∴∠C= 39º.
总结
性质1 两条平行线被第三条直线所截,同位角相等. 性质2 两条平行线被第三条直线所截,内错角相等.
性质3 两条平行线被第三条直线所截,同旁内角互补.
自主练习
1.梳理旧知,引入新课 问题1 (1)平行线的性质是什么?
这三个性质中条件和结论分别是什么? 性质1 两直线平行,同位角相等. 性质2 两直线平行,内错角相等. 性质3 两直线平行,同旁内角互补.
性质3 两条平行线被第三条直 线 所截,同旁内角互补.
4.巩固新知,深化理解
例1 如图,平行线AB,CD被直线AE所截.
(3)从∠1=110º可以知道∠4是多少度吗?为什么?
答:∠4=70º.因为AB∥CD , ∠1和∠4是同旁内 角,根据两直线平行,同旁内角互补,得到 ∠1+∠4=180º.因为∠1=110º,所以∠4=70Cº.
【最新】人教版七年级数学下册第五章《平行线的性质 》公开课课件.ppt

(2)测量上面八个角的大小,记录下 来.从中你能发现什么?
问题
如果两条直线平行,那么这两条平行线被 第三条直线所截而成的同位角有什么数量关系?
演示……
平行线的性质1(公理)
结论 两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
性质2
E
C
P
D
2
A
1B
F
E’ E
C64 8
两直线平行
方法4:如果两条直线都与第三条直线平行, 那么这两条直线也互相平行.
问题2:
根据同位角相等可以判定两直线平 行,反过来如果两直线平行同位角之间 有什么关系呢?
内错角,同旁内角之间又有什么关 系呢?
动手画一画!
(1)用直尺和三角学科尺网 画出两条平行线 a∥b,再画一条截线c,使之与直线 a,b相交,并标出所形成的八角.
9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/162020/12/16Wednesday, December 16, 2020
10、人的志向通常和他们的能力成正比例。2020/12/162020/12/162020/12/1612/16/2020 7:33:49 AM 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2020/12/162020/12/162020/12/16Dec-2016-Dec-20 12、越是无能的人,越喜欢挑剔别人的错儿。2020/12/162020/12/162020/12/16Wednesday, December 16, 2020 13、志不立,天下无可成之事。2020/12/162020/12/162020/12/162020/12/1612/16/2020
问题
如果两条直线平行,那么这两条平行线被 第三条直线所截而成的同位角有什么数量关系?
演示……
平行线的性质1(公理)
结论 两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
性质2
E
C
P
D
2
A
1B
F
E’ E
C64 8
两直线平行
方法4:如果两条直线都与第三条直线平行, 那么这两条直线也互相平行.
问题2:
根据同位角相等可以判定两直线平 行,反过来如果两直线平行同位角之间 有什么关系呢?
内错角,同旁内角之间又有什么关 系呢?
动手画一画!
(1)用直尺和三角学科尺网 画出两条平行线 a∥b,再画一条截线c,使之与直线 a,b相交,并标出所形成的八角.
9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/162020/12/16Wednesday, December 16, 2020
10、人的志向通常和他们的能力成正比例。2020/12/162020/12/162020/12/1612/16/2020 7:33:49 AM 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2020/12/162020/12/162020/12/16Dec-2016-Dec-20 12、越是无能的人,越喜欢挑剔别人的错儿。2020/12/162020/12/162020/12/16Wednesday, December 16, 2020 13、志不立,天下无可成之事。2020/12/162020/12/162020/12/162020/12/1612/16/2020
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
且只有一条直线与这条直线平行 . 画直线 a 的平行线,怎么画?能画几条?
一落
zxxkw
C
二靠 B 三移
a
平行公理的推论:如果两条直线都 你能过点C画直线 a 的平行线吗? 与第三条直线平行,那么这两条直 线也互相平行.
Zx、xk
四画
应用交流
1.下列说法正确的是(A ) A .同一平面内,两条直线的位置关系 只有相交、平行两种 B .同一平面内,不相交的两条线段互 相平行 C .不相交的两条直线是平行线 D .同一平面内,不相交的两条射线互 相平行 2.在同一平面内,三条直线的交点个数 可能是 0、1、2、3 .
a b
· ·
D
AB ∥ CD
a∥b
找一找
日常生活中还有哪些实 物给我们以平行线的形象?
黑 板
zxxkw
同一平面内的两条直 线的位置关系有几种? 相交或平行
在转动木条 a 的过程中, 有几个位置能使 a 与 b 平行?
c
a
a a a a
b
结论:只有一个位置能使 a 与 b 平行 .
已知直线 和直线 a 外的点 B ,过点 B a 平行公理:经过直线外一点,有
应用交流
3.读下列语句,并画出图形:
(1)点P是直线AB外一点,直线CD经过
点P,且与直线AB平行;
(2)直线AB,CD是相交直线,点P是直
线AB、CD外一点,直线EF经过点P且与
直线AB平行,与直线CD相交于点E.
反思小结
1.本节课主要学习了平行线的定义、 表示方法和平行公理及其推论.
zxxkw
点D是△ABC中AB边上的 中点.①过点D作BC的平行线,交AC 于E;②量一量AE、CE的长度,它们 相等吗?③量一量DE、BC的长度, 它们有何关系?
2.在学习的过程中用到了类比的 思想方法.
3.要注意总结平行线的画法.
布置作业
1.在同一平面内,直线l与两条平行线a、b的位置关系 是( ) A.l一定与a、b都平行 B.l可能与a平行,与b相交 C.l一定与a、b都相交 D.l与a、b都平行或都相交 2.在同一平面内,若两条直线没有公共点,则两条直 线_________;若有一个公共点,则两条直线 ___________.
第五章 相交线与平行线
5.2 平行线及其判定
zxxkw 学科网
5.2.1 平行线
学.科.网
c
学科网
a
a a a a
b
平行线的定义:
c 平行线有什么特征?
1.在同一平面内 2.不相交
zxxk
在同一平面内,不相交的 两条直线叫做平行线.
a
b
平行线的表示:
我们通常用符号“//”表示平行.
A
· ·
C
B
一落
zxxkw
C
二靠 B 三移
a
平行公理的推论:如果两条直线都 你能过点C画直线 a 的平行线吗? 与第三条直线平行,那么这两条直 线也互相平行.
Zx、xk
四画
应用交流
1.下列说法正确的是(A ) A .同一平面内,两条直线的位置关系 只有相交、平行两种 B .同一平面内,不相交的两条线段互 相平行 C .不相交的两条直线是平行线 D .同一平面内,不相交的两条射线互 相平行 2.在同一平面内,三条直线的交点个数 可能是 0、1、2、3 .
a b
· ·
D
AB ∥ CD
a∥b
找一找
日常生活中还有哪些实 物给我们以平行线的形象?
黑 板
zxxkw
同一平面内的两条直 线的位置关系有几种? 相交或平行
在转动木条 a 的过程中, 有几个位置能使 a 与 b 平行?
c
a
a a a a
b
结论:只有一个位置能使 a 与 b 平行 .
已知直线 和直线 a 外的点 B ,过点 B a 平行公理:经过直线外一点,有
应用交流
3.读下列语句,并画出图形:
(1)点P是直线AB外一点,直线CD经过
点P,且与直线AB平行;
(2)直线AB,CD是相交直线,点P是直
线AB、CD外一点,直线EF经过点P且与
直线AB平行,与直线CD相交于点E.
反思小结
1.本节课主要学习了平行线的定义、 表示方法和平行公理及其推论.
zxxkw
点D是△ABC中AB边上的 中点.①过点D作BC的平行线,交AC 于E;②量一量AE、CE的长度,它们 相等吗?③量一量DE、BC的长度, 它们有何关系?
2.在学习的过程中用到了类比的 思想方法.
3.要注意总结平行线的画法.
布置作业
1.在同一平面内,直线l与两条平行线a、b的位置关系 是( ) A.l一定与a、b都平行 B.l可能与a平行,与b相交 C.l一定与a、b都相交 D.l与a、b都平行或都相交 2.在同一平面内,若两条直线没有公共点,则两条直 线_________;若有一个公共点,则两条直线 ___________.
第五章 相交线与平行线
5.2 平行线及其判定
zxxkw 学科网
5.2.1 平行线
学.科.网
c
学科网
a
a a a a
b
平行线的定义:
c 平行线有什么特征?
1.在同一平面内 2.不相交
zxxk
在同一平面内,不相交的 两条直线叫做平行线.
a
b
平行线的表示:
我们通常用符号“//”表示平行.
A
· ·
C
B
