必修一第一章章末复习
必修一第一章复习资料

必修一第一章复习资料1-1化学实验基本方法一.化学实验安全包括哪些内容?1.遵守实验室规则。
2.了解安全措施。
(实验室安全规则、药品安全存放、实验安全操作、实验事故处理)“六防”:防爆炸、防暴沸、防失火、防中毒、防倒吸、防污染练习:1、下列试剂保存方法中正确的是()A.浓硫酸难挥发,可以敞口放置B.浓硝酸见光易分解,可以放在棕色广口瓶中C.酒精应密封存放,并远离火源D.白磷不易挥发,不需密封存放2、二、混合物的分离和提纯分离和提纯“四原则”和“三必须”“四原则”不增、不减、易分离、易复原*课本实验实例:粗盐的提纯⑴步骤:溶解、过滤、蒸发⑵玻璃棒在三个步骤中的作用分别为:________________、________________________、_____________________________。
⑶粗盐中可溶性杂质的去除:①Na2CO3除去CaCl2;②BaCl2除去硫酸盐;③NaOH除去MgCl2;④盐酸除去过量Na2CO3和NaOH杂质;⑤过滤,调节溶液酸碱性。
⑷试剂填加顺序_____________ __________________________*几种常见离子的检验SO42-CI—【练习】1.下列实验基本操作(或实验注意事项)中,主要是出于实验安全考虑的是()A.实验剩余的药品不能放回原试剂瓶B.可燃性气体的验纯C.气体实验装置在实验前进行气密性检查D.滴管不能交叉使用2.下列实验仪器不宜直接用来加热的是()A.试管B.坩埚C.蒸发皿D.烧杯3.在盛放浓硫酸的试剂瓶的标签上应印有下列警示标记中的()4.现有三组溶液:①汽油和氯化钠溶液②39%的乙醇溶液⑧氯化钠和单质溴的水溶液,分离以上各混合液的正确方法依次是()A.分液、萃取、蒸馏 B.萃取、蒸馏、分液 C.分液、蒸馏、萃取D.蒸馏、萃取、分液5.能够用来鉴别BaCl2、NaCl 、Na2CO3三种物质的试剂是()A.AgNO3溶液B.稀硫酸C.稀盐酸D.稀硝酸6.某溶液中含有较大量的Cl-、CO32-、OH-等3种阴离子,如果只取一次该溶液就能够分别将3种阴离子依次检验出来,下列实验操作顺序正确的是()①滴加Mg(NO3)2溶液;②过滤;③滴加AgNO3溶液;④滴加Ba(NO3)2溶液A.①②④②③B.④②①②③C.①②③②④D.④②③②①7.下列实验操作均要用玻璃棒,其中玻璃棒作用相同的是()①过滤②蒸发③溶解④向容量瓶转移液体A.①和②B.①和③C.③和④D.①和④8.下列图示的实验正确的是().A.除去粗盐中的不溶物 B 除去CO中的CO2 C除去CO中的CO2 D苯萃取碘水中的I2,分出水层后的操作①从A.D的混合物中分离提纯D,需进行的操作是:a:溶解;b:__ ____(填操作名称,下同);c:____ __.②上述a、b、c操作过程中均需用到的一种玻璃仪器为______;从B的水溶液中分离出B的操作名称为______.(2)从C与水的混合物中分离提纯C所需的玻璃仪器有____ __.1-2化学计量在实验中的应用一、物质的量(n )物质的量(n)是表示含有_____________粒子的_____________。
高一化学必修一第一章物质及其变化章末综合复习测试卷含答案解析(29)

高一化学必修一第一章物质及其变化章末综合复习测试卷含答案解析(1)在小烧杯中加入20mL__________,加热到沸腾后,向其中滴入几滴饱和FeCl3溶液,继续煮沸至溶液呈红褐色,即制得Fe(OH)3胶体。
(2)取另一小烧杯也加入20mL蒸馏水后,向烧杯中加入1mLFeCl3溶液,振荡均匀后,将此烧杯(编号甲)与盛有上述操作(1)中制取的物质的烧杯(编号乙)一起放置暗处:分别用激光笔照射两烧杯中的液体,可以看到_____(填“甲”或“乙” )烧杯中的液体会产生_________效应。
这个实验可以用区别溶液和胶体。
【答案】蒸馏水乙丁达尔【分析】(1)将饱和三氯化铁溶液滴人沸蒸馏水中来制取氢氧化铁胶体;(2)胶体具有丁达尔效应。
【详解】(1)胶体的制备过程中必须用蒸馏水,其它水中含有的盐,能使胶体聚沉;(2)只有胶体具有丁达尔效应,可以用来区别溶液和胶体。
82.双线桥法标出电子转移并填空。
3Cu+8HNO3=3Cu(NO3)2+2NO+4H2O,______。
被还原的物质为______,还原剂为______。
【答案】HNO3Cu【分析】反应3Cu+8HNO3(稀)=3Cu(NO3)2+2NO↑+4H2O中,N元素的化合价从+5价降低到+2价,Cu元素的化合价从0价升高到+2价,结合氧化还原反应的规律分析解答。
【详解】(1) 反应3Cu+8HNO3(稀)=3Cu(NO3)2+2NO↑+4H2O中,N元素的化合价从+5价降低到+2价,Cu元素的化合价从0价升高到+2价,转移电子数为6mol,电子转移的方向和数目用双线桥法表示为;化合价降低的元素是氮元素,被还原,因此被还原的物质是硝酸;化合价升高的是铜元素,被氧化,Cu为还原剂,故答案为:;HNO3;Cu。
83.在酸性条件下,KBrO3能将KI氧化成I2或KIO3,KBrO3本身被还原成Br-或Br2,KIO3能将KI氧化成I2或将Br-氧化成Br2(KIO3本身均被还原为I2)。
高一化学必修一第一章物质及其变化章末综合复习测试卷含答案解析(39)

高一化学必修一第一章物质及其变化章末综合复习测试卷含答案解析有一包白色固体粉末,可能含有K2SO4、Na2CO3、NH4Cl、BaCl2、CuSO4中的一种或几种,按以下步骤进行实验:①取少量固体粉末加到足量水中,得到无色溶液;②取①中溶液少量继续往其中加入足量稀硫酸,有气泡产生;③继续向②中的溶液加Ba(NO3)2溶液,有白色沉淀生成;④取①中溶液少量,加入NaOH溶液并加热,产生刺激性气味的气体,并用湿润的红色石蕊试纸检验气体,试纸变蓝。
根据以上事实判断:(1)肯定存在的是_______。
(2)肯定不存在的是_______。
(3)不能确定是否存在的是_______。
请简述证明该物质是否存在的实验方案(实验方法、现象、结论)_______。
(4)写出上述实验④中产生刺激性气味反应的离子方程式:_______。
【答案】Na2CO3、NH4Cl BaCl2、CuSO4K2SO4用洁净铂丝蘸取少量①中溶液进行灼烧,透过蓝色钴玻璃观察到火焰呈紫色,说明有K2SO4,否则没有NH+4+OH-ΔNH3↑+H2O【详解】(1)①取少量固体粉末加到足量水中,得到无色溶液,说明不含有CuSO4,由于Na2CO3、BaCl2会发生反应形成沉淀,所以二者不能大量共存;根据实验②可知固体中有Na2 CO3 ,则原固体中不含有BaCl2溶液;④取①中溶液少量,加入NaOH溶液并加热,产生刺激性气味的气体,并用湿润的红色石蕊试纸检验气体,试纸变蓝。
则产生的气体是NH3,原物质中含有NH4Cl;根据以上事实判断:(1)肯定存在的是Na2CO3、NH4Cl;(2)肯定不存在的是BaCl2、CuSO4;(3)不能确定是否存在的是K2SO4;证明该物质是否存在的实验方案是用洁净铂丝蘸取少量①中溶液进行灼烧,透过蓝色钴玻璃观察到火焰呈紫色,说明有K2SO4,否则不含有K2SO4。
也可以用检验SO42-的方法检验,方法是取①中溶液加盐酸酸化,(无沉淀生成),再继续加入BaCl2溶液,有白色沉淀生成,说明原样品中有K2SO4,否则没有K2SO4。
数学必修一第一章 章末复习提升

章末复习提升
13
例2
已知集合A={x|0≤x≤2},B={x|a≤x≤a+3}.
(1)若(∁RA)∪B=R,求a的取值范围.
解 (1)A={x|0≤x≤2},
∴∁RA={x|x<0,或x>2}.
∵(∁RA)∪B=R.
a≤0, ∴ ∴-1≤a≤0. a+3≥2,
章末复习提升
14
(2)是否存在a使(∁RA)∪B=R且A∩B=∅? 解 由(1)知(∁RA)∪B=R时, -1≤a≤0,而a+3∈[2,3], ∴A⊆B,这与A∩B=∅矛盾.即这样的a不存在.
集合中的元素不能有重复 , 含求有参数的集合元素时利 用互异性来进行讨论,从而达到确定集合的目的.
章末复习提升
4
2.空集的特殊性和特殊作用
空集是一个特殊的集合,它不含任何元素,是任何集合的子集,
是任何非空集合的真子集 ,在解决集合之间关系问题时 ,它往
往被忽视而导致解题出现失误.
3.集合的运算
集合的运算有交集(∩)、并集(∪)、补集(∁)三种.在集合运算 过程中应力求做到“三化”;
章末复习提升
15
跟踪演练2 (1)设集合M={-1,0,1},N={x|x2≤x},则M∩N等于( B )
A.{0}
B.{0,1}
C.{-1,1}
D.{-1,0,1}
解析 由x2≤x,解得0≤x≤1,∴M∩N={0,1}.
(2) 已 知 集 合 U = {2,3,6,8},A = {2,3},B = {2,6,8}, 则 ( ∁ UA)∩B = {6,8} ________. 解析 先计算∁UA,再计算(∁UA)∩B.
∵U={2,3,6,8},A={2,3},∴∁UA={6,8}.
高中数学必修一第一章 章末复习课课件

反思与感悟
解析答案
跟踪训练2 某粮店销售大米,若一次购买大米不超过50 kg时,单价 为m元;若一次购买大米超过50 kg时,其超出部分按原价的90%计算, 某人一次购买了x kg大米,其费用为y元,则y与x的函数关系式y=
mx,0≤x≤50, __0_.9_m__x_+__5_m_,__x_>__5_0___. 解析 当0≤x≤50时,y=mx; 当x>50时,y=50m+(x-50)×90%·m=0.9mx+5m.
2.数学四大思想:函数与方程、转化与化归、分类讨论、数形结合思想, 本章用到以下思想方法: (1)函数与方程思想体现在函数解析式部分,将实际问题中的条件转化为 数学模型,再通过研究函数性质解决诸如最大、最优等问题. (2)转化与化归主要体现在集合部分符号语言、文字语言、图形语言的转 化,函数中求定义域大多转化成解不等式,求值域大多可以化归为求二 次函数等基本函数的值域. (3)分类讨论主要体现在集合中对空集和区间端点的讨论,函数中主要是 欲去绝对值而正负不定,含参数的函数式的各种性质的探讨. (4)数形结合主要体现在用数轴求并交补集,借助函数图象研究函数性质.
(5)数学交流体现在使用了大量的文字、符号、图形语言,用以刻画集 合的关系运算及函数表示和性质,往往还需要在三种语言间灵活转换, 有意识地培养灵活选择语言,清晰直观而又严谨地表达自己的想法, 听懂别人的想法,从而进行交流与合作. (6)运用信息技术的技能主要表现在应用网络资源拓展知识,了解数学 史及发展前沿,以及应用计算机强大的计算能力描点作图探究新知等 方面.
所以 Q P.
解析答案
1 234
3.设函数 f(x)=x22x+,2x,>2x,≤2, 则 f(-4)=____1_8___,若 f(x0)=8,则 x0 =__-___6_或___4_____. 解析 f(-4)=(-4)2+2=18,由 f(x0)=8,得xx020≤ +22, =8, 或x20x>0=2,8, 得 x0=- 6,或 x0=4.
必修一第一章章末总结

一、速度、加速度与物体的运动例1 关于速度、速度变化、加速度,以下说法正确的选项是( )A .加速度方向与规定正方向相反,物体速度一定减小B .加速度不为零,物体速度一定增加C .加速度不断减小,速度一定不断减小D .速度变化越快,加速度越大[总结提升]二、匀变速直线运动的常用解题方法例2 一物体以某一速度冲上一光滑斜面,前4 s 的位移为1.6 m ,随后4 s 的位移为零,那么物体的加速度多大?[方法总结]1.公式法匀变速直线运动的常用公式有:v t =v 0+at x =v 0t +12at 2 v 2t -v 20=2ax 使用时应注意它们都是矢量,一般以v 0方向为正方向,其余物理量与正方向相同的为正,与正方向相反的为负.2.平均速度法(1)v =x t,此式为平均速度的定义式,适用于任何直线运动. (2)v =v t 2=12(v 0+v ),只适用于匀变速直线运动. 3.比例法对于初速度为零的匀加速直线运动或末速度为零的匀减速直线运动,可利用初速度为零的匀加速直线运动的推论,用比例法解题.4.逆向思维法把运动过程的“末态〞作为“初态〞的反向研究问题的方法.例如,末速度为零的匀减速直线运动可以看做反向的初速度为零的匀加速直线运动.5.图像法应用v-t图像,可把复杂的物理问题转化为较为简单的数学问题解决,尤其是用图像定性分析,可防止繁杂的计算,快速求解.三、运动图像的意义及应用例3如图1所示是在同一直线上运动的甲、乙两物体的x—t图像,以下说法中正确的选项是()图1A.甲启动的时刻比乙早t1 B.两车都运动起来后甲的速度大C.当t=t2时,两物体相距最远D.当t=t3时,两物体相距x1[总结提升]通过“看〞寻找规律及解题的突破口.为方便记忆,这里总结为六看:一看“轴〞,二看“线〞,三看“斜率〞,四看“面〞,五看“截距〞,六看“特殊值〞.(1)“轴〞:纵、横轴所表示的物理量,特别要注意纵轴是位移x,还是速度v.(2)“线〞:从线反映运动性质,如x-t图像为倾斜直线表示匀速运动,v-t图像为倾斜直线表示匀变速运动.(3)“斜率〞:“斜率〞往往代表一个物理量.x-t图像斜率表示速度;v-t图像斜率表示加速度.(4)“面〞即“面积〞:主要看纵、横轴物理量的乘积有无意义.如x-t图像面积无意义,v-t图像与t轴所围面积表示位移.(5)“截距〞:初始条件、初始位置x0或初速度v0.(6)“特殊值〞:主要看图线交点.如x-t图像交点表示相遇,v-t图像交点表示速度相等.四、研究匀变速直线运动实验中数据处理的方法例4如图2所示为“探究小车速度随时间变化的规律〞实验中打点计时器打出的纸带,相邻两计数点间还有两个点未画出(电源频率为50 Hz).由图知纸带上D点的瞬时速度v D=________;加速度a =________;E 点的瞬时速度v E =__________.(小数点后均保存两位小数)图2[方法提升]研究匀变速直线运动实验,主要研究两个方向:(1)利用纸带求某点的瞬时速度:v n =x n +x n +12T. (2)利用纸带求物体的加速度,方法有以下两个:①逐差法如图3所示,纸带上有六个连续相等的时间T 内的位移x 1、x 2、x 3、x 4、x 5、x 6.图3由Δx =aT 2可得:x 4-x 1=(x 4-x 3)+(x 3-x 2)+(x 2-x 1)=3aT 2x 5-x 2=(x 5-x 4)+(x 4-x 3)+(x 3-x 2)=3aT 2x 6-x 3=(x 6-x 5)+(x 5-x 4)+(x 4-x 3)=3aT 2所以a =(x 6-x 3)+(x 5-x 2)+(x 4-x 1)9T 2=(x 6+x 5+x 4)-(x 3+x 2+x 1)9T 2由此可以看出,各段位移都用上了,有效地减小了偶然误差,所以利用纸带计算加速度时,可采用逐差法.②v -t 图像法先求出各时刻的瞬时速度v 1、v 2、v 3、…、v n ,然后作v -t 图像,求出该v -t 图线的斜率k ,那么k =a .这种方法的优点是可以舍掉一些偶然误差较大的测量值,因此求得值的偶然误差较小.。
高中物理人教版必修一:第一章章末复习课

高中物理人教版必修一:第一章章末复习课【知识体系】[答案填写]①有质量②大小、外形③作为参考④空中⑤位置变化⑥点⑦线段⑧位置变化⑨初位置⑩运动轨迹⑪位移⑫v=ΔxΔt⑬物体运动⑭运动快慢⑮瞬时速度⑯变化量⑰a=ΔvΔt⑱m/s2⑲速度变化快慢⑳相反○21相反○22方向○23方向○24速度○25性质○26方向○27大小○28交流○29计时主题1三组概念的比拟1.位移和路程的比拟.(1)速度是位移对时间的变化率,速度的变化量是指速度改动的多少,减速度是速度对时间的变化率.(2)速度的变化量表示速度变化的大小和变化的方向,减速度的大小由速度变化的大小与发作这一变化所用时间的多少共同决议,减速度的方向与速度变化的方向相反.(3)减速度与速度以及速度的变化量没有直接的关系,减速度很大时速度可以很大、很小,也可以为零;速度的变化量可以很大也可以很小.(4)物体做减速还是减速运动取决于减速度方向与速度方向的关系,与减速度的大小有关.【典例1】阿祥学习有关直线运动的物理概念后,找到小明、小强、小梅和小雪离开校园展开了〝讨论与交流〞活动,他们提出了以下几个观念,你以为正确的选项是()A.速度变化得越多,减速度就越大B.速度变化得越快,减速度就越大C .运植物体在某段时间内位移为零,那么其运动速率也一定为零D .物体在某一时辰的瞬时速度就是瞬时速率解析:减速度的定义是:物体速度变化量与时间的比值.减速度的方向与速度变化量的方向是分歧的,只需有减速度,物体的速度一定发作变化,速度变化得多不表示减速度大,所以A 错,B 对.如物体做圆周运动,当其回到动身点后其位移为零,但在其运动时间内速率和速度都不为零,那么C 错.瞬时速率和瞬时速度大小相等,但速度是矢量有方向,速率是标量有方向,那么D 错.答案:B针对训练1.如下图,小球从高出空中h =15 m 的位置,在t =0时辰竖直向上抛出,经1 s 小球上升到距抛出点5 m 最高处,之后就末尾竖直回落,经0.5 s 刚好经过距最高点1.25 m 处位置,再经过1.5 s 抵达空中.求:(1)前1.5 s 内平均速度是多少.(2)全进程的平均速率是多少.(结果仅保管一位小数)解析:(1)由题图可知:前1.5 s 小球的位移为:x =H -h ′=5 m -1.25 m =3.75 m所以前1.5 s 内平均速度v =x t =3.751.5m/s =2.5 m/s (2)由题图可知:全进程小球的路程为s =5 m +5 m +15 m =25 m全进程的平均速率为v ′=s t =253m/s ≈8.3 m/s 答案:(1)2.5 m/s (2)8.3 m/s主题2 v-t 图象的了解及运用1.图象的含义.v-t图象描画的是物体速度随时间的变化规律.如下图,甲图中a、b 物体的速度随时间平均变化,乙图中c、d物体的速度随时间变化不平均.2.图象的运用.(1)判别物体的运动性质.甲图中物体a做匀减速直线运动,b做匀减速直线运动,它们的运动方向相反.(2)依据图象的纵坐标确定物体在某时辰速度的大小和方向.纵坐标的相对值为瞬时速度的大小,正负号表示瞬时速度的方向.(3)依据图象中图线的斜率确定物体运动减速度的大小和方向.假定v-t 图象为曲线,那么曲线上某点的切线的斜率表示此时减速度的大小和方向,如图乙中物体d的运动图象所示.[典例❷]在如下图的v-t图象中,A、B两质点同时从同一点沿一条直线末尾运动,运动规律用A、B两图线表示,以下表达正确的选项是() A.t=1 s时,B质点运动方向发作改动B.t=2 s前后,B质点运动方向和减速度方向均发作改动C.A、B同时从运动动身,朝相反的方向运动D.在t=4 s时,A、B速度相等解析:质点的运动方向发作改动,即速度的正、负发作变化,显然在t =2 s时,B质点改动运动方向,但减速度方向并没发作变化,故A、B错误.由题图可知,t=0时,A、B两质点v=0,尔后2 s内v A>0,v B<0,那么C正确.t=4 s时,两者速度相等,故D正确.答案:CD针对训练2.甲、乙两物体同时、同地动身,它们的〝速度—时间〞图象如下图.那么以下说法正确的选项是()A.甲、乙两图线的交点表示两物体相遇B.甲、乙两物体做曲线运动C.甲物体先减速后减速,乙物体不时做减速运动D.甲、乙两物体都做减速运动,甲物体的减速度不时减小,乙物体的减速度不时增大解析:v-t图象只表示两个方向即正方向和负方向,所以只能表示物体做直线运动的状况,B错;图象上的交点表示该时辰两物体速度相等,A 错;由图象知甲、乙两物体速度都添加,故C错;v-t图象中图线上每一点的切线的斜率为该点的瞬时减速度,甲物体的曲线上每点的切线的斜率不时减小,所以甲物体做减速度减小的减速运动,D对.答案:D统揽考情本章知识基础概念较多,在高考中简直不会独自命题,都是和其他章节统筹考察.本章的重点同时也是热点,就是减速度、速度概念的了解和v-t图象的了解运用.假定有考试题,基本上都是选择题,分值6分以内.真题例析(2021·浙江卷)如下图,气垫导轨上滑块经过光电门时,其上的遮光条将光遮住,电子计时器可自动记载遮光时间Δt.测得遮光条的宽度为Δx,用ΔxΔt近似代表滑块经过光电门时的瞬时速度.为使ΔxΔt更接近瞬时速度,正确的措施是()A.换用宽度更窄的遮光条B.提高测量遮光条宽度的准确度C.使滑块的释放点更接近光电门D .增大气垫导轨与水平面的夹角 解析:Δx Δt表示的是Δt 时间内的平均速度,遮光条的宽度Δx 越窄,那么记载遮光时间Δt 越小,Δx Δt越接近滑块经过光电门时的瞬时速度,选项A 正确.答案:A针对训练一质点沿直线Ox 方向做变速直线运动,它分开O 点的距离x 随时间变化的关系为x =6t -2t 3 (m),它的速度v 随时间t 变化的关系为v =6-6t 2 (m/s),那么该质点在t =2 s 时的瞬时速度、t =0到t =2 s 间的平均速度、平均速率区分为( )A .-18 m/s 、-2 m/s 、2 m/sB .-18 m/s 、-2 m/s ,6 m/sC .-2 m/s 、- 2 m/s 、-18 m/sD .-18 m/s 、6 m/s ,6 m/s解析:该质点在t =2 s 时的瞬时速度v 2=6-6×22=-18 (m/s);t =0时,x 0=0 m ,t =2 s 时,x 2=-4 m ,故2 s 内的位移为Δx =x 2-x 0=-4 m ,2 s 内的平均速度v =Δx t2=-2 m/s ;当v =0时,由v =6-6t 2 (m/s),得t =1 s ,此时x 1=4 m ,在前1 s 内质点经过的路程s 1=x 1=4 m ,在后1 s 内经过的路程为s 2=|x 2-x 1|=8 m ,那么平均速率v 速率=s 1+s 2t 2=6 m/s ,选B. 答案:B1.物体沿直线A 到B ,前一半位移以速度v 1匀速运动,接着的后一半位移以速度v 2匀速运动,那么全程的平均速度是( )A.v 1+v 22B.v 1v 2C.v 1v 2v 1+v 2D.2〔v 1v 2〕〔v 1+v 2〕解析:由速度公式的变形公式求出物体前半程的运动时间与后半程的运动时间,然后由平均速度公式求出全程的平均速度.设一半位移为x ,那么关于前一半位移所用时间为:t 1=x v 1,关于后一半位移所用时间为t 2=x v 2,故全程平均速度为v =x +x t 1+t 2=2x x v 1+x v 2=2〔v 1v 2〕〔v 1+v 2〕,D 正确. 答案:D2.A 、B 两物体在同不时线上做变速直线运动,它们的速度—时间图象如下图,那么( )A .A 、B 两物体的运动方向一定相反B .0~6 s 内A 比B 物体运动得快C .t =4 s 时,A 、B 两物体的速度相反D .A 物体的减速度比B 物体的减速度大解析:两物体的速度都为正值,所以运动方向相反,A 错误;0~4 s ,B 的速度大,B 运动得快,4~6 s ,A 的速度大,A 运动得快,B 错误;t =4 s 时,A 、B 两物体的速度都为5 m/s ,所以两物体的速度相反,C 正确;从图象上可以看出,B 的斜率比A 的斜率大,所以B 的减速度大于A 的减速度,D 错误.答案:C3.一物体做直线运动,其减速度随时间变化的a -t 图象如右图所示.以下v-t 图象中,能正确描画此物体运动的是( )解析:解答此题的打破口是T ~2T 时间内的减速度与0~T 2时间内的减速度大小相等,方向相反,而对应时间内v-t 图象斜率的相对值相等,斜率正负不同,从而扫除选项A 、B 、C ,故正确答案为D.答案:D4.(多项选择)某日,亚丁湾索马里海域六艘海盗快艇试图接近中国海军护航编队维护的商船,中国特战队员发射爆震弹成功将其驱离.假设其中一艘海盗快艇在海面上运动的v -t 图象如下图,设运动进程中海盗快艇所受阻力不变.那么以下说法正确的选项是( )A .海盗快艇在0~66 s 内从运动动身做减速度增大的减速直线运动B .海盗快艇在96 s 末末尾调头逃离C .海盗快艇在66 s 末离商船最近D .海盗快艇在96 s ~116 s 的减速度为a =-0.75 m/s 2解析:在0~66 s 内图象的斜率越来越小,减速度越来越小,故海盗快艇做减速度减小的减速运动,A 错误;海盗快艇在96 s 末,速度由正变负,即改动运动的方向,末尾掉头逃跑,此时海盗快艇离商船最近,B 正确,C错误;依据a =Δv Δt 可得,a =Δv Δt =-15-0116-96m/s 2=-0.75 m/s 2,所以D 正确.答案:BD5.如下图,装置甲中挂有小桶的细线绕过定滑轮,固定在小车上;装置乙中橡皮筋的一端固定在导轨的左端,另一端系在小车上.一同窗用装置甲和乙区分停止实验,经正确操作取得两条纸带①和②,纸带上的a 、b 、c ……均为打点计时器打出的点.(1)任选一条纸带读出b 、c 两点间的距离为________.(2)任选一条纸带求出c 、e 两点间的平均速度大小为________,纸带①和②上c 、e 两点间的平均速度v -①______v -②(填〝大于〞〝等于〞或〝小于〞).解析:(1)由于刻度尺的最小刻度是1 mm ,读数要估读到0.1 mm.选①纸带读出b 、c 两点间的距离为6.00 cm -3.90 cm =2.10 cm.选②纸带读出b 、c 两点间的距离为6.50 cm -4.10 cm =2.40 cm.(2)选①纸带读出c 、e 两点间的距离为4.50 cm ,相对应的平均速度v -①=4.50 cm 0.04 s≈1.13 m/s.选②纸带读出c 、e 两点间的距离为5.00 cm ,相对应的平均速度v -②=5.00 cm 0.04 s=1.25 m/s.所以平均速度v -①小于v -②. 答案:(1)2.10 cm(或2.40 cm)(2)1.13 m/s(或1.25 m/s) 小于。
高中生物必修一(新教材) 章末总结(共6章)

答案 (1)Mg2+是构成叶绿素的成分。 (2)培养液浓度过高,细胞会失水皱缩,影响其正常生长。 (3)缺少与缺 K 培养液形成的二次对照实验。在缺 K 的培养液中加入 K, 看幼苗生长发育恢复情况。 (4)适当补施钾肥等。
答准 概念 1 细胞是生物体结构与生命活动的基本单位 1.3 细胞各部分结构既分工又合作,共同执行细胞的各项生命活动 1.3.1 概述细胞都由质膜包裹,质膜将细胞与其生活环境分开,能控 制物质进出,并参与细胞间的信息交流。 1.3.2 阐明细胞内具有多个相对独立的结构,担负着物质运输、合成 与分解、能量转换和信息传递等生命活动。 1.3.3 阐明遗传信息主要储存在细胞核中。 1.3.4 举例说明细胞各部分结构之间相互联系、协调一致,共同执行 细胞的各项生命活动。
请回答下列问题: (1)上述图片中的细胞,放大倍数由小到大依次是________(填序号)。 (2)实际上,图①中的细胞不是完整的细胞结构,只剩下“轮廓”,这是 细胞的哪个结构?具有什么功能? (3)图②、图③所示的细胞中能够清楚看到的结构有哪些?根据你学过的 生物学知识,能否判断出这两种细胞是植物细胞还是动物细胞?说明判断的 依据。 (4)施莱登和施旺基于对不同细胞的观察,提出了________,其内容能否 为“生物起源于共同的祖先”这一观点提供支持?请说明理由。
新课程理念导读 学科核心素养 1.通过观察不同的生物体,说明有些生物体只有一个细胞,而有些由很 多细胞构成。能够运用细胞学说解释细胞形态和功能的多样性,认识细胞生 命系统。 2.基于细胞学说建立的科学史资料,运用归纳与概括等科学思维方法, 说明人类在探索细胞的过程中运用的逻辑方法,阐述对科学发展过程和科学 本质的理解。
第一章 章末总结
知识构建
课程内容标准 概念 1 细胞是生物体结构与生命活动的基本单位 1.1 各种细胞具有相似的基本结构,但在形态与功能上有所差异 1.1.1 说明有些生物体只有一个细胞,而有的由很多细胞构成,这些 细胞形态和功能多样,但都具有相似的基本结构。 1.1.2 描述原核细胞与真核细胞的最大区别是原核细胞没有由核膜包 被的细胞核。
高一化学必修一第一章物质及其变化章末综合复习测试卷含答案解析(101)

高一化学必修一第一章物质及其变化章末综合复习测试卷含答案解析111.下列依据实验目的所设计的实验操作中,正确的是A.A B.B C.C D.D【答案】B【详解】A.氯化钠和碳酸钠都能溶于水,现象相同不能鉴别,A错误;B.Na2CO3不和氢氧化钠的反应、Na2CO3和氢氧化钙溶液反应生成白色沉淀碳酸钙,可以鉴别,B正确;C.氧化钙、碳酸钙均能和盐酸反应,因此稀盐酸不适宜除去CaO 中的CaCO3,C错误;D.二氧化碳能和氢氧化钠溶液反应被吸收、一氧化碳不吸收。
因此,NaOH溶液不适宜除去CO2中的CO,D错误;答案选B。
2.下列叙述中,不正确的是A.CaCO3、Ca(HCO3)2、Cu2(OH)2CO3都属于碳酸盐B.盐酸、纯碱、醋酸钠和生石灰分别属于酸、碱、盐和氧化物C.蓝矾(CuSO4·5H2O)和干冰属于化合物,铁矿石属于混合物D.通过化学反应,可由Ba(OH)2一步转化生成NaOH【答案】B【详解】A.CaCO3是碳酸的正盐、Ca(HCO3)2是碳酸的酸式盐、Cu2(OH)2CO3是碳酸的碱式盐,三者都属于碳酸盐,故A正确,不符合题意;B.纯碱属于盐类,故B错误,符合题意;C.蓝矾是含结晶水的化合物,干冰是固态CO2,二者都属于化合物,铁矿石含有多种物质是混合物,故C正确,不符合题意;D.Ba(OH)2+Na2CO3═BaCO3↓+2NaOH,对溶液过滤可得NaOH 溶液,能够一步制取,故D正确,不符合题意;故答案选B。
3.下列液体中,属于分散系,但不会出现丁达尔效应的是①淀粉溶液②乙醇③硅酸胶体④火碱溶液⑤Fe(OH)3胶体⑥肥皂水A.②④B.①③C.⑤⑥D.④【分析】只有胶体才有丁达尔效应,而常见的胶体有鸡蛋清溶液、淀粉溶液、血液、牛奶、豆浆、肥皂水、河水、大气、土壤等,据此分析。
【详解】分散系是将一种物质分散到另一种物质中所得到的体系,故为混合物,分为溶液、胶体和浊液,只有胶体才有丁达尔效应。
高一化学必修一第一章物质及其变化章末综合复习测试卷含答案解析(150)

高一化学必修一第一章物质及其变化章末综合复习测试卷含答案解析通常将__________称作标准状况,标准状况下的气体摩尔体积约为_____________,若标准状况下CO 和CO 2混合气体的密度为1.607g/L ,则混合气体的平均相对分子质量为_____________;其中CO 的质量分数为__________________;若将0.1mol 该混合气体通入含0.1molCa (OH )2的澄清石灰水中,写出反应的离子方程式:________________________。
【答案】0℃101kPa 22.4L/mol 36 38.89% CO 2+Ca 2++2OH -=CaCO 3↓+H 2O【详解】试题分析:通常将0℃称作标准状况,标准状况下的气体摩尔体积约为22.4L/mol ;若标准状况下CO 和CO 2混合气体的密度为1.607g/L ,则混合气体的平均相对分子质量为1.607×22.4=36;则284436x y x y +=+,解答x :y =1:1,所以CO 的质量分数为2872×100%=38.89%;0.1mol该混合气体中CO 2是0.05mol ,通入含0.1molCa (OH )2的澄清石灰水中,氢氧化钙过量,反应的离子方程式为CO 2+Ca 2++2OH - = CaCO 3↓+H 2O 。
考点:考查物质的量的有关计算92.A 、B 、C 、D 、E 五瓶透明溶液,分别是HCl 、BaCl 2、NaHSO 4、Na 2CO 3和AgNO 3中的一种。
已知:①A 与B 反应有气体生成 ②B 与C 反应有沉淀生成 ③C 与D 反应有沉淀生成 ④D 与E 反应有沉淀生成⑤A与E反应有气体生成⑥在②和③的反应中生成的沉淀是同一种物质请填空:⑴在⑴和⑴的反应中,生成的沉淀物质的化学式(分子式)是__________。
⑴A是________,B是_______,C是_______,D是_______,E是________。
高一化学必修一第一章物质及其变化章末综合复习测试卷含答案解析(198)

高一化学必修一第一章物质及其变化章末综合复习测试卷含答案解析25℃、101kPa 下:℃2Na(s)+1/2O2(g)=Na2O(s) ℃H=-414kJ·mol-1℃2Na(s)+ O2(g)=Na2O2(s) ℃H=-511kJ·mol-1下列说法正确的是A.℃和℃产物的阴阳离子个数比不相等B.℃和℃生成等物质的量的产物,转移电子数不同C.常温下Na与足量O2反应生成Na2O,随温度升高生成Na2O 的速率逐渐加快D.25℃、101kPa 下:Na2O2(s)+2 Na(s)= 2Na2O(s)℃H =-317kJ/mol【答案】D【详解】A、氧化钠中阴阳离子个数比为1:2,过氧化钠的电子式为:,阴阳离子个数比为1:2,故错误;B、生成等物质的量的产物,即消耗的Na的物质的量相等,转移电子物质的量相等,故错误;C、温度升高,钠和氧气反应生成过氧化钠,故错误;D、①×2-②得2Na(s)+Na2O2(s)=2Na2O(s) △H=(-414×2+511)kJ·mol-1=-317kJ·mol-1,故正确。
答案选D。
72.已知℃N 2+3H 2催化剂高温高压2NH 3;℃3Cl 2+8NH 3=N 2+6NH 4Cl ,判断下列物质的还原性从强到弱的顺序是A .NH 4Cl>NH 3>H 2B .H 2>NH 3>NH 4ClC .NH 3>NH 4Cl>H 2D .H 2>NH 4Cl>NH 3 【答案】B【详解】在反应△中还原性为:H 2(还原剂)>NH 3(还原产物),在反应△中还原性:NH 3(还原剂)>NH 4Cl (还原产物),即还原性:H 2>NH 3>NH 4Cl ,故选B 。
73.科学家首次用CO 2高效合成乙酸,其反应路径如图所示,下列叙述不正确的是A .HI 、LiOH 、CH 3I 、CH 3Rh*I 、CH 3COORh*I 为反应的中间产物B .第4步反应的氧化剂是CH 3COORh*IC .反应过程中碳元素的化合价始终不变D .催化循环的总反应为CH 3OH+CO 2+H 2*Li Rh 、CH 3COOH+H 2O【答案】C【详解】A .根据步骤反应知,HI 、LiOH 、CH 3I 、CH 3Rh*I 、CH 3COORh*I 都是先生成后反应掉的物质,则都是反应的中间产物,故A 正确;B .第4步反应为:CH 3COORh*I+H 2= CH 3COOH+Rh*+HI ,氧化剂是CH 3COORh*I ,故B 正确;C .碳元素在CH 3OH 中显-2价,在CH 3COOH 中显0价,碳元素的化合价根成键原子的非金属性有关,故C 错误;D .根据图示,CH 3OH 、CO 2、H 2反应生成CH 3COOH 和H 2O ,化学方程式为:CH 3OH+CO 2+H 2*Li Rh 、CH 3COOH+H 2O ,故D 正确;故选:C 。
苏教版高中数学必修一 第一章 章末知识整合(附答案)

章末知识整合一、元素与集合的关系[例1] 设集合B =⎩⎨⎧⎭⎬⎫x ∈N ⎪⎪⎪62+x ∈N . (1)试判断1和2与集合B 的关系;(2)用列举法表示集合B .解:(1)当x =1时,62+1=2∈N ,所以1∈B . 当x =2时,62+2=32∉N ,2∉B . (2)令x =0,1,2,3,4,代入62+x ,检验62+x∈N 是否成立,可得B ={0,1,4}. 规律方法1.判断所给元素a 是否属于给定集合时,若a 在集合内,用符号“∈”;若a 不在集合内,用符号“∉”.2.当所给的集合是常见数集时,要注意符号的书写规范.[即时演练] 1.已知集合A ={x |ax 2-3x +2=0}.(1)若A =∅,求实数a 的取值范围;(2)若A 中只有一个元素,求实数a 的值,并把这个元素写出来. 解:(1)A =∅,则方程ax 2-3x +2=0无实根,即Δ=9-8a <0,所以a >98. 所以a 的取值范围是⎩⎨⎧⎭⎬⎫a ⎪⎪⎪a >98. (2)因为A 中只有一个元素,所以①a =0时,A =⎩⎨⎧⎭⎬⎫23满足要求. ②a ≠0时,则方程ax 2-3x +2=0有两个相等的实根.故Δ=9-8a =0,所以a =98,此时A =⎩⎨⎧⎭⎬⎫43满足要求. 综上可知:a =0或a =98. 二、集合与集合的关系[例2] A ={x |x <-1或x >2},B ={x |4x +p <0},当B ⊆A 时,求实数p 的取值范围.分析:首先求出含字母的不等式,其次利用数轴解决.解:由已知解得,B =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <-p 4. 又因为因为A ={x |x <-1或x >2},且B ⊆A ,利用数轴所以-p 4≤-1.所以p≥4,故实数p的取值范围为{p|p≥4}.规律方法1.在解决两个数集的包含关系问题时,避免出错的一个有效手段是合理运用数轴帮助分析与求解.2.注意端点值的取舍,这是同学易忽视失误的地方.[即时演练] 2.设集合P={(x,y)|x+y<4,x,y∈N*},则集合P 的非空子集的个数是()A.2 B.3 C.7 D.8解析:当x=1时,y<3,又y∈N*,因此y=1或y=2;当x=2时,y<2,又y∈N*,因此y=1;当x=3时,y<1,又y∈N*,因此这样的y不存在;当x≥4时,y<0,也不满足y∈N*.综上所述,集合P中的元素有(1,1),(1,2),(2,1),所以P 的非空子集的个数是23-1=7.故选C.答案:C三、集合的运算[例3]已知集合A={x|x-2>3},B={x|2x-3>3x-a},求A∪B,分析:先确定集合A,B,然后讨论a的范围对结果的影响.解:A={x|x-2>3}={x|x>5},B={x|2x-3>3x-a}={x|x<a-3}.借助数轴表示如图所示.(1)当a-3≤5,即a≤8时,A∪B={x|x<a-3或x>5}.(2)当a-3>5,即a>8时,A∪B={x|x>5}∪{x|x<a-3}={x|x∈R}=R.综上可知,当a≤8时,A∪B={x|x<a-3或x>5};当a>8时,A∪B=R.规律方法解集合问题关键是读懂集合语言,明确意义,用相关的代数或几何知识进行解决.[即时演练] 3.设集合A={x||x|<4},B={x|x2-4x+3>0},则集合∁A(A∩B)=________.解析:因为A={x|-4<x<4},B={x|x<1或x>3},所以A∩B={x|-4<x<1或3<x<4}.所以∁A(A∩B)={x|1≤x≤3}.答案:{x|1≤x≤3}四、利用集合的运算求参数[例4]设集合M={x|-2<x<5},N={x|2-t<x<2t+1,t∈R},若M∪N=M,求实数t的取值范围.分析:由M∪N=M,知N⊆M.根据子集的意义,建立关于t的不等式关系来求解.解:由M∪N=M得N⊆M,故当N =∅,即2t +1≤2-t ,t ≤13时,M ∪N =M 成立. 当N ≠∅时,由数轴图可得⎩⎪⎨⎪⎧2-t <2t +1,2t +1≤5,2-t ≥-2,解得13<t ≤2.综上可知,所求实数t 的取值范围是{t |t ≤2}.规律方法1.用数轴表示法辅助理解,若右端点小于等于左端点,则不等式无解, N =∅.2.列不等式组的依据是左端点小于右端点,即2t +1在5的左侧(相等时也符合题意),2-t 在-2的右侧(相等时也符合题意).[即时演练] 4.集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1}.(1)若A ∩B =B ,求实数m 的取值范围;(2)若A ∩B =∅,求实数m 的取值范围.解:(1)A ∩B =B ⇔B ⊆A ,当m +1>2m -1,即m <2时,B =∅,满足B ⊆A ;当m +1≤2m -1时,要使B ⊆A .则⎩⎪⎨⎪⎧m +1≥-2,2m -1≤5,m +1≤2m -1⇒2≤m ≤3.综上,m 的取值范围为{m |m ≤3}.(2)当m +1>2m -1,即m <2时,B =∅,满足A ∩B =∅; 当B ≠∅时,要使A ∩B =∅,则必须⎩⎨⎧m +1≤2m -1,m +1>5或⎩⎨⎧m +1≤2m -1,2m -1<-2⇒m >4. 综上,m 的取值范围是{m |m <2或m >4}.五、集合的实际应用[例5] 某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有________人.分析:每名同学至多参加两个小组―→画出相应的Venn图―→根据全班有36名同学列等式―→得答案解析:设参加数学、物理、化学小组的人数构成的集合分别为A,B,C,同时参加数学和化学小组的有x人,由题意可得如图所示的Venn图.由全班共36名同学可得(26-6-x)+6+(15-10)+4+(13-4-x)+x=36,解得x=8,故同时参加数学和化学小组的有8人.答案:8规律方法解决有关集合的实际应用题时,首先要将文字语言转化为集合语言,然后结合集合的交、并、补运算来处理.此外,由于Venn图简明、直观,因此很多集合问题往往借助Venn图来分析.[即时演练] 5.某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜欢,则喜爱篮球运动但不喜爱乒乓球运动的人数为________.解析:设A,B分别表示喜爱篮球运动、乒乓球运动的人数构成的集合,集合U表示全班人数构成的集合.设同时喜爱乒乓球和篮球运动的有x人.依题意,画出如图所示的Venn图.根据Venn图,得8+x+(15-x)+(10-x)=30.解得x=3.故喜爱篮球运动但不喜爱乒乓球运动的人数为15-3=12.答案:12。
必修一第一章复习

设A S ,由S中不属于A的所有元素组成的集合称为S的 子集A的 补集 (complement set ), 记为 s A (读作" A在S ary 中的补集" ), 即 s A x | x S , 且 x A.
A 可用右图中的阴影部分 来表示. 对于例2, 我们有B s A, A s B
A B可用右图中的阴影部分来表示 .
U
A B
一般地,由所有属于集合 A 或者属于集合B的元素构成的 集合, 称为 A与B的并集( int er section set ) , 记作 A B (读 作" A" 并B " ), 即 A B x | x A, 或x B .sS NhomakorabeaA
如果集合S包含我们所要研究的各个集合, 这时S可以看
全集 universal, 全集通常记作U . 做一个
一般地,由所有属于集合A且属于集合B的元素构成的集 合, 称为A与B的交集( int er section set ) , 记作 A B (读作 " A"交B " ), 即 A B x | x A, 且x B .
A B 可用右图中的阴影 部分来表示, 显然有
U
A B
集合的两种表示方法: 列举法 集合的表示方法还有Venn图示法
描述法
如果集合A的每一个元素都是集合B的元素 (若a A, 则a B) , 则称集合A是集合B的 子
集 subset , 记为 A B 或 B A , 读作" 集
合A包含于集合B "或 " 集合B包含集合A".
如果 A B, 并且 A B, 这时集合 A 称为B 的 真子集 proper set , 记为 A B 或 B A , 读作" A真包含于B " 或 " B真包含A" , 如a a, b.
高中生物 选择性必修一 第1章 章末复习提纲(教师版含答案)

第1章人体的内环境与稳态第1节细胞生活的环境1.多细胞动物的细胞都必须通过内环境与外界进行物质交换,对吗?答案:不对,虽然绝大部分细胞没有直接与外界环境接触,需通过内环境与外界环境进行物质交换。
但还有少部分细胞可以直接与外界环境进行物质交换,例如肺泡细胞、小肠粘膜等。
2.皮肤细胞与外界环境直接接触,可以与外界环境直接进行物质交换,对吗?答案:不对,皮肤需要的氧气与营养物质还是需从内环境中获得。
当受伤后错误的用不透气的膜包裹伤口,不会影响受伤部位细胞的氧气来源。
3.草履虫等单细胞生物生活的内环境是外界,对吗?答案:不对,草履虫没有内环境。
没有内环境的生物:单细胞(如草履虫)直接从水中获取养分和氧气;简单的多细胞生物(如水螅)也直接与外界进行物质交换;4.体液的组成示意图默写;分类标准是什么?体液细胞内液(2/3)存在细胞内细胞外液(1/3)组织液=组织间隙液(血浆通过毛细血管壁渗出到细胞间而形成,可回流)血浆=血液-血细胞淋巴=组织液经毛细淋巴管壁进入毛细淋巴管,最终汇入血浆5.组织液+血浆+淋巴液>细胞内液,对吗?答案:不对,不能因3项就判断多于1项。
组织液+血浆+淋巴液是细胞外液的一部分,细胞外液占体液的1/3,小于细胞内液的2/3。
6.辨析:体液细胞内液细胞外液细胞液答案:体液是体内以水为基础的液体。
体液又包括细胞内液和细胞外液。
细胞内液主要包括细胞质基质,细胞外液主要包括组织液(组织间隙液的简称)、血浆(血液的液体部分)和淋巴、脑脊液等。
细胞内液并不是细胞液,细胞液是指液泡内的液体,成熟的植物细胞有。
7.细胞外液只包含组织液、血浆、淋巴液对吗?答案:不对,主要包括,除此之外脑脊液、房水等也属于细胞外液。
8.细胞之外的液体统称为细胞外液,对吗?答案:不对,消化液、尿液等也是细胞之外,但它们不属于细胞外液。
9.辨析:血液血浆血清答案:血浆经抗凝处理后获得的不含细胞成分的液体,内含纤维蛋白原。
血清:指血液凝固后渗出的淡黄色透明液体或指纤维蛋白原已被除去的血浆。
人教课标版高中数学必修一《第一章》章末复习教案(1)-新版
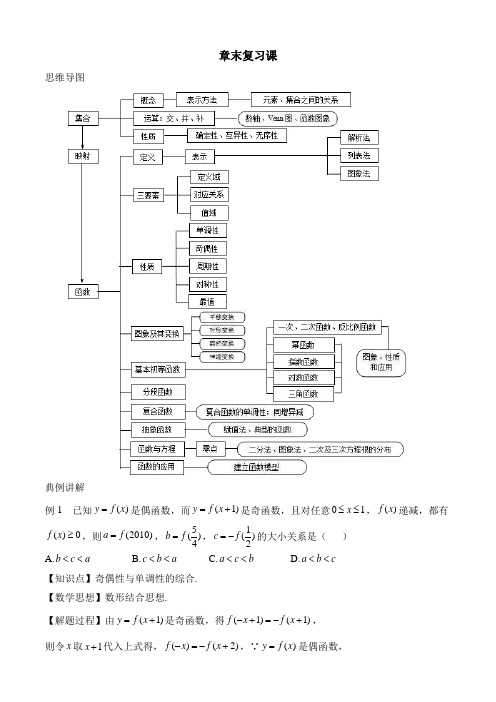
章末复习课思维导图典例讲解例1 已知)(x f y =是偶函数,而)1(+=x f y 是奇函数,且对任意10≤≤x ,)(x f 递减,都有0)(≥x f ,则)2010(f a =,)45(f b =,)21(f c -=的大小关系是( ) A.a c b << B.a b c << C.b c a << D.c b a <<【知识点】奇偶性与单调性的综合.【数学思想】数形结合思想.【解题过程】由)1(+=x f y 是奇函数,得)1()1(+-=+-x f x f ,则令x 取1+x 代入上式得,)2()(+-=-x f x f ,∵)(x f y =是偶函数,∴)()()2(x f x f x f -=--=+,则)()2()4(x f x f x f =+-=+,∴)(x f 是以4为周期的一个周期函数,则)0()2()25024()2010(f f f f a -==+⨯==,)43()243()45(f f f b -=+-==, )21(-=f c , ∵43210<<,且对任意0≤x ≤1,f (x )递减, ∴)43()21()0(f f f >>,则)43()21()0(f f f -<-<-,即b c a <<,故选:C . 【思路点拨】由函数奇偶性可推断出=f (x )是周期为4的函数,由这些性质将三数化简为自变量在0≤x≤1的函数值,再利用单调性比较大小.【答案】C例2 已知集合A ={x |3<x <7},B ={x |2<x <10},C ={x |5-a <x <a }.(1)求B A C R; (2)若⊆C )(B A ,求a 的取值范围.【知识点】交集,并集,补集及运算.【数学思想】【解题过程】(1)∵A ={x |3<x <7},B={x |2<x <10},∴A C R ={x|x ≤3或x ≥7},∴(∁R A )∩B={x |2<x ≤3或7≤x <10} .(2)由(1)知,A ∪B ={x |2<x <10},当C ≠∅时,要使C ⊆)(B A ,须55210a a a a -⎧⎪-⎨⎪⎩<≥,≤,解得25<a ≤3; 当C =∅时,5-a ≥a ,解得a ≤25. ∴a 的取值范围是a ≤3. 【思路点拨】根据交集与并集和补集的定义即可求出; 根据分两种情况讨论,解不等式组即可.【答案】(1){x |2<x ≤3或7≤x <10};(2)a ≤25.例3 已知函数f (x )=11+-x x e e . (1)判断f (x )的奇偶性;(2)判断f (x )在R 上的单调性,并用定义证明;(3)是否存在实数t ,使不等式f (x -t )+f (22t x -)≥0对一切x ∈[1,2]恒成立?若存在,求出t 的取值范围;若不存在,请说明理由.【知识点】函数奇偶性的判断,函数单调性的判断与证明.【数学思想】数形结合思想,转化思想.【解题过程】(1)函数的定义域为(-∞,+∞),则f (-x )=11+---x x e e =x x e e +-11=11+--x x e e =-f (x ),则f (x )为奇函数. (2)f (x )=11+-x x e e =121+-+x x e e =112+-x e ,则f (x )在R 上的单调性递增, 证明:设x 1<x 2,则f (1x )-f (2x )=121212+-+x x e e =)1)(1()(22121++-x x x x e e e e ,∵x 1<x 2, ∴21x x e e <, ∴021<-x x e e ,即f (1x )-f (2x )<0,即f (1x )<f (2x ),即函数为增函数.(3)若存在实数t ,使不等式f (x -t )+f (22t x -)≥0对一切x ∈[1,2]恒成立,则f (22t x -)≥-f (x -t )=f (t -x ). 即22t x -≥t -x .即2x +x ≥2t +t 恒成立,设y =2x +x =)21(+x -14,∵x ∈[1,2],∴y ∈[2,6], 即2t +t ≤2,即2t +t -2≤0. 解得-2≤t ≤1,即存在实数t ,当-2≤t ≤1时使不等式f (x -t )+f (22t x -)≥0对一切x ∈[1,2]恒成立.【思路点拨】根据就行单调性定义证明即可,结合函数奇偶性和单调性的性质将不等式进行转化,利用参数分离法进行求解.【答案】 (1)奇函数;(2)略;(3)存在实数t ,当-2≤t ≤1时即可.章末检测题一、选择题1.设全集U ={1,2,3,4,5,6,7,8,9},若A C U ={1,3,5,7,9},则集合A =( )A.{2,6,8}B.{2,4,6,8}C.{0,2,4,6,8}D.{0,2,6,8}【知识点】补集及其运算.【解题过程】全集U ={1,2,3,4,5,6,7,8,9},当A C U ={1,3,5,7,9}时,集合A ={2,4,6,8}.故选:B .【思路点拨】根据补集的定义写出集合A 即可.【答案】B2.函数的定义域为( ) A.B.C.D. 【知识点】函数的定义域及其求法. 【解题过程】,,故选C .【思路点拨】算术平方根被开方数非负,分母不为0.【答案】C3.设函数,若,则实数a =( )A.-4或-2B.-4或2C.-2或4D.-2或2【知识点】函数的对应法则【数学思想】分类讨论思想.【解题过程】 由 或得或a =2,故选B.【思路点拨】分类讨论,解不等式求交集即可.【答案】B4.某部队官兵从驻地出发前往目的地训练,按计划先乘车行进一段路程,再步行至目的地,下图中横轴表示出发后的时间,纵轴表示官兵离目的地的距离,则较符合的图象是( ) A.B. C. D.【知识点】函数的图象与图象变化.【数学思想】数形结合思想.【解题过程】随着时间的增加,距目的地的距离在减小,即函数图象应为减函数,排除A 、C ,曲线的斜率反映行进的速度,斜率的绝对值越大速度越大,步行后速度变小,故排除B. 故选D.【思路点拨】借助函数单调性,考虑图像倾斜程度的实际意义.【答案】D5.满足条件},,{c b a M ⊆⊂∅≠的集合M 的个数为( ) A.6B.7C.8D.9【知识点】子集与真子集.【解题过程】:{a,b,c }的非空子集有7个,故选B .【思路点拨】确定集合M 的可能元素,结合子集的定义进行计算.【答案】B6、二次函数中,若,则其图象必经过点( ) A.B.C.D. 【知识点】函数的图象,函数的定义. 【解题过程】因为,所以,即函数图象过点,故选C .【思路点拨】结合题目所给二次函数信息,代入特殊值进行构造.【答案】C7.已知函数y =f (x )在定义域(-1,1)上是减函数,且f (2a -1)<f (1-a ),则实数a 的取值范围是( ) A.),32(+∞ B.)1,32( C.)2,0(D.(0,+∞)【知识点】函数的图象与函数单调性【数学思想】数形结合思想,转化的思想【解题过程】函数y =f (x )在定义域(-1,1)上是减函数,则有:1121->->a , 111<-<-a ,a a ->-112三者同时成立,故选B.【思路点拨】利用函数y =f (x )在定义域(-1,1)上是减函数,将f (2a -1)<f (1-a )转化为:2a -1>1-a 求解.【答案】B8.已知函数5()2b f x ax x=+-,若(2019)2f =,则(2019)f -=( ) A.6B.-6C.0D.无法确定【知识点】函数奇偶性的性质.【解题过程】由题知f(x)+2是奇函数, 则2)2019(2)2019(--=+-f f ⇒6)2019(-=-f 故选B.【思路点拨】根据函数解析式,分析奇偶性求值.【答案】B9.设函数满足,则的表达式为( ) A.B.C.D. 【知识点】函数解析式的求解及常用方法. 【解题过程】设,则,所以,所以,故选C .【思路点拨】换元法求出函数解析式.【答案】C10.若函数在区间上单调递增,则实数a 的取值范围为( ) A.B.C.D. 【知识点】函数的单调性的性质.【解题过程】,在区间上单调递增,则,,故选A . 【思路点拨】分离常数,结合反比例函数的单调性解不等式.【答案】A11.定义在R 上的函数f (x )满足)4()(x f x f -=,)2,(,21-∞∈∀x x )(21x x ≠,有[]0)()()(2121<--x x x f x f 成立,若)25(f a =,)2(f b =,)3(-=f c ,则( ) A.b<a<cB.c<a<bC.b<c<aD.c<b<a 【知识点】函数的单调性的性质,函数的图象.【解题过程】因为)4()(x f x f -=,所以对称轴为x =2,由题意可知f(x)在x <2时,f (x )递减, 则f (x )在x >2时,f (x )递增,f (-3)=f (4-7)=f (7),因为7252<<,所以b<a<c.故选A. 【思路点拨】根据信息,得到函数的单调性和对称性,将各个函数值对应在对称轴同侧即可.【答案】A12.已知平面直角坐标系内两点),(),,(222111y x A y x A 间距离12||A A =P 是二次函数图像)(122R k k x x y ∈+++=上的动点,M 是该二次函数图像的顶点,定点错误!未找到引用源。
高中物理必修一 第一章 运动的描述 章末复习课件(共37张PPT)

0
12
34
56
-1
7 t/s
-2
-3
远离时间轴为加速,靠近时
间轴为减速
思考:v-t图象如图所示,代表物体做什么运动?
速 度
4 v/ms-1
物体的初速度
图
3
象
2
1
0
12
34
56
-1
7 t/s
-2 A:匀速直线运动的v-t图象
-3
思考:求出物体的加速度
思考:v-t图象如图所示,代表物体做什么运动?
速 度 图
2、下列描述中指时间的是 A.会议准备在什么时间召开 B.会议准备召开多长时间 C.主席在什么时间作报告 D.主席的报告预计多长时间
3. 小球从距地面5m高处落下,碰到地面反 弹 后,在距地面2m高处被接住,则小球从高处落下 到被接住这一过程中通过的路程和位移的大小
分别是( D ) A、7m、7m B、5m、2m C、5m、3m D、7m、3m
(1)都是描述质点运动的空间特征
联系 (2)都是过程量
(3)一般来说,位移的大小不大于相应的路程,只有质点做单向直线
运动时,位移的大小才等于路程
对
3.平均速度和瞬时速度
比
平均速度
瞬时速度
易
物体的位移与发生这一位移所用 定
物体在某一时刻或经过某一位置
混
时间的比值.与一段时间或位移 义
对应
的速度,与某一时刻或某一位置 对应
a
v t
(3)物理意义:加速度是表示速度变化快慢的
物理量。 (4)单位:米每二次方秒,符号是m/s2 (m·s-2)
对
1.时刻和时间间隔
比
易
高中数学必修一第一章复习

必修一 第一章 集合与函数概念(1)一、集合有关概念 1. 集合的含义2. 集合的中元素的三个特性:元素的确定性,互异性,无序性3.集合的表示: ※注意:常用数集及其记法:非负整数集(即自然数集):N 正整数集:N*或 N+ 整数集Z 有理数集Q 实数集R 1) 列举法:{a,b,c ……}2) 描述法:将集合中的元素的公共属性描述出来,写在大括号内表示集合的方法。
{x ∈R| x-3>2} ,{x| x-3>2}3) 语言描述法:例:{不是直角三角形的三角形} 4) Venn 图: 二、集合间的基本关系 1.“包含”关系—子集注意:B A ⊆有两种可能(1)A 是B 的一部分,;(2)A 与B 是同一集合。
2.“相等”关系:A=B (5≥5,且5≤5,则5=5)即:① 任何一个集合是它本身的子集。
A ⊆A ②真子集 3. 不含任何元素的集合叫做空集,记为Φ规定: 空集是任何集合的子集, 空集是任何非空集合的真子集。
有n 个元素的集合,含有2n 个子集,2n-1个真子集1.集合{a ,b ,c }的真子集共有 个2.若集合M={y|y=x 2-2x+1,x ∈R},N={x|x ≥0},则M 与N 的关系是 .3.设集合A=}{12x x <<,B=}{x x a <,若A ⊆B ,则a 的取值范围是4.已知集合A={x| x 2+2x-8=0}, B={x| x 2-5x+6=0}, C={x| x 2-mx+m 2-19=0}, 若B ∩C ≠Φ,A ∩C=Φ,求m 典型例题:例1 参数取值及范围 例2 空集优先原则及分类讨论二、函数的有关概念1.函数的概念:注意:1.定义域:能使函数式有意义的实数x 的集合称为函数的定义域。
求函数的定义域时列不等式组的主要依据是:(1)分式的分母不等于零;(2)偶次方根的被开方数不小于零; (3)对数式的真数必须大于零;(4)指数、对数式的底必须大于零且不等于1. (5)指数为零底不可以等于零,(6)实际问题中的函数的定义域还要保证实际问题有意义.相同函数的判断方法:①表达式相同(与表示自变量和函数值的字母无关);②定义域一致 (两点必须同时具备) 2.值域 : 先考虑其定义域 3. 函数图象知识归纳(1) 画法:描点法;图象变换法常用变换方法有三种:(1)平移变换(2)伸缩变换 (2)对称变换 4.分段函数(1)在定义域的不同部分上有不同的解析表达式的函数。
高一物理必修1第一章复习

例.一物体由A点出发沿直线运动到20m处的B点花了5秒钟,然后又以4m/s的速度回到A点。求整个过程的平均速度、平均速率?
两种打点计时器的比较
类型比较
电磁打点计时器
电火花打点计时器
所用 电源
4~6 V低压交流
220 V交流
打点 方式
振针打点
电火花打点
时间 间隔
每隔0.02 s打一次点
每隔0.02 s打一次点
5πR/2
√2R
正东南方向
例.下列说法正确的是( ) A.位移是矢量,位移的方向即为质点运动的方向 B.路程是标量,其值是位移的大小 C.质点做单向直线运动时,路程等于位移的大小 D.位移的值不会比路程大
CD
例.气球升到离地面80 m的高空时,从上掉下一物体,物体又上升了10 m高后开始下落。若取向上为正方向,则物体从离开气球开始到落到地面的位移大小为________m,通过的路程为________m
D
结论:选择不同的参考系观察同一物体的运动,其结果可能不同。但是对于同一个参考系物体的运动的是确定的。
时刻与时间
1.时刻(某一瞬间): 时间轴上的点表示时刻 2.时间间隔(一段时间): 时间轴上的一条线段表示时间间隔
0 1 2 3 4 5 6
t/s
A B C D E F G
判断质点的条件:
地球的自转运动。
绕太阳运转的地球。
做花样滑冰的运动员。
转动的门。
运动员发出的弧旋乒乓球。
沿曲线飞行的空中的乒乓球。
上海开往吉首的火车。
火车通过站牌所用的时间。
研究汽车行驶的速度。
研究汽车轮上的一点运动情况的车轮。
下列哪些情况下的物体可以看成是质点:
必修第一册第一章章末复习

必修第一册第一章章末复习试卷一、单项选择题:在每小题给出的选项中,有且只有一项符合题目要求1、已知全集{110}U x Z x =∈≤<,,A U B U ⊆⊆,且(){}{}()(){}1,8,2,3,6,9U U U C A B A B C A C B ⋂=⋂=⋂=,那么集合A =( )A .{4,5,7}B .{2,4,5,7}C .{2,4,6,9}D .{2,3,4,8}2.集合U 、M 、N 、P 如图所示,则图中阴影部分所表示的集合是( )A .()M N P ⋂⋃B .()U MC N P ⋂⋃ C .()U M C N P ⋃⋂D .()U M C N P ⋃⋃3.若集合{}220,A x ax x a a R =++=∈∣,若集合A 有且仅有两个子集,则a 的值是( )A .1B .-1C .0,1D .-1,0,14.已知集合A 、B 均为非空集合,定义{*|()A B x x A B =∈⋃且}()x A B ∉⋂,若{}1,0,1,2,3A =-,{}2|1,B x x t t A ==+∈,则集合*A B 的子集共( )A .64个B .63个C .32个D .31个5.已知集合{}2560A xx x =-+=∣,{}06,B x x x N =<<∈∣,则满足A C B ⊆⊆的集合C 的个数为( )A .4B .8C .7D .166. 集合{|2}M x x k k Z ==∈,,{|21}N x x k k Z ==+∈,,{|41}O x x k k Z ==+∈,,则对任意的m M n N o O ∈∈∈,,,有下列四种说法:①m n O ⋅∈;②m n O +∈;③o m N -∈;④o n O ⋅∈,其中一定正确的个数为( )A .1个B .2个C .3个D .4个7.用()n A 表示非空集合A 中元素个数,定义()()()()()()()(),*,n A n B n A n B A B n B n A n A n B ⎧-≥⎪=⎨-<⎪⎩当当,若{}220,A x x ax a R =--=∈,{}222,B x x mx m R =++=∈,且*2A B =,则实数m 的取值范围是( )A .22m ≤-或22m ≥B .22m <-或22m >C .4m ≤-或4m ≥D .4m <-或4m >8.设非空数集M 同时满足条件:①M 中不含元素-1,0,1;②若a ∈M ,则11a a +-∈M .则下列结论正确的是( )A .集合M 中至多有2个元素;B .集合M 中至多有3个元素C .集合M 中有且仅有4个元素;D .集合M 中至少有4个元素二、多项选择题:在每小题给出的选项中,有多项符合题目要求.9. 下列说法正确的是( )A.“A B =B ”是“B =∅”的必要不充分条件B .“x =3”的一个必要不充分条件是“2230x x --=”C.“m 是实数”的充分不必要条件是“m 是有理数”D .“|x|=1”是“x =1”的充分条件10.设集合{}22,2,1A a a a =-+-,若4A ∈,则a 的值可以为( ).A .-3B .-2C .-1D .211.在整数集Z 中,被5除所得余数为k 的所有整数组成一个“类”,记为[]k ,即[]{}5|Z k n k n =+∈,0k =,1,2,3,4,给出如下四个结论,其中,正确结论的是( )A .[]20211∈B .[]33-∈C .若整数a ,b 属于同一“类”,则[]0a b -∈D .若[]0a b -∈,则整数a ,b 属于同一“类”12. 取整函数:[x ]表示不超过x 的最大整数,如[1.2]=1,[2]=2,[-1.2]=-2.取整函数在现实生活中有着广泛的应用,诸如停车收费、出租车收费等都是按照“取整函数”进行计费的..以下关于“取整函数”的性质是真命题的有 ( )A.,[2]2[]x R x x ∀∈=B.,[2]2[]x R x x ∃∈=C .,,[][],1x y R x y x y ∀∈=-<则 D.1,[]+[][2]2x R x x x ∀∈+=三、填空题:13.命题“N x ∃∈,221x x ≥+”的否定为_____________________14、若α是β的必要非充分条件,β是γ的充要条件,γ是δ的必要非充分条件,则δ是α的_______条件.15.集合2{|290}A x x x a =-+-=,2{|410,0}B x ax x a =-+=≠,若集合A ,B 中至少有一个非空集合,则实数a 的取值范围为___________________ 16.集合{}66,11,23,10,911,1,18,100,0,πM =---有10个元素,设M 的所有非空子集为i M ()1,2,,1023i =每一个i M 中所有元素乘积为i m ()1,2,,1023i =,则1231023m m m m ++++=___________.四、解答题:17.已知集合{1,1,A x x a a =-≤≤>-∣且}a R ∈,{21,}B y y x x A ==-∈∣,{}2,C z z x x A ==∈∣.是否存在a ,使C B ⊆?若存在,求出a 的取值范围;若不存在,说明理由.18.已知集合1{|015},{|2}2A x ax B x x =<-≤=-<≤(1)若1a =,求AB (2)若AB =∅,求实数a 的取值范围19.已知函数21122,2y x y x m ==--,若1{|13}x x x ∀∈-≤≤,2{|02}x x x ∃∈≤≤,使得12y y ≤,求实数m 的取值范围20.在①A B B ⋃=;②“x A ∈”是 “x B ∈”的充分不必要条件;③A B =∅这三个条件中任选一个,补充到本题第(2)问的横线处,求解下列问题:已知集合{}11A x a x a =-≤≤+,{}2230B x x x =--≤ (1)当2a =时,求A B ;(2)若______,求实数a 的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
章末复习课1.正确理解集合的概念必须掌握构成集合的两个必要条件:研究对象是具体的,其属性是确定的.2.在判定给定对象能否构成集合时,特别要注意它的“确定性”;在表示一个集合时,要特别注意它的“互异性”.3.在集合运算中必须注意组成集合的元素应具备的性质.4.若集合中的元素是用坐标形式给出的,要注意满足条件的点构成的图形是什么,用数形结合法解之.5.若集合中含有参数,须对参数进行分类讨论,讨论时要不重不漏.6.相同函数的判定方法:(1)定义域相同;(2)对应关系相同(两点必须同时具备).7.函数的定义域的求法:使函数有意义的自变量的不等关系式,求解即可求得函数的定义域.常涉及的依据为:(1)分母不为0;(2)偶次根式中被开方数不小于0;(3)零指数幂的底数不等于零;(4)实际问题要考虑实际意义等.8.函数值域的求法:(1)配方法(二次或四次);(2)数形结合;(3)函数的单调性法等.9.单调性的判断步骤:(1)设x1,x2是所研究区间内的任意两个自变量,且x1<x2;(2)作差比较或作商比较判定f(x1)与f(x2)的大小;(3)得出结论.10.奇偶性的判断步骤:(1)先求函数的定义域,若定义域关于坐标原点对称,继续以下步骤,若不对称,则为非奇非偶函数;(2)计算f(-x)的值;(3)判断f(-x)与±f(x)中的哪一个相等;(4)下结论.一、集合中空集的特殊性及特殊作用空集是一个特殊的集合,它不含任何元素,是任何集合的子集,是任何非空集合的真子集,在解决集合之间的关系问题时,它往往易被忽视而引起解题失误.例1 已知A ={x |x 2-3x +2=0},B ={x |ax -2=0},且A ∪B =A ,求实数a 组成的集合C分析 B ⊆A 包括两种情况,即B =∅和B ≠∅. 解 (1)当B ≠∅时,由x 2-3x +2=0,得x =1或2. 当x =1时,a =2;当x =2时,a =1.(2)当B =∅时,即当a =0时,B =∅,符合题设,故实数a 组成的集合C ={0,1,2}.二、集合中元素的互异性集合中元素的互异性是集合中元素的重要属性,这一属性在解题过程中常被忽略而造成错误.因此在涉及集合中元素的有关性质时,要有问题被解决后作检验这一意识. 例2 已知集合A ={a ,a +b ,a +2b },B ={a ,ac ,ac 2},若A =B ,求c 的值.分析 要求c 的值,根据集合相等,转化为解方程问题来解决.集合A ,B 有公共元素a ,所以使余下的元素相等即可.解 若a +b =ac ,且a +2b =ac 2, 消去b ,则有a -2ac +ac 2=0.显然a ≠0,否则集合B 的元素均为0,与集合中元素的互异性矛盾,所以1-2c +c 2=0,得c =1,这时B ={a ,a ,a },仍与集合中元素的互异性矛盾; 若a +b =ac 2,且a +2b =ac ,消去b ,则有2ac 2-ac -a =0,又a ≠0, 则有2c 2-c -1=0,即(c -1)(2c +1)=0,又c ≠1,所以c =-12.三、函数的性质及应用研究函数往往从定义域、值域、单调性、奇偶性、对称性及解析式等方面入手,通过对函数性质的应用使问题得以解决.例3 已知函数f (x )=mx 2+23x +n是奇函数,且f (2)=53.(1)求实数m 和n 的值;(2)判断函数f (x )在(-∞,0)上的单调性,并加以证明.解 (1)∵f (x )是奇函数,∴f (-x )=-f (x ), ∴mx 2+2-3x +n =-mx 2+23x +n =mx 2+2-3x -n . 比较得n =-n ,n =0.又f (2)=53,∴4m +26=53,解得m =2.即实数m 和n 的值分别是2和0.(2)函数f (x )在(-∞,-1]上为增函数,在(-1,0)上为减函数. 证明如下:由(1)可知f (x )=2x 2+23x =2x 3+23x .设x 1<x 2<0,则f (x 1)-f (x 2)=23(x 1-x 2)⎝⎛⎭⎫1-1x 1x 2 =23(x 1-x 2)·x 1x 2-1x 1x 2. 当x 1<x 2≤-1时,x 1-x 2<0,x 1x 2>0,x 1x 2-1>0, ∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), ∴函数f (x )在(-∞,-1]上为增函数; 当-1<x 1<x 2<0时,x 1-x 2<0,x 1x 2>0,x 1x 2-1<0, ∴f (x 1)-f (x 2)>0,即f (x 1)>f (x 2), ∴函数f (x )在(-1,0)上为减函数.四、函数图象及应用函数的图象是函数的重要表示方法,它具有明显的直观性,通过函数的图象能够掌握函数重要的性质,如单调性、奇偶性等.反之,掌握好函数的性质,有助于图象正确的画出.函数图象广泛应用于解题过程中,利用数形结合解题具有直观、明了、易懂的优点,在历届高考试题中,常出现有关函数图象和利用图象解题的试题. 例4 设函数f (x )=x 2-2|x |-1 (-3≤x ≤3), (1)证明f (x )是偶函数; (2)画出这个函数的图象;(3)指出函数f (x )的单调区间,并说明在各个单调区间上f (x )是增函数还是减函数; (4)求函数的值域.(1)证明 f (-x )=(-x )2-2|-x |-1 =x 2-2|x |-1=f (x ),即f (-x )=f (x ),∴f (x )是偶函数.(2)解 当x ≥0时,f (x )=x 2-2x -1=(x -1)2-2,当x<0时,f(x)=x2+2x-1=(x+1)2-2,即f(x)=()()()()⎪⎩⎪⎨⎧<≤--+≤≤--03,2130,2122x x x x根据二次函数的作图方法,可得函数图象如图.(3)解 函数f(x)的单调区间为 [-3,-1),[-1,0),[0,1),[1,3]. f(x)在区间[-3,-1)和[0,1)上为减函数,在[-1,0),[1,3]上为增函数.(4)解 当x ≥0时,函数f(x)=(x-1)2-2的最小值为-2,最大值为f(3)=2;当x<0时,函数f(x)=(x+1)2-2的最小值为-2,最大值为f(-3)=2.故函数f(x)的值域为[-2,2].一、选择题1.若偶函数f (x )在区间(-∞,-1]上是增函数,则( )A .f ⎝⎛⎭⎫-32<f (-1)<f (2) B .f (-1)<f ⎝⎛⎭⎫-32<f (2) C .f (2)<f (-1)<f ⎝⎛⎭⎫-32 D .f (2)<f ⎝⎛⎭⎫-32<f (-1) 答案 D解析 由f (x )是偶函数,得f (2)=f (-2), 又f (x )在区间(-∞,-1]上是增函数,且-2<-32<-1,则f (2)<f ⎝⎛⎭⎫-32<f (-1). 二、填空题2.有下列四个命题:①函数f (x )=|x ||x -2|为偶函数;②函数y =x -1的值域为{y |y ≥0};③已知集合A ={-1,3},B ={x |ax -1=0,a ∈R },若A ∪B =A ,则a 的取值集合为⎩⎨⎧⎭⎬⎫-1,13;④集合A ={非负实数},B ={实数},对应法则f :“求平方根”,则f 是A 到B 的映射. 你认为正确命题的序号为:________.答案 ②④解析 函数f (x )=|x ||x -2|的定义域为(-∞,2)∪(2,+∞),它关于坐标原点不对称,所以函数f (x )=|x ||x -2|既不是奇函数也不是偶函数,即命题①不正确;函数y =x -1的定义域为{x |x ≥1},当x ≥1时,y ≥0,即命题②正确;因为A ∪B =A ,所以B ⊆A ,若B =∅,满足B ⊆A ,这时a =0;若B ≠∅,由B ⊆A ,得a =-1或a =13.因此,满足题设的实数a 的取值集合为⎩⎨⎧⎭⎬⎫-1,0,13,即命题③不正确.依据映射的定义知,命题④正确.三、解答题 3.已知集合A ={x |-2<x <-1或x >0},B ={x |a ≤x ≤b },满足A ∩B ={x |0<x ≤2},A ∪B ={x |x >-2}.求a 、b 的值.解 将集合A 、A ∩B ,A ∪B 分别在数轴上表示, 如图所示由A ∩B ={x |0<x ≤2},知b =2且-1≤a ≤0. 由A ∪B ={x |x >-2}知-2<a ≤-1.综上可知:a =-1,b =2.4.设全集U =R ,A ={x |x >1};B ={x |x +a <0},且B ∁U A ,求实数a 的取值范围. 解∵U=R ,A={x|x>1}, ∴∁UA={x|x ≤1}.∵x+a<0,x<-a ,∴B={x|x<-a}.又∵B ∁UA ,∴-a ≤1,∴a ≥-1.5.已知集合A ={x |ax 2+2x +1=0,a ∈R }至多有一个真子集,求a 的取值范围. 解 集合A 是关于x 的方程的解集.至多有一个真子集的集合有两种情况:一是恰有一个真子集,二是没有真子集,即集合A 为空集.若A =∅,则集合A 无真子集,这时关于x 的方程ax 2+2x +1=0无实数解,则a ≠0,且Δ=4-4a <0,解得a >1.若集合A 恰有一个真子集,这时集合A 必为单元素集. 可分为两种情况:(1)a =0时,方程为2x +1=0,x =-12;(2)a ≠0时,则Δ=4-4a =0,a =1.综上,当集合A 至多有一个真子集时,实数a 的取值范围为a ≥1或a =0.6.已知f (x )=⎩⎪⎨⎪⎧x 2-2x +4, x <-1,-2x +5, -1≤x <1,3, x ≥1,(1)求:f (-2),f (0),f (1),f (4);(2)画出函数图象; (3)指出函数的值域.解 2x ,x ≠0,x ∈R ;=-2包含在区间(-∞,-1)中, ∴f (-2)=(-2)2-2(-2)+4=12. x =0包含在区间[-1,1)中,∴f (0)=5.x =1包含在区间[1,+∞)中,∴f (1)=3. x =4包含在区间[1,+∞)中,∴f (4)=3. (2)如图所示(3)由图象知,函数的值域为[3,+∞).7.已知函数f (x )=x +mx,且f (1)=2,(1)判断f (x )的奇偶性;(2)判断f (x )在(1,+∞)上的增减性,并证明; (3)若f (a )>2,求a 的取值范围.解 (1)∵f (1)=2,∴f (1)=1+m =2,∴m =1,∴f (x )=x +1x,则f (-x )=-x +1-x =-⎝⎛⎭⎫x +1x =-f (x ), 又f (x )的定义域为{x |x ≠0},关于原点对称, ∴函数f (x )是奇函数. (2)设1<x 1<x 2,则f (x 1)-f (x 2)=x 1+1x 1-x 2-1x 2=x 1-x 2+1x 1-1x 2=x 1-x 2+x 2-x 1x 1x 2=(x 2-x 1)⎝⎛⎭⎫1x 1x 2-1=(x 2-x 1)(1-x 1x 2)x 1x 2.∵1<x 1<x 2,∴x 2-x 1>0,x 1x 2>0,x 1x 2>1, ∴1-x 1x 2<0,∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2),∴f (x )在(1,+∞)上是增函数.(3)同理可证f(x)在(0,1)上是减函数,由于函数是奇函数,可得简图. ∵f(a.)>2,即f(a.)>f(1), ∴a.>1或0<a.<1,∴a 的取值范围是(0,1)∪(1,+∞).章末检测一、选择题(本大题共12小题,每小题5分,共60分)1.设集合U ={1,2,3,4,5},M ={1,2,3},N ={2,5},则M ∩(∁U N )等于( ) A .{2} B .{2,3} C .{3} D .{1,3} 答案 D解析 ∁U N ={1,3,4},M ∩(∁U N )={1,2,3}∩{1,3,4}={1,3}. 2.下列集合不同于其他三个集合的是( ) A .{x |x =1} B .{y |(y -1)2=0} C .{x =1} D .{1} 答案 C解析 A 、B 、D 都表示元素是1的集合,C 表示元素为“x =1”的集合. 3.下列集合不能用区间形式表示的是( ) ①A ={1,2,3,4};②{x |x 是三角形}; ③{x |x >1,且x ∈Q };④∅;⑤{x |x ≤0,或x ≥3};⑥{x |2<x ≤5,x ∈N }. A .①②③ B .③④⑤ C .⑤⑥ D .①②③④⑥ 答案 D解析 根据区间的意义知只有⑤能用区间表示,其余均不能用区间表示. 4.下列各图中,可表示函数y =f (x )的图象的只可能是图中的( )答案 A解析 根据函数的概念知,只有“一对一”或“多对一”的对应才能构成函数关系. 5.下列函数表示同一函数的是( ) A .f (x )=|x |,g (x )=xB .f (x )=|x |,g (x )=⎩⎪⎨⎪⎧x ,x ≥0-x ,x <0C .f (x )=x ,g (x )=x 2xD .f (x )=x (x -1),g (x )=x 2-x (x >1) 答案 B解析 选项A 中两函数的对应关系不同,选项C 、D 中两函数的定义域不同. 6.函数f (x )=|x -1|的图象是( )答案 B解析 f(x)=|x-1|=⎩⎨⎧<-≥-1,11,1x x x x ,由分段函数的作图方法可知选项B 正确.7.设f (x )=2x +3,g (x +2)=f (x ),则g (x )等于( ) A .2x +1 B .2x -1 C .2x -3 D .2x +7 答案 B解析 g (x +2)=f (x )=2x +3=2(x +2)-1.∴g (x )=2x -1.8.下列函数中,在区间(0,2)上为增函数的是( ) A .y =3-x B .y =x 2+1C .y =1xD .y =-|x |答案 B解析 y =3-x 在(0,2)上为减函数,y =1x 在(0,2)上为减函数,y =-|x |在(0,2)上亦为减函数.9.已知函数f (x )=⎩⎪⎨⎪⎧x (x ≥0)x 2 (x <0),则f (f (-2))的值是( )A .2B .-2C .4D .-4 答案 C解析 ∵x =-2<0,∴f (-2)=(-2)2=4,又4>0,∴f (f (-2))=f (4)=4.10.设A ={x |1<x <2},B ={x |x <a },若A B ,则实数a 的取值范围是( ) A .{a |a ≥2} B .{a |a ≤1} C .{a |a ≥1} D .{a .|a ≤2} 答案 A解析 如图所示,∴a ≥2.11.已知集合M =⎩⎨⎧⎭⎬⎫x |x =m +16,m ∈Z ,N =⎩⎨⎧⎭⎬⎫x |x =n 2-13,n ∈Z ,P =⎩⎨⎧⎭⎬⎫x |x =p 2+16,p ∈Z ,则M 、N 、P 的关系是( )A .M =N PB .M N =PC .M N PD .N P M 答案 B解析 m +16=6m +16,n 2-13=3n -26,p 2+16=3p +16, ∵m ,n ,p ∈Z ,∴3n -2、3p +1都是3的倍数加1,6m +1是6的倍数加1. ∴M N =P .12.设f (x )=11-x,则f {f [f (x )]}的解析式为( )A.11-xB.1(1-x )3 C .-x D .x 答案 D解析 f [f (x )]=11-f (x )=x -1x∴f {f [f (x )]}=11-x -1x=x .二、填空题(本大题共4小题,每小题4分,共16分)13.函数y =x +1+12-x的定义域为________.答案 [-1,2)∪(2,+∞)解析 由题意知⎩⎪⎨⎪⎧x +1≥02-x ≠0,∴x ≥-1且x ≠2.14.用列举法表示集合:M =⎩⎨⎧⎭⎬⎫m |10m +1∈Z ,m ∈Z =________________________.答案 {-11,-6,-3,-2,0,1,4,9}解析 由10m +1∈Z ,且m ∈Z ,知m +1是10的约数,故|m +1|=1,2,5,10,从而m 的值为-11,-6,-3,-2,0,1,4,9.15.已知集合{2x ,x +y }={7,4},则整数x =________,y =________. 答案 2 5解析 由集合相等的定义知,⎩⎪⎨⎪⎧ 2x =7x +y =4或⎩⎪⎨⎪⎧2x =4x +y =7,解得⎩⎨⎧x =72y =12或⎩⎪⎨⎪⎧x =2y =5, 又x ,y 是整数,所以x =2,y =5.16.若函数f (x )=kx 2+(k -1)x +2是偶函数,则f (x )的递减区间是________.答案 (-∞,0]解析 ∵f (x )是偶函数, ∴f (-x )=kx 2-(k -1)x +2 =kx 2+(k -1)x +2=f (x ),∴k =1,∴f (x )=x 2+2,其递减区间为(-∞,0]. 三、解答题(本大题共6小题,共74分)17.(12分)已知集合A ={x |2≤x ≤8},B ={x |1<x <6},C ={x |x >a },U =R . (1)求A ∪B ,(∁U A )∩B ;(2)若A ∩C ≠∅,求a 的取值范围. 解 (1)A ∪B ={x |2≤x ≤8}∪{x |1<x <6} ={x |1<x ≤8}.∵∁U A ={x |x <2或x >8}. ∴(∁U A )∩B ={x |1<x <2}.(2)∵A ∩C ≠∅,∴a <8.18.(12分)若A ={x |-3≤x ≤4},B ={x |2m -1≤x ≤m +1},B ⊆A ,求实数m 的取值范围.解 ∵B ⊆A ,当B =∅时,得2m -1>m +1,m >2, 当B ≠∅时,得⎩⎪⎨⎪⎧2m -1≤m +1,2m -1≥-3,m +1≤4.解得-1≤m ≤2.综上所述,m 的取值范围为m ≥-1.19.(12分)已知函数f (x )=ax 2+bx +3a +b 为偶函数,其定义域为[a -1,2a ],求f (x )的值域.解 ∵f (x )是偶函数,∴定义域[a -1,2a ]关于原点对称.∴⎪⎩⎪⎨⎧≤+-≥-+≥-a a a a a 1,312,112 ∴a =13,b =0.∴f (x )=13x 2+1,x ∈⎣⎡⎦⎤-23,23. ∴f (x )的值域为⎣⎡⎦⎤1,3127. 20.(12分)判断并证明f (x )=11+x 2在(-∞,0)上的增减性. 解 在(-∞,0)上单调递增.证明如下: 设x 1<x 2<0,f (x 1)-f (x 2)=11+x 21-11+x 22=x 22-x 21(1+x 21)(1+x 22)=(x 2-x 1)(x 2+x 1)(1+x 21)(1+x 22)∵x 2-x 1>0,x 1+x 2<0,1+x 21>0,1+x 22>0,∴f (x 1)-f (x 2)<0,∴f (x 1)<f (x 2),∴f (x )在(-∞,0)上单调递增.21.(12分)定义在实数集R 上的函数y =f (x )是偶函数,当x ≥0时,f (x )=-4x 2+8x -3.(1)求f (x )在R 上的表达式;(2)求y =f (x )的最大值,并写出f (x )在R 上的单调区间(不必证明).解 (1)设x <0,则-x >0,f (-x )=-4(-x )2+8(-x )-3=-4x 2-8x -3.∵f (x )是R 上的偶函数,∴f (-x )=f (x ),∴当x <0时,f (x )=-4x 2-8x -3.∴f (x )=⎩⎪⎨⎪⎧ -4x 2+8x -3 (x ≥0)-4x 2-8x -3 (x <0), 即f (x )=⎩⎪⎨⎪⎧-4(x -1)2+1 (x ≥0)-4(x +1)2+1 (x <0). (2)∵y =f (x )开口向下,∴y =f (x )有最大值,f (x )max =f (-1)=f (1)=1.函数y =f (x )的单调递增区间是(-∞,-1]和[0,1],单调递减区间是[-1,0]和[1,+∞).22.(14分)已知函数f (x )的定义域为(-2,2),函数g (x )=f (x -1)+f (3-2x ).(1)求函数g (x )的定义域;(2)若f (x )是奇函数,且在定义域上单调递减,求不等式g (x )≤0的解集.解 (1)由题意可知⎩⎪⎨⎪⎧ -2<x -1<2,-2<3-2x <2,∴⎩⎪⎨⎪⎧-1<x <3,12<x <52. 解得12<x <52. 故函数g (x )的定义域为⎝⎛⎭⎫12,52.(2)由g (x )≤0,得f (x -1)+f (3-2x )≤0,∴f (x -1)≤-f (3-2x ).∵f (x )为奇函数,∴f (x -1)≤f (2x -3).而f (x )在(-2,2)上单调递减. ∴⎩⎪⎨⎪⎧x -1≥2x -3,12<x <52.解得12<x ≤2. ∴g (x )≤0的解集为⎝⎛⎦⎤12,2.。
