常用幂次数列
公务员考试之数量关系
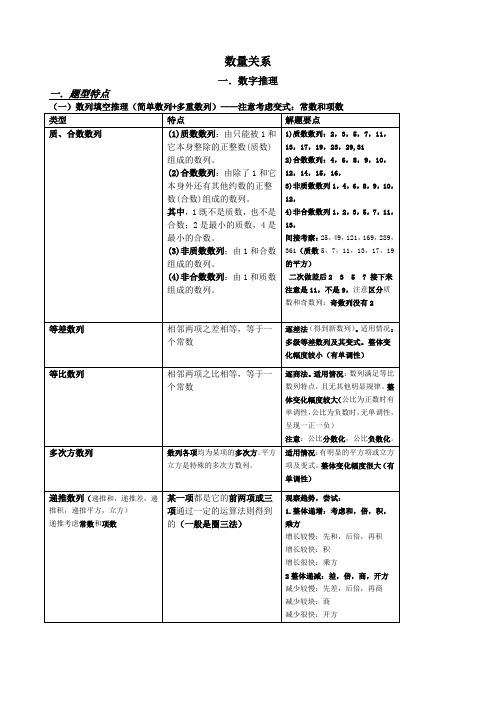
数量关系一.数字推理一.题型特点(一)数列填空推理(简单数列+多重数列)——注意考虑变式:常数和项数类型特点解题要点质、合数数列(1)质数数列:由只能被1和它本身整除的正整数(质数)组成的数列。
(2)合数数列:由除了1和它本身外还有其他约数的正整数(合数)组成的数列。
其中,1既不是质数,也不是合数;2是最小的质数,4是最小的合数。
(3)非质数数列:由1和合数组成的数列。
(4)非合数数列:由1和质数组成的数列。
1)质数数列:2,3,5,7,11,13,17,19,23,29,312)合数数列:4,6,8,9,10,12,14,15,16,3)非质数数列1,4,6,8,9,10,12,4)非合数数列1,2,3,5,7,11,13,间接考察:25,49,121,169,289,361(质数5,7,11,13,17,19的平方)二次做差后2 3 5 7 接下来注意是11,不是9,注意区分质数和奇数列:奇数列没有2等差数列相邻两项之差相等,等于一个常数逐差法(得到新数列)。
适用情况:多级等差数列及其变式。
整体变化幅度较小(有单调性)等比数列相邻两项之比相等,等于一个常数逐商法。
适用情况:数列满足等比数列特点,且无其他明显规律。
整体变化幅度较大(公比为正数时有单调性,公比为负数时,无单调性,呈现一正一负)注意:公比分数化,公比负数化。
多次方数列数列各项均为某项的多次方。
平方立方是特殊的多次方数列。
适用情况:有明显的平方项或立方项及变式。
整体变化幅度很大(有单调性)递推数列(递推和,递推差,递推积,递推平方,立方)递推考虑常数和项数某一项都是它的前两项或三项通过一定的运算法则得到的(一般是圈三法)观察趋势,尝试:1.整体递增:考虑和,倍,积,乘方增长较慢:先和,后倍,再积增长较快:积增长很快:乘方2整体递减:差,倍,商,开方减少较慢:先差,后倍,再商减少较块:商减少很快:开方根式数列数列中含根式的数列1根次之间存在关系2根次相同时,可以把根号外面的数化到根号里面去(或把根号里面的数化到外面去),看底数关系3根式的底数存在关系4.根次,底数分别存在一定的关系。
行测:负幂次数列和幂次数列

负幂次数列和幂次数列幂次数列是数字推理部分中对数字敏感性要求最高的一部分,也是出题率最高的一部分之一,需要记忆一些常规数字幂次知识。
本文通过对近十年的考题回放,得出了幂次数列的出规律及解题技巧,以期对参加国考的同学起到参考作用。
(一)真题回放及答案详解:2009年第102题、105题1. 7,7,9,17,43,()A. 119B. 117C. 123D. 121【解析】C。
这是一道幂数列。
规律是:原数列后项与前项的差依次是0、2、8、26;新数列依次可以化成:3的0次方减1,3的1次方减1,3的2次方减1,3的3次方减1;所以()=43+80(3的4次方减1)=123。
2. 153,179,227,321,533,()A. 789B. 919C. 1229D. 1079【解析】D。
这是一道幂数列。
规律是:原数列各项依次可以化成:150+31,170+32,200+33,240+34,290+35,其中新数列150,170,200,240,290后项与前项做差得20,30,40,50,故()=60+290+36=1079。
2008年第44题、45题3. 67,54,46,35,29,()A. 13B. 15C. 18D. 20【解析】D。
这是一道幂数列变形题。
题干中数列的每两项之和是:121,100,81,64,49,分别是:11、10、9、8、7的平方。
所以()里就是7的平方-29,即20。
4. 14,20,54,76,()A. 104B. 116C. 126D. 144【解析】C。
这是一道幂数列的变形题。
题干中数列各项分别是:3的平方加5,5的平方减5,7的平方加5,9的平方减5,所以()里就是11的平方加5,即126。
2007年第42题、43题、45题5. 1,3,4,1,9,()A.5 B.11 C.14 D.64【解析】D。
本题规律为:(第二项-第一项)的平方=第三项,所以()里应为:(1-9)的平方,即64。
数量关系--数字推理重点

执教人
周为响
什么是数量关系
大纲界定: 数量关系:主要测试应试人员理解、把握事 物间量化关系和解决数量关系问题的技能,重 点涉及数字和数据关系的分析、推理、判断、 运算等。 题型:数 字 推 理、数 学 运 算
数字推理的命题特点和趋势
题量的变化 试题的难易程度 解题时间 试题的重点和难点
64
18 324 28 784
81
19 361 29 841
100
20 400 30 900
“单数字发散”必备技能
“单数字发散”必备技能
“单数字发散”必备技能
质因数分解:牢记200以内一些特殊数字的分解有时可以 起到意想不到的效果,可将其看作一种特殊意义上的 “基准数”。
知识运用
【例1】(江苏2004A类-4)4,6,10,14,22,( )。 A. 30 B. 28 C. 26 D. 24 【例2】(国家05一类-32)2,3,10,15,26,( )。 A. 29 B. 32 C. 35 D. 37 【例3】(国家07-43)0,9,26,65,124,( )。 A. 165 B. 193 C. 217 D. 239 【例4】3,4,8,26,122,( )。 A. 722 B. 727 C. 729 D. 731 【例5】(08省)2,6,15,28,( ),78 A.45 B.48 C.55 D.56 【例6】(10国)1,6,20,56,144,() A.256 B.312 C.352 D.384
多级数列
基本知识点: 1、多级数列是指对数列相邻两项进行“-、+、 ×、÷”四则运算从而形成规律的数列。 2、做差数列是多级数列的主体内容,做和和做 积数列一般很少考到。 3、运算后得到的新数列可能是等差、等比数列, 也可能是其它特殊数列,包括质数、周期、幂 次、基础递推数列。
形式幂级数的基础理论和应用

形式幂级数的基础理论和应用形式幂级数是现代数学基础理论中的一个重要分支,是研究无穷级数的一个重要手段。
本文将从形式幂级数的定义、性质等方面来探讨其基础理论和应用。
一、形式幂级数的定义与基本性质形式幂级数指的是由一系列形如$a_n x^n$的项所组成的级数,其中$x$为未定元,系数$a_n$可以取任意实数或复数。
例如:$$f(x)=\sum_{n=0}^{\infty} a_n x^n=a_0+a_1 x+a_2 x^2+...+a_n x^n+... (a_n\in \mathbb{C})$$其中$f(x)$为形式幂级数,如果其中某一项$a_nx^n=a_mx^m(m\neq n)$,则称其为一项余项。
形式幂级数不是函数,只是一个由一系列项组成的形式化级数。
针对形式幂级数,有一些基本性质:1. 形式幂级数的加法运算:设$f(x)=\sum_{n=0}^{\infty}a_n x^n,g(x)=\sum_{n=0}^{\infty} b_n x^n$,则它们之和为:$$f(x)+g(x)=\sum_{n=0}^{\infty}(a_n+b_n)x^n$$2. 形式幂级数的乘法运算:设$f(x)=\sum_{n=0}^{\infty}a_n x^n,g(x)=\sum_{n=0}^{\infty} b_n x^n$,则它们的乘积为:$$f(x) \cdot g(x)=\sum_{n=0}^{\infty}c_n x^n$$其中:$$c_n=\sum_{k=0}^n a_k b_{n-k}$$3. 形式幂级数的复合运算:设$f(x) =\sum_{n=0}^{\infty} a_n x^n,g(x)=\sum_{n=0}^{\infty}b_n x^n$,则它们的复合为:$$f(g(x))=\sum_{n=0}^{\infty} a_n g^n(x)$$其中$a_n g^n(x)$表示对于形式幂级数$g(x)$,将其代入到 $a_n x^n$ 中,再对一系列项进行求和。
真题分类-数资-3数字推理-破题之术-考点05幂次数列

1.根据以下数字的规律,空缺处应填入的是( )。
1,4,9,25,49,121,( )********【答案】C 。
根据题干分析,数列可以变形为12,22,32,52,72,112,( ),底数构成规律1,1,2,2,4,(4),所求项为(11+4)2=225。
C 项正确,A 、B 、D 选项不符合题意,故本题正确答案选择C 项。
【题源】2018光大秋招**,27,37,12,24,( )********【答案】B 。
两两相加得到二级数列81,64,49,36为简单幂次数列,依次为9,8,7,6的平方,下一项为5的平方25,则括号内应为25-24=1。
B 选项正确,A 、C 、D 选项错误。
故本题应选B 。
【题源】2017建行秋招**,7,36,( ),256,243********【答案】A 。
根据题干,可得A 项正确;该数列的规律为:0123418,77,366,(1255),256=4====,A 选项符合题意。
B 、C 、D 选项错误。
故本题应选A 项。
【题源】2017建行秋招**,32,81,64,25,( )********【答案】C。
根据题干,可推得C项正确;依次分别是16,25,34,43,52,未知项为61=6,C选项符合题意。
A、B、D选项错误。
故本题应选C项。
【题源】2018建行秋招5. 34,18,10,(),4,3********【答案】A。
根据题干,可得A项正确;34=25+2,18=24+2,10=23+2,4=21+2,3=20+2,因此,未知项为22+2=6,A选项符合题意。
B、C、D选项错误。
故本题应选A项。
【题源】2018建行秋招**,9,26,65,124,()********【答案】D。
题干规律为1^3-1=0,2^3+1=9,3^3-1=26,4^3+1=65,5^3-1=124,6^3+1=127。
D选项正确,A、B、C选项错误。
答案选择D。
【题源】2018建行秋招**、4、8、9、27、16、64、()********【答案】A。
数字推理

数字推理2011年国考没有数字推理,可能安徽也会跟着中央走,更何况安徽的数字推理是有名的弱智,完全可以随便看看。
所以我这部分也就没整理太多。
数字敏感记熟常用的幂次数3,多次方因数分解法有的数列,必须要把每项拆成2个数字的积,这2个数字分别构成数列。
这种数列,还是有迹可循的。
注意看所给的数字是不是很明显地某个数的倍数。
这是华图弄得数推思维过程,新手可以看看,一般的题基本这么就可以了。
难题其实顶多也就1个,为这1分花大工夫我觉得挺不值的~~真要全对,那就多接触接触各种题目,开阔思路。
1,等差数列及其变式这个是最基本的了,一般数字变化不大的都是此类。
不过现在为了增加难度,一般都是二级,三级,而且最后一级可能不只是等差数列2,等比数列及其变式观察数列各项间有大致的倍数关系,则易解,顶多是多了个修正数列3,平方,立方数列及其变式1,这个要求对基本的平方,立方非常熟悉,然后要有一定的数字敏感性——比如说26,就得想到26=25+1=27-1等等。
2,这种数列一般跳跃较大,而且前后没什么明显关系。
这可能是解题突破口。
3,可以在数列的中后部找到一数字,因为此时未修正数很大,修正数列已经无法掩盖其原貌。
4,一般不会直接考,会加个修正数列(注意修正数列特别大的情况,比如09年国考)或者是前面2项之差的平方等于第三项这类的规律5,有可能会与项数相联系,形成有通项公式的数列。
如:-2,-8,0,64,(250)为n*n*n*(n-5)4,做和数列(同理有可能是积数列,就不单列了)1,这种数列需要两项(甚至三项)做和,得到的和构成一个新数列2,如果数字彼此差距不大,而且不是等差,有的会“高低起伏”,那么可以尝试做和3,这种数列的难点就在于如何想到这是做和数列4,这种数列有的数字都很小,而且参差不齐,这或许可以作为突破口5,有的含有负数,不大6,在最开始的做差如果发现差跳来跳去,那么可以从这方面考虑5,递推和数列及其变式1,前2项和等于第三项,这是最普通的,可能会加个修正数列,如+1,-1。
数字推理22

数字推理第01讲数列概述一、考区范围数字推理是数量关系当中非常重要的传统题型,然而国考、联考和大部分地方考试已经多年没有涉及,所以对于大部分考生来说,数字推理的课程可以简单轻松地看一看即可。
但是,数字推理仍会出现在部分省级考试中,譬如浙江和江苏每年都有比重不小的数字推理试题,所以这两个地区的考生一定要非常认真的复习本篇课程。
除此之外,陕西、天津、河北、新疆、吉林、广东、深圳等省市的考试,也有很大的概率要考到数字推理,所以这些地区的考生也不能轻视数字推理的复习。
二、基础数列数字推理的主体内容可以归纳为五大题型,而这些题型是建立在“基础数列”之上的。
“基础数列”包括等差数列、等比数列、质数型数列、周期数列和直接递推数列五种形态:● 等差数列:相邻两项之差(后项减去前项)等于定值的数列。
【例1】(河北2013-38)1,5,9,(),17,21C. 14A. 12B. 13 D. 15[答案]B● 等比数列:相邻两项之比(后项除以前项)等于定值的数列。
【例2】(广东2013C-1)160,80,40,20,( )A. 4B. 6C. 8D. 10[答案]D● 质数型数列质数数列:由质数构成的数列叫做质数数列。
譬如:2、3、5、7、11、13…合数数列:由合数构成的数列叫做合数数列。
譬如:4、6、8、9、10、12…● 周期数列:自某一项开始,重复出现前面相同(相似)项的数列。
譬如:①2、5、4、2、5、4…②2、4、2、4、2、4…● 直接递推数列:数列当中每一项直接等于其前两项的和、差、积或者商。
譬如:①②0、1、1、2、3、5…-1、3、2、5、7…三、五大题型数字推理的主体内容主要包括以下五大题型:1.2.3.4.5. 多级数列:数列中相邻项通过四则运算,得到的结果形成某种特定的规律。
多重数列:数列中数字通过交叉或者分组,从而形成某种特定的规律。
分式数列:数列中的数通过自然分隔,形成某种特定的规律。
公务员考试行测讲义-数量关系

【行测讲义】数量关系一、数量关系简介数量关系主要是考查应试者对数量关系的理解,其主要有两大题型,一是数字推理,二是数学运算。
数字推理主要是考察应试者对数字和运算的敏感程度。
本质上来看,是考察是考生对出题考官的出题思路的把握,因为在数字推理中的规律并非“客观规律”,而是出题考官的“主观规律”,也就是说,在备考过程中,不能仅从数字本身进行思考,还必须深入地理解出题者的思路与规律。
数学运算基本题型众多,每一基本题型都有其核心的解题公式或解题思路,应通过练习不断熟练。
在此基础上,有意识培养自己的综合分析能力,即在复杂数学运算题面前,能够透过现象看到本质,挖掘其中深层次的等量关系。
从备考内容来看,无论是数字推理还是数学运算,都需要从思路和技巧两方面来着手准备。
上篇数字推理数字推理的题目通常状况下是给你一个数列,但整个数列中缺少一项(中间或两边),要求应试者仔细观察这个数列各数字之间的关系,判断其中的规律,然后在四个选择答案中选择最合理的答案。
一、数字推理要点简述(一)解题关键点1.培养数字、数列敏感度是应对数字推理的关键2.熟练掌握各种基本数列(自然数列、平方数列、立方数列等)3.熟练掌握常见的简单数列,并深刻理解“变式”的概念(1)应掌握的基本数列如下:常数数列7,7,7,7, 7,7,7 …自然数列:1,2,3,4,5,6,7……奇数列:1,3,5,7,9,11……偶数列:2,4,6,8,10,12……自然数平方数列:1,4,9,16,25,36……自然数立方数列:1,8,27,64,125,216……等差数列:1,6,11,16,21,26……等比数列:1,3,9,27,81,243……质数数列2,3,5,7,11,13,17,19…《质数是指只能被1和其本身整除的数(1既不是质数,也不是合数)》合数数列4,6,8,9,10,12,14,15…合数是指除1和质数之外的自然数。
周期数列1,3,4,1,3,4…幂次数列1,4,9,16,25,…1,8,27,64,125,…递推数列1,1,2,3,5,8,13…对称数列1,3,2,5,2,3,1…1,3,2,5,-5,-2,-3,-1…4.进行大量的习题训练(二)熟练掌握数字推理的解题技巧1、观察题干,大胆假设。
【第3季-数资】数字推理特色题(苏、新)(讲义笔记)

1.7.1,24.8,41.32,58.73,()A.75.131B.65.131C.75.121D.85.1212.1/6,6/7,42/13,546,55,()A.7098/559B.30030/559C.7098/601D.30030/6013.3,1,8,18,52,()A.138B.140C.142D.1444.36,125,1024,2187,2048,()A.49B.512C.1D.05.2,,4,7,()A.17B.C. D.【知识点】数字推理:1.基础数列:直接做。
2.特征数列:(1)多重数列:①特征:项数较多。
②方法:先交叉,再分组。
(2)机械划分数列:①特征:有小数点、*号等特殊符号。
②方法:以特殊符号为分界线,先分开再组内。
(3)分数数列:①特征:一般全部或大部分是分数。
②方法:观察趋势:a.先分开,再一起。
b.反约分。
(4)作商数列:①特征:两两倍数关系明显。
②方法:两两作商找规律。
(5)幂次数列:①特征:本身是或附近有幂次数。
②方法:a.普通幂次:直接找规律。
b.修正幂次:转化为普通幂次±修正项。
3.非特征数列:(1)多级数列:①特征:无明显特征,变化趋势平缓。
②方法:两两作差,一次不行作两次。
(2)递推数列:①特征:无明显特征,非多级数列。
②方法:圈仨数——找规律——做验证。
1.7.1,24.8,41.32,58.73,()A.75.131B.65.131C.75.121D.85.121【解析】1.观察数列有两部分组成(整数和小数),是机械划分数列。
方法一:先分开找规律,整数:7、24、41、58,是基础数列,如果看不出来,变化缓慢,可以做减法,后-前都是 17,则下项=58+17=75,排除 B、D 项;小数:1、8、32、73,后-前得到 7、24、41,再次作差均为 17,则接着是 41+17=58,因此小数部分=73+58=131,结果为 75.131,对应 A 项。
职测a类知识点总结

职测a类知识点总结一、常识判断。
1. 政治常识。
- 马克思主义基本原理:包括辩证唯物主义(物质与意识的辩证关系、唯物辩证法的三大规律等)和历史唯物主义(社会存在与社会意识的辩证关系、人民群众是历史的创造者等)。
- 中国特色社会主义理论体系:邓小平理论(改革开放、社会主义市场经济等核心思想)、“三个代表”重要思想(始终代表中国先进生产力的发展要求、始终代表中国先进文化的前进方向、始终代表中国最广大人民的根本利益)、科学发展观(以人为本,全面、协调、可持续的发展观)、习近平新时代中国特色社会主义思想(新时代我国社会主要矛盾的转化、“四个全面”战略布局、“五位一体”总体布局等)。
- 时事政治:关注近一年来国内外重大政治事件,如重要国际会议(如G20峰会等)、国内的重大政策出台(如乡村振兴战略的推进举措等)。
2. 经济常识。
- 微观经济:供求关系(影响价格的因素、均衡价格等)、市场结构(完全竞争市场、垄断竞争市场、寡头垄断市场、完全垄断市场的特点)、企业经营(企业成本、利润、市场竞争策略等)。
- 宏观经济:宏观调控目标(促进经济增长、稳定物价、增加就业、保持国际收支平衡)、财政政策(财政收入与支出、税收政策等)、货币政策(货币供应量、利率、汇率等货币政策工具)、经济全球化(国际贸易、国际投资等相关概念和影响)。
3. 法律常识。
- 宪法:国家的基本制度(国体、政体等)、公民的基本权利和义务、国家机构的组成和职能。
- 民法:民事主体(自然人、法人、非法人组织)、民事法律行为(有效、无效、可撤销等情形)、物权(所有权、用益物权、担保物权)、债权(合同之债、侵权之债等)、婚姻家庭法(结婚、离婚的条件和程序等)、继承法(法定继承、遗嘱继承等)。
- 刑法:犯罪构成(犯罪主体、犯罪主观方面、犯罪客体、犯罪客观方面)、刑罚种类(主刑和附加刑)、常见犯罪类型(如盗窃、抢劫、贪污受贿等犯罪的认定)。
- 行政法:行政主体、行政行为(具体行政行为和抽象行政行为)、行政许可、行政处罚、行政复议、行政诉讼等。
17个常见的生成函数

17个常见的生成函数生成函数是一个重要的工具,用于描述数列的性质和计算数列的各项值。
在数学中,有很多常见的生成函数用于解决各种数学问题。
下面列举了17个常见的生成函数,详细介绍它们的定义和用途。
1.普通生成函数:普通生成函数是最简单的类型之一,用于描述数列的全部项。
它的形式为:G(x)=a0+a1x+a2x^2+...其中,ai表示数列的第i项,x是一个变量。
通过普通生成函数可以求得数列的各项值,或者求得数列的一些性质。
2.整数拆分生成函数:整数拆分是将一个正整数拆分成多个正整数之和的过程。
整数拆分生成函数用于描述整数拆分的性质。
它的形式为:G(x)=(1+x+x^2+...)*(1+x^2+x^4+...)*(1+x^3+x^6+...)*...其中,括号内的每一项分别表示用1、2、3等整数进行拆分的情况,每一项都是一个无穷级数,通过展开括号可以得到拆分的每一种可能。
3.斐波那契数列生成函数:斐波那契数列是一个经典的数列,每一项等于前两项的和。
斐波那契数列生成函数用于描述斐波那契数列的性质。
它的形式为:G(x)=1/(1-x-x^2)通过展开这个生成函数,可以得到斐波那契数列的每一项。
4.格式幂级数生成函数:格式幂级数生成函数用于描述从序列中选取元素进行组合的情况。
它的形式为:G(x)=1/(1-a1x)*1/(1-a2x)*1/(1-a3x)*...通过展开这个生成函数,可以得到选取元素进行组合的每一种可能。
5.幂方数列生成函数:幂方数列是一个特殊的数列,每一项等于一个常数的幂次方。
幂方数列生成函数用于描述幂方数列的性质。
它的形式为:G(x) = 1/(1-ax)通过展开这个生成函数,可以得到幂方数列的每一项。
6.斐波那契幂级数生成函数:斐波那契幂级数是一个特殊的数列,每一项等于斐波那契数列的幂次方。
斐波那契幂级数生成函数用于描述斐波那契幂级数的性质。
它的形式为:G(x)=1/(1-x-x^2)通过将斐波那契数列生成函数中的x替换为x^k,然后展开这个生成函数,可以得到斐波那契幂级数的每一项。
公务员备考技巧:推理之幂次数列

事业单位备考技巧: 推理之幂次数列数字推理比较明显的两个特征是大家前面学过的多重数列与分数数列,我们拿到一道题,先要根据特征对于题型进行排除,很容易能排除是否是多重数列和分数数列,那么接下来就要按幂次数列的特征来有针对性的排除了。
下面给大家列举出一些常用必背的幂次数,希望大家能牢记并在事业单位考试中灵活应用。
一、20以内数的平方数:1、4、9、16、25、36、49、64、81、100121、144、169、196、225、256、289、324、361、400 二、10以内数的立方:1、8、27、64、125、216、343、512、729、1000 三、2、3、4、5的多次方:2的1-10次幂:2、4、8、16、32、64、128、256、512、1024 3的1--5次幂:3、9、27、81、243 4的1--5次幂:4、16、64、256、1024 5的1--5次幂:5、25、125、625、3125 四、关于常数0和1N 00=:0是0的任意自然数次方(0的0次方没有意义!即此处0≠N );a a 20)1(1N 1-===(0≠N )1是任意非零数的0次方,是1的任意次方,是-1的任意偶次方。
五、16、64、81、256的多种分解方式16= 42, 24;64= 62,34,28;81= 43,29;256= 82,44,216六、负幂次11-=a a(0≠a ),例如3113271;771;551---=== 唐山华图教育将就这一问题进行阐释,让考生梳理出其中某个特定的逻辑关系。
接下来我们在例题中感受一下这类题型的解题过程,希望大家能在考试中快速解决此类题型:【例1】343,216,125,64,27,( ) A .8 B .9 C .10D .12【题型识别】全部课转化为幂次数,幂次数列。
【唐山华图解析】整个数列可转化为37,36,35,34,33,(32),选择A 选项。
【胖虎提示】明显的幂次数需要靠大家平时对于幂次数的熟悉并牢记,可通过一些特殊的方法来辅助记忆,例如343=334+()等等,。
数字推理之幂次数列

数字推理之幂次数列华图教育邹维丽幂数列是公务员考试数字推理部分的重要题型之一,从2007至2010年每年都考过。
其中难度也是逐渐加大,基本的幂数列考上的越来越少,取而代之的是幂次修正数列。
幂次修正数列就是在基本的幂数列的基础上进行了一定的转换,形式不同,而本质相同的数列。
如果把幂次数列掌握了,那么幂次修正数列也很容易了。
这就要求考生把1-30内的平方数熟练记住,从而培养对数字的敏感。
比如说如果题目中给出了126,那么就需要立刻联系到126=125+1=53+1,126=121+5=112+5,126=128-2=27-2。
幂次修正数列包括常数修正、等差修正、正负修正、等差正负混合修正四种情况。
下面我们分别来学习一下这几种幂次修正数列。
一、常数修正【例1】0,7,26,63,124,()【浙江2008-5】A.209B.215C.224D.262[答案]B[解析]各项分别为 1-1, 8-1, 27-1, 64-1,125-1。
故空缺项为216-1=215,本题选B。
【例2】2,7,23,47,119,()【江苏2009B类-61】A.125B.167C.168D.170[答案]B[解析]各项为 4-2, 9-2, 25-2, 49-2, 121-2。
故空缺项为169-2=167,本题选B。
二、等差修正【例1】2,10,30,68,(),222【上海2009-5】A.130B.150C.180D.200[解析]各项分别为:13+1,23+2,33+3,43+4,()63+6,所以空缺项为53+5=130,本题选A。
【例2】1,3,11,67,629,()【浙江2009-38】A.2350B.3130C.4783D.7781[答案]D[解析]各项分别为:10+0,21+1,32+2,43+3,54+4故空缺项为65+5=7781,本题选D。
三、正负修正【例1】6,7,18,23,38 ()【浙江2010-73】A.47B.53C.62D.76[答案]A[解析]各项分别为:22+2, 32-2,42+2,52-2,62+2,空缺项为72-2,故选A 。
数学物理基本方法4.1数项级数、幂级数

幂级数在物理学中的应用
弹性力学
幂级数在弹性力学中用于 描述弹性体的应力和应变 关系。
热力学
热力学中的理想气体状态 方程就是通过幂级数来表 达的。
电磁学
在电磁学中,幂级数用于 描述电磁波的传播和电磁 场的分布。
数项级数与幂级数在金融领域的应用
复利计算
通过使用幂级数和数项级数,可以更精确地计算 复利,这对于金融投资和保险非常重要。
定义
数项级数与幂级数的乘法运算是 将两个级数的对应项相乘,得到
一个新的级数。
规则
乘法运算有特定的规则,如合并 同类项、调整系数等,需要细心
操作避免出错。
应用
数项级数与幂级数的乘法运算在 数学、物理、工程等领域有广泛 应用,如求解物理问题、研究复
合材料的性质等。
Part
05
数项级数与幂级数的应用实例
数学物理基本方法 4.1数项级数、幂级 数
• 数项级数简介 • 幂级数简介 • 数项级数与幂级数的联系与区别 • 数项级数与幂级数的运算方法 • 数项级数与幂级数的应用实例
目录
Part
01
数项级数简介
数项级数的定义
01
数项级数是无穷序列的和,表示为 $sum_{n=0}^{infty} a_n$,其中 $a_n$是序列中的第$n$项。
的时间序列数据。
Part
03
数项级数与幂级数的联系与区 别
数项级数与幂级数的共同点
01
两者都是无穷序列
数项级数和幂级数都是无穷序列,可以表示为无限多个项的和或乘积。
02
两者都有收敛和发散的概念
数项级数和幂级数都有收敛和发散的概念,收敛的级数或幂级数具有确
定的极限值,而发散的级数或幂级数则没有确定的极限值。
求数列的常用方法

求数列的常用方法数列是数学中的一个重要概念,它是有规律的数的排列。
数列的研究对于数学的发展和应用有着重要的意义。
在数学中,常用的数列方法包括等差数列、等比数列、递推数列、斐波那契数列、调和数列等等。
接下来,我将详细介绍这些常用数列方法。
一、等差数列:等差数列是指数列中的每一项与前一项之差保持一致的数列。
其通项公式为:an = a1 + (n-1)d,其中an表示数列的第n项,a1为第一项,d为公差(即每一项与前一项之差)。
等差数列的性质有:任意三项成等差中项;任意两项之和等于中间项的两倍;相邻项和恒等于首尾项和的一半等等。
二、等比数列:等比数列是指数列中的每一项与前一项之比保持一致的数列。
其通项公式为:an = a1 * r^(n-1),其中an表示数列的第n项,a1为第一项,r为公比(即每一项与前一项之比)。
等比数列的性质有:任意三项成等比中项;任意两项之商等于中间项的n-1次幂;相邻两项的平方等于首尾项的乘积等等。
三、递推数列:递推数列是指数列中的每一项都是依赖于前一项的值得到的数列。
递推数列有很多不同的构成方法,其中最常见的是斐波那契数列。
斐波那契数列的定义为:F(1)=1,F(2)=1,F(n)=F(n-1)+F(n-2)(n≥3)。
斐波那契数列的性质包括前两项之和等于后一项、前一项无限逼近后一项的比例等等。
四、调和数列:调和数列是指数列中的每一项的倒数都是等差的数列。
调和数列的通项公式为:an = 1/n。
调和数列的性质有:任意两项之和等于首尾项之积的倒数;调和数列的和发散,也就是无穷大。
除了上述常用的数列方法外,还有一些其他的数列方法如泰勒级数、阶乘数列、幂次数列等等。
泰勒级数是一种将函数展开为无穷级数的方法,用于近似计算;阶乘数列是指数列中的每一项都是阶乘的结果;幂次数列是指数列中的每一项都是底数的幂次运算结果。
总结起来,数列是数学中的重要概念,常用的数列方法包括等差数列、等比数列、递推数列、斐波那契数列、调和数列等等。
迭代幂次函数

迭代幂次函数一、引言迭代幂次函数是数学中常见的一类函数,它通过多次迭代幂次运算来产生数列或序列。
这类函数具有一定的规律和性质,常被用于解决问题和分析数学模型。
本文将详细探讨这一主题,从基本概念到应用实例,全面介绍迭代幂次函数的相关知识。
二、基本概念迭代幂次函数是由幂函数构成的一族函数,其形式为 f(x) = a^x,其中 a 是一个常数。
幂函数是一种常见的函数形式,其特点是自变量 x 出现在指数位置上。
迭代幂次函数则通过多次迭代幂函数运算,生成一个序列或数列。
三、迭代幂次函数的性质3.1 收敛性迭代幂次函数的重要性质之一是其收敛性。
对于某个给定的初始值,通过多次迭代幂次运算,函数值可能逐渐趋近于一个确定的极限值。
收敛性的研究对于理解迭代幂次函数的行为和应用具有重要意义。
3.2 极限值的计算在迭代幂次函数的研究中,计算极限值是一个关键的问题。
针对不同的初始值和参数,迭代幂次函数可能收敛到不同的极限值,或者发散不收敛。
解析计算极限值是一项重要的技巧,常用的方法有泰勒展开、二分法等。
3.3 动态行为迭代幂次函数的动态行为是指函数值随迭代次数的变化情况。
通过绘制函数值与迭代次数的关系图像,可以观察到函数的周期性、振荡性以及其他动态特征。
动态行为的研究有助于深入理解迭代幂次函数的性质和变化规律。
四、迭代幂次函数的应用迭代幂次函数在科学、工程和金融等领域具有广泛的应用。
以下列举几个典型的应用实例。
4.1 分形几何迭代幂次函数的动态行为常常具有一种自相似性质,这与分形几何的概念相契合。
通过迭代幂次函数的运算,可以生成分形图形,如科赫曲线、谢尔宾斯基三角形等。
这些分形图形具有独特的几何形态和结构特征,应用于图像处理、数据压缩等领域。
4.2 数值计算迭代幂次函数可以用于数值计算的近似求解。
通过迭代幂次运算,可以逼近复杂的数学函数,例如平方根函数、对数函数等。
这种数值计算方法在计算机模拟、优化算法等领域具有重要的应用价值。
数量——数字推理

数量——数字推理一、基础数列(2018 广东)14、28、56、112、(C )A.155B.186C.224D.320(2015 广州)3、4、7、11、18、(C )A.21B.25C.29D.35二、分数数列1.题型特征:全部或大多数是分数。
2.解题思路:观察分子、分母是否递增或递减。
3.如果是递增或递减:(1)分开看:分子、分母分别成规律。
(2)一起看:前后两个分数(分子、分母)四则运算。
4.如果不是递增或递减:反约分为递增递减的数列。
例如:2/4 可以约分为1/2,将1/2 变为2/4、3/6、4/8 的过程就叫反约分(2018 吉林)1/4,1/4,3/16,(),5/64,3/64 ( D )A.3/32B.6/32C.5/32D.4/32(2015 吉林)0,1,4/5(),8/17,()(A )A.6/10,10/26B.3/5,8/13C.6/10,7/20D.2/5,9/19三、多重数列1.一般多重数列:(1)题型特征:数列项数较多,一般在7 项或7 项以上(包括未知项)。
(2)解题思路:①先交叉:奇数项和偶数项分别成规律;②再分组:两两分组或三三分组2.特殊多重数列(2018 新疆)2,2,5,4,8,6,11,8,14,10,( B )A.15B.17C.12D.16(2014 广东)8、3、17、5、24、9、26、18、30、(A )A.22B.25C.33D.36→奇数项:8、17、24、26、30,相减为:9、7、2、4,没有规律。
考虑分组,优先两两分组,再组内做加减法。
(8,3)相加得到 11,(17,5)相加得到 22,(24,9)相加得到 33,(26,18)相加得到 44,即等差数列,下一组相加得到 55【知识点】特殊多重数列:1.题型特征一:复杂小数、特殊符号(ln,根号、log)加减。
2.解题思路:机械拆分,小数点或“+、-”前后分别拆成两个数列分开求规律。
