抛物线地性质归纳和证明
抛物线及其性质知识点及题型归纳总结

抛物线及其性质知识点及题型归纳总结知识点精讲一、抛物线的定义平面内与一个定点F 和一条定直线)(l F l ∉的距离相等的点的轨迹叫做抛物线,定点F 叫抛物线的焦点,定直线l 叫做抛物线的准线.注 若在定义中有l F ∈,则动点的轨迹为l 的垂线,垂足为点F . 二、抛物线的方程、图形及性质抛物线的标准方程有4种形式:)0(2,2,2,22222>-==-==p py x py x px y px y ,其中一次项与对称轴一致,一次项系数的符号决定开口方向(如表10-3所示)1. 点),(00y x P 与抛物线)0(22>=p px y 的关系(1)P 在抛物线内(含焦点)0202px y <⇔. (2)P 在抛物线上0202px y =⇔. (3)P 在抛物线外0202px y >⇔.2. 焦半径抛物线上的点),(00y x P 与焦点F 的距离称为焦半径,若)0(22>=p px y ,则焦半径20px PF +=,2max p PF =. 3. )0(>p p 的几何意义p 为焦点F 到准线l 的距离,即焦准距,p 越大,抛物线开口越大.4. 焦点弦若AB 为抛物线)0(22>=p px y 的焦点弦,),(11y x A ,),(22y x B ,则有以下结论:(1)4221p x x =.(2)221p y y -=.(3)焦点弦长公式1:p x x AB ++=21,p x x x x =≥+21212,当21x x =时,焦点弦取最小值p 2,即所有焦点弦中通径最短,其长度为p 2.焦点弦长公式2:α2sin 2pAB =(α为直线AB 与对称轴的夹角).(4)AOB ∆的面积公式:αsin 22p S AOB =∆(α为直线AB 与对称轴的夹角). 5.抛物线的弦若AB 为抛物线22(p 0)y px => 的任意一条弦,1122(x ,y ),B(x ,y )A ,弦的中点为000(x ,y )(y 0)M ≠ ,则(1) 弦长公式:1212(k k 0)AB AB x y y =-=-=≠ (2) 0AB p k y =(3) 直线AB 的方程为000(x x )py y y -=- (4) 线段AB 的垂直平分线方程为000(x x )y y y p-=-- 6.求抛物线标准方程的焦点和准线的快速方法(4A法) (1)2(A 0),y Ax =≠ 焦点为(,0)4A ,准线为4A x =-(2) 2(A 0),x Ay =≠ 焦点为(0,)4A ,准线为4A y =-如24y x =,即24y x =,焦点为1(0,)16 ,准线方程为116y =-7.参数方程22(p 0)y px => 的参数方程为222x pt y pt ⎧=⎨=⎩(参数t R ∈)8.切线方程和切点弦方程抛物线22(p 0)y px =>的切线方程为0000(x x ),(x ,y )y y p =+为切点切点弦方程为00(x x ),y y p =+点00(x ,y )在抛物线外与中点弦平行的直线为00(x x ),y y p =+此直线与抛物线相离,点00(x ,y )(含焦点)是弦AB 的中点,中点弦AB 的斜率与这条直线的斜率相等,用点差法也可以得到同样的结果。
(完整版)抛物线的性质归纳及证明

抛物线的常见性质及证明概念焦半径:抛物线上一点与其焦点的连线段;焦点弦:两端点在抛物线上且经过抛物线的焦点线段称为焦点弦.性质及证明过抛物线y 2=2px (p >0)焦点F 的弦两端点为),(11y x A ,),(22y x B ,倾斜角为α,中点为C(x 0,y 0), 分别过A 、B 、C 作抛物线准线的垂线,垂足为A ’、B ’、C ’. 1.求证:①焦半径αcos 12||1-=+=p p x AF ;②焦半径αcos 12||2+=+=pp x BF ; ③1| AF |+1| BF |=2p ; ④弦长| AB |=x 1+x 2+p =α2sin 2p ;特别地,当x 1=x 2(α=90︒)时,弦长|AB|最短,称为通径,长为2p ;⑤△AOB 的面积S △OAB =αsin 22p .证明:根据抛物线的定义,| AF |=| AD |=x 1+p 2,| BF |=| BC |=x 2+p2,| AB |=| AF |+| BF |=x 1+x 2+p如图2,过A 、B 引x 轴的垂线AA 1、BB 1,垂足为 A 1、B 1,那么| RF |=| AD |-| FA 1 |=| AF |-| AF |cos θ, ∴| AF |=| RF |1-cos θ=p1-cos θ同理,| BF |=| RF |1+cos θ=p1+cos θ∴| AB |=| AF |+| BF |=p 1-cos θ+p 1+cos θ=2psin 2θ.S △OAB =S △OAF +S △OBF =12| OF || y 1 |+12| OF || y 1 |=12·p2·(| y 1|+| y 1 |)∵y 1y 2=-p 2,则y 1、y 2异号,因此,| y 1 |+| y 1 |=| y 1-y 2 |∴S △OAB =p 4| y 1-y 2 |=p 4(y 1+y 2)2-4y 1y 2=p 44m 2p 2+4p 2=p 221+m 2=p 22sin θ.2.求证:①2124p x x =;②212y y p =-;③ 1| AF |+1| BF |=2p .当AB ⊥x 轴时,有 AF BF p ==,成立; 当AB 与x 轴不垂直时,设焦点弦AB 的方程为:2p y k x ⎛⎫=-⎪⎝⎭.代入抛物线方程: 2222p k x px ⎛⎫-= ⎪⎝⎭.化简得:()()222222014p k x p k x k -++=∵方程(1)之二根为x 1,x 2,∴1224k x x ⋅=.(122111212111111222x x p p pp AF BF AA BB x x x x +++=+=+=+++()()121222121222424x x p x x p p p p p p x x p x x ++++===+++++. 3.求证:=∠=∠'''FB A B AC Rt ∠.先证明:∠AMB =Rt ∠【证法一】延长AM 交BC 的延长线于E ,如图3,则△ADM ≌△ECM ,∴| AM |=| EM |,| EC |=| AD | ∴| BE |=| BC |+| CE |=| BC |+| AD | =| BF |+| AF |=| AB |∴△ABE 为等腰三角形,又M 是AE 的中点, ∴BM ⊥AE ,即∠AMB =Rt ∠ 【证法二】取AB 的中点N ,连结MN ,则| MN |=12(| AD |+| BC |)=12(| AF |+| BF |)=12| AB |,∴| MN |=| AN |=| BN |∴△ABM 为直角三角形,AB 为斜边,故∠AMB =Rt ∠.【证法三】由已知得C (-p 2,y 2)、D (-p 2,y 1),由此得M (-p 2,y 1+y 22).∴k AM =y 1-y 1+y 22x 1+p 2=y 1-y 22·y 212p +p =p (y 1-y 2)y 21+p 2=p (y 1--p 2y 1)y 21+p 2=p y 1,同理k BM =py 2 ∴k AM ·k BM =p y 1·p y 2=p 2y 1y 2=p 2-p 2=-1∴BM ⊥AE ,即∠AMB =Rt ∠.【证法四】由已知得C (-p 2,y 2)、D (-p2,y 1),由此得M (-p 2,y 1+y 22). ∴MA →=(x 1+p 2,y 1-y 22),MB →=(x 3+p 2,y 2-y 12)∴MA →·MB →=(x 1+p 2)(x 2+p 2)+(y 1-y 2)(y 2-y 1)4=x 1x 2+p 2(x 1+x 2)+p 24-(y 1-y 2)24=p 24+p 2(y 212p +y 222p )+p 24-y 21+y 22-2y 1y 24=p 22+y 1y 22=p 22+-p 22=0 ∴MA →⊥MB →,故∠AMB =Rt ∠.【证法五】由下面证得∠DFC =90 ,连结FM ,则FM =DM .又AD =AF ,故△ADM ≌△AFM ,如图4 ∴∠1=∠2,同理∠3=∠4∴∠2+∠3=12×180︒=90︒∴∠AMB =Rt ∠. 接着证明:∠DFC =Rt ∠【证法一】如图5,由于| AD |=| AF |,AD ∥RF ,故可设∠AFD =∠ADF =∠DFR =α, 同理,设∠BFC =∠BCF =∠CFR =β, 而∠AFD +∠DFR +∠BFC +∠CFR =180︒ ∴2(α+β)=180︒,即α+β=90︒,故∠DFC =90︒ 【证法二】取CD 的中点M ,即M (-p 2,y 1+y 22)由前知k AM =py 1,k CF =-y 2+p 2+p 2=-y 2p =p y 1∴k AM =k CF ,AM ∥CF ,同理,BM ∥DF ∴∠DFC =∠AMB =90︒.【证法三】∵DF →=(p ,-y 1),CF →=(p ,-y 2),∴DF →·CF →=p 2+y 1y 2=0 ∴DF →⊥CF →,故∠DFC =90︒.【证法四】由于| RF |2=p 2=-y 1y 2=| DR |·| RC |,即| DR || RF |=| RF || RC |,且∠DRF =∠FRC =90︒ ∴ △DRF ∽△FRC∴∠DFR =∠RCF ,而∠RCF +∠RFC =90︒ ∴∠DFR +∠RFC =90︒ ∴∠DFC =90︒4. C ’A 、C ’B 是抛物线的切线【证法一】∵k AM =p y 1,AM 的直线方程为y -y 1=p y 1(x -y 212p)图6与抛物线方程y 2=2px 联立消去x 得y -y 1=p y 1(y 22p -y 212p),整理得y 2-2y 1y +y 21=0可见△=(2y 1)2-4y 21=0,故直线AM 与抛物线y 2=2px 相切, 同理BM 也是抛物线的切线,如图8.【证法二】由抛物线方程y 2=2px ,两边对x 求导,(y 2)'x=(2px )'x , 得2y ·y 'x=2p ,y 'x =py,故抛物线y 2=2px 在点A (x 1,y 1)处的切线的斜率为k 切=y 'x | y =y 1=p y 1. 又k AM =py 1,∴k 切=k AM ,即AM 是抛物线在点A 处的切线,同理BM 也是抛物线的切线.【证法三】∵过点A (x 1,y 1)的切线方程为y 1y =p (x +x 1),把M (-p 2,y 1+y 22)代入左边=y 1·y 1+y 22=y 21+y 1y 22=2px 1-p 22=px 1-p 22,右边=p (-p 2+x 1)=-p 22+px 1,左边=右边,可见,过点A 的切线经过点M ,即AM 是抛物线的切线,同理BM 也是抛物线的切线.5. C ’A 、C ’B 分别是∠A ’AB 和∠B ’BA 的平分线. 【证法一】延长AM 交BC 的延长线于E ,如图9,则△ADM ≌△ECM ,有AD ∥BC ,AB =BE , ∴∠DAM =∠AEB =∠BAM ,即AM 平分∠DAB ,同理BM 平分∠CBA . 【证法二】由图9可知只须证明直线AB 的倾斜角α是直线AM 的倾斜角β的2倍即可,即α=2β. 且M (-p 2,y 1+y 22)图9∵tan α=k AB =y 2-y 1x 2-x 1=y 2-y 1 y 222p -y 212p=2py 1+y 2. tan β=k AM =y 1-y 1+y 22x 1+p 2=y 1-y 22·y 212p +p =p (y 1-y 2)y 21+p 2=p (y 1--p 2y 1)y 21+p 2=py 1. ∴tan 2β=2tan β1-tan 2β=2py 11-(p y 1)2=2py 1y 22-p 2=2py 1y 22+y 1y 2=2py 1+y 2=tan α ∴α=2β,即AM 平分∠DAB ,同理BM 平分∠CBA .6. AC ’、A ’F 、y 轴三线共点,BC ’、B ’F 、y 轴三线共点 【证法一】如图10,设AM 与DF 相交于点G 1,由以上证明知| AD |=| AF |,AM 平分∠DAF ,故AG 1也是DF 边上的中线, ∴G 1是DF 的中点.设AD 与y 轴交于点D 1,DF 与y 轴相交于点G 2, 易知,| DD 1 |=| OF |,DD 1∥OF , 故△DD 1G 2≌△FOG 2∴| DG 2 |=| FG 2 |,则G 2也是DF 的中点.∴G 1与G 2重合(设为点G ),则AM 、DF 、y 轴三线共点,同理BM 、CF 、y 轴也三线共点.【证法二】AM 的直线方程为y -y 1=p y 1(x -y 212p),令x =0得AM 与y 轴交于点G 1(0,y 12),又DF 的直线方程为y =-y 1p (x -p 2),令x =0得DF 与y 轴交于点G 2(0,y 12)∴AM 、DF 与y 轴的相交同一点G (0,y 12),则AM 、DF 、y 轴三线共点,同理BM 、CF 、y 轴也三线共点H .由以上证明还可以得四边形MHFG 是矩形.图107. A 、O 、B ’三点共线,B 、O 、A ’三点共线. 【证法一】如图11,k OA =y 1x 1=y 1 y 212p=2py 1,k OC =y 2 -p 2 =-2y 2p =-2py 2p 2=-2py 2-y 1y 2=2p y 1∴k OA =k OC ,则A 、O 、C 三点共线, 同理D 、O 、B 三点也共线.【证法二】设AC 与x 轴交于点O ',∵AD ∥RF ∥BC∴| RO ' || AD |=| CO ' || CA |=| BF || AB |,| O 'F || AF |=| CB || AB |, 又| AD |=| AF |,| BC |=| BF |,∴| RO ' || AF |=| O 'F || AF |∴| RO ' |=| O 'F |,则O '与O 重合,即C 、O 、A 三点共线,同理D 、O 、B 三点也共线.【证法三】设AC 与x 轴交于点O ',RF ∥BC ,| O 'F || CB |=| AF || AB |,∴| O 'F |=| CB |·| AF || AB |=| BF |·| AF || AF |+| BF |=1 1| AF |+1| BF |=p2【见⑵证】∴O '与O 重合,则即C 、O 、A 三点共线,同理D 、O 、B 三点也共线. 【证法四】∵OC →=(-p 2,y 2),OA →=(x 1,y 1),∵-p 2·y 1-x 1 y 2=-p 2·y 1-y 212p y 2=-py 12-y 1y 2y 12p =-py 12+p 2y 12p =0∴OC →∥OA →,且都以O 为端点∴A 、O 、C 三点共线,同理B 、O 、D 三点共线.【推广】过定点P (m ,0)的直线与抛物线y 2=2px (p >0)相交于点A 、B ,过A 、B 两点分别作直线l :x =-m 的垂线,垂足分别为M 、N ,则A 、O 、N 三点共线,B 、O 、M 三点也共线,如下图:图118. 若| AF |:| BF |=m :n ,点A 在第一象限,θ为直线AB 的倾斜角. 则cos θ=m -nm +n ;【证明】如图14,过A 、B 分别作准线l 的垂线,垂足分别为D ,C ,过B 作BE ⊥AD于E ,设| AF |=mt ,| AF |=nt ,则| AD |=| AF |,| BC |=| BF |,| AE |=| AD |-| BC |=(m -n )t ∴在Rt △ABE 中,cos ∠BAE =| AE || AB |= (m -n )t (m +n )t =m -nm +n∴cos θ=cos ∠BAE =m -nm +n.【例6】设经过抛物线y 2=2px 的焦点F 的直线与抛物线相交于两点A 、B ,且| AF |:| BF |=3:1,则直线AB 的倾斜角的大小为 .则E 的坐标为( p2+x 1 2,y 12),则点E 到y 轴的距离为d = p2+x 1 2=12| AF |故以AF 为直径的圆与y 轴相切, 同理以BF 为直径的圆与y 轴相切.【说明】如图15,设M 是AB 的中点,作MN ⊥准线l 于N ,则| MN |=12(| AD |+| BC |)=12(| AF |+| BF |)=12| AB |则圆心M 到l 的距离| MN |=12| AB |,故以AB 为直径的圆与准线相切. 10. MN 交抛物线于点Q ,则Q 是MN 的中点.【证明】设A (y 212p ,y 1),B (y 222p ,y 1),则C (-p 2,y 2),D (-p 2,y 1),M (-p 2,y 1+y 22),N (y 21+y 224p ,y 1+y 22),设MN 的中点为Q ',则Q ' ( -p 2+y 21+y 224p 2,y 1+y 22)∵ -p 2+y 21+y 224p 2= -2p 2+y 21+y 22 8p = 2y 1y 2+y 21+y 228p = ⎝⎛⎭⎫y 1+y 222 2p∴点Q ' 在抛物线y 2=2px 上,即Q 是MN 的中点.图16。
抛物线知识点高考

抛物线知识点高考高中数学中的抛物线知识点在高考中占据了重要的位置。
抛物线是数学中的一种曲线,具有很多有趣的性质和应用。
在本文中,我们将深入探讨抛物线的定义、性质以及高考中常见的相关考点。
首先,我们来介绍一下抛物线的定义。
抛物线是由一个定点(焦点)和一条直线(准线)确定的曲线。
对于抛物线上的任意一点P,它到焦点的距离等于它到准线的距离。
这个定义能够很好地解释抛物线的形状,以及抛物线上各个点的位置关系。
接下来,我们来探讨抛物线的性质。
首先是对称性。
抛物线具有对称轴,对称轴是通过焦点垂直于准线的直线。
抛物线的形状在对称轴两侧完全相同,即左右对称。
其次是焦点与准线之间的距离关系。
抛物线上任意一点到焦点与准线的距离之差保持不变。
这个性质在物理学中有广泛的应用,例如反射和聚焦。
最后是切线和法线。
抛物线上每一点处都有唯一的切线和法线,切线与法线相互垂直。
在高考中,抛物线相关的知识点主要包括方程求解、性质应用以及相关的解析几何问题。
首先是方程求解,即给定一个抛物线的方程,要求求解其焦点、准线以及对称轴等相关的信息。
其次是性质应用,例如给定一个抛物线上的一点,要求计算它到焦点和准线的距离之差。
另外,还会出现一些解析几何的问题,例如给定一个抛物线和一条直线,要求求解它们的交点等等。
在解决这些问题的过程中,我们可以运用一些有效的方法和技巧。
其中,最重要的是熟练掌握抛物线的标准方程和一般方程。
标准方程是y^2=4ax,其中a是抛物线的参数。
一般方程是y=ax^2+bx+c。
通过这两个方程,我们可以很方便地确定抛物线的性质和解析几何问题的解。
另外,还要注意抛物线的对称性质和距离关系,这些特性对于解题至关重要。
总之,抛物线是高中数学中一个重要的知识点,也是高考中经常出现的考点之一。
通过深入了解抛物线的定义、性质以及运用方法,我们可以更好地应对高考中的相关题目。
希望本文的介绍和解析能够帮助到同学们更好地掌握抛物线知识,取得优异的成绩。
完整版抛物线的性质归纳及证明

抛物线的常见性质及证明概念焦半径:抛物线上一点与其焦点的连线段;焦点弦:两端点在抛物线上且经过抛物线的焦点线段称为焦点弦性质及证明y 2= 2px (p >0)焦点F 的弦两端点为 A(x 1, y 1), B(x 2, y 2),倾斜角为 ,中点为时,弦长|AB|最短,称为通径,长为 鸟卩:⑤^ AOB 的面积S ^OAB =2sin证明:根据抛物线的定义,I AF |= I AD |= x i + p , I BF |= I BC |= X 2+号,| AB |= | AF 1+ | BF |= X 1 + X 2+P如图2,过A 、B 引X 轴的垂线AA i 、BB I ,垂足为A i 、B i ,那么 I RF |= | AD I —I FA 1 |= | AF |- | AF |cos ,•j AF = 1—o^=1—cos同理,I BF |=I RF I=―p—1 + cos 1 + cos•j AB =I AF I+ I BF=血 + 1 + cos = sin 2S5 = SS AF + &OBF = 2| OF II y i |+1OF || y i | =舟-p - (I y i1+1 y i I)■ yi y 2=—P 2,贝y y i 、y 2异号,因此,I y i |+ | y i |= | y i — y 2 |C(x o ,y 0), 1.求证: 分别过A 、B 、C 作抛物线准线的垂线,垂足为 A'、B'、C . ①焦半径I AF I X i 当 一p —:②焦半径|BF I X 2占 2 1 cos2 ③备 +帀十厂p ;④弦长I AB| = X i + X 2+ p =—;特别地,| AF | | BF 丨 psin 2_p_1 cos当 x i =X 2( =90 )过抛物线2p二SgAB = p| y i —y2 | =艸(y i + y2)2—4y i y2 =哲4m2p2+4p2=^p/ i+m2=2Sn32.求证:①XX2 P:②yy4当AB丄x轴时,有AF BF P,成立;当AB与x轴不垂直时,设焦点弦AB的方程为: •代入抛物线方程:k2X22 2PX.化简得: k2x2k22•••方程(1 )之二根为k2AF BFX1 X2 p 2P PX1 4 2 1X2X1 , X2, •-X1X2X1 X2BB1X13.求证:AC'BX2X2 X1X2P1 X2X1 X2 p2A'FB' Rt / .则先证明:/ AMB = Rt /•••△ ABE 为等腰三角形,又 M 是AE 的中点,••• BM 丄 AE ,即/ AMB = Rt / 【证法二】取 AB 的中点N ,连结MN ,则 | MN |= 2(| AD 汁 I BC |)= 2(1 AF |+ | BF |)=弓 AB |,A | MN |= | AN |= | BN |=齐瞪+i +臭沁4P!+ 迤=P!+» = 0•••MA 丄1M B ,故/ AMB = Rt / .【证法五】由下面证得/ DFC = 90,连结FM ,贝U FM = DM .又 AD = AF ,故△ ADMAFM ,如图 4•••/ 1 = / 2,同理/ 3 =/ 4•••△ ABM 为直角三角形,AB 为斜边,AMB = Rt / .【证法三】由已知得 C(— 2, y 2)、D( — 2, y i ).由此得M (—2,宁). --k AM =y i + y 2y i - 2 y i — y 2 p(y 1 — y 2) -P 2p(yi —=) y 1 X 1 + Py 2+p 22- S + p2 2卫=卫一=4 =— 1y 2+p 2 y ,,同理k BM =y • I_p --kAM - kBM = • P2,p p 2 (y 1 — y 2)2=X 1X 2 + 2(X 1 + X 2)+ 4 — —•••/ 2+/ 3 = 2X 180 = 90 •••/ AMB = Rt / .接着证明:/ DFC = Rt /【证法一】如图5,由于I AD |= | AF |, AD // RF,同理,设/ BFC =/ BCF = / CFR =, 而/ AFD + / DFR + /BFC +/ CFR = 180故可设/ AFD =/ ADF =/ DFR =••• 2( + ) = 180,即 + = 90,故/ DFC = 90 【证法二】取CD的中点M,即M(—2,豊产)由前知k AM=弗k cF =^—」—Ry i••• k AM = k CF, AM // CF,同理, BM // D F•••/ DFC =/ AMB = 90 .【证法三】••• "DF = (p, —y1), "C F=(P, -y2),• - DF • CF = p2+ y i y2 = 0•••"D F丄"C F,故/ DFC = 90 .【证法四】由于I RF 2= p2=—y i y2= I DR I - I RC |,即IR-j,且/ DRF = / FRC = 90••• △ DRF F RC•••/DFR = / RCF,而/ RCF+/ RFC = 90•••/ DFR + / RFC= 90•••/ DFC = 904. C ' A、C' B是抛物线的切线【证法一】••• k AM=y1,AM的直线方程为y- y1=y^与抛物线方程y2= 2px联立消去x得2 2y—y i=y i(2p―2p),整理得y2—2y i y+ y2= 0可见△= (2y i)2—4y2= 0,故直线AM与抛物线y2= 2px相切,同理BM也是抛物线的切线,如图8.【证法二】由抛物线方程y2= 2px,两边对x求导, 得2y • y x= 2p, y = p,故抛物线y2= 2px在点=yi = Py i(y2)x= (2p x)x,A(x i, y i)处的切线的斜率为k切=y x| y切线.又k AM =牛,• k切=K AM,即AM是抛物线在点A处的切线,同理BM也是抛物线的【证法三】•••过点A(x i, y i)的切线方程为y i y =p(x + x i),把M(—号,左边=y i •呼=y^=沁』=px i —^2,2右边=p(—p + x i)=—p + px i,左边=右边,可见,过点A的切线经过点M,即AM是抛物线的切线,同理BM也是抛物线的切线.5. C'A、C'B分别是/ A 'AB和/ B 'BA的平分线.【证法一】延长AM交BC的延长线于E,如图9,则^ ADM ECM,有AD // BC, AB= BE,•••/ DAM = / AEB = / BAM ,即AM平分/ DAB,同理BM平分/ CBA.【证法二】由图9可知只须证明直线AB的倾斜角是直线AM的倾斜角的2倍即可,即=2.且M( - p,宁)「tan =k AB=x 2—i= y ¥y 2.2p —环,即AM 平分/ DAB ,同理 BM 平分/ CBA.【证法一】如图10,设AM 与DF 相交于点G i ,由以上证明知I AD |= I AF I , AM 平分/ DAF ,故AG i 也是 • G i 是DF 的中点.设AD 与y 轴交于点D i , DF 与y 轴相交于点 易知,I DD i I = I OF I , DD i // OF ,故^ DD I G 2BA FOG 2 •••I DG 2 |= | FG 2 I ,则 G 2也是 DF 的中点.•- G i 与G 2重合(设为点 G ),贝U AM 、DF 、线共点,y i + y 2y i —tan = k AM =x i + P—P 2=p(yiF=p y 2+p 2 =y i + P 2 = y i••• tan 2=2ta n_ 1 —tan 22 y i— y 2p(y i — y 2) = 2 = 2・ 2■+ p2py i 2py i 2py i 2pi—(P )2 y 2— p y 2+ yi y 2 屮 + y 2 (y i ) =tan6. AC ' A '、 y 轴三线共点,BC ' B '、y 轴三线共点同理BM 、CF 、y 轴也三线共点.G 2(0 ,DF 边上的中线,••• 0与0重合,则即 C 、0、A 三点共线,同理 D 、0、B 三点也共线.【证法四】••• 0C = (-p2^y 2), 0A =(x i , y i ),p p y 2py i y i y 2y i—2 - y i — x i y 2= — 2 - y i — y 2 =—牙一 2p 叫血=02 2p••• OC // OA ,且都以0为端点••• A 、0、C 三点共线,同理 B 、0、D 三点共线.【推广】过定点 P(m , 0)的直线与抛物线 y 2= 2px ( p > 0) 相交于点A 、B ,过A 、B 两 点分别作直线I : x =- m 的垂线,垂足分别为 M 、N ,贝U A 、0、N 三点共线, B 、0、M三点也共线,如下图:7. A 、0、B '三点共线,B 、0、A '三点共线.=I C0 |= I BF I I 0F |= I CB I • I AD I = I CA I = I ABI , I AF | = | AB |,又I AD |= I AF I ,I BC |= I BF |,A 罟古辭共线.【证法三】设 AC 与x 轴交于点0,RF // BC ,I0^= ^TZ-*,1 CB 1 1 AB 1=I AF |+ I BF 1= 丄= 2【见⑵证】 I AF I I BF I【证法一】如图11, k 0A =2p =2py ik 0C ==—p 22y 22py 22py 2 = 2p —y 1y 2 y 1--k oA = k oc , A 、0、C 三点共线,同理D 、 0、 B 三点也共线.【证法二】设 AC 与 x 轴交于点 0 ,••• AD // RF // BC••• I R0 I = I OF I ,贝U 0与0重合,即C 、0、A 三点共线,同理 D 、0、 B 三点也...* 0 F *= I CB • I AF I I BF I • I AF |I AB I于 E ,设 I AF |= mt , | AF |= nt ,则| AD |= I AF I , I BC |= I BF |, | AE |= | AD |- | BC | = (m —n)t•••在 Rt △ ABE 中, cos / BAE =仏口 =血皿 吩 n/• cos = cos / BAE=m —nm + n【例6】设经过抛物线 y 2= 2px 的焦点F 的直线与抛物线相交于两点A 、B ,且I AF I : I BF |= 3: 1,则直线AB 的倾斜角的大小为8.若I AF I : I BF |= m : n , 点A 在第一象限,为直线AB 的倾斜角.则cosm + n【证明】如图14,过A 、B 分别作准线I 的垂线,垂足分别为 D ,C , 过B 作BE 丄ADI AB I (m + n)t m +n【答案】60或120 .9.以AF为直径的圆与y轴相切, 以BF为直径的圆与y轴相切;以AB为直径的圆与准线相切;A' B'为直径的圆与焦点弦A'y -—C' / / 1■bK B' 'O4-/X.IIA'.C'.【说明】如图15,设E是AF的中点,AB相切.11同理以BF 为直径的圆与y 轴相切.【说明】如图15,设M 是AB 的中点,作 MN 丄准线I 于N ,则1 1 11 MN |= 1(| AD 汁丨 BC |)= 1(| AF |+ | BF |)=刁 AB |2 【证法二】AM 的直线方程为y — y i =十(x —稽),令x = 0得AM 与y 轴交于点G i (0, y i ),又DF 的直线方程为y =— W (x — p),令x = 0得DF 与y 轴交于点p 2 ••• AM 、DF 与y 轴的相交同一点 G (0,罗),贝U AM 、DF 、8p y 1+ y 22 2pp 十X1 则E 的坐标为(勺一则点E 到y 轴的距离为故以AF 为直径的圆与 y 轴相切,1则圆心M 到I 的距离I MN | = 2| AB故以AB 为直径的圆与准线相切.10. MN 交抛物线于点 Q ,则Q 是MN 的中点.2 2【证明】设 A (21 , y 1), B (22, y 1),则 C (-2,y i ),M(-2,导 N<y 24p y 2 设MN 的中点为 Q ,则 Q ( y 1 + y 2)2 ), -2 . y 1 + y 2—2 十 4p 2 2y轴三线共点,同理BM、CF、y轴也三线共点H .由以上证明还可以得四边形MHFG_ - 2p2+ y2+ y2 2y1y2+ y i + y28p•••点Q在抛物线y2= 2px上,即Q是MN的中点.12。
抛物线几何性质(抛物线几何性质总结)

思考: “一条直线和抛物线 y2 2 px( p 0) 相交, 两个交点的纵坐标为 y1 、y2 ,且 y1 y2 p2 .则 这条直线过焦点.”成立吗?
例2. 求证: 以抛物线的焦点弦为直径的圆与
抛物线的准线相切.
证明:取AB的中点M, 过A、B、C点作准线的
垂线, 垂足为A1、B1、M1, 则
x+5=0的距离小1,求点M的轨迹方程.
分析:如图可知原条件等价于M点到F(4, 0)和到
x=-4距离相等,由抛物线的定义,
点M的轨迹是以F(4, 0)为焦点,x=-4为准
线的抛物线.
y
因为p/2=4, 所以p=8,
M(x , y)
所求方程是 y2=16x.
-5 -4
F(4,0) x
例2. M是抛物线y2 = 2px (p>0)上一点, 若点M的
2
∴直线 AB 的方程为 x
y cot
p
由
x
y cot
p 2
消去
x
并整理
2
y2 2 px
得 y2 2 py cot p2 0
∴ y1 y2 2 p cot , y1 y2 p2
( x1 , y1 )
( x2 , y2 )
与直线 的倾斜角 无关!
AB ( x1 x2 )2 ( y1 y2 )2 = (1 cot2 )( y1 y2很)2奇怪!
三角形,那么∠CFD的大小如何?
yA C
90°
OF
x
D
B
形成结论
过抛物线y2=2px的焦点F作直线交抛物线于A、 B两点,焦点弦AB具有如下性质.
1
AB
x1
x2
p
2p
超详细抛物线知识点归纳总结

超详细抛物线知识点归纳总结抛物线是一个经典的二次曲线,它的形状类似于一个向上开口或向下开口的U 形曲线。
在数学和物理学中,抛物线具有许多重要的性质和应用。
下面是超详细的抛物线知识点总结:1. 基本定义:抛物线是平面上到定点(焦点)和定直线(准线)之距离相等的点的轨迹。
准线与抛物线的交点被称为顶点,准线上两个焦点和顶点的中垂线被称为对称轴。
2. 标准方程:一般抛物线的标准方程为 y = ax^2 + bx + c,其中 a、b、c 是常数。
通过变换可以将一般方程转化为其他形式,如顶点形式、焦点形式和准线形式。
3. 顶点形式:顶点形式的抛物线方程为 y = a(x-h)^2 + k,其中 (h,k) 是顶点的坐标。
通过平移和缩放可以将一般方程转化为顶点形式。
4. 焦点形式:焦点形式的抛物线方程为 (x-h)^2 = 4p(y-k),其中 (h,k) 是顶点的坐标,p 是焦距的一半。
焦点形式可以直接得到焦点坐标。
5. 准线形式:准线形式的抛物线方程为 y = px^2,其中 p 是焦距的一半。
准线形式的焦点在原点,并且准线是 x 轴。
6. 直径和焦距:抛物线的直径是通过顶点且与曲线相切的直线段。
焦距是焦点到准线的垂直距离。
7. 对称性:抛物线是关于对称轴对称的。
即曲线上任意一点关于对称轴对称的点,其到焦点和准线的距离相等。
8. 切线与法线:抛物线上任意一点处的切线是通过该点且与曲线相切的直线。
切线的斜率等于该点处的导数。
法线是与切线垂直的直线,其斜率是切线斜率的负倒数。
9. 焦点与直角焦点:焦点是到准线距离等于到抛物线上一点距离的点。
直角焦点是到准线距离等于到抛物线上一点距离的点,并且该点与焦点、准线之间的连线与准线垂直。
10. 焦半径:焦半径是焦点与抛物线上任意一点的连线与准线的夹角的二倍。
11. 焦散性质:抛物线的焦点到抛物线上任意一点的距离可以通过反射性质来得到。
即经过抛物线上某点的光线经过反射后都通过焦点。
抛物线经典性质总结30条

抛物线经典性质总结30条1.已知抛物线y=2px(p>0),AB是抛物线的焦点弦,点C 是AB的中点。
AA’垂直准线于A’,BB’垂直准线于B’,CC’垂直准线于C’,CC’交抛物线于点M,准线交x轴于点K。
证明:CC’是梯形AA’BB’的中位线,即|AB|=2|CC’|。
2.证明:|BF|=x^2/(2p)。
3.证明:CC’=AB=(AA’+BB’)/2.4.证明:以AB为直径的圆与准线L相切。
5.证明:∠A’FB’=90°。
6.证明:AA’FK,∴∠A’FK=∠FA’A;|AF|=|AA’|,∴∠AA’F=∠AFA’;同理可证∠B’FK=∠XXX,得证。
7.证明:C’F= A’B’=C’A’=C’B’。
8.证明:AC’平分∠A’AF,BC’平分∠B’BF,A’F平分∠AFK,B’F平分∠XXX。
9.证明:C’F垂直AB,即C’F⋅AB=0.10.证明:AF=(y+y1)/2p(1-cosα),BF=(y2-y)/(2p(1+cosα))。
11.证明:AF/BF=p/(1-cosα)。
12.证明:点A处的切线为y=y1+p(x+x1)。
1.证明y = 2px的两种方法:方法一:代入y = kx^2求解k,得到k = 2p,证毕。
方法二:对y = 2px两边求导得到2yy' = 2p,解出y' = p/x,证毕。
2.证明切线AC'和BC'交于焦点F:易证点A处的切线为y = px + py1,点B处的切线为y = px + py2,解得两切线的交点为C'(-p(y1-y2)。
(y1+y2)/2),证毕。
3.对于抛物线y^2 = 2px,过准线上任一点P(-2p。
t)作切线,证明过两切点Q1、Q2的弦必过焦点,且PQ1⊥PQ2:设切点为Q(x。
y),则有y' = p/x,代入y^2 = 2px得到x = y^2/(2p),进而得到Q1、Q2的坐标。
抛物线性质和知识点总结

抛物线性质和知识点总结1. 抛物线的定义和基本形式抛物线是指平面上满足二次方程y=ax^2+bx+c(a≠0)的曲线。
其基本形式是y=ax^2+bx+c,其中a、b、c是常数,称为抛物线的系数。
a决定抛物线的开口方向,当a>0时抛物线开口朝上,当a<0时抛物线开口朝下;b决定抛物线的位置,c决定抛物线与y轴的交点。
2. 抛物线的顶点和对称轴抛物线的顶点是抛物线的最低点(开口向上)或者最高点(开口向下),对于标准形式的抛物线y=ax^2+bx+c,它的顶点坐标为(-b/2a, c-b^2/4a)。
抛物线的对称轴是通过顶点并垂直于x轴的直线,对称轴方程为x=-b/2a。
3. 抛物线的焦点和直线方程抛物线的焦点是到抛物线上所有点的距离到抛物线的对称轴的距离相等的点,焦点的坐标为(-b/2a, 1-1/4a)。
抛物线的直线方程是y=mx+n,其中m和n是常数,直线与抛物线有两个交点。
当直线与抛物线相切时,两个交点重合。
当直线与抛物线没有交点时,这个抛物线不与这条直线相交。
4. 抛物线的焦距和离心率抛物线的焦距是抛物线的顶点到焦点的距离,焦距的大小是2|a|;抛物线的离心率是焦距与顶点到焦点的距离的比值,离心率的大小是1。
5. 抛物线的性质抛物线的性质是抛物线的特征,对于抛物线y=ax^2+bx+c,它的性质包括:a)抛物线的开口方向是由a的符号决定的,a>0时开口向上,a<0时开口向下;b)抛物线的顶点在对称轴上;c)焦点在对称轴上的顶点的上方,离心率等于1;d)与y轴的交点是常数项c;e)抛物线的焦点到直线方程的距离等于抛物线到直线方程的对称轴的距离。
6. 抛物线的知识点抛物线的知识点是在解决抛物线问题时需要掌握的知识,包括:a)抛物线的标准形式、一般形式、顶点形式和焦点形式的相互转化;b)抛物线的顶点、对称轴、焦点和直线方程的求法;c)抛物线与直线的交点和相切点的求法;d)抛物线的焦距和离心率的求法;e)抛物线的方程的实际应用问题。
高中数学抛物线的性质归纳及证明

每一个人的成功之路或许都不尽相同,但我相信,成功都需要每一位想成功的人去努力、去奋斗,而每抛物线的常见性质及证明概念焦半径:抛物线上一点与其焦点的连线段;焦点弦:两端点在抛物线上且经过抛物线的焦点线段称为焦点弦.性质及证明过抛物线y 2=2px (p >0)焦点F 的弦两端点为),(11y x A ,),(22y x B ,倾斜角为α,中点为C(x 0,y 0), 分别过A 、B 、C 作抛物线准线的垂线,垂足为A ’、B ’、C ’. 1.求证:①焦半径αcos 12||1-=+=p p x AF ;②焦半径αcos 12||2+=+=pp x BF ; ③1| AF |+1| BF |=2p ; ④弦长| AB |=x 1+x 2+p =α2sin 2p ;特别地,当x 1=x 2(α=90︒)时,弦长|AB|最短,称为通径,长为2p ;⑤△AOB 的面积S △OAB =αsin 22p .证明:根据抛物线的定义,| AF |=| AD |=x 1+p 2,| BF |=| BC |=x 2+p2,| AB |=| AF |+| BF |=x 1+x 2+p如图2,过A 、B 引x 轴的垂线AA 1、BB 1,垂足为 A 1、B 1,那么| RF |=| AD |-| FA 1 |=| AF |-| AF |cos θ, ∴| AF |=| RF |1-cos θ=p1-cos θ同理,| BF |=| RF |1+cos θ=p1+cos θ∴| AB |=| AF |+| BF |=p 1-cos θ+p 1+cos θ=2psin 2θ.S △OAB =S △OAF +S △OBF =12| OF || y 1 |+12| OF || y 1 |=12·p2·(| y 1|+| y 1 |)∵y 1y 2=-p 2,则y 1、y 2异号,因此,| y 1 |+| y 1 |=| y 1-y 2 |∴S △OAB =p 4| y 1-y 2 |=p 4(y 1+y 2)2-4y 1y 2=p 44m 2p 2+4p 2=p 221+m 2=p 22sin θ.2.求证:①2124p x x =;②212y y p =-;③ 1| AF |+1| BF |=2p .当AB⊥x 轴时,有 AF BF p ==,成立; 当AB 与x 轴不垂直时,设焦点弦AB 的方程为:2p y k x ⎛⎫=-⎪⎝⎭.代入抛物线方程: 2222p k x px ⎛⎫-= ⎪⎝⎭.化简得:()()222222014p k x p k x k -++=∵方程(1)之二根为x 1,x 2,∴1224k x x ⋅=.(122111212111111222x x p p pp AF BF AA BB x x x x +++=+=+=+++()()121222121222424x x p x x p p p p p p x x p x x ++++===+++++. 3.求证:=∠=∠'''FB A B AC Rt ∠.先证明:∠AMB =Rt ∠【证法一】延长AM 交BC 的延长线于E ,如图3,则△ADM ≌△ECM ,∴| AM |=| EM |,| EC |=| AD | ∴| BE |=| BC |+| CE |=| BC |+| AD | =| BF |+| AF |=| AB |每一个人的成功之路或许都不尽相同,但我相信,成功都需要每一位想成功的人去努力、去奋斗,而每∴△ABE 为等腰三角形,又M 是AE 的中点, ∴BM ⊥AE ,即∠AMB =Rt ∠ 【证法二】取AB 的中点N ,连结MN ,则| MN |=12(| AD |+| BC |)=12(| AF |+| BF |)=12| AB |,∴| MN |=| AN |=| BN |∴△ABM 为直角三角形,AB 为斜边,故∠AMB =Rt ∠.【证法三】由已知得C (-p 2,y 2)、D (-p 2,y 1),由此得M (-p 2,y 1+y 22).∴k AM =y 1-y 1+y 22x 1+p 2=y 1-y 22·y 212p +p =p (y 1-y 2)y 21+p 2=p (y 1--p 2y 1)y 21+p 2=p y 1,同理k BM =py 2 ∴k AM ·k BM =p y 1·p y 2=p 2y 1y 2=p 2-p 2=-1∴BM ⊥AE ,即∠AMB =Rt ∠.【证法四】由已知得C (-p 2,y 2)、D (-p2,y 1),由此得M (-p 2,y 1+y 22). ∴MA →=(x 1+p 2,y 1-y 22),MB →=(x 3+p 2,y 2-y 12)∴MA →·MB →=(x 1+p 2)(x 2+p 2)+(y 1-y 2)(y 2-y 1)4=x 1x 2+p 2(x 1+x 2)+p 24-(y 1-y 2)24=p 24+p 2(y 212p +y 222p )+p 24-y 21+y 22-2y 1y 24=p 22+y 1y 22=p 22+-p 22=0 ∴MA →⊥MB →,故∠AMB =Rt ∠.【证法五】由下面证得∠DFC =90 ,连结FM ,则FM =DM .又AD =AF ,故△ADM ≌△AFM ,如图4 ∴∠1=∠2,同理∠3=∠4每一个人的成功之路或许都不尽相同,但我相信,成功都需要每一位想成功的人去努力、去奋斗,而每∴∠2+∠3=12×180︒=90︒∴∠AMB =Rt ∠. 接着证明:∠DFC =Rt ∠【证法一】如图5,由于| AD |=| AF |,AD ∥RF ,故可设∠AFD =∠ADF =∠DFR =α, 同理,设∠BFC =∠BCF =∠CFR =β, 而∠AFD +∠DFR +∠BFC +∠CFR =180︒ ∴2(α+β)=180︒,即α+β=90︒,故∠DFC =90︒ 【证法二】取CD 的中点M ,即M (-p 2,y 1+y 22)由前知k AM =py 1,k CF =-y 2+p 2+p 2=-y 2p =p y 1∴k AM =k CF ,AM ∥CF ,同理,BM ∥DF ∴∠DFC =∠AMB =90︒.【证法三】∵DF →=(p ,-y 1),CF →=(p ,-y 2),∴DF →·CF →=p 2+y 1y 2=0 ∴DF →⊥CF →,故∠DFC =90︒.【证法四】由于| RF |2=p 2=-y 1y 2=| DR |·| RC |,即| DR || RF |=| RF || RC |,且∠DRF =∠FRC =90︒ ∴ △DRF ∽△FRC∴∠DFR =∠RCF ,而∠RCF +∠RFC =90︒ ∴∠DFR +∠RFC =90︒ ∴∠DFC =90︒4. C ’A 、C ’B 是抛物线的切线图6每一个人的成功之路或许都不尽相同,但我相信,成功都需要每一位想成功的人去努力、去奋斗,而每【证法一】∵k AM =p y 1,AM 的直线方程为y -y 1=p y 1(x -y 212p)与抛物线方程y 2=2px 联立消去x 得y -y 1=p y 1(y 22p -y 212p),整理得y 2-2y 1y +y 21=0可见△=(2y 1)2-4y 21=0,故直线AM 与抛物线y 2=2px 相切, 同理BM 也是抛物线的切线,如图8.【证法二】由抛物线方程y 2=2px ,两边对x 求导,(y 2)'x =(2px )'x ,得2y ·y 'x=2p ,y 'x =p y ,故抛物线y 2=2px 在点A (x 1,y 1)处的切线的斜率为k 切=y 'x| y =y 1=py 1. 又k AM =py 1,∴k 切=k AM ,即AM 是抛物线在点A 处的切线,同理BM 也是抛物线的切线.【证法三】∵过点A (x 1,y 1)的切线方程为y 1y =p (x +x 1),把M (-p 2,y 1+y 22)代入左边=y 1·y 1+y 22=y 21+y 1y 22=2px 1-p 22=px 1-p 22,右边=p (-p 2+x 1)=-p 22+px 1,左边=右边,可见,过点A 的切线经过点M ,即AM 是抛物线的切线,同理BM 也是抛物线的切线.5. C ’A 、C ’B 分别是∠A ’AB 和∠B ’BA 的平分线. 【证法一】延长AM 交BC 的延长线于E ,如图9,则△ADM ≌△ECM ,有AD ∥BC ,AB =BE , ∴∠DAM =∠AEB =∠BAM ,即AM 平分∠DAB ,同理BM 平分∠CBA . 【证法二】由图9可知只须证明直线AB 的倾斜角α是直线AM 的倾斜角β的2倍即可,即α图9图8每一个人的成功之路或许都不尽相同,但我相信,成功都需要每一位想成功的人去努力、去奋斗,而每=2β. 且M (-p 2,y 1+y 22)∵tan α=k AB =y 2-y 1x 2-x 1=y 2-y 1 y 222p -y 212p=2py 1+y 2. tan β=k AM =y 1-y 1+y 22x 1+p 2=y 1-y 22·y 212p +p =p (y 1-y 2)y 21+p 2=p (y 1--p 2y 1)y 21+p 2=py 1. ∴tan 2β=2tan β1-tan 2β=2py 11-(p y 1)2=2py 1y 22-p 2=2py 1y 22+y 1y 2=2py 1+y 2=tan α ∴α=2β,即AM 平分∠DAB ,同理BM 平分∠CBA .6. AC ’、A ’F 、y 轴三线共点,BC ’、B ’F 、y 轴三线共点 【证法一】如图10,设AM 与DF 相交于点G 1,由以上证明知| AD |=| AF |,AM 平分∠DAF ,故AG 1也是DF 边上的中线, ∴G 1是DF 的中点.设AD 与y 轴交于点D 1,DF 与y 轴相交于点G 2, 易知,| DD 1 |=| OF |,DD 1∥OF , 故△DD 1G 2≌△FOG 2∴| DG 2 |=| FG 2 |,则G 2也是DF 的中点.∴G 1与G 2重合(设为点G ),则AM 、DF 、y 轴三线共点,同理BM 、CF 、y 轴也三线共点.【证法二】AM 的直线方程为y -y 1=p y 1(x -y 212p),令x =0得AM 与y 轴交于点G 1(0,y 12),又DF 的直线方程为y =-y 1p (x -p 2),令x =0得DF 与y 轴交于点G 2(0,y 12)∴AM 、DF 与y 轴的相交同一点G (0,y 12),则AM 、DF 、y 轴三线共点,图10每一个人的成功之路或许都不尽相同,但我相信,成功都需要每一位想成功的人去努力、去奋斗,而每同理BM 、CF 、y 轴也三线共点H .由以上证明还可以得四边形MHFG 是矩形. 7. A 、O 、B ’三点共线,B 、O 、A ’三点共线. 【证法一】如图11,k OA =y 1x 1=y 1 y 212p=2py 1,k OC =y 2 -p 2 =-2y 2p =-2py 2p 2=-2py 2-y 1y 2=2p y 1∴k OA =k OC ,则A 、O 、C 三点共线, 同理D 、O 、B 三点也共线.【证法二】设AC 与x 轴交于点O ',∵AD ∥RF ∥BC∴| RO ' || AD |=| CO ' || CA |=| BF || AB |,| O 'F || AF |=| CB || AB |, 又| AD |=| AF |,| BC |=| BF |,∴| RO ' || AF |=| O 'F || AF |∴| RO ' |=| O 'F |,则O '与O 重合,即C 、O 、A 三点共线,同理D 、O 、B 三点也共线.【证法三】设AC 与x 轴交于点O ',RF ∥BC ,| O 'F || CB |=| AF || AB |,∴| O 'F |=| CB |·| AF || AB |=| BF |·| AF || AF |+| BF |=1 1| AF |+1| BF |=p2【见⑵证】∴O '与O 重合,则即C 、O 、A 三点共线,同理D 、O 、B 三点也共线. 【证法四】∵OC →=(-p 2,y 2),OA →=(x 1,y 1),∵-p 2·y 1-x 1 y 2=-p 2·y 1-y 212p y 2=-py 12-y 1y 2y 12p =-py 12+p 2y 12p =0∴OC →∥OA →,且都以O 为端点∴A 、O 、C 三点共线,同理B 、O 、D 三点共线.【推广】过定点P (m ,0)的直线与抛物线y 2=2px (p >0)相交于点A 、B ,过A 、B 两点分别作直线l :x =-m 的垂线,垂足分别为M 、N ,则A 、O 、N 三点共线,B 、O 、M图11每一个人的成功之路或许都不尽相同,但我相信,成功都需要每一位想成功的人去努力、去奋斗,而每三点也共线,如下图:8. 若| AF |:| BF |=m :n ,点A 在第一象限,θ为直线AB 的倾斜角. 则cos θ=m -nm +n ;【证明】如图14,过A 、B 分别作准线l 的垂线,垂足分别为D ,C ,过B 作BE ⊥AD于E ,设| AF |=mt ,| AF |=nt ,则| AD |=| AF |,| BC |=| BF |,| AE |=| AD |-| BC |=(m -n )t ∴在Rt △ABE 中,cos ∠BAE =| AE || AB |= (m -n )t (m +n )t =m -nm +n∴cos θ=cos ∠BAE =m -nm +n.【例6】设经过抛物线y 2=2px 的焦点F 的直线与抛物线相交于两点A 、B ,且| AF |:| BF |=3:1,则直线AB 的倾斜角的大小为 .每一个人的成功之路或许都不尽相同,但我相信,成功都需要每一位想成功的人去努力、去奋斗,而每则E 的坐标为( p2+x 1 2,y 12),则点E 到y 轴的距离为d = p2+x 1 2=12| AF |故以AF 为直径的圆与y 轴相切, 同理以BF 为直径的圆与y 轴相切.【说明】如图15,设M 是AB 的中点,作MN ⊥准线l 于N ,则| MN |=12(| AD |+| BC |)=12(| AF |+| BF |)=12| AB |则圆心M 到l 的距离| MN |=12| AB |,故以AB 为直径的圆与准线相切. 10. MN 交抛物线于点Q ,则Q 是MN 的中点.【证明】设A (y 212p ,y 1),B (y 222p ,y 1),则C (-p 2,y 2),D (-p 2,y 1),M (-p 2,y 1+y 22),N (y 21+y 224p ,y 1+y 22),设MN 的中点为Q ',则Q ' ( -p 2+y 21+y 224p 2,y 1+y 22)∵ -p 2+y 21+y 224p 2= -2p 2+y 21+y 22 8p = 2y 1y 2+y 21+y 228p = ⎝⎛⎭⎫y 1+y 222 2p∴点Q ' 在抛物线y 2=2px 上,即Q 是MN 的中点.图16。
抛物线30条经典性质及其证明

AB
2p sin2
、 SAOB
p2 2sin
得证.
20. SABC
p2 sin2
证明: SABC
1 2
|
AB
| | PF
|
1 2
2p
1
1 k2
p2(
y1 2
y2 ) 2
p
1
1 k2
p2
(
p k
)2
p 2(1
1 k2
)
p2 sin2
21. AB 2 p ;
证明:由
AB
2p sin2
得证.
2 px,
y1y2
2
pm,
2
px1
2
px2 4
4 pm
2 px,
x
x1
x2 4
2m
.
所以点 M 的横坐标为 x
x1 x2 2m 4
. 点 M 是 PC 的中点.
28.设点 A、B 在准线上的射影分别是 A1,B1,则 PA 垂直平分 A1F, PB 垂直平分 B1F,从而 PA 平
分 A1AF ,PB 平分 B1BF
y1)
p(x2 x1)
y12 y22 2
y22 2
y12 2
y12 y22 2
0
10.
AF
P 1 cos
;
BF
P 1 cos
;
关注公众号“品数学”,获取更多干货
证明:作 AH 垂直 x 轴于点 H,则 |
AF
||
AA || KF
| | FH
|
p |
AF
| cos ,|
AF
|
p 1 cos
抛物线的简单几何性质

y
1 y2
k
(x 4x
2)
Y
可得ky2 4 y 4(2k 1) 0 (1)当k 0时,由方程得 y 1.
P·
把y 1代入y2 4x,得x 1 .
O
X
4
这时,直线l与抛物线只有一个公共点(1 ,1) 4
例1 已知抛物线的方程为y²=4x,直线l过定点P(-2,1),斜率为k,k 为何值时,直线l与抛物线y²=4x:只有一个公共点;有两个公共 点;没有公共点?
(0,0)
e=1
x2 2 py ( p 0)
y 0, xR
关于y 轴 对称,无 对称中心
(0,0)
e=1
x2 2 py y 0,
关于y 轴 对称,无
(0,0) e=1
( p 0) x R 对称中心
例3 已知抛物线关于x轴对称,它的顶点在坐标原点, 并且经过点(2,2 2),求它的标准方程。
(5)一次项系数的绝对值越大,开口越大
课堂小结
(1)抛物线的简单几何性质 (2)抛物线与椭圆、双曲线几何性质的不同点 (3)应用性质求标准方程的方法和步骤
小结:
1、抛物线的定义,标准方程类型与图象的对应 关系以及判断方法
2、抛物线的定义、标准方程和它 的焦点、准线、方程
3、注重数形结合的思想。
例5 过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的 直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴。
证明:以抛物线的对称轴为x轴,它的顶点为原点,
建立直角坐标系。设抛物线的方程为y2 2 px,
点A的坐标为(
y02 2p
,
y0
),则直线OA的方程为y
抛物线的准线是x p
(完整版)抛物线的性质归纳及证明(最新整理)

抛物线的常见性质及证明概念焦半径:抛物线上一点与其焦点的连线段;焦点弦:两端点在抛物线上且经过抛物线的焦点线段称为焦点弦.性质及证明过抛物线y 2=2px (p >0)焦点F 的弦两端点为,,倾斜角为,中点为),(11y x A ),(22y x B αC(x 0,y 0), 分别过A 、B 、C 作抛物线准线的垂线,垂足为A’、B’、C’.1.求证:①焦半径;②焦半径;αcos 12||1-=+=p p x AF αcos 12||2+=+=pp x BF ③+=; ④弦长| AB |=x 1+x 2+p =;特别地,当x 1=x 2(1| AF |1| BF |2p α2sin 2p =90︒)时,弦长|AB|最短,称为通径,长为2p ;⑤△AOB 的面积S △OAB =.ααsin 22p 证明:根据抛物线的定义,| AF |=| AD |=x 1+,| BF |=| BC |=x 2+,p2p2| AB |=| AF |+| BF |=x 1+x 2+p如图2,过A 、B 引x 轴的垂线AA 1、BB 1,垂足为A 1、B 1,那么| RF |=| AD |-| FA 1 |=| AF |-| AF |cos θ,∴| AF |==| RF |1-cos θp1-cos θ同理,| BF |==| RF |1+cos θp1+cos θ∴| AB |=| AF |+| BF |=+=.p1-cos θp1+cos θ2psin 2θS △OAB =S △OAF +S △OBF =| OF || y 1 |+| OF || y 1 |=·121212p2·(| y 1 |+| y 1 |)∵y 1y 2=-p 2,则y 1、y 2异号,因此,| y 1 |+| y 1 |=| y 1-y 2 |∴S △OAB =| y 1-y 2 |====.p 4p4(y 1+y 2)2-4y 1y 2p44m 2p 2+4p 2p 221+m2p 22sin θ2.求证:①;②;③ +=.2124p x x =212y y p =-1| AF |1| BF |2p 当AB ⊥x 轴时,有成立;AF BF p ==,当AB 与x 轴不垂直时,设焦点弦AB 的方程为:.代入抛物线方程:2p y k x ⎛⎫=-⎪⎝⎭.化简得:2222p k x px ⎛⎫-= ⎪⎝⎭()()222222014p k x p k x k -++=∵方程(1)之二根为x 1,x 2,∴.1224k x x ⋅=111211111122p pAF BF AA BB x x +=+=+=++.()()121222121222424x x p x x p p p p p p x x p x x ++++===+++++3.求证:Rt ∠.=∠=∠'''FB A B AC 先证明:∠AMB =Rt ∠【证法一】延长AM 交BC 的延长线于E ,如图3,则△ADM ≌△ECM ,∴| AM |=| EM |,| EC |=| AD |∴| BE |=| BC |+| CE |=| BC |+| AD |=| BF |+| AF |=| AB |∴△ABE 为等腰三角形,又M 是AE 的中点,∴BM ⊥AE ,即∠AMB =Rt ∠【证法二】取AB 的中点N ,连结MN ,则| MN |=(| AD |+| BC |)=(| AF |+| BF |)=| AB |,∴| MN |=| AN |=| BN |121212∴△ABM 为直角三角形,AB 为斜边,故∠AMB =Rt ∠.【证法三】由已知得C (-,y 2)、D (-,y 1),由此得M (-,).p 2p 2p 2y 1+y 22∴k AM =====,同理k BM =y 1-y 1+y 22x 1+p2y 1-y 22·y 212p+pp (y 1-y 2)y 21+p 2p (y 1-\f(-p 2,y 1))y 21+p2py 1p y 2∴k AM ·k BM =·===-1p y 1p y 2p 2y 1y 2p 2-p 2∴BM ⊥AE ,即∠AMB =Rt ∠.【证法四】由已知得C (-,y 2)、D (-,y 1),由此得M (-p 2p2,).p 2y 1+y 22∴=(x 1+,),=(x 3+,)MA →p 2y 1-y 22MB → p 2y 2-y 12∴·=(x 1+)(x 2+)+MA → MB →p 2p 2(y 1-y 2)(y 2-y 1)4=x 1x 2+(x 1+x 2)+-p 2p 24(y 1-y 2)24=+(+)+-p 24p 2y 212p y 222p p 24y 21+y 22-2y 1y 24=+=+=0p 22y 1y 22p 22-p 22∴⊥,故∠AMB =Rt ∠.MA → MB →【证法五】由下面证得∠DFC =90 ,连结FM ,则FM =DM .又AD =AF ,故△ADM ≌△AFM ,如图4∴∠1=∠2,同理∠3=∠4∴∠2+∠3=×180︒=90︒12∴∠AMB =Rt ∠.接着证明:∠DFC =Rt ∠【证法一】如图5,由于| AD |=| AF |,AD ∥RF ,故可设∠AFD =∠ADF =∠DFR =α,同理,设∠BFC =∠BCF =∠CFR =β,而∠AFD +∠DFR +∠BFC +∠CFR =180︒∴2(α+β)=180︒,即α+β=90︒,故∠DFC =90︒【证法二】取CD 的中点M ,即M (-,)p 2y 1+y 22由前知k AM =,k CF ===p y 1-y 2+p 2+p 2-y 2p py1∴k AM =k CF ,AM ∥CF ,同理,BM ∥DF ∴∠DFC =∠AMB =90︒.【证法三】∵=(p ,-y 1),=(p ,-y 2),DF → CF →∴·=p 2+y 1y 2=0DF → CF →∴⊥,故∠DFC =90︒.DF → CF →【证法四】由于| RF |2=p 2=-y 1y 2=| DR |·| RC |,即| DR || RF |=,且∠DRF =∠FRC =90︒| RF || RC |∴ △DRF ∽△FRC∴∠DFR =∠RCF ,而∠RCF +∠RFC =90︒∴∠DFR +∠RFC =90︒∴∠DFC =90︒4. C ’A 、C ’B 是抛物线的切线图6【证法一】∵k AM =,AM 的直线方程为y -y 1=(x -)p y 1p y1y 212p 与抛物线方程y 2=2px联立消去x 得y -y 1=(-),整理得y 2-2y 1y +=0p y 1y 22p y 212py 2 1可见△=(2y 1)2-4=0,y21故直线AM 与抛物线y 2=2px 相切,同理BM 也是抛物线的切线,如图8.【证法二】由抛物线方程y 2=2px ,两边对x求导,=,(y 2)'x(2px )'x得2y ·=2p ,=,故抛物线y 2=2px 在点A (x 1,y 1)处的切线的斜率为k 切=| y 'x y ' x p y y 'x y =y 1=.py1又k AM =,∴k 切=k AM ,即AM 是抛物线在点A 处的切线,同理BM 也是抛物线的py1切线.【证法三】∵过点A (x 1,y 1)的切线方程为y 1y =p (x +x 1),把M (-,)代入p 2y 1+y 22左边=y 1·===px 1-,y 1+y 22y 21+y 1y 222px 1-p 22p 22右边=p (-+x 1)=-+px 1,左边=右边,可见,过点A 的切线经过点M ,p 2p 22即AM 是抛物线的切线,同理BM 也是抛物线的切线.5. C’A 、C’B 分别是∠A’AB 和∠B’BA 的平分线.【证法一】延长AM 交BC 的延长线于E ,如图9,则△ADM ≌△ECM ,有AD ∥BC ,AB =BE ,∴∠DAM =∠AEB =∠BAM ,E图8即AM 平分∠DAB ,同理BM 平分∠CBA .【证法二】由图9可知只须证明直线AB 的倾斜角α是直线AM 的倾斜角β的2倍即可,即α=2β. 且M (-,)p 2y 1+y 22∵tan α=k AB ===.y 2-y 1x 2-x 1y 2-y 1y 2 22p -y 212p 2py 1+y 2tan β=k AM =====.y 1-y 1+y 22x 1+p 2y 1-y 22·y 2 12p +pp (y 1-y 2)y 2 1+p 2p (y 1-\f(-p 2,y 1))y 2 1+p 2py 1∴tan 2β======tan α2tan β1-tan 2β2p y 11-(\f(p ,y 1))22py 1y 2 2-p 22py 1y 2 2+y 1y 22p y 1+y 2∴α=2β,即AM 平分∠DAB ,同理BM 平分∠CBA .6. AC’、A’F 、y 轴三线共点,BC’、B’F 、y 轴三线共点【证法一】如图10,设AM 与DF 相交于点G 1,由以上证明知| AD |=| AF |,AM 平分∠DAF ,故AG 1也是DF 边上的中线,∴G 1是DF 的中点.设AD 与y 轴交于点D 1,DF 与y 轴相交于点G 2,易知,| DD 1 |=| OF |,DD 1∥OF ,故△DD 1G 2≌△FOG 2∴| DG 2 |=| FG 2 |,则G 2也是DF 的中点.∴G 1与G 2重合(设为点G ),则AM 、DF 、y 轴三线共点,同理BM 、CF 、y 轴也三线共点.【证法二】AM 的直线方程为y -y 1=(x -),py 1y 212p图10令x =0得AM 与y 轴交于点G 1(0,),y 12又DF 的直线方程为y =-(x -),令x =0得DF 与y 轴交于点G 2(0,)y 1p p 2y 12∴AM 、DF 与y 轴的相交同一点G (0,),则AM 、DF 、y 轴三线共点,y 12同理BM 、CF 、y 轴也三线共点H .由以上证明还可以得四边形MHFG 是矩形.7. A 、O 、B’三点共线,B 、O 、A’三点共线.【证法一】如图11,k OA ===,y 1x 1y 1y 212p2py1k OC ==-=-=-=y 2-p22y 2p 2py 2p 22py 2-y 1y 22p y 1∴k OA =k OC ,则A 、O 、C 三点共线,同理D 、O 、B 三点也共线.【证法二】设AC 与x 轴交于点O ',∵AD ∥RF ∥BC∴==,=,| RO ' || AD || CO ' || CA || BF || AB || O 'F || AF || CB || AB |又| AD |=| AF |,| BC |=| BF |,∴=| RO ' || AF || O 'F || AF |∴| RO ' |=| O 'F |,则O '与O 重合,即C 、O 、A 三点共线,同理D 、O 、B 三点也共线.【证法三】设AC 与x 轴交于点O ',RF ∥BC ,=,| O 'F || CB || AF || AB |∴| O 'F |====【见⑵证】| CB |·| AF || AB || BF |·| AF || AF |+| BF |11| AF |+1| BF |p 2∴O '与O 重合,则即C 、O 、A 三点共线,同理D 、O 、B 三点也共线.【证法四】∵=(-,y 2),=(x 1,y 1),OC → p 2OA →∵-·y 1-x 1 y 2=-·y 1- y 2=--=-+=0p 2p2y 212p py 12y 1y 2y 12p py 12p 2y 12p图11∴∥,且都以O 为端点OC → OA →∴A 、O 、C 三点共线,同理B 、O 、D 三点共线.【推广】过定点P (m ,0)的直线与抛物线y 2=2px (p >0)相交于点A 、B ,过A 、B 两点分别作直线l :x =-m 的垂线,垂足分别为M 、N ,则A 、O 、N 三点共线,B 、O 、M 三点也共线,如下图:8. 若| AF |:| BF |=m :n ,点A 在第一象限,θ为直线AB 的倾斜角. 则cos θ=;m -nm +n【证明】如图14,过A 、B 分别作准线l 的垂线,垂足分别为D ,C ,过B 作BE ⊥AD于E ,设| AF |=mt ,| AF |=nt ,则| AD |=| AF |,| BC |=| BF |,| AE |=| AD |-| BC |=(m -n )t ∴在Rt △ABE 中,cos ∠BAE ===| AE || AB |(m -n )t (m +n )t m -nm +n∴cos θ=cos ∠BAE =.m -nm +n 【例6】设经过抛物线y 2=2px 的焦点F 的直线与抛物线相交于两点A 、B ,且| AF |:| BF |=3:1,则直线AB 的倾斜角的大小为.【说明】如图15,设E 是AF 的中点,则E 的坐标为(,),p2+x 12y 12则点E 到y 轴的距离为d ==| AF |p2+x 1212故以AF 为直径的圆与y 轴相切,同理以BF 为直径的圆与y 轴相切.【说明】如图15,设M 是AB 的中点,作MN ⊥准线l 于N ,则| MN |=(| AD |+| BC |)=(| AF |+| BF |)=| AB |121212则圆心M 到l 的距离| MN |=| AB |,12故以AB 为直径的圆与准线相切. 10. MN 交抛物线于点Q ,则Q 是MN 的中点.【证明】设A (,y 1),B (,y 1),则C (-,y 2),D (-,y 1),y 212p y 222p p 2p2M (-,),N (,),p 2y 1+y 22y 2 1+y 224p y 1+y 22设MN 的中点为Q ',则Q ' (,)-p 2+y 21+y 224p 2y 1+y 22∵ ===-p 2+y 21+y 224p 2-2p 2+y 2 1+y 2 28p 2y 1y 2+y 2 1+y 228p (y 1+y 22)22p图16∴点Q 在抛物线y2=2px上,即Q是MN的中点.。
抛物线其性质知识点大全
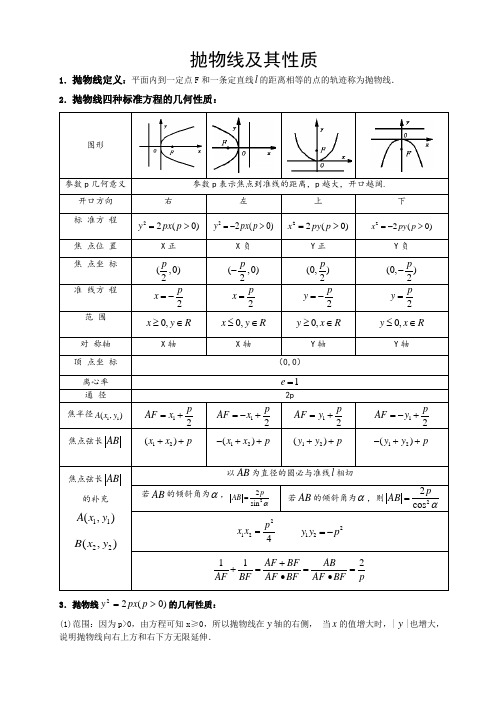
抛物线及其性质1.抛物线定义:平面内到一定点F 和一条定直线l 的距离相等的点的轨迹称为抛物线. 2.抛物线四种标准方程的几何性质:图形参数p 几何意义 参数p 表示焦点到准线的距离,p 越大,开口越阔.开口方向 右左上下 标 准方 程 22(0)y px p => 22(0)y px p =-> 22(0)x py p =>22(0)x py p =->焦 点位 置 X 正X 负Y 正Y 负焦 点坐 标 (,0)2p (,0)2p -(0,)2p(0,)2p -准 线方 程 2p x =-2p x =2p y =-2p y =范 围 0,x y R ≥∈0,x y R ≤∈0,y x R ≥∈0,y x R ≤∈对 称轴 X 轴X 轴Y 轴Y 轴顶 点坐 标 (0,0)离心率 1e =通 径 2p焦半径11(,)A x y 12p AF x =+12p AF x =-+12p AF y =+12p AF y =-+焦点弦长AB12()x x p ++ 12()x x p -++ 12()y y p ++ 12()y y p -++焦点弦长AB 的补充11(,)A x y22(,)B x y以AB 为直径的圆必与准线l 相切若AB 的倾斜角为α,22sin p AB α=若AB 的倾斜角为α,则22cos pAB α=2124p x x = 212y y p =-112AF BF AB AF BF AF BF AF BF p++===•• 3.抛物线)0(22>=p px y 的几何性质:(1)范围:因为p>0,由方程可知x ≥0,所以抛物线在y 轴的右侧, 当x 的值增大时,|y |也增大,说明抛物线向右上方和右下方无限延伸.(2)对称性:对称轴要看一次项,符号决定开口方向. (3)顶点(0,0),离心率:1=e ,焦点(,0)2p F ,准线2px -=,焦准距p . (4) 焦点弦:抛物线)0(22>=p px y 的焦点弦AB ,),(11y x A ,),(22y x B ,则p x x AB ++=21||. 弦长|AB|=x 1+x 2+p,当x 1=x 2时,通径最短为2p 。
抛物线及其性质知识点大全

抛物线及其性质1.抛物线定义:平面内到一定点F 和一条定直线l 的距离相等的点的轨迹称为抛物线. 2.抛物线四种标准方程的几何性质:3.抛物线)0(22>=p px y 的几何性质:(1)范围:因为p>0,由方程可知x ≥0,所以抛物线在y 轴的右侧, 当x 的值增大时,|y |也增大,说明抛物线向右上方和右下方无限延伸.(2)对称性:对称轴要看一次项,符号决定开口方向. (3)顶点(0,0),离心率:1=e ,焦点(,0)2p F ,准线2px -=,焦准距p . (4) 焦点弦:抛物线)0(22>=p px y 的焦点弦AB ,),(11y x A ,),(22y x B ,则p x x AB ++=21||. 弦长|AB|=x 1+x 2+p,当x 1=x 2时,通径最短为2p 。
4.焦点弦的相关性质:焦点弦AB ,),(11y x A ,),(22y x B ,焦点(,0)2pF (1) 若AB 是抛物线22(0)y px p =>的焦点弦(过焦点的弦),且11(,)A x y ,22(,)B x y ,则:2124p x x =,212y y p =-。
(2) 若AB 是抛物线22(0)y px p =>的焦点弦,且直线AB 的倾斜角为α,则22sin P AB α=(α≠0)。
(3) 已知直线AB 是过抛物线22(0)y px p =>焦点F ,112AF BF AB AF BF AF BF AF BF p++===∙∙ (4) 焦点弦中通径最短长为2p 。
通径:过焦点垂直于焦点所在的轴的焦点弦叫做通径.(5) 两个相切:○1以抛物线焦点弦为直径的圆与准线相切.○2过抛物线焦点弦的两端点向准线作垂线,以两垂足为直径端点的圆与焦点弦相切。
5.弦长公式:),(11y x A ,),(22y x B 是抛物线上两点,则AB =||11||1212212y y k x x k -+=-+=6.直线与抛物线的位置关系 直线,抛物线,,消y 得:(1)当k=0时,直线l 与抛物线的对称轴平行,有一个交点; (2)当k ≠0时,Δ>0,直线l 与抛物线相交,两个不同交点; Δ=0, 直线l 与抛物线相切,一个切点; Δ<0,直线l 与抛物线相离,无公共点。
抛物线的概念

抛物线的概念抛物线的概念及其应用1. 引言抛物线是数学中一个重要的曲线,其形状独特而美妙。
在几何学和物理学中,抛物线广泛应用于各种领域,包括力学、光学、天文学等。
本文将深入探讨抛物线的概念、性质和应用,以便更深入地理解这一曲线。
2. 抛物线的定义抛物线是所有离一个定点(称为焦点)距离与其到一条直线(称为准线)的距离成正比的点构成的曲线。
准线和焦点之间的距离称为焦距,并用字母p表示。
3. 抛物线的性质3.1 对称性抛物线具有关于准线对称的性质。
如果抛物线上的点P到准线的距离为d,则点P'到准线的距离也为d并且两点在准线的同一侧。
3.2 焦点与准线的距离关系对于抛物线上的任意一点P,其距离焦点的距离与其到准线的距离之间存在以下关系:d = |PF| = |PL| = p,其中PF表示点P到焦点的距离,PL表示点P到准线的距离。
3.3 焦点的确定方法通过对称性和焦点与准线的距离关系,可以确定焦点的位置。
以焦点为圆心、焦距为半径作圆与准线相交于点O,连接PO即可确定焦点的位置。
4. 抛物线的方程抛物线的方程可以通过焦点、准线和直角坐标系来求得。
一般来说,抛物线的顶点位于坐标轴上,其坐标表示为(h,k)。
根据抛物线的定义,可以得到一般式方程:y = ax^2 + bx + c。
5. 抛物线的重要应用5.1 物体的抛射运动在力学中,抛物线被广泛应用于描述物体的抛射运动。
当物体在水平面上以一定初速度和发射角度被抛出时,其运动轨迹正是一个抛物线。
通过抛物线方程,可以计算物体的运动轨迹、最大高度和最远距离等参数。
5.2 反射聚焦在光学中,抛物线被用于反射聚焦。
抛物面反射器是一种利用抛物线形状的曲面来聚焦光线的光学器件。
这种曲面具有将接近光轴的入射平行光束反射到焦点上的特点,因此被广泛应用于望远镜、卫星接收器等光学设备中。
5.3 天体运动轨迹在天文学中,抛物线也用于描述天体的运动轨迹。
彗星经常沿着抛物线轨道绕太阳运行,其中太阳位于焦点上。
抛物线30条经典性质及其证明

抛物线的30条经典性质及证明已知抛物线22(0)y px p =>,AB 是抛物线的焦点弦,点C 是AB 的中点.AA’垂直准线于A’,BB’垂直准线于B’,CC’垂直准线于C’,CC’交抛物线于点M ,准线交x 轴于点K.求证:1.12||,||,22p pAF x BF x =+=+2.11()22CC AB AA BB '''==+;3.以AB 为直径的圆与准线L 相切;证明:CC’是梯形AA’BB’的中位线,||||||||||2||2AB AF BF AA BB CC r'''=+=+==4.90AC B '∠=;(由1可证)5.90A FB ''∠= ;,,||||,,1,2AA FK A FK FA A AF AA AA F AFA A FK AFK '''∴∠=∠'''=∴∠=∠'∴∠=∠ 证明:同理:1,2B FK BFK '∠=∠得证.6.1C F A B 2'''=.证明:由90A FB ''∠=得证.7.AC '垂直平分A F ';BC '垂直平分B F ';证明:由1C F A B 2'''=可知,1||||||,2C F A B C A '''''==||||,.AF AA '=∴ 又得证同理可证另一个.8.AC '平分A AF '∠,BC '平分B BF '∠,A’F 平分AFK ∠,B’F 平分BFK ∠.证明:由AC '垂直平分A F '可证.9.C F 'AB ⊥;证明:122121(,)(,)2y y C F AB p x x y y +'⋅=-⋅-- 22222212211221()02222y y y y y y p x x --=-+=-+=10.1cos P AF α=-;1cos PBF α=+;证明:作AH 垂直x 轴于点H,则||||||||||cos ,||1cos pAF AA KF FH p AF AF αα'==+=+∴=-.同理可证另一个.11.112AF BF P+=;证明:由1cos P AF α=-;1cos PBF α=+;得证.12.点A 处的切线为11()y y p x x =+;证明:(方法一)设点A 处切线方程为11()y y k x x -=-,与22y px =联立,得21122()0,ky py p y kx -+-=由2110220,x k y k p ∆=⇒-+=解这个关于k 的一元二次方程(它的差别式也恰为0)得:111,2y pk x y ==得证.证法二:(求导)22y px =两边对x 求导得1122,,|x x p pyy p y y y y ='''==∴=得证.13.AC’是切线,切点为A;BC’是切线,切点为B;证明:易求得点A 处的切线为11()y y p x x =+,点B 处的切线为22()y y p x x =+,解得两切线的交点为12(,22y y p C +'-,得证.14.过抛物线准线上任一点P 作抛物线的切线,则过两切点Q 1、Q 2的弦必过焦点;并且12.PQ PQ ⊥证明:设点(,)()2pP t t R -∈为准线上任一点,过点P 作抛物线的切线,切点为2(,)2y Q y p ,22y px =两边对x 求导得22222,,,20,22PQ p p y tyy p y K y ty p y y y pp -''==∴==∴--=+显然22440,t p ∆=+>切点有两个,设为2221211221212(,),(,),2,,22y y Q y Q y y y t y y p p p+==-则1212122222221212222222FQ FQ y y py py k k y y y p y p pp p p ∴-=-=----1222121211221222220,py py p py y y y y y y y y y =-=-=++++所以Q 1Q 2过焦点.22222222121212*********(,)(,)()2222444y y y y y y p p p PQ PQ y t y t y y t y y tp p p +⋅=+-⋅+-=++-++ 22222222222121212()2420,242424y y y y y y p p p t p t t t ++-+=-+-=-+-=-+-=12.PQ PQ ∴⊥15.A 、O 、B '三点共线;B 、O 、A '三点共线;证明:A 、O 、B '三点共线2211212112.222OA OB y p pk k x y y y y y y p p '⇐=⇐=-⇐=-⇐=-同理可证:B 、O 、A '三点共线.16.122y y p ⋅=-;1224p x x ⋅=证明:设AB 的方程为(2py k x =-,与22y px =联立,得2220,ky py kp --=212122,,py y y y p k∴+==-224212122.2244y y p p x x p p p ∴=⋅==17.1222sin p AB x x p α=++=证明:1212,22p pAB AF FB x x x x p =+=+++=++||2AB p =222sin pα==得证.18.22sin AOBp S α∆=;证明:122AOB OFA OFB p S S S ∆∆∆=+=⋅⋅22sin p α==.19.322AOBS pAB∆⎛⎫= ⎪⎝⎭(定值);证明:由22sinpABα=、22sinAOBpSα∆=得证.20.22sinABCp Sα'∆=证明:11||||222 ABCS AB PF'∆=⋅=⋅22221(1)sinppkα==+=21.2AB p≥;证明:由22sinpABα=得证.22.122ABpky y=+;证明:由点差法得证.23.121222tanP Py yx xα==--;证明:作AA2垂直x轴于点A2,在2AA F∆中,2121tan,2AA yFA pxα==-同理可证另一个.24.2A B4AF BF''=⋅;证明:2212124||4()()22p pA B AF BF y y x x''=⋅⇔-=++2222121212121212242224y y y y x x px px p y y x x p⇔+-=+++⇔-=+,由122y y p⋅=-,1224px x⋅=得证.25.设CC’交抛物线于点M,则点M是CC’的中点;证明:12121212 (,),(),CC, 22224x x y y y y x x ppC C++++-''-∴中点横坐标为把122y yy+=代入22y px=,得2221212121222222,2,.444y y y y px px p x x ppx px x+++-+-=∴==所以点M的横坐标为12.4x x px+-=点M是CC’的中点.当弦AB 不过焦点时,设AB 交x 轴于点(,0)(0)D m m >,设分别以A 、B 为切点的切线相交于点P ,求证:26.点P 在直线x m =-上证明:设:,AB x ty m =+与22y px =联立,得21212220,2,2y pty pm y y pt y y pm --=∴+==-,又由221112121222:()(),,222:()PA y y p x x y y y y y y y y PB y y p x x =+⎧+-=-∴=⎨=+⎩,相减得代入11()y y p x x =+得,22112112,2,,22y y y y px y y px x m +=+∴=∴=-得证.27.设PC 交抛物线于点M ,则点M 是PC 的中点;证明:121212122(,),(,),,2224x x y y y y x x mC P m PC ++++--∴中点横坐标为把122y y y +=代入22y px =,得221212121212222422,2,2,.444y y y y px px pm x x mpx y y pm px x +++-+-==-∴== 所以点M 的横坐标为122.4x x mx +-=点M 是PC 的中点.28.设点A 、B 在准线上的射影分别是A 1,B 1,则PA 垂直平分A 1F ,PB 垂直平分B 1F ,从而PA 平分1A AF ∠,PB 平分1B BF∠证明:1111110()1,,()22PA A F y y p p k k PA A F y p p y p-⋅=⋅=⋅-=-∴⊥--又1||||AF AA =,所以PA 垂直平分A 1F.同理可证另一个.证法二:1112221112,,0,22AF AP AA y py pk k k y y y p p p ====--111tan tan 11AP AA AF APAF AP AP AA k k k k FAP PAA k k k k --∴∠-∠=-+⋅+⋅12222231111111222221111111122111202()022()101py p p p py y p y y p y y py p p p p ppy p y y y y p y p p y y p y y y p -----+=-==--=-+++⋅+⋅-11tan tan ,.FAP PAA FAP PAA ∴∠=∠∴∠=∠同理可证另一个29.PFA PFB∠=∠证明:11111,,,PAA PAF PFA PA A PFB PB B PA A PB B ∆≅∆⇒∠=∠∠=∠∴∠=∠同理:只需证易证:111111||||||,,PA PF PB PA B PB A ==∴∠=∠11,PA A PB B ∴∠=∠30.2||||||FA FB PF ⋅= 证明:22222212121212122||||()()(),2224444y y y y p p p p p AF BF x x x x x x p+⋅=++=+++=++1212(,),22y y y y P p + 22222222121212122||,222444y y y y y y y y p p PF p p ++⎛⎫⎛⎫∴=-+= ⎪ ⎝⎭⎝⎭得证.例1:(2007江苏高考第19题)如图,过C(0,c)(c>0)作直线与抛物线y=x 2相交于A、B 两点,一条垂直于x 轴的直线,分别与线段AB 和直线y+c=0交于P、Q。
抛物线性质归纳、证明和应用

抛物线性质归纳、证明和应用抛物线是平面到定点的距离等于到定直线(定点在定直线外)的距离的点的轨迹,它是椭圆过渡到双曲线的瞬间曲线,它只有一支(双曲线有两支),只有一条对称轴,没有渐近线和对称中心,属于无心曲线.抛物线的焦半径、焦点弦性质丰富多彩,此外还有定点、定值、定弦、最值等问题也值得探讨,抛物线的许多性质也是历年高考的重点和热点,这里就它的一些性质加以归纳,说明和证明,及其在历年高考和模拟考试出现的典例. 一、焦半径、焦点弦性质如图,AB 是过抛物线 y 2=2px (p >0)焦点F 的弦,AD 、BC 是准线的垂线,垂足分别为D 、C ,M 是CD 的中点,N 是AB 的中点.设点A (x 1,y 1)、点B (x 2,y 2),直线AB 交y 轴于点K (0,y 3),则:⑴ ① y 1y 2=-p 2;② x 1x 2=p 24;③ 1y 1+1y 2=1y 3;④ | AB |=x 1+x 2+p =2psin 2θ (θ为AB 的倾斜角);⑤ S △OAB =p22sin θ,S 梯形ABCD =2p2sin 3θ..⑵1| AF |+1| BF |=2p ; ⑶ ∠AMB =∠DFC =Rt ∠; ⑷ AM 、BM 是抛物线的切线;⑸ AM 、BM 分别是∠DAB 和∠CBA 的平分线; ⑹ AM 、DF 、y 轴三线共点,BM 、CF 、y 轴三线共点;⑺ A 、O 、C 三点共线,B 、O 、D 三点共线; ⑻ 若| AF |:| BF |=m :n ,点A 在第一象限,θ为直线AB 的倾斜角. 则cos θ=m -nm +n;⑼ 以AF 为直径的圆与y 轴相切,以BF 为直径的圆与y 轴相切; 以AB 为直径的圆与准线相切.⑽ MN 交抛物线于点Q ,则,Q 是MN 的中点.★⑴ ① y 1y 2=-p 2;② x 1x 2=p 24;③ 1y 1+1y 2=1y 3④ | AB |=x 1+x 2+p =2p sin 2θ (θ为AB 的倾斜角);⑤S △OAB =p 22sin θ,S 梯形ABCD =2p2sin 3θ.【证明】设过焦点F (p 2,0)的AB 的直线方程为x =my +p2,代入抛物线方程y 2=2px 得y 2-2pmy -p 2=0,因此 ① y 1y 2=-p 2,y 1+y 2=2pm . 另由⑶得在Rt △CFD 中,FR ⊥CD , 有| RF |2=| DR |·| RC |,而| DR |=| y 1 |,| RC |=| y 2 |,| RF |=p ,且y 1 y 2<0 ∴y 1y 2=-p 2.② 又点A 、B 在抛物线上,有x 1=y 212p ,x 2=y 222p ,因此x 1x 2=y 212p ·y 222p =(y 1y 2)24p 2=p24. ③ 1y 1+1y 2=y 1+y 2y 1y 2=2pm -p 2=-2mp, 在直线AB 方程x =my +p2中令x =0,得y 3=-p 2m ,代入上式得1y 1+1y 2=1y 3④【证法一】根据抛物线的定义,| AF |=| AD |=x 1+p 2,| BF |=| BC |=x 2+p2,| AB |=| AF |+| BF |=x 1+x 2+p又| AB |=(x 2-x 1)2+(y 2-y 1)2=1+m 2| y 2-y 1 |=1+m 2(y 1+y 2)2-4y 1y 2 =1+m24m 2p 2+4p 2=2p (1+m 2)当m ≠0时,m =1k =1tan θ=cos θsin θ,有1+m 2=1+cos 2θsin 2θ=1sin 2θ(k 为直线AB 的斜率)当m =0时,θ=90︒,1+m 2=1也满足1+m 2=1sin 2θ∴| AB |=2p (1+m 2)=2p sin 2θ.【证法二】如图2,过A 、B 引x 轴的垂线AA 1、BB 1,垂足为A 1、B 1,那么| RF |=| AD |-| FA 1 |=| AF |-| AF |cos θ,∴| AF |=| RF |1-cos θ=p1-cos θ同理,| BF |=| RF |1+cos θ=p1+cos θ∴| AB |=| AF |+| BF |=p 1-cos θ+p 1+cos θ=2psin 2θ.【证法三】极坐标法,设抛物线的极坐标方程为ρ=p1-cos θ,则| AF |=ρ1=p 1-cos θ ,| BF |=ρ2=p 1-cos(π+θ )=p1+cos θ.∴| AB |=| AF |+| BF |=p 1-cos θ+p 1+cos θ=2psin 2θ.⑤S △OAB =S △OAF +S △OBF =12| OF || y 1 |+12| OF || y 1 |=12·p2·(| y 1 |+| y 1 |)∵y 1y 2=-p 2,则y 1、y 2异号,因此,| y 1 |+| y 1 |=| y 1-y 2 |∴S △OAB =p 4| y 1-y 2 |=p4(y 1+y 2)2-4y 1y 2=p44m 2p 2+4p 2=p 221+m 2=p 22sin θ .又∵| CD |=| AB |sin θ=2p sin θ ,| AD |+| BC |=| AB |=2psin 2θ.∴S 梯形ABCD =12(| AD |+| BC |)·| CD |=12×2p sin θ×2p sin 2θ=p2sin 3θ.【例1】(2001年新课程高考文)设坐标原点为O ,抛物线y 2=2x 与过焦点的直线交于A 、B 两点,则OA →·OB →= ································································································································ ( )A. 34B. -34C. 3D. -3【解】设A (x 1,y 1),B (x 2,y 2),则OA →·OB →=x 1x 2+y 1y 2=p 24-p 2=-34,故选B.【例2】(2009年理)过抛物线y 2=2px (p >0)的焦点F 作倾斜角为45︒的直线交抛物线于A 、B 两点,若线段AB 的长为8,则p = .【解】由性质⑴得| AB |=2p sin 2θ=2psin 245︒=8,∴p =8×122=4.★⑵1| AF |+1| BF |=2p 【证法一】由⑴x 1x 2=p 24,且| AF |=x 1+p 2,| BF |=x 2+p2.∴1| AF |+1| BF |=1x 1+p 2+1x 2+p 2=x 1+x 2+p (x 1+p 2)·(x 2+p 2)=x 1+x 2+p x 1x 2+p 2(x 1+x 2)+p 24=x 1+x 2+p p 24+p 2(x 1+x 2)+p 24=x 1+x 2+p p 2(x 1+x 2+p )=2p【证法二】由| AF |=ρ1=p 1-cos θ ,| BF |=ρ2=p 1-cos(π+θ )=p1+cos θ.. 资料∴1| AF |+1| BF |=1ρ1+1ρ2=1-cos θp +1+cos θp =2p【例3】(2000全国)过抛物线y =ax 2(a >0)的焦点F 用一直线交抛物线于P 、Q 两点,若线段PF 与FQ 的长分别是p 、q ,则1p +1q等于 ······················································································· ( )A. 2aB.12aC.4aD. 4a【解】由y =ax 2得x 2=1a y ,(抛物线焦点到准线的距离为12a ),由此得1p +1q =4a ,故选C.★⑶ ∠AMB =∠DFC =Rt ∠,先证明:∠AMB =Rt ∠ 【证法一】延长AM 交BC 的延长线于E ,如图3,则△ADM ≌△ECM ,∴| AM |=| EM |,| EC |=| AD | ∴| BE |=| BC |+| CE |=| BC |+| AD | =| BF |+| AF |=| AB |∴△ABE 为等腰三角形,又M 是AE 的中点, ∴BM ⊥AE ,即∠AMB =Rt ∠ 【证法二】取AB 的中点N ,连结MN ,则| MN |=12(| AD |+| BC |)=12(| AF |+| BF |)=12| AB |,∴| MN |=| AN |=| BN |∴△ABM 为直角三角形,AB 为斜边,故∠AMB =Rt ∠.【证法三】由已知得C (-p 2,y 2)、D (-p 2,y 1),由此得M (-p 2,y 1+y 22).∴k AM =y 1-y 1+y 22x 1+p 2=y 1-y 22·y 212p +p =p (y 1-y 2)y 21+p 2=p (y 1--p 2y 1)y 21+p2=p y 1,同理k BM =py 2 ∴k AM ·k BM =p y 1·p y 2=p 2y 1y 2=p 2-p 2=-1∴BM ⊥AE ,即∠AMB =Rt ∠.【证法四】由已知得C (-p 2,y 2)、D (-p 2,y 1),由此得M (-p 2,y 1+y 22).∴MA →=(x 1+p 2,y 1-y 22),MB →=(x 3+p 2,y 2-y 12)∴MA →·MB →=(x 1+p 2)(x 2+p 2)+(y 1-y 2)(y 2-y 1)4图3. 资料=x 1x 2+p 2(x 1+x 2)+p 24-(y 1-y 2)24=p 24+p 2(y 212p +y 222p )+p 24-y 21+y 22-2y 1y 24=p 22+y 1y 22=p 22+-p 22=0 ∴MA →⊥MB →,故∠AMB =Rt ∠.【证法五】由下面证得∠DFC =90︒,连结FM ,则FM =DM .又AD =AF ,故△ADM ≌△AFM ,如图4 ∴∠1=∠2,同理∠3=∠4 ∴∠2+∠3=12×180︒=90︒∴∠AMB =Rt ∠. 接着证明:∠DFC =Rt ∠【证法一】如图5,由于| AD |=| AF |,AD ∥RF ,故可设∠AFD =∠ADF =∠DFR =α, 同理,设∠BFC =∠BCF =∠CFR =β, 而∠AFD +∠DFR +∠BFC +∠CFR =180︒ ∴2(α+β)=180︒,即α+β=90︒,故∠DFC =90︒【证法二】取CD 的中点M ,即M (-p 2,y 1+y 22)由前知k AM =p y 1,k CF =-y 2+p 2+p 2=-y 2p =py 1∴k AM =k CF ,AM ∥CF ,同理,BM ∥DF ∴∠DFC =∠AMB =90︒.【证法三】∵DF →=(p ,-y 1),CF →=(p ,-y 2),∴DF →·CF →=p 2+y 1y 2=0 ∴DF →⊥CF →,故∠DFC =90︒.【证法四】由于| RF |2=p 2=-y 1y 2=| DR |·| RC |,即| DR || RF |=| RF || RC |,且∠DRF =∠FRC =90︒∴ △DRF ∽△FRC∴∠DFR =∠RCF ,而∠RCF +∠RFC =90︒ ∴∠DFR +∠RFC =90︒ ∴∠DFC =90︒【例4】(2009年文)如图7,过抛物线y 2=2px (P >0)的焦点F 的直图6线与抛物线相交于M 、N 两点,自M 、N 向准线l 作垂线,垂足分别为M 1、N 1,求证:FM 1⊥FN 1★⑷ AM 、BM 是抛物线的切线【证法一】∵k AM =p y 1,AM 的直线方程为y -y 1=py 1(x -y 212p)与抛物线方程y 2=2px 联立消去x 得y -y 1=p y 1(y 22p -y 212p),整理得y 2-2y 1y +y 21=0可见△=(2y 1)2-4y 21=0,故直线AM 与抛物线y 2=2px 相切, 同理BM 也是抛物线的切线,如图8.【证法二】由抛物线方程y 2=2px ,两边对x 求导,(y 2)'x =(2px )'x ,得2y ·y 'x =2p ,y 'x =py ,故抛物线y 2=2px 在点A (x 1,y 1)处的切线的斜率为k 切=y 'x | y =y 1=p y 1.又k AM =p y 1,∴k 切=k AM ,即AM 是抛物线在点A 处的切线,同理BM 也是抛物线的切线.【证法三】∵过点A (x 1,y 1)的切线方程为y 1y =p (x +x 1),把M (-p 2,y 1+y 22)代入左边=y 1·y 1+y 22=y 21+y 1y 22=2px 1-p 22=px 1-p 22,右边=p (-p 2+x 1)=-p 22+px 1,左边=右边,可见,过点A 的切线经过点M ,即AM 是抛物线的切线,同理BM 也是抛物线的切线. ★⑸ AM 、BM 分别是∠DAB 和∠CBA 的平分线 【证法一】延长AM 交BC 的延长线于E ,如图9,则△ADM ≌△ECM ,有AD ∥BC ,AB =BE , ∴∠DAM =∠AEB =∠BAM ,即AM 平分∠DAB ,同理BM 平分∠CBA .【证法二】由图9可知只须证明直线AB 的倾斜角α是直线AM图8的倾斜角β的2倍即可,即α=2β. 且M (-p 2,y 1+y 22)∵tan α=k AB =y 2-y 1x 2-x 1=y 2-y 1 y 222p -y 212p=2py 1+y 2. tan β=k AM =y 1-y 1+y 22x 1+p 2=y 1-y 22·y 212p+p =p (y 1-y 2)y 21+p 2=p (y 1--p2y 1)y 21+p 2=py 1. ∴tan 2β=2tan β1-tan 2β=2py 11-(p y 1)2=2py 1y 22-p 2=2py 1y 22+y 1y 2=2py 1+y 2=tan α ∴α=2β,即AM 平分∠DAB ,同理BM 平分∠CBA .★⑹ AM 、DF 、y 轴三线共点,BM 、CF 、y 轴三线共点 【证法一】如图10,设AM 与DF 相交于点G 1,由以上证明知| AD |=| AF |,AM 平分∠DAF ,故AG 1也是DF 边上的中线, ∴G 1是DF 的中点.设AD 与y 轴交于点D 1,DF 与y 轴相交于点G 2, 易知,| DD 1 |=| OF |,DD 1∥OF , 故△DD 1G 2≌△FOG 2∴| DG 2 |=| FG 2 |,则G 2也是DF 的中点.∴G 1与G 2重合(设为点G ),则AM 、DF 、y 轴三线共点, 同理BM 、CF 、y 轴也三线共点.【证法二】AM 的直线方程为y -y 1=py 1(x -y 212p),令x =0得AM 与y 轴交于点G 1(0,y 12), 又DF 的直线方程为y =-y 1p (x -p 2),令x =0得DF 与y 轴交于点G 2(0,y 12)∴AM 、DF 与y 轴的相交同一点G (0,y 12),则AM 、DF 、y 轴三线共点,同理BM 、CF 、y 轴也三线共点H .由以上证明还可以得四边形MHFG 是矩形.★⑺ A 、O 、C 三点共线,B 、O 、D 三点共线图10【证法一】如图11,k OA =y 1x 1=y 1 y 212p=2py 1, k OC =y 2 -p 2=-2y 2p =-2py 2p 2=-2py 2-y 1y 2=2p y 1∴k OA =k OC ,则A 、O 、C 三点共线, 同理D 、O 、B 三点也共线.【证法二】设AC 与x 轴交于点O ',∵AD ∥RF ∥BC∴| RO ' || AD |=| CO ' || CA |=| BF || AB |,| O 'F || AF |=| CB || AB |, 又| AD |=| AF |,| BC |=| BF |,∴| RO ' || AF |=| O 'F || AF |∴| RO ' |=| O 'F |,则O '与O 重合,即C 、O 、A 三点共线,同理D 、O 、B 三点也共线. 【证法三】设AC 与x 轴交于点O ',RF ∥BC ,| O 'F || CB |=| AF || AB |,∴| O 'F |=| CB |·| AF || AB |=| BF |·| AF || AF |+| BF |=1 1| AF |+1| BF | =p2【见⑵证】∴O '与O 重合,则即C 、O 、A 三点共线,同理D 、O 、B 三点也共线.【证法四】∵OC →=(-p 2,y 2),OA →=(x 1,y 1),∵-p2·y 1-x 1 y 2=-p2·y 1-y 212p y 2=-py 12-y 1y 2y 12p =-py 12+p 2y 12p=0∴OC →∥OA →,且都以O 为端点∴A 、O 、C 三点共线,同理B 、O 、D 三点共线.【推广】过定点P (m ,0)的直线与抛物线y 2=2px (p >0)相交于点A 、B ,过A 、B 两点分别作直线l :x =-m 的垂线,垂足分别为M 、N ,则A 、O 、N 三点共线,B 、O 、M 三点也共线,如下图:【例5】(2001A 、B 两点,点C 在抛物线的准线上,且BC ∥x 轴. 证明直线AC 经过原点O .【证法一】因为抛物线y 2=2px (p >0)的焦点为F (-p2,0),所以经过点F 的直线AB 的方程可设为x =my +p2;代入抛物线方程得y 2-2pmy -p 2=0设A (x 1,y 1),B (x 2,y 2),则y 1,y 2是该方程的两个根, ∴y 1y 2=-p 2因为BC ∥x 轴,且点C 在准线x =-p 2上,故C (-p2,y 2),∴直线CO 的斜率为 k OC =y 2 -p 2=2p y 1=y 1x 1=k OA .∴直线AC 经过原点O .【证法二】如图13,过A 作AD ⊥l ,D 为垂足,则:AD ∥EF ∥BC连结AC 与EF 相交于点N ,则| EN | | AD | =| CN | | AC | =| BF | | AB | ,| NF | | BC | =| AF | | AB | 由抛物线的定义可知:| AF |=| AD |,| BF |=| BC | ∴| EN |=| AD |·| BF | | AB | =| AF |·| BC || AB |=| NF |.即N 是EF 的中点,与抛物线的顶点O 重合,所以直线AC 经过原点O .★⑻ 若| AF |:| BF |=m :n ,点A 在第一象限,θ为直线AB 的倾斜角. 则cos θ=m -nm +n; 【证明】如图14,过A 、B 分别作准线l 的垂线,垂足分别为D ,C ,过B 作BE ⊥AD 于E ,设| AF |=mt ,| AF |=nt ,则| AD |=| AF |,| BC |=| BF |,| AE |=| AD |-| BC |=(m -n )t ∴在Rt △ABE 中,cos ∠BAE =| AE || AB |= (m -n )t (m +n )t =m -nm +n∴cos θ=cos ∠BAE =m -nm +n. 【例6】设经过抛物线y 2=2px 的焦点F 的直线与抛物线相交于两点A 、B ,且| AF |:| BF |=3:1,则直线AB 的倾斜角的大小为 . 【答案】60︒或120︒.★⑼ 以AF 为直径的圆与y 轴相切,以BF 为直径的圆与y 轴相切;以AB 为直径的圆与准线相切. 【说明】如图15,设E 是AF 的中点,图12图13则E 的坐标为( p2+x 1 2,y 12),则点E 到y 轴的距离为d = p2+x 12=12| AF |故以AF 为直径的圆与y 轴相切, 同理以BF 为直径的圆与y 轴相切.【说明】如图15,设M 是AB 的中点,作MN ⊥准线l 于N ,则| MN |=12(| AD |+| BC |)=12(| AF |+| BF |)=12| AB |则圆心M 到l 的距离| MN |=12| AB |,故以AB 为直径的圆与准线相切. ★⑽ MN 交抛物线于点Q ,则Q 是MN 的中点.【证明】设A (y 212p ,y 1),B (y 222p ,y 1),则C (-p 2,y 2),D (-p2,y 1),M (-p 2,y 1+y 22),N (y 21+y 224p ,y 1+y 22),设MN 的中点为Q ',则Q ' (-p 2+y 21+y 224p 2,y 1+y 22)∵ -p 2+y 21+y 224p 2= -2p 2+y 21+y 22 8p = 2y 1y 2+y 21+y 22 8p = ⎝ ⎛⎭⎪⎫y 1+y 2222p∴点Q ' 在抛物线y 2=2px 上,即Q 是MN 的中点.C DBR Axy O F图15 l M N E图16二、定点、定值、定直线问题(共9个结论)★⑴平行于抛物线对称轴的光线,被抛物面反射后会聚焦于抛物线的焦点,如图17. 【证明】如图17,设抛物线方程为y 2=2px (p >0),直线AB ∥x 轴,点A 的坐标为(x 0,y 0),则过A 点的切线方程为y 0y =p (x +x 0),直线l 的斜率为k 0=p y 0,设直线AB 到l 的角为α,则tan α=py 0,设直线AF 的斜率为k 1,则k 1=y 0x 0-p 2=2py 0y 20-p 2,设直线l 到AF 的角为β,则tan β=k 1-k 01+k 0k 1=2py 0y 20-p 2-py 01+p y 0·2py 0y 20-p2=p (y 20+p 2)y 0(y 20+p 2)=p y 0. ∴tan α=tan β,又α、β∈[0,π),则α=β,也就是说平行于抛物线对称轴的光线,被抛物面反射后会聚焦于抛物线的焦点. 【例7】(2004年省质检)如图18,从点M (x 0,2)发出的光线沿平行于抛物线y 2=4x 的轴的方向射向抛物线的点P ,反射后经焦点F 又射向直线l :x -2y -7=0上的点N ,再反射后又设回点M ,则x 0= .【解】PM ∥x 轴,点P 在抛物线上,得P 的坐标为(1,2),经过F (1,0)点后反射在Q 点,则Q 的坐标为(1,-2),经Q 反射后点N 的坐标为(3,-2),设M 关于l 对称的点为M ',依题意,Q 、N 、M '共线.故可设M '(x 1,-2),由此得 ⎩⎪⎨⎪⎧2+2x 0-x 1·12=-1x 0+x 12―2·2-22―7=0 ,解得x 0=6.【另解】若设Q 关于直线l 的对称点为Q ',设Q ' (a ,b ),由于Q 、Q '关于直线l 对称,由此得⎩⎪⎨⎪⎧b +2a -1·12=-1a +12―2·b -22―7=0 ,解得⎩⎪⎨⎪⎧a =95b =-185 则Q '的坐标为(95,-185), 又M 、N 、Q '三点共线,k MN =k NQ ',即-185+195-3=2+2x 0-3,∴x 0=6.★⑵若C (x 0,y 0)是抛物线y 2=2px (p >0)上的任一点,过C 引两条互相垂直的直线交抛物线于A 、B ,则直线AB 过定点(2p +x 0,-y 0).【证明】设A (s 22p ,s )、B (t 22p,t )(s ,t ,y 0互不相等)那么,由AC ⊥BC 得k AC ·k BC =y 0-s x 0-s 22p ·y 0-tx 0-t 22p=y 0-s y 202p -s 22p ·y 0-t y 202p -t 22p=4p2(y 0+s )(y 0+t )=-1∴4p 2=-(y 0+s )(y 0+t )∴st =-4p 2-(s +t )y 0-y 20 ····························· ①又直线AB 的方程为y -s t -s =x -s 22p t 22p -s 22p,整理得,y =2px +sts +t· ② 把①代入②得 y =2px -4p 2-(s +t )y 0-y 20s +t =2px -4p 2-2px 0s +t -y 0=2ps +t (x -2p -x 0)-y 0令x -2p -x 0=0,即x =2p +x 0,得y =-y 0. 故直线AB 过定点(2p +x 0,-y 0).特别地,当C 是抛物线的顶点时,定点P 的坐标为(2p ,0).【拓展】C (x 0,y 0)是抛物线y 2=2px (p >0)上的一定点,直线AB 与抛物线相交于A 、B 两点(都异于C ),若直线CA 、CB 的斜率k CA 、k CB 的乘积为定值m ,那么,直线AB 过定点(x 0-2pm,-y 0).【例8】(2000京皖春季高考)如图20,设点A 和B 为抛物线y 2=4px (p >0)上原点以外的两个动点,已知OA ⊥OB ,OM ⊥AB ,求点M 的轨迹方程,并说明它表示什么曲线. 【解法一】点A ,B 在抛物线y 2=4px 上,设A (y 2A 4p ,y A ),B (y 2B4p ,y B ),OA 、OB 的斜率分别为k OA 、k OB .∴k OA =y A y 2A 4p =4p y A ,k OA =4p y B ,k AB =y B -y A y 2B 4p -y 2A 4p=4p y A +y B. 由OA ⊥OB ,得k OA ·k OB =16p2y A y B=-1 ············································· ①(s 22p,s ) 图19 B (t 2p,t )图20∴直线AB 方程为,y -y A =4py A +y B (x -y 2A 4p ),即(y A +y B )(y -y A )=4p (x -y 2A 4p) ·························· ②由OM ⊥AB ,得直线OM 方程y = y A +y B4p ················································ ③设点M (x ,y ),则x ,y 满足②、③两式,将②式两边同时乘以-x4p ,并利用③式整理得,x4p y A 2+yy A -(x 2+y 2)=0 ·········································································· ④由③、④两式得-x4p +y B y A -(x 2+y 2)=0,由①式知,y A y B =-16p 2,所以x 2+y 2-4px =0. 因为A 、B 是原点以外的两点,所以x ≠0.所以点M 的轨迹是以(2p ,0)为圆心,以2p 为半径的圆,去掉坐标原点.【解法二】由性质(2)易知AB 经过定点P (4p ,0),由于OM ⊥AB ,那么,M 的轨迹以(2p ,0)为圆心,以2p 为半径的圆,去掉坐标原点.其轨迹方程为x 2+y 2-4px =0(x ≠0).★⑶抛物线y 2=2px (p >0)的弦AB 的中点D 恰好在定直线l :x =m (m >0)上,则线段AB 的垂直平分线过定点M (m +p ,0).【证明】如图22,设A (x 1,y 1),B (x 2,y 2),D (m ,y 0),那么⎩⎨⎧y 21=2px 1…………①y 22=2px 2…………② ①-②得y 21-y 22=2p (x 1-x 2)∴直线AB 的斜率k AB =y 1-y 2x 1-x 2=2p y 1+y 2=p y 0∴直线DM 的斜率k DM =-1k AB=-y 0p∴DM 的直线方程为y -y 0=-y 0p(x -m ) 令y =0,得x =m +p∴直线AB 的垂直平分线恒过定点(m +p ,0).【例9】(2008理科高考)若A 、B 是抛物线y 2=4x 上的不同两点,弦AB (不平行于y 轴)的垂直平分线与x 轴相交于点P ,则称弦AB 是点P 的一条“相关弦”.已知当x >2时,点P (x ,0)存在无穷多条“相关弦”.给定x 0>2.⑴证明:点P (x 0,0)的所有“相关弦”的中点的横坐标相同;⑵(略)图21xyOA (x A ,y A )B (x B ,y B )M P 图22【说明】应用性质⑶,由已知得p=2,由定点P(x0,0)得m+p=x0,故m=x0-2 ∴“相关弦”的中点的横坐标为x0-2.★⑷设直线l 与抛物线y 2=2px (p >0)相交于点A (x 1,y 1)、B (x 2,y 2),那么①若直线l 过抛物线对称轴的定点M (a ,0),则y 1y 2=-2ap ,x 1x 2=a 2;反之 ②若y 1y 2=k (定值),则直线l 恒过定点N (-k2p ,0).③若直线l 与y 轴相交于点(0,y 3),则1y 1+1y 2=1y 3.【证明】①设过点M (a ,0)的直线方程为x =my +a ,代入抛物线方程y 2=2px 得y 2-2pmy -2pa =0,因此y 1y 2=-2ap ,x 1x 2=y 212p ·y 222p =(y 1y 2)24p 2=4a 2p 24p2=a 2.②设直线l 方程为x =my +b ,代入抛物线方程y 2=2px 得 y 2-2pmy -2pb =0,即方程的根y 1、y 2是P 、Q 两点的纵坐标 ∴y 1y 2=-2pb ,又y 1y 2=k .∴-2pb =k ,即b =-k 2p ,则直线l 方程为x =my -k2p 令y =0,得x =-k 2p ,则直线l 恒过定点N (-k2p ,0). ③由l 的方程x =my +a 中,令x =0得y 3=-am,y 1+y 2=2pm ∴1y 1+1y 2=y 1+y 2y 1y 2=2pm -2ap =-m a =1y 3.【例10】(2005年春季高考理科)如图24,O 为坐标原点,直线l 在x 轴和y 轴上的截距分别为a 和b (a >0,b ≠0),且交抛物线y 2=2px (p >0)于M (x 1,y 1)、N (x 2,y 2)两点. ⑴写出直线l 的截距式方程; ⑵证明:1y 1+1y 2=1b.⑴【解】直线l 的截距式方程为x a +yb=1.⑵由上面性质⑶证明可得1y 1+1y 2=1b.图23★⑸过抛物线y 2=2px (p >0)的焦点F 作直线l 与抛物线交于A 、B 两点,且与准线交于点M ,设MA →=λAF →,MB →=μBF →,则λ+μ=0.【证法一】设过点F (p 2,0)的直线方程为x =my +p2,代入抛物线方程y 2=2px 得y 2-2pmy -p 2=0,因此y 1y 2=-p 2,y 1+y 2=2pm 令x =-p 2,得y M =-pm由MA →=λAF →得(x 1+p 2,y 1+p m )=λ (p 2-x 1,-y 1)∴y 1+pm =-λ y 1,λ=1+p my 1,同理,μ=1+p my 2∴λ+μ=2+p my 1+p my 2=2+p (y 1+y 2)my 1 y 2=2+p ·2pmm ·(-p 2)=2-2=0. 【证法二】由已知MA →=λAF →,MB →=μBF →,得λ·μ<0.则|MA →| |MB →| =-λ|AF →| μ|BF →| ··················································· ①过点A ,B 分别作准线l 的垂线,垂足分别为A 1,B 1, 则有:|MA →| |MB →| =|AA 1→| |BB 1→| =|AF →||BF →| ································· ②由①②得-λ|AF →|μ|BF →| =|AF →||BF →|,即λ+μ=0.【例11】(2007年理科高考)如图27,已知点F (1,0),直线l :x =-1,P 为平面上的动点,过P 作直线l 的垂线,垂足为点Q ,且QP →·QF →=FP →·FQ →. ⑴求动点P 的轨迹C 的方程;⑵过点F 的直线交轨迹C 于A ,B 两点,交直线l 于点M ,已知 MA →=λ1AF →,MB →=λ2BF →,求λ1+λ2的值; 【略解】⑴动点P 的轨迹C 的方程为:y 2=4x ;⑵λ1+λ2=0.AB图27★⑹定长为l 的弦AB 的两个端点在抛物线y 2=2px 上,M 是AB 的中点,M 到y 轴的距离为d ,那么,M 的轨迹方程为:4(y 2+p 2)(2px -y 2)=p 2l 2,且①当0<l <2p 时,d 的最小值为l 28p,此时,AB ∥y 轴;②当l ≥2p 时,d 的最小值为l -p2,此时,弦AB 过焦点F .【解】设A (x 1,y 1),B (x 2,y 2),弦AB 的中点M 的坐标为(x 0,y 0),AB 的直线方程为x =my +b ,代入抛物线方程y 2=2px得y 2-2pmy -2pb =0. ∴y 1+y 2=2pm ,y 1y 2=-2pb . 又AB 的中点为M (x 0,y 0),且点M 在直线AB 上,∴y 0=y 1+y 22=pm ,x 0=my 0+b ,m =y 0p ,b =x 0-my 0=x 0-y 20p.∴| AB |2=l 2=(x 1-x 2)2+(y 1-y 2)2=(my 1+b -my 2-b )2+(y 1-y 2)2=(1+m 2)(y 1-y 2)2=(1+m 2)[(y 1+y 2)2-4y 1y 2]=(1+y 20p 2)[4y 20+8pb ]=(1+y 20p 2)[4y 20+8p (x 0-y 20p)]整理得,4(y 20+p 2)(2px 0-y 20)=p 2l 2. 故中点M 的轨迹方程为:4(y 2+p 2)(2px -y 2)=p 2l 2.由上可知d =x =pl 28(y 2+p 2)+y 22p ,令t =y 2+p 2≥p 2,即y 2=t -p 2,则 d =x =pl 28t +t -p 22p =pl 28t +t 2p -p 2(t ≥p 2).令pl 28t =t 2p ,得t =pl 2.①当0<l <2p 时,p 2>pl2,d 在t ∈[ p 2,+∞)上是增函数,∴当t =p 2,即y =0时,d min =pl 28p 2+p 22p -p 2=l 28p,此时,m =0,即AB ∥y 轴.②当l ≥2p 时,p 2≤pl2,∴d =pl 28t +t 2p -p 2≥2ptt pl 282⨯-p 2=l -p 2.当且仅当pl 28t =t 2p ,即t =pl 2≥p 2时取等号,故d 的最小值为l -p2.②【证法二】当l ≥2p 时,过A 、B 、M 作准线x =-p2的垂线,垂足为A '、B '、M ',则| MM ' |=d +p 2=12(| AA ' |+| BB ' |)=12(| AF |+| BF |)≥12| AB |=12l .上式当且仅当| AF |+| BF |=| AB |,即弦AB 过抛物线的焦点M 时取等号,则d 的最小值为12l -p 2=l -p2.【说明】经过焦点F 的最短弦是通经2p ,因此当弦AB 的长l <2p 时,图28不能用证法二证明d 的最小值为l 28p.【例12】长度为a 的线段AB 的两个端点在抛物线x 2=2py (a ≥2p >0)上运动,以AB 的中点C 为圆心作圆与抛物线的准线相切,求圆C 的最小半径.【解】依题意,问题转化为定长的弦的两个端点在抛物线上,弦的中点C 到y 轴的距离的最值问题,由上面的性质可知当弦AB 经过焦点F 时,点C 到准线的距离为最小值. 如图30.∴圆C 的最小半径为r =a2.★⑺过抛物线y 2=2px (p >0)的对称轴上的定点M (m ,0)(m >0),作直线AB 与抛物线相交于A ,B 两点.点N 是定直线l :x =-m 上的任一点,则直线AN ,MN ,BN 的斜率成等差数列.【证明】设A (x 1,y 1),B (x 2,y 2),N (-m ,n ), 由性质⑶有y 1y 2=-2pm ,则直线AN 、BN 的斜率为k AN =y 1-n x 1+m ,k BN =y 2-nx 2+m∴k AN +k BN =y 1-n y 212p +m +y 2-ny 222p+m=2p (y 1-n )y 21+2pm +2p (y 2-n )y 22+2pm =2p (y 1-n )y 21-y 1y 2+2p (y 1-n )y 22-y 1y 2=2p [y 2(y 1-n )-y 1(y 2-n )]y 1y 2(y 1-y 2)=2pn (y 1-y 2)y 1y 2(y 1-y 2)=2pn y 1y 2=2pn -2pm =-n m又∵直线MN 的斜率为k MN =n -0-m -m =-n2m.∴k AN +k BN =2k MN∴直线AN ,MN ,BN 的斜率成等差数列.★⑻抛物线的一组平行弦的中点共线,且所在直线平行于对称轴或与对称轴重合.【证明】设斜率为k (k 为常数)的一组平行线与抛物线y 2=2px (p >0)交于点A i 、B i(i =1,2,…),弦A i B i 的中点为M i ,(即M 1,M 2,…,M n ),且A i B i 的直线方程为y =kx +b i (b i 为直线A i B i 在y 轴上的截距),A i (x 1,y 1),B i (x 2,y 2),M i (x i ,y i ).(-联立方程组⎩⎨⎧y 2=2px y =kx +b i,消去x 得k 2p y 2-y +b i =0∴y 1+y 2=2pk,又M i 是A i B i 的中点∴y i =y 1+y 22=p k ,则M 1,M 2,…,M n 在平行于x 轴的直线y =pk上. 当直线A i B i 与x 轴垂直(即直线A i B i 的斜率不存在时),易知M 1,M 2,…,M n 在x 轴上. 【例13】(2009年卷理20文21)已知抛物线C :y =2x 2,直线y =kx +2交C 于A ,B 两点,M 是线段AB 的中点,过M 作x 轴的垂线交C 于点N . ⑴证明:抛物线C 在点N 处的切线与AB 平行; 【证明】如图34,设A (x 1,2x 21),B (x 1,2x 22),把y =kx +2代入y =2x 2得2x 2-kx -2=0, 由韦达定理得x 1+x 2=k2,x 1x 2=-1,∴x N =x M =x 1+x 22=k4,即N 点的坐标为(k 4,k 28) 设抛物线在点N 处的切线l 的方程为y -k 28=m (x -k4),将y =2x 2代入上式得2x 2-mx +mk 4-k 28=0, ∵直线l 与抛物线C 相切, ∴∆=m 2-8(mk 4-k 28)=0, 解得m =k ,即l ∥AB .【说明】其实,也就是与AB 平行的弦,它们的中点在过AB 中点且与对称轴(x 轴)平行的直线上,它与C 的交点N ,此时的切点就是这些弦的缩点,故过N 点的抛物线C 的切线与AB 平行. ★⑼过定点P (x 0,y 0)作任一直线l 与抛物线y 2=2px (p >0)相交于A 、B 两点,过A 、B 两点作抛物线的切线l 1、l 2,设l 1,l 2相交于点Q ,则点Q 在定直线px -y 0y +px 0=0上. 【证明】设A (x 1,y 1)、B (x 2,y 2),因为过点P 与x 轴平行的直线与抛物线只有一个交点,所以直线AB 与x 轴不平行,故可设AB 的方程为x -x 0=m (y -y 0).联立方程组⎩⎨⎧y 2=2pxx -x 0=m (y -y 0),消去x 得12py 2-my +my 0-x 0=0 ∴y 1y 2=2p (my 0-x 0)又过A 、B 两点的抛物线的切线方程为图34y 1y =p (x +x 1)和y 2y =p (x +x 2),联立方程组⎩⎨⎧y 1y =p (x +x 1)y 2y =p (x +x 2)解得x Q =x 1y 2-x 2y 1y 1-y 2=- y 212p ·y 2-y 222p ·y 1 y 1-y 2=y 1y 22p =my 0-x 0 ······································ ①y Q =p ·x 1-x 2y 1-y 2=pm ·································································································· ②由②得m =y Qp 代入①得x Q =y Q py 0-x 0,∴点Q 在直线px -y 0y +px 0=0上.【例14】(2007年文科高考题)如图36,对每个正整数 n ,A n (x n ,y n )是抛物线x 2=4y 上的点,过焦点F 的直线FA n 交抛物线于另一点B n (s n ,t n ). ⑴试证:x n s n =-4(n ≥1);⑵取x n =2n,并记C n 为抛物线上分别以A n 与B n 为切点的两条切线的交点.试证:| FC 1 |+| FC 2 |+…+| FC n |=2n-2-n +1+1.【说明】本题第⑴小题就是抛物线的焦点弦的性质y 1y 2=-p 2.第⑵小题两条切线的交点C n 就是上面抛物线的性质,即点C n 必在直线y =-1上.【例15】(2008年理科高考)如图,设抛物线方程为x 2=2py(p >0),M 为 直线y =-2p 上任意一点,过M 引抛物线的切线,切点分别为A ,B .⑴求证:A ,M ,B 三点的横坐标成等差数列;⑵⑶略.【证明】由题意设A (x 1,x 212p ),B (x 2,x 222p),x 1<x 2,M (x 0,-2p )由x 2=2py 得y =x22p ,y '=xp所以,k MA =x 1p ,k MB =x 2p,因此直线MA 的方程为y +2p =x 1p (x -x 0),直线MB 的方程为y +2p =x 2p(x -x 0),所以,x 212p +2p =x 1p(x 1-x 0)…………①,x 222p +2p =x 2p(x 2-x 0)…………②, ①-②得,(x 1+x 2)(x 1-x 2)2p =(x 1+x 2)(x 1-x 2)p -x 0(x 1-x 2)p∴x 1+x 22=x 1+x 2-x 0,即2x 0=x 1+x 2图37所以A ,M ,B 三点的横坐标成等差数列.★⑽过抛物线y 2=2px (p >0)的焦点F 的直线l 与抛物线交于A 、B 两点,线段AB 的垂直平分线交x 轴于点M ,则| AB || FM |=2. 【证明】设过焦点F (p 2,0)的直线AB 的方程为x =my +p2(m ≠0),且A (x 1,y 1)、B (x 2,y 2),把x =my +p2代入y 2=2px ,得y 2=2pmy +p 2, 即y 2-2pmy -p 2=0 ∴y 1+y 2=2pm ,y 1·y 2=-p 2∴x 1+x 2=m (y 1+y 2)+p =2pm 2+p , ∴AB 的中点N 的坐标为(pm 2+p2,pm )AB 的垂直平分线方程为y -pm =-m (x -pm 2-p2)令y =0,得M 的横坐标为x =pm 2+3p 2∴| FM |=| x M -p2 |=pm 2+p =p (m 2+1),又| AB |=x 1+x 2+p =2p (m 2+1).∴| AB || FM |=2p (m 2+1)p (m 2+1)=2 【证法二】设A (x 1,y 1)、B (x 2,y 2),过A 、B 分别作准线的垂线,垂足分别为C 、D ,则C (-p2,y 1)、D (-p 2,y 2),则CD 的中点E 的坐标为(-p 2,y 1+y 22),由证法一知y 1+y 2=2pm ,∴E (-p 2,pm ),所以k EF =pm-p 2-p2=-m又k AB =1m ,所以k AB ·k EF =(-m )·1m=-1∴EF ⊥AB ,又MN ⊥AB ,所以EF ∥MN 又EN ∥x 轴,所以四边形EFMN 为平行四边形 ∴| FM |=| EN |=12(| AC |+| B D |)=12| AB |所以| AB || FM |=2★⑾P 是过抛物线y 2=2px (p >0)上的一定点,过P 作与x 轴平行的直线m ,过OP 的直线为n ,直线l ⊥x 轴,l 与m 、n 分别相交于A 、B 两点,则AB 的中点M 在点P 处的切线.【证明】设P (t 22p,t ),则m 的方程为y =t ,直线n (即OP )的方程为y =2ptx ,设直线l 的方程为x =s (s ≠t 22p),那么A 的坐标为(s ,t ),B 的坐标为(s ,2pst),AB 的中点M 的坐标为(t ,t +2pst2),即(t ,2ps +t22t)又过点P (t 22p ,t )的抛物线的切线方程为yt =p (x +t 22p )∴y =p t (x +t 22p)当x =x M =s 时,y =p t (s +t 22p )=ps t +t 2=2ps +t 22t=y M可见点M 在点P 处的切线n 上.★⑿点P (a ,0)(a ≠0)是抛物线y 2=2px (p >0)的对称轴上的一点,过P 的直线l 与抛物线相交于两点A 、B ,A 关于x 轴的对称的点为A ',又点Q (-a ,0),那么A '、B 、Q 三点共线. 【证明】设直线l 的方程为x =my +a ,A (x 1,y 1),B (x 2,y 2)则A '(x 1,-y 1),联立方程组⎩⎨⎧y 2=2pxx =my +a,消去x 得 y 22p-my -a =0,那么y 1 y 2=-2pa ,又QA '→=(x 1+a ,-y 1),QB '→=(x 2+a ,y 2), ∵(x 1+a )y 2+(x 2+a )y 1=(y 212p +a )y 2+(y 222p+a )y 1=y 21y 22p +y 22y 12p +a (y 1+y 2)=y 1y 2(y 1+y 2)2p +a (y 1+y 2)=(y 1+y 2)(y 1y 22p +a )=(y 1+y 2)(-2pa 2p+a )=0 ∴QA '→∥QB '→∴Q 、A '、B 三点共线.【例16】给出一个抛物线,根据其性质,用尺规作图求出该抛物线的对称轴、顶点和焦点.2图a 图b【作法】1.任意作两条平行弦A1B1和A2B2;2.分别取A1B1和A2B2的中点M、N,过M、N作直线m;3.作直线CD⊥m,交抛物线于C、D;4.取CD的中点E;5.过E作直线l∥m,交抛物线于点O.则直线l为抛物线的对称轴,O为抛物线的顶点,如图a.6.过顶点O作两条互相垂直的弦OP、OQ;7.设PQ与对称轴l相交于点G;8.取OG的靠近O的四等分点F.则F为抛物线的焦点.【说明】1.根据性质⑻,平行弦的中点共线,且与对称轴平行;2.垂直于对称轴的弦CD的中点在对称轴上,故l为抛物线的对称轴;3.根据性质⑵得PQ过顶点(2p,0),故F为抛物线的焦点.。
抛物线性质归纳、证明和应用(K12教育文档)

抛物线性质归纳、证明和应用(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(抛物线性质归纳、证明和应用(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为抛物线性质归纳、证明和应用(word版可编辑修改)的全部内容。
抛物线性质归纳、证明和应用抛物线是平面内到定点的距离等于到定直线(定点在定直线外)的距离的点的轨迹,它是椭圆过渡到双曲线的瞬间曲线,它只有一支(双曲线有两支),只有一条对称轴,没有渐近线和对称中心,属于无心曲线.抛物线的焦半径、焦点弦性质丰富多彩,此外还有定点、定值、定弦、最值等问题也值得探讨,抛物线的许多性质也是历年高考的重点和热点,这里就它的一些性质加以归纳,说明和证明,及其在历年高考和模拟考试出现的典例.一、焦半径、焦点弦性质如图,AB是过抛物线 y2=2px(p>0)焦点F的弦,AD、BC是准线的垂线,垂足分别为D、C,M是CD的中点,N是AB的中点.设点A(x1,y1)、点B(x2,y2),直线AB交y轴于点K(0,y3),则:⑴①y1y2=-p2;②x1x2=p24;③错误!+错误=错误!;④ | AB |=x1+x2+p=错误!(为AB的倾斜角);⑤S△OAB=错误!,S梯形ABCD=错误!。
.⑵1| AF |+错误!=错误!;⑶∠AMB=∠DFC=Rt∠;⑷AM、BM是抛物线的切线;⑸AM、BM分别是∠DAB和∠CBA的平分线;⑹AM、DF、y轴三线共点,BM、CF、y轴三线共点;⑺A、O、C三点共线,B、O、D三点共线;⑻若| AF|:|BF|=m:n,点A在第一象限,为直线AB的倾斜角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
抛物线的常见性质及证明概念焦半径:抛物线上一点与其焦点的连线段;焦点弦:两端点在抛物线上且经过抛物线的焦点线段称为焦点弦.性质及证明过抛物线y 2=2px (p >0)焦点F 的弦两端点为),(11y x A ,),(22y x B ,倾斜角为α,中点为C(x 0,y 0), 分别过A 、B 、C 作抛物线准线的垂线,垂足为A ’、B ’、C ’. 1.求证:①焦半径||1=+=p p x AF ;②焦半径||2=+=p p x BF ; ③1| AF |+1| BF |=2p ; ④弦长| AB |=x 1+x 2+p =α2sin 2p ;特别地,当x 1=x 2(α=90︒)时,弦长|AB|最短,称为通径,长为2p ;⑤△AOB 的面积S △OAB =αsin 22p .证明:根据抛物线的定义,| AF |=| AD |=x 1+p 2,| BF |=| BC |=x 2+p2,| AB |=| AF |+| BF |=x 1+x 2+p 如图2,过A 、B 引x 轴的垂线AA 1、BB 1,垂足为A 1、B 1,那么| RF |=| AD |-| FA 1 |=| AF |-| AF|cos θ,∴| AF |=| RF |1-cos θ=p1-cos θ同理,| BF |=| RF |1+cos θ=p1+cos θ∴| AB |=| AF |+| BF |=p1-cos θ+p1+cos θ=2psin 2θ. S △OAB =S △OAF +S △OBF =12| OF || y 1 |+12| OF || y 1 |=12·p2·(| y 1 |+| y 1 |)∵y 1y 2=-p 2,则y 1、y 2异号,因此,| y 1 |+| y 1 |=| y 1-y 2 |∴S △OAB =p 4| y 1-y 2 |=p4(y 1+y 2)2-4y 1y 2=p44m 2p 2+4p 2=p 221+m 2=p 22sin θ.2.求证:①2124p x x =;②212y y p =-;③ 1| AF |+1| BF |=2p .当AB ⊥x 轴时,有 AF BF p ==,成立; 当AB 与x 轴不垂直时,设焦点弦AB 的方程为:2p y k x ⎛⎫=-⎪⎝⎭.代入抛物线方程: 2222p k x px ⎛⎫-= ⎪⎝⎭.化简得:()()222222014p k x p k x k -++=∵方程(1)之二根为x 1,x 2,∴1224k x x ⋅=.(12111212111111222x x p p pp AF BF AA BB x x x x +++=+=+=+++()()121222121222424x x p x x p p p p pp x x p x x ++++===+++++. 3.求证:=∠=∠'''FB A B AC Rt ∠.先证明:∠AMB =Rt ∠【证法一】延长AM 交BC 的延长线于E ,如图3,则△ADM ≌△ECM ,∴| AM |=| EM |,| EC |=| AD | ∴| BE |=| BC |+| CE |=| BC |+| AD |=| BF |+| AF |=| AB |∴△ABE 为等腰三角形,又M 是AE 的中点, ∴BM ⊥AE ,即∠AMB =Rt ∠ 【证法二】取AB 的中点N ,连结MN ,则| MN |=12(| AD |+| BC |)=12(| AF |+| BF |)=12| AB |,∴| MN |=| AN |=| BN |∴△ABM 为直角三角形,AB 为斜边,故∠AMB =Rt ∠. 【证法三】由已知得C (-p 2,y 2)、D (-p 2,y 1),由此得M (-p 2,y 1+y 22).∴k AM =y 1-y 1+y 22x 1+p2=y 1-y 22·y 212p+p =p (y 1-y 2)y 21+p 2=p (y 1--p 2y 1)y 21+p2=p y 1,同理k BM =py 2 ∴k AM ·k BM =p y 1·p y 2=p 2y 1y 2=p 2-p 2=-1∴BM ⊥AE ,即∠AMB =Rt ∠.【证法四】由已知得C (-p 2,y 2)、D (-p2,y 1),由此得M (-p 2,y 1+y 22).∴MA →=(x 1+p 2,y 1-y 22),MB →=(x 3+p 2,y 2-y 12)∴MA →·MB →=(x 1+p 2)(x 2+p 2)+(y 1-y 2)(y 2-y 1)4=x 1x 2+p 2(x 1+x 2)+p 24-(y 1-y 2)24=p 24+p 2(y 212p +y 222p )+p 24-y 21+y 22-2y 1y 24 =p 22+y 1y 22=p 22+-p 22=0 ∴MA →⊥MB →,故∠AMB =Rt ∠.【证法五】由下面证得∠DFC =90 ,连结FM ,则FM =DM .又AD =AF ,故△ADM ≌△AFM ,如图4∴∠1=∠2,同理∠3=∠4 ∴∠2+∠3=12×180︒=90︒∴∠AMB =Rt ∠. 接着证明:∠DFC =Rt ∠【证法一】如图5,由于| AD |=| AF |,AD ∥RF ,故可设∠AFD =∠ADF =∠DFR =α, 同理,设∠BFC =∠BCF =∠CFR =β, 而∠AFD +∠DFR +∠BFC +∠CFR =180︒∴2(α+β)=180︒,即α+β=90︒,故∠DFC =90︒ 【证法二】取CD 的中点M ,即M (-p 2,y 1+y 22)由前知k AM =p y 1,k CF =-y 2+p 2+p 2=-y 2p =py 1∴k AM =k CF ,AM ∥CF ,同理,BM ∥DF ∴∠DFC =∠AMB =90︒.【证法三】∵DF →=(p ,-y 1),CF →=(p ,-y 2),∴DF →·CF →=p 2+y 1y 2=0 ∴DF →⊥CF →,故∠DFC =90︒.【证法四】由于| RF |2=p 2=-y 1y 2=| DR |·| RC |,即| DR || RF |=| RF || RC |,且∠DRF =∠FRC =90︒∴ △DRF ∽△FRC∴∠DFR =∠RCF ,而∠RCF +∠RFC =90︒ ∴∠DFR +∠RFC =90︒ ∴∠DFC =90︒4. C ’A 、C ’B 是抛物线的切线图6【证法一】∵k AM =p y 1,AM 的直线方程为y -y 1=py 1(x -y 212p)与抛物线方程y 2=2px 联立消去x 得y -y 1=p y 1(y 22p -y 212p),整理得y 2-2y 1y +y 21=0可见△=(2y 1)2-4y 21=0, 故直线AM 与抛物线y 2=2px 相切, 同理BM 也是抛物线的切线,如图8.【证法二】由抛物线方程y 2=2px ,两边对x 求导,(y 2)'x =(2px )'x, 得2y ·y 'x=2p ,y 'x =py,故抛物线y 2=2px 在点A (x 1,y 1)处的切线的斜率为k 切=y 'x| y =y 1=p y 1. 又k AM =p y 1,∴k 切=k AM ,即AM 是抛物线在点A 处的切线,同理BM 也是抛物线的切线.【证法三】∵过点A (x 1,y 1)的切线方程为y 1y =p (x +x 1),把M (-p 2,y 1+y 22)代入左边=y 1·y 1+y 22=y 21+y 1y 22=2px 1-p 22=px 1-p 22,右边=p (-p 2+x 1)=-p 22+px 1,左边=右边,可见,过点A 的切线经过点M ,即AM 是抛物线的切线,同理BM 也是抛物线的切线.5. C ’A 、C ’B 分别是∠A ’AB 和∠B ’BA 的平分线.【证法一】延长AM 交BC 的延长线于E ,如图9,则△ADM ≌△ECM ,有AD ∥BC ,AB =BE , ∴∠DAM =∠AEB =∠BAM ,即AM 平分∠DAB ,同理BM 平分∠CBA . 【证法二】由图9可知只须证明直线AB 的倾斜角α是直线AM 的倾斜角β的2倍即可,即α=2β. 且M (-p 2,y 1+y 22)图9图8∵tan α=k AB =y 2-y 1x 2-x 1=y 2-y 1 y 222p -y 212p=2py 1+y 2. tan β=k AM =y 1-y 1+y 22x 1+p 2=y 1-y 22·y 212p +p =p (y 1-y 2)y 21+p 2=p (y 1--p 2y 1)y 21+p 2=py 1. ∴tan 2β=2tan β1-tan 2β=2py 11-(p y 1)2=2py 1y 22-p 2=2py 1y 22+y 1y 2=2py 1+y 2=tan α ∴α=2β,即AM 平分∠DAB ,同理BM 平分∠CBA .6. AC ’、A ’F 、y 轴三线共点,BC ’、B ’F 、y 轴三线共点 【证法一】如图10,设AM 与DF 相交于点G 1,由以上证明知| AD |=| AF |,AM 平分∠DAF ,故AG 1也是DF 边上的中线, ∴G 1是DF 的中点.设AD 与y 轴交于点D 1,DF 与y 轴相交于点G 2, 易知,| DD 1 |=| OF |,DD 1∥OF , 故△DD 1G 2≌△FOG 2∴| DG 2 |=| FG 2 |,则G 2也是DF 的中点. ∴G 1与G 2重合(设为点G ),则AM 、DF 、y 轴三线共点,同理BM 、CF 、y 轴也三线共点.【证法二】AM 的直线方程为y -y 1=py 1(x -y 212p ),令x =0得AM 与y 轴交于点G 1(0,y 12),又DF 的直线方程为y =-y 1p (x -p 2),令x =0得DF 与y 轴交于点G 2(0,y 12)∴AM 、DF 与y 轴的相交同一点G (0,y 12),则AM 、DF 、y 轴三线共点,同理BM 、CF 、y 轴也三线共点H .由以上证明还可以得四边形MHFG 是矩形.图107. A 、O 、B ’三点共线,B 、O 、A ’三点共线. 【证法一】如图11,k OA =y 1x 1=y 1 y 212p=2p y 1, k OC =y 2 -p 2=-2y 2p =-2py 2p 2=-2py 2-y 1y 2=2py 1∴k OA =k OC ,则A 、O 、C 三点共线, 同理D 、O 、B 三点也共线.【证法二】设AC 与x 轴交于点O ',∵AD ∥RF ∥BC∴| RO ' || AD |=| CO ' || CA |=| BF || AB |,| O 'F || AF |=| CB || AB |, 又| AD |=| AF |,| BC |=| BF |,∴| RO ' || AF |=| O 'F || AF |∴| RO ' |=| O 'F |,则O '与O 重合,即C 、O 、A 三点共线,同理D 、O 、B 三点也共线.【证法三】设AC 与x 轴交于点O ',RF ∥BC ,| O 'F || CB |=| AF || AB |,∴| O 'F |=| CB |·| AF || AB |=| BF |·| AF || AF |+| BF |=11| AF |+1| BF |=p2【见⑵证】∴O '与O 重合,则即C 、O 、A 三点共线,同理D 、O 、B 三点也共线.【证法四】∵OC →=(-p 2,y 2),OA →=(x 1,y 1),∵-p2·y 1-x 1 y 2=-p2·y 1-y 212p y 2=-py 12-y 1y 2y 12p =-py 12+p 2y 12p=0∴OC →∥OA →,且都以O 为端点∴A 、O 、C 三点共线,同理B 、O 、D 三点共线.【推广】过定点P (m ,0)的直线与抛物线y 2=2px (p >0)相交于点A 、B ,过A 、B 两点分别作直线l :x =-m 的垂线,垂足分别为M 、N ,则A 、O 、N 三点共线,B 、O 、M 三点也共线,如下图:图118. 若| AF |:| BF |=m :n ,点A 在第一象限,θ为直线AB 的倾斜角. 则cos θ=m -nm +n; 【证明】如图14,过A 、B 分别作准线l 的垂线,垂足分别为D ,C ,过B 作BE ⊥AD 于E ,设| AF |=mt ,| AF |=nt ,则| AD |=| AF |,| BC |=| BF |,| AE |=| AD |-| BC |=(m -n )t∴在Rt △ABE 中,cos ∠BAE =| AE || AB |= (m -n )t (m +n )t =m -nm +n∴cos θ=cos ∠BAE =m -nm +n.【例6】设经过抛物线y 2=2px 的焦点F 的直线与抛物线相交于两点A 、B ,且| AF |:| BF |=3:1,则直线AB 的倾斜角的大小为 .则E 的坐标为( p2+x 1 2,y 12),则点E 到y 轴的距离为d = p2+x 12=12| AF |故以AF 为直径的圆与y 轴相切, 同理以BF 为直径的圆与y 轴相切.【说明】如图15,设M 是AB 的中点,作MN ⊥准线l 于N ,则| MN |=12(| AD |+| BC |)=12(| AF |+| BF |)=12| AB |则圆心M 到l 的距离| MN |=12| AB |,故以AB 为直径的圆与准线相切. 10. MN 交抛物线于点Q ,则Q 是MN 的中点.【证明】设A (y 212p ,y 1),B (y 222p ,y 1),则C (-p 2,y 2),D (-p2,y 1),M (-p 2,y 1+y 22),N (y 21+y 224p ,y 1+y 22),设MN 的中点为Q ',则Q ' (-p 2+y 21+y 224p 2,y 1+y 22)∵ -p 2+y 21+y 224p 2= -2p 2+y 21+y 22 8p = 2y 1y 2+y 21+y 22 8p = ⎝ ⎛⎭⎪⎫y 1+y 222 2p∴点Q ' 在抛物线y 2=2px 上,即Q 是MN 的中点.图16。
