第2章 原子结构
结构化学第二章

8h2224Z e20rE
精选可编辑ppt
17
球极坐标与笛卡儿坐标的关系
精选可编辑ppt
18
Schrödinger方程在球极坐标中的形式
精选可编辑ppt
19
2. 变数分离法
令 (r,)R( r())(),代入上式 r2si并 2n 乘以
R
s R 2 i r n r 2 R r s i n si n 1 2 2 8 h 2 2( E V ) r 2 s2 i 0 n
这样的原子称为Rydberg原子。在实验室里已造出n 约为105的H原子, n 约为104的Ba原子; 在宇宙中也观察到了n 从301到300之间的跃迁。
毋庸置疑, Rydberg原子是个大胖子。事实上, 它的半径大约相当于基态 原子的十万倍! 这样一个胖原子, 即使受到微弱的电场或磁场作用, 也会显著 变形。
第二章 原子的结构和性质
精选可编辑ppt
1
精选可编辑ppt
2
在本章中,将用Schrödinger方程处理真实的化学物种, 这自然要从最简单的H原子入手。为了更具一般性,也包括 类氢离子,如He+、Li2+等,它们的区别仅在于原子序数Z的 不同。
氢是化学中最简单的物种,也是宇宙中最丰富的元素。 无论在矿石、海洋或生物体内,氢无所不在。
精选可编辑ppt
20
2. 变量分离
设ψ(r,θ,φ)=R(r)Θ(θ)Φ(φ)= R(r) Y (θ,φ). 方程两边同乘以r2/(RΘΦ)
R方程:
Y方程:
Y=ΘΦ.方程两边同乘以 sin2θ/(ΘΦ)并移项
精选可编辑ppt
21
经变数分离得到的三个分别只含,和r变量的方程依次称 为方程、方程和R方程,将方程和方程合并,Y(,) =()(),代表波函数的角度部分。
普通化学:第二章-原子结构、分子结构与化学键4

作业:P71:2,3,4,5,6;P83:2;3;P81:9; 更正:P71: 3. 给出电子在l = 4的5g 轨道的所有可能的量子数。
说明为什么不存在3f 轨道或4g 轨道。
为什么说只有原子序数从122 (121)开始的元素,5g 轨道才被电子所占有。
五、 多电子原子的核外电子排布i) 处理多电子原子的结构,必须采用近似方法 中心场近似只考察其中一个电子的运动,而把原子核对它的库仑吸引以及其他N -1个电子对它的库仑排斥笼统地看成是一个处在原子中心的正电荷Z* 对它的库仑吸引:V = -*2Z e 4r πε通过这个势函数,多电子原子就可以简单地当作单电子原子来处理。
这样,上一节处理单电子原子的全部结果,只要略作修正,都适用于多电子原子。
在多电子原子中,电子的运动状态也是由n , l , m l 和m s 四个量子数决定的,电子在由这四个量子数所决定的各运动状态上的空间分布特征完全和在单电子原子中一样。
在电荷为Z*的中心场作用下运动的电子的能量为:E = -Z m e h e *2422028n ε=-Z Eh *222nZ*称为作用在电子上的有效核电荷:Z* = Z -σσ称为屏蔽常数,其意义是:一个核电荷为Z (>1) 的多电子原子,作用在电子上的电荷不再是核电荷Z,而是扣除了其它电子的屏蔽作用以后的有效核电荷Z*。
要了解多电子原子的电子结构,关键在于确定其它电子对被考察的电子的屏蔽常数。
电子的“屏蔽作用”是广义的,它包括了内层电子的真实的屏蔽作用,也包括了同层电子及外层电子的排斥作用。
这是氢原子的1s, 2s, 3s轨道的边界图,每个球包含约90%的电子密度。
简单地讲,轨道尺寸正比于n2。
内层电子对外层电子的屏蔽效应大,外层电子对内层电子的屏蔽效应小。
ii) 斯莱特规则在量子力学中,这个屏蔽作用是通过光谱实验数据得到的。
1930年,美国的斯莱特(J. C. Slater) 提出了一套估算屏蔽常数的半经验规则,按量子数n和l的递增,把多电子原子的原子轨道按如下的顺序分组:(1s) (2s, 2p) (3s, 3p) (3d) (4s, 4p) (4d) (4f) (5s, 5p)……可以按下面的简单规则估算一个电子对另一个电子的屏蔽系数:1. 处在右面的各轨道组内的电子对左面轨道组内的电子没有屏蔽作用,屏蔽系数为0;2. 在同一轨道组内的电子,除(1s)组的二个电子间的屏蔽系数为0.30外,其它各轨道组内电子间的屏蔽系数都是0.35;3. 主量子数为n-1的各轨道组内的电子对(ns, np)组各电子的屏蔽系数为0.85;4. 主量子数等于和小于n-2的各轨道组内的电子对(ns, np)组各电子的屏蔽系数均为1.00;5. 处在(nd)或(nf)组左面的各轨道组内的电子对(nd)或(nf)组内电子的屏蔽系数均为1.00。
第2章原子结构和原子光谱[3]
![第2章原子结构和原子光谱[3]](https://img.taocdn.com/s3/m/cb0841641eb91a37f1115c57.png)
3S 1S
m
1 0
l
-1
m
1
l
m
1 1 1 0 0 0 0 0 0 0 0 0 -1 -1 -1
s
↑
↑
-1 0 0 -1 2
↑
1
↓
↓↑
0 1 0 1 0
↑
↓
↓
Atomic terms symbols for two equivalent electrons
12
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
l - l coupling
Summary
s-s coupling
L-S coupling
Magnetic field
20112011-9-30 Chemistry Department of Fudan University 13
L - Scoupling: the orbital momenta for all electrons is coupled to obtain a total orbital angular momentum L and then the individual spin angular momenta is coupled to obtain the total spin angular momentum S. The total angular momentum J is then obtained by vector addition of L and S.
无机化学2原子结构与元素周期律

第二章 原子结构与元素周期律
表2-4
n、l、m的关系
第二章 原子结构与元素周期律
六、多电子原子轨道的能级
用图形把原 子轨道能级 高低顺序表 示出来,就 是原子轨道 能级图。
第二章 原子结构与元素周期律
第二节 核外电子的排布
多电子原子中,电子不仅受核的吸引,而且还存在 电子间的相互排斥,这些都影响到原子核外电子的排布, 而核外电子的排布又直接决定着元素的性质。因此,核 外电子排布是多电子原子结构中的一个重要问题。 人们根据光谱实验结果,并结合对元素周期律的分 析,归纳、总结出基态原子核外电子排布的三个基本原 理。
第二章 原子结构与元素周期律
五、薛定谔方程和四个量子数
为了描述电子的运动状态,1926年薛定谔把电子运动和 光的波动理论联系起来,提出了一种波动方程,该方程 称为薛定谔方程。
为了得到电子运动状态合理的解,必须引用三个参数,主 量子数n、角量子数l和磁量子数m,它们的取值是相互制 约的。此外,还有用来描述电子自旋运动的自旋量子数ms。
第二章 原子结构与元素周期律
迄今为止,人类已发现了一百多种元素,而这些元
素形成了数以百万计的物质,组成了丰富多彩的物质世 界。要了解这些物质的性质和变化规律,就必须要认识 其结构,从原子、分子水平上研究物质结构、性质及其 变化规律之间的关系。
第二章 原子结构与元素周期律
第一节 核外电子运动状态 一、氢原子光谱和玻尔理论
第二章 原子结构与元素周期律
(一)主量子数n
主量子数表示电子离核的平均距离,n越大,电子离核平 均距离越远,n相同的电子离核平均距离比较接近,即所 谓电子处于同一电子层。
电子层能量高低顺序: K<L<M<N<O<P。
高中物理 第2章 原子结构 2.1 电子的发现与汤姆孙模型教案

第1节电子的发现与汤姆孙模型●课标要求1.知道阴极射线是由电子组成的,电子是原子的组成部分,是比原子更基本的物质单元.2.体会电子的发现过程中蕴含的科学方法及人类探索原子结构的重大意义.3.知道汤姆孙的原子模型,认识19世纪末三大发现的物理意义.●教学地位本节教科书由阴极射线、电子的发现和汤姆孙模型三部分内容组成.重点是电子的发现过程蕴含的科学方法.首先通过实验说明阴极射线的存在,然后指出“19世纪后期”,物理学家对阴极射线的本质的认识有两种观点”,最后仍然通过实验研究发现了电子.电子的发现说明原子不是组成物质的最小微粒,对揭示原子结构有重大意义,是近代物理三大发现(X射线、放射性、电子)之一.电子的发现是一个很好的培养学生分析问题和解决问题能力的内容.认识电子发现的重大意义,体会电子的发现过程中蕴含的科学方法,是教学中的重点.●新课导入建议实验引入给阴极射线管加上高压,并将磁铁靠近阴极射线管,你会观察到什么现象?为什么会出现这种现象?阴极射线到底是什么?本节课我们重复着科学家的足迹进行探究.●教学流程设计课前预习安排:1.看教材2.填写【课前自主导学】同学之间可进行讨论⇒步骤1:导入新课,本节教学地位分析⇒步骤2:老师提问,检查预习效果可多提问几个学生⇒步骤3:师生互动完成“探究1”除例1外可再变换命题角度,补充一个例题以拓展学生思路⇓步骤7:先由学生自己总结本节的主要知识,教师点评,安排学生课下完成【课后知能检测】⇐步骤6:指导学生完成【当堂双基达标】,验证学习情况⇐步骤5:师生互动完成“探究2”重在分析错误的原因⇐步骤4:让学生完成【迁移应用】,检查完成情况并点评课标解读重点难点1.了解物质结构早期探究的基本历程.2.知道阴极射线的产生及其本质,理解汤姆孙对阴极射线研究的方法及电子发现的意义.3.了解汤姆孙原子模型. 1.理解阴极射线的研究过程.(重点)2.汤姆孙发现电子的理论推导.(难点)3.电子电荷量的测定.(难点)物质结构的早期探究(1)古人对物质的认识①我国西周的“五行说”认为万物是由金、木、水、火、土5种基本“元素”组成的.②古希腊的亚里士多德认为万物的本质是土、水、火、空气四种“元素”,天体则由第五种“元素”——“以太”构成.③古希腊哲学家德谟克利特等人建立了早期的原子论,认为宇宙间存在一种或多种微小的实体,叫做“原子”.(2)通过实验了解物质的结构①1661年,玻意耳以化学实验为基础建立了科学的元素论.②19世纪初,道尔顿提出了原子论,认为原子是元素的最小单位.③1811年,意大利化学家阿伏伽德罗提出了分子假说,指出分子可以由多个相同的原子组成.(3)结论在物质的结构中存在着分子、原子这样的层次,宏观物质的化学性质决定于分子,而分子则由原子组成.原子是构成物质的不可再分割的最小颗粒,它既不能创生,也不能消灭.2.思考判断(1)玻意耳认为万物的本质是土、水、火、空气四种元素的元素论.(×)(2)阿伏伽德罗提出分子可以由多个原子组成.(√)(3)19世纪初期形成的原子论观点认为原子是构成物质的最小颗粒是不可分的.(√)3.探究交流试简述道尔顿提出原子论的依据.【提示】18世纪一系列重要的实验结果,如化学反应遵从质量守恒定律,元素形成化合物时遵从定比定律、倍比定律等,启示人们推想物质是由一些不可毁灭的微粒构成的,而且各种不同的元素微粒按照一定的比例形成化合物,在此基础上,19世纪初,道尔顿提出了原子论,认为原子是元素的最小单元.电子的发现及汤姆孙模型1.(1)汤姆孙的探究方法①让阴极射线分别通过电场或磁场,根据偏转现象,证明它是带负电的粒子流,通过静电偏转力与磁场偏转力相抵消等方法,确定了阴极射线粒子的速度,并测量出了其比荷.②换用不同金属的阴极,所得粒子的比荷值大体相同.③粒子带负电,阴极射线的电荷与氢离子的电荷大小基本相同,比荷是氢离子的近两千倍,说明阴极射线粒子的质量远小于氢离子质量.④组成阴极射线的粒子称为电子.(2)结论①阴极射线是高速电子流.②不同物质都能发射这种带电粒子,它是各种物质中共有的成分,比最轻的氢原子的质量还要小的多,汤姆孙将这种带电粒子称为电子.(3)电子发现的意义以前人们认为物质由分子组成,分子由原子组成,原子是不可再分的最小微粒.现在人们发现了各种物质里都有电子,而且电子的质量比最轻的氢原子质量小得多,这说明电子是原子的组成部分.电子带负电,而原子是电中性的,可见原子内还有带正电的物质,这些带正电的物质和带负电的电子如何构成原子呢?电子的发现大大激发了人们研究原子内部结构的热情,拉开了人们研究原子结构的序幕.(4)19世纪末物理学的三大发现①1895年伦琴发现了X 射线;②X 射线发现后不久,贝克勒尔发现了放射性;③1897年汤姆孙发现了电子.(5)汤姆孙的原子模型原子带正电的部分充斥整个原子,很小很轻的电子镶嵌在球体的某些固定位置,正像葡萄干嵌在面包中那样.2.思考判断(1)电子的发现,说明原子具有一定的结构.(√)(2)电子是第一种被人类发现的微观粒子.(√)(3)电子的发现,是19世纪末的三大著名发现之一.(√)3.探究交流为什么汤姆孙要通过电场和磁场研究阴极射线?【提示】 当时对阴极射线本质的认识存在两种认识:一是认为是带电粒子,二是认为是以太波.而汤姆孙认为阴极射线是带电粒子,而带电粒子可受电场力和磁场力.“阴极射线”性质的研究1.如何确定阴极射线的带电性质?2.如何确定阴极射线的比荷? 3.阴极射线的本质是什么?1.电性的确定 方法一:让阴极射线进入已知电场,由所受电场力方向确定带电的性质.方法二:让阴极射线进入磁场,由所受洛伦兹力的方向,根据左手定则确定带电的性质.2.比荷的测定方法图2-1-1(1)让粒子通过正交的电磁场,如图2-1-1所示,让其做直线运动,根据二力平衡条件,即F 洛=F 电(Bqv =qE )得到粒子的运动速度v =E B.图2-1-2(2)在其他条件不变的情况下,撤去电场,如图2-1-2所示,保留磁场,让粒子只在磁场中运动,由洛伦兹力提供向心力即Bqv =mv 2R,根据磁场情况和轨迹偏转情况,由几何知识求出其半径R .(3)由以上方法确定粒子比荷的表达式:q m =E B 2R. 3.电子的发现(1)汤姆孙测得阴极射线粒子的比荷约为1011 C/kg ,电荷量与氢离子基本相同,质量为氢离子的11 800. (2)最后经定量计算,汤姆孙认定组成阴极射线的粒子为电子.1.阴极射线的来源:若放电管的真空度高,阴极射线的粒子主要来自阴极;若放电管的真空度不高,粒子还可能来自管中气体.2.阴极射线不是X 射线.(2012·文昌检测)1897年,物理学家汤姆孙正式测定了电子的比荷,打破了原子是不可再分的最小单位的观点.因此,汤姆孙的实验是物理学发展史上最著名的经典实验之一.在汤姆孙测电子比荷的实验中,采用了如图2-1-3所示的阴极射线管,从电子枪C 出来的电子经过A 、B 间的电场加速后,水平射入长度为L 的D 、G 平行板间,接着在荧光屏中心F 出现荧光斑.若在D 、G 间加上方向向下,场强为E 的匀强电场,电子将向上偏转;如果再利用通电线圈在D 、G 电场区加上一垂直纸面的、磁感应强度为B 的匀强磁场(图中未画),荧光斑恰好回到荧光屏中心,接着再去掉电场,电子向下偏转,偏转角为θ,试解决下列问题. 图2-1-3(1)说明图中磁场沿什么方向;(2)根据L 、E 、B 和θ,求出电子的比荷.【审题指导】 阴极射线带负电,根据运动的速度方向及在磁场中的偏转方向利用左手定则判断磁场方向,并利用几何关系计算比荷.【解析】 (1)由于所加磁场使电子受到向下的洛伦兹力,因此磁场的方向垂直纸面向里.(2)如图,当电子在DG 间做匀速直线运动时,有eE =evB ①当电子在DG 间的磁场中偏转时,有evB =mv 2r② 同时又有L =r sin θ③由①②③式得e m =E sin θB 2L. 【答案】 见解析1.比荷的测定问题只是带电粒子在磁场和电场中运动的一类典型例子,这种方法可以推广到带电粒子在复合场中的运动,求其他相关的问题.2.解决带电粒子在电磁场中运动的问题时要注意以下几点:(1)带电粒子的带电性质.(2)正确描绘运动轨迹.(3)能确定半径、圆心.(4)会利用几何知识把有关线段与半径联系起来.(2013·琼海检测)如图2-1-4所示是汤姆孙的气体放电管的示意图,下列说法中正确的是( )汤姆孙的气体放电管的示意图图2-1-4A .若在D 1、D 2之间不加电场和磁场,则阴极射线应打到最右端的P 1点B .若在D 1、D 2之间加上竖直向下的电场,则阴极射线应向下偏转C .若在D 1、D 2之间加上竖直向下的电场,则阴极射线应向上偏转D .若在D 1、D 2之间加上垂直纸面向里的磁场,则阴极射线不偏转【解析】 实验证明,阴极射线是电子流,它在电场中偏转时应偏向带正电的极板一侧,可知选项C 正确,选项B 错误.加上磁场时,电子在磁场中受洛伦兹力作用,要发生偏转,因而选项D 错误.当不加电场和磁场时,电子所受的重力可以忽略不计,因而不发生偏转,选项A 的说法正确.【答案】 AC易错案例警示——对汤姆孙原子模型的意义认识不清导致错误 下列说法正确的是 ( )A.汤姆孙研究阴极射线,用测定粒子比荷的方法发现了电子B.电子的发现证明了原子是可分的C.汤姆孙认为原子里面带正电荷的物质应充斥整个原子,而带负电的电子,则镶嵌在球体的某些固定位置D.汤姆孙原子模型是正确的【正确解答】通过物理学史可得,选项A正确;根据电子发现的重要意义可得,选项B正确;选项C描述的是汤姆孙原子模型,选项C正确;汤姆孙原子模型本身是错的,选项D错误.【答案】ABC【易错分析】本题易错选项及错误原因分析如下:电子电荷量的测定——密立根油滴实验1.密立根油滴实验的原理电子所带的电荷量最早是由美国科学家密立根所做的油滴实验测出的.密立根实验的原理如图教2-1-1所示.图教2-1-1(1)两块水平放置的平行金属板A、B与电源相接,使上板带正电,下板带负电,油滴从喷雾器喷出后,经上面金属板中间的小孔,落到两板之间的匀强电场中.(2)大多数油滴在经过喷雾器喷嘴时,因摩擦而带负电,油滴在电场力、重力和空气阻力的作用下下降.观察者可在强光照射下,借助显微镜进行观察.2.方法(1)两板间的电势差、两板间的距离都可以直接测得,从而确定极板间的电场强度E,但是由于油滴太小,其质量很难直接测出.密立根通过测量油滴在空气中下落的终极速度来测量油滴的质量.没加电场时,由于空气的黏性,油滴所受的重力大小很快就等于空气给油滴的摩擦力而使油滴匀速下落,可测得速度v1.(2)再加一足够强的电场,使油滴做竖直向上的运动,在油滴以速度v2匀速运动时,油滴所受的静电力与重力、阻力平衡.根据空气阻力遵循的规律,即可求得油滴所带的电荷量.3.结论密立根测定了数千个带电油滴的电荷量,发现这些电荷量都等于某个最小电荷量的整数倍,从而证实了电荷是量子化的,并求得了元电荷即电子或质子所带的电荷量e.1.历史上第一个发现电子的科学家是( )A.贝可勒尔 B.道尔顿C.伦琴D.汤姆孙【解析】贝可勒尔发现了天然放射现象,道尔顿提出了原子论,伦琴发现了X射线,汤姆孙发现了电子.【答案】 D图2-1-52.如图2-1-5所示,在阴极射线管正上方平行放一通有强电流的长直导线,则阴极射线将( )A.向纸内偏转B.向纸外偏转C.向下偏转D.向上偏转【解析】本题综合考查电流产生的磁场、左手定则和阴极射线的产生及性质.由题目条件不难判断阴极射线所在处磁场垂直纸面向外,电子从负极端射出,根据左手定则可判定阴极射线(电子)向上偏转.【答案】 D3.关于电荷的电荷量,下列说法错误的是( )A.电子的电荷量是由密立根油滴实验测得的B.物体所带电荷量可以是任意值C.物体所带电荷量最小值为1.6×10-19 CD.物体所带的电荷量都是元电荷的整数倍【解析】密立根油滴实验测出了电子的电荷量为1.6×10-19C,并提出了电荷量量子化的观点,因而A、C对,B错;任何物体的电荷量都是e的整数倍,故D对;因此选B.【答案】 B4.关于阴极射线的性质,下列说法正确的是 ( )A.阴极射线带负电B.阴极射线带正电C.阴极射线中的负电粒子的比荷与氢离子的基本相同D.阴极射线中的负电粒子的带电荷量与氢离子的相同【解析】阴极射线是电子流,故带负电,A对B错.电子与氢离子的带电荷量相同,但质量不同,故C错D对.【答案】AD5.阴极射线是从阴极射线管的阴极发出的高速运动的图2-1-6粒子流,这些微观粒子是________.若在如图2-1-6所示的阴极射线管中部加垂直于纸面向里的磁场,阴极射线将________(选填“向上”、“向下”或“向外”)偏转.【解析】阴极射线即为电子流.当电子流穿过垂直纸面向里的磁场时,将受到洛伦兹力的作用而向下偏转(注意电流方向与电子流方向相反).【答案】电子向下。
2原子的结构与性质

1 m 0, 0 2
本章目录 总目录 阅读帮助
第二章 原子的结构和性质
根据态叠加原理,两个独立特解的线性组合仍然是 方程的解。可由此得实函数解。
1 im 1 m e cos m i sin m 2 2
m
1 im 1 e cos m i sin m 2 2
(2.1.8)
本章目录 总目录 阅读帮助
第二章 原子的结构和性质
按照偏微分关系运算可得几个典型算符在极坐标内 的情况:
ih ˆ M z 2π ih ˆ Mx sin cos cos 2π
ih ˆ My cos cos sin 2π
z r cos
: [0,2]
2 2
r x y z
2 2
(2.1.4)
cos
x
z
2
y z
2
2
1
2
(2.1.5) (2.1.6)
tan y
本章目录
x
阅读帮助
总目录
第二章 原子的结构和性质
按偏微分关系分别对式(2.1.4)、(2.1.5)、(2.1.6) 求导并 代入式(2.1.3) ,利用偏微分关系式:
单电子原子:H、 He+、 Li2+、Be3+都是只有1个 核外电子的简单体系,称为单电子原子或类氢离子。
核电荷数为 Z 的单电子原子,电子距核 r 处绕核 运动,电子和原子核吸引的位能由库仑定律可求得:
Ze 2 V 4π 0 r
体系的全能量算符(Hamilton):
2 2 2 h h Ze 2 2 ˆ H N 2 e 2 8 M N 8 me 4 0 r
高中物理 第2章 原子结构 第4讲 氢原子光谱与能级结构

解析 巴尔末公式只确定了氢原子发光中的一个线系波长, 不能描述氢原子发出的各种光的波长,也不能描述其他原 子发出的光,故D错误. 巴尔末公式是由当时已知的可见光中的部分谱线总结出来 的,但它适用于整个巴尔末线系,故A、B错误,C正确. 答案 C
借题发挥 巴尔末公式的应用方法及注意问题 (1)巴尔末公式反映了氢原子发光的规律特征,不能描述其他 原子. (2)公式中n只能取大于等于3的整数,不能连续取值,因此波 长也只是分立的值. (3)公式是在对可见光区的四条谱线分析时总结出的,但在紫 外区的谱线也适用. (4)应用时熟记公式,当n取不同值时求出对应的波长λ.
第2章——
第4讲 氢原子光谱与能级结构
目标定位 1.知道氢原子光谱的实验规律,了解巴尔末公式及里德伯 常量. 2.理解玻尔理论对氢原子光谱规律的解释.
1 预习导学 2 课堂讲义 3 对点练习
梳理·识记·点拨 理解·深化·探究 巩固·应用·反馈
预习导学
梳理·识记·点拨
一、氢原子光谱 1.氢原子光谱的特点: (1)从红外区到紫外区呈现多条具有确定 波长 的谱线; (2)从长波到短波,Hα~Hδ等谱线间的距离 越来越小 , 表 现出明显的 规律性 .
2.玻尔理论的成功之处 (1)运用经典理论和量子化观念确定了氢原子的各个定态的能 量,并由此画出了氢原子的能级图. (2)处于激发态的氢原子向低能级跃迁辐射出光子,辐射光子 的能量与实际符合得很好,由于能级是分立的,辐射光子的 波长是不连续的. (3)导出了巴尔末公式,并从理论上算出了里德伯常量R的值, 并很好地解释甚至预言了氢原子的其他谱线系.
氢原子光谱的实验规律 3.下列对于巴尔末公式的说法正确的是( ) A.所有氢原子光谱的波长都与巴尔末公式相对应 B.巴尔末公式只确定了氢原子发出的可见光部分的光的波长 C.巴尔末公式确定了氢原子发光的一个线系的波长,其中既 有可见光,又有紫外光 D.巴尔末公式确定了各种原子发光中的光的波长
选修3-5 第二章 第1讲 原子结构 氢原子光谱

3.光谱分析
特征谱线 可以用来鉴别物质和确定 利用每种原子都有自己的_________
物质的组成成分,且灵敏度很高。在发现和鉴别化学元素上有
着重大的意义。
知识点 2
氢原子的能级结构、能级公式
Ⅰ
1.玻尔理论
不连续 的能量状态中,在这 (1)定态:原子只能处于一系列_______
稳定 的,电子虽然绕核运动,但并不向 些能量状态中原子是_____
表示电子由较高能级向较低能级跃迁,电 子跃迁的条件为hν =Em-En
带箭头的竖线
2.对电子跃迁条件hν =Em-En的说明
(1)电子跃迁条件hν =Em-En只适用于光子和原子作用而使原子
在各定态之间跃迁的情况。
(2)当光子能量大于或等于13.6 eV时,也可以被处于基态的氢 原子吸收,使氢原子电离;当处于基态的氢原子吸收的光子能量 大于13.6 eV时,氢原子电离后,电子具有一定的初动能。 (3)原子还可吸收外来实物粒子(例如自由电子)的能量而被 激发。由于实物粒子的动能可全部或部分被原子吸收,所以只要 入射粒子的能量大于或等于两能级的能量差值(E=Em-En),均
②利用原子能量公式En=Ekn+Epn判断,当轨道半径增大时,原
子能量增大,电子动能减小,故原子的电势能增大。反之,当
轨道半径减小时,原子能量减小,电子动能增大,故原子的电 势能减小。
【典例透析2】氢原子辐射出一个光子后,根据玻尔理论,下 述说法正确的是( )
A.电子绕核旋转的半径增大
B.电子的动能增大
【典例透析1】如图所示为氢原子能级
图,下列说法正确的是(
的光谱
)
A.玻尔理论也能很好地解释复杂原子 B.玻尔理论认为原子的能量是连续的, 电子的轨道半径是不连续的
原子结构讲解

原子结构讲解
原子结构是指原子的组成以及各组成部分之间的相对位置。
原子是由原子核和核外电子组成的,原子核位于原子的中心,核外电子围绕原子核高速旋转。
原子结构示意图是一种表示原子结构的图示,它用圆圈和小圈分别表示原子核和核内质子数,弧线表示电子层,弧线上的数字表示该层的电子数。
原子的核外电子是分层排列的,从里到外分别称为第一层、第二层、第三层等。
每层最多可以排2×(n)^2个电子,其中n表示层数。
最外层电子数不
超过8个,次外层电子数不超过18个,倒数第三层不超过32个。
原子的性质由其核外电子的排布决定。
根据电子排布的不同,原子可以分为金属原子、非金属原子和稀有气体原子。
金属原子的最外层电子数一般小于4,容易失去电子,表现出金属的特性;非金属原子的最外层电子数一般大
于或等于4,容易得到电子,表现出非金属的特性;稀有气体原子的最外层电子数为8个(氦为2个),是一种稳定结构,表现出稀有气体的特性。
以上就是原子结构的简要介绍,如需获取更多信息,建议查阅化学书籍或咨询化学专家。
第二章 原子的结构和性质2.3-2.4

作图方法主要包括:
函数-变量对画图 等值面(线)图 界面图 网格图 黑点图
有些图形只能用某一种方式来画, 有些图形则可 能用几种不同方式来画。作图对象与作图方法结合 起来, 产生了错综复杂的许多种图形。
采用列表的形式, 可使这种关系变得一目了然。
2.3 原子轨道和电子云的图形表示
波函数 ( ,原子轨道) 电子云 ( ||2 ,概率密度)
当n相同,l不同时, l越 大,主峰离核越近; l越小 峰越多,而且第一个峰离 核越近,俗称钻得越深。 钻穿效应
2.3.2 原子轨道 和电子云 ||2 的角度分布
角度分布是以角度波函数 Y ,m ( , ) 在球坐标系中对 θ、角作图,其做法是在坐标系中,选原子核作为 坐标原点,在每一个(θ, )方向上引一条直线,取长 度为|Y|的线段,将这些线段的端点连接起来,在空 间形成一个曲面,根据 Y值的大小标明正负号。若 取直线的长度为|Y|2,所以直线端点构成的曲面称 为电子云 的角2 度分布。
毋庸置疑, Rydberg原子一定是个大胖子. 事实上, 它的半径 大约相当于基态原子的十万倍! 这样一个胖原子, 即使受到微弱 的电场或磁场作用, 也会显著变形.
由于 Yl,m (q ,f )只与角量子数 l 和磁量子数m有关,而 与主量子数n无关,因此 l,m 相同的状态,其原子轨 道的角度分布图都相同。如2pz, 3pz, 4pz角度部分图 形都完全相同。
原子轨道ψ的角度分布
s 00
1
4
对s-型轨道而言,只
与r有关,没有角度依赖
+
性,所以从原点到曲线
数的形式。
5. 磁量子数及角动量在磁场方向的分量
角动量在Z方向(磁场方向)的分量Lz的算符 作用于单电子原子波函数ψ,得:
结构化学讲义教案2原子结构和性质

第二章 原子结构和性质教学目的:通过H 原子薛定谔方程的求解,了解原子结构中量子数的来源,类氢离子波函数的图形及其物理意义。
掌握多电子原子的原子轨道能级等,推导原子基态光谱项。
教学重点:1.类氢离子波函数量子数的物理意义。
2.掌握多电子原子的原子轨道能级、电离能的求解。
3.推导等价、非等价电子的原子光谱项,掌握基态原子谱项的快速推算法。
第一节 单电子原子的薛定谔方程及其解引言:前面介绍了量子力学的概念,建立了量子力学的基础,下面我们要讨论原子结构的核心问题,即原子中电子的运动状态,其中最简单的体系就是原子核外只有一个电子的体系,也叫单电子原子结构,如氢原子和类氢离子(H ,Li 2+,He +,Be 3+……)。
一.建立单电子原子的Schrodinger 方程r Ze mh M h H e N 022********ˆπεππ-∇-∇-= 假设在研究电子运动时核固定不动,r Ze mh H 0222248ˆπεπ-∇-= 为了解题方便通常将x,y ,z 变量变换成极坐标变量r ,θ,φ由图可得如下关系:⎪⎭⎪⎬⎫⋅=⋅⋅=⋅⋅=θφθφθcos sin sin cos sin r z r y r x得极坐标形式的Schrodinger 方程:048sin 1sin sin 110222222222=⎪⎪⎭⎫⎝⎛++∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂ψπεπφψθθψθθθψr Ze E h m r r r r r r二、单电子Schrodinger 方程的一般解。
1. 变数分离法把含三个变量的微分方程化为三个各含一个变量的常微分方程来求解。
令()()r R r =φθψ,,Θ(θ)Φ(φ)()()φθ,,Y r R =代入薛定鄂方程,经过数学变换得三个方程:R(r)方程 ()()k E r hm r h mZe r r R r r r R =++⎪⎭⎫ ⎝⎛∂∂∂∂⋅2222022821πεπ Θ方程22sin )(sin )(sin m k =+⎪⎭⎫ ⎝⎛∂Θ∂⋅∂∂⋅Θθθθθθθθ Φ方程222)()(1m =∂Φ∂⋅Φ-φφφ 2. Φ方程的解Φ方程整理得:0222=Φ+Φm a a φ这是一个常系数2阶齐次线性方程,它的特征方程为022=+m p i m p ±=微分方程的两个特解为φim Ae m =Φ m m ±= A 由归一化求得: π21=A ∴φπim e m 21=Φ 这是解的复数形式,由于Φ是循环坐标所以()()πφφ2+Φ=Φm m 于是πφπφφ2)2(im im im im e e e e ⋅==+ 即12=πim e由欧拉公式12sin 2cos 2=+=m i m e im πππ故m 的取值必须为: 2,1,0±±=m 即取值是量子化的称为磁量子数。
大学无机化学第二章(原子结构)试题及答案

第五章 原子结构和元素周期表本章总目标:1:了解核外电子运动的特殊性,会看波函数和电子云的图形2:能够运用轨道填充顺序图,按照核外电子排布原理,写出若干元素的电子构型。
3:掌握各类元素电子构型的特征4:了解电离势,电负性等概念的意义和它们与原子结构的关系。
各小节目标:第一节:近代原子结构理论的确立 学会讨论氢原子的玻尔行星模型213.6E eV n =。
第二节:微观粒子运动的特殊性1:掌握微观粒子具有波粒二象性(h h P mv λ==)。
2:学习运用不确定原理(2h x P mπ∆∙∆≥)。
第三节:核外电子运动状态的描述1:初步理解量子力学对核外电子运动状态的描述方法——处于定态的核外电子在核外空间的概率密度分布(即电子云)。
2:掌握描述核外电子的运动状态——能层、能级、轨道和自旋以及4个量子数。
3:掌握核外电子可能状态数的推算。
第四节:核外电子的排布1:了解影响轨道能量的因素及多电子原子的能级图。
2;掌握核外电子排布的三个原则:○1能量最低原则——多电子原子在基态时,核外电子尽可能分布到能量最低的院子轨道。
○2Pauli 原则——在同一原子中没有四个量子数完全相同的电子,或者说是在同一个原子中没有运动状态完全相同的电子。
○3Hund 原则——电子分布到能量简并的原子轨道时,优先以自旋相同的方式分别占据不同的轨道。
3:学会利用电子排布的三原则进行第五节:元素周期表认识元素的周期、元素的族和元素的分区,会看元素周期表。
第六节:元素基本性质的周期性掌握元素基本性质的四个概念及周期性变化1:原子半径——○1从左向右,随着核电荷的增加,原子核对外层电子的吸引力也增加,使原子半径逐渐减小;○2随着核外电子数的增加,电子间的相互斥力也增强,使得原子半径增加。
但是,由于增加的电子不足以完全屏蔽增加的核电荷,因此从左向右有效核电荷逐渐增加,原子半径逐渐减小。
2:电离能——从左向右随着核电荷数的增多和原子半径的减小,原子核对外层电子的引力增大,电离能呈递增趋势。
print 第2章.原子的结构和性质
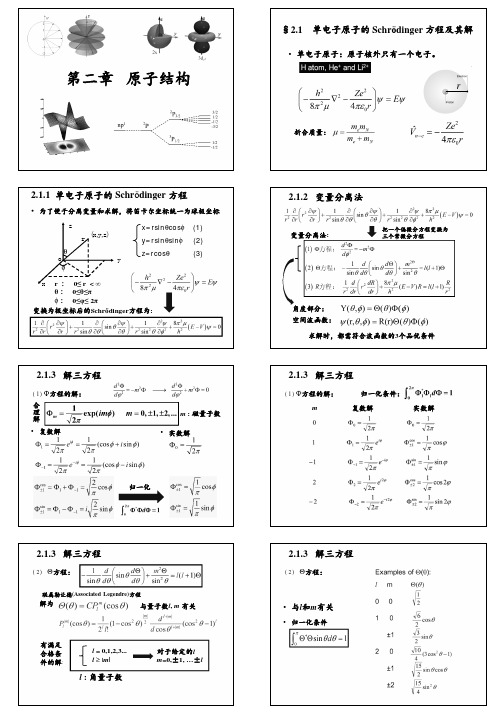
三个量子数n, l和m具有如下的关系
• 主量子数
n = 1, 2, 3, …, n;
• 角量子数
l = 0, 1, 2, …, n-1;
• 磁量子数
m= 0, ±1, ±2,…, ±l
每套量子数n, l和m决定一个波函数ψnlm的形式,即 决定了单电子原子体系的一种状态,因此简称为原子轨
道(AO, Atomic Orbital)。
• 两个径向节面,
3s
即n-l-1=2,所以n=3
§2.4 多电子原子的结构
2.4.1 多电子原子的Schrödinger方程
• 原子单位 atomic unit, a.u.
定核近似
r
2.4.1 多电子原子的Schrödinger方程
两个电子的 电子与原子核相互 两电子之间相互作 动能算符 作用的势能算符 用的势能算符
能级交错
2.4.1 多电子原子的Schrödinger方程
• 单电子波函数求 解结果与类氢粒 子波函数一样
n例:He原子基态
零级近似的计算结果:
实验值:
结论:零级近似的计算结果与实验值相差很大, 说明电子间的相互作用不可忽略。
2.4.2 单电子原子轨道能
和单电子波函数 Ψi 相应的能量 Ei
2. 由屏蔽常数近似计算原子轨道能
l 单电子原子的能级公式:
单电子原子的 能量E只与主量 子数n有关
1. 主量子数
• 能量量子化 • 能量为负,电子离
核无穷远时作为位 能的零点 • 简并度:在相同n 下,而l, m不同的 AO有n2个 例如,n=2时,空间波函数有
2. 角量子数 l:决定电子的原子轨道角动量的大小。
• 原子只要有角动量 也就有磁距
第二章原子结构习题及解答

第二章、原子结构习题及解答一、填空题(在划线处填上正确答案)2101、在直角坐标系下,Li 2+ 的Schr ödinger 方程为________________ 。
2102、已知类氢离子 He +的某一状态波函数为:()022-023021e 222241a r a r a ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛π 则此状态的能量为 )(a ,此状态的角动量的平方值为 )(b ,此状态角动量在 z 方向的分量为 )(c ,此状态的 n , l , m 值分别为 )(d ,此状态角度分布的节面数为 )(e 。
2103、写出 Be 原子的 Schr ödinger 方程 。
2104、已知类氢离子 He +的某一状态波函数为ψ= ()02-023021e 222241a r a r a ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛π 则此状态最大概率密度处的 r 值为 )(a ,此状态最大概率密度处的径向分布函数值为 )(b ,此状态径向分布函数最大处的 r 值为 )(c 。
2105、原子轨道是原子中的单电子波函数, 每个原子轨道只能容纳 ______个电子。
2106、H 原子的()υr,θψ,可以写作()()()υθr R ΦΘ,,三个函数的乘积,这三个函数分别由量子数 (a) ,(b), (c) 来规定。
2107、给出类 H 原子波函数()θa r Z a Zr a Z a Zr cos e6812032022023021-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛π=ψ 的量子数 n ,l 和 m 。
2108、H 原子 3d 电子轨道角动量沿磁场方向分量的可能值 。
2109、氢原子的波函数131321122101-++=ψψψψc c c 其中 131211210-ψψψψ和,, 都是归一化的。
那么波函数所描述状态的能量平均值为(a ),角动量出现在π22h 的概率是(b ),角动量 z 分量的平均值为(c )。
第二章 原子结构与性质

③ 电子填入顺序 基态原子: ns →(n–2)f→ (n–1)d→ np 价电子电离: np →ns→(n1)d → (n–2)f 徐光宪: 原子 (n+0.7l), 离子(n+0.4l) 越大能级越高
28
ⅠA-ⅡA ⅠB-ⅡB
ⅢA-ⅧA ⅢB-Ⅷ
La系 Ac系
例:氩(Z=18)的电子组态 1s2 2s22p6 3s23p6 Fe (Z=26) Cu (Z=29)
轨道角动量与z轴的夹角
e m mμB 2. 磁矩在磁场方向的分量量子化: μz 2me
3. m决定磁场中轨道的空间方向,磁矩与外磁场的作用能
18
2.4 电子的自旋运动与泡利原理
一. 电子的自旋运动
19
●自旋角动量量子化
Ls s(s 1)
电子的自旋量子数 s ≡1/2
26
四. 原子核外电子的排布规则 1. Pauli不相容原理 2. 能量最低原理 3. Hund规则:简并轨道上全充满、半充满或全空较稳定 4. 原子的构造: ① 电子组态:确定每个电子的n,l ② 电子层:ns2到ns2np6构成一个能级组 4(N) 3(M) 2(L) 1 2 0 1 2 3 0 1 0 2s 2p 3s 3p 3d 4s 4p 4d 4f 0 0 0 0 0 0 0 0 0 ±1 ±1 ±1 ±1 ±1 ±1 ±2 ±2 ±2 ±3 亚层轨道数 1 1 3 5 7 3 5 1 3 1 42 12 22 32 电子层轨道数 27 第n能层有n2个“轨道”,可以容纳2n2个电子 电子层 1(K) 角量子数l 0 电子亚层符号 1s 0 磁量子数m 可能取值
7
氢原子或类氢离子的轨道波函数举例 轨道 n
1s 2s
基础化学-第二章物质结构

③γ-射线:不带电的光子流,穿透能力很强。
• 2.放射性同位素的应用:
①示踪原子,例如125I、32P、60Co等。
②微量物质的含量测定。
1.某离子X3-质量数是75,中子数是42,那么 它的核外电子数是 ( C )
A. 30
B. 33 C. 36
D. 39
2.同位素间不相等的是 ( B ) A. 质子数 B.中子数 C. 电子数 D. 核电荷数
还原剂具有失去电子的性质,即还原 性。物质失去电子能力越强,其还原性 就越强。
• 卤素单质都是氧化剂,均具有氧化性,其 氧化性的强弱顺序见下: F→Cl→Br→I(强→弱),得电子的能力 逐渐减弱。
• 碱金属都是还原剂,具有还原性,其还原 性强弱顺序是: Cs→Rb→K→Na→Li(强→弱),失电子 的能力逐渐减弱。
的电子层结构,从而成为正价离子。 3.非金属元素
①其原子最外层电子数目一般多于4个。 ②化学反应中,易得到电子而达到稳定的电子层 结构,从而成为负价离子。
e
Na
Na +
+11 2 8 1
+11 2 8
e Cl
+17 2 8 7
Cl -
+17 2 8 8
1. 某原子最外层电子排布是3S23P4,这种原子 的核外电子数是( C )
Cu + H2O
得到 2 e ,被还原,化合价降低
当物质跟氧化合时,总是失去电子被氧化,其化合价升高; 当含氧物质失去氧时,总是得到电子被还原,化合价降低。
• 结论: 物质失去电子,化合价升高的反应,是
氧化反应;物质得到电子,化合价下降的 反应,是还原反应。
凡是有电子得失,化合价变化的反应, 叫做氧化还原反应。
第二章 原子结构与性质

第二章原子结构与性质1. 填空题(1) He+离子的薛定谔方程为。
(2) 用分离变量法解类氢原子薛定谔方程采用的主要近似是。
(3) 已知Cu 的原子序数为29,写出核外电子排布。
(4) He+的2s电子能量比He(1s12s1)中2s电子能量。
(填高或低)(5) 钠的电子组态为1s22s22p63s1,其光谱项为,光谱支项为。
(6) 写出d2可能的总轨道角量子数。
(7) 离核越近径向函数R1s(r)其值,离核越近径向分布函数D=r2R1s2(r) 。
(8) 氢原子态函数Ψ(r,θ,φ) 可以写作R(r),Θ(θ), (φ) 三个函数的乘积,它们由量子数; ; 来规定。
(9) 如一原子的轨道磁量子数m=0, 主量子数n≤2,则可能的轨道为。
(10) 在一定电子组态下,描写多电子原子状态的量子数是。
(11) 两个氢原子,第一个的电子处于主量子数n=1的轨道,第二个处于n=4的轨道,原子势能较低的是,原子电离能较低的是。
(12) 多电子原子中的一个光谱项支项3D2,据此给出原子的总轨道角动量量子数,原子的总自旋角动量量子数,原子总角动量量子数,在磁场中分裂出个塞曼能级。
(13) 氢原子的态函数Ψ3,2,1,其轨道能量为,轨道角动量,轨道角动量在磁场方向的分量为。
(14) 氢原子3d电子轨道角动量沿磁场方向分量的可能值为。
(15) 对于氢原子及类氢离子的1s电子来说,出现在半径为r,厚度为d r的球壳内,各个方向的概率密度(填相等或不相等),对于2p x电子(填相等或不相等)。
(16) 同电子组态光谱项稳定性比较:3P1D; 3P21P02. 选择题(1) 关于四个量子数n, l, m, m s,下列叙述正确的是: ·············································· ( )A、由实验测定;B、解类氢原子薛定谔方程得到的;C、解类氢原子薛定谔方程得到的n, l, m, 由电子自旋假设引入m sD、由自旋假设引入的(2) 决定多电子原子轨道的能量是: ···································································( )A、nB、n, l, ZC、n+0.4lD、n, m(3) 用来表示核外某电子运动状态的下列各组量子数(n,l,m,m s)合理的是: ··················· ( )A、2, 1, 0, 0B、0, 0, 0, 12C、3, 1, 2,12D、2, 1, -1, -12(4) 氢原子3d状态轨道角动量沿磁场方向的分量最大值是:····································( )A、5B、4C、3D、2(5) 如下表达式为径向分布函数的是: ·······························································( )A、R2B、R2drC、r2R2D、r2R2d r(6) R n,l(r)-r图中,节点数为·············································································· ( )A、n-1个B、n-l-1个C、n-l+1个D、n-l-2个(7) 原子的电子云角度分布图应该用如下哪一个函数对参数作图······························ ( )A、|Y l,m(θ,φ)|2B、R n,l(r)C、Y l,m(θ,φ)D、|R n,l(r)Y l,m(θ,φ)|2(8) 对于单电子原子,在无外场时,能量相同的轨道数是: ······································· ( )A、n2B、2(l+1)C、n-1D、n-l-1(9) 已知Ca的第一激发态的电子组态为[Ar]3d14s1, 其光谱支项有如下四种,指出能量最低的光谱项:A、1D2B、3D3C、3D2D、3D1(10) 求解氢原子薛定谔方程,我们常采用下列哪些近似?······································( )①核固定②变数分离③以电子质量代替折合质量④球极坐标A、①③B、①②C、①④D、①②③④(11) 基态铬原子(原子序数是24)的核外电子排布为: ············································( )A、[Ar]3d44s2B、[Ar]3d54s1C、[Ar]3d64s0D、4s24p4(12) 某多电子原子中电子具有下列量子数(n,l,m,m s),其中轨道角动量最大的是: ·······( )A、2,1,-1,12B、2,0,0,-12C、3,1,1,-12D、3,2,-1,12(13)描述原子轨道3d z2的一组量子数是: ····························································· ( )A、2,1,0B、3,2,0C、3,1,0D、3,2,1(14)3d z2轨道的角动量大小为: ·········································································( )A、B、 C、0 D(15) He+中一个电子处于径向分布图中总节面为3的d态,则该电子的能量应为:·······( )A、1E1B、19E1C、14E1D、116E1(16) 氢原子中处于Ψ2pz状态,其角动量在下列哪一个轴上的投影有确定值?···············( )A、x轴B、y轴C、z轴D、x轴和y轴(17) 对于类氢原子的基态, 下列结论不正确的是: ·················································( )A、E相同B、M z相同C、简并度相同D、l相同(18) Be3+ 的一个电子所处的轨道,能量等于氢原子1s轨道能,该轨道可能是: ······( )A、1sB、2sC、4dD、3p(19) 4d 的径向分布函数图的极大值数与节面数分别是: ··········································( )A、2,1B、2, 3C、4,2D、1,3(20) 下列是关于s轨道波函数ψ的认识,正确的是:················································( )A、ψ的值随着r的增大而减小B、ψ的节面数为nC、当r趋于无穷大时,ψ趋于0D、ψ2s-r曲线在r=2a0处达到最低点(21) 对氢原子和类氢离子的量子数l,下列叙述不正确的是:·····································( )A、l的取值规定了m的取值范围B、它的取值与体系能量大小有关C、它的最大可能取值由解R方程决定D、它的取值决定了M=(22) 对于氢原子和类氢离子的径向分布D(r)-r图,下列叙述错误的是:························( )A、径向峰数与节面数都与n,l有关B、l相同,n愈大,则最高峰离核愈远C、核周围电子出现的概率为0D、最高峰所对应的r处,电子出现的概率密度最大(23) 电子在核附近有非零概率密度的原子轨道是:··············································( )A、ψ3pB、ψ4dC、ψ2pD、ψ2s(24) 电子云图是下列哪一种函数的图形?··························································( )A、D(r)B、ψ2(r,θ,φ)C、R2(r)D、ψ(r,θ,φ)(25) 已知类氢波函数ψ2px的各种图形,推测ψ3px图形,下列说法错误的是:····················( )A、角度部分的图形相同B、电子云图相同C、径向分布函数图不同D、界面图不同(26) He+离子的3d和4s的能级次序为:······························································( )A、3d >4sB、3d < 4sC、3d = 4sD、存在交叉(27) 电子组态d9s1的光谱项是: ········································································ ( )A、3F,1DB、1D,3DC、2P,3PD、1S,2P(28) Fe的电子组态为[Ar]3d64s2,其能量最低的光谱支项是:····································( )A、5D4B、3P2C、5D0D、1S0(29) Cu的基谱项为,与其基谱项不同的原子是:····································( )A、AgB、AuC、ZnD、K(30) 已知Rh的基谱项为4F9/2,则它的价电子组态是:··········································( )A、s1d8B、s0d9C、s2d8D、s0d103. 简答题(1) 请用光谱项语言叙述洪特规则。
原子结构知识点

原子结构知识点前言原子结构是化学中一个非常重要的概念,它解释了物质的性质和行为。
本文将重点介绍原子结构相关的知识点,包括原子的组成、结构和性质,希望能帮助读者更深入地了解原子的奥秘。
原子的组成原子是构成所有物质的基本单位,它由三种基本粒子组成:质子、中子和电子。
质子带正电荷,中子是中性粒子,而电子带负电荷。
质子和中子位于原子核中,形成原子的核心,而电子则绕核壳层运动。
原子的结构原子的结构包括原子核和电子壳层。
原子核由质子和中子组成,电子围绕在原子核外部的不同能级壳层上运动。
原子核的直径约为电子壳层的万分之一,但其中包含原子99.9%以上的质量。
电子结构电子壳层的能级分为K、L、M、N等,每个能级壳层可以容纳不同数量的电子。
根据泡利不相容原理和居里原理,每个电子轨道最多容纳2个电子,且必须填满低能级轨道后才能填满高能级轨道。
原子物理性质原子的物理性质主要由其原子序数(核电荷数)和电子结构决定。
原子序数越大,原子核中的质子数目越多,电子结构也更加稳定。
原子的性质还受到元素化学属性的影响,如电负性、原子半径、离子半径等。
原子结构的应用原子结构不仅在化学领域有重要应用,还在物理、材料科学等领域发挥关键作用。
人们通过深入研究原子结构,可以设计新材料、开发新技术,甚至探索宇宙奥秘。
结语原子结构是一个精彩而复杂的领域,本文只是对其进行了简要介绍,希望读者在学习过程中能够继续深入探索原子结构的奥秘,拓展对自然世界的认识,为科学发展做出贡献。
以上就是有关原子结构知识点的介绍,希望能对你有所启发。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 玻尔的氢原子模型
三点假设:
①定态假设
2.1791018 E J 2 n
②量子化条件
+ n=1
-
m r nh / 2
n=1,2,3,„ ③频率假设 hv=En'−En
n=2 n=3
2.179 1018 E J 2 n 1 18 1 E 2.179 10 2 2 n1 n2 2.179 1018 1 1 2.179 1018 1 1 2 2 2 34 2 h n1 n2 6.626 10 n1 n2 吸收或辐射光的频率为:
能量 动量
E = hv P = h/λ
粒子性 波动性
频率 波长
德布罗意假设
1924年de Broglie假设: 所有的实物微观粒子,如电子、 原子、分子等和光子一样,也具有波 粒二象性,并且预言
h h p m
Louis de Brogile (1892-1987)
1929年获得诺贝尔物理学奖
3. 波函数的有关图形表示
坐标变换: z
(x, y,z) (r, , )
P
r2=x2+y2+z2 x = r sin cos y = r sin sin z = r cos
θ
Байду номын сангаас
r y P′
O
φ x
0≤r∞ 0≤ ≤π 0≤ ≤2π
n,l ,m r, , =Rn,l r Yl ,m ,
4. 电子像行星绕着太阳那样绕核运动。
根据当时的物理学概念,带电 微粒在力场中运动时总要产生电磁
辐射并逐渐失去能量,运动着的电
子轨道会越来越小,最终将与原子 核相撞并导致原子毁灭。由于原子 毁灭的事实从未发生,将经典物理 学概念推到前所未有的尴尬境地。
19世纪末人类科学天空的三朵乌云: 氢原子光谱、黑体辐射、光电效应
λ:波长 m:粒子的质量 υ:粒子运动的速度
与实物粒子相关联的波称为物质 波,也叫德布罗意波。
电子衍射实验示意图
电子枪发射高速电子通过薄晶体片射击感光荧屏, 得到明暗相间的环纹,类似于光波的衍射环纹。 电 子 枪 电 子 束
薄晶体片 感光屏幕 衍射环纹
物质波是几率波
2. 不确定原理
不能同时测准微观粒子的位置和动量
标上Y的正、负号,就得到波函数的角度分布
图。
例如:s轨道的角度波函数为:
玻尔理论的不足之处
不能解释氢原子光谱的精细结构 不能解释氢原子光谱在磁场中的分裂 不能解释多电子原子光谱
Niels Bohr (1885-1962)
1922年获得诺贝尔物理学奖
2.3 微观粒子的运动属性
1 2
波粒二象性
不确定原理
1. 波粒二象性
光的波粒二象性
光的波动性:光在传播时体现。如干涉、衍射 光的粒子性:光与实物相互作用时体现。如辐 射、吸收、光电效应
物理意义: 决定原子轨道或电子云在空间的取向(或伸展方向)
s 轨道(l = 0, m = 0 ) m一种取值,空间一种取向,一条 s 轨道
p 轨道(l = 1,m = +1,
0,
-1)
m 三种取值,三种取向,三条等价(简并) p 轨道
d 轨道(l = 2,m = +2,+1,0,-1,-2) m 五种取值,空间五种取向,五条等价(简并) d 轨道
x Px h
Δx:粒子所在位置的不确定度 Δpx:粒子动量的不确定度 Heisenberg (1901-1976)
1932年获得诺贝尔物理学奖
不确定原理是微观粒子运动的固有特 性,对于宏观物体没有实际意义。
粒子 m/kg Δx/m Δυ/m· s-1
电子
子弹
9.1×10-31
1.0×10-2
例题:下列各组量子数哪些不合理? 1. n = 2, l = 1, m = 0 2. n = 2, l = 0, m = -1 3. n = 2, l = 2, m = -1 4. n = 2, l = 3, m = 2 5. n = 3, l = 1, m = 1 6. n = 3, l = 0, m = -1 2 3 4 6
1 1 3.289 10 2 2 n1 n2
15
0h 2 另外:rn n 2 me
2
例题:求激发态氢原子的电子从n=4能级跃迁到
n=2能级时所发射的辐射能的频率、波长及能量?
1 1 1 15 1 解:由 3.28910 n2 n2 3.28910 22 42 2 1
Ψ: 波函数 E:能量 V:势能
Erwin SchrÖ dinger (1887-1961)
1933年获得诺贝尔物理学奖
m:质量 h:Planck常数 x, y, z:空间直角坐标
解薛定谔方程时的几点说明: ①将直角坐标变成球坐标,解得的波函数由ψ(x,
y,z)转换成ψ(r,θ,φ)
②Schrö dinger方程的解为系列解,每一个解都有
测试电子自旋现象的实验装置
综上所述:
描述一个原子轨道要用三个量子数(n、l、m), 而描述一个原子轨道上运动的电子,要用四个量子 数(n、l、m、ms)。
• 主量子数n决定原子轨道的大小(即电子层数) 和电子的能量; • 角量子数l决定原子轨道或电子云的形状同时 也影响电子的能量; • 磁量子数m决定原子轨道或电子云在空间的伸 展方向; • 自旋量子数ms决定电子的自旋方向。
15
6.1671014 s 1
2.9979 108 109 486.1nm 14 6.16710 c
E h 6.6262 1034 6.1671014 4.08610-19 (J)
玻尔理论的成功之处
量子化概念引入原子结构 说明了原子的稳定性 解释了H及He+、Li2+、B3+ 的原子光谱
z
x
多电子原子轨道能量
E=E (n,l)
• n相同,l越大,E越高
E3s<E3p<E3d E4s<E4p<E4d<E4f
从能量角度看,亚层也可以称为能级 • l相同,n越大,E越高
E1s<E2s<E3s<E4s E2p<E3p<E4p
• n,l都不同,有时发生能级交错
E4s<E3d
单电子原子轨道能量
1. 汤姆逊(Thomson)模型
汤姆逊1897年发现电子,1903年提出西瓜模型
汤姆逊阴极射线管
西瓜模型
2. 卢瑟福(Rutherford)模型
1908年获得诺贝尔化学奖
卢瑟福1911年提出核式结构模型
太阳-行星模型
1. 所有原子都有一个核即原子核(nucleus); 2. 核的体积只占整个原子体积极小的一部分; 3. 原子的正电荷和绝大部分质量集中在核上;
1 1 RH 2 2 2 n 1
RH称为里德堡常数,其数值为1.09677×107m-1。
2. 能量量子化和光子学说
能量量子化
Planck的量子假说(1900年): ① 能量有一最小单位E0,称为能 量子或量子, E0 = hv; v:电磁波频率 h:Planck常数,等于6.626×10-34 J· s ② 宇宙中的任何振动所具有的能 量都是量子hv的整数倍: Max K.E.L. Planck (1858-1947)
一定能量E和其对应
③为了得到合理解,必须引入三个常数项n,l, m,称为量子数
2. 原子轨道、波函数及量子数
原子轨道和波函数
•在量子力学中用 和E描述微观粒子运动状态
•通常把一个波函数 称作一个原子轨道 注意
这里的轨道(orbital),不是经典力学意义上的轨 道(orbit),而是服从量子力学意义上的轨道。
第2章 原子结构
2.1经典核模型的建立 2.2氢原子光谱与玻尔的氢原子模型 2.3微观粒子的运动属性 2.4氢原子的量子力学模型 2.5多电子原子结构 2.6元素周期表与核外电子构型 2.7元素基本性质的周期性
2.1 经典核模型的建立
1 2
汤姆逊(Thomson)模型
卢瑟福(Rutherford)模型
1918年获得诺贝尔物理学奖
ε=nhv
光子学说
Einstein的光子学说(1905年): ① 一束光是由光子组成,光的能 量是不连续的,光能的最小单 位是光子; ② 光子的能量E0 = hv Albert Einstein (1879-1955)
1921年获得诺贝尔物理学奖
v:光的频率, h:Planck常数,等于6.626×10-34 J· s。
2
E=E (n)
Z En 13.6 2 (ev) n
氢原子或类氢原子只有一个电子,n相同,E相同。
如:n=4
E4s=E4p=E4d=E4f
能级由n,l共同定义,一组(n,l)对应于一
个能级(氢原子的能级由n定义);能量相同的 轨道称为简并轨道。
⑶磁量子数m (magnetic quantum number)
1.0×10-11
1.0×10-6
7.3×107
6.6×10-26
卢瑟福行星模型
普朗克定律
德布罗意假设
光子学说
海森堡不确定原理
玻尔的氢原子模型
2.4 氢原子的量子力学模型
1
薛定谔方程
2
3
原子轨道、波函数及量子数
波函数的有关图形表示
1. 薛定谔方程
2Ψ 2Ψ 2Ψ 8π 2 m 2 2 2 E V Ψ 0 2 x y z h
