人教版八年级上第十二章全等三角形章节复习 (共16页)

合集下载

人教版八年级数学上册第12章全等三角形单元复习课件

∵BF∥AC，DE⊥AC，∴BF⊥DF，
∵BC平分∠ABF，DH⊥AB，DF⊥BF，∴DH＝DF，
∴DE＝DF，
∴点D为EF的中点．
(2)∵BF∥AC，∴∠C＝∠DBF，
∵BC平分∠ABF，∴∠ABD＝∠DBF，∴∠C＝∠ABD，
∵AD平分∠BAC，∴∠CAD＝∠BAD，
又AD＝AD，∴△DCA≌△DBA，∴∠CDA＝∠BDA，
应角与对角的概念．一般地，对应边、对应角是对两个三
角形而言，而对边、对角是对同一个三角形的边和角而言，
对边是指角的对边，对角是指边的对角．
1．已知△ABC≌△A1B1C1，A和A1对应，B和B1对应，
∠A＝70°，∠B1＝50°，则∠C的度数为( D )
A．70°
B．50°
C．120°
D．60°
2．(全国视野)(2022南京模拟)如图，四边形ABCD的对角
证明：(1)在Rt△BOF和Rt△COE中，
∵OF＝OE，OB＝OC，
∴Rt△BOF≌Rt△COE(HL)．
∴∠FBO＝∠ECO，即∠ABO＝∠ACO．
(2)连接AO．∵OF⊥AB，OE⊥AC，且OF＝OE，
∴∠BAO＝∠CAO．
∵∠ABO＝∠ACO，AO＝AO，
∴△BOA≌△COA(AAS)，∴AB＝AC．
则BD＝
1 ．
22．如图，过点B，D分别向线段AE作垂线段BQ和DF，
点Q和F是垂足，连接AB，DE，BD，BD交AE于点C，且
AB＝DE，AF＝EQ．
(1)求证：△ABQ≌△EDF；
(2)求证：点C是BD的中点．
证明：(1)∵AF＝EQ，∴AQ＝EF，在Rt△ABQ和Rt△EDF中，
＝

人教版八年级上册第十二章全等三角形(复习课)课件

3
4
考点3. 角平分线的性质与判定
1、作已知角的平分线？作法：（1）以点O为圆心，适当长为半径画弧线，交OA 于点N，交OB于点M.
1 2
（2）分别以M、N为圆心，大于 MN的长为半径画弧，两弧在∠AOB的内部相交于点C.
（3）画射线OC，射线OC即为所求.
2. 角的平分线的性质角的平分线的判定
∴DM⊥AM.
4.如图，在△ABC中，点D在边BC上，DE⊥AB，DF⊥AC，垂足分别为E，F，请你添
加一个条件使得AD⊥EF.
（1）你添加的条件是（
），并证明AD⊥EF.
（2）如图，AD为∠BAC的平分线，当有一点G从点D向点A运动时，GE⊥AB，
GF⊥AC，垂足分别为E、F.这时AD是否垂直于EF？
∠CMA＝∠BMN， CM＝BM，
3．在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN 于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图1的位置时，求证： ①△ADC≌△CEB；②DE＝AD+BE；（2）当直线MN绕点C旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由．
（1）证明：①∵∠ACD+∠BCE＝90°∠DAC+∠ACD＝90°， ∴∠DAC＝∠BCE．又AC＝BC，∠ADC＝∠BEC＝90°， ∴△ADC≌△CEB．②∵△ADC≌△CEB，∴CD＝BE，AD＝ CE．∴DE＝CE+CD＝AD+BE．（2）△ADC≌△CEB成立，DE＝
AD+BE．不成立，此时应有DE＝AD﹣BE．证明： ∵∠ACD+∠BCE＝90°∠DAC+∠ACD＝90°，∴∠DAC＝ ∠BCE．又AC＝BC，∠ADC＝∠BEC＝90°， ∴△ADC≌△CEB．∴CD＝BE，AD＝CE．∴DE＝AD﹣BE．

人教版八年级上册第十二章全等三角形知识点总结及复习

全等三角形知识点总结及复习一、知识网络⎧⎧⎨⎪⎩⎪⎪⎧⎪⎪→⇒⎨⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩⎩⎧⎨⎩对应角相等性质对应边相等边边边 SSS 全等形全等三角形应用边角边 SAS 判定角边角 ASA 角角边 AAS 斜边、直角边 HL 作图角平分线性质与判定定理二、基础知识梳理（一）、基本概念1、“全等”的理解全等的图形必须满足：（1）形状相同的图形；（2）大小相等的图形；即能够完全重合的两个图形叫全等形。

同样我们把能够完全重合的两个三角形叫做全等三角形。

全等三角形定义：能够完全重合的两个三角形称为全等三角形。

（注：全等三角形是相似三角形中的特殊情况）当两个三角形完全重合时，互相重合的顶点叫做对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角。

由此，可以得出：全等三角形的对应边相等，对应角相等。

(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边； (2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角； (3)有公共边的，公共边一定是对应边； (4)有公共角的，角一定是对应角；(5)有对顶角的，对顶角一定是对应角； 2、全等三角形的性质（1）全等三角形对应边相等；（2）全等三角形对应角相等； 3、全等三角形的判定方法（1）三边对应相等的两个三角形全等。

（2）两角和它们的夹边对应相等的两个三角形全等。

（3）两角和其中一角的对边对应相等的两个三角形全等。

（4）两边和它们的夹角对应相等的两个三角形全等。

（5）斜边和一条直角边对应相等的两个直角三角形全等。

4、角平分线的性质及判定性质：角平分线上的点到这个角的两边的距离相等判定：到一个角的两边距离相等的点在这个角平分线上（二）灵活运用定理1、判定两个三角形全等的定理中，必须具备三个条件，且至少要有一组边对应相等，因此在寻找全等的条件时，总是先寻找边相等的可能性。

2、要善于发现和利用隐含的等量元素，如公共角、公共边、对顶角等。

人教版八年级上册数学第十二章全等三角形复习课件

先在过点B的AB的垂线上取两点C、D，使得CD＝
BC，再在过点D的垂线上取点E，使A、C、E三点
在一条直线上，可以证明△EDC≌△ABC，所以测
得ED的长就是A、B两点间的距离，这里判定
△EDC≌△ABC的理由是（ C ）
A．SAS
B．SSS
C．ASA
D．AAS
第十二章全等三角形
16．如图，AB，CD表示两根长度相等的铁条，若 O是AB，CD的中点，经测量AC＝15cm，则容器的
在△AOD和△BO
第十二章全等三角形
9．如图，已知AB∥CD，AE⊥BD，CF⊥BD，垂足分别E，F，BF＝DE. 求证：AB＝CD. ∵AE⊥BD，CF⊥BD，∴∠AEB＝∠CFD＝90°. ∵BF＝DE，∴BF＋FE＝DE＋EF，即BE＝DF， ∵AB∥CD，∴∠D＝∠B.
∵BE＝CF，∴BE＋EF＝CF＋EF，即BF＝CE，
在△ABF和△DCE中，
，
∴△ABF≌△DCE(SAS).
第十二章全等三角形
8．如图，已知AD＝BC，AC＝BD，求证：（1）△ADB≌△BCA；（2）△AOD≌△BOC.
(1) 在△ADB与△BCA中，
，
∴△ADB≌△BCA(SSS)； (2) ∵由(1)得△ADB≌△BCA，∴∠D＝∠C，
第十二章全等三角形
22．如图：已知BD＝CD，BF⊥AC， CE⊥AB，求证：AD平分∠BAC.
∵BF⊥AC，CE⊥AB， ∴∠BED＝∠CFD＝90°，
在△BED和△CFD中，
，
∴△BED≌△CFD(AAS)，∴DE＝DF，又∵DE⊥AB，DF⊥AC，∴AD平分∠BAC.
感谢聆听
内径长为（ D ）

人教版八年级上册第十二章全等三角形知识点复习

A. ①④
B.①②
C.②③
D.③④
2．如图，ABD ≌ CDB ，且 AB 和 CD 是对应边，下面四个结论中不正确的是（）
A. ABD和CDB 的面积相等
A
D
B. ABD和CDB 的周长相等 C. A + ABD = C + CBD
B
C
D.DAD//BC 且 AD=BC
3．如图， ABC ≌ BAD ，A 和 B 以及 C 和 D 分别是对应点，如果
4．全等三角形的判定（一）：三边对应相等的两个三角形全等，简与成“边边边”或“SSS”．
AB = DE 如图，在 ABC 和 DEF 中 BC = EF
AC =
【典型例题】
例1．如图， ABC ≌ ADC ，点 B 与点 D 是对应点， BAC = 26 ，且 B = 20 ， SABC = 1，求 CAD , D, ACD 的度数及 ACD 的面积．
数及 BC 的长．
E
F
A
BC
D
本文来源于网络，如果侵权行为，请联系删除！
精品文档，助力人生，欢迎关注小编！
11．如图，在 ABC与ABD 中，AC=BD，AD=BC，求证： ABC ≌ ABD
D A
C B
全等三角形（一）作业
1．如图， ABC ≌ CDA ，AC=7cm，AB=5cm.，则 AD 的长是（）
求证：（1） DE ⊥ AB ；（2）BD 平分 ABC （角平分线的相关证明及性质）
B
A E
D
C
【巩固练习】 1．下面给出四个结论：①若两个图形是全等图形，则它们形状一定相同；②若两个图形的
形状相同，则它们一定是全等图形；③若两个图形的面积相等，则它们一定是全等图形； ④若两个图形是全等图形，则它们的大小一定相同，其中正确的是（）

人教版初中八年级数学上册第十二章《全等三角形》复习题(含答案解析)

一、选择题1．如图，在ABC 中，8AB AC ==厘米，6BC =厘米，点D 为AB 的中点．如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动，同时，点Q 在线段CA 上，由C 点向A 点运动，为了使BPD CPQ △≌△，点Q 的运动速度应为（）A ．1厘米/秒B ．2厘米/秒C ．3厘米/秒D ．4厘米/秒D解析：D【分析】根据三角形全等的性质与路程、速度、时间的关系式求解．【详解】解：设△BPD ≌△CPQ 时运动时间为t ，点Q 的运动速度为v ，则由题意得：BP CP BD CQ =⎧⎨=⎩，即3634t t vt =-⎧⎨=⎩，解之得：14t v =⎧⎨=⎩， ∴点Q 的运动速度为4厘米/秒，故选D ．【点睛】本题考查三角形全等的综合应用，熟练掌握三角形全等的判定与性质、路程、速度、时间的关系式及方程的思想方法是解题关键．2．如图，OM 、ON 、OP 分别是AOB ∠，BOC ∠，AOC ∠的角平分线，则下列选项成立的（）A ．AOP MON ∠>∠B ．AOP MON ∠=∠C ．AOP MON ∠<∠D ．以上情况都有可能B 解析：B【分析】根据角平分线的定义可得∠AOP=12∠AOC ，∠AOM=∠MOB=12∠AOB ，∠CON=∠BON=12∠BOC ，进而可得∠MON=12∠AOB+12∠BOC=12∠AOC ，从而可得∠AOP=∠MON ．【详解】解：∵OP 平分∠AOC ，∴∠AOP=12∠AOC ， ∵OM 、ON 分别是∠AOB 、∠BOC 的平分线， ∴∠AOM=∠MOB=12∠AOB ，∠CON=∠BON=12∠BOC ， ∴∠MON=12∠AOB+12∠BOC=12∠AOC ， ∴∠AOP=∠MON ．故选B ．【点睛】此题主要考查了角平分线的定义，关键是掌握角平分线把角分成相等的两部分． 3．工人师傅常用直角尺平分一个角，做法如下：如图所示，在∠AOB 的边OA ，OB 上分别取OM ＝ON ，移动直角尺，使直角尺两边相同的刻度分别与M ，N 重合（即CM ＝CN ）．此时过直角尺顶点C 的射线OC 即是∠AOB 的平分线．这种做法的道理是（）A ．HLB ．SASC ．SSSD ．ASA C【分析】根据题中的已知条件确定有三组边对应相等，由此证明△OMC ≌△ONC(SSS)，即可得到结论.【详解】在△OMC 和△ONC 中，OM ON CM CN OC OC =⎧⎪=⎨⎪=⎩, ∴△OMC ≌△ONC(SSS)，∴∠MOC=∠NOC ，∴射线OC 即是∠AOB 的平分线，故选：C.【点睛】此题考查了全等三角形的判定及性质，比较简单，注意利用了三边对应相等，熟记三角形全等的判定定理并解决问题是解题的关键.4．如图，点O 在ABC 内，且到三边的距离相等．若110BOC ∠=°，则A ∠的度数为( )A ．40︒B ．45︒C ．50︒D ．55︒A解析：A【分析】由条件可知BO 、CO 平分∠ABC 和∠ACB ，利用三角形内角和可求得∠A ．【详解】解：∵点O 到ABC 三边的距离相等，∴BO 平分ABC ∠，CO 平分ACB ∠，∴ ()180A ABC ACB ∠=︒-∠+∠()1802OBC OCB =︒-∠+∠()1802180BOC =︒-⨯︒-∠()1802180110︒=︒-⨯-︒40=︒．【点睛】本题主要考查角平分线的性质，掌握角平分线的交点到三角形三边的距离相等是解题的关键．5．如图所示，下面甲、乙、丙三个三角形和ABC全等的图形是（）A．甲和乙B．乙和丙C．只有丙D．只有乙B解析：B【分析】甲只有2个已知条件，缺少判定依据；乙可根据SAS判定与△ABC全等；丙可根据AAS判定与△ABC全等，可得答案．【详解】解：甲三角形只知道两条边长无法判断是否与△ABC全等；乙三角形夹50°内角的两边分别与已知三角形对应相等，故乙与△ABC全等；丙三角形72°内角及所对边与△ABC对应相等且均有50°内角，可根据AAS判定乙与△ABC 全等；则与△ABC全等的有乙和丙，故选：B．【点睛】本题主要考查全等三角形的判定定理，熟练掌握并充分理解三角形全等的判定定理，注意对应二字的理解很重要．6．下列判断正确的个数是（）①三角形的三条高都在三角形的内部，并且相交于一点；②两边及一角对应相等的两个三角形全等；③两角及一边对应相等的两个三角形全等；④到三角形的三边所在的直线距离相等的点有三个；⑤两边及第三边上的高对应相等的两个三角形全等．A．4 B．3 C．2 D．1D解析：D【分析】根据三角形的高线、角平分线的性质及全等三角形的判定分析各个选项即可．【详解】解：①只有当三角形是锐角三角形时，三条高才在三角形的内部，此选项错误；②有两边及一角对应相等的两个三角形全等，此选项错误；③有两角和一边对应相等，满足AAS或ASA，此选项正确；④在三角形内部到三边距离相等的点是三条内角平分线的交点，交点重合，只有一点；在三角形的外部到三条边所在直线距离相等的点是外角平分线的交点，交点不重合，有三个．则到三角形三边所在直线距离相等的点有4个，此选项错误；⑤两边及第三边上的高对应相等的两个三角形不一定全等，此选项错误．正确的有一个③，故选：D ．【点睛】本题考查了全等三角形的判定方法及三角形的角平分线，垂心等概念，熟练掌握概念和性质是解题的关键．7．如图，OB 平分∠MON ，A 为OB 的中点，AE ⊥ON ，EA=3，D 为OM 上的一个动点，C 是DA 延长线与BC 的交点，BC //OM ，则CD 的最小值是（）A ．6B ．8C ．10D ．12A解析：A【分析】根据两条平行线之间的距离可知当CD ⊥OM 时，CD 取最小值，先利用角平分线的性质得出AD =AE =3，利用全等三角形的判定和性质得出AC =AD =AE =3，进而解答即可．【详解】解：由题意得，当CD ⊥OM 时，CD 取最小值，∵OB 平分∠MON ，AE ⊥ON 于点E ，CD ⊥OM ，∴AD =AE =3，∵BC ∥OM ，∴∠DOA =∠B ，∵A 为OB 中点，∴AB =AO ，在△ADO 与△ABC 中B DOA AB AO BAC DAO ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ADO ≌△ABC (SAS ),∴AC =AD =3，∴336CD AC AD =+=+=，【点睛】此题考查角平分线的性质、全等三角形的判定和性质、平行线之间的距离，关键是利用全等三角形的判定和性质得出AC =AD =AE =3．8．如图，AC 与DB 相交于E ，且BE CE =，如果添加一个条件还不能判定ABE △≌DCE ，则添加的这个条件是（）．A ．AC DB =B ．A D ∠=∠C ．B C ∠=∠D ．AB DC = D解析：D【分析】根据全等三角形的判定定理，对每个选项分别分析、解答出即可．【详解】根据题意：BE=CE ，∠AEB=∠DEC ，∴只需要添加对顶角的邻边，即AE=DE （由AC=BD 也可以得到），或任意一组对应角，即∠A=∠D ，∠B=∠C ，∴选项A 、B 、C 可以判定，选项D 不能判定，故选：D ．【点睛】此题考查全等三角形的判定定理，熟记判定定理并熟练应用是解题的关键．9．如图，在OAB 和OCD 中，OA OB =，OC OD =，OA OC >，40AOB COD ∠=∠=︒，连接AC 、BD 交于点M ，连接OM ，下列结论：①AC BD =；②40AMB ∠=︒；③OM 平分BOC ∠；④MO 平分BMC ∠，其中正确的为（）A ．①②③B ．①②④C ．②③④D ．①②③④B解析：B由SAS 证明AOC BOD ≅得出OCA ODB ∠=∠，=AC BD ，①正确；由全等三角形的性质得出OAC OBD ∠=∠，由三角形的外角性质得：AMB OAC AOB OBD ∠+∠=∠+∠，得出40AOB COD ∠=∠=︒，②正确；作OG MC ⊥于G ，OH MB ⊥于H ，如图所示：则90OGC OHD ∠=∠=，由AAS 证明OCG ODH ≅（AAS ），得出OG=OH ，由角平分线的判定方法得出MO 平分BOC ∠，④正确；由AOB COD ∠=∠，得出当∠=∠DOM AOM 时，OM 平分BOC ∠，假设∠=∠DOM AOM ，由AOC BOD ≅得出COM BOM ，由MO 平分BMC ∠得出∠=∠CMO BMO ，推出COM BOM ≅，得出OB=OC ，OA=OB ，所以OA=OC ，而OA OC >，故③错误；即可得出结论．【详解】∵40AOB COD ∠=∠=︒，∴AOB AOD COD AOD ∠+∠=∠+∠即AOC BOD ∠=∠在AOC △和BOD 中OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴AOC BOD ≅（SAS ）∴OCA ODB ∠=∠，=AC BD ，①正确；∴OAC OBD ∠=∠，由三角形的外角性质得：AMB OAC AOB OBD ∠+∠=∠+∠，∴40AOB COD ∠=∠=︒，②正确；作OG MC ⊥于G ，OH MB ⊥于H ，如图所示：则90OGC OHD ∠=∠=，在OCG 和ODH 中OCA ODB OGC OHD OC OD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴OCG ODH ≅（AAS ），∴OG=OH∴MO 平分BOC ∠，④正确；∴AOB COD ∠=∠∴当∠=∠DOM AOM 时，OM 平分BOC ∠，假设∠=∠DOM AOM∵AOC BOD ≅ ∴COM BOM ，∵MO 平分BMC ∠∴∠=∠CMO BMO ，在COM 和BOM 中OCM BOM OM OMCMO BMO ∠=∠⎧⎪=⎨⎪∠=∠⎩∴COM BOM ≅（ASA ）∴OB=OC ，∵OA=OB ，∴OA=OC ，与OA OC >矛盾，∴③错误；正确的有①②④；故选：B【点睛】本题考查了全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识；证明三角形全等是解题的关键．10．如图，△ACB ≌△A 'CB '，∠BCB '=25°，则∠ACA '的度数为（）A ．35°B ．30°C ．25°D ．20°C解析：C【分析】利用全等三角形的性质可得∠A′CB′=∠ACB ，再利用等式的性质可得答案．【详解】解：∵△ACB ≌△A′CB′，∴∠A′CB′=∠ACB ，∴∠A′CB′-∠A′CB=∠ACB-∠A′CB ，∴∠ACA′=∠BCB′=25°，故选：C ．【点睛】此题主要考查了全等三角形的性质，关键是掌握全等三角形对应角相等．二、填空题11．如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝12，BC＝18，CD＝8，则四边形ABCD的面积是____．【分析】过点D作DE⊥BA的延长线于点E利用角平分线的性质可得出DE＝DC＝8再利用三角形的面积公式结合S四边形ABCD ＝S△ABD＋S△BCD可求出四边形ABCD的面积【详解】解：过点D作DE⊥B 解析：120【分析】过点D作DE⊥BA的延长线于点E，利用角平分线的性质可得出DE＝DC＝8，再利用三角形的面积公式结合S四边形ABCD＝S△ABD＋S△BCD，可求出四边形ABCD的面积．【详解】解：过点D作DE⊥BA的延长线于点E，如图所示．又∵BD平分∠ABC，∠BCD＝90°，∴DE＝DC＝8，∴S四边形ABCD＝S△ABD＋S△BCD，＝12AB•DE＋12BC•CD，＝12×12×8＋12×18×8，＝120．故答案为：120．【点睛】本题考查了角平分线的性质以及三角形的面积，利用角平分线的性质，找出DE＝8是解题的关键．12．如图，把等腰直角三角板放平面直角坐标系内，已知直角顶点C的坐标为()0,3，另一个顶点B的坐标为()8,8，则点A的坐标为____________（5－5）【分析】根据余角的性质可得∠BCP=∠CAQ 根据全等三角形的判定与性质可得AQCQ 根据线段的和差可得OQ 可得答案【详解】解：作BP ⊥y 轴AQ ⊥y 轴如图∴∠BPC=∠AQC=90°∵BC=A解析：（5，－5）【分析】根据余角的性质，可得∠BCP=∠CAQ ，根据全等三角形的判定与性质，可得AQ ，CQ ，根据线段的和差，可得OQ ，可得答案．【详解】解：作BP ⊥y 轴，AQ ⊥y 轴，如图，∴∠BPC=∠AQC=90°∵BC=AC ，∠BCA=90°，∴∠BCP+∠ACQ=90°．又∠CAQ+∠ACQ=90°∴∠BCP=∠CAQ ．在△BPC 和△CQA 中，BPC CQA BCP CAQ BC AC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝ Rt △BPC ≌Rt △ACQ （AAS ），AQ=PC=8-3=5；CQ=BP=8．∵QO=QC-CO=8-3=5，∴A （5，-5），故答案为：（5，-5）．【点睛】本题考查了坐标与图形，全等三角形的判定与性质，利用全等三角形的判定与性质得出AQ ，CQ 是解题关键．13．如图，△ABE ≌△ADC ≌△ABC ，若∠1＝130°，则∠α的度数为________．100°【分析】根据全等三角形对应角相等可得然后根据周角等于求出再根据三角形的内角和定理求出从而得解【详解】解：（对顶角相等）故答案为：【点睛】本题考查了全等三角形对应角相等的性质三角形的内角和定理解析：100°【分析】根据全等三角形对应角相等可得1BAE ∠=∠，ACB E ∠=∠，然后根据周角等于360︒求出2∠，再根据三角形的内角和定理求出2α∠=∠，从而得解．【详解】解：ABE ADC ABC ∆≅∆≅∆，1130BAE ∴∠=∠=︒，ACB E ∠=∠，23601360130130100BAE ∴∠=︒-∠-∠=︒-︒-︒=︒，180DFE E α∴∠=︒-∠-∠，1802AFC ACD ∠=︒-∠-∠，DFE AFC ∠=∠（对顶角相等），1801802E ACD α∴︒-∠-∠=︒-∠-∠，2100α∴∠=∠=︒．故答案为：100︒．【点睛】本题考查了全等三角形对应角相等的性质，三角形的内角和定理，对顶角相等的性质，准确识图，找出对应角是解题的关键．14．如图，AB ＝4cm ，AC ＝BD ＝3cm ，∠CAB ＝∠DBA ，点P 在线段AB 上以1cm/s 的速度由点A 向点B 运动，同时，点Q 在线段BD 上由点B 向点D 运动．设运动时间为t （s ），则当△ACP 与△BPQ 全等时，点Q 的运动速度为__cm/s ．1或15【分析】分两种情况讨论：当△ACP ≌△BPQ 时从而可得点的运动速度；当△ACP ≌△BQP 时可得：从而可得点的运动速度从而可得答案【详解】解：当△ACP ≌△BPQ 时则AC ＝BPAP ＝BQ ∵AC解析：1或1.5【分析】分两种情况讨论：当△ACP ≌△BPQ 时，1AP BQ ==，从而可得Q 点的运动速度；当△ACP ≌△BQP 时，可得：23AP BP BQ ===，，从而可得Q 点的运动速度，从而可得答案．【详解】解：当△ACP ≌△BPQ 时，则AC ＝BP ，AP ＝BQ ，∵AC ＝3cm ，∴BP ＝3cm ，∵AB ＝4cm ，∴AP ＝1cm ，∴BQ ＝1cm ，∴点Q 的速度为：1÷（1÷1）＝1（cm/s ）；当△ACP ≌△BQP 时，则AC ＝BQ ，AP ＝BP ，∵AB ＝4cm ，AC ＝BD ＝3cm ，∴AP ＝BP ＝2cm ，BQ ＝3cm ，∴点Q 的速度为：3÷（2÷1）＝1.5（cm/s ）；故答案为：1或1.5．【点睛】本题考查的是全等三角形的判定与性质，分类讨论的数学思想，掌握利用分类讨论解决全等三角形问题是解题的关键．15．如图，线段AB ，CD 相交于点O ，AO=BO ，添加一个条件，能使AOC BOD ≅，所添加的条件的是___________________________．或或或【分析】先根据对顶角相等可得再根据三角形全等的判定定理即可得【详解】由对顶角相等得：当时由定理可证当时由定理可证当时由定理可证当时则由定理可证故答案为：或或或【点睛】本题考查了对顶角相等三角形解析：CO DO =或A B ∠=∠或C D ∠=∠或//AC BD【分析】先根据对顶角相等可得AOC BOD ∠=∠，再根据三角形全等的判定定理即可得．【详解】由对顶角相等得：AOC BOD ∠=∠，AO BO =，∴当CO DO =时，由SAS 定理可证AOC BOD ≅，当A B ∠=∠时，由ASA 定理可证AOC BOD ≅，当C D ∠=∠时，由AAS 定理可证AOC BOD ≅，当//AC BD 时，则A B ∠=∠，由ASA 定理可证AOC BOD ≅，故答案为：CO DO =或A B ∠=∠或C D ∠=∠或//AC BD ．【点睛】本题考查了对顶角相等、三角形全等的判定定理等知识点，熟练掌握三角形全等的判定定理是解题关键．16．如图，△ABC ≌△A'B'C'，其中∠A ＝35°，∠C ＝25°，则∠B'＝_____．120°【分析】根据三角形内角和定理求出∠B 根据全等三角形的性质得出∠B=∠B′即可【详解】解：∵△ABC ∠A ＝35°∠C ＝25°∴∠B ＝180°﹣∠A ﹣∠C ＝180°﹣25°﹣35°＝120°∵△解析：120°【分析】根据三角形内角和定理求出∠B ，根据全等三角形的性质得出∠B=∠B′即可．【详解】解：∵△ABC ，∠A ＝35°，∠C ＝25°，∴∠B ＝180°﹣∠A ﹣∠C ＝180°﹣25°﹣35°＝120°，∵△ABC ≌△A'B'C'，∴∠B ＝∠B′＝120°，故答案为：120°．【点睛】本题考查了三角形内角和定理，全等三角形的性质的应用，注意：全等三角形的对应边相等，对应角相等．17．如图，90,,,ACB AC BC AD CE BE CE ∠=︒=⊥⊥，垂足分别为,D E ，若9,6AD DE ==，则BE 的长为________________________．3【分析】由AD ⊥CEBE ⊥CE 可以得到∠BEC=∠CDA=90°再根据∠ACB=90°可以得到∠BCE=∠CAD 从而求得△CEB ≌△ADC 然后利用全等三角形的性质可以求得BE 的长【详解】解：∵∠A解析：3【分析】由AD ⊥CE ，BE ⊥CE ，可以得到∠BEC=∠CDA=90°，再根据∠ACB=90°，可以得到∠BCE=∠CAD ，从而求得△CEB ≌△ADC ，然后利用全等三角形的性质可以求得BE 的长．【详解】解：∵∠ACB=90°，BE ⊥CE ，AD ⊥CE ，∴∠BCE+∠DCA=90°，∠BEC=∠CDA=90°，∴∠ACD+∠CAD=90°，∴∠BCE=∠CAD ，在△CEB 和△ADC 中，BCE CAD BEC CDA AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△CEB ≌△ADC （AAS ）；∴BE=CD ，CE=AD=9．∵DC=CE-DE ，DE=6，∴DC=9-6=3，∴BE=3．故答案为：3【点睛】本题考查全等三角形的判定与性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．18．如图，∠1＝∠2，要使△ABC ≌△ADC ，还需添加条件：_____．（填写一个你认为正确的即可）AB ＝AD （答案不唯一）【分析】根据题目中条件和图形可以得到∠1＝∠2AC ＝AC 然后即可得到使得△ABC ≌△ADC 需要添加的条件本题得以解决【详解】由已知可得∠1＝∠2AC ＝AC ∴若添加条件AB ＝A解析：AB ＝AD （答案不唯一）【分析】根据题目中条件和图形，可以得到∠1＝∠2，AC ＝AC ，然后即可得到使得△ABC ≌△ADC 需要添加的条件，本题得以解决．【详解】由已知可得，∠1＝∠2，AC ＝AC ，∴若添加条件AB ＝AD ，则△ABC ≌△ADC （SAS ）；若添加条件∠ACB ＝∠ACD ，则△ABC ≌△ADC （ASA ）；若添加条件∠ABC ＝∠ADC ，则△ABC ≌△ADC （AAS ）；故答案为：AB ＝AD （答案不唯一）．【点睛】本题考查全等三角形的判定，解答本题的关键是明确题意，利用数形结合的思想解答． 19．如图所示，AB AC =，AD AE =，BAC DAE ∠=∠，点D 在线段BE 上．若125∠=︒，230∠=︒，则3∠=______．55°【分析】先证明△ABD ≌△ACE （SAS ）；再利用全等三角形的性质：对应角相等求得∠2=∠ABE ；最后根据三角形内角与外角的性质即可求出答案【详解】∵∴∠1+∠CAD=∠CAE+∠CAD ∴∠1解析：55°【分析】先证明△ABD ≌△ACE （SAS ）；再利用全等三角形的性质：对应角相等，求得∠2=∠ABE ；最后根据三角形内角与外角的性质即可求出答案．【详解】∵BAC DAE ∠=∠，∴∠1+∠CAD=∠CAE+∠CAD ，∴∠1=∠CAE ；在△ABD 与△ACE 中，1AD AE CAE AB AC =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ACE （SAS ）；∴∠2=∠ABE ；∵∠3=∠ABE+∠1=∠1+∠2，∠1=25°，∠2=30°，∴∠3=55°．故答案为：55°．【点睛】本题考查了全等三角形的判定及性质，三角形的外角性质；将所求的角与已知角通过全等及内角、外角之间的关系联系起来是解答此题的关键．20．如图，已知AB AC =，D 为BAC ∠的角平分线上面一点，连接BD ，CD ；如图，已知AB AC =，D 、E 为BAC ∠的角平分线上面两点，连接BD ，CD ，BE ，CE ；如图，已知AB AC =，D 、E 、F 为BAC ∠的角平分线上面三点，连接BD ，CD ，BE ，CE ，BF ，CF ；…，依此规律，第n 个图形中有全等三角形的对数是______．【分析】根据图形得出当有1点D 时有1对全等三角形；当有2点DE 时有3对全等三角形；当有3点DEF 时有6对全等三角形；根据以上结果得出当有n 个点时图中有个全等三角形即可【详解】解：当有1点D 时有1对全解析：)(12n n +【分析】根据图形得出当有1点D 时，有1对全等三角形；当有2点D 、E 时，有3对全等三角形；当有3点D 、E 、F 时，有6对全等三角形；根据以上结果得出当有n 个点时，图中有)(12n n +个全等三角形即可．【详解】解：当有1点D 时，有1对全等三角形；当有2点D 、E 时，有3对全等三角形；当有3点D 、E 、F 时，有6对全等三角形；当有4点时，有10个全等三角形；…当有n 个点时，图中有)(12n n +个全等三角形．故答案为：)(12n n +．【点睛】本题考查了对全等三角形的应用，关键是根据已知图形得出规律，题目比较典型，但有一定的难度．三、解答题 21．在正方形网格中，网格线的交点叫做格点，三个顶点均在格点上的三角形叫做格点三角形．（1）在图1中计算格点三角形ABC 的面积是__________；（每个小正方形的边长为1）（2）ABC 是格点三角形．①在图2中画出一个与ABC 全等且有一条公共边BC 的格点三角形；②在图3中画出一个与ABC 全等且有一个公共点A 的格点三角形．解析：（1）6；（2）①见解析；②见解析【分析】（1）用割补法求解即可；（2）根据“SSS”画图即可；（3）根据“SSS”画图即可；【详解】解：（1）5×3-12×3×3-12×2×2-12×5×1=6，故答案为：6；（2）①如图，'A BC即为所求，AB C即为所求，②如图，''【点睛】本题考查了“格点三角形的定义”以及全等三角形的判定方法，熟练掌握“SSS”是解答本题的关键．22．如图，在△ABC中，∠BAC的平分线AD交BC于点D，过点D作DE⊥AB，DF⊥AC，垂足分别是E，F，连接EF．写出两个结论（∠BAD＝∠CAD和DE＝DF除外），并选择一个结论进行证明．（1）____________；（2）____________．解析：（1）∠ADE=∠ADF；证明见解析；（2）AE=AF；证明见解析．【分析】（1）∠ADE=∠ADF，根据DE⊥AB，DF⊥AC及AD为∠BAC的角平分线，即可证得∠ADE=∠ADF；（2）AE=AF，根据（1）可知证明△AED≌△AFD，即可证得AE=AF．【详解】（1）结论1：∠ADE=∠ADF，证明如下：∵DE⊥AB，DF⊥AC，∴∠AED=∠AFD=90︒，∵AD 为∠BAC 的角平分线，∴∠EAD=∠FAD ，∴∠ADE=∠ADF ；（2）结论2：AE=AF ，证明如下：由（1）可知：△AED ≌△AFD ，∴AE=AF ．【点睛】本题考查全等三角形的性质和判定，解题的关键是灵活运用全等三角形的判定和性质解决问题．23．在Rt ABC △中，90C ∠=︒，8cm AC =，6cm BC =，点D 在AC 上，且6cm AD =，过点A 作射线AE AC ⊥（AE 与BC 在AC 同侧），若点P 从点A 出发，沿射线AE 匀速运动，运动速度为1cm/s ，设点P 运动时间为t 秒．连结PD 、BD ．（1）如图①，当PD BD ⊥时，求证：PDA DBC △≌△；（2）如图②，当PD AB ⊥于点F 时，求此时t 的值．解析：（1）见解析；（2）8秒【分析】（1）根据垂直及角之间的关系证明出PDA CBD ∠=∠，又有90PAD C ∠=∠=︒，=6AD BC =，根据三角形全等的判定定理则可证明PDA DBC △≌△．（2）根据垂直及角之间的关系证明APF DAF ∠=∠，又因为90PAD C ∠=∠=︒，AD BC =，则可证明PAD ACB △≌△，所以8cm AP AC ==，即t=8秒．【详解】（1）证明：PD BD ⊥，90PDB ∴∠=︒，即90BDC PDA ∠+∠=︒又90C ∠=︒，90BDC CBD ∠+∠=︒ PDA CBD ∴∠=∠又AE AC ⊥，90PAD ∴∠=︒90PAD C ∴∠=∠=︒又6cm BC =，6cm AD =AD BC ∴=在PAD △和DCB 中PAD C AD CBPDA DBC ∠=∠⎧⎪=⎨⎪∠=∠⎩()PDA DBC ASA ∴△≌△（2）PD AB ⊥，90AFD AFP ∴∠=∠=︒，即90PAF APF ∠+∠=︒又AE AC ⊥， 90PAF DAF ∴∠+∠=︒APF DAF ∴∠=∠又90PAD C ∠=∠=︒，AD BC =在APD △和CAB △中APD CAB PAD C AD BC ∠=∠⎧⎪∠=∠⎨⎪=⎩()PAD ACB AAS ∴△≌△8cm AP AC ∴==即8t =秒．【点睛】本题主要考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理，灵活运用角之间的关系是解题关键．24．如图，点B 、E 、C 、F 在同一条直线上，A D ∠=∠，//AB DE ，BE CF =．求证：//AC DF ．解析：见解析．【分析】根据//AB DE 可知B DEF ∠=∠，又根据∠A=∠D ，BE=CF 可以判定ABC DEF △≌△，即可求证//AC DF ；【详解】∵//AB DE ，∴B DEF ∠=∠，∵BE CF =，∴BC EF =，∴在ABC 和DEF 中，A DB DEF BC EF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ABC DEF △≌△，∴ACB F ∠=∠，∴//AC DF ．【点睛】本题考查了三角形全等的性质与判定的应用以及两直线平行的判定定理，解此题的关键是推出ABC DEF △≌△，注意全等三角形的对应边相等；25．如图，已知在ABC 中，AB AC =，90BAC ∠=︒，别过B 、C 两点向过A 的直线作垂线，垂足分别为E 、F ．求证：EF BE CF =+．解析：见解析【分析】证明△BEA ≌△AFC ，得到AE=CF ，BE=AF ，即可得到结论．【详解】证明：BE EA ⊥，CF AF ⊥，90BAC BEA AFC ∴∠=∠=∠=︒，90EAB CAF ∴∠+∠=︒，90EBA EAB ∠+∠=︒，CAF EBA ∴∠=∠，在ABE △和AFC △中，BEA AFC EBA CAF AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，(AAS)BEA AFC ∴△≌△．AE CF ∴=，BE AF =．EF AF AE BE CF ∴=+=+．．【点睛】此题考查全等三角形的判定及性质，熟记三角形的判定定理是解题的关键．26．已知矩形ABCD 中，点E 是AD 中点，连接CE ，经过点A ，B ，E 三点作O ，交BC 于点F ，过点F 作FH CE ⊥于H ．（1）求证：直线FH 是O 的切线；（2）若42AD =，且点H 恰好为CE 中点时，判断此时CE 与O 的位置关系？说明理由，并求出弧EF ，线段EH ，FH 围成的图形的面积．解析：（1）见解析；（2）EC 与O 相切，理由见解析，4π-【分析】（1）连接BE ，OF ，易得出BE 是圆的直径，根据全等三角形的判定证得△EAB ≌△EDC ，继而根据平行线的性质和切线的判定即可求证结论；（2）连接EF ，易求得四边形OFHE 的边长，再利用面积的和差即可求解．【详解】（1）连接BE ，OF∵四边形ABCD 是矩形，∴90A D ∠=∠=︒，AB CD =，∵90A ∠=︒，∴BE 是O 的直径，∵点E 是AD 中点，∴EA EC =，∴△EAB ≌△EDC ，∴EB EC =，∴EBC ECB ∠=∠，∵OB OF =，∴ECB OFB ∠=∠，∴ECB OFB ∠=∠，∴//OF EC ，∴OFH FHC ∠=∠，∵FH CE ⊥，∴90FHC OFH ∠=∠=︒，又∵OF 是O 的半径，∴直线FH 是O 的切线．（2）EC 与O 相切．理由如下：连接EF ，由（1）知，BE 是O 直径，∴90EFB EFC ∠=∠=︒，∵点H 是CE 中点，∴FH EH HC ==，∵FH CE ⊥，∴90FHC ∠=︒，∴45ECF HFC ∠=∠=︒，∴90BEC ∠=︒，又∵OE 是O 的半径，∴直线EC 与圆O 相切．由上可知四边形ABFE 和四边形OFHE 都是正方形， ∴11422222AE AB AD ===⨯= ∴224BE AB AE =+=，∴2OE OF ==， ∴2290π224π360OFHE OEFS S S ⨯=-=-=-正方形扇形．【点睛】本题考查直线与圆的位置关系，矩形的性质，全等三角形的判定和性质、切线的判定、勾股定理，解题的关键是综合运用所学知识．27．已知ABC 是等腰直角三角形，90ACB ∠=︒，BC AC =．直角顶点C 在x 轴上，锐角顶点B 在y 轴上，过点A 作AD x ⊥轴，垂足为点D ．当点B 不动，点C 在x 轴上滑动的过程中．（1）如图1，当点C 的坐标是()1,0-，点A 的坐标是()3,1-时，请求出点B 的坐标；（2）如图2，当点C 的坐标是()1,0时，请写出点A 的坐标；（3）如图3，过点A 作直线AE y ⊥轴，交y 轴于点E ，交BC 延长线于点F ．AC 与y 轴交于点G ．当y 轴恰好平分ABC ∠时，请写出AE 与BG 的数量关系．解析：（1）（0，2）；（2）（-1，-1）；（3）BG=2AE ，理由见详解【分析】（1）先证明Rt∆ADC ≅Rt∆COB ，结合条件，即可得到答案；（2）先证明∆ADC ≅∆COB ，结合点B ，C 的坐标，求出AD ，OD 的长，即可得到答案；（3）先证明∆BGC ≅∆AFC ，再证明∆ABE ≅∆FBE ，进而即可得到答案．【详解】（1）∵点C 的坐标是()1,0-，点A 的坐标是()3,1-，∴AD=OC ，又∵AC=BC ，∴Rt∆ADC ≅ Rt∆COB （HL ），∴OB=CD=2，∴点B 的坐标是（0，2）；（2）∵AD ⊥x 轴，∴∠DAC+∠ACD=90°，又∵∠OCB+∠ACD=90°，∴∠DAC=∠OCB ，又∵∠ADC=∠COB=90°，AC=BC ，∴∆ADC ≅ ∆COB （AAS ），∵点C 的坐标是()1,0∴AD=OC=1，∵点B 的坐标是（0，2），∴CD=OB=2，∴OD=2-1=1，∴点A 的坐标是（-1，-1）；（3）BG=2AE ，理由如下：∵ABC 是等腰直角三角形，90ACB ∠=︒，BC AC =，AE y ⊥轴，∴∠BCA=∠ACF=90°，∠AEG=90°，∴∠GBC+∠BGC=90°，∠GAE+∠AGE=90°，又∵∠BGC=∠AGE ，∴∠GBC=∠FAC ，在∆BGC 和 ∆AFC 中，∵∠GBC=∠FAC ，BC AC =， ∠GBC=∠FAC ，∴∆BGC ≅∆AFC （ASA ），∴BG=AF ，∵BE ⊥AF ，y 轴恰好平分ABC ∠，∴∠ABE=∠FBE ，∠AEB=∠FEB=90°，BE=BE ，∴∆ABE ≅∆FBE ，∴AE=FE ，∴AF=2AE∴BG=2AE ．【点睛】本题主要考查等腰直角三角形的性质，全等三角形的判定和性质，熟练掌握“一线三垂直”模型，是解题的关键．28．如图，在四边形ABCD 中，//AD BC ，E 为AC 的中点，连接DE 并延长，交BC 于点F ．（1）求证：DE EF =．（2）若12AD =，:2:3BF CF =，求BC 的长．解析：（1）见解析；（2）20【分析】（1）根据平行线的性质可得：EAD ECF ∠=∠，EDA EFC ∠=∠，继而根据全等三角形的判定证得()ADE CFE AAS ≅△△，继而即可求证结论；（2）由全等三角形的性质可得：12AD CF ==，求得8BF =，继而即可求解．【详解】（1）证明：∵//AD BC ，∴EAD ECF ∠=∠，EDA EFC ∠=∠．∵E 为AC 的中点，∴AE CE =．在ADE 和CFE 中，,,,EAD ECF EDA EFC AE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()ADE CFE AAS ≅△△．∴DE EF =．（2）解：∵ADE CFE ≅，∴12AD CF ==．∵:2:3BF CF =，∴8BF =，∴81220BC BF CF =+=+=．【点睛】本题考查全等三角形的判定和性质，平行线的性质，解题的关键是熟练掌握全等三角形的判定方法和性质．。

人教版数学八年级上册第十二章全等三角形章节专题复习

经过大海的一番磨砺,卵石才变得更加美丽光滑。

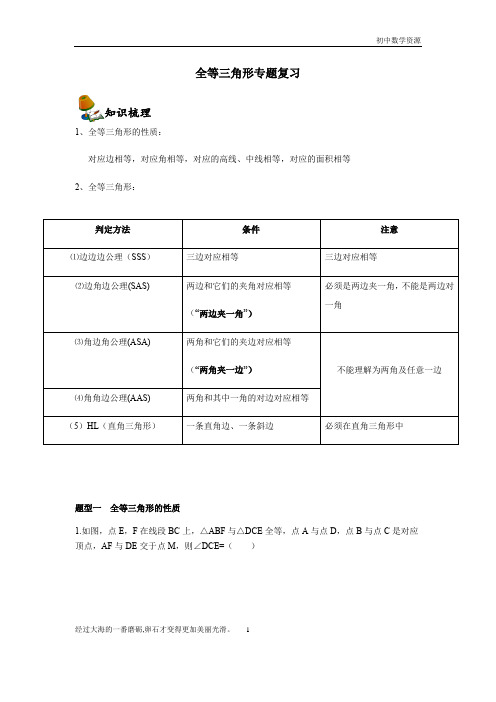
1全等三角形专题复习1、全等三角形的性质：对应边相等，对应角相等，对应的高线、中线相等，对应的面积相等 2、全等三角形：题型一全等三角形的性质1.如图，点E ，F 在线段BC 上，△ABF 与△DCE 全等，点A 与点D ，点B 与点C 是对应顶点，AF 与DE 交于点M ，则∠DCE=（）判定方法条件注意⑴边边边公理（SSS ）三边对应相等三边对应相等⑵边角边公理(SAS)两边和它们的夹角对应相等（“两边夹一角”）必须是两边夹一角，不能是两边对一角⑶角边角公理(ASA) 两角和它们的夹边对应相等（“两角夹一边”）不能理解为两角及任意一边⑷角角边公理(AAS) 两角和其中一角的对边对应相等（5）HL （直角三角形）一条直角边、一条斜边必须在直角三角形中知识梳理A．∠B B．∠A C．∠EMF D．∠AFB2.如图，AB∥ED，CD=BF，若△ABC≌△EDF，则还需要补充的条件可以是（）A．AC=EF B．BC=DF C．AB=DE D．∠B=∠E3.如图，△ACB≌△A′CB′，∠ACA′=30°，则∠BCB′的度数为（）A．20°B．30°C．35°D．40°4.已知四边形ABCD各边长如图所示，且四边形OPEF≌四边形ABCD．则PE的长为（）A．3B．5C．6D．105.如图，△ABC≌△AEF，AB=AE，∠B=∠E，则对于结论①AC=AF，②∠FAB=∠EAB，③EF=BC，④∠EAB=∠FAC，其中正确结论的个数是（）经过大海的一番磨砺,卵石才变得更加美丽光滑。

2A．1个B．2个C．3个D．4个6.如图，在△ABC中，D、E分别是AC、AB上的点，在△ADE≌△BDE≌△BDC，则∠A 的度数是（）A．15°B．20°C．25°D．30°7.如图，△ABC≌△AEF，那么与∠EAC相等的角是（）A．∠ACB B．∠BAF C．∠CAF D．∠AFE8.如图，已知D、E分别是△ABC的边AB、AC上的一点，若△ADE≌△CFE，则下列结论中不正确的是（）A．AD=CF B．AB∥CF C．AC⊥DF D．E是AC的中点9.如图，△ABC≌△A′B′C′，其中∠A=36°，∠C′=24°，则∠B=．经过大海的一番磨砺,卵石才变得更加美丽光滑。

人教版数学八年级上册-第十二章全等三角形复习课件(共16张PPT)

3.如图，已知∠A =∠C，∠B =∠D，要使△ABO≌△CDO，需要补充的一个条件是 _____
思路：
已知两角---
找两角的夹边
AB=CD （ASA）
找已知任一角的对边
OB=OD 或OA=OC（AAS）
4.如图，A，B，C三点在同一直线上， ∠A= ∠C=90°，AB=CD,
请添加一个适当的条件
(3) 已知两角---
找两角的夹边
( AS A )
找已知任一角的对边 ( AA S )
1.如图，已知AD=AB, 要使△ABC ≌△ADC 需要
添加一个条件是____ D
A
C
B
隐含条件——公共边
思路：
找第三边
DC=CB （SSS）
已知两边：找两边的夹角
∠ DAC=∠CAB （SAS）
找直角
∠ D=∠B=90°（HL）
八年级上册
第十二章全等三角形复习课(1)
本章知识框架
只适合直角三角形奥！
SSS、SAS、ASA、AAS、HL
判定
全等形全等三角形
应用
性质
对应边相等，对应角相等
一、全等三角形
1.什么是全等三角形？
能够完全重合的两个三角形叫做全等三角形. 一个三角形经过哪些变化可以得到它的全等形？
2.全等三角形有哪些性质？ (1)全等三角形的对应边相等、对应角相等. (2)全等三角形的周长相等、面积相等. (3)全等三角形的对应边上的对应中线、角平分线、高线分别相等.
方法指引证明两个三角形全等的基本思路：
（1）已知两边-- --
找第三边 (S S S ) 找两边的夹角 (SAS) 找是否有直角 (HL)

人教版初中数学八年级上册第十二章全等三角形复习习题 (含答案解析)

A．②③B．②④C．①②③D．②③④
19．如图，在Rt△AEB和Rt△AFC中，BE与AC相交于点M，与CF相交于点D，AB与CF相交于N，∠E＝∠F＝90°，∠EAC＝∠FAB，AE＝AF.给出下列结论：①∠B＝∠C；②CD＝DN；③BE＝CF；④△ACN≌△ABM.其中正确的结论是()
A．①③④B．②③④C．①②③D．①②④
A．6B．5C．4D．3
4．一块三角形玻璃板不慎被小强同学碰破,成了如图所示的四块,聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃板,你认为可行的方案是( )
A．带其中的任意两块去都可以B．带①、②或②、③去就可以了
C．带①、④或③、④去就可以了D．带①、④或①、③去就可以了
20．已知∠AOB＝20°，∠AOC＝4∠AOB，OD平分∠AOB，OM平分∠AOC，则∠MOD的度数是( )
A．20°或50°B．ຫໍສະໝຸດ 0°或60°C．30°或50°D．30°或60°
21．如图，AB是⊙O的直径，AB=10，P是半径OA上的一动点，PC⊥AB交⊙O于点C，在半径OB上取点Q，使得OQ=CP，DQ⊥AB交⊙O于点D，点C，D位于AB两侧，连接CD交AB于点E，点P从点A出发沿AO向终点O运动，在整个运动过程中，△CEP与△DEQ的面积和的变化情况是（）
人教版初中数学八年级上册第十二章全等三角形复习习题（含答案解析）
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（）
A．甲和乙B．乙和丙C．甲和丙D．只有丙

人教版数学八年级上册第十二章全等三角形复习课件

证明：过点P作PD⊥AB于D， PE⊥BC于E，PF⊥AC于F
∵BM是△ABC的角平分线,点P在
BM上, PD⊥AB于D，PE⊥BC于E
A
ND
M
PF
∴PD=PE(角平分线上的点到这个B角的两边E距 C
离相等).
同理,PE=PF.
∴PD＝PE=PF.
即点P到三边AB、BC、CA的距离相等
2.如图，已知△ABC的外角∠CBD和∠BCE的平分线相
总结提高
学习全等三角形应注意以下几个问题：
（1):要正确区分“对应边”与“对边”，“对应
角”与
“对角”的不同含义；
（2）：表示两个三角形全等时，表示对应顶点的字母要写在对应的位置上；
（3）：要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等；
（4）：时刻注意图形中的隐含条件，如 “公共角” 、 “公共边”、“对顶角”
4.已知：如图：在△ABC中，BE、CF 分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取 CG=AB，连结AD、AG。
求证：△ ADG 为等腰直角三角形。
G F
A
E D H
Bபைடு நூலகம்
C
5.已知：如图21，AD平分 ∠BAC，DE⊥AB于E，DF⊥AC于 F，DB=DC，求证：EB=FC
c
D
A
B E
4.已知，△ABC和△ECD都是等边三角形，且点B，C，D在一条
直线上求证：BE=AD 证明：
E
∵ △ABC和△ECD都是等边三角形
A
∴ AC=BC DC=EC ∠BCA=∠DCE=60°
∴ ∠BCA+∠ACE=∠DCE+ ∠ACE

人教版八年级上册第十二章全等三角形全章复习课件

如何寻找全等三角形的对应边和对应角呢？
例如图，△ABC≌△DEF.请指出图中对应边和对应角.
边 AC=DF 边 AB=DE 边 BC=EF 角 ∠A=∠D 角 ∠B=∠E 角 ∠C=∠F
如何根据需要寻找条件证明三角形全等，进而利用全等三角形的性质证明线段相等、角相等、直线平行等结论？
例如图，AB和CD相交于E，AE=EC，EB=ED.
B
C
如何根据需要寻找条件证明三角形全等，进而利用全等三角形的性质证明线段相等、角相等、直线平行等结论？
例如图，AD=AE，∠B=∠C.
求证：△ABE≌△ACD．
A
分析：根据条件一边一角对应相等找夹边或者一个角.
D
E
O
B
C
如何根据需要寻找条件证明三角形全等，进而利用全等三角形的性质证明线段相等、角相等、直线平行等结论？
边角边（SAS）的判定方法；
角边角（ASA）斜边和一条直角
全等三角形的判定角角边（AAS）边对应相等（HL）
注意: 判定两个三角形全等必须有一组边对应相等
全等三角形的性质对应边相等、对应角相等
全等三角形这一章我们学习了哪些知识呢？
两个三角形中对应相等的边或角
是否全等全等：√ 不全等：
E
C
课堂小结
复习了全等三角形判定及性质. 学会执果索因分析几何问题的方法. 学会利用二次全等证明几何问题.
作业如图，∠A=∠D=90°，AC=BD. 求证：△AOB≌△DOC．
A
D
O
B
C
同学们，再见！
全等三角形这一章我们学习了哪些知识呢？ 1.全等形的相关概念
全等形、对应顶点、对应边、对应角．

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

B C
在BDA和AEC中 BDA AEC已证 DBA EAC已证 AB AC 已知 BDA AECAAS BD AE，DA EC DE AE AD BD EC
能力提升
如图，△ABC中，AB＝AC，∠BAC＝90°，DE是过点A的直线，BD⊥DE于D，CE⊥DE于E，（2）若B、C在DE的两侧（如图2），其他条件不变，DE、 DB、EC三条线段之间满足什么关系？写出你的猜测，并说明你的理由．
基础训练 1.已知：如图 B DEF，BC EF，
AB DE, AC DF 1若要以“ SSS”为依据，还缺条件 __________ __ 2若要以“ SAS”为依据，还缺条件 __________ AB DE __ ACB DFE 3若要以“ ASA”为依据，还缺条件 __________ __ 4若要以“ AAS ”为依据，还缺条件 __________ __ A D
能力提升
如图，△ABC中，AB＝AC，∠BAC＝90°，DE是过点A的直线，BD⊥DE于D，CE⊥DE于E，（1）若B、C在DE的同侧（如图1），求证：DE＝DB＋EC 解： BD DE，CE DE 已知
BDA AEC 90
D A E
DBA DAB 90 又 BAC 90 DAB EAC 90 DBA EAC
4.中点——边相等
5.公共边——边相等
6.平移、翻折、旋转——角相等，边相等
小
结
1.经过本节课的学习你有什么收获？
2.你体会了什么数学思想？
基础训练
6.如图，BE⊥AE，CF⊥AE，垂足分别是E、F， D是EF的中点，△BED与△CFD全等吗？为什么？
解： BE AE，CF AE已知 BED CFD 90 又 D是EF的中点 ED FD 在BED和CFD中 BED CFD已证 ED FD已证 BDE CDF对顶角相等 BED CFDAAS
AEH=DH或Fra bibliotekAE=CD
E H D C
B
第 4 题图
基础训练
3.如图AB CD，AC BD，则ABC DCB吗？说明理由。
解：在ABC和DCB中 AB DC已知 AC DB已知 BC CB公共边
ABC DCBSSS
基础训练
A D B E C
BD DE EC
方法规律总结
全等三角形，是证明两条线段或两个角相等的重要方法之一，证明时
①要观察待证线段或角，在哪两个可能全等的三角形中
②分析要证两个三角形全等，已有什么条件，还缺什么条件。
感悟与反思： 1.对顶角——角相等 2.公共角——角相等 3.垂直——角相等
4.已知：如图，AB=AC,AD=AE, ∠1=∠3,那么∠E=∠D吗？为什么？ .
3 2 1 2等式性质即EAC DAB 在EAC和DAB中 AC AB已证 EAC DAB已证 AE AD已知 EAC DABSAS 解： 1 3已知
E D全等三角形的性质
基础训练
5.如图，AC与BD相交于点O，且AC=BD，DA⊥AC， BC⊥BD，垂足分别是A，B.求证：AD=BC.
基础训练
5.如图，AC与BD相交于点O，且AC=BD，DA⊥AC， BC⊥BD，垂足分别是A，B.求证：AD=BC.
证明：连接DC DA AC，BC BD DAC DBC 90 在RtDAC和RtCBD中， DC CD AC BD RtDAC RtCBDHL AD BC
补充条件求证： ABC DEF
5若B DEF 90 , 要以“HL”为依据，还缺 AC DF __ 条件 __________
基础训练
2.如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件： AH=CH或，使△AEH≌△CDH．
一、全等三角形的定义？能够完全重合的两个三角形叫全等三角形二、全等三角形的性质？
A
A’
B
C
B’
C’
全等三角形对应边相等，对应角相等
∠A=∠A’ ∠B=∠B’ ∠C=∠C’ AB=A’B’ BC=B’C’ AC=A’C’
3、全等三角形的判定方法
一般三角形
三、全等三角形的判定方法
特殊方法1 斜边和一条直角边对应相等的两个直角三角形全等(可以简写为“斜边、直角边”或 “HL” )

人教版八年级上第十二章全等三角形章节复习 (共16页)

人教版八年级数学上册第12章 全等三角形 单元复习 课件

人教版八年级上册第十二章 全等三角形(复习课)课件